过程控制作业答案
中级 统计过程控制作业答案

一、单选1、你的答案:标准答案:b2、你的答案:标准答案:a解析:偶然因素是过程固有的难以消除的;异常因素不是过程固有的,容易发现和消除3你的答案:标准答案:d4、你的答案:标准答案:b5、你的答案:标准答案:c6、你的答案:标准答案:c7、你的答案:标准答案:a8、你的答案:标准答案:b解析:由过程能力定义可知,是指过程加工质量的能力,是稳态下的最小波动,因而过程能力指数应在统计控制状态下收集数据。
9、你的答案:标准答案:a解析:在此状态下,过程是无偏移的正态分布,故在此时,不合格品率减小,过程能力指数增大。
10、你的答案:标准答案:c解析:由过程改进策略图可知,改进策略包括判断过程是否处于统计控制状态和评价过程能力两个环节。
是否处于统计控制状态就是判稳。
11、你的答案:标准答案:b解析:过程性能指数是长期的过程能力指数,可以反映出过程当前的实际状态,而不要求在稳态的条件下进行计算12、你的答案:标准答案:d解析:一定面积、一定长度的不合格数时用C图,而当样品规格有变化时,应换算成每单位不合格数控制图,即u图;当控制图的质量指标为不合格品率时,用p控制图,当控制对象为不合格品数时,用np图。
13、你的答案:标准答案:a解析:由于均值控制图中的上、下控制限中包含有极差参数,故必须先做极差控制图,在极差控制图判稳的情况下才能再作均值控制图。
14、你的答案:标准答案:b解析:无论每一种控制图的中心线,其值都为这一参数的均值,故均值图的中心线是其总体均值。
15、你的答案:标准答案:b解析:16、你的答案:标准答案:b解析:手表齿轮轴直径是计量值,其中只有均值-极差控制图是计量值控制图。
17、你的答案:标准答案:c解析:这是均值-极差控制图和均值-标准差控制图应用的区别,由于σ不知只能通过估计获得,故两种控制图分别对极差和标准差的值进行估计。
18、你的答案:标准答案:d解析:休哈特控制图就是要求在偶然因素作用下的稳态,出现异常因素时造成产品质量的波动,故其目的是区分偶然因素和异常因素19、你的答案:标准答案:c解析:我们说U控制图适用于样品规格有变化时的单位不合格数,由于话务员每天的话务量不同,故采用平均差错数时,应适用U控制图。
1080《过程控制》西南大学网教23秋季作业参考答案

108020232单项选择题1、串级控制系统的主回路是一个(),因此对于设计中的主参数的选择,可以按照单回路控制系统的设计原则进行。
.随动控制系统 . 定值控制系统. 程序控制系统 .以上都不是2、比例调节的缺点是存在静态误差,因此也称为()。
. 误差调节 . 动态调节. 有差调节.静态调节3、实验法建模时,为了获得被控对象的(),应加入激励信号使被控对象处于被激励的状态。
. 动态特性. 静态特性. 物理属性 .化学特性4、利用阶跃响应曲线法建立被控对象的数学模型,需求取被控对象输入与输出之间的()。
.大小关系.最大值.最小值.传递函数5、比例积分调节规律中,积分调节可以消除()。
.振荡.比例系数.调节时间.静态误差6、比例积分微分调节的缩写为()。
.DCS.PID.PI.PD7、若调节对象的特性是线性的,应选择具有()流量特性的调节阀。
.双曲线.抛物线.直线.等百分比8、为了减小调节阀()的影响,一般采用阀门定位器克服阀杆摩擦力。
.流量.重量.间隙特性.尺寸9、弹性式压力表是利用各种弹性元件,在被测介质压力作用下产生弹性变形的原理来测量压力的,服从()。
.法拉第电磁感应定律.胡克定律.质量守恒定律.惯性定律10、变送器一般由输入转换部分、放大器和()组成。
.控制器.反馈部分.传感器.执行单元11、关于压力检测仪表的安装,下列叙述错误的是()。
.压力检测仪表必须经检验合格后才能安装.压力检测仪表应水平安装.取压点应能如实反映被测压力的真实情况.压力检测仪表的连接处,应选择适当的材料作为密封垫圈12、串级控制系统是把两个调节器串接在一起,其中一个调节器的输出作为另一个调节器的(),共同稳定一个被控变量所组成的闭合回路。
.输入值.给定值.扰动量.以上都不是13、阶跃响应曲线法适用于处于()的被控对象。
.C. 开环、非稳态.开环、稳态.闭环、稳态.闭环、非稳态14、调节器的调节规律是指调节器输出信号与输入信号之间随()变化的规律。
过程控制作业答案(精品)

第一章 概述1.1 过程控制系统由哪些基本单元构成?画出其基本框图。
控制器、执行机构、被控过程、检测与传动装置、报警,保护,连锁等部件1.2 按设定值的不同情况,自动控制系统有哪三类? 定值控制系统、随机控制系统、程序控制系统1.3 简述控制系统的过渡过程单项品质指标,它们分别表征过程控制系统的什么性能?a.衰减比和衰减率:稳定性指标;b.最大动态偏差和超调量:动态准确性指标;c.余差:稳态准确性指标;d.调节时间和振荡频率:反应控制快速性指标。
第二章 过程控制系统建模方法习题2.10某水槽如图所示。
其中F 为槽的截面积,R1,R2和R3均为线性水阻,Q1为流入量,Q2和Q3为流出量。
要求:(1) 写出以水位H 为输出量,Q1为输入量的对象动态方程;(2) 写出对象的传递函数G(s),并指出其增益K 和时间常数T 的数值。
(1)物料平衡方程为123d ()d HQ Q Q Ft-+= 增量关系式为 123d d H Q Q Q F t∆∆-∆-∆= 而22h Q R ∆∆=, 33hQ R ∆∆=, 代入增量关系式,则有23123()d d R R hh F Q t R R +∆∆+=∆ (2)两边拉氏变换有:23123()()()R R FsH s H s Q s R R ++=故传函为:232323123()()()11R R R R H s KG s R R Q s Ts F s R R +===+++ K=2323R R R R +, T=2323R R F R R +第三章 过程控制系统设计1. 有一蒸汽加热设备利用蒸汽将物料加热,并用搅拌器不停地搅拌物料,到物料达到所需温度后排出。
试问:(1) 影响物料出口温度的主要因素有哪些?(2) 如果要设计一温度控制系统,你认为被控变量与操纵变量应选谁?为什么?(3) 如果物料在温度过低时会凝结,据此情况应如何选择控制阀的开、闭形式及控制器的正反作用?解:(1)物料进料量,搅拌器的搅拌速度,蒸汽流量(2)被控变量:物料出口温度。
过程控制技术课后作业答案详解
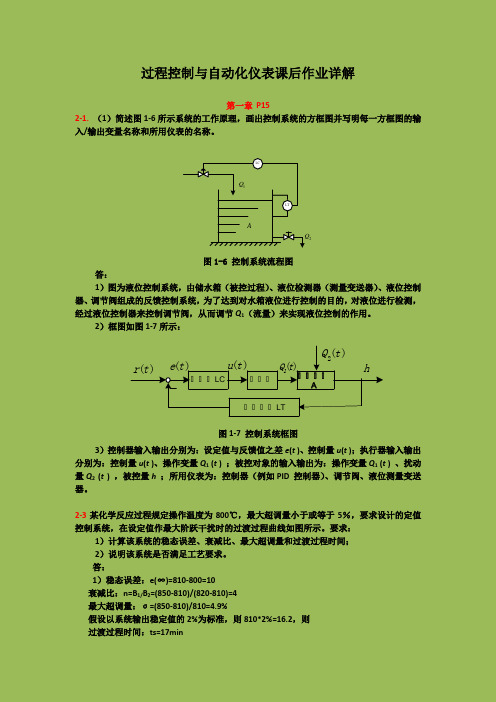
过程控制与自动化仪表课后作业详解第一章 P152-1. (1)简述图1-6所示系统的工作原理,画出控制系统的方框图并写明每一方框图的输入/输出变量名称和所用仪表的名称。
LTLC1Q 2Q A图1-6 控制系统流程图答:1)图为液位控制系统,由储水箱(被控过程)、液位检测器(测量变送器)、液位控制器、调节阀组成的反馈控制系统,为了达到对水箱液位进行控制的目的,对液位进行检测,经过液位控制器来控制调节阀,从而调节Q 1(流量)来实现液位控制的作用。
2)框图如图1-7所示:控控控LC控控控控控控控A控控控控LT_2()Q t ()1Q t ()r t ()e t ()u t h图1-7 控制系统框图3)控制器输入输出分别为:设定值与反馈值之差e (t )、控制量u (t );执行器输入输出分别为:控制量u (t )、操作变量Q 1 (t ) ;被控对象的输入输出为:操作变量Q 1 (t ) 、扰动量Q 2 (t ) ,被控量h ;所用仪表为:控制器(例如PID 控制器)、调节阀、液位测量变送器。
2-3某化学反应过程规定操作温度为800℃,最大超调量小于或等于5%,要求设计的定值控制系统,在设定值作最大阶跃干扰时的过渡过程曲线如图所示。
要求:1)计算该系统的稳态误差、衰减比、最大超调量和过渡过程时间; 2)说明该系统是否满足工艺要求。
答:1)稳态误差:e(∞)=810-800=10衰减比:n=B 1/B 2=(850-810)/(820-810)=4 最大超调量:σ=(850-810)/810=4.9%假设以系统输出稳定值的2%为标准,则810*2%=16.2,则 过渡过程时间:ts=17min2)由于规定操作温度为800︒C ,而系统稳态值为810︒C 所以不满足工艺要求。
第二章P711-3 某台测温仪表测量的上下限为500℃~1000℃,它的最大绝对误差为±2℃,试确定该仪表的精度等级;答:根据题意可知:最大绝对误差为±2℃则精度等级%4.0%1005002±=⨯±=δ 所以仪表精度等级为0.4级1-4某台测温仪表测量的上下限为100℃~1000℃,工艺要求该仪表指示值的误差不得超过±2℃,应选精度等级为多少的仪表才能满足工艺要求?答:由题可得:%22.0%10010010002±=⨯-±=δ仪表精度等级至少0.2以上。
2020年中国石油大学北京网络学院 过程控制工程-第二次在线作业 参考答案

中国石油大学北京网络学院
过程控制工程-第二次在线作业
参考答案
1.(
2.5分)串级控制系统中的主控制器对下列的哪个环节具有鲁棒性
A、副回路反馈通道
B、副对象
C、主对象
我的答案:B 此题得分:2.5分
2.(2.5分)某个串级控制系统中,调节阀为气开阀,副对象为反作用,则副控制器为
A、正作用
B、反作用
C、正反作用均可
我的答案:A 此题得分:2.5分
3.(2.5分)某个串级控制系统中,调节阀为气开阀,副对象为反作用,主对象为正作用,则主控制器为
A、正作用
B、反作用
C、正反作用均可
我的答案:B 此题得分:2.5分。
过程控制复习要点和习题答案(3,4)

第三章调节器1.掌握P、PI、PD,PID调节的特点,各调节规律定义公式,其阶跃响应。
积分时间的大小相应的积分作用怎样微分时间的大小其作用怎样比例度如何求取2.无扰动切换是指什么3.了解微分先行的PID算法主要用于解决什么问题对什么有微分作用4.了解比例先行的PID算法有什么特点5.掌握PID微分方程及差分方程6.掌握调节器的正反作用判断。
执行器7.掌握解执行器的作用、类型、由哪两部分组成各部分的作用是什么8.了解气动执行器和电动执行器各有什么特点9.掌握什么是气开阀,什么是气关阀。
按什么原则、如何来选择气开或气关方式10.掌握调节阀流量特性的定义;理想流量特性的定义、分类和特点;11.工作流量特性的定义,串联管道中调节阀流量特性的变化12.S值是指什么S值的大小对流量特性的影响13.掌握选择调节阀的流量特性的三原则14.了解电-气转换器起什么作用为什么要用阀门定位器15.掌握构成一个安全火花型防爆系统的充要条件是什么安全火花型防爆系统的组成结构。
16.了解防爆栅有哪几种类型17.了解危险场所分为哪几类危险程度最高的是哪一类第一类危险场所又分为哪几级第四章控制对象的特性测试1.掌握利用机理法建立单容/双容对象的数学模型。
2.掌握什么是具有自衡能力的对象具有滞后的一阶二阶特性的表示式;什么是无自衡能力的对象具有滞后的一阶二阶特性的表示式。
3.掌握什么是飞升曲线单容对象或多容对象的飞升曲线可用哪些参数来表征4.掌握如何测定飞升曲线和方波响应曲线测得方波响应曲线后如何获得飞升曲线(获取飞升曲线的原理和方法)。
5.掌握由飞升曲线来确定一阶对象,了解确定二阶对象的传递函数的方法。
6.掌握测定对象动特性的方法分类第三次作业(P108)1(2)某比例积分调节器的输入,输出范围均为4~20mA DC,若设ó=100%,T1=2MIN,稳态时其输出为6mA,若在某一时刻输入阶跃增加1mA,试求经过4min后调节器的输出。
过程控制作业(部分)

第一章绪论1)什么是过程控制系统?试用框图表示其一般组成?常用的过程控制系统可以分为哪几类?2)衡量过程控制系统过度过程的好坏,通过静态质量指标和动态质量指标,他们分别是什么?3)两个流量控制系统如下图所示。
试说明它们分别属于哪个过程控制系统?并画出各自的系统方框图。
4)某发酵过程工艺规定操作温度为(40±2)℃。
考虑到发酵效果,控制过程中温度偏离给定值最大不能超过6℃。
现设计一定值控制系统,在阶跃扰动作用下发酵罐及反应曲线如下图所示。
试①绘制系统方框图;②确定该系统的最大动态偏差、衰减比、余差、过度时间(按进入新稳态值±2%范围内)和振荡周期等过度过程指标,并回答是否满足工艺要求。
第二章检测及变送1)衡量一块仪表的性能指标有哪些?其中仪表精度和那个误差有关系?2)已知某S型热电偶在工作时冷端温度t0=30℃,现测得热电偶的热电动势为7.5mV,求被测介质的实际温度。
(已知E(30,0)=0.173mV)3)某台测温仪表的测温范围为200~700℃,校验该表时得到的最大绝对误差为+4℃,试确定该仪表的精度等级。
4)试简述热电偶工作原理及热电偶冷端温度补偿的几种主要方法和补偿原理。
5)试简述静压式液位计及电容式液位计测量原理?用电容式液位计在测量导电介质与非导电介质的液位时有何不同?6)某测温仪表的测量范围为0-500℃,输出信号为4-20mA,欲将该仪表用于测量200-1000℃的某信号,试问应该做如何调整迁移?7)某台测温仪表的测温范围为0~1000℃。
根据工艺要求,温度指示值的误差不允许超过±7℃,试问应该如何选择仪表的精度等级才能满足要求?8)某台往复式压缩机的出口压力范围为25~28MPa,测量误差不得大于1MPa。
工艺上要求就地观察,并能高低限报警,试正确选择一台压力表,指出其测量范围及精度等级要求。
9)利用弹簧管压力表测量某容器中的压力,工艺要求其压力为1.3±0.06MPa,现可提供选择压力表的量程有0~1.6MPa、0~2.5MPa及0~4MPa,其精度为1.0,1.5,2.0,2.5及4.0级,试合理选用压力表的量程和精度等级。
大学_过程控制工程课后作业试题以及答案(邵裕森)

过程控制工程课后作业试题以及答案(邵裕森)过程控制工程课后作业试题以及答案(邵裕森版)《过程控制工程第2版》是06月机械工业出版社出版的图书,作者是邵裕森图书简介:编辑作/译者:邵裕森出版社:机械工业出版社出版日期:06月 ISBN:9787111076025 [十位:7111076028]内容提要:编辑过程控制作为自动化技术的重要组成部分,其发展很快,并已广泛地应用于石油、化工、电力、冶金、机械、轻工、原子能、环保等许多国民经济的重要领域。
.具有跨世纪学科特色的规划教材--《过程控制工程》,不仅介绍了过程建模,将数字检测、数字控制仪表与计算机控制贯穿于全书的各章节,使模拟与数字技术融于全书,而且突出了系统的工程设计与工程应用。
教材主要内容包括过程建模,模拟及数字检测控制仪表,简单系统与复杂系统设计,dcs和工程应用举例等。
..本书内容丰富新颖,能适应跨世纪人才培养需要,是工业自... [显示全部]图书目录:编辑前言.第一章绪论第一节过程控制发展概况第二节过程控制的特点第三节过程控制系统的组成及其分类第四节“过程控制工程”课程的性质和任务思考题与习题第二章过程建模和过程检测控制仪表第一节过程建模第二节过程变量检测及变送第三节过程控制仪表第四节其它数字式过程控制装置思考题与习题第三章简单过程控制系统--单回路控制系统的工程设计第一节过程控制系统工程设计概述第二节控制方案设计第三节检测过程控制工程第2版简介课程内容主要包括过程动态测试和建模、控制器的参数整定、单回路控制系统、复杂控制系统、先进控制系统以及典型的工业过程控制系统。
通过学习,要求掌握过程控制系统的控制原理和分析设计方法,具备分析和设计能满足实际工业生产需要的控制系统的技能;掌握常用控制仪表选用,能熟练地操作、运行、安装、校验与维护常用控制仪表,能熟练地调试并进行技术改造,能熟练地正确调试简单控制系统及常用复杂控制系统,较熟练地掌握简单控制系统的开发与组织实施能力。
过程控制(专升本)阶段性作业3

过程控制(专升本)阶段性作业3总分: 100分考试时间:分钟单选题1. 选择被控变量应尽量使控制通道_____。
(4分)(A) 放大系数适当大、时间常数适当小、功率比较大(B) 放大系数大、时间常数适当小、滞后时间尽量小(C) 时间常数适当小、滞后时间尽量小、偏差信号尽量小(D) 滞后时间尽量小、偏差信号尽量小、功率比较大参考答案:B2. 只要偏差存在,积分调节就起作用,直至_____消失为止。
(4分)(A) 测量值(B) 正偏差(C) 余差(D) 负偏差参考答案:C3. 在自控系统中,确定调节器、调节阀、被控对象的正、反作用方向必须按步骤进行,其先后排列次序为_____。
(4分)(A) 调节器、调节阀、被控对象(B) 调节阀、被控对象、调节器(C) 被控对象、调节器、调节阀(D) 被控对象、调节阀、调节器参考答案:D4. PID调节器变为纯比例作用,则_____。
(4分)(A) 积分时间置∞、微分时间置∞(B) 积分时间置0、微分时间置∞(C) 积分时间置∞,微分时间置0(D) 积分时间置0,微分时间置0参考答案:C5. 某控制系统采用比例积分作用调节器。
某人用先比例后加积分的凑试法来整定调节器的参数。
若比例带的数值已基本合适,再加入积分作用的过程中,则_____(4分)(A) 应适当减少比例带(B) 适当增加比例带(C) 无需改变比例带(D) 与比例带无关参考答案:B6. 串级控制系统主、副对象的时间常数之比,T01/T02=_____为好,主、副回路恰能发挥其优越性,确保系统高质量的运行。
(4分)(A) 3~10(B) 2~8(C) 1~4(D) 1~2参考答案:A7. 通常串级控制系统主调节器正反作用选择取决于_____。
(4分)(A) 调节阀(B) 副调节器(C) 副对象(D) 主对象参考答案:D8. _____存在纯滞后,但不会影响调节品质。
(4分)(A) 调节通道;(B) 测量元件;(C) 变送器;(D) 干扰通道。
过程控制系统作业答案(全)

比值控制系统
2、如图所示一氧化氮生产串级比值控制系统, 要保证产品质量,需要稳定氧化炉出口温度。 回答以下问题 。 (1)图中除法器的输出代表什么? (2)系统中开方器有什么作用? (3)图中Q1是主流量还是副流量? (4)系统主副流量无变化,当扰动作用使氧 化炉出口温度偏离设定值时,系统如何调节?
串级控制系统
2、某一温度-压力串级控制系统采用两步法整 定控制器参数,测得4:1衰减过程的参数为: δ 8% 、 100 s 、δ 40% 、 T 10 s T 主控制器采用PI控制规律,副控制器采用P控 制,确定系统整定参数。
s1
s1
s2
s2
(1)4:1衰减法参数整定表
(2)临界比例度法参数整定表
m1 m2
c1 c2
双输入双输出系统,输入输出关系如下:
c1 2 m 1 3 m 2 c 2 4 m1 m 2
(1)求相对增益矩阵。 (2)求正确的变量配对。
多变量解耦控制系统
c1 2 m 1 3 m 2 c 2 4 m1 m 2
dh Q i Q o1 Q o 2 C dt h Q o1 R1 h Qo2 R2 Q ( s ) Q o1 ( s ) Q o 2 ( s ) CsH ( s ) i H (s) Q o1 ( s ) R1 H (s) Qo2 (s) R2
m 2 c 2 4m1
解:(1)由式 c 2 4 m1 m 2 ,得 代入 c 2 m 3 m 式中,得
1 1 2
过程控制技术课后作业答案详解

过程控制与自动化仪表课后作业详解第一章P152-1. (1)简述图1-6所示系统的工作原理,画出控制系统的方框图并写明每一方框图的输入/输出变量名称和所用仪表的名称。
答:1)图为液位控制系统,由储水箱(被控过程X液位检测器(测量变送器)、液位控制器、调节阀组成的反馈控制系统,为了达到对水箱液位进行控制的目的,对液位进行检测,经过液位控制器来控制调节阀,从而调节Q 1 (流量)来实现液位控制的作用。
2)框图如图1-7所示:图1-7控制系统框图3)控制器输入输出分别为:设定值与反馈值之差e (t )、控制量u(t );执行器输入输出分别为:控制量u(t)、操作变量Q 1(t);被控对象的输入输出为:操作变量Q 1(t)、扰动量Q2 (t),被控量h;所用仪表为:控制器(例如PID控制器)、调节阀、液位测量变送器。
2-3某化学反应过程规定操作温度为800℃,最大超调量小于或等于5%,要求设计的定值控制系统,在设定值作最大阶跃干扰时的过渡过程曲线如图所示。
要求:1)计算该系统的稳态误差、衰减比、最大超调量和过渡过程时间;2)说明该系统是否满足工艺要求。
答:1)稳态误差:e(8)=810-800=10衰减比:n=B1/B2=(850-810)/(820-810)=4最大超调量:。
=(850-810)/810=4.9%假设以系统输出稳定值的2%为标准,则810*2%=16.2,则过渡过程时间:ts=17min2)由于规定操作温度为800 °C,而系统稳态值为810 ℃所以不满足工艺要求。
第二章P711-3某台测温仪表测量的上下限为500℃~1000℃,它的最大绝对误差为±2℃,试确定该仪 表的精度等级;答:根据题意可知:最大绝对误差为±2℃ 则精度等级5 =±烹义100% = ±0.4% 所以仪表精度等级为0.4级1-4某台测温仪表测量的上下限为100℃~1000℃,工艺要求该仪表指示值的误差不得超过土 2℃,应选精度等级为多少的仪表才能满足工艺要求?答: 由题可得:5=± ——2—— x 100% = ±0.22%1000 -100仪表精度等级至少0.2以上。
过程控制 第一到三章 作业

第一章作业1.1 常用的评价控制系统动态性能的单项性能指标有哪些?它与误差积分指标各有何特点?答:(1)衰减率ψ、超调量σ、稳态误差e ss、调节时间t s、振荡频率ω;(2)单项指标用若干特征参数评价系统优劣,积分指标用误差积分综合评价系统优劣。
1.2 什么是对象的动态特性?为什么要研究对象的动态特性?答:(1)指被控对象的输入发生变化时,其输出(被调量)随时间变化的规律;(2)实现生产过程自动化时,对象的动态特性可以为控制工程师设计出合理的控制系统满足要求提高主要依据。
1.3 通常描述对象动态特性的方法有哪些?答:微分方程或传递函数。
1.4 过程控制中被控对象动态特性有哪些特点?答:无振荡、稳定或中性稳定、有惯性或迟延、非线性但在工作点附近可线性化。
1.11 某水槽水位阶跃响应实验为:其中阶跃扰动量Δµ=20%。
(1)画出水位的阶跃响应曲线;(2)若该水位对象用一阶惯性环节近似,试确定其增益K和时间常数T。
解:MATLAB编程如下:%作出标幺后的响应曲线t=[ 0 10 20 40 60 80 100 150 200 300 400 ];h=[ 0 9.5 18 33 45 55 63 78 86 95 98 ];x=0:0.01:400;y=interp1(t,h,x,'spline'); %三次样条函数据己知的t、h插出x的值yy=y/y(end); %输出标幺plot(x,yy,'k');xlabel('t/s');ylabel('h/mm');title('阶跃响应曲线','fontsize',10);grid;%找出最接近0.39和0.63的点 less1=find(yy<=0.39); more1=find(yy>=0.39); front1=less1(1,end); behind1=more1(1,1);cha11=0.39-yy(1,front1); cha12=yy(1,behind1)-0.39; if cha11<=cha12 t1=x(1,front1) elset1=x(1,behind1) endless2=find(yy<=0.63); more2=find(yy>=0.63); front2=less2(1,end); behind2=more2(1,1);cha21=0.63-yy(1,front2); cha22=yy(1,behind2)-0.63; if cha21<=cha22 t2=x(1,front2) elset2=x(1,behind2) end%求增益K 和时间常数T K=y(end)/20 T=2*(t2-t1)(1)水位的阶跃响应曲线如图:t/sh /m m阶跃响应曲线(2)计算结果如下:>> GK1_11 t1 =48.1700t2 =96.5900K =4.9T =96.8400则该水位对象用一阶惯性环节近似后,得其增益K=4.9,时间常数T≈96.84。
过程控制复习要点和习题答案(3,4)

17。95
18。1
画图并求得
•t=0:20:400;
•h1=[0,0.2,0.8,2。0,3。6,5。4,7.4,9。3,11,12。6,13.6,14.4,15。1,15.8,16。4,
17,17.4,17.6,17。8,17.95,18。1];
•h=h1/0。2;
x2(t)= —x1(t-Δt)
y(t)=y1(t)+y2(t)
=y1(t)-y1(t-Δt)
t
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
h1
0
0。2
0.8
2.0
3.6
5.4
7。4
9。3
11
12。6
13。6
14.4
15。1
15。8
16。4
300
320
340
360
380
2(5)如图所示,冷物料通过加热器用蒸汽对其加热。在事故状态下,为了保护加热器设备的安全,即耐热材料不被损坏,现在蒸汽管道上有一个气动执行器,试确定其气开,气关形式,并画出由PID调节器构成的控制系统结构框图。
解:为了保护加热设备的安全,应该选择气开阀.
(6)现测得三种流量特性的有关数据见表。试分别计算其相对开度在10%,50%,80%各变化10%时的相对流量的变化量,并据此分析它们对控制质量的影响和一些选用原则.
液位h为输出变量进水流量qi为输入变量111idhaqqdt?????111hqr???2212dhaqqdt?????223hqr???12211122111iqshsrgsqsqsarsars??????2101104222121ishkqtgses??????????????121oofoorgsgsrfs???干扰通道特性对控制质量的影响当干扰是幅值为f的阶跃信号6
《过程控制工程(专科)》17年9月在线作业满分答案

《过程控制工程(专科)》17年9月在线作业一、单选题(共 30 道试题,共 60 分。
)1. 下面对过程的控制质量没有影响的是()A. 控制通道放大倍数KoB. 扰动通道放大倍数KfC. 扰动通道时间常数D. 扰动通道纯滞后时间正确答案:D2. 在单回路控制中,控制阀的结构形式的选择很重要,在分流或合流控制时选用()A. 角形控制阀B. 隔膜控制阀C. 三通控制阀D. 蝶阀正确答案:C3. 在单回路控制中,控制阀的结构形式的选择很重要,在高压差时选用()A. 角形控制阀B. 隔膜控制阀C. 三通控制阀D. 蝶阀正确答案:A4. 在比例控制器中,放大倍数Kc和控制器的比例度δ之间的关系是()A. δ越大,Kc也越大B. δ越大,Kc越小C. δ变化与Kc无关D. δ与Kc都是定值正确答案:B5. 在某温度控制系统中,采用4:1衰减曲线法整定控制器的参数,得δs=20%,当控制器为比例作用时,其整定参数值为()A. 0.2B. 0.4C. 0.6D. 0.8正确答案:A6. 控制器负作用时,其放大系数Kc满足( )A. Kc<0B. Kc<-1C. Kc>0D. Kc=0正确答案:A7. 在过程控制系统中,系统的设定值保持不变的系统属于()A. 随动系统B. 定值系统C. 程序系统D. 以上都不是正确答案:B8. 在控制阀的正作用下,控制阀是气开式,则Kv满足()A. 等于0B. 大于0C. 小于 0D. 不能确定正确答案:B9. 在控制阀的负作用下,控制阀是气关式,则Kv满足()A. 等于0B. 大于0C. 小于 0D. 不能确定正确答案:C10. 串级控制系统中控制器的作用正确的是()A. 主粗副粗B. 主粗副细C. 主细副粗D. 主细副细正确答案:C11. 过程控制设计中,系统设计的核心是()A. 控制方案设计B. 工程设计C. 工程安装D. 仪表调校正确答案:A12. 在过程控制系统中,既能使控制变量不存在余差又使系统具有超前性控制应选用()控制规律A. PB. PIC. PIDD. PD正确答案:C13. 在控制系统中,能准确、快速、及时地跟踪设定值的变化的系统属于()A. 随动系统B. 定值系统C. 程序系统D. 以上都不是正确答案:A14. 串级控制系统系统中存在的一次扰动来源于它的()A. 主回路B. 副回路C. 主副回路都有D. 不能确定正确答案:A15. 在控制器上对所求得的整定参数设置的顺序是()A. P,I,DB. P,D,IC. I,P,DD. I,D,P正确答案:A16. 在单回路控制中,控制阀的结构形式的选择很重要,在控制强腐蚀性介质时选用()A. 角形控制阀B. 隔膜控制阀C. 三通控制阀D. 蝶阀正确答案:B17. 串级控制系统中主控制器的正、反作用的选择顺序()A. 先副后主B. 先主后副C. 主、副同样D. 不确定正确答案:A18. 在过程控制系统过渡过程的质量指标中,()是描述被控变量偏离设定值最大程度的物理量A. 最大偏差B. 超调量C. 衰减比D. 振荡周期正确答案:A19. 为了使过程控制系统能够正常工作,则必须使系统的各个环节的静态放大系数相乘必须满足()A. 等于 0B. 大于0C. 小于 0D. 不能确定正确答案:C20. 二阶过程控制系统稳定条件是()A. 特征根实部为负,微衰减系数小于零,分方程系数都大于零B. 特征根实部为正,微衰减系数小于零,分方程系数都大于零C. 特征根实部为正,微衰减系数大于零,分方程系数都大于零D. 特征根实部为负,微衰减系数大于零,分方程系数都大于零正确答案:D21. 一阶过程控制系统稳定条件是()A. 特征根为正,微分方程系数都大于零B. 特征根为负,微分方程系数都大于零C. 特征根为正,微分方程系数都小于零D. 特征根为负,微分方程系数都小于零正确答案:B22. 在过程控制系统中,若使控制变量最终不存在余差但系统的稳定性要下降应选用()A. 比例控制器B. 比例积分控制器C. 比例微分控制器D. 比例积分微分控制器正确答案:B23. 控制器正作用时,其放大系数Kc满足( )A. Kc<0B. Kc<-1C. Kc>0D. Kc=0正确答案:C24. 下列中对干扰通道特性对控制质量影响描述错误的是()A. Kf增加,余差增加,系统稳定性不变B. Tf增加,过渡过程时间减小C. Tf增加,振荡幅值减小D. τf增加,余差减小正确答案:D25. 串级控制系统中主回路的控制器包括()A. 主控制器B. 副控制器C. 主、副控制器D. 不确定正确答案:C26. 串级控制系统系统中副环是一个()系统A. 定值系统B. 随动系统C. 程序系统D. 分时系统正确答案:B27. 在比例控制规律中,衰减系数与系统的稳定性之间的关系应满足()A. 衰减系数越大系统越稳定B. 衰减系数越大系统越不稳定C. 衰减系数与系统稳定无关正确答案:A28. 一阶环节的传递函数是()A. K/(Ts+l)B. K/TisC. KD. Tds正确答案:A29. 在过程控制系统中,系统的设定值有规律变化的系统属于()A. 随动系统B. 定值系统C. 程序系统D. 以上都不是正确答案:C30. 在某温度控制系统中,采用4:1衰减曲线法整定控制器的参数,得δs=20%,当控制器为比例积分微分作用时,其整定参数值为()A. 0.2B. 0.4C. 0.16D. 0.32正确答案:C《过程控制工程(专科)》17年9月在线作业二、多选题(共 20 道试题,共 40 分。
西安石油大学函授《过程控制设备基础》作业1-4全答案

2024年秋+过程控制设备基础+作业一1 / 30 单选题(5分)正确答案 BA自上而下B自下而上C循环流动D单相流动2 / 30 单选题(5分)正确答案 AA2B3C4D53 / 30 单选题(5分)正确答案 B( )类。
A1B2C3D44 / 30 单选题(5分)正确答案 B计量( )。
A转子流量计B椭圆齿轮流量计C靶式流量计D涡轮流量计5 / 30 单选题(5分)正确答案 BA大B小C相等D与外部条件有关6 / 30 单选题(5分)正确答案 AA交流供电方式B动态供电方式C间接供电方式D直接供电方式7 / 30 单选题(5分)正确答案 C,静压式液位测量读数需要正迁移修正。
下列哪个为正确的修正公式?( )AA. Δp = Hρg + hBΔp = Hρg-hCΔp =(H+h)ρgDΔp =(H-h)ρg8 / 30 单选题(5分)正确答案 D量,大多采用热电偶进行测量。
A100B200C300D5009 / 30 单选题(5分)正确答案 AAProportional Integral DerivativeBProportional Internal DivisionCProcess Input DisplayDProcess Instrumentation Device10 / 30 单选题(5分)正确答案 A用电子电位差计测热电偶温度,如果热端温度升高20℃,室温冷端下降20℃则仪表的指示( ) A升高20℃B下降20℃C不变D升高40℃11 / 30 多选题(3分)正确答案 BCD。
A检测误差B系统误差C随机误差D粗大误差12 / 30 多选题(3分)正确答案 ABCA现场类B控制室类C自动化类D电气类13 / 30 多选题(3分)正确答案 ABCA系统的构成B控制方式C控制规律D控制过程14 / 30 多选题(3分)正确答案 ABA接触电势B温差电势C霍尔电势D感应电势15 / 30 多选题(3分)正确答案 ABCDA高温辐射温度计B低温辐射温度计C光电温度计D力温度计16 / 30 多选题(3分)正确答案 ABCDA确定合理的控制方案B选择正确的参数检测方法C过程控制仪表的选型D调节器的参数整定17 / 30 多选题(3分)正确答案 ABCA被控过程B过程检测C控制仪表D控制对象18 / 30 多选题(3分)正确答案 ABCA液动B气动C电动D固动19 / 30 多选题(3分)正确答案 ABD点选择时,下列各项中的哪几项为正确的注意事项?( )A流动介质测量时,尽量选择安装在直管部分B流动介质测量时,尽量使取压点与流动方向垂直C气体压力测量时,取压点应在管道下方D导压管长度要尽量短20 / 30 多选题(3分)正确答案 BCEAS 型B直线型C等百分比Dx 型E快开型21 / 30 判断题(2分)系统。
过程控制作业答案

作 业第二章:2-6某水槽如题图2-1所示。
其中A 1为槽的截面积,R 1、R 2均为线性水阻,Q i 为流入量,Q 1和Q 2为流出量要求:(1)写出以水位h 1为输出量,Q i 为输入量的对象动态方程;(2)写出对象的传递函数G(s)并指出其增益K 和时间常数T 的数值。
图2-1解:1)平衡状态: 02010Q Q Q i +=2)当非平衡时: i i i Q Q Q ∆+=0;1011Q Q Q ∆+=;2022Q Q Q ∆+= 质量守恒:211Q Q Q dthd A i ∆-∆-∆=∆ 对应每个阀门,线性水阻:11R h Q ∆=∆;22R h Q ∆=∆ 动态方程:i Q R hR h dt h d A ∆=∆+∆+∆2113) 传递函数:)()()11(211s Q s H R R S A i =++1)11(1)()()(211+=++==Ts KR R S A s Q s H s G i这里:21121212111111R R A T R R R R R R K +=+=+=;2Q112-7建立三容体系统h 3与控制量u 之间的动态方程和传递数,见题图2-2。
解:如图为三个单链单容对像模型。
被控参考△h 3的动态方程: 3233Q Q dth d c ∆-∆=∆;22R h Q ∆=∆;33R hQ ∆=∆; 2122Q Q dth d c ∆-∆=∆;11R h Q ∆=∆ 111Q Q dth d c i ∆-∆=∆ u K Q i ∆=∆ 得多容体动态方程:uKR h dth d c R c R c R dt h d c c R R c c R R c c R R dt h d c c c R R R ∆=∆+∆+++∆+++∆333332211232313132322121333321321)()(传递函数:322133)()()(a s a s a s Ks U s H s G +++==; 这里:32132133213213321321332211232132131313232212111;c c c R R R kR K c c c R R R a c c c R R R c R c R c R a c c c R R R c c R R c c R R c c R R a ==++=++=2-8已知题图2-3中气罐的容积为V ,入口处气体压力,P 1和气罐 内气体温度T 均为常数。
过程控制系统章节练习题及答案 习题解答

过程控制系统章节练习题及答案习题解答1. 什么是过程控制系统?过程控制系统是一种用于监测、控制和优化工业过程的系统。
它通常由传感器、执行器、控制器和人机界面等组成。
过程控制系统的主要功能是收集过程数据、分析数据、做出决策并自动调整参数,以提高生产效率、产品质量和工作安全性。
2. 过程控制系统的主要组成部分有哪些?过程控制系统主要由以下几个组成部分组成:•传感器:用于收集流程中的各种参数,如温度、压力、流量等。
•执行器:根据控制器的指令,调整流程中的参数,如开关阀门、调节电动机速度等。
•控制器:根据传感器的反馈信号和设定值,计算控制算法,并生成控制信号送给执行器。
•人机界面:供操作人员监视和操作过程控制系统,如显示仪表盘、报警信息和设定参数等。
3. 过程控制系统的工作原理是什么?过程控制系统的工作原理可以简单描述为以下几个步骤:1.传感器收集流程中的各种参数,并将数据传输给控制器。
2.控制器接收传感器数据,与设定值进行比较,并计算出控制信号。
3.控制信号送给执行器,执行器根据控制信号的大小和方向来调整流程中的参数。
4.执行器调整参数后,传感器再次收集参数,并将数据传输给控制器。
5.控制器不断进行数据分析,判断是否需要调整控制算法,并生成新的控制信号。
6.过程控制系统循环执行上述步骤,以实现对工业过程的监控和控制。
4. 什么是开环控制和闭环控制?•开环控制:也称为无反馈控制,是指控制器输出信号不受过程参数变化的影响。
开环控制系统只根据预先设定的参数进行控制,没有考虑实际过程的反馈信息。
这种控制方式比较简单,但容易受到外界因素的干扰,控制精度较低。
•闭环控制:也称为有反馈控制,是指控制器根据过程的反馈信息来调整输出信号。
闭环控制系统通过与设定值进行比较,获取过程的实际状态,并根据反馈信息调整控制算法,从而实现对过程的精确控制。
闭环控制具有良好的鲁棒性和可靠性。
5. 过程控制系统常见的控制策略有哪些?过程控制系统常见的控制策略包括以下几种:•比例控制:根据当前误差的大小,按比例调整控制器输出信号。
过程控制及自动化仪表 作业1-2答案

过程控制及自动化仪表——作业11. 用分度号为S的热电偶测温,冷端温度为20℃。
测得热电势E(t, 20) = 11.30 mV,求被测温度t。
E(t, 0)=E(t, 20)+E(20, 0)=11.30+0.113=11.413 mV查询附表A-1,t1=1150, E1=11.348t2=1160, E2=11.467(E-E1)/(E2-E1)=(t-t1)/(t2-t1)=> t=1155.46 ℃2. 用分度好为K的热电偶测试,冷端温度为25℃,热端温度为750℃,则产生的热电势是多少。
查附表A-3E(750, 0)=31.214 mVE(20, 0)=0.798 mVE(30, 0)=1.203 mV由内插法,得E(25, 0)=(0.798+1.203)/2=1.0005 mVE(750, 25)=E(750, 0)-E(25, 0)=31.214-1.0005=30.2135 mV过程控制及自动化仪表——作业23. 弹簧管测蒸汽管道内压力,仪表低于管道安装,二者标高分别为1.6m和6m,若仪表读数为0.7 MPa,已知蒸汽冷凝水密度ρ= 966 kg/m^3,g = 9.8 m^2/s,求管道内蒸汽的实际压力。
当前仪表的绝对压力:p=Δp+p0 = 0.8 MPa管道内压力按力平衡:p' = p - ρgh = 0.8 - 966*9.8*(6-1.6)*1e-6=0.7583 MPa4. 被测压力波动范围0.5~1.4 MPa,要求测量误差不大于压力示值的±5%,确定压力表量程和精度等级。
1/3*A<=(0.5~1.4) <= 2/3*AA<=1.5 MPa && A>=2.1 MPa这两个条件相互矛盾,即量程选择不能同时满足低限和高限要求,以高限优先则取量程A =0 ~ 2.5MPa >= 2.1P=(1.4*0.05)/(2.5-0)*100% = 2.8%取精度等级时按系列小于等于的最大值取,即P=2.5级。
最新过程控制-李文涛-课后习题答案

最新过程控制-李⽂涛-课后习题答案不知道谁弄的和我们要求的课后作业相似度很⼤,值得参考,另外答案准确度应该还⾏超调量B —第⼀个波峰值与新稳定值之差 B=843-808=35 C衰减⽐B1 : B2 — 相邻两个波峰值之⽐ (843-808)/(815-808)=5余差值被控变量的新稳定值与给定值之偏差C=808-800=8 C 振荡周期过渡过程同向两个波峰间间隔时间为周期T=20-5=15min⼯艺规定的操作温度为 800± 9) C ,表⽰给定值为800 C ,余差为9 C ,由(1)得出的最⼤偏差A=43 C <50 C ,余差C=8 C <9 C ,所以该系统满⾜要求 T2.8(2)由图可知:.=30s,T =250 -30 =220s, k =[y(::) - y(0)] / ? :x = (196 - 0)/(196* 10%) =10(阶跃扰动为稳态值的 10%,即k=10)(P36)计算法:阶跃响应表达式y°(t)⼆y(t)/yC :)0(t<£)Yt-2).1 _e"^(ti )T1.6(1)最⼤偏差A —被控变量偏离给定值的最⼤数值(给定值为 800) A=843-800=43 C y °(t )(1.1)T3.10⼤修后变送器的量程由500C 变为300-200=100C ,变送器的放⼤倍数将发⽣变化,从⽽导致⼴义对象特性放⼤倍数发⽣变化:选取 t1=140s,t2=250s 对应h o(t 1),h o(t 2),其中t2>t1> . _(t1⑵」2⼯)由式(门)可得h o (tl ) =1 —e F , h o (t2) =1 —e F取⾃然对数并联⽴求解,得t2-11t2 In [1-4如)]七 In [1-h °(t2)]h (h(1.3)为计算⽅便,选取 h 0(t1) =0.39,h °(t2) =0.632代⼊式(1.2)和(1.3)则T=2( t2-t1)= 2 (250 -140) = 220s ;.=2t1 -12 = 2 140—250 = 30s ;k ⼆[y (:J - y (0)]/ :x=(196-0"T3.9(1) 影响物料岀⼝温度的主要因素有:蒸汽压⼒、流量,冷物料温度、压⼒、流量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作 业第二章:2-6某水槽如题图2-1所示。
其中A 1为槽的截面积,R 1、R 2均为线性水阻,Q i 为流入量,Q 1和Q 2为流出量要求:(1)写出以水位h 1为输出量,Q i 为输入量的对象动态方程;(2)写出对象的传递函数G(s)并指出其增益K 和时间常数T 的数值。
图2-1解:1)平衡状态: 02010Q Q Q i +=2)当非平衡时: i i i Q Q Q ∆+=0;1011Q Q Q ∆+=;2022Q Q Q ∆+= 质量守恒:211Q Q Q dthd A i ∆-∆-∆=∆ 对应每个阀门,线性水阻:11R h Q ∆=∆;22R h Q ∆=∆ 动态方程:i Q R hR h dt h d A ∆=∆+∆+∆2113) 传递函数:)()()11(211s Q s H R R S A i =++1)11(1)()()(211+=++==Ts KR R S A s Q s H s G i这里:21121212111111R R A T R R R R R R K +=+=+=;2Q112-7建立三容体系统h 3与控制量u 之间的动态方程和传递数,见题图2-2。
解:如图为三个单链单容对像模型。
被控参考△h 3的动态方程: 3233Q Q dth d c ∆-∆=∆;22R h Q ∆=∆;33R hQ ∆=∆; 2122Q Q dth d c ∆-∆=∆;11R h Q ∆=∆ 111Q Q dth d c i ∆-∆=∆ u K Q i ∆=∆ 得多容体动态方程:uKR h dth d c R c R c R dt h d c c R R c c R R c c R R dt h d c c c R R R ∆=∆+∆+++∆+++∆333332211232313132322121333321321)()(传递函数:322133)()()(a s a s a s Ks U s H s G +++==; 这里:32132133213213321321332211232132131313232212111;c c c R R R kR K c c c R R R a c c c R R R c R c R c R a c c c R R R c c R R c c R R c c R R a ==++=++=2-8已知题图2-3中气罐的容积为V ,入口处气体压力,P 1和气罐 内气体温度T 均为常数。
假设罐内气体密度在压力变化不大的情况下,可视为常数,并等于入口处气体的密度;R 1在进气量Q 1变化不大时可近似看作线性气阻。
求以用气量Q 2为输入量、气罐压力P 为输出量对象的动态方程。
解: 根据题意:假设:1)ρ在P 变化不大时为常数 2) R 1近似线性气阻;3)气罐温度不变,压力的变化是进出流量的变化引起; 平衡时:211Q Q p p ==非平衡时: 21GQ Q dtd C∆-∆= 气容:容器内气体变化量量容器内气体重量的变化=CdtdGdt p d Cpd dGC =∆∆=111)(1R p p P P R G ∆-=∆--=∆ 动态方程:211p Q Rp dt d C ∆-=∆+∆;2-10有一复杂液位对象,其液位阶跃响应实验结果为:(1) 画出液位的阶跃响应曲线;题图2-3(2) 若该对象用带纯延迟的一阶惯性环节近似,试用作图法确定纯延迟时间τ和时间常数T。
(3) 定出该对象,增益K 和响应速度ε设阶跃扰动量△μ=20% 。
解:1)画出液位动态曲线:2) 切线近似解:τ=40s T=180-40=140(s) 1002.020)0()(==∆-∞=u y y Kss e s e Ts K s G 4011401001)(--+=+=∴τ3)采用两点法:取【t 1, y*(t 1)】, 【t 2, y*(t 2)】 无量纲化: )(201)()(*t y y t y y =∞=则: ⎪⎩⎪⎨⎧≥--<=T t T t T t t y )exp(10)(*τ取两点:⎪⎩⎪⎨⎧--=--=)exp(18.0)exp(14.021T t T t ττ解得:⎩⎨⎧=-=-T t Tt 61.151.021ττ ⎪⎩⎪⎨⎧-=-=∴1.151.061.11.12112t t t t T τ2-12 知矩阵脉冲宽度为1s ,幅值为,测得某对象的脉冲响应曲线数据如下表:试求阶跃响应曲线。
解:设脉冲响应y(t),阶跃输入R(t); 1) 列关系式:122111()()()()()()()()u t u t u t u t u t t u t u t u t t =+=--∆=--∆1211()()()()()y t y t y t y t y t t =+=--∆ 即 11()()()y t y t y t t =+-∆从题意知:△t =1秒 一拍; 可列表格:2)表格计算:yu0u)(t )t ∆-)t ∆-3) 做图:2-14已知被控对象的单位阶跃响应曲线试验数据如下表所示:分别用切线法,两点法求传递函数,并用仿真计算过渡过程,所得结果与实际曲线进行比较。
解:1)对实验曲线描图:60 30 30090 120 150 180 210 240 270 330t2) 切线法: 找拐点:)(130********)0()(s T uy y k =-===∆-∞=τ s e s s G 8011301)(-+=3) 两点法:)()()(63.0)(*)()()(39.0)(*222111t y y t y t y t y y t y t y =∞===∞==)(220)(5.15321s t s t ==得: 862133)(22112=-==-=t t t t T τ ∴ s e s s G 8611331)(-+=2-17 根据热力学原理,对给定质量的气体,压力p 与体积V 之间的关间为。
pV α=β, 其中α和β为待定参数。
经实验获得如下一批数据,V 单位为立方英寸,p 的单位为帕每平方英寸。
试用最小二乘法确定参数α和β。
解: 由 βα=PV 取对数:βαln ln ln =+V P V P ln ln ln αβ-=方法1:矩阵解: Θ=X Y[]TV V V X P P P Y αβln ln ln ln 111ln ln ln 621621=Θ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=M M M M M M由定义:Θ-=X Y εΘΘ+Θ-Θ-=Θ-Θ-===∑=X X X Y Y X Y Y X Y X Y J TT T T T T T mj j )()()(12εεε0ˆ22ˆ=Θ+-=Θ∂∂Θ=ΘX X Y X J T T 得:Y X X X Y X X X T T T T 1)(ˆ;ˆ-=Θ=Θ(1) 带入数值到(1)式:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎦⎤⎢⎣⎡---=53.15123.2923.29657.7112.4194.3157.712.494.3111M M ΛΛX X T⎥⎦⎤⎢⎣⎡=-11.0534.0534.077.2)(1X X T ∴ ⎥⎦⎤⎢⎣⎡-=-319.0008.0040.0063.0081.0095.0272.1217.0372.0484.0570.0639.0)(1X X X X TT⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-==Θ-445.0624.531.295.245.363.390.311.4319.0008.0040.0063.0081.0095.0272.1217.0372.0484.0570.0639.0ln )(ˆ1αβY X X X T T ∴ ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡445.0277αβ方法二:采用代数式求解: ∑=-+=612)ln ln (ln i i i V P J βα01)ln ln (ln 20ln )ln ln (ln 26161=-+=∂∂=-+=∂∂∑∑==i i i i i i i V P J V V P Jββαββαα解得:ln )(ln ln 0ln ln )(ln ln ln 61616161261=++=-+⋅∑∑∑∑∑=====βαβαi ii ii i i ii iiV P V V V P把值代入:0ln 623.2925.200ln 23.295.1516.94=-+=-+βαβα 57.5ln 45.0==∴βα4.26245.0==∴βα2-18求下列所示各系统输出Y(z)的表达式。
a)解:)()(1)()()(2112z G z H G z R G z G z Y +=b)解:1)在R(s)作用下: )(1)()(2122z G H z G z +=Φ )()()(1)()()()(1)()()(22212222z G z H z G H z R z G z z H z R z z Y R ++=Φ+Φ=2)在N(s)的作用下:()z H z G z G H z N G z Y N ())(1)()(12212++=3)总解:()z H z G z G H z N G z R z G z Y z Y z Y N R ())(1)()()()()()(122122+++=+=c)解:1)在R(s)作用下:)()()(1)()]()([)()()()()]()()[()()(2112121212211z R z G G G z D z G G G z D z D z Y z R z G G G z D z Y z R z G G G z D z Y k k R k R k R ++=+-=2)在N(s)作用下:)()(1)()()()()()()(21121212z G G G z D z NG z Y z Y z D z G G G z NG z Y k N N k N +=-=3) 总输出:)()(1)()()()(1)()]()([)()()(21122112121z G G G z D z NG z R z G G G z D z G G G z D z D z Y z Y z Y k k k N R ++++=+=第四章:4-2试确定题图4-1中各系统调节器的正反作用方式。
设燃料调节阀为气开式,给水调节阀为气关式。
蒸汽(b )(a )题图4-1 控制系统(a )加热炉温度控制系统 (b )锅炉汽包液位控制系统解:(a )对加热调节控制系统,依题意采用气开式,当偏差越大,输出控制量越大,(即e ↗——u ↗——阀气开)而阀打开,燃料才加大,通常应关闭,则输出为反作用。
