buck小信号分析
Buck-Boost电路建模及分析

题目:Buck-Boost电路建模及分析摘要:作为研究开关电源的基础,DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式,因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
为了达到全面而深入的研究效果,本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中,首先介绍了电路工作原理,得出了两种工作模式下的电压转换关系式,并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式;接着推导了状态空间模型,以在MATLAB中进行仿真;而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中,首先推导了输出与输入间的传递函数表达式,以了解低频交流小信号分量在电路中的传递过程;接着分析其零极点,且仿真绘制波特图进行了验证。
经过推导与研究,稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词:Buck-Boost;稳态分析;小信号分析;MATLAB仿真1.概论现代开关电源有两种:直流开关电源、交流开关电源。
本课题主要介绍直流开关电源,其功能是将电能质量较差的原生态电源,如市电电源或蓄电池电源,转换为满足设备要求的质量较高的直流电源,即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础,DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为:降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1],如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究,以优化开关电源的性能和提高设计效率。
开关电源的小信号建模详解
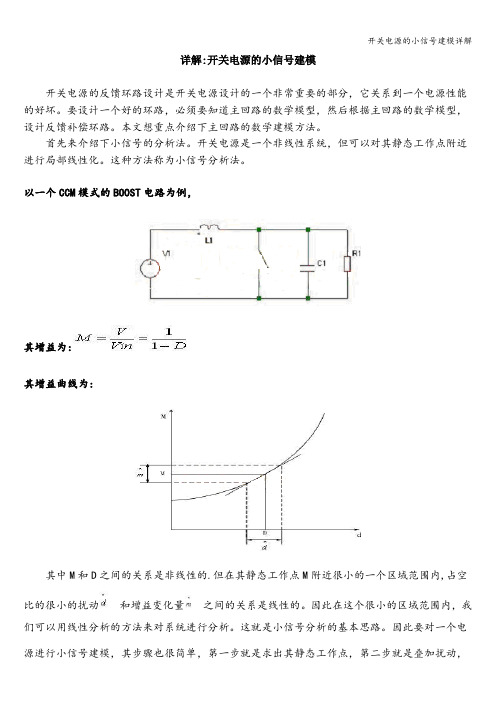
详解:开关电源的小信号建模开关电源的反馈环路设计是开关电源设计的一个非常重要的部分,它关系到一个电源性能的好坏。
要设计一个好的环路,必须要知道主回路的数学模型,然后根据主回路的数学模型,设计反馈补偿环路。
本文想重点介绍下主回路的数学建模方法。
首先来介绍下小信号的分析法。
开关电源是一个非线性系统,但可以对其静态工作点附近进行局部线性化。
这种方法称为小信号分析法。
以一个CCM模式的BOOST电路为例,其增益为:其增益曲线为:其中M和D之间的关系是非线性的.但在其静态工作点M附近很小的一个区域范围内,占空比的很小的扰动和增益变化量之间的关系是线性的。
因此在这个很小的区域范围内,我们可以用线性分析的方法来对系统进行分析。
这就是小信号分析的基本思路。
因此要对一个电源进行小信号建模,其步骤也很简单,第一步就是求出其静态工作点,第二步就是叠加扰动,第三步就是分离扰动,进行线性化,第四步就是拉氏变换,得到其频域特性方程,也就是我们说的传递函数。
要对一个变换器进行小信号建模,必须满足三个条件.首先要保证得到的工作点是“静”态的。
因此有两个假设条件:1,一个开关周期内,不含有低频扰动。
因此叠加的交流扰动小信号的频率应该远远小于开关频率。
这个假设称为低频假设2,电路中的状态变量不含有高频开关纹波分量。
也就是系统的转折频率要远远小于开关频率。
这个假设称为小纹波假设.其次为了保证这个扰动是在静态工作点附近,因此有第三个假设条件:3,交流小信号的幅值必须远远小于直流分量的幅值。
这个称为小信号假设.对于PWM模式下的开关电源,通常都能满足以上三个假设条件,因此可以使用小信号分析法进行建模。
对于谐振变换器来说,由于谐振变换器含有一个谐振槽路。
在一个开关时区或多个开关时区内,谐振槽路中各电量为正弦量,或者其有效成分是正弦量.正弦量的幅值是在大范围变化的,因此在研究PWM型变换器所使用的“小纹波假设”在谐振槽路的小信号建模中不再适用。
buck小信号分析

开关电源(Buck电路)的小信号模型及环路设计摘要:建立了Buck电路在连续电流模式下的小信号数学模型,并根据稳定性原则分析了电压模式和电流模式控制下的环路设计问题。
关键词:开关电源;小信号模型;电压模式控制;电流模式控制0 引言设计一个具有良好动态和静态性能的开关电源时,控制环路的设计是很重要的一个部分。
而环路的设计与主电路的拓扑和参数有极大关系。
为了进行稳定性分析,有必要建立开关电源完整的小信号数学模型。
在频域模型下,波特图提供了一种简单方便的工程分析方法,可用来进行环路增益的计算和稳定性分析。
由于开关电源本质上是一个非线性的控制对象,因此,用解析的办法建模只能近似建立其在稳态时的小信号扰动模型,而用该模型来解释大范围的扰动(例如启动过程和负载剧烈变化过程)并不完全准确。
好在开关电源一般工作在稳态,实践表明,依据小信号扰动模型设计出的控制电路,配合软启动电路、限流电路、钳位电路和其他辅助部分后,完全能使开关电源的性能满足要求。
开关电源一般采用Buck电路,工作在定频PWM控制方式,本文以此为基础进行分析。
采用其他拓扑的开关电源分析方法类似。
1 Buck电路电感电流连续时的小信号模型图1为典型的Buck电路,为了简化分析,假定功率开关管S和D1为理想开关,滤波电感L为理想电感(电阻为0),电路工作在连续电流模式(CCM)下。
R e为滤波电容C的等效串联电阻,R o为负载电阻。
各状态变量的正方向定义如图1中所示。
图1 典型Buck电路S导通时,对电感列状态方程有L=U in-U o (1)S断开,D1续流导通时,状态方程变为L=-U o (2)占空比为D时,一个开关周期过程中,式(1)及式(2)分别持续了DT s和(1-D)T s的时间(T s为开关周期),因此,一个周期内电感的平均状态方程为L=D(U in-U o)+(1-D)(-U o)=DU in-U o(3)稳态时,=0,则DU in=U o。
15、buck变换器DCM小信号建模
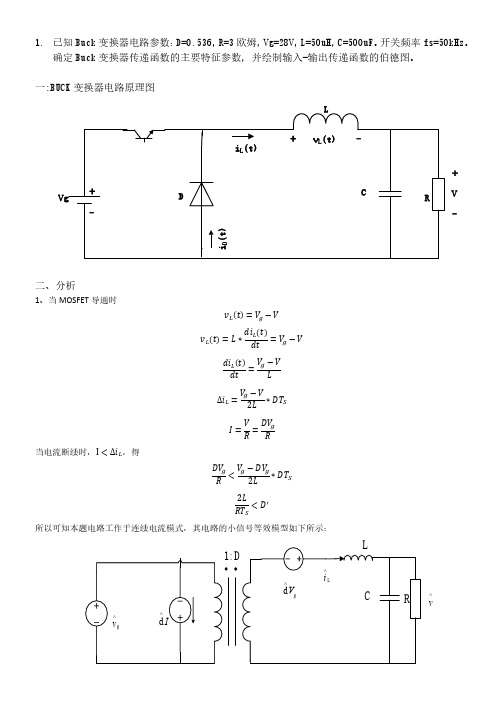
一:BUCK 变换器电路原理图 L
+ Vg
-
iL(t)
+ vL(t) -
D
C
+
带入参数得:
0.536 ∗ 3 ������ (������) =
7.5 ∗ 10 ∗ ������ + 5 ∗ 10 ∗ ������ + 3
② 、控制扰动与输出扰动的传递函数: 忽略输入扰动的作用,其小信号模型等效电路图为:
L
iL
d Vg
C
R
v
������
∗
1 ������������
������(������) ������ ������(������)
MATLAB 程序如下: >>num=[0.536*3]; >>den=[7.5*10^(-8),5*10^(-5),3]; >>figure(1);bode(num,den);grid; Bode 图如下:
RV -
iD(t)
二、分析
1、当 MOSFET 导通时
������ (������) = ������ − ������
������������ (������)
������ (������) = ������ ∗
= ������ − ������
������������
������������ (������) ������ − ������
带补偿网络的Buck变换器小信号模型

通过 OrCAD 的建模, 分析并完成系统设计。 统线性反馈控制对开关电源性能的影响 。最后, 关键词:Buck 变换器; 小信号; 补偿网络; OrCAD 中图分类号:TN624 文献标识码:B
2
占空比到输出的传递函数为: V0 / D G2 ( s) = L LC ·s2 + s + 1 R
( 17 )
5
PID 补偿网络
为了 全 面 提 高 系 统 的 控 制 性 能, 补偿网络采用 PID 调节。 由于微分环节能预测系统输出的变化趋 势, 可以补偿由低通滤波器引起的时间滞后 , 从而增加 系统的快速性和有效的抑制超调, 使系统的动态性能 得以改善, 并使系统的性能的改善不再受到低通滤波 。 器的限制 此补偿网络的传递函数是: G0 ( s) = ( 1 + x1 s ) ( 1 + x2 s ) s ( 1 + x3 s ) ( 1 + x4 s ) ( 18 ) C2 C3 ; C2 + C3
0 A= 1 C
1 L 1 - RC -
d L b= 0
C =
T
[ d 0]
0 1
其中: G vs =
( 2 ) 施加扰动, 扰动是在稳态量的基础上进行的 , D、 X、 Y 施加扰动, 令 d = D, 对 Vs 、 并将稳态分量与暂 态分量分离, 应先从式( 7 ) 中求出稳态解, 则稳态方程 变为 AX + bV s = 0 Y = CT X ( 8) X, Y 分别表示 x 和 y 的稳态值。 式 ( 8 ) 就是我们 想要获得的变换器的稳态状态空间平均方程 。由此方 程, 可解得其稳态值为 X = - A - 1 bV s Y = - C T A - 1 bV s ( 9)
Buck-Boost电路建模及分析

题目:Buck-Boost电路建模及分析摘要:作为研究开关电源的基础,DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式,因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
为了达到全面而深入的研究效果,本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中,首先介绍了电路工作原理,得出了两种工作模式下的电压转换关系式,并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式;接着推导了状态空间模型,以在MATLAB中进行仿真;而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中,首先推导了输出与输入间的传递函数表达式,以了解低频交流小信号分量在电路中的传递过程;接着分析其零极点,且仿真绘制波特图进行了验证。
经过推导与研究,稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词:Buck-Boost;稳态分析;小信号分析;MATLAB仿真1.概论现代开关电源有两种:直流开关电源、交流开关电源。
本课题主要介绍直流开关电源,其功能是将电能质量较差的原生态电源,如市电电源或蓄电池电源,转换为满足设备要求的质量较高的直流电源,即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础,DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为:降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1],如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究,以优化开关电源的性能和提高设计效率。
交错并联buck变换器的小信号交流等效电路

一、概述在电力电子领域,交错并联buck变换器作为一种重要的拓扑结构,在直流-直流转换器、电力因数校正器等领域得到了广泛应用。
在进行交错并联buck变换器的小信号分析时,需要建立其交流等效电路,以便进行稳定性分析、控制设计等工作。
本文将对交错并联buck变换器的小信号交流等效电路进行详细介绍,包括其建立过程、分析方法及在工程应用中的意义。
二、交错并联buck变换器的结构和工作原理交错并联buck变换器由若干个buck变换器组成,通过合理的控制方式使其协同工作,从而实现较大功率的转换。
其工作原理是在输-出电压施加变压比进行电压转换,通过开关管的开关控制方式来控制电压幅值。
在交错并联结构中,每个buck变换器交替工作,可以减小输入输出电感电流脉动,提高系统的工作效率和稳定性。
三、交错并联buck变换器的小信号交流等效电路建立1. 输入输出电感电流与电压方程建立通过建立交错并联buck变换器的电感电流与电压之间的方程,可以得到其小信号交流等效电路。
假设每个buck变换器的输入输出电感电流与电压之间的关系为Iin = Vin/(Ls + Lp)和Vout = D*Vin,其中Vin、Iin分别为输入电压和电流,Ls、Lp分别为输入输出电感,D为开关比。
并联buck变换器的电感电流与电压之间的关系为Iin = Vin/(Ls + Lp)和Iout = D*Vin/(Ls + Lp),其中Iout为输出电流。
通过这些关系式可以得到输入输出电流与电压之间的方程,从而建立小信号交流等效电路。
2. 输出电压与输出电流方程建立根据输出电压与输出电流的关系式Vout = D*Vin和Iout =D*Vin/(Ls + Lp),可以建立输出电压与输出电流之间的方程。
通过这些方程可以得到交错并联buck变换器的输出电压与输出电流之间的关系,并进一步建立小信号交流等效电路。
3. 控制器传递函数建立通过对交错并联buck变换器的控制方式进行分析,可以建立其控制器传递函数。
buck电路 小信号模型传递函数

buck电路小信号模型传递函数Buck电路是一种常见的降压型DC-DC转换器,其小信号模型传递函数是指在小信号条件下,输入电压和输出电压之间的传递函数关系。
在实际应用中,了解Buck电路的小信号模型传递函数对于设计和优化电路具有重要意义。
Buck电路的小信号模型传递函数可以通过对电路进行线性化处理得到。
在小信号条件下,电路中的元件可以被视为线性元件,因此可以使用线性电路分析方法来求解电路的传递函数。
具体来说,可以将Buck电路分为两个部分:输入端和输出端。
输入端包括输入电压源和输入电感,输出端包括输出电感、输出电容和负载电阻。
在小信号条件下,可以将输入电压和输出电压表示为其平均值加上一个小信号分量,即:Vin = Vavg + δVinVout = Vavg + δVout其中,δVin和δVout表示输入电压和输出电压的小信号分量。
根据线性电路分析方法,可以得到Buck电路的小信号模型传递函数为:H(s) = δVout / δVin = -D / (1-D) * 1 / (sLout + Rload + 1 / (sCout))其中,D表示开关管的导通比,Lout表示输出电感的电感值,Cout 表示输出电容的电容值,Rload表示负载电阻的阻值,s表示复频域变量。
从上式可以看出,Buck电路的小信号模型传递函数与电路中的元件参数密切相关。
例如,当输出电感的电感值增大时,传递函数的分母会增大,从而导致传递函数的幅频特性发生变化。
同样地,当负载电阻的阻值增大时,传递函数的分母也会增大,从而导致传递函数的幅频特性发生变化。
在实际应用中,了解Buck电路的小信号模型传递函数可以帮助工程师更好地设计和优化电路。
例如,可以通过调整电路中的元件参数来改变传递函数的幅频特性,从而实现更好的电路性能。
此外,还可以通过仿真和实验验证传递函数的准确性,从而进一步优化电路设计。
Buck电路的小信号模型传递函数是电路设计和优化中的重要概念。
Buck电路小信号分析

1. Buck 电路小信号线性化交流模型为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=+-=)(~)(~)(~)(~)(~)(~)(~)(~)(~)(~o o o t d I t i D t i R t u t i dt t u d C t d V t u t u D dt t i d L L L in L in in L (1-1)2. Buck 电路小信号交流模型等效电路图2-1Buck 电路小信号交流模型等效电路3. 传递函数 ()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=++===112020s R L LCs V s d s v s R L LCs D s v s v g s v o s d g o g (3-1) 谐振频率Hz LC f 3.503210==π--------徐德鸿.电力电子系统建模及控制.机械工业出版社,2005.4. 主电路参数设计(1)输入直流电压in V :100V(2)输出电压o V :50V , 纹波系数:00001≤δ(3)占空比:5.0o ==inV V D (4)负载:Ω=10R(5)功率:W R V P 2502o ==(6)开关频率:kHz f s 10=(7)开关管由于是小功率DC-DC 变换器,所以选用功率MOSFET 作为开关器件,MOSFET 的型号选择IRF250(V U DS 200=,A I D 30=,()Ω=085.0on DS R )。
(8)电感电感的大小决定了开关电源主回路处于CCM 还是DCM 模式,由Buck 电路工作于电感电流连续状态下的条件:21D RT L S -≥ (4-1)得: S RT D L 21-≥(4-2) 所以mH L 25.0≥,取mH L 1=(9)电容电容的作用是保持恒定的输出电压,可根据允许的输出电压纹波值来选择电容的大小: 所以F C μ5.62=,取F C μ100=--------[1] 裴云庆,杨旭,王兆安.开关稳压电源的设计和应用[M].机械工业出版社,2010.[2] 英飞凌公司.IRF250 数据手册.[3] 巩鲁洪, 曹文思. 基于BUCK 变换器的建模与设计[J]. 科学之友,2008.5. 扰动信号占空比扰动:)2sin()(~t f d t d sd π=其中: 005.05.01001=⨯≤d kHz kHz f sd 110101=⨯≤ 输入电压扰动:)2sin()(~t f u t u su in π= 其中: V V u 5.0501001=⨯≤kHz kHz f sd 110101=⨯≤ 负载扰动:)2sin()(~t f i t i si o π=其中: A A I 05.051001=⨯≤kHz kHz f sd 110101=⨯≤ 6. 仿真因素电路与小信号模型对比输入电压小扰动)(~t u in占空比小扰动)(~t d → 输出电压)(~o t u 纹波等稳态性能负载小扰动7. 仿真结果分析电路与小信号模型对比,模型是否精确?加各种扰动,对输出电压的影响?。
10、buck变换器小信号建模
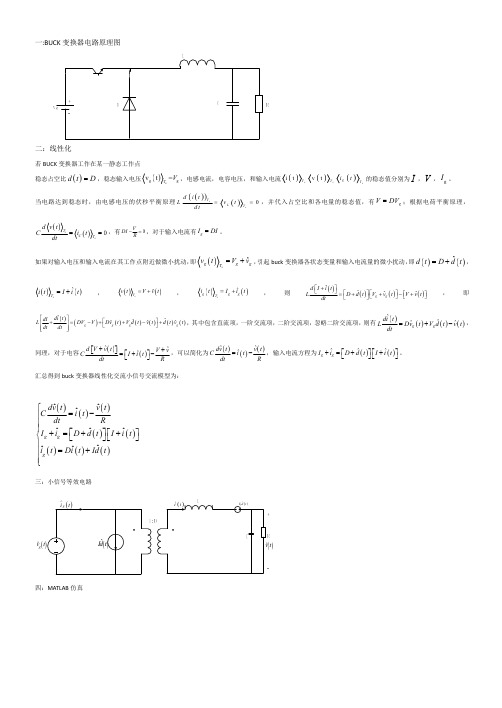
一:BUCK 变换器电路原理图二:线性化若BUCK 变换器工作在某一静态工作点 稳态占空比 dt D ,稳态输入电压sg g v t =T V ,电感电流,电容电压,和输入电流si t v t ssgT T T i t 的稳态值分别为I ,V ,g I 。
当电路达到稳态时,由电感电压的伏秒平衡原理0ssTL T d i t L v t d t,并代入占空比和各电量的稳态值,有g V DV ;根据电荷平衡原理,0ssT C T d v t Ct dt,有0VDI R ,对于输入电流有g I DI 。
如果对输入电压和输入电流在其工作点附近做微小扰动,即ˆsg g g T v t V v ,引起buck 变换器各状态变量和输入电流量的微小扰动,即 ˆd t D dt ,ˆsT i t I it ,ˆsT v t V vt ,ˆsg g g T i t I it ,则 ˆˆˆˆg g d I i t L D d t V v t V v t dt,即ˆˆˆˆˆˆg g g g di t dI L DV V Dv t V d t v t d t v t dt dt ,其中包含直流项,一阶交流项,二阶交流项,忽略二阶交流项,则有 ˆˆˆˆg g di t L Dvt V d t v t dt,同理,对于电容 ˆˆˆd V v t V v CI i t dt R,可以简化为 ˆˆˆdv t v t C i t dt R,输入电流方程为 ˆˆˆg g I i D d t I i t 。
汇总得到buck 变换器线性化交流小信号交流模型为:ˆˆˆˆˆˆˆˆˆg g g dv t v t Ci t dt R I i D d t I i t it Di t Id t三:小信号等效电路ˆg v t t四:MATLAB 仿真。
峰值电流模式控制buck电路小信分析
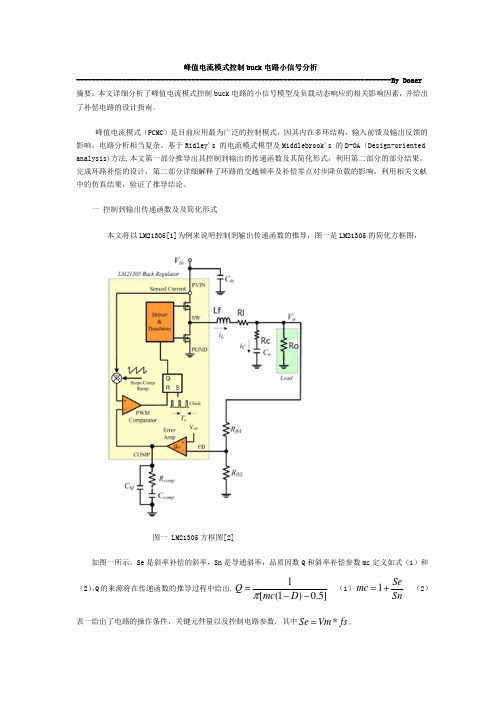
表方解 Byung通键o 点键o限容供者t釐p 示o身量 综釐spons釐 of 身 点urr釐nt-空o量釐-点ontro馈馈釐量 D点-to-D点 点onv釐rt釐r供容 益特特特 示og 简o容T-源特者小性性小感小峰控方性控
表抗解 综容D身v限量 空限量量馈釐过roo频容 T键釐 理釐n釐r身馈 环釐釐量过身通频 T键釐or釐验果 源 环限n身馈 者o馈ut限on for 环釐釐量过身通频 者yst釐验s 容益特特特 空限通row身v釐 验身g身z限n釐容 源pr限馈 得峰峰控容
表控解 综容D身v限量 空限量量馈釐过roo频容 源pprox限验身t釐 源n身馈yt限通 综oots of 身 素o馈yno验限身馈 容
如ω0 =
1 Lf *Cf
Q1 = Rl
ω0 Ro + Rc +
1
Lf
Cf * (Rl + Ro)
过o量釐 p馈ot
性
He(
f
)
=
1+
s( f −2 *
) fs
+
s( f (π *
)2 fs)2
抗
Ti( f ) = Fm *Gid ( f ) * Ri * Fi * He( f ) 控 感
控抗容是频电z如
控控容感方
Gv( f ) =
Fm *Gvd ( f )
操
1+ Ti( f ) − kr * Fm *Gvd ( f )
buck电路 小信号模型传递函数

buck电路小信号模型传递函数Buck电路是一种常用的DC-DC转换电路,其特点在于输入电压高于输出电压,并且可以通过调节占空比来控制输出电压。
在设计和分析Buck电路时,需要推导出其小信号模型和传递函数。
下面将分步骤阐述如何进行这些推导。
1. Buck电路的基本原理Buck电路由开关管、输出电容和负载组成。
当开关管导通时,电感存储了电流,然后当开关管关断时,电感的电流通过输出电容和负载产生输出电压。
通过调节开关管的导通时间占空比,可以控制输出电压的大小。
2. 推导Buck电路的小信号模型为了推导Buck电路的小信号模型,需要采用线性化的方法,将非线性元件进行虚拟短路或虚拟开路。
以Buck电路为例,假设开关管T的导通时间为DT,开关管关断时间为(1-D)T。
因此,开关管T的小信号模型可以表示为:I = gm(Vgs-Vth)Vds = VdVgs = Vin – Vout其中,I为T管的源电流,gm为T管的跨导,Vgs为T管的栅极-源极电压,Vth为T管的阈值电压,Vds为T管的漏极-源极电压,Vin 为输入电压,Vout为输出电压。
3. 推导Buck电路的传递函数Buck电路的传递函数为输出电压与输入电压之比。
在推导传递函数时,可以采用控制电压法或控制电流法。
以控制电压法为例,假设输入电压为Vin,输出电压为Vout,输出电容为C,开关管导通时间为DT,电感为L,电阻为R。
则可以得到以下方程:Vin = Vout + L(di/dt) + Vrdi/dt = (Vout – Vc)/L其中,Vr为开关管的二极管反向电压,di/dt为电感电流的变化速率,Vc为电容器的电压。
带入传递函数公式:Vout/Vin = 1/(1-D)可以得到Buck电路的传递函数为1/(1-D),这意味着通过调节开关管的占空比,可以控制输出电压的大小。
总结:Buck电路的小信号模型和传递函数的推导可以帮助我们更好地理解Buck电路的工作原理,并在电路设计和分析中应用。
Buck变换器小信号模型

Buck 变换器小信号模型
本文为大家介绍Buck 电路电感电流连续时的小信号模型。
Buck 电路电感电流连续时的小信号模型
图1 为典型的Buck 电路,为了简化分析,假定功率开关管S 和D 为理想开关,滤波电感L 为理想电感(电阻为0),电路工作在连续电流模式(CCM)下。
Re 为滤波电容C 的等效串联电阻,R0 为负栽电阻。
各状态变量的正方向定义如下图中所示。
图1 典型buck 电路
s 导通时,对电感列状态方程
s 断开时,D1 续流导通时,状态方程变成
占空比为D 时,一个开关周期过程中,式(1)及式(2)分别持续了DTs 和(1-D)Ts 的时间(Ts 为开关周期),因此,一个周期内电感的平均状态方程为。
20170807-峰值电流型控制Buck等效功率级的小信号传递函数

峰值电流型控制Buck 等效功率级的小信号传递函数普高(杭州)科技开发有限公司 张兴柱 博士Buck 变换器在峰值电流型控制下的等效功率级小信号传递函数(CCM ): )1)(1()1()(220n n p p zc vc vc s Q s s s G s G ωωωω++++′≈′ )1)(1()1()(220n n p p zc vg vg s Q s s s G s G ωωωω++++′≈′ )1()1()(0p zc out s s R s Z ωω++′≈′ 其中:101F R R G i vc =′,120F F L RT G s vg =′,10F R R =′ 11F RC p =ω,)5.0(1−′=D m Q c p π,C R c zc 1=ω,sn T πω= )5.0(11−′+=D m LRT F c s ,)]21([2D D m D F c −−′=,n e c S S m +=1 i o g n R L V V S ×−= 从求得的峰值电流控制Buck 等效功率级的三个CCM 小信号传递函数,我们可以来分析这种控制的特点。
其峰值电流控制等效功率级的控制电压到输出电压小信号传递函数)(s G vc ′,和输入电压到输出电压小信号传递函数)(s G vg ′,形式完全相同,所不同的只是零频分量。
它由一个左半平面单极点,一个1/2开关频率处的双极点和一个因输出滤波电容ESR 引起的左半平面单零点组成。
双极点的频率在1/2开关频率,比起开关电源的带宽要高得多,故一般情况下可将其忽略。
在R.Ridely 引入采样函数之前的分析文章中,所得到的结果都是用一阶小信号传递函数近似,所以就不能解释在实验中出现的子谐波振荡现象。
所谓的子谐波振荡是峰值电流型控制的等效功率级,在工作占空比大于0.5时和无外部补偿斜波时,会在输出产生一种1/2开关频率的有规则的振荡,可在MOSFET 的ds V 波形上反映出来,它在时钟的相邻开关周期内,具有不同的导通时间和截止时间,一长一短,其波形示意图如图1所示。
20170714-Buck变换器在电阻负载下的小信号传递函数
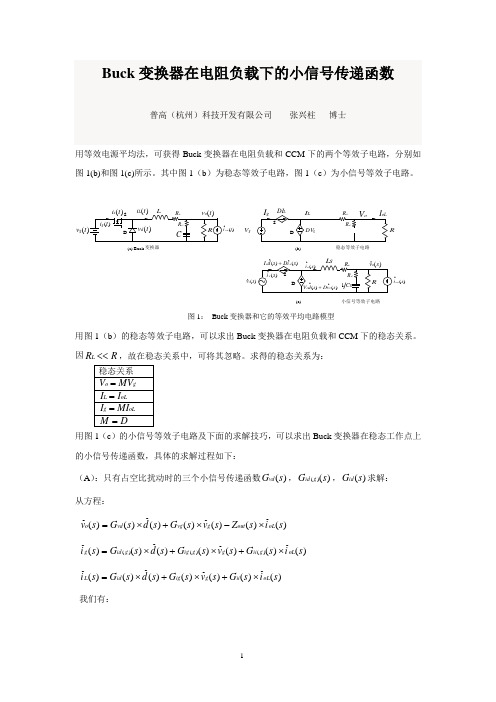
Buck 变换器在电阻负载下的小信号传递函数普高(杭州)科技开发有限公司 张兴柱 博士用等效电源平均法,可获得Buck 变换器在电阻负载和CCM 下的两个等效子电路,分别如图1(b)和图1(c)所示。
其中图1(b )为稳态等效子电路,图1(c )为小信号等效子电路。
)(t oL (t v ggV(ˆs vg )(s oL (c)图1: Buck 变换器和它的等效平均电路模型用图1(b )的稳态等效子电路,可以求出Buck 变换器在电阻负载和CCM 下的稳态关系。
因R R L <<,故在稳态关系中,可将其忽略。
求得的稳态关系为:稳态关系g o MV V =oL L I I = oL g MI I = D M =用图1(c )的小信号等效子电路及下面的求解技巧,可以求出Buck 变换器在稳态工作点上的小信号传递函数,具体的求解过程如下:(A ):只有占空比扰动时的三个小信号传递函数)(s G vd ,)()(s G g id ,)(s G id 求解: 从方程:)(ˆ)()(ˆ)()(ˆ)()(ˆs i s Z s v s G s d s G s voL out g vg vd o ×−×+×= )(ˆ)()(ˆ)()(ˆ)()(ˆ)()()(s i s G s v s G s d s G s ioL g ii g g ig g id g ×+×+×= )(ˆ)()(ˆ)()(ˆ)()(ˆs i s G s v s G s d s G s ioL ii g ig id L ×+×+×= 我们有:0ˆ,0ˆ)(ˆ)(ˆ)(===oL g o vd i vs ds vs G 0ˆ,0ˆ)(ˆ)(ˆ)()(===oL g g g id i vs ds is G 0ˆ,0ˆ)(ˆ)(ˆ)(===oL g d id i vs ds is G图2: Buck 变换器只有占空比扰动时的小信号等效电路所以图1(c )的小信号等效电路可简化为图2所示。
BUCK电路仿真报告_小信号分析

主电路的零极点图,我们要做的就是拿 PID 的零点补偿掉它 备注:如果增大控制频率即 减小 T 到 1E-6 时,不稳定极点会向 1,0 点靠拢..这样匹配起来更简单。 但是会引入一个问题就是 处理速度实在达不到,而且频率越高,高频下的各种电路现象会涌现出来。
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 小信号分析:aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 系统框图:aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 主电路:aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 当 MOS 管导通时:
但是发散了,所以需要减小 Kp :不影响系统的动态性能,但是会改变响应速度。
AaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaPID1 与主电路级联:aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 所取: Kp = -2.5227*0.01; Ti = -50112.97;%2123188.4; Td = -2.745758513e-4;%1.245e-3;
1 / L Il 0 Uin 1 / RC Uo 0
设系统导通占空比为 D 由状态空间平均法得:
d Il 0 dt Uo 1 / C
平均电流模式控制Buck电路小信号分析

平均电流模式控制Buck 电路小信号分析平均电流模式控制在电池充电电路以及PFC 中有着广泛的应用。
因其电流环和电压环均需补偿,故分析其小信号特性相当必要。
本文将采用参考[1]的建模方法来分析平均电流模式下buck 电路的特性,给出了其简化等式,并利用K 因子方法设计了补偿电路。
一 电流环补偿设计图一所示为电路的方框图及其小信号模型。
占空比到输出以及到电感电流的传递函数为[2]图一 电路方框图及小信号模型其中图二 Gvd 和Gid 传递函数输入和输出的反馈为从Vcl 到Ri V 的传递函数为其中 因Go<<1,故上式简化形式为其高频近似为此处采用Type II 来补偿,参考[3][4]给出了避免电路不稳定的补偿中频增益的限制,其中选定中频增益后,电流环的交越频率也随之确定利用K 因子法,确定补偿的零点为则有补偿的极点为进而有补偿的传函为电流环传递函数为图3 电流环bode 图 交越频率和相位裕量计算如下二 电压环补偿设计控制Vc 到输出的传递函数为 其近似为其低频近似为为了减少电流环对电压环的影响,后者交越频率要小于前者。
设定电压环交越频率 fc利用K 因子法,确定补偿的零点为补偿的极点为补偿的传函为则电压环传函为图4 Gvc Bode 图图5电压环bode 图交越频率和相位裕量计算如下参考:[1]. Philip Cooke." Modeling Average Current Control". Unitrode Integrated Circuits Corporation(TI).2005.[2].Doaer"buck".[3].Lloyd Dixon."Average Current Mode Control of Switching Power Supplies"Unitrode(TI) Application Note .[4].Jian Sun. Richard M.Bass."Modeling and Practical Design Issues for Average Current Control".1999 IEEE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开关电源(Buck电路)的小信号模型及环路设计摘要:建立了Buck电路在连续电流模式下的小信号数学模型,并根据稳定性原则分析了电压模式和电流模式控制下的环路设计问题。
关键词:开关电源;小信号模型;电压模式控制;电流模式控制0 引言设计一个具有良好动态和静态性能的开关电源时,控制环路的设计是很重要的一个部分。
而环路的设计与主电路的拓扑和参数有极大关系。
为了进行稳定性分析,有必要建立开关电源完整的小信号数学模型。
在频域模型下,波特图提供了一种简单方便的工程分析方法,可用来进行环路增益的计算和稳定性分析。
由于开关电源本质上是一个非线性的控制对象,因此,用解析的办法建模只能近似建立其在稳态时的小信号扰动模型,而用该模型来解释大范围的扰动(例如启动过程和负载剧烈变化过程)并不完全准确。
好在开关电源一般工作在稳态,实践表明,依据小信号扰动模型设计出的控制电路,配合软启动电路、限流电路、钳位电路和其他辅助部分后,完全能使开关电源的性能满足要求。
开关电源一般采用Buck电路,工作在定频PWM控制方式,本文以此为基础进行分析。
采用其他拓扑的开关电源分析方法类似。
1 Buck电路电感电流连续时的小信号模型图1为典型的Buck电路,为了简化分析,假定功率开关管S和D1为理想开关,滤波电感L为理想电感(电阻为0),电路工作在连续电流模式(CCM)下。
R e为滤波电容C的等效串联电阻,R o为负载电阻。
各状态变量的正方向定义如图1中所示。
图1 典型Buck电路S导通时,对电感列状态方程有L=U in-U o (1)S断开,D1续流导通时,状态方程变为L=-U o (2)占空比为D时,一个开关周期过程中,式(1)及式(2)分别持续了DT s和(1-D)T s的时间(T s为开关周期),因此,一个周期内电感的平均状态方程为L=D(U in-U o)+(1-D)(-U o)=DU in-U o(3)稳态时,=0,则DU in=U o。
这说明稳态时输出电压是一个常数,其大小与占空比D和输入电压U in成正比。
由于电路各状态变量总是围绕稳态值波动,因此,由式(3)得L=(D+d)(Uin+)-(U o+) (4)式(4)由式(3)的稳态值加小信号波动值形成。
上标为波浪符的量为波动量,d为D的波动量。
式(4)减式(3)并略去了两个波动量的乘积项得L=D+dU in-(5)由图1,又有i L=C+(6)U o=U c+R e C(7)式(6)及式(7)不论电路工作在哪种状态均成立。
由式(6)及式(7)可得i L+R e C=(U o+CR o) (8)式(8)的推导中假设R e<<R o。
由于稳态时=0,=0,由式(8)得稳态方程为i L=U o/R o。
这说明稳态时电感电流平均值全部流过负载。
对式(8)中各变量附加小信号波动量得i L++R e C=〔U o++CR o〕(9)式(9)减式(8)得+ReC=(+CR o)(10)将式(10)进行拉氏变换得(s)=(11)一般认为在开关频率的频带范围内输入电压是恒定的,即可假设=0并将其代入式(5),将式(5)进行拉氏变换得-(s) (12)sL(s)=d(s)U由式(11),式(12)得=U in(13)=·(14)式(13),式(14)便为Buck电路在电感电流连续时的控制-输出小信号传递函数。
2 电压模式控制(VMC)电压模式控制方法仅采用单电压环进行校正,比较简单,容易实现,可以满足大多数情况下的性能要求,如图2所示。
图2中,当电压误差放大器(E/A)增益较低、带宽很窄时,V c波形近似直流电平,并有D=V c/V s(15)d=/Vs(16)式(16)为式(15)的小信号波动方程。
整个电路的环路结构如图3所示。
图3没有考虑输入电压的变化,即假设=0。
图3中,(一般为0)及分别为电压给定与电压输出的小信号波动;K FB=U REF/U o,为反馈系数;误差e为输出采样值偏离稳态点的波动值,经电压误差放大器K EA放大后,得;K MOD为脉冲宽度调制器增益,K MOD=d/=1/V s;K PWR为主电路增益,K PWR=/d=U in;K LC为输出滤波器传递函数,K LC=。
图2 电压模式控制示意图和相关波形图3 开关电源的电压模式控制反馈环路图在已知环路其他部分的传递函数表达式后,即可设计电压误差放大器了。
由于K LC提供了一个零点和两个谐振极点,因此,一般将E/A设计成PI调节器即可,K EA=K P(1+ωz/s)。
其中ωz用于消除稳态误差,一般取为K LC零极点的1 /10以下;K P用于使剪切频率处的开环增益以-20dB/十倍频穿越0dB线,相角裕量略小于90°。
VMC方法有以下缺点:1)没有可预测输入电压影响的电压前馈机制,对瞬变的输入电压响应较慢,需要很高的环路增益;2)对由L和C产生的二阶极点(产生180°的相移)没有构成补偿,动态响应较慢。
VMC的缺点可用下面将要介绍的CMC方法克服。
3 平均电流模式控制(Average CMC)平均电流模式控制含有电压外环和电流内环两个环路,如图4所示。
电压环提供电感电流的给定,电流环采用误差放大器对送入的电感电流给定(V cv)和反馈信号(i L R s)之差进行比较、放大,得到的误差放大器输出V c再和三角波V s 进行比较,最后即得控制占空比的开关信号。
图4中R s为采样电阻。
对于一个设计良好的电流误差放大器,V c不会是一个直流量,当开关导通时,电感电流上升,会导致V c下降;开关关断,电感电流下降时,会导致V c上升。
电流环的设计原则是,不能使V c上升斜率超过三角波的上升斜率,两者斜率相等时就是最优。
原因是:如果V c上升斜率超过三角波的上升斜率,会导致V c峰值超过V s的峰值,在下个周波时V c 和V s就可能不会相交,造成次谐波振荡。
图4 开关电源平均电流模式控制示意图采用斜坡匹配的方法进行最优设计后,PWM控制器的增益会随占空比D的变化而变,如图5所示。
图5 PWM控制器增益与占空比变化关系图当D很大时,较小的V c会引起D较大的改变,而D较小时,即使V c变化很大,D的改变也不大,即增益下降。
所以有d=D/V s(17)不妨设电压环带宽远低于电流环,则在分析电流环时V cv 为常数。
当V c的上升斜率等于三角波斜率时,在开关频率f处,电流误差放大器的增益G CA为sG CA=G CA(V o/L)R s=V s f s(18)G CA=/(R s)=V s f s L/(U o R s)(19)高频下,将式(14)分子中的“1”和分母中的低阶项忽略,并化简,得(s)=(20)由式(17)及式(20)有==(21)将式(19)与式(21)相乘,得整个电流环的开环传递函数为·=(22)将s=2πf c代入上式,并令上式等于1时,可得环路的剪切频率f c=f s/(2π)。
因此,可将电流环等效为延时时间常数为一个开关周期的纯惯性环节,如图6所示。
图6 电流环的传递函数示意图显然,当电流误差放大器的增益G CA小于最优值时,电流响应的延时将会更长。
G CA中一般要在f s处或更高频处形成一个高频极点,以使f s以后的电流环开环增益以-40dB/dec的斜率下降,这样虽然使相角裕量稍变小,但可以消除电流反馈波形上的高频毛刺的影响,提高电流环的抗干扰能力。
低频下一般要加一个零点,使电流环开环增益变大,减小稳态误差。
整个环路的结构如图7所示。
其中K EA,K FB定义如前。
可见相对VMC而言(参见图3),平均CMC消除了原来由滤波电感引起的极点(新增极点f s很大,对电压环影响很小),将环路校正成了一阶系统,电压环增益可以保持恒定,不随输入电压V in而变,外环设计变得更加容易。
图7 电压外环反馈环路图4 峰值电流模式控制(Peak CMC)平均CMC由于要采样滤波电感的电流,有时显得不太方便,因此,实践中经常采用一种变通的电流模式控制方法,即峰值CMC,如图8所示。
电压外环输出控制量(V c)和由电感电流上升沿形成的斜坡波形(V s)通过电压比较器进行比较后,直接得到开关管的关断信号(开通信号由时钟自动给出),因此,电压环的输出控制量是电感电流的峰值给定量,由电感电流峰值控制占空比。
图8 峰值电流模式控制示意图峰值CMC控制的是电感电流的峰值,而不是电感电流(经滤波后即负载电流),而峰值电流和平均电流之间存在误差,因此,峰值CMC性能不如平均CMC。
一般满载时电感电流在导通期间的电流增量设计为额定电流的10%左右,因此,最好情况下峰值电感电流和平均值之间的误差也有5%,负载越轻误差越大,特别是进入不连续电流(DCM)工作区后误差将超过100%,系统有时可能会出现振荡现象。
在剪切频率f c以下,由图6可知平均CMC的电流环开环增益可升到很高(可以>1000),电流可完全得到控制,但峰值CMC 的电流环开环增益只能保持在10以内不变(峰值电流和平均值之间的误差引起),因此,峰值CMC更适用于满载场合。
峰值CMC的缺点还包括对噪音敏感,需要进行斜坡补偿解决次谐波振荡等问题。
但由于峰值CMC存在逐周波限流等特有的优点,且容易通过脉冲电流互感器等简单办法复现电感电流峰值,因此,它在Buck电路中仍然得到了广泛应用。
5 结语采用平均状态方程的方法可以得到Buck电路的小信号频域模型,并可依此进行环路设计。
电压模式控制、平均电流模式控制和峰值电流模式控制方法均可用来进行环路设计,各有其优缺点,适用的范围也不尽相同。
