大学物理第15章习题解答
大学物理上册(第五版)重点总结归纳及试题详解第十五章狭义相对论基础

⼤学物理上册(第五版)重点总结归纳及试题详解第⼗五章狭义相对论基础第⼗五章狭义相对论基础⼀、基本要求1. 理解爱因斯坦狭义相对论的两个基本假设。
2. 了解洛仑兹变换及其与伽利略变换的关系;掌握狭义相对论中同时的相对性,以及长度收缩和时间膨胀的概念,并能正确进⾏计算。
3. 了解相对论时空观与绝对时空观的根本区别。
4. 理解狭义相对论中质量和速度的关系,质量和动量、动能和能量的关系,并能分析计算⼀些简单问题。
⼆、基本内容1.⽜顿时空观⽜顿⼒学的时空观认为,物体运动虽然在时间和空间中进⾏,但时间的流逝和空间的性质与物体的运动彼此没有任何联系。
按⽜顿的说法是“绝对空间,就其本性⽽⾔,与外界任何事物⽆关,⽽永远是相同的和不动的。
”,“绝对的,真正的和数学的时间⾃⼰流逝着,并由于它的本性⽽均匀地与任何外界对象⽆关地流逝着。
”以上就构成了⽜顿的绝对时空观,即长度和时间的测量与参照系⽆关。
2.⼒学相对性原理所有惯性系中⼒学规律都相同,这就是⼒学相对性原理(也称伽利略相对性原理)。
⼒学相对性原理也可表述为:在⼀惯性系中不可能通过⼒学实验来确定该惯性系相对于其他惯性系的运动。
3. 狭义相对论的两条基本原理(1)爱因斯坦相对性原理:物理规律对所有惯性系都是⼀样的,不存在任何⼀个特殊的(例如“绝对静⽌”的)惯性系。
爱因斯坦相对论原理是伽利略相对性原理(或⼒学相对性原理)的推⼴,它使相对性原理不仅适⽤于⼒学现象,⽽且适⽤于所有物理现象。
(2)光速不变原理:在任何惯性系中,光在真空中的速度都相等。
光速不变原理是当时的重⼤发现,它直接否定了伽利略变换。
按伽利略变换,光速是与观察者和光源之间的相对运动有关的。
这⼀原理是⾮常重要的。
没有光速不变原理,则爱因斯坦相对性原理也就不成⽴了。
这两条基本原理表⽰了狭义相对论的时空观。
4. 洛仑兹变换()--='='='--='2222211c u xc u t t z z y y c u ut x x (K 系->'K 系)()-'+'='='=-'+'=2222211c u x c u t t z z y y c u t u x x (K 系->'K 系)令u c β=,γ=①当0→β,γ=1得ut x x -=',,',','t t z z y y ===洛仑兹变换就变成伽利略变换。
大学物理

第九章9-4 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C·m -1,求:(1)棒的延长线上与棒的近端相距d 1 = 8cm 处的场强; (2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强。
解:(1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m)。
在细棒上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产生的场强的大小为1220d d d 4()q lE krx l ==-λπε场强的方向沿x 轴正向.因此P 1点的总场强大小 通过积分得12d 4()LLl E x l λπε-=-⎰014LLx lλπε-=-011()4x Lx Lλπε=--+220124L x Lλπε=-①将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯-= 2.41×103(N·C -1)方向沿着x 轴正向。
(2)建立坐标系,y = d 2。
在细棒上取一线元d l ,所带的电量为d q = λd l 在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE krrλπε==由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ。
由图可知:r = d 2/sin θ,l = d 2cot θ所以 d l = -d 2d θ/sin 2θ 因此 02d sin d 4y E d λθθπε-=总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N·C -1)方向沿着y 轴正向9-6 一宽为b 的无限长均匀带电平面薄板,其电荷密度为σ,如习题9-6图所示。
《大学物理》习题课14-15章

I
1 r2
• 波函数(正弦、余弦表示)
D Asin(kx t )
• 振动与波的关系
y(x,t) Acos[(t
x v
)
0
]
由波写出振源振动表达式,由振源写出波函数
• 波的叠加、干涉、驻波
y y(x,t)
各质点相对平衡位置的 位移
波线上各质点平衡位置
yP
A cos[ (t
47
f
设原点处的振动方程
y Acos(2 ft ) y Acos[2 f (t t) ]
2
波的表达式 y Acos[2 f (t t x) ]
u2
2k
2
1
2
r2 r1
2
1
2
r1
r2
36
(A) 均为零.
(B) 均为π / 2 (C) 均为 π / 2
y
y
u A
O
x0
t
图A
图B
(D) 依次分别为 π / 2 与 π / 2
(E) 依次分别为 π / 2 与π / 2
[D]
11
O
y
A
+
2l
O处的相位比P点相位超前 l
u
C处的相位比P点相位落后 2l
u
u 沿x 轴正向
C点振动的相位差
r2
(2k 1) π
2
1
2
π
r2
r1
3 r1 2
/2
M点振动的相位差
(2k 1) π
大学物理2,15.第十五章思考题

1、一束光垂直入射在偏振片上,以入射光线为轴转动偏振片,观察通过偏振片后的光强变化过程。
如果观察到光强不变,则入射光是什么光?如果观察到明暗交替变化,有时出现全暗,则入射光是什么光?如果观察到明暗交替变化,但不出现全暗,则入射光是什么光?【答案:自然光;完全偏振光;部分偏振光】详解:当一束光垂直入射在偏振片上时,以入射光线为轴转动偏振片,如果观察到通过偏振片后的光强不发生变化,入射光是由自然光;如果观察到光强有明暗交替变化,并且有时出现全暗,则入射光是完全偏振光;如果观察到光强有明暗交替变化,但不出现全暗,则入射光是部分偏振光。
2、一束光是自然光和线偏振光的混合光,让它垂直通过一个偏振片。
若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光与线偏振光的光强比值为多少?【答案:1/2】详解:设该光束中自然光和线偏振光的强度分别为I 1和I 2。
当以此入射光束为轴旋转偏振片时,透射光强度的最大值和最小值分别为21max 21I I I +=1min 21I I = 依题意有I max =5I min ,即 12121521I I I ⨯=+ 解之得2121=I I 即入射光束中自然光与线偏振光的光强比值等于1/2。
3、一束光强为I 0的自然光相继通过三个偏振片P 1、P 2、P 3后,出射光的光强为0.125I 0 。
已知P 1和P 2的偏振化方向相互垂直,若以入射光线为轴旋转P 2,要使出射光的光强为零,P 2最少要转过多大的角度?【答案:45°】详解:由于P 1和P 2的偏振化方向相互垂直,而自然光相继通过三个偏振片后的光强不等于零,说明自然光通过偏振片的顺序为P 1、P 3、P 2。
如图所示,设偏振片P 1和P 3的夹角为θ,由马吕斯定律得出射光强为 )09(cos cos 2220θθ-= I I θ2sin 820I = 由于I =0.125I 0 ,代入上式解得 45=θ要使出射光强为零,应使P 2和P 3的偏振化方向垂直,因此P 2最少要转过的角度也等于45°。
华东理工大学大学物理作业答案2

2f 2 1 600 10 9 3 10 3 m a 0.4 10 3 (2)由 a sin k (k 1) 得 x sin 1.5 10 3 r a d a
44
大学物理习题册解答
7、用 1mm 内有 500 条刻痕的平面透射光栅观察钠光谱(λ =589nm) ,问: (1)光线垂直入射时,最多能看到第几级光谱; (2)光线以入射角 300 入射时,最多能看到第几级光谱。 解: (1) d
1 2 10 3 mm 500 由 d sin k 及最多能看到的谱线时 sinθ ~1 可得 d 2 10 3 k m ax 3.4 589 10 6
0
(3)最多能看到的谱线级数 sinθ ~1
k d 2400 4 600
∴
k=0,±1,±2
共5条谱线
45
大学物理习题册解答
9、一双缝,缝间距 d=0.1mm,缝宽 a=0.02mm,用波长λ =480nm 的平行单色光垂直入 射双缝,双缝后放一焦距为 50cm 的透镜,试求: (1)透镜焦平面上,干涉条纹的间距; (2)单缝衍射中央亮纹的宽度; (3)单缝衍射的中央包线内有多少条干涉的主极大? x 解: (1)由双缝干涉明条纹条件 d sin d k 得 f
12、一束自然光,入射到由 4 片偏振片构成的偏振片组上。每一片偏振片的偏振化方向 0 相对于前面一片的偏振化方向沿顺时针方向转过 30 角。问通过偏振片组后的光强是入 射光强的百分之几? 解: 设入射光强为 I0,通过偏振片的光强为 I1、I2、I3、I4 1 I1 I 0 2
大学物理下毛峰版光的衍射习题及答案

第15章 光的衍射 习题解答1.为什么声波的衍射比光波的衍射更加显着解:因为声波的波长远远大于光的波长,所以声波衍射比光波显着;2.衍射的本质是什么衍射和干涉有什么联系和区别解:波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象.其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生.而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成.3.什么叫半波带单缝衍射中怎样划分半波带对应于单缝衍射第三级明条纹和第四级暗条纹,单缝处波阵面各可分成几个半波带解:半波带由单缝A 、B 首尾两点向ϕ方向发出的衍射线的光程差用2λ来划分.对应于第三级明条纹和第四级暗条纹,单缝处波阵面可分成7个和8个半波带. ∵由272)132(2)12(sin λλλϕ⨯=+⨯=+=k a4.在单缝衍射中,为什么衍射角ϕ愈大级数愈大的那些明条纹的亮度愈小 解:因为衍射角ϕ愈大则ϕsin a 值愈大,分成的半波带数愈多,每个半波带透过的光通量就愈小,而明条纹的亮度是由一个半波带的光能量决定的,所以亮度减小.5.若把单缝衍射实验装置全部浸入水中,衍射图样将发生怎样的变化如果此时用公式),2,1(2)12(sin =+±=k k a λϕ来测定光的波长,问测出的波长是光在空气中的还是在水中的波长解:当全部装置浸入水中时,由于水中波长变短,对应='='λϕk a sin n k λ,而空气中为λϕk a =sin ,∴ϕϕ'=sin sin n ,即ϕϕ'=n ,水中同级衍射角变小,条纹变密.如用)12(sin +±=k a ϕ2λ),2,1(⋅⋅⋅=k 来测光的波长,则应是光在水中的波长.因ϕsin a 只代表光在水中的波程差.6.单缝衍射暗纹条件与双缝干涉明纹的条件在形式上类似,两者是否矛盾怎样说明解:不矛盾.单缝衍射暗纹条件为k k a 2sin ==λϕ2λ,是用半波带法分析子波叠加问题.相邻两半波带上对应点向ϕ方向发出的光波在屏上会聚点一一相消,而半波带为偶数,故形成暗纹;而双缝干涉明纹条件为λθk d =sin ,描述的是两路相干波叠加问题,其波程差为波长的整数倍,相干加强为明纹.7.光栅衍射与单缝衍射有何区别为何光栅衍射的明纹特别明亮而暗区很宽解:光栅衍射是多缝干涉和单缝衍射的总效果.其明条纹主要取决于多缝干涉.光强与缝数2N 成正比,所以明纹很亮;又因为在相邻明纹间有)1(-N 个暗纹,而一般很大,故实际上在两相邻明纹间形成一片黑暗背景.8. 试指出当衍射光栅的光栅常数为下述三种情况时,哪些级次的衍射明纹缺级12a b a +=;23a b a +=;34a b a +=解:由光栅明纹条件和单缝衍射暗纹条件同时满足时,出现缺级.即可知,当k ab a k '+=时明纹缺级. 1a b a 2=+时,⋅⋅⋅=,6,4,2k 偶数级缺级;2a b a 3=+时,⋅⋅⋅=,9,6,3k 级次缺级;3a b a 4=+,⋅⋅⋅=,12,8,4k 级次缺级.9.若以白光垂直入射光栅,不同波长的光将会有不同的衍射角;1零级明纹能否分开不同波长的光2在可见光中哪种颜色的光衍射角最大3不同波长的光分开程度与什么因素有关解:1零级明纹不会分开不同波长的光.因为各种波长的光在零级明纹处均各自相干加强.2可见光中红光的衍射角最大,因为由λϕk b a =+sin )(,对同一k 值,衍射角λϕ∞.3对于同一级明纹,波长相差越大条纹分开程度越大;10.为什么天文望远镜物镜的孔径做得很大射电天文望远镜和光学望远镜,哪种分辨率更高 解:光学仪器的最小分辨角为0 1.22D λθ=,它的倒数为分辨率,当D 越大或者λ越小,分辨率就越大,所以用的天文望远镜物镜的孔径很大,提高了分辨率;由于微波的波长比可见光的波长要小,故射电天文望远镜的分辨率更高;11.单缝宽0.40mm,透镜焦距为1m,用600λ=nm 的单色平行光垂直照射单缝;求:1屏上中央明纹的角宽度和线宽度;2单缝上、下端光线到屏上的相位差恰为4π的P 点距离中央明纹中心的距离;3屏上第一级明纹的线宽度;解:1第1级暗条纹中心对应的衍射角1ϕ为故中央明纹的角宽度为而中央明纹的线宽度为2相位差为4π,则对应的光程差为2λ,即故屏上P 点应形成第二级暗纹,它到中央明纹中心的距离为3屏上第一级明纹的线宽度为中央明纹线宽度的1/2,解之得12.在单缝夫琅禾费衍射实验中,用波长1650nm λ=的单色平行光垂直入射单缝,已知透镜焦距2.00f m =,测得第二级暗纹距中央明纹中心33.2010m -⨯;现用波长为2λ的单色平行光做实验,测得第三级暗纹距中央明纹中心34.5010m -⨯.求缝宽a 和波长2λ; 解:1当用1650nm λ=入射时,第二级暗纹对应的衍射角设为1ϕ由暗纹公式得: 11sin 2a ϕλ=而第二级暗纹距中中央明纹中心距离则 9413122650102.008.13103.210a f m m x λ---⨯⨯==⨯=⨯⨯ 2当用2λ入射时,第三级暗纹对应的衍射角设为2ϕ由暗纹公式得: 22sin 3a ϕλ=而第三级暗纹距中央明纹中心距离则 34722 4.5108.1310 6.091060933 2.00x a m m nm f λ---⨯⨯⨯===⨯=⨯ 13.一单色平行光垂直照射一单缝,若其第三级明纹位置正好与600nm 的单色平行光的第二级明纹位置重合,求此单色光的波长;解:单缝衍射的明纹公式为当600=λnm 时,2=kx λλ=时,3=k重合时ϕ角相同,所以有得 6.42860075=⨯=x λnm 14.用橙黄色的平行光垂直照射一缝宽为0.60mm 的单缝,缝后凸透镜的焦距为40.0cm,观察屏幕上形成的衍射条纹;若屏上离中央明纹中心1.40mm 处的P 点为一明纹;求:1入射光的波长;2P 点处条纹的级数;3从P 点看,对该光波而言,狭缝处的波阵面可分成几个半波带解:1由于P 点是明纹,故有2)12(sin λϕ+=k a ,⋅⋅⋅=3,2,1k由ϕϕsin tan 105.34004.13≈=⨯==-f x 故3105.3126.0212sin 2-⨯⨯+⨯=+=k k a ϕλ 当 3=k ,得600=λnm2 3=k P 点是第3级明纹;3由2)12(sin λϕ+=k a 可知, 当3=k 时,单缝处的波面可分成712=+k 个半波带;15.以白光垂直照射光栅常数d=×10-6m 的透射光栅,在衍射角为30°处会出现什么波长的可见光可见光的波长范围为400~700nm解:由光栅方程:λθk d ±=sin , 3,2,1,0=k讨论:当1=k 时,nm k d 17002==λ 当2=k时,nm k d 8502==λ 当3=k时,nm k d 5672==λ 当4=k时,nm k d 4252==λ 当5=k 时,nm kd 3402==λ 所以,在衍射角为30°处会出现波长为567nm 和425nm 的可见光16.用波长1400nm λ=和2760nm λ=的两种平行光,垂直入射在光栅常数为52.010m -⨯的光栅上,若紧接光栅后用焦距为f =2.0m 的透镜把光会聚在屏幕上;求屏幕上两种平行光第二级主极大之间的距离;解:光栅方程:sin d k ϕλ=±, 3,2,1,0=k屏幕上第k 级主极大的位置为屏幕上两种光第二级主极大之间的距离为17.波长600λ=nm 的单色平行光垂直入射到一光栅上,第二、三级明纹分别出现在20.0sin =ϕ与30.0sin =ϕ处,第四级缺级;求:1光栅常数d ;2光栅上狭缝的最小宽度a ;3在9090ϕ-<<范围内,实际呈现的全部级数;解:1由λϕk b a =+sin )(式对应于20.0sin 1=ϕ与30.0sin 2=ϕ处满足:得 6100.6-⨯=+=b a d m2因第四级缺级,故此须同时满足解得 k k b a a '⨯='+=-6105.14取1='k ,得光栅狭缝的最小宽度为6105.1-⨯m3由λϕk b a =+sin )( 当2πϕ=,对应max k k =∴ 1010600100.696max =⨯⨯=+=--λb a k 因4±,8±缺级,所以在︒︒<<-9090ϕ范围内实际呈现的全部级数为9,7,6,5,3,2,1,0±±±±±±±=k 共15条明纹10±=k 在︒±=90k 处看不到.18.一束平行光含有两种不同波长成份1λ和2λ;此光束垂直照射到一个衍射光栅上,测得波长1λ的第二级主极大与波长2λ的第三级主极大位置相同,它们的衍射角均满足sin 0.3ϕ=;已知nm 6301=λ;1求光栅常数d ;2求波长2λ;3对波长1λ而言,最多能看到第几级明纹解:由光栅方程 λθk d ±=sin , 3,2,1,0=k1光栅常数为m d 61102.4sin 2-⨯==θλ 22132sin λλθ==d 37.6sin 11=≤=λλθd d k最多能看到第6级明纹19.波长范围为400760nm 的白光垂直照射入射某光栅,已知该光栅每厘米刻有5000条透光缝,在位于透镜焦平面的显示屏上,测得光栅衍射第一级光谱的宽度约为56.5mm,求透镜的焦距;解:由题设可知光栅常数为由光栅方程可得波长为400nm 和760nm 的第一级谱线的衍射角分别为第一级光谱的宽度为则有 0.18x f ∆==0.31m 20.在圆孔夫琅禾费衍射中,设圆孔半径为0.10mm,透镜焦距为50cm,所用单色光波长为500nm,求在透镜焦平面处屏幕上呈现的爱里斑半径;解:由爱里斑的半角宽度爱里斑半径53.1105.30500tan 24=⨯⨯=≈=-θθf f d mm 21.已知天空中两颗星相对于一望远镜的角距离为64.8410rad -⨯,它们都发出波长为550nm 的光,试问望远镜的口径至少要多大,才能分辨出这两颗星解:由最小分辨角公式22.已知入射的X 射线束含有从~范围内的各种波长的X 射线,晶体的晶格常数为,当X 射线以45°角入射到晶体时,问晶体对哪些波长的X 射线能产生强反射解:由布喇格公式 λϕk d =sin 2 得kd ϕλsin 2=时满足干涉相长 当1=k 时, nm 389.045sin 75.22=⨯⨯=︒λ2=k 时,nm 194.0245sin 75.22=⨯⨯=︒λ 3=k 时,nm 13.0389.3==λ 4=k 时, nm 097.0489.3==λ 故只有nm 13.03=λ和nm 097.04=λ的X 射线能产生强反射.。
【大学物理】第15章热力学第一定律

例补:20mol氧气由状态1变化到状态2所经历的过程
如图,(1)沿1-m-2路径;(2)沿1-2直线。试分
别求出这两过程中的A与Q及氧气内能的变化 氧气分子当成刚性分子理想气体看待。
E2
E1
p(1.03105 pa)
20 2
m
5 0 10
1
50 V (L)
解(1)1-m-2过程:
对于1-m过程,由于体积不变(等容过程),所以
I绝热膨胀:V2 V1 T2 T1
II绝热压缩:V2 V1 T2 T1
四、绝热过程的P-V图
1、P-V图: 将绝热方程代入
A V2 PdV 可得: V1
A P1V1 P2V2
1
A
p1V1
1
1
V1 V2
1
dQ dE dA dE PdV
dE 0
PV M RT
( dQ)T dA PdV
QT
A
V2 PdV
V1
代入上式
QT
M
RT
V2 dV V V1
M
RT ln V2 V1
P1V1 P2V2
QT
M
RT
ln
P1 P2
3、理想气体等温过程作功图示:
对于AB过程,因为热力学第一定律得气体吸收的热量应等于气体对外做的功, 功可以通过过程曲线下的面积求得
QAB
WAB
1 2 (pA
pB )(VB
VA )
大学物理 第十五章 磁介质的磁化
临界温度Tc。在Tc以上,铁磁性完全消失而 成为顺磁质,Tc称为居里温度或居里点。不 同 的 铁 磁 质 有 不 同 的 居 里 温 度 Tc 。 纯 铁 : 770ºC,纯镍:358ºC。
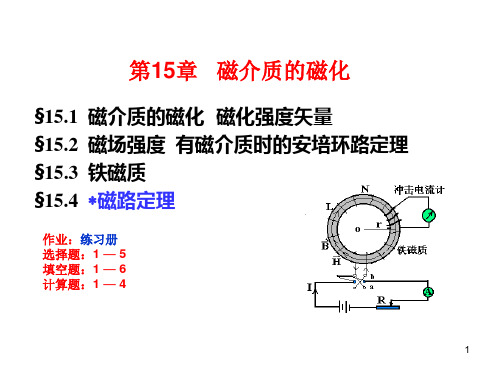
居里
装置如图所示:将悬挂着的镍片移近永 久磁铁,即被吸住,说明镍片在室温下 具有铁磁性。用酒精灯加热镍片,当镍 片的温度升高到超过一定温度时,镍片 不再被吸引,在重力作用下摆回平衡位 置,说明镍片的铁磁性消失,变为顺磁 性。移去酒精灯,稍待片刻,镍片温度 下降到居里点以下恢复铁磁性,又被磁 铁吸住。
第15章 磁介质的磁化
§15.1 磁介质的磁化 磁化强度矢量 §15.2 磁场强度 有磁介质时的安培环路定理 §15.3 铁磁质 §15.4 磁路定理
作业:练习册 选择题:1 — 5 填空题:1 — 6 计算题:1 — 4
1
§1 磁介质的磁化 磁化强度矢量
1. 磁介质 磁介质:实体物质在磁场作用下呈现磁性,该物体称磁介质。 磁化:磁介质在磁场中呈现磁性(在磁场的作用下产生附加 磁场)的现象称为磁化。
B B0 B
I
I
磁介质
抗磁质: r 1, B B0
B与B0 反方向,
如氮、水、铜、银、金、铋等。
I
I
铁磁质: r 1, B B0 B与B0 同方向,
如铁、钴、镍等,
超导体是理想的抗磁体。
B0 B
3
2.分子电流模型和分子磁矩
原子中电子参与两种运动:自
pm B
旋及绕核的轨道运动,对应有轨道
矢量和为零。
极化、位移极化。
4
加外磁场时 : M Pm B
B B0 B
当外磁场存在时,各分子固有磁矩受磁场力矩的作用,或
大学物理下册11-15章答案(修改过,红色为修正地方还有以下解释)
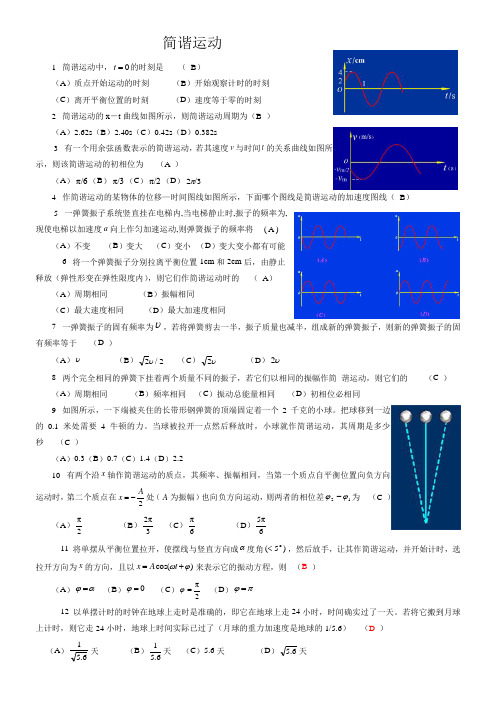
简谐运动1 简谐运动中,0=t 的时刻是 ( B )(A )质点开始运动的时刻 (B )开始观察计时的时刻(C )离开平衡位置的时刻 (D )速度等于零的时刻2 简谐运动的x -t 曲线如图所示,则简谐运动周期为(B )(A )2.62s (B )2.40s (C )0.42s (D )0.382s3 有一个用余弦函数表示的简谐运动,若其速度v 与时间t 的关系曲线如图所示,则该简谐运动的初相位为 (A )(A )π/6(B )π/3(C )π/2(D )/32π4 作简谐运动的某物体的位移—时间图线如图所示,下面哪个图线是简谐运动的加速度图线( B )5 一弹簧振子系统竖直挂在电梯内,当电梯静止时,振子的频率为,现使电梯以加速度a 向上作匀加速运动,则弹簧振子的频率将 ( A )(A )不变 (B )变大 (C )变小 (D )变大变小都有可能6 将一个弹簧振子分别拉离平衡位置1cm 和2cm 后,由静止释放(弹性形变在弹性限度内),则它们作简谐运动时的 ( A )(A )周期相同 (B )振幅相同(C )最大速度相同 (D )最大加速度相同7 一弹簧振子的固有频率为υ,若将弹簧剪去一半,振子质量也减半,组成新的弹簧振子,则新的弹簧振子的固有频率等于 (D )(A )υ (B )2/2υ (C )υ2 (D )υ28 两个完全相同的弹簧下挂着两个质量不同的振子,若它们以相同的振幅作简 谐运动,则它们的 (C ) (A )周期相同 (B )频率相同 (C )振动总能量相同 (D )初相位必相同9 如图所示,一下端被夹住的长带形钢弹簧的顶端固定着一个2千克的小球。
把球移到一边的0.1米处需要4牛顿的力。
当球被拉开一点然后释放时,小球就作简谐运动,其周期是多少秒 (C )(A )0.3(B )0.7(C )1.4(D )2.210 有两个沿x 轴作简谐运动的质点,其频率、振幅相同,当第一个质点自平衡位置向负方向运动时,第二个质点在2A x -=处(A 为振幅)也向负方向运动,则两者的相位差12ϕϕ-为 (C ) (A )2π (B )3π2 (C )6π (D )6π5 11 将单摆从平衡位置拉开,使摆线与竖直方向成α度角)5(o <,然后放手,让其作简谐运动,并开始计时,选拉开方向为x 的方向,且以)cos(ϕω+=t A x 来表示它的振动方程,则 (B )(A )αϕ= (B )0=ϕ (C )2π=ϕ (D )πϕ= 12 以单摆计时的时钟在地球上走时是准确的,即它在地球上走24小时,时间确实过了一天。
大学物理学(下册)第15章 量子物理基础

5、爱因斯坦的光子假说和光电效应方程
1).爱因斯坦光子假设 ①.光是一束以光速c运动的粒子流,这些粒子称为光子;
②.光子的能量: h
③.光的强度: SNh
2).爱因斯坦光电效应方程
爱因斯坦认为:在光电效应中,金属中的电子吸收
一个光子的能量h,一部分消耗在使金属中电子挣脱原子
2020/12/10
2. 普朗克理论与经典理论不同
经典理论的基本观点
普朗克能量子假设
(1)电磁波辐射来源于 带电粒子的振动,电磁波 频率与带电粒子振动频率 相同。 (2)振子辐射电磁波含 各种波长,是连续的,辐 射能量也是连续的。
对于频率为的振子,
振子辐射的能量不是 连续的,而是分立的, 它的取值是某一最小 能量 的整数倍
出的、在波长 附近单位波长间隔内的能量。称为单色辐
射出射度或单色辐出度。
M(T)
dM(T)
d
单位: W / m 3
2020/12/10
温度为 T 的物体,在单位时间内,从单位面积上所辐射
出的各种波长的电磁波的能量总和。称为辐射出射度或辐
出度。
M(T) 0M(T)d
单位: W / m 2
太阳和钨丝的单色 辐出度曲线
即:光电子的最大初动能与入射光的强度成正比关系,而 与光的频率无关。与实验结果不符。
2020/12/10
红限问题
按上述理论,无论何种频率的入射光,只要其强 度足够大,就能使电子具有足够的能量逸出金属,不 存在红限问题。与实验结果不符。
驰豫时间
按上述理论,如果入射光强很弱,则电子逸出金 属所需的能量,需要有一定的时间来积累。与实验结 果不符。
光的波动性用光波的波长 和频率 描述,光
湖南大学物理(2)第14,15章课后习题参考答案

第14章 稳恒电流的磁场 一、选择题1(B),2(D),3(D),4(B),5(B),6(D),7(B),8(C),9(D),10(A) 二、填空题(1). 最大磁力矩,磁矩 ; (2). πR 2c ; (3). )4/(0a I μ; (4).RIπ40μ ;(5). μ0i ,沿轴线方向朝右. ; (6). )2/(210R rI πμ, 0 ; (7). 4 ; (8). )/(lB mg ; (9). aIB ; (10). 正,负.三 计算题1.一无限长圆柱形铜导体(磁导率μ0),半径为R ,通有均匀分布的电流I .今取一矩形平面S (长为1 m ,宽为2 R ),位置如右图中画斜线部分所示,求通过该矩形平面的磁通量.解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定 律可得:)(220R r r RIB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r R I Rd 2020⎰π=μπ=40Iμ 在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+Iμ1 m2. 横截面为矩形的环形螺线管,圆环内外半径分别为R 1和R 2,芯子材料的磁导率为μ,导线总匝数为N ,绕得很密,若线圈通电流I ,求.(1) 芯子中的B 值和芯子截面的磁通量. (2) 在r< R 1和r > R 2处的B 值.解:(1) 在环内作半径为r 的圆形回路, 由安培环路定理得NI r B μ=π⋅2, )2/(r NI B π=μ 在r 处取微小截面d S = b d r , 通过此小截面的磁通量r b rNIS B d 2d d π==μΦ穿过截面的磁通量⎰=SS B dΦr b rNId 2π=μ12ln2R R NIbπ=μ (2) 同样在环外( r < R 1 和r > R 2 )作圆形回路, 由于0=∑iI02=π⋅r B ∴ B = 03. 一根很长的圆柱形铜导线均匀载有10 A 电流,在导线内部作一平面S ,S 的一个边是导线的中心轴线,另一边是S 平面与导线表面的交线,如图所示.试计算通过沿导线长度方向长为1m 的一段S 平面的磁通量.(真空的磁导率μ0 =4π×10-7 T ·m/A ,铜的相对磁导率μr ≈1)解:在距离导线中心轴线为x 与x x d +处,作一个单位长窄条, 其面积为 x S d 1d ⋅=.窄条处的磁感强度 202RIxB r π=μμ所以通过d S 的磁通量为 x RIxS B r d 2d d 20π==μμΦ通过1m 长的一段S 平面的磁通量为⎰π=Rr x RIx20d 2μμΦ60104-=π=Ir μμ Wb4. 计算如图所示的平面载流线圈在P 点产生的磁感强度,设线圈中的电流强度为I .解:如图,CD 、AF 在P 点产生的 B = 0x2EF D E BC AB B B B B B+++= )sin (sin 4120ββμ-π=aIB AB , 方向⊗其中 2/1)2/(sin 2==a a β,0sin 1=β∴ a I B AB π=240μ, 同理, a IB BC π=240μ,方向⊗.同样)28/(0a I B B EF D E π==μ,方向⊙.∴ aI B π=2420μaIπ-240μaIπ=820μ 方向⊗.5. 如图所示线框,铜线横截面积S = 2.0 mm 2,其中OA 和DO '两段保持水平不动,ABCD 段是边长为a 的正方形的三边,它可绕OO '轴无摩擦转动.整个导线放在匀强磁场B 中,B 的方向竖直向上.已知铜的密度ρ = 8.9×103 kg/m 3,当铜线中的电流I =10 A 时,导线处于平衡状态,AB 段和CD 段与竖直方向的夹角α =15°.求磁感强度B的大小.解:在平衡的情况下,必须满足线框的重力矩与线框所受的磁力矩平衡(对OO '轴而言).重力矩 αραρsin sin 2121gSa a a gS a M +⋅= αρsin 22g Sa =磁力矩 ααcos )21sin(222B Ia BIa M =-π=平衡时 21M M =所以 αρsin 22g Sa αcos 2B Ia = 31035.9/tg 2-⨯≈=I g S B αρ T6. 如图两共轴线圈,半径分别为R 1、R 2,电流为I 1、I 2.电流的方向相反,求轴线上相距中点O 为x 处的P 点的磁感强度. 解:取x 轴向右,那么有 2/322112101])([2x b R I R B ++=μ 沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0,则B 方向为沿x 轴正方向.若B < 0,则B的方向为沿x 轴负方向.P7. 如图所示.一块半导体样品的体积为a ×b ×c .沿c 方向有电流I ,沿厚度a 边方向加有均匀外磁场B (B 的方向和样品中电流密度方向垂直).实验得出的数据为 a =0.10 cm 、b =0.35 cm 、c =1.0 cm 、I =1.0 mA 、B =3.0×10-1 T ,沿b 边两侧的电势差U =6.65 mV ,上表面电势高.(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)?(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数).解:(1) 根椐洛伦兹力公式:若为正电荷导电,则正电荷堆积在上表面,霍耳电场的方向由上指向下,故上表面电势高,可知是p 型半导体。
大学物理学下册(赵近芳)第15章习题解答

1习 题1515.1选择题(1)用一定频率的单色光照射在某种金属上,测出其光电流I 与电势差U 的关系曲线如题16.1图中实线所示.然后在光强度I 不变的条件下增大照射光的频率,测出其光电流的曲线用虚线表示.符合题意的图是: [ ][答案:D 。
光强度I φ不变,光的频率v 增大,光子数(光子密度)N φ减少,则逸出光电子数 N e 减少,饱和光电流I e 减少;光的频率v 增大,由爱因斯坦光电效应方程21A 2m m hv υ=-知初动能增大,则遏止电压增加。
](2) 康普顿散射的主要特点是: [ ](A) 散射光的波长均与入射光的波长相同,与散射角、散射体性质无关.(B) 散射光中既有与入射光波长相同的,也有比入射光波长长的和比入射光波长短的.这与散射体性质有关.(C) 散射光的波长均比入射光的波长短,且随散射角增大而减小,但与散射体的性质无关.(D) 散射光中有些波长比入射光的波长长,且随散射角增大而增大,有些散射光波长与入射光波长相同.这都与散射体的性质无关.[答案:D 。
](3)假定氢原子原是静止的,质量为1.67×10-27 kg ,则氢原子从n = 3 的激发状态直接通过辐射跃迁到基态时的反冲速度大约是 [ ](A) 4 m/s . (B) 10 m/s . (C) 100 m/s . (D) 400 m/s .[答案:A 。
动量守恒 -m υ+h/λ34722711 6.62610 1.096108()13 1.67109H h R m υ--⨯⨯⨯=-=⨯⨯≈4m/s](4) 关于不确定关系2x p x ∆∆≥,有以下几种理解: (a ) 粒子的动量不可能确定.(b ) 粒子的坐标不可能确定.(c ) 粒子的动量和坐标不可能同时准确地确定.(d ) 不确定关系不仅适用于电子和光子,也适用于其它粒子.其中正确的是: [ ]O(A ) (B ) (C ) (D )题15.1图。
大学物理第15章

外力克服f m作功(消耗机械能) 通过fm转换为感应电流的能量。
15
例长为L的铜棒,在磁感强度为B 的均匀磁场中以角速 度 在与磁场方向垂直的平面内绕棒的一端o 匀速转动,
解: 取线元 d l ,方向沿o指向A
求棒中的动生电动势。
v l d i (v B) d l vB d l
动生电动势的计算公式:
i v B dl
L
v B dl v
fL
(3)说明
L
v
dl
动生电动势的计算公式是普遍的。 动生电动势不依赖于导体回路的存在而产生。 电动势是非静电力对单位电荷所做的功。 动生电动势与“洛伦兹力不做功”并不矛盾。
金属棒上总电动势为
i Bv d l Bl d l BL
L 0 L 0 1 2
2
方向为A0,即o点电势较高。
16
另解:
1 2 S L 2
L
S
Φ BS
dΦ 1 2 d 1 2 BL i BL 2 dt 2 dt
讨论 法拉第圆盘发电机 ——铜盘在磁场中转动。
d ( B) dl
0
B sin 90 dl cos dl Rd 2 BR 2 cos d B2R
方向:
d θ dl
θ
B
R
ab
23
§15-3 感生电动势和感生电场
(1)感生电动势
考虑随时间变化的磁场,即 B Bt ,代入 B dS
分析指出:两种电动势的非静电力不同。
大学物理习题解答12~15章

第十二章 恒定磁场 (Steady Magnetic Field)一、选择题12.1 均匀磁场的磁感强度B垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为 (A) B r 22π. (B)B r 2π.(C) 0. (D) 无法确定的量. [ B ]12.2 载流的圆形线圈(半径a 1 )与正方形线圈(边长a 2 )通有相同电流I .若两个线圈的中心O 1 、O 2处的磁感强度大小相同,则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B)π2∶ 1(C)π2∶4 (D)π2∶8 [ D ]12.3 如题图12.1,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅LlB d 等于(A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ. [ D ]II a bcdL120°题图12.1I 1I 212.4 如题图12.2,在一固定的载流大平板附近有一载流小线框能自由转动或平动.线框平面与大平板垂直。
大平板的电流与线框中电流方向如图所示。
则在同一侧且对着大平板看,通电线框的运动情况是:(A) 靠近大平板. (B) 顺时针转动.(C) 逆时针转动. (D) 离开大平板向外运动. [ B ]12.5 在匀强磁场中,有两个平面线圈,其面积A 1 = 2 A 2,通有电流I 1 = 2 I 2,它们所受的最大磁力矩之比M 1 / M 2等于 (A) 1. (B) 2.(C) 4. (D) 1/4. [ C ]12.6 如题图12.3所示,无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于 (A)RIπ20μ; (B)RI40μ; (C)RIπ20μ ;(D))11(20π-R Iμ; (E) )11(40π+R I μ。
大学物理课本答案习题 第十五章习题解答

习题十五15-1 某物体辐射频率为146.010Hz ⨯的黄光,问这种辐射的能量子的能量是多大? 解: 根据普朗克能量子公式有:-3414196.6310 6.010 4.010(J)h εν-==⨯⨯⨯=⨯15-2 假设把白炽灯中的钨丝看做黑体,其点亮时的温度为K 2900. 求:(1) 电磁辐射中单色辐出度的极大值对应的波长; (2) 据此分析白炽灯发光效率低的原因. 解 (1)由维恩位移定律,得-3-72.89810=9.9910(m)=999(nm)2900b T λ⨯==⨯(2)因为电磁辐射中单色辐出度的极大值对应的波长在红外区域,所以白炽灯的发光效率较低。
15-3 假定太阳和地球都可以看成黑体,如太阳表面温度T S =6000K ,地球表面各处温度相同,试求地球的表面温度(已知太阳的半径R 0=6.96×105km ,太阳到地球的距离r =1.496×108km )。
解: 由 40T M σ=太阳的辐射总功率为2428482002644 5.671060004(6.9610)4.4710(W)S S S P M R T R πσππ-===⨯⨯⨯⨯⨯=⨯地球接受到的功率为62226221117 6.3710() 4.4710()422 1.496102.0010(W)S E E E S P R P R P d d ππ⨯===⨯⨯⨯=⨯ 把地球看作黑体,则 24244E E E E E R T R M P πσπ==290(K)E T ===15-4 一波长nm 2001=λ的紫外光源和一波长nm 7002=λ的红外光源,两者的功率都是400W 。
问:(1)哪个光源单位时间内产生的光子多?(2)单位时间内产生的光子数等于多少? 解: (1)光子的能量λνchh E ==设光源单位时间内产生的光子数为n ,则光源的功率hcw n nhcnE w λλ===, 可见w 相同时,λ越大,n 越大,而12λλ>,所以红外光源产生的光子数多。
大学物理学 第15章_光的干涉 习题解答 [王玉国 康山林 赵宝群]
![大学物理学 第15章_光的干涉 习题解答 [王玉国 康山林 赵宝群]](https://img.taocdn.com/s3/m/daedcac3a1c7aa00b52acb9a.png)
2n油e (2k 1) , k 1,, 2 2
1 2 n e (2 k 1) 油 1 2k 1 2 7 1 500 nm 2 , 当 时, 1 700 nm k 2 1 5 2 2 2 1 2n e (2k 1) 2 油 2
对于 2 =532nm 的光波,条纹间距为:
x2
两组条纹的同侧第 8 级条纹之间的距离为:
x k
D D 1 k 2 k (x1 x2 ) 8 (0.433 0.355) 103 m 0.624 103 m d d
已知对于波长为 500nm 和 15-8 在玻璃板(折射率为1.50 )上有一层油膜(折射率1.30 )。 700nm 的垂直入射光都发生反射相消,而这两波长之间无别的波长的光反射相消,求此油 膜的厚度。 解:因为油膜( n油 1.3 )在玻璃( n玻 1.5 )上,所以不考虑半波损失,由反射相消条件 有:
r2 e ne r1 r2 r1 (n 1)e 0
解得
k
(n 1)e
(1.58 1) 6.6 10 6 7 5.5 10 7
即零级明纹移到覆盖云母片的狭缝这一侧的原来的第 7 级明纹处。 15-7 在杨氏干涉实验中,两小孔的距离为1.5mm ,观察屏离小孔的垂直距离为 1m , 若所用光源发出波长 1=650nm 和 2=532nm 的两种光波,试求两光波分别形成的条纹间 距以及两组条纹的同侧两个第 8 级亮纹之间的距离。 解:第 k 明纹中心位置为
《大学物理学》习题解答
第 15 章
15-1 一单色光从空气射入水中,其频率、波速、波长是否变化?怎样变化? 答:单色光从空气射入水中,其频率不变;波速变大;波长变长。 15-2 什么是光程?在不同的均匀媒质中,若单色光通过的光程相等时,其几何路程是 否相同?其所需时间是否相同?在相位差与光程差的关系式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五章习题解答
1选择题:⑴ B ;⑵ C ;⑶ B ;⑷ B 。
2填空题:⑴ 线偏振光(或完全偏振光,或平面偏振光),光(矢量)振动,偏振化(或透光轴);
⑵ 完全偏振光(或线偏振光),垂直; ⑶ ; ⑷ 波动,横波;
3计算题:
1 自然光入射到两个重叠的偏振片上.如果透射光强为,(1)透射光最大强度的三分之一,(2)入射光强的三分之一,则这两个偏振片透光轴方向间的夹角为多少? 解:(1) max 12013
1cos 2I I I ==α 又 20max I I =
∴ ,6
01I I = 故 'ο11124454,3
3cos ,31cos ===ααα. (2) 022023
1cos 2I I I ==α ∴ 'ο221635,32cos ==
αα
2 投射到起偏器的自然光强度为I 0,开始时,起偏器和检偏器的透光轴方向平行.然后使检偏器绕入射光的传播方向转过30°,45°,60°,试分别求出在上述三种情况下,透过检偏器后光的强度是I 0的几倍?
解:由马吕斯定律有:0o 2018
330cos 2I I I ==
, 0ο2024145cos 2I I I ==,0ο2038
160cos 2I I I == 所以透过检偏器后光的强度分别是I 0的38,14,18倍。
3 使自然光通过两个偏振化方向夹角为60°的偏振片时,透射光强为I 1,今在这两个偏振片之间再插入一偏振片,它的偏振化方向与前两个偏振片均成30°,问此时透射光I 与I 1之比为多少?
解:由马吕斯定律:
ο20160cos 2I I =
80I =,32
930cos 30cos 20ο2ο20I I I == ∴ 194 2.25I I == 4 一束自然光从空气入射到折射率为1.40的液体表面上,其反射光是完全偏振光.试求:(1)入射角等于多少? (2)折射角为多少?
解:⑴ 0tan 1.401i =,∴ 'ο02854=i
⑵ οο'0903532i γ=-=
5 自然光从空气中射向介质,测得布儒斯特角058i =.(1)求介质的折射率和折射角.
(2)如果实验在水中进行,水的折射率为 1.33n =水,求这种情况下的布儒斯特角.(3)若介质是透明的,当光从介质射向与空气的分界面时,起偏角是多少?(4)若从空气中射向介质的是振动方向在入射面内的偏振光,仍以058i =入射,问反射光是什么性质的光?
解:(1)00tan tan 58 1.6n i ===折射角:οο
09032i γ=-=
(2)0 1.6tan 1.2031.33
i ==,ο050.26i = (3)01tan 0.6251.6i ==,ο
032i = (4)无反射光。
