耦合电感的电路
耦合电感的去耦等效电路
ห้องสมุดไป่ตู้
Lb )
di1 dt
Lb
di2 dt
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
图10-11 由此解得: 图10-11(d)
例10-3 用去耦等效电路求图(a)单口网络的等效电感。
图10-12
解:若将耦合电感 b、d两端相连,其连接线中的电流为零,不会 影响单口网络的端口电压电流关系,此时可用图
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
La L1 M
Lb M
L c L 2 M
L1 La Lb
L2
Lb
L
c
M L b
La L1 M
Lb M
L c L 2 M
u1
L1
di1 dt
M
di2 dt
u2
M
di1 dt
L2
di2 dt
u1
(La
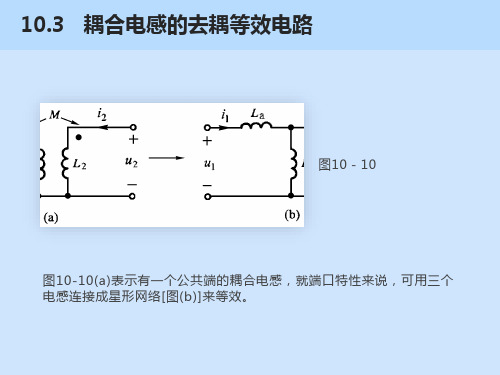
10.3 耦合电感的去耦等效电路
图10-10
图10-10(a)表示有一个公共端的耦合电感,就端口特性来说,可用三个 电感连接成星形网络[图(b)]来等效。
u1
L1
d i1 dt
M
di2 dt
u2
M
d i1 dt
L2
di2
dt
u1
(La
Lb )
di1 dt
Lb
di2 dt
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
列出图(a)和(b)电路的电压、电流关系方程: 图10-10
令以上两式 各系数分别 相等,得到:
耦合电感_精品文档

线圈电流产生的磁通全部与耦合线圈交链Mmax =
;
K 近于1时称为紧耦合;K 值较小时称为松耦合;K=0 称
为无耦合。
上一页 返回
第二节 有耦合电感的正弦电路
含有耦合电感电路(简称互感电路)的正弦稳态计算可采用 相量法。分析时要注意耦合电感上的电压是由自感电压和互 感电压叠加而成的。根据电压、电流的参考方向及耦合电感 的同名端确定互感电压的方向是互感电路分析计算的难点。 由于耦合电感支路的电压不仅与本支路电流有关,还和与之 有耦合支路的电流有关,列写节点电压方程较困难,所以互 感电路的分析计算一般采用支路电流法(网孔法)。
第六章 耦 合 电 路
第一节 耦合电感 第二节 有耦合电感的正弦电路 第三节 空心变压器 第四节 理想变压器
第一节 耦合电感
一、互感
1. 互感现象 我们先观察下面这个实验。图6−1 所示的实验电路中,线
圈2 两端接一灵敏检流计。当开关S 闭合瞬间,可以观察到 检流计指针偏转一下之后又回到零位。发生这种现象的原因 是由于开关S 闭合的瞬间,线圈1 产生变化的磁通Φ 11,其 中的一部分磁通Φ 12与线圈2 交链,使线圈2 产生感应电动 势,因而产生感应电流使检流计指针偏转。S 闭合后,线圈 1 的电流不再发生变化,虽然仍有磁通与线圈2 交链,但该 磁通是不变化的,所以不产生感应电动势,没有电流流过检 流计,因而检流计的指针回到零位。
上一页 下一页 返回
第一节 耦合电感
在同频正弦稳态电路中,耦合电感的伏安关系可以用相量形 式表示,式(6−5)可表示为
(6−8)
例6−3 电路如图6−8 所示,已知R1=1 Ω,L1=L2=1 H, M=0.5 H,uS=10sin 4t。试求u2。
第十章含耦合电感的电路

r R
E
(a)
r R
E
(b)
直接连接
P
I
2
R
E R
r
2
R
8
6 100
2
8
25mW
用匝比为n = 3的变压器耦合
扬声器的反射阻抗
R'
N1 N2
2
R
300 100
i1 * N1
n :1
i2
பைடு நூலகம்
+
N2
u2
*
-
实际变压器与理想变压器近似的条件
变压器原、副边线圈自电感 :L1、L2 耦合电感 : M k L1L2 近似条件: k M 1 L1、L2很大
L1L2
n n1 n2
例题
一个理想变压器的额定值是2400V/120V,9.6kVA且 在次级有50匝。计算:(a)匝数比,(b)初级的匝 数,(c)初级绕组和次级绕组的额定电流值。
原、副边匝比: 初级匝数:
n V1 2400 20 V2 120
n1 n 50 2050 1000 匝
初级绕组和次级绕组的额定电流值
I1
9600 V1
9600 2400
4A
I2
9600 V2
9600 120
80A
例题
求负载的端电压 U 2。
副边电压、电流关系。 配合电阻元件等,可模拟实际变压器
电工原理之含有耦合电感电路介绍课件

频率响应分析:通过分析频 率响应曲线,可以了解电路 的滤波特性、增益、相位等 参数,从而优化电路设计。
频率响应的应用:耦合电感 电路的频率响应分析在电子 技术、通信工程、电力电子 等领域具有广泛的应用。
3
耦合电感电路 的应用实例
耦合电感电路在滤波器中的应用
01 滤波器类型:低通滤波器、高通 滤波器、带通滤波器等
03
耦合电感的大小与线圈的几何形状、相对位 04
耦合电感在电路中起到能量传递、信号处
置、绕线方式等因素有关。
理等作用。
耦合电感的作用
1
耦合电感是电 路中两个或多 个电感之间的
相互影响
3Байду номын сангаас
耦合电感可以 减小电路的噪
声干扰
2
耦合电感可以 增强电路的滤
波性能
4
耦合电感可以 提高电路的功
率传输效率
耦合电感的分类
电工原理之含有 耦合电感电路介 绍课件
目录
01. 耦合电感电路的基本概念 02. 耦合电感电路的分析方法 03. 耦合电感电路的应用实例
1
耦合电感电路 的基本概念
耦合电感的定义
01
耦合电感是两个或多个电感线圈之间通过
02
耦合电感是电路中一种重要的元件,常用于
磁场相互影响的现象。
滤波、调谐、阻抗匹配等电路中。
自感耦合:两个电感线圈之 间通过磁场相互耦合
变压器耦合:两个电感线圈 之间通过变压器相互耦合
互感耦合:两个电感线圈之 间通过电流相互耦合
电容耦合:两个电感线圈之 间通过电容相互耦合
2
耦合电感电路 的分析方法
电路分析的基本方法
电路图分析:了
1 解电路的结构和 功能
电路第10章耦合电感电路
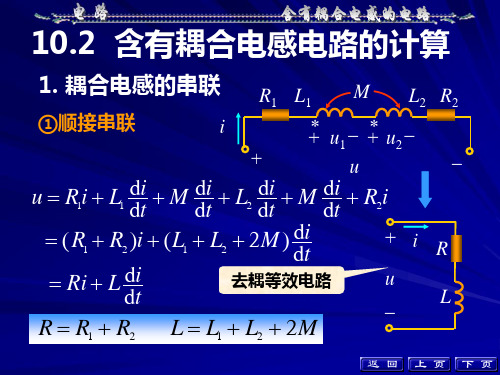
1. 耦合电感的串联
①顺接串联 i + R1 L1 M L2 R2 – * – * – + u1 + u2 u
u = Ri + L di + M di + L2 di + M di + R2i 1 1 dt dt dt dt + i = ( R + R2 )i + (L + L2 + 2M) di 1 1 R dt u 去耦等效电路 = Ri + L di L dt – R = R1 + R2 L = L1 + L2 + 2M
返 回
上 页
下 页
作出去耦等效电路, 一对一对消): 解2 作出去耦等效电路,(一对一对消):
M12 • ∆ L1 L3 ∆ * L2 • * M23 L1–M12 ∆ L3+M12 M31 ∆ * L2–M12 *
M31
M23
L1–M12 +M23 –M13 L2–M12–M23 +M13 L3+M12–M23 –M13
返 回
上 页
下 页
作业: 作业:
习题10-4 习题
M=4H 5H 6H
3H M=1H 2H 3H
4H
返 回 上 页 下 页
5. 有互感电路的计算
①在正弦稳态情况下,有互感的电路的计算仍应用 在正弦稳态情况下, 前面介绍的相量分析方法。 前面介绍的相量分析方法。 ②注意互感线圈上的电压除自感电压外,还应包含 注意互感线圈上的电压除自感电压外, 互感电压。 互感电压。 一般采用支路法和回路法计算。 ③一般采用支路法和回路法计算。
R = R1 + R2
耦合电感的等效电路

耦合电感的等效电路耦合电感通常用于电子电路中的方式是将两个电感互相连接在一起,以达到某种特定的电磁共振的效果。
可以将两个电感的线圈安置在同一轴向,这时谐振点的频率相对较低,也可以将两个电感的线圈安置在互相垂直的两个面上,这时谐振点的频率相对较高。
耦合电感与普通电感的不同之处在于,耦合电感可以看做是两个独立的电感的复合体,其等效电路可以用两个独立的电感和一个耦合系数来描述。
如果耦合系数为零,那么就相当于两个电感独立起作用。
如果耦合系数为1,那么两个电感就完全耦合在一起。
在实际应用中,耦合系数通常介于0和1之间。
下面是一个简单的电路图,它展示了一个由两个耦合电感组成的电路。
这个电路包含两个电感L1和L2,它们通过一个互感器M1连接在一起。
该互感器可以理解为是一种特殊的变压器,它将来自信号源的电流分成两部分,分别流过L1和L2,并给它们带来一个附加的磁耦合效应。
根据基尔霍夫定律和欧姆定律,可以得到下面的等效电路:其中,L1和L2分别表示电感L1和L2的自感,M表示它们的磁耦合系数。
对于互感器M1,理论上可以用变压器的数学模型进行计算,但在实际应用中,一般使用一组简单的参数来描述其特性,比如M1的参数可以表示为M1=k√L1L2,其中k为磁耦合系数,√L1L2为它们的几何平均值。
通过等效电路,我们可以计算出这个电路的整体阻抗和传输特性。
下面是一些基本的计算公式:总自感:L= L1+ L2+2M谐振频率:f0= 1/2π√LC品质因数 Q:Q= R/ωL在通信电路中,耦合电感通常用来实现滤波和共振器的功能,比如说,可以通过一组耦合电感来构成一个调制器。
这种方法可以将两个频率相差较大的信号合成到一个相对较低的频率带宽内,从而实现调制操作。
类似地,在雷达和无线电设备中,耦合电感也可以提供必要的信号处理和调谐功能。
具有耦合电感的电路教案

近饱和区,其磁导率高,磁阻小,建立相同的磁通,需要的电
流小。耦合系数大。实际中得到广泛应用。
第三节 空心变压器
一、空 芯变压器的伏安关系
变压器一般有两个线圈,与电源 1 i1
i2 2
相联的称为原线圈,与负载相联的
找到施感电流i2从同名端流入,则本线圈同名端处为正。
7、互感元件的VAR的相量形式 (计电阻电压时) U1 R1 jL1I1 jMI2 U 2 R2 jL2 I2 jMI2
1
U1
I1
R1
jMR2 I2*Fra bibliotekjL1
*
jL2
2
U 2
1'
2'
例:写出图示电路VAR
1
M
*
*
i2
u1
L1
L2
i1
建立模型时:自感电压的方向由自 身电压电流参考方向是否一致决定。 互感电压方向则由自身参考方向与 施感电流的参考方向相对于同名端
1
u1
i1
u L1
* u M 12L1
是否一致(关联)来决定。
1'
M
i2
*
2
L2 uM 21 u L2 u 2
2'
如判断uM1( 2 线圈2在线圈1中产生的互感电压)的方向,
U S
jMI1
jL2 I2
R2
R3
I3
C
U a jMI1 (R2 jL2 )I2 0
I1 R1
a jM
3、互感消取法(两线圈有公共节点)
耦合电感的电路分析10

第十三章 含耦合电感的电路分析
磁耦合线圈在电子工程、通信工程和测量仪器等方面得到了广泛应用。 为了得到实际耦合线圈的电路模型,现在介绍一种动态双口元件——耦合电 感,并讨论含耦合电感的电路分析。
在介绍耦合电感元件以前,下面先用示波器观察磁耦合线圈初级和次 级的波形。
在环形磁芯上用漆包线绕一个耦合电感,初级60匝,次级30匝,如图所示。
在前面的实验中已经测量出上图所示耦合电 感初级线圈自电感L1=0.66mH和耦合电感线圈次 级的等效自电感L2=0.17mH。由此可以计算出该 耦合线圈的耦合系数为
k M 0.26 0.776 L1L2 0.66 0.17
该耦合线圈接近紧耦合,其原因是磁环的导磁系数很高。
例13-2 图13-9电路原已稳定。已知R=20, L1=L2=4H, k=0.25, US=8V。t=0时开关闭合,求t>0时的i(t)和 u(t)。
图13-1(a)
对于图(a)的情况,根据电磁感应定律可以得到:
u1
d 1
dt
d 11
dt
d 12
dt
L1
di1 dt
M
di2 dt
u2
d 2
dt
d 21
dt
d 22
dt
M
di1 dt
L2
di2
dt
(13 3)
图13-1(b)
与此相似,对于图(b)情况可以得到:
u1
d 1
dt
d 11
dt
d 12
di dt
M
di dt
M
di dt
L2
di dt
( L1
L2
2M )
di dt
耦合电感的等效电路

11
并联去耦等效(异名端共一节点)
M
L1
L2
-M L1+M
L2+M
电磁耦合
-jωM
电耦合
jω(L1+M)
jω(L2+M)
正弦稳态模型
12
Lc
di2 dt
6
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
• 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
M
i2
+
+
u1
L1
L2
u2
-
-
+ i1 L1+M
u1 -
L2+M i2
+
-M
u2
-
3
3.耦合电感的顺接串联等效
i
.+
M
+
u1 L1 L2
u-
_
KVL:u=u1+u2
u2
u1=
L1
di dt
M udi2=
dt
L2
di dt
M di dt
+
∴u=
L1
L2
2 M= di
dt
L di dt
i
L=L1+L2+2M — 等效电路
+
u
L
_
4
4.反接串联
i
+ + u1 L1
电路PPT课件第10章含有耦合电感的电路

由同名端及u、i参考方向确定互感线圈的特性方程
有了同名端,以后表示两个线圈相互作用,就不再考虑实际绕向,而只画 出同名端及参考方向即可。
M
*
*
i1
+ u21 –
M
*
*
i1
– u21 +
u21
M
di1 dt
u21
M
di1 dt
例
i1
M
i2
+*
*+
u1 L1 _
L2 u2 _
u1
L1
di1 dt
M
di2 dt
u
L1
L2
–
i1
M
i2
+
**
+
u
L1
L2
u
–
–
•
I
jM
j(L1-M)
•
•
I1 I2
j(L2-M)
•
I1
j(L1-M)
•
I2
j(L2-M)
jM
4. 受控源等效电路
i1
M
i2
+
**
+
u
L1
L2 u
–
–
•
I1
+
j L1
•
U1
+
•
jM
–
I–2
•
I2
+
j L2
•
+
U2
•
jMI 1
–
–
•
•
•
U 1 jL1 I 1 jM I 2
US
j (L1 L3 2M31)
《具有耦合电感电路》课件

用于选择信号和消除干扰,例如收音机的调谐电 路。
并联谐振电路
并联谐振电路
在具有耦合电感的并联电路中,当电路的输入频率等于电路的固 有频率时,电路发生谐振。
并联谐振的特点
阻抗最大,电流最小,电感与电容上的电压相位相同。
应用
用于信号源的负载匹配和放大器的反馈电路。
滤波器电路
滤波器电路
01
利用具有耦合电感的电路设计的一种电子设备,用于通过、阻
自动控制系统
在自动控制系统中,耦合电感 常用于实现传感器和执行器之
间的信号传输和隔离。
02
CATALOGUE
耦合电感的工作原理
磁耦合原理
磁耦合原理是耦合电感电路的基本工作原理,它描述了两个线圈之间的相互作用 。当一个线圈中的电流发生变化时,会在另一个线圈中产生感应电动势,从而产 生电流。
磁耦合原理的应用广泛,包括变压器、电动机、发电机等。
新型材料的应用
铁硅铝材料
具有高磁导率、低损耗的特点, 可应用于高频耦合电感器中,提 高电路性能。
磁性薄膜材料
通过先进的薄膜制备技术,实现 高性能、微型化的磁性薄膜耦合 电感,满足小型化设备的需求。
高频化与小型化的发展趋势
高频化
随着通信技术的发展,耦合电感在高 频领域的应用越来越广泛,需要不断 提升高频性能以满足系统需求。
小型化
随着便携式电子设备的普及,耦合电 感的小型化成为发展趋势,需要优化 设计、减小体积并保持性能。
智能化与自动化的技术革新
智能化
通过集成传感器和微控制器等智能化技术,实现耦合电感的自适应调节和控制,提升系 统的智能化水平。
自动化
采用自动化生产线和机器人技术,实现耦合电感的快速、高效生产,降低成本并提高生 产效率。
耦合电感电路的等效6种模型

耦合电感电路的等效6种模型
耦合电感电路的等效模型有以下6种:
1. 互感耦合模型:将耦合电感电路分解为两个互感元件(互感电感),通过互感系数来描述电感之间的耦合程度。
2. 理想变压器模型:将耦合电感电路看作是一个理想变压器,将互感耦合转化为变压器变比。
3. T模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个串联电感,表示耦合电感。
4. π模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个并联电感,表示耦合电感。
5. 串联模型:将耦合电感电路看作是一个串联电感,将多个电感元件串联连接。
6. 并联模型:将耦合电感电路看作是一个并联电感,将多个电感元件并联连接。
以上是耦合电感电路的常见等效模型,根据具体情况选择适合的模型进行分析和计算。
记得具体情况具体分析,如果需要更详细的解答,可以提供具体的电路图等信息。
耦合电感电路

单元五具有耦合电感的电路(互感电路)互感现象:线圈电流在邻近线圈产生感应电动势的现象。
线圈间存在互感或耦合电感,有互感的两个(几个)线圈的电路模型称为互感元件,其为双端口(多端口)元件。
1i11φ-+1Lu-+12Mu-+21Mu2i22φ-+2Lu21φ12φ1'12'2自感现象:线圈电流在自身线圈产生感应电动势的现象。
其元件称为自感元件(电感元件)含有互感元件的电路称为互感电路。
1、自感电压。
dtdi L u L 111=2、互感电压。
dtdi M u M 12121=dtdi L u L 222=一、互感电压1i 11φ-+1L u -+12M u -+21M u 2i 22φ-+2L u 21φ12φ1'12'2dtdi M u M 21212=可以证明:对于线性电感,M 12= M 21= M 。
3. 互感的性质①对于线性电感M 12=M 21=M②互感系数M 只与两个线圈的几何尺寸、匝数、相互位置和周围的介质磁导率有关。
4. 耦合系数k全耦合:即F 11= F 21 ,F 22 =F 121, : 21==k L L M 全耦合时k 表示两个线圈磁耦合的紧密程度。
21defL L M k =可以证明,k ≤1。
1i 11φ-+1L u -+1u -+12M u -+2u -+21M u 2i 22φ-+2L u 21φ12φ1'12'2二、线圈电压dtdi Mdt di L u u u dt di Mdt di L u u u M L M L122122211211+=+=+=+=若线圈N 2与线圈N 1的绕向不同或注入的电流的方向不同则有:dtdi Mdt di L u u u dt di Mdt di L u u u M L M L 122122211211-=+=-=+=如何判断互感电压的正负?通常在线圈的端子上标以星标“*”用以表示线圈的绕向。
含有耦合电感的电路分析

耦合电感的参数包括自感、互感、耦 合系数等,这些参数用于描述耦合电 感的电气特性。
02
耦合电感的等效电路
耦合电感的串联等效电路
总结词
在串联等效电路中,耦合电感被视为一个整体,其等效阻抗由两个电感线圈的互 感和总自感共同决定。
详细描述
在串联等效电路中,耦合电感器被视为一个整体,其等效阻抗由两个电感线圈之 间的互感和总自感共同决定。互感是指一个线圈的磁场对另一个线圈产生感应电 动势的能力,总自感则是每个线圈单独存在时的自感之和。
戴维南定理是电路分析的重要定理之一,适用于含有耦合电感的电路。通过将复杂电路等效为简单电 路,简化分析过程。
详细描述
在含有耦合电感的电路中,将电路划分为待求支路和入端电阻网络。然后通过设定入端电阻网络的参 考方向,利用戴维南定理求出等效电源电动势和内阻,从而得到待求支路的电压和电流。
04
耦合电感在电路中的应用
成持续的振荡波形。
设计要素
02
振荡器的设计需要考虑反馈系数、放大倍数、选频网络等要素。
耦合电感在振荡器中的作用
03
耦合电感作为选频网络的一部分,决定了振荡器的振荡频率和
稳定性。
THANKS
05
含有耦合电感的电路实例分 析
变压器的工作原理分析
变压器原理
变压器是利用耦合电感原理,通过磁场传递能量,实现电压、电流和阻抗的变换。
工作过程
当交流电源施加在变压器的一次绕组时,产生交变磁场,在二次绕组中产生感应电动势,从而实 现了电压的变换。
变压比
变压器一次绕组与二次绕组的匝数比决定了输出电压与输入电压的比值。
耦合电感在电路中的作用
1 2
3
实现电能转换
含耦合电感电路的基本概念

含耦合电感电路的基本概念1. 电感和耦合的基础知识1.1 什么是电感?好嘞,咱们先聊聊电感。
这玩意儿呢,其实就是一种能储存电能的元件。
简单来说,当电流通过一根线圈时,它会在周围产生磁场,就像一个小小的磁铁!嘿,你有没有想过,为什么老奶奶的缝纫机里有那种线圈?不就是用来储存电能,保持机器平稳运行吗?电感的单位是亨利(Henry),听起来挺高大上的,但其实就是个简单的存能器。
1.2 耦合的概念接下来我们聊聊耦合。
你可以把耦合想象成两个电感之间的“握手”。
当一个电感的磁场影响到另一个电感时,它们就“耦合”在一起了。
这就好比你和朋友一起打游戏,你的操作会影响他的角色。
耦合电感的关键就在于这种互相影响的关系,它们的磁场相互作用,就像一对老夫妻,心有灵犀一点通。
2. 耦合电感的工作原理2.1 磁场的秘密那么,耦合电感到底是怎么工作的呢?首先得知道,电感的工作原理与它周围的磁场密不可分。
想象一下,两根电感在同一个空间里,彼此产生的磁场就像两条相互缠绕的绳子。
当电流流过其中一根电感时,它产生的磁场会影响到另一根电感,从而在其上感应出电流。
这种现象就是“电磁感应”,听起来就像魔法,但其实是科学的魅力!2.2 耦合系数的重要性接下来谈谈耦合系数,这可是个关键指标。
它的值从0到1,0代表完全不耦合,1则表示完全耦合。
你想象一下,假设两个电感之间有很多空隙,耦合系数就低得可怜;但如果它们紧紧相依,耦合系数就会飙升。
越高的耦合系数,电路的性能就越好,这就像一对恩爱的小夫妻,心心相印,合作无间。
3. 耦合电感电路的应用3.1 实际应用场景说到耦合电感的应用,那可真是五花八门。
比如,咱们的电视机、无线电和电源变换器里,都能找到它的身影。
想象一下,你的音响系统中,那些震撼人心的低音效果,背后离不开耦合电感的默默付出。
正因为它的存在,才让我们的耳朵能享受到如此美妙的音乐,简直是无声的英雄!3.2 未来的发展方向未来,耦合电感可能会在电动汽车、无线充电等高科技领域大展拳脚。
含有耦合电感的电路计算

THANKS
感谢观看
互感系数
定义
互感系数是衡量两个线圈之间磁耦合强度的物理量,用符 号M表示。
计算公式
互感系数M与线圈的匝数、线圈之间的距离、线圈的相对位 置等因素有关,计算公式为M=k*sqrt(L1*L2)。
应用
互感系数在含有耦合电感的电路计算中具有重要意义,是 计算感应电动势和磁能量传递的关键参数。
02
含有耦合电感的电路分析
VS
磁路平衡方程
在含有耦合电感的电路中,磁路平衡方程 是描述磁场能量守恒的方程。对于两个串 联耦合电感,其磁路平衡方程为:$H = NPhi$,其中H是磁场强度,N是线圈匝数, $Phi$是磁通量;对于两个并联耦合电感, 其磁路平衡方程为:$B = mu H$,其中B 是磁感应强度,$mu$是磁导率,H是磁场 强度。
01 总结词
直接计算法是一种基本的电路 计算方法,适用于简单的电路 系统。
02
详细描述
直接计算法是根据电路的基本 定律(如基尔霍夫定律)和元 件的特性方程,直接求解电路 变量的方法。对于含有耦合电 感的电路,可以通过建立和解 决相应的方程组来找到电流和 电压。
03
适用范围
04
适用于耦合系数较小、电路结构 简单的系统。
ERA
在电力系统的应用
用于实现高压输电的变压器
耦合电感在电力系统中主要用于实现高压输电。通过变压器,可以将低电压转换 为高电压,以减少电流的损失,从而降低线路损耗。
在通信系统的应用
用于信号传输和接收的设备
在通信系统中,耦合电感常用于信号传输和接收设备,如无线电和电视接收器。通过调整耦合电感的参数,可以控制信号的 传输和接收质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在正弦交流电路中,其相量形式的方程为:
1 jM I 2 U 1 jL1 I U j M I j L I 1 2 2 2
克服:合理布置线圈相互位置或增加屏蔽减少互感作用。
电抗器
上 页 下 页
电抗器磁场
铁磁材料屏蔽磁场
上 页 下 页
3. 耦合电感上的电压、电流关系
当 i1 为时变电流时,磁通也将随时间变化,从 而在线圈两端产生感应电压。 当 i1 、 u11 、 u21 方向与 符合右手螺旋时,根 据电磁感应定律和楞次定律:
I
3
-jM
I
U 13 jL1 I 1 jM I 2 jω( L1 M ) I 1 jM I
U 23 jL2 I 2 jM I 1 jω( L2 M ) I 2 jM I
I I1 I 2
上 页 下 页
i
上 页
下 页
空心线圈, 与i 成正比。当只有一个线圈时:
1 11 L1i1 L1为自感系数,单位亨(H)。
当两个线圈都有电流时,每一线圈的磁链为 自磁链与互磁链的代数和:
1 11 12 L1i1 M12i2 2 22 21 L2i2 M 21i1
di1 di2 u1 L1 M dt dt di1 di2 u2 M L2 dt dt i1 M i 2 _ + * u1 L1 L2 u2 _ * +
上 页
写 出 图 示 电 路 电 压、 电 流 关 系 式
下 页
例 已知R1 10, L1 5H, L2 2H, M 1H, 求u(t )和u2 (t )
2
上 页 下 页
3.耦合电感的T型等效
①同名端为共端的T型去耦等效 1
2 1 j M I I
* jL1
3
*
2
1
jL2
j(L1-M)
1 I
2 I2 j(L2-M)
I
3
jM
I
U 13 jL1 I 1 jM I 2 jω( L1 M ) I 1 jM I
2
4M
0
顺接
反接
上 页
下 页
在正弦激励下: R1 j L1 + U * 1 I +
j M
– *+
j L 2
U2 –
–
U
( R1 R2 ) I jω( L1 L2 – U 2M ) I
上 页
下 页
相量图: (a) 顺接
U
R1 j L1 + U 1* I +
当两组线圈装在黑盒里,只引出四个端线 组,要确定其同名端,就可以利用上面的结论 来加以判断。
上 页 下 页
由同名端及u、i参考方向确定互感线圈的特性方程 有了同名端,表示两个线圈相互作用时,就 不需考虑实际绕向,而只画出同名端及u、i参考 方向即可。 M di1 * * u21 M dt i1 + u21 – M * i1 * – u21 +
上 页 下 页
10.2
含有耦合电感电路的计算
R1 L1 + + u1 * M – +* u L2 R2 i
1. 耦合电感的串联
①顺接串联
u2 – –
u R1i L1 di M di L2 di M di R2i dt dt dt dt + i ( R1 R2 )i ( L1 L2 2M ) di R dt u 去耦等效电路 Ri L di L dt – R R1 R2 L L1 L2 2M
M + u _ 解 R1 * L1 * R2 L2 + u2 _ 10 0 1 2 t/s i1/A
i1
10V 0 t 1s 0 t 1s 10t di1 u2 (t ) M 10V 1 t 2s i1 20 10t 1 t 2s dt 2t 2t 0 0 0 t 1s 100 t 50V di1 u (t ) R1i1 L 100 t 150 V 1 t 2s dt 2t 0
上 页
下 页
变压器
上 页 下 页
变压器
上 页 下 页
有载调压变压器
上 页 下 页
小变压器
上 页 下 页
调压器
整流器
电流互感器
牵引电磁铁
上 页
下 页
1. 互感
11
21
i1 N1 N2
+ u11 –
+ u21 –
线圈 1 中通入电流 i1 时,在线圈 1 中产生磁通, 同时,有部分磁通穿过临近线圈 2,这部分磁通称 为互感磁通。两线圈间有磁的耦合。 定义 :磁链 , =N
i1 u11
上式说明,对于自感电压由于电压电流为同 一线圈上的,只要参考方向确定了,其数学描述 便可容易地写出,可不用考虑线圈绕向。
上 页
下 页
对互感电压,因产生该电压的电流在另一线圈 上,因此,要确定其符号,就必须知道两个线圈 的绕向。这在电路分析中显得很不方便。为解决 这个问题引入同名端的概念。 同名端 当两个电流分别从两个线圈的对应端子同 时流入或流出,若所产生的磁通相互加强时, 则这两个对应端子称为两互感线圈的同名端。
上 页 下 页
注意
两线圈的自磁链和互磁链相助,互感电压 取正,否则取负。表明互感电压的正、负: (1)与电流的参考方向有关。
(2)与线圈的相对位置和绕向有关。
上 页
下 页
4.互感线圈的同名端
对自感电压,当 u, i 取关联参考方向, u、i 与 符合右螺旋定则,其表达式为:
dΨ 11 dΦ11 di1 u11 N1 L1 dt dt dt
R R1 R2
L L1 L2 2M
注意 L L1 L2 2M 0
M 1 ( L1 L2 ) 2
上 页 下 页
互感的测量方法:
顺接一次,反接一次,就可以测出互感:
L顺 L反 M 4
全耦合时
M L1L2
当 L=
L1=L2 时 , M=L
L L1 L2 2 M L1 L2 2 L1 L2 ( L1 L2 )
上 页
下 页
11
s 0
i1
* + u11
N1
N N 2 3 * i2 i3 △ △ – + u21 – + u31 –
di1 u21 M 21 dt
di1 u31 M 31 dt
注意 线圈的同名端必须两两确定。
上 页
下 页
确定同名端的方法: (1) 当两个线圈中电流同时由同名端流入 ( 或流出 ) 时,两个电流产生的磁场相互增强。
di1 u21 M dt
上 页
下 页
例
i1
M
i2
i1 + * u1 L1 _
+ * u1 L1 _
M L2 *
i2 + u2 _
* + L2 u2 _
di1 di2 u2 M L2 dt dt
i1 + * u1 L1 _ M L2 * i2 + u2 _
di1 di2 u1 L1 M dt dt
k
def
M 1 L1 L2
11= 21 ,22 =12
2
M M ( Mi1 )( Mi2 ) 12 21 k 1 L1 L2 L1i1 L2i2 11 22 L1 L2
注意 耦合系数k与线圈的结构、相互几何位置、
空间磁介质有关。
上 页 下 页
互感现象
利用——变压器:信号、功率传递 避免——干扰
jM I
U2
j M – +
j L 2
* 2 – U
–
U
(b) 反接
jL2 I
jL1 I
jM I
R2 I
U1
jL2 I
jM I
R1 I
jM I U
U2
R2 I
I
R1 I jL1 I
I
U1
上 页
下 页
思考题
同名端的实验测定: 黑 盒 子
第10章 含有耦合电感的电路
重点
1.互感和互感电压 2.有互感电路的计算
3.空心变压器和理想变压器原理
下 页
10.1
互感
耦合电感元件属于多端元件,在实际电 路中,如收音机、电视机中的中周线圈、振荡线 圈,整流电源里使用的变压器等都是耦合电感元 件,熟悉这类多端元件的特性,掌握包含这类多 端元件的电路问题的分析方法是非常必要的。
例
1'
1*
i
*21源自*23
2'
1'
2'
*
3'
(2)当随时间增大的时变电流从一线圈的一端流入 时,将会引起另一线圈相应同名端的电位升高。
上 页 下 页
同名端的实验测定:
+ R S 1i i *
2 * 2'
