与圆有关的中考试题集锦附答案

合集下载

中考数学总复习《圆的综合题》练习题(附答案)

中考数学总复习《圆的综合题》练习题（附答案）班级:___________姓名：___________考号：_____________一、单选题1．在平面直角坐标系xOy中以点(3,4)为圆心，4为半径的圆（）A．与x轴相交，与y轴相切B．与x轴相离，与y轴相交C．与x轴相切，与y轴相交D．与x轴相切，与y轴相离2．如图，在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点，则弦BC的长的最小值为()A．22B．24C．10√5D．12√33．如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DCB等于（）A．90°B．100°C．130°D．140°4．如图，在正五边形ABCDE中连接AD，则∠DAE的度数为（）A．46°B．56°C．36°D．26°5．如图，PA、PB为∠O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交∠O 于点D．下列结论不一定成立的是（）A．△BPA为等腰三角形B．AB与PD相互垂直平分C．点A，B都在以PO为直径的圆上D．PC为△BPA的边AB上的中线6．如图，四边形ABCD内接于半径为6的∠O中连接AC，若AB＝CD，∠ACB＝45°，∠ACD＝12∠BAC，则BC的长度为（）A．6 √3B．6 √2C．9 √3D．9 √27．如图，点A，B，D，C是∠O上的四个点，连结AB，CD并延长，相交于点E，若∠BOD=20°，∠AOC=90°，则∠E的度数为()A．30°B．35°C．45°D．55°8．∠ABC中∠C=Rt∠，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB，BC分别交于点E，D，则AE的长为()A．95B．125C．185D．3659．如图，AB为∠O的直径，点C在∠O上，若∠B=60°，则∠A等于（）A．80°B．50°C．40°D．30°10．两个圆的半径分别是2cm和7cm，圆心距是5cm，则这两个圆的位置关系是() A．外离B．内切C．相交D．外切11．已知正三角形的边长为12，则这个正三角形外接圆的半径是()A．B．C．D．12．一个扇形的弧长为4π，半径长为4，则该扇形的面积为（）A．4πB．6πC．8πD．12π二、填空题13．在Rt∠ABC中∠C=90°，AB=5，BC=4，求内切圆半径14．如图，∠C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内弧OB上一点，∠BMO=120°，则∠C的半径为．15．一个立体图形的三视图如图所示，根据图中数据求得这个立体图形的侧面积为.16．一个半径为5cm的球形容器内装有水，若水面所在圆的直径为8cm，则容器内水的高度为cm.17．如图，在直角坐标系中以点P为圆心的圆弧与x轴交于A，B两点，已知P（4，2）和A（2，0），则点B的坐标是．18．下面是“作一个30°角”的尺规作图过程．已知：平面内一点A．求作：∠A，使得∠A=30°．作法：如图①作射线AB；②在射线AB取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；③以C为圆心，OC C为半径作弧，与⊙O交于点D，作射线AD．则∠DAB即为所求的角．请回答：该尺规作图的依据是．三、综合题19．如图，在△ABC中AC=BC=BD，点O在AC边上，OC为⊙O的半径，AB是⊙O 的切线，切点为点D，OC=2，OA=2√2．（1）求证：BC是⊙O的切线；（2）求阴影部分的面积．20．如图，△ABC内接于⊙O，CD是直径，∠CBG=∠BAC，CD与AB相交于点E，过点E作EF⊥BC，垂足为F，过点O作OH⊥AC，垂足为H，连接BD、OA．（1）求证：直线BG与⊙O相切；（2）若BEOD=54，求EFAC的值．21．如图，四边形ABCD 内接于∠O，BD是∠O的直径，过点A作∠O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE∠CD；（2）已知AE=4cm，CD=6cm，求∠O的半径．22．如图，∠O是∠ABC的外接圆，BC为∠O的直径，点E为∠ABC的内心，连接AE并延长交∠O 于D点，连接BD并延长至F，使得BD=DF，连接CF、BE．（1）求证：DB=DE；（2）求证：直线CF为∠O的切线．23．公元前5世纪，古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱，在狱中他对方铁窗和圆月亮产生了兴趣．他不断变换观察的位置，一会儿看见圆比正方形大，一会儿看见正方形比圆大，于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了：作一个正方形，使它的面积等于已知圆的面积（1）设有一个半径为√3的圆，则这个圆的周长为，面积为，作化圆为方得到的正方形的边长为(计算结果保留π)（2）由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图)，包括化圆为方在内的几何三大问题都已被证明是不可能的．但若不受标尺的限制，化圆为方并非难事。

2024中考数学全国真题分类卷第二十一讲与圆有关的计算强化训练(含答案)

2024中考数学全国真题分类卷第二十一讲与圆有关的计算强化训练命题点1扇形的相关计算类型一弧长的计算1.(2023甘肃省卷)如图，一条公路(公路的宽度忽略不计)的转弯处是一段圆弧( AB )，点O 是这段弧所在圆的圆心，半径OA ＝90m ，圆心角∠AOB ＝80°，则这段弯路( AB )的长度为()第1题图A.20πmB.30πmC.40πmD.50πm2.(2023黄冈)如图，在Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝8，以点C 为圆心，CA 的长为半径画弧，交AB 于点D ，则弧AD 的长为()第2题图A.πB.43πC.53πD.2π3.(2023丽水)某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为2m ，高为23m ，则改建后门洞的圆弧长是()第3题图A.5π3mB.8π3mC.10π3m D.(5π3＋2)m 4.(2023攀枝花)如图，在半径为1的⊙O 上顺次取点A ，B ，C ，D ，E ，连接AB ，AE ，OB ，OC ，OD ，OE .若∠BAE ＝65°，∠COD ＝70°，则 BC与 DE 的长度之和为________(结果保留π).第4题图5.(新趋势)·跨学科知识(2023衡阳)如图，用一个半径为6cm的定滑轮拉动重物上升，滑轮旋转了120°，假设绳索粗细不计，且与轮滑之间没有滑动，则重物上升了________cm.(结果保留π)第5题图6.(2023宜昌)如图，点A，B，C都在方格纸的格点上，△ABC绕点A顺时针方向旋转90°BB'的长为________．后得到△AB′C′，则点B运动的路径第6题图7.(2023福建)如图，△ABC内接于⊙O，AD∥BC交⊙O于点D，DF∥AB交BC于点E，交⊙O于点F，连接AF，CF.(1)求证：AC＝AF；(2)若⊙O的半径为3，∠CAF＝30°，求 AC的长(结果保留π).第7题图类型二扇形面积的计算8.(2023凉山州)家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件，已知扇形的圆心角∠BAC＝90°，则扇形部件的面积为()A.1 2π米2B.14π米2 C.18π米2 D.116π米2第8题图9.(2023台州)一个垃圾填埋场，它在地面上的形状为长80m，宽60m的矩形，有污水从该矩形的四周边界．．．．向外渗透了3m，则该垃圾填埋场外围受污染土地的面积为()A.(840＋6π)m2B.(840＋9π)m2C.840m2D.876m210.(2023玉林)数学课上，老师将如图边长为1的正方形铁丝框变形成以A为圆心，AB为半径的扇形(铁丝的粗细忽略不计)，则所得扇形DAB的面积是________．第10题图11.(2023盐城)如图，在矩形ABCD中，AB＝2BC＝2，将线段AB绕点A按逆时针方向旋转，使得点B落在边CD上的点B′处，线段AB扫过的面积为________.第11题图命题点2与扇形有关的阴影部分面积计算类型一直接和差法12.(2023兰州)如图①是一块弘扬“社会主义核心价值观”的扇面宣传展板，该展板的部分示意图如图②所示，它是以O为圆心，OA，OB长分别为半径，圆心角∠O＝120°形成的扇面，若OA＝3m，OB＝1.5m，则阴影部分的面积为()第12题图A.4.25πm 2B.3.25πm 2C.3πm 2D.2.25πm 213.(2023泰安)如图，四边形ABCD 中，∠A ＝60°，AB ∥CD ，DE ⊥AD 交AB 于点E ，以点E 为圆心，DE 为半径，且DE ＝6的圆交CD 于点F ，则阴影部分的面积为()第13题图A.6π－93B.12π－93C.6π－932D.12π－93214.(2023山西)如图，扇形纸片AOB 的半径为3，沿AB 折叠扇形纸片，点O 恰好落在 AB 上的点C 处，图中阴影部分的面积为()第14题图A.3π－33B.3π－932C.2π－33D.6π－93215.(2023重庆A 卷)如图，菱形ABCD 中，分别以点A ，C 为圆心，AD ，CB 长为半径画弧，分别交对角线AC 于点E ，F .若AB ＝2，∠BAD ＝60°，则图中阴影部分的面积为________．(结果不取近似值)第15题图类型二构造和差法16.(2023赤峰)如图，AB 是⊙O 的直径，将弦AC 绕点A 顺时针旋转30°得到AD ，此时点C 的对应点D 落在AB 上，延长CD ，交⊙O 于点E ，若CE ＝4，则图中阴影部分的面积为()第16题图A.2πB.22C.2π－4D.2π－2217.(2022资阳)如图，在矩形ABCD 中，AB ＝2cm ，AD ＝3cm ，以点B 为圆心，AB 长为半径画弧，交CD 于点E ，则图中阴影部分的面积为________cm 2.第17题图18.(2023河南)如图，将扇形AOB 沿OB 方向平移，使点O 移到OB 的中点O ′处，得到扇形A ′O ′B ′.若∠O ＝90°，OA ＝2，则阴影部分的面积为__________．第18题图19.(2023梧州)如图，四边形ABCD 是⊙O 的内接正四边形．分别以点A ，O 为圆心，取大于12OA 的定长为半径画弧，两弧相交于点M ，N ，作直线MN ，交⊙O 于点E ，F .若OA ＝1，则 BE，AE ，AB 所围成的阴影部分面积为________．第19题图类型三等积转化法20.(2023遵义)如图，在正方形ABCD 中，AC 和BD 交于点O ，过点O 的直线EF 交AB 于点E(E不与A，B重合)，交CD于点F.以点O为圆心，OC为半径的圆交直线EF于点M，N.若AB＝1，则图中阴影部分的面积为()A.π8－18B.π8－14C.π2－18D.π2－14第20题图21.(2022泰安)若△ABC为直角三角形，AC＝BC＝4，以BC为直径画半圆如图所示，则阴影部分的面积为________．第21题图22.(2023广元)如图，将⊙O沿弦AB折叠， AB恰经过圆心O，若AB＝23，则阴影部分的面积为________.第22题图类型四容斥原理法23.(2022荆门)如图，正方形ABCD的边长为2，分别以B，C为圆心，以正方形的边长为半径的圆相交于点P，那么图中阴影部分的面积为________．第23题图命题点3圆切线与求阴影部分面积结合24.(2023齐齐哈尔)如图，在△ABC中，AB＝AC，以AB为直径作⊙O，AC与⊙O交于点D，BC与⊙O交于点E，过点C作CF∥AB，且CF＝CD，连接BF.(1)求证：BF是⊙O的切线；(2)若∠BAC＝45°，AD＝4，求图中阴影部分的面积．第24题图25.(2023益阳)如图，C是圆O被直径AB分成的半圆上一点，过点C的圆O的切线交AB 的延长线于点P，连接CA，CO，CB.(1)求证：∠ACO＝∠BCP；(2)若∠ABC＝2∠BCP，求∠P的度数；(3)在(2)的条件下，若AB＝4，求图中阴影部分的面积(结果保留π和根号).第25题图命题点4圆锥、圆柱的相关计算26.(2023无锡)在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以AC所在直线为轴，把△ABC 旋转1周，得到圆锥，则该圆锥的侧面积为()A.12πB.15πC.20πD.24π27.(2023赤峰)如图所示，圆锥形烟囱帽的底面半径为12cm，侧面展开图为半圆形，则它的母线长为()A.10cmB.20cmC.5cmD.24cm第27题图28.(2023云南)某中学开展劳动实习，学生到教具加工厂制作圆锥．他们制作的圆锥，母线长为30cm，底面圆的半径为10cm，这种圆锥的侧面展开图的圆心角度数是________．29.(2022广西北部湾经济区)如图，从一块边长为2，∠A＝120°的菱形铁片上剪出一个扇形，这个扇形在以A为圆心的圆上(阴影部分).且圆弧与BC，CD分别相切于点E，F，将剪下来的扇形围成一个圆锥．则圆锥的底面圆半径是________．第29题图命题点5圆与正多边形的相关计算30.(2022贵阳)如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，C两点，则∠AOC 的度数是()A.144°B.130°C.129°D.108°第30题图31.(2023雅安)如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为()第31题图A.33B.32 C.332 D.332.(2022山西)如图，正六边形ABCDEF 的边长为2，以A 为圆心，AC 的长为半径画弧，得 EC ，连接AC ，AE ，则图中阴影部分的面积为()第32题图A.2πB.4πC.33πD.233π33.(2022绥化)边长为4cm 的正六边形，它的外接圆与内切圆半径的比值是________．参考答案与解析1.C 【解析】根据弧长公式l ＝n πr 180＝80×π×90180＝40π.2.B 【解析】如解图，连接CD ，∵∠B ＝30°，∠ACB ＝90°，AB ＝8，∴∠CAB ＝60°，AC ＝4.∵AC ＝CD ，∴△ACD 是等边三角形，∴∠ACD ＝60°.∴弧AD 的长为60π×4180＝43π.第2题解图3.C 【解析】∵圆弧所在圆外接于矩形，且矩形四个角均为直角，∴直角所对的弦为直径，∴如解图，连接矩形对角线的交点O 即为圆心，∵AB ＝2，AD ＝23，∴BD ＝AB 2＋AD 2＝4，∴∠ADB ＝30°，∴∠ABD ＝60°，∵OA ＝OD ＝OB ＝OC ＝2，∴∠AOB ＝∠DOC ＝60°，∴圆弧长为300π×2180＝10π3.第3题解图4.π3【解析】∵∠BAE ＝65°，∴∠BOE ＝2∠BAE ＝130°，∵∠COD ＝70°，∴∠BOC ＋∠DOE ＝∠BOE －∠COD ＝130°－70°＝60°，∴ BC 与 DE 的长度之和为60π×1180＝π3.5.4π【解析】由题意可知，重物上升的高度即为120°的圆心角所对应的弧长，∴重物上升的高度为120π×6180＝4π.6.52π【解析】由题可得旋转角∠BAB ′＝90°，AB ＝AB ′，∵在Rt △ABC 中，BC ＝3，AC＝4，∴AB ＝5，∴路径 BB'的长为90π×5180＝52π.7.(1)证明：∵AD ∥BC ，DF ∥AB ，∴四边形ABED 是平行四边形，∴∠B ＝∠D .又∵∠AFC ＝∠B ，∠ACF ＝∠D ，∴∠AFC ＝∠ACF ，∴AC ＝AF ；(2)解：如解图，连接AO ，CO .由(1)得∠AFC ＝∠ACF ，又∵∠CAF ＝30°，∴∠AFC ＝180°－30°2＝75°，∴∠AOC ＝2∠AFC ＝150°.∴ AC 的长为150π×3180＝52π.第7题解图8.C【解析】如解图，连接BC ，OA .∵∠BAC ＝90°，∴BC 为⊙O 的直径．∵BC ＝1米，∴OA ＝OB ＝12米，由题意可知AB ＝AC ，∴△ABC 为等腰直角三角形，∴AB ＝22米，∴S扇形＝90π×（22）2360＝18π米2.第8题解图9.B【解析】如解图，该垃圾填埋场外围受污染土地的面积＝80×3×2＋60×3×2＋32π＝(840＋9π)m 2.第9题解图10.1【解析】∵正方形ABCD 的边长为1，∴AB ＝AD ＝1， BD的长为2，∴S 扇形DAB ＝12lr＝12×2×1＝1.11.π3【解析】如解图，过点B ′作B ′H ⊥AB 于点H ，∵B ′H ＝BC ＝1，AB ′＝AB ＝2，∴∠B ′AH＝30°，∴线段AB 所扫过的面积为30π×22360＝π3.第11题解图12.D【解析】S 阴影＝S 扇形AOD －S 扇形BOC ＝120π×32360－120π×1.52360＝13×π×(9－2.25)＝2.25π(m 2).13.B【解析】如解图，过点E 作EG ⊥CD 于点G ，∵∠A ＝60°，AD ⊥DE ，∴∠AED ＝30°.∵AB ∥CD ，∴∠EDF ＝∠AED ＝30°.又∵DE ＝EF ，∴∠DFE ＝∠EDF ＝30°，∴∠DEF ＝180°－∠DFE －∠EDF ＝120°.在Rt △DEG 中，DE ＝6，∠EDF ＝30°，∴EG ＝DE ·sin ∠EDF ＝3，DG ＝DE ·cos ∠EDF ＝33，∴DF ＝2DG ＝63，∴S 阴影＝S 扇形DEF －S △DEF ＝120π×62360－12×63×3＝12π－93.第13题解图14.B 【解析】如解图，连接OC ，∵扇形AOB 沿着AB 折叠，点O 落在 AB 上的点C 处，∴四边形OACB 是菱形．又∵OA ＝AC ＝OC ，∴△AOC 是等边三角形，∴∠AOC ＝60°，∴∠AOB ＝120°.∵S 菱形OACB ＝2S △AOC ，∴S 阴影＝S 扇形AOB －S 菱形OACB ＝120π×32360－2×34×32＝3π－932.第14题解图15.23－2π3【解析】如解图，连接BD 交AC 于点M .∵四边形ABCD 是菱形，∠BAD＝60°，∴∠AMD ＝90°，∠DAM ＝12∠BAD ＝30°，AM ＝12AC ，DM ＝12BD ，∴在Rt △ADM中，DM ＝12AD ＝1，AM ＝32AD ＝3，∴AC ＝2AM ＝23，BD ＝2DM ＝2，∴S 菱形ABCD ＝12AC ·BD ＝12×23×2＝23，S 扇形DAE ＝S 扇形BCF ＝30π×22360＝π3，∴S 阴影＝S 菱形ABCD －S 扇形DAE－S 扇形BCF ＝23－π3－π3＝23－2π3.第15题解图16.C 【解析】如解图，连接OC ，OE ，过点O 作ON ⊥CE 于点N ，∵AC ＝AD 且∠A ＝30°，∴∠ADC ＝∠ACD ＝75°，∵OA ＝OC ，∴∠ACO ＝∠A ＝30°，∴∠OCD ＝∠ACD －∠ACO ＝45°，∵OC ＝OE ，∴∠OCE ＝∠OEC ＝45°，∴∠EOC ＝90°，∵CE ＝4，∴ON ＝EN ＝CN ＝2，OE ＝OC ＝22，∴S 阴影＝S 扇形COE －S △OEC ＝90π×（22）2360－12×4×2＝2π－4.第16题解图17.332－2π3【解析】如解图，连接BE ，由题意得BE ＝AB ＝2cm ，∵四边形ABCD是矩形，∴∠ABC ＝∠C ＝90°，BC ＝AD ＝3cm ，∴cos ∠EBC ＝BC BE ＝32，∴∠EBC ＝30°，∴∠ABE ＝60°，CE ＝1cm ，∴S 阴影＝S 矩形ABCD －S 扇形ABE －S △ECB ＝2×3－60π×22360－12×1×3＝(332－2π3)cm 2.第17题解图18.π3＋32【解析】如解图，设O ′A ′与 AB 交于点C ，连接OC ，∵点O ′是OB 的中点，∴OO ′＝12OB ＝12OA ＝1，由平移可得∠CO ′O ＝90°，∴cos ∠COO ′＝OO ′OC ＝12，∴∠COO ′＝60°，∴CO ′＝3OO ′＝3，∴S 阴影＝S 扇形A ′O ′B ′＋S △COO ′－S 扇形COB ＝90π×22360＋12×3×1－60π×22360＝π3＋32.第18题解图19.π12－2－34【解析】如解图，连接OE ，OB ，∵四边形ABCD 是⊙O 的内接正四边形，∴∠AOB ＝90°，由尺规作图知MN 垂直平分OA ，∴AE ＝OE ，∵OA ＝OE ，∴△OAE 是等边三角形，∴AE ＝OE ＝OA ＝1，∠AOE ＝60°，设MN 与OA 交于点G ，则EG ＝OE ·sin ∠AOE ＝1×sin 60°＝32，∴S 阴影＝S 扇形AOB －S △OAB －S 弓形AE ＝S 扇形AOB －S △OAB －(S 扇形AOE －S △OAE )＝90π×12360－12×1×1－(60π×12360－12×1×32)＝π4－12－π6＋34＝π12－2－34.第19题解图20.B 【解析】如解图，以点O 为圆心，以OD 为半径作 DN，∵四边形ABCD 是正方形，AB ＝1，∴OB ＝OD ＝OC ＝22，∠DOC ＝90°，∵∠EOB ＝∠FOD ，∴S 扇形BOM ＝S 扇形DON ，易知△BOE ≌△DOF ，∴S 阴影＝S 扇形COD －S △COD ＝90π×（22）2360－14×1×1＝π8－14.第20题解图【一题多解】∵在正方形ABCD 中，AB ＝1，∴⊙O 的半径为OB ＝22AB ＝22，∵EF 过点O ，∴由中心对称可得四边形EBCF 的面积等于正方形面积的一半，又∵S △OBC ＝14S 正方形ABCD ，∴S阴影＝S半圆－12S 正方形ABCD －(S扇形BOC －S △OBC )＝12π×(22)2－12×1×1－90π×（22）2360＋14×1×1＝π4－12－π8＋14＝π8－14.21.4【解析】如解图，连接CD ，则阴影部分面积为△ABC 面积的一半，即12×4×4×12＝4.第21题解图22.2π3【解析】如解图，过点O 作OD ⊥AB 于点D ，交劣弧AB 于点E ，连接AO ，AE ，根据垂径定理得AD ＝BD ＝12AB ＝3，∵将⊙O 沿弦AB 折叠， AB 恰经过圆心O ，∴OD＝DE ＝12OA ，∴∠OAD ＝30°，∴∠OAE ＝60°，∵OA ＝OE ，∴△AOE 是等边三角形，∴∠E＝60°，在Rt △AOD 中，AO ＝ADcos 30°＝332＝2，∵AD ＝BD ，∠ADE ＝∠BDO ＝90°，DE＝OD ，∴△ADE ≌BDO (SAS)，∴S 阴影＝S 扇形AEO ＝60π×22360＝2π3.第22题解图【一题多解】如解图，过点O 作OD ⊥AB 于点D ，交劣弧AB 于点E ，连接AO ，AE ，∴AD＝BD ＝3，∠ODB ＝90°，由折叠可知，OD ＝DE ＝12OB ，可得∠OBD ＝30°，∠AOB ＝120°，∴OB ＝BD cos ∠OBD ＝2，∴S 扇形AOB ＝120π×22360＝4π3，S △AOB ＝12×23×1＝3，S 扇形AOB－S △AOB ＝4π3－3.OE 左边阴影部分面积为12(S 扇形AOB －S △AOB )＝2π3－32，OE 右边阴影部分面积为12S △AOB ＝32，整体阴影部分面积为两部分阴影面积之和即为2π3.23.23－2π3【解析】如解图，连接PB ，PC ，过点P 作PF ⊥BC 于点F ，∵PB ＝BC ＝PC ，∴△PBC 为等边三角形，∴∠PBC ＝60°，∠PBA ＝30°，∴BF ＝PB ·cos 60°＝12PB ＝1，PF ＝PB ·sin 60°＝3，∴S 阴影＝[S 扇形ABP －(S 扇形BPC －S △BPC )]×2＝[30π×22360－(60π×22360－12×2×3)]×2＝23－2π3.第23题解图24.(1)证明：如解图，连接BD ，第24题解图∵AB 是⊙O 的直径，∴∠BDA ＝90°，∴∠BDC ＝90°，∵AB ＝AC ，∴∠ABC ＝∠ACB .∵CF ∥AB ，∴∠FCB ＝∠ABC ，∠ABF ＋∠F ＝180°，∴∠FCB ＝∠ACB ，∵CF ＝CD ，BC ＝BC ，∴△BCF ≌△BCD (SAS).∴∠F ＝∠BDC ＝90°，又∵∠ABF ＋∠F ＝180°，∴∠ABF ＝90°，且AB 是⊙O 的直径，∴BF 是⊙O 的切线；(2)解：如解图，连接OE ，与BD 交于点M ，∵∠BDA ＝90°，∠BAC ＝45°，AD ＝4，∴BD ＝AD ＝4，∴AB ＝AD 2＋BD 2＝42，∴OB ＝22，∴OE ＝OB ＝22，∴∠OEB ＝∠ABC .∵AB ＝AC ，∠BAC ＝45°，∴∠BOE ＝∠BAC ＝45°，∴OE ∥AC ，∴∠OMB ＝∠ADB ＝90°，∴BM ＝OM ＝2，∴S 阴影＝S 扇形BOE －S △OBE ＝45π×（22）2360－2×222＝π－22.25.(1)证明：∵AB 为半圆O 的直径，∴∠ACB ＝90°，又∵CP 为半圆O 的切线，OC 为半圆O 的半径，∴∠OCP ＝90°，∴∠ACB ＝∠OCP ，∴∠ACO ＋∠OCB ＝∠OCB ＋∠BCP ，∴∠ACO ＝∠BCP ；(2)解：∵OA ＝OC ，∴∠OAC ＝∠OCA ，∴∠COB ＝∠OAC ＋∠OCA ＝2∠ACO ，∵∠ABC ＝2∠BCP ，∠ACO ＝∠BCP ，∴∠ABC ＝∠COB ，又∵OB ＝OC ，∴∠ABC ＝∠COB ＝∠OCB ＝60°，∴∠P ＝90°－∠COB ＝30°；(3)解：由(2)知∠OAC ＝30°，∴BC ＝12AB ，又∵AB ＝4，∴BC ＝2，∴AC ＝AB 2－BC 2＝42－22＝23，∴S △ABC ＝12×2×23＝23，∴S 阴影＝S 半圆－S △ABC ＝12π×22－23＝2π－23.26.C 【解析】由题意得AB ＝32＋42＝5，∴以AC 所在直线为轴将△ABC 旋转一周得到一个圆锥，圆锥的底面圆半径为4，母线长为5，∴圆锥的侧面积为π×4×5＝20π.27.D 28.120°【解析】由题意可知n π×30180＝2π×10，解得n ＝120，即这种圆锥的侧面展开图的圆心角度数是120°.29.33【解析】如解图，连接AE ，AF ，AC .∵四边形ABCD 是菱形，∠BAD ＝120°，∴∠ACD ＝∠ACB ＝60°，∴AD ＝AB ＝BC ＝CD ＝AC ＝2，∵BC ，CD 是切线，∴AE ⊥BC ，AF ⊥CD ，∴AE ＝AF ＝AC ·sin 60°＝3，设圆锥的底面圆半径为r ，则2πr ＝120π·AE180＝120π×3180＝23π3，解得r ＝33.第29题解图30.A【解析】正五边形的内角和为(5－2)×180°＝540°，∴∠E ＝∠D ＝108°，∵AE ，CD分别与⊙O 相切于A ，C 两点，∴∠OAE ＝∠OCD ＝90°，∴∠AOC ＝540°－90°－90°－108°－108°＝144°.31.C 【解析】如解图，连接OC ，OD ，∵圆的周长为6π，∴2πr ＝6π，∴r ＝3，∴OC ＝OD ＝3.∵六边形ABCDEF 是正六边形，∴∠COD ＝60°，∴∠OCD ＝60°.∵OG ⊥CD ，∴OG ＝OC ·sin ∠OCD ＝3×sin 60°＝332.第31题解图32.A 【解析】如解图，过点B 作BG ⊥AC 于点G ，∵六边形ABCDEF 是正六边形，∴∠F ＝∠FAB ＝∠ABC ＝120°，AB ＝BC ＝AF ＝EF ＝2，∴∠BAC ＝∠EAF ＝30°，∴∠EAC ＝60°.∵BG ⊥AC ，∴AG ＝CG ＝AB ·cos 30°＝2×32＝3，∴AC ＝23，∴S 阴影＝60π·（23）2360＝2π.第32题解图33.233【解析】如解图，连接OA ，OB ，过点O 作OG ⊥AB 于点G ，∵正六边形的边长为4cm ，∴正六边形的外接圆的半径4cm ，内切圆的半径是正六边形的边心距，因而是GO ＝32×4＝23，因而正六边形的外接圆的半径与内切圆的半径之比为423＝233.第33题解图。

人教中考数学圆的综合综合题含详细答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E．（1）求证：AC∥OD；（2）如果DE⊥BC，求AC的长度．【答案】（1）证明见解析；（2）2π．【解析】试题分析：（1）由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；（2）BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度．试题解析：（1）证明：∵OC=OD，∴∠OCD=∠ODC．∵CD平分∠ACO，∴∠OCD=∠ACD，∴∠ACD=∠ODC，∴AC∥OD；（2）∵BC切⊙O于点C，∴BC⊥OC．∵DE⊥BC，∴OC∥DE．∵AC∥OD，∴四边形ADOC 是平行四边形．∵OC=OD，∴平行四边形ADOC是菱形，∴OC=AC=OA，∴△AOC是等边三角形，∴∠AOC=60°，∴弧AC的长度=606180π⨯=2π．点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式．此题难度适中，注意掌握数形结合思想的应用．2．如图，AB是半圆的直径，过圆心O作AB的垂线，与弦AC的延长线交于点D，点E在OD上DCE B∠=∠．（1）求证：CE是半圆的切线；（2）若CD=10，2tan3B=，求半圆的半径．【答案】（1）见解析；(2)13【解析】分析: （1）连接CO ，由DCE B ∠=∠且OC=OB,得DCE OCB ∠=∠,利用同角的余角相等判断出∠BCO+∠BCE=90°，即可得出结论；（2）设AC=2x ，由根据题目条件用x 分别表示出OA 、AD 、AB ，通过证明△AOD ∽△ACB ，列出等式即可.详解：（1）证明：如图，连接CO .∵AB 是半圆的直径，∴∠ACB =90°.∴∠DCB =180°-∠ACB =90°.∴∠DCE+∠BCE=90°.∵OC =OB ,∴∠OCB =∠B.∵=DCE B ∠∠，∴∠OCB =∠DCE .∴∠OCE =∠DCB =90°.∴OC ⊥CE .∵OC 是半径，∴CE 是半圆的切线.（2）解：设AC =2x ，∵在Rt △ACB 中，2tan 3AC B BC ==, ∴BC =3x .∴()()222313AB x x x =+=.∵OD ⊥AB ,∴∠AOD =∠A CB=90°.∵∠A =∠A ，∴△AOD ∽△ACB .∴AC AO AB AD=. ∵11322OA AB x ==，AD =2x +10, ∴113221013x x x =+. 解得 x =8.∴1384132OA=⨯=.则半圆的半径为413.点睛：本题考查了切线的判定与性质，圆周角定理，相似三角形.3．如图，已知四边形ABCD是矩形，点P在BC边的延长线上，且PD=BC，⊙A经过点B，与AD边交于点E，连接CE .（1）求证：直线PD是⊙A的切线；（2）若PC=25，sin∠P=23，求图中阴影部份的面积（结果保留无理数）．【答案】（1）见解析；（2）20-4π.【解析】分析：（1）过点A作AH⊥PD，垂足为H，只要证明AH为半径即可.（2）分别算出Rt△CED的面积，扇形ABE的面积，矩形ABCD的面积即可.详解：（1）证明：如图，过A作AH⊥PD，垂足为H，∵四边形ABCD是矩形，∴AD=BC，AD∥BC，∠PCD=∠BCD=90°，∴∠ADH=∠P，∠AHD=∠PCD=90°，又PD=BC，∴AD=PD，∴△ADH≌△DPC，∴AH=CD，∵CD=AB，且AB是⊙A的半径，∴AH=AB,即AH是⊙A的半径，∴PD是⊙A的切线.（2）如图，在Rt△PDC中，∵sin∠P=23CDPD=，5，令CD=2x，PD=3x，由由勾股定理得：（3x）2-(2x)252，解得：x=2，∴CD=4，PD=6，∴AB=AE=CD=4，AD=BC=PD=6，DE=2，∵矩形ABCD 的面积为6×4=24，Rt △CED 的面积为12×4×2=4，扇形ABE 的面积为12π×42=4π， ∴图中阴影部份的面积为24-4-4π=20-4π.点睛：本题考查了全等三角形的判定，圆的切线证明，三角形的面积，扇形的面积，矩形的面积.4．对于平面直角坐标系xOy 中的线段MN 和点P ，给出如下定义：点A 是线段MN 上一个动点，过点A 作线段MN 的垂线l ，点P 是垂线l 上的另外一个动点．如果以点P 为旋转中心，将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点，我们就称点P 是线段MN 的“关联点”．如图，M （1，2），N （4，2）．（1）在点P 1（1，3），P 2（4，0），P 3（3，2）中，线段MN 的“关联点”有；（2）如果点P 在直线1y x =+上，且点P 是线段MN 的“关联点”，求点P 的横坐标x 的取值范围；（3）如果点P 在以O （1，1-）为圆心，r 为半径的⊙O 上，且点P 是线段MN 的“关联点”，直接写出⊙O 半径r 的取值范围．【答案】（1）P 1和P 3；（2）3311x -≤≤；（3333 3.r +≤ 【解析】【分析】（1）先根据题意求出点P 的横坐标的范围，再求出P 点的纵坐标范围即可得出结果；（2）由直线y=x+1经过点M （1，2），得出x≥1，设直线y=x+1与P 4N 交于点A ，过点A 作AB ⊥MN 于B ，延长AB 交x 轴于C ，则在△AMN 中，MN=3，∠AMN=45°，∠ANM=30°，设AB=MB=a ，tan ∠ANM=AB BN ，即tan30°=3a a-，求出a 即可得出结果；（3）圆心O 到P 4的距离为r 的最大值，圆心O 到MP 5的距离为r 的最小值，分别求出两个距离即可得出结果．【详解】（1））如图1所示：∵点A 是线段MN 上一个动点，过点A 作线段MN 的垂线l ，点P 是垂线l 上的另外一个动点，M （1，2），N （4，2），∴点P 的横坐标1≤x≤4，∵以点P 为旋转中心，将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点，当∠MPN=60°时，PM=60MN tan ︒=3=3，同理P′N=3，∴点P 的纵坐标为2-3或2+3，即纵坐标2-3≤y≤2+3，∴线段MN 的“关联点”有P 1和P 3；故答案为：P 1和P 3；（2）线段MN 的“关联点”P 的位置如图所示，∵ 直线1y x =+经过点M （1，2），∴ x ≥1.设直线1y x =+与P 4N 交于点A .过点A 作AB ⊥MN 于B ，延长AB 交x 轴于C .由题意易知，在△AMN 中，MN = 3，∠AMN = 45°，∠ANM = 30°.设AB = MB = a ，∴ tan AB ANM BN ∠=，即tan303a a ︒=-，解得333a -=∴ 点A 的横坐标为33333111.22x a --=+=+= ∴331.x -≤ 综上 3311.2x -≤≤（3）点P 在以O （1，-1）为圆心，r 为半径的⊙O 上，且点P 是线段MN 的“关联点”，如图3所示：连接P 4O 交x 轴于点D ，P 4、M 、D 、O 共线，则圆心O 到P 4的距离为r 的最大值，由（1）知：MP 4=NP 53即OD+DM+MP 433圆心O 到MP 5的距离为r 的最小值，作OE ⊥MP 5于E ，连接OP 5，则OE 为r 的最小值，MP 5225MN NP +223(3)+3OM=OD+DM=1+2=3， △OMP 5的面积=12OE•MP 5=12OM•MN ，即12312×3×3，解得：33 ∴3323 【点睛】本题是圆的综合题，考查了旋转、直角三角形的性质、勾股定理、最值等知识，熟练掌握“关联点”的含义，作出关于MN 的“关联点”图是关键．5．如图，在直角坐标系中，⊙M 经过原点O(0，0)，点6，0)与点B(02)，点D 在劣弧OA 上，连结BD 交x 轴于点C ，且∠COD ＝∠CBO.(1)求⊙M 的半径；(2)求证：BD 平分∠ABO ；(3)在线段BD 的延长线上找一点E ，使得直线AE 恰为⊙M 的切线，求此时点E 的坐标．【答案】（1）M 的半径r ＝2；（2）证明见解析；（3）点E 的坐标为(263，2)．【解析】试题分析：根据点A 和点B 的坐标得出OA 和OB 的长度，根据Rt △AOB 的勾股定理得出AB 的长度，然后得出半径；根据同弧所对的圆周角得出∠ABD=∠COD ，然后结合已知条件得出角平分线；根据角平分线得出△ABE ≌△HBE ，从而得出BH=BA=22，从而求出OH 的长度，即点E 的纵坐标，根据Rt △AOB 的三角函数得出∠ABO 的度数，从而得出∠CBO 的度数，然后根据Rt △HBE 得出HE 的长度，即点E 的横坐标.试题解析：（1）∵点A 为（6，0），点B 为（0，－2） ∴OA=6OB=2 ∴根据Rt △AOB 的勾股定理可得：AB=22∴M 的半径r=12AB=2. （2）根据同弧所对的圆周角相等可得：∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO ∴BD 平分∠ABO（3）如图，由（2）中的角平分线可得△ABE ≌△HBE ∴BH=BA=22∴OH=22－2=2在Rt △AOB 中，3OA OB=∴∠ABO=60° ∴∠CBO=30° 在Rt △HBE 中，HE=2633=∴点E 的坐标为（263，2）考点：勾股定理、角平分线的性质、圆的基本性质、三角函数.6．在O 中，AB 为直径，C 为O 上一点.（Ⅰ）如图①，过点C 作O 的切线，与AB 的延长线相交于点P ，若28CAB ∠=︒，求P ∠的大小；（Ⅱ）如图②，D 为弧AC 的中点，连接OD 交AC 于点E ，连接DC 并延长，与AB 的延长线相交于点P ，若12CAB ∠=︒，求P ∠的大小.【答案】（1）∠P ＝34°；（2）∠P ＝27°【解析】【分析】（1）首先连接OC ，由OA=OC ，即可求得∠A 的度数，然后由圆周角定理，求得∠POC 的度数，继而求得答案；（2）因为D 为弧AC 的中点，OD 为半径，所以OD ⊥AC ，继而求得答案．【详解】（1）连接OC ，∵OA ＝OC ，∴∠A ＝∠OCA ＝28°，∴∠POC ＝56°，∵CP 是⊙O 的切线，∴∠OCP ＝90°，∴∠P ＝34°；（2）∵D 为弧AC 的中点，OD 为半径，∴OD ⊥AC ，∵∠CAB ＝12°，∴∠AOE ＝78°，∴∠DCA ＝39°，∵∠P ＝∠DCA ﹣∠CAB ，∴∠P ＝27°．【点睛】本题考查切线的性质以及等腰三角形的性质．注意准确作出辅助线是解此题的关键．7．如图，等边△ABC 内接于⊙O ，P 是弧AB 上任一点（点P 不与A 、B 重合），连AP ，BP ，过C 作CM ∥BP 交PA 的延长线于点M ，（1）求证：△PCM 为等边三角形；（2）若PA ＝1，PB ＝2，求梯形PBCM 的面积．【答案】（1）见解析；（21534【解析】【分析】（1）利用同弧所对的圆周角相等即可求得题目中的未知角，进而判定△PCM 为等边三角形；（2）利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等，进而利用△PCM 为等边三角形，进而求得PH 的长，利用梯形的面积公式计算梯形的面积即可．【详解】（1）证明：作PH ⊥CM 于H ，∵△ABC 是等边三角形，∴∠APC=∠ABC=60°，∠BAC=∠BPC=60°，∵CM ∥BP ，∴∠BPC=∠PCM=60°，∴△PCM 为等边三角形；（2）解：∵△ABC 是等边三角形，△PCM 为等边三角形，∴∠PCA+∠ACM=∠BCP+∠PCA ，∴∠BCP=∠ACM ，在△BCP 和△ACM 中， BC AC BCP ACM CP CM =⎧⎪∠=∠⎨⎪=⎩，∴△BCP ≌△ACM （SAS ），∴PB=AM ，∴CM=CP=PM=PA+AM=PA+PB=1+2=3，在Rt△PMH中，∠MPH=30°，∴PH=332，∴S梯形PBCM=12（PB+CM）×PH=12×（2+3）×33=1534．【点睛】本题考查圆周角定理、等边三角形的判定、全等三角形的性质及梯形的面积计算方法，是一道比较复杂的几何综合题．8．如图，AB是半圆⊙O的直径，点C是半圆⊙O上的点，连接AC，BC，点E是AC的中点，点F是射线OE上一点．（1）如图1，连接FA，FC，若∠AFC＝2∠BAC，求证：FA⊥AB；（2）如图2，过点C作CD⊥AB于点D，点G是线段CD上一点（不与点C重合），连接FA，FG，FG与AC相交于点P，且AF＝FG．①试猜想∠AFG和∠B的数量关系，并证明；②连接OG，若OE＝BD，∠GOE＝90°，⊙O的半径为2，求EP的长．【答案】（1）见解析；（2）①结论：∠GFA＝2∠ABC．理由见解析；②PE 3．【解析】【分析】（1）证明∠OFA＝∠BAC，由∠EAO+∠EOA＝90°，推出∠OFA+∠AOE＝90°，推出∠FAO＝90°即可解决问题．（2）①结论：∠GFA＝2∠ABC．连接FC．由FC＝FG＝FA，以F为圆心FC为半径作⊙F．因为AG AG，推出∠GFA＝2∠ACG，再证明∠ACG＝∠ABC．②图2﹣1中，连接AG，作FH⊥AG于H．想办法证明∠GFA＝120°，求出EF，OF，OG即可解决问题．【详解】（1）证明：连接OC．∵OA＝OC，EC＝EA，∴OF⊥AC，∴FC＝FA，∴∠OFA＝∠OFC，∵∠CFA＝2∠BAC，∴∠OFA＝∠BAC，∵∠OEA＝90°，∴∠EAO+∠EOA＝90°，∴∠OFA+∠AOE＝90°，∴∠FAO＝90°，∴AF⊥AB．（2）①解：结论：∠GFA＝2∠ABC．理由：连接FC．∵OF垂直平分线段AC，∴FG＝FA，∵FG＝FA，∴FC＝FG＝FA，以F为圆心FC为半径作⊙F．∵AG AG，∴∠GFA＝2∠ACG，∵AB是⊙O的直径，∴∠ACB＝90°，∵CD⊥AB，∴∠ABC+∠BCA＝90°，∵∠BCD+∠ACD＝90°，∴∠ABC＝∠ACG，∴∠GFA ＝2∠ABC ．②如图2﹣1中，连接AG ，作FH ⊥AG 于H ．∵BD ＝OE ，∠CDB ＝∠AEO ＝90°，∠B ＝∠AOE ，∴△CDB ≌△AEO （AAS ），∴CD ＝AE ，∵EC ＝EA ，∴AC ＝2CD ．∴∠BAC ＝30°，∠ABC ＝60°，∴∠GFA ＝120°，∵OA ＝OB ＝2，∴OE ＝1，AE ＝，BA ＝4，BD ＝OD ＝1， ∵∠GOE ＝∠AEO ＝90°，∴OG ∥AC ， 323DG OG ∴==, 222213AG DG AD ∴=+=， ∵FG ＝FA ，FH ⊥AG ，∴AH ＝HG 21∠AFH ＝60°， ∴AF ＝27sin 60AH ︒=，在Rt △AEF 中，EF 2213AF AE -=， ∴OF ＝OE +EF ＝43 ， ∵PE ∥OG ， ∴PE EF OG 0F=， ∴134233=，∴PE ＝36 ．【点睛】圆综合题，考查了垂径定理，勾股定理，圆周角定理，全等三角形的判定和性质，锐角三角函数，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.9．如图，已知AB 是⊙O 的直径，直线CD 与⊙O 相切于C 点，AC 平分∠DAB ．（1）求证：AD ⊥CD ；（2）若AD ＝2，AC=6，求⊙O 的半径R 的长．【答案】（1）证明见解析（2）32【解析】试题分析：（1）连接OC ，由题意得OC ⊥CD ．又因为AC 平分∠DAB ，则∠1=∠2=12∠DAB ．即可得出AD ∥OC ，则AD ⊥CD ；（2）连接BC ，则∠ACB =90°，可证明△ADC ∽△ACB ．则2AD AC AC R ，从而求得R ．试题解析：（1）证明：连接OC ，∵直线CD 与⊙O 相切于C 点，AB 是⊙O 的直径，∴OC ⊥CD ．又∵AC 平分∠DAB ，∴∠1=∠2=12∠DAB ．又∠COB =2∠1=∠DAB ，∴AD ∥OC ，∴AD ⊥CD ．（2）连接BC ，则∠ACB =90°，在△ADC 和△ACB 中∵∠1=∠2，∠3=∠ACB =90°，∴△ADC ∽△ACB ． ∴2AD AC AC R= ∴R =2322AC AD =10．如图，AN 是⊙M 的直径，NB ∥x 轴，AB 交⊙M 于点C ．（1）若点A （0，6），N （0，2），∠ABN=30°，求点B 的坐标；（2）若D 为线段NB 的中点，求证：直线CD 是⊙M 的切线．【答案】(1) B （，2）．(2)证明见解析.【解析】试题分析：（1）在Rt △ABN 中，求出AN 、AB 即可解决问题；（2）连接MC ，NC ．只要证明∠MCD=90°即可试题解析：（1）∵A 的坐标为（0，6），N （0，2）， ∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=，∴B （，2）．（2）连接MC ，NC∵AN 是⊙M 的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt △NCB 中，D 为NB 的中点，∴CD=NB=ND ，∴∠CND=∠NCD ，∵MC=MN ，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．考点：切线的判定；坐标与图形性质．。

中考数学-圆经典必考题型中考试题集锦(附答案)解答题

中考数学圆经典必考题型中考试题（附答案）解答题1.（已知：如图，△ ABC 内接于O O 过点B 作的切线，交 CA 的延长线于点 E / EB & 2① 求证：AB= AC1AB ② 若tan / ABE=丄，（i ）求的值；（ii ）求当 AC= 2时，AE 的长. 2BC=4cm 求O o 的半径.2.如图,PA 为O O 的切线, A 为切点，O 0的割线PBC 过点0与O O 分别交于B 、C, PA= 8cm PB3.已知：如图，BC 是O 0的直径，AC 切O 0于点C AB 交O 0于点D,若AD ： DB= 2 : 3, AC= 10,求 sin B 的值.4.如图，PC 为O 0的切线，C 为切点，PAB 是过0的割线,1若tan B= _ , PC= 10cm 求三角形BCD的面积.25•如图，在两个半圆中，大圆的弦MNW小圆相切，D为切点，且MN AB MN a, ON CD分别为两圆的半径，求阴影部分的面积.6.已知，如图，以△ ABC的边AB作直径的O O分别并AC BC于点D E,弦FG// AB S A CDE S△ ABC= 1 : 4, DE= 5cm FG= 8cm,求梯形AFG啲面积.7.如图所示：PA为O O的切线，A为切点，PBC是过点O的割线,PA= 10, PB= 5，求：(1)O O的面积(注：用含n的式子表示)；(2)cos / BAP的值.参考答案1.( 1)v BE 切O O 于点 B ,「. / ABE=Z C./ EBC= 2/ C,即 / ABH / ABC= 2/C,/ C +Z ABO 2 / C,/ ABC=Z C, ••• AB= AC.(2)①连结AO 交BC 于点F ,AB- AC, AOL BC 且 BF = FC.AF 在 Rt A ABF 中， =tan / ABF BF1 又 tan / ABF= tan C = tan / ABE=2 AF = 1 BF.AB AB .5BC 2BF4 ②在△ EBA M^ ECB 中 ,^EA 2- EA- (EA^ AC ),又 EA M 0 , 5 11EA= AC EA= — x 2 = 10 .5 11 11 22 •设O 的半径为r ,由切割线定理，得 PA = PB- PCAC 切O O 于点C,线段ADB 为O O 的割线,2AC = AD- ABAB= AM DB= 2k + 3k = 5k ,2 210 = 2k X 5k,••• k = 10,AB= AF 2 * * * BF 2BF 2 AF = 1BF 2/ E =Z E , / EBA=Z ECB△ EBA^A ECBEAEBBE 2 AB BC ,解之，得 EA ECk> 0,「. k= 10 .AB= 5k= 10 .AC切O O于C, BC为O O的直径,ACL BC在Rt A ACB中, sin B=虫10 10 .AB 5 屁5CD L AB于点D,/ADC=Z BD= 90°,/ 2= 90°—/ BAC=Z B.1tan B=2tan / 2=—.2AD CD 1 ACCD DB 2 CB .设AD= x (x > 0), CD= 2x, DB= 4x, AB= 5x .•/ PC切O O于点C,点B在O O上，• / 1 = / B./ P=/ P,「. △ PAC^ PCBPA AC 1PC CB 2 .PC= 10,「. PA= 5,PC 切O O 于点C, PAB 是O 0的割线,2PC = PA- PB210 = 5 (5 + 5 x ).解得 x = 3.AD= 3, CD= 6, DB= 12.1 1S ^BCD = CD" DB= — x 6X 12 = 36.2 22即三角形BCD 的面积36cm .PA= 10,二 PB= 20.2由切割线定理，得 PC = PA- PBA 內 DB= x + 4x = 15,解得 x = 3,CD= 2x = 6, DB= 4x = 12.S A BCD = ^CD- DB= 1 x 6X 12= 36.2 22即三角形BCD 的面积36cm .5.解：如图取 MN 的中点E 连结OE解法二：同解法一，由△ PAC^A PCB 得 PA PC AC CBPB 101220 AB= PB- PA= 15,2 2 2 a在 Rt A NOE 中 NO- OE = EN =2 6.解：T / CDE=/ CBA / DCE=/ BCA /• △ CDE^A ABC2S CDEDE S ABC AB DE = S CDE =任=1AB S ABC ' 42 ' 51 即，解得 AB= 10 (cm ,AB 2作OML FG 垂足为M11 则 FM= ^FG=丄^ 8= 4 (cm),22连结OF 11 OA= AB= — x 10= 5 (cm ).2 2OF= OA= 5 (cm ).在Rt A OMF 中由勾股定理，得 OM = . OF 2 FM 2 = -52 42 = 3 (cm ).A B FG10 Q 2 ••• 梯形 AFG 啲面积= -------------- • OM= -------- x 3 = 27 (cm ).2 27. 2 1 a n2 n ・ — =—a 2 2 8 2 2 1n( NO — OE ) 2 （平方单位）. (2) CBAP AC PA △ ACP^A BAP —— P P AB PBAC 2AB 1S阴影 ⑴PA 是。

初三数学有关圆的各地中考题汇编(含答案)

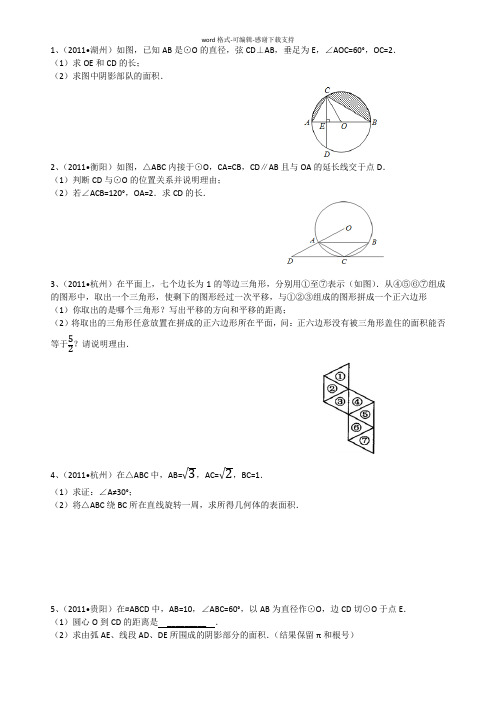
1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．2、（2011•衡阳）如图，△ABC 内接于⊙O ，CA=CB ，CD ∥AB 且与OA 的延长线交于点D ．（1）判断CD 与⊙O 的位置关系并说明理由；（2）若∠ACB=120°，OA=2．求CD 的长．3、（2011•杭州）在平面上，七个边长为1的等边三角形，分别用①至⑦表示（如图）．从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形（1）你取出的是哪个三角形？写出平移的方向和平移的距离；（2）将取出的三角形任意放置在拼成的正六边形所在平面，问：正六边形没有被三角形盖住的面积能否等于52？请说明理由．4、（2011•杭州）在△ABC 中，AB=√3，AC=√2，BC=1．（1）求证：∠A≠30°；（2）将△ABC 绕BC 所在直线旋转一周，求所得几何体的表面积．5、（2011•贵阳）在▱ABCD 中，AB=10，∠ABC=60°，以AB 为直径作⊙O ，边CD 切⊙O 于点E ．（1）圆心O 到CD 的距离是 _________ ．（2）求由弧AE 、线段AD 、DE 所围成的阴影部分的面积．（结果保留π和根号）6、（2011•抚顺）如图，AB 为⊙O 的直径，弦CD 垂直平分OB 于点E ，点F 在AB 延长线上，∠AFC=30°．（1）求证：CF 为⊙O 的切线．（2）若半径ON ⊥AD 于点M ，CE=√3，求图中阴影部分的面积．7、（2011•北京）如图，在△ABC ，AB=AC ，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，点F 在AC 的延长线上，且∠CBF=12∠CAB ．（1）求证：直线BF 是⊙O 的切线；（2）若AB=5，sin ∠CBF=√55，求BC 和BF 的长．8、（2010•义乌市）如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE ̂的中点，OM 交AC 于点D ，∠BOE=60°，cosC=12，BC=2√3．（1）求∠A 的度数；（2）求证：BC 是⊙O 的切线（3）求MD 的长度．9、（2010•沈阳）如图，AB 是⊙O 的直径，点C 在BA 的延长线上，直线CD 与⊙O 相切与点D ，弦DF ⊥AB 于点E ，线段CD=10，连接BD ．（1）求证：∠CDE=2∠B ；（2）若BD ：AB=√3：2，求⊙O 的半径及DF 的长．10、（2010•绍兴）如图，已知△ABC 内接于⊙O ，AC 是⊙O 的直径，D 是AB ̂的中点，过点D 作直线BC的垂线，分别交CB 、CA 的延长线E 、F ．（1）求证：EF 是⊙O 的切线；（2）若EF=8，EC=6，求⊙O 的半径．11、（2010•丽水）如图，直线l 与⊙O 相交于A ，B 两点，且与半径OC 垂直，垂足为H ，已知AB=16cm ，．（1）求⊙O 的半径；（2）如果要将直线l 向下平移到与⊙O 相切的位置，平移的距离应是多少？请说明理由．1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．考点：扇形面积的计算；垂径定理。

中考数学《圆的综合题》专项练习题及答案

中考数学《圆的综合题》专项练习题及答案一、单选题1．如图，在一块正三角形飞镖游戏板上画一个正六边形（图中阴影部分），假设飞镖投中游戏板上的每一点是等可能的（若投中边界或没有投中游戏板，则重投1次），任意投掷飞镖1次，则飞镖投中阴影部分的概率为（）A．13B．49C．12D．232．如图，AB为⊙O的直径，弦DC垂直AB于点E，⊙DCB=30°，EB=3，则弦AC的长度为（）A．3 √3B．4√3C．5√3D．6√33．如图，AB是⊙O的弦，半径OC⊙AB于点D，且AB=6cm，OD=4cm。

则DC的长为（）A．cm B．1cm C．2cm D．5cm4．如图，四边形ABCD内接于⊙ O，AB为⊙ O的直径，∠ABD=20∘，则∠BCD的度数是（）A．90°B．100°C．110°D．120°5．如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则⊙ABD=（）A．⊙ACD B．⊙ADB C．⊙AED D．⊙ACB6．如图，在⊙O中，弦AB⊙CD，若⊙ABC=40°，则⊙BOD=（）A．20°B．40°C．50°D．80°7．下列判断结论正确的有（）（1）直径是圆中最大的弦．（2）长度相等的两条弧一定是等弧．（3）面积相等的两个圆是等圆．（4）同一条弦所对的两条弧一定是等弧．（5）圆上任意两点间的部分是圆的弦．A．1个B．2个C．3个D．4个8．已知如图，PA、PB切⊙O于A，B，MN切⊙O于C，交PB于N；若PA=7.5cm，则⊙PMN的周长是（）A．7.5cm B．10cm C．15cm D．12.5cm9．若小李同学掷出的铅球在场地航砸出一个直径为10厘米，深2厘米的小坑，则该铅球的直径为（）A．20厘米B．19.5厘米C．14.5厘米D．10厘米10．如图，如果从半径为9cm的圆形纸片剪去13圆周的一个扇形，将留下的扇形（阴影部分）围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）A．6cm B．5√3cm C．8cm D．3√5cm11．如图，△ABC内接于⊙O，∠B=65o，∠C=70o，若BC=2√2，则弧BC长为（）A．πB．√2πC．2πD．√2π12．如下图，点B，C，D在⊙O上，若⊙BCD＝130°，则⊙BOD的度数是（）A．96°B．98°C．102°D．100°二、填空题13．如图，在扇形AOB中，OA＝4，⊙AOB＝90°，点P是弧AB上的动点，连接OP，点C是线段OP的中点，连接BC并延长交OA于点D，则图中阴影部分面积最小值为.14．如图，在边长为√2的正方形ABCD中，分别以四个顶点为圆心，以边长为半径画弧，分别与正方形的边和对角线相交，则图中阴影部分的面积为（结果保留π）.15．如图，⊙ABC的顶点A，B，C均在⊙O上，若⊙ABC+⊙AOC=90°，则⊙AOC的大小是．16．如图：⊙O为⊙ABC的内切圆，⊙C＝90°，AO的延长线交BC于点D，AC＝4，CD＝1，则⊙O的半径为.17．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则tan⊙ACG=．18．如图，菱形ABCD中，已知AB=2，∠DAB=60°将它绕着点A逆时针旋转得到菱形ADEF，使AB与AD重合，则点C运动的路线CE⌢的长为．三、综合题19．如图，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，点D为AP的中点，连结AC．求证：（1）⊙P=⊙BAC（2）直线CD是⊙O的切线．20．如图，以△ABC的边AB为直径的⊙O交AC于点F，点E是BF⌢的中点，连接BE并延长交AC于点D，若∠CBD=12∠CAB．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为2，cos∠BAC=25，求CD的长．21．如图，⊙O是⊙ABC的外接圆，AC是O的直径，BD＝BA＝12，BC＝5，BE⊙DC，交D的延长线于点E，BD交直径AC于点F．（1）求证：⊙BCA＝⊙BAD．（2）求证：BE是⊙O的切线．（3）若BD平分⊙ABC，交⊙O于点D，求AD的长．22．如图，⊙OAB中，OA=OB=10cm，⊙AOB=80°，以点O为圆心，半径为6cm的优弧弧MN分别交OA，OB于点M，N．（1）点P在右半弧上（⊙BOP是锐角），将OP绕点O逆时针旋转80°得OP′．求证：AP=BP′；（2）点T在左半弧上，若AT与弧相切，求A T的长．23．如图，有一直径是√2米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米.⌢的中点，CE⊥AB于点E，BD交CE于点F．24．如图，AB是⊙O的直径，C是BD（1）求证：CF=BF；（2）若CD﹦5，AC﹦12，求⊙O的半径和CE的长．参考答案1．【答案】D2．【答案】D3．【答案】B4．【答案】C5．【答案】A6．【答案】D7．【答案】B8．【答案】C9．【答案】C10．【答案】D11．【答案】A12．【答案】D13．【答案】4π−8√3314．【答案】4-π15．【答案】60°16．【答案】0.817．【答案】118．【答案】2√33π19．【答案】（1）解：证明：∵AB是⊙O的直径∴⊙ACB=90°∴⊙ACP=90°∴⊙P+⊙CAP=90°∵AP⊙O是切线∴⊙BAP=90°即⊙CAP+⊙BAC=90°∴⊙P=⊙BAC；（2）解：∵CD是Rt⊙PAC斜边PA的中线∴CD=AD∴⊙DCA=⊙DAC连接OC∵OC=OA∴⊙OCA=⊙OAC∴⊙DCO=⊙DAO=90°∴CD是⊙O的切线．20．【答案】（1）证明：连接AE，如图所示：∵AB是⊙O的直径∴∠AEB=90°∴∠BAE+∠ABE=90°．∵点E为弧BF的中点∴EF⌢=EB⌢∴∠BAE=∠DAE=12∠CAB．又∵∠CBD=12∠CAB∴∠BAE=∠CBD∴∠CBD+∠ABE=90°∴AB⊥CB∴BC是⊙O的切线．（2）解：∵∠BAE=∠DAE，∠AED=∠AEB=90°∴∠ADE=∠ABE∴AD=AB=2×2=4．∵cos∠BAC=2 5∴在Rt△ABC中即4AC=25，得AC=10∴CD=AC−AD=10−4=6．21．【答案】（1）证明：∵BD=BA ∴∠BDA=∠BAD．∵∠BCA=∠BDA∴∠BCA=∠BAD．（2）证明：连结OB，如图∵∠BCA=∠BAD又∵∠BCE=∠BAD∴∠BCA=∠BCE∵OB=OC∴∠BCO=∠CBO∴∠BCE=∠CBO∴OB//ED．∵BE⊥ED∴EB⊥BO．∴BE是⊙O的切线．（3）解：∵AC是⊙O的直径∴∠ABC=90°∴AC=√AB2+BC2=√122+52=13．∵∠BDE=∠CAB∴△BED∽△CBA∴BDAC=DEAB，即1213=DE12∴DE=14413∴BE=√BD2−DE2=6013∴CE=√BC2−BE2=2513∴CD=DE−CE=119 13∵BD平分⊙ABC ∴∠CBD=∠ABD∴AD=CD=119 13．22．【答案】（1）证明：∵⊙AOB=⊙POP′=80°∴⊙AOB+⊙BOP=⊙POP′+⊙BOP即⊙AOP=⊙BOP′在⊙AOP 与⊙BOP′中 OA=OB ⊙AOP=⊙BOP OP=OP′∴⊙AOP⊙⊙BOP′ ∴AP=BP′（2）解：∵A T 与弧相切，连结OT ．∴OT⊙A T在Rt⊙AOT 中，根据勾股定理得，A T= √OA 2−OT 2 ∵OA=10，OT=6 ∴AT=823．【答案】（1）1 （2）1424．【答案】（1）证明：∵AB 是 ⊙O 的直径∴∠ACB =90° ∴∠A +∠ABC =90° 又∵CE ⊥AB ∴∠CEB =90° ∴∠BCE +∠ABC =90° ∴∠BCE =∠A∵C 是 BD ⌢ 的中点 ∴CD⌢=CB ⌢ ∴∠DBC =∠A ∴∠DBC =∠BCE ∴CF =BF（2）解：∵CD⌢=CB ⌢，CD =5 ∴∠DBC =∠BDC∴BC=CD=5∵∠ACB=90°∴AB=√AC2+BC2=√122+52=13∴AO=6.5∵∠BCE=∠A，∠ACB=∠CEB=90°∴△CEB⊙ △ACB∴CE=AC⋅BCAB=12×513=6013故⊙O的半径为6.5，CE的长是6013.第11页共11。

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练(含答案)

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1. (2023江西)如图，点A，B，C，D均在直线l上，点P在直线l外，则经过其中任意三个点，最多可画出圆的个数为()A. 3B. 4C. 5D. 6第1题图2. (2023广东省卷)如图，AB是⊙O的直径，∠BAC＝50°，则∠D＝()第2题图A. 20°B. 40°C. 50°D. 80°3. (2023广元)如图，AB是⊙O的直径，点C，D在⊙O上，连接CD，OD，A C.若∠BOD＝124°，则∠ACD的度数是()A. 56°B. 33°C. 28°D. 23°第3题图4. (2023山西)如图，四边形ABCD内接于⊙O，AC，BD为对角线，BD经过圆心O.若∠BAC ＝40°，则∠DBC的度数为()第4题图A. 40°B. 50°C. 60°D. 70°5. (2023安徽)如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE－∠COD＝()A. 60°B. 54°C. 48°D. 36°第5题图6. (2023赤峰)如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC ＝2∠COD，则∠CBD的度数是()第6题图A. 25°B. 30°C. 35°D. 40°7. [新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题：“今有圆材，径二尺五寸．欲为方版，令厚七寸，问广几何？”结合下图，其大意是：今有圆形材质，直径BD为25寸，要做成方形板材，使其厚度CD达到7寸，则BC的长是() A. 674寸 B. 25寸C. 24寸D. 7寸第7题图8. (2023杭州)如图，在⊙O中，半径OA，OB互相垂直，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝()第8题图A. 23°B. 24°C. 25°D. 26°9. (2023广西)赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥．如图，主桥拱呈圆弧形，跨度约为37 m，拱高约为7 m，则赵州桥主桥拱半径R约为()第9题图A. 20 mB. 28 mC. 35 mD. 40 m10. (2023凉山州)如图，在⊙O中，OA⊥BC，∠ADB＝30°，BC＝23，则OC＝()A. 1B. 2C. 2 3D. 4第10题图11. 如图，点A，B，D在⊙O上，CD垂直平分AB于点C.现测得AB＝CD＝16，则圆形宣传图标的半径为()第11题图A. 12B. 10C. 8D. 612. 如图，在平面直角坐标系中，⊙O的半径为4，弦AB的长为3，过O作OC⊥AB于点C，则OC的长度是________；⊙O内一点D的坐标为(－2，1)，当弦AB绕O点顺时针旋转时，点D到AB的距离的最小值是________．第12题图13. (2023武汉)如图，OA，OB，OC都是⊙O的半径，∠ACB＝2∠BA C.(1)求证：∠AOB＝2∠BOC；(2)若AB＝4，BC＝5，求⊙O的半径．第13题图拔高题14. (2023吉林省卷)如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点(点P不与点B重合)，连接CP.若∠BAC＝70°，则∠BPC的度数可能是()A. 70°B. 105°C. 125°D. 155°第14题图15. 如图，正方形ABCD 内接于⊙O ，点E 为弧AB 的中点，连接DE 与AB 交于点F .若AB＝1，记△ADF 的面积为S 1，△AEF 的面积为S 2，则S 1S 2的值为________．第15题图16. 如图，以原点O 为圆心的圆交x 轴于A ，B 两点，交y 轴的正半轴于点C ，且点A 的坐标为(－2，0)，D 为第一象限内⊙O 上的一点，若∠OCD ＝75°，则AD 的长为________．第16题图参考答案与解析1. D 【解析】本题考查了确定圆的条件及圆的有关定义及性质．∵过不在同一直线上的三个点一定能作一个圆，∴要经过题中所给的3个点画圆，除选定直线l 外的点P 外，再在直线l 上的A ，B ，C ，D 四个点中任选其中2个即可画圆．∵从A ，B ，C ，D 四个点中任选其中2个点的方法可以是AB ，AC ，AD ，BC ，BD ，CD ，共6种，∴最多可以画出圆的个数为6.2. B 【解析】∵AB 是⊙O 的直径，∠BAC ＝50°，∴∠ACB ＝90°，∠B ＝180°－50°－90°＝40°.∵AC ＝AC ，∴∠D ＝∠B ＝40°.3. C 【解析】∵∠BOD ＝124°，∴∠AOD ＝180°－124°＝56°，∴∠ACD ＝12∠AOD ＝28°. 4. B 【解析】∵BD 经过圆心O ，∴∠BCD ＝90°.∵∠BDC ＝∠BAC ＝40°，∴∠DBC ＝90°－∠BDC ＝50°.5. D 【解析】∵五边形ABCDE 是正五边形，∴∠BAE ＝（5－2）×180°5＝108°，∠COD ＝360°5＝72°，∴∠BAE －∠COD ＝108°－72°＝36°. 6. A 【解析】∵∠BCD ＝105°，∴∠BAD ＝180°－105°＝75°，∴∠BOD ＝150°.∵∠BOC＝2∠COD ，∴∠COD ＝13 ∠BOD ＝50°，∴∠CBD ＝12∠COD ＝25°. 7. C 【解析】∵BD 是圆的直径，∴∠BCD ＝90°.∵BD ＝25，CD ＝7，∴在Rt △BCD 中，由勾股定理得，BC ＝252－72 ＝24(寸).8. D 【解析】如解图，连接OC ，∵∠ABC ＝19°，∴∠AOC ＝2∠ABC ＝38°.∵半径OA ，OB 互相垂直，∴∠AOB ＝90°，∴∠BOC ＝90°－38°＝52°，∴∠BAC ＝12∠BOC ＝26°.第8题解图9. B 【解析】如解图，在Rt △OAB 中，由勾股定理，得AO 2＋AB 2＝OB 2，即(R －7)2＋(372)2＝R 2，解得R ≈28(m).第9题解图10. B 【解析】如解图，连接OB ，设OA 交BC 于点E ，∵∠ADB ＝30°，∴∠AOB ＝60°.∵OA ⊥BC ，BC ＝23 ，∴BE ＝12 BC ＝3 .在Rt △BOE 中，sin ∠AOB ＝BE OB，∴sin 60°＝3OB ＝32，∴OB ＝2，∴OC ＝2.第10题解图11. B 【解析】如解图，连接OA ，设圆形宣传图标的半径为R ，∵CD 垂直平分AB ，AB＝CD ＝16，∴CD 过点O ，AC ＝BC ＝12 AB ＝12×16＝8，∠DCA ＝90°.∵AO ＝OD ＝R ，∴在Rt △AOC 中，由勾股定理，得OC 2＋AC 2＝OA 2，即(16－R )2＋82＝R 2，解得R ＝10，即圆形宣传图标的半径为10.第11题解图 12. 552 ；552 －5 【解析】如解图，连接OB ，∵OC ⊥AB ，∴BC ＝12 AB ＝32.由勾股定理，得OC ＝OB 2－BC 2 ＝552.当OD ⊥AB 时，点D 到AB 的距离最小，由勾股定理，得OD ＝22＋12 ＝5 ，∴点D 到AB 的距离的最小值为552 －5 .第12题解图13. (1)证明：由圆周角定理，得∠ACB ＝12 ∠AOB ，∠BAC ＝12∠BOC . ∵∠ACB ＝2∠BAC ，∴∠AOB ＝2∠BOC ；(2)解：如解图，过点O 作半径OD ⊥AB 于点E ，连接BD .则∠DOB ＝12∠AOB ，AE ＝BE . ∵∠AOB ＝2∠BOC ，∴∠DOB ＝∠BOC .∴BD ＝BC .∵AB ＝4，BC ＝5 ，∴BE ＝2，DB ＝5 .在Rt △BDE 中，∵∠DEB ＝90°，∴DE ＝BD 2－BE 2 ＝1.在Rt △BOE 中，∵∠OEB ＝90°，∴OB 2＝(OB －1)2＋22，∴OB ＝52，即⊙O 的半径是 52.第13题解图14. D 【解析】如解图，连接BC ，∵∠BAC ＝70°，∴∠BOC ＝2∠BAC ＝140°.∵OB ＝OC ，∴∠OBC ＝∠OCB ＝180°－140°2＝20°.∵点P 为OB 上任意一点(点P 不与点B 重合)，∴0°<∠OCP <20°.∵∠BPC ＝∠BOC ＋∠OCP ＝140°＋∠OCP ，∴140°<∠BPC <160°，故选D.第14题解图15. 2(2 ＋1) 【解析】如解图，连接OE 交AB 于点G ，连接AC .根据垂径定理的推论，得OE ⊥AB ，AG ＝BG .由题意可得，AC 为⊙O 的直径，AC ＝2 ，则圆的半径是22.根据正方形的性质，得∠OAF ＝45°，∴OG ＝12 ，EG ＝2－12.∵OE ∥AD ，∴△ADF ∽△GEF ，∴FE FD ＝EG DA ＝2－12 .∵△ADF 与△AEF 等高，∴S 1S 2 ＝S △ADF S △AEF＝DF EF ＝2(2 ＋1).第15题解图16. 23 【解析】如解图，连接OD ，BD .∵A (－2，0)，∴OA ＝OB ＝2，∴AB ＝4.∵OC ＝OD ，∴∠OCD ＝∠ODC ＝75°，∴∠DOC ＝180°－2×75°＝30°，∴∠DOB ＝90°－30°＝60°，∴∠DAB ＝12∠DOB ＝30°.∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴AD ＝AB ·cos 30°＝23 .第16题解图。

圆中考试题集锦(附答案)

圆中考试题集锦(附答案)圆中考试题1.如图所示，BC是圆O的直径，点P在CB的延长线上，PA与圆O相切于点A。

已知PA=3，PB=1，求∠APC的度数。

2.若圆柱的高为20厘米，底面半径等于侧面积除以高，求底面半径的长度。

3.“圆材埋壁”是《九章算术》中的一个古代数学问题。

如图所示，CD为圆O的直径，弦AB⊥CD，垂足为E，CE=1寸，AB=10寸，求直径CD的长度。

4.已知圆O的半径为5，PC切圆O于点C，PO交圆O于点A，PA=4，求PC的长度。

5.若圆锥的侧面积为20π平方厘米，母线长为5厘米，求底面半径的长度。

6.两个圆相交，公共弦长为16厘米，圆的半径分别为10厘米和17厘米，求两圆的圆心距离。

7.如图所示，圆O是△ABC的内切圆，∠C=90度，AO的延长线交BC于点D，AC=4，DC=1，求圆O的半径长度。

8.一个居民小区有一个正多边形的活动场。

为了迎接“AAPP”会议在重庆市的召开，小区决定在多边形的每个顶点处修建一个半径为2米的扇形花台，花台以多边形的顶点为圆心，比多边形的内角为圆心角，花台占地面积共为12π平方米。

若每个花台的造价为400元，求修建这些花台的总费用。

9.如图所示，AB是圆O的直径，CD是弦。

若AB=10厘米，CD=8厘米，求A、B两点到直线CD的距离之和。

10.某工件的形状如图所示：[图片] 圆弧BC的度数为60，AB=6厘米，点B到点C的距离等于AB，∠BAC=30.求工件的面积。

11.如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA=4，PB=2.求⊙O的半径。

12.已知⊙O的半径为35厘米，⊙O'的半径为5厘米。

⊙O与⊙O'相交于点D、E。

若两圆的公共弦DE的长是6厘米（圆心O、O'在公共弦DE的两侧），则两圆的圆心距OO'的长为多少？13.如图，两个等圆⊙O和⊙O'的两条切线OA、OB，A、B是切点。

求∠AOB的度数。

中考数学专题练——专题11 圆(试题精选,含答案)

专题十一圆一、单选题1.（2019·高新模拟）如图，O为圆心，是直径，是半圆上的点，是上的点.若，则的大小为（）A. B. C. D.2.（2020·南通模拟）如图，点A，B，C，D都在⊙O上，BD为直径，若∠A＝65°，则∠DBC的值是（）A. 65°B. 25°C. 35°D. 15°3.如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是( )A. B. 2 C. 6 D. 84.（2020九上·奉化期末）如图，在菱形ABCD中，已知AB=4，∠B=60°，以AC为直径的⊙O与菱形ABCD 相交，则图中阴影部分的面积为( )A. B. C. D.5.（2019九上·温州月考）如图，△ABC内接于⊙O中，AB=AC，=60°，则∠B=( )A. 30°B. 45°C. 60°D. 75°6.（2020九上·中山期末）如图，AD是半圆的直径，点C是弧BD的中点，∠ADC=55°，则∠BAD等于（）A. 50°B. 55°C. 65°D. 70°7.（2020九上·海曙期末）平面直角坐标系中，⊙P的圆心坐标为(-4，-5)，半径为5，那么⊙P与y轴的位置关系是（）A. 相交B. 相离C. 相切D. 以上都不是8.（2019九上·驻马店期末）如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（）A. 3πB.C. 6πD. 24π9.（2020九上·北仑期末）下列四个结论，不正确的是（）①过三点可以作一个圆；②圆内接四边形对角相等③平分弦的直径垂直于弦；④相等的圆周角所对的弧也相等A. ②③B. ①③④C. ①②④D. ①②③④10.（2020九上·诸暨期末）如图，是圆内接四边形的一条对角线，点关于的对称点在边上，连接.若，则的度数为（）A. 106°B. 116°C. 126°D. 136°11.（2019九上·武汉月考）如图，O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB 于点C，则△ABC的最大面积是（）A. B. C. D.12.如图，在⊙O中，点C在优弧AB上，将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为，AB=8，则BC的长是（）A. B. C. D.13.（2019九上·如皋期末）如图，▱ABCD中，，，，是边AB上的两点，半径为2的过点A，半径为1的过点、E、F分别是边CD，和上的动点则的最小值等于A. B. 6 C. D. 914.（2019·武汉模拟）点G为△ABC的重心（△ABC三条中线的交点），以点G为圆心作⊙G与边AB，AC相切，与边BC相交于点H，K，若AB＝4，BC＝6，则HK的长为（）A. B. C. D.15.（2019·武汉模拟）如图，⊙O内切于正方形ABCD，边AD，CD分别与⊙O切于点E，F，点M、N 分别在线段DE，DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（）A. B. 2 C. D. 216.（2020·长兴模拟）如图，AB为☉O的直径，P为弦BC上的点，∠ABC=30°，过点P作PD⊥OP交☉O 于点D，过点D作DE∥AB交AB的延长线于点E.若点C恰好是的中点，BE=6，则PC的长是（）A. -8B. -3C. 2D. 12-17.（2019九上·宜兴月考）在平面直角坐标系中，直线经过点A（－3，0），点B（0，），点P的坐标为（1，0），与轴相切于点O，若将⊙P沿轴向左平移，平移后得到（点P的对应点为点P′），当⊙P′与直线相交时，横坐标为整数的点P′共有（）A. 1个B. 2个C. 3个D. 4个18.（2019·海州模拟）如图，菱形ABCD的边AB=5，面积为20，∠BAD＜90°，⊙O与边AB、AD都相切，AO=2，则⊙O的半径长等于（）A. B. C. D.19.（2019·高台模拟）如图，AB与⊙O相切于点C，OA＝OB，⊙O的直径为6cm，AB＝6 cm，则阴影部分的面积为（）A. B. C. D.20.（2019九下·深圳月考）如图，△ABC内接于圆O，∠BOC=120°，AD为圆O的直径．AD交BC于P 点且PB=1，PC=2，则AC的长为( )A. B. C. 3 D. 2二、填空题21.（2019·嘉定模拟）如图，的半径长为5cm，内接于，圆心O在的内部，如果，cm，那么的面积为________cm22.（2019九上·黄石期末）如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC=25°.求∠P的度数________.23.（2020九上·东台期末）如图，⊙O是△ABC的外接圆，已知∠ABO=40°，则∠ACB的大小为________．24.（2019·台江模拟）如图，⊙O是Rt△ABC的外接圆，∠ACB＝90°，∠A＝25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是________．25.（2019九上·道里期末）如图，已知，在中，，，，是ABC的内切圆，则这个圆的半径是________．26.（2020九上·北仑期末）如图，四边形ABCD中，∠BAD=∠BCD=90°，∠B=45°，DE⊥AC于E交AB 于F，若BC=2CD，AE=2，则线段BF=________。

2024年中考数学真题汇编专题22 圆的相关性质+答案详解

2024年中考数学真题汇编专题22 圆的相关性质+答案详解（试题部分）一、单选题1．（2024·湖南·中考真题）如图，AB ，AC 为O 的两条弦，连接OB ，OC ，若45A ∠=︒，则BOC ∠的度数为（）A ．60︒B ．75︒C ．90︒D ．135︒2．（2024·甘肃临夏·中考真题）如图，AB 是O 的直径，35E ∠=︒，则BOD ∠=（）A ．80︒B ．100︒C ．120︒D ．110︒3．（2024·江苏连云港·中考真题）如图，将一根木棒的一端固定在O 点，另一端绑一重物．将此重物拉到A 点后放开，让此重物由A 点摆动到B 点．则此重物移动路径的形状为（）A ．倾斜直线B ．抛物线C ．圆弧D ．水平直线4．（2024·四川凉山·中考真题）数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点,A B ，连接AB ，作AB 的垂直平分线CD 交AB 于点D ，交AB 于点C ，测出40cm 10cm AB CD ==,，则圆形工件的半径为（）A ．50cmB ．35cmC ．25cmD ．20cm5．（2024·内蒙古赤峰·中考真题）如图，AD 是O 的直径，AB 是O 的弦，半径OC AB ⊥，连接CD ，交OB 于点E ，42BOC ∠=︒，则OED ∠的度数是（）A ．61︒B ．63︒C ．65︒D ．67︒6．（2024·湖北·中考真题）AB 为半圆O 的直径，点C 为半圆上一点，且50CAB ∠=︒．①以点B 为圆心，适当长为半径作弧，交,AB BC 于,D E ；②分别以DE 为圆心，大于12DE 为半径作弧，两弧交于点P ；③作射线BP ，则ABP ∠=（）A ．40︒B ．25︒C ．20︒D ．15︒7．（2024·四川宜宾·中考真题）如图，AB 是O 的直径，若60CDB ∠=︒，则ABC ∠的度数等于（）A ．30︒B ．45︒C ．60︒D ．90︒8．（2024·四川广元·中考真题）如图，已知四边形ABCD 是O 的内接四边形，E 为AD 延长线上一点，128AOC ∠=︒，则CDE ∠等于（）A ．64︒B ．60︒C ．54︒D ．52︒9．（2024·云南·中考真题）如图，CD 是O 的直径，点A 、B 在O 上．若AC BC =，36AOC ∠=，则D ∠=（）A ．9B ．18C ．36oD ．4510．（2024·黑龙江绥化·中考真题）下列叙述正确的是（）A ．顺次连接平行四边形各边中点一定能得到一个矩形B ．平分弦的直径垂直于弦CD ．相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等11．（2024·广东广州·中考真题）如图，O 中，弦AB 的长为点C 在O 上，OC AB ⊥，30ABC ∠=︒．O 所在的平面内有一点P ，若5OP =，则点P 与O 的位置关系是（）A ．点P 在O 上B ．点P 在O 内C ．点P 在O 外D ．无法确定12．（2024·黑龙江牡丹江·中考真题）如图，四边形ABCD 是O 的内接四边形，AB 是O 的直径，若20BEC ∠=︒，则ADC ∠的度数为（）A ．100︒B ．110︒C ．120︒D ．130︒13．（2024·湖北武汉·中考真题）如图，四边形ABCD 内接于O ，60ABC ∠=︒，45BAC CAD ∠=∠=︒，2AB AD +=，则O 的半径是（）A B C D二、填空题14．（2024·四川南充·中考真题）如图，AB 是O 的直径，位于AB 两侧的点C ，D 均在O 上，30BOC ∠=︒，则ADC ∠= 度．15．（2024·北京·中考真题）如图，O 的直径AB 平分弦CD （不是直径）.若35D ∠=︒，则C ∠= ︒16．（2024·江苏苏州·中考真题）如图，ABC 是O 的内接三角形，若28OBC ∠=︒，则A ∠= ．17．（2024·黑龙江大兴安岭地·中考真题）如图，ABC 内接于O ，AD 是直径，若25B ∠=︒，则CAD ∠ ︒．18．（2024·四川眉山·中考真题）如图，ABC 内接于O ，点O 在AB 上，AD 平分BAC ∠交O 于D ，连接BD ．若10AB =，BD =BC 的长为．19．（2024·陕西·中考真题）如图，BC 是O 的弦，连接OB ，OC ，A ∠是BC 所对的圆周角，则A ∠与OBC ∠的和的度数是．20．（2024·黑龙江牡丹江·中考真题）如图，在O 中，直径AB CD ⊥于点E ，6,1CD BE ==，则弦AC 的长为．21．（2024·江西·中考真题）如图，AB 是O 的直径，2AB =，点C 在线段AB 上运动，过点C 的弦DE AB ⊥，将DBE 沿DE 翻折交直线AB 于点F ，当DE 的长为正整数时，线段FB 的长为．22．（2024·河南·中考真题）如图，在Rt ABC △中，90ACB ∠=︒，3CA CB ==，线段CD 绕点C 在平面内旋转，过点B 作AD 的垂线，交射线AD 于点E ．若1CD =，则AE 的最大值为，最小值为 .三、解答题23．（2024·四川甘孜·中考真题）如图，AB 为⊙O 的弦，C 为AB 的中点，过点C 作CD AB ∥，交OB 的延长线于点D ．连接OA OC ，．(1)求证：CD 是⊙O 的切线；(2)若32OA BD ==，，求OCD 的面积．24．（2024·内蒙古包头·中考真题）如图，AB 是O 的直径，,BC BD 是O 的两条弦，点C 与点D 在AB 的两侧，E 是OB 上一点（OE BE >），连接,OC CE ，且2BOC BCE ∠=∠．(1)如图1，若1BE =，CE =O 的半径；(2)如图2，若2BD OE =，求证：BD OC ∥．（请用两种证法解答）25．（2024·安徽·中考真题）如图，O 是ABC 的外接圆，D 是直径AB 上一点，ACD ∠的平分线交AB 于点E ，交O 于另一点F ，FA FE =．(1)求证：CD AB ⊥；(2)设FM AB ⊥，垂足为M ，若1OM OE ==，求AC 的长．26．（2024·四川眉山·中考真题）如图，BE 是O 的直径，点A 在O 上，点C 在BE 的延长线上，EAC ABC ∠=∠，AD 平分BAE ∠交O 于点D ，连结DE ．(1)求证：CA 是O 的切线；(2)当8,4AC CE ==时，求DE27．（2024·江苏扬州·中考真题）如图，已知PAQ ∠及AP 边上一点C ．(1)用无刻度直尺和圆规在射线AQ 上求作点O ，使得2COQ CAQ ∠=∠；（保留作图痕迹，不写作法）(2)在（1）的条件下，以点O 为圆心，以OA 为半径的圆交射线AQ 于点B ，用无刻度直尺和圆规在射线CP 上求作点M ，使点M 到点C 的距离与点M 到射线AQ 的距离相等；（保留作图痕迹，不写作法）(3)在（1）、（2）的条件下，若3sin 5A =，12CM =，求BM 的长． 28．（2024·河南·中考真题）如图1，塑像AB 在底座BC 上，点D 是人眼所在的位置．当点B 高于人的水平视线DE 时，由远及近看塑像，会在某处感觉看到的塑像最大，此时视角最大．数学家研究发现：当经过A ，B 两点的圆与水平视线DE 相切时（如图2），在切点P 处感觉看到的塑像最大，此时APB ∠为最大视角．(1)请仅就图2的情形证明APB ADB ∠>∠．(2)经测量，最大视角APB ∠为30︒，在点P 处看塑像顶部点A 的仰角APE ∠为60︒，点P 到塑像的水平距离PH 为6m ．求塑像AB 的高（结果精确到0.1m 1.73≈）．29．（2024·江西·中考真题）如图，AB 是半圆O 的直径，点D 是弦AC 延长线上一点，连接BD BC ，，60D ABC ∠=∠=︒．(1)求证：BD 是半圆O 的切线；(2)当3BC =时，求AC 的长．30．（2024·广东深圳·中考真题）如图，在ABD △中，AB BD =，O 为ABD △的外接圆，BE 为O 的切线，AC 为O 的直径，连接DC 并延长交BE 于点E ．(1)求证：DE BE ⊥；(2)若AB =5BE =，求O 的半径．31．（2024·四川广元·中考真题）如图，在ABC 中，AC BC =，90ACB ∠=︒，O 经过A 、C 两点，交AB 于点D ，CO 的延长线交AB 于点F ，DE CF ∥交BC 于点E ．(1)求证：DE 为O 的切线；(2)若4AC =，tan 2CFD ∠=，求O 的半径．32．（2024·内蒙古呼伦贝尔·中考真题）如图，在ABC 中，以AB 为直径的O 交BC 于点,D DE AC ⊥，垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证：DE 是O 的切线；(2)若30,C CD ∠=︒=OBD 的面积．33．（2024·江苏扬州·中考真题）在综合实践活动中，“特殊到一般”是一种常用方法，我们可以先研究特殊情况，猜想结论，然后再研究一般情况，证明结论．如图，已知ABC ，CA CB =， O 是ABC 的外接圆，点D 在O 上（AD BD >），连接AD 、BD 、CD ．【特殊化感知】（1）如图1，若60ACB ∠=︒，点D 在AO 延长线上，则AD BD −与CD 的数量关系为________；【一般化探究】（2）如图2，若60ACB ∠=︒，点C 、D 在AB 同侧，判断AD BD −与CD 的数量关系并说明理由；【拓展性延伸】（3）若ACB α∠=，直接写出AD 、BD 、CD 满足的数量关系．（用含α的式子表示）34．（2024·浙江·中考真题）如图，在圆内接四边形ABCD 中，AD AC ADC BAD <∠<∠，，延长AD 至点E ，使AE AC =，延长BA 至点F ，连结EF ，使AFE ADC ∠=∠．(1)若60AFE ∠=︒，CD 为直径，求ABD ∠的度数．(2)求证：①EF BC ∥；②EF BD =．2024年中考数学真题汇编专题22 圆的相关性质+答案详解（答案详解）一、单选题1．（2024·湖南·中考真题）如图，AB ，AC 为O 的两条弦，连接OB ，OC ，若45A ∠=︒，则BOC ∠的度数为（）A ．60︒B ．75︒C ．90︒D ．135︒ 45A ∠=BOC ∴∠故选：C ．2．（2024·甘肃临夏·中考真题）如图，AB 是O 的直径，35E ∠=︒，则BOD ∠=（）A ．80︒B ．100︒C ．120︒D ．110︒【答案】D 【分析】本题考查圆周角定理，关键是由圆周角定理推出2AOD E ∠=∠．由圆周角定理得到270AOD E ∠=∠=︒，由邻补角的性质求出18070110BOD ∠=︒−︒=°．【详解】解：35E ∠=︒，270AOD E ∴∠=∠=︒，18070110BOD ︒∴∠=−︒=︒．故选：D ．3．（2024·江苏连云港·中考真题）如图，将一根木棒的一端固定在O 点，另一端绑一重物．将此重物拉到A 点后放开，让此重物由A 点摆动到B 点．则此重物移动路径的形状为（）A ．倾斜直线B ．抛物线C ．圆弧D ．水平直线【答案】C 【分析】本题考查动点的移动轨迹，根据题意，易得重物移动的路径为一段圆弧．【详解】解：在移动的过程中木棒的长度始终不变，故点A 的运动轨迹是以O 为圆心，OA 为半径的一段圆弧，故选：C ．4．（2024·四川凉山·中考真题）数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点,A B ，连接AB ，作AB 的垂直平分线CD 交AB 于点D ，交AB 于点C ，测出40cm 10cm AB CD ==,，则圆形工件的半径为（）A ．50cmB ．35cmC ．25cmD ．20cm【答案】C 【分析】本题考查垂径定理，勾股定理等知识．由垂径定理，可得出BD 的长；设圆心为O ，连接OB ，在Rt OBD △中，可用半径OB 表示出OD 的长，进而可根据勾股定理求出得出轮子的半径，即可得出轮子的直径长．【详解】解：∵CD 是线段AB 的垂直平分线，∴直线CD 经过圆心，设圆心为O ，连接OB ．Rt 根据勾股定理得：222OD BD OB +=，即：)2221020OB OB −+=，解得：25OB =；5．（2024·内蒙古赤峰·中考真题）如图，AD 是O 的直径，AB 是O 的弦，半径OC AB ⊥，连接CD ，交OB 于点E ，42BOC ∠=︒，则OED ∠的度数是（）A ．61︒B ．63︒C ．65︒D ．67︒6．（2024·湖北·中考真题）AB 为半圆O 的直径，点C 为半圆上一点，且50CAB ∠=︒．①以点B 为圆心，适当长为半径作弧，交,AB BC 于,D E ；②分别以DE 为圆心，大于12DE 为半径作弧，两弧交于点P ；③作射线BP ，则ABP ∠=（）A ．40︒B ．25︒C ．20︒D ．15︒7．（2024·四川宜宾·中考真题）如图，AB 是O 的直径，若60CDB ∠=︒，则ABC ∠的度数等于（）A ．30︒B ．45︒C ．60︒D ．90︒【答案】A 【分析】本题考查了直径所对的圆周角为直角，同弧或等弧所对的圆周角相等．根据直径所对的圆周角为直角得到90ACB ∠=︒，同弧或等弧所对的圆周角相等得到60CDB A ∠=∠=︒，进一步计算即可解答．【详解】解：AB 是O 的直径，90ACB ∴∠=︒，60CDB ∠=︒，60A CDB ∴∠=∠=︒，9030ABC A ∴∠=︒−∠=︒，故选：A ．8．（2024·四川广元·中考真题）如图，已知四边形ABCD 是O 的内接四边形，E 为AD 延长线上一点，128AOC ∠=︒，则CDE ∠等于（）A ．64︒B ．60︒C ．54︒D ．52︒ 【详解】解：ABC ∠是圆周角，与圆心角12AOC ∠=又四边形ABCD 是O 的内接四边形，180ADC =︒，又180CDE ADC ∠+∠=︒，64CDE ∴∠=∠︒，故选：A ．9．（2024·云南·中考真题）如图，CD 是O 的直径，点A 、B 在O 上．若AC BC =，36AOC ∠=，则D ∠=（）A ．9B ．18C ．36oD ．4510．（2024·黑龙江绥化·中考真题）下列叙述正确的是（）A ．顺次连接平行四边形各边中点一定能得到一个矩形B ．平分弦的直径垂直于弦C ．物体在灯泡发出的光照射下形成的影子是中心投影D ．相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等【答案】C【分析】本题考查了矩形的判定，垂径定理，中心投影，弧、弦与圆心角的关系，根据相关定理逐项分析判断，即可求解．【详解】A. 顺次连接平行四边形各边中点不一定能得到一个矩形，故该选项不正确，不符合题意；B. 平分弦（非直径）的直径垂直于弦，故该选项不正确，不符合题意；C. 物体在灯泡发出的光照射下形成的影子是中心投影，故该选项正确，符合题意；D. 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等，故该选项不正确，不符合题意；故选：C ．11．（2024·广东广州·中考真题）如图，O 中，弦AB 的长为点C 在O 上，OC AB ⊥，30ABC ∠=︒．O 所在的平面内有一点P ，若5OP =，则点P 与O 的位置关系是（）A ．点P 在O 上B ．点P 在O 内C ．点P 在O 外D ．无法确定，再结合特殊角的正弦值，求出O 的OC 为半径，12AD ∴=ABC =∠AOC ∴∠=在ADO △sin AOD ∠sin AD OA ∴=，即O 的半径为5OP =>∴点P 在O 外，故选：C ．12．（2024·黑龙江牡丹江·中考真题）如图，四边形ABCD 是O 的内接四边形，AB 是O 的直径，若20BEC ∠=︒，则ADC ∠的度数为（）A ．100︒B ．110︒C ．120︒D ．130︒ 【答案】B 【分析】此题考查了圆周角定理、圆内接四边形的性质，连接AC ，由AB 是O 的直径得到90ACB ∠=︒，根据圆周角定理得到20CAB BEC ∠=∠=︒，得到9070ABC BAC ∠=︒−∠=︒，再由圆内接四边形对角互补得到答案.【详解】解：如图，连接AC ，∵AB 是O 的直径，∴90ACB ∠=︒，∵20BEC ∠=︒，∴20CAB BEC ∠=∠=︒∴9070ABC BAC ∠=︒−∠=︒∵四边形ABCD 是O 的内接四边形，∴180110ADC ABC ∠=︒−∠=︒，故选：B13．（2024·湖北武汉·中考真题）如图，四边形ABCD 内接于O ，60ABC ∠=︒，45BAC CAD ∠=∠=︒，2AB AD +=，则O 的半径是（）A B C 2 D 并延长交O 于点F ()SAS ADC EBC ≌，再利用圆周角定理得到函数即可求解．【详解】解：延长AB 并延长交O 于点F∵四边形ABCD 内接于O ，∴ADC ABC ABC CBE ∠+∠=∠+∠∴ADC CBE ∠=∠∵45BAC CAD ∠=∠=︒︒，DAB ∠是O 的直径，90DCB =︒DCB 是等腰直角三角形，BCAD∴()SAS ADC EBC ≌ACD ECB ∠=∠，AC 2AB AD +=2AB BE AE +==又∵90DCB ∠=︒二、填空题14．（2024·四川南充·中考真题）如图，AB是O的直径，位于AB两侧的点C，D均在O上，30∠=︒，BOC ∠=度．则ADC是O的直径，位于均在O上，∠BOC=︒，15075︒；15．（2024·北京·中考真题）如图，O的直径AB平分弦CD（不是直径）.若35∠=︒，则C∠=D︒【答案】55【分析】本题考查了垂径定理的推论，圆周角定理，直角三角形的性质，熟练掌握知识点是解题的关键．先由垂径定理得到AB CD ⊥，由BC BC =得到35A D ∠=∠=︒，故903555C ︒︒∠=−=︒．【详解】解：∵直径AB 平分弦CD ，∴AB CD ⊥，∵BC BC =，∴35A D ∠=∠=︒，∴903555C ︒︒∠=−=︒，故答案为：55．16．（2024·江苏苏州·中考真题）如图，ABC 是O 的内接三角形，若28OBC ∠=︒，则A ∠= ．∵OB OC =，OBC ∠∴OCB OBC ∠=∠∴180BOC ∠=︒−∠117．（2024·黑龙江大兴安岭地·中考真题）如图，ABC 内接于O ，AD 是直径，若25B ∠=︒，则CAD ∠ ︒．【答案】65【分析】本题考查了圆周角定理，直角三角形的两个锐角互余，连接CD ，根据直径所对的圆周角是直角得出=90ACD ∠︒，根据同弧所对的圆周角相等得出25D B ∠=∠=︒，进而根据直角三角形的两个锐角互余，即可求解．【详解】解：如图所示，连接CD ，∵ABC 内接于O ，AD 是直径，∴=90ACD ∠︒，∵AC AC =,25B ∠=︒，∴25D B ∠=∠=︒∴902565CAD ∠=︒−︒=︒，故答案为：65．18．（2024·四川眉山·中考真题）如图，ABC 内接于O ，点O 在AB 上，AD 平分BAC ∠交O 于D ，连接BD ．若10AB =，BD =BC 的长为．可证明(ASA ABD AED ≌BCE ∽△，得到BE AB 【详解】解：延长AC ，BD AB 是O 的直径，90ADB ADE ∴∠=∠=︒，∠AD 平分BAD ∴∠=又∵AD =∴(ASA ABD AED ≌25BD DE ∴==，45BE =，10AB =，25BD =，AD ∴=DAC ∠=又∵BAD ∠∴BAD ∠ADB ∠=ABD BEC ∴∽，BE BC AB AD∴=， 451045BC ∴=， 8BC ∴=，19．（2024·陕西·中考真题）如图，BC 是O 的弦，连接OB ，OC ，A ∠是BC 所对的圆周角，则A ∠与OBC ∠的和的度数是．【答案】90︒/90度【分析】本题考查了圆周角定理，等腰三角形的性质，三角形内角和定理，熟练掌握圆周角定理是解题的关键．根据圆周角定理可得2BOC A ∠=∠，结合三角形内角和定理，可证明2180A OBC OCB ∠+∠+∠=︒，再根据等腰三角形的性质可知OBC OCB ∠=∠，由此即得答案．【详解】A ∠是BC 所对的圆周角，BOC ∠是BC 所对的圆心角，2BOC A ∴∠=∠，180BOC OBC OCB ∠+∠+∠=︒，2180A OBC OCB ∴∠+∠+∠=︒，OB OC =，OBC OCB ∴∠=∠，2180A OBC OBC ∴∠+∠+∠=︒，22180A OBC ∴∠+∠=︒，90A OBC ∴∠+∠=︒．故答案为：90︒．20．（2024·黑龙江牡丹江·中考真题）如图，在O 中，直径AB CD ⊥于点E ，6,1CD BE ==，则弦AC 的长为．，设O 的半径为Rt OED 中，由勾股定9=，在Rt AEC 中，由勾股定理即可求解．设O的半径为Rt OED中，由勾股定理得：r，解得：=5==5,OA OE=+AE OA OERt AEC中，由勾股定理得：故答案为：321．（2024·江西·中考真题）如图，AB是O的直径，2⊥，AB=，点C在线段AB上运动，过点C的弦DE AB 将DBE沿DE翻折交直线AB于点F，当DE的长为正整数时，线段FB的长为．【详解】解：AB为直径，的长为正整数时，时，即DE为直径，∵22．（2024·河南·中考真题）如图，在Rt ABC △中，90ACB ∠=︒，3CA CB ==，线段CD 绕点C 在平面内旋转，过点B 作AD 的垂线，交射线AD 于点E ．若1CD =，则AE 的最大值为，最小值为 .与C在ABC 内部时，与C 相切于点在ABC AE 最小，分别画出图形，求出结果即可．90=︒，CA 9045︒=︒，在平面内旋转，与C 相切于点在ABC 内部时，则CD AE ⊥，∴90ADC CDE ∠=∠=︒，∴22231AD AC CD =−=−∵AC AC =，∴45CED ABC ==︒∠∠，∵90CDE ∠=︒，∴CDE 为等腰直角三角形，DE CD =AE AD =AE 的最大值为AE 与C 相切于点在ABC 外部时，则CD AE ⊥，∴90CDE ∠=︒，∴222231AD AC CD =−=−=∵四边形ABCE 为圆内接四边形，∴180135CEA ABC =︒−=︒∠∠∴18045CED CEA =︒−=︒∠∠，∵90CDE ∠=︒，∴CDE 为等腰直角三角形，DE CD =AE AD =AE 的最小值为故答案为：三、解答题23．（2024·四川甘孜·中考真题）如图，AB 为⊙O 的弦，C 为AB 的中点，过点C 作CD AB ∥，交OB 的延长线于点D ．连接OA OC ，．(1)求证：CD 是⊙O 的切线；(2)若32OA BD ==，，求OCD 的面积．24．（2024·内蒙古包头·中考真题）如图，AB 是O 的直径，,BC BD 是O 的两条弦，点C 与点D 在AB 的两侧，E 是OB 上一点（OE BE >），连接,OC CE ，且2BOC BCE ∠=∠．(1)如图1，若1BE =，CE =O 的半径；(2)如图2，若2BD OE =，求证：BD OC ∥．（请用两种证法解答） Rt OCE 中，利用勾股定理求解即可；，利用垂径定理等可得出BF =Rt Rt CEO OFB ≌，得出，然后利用平行线的判定即可得证；法二：连接AD ，证明CEO ADB ∽，得出ABD ∠，然后利用平行线的判定即可得证【详解】（1）解∶∵OC OB =，()11802OBC OCB BOC ∠=∠=︒−∠， 2BOC BCE ∠=∠，)90BCE BCE ∠=︒−∠即O 的半径为2）证明：法一：过∴12BF BD =， ∵2BD OE =∴OE BF =，又OC OB =，OEC ∠=∠()Rt Rt HL CEO OFB ≌，COE OBF =∠，BD OC ∥；法二：连接AD ， ∵AB 是直径，∴90ADB ∠=︒，∴22AD AB BD =−=∴1OC CE OE ===，∴CEO ADB ∽，COE ABD ∠=∠，BD OC ∥．【点睛】本题考查了垂径定理，相似三角形的判定与性质，等腰三角形的性质，三角形的内角和定理，全等三角形的判定与性质等知识，明确题意，灵活运用所学知识解题是解题的关键．25．（2024·安徽·中考真题）如图，O 是ABC 的外接圆，D 是直径AB 上一点，ACD ∠的平分线交AB 于点E ，交O 于另一点F ，FA FE =．(1)求证：CD AB ⊥；(2)设FM AB ⊥，垂足为M ，若1OM OE ==，求AC 的长．在ABC中．AB OA==2=AC ABAC的长为26．（2024·四川眉山·中考真题）如图，BE是O的直径，点A在O上，点C在BE的延长线上，EAC ABC ∠=∠，AD 平分BAE ∠交O 于点D ，连结DE ．(1)求证：CA 是O 的切线；(2)当8,4AC CE ==时，求DE 的长． BE 是O 的直径，OA OB =ABC ∴∠EAC ∠=CAE ∴∠=CAE ∴∠+OAC ∴∠OA 是O 的半径，是O 的切线；）解：EAC ∠=ABC EAC ∽△，CE AC， 4，，AD 平分BAD \?∴BD DE =BD DE ∴=BE 是O 的直径，90BDE ∴∠=︒，22DE BD ∴==27．（2024·江苏扬州·中考真题）如图，已知PAQ ∠及AP 边上一点C ．(1)用无刻度直尺和圆规在射线AQ 上求作点O ，使得2COQ CAQ ∠=∠；（保留作图痕迹，不写作法）(2)在（1）的条件下，以点O 为圆心，以OA 为半径的圆交射线AQ 于点B ，用无刻度直尺和圆规在射线CP 上求作点M ，使点M 到点C 的距离与点M 到射线AQ 的距离相等；（保留作图痕迹，不写作法）(3)在（1）、（2）的条件下，若3sin 5A =，12CM =，求BM 的长．【答案】(1)作图见详解的值，在直角BCM 中运用勾股定理即可求解．()1Rt BCM Rt BB M HL ≌，1CM B M =，Rt AMW 中，53WM ==AM CM =−是直径，90ACB =︒，Rt ABC 中，2x =（负值舍去）36x ==，Rt BCM 中，【点睛】本题主要考查尺规作角等于已知角，掌握以上知识的综合运用是解题的关键．28．（2024·河南·中考真题）如图1，塑像AB 在底座BC 上，点D 是人眼所在的位置．当点B 高于人的水平视线DE 时，由远及近看塑像，会在某处感觉看到的塑像最大，此时视角最大．数学家研究发现：当经过A ，B 两点的圆与水平视线DE 相切时（如图2），在切点P 处感觉看到的塑像最大，此时APB ∠为最大视角．(1)请仅就图2的情形证明APB ADB ∠>∠．(2)经测量，最大视角APB ∠为30︒，在点P 处看塑像顶部点A 的仰角APE ∠为60︒，点P 到塑像的水平距离PH 为6m ．求塑像AB 的高（结果精确到0.1m 1.73≈）． Rt AHP 中，利用正切的定义求出1）证明：如图，连接Rt AHP 中，AH PH， tan606︒=⨯，APH APB −∠29．（2024·江西·中考真题）如图，AB 是半圆O 的直径，点D 是弦AC 延长线上一点，连接BD BC ，，60D ABC ∠=∠=︒．(1)求证：BD 是半圆O 的切线；(2)当3BC =时，求AC 的长．【答案】(1)见解析(2)2π【分析】本题考查了直径所对的圆周角为直角，等边三角形的判定和性质，弧长公式，熟知相关性质和计算公式是解题的关键．（1）根据直径所对的圆周角为直角结合已知条件，可得30CAB ∠=︒，即可得90ABD??，进而可证得结论；（2）连接OC ，证明OBC △为等边三角形，求得120AOC ∠=︒，利用弧长公式即可解答．【详解】（1）证明：AB 是半圆O 的直径，90ACB ∴∠=︒， 60D ABC ∠=∠=︒，9030CAB ABC ∴∠=︒−∠=︒，18090ABD CAB D ∴∠=︒−∠−∠=︒，BD ∴是半圆O 的切线；（2）解：如图，连接OC ，,60OC OB CBA =∠=︒，OCB ∴为等边三角形，COB ∴∠=180AOC ∴∠=120360AC l ∴=30．（2024·广东深圳·中考真题）如图，在ABD △中，AB BD =，O 为ABD △的外接圆，BE 为O 的切线，AC 为O 的直径，连接DC 并延长交BE 于点E ．(1)求证：DE BE ⊥；(2)若AB =5BE =，求O 的半径．的长，设O 的半径为OD ，∵AB BD =，OA OD =，∴BO 垂直平分AD ，为O 的切线，BE ，为O 的直径，90ADC =︒，∴四边形BHDE 为矩形，BE ；）由（1）知四边形设O 的半径为Rt AOH △解得：3r =即：O 的半径为31．（2024·四川广元·中考真题）如图，在ABC 中，AC BC =，90ACB ∠=︒，O 经过A 、C 两点，交AB 于点D ，CO 的延长线交AB 于点F ，DE CF ∥交BC 于点E ．(1)求证：DE 为O 的切线；(2)若4AC =，tan 2CFD ∠=，求O 的半径．DE CFDE CF为O的切线．）过点C作CHACB为等腰直角三角形，42，AH=22【点睛】本题考查了切线的判定，圆周角定理，正切，勾股定理等知识以及等腰三角形的性质等知识，问题难度不大，正确作出合理的辅助线，是解答本题的关键．32．（2024·内蒙古呼伦贝尔·中考真题）如图，在ABC 中，以AB 为直径的O 交BC 于点,D DE AC ⊥，垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证：DE 是O 的切线；(2)若30,C CD ∠=︒=OBD 的面积．是O 的半径；是O 的切线；）解：∵C ∠=132CD =DE ，180BDO =︒−∠33．（2024·江苏扬州·中考真题）在综合实践活动中，“特殊到一般”是一种常用方法，我们可以先研究特殊情况，猜想结论，然后再研究一般情况，证明结论．如图，已知ABC ，CA CB =， O 是ABC 的外接圆，点D 在O 上（AD BD >），连接AD 、BD 、CD ．【特殊化感知】（1）如图1，若60ACB ∠=︒，点D 在AO 延长线上，则AD BD −与CD 的数量关系为________；【一般化探究】（2）如图2，若60ACB ∠=︒，点C 、D 在AB 同侧，判断AD BD −与CD 的数量关系并说明理由；【拓展性延伸】（3）若ACB α∠=，直接写出AD 、BD 、CD 满足的数量关系．（用含α的式子表示））根据题意得出ABC 是等边三角形，则CE =，设BD ，证明(AAS AFB CDB ≌①当D 在BC 上时，在AD 上截取证明CAB DEB ∽，ABE V AB ⊥于点F ，得出2AB BC =进而即可得出结论；②当D AG ，证明CAB DAG ∽，CAD BAG ∽，同①可得AB =∴ABC 是等边三角形，则∵O 是ABC 的外接圆，AD 是BAC ∠的角平分线，则AD BC ⊥∵四边形ACDB 是圆内接四边形，120CDB ∠=︒DBC =∠=在Rt BDE △中，∴cos30BE BD =︒⋅=∴3BC =，∵AD 是直径，则ABD ?∵AB AB =∴60ADB ACB ∠=∠=∴DBF 是等边三角形，∴BF BD =，则BFD ∠∴120AFB ∠=︒∵四边形ACDB CDB ∠=∴ABC 是等边三角形，则在,AFB CDB 中AFB CDB BAF BCD AB CB ∠=∠∠=∠= ∴(AAS AFB CDB ≌AF CD =，AD BD AD DF −=−AD BD CD −=；3）解：①如图所示，当在AD 上截取DE BD =∵AB AB =∴ACB ADB ??又∵,CA CB DE DB ==∴CAB DEB ∽，则∠AB BC EB BD =即AB BC =又∵ABC EBD ∠=∠ABE CBD ∠=∠ABE CBD V V ∽Rt BCF 中，sin 2BC α⋅=∴2sin2AB BC α=⋅ ∴2sin 2AD BD CD α−=，即②当D 在AB 上时，如图所示，延长∵四边形ACDB 是圆内接四边形，∴180GDA ACB ∠=∠=又∵,CA CB DG DA ==∴CAB DAG ∽，则∴AC AB AD AG =即AC AB =又∵CAB DAG ∠=∠CAD BAG ∠=∠∴CAD BAG ∽CD AC BG AB=， BG BD DG BD =+=同①可得2sin AB AC =⋅CD AC ==34．（2024·浙江·中考真题）如图，在圆内接四边形ABCD 中，AD AC ADC BAD <∠<∠，，延长AD 至点E ，使AE AC =，延长BA 至点F ，连结EF ，使AFE ADC ∠=∠．(1)若60AFE ∠=︒，CD 为直径，求ABD ∠的度数．(2)求证：①EF BC ∥；②EF BD =．可证明ADG AEF ∽，CDA △60AFE =︒，∽，，ADG AEF，=∠，ABD ACDBGD，∽，∵ADG AEFAD GD=，AE EFAD AE=，GD EFAC AE=，BD EF=，AE AC。

2023年中考真题与圆有关的压轴题汇编(附详解)

2023年中考真题与圆有关的压轴题汇编(附详解)1.(2023·安徽)已知四边形ABCD 内接于O ,对角线BD 是O 的直径．（1）如图1,连接,OA CA ,若OA BD ⊥,求证;CA 平分BCD ∠;（2）如图2,E 为O 内一点,满足,AE BC CE AB ⊥⊥,若33BD =,3AE =,求弦BC的长． 2.(2023·北京)如图,圆内接四边形ABCD 的对角线AC ,BD 交于点E ,BD 平分ABC ∠,BAC ADB ∠=∠．（1）求证DB 平分ADC ∠,并求BAD ∠的大小;（2）过点C 作CF AD ∥交AB 的延长线于点F ．若AC AD =,2BF =,求此圆半径的长．3.(2023·福建)如图,已知ABC ∆内接于,O CO 的延长线交AB 于点D ,交O 于点E ,交O 的切线AF 于点F ,且AF BC ∥．（1）求证：AO BE ∥;（2）求证：AO 平分BAC ∠．4.(2023·广东)综合探究如图1,在矩形ABCD 中()AB AD >,对角线AC BD ，相交于点O ,点A 关于BD 的对称点为A ',连接AA '交BD 于点E ,连接CA '．（1）求证：AA CA '⊥';（2）以点O 为圆心,OE 为半径作圆．①如图2,O 与CD 相切,求证：3AA CA '='; ①如图3,O 与CA '相切,1AD =,求O 的面积．5.(2023·广西) 如图,PO 平分APD ∠,PA 与O 相切于点A ,延长AO 交PD 于点C ,过点O 作OB PD ⊥,垂足为B ．（1）求证：PB 是O 的切线; （2）若O 的半径为4,5OC =,求PA 的长．6.(2023·贵州) 如图,已知O 是等边三角形ABC 的外接圆,连接CO 并延长交AB 于点D ,交O 于点E ,连接EA ,EB ．（1）写出图中一个度数为30︒的角：_______,图中与ΔACD 全等的三角形是_______; （2）求证：AED CEB ∽△△;（3）连接OA ,OB ,判断四边形OAEB 的形状,并说明理由．7.(2023·河北)如图,点18~P P 是O 的八等分点．若137PP P ,四边形3467P P P P 的周长分别为a ,b ,则下列正确的是( )A. a b <B. a b =C. a b >D. a ,b 大小无法比较8.(2023·河北)装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,50cm AB =,如图1和图2所示,MN 为水面截线,GH 为台面截线,MN GH ∥．计算：在图1中,已知48cm MN =,作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动,使水流出一部分,当30ANM ∠=︒时停止滚动,如图2．其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D ．探究：在图2中（2）操作后水面高度下降了多少？（3）连接OQ 并延长交GH 于点F ,求线段EF 与EQ 的长度,并比较大小．9.(2023·河南)如图,PA 与O 相切于点A ,PO 交O 于点B ,点C 在PA 上,且CB CA =．若5OA =,12PA =,则CA 的长为______．10.(2023·上海)在ABC ∆中7,3,90AB BC C ==∠=︒,点D 在边AC 上,点E 在CA 延长线上,且CD DE =,如果B 过点A ,E 过点D ,若B 与E 有公共点,那么E 半径r 的取值范围是________．11.(2023·上海)如图,在O 中,弦AB 的长为8,点C 在BO 延长线上,且41cos ,52ABC OC OB ∠==．（1）求O 的半径;（2）求BAC ∠的正切值．12.(2023·苏州)如图,AB 是半圆O 的直径,点,C D 在半圆上,CD DB =,连接,,OC CA OD ,过点B 作EB AB ⊥,交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ,若1223S S =,则tan ACO ∠的值为（）A.2 B. 223 C. 75 D. 32∆是O的内接三角形,AB是O的直径, 13.(2023·苏州)如图,ABC==,点F在AB上,连接CF并延长,交O于点D,连接BD,作AC BC5,25⊥,垂足为E．BE CD△∽△;（1）求证：DBE ABCAF=,求ED的长．（2）若214.(2023·天津)如图,在每个小正方形的边长为1的网格中,等边三角形ABC内接于圆,且顶点A,B均在格点上．（1）线段AB的长为________;（2）若点D在圆上,AB与CD相交于点P．请用无刻度．．．的直尺,在如图所示的网格中,画出∆为等边三角形,并简要说明点Q的位置是如何找到的（不要求证明）________．点Q,使CPQ15.(2023·天津)在O 中,半径OC 垂直于弦AB ,垂足为D ,60AOC ∠=︒,E 为弦AB 所对的优弧上一点．（1）如图①,求AOB ∠和CEB ∠的大小;（2）如图②,CE 与AB 相交于点F ,EF EB =,过点E 作O 的切线,与CO 的延长线相交于点G ,若3OA =,求EG 的长． 16.(2023·无锡)如图,AB 是O 的直径,CD 与AB 相交于点E ．过点D 的圆O 的切线DF AB ∥,交CA 的延长线于点F ,CF CD =．（1）求F ∠的度数;（2）若8DE DC ⋅=,求O 的半径．17.(2023·武汉)如图,,,OA OB OC 都是O 的半径,2ACB BAC ∠=∠．（1）求证：2AOB BOC ∠=∠;（2）若4,5AB BC ==,求O 的半径．18.(2023·杭州) 如图,在O 中,直径AB 垂直弦CD 于点E ,连接,,AC AD BC ,作CF AD ⊥于点F ,交线段OB 于点G （不与点,O B 重合）,连接OF ．（1）若1BE =,求GE 的长．（2）求证：2BC BG BO =⋅．（3）若FO FG =,猜想CAD ∠的度数,并证明你的结论．19.(2023·宜宾)如图,以AB 为直径的O 上有两点E ,F ,BE EF =,过点E 作直线CD AF ⊥交AF 的延长线于点D ,交AB 的延长线于点C ,过C 作CM 平分ACD ∠交AE 于点M ,交BE 于点N ．（1）求证：CD 是O 的切线;（2）求证：EM EN =;（3）如果N 是CM 的中点,且95AB =,求EN 的长．20.(2023·内江)如图,以线段AB 为直径作O ,交射线AC 于点C ,AD 平分CAB ∠交O 于点D ,过点D 作直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F ．连接BD 并延长交AC 的延长线于点M ．（1）求证：直线DE 是O 的切线;（2）当30F ∠=︒时,判断ABM 的形状,并说明理由;（3）在（2）的条件下,1ME =,连接BC 交AD 于点P ,求AP 的长．21.(2023·乐山)如图,在平面直角坐标系xOy 中,直线2y x =--与x 轴,y 轴分别交于A ,B 两点,C ,D 是半径为1的O 上两动点,且2CD =,P 为弦CD 的中点．当C ,D 两点在圆上运动时,PAB 面积的最大值是（）A. 8B. 6C. 4D. 322.(2023·乐山)如图,已知O 是Rt ABC △的外接圆,90ACB ∠=︒,D 是圆上一点,E 是DC 延长线上一点,连结AD AE ，,且AD AE CA CE ==，．（1）求证：直线AE 是O 是的切线; （2）若2sin 3E =,O 的半径为3,求AD 的长．23.(2023·广元) 如图,45ACB ∠=︒,半径为2的O 与角的两边相切,点P 是⊙O 上任意一点,过点P 向角的两边作垂线,垂足分别为E ,F ,设2t PE PF =+,则t 的取值范围是 _____．24.(2023·广元)如图,AB 为O 的直径,C 为O 上一点,连接AC BC ，,过点C 作O 的切线交AB 延长线于点D ,OF BC ⊥于点E ,交CD 于点F ．（1）求证：BCD BOE ∠=∠;（2）若3sin 5CAB ∠=,10AB =,求BD 的长．25.(2023·滨州) 如图,点E 是ABC ∆的内心,AE 的延长线与边BC 相交于点F ,与ABC ∆的外接圆相交于点D ．（1）求证：::ABF ACF S S AB AC =△△;（2）求证：::AB AC BF CF =;（3）求证：2AF AB AC BF CF =⋅-⋅;（4）猜想：线段,,DF DE DA 三者之间存在的等量关系．（直接写出,不需证明．）26.(2023·东营) 如图,在ABC 中,AB AC =,以AB 为直径的O 交BC 于点D ,DE AC ⊥,垂足为E ．（1）求证：DE 是O 的切线;（2）若30C ∠=︒,23CD =,求BD 的长．27.(2023·济宁) 如图,已知AB 是O 的直径,CD CB =,BE 切O 于点B ,过点C 作CF OE ⊥交BE 于点F ,若2EF BF =．（1）如图1,连接BD ,求证：ADB OBE △≌△;（2）如图2,N 是AD 上一点,在AB 上取一点M ,使60MCN ∠=︒,连接MN ．请问：三条线段MN BM DN ，，有怎样的数量关系？并证明你的结论．28.(2023·烟台)如图,在菱形ABCD 中,对角线,AC BD 相交于点,E O 经过,A D 两点,交对角线AC 于点F ,连接OF 交AD 于点G ,且AG GD =．（1）求证：AB 是O 的切线; （2）已知O 的半径与菱形的边长之比为5:8,求tan ADB ∠的值．29.(2023·临沂)如图,O 是ABC 的外接圆,BD 是O 的直径,,AB AC AE BC =∥,E 为BD 的延长线与AE 的交点．（1）求证：AE 是O 的切线;（2）若75,2ABC BC ∠=︒=,求CD 的长．30.(2023·聊城) 如图,在Rt ABC △中,90ACB ∠=︒,BAC ∠的平分线AD 交BC 于点D ,ADC ∠的平分线DE 交AC 于点E ．以AD 上的点O 为圆心,OD 为半径作O ,恰好过点E ．（1）求证：AC 是O 的切线;（2）若12CD =,3tan 4ABC ∠=,求O 的半径．2023年中考真题与圆有关的压轴题汇编详解1.(2023·安徽)已知四边形ABCD 内接于O ,对角线BD 是O 的直径．（1）如图1,连接,OA CA ,若OA BD ⊥,求证;CA 平分BCD ∠;（2）如图2,E 为O 内一点,满足,AE BC CE AB ⊥⊥,若33BD =,3AE =,求弦BC 的长．【答案】（1）见解析（2）32BC =【小问1详解】∵对角线BD 是O 的直径,OA BD ⊥ ∴AB AD =.∴BCA DCA ∠=∠.∴CA 平分BCD ∠．【小问2详解】∵对角线BD 是O 的直径.∴90BAD BCD ∠=∠=︒.∴,DC BC DA AB ⊥⊥∵,AE BC CE AB ⊥⊥.∴，，CE DA AE DC ////∴四边形AECD 平行四边形.∴DC AE =.∵33BD =,3AE =.∴33BD =,3DC =.∴BC ==2.(2023·北京)如图,圆内接四边形ABCD 的对角线AC ,BD 交于点E ,BD 平分ABC ∠,BAC ADB ∠=∠．（1）求证DB 平分ADC ∠,并求BAD ∠的大小;（2）过点C 作CF AD ∥交AB 的延长线于点F ．若AC AD =,2BF =,求此圆半径的长．【答案】（1）见解析,90BAD ∠=︒（2）4【小问1详解】解：①BAC ADB ∠=∠∴AB BC =.∴ADB CDB ∠=∠,即DB 平分ADC ∠．∵BD 平分ABC ∠.①ABD CBD ∠=∠.①AD CD =.①AB AD BC CD +=+,即BAD BCD =.①BD 是直径.①90BAD ∠=︒;【小问2详解】解：∵90BAD ∠=︒,CF AD ∥.①180F BAD ∠+∠=︒,则90F ∠=︒．①AD CD =.①AD DC =．①AC AD =.∴AC AD CD ==.∴ADC △是等边三角形,则60ADC ∠=︒．∵BD 平分ADC ∠. ∴1302CDB ADC ∠=∠=︒． ∵BD 是直径. ∴90BCD ∠=︒,则12BC BD =． ∵四边形ABCD 是圆内接四边形.∴180ADC ABC ∠+∠=︒,则120ABC ∠=︒.∴60FBC ∠=︒.∴906030FCB ∠=︒-︒=︒. ∴12FB BC =． ∵2BF =.∴4BC =.∴28BD BC ==．∵BD 是直径. ∴此圆半径的长为142BD =． 3.(2023·福建)如图,已知ABC 内接于,O CO 的延长线交AB 于点D ,交O 于点E ,交O 的切线AF 于点F ,且AF BC ∥．（1）求证：AO BE ∥;（2）求证：AO 平分BAC ∠．【答案】（1）见解析（2）见解析【小问1详解】证明AF 是O 的切线.AF OA ∴⊥,即90OAF ∠=︒． CE 是O 的直径.90CBE ∴∠=︒．∴90OAF CBE ∠=∠=︒．AF BC ∥.BAF ABC ∴∠=∠.OAF BAF CBE ABC ∴∠-∠=∠-∠,即OAB ABE ∠=∠.AO BE ∴∥．【小问2详解】解：ABE ∠与ACE ∠都是AE 所对的圆周角.ABE ACE ∴∠=∠．OA OC =.ACE OAC ∴∠=∠.ABE OAC ∴∠=∠．由（1）知OAB ABE ∠=∠.OAB OAC ∴∠=∠.AO ∴平分BAC ∠．4.(2023·广东)综合探究如图1,在矩形ABCD 中()AB AD >,对角线AC BD ，相交于点O ,点A 关于BD 的对称点为A ',连接AA '交BD 于点E ,连接CA '．（1）求证：AA CA '⊥';（2）以点O 为圆心,OE 为半径作圆．①如图2,O 与CD 相切,求证：3AA CA '='; ①如图3,O 与CA '相切,1AD =,求O 的面积．【答案】（1）见解析（2）①见解析;①224π+. 【小问1详解】∵点A 关于BD 的对称点为A '.∴点E 是AA '的中点,90AEO ∠=︒.又∵四边形ABCD 是矩形.∴O 是AC 的中点.∴OE 是ACA '的中位线.∴OE A C '∥∴90AAC AEO ∠'=∠=︒.∴AA CA '⊥'【小问2详解】①过点O 作OF AB ⊥于点F ,延长FO 交CD 于点G ,则90OFA ∠=︒.∵四边形ABCD 是矩形.∴AB CD ,AO BO CO DO ===.∴OCG OAF ∠=∠,90OGC OFA ∠=∠=︒．∵OCG OAF ∠=∠,90OGC OFA ∠=∠=︒,AO CO =.∴()AAS OCG OAF ≌.∴OG OF =．∵O 与CD 相切,OE 为半径,90OGC ∠=︒.∴OG OE =.∴OE OF =又∵90AEO ∠=︒即OE AE ⊥,OF AB ⊥.∴AO 是EAF ∠的角平分线,即OAE OAF ∠=∠.设OAE OAF x ∠=∠=,则OCG OAF x ∠=∠=.又∵CO DO =∴OCG ODG x ∠=∠=∴2AOE OCG ODG x ∠=∠+∠=又∵90AEO ∠=︒,即AEO △是直角三角形.∴90AOE OAE ∠+∠=︒,即290x x +=︒解得：30x =︒.∴30OAE ∠=︒,即30A AC '∠=︒.在Rt A AC '△中,30A AC '∠=︒,90AA C '∠=︒.∴2AC CA '=. ∴()222223AA AC CA CA CA CA ''''=-=-=';①过点O 作OH A C '⊥于点H .∵O 与CA '相切.∴OE OH =,90A HO '∠=︒∵90AAC AEO A EO A HO ''∠'=∠=∠=∠=︒∴四边形A EOH '是矩形.又∵OE OH =.∴四边形A EOH '是正方形.∴OE OH A H '==.又∵OE 是ACA '的中位线. ∴12OE A C '= ∴12A H CH A C ''==∴OH CH = 又∵90A HO '∠=︒.∴45OCH ∠=︒又∵OE A C '∥.∴45AOE ∠=︒又∵90AEO ∠=︒.∴AEO △是等腰直角三角形,AE OE =.设AE OE r ==,则AO DO ==∴)1DE DO OE r r =-=-= 在Rt ADE △中,222AE DE AD +=,1AD =即)222211r r +=∴()2212411r ===+∴O 的面积为：224S r π==. 5.(2023·广西) 如图,PO 平分APD ∠,PA 与O 相切于点A ,延长AO 交PD 于点C ,过点O 作OB PD ⊥,垂足为B ．（1）求证：PB 是O 的切线; （2）若O 的半径为4,5OC =,求PA 的长．【答案】（1）见解析（2）12AP =【小问1详解】①PA 与O 相切于点A .①OA PA ⊥.①PO 平分APD ∠,OB PD ⊥.①OA OB =.①PB 是O 的切线;【小问2详解】①O 的半径为4.①4OA OB ==.①OB PD ⊥,5OC =. ①223BC OC OB =-=,459AC OA OC =+=+=.①BCO ACP ∠=∠.①tan tan BCO ACP ∠=∠.①BO AP BC AC =,即439AP =. ①12AP =．6.(2023·贵州) 如图,已知O 是等边三角形ABC 的外接圆,连接CO 并延长交AB 于点D ,交O 于点E ,连接EA ,EB ．（1）写出图中一个度数为30︒的角：_______,图中与ACD 全等的三角形是_______; （2）求证：AED CEB ∽△△;（3）连接OA ,OB ,判断四边形OAEB 的形状,并说明理由．【答案】（1）1∠,2∠,3∠,4∠;BCD △;（2）证明见详解; （3）四边形OAEB 是菱形;【小问1详解】解：∵O 是等边三角形ABC 的外接圆.∴CO 是ACB ∠的角平分线,60ACB ABC CAB ∠=∠=∠=︒.∴1230∠=∠=︒.∵CE 是O 的直径.∴90CAE CBE ∠=∠=︒.∴3430∠=∠=︒.∴30︒的角有：1∠,2∠,3∠,4∠.∵CO 是ACB ∠的角平分线.∴90ADC BDC ∠=∠=︒,56903060∠=∠=︒-︒=︒.在ACD 与BCD △中.∵1290CD CD ADC BDC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩.∴ACD BCD ≌.故答案为：1∠,2∠,3∠,4∠,BCD △;【小问2详解】证明：∵56∠=∠,3=230∠∠=︒.∴AED CEB ∽△△;【小问3详解】解：连接OA ,OB .∵OA OE OB r ===,5660∠=∠=︒.∴OAE △ ,OBE △是等边三角形.∴OA OB AE EB r ====.∴四边形OAEB 是菱形．7.(2023·河北)如图,点18~P P 是O 的八等分点．若137PP P ,四边形3467P P P P 的周长分别为a ,b ,则下列正确的是( )A. a b <B. a b =C. a b >D. a ,b 大小无法比较【答案】A【详解】连接1223,PP P P .∵点18~P P 是O 的八等分点,即1223345566778148PP P P P P P P P P P P P P P P ======= ∴12233467PP P P P P P P ===,464556781178P P P P P P P P P P PP =+=+= ∴4617P P PP =又∵137PP P 的周长为131737a PPPP P P ++=.四边形3467P P P P 的周长为34466737b PP P P P P P P ++=+. ∴()()34466737131737b a P P P P P P P P PP PP P P ++-++=+-()()12172337131737PP PP P P P P PP PP P P =+++-++122313PP P P PP =-+在123PP P 中有122313PPP P PP >+ ∴1223130b a PP P P PP -=+>-故选A ．8.(2023·河北)装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,50cm AB =,如图1和图2所示,MN 为水面截线,GH 为台面截线,MN GH ∥．计算：在图1中,已知48cm MN =,作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动,使水流出一部分,当30ANM ∠=︒时停止滚动,如图2．其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D ．探究：在图2中（2）操作后水面高度下降了多少？（3）连接OQ 并延长交GH 于点F ,求线段EF 与EQ 的长度,并比较大小．【答案】（1）7cm ;（2）11cm 2;（3）253cm 3EF =,25π=cm 6EQ ,EF EQ >．【详解】解：（1）连接OM .∵O 为圆心,OC MN ⊥于点C ,48cm MN =.∴124cm 2MC MN ==. ∵50cm AB =. ∴125cm 2OM AB ==. ∴在Rt OMC 中.222225247cm OC OM MC =-=-=．（2）∵GH 与半圆的切点为E .∴OE GH ⊥∵MN GH ∥∴OE MN ⊥于点D .∵30ANM ∠=︒,25cm ON =.∴125cm 22OD ON ==. ∴操作后水面高度下降高度为：25117cm 22-=．（3）∵OE MN ⊥于点D ,30ANM ∠=︒∴60DOB ∠=︒.∵半圆的中点为Q .∴AQ QB =.∴90QOB ∠=︒.∴30QOE ∠=︒.∴tan EF QOE OE =∠⋅=. 30π2525π==cm 1806EQ ⨯⨯.()25π25π066==>.∴EF EQ >．9.(2023·河南)如图,PA 与O 相切于点A ,PO 交O 于点B ,点C 在PA 上,且CB CA =．若5OA =,12PA =,则CA 的长为______．【答案】103【详解】如图,连接OC .∵PA 与O 相切于点A .∴90OAC ∠=︒;∵OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩.∴OAC OBC ≌.∴90OAC OBC ∠=∠=︒.∴90PAO PBC ∠=∠=︒.∵P P ∠=∠.∴PAO PBC ∽. ∴PO AO PC BC=. ∵5OA =,12PA =.∴13PO =.设CB CA x ==,则12PC PA CA x =-=-. ∴13512x x=-. 解得103x =. 故CA 的长为103. 故答案为：103． 10.(2023·上海)在ABC 中7,3,90AB BC C ==∠=︒,点D 在边AC 上,点E 在CA 延长线上,且CD DE =,如果B 过点A ,E 过点D ,若B 与E 有公共点,那么E 半径r 的取值范围是________．【答案】10210r <≤【详解】解：由题意画出图形如下：连接BE .B 过点A ,且7AB =.B 的半径为7. E 过点D ,它的半径为r ,且CD DE =.2CE CD DE r ∴=+=.3,90BC C =∠=︒. 22294BE BC CE r ∴=+=+,22210AC AB BC =-=.D 在边AC 上,点E 在CA 延长线上.CD AC CE AC ≤⎧∴⎨>⎩,即2102210r r ⎧≤⎪⎨>⎪⎩. 10210r ∴<≤.B 与E 有公共点.AB DE BE AB DE ∴-≤≤+,即22947794r r r r ⎧+≤+⎪⎨-≤+⎪⎩①②. 不等式①可化为2314400r r --≤.解方程2314400r r --=得：2r =-或203r =. 画出函数231440y r r =--的大致图象如下：由函数图象可知,当0y ≤时,2023r -≤≤. 即不等式①的解集为2023r -≤≤.同理可得：不等式②的解集为2r ≥或203r ≤-. 则不等式组的解集为2023r ≤≤.又10r <≤①①r r <≤.r <≤11.(2023·上海)如图,在O 中,弦AB 的长为8,点C 在BO 延长线上,且41cos ,52ABC OC OB ∠==．（1）求O 的半径;（2）求BAC ∠的正切值．【答案】（1）5 （2）94 【小问1详解】解：如图,延长BC ,交O 于点D ,连接AD .由圆周角定理得：90BAD ∠=︒.弦AB 的长为8,且4cos 5ABC ∠=. 845AB BD BD ∴==. 解得10BD =.O ∴的半径为152BD =．【小问2详解】解：如图,过点C 作CE AB ⊥于点E .O 的半径为5.5OB ∴=.12OC OB =. 31522BC OB ∴==. 4cos 5ABC ∠=. 45BE BC ∴=,即41552BE =. 解得6BE =.2AE AB BE ∴=-=,2292CE BC BE =-=. 则BAC ∠的正切值为99224CE AE ==． 12.(2023·苏州)如图,AB 是半圆O 的直径,点,C D 在半圆上,CD DB =,连接,,OC CA OD ,过点B 作EB AB ⊥,交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ,若1223S S =,则tan ACO ∠的值为（）A. 2B. 223 C . 75 D. 32 【答案】A【详解】解：如图,过C 作CH AO ⊥于H .∵CD BD =.∴COD BOE CAO ∠=∠=∠.∵1223S S =,即122132OA CH OB BE =. ∴23CH BE =. ∵A BOE ∠=∠.∴tan tan A BOE ∠=∠.∴CH BE AH OB =,即23CH AH BE OB ==. 设2AH m =,则3BO m AO CO ===.∴32OH m m m =-=.∴22922CH m m m =-=.∴22tan 22CH m A AH m∠===.∵OA OC =.∴A ACO ∠=∠.∴tan ACO ∠=; 故选A.13.(2023·苏州)如图,ABC 是O 的内接三角形,AB 是O 的直径,5,25AC BC ==,点F 在AB 上,连接CF 并延长,交O 于点D ,连接BD ,作BE CD ⊥,垂足为E ．（1）求证：DBE ABC △∽△;（2）若2AF =,求ED 的长．【答案】（1）证明见解析（2）355【小问1详解】证明：∵AB 是O 的直径,BE CD ⊥.∴90ACB BED ∠=︒=∠.∵CAB CDB ∠=∠.∴DBE ABC △∽△．【小问2详解】∵5,25AC BC ==,90ACB ∠=︒. ∴225AB AC BC =+=,1tan 2AC ABC BC ∠==. ∵2AF =.∴3BF =.∵DBE ABC △∽△.∴ABC DBE ∠=∠. ∴1tan tan 2DE ABC DBE BE ∠=∠==.设DE x =,则2BE x =,BD =. ∵AFC BFD ∠=∠,CAB CDB ∠=∠.∴ACF DBF ∽. ∴AC AF CF BD DF BF==.2DF=,则2DF x =. ∴EF x DE ==.∴3BD BF ==.∴5DE =． 14.(2023·天津)如图,在每个小正方形的边长为1的网格中,等边三角形ABC 内接于圆,且顶点A ,B 均在格点上．（1）线段AB 的长为________;（2）若点D 在圆上,AB 与CD 相交于点P ．请用无刻度．．．的直尺,在如图所示的网格中,画出点Q ,使CPQ 为等边三角形,并简要说明点Q 的位置是如何找到的（不要求证明）________．【答案】（1）29（2）画图见解析;如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求【小问1详解】解：222529AB =+=;故答案为：29．【小问2详解】解：如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求;连接PQ ,,AD BK ,过点E 作ET ⊥网格线,过点G 作GS ⊥网格线.由图可得：∵AJF BLF ∠=∠,AFJ BFL ∠=∠,AJ BL =.①()Rt Rt AAS AJF BLF ≌.①FJ FL =,AF BF =.①MJ NL =.①FJ MJ FL NL -=-,即FM FN =.①IMF HNF ∠=∠,IFM HFN ∠=∠.①()Rt Rt ASA IMF HNF ≌.①FI FH =.①AFI BFH ∠=∠,AF BF =.①()SAS AIF BHF ≌.①FAI FBH ∠=∠.①AD BK =.①12∠=∠.①ABC 是等边三角形.①60ACB ∠=︒,即1+60PCB ∠∠=︒.①2+60PCB ∠∠=︒,即60PCQ ∠=︒.①ET GS =,ETF GSF ∠=∠,EFT GFS ∠=∠.①()Rt Rt AAS ETF GSF ≌.①EF GF =.①AF BF =,AFE BFG ∠=∠.①()SAS AFE BFG ≌.①EAF GBF ∠=∠.①60GBF EAF CBA ∠=∠=∠=︒.①18060CBQ CBA GBF ∠=︒-∠-∠=︒.①CBQ CAB ∠=∠.①CA CB =.①()ASA CAP CBQ ≌.①CQ CP =.①60PCQ ∠=︒.①PCQ △是等边三角形,此时点Q 即为所求;故答案为：如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求．15.(2023·天津)在O 中,半径OC 垂直于弦AB ,垂足为D ,60AOC ∠=︒,E 为弦AB 所对的优弧上一点．（1）如图①,求AOB ∠和CEB ∠的大小;（2）如图②,CE 与AB 相交于点F ,EF EB =,过点E 作O 的切线,与CO 的延长线相交于点G ,若3OA =,求EG 的长．【答案】（1）120AOB ∠=︒,30CEB ∠=︒ （2）3 【小问1详解】解：在O 中,半径OC 垂直于弦AB .∴AC BC =,得AOC BOC ∠=∠．∵60AOC ∠=︒.∴2120AOB AOC ∠=∠=︒．∵1122CEB BOC AOC ∠=∠=∠. ∴30CEB ∠=︒．【小问2详解】解：如图,连接OE ．同（1）得30CEB ∠=︒．∵在BEF △中,EF EB =.∴75EBF EFB ∠=∠=︒．∴2150AOE EBA ∠=∠=︒．又180120AOG AOC ∠=︒-∠=︒.∴30GOE AOE AOG ∠=∠-∠=︒．∵GE 与O 相切于点E .∴OE GE ⊥,即90OEG ∠=︒．在Rt OEG △中,tan ,3EG GOE OE OA OE∠===. ∴3tan 303EG =⨯︒=．16.(2023·无锡)如图,AB 是O 的直径,CD 与AB 相交于点E ．过点D 的圆O 的切线DF AB ∥,交CA 的延长线于点F ,CF CD =．（1）求F ∠的度数;（2）若8DE DC ⋅=,求O 的半径．【答案】（1）67.5︒（2）2【小问1详解】如图,连接OD ．FD 为O 的切线.∴90ODF ∠=︒．DF AB ∥.∴90AOD ∠=︒．AD AD =. ∴1452ACD AOD ∠=∠=︒． CF CD =.∴1(180)67.52F ACD ∠∠=⨯-=︒．【小问2详解】如图,连接AD .AO OD =,90AOD ∠=︒.∴45EAD ∠=︒．45ACD ∠=︒.∴ACD EAD ∠=∠,且ADE CDA ∠=∠.∴DAE DCA ∽.∴DE DA DA DC=,即28DA DE DC =⋅=. ∴22DA =.∴222OA OD AD ===,即半径为2． 17.(2023·武汉)如图,,,OA OB OC 都是O 的半径,2ACB BAC ∠=∠．（1）求证：2AOB BOC ∠=∠;（2）若4,5AB BC ==,求O 的半径．【答案】（1）见解析（2）52 【小问1详解】证明：∵AB AB =.∴12ACB AOB ∠=∠. ∵BC BC =.∴12BAC BOC ∠=∠. 2ACB BAC ∠=∠.2AOB BOC ∴∠=∠．【小问2详解】解：过点O 作半径OD AB ⊥于点E ,则1,2∠=∠=DOB AOB AE BE . BOC AOB ∠=∠2 .∴DOB BOC ∠=∠.BD BC ∴=.4,5==AB BC .2,5∴==BE DB .在Rt BDE △中,90DEB =︒∠221∴=-=DE BD BE .在Rt BOE 中,90OEB ∠=︒.222(1)2∴=-+OB OB .52OB ∴=,即O 的半径是52．18.(2023·杭州) 如图,在O 中,直径AB 垂直弦CD 于点E ,连接,,AC AD BC ,作CF AD ⊥于点F ,交线段OB 于点G （不与点,O B 重合）,连接OF ．（1）若1BE =,求GE 的长．（2）求证：2BC BG BO =⋅．（3）若FO FG =,猜想CAD ∠的度数,并证明你的结论．【答案】（1）1 （2）见解析（3）45CAD ∠=︒,证明见解析【小问1详解】解：直径AB 垂直弦CD .∴90AED ∠=︒.∴90DAE D ∠+∠=︒.CF AD ⊥.∴90FCD D ∠+∠=︒.∴DAE FCD ∠=∠.由圆周角定理得：DAE BCD ∠=∠.∴BCD FCD ∠=∠.在BCE 和GCE 中.BCE GCE CE CEBEC GEC ∠=∠⎧⎪=⎨⎪∠=∠⎩. ∴BCE GCE≌()ASA .∴1GE BE ==; 【小问2详解】证明：AB 是O 的直径.∴90ACB ∠=︒.在ACB △和CEB 中.90ACB CEB ABC CBE∠=∠=︒⎧⎨∠=∠⎩. ∴ACB △CEB ∽.∴BC BA BE BC=. ∴2BC BA BE =⋅.由（1）知GE BE =.∴12BE BG =. 又2AB BO =. ∴2122BC BA BE BO BG BG BO =⋅=⋅=⋅; 【小问3详解】解：45CAD ∠=︒,证明如下：如图,连接OC .FO FG=.∴FOG FGO∠=∠.直径AB垂直弦CD.∴CE DE=,90AED AEC∠=∠=︒,又AE AE=.∴ACE△ADE≌()SAS.∴DAE CAE∠=∠.设DAE CAEα∠=∠=,FOG FGOβ∠=∠=.则FCD BCD DAEα∠=∠=∠=,OA OC=.∴OCA OACα∠=∠=.又90ACB∠=︒.∴903OCF ACB OCA FCD BCDα∠=∠-∠-∠-∠=︒-.CGE OGFβ∠=∠=,GCEα∠=,90CGE GCE∠+∠=︒∴90βα+=︒.∴90αβ=︒-.2COG OAC OCAααα∠=∠+∠=+=.∴()2290180 COF COG GOFαββββ∠=∠+∠=+=︒-+=︒-. ∴COF AOF∠=∠.COF和AOF中.CO AOCOF AOFOF OF=⎧⎪∠=∠⎨⎪=⎩∴()SASCOF AOF≌,∴OCF OAF∠=∠.即903αα︒-=.∴22.5α=︒.∴245CADα∠==︒．19.(2023·宜宾)如图,以AB 为直径的O 上有两点E ,F ,BE EF =,过点E 作直线CD AF ⊥交AF 的延长线于点D ,交AB 的延长线于点C ,过C 作CM 平分ACD ∠交AE 于点M ,交BE 于点N ．（1）求证：CD 是O 的切线;（2）求证：EM EN =;（3）如果N 是CM 的中点,且95AB =,求EN 的长．【答案】（1）见解析（2）见解析（3）6【小问1详解】证明：如图所示.①BE EF =.∴12∠=∠.∵OA OE =∴13∠=∠.∴23∠∠=.∴OE AF ∥∵CD AF ⊥.∴OE CD ⊥.∴CD 是O 的切线;【小问2详解】证明：如图所示.①CM 平分ACD ∠ ∴1562DCA ∠=∠=∠ 又∵1122DAC ∠=∠=∠,AD CD ⊥ 则90ADC ∠=︒.∴EMC =∠()()11151804522DAC DCA ADC ∠+∠=∠+∠=︒-∠=︒. ∵AB 是O 的直径.∴90MEN AEB ∠=∠=︒.∴45ENM EMN ∠=∠=︒.∴EM EN =;【小问3详解】解：如图所示,取EC 的中点P ,连接PN .①CD 是O 的切线.∴90CEB OEB ∠+∠=︒.∵90AEB AEO OEB ∠=∠+∠=︒.∴AEO BEC ∠=∠.又OAE OEA ∠=∠.∴BEC OAE ∠=∠.∵N 是MC 的中点,P 是EC 的中点. ∴11,22PN EM PN EM EN ==∥. ∵AE EB ⊥.∴PN EB ⊥.在Rt PEN △中,1tan 2PN PEN EN ∠==. ∵BEC OAE ∠=∠. ∴1tan tan 2EB EAB PEN AE ∠==∠= 设BE b =,则2AE b =.∴AB =∵AB =∴9b =∴18AE =,9EB =.∵BEC EAC ∠=∠,ECB ACE ∠=∠.∴ECB ACE ∽. ∴2AE CE EB CB==. ∵CM 是ACD ∠的角平分线.∴N 到,CD AC 的距离相等,设为d ,在EBC ,设点C 到EB 的距离为h . ∴11221122ENC BNC EC d EN h S S BC d BN h ⨯⨯==⨯⨯. ∴2EN EC BN BC==. ∴263EN EB ==．20.(2023·内江)如图,以线段AB 为直径作O ,交射线AC 于点C ,AD 平分CAB ∠交O 于点D ,过点D 作直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F ．连接BD 并延长交AC 的延长线于点M ．（1）求证：直线DE 是O 的切线;（2）当30F ∠=︒时,判断ABM 的形状,并说明理由;（3）在（2）的条件下,1ME =,连接BC 交AD 于点P ,求AP 的长．【答案】（1）见解析（2）ABM 是等边三角形,理由见解析（3）433AP =．【小问1详解】证明：连接OD .∵AD 平分CAB ∠.∴12∠=∠.∵OA OD =.∴32∠=∠.∴31∠=∠.∴OD AC ∥.∵DE AC ⊥.∴OD DE ⊥.∵OD 是O 的半径.。

初三圆经典试题及答案

初三圆经典试题及答案一、选择题1. 已知圆的半径为r，圆心为O，点P在圆上，则OP的长度为（）。

A. rB. 2rC. r/2D. 无法确定答案：A2. 下列说法中，正确的是（）。

A. 圆的半径是直径的一半B. 圆的直径是半径的两倍C. 圆的半径和直径相等D. 圆的周长是直径的四倍答案：B3. 圆的周长公式为（）。

A. C = 2πrB. C = πrC. C = 4πrD. C = 2πd答案：A4. 圆的面积公式为（）。

A. S = πr^2B. S = 2πrC. S = πdD. S = 4πr答案：A5. 如果一个圆的半径增加1倍，那么它的面积将增加（）倍。

A. 1B. 2C. 4D. 8答案：C二、填空题6. 已知圆的半径为3cm，那么它的直径为_______cm。

答案：67. 圆的周长与直径的比值为______。

答案：π8. 如果一个圆的周长为12πcm，那么它的半径为_______cm。

答案：69. 圆的面积与半径的平方成正比，比例常数为______。

答案：π10. 已知圆的半径为5cm，那么它的面积为_______cm²。

答案：25π三、解答题11. 已知圆的半径为4cm，求圆的周长和面积。

解答：根据圆的周长公式C = 2πr，代入r = 4cm，得：C = 2π × 4 = 8π cm根据圆的面积公式S = πr^2，代入r = 4cm，得：S = π × 4^2 = 16π cm²12. 已知圆的直径为10cm，求圆的半径和面积。

解答：根据直径与半径的关系d = 2r，得：r = d / 2 = 10 / 2 = 5 cm根据圆的面积公式S = πr^2，代入r = 5cm，得：S = π × 5^2 = 25π cm²13. 已知一个圆的周长比另一个圆的周长大6πcm，且大圆的半径比小圆的半径大3cm，求两个圆的半径。

初三圆的测试题及答案

初三圆的测试题及答案一、选择题（每题3分，共30分）1. 若圆的半径为r，则圆的周长为：A. 2πrB. πrC. 2rD. πr²答案：A2. 圆的直径是半径的：A. 2倍B. 4倍C. 3倍D. 1/2倍答案：A3. 圆的面积公式为：A. πr²B. 2πrC. r²D. 2r答案：A4. 圆心角为90°的扇形面积是圆面积的：A. 1/4B. 1/2C. 3/4D. 1/3答案：A5. 圆内接四边形的对角互补，那么该四边形是：A. 矩形B. 菱形C. 平行四边形D. 梯形答案：C6. 圆的切线与半径垂直相交于：A. 圆心B. 圆周C. 切点D. 直径答案：C7. 圆的弦长公式为：A. 2r * sin(θ/2)B. 2r * cos(θ/2)C. r * sin(θ)D. r * cos(θ)答案：A8. 圆的弧长公式为：A. r * θB. r * θ/180C. r * θ * πD. r * θ/π答案：B9. 圆周角定理指出，圆周上任意两点与圆心连线所成的角是：A. 直角B. 锐角C. 钝角D. 任意角答案：A10. 圆的切线与圆心的距离等于：A. 半径B. 直径C. 弦长D. 弧长答案：A二、填空题（每题3分，共30分）1. 半径为5cm的圆的周长是______。

答案：10π cm2. 圆的直径是半径的______倍。

答案：23. 半径为4cm的圆的面积是______。

答案：16π cm²4. 圆心角为120°的扇形面积是圆面积的______。

答案：1/35. 圆内接四边形的对角互补，那么该四边形是______。

答案：平行四边形6. 圆的切线与半径垂直相交于______。

答案：切点7. 半径为3cm的圆的弦长为4cm，那么弦所对的圆心角是______。

答案：60°8. 半径为6cm的圆的弧长为2πcm，那么弧所对的圆心角是______。

中考数学真题《圆的有关位置关系》专项测试卷(附答案)

中考数学真题《圆的有关位置关系》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（45题）一、单选题1．（2023·四川眉山·统考中考真题）如图，AB 切O 于点B 连接OA 交O 于点C BD OA ∥交O 于点D 连接CD 若25OCD ∠=︒则，A ∠的度数为（）A ．25︒B ．35︒C ．40︒D ．45︒2．（2023·重庆·统考中考真题）如图，AC 是O 的切线 B 为切点连接OA OC ，．若30A ∠=︒ 23AB = 3BC =则，OC 的长度是（）A ．3B ．3C 13D ．63．（2023·重庆·统考中考真题）如图，AB 为O 的直径直线CD 与O 相切于点C 连接AC若50ACD ∠=︒则，BAC ∠的度数为（）A ．30︒B ．40︒C ．50︒D ．60︒4．（2023·湖北武汉·统考中考真题）如图，在四边形ABCD 中 ,AB CD AD AB ⊥∥ 以D 为圆心 AD 为半径的弧恰好与BC 相切切点为E ．若13AB CD =则，sin C 的值是（）A ．23 B 5C ．34 D 75．（2023·四川泸州·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ 点D 在斜边AB 上以AD 为直径的半圆O 与BC 相切于点E 与AC 相交于点F 连接DE ．若8AC = 6BC =则，DE 的长是（）A 410B 810C ．8027D ．83二填空题6．（2023·浙江嘉兴·统考中考真题）如图，点A 是O 外一点 AB AC 分别与O 相切于点B C 点D 在BDC 上已知50A ∠=︒则，D ∠的度数是___________．7．（2023·黑龙江·统考中考真题）如图，AB 是O 的直径 PA 切O 于点A PO 交O 于点C 连接BC 若28B ∠=︒则，P ∠=__________︒．8．（2023·湖南·统考中考真题）如图，AD 是O 的直径 AB 是O 的弦 BC 与O 相切于点B 连接OB 若65ABC ∠=︒则，BOD ∠的大小为__________．9．（2023·山东滨州·统考中考真题）如图，,PA PB 分别与O 相切于,A B 两点且56APB ∠=︒．若点C 是O 上异于点,A B 的一点则，ACB ∠的大小为___________．10．（2023·浙江宁波·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ E 为AB 边上一点以AE 为直径的半圆O 与BC 相切于点D 连接AD 3,35BE BD ==P 是AB 边上的动点当ADP △为等腰三角形时 AP 的长为_____________．11．（2023·河南·统考中考真题）如图，PA 与O 相切于点A PO 交O 于点B 点C 在PA 上且CB CA =．若5OA = 12PA =则，CA 的长为______．12．（2023·湖北·统考中考真题）如图，在ABC 中 70ACB ABC ∠=︒，△的内切圆O 与AB BC ，分别相切于点D E 连接DE AO ，的延长线交DE 于点F 则，AFD ∠=_________．13．（2023·湖南·统考中考真题）如图，在Rt ABC △中 90,8,6ACB AC BC ∠=︒==．以点C 为圆心 r 为半径作圆当所作的圆与斜边AB 所在的直线相切时 r 的值为________．14．（2023·山东烟台·统考中考真题）如图，在直角坐标系中 A 与x 轴相切于点,B CB 为A 的直径点C 在函数(0,0)ky k x x =>>的图象上 D 为y 轴上一点 ACD 的面积为6则，k 的值为________．15．（2023·四川·统考中考真题）如图，45ACB ∠=︒ 半径为2的O 与角的两边相切点P 是⊙O 上任意一点过点P 向角的两边作垂线垂足分别为E F 设2t PE PF =则，t 的取值范围是 _____．16．（2023·湖南岳阳·统考中考真题）如图，在O 中 AB 为直径 BD 为弦点C 为BD 的中点以点C 为切点的切线与AB 的延长线交于点E ．（1）若30,6A AB ∠=︒=则，BD 的长是_________（结果保留π）（2）若13CF AF =则，CE AE =_________．17．（2023·上海·统考中考真题）在ABC 中7,3,90AB BC C ==∠=︒ 点D 在边AC 上点E 在CA 延长线上且CD DE = 如果B 过点A E 过点D 若B 与E 有公共点那么E 半径r 的取值范围是________．三解答题18．（2023·浙江绍兴·统考中考真题）如图，AB 是O 的直径 C 是O 上一点过点C 作O 的切线CD 交AB 的延长线于点D 过点A 作AE CD ⊥于点E ．(1)若25EAC ∠=︒ 求ACD ∠的度数．(2)若2,1OB BD == 求CE 的长．19．（2023·湖南张家界·统考中考真题）如图，O 是ABC 的外接圆 AD 是O 的直径F 是AD 延长线上一点连接CD CF ，且DCF CAD ∠=∠．(1)求证：CF 是O 的切线(2)若直径310,cos 5AD B == 求FD 的长．20．（2023·江西·统考中考真题）如图，在ABC 中 464AB C =∠=︒，以AB 为直径的O 与AC 相交于点D E 为ABD 上一点且40ADE ∠=︒．(1)求BE 的长(2)若76EAD ∠=︒ 求证：CB 为O 的切线．21．（2023·江苏连云港·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交边AC 于点D 连接BD 过点C 作CE AB ∥．(1)请用无刻度的直尺和圆规作图：过点B 作O 的切线交CE 于点F （不写作法保留作图痕迹标明字母）(2)在（1）的条件下求证：BD BF =．22．（2023·辽宁·统考中考真题）如图，AB是O的直径点C E，在O上2CAB EAB∠=∠点F在线段AB的延长线上且AFE ABC∠=∠．(1)求证：EF与O相切(2)若41sin5BF AFE=∠=，求BC的长．23．（2023·山东东营·统考中考真题）如图，在ABC中AB AC=以AB为直径的O交BC于点D DE AC⊥垂足为E．(1)求证：DE是O的切线(2)若30C∠=︒23CD=求BD的长．24．（2023·内蒙古赤峰·统考中考真题）如图，AB 是O 的直径 C 是O 上一点过点C 作CD AB ⊥于点E 交O 于点D 点F 是AB 延长线上一点连接CF AD 2FCD DAF ∠=∠．(1)求证：CF 是O 切线(2)若10AF2sin 3F = 求CD 的长．25．（2023·湖南常德·统考中考真题）如图，四边形ABCD 是O 的内接四边形 AB 是直径 C 是BD 的中点过点C 作CE AD ⊥交AD 的延长线于点E ．(1)求证：CE 是O 的切线(2)若6BC = 8AC = 求,CE DE 的长．26．（2023·内蒙古通辽·统考中考真题）如图，AB 为O 的直径 D E 是O 上的两点延长AB 至点C 连接CD BDC A∠=∠．(1)求证：ACD DCB∽(2)求证：CD是O的切线(3)若3tan,105E AC==求O的半径．27．（2023·广东深圳·统考中考真题）如图，在单位长度为1的网格中点O A B均在格点上3OA= 2AB=以O为圆心OA为半径画圆请按下列步骤完成作图并回答问题：⊙过点A作切线AC且4AC=（点C在A的上方）⊙连接OC交O于点D⊙连接BD与AC交于点E．(1)求证：BD为O的切线(2)求AE的长度．28．（2023·黑龙江绥化·统考中考真题）已知：点P是O外一点．(1)尺规作图：如图，过点P 作出O 的两条切线PE PF 切点分别为点E 点F ．（保留作图痕迹不要求写作法和证明）(2)在（1）的条件下若点D 在O 上（点D 不与E F 两点重合）且30EPF ∠=︒．求EDF ∠的度数．29．（2023·黑龙江齐齐哈尔·统考中考真题）如图，在Rt ABC △中 90B AD 平分BAC ∠交BC 于点D 点E 是斜边AC 上一点以AE 为直径的O 经过点D 交AB 于点F 连接DF ．(1)求证：BC 是O 的切线(2)若5BD = tan 3ADB ∠= 求图中阴影部分的面积（结果保留π）．30．（2023·福建·统考中考真题）如图，已知ABC 内接于,O CO 的延长线交AB 于点D 交O 于点E 交O 的切线AF 于点F 且AF BC ∥．(1)求证：AO BE ∥(2)求证：AO 平分BAC ∠．31．（2023·湖北荆州·统考中考真题）如图，在菱形ABCD 中 DH AB ⊥于H 以DH 为直径的O 分别交AD BD 于点E F 连接EF ．(1)求证：⊙CD 是O 的切线⊙DEF DBA ∽(2)若5AB = 6DB = 求sin DFE ∠．32．（2023·广西·统考中考真题）如图，PO 平分APD ∠ PA 与O 相切于点A 延长AO 交PD 于点C 过⊥垂足为B．点O作OB PD(1)求证：PB是O的切线(2)若O的半径为4 5OC=求PA的长．33．（2023·湖北黄冈·统考中考真题）如图，ABC中以AB为直径的O交BC于点D DE是O的切线⊥垂足为E延长CA交O于点F．且DE AC=(1)求证：AB AC(2)若3,6AE DE==求AF的长．34．（2023·湖南郴州·统考中考真题）如图，在O中AB是直径点C是圆上一点．在AB的延长线上取一点D 连接CD 使BCD A ∠=∠．(1)求证：直线CD 是O 的切线(2)若120ACD ∠=︒ 3CD = 求图中阴影部分的面积（结果用含π的式子表示）．35．（2023·湖北十堰·统考中考真题）如图，在Rt ABC △中 90,C AC BC ∠=︒= 点O 在AB 上以O 为圆心 OA 为半径的半圆分别交,AC BC AB 于点,,D E F 且点E 是弧DF 的中点．(1)求证：BC 是O 的切线(2)若2CE 求图中阴影部分的面积（结果保留π）．36．（2023·四川内江·统考中考真题）如图，以线段AB 为直径作O 交射线AC 于点C AD 平分CAB ∠交O 于点D 过点D 作直线DE AC ⊥ 交AC 的延长线于点E 交AB 的延长线于点F ．连接BD 并延长交AC的延长线于点M．(1)求证：直线DE是O的切线(2)当30F∠=︒时判断ABM的形状并说明理由(3)在（2）的条件下1ME=连接BC交AD于点P求AP的长．37．（2023·湖北随州·统考中考真题）如图，AB是O的直径点E C在O上点C是BE的中点AE 垂直于过C点的直线DC垂足为D AB的延长线交直线DC于点F．(1)求证：DC是O的切线(2)若2AE=1sin3AFD∠=⊙求O的半径⊙求线段DE的长．38．（2023·山东枣庄·统考中考真题）如图，AB为O的直径点C是AD的中点过点C做射线BD的垂线垂足为E．(1)求证：CE 是O 切线(2)若34BE AB ==，求BC 的长(3)在（2）的条件下求阴影部分的面积（用含有π的式子表示）．39．（2023·山东临沂·统考中考真题）如图，O 是ABC 的外接圆 BD 是O 的直径 ,AB AC AE BC =∥ E 为BD 的延长线与AE 的交点．(1)求证：AE 是O 的切线(2)若75,2ABC BC ∠=︒= 求CD 的长．40．（2023·湖南永州·统考中考真题）如图，以AB 为直径的O 是ABC 的外接圆延长BC 到点D ．使得BAC BDA ∠=∠ 点E 在DA 的延长线上点AM 在线段AC 上 CE 交BM 于N CE 交AB 于G ．(1)求证：ED 是O 的切线(2)若,65,AC BD AC CD ==> 求BC 的长(3)若DE AM AC AD ⋅=⋅ 求证：BM CE ⊥．41．（2023·山东烟台·统考中考真题）如图，在菱形ABCD 中对角线,AC BD 相交于点,E O 经过,A D 两点交对角线AC 于点F 连接OF 交AD 于点G 且AG GD =．(1)求证：AB 是O 的切线(2)已知O 的半径与菱形的边长之比为5:8 求tan ADB ∠的值．42．（2023·江苏扬州·统考中考真题）如图，在ABC 中 90ACB ∠=︒ 点D 是AB 上一点且12BCD A ∠=∠ 点O 在BC 上以点O 为圆心的圆经过C D 两点．(1)试判断直线AB 与O 的位置关系并说明理由(2)若3sin ,5B O =的半径为3 求AC 的长．43．（2023·四川乐山·统考中考真题）如图，已知O 是Rt ABC △的外接圆 90ACB ∠=︒ D 是圆上一点 E 是DC 延长线上一点连结AD AE ，且AD AE CA CE ==，．(1)求证：直线AE 是O 是的切线(2)若2sin 3E =O 的半径为3 求AD 的长．44．（2023·甘肃兰州·统考中考真题）如图，ABC 内接于O AB 是O 的直径 BC BD = DE AC ⊥于点E DE 交BF 于点F 交AB 于点G 2BOD F ∠=∠ 连接BD ．(1)求证：BF是O的切线(2)判断DGB的形状并说明理由(3)当2BD=时求FG的长．=BD是边AC上的中线过点C作45．（2023·湖北·统考中考真题）如图，等腰ABC内接于O AB ACAE FC．AB的平行线交BD的延长线于点E BE交O于点F连接,(1)求证：AE为O的切线BC=求FC的长．(2)若O的半径为56参考答案一单选题1．（2023·四川眉山·统考中考真题）如图，AB切O于点B连接OA交O于点C BD OA∥交O于点∠的度数为（）D连接CD若25OCD∠=︒则，AA ．25︒B ．35︒C ．40︒D ．45︒【答案】C 【分析】如图，连接OB 证明90∠=︒ABO 25CDB ∠=︒ 可得250BOC BDC ∠=∠=︒ 从而可得40A ∠=︒．【详解】解：如图，连接OB⊙AB 切O 于点B⊙90∠=︒ABO⊙BD OA ∥ 25OCD ∠=︒⊙25CDB ∠=︒⊙250BOC BDC ∠=∠=︒⊙40A ∠=︒故选：C.【点睛】本题考查的是切线的性质圆周角定理的应用三角形的内角和定理的应用掌握基本图形的性质是解本题的关键．2．（2023·重庆·统考中考真题）如图，AC 是O 的切线 B 为切点连接OA OC ，．若30A ∠=︒ 23AB = 3BC =则，OC 的长度是（）A ．3B ．3C 13D ．6【答案】C 【分析】根据切线的性质及正切的定义得到2OB = 再根据勾股定理得到13OC =【详解】解：连接OB⊙AC 是O 的切线 B 为切点⊙OB AC ⊥⊙30A ∠=︒ 23AB =⊙在Rt OAB 中 3tan 232OB AB A =⋅∠== ⊙3BC =⊙在Rt OBC 中 2213OC OB BC +故选：C ．【点睛】本题考查了切线的性质锐角三角函数勾股定理掌握切线的性质是解题的关键．3．（2023·重庆·统考中考真题）如图，AB 为O 的直径直线CD 与O 相切于点C 连接AC 若50ACD ∠=︒则，BAC ∠的度数为（）A ．30︒B ．40︒C ．50︒D ．60︒【答案】B 【分析】连接OC 先根据圆的切线的性质可得90OCD ∠=︒ 从而可得40OCA ∠=︒ 再根据等腰三角形的性质即可得．【详解】解：如图，连接OC直线CD 与O 相切OC CD ∴⊥90OCD ∴∠=︒50ACD ∠=︒40OCA ∴∠=︒OA OC =40BAC OCA ∴∠=∠=︒故选：B ．【点睛】本题考查了圆的切线的性质等腰三角形的性质熟练掌握圆的切线的性质是解题关键． 4．（2023·湖北武汉·统考中考真题）如图，在四边形ABCD 中 ,AB CD AD AB ⊥∥ 以D 为圆心 AD 为半径的弧恰好与BC 相切切点为E ．若13AB CD =则，sin C 的值是（）A ．23B 5C ．34D 7【答案】B 【分析】作CF AB ⊥延长线于F 点连接DE 根据圆的基本性质以及切线的性质分别利用勾股定理求解在Rt DEC △和Rt BFC △ 最终得到DE 即可根据正弦函数的定义求解．【详解】解：如图所示作CF AB ⊥延长线于F 点连接DE⊙AD AB ⊥ AB CD ∥⊙90FAD ADC F ∠=∠=∠=︒⊙四边形ADCF 为矩形 AF DC = AD FC =⊙AB 为D 的切线由题意 BE 为D 的切线⊙DE BC ⊥ AB BE = ⊙13AB CD = ⊙设AB BE a 3CD a = CE x =则2BF AF AB CD AB a =-=-= BC BE CE a x =+=+在Rt DEC △中 222229DE CD CE a x =-=-在Rt BFC △中 ()()222222FC BC BF a x a =-=+-⊙DE DA FC ==⊙()()222292a x a x a -=+-解得：2x a =或3x a =-（不合题意舍去）⊙2CE a = ⊙2222945DE CD CE a a a --= ⊙55sin DE a C DC === 故选：B ．【点睛】本题考查圆的切线的判定与性质解直角三角形以及正弦函数的定义等综合性较强熟练运用圆的相关性质以及切线的性质等是解题关键．5．（2023·四川泸州·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ 点D 在斜边AB 上以AD 为直径的半圆O 与BC 相切于点E 与AC 相交于点F 连接DE ．若8AC = 6BC =则，DE 的长是（）A 410B 810C ．8027 D ．83【答案】B【分析】连接OE AE 首先根据勾股定理求出2210AB AC BC + 然后证明出BCA BEO ∽利用相似三角形的性质得到409OE = 103BE = 证明出DBE EBA ∽ 利用相似三角形的性质求出810DE =【详解】如图所示连接OE AE⊙90C ∠=︒ 8AC = 6BC = ⊙2210AB AC BC +⊙以AD 为直径的半圆O 与BC 相切于点E⊙OE BC ⊥⊙90C ∠=︒⊙90C OEB ︒∠=∠=⊙AC OE ∥⊙A EOB ∠=∠⊙BCA BEO ∽ ⊙6OE OB BE AC AB == 即108106OE OEBE-== ⊙409OE = 103BE = ⊙108633CE CB BE =-=-=⊙228103AE AC CE =+=⊙90OEB ∠=︒ ⊙90OED DEB ∠+∠=︒⊙90ODE EAD ∠+∠=︒ ODE OED ∠=∠⊙EAD DEB ∠=∠又⊙B B ∠=∠⊙DBE EBA ∽ ⊙DE BE AE AB = 即103810103DE = ⊙解得810DE =故选：B ．【点睛】此题考查了圆与三角形综合题切线的性质定理相似三角形的性质和判定勾股定理等知识解题的关键是熟练掌握以上知识点．二填空题6．（2023·浙江嘉兴·统考中考真题）如图，点A 是O 外一点 AB AC 分别与O 相切于点B C 点D 在BDC 上已知50A ∠=︒则，D ∠的度数是___________．【答案】65︒【分析】连接,CO BO 根据切线的性质得出90ACO ABO ∠=∠=︒ 根据四边形内角和得出130COB ∠=︒ 根据圆周角定理即可求解．【详解】解：如图,CO BO⊙AB AC 分别与O 相切于点B C⊙90ACO ABO ∠=∠=︒⊙50A ∠=︒⊙360909050130COB ∠=︒-︒-︒-︒=︒⊙BC BC = ⊙1652D BOC ∠=∠=︒ 故答案为：65︒．【点睛】本题考查了切线的性质圆周角定理求得130COB ∠=︒是解题的关键．7．（2023·黑龙江·统考中考真题）如图，AB 是O 的直径 PA 切O 于点A PO 交O 于点C 连接BC 若28B ∠=︒则，P ∠=__________︒．【答案】34【分析】首先根据等边对等角得到28B OCB ∠=∠=︒ 然后利用外角的性质得到56AOC B OCB ∠=∠+∠=︒ 利用切线的性质得到90OAP ∠=︒ 最后利用三角形内角和定理求解即可．【详解】解：⊙28B ∠=︒ OB OC =⊙28B OCB ∠=∠=︒⊙56AOC B OCB ∠=∠+∠=︒⊙PA 切O 于点A⊙90OAP ∠=︒⊙18034P OAP AOP ∠=︒-∠-∠=︒．故答案为：34．【点睛】此题考查了切线的性质和三角形的外角的性质三角形内角和定理等知识解题的关键是熟练掌握以上知识点．8．（2023·湖南·统考中考真题）如图，AD 是O 的直径 AB 是O 的弦 BC 与O 相切于点B 连接OB 若65ABC ∠=︒则，BOD ∠的大小为__________．【答案】50︒【分析】证明90OBC ∠=︒ 可得906525OBD ∠=︒-︒=︒ 结合OB OA = 证明25A OBA ∠=∠=︒ 再利用三角形的外角的性质可得答案．【详解】解：⊙BC 与O 相切于点B⊙90OBC ∠=︒⊙65ABC ∠=︒⊙906525OBD ∠=︒-︒=︒⊙OB OA =⊙25A OBA ∠=∠=︒⊙22550BOD ∠=⨯︒=︒故答案为：50︒【点睛】本题考查的是圆的切线的性质等腰三角形的性质三角形的外角的性质熟记基本图形的性质是解本题的关键．9．（2023·山东滨州·统考中考真题）如图，,PA PB 分别与O 相切于,A B 两点且56APB ∠=︒．若点C 是O 上异于点,A B 的一点则，ACB ∠的大小为___________．【答案】62︒或118︒【分析】根据切线的性质得到90∠=∠=︒PAO PBO 根据四边形内角和为360︒ 得出AOB ∠ 然后根据圆周角定理即可求解．【详解】解：如图所示连接,AC BC 当点C 在优弧AB 上时⊙,PA PB 分别与O 相切于,A B 两点⊙90∠=∠=︒PAO PBO⊙56APB ∠=︒．⊙360909056124AOB ∠=︒-︒-︒-︒=︒⊙AB AB = ⊙1622ACB AOB ∠=∠=︒ 当点C '在AB 上时⊙四边形AC BC '是圆内接四边形⊙180118C C '∠=︒-∠=︒故答案为：62︒或118︒．【点睛】本题考查了切线的性质圆周角定理多边形内角和熟练掌握切线的性质与圆周角定理是解题的关键．10．（2023·浙江宁波·统考中考真题）如图，在Rt ABC △中 90C ∠=︒ E 为AB 边上一点以AE 为直径的半圆O 与BC 相切于点D 连接AD 3,35BE BD ==P 是AB 边上的动点当ADP △为等腰三角形时 AP 的长为_____________．【答案】2306【分析】连接OD 勾股定理求出半径平行线分线段成比例求出CD 的长勾股定理求出AC 和AD 的长分AP AD =和AP PD =两种情况进行求解即可．【详解】解：连接OD⊙以AE 为直径的半圆O 与BC 相切于点D⊙OD BC ⊥ OA OE OD ==⊙90ODB ∠=︒设OA OE OD r ===则，3OB OE BE r =+=+在Rt ODB △中：222OD BD OB += 即：(()222353r r +=+ 解得：6r =⊙6OA OE OD ===⊙9OB = 15AB = 12AE =⊙90C ODB ∠=∠=︒⊙OD AC ∥ ⊙9362OB DB OA DC === ⊙35DB = ⊙5CD = ⊙5BC DB CD =+= ⊙2210AC AB BC -= ⊙22230AD AC CD +=⊙ADP △为等腰三角形当AD AP =时 30AP =当PA PD =时⊙OA OD =⊙点P 与点O 重合⊙6AP OA ==不存在PD AD =的情况综上：AP 的长为306．故答案为：2306．【点睛】本题考查切线的性质平行线分线段成比例勾股定理等腰三角形的定义．熟练掌握切线的性质等腰三角形的定义确定点P 的位置是解题的关键．11．（2023·河南·统考中考真题）如图，PA 与O 相切于点A PO 交O 于点B 点C 在PA 上且CB CA =．若5OA = 12PA =则，CA 的长为______．【答案】103【分析】连接OC 证明OAC OBC ≌ 设CB CA x ==则，12PC PA CA x =-=- 再证明PAO PBC ∽ 列出比例式计算即可．【详解】如图，连接OC⊙PA 与O 相切于点A⊙90OAC ∠=︒⊙OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩, ⊙OAC OBC ≌⊙90OAC OBC ∠=∠=︒⊙90PAO PBC ∠=∠=︒⊙P P ∠=∠⊙PAO PBC ∽ ⊙PO AO PC BC= ⊙5OA = 12PA = ⊙2251213PO +设CB CA x ==则，12PC PA CA x =-=- ⊙13512x x=- 解得103x =故CA 的长为103故答案为：103．【点睛】本题考查了切线的性质三角形全等的判定和性质勾股定理三角形相似的判断和性质熟练掌握性质是解题的关键．12．（2023·湖北·统考中考真题）如图，在ABC 中 70ACB ABC ∠=︒，△的内切圆O 与AB BC ，分别相切于点D E 连接DE AO ，的延长线交DE 于点F 则，AFD ∠=_________．【答案】35︒【分析】如图所示连接OE OD OB ，，设OB DE 、交于H 由内切圆的定义结合三角形内角和定理求出125AOB ∠=︒ 再由切线长定理得到BD BE = 进而推出OB 是DE 的垂直平分线即90OHF ∠=︒则，35AFD AOH OHF =-=︒∠∠∠．【详解】解：如图所示连接OE OD OB ，，设OB DE 、交于H⊙O 是ABC 的内切圆⊙OA OB 、分别是CAB CBA ∠、∠的角平分线 ⊙1122OAB CAB OBA CBA ==∠∠，∠∠ ⊙70ACB ∠=︒⊙180110CAB CBA ACB +=︒-=︒∠∠∠ ⊙115522OAB OBA CBA CAB +=+=︒∠∠∠∠ ⊙180125AOB OAB OBA =︒--=︒∠∠∠⊙O 与AB BC ，分别相切于点D E⊙BD BE =又⊙OD OE =⊙OB 是DE 的垂直平分线⊙OB DE ⊥ 即90OHF ∠=︒⊙35AFD AOH OHF =-=︒∠∠∠故答案为：35︒．【点睛】本题主要考查了三角形内切圆切线长定理三角形内角和定理线段垂直平分线的判定三角形外角的性质正确作出辅助线是解题的关键．13．（2023·湖南·统考中考真题）如图，在Rt ABC △中 90,8,6ACB AC BC ∠=︒==．以点C 为圆心 r 为半径作圆当所作的圆与斜边AB 所在的直线相切时 r 的值为________．【答案】245【分析】根据勾股定理得228610AB =+= 根据切线的性质得到圆的半径等于AB 边上的高根据直角三角形的面积不变性计算即可．【详解】⊙90,8,6ACB AC BC ∠=︒== ⊙228610AB +=根据切线的性质得到圆的半径等于AB 边上的高 ⊙1122AB r AC BC ⨯=⨯, ⊙8624105AC BCr AB ⨯⨯=== 故答案为：245．【点睛】本题考查了勾股定理切线的性质熟练掌握勾股定理切线的性质是解题的关键． 14．（2023·山东烟台·统考中考真题）如图，在直角坐标系中 A 与x 轴相切于点,B CB 为A 的直径点C 在函数(0,0)ky k x x =>>的图象上 D 为y 轴上一点 ACD 的面积为6则，k 的值为________．【答案】24 【分析】设,k C a a ⎛⎫⎪⎝⎭则，,k OB a AC a ==则，122kAC BC a == 根据三角形的面积公式得出162ACD S AC OB =⋅= 列出方程求解即可．【详解】解：设,k C a a ⎛⎫⎪⎝⎭⊙A 与x 轴相切于点B⊙BC x ⊥轴 ⊙,kOB a AC a ==则，点D 到BC 的距离为a⊙CB 为A 的直径⊙122k AC BC a == ⊙16224ACD k k S a a =⋅⋅== 解得：24k =故答案为：24．【点睛】本题主要考查了切线的性质反比例函数的图象和性质解题的关键掌握切线的定义：经过半径外端且垂直于半径的直线是圆的切线以及反比例函数图象上点的坐标特征．15．（2023·四川·统考中考真题）如图，45ACB ∠=︒ 半径为2的O 与角的两边相切点P 是⊙O 上任意一点过点P 向角的两边作垂线垂足分别为E F 设2t PE PF =则，t 的取值范围是 _____．【答案】22224t ≤ 【分析】利用切线的性质以及等腰直角三角形的性质求得222CD DH == 再求得t PE PQ EQ =+= 分两种情况讨论画出图形利用等腰直角三角形的性质即可求解．【详解】解：设O 与ACB ∠两边的切点分别为D G 连接OG OD 、延长DO 交CB 于点H由90OGC ODC OGH ∠=∠=∠=︒⊙45ACB ∠=︒⊙45OHC ∠=︒ ⊙222OH OG == ⊙222CD DH ==如图，延长EP 交CB 于点Q同理2PQ PF = ⊙2t PE PF =⊙t PE PQ EQ =+=当EQ 与O 相切时 EQ 有最大或最小值连接OP⊙D E 都是切点⊙90ODE DEP OPE ∠=∠=∠=︒⊙四边形ODEP 是矩形⊙OD OP =⊙四边形ODEP 是正方形⊙t 的最大值为24EQ CE CD DE ==+=如图，同理 t 的最小值为2EQ CE CD DE ==-=综上 t 的取值范围是22224t ≤≤．故答案为：22224t ≤．【点睛】本题考查了切线的性质等腰直角三角形的性质勾股定理求得t EQ =是解题的关键． 16．（2023·湖南岳阳·统考中考真题）如图，在O 中 AB 为直径 BD 为弦点C 为BD 的中点以点C 为切点的切线与AB 的延长线交于点E ．（1）若30,6A AB ∠=︒=则，BD 的长是_________（结果保留π）（2）若13CF AF =则，CE AE =_________．【答案】2π12 【分析】（1）连接,OC OD 根据点C 为BD 的中点根据已知条件得出120BOD ∠=︒ 然后根据弧长公式即可求解（2）连接OC 根据垂径定理的推论得出OC BD ⊥ EC 是O 的切线则，OC EC ⊥,得出EC BD ∥ 根据平行线分线段成比例得出13EB AB = 设2EB a =则，6AB a = 勾股定理求得EC ,J 进而即可求解．【详解】解：（1）如图，连接,OC OD⊙点C 为BD 的中点⊙BC CD =又⊙30A ∠=︒⊙260BOC COD A ∠=∠=∠=︒⊙120BOD ∠=︒⊙6AB = ⊙132OB AB == ⊙120π32π180BD l =⨯⨯= 故答案为：2π．（2）解：如图，连接OC⊙点C 为BD 的中点⊙BC CD =⊙OC BD ⊥⊙EC 是O 的切线⊙OC EC ⊥,⊙EC BD ∥ ⊙CF EB AF AB = ⊙13CF AF = ⊙13EB AB = 设2EB a =则，6AB a = 3,5BO a EO EB BO a ==+= ⊙2222534EC EO CO a a --= 268AE a a a =+= ⊙4182CE a AE a ==．故答案为：12．【点睛】本题考查了垂径定理圆周角定理切线的性质弧长公式平行线分线段成比例定理等知识综合性较强熟练掌握和灵活运用相关知识是解题的关键．17．（2023·上海·统考中考真题）在ABC 中7,3,90AB BC C ==∠=︒ 点D 在边AC 上点E 在CA 延长线上且CD DE = 如果B 过点A E 过点D 若B 与E 有公共点那么E 半径r 的取值范围是________． 1010r ≤【分析】先画出图形连接BE 利用勾股定理可得294BE r + 210AC = 10210r <≤ 再根据B 与E 有公共点可得一个关于r 的不等式组然后利用二次函数的性质求解即可得．【详解】解：由题意画出图形如下：连接BEB 过点A 且7AB =B ∴的半径为7 E 过点D 它的半径为r 且CD DE =2CE CD DE r ∴=+=3,90BC C =∠=︒22294BE BC CE r ∴++ 22210AC AB BC - D 在边AC 上点E 在CA 延长线上CD AC CE AC ≤⎧∴⎨>⎩ 即2102210r r ⎧≤⎪⎨>⎪⎩10210r <≤ B 与E 有公共点AB DE BE AB DE ∴-≤≤+ 即22947794r r r r ++-≤+⎪⎩①②不等式⊙可化为2314400r r --≤解方程2314400r r --=得：2r =-或203r = 画出函数231440y r r =--的大致图象如下：由函数图象可知当0y ≤时 2023r -≤≤即不等式⊙的解集为2023r -≤≤ 同理可得：不等式⊙的解集为2r ≥或203r ≤-则不等式组的解集为2023r ≤≤又10210r <≤ 半径r 1010r ≤ 1010r ≤．【点睛】本题考查了勾股定理圆与圆的位置关系二次函数与不等式根据圆与圆的位置关系正确建立不等式组是解题关键．三解答题18．（2023·浙江绍兴·统考中考真题）如图，AB 是O 的直径 C 是O 上一点过点C 作O 的切线CD 交AB 的延长线于点D 过点A 作AE CD ⊥于点E ．(1)若25EAC ∠=︒ 求ACD ∠的度数．(2)若2,1OB BD == 求CE 的长．【答案】(1)115︒ (2)253CE = 【分析】（1）根据三角形的外角的性质 ACD AEC EAC ∠=∠+∠即可求解．（2）根据CD 是O 的切线可得90OCD ∠=︒ 在Rt OCD △中勾股定理求得5CD 根据OC AE ∥ 可得CDODCE OA = 进而即可求解．【详解】（1）解：⊙AE CD ⊥于点E⊙90AEC ∠=︒⊙9025115ACD AEC EAC ∠=∠+∠=︒+︒=︒．（2）⊙CD 是O 的切线 OC 是O 的半径⊙90OCD ∠=︒．在Rt OCD △中⊙2,3OC OB OD OB BD ===+= ⊙225CD OD OC -⊙90OCD AEC ∠=∠=︒⊙OC AE ∥ ⊙CD OD CE OA = 532= ⊙253CE =．【点睛】本题考查了三角形外角的性质切线的性质勾股定理平行线分线段成比例熟练掌握以上知识是解题的关键．19．（2023·湖南张家界·统考中考真题）如图，O 是ABC 的外接圆 AD 是O 的直径 F 是AD 延长线上一点连接CD CF ，且DCF CAD ∠=∠．(1)求证：CF 是O 的切线(2)若直径310,cos 5AD B == 求FD 的长．【答案】(1)详见解析 (2)907【分析】(1)根据直径所对的圆周角是直角余角的性质即可求得结论(2)根据已知条件可知FCD FAC ∽ 再根据正切的定义和相似三角形的性质得到线段的关系即可求得线段FD 的长度．【详解】（1）证明：连接OC⊙AD 是O 的直径⊙90ACD ∠=︒⊙90ADC CAD ∠+∠=︒又⊙OC OD =⊙ADC OCD ∠=∠又⊙DCF CAD ∠=∠⊙90DCF OCD ∠+∠=︒即OC FC ⊥⊙FC 是O 的切线（2）解：⊙3,cos 5B ADC B ∠=∠=⊙3cos 5ADC ∠= ⊙在Rt ACD 中 3cos ,10,5CD ADC AD AD∠=== ⊙3cos 106,5CD AD ADC =⋅∠=⨯= ⊙228AC AD CD - ⊙34CD AC = ⊙FCD FAC F F ∠=∠∠=∠，⊙FCD FAC ∽ ⊙34CD FC FD AC FA FC === 设3FD x =则，4310FC x AF x ==+，又⊙2FC FD FA =⋅即2(4)3(310)x x x =+ 解得307x =（取正值） ⊙9037FD x ==【点睛】本题考查了圆周角的性质切线的判定定理正切的定义相似三角形的性质和判定找出正切的定义与相似三角形相似比的关联是解题的关键．20．（2023·江西·统考中考真题）如图，在ABC 中 464AB C =∠=︒，以AB 为直径的O 与AC 相交于点D E 为ABD 上一点且40ADE ∠=︒．(1)求BE 的长(2)若76EAD ∠=︒ 求证：CB 为O 的切线．【答案】(1)109π (2)见解析【分析】（1）如图所示连接OE 先求出2OE OB OA === 再由圆周角定理得到280AOE ADE ==︒∠∠进而求出100∠=︒BOE 再根据弧长公式进行求解即可（2）如图所示连接BD 先由三角形内角和定理得到64AED ∠=︒则，由圆周角定理可得64ABD AED ==︒∠∠ 再由AB 是O 的直径得到90ADB ∠=︒ 进而求出26BAC ∠=︒ 进一步推出90ABC ∠=︒ 由此即可证明BC 是O 的切线．【详解】（1）解：如图所示连接OE⊙AB 是O 的直径且4AB =⊙2OE OB OA ===⊙E 为ABD 上一点且40ADE ∠=︒⊙280AOE ADE ==︒∠∠⊙180100BOE AOE ∠=︒-=︒∠⊙BE 的长1002101809ππ⨯⨯==（2）证明：如图所示连接BD⊙76EAD ∠=︒ 40ADE ∠=︒⊙18064AED EAD ADE =︒--=︒∠∠∠⊙64ABD AED ==︒∠∠⊙AB 是O 的直径⊙90ADB ∠=︒⊙9026BAC ABD =︒-=︒∠∠⊙64C ∠=︒⊙18090ABC C BAC =︒--=︒∠∠∠ 即AB BC ⊥⊙OB 是O 的半径⊙BC 是O 的切线．【点睛】本题主要考查了切线的判定求弧长圆周角定理三角形内角和定理等等正确作出辅助线是解题的关键．21．（2023·江苏连云港·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交边AC 于点D 连接BD 过点C 作CE AB ∥．(1)请用无刻度的直尺和圆规作图：过点B 作O 的切线交CE 于点F （不写作法保留作图痕迹标明字母）(2)在（1）的条件下求证：BD BF =．【答案】(1)见解析(2)见解析【分析】（1）根据尺规作图过点B 作AB 的垂线交CE 于点F 即可求解（2）根据题意切线的性质以及直径所对的圆周角是直角证明BDC BFC ∠=∠ 根据平行线的性质以及等腰三角形的性质得出BCD BCF =∠ 进而证明()AAS BCD BCF ≌ 即可得证．【详解】（1）解：方法不唯一如图所示．（2）⊙AB AC =⊙A ABC CB =∠∠．又⊙CE AB ∥⊙ABC BCF ∠=∠⊙BCF ACB =∠∠．⊙点D 在以AB 为直径的圆上⊙90ADB ∠=︒⊙=90BDC ∠︒．又⊙BF 为O 的切线⊙90ABF ∠=︒．⊙CE AB ∥⊙180BFC ABF ∠+∠=︒⊙90BFC ∠=︒⊙BDC BFC ∠=∠．⊙在BCD △和BCF △中,,,BCD BCF BDC BFC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩⊙()AAS BCD BCF ≌．⊙BD BF =．【点睛】本题考查了作圆的切线切线的性质直径所对的圆周角是直角全等三角形的性质与判定熟练掌握以上知识是解题的关键．22．（2023·辽宁·统考中考真题）如图，AB 是O 的直径点C E ，在O 上 2CAB EAB ∠=∠ 点F 在线段AB 的延长线上且AFE ABC ∠=∠．(1)求证：EF 与O 相切(2)若41sin 5BF AFE =∠=，求BC 的长．【答案】(1)见解析 (2)245BC = 【分析】（1）利用圆周角定理得到2EOB EAB ∠=∠ 结合已知推出CAB EOB ∠=∠ 再证明OFE ABC ∽△△ 推出90OEF C ∠=∠=︒ 即可证明结论成立（2）设O 半径为x 则，1=+OF x 在Rt OEF △中利用正弦函数求得半径的长再在Rt ABC △中解直角三角形即可求解．【详解】（1）证明：连接OE⊙=BE BE ⊙2EOB EAB ∠=∠⊙2CAB EAB ∠=∠⊙CAB EOB ∠=∠⊙AB 是O 的直径⊙90C ∠=︒⊙AFE ABC ∠=∠⊙OFE ABC ∽△△⊙90OEF C ∠=∠=︒⊙OE 为O 半径⊙EF 与O 相切（2）解：设O 半径为x 则，1=+OF x⊙AFE ABC ∠=∠ 4sin 5AFE ∠=⊙4sin 5ABC ∠= 在Rt OEF △中 90OEF ∠=︒ 4sin 5AFE ∠=⊙45OE OF = 即415x x =+ 解得4x =经检验 4x =是所列方程的解⊙O 半径为4则，8AB =在Rt ABC △中 90C ∠=︒ 4sin 5ABC ∠=8AB = ⊙32sin 5A AB C AB C ∠==⋅ ⊙22245BC AB AC =-=．【点睛】本题考查了圆的切线的判定圆周角定理解直角三角形以及相似三角形的判定和性质等知识熟练掌握圆的相关知识和相似三角形的判定和性质是解题的关键．23．（2023·山东东营·统考中考真题）如图，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D DE AC ⊥ 垂足为E ．(1)求证：DE 是O 的切线(2)若30C ∠=︒ 23CD = 求BD 的长．【答案】(1)见解析 (2)43π 【分析】（1）如图：OD 然后根据等边对等角可得B ODB ∠=∠ B C ∠=∠即ODB C ∠=∠ 再根据OD AC ∥可得ODE DEC ∠=∠ 进而得到90ODE ∠=︒即可证明结论（2）如图：连接AD 有圆周角定理可得AD BC ⊥ 再解直角三角形可得4AC = 进而得到11222OB AB AC === 然后说明120BOD ∠=︒ 最后根据弧长公式即可解答．【详解】（1）证明：如图：连接OD⊙OB OD =⊙B ODB ∠=∠,⊙AB AC =⊙B C ∠=∠,⊙ODB C ∠=∠,⊙OD AC ∥,⊙ODE DEC ∠=∠。

中考试题数学圆及答案

中考试题数学圆及答案
一、选择题
1. 若圆的半径为3，则该圆的面积是多少？
A. 9π
B. 12π
C. 18π
D. 27π
答案：C
2. 已知圆心为O，半径为5，点A在圆上，若OA=6，则点A与圆的位
置关系是？
A. 点A在圆内
B. 点A在圆上
C. 点A在圆外
D. 无法确定
答案：C
二、填空题
3. 圆的周长公式为C=2πr，若半径r=4，则该圆的周长为______。

答案：8π
4. 已知圆的直径为10cm，求该圆的半径为______。

答案：5cm
三、解答题
5. 已知圆的方程为(x-2)^2 + (y-3)^2 = 16，求该圆的圆心坐标和半径。

答案：圆心坐标为(2, 3)，半径为4。

6. 已知圆的半径为5，求该圆的内接正方形的边长。

答案：边长为5√2。

四、证明题
7. 证明：若两圆相切，则两圆心之间的距离等于两圆半径之和或之差。

答案：证明过程略。

以上为中考数学试题中关于圆的部分题目及答案，供参考。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

与圆有关的中考试题集锦附答案一、选择题1．（北京市西城区）如图，BC 是⊙O 的直径，P 是CB 延长线上一点，PA 切⊙O 于点A ，如果PA ＝3，PB ＝1，那么∠APC 等于（）（A ）15 （B ）30 （C ）45 （D ）60第1题第2 题第3题 2．（北京市西城区）如果圆柱的高为20厘米，底面半径是高的41，那么这个圆柱的侧面积是（）（A ）100π平方厘米（B ）200π平方厘米（C ）500π平方厘米（D ）200平方厘米3．（北京市西城区）“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何”用现在的数学语言表述是：“如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，CE ＝1寸，AB ＝寸，求直径CD 的长”．依题意，CD 长为（）（A ）225寸（B ）13寸（C ）25寸（D ）26寸 4．（北京市朝阳区）已知：如图，⊙O 半径为5，PC 切⊙O 于点C ，PO 交⊙O 于点A ，PA ＝4，那么PC 的长等于（）（A ）6 （B ）25 （C ）210 （D ）2145．（北京市朝阳区）如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于（）（A ）2厘米（B ）22厘米（C ）4厘米（D ）8厘米6．（天津市）相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘米和17厘米，则这两圆的圆心距为（）（A ）7厘米（B ）16厘米（C ）21厘米（D ）27厘米7．（重庆市）如图，⊙O 为△ABC 的内切圆，∠C ＝90，AO 的延长线交BC 于点D ，AC ＝4，DC ＝1，，则⊙O 的半径等于（）（A ）54 （B ）45 （C ）43 （D ）658．（重庆市）一居民小区有一正多边形的活动场．为迎接“AAPP ”会议在重庆市的召开，小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台，花台都以多边形的顶点为圆心，比多边形的内角为圆心角，花台占地面积共为12π平方米．若每个花台的造价为400元，则建造这些花台共需资金（）（A ）2400元（B ）2800元（C ）3200元（D ）3600元9．（河北省）如图，AB 是⊙O 直径，CD 是弦．若AB ＝10厘米，CD ＝8厘米，那么A 、B 两点到直线CD 的距离之和为（）（A ）12厘米（B ）10厘米（C ）8厘米（D ）6厘米第9题第10题第11题10．（河北省）某工件形状如图所示，圆弧BC 的度数为60，AB ＝6厘米，点B 到点C 的距离等于AB ，∠BAC ＝30，则工件的面积等于（）（A ）4π （B ）6π （C ）8π （D ）10π11．（沈阳市）如图，PA 切⊙O 于点A ，PBC 是⊙O 的割线且过圆心，PA ＝4，PB ＝2，则⊙O 的半径等于（）（A ）3 （B ）4 （C ）6 （D ）812．（哈尔滨市）已知⊙O 的半径为35厘米，⊙O '的半径为5厘米．⊙O 与⊙O '相交于点D 、E ．若两圆的公共弦DE 的长是6厘米（圆心O 、O '在公共弦DE 的两侧），则两圆的圆心距O O '的长为（）（A ）2厘米（B ）10厘米（C ）2厘米或10厘米（D ）4厘米13．（陕西省）如图，两个等圆⊙O 和⊙O '的两条切线OA 、OB ，A 、B 是切点，则∠AOB 等于（）（A ）30 （B ）45 （C ）60 （D ）90第13题第14题14．（甘肃省）如图，AB 是⊙O 的直径，∠C ＝30，则∠ABD ＝（）（A ）30 （B ）40 （C ）50 （D ）6015．（甘肃省）弧长为6π的弧所对的圆心角为60，则弧所在的圆的半径为（）（A ）6 （B ）62 （C ）12 （D ）1816．（甘肃省）如图，在△ABC 中，∠BAC ＝90，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为（）（A ）1 （B ）2 （C ）1+4π（D ）2－4π 17．（宁夏回族自治区）已知圆的内接正六边形的周长为18，那么圆的面积为（）（A ）18π （B ）9π （C ）6π （D ）3π18．（山东省）如图，点P 是半径为5的⊙O 内一点，且OP ＝3，在过点P 的所有弦中，长度为整数的弦一共有（）（A ）2条（B ）3条（C ）4条（D ）5条19．（南京市）如图，正六边形ABCDEF 的边长的上a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是（）（A ）261a π （B ）231a π （C ）232a π （D ）234a π 20．（杭州市）过⊙O 内一点M 的最长的弦长为6厘米，最短的弦长为4厘米，则OM 的长为（）（A ）3厘米（B ）5厘米（C ）2厘米（D ）5厘米21．（安徽省）已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是（）（A ）12π （B ）15π （C ）30π （D ）24π22．（安微省）已知⊙O 的直径AB 与弦AC 的夹角为30，过C 点的切线PC 与AB 延长线交P ．PC ＝5，则⊙O 的半径为（）（A ）335 （B ）635 （C ）10 （D ）5第22题第23题第24题23．（福州市）如图：PA 切⊙O 于点A ，PBC 是⊙O 的一条割线，有PA ＝32，PB ＝BC ，那么BC 的长是（）（A ）3 （B ）32 （C ）3 （D ）3224．（河南省）如图，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）（A ）π （B ）π （C ）2π （D ）π 25．（四川省）正六边形的半径为2厘米，那么它的周长为（）（A ）6厘米（B ）12厘米（C ）24厘米（D ）122厘米26．（四川省）一个圆柱形油桶的底面直径为米，高为1米，那么这个油桶的侧面积为（）（A ）π平方米（B ）π平方米（C ）平方米（D ）π平方米27．（贵阳市）一个形如圆锥的冰淇淋纸筒，其底面直径为6厘米，母线长为5厘米，围成这样的冰淇淋纸筒所需纸片的面积是（）（A ）66π平方厘米（B ）30π平方厘米（C ）28π平方厘米（D ）15π平方厘米28．（新疆乌鲁木齐）在半径为2的⊙O 中，圆心O 到弦AB 的距离为1，则弦AB 所对的圆心角的度数可以是（）（A ）60 （B ）90 （C ）120 （D ）15029．（新疆乌鲁木齐）将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面，（接口损耗不计），则桶底的面积为（）（A ）π1600平方厘米（B ）1600π平方厘米（C ）π6400平方厘米（D ）6400π平方厘米30．（成都市）如图，已知AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10厘米，AP ∶PB ＝1∶5，那么⊙O 的半径是（）（A ）6厘米（B ）53厘米（C ）8厘米（D ）35厘米31．（成都市）在Rt △ABC 中，已知AB ＝6，AC ＝8，∠A ＝90．如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1；把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，那么S 1∶S 2等于（）（A ）2∶3 （B ）3∶4 （C ）4∶9 （D ）5∶1232．（苏州市）如图，⊙O 的弦AB ＝8厘米，弦CD 平分AB 于点E ．若CE ＝2厘米．ED 长为（）（A ）8厘米（B ）6厘米（C ）4厘米（D ）2厘米33．（苏州市）如图，四边形ABCD 内接于⊙O ，若∠BOD ＝ 160，则∠BCD ＝（）（A ）160 （B ）100 （C ）80 （D ） 20第33题第34题第35题34．（镇江市）如图，正方形ABCD 内接于⊙O ，E 为DC 的中点，直线BE 交⊙O 于点F ．若⊙O 的半径为2，则BF 的长为（）（A ）23 （B ）22 （C ）556 （D ）55435．（扬州市）如图，AB 是⊙O 的直径，∠ACD ＝15，则∠BAD 的度数为（）（A ）75 （B ）72 （C ）70 （D ）6536．（扬州市）已知：点P 直线l 的距离为3，以点P 为圆心，r 为半径画圆，如果圆上有且只有两点到直线l 的距离均为2，则半径r 的取值范围是（）（A ）r ＞1 （B ）r ＞2 （C ）2＜r ＜3 （D ）1＜r ＜537．（绍兴市）边长为a 的正方边形的边心距为（）（A ）a （B ）23a （C ）3a （D ）2a 38．（绍兴市）如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为（）（A ）30π （B ）76π （C ）20π （D ）74π39．（昆明市）如图，扇形的半径OA ＝20厘米，∠AOB ＝135，用它做成一个圆锥的侧面，则此圆锥底面的半径为（）（A ）厘米（B ）厘米（C ）15厘米（D ）30厘米40．（昆明市）如图，正六边形ABCDEF 中．阴影部分面积为123平方厘米，则此正六边形的边长为（）（A ）2厘米（B ）4厘米（C ）6厘米（D ）8厘米41．（温州市）已知扇形的弧长是2π厘米，半径为12厘米，则这个扇形的圆心角是（）（A ）60 （B ）45 （C ）30 （D ）2042．（温州市）圆锥的高线长是厘米，底面直径为12厘米，则这个圆锥的侧面积是（）（A ）48π厘米（B ）24π13平方厘米（C ）48π13平方厘米（D ）60π平方厘米43．（温州市）如图，AB 是⊙O 的直径，点P 在BA 的延长线上，PC 是⊙O 的切线，C 为切点，PC ＝26，PA ＝4，则⊙O 的半径等于（）（A ）1 （B ）2 （C ）23（D ）2644．（常州市）已知圆柱的母线长为5厘米，表面积为28π平方厘米，则这个圆柱的底面半径是（）（A ）5厘米（B ）4厘米（C ）2厘米（D ）3厘米45．（常州市）半径相等的圆内接正三角形、正方形、正六边形的边长之比为（）（A ）1∶2∶3 （B ）3∶2∶1（C ）3∶2∶1 （D ）1∶2∶346．（广东省）如图，若四边形ABCD 是半径为1和⊙O 的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为（）（A ）（2π－2）厘米（B ）（2π－1）厘米（C ）（π－2）厘米（D ）（π－1）厘米47．（武汉市）如图，已知圆心角∠BOC ＝100，则圆周角∠BAC 的度数是（）（A ）50 （B ）100 （C ）130 （D ）20048．（武汉市）半径为5厘米的圆中，有一条长为6厘米的弦，则圆心到此弦的距离为（）（A ）3厘米（B ）4厘米（C ）5厘米（D ）6厘米49．已知：Rt △ABC 中，∠C ＝90，O 为斜边AB 上的一点，以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ，若AC ＝1，BC ＝3，则⊙O 的半径为（）（A ）21 （B ）32 （C ）43 （D ）5450．（武汉市）已知：如图，E 是相交两圆⊙M 和⊙O 的一个交点，且ME ⊥NE ，AB 为外公切线，切点分别为A 、B ，连结AE 、BE ．则∠AEB 的度数为（）（A ）145° （B ）140° （C ）135° （D ）130° 二、填空题1．（北京市东城区）如图，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D 是优弧上的一点，已知∠BAC ＝80，那么∠BDC ＝__________度．2．（北京市东城区）在Rt △ABC 中，∠C ＝90，A Ｂ＝3，BC ＝1，以AC 所在直线为轴旋转一周，所得圆锥的侧面展开图的面积是__________．3．（北京市海淀区）如果圆锥母线长为6厘米，那么这个圆锥的侧面积是_______平方厘米4．（北京市海淀区）一种圆状包装的保鲜膜，如图所示，其规格为“20厘米×60米”，经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为厘米、厘米，则该种保鲜膜的厚度约为_________厘米（π取，结果保留两位有效数字）．5．（上海市）两个点O 为圆心的同心圆中，大圆的弦AB 与小圆相切，如果AB 的长为24，大圆的半径OA 为13，那么小圆的半径为___________． 6．（天津市）已知⊙O 中，两弦AB 与CD 相交于点E ，若E 为AB 的中点，CE ∶ED ＝1∶4，AB ＝4，则CD的长等于___________．7．（重庆市）如图，AB 是⊙O 的直径，四边形ABCD 内接于⊙O ，，，的度数比为3∶2∶4，MN是⊙O 的切线，C 是切点，则∠BCM 的度数为___________．第7题第8题第9题8．（重庆市）如图，P 是⊙O 的直径AB 延长线上一点，PC 切⊙O 于点C ，PC ＝6，BC ∶AC ＝1∶2，则AB 的长为___________．9．9．（重庆市）如图，四边形ABCD 内接于⊙O ，AD ∥BC ，＝，若AD ＝4，BC ＝6，则四边形ABCD 的面积为__________．10．(山西省)若一个圆柱的侧面积等于两底面积的和，则它的高h 与底面半径r 的大小关系是__________． 11．（沈阳市）要用圆形铁片截出边长为4厘米的正方形铁片，则选用的圆形铁片的直径最小要___________厘米．12．（沈阳市）圆内两条弦AB 和CD 相交于P 点，AB 长为7，AB 把CD 分成两部分的线段长分别为2和6，那么＝__________．13．（沈阳市）△ABC 是半径为2厘米的圆内接三角形，若BC ＝23厘米，则∠A 的度数为________． 14．（沈阳市）如图，已知OA 、OB 是⊙O 的半径，且OA ＝5，∠AOB ＝15，AC ⊥OB 于C ，则图中阴影部分的面积（结果保留π）S ＝_________．第14题第15题15．（哈尔滨市）如图，圆内接正六边形ABCDEF 中，AC 、BF 交于点M ．则ABM S △∶AFM S △＝_________． 16．(哈尔滨市)两圆外离，圆心距为25厘米，两圆周长分别为15π厘米和10π厘米．则其内公切线和连心线所夹的锐角等于__________度．17．（哈尔滨市）将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周，所得圆柱体的表面积为_________平方厘米．18．（陕西省）如图，在⊙O 的内接四边形ABCD 中，∠BCD ＝130，则∠BOD 的度数是________． 19．（陕西省）已知⊙O 的半径为4厘米，以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积，则这个小圆的半径是______厘米．20．（陕西省）如图，⊙O 1的半径O 1A 是⊙O 2的直径，C 是⊙O 1上的一点，O 1C 交⊙O2于点B ．若⊙O1的半径等于5厘米，的长等于⊙O 1周长的101，则的长是_________．21．（甘肃省）正三角形的内切圆与外接圆面积之比为_________．22．（甘肃省）如图，AB ＝8，AC ＝6，以AC 和BC 为直径作半圆，两圆的公切线MN 与AB 的延长线交于D ，则BD 的长为_________．23．（宁夏回族自治区）圆锥的母线长为5厘米，高为3厘米，在它的侧面展开图中，扇形的圆心角是_________度．24．（南京市）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF ＝2，AF ＝3，则EF 的长是_________．25．（福州市）在⊙O 中，直径AB ＝4厘米，弦CD ⊥AB 于E ，OE ＝3，则弦CD 的长为__________厘米． 26．（福州市）若圆锥底面的直径为厘米，线线长为5厘米，则它的侧面积为__________平方厘米（结果保留π）．27．（河南省）如图，AB 为⊙O 的直径，P 点在AB 的延长线上，PM 切⊙O 于M 点．若OA ＝a ，PM ＝3a ，那么△PMB 的周长的__________．28．（长沙市）在半径9厘米的圆中，60的圆心角所对的弧长为__________厘米． 29．（四川省）扇形的圆心角为120，弧长为6π厘米，那么这个扇形的面积为_________．30．（贵阳市）如果圆O 的直径为10厘米，弦AB 的长为6厘米，那么弦AB 的弦心距等于________厘米． 31．（贵阳市）某种商品的商标图案如图所求（阴影部分），已知菱形ABCD 的边长为4，∠A ＝60，是以A 为圆心，AB 长为半径的弧，是以B 为圆心，BC 长为半径的弧，则该商标图案的面积为_________．32．（云南省）已知，一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周，所得圆锥的表面积是__________．33．（新疆乌鲁木齐）正六边形的边心距与半径的比值为_________．34．（新疆乌鲁木齐）如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OA 上一点，以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切，则半圆1O 的半径为__________．35．（成都市）如图，PA 、PB 与⊙O 分别相切于点A 、点B ，AC 是⊙O 的直径，PC 交⊙O 于点D ．已知∠APB ＝60，AC ＝2，那么CD 的长为________．36．（苏州市）底面半径为2厘米，高为3厘米的圆柱的体积为_________立方厘米（结果保留π）． 37．（扬州市）边长为2厘米的正六边形的外接圆半径是________厘米，内切圆半径是________厘米（结果保留根号）．38．（绍兴市）如图，PT 是⊙O 的切线，T 为切点，PB 是⊙O 的割线交⊙O 于A 、B 两点，交弦CD 于点M ，已知：CM ＝10，MD ＝2，PA ＝MB ＝4，则PT 的长等于__________．39．（温州市）如图，扇形OAB 中，∠AOB ＝90，半径OA ＝1，C 是线段AB 的中点，CD ∥OA ，交于点D ，则CD ＝________．40．（常州市）已知扇形的圆心角为150，它所对的弧长为20π厘米，则扇形的半径是________厘米，扇形的面积是__________平方厘米．41．（常州市）如图，AB 是⊙O 直径，CE 切⊙O 于点C ，CD ⊥AB ，D 为垂足，AB ＝12厘米，∠B ＝30，则∠ECB ＝__________；CD ＝_________厘米．42．（常州市）如图，DE 是⊙O 直径，弦AB ⊥DE ，垂足为C ，若AB ＝6，CE ＝1，则CD ＝________，OC ＝_________．43．（常州市）如果把人的头顶和脚底分别看作一个点，把地球赤道作一个圆，那么身高压2米的汤姆沿着地球赤道环道环行一周，他的头顶比脚底多行________米．44．（海南省）已知：⊙O 的半径为1，M 为⊙O 外的一点，MA 切⊙O 于点A ，MA ＝1．若AB 是⊙O 的弦，且AB ＝2，则MB 的长度为_________．45．（武汉市）如果圆的半径为4厘米，那么它的周长为__________厘米．三、解答题：1．（苏州市）已知：如图，△ABC 内接于⊙O ，过点B 作⊙O 的切线，交CA 的延长线于点E ，∠EBC ＝2∠C ．①求证：AB ＝AC ； ②若tan ∠ABE ＝21，（ⅰ）求BCAB的值；（ⅱ）求当AC ＝2时，AE 的长．2．（广州市）如图，PA 为⊙O 的切线，A 为切点，⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ，PA ＝8cm ，PB ＝4cm ，求⊙O 的半径．3．（河北省）已知：如图，BC 是⊙O 的直径，AC 切⊙O 于点C ，AB 交⊙O 于点D ，若AD ︰DB ＝2︰3，AC ＝10，求s4．（北京市海淀区）如图，PC 为⊙O 的切线，C 为切点，PAB 是过O 的割线，CD ⊥AB 于点D ，若tan B ＝21，PC ＝10cm ，求三角形BCD 的面积．5．（宁夏回族自治区）如图，在两个半圆中，大圆的弦MN 与小圆相切，D 为切点，且MN ∥AB ，MN ＝a ，ON 、CD 分别为两圆的半径，求阴影部分的面积．6．（四川省）已知，如图，以△ABC 的边AB 作直径的⊙O ，分别并AC 、BC 于点D 、E ，弦FG ∥AB ，S △CDE ︰S △ABC ＝1︰4，DE ＝5cm ，FG ＝8cm ，求梯形AFGB 的面积．7．（贵阳市）如图所示：PA 为⊙O 的切线，A 为切点，PBC 是过点O 的割线，PA ＝10，PB ＝5，求：（1）⊙O 的面积（注：用含π的式子表示）；（2）cos ∠BAP 的值．参考答案一、选择题1．B 2．B 3．D 4．D 5．C 6．C 7．A 8．C 9．D 10．B 11．A 12．B 13．C 14．D 15．D16．A 17．B 18．C 19．C 20．B 21．C 22．A 23．A 24．B 25．B 26．D 27．D 28．C 29．A30．B 31．A 32．A 33．B 34．C 35．A 36．D 37．B 38．B 39．B 40．B 41．C 42．D 43．A44．C 45．B 46．C 47．A 48．B 49．C 50．C二、填空题1．50 2．2π 3．18π 4．4105.7-⨯ 5．5 6．5 7．30° 8．9 9．25 10．h ＝r 11．42 12．3或4 13．60°或120° 14．8252425-π 15．1:2 16．30 17．80π或120π 18．100° 19．22 20．π 21．1:4 22．1 23．288 24．4 25．2 26．15π 27．()a 23+ 28．3π 29．27π平方厘米 30．4 31．34 32．24π平方厘米或36π平方厘米 33．23 34．4 35．774 36．12π 37．2，3 38．132 39．213- 40．24，240π 41．60°，33 42．9，4 43．4π 44．1或5 45．8π三、解答题：1．（1）∵ BE 切⊙O 于点B ，∴ ∠ABE ＝∠C ． ∵ ∠EBC ＝2∠C ，即 ∠ABE ＋∠ABC ＝2∠C ，∴ ∠C ＋∠ABC ＝2∠C ，∴ ∠ABC ＝∠C ，∴ AB ＝AC ．（2）①连结AO ，交BC 于点F ，∵ AB ＝AC ，∴ ＝，∴ AO ⊥BC 且BF ＝FC ．在Rt △ABF 中，BFAF ＝tan ∠ABF ，又 tan ∠ABF ＝tan C ＝tan ∠ABE ＝21，∴ BF AF ＝21， ∴ AF ＝21BF ． ∴ AB ＝22BF AF +＝2221BF BF +⎪⎭⎫ ⎝⎛＝25BF ． ∴ 452==BF AB BC AB ． ②在△EBA 与△ECB 中，∵ ∠E ＝∠E ，∠EBA ＝∠ECB ，∴ △EBA ∽△ECB ．∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2，解之，得516EA 2＝EA ·（EA ＋AC ），又EA ≠0， ∴ 511EA ＝AC ，EA ＝115×2＝1110． 2．设⊙的半径为r ，由切割线定理，得PA 2＝PB ·PC ，∴ 82＝4（4＋2r ），解得r ＝6（cm ）．即⊙O 的半径为6cm ．3．由已知AD ︰DB ＝2︰3，可设AD ＝2k ，DB ＝3k （k ＞0）．∵ AC 切⊙O 于点C ，线段ADB 为⊙O 的割线，∴ AC 2＝AD ·AB ，∵ AB ＝AD ＋DB ＝2k ＋3k ＝5k ，∴ 102＝2k ×5k ，∴ k 2＝10，∵ k ＞0，∴ k ＝10．∴ AB ＝5k ＝510．∵ AC 切⊙O 于C ，BC 为⊙O 的直径，∴ AC ⊥BC ．在Rt △ACB 中，sin B ＝51010510==AB AC ． 4．解法一：连结AC ．∵ AB 是⊙O 的直径，点C 在⊙O 上，∴ ∠ACB ＝90°．CD ⊥AB 于点D ，∴ ∠ADC ＝∠BDC ＝90°，∠2＝90°－∠BAC ＝∠B ． ∵ tan B ＝21， ∴ tan ∠2＝21． ∴ CB AC DB CD CD AD ===21．设AD ＝x （x ＞0），CD ＝2x ，DB ＝4x ，AB ＝5x ．∵ PC 切⊙O 于点C ，点B 在⊙O 上，∴ ∠1＝∠B ．∵ ∠P ＝∠P ，∴ △PAC ∽△PCB ，∴ 21==CB AC PC PA ． ∵ PC ＝10，∴ PA ＝5，∵ PC 切⊙O 于点C ，PAB 是⊙O 的割线，∵ PC 2＝PA ·PB ，∴ 102＝5（5＋5 x ）．解得x ＝3．∴ AD ＝3，CD ＝6，DB ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．解法二：同解法一，由△PAC ∽△PCB ，得21==CB AC PC PA ． ∵ PA ＝10，∴ PB ＝20．由切割线定理，得PC 2＝PA ·PB ． ∴ PA ＝201022-PB PC ＝5，∴ AB ＝PB －PA ＝15， ∵ AD ＋DB ＝x ＋4x ＝15，解得x ＝3，∴ CD ＝2x ＝6，DB ＝4x ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．5．解：如图取MN 的中点E ，连结OE ，∴ OE ⊥MN ，EN ＝21MN ＝21a ．在四边形EOCD 中，∵ CO ⊥DE ，OE ⊥DE ，DE ∥CO ，∴ 四边形EOCD 为矩形．∴ OE ＝CD ，在Rt △NOE 中，NO 2－OE 2＝EN 2＝22⎪⎭⎫ ⎝⎛a ． ∴ S 阴影＝21π（NO 2－OE 2）＝21π·22⎪⎭⎫ ⎝⎛a ＝28πa ．6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ．∴ 2⎪⎭⎫ ⎝⎛=∆∆AB DE S S ABC CDE ∴ AB DE ＝ABCCDE S S ∆∆＝41＝21，即215=AB ，解得 AB ＝10（cm ），作OM ⊥FG ，垂足为M ，则FM ＝21FG ＝21×8＝4（cm ），连结OF ，∵ OA ＝21AB ＝21×10＝5（cm ）．∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）． ∴ 梯形AFGB 的面积＝2FGAB +·OM ＝2810⨯×3＝27（cm 2）．7．⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(PA 2＝PB ·PC PC ＝20半径为圆面积为π4225（或π）（平方单位）． ⎭⎬⎫∠=∠∠=∠P P BAP C )2(△ACP ∽△BAPPB PA AB AC=12=AB AC．解法一：设AB ＝x ，AC ＝2x ，BC 为⊙O 的直径∠CAB ＝90°，则 BC ＝5x ． ∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==x x BC AC解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65， ∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC。