第十二章 波动光学2
第12章波动光学

第12章 波动光学一、选择题1. 如T12-1-1图所示,折射率为2n 、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为1n 和3n ,已知321n n n <<.若波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束①与②的光程差是:[ ] (A) e n 22 (B) λ2122-e n(C) λ-22n (D) 2222n e n λ-2. 如T12-1-2图所示,1S 、2S 是两个相干光源,他们到P 点的距离分别为 1r 和 2r .路径P S 1垂直穿过一块厚度为1t ,折射率为1n 的一种介质;路径P S 2垂直穿过一块厚度为2t 的另一介质;其余部分可看作真空.这两条光路的光程差等于: [ ] (A) )()(111222t n r t n r +-+(B) ])1([])1([121222t n r t n r -+--+ (C) )()(111222t n r t n r ---(D) 1122t n t n -3. 在相同的时间内,一束波长为的单色光在空气和在玻璃中[ ] (A) 传播的路程相等,走过的光程相等(B) 传播的路程相等,走过的光程不相等 (C) 传播的路程不相等,走过的光程相等 (D) 传播的路程不相等,走过的光程不相等4. 频率为f 的单色光在折射率为n 的媒质中的波速为v , 则在此媒质中传播距离为l 后, 其光振动的相位改变了 [ ] (A)vlfπ2 (B)lfv π2 (C)vnlfπ2 (D)π2lfv5. 波长为λ的单色光在折射率为n 的媒质中由a 点传到b 点相位改变了π, 则光从a 点到b 点的几何路程为: [ ] (A)n2λ(B)2nλ (C)2λ(D) λn6. 真空中波长为λ的单色光, 在折射率为n 的均匀透明媒质中从a 点沿某一路径传到b 点.若将此路径的长度记为l , a 、b 两点的相位差记为∆ϕ , 则λe1n 2n 3n )1()2(T12-1-1图1S S 1t 1r 1n 2t 2n 2r PT12-1-2图[ ] (A) π3,23=∆=ϕλl (B) π3,23n n l =∆=ϕλ(C) π3,23=∆=ϕλn l (D) π3,23n n l =∆=ϕλ7. 两束平面平行相干光, 每一束都以强度I 照射某一表面, 彼此同相地并合在一起, 则合光照在该表面的强度为 [ ] (A) I(B) 2I (C) 4I (D)I 28. 相干光是指[ ] (A) 振动方向相同、频率相同、相位差恒定的两束光(B) 振动方向相互垂直、频率相同、相位差不变的两束光 (C) 同一发光体上不同部份发出的光 (D) 两个一般的独立光源发出的光9. 两个独立的白炽光源发出的两条光线, 各以强度I 照射某一表面.如果这两条光线同时照射此表面, 则合光照在该表面的强度为 [ ] (A) I(B) 2I (C) 4I (D) 8I10. 相干光波的条件是振动频率相同、相位相同或相位差恒定以及 [ ] (A) 传播方向相同 (B) 振幅相同(C) 振动方向相同 (D) 位置相同11. 用厚度为d 、折射率分别为n 1和n 2 (n 1<n 2)的两片透明介质分别盖住杨氏双缝实验中的上下两缝, 若入射光的波长为λ, 此时屏上原来的中央明纹处被第三级明纹所占据, 则该媒质的厚度为 [ ] (A) λ3(B)123n n -λ(C) λ2(D) 122n n -λ12. 一束波长为 λ 的光线垂直投射到一双缝上, 在屏上形成明、暗相间的干涉条纹, 则下列光程差中对应于最低级次暗纹的是 [ ] (A) λ2(B)λ23 (C)λ(D)2λ13. 在杨氏双缝实验中, 若用白光作光源, 干涉条纹的情况为 [ ] (A) 中央明纹是白色的(B) 红光条纹较密 (C) 紫光条纹间距较大(D) 干涉条纹为白色T12-1-11图14. 在双缝干涉实验中,屏幕E 上的P 点处是明条纹.若将缝2S 盖住,并在21S S 连线的垂直平面出放一反射镜M ,如图所示,则此时 [ ] (A) P 点处仍为明条纹(B) P 点处为暗条纹(C) 不能确定P 点处是明条纹还是暗条纹 (D) 无干涉条纹15. 在双缝干涉实验中,入射光的波长为,用玻璃纸遮住双缝中的一个缝,若玻璃纸中光程比相同厚度的空气的光程大 2.5,则屏上原来的明纹处 [ ] (A) 仍为明条纹(B) 变为暗条纹(C) 既非明条纹也非暗条纹(D) 无法确定是明纹还是暗纹16. 把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d , 双缝到屏的距离为D (d D >>),所用单色光在真空中的波长为,则屏上干涉条纹中相邻的明纹之间的距离是: [ ] (A)ndDλ (B)dDn λ (C)nDd λ (D)ndD 2λ17. 如T12-1-17图所示,在杨氏双缝实验中, 若用一片厚度为d 1的透光云母片将双缝装置中的上面一个缝挡住; 再用一片厚度为d 2的透光云母片将下面一个缝挡住, 两云母片的折射率均为n , d 1>d 2, 干涉条纹的变化情况是[ ] (A) 条纹间距减小(B) 条纹间距增大 (C) 整个条纹向上移动(D) 整个条纹向下移动18. 在杨氏双缝实验中, 若用一片能透光的云母片将双缝装置中的上面一个缝盖住, 干涉条纹的变化情况是 [ ] (A) 条纹间距增大(B) 整个干涉条纹将向上移动 (C) 条纹间距减小(D) 整个干涉条纹将向下移动19. 当单色光垂直照射杨氏双缝时, 屏上可观察到明暗交替的干涉条纹.若减小 [ ] (A) 缝屏间距离, 则条纹间距不变 (B) 双缝间距离, 则条纹间距变小 (C) 入射光强度, 则条纹间距不变 (D) 入射光波长, 则条纹间距不变20. 在保持入射光波长和缝屏距离不变的情况下, 将杨氏双缝的缝距减小, 则 [ ] (A) 干涉条纹宽度将变大 (B) 干涉条纹宽度将变小(C) 干涉条纹宽度将保持不变 (D) 给定区域内干涉条纹数目将增加21. 有两个几何形状完全相同的劈形膜:一个由空气中的玻璃形成玻璃劈形膜; 一个由玻璃中的空气形成空劈形膜.当用相同的单色光分别垂直照射它们时, 从入射光方向观察到干涉条纹间距较大的是1S 2SMT12-1-14图T12-1-17图T12-1-18图[ ] (A) 玻璃劈形膜(B) 空气劈形膜(C) 两劈形膜干涉条纹间距相同(D) 已知条件不够, 难以判定22. 用波长可以连续改变的单色光垂直照射一劈形膜, 如果波长逐渐变小, 干涉条纹的变化情况为[ ] (A) 明纹间距逐渐减小, 并背离劈棱移动(B) 明纹间距逐渐变小, 并向劈棱移动 (C) 明纹间距逐渐变大, 并向劈棱移动 (D) 明纹间距逐渐变大, 并背向劈棱移动23. 在单色光垂直入射的劈形膜干涉实验中, 若慢慢地减小劈形膜夹角, 则从入射光方向可以察到干涉条纹的变化情况为 [ ] (A) 条纹间距减小(B) 给定区域内条纹数目增加 (C) 条纹间距增大(D) 观察不到干涉条纹有什么变化24. 两块平玻璃板构成空气劈尖,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的 [ ] (A) 间隔变小,并向棱边方向平移(B) 间隔变大,并向远离棱边方向平移 (C) 间隔不变,向棱边方向平移(D) 间隔变小,并向远离棱边方向平移25. 检验滚珠大小的干涉试装置示意如T12-1-25(a)图.S 为光源,L 为汇聚透镜,M 为半透半反镜.在平晶T 1、T 2之间放置A 、B 、C 三个滚珠,其中A 为标准,直径为0d .用波长为的单色光垂直照射平晶,在M 上方观察时观察到等厚条纹如T12-1-25(b)图所示,轻压C 端,条纹间距变大,则B 珠的直径1d 、C 珠的直径2d 与0d 的关系分别为:[ ] (A) ,01λ+=d d λ302+=d d (B) ,01λ-=d d λ302-=d d(C) ,201λ+=d d 2302λ+=d d (D) ,201λ-=d d 2302λ-=d dT12-1-23图S f 45M1T 2T L B•C AT12-1-25(a)图 T12-1-25(b)图26. 如T12-1-26(a)图所示,一光学平板玻璃A 与待测工件B 之间形成空气劈尖,用波长=500nm(1nm = 10-9m)的单色光垂直照射.看到的反射光的干涉条纹如T12-1-26(b)图所示.有些条纹弯曲部分的顶点恰好与其右边条纹的直线部分的切线相切.则工件的上表面缺陷是 [ ] (A) 不平处为凸起纹,最大高度为500nm(B) 不平处为凸起纹,最大高度为250nm (C) 不平处为凹槽,最大深度为500nm (D) 不平处为凹槽,最大深度为250nm27. 设牛顿环干涉装置的平凸透镜可以在垂直于平玻璃的方向上下移动, 当透镜向上平移(即离开玻璃板)时, 从入射光方向可观察到干涉条纹的变化情况是 [ ] (A) 环纹向边缘扩散, 环纹数目不变(B) 环纹向边缘扩散, 环纹数目增加 (C) 环纹向中心靠拢, 环纹数目不变(D) 环纹向中心靠拢, 环纹数目减少28. 牛顿环实验中, 透射光的干涉情况是 [ ] (A) 中心暗斑, 条纹为内密外疏的同心圆环(B) 中心暗斑, 条纹为内疏外密的同心圆环 (C) 中心亮斑, 条纹为内密外疏的同心圆环 (D) 中心亮斑, 条纹为内疏外密的同心圆环29. 在牛顿环装置中, 若对平凸透镜的平面垂直向下施加压力(平凸透镜的平面始终保持与玻璃片平行), 则牛顿环[ ] (A) 向中心收缩, 中心时为暗斑, 时为明斑, 明暗交替变化(B) 向中心收缩, 中心处始终为暗斑 (C) 向外扩张, 中心处始终为暗斑 (D) 向中心收缩, 中心处始终为明斑30. 关于光的干涉,下面说法中唯一正确的是[ ] (A) 在杨氏双缝干涉图样中, 相邻的明条纹与暗条纹间对应的光程差为2λ (B) 在劈形膜的等厚干涉图样中, 相邻的明条纹与暗条纹间对应的厚度差为2λ (C) 当空气劈形膜的下表面往下平移2λ时, 劈形膜上下表面两束反射光的光程差将增加2λ (D) 牛顿干涉圆环属于分波振面法干涉T12-1-26(a)图T12-1-26(b)图T12-1-29图31. 根据第k 级牛顿环的半径r k 、第k 级牛顿环所对应的空气膜厚d k 和凸透镜之凸面半径R 的关系式Rr d k k 22=可知,离开环心越远的条纹[ ] (A) 对应的光程差越大,故环越密(B) 对应的光程差越小,故环越密(C) 对应的光程差增加越快,故环越密(D) 对应的光程差增加越慢,故环越密32. 如果用半圆柱形聚光透镜代替牛顿环实验中的平凸透镜, 放在平玻璃上, 则干涉条纹的形状 [ ] (A) 为内疏外密的圆环(B) 为等间距圆环形条纹 (C) 为等间距平行直条纹(D)为以接触线为中心,两侧对称分布,明暗相间, 内疏外密的一组平行直条纹33. 劈尖膜干涉条纹是等间距的,而牛顿环干涉条纹的间距是不相等的.这是因为: [ ] (A) 牛顿环的条纹是环形的(B) 劈尖条纹是直线形的 (C) 平凸透镜曲面上各点的斜率不等(D) 各级条纹对应膜的厚度不等34. 如T12-1-34图所示,一束平行单色光垂直照射到薄膜上,经上、下两表面反射的光束发生干涉.若薄膜的厚度为e ,且n 1 < n 2 > n 3,λ为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为: [ ] (A)e n n 12π2⋅λ(B)ππ421+⋅e n n λ (C)ππ412+⋅e n n λ (D)e n n 12π4⋅λ35. 用白光垂直照射厚度e = 350nm 的薄膜,若膜的折射率n 2 = 1.4 ,薄膜上面的媒质折射率为n 1,薄膜下面的媒质折射率为n 3,且n 1 < n 2 < n 3.则反射光中可看到的加强光的波长为: [ ] (A) 450nm(B) 490nm (C) 690nm(D) 553.3nm36. 已知牛顿环两两相邻条纹间的距离不等.如果要使其相等, 以下所采取的措施中不可行的是[ ] (A) 将透镜磨成半圆柱形(B) 将透镜磨成圆锥形 (C) 将透镜磨成三棱柱形(D) 将透镜磨成棱柱形37. 欲使液体(n > 1)劈形膜的干涉条纹间距增大,可采取的措施是: [ ] (A) 增大劈形膜夹角(B) 增大棱边长度(C) 换用波长较短的入射光(D) 换用折射率较小的液体T12-1-32图38. 若用波长为λ的单色光照射迈克尔逊干涉仪,并在迈克尔逊干涉仪的一条光路中放入厚度为l 、折射率为n 的透明薄片.放入后,干涉仪两条光路之间的光程差改变量为 [ ] (A) (n -1)l (B) nl(C) 2nl (D) 2(n -1)l39. 若用波长为λ的单色光照射迈克尔逊干涉仪, 并在迈克尔逊干涉仪的一条光路中放入一厚度为l 、折射率为n 的透明薄片, 则可观察到某处的干涉条纹移动的条数为 [ ] (A)λln )1(4-(B)λln(C)λln )1(2-(D)λln )1(-40. 如图所示,用波长为λ的单色光照射双缝干涉实验装置,若将一折射率为n 、劈角为α的透明劈尖b 插入光线2中,则当劈尖b 缓慢向上移动时(只遮住S 2),屏C 上的干涉条纹 [ ] (A) 间隔变大,向下移动(B) 间隔变小,向上移动(C) 间隔不变,向下移动 (D) 间隔不变,向上移动41. 根据惠更斯--菲涅耳原理, 若已知光在某时刻的波阵面为S , 则S 的前方某点P 的光强度取决于波阵面S 上所有面积元发出的子波各自传到P 点的 [ ] (A) 振动振幅之和 (B) 振动振幅之和的平方(C) 光强之和 (D) 振动的相干叠加42. 无线电波能绕过建筑物, 而可见光波不能绕过建筑物.这是因为[ ] (A) 无线电波是电磁波 (B) 光是直线传播的 (C) 无线电波是球面波 (D) 光波的波长比无线电波的波长小得多43. 光波的衍射现象没有显著, 这是由于 [ ] (A) 光波是电磁波, 声波是机械波(B) 光波传播速度比声波大 (C) 光是有颜色的(D) 光的波长比声波小得多44. 波长为λ 的单色光垂直入射在缝宽为a 的单缝上, 缝后紧靠着焦距为f 的薄凸透镜, 屏置于透镜的焦平面上, 若整个实验装置浸入折射率为n 的液体中, 则在屏上出现的中央明纹宽度为 [ ] (A)na f λ (B)na f λ (C) naf λ2(D) anf λ245. 在单缝衍射中, 若屏上的P 点满足a sin ϕ = 5/2则该点为 [ ] (A) 第二级暗纹(B) 第五级暗纹 (C) 第二级明纹(D) 第五级明纹S 1S 2S OCb12λT12-1-40图T12-1-44图46. 在夫琅和费单缝衍射实验中, 欲使中央亮纹宽度增加, 可采取的方法是 [ ] (A) 换用长焦距的透镜 (B) 换用波长较短的入射光(C) 增大单缝宽度 (D) 将实验装置浸入水中47. 夫琅和费单缝衍射图样的特点是[ ] (A) 各级亮条纹亮度相同(B) 各级暗条纹间距不等(C) 中央亮条纹宽度两倍于其它亮条纹宽度(D) 当用白光照射时, 中央亮纹两侧为由红到紫的彩色条纹48. 在夫琅和费衍射实验中,对给定的入射单色光,当缝宽变小时,除中央亮纹的中心位置不变,各衍射条纹[ ] (A) 对应的衍射角变小 (B) 对应的衍射角变大(C) 对应的衍射角不变 (D) 光强也不变49. 一束波长为λ的平行单色光垂直入射到一单缝AB 上,装置如T12-1-49图所示,在屏幕E 上形成衍射图样.如果P 是中央亮纹一侧第一个暗纹所在的位置,则BC 的长度为 [ ] (A)λ(B)2λ(C)23λ(D) λ250. 在单缝夫琅和费衍射实验中,若增大缝宽,其它条件不变,则中央明纹 [ ] (A) 宽度变小 (B) 宽度变大(C) 宽度不变,且中心强度也不变(D) 宽度不变,但中心强度增大51. 在如T12-1-51图所示的在单缝夫琅和费衍射装置中,设中央明纹的衍射角范围很小.若单缝a 变为原来的23,同时使入射的单色光的波长变为原来的43,则屏幕E 上的单缝衍射条纹中央明纹的宽度△x 将变为原来的 [ ] (A)43倍 (B)32倍 (C)89倍 (D)21倍52. 一单缝夫琅和费衍射实验装置如T12-1-52图所示,L 为透镜,E 为屏幕;当把单缝向右稍微移动一点时,衍射图样将[ ] (A) 向上平移 (B) 向下平移(C) 不动 (D) 消失PT12-1-49图T12-1-51图λλ53. 在T12-1-53图所示的单缝夫琅和费衍射实验中,)方向稍微平移,则 [ ] (A) 衍射条纹移动,条纹宽度不变(B) 衍射条纹移动,条纹宽度变动(C) 衍射条纹中心不动,条纹变宽 (D) 衍射条纹不动,条纹宽度不变54. 在T12-1-54图所示的单缝夫琅和费衍射实验中,将单缝宽度 a 稍稍变宽,同时使单缝沿x 轴正向作微小移动,则屏幕E 的中央衍射条纹将[ ] (A) 变窄,同时上移 (B) 变窄,同时下移(C) 变窄,不移动 (D) 变宽,同时上移55. 在T12-1-55图所示的单缝夫琅和费衍射实验中,将单缝宽度a 稍稍变窄,同时使会聚透镜L 2沿x 轴正方向作微小移动,则屏幕E 上的中央衍射条纹将[ ] (A) 变宽,同时上移 (B) 变宽,同时下移(C) 变宽,不移动 (D) 变窄,同时上移56. 一衍射光栅由宽300 nm 、中心间距为900 nm 的缝构成, 当波长为600 nm 的光垂直照射时, 屏幕上最多能观察到的亮条纹数为:[ ] (A) 2条 (B) 3条 (C) 4条 (D) 5条57. 白光垂直照射到每厘米有5000条刻痕的光栅上, 若在衍射角ϕ = 30°处能看到某一波长的光谱线, 则该光谱线所属的级次为[ ] (A) 1 (B) 2 (C) 3 (D) 458. 波长为λ的单色光垂直入射于光栅常数为d 、缝宽a 、 总缝数为N 的光栅上.取0=k ,1±,2±,……,则决定出现主级大的衍射角θ的公式可写成 [ ] (A) λθk Na =sin (B) λθk a =sin(C) λθk Nd =sin (D) λθk d =sin59. 一衍射光栅对某一定波长的垂直入射光,在屏幕上只能出现零级和一级主极大,欲使屏幕出现更高级次的主极大,应该[ ] (A) 换一个光栅常数较小的光栅 (B) 换一个光栅常数较大光栅(C) 将光轴向靠近屏幕的方向移动 (D) 将光轴向远离屏幕的方向移动T12-1-53图T12-1-54图T12-1-55图60. 为测量一单色光的波长,下列方法中最准确的是( )实验. [ ] (A) 双缝干涉 (B) 牛顿环干涉 (C) 单缝衍射 (D) 光栅衍射 61. 一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是[ ] (A) 紫光 (B) 绿光 (C) 黄光 (D) 红光62. 在光栅光谱中,假设所有的偶数极次的主级大都恰好在每缝衍射的暗纹方向上,因而实际上不出现,那么光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系 [ ] (A) a = b (B) a =2b (C) a = 3b (D) b = 2a63. 若用衍射光栅准确测量一单色可见光的波长,在下列各种光栅常数的光栅中选那一种最好?[ ] (A) 1100.1-⨯mm(B) 1100.5-⨯mm (C) 2100.1-⨯mm(D) 3100.1-⨯mm64. 在一光栅衍射实验中,如果光栅、透镜均与屏幕平行,则当入射的平行单色光从垂直于光栅平面入射变为斜入射时,能观察到的光谱线的最高级数k [ ] (A) 变小 (B) 变大 (C) 不变 (D) 改变无法确定65. 在一光栅衍射实验中,若衍射光栅单位长度上的刻痕数越多, 则在入射光波长一定的情况下, 光栅的[ ] (A) 光栅常数越小 (B) 衍射图样中亮纹亮度越小 (C) 衍射图样中亮纹间距越小 (D) 同级亮纹的衍射角越小66. 以平行可见光(400nm ~700nm)照射光栅, 光栅的第一级光谱与第二级光谱将会出现什么现象?[ ] (A) 在光栅常数取一定值时, 第一级与第二级光谱会重叠起来(B) 不论光栅常数如何, 第一级与第二级光谱都会重合 (C) 不论光栅常数如何, 第一级与第二级光谱都不会重合(D) 对于不同光栅常数的光栅, 第一级与第二级光谱的重叠范围相同67. 用单色光照射光栅,屏幕上能出现的衍射条纹最高级次是有限的.为了得到更高衍射级次的条纹,应采用的方法是: [ ] (A) 改用波长更长的单色光 (B) 将单色光斜入射(C) 将单色光垂直入射 (D) 将实验从光密媒质改为光疏媒质68. 已知一衍射光栅上每一透光狭缝的宽度都为a , 缝间不透明的那一部分宽度为b ;若b = 2a , 当单色光垂直照射该光栅时, 光栅明纹的情况如何(设明纹级数为k )? [ ] (A) 满足k = 2 n 的明条纹消失( n =1、2、...)(B) 满足k = 3 n 的明条纹消失( n =1、2、...) (C) 满足k = 4 n 的明条纹消失( n =1、2、...)69. 用波长为λ的光垂直入射在一光栅上, 发现在衍射角为ϕ 处出现缺级, 则此光栅上缝宽的最小值为 [ ] (A)ϕλsin 2 (B)ϕλsin (C)ϕλsin 2 (D)λϕsin 270. 一束平行光垂直入射在一衍射光栅上, 当光栅常数)(b a +为下列哪种情况时(a 为每条缝的宽度, b 为不透光部分宽度) , k = 3、6、9⋯等级次的主极大均不出现. [ ] (A) a b a 2=+(B) a b a 3=+ (C) a b a 4=+(D) a b a 6=+71. 在双缝衍射实验中,若保持双缝S 1和S 2的中心之间的距离d 不变,而把两条缝的宽度a 略为加宽,则[ ] (A) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变少(B) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变多 (C) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目不变 (D) 单缝衍射的中央主极大变窄,其中所包含的干涉条纹数目变少 72. 一束光垂直入射到一偏振片上, 当偏振片以入射光方向为轴转动时, 发现透射光的光强有变化, 但无全暗情形, 由此可知, 其入射光是 [ ] (A) 自然光 (B) 部分偏振光(C) 全偏振光 (D) 不能确定其偏振状态的光73. 把两块偏振片紧叠在一起放置在一盏灯前, 并使其出射光强变为零.当把其中一块偏振片旋转 180°时, 出射光强的变化情况是 [ ] (A) 光强由零逐渐变为最大(B) 光强由零逐渐增为最大, 然后由最大逐渐变为零 (C) 光强始终为零(D) 光强始终为最大值 74. 自然光通过两个主截面正交的尼科尔棱镜后, 透射光的强度为 [ ] (A) I = 0 (B) 与入射光的强度相同(C) I ≠ 0 (D) 与入射光强度不相同75. 在双缝干涉实验中, 用单色光自然光在屏上形成干涉条纹.若在两缝后面放一块偏振片, 则[ ] (A) 干涉条纹间距不变, 但明条纹亮度加强(B) 干涉条纹间距不变, 但明条纹亮度减弱 (C) 干涉条纹间距变窄, 且明条纹亮度减弱 (D) 无干涉条纹 76. 在双缝干涉实验中, 用单色光自然光在屏上形成干涉条纹.若在两缝后面分别放置一块偏振片, 且两偏振片的偏振化方向相互垂直,则T12-1-72图[ ] (A) 干涉条纹间距不变, 但明条纹亮度加强(B) 干涉条纹间距不变, 但明条纹亮度减弱 (C) 干涉条纹间距变窄, 且明条纹亮度减弱 (D) 无干涉条纹77. 有两种不同的媒质, 第一媒质的折射率为n 1 , 第二媒质的折射率为n 2 ; 当一束自然光从第一媒质入射到第二媒质时, 起偏振角为i 0 ; 当自然光从第二媒质入射到第一媒质时, 起偏振角为i .如果i 0>i , 则光密媒质是[ ] (A) 第一媒质 (B) 第二媒质(C) 不能确定 (D) 两种媒质的折射率相同 78. 设一纸面为入射面.当自然光在各向同性媒质的界面上发生反射和折射时, 若入射角不等于布儒斯特角, 反射光光矢量的振动情况是 [ ] (A) 平行于纸面的振动少于垂直于纸面的振动 (B) 平行于纸面的振动多于垂直于纸面的振动 (C) 只有垂直于纸面的振动(D) 只有平行于纸面的振动79. 自然光以60 的入射角照射到不知其折射率的某一透明介质表面时,反射光为线偏振光,则[ ] (A) 折射光为线偏振光,折射角为(B) 折射光为部分线偏振光,折射角为 (C) 折射光为线偏振光,折射角不能确定 (D) 折射光为部分线偏振光,折射角不能确定80. 自然光以布儒斯特角由空气入射到一玻璃表面上,则反射光是 [ ] (A) 在入射面内振动的完全线偏振光(B) 平行于入射面的振动占优势的部分偏振光 (C) 垂直于入射面的振动的完全偏振光(D) 垂直于入射面的振动占优势的部分偏振光81. 一束自然光由空气射向一块玻璃,[ ] (A) 自然光 (B) 完全偏振光且光矢量的振动方向垂直于入射面 (C) 完全偏振光且光矢量的振动方向平行于入射面 (D) 部分偏振光 82. 强度为I 0的自然光经两个平行放置的偏振片后, 透射光的强度变为I 0/4, 由此可知, 这两块偏振片的偏振化方向夹角是 [ ] (A) 30° (B) 45°(C) 60° (D) 90°0IT12-1-82图4/0I83. 起偏器A 与检偏器B 的偏振化方向相互垂直,偏振片C 位于A 、B 中间且与A 、B 平行,其偏振化方向与A 的偏振化方向成30°夹角. 当强度为I 的自然光垂直射向A 片时,最后的出射光强为[ ] (A) 0 (B) I /2(C) I /8 (D) 以上答案都不对 84. 一束光强为I 0的自然光相继通过三块偏振片P 1、P 2、P 3后,其出射光的强度为I = I 0/8.已知P 1和P 3的偏振化方向相互垂直.若以入射光线为轴转动P 2, 问至少要转过多少角度才能出射光的光强度为零?[ ] (A) 30° (B) 45° (C) 60° (D) 90°85. 光强为I 0的自然光垂直通过两个偏振片,他们的偏振化方向之间的夹角60=α.设偏振片没有吸收,则出射光强I 与入射光强0I 之比为 [ ] (A) 1/4 (B) 3/4 (C) 1/8 (D) 3/886. 两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过.当其中一偏振片慢慢转动时, 投射光强度发生的变化为: [ ] (A) 光强单调增加(B) 光强先增加,后又减小至零 (C) 光强先增加,后减小,再增加(D) 光强先增加,然后减小,再增加,再减小至零87. 如T12-1-87图所示,ABCD 一块方解石的一个截面,AB 垂直于纸面的晶体平面与纸面的交线.光轴的方向在纸面内与AB 成一锐角.一束平行的单色自然光垂直于AB 端面入射.在方解石内折射光分为O 光和e 光,O 光和e 光的 [ ] (A) 传播方向相同,电场强度的振动方向相互垂直(B) 传播方向相同,电场强度的振动方向不相互垂直 (C) 传播方向不同,电场强度的振动方向相互垂直 (D) 传播方向不同,电场强度的振动方向不相互垂直 88. 一束自然光通过一偏振片后,射到一块方解石晶体上,入射角为i 0.关于折射光,下列的说法正确的是 [ ] (A) 是是e 光,偏振化方向垂直于入射面(B) 是e 光,偏振化方向平行于入射面 (C) 是O 光,偏振化方向平行于入射面 (D) 是O 光,偏振化方向垂直于入射面89. 用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则IT12-1-83图ABC IT12-1-84图1P 3P 2PθT12-1-87图C A B D••iT12-1-88图[ ] (A) 干涉条纹的宽度将发生改变(B) 产生红光和蓝光的两套彩色干涉条纹 (C) 干涉条纹的亮度将发生改变 (D) 不产生干涉条纹90. 在扬氏双缝实验中,屏幕中央明纹处的最大光强是I 1.当其中一条缝被盖住时,该位置处的光强变为I 2.则I 1 : I 2为[ ] (A) 1 (B) 2 (C) 3 (D) 4二、选择题1. 如T12-2-1图所示,折射率为2n 、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为1n 和3n ,已知321n n n ><,若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下表面反射的光束(用①与②示意)的光程差是 .2. 真空中波长 λ = 400 nm 的紫光在折射率为 n =1.5 的媒质中从A 点传到B 点时, 光振动的相位改变了5π, 该光从A 到B 所走的光程为 .3. 如T12-2-3图所示,两缝S 1和S 2之间的距离为d ,介质的折射率为n =1,平行单色光斜入射到双缝上,入射角为,则屏幕上P 处,两相干光的光程差为 ________________.4. 如T12-2-4图所示,在双缝干涉实验中SS 1=SS 2用波长为的光照射双缝S 1和S 2,通过空气后在屏幕E 上形成干涉条纹.已知P 点处为第三级明条纹,则S 1和S 2到P 点的光程差为 _________.若将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率n = ____________.5. 两条狭缝相距2mm, 离屏300cm, 用600nm 的光照射时, 干涉条纹的相邻明纹间距为___________mm?6. 将一块很薄的云母片(n = 1.58)覆盖在扬氏双缝实验中的一条缝上,这时屏幕上的中央明纹中心被原来的第7级明纹中心占据.如果入射光的波长 = 550nm, 则该云母片的厚度为___________.λe1n 2n 3n )1()2(T12-2-3图θθλ1S 2S d1r 2r )1(=n 1S 2S PET12-2-4图。
大学物理波动光学课件

麦克斯韦电磁理论:19 世纪中叶,英国物理学 家麦克斯韦建立了电磁 理论,揭示了光是一种 电磁波,为波动光学提 供了更加深入的理论根 据。
在这些重要人物和理论 的推动下,波动光学逐 渐发展成为物理学的一 个重要分支,并在现代 光学、光电子学等领域 中发挥了重要作用。
02 光的干涉
干涉的定义与分类
定义 分类 分波前干涉 分振幅干涉
干涉是指两个或多个相干光波在空间某一点叠加产生加强或减 弱的现象。
根据光源的性质,干涉可分为两类,分别是ห้องสมุดไป่ตู้波前干涉和分振 幅干涉。
波前上不同部位发出的子波在空间某点相遇叠加产生的干涉。 如杨氏双缝干涉、洛埃镜、菲涅尔双面镜以及菲涅尔双棱镜等
。
一束光的振幅分成两部分(或以上)在空间某点相遇时产生的 干涉。例如薄膜干涉、等倾干涉、等厚干涉以及迈克耳孙干涉
波动光学与几何光学的比较
几何光学
几何光学是研究光线在介质中传播的光学分支,它主要关注 光线的方向、成像等,基于光的直线传播和反射、折射定律 。
波动光学与几何光学的区分
波动光学更加关注光的波动性质,如光的干涉、衍射等现象 ,而几何光学则更加关注光线传播的几何特性。两者在研究 对象和方法上存在差异,但彼此相互补充,构成了光学的完 整体系。
VS
马吕斯定律
当一束光线通过两个偏振片时,只有当两 个偏振片的透振方向夹角为特定值时,光 线才能通过。这就是马吕斯定律,它描述 了光线通过偏振片时的透射情况。这两个 定律在光学和物理学中都有着广泛的应用 。
THANKS
感谢观看
分类
根据障碍物的大小和光波波长的相对 关系,衍射可分为菲涅尔衍射和夫琅 禾费衍射。
单缝衍射与双缝衍射
单缝衍射
第12章-2波动光学

对纵波而言, 对纵波而言,由于振动方向和波的传播方 向一致,如果过波的传播方向做很多平面, 向一致,如果过波的传播方向做很多平面, 振动方向总包含在此平面内。 振动方向总包含在此平面内。因此没有振 动的取向问题,即纵波没有偏振性的问题。 动的取向问题,即纵波没有偏振性的问题。 要区别横波还是纵波, 要区别横波还是纵波,主要就是讨论这种 波动是否具有偏振性。 波动是否具有偏振性。
§12-5 光的偏振 1212-5-1 自然光与偏振光
E
H
光是一种电磁波(横波)。电矢量 光是一种电磁波(横波)。电矢量 E与磁矢量 H相 )。 互垂直,它们分别又与电磁波的传播方向垂直。 互垂直,它们分别又与电磁波的传播方向垂直。
光振动: 振动。 光振动:电磁波的 E振动。 光矢量: 矢量。 光矢量:电磁波的 E矢量。
E
v
自然光: 自然光:在垂直于光传播方向上的所有可能方向 上,E 振动的振幅都相等。 振动的振幅都相等。
v
Ey
v
Ex
线偏振光:某一光束只含有一个方向的光振动。 线偏振光:某一光束只含有一个方向的光振动。 振动面:光振动方向与传播方向所确定的那平面。 振动面:光振动方向与传播方向所确定的那平面。
部分偏振光: 部分偏振光:某一方向的光振动比与之相垂直的另 一方向的光振动占优势。 一方向的光振动占优势。
12-5-2 偏振片 马吕斯定律
偏振片:能吸收某一方向的光振动, 偏振片:能吸收某一方向的光振动,而只让与之垂 直方向上的光振动通过的一种透明薄片。 直方向上的光振动通过的一种透明薄片。 偏振化方向: 偏振化方向: 允许通过的光振 动方向。 动方向。
偏振片的用途: 起偏” 偏振片的用途:“起偏”和“检偏” 检偏”
12-07 单缝夫琅禾费衍射
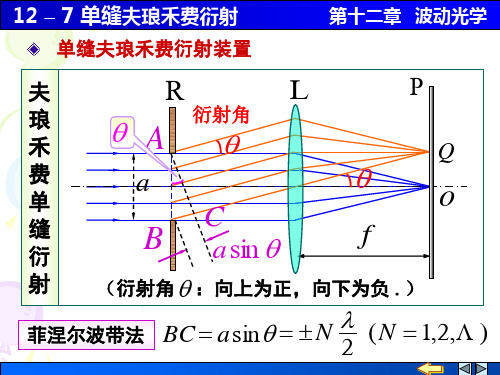
o
a
2
a
3
a
sin
12 – 7 单缝夫琅禾费衍射
S
L1 R
L2
a
第十二章 波动光学
Px
f
x
O
I 当 较小时,sin
x f tan f
3
a
2
a
a
o
a
2
a
3
a
sin
3
a
f
2
a
f
a
f
a
f
2
a
f
3
a
f
x
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
a sin 2k k 干涉相消(暗纹)
发射的微波波长是18mm ,则在它监视范围内的公路长 度大约是多少?
解 将雷达天线输出口看成是发出衍射波的单缝, 衍射波能量主要集中在中央明纹范围内.
d 15m
15 a 0.10m
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
s1
s s2
1 15
2
d 15m
a 0.10m
根据暗纹条件 a sin , arcsin 10.37
a
s2 s s1 d (cot2 cot1)
d[cot(15 ) cot(15 )] 153m
解 AD BC
a(sin sin)
由暗纹条件
a(sin sin) k
(k 1,2,3, )
A
a
D
C
B
arcsin(
k
a
sin )
12 – 7 单缝夫琅禾费衍射
第十二章 波动光学
例3 如图,一雷达位于路边 15m 处,它的射束与
波动光学(二)答案

一. 选择题[ D ]1. 一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是(A) 紫光. (B) 绿光. (C) 黄光. (D) 红光. 注:λθk d =sin 波长越长,偏离中心越远.[ B ]2. 在单缝夫琅禾费衍射实验中,波长为λ的单色光垂直入射在宽度为a =4 λ的单缝上,对应于衍射角为30°的方向,单缝处波阵面可分成的半波带数目为 (A) 2 个. (B) 4 个. (C) 6 个. (D) 8 个.注:24sin λθ⨯=a[ B ]3. 一束平行单色光垂直入射在光栅上,当光栅常数(a + b )为下列哪种情况时(a 代表每条缝的宽度),k =3、6、9 等级次的主极大均不出现?(A) a +b =2 a . (B) a +b =3 a . (C) a +b =4 a . (A) a +b =6 a .注:,'/k k ad=当此比值为整数时,该整数即为第一个缺级. [ C ]4. 在如图所示的单缝夫琅禾费衍射装置中,将单缝宽度a 稍梢变宽,同时使单缝沿y 轴正方向作微小平移(透镜屏幕位置不动),则屏幕C 上的中央衍射条纹将(A) 变窄,同时向上移; (B) 变窄,同时向下移; (C) 变窄,不移动;(D) 变宽,同时向上移;(E) 变宽,不移. 注: λθ=sin a[ D ]5. 根据惠更斯-菲涅耳原理,若已知光在某时刻的波阵面为S ,则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的 (A) 振动振幅之和. (B) 光强之和.(C) 振动振幅之和的平方. (D) 振动的相干叠加. 注:惠更寺原理[ D ]6. 某元素的特征光谱中含有波长分别为λ1=450 nm 和λ2=750 nm (1 nm =10-9m)的光谱线.在光栅光谱中,这两种波长的谱线有重叠现象,重叠处λ2的谱线的级数将是 (A) 2 ,3 ,4 ,5 ...... (B) 2 ,5 ,8 ,11......(C) 2 ,4 ,6 ,8 ...... (D) 3 ,6 ,9 ,12...... 注:同一角度对应同一种光栅2211sin λλθk k d ==∴找最小公倍数即可.[ B ]7. 设光栅平面、透镜均与屏幕平行.则当入射的平行单色光从垂直于光栅平面入射变为斜入射时,能观察到的光谱线的最高级次k(A) 变小. (B) 变大. (C) 不变. (D) 的改变无法确定.λ注:公式从λθk d =sin 变成λθk d =sin λθk d =sin[ B ]8. 在单缝夫琅禾费衍射实验中,波长为λ的单色光垂直入射在宽度为a =4 λ的单缝上,对应于衍射角为30°的方向,单缝处波阵面可分成的半波带数目为 (A) 2 个. (B) 4 个. (C) 6 个. (D) 8 个. 二. 填空题1. 在单缝的夫琅禾费衍射实验中,屏上第三级暗纹对应于单缝处波面可划分为6 个半波带,若将缝宽缩小一半,原来第三级暗纹处将明_纹.注:,23sin ',2',26sin λθλθ⨯=∴=⨯=a a a a 奇数个半波带对应明纹 2. He -Ne 激光器发出λ=632.8 nm (1nm=10-9m)的平行光束,垂直照射到一单缝上,在距单缝3 m 远的屏上观察夫琅禾费衍射图样,测得两个第二级暗纹间的距离是10 cm ,则单缝的宽度a =__75900nm______.注: 2224,4,2tan x fa afx aff x ∆==∆∴==λλλθ注意单位统一.3. 波长为λ=550 nm(1nm=10-9m)的单色光垂直入射于光栅常数d =2×10-4cm 的平面衍射光栅上,可能观察到光谱线的最高级次为第3级。
第12章-波动光学(二)概论

bsin 2k 1 k 1,2,3, 明纹
2
• 缝宽 b 越小,衍射角 越大,衍射越显著; • 缝宽 b 越大,衍射角 越小,衍射越不明显;
• 当 b >>λ时,不发生衍射现象。
12
结论:几何光学是波动光学在 b 0 时的极
限情况。 2 1
0
b sin (2k 1) 明纹
2
bsin k
解: bsin
sin
b
L 2x 2D tg
2D 2 D
D
b
2 5.460107 0.40 1.0103 m
0.437 103
19
12-4-4 单缝衍射的光强分布
将狭缝分为N个小波 带。
各光振动矢量: E1 , E2 , , En
设 E1 E2 En E0
相邻两光振动的相位差:
sin 2 u u2
sin 23 2 3 22
0.045
I2 I0
sin 2 u u2
sin 25 2 5 22
0.016
24
12-4-5 圆孔衍射 光学仪器的分辨本领
25
爱里斑:圆孔衍射的中央亮斑,其上集中了全部 衍射光能的84%。
E
E0
sin bsin sin bsin
N
因为N 很大,所以有 sin bsin N bsin N
sin bsin
E NE0 b sin
I E2 令: u bsin
I0 NE0 2
22
P点处的光强:
I
I0
sin 2 u2
u
当 u bsin k I 0
孔或狭缝以及屏幕P距小孔或狭缝 都在无限远处。
P
大学物理 第十二章 波动光学2

2 又,明纹所在处x满足: x tg 1.5 0.003 , f 500
2 0.5 1.5 3 104 2ax / f 107 m A λ (2k 1) 500 2k 1 2k 1
白光波长范围4000—7000Å,满足上式的波长值即为所求:
• • • •
例题:已知单缝宽a=0.5mm,透镜焦距f=50cm,今以白光垂直照 射狭缝,在观察屏上x=1.5mm处看到明纹极大,求: (1)入射光的波长及衍射级数; (2)单缝所在处的波阵面被分成的波带数目。
[解]: (1)由明纹条件: a sin (2k 1)
x 很小 。 sin ≈ tg f
sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称次极大。
2、明暗纹中心位置坐标
(1)中央明纹中心位置 x=0
xk t g k f
tgk sin k
x xk
k
中 O 央 明 纹
k2
k 1
(1)
(2)
f
(2)暗纹中心位置坐标
由 a sin k k 及式(1)、(2) 得
二、光学仪器的分辨本领
1.22 1 D
D
瑞 利 判 据
定义
分辨本领
D R 1.22
1
刚可分辨
非相干叠加
不可分辨
瑞利判据 : 对于两个等光强的非相
干物点,若其中一点的象斑中心恰好落 在另一点的象斑的边缘(第一暗纹处), 则此两物点被认为是刚刚可以分辨。
当 再 , =3/2时,可将缝分成三个“半波带”,
B a A θ a B θ
波动光学 (2)

加强(明纹)k=0,1,2, …
2k 1 消弱(暗纹)k=1,2,3, …
2
1.3 杨氏双缝干涉实验
条纹分布规律:
k D
加强(明纹)k=0,1,2, …
x
d
2k 1 D 消弱(暗纹)k=1,2,3, …
d2
k为干涉级数,k=0时,O点对应中央明条纹,正 负号代表明暗条纹在中央明纹两侧对称分布。
单色光在真空中经过时间t传播的路程: s ct
若单色光在真空中的波长为λ,传播路程s对应的
相位变化:
2
s
该单色光通过折射率为n的介质时,经过时间t传
播的路程: l vt n c v s nl
相位变化:
2
nl
可见光在折射率为n的介质中传播的路程l等效于
在真空中传播的路程nl。
1.2 光程、光程差和相位差
r
S1和S2的相位差:
2
n
1l
两列光的光程差决定它们的相位差。 2
1.2 光程、光程差和相位差 注意: 1、在真空中,n=1,此时的光程等于几何路程。 2、决定光波相位变化的是光程或光程差而不是几 何路程。
3、就相位变换而言,单色光在介质中通过l路程 相当于在真空中通过nl。 4、理想透镜不产生附加光程差。
1.3 杨氏双缝干涉实验
两相邻明(暗)纹中心间距:
x D
d
xk+1
Δx xk
k+1 k
该式表明:
O
1、条纹间距Δx与级数k无
关,干涉条纹等间距分布。
2、若λ一定,减小d或增大D,会使Δx 变大,即条纹变稀,反之变密。
3、若d和D一定,则λ越大条纹越稀,反之变密。 若白光做光源,则中央明纹是白色,其他各级形
12-13 反射和折射光的偏振
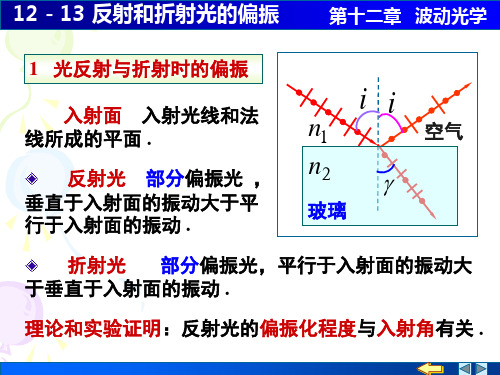
第十二章 波动光学
1 光反射与折射时的偏振
入射面 入射光线和法 线所成的平面 .
反射光 部分偏振光 , 垂直于入射面的振动大于平 行于入射面的振动 .
ii
n1
空气
n2
玻璃
折射光 部分偏振光,平行于入射面的振动大 于垂直于入射面的振动 .
理论和实验证明:反射光的偏振化程度与入射角有关 .
cosi0
sin
cos(π 2
)
i0
2
12 - 13 反射和折射光的偏振
第十二章 波动光学
i0 i0 n1
n2
玻璃
i0
n1
玻璃
n2
2)根据光的可逆性,当入射光以 角从 n2 介
质入射于界面时,此 角即为布儒斯特角 .
tan i0
n2 n1
cot i0
n1 n2
tan( π 2
i0 )
tan
i1 53.12 i2 51.58
90 i1
又在三角形OAB中有
i1
n空 气
O A
i2 n水
B
n介
(90 ) (90 i2 ) 180 i2 (90 i1)
53.12 51.58 90 14.7
12 - 13 反射和折射光的偏振
第十二章 波动光学
例 一自然光自空气射向一块平板玻璃,入射角
解 在空气和水的界面上
的布儒斯特角i1 满足
tan i1
n水 n空
1斯特角i2满足
tan i2
n介 n水
1.681 1.333
1.261
i1
n空 气
O A
i2 n水
波动光学

r 2 nr
2
从相位改变的角度来看,光在折射率为n的 介质中通过了几何路程r,相当于它在真空中通过了nr的几何路程。
'
第十二章 波动光学
光程:折射率n和光所通过的几何路程r的乘积
L nr
2.光程差 • 两束光的光程之差称为光程差,常用 表示。 • 决定光波相位和相位变化的不只是几何路程,而是光 程和光程差。 2 • 相位差与光程差的关系为:
第十二章 波动光学
3.条纹位置 • 第k级暗纹位置: xk f tg f sin k f
a
• 第k级明纹位置: xk (2k 1) f
2a
k=1, 2, 3, ……
k=1, 2, 3, ……
• 明条纹宽度:即相邻两暗纹中心间距。
x ' x k 1 x k
2 k x 2 d sin d D (2k 1) 2
x δ= r2 r1 d sin d tan d D
( k 0,1, 2,) 相干加强,明纹 ( k 1, 2, 3,) 相干削弱 , 暗纹
(r1 l n l ) r2 (n 1) l
(n 1) l k
(1.30 1) 0.01 103 5 7 6.00 10
第十二章 波动光学
四、劳埃德镜实验
S1 和 S2相当于两个相干光源,屏上相遇区域观 察到明暗相间的干涉条纹。 实验结果还表明:光从空气射向玻璃发生反射 时,反射光有大小为 的相位突变。 相当于光波多走(或少走)了半个波长的距离, 这个现象称为半波损失。
波动光学2

费马原理:从垂直于平行光的任一平面算起,各平行光线到 会聚点的光程相等(即透镜不附加光程差)。
10
讨论 把一条缝加宽,条纹如何变化? 若d不变, 则条纹位置不变。 E10 E20 暗纹强度不为0, 明纹强度也变大 条纹反差小(有衬底) 若把s向上移, 条纹如何变化?
x
I
s s
11
s1
s2
2
{(2k 1)
k
max
min
(k 0,1,2)
将屏移到 B处,证实了半波损失的存在。
半波损失 :光从光速较大的介质射向光速较小的介质时反射光 的相位较之入射光的相位跃变了 π ,相当于反射光与入射光之间 附加了半个波长的波程差。
2
3) 菲涅耳双镜(A. Fresnel,1818年) P
相干
I I1 I 2 2 I1I 2 cos
2 k
干涉项
2
( nr2 nr1 ) ( 20 10 )
明纹
暗纹
(2k 1)
2
( nr2 nr1 ) ( 20 10 ) 设初位相相同:
2
光程差表示的明暗纹条件
1 5.74
注意
20.0cm 1 arcsin arcsin 0.1 4 0.5m
考虑半波损失时,附加波程差取 / 2 均可, 符号不同,k 取值不同,对问题实质无影响.
17
二、时间相干性和空间相干性
s
s1
r1
r2
r
B
p
o
s2
如果光程差过大,大于波列的长度(L),或者 两列光波到达P点的时间相差过大,P点振动非相 干叠加——时间相干性 2 c
第十二章(二)波动光学

第十二章(二) 波动光学班号 学号 姓名 日期一、选择题1.一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是(A) 紫光; (B) 绿光; (C) 黄光; (D) 红光。
( )2.在光栅光谱中,假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,因而实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为(A) b a =; (B) b a 2=; (C) b a 3=; (D) a b 2=。
( )3.设一平面透射光栅,当入射的平行单色光从垂直于光栅平面入射变为斜入射时,能观察到的光谱线的最高级次k(A) 变小; (B) 变大; (C) 不变; (D) 无法确定。
( )4.一束光强度为I 0的自然光垂直穿过两个偏振片,此两偏振片的偏振化方向成45︒角,若不考虑偏振片的反射和吸收,则穿过这两个偏振片后的光强度I 为(A) 420I ; (B) 40I ; (C) 20I ; (D) 220I 。
( )5.自然光以60︒的入射角照射到某两介质交界面时,反射光为完全偏振光,则知折射光为(A) 完全偏振光且折射角是30︒;(B) 部分偏振光、且只是在该光由真空入射到折射率为3的介质时,折射角是30︒;(C) 部分偏振光,但须知两种介质的折射率才能确定折射角;(D) 部分偏振光、且折射角是30︒。
( )6.一束光强度为I 0的自然光,相继通过三个偏振片P 1、P 2、P 3后,出射光的光强度为80I I =,已知P 1和P 3的偏振化方向相互垂直,若以入射光线为轴,旋转P 2,则它至少要转过多大角度,才能使出射光的光强度为零。
(A) 30︒; (B) 45︒; (C) 60︒; (D) 90︒ 。
()7.一束自然光自空气射向一块平板玻璃(如图所示),设入射角等于布儒斯特角i 0,则在界面2的反射光为(A) 自然光; (B) 完全偏振光、且光矢量的振动方向垂直于入射面;(C) 完全偏振光、且光矢量的振动方向平行于入射面; (D) 部分偏振光。
第十二章 光学2 衍射

L′
缝平 面
L
观察 屏
*
f′
S
a
B θ
·
θ
p
A f
θ:衍射角 AB = a (缝宽) 缝宽) S:单色光源 光线正入射
单缝衍射a=0.15mm, f=400mm, 例3 单缝衍射a=0.15mm, f=400mm,屏上两个第三 级暗纹相距8mm 求入射光的波长? 8mm。 级暗纹相距8mm。求入射光的波长?
光源 S 单缝K
屏 幕
E
a b
(a)
若将缝的宽度减小 及更小时, 到约10−4m及更小时,缝 后几何阴影区的光屏上 将出现衍射条纹, 将出现衍射条纹,如图 (b)所示,这就是光的 b)所示, 所示 衍射现象。 衍射现象。
(b) 光源 S
a′
E′
屏 幕
b′
二、菲涅耳衍射和夫琅禾费衍射
按 光源, 障碍物, 屏 , 三者相对位置分 光源, 障碍物,
三、惠更斯-菲涅耳原理 惠更斯 菲涅耳原理
内容:在任一时刻,波阵面上每一未被阻挡的点均起着 次级球面子波波源的作用,障碍物后任一点上光场的振 幅是所有这些子波源所发出的球面子波的相干叠加。 子波在P点引起的振动振幅矢量 与距离 、面 子波在 点引起的振动振幅矢量dA与距离 点引起的振动振幅矢量 与距离r、 积元dS、 角有关。 积元 、θ角有关。 若已知某时刻的波阵面
级数K的影响:越大;条纹亮度越小. 级数K的影响:越大;条纹亮度越小.
ϕ
ϕ
半波带 少而宽
λ
λ λ λ 2
2 2
C
B
C
半波带 多而窄
B
λ 2
2
λ 2
λ 2
λ 2
各级亮纹的强度分布
12-04 薄膜干涉
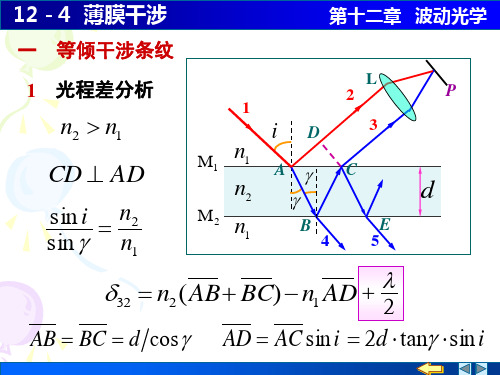
则他将观察到油层呈什么颜色?
(2)如果一潜水员潜入该区域水下,又将看到油
层呈什么颜色?
解(1) r 2dn1 k
2n1d , k 1,2,
k
k 1, 2n1d 1104 nm
k 2, n1d 552 nm 绿色
k 3,
2 3
n1d
368 nm
12 - 4 薄膜干涉
第十二章 波动光学
B
E
45
d
12 - 4 薄膜干涉
第十二章 波动光学
反 2d
n22
n12
sin 2
i
2
根据具体 情况而定
n2 n1
1
M1 n1 n2
M2 n1
iD
A B 4
L 2
3 C
E 5
透射光的光程差
P
t 2d n22 n12 sin2 i
d
注意:透射光和反 射光干涉具有互补性,
符合能量守恒定律。
12 - 4 薄膜干涉
当d 变小时,r 减小,
圆形干涉条纹一个个向中 心缩进,干涉条纹变疏。
当d 变大时,r 增大,
圆形干涉条纹从中心一个 个冒出,并向外扩张,干 涉条纹变密。
12 - 4 薄膜干涉
第十二章 波动光学
讨论
2d
n22
n12
sin 2
i
2
k
当光线垂直入射时 i 0
当 n2 n1 时
r
2dn2
2
n1
n2 n1
3 增透膜和增反膜
利用薄膜干涉可以提高光学器件的透光率 .
例 为了增加透射率;求:氟化镁膜的最小厚度 .
已知 空气 n1 1.00 ,氟化镁 n2 1.38 , 550nm
大学物理高校出版社罗圆圆主编-第12章波动光学PPT课件

现象:一系列平行的明暗相间的条纹; 不太大时条纹等间距.
24
干涉条纹定量分析:
(1)条纹(中心)的位置
s
s
d
1
(在 较小的情况下) s 2
波程差:
r1
p
r2
x
o
D
r2r1dsin dt gdD x
Δ20 10 2 π(r2r1) 现已有 20 - 10=0
25
亮纹: (相长干涉)
2kπ (k0,1,2, ) 或波程 r2差 r1k
13
P点处:
E 1E 1c 0 o ts (1)
E 2E 2c 0 o ts (2)
r1
· 1
r2
· 2
E20
·P
E0
EE1E2
EE0cos(t)
2 1 E10
14
E 0 2E 1 2 0E 2 2 02E 1E 0 2c 0 os
其中:21
I E 0 2 = 1 0 E 2 0 d t = 1 0 [E 1 2 0 E 2 2 0 2 E 1 0 E 2 0 c o s ] d t
电磁谐波 EE0cots(k)x
电磁波的强度:
I
wu1
2
E02u
在同一介质中通常把强度直接写成
I
E
2 0
说明:与物质作用的主要物理量是电矢量 通常称 E为光矢量
按波长或频率的次序把这些电磁波排列成谱
----称为电磁波谱。
可见光的范围
4000埃~7600埃,
:40~076n0m只占很小的一段 :7.51104~4.31104Hz 8
2
波动光学
第一部分 光的干涉 第二部分 光的衍射 第三部分 光的偏振
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章波动光学(二)
高玉梅编
姓名学号班级
1、平行单色光垂直入射到单缝上,观察夫朗和费衍射。
若屏上P点处为第2级暗纹,则单缝处波面相应地可划分为几个半波带( )
A 一个 B. 两个 C. 三个 D. 四个
2、波长为λ的单色光垂直入射到狭缝上,若第1级暗纹的位置对应的衍射角为θ=±π/6,则缝宽的大小为( )
A. λ/2
B. λ
C. 2λ
D. 3λ
3、波长λ=550nm的单色光垂直入射于光栅常数d=2×10−4cm的平面衍射光栅上,可能观察到的光谱线的最大级次为( )
A. 2
B. 3
C. 4
D. 5
4、一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是( )
A 紫光 B. 绿光 C.黄光 D. 红光
5、一束单色光垂直入射在平面光栅上,衍射光谱中共出现了5条明纹。
若已知此光栅缝宽度与不透明宽度相等,那么在中央明纹一侧的第二条明纹是第几级?( )
A. 1级
B. 2级
C. 3级
D. 4级
6、波长为λ的单色光垂直照射在缝宽为a=4λ的单缝上,对应θ=30°衍射角,单缝处的波面可划分为半波带,对应的屏上条纹为纹。
7、在单缝实验中,如果上下平行移动单缝的位置,衍射条纹的位置。
8、平行单色光垂直入射到平面衍射光栅上,若增大光栅常数,则衍射图样中明条纹的间距将,若增大入射光的波长,则明条纹间距将。
9、波长为500nm的平行单色光垂直入射在光栅常数为2×10−3mm的光栅上,光栅透光缝宽度为1×10−3mm,则第级主极大缺级,屏上将出现条明条纹。
10、在单缝衍射实验中,透镜焦距为0.5m,入射光波长λ=500nm,缝宽a=0.1mm。
求:(1)中央明条纹宽度;(2)第1级明条纹宽度。
11、一束具有两种波长λ1和λ2的平行光垂直照射到一个衍射光栅上,测得波长λ1的第3级主极大与λ2的第4级主极大衍射角均为30°,已知λ1=560nm,求:(1)光栅常数d;(2)波长λ2。
12、用波长λ=700nm的单色光,垂直入射在平面透射光栅上,光栅常数为3×10−6m的光栅观察,试问:(1)最多能看到第几级衍射明条纹?(2)若缝宽0.001mm,第几级条纹缺级?。
