全国高考文科数学试题及答案全国卷3
高考全国卷3文科数学及答案(word精校版)之欧阳理创编

2019年普通高等学校招生全国统一考试全国卷3文科数学考试时间:2019年6月7日15:00——17:00使用省份:云南、广西、贵州、四川、西藏本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2,,则A B=()=-=≤{1,0,1,2}{1}A B x xA.{}1,0,1-B.{}0,1C.{}1,1-D.{}0,1,22.若(1i)2iz+=,则z=()A.1i--B.1+i-C.1i-D.1+i3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是()A.16B.14C.13D.124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为()A.0.5 B.0.6C.0.7D.0.85.函数()2sin sin2f x x x=-在[0,2π]的零点个数为()A.2B.3C.4D.56.已知各项均为正数的等比数列{a n}的前4项和为15,且a5=3a3+4a1,则a3=()A. 16B. 8C.4 D. 27.已知曲线e lnxy a x x=+在点(1,a e)处的切线方程为y=2x+b,则()A.a=e,b=-1B.a=e,b=1C.a=e-1,b=1D.a=e-1,1b=-8.如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于( ) A.4122- B.5122- C.6122- D.7122- 10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为( )A .32B .52C .72D .92 11.记不等式组6,20x y x y +⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+;命题:(,),212q x y D x y ∀∈+.下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是( )A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则( )A .f (log 314)>f (322-)>f (232-) B .f (log 314)>f (232-)>f (322-) C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314) 第Ⅱ卷(非选择题,共90分)二、填空题:本题共4小题,每小题5分,共20分。
2020年普通高等学校招生全国统一考试文科数学试卷(全国Ⅲ卷)(含解析)

2020年普通高等学校招生全国统一考试
文科数学(全国Ⅲ卷)(含解析)
1. 答卷前,考生务必将自己的姓名,准考证号填写在答题卡上。 2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案 标号涂黑。如需改动,用橡皮擦干净后,在选涂其他答案标号。回答选择 题时 , 将答案写在答题卡上。写在本试卷上无效。 3. 考试结束后,将本试卷和答题卡一并交回。 一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项 中,只有一项是符合题目要求的。
x2 y2 14. 设双曲线 C : a2 b2 1 a 0, b 0 的一条渐近线为 y
2x , 则 C 的离心率
为 ______.
15. 设函数 f x
ex ,若 f 1
e ,则 a=____.
xa
4
16. 已知圆锥的底面半径为 1,母线长为 3,则该圆锥内半径最大的切球表面积
为
.
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21
A. f ( x) 的最小值为 2
B.
f ( x) 的图像关于 y 轴对称
C. f ( x) 的图像关于直线 x 对称 D.
f ( x) 的图像关于直线 x 对称 2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13. 若 x, y 满足约束条件
xy0 2x y 0 ,则 z=3x+2y 的最大值为 _____. x1
的中点值为代表);
( 3) 若某天的空气质量等级为 1 或 2,则称这天“空气质量好”;若某天的空 气质量等级为 3 或 4,则称这天“空气质量不好”。根据所给数据,完成 下面的 2 2 列联表,并根据列联表,判断是否有 95%的把握认为一天中到 该公园锻炼的人次与该市当天的空气质量有关?
高考全国卷3文科数学及答案(word精校版)之欧阳文创编

2019年普通高等学校招生全国统一考试全国卷3文科数学考试时间:2019年6月7日15:00——17:00使用省份:云南、广西、贵州、四川、西藏本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x=-=≤,,则A B=()A.{}1,0,1-B.{}0,1C.{}1,1-D.{}0,1,22.若(1i)2iz+=,则z=()A.1i--B.1+i-C.1i-D.1+i3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是()A.16B.14C.13D.124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )A .0.5B .0.6C .0.7D .0.85.函数()2sin sin2f x x x =-在[0,2π]的零点个数为( )A .2B .3C .4D .56.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=( )A . 16B . 8C .4D . 27.已知曲线e ln x y a x x =+在点(1,a e )处的切线方程为y =2x +b ,则( )A .a=e ,b =-1B .a=e ,b =1C .a=e -1,b =1D .a=e -1,1b =- 8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则( )A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于( ) A.4122- B.5122- C.6122- D.7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为( )A .32B .52C .72D .9211.记不等式组6,20x y x y +⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+;命题:(,),212q x y D x y ∀∈+.下面给出了四个命题 ①p q ∨②p q ⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是( )A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则( )A .f (log 314)>f(322-)>f (232-)B .f (log 314)>f(232-)>f (322-)C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314)第Ⅱ卷(非选择题,共90分)二、填空题:本题共4小题,每小题5分,共20分。
高考全国卷3文科数学及答案(word精校版)之欧阳德创编

2019年普通高等学校招生全国统一考试全国卷3文科数学考试时间:2019年6月7日15:00——17:00使用省份:云南、广西、贵州、四川、西藏本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x=-=≤,,则A B=()A.{}1,0,1-B.{}0,1C.{}1,1-D.{}0,1,22.若(1i)2iz+=,则z=()A.1i--B.1+i-C.1i-D.1+i3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是()A.16B.14C.13D.124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为()A.0.5 B.0.6C.0.7D.0.85.函数()2sin sin2f x x x=-在[0,2π]的零点个数为()A.2B.3C.4D.56.已知各项均为正数的等比数列{a n}的前4项和为15,且a5=3a3+4a1,则a3=()A. 16B. 8C.4 D. 27.已知曲线e lnxy a x x=+在点(1,a e)处的切线方程为y=2x+b,则()A.a=e,b=-1B.a=e,b=1C.a=e-1,b =1D .a=e -1,1b =-8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则( )A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于( ) A.4122- B.5122- C.6122- D.7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为( )A .32B .52C .72D .9211.记不等式组6,20x y x y +⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+;命题:(,),212q x y D x y ∀∈+.下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是( )A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则( ) A .f (log 314)>f (322-)>f (232-) B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314) 第Ⅱ卷(非选择题,共90分) 二、填空题:本题共4小题,每小题5分,共20分。
高考文科数学全国3卷试题及答案(Word版)(20200618130547)

( C)三月和十一月的平均最高气温基本相同
( D)平均最高气温高于 20℃的月份有 5 个
( 5)小敏打开计算机时 , 忘记了开机密码的前两位 , 只记得第一位是 M, I,N 中的一个字
母 , 第二位是 1,2,3,4,5 中的一个数字 , 则小敏输入一次密码能够成功开机的概率是
8
1
1
1
( A) 15 ( B) 8 ( C) 15 ( D) 30
.
所以预测 2016 年我国生活垃圾无害化处理量将约 1.82 亿吨 . .........12 分
19 、(Ⅰ) 由已知得
, 学 .科网取 的中点 , 连接
,由 为
中点知
,
. ......3 分
又
, 故 平行且等于
, 四边形
为平行四边形 , 于是
.
因为
平面
,
平面
, 所以
平面
. ........6 分
(II )证明当 x (1, ) 时 , 1 x 1 x ; ln x
(III )设 c
1 , 证明当 x
(0,1)时 , 1 (c 1)x
x
c.
请考生在 22、23、 24 题中任选一题作答 ,如果多做 ,则按所做的第一题计分 , (22)(本小题满分 10 分)选修 4— 1:几何证明选讲
如图 , ⊙ O 中 的中点为 P, 弦 PC, PD 分别交 AB 于 E, F 两点。 (Ⅰ)若∠ PFB =2∠ PCD, 求∠ PCD 的大小; (Ⅱ)若 EC 的垂直平分线与 FD 的垂直平分线交于点 G, 证明 OG ⊥ CD 。 (23)(本小题满分 10 分)选修 4— 4:坐标系与参数方程 在直线坐标系 xoy 中 , 曲线 C1的参数方程为 错误 ! 未找到引用源。 ( 错误 ! 未找到引用源。 为参数) 。以坐标原点为极点 , x 轴正半轴为极轴 , 建立极 坐标系 , 曲线 C2 的极坐标方程为 ρsin (错误 ! 未找到引用源。 ) =错误 !未找到引用源。 . (I )写出 C1 的普通方程和 C2 的直角坐标方程; (II )设点 P 在 C1 上, 点 Q 在 C2 上 , 求∣ PQ ∣的最小值及此时 P 的直角坐标 . (24)(本小题满分 10 分) , 选修 4—5:不等式选讲 已知函数 f(x)=∣ 2x-a∣ +a. (I )当 a= 2 时 , 求不等式 f(x)≤6 的解集; (II )设函数 g(x)=∣ 2x-1∣ .当 x∈ R 时 , f( x)+g(x)≥ 3, 求 a 的取值范围。
2020年高考数学文科全国三试卷及答案解析
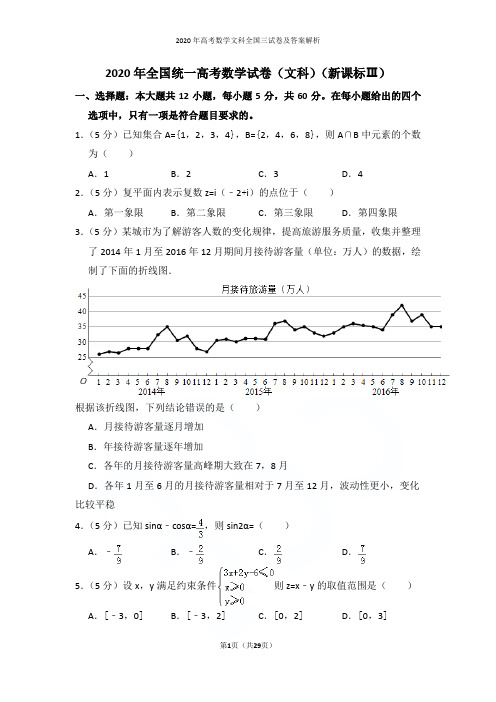
2020年全国统一高考数学试卷(文科)(新课标Ⅲ)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1B.2C.3D.42.(5分)复平面内表示复数z=i(﹣2+i)的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)已知sinα﹣cosα=,则sin2α=()A.﹣B.﹣C.D.5.(5分)设x,y满足约束条件则z=x﹣y的取值范围是()A.[﹣3,0]B.[﹣3,2]C.[0,2]D.[0,3]6.(5分)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.B.1C.D.7.(5分)函数y=1+x+的部分图象大致为()A.B.C.D.8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为()A.5B.4C.3D.29.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.C.D.10.(5分)在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC 11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.12.(5分)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A.﹣B.C.D.1二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A=.16.(5分)设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是.三、解答题17.(12分)设数列{a n}满足a1+3a2+…+(2n﹣1)a n=2n.(1)求{a n}的通项公式;(2)求数列{}的前n项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx﹣2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x﹣2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.2017年全国统一高考数学试卷(文科)(新课标Ⅲ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分。
2020年高考数学全国卷3-文科数学试题参考答案

1.B2.D3.C4.C5.B6.A7.B8.B9.C 10.A 11.C 12.D 13.7 14.3 15.1 16.23π17.解:(1)设{a n }的公比为q ,则a n =a 1qn -1.由己知得a 1+a 1q =4,a 1q 2-a 1=8.解得a 1=1,q =3.所以{a n }的通项公式为a n =3n -1.(2)由(1)知l o g 3a n =n -1.故S n =n (n -1)2.由Sm+Sm +1=S m +3得m (m -1)+(m +1)m =(m +3)(m +2),即m 2-5m -6=0.解得m =-1(舍去),m =6.18.解:(1)由所给数据,该市一天的空气质量等级为1,2,3,4的概率的估计值如下表:空气质量等级1234概率的估计值0.430.270.210.09(2)一天中到该公园锻炼的平均人次的估计值为1100(100ˑ20+300ˑ35+500ˑ45)=350.(3)根据所给数据,可得2ˑ2列联表:人次ɤ400人次>400空气质量好3337空气质量不好228根据列联表得K 2=100ˑ(33ˑ8-22ˑ37)255ˑ45ˑ70ˑ30ʈ5.820.由于5.820>3.841,故有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.19.解:(1)如图,连结B D ,B 1D 1.因为AB =B C ,所以四边形AB C D 为正方形,故AC ʅB D .又因为B B 1ʅ平面AB C D ,于是AC ʅB B 1.所以AC ʅ平面B B 1D 1D .由于E F 平面B B 1D 1D ,所以E F ʅAC.(2)如图,在棱A A 1上取点G ,使得AG =2GA 1,连结GD 1,F C 1,F G .2020年普通高等学校招生全国统一考试试题参考答案数 学(文科)因为D 1E =23D D 1,AG =23A A 1,D D 1A A 1,所以E D 1AG ,于是四边形E D 1GA 为平行四边形,故AE ʊGD 1.因为B 1F =13B B 1,A 1G =13A A 1,B B 1A A 1,所以F G A 1B 1,F GC 1D 1,四边形F GD 1C 1为平行四边形,故GD 1ʊF C 1.于是AE ʊF C 1.所以A ,E ,F ,C 1四点共面,即点C 1在平面AE F 内.20.解:(1)f '(x )=3x 2-k .当k =0时,f (x )=x 3,故f (x )在(-ɕ,+ɕ)单调递增;当k <0时,f '(x )=3x 2-k >0,故f (x )在(-ɕ,+ɕ)单调递增.当k >0时,令f '(x )=0,得x =ʃ3k3,当x ɪ -ɕ,-3k 3时,f '(x )>0;当x ɪ -3k 3,3k 3时,f '(x )<0;当x ɪ3k3,+ɕ 时,f '(x )>0.故f (x )在 -ɕ,-3k 3,3k3,+ɕ单调递增,在-3k 3,3k 3单调递减.(2)由(1)知,当k ɤ0时,f (x )在(-ɕ,+ɕ)单调递增,f (x )不可能有三个零点,当k >0时,x =-3k3为f (x )的极大值点,x =3k3为f (x )的极小值点,此时,-k -1<-3k3<3k3<k +1且f (-k -1)<0,f (k +1)>0,f-3k 3>0.根据f (x )的单调性,当且仅当f3k 3<0,即k 2-2k 3k9<0时,f (x )有三个零点,解得k <427.因此k 的取值范围为 0,427.21.解:(1)由题设可得25-m25=154,得m 2=2516,所以C 的方程为x 225+y 22516=1.(2)设P (x P ,y P ),Q (6,y Q ),根据对称性可设y Q >0,由题意知y P >0.由己知可得B (5,0),直线B P 的方程为y =-1y Q(x -5),所以|B P |=y P 1+y 2Q ,|B Q |=1+y 2Q .因为|B P |=|B Q |,所以y P =1,将y P =1代入C 的方程,解得x P =3或-3.由直线B P 的方程得y Q =2或8.所以点P ,Q 的坐标分别为P 1(3,1),Q 1(6,2);P 2(-3,1),Q 2(6,8).|P 1Q 1|=10,直线P 1Q 1的方程为y =13x ,点A (-5,0)到直线P 1Q 1的距离为102,故әA P 1Q 1的面积为12ˑ102ˑ10=52.|P 2Q 2|=130,直线P 2Q 2的方程为y =79x +103,点A 到直线P 2Q 2的距离为13026,故әA P 2Q 2的面积为12ˑ13026ˑ130=52.综上,әA P Q 的面积为52.试题参考答案数 学(文科)22.解:(1)因为tʂ1,由2-t-t2=0得t=-2,所以C与y轴的交点为(0,12);由2-3t+t2=0得t=2,所以C与x轴的交点为(-4,0).故|AB|=410.(2)由(1)可知,直线AB的直角坐标方程为x-4+y12=1,将x=ρcosθ,y=ρsi nθ代入,得直线AB的极坐标方程3ρcosθ-ρsi nθ+12=0.23.解:(1)由题设可知,a,b,c均不为零,所以ab+b c+ca=12[(a+b+c)2-(a2+b2+c2)]=-12(a2+b2+c2)<0.(2)不妨设m ax{a,b,c}=a,因为ab c=1,a=-(b+c),所以a>0,b<0,c<0.由b cɤ(b+c)24,可得ab cɤa3 4,故aȡ34,所以m ax{a,b,c}ȡ34.试题参考答案数学(文科)。
2020年普通高等学校招生全国统一考试文科数学(全国III卷)(含答案) (3)

2020年普通高等学校招生全国统一考试文科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}1,2,3,5,7,11A =,{}|315B x x =<<,则A B 中元素的个数为A. 2B. 3C. 4D. 52. 若(1)1z i i +=-,则z = A. 1i - B. 1i + C.i - D.i3.设一组样本数据12,,...,n x x x 的方差为0.01,则数据12n 10,10,...,10x x x 的方差为 A .0.01 B .0.1 C .1 D .104. Logistic 模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()t I (t 的单位:天)的Logistic 模型:()()0.23531t KI t e--=+,其中K 为最大确诊病例数.当()0.95I t K *=时,标志着已初步遏制疫情,则t *约为(In19≈3) A.60 B.63 C.66 D.695.已知sin sin()13πθθ++=,则sin()6πθ+= A.12C.23D.26.在平面内,,A B 是两个定点,C 是动点,若1AC BC ⋅=,则点C 的轨迹为 A. 圆 B. 椭圆 C. 抛物线 D. 直线7.设O 为坐标原点,直线2x =与抛物线2:2(0)C y px p =>交于,D E 两点,若OD OE ⊥,则C 的焦点坐标为A .1(,0)4B .1(,0)2C .(1,0)D .(2,0)8.点(0,1)-到直线(1)y k x =+距离的最大值为 A .1 B .2 C .3 D .29.右图为某几何体的三视图,则该几何体的表面积是A. 6+42B. 4+42C. 6+23D. 4+2310.设3log 2a =,5log 3b =,23c =,则 A .a c b << B.a b c << C. b c a << D. c a b <<11. 在ABC ∆中,2cos 3C =,4,3AC BC ==,则tan B =12. 已知函数1()sin sin f x x x=+,则 A. ()f x 的最小值为2B. ()f x 的图像关于y 轴对称C. ()f x 的图像关于直线x π=对称D. ()f x 的图像关于直线2x π=对称二、填空题:本题共4小题,每小题5分,共20分。
(版)高考全国3卷文科数学与答案

绝密★启用前2021年普通高等学校招生全国统一考试文科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
考前须知:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:此题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项是符合题目要求的。
1.集合 A { 1,0,1,2},B {xx21},那么ABA. 1,0,1 B. 0,1 C. 1,1 D. 0,1,22.假设z(1 i) 2i,那么z=A.1 i B.1+i C.1 i D. 1+i3.两位男同学和两位女同学随机排成一列,那么两位女同学相邻的概率是1 1 1 1A. B. C.D.6 4 3 24.?西游记??三国演义??水浒传?和?红楼梦?是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过?西游记?或?红楼梦?的学生共有90位,阅读过?红楼梦?的学生共有80位,阅读过?西游记?且阅读过?红楼梦?的学生共有60位,那么该校阅读过?西游记?的学生人数与该校学生总数比值的估计值为A.0.5 B.0.6 C.0.7 D.0.85.函数 f(x) 2sinxsin2x 在[0,2π]的零点个数为A.2B.3C.4D.56.各项均为正数的等比数列{an}的前4项和为15,且a5=3a3+4a1,那么a3=A.16B.8C.4D.27x1aey=2x+b.曲线y ae xlnx在点〔,〕处的切线方程为,那么-1,b=1D.a=e-1,A.a=e,b=-1B.a=e,b=1C.a=e b1文科数学试题第1页〔共9页〕8.如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M 是线段ED的中点,那么A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线为,那么输出s的值等于9.执行下边的程序框图,如果输入的1A.2241B.2251C.2261D.22710.F是双曲线C:x2y21的一个焦点,点P在C上,O为坐标原点,假设OP=OF,45那么△OPF的面积为3579A.B.C.D .222211.记不等式组xy?6,表示的平面区域为D.命题p:(x,y)D,2xy?9;命题2x y0q:(x,y)D,2x y,12.下面给出了四个命题①pq②pq③pq④p q这四个命题中,所有真命题的编号是A.①③B.①②C.②③D.③④12.设fx是定义域为R的偶函数,且在0, 单调递减,那么132A.f〔log32〕>f〔23〕B.f〔log3〕>f〔2423〕>f〔23〕>f〔22〕3C.f〔22223〕>f〔23〕>f〔log31〕D.f〔23〕>f〔22〕>f〔log31〕44文科数学试题第2页〔共9页〕二、填空题:此题共4小题,每题5分,共20分。
高考文科数学全国卷3试题及详细解析答案Word版

- 1 - 2018年一般高等学校招生全国一致考试全国卷III 文科数学注意事项1答题前先将自己的姓名、准考据号填写在试题卷和答题卡上并将准考据号条形码粘贴在答题卡上的指定地点。
2选择题的作答每题选出答案后用2B铅笔把答题卡上对应题目的答案标号涂黑写在试题卷、底稿纸和答题卡上的非答题地区均无效。
3非选择题的作答用署名笔挺接答在答题卡上对应的答题地区内。
写在试题卷、底稿纸和答题卡上的非答题地区均无效。
4考试结束后请将本试题卷和答题卡一并上交。
一、选择题此题共12小题每题5分共60分在每题给的四个选项中只有一项切合1已知会合|10Axx≥012B则ABA0 B1 C12 D012分析∵{|10}{|1}Axxxx{0,1,2}B∴{1,2}AB.故答案为C.212iiA3iB3i C3i D3i分析2(1)(2)23iiiii故答案为D.3中国古建筑借助榫卯将木构件连结起来构件的凸出部分叫棒头凹进部分叫卯眼图中木构件右侧的小长方体是棒头若如图摆放的木构件与某一带卯眼的木构件咬合成长方体则咬合时带卯眼的木构件的俯视图能够是- 2 - 分析由几何体及选项可知答案为A.4若1sin3则cos2A89 B79 C79D89分析227cos212sin199.故答案为B.5既用现金支付也用非现金支付的概率为则不用现金支付的概率为A0.3 B0.4 C0.6 D0.7分析由题意.故答案为B.6函数2tan1tanxfxx的最小正周期为A4 B2 C D2分析 22222sintansincos1cos()sincossin2sin1tansincos21cosxxxxxfxxxxxxxxx∴()fx的周期22T.故答案为C.7以下函数中其图像与函数lnyx的图像对于直线1x对称的是Aln1yx B ln2yx C ln1yx D ln2yx 分析()fx对于1x对称则()(2)ln(2)fxfxx.故答案为B.8直线20xy分别与x轴y轴交于A B两点点P在圆 2222xy上则ABP面积的取值范围是A26 B48 C232D2232分析由直线20xy得(2,0),(0,2)AB∴22||2222AB圆22(2)2xy的圆心为(2,0)∴圆心到直线20xy的距离为222211∴点P- 3 - 到直线20xy的距离的取值范围为222222d即232d∴1||[2,6]2ABPSABd.故答案为A .9函数422yxx的图像大概为分析清除法。
高考文科数学全国卷三真题试卷及答案(新课标)
绝密★启用前2021年普通高等学校招生全国统一考试〔新课标Ⅲ〕文科数学考前须知:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答复选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答复非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
1.集合A={1,2,3,4},B={2,4,6,8},那么A⋂B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游效劳质量,收集并整理了2021年1月至2021年12月期间月接待游客量〔单位:万人〕的数据,绘制了下面的折线图.根据该折线图,以下结论错误的选项是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量顶峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比拟平稳4.4sin cos3αα-=,那么sin2α=A .79-B .29-C .29D .795.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,那么z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .157.函数y =1+x +2sin xx的局部图像大致为A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,那么输入的正整数N 的最小值为A .5B .4C .3D .29.圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,那么该圆柱的体积为 A .πB .3π4C .π2D .π410.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,那么A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.椭圆C :22221x y a b+=,〔a >b >0〕的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,那么C 的离心率为AB C D .1312.函数211()2()x x f x x x a ee --+=-++有唯一零点,那么a =A .12-B .13C .12D .1二、填空题:此题共4小题,每题5分,共20分。
2020年全国统一高考数学试卷(文科)(新课标ⅲ)(含解析版)

【点睛】本题考查等比数列通项公式基本量的计算,以及等差数列求和公式的应用,考查计算求解能力,属于基础题目.
18.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次
空气质量等级
[0,200]
(200,400]
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 , ,则A∩B中元素的个数为()
A.2B.3C.4D.5
【答案】B
【解析】
【分析】
采用列举法列举出 中元素的即可.
【详解】由题意, ,故 中元素的个数为3.
故选:B
【点晴】本题主要考查集合 交集运算,考查学生对交集定义的理解,是一道容易题.
【详解】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,
其中 ,且点M为BC边上的中点,
设内切圆的圆心为 ,
由于 ,故 ,
设内切圆半径为 ,则:
,
解得: ,其体积: .
故答案为: .
【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.
2.若 ,则z=()
A. 1–iB. 1+iC. –iD.i
【答案】D
【解析】
【分析】
先利用除法运算求得 ,再利用共轭复数的概念得到 即可.
【详解】因为 ,所以 .
2020年普通高等学校招生全国统一考试(全国III卷文科) 数学试题及答案(学生版)

2020年普通高等学校招生全国统一考试(全国III 卷文科)数学试题注意事项:1.答题前,考生务必将自己的姓名、考生号、座位号填写在答题卡上。
本试卷满分150分。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合,,则A ∩B 中元素的个数为( ) A. 2 B. 3 C. 4 D. 52.若,则z =( )A. 1–iB. 1+iC. –iD. i3.设一组样本数据x 1,x 2,…,x n 的方差为0.01,则数据10x 1,10x 2,…,10x n 的方差为( )A. 0.01B. 0.1C. 1D. 104.Logistic 模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:,其中K 为最大确诊病例数.当I ()=0.95K 时,标志着已初步遏制疫情,则约为( )(ln19≈3)A. 60B. 63C. 66D. 695.已知,则( )A.C.D.6.在平面内,A,B 是两个定点,C 是动点,若,则点C 的轨迹为( )A. 圆B. 椭圆C. 抛物线D. 直线7.设O 为坐标原点,直线x =2与抛物线C :y 2=2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为( )A. (,0) B. (,0) C. (1,0) D. (2,0){}1235711A =,,,,,{}315|B x x =<<()11+=-z i i 0.23(53)()=1et I K t --+*t *t πsin sin =31θθ⎛⎫++ ⎪⎝⎭πsin =6θ⎛⎫+ ⎪⎝⎭12232=1AC BC ⋅14128.点(0,﹣1)到直线距离的最大值为( )A. 1B.C.D. 29.下图为某几何体的三视图,则该几何体的表面积是( )A. 6+4B. 4+4C. 6+2D. 4+210.设a =log 32,b =log 53,c =,则( ) A. a<c<b B. a<b<c C. b<c<a D. c<a<b 11.在△ABC 中,cos C =,AC =4,BC =3,则tan B =( ) A.B. 2C. 4D. 812.已知函数f (x )=sin x +,则( ) A. f(x)的最小值为2B. f(x)的图像关于y 轴对称C. f(x)的图像关于直线对称D. f(x)的图像关于直线对称二、填空题(本题共4小题,每小题5分,共20分.)13.若x ,y 满足约束条件 ,则z =3x +2y 的最大值为_________.14.设双曲线C : (a >0,b >0)的一条渐近线为y =x ,则C 的离心率为_________.15.设函数.若,则a =_________.16.已知圆锥底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________. 三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分.17.设等比数列{a n }满足,. (1)求{a n }的通项公式;()1y k x =+232233232355551sin xx π=2x π=0,201,x y x y x +≥⎧⎪-≥⎨⎪≤⎩,22221x y a b -=2e ()xf x x a =+(1)4e f '=124a a +=318a a -=(2)记为数列{log 3a n }的前n 项和.若,求m .18.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(1(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:,n S 13m m m S S S +++=2()()()()()n ad bc K a b c d a c b d -=++++P (K 2≥k ) 0.050 0.010 0.001 k 3.8416.63510.82819.如图,在长方体中,点,分别在棱,上,且,.证明: (1)当时,; (2)点在平面内.20.已知函数. (1)讨论的单调性;(2)若有三个零点,求的取值范围.1111ABCD A B C D -E F 1DD 1BB 12DE ED =12BF FB =AB BC =EF AC ⊥1C AEF 32()f x x kx k =-+()f x ()f x k21.已知椭圆的离心率为,,分别为的左、右顶点.(1)求的方程;(2)若点在上,点在直线上,且,,求的面积.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.)[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数且t ≠1),C 与坐标轴交于A ,B 两点. (1)求||:(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求直线AB 的极坐标方程.222:1(05)25x y C m m +=<<4A B C C P C Q 6x =||||BP BQ =BP BQ ⊥APQ 2222x t t y t t ⎧=--⎨=-+⎩,AB[选修4-5:不等式选讲]23.设a,b,c R,a+b+c=0,abc=1.(1)证明:ab+bc+ca<0;(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c2020年普通高等学校招生全国统一考试(全国III 卷文科)数学试题参考答案1-5.BDCCB 6-10ABBCA 11-12.CD 13.715.116.17.(1)设等比数列的公比为,根据题意,有,解得,所以;(2)令, 所以, 根据,可得, 整理得,因为,所以18.(1)由频数分布表可知,该市一天空气质量等级为的概率为,等级为的概率为,等级为的概率为,等级为的概率为; (2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为(3)列联表如下:3{}n a q 1121148a a q a q a +=⎧⎨-=⎩113a q =⎧⎨=⎩13-=n n a 313log log 31n n n b a n -===-(01)(1)22n n n n n S +--==13m m m S S S +++=(1)(1)(2)(3)222m m m m m m -++++=2560m m --=0m >6m =的1216250.43100++=2510120.27100++=36780.21100++=47200.09100++=100203003550045350100⨯+⨯+⨯=22⨯空气质量好,因此,有的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关. 19.(1)因为长方体,所以平面, 因为长方体,所以四边形为正方形 因为平面,因此平面,因为平面,所以;(2)在上取点使得,连, 因为,所以所以四边形为平行四边形,因为所以四边形为平行四边形, 因此在平面内20. (1)由题,,当时,恒成立,所以在上单调递增; 当时,令,得,令,得, 令,得或,所以在上单调递减,在 ,上单调递增. (2)由(1)知,有三个零点,则,且228()21003383722 5.820 3.84155457030K ⨯⨯-⨯=≈>⨯⨯⨯95%1111ABCD A B C D -1BB ⊥ABCD ∴1AC BB ⊥1111,ABCD A B C D AB BC -=ABCD AC BD ∴⊥11,BB BD B BB BD =⊂、11BB D D AC ⊥11BB D D EF ⊂11BB D D AC EF ⊥1CC M 12CM MC =,DM MF 111112,//,=D E ED DD CC DD CC =11,//,ED MC ED MC =1DMC E 1//DM EC ∴//,=,MF DA MF DA MFAD 1//,//DM AF EC AF ∴∴1C AEF '2()3f x x k =-0k ≤'()0f x ≥()f x (,)-∞+∞0k >'()0f x =3k x =±'()0f x <33kkx -<<'()0f x >3kx <-3k x >()f x (,)33k k-(,)3k -∞-(,)3k+∞()f x 0k >()03()03kf kf ⎧->⎪⎪⎨⎪<⎪⎩即,解得, 当时,,且, 所以在上有唯一一个零点,同理,, 所以在上有唯一一个零点,又在上有唯一一个零点,所以有三个零点, 综上可知的取值范围为. 21.(1),,根据离心率, 解得或(舍), 的方程为:,即; (2)点在上,点在直线上,且,,过点作轴垂线,交点为,设与轴交点为根据题意画出图形,如图2220332033kk kk k k ⎧+>⎪⎪⎨⎪-<⎪⎩4027k <<4027k <<3kk >2()0f k k =>()f x (,)3kk 13kk --<-32(1)(1)0f k k k --=--+<()f x (1,)3kk ---()f x (,)33k k-()f x k 4(0,)27222:1(05)25x y C m m +=<<∴5a =b m =22154115c b m e a a ⎛⎫⎛⎫==-=-= ⎪ ⎪⎝⎭⎝⎭54m =54m =-∴C 22214255x y ⎛⎫ ⎪⎝⎭+=221612525x y +=P C Q 6x =||||BP BQ =BP BQ ⊥P x M 6x =x N,,,又,,,根据三角形全等条件“”, 可得:,, ,,设点为,可得点纵坐标为,将其代入,可得:,解得:或,点为或,①当点为时, 故,, ,可得:点为, 画出图象,如图,,可求得直线的直线方程为:, 根据点到直线距离公式可得到直线的距离为:, 根据两点间距离公式可得:,||||BP BQ =BP BQ ⊥90PMB QNB ∠=∠=︒90PBM QBN ∠+∠=︒90BQN QBN ∠+∠=︒∴PBM BQN ∠=∠AAS PMB BNQ ≅△△221612525x y +=∴(5,0)B ∴651PM BN ==-=P (,)P P x y P 1P y =221612525x y +=21612525P x +=3P x =3P x =-∴P (3,1)(3,1)-P (3,1)532MB =-=PMB BNQ ≅△△∴||||2MB NQ ==Q (6,2)(5,0)A -(6,2)Q AQ 211100x y -+=P AQ 22231111055125211d ⨯-⨯+===+()()22652055AQ =++-=面积为:;②当点为时,故,,,可得:点为,画出图象,如图,可求得直线的直线方程为:,根据点到直线距离公式可得到直线的距离为:,根据两点间距离公式可得:,面积为:,综上所述,面积为:.22.(1)令,则,解得或(舍),则,即. 令,则,解得或(舍),则,即.;(2)由(1)可知,则直线的方程为,即.由可得,直线的极坐标方程为.23.(1),.均不为,则,;(2)不妨设,∴APQ15555252⨯⨯=P(3,1)-5+38MB==PMB BNQ≅△△∴||||8MB NQ==Q(6,8)(5,0)A-,(6,8)Q AQ811400x y-+=P AQ()2283111405185185811d⨯--⨯+===+()()226580185AQ=++-=∴APQ1518522185⨯⨯=APQ520x=220t t+-=2t=-1t=26412y=++=(0,12)A 0y=2320t t-+=2t=1t=2244x=--=-(4,0)B-22(04)(120)410AB∴=++-=12030(4)ABk-==--AB3(4)y x=+3120x y-+=cos,sinx yρθρθ==AB3cos sin120ρθρθ-+=2222()2220a b c a b c ab ac bc++=+++++=()22212ab bc ca a b c∴++=-++,,a b c02220a b c++>()22212ab bc ca a b c∴++=-++<max{,,}a b c a=由可知,,,. 当且仅当时,取等号,,即.0,1a b c abc ++==0,0,0a b c ><<1,a b c a bc =--=()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=b c =a ∴≥3max{,,}4a b c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年普通高等学校招生全国统一考试文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B I 中元素的个数为 A .1B .2C .3D .42.复平面内表示复数(2)z i i =-+的点位于 A .第一象限B .第二象限C .第三象限D .第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 4.已知4sin cos 3αα-=,则sin 2α=A .79-B .29-C .29D .795.设,x y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z x y =-的取值范围是A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]6.函数1()sin()cos()536f x x x ππ=++-的最大值为 A .65 B .1 C .35D .157.函数2sin 1xy x x=++的部分图像大致为A .B .C .D .8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为 A .5 B .4 C .3 D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .34π C .2πD .4π10.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为12,A A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A BC .3D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量(2,3),(3,)a b m =-=,且a b ⊥,则m = .14.双曲线2221(0)9x y a a -=>的一条渐近线方程为35y x =,则a = .15.ABC ∆的内角,,A B C 的对边分别为,,a b c 。
已知60,3C b c ===o,则A =_________。
16.设函数1,0,()2,0,xx x f x x +≤⎧=⎨>⎩ 则满足1()()12f x f x +->的x 的取值范围是__________。
三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-=K . (1)求{}n a 的通项公式; (2)求数列{}21na n +的前n 项和. 18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表: 最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.19.(12分)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比. 20.(12分)在直角坐标系xOy 中,曲线22y x mx =+-与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 21.(12分)已知函数()2(1)ln 2x ax a x f x =+++.(1)讨论()f x 的单调性;(2)当0a <时,证明3()24f x a≤--. (二)选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线1l 的参数方程为2,x t y kt =+⎧⎨=⎩(t 为参数),直线2l 的参数方程为2,x m my k =-+⎧⎪⎨=⎪⎩(m 为参数),设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程:(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l:(cos sin )0ρθθ+-=,M 为3l 与C 的交点,求M 的极径.23.[选修4—5:不等式选讲](10分)已知函数()||||f x x x =+1--2. (1)求不等式()f x ≥1的解集;(2)若不等式()f x x x m 2≥-+的解集非空,求m 的取值范围.2017年普通高等学校招生全国统一考试文科数学参考答案一、选择题1.B 2.C 3.A 4.A5.B6.A7.D 8.D9.B10.C 11.A 12.C二、填空题13.2 14.515.75°16.1(,)4-+∞三、解答题 17.解:(1)因为123(21)2n a a n a n +++-=K ,故当2n ≥时,1213(23)2(1)n a a n a n -+++-=-K两式相减得(21)2n n a -= 所以2(2)21n a n n =≥- 又由题设可得12a = 从而{}n a 的通项公式为221n a n =- (2)记{}21na n +的前n 项和为n S 由(1)知21121(21)(21)2121n a n n n n n ==-++--+ 则1111112 (1335212121)n nS n n n =-+-++-=-++ 18.解:(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为216360.690++=,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6(2)当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则64504450900Y =⨯-⨯=;若最高气温位于区间[20,25),则63002(450300)4450300Y =⨯+--⨯=;若最高气温低于20,则62002(450200)4450100Y =⨯+--⨯=- 所以,Y 的所有可能值为900,300,-100Y 大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为3625740.890+++=,因此Y 大于零的概率的估计值为0.819.解:(1)取AC 的中点O ,连结,DO BO ,因为AD CD =,所以AC DO ⊥ 又由于ABC ∆是正三角形,故BO AC ⊥ 从而AC ⊥平面DOB ,故AC BD ⊥ (2)连结EO由(1)及题设知90ADC ∠=o,所以DO AO = 在Rt AOB ∆中,222BO AO AB += 又AB BD =,所以222222BO DO BO AO AB BD +=+==,故90DOB ∠=o由题设知AEC ∆为直角三角形,所以12EO AC =又ABC ∆是正三角形,且AB BD =,所以12EO BD =故E 为BD 的中点,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1:1 20.解:(1)不能出现AC BC ⊥的情况,理由如下:设12(,0),(,0)A x B x ,则12,x x 满足220x mx +-=,所以122x x =-又C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为121112x x --⋅=-,所以不能出现AC BC ⊥的情况 (2)BC 的中点坐标为21(,)22x ,可得BC 的中垂线方程为221()22x y x x -=-ODABCE由(1)可得12x x m +=-,所以AB 的中垂线方程为2m x =-联立22,21()22m x x y x x ⎧=-⎪⎪⎨⎪-=-⎪⎩又22220x mx +-=,可得,212m x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以过A,B,C 三点的圆的圆心坐标为1(,)22m --,半径2r =故圆在y轴上截得的弦长为3=,即过A,B,C 三点的圆在y 轴上截得的弦长为定值。
21.解:(1)f(x)的定义域为(0,)+∞,1(1)(21)()221x ax f x ax a x x++'=+++=若0a ≥,则当(0,)x ∈+∞时,()0f x '>,故()f x 在(0,)+∞单调递增若0a <,则当1(0,)2x a ∈-时,()0f x '>;当1(,)2x a∈-+∞时,()0f x '< 故()f x 在1(0,)2a -单调递增,在1(,)2a-+∞单调递减。
