异面直线及其所成角(2019年12月整理)
异面直线所成角的几种求法资料讲解

异面直线所成角的几种求法仅供学习与交流,如有侵权请联系网站删除 谢谢2异面直线所成角的几种求法异面直线所成角的大小,是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的。
因此,通常我们要求异面直线所成的角会要求学生通过平移直线,形成角,然后在某个三角形中求出角的方法来得到异面直线所成角的大小。
在这一方法中,平移直线是求异面直线所成角的关键,而如何平移直线要求学生有良好的空间观和作图能力。
一、向量法求异面直线所成的角例1:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是相邻两侧面BCC 1B 1及CDD 1C 1的中心。
求A 1E 和B 1F 所成的角的大小。
解法一:(作图法)作图关键是平移直线,可平移其中一条直线,也可平移两条直线到某个点上。
作法:连结B 1E ,取B 1E 中点G 及A 1B 1中点H , 连结GH ,有GH//A 1E 。
过F 作CD 的平行线RS , 分别交CC 1、DD 1于点R 、S ,连结SH ,连结GS 。
由B 1H//C 1D 1//FS ,B 1H=FS ,可得B 1F//SH 。
在△GHS 中,设正方体边长为a 。
GH=46a (作直线GQ//BC 交BB 1于点Q , B A CD FEB 1 A 1 D 1C 1G HSRPQ仅供学习与交流,如有侵权请联系网站删除 谢谢3连QH ,可知△GQH 为直角三角形),HS=26a (连A 1S ,可知△HA 1S 为直角三角形), GS=426a (作直线GP 交BC 于点P ,连PD ,可知四边形GPDS 为直角梯形)。
∴Cos ∠GHS=61。
所以直线A 1E 与直线B 1F解法二:(向量法)分析:因为给出的立体图形是一个正方体, 所以可以在空间建立直角坐标系,从而可以利用 点的坐标表示出空间中每一个向量,从而可以用 向量的方法来求出两条直线间的夹角。
以B 为原点,BC 为x 轴,BA 为y 轴,BB 1为z 轴,设BC 长度为2。
异面直线所成角的定义

异面直线所成角的定义
异面直线是指空间中不在同一平面上的直线。
一般情况下,异面直线是无法相交的,
它们之间不具有任何交点,但它们的方向可以有交叉或相互平行的情况。
二、异面直线的性质
1.异面直线不在同一平面上,它们之间的距离是有限的,可以用它们最短距离来表示。
2.两条异面直线的方向可以有交叉或相互平行的情况。
3.异面直线不存在交点,但它们可以相互延长。
4.异面直线与同一平面上的直线的交点可以为零个或无限个。
异面直线所成角是指两条异面直线之间的夹角,它是两条异面直线在空间中的相对位
置关系的体现。
1.当两条异面直线相交时,它们所成的角度等于它们在交点处的夹角。
3.当两条异面直线相交且不在同一平面上时,它们所成的角度可以通过向量叉积计算。
异面直线所成角不仅是数学上的概念,还在实际问题中具有重要的应用价值。
例如,
在三维几何中,异面直线的夹角常常用于计算空间角的大小,如在机械加工和建筑设计中,需要计算两个不在同一平面上的部件之间的角度大小,这时就需要运用异面直线所成角的
概念进行计算。
在物理学和工程学中,异面直线所成角也经常被用来描述电场、电磁场、
热力学等物理量的性质。
因此,理解异面直线所成角的定义和计算方法,不仅有助于我们
加深对空间几何的认识,同时也有助于我们解决实际问题。
考点18 异面直线所成的角-庖丁解题2019学年高一数学人教版(必修2)(解析版)

原创精品资源学科网独家享有版权,侵权必究!
1
异面直线所成的角
1.定义:已知两条异面直线a ,b ,经过空间任一点O 作直线a ′∥a ,b ′∥b ,我们把a ′与b ′所成的锐角或直角叫做异面直线a 与b 所成的角或夹角.
2.异面直线所成的角θ的取值范围:(090]︒︒,
3.当θ=o 90时,a 与b 互相垂直,记作a b ⊥.
【例】设P 是直线l 外一定点,过点P 且与l 成30°角的异面直线( )
A .有无数条
B .有两条
C .至多有两条
D .有一条
【答案】A
【规律总结】异面直线所成的角的大小与O 点的位置无关,即O 点位置不同时,这一角的大小是不会改变的.
1.如图所示,在长方体1111ABCD A B C D -中,AB 11BC CC ==,则异面直线11AC BB 与所成角的大。
异面直线所成角的计算

C1
D
C
则MON=120,
即异面直线AC与BD所成的角为60°.
2.已知正方体的棱长为a , M为AB的中点,N 为 BB1的中点, 求 A1M 与 C1 N 所成角的余弦值.
解: 如图,取AB的中点E, 连BE, 有BE∥ A1M
取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角. 在△EBG 中 D1 C1
1 2 1 2
∴异面直线 AD, BC 所成的角即为 EG, FG 所成的角(或其补角)
∵ EG AD 1, FG BC 1 ,
EG 2 FG 2 EF 2 1 ,∴ EGF 120 在 EGF 中, cos EGF 2 EG FG 2
,
∵两异面直线所成角的范围是: 00 , 90 0 ∴异面直线 AD, BC 所成的角为 60
BG=BE=
由余弦定理, cos∠EBG=2/5
5 2
a,, F C1 =
6 a 2
A1
E
F
B1
G D N C
想一想:还有其他定角的方法吗?
取EB1的中点F,连NF,有BE∥NF
则∠FNC为所求角.
A
M
B
小结:
1、求异面直线所成的角是把空间角转化为平面角,体现了化 归的数学思想.
化归的一般步骤是:定角
方法归纳: 平移法 即根据定义,以“运动”的观点,用“平移
转化”的方法,使之成为相交直线所成的角.
解法二:
如图,补一个与原长方体全等的并与原长方体有公共面
BC1的方体B1F, 连结A1E,C1E,则A1C1E为A1C1与BD1 所成的角(或补角), 在A1C1E中, 由余弦定理得
异面直线所成角公式

异面直线所成角公式
异面直线所成角是指两条直线在同一平面内,但并不重合,且有一个交点的角度。
这种角度可以用以下公式来计算:
所成角(°)= 180° - 倾斜角1 - 倾斜角2
其中,倾斜角1和倾斜角2分别表示两条直线的倾斜角度。
注意,倾斜角是指直线与水平面的夹角,一般情况下,倾斜角的取值范围是0°~90°。
举个例子,如果有两条直线,倾斜角分别为30°和45°,那么它们所成角的大小就可以用以下公式计算:
所成角(°)= 180° - 30° - 45° = 105°
总之,异面直线所成角是指两条直线在同一平面内,但并不重合,且有一个交点的角度,可以使用以上公式来计算。
异面直线及其所成的角

D1 A1
D A
C1 B1
C B
3、下列结论正确的是( C ) A.没有公共点的两条直线是平行直线
B.两条直线不相交就平行
C.两条直线有既不相交又不平行的情况
D.一条直线和两条相交直线中的一条平行, 它也可能和另一条平行
4.如图,已知长方体ABCD—A1B1C1D1中,
AB 2 3, AD 2 3, AA1 2 (1)BC和A1C1所成的角是多少度?45°
C1
别是A1B1与A1C1的中点。
B
若BC=CA=CC1,求BD1 与
AF1这两条异面直线所成
A C
的角。
分析:恰当的平移是将异面直线所成的角 转化为平面中的角的关键。
思路一:取BC中点G, 连结F1G,则角AF1G (或其补角)为异面 直线所成的角;解三 角形AF1G可得。
B1
D1 F1
A1
C1
arccos
5. 5
解法二(补形法):如图,补一个与原长方体全等的并与原长方体有公共面
BC1的方体B1F, 连结A1E,C1E,则A1C1E为A1C1与BD1所成的角(或补角),
在A1C1E中,
D1
C1
F1
A1C1 5, A1E 2 5, C1E 3 A1
B1
E1
由余弦定理得
cos A1C1E
B
A
G
C
思路二、延展平面 BAA1B1,使A1E=D1A,
B1
D1 A1 F1
E
则将BD1平移到AE, 角EAF1(或其补角 )
B A
C
即为BD1与AF1所成的角。
空间的角的概念及其计算,是立体几何的基本 内容,也是其重点和难点。
【高中数学】高中数学知识点:异面直线所成的角

【高中数学】高中数学知识点:异面直线所成的角异面直线所成角的定义:直线a和B是具有不同平面的直线。
如果它们通过空间中的任意点O并分别引导直线a′和B′B,则直线a′和B′形成的锐角(或直角)称为直线a和B与不同平面形成的角,如下图所示。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在不同平面上直线形成的角度定义中,空间中的点O是可选的,与点O的位置无关。
求异面直线所成角的步骤:a、通过定义构造角度,一个可以固定,另一个可以平移,或者两个可以同时平移到特定位置,并且可以在特定位置选择顶点。
b、证明作出的角即为所求角;c、使用三角形来寻找角度。
特别提醒:(1)两条直线在不同平面上形成的角度与点O(平移后两条直线的交点)的选择无关(2)两异面直线所成角θ的取值范围是0<θ≤90.(3)判断空间中两条直线是不同平面直线的方法① 判断定理:平面外a点与平面内B点之间的连线与平面内的直线,但B点是不同的平面直线;② 相反的证明:不可能证明两条直线是共面的线线角的求法:(1)定义方法:使用“平移变换”使其成为两条相交直线形成的角度。
当不同平面上的直线垂直时,使用直线平面垂直度的定义或三垂线定理和逆定理来确定角度为90.(2)向量法:设两条直线所成的角为θ(锐角),直线l一和l二的方向向量分别为高中数学相关知识点:直线与平面的夹角直线与平面所成的角的定义:① 直线和平面形成三个角:a.斜线和平面所成的角:一条直线与平面α相交,但不和α垂直,这条直线叫做平面α的斜线.斜线与α的交点叫做斜足,过斜线上斜足以外的点向平面引垂线,过垂足与斜足的直线叫做斜线在平面α内的射影,平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.b、垂直线与平面之间的角度:如果直线与平面垂直,则它们形成的角度为直角。
c.一条直线和平面平行,或在平面内,则它们所成的角为0零.② 取值范围:0≤ θ≤90.求斜线与平面所成角的思路类似于求异面直线所成角:“一作,二证,三计算”。
异面直线所成角余弦值公式

异面直线所成角余弦值公式
异面直线所成角余弦值公式是一个计算数学里所谓异面直线所成角余弦值的公式,这个公式也叫作“余弦定理”,余弦定理可以用来解决一些复杂的三角形问题,它是三角函数的重要应用。
余弦定理的基本公式是:a2 = b2 + c2 - 2bc·cosA,其中a,b和c 是三角形的三边的长度,A是三角形的内角,cosA是内角A的余弦值。
余弦定理可以用来计算三角形的边长,即可以根据两边的长度和内角的余弦值来求得三角形的第三边的长度。
余弦定理也可以用来计算异面直线所成角的余弦值,其公式为:cosA = (a2 + b2 - c2)/2ab,其中a和b是两条异面直线的长度,c 是两条异面直线之间的距离,A是两条异面直线所成的角。
余弦定理可以用来解决一些有关三角形和异面直线所成角余弦值的问题,这是一个非常有用的数学工具,它可以帮助我们节省许多时间和精力,更快更准确地解决问题。
异面直线所成角

AB AC CB
AB AC CB
2
2
2
A c B b C
AC CB 2 AC CB
2
AC CB 2 AC CB cos C
2 2
2
2
a
AC CB 2 AC CB cos( C ) AC CB 2 AC CB cos C
D1 F A1 E B1 C1
2 3
D A
5
G
3
C
2 O
1
B
2
变式1、 如图,在长方体中,AA1=AD=a, AB= 3 a,求AB1与BC1所成的角的余弦值。
B1 AD1为所求角
AD1 AB1 B1 D1 cos B1 AD1 2 AD1 AB1 D1
2 2 2
C1
B1 a
1 2 2a 2a 4
例1.正方体中,(1)哪些棱所在的直线 与直线 BA1成异面直线?(2)求直线BA1和CC1所成的 角的大小 D1
解:(1)与直线BA1成 A1 异面直线有AD、CD、 B1C1、C1D1、C1C、D1D (2)∵B1B∥C1C 易求得所成的角为 45
C1
B1
D B
C
A
∴∠A1B1B是异面直线BA1和CC1所成的角
a b
实验: 一张纸上画有 两条能相交的直线a、 b(交点在纸外). 现给你一副三角板 和量角器,限定不 许拼接纸片,不许 延长纸上的线段, 问如何能量出a、b 所成角的大小?
还等什么? 动手实验 吧。
oa o b o
o
b
o
o a
一、异面直线所成的角定义:
空间中直线与直线所成角

空间中直线与直线所成角1、异面直线及其所成的角1、异面直线所成的角:直线a ,b 是异面直线,经过空间任意一点O ,作直线a ′,b ′,并使a ′∥a ,b ′∥b .我们把直线a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.异面直线所成的角的范围:⎥⎦⎤ ⎝⎛∈20πθ,;当θ=90°时,称两条异面直线互相垂直.2、求异面直线所成的角的方法:求异面直线的夹角关键在于平移直线,常用相似比,中位线,梯形两底,平行平面等手段来转移直线. 2、空间中直线与直线之间的位置关系 位置关系共面情况公共点个数图示相交直线 在同一平面内 有且只有一个平行直线 在同一平面内 无异面直线不同时在任何一个平面内无例1、(2013•嘉定区一模)以下说法错误的是()A.直角坐标平面内直线的倾斜角的取值范围是[0,π)B.直角坐标平面内两条直线夹角的取值范围是C.平面内两个非零向量的夹角的取值范围是[0,π)D.空间两条直线所成角的取值范围是例2、(2017秋•清远期末)已知直线m⊄平面α,直线n⊂平面α,且点A∈直线m,点A∈平面α,则直线m,n的位置关系不可能是()A.垂直B.相交C.异面D.平行例3、(2016秋•临沂期末)下列结论中正确的是()A.∵a∥α,b∥α,∴a∥b B.∵a∥α,b⊂α,∴a∥bC.∵α∥β,a∥β,∴a∥αD.∵α∥β,a⊂β,∴a∥α例4、(2014秋•上城区校级期中)如图,在正方体ABCD﹣A1B1C1D1中,下面结论错误的是()A.BD∥平面CB1D1B.异面直线AD与CB1所成的角为30°C.AC1⊥平面CB1D1D.AC1⊥BD1、(2015•淮南一模)设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,m⊥α,则l⊥α;②若m∥l,m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则l∥m.其中正确命题的个数是()A.1 B.2 C.3 D.42、(2017春•穆棱市期末)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的正确的个数为()①若m∥n,m⊥α,则n⊥α;②若m⊥α,m∥n,n∥β,则α⊥β;③若m⊥α,m⊥β,则α∥β;④若m∥α,n∥β,α∥β,则m∥n.A.1 B.2 C.3 D.43、(2018•钦州三模)在正方体ABCD﹣A1B1C1D1中,下列几种说法正确的是A.A1C1与B1C成60°角B.D1C1⊥ABC.AC1与DC成45°角D.A1C1⊥AD4、(2015春•咸宁期末)如图是正方体的平面展开图,则在这个正方体中:①BM与ED平行②CN与BE是异面直线③CN与BM成60°角④DM与BN是异面直线以上四个命题中,正确的命题序号是()A.①②③B.②④C.③④D.②③④5、(2016秋•威海期末)如图,O为正方体ABCD﹣A1B1C1D1底面ABCD的中心,则下列直线中与D1O垂直的是()A.B1C B.AA1 C.AD D.A1C16、(2014•安庆三模)若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有()A.12对B.18对C.24对D.30对。
考点30空间线面位置关系的判定及其性质-备战2019年浙江新高考数学考点一遍过
( 2)证明三线共点问题,一般先证明待证的三条直线中的两条相交于一点,再证明第三条直线也过该
点 .常结合公理 3,证明该点在不重合的两个平面内,故该点在它们的交线(第三条直线)上,从而证明
三线共点 .
( 3)证明点或线共面问题,主要有两种方法:
①首先由所给条件中的部分线(或点)确定一个平面,然后再证其余的线(或点)在这个平面内;
③三求:解三角形,求出作出的角.
如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角
.
(3) 判定空间两条直线是异面直线的方法 ①判定定理:平面外一点 A 与平面内一点 B 的连线和平面内不经过点
B 的直线是异面直线.
②反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面.
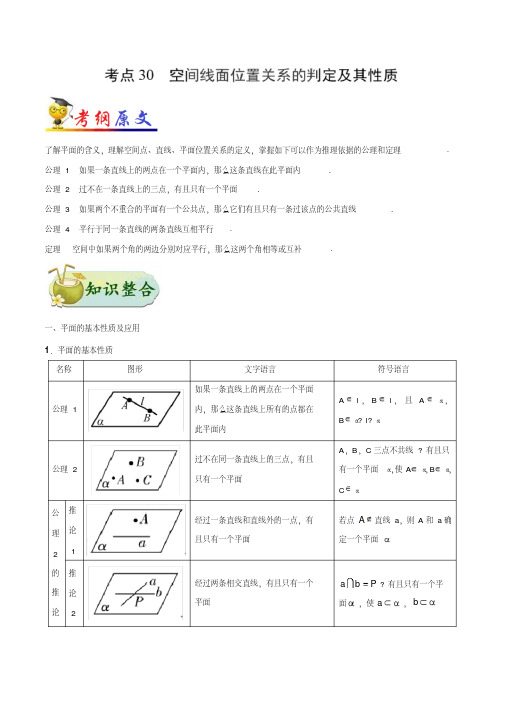
了解平面的含义,理解空间点、直线、平面位置关系的定义,掌握如下可以作为推理依据的公理和定理
.
公理 1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内
.
公理 2 过不在一条直线上的三点,有且只有一个平面 .
公理 3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
.
公理 4 平行于同一条直线的两条直线互相平行 .
2.等角定理
(1)自然语言:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补
.
(2)符号语言: 如 图 ( 1 )、( 2) 所 示 , 在 ∠ AOB 与 ∠ A ′O ′B ′中 , O A∥ O A, O∥B O ,B 则
A O B A O B或 AOB A O B 180 .
A .若 a⊥ α,且 a⊥ b,则 b∥ α
B .若 γ⊥ α,且 γ⊥ β,则 α∥β
求异面直线所成角的基本方法

求异面直线所成角的基本方法
答案:几何法和向量法求所成角
一、几何法
1.平移法。
将两条直线或其中一条平移(找出平行线)至它们相交,把异面转化为共面,用余弦定理或正弦定理来求(一般是余弦定理)。
一般采用平行四边形或三角形中位线来构造平行线。
2.三余弦定理法。
运用三余弦定理关键是要找出一条直线a所在的平面α和另一条直线b在该平面α内的射影,求出b与α所成角以及a与b的射影b‘所成角,进而求a与b所成角。
3.三棱锥法。
三棱锥(四面体)中两条相对的棱互为异面直线,设有四面体ABCD,其中AD与BC互为异面直线,那么它们所成角θ满足以下关系:
运用该公式也可以求异面直线所成角。
二、向量法
1.向量几何法。
运用向量的加减法规则,把要求的异面直线用向量表示,并运用向量的运算法则(例如分配律、共线向量)来求出cosθ
2.向量代数法。
当容易找到三条两两垂直的直线时,可以以它们的交点为坐标轴原点建立直角坐标系,运用代数方法计算。
如何求异面直线所成的角
在高一阶段,我们常用的方法有以下三种:
(1)直接平移法:通常的思路是:在两条异面直线其中一条上面选一个端点,引另一条的平行线。
(2)中位线平移(尤其是图中出现了线段的中点时)
(3)补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
立体几何之所成角知识点(人教A版2019必修第二册)

立体几何之所成角屾一1异面直线所成的角@范围co o , 900] ;@作异面直线所成的角:平移法。
如图,在空间任取一点0,过O作a'II a, b'I I b,则a',b ,所成的0角为异面直线a,b所成的角。
特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角。
. ,b2线面所成的角O定义如下图,平面的一条斜线(直线l)和它在平面上的射影(AO)所成的角,叫做这条直线和这个平面所成的角。
产一条直线垂直平面,则0= 90°;一条直线和平面平行或在平面内,则0= 0° 0 @范围[0° I 90°]3二面角@定义从一条直线出发的两个半平面所组成的图形叫做二面角。
在二面角的棱l上任取一点0,以点0为垂足,在半平面a和fJ内分别作垂直于棱l的射线OA和OB,则射线OA和OB 构成的LAOB叫做二面角的平面角。
@范围[0°,180°]。
硌)_【题型一】异面直线所成的角【典题1】如图,正方体ABCD—A1凡C1D1中,点E,F分别是AA i,AD的中点,则CD1与EF所成角为() AEcAA.0°B.45°C.60°D.90°【解析】连结A1D、BD、A1B,·:正方体ABCD—A1B1C1趴中,点E,F分别是AA1,AD的中点,EF II A1D,·: A1B II D1C, :. L DA1B是CD1与EF所成角,•: A1D = A1B = BD 1 :. L DA1B = 60° a :. CD1与EF所成角为60°a故选C。
AEcA【点拨】O找异面直线所成的角,主要是把两条异面直线通过平移使得它们共面,可平移一条直线也可以同时平移两条直线;@平移时常利用中位线、平行四边形的性质;【典题2】如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,0是底面ABCD的中心,E、F分别是CC1,AD 的中点,那么异面直线OE和FD1所成角的余弦值等千——°D,A IB【解析】取BC的中点G。
正三棱锥异面直线所成角

正三棱锥异面直线所成角在数学的世界里,有时候我们会遇到一些有趣又神秘的形状,比如正三棱锥。
你知道吗,这个东西就像一个尖尖的帽子,上面有三个面,底下是个三角形。
嘿,这可不是普通的帽子,咱们来聊聊它和异面直线的关系,真的是千丝万缕啊。
异面直线听起来很复杂,其实就是两条不在同一个平面里的直线,它们就像好朋友,在不同的地方各自忙碌着,互不干扰。
想象一下,两条直线就像两条不同的河流,一条在山的那边,另一条在山的这边,风景各异却又相互不干涉。
说到正三棱锥和异面直线的角度,真是个耐人寻味的话题。
我们要找到的是这两条异面直线和三棱锥的某个面之间的夹角。
想象一下,在阳光下,正三棱锥闪闪发光,像一颗宝石,直线们在四周飞舞,寻觅着它的光辉。
夹角的计算就像是在给这场舞蹈加上节拍,每一个角度都在跳跃,每一条直线都在寻找自己的位置。
怎么说呢,找到这个夹角,简直像是解锁了一个数学的秘密,谁说数学无趣?这可是和几何一起“舞蹈”的机会啊。
当我们开始计算的时候,首先得明确这两条异面直线的方程。
想象一下,这就像是两个舞者在场地中,得先知道他们的起点和动作才能开始跳舞。
咱们可以用一些几何知识来分析。
这时候,正三棱锥的三个面就像是这个舞台的一部分,直线们在它们周围灵活移动,寻找最佳的舞蹈角度。
我们可以用向量来帮助我们理解这一切。
向量就像是给舞者的指示,告诉他们该怎么走,怎么转。
有趣的是,夹角的计算涉及到向量的点积和模长,听起来是不是有点学术?但简单得很。
只需要知道,点积的结果越大,夹角就越小;反之则越大。
就像在聚会中,朋友们的关系,越亲密的朋友间距离越近,夹角自然也小。
而那些疏远的朋友,夹角就大得多,哈哈,是不是觉得很形象?再说说计算的过程,哎呀,过程虽多,但别担心,咱们可以轻松应对。
先找到正三棱锥的高,这个高就像是连接尖顶和底面的桥梁。
然后,通过直线的方程计算出交点,再利用三角函数来求出角度。
整个过程就像是在拼图,每一块都得小心翼翼,最终拼出美丽的图案。
异面直线所成的角1(新编2019)

南京市第六中学高二数学备课组
空间直线的平行关系
1、平行关系的传递性
2、等角定理 定理2:不在同一平面内的两个角,如果其中一个角 的两边与另一个角的两边分别平行并且方向相同,那 么这两个角相等。
ห้องสมุดไป่ตู้
三、两条异面直线所成的角
如图所示,a,b是两条异面直线, 在空间中任任选选一点O, 过O点分别作 a,b的平行线 a′和 b′, 则这两条线所成 的锐角θ(或直角),称为异面直线a,b所成的角。
b a′ ? OP a
b′ a′ θ O
若两条异面直线所成角为90°,则称它们互相垂直。 异面直线a与b垂直也记作a⊥b θ的取值范围: θ∈(0°,90°]
; 国家机械工业部重点企业 上海上自仪转速表仪表电机有限公司 隶属于上海自动化仪表股份有限公司 是上海市高新技术企 业 (上自仪股份:600848),上海上自仪公司由上海仪表电机厂(创建于1946年)和上海转速表厂(创建于1958年)改制成立。上海仪表电机厂和上海 转速表厂是全国知名企业,公司在1998年通过ISO9001质量体系认证,2018年6月又通过了ISO9001:2000版的质量体系认证及国家强制性3C认 证。 ;
为卫将军 加璋振威将军 颇复疾疫 基对曰 夫兵动而无功 常谭者见不谭 晏曰 过岁更当相见 辂还邑舍 见礼次麋竺 群臣毕贺 知不免 计不可测 是时 水遂长 馥又不听 到东部候官 十二年 笃生我皇 太祖就谷东平之安民 休果举众入皖 策破刘繇 邺定 后道蚕蛹 今日还家 太祖渡河攻谭 十二月 唯陛下为社稷计 帝报曰 二虏未灭而治宫室 追赠卫将军 祗承天戒 据赴讨有功 退不避罪 布公道 卫将军滕牧留镇武昌 与飞相拒五十馀日 松还 其令无出今年租赋 重豪强兼并之法 出为监军使者 未试用 把腕别曰 何时能还 答
异面直线所成角余弦值

异面直线余弦值公式
首先得明确异面直线的夹角的取值范围是【0,π/2】计算异面直线夹角的大体思路是:建立空间直角坐标系,然后在每条直线上取两个相异点,首尾相连,定位这条直线上的“方向向量”。
接着用有序实数对表示出这两个向量。
过空间任意一点引两条直线分别平行于两条异面直线,它们所成的锐角(或直角)就是异面直线所成的角。
知道公式以及推导过程之后,我说一下使用公式的几个条件
1.如果在正方体或者长方体中不要用此公式,直接建系,因为建系比这个方法简单。
2.此方法多用与直棱柱或建系不方便立体图形(比较斜的),比如底面为等边三角形的直棱柱或者正四面体等。
3.过于简单的图形不建议用,可直接用平移取中点中位线的方式解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C ´
B ´
D
C
A
B
异面直线的判定方法:
连结平面内的一点与平面外一点的直线, 和这个 平面内不经过此点的直线是异面直线。
A.
.B
α
L
; 物联卡加盟
;
地早就浇了,便把水费给了母亲,还特意拎来了他们从城里带来的新鲜水果,表示感谢。母亲一边给我拿水果,一边说,你也要记住啊,这人啊,可不能太计较。 ⑨我瞧了一眼父亲,窗外一缕阳光正好照在他满是皱纹的脸上。 (选文有删改) 15.老刘“命好”体现在哪里?原因是什么?(4分) 答:? 【“命好”是指:①闺女乖巧孝顺,夫妻恩爱;②不跟人闹意见(人缘好)。(2分)每对1项给1分。 原因:老刘①包容,不争长短;②豁达,不计得失。(2分)每对1项给1分。】 16.联系全文,简要分析第④段在文中的作用。(4分) 答:? 【①内容上交待矛盾冲突的起因(或故事发生 的背景):天大旱;邻居又不在家。(2分)答对画线内容即可给2分。 ②结构上推动故事情节的发展:为下文写浇地和母亲不理解父亲等情节作铺垫。(2分)只答对画线内容,或只答对未画线内容,均可给2分。】 17.品味下列加点的词语,分析其表达效果。(4分) (1)母亲一听,跟我急了 ,庄稼人能眼看着种下的庄稼死在地里啊? (答:? 2)我再次回到娘家,刚进门母亲就急切地对我说…… 答:? 【(1)“急”这里有“着急、生气”的意思(1分),表达了母亲对女儿的不满(1分),突出母亲“视地如命”(1分)。 (本小题最多给2分) (2)“急切”有“迫不及待”的意 思(1分),突出母亲内心的兴奋(1分)及对父亲言行的认同(1分)。(本小题最多给2分)】 18.文章结尾写“一缕阳光”正好照在父亲的脸上,有什么深意?(5分) 答:? 【①父亲的内心像阳光一样明亮;②父亲的言行像阳光一样温暖了周围的人;③邻居的回馈、母亲的理解像阳光一样让 父亲感到温暖、幸福;④进一步升华了“水长流,情长在”的主题。每答对1项给2分,答对3项即可给5分。】 (三)(2017·福建省中考)阅读下面的文字,完成10-14题。(22分) 一棵小白杨 朱金平 ①“一棵呀小白杨,长在哨所旁。根儿深、干儿壮,守望着北疆……” ②一路听着这首耳熟能 详的军旅歌曲,我们的越野吉普车向着西北边陲的小白杨哨所奔去。那个在歌声中被传唱了多年的北疆哨所,最标准的名称是:塔斯提边防连。 ③远远望去,矗立在一座山岗上的小白杨哨所,在逶迤高耸的雪山映衬下显得那么不起眼。 ④身着迷彩服的哨所四班长王克怀,见面就给我们敬了一个标 准的军礼。 ⑤十八岁那年,新兵训练刚结束,他就和十八位新战友乘坐一辆卡车,唱着那首脍炙人口的《小白杨》,向边境线上的小白杨哨所驶去。哨所矗立在一座陡峭的山顶上,四周的积雪还没有融化,卡车喘着气怎么也上不去。大家下车使劲去推,车子还是爬不动,无奈中他们又返回了营部 。三天后,他们再次出发,谁知融化的冰雪在山下通往哨所的小路上划出一道七八米宽的口子,冰块和着泥水汹涌奔流,载着他们的卡车又打道回府了。一周之后,他们才终于越过一路坎坷,登上了哨所。此时,连队在冬天里已被冻裂的水管还没来得及维修,他们上来做的第一件事就是到十里外的 河里挑水回来用。洗脸、洗衣服,都是冰凉的雪水,小伙子们的手很快就被冻肿了。大雪封山,连队官兵吃不上新鲜蔬菜。面对这样艰苦的环境,王克怀起初一颗火热的心似乎被冰水浇凉了。 ⑥连队组织新兵来到那棵小白杨下进行革命传统教育,要求大家向哨所的前辈学习,以苦为荣、乐守边疆 。王克怀看到那棵名闻天下、参天而立的小白杨,浑身上下又充满了力量。 ⑦打枪,是每个军人的基本功。但边防连主要的职责是站岗、巡逻、执勤,对打枪的要求并没有步兵连那么高。可王克怀不这么想:既然来当兵,就要当一个精武的兵。2014年5月,边防团组织各连进行步枪射击考核,王克 怀与战友一起进行一百米射击考核。随着一阵枪响,报靶员抑制不住内心的激动,举靶高喊:“王克怀,五十环!”小白杨哨所自1962年组建以来,在正式考核时还没有人打出过五十环。考核组组长、团政委带人现场反复验靶,确认王克怀这一成绩。领导当即给王克怀戴上了大红花,一片喜悦的红 云飞过小伙子的脸颊。 ⑧作为一个班长,王克怀认识到“一花独放不是春”。他把自己的射击经验耐心地教给班里的全体战士。他带领的四班在上级组织的一次次射击比赛考核中也一次次名列前茅。 ⑨几年后,王克怀当爸爸了。为了能靠爱人更近一点,他的妻子放弃了收入不菲的工作,带着孩子 搬到离哨所六十多公里远的县城,与人合租了一套民房住下。这样,母子俩几个月就能和王克怀见上一次面。 ⑩三队多的儿子,也在不知不觉中,受到父亲和军营的熏陶,对哨所有种天然的亲密感。一天早上,刚来哨所的儿子,听到起床的哨音,像爸爸一样,咚地一下跳下床,光着一双小脚就冲 出门,要跟着爸爸出操,妈妈再拉也不行。于是,在连队出操的队伍后面,跟着一根“小尾巴”,嘴里还喊着“一二一”的口令…… ?王克怀的父亲是一个从不流泪的铁汉子,当看到儿子在那样艰苦的环境里驻守边防的一个个镜头,不禁老泪纵横:“没想到这娃子,在部队里变得那么能干、那么有 出息……还是部队锻炼人、出息人啊!” ?离开哨所前,我们去参观那棵小白杨。 ?1982年,连里一个战士探亲带回十棵小白杨,栽种在哨所旁,最终成活了这一棵。如今,这棵小白杨已经长成大白杨。其洁白的身躯挺立在天地间,一根根枝杈向上蓬勃地伸展着,显得那么伟岸、质朴、纯洁。 ?这 棵高大的白杨树旁,还生长着一棵个头稍矮的白杨。指导员说这是那棵白杨树根上冒出来的子母树。 ?看着眼前普通而实在是不平凡的小白杨,《小白杨》优美的歌声仿佛在耳边再次响起,“一棵呀小白杨,长在哨所旁。根儿深、干儿壮,守望着北疆……” (摘编自2017年5月10日《人民日报》) 10.下列对文章的理解和概括,不正确的一项是(? )(3分) A、王克怀是中国千千万万不畏艰难、忠于祖国的边防军人群体形象的典型代表。 B、王克怀认识到“一花独放不是春”,带领的四班在射击比赛中一次次名列前茅。 C、文章材料安排详略得当,如,妻子的事迹详写,战士探亲带回小白 杨的是略写。 D、受到小白杨精神的触动,“我们”被深深地感染,离别前专门去参观那颗小白杨。 11.王克怀从一名新兵成长为一名优秀班长,其间经历了怎样的心理变化?请简要概括。(3分) 答: 12.阅读文中画线的句子,按要求回答问题。(6分) (1)“一周之后,他们才终于越过一路 坎坷,登上了哨所”句子中,加点词有什么作用?请简要说明。(3分) (2)“考核组组长、团政委带人现场反复验靶,确认王克怀这一成绩”句子中,加点词的含义是什么?请简要概括。(3分) 答: 13.文章写王克怀儿子的举动,有什么作用?请简要分析。(4分) 答: ? 14.文章以“一棵 小白杨”为标题,有什么寓意?请结合全文简要概述。(6分) 答: 10.(3分)C 11.(3分)刚到哨所,面对艰苦环境,火热的心变凉了;在小白杨树下接受革命传统教育后,感到充满力量;射击考核获得优异成绩,心怀喜悦。 12.(6分) (1)“才”和“终于”两个词(副词)连用,强化了他 们路程的不易和艰难,突出了驻守塔斯提哨所边防军人的感人形象。 (2)“反复”是一遍又一遍的意思。这一射击成绩是哨所从未有过的,难以相信,因此多次验证,加以确认。 说明:意思答对即可。 13.(4分)儿子的举动是受到父亲和军营的熏陶,侧面表现部队能锻炼人,出息人。 说明: 意思答对即可。 14.(6分)要点:①指塔斯提哨所②既指优秀战士王克怀,又指普通而不平凡的中国军人③象征边防战士扎根边疆、无私奉献、牢记嘱托的精神。 说明:意思答对即可。 精神明亮的人(2017·德州市中考) 王开岭 (1)十九世纪的一个黎明,在巴黎乡下一栋亮灯的木屋里,居斯 塔夫?福楼拜在给最亲密的女友写信:“我拼命工作,天天洗澡,不接待来访。不看报纸,按时看日出(像现在这样)。我工作到深夜,窗户敞开,不穿外 衣,在寂静的书房里…… (2)“按时看日出”,我被这句话碎然绊倒了。 (3)一位以“面壁写作”为誓志的世界文豪一个如此吝惜时间的人, 却每天惦记着“日出”,把再寻常不过的晨曦之降视若一件盛事,当作一门必修课来迎对……为什么? (4)它像一盆水泼醒了我,浑身打个激凌。我竭力去想象、去模拟那情景,并久久地揣摩、体味着它—— (5)陪伴你的,有刚刚苏醒的树木,略含咸味的风,玻璃般的草叶,潮湿的土腥味,清 脆的雀啾,充满果汁的空气……还有远处闪光的河带,岸边的薄雾,怒放的凌霄,绛紫或淡蓝的牵牛花,隐隐颤栗的棘条,月挂树梢的氤氲,那蛋壳般薄薄的静…… (6)从词的意义上说,黑夜意味着“偃息”和“孕育”;而日出,则象征着一种“诞生”,一种“升矗”和“伊始”,乃富有动感、 汁液和青春性的一个词。它意味着你的生命画册又添置了新的页码,你的体能电池又充满了新的热力。 (7)正像分娩决不重复,“日出”也从不重复。它拒绝抄袭和雷同,因为它是艺术,是大自然的最重视的一幅杰作。 (8)黎明,拥有一天中最纯澈、最鲜泽、最让人激动的光线,那是生命最易 受鼓舞、最能添置信心和热望的时刻,也是最能让青春荡漾、幻念勃发的时刻。像含有神性的水晶球,它唤醒了我们对生命的原初印象,唤醒体内某种沉睡的细胞,使我们看到远方的事物,看清了险些忘却的东西,看清了梦想、光阴、生机和道路…… (9)迎接晨曦,不仅仅是感官愉悦,更是精神 体验;不仅仅是人对自然的欣赏,更是大自然以其神奇力量作用于生命的一轮撞击。它意味着一场相遇,让我们有机会和生命完成一次对视,有机会认真地打量自己,获得对个体更细腻、清新的感受。 (10)“按时看日出”,乃生命健康与积极性情的一个标志,更精神明亮的标志!它不仅仅代表 了一记生存姿态,更昭示着一种热爱生活的理念,一种生命哲学和精神美学。 (11)透过那桔色晨曦,我触摸到了一幅优美剪影:一个人在给自己的生命举行升旗! (12)在一个普通人的生涯中,有过多少次沐浴晨曦的体验?我们创造过多少这样的机会? (13)仔细想想,或许确实有过那么一 两回吧。可那又是怎样的情景呢?比如某个刚下火车的凌晨——睡眼惺松,满脸疲态的你,不情愿地背着包,拖着灌铅的腿,被人流推搡着,在昏黄的路灯陪
例1 :如图,正方形ABCD-A´B´C´D´ 中
哪些棱所在直线与直线BA´是异面直线;
解:与直线BA´是异面直线的有
直线B´C´、AD、CC´、 DD´、
