时间序列分析期末考试B
最新时间序列分析期末考试B

精品文档浙江农林大学 2009 - 2010 学年第 二 学期考试卷(A 卷)课程名称: 应用时间序列分析 课程类别: 必修 考试方式: 闭卷注意事项:1、本试卷满分100分。
2、考试时间 120分钟。
一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的选项填在题后的括号内。
每小题2分,共12分)1. 关于严平稳与(宽)平稳的关系,不正确的为 。
( ) A. 严平稳序列一定是宽平稳序列 B. 当序列服从正态分布时,两种平稳性等价 C. 二阶矩存在的严平稳序列一定为宽平稳的 D. MA(p)模型一定是宽平稳的2. 下图为某时间序列的相关检验图,图1为自相关函数图,图2为偏自相关函数图,请选择模型 。
( )图1图2学院: 专业班级: 姓名: 学号:装 订 线 内 不 要 答 题A. AR(1)B. AR(2)C. MA(1)D. MA(2)3. 下图中,图3为某序列一阶差分后的自相关函数图,图4为某序列一阶差分后的偏自相关函数图,请对原序列选择模型。
( )图3图4A.ARIMA(4,1,0)B. ARIMA(0,2,1)C. ARIMA(0,1,2)D.ARI MA(0,1,4) 4. 记B 为延迟算子,则下列不正确的是 。
( ) A. 01B = B. (1)kt t k t X X B X --=- C. 12t t BX X --= D. 11()t t t t B X Y X Y --±=±5.对于平稳时间序列,下列错误的是 ( ) A.)(212εσεE = B.),(),(k t t k t t y y Cov y y Cov -+=C.k k -=ρρD.)(ˆ)1(ˆ1k y k yt t +=+ 6.下图为对某时间序列的拟合模型进行显著性水平0.05α=的显著性检验,请选择该序列的拟合模型 。
( )A. 151.261690.42481t t t X X a -=-+B.173.038290.42481t t t X X a -=-+C. 151.261690.42481t t t X a a -=++D. 173.038290.42481t t t X a a -=++二、检验下列模型的平稳性与可逆性,写出详细过程。
时间序列分析考试卷及答案

考核课程 时间序列分析(B 卷) 考核方式 闭卷 考核时间 120 分钟注:B 为延迟算子,使得1-=t t Y BY ;∇为差分算子,。
一、单项选择题(每小题3 分,共24 分。
)1. 若零均值平稳序列{}t X ,其样本ACF 和样本PACF 都呈现拖尾性,则对{}t X 可能建立( B )模型。
A. MA(2)B.ARMA(1,1)C.AR(2)D.MA(1)2.下图是某时间序列的样本偏自相关函数图,则恰当的模型是( B )。
A. )1(MAB.)1(ARC.)1,1(ARMAD.)2(MA3. 考虑MA(2)模型212.09.0--+-=t t t t e e e Y ,则其MA 特征方程的根是( C )。
(A )5.0,4.021==λλ (B )5.0,4.021-=-=λλ (C )5.2221==λλ, (D ) 5.2221=-=λλ,4. 设有模型112111)1(----=++-t t t t t e e X X X θφφ,其中11<φ,则该模型属于( B )。
A.ARMA(2,1) B.ARIMA(1,1,1) C.ARIMA(0,1,1) D.ARIMA(1,2,1)5. AR(2)模型t t t t e Y Y Y +-=--215.04.0,其中64.0)(=t e Var ,则=)(t t e Y E ( B )。
A.0 B.64.0 C. 16.0 D. 2.06.对于一阶滑动平均模型MA(1): 15.0--=t t t e e Y ,则其一阶自相关函数为( C )。
A.5.0- B. 25.0 C. 4.0- D. 8.07. 若零均值平稳序列{}t X ∇,其样本ACF 呈现二阶截尾性,其样本PACF 呈现拖尾性,则可初步认为对{}t X 应该建立( B )模型。
A. MA(2)B.)2,1(IMAC.)1,2(ARID.ARIMA(2,1,2)8. 记∇为差分算子,则下列不正确的是( C )。
时间序列期末精彩试题B卷
成都信息工程学院考试试卷2012——2013学年第2学期课程名称:《金融时间序列分析》 班级:金保111本01、02、03班一、判断题(每题1分,正确的在括号内打√,错误的在括号内打×,共15分) 1.模型检验即是平稳性检验( )。
2.模型方程的检验实质就是残差序列检验( )。
3.矩法估计需要知道总体的分布( )。
4.ADF 检验中:原假设序列是非平稳的( )。
5.最优模型确定准则:AIC 值越小、SC 值越大,说明模型越优( )。
6.对具有曲线增长趋势的序列,一阶差分可剔除曲线趋势( )。
7.严平稳序列与宽平稳时序区分主要表现在定义角度不同( )。
8.某时序具有指数曲线增长趋势时,需做对数变换,才能剔除曲线趋势( )。
9.时间序列平稳性判断方法中 ADF 检验优于序时图法和自相关图检验法( )。
10.时间序列的随机性分析即是长期趋势分析( )。
11.ARMA (p,q )模型是ARIMA(p,d,q)模型的特例( )。
12.若某序列的均值和方差随时间的平移而变化,则该序列是非平稳的( )。
13. MA(2)模型的3阶偏自相关系数等于0( )。
14.ARMA(p,q)模型自相关系数p 阶截尾,偏自相关系数拖尾( )。
15.MA(q)模型平稳的充分必要条件是关于后移算子B 的q 阶移动自回归系数多项式根的绝对值均在单位圆内( )。
二、填空题。
(每空2分,共20分) 1.t X 满足ARMA (1,2)模型即:t X =0.43+0.341-t X +t ε+0.81-t ε–0.22-t ε,则均值= ,1θ(即一阶移动均值项系数)= 。
2.设{x t }为一时间序列,B 为延迟算子,则B 2X t = 。
3.在序列y 的view 数据窗,选择 功能键,可对序列y 做ADF 检验。
4.若某平稳时序的自相关图拖尾,偏相关图1阶截尾,则该拟合 模型。
5. 已知AR (1)模型:t X +0.81-t X =t ε,t ε服从N(0,0.36),则一阶自相关系数= ,方差= 。
时间序列分析期末复习题

时间序列分析期末复习题时间序列分析期末复习题时间序列分析是一种用来研究时间序列数据的统计方法。
它可以帮助我们理解和预测时间序列数据的趋势、季节性和周期性变化。
在期末复习中,我们可以通过解答一些典型的时间序列分析问题来加深对这一概念的理解。
1. 如何确定时间序列数据的趋势?时间序列数据的趋势是指数据随时间变化的长期趋势。
我们可以使用移动平均法或指数平滑法来确定趋势。
移动平均法是将数据按照一定的时间窗口进行平均,以减少随机波动。
指数平滑法则是通过对数据进行加权平均,使得最近的数据对趋势的影响更大。
通过观察平滑后的数据,我们可以确定时间序列数据的趋势。
2. 如何检测时间序列数据的季节性?时间序列数据的季节性是指数据在特定时间段内周期性变化的模式。
我们可以使用季节性分解方法来检测季节性。
季节性分解方法将时间序列数据分解为趋势、季节性和随机成分三个部分。
通过观察季节性成分,我们可以确定时间序列数据的季节性。
3. 如何预测未来的时间序列数据?预测未来的时间序列数据是时间序列分析的一个重要应用。
我们可以使用平稳性检验来确定时间序列数据是否具有稳定性,如果数据不稳定,我们需要进行差分运算来使其稳定。
然后,我们可以使用自回归移动平均模型(ARMA)或自回归积分移动平均模型(ARIMA)来建立预测模型。
这些模型可以根据过去的数据来预测未来的数据。
4. 如何评估时间序列预测模型的准确性?评估时间序列预测模型的准确性是非常重要的。
我们可以使用均方根误差(RMSE)或平均绝对百分比误差(MAPE)来评估模型的预测准确性。
这些指标可以帮助我们了解模型的误差大小和方向,从而判断模型的有效性。
5. 如何处理异常值和缺失值?在时间序列分析中,异常值和缺失值可能会对结果产生不良影响。
对于异常值,我们可以使用平滑技术或插值方法来修正。
平滑技术可以通过对数据进行平均或加权平均来减少异常值的影响。
插值方法可以通过使用相邻数据的平均值或线性插值来填补缺失值。
南开大学时间序列分析往年期末试题考题

南开大学经济学院2002年第一学期计量经济学期末开卷试题五、下图一是yt 的差分变量Dyt的相关图和偏相关图;图二是以Dyt为变量建立的时间序列模型的输出结果。
(22 分)其中Q统计量Q-statistic(k=15)=5.4871.根据图一,试建立Dyt的ARMA模型。
(限选择两种形式)( 6 分)2.根据图二,试写出模型的估计式,并对估计结果进行诊断检验。
(8 分)3.与图二估计结果相对应的部分残差值见下表,试用(2)中你写出的模型估计式预测1998年的Dyt的值(计算过程中保留四位小数)。
( 6 分)五、( 6 分,8 分, 6 分)1.由图一的偏相关图和相关图的特点,可知原序列可能是ARIMA(1,1,1) ;ARIMA(1,1,2)等过程。
2.模型的估计式为:△y t=0.978038 △ yt-1+ut-0.313231ut-2 。
此结果可取,因为所有系数都通过了t 检验,并且Q 值非常小( 5.487),远小于Q 检验的临界值χ20.05(15-1-2)=21 。
3.利用yt=0.978038 △ yt-1+ut-0.313231ut-2 ,可得:Δ y? 1998 = 0.9780 Δ y1997 - 0.3132u ? 1996 =0.9780 × 0.1237-0.3132 × (-0.0013)=0.1214 。
y? 1998 = y1997 + Δ y? 1998 =12.3626+0.1214=12.48402004年计量经济学试题五、(20 分)图 1 是我国1978 年—1999 年的城镇居民消费水平取对数后(记为LPI )的差分变量DLPI 相关图和偏相关图;图 2 是以DLPI 为变量建立的时间序列模型的输出结果。
其中Q 统计量Q-statistic(k=12)=11.7351.根据图1,建立DLPI 的ARMA模型。
(限选两种形式)( 6 分)2.根据图2,试写出模型的估计式,并对估计结果进行诊断检验。
12-13时间序列分析期末试卷

诚信应考 考出水平 考出风格浙江大学城市学院2012— 2013学年第二学期期末考试试卷《时间序列分析》开课单位:计算学院 ;考试形式:闭卷;考试时间:2013年7月7日; 所需时间:120分钟一.简答和计算题(本大题共9题,第1到5题每题5分,第6到9题每题7分,共53分。
)1. 写出(,,)ARIMA p d q 模型的结构。
2. 写出(,)ARMA p q 模型的传递形式和格林函数的递推式。
3. 写出(,)ARMA p q 模型的逆转形式和逆函数的递推式。
第1页共5页4.计算模型120.5t t t tx x x ε--=--+的偏自相关系数。
5.判断模型1210.80.5 1.1t t t t t x x x εε---=-++-的平稳性与可逆性。
6. 对于(1)AR 模型:11()t t tx x μφμε--=-+,根据t 个历史观察值数据:,10.1,9,6,已求出ˆ10μ=,1ˆ0.3φ=,29εσ=,求:(1)之后3期的预测值及95%置信区间。
(2)假定获得新的观察值数据为110.5t x +=,求之后2期的预测值及95%置信区间。
第2页共5页7.已知某地区每年常住人口数量近似服从(3)MA 模型(单位:万人):21231000.80.60.2,25t t t t t x εεεεεσ---=+-+-=最近3年的常住人口数量及一步预测数量如下:年份 统计人数 预测人数 2002 104 110 2003 108 100 2004 105 109请预测未来5年该地区常住人口的95%置信区间。
8. 使用指数平滑法得到ˆ5t x=,2ˆ 5.26t x+=,已知序列观察值5.25t x =,1 5.5t x +=,求指数平滑系数α。
9. 某一10期观察值序列为5.43, 6.19, 6.63, 7.18, 8.95, 10.14, 11.74, 12.60, 17.26, 21.07(1)使用6期移动平均法预测12ˆx。
(完整word版)《时间序列》试卷

《时间序列分析》试卷注意:请将答案直接写在试卷上一、填空题(1分*20空=20分)1. 德国药剂师、业余天文学家施瓦尔发现太阳黑子的活动具有11年周期依靠的是 时序分析方法。
2. 时间序列预处理包括 和 。
3. 平稳时间序列有两种定义,根据限制条件的严格程度,分为和 。
使用序列的特征统计量来定义的平稳性属于 。
4. 统计时序分析方法分为 和 。
5. 为了判断一个平稳的序列中是否含有信息,即是否可以继续分析,需对该序列进行 检验,该检验用到的统计量服从 分布;原假设和备择假设分别是 和 。
6. 图1为2000年1月——2007年12月中国社会消费品零售总额时间序列图,据此判断,该序列{}t X 是否平稳(填“是”或者“否”) ;要使其平稳化,应该对原序列进行 和 差分处理。
用Eviews 软件对该序列做差分运算的表达式是 。
7. ARIMA 模型的实质 是和的结合。
8. 差分运算的实质是使用的方式提取确定性信息。
9. 用延迟算子表示中心化的AR(P)模型是 。
二、不定项选择题(下列每小题至少有一个答案是正确的,请将正确答班级 姓名 学号50010001500200025003000350040009394959697989900图1案代码填入相应括号内,2分*5题=10分)1.下列属于白噪声序列{}t ε所满足的条件的是( )A. 任取T t ∈,有με=)(t E (μ为常数)B. 任取T t ∈,有0)(=t E εC.)(0),(s t Cov s t ≠∀=εεD. 2)(εσε=t Var (2εσ为常数) 2.使用n 期中心移动平均法对序列{}t x 进行平滑时,下列表达式正确的是( )A.n x x x x x n x n t n t t n t n t t ),(1~2112112121-+--++----++++++=ΛΛ为奇数;B. n x x x x x n x n t n t t n t n t t ),(1~212122+-++--++++++=ΛΛ为偶数;C. )(1~11+--+++=n t t t t x x x n x Λ; D. n x x x x x n x n t n t t n t n t t ),2121(1~212122+-++--++++++=ΛΛ为偶数。
(整理)时间序列分析试题

B.大于100%表示各月(季)水平比全期平均水平高,现象处于旺季
C.小于100%表示各月(季)水平比全期水平低,现象处于淡季
D.小于100%表示各月(季)水平比全期平均水平低,现象处于淡季
E.等于100%表示无季节变化
答案:BD.E
12、循环变动指数C%()。
3月
4月
5月
6月
7月
月初应收账款余额
(万元)
690
850
930
915
890
968
1020
则该企业2005年上半年平均每个月的应收账款余额为()。
A.
B.
C.
D.
答案:A
10、采用几何平均法计算平均发展速度时,侧重于考察()。
A.现象的全期水平,它要求实际各期水平等于各期计算水平
B.现象全期水平的总和,它要求实际各期水平之和等于各期计算水平之和
答案:A
14、元宵的销售一般在“元宵节”前后达到旺季,1月份、2月份的季节指数将()。
A.小于100% B.大于100%
C.等于100% D.大于1200%
答案:B
15、空调的销售量一般在夏季前后最多,其主要原因是空调的供求(),可以通过计算()来测定夏季期间空调的销售量高出平时的幅度。
A.受气候变化的影响;循环指数
答案:D.
17、当时间序列的二级增长量大体相同时,适宜拟合()。
A.抛物线B.指数曲线
C.直线D.对数曲线
答案:A
18、国家统计局2005年2月28日公告,经初步核算,2004年我国的国内生产总值按可比价格计算比上年增长9.5%。这个指标是一个()。
时间序列分析试卷及答案

时间序列分析试卷及答案时间序列分析试卷1一、填空题(每小题2分, 共计20分)1.ARMA(p,q)模型是一种常用的时间序列模型, 其中模型参数为p和q。
2.设时间序列{Xt}, 则其一阶差分为Xt-Xt-1.3.设ARMA (2.1): Xt=0.5Xt-1+0.4Xt-2+εt-0.3εt-1, 则所对应的特征方程为1-0.5B-0.4B^2+0.3B。
4.对于一阶自回归模型AR(1):Xt=10+φXt-1+εt, 其特征根为φ, 平稳域是|φ|<1.5.设ARMA(2.1):Xt=0.5Xt-1+aXt-2+εt-0.1εt-1, 当a满足|a|<1时, 模型平稳。
6.对于一阶自回归模型Xt=φXt-1+εt, 其平稳条件是|φ|<1.7.对于二阶自回归模型AR(2):MA(1):Xt=εt-0.3εt-1, 其自相关函数为Xt=0.5Xt-1+0.2Xt-2+εt, 则模型所满足的XXX-Walker方程是ρ1-0.5ρ2=0.2, ρ2-0.5ρ1=1.8.设时间序列{Xt}为来自ARMA(p,q)模型: Xt=φ1Xt-1+。
+φpXt-p+εt+θ1εt-1+。
+θqεt-q, 则预测方差为σ^2(1+θ1^2+。
+θq^2)。
9.对于时间序列{Xt}, 如果它的差分序列{ΔXt}是平稳的, 则Xt~I(d)。
10.设时间序列{Xt}为来自GARCH(p,q)模型, 则其模型结构可写为σt^2=α0+α1εt-1^2+。
+αpεt-p^2+β1σt-1^2+。
+βqσt-q^2.二、(10分)设时间序列{Xt}来自ARMA(2,1)过程, 满足(1-B+0.5B^2)Xt=(1+0.4B)εt, 其中{εt}是白噪声序列, 并且E(εt)=0, Var(εt)=σ^2.1)判断ARMA(2,1)模型的平稳性。
根据特征方程1-φ1B-φ2B^2, 求得其根为0.5±0.5i, 因此模型的平稳条件是|φ1-0.5i|<1和|φ1+0.5i|<1, 即-1<φ1<1.因为0.5i不在实轴上, 所以模型不是严平稳的, 但是是宽平稳的。
时间序列分析期末试卷AB卷

卷A一、 判定下列模型的稳定性和可逆性。
(10)1.t t t a X X =--11.12.14.0--=t t t a a X3.1218.04.03.1----=+-t t t t t a a X X X二、简述(25)1.宽平稳的定义是什么?它和严平稳有什么联系?(10)2.写出AR (1),MA (1),ARMA (2,1)模型的表达式,并分别说明它们的基本假设。
(15)三、计算(65)1.根据下面AR (4)模型的估计值求关于一个ARMA (2,1)模型的可逆初始猜测值6.01=ϕ,2.02-=ϕ,2.03-=ϕ,8.04=ϕ (10)2. 求模型2114.03.15.0---+-=-t t t t t a a a X X 的前5个格林函数和逆函数。
(10)3.对于ARMA (2,1)模型 1214.03.0---+=+-t t t t t a a X X X ,t a ~NID (0,100),给定345=-t X ,364=-t X ,=-3t X 12=-t X ,3.01=-t X ,10-=t X ,并假定1-t a =-25(a )计算)(ˆl X t )2,1(=l 及)1(ˆtX 的95%的概率限。
(b )给定09.111-=+t X ,4.11=G ,修正)2(ˆtX 。
4. 有t=1,2,3,4,5的数据序列如下:7.0,6.8,7.2,6.9,7.1 (a )求零均值化后的序列t X(b )用AR(1)模型拟合t X ,求1ϕ的估计。
5. 某过程的逆函数2,)7.0(3.0,5.021≥==-j I I j j ,试求相应的ARMA 模型的表达式。
卷B二、 判定下列模型的稳定性和可逆性。
(10)1.t t t a X X =--15.02.12.1--=t t t a a X3.21216.07.11.07.0----+-=+-t t t t t t a a a X X X二、简述(25)1.宽平稳的定义是什么?它和严平稳有什么联系?(10)2.写出AR (1),MA (1),ARMA (2,1)模型的表达式,并分别说明它们的基本假设。
10-11上学期时间序列分析B卷及答案
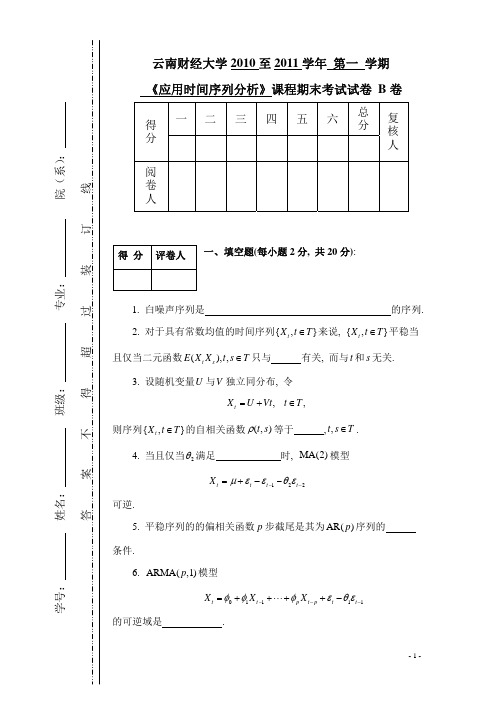
函数 { (k ), k 0,1, 2,} 表示).
3.试求极限 lim E[et (l ) 2 ] .
l
-5-
-6-
得 分
评卷人
五、 计算证明题(每小题 5 分, 共 15 分) 设 { t , t 1, 2,} ~ WN (0, 2 ) , 令
X t t k , t 1, 2,.
k
10. 设 { X t , t 0, 1, 2,} 是满足 MA(q) 模型 X t t 1 t 1 q t q
ˆ (l ) 的均方误差为 的 MA(q) 序列, 则已知 X t , X t 1 , X t 2 , 时, X t l 的最佳线性预测 X t
可逆.
5. 平稳序列的的偏相关函数 p 步截尾是其为 AR( p) 序列的 充要 条件. 6. ARMA( p,1) 模型 X t 0 1 X t 1 p X t p t 1 t 1
的可逆域是 | 1 | 1 .
7. ARMA(2, q) 模型 X t 0 1 X t 1 2 X t 2 t 1 t 1 q t q
k 0
t 1
1.试求序列 { X t , t 1, 2,} 的自相关函数 (t , s), t , s 1, 2, . 2.试求极限 lim (t , s), t 1, 2, .
s
3.试证明序列 { X t , t 1, 2,} 不平稳.
-7-
得 分
评卷人
ˆ (l ) 的均方误差为 的 MA(q) 序列, 则已知 X t , X t 1 , X t 2 , 时, X t l 的最佳线性预测 X t
《时间序列》试卷答案

《时间序列》试卷答案【篇一:时间序列分析试卷及答案3套】>一、填空题(每小题2分,共计20分)1. arma(p, q)模型_________________________________,其中模型参数为____________________。
2. 设时间序列?xt?,则其一阶差分为_________________________。
3. 设arma (2, 1):xt?0.5xt?1?0.4xt?2??t?0.3?t?1则所对应的特征方程为_______________________。
4. 对于一阶自回归模型ar(1): xt?10+?xt?1??t,其特征根为_________,平稳域是_______________________。
5. 设arma(2, 1):xt?0.5xt?1?axt?2??t?0.1?t?1,当a满足_________时,模型平稳。
6. 对于一阶自回归模型______________________。
7. 对于二阶自回归模型ar(2):xt?0.5xt?1?0.2xt?2??tma(1):xt??t?0.3?t?1,其自相关函数为则模型所满足的yule-walker方程是______________________。
8. 设时间序列?xt?为来自arma(p,q)模型:xt??1xt?1?l??pxt?p??t??1?t?1?l??q?t?q则预测方差为___________________。
9. 对于时间序列?xt?,如果___________________,则xt~i?d?。
10. 设时间序列?xt?为来自garch(p,q)模型,则其模型结构可写为_____________。
二、(10分)设时间序列?xt?来自arma?2,1?过程,满足1b0.5bx2t1?0.4bt,2其中??t?是白噪声序列,并且e??t??0,var??t。
(1)判断arma?2,1?模型的平稳性。
统计学考试题目 时间序列分析

统计学考试题目时间序列分析(总3页)-本页仅作为预览文档封面,使用时请删除本页-B C C A A, A C B D D , B B D B D , B A第六章时间序列分析一、单项选择题1.某地区1990—1996年排列的每年年终人口数动态数列是( b)。
A、绝对数动态数列B、绝对数时点数列C、相对数动态数列D、平均数动态数列2.某工业企业产品年生产量为20 万件,期末库存万件,它们( c)。
A、是时期指标 B、是时点指标C、前者是时期指标,后者是时点指标D、前者是时点指标,后者是时期指标3.间隔相等的不连续时点数列计算序时平均数的公式为(c )。
4.某地区连续4 年的经济增长率分别为%,9%,8%,%,则该地区经济的年平均增长率为( a)。
5.某工业企业生产的产品单位成本从2005年到2007年的平均发展速度为98%,说说明该产品单位成本( a)。
A、平均每年降低2%B、平均每年降低1%C、2007 年是2005 年的98%D、2007年比2005年降低98%6.根据近几年数据计算所的,某种商品第二季度销售量季节比率为,表明该商品第二季度销售( a)。
A、处于旺季B、处于淡季C、增长了70%D、增长了170%7.对于包含四个构成因素(T,S,C,I)的时间序列,以原数列各项数值除以移动平均值(其平均项数与季节周期长度相等)后所得比率(c )。
A、只包含趋势因素B、只包含不规则因素C、消除了趋势和循环因素D、消除了趋势和不规则因素8.当时间序列的长期趋势近似于水平趋势时,测定季节变动时(b )。
A、要考虑长期趋势的影响B、可不考虑长期趋势的影响C、不能直接用原始资料平均法D、剔除长期趋势的影响9.在对时间序列作季节变动分析时,所计算的季节比率是( d)。
A、某一年月或季平均数相对于本年度序列平均水平变动的程度B、某一年月或季平均数相对于整个序列平均水平变动的程度C、各年同期(月或季)平均数相对于某一年水平变动的程度D、各年同期(月或季)平均数相对于整个序列平均水平变动的程度10.企业5月份计划要求销售收入比上月增长8%。
时间序列期末考试A卷答案

第(-)学期考试试卷课程代码6024000课程名称时间序列分析B(A卷)考试时间____________(注:匕}为均值为零的白噪声序列)一、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其字母代号写在该题【1 内。
答案错选或未选者,该题不得分。
每小题4分,共20分。
)1.X,的k阶差分是【C】(A) Px严Xt—X.k(B) 丁X严P-'X厂p-'Xj(c) =v A-,x/-v A-'x/_1(D)v*x r=V A-,X,_1-V A-,X/_22.MA⑵模型X f=^-1.1£-Z_I+0.24^_2,则移动平均部分的特征根是【A】(A)人=0.8, /U=0.3 (B) =-0.8, /U=0.3(C)人=-0.8, = -0.3 (D) & =一0.8,入=0.23•关于差分X,—1.3Xi+0.4X一2=0,其通解是【D】(A) q(08+0.3‘)(B) q(o.&+o.5『)(C) qO.S+C/O.M (D) Cfi.S1+C20S4.AR(2)模型X, =£—l.lXj+0.24X_2,其中£>£=0.04,则EX 禺=[B 】(A) 0 (B) 0.04(C) 0.14 (D) 0.25.ARMA(2,l)tMgy X, -X,., -0.24X z_2 =^; -0.8^,.,,其延迟表达式为【A 】(A) (l-B-0.24B2)X, =(l-0.8BX (B) (B2-B-0.24)%, =(B-0.8X(C) (B2-B-0.24)X f =0.8V^ (D) (1 -B-0.24/?2)X f = Vf r二、简答题(10分)对于均值为零的平稳序列,其自相关系数存在两个估计量,请写出两个估计量,并说出它们各自优缺点。
三、(15 分)已知 MA (2)模型为 X r =^-0.6^_,+0.5^_2,其中 Ds, = 0.04 ,(1)计算前3个逆函数,/…; = 1,2,3; -------------------------- (8分) (2)计算Var{X t );------------------------------------ (7 分)解答:(1) X 」勺逆转形式为:或J 壬 --------------------------------------------------------- (1分) /■]J-0将其代入原模型得:X, = (1 -0.6B + 0.5B 2)(1 -I.B- I 2B 2 • • •)%, -------- (1 分) 比较B 的同次幕系数得:B:-Z 1-0.6 = 0=>/l =-0.6 ---------------- (2 分) B 2:-Z 2 + 0.6/, + 0.5 = 0 Z 2 = 0.14 ---------------- (2 分)肝:一人+0・6厶+0・5人=0=>厶=0.384 ------ (2分)(2) EX t = E (s j -0.6^ + 0.5^_2) = 0 ---------- (1 分)EX ; = E[(£ _0・6吕-]+0・5名-2)(吕 _0・6吕-]+0・5爲_2)](2分)所以:Var (X z ) = EX ; = (1 + 0.62 + 0.52)x0.04 = 0.0644 -- (2 分) 四、(15 分)已知 AR (2)模型为(1—0・53)(1-0・33)/=爲 Ds. =a ;= 0.5(1)计算偏相关系数%伙=123); -------------------------------- (8分)(2) W/r (XJ ; ----------------------------------------- (7 分) 解答(1) (l-0・5B )(l-0・3B )X 『 =X 『—O ・8X"i+O ・15X_=£,所以:% =0.=-0」5对于A&2)模型其系数满足2阶Yule-Walker 方程:姑金“69565 和/金+ *“40652,产生偏相关系数的相关序列为,相应Yule-Wolker 方程为:‘1 p\/ 、 '1 P\ V 0.8、(PC<P1 16l.Pi 1315丿4所以:(2分)当£ = 2时, P\ P\Po >2ij =rpi~他」一1因为0, m b ; = 0.04, t= s将其代入原模型得:(1-加-02肝)丘手一广吕一(1分)7-0比较B 的同次幕系数得:G° = lB :G\- %G ()= 0 => G] = (p 、= £ -------- ( 2 分)3’ : G, — %G] +(P 、G Q = 0 => G? = --------- ( 2 分) 225 553G 3 —(pfi 2 一(p 2G } =0=>G 3= 〜0」6385 -------- (2 分)^7P\=(P\\P Q 即 ®I =ZV 所以(Pw= P\ 0.69565% =[。
广西科技大学时间序列分析考试卷2013B卷答案最新版

广西科技大学 2012 — 2013 学年第 2 学期考试题考核课程 时间序列分析(B 卷)考核班级 统计101,102 学生数 73 印数 78 考核方式 闭卷 考核时间 120 分钟一、单项选择题(每小题3 分,共24 分) 1. X 的k 阶差分是 ( C )A. k t t t k X X X -∇=-B.11k k k t t t kX X X ---∇=∇-∇ C.111k k k t t t X X X ---∇=∇-∇ D. 1112k k k t t t X X X ----∇=∇-∇2. ARMA(2,1)模型1210.240.8t t t t t X X X εε-----=-,其延迟表达式为( A )(其中B 为延迟算子)。
A .2(10.24)(10.8)t t B B X B ε--=- B. 2(0.24)(0.8)t tB B X B ε--=- C.2(0.24)0.8t t BB X ε--=∇ D. 2(10.24)t t B B X ε--=∇3. 若零均值平稳序列{}t X ,其样本ACF 呈现拖尾性,其样本PACF 呈现一阶截尾性,则可初步认为对{}t X 应该建立( C )模型。
A. MA(1)B.ARMA(1,1)C.AR(1)D.ARIMA(0,1,0)4.对于平稳时间序列,下列错误的是 ( D )A.)(22t e e E =σ B.),(),(k t t k t t y y Cov y y Cov -+= C.k k -=ρρ D.)(ˆ)1(ˆ1k y k y t t +=+5. AR(2)模型t t t t e Y Y Y +-=--2105.045.0,其中04.0)(=t e Var ,则=)(t t e Y E ( B ) A.08.0 B 0.04 C. 0 D. 0.26. 在进行平稳性检验时,常采用DF 单位根检验,其形式为:.1:,1:,101<=+=-ρρρH H e X X t t t 则接受假设0H 意味着:( D )A. 无单位根,平稳B.有单位根,平稳C.无单位根,非平稳D.有单位根,非平稳7. 下列四个MA 模型中,可逆的是( C )A. 12t t t x εε-=- ;B. ;221--+-=t t t t x εεεC. 10.5t t t x εε-=-; D. 215.05.1--+-=t t t t x εεε.8. 考虑AR(2)模型t t t t e Y Y Y +-=--2115.08.0,则其AR 特征方程的根是( B )(A )5.01=λ,20.3λ= (B )310,221==λλ(C )5.01-=λ,20.3λ=- (D ) 310,221-=-=λλ二、填空题(每题3分,共24分);1. 设{}x t 为一时间序列,且)(,t t 21-t t t x x x x x ∇∇=∇-=∇=________________。
时间序列分析试卷及答案

时间序列分析试卷1一、 填空题(每小题2分,共计20分)1. ARMA(p, q)模型_________________________________,其中模型参数为____________________。
2. 设时间序列{}t X ,则其一阶差分为_________________________。
3. 设ARMA (2, 1):1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。
4. 对于一阶自回归模型AR(1): 110t t t X X φε-=++,其特征根为_________,平稳域是_______________________。
5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-,当a 满足_________时,模型平稳。
6. 对于一阶自回归模型MA(1):10.3t t t X εε-=-,其自相关函数为______________________。
7. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。
8. 设时间序列{}t X 为来自ARMA(p,q)模型:1111t t p t p t t q t q X X X φφεθεθε----=++++++L L则预测方差为___________________。
9. 对于时间序列{}t X ,如果___________________,则()~t X I d 。
10. 设时间序列{}t X 为来自GARCH(p ,q)模型,则其模型结构可写为_____________。
二、(10分)设时间序列{}t X 来自()2,1ARMA 过程,满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列,并且()()2t t 0,E Var εεσ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析期末考试B
浙江农林大学 2009 - 2010 学年第 二 学期考试卷(A 卷)
课程名称: 应用时间序列分析 课程类别: 必修 考试方式: 闭
卷
注意事项:1、本试卷满分100分。
2、考试时间 120分钟。
一、单项选择题(在每小题
的四个备选答案中,选出一个正确答案,并将正确答案的选项填在题后的括号内。
每小题2分,共12分)
1. 关于严平稳与(宽)平稳的关系,不正确的为 。
( )
A. 严平稳序列一定是宽平稳序列
B. 当序列服从正态分布时,两种平稳性等价
C. 二阶矩存在的严平稳序列一定为宽平稳的
D. MA(p)模型一定是宽平稳的
2. 下图为某时间序列的相关检验图,图1为自相关函数图,图2
为偏自相关函数图,请选择模型 。
学院: 专业班级: 姓名: 学号:
装 订 线 内 不 要 答 题
( )
图1
图2
A. AR(1)
B. AR(2)
C. MA(1)
D. MA(2)
3. 下图中,图3为某序列一阶差分后的自相关函数图,图4为某序列一阶差分后的偏自相关函数图,请对原序列选择模型。
( )
图3
图4
A.ARIMA(4,1,0)
B. ARIMA(0,2,1)
C. ARIMA(0,1,2)
D.ARI MA(0,1,4)
4. 记B为延迟算子,则下列不正确的是。
( ) A. 0
1B = B. (1)k
t t k t X X B X --=- C.
12
t t BX X --= D.
11()t t t t B X Y X Y --±=±
5.对于平稳时间序列,下列错误的是 ( ) A.)(212εσεE = B.),(),(k t t k t t y y Cov y y Cov -+= C.k k
-=ρρ D.)(ˆ)1(ˆ1k y k y
t t +=+ 6.下图为对某时间序列的拟合模型进行显著性水平0.05α=的显著
性检验,请选择该序列的拟合模型 。
( )
A. 151.261690.42481t t t X X a -=-+
B.173.038290.42481t t t X X a -=-+
C.
151.261690.42481t t t X a a -=++ D. 173.038290.42481t t t X a a -=++
得分
二、检验下列模型的平稳性与可逆性,写出详细过程。
(每小题4分,共16分) 1.
12t t t
X X a -=-+ 2.
10.7t t t X a a -=-
3.
11
1.50.4t t t t X X a a --=+- 4.
1211.40.40.5t t t t t X X X a a ---=-+-
三、解差分方程(每小题3分,共6分) 1. (2)2()0y k y k +-=
2. (2)5(1)6()0y k y k y k +-++=
四、计算题(第1题11分,第2-6题每题9分,共56分)
1.一个序列适应如下模型:
121t 32120.80.50.3,1,2, 2.5,0.6,0,
ˆ(),1,2.t t t t t t t t t t
X X X a a X X X X a l l --------+=-=-=====已知求X
2.已知某序列服从MA(3)模型:
2
123121000.80.60.2,25,4,8,6
t t t t t a t t t a a a a a a a σ-----=+-+-==-==-X 预测未来2期的值及95%的置信区间.
1234t 2
~
2.
{}55,7,4,6,8.
ˆ(1)5;(2)t t t t t t t X X X X X X X
X ----+-=====3.某一观察值序列最后期观测值分别为:使用期移动平均法预测使用5期中心移动平均法求
4.对一观察值序列{
t X }使用指数平滑法.已知23,t X =且前一期的
平滑值为24.5,平滑系数为0.30.求2期预测值
12k 5.0.6,(1).t t t t a a a k ρ--=+-≥对于MA(2)模型:X 求其自相关函数
6.获得100个ARIMA(0,1,1)序列的观测值
(1).已知50)1(ˆ,45,5.01001001===X X θ求)2(ˆ100
X 的值
2.假定新获得51101=X 求)1(ˆ101X 的值
五、证明题(10分)
对于一个中心化AR(1)模型,证明22
1
var()1a
t X σφ=- 若已知25t X =,且ˆ(1)t
X 的95%的置信区间为(16,9),求模型中2a σ和1φ值.。
