1.1 直角坐标系中的平移变换与伸缩变换
直角坐标系中的平移

课前检测
在平面内,把一个图形的整体沿某一直 线方向移动一定的距离,会得到一个新图形。
图形的这种移动叫做平移变换,简称平移。
2)图形平移的性质是什么?
新图形与原图形形状和大小完全相同。
对应点的连线平行且相等。
对应线段平行且相等。
对应角相等。
仔细观察,点A、 A1、 A2的位置与 坐标之间的关系,你发现了什么?
-5
-4
-3
-2
-1 0 -1-1
1
2 3 4x
不变,
-2-2
-3 -3
则有A1 (-2,3) ,B1 (-3,1) ,C1 (-5,2) 。 猜想: △ A1B1C1与△ABC的大小、 形状
和位置上有什么关系,为什么?
1.例题探索
如图, △ ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(4)将点A向左平移a(a>o)个单位长度得到点
An´,则 点An ´点的坐标是 (-2-a ,-3) ;
在坐标系中描出点A(-2,-3)并进行如下平移:
(1)将点A向上平移5个单位长度得到点A1,
则 点A1点的坐标是 (-2,2) ;
(2)将点A向上平移6个单位长度得到点A2,
则 点A2点的坐标是 (-2,3) ;
应点P的坐标应为(__4,__2_.2_)_;
y4
P
●
3
2
4y
3
P
●
2
1
1
O 12 34 5 -1
ⅹ
O 12 34 5 -1
ⅹ
-2
-2
-3
-3
图1
图2
8、在直角坐标系中描出以下各点:
平面直角坐标系伸缩变换课件

伸缩变换的矩阵表示
伸缩变换
将平面中的点按照某个方向进行缩放,通常称为放缩变换。
伸缩变换矩阵
放缩变换可以通过一个二阶实对称矩阵来实现,该矩阵称为伸缩变 换矩阵。
伸缩变换矩阵的性质
具有正定的对角线元素,并且其特征值分别对应于放缩变换的两个 方向上的缩放因子。
平面直角坐标系伸 缩变换的优缺点及 展望
平面直角坐标系伸缩变换的优点
便于解决几何问题
通过伸缩变换,可以将复杂的几 何问题转化为简单的代数问题,
从而更便于解决。
丰富数学内容
伸缩变换是一种新的数学方法,可 以丰富数学的教学内容,提高学生 的学习兴趣。
应用广泛
伸缩变换在物理学、工程学等领域 都有广泛的应用,可以帮助学生更 好地理解这些领域的基础知识。
平面直角坐标系伸缩 变换课件
目录
CONTENTS
• 平面直角坐标系基础 • 伸缩变换的基本原理 • 伸缩变换的应用 • 伸缩变换的数学模型 • 伸缩变换的实现方法 • 平面直角坐标系伸缩变换的优缺
点及展望
01
平面直角坐标系基 础
定义与性质
定义
平面直角坐标系是一个二维的数 轴系统,它由两个互相垂直的坐 标轴构成。
伸缩变换的逆变换与等价变换
01
02
03
04
逆变换
如果一个变换可以通过逆变换 还原到原始状态,那么这个变
换就称为可逆的。
等价变换
两个变换可以相互转换,并且 它们对所有点的作用相同,那
么它们称为等价的。
伸缩变换的逆变换
通过伸缩变换矩阵的逆矩阵可 以获得逆变换矩阵。
等价变换的证明
曲线在直角坐标系中的平移和伸缩变换

J( 一 日, ’
) 一 0;
C: x, f( )一 0
以 — b代 Y. 线 沿 Y 轴 向 上 平 移 b个 单 位 曲
b) 一 0.
O )的 图 像 ) 直 线 、 锥 曲线 等 方 程 的 化 简 是 通 ; 圆
f( Y — x,
过 坐 标 轴 的 平 移 和 旋 转 ( 实 质 是 同 一 曲 线 在 其
用 上 述 命 题 提 供 的 方 法 解 决 点 的 平 移 变 换 、 线 的平移变 换、 曲 曲线 的 伸 缩 变 换 , 非 常 是 容 易 的 . 其 是 高 三 的综 合 复 习 阶段 , 用 上 述 尤 采
( )沿 轴 向左 平 移 n个 单 位 后 , 得 曲线 2 所
C2 方 程 是 f x+ 口 ) 的 ( , ;
方 法 , 将 函 数 的 图 像 、 线 、 锥 曲线 和 复 平 可 直 圆 面 内 曲 线 的平 移 变 换 、 缩 变 换 融 合 在 一 起 , 伸 达
维普资讯
・ 6・ 重 庆 4 《 学 教 学 通 讯 > 0 2年 第 8期 ( 第 1 3期 ) 数 > 0 2 总 5
是 数 学 等 自然 学 科 中 经 常 遇 到 的 问题 . 究 它 , 研
碧 李Biblioteka 叔 珉 ( )沿 y轴 向 上 平 移 b 单 位 后 , 得 曲线 3 个 所
C 的 方 程 是 f x, ( Y一 6 ; )
不 仅 可 以 深 化 数 形 结 合 、 价 转 换 的 数 学 思 想 等
命 题 1 将 点 M ( ) x,
( )沿 轴 向 右 平 移 n个 单 位 后 , 得 点 1 所
M 坐 标 是 ( + 口 Y ; 的 , )
讲坐标系平面直角坐标系中的伸缩变换

2023讲坐标系平面直角坐标系中的伸缩变换contents •引言•平面直角坐标系的基本概念•伸缩变换的基本原理•伸缩变换的应用实例•平面直角坐标系中的伸缩变换•结论与展望目录01引言伸缩变换是指对平面直角坐标系中的点进行有比例的放大或缩小,可以用一个矩阵来表示这种变换。
伸缩变换的主要特点是,原点保持不变,且每个轴上的单位长度发生了变化。
伸缩变换的定义伸缩变换在图像处理、计算机视觉和机器学习等领域具有广泛应用。
通过伸缩变换,可以将图像或数据集的大小调整为适合分析或处理的要求,从而提高算法的准确率和效率。
伸缩变换的重要性伸缩变换的应用场景图像缩放01在图像处理中,通过伸缩变换可以调整图像的大小,以满足不同应用的需求。
数据预处理02在机器学习中,为了提高算法的准确性,通常需要对数据进行预处理,其中包括对数据进行缩放。
通过伸缩变换,可以将数据调整为同一尺度,减少计算误差。
计算机视觉03在计算机视觉中,伸缩变换被广泛应用于目标检测、识别和跟踪等领域。
通过对图像进行伸缩变换,可以增强目标特征,提高检测准确率。
02平面直角坐标系的基本概念在平面直角坐标系中,每个点都可以由两个数值,即横坐标和纵坐标,来表示。
例如,点A的坐标为(3,4)。
点的坐标表示点的坐标平面直角坐标系的原点是(0,0)。
原点平面直角坐标系中有两条相互垂直的坐标轴,分别是x轴和y轴。
坐标轴点到点的距离在平面直角坐标系中,两点之间的距离可以通过欧几里得距离公式来计算。
例如,点A(3,4)到点B(1,2)的距离是[(3-1)^2 + (4-2)^2]^0.5 = 2.8284。
向量的模一个向量的模等于其终点与原点之间的距离。
例如,向量OA的模是[(3^2 + 4^2)^0.5] = 5。
距离与向量的计算平面几何的基本定理勾股定理在直角三角形中,勾股定理表述了两条直角边的平方和等于斜边的平方。
平行线之间的距离两条平行线之间的距离等于两直线上的对应点之间的距离。
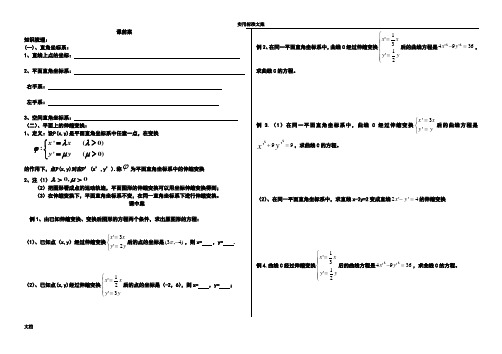
1_1_2、平面直角坐标系中的伸缩变换

纵坐标不变,横坐标缩短到原来的 1, a
2)当0 < a <1时,将y = f(x)图象上每一个点的
纵坐标不变,横坐标伸长到原来的 1 倍,
即得函数y = f(ax)的图象;a
特殊地:y=sin x, x R( >0, 1)的图象能够由y=sinx
1.1.2平面直角坐标 系中的伸缩变换
• 教学目标:
• (1)学会用坐标法来解决几何问题。
• (2)能用变换的观点来观察图形之间的因果联 系,知道图形之间是能够类与类变换的。
• (3)掌握变换公式,能求变换前后的图形或变 换公式。
• 教学重点:应用坐标法的思想及掌握变换公式。
• 教学难点:掌握坐标法的解题步骤与应用,总结 体会伸缩变换公式的应用。通过典型习题的讲解、 剖析,及设置相关问题引导学生思考来突破难点。
(C)纵坐标伸长到原来的2倍,横坐标不变
(D)纵坐标缩短到原来的1 倍,横坐标不变 2
1.选择题 :已知函数y 3sin( x )的图象为C.
5
(3)为了得到函数y 4sin( x )的图象,只要
5
把C上所有的点 C
( A)横坐标伸长到原来的4 倍,纵坐标不变 3
(B)横坐标缩短到原来的3 倍,纵坐标不变 4
亿元上升到1995年6月的18.281亿元,能够用图1和图2来
表示增长幅度。
贷款/亿元
20
贷款/亿元
18
18 16
图1 16
14
14
图2
3 6 月份
3 6 月份
这两个图中所表示的数据是相同的,但是给我们的感
觉是图2显示的增长的幅度要大,产生这种误解的原因是
三种图象变换:平移变换、对称变换和伸缩变换

三种图象变换:平移变换、对称变换和伸缩变换①平移变换:(h>0)Ⅰ、水平平移:函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向左(0)a >或向右(0)a <平移||a 个单位即可得到;1)y=f(x)h 左移→y=f(x+h);2)y=f(x) h 右移→y=f(x -h);Ⅱ、竖直平移:函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向上(0)a >或向下(0)a <平移||a 个单位即可得到;1)y=f(x) h 上移→y=f(x)+h ;2)y=f(x) h下移→y=f(x)-h 。
②对称变换:Ⅰ、函数()y f x =-的图像可以将函数()y f x =的图像关于y 轴对称即可得到; y=f(x) 轴y →y=f(-x)Ⅱ、函数()y f x =-的图像可以将函数()y f x =的图像关于x 轴对称即可得到;y=f(x) 轴x →y= -f(x)Ⅲ、函数()y f x =--的图像可以将函数()y f x =的图像关于原点对称即可得到;y=f(x) 原点→y= -f(-x)Ⅳ、函数)(y f x =的图像可以将函数()y f x =的图像关于直线y x =对称得到。
y=f(x) x y =→直线x=f(y)Ⅴ、函数)2(x a f y -=的图像可以将函数()y f x =的图像关于直线a x =对称即可得到;y=f(x) a x =→直线y=f(2a -x)。
③翻折变换:Ⅰ、函数|()|y f x =的图像可以将函数()y f x =的图像的x 轴下方部分沿x 轴翻折到x 轴上方,去掉原x 轴下方部分,并保留()y f x =的x 轴上方部分即可得到;Ⅱ、函数(||)y f x =的图像可以将函数()y f x =的图像右边沿y 轴翻折到y 轴左边替代原y 轴左边部分并保留()y f x =在y 轴右边部分即可得到④伸缩变换:Ⅰ、函数()y af x =(0)a >的图像可以将函数()y f x =的图像中的每一点横坐标不变纵坐标伸长(1)a >或压缩(01a <<)为原来的a 倍得到;y=f(x)ay ⨯→y=af(x)Ⅱ、函数()y f ax =(0)a >的图像可以将函数()y f x =的图像中的每一点纵坐标不变横坐标压缩(1)a >或伸长(01a <<)为原来的1a倍得到。
平面直角坐标系知识点平面直角坐标系中的伸缩变换坐标系的作用

一、平面直角坐标系中的伸缩变换设点P(x,y)是平面直角坐标系中任意一点,在变换的作用下,点P(x,y)对应到P'(x',y'),称为平面直角坐标系中的伸缩变换。
在平面上取两条互相垂直并选定了方向的直线,一条称为x轴,一条称为y轴,交点O为原点。
再取一个单位长度,如此取定的两条互相垂直的且有方向的直线和长度单位构成平面上的一个直角坐标系,即为xOy。
数轴(直线坐标系):在直线上取定一点O,取定一个方向,再取一个长度单位,点O,长度单位和选定的方向三者就构成了直线上的坐标系,简称数轴.如图,平面直角坐标系:在平面上取两条互相垂直并选定了方向的直线,一条称为x轴,一条称为y轴,交点O为原点。
再取一个单位长度,如此取定的两条互相垂直的且有方向的直线和长度单位构成平面上的一个直角坐标系,即为xOy。
如图:建立坐标系必须满足的条件:任意一点都有确定的坐标与它对应;反之,依据一个点的坐标就能确定这个点的位置.坐标系的作用:①坐标系是刻画点的位置与其变化的参照物;②可找到动点的轨迹方程,确定动点运动的轨迹(或范围);③可通过数形结合,用代数的方法解决几何问题。
平面直角坐标系知识点(1)平面直角坐标系:在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称直角坐标系。
(2)两条数轴分别置于水平位置与垂直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴叫做x轴或横轴,垂直的数轴叫做y轴或纵轴,x轴y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
(3)x轴y轴将坐标平面分成了四个象限,右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。
第一、三象限角平分线上的点横、纵坐标相等;第二、四象限角平分线上的点横、纵坐标互为相反数。
(4)坐标平面内的点与有序实数对一一对应。
有序数对:有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b)。
平面直角坐标系中的伸缩变换

平面直角坐标系中的伸缩变换【知识要点归纳】(1) 以坐标法为工具,用代数方法研究几何图形是解析几何的主要问题,它的特点是“数形结合”。
(2) 能根据问题建立适当的坐标系又是能否准确解决问题的关键。
(3) 设点P (x,y )是平面直角坐标系中的任意一点,在变换⎩⎨⎧>⋅='>⋅='),0(,),0(,:μμλλϕy y x x 的作用下,点P(x,y)对应到点),(y x P ''',称ϕ为平面直角坐标系中的坐标伸缩变换。
【典型例题】 在同一直角坐标系中,求满足下列图形变换的伸缩变换。
(1) 将直线22=-y x 变成直线42='-'y x ,(2) 曲线0222=--x y x 变成曲线0416/22=-'-'x y x【解题能力测试】1、已知x x f x x f ωsin )(,sin )(21==()0>ω)(2x f 的图象可以看作把)(1x f 的图象在其所在的坐标系中的横坐标压缩到原来的31倍(纵坐标不变)而得到的,则ω为( ) A .21 B .2 C.3 D.312.在同一直角坐标系中,经过伸缩变换⎩⎨⎧='='yy x x 35后,曲线C 变为曲线18222='+'y x 则曲线C 的方程为( )A .1725022=+y x B.1100922=+y x C .12410=+y x D.19825222=+y x 3.在同一平面坐标系中,经过伸缩变换⎩⎨⎧='='yy x x ,3后,曲线C 变为曲线9922='+'y x ,求曲线C 的方程并画出图象。
4.在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换⎪⎩⎪⎨⎧='='yy xx 3121后的图形。
求: (1);025=+y x (2)122=+y x 。
平面直角坐标系及伸缩变换

=4.动圆 M 与圆 O1 内切,又与圆 O2 外切,建立适当的坐标系,
求动圆圆心 M 的轨迹方程,并说明轨迹是何种曲线.
解: 如图所示,以 O1O2 的中点 O 为原点,O1O2 所在直线为
x 轴建立平面直角坐标系.
y
由由|O|O1O1O2|=2|=4,4,得得OO11((- -22, ,00)),、OO2(22(,20,0))..
A1(- a,0),A2(a,0)
ec (e1) a
y b x a
A1(0,-a),A2(0,a)
ec (e1) a
y a x b
图形 ly
OF x
标准方程
y2=2px (p>0)
焦点坐标 准线方程
( p ,0 ) x p
2
2
二 抛
物
yl
FO
y2=-2px x (p>0)
( p ,0) 2
lll和和和lll的的的距距距离离离的的的最最最小小小值值值为为为|1|122||1±5±52441|±5.2|.45|.4 | .
O
x
∴∴∴点点点QQQ与与与ll的l的的最最最小小小值值值为为为88558555..5.
题 型 三 定义法求轨迹方程
【例 3】已知两个定圆 O1和 O2,它们的半径分别是 1 和 2,且|O1O2|
所以有 x02
4
把①代入②,
y02
得
4
1.
(2x)2
②
(2y)2 1,
4
整理, 得 x24y21.
MP
O
x
所以点M的轨迹方程是 x24y21.
课堂小结
平面直角坐标系建系时,根据几何特点选 择适当的直角坐标系。
平面直角坐标系变化规律

平面直角坐标系变化规律一、平面直角坐标系中的平移变化规律1. 点的平移- 在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x + a,y)(或(x - a,y));- 将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y + b)(或(x,y - b))。
- 例如:点A(2,3)向右平移3个单位长度,得到点A'(2 + 3,3)=(5,3);点A(2,3)向下平移2个单位长度,得到点A''(2,3 - 2)=(2,1)。
2. 图形的平移- 图形的平移实际上就是图形上各个点的平移。
例如,三角形ABC三个顶点A(x_1,y_1)、B(x_2,y_2)、C(x_3,y_3),将三角形ABC向右平移a个单位长度,再向上平移b个单位长度,则A点变为A'(x_1 + a,y_1 + b),B点变为B'(x_2+a,y_2 + b),C点变为C'(x_3 + a,y_3 + b),新的三角形A'B'C'就是原三角形ABC平移后的图形。
二、平面直角坐标系中的对称变化规律1. 关于x轴对称- 点(x,y)关于x轴对称的点的坐标为(x,-y)。
- 例如:点P(3,4)关于x轴对称的点P'(3,-4)。
- 对于图形来说,图形关于x轴对称,就是图形上所有点关于x轴对称后得到的新图形。
如三角形ABC关于x轴对称,A(x_1,y_1)变为A''(x_1,-y_1),B(x_2,y_2)变为B''(x_2,-y_2),C(x_3,y_3)变为C''(x_3,-y_3),新的三角形A''B''C''就是三角形ABC关于x轴对称后的图形。
2. 关于y轴对称- 点(x,y)关于y轴对称的点的坐标为( - x,y)。
第1章 1.1 直角坐标系,平面上的伸缩变换

3
【尝试解答】 法一 (坐标法)以A为坐标原点O,AB所 在的直线为x轴,建立平面直角坐标系xOy,则A(0,0),
设B(a,0),C(b,c), 则AC的中点E(,), 由对称性知D(b-a,c), 所以|AB|2=a2,|AD|2=(b-a)2+c2, |AC|2=b2+c2,|BD|2=(b-2a)2+c2, |AC|2+|BD|2=4a2+2b2+2c2-4ab =2(2a2+b2+c2-2ab), |AB|2+|AD|2=2a2+b2+c2-2ab, ∴|AC|2+|BD|2=2(|AB|2+|AD|2). 法二 (向量法) 在▱ABCD中,=+, 两边平方得2=||2=2+2+2· , 同理得2=||2=2+2+2· , 以上两式相加,得 ||2+||2=2(||2+||2)+2· (+)=2(||2+||2), 即|AC|2+|BD|2=2(|AB|2+|AD|2).
[再练一题] 2.已知B村位于A村的正西方向1千米处,原计划经过B村沿着北偏东60°的方 向埋设一条地下管线m,但A村的西北方向400米处,发现一古代文物遗址W.根 据初步勘察的结果,文物管理部门将遗址W周围100米范围划为禁区.试问:埋设 地下管线m的计划需要修改吗? 【解】 如图所示,以A为坐标原点,AB所在直线为x轴. 垂直于AB的直线为y轴建立坐标系, 则A(0,0),B(-1 000,0). 由W位于A的西北方向, 且|AW|=400, ∴点W(-200,200), 由直线m过点B,且倾斜角 =90°-60°=30°, ∴直线m的方程是x-y+1 000=0. 于是,点W到直线m的距离为 =100×(5--)≈113.6>100. 所以,埋设地下管线m的计划不需修改. 类型三 已知伸缩变换求点的坐标和曲线方程
一讲坐标系一平面直角坐标系及伸缩变换15页PPT

由题意构图如下:
P C
B
A
信息中心
C1
如何建立直角坐标系才能有利于解决这 个问题呢?
由题意构图如下: y
P C
B
o
C1
A x
l
意请同意学们注意:在这个声音定位问题中点P的位置除了用 直角坐标系下的坐标来刻画外,还能用什么其它的方法来确定?
基点(O)、角度(以正西为正方向)和距离(|OP|)
例1.已知△ABC的三边a 、b 、c满足
课本P8 习题1.1
再 见
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
b2+c2=5a2,BE,CF分别为边AC,AB的
中线,建立适当的平面直角坐标系探究
BE与CF的位置关系。
C
y
C
E E
问题:
OA
F
BX
AFBFra bibliotek1.你能建立不同的直角坐标系来解决这个问题吗?
2.不建立直角坐标系,你是否也可以解决这个问 题呢?
学生练习:
1.已知△ABC的周长为10 ,且BC=4, 求点A的轨迹方程。
一讲坐标系一平面直角坐标系及伸缩变 换
56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
直角坐标系、伸缩变换(最终)
文档课后案1.将点(2,3)变成点(3,2)的伸缩变换是( )A.⎪⎪⎩⎪⎪⎨⎧==y y x x 23'32'B.⎪⎪⎩⎪⎪⎨⎧==y y x x 32'23' C.⎩⎨⎧==x y y x '' D.⎩⎨⎧-=+=1'1'y y x x 2.将点),(y x P 的横坐标伸长到原来的2倍,纵坐标压缩为原来的31,得到点P '的坐标为( ) A.)3,2(y x B.)3,2(y x C.)2,3(y x D.)2,3(y x3.曲线C 经过伸缩变换⎪⎩⎪⎨⎧='='y y xx 31后得到曲线C '的方程为)2(log 2+=x y ,则曲线C 的方程为 ( ) A.)2(log 312+=x y B.)2(log 32+=x yC.)231(log 2+=x y D.)23(log 2+=x y4.把函数sin 2y x =的图像作怎样的变换能得到sin(2)3y x π=+的图像 ( )A .向左平移6π B .向右平移6π C .向左平移3π D .向右平移3π 5.将()y f x =的图像横坐标伸长到原来的3倍,纵坐标缩短到原来的31,则所得函数的解析式为( )A .3(3)y f x = B. 1(3)3y f x =C. 13()3y f x =D. 11()33y f x = 6.点),(y x 经过伸缩变换⎪⎩⎪⎨⎧==yy xx 3'21'后的点的坐标是(-2,6),则=x ,=y ; 7.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 . 8.为了得到函数R x x y ∈+=),63sin(2π的图像,只需将函数R x x y ∈=,sin 2的图像上所有的点( ) A.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) B.向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) C.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) D.向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)9.曲线)6sin(π+=x y 经过伸缩变换⎩⎨⎧==y y x x 2'3'后的曲线方程是 ;10.曲线0222=+-x y x 变成曲线0'4'16'22=+-x y x 的伸缩变换是 .11.曲线364922=+y x 经过伸缩变换⎪⎪⎩⎪⎪⎨⎧==y y x x 31'21'后的曲线方程是 .12.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 .13.函数R x x x x y ∈++=,1cos sin 23cos 212. (1)当函数y 取得最大值时,求自变量x 的集合;(2)该函数的图像可由)(sin R x x y ∈=的图像经过怎样的平移和伸缩变换得到?实用标准文案文档1.点)1,2(π经过伸缩变换⎩⎨⎧==y y xx 3'2'后的点的坐标是 ;3.在伸缩变换⎩⎨⎧==y y x x '2'与⎩⎨⎧==yy xx 2'2'的作用下,单位圆122=+y x 分别变成什么图形?4. 函数31x y x =-,经过怎样的平移变换与伸缩变换才能得到函数1y x=? 1.点),(y x 经过伸缩变换⎩⎨⎧==yy xx 2'3'后的点的坐标是)4,3(-π,则=x ,=y .2.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 . 3.为得到函数R x x y ∈+=),63sin(2π的图像,需将R x x y ∈=,sin 2的图像上所有的点( )A.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) B.向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变)C.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) D.向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)4.曲线)6sin(π+=x y 经过伸缩变换⎩⎨⎧==yy xx 2'3'后的曲线方程是 ; 5.将曲线0222=+-x y x 变成曲线0'4'16'22=+-x y x 的伸缩变换是 . 6.函数()f x 的图像是将函数2log (1)x +的图像上各点的横坐标变为原来的13,纵坐标变为原来的12而得到的,则与()f x 的图像关于原点对称的图像的解析式是 。
平面直角坐标系中的伸缩变换

x y
' '
x y
( 0) ( 0)
的作用下,点P(x,y)对应 P' (x', y') 称 为平面直角坐
标系中的伸缩变换。
注 : (1)λ>0,μ>0
(2)把图形看成点的运动轨迹,平面图形的伸缩 变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同 一直角坐标系下进行伸缩变换。
坐标伸长变换
8
6
4 2
- 10
-5 -2 -4
5
10
-6
-8
设P( x, y)是平面直角坐标系中的任意一点,保持
横坐标x不变,将纵坐标y伸长为原来的3倍,得到
点P '
(
x'
,
y'
),那么{
x' x y' 3 y
(2)
我们把(2)式叫做平面直角坐标系中的一个坐标
伸长变换。
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写 出其坐标变换
平面直角坐标系的伸缩变换
定义:设点P( x, y)是平面直角坐标系中的
任意一点,在变换
φ:{ yx
λ μ
x( y(
λ μ
0) 0)
的作用下,点P( x, y)对到应点P( x, y),称 为
平面直角坐标系中的坐 标伸缩变换简称伸缩变 换
定义:设P(x,y)是平面直角坐标系中任意一点,在变
换
:
压缩变换。
(2)怎样由正弦曲线y sin x得到曲线y 3sin x?
如图,在正弦曲线 y sin x上任取一点P( x, y), 保持横坐标x不变,将纵坐标 y伸长原来的3倍, 那么正弦曲线y sin x就变成曲线y 3sin x
直角坐标系中的平移变换与伸缩变换

如有你有帮助,请购买下载,谢谢!1.1 直角坐标系中的平移变换与伸缩变换目标:平移变换与伸缩变换的应用与理解一.直角坐标系1.直线上,取定一个点为原点,规定一个长度为单位长度,规定直线的一个方向为正方向。
这样我们就建立了直线上的坐标系 (即数轴)。
它使直线上任意一点P 都可以由惟一的实数x 来确定。
2.平面上,取定两条互相垂直的直线作为x 、y 轴,它们的交点作为坐标原点,并规定好长度单位和这两条直线的正方向。
这样我们就建立了平面直角坐标系。
它使平面上任意一点P 都可以由惟一的二元有序实数对),(y x 来确定。
3.在空间中,选择三条两两垂直且交于一点的直线,以这三条直线分别作为x 、y 、z 轴,它们的交点作为坐标原点,并规定好长度单位和这三条直线的正方向。
这样我们就建立了空间直角坐标系。
它使空间中任意一点P 都可以由惟一的三元有序实数对),,(z y x 来确定。
事实上,直线上所有点的集合与全体实数的集合一一对应;平面上所有点的集合与全体二元有序数对),(y x 的集合一一对应;空间中所有点的集合与全体三元有序数对),,(z y x 的集合一一对应.二.平面直角坐标系中图形的平移变换1.平移变换在平面内,将图形F 上所有点按照同一个方向,移动同样长度,称为 图形F 的平移。
若以向量a 表示移动的方向和长度,我们也称图形F 按向量a 平移.在平面直角坐标系中,设图形F 上任意一点P 的坐标为),(y x ,向量),(k h a = ,平移后的对应点为),(y x P '''.则有:),(),(),(y x k h y x ''=+即有:⎩⎨⎧'=+'=+y k y x h x . 因此,我们也可以说,在平面直角坐标系中,由⎩⎨⎧'=+'=+y k y x h x 所确定的变换是一个平移变换。
因为平移变换仅改变图形的位置,不改变它的形状和大小.所以,在 平移变换作用下,曲线上任意两点间的距离保持不变。
直角坐标系中的伸缩变换课件PPT

03 伸缩变换的矩阵表示
二维伸缩变换的矩阵表示
总结词
描述二维平面上的点通过伸缩变换后的坐标变化。
详细描述
在二维直角坐标系中,伸缩变换可以通过一个矩阵来表示。假设原点为 $(x, y)$, 经过伸缩变换后变为 $(x', y')$,则变换矩阵可以表示为
二维伸缩变换的矩阵表示
• $\begin{pmatrix}
02
在直角坐标系中,设原点为 $O(0,0)$,点$P(x,y)$经过伸缩变 换后变为点$P'(x',y')$,则变换公 式为:$x' = kx, y' = ky$,其中 $k$为伸缩系数。
伸缩变换的性质
伸缩变换保持点之间 的距离不变,即 $|OP| = |OP'|$。
伸缩变换可以同时对 x和y进行放大或缩小, 但比例系数必须相同。
伸缩变换的理论研究
01
02
03
理论框架
深入探讨伸缩变换的基本 原理、数学表达和推导过 程,建立完善的理论框架。
性质研究
研究伸缩变换的性质,如 线性、可逆性、连续性和 可微性等,并探讨其在不 同坐标系下的表现。
几何意义
从几何角度解释伸缩变换, 探究其在图形、曲线和曲 面等几何对象上的应用和 表现。
伸缩变换的应用研究
02 伸缩变换在直角坐标系中 的应用
横向伸缩变换
总结词
在直角坐标系中,横向伸缩变换 是指沿x轴方向的伸长或缩短。
详细描述
横向伸缩变换通过乘以一个大于1 的系数来增加x轴上的长度,或者 乘以一个小于1的系数来减小x轴 上的长度。这种变换不会改变点 在y轴上的坐标。
纵向伸缩变换
总结词
纵向伸缩变换是指沿y轴方向的伸长或缩短。
(完整版)直角坐标系中的变换知识点归纳总结

(完整版)直角坐标系中的变换知识点归纳总结直角坐标系中的变换知识点归纳总结直角坐标系是一个用于描述平面或空间中点位置的坐标系统,常见的变换包括平移、旋转和缩放。
下面是与直角坐标系变换相关的几个知识点的总结:平移变换平移变换是指将一个点沿着指定方向和距离移动。
在二维直角坐标系中,平移操作可以表示为:x' = x + dxy' = y + dy其中,(x, y)是原始点的坐标,(x', y')是移动后的点的坐标,dx 和dy分别是沿x轴和y轴的平移距离。
在三维直角坐标系中,平移操作可以表示为:x' = x + dxy' = y + dyz' = z + dz旋转变换旋转变换是指将一个点围绕某个中心点按照指定角度进行旋转。
在二维直角坐标系中,旋转操作可以表示为:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ其中,(x, y)是原始点的坐标,(x', y')是旋转后的点的坐标,θ是旋转角度。
在三维直角坐标系中,旋转操作可以使用旋转矩阵来表示,旋转矩阵的计算涉及到复杂的线性代数运算。
缩放变换缩放变换是指将一个点按照指定比例进行放大或缩小。
在二维直角坐标系中,缩放操作可以表示为:x' = x * sxy' = y * sy其中,(x, y)是原始点的坐标,(x', y')是缩放后的点的坐标,sx 和sy分别是沿x轴和y轴的缩放比例。
在三维直角坐标系中,缩放操作可以表示为:x' = x * sxy' = y * syz' = z * sz变换组合在实际应用中,常常需要将多个变换组合在一起进行操作。
变换的组合顺序会影响最终结果。
通常,变换的顺序是从右到左进行计算。
例如,如果要先进行平移,再进行旋转,最后进行缩放,可以表示为:(x', y') = S * R * T * (x, y)其中,T表示平移变换,R表示旋转变换,S表示缩放变换。
直角坐标系中的变换知识点归纳总结

直角坐标系中的变换知识点归纳总结1.平移变换:平移是直角坐标系中最简单的变换之一,它保持点的形状和大小不变,只改变其位置。
平移变换可以表示为(X',Y')=(X+a,Y+b),其中(a,b)是平移的位移向量。
2.缩放变换:缩放是改变图形大小的变换,可以将图形按照比例放大或缩小。
缩放变换可以表示为(X',Y')=(sX,sY),其中s是缩放的因子。
3. 旋转变换:旋转是将图形绕着一个固定点旋转一定角度的变换。
旋转变换可以表示为(X', Y') = (Xcosθ - Ysinθ, Xsinθ + Ycosθ),其中θ是旋转的角度。
4.矩阵变换:矩阵变换是直角坐标系中一种通用的线性变换方法,可以表示平移、缩放、旋转和剪切等复合变换。
矩阵变换可以用一个2×2的矩阵表示,对于一个点(X,Y)的变换,可以表示为(X',Y')=(a11X+a12Y,a21X+a22Y),其中矩阵A=[a11a12;a21a22]表示变换的系数。
5.对称变换:对称变换是指将图形绕着一个直线对称成对称图形的变换。
常见的对称变换包括关于x轴对称、y轴对称、原点对称、直线对称等,对称变换可以通过变换矩阵来表示。
6.剪切变换:剪切变换是指将图形按照一定比例沿着一些方向延伸或收缩的变换。
剪切变换可以表示为(X',Y')=(X+aY,Y+bX),其中(a,b)是两个剪切因子。
7.一般线性变换:一般线性变换是指包括平移、旋转、缩放、剪切等多种变换同时进行的复合变换。
一般线性变换可以表示为(X',Y')=(aX+bY+c,dX+eY+f),其中(a,b,c,d,e,f)是六个变换系数。
8.坐标轴变换:坐标轴变换是指将直角坐标系中的坐标轴按照一定角度旋转或者倾斜得到的新的坐标系。
在坐标轴变换中,点的坐标可以通过坐标轴旋转矩阵或者倾斜矩阵来进行变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1 直角坐标系中的平移变换与伸缩变换目标:平移变换与伸缩变换的应用与理解一.直角坐标系1.直线上,取定一个点为原点,规定一个长度为单位长度,规定直线的一个方向为正方向。
这样我们就建立了直线上的坐标系 (即数轴)。
它使直线上任意一点P 都可以由惟一的实数x 来确定。
2.平面上,取定两条互相垂直的直线作为x 、y 轴,它们的交点作为坐标原点,并规定好长度单位和这两条直线的正方向。
这样我们就建立了平面直角坐标系。
它使平面上任意一点P 都可以由惟一的二元有序实数对),(y x 来确定。
3.在空间中,选择三条两两垂直且交于一点的直线,以这三条直线分别作为x 、y 、z 轴,它们的交点作为坐标原点,并规定好长度单位和这三条直线的正方向。
这样我们就建立了空间直角坐标系。
它使空间中任意一点P 都可以由惟一的三元有序实数对),,(z y x 来确定。
事实上,直线上所有点的集合与全体实数的集合一一对应;平面上所有点的集合与全体二元有序数对),(y x 的集合一一对应;空间中所有点的集合与全体三元有序数对),,(z y x 的集合一一对应.二.平面直角坐标系中图形的平移变换 1.平移变换在平面内,将图形F 上所有点按照同一个方向,移动同样长度,称为图形F 的平移。
若以向量a表示移动的方向和长度,我们也称图形F 按向量a平移.在平面直角坐标系中,设图形F 上任意一点P 的坐标为),(y x ,向量),(k h a =,平移后的对应点为),(y x P '''.则有:),(),(),(y x k h y x ''=+即有:⎩⎨⎧'=+'=+y k y x h x . 因此,我们也可以说,在平面直角坐标系中,由⎩⎨⎧'=+'=+y k y x h x 所确定的变换是一个平移变换。
因为平移变换仅改变图形的位置,不改变它的形状和大小.所以,在 平移变换作用下,曲线上任意两点间的距离保持不变。
例1.①.已知点)3,4(-P 按向量)5,1(=a平移至点Q ,求点Q 的坐标;②.求直线01223:=+-y x l 按向量)3,2(-=a平移后的方程。
一般地我们有如下关于平移变换的结论:①.将点),(y x P 按向量),(00y x a =平移, 所得点P '的坐标为:),(00y y x x P ++'.②.将曲线0),(:=y x f C 按向量),(00y x a =平移, 所得曲线C '的方程为0),(:00=--'y y x x f C .注:点)3,4(-P 按向量)5,1(=a平移,得点)53,14(++-'P ,即:)8,3(-'P ;直线01223:=+-y x l 按向量)3,2(-=a平移,得直线012)3(2)2(3:=++--'y x l ,即:023:=-'y x l .2.有关曲线平移的一般性结论①.直线0:=+by ax l ,按向量),(00y x a =平移后得直线0)()(:00=-+-'y y b x x a l . → 过点),(00y x .②.曲线222:r y x C =+,按向量),(00y x a = 平移后得曲线22020)()(:r y y x x C =-+-' → 中心为),(00y x .③.曲线1:2222=+by a xC ,按向量),(00y x a = 平移后得曲线1)()(:220220=-+-'by y a x x C → 中心为),(00y x .④.曲线1:2222=-by a xC ,按向量),(00y x a = 平移后得曲线1)()(:220220=---'by y a x x C → 中心为),(00y x .⑤.曲线px y C 2:2=,按向量),(00y x a =平移后得曲线)(2)(:020x x p y y C -=-' → 顶点为),(00y x .例2.说明方程01118169422=-+-+y x y x 表示什么曲线,求这个曲线的顶点、中心、焦点、渐近线和离心率.三.平面直角坐标系中的伸缩变换 1. 伸缩变换例3.我们已经知道,方程x y 2sin =所表示的曲线可以看作由方程x y sin =所表示的曲线上所有点的纵坐标不变,横坐标变为原来的21得到的曲线;同理,将方程x y 2s i n =所表示的曲线上所有点的纵坐标保持不变,而横坐标变为原来的2倍,也可以得到方程x y sin =所表示的曲线. 这也就是说,方程x y 2sin =所表示的曲线可以通过伸缩变换得到方程x y sin =所表示的曲线.实际上,设y y x x '='=,2,则x y 2sin = 可以化为 x y '='sin .由⎩⎨⎧'='=y y x x 2 ,所确定的变换,是曲线上所有点的纵坐标不变,横坐标变为原来的2倍,也可以称为曲线按伸缩系数为2向着y 轴的伸缩变换(这里),(y x P 是变换前的点,),(y x P '''是变换后的点).一般地,由⎩⎨⎧'='=y y x x λ ,所确定的伸缩变换,是按伸缩系数为λ向着y 轴的伸缩变换(当λ>1时,表示伸长;当λ<1时,表示压缩),即曲线上所 有点的纵坐标不变,横坐标变为原来的λ倍(这里),(y x P 是变换前的点,),(y x P '''是变换后的点).同理,由⎩⎨⎧'='=y y x x μ ,所确定的伸缩变换,是按伸缩系数为μ向着x 轴的伸缩变换(当μ>1时,表示伸长;当μ<1时,表示压缩),即曲线上所有点的横坐标不变,纵坐标变为原来的μ倍(这里),(y x P 是变换前的点,),(y x P '''是变换后的点).由⎩⎨⎧'='=y y x x λμ ,所确定的伸缩变换,是按伸缩系数λ向着x 轴和按伸缩系数μ向着y 轴的伸缩变换(当1>λ时,表示伸长,1<λ时,表示压缩;当1>μ时,表示伸长,当μ<1时,表示压缩),即曲线上所有点的横坐标和纵坐标分别变为原来的λ倍和μ倍(这里),(y x P 是变换前的点,),(y x P '''是变换后的点).在伸缩变换中,曲线上任意两点间距离的不变性已不存在.那么缩变换有什么特征呢?我们来考察直线与圆在伸缩变换作用下的变化.例4.对下列曲线向着x 轴进行伸缩变换,伸缩系数是41=k . ①.0632=-+y x ;②.1622=+y x .(设),(y x P 是变换前的点,),(y x P '''是变换后的点).注:①.直线0632=-+y x 经过伸缩变换后的方程为036=-+y x , 它仍然表示一条直线;②.圆1622=+y x 经过伸缩变换后的方程为11622=+y x ,它变为椭圆.2.有关曲线伸缩变换的一般性结论①.直线经过伸缩变换后,仍是直线.因此,在伸缩变换作用下,点的共线性质保持不变。
②.曲线0),(:=y x f C 在伸缩变换⎩⎨⎧'='=y y x x λ(或⎩⎨⎧'='=y y x x μ或⎩⎨⎧'='=y y x x μλ)作用下(1,>μλ时表示拉伸,1,<μλ时表示压缩),所得曲线C '的方程为::C '0),1(=y x f λ(或0)1,(=y x f μ或0)1,1(=y x f μλ).③.曲线0),(:=y x f C 上各点的横坐标(或纵坐标、或横坐标和纵坐标)压缩为原来的λ1,可得曲线:C '0),(=y x f λ(或0),(=y x f λ或0),(=y x f λλ,1>λ时表示压缩,1<λ时表示拉伸).例5.设曲线x y C 2log :=,1log :21-=x y C ,x y C 22log 32:=,9log log 2:223-=x y C .由曲线C 经过何种变换可以得到曲线1C 、2C 、3C .例6.设1M 是),(111y x A 与),(221y x B 的中点,经过伸缩变换⎩⎨⎧'='=y y k x x k 21后,它 们分别为222,,B A M ,求证:2M 是22B A 的中点. (设),(y x P 是变换前的点,),(y x P '''是变换后的点).四.典型例题1.两个定点的距离为4,点M 到这两个定点的距离的平方和为16,则点M 的轨迹是 ( ) A.圆 B.椭圆 C.双曲线 D.抛物线2.将函数x y sin =图象上所有点的横坐标扩大为原来的2倍,纵坐标拉伸为原来的2倍,得到的函数图象的解析式为 ( ) A.x y 2sin 21=B.x y 21sin 21= C.x y 2sin 2= D.x y 21sin 2=3.将点)2,2(-P 变换为点)1,6(-'P 所用的伸缩变换公式是 ( )A.⎪⎩⎪⎨⎧='='yy x x 231 B.⎪⎩⎪⎨⎧='='y y x x 321 C.⎪⎩⎪⎨⎧='='y y x x 213 D.⎩⎨⎧='='y y x x 234.①已知点)3,2(-P 按向量)4,1(-=a平移至点Q ,求点Q 的坐标;②已知点)2,3(-P 按向量a 平移至点)0,2(Q ,求平移向量a.5.将对数函数x y 3log =曲线的横坐标拉伸为原来的2倍, 求所得曲线的方程.6.在同一直角坐标系中,已知伸缩变换⎩⎨⎧='='yy xx 23:ϕ. ①.求点)2,31(-A 经过ϕ变换所得到的点A '的坐标; ②.点B 经过ϕ变换得到点)21,3(-'B ,求点B 的坐标③.求直线x y l 6:=经过ϕ变换后所得到的直线l '的方程;④.求双曲线164:22=-y x C 经过ϕ变换后所得到的曲线C '的焦点坐标.7.在平面直角坐标系中求将曲线1:22=+y x C 变为曲线149:22='+''y x C 的伸缩变换.8.方程07161843:22=++-+y x y x C 表示何种曲线,求它的中心坐标、焦点坐标、准线方程、离心率.五.课外练习六.补充练习1.将点),(y x P 的横坐标伸长到原来的2倍,纵坐标压缩为原来的31,得到点P '的坐标为 ( )A.)3,2(y xB.)3,2(y x C.)2,3(y x D.)2,3(y x2.曲线C 经过伸缩变换⎪⎩⎪⎨⎧='='y y xx 31后得到曲线C '的方程为)2(log 2+=x y , 则曲线C 的方程为 ( )A.)2(log 312+=x y B.)2(log 32+=x yC.)231(log 2+=x y D.)23(l og 2+=x y3.①已知点)2,3(-P 按向量)4,1(-=a平移至点Q ,求点Q 的坐标;②已知点)3,1(P 按向量a 平移至点)1,3(Q ,求向量a.4.写出曲线按向量)3,4(-平移后的方程. ①.0543=+-y x ; ②.x y 82=5.求下列方程所表示的曲线的顶点、焦点、中心及准线方程. ①.884422=-+-y x y x ; ②.05242=++-y x y .6.对下列曲线向着y 轴进行伸缩变换,伸缩系数21=k .①.x y 3sin 2=;②.14822=-y x .7.对012422=++-+y x y x 曲线向着x 轴进行伸缩变换,伸缩系数2=k .8.在平面直角坐标系中求将曲线0142:22=+--+y x y x C 变为曲线012444:22=+'-'-'+''y x y x C 的伸缩变换.。
