初中数学课件-切线长定理课堂课件北师大版1
合集下载
初中数学课件-切线长定理课件模板北师大版1

(5)图中所有的等腰三角形: △ABP △AOB
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
例题讲解
例 已知:如图,四边形ABCD的边AB,BC,CD,DA和
⊙O分别相切于点E,F,G,H. 求证: AB + CD = DA + BC.
证明:∵ AB,BC,CD,DA都与⊙O相切, E,F,G,H是切点,
切线长定理:
A
过圆外一点所画的圆的两条切线
的切线长相等,圆心和这一点的连
O.
线平分两条切线的夹角.
P
几何语言:
PA、PB分别切☉O于A、B
B PA = PB ∠OPA=∠OPB
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
4. 如图,过☉O外一点P作圆的切线PA,PB,F是劣弧AB上任意一点,
过点F作☉O的切线分别交PA,PB于点D,E,如果PA=10,∠P=42°. 求:(1)△PED的周长; (2)∠DOE的度数.
(2)∵DA,DF分别切☉O于点A,F,
∴∠DAO=∠DFO=90°.
在Rt△AOD与Rt△FOD中,
∵AO=FO,OD=OD,
∴Rt△AOD≌Rt△FOD,
∴∠AOD=∠FOD = 1 ∠AOF,
2
同理∠EOF=∠BOE= 1 ∠BOF,
2
∴∠DOE=∠FOD+∠EOF=12∠AOF+12∠BOF
2. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB. 下列结论不一定正确的是( D ) A.PA=PB B.OP垂直平分AB C.∠OPA=∠OPB D.PA=AB
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
例题讲解
例 已知:如图,四边形ABCD的边AB,BC,CD,DA和
⊙O分别相切于点E,F,G,H. 求证: AB + CD = DA + BC.
证明:∵ AB,BC,CD,DA都与⊙O相切, E,F,G,H是切点,
切线长定理:
A
过圆外一点所画的圆的两条切线
的切线长相等,圆心和这一点的连
O.
线平分两条切线的夹角.
P
几何语言:
PA、PB分别切☉O于A、B
B PA = PB ∠OPA=∠OPB
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
初中数学课件-切线长定理课件模板北 师大版 1(精 品课件 )
4. 如图,过☉O外一点P作圆的切线PA,PB,F是劣弧AB上任意一点,
过点F作☉O的切线分别交PA,PB于点D,E,如果PA=10,∠P=42°. 求:(1)△PED的周长; (2)∠DOE的度数.
(2)∵DA,DF分别切☉O于点A,F,
∴∠DAO=∠DFO=90°.
在Rt△AOD与Rt△FOD中,
∵AO=FO,OD=OD,
∴Rt△AOD≌Rt△FOD,
∴∠AOD=∠FOD = 1 ∠AOF,
2
同理∠EOF=∠BOE= 1 ∠BOF,
2
∴∠DOE=∠FOD+∠EOF=12∠AOF+12∠BOF
2. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB. 下列结论不一定正确的是( D ) A.PA=PB B.OP垂直平分AB C.∠OPA=∠OPB D.PA=AB
北师大版九年级下册数学课件3.7切线长定理(共21张PPT)

A
O
D
P
图10B
• 3、为了测量一个圆形锅盖的半径,某同学 采用了如下办法:将锅盖平放在水平桌面 上,用一个锐角为30°的三角板和一个刻 度尺,按图中所示的方法得到相关数据,
进而可求得锅盖的半径,若测得PA=5cm,
则锅盖的半径长是多少?
•
O B
AP
四、梳理小结,盘点收获
1、你的学习心得、体会是什么? 2、你有哪些好的经验可推广? 3、你还存在哪些困难、疑问?
二、 合作学习,探究新知
线段PA或线段PB
二、 合作学习,探究新知
二、 合作学习,探O究新知
O
O
(1)若PB=12,PO=13,则AO=
而切线长是线段,指过圆外一点做圆的切线,该点到切点的距离。
(4)既然点P到⊙O的切线长可以用两条不同的线段的长来表示图,8那么这两条线段之间一定存在着某种关系,是什么关系呢?
(1)已知:如图1,PC和⊙O相切于点A ,点P到⊙O的切线长可以用哪一条线段的长来表示? (3) 如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三角形的内切圆,图8中存在切线长定理吗?.
二、 合作学习,探究新知
四、梳理小结,盘点收获
A
而切线长是线段,指过圆外一点做圆的切线,该点到切点的距离。
线段PA或线段PB
画一画:画圆O,在圆外取一点P,过点P作圆O的切线PA,切点为A。
例题1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。
(3) 如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三角形的内切圆,图8中存在切线长定理吗?.
线段PA或线段PB (3)如图2,思考:点P到⊙O的切线长可以用三条或三条以 上不同的线段的长来表示吗?这样的线段最多可以有几条? 为什么?
O
D
P
图10B
• 3、为了测量一个圆形锅盖的半径,某同学 采用了如下办法:将锅盖平放在水平桌面 上,用一个锐角为30°的三角板和一个刻 度尺,按图中所示的方法得到相关数据,
进而可求得锅盖的半径,若测得PA=5cm,
则锅盖的半径长是多少?
•
O B
AP
四、梳理小结,盘点收获
1、你的学习心得、体会是什么? 2、你有哪些好的经验可推广? 3、你还存在哪些困难、疑问?
二、 合作学习,探究新知
线段PA或线段PB
二、 合作学习,探究新知
二、 合作学习,探O究新知
O
O
(1)若PB=12,PO=13,则AO=
而切线长是线段,指过圆外一点做圆的切线,该点到切点的距离。
(4)既然点P到⊙O的切线长可以用两条不同的线段的长来表示图,8那么这两条线段之间一定存在着某种关系,是什么关系呢?
(1)已知:如图1,PC和⊙O相切于点A ,点P到⊙O的切线长可以用哪一条线段的长来表示? (3) 如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三角形的内切圆,图8中存在切线长定理吗?.
二、 合作学习,探究新知
四、梳理小结,盘点收获
A
而切线长是线段,指过圆外一点做圆的切线,该点到切点的距离。
线段PA或线段PB
画一画:画圆O,在圆外取一点P,过点P作圆O的切线PA,切点为A。
例题1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。
(3) 如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三角形的内切圆,图8中存在切线长定理吗?.
线段PA或线段PB (3)如图2,思考:点P到⊙O的切线长可以用三条或三条以 上不同的线段的长来表示吗?这样的线段最多可以有几条? 为什么?
北师大初中数学九下《3.7切线长定理》PPT课件 (1)

PA = PB ∠OPA=∠OPB
如图:PA、PB是⊙O的两条切线,A、B为切点。 B
思考:由切线长定
O。 C
P
理可以得出哪些结
论?
A
例:已知:在△ABC中,BC=14, AC=13,AB=9,它的内切圆分别和 BC、AC、AB切于点D、E、F,求AF、 BD和CE的长。
B
A
x
F . I
yD
E
z
C
分析:设 AF=x,BD=y,
CE=z
y+z=14
x+z=13
x+y=9
如图:从⊙O外的定点P作 ⊙O 的点A两在条弧切线AB上,任分取别切一点⊙CO,于过 和点BC,作⊙O的切线,分别交PA、 PB于点D、E。PA =12
求:⑴ △PDE的周长
(提示AD=DC)
D
C
O
E
A
。
O
B
C
1
C
D r. O
探究:
如图,纸上有一⊙o, PA为⊙0的一条切线, 沿着直线PO将纸对折, 设圆上与点A重合的点 为B,这时,OB是⊙o 的一条半径吗?PB是 ⊙o的切线吗?利用图形 的轴对称性说明图中PA 与PB,∠APO与∠BPO 有什么关系?
切线长的定义
经过圆外一点作圆的切线,这点和切点之间 的线段长叫做这点到圆的切线长。
A B
2
通过这节课的学习,你有什么收获或体会?
如图PA、PB是⊙O的两条切线, ∴OA⊥AP,OB⊥BP 又OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP ∴PA=PB,∠OPA=∠OPB。
定理:从圆外一点可以引圆的两条切线,它 们的切线长相等,这一点和圆心的连线平分 这两条切线的夹角。
九下数学(北师大)课件-切线长定理
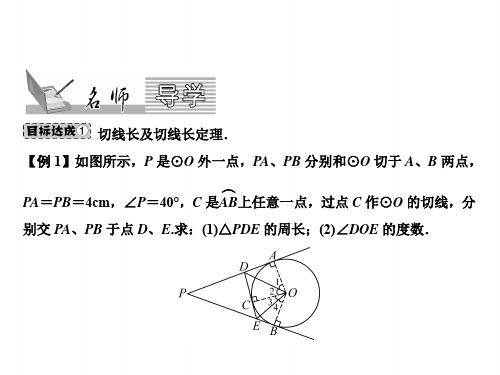
解:(1)连接 CB、CE、CF、AC,则∠BAC=∠EAC=∠BCA,∴AB=BC =5,CE=OB=3,∴C 的坐标为(-5,3);
(2)连接 CD、CE、CF,∵∠CEO=∠CDO=90°,又∠DOE=90°,∴四边 形 CEOD 为矩形,又∵CE=CD,得正方形 CEOD,∴CE=DO=R,又 BO =3,∴BD=3-R,∵BF、BD 为切线,∴FB=BD=3-R,同理 AE=AF, 即 R+4=3-R+5,∴R=2.
(2)连接 OB、OC、OD、OF,如图,∵等腰三角形 ABC 中,AE⊥EC,∴E OD=OF
是 BC 中点,BE=CE,∵在 Rt△AOF 和 Rt△AOD 中,OA=OA , ∴Rt△AOF≌Rt△AOD,∴AF=AD,同理 Rt△COF≌Rt△COE,CF=CE =2,Rt△BOD≌Rt△BOE,BD=BE,∴AD=AF,BD=CF,∴DF∥BC, ∴AAME =AAFC=32,∵AE= AC2-CE2=4 2,∴AM=32AE=4 2×32=83 2.
7.(益阳中考)如图,PA、PB 为圆 O 的切线,切点分别为 A、B,PO 交 AB
于点 C,PO 的延长线交圆 O 于点 D,下列结论不一定成立的是( D )
A.PA=PB
B.∠BPD=∠APD
C.AB⊥PD
D.AB 平分 PD
8.(广州中考)平面内,⊙O 的半径为 1,点 P 到 O 的距离为 2,过点 P 可作
切线长及切线长定理.
【例 1】如图所示,P 是⊙O 外一点,PA、PB 分别和⊙O 切于 A、B 两点,
︵ PA=PB=4cm,∠P=40°,C 是AB上任意一点,过点 C 作⊙O 的切线,分
别交 PA、PB 于点 D、E.求:(1)△PDE 的周长;(2)∠DOE 的度数.
切线长定理课件北师大版数学九年级下册

由切线长定理可知,∠FEO=∠OEA,∠EFO=∠OFB, . ∠FEO+∠EFO=115°
∠EOF=180°-115°=65°
当堂练习
1.如图,PA 、PB 是⊙O的两条切线,切点分别是A 、B,
如 果AP=4,∠A PB= 40°, 则∠APO= 20° ,PB= 4
第1题
2.如图,已知点0是△ABC的内心,且∠ABC=60°
切线长定理
【新知探究】
经过圆外一点的圆的切线上,这 点和切点之间线段的长,叫做这 点到圆的切线长.
特别注意: 切线是直线,无法度量长度; 切线长是切线上一条线段的长, 即圆外一点与切点之间的距离,可以度量。
0
B
【新知探究】
已知,如图PA、PB是⊙0的两条切线, A、B 为切点.
D
求证:PA=PB,∠APO=∠BPO.
感谢聆听,同学们再见!
注 意 :过圆外任意一点都可以引圆的两条切线;过圆上一点只能引圆的一条切线。
【解决问题】
如图,已知PA,PB,EF 分别切⊙0于点A,
B,D. 若PA=15 cm,
(1)PB= cm.
(2)若∠AEF=120°, 则 ∠FEO=
(3)△PEF 的周长是
cm.
(4)若∠P=50°, 则∠EOF=
【解决问题】
∠ACB=80°,则∠BOC= 110°
3.如图,PA、PB是⊙O的切线,切点分别为A、B, 点 C在⊙0上,如果∠ACB=70°, 那么∠OPA的度数是
20 度.
4.如图,PA 、PB是⊙0的两条切线,切点为A 、B, ∠P=50°, 点C是⊙0上异于A 、B的点,则
∠ACB=65°或115?
边形BODC为正方形.
∠EOF=180°-115°=65°
当堂练习
1.如图,PA 、PB 是⊙O的两条切线,切点分别是A 、B,
如 果AP=4,∠A PB= 40°, 则∠APO= 20° ,PB= 4
第1题
2.如图,已知点0是△ABC的内心,且∠ABC=60°
切线长定理
【新知探究】
经过圆外一点的圆的切线上,这 点和切点之间线段的长,叫做这 点到圆的切线长.
特别注意: 切线是直线,无法度量长度; 切线长是切线上一条线段的长, 即圆外一点与切点之间的距离,可以度量。
0
B
【新知探究】
已知,如图PA、PB是⊙0的两条切线, A、B 为切点.
D
求证:PA=PB,∠APO=∠BPO.
感谢聆听,同学们再见!
注 意 :过圆外任意一点都可以引圆的两条切线;过圆上一点只能引圆的一条切线。
【解决问题】
如图,已知PA,PB,EF 分别切⊙0于点A,
B,D. 若PA=15 cm,
(1)PB= cm.
(2)若∠AEF=120°, 则 ∠FEO=
(3)△PEF 的周长是
cm.
(4)若∠P=50°, 则∠EOF=
【解决问题】
∠ACB=80°,则∠BOC= 110°
3.如图,PA、PB是⊙O的切线,切点分别为A、B, 点 C在⊙0上,如果∠ACB=70°, 那么∠OPA的度数是
20 度.
4.如图,PA 、PB是⊙0的两条切线,切点为A 、B, ∠P=50°, 点C是⊙0上异于A 、B的点,则
∠ACB=65°或115?
边形BODC为正方形.
九年级数学北师大版下册课件:第三章 3.7 切线长定理(共26张PPT)

连接 OD, ∵OD=OA,∴∠OAD=∠ODA=50°.
∵∠CBA=70°,∴∠ADC=110°,∠ODC=60
°.又∵OP⊥CD,∴∠OQD=90°. ∴OQ=OD·sin60°=2× 23= 3. ∴DQ=OD·cos60°=1. ∵PD 是切线,∴∠PDO=90°.∴∠PDC=30°. ∴PQ=DQ·tan30°=1× 33= 33. ∴OP=PQ+QO=4 3 3.
探究二:如图,△ABC 的内切圆⊙O 与 BC,CA,
AB 分别相切于点 D,F,E,且 AB=9 cm,BC=14 cm, CA=13 cm,求 AE,BD,CF 的长.
解:设 AE=x,BD=y,CF=z,
由切线长定理列方程组xy+ +yz= =91, 4,得xy= =45, , x+z=13, z=9.
∴OD=CD=4-x,∵∠A=∠A,∠ADO=∠ACB,∴
△ADO∽△ACB,∴AADC=BODC,即x4=4-6 x,∴x=1.6.
7. (2018·绵阳)如图,AB 是⊙O 的直径,点 D 在 ⊙O 上(点 D 不与 A,B 重合),直线 AD 交过点 B 的切
线于点 C,过点 D 作⊙O 的切线 DE 交 BC 于点 E. (1)求证:BE=CE; (2)若 DE∥AB,求 sin∠ACO 的值.
∴BC=2r,AC=2 2r, 在 Rt△COB 中,∴OC= 5r,
又∵S△ACO=21·AO·BC=21·AC·OH,
∴r×2r=2 2r×OH,∴OH= 22r,
在
Rt△COH
OH 中,∴sin∠ACO=OC=
225rr=
1100.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
∵∠CBA=70°,∴∠ADC=110°,∠ODC=60
°.又∵OP⊥CD,∴∠OQD=90°. ∴OQ=OD·sin60°=2× 23= 3. ∴DQ=OD·cos60°=1. ∵PD 是切线,∴∠PDO=90°.∴∠PDC=30°. ∴PQ=DQ·tan30°=1× 33= 33. ∴OP=PQ+QO=4 3 3.
探究二:如图,△ABC 的内切圆⊙O 与 BC,CA,
AB 分别相切于点 D,F,E,且 AB=9 cm,BC=14 cm, CA=13 cm,求 AE,BD,CF 的长.
解:设 AE=x,BD=y,CF=z,
由切线长定理列方程组xy+ +yz= =91, 4,得xy= =45, , x+z=13, z=9.
∴OD=CD=4-x,∵∠A=∠A,∠ADO=∠ACB,∴
△ADO∽△ACB,∴AADC=BODC,即x4=4-6 x,∴x=1.6.
7. (2018·绵阳)如图,AB 是⊙O 的直径,点 D 在 ⊙O 上(点 D 不与 A,B 重合),直线 AD 交过点 B 的切
线于点 C,过点 D 作⊙O 的切线 DE 交 BC 于点 E. (1)求证:BE=CE; (2)若 DE∥AB,求 sin∠ACO 的值.
∴BC=2r,AC=2 2r, 在 Rt△COB 中,∴OC= 5r,
又∵S△ACO=21·AO·BC=21·AC·OH,
∴r×2r=2 2r×OH,∴OH= 22r,
在
Rt△COH
OH 中,∴sin∠ACO=OC=
225rr=
1100.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
初三下数学课件(北师大)-切线长定理
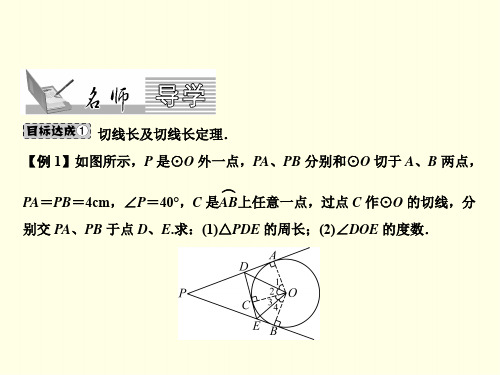
︵ 过劣弧DE (不包括端点 D、E)上任一点作⊙O 的切线 MN 与 AB、BC 分别 交于点 M、N.若⊙O 的半径为 r,则 Rt△MBN 的周长为 2r .
12.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,
A、B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD、BE 于点 M、 3
解:(1)△ABC 为等腰三角形,∵△ABC 的内切圆⊙O 与 AB、BC、AC 分 别相切于点 D、E、F,∴∠CFO=∠CEO=∠BDO=∠BEO=90°,∵四边
︵︵ 形内角和为 360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵EF=DE, ∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC 为等腰三角形;
切线长定理的综合运用. 【例 2】如图所示,在△ABC 中,∠C=90°,AC=8,AB=10,点 P 在 AC 上,AP=2,若⊙O 的圆心在线段 BP 上,且⊙O 与 AB、AC 都相切,则⊙ O 的半径是( A )
A.1 C.172
B.45 D.94
【思路分析】如图所示,过点 O 作 OD⊥AC,OE⊥AB,OF⊥BC,垂足分 别为 D、E、F,CP=AC-AP=8-2=6,BC= AB2-AC2= 102-82=6. ∴CP=CB,∴∠CPB=∠CBP=45°,设⊙O 的半径为 r,则 OD=OE=DP =r,BF=OF=6-r,AD=AE=r+2,BE=8-r,在 Rt△BOE 中,由勾 股定理,得 BE2+OE2=BO2,而 BO2=BF2+OF2,即(8-r)2+r2=2(6-r)2, ∴r=1.
⊙O 的切线条数为( C )
A.0 条
B.1 条
C.2 条
D.无数条
12.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,
A、B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD、BE 于点 M、 3
解:(1)△ABC 为等腰三角形,∵△ABC 的内切圆⊙O 与 AB、BC、AC 分 别相切于点 D、E、F,∴∠CFO=∠CEO=∠BDO=∠BEO=90°,∵四边
︵︵ 形内角和为 360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵EF=DE, ∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC 为等腰三角形;
切线长定理的综合运用. 【例 2】如图所示,在△ABC 中,∠C=90°,AC=8,AB=10,点 P 在 AC 上,AP=2,若⊙O 的圆心在线段 BP 上,且⊙O 与 AB、AC 都相切,则⊙ O 的半径是( A )
A.1 C.172
B.45 D.94
【思路分析】如图所示,过点 O 作 OD⊥AC,OE⊥AB,OF⊥BC,垂足分 别为 D、E、F,CP=AC-AP=8-2=6,BC= AB2-AC2= 102-82=6. ∴CP=CB,∴∠CPB=∠CBP=45°,设⊙O 的半径为 r,则 OD=OE=DP =r,BF=OF=6-r,AD=AE=r+2,BE=8-r,在 Rt△BOE 中,由勾 股定理,得 BE2+OE2=BO2,而 BO2=BF2+OF2,即(8-r)2+r2=2(6-r)2, ∴r=1.
⊙O 的切线条数为( C )
A.0 条
B.1 条
C.2 条
D.无数条
初中数学《切线长定理》PPT北师大版1

为切点。
B
思考:由切线长定
O。 C
P
理可以得出哪些结
论?
A
(1)写出图中所有的垂直关系; (2)写出图中所有的全等三角形; (3)写出图中所有的等腰三角形.
练习
1、如图,已知⊙O的半径为3cm,
PO=6cm,PA,PB分别切⊙O于A,B,
(1)PA= .
(2)若PO交⊙O于点Q,直线CD切⊙O
于点Q,交PA、PB于点C、D,则
1探、究切: 线长的概念.
经经过平过面圆上外的一已点知作点圆作的已知切圆线的,这切点线和,切会有点怎之 样间的的情线形段呢的?长叫做这点到圆的切线长.
如 图 , 线 段 PA ,
PB的长就是点P到
⊙O的切线长.
A
O P
O
A P
O
P
B
比一比
A
O
P
B
切线和切线长是两个不同的概念: 1、切线是一条与圆相切的直线,不能度量; 2、切线长是线段的长,这条线段的两个端点 分别是圆外一点和切点,可以度量。
•
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
•
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
•
8.少年时阅历不够丰富,洞察力、理 解力有 所欠缺 ,所以 在读书 时往往 容易只 看其中 一点或 几点, 对书中 蕴含的 丰富意 义难以 全面把 握。
•
9.自信让我们充满激情。有了自信, 我们才 能怀着 坚定的 信心和 希望, 开始伟 大而光 荣的事 业。自 信的人 有勇气 交往与 表达, 有信心 尝试与 坚持, 能够展 现优势 与才华 ,激发 潜能与 活力, 获得更 多的实 践机会 与创造 可能。
《切线长定理》示范公开课PPT教学课件【九年级数学下册北师大版】

只要证明OC1CD,即LOCD = 90°即可,由LOCD LOCB + LBCD,已知LBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了,但LOCB与LBAC既没有共同的顶点,又不在同一个三角形中,故可延长CO交O0于点E,连接EB,由圆周角定理的推论,可Q LBAC =LBEC.而LBCELBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了,但LOCB与LBAC既没有共同的顶点,又不在同一个三角形中,故可延由LOCD LOCB + LBCD,已知LBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了长CO交O0于点E,连接EB,由圆周角定理的推论,可Q LBAC =LBEC.而LBCE与LBEC都是同一个三角形的内角,因此只要证明LCBE = 90°就行了x这是很角形的内角,因此只要证明LCBE = 90°就行了x这是很
例 如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
分析:
A
O
设 ⊙O的半径为r,连接OD,OE,OF
由切线的性质及切线长定理可得四边形OECF为正方形.
从而CF=CE=OE=OF=r,所以AF=10-r,BE=24-r,
再由切线长定理可得,AD=AF=10-r,BD=BE=24-r,
∠BIC
2.如图,PA,PB分别与⊙O相切于A,B两点.C是弧AB上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA = PB =5 cm,求△PDE的周长.
O
P
A
B
C
D
E
解:∵PA,PB,DE是圆的切线∴PA=PB,DC=DA,CE=BE,
例 如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
分析:
A
O
设 ⊙O的半径为r,连接OD,OE,OF
由切线的性质及切线长定理可得四边形OECF为正方形.
从而CF=CE=OE=OF=r,所以AF=10-r,BE=24-r,
再由切线长定理可得,AD=AF=10-r,BD=BE=24-r,
∠BIC
2.如图,PA,PB分别与⊙O相切于A,B两点.C是弧AB上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA = PB =5 cm,求△PDE的周长.
O
P
A
B
C
D
E
解:∵PA,PB,DE是圆的切线∴PA=PB,DC=DA,CE=BE,
北师大版数学九年级下册切线长定理课件
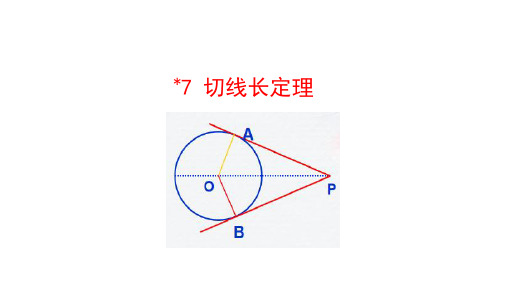
A
O 130°
B
P
50°
如何用圆规和直尺
作出这两条
A
切线呢?
O.
P
B 思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°, 连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?
A
OO ·
P
B
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段长叫 做这点到圆的切线长.
A
O
·
P
B
切线与切线长是一回事吗?它们有什么区分与联系呢?
C
求证:AD+BC=AB+CD.
N
证明:由切线长定理得
D
AL=AP,LB=MB,NC=MC,
M O
DN=DP,
P
∴AP+MB+MC+DP=AL+LB+NCA L
B
+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
【跟踪训练】
1.如果PA=4cm,PD=2cm, 求半径OAB
定理 圆的切线垂直于过切点的半径
●
∵CD与⊙O相切与点A,且OA是半
O
径∴CD⊥OA.
提示:
CAD
“见切点,连圆心”是常用辅助线之一.
你还记得内切圆与内心吗?
A
F
E
I
●●
B
┓
C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内 切圆的圆心叫做三角形的内心,是三角形三条角平分线的 交点.
1.理解切线长的概念,掌握切线长定理. 2.学会运用切线长定理解有关问题. 3.通过对例题的分析,培养学生分析总结问题的习 惯,提高学生综合运用知识解题的能力,培养数形 结合的思想.
O 130°
B
P
50°
如何用圆规和直尺
作出这两条
A
切线呢?
O.
P
B 思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°, 连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?
A
OO ·
P
B
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段长叫 做这点到圆的切线长.
A
O
·
P
B
切线与切线长是一回事吗?它们有什么区分与联系呢?
C
求证:AD+BC=AB+CD.
N
证明:由切线长定理得
D
AL=AP,LB=MB,NC=MC,
M O
DN=DP,
P
∴AP+MB+MC+DP=AL+LB+NCA L
B
+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
【跟踪训练】
1.如果PA=4cm,PD=2cm, 求半径OAB
定理 圆的切线垂直于过切点的半径
●
∵CD与⊙O相切与点A,且OA是半
O
径∴CD⊥OA.
提示:
CAD
“见切点,连圆心”是常用辅助线之一.
你还记得内切圆与内心吗?
A
F
E
I
●●
B
┓
C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内 切圆的圆心叫做三角形的内心,是三角形三条角平分线的 交点.
1.理解切线长的概念,掌握切线长定理. 2.学会运用切线长定理解有关问题. 3.通过对例题的分析,培养学生分析总结问题的习 惯,提高学生综合运用知识解题的能力,培养数形 结合的思想.
北师大版九年级下册数学:3.7切线长定理课件(共30张PPT)

AD+BC(>,<,=)
∴ PA = PB ∠OPA=∠OPB
根据切线长定理说出图中可以得到的结论。 如图,PA、AB与⊙O相切于点A、B,
例:如图, △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。
例:如图, △ABC的内切圆⊙O与BC、CA、 AB分别相切于点D、E、F,且AB=9cm, BC=14cm,CA=13cm,求AF、BD、CE的长。
O
CD
P
(1)写出图中所有的垂直关系
B
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
(3)写出图中所有相等的线段
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
如图,△ABC的内切圆⊙O与各边分别相切于点D、 E、F,图中有切线长定理的基本图形吗?
∴Rt△AOP≌Rt△BOP(HL)
① 分别连接圆心和切点;
辅助线 OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
∠OAC=∠OBC=∠APC=∠BPC 圆的内接四边形:角的关系
猜想:PA、PB有怎样的数量关系?如何证明? 猜想:PA、PB有怎样的数量关系?如何证明?
② 连接两切点; ③ 连接圆心和圆外一点.
x A x F 9﹣x
E
B
O
13﹣x
D 9﹣x
13﹣x
C
例 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm, 求AF、BD、CE的长.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PO平分∠APB
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
2.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这
一点的连线平分两条切线的夹角。
A
推导格式 :∵PA、PB分别切⊙O于A、B,
O B
1 2
P
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
o.
o.
.
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
【探究1】如图,☉I是△ABC的内切圆,那么线段IA、IB、IC有什
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
反思:在解决有关 圆的切线长问题时, 往往需要我们构建 基本图形。
反思:在解决有关圆的切线长
A 的问题时,往往需要我们构建
基本图形。
。
O
P
B
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
练一练
1.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则
∠BOC的度数为( )
A.130° B.120° C.110° D.100°
【答案】C 【详解】 ∵AB、AC是⊙O的两条切线,B、C是切点, ∴∠B=∠C=90°,∠BOC=180°-∠A=110°. 故选C.
A
2.三角形的内心:
定义:内切圆的圆心叫做这个三角形的内心。
O
作图:三角形的内心在三角形的角平分线上。 B
C
性质:三角形的内心到三角形的三边距离相等。
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 ) 初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
例1.PA、PB是⊙O的两条 切线,A、B为切点,直线
A
OP交于⊙O于点D、E,交 A(B1于)写C出。图中所有的垂直关系
E
O CD
P
OA⊥PA,OB ⊥PB,AB ⊥OP
B
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
3.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这
一点的连线平分两条切线的夹角。
A
推导格式 :∵PA、PB分别切⊙O于A、B,
O B
1 2
P
∴PA=PB,∠OPA=∠OPB.
切线长定理为证明线段相
等,角相等提供新的方法
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
2.如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点 作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长。
易证EQ=EA,FQ=FB,PA=PB
A P
B
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
问题1:如何过⊙O外一点P画出⊙O的切线?
连接OP,以OP为直径作圆,与⊙O 交于A、B两点。 连接PA、PB, 则PA、PB即为⊙O切线。
A
O
P
B
连接OA、OB,可证∠PAO=∠PBO=90°,从而可证PA、PB为⊙O切线。
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
小结
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
A
P
B
切线
A
P
B
切线长
实质 直线 线段
长度 不可测量 可测量(线段PA)
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
∴PA=PB,∠OPA=∠OPB.
切线长定理为证明线段相
等,角相等提供新的方法
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
我们学过的切线,常有 五六个 性质:
1、切线和圆只有一个公共点; 2、切线和圆心的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。 6、从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC (3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
(5)若PA=4、PD=2,求半径OA
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
第二十四章 圆 24.2.2直线和圆的位置关系
第4课时 切线长定理
同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一 瞬间,你能从中抽象出什么样数学图形?
学
1 掌握切线长的定义及切线长定理.(重点)
习
思考
过圆外一点可以作圆的___2___条切线;过圆上一点可以作圆的___1__条切线; 过圆内一点的圆的切线___0___.
∴ PE+EQ=PA=12cm PF+FQ=PB=PA=12cm
∴△PEF周长为24cm
P
A E
O Q
FB
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
三、三角形的内切圆
1.与三角形三边都相切的圆叫作三角形的内切圆.
这个三角形叫做这个圆的外切三角形.
二、切线长定理及应用
问题2:PA、PB有什么数量关系?
解:PA=PB,理由如下: ∵PA,PB分别与⊙O相切于A,B ∴OA⊥PA,OB⊥PB ∴∠OAP=∠OBP=90° ∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB
A
O
P
B
问题3:观察PO的位置,你还有什么发现?
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
2.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这
一点的连线平分两条切线的夹角。
A
推导格式 :∵PA、PB分别切⊙O于A、B,
O B
1 2
P
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
o.
o.
.
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
【探究1】如图,☉I是△ABC的内切圆,那么线段IA、IB、IC有什
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
反思:在解决有关 圆的切线长问题时, 往往需要我们构建 基本图形。
反思:在解决有关圆的切线长
A 的问题时,往往需要我们构建
基本图形。
。
O
P
B
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
练一练
1.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则
∠BOC的度数为( )
A.130° B.120° C.110° D.100°
【答案】C 【详解】 ∵AB、AC是⊙O的两条切线,B、C是切点, ∴∠B=∠C=90°,∠BOC=180°-∠A=110°. 故选C.
A
2.三角形的内心:
定义:内切圆的圆心叫做这个三角形的内心。
O
作图:三角形的内心在三角形的角平分线上。 B
C
性质:三角形的内心到三角形的三边距离相等。
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 ) 初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
例1.PA、PB是⊙O的两条 切线,A、B为切点,直线
A
OP交于⊙O于点D、E,交 A(B1于)写C出。图中所有的垂直关系
E
O CD
P
OA⊥PA,OB ⊥PB,AB ⊥OP
B
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
3.切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这
一点的连线平分两条切线的夹角。
A
推导格式 :∵PA、PB分别切⊙O于A、B,
O B
1 2
P
∴PA=PB,∠OPA=∠OPB.
切线长定理为证明线段相
等,角相等提供新的方法
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
2.如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点 作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长。
易证EQ=EA,FQ=FB,PA=PB
A P
B
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
问题1:如何过⊙O外一点P画出⊙O的切线?
连接OP,以OP为直径作圆,与⊙O 交于A、B两点。 连接PA、PB, 则PA、PB即为⊙O切线。
A
O
P
B
连接OA、OB,可证∠PAO=∠PBO=90°,从而可证PA、PB为⊙O切线。
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
小结
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
A
P
B
切线
A
P
B
切线长
实质 直线 线段
长度 不可测量 可测量(线段PA)
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
∴PA=PB,∠OPA=∠OPB.
切线长定理为证明线段相
等,角相等提供新的方法
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
我们学过的切线,常有 五六个 性质:
1、切线和圆只有一个公共点; 2、切线和圆心的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。 6、从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC (3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
(5)若PA=4、PD=2,求半径OA
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
第二十四章 圆 24.2.2直线和圆的位置关系
第4课时 切线长定理
同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一 瞬间,你能从中抽象出什么样数学图形?
学
1 掌握切线长的定义及切线长定理.(重点)
习
思考
过圆外一点可以作圆的___2___条切线;过圆上一点可以作圆的___1__条切线; 过圆内一点的圆的切线___0___.
∴ PE+EQ=PA=12cm PF+FQ=PB=PA=12cm
∴△PEF周长为24cm
P
A E
O Q
FB
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
初中数学课件-切线长定理课堂课件北 师大版 1(精 品课件 )
三、三角形的内切圆
1.与三角形三边都相切的圆叫作三角形的内切圆.
这个三角形叫做这个圆的外切三角形.
二、切线长定理及应用
问题2:PA、PB有什么数量关系?
解:PA=PB,理由如下: ∵PA,PB分别与⊙O相切于A,B ∴OA⊥PA,OB⊥PB ∴∠OAP=∠OBP=90° ∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB
A
O
P
B
问题3:观察PO的位置,你还有什么发现?
