中考与圆有关的计算和证明

合集下载

圆的相关证明与计算(复习讲义)(原卷版)-中考数学重难点题型专题汇总

题型五--圆的相关证明与计算（复习讲义）【考点总结|典例分析】考点01圆的有关概念1．与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．（4）圆心角：顶点在圆心的角叫做圆心角．（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．（6）弦心距：圆心到弦的距离．考点02垂径定理及其推论1．垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．2．推论（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．考点03圆心角、弧、弦的关系1．定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．2．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．考点04圆周角定理及其推论1．定理一条弧所对的圆周角等于它所对的圆心角的一半．2．推论（1）在同圆或等圆中，同弧或等弧所对的圆周角相等．（2）直径所对的圆周角是直角．考点05与圆有关的位置关系1．点与圆的位置关系设点到圆心的距离为d．(1)d<r⇔点在⊙O内；(2)d=r⇔点在⊙O上；(3)d>r ⇔点在⊙O 外．判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．2．直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r考点06切线的性质与判定1．切线的性质（1）切线与圆只有一个公共点．（2）切线到圆心的距离等于圆的半径．（3）切线垂直于经过切点的半径．利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题．2．切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）．（2）到圆心的距离等于半径的直线是圆的切线．（3）经过半径外端点并且垂直于这条半径的直线是圆的切线．切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．考点07三角形与圆1.三角形外接圆外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等．2．三角形的内切圆内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等．1.如图，点,,,,A B C D E 在O 上，,42AB CD AOB =∠=︒，则CED ∠=（）A．48︒B．24︒C．22︒D．21︒2.如图，A，B，C 是半径为1的⊙O 上的三个点，若，∠CAB＝30°，则∠ABC 的度数为（）A．95°B．100°C．105°D．110°3.如图，AB 是⊙O 的直径，AC，BC 是⊙O 的弦，若20A ∠=︒，则B Ð的度数为（）A．70°B．90°C．40°D．60°4.如图，Rt ABC 中，90ACB ∠=︒，AC =3BC =．点P 为ABC ∆内一点，且满足22PA PC +2AC =．当PB 的长度最小时，ACP ∆的面积是（）A．3B．C．4D．25.如图，已知在⊙O 中， AB BCCD ＝＝，OC 与AD 相交于点E．求证：（1）AD∥BC（2）四边形BCDE 为菱形．6.如图，A，B 是O 上两点，且AB OA =，连接OB 并延长到点C，使BC OB =，连接AC．（1）求证：AC 是O 的切线．（2）点D，E 分别是AC，OA 的中点，DE 所在直线交O 于点F，G，4OA =，求GF 的长．7.如图，Rt ABC 中，90ABC ∠=︒，以点C 为圆心，CB 为半径作C ，D 为C 上一点，连接AD 、CD ，AB AD =，AC 平分BAD ∠．（1）求证：AD 是C 的切线；（2）延长AD 、BC 相交于点E，若2EDC ABC S S = ，求tan BAC ∠的值．8.如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．9.如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．10.如图，已知点C 是以AB 为直径的圆上一点，D 是AB 延长线上一点，过点D 作BD 的垂线交AC 的延长线于点E ，连结CD ，且CD ED =．（1）求证：CD 是O 的切线；（2）若tan 2DCE ∠=，1BD =，求O 的半径．11.如图，AB 是⊙O 的直径，C 为⊙O 上一点，连接AC，CE⊥AB 于点E，D 是直径AB 延长线上一点，且∠BCE＝∠BCD．（1）求证：CD 是⊙O 的切线；（2）若AD＝8，BE CE=12，求CD的长．12.如图，△ABC内接于⊙O，AB为⊙O的直径，AB＝10，AC＝6，连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．13.如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO并延长，与⊙O 交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．=CD =DB ，连接AD，过点D作14.如图，AB为⊙O的直径，C、D为⊙O上的两个点，ACDE⊥AC交AC的延长线于点E．（1）求证：DE是⊙O的切线．（2）若直径AB＝6，求AD的长．15.如图，AB是半圆O的直径，C，D是半圆O上不同于A，B的两点，AD＝BC，AC与BD相交于点F．BE是半圆O所在圆的切线，与AC的延长线相交于点E．（1）求证：△CBA≌△DAB；（2）若BE＝BF，求证：AC平分∠DAB．16.如图，AB为⊙O的直径，C为⊙O上一点，AD与过C点的直线互相垂直，垂足为D，AC 平分∠DAB．（1）求证：DC为⊙O的切线．（2）若AD＝3，DC=3，求⊙O的半径．17.如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作⊙O的切线交AC于点E．（1）求证：DE⊥AC；（2）若⊙O的半径为5，BC＝16，求DE的长．。

2023年数学中考真题：圆的有关计算及证明精选(一)

圆的有关计算及证明2023年数学中考试题精选（一）1.（2023.营口23题）如图，在△ABC中，AB=BC，以BC为直径作圆O与AC将于点D，过点D作DE⊥AB，交CB延长线于点F，垂足为点E.（1）求证：DF为圆O的切线；，求BF的长。

（2）若BE=3，cosC=452.（2023.本溪铁岭辽阳24题）如图，AB是圆O的直径，点C，E在圆O上，∠CAB=2∠EAB，点F在线段AB的延长线上，且∠AFE=∠ABC.（1）求证：EF与圆O相切；，求BC的长。

（2）若BF=1，sin∠AFE=453.(2023.沈阳22题)如图，BE是圆O的直径，点A和点D是圆O上的两点，过点A作圆O的切线交BE延长线于点C.（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求圆O半径的长.4.(2023.大连市23题)如图1，在圆O中，AB为圆O的直径，点C为圆O上一点，AD为∠CAB的平分线交圆O于点D，连接OD交BC于点E.（1）求∠BED的度数；（2）如图2，过点A作圆O的切线BC延长线于点F，过点D作DG ∥AF交AB于点G.若AD=2√35,DE=4，求DG的长。

5.(2023.湖北省恩施州23题)如图，△ABC是等腰直角三角形，∠ACB=90°，点O为AB的中点，连接CO交圆O于点E，圆O与AC 相切于点D.（1）求证：BC是圆O的切线；（2）延长CO交圆O于点G，连接AC交圆O于点F，若AC=4√(2)，求FG的长.6.（2023.贵州省23题）如图，已知圆O是等边三角形ABC的外接圆，连接CO并延长交AB于点D，交圆O于点E，连接EA，EB.（1）写出图中一个度数为30°的角；____，图中与△ACD全等的三角形是______；（2）求证：△AED∽△CEB;（3）连接OA，OB，判断四边形OAEB的形状，并说明理由。

7.(2023.江苏省24题)如图，在△ABC中，AB=AC，以AB为直径的圆O交边AC于点D，连接BD，过点C作CE∥AB.（1）请用无刻度的直尺和圆规作图：过点B作圆O的切线，交CE 于点F；（不写作法，保留作图痕迹，标明字母）（2）在（1）的条件下，求证：BD=BF.8.(2023.江西省20题)如图，在△ABC中，AB=4,∠C=64°，以AB为直径的圆O与AC相交于点D，E为优弧ABD上一点，且∠ADE=40°.（1）求BE的长；（2）若∠EAD=76°，求证：CB为圆O的切线.9.(2023.沈阳22题)如图，AB是圆O的直径，点C是圆O上的一点（点C不与点A，B重合），连接AC，BC，点D是AB上的一点，AC=AD，BE交CD的延长线于点E，且BE=BC.（1）求证：BE是圆O的切线；（2）若圆O的半径为5，tanE=1，则BE的长为_____.210.(2023.扬州市25题)如图，在△ABC中，∠ACB=90°，点D是AB∠A，点O在BC上，以点O为圆心的圆经过C、上一点，且∠BCD=12D两点.（1）试判断直线AB与圆O的位置关系，并说明理由；，圆O的半径为3，求AC的长.（2）若sinB=3511.(2023.广西壮族自治区23题)如图，PO平分∠APD，PA与圆O相切于点A，延长AO交PD于点C，过点O作OB⊥PD，垂足为B.（1）求证：PB是圆O的切线；（2）若圆O的半径为4，OC=5，求PA的长.12.（2023.广东省22题）如图1，在矩形ABCD中（AB>AD），对角线AC，BD相交于点O，点A关于BD的对称点为A`，连接AA`交BD于点E，连接CA`.（1）求证：AA`⊥CA`；（2）以点O为圆心，OE为半径作圆.①如图2，圆O与CD相切，求证：AA`=√3CA`；②如图3，圆O与CA`相切，AD=1，求圆O的面积.13.(2023.安徽省20题)已知四边形ABCD内接于圆O，对角线BD是圆O的直径.（1）如图1，连接OA，CA，若OA⊥BD，求证：CA平分⊥BCD; （2）如图2，E为圆O内一点，满足AE⊥BC，CE⊥AB，若BD=3√3，AE=3.求弦BC的长.14.(2023.湖北黄冈市20题)如图，⊥ABC 中，以AB 为直径的圆O 交BC 于点D ，DE 是圆O 的切线，且DE⊥AC ，垂足为E ，延长CA 交圆O 于点F.（1）求证：AB=AC ；（2）若AE=3，ED=6，求AF 的长。

中考压轴题圆的切线证明与计算(中考真题)

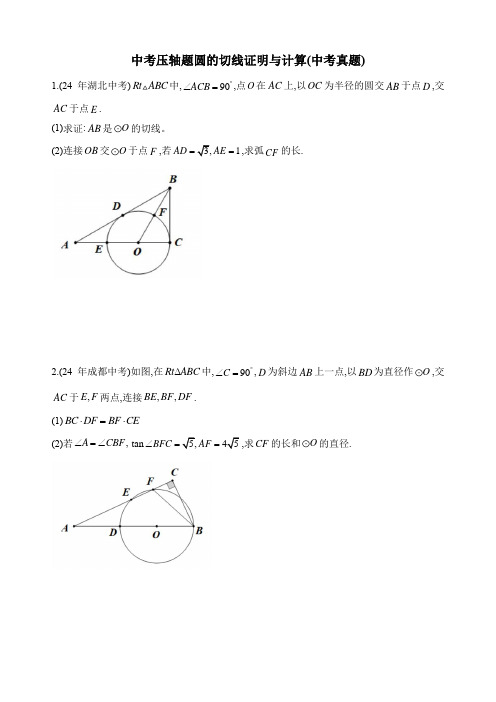
中考压轴题圆的切线证明与计算(中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。

(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF 的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE ⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD中,AD<AC,ADC BAD∠<∠,延长AD至点E,使AE=AC,延长BA至点F,连结EF,使AFE ADC∠=∠.(1)若60O∠的度数.∠=,CD为直径,求ABDAFE(2)求证:①EF∥BC ②EF=BD.4.(24年辽宁中考)如图,O是ABC的外接圆,AB是O的直径,点D在BC上,AC BD=,E ∠=∠．在BA的延长线上,CEA CAD(1)如图1,求证:CE是O的切线OA=,求BD的长．(2)如图2,若2CEA DAB∠=∠,85.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E,AD BD =.(1)求证：△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ，,60D ABC ∠=∠=︒．(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求AC 的长．8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积．9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论．如图,已知ABC ,CA CB =, O 是ABC 的外接圆,点D 在O 上(AD BD >),连接AD ,BD ,CD ．【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系．(用含α的式子表示)10.(24年赤峰中考)如图,ABC中,90ACB∠=︒,AC BC=,O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交O于点D,过点E作EF CD∥,交AC于点F．(1)求证:EF是O的切线;(2)若BM=,1tan2BCD∠=,求OM的长．11.(24年绥化中考)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的O 与AD相切于点E,与AC相交于点F．(1)求证:AB与O相切．(2)若正方形ABCD1,求O的半径．(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN OC⊥交CE于点N．当:1:4CM FM=时,求CN的长．12.(24年河北中考)已知O的半径为3,弦MN=ABC中.∠=︒==在平面上,先将ABC和O按图1位置摆放(点B与点N重90,3,ABC AB BC合,点A在O上,点C在O内),随后移动ABC,使点B在弦MN上移动,点A始终在O上=．随之移动,设BN x(1)当点B与点N重合时,求劣弧AN的长.(2)当OA MN∥时,如图2,求点B到OA的距离,并求此时x的值.(3)设点O到BC的距离为d．①当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.①直接写出d的最小值．13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题: 如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系．(提示:分别作AB 和BC 边上的高．)【得出结论】sin sin sin a b c A B C==．【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C===(R 为ABC 外接圆的半径)．请利用图1证明:2sin sin sin a b c R A B C ===．【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒．求过A,B,D 三点的圆的半径．14.(24年苏州中考)如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠cos ADC ∠=. O 是ACD 的外接圆．(1)求BC 的长(2)求O 的半径．15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为CB 上一点,且AC CE =．(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积．16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点．(1)求证:AB 与半圆O 相切(2)连接OA ．若4CD =,2CF =,求sin OAC ∠的值．17.(24年甘肃武威中考)如图,AB 是O 的直径,BC BD =,点E 在AD 的延长线上,且ADC AEB ∠=∠．(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值．18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E ．(1)求证:DE BE ⊥(2)若AB =5BE =,求O 的半径．19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、．(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径．20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =．点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF ．(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径． 21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠．(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长．22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠．(1)求证:AD 是O 的切线．(2)若4,BE AD ==求O 的半径长．23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F ．(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长．24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明:点D 为BC 上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系,并说明理由;①若ABC 为锐角三角形,求DF 的取值范围．25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD ．(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长．26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD ．(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径．27.(24年四川达州中考)如图,BD 是O 的直径．四边形ABCD 内接于O ．连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F ．(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E ．若3CD DE =,求cos ABC ∠的值．28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G ．(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM ．①求证:AM 是O 的切线;①若6DG =,5DF =,求O 的半径．29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠．(1)如图1,若1BE =,CE =求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥．(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F ．(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N ．求证:MN 是O 的切线．31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===．以点A 为圆心,以AD 为半径作DE 交AB 于点E ,以点B 为圆心,以BE 为半径作EF 所交BC 于点F ,连接FD 交EF 于另一点G ,连接CG ．(1)求证：CG 为EF 所在圆的切线(2)求图中阴影部分面积．(结果保留π)32.(24年青海中考) 如图,直线AB经过点C,且OA OB=．=,CA CB(1)求证:直线AB是O的切线;(2)若圆的半径为4,30∠=︒,求阴影部分的面积．B中考压轴题圆的切线证明与计算答案1.(24年湖北中考)【答案】(1)略 (2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解 (2)2π5.(24年安徽中考)【答案】(1)略 (2).6.(24年新疆中考)【答案】(1) 略 (2)CE =.7.(24年江西中考)【答案】(1)见解析 (2)2π8.(24年呼伦贝尔中考)【答案】(1)略 (2)43π 9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在BC 上时,2sin 2CD AD BD α⋅=-.当D 在AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略 (2)OM =11.(24年绥化中考)【答案】(1)证明略 (2)12.(24年河北中考)【答案】(1)π (2)点B 到OA 的距离为2;3 (3)①3d =2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:AB =;推广证明:见解析;拓展应用:6R =．14.(24年苏州中考)【答案】(1)4BC = (2)O 的半径为715.(24年乐山中考)【答案】(1)略 (2)3π-16.(24年武汉中考)【答案】(1)略 (2)4517.(24年甘肃武威中考)【答案】(1)略 (2)tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略 (2)19.(24年盐城中考)【答案】(1)略 (2)25620.(24年广西中考)【答案】(1)略 (2)略 (3)1021.(24年四川广安中考)【答案】(1)略 (2)1422.(24年四川南充中考)【答案】(1)略 (2)23.(24年四川泸州中考)【答案】(1)证明略 (2)45 24.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;①DF 的取值范围为2DF <<25.(24年四川宜宾中考)【答案】(1)略 (2)CD =DE =． 26.(24年内蒙古通辽中考)【答案】(1)证明略 (2)327.(24年四川达州中考)【答案】(1)证明略 28.(24年四川遂宁中考)【答案】(1)证明略 (2)①证明略,①O 的半径为203． 29.(24年包头中考)【答案】(1)3 (2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1 (2)略31.(24年山东枣庄中考)【答案】(1)略 3π32.(24年青海中考) 【答案】(1)详见解析 (2) 83S π=阴影。

圆的有关计算与证明问题(真题10道+模拟30道)中考数学重难题型押题培优导练案【解析版】

专题15圆的有关计算与证明问题（北京真题10道+模拟30道）【方法归纳】题型概述，方法小结，有的放矢考点考查年份考查频率圆的有关计算与证明问题（大题） 2013.2014.2015.2016.2017十年10考2018.2019.2020.2021.2022圆的证明与计算是中考取的一类重要的问题，在北京市的2013-2022年10年中考中出现了10次，常见的圆的基础知识和解题技巧如下：1、圆中的重要定理:(1)圆的定义: 主要用来证明四点共圆和点到或直线圆的最值距离问题.(2)垂径定理: 主要用来证明——弧相等、线段相等、垂直关系等等.(3)三者之间的关系定理: 主要用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推论 : 主要用来证明——直角、角相等、弧相等.(5)切线的性质定理: 主要用来证明垂直关系 .(6)切线的判断定理: 主要用来证明直线是圆的切线 .(7)切线长定理:线段相等、垂直关系、角相等 .2.圆中几个要点元素之间的相互转变 : 弧、弦、圆心角、圆周角等都能够经过相等来相互转变 . 这在圆中的证明和计算中常常用到 .3.判断切线的方法：（ 1）若切点明确，则“连半径，证垂直”。

常有手法有：全等转变；平行转变；直径转变；中线转变等；有时可经过计算联合相像、勾股定理证垂直；（ 2）若切点不明确，则“作垂直，证半径”。

常有手法：角均分线定理；等腰三角形三线合一，隐蔽角均分线；4、考题形式剖析：主要以解答题的形式出现, 第 1 问主要判断切线、证明角或线段相等；第2 问主要与圆有关的计算：①求线段长（或面积）；②求线段比；③求角度的三角函数值（本质仍是求线段比）【典例剖析】典例精讲，方法提炼，精准提分【例1】（2021·北京·中考真题）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E．（1）求证：∠BAD=∠CAD；（2）连接BO并延长，交AC于点F，交⊙O于点G，连接GC．若⊙O的半径为5，OE=3，求GC和OF的长．【答案】（1）见详解；（2）GC=6，OF=2511【解析】【分析】（1）由题意易得BD⌢=CD⌢，然后问题可求证；（2）由题意可先作图，由（1）可得点E为BC的中点，则有OE=12CG,OE//CG，进而可得△AOF∽△CGF，然后根据相似三角形的性质可进行求解．【详解】（1）证明：∵AD是⊙O的直径，AD⊥BC，∵BD⌢=CD⌢，∵∠BAD=∠CAD；（2）解：由题意可得如图所示：由（1）可得点E为BC的中点，∵点O是BG的中点，∵OE=12CG,OE//CG，∵△AOF∽△CGF，∵OA CG =OFGF，∵OE=3，∵CG=6，∵⊙O的半径为5，∵OA=OG=5，∵5 6=OFGF，∵OF=511OG=2511．【点睛】本题主要考查垂径定理、三角形中位线及相似三角形的性质与判定，熟练掌握垂径定理、三角形中位线及相似三角形的性质与判定是解题的关键．【例2】（2022·北京·中考真题）如图，AB是⊙O的直径，CD是⊙O的一条弦，AB⊥CD,连接AC,OD.(1)求证：∠BOD=2∠A;(2)连接DB,过点C作CE⊥DB,交DB的延长线于点E，延长DO,交AC于点F，若F为AC的中点，求证：直线CE为⊙O的切线．【答案】(1)答案见解析(2)答案见解析【解析】【分析】（1）设AB交CD于点H，连接OC，证明RtΔCOH≅RtΔDOH，故可得∠COH=∠DOH，于是BC⌢=BD⌢，即可得到∠BOD=2∠A；（2）连接，解出∠COB=60°，根据AB为直径得到∠ADB=90°，进而得到∠ABD=60°，即可证明OC//DB，故可证明直线CE为⊙O的切线．(1)证明：设AB交CD于点H，连接OC，由题可知，∴OC=OD，∠OHC=∠OHD=90°，∵OH=OH，∴RtΔCOH≅RtΔDOH(HL)，∴∠COH=∠DOH，∴BC⌢=BD⌢，∴∠COB=∠BOD，∵∠COB=2∠A，∴∠BOD=2∠A；(2)证明：连接AD，∵OA=OD，∴∠OAD=∠ODA，同理可得：∠OAC=∠OCA,∠OCD=∠ODC，∵点H是CD的中点，点F是AC的中点，∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC，∵∠OAD+∠ODA+∠OAC+∠OCA+∠OCD+∠ODC=180°，∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC=30°，∴∠COB=2∠CAO=2×30°=60°，∵AB为⊙O的直径，∴∠ADB=90°，∴∠ABD=90−∠DAO=90°−30°=60°，∴∠ABD=∠COB=60°，∴OC//DE，∵CE⊥BE，∴CE⊥OC，∴直线CE为⊙O的切线．【点睛】本题主要考查三角形全等的判定与性质，同弧所对的圆周角相等，圆周角定理，直线平行的判定与性质，三角形的内角和公式，证明三角形全等以及证明平行线是解题的关键．【真题再现】必刷真题，关注素养，把握核心1．（2013·北京·中考真题）如图，AB是∵O的直径，PA，PC分别与∵O 相切于点A，C，PC交AB的延长线于点D，DE∵PO交PO的延长线于点E．（1）求证：∵EPD=∵EDO（2）若PC=6，tan∵PDA=，求OE的长．【答案】（1）见解析（2）√5【解析】【详解】试题分析：（1）根据切线长定理和切线的性质即可证明：∵EPD=∵EDO；（2）连接OC，利用tan∵PDA=34，可求出CD=4，再证明∵OED∵∵DEP，根据相似三角形的性质和勾股定理即可求出OE的长．试题解析：（1）证明：PA，PC与∵O分别相切于点A，C，∵∵APO=∵EPD且PA∵AO，∵∵PAO=90°，∵∵AOP=∵EOD，∵PAO=∵E=90°，∵∵APO=∵EDO，∵∵EPD=∵EDO；（2）解：连接OC，∵PA=PC=6，∵tan∵PDA=34，∵在Rt∵PAD中，AD=8，PD=10，∵CD=4，∵tan∵PDA=34，∵在Rt∵OCD中，OC=OA=3，OD=5，∵∵EPD=∵ODE，∵∵OED∵∵DEP，∵PD DO =PEDE=EDOE=2，∵DE=2OE在Rt∵OED中，OE2+DE2=OD2，即5OE2=52，∵OE=√5．考点：1．切线的性质；2．相似三角形的判定与性质．⌢的中点，⊙O的切线BD交AC的延长线于点D，E是2．（2014·北京·中考真题）如图，AB是⊙O的直径，C是ABOB的中点，CE的延长线交切线BD于点F，AF交⊙O于点H，连接BH.（1）求证：AC=CD；（2）若OB=2，求BH的长.【答案】(1)证明见解析(2)BH=4√55【解析】【分析】⌢的中点，可知OC∵AB，又BD是切(1)连接OC，若要证明C为AD的中点，只需证OC//BD，已知C是AB线，可知BD∵AB，问题得证(2)由（1）及E为OB中点可知∵COE∵∵FBE，从而可知BF=CO=BO=2，由勾股定理可得AF的长，由面积法即可求出BH的长【详解】（1）连接OC⌢的中点，AB是∵O的直径∵C是AB∵OC∵AB∵BD是∵O的切线∵BD∵AB∵OC//BD∵AO=BO∵AC=CD（2）∵E是OB的中点∵OE=BE在∵COE和∵FBE中{∠CEO=∠FEB OE=BE ∠COE=∠FBE∵∵COE∵∵FBE（ASA)∵BF=CO∵OB=2∵BF=2∵AF=√AB2+BF2=2√5∵AB是直径∵BH∵AFBH=AB⋅BFAF=2√5=4√55考点：1、平行线分线段成比例定理；2、切线的性质；3勾股定理；4、全等三角形3．（2015·北京·中考真题）如图，AB是∵O的直径，过点B作∵O的切线BM，弦CD//BM，交AB于点F，且DA⌢=DC⌢，连接AC，AD，延长AD交BM于点E．（l）求证：∵ACD是等边三角形；（2）连接OE，若DE＝2，求OE的长．【答案】（1）见解析；（2）2√7【解析】【分析】（1）根据切线的定义可知AB∵BM，又∵BM//CD，∵AB∵CD，根据圆的对称性可得AD=AC，再根据等弧对等弦得DA=DC，即DA=DC=AC，所以可得∵ACD是等边三角形；（2）∵ACD为等边三角形，AB∵CD，由三线合一可得∵DAB=30°，连接BD，根据直径所对的角是直角和三角形的内角和可得∵∵EBD＝∵DAB＝30°，因为DE＝2，求出BE＝4，根据勾股定理得BD=2√3，直角三角形中30°角所对的直角边等于斜边的一半得，AB=4√3，OB=2√3，在Rt∵OBE中，根据勾股定理即可得出OE的长．【详解】解：（1）∵BM是∵O切线，AB为∵O直径，∵AB∵BM，∵BM//CD，∵AB∵CD，∵AD＝AC，∵AD＝AC，∵DA＝DC，∵DC＝AD，∵AD＝CD＝AC，∵∵ACD为等边三角形.（2）∵ACD为等边三角形，AB∵CD，∵∵DAB＝30°，连结BD，∵BD∵AD.∵EBD＝∵DAB＝30°，∵DE＝2，∵BE＝4，BD=2√3，AB=4√3，OB=2√3，在Rt∵OBE中，OE=√OB2+BE2=√12+16=2√7．【点睛】本题考查圆的有关性质，直角三角形的性质；勾股定理．4．（2016·北京·中考真题）如图，AB为∵O的直径，F为弦AC的中点，连接OF并延长交AC⌢于点D，过点D作∵O的切线，交BA的延长线于点E．（1）求证：AC∵DE；（2）连接CD，若OA=AE=a，写出求四边形ACDE面积的思路．【答案】（1）证明见解析；（2）32a2.【解析】【详解】试题分析：（1）欲证明AC∵DE，只要证明AC∵OD，ED∵OD即可．（2）作DM∵OA于M，连接CD，CO，AD，首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可．试题解析：（1）∵ED与∵O相切于D，∵OD∵DE，∵F为弦AC中点，∵OD∵AC，∵AC∵DE．（2）作DM∵OA于M，连接CD，CO，AD．首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可．∵AC∵DE，AE=AO，∵OF=DF，∵AF∵DO，∵AD=AO，∵AD=AO=OD，∵∵ADO是等边三角形，同理∵CDO 也是等边三角形，∵∵CDO=∵DOA=60°，AE=CD=AD=AO=DD=a，∵AO∵CD，又AE=CD，∵四边形ACDE是平行四边形，易知DM=√32a，∵平行四边形ACDE面积=√32a2．考点：切线的性质．5．（2017·北京·中考真题）如图，AB是∵O的一条弦，E是AB的中点，过点E作EC∵OA于点C，过点B 作∵O的切线交CE的延长线于点D．（1）求证：DB=DE;（2）若AB=12，BD=5，求∵O的半径.【答案】（1）证明见解析；（2）152【解析】【详解】试题分析:(1)由切线性质及等量代换推出∵4=∵5，再利用等角对等边可得出结论；（2）由已知条件得出sin∵DEF和sin∵AOE的值，利用对应角的三角函数值相等推出结论.试题解析：（1）∵DC∵OA，∵∵1+∵3=90°，∵BD为切线，∵OB∵BD，∵∵2+∵5=90°，∵OA=OB，∵∵1=∵2，∵∵3=∵4，∵∵4=∵5，在∵DEB中，∵4=∵5，∵DE=DB.(2)作DF∵AB于F，连接OE，∵DB=DE，∵EF=12BE=3，在RT∵DEF中，EF=3，DE=BD=5，EF=3 ，∵DF=√52−32=4∵sin∵DEF=DFDE = 45，∵∵AOE=∵DEF，∵在RT∵AOE中，sin∵AOE=AEAO =45，∵AE=6，∵AO=152.【点睛】本题考查了圆的性质，切线定理，三角形相似，三角函数等知识，结合图形正确地选择相应的知识点与方法进行解题是关键.6．（2018·北京·中考真题）如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．【答案】（1）证明见解析；（2）4√33.【解析】【分析】（1）根据切线的性质定理得到PC=PD，OP平分∠CPD．根据等腰三角形的性质即可得到PQ⊥CD于Q，即OP⊥CD．（2）连接OC、OD．根据等腰三角形的性质和平角的性质得到∠COD=180°−∠AOD−∠BOC=60°．进而得到∠DOQ=12∠COD=30°．在Rt△ODP中，解直角三角形即可.【详解】（1）证明：∵PC、PD与⊙O相切于C、D．∵PC=PD，OP平分∠CPD．在等腰△PCD中，PC=PD，PQ平分∠CPD．∵PQ⊥CD于Q，即OP⊥CD．（2）解：连接OC、OD．∵OA=OD∵∠OAD=∠ODA=50°∵∠AOD=180°−∠OAD−∠ODA=80°同理：∠BOC=40°∵∠COD=180°−∠AOD−∠BOC=60°．在等腰△COD中，OC=OD．OQ⊥CD∵∠DOQ=12∠COD=30°．∵PD与⊙O相切于D．∵OD⊥DP．∵∠ODP=90°．在Rt△ODP中，∠ODP=90°，∠POD=30°∵OP=ODcos∠POD=OAcos30°=√32=43√3．【点睛】本题考查了切线的性质和判定，圆周角定理，解直角三角形等，题目比较典型，综合性比较强，难度适中．7．（2019·北京·中考真题）在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C 的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G，∠ABC的平分线交图形G于点D，连接AD，CD．（1）求证：AD=CD；（2）过点D作DE⊥BA，垂足为E，作DF⊥BC，垂足为F，延长DF交图形G于点M，连接CM．若AD=CM，求直线DE与图形G的公共点个数．【答案】依题意画出图形G为∵O，如图所示,见解析；（1）证明见解析；（2）直线DE与图形G的公共点个数为1个.【解析】【分析】（1）根据线段垂直平分线的性质得出图形G为∵O，再根据在同圆或等圆中相等的圆周角所对的弧相等得⌢=CD⌢；从而得出弦相等即可．出AD（2）先根据HL得出△CDF∵∵CMF，得出DF=MF，从而得出BC为弦DM的垂直平分线，根据圆心角和圆周角之间的关系定理得出∵ABC=∵COD，再证得DE为∵O的切线即可【详解】如图所示，依题意画出图形G为∵O，如图所示（1）证明：∵BD平分∵ABC，∵∵ABD=∵CBD，⌢=CD⌢，∵AD=CD∵AD（2）解：∵AD=CD，AD=CM，∵CD=CM.∵DF∵BC，∵∵DFC=∵CFM=90°在Rt△CDF和Rt△CMF中{CD=CMCF=CF，∵Rt△CDF∵Rt△CMF（HL），∵DF=MF，∵BC为弦DM的垂直平分线∵BC为∵O的直径，连接OD∵∵COD=2∵CBD，∵ABC=2∵CBD，∵∵ABC=∵COD，∵OD∵BE.又∵DE∵BA，∵∵DEB=90°，∵∵ODE=90°，即OD∵DE，∵DE为∵O的切线.∵直线DE与图形G的公共点个数为1个.【点睛】本题考查了垂直平分线的性质，圆心角和圆周角之间的关系定理，切线的判定，熟练掌握相关的知识是解题的关键．8．（2020·北京·中考真题）如图，AB为∵O的直径，C为BA延长线上一点，CD是∵O的切线，D为切点，OF∵AD于点E，交CD于点F．（1）求证：∵ADC=∵AOF；（2）若sinC=13，BD=8，求EF的长．【答案】（1）见解析；（2）2．【解析】【分析】（1）连接OD，根据CD是∵O的切线，可推出∵ADC+∵ODA=90°，根据OF∵AD，∵AOF+∵DAO=90°，根据OD=OA，可得∵ODA=∵DAO，即可证明；（2）设半径为r，根据在Rt∵OCD中，sinC=13，可得OD=r，OC=3r，AC=2r，由AB为∵O的直径，得出∵ADB=90°，再根据推出OF∵AD，OF∵BD，然后由平行线分线段成比例定理可得OEBD =OAAB=12，求出OE，OFBD =OCBC=34，求出OF，即可求出EF．【详解】（1）证明：连接OD，∵CD是∵O的切线，∵OD∵CD，∵∵ADC+∵ODA=90°，∵OF∵AD，∵∵AOF+∵DAO=90°，∵OD=OA，∵∵ODA=∵DAO，∵∵ADC=∵AOF；（2）设半径为r，在Rt∵OCD中，sinC=13，∵OD OC =13，∵OD=r，OC=3r，∵OA=r，∵AC=OC-OA=2r，∵AB为∵O的直径，∵∵ADB=90°，又∵OF∵AD，∵OF∵BD，∵OE BD =OAAB=12，∵OE=4，∵OF BD =OCBC=34，∵OF=6，∵EF=OF−OE=2．【点睛】本题考查了平行线分线段成比例定理，锐角三角函数，切线的性质，直径所对的圆周角是90°，灵活运用知识点是解题关键．【模拟精练】押题必刷，巅峰冲刺，提分培优一、解答题1．（2022·北京市广渠门中学模拟预测）如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，E为BC⌢上一点，过点E作⊙O的切线，分别交DC,AB的延长线于点F，G连接AE，交CD于点P．(1)求证：EF=FP；(2)连接AD，若AD∥FG,CD=8,cosF=45，求⊙O半径．【答案】(1)见解析(2)256【解析】【分析】（1）连接OE，要使EF=FP，需要∵FEP=∵FPE，通过切线和垂直的已知条件，利用等角的余角相等可得∵FEP=∵FPE，结论可得．（2）设圆的半径为r，在Rt∵ODH中，利用勾股定理可以求得半径r．(1)证明：连接OE，∵EF是圆的切线，∵OE∵EF．∵∵OEF=90°．∵∵OEA+∵AEF=90°．∵CD∵AB，∵∵AHC=90°．∵∵OAE+∵APH=90°．∵OA=OE，∵∵OAE=∵OEA．∵∵AEF=∵APH．∵∵APH=∵EPF，∵∵EPF=∵AEF．∵EF=PF．(2)连接OD，设圆的半径为r，∵直径AB∵CD于H，CD=8，∵CH=DH=4．∵AD∵FG，∵∵ADH=∵F．∵cos∵ADH=cos F=45∴AD=CHcos∠ADH=5∴AH=√AD2−DH2=3∵OH=OA-AH=r-3．在Rt∵ODH中，∵OH2+DH2=OD2,∵（r-3）2+42=r2．∴OE=r=25 6【点睛】本题主要考查了圆的切线的性质，勾股定理，垂径定理，圆周角定理和解直角三角形的知识．使用添加圆中常添加的辅助线是解题的关键．2．（2022·北京房山·二模）如图，已知AB是半⊙O的直径，点H在⊙O上，E是HB⌢的中点，连接AE，过点E作EC⊥AH交AH的延长线于点C．过点E作EF⊥AB于点F．(1)求证：CE是⊙O的切线；(2)若FB=2,EFAF =√22，求OF的长．【答案】(1)见解析(2)OF=1【解析】【分析】（1）连接OE，由于E为HB⌢的中点，根据圆周角定理可知∵1=∵2，而AO=EO，则∵3=∵2，于是∵1=∵3，根据平行线的判定知OE∥AC，而AC∵CE，根据平行线的性质知∵OEC=90°，即OE∵CE，根据切线的判定可知CE是∵O的切线；（2）由于AB是直径，故∵AED=90°，而EF∵AB，易知∵2=∵4=∵1，那么tan∵1=tan∵2=tan∵4=EFAF =√22，在Rt∵EFB中，利用正切可求出EF，同理在Rt∵AEF中，可求出AF，得半径OB=3，进而可求出OF．(1)证明：连结OE，∵点E为HB⌢的中点，∵ ∵1=∵2，∵OE=OA，∵∵3=∵2，∵∵3=∵1，∵OE∵AC，∵AC∵CE，∵OE∵CE，∵点E在∵O上，∵CE是∵O的切线．(2)连结EB，∵AB是∵O的直径，∵∵AEB=90°，∵EF∵AB于点F，∵∵AFE=∵EFB=90°，∵∵2+∵AEF=∵4+∵AEF=90°，∵∵2=∵4=∵1，∵EF AF =√22，∵tan∠1=√22，∵tan∵4 =√22，在Rt∵EFB中，∵EFB=90°，FB=2，tan∵4 =√22，∵EF=2√2，设OE=x，则OB= x．∵FB=2，∵OF=x-2，∵在Rt∵OEF中，∵EFO=90°，∵x2=(x-2)2+(2√2)2，∵x=3，∵OF=1．【点睛】本题主要考查了切线的判定，圆周角定理，平行线的性质，等腰三角形的性质，勾股定理，三角函数的定义，作出辅助线，熟练掌握圆的切线判定方法，是解题的关键．3．（2022·北京朝阳·二模）如图，AB为∵O的直径，C为∵O上的一点，OD⊥AB交AC于点E，DE=DC．(1)求证：DC是∵O的切线；(2)若OA=4，OE=2，求cos D．【答案】(1)见解析(2)35【解析】【分析】（1）连接OC．证∵OCD=90°，即可得出结论；（2）先求出OC=4．再同由勾股定理求出DC=3，OD=5，最后由余弦定义cosD=DC求解．OD(1)证明：如图，连接OC．∵OD⊥AB交AC于点E，∵∠AOD=90∘,∵∠A+∠AEO=90∘．∵∠AEO=∠DEC，∵∠A+∠DEC=90∘．∵DE=DC，∵∠DEC=∠DCE,∵OA=OC，∵∠A=∠ACO，∵∵OCD=∠ACO+∠DCE=90∘，∵DC⊥OC，∵DC是∵O的切线，(2)解：∵∠OCD=90∘，∵DC2+OC2=OD2，∵OA=4，∵OC=4．设DC=x，∵OE=2，∵x2+42=(x+2)2．解得x=3，∵DC=3，OD=5．∵在Rt∵OCD中，cosD=DCOD =35．【点睛】本师考查切线的判定，解直角三角形，掌握切线的判定定理是解题的关键．4．（2022·北京东城·二模）如图，在△ABC中，AB>AC，∠BAC=90°，在CB上截取CD=CA，过点D作DE⊥AB 于点E，连接AD，以点A为圆心、AE的长为半径作⊙A．(1)求证：BC是∵A的切线；(2)若AC=5，BD=3，求DE的长．【答案】(1)见解析(2)158【解析】【分析】（1）过点A作AF⊥BC于F，根据同旁内角互补证得DE//AC，可证得∠DAC=∠ADE，利用AAS可证得△ADE≅△ADF，则可证得AF=AE，根据切线的判定即可求证结论．（2）根据角相等即可得△BDE∼△BCA，利用相似三角形的性质即可求解．(1)过点A作AF⊥BC于F，如图所示，∵DE⊥AB，∴∠AED=90°，∵∠BAC=90°，∴∠AED+∠BAC=180°，∴DE//AC，∴∠DAC=∠ADE，∵CD=AC，∴∠DAC=∠ADC，∴∠ADE=∠ADC，在△ADE和△ADF中，{∠AED=∠AFD ∠ADE=∠ADFAD=AD，∴△ADE≅△ADF(AAS)，∴AF=AE，且AE为⊙A的半径，∴AF是⊙A的半径，∴BC是⊙A的切线．(2)∵AC=5，∴CD=AC=5，∴BC=BD+CD=3+5=8，∵∠DEB=∠BAC=90°，∠B=∠B，∴△BDE∼△BCA，∴DEAC =BDBC，∴DE5=38，解得DE=158，∴DE的长为158．【点睛】本题考查了切线判定、三角形全等的判定及性质、相似三角形的判定及性质，熟练掌握全等三角形的判定及性质，切线的判定及相似三角形判定及性质是解题的关键．5．（2022·北京平谷·二模）如图，AB是∵O的直径，过B作∵O的切线，与弦AD的延长线交于点C，AD=DC，E是直径AB上一点，连接DE并延长与直线BC交于点F，连接AF．(1)求证：AD⌢=BD⌢；(2)若tan∠BAF=14，∵O的半径长为6，求EF的长．【答案】(1)证明见解析(2)√13【解析】【分析】（1）连接BD，根据圆周角定理、切线性质以及题中AD=DC可得∠BAD=∠ABD=∠CBD=∠C=45°，从而得出结论；（2）连接OD，由（1）知DO⊥AB，得出ΔDOE∼ΔFBE，得出DOBF =OEBE，在RtΔABF中，tan∠BAF=14，∵O的半径长为6，解得BF=3，从而63=OEBE，设BE=x,OE=2x，则BE+OE=OB=6，解得x=2，即BE=2，在RtΔEBF中，利用勾股定理得结论．(1)证明：连接BD，如图所示：∵AB是∵O的直径，∴∠ABD=90°，即BD⊥AC，∵过B作∵O的切线，∴AB⊥BC，∵AD=DC，∴∠BAD=∠ABD=∠CBD=∠C=45°，∴BD=AD，∴AD⌢=BD⌢；(2)解：连接OD，如图所示：在等腰RtΔABD中，∠ADB=90°，∴DO⊥AB，∵∠DEO=∠BEF,∠DOE=∠FBE=90°，∴ΔDOE∼ΔFBE，∴DOBF =OEBE，在RtΔABF中，tan∠BAF=14，∵O的半径长为6，则tan∠BAF=14=BFAB=BF12，解得BF=3，∴63=OEBE，设BE=x,OE=2x，则BE+OE=x+2x=OB=6，解得x=2，在RtΔEBF中，∠EBF=90°，BE=2,BF=3，则利用勾股定理得EF=√BE2+BF2=√22+32=√13．【点睛】本题考查圆综合，涉及到圆周角定理、直角三角形的性质、切线的性质、相似三角形的判定与性质、正切函数求线段长、勾股定理等知识点，根据题意准确作出辅助线是解决问题的关键．6．（2022·北京北京·二模）如图，AB为⊙O的直径，BD⌢=CD⌢，过点A作⊙O的切线，交DO的延长线于点E．(1)求证：AC∥DE；(2)若AC=2，t an E=1，求OE的长．2【答案】(1)见解析(2)5【解析】【分析】（1）根据同圆中，等弧相等性质可得∠BAD=∠CAD，再利用等边对等角及等量代换即可证得∠CAD=∠D从而证得结论．（2）连接BC，利用直径所对的圆周角是直角结合（1）中平行线的性质可求得∠B=∠E，从而得到tanB=tanE，根据直角三角形的锐角三角函数的值结合勾股定理即可求得答案．(1)⌢=CD⌢，证明：∵BD∵∠BAD=∠CAD，∵OA=OD，∵∠D=∠BAD，∵∠CAD=∠D，∵AC∥DE．(2)如图，连接BC，∵AB为⊙O的直径，∵∠C=90°，∵AC∥DE，∵∠BAC=∠AOE，∵AE是⊙O的切线，∵OA⊥AE，∵∠C=∠OAE=90°，∵∠B=∠E，∵tanB=tanE=12，在Rt△OAE中，tanB=12，AC=2，∵tanB=ACBC =2BC=12，解得BC=4，∴AB=√AC2+BC2=√22+C2=2√5，∵OA=√5，∵在Rt△OAE中，tanE=12，∵tanE=AOAE =√5AE=12，解得AE=2√5，∵OE=√OA2+AE2=√(√5)2+(2√5)2=5．【点睛】本题考查了平行线的判定及性质、切线的性质、圆周角定理、锐角三角函数值及勾股定理解直角三角形的应用，熟练掌握圆周角定理及平行线的判定及锐角三角函数值及勾股定理解直角三角形的应用是解题的关键．7．（2022·北京丰台·二模）如图，AB是∵O的直径，C为BA延长线上一点，过点C作∵O的切线，切点为D，过点B作BE∵CD于点E，连接AD，BD．(1)求证：∠ABD=∠DBE；(2)如果CA＝AB，BD＝4，求BE的长．【答案】(1)证明见解析；(2)43√6．【解析】【分析】（1）如图1，连接OD，由CD切∵O于点A得OD⊥CD，从而得OD∥BE，进而得∠ODB=∠DBE，另外由∠ODB=∠ABD即可得出结论；（2）解：设OA=x，则CA=AB=2x，CO=CA+OA=3x，先证明△COD∽△CBE，得ODBE =COCB=3x4x从而有x=34BE，另外由△ABD∽△DBE得ABBD =DBBE，即可求得BE=43√6．(1)证明：如图，连接OD，∵CD切∵O于点A，∴OD⊥CD，∵BE∵CD，∴OD∥BE，∴∠ODB=∠DBE，∵OD=OB，∴∠ODB=∠ABD，∴∠ABD=∠DBE；(2)解：如图，设OA=x，则CA=AB=2x，CO=CA+OA=3x，∵OD∥BE，∴∠CDO=∠E,∠COD=∠CBE，∴△COD∽△CBE，∴ODBE =COCB=3x4x即xBE=34，∴x=34BE，∵AB是∵O的直径，∴∠ADB=90°，∵BE∵CD，∴∠E=∠ADB=90°，∵∠ABD=∠DBE，∴△ABD∽△DBE，∴ABBD =DBBE，∵BD＝4，∴2×34BE4=4BE，解得BE=43√6．【点睛】本题主要考查了圆的切线、勾股定理、相似三角形的判定及性质以及平行线的判定及性质，熟练掌握相似三角形的判定及性质是解题的关键．8．（2022·北京密云·二模）如图，在△ABC中，AB=BC，以BC为直径的∵O与AC交于点D，DE是∵O的切线．(1)计算∠AED的度数；(2)若tanA=12，BC=2√5，求线段DE的长．【答案】(1)90°(2)4√55【解析】【分析】（1）连接OD，BD，由直径所对圆周角等于90度得∵BDO+∵ODC=∵BDC=90°，再由切线的性质得∵BDE+∵BDO=∵ODE=90°，所以∵BDE=∵ODC，∵ADE=∵BDO，然后由OB-OC，则∵C=∵ODC，BA=BC，则∵C=∵A，所以∵A+∵ADE=90°，最后由三角形内角和定理即可求解；（2）由（1）知：∵AED=∵ADB=90°，则tan∵A=DEAE =BDAD=12，所以AD=2BD，AE=2DE，又因为AB=BC=2√5，在Rt△ADB中，由勾股定理，可求出BD=2，AD=4，再在Rt△ADE中，由勾股定理可求出DE长．(1)解：如图，连接OD，BD，∵BC是∵O的直径，∵∵BDO+∵ODC=∵BDC=90°，∵∵BDE+∵ADE=∵BDA=90°，∵DE是∵O的切线，∵∵BDE+∵BDO=∵ODE=90°，∵∵BDE=∵ODC，∵ADE=∵BDO，∵OD=OC，∵∵C=∵ODC，∵∵C+∵ADE=∵C+∵BDO=90°，∵BA=BC，∵∵C=∵A，∵∵A+∵ADE=90°，∵∵AED=180°-（∵A+∵ADE）=90°；(2)解：由（1）知：∵AED=∵ADB=90°，∵tan∵A=DEAE =BDAD=12，∵AD=2BD，AE=2DE，∵AB=BC=2√5，∵在Rt△ADB中，由勾股定理，得AD2+BD2=AB2，∵（2BD）2+BD2=（2√5）2，∵BD=2，∵AD=4，在Rt△ADE中，由勾股定理，得AE2+DE2=AD2，（2DE）2+DE2=42，∵DE=4√5．5【点睛】本题考查切线的性质，圆周角定理的推论，勾股定理，正切的定义，熟练掌握切线的性质、圆周角定理的推论、正切的定义是解题的关键．9．（2022·北京大兴·二模）如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA 为半径的⊙O经过点D．(1)求证：BC是⊙O切线；(2)若BD=5,DC=3，求AC的长．【答案】(1)见解析(2)6【解析】【分析】（1）要证BC是∵O的切线，只要连接OD，再证OD∵BC即可．（2）过点D作DE∵AB，根据角平分线的性质可知CD=DE=3，由勾股定理得到BE的长，再通过证明△BDE∵∵BAC，根据相似三角形的性质得出AC的长．(1)连接OD；∵AD是∵BAC的平分线，∵∵1=∵3．∵OA=OD，∵∵1=∵2．∵∵2=∵3．∵OD∵AC．∵∵ODB=∵ACB=90°．∵OD∵BC．∵OD是∵O的半径，∵BC是∵O切线．(2)过点D作DE∵AB，∵AD是∵BAC的平分线，∵CD=DE=3．在Rt△BDE中，∵BED=90°，由勾股定理得：BE=√BD2−DE2=√52−32=4,∵∵BED=∵ACB=90°，∵B=∵B，∵∵BDE∵∵BAC．∵BE BC =DEAC．∵4 8=3AC．∵AC=6．【点睛】^$本题综合性较强，既考查了切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．同时考查了角平分线的性质，勾股定理得到BE的长，及相似三角形的性质．10．（2022·北京西城·二模）如图，AB是⊙O的直径，CB，CD分别与⊙O相切于点B，D，连接OC，点E 在AB的延长线上，延长AD，EC交于点F．(1)求证：FA∥CO；(2)若FA=FE，CD=4，BE=2，求F A的长．【答案】(1)见解析(2)3√5【解析】【分析】（1）连接OD，证明△CDO∵△CBO（SSS），得∵COD=∵COB，即∵BOD=2∵COB，又因为OD=OA，得∵OAD=∵ODA，所以∵BOD=∵OAD+∵ODA=2∵OAD，即可证得∵COB=∵OAD，即可由平行线的判定定理，得出结论；（2）由F A=FE，得∵F AE=∵FEA，又由（1）知：∵COB=∵OAD，所以∵COE=∵CEO，则CO=CE，又由切线的性质得OB∵CB，根据等腰三角形“三线合一”性质得OB=BE=2，从而求出AE=6，OE=4，再由切线性质得CB=CD=4，然后在Rt△CBE中，由勾股定理，得CF=√CB2+BE2=√42+22=2√5，最后证△EOC∵△EAF，得OEAE =CEFE，即46=2√5FE，可求得FE=3√5，即可由F A=FE得出答案．(1)证明：如图，连接OD，∵CB，CD分别与⊙O相切于点B，D，∵CD=CB，∵OD=OB，OC=OC，∵∵CDO∵△CBO（SSS），∵∵COD=∵COB，即∵BOD=2∵COB，∵OD=OA，∵∵OAD=∵ODA，∵∵BOD=∵OAD+∵ODA=2∵OAD，∵2∵COB=2∵OAD，即∵COB=∵OAD，∵F A∥OC；(2)解：∵F A=FE，∵∵F AE=∵FEA，由（1）知：∵COB=∵OAD，∵∵COE=∵CEO，∵CO=CE，∵CB是∵O的切线，∵OB∵CB，∵OB=BE=2，∵OA=OB=2，∵AE=6，OE=4，∵CB、CD是∵O的切线，∵CB=CD=4，在Rt△CBE中，由勾股定理，得CE=√CB2+BE2=√42+22=2√5，∵F A∥OC，∵∵EOC∵∵EAF，∵OE AE =CEFE，即46=2√5FE，∵FE=3√5，∵F A=FE=3√5．【点睛】本题考查切线的性质，全等三角形的判定与性质，相似三角形的判定与性质，等腰三角形的判定与性质，熟练掌握相关性质与判定是解题的关键．11．（2022·北京顺义·二模）如图，△ABC内接于⊙O，AB是⊙O的直径，点D在AB的延长线上，且∠BCD=∠A，点E为AC的中点，连接OE并延长与DC的延长线交于点F．(1)求证：CD是⊙O的切线；(2)若CD=4，tanA=12，求CF的长．【答案】(1)见解析(2)6【解析】【分析】（1）根据AB是⊙O的直径，可得∠ACB=90°，由OA=OC得∠A=∠ACO，结合已知条件，根据可得∠BCD+∠OCB=90°，即可得证；（2）证明△DCB∽△DAC，得出CDAD =DBDC=CBAC，根据tanA=12，可得CBAC=12，从而求得DB的长，进而求得OD的长，由点E为AC的中点，根据垂径定理以及∠ACB=90°，证明OF∥BC，根据平行线分线段成比例即可求解．(1)证明：如图，连接OC，∵OA=OC，∴∠A=∠ACO，∵∠BCD=∠A，∴∠BCD=∠ACO∵AB是⊙O的直径，∴∠ACB=90°,∴∠ACO+∠OCB=90°，∴∠BCD+∠OCB=90°，即∠OCD=90°，∵OC是半径，∴CD是⊙O的切线；(2)∵∠BCD=∠A，∠D=∠D，∴△DCB∽△DAC，∴CDAD =DBDC=CBAC，∵tanA=12，可得CBAC=12，∴4AD =DB4=12，∴AD=8,DB=2，∴OB=12AB=12(AD−BD)=3，∵点E为AC的中点，∴OF⊥AC，又∵∠ACB=90°，∴OF∥BC，∴DCCF =BDOB，即4CF=23，∴CF=6．【点睛】本题考查了切线的判定，直径所对的圆周角是直角，垂径定理的推论，相似三角形的性质与判定，正切，平行线分线段成比例，掌握以上知识是解题的关键．12．（2022·北京房山·二模）如图，在△ABC中，∠C=90°,∠ABC的平分线BE交AC于点E，过点E作直线BE 的垂线于交AB于点F，⊙O是△BEF的外接圆．(1)求证：AC是⊙O的切线；(2)过点E作EH⊥AB于点H，若CD=2，求HF的长度．【答案】(1)见详解(2)2【解析】【分析】（1）连接OE，先证明BF是圆的直径，OE是圆的半径，再证明OE∥BC在，则有∵OEA=∵C=90°，结论得证；（2）连接ED，根据角平分线的性质证明EH=EC，再证∵EHF∵∵ECD，则HF可求．(1)连接OE，如图，∵EF∵BE，∵∵BEF=90°，∵∵O是∵BEF的外接圆，∵BF是∵O的直径，OE是∵O的半径，∵∵OEB=∵OBE，∵BE是∵ABC的角平分线，∵∵OBE=∵CBE，∵∵OEB=∵CBE，∵OE∥BC，∵∵OEA=∵C=90°，即OE∵AC，∵OE是半径，∵AC是∵O的切线；(2)连接ED，如图，∵BE平分∵ABC，且EH∵BA，EC∵BC，∵EH=EC，∵四边形BDEF是∵O的内接四边形，∵∵EFH=∵EDC，∵∵EHF=∵C=90°，∵∵EHF∵∵ECD，∵HF=CD=2，即HF的值为2．【点睛】此题考查了圆的切线的判定、圆周角定理、平行线的判定与性质、全等三角形的判定与性质等知识，解题的关键是正确的作出所需辅助线．13．（2022·北京昌平·二模）如图，在△ABC中，∠C=90°，BC，AC与⊙O交于点F，D，BE为⊙O直径，点E在AB上，连接BD，DE，∠ADE=∠DBE．(1)求证：AC是⊙O的切线；(2)若sinA=35，⊙O的半径为3，求BC的长．【答案】(1)过程见详解(2)245【解析】【分析】（1）连接OD，OD=OB=OE，即有∵OBD=∵ODB，∵ODE=∵OED，再根据BE是直径，得到∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE，即有∵DBE+∵ODE=90°，再根据∵ADE=∵DBE，有∵ADE+∵ODE=90°，即有OD∵AC，则结论得证；（2）先证OD∥BC，则有BCOD =ABOA，利用sinA=ODOA=35可求出OA，即可求出BC的值．(1)连接OD，如图，∵OD=OB=OE，∵∵OBD=∵ODB，∵ODE=∵OED，∵BE是直径，∵∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE，∵∵DBE+∵ODE=90°，∵∵ADE=∵DBE，∵∵ADE+∵ODE=90°，∵OD∵AC，∵OD为半径，∵AC是∵O的切线；(2)根据（1）的结论，有OD∵AC，∵∵C=90°，∵BC∵AC，∵OD∥BC，∵BC OD =ABOA，∵在Rt△ADO中，sinA=ODOA =35，又∵OD=OB=3，∵OA=5，∵AB=OA+OB=8，∵BC OD =ABOA，∵BC=ABOA ×OD=85×3=245．即BC为245．【点睛】本题考查了切线的判定与性质、直径作对圆周角为90°、平行的性质、勾股定理、三角函数等知识，证明切线是解答本题的关键．14．（2022·北京海淀·二模）如图，AB为∵O的直径，CD为弦，CD∵AB于点E，连接DO并延长交∵O于点F，连接AF交CD于点G，CG =AG，连接AC．(1)求证：AC∵DF；(2)若AB = 12，求AC和GD的长．【答案】(1)见解析(2)AC =6，DG=4√3【解析】【分析】（1）根据圆周角定理得到∵C=∵F，由GA=GC推出∵CAF=∵C，得到∵CAF=∵F，即可得到结论AC∵DF．∠2，进而证得△AOD是等边三角形，（2）连接AD，利用AC∵DF推出∵C=∵1，根据圆周角定理得到∠C=12AB=6．利用垂径定理求出AC=AD=6，利用三角函数求出AG．得到AD=AO=12(1)证明：∵ C，F都在∵O上，∵ ∵C=∵F．∵ GA=GC，∵ ∵CAF=∵C．∵ ∵CAF=∵F．∵ AC∵DF．(2)解：连接AD．∵ AC∵DF，∵ ∵C=∵1，⌢=AD⌢，∵AD∠2．∵∠C=12∠2．∵∵∠1=12∵ AB∵CD于E，∵ ∵BED=90°．∵∠1+∠2=90°．∵∵由∵，∵得∵1=30°，∵2=60°．∵ OA=OD，∵ ∵AOD是等边三角形．AB=6．∵AD=AO=12∵直径AB∵CD于E，∵AC⌢=AD⌢．∵ AC=AD=6．∵ ∵AOD是等边三角形，∵ ∵ADO=60°，∵1=30°．∵ ∵3=∵AOD-∵1=30°∵ DF是∵O的直径，∵ ∵F AD=90°．=4√3．∵ 在Rt∵GAD中，DG=ADcos∠3【点睛】此题考查了圆周角定理，垂径定理，等边三角形的判定及性质，锐角三角函数，平行线的判定定理，熟记圆周角定理及垂径定理是解题的关键．15．（2022·北京市十一学校模拟预测）如图，AB 是⊙O 的弦，C 为⊙O 上一点，过点C 作AB 的垂线与AB 的延长线交于点D ，连接BO 并延长，与⊙O 交于点E ，连接EC ，CD 是⊙O 的切线．(1)求证：∠ABE =2∠E ；(2)若tanE =13，AB =8，求BD 的长．【答案】(1)证明见解析(2)1【解析】【分析】（1）连接OC ，根据切线的性质易得AD ∥CO ，由平行线的性质得到∠ABE =∠BOC ，再结合等腰三角形的性质得到∠OCE =∠OEC ，由三角形外角性质易得∠BOC =∠OCE +∠OEC =2∠BCE 即可求解；（2）连接BC 和AC ，CO ，根据BE 是⊙O 的直径和切线的性质易得∠BCD =∠E ，由圆周角定理得到∠A =∠E ，结合tanE =13得到BD CD =DC AD =13，进而可得CD =3BD ，将AB =8，AD =AB +BD =8+BD 代入即可求解．（1）证明：连接OC ，如下图．∵CD 是⊙O 的切线，过点C 作AB 的垂线与AB 的延长线交于点D ，∵∠CDA =∠DCO =90°，∵AD ∥CO ，∵∠ABE =∠BOC ．∵OC =OE ，∵∠OCE =∠OEC ，∵∠BOC =∠OCE +∠OEC =2∠BCE，∵∠ABE=2∠E；（2）解：连接BC和AC，CO，如下图．∵BE是⊙O的直径，∵∠BCE=90°，∵∠OCE+∠OCB=90°．∵CD是⊙O的切线，∵∠OCB+∠BCD=90°，∵∠BCD=∠OCE，∵∠BCD=∠E，∵∠A=∠E，tanE=13，∵BDCD=DC AD =13，∵CD=3BD．∵AB=8，AD=AB+BD=8+BD，∵3BD8+BD=13，∵BD=1．【点睛】本题主要考查了圆周角定理、切线的性质，平行线的性质，等腰三角形的性质，三角形外角性质，锐角三角函数值的求法，作出辅助线是解答关键．16．（2022·北京东城·一模）如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交AC于点E，过点B作⊙O的切线交OD的延长线于点F．(1)求证：∠A=∠BOF；(2)若AB=4，DF=1，求AE的长．【答案】(1)见解析(2)AE=83【解析】【分析】(1)首先根据等边对等角可证得∠C=∠ODB，再根据平行线的判定与性质，即可证得结论；(2)首先根据圆周角定理及切线的性质，可证得∠AEB=∠OBF，即可证得△ABE∽△OFB，再根据相似三角形的性质即可求得．(1)证明：∵AB=AC∴∠C=∠ABC∵OB=OD∴∠ODB=∠OBD∴∠C=∠ODB∴AC∥OD∴∠A=∠BOF(2)解：如图：连接BE∵AB是⊙O的直径，AB=4AB=2∴∠AEB=90°，OB=OD=12∵BF是⊙O的切线∴∠OBF=90°。

第26课时与圆有关的计算课件 2025年中考数学一轮总复习

成一个圆锥，则该圆锥底面圆的半径
是；
图2
（3）（2024·湖北改编）如图3，在
Rt△ABC中，∠ACB＝90°，点O在
AC上，以OC为半径的圆交AB于点D，
交AC于点E，且BD＝BC. 连接OB交
☉O于点F. 若AD＝，AE＝1，则☉O的直径EC＝，弧CF的长为 .
有
关概
念
正多边形每一边所对的圆心角叫做
正多边形的
正多边形的中心到正多边形的一边
的距离叫做正多边形的
半径
中心角
边心距
知识点3 与圆有关的阴影部分面积把不规则图形的面积转化为规则图
题型：（1）根据扇形面积（弧长）公式，已知
圆心角、半径、面积（弧长）三个量中
的两个，求第三个量；（2）根据扇形面积公式，已知弧长、
半径、面积三个量中的两个，求第三
个量；
（3）用分段的方法计算由弧长组成的路
径长；（4）用割补法计算与扇形有关的阴影部
分的面积.
考点一正多边形和圆
例1 （1）如图1，正五边形ABCDE内
第一部分考点梳理
第四章图形的性质第26课时与圆有关的计算
知识点1 与圆有关的计算公式
公式
备注
圆周长
C＝2πR
R为圆的半径
圆面积
S＝πR2
弧长
l＝
R为弧所在圆的半
径，n为弧所对的圆心角的度数
扇形面积
S扇＝ πR2S扇＝ lR
R为圆的半径，l为弧长，n为扇形的圆心角度数
知识点2 正多边形和圆
A. π
B. π
C. 2 π
D. π
D
1. （2024·甘孜州）如图，正六边形

二、解答重难题型突破+题型5 圆的综合++++课件+2025年中考数学总复习人教版(山东)

2
P在半圆弧AB上运动(不与A,B两点重合),过点C作直线PB的垂线CD交PB于点D.
(1)如图1,求证:△PCD∽△ABC.
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由.
(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.
28
【解析】(1)∵AB是☉O的直径,
∴∠BCD=30°.
31
本课结束
∴BF=BE=5.
∵∠ABE=∠AMF=90°,∠BAE=∠MAF,
∴△AMF∽△ABE,

∴ = ,即 = = =2.

设MF=x,则AM=2x,
∴BM=10-2x.
5
∵BM2+MF2=BF2,
∴(10-2x)2+x2=52,解得x=3,x=5(不符合题意,舍去),即MF=3.
∴∠PCD=60°.
∵四边形ABDC内接于☉O,
∴∠B=∠PCD=60°.
9
෽
(2)∵点C为的中点,
∴∠CAD=∠CDA,∴AC=CD.
∵∠ADB=90°,
∴∠CDA+∠CDP=90°.
在Rt△ADP中,∠CAD+∠P=90°,
∴∠CDP=∠P,
∴CD=PC=2 ,
∴AC=CD=PC=2 ,
෽ ,对角线AC为☉O
෽
【例2】(2024·济南三模)如图,四边形ABCD内接于☉O,=
的直径,延长BC交过点D的切线于点E.
(1)求证:DE⊥BE;
3
(2)若☉O的半径为5,tan∠DAC= ,求DE的长.
4
12
【自主解答】(1)连接DO并延长交AB于F,

考点20 与圆有关的位置关系及计算(精讲)(解析版)

考点20.与圆有关的位置关系及计算（精讲）【命题趋势】与圆相关的位置关系也是各地中考数学中的必考考点之一，主要内容包括点、直线与圆的位置关系、切线的性质和判定、三角形的内切圆和外接圆三块，在解答题中想必还会考查切线的性质和判定，和直角三角形结合的求线段长的问题和三角函数结合的求角度的问题等知识点综合，考查形式多样，多以动点、动图的形式给出，难度较大。

关键是掌握基础知识、基本方法，力争拿到全分。

【知识清单】1：点、直线与圆的位置关系类（☆☆）1）点和圆的位置关系：已知⊙O的半径为r，点P到圆心O的距离为d，则：图1图2(1)d<r⇔点在⊙O内，如图1；(2)d=r⇔点在⊙O上，如图2；(3)d>r⇔点在⊙O外，如图3．解题技巧：掌握已知点的位置，可以确定该点到圆心的距离与半径的关系，反过来已知点到圆心的距离与半径的关系，可以确定该点与圆的位置关系。

2）直线和圆的位置关系：设⊙O的半径为r，圆心到直线l的距离为d，则直线和圆的位置关系如下：图1图2图3(1)d>r⇔相离，如图1；(2)d=r⇔相切，如图2；(3)d<r⇔相交，如图3。

2：切线的性质与判定（☆☆☆）1）切线的性质：（1）切线与圆只有一个公共点；（2）切线到圆心的距离等于圆的半径；（3）切线垂直于经过切点的半径。

解题技巧：利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题。

2）切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）；（2）到圆心的距离等于半径的直线是圆的切线（数量关系法）；（3）经过半径外端点并且垂直于这条半径的直线是圆的切线（判定定理法）。

切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径。

3）切线长定理定义：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长。

定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

第40讲与圆有关的计算与证明题课件(共74张ppt) 2024年中考数学总复习专题突破.ppt

复习讲义
（2）若 = 5 ， cos ∠ =
4
，求的长.
5
∘
解： ∵ ∠ = 90∘ ， ∴ ∠ + ∠ = 90 .
由（1）知， = 2 = 10 ， ∠ = 90∘ ，
∴ ∠ + ∠ = 90∘ .
图3
∴ ∠ = ∠.
4
.
5
∴ cos = cos ∠ =
复习讲义
（2）若 = 10 ， = 12 ， = 2 ，求 ⊙ 的半径．
思路点拨由（1）知 ⊥ ，因此可在 Rt △
中利用勾股定理列方程求解.
解： ∵ = ， ⊥ ， ∴ = =
1

2
= 6.
图1
∴ = 2 − 2 = 102 − 62 = 8.
∴ = 6 .
目录导航
9
第40讲与圆有关的计算与证明题
复习讲义
2.（2022·鄂尔多斯）如图3，以为直径的
⊙ 与 △ 的边相切于点，且与边
交于点，点为的中点，连接，，
.
（1）求证：是 ⊙ 的切线.
1.（2022·衡阳）如图2，为 ⊙ 的直径，过圆上一
点作 ⊙ 的切线交的延长线于点，过点
作 // 交于点，连接．
（1）直线与 ⊙ 相切吗？请说明理由.
图2
目录导航
7
第40讲与圆有关的计算与证明题
复习讲义
解：直线与 ⊙ 相切.
，的点，连接，，点在的延长线
上，且 ∠ = ∠ ，点在的延长线上，

陕西中考圆的证明与计算(2023版)

陕西中考圆的证明与计算（2023版）知识总结1．切线的性质：垂直于过切点的半径．（连半径，得垂直）2．切线的判定：（1）定义法：和圆只有一个交点的直线是圆的切线；（2）距离法：到圆心距离等于半径的直线是圆的切线；证明d =r 即可，常用于已知数据的计算，比如动圆相切问题．（3）判定定理：经过半径外端且垂直于这条半径的直线是圆的切线．换个说法：⎧⎨⎩有交点：连半径,证垂直无交点：作垂直,证半径，多用于几何证明．多数情况为有交点，重点考虑如何证垂直：①证明和已知垂线平行；②证明夹角为直角．3．常见相切图（1）角分+等腰得平行：点C 在以AB 为直径的圆O 上，AH ⊥CH ，且AC 平分∠HAB ．【证明】连接OC，则OC=OA，∴∠OCA=∠OAC，又∠OAC=∠HAC，∴∠OCA=∠HAC，∴OC∥AH，∴OC⊥CH，∴CH是圆O的切线．（2）证明和已知直角相等．证明△PCO≌△PAO，可得∠PCO=∠PAO=90°．（3）证明夹角为直角．（弦切角定理）如图，若∠BAC=∠D，则AB是圆O切线．如图，连接AO并延长交圆O于点P，则∠P=∠D=∠BAC，∵∠P+∠PAC=90°，∴∠BAC+∠PAC=90°，即AB⊥AP，∴AB是圆O的切线．1．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC 于点E．（1）求证：DE＝AE；（2）若AD＝8，DE＝5，求BC的长度．2．如图，在Rt△ABC中，∠ABC＝90°，以BC为直径的⊙O交AC于点E，⊙O的切线DE交AB于点D．（1）求证：DA＝DB；（2）连接BE，OD，交点为F，若cos A＝，BC＝6，求OF的长．3．如图，AB是⊙O的直径，经过⊙O上一点D，作⊙O的切线EF，交AB的延长线于点F，AE⊥EF，交BD的延长线于点C．（1）求证：AB＝AC．（2）若⊙O的半径为3，，求BF的长．4．如图，AB为⊙O的直径，C、E为⊙O上的两点，过点E的切线交CB的延长线于点D，且CD⊥DE，连接CE，AE．（1）求证：∠ABC＝2∠A；（2）若⊙O半径为，AB：BD＝5：1，求AE的长．5．已知：如图，AB为⊙O的直径，CD与⊙O相切于点C，交AB延长线于点D，∠D＝30°，连接AC、BC，CE平分∠ACB交⊙O于点E，过点B作BF⊥CE，垂足为F．（1）求证：CA＝CD；（2）若AB＝12，求线段BF的长．6．已知：如图，⊙O过正方形ABCD的顶点A，B，且与CD边相切于点E．点F是BC与⊙O的交点，连接OB，OF，AF，点G是AB延长线上一点，连接FG，且∠G+∠BOF＝90°．（1）求证：FG是⊙O的切线；（2）如果正方形边长为8，求⊙O的半径．7．如图，在△AOB中，以点O为圆心的⊙O与AB相切于点D，延长AO交⊙O于点C，连接CD，过点A作AF⊥BO，交BO的延长线于点H，交⊙O于点F，∠B＝∠C．求证：（1）AF∥CD；（2）AH2＝OH⋅BH．8．如图，AB是⊙O的直径，已知点D是弧BC的中点，连接DO并延长，在延长线上有一点E，连接AE，且∠E＝∠B．（1）求证：AE是⊙O的切线；（2）连接AC，若AC＝6，CF＝4，求OE的长．9．如图，AB是⊙O的直径，C在AB的延长线上，⊙O与CD相切于点D，过点A作AE ⊥CD，垂足为E．（1）求证：AD平分∠EAC．（2）若BC＝3，，求⊙O的半径以及线段ED的长．10．如图，AB是⊙O的直径，点D是直径AB上不与A，B重合的一点，过点D作CD⊥AB，且CD＝AB，连接BC交⊙O于点F，在CD上取一点E，使EF＝EC．（1）求证：EF是⊙O的切线；（2）当D是OA的中点时，AB＝4，求BF的长．11．如图，△ABC内接于⊙O，AB＝AC，过点A作BC平行线AM，连接BO并延长，交AM于点D，连接AO、CO．（1）求证：AM是⊙O的切线；（2）若BC＝10，AD＝8，求⊙O的半径．12．如图，已知△ABC的边AB所在的直线是⊙O的切线，切点为B，AC经过圆心O并与圆交于点D、C，E为AB延长线上一点，连接CE交⊙O于点F，且∠BCE＝∠ACB．（1）求证：CE⊥AB；（2）若⊙O的半径是6，AB＝8，求EF的长．13．如图，在△ABC中，∠C＝90°，以FB为直径作⊙O，⊙O与直角边AC相切，切点为E．（1）求证：∠DBE＝∠EBA；（2）若AB＝10，DB＝4，求EB的长．14．如图，已知AB是⊙O的直径，C是⊙O上一点，OD⊥BC，垂足为D，连接AD，过点A作⊙O的切线与DO的延长线相交于点E．（1）求证：∠B＝∠E；（2）若⊙O的半径为4，OE＝6，求AD的长．15．如图，AB是⊙O的直径，点D、E均在⊙O上，连接AD、BD、BE、DE，过点D作⊙O的切线，交AB的延长线于点C．（1）求证：∠DEB＝∠CDB；（2）若BD＝DE＝6，BE＝9.6，求⊙O的半径．16．如图，△ABC是⊙O的内接三角形，BC为⊙O的直径，点E是⊙O上一点，连接OE 并延长交过点C的切线CD于点D，∠B＝∠D．（1）求证：OD∥AC；（2）延长EO交AB于点F，AF＝2，⊙O的直径为2，求OD的长．17．如图，已知△ABC的外接圆直径是AB，点O是圆心，点D在⊙O上，且＝，过点D作⊙O的切线，与CA、CB的延长线分别交于点E、F．（1）求证：AB∥EF；（2）若⊙O的半径为5，BC＝8，求DF的长度．18．如图，AB为⊙O的直径，C为⊙O上一点，AD⊥CE，垂足为D，AC平分∠DAB．（1）判定直线CE与⊙O的位置关系，并说明你的理由；（2）若AD＝3，AC＝4，求圆的半径．19．如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，与AC边的交点为F，过点D作DE⊥AC于点E．（1）求证：直线DE是⊙O的切线；（2）若AB＝5，tan∠ACB＝2，求弦AF的长度．20．如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D．过点D作DE⊥AC，垂足为E，延长CA交⊙O于点F．（1）求证：DE是⊙O的切线；（2）若tan B＝，⊙O的半径为5，求线段CF的长．21．如图，AB为⊙O的直径，OD为⊙O的半径，⊙O的弦CD与AB相交于点F，⊙O的切线CE交AB的延长线于点E，EF＝EC．（1）求证：OD垂直平分AB；（2）若⊙O的半径长为3，且BF＝BE，求OF的长．22．如图，AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，BD⊥CD，DB的延长线与⊙O交于点E．（1）求证：∠ABE＝2∠A；（2）若，BD＝4，求BE的长．23．如图，在△ABC中，AC＝AB，以AB为直径的⊙O交BC于点D，过点D作ED⊥AC 点E，交AB延长线于点F．（1）求证：EF是⊙O的切线；（2）若DF＝4，tan∠BDF＝，求AC的长．24．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD．（1）求证：CF是⊙O的切线；（2）若直径AD＝10，cos B＝，求FD的长．25．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CAD＝∠CDE；（2）若CD＝6，tan∠BAD＝，求⊙O的半径．26．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为⊙O的直径，过点A作AE ⊥CD，与CD的延长线交于点E，且DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若⊙O的半径为5，CD＝6，求AD的长．27．如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是的中点，过点B的切线与AC的延长线交于点D．①求证：BD⊥AD；②若AC＝9，tan∠ABC＝，求⊙O的半径．28．如图，△ABC中，∠C＝90°，点O在AB上，⊙O经过点A，且与BC相切于点D．（1）求证：AD平分∠BAC；（2）若AC＝6，cos∠BAC＝，求⊙O的半径．29．如图，AB是⊙O的直径，点C为⊙O上一点，CD平分∠ACB，交AB于点E，交⊙O 于点D，延长BA到点P，使得PE＝PC．（1）求证：PC与⊙O相切；（2）若⊙O的半径3，PC＝4，求CD的长．30．如图，AB是⊙O的直径，点C、D是⊙O上两点，CE与⊙O相切，交DB延长线于点E，且DE⊥CE，连接AC，DC．（1）求证：∠ABD＝2∠A；（2）若DE＝2CE，AC＝8，求⊙O的半径．31．如图，AB是⊙O的直径，AC是弦，且OD⊥AC于点E，OD交⊙O于点F，连接CF、BF，若∠BFC＝∠ODA．（1）求证：AD是⊙O的切线：（2）若AB＝10，AC＝8，求AD的长．32．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，连接OD，过点D作⊙O的切线DE，交AC于点E，延长CA交⊙O于点F，连接BF．（1）求证：DE⊥AC；（2）若⊙O的直径为5，cos C＝，求CF的长．33．如图，在⊙O中，PA是直径，PC是弦，PH平分∠APB且与⊙O交于点H，过H作HB⊥PC交PC的延长线于点B．（1）求证：HB是⊙O的切线；（2）若HB＝4，BC＝2，求⊙O的半径．34．如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB，且CD＝AB，连接CB，与⊙O交于点F，在CD上取一点E，使得EF＝EC．（1）求证：EF是⊙O的切线；（2）若D是OA的中点，AB＝4，求CF的长．35．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为直径，过点A作⊙O的切线AE，与CD的延长线交于点E，已知DA平分∠BDE．（1）求证：AE⊥DE；（2）若⊙O的半径为5，CD＝6，求AD的长．36．如图，在Rt△ACD中，∠ACD＝90°，点O在CD上，作⊙O，使⊙O与AD相切于点B，⊙O与CD交于点E，过点D作DF∥AC，交AO的延长线于点F，且∠OAB＝∠F．（1）求证：AC是⊙O的切线；（2）若OC＝3，DE＝2，求DF的长．37．如图，在Rt△ABC中，∠ACB＝90°，点D是AB的中点，以CD为直径作⊙O，与BC交于点E，过点E作⊙O的切线EF，交AB于点F．（1）求证：EF⊥AB；（2）若⊙O的半径是，cos∠ACD＝，求DF的长．38．如图，⊙O是△ABC的外接圆，＝，过点A作AD∥BC交⊙O于点D，连接CD，延长DA到点E，连接CE，∠D＝∠E．（1）求证：CE是⊙O的切线；（2）若CE＝8，AE＝5，求⊙O半径的长．39．如图，BD为⊙O的直径，∠ABE＝∠BCA，过点A的直线与⊙O分别交于点E，C，与BD交于点F，连接BE，BC．（1）求证：AB为⊙O的切线．（2）若∠A＝∠ABE，BE＝5，BC＝8，求⊙O的半径．40．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CDE＝∠CAD；（2）若CD＝4，tan B＝，求⊙O的半径．。

专题25 圆的有关计算与证明(共20道)(原卷版)-2023年中考数学真题分项汇编(全国通用)

专题25圆的有关计算与证明（20道）一、填空题1．（2023·江苏徐州·统考中考真题）如图，在O 中，直径AB 与弦CD 交于点 ,2E AC BD=．连接AD ，过点B 的切线与AD 的延长线交于点F ．若68AFB ∠=︒，则DEB ∠=°．2．（2023·湖南常德·统考中考真题）沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图． AB 是以O 为圆心，OA 为半径的圆弧，C 是弦AB 的中点，D 在 AB 上，CD AB ⊥．“会圆术”给出 AB 长l 的近似值s 计算公式：2CD s AB OA =+，当2OA =，90AOB ∠=︒时，l s -=．（结果保留一位小数）二、解答题3．（2023·辽宁盘锦·统考中考真题）如图，ABC 内接于O ，AB 为O 的直径，延长AC 到点G ，使得CG CB =，连接GB ，过点C 作CD GB ∥，交AB 于点F ，交点O 于点D ，过点D 作DE AB ∥．交GB 的延长线于点E ．(1)求证：DE 与O 相切．(2)若4AC =，2BC =，求BE 的长．4．（2023·江苏南通·统考中考真题）如图，等腰三角形OAB 的顶角120AOB ∠=︒，O 和底边AB 相切于点C ，并与两腰OA ，OB 分别相交于D ，E 两点，连接CD ，CE ．(1)求证：四边形ODCE 是菱形；(2)若O 的半径为2，求图中阴影部分的面积．5．（2023·辽宁鞍山·统考中考真题）如图，四边形ABCD 内接于O ，AB 为O 的直径，过点D 作DF BC ⊥，交BC 的延长线于点F ，交BA 的延长线于点E ，连接BD ．若180EAD BDF ∠+∠=︒．(1)求证：EF 为O 的切线．(2)若10BE =，2sin 3BDC ∠=，求O 的半径．6．（2023·辽宁阜新·统考中考真题）如图，AB 是O 的直径，点C ，D 是O 上AB 异侧的两点，DE CB ⊥，交CB 的延长线于点E ，且BD 平分ABE ∠．(1)求证：DE 是O 的切线．(2)若60ABC ∠=︒，4AB =，求图中阴影部分的面积．(1)如图①，求证2BC OH =；(2)如图②，点D 在O 上，连接DB ，DO ，DC ，DC 交OH 于点E ，若(3)如图③，在（2）的条件下，点F 在BD 上，过点F 作FG DO ⊥，交DO 于点G 垂足为R ，连接EF ，EA ，32EF DF =::，点T 在BC 的延长线上，连接AT 的延长线于点M ，若42FR CM AT ==，，求AB 的长．8．（2023·江苏徐州·统考中考真题）两汉文化看徐州，桐桐在徐州博物馆“壁，玉环为我国的传统玉器，通常为正中带圆孔的扇圆型器物，据《尔雅肉好若一，调之环．”如图1，“肉”指边（阴影部分），“好”指孔，其比例关系见图示，以考古发现看，这两种玉器的“肉”与“好”未必符合该比例关系．(1)若图1中两个大圆的直径相等，则璧与环的“肉”的面积之比为；(2)利用圆规与无刻度的直尺，解决下列问题（保留作图痕迹，不写作法）．①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图，试判断该件玉器的比例关系是否符合一”？②图3表示一件圆形玉坯，若将其加工成玉璧，且比例关系符合“肉倍好”，请画出内孔．9．（2023·辽宁·统考中考真题）如图，AB 是O 的直径，点C E ，在O 上，2CAB EAB ∠=∠，点F 在线段AB 的延长线上，且AFE ABC ∠=∠．(1)求证：EF 与O 相切；(2)若41sin 5BF AFE =∠=，，求BC 的长．10．（2023·贵州·统考中考真题）如图，已知O 是等边三角形ABC 的外接圆，连接CO 并延长交AB 于点D ，交O 于点E ，连接EA ，EB ．(1)写出图中一个度数为30︒的角：_______，图中与ACD 全等的三角形是_______；(2)求证：AED CEB ∽△△；(3)连接OA ，OB ，判断四边形OAEB 的形状，并说明理由．11．（2023·湖北鄂州·统考中考真题）如图，AB 为O 的直径，E 为O 上一点，点C 为»EB 的中点，过点C 作CD AE ⊥，交AE 的延长线于点D ，延长DC 交AB 的延长线于点F ．(1)求证：CD 是O 的切线；(2)若1DE =，2DC =，求O 的半径长．12．（2023·吉林长春·统考中考真题）【感知】如图①，点A 、B 、P 均在O 上，90AOB ∠=︒，则锐角APB ∠的大小为__________度．【探究】小明遇到这样一个问题：如图②，O 是等边三角形ABC 的外接圆，点P 在 AC 上（点P 不与点A 、C 重合），连结PA 、PB 、PC ．求证：PB PA PC =+．小明发现，延长PA 至点E ，使AE PC =，连结BE ，通过证明PBC EBA ≌△△，可推得PBE 是等边三角形，进而得证．下面是小明的部分证明过程：证明：延长PA 至点E ，使AE PC =，连结BE ，四边形ABCP 是O 的内接四边形，180BAP BCP ∴∠+∠=︒．180BAP BAE ∠+∠=︒ ，BCP BAE ∴∠=∠．ABC 是等边三角形．BA BC ∴=，(SAS)PBC EBA ∴ ≌请你补全余下的证明过程．【应用】如图③，O 是ABC 的外接圆，90ABC AB BC ∠=︒=，，点P 在O 上，且点P 与点B 在AC 的两侧，连结PA 、PB 、PC ．若22PB PA =，则PB PC的值为__________．13．（2023·甘肃兰州·统考中考真题）如图，ABC 内接于O ，AB 是O 的直径， BCBD =，DE AC ⊥于点E ，DE 交BF 于点F ，交AB 于点G ，2BOD F ∠=∠，连接BD ．(1)求证：BF 是O 的切线；(2)判断DGB 的形状，并说明理由；(3)当2BD =时，求FG 的长．14．（2023·山东东营·统考中考真题）如图，在ABC 中，AB AC =，以AB 为直径的O 交BC 于点D ，(1)求证：DE 是O 的切线；(2)若30C ∠=︒，23CD =，求 BD的长．(1)求证：CF 是O 切线；(2)若10AF =，2sin 3F =，求一点，连接,,AD DC CP ．(1)求证：90ADC BAC ∠-∠=︒；（请用两种证法解答）(2)若ACP ADC ∠=∠，O 的半径为3，4CP =，求AP 的长．17．（2023·湖南·统考中考真题）问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图①）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都按逆时针做匀速圆周运动，每旋转一周用时120秒．问题设置：把筒车抽象为一个半径为r 的O ．如图②，OM 始终垂直于水平面，设筒车半径为2米．当0=t 时，某盛水筒恰好位于水面A 处，此时30AOM ∠=︒，经过95秒后该盛水筒运动到点B 处．（参考数据，2 1.4143 1.732，≈≈）问题解决：(1)求该盛水筒从A 处逆时针旋转到B 处时，BOM ∠的度数；(2)求该盛水筒旋转至B 处时，它到水面的距离．（结果精确到0.1米）18．（2023·湖南常德·统考中考真题）如图，四边形ABCD 是O 的内接四边形，AB 是直径，C 是 BD 的中点，过点C 作CE AD ⊥交AD 的延长线于点E ．(1)求证：CE 是O 的切线；(2)若6BC =，8AC =，求CE 19．（2023·内蒙古通辽·统考中考真题）如图，连接CD ，BDC A ∠=∠．(1)求证：ACD DCB ∽；(2)求证：CD 是O 的切线；(3)若3tan ,105E AC ==，求O 的半径．11①过点A 作切线AC ，且4AC （点C 在A 的上方）；②连接OC ，交O 于点D ；③连接BD ，与AC 交于点E ．(1)求证：BD 为O 的切线；(2)求AE 的长度．。

重难点圆中的计算及其综合专项中考数学

重难点圆中的计算及其综合考点一：圆中的角度计算圆中角度的相关考点主要是圆周角定理和圆心角定理，这两个定理都有对应推论，考察难度不大，题型基本以选择、填空题为主，所以重点是要把这两个定理及其推论熟练掌握即可！题型01 圆中常见的角度计算易错点：圆中角度定理都有一个大前提——在同圆或等圆中，特别是一些概念性选择题，没有这个前提的话，对应结论是不正确的。

解题大招01：圆中角度计算口诀——圆中求角度，同弧或等弧＋直径所对圆周角是90度圆心角定理、圆周角定理以及其推论为圆中角的计算提供了等量关系，圆中的等角也是解决角度问题中常见的转化关系，所以特别要注意同弧或等弧所对的圆周角相等，以及直径所对圆周角=90°的固定关系解题大招01：圆中求角度常用的其他规律：圆内接四边形的一个外角=其内对角折叠弧过圆心→必有30°角以等腰三角形的腰长为直径的圆→必过底边中点圆中出现互相垂直的弦，常作两弦心距→必有矩形（当弦相等，则得正方形）【中考真题练】1．（2023•河南）如图，点A，B，C在⊙O上，若∠C＝55°，则∠AOB的度数为（）A．95°B．100°C．105°D．110°2．（2023•吉林）如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点（点P不与点B重合），连接CP．若∠BAC＝70°，则∠BPC的度数可能是（）A．70°B．105°C．125°D．155°3．（2023•枣庄）如图，在⊙O中，弦AB，CD相交于点P．若∠A＝48°，∠APD＝80°，则∠B的度数为（）A．32°B．42°C．48°D．52°4．（2023•眉山）如图，AB切⊙O于点B，连结OA交⊙O于点C，BD∥OA交⊙O于点D，连结CD，若∠OCD＝25°，则∠A的度数为（）A．25°B．35°C．40°D．45°5．（2023•湖北）如图，在△ABC中，∠ACB＝70°，△ABC的内切圆⊙O与AB，BC分别相切于点D，E，连接DE，AO的延长线交DE于点F，则∠AFD＝．【中考模拟练】1．（2024•连云区一模）如图，正五边形ABCDE内接于⊙O，点P是劣弧上一点（点P不与点C重合），则∠CPD＝（）A．45°B．36°C．35°D．30°2．（2024•岱岳区一模）如图，AB是⊙O的直径，点D是的中点，∠BAC＝40°，则∠ACD的度数是（）A．40°B．25°C．40°．D．30°3．（2024•甘井子区校级一模）如图，在⊙O中，OA、OB、OC为半径，连接AB、BC、AC．若∠ACB＝53°，∠CAB ＝17°，则∠OAC 的度数为（）A ．10°B ．15°C ．20°D ．25°4．（2024•连云区一模）如图，一块直角三角板的30°角的顶点P 落在⊙O 上，两边分别交⊙O 于A ，B 两点，连结AO ，BO ，则∠AOB 的度数 °．5．（2024•新城区模拟）如图，在△ABC 中，∠B ＝70°，⊙O 是△ABC 的内切圆，M ，N ，K 是切点，连接OA ，OC ．交⊙O 于E ，D 两点．点F 是上的一点，连接DF ，EF ，则∠EFD 的度数是．题型02 “知1得4”模型的常见题型解题大招：圆中模型“知1得4”由图可得以下5点：①AB=CD；②⋂⋂=CD AB ；③OM=ON；④F E ∠=∠；⑤COD AOB ∠=∠；以上5个结论，知道其中任意1个，剩余的4个都可以作为结论使用。

初中数学中考复习正多边形与圆的有关的证明和计算

初中数学中考复习正多边形与圆的有关的证明和计算正多边形与圆的有关证明和计算是初中数学中的基础知识，掌握这些知识将有助于学生在中考中取得好成绩。

下面将详细介绍正多边形与圆的证明和计算相关内容。

一、多边形的内角和在初中数学中，我们首先要了解正多边形的内角和的计算方式。

一个n边形（n≥3）的内角和公式为：(n-2)×180度，也可以写成(n-2)×π弧度。

例如，一个三角形的内角和为(3-2)×180度=180度；一个四边形的内角和为(4-2)×180度=360度。

二、正多边形的性质1.正多边形的内角是相等的。

这是因为正多边形的所有边长和内角都相等。

2.正多边形的外角是相等的。

外角是指在多边形外部，相邻两边的夹角。

3.正多边形的对角线个数为n(n-3)/2，其中n为多边形的边数。

例如，一个六边形有6(6-3)/2=9条对角线。

4.正多边形的对角线长度相等。

如果我们连接正多边形的一个顶点和非相邻顶点，得到的线段即为对角线。

所有对角线的长度均相等。

5.正多边形的中心到顶点的距离称为半径，正多边形的中心到边的距离称为中线。

一个正多边形的半径和中线相等。

三、正多边形的外接圆和内切圆1. 正n边形的外接圆半径r的计算公式为：r = a/2sin(π/n)，其中a为正n边形的边长。

例如，一个正六边形的边长为a，那么它的外接圆的半径为r = a/2sin(π/6)。

2. 正n边形的内切圆半径R的计算公式为：R = a/2tan(π/n)。

例如，一个正六边形的边长为a，那么它的内切圆的半径为R =a/2tan(π/6)。

四、正多边形与圆的面积1. 正n边形的面积公式为：S = (1/4) × n × a² × cot(π/n)，其中a为正n边形的边长。

例如，一个正六边形的边长为a，那么它的面积为S = (1/4) × 6 × a² × cot(π/6)。

圆的有关计算与证明(共50题)(解析版)-2023年中考数学真题分项汇编(全国通用)

圆的有关计算与证明(50题)一、单选题1.(2023·新疆·统考中考真题)如图，在⊙O 中，若∠ACB =30°，OA =6，则扇形OAB (阴影部分)的面积是()A.12πB.6πC.4πD.2π【答案】B【分析】根据圆周角定理求得∠AOB =60°，然后根据扇形面积公式进行计算即可求解．【详解】解：∵AB=AB，∠ACB =30°，∴∠AOB =60°，∴S =60360π×62=6π．故选：B .【点睛】本题考查了圆周角定理，扇形面积公式，熟练掌握扇形面积公式以及圆周角定理是解题的关键．2.(2023·江苏连云港·统考中考真题)如图，矩形ABCD 内接于⊙O ，分别以AB 、BC 、CD 、AD 为直径向外作半圆．若AB =4,BC =5，则阴影部分的面积是()A.414π-20 B.412π-20 C.20πD.20【答案】D【分析】根据阴影部分面积为2个直径分别为AB ,BC 的半圆的面积加上矩形的面积减去直径为矩形对角线长的圆的面积即可求解．【详解】解：如图所示，连接AC ，∵矩形ABCD 内接于⊙O ，AB =4,BC =5∴AC 2=AB 2+BC 2∴阴影部分的面积是S 矩形ABCD +π×AB 2 2+π×BC22-πAC22S 矩形ABCD +π×14AB 2+BC 2-AC 2=S 矩形ABCD=4×5=20，故选：D ．【点睛】本题考查了勾股定理，矩形的性质，熟练掌握勾股定理是解题的关键．3.(2023·湖北荆州·统考中考真题)如图，一条公路的转弯处是一段圆弧(AC)，点O 是这段弧所在圆的圆心，B 为AC上一点，OB ⊥AC 于D ．若AC =3003m ，BD =150m ，则AC 的长为()A.300πmB.200πmC.150πmD.1003πm【答案】B【分析】根据垂径定理求出AD 长度，再根据勾股定理求出半径长度，最后利用弧长公式即可求出答案.【详解】解：∵OB ⊥AC ，点O 是这段弧所在圆的圆心，∴AD =CD ，，∵OD =OD ，OA =OC ，∴△ADO ≌△CDO ，∴∠AOD =∠COD .∵AC =3003m ，AD =CD ，∴AD =CD =1503m .设OA =OC =OB =x ，则DO =x -150，在Rt △ADO 中，x 2=x -150 2+1503 2，∴x =300m ，∴sin ∠AOD =AD AO=1503300=32.∴∠AOD =60°，∴∠AOC =120°，∴AC =n πR 180=120×π×300180=200πm .故选：B .【点睛】本题考查了圆的垂径定理，弧长公式，解题的关键在于通过勾股定理求出半径长度，从而求出所求弧长所对应的圆心角度数.4.(2023·山东滨州·统考中考真题)如图，某玩具品牌的标志由半径为1cm 的三个等圆构成，且三个等圆⊙O 1,⊙O 2,⊙O 3相互经过彼此的圆心，则图中三个阴影部分的面积之和为()A.14πcm 2 B.13πcm 2 C.12πcm 2 D.πcm 2【答案】C 【分析】根据圆的对称性可知：图中三个阴影部分的面积相等，只要计算出一个阴影部分的面积即可，如图，连接AO 1,AO 2,O 1O 2，阴影AO 1O 2的面积=扇形AO 1O 2的面积，据此即可解答.【详解】解：根据圆的对称性可知：图中三个阴影部分的面积相等；如图，连接AO 1,AO 2,O 1O 2，则AO 1=AO 2=O 1O 2，△AO 1O 2是等边三角形，∴∠AO 1O 2=60°，弓形AO 1,AO 2,O 1O 2的面积相等，∴阴影AO 1O 2的面积=扇形AO 1O 2的面积=60π×12360=16πcm 2，∴图中三个阴影部分的面积之和=3×16π=12πcm 2；故选：C .【点睛】本题考查了不规则图形面积的计算，正确添加辅助线、掌握求解的方法是解题关键.5.(2023·四川达州·统考中考真题)如图，四边形ABCD 是边长为12的正方形，曲线DA 1B 1C 1D 1A 2⋯是由多段90°的圆心角的圆心为C ，半径为CB 1；C 1D 1 的圆心为D ，半径为DC 1⋯,DA 1 、A 1B 1 、B 1C 1、C 1D 1⋯的圆心依次为A 、B 、C 、D 循环，则A 2023B 2023�的长是()A.4045π2B.2023πC.2023π4D.2022π【答案】A【分析】曲线DA 1B 1C 1D 1A 2⋯是由一段段90度的弧组成的，半径每次比前一段弧半径+12，得到AD n -1=AA n =4×12(n -1)+12，BA n =BB n =4×12(n -1)+1，得出半径，再计算弧长即可．【详解】解：由图可知，曲线DA 1B 1C 1D 1A 2⋯是由一段段90度的弧组成的，半径每次比前一段弧半径+12，∴AD =AA 1=12，BA 1=BB 1=1，CB 1=CC 1=32，DC 1=DD 1=2，AD 1=AA 2=2+12，BA 2=BB 2=2+1，CB 2=CC 2=2+32，DC 2=DD 2=2+2，⋯⋯，AD n -1=AA n =4×12(n -1)+12，BA n =BB n =4×12(n -1)+1，故A 2023B 2023 的半径为BA 2023=BB 2023=4×12×2023-1 +1=4045，∴A 2023B 2023 的弧长=90180×4045π=40452π．故选：A .【点睛】此题主要考查了弧长的计算，弧长的计算公式：l =n πr180，找到每段弧的半径变化规律是解题关键．6.(2023·四川广安·统考中考真题)如图，在等腰直角△ABC 中，∠ACB =90°,AC =BC =22，以点A 为圆心，AC 为半径画弧，交AB 于点E ，以点B 为圆心，BC 为半径画弧，交AB 于点F ，则图中阴影部分的面积是()A.π-2B.2π-2C.2π-4D.4π-4【答案】C【分析】先利用扇形的面积公式求出扇形ACE 和扇形BCF 的面积，再减去△ABC 的面积即可得．【详解】解：∵△ABC 是等腰直角三角形，∴∠A =∠B =45°，∵AC =BC =22，∴图中阴影部分的面积是S 扇形ACE +S 扇形BCF -S Rt △ABC =45π×22 2360+45π×22 2360-12×22 ×22=2π-4，故选：C ．【点睛】本题考查了扇形的面积，熟练掌握扇形的面积公式是解题关键．7.(2023·江苏苏州·统考中考真题)如图，AB 是半圆O 的直径，点C ,D 在半圆上，CD=DB，连接OC ,CA ,OD ，过点B 作EB ⊥AB ，交OD 的延长线于点E ．设△OAC 的面积为S 1,△OBE 的面积为S 2，若S 1S 2=23，则tan ∠ACO 的值为()A.2B.223C.75D.32【答案】A【分析】如图，过C 作CH ⊥AO 于H ，证明∠COD =∠BOE =∠CAO ，由S 1S 2=23，即12OA ∙CH 12OB ∙BE =23，可得CH BE =23，证明tan ∠A =tan ∠BOE ，可得CH BE =AH OB =23，设AH =2m ，则BO =3m =AO =CO ，可得OH =3m -2m =m ，CH =9m 2-m 2=22m ，再利用正切的定义可得答案．【详解】解：如图，过C 作CH ⊥AO 于H ，∵CD=BD，∴∠COD =∠BOE =∠CAO ，∵S 1S 2=23，即12OA ∙CH 12OB ∙BE =23，∴CH BE=23，∵∠A =∠BOE ，∴tan ∠A =tan ∠BOE ，∴CH AH=BE OB ，即CH BE =AH OB =23，设AH =2m ，则BO =3m =AO =CO ，∴OH =3m -2m =m ，∴CH =9m 2-m 2=22m ，∴tan ∠A =CH AH=22m2m =2，∵OA =OC ，∴∠A =∠ACO ，∴tan ∠ACO =2；故选：A .【点睛】本题考查的是圆周角定理的应用，勾股定理的应用，锐角三角函数的应用，作出合适的辅助线构建直角三角形是解本题的关键．二、填空题8.(2023·重庆·统考中考真题)如图，在矩形ABCD 中，AB =2，BC =4，E 为BC 的中点，连接AE ，DE ，以E 为圆心，EB 长为半径画弧，分别与AE ，DE 交于点M ，N ，则图中阴影部分的面积为．(结果保留π)【答案】4-π【分析】利用矩形的性质求得AB =CD =2,BE =CE =2，进而可得∠BAE =∠AEB =∠DEC =∠CDE =45°，然后根据S 阴影=2S △ABE -S 扇形BEM 解答即可．【详解】解：∵四边形ABCD 是矩形，AB =2，BC =4，E 为BC 的中点，∴AB =CD =2,BE =CE =12BC =2，∠ABC =∠DCB =90°，∴∠BAE =∠AEB =∠DEC =∠CDE =45°，∴S 阴影=2S △ABE -S 扇形BEM =2×12×2×2-45π×22360 =2×2-12π=4-π；故答案为：4-π．【点睛】本题考查了矩形的性质和不规则面积的计算，熟练掌握矩形的性质、明确阴影面积为两个全等的等腰直角三角形的面积减去两个圆心角为45°的扇形面积是解题关键．9.(2023·黑龙江绥化·统考中考真题)如图，⊙O 的半径为2cm ，AB 为⊙O 的弦，点C 为AB上的一点，将AB沿弦AB 翻折，使点C 与圆心O 重合，则阴影部分的面积为．(结果保留π与根号)【答案】23π-3cm 2【分析】根据折叠的性质得出△AOC 是等边三角形，则∠AOC =60°，OD =CD =1，根据阴影部分面积=S 扇形AOC -S △AOC 即可求解．【详解】解：如图所示，连接OA ,OC ，设AB ,CO 交于点D∵将AB沿弦AB 翻折，使点C 与圆心O 重合，∴AC =AO ，OC ⊥AB 又OA =OC ∴OA =OC =AC ，∴△AOC 是等边三角形，∴∠AOC =60°，OD =CD =1，∴AD =AO 2-CD 2=3,∴阴影部分面积=S 扇形AOC -S △AOC =60360π×22-12×2×3=23π-3cm 2 故答案为：23π-3cm 2．10.(2023·重庆·统考中考真题)如图，⊙O 是矩形ABCD 的外接圆，若AB =4,AD =3，则图中阴影部分的面积为．(结果保留π)【答案】254π-12【分析】根据直径所对的圆周角是直角及勾股定理得到BD =5，再根据圆的面积及矩形的性质即可解答．【详解】解：连接BD ，∵四边形ABCD 是矩形，∴BD 是⊙O 的直径，∵AB =4,AD =3，∴BD =AB 2+AD 2=5，∴⊙O 的半径为52，∴⊙O 的面积为254π，矩形的面积为3×4=12，∴阴影部分的面积为254π-12；故答案为：254π-12.【点睛】本题考查了矩形的性质，圆的面积，矩形的面积，勾股定理，掌握矩形的性质是解题的关键．11.(2023·江苏扬州·统考中考真题)用半径为24cm ，面积为120πcm 2的扇形纸片，围成一个圆锥的侧面，则这个圆锥的底面圆的半径为cm ．【答案】5【分析】应为圆锥侧面母线的长就是侧面展开扇形的半径，利用圆锥侧面面积公式：S =π⋅r ⋅l ，就可以求出圆锥的底面圆的半径．【详解】解：设圆锥底面圆的半径为r ，l =24，由扇形的面积：S =π⋅r ⋅l =120π，得：r =5故答案为：5.【点睛】本题考查了圆锥侧面面积的相关计算，熟练掌握圆锥侧面面积的计算公式是解题的关键，注意用扇形围成的圆锥，扇形的半径就是圆锥的母线．12.(2023·浙江温州·统考中考真题)若扇形的圆心角为40°，半径为18，则它的弧长为．【答案】4π【分析】根据弧长公式l =n πr180即可求解．【详解】解：扇形的圆心角为40°，半径为18，∴它的弧长为40180×18π=4π，故答案为：4π．【点睛】本题考查了求弧长，熟练掌握弧长公式是解题的关键．13.(2023·浙江宁波·统考中考真题)如图，圆锥形烟囱帽的底面半径为30cm，母线长为50cm，则烟囱帽的侧面积为cm2．(结果保留π)【答案】1500π【分析】根据圆锥侧面展开图是一个扇形，由扇形面积公式S=12lr代值求解即可得到答案．【详解】解：∵圆锥形烟囱帽的底面半径为30cm，母线长为50cm，∴烟囱帽的侧面积S=12lr=12×2π×30×50=1500π(cm2)，故答案为：1500π．【点睛】本题考查圆锥侧面展开图及扇形面积公式S=12lr，熟记扇形面积公式是解决问题的关键．14.(2023·天津·统考中考真题)如图，在每个小正方形的边长为1的网格中，等边三角形ABC内接于圆，且顶点A，B均在格点上．(1)线段AB的长为；(2)若点D在圆上，AB与CD相交于点P．请用无刻度的直尺，在如图所示的网格中，画出点Q，使△CPQ为等边三角形，并简要说明点Q的位置是如何找到的(不要求证明)．【答案】(1)29(2)画图见解析；如图，取AC,AB与网格线的交点E，F，连接EF并延长与网格线相交于点G；连接DB与网格线相交于点H，连接HF并延长与网格线相交于点I，连接AI并延长与圆相交于点K，连接CK并延长与GB的延长线相交于点Q，则点Q即为所求【分析】(1)在网格中用勾股定理求解即可；(2)取AC,AB与网格线的交点E，F，连接EF并延长与网格线相交于点M，连接MB；连接DB与网格线相交于点G，连接GF并延长与网格线相交于点H，连接AH并延长与圆相交于点I，连接CI并延长与MB的延长线相交于点Q，则点Q即为所求，连接PQ，AD,BK，过点E作ET⊥网格线，过点G作GS ⊥网格线，由图可得Rt △AJF ≌Rt △BLF AAS ，根据全等三角形的性质可得Rt △IMF ≌Rt △HNF ASA 和△AIF ≌△BHF SAS ，根据同弧所对圆周角相等可得AD=BK，进而得到∠1=∠2和∠PCQ =60°，再通过证明△CAP ≌△CBQ ASA 即可得到结论．【详解】(1)解：AB =22+52=29；故答案为：29．(2)解：如图，取AC ,AB 与网格线的交点E ，F ，连接EF 并延长与网格线相交于点G ；连接DB 与网格线相交于点H ，连接HF 并延长与网格线相交于点I ，连接AI 并延长与圆相交于点K ，连接CK 并延长与GB 的延长线相交于点Q ，则点Q 即为所求；连接PQ ，AD ,BK ，过点E 作ET ⊥网格线，过点G 作GS ⊥网格线，由图可得：∵∠AJF =∠BLF ，∠AFJ =∠BFL ，AJ =BL ，∴Rt △AJF ≌Rt △BLF AAS ，∴FJ =FL ，AF =BF ，∵MJ =NL ，∴FJ -MJ =FL -NL ，即FM =FN ，∵∠IMF =∠HNF ，∠IFM =∠HFN ，∴Rt △IMF ≌Rt △HNF ASA ，∴FI =FH ，∵∠AFI =∠BFH ，AF =BF ，∴△AIF ≌△BHF SAS ，∴∠FAI =∠FBH ，∴AD=BK，∴∠1=∠2，∵△ABC 是等边三角形，∴∠ACB =60°，即∠1+∠PCB =60°，∴∠2+∠PCB =60°，即∠PCQ =60°，∵ET =GS ，∠ETF =∠GSF ，∠EFT =∠GFS ，∴Rt △ETF ≌Rt △GSF AAS ，∴EF =GF ，∵AF =BF ，∠AFE =∠BFG ，∴△AFE ≌△BFG SAS ，∴∠EAF =∠GBF ，∴∠GBF =∠EAF =∠CBA =60°，∴∠CBQ =180°-∠CBA -∠GBF =60°，∴∠CBQ =∠CAB ，∵CA =CB ，∴△CAP ≌△CBQ ASA ，∴CQ =CP ，∵∠PCQ =60°，∴△PCQ 是等边三角形，此时点Q 即为所求；故答案为：如图，取AC ,AB 与网格线的交点E ，F ，连接EF 并延长与网格线相交于点G ；连接DB 与网格线相交于点H ，连接HF 并延长与网格线相交于点I ，连接AI 并延长与圆相交于点K ，连接CK 并延长与GB 的延长线相交于点Q ，则点Q 即为所求．【点睛】本题考查作图-复杂作图，勾股定理、等边三角形的判定、全等三角形的判定与性质等知识，解题关键是理解题意，灵活运用所学知识是关键．15.(2023·江苏苏州·统考中考真题)如图，在▱ABCD 中，AB =3+1,BC =2,AH ⊥CD ，垂足为H ,AH =3．以点A 为圆心，AH 长为半径画弧，与AB ,AC ,AD 分别交于点E ,F ,G ．若用扇形AEF 围成一个圆锥的侧面，记这个圆锥底面圆的半径为r 1；用扇形AHG 围成另一个圆锥的侧面，记这个圆锥底面圆的半径为r 2，则r 1-r 2=．(结果保留根号)【答案】324【分析】由▱ABCD ，AB =3+1,BC =2,AH ⊥CD ，AH =3，AD =BC =2，DH =22-3 2=1，cos DAH =AH AD=32，AB =CD =3+1，AB ∥CD ，求解∠DAH =30°，CH =3=AH ，证明∠ACH =∠CAH =45°，可得∠BAC =45°，再分别计算圆锥的底面半径即可．【详解】解：∵在▱ABCD 中，AB =3+1,BC =2,AH ⊥CD ，AH =3，∴AD =BC =2，DH =22-3 2=1，∵cos ∠DAH =AHAD=32，AB =CD =3+1，∴∠DAH =30°，CH =3=AH ，∴∠ACH =∠CAH =45°，∵AB ∥CD ，∴∠BAC =45°，∴45π×3180=2πr 1，30π×3180=2πr 2，解得：r 1=38，r 2=312，∴r 1-r 2=3324-2324=324；故答案为：324【点睛】本题考查的是平行四边形的性质，勾股定理的应用，锐角三角函数的应用，扇形的弧长的计算，圆锥的底面半径的计算，熟记圆锥的侧面展开图的扇形弧长等于底面圆的周长是解本题的关键．16.(2023·四川自贡·统考中考真题)如图，小珍同学用半径为8cm ，圆心角为100°的扇形纸片，制作一个底面半径为2cm 的圆锥侧面，则圆锥上粘贴部分的面积是cm 2．【答案】169π【分析】由题意知，底面半径为2cm 的圆锥的底面周长为4πcm ，扇形弧长为100π×8180=409πcm ，则扇形中未组成圆锥底面的弧长l =409π-4π=49πcm ，根据圆锥上粘贴部分的面积为扇形中未组成圆锥的弧长部分所对应的扇形面积可得圆锥上粘贴部分的面积为12lr =12×49π×8，计算求解即可．【详解】解：由题意知，底面半径为2cm 的圆锥的底面周长为4πcm ，扇形弧长为100π×8180=409πcm ，∴扇形中未组成圆锥底面的弧长l =409π-4π=49πcm ，∵圆锥上粘贴部分的面积为扇形中未组成圆锥的弧长部分所对应的扇形面积，∴圆锥上粘贴部分的面积为12lr =12×49π×8=169πcm 2，故答案为：169π．【点睛】本题考查了扇形的弧长、面积公式．解题的关键在于熟练掌握S 扇形=12lr ，l 扇形=n πr180，其中n 为扇形的圆心角，r 为扇形的半径．三、解答题17.(2023·四川南充·统考中考真题)如图，AB 与⊙O 相切于点A ，半径OC ∥AB ，BC 与⊙O 相交于点D ，连接AD ．(1)求证：∠OCA =∠ADC ；(2)若AD =2,tan B =13，求OC 的长．【答案】(1)见解析(2)5【分析】(1)连接OA ，根据切线的性质得出∠OAB =90°，再由平行线的性质得出∠AOC =90°，利用圆周角定理及等腰直角三角形的性质即可证明；(2)过点A 作AH ⊥BC ，过点C 作CF ⊥BA 的延长线于点F ，根据勾股定理及等腰直角三角形的性质得出AH =DH =2，再由正切函数确定BH =32，AB =25，再由正方形的判定和性质及相似三角形的判定和性质求解即可．【详解】(1)证明：连接OA ，如图所示：∵AB 与⊙O 相切于点A ，∴∠OAB =90°，∵OC ∥AB ，∴∠AOC =90°，∴∠ADC =45°，∵OC =OA ，∴∠OCA =45°，∴∠OCA =∠ADC ；(2)过点A 作AH ⊥BC ，过点C 作CF ⊥BA 交BA 的延长线于点F ，如图所示：由(1)得∠OCA =∠ADC =45°，∴ΔAHD 为等腰直角三角形，∵AD =2，∴AH =DH =2，∵tan B =13，∴BH =32，AB =AH 2+BH 2=25，由(1)得∠AOC =∠OAF =90°，∵CF ⊥BA ，∴四边形OCFA 为矩形，∵OA =OC ，∴四边形OCFA 为正方形，∴CF =FA =OC =r ，∵∠B =∠B ,∠AHB =∠CFB =90°，∴△ABH ∽△CBF ,∴BH BF =AH CF 即3225+r=2r ，解得：r =5，∴OC =5．【点睛】题目主要考查圆周角定理，解直角三角形及正方形与相似三角形的判定和性质，理解题意，作出辅助线，综合运用这些知识点是解题关键．18.(2023·四川成都·统考中考真题)如图，以△ABC 的边AC 为直径作⊙O ，交BC 边于点D ，过点C 作CE ∥AB 交⊙O 于点E ，连接AD ，DE ，∠B =∠ADE ．(1)求证：AC=BC；(2)若tan B=2，CD=3，求AB和DE的长．【答案】(1)见解析(2)AB=25，DE=25【分析】(1)根据CE∥AB，得到∠ACE=∠BAC，再根据同弧所对的圆周角相等，得到∠ACE=∠ADE=∠B，可证明△ABC是等腰三角形，即可解答；(2)根据直径所对的圆周角为直角，得到tan B=2=ADBD，设BD=x，根据勾股定理列方程，解得x 的值，即可求出AB；解法一：过点E作DC的垂线段，交DC的延长线于点F，证明∠B=∠ECF，求出EF,DF的长，根据勾股定理即可解出DE的长；解法二：连接AE,得到角相等，进而证得△ABC∽△ADE，根据对应边成比例即可解出DE的长．【详解】(1)证明：∵CE∥AB，∴∠BAC=∠ACE，∴∠BAC=∠ACE=∠ADE，∵∠B=∠ADE，∴∠B=∠BAC，∴AC=BC；(2)解：设BD=x，∵AC是⊙O的直径，∴∠ADC=∠ADB=90°，∵tan B=2，=2，即AD=2x，∴ADBD根据(1)中的结论，可得AC=BC=BD+DC=x+3，根据勾股定理，可得AD2+DC2=AC2，即2x2，2+32=x+3解得x1=2，x2=0(舍去)，∴BD=2，AD=4,根据勾股定理，可得AB=AD2+BD2=25；解法一：如图，过点E作DC的垂线段，交DC的延长线于点F，∵CE∥AB，∴∠ECF=∠B，∵EF⊥CF，∴tan∠ECF=tan∠B=2，即EF=2，CF∵∠B+∠BAD=90°，∠ADE+∠EDF=90°，∠B=∠ADE，∴∠BAD=∠EDF，∴∠DEF =90°-∠EDF =90°-∠BAD =∠B ，∴DF EF=2，设CF =a ，则DF =DC +CF =a +3，∴EF =2a ，可得方程a +32a=2，解得a =1，∴EF =2，DF =4，根据勾股定理，可得DE =DF 2+EF 2=25．解法二：如图，连接AE ,∵∠B =∠ADE ，∠ACB =∠AED ，∴△ABC ∽△ADE ，∴AB AD=BC DE ，又∵BC =5，AD =4，AB =25，∴254=5DE ，∴DE =25．【点睛】本题考查了圆周角定理，等腰三角形的判定和性质，相似三角形的判定及性质，平行线的性质，勾股定理，正切，利用等量代换证明相关角相等是解题的关键．19.(2023·内蒙古·统考中考真题)如图，AB 是⊙O 的直径，AC 是弦，D 是AC上一点，P 是AB 延长线上一点，连接AD ,DC ,CP ．(1)求证：∠ADC -∠BAC =90°；(请用两种证法解答)(2)若∠ACP =∠ADC ，⊙O 的半径为3，CP =4，求AP 的长．【答案】(1)证明见解析(2)8【分析】(1)证法一：连接BD ，得到∠ADB =90°，因为∠BAC =∠BDC ，所以∠ADC -∠BAC =90°；证法二：连接BC ，可得∠ADC +∠ABC =180°，则∠ABC =180°-∠ADC ，根据∠ACB =90°，可得∠BAC +∠ABC =90°，即可得到结果；(2)连接OC ，根据角度间的关系可以证得△OCP 为直角三角形，根据勾股定理可得边OP 的长，进而求得结果．【详解】(1)证法一：如图，连接BD ，∵BC=BC，∴∠BDC=∠BAC，∵AB是⊙O的直径，∴∠ADB=90°，∴∠ADC=∠ADB+∠BDC∵∠BAC=∠BDC，∴∠ADC=90°+∠BAC，∴∠ADC-∠BAC=90°，证法二：如图，连接BC，∵四边形ABCD是⊙O的内接四边形，∴∠ADC+∠ABC=180°，∴∠ABC=180°-∠ADC，∵AB是⊙O的直径，∴∠ACB=90°，∴∠BAC+∠ABC=90°，∴∠BAC+180°-∠ADC=90°，∴∠ADC-∠BAC=90°，(2)解：如图，连接OC，∵∠ACP=∠ADC，∠ADC-∠BAC=90°，∴∠ACP-∠BAC=90°，∵OA=OC，∴∠BAC=∠ACO，∴∠ACP-∠ACO=90°，∴∠OCP=90°．∵⊙O的半径为3，∴AO=OC=3，在Rt△OCP中，OP2=OC2+CP2，∵CP=4，∴OP2=32+42=25，∴OP=5，∴AP=AO+OP=8，【点睛】本题考查了圆周角定理，直径所对的圆周角为直角，勾股定理，找到角度之间的关系是解题的关键．20.(2023·辽宁大连·统考中考真题)如图1，在⊙O中，AB为⊙O的直径，点C为⊙O上一点，AD为∠CAB的平分线交⊙O于点D，连接OD交BC于点E．(1)求∠BED 的度数；(2)如图2，过点A 作⊙O 的切线交BC 延长线于点F ，过点D 作DG ∥AF 交AB 于点G ．若AD =235,DE =4，求DG 的长．【答案】(1)90°(2)210【分析】(1)根据圆周角定理证明两直线平行，再利用平行线的性质证明角度相等即可；(2)由勾股定理找到边的关系，求出线段长，再利用等面积法求解即可．【详解】(1)∵AB 是⊙O 的直径，∴∠ACB =90°，∵AD 平分∠CAB ，∴∠BAD =12∠BAC ，即∠BAC =2∠BAD ，∵OA =OD ，∴∠BAD =∠ODA ，∴∠BOD =∠BAD +∠ODA =2∠BAD ，∴∠BOD =∠BAC ，∴OD ∥AC ，∴∠OEB =∠ACB =90°，∴∠BED =90°，(2)如图，连接BD ，设OA =OB =OD =r ，则OE =r -4，AC =2OE =2r -8，AB =2r ，∵AB 是⊙O 的直径，∴∠ADB =90°，在Rt △ADB 中，有勾股定理得：BD 2=AB 2-AD 2由(1)得：∠BED =90°，∴∠BED =∠BEO =90°，由勾股定理得：BE 2=OB 2-OE 2，BE 2=BD 2-DE 2，∴BD 2=AB 2-AD 2=BE 2+DE 2=OB 2-OE 2+DE 2，∴2r 2-235 2=r 2-r -4 2+42，整理得：r 2-2r -35=0，解得：r =7或r =-5(舍去)，∴AB =2r =14，∴BD =AB 2-AD 2=142-235 2=214，∵AF是⊙O的切线，∴AF⊥AB，∵DG∥AF，∴DG⊥AB，∴S△ABD=12AD·BD=12AB·DG，∴DG=AD·BDAB =235×21414=210．【点睛】此题考查了圆周角定理和勾股定理，三角形中位线定理，切线的性质，解一元二次方程，熟练掌握圆周角定理和勾股定理是解题的关键．21.(2023·浙江杭州·统考中考真题)在边长为1的正方形ABCD中，点E在边AD上(不与点A，D重合)，射线BE与射线CD交于点F．(1)若ED=13，求DF的长．(2)求证：AE⋅CF=1．(3)以点B为圆心，BC长为半径画弧，交线段BE于点G．若EG=ED，求ED的长．【答案】(1)1 2(2)见解析(3)14【分析】(1)证明△AEB∽△DEF，利用相似三角形的对应边成比例求解；(2)证明△AEB∽△CBF，利用相似三角形的对应边成比例证明；(3)设EG=ED=x，则AE=1-x，BE=1+x，在Rt△ABE中，利用勾股定理求解．【详解】(1)解：由题知，AB=BC=CD=DA=1，若ED=13，则AE=AD-ED=23．∵四边形ABCD是正方形，∴∠A=∠FDE=90°，又∵∠AEB=∠FED，∴△AEB∽△DEF，∴AB DF =AE ED，即1DF=2313，∴DF=12．(2)证明：∵四边形ABCD是正方形，∴∠A=∠C=90°，AB∥CD，∴∠ABE=∠F，∴△ABE∽△CFB，∴AB CF =AE BC，∴AE⋅CF=AB⋅BC=1×1=1．(3)解：设EG=ED=x，则AE=AD-AE=1-x，BE=BG+GE=BC+GE=1+x．在Rt△ABE中，AB2+AE2=BE2，即12+(1-x)2=(1+x)2，解得x=1 4．∴ED=14．【点睛】本题考查了相似三角形的性质与判定，勾股定理的应用，正方形的性质等，熟练掌握相关性质定理是解题的关键．22.(2023·河北·统考中考真题)装有水的水槽放置在水平台面上，其横截面是以AB为直径的半圆O，AB=50cm，如图1和图2所示，MN为水面截线，GH为台面截线，MN∥GH．计算：在图1中，已知MN=48cm，作OC⊥MN于点C．(1)求OC的长．操作：将图1中的水面沿GH向右作无滑动的滚动，使水流出一部分，当∠ANM=30°时停止滚动，如图2．其中，半圆的中点为Q，GH与半圆的切点为E，连接OE交MN于点D．探究：在图2中(2)操作后水面高度下降了多少？(3)连接OQ 并延长交GH 于点F ，求线段EF 与EQ的长度，并比较大小．【答案】(1)7cm (2)112cm(3)EF =2533cm ，EQ =25π6cm ，EF >EQ ．【分析】(1)连接OM ，利用垂径定理计算即可；(2)由切线的性质证明OE ⊥GH 进而得到OE ⊥MN ，利用锐角三角函数求OD ，再与(1)中OC 相减即可；(3)由半圆的中点为Q 得到∠QOB =90°，得到∠QOE =30°分别求出线段EF 与EQ的长度，再相减比较即可．【详解】解：(1)连接OM ，∵O 为圆心，OC ⊥MN 于点C ，MN =48cm ，∴MC =12MN =24cm ，∵AB =50cm ，∴OM =12AB =25cm ，∴在Rt △OMC 中，OC =OM 2-MC 2=252-242=7cm ．(2)∵GH 与半圆的切点为E ，∴OE ⊥GH ∵MN ∥GH∴OE ⊥MN 于点D ，∵∠ANM =30°，ON =25cm ，∴OD =12ON =252cm ，∴操作后水面高度下降高度为：252-7=112cm ．(3)∵OE ⊥MN 于点D ，∠ANM =30°∴∠DOB =60°，∵半圆的中点为Q ，∴AQ=QB，∴∠QOB =90°，∴∠QOE =30°，∴EF =tan ∠QOE ⋅OE =2533cm ，EQ =30×π×25180=25π6cm ，∵2533-25π6=503-25π6=2523-π 6>0，∴EF >EQ．【点睛】本题考查了垂径定理、圆的切线的性质、求弧长和解直角三角形的知识，解答过程中根据相关性质构造直角三角形是解题关键．23.(2023·湖北武汉·统考中考真题)如图，OA ,OB ,OC 都是⊙O 的半径，∠ACB =2∠BAC ．(1)求证：∠AOB =2∠BOC ；(2)若AB =4,BC =5，求⊙O 的半径．【答案】(1)见解析(2)52【分析】(1)由圆周角定理得出，∠ACB =12∠AOB ,∠BAC =12∠BOC ，再根据∠ACB =2∠BAC ，即可得出结论；(2)过点O 作半径OD ⊥AB 于点E ，根据垂径定理得出∠DOB =12∠AOB ,AE =BE ，证明∠DOB =∠BOC ，得出BD =BC ，在Rt △BDE 中根据勾股定理得出DE =BD 2-BE 2=1，在Rt △BOE 中，根据勾股定理得出OB 2=(OB -1)2+22，求出OB 即可．【详解】(1)证明：∵AB=AB，∴∠ACB =12∠AOB ，∵BC =BC ，∴∠BAC =12∠BOC ，∵∠ACB =2∠BAC ，∴∠AOB =2∠BOC ．(2)解：过点O 作半径OD ⊥AB 于点E ，则∠DOB =12∠AOB ,AE =BE ，∵∠AOB =2∠BOC ，∴∠DOB =∠BOC ，∴BD =BC ，∵AB =4,BC =5，∴BE =2,DB =5，在Rt △BDE 中，∵∠DEB =90°∴DE =BD 2-BE 2=1，在Rt △BOE 中，∵∠OEB =90°，∴OB 2=(OB -1)2+22，∴OB =52，即⊙O 的半径是52．【点睛】本题主要考查了勾股定理，垂径定理，圆周角定理，解题的关键是作出辅助线，熟练掌握圆周角定理．24.(2023·湖南·统考中考真题)如图所示，四边形ABCD 是半径为R 的⊙O 的内接四边形，AB 是⊙O 的直径，∠ABD =45°，直线l 与三条线段CD 、CA 、DA 的延长线分别交于点E 、F 、G ．且满足∠CFE =45°．(1)求证：直线l ⊥直线CE ；(2)若AB =DG ；①求证：△ABC ≌△GDE ；②若R =1，CE =32，求四边形ABCD 的周长．【答案】(1)见解析(2)①见解析，②72+2【分析】(1)在⊙O 中，根据同弧所对的圆周角相等可得∠ACD =∠ABD =45°，结合已知在△CFE 中根据三角形内角和定理可求得∠FEC =90°；(2)①根据圆内接四边形的性质和邻补角可得∠ABC =∠GDE ，由直径所对的圆周角是直角和(1)可得∠ACB =∠GED ，结合已知即可证得△ABC ≌△GDE AAS ；②在⊙O 中由R =1，可得AB =2，结合题意易证DA =DB ，在Rt △ABC 中由勾股定理可求得DA =2，由①可知易得BC +CD =DE +CD =CE ，最后代入计算即可求得周长．【详解】(1)证明：在⊙O 中，∵AD =AD，∴∠ACD =∠ABD =45°，即∠FCE =45°，在△CFE 中，∵∠CFE =45°，∴∠FEC =180°-∠FCD +∠CFE =90°，即直线l ⊥直线CE ；(2)①四边形ABCD 是半径为R 的⊙O 的内接四边形，∴∠ADC +∠ABC =180°，∵∠ADC +∠GDE =180°，∴∠ABC =∠GDE ，∵AB 是⊙O 的直径，∴∠ACB =90°，由(1)可知∠GED =90°，∴∠ACB=∠GED，在△ABC与△GDE中，∠ABC=∠GDE ∠ACB=∠GED AB=DG，∴△ABC≌△GDE AAS，②在⊙O中，R=1，∴AB=2R=2，∵AB是⊙O的直径，∴∠ADB=90°，∵∠ABD=45°，∴∠BAD=90°-∠ABD=45°，∴DA=DB，在Rt△ABC中，∴DA2+DB2=AB2，即2DA2=22，解得：DA=2，由①可知△ABC≌△GDE，∴BC=DE，∴BC+CD=DE+CD=CE=32，∴四边形ABCD的周长为：DA+AB+BC+CD=DA+AB+CE=2+2+32=72+2．【点睛】本题考查了同弧所对的圆周角相等、三角形内角和定理、垂直的定义、圆内接四边形的性质、邻补角互补、直径所对的圆周角是直角、全等三角形的判定和性质、勾股定理解直角三角形以及周长的计算；解题的关键是灵活运用以上知识，综合求解．25.(2023·天津·统考中考真题)在⊙O中，半径OC垂直于弦AB，垂足为D，∠AOC=60°，E为弦AB所对的优弧上一点．(1)如图①，求∠AOB和∠CEB的大小；(2)如图②，CE与AB相交于点F，EF=EB，过点E作⊙O的切线，与CO的延长线相交于点G，若OA=3，求EG的长．【答案】(1)∠AOB=120°，∠CEB=30°(2)3【分析】(1)根据半径OC 垂直于弦AB ，可以得到AC =BC，从而得到∠AOC =∠BOC ，结合已知条件∠AOC =60°即可得到∠AOB =2∠AOC =120°，根据∠CEB =12∠AOC 即可求出∠CEB =30°；(2)根据∠CEB =30°，结合EF =EB ，推算出∠EBF =∠EFB =75°，进一步推算出∠GOE =∠AOE-∠AOG =30°，在Rt △OEG 中，tan ∠GOE =EG OE,OE =OA =3，再根据EG =3×tan30°即可得到答案．【详解】(1)解：在⊙O 中，半径OC 垂直于弦AB ，∴AC =BC ，得∠AOC =∠BOC ．∵∠AOC =60°，∴∠AOB =2∠AOC =120°．∵∠CEB =12∠BOC =12∠AOC ，∴∠CEB =30°．(2)解：如图，连接OE ．同(1)得∠CEB =30°．∵在△BEF 中，EF =EB ，∴∠EBF =∠EFB =75°．∴∠AOE =2∠EBA =150°．又∠AOG =180°-∠AOC =120°，∴∠GOE =∠AOE -∠AOG =30°．∵GE 与⊙O 相切于点E ，∴OE ⊥GE ，即∠OEG =90°．在Rt △OEG 中，tan ∠GOE =EG OE,OE =OA =3，∴EG =3×tan30°=3．【点睛】本题考查圆周角定理、切线的性质和直角三角函数，解题的关键是灵活运用相关知识．26.(2023·江苏苏州·统考中考真题)如图，△ABC 是⊙O 的内接三角形，AB 是⊙O 的直径，AC =5,BC =25，点F 在AB 上，连接CF 并延长，交⊙O 于点D ，连接BD ，作BE ⊥CD ，垂足为E ．(1)求证：△DBE ∽△ABC ；(2)若AF =2，求ED 的长．【答案】(1)证明见解析(2)355【分析】(1)分别证明∠ACB=90°=∠BED，∠CAB=∠CDB，从而可得结论；(2)求解AB=AC2+BC2=5，tan∠ABC=ACBC =12，可得BF=3，证明tan∠ABC=tan∠DBE=DE BE =12，设DE=x，则BE=2x，BD=5x，证明△ACF∽△DBF，可得ACBD=AFDF=CFBF，可得DF=2x，EF=x=DE，BD=BF=3，从而可得答案．【详解】(1)证明：∵AB是⊙O的直径，BE⊥CD，∴∠ACB=90°=∠BED，∵∠CAB=∠CDB，∴△DBE∽△ABC．(2)∵AC=5,BC=25，∠ACB=90°，∴AB=AC2+BC2=5，tan∠ABC=ACBC =12，∵AF=2，∴BF=3，∵△DBE∽△ABC，∴∠ABC=∠DBE，∴tan∠ABC=tan∠DBE=DEBE =12，设DE=x，则BE=2x，BD=5x，∵∠AFC=∠BFD，∠CAB=∠CDB，∴△ACF∽△DBF，∴AC BD =AFDF=CFBF，∴55x =2DF，则DF=2x，∴EF=x=DE，∴BD=BF=3，∴DE=355．【点睛】本题考查的是圆周角定理的应用，相似三角形的判定与性质，锐角三角函数的应用，熟记圆的基本性质与重要定理是解本题的关键．27.(2023·四川达州·统考中考真题)如图，△ABC、△ABD内接于⊙O，AB=BC，P是OB延长线上的一点，∠PAB=∠ACB，AC、BD相交于点E．(1)求证：AP 是⊙O 的切线；(2)若BE =2，DE =4，∠P =30°，求AP 的长．【答案】(1)见解析(2)6【分析】(1)由AB =BC ，OB 为半径，可知OB ⊥AC ，∠CAB =∠ACB ，则∠CAB +∠ABO =90°，∠ACB +∠ABO =90°，∠PAB +∠ABO =90°，如图1，连接OA ，由OA =OB ，可得∠OAB =∠ABO ，则∠PAB +∠OAB =90°，即∠OAP =90°，进而结论得证；(2)如图2，记OB 与AC 交点为M ，连接OD ，过O 作ON ⊥DB 于N ，证明△ABO 是等边三角形，则AB =OB =OA ，∠ABM =60°，设⊙O 半径为r ，则BM =AB ⋅cos ∠ABM =12r ，由OB =OD ，ON ⊥DB ，可得BN =12BD =3，证明△BME ∽△BNO ，则BM BN =BE BO ，即12r 3=2r ，解得r =23或r =-23(舍去)，根据AP =OA tan ∠P，计算求解即可．【详解】(1)解：如图，连接OA ,OC ，∵AB =BC ，∴AB �=BC �，∴∠AOB =∠COB ，∴OB ⊥AC ，由等边对等角可得∠CAB =∠ACB ，∴∠CAB +∠ABO =90°，∴∠ACB +∠ABO =90°，∵∠PAB =∠ACB ，∴∠PAB +∠ABO =90°，∵OA =OB ，∴∠OAB =∠ABO ，∴∠PAB +∠OAB =90°，即∠OAP =90°，又∵OA 是半径，∴AP 是⊙O 的切线；(2)解：如图2，记OB 与AC 交点为M ，连接OD ，过O 作ON ⊥DB 于N ，∵∠P =30°，∴∠AOP =60°，∴△ABO 是等边三角形，∴AB =OB =OA ，∠ABM =60°，设⊙O 半径为r ，∵AM ⊥BM ，∴BM =AB ⋅cos ∠ABM =12r ，∵OB =OD ，∴△BOD 是等腰三角形，又∵ON ⊥DB ，∴BN =12BD =BE +DE 2=3，∵∠BME =∠BNO =90°，∠EBM =∠OBN ，∴△BME ∽△BNO ，∴BM BN =BE BO ，即12r 3=2r ，解得r =23或r =-23(舍去)，∴AP =OA tan ∠P =r 33=6，∴AP 的长为6．【点睛】本题考查了垂径定理，等腰三角形的判定与性质，切线的判定，等边三角形的判定与性质，相似三角形的判定与性质，余弦、正切等知识．解题的关键在于对知识的熟练掌握与灵活运用．28.(2023·湖南·统考中考真题)如图，AB 是⊙O 的直径，AC 是一条弦，D 是AC的中点，DE ⊥AB 于点E ，交AC 于点F ，交⊙O 于点H ，DB 交AC 于点G ．(1)求证：AF =DF ．(2)若AF =52,sin ∠ABD =55，求⊙O 的半径．【答案】(1)见解析(2)5【分析】(1)根据D 是AC 的中点，DE ⊥AB 于点E ，得到CD =DA =AH ,得到∠ADH =∠DAC 即可得证．(2)根据sin ∠ABD =55=AD AB，设AD =5x ,AB =5x ，运用勾股定理，得到BD =5x 2-5x 2=25x ，结合sin ∠ABD =55=DE BD ，得到DE =2x ，运用勾股定理，得到BE =25x 2-2x 2=4x ，从而得到AE =x ,EF =ED -DF =DE -AF =2x -52，在Rt △AEF 中，利用勾股定理计算x 即可．【详解】(1)∵D 是AC 的中点，∴CD =DA ，∵DE ⊥AB ，AB 是⊙O 的直径，∴DA =AH ，∴CD =DA =AH，∴∠ADH =∠DAC ，∴AF =DF ．(2)∵DE ⊥AB ，AB 是⊙O 的直径，。

2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)

2024年中考数学复习重难点题型训练—圆的相关证明与计算（含答案解析）类型一基本性质有关的1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．(1)求证：直线PE是⊙O的切线；(2)若⊙O的半径为6，∠P=30°，求CE的长．【答案】(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，可得BD=CD=12BC=6，在Rt△CDE中，即得CE的长是3．本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．(1)求证：CE与⊙O相切；(2)若AD=4，∠D=60°，求线段AB，BC的长．【答案】(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，60°，即得AB=3BD=23，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=2AB= 6，又△AOC是等腰直角三角形，OA=OC=2，得AC=22，故CF=AC2−AF2=2，从而BC=BF+CF=6+2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．3.（2021·山东临沂市·中考真题）如图，已知在⊙O中，＝＝，OC与AD相交于点AB BC CDE．求证：（1）AD∥BC（2）四边形BCDE为菱形．【答案】（1）见解析；（2）见解析【分析】（1）连接BD ，根据圆周角定理可得∠ADB=∠CBD ，根据平行线的判定可得结论；（2）证明△DEF ≌△BCF ，得到DE=BC ，证明四边形BCDE 为平行四边形，再根据 BCCD =得到BC=CD ，从而证明菱形．【详解】解：（1）连接BD ，∵ AB BCCD ==，∴∠ADB=∠CBD ，∴AD ∥BC ；（2）连接CD ，∵AD ∥BC ，∴∠EDF=∠CBF ，∵ BCCD =，∴BC=CD ，∴BF=DF ，又∠DFE=∠BFC ，∴△DEF ≌△BCF （ASA ），∴DE=BC ，∴四边形BCDE 是平行四边形，又BC=CD ，∴四边形BCDE 是菱形．【点睛】本题考查了垂径定理，圆周角定理，弧、弦、圆心角的关系，全等三角形的判定和性质，菱形的判定，解题的关键是合理运用垂径定理得到BF=DF ．4.（2021·四川南充市·中考真题）如图，A ，B 是O 上两点，且AB OA =，连接OB 并延长到点C ，使BC OB =，连接AC ．（1）求证：AC 是O 的切线．（2）点D ，E 分别是AC ，OA 的中点，DE 所在直线交O 于点F ，G ，4OA =，求GF 的长．【答案】（1）见解析；（2）【分析】（1）先证得△AOB 为等边三角形，从而得出∠OAB=60°，利用三角形外角的性质得出∠C=∠CAB=30°，由此可得∠OAC=90°即可得出结论；（2）过O 作OM ⊥DF 于M ，DN ⊥OC 于N ，利用勾股定理得出AC=30°的直角三角形的性质得出DN ，再根据垂径定理和勾股定理即可求出GF 的长．【详解】（1）证明：∵AB=OA ，OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°，∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线；（2）∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点，∴OE//BC ，DC=过O 作OM ⊥DF 于M ，DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中，∠C=30°，∴DN=12DC=∴OM=3连接OG ，∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定，熟练掌握相关的知识是解题的关键．5.（2021·安徽中考真题）如图，圆O 中两条互相垂直的弦AB ，CD 交于点E ．（1）M 是CD 的中点，OM ＝3，CD ＝12，求圆O 的半径长；（2）点F 在CD 上，且CE ＝EF ，求证：AF BD ⊥．【答案】（1）35；（2）见解析．【分析】（1）根据M 是CD 的中点，OM 与圆O 直径共线可得OM CD ⊥，OM 平分CD ，则有6MC =，利用勾股定理可求得半径的长；（2）连接AC ，延长AF 交BD 于G ，根据CE EF =，AE FC ⊥，可得AF AC =，12∠=∠，利用圆周角定理可得2D ∠=∠，可得1D ∠=∠，利用直角三角形的两锐角互余，可证得90AGB ∠=︒，即有AF BD ⊥．【详解】（1）解：连接OC ，∵M 是CD 的中点，OM 与圆O 直径共线∴OM CD ⊥，OM 平分CD ，90OMC ∴∠=︒12CD = 6MC ∴=．在Rt OMC △中．OC ===∴圆O 的半径为（2）证明：连接AC ，延长AF 交BD 于G ．CE EF = ，AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理，圆周角定理，直角三角形的两锐角互余，勾股定理等知识点，熟练应用相关知识点是解题的关键．∠是 AD所对的圆周角，6.（2021·浙江中考真题）如图，已知AB是⊙O的直径，ACD∠=︒．30ACD∠的度数；（1）求DABAB=，求DF的（2）过点D作DE AB⊥，垂足为E，DE的延长线交⊙O于点F．若4长．【答案】（1）60︒；（2）23【分析】（1）连结BD ，根据圆周角性质，得B ACD ∠=∠；根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算，即可得到答案；（2）根据含30°角的直角三角形性质，得12AD AB =；根据垂径定理、特殊角度三角函数的性质计算，即可得到答案．【详解】（1）连结BD ，30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径，90ADB ∴∠=︒，9060DAB B ∴∠=︒-∠=︒（2）90ADB ∠=︒ ，30B ∠=︒，4AB =∴122AD AB ==60DAB ∠=︒ ，DE AB ⊥，且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=．【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识；解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质，从而完成求解．7.（2021·湖南中考真题）如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．【答案】（1）见解析；（2）5CE =．【分析】（1）连接OD ，由点D 是 BC的中点得OD ⊥BC ，由DE//BC 得OD ⊥DE ，由OD 是半径可得DE 是切线；（2）证明△ODE 是等腰直角三角形，可求出OE 的长，从而可求得结论．【详解】解：（1）连接OD 交BC 于点F ，如图，∵点D 是 BC的中点，∴OD ⊥BC ，∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切；（2）∵AC 是O 的直径，且AB=10,∴∠ABC=90°，152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得，OE =∴5CE OE OC =-=．【点睛】此题主要考查了切线的判定与性质的综合运用，熟练掌握切线的判定与性质是解答此题的关键．8.（2021·湖南张家界市·中考真题）如图，在Rt AOB 中，90∠=︒ABO ，30OAB ∠=︒，以点O 为圆心，OB 为半径的圆交BO 的延长线于点C ，过点C 作OA 的平行线，交O 于点D ，连接AD ．（1）求证：AD 为O 的切线；（2）若2OB =，求弧CD 的长．【答案】（1）见解析；（2）23π【分析】（1）连接OB ，先根据直角三角形的性质得到∠AOB=60°，再运用平行线的性质结合已知条件可得60AOD ∠=︒，再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可；（2）先求出∠COD ，然后再运用弧长公式计算即可．【详解】（1）证明：连接OD∵30OAB ∠=︒，90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线；（2）∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=．【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点，掌握圆的切线的证明方法成为解答本题的关键．9.（2020•齐齐哈尔）如图，AB 为⊙O 的直径，C 、D 为⊙O 上的两个点，AC=CD =DB ，连接AD ，过点D 作DE ⊥AC 交AC 的延长线于点E ．（1）求证：DE 是⊙O 的切线．（2）若直径AB ＝6，求AD 的长．【分析】（1）连接OD ，根据已知条件得到∠BOD =13×180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．【解析】（1）证明：连接OD，=CD =DB ，∵AC∴∠BOD=13×180°＝60°，=DB ，∵CD∴∠EAD＝∠DAB=12∠BOD＝30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∵∠DAB＝30°，AB＝6，∴BD=12AB＝3，∴AD=62−32=33．10.（2020•深圳）如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝10，BC＝6，求CD的长．【分析】（1）证明：连接AC、OC，如图，根据切线的性质得到OC⊥CD，则可判断OC∥AD，所以∠OCB＝∠E，然后证明∠B＝∠E，从而得到结论；（2）利用圆周角定理得到∠ACB＝90°，则利用勾股定理可计算出AC＝8，再根据等腰三角形的性质得到CE＝BC＝6，然后利用面积法求出CD的长．【解析】（1）证明：连接AC、OC，如图，∵CD为切线，∴OC⊥CD，∴CD⊥AD，∴OC∥AD，∴∠OCB＝∠E，∵OB＝OC，∴∠OCB＝∠B，∴∠B＝∠E，∴AE＝AB；（2）解：∵AB为直径，∴∠ACB＝90°，∴AC=102−62=8，∵AB＝AE＝10，AC⊥BE，∴CE＝BC＝6，∵12CD•AE=12AC•CE，∴CD=6×810=245．11.（2020•陕西）如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°．连接AO并延长，交⊙O于点D，连接BD．过点C作⊙O的切线，与BA的延长线相交于点E．（1）求证：AD∥EC；（2）若AB＝12，求线段EC的长．【分析】（1）连接OC，由切线的性质可得∠OCE＝90°，由圆周角定理可得∠AOC＝90°，可得结论；（2）过点A作AF⊥EC交EC于F，由锐角三角函数可求AD＝83，可证四边形OAFC是正方形，可得CF＝AF＝43，由锐角三角函数可求EF＝12，即可求解．【解析】证明：（1）连接OC，∵CE与⊙O相切于点C，∴∠OCE＝90°，∵∠ABC＝45°，∴∠AOC＝90°，∵∠AOC+∠OCE＝180°，∴∴AD∥EC（2）如图，过点A作AF⊥EC交EC于F，∵∠BAC＝75°，∠ABC＝45°，∴∠ACB＝60°，∴∠D＝∠ACB＝60°，∴sin∠ADB=AB AD==83，∴AD=∴OA＝OC＝43，∵AF⊥EC，∠OCE＝90°，∠AOC＝90°，∴四边形OAFC是矩形，又∵OA＝OC，∴四边形OAFC是正方形，∴CF＝AF＝43，∵∠BAD＝90°﹣∠D＝30°，∴∠EAF＝180°﹣90°﹣30°＝60°，∵tan∠EAF=EF AF=3，∴EF=3AF＝12，∴CE＝CF+EF＝12+43．类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．(1)求证：∠D=∠EBC；(2)若CD=2BC，AE=3，求⊙O的半径．【答案】(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．13.（2022·北部湾）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E，延长BA交⊙O于点F.（1）求证：DE是⊙O的切线（2）若AE DE=23，AF=10，求⊙O的半径.【答案】（1）证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线（2）解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD=CD，即OD是△ABC的中位线，∵AC是⊙O的直径，∴∠CFA=90°，∵DE⊥AB，∴∠BED=90°，∴∠CFA=∠BED=90°，∴DE∥CF，∴BE=EF，即DE是△FBC的中位线，∴CF=2DE，∵AE DE=23，∴设AE=2x，DE=3k，CF=6k，∵AF=10，∴BE=EF=AE+AF=2k+10，∴AC=BA=EF+AE=4k+10，在Rt△ACF中，由勾股定理，得AC2=AF2+CF2，即(4k+10)2=102+(6k)2，解得：k=4，∴AC=4k+10=4×4+10=26，∴OA=13，即⊙O的半径为13.【知识点】平行线的判定与性质；等腰三角形的性质；圆周角定理；切线的判定；三角形的中位线定理【解析】【分析】（1）连接OD ，根据等腰三角形的性质可得∠C=∠ODC ，∠B=∠C ，则∠B=∠ODC ，推出OD ∥AB ，由平行线的性质可得∠ODE=∠DEB=90°，即DE ⊥OD ，据此证明；（2）连接CF ，由（1）知OD ⊥DE ，则OD ∥AB ，易得OD 是△ABC 的中位线，根据圆周角定理可得∠CFA=90°，根据垂直的概念可得∠BED=90°，则DE ∥CF ，推出DE 是△FBC的中位线，得CF=2DE ，设AE=2x ，DE=3k ，CF=6k ，则BE=EF=2k+10，AC=BA=4k+10，根据勾股定理可得k 的值，然后求出AC 、OA ，据此可得半径.14.（2021·江苏无锡市·中考真题）如图，四边形ABCD 内接于O ，AC 是O 的直径，AC 与BD 交于点E ，PB 切O 于点B ．（1）求证：PBA OBC ∠=∠；（2）若20PBA Ð=°，40ACD ∠=︒，求证：OAB CDE V V ∽．【答案】（1）见详解；（2）见详解【分析】（1）由圆周角定理的推论，可知∠ABC=90°，由切线的性质可知∠OBP=90°，进而即可得到结论；（2）先推出20OCB OBC ∠=∠=︒，从而得∠AOB=40°，继而得∠OAB=70°，再推出∠CDE=70°，进而即可得到结论．【详解】证明：（1）∵AC 是O 的直径，∴∠ABC=90°，∵PB 切O 于点B ，∴∠OBP=90°，∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒，∴PBA OBC ∠=∠；（2）∵20PBA Ð=°，PBA OBC ∠=∠，∴20OBC ∠=︒，∵OB=OC ，∴20OCB OBC ∠=∠=︒，∴∠AOB=20°+20°=40°，∵OB=OA ，∴∠OAB=∠OBA=(180°-40°)÷2=70°，∴∠ADB=12∠AOB=20°，∵AC 是O 的直径，∴∠ADC=90°，∴∠CDE=90°-20°=70°，∴∠CDE=∠OAB ，∵40ACD ∠=︒，∴40ACD AOB ∠=∠=︒，∴OAB CDE V V ∽．【点睛】本题主要考查圆的性质以及相似三角形的判定定理，掌握圆周角定理的推论，相似三角形的判定定理，切线的性质定理，是解题的关键．15.（2020•衢州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝10，AC ＝6，连结OC ，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．【分析】（1）利用垂径定理以及圆周角定理解决问题即可．（2）证明△AEC∽△BCA，推出CE AC=AC AB，求出EC即可解决问题．【解析】（1）证明：∵AE＝DE，OC是半径，=CD ，∴AC∴∠CAD＝∠CBA．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE，∴OC⊥AD，∴∠AEC＝90°，∴∠AEC＝∠ACB，∴△AEC∽△BCA，∴CE AC=AC AB，∴CE6=610，∴CE＝3.6，∵OC=12AB＝5，∴OE＝OC﹣EC＝5﹣3.6＝1.4．16.（2020•铜仁市）如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D 是直径AB延长线上一点，且∠BCE＝∠BCD．（1）求证：CD是⊙O的切线；（2）若AD＝8，BE CE=12，求CD的长．【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【解析】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD是⊙O的切线；（2）解：∵∠A＝∠BCE，∴tanA=BC AC=tan∠BCE=BE CE=12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC=CD AD=12，∵AD＝8，∴CD＝4．17.（2020•衡阳）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【分析】（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；（2）连接DE，根据圆周角定理得到∠ADE＝90°，根据相似三角形的性质得到AC=325，根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论．【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AE AD=AD AC，108=8AC，∴AC=325，∴CD=AD2−AC2==245，∵OD⊥BC，AC⊥BC，∴△OBD∽△ABC，∴OD AC=BD BC，∴5325=BD BD+245，∴BD=1207．18.（2020•遵义）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交BC 于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【解析】（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BA=BF BD，∴BD2＝BF•BA＝2×6＝12．∴BD＝23．19.（2019•陕西）如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．【分析】（1）根据切线的性质得到∠OAP＝90°，根据圆周角定理得到∠BCD＝90°，根据平行线的性质和判定定理即可得到结论；（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．【解析】（1）证明：∵AP是⊙O的切线，∴∠OAP＝90°，∵BD是⊙O的直径，∴∠BCD＝90°，∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO，∴DC∥AP；（2）解：∵AO∥BC，OD＝OB，∴延长AO交DC于点E，则AE⊥DC，OE=12BC，CE=12CD，在Rt△AOP中，OP=62+82=10，由（1）知，△AOP∽△CBD，∴DB OP=BC OA=DC AP，即1210=BC6=DC8，∴BC=365，DC=485，∴OE=185，CE=245，在Rt△AEC中，AC=AE2+CE2==20（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC 是O 的切线：（2）若2,33OA BE OD ==，求DA 的长．【答案】（1）见解析；（2）910【分析】（1）连接OC ，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC 是圆O 的切线；（2）根据已知得到OA=2DA ，证明△DCO ∽△DEB ，得到DO CO DB EB =，可得DA=310EB ，即可求出DA 的长．【详解】解：（1）如图，连接OC ，由题意可知：∠ACB 是直径AB 所对的圆周角，∴∠ACB=90°，∵OC ，OB 是圆O 的半径，∴OC=OB ，∴∠OCB=∠ABC ，又∵∠DCA=∠ABC ，∴∠DCA=∠OCB ，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC ⊥DC ，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB+===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．21.（2021·江苏扬州市·中考真题）如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ．（1）试判断CD 与B 的位置关系，并说明理由；（2）若AB =，60BCD ∠=︒，求图中阴影部分的面积．【答案】（1）相切，理由见解析；（2）π-【分析】（1）过点B 作BF ⊥CD ，证明△ABD ≌△FBD ，得到BF=BA ，即可证明CD 与圆B 相切；（2）先证明△BCD 是等边三角形，根据三线合一得到∠ABD=30°，求出AD ，再利用S △ABD -S 扇形ABE 求出阴影部分面积．【详解】解：（1）过点B 作BF ⊥CD ，∵AD ∥BC ，∴∠ADB=∠CBD ，∵CB=CD ，∴∠CBD=∠CDB ，∴∠ADB=∠CDB ，又BD=BD ，∠BAD=∠BFD=90°，∴△ABD ≌△FBD （AAS ），∴BF=BA ，则点F 在圆B 上，∴CD 与圆B 相切；（2）∵∠BCD=60°，CB=CD ，∴△BCD 是等边三角形，∴∠CBD=60°∵BF ⊥CD ，∴∠ABD=∠DBF=∠CBF=30°，∴∠ABF=60°，∵AB=BF=，∴AD=DF=tan30AB ⋅︒=2，∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-．【点睛】本题考查了切线的判定，全等三角形的判定和性质，等边三角形的判定和性质，扇形面积，三角函数的定义，题目的综合性较强，难度不小，解题的关键是正确做出辅助线．22.（2020•上海）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC 于点D．（1）求证：∠BAC＝2∠ABD；（2）当△BCD是等腰三角形时，求∠BCD的大小；（3）当AD＝2，CD＝3时，求边BC的长．【分析】（1）连接OA．利用垂径定理以及等腰三角形的性质解决问题即可．（2）分三种情形：①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD．③若DB＝DC，则D与A重合，这种情形不存在．分别利用三角形内角和定理构建方程求解即可．（3）如图3中，作AE∥BC交BD的延长线于E．则AE BC=AD DC=23，推出AO OH=AE BH=43，设OB＝OA＝4a，OH＝3a，根据BH2＝AB2﹣AH2＝OB2﹣OH2，构建方程求出a即可解决问题．【解析】（1）证明：连接OA．A∵AB＝AC，=AC ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠BAD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC+∠C+∠BDC＝180°，∴8∠ABD＝180°，∴∠C＝3∠ABD＝67.5°．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠C ＝4∠ABD ，∵∠DBC+∠C+∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23，∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ，∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =∴BC ＝2BH =23.（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC是O的切线：（2）若2,33OA BEOD==，求DA的长．【答案】（1）见解析；（2）9 10【分析】（1）连接OC，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC是圆O的切线；（2）根据已知得到OA=2DA，证明△DCO∽△DEB，得到DO CODB EB=，可得DA=310EB，即可求出DA的长．【详解】解：（1）如图，连接OC，由题意可知：∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∵OC，OB是圆O的半径，∴OC=OB，∴∠OCB=∠ABC，又∵∠DCA=∠ABC，∴∠DCA=∠OCB，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC⊥DC，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB +===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．(1)求证：BF与⊙O相切；(2)若AP=OP，cosA=45，AP=4，求BF的长．【答案】(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD，然后利用等腰三角形的性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE= 90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．25.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD ，∠BDC =∠BAD ．(1)求证：CD 是⊙O 的切线．(2)若tan∠BED =23，AC =9，求⊙O 的半径．【答案】（1）连接OD ，由圆周角定理得出∠ADB =90°，证出OD ⊥CD ，由切线的判定可得出结论；(2)证明△BDC∽△DAC ，由相似三角形的性质得出CD AC =BC CD =BD DA =23，由比例线段求出CD 和BC 的长，可求出AB 的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.（2021·山东菏泽市·中考真题）如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．【答案】（1）见解析；（2）=2BG 【分析】（1）连接OE ，证明OE ⊥EF 即可；（2）由3sin 5F =证得4sin 5G =，运用正弦的概念可得结论．【详解】解：（1）证明：连接OE ，如图，∵OA=OE∴∠OAE=∠OEA ．∵EF=PF ，∴∠EPF=∠PEF∵∠APH=∠EPF ，∴∠APH=∠EPF ，∴∠AEF=∠APH ．∵CD ⊥AB ，∴∠AHC=90°．∴∠OAE+∠APH=90°．∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF ．∵OE 是O 的半径∴EF 是圆的切线，（2）∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =，则5FG x=由勾股定理得，4FH x=由（1）得，OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =，即45OE OE BG =+∵8OE =∴8485BG =+解得，2BG =【点睛】此题主要考查了圆的切线的判定，勾股定理和解直角三角形等知识，熟练掌握切线的判定是解答此题的关键．27.（2022·黔东南）（1）请在图中作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹，不写作法）；的中点，过点B的（2）如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE切线与AC的延长线交于点D.①求证：BD⊥AD；②若AC=6，tan∠ABC=34，求⊙O的半径.【答案】（1）解：如下图所示（2）解：①如下图所示，连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角，∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示，连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理；三角形的外接圆与外心；切线的性质；解直角三角形；作图-线段垂直平分线【解析】【解答】（1）∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点，半径为交点到任意顶点的距离，∴做AB、AC的垂直平分线交于点O，以OB为半径，以O为圆心做圆即可得到△ABC 的外接圆；【分析】（1）利用尺规作图分别作出AC，AB的垂直平分线，两垂直平分线交于点O，然后以点O为圆心，OB的长为半径画圆即可.（2）①连接OC，OB，利用切线的性质可证得OB⊥BD，利用圆周角定理可证得∠COE=2∠CAE，由点B是弧CE的中点，可推出∠CAE=∠BOE，利用平行线的判定定理可证得AD∥OB，由此可证得结论；②连接CE，利用同弧所对的圆周角相等，可证得∠ABC=∠AEC，利用直径所对的圆周角是直角，可推出∠ACE=90°；再利用解直角三角形求出CE的长，利用勾股定理求出AE的长.28.（2022·鄂州）如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB=∠OAC，过点O作BC的平行线交PC的延长线于点D.（1）试判断PC与⊙O的位置关系，并说明理由；（2）若PC＝4，tanA＝12，求△OCD的面积.【答案】（1）解：PC与⊙O相切，理由如下：∵AB是圆O的直径，∴∠ACB=90°，∴∠OCB+∠OCA=90°，∵OA=OC，∴∠OCA=∠OAC，∵∠PCB=∠OAC，∴∠PCB=∠OCA，∴∠PCB+∠OCB=∠OCA+∠OCB=90°，即∠PCO=90°，∴PC与⊙O相切（2）解：∵∠ACB=90°，tanA=12，∴BC AC=12，∵∠PCB=∠OAC，∠P=∠P，∴△PBC∽△PCA，∴PC PA=PB PC=BC CA=12，∴PA=8，PB=2，∴AB=6，∴OC=OB=3，∴OP=5，∵BC∥OD，∴△PBC∽△POD，∴PB OP=PC PD，即25=4PD，∴PD=10，∴CD=6，∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质；圆周角定理；切线的判定；相似三角形的判定与性质；锐角三角函数的定义【解析】【分析】（1）由圆周角定理得∠ACB=90°，根据等腰三角形的性质可得∠OCA=∠OAC，结合∠PCB=∠OAC得PCB=∠OCA，结合∠OCB+∠OCA=90°可得∠PCO=90°，据此证明；（2）根据三角函数的概念可得BC AC=12，易证△PBC∽△PCA，根据相似三角形的性质可得PA、PB，然后求出AB、OP，证明△PBC∽△POD，根据相似三角形的性质可得PD，由PD-PC=CD可得CD，然后根据三角形的面积公式进行计算.29.（2022·毕节）如图，在△ABC中，∠ACB=90∘，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F.（1）求证：BF=BD；（2）若CF=1，tan∠EDB=2，求⊙O直径.【答案】（1）证明：连接OE，如下图所示：∵AC为圆O的切线，∴∠AEO=90°，∵AC⊥BC，∴∠ACB=90°，∴OE∥BC，∴∠F=∠DEO，又∵OD=OE，∴∠ODE=∠DEO，∴∠F=∠ODE，∴BD=BF.（2）解：连接BE，如下图所示：由(1)中证明过程可知：∠EDB=∠F，。

中考数学点对点-涉及圆的证明与计算问题(解析版)

专题27 涉及圆的证明与计算问题专题知识点概述圆的证明与计算是中考必考点，也是中考的难点之一。

纵观全国各地中考数学试卷，能够看出，圆的证明与计算这个专题内容有三种题型：选择题、填空题和解答题。

一、与圆有关的概念1．圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

圆的半径或直径决定圆的大小，圆心决定圆的位置。

2．圆心角：顶点在圆心上的角叫做圆心角。

圆心角的度数等于它所对弧的度数。

3.圆周角：顶点在圆周上，并且两边分别与圆相交的角叫做圆周角。

4. 外接圆和外心：经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆。

外接圆的圆心，叫做三角形的外心。

外心是三角形三条边垂直平分线的交点。

外心到三角形三个顶点的距离相等。

5．若四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个圆叫做这个四边形的外接圆。

6.和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。

内心是三角形三个角的角平分线的交点。

内心到三角形三边的距离相等。

二、与圆有关的规律1.圆的性质：（1）圆具有旋转不变性；（2）圆具有轴对称性；（3）圆具有中心对称性。

2.垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。

3．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．4．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弧相等，那么他们所对的圆心角相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角相等，所对的弧相等，所对的弦心距也相等。

5.在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．7．圆内接四边形的特征①圆内接四边形的对角互补；②圆内接四边形任意一个外角等于它的内对角。

2025年广东中考数学第一部分中考考点梳理第六章圆

算
T22(2)②/4分切求圆的面积
扇形面积的
2022
计算
填空，
T15/3分
已知扇形半径和圆心角
求面积
为什么考
核心素养
/
返回
目录
考什么
年份
2021
考点
题型/分值
设问角度
扇形面积的计
填空，与等腰直角三角形结合
算
T13/4分求阴影部分面积
2020 扇形弧长公式
2019
怎么考
扇形面积的
计算
填空，把扇形围成圆锥求底面
课标要求
会计算圆的弧长、扇形的面积.了解正多边形的概念及正多边形与圆的关
系.
返回
目录
近6年考情分析表
考什么
年份
考点
题型/分值
怎么考
设问角度
图形
圆锥体积公
解答，
(2)综合与实践，求滤纸
2024
式
T21(2)/4分围成圆锥形的体积
几何直观
运算能力
推理能力
圆面积的计
解答，
(2)②圆与三角形的边相
2023
【说明】基于直线和圆的位置关系，一条直线与一个圆的位置关系有三种可能
情况：不相交、交于两点、交于一点.这里只需要分析后两种情况.
交于两点：如图(a)，直线l与☉O交于两点P和Q，连接OP，OQ，则△OPQ为等
腰三角形.
交于一点：如图(b)，直线l与☉O只有一个交点P.此时称l为☉O在点P处的切
线，称点P为切点.因为l上的其他点到点O的距离
2025年广东中考数学第一部分中考考点梳理
第六章
第21讲
圆
圆的基本性质
课标要求

2024中考数学一轮复习核心知识点精讲—与圆有关的计算

2024中考数学一轮复习核心知识点精讲—与圆有关的计算1.掌握弧长和扇形面积计算公式；2.会利用弧长和扇形面积计算公式进弧长和扇形面积的计算考点1：圆内正多边形的计算（1）正三角形在⊙O 中△ABC 是正三角形，有关计算在Rt BOD ∆中进行：::1:2OD BD OB =；（2）正四边形同理，四边形的有关计算在Rt OAE ∆中进行，::OE AE OA =（3）正六边形同理，六边形的有关计算在Rt OAB ∆中进行，::2AB OB OA =.考点2：扇形的弧长和面积计算扇形：（1）弧长公式：180n Rl π=；（2）扇形面积公式：213602n R S lRπ==n ：圆心角R ：扇形多对应的圆的半径l ：扇形弧长S ：扇形面积注意：（1）对于弧长公式，关键是要理解1°的圆心角所对的弧长是圆周长的，即；（2）公式中的ｎ表示1°圆心角的倍数，故ｎ和180都不带单位，R 为弧所在圆的半径；（3）弧长公式所涉及的三个量：弧长、圆心角度数、弧所在圆的半径，知道其中的两个量就可以求出第三个量.(4)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即；(5)在扇形面积公式中，涉及三个量：扇形面积S 、扇形半径R 、扇形的圆心角，知道其中的两个量就可以求出第三个量.考点3：扇形与圆柱、圆锥之间联系1、圆柱：（1）圆柱侧面展开图2S S S =+侧表底=222rh rππ+C 1D 1（2）圆柱的体积：2V r hπ=2、圆锥侧面展开图（1）S S S =+侧表底=2Rr r ππ+（2）圆锥的体积：213V r hπ=注意：圆锥的底周长=扇形的弧长（180r 2Rn ΠΠ=）【题型1：正多边形和圆的有关计算】【典例1】（2023•福建）我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率π的近似值为3.1416．如图，⊙O 的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计⊙O 的面积，可得π的估计值为，若用圆内接正十二边形作近似估计，可得π的估计值为（）A．B ．2C ．3D ．2【答案】C【解答】解：如图，AB是正十二边形的一条边，点O是正十二边形的中心，过A作AM⊥OB于M，在正十二边形中，∠AOB＝360°÷12＝30°，∴AM＝OA＝，＝OB•AM＝＝，∴S△AOB∴正十二边形的面积为12×＝3，∴3＝12×π，∴π＝3，∴π的近似值为3，故选：C．【变式1-1】（2023•临沂）将一个正六边形绕其中心旋转后仍与原图形重合，旋转角的大小不可能是（）A．60°B．90°C．180°D．360°【答案】B【解答】解：由于正六边形的中心角为＝60°，所以正六边形绕其中心旋转后仍与原图形重合，旋转角可以为60°或60°的整数倍，即可以为60°，120°，180°，240°，300°，360°，不可能是90°，故选：B．【变式1-2】（2023•安徽）如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE﹣∠COD＝（）A．60°B．54°C．48°D．36°【答案】D【解答】解：∵五边形ABCDE是正五边形，∴∠BAE＝＝108°，∠COD＝＝72°，∴∠BAE﹣∠COD＝108°﹣72°＝36°，故选：D．【变式1-3】（2023•山西）蜂巢结构精巧，其巢房横截面的形状均为正六边形．如图是部分巢房的横截面图，图中7个全等的正六边形不重叠且无缝隙，将其放在平面直角坐标系中，点P，Q，M均为正六边形的顶点．若点P，Q的坐标分别为，（0，﹣3），则点M的坐标为（）A．（3，﹣2）B．（3，2）C．（2，﹣3）D．（﹣2，﹣3）【答案】A【解答】解：设中间正六边形的中心为D，连接DB．∵点P，Q的坐标分别为，（0，﹣3），图中是7个全等的正六边形，∴AB＝BC＝2，OQ＝3，∴OA＝OB＝，∴OC＝3，∵DQ＝DB＝2OD，∴OD＝1，QD＝DB＝CM＝2，∴M（3，﹣2），故选：A．【变式1-4】（2023•内江）如图，正六边形ABCDEF内接于⊙O，点P在上，点Q是的中点，则∠CPQ 的度数为（）A．30°B．45°C．36°D．60°【答案】B【解答】解：如图，连接OC，OD，OQ，OE，∵正六边形ABCDEF，Q是的中点，∴∠COD＝∠DOE＝＝60°，∠DOQ＝∠EOQ＝∠DOE＝30°，∴∠COQ＝∠COD+∠DOQ＝90°，∴∠CPQ＝∠COQ＝45°，故选：B．【题型2：弧长和扇形面积的有关计算】【典例2】（2023•张家界）“莱洛三角形”也称为圆弧三角形，它是工业生产中广泛使用的一种图形．如图，分别以等边△ABC的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的封闭图形是“莱洛三角形”．若等边△ABC的边长为3，则该“莱洛三角形”的周长等于（）A．πB．3πC．2πD．2π﹣【答案】B【解答】解：∵△ABC是等边三角形，∴AB＝BC＝AC＝3，∠A＝∠B＝∠C＝60°，∴＝＝，∵的长＝＝π，∴该“莱洛三角形”的周长是3π．故选：B．【变式2-1】（2022•广西）如图，在△ABC中，CA＝CB＝4，∠BAC＝α，将△ABC绕点A逆时针旋转2α，得到△AB′C′，连接B′C并延长交AB于点D，当B′D⊥AB时，的长是（）A．πB．πC．πD．π【答案】B【解答】解：∵CA＝CB，CD⊥AB，∴AD＝DB＝AB′．∴∠AB′D＝30°，∴α＝30°，∵AC＝4，∴AD＝AC•cos30°＝4×＝2，∴，∴的长度l＝＝π．故选：B．【变式2-2】（2022•丽水）某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为2m，高为2m，则改建后门洞的圆弧长是（）A．m B．m C．m D．（+2）m【答案】C【解答】解：连接AC，BD，AC和BD相交于点O，则O为圆心，如图所示，由题意可得，CD＝2m，AD＝2m，∠ADC＝90°，∴tan∠DCA＝＝＝，AC＝＝4（m），∴∠ACD＝60°，OA＝OC＝2m，∴∠ACB＝30°，∴∠AOB＝60°，∴优弧ADCB所对的圆心角为300°，∴改建后门洞的圆弧长是：＝（m），故选：C．【变式2-3】（2023•锦州）如图，点A，B，C在⊙O上，∠ABC＝40°，连接OA，OC．若⊙O的半径为3，则扇形AOC（阴影部分）的面积为（）A．πB．πC．πD．2π【答案】D【解答】解：∵∠ABC＝40°，∴∠AOC＝2∠ABC＝80°，∴扇形AOC的面积为，故选：D．【题型3：有圆有关的阴影面积的计算】【典例3】（2023•广元）如图，半径为5的扇形AOB中，∠AOB＝90°，C是上一点，CD⊥OA，CE⊥OB，垂足分别为D，E，若CD＝CE，则图中阴影部分面积为（）A．B．C．D．【答案】B【解答】解：连接OC，如图所示，∵∠AOB＝90°，CD⊥OA，CE⊥OB，∴∠AOB＝∠ODC＝∠OEC＝90°，∴四边形OECD是矩形，∵CD ＝CE ，∴四边形OECD 是正方形，∴∠DCE ＝90°，△DCE 和△OEC 全等，∴S 阴影＝S △DCE +S 半弓形BCE＝S △OCE +S 半弓形BCE＝S 扇形COB＝＝，故选：B ．【变式3-1】（2023•雅安）如图，某小区要绿化一扇形OAB 空地，准备在小扇形OCD 内种花，在其余区域内（阴影部分）种草，测得∠AOB ＝120°，OA ＝15m ，OC ＝10m ，则种草区域的面积为（）A ．B ．C ．D ．【答案】B 【解答】解：S 阴影＝S 扇形AOB ﹣S 扇形COD ＝＝（m 2）．故选：B．【变式3-2】（2023•鄂州）如图，在△ABC中，∠ABC＝90°，∠ACB＝30°，AB＝4，点O为BC的中点，以O为圆心，OB长为半径作半圆，交AC于点D，则图中阴影部分的面积是（）A．5πB．5﹣4πC．5﹣2πD．10﹣2π【答案】C【解答】解：连接OD．在△ABC中，∠ABC＝90°，∠ACB＝30°，AB＝4，∴BC＝AB＝4，∴OC＝OD＝OB＝2，∴∠DOB＝2∠C＝60°，∴S阴＝S△ACB﹣S△COD﹣S扇形ODB＝×4×4﹣﹣＝8﹣3﹣2π＝5﹣2π．故选：C．【变式3-3】（2022•凉山州）家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件，已知扇形的圆心角∠BAC＝90°，则扇形部件的面积为（）A．米2B．米2C．米2D．米2【答案】C【解答】解：连结BC，AO，如图所示，∵∠BAC＝90°，∴BC是⊙O的直径，∵⊙O的直径为1米，∴AO＝BO＝（米），∴AB＝＝（米），∴扇形部件的面积＝π×（）2＝（米2），故选：C．【题型4：圆锥的有关计算】【典例4】（2023•东营）如果圆锥侧面展开图的面积是15π，母线长是5，则这个圆锥的底面半径是（）A．3B．4C．5D．6【答案】A【解答】解：设底面半径为R，则底面周长＝2πR，圆锥的侧面展开图的面积＝×2πR×5＝15π，∴R＝3．故选：A．【变式4-1】（2022•牡丹江）圆锥的底面圆半径是1，母线长是3，它的侧面展开图的圆心角是（）A．90°B．100°C．120°D．150°【答案】C【解答】解：圆锥侧面展开图的弧长是：2π×1＝2π，设圆心角的度数是n度．则＝2π，解得：n＝120．故选：C．【变式4-2】（2022•广安）蒙古包可以近似地看作由圆锥和圆柱组成．下图是一个蒙古包的示意图，底面圆半径DE＝2m，圆锥的高AC＝1.5m，圆柱的高CD＝2.5m，则下列说法错误的是（）A．圆柱的底面积为4πm2B．圆柱的侧面积为10πm2C．圆锥的母线AB长为2.25mD．圆锥的侧面积为5πm2【答案】C【解答】解：∵底面圆半径DE＝2m，∴圆柱的底面积为4πm2，所以A选项不符合题意；∵圆柱的高CD＝2.5m，∴圆柱的侧面积＝2π×2×2.5＝10π（m2），所以B选项不符合题意；∵底面圆半径DE＝2m，即BC＝2m，圆锥的高AC＝1.5m，∴圆锥的母线长AB＝＝2.5（m），所以C选项符合题意；∴圆锥的侧面积＝×2π×2×2.5＝5π（m2），所以D选项不符合题意．故选：C．【变式4-3】（2022•赤峰）如图所示，圆锥形烟囱帽的底面半径为12cm，侧面展开图为半圆形，则它的母线长为（）A．10cm B．20cm C．5cm D．24cm【答案】D【解答】解：设母线的长为R，由题意得，πR＝2π×12，解得R＝24，∴母线的长为24cm，故选：D．一．选择题（共10小题）1．如图，五边形ABCDE是⊙O的内接正五边形，则正五边形的中心角∠COD的度数是（）A．72°B．60°C．48°D．36°【答案】A【解答】解：∵五边形ABCDE是⊙O的内接正五边形，∴五边形ABCDE的中心角∠COD的度数为＝72°，故选：A．2．如图，正六边形ABCDEF内接于⊙O，⊙O的半径为4，则这个正六边形的边心距OM和的长分别为（）A．2，B．，πC．2，D．2，【答案】D【解答】解：如图所示，连接OC、OB，∵多边形ABCDEF是正六边形，∴∠BOC＝60°，∵OC＝OB，∴△BOC是等边三角形，∴∠OBM＝60°，∴OM＝OB sin∠OBM＝4×＝2，的长＝＝；故选：D．3．如图，⊙O的半径为1，点A、B、C都在⊙O上，∠B＝45°，则的长为（）A．πB．πC．πD．π【答案】C【解答】解：∵∠B＝45°，∴∠AOC＝90°，∵⊙O的半径为1，∴的长＝＝＝π，故选：C．4．如图，AB是半圆O的直径，C、D是半圆上两点，且满足∠ADC＝120°，BC＝1，则的长为（）A．B．C．D．【答案】A【解答】解：如图，连接OC．∵∠ADC＝120°，∴∠ABC＝60°，∵OB＝OC，∴∠OCB＝∠OBC＝∠B＝60°，OB＝OC＝BC＝1，∴的长为＝，故选：A．5．如图，等边△ABC的边长为4，D、E、F分别为边AB、BC、AC的中点，分别以A、B、C三点为圆心，以AD长为半径作三条圆弧，则图中三条圆弧的弧长之和是（）A．πB．2πC．4πD．6π【答案】B【解答】解：依题意知：图中三条圆弧的弧长之和＝×3＝2π．故选：B．6．若扇形的半径是12cm弧长是20πcm，则扇形的面积为（）A．120πcm2B．240πcm2C．360πcm2D．60πcm2【答案】A【解答】解：该扇形的面积为：（cm2）．故选：A．7．如图，将含60°角的直角三角板ABC绕顶点A顺时针旋转45°后得到△AB'C'，点B经过的路径为弧BB′，若∠BAC＝60°，AC＝3，则图中阴影部分的面积是（）A．B．C．D．3π【答案】C【解答】解：在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝3，∴∠ABC＝30°．∴AB＝2AC＝6．根据旋转的性质知△ABC≌△AB′C′，则S△ABC＝S△AB′C′，AB＝AB′．∴S阴影＝S扇形ABB′+S△AB′C′﹣S△ABC＝＝．故选：C．8．如图，四边形ABCD为正方形，边长为4，以B为圆心、BC长为半径画，E为四边形内部一点，且BE⊥CE，∠BCE＝30°，连接AE，则阴影部分面积（）A．B．6πC．D．【答案】C【解答】解：如图，作EF⊥AB于点F，∵BE⊥CE，∠BCE＝30°，∴BE＝BC＝2，∠CBE＝60°，∴CE＝BE＝2，∠EBF＝30°，∴EF＝BE＝1，∴S阴影＝S扇形ABC﹣S△BCE﹣S△ABE＝﹣×2×﹣×1＝4π﹣2﹣2．故选：C．9．如图，圆锥的母线长为5cm，高是4cm，则圆锥的侧面展开扇形的圆心角是（）A．180°B．216°C．240°D．270°【答案】B【解答】解：∵圆锥的母线长为5cm，高是4cm，∴圆锥底面圆的半径为：＝3（cm），∴2π×3＝，解得n＝216°．故选：B．10．已知圆锥的底面半径是4，母线长是5，则圆锥的侧面积是（）A．10πB．15πC．20πD．25π【答案】C【解答】解：圆锥的侧面积＝×2π×4×5＝20π，故选：C．二．填空题（共8小题）11．AB是⊙O的内接正六边形一边，点P是优弧AB上的一点（点P不与点A，B重合）且BP∥OA，AP 与OB交于点C，则∠OCP的度数为90°．【答案】90°．【解答】解：∵AB是⊙O的内接正六边形一边，∴∠AOB＝＝60°，∴＝30°，∵BP∥OA，∴∠OAC＝∠P＝30°，∴∠OCP＝∠AOB+∠OAC＝60°+30°＝90°．故答案为：90°．12．已知正六边形的内切圆半径为，则它的周长为12．【答案】见试题解答内容【解答】解：如图，连接OA、OB，OG；∵六边形ABCDEF是边长等于正六边形的半径，设正六边形的半径为a，∴△OAB是等边三角形，∴OA＝AB＝a，∴OG＝OA•sin60°＝a×＝，解得a＝2，∴它的周长＝6a＝12．故答案为：12．13．如图，一条公路（公路的宽度忽略不计）的转弯处是一段圆弧，点O是这段弧所在圆的圆心，半径OA＝90m，圆心角∠AOB＝80°，则这段弯路的长度为40πm．【答案】见试题解答内容【解答】解：由题意得，这段弯路的长度为，故答案为：40π．14．已知扇形的圆心角为120°，面积为27πcm2，则该扇形所在圆的半径为9cm．【答案】见试题解答内容【解答】解：∵扇形的圆心角为120°，面积为27πcm2，∴由S＝得：r＝＝＝9cm，故答案为：9cm．15．圆锥的侧面积是10πcm2，底面半径是2cm，则圆锥的母线长为5cm．【答案】见试题解答内容【解答】解：底面半径是2cm，则扇形的弧长是4π．设母线长是l，则×4πl＝10π，解得：l＝5．故答案为：5．16．如图，用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽，则这个纸帽的高是4 cm．【答案】见试题解答内容【解答】解：∵圆心角为120°，半径为6cm的扇形的弧长＝＝4π，∴圆锥的底面圆的周长为4π，∴圆锥的底面圆的半径为2，∴这个纸帽的高＝＝4（cm）．故答案为4．17．如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是6π．【答案】见试题解答内容【解答】解：阴影部分的面积＝以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积＝扇形ABB′的面积，则阴影部分的面积是：＝6π，故答案为：6π．18．如图，将边长相等的正六边形和正五边形拼接在一起，则∠ABC的度数为132°．【答案】见试题解答内容【解答】解：由题意得：正六边形的每个内角都等于120°，正五边形的每个内角都等于108°，∴∠ABC＝360°﹣120°﹣108°＝132°，故答案为：132．一．选择题（共7小题）1．在2022年北京冬奥会开幕式和闭幕式中，一片“雪花”的故事展现了“世界大同、天下一家”的主题，让世界观众感受到中国人的浪漫，如图，将“雪花”图案（边长为4的正六边形ABCDEF）放在平面直角坐标系中，“雪花”中心与原点重合，C，F在y轴上，则顶点B的坐标为（）A．（4，2）B．（4，4）C．D．【答案】C【解答】解：连接OB，OA，如图所示：∵正六边形是轴对称图形，中心与坐标原点重合，∴△AOB是等边三角形，AO＝BO＝AB＝4，AB⊥x轴，AM＝BM，∵AB＝4，∴AM＝BM＝2，∴OM＝，∴点B的坐标为：（2，2），故选：C．2．如图，正五边形ABCDE内接于⊙O，点F在弧AE上．若∠CDF＝95°，则∠FCD的大小为（）A．38°B．42°C．49°D．58°【答案】C【解答】解：如图，连接OE，OD，CE，∵五边形ABCDE是正五边形，∴∠CDE＝（5﹣2）×180°÷5＝108°，∵∠CDF＝95°，∴∠FDE＝∠CDE﹣∠CDF＝108°﹣95°＝13°，∴∠FCE＝13°，∵正五边形ABCDE内接于⊙O，∴∠EOD＝360°÷5＝72°，∴∠ECD＝＝36°，∴∠FCD＝∠FCE+∠ECD＝36°+13°＝49°，故选：C．3．如图，在⊙O中，点C在优弧上，将沿BC折叠后刚好经过AB的中点D．若⊙O的半径为5，AB＝4，则的长是（）A．B．C．D．4π【答案】A【解答】解：连接AC，OB，OD，CD，作CF⊥AB于点F，作OE⊥CF于点E，由垂定理可知OD⊥AB于点D，AD＝BD＝＝．又OB＝5，∴OD＝＝＝，∵CA、CD所对的圆周角为∠CBA、∠CBD，且∠CBA＝∠CBD，∴CA＝CD，△CAD为等腰三角形．∴AF＝DF＝＝，又四边形ODFE为矩形且OD＝DF＝，∴四边形ODFE为正方形．∴，∴CE＝＝＝2，∴CF＝CE+EF＝3＝BF，故△CFB为等腰直角三角形，∠CBA＝45°，∴所对的圆心角为90°，∴＝＝．故选：A．4．如图，将直径为4的半圆形分别沿CD，EF折叠使得直径两端点A，B的对应点都与圆心O重合，则图中阴影部分的面积为（）A．B．C．D．【答案】A【解答】解：连接AC，OC，OE，BE，由题意得：CD垂直平分OA，∴AC＝OC，∴△OAC是等边三角形，同理△BOE是等边三角形，∴∠AOC＝∠BOE＝60°，∴∠COE＝60°，∴弓形AMC、弓形ONC、弓形OPE的面积相等，∵圆的直径是4，∴OA＝2，∴扇形OAC的面积＝＝，△OAC的面积＝OA2＝，∴扇形OCE的面积＝扇形OAC的面积＝，∴弓形AMC的面积＝扇形OAC的面积﹣△OAC的面积＝﹣，∴阴影的面积＝扇形OCE的面积﹣弓形AMC的面积×2＝﹣2×（﹣）＝2﹣．故选：A．5．如图，扇形AOB中，∠AOB＝90°，点C，D分别在OA，上，连接BC，CD，点D，O关于直线BC 对称，的长为π，则图中阴影部分的面积为（）A．B．C．D．【答案】A【解答】解：连接BD、OD，交BC与E，由题意可知，BD＝BO，∵OD＝OB，∴OD＝OB＝DB，∴∠BOD＝60°，∵∠AOB＝90°，∴∠AOD＝30°，∵的长为π，∴，∴r＝6，∴OB＝6，∴OE＝＝3，BE＝OB＝3，∴CE＝OE＝，+S△COE﹣S△BOE＝+﹣＝6π﹣3．∴阴影部分的面积＝S扇形BOD故选：A．6．如图，点O是半圆圆心，BE是半圆的直径，点A，D在半圆上，且AD∥BO，∠ABO＝60°，AB＝8，过点D作DC⊥BE于点C，则阴影部分的面积是（）A．B．C．D．【答案】B【解答】解：如图，连接OA，∵∠ABO＝60°，OA＝OB，∴△AOB是等边三角形，∴OA＝OB＝AB＝8，∵AD∥BO，∴∠OAD＝∠AOB＝60°，∵OA＝OD，∴△AOD是等边三角形，∴∠AOD＝60°，∵△OAD与△ABD与△AOB是等底等高的三角形，∴S阴影＝S扇形AOB＝＝π．故选：B．7．如图，一个圆锥的母线长为6，底面圆的直径为8，那么这个圆锥的侧面积是（）A．24πB．40πC．48πD．【答案】A【解答】解：根据题意，这个圆锥的侧面积＝×8π×6＝24π．故选：A．二．填空题（共5小题）8．如图，已知正方形ABCD的边长为4cm，以AB，AD为直径作两个半圆，分别取弧AB，弧AD的中点M，N，连结MC，NC，则图中阴影部分的周长为（4）cm．【答案】（4）．【解答】解：解法一：如图，取AD的中点O，连接NO，设CN交AD于点E，∵N是弧AD的中点，∴NO⊥AD，∵CD⊥AD，∴NO∥CD，∴△NOE∽△CDE，∴＝＝＝＝，∴OE＝OD＝，在Rt△NOE中，NE＝＝＝，∴CM＝CN＝3NE＝2，∵点M，N分别为弧AB，弧AD的中点∴弧AB，弧AD的长度和为2×＝2π，∴图中阴影部分的周长为（4）cm．解法二：作NH⊥BC于点H，则CH＝2，NH＝6，在Rt△NHC中，NC＝＝＝2，∴CM＝CN＝2，∵点M，N分别为弧AB，弧AD的中点∴弧AB，弧AD的长度和为2×＝2π，∴图中阴影部分的周长为（4）cm．故答案为：（4）．9．如图，△ABC是边长为1的等边三角形，曲线CC1C2C3C4…是由多段120°的圆心角所对的弧组成的，其中的圆心为A，半径为AC；的圆心为B，半径为BC1；的圆心为C，半径为CC2；的圆心为A，半径为AC3……，，，，…的圆心依次按点A，B，C循环，则的长是．（结果保留π）【答案】．【解答】解：∵△ABC是边长为1的等边三角形，∴AC＝AC1＝1，∠CAB＝∠ABC＝∠BCA＝60°，；∴BC2＝BC1＝AB+AC1＝2，CC3＝CC2＝BC2+AB＝3，∠CAC1＝∠C1BC2＝C2CC3＝120°，∴的半径为1；的半径为2；的半径为3；所对的圆心角为120°，∴的半径为n，所对的圆心角为120°，∴所在圆的半径为2023，所对的圆心角为120°，∴的长为．故答案为：．10．如图，已知矩形纸片ABCD，AD＝2，，以A为圆心，AD长为半径画弧交BC于点E，将扇形AED剪下围成一个圆锥，则该圆锥的底面半径为．【答案】见试题解答内容【解答】解：cos∠BAE＝，∴∠BAE＝30°，∴∠DAE＝60°，∴圆锥的侧面展开图的弧长为：＝π，∴圆锥的底面半径为π÷2π＝．11．如图，从一块半径为20的圆形纸片上剪出一个圆心角是90°的扇形ABC，如果将剪下来的扇形ABC围成一个圆锥，则该圆锥的底面半径是．【答案】．【解答】解：连接BC，如图，∵∠BAC＝90°，∴BC为⊙O的直径，即BC＝20，∴AB＝10，设该圆锥的底面圆的半径为r，根据题意得2πr＝，解得r＝，即该圆锥的底面圆的半径为m．故答案为：．12．如图，AB是圆锥底面的直径，AB＝6cm，母线PB＝9cm，点C为PB的中点，若一只蚂蚁从A点处出发，沿圆锥的侧面爬行到C点处，则蚂蚁爬行的最短路程为cm．【答案】cm．【解答】解：由题意知，底面圆的直径AB＝6cm，故底面周长等于6πcm，设圆锥的侧面展开后的扇形圆心角为n°，根据底面周长等于展开后扇形的弧长得6π＝，解得n＝120°，所以展开图中∠APD＝120°÷2＝60°，因为半径PA＝PB，∠APB＝60°，故三角形PAB为等边三角形，又∵D为PB的中点，所以AD⊥PB，在直角三角形PAD中，PA＝9cm，PD＝cm，根据勾股定理求得AD＝（cm），所以蚂蚁爬行的最短距离为cm．故答案为：cm．1．（2023•连云港）如图，矩形ABCD内接于⊙O，分别以AB、BC、CD、AD为直径向外作半圆．若AB＝4，BC＝5，则阴影部分的面积是（）A．π﹣20B．π﹣20C．20πD．20【答案】D【解答】解：如图，连接BD，则BD过点O，在Rt△ABD中，AB＝4，BC＝5，∴BD2＝AB2+AD2＝41，S阴影部分＝S以AD为直径的圆+S以AB为直径的圆+S矩形ABCD﹣S以BD为直径的圆＝π×（）2+π×（）2+4×5﹣π×（）2＝+20﹣＝20，故选：D．2．（2023•广安）如图，在等腰直角△ABC中，∠ACB＝90°，AC＝BC＝2，以点A为圆心，AC为半径画弧，交AB于点E，以点B为圆心，BC为半径画弧，交AB于点F，则图中阴影部分的面积是（）A．π﹣2B．2π﹣2C．2π﹣4D．4π﹣4【答案】C【解答】解：在等腰直角△ABC中，∠ACB＝90°，AC＝BC＝2，∴∠A＝∠B＝45°，+S扇形CBF﹣S△ABC∴阴影部分的面积S＝S扇形CAE＝×2﹣＝2π﹣4．故选：C．3．（2023•上海）如果一个正多边形的中心角是20°，那么这个正多边形的边数为18．【答案】见试题解答内容【解答】解：360°÷20°＝18．故这个正多边形的边数为18．故答案为：18．4．（2023•衡阳）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是10．【答案】10．【解答】解：∵多边形是正五边形，∴正五边形的每一个内角为：×180°×（5﹣2）＝108°，∴∠O＝180°﹣（180°﹣108°）×2＝36°，∴正五边形的个数是360°÷36°＝10．故答案为：10．5．（2023•宿迁）若圆锥的底面半径为2cm，侧面展开图是一个圆心角为120°的扇形，则这个圆锥的母线长是6cm．【答案】见试题解答内容【解答】解：设圆锥的母线长为x cm，根据题意得＝2π•2，解得x＝6，即圆锥的母线长为6cm．故答案为6．6．（2023•徐州）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形．若母线长l为6cm，扇形的圆心角θ为120°，则圆锥的底面圆的半径r为2cm．【答案】2．【解答】解：由题意得：母线l＝6，θ＝120°，2πr＝，∴r＝2（cm）．故答案为：2．7．（2022•广元）如图，将⊙O沿弦AB折叠，恰经过圆心O，若AB＝2，则阴影部分的面积为．【答案】．【解答】解：如图，过点O作AB的垂线并延长，垂足为C，交⊙O于点D，连结AO，AD，根据垂径定理得：AC＝BC＝AB＝，∵将⊙O沿弦AB折叠，恰经过圆心O，∴OC＝CD＝r，∴OC＝OA，∴∠OAC＝30°，∴∠AOD＝60°，∵OA＝OD，∴△AOD是等边三角形，∴∠D＝60°，在Rt△AOC中，AC2+OC2＝OA2，∴（）2+（r）2＝r2，解得：r＝2，∵AC＝BC，∠OCB＝∠ACD＝90°，OC＝CD，∴△ACD≌△BCO（SAS），＝×π×22＝．∴阴影部分的面积＝S扇形ADO故答案为：．8．（2023•金华）如图，在△ABC中，AB＝AC＝6cm，∠BAC＝50°，以AB为直径作半圆，交BC于点D，交AC于点E，则弧DE的长为πcm．【答案】π．【解答】解：连接OE，OD，∵OD＝OB，∴∠B＝∠ODB，∵AB＝AC，∴∠B＝∠C，∴∠C＝∠ODB，∴OD∥AC，∴∠EOD＝∠AEO，∵OE＝OA，∴∠OEA＝∠BAC＝50°，∴∠EOD＝∠BAC＝50°，∵OD＝AB＝×6＝3（cm），∴的长＝＝π（cm）．故答案为：π．9．（2023•温州）图1是4×4方格绘成的七巧板图案，每个小方格的边长为，现将它剪拼成一个“房子”造型（如图2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形CDEF作为题字区域（点A，E，D，B在圆上，点C，F在AB上），形成一幅装饰画，则圆的半径为5．若点A，N，M在同一直线上，AB∥PN，DE＝EF，则题字区域的面积为．【答案】5；．【解答】解：如图所示，依题意，GH＝2＝GQ，∵过左侧的三个端点Q，K，L作圆，QH＝HL＝4，又NK⊥QL，∴O在KN上，连接OQ，则OQ为半径，∵OH＝r﹣KH＝r﹣2，在Rt△OHQ中，OH2+QH2＝QO2，∴（r﹣2）2+42＝r2，解得：r＝5；连接OE，取ED的中点T，连接OT，交AB于点S，连接PB，AM，过点O作OU⊥AM于点U.连接OA．由△OUN∽△NPM，可得＝＝，∴OU＝．MN＝2，∴NU＝，∴AU＝＝，∴AN＝AU﹣NU＝2，∴AN＝MN，∵AB∥PN，∴AB⊥OT，∴AS＝SB，∴NS∥BM，∴NS∥MP，∴M，P，B共线，又NB＝NA，∴∠ABM＝90°，∵MN＝NB，NP⊥MP，∴MP＝PB＝2，∴NS＝MB＝2，∵KH+HN＝2+4＝6，∴ON＝6﹣5＝1，∴OS＝3，∵，设EF＝ST＝a，则，在Rt△OET中，OE2＝OT2+TE2，即，整理得5a2+12a﹣32＝0，即（a+4）（5a﹣8）＝0，解得：或a＝﹣4，∴题字区域的面积为．故答案为：．。

中考数学复习《圆的证明与计算》经典题型及测试题(含答案)

中考数学复习《圆的证明与计算》经典题型及测试题（含答案）阅读与理解圆的相关知识的考查是中考数学中的一个重要内容，圆作为一个载体，常与三角形、四边形结合，考查切线的性质及判定、相似三角形的性质与判定、解直角三角形、求阴影面积等．解题时要先分析题干中的条件，然后从图象中挖掘隐含条件，最后再解题．类型一切线的判定判定一条直线是圆的切线，首先看圆的半径是否过直线与圆的交点，有半径则证垂直；没有半径，则连接圆心与切点，构造半径证垂直．例1 (2016·黄石)如图，⊙O的直径为AB，点C在圆周上(异于A，B)，AD⊥CD.(1)若BC＝3，AB＝5，求AC的值；(2)若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．【分析】（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得AC的长即可；（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得⊥OCA=⊥CAD，即可得到OC⊥AD，由于AD⊥CD，那么OC⊥CD，由此得证．【自主解答】（1）解：⊥AB是⊥O直径，C在⊥O上，⊥⊥ACB=90°，又⊥BC=3，AB=5，⊥由勾股定理得AC=4；（2）证明：⊥AC是⊥DAB的角平分线，⊥⊥DAC=⊥BAC，又⊥AD⊥DC，⊥⊥ADC=⊥ACB=90°，⊥⊥ADC⊥⊥ACB，⊥⊥DCA=⊥CBA，又⊥OA=OC，⊥⊥OAC=⊥OCA，⊥⊥OAC+⊥OBC=90°，⊥⊥OCA+⊥ACD=⊥OCD=90°，⊥DC是⊥O的切线．变式训练1．(2017·白银) 如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．解：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB==，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．类型二切线的性质已知某条直线是圆的切线，当圆心与切点有线段连接时，直接利用切线的性质：圆的切线垂直于过切点的半径；当圆心与切点没有线段相连时，则作辅助线连接圆心与切点，再利用切线的性质解题．例2 (2016·资阳) 如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连接BD.(1)求证：∠A＝∠BDC；(2)若CM平分∠ACD，且分别交AD，BD于点M，N，当DM＝1时，求MN的长．【分析】(1)连接OD，由切线的性质可得∠CDB＋∠ODB＝90°，由AB是直径，可得∠ADB＝90°，进而可得∠A＋∠ABD＝90°，进而求得∠A＝∠BDC；(2)由角平分线及三角形外角性质可得∠A＋∠ACM＝∠BDC＋∠DCM，即∠DMN＝∠DNM，再根据勾股定理求得MN的长．【自主解答】(1)如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，∴∠BDC＋∠ODB＝90°.∵AB是⊙O的直径，∴∠ADB＝90°，∴∠A＋∠ABD＝90°.∵OB＝OD，∴∠OBD＝∠ODB，∴∠A＋∠ODB＝90°，∴∠A＝∠BDC.(2)∵CM平分∠ACD，∴∠DCM＝∠ACM.∵∠A＝∠BDC，∴∠A＋∠ACM＝∠BDC＋∠DCM.即∠DMN＝∠DNM.∵∠ADB＝90°，DM＝1，∴DN＝DM＝1，∴MN＝变式训练2．(2017·长沙)如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E，=（1）求证：OA=OB；（2）已知AB=4，OA=4，求阴影部分的面积．解：（1）连接OC，∵AB与⊙O相切于点C∴∠ACO=90°，由于=，∴∠AOC=∠BOC，∴∠A=∠B∴OA=OB，（2）由（1）可知：△OAB是等腰三角形，∴BC=AB=2，∴sin∠COB==，∴∠COB=60°，∴∠B=30°，∴OC=OB=2，∴扇形OCE的面积为：=，△OCB的面积为：×2×2=2=2﹣π∴S阴影类型三圆与相似的综合圆与相似的综合主要体现在圆与相似三角形的综合，一般结合切线的判定与性质综合考查，求线段长或半径．一般的解题思路是利用切线的性质构造角相等，进而构造相似三角形，利用相似三角形对应边成比例求出所求线段或半径．例3 (2017·兰州) 如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD，∠D=∠BAF．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2，求EF的长．【分析】（1）由BC是⊙O的直径，得到∠BAF+∠FAC=90°，等量代换得到∠D+∠AOD=90°，于是得到结论；（2）连接BF，根据相似三角形的判定和性质即可得到结论．【自主解答】解：（1）∵BC是⊙O的直径，∴∠BAF+∠FAC=90°，∵∠D=∠BAF，∠AOD=∠FAC，∴∠D+∠AOD=90°，∴∠OAD=90°，∴AD是⊙O的切线；（2）连接BF，∴∠FAC=∠AOD，∴△ACE∽△OCA，∴，∴，∴AC=AE=，∵∠CAE=∠CBF，∴△ACE∽△BFE，∴，∴=，∴EF=．变式训练3．(2016·丹东)如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.(1)求证：∠BDC＝∠A；(2)若CE＝4，DE＝2，求AD的长．(1)证明：如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，即∠ODB＋∠BDC＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°. ∴∠BDC＝∠ADO.∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A.(2)解：∵CE⊥AE，∴∠E＝90°，∴DB∥EC，∴∠DCE＝∠BDC.∵∠BDC＝∠A，∴∠A＝∠DCE.∵∠E＝∠E，∴△AEC∽△CED，∴∴CE2＝DE·AE，即16＝2(2＋AD)，∴AD＝6.。

2023年中考专题训练——圆的计算和证明(含答案)

2023年中考专题训练——圆的计算和证明1．如图，AB是⊙O的弦，点C在过点B的切线上，且OC⊥OA，OC交AB于点D．(1)判断△CBD的形状，并说明理由；(2)若CD＝3OD，AD＝8，求⊙O的半径．2．如图，Rt ABC中，90∠=︒，点O为AB上一点，以点O为圆心，以OA为半径，作OACB交AB于点E，边BC与O相切于点D．过点C作CF//AB交AD延长线于点F．(1)求证：AC CF=；(2)若4AC=，求O的半径．AE BE=，103．如图，AB是O的直径，弦CD AB⊥于点G．点F是CG的中点，连接AF并延长交O于点E，连接AD，DE．(1)求证：2=⋅；AD AE AF(2)若2AF=，求DEF的面积．CF=，34．如图，⊙O是ABC的外接圆，AB是O的直径，过点A作O的切线，交BC的延长线与点D，点E是劣弧BC上的一点，连接AE，CE．(1)求证：DAC AEC ∠=∠；(2)若4sin 5AEC ∠=，10AD =，求O 的半径． 5．如图，以ABC 的边AB 为直径作O ，交边AC 于点D ，BC 为O 的切线，弦DE AB ⊥于点F ，连结BE ．(1)求证：ABE C ∠=∠．(2)若点F 为OB 中点，且1OF =，求线段BC 的长．6．如图，AB 为O 的直径，点C 在O 上，过点C 作O 切线CD 交BA 的延长线于点D ，过点O 作OE AC ∥交切线DC 于点E ，交BC 于点F ．(1)求证：B E ∠=∠；(2)若10AB =，4cos 5B =，求EF 的长．7．如图，AB 是⊙O 的直径，点E 为线段OB 上一点（不与O ，B 重合），作CE ⊥OB ，交⊙O 于点C ，垂足为点E ，作直径CD ，过点C 的切线交DB 的延长线于点P ，作AF ⊥PC 于点F ，连接CB ．(1)求证：△CBE∽△CPB；(2)当3AB=34CFCP=时，求扇形COB的面积．8．如图，ABC内接于⊙O，10AB AC==，12BC=，点E为AC上一点，点F为CE的中点，连结BF并延长与AE交于点G，连结AF，CF．(1)求证：AFC AFG∠=∠．(2)当BG经过圆心O时，求FG的长．9．如图，已知AB为⊙O的直径，E是AB延长线上一点，点C是⊙O上的一点，连接EC、BC、AC，且EC是⊙O的切线，C为切点．(1)求证：∠BCE＝∠A；(2)过点A作AD垂直于直线EC于D，若AD＝3，DE＝4，求⊙O的半径．10．如图，点C是以O为圆心，AB为直径的半圆上一动点（不与A，B重合），8AB=，连接AC 并延长至点D，使CD AC=，过点D作AB的垂线DH，分别交ACB，CB，AB于点E，F，H，连接OC．记ABCθ∠=，θ随点C的移动而变化．(1)当45θ︒⋅=⋅；<时，求证：BH AH DH FH(2)连接OD，当2ADOθ=∠时，求OH的长．11．如图，AB是O的直径，BC是O的弦，直线MN与O相切于点C，过点B作BD MN⊥于点D．(1)求证：ABC CBD∠=∠；(2)若BC=4CD=，求O的半径．12．如图，O的直径18AB=，点E是AB上的动点，CD是经过点E的弦，过点B作O的切线交AC的延长线于点F，且CD//BF．(1)若AC=BC，分别求AE，CD的长；(2)当点E位于OB的什么位置时，以,,,O C B D为顶点的四边形是菱形？请说明理由．13．如图，AB是O的直径，过点B作AB的垂线BC，连接AC，交O于点D，O的切线DE 交BC于E．(1)求证：点E 为BC 的中点；(2)若O 的直径为3，2DE =，求AD 的长．14．如图，□OABC 的对角线相交于点D ，O 经过A 、D 两点，与BO 的延长线相交于点E ，点F 为AE 上一点，且=AF AD ．连接AE 、DF 相交于点G ，若3AG =，6EG =．(1)求□OABC 对角线AC 的长；(2)求证：□OABC 为矩形．15．读下面材料，并完成相应的任务切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．下面是不完整的证明过程，请补充完整．已知：P 为O 外一点，P A 与O 交于A ，B 两点，PM 与O 相切于点M ．求证：2PM PB PA =⋅．证明：如图，连接AM ，BM ，连接MO 并延长交O 于点C ，连接BC ．∵PM 为O 的切线，∴_______90=︒，∴90CMB BMP ∠+∠=︒，∵CM 为O 的直径，∴_______90=︒，∴90CMB MCB ∠+∠=︒，∴MCB ∠=_______，∵MAB MCB ∠=∠，∴BMP MAB ∠=∠．∵P P ∠=∠，∴PBM ∽△_______．∴PM PB PA PM =，∴2PM PB PA =⋅．学习任务：如图，若线段AB 与O 相交于C ，D 两点，且AC BD =，射线AB ，BF 为O 的两条切线，切点分别为E ，F ，连接CF ．(1)求证：AE BF =；(2)若6BF =，2CD BD =，60FBC ∠=︒，求BCF △的面积．16．如图，在O 中，B ，C 是AD 的三等分点，弦AC ，BD 相交于点E ．(1)求证：AC BD =；(2)连接CD ，若25BDC ∠=︒，求BEC ∠的度数．17．已知点C 是△ABD 的边AB 上一点，且12BC AC =，AC 为O 的直径，BD 切O 于点D ，连接DO 并延长交O 于点E ，连接BE 交O 于点M ．(1)求证：BAD ABD ∠=∠；(2)若O 的半径为1，求线段EM 的长．18．如图，在AOB 中，AO BO =，AB 与O 相切于点C ，延长BO 交O 于点P 、Q ．连接CP ，CQ ．(1)若30A ∠=︒，求CPQ ∠的大小．(2)若1tan 2CPQ ∠=，O 的半径为35AB 的长度．19．如图，AC 是⊙O 的直径，OD AB ⊥，点E 是射线DO 上一点且OE BC =，过点E 作FE DE ⊥交射线AC 于点F ．(1)求证：2OE OD =；(2)求证：ABC FEO ≌△△；(3)当EF 与⊙O 相切时，若⊙O 的半径为2，求弧BC 的长．20．如图，P A 和PB 是O 的两条切线，A ，B 为切点，点D 在AB 上，点E 和点F 分别在PB 和P A 上，且AD BE =．(1)求证：PA PB=(2)若40∠=︒，当EDFP∠是多少度时，BD AF=？请说明理由．(3)若APBα∠=，当α=__________时，四边形DEPF为菱形．参考答案：1．(1)△CBD 是等腰三角形，理由见解析 (2)14【分析】（1）由点C 在过点B 的切线上，且OC ⊥OA ，根据等角的余角相等，易证得∠CBD =∠CDB ，即可证得△CBD 是等腰三角形；（2）设OD =x ，则BC =DC =3x ，由勾股定理求出7OB x =，在Rt AOD ∆中，由勾股定理得222(7)8x x +=，求出x 的值即可得解．【解析】（1）△CBD 是等腰三角形，∵OC ⊥OA ，∴∠AOC =90°，∴∠A +∠ADO =90°，∵BC 切⊙O 于点B ，∴∠OBC =90°，∴∠OBA +∠CBD =90°，∵OA =OB ，∴∠A =∠OBA ，∴∠ADO =∠CBD ，∵∠ADO =∠CDB ，∴∠CDB =∠CBD ，∴CD =CB ；∴△CBD 是等腰三角形；（2）∵CD ＝3OD ，AD ＝8，∴设OD x =，则34CD x OC x ==，，∴BC =3x ，在Rt OBC △中，227OB OC BC x -， ∴7OA x =，在Rt AOD △中，222AD AO DO =+， ∴222(7)8x x +=，解得，2x =22x =-， ∴2714AO ==【点评】本题主要考查了切线的性质，等腰三角形的判定与性质以及勾股定理，正确识图是解答本题的关键．2．(1)见解析；(2)⊙O 的半径为6【分析】（1）连结OD ，BC 与⊙O 相切于点D ，90ODB ∠=︒，由90ACB ∠=︒，得到OD AC ，13∠=∠，由OD OA =，进一步得23∠∠=，由CF AB ∥得2F ∠=∠，则3F ∠=∠，得到结论；（2）设⊙O 的半径为r ，则2AE r =．由4AE BE =可以得到32OB r =，52AB r =，由OD AC 得到BOD BAC ∽，得到OB OD AB AC=，进一步即可得解．（1）证明：连结OD ，∵BC 与⊙O 相切于点D ，∴OD ⊥BC ，∴90ODB ∠=︒，∵90ACB ∠=︒，∴90ODB ACB ∠=∠=︒，∴OD AC ，∴13∠=∠，又∵OD OA =，∴12∠=∠，∴23∠∠=，又∵CF AB ∥，∴2F ∠=∠，∴3F ∠=∠，∴△ACF 是等腰三角形，∴AC CF =．（2）解：设⊙O 的半径为r ，则2AE r =．∵4AE BE =， ∴12BE r =， ∴32OB r =，52AB r =，由（1）知：OD AC ，∴∠BOD ＝∠BAC ，∵∠B ＝∠B ，∴BOD BAC ∽， ∴OB OD AB AC=， ∵10AC =， ∴325102r r r =， ∴6r =，即⊙O 的半径为6．【点评】此题考查了切线的性质定理，相似三角形的判定和性质、等腰三角形的判定和性质等知识，证明BOD BAC ∽是求O 的半径的关键．3．(1)见解析 (2)5【分析】（1）证明ADF AED △△∽即可；（2）先求出ADF S △，再利用相似求出AED S，最后根据DEF AED ADF S S S =-计算即可．(1)∵AB 是O 的直径，弦CD AB ⊥，∴AD AC =，DG CG =，∴ADF AED ∠=∠，∵FAD DAE ∠=∠（公共角），∴ADF AED △△∽，∴AD AF AE AD=， ∴2AD AE AF =⋅；(2)∵点F 是CG 的中点，2CF =，∴2FG =，AG∵CD AB ⊥于点G ，∴4CG DG ==，∴6FD =，AD =∴11622ADF S DF AG =⨯⋅=⨯△ ∵ADF AED △△∽， ∴2ADF AED S AF SAD ⎛⎫= ⎪⎝⎭，37AED =，∴AED S=， ∴45DEF AED ADF S S S =-=【点评】本题主要考查垂径定理、相似三角形的判定和性质，由垂径定理得到G 是CD 的中点是解题的关键．本题所考查知识点较多，综合性较强，解题时注意知识的灵活运用．4．(1)见解析(2)154【分析】（1）AD 与⊙O 相切于点E ，90DAC BAC ∠+∠=︒，AB 是O 的直径，则∠ABC ＋∠BAC ＝90°，DAC ABC ∠=∠，又ABC AEC ∠=∠，结论得证；（2）在ABD △，90BAD ∠=︒，10AD =，4sin sin 5ABD AEC ∠=∠=，求得BD ，由勾股定理得到AB ，即得O 的半径．(1)证明：∵AD 与⊙O 相切于点E ，∴AB ⊥AD ，∴∠BAD ＝90°，∴90DAC BAC ∠+∠=︒∵AB 是O 的直径，∴90ACB ∠=︒，∴90ABC BAC ∠+∠=︒，∴DAC ABC ∠=∠∵ABC AEC ∠=∠，∴DAC AEC ∠=∠．(2)解：在ABD △，90BAD ∠=︒，10AD =，4sin sin 5ABD AEC ∠=∠=， ∴52510sin 42AD BD ABD ==⨯=∠，由勾股定理得，222225151022AB BD AD ⎛⎫=-- ⎪⎝⎭， ∴O 的半径为154．【点评】此题考查了切线的性质定理、圆周角定理及其推论、锐角三角函数、勾股定理等知识，熟练掌握定理的应用是解题的关键．5．(1)见解析； 43【分析】（1）根据切线的性质以及DE AB ⊥，可得BC DE ∥，可得ADE C ∠=∠，根据同弧所对的圆周角相等，可得ADE ABE ∠=∠，进而即可得证；（2）连接OE ，垂径定理求得EF ，进而证明AFD ∆∽ABC ∆，根据相似三角形的性质，列出比例式，代入数值即可求解．（1）证明 ∵AB 是⊙O 的直径，BC 为⊙O 的切线，∴AB ⊥BC ，∵DE ⊥AB ，∴DE //BC ，∴ADE C ∠=∠，∵弧AE 所对圆周角是ABE ∠和ADE ∠，∴ABE ADE ∠=∠，∴ABE C ∠=∠；（2）连接OE ，∵点F 为OB 中点，AB ⊥BC ，∴OF =12OE ， 1OF =，∴2OE =，∴EF =FD∴ AF =AO OF OE OF +=+=3，ED FD ∥ ，∴AFD ∆∽ABC ∆，∴AF FD AB BC =，即34=，得，BC =．【点评】本题考查了切线的性质、等弧所对的圆周角相等、垂径定理、相似三角形的性质与判定，综合运用以上知识是解题的关键．6．(1)见解析 (2)163【分析】（1）证明：连接OC ，利用圆周角定理及切线的性质定理求出OCB ACD ∠=∠，由圆的半径相等求出B OCB ∠=∠，利用平行线的性质求出ACD E ∠=∠，即可得到结论B E ∠=∠；（2）由4cos 5BC B AB ==求出8BC =，AC =6，证明ACB OCE ∽△△求出OE ，根据三角形中位线的性质求出OF ，即可得到EF ．（1）证明：连接OC ，如图所示：∵AB 为⊙O 的直径，∴90ACB ACO OCB ∠=∠+∠=︒．∵DE 是⊙O 的切线，∴90OCD ACO ACD ∠=∠+∠=︒，∴OCB ACD ∠=∠，∵OB ，OC 是⊙O 的半径，∴OB OC =，∴B OCB ∠=∠，∵OE AC ∥，∴ACD E ∠=∠，∴B E ∠=∠；（2）解：在Rt ACB 中，4cos 5BC B AB ==，10AB =， ∴8BC =，∵OC OA OB ==， ∴1110522OC AB ==⨯=， ∴22221086AC AB BC --，∵90ACB OCE ∠=∠=︒，B E ∠=∠，∴ACB OCE ∽△△， ∴AC AB OC OE=，即6105OE =， ∴253OE =， ∵OF AC ∥，O 为AB 中点， ∴132OF AC ==， ∴2516333EF OE OF =-=-=．【点评】此题考查了圆周角定理、切线的性质定理、相似三角形的判定及性质、勾股定理、三角函数，熟练掌握各知识点并应用解决问题是解题的关键．7．(1)见解析(2)2π【分析】（1）先证明∠CEB=∠CBP＝90°，再由∠D+∠P=90°，∠CAB＋∠CBE＝90°，∠CAB=∠D，推出∠CBE=∠P，即可证明结论；（2）设CF=3k，CP=4k，先证明∠F AC=∠CAB，得到CE=CF=3k，再由相似三角形的性质得到BC2＝CE•CP；从而求出sin∠CBE=∠CBE=60°，即可证明△OBC是等边三角形，得到∠COB=60°，据此求解即可．（1）解：∵CE⊥OB，CD为圆O的直径，∴∠CEB=∠DBC＝90°，∴∠CEB=∠CBP＝90°，∵PF是切线，∴∠DCP=90°，∴∠D+∠P=90°，∵AB是直径，∴∠ACB=90°∴∠CAB＋∠CBE＝90°，∵∠CAB=∠D，∴∠CBE=∠P，∴△CBE∽△CPB；（2）解：∵34 CFCP=，∴设CF=3k，CP=4k，∵PF是切线，∴OC ⊥PF ，∵AF ⊥PF ，∴AF ∥OC ．∴∠F AC =∠ACO ，∵OA =OC ，∴∠OAC =∠ACO ，∴∠F AC =∠CAB ，∴CE =CF =3k ，∵△CBE ∽△CPB ， ∴CB CE CP CB=， ∴BC 2＝CE •CP ；∴BC =23k∴sin ∠CBE 323k= ∴∠CBE =60°，∵OB =OC ，∴△OBC 是等边三角形，∴∠COB =60°， ∵43AB =∴扇形COB 的面积260232360ππ⨯=（）【点评】本题主要考查了圆切线的性质，相似三角形的性质与判定，圆周角定理，角平分线的性质，解直角三角形，扇形面积，等边三角形的性质与判定等等，熟练掌握圆的相关知识是解题的关键．8．(1)见解析； (2)72【分析】(1)根据等腰三角形的性质，圆内接四边形的性质，补角的性质证明即可；(2) 利用勾股定理，三角形中位线定理，三角形全等性质计算即可．（1）证明：∵AB AC =，∴A ABC CB =∠∠，∵ACB AFB ∠=∠，∴ABC AFB ∠=∠，∵180ABC AFC ∠+∠=︒，180AFG AFB ∠+∠=︒，∴AFC AFG ∠=∠；（2）连结AO 并延长AO 交于点H ，∵AB AC =，∴AH BC ⊥，6BH CH ==，∴8AH =，连结OC ，设OH x =，则8OA OC x ==-，在Rt OCH 中，()22268x x +=-，解得74x =， ∵OH 是Rt BCF 的中位线， ∴722CF OH ==，∵点F 为CE 的中点，∴EAF CAF ∠=∠，∵AFC AFG ∠=∠，AF AF =，∴()ACF AGF ASA ≌△△， ∴72FG CF ==．【点评】本题考查了圆的内接四边形的性质，勾股定理，等腰三角形的性质，三角形中位线定理，三角形全等的判定和性质，熟练掌握圆的性质和勾股定理是解题的关键．9．(1)见解析(2)⊙O 的半径为158【分析】（1）连结OC ，根据圆周角定理由AB 是⊙O 的直径得∠1+∠2=90°，根据切线的性质即可得到∠BCE +∠2=90°，所以∠BCE =∠1，而∠1=∠A ，即∠A =∠BCE（2）设⊙O 的半径为r ，在Rt △ADE 中利用勾股定理计算出AE =5，则OE =5-r ，OC =r ，证明△EOC ∽△EAD ，利用相似比得到EO OC EA AD =，即553r r -=，然后解方程即可得到圆的半径．（1）如图，连接OC ，∵AB 是⊙O 的直径，∴∠ACB ＝90°，即∠1＋∠2＝90°又∵EC 是⊙O 的切线∴OC ⊥EC即∠BCE ＋∠2＝90°∴∠BCE ＝∠1∵OC ＝OA∴∠1＝∠A∴∠A ＝∠BCE（2）∵OC ⊥EC又AD ⊥EC∴OC ∥AD∴EOC EAD ∠=∠，ECO EDA=∠∠∴△EOC ∽△EAD ∴EOOCEA AD =设⊙O 的半径为r在Rt △ADE 中AD ＝3，ED ＝4则AE 22AD DE +∴OE ＝5－r ；OC ＝r ∴553r r -= ∴158r =即⊙O 的半径为158【点评】本题考察了圆的切线性质及相似三角形的判定与性质，利用圆的切线性质是解决本题的关键点．10．(1)见解析(2)3【分析】（1）证△BHF ∽△DHA ，根据线段比例关系即可证；（2）过点O 作OG AD ⊥于点G ，可得OH OG =，设OH OG x ==，AG y =，由正弦定义，4sin 4x yθ+=，sin 4y θ=，则444x y y +=，即2120x x +-=，由勾股定理，得2224x y +=，解得OH 的长为3．（1） AB 是直径，90ACB DCB ︒∴∠=∠=．DH AB ⊥，CFD BFH ∠=∠，CDH ABC θ∴∠=∠=．90DCB DHB ACB ︒∠=∠=∠=，BHF DHA ∴∆∆∽．::BH DH FH AH ∴=．BH AH DH FH ∴⋅=⋅．（2）解：如图，过点O 作OG AD ⊥于点G ．由（2）知，CDH ABC θ∠=∠=．2ADO θ=∠，OD ∴平分CDH ∠．OH OG ∴=．设OH OG x ==，AG y =，则4AH x =+，2AC y =，24AD AC y ==．在Rt AGO ∆中，由勾股定理，得2224x y +=．①在Rt AHD ∆中，sin AH ADH AD ∠=，即4sin 4x y θ+=．② 在Rt ABC ∆中，sin AC ABC AB∠=，即sin 4y θ=．③ 由②③，得444x y y +=， 24y x ∴=+．代入①中，得2120x x +-=，解得3x =或4x =-（舍去）．故OH 的长为3．【点评】本题考查了相似三角形的判定和性质，圆周角定理，运用相似三角形的判定和性质解题是关键．11．(1)证明见解析(2)5【分析】（1）连接OC ，由切线的性质可得OC MN ⊥，即可证得OC BD ⊥，由平行线的性质和等腰三角形的性质可得CBD BCO ABC ∠=∠=∠，即可证得结论；（2）连接AC ，由勾股定理求得BD ，然后通过证得C ABC BD ∽△△，求得直径AB ，从而求得半径．（1）证明：连接OC ，∵MN 为O 的切线，∴OC MN ⊥，∵BD MN ⊥，∴//OC BD ，∴CBD BCO ∠=∠，又∵OC OB =，∴BCO ABC ∠=∠，∴CBD ABC ∠=∠．（2）解：连接AC ，∵BD MN ⊥，∴BCD △是直角三角形，∵BC =4CD =，∴8BD ，∵AB 是O 的直径，∴90ACB ∠=︒，∴90ACB CDB ∠=∠=︒，∵ABC CBD ∠=∠，∴C ABC BD ∽△△，∴AB CBBC BD == ∴10AB =，∴O 的半径是5．【点评】本题考查了切线的性质和圆的基本性质、三角形相似的判定和性质以及解直角三角形.通过作辅助线构建等腰三角形、直角三角形是解题的关键．12．(1)16AE =；CD =(2)当点E 位于OB 的中点位置时，以,,,O C B D 为顶点的四边形为菱形，理由见解析【分析】（1）利用勾股定理得出BC 的长，再证明AEC ACB △△得出AE 的长，由勾股定理得CE 的长，再由垂径定理即可得出答案；（2）利用对角线互相垂直且互相平分的四边形是菱形求出即可．(1)解：∵O 的直径，∴90ACB ∠=︒，∵O 的直径12218,AB AC == ∴226BC AB AC -∵过点B 的O 的切线交AC 的延长线于点F ，且CD FB ∥.∴90AEC ABF ∠=∠=︒，∴AEC ACB ∠=∠∵A A ∠=∠，∴AEC ACB △△， ∴AC AE AB AC =， ∴12218122∴16AE = ∴2242CE AC AE =-=∵OE CD ⊥，∴CE DE = ∴282CD CE ==(2)解：当点E 位于OB 的中点位置时，以,,,O C B D 为顶点的四边形为菱形．如图，理由：由（1）得CE DE =，当EO BE =时，四边形OCBD 为平行四边形，又∵OB CD ⊥，∴以点,,,O C B D 为顶点的四边形为菱形. 【点评】此题考查了切线的性质、相似三角形的判定与性质、垂径定理以、菱形的的判定、勾股定理等知识．此题难度适中，注意掌握数形结合思想与方程思想的应用．13．(1)见解析 (2)95【分析】（1）连接OD ，BD ，分别证明BE DE =和DE EC =，从而可得结论；（2）根据勾股定理求出5AC =，再证明Rt ADB Rt ABC ∆∆∽，根据相似三角形的性质可得结论．（1）连接OD ，BD ，∵DE 是圆的切线，∴90ODE ∠=︒，∵AB 是O 的直径，∴90ADB ∠=︒又90ABC ∠=︒∴90ABC ODE ADB ︒∠=∠=∠=，∵OA OD =，OB OD =∴A ODA ∠=∠，ODB OBD ∠=∠，∵90A ABD ABD DBE ADO ODB ∠+∠=∠+∠=∠+∠=︒，DBE A ODA BDE ∴∠=∠=∠=∠，BE DE ∴=，∵90DBC C BDE CDE ∠+∠=∠+∠=︒，又C OBD ODB EDC ∠=∠=∠=∠，DE EC ∴=，12BE BC ∴=， ∴点E 为BC 的中点；（2）2DE =，24BC DE ∴==，在Rt ABC ∆中，5AC ==．BAD CAB ∠=∠，ADB ABC ∠=∠·Rt ADB Rt ABC ∴∆∆∽，AD AB AB AC∴=， 295AB AD AC ∴== 【点评】本题主要考查了切线的性质，圆周角定理，相似三角形的判定与性质，熟练掌握相关性质是解答本题的关键．14．(1)63(2)见解析【分析】（1）利用弧相等，由圆周角定理推论推出ADE AGD △∽△，由相似三角形的性质可求AD 的长度，再利用平行四边形的性质可求出AC 的长度；（2）利用对角线相等的平行四边形是矩形可得证．(1)解：∵DE 是直径，3AG =，6EG =，∴90EAD ∠=︒，9AE AG EG =+=，∵=AF AD ，∴ADF AFD AED ∠=∠=∠，又∵90DAE GAD ∠=∠=︒，∴ADE AGD △∽△， ∴AD AG AE AD=， ∴23927AD AG AE =⨯=⨯=， ∴33AD =∵四边形OABC 是平行四边形， ∴263AC AD ==(2)由（1）可知：90EAD ∠=︒，∴AED △是直角三角形， ∴()222293363DE AE AD ++∵四边形OABC 是平行四边形，∴263OB OD DE ===∴AC OB =，∴□OABC 为矩形．【点评】本题考查了圆的基本性质，相似三角形的判定及性质、平行四边形的性质、矩形的判定、勾股定理．理解和掌握圆周角定理的推论及相似三角形判定及性质并能进行灵活应用是解决本题的关键．15．(1)∠CMP ；∠CBM ；∠BMP ；△PMA ；见解析(2)27【分析】阅读材料：连接AM ，BM ，连接MO 并延长交O 于点C ，连接BC ，证PBM ∽△△PMA 即可得出结论；（1）由阅读材料得2AE AC AD =⋅，2BF BD BC =⋅，再由AC =BD ，证AD =BC ，即可得出结论；（2）由阅读材料得2BF BD BC =⋅，从而求出BC =F 作FG BC ⊥于点G ，解Rt BFG △求出6FG ==，最后利用12BCF S BC FG =⋅△计算即可求解．（1）阅读材料证明：如图，连接AM ，BM ，连接MO 并延长交O 于点C ，连接BC ．∵PM 为O 的切线，∴∠CMP 90=︒，∴90CMB BMP ∠+∠=︒，∵CM 为O 的直径，∴∠CBM 90=︒，∴90CMB MCB ∠+∠=︒，∴MCB ∠=∠BMP ，∵MAB MCB ∠=∠，∴BMP MAB ∠=∠．∵P P ∠=∠，∴PBM ∽△△PMA ． ∴PM PB PA PM=， ∴2PM PB PA =⋅．故答案为：∠CMP ，∠CBM ，∠BMP ，△PMA ．（1）证明：∵AE ，BF 为O 的两条切线，∴2AE AC AD =⋅，2BF BD BC =⋅．∵AC BD =，∴AC CD BD CD +=+，即AD BC =．∴22AE BF =，∴AE BF =．（2）解：∵2CD BD =，设BD m =，则2CD m =，3BC m =，由由阅读材料得，2BF BD BC =⋅，即2236m =，解得3m = ∴3BC =如图1，过点F 作FG BC ⊥于点G ，在Rt BFG △中，sin FG FB B =，即3633FG == ∴12BCF S BC FG =⋅△16333272=⨯=．【点评】本题考查切线的性质，相似三角形的判定与性质，解直角三角形，本题属阅读材料题，通过阅读，探究出一个结论，再运用结论解决其他问题，属中考试常用考类型．16．(1)见解析(2)130°【分析】（1）根据B ，C 是AD 的三等分点，求出ABC BCD =，再根据圆心角、弧、弦之间的关系得出即可；（2）根据圆周角定理得出∠CAD =∠BDA =∠BDC =25°，根据三角形内角和定理求出∠AED ，再求出答案即可．【解析】（1）证明：B ，C 是AD 的三等分点，AB BC CD ∴==AB BC BC CD ∴+=+∴ABC BCD =∴AC =BD ；（2）连接AD ，∵∠BDC =25°，AB BC CD ==∴∠CAD =∠BDA =∠BDC =25°，∵∠AED +∠CAD +∠BDA =180°，∴∠AED =180°-∠CAD -∠BDA =180°-25°-25°=130°，∴∠BEC =∠AED =130°，故答案为：130°．【点评】本题考查了圆心角、弧、弦之间的关系和圆周角定理，能熟记圆心角、弧、弦之间的关系是解此题的关键．17．(1)见解析(2)EM【分析】（1）连接CD ，根据题意可得出BC =OA ，CD =OD ，∠AOD =∠BCD ，利用SAS 证明△AOD ≌△BCD 即可得出结论；（2）由△AOD ≌△BCD 知AD =BD ，运用勾股定理可得出BD AD ==BE =，连接DM ，证明BDM BED ∆∆得BD BM BE BD=，即2BD BM BE =，设EM =x ，BM x =，代入相关数据得方程7(7)3x -=，求出x 的值即可．(1)连接CD ，如图，∵BD 是切线，DE 是圆的直径，∴DE BD ⊥，∴BDO ∆是直角三角形. ∵12BC AC =， ∴=BC OC OA =，∴点C 为OB 的中点，CD 为OB 边上的中线，∴CD OC OD ==，∴DCO DOC ∠=∠，∴DOA DCB ∠=∠，在DOA ∆和BCD ∆中，AO BC AOD BCD CD OD =⎧⎪∠=∠⎨⎪=⎩，∴DOA DCB ∆≅∆，∴BAD ABD ∠=∠．(2)∵AC 是圆的直径，∴=90ADC ∠︒，∴ADC ∆是直角三角形，∵1AO OC CD ===，∴2AC =，由勾股定理得，2222213AD AC CD --由（1）知DOA DCB ∆≅∆， ∴3BD AD ==在Rt BDE ∆中，2,3DE BD == ∴22222(3)7BE DE BD =++连接DM ，∵DE 是圆的直径，∴90BMD EMD ∠=∠=︒，∵90EDB ∠=︒，∴BMD EDB ∠=∠，又MBD DBE ∠=∠，∴BDM BED ∆∆，∴BD BM BE BD=，即2BD BM BE =，设EM =x ，则BM x =，(7)3x -=，解得，x =∴EM = 【点评】本题主要考查了切线的性质，直角三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质，正确证明BDMBED ∆∆是解答本题的关键． 18．(1)30°(2)【分析】（1）根据切线的性质求出60COB ∠=︒，再根据圆周角定理求CPQ ∠的大小即可；（2）证明BQC BCP △∽△结合1tan 2CPQ ∠=即可求出BQ 的长度，再由相似得到的比例即可求出BC 的长度，最后根据AB =2BC 求值即可．（1）如图，连接CO ．∵AB 与O 相切于点C ，∴CO AB ⊥．∵,30AO BO A =∠=︒，∴30,60B A COB ∠=∠=︒∠=︒，∴1302CPQ COB ∠=∠=︒．（2）∵PQ 是O 的直径，∴90PCQ ∠=︒．∵1tan 2CPQ ∠=， ∴12CQ CP =∵90PCQ OCB ∠=∠=︒， OC OP =，∴OPC OCP BCQ ∠=∠=∠．∵B B ∠=∠，∴BQC BCP △∽△， ∴12BQ BC CQ BC BP CO ===， ∴2,2BP BC BC BQ ==， ∴45BP BQ BQ ==+25BQ = ∴45BC = ∴85AB =【点评】本题综合考查切线的性质、圆周角定理、正切、相似三角形的性质与判定、等腰三角形的性质，考查的知识点比较多，但是都比较简单，正确的作出辅助线是解题的关键．19．(1)见解析(2)见解析 (3)23π【分析】（1）由垂径定理及三角形中位线定理即可求解；（2）先证明AB EF ∥，再根据平行线的性质得出OAB F ∠=∠，即可证明()ABC FEO AAS ≌△△；（3）连接OB ，先证明OBC △为等边三角形，再利用弧长公式计算即可．(1)证明：∵OD AB ⊥，∴点D 是AB 的中点，∵点O 是AC 的中点，∴2BC OD =，∵OE BC =，∴2OE OD =，(2)证明∵OD AB ⊥，EF DE ⊥，∴90EDB ∠=︒，90DEF ∠=︒，∴180EDB DEF ∠+∠=︒，∴AB EF ∥，∴OAB F ∠=∠，∵AC 是⊙O 的直径，∴90ABC ∠=︒，∴ABC E ∠=∠，∵OE BC =，∴()AAS ABC FEO ≌△△，(3)解：连接OB ，∵EF 与⊙O 相切时，∴2OE =，∴2BC OE ==，∵在OBC △中，OC OB BC ==，∴OBC △为等边三角形，∴60BOC ∠=︒， ∴60221803BC L ππ⨯⨯==．【点评】本题考查了垂径定理、三角形中位线定理、平行线的性质、切线的性质、全等额三角形的判定、等边三角形的判定与性质及弧长公式，熟练掌握知识点是解题的关键．20．(1)见解析(2)70°，理由见解析(3)60°【分析】（1）连接AO 、BO 、OP ，根据切线的性质及全等三角形的判定证明△APO ≌△BPO ，即可求解；（2）由（1）得到AP =BP ，根据三角形内角和定理得到∠P AB ＝∠PBA ＝70°，证明△AFD ≌△BDE ，根据全等三角形的性质得到∠AFD ＝∠BDE ，根据三角形的内角和，得到答案；（3）根据菱形的性质与直角三角形的性质证明BD =BE =DE ，得到△BDE 是等边三角形，根据三角形内角和即可求解．（1）连接AO 、BO 、OP ，∵P A 和PB 是O 的两条切线，A ，B 为切点，∴OA ⊥AP ，OB ⊥BP ，∴∠OAP =∠OBP =90°，又∵AO =BO ，OP =OP ，∴△APO ≌△BPO （HL ），∴AP =BP ；（2）当EDF ∠是70度时，BD AF =，证明如下：由（1）可得P A ＝PB ，∴∠P AB ＝∠PBA ＝12（180°−40°）＝70°，在△AFD 和△BDE 中， AD BE FAD DBE AF BD =⎧⎪∠=∠⎨⎪=⎩，∴△AFD ≌△BDE （SAS ）∴∠AFD ＝∠BDE ，∴∠EDF ＝180°−∠BDE −∠ADF ＝180°−∠AFD −∠ADF ＝∠F AD ＝70°，故EDF ∠是70度时，BD AF =．（3）如图，当四边形DEPF为菱形时，∠APD=∠BPD，EP=DE=DF=PF，∵AP=BP，DP=DP，∴△APD≌△BPD（SAS），∴AD=BD，∴DP⊥AB，△BDP是直角三角形，∵DE=EP，∴∠DPE=∠PDE，∴∠DPB+∠DBP=∠PDE+∠BDE=90°，∴∠DBP=∠BDE，∴DE=BE，∵AD BE，∴BD=BE=DE，∴△BDE是等边三角形，∴∠DBE=60°=∠P AD，∴∠APB=180°-∠DBE-∠P AD =60°，故答案为：60°．【点评】本题考查的是切线的性质、菱形的判定与性质、全等三角形的判定和性质，掌握圆的切线垂直于经过切点的半径是解题的关键.。