SPSS操作实验作业1

合集下载

spss_实验指导书学生作业

《SPSS 及在医学中的应用》实验指导书任课教师：谭建军应用专业：生物技术专业实验学时：32实验一认识SPSS一、实验目的通过本次实验，了解SPSS的基本特征、结构、运行模式、主要窗口等，对SPSS 有一个浅层次的综合认识。

要求掌握SPSS的基本运行程序，了解如何录入数据和建立数据文件，掌握基本的数据文件编辑与修改方法。

二、实验性质基础三、主要仪器及试材计算机及SPSS软件四、实验内容[1]打开SPSS的基本方法；[2]打开文件、保存文件；[3]认识各种窗口类型；[4]练习系统参数设置；[5]录入数据；[6]保存数据文件；[7]编辑数据文件；五、实验学时10学时六、实验方法与步骤[1]找到SPSS的快捷按纽或在程序中找到SPSS，打开SPSS；[2]认识SPSS数据编辑窗、结果输出窗、帮助窗口、图表编辑窗、语句编辑窗；[3]练习系统参数设置；[4]认识SPSS数据编辑窗；[5]按要求录入数据；[6]联系基本的数据修改编辑方法；[7]保存数据文件。

七、实验注意事项遇到各种难以处理的问题，请询问指导老师。

八、上机作业试录入以下数据文件，并按要求进行变量定义。

数据：要求：(a) 变量名同表格名，以“（）”内的内容作为变量标签。

对性别（Sex）设值标签“男=0；女=1”。

(b) 正确设定变量类型。

其中学号设为数值型；日期型统一用“mm/dd/yyyy“型号；生活费用货币型。

实验二数据文件的整理一、实验目的通过本次实验，掌握数据文件的基本整理技巧。

二、实验性质基础三、主要仪器及试材计算机及SPSS软件四、实验内容[1]排序[2]文件拆分与合并[3]重编码[4]计算产生新变量[5]缺失值的处理五、实验学时10学时六、实验方法与步骤[1]找到SPSS的快捷按纽或在程序中找到SPSS，打开SPSS；[2]打开一个已经存在的数据文件；[3]按要求完成上机作业；[4]关闭SPSS。

SPSS实验指导书(全)

《SPSS统计软件应用》实验指导书目录1.实验一 SPSS的数据管理2.实验二描述性统计分析3.实验三均值检验4.实验四相关分析5.实验五因子分析6.实验六聚类分析7.实验七回归分析8.实验八判别分析实验一SPSS的数据管理一、实验目的1．熟悉SPSS的菜单和窗口界面，熟悉SPSS各种参数的设置；2．掌握SPSS的数据管理功能。

二、实验内容及步骤统计分析离不开数据，因此数据管理是SPSS的重要组成部分。

详细了解SPSS 的数据管理方法，将有助于用户提高工作效率。

SPSS的数据管理是借助于数据管理窗口和主窗口的File、Data、Transform等菜单完成的。

(一) SPSS进行统计处理的基本过程SPSS是Statistics Package for Social Sciences（社会科学统计软件包）的缩写，被广泛应用于社会科学和自然科学的各个领域中。

SPSS功能强大，但操作简单，这一特点突出地体现在它统一而简单的使用流程中。

SPSS进行统计处理的基本过程如图6-1所示：其基本步骤如下：1. 数据的录入将数据以电子表格的方式输入到SPSS中(*.sav, 是SPSS独有的格式)，也可以从其它可转换的数据文件中读出数据。

数据录入的工作分两个步骤，一是定义变量，二是录入变量值。

2. 数据的预分析在原始数据录入完成后，要对数据进行必要的预分析，如数据分组、排序、分布图、平均数、标准差的描述等，以掌握数据的基本特点和基本情况，保证后续工作的有效性，也为确定应采用的统计检验方法提供依据。

3. 统计分析按研究的要求和数据的情况确定统计分析方法，然后对数据进行统计分析。

4. 统计结果可视化在统计过程进行完后，SPSS会自动生成一系列数据表，其中包含了统计处理产生的整套数据。

为了能更形象地呈现数据，需要利用SPSS提供的图形生成工具将所得数据可视化。

如前所述，SPSS提供了许多图形来进行数据的可视化处理，使用时可根据数据的特点和研究的需求来进行选择。

SPSS操作实验作业1(附答案)

SPSS操作实验 (作业1)作为华夏儿女都曾为有着五千年的文化历史而骄傲过，作为时代青年都曾为中国所饱受的欺压而愤慨过，因为我们多是炎黄子孙。

然而，当代大学生对华夏文明究竟知道多少呢某研究机构对大学电气、管理、电信、外语、人文几个学院的同学进行了调查，各个学院发放问卷数参照各个学院的人数比例，总共发放问卷250余份，回收有效问卷228份。

调查问卷设置了调查大学生对传统文化了解程度的题目，如“佛教的来源是什么”、“儒家的思想核心是什么”、“《清明上河图》的作者是谁”等。

调查问卷给出了每位调查者对传统文化了解程度的总得分，同时也列出了被调查者的性别、专业、年级等数据信息。

请利用这些资料，分析以下问题。

问题一：分析大学生对中国传统文化的了解程度得分，并按了解程度对得分进行合理的分类。

问题二：研究获得文化来源对大学生了解传统文化的程度是否存在影响。

要求：直接导出查看器文件为.doc后打印（导出后不得修改）对分析结果进行说明，另附(手写、打印均可)。

于作业布置后，1周内上交本次作业计入期末成绩答案问题一操作过程1.打开数据文件作业。

同时单击数据浏览窗口的【变量视图】按钮，检查各个变量的数据结构定义是否合理，是否需要修改调整。

2.选择菜单栏中的【分析】→【描述统计】→【频率】命令，弹出【频率】对话框。

在此对话框左侧的候选变量列表框中选择“X9”变量，将其添加至【变量】列表框中，表示它是进行频数分析的变量。

3.单击【统计量】按钮，在弹出的对话框的【割点相等组】文本框中键入数字“5”，输出第20％、40％、60％和80％百分位数，即将数据按照题目要求分为等间隔的五类。

接着，勾选【标准差】、【均值】等选项，表示输出了解程度得分的描述性统计量。

再单击【继续】按钮，返回【频率】对话框。

4.单击【图表】按钮，勾选【直方图】和【显示正态曲线】复选框，即直方图中附带正态曲线。

再单击【继续】按钮，返回【频率】对话框。

最后，单击【确定】按钮，操作完成。

SPSS简单的练习作业

（3）
在上图中，分别显示了两两广告形式下销售额均值检验的结果。在SPSS中全部采用了LSD方法中的分布标准误，因此各种方法的前两列计算结果完全相同。表中第三列是检验统计量观测值在不同分布中概率值p，可以发现各种方法在检验敏感度上市存在差异的。以报纸广告与其他三种广告形式的两两检验结果为例，如果显著性水平α=0.05，在LSD方法中，报纸广告和广播广告的效果没有显著性差异，p值为0.412，与宣传品和体验均有显著性差异，概率p值分别是0.00，接近和0.021；但是在其他三种方法中，报纸广告只与宣传品广告存在显著性差异，而与体验无显著性差异。表中第一列星号的含义是，在显著性水平α=0.05的情况下，相应两总体的均值存在显著性差异，与第三列的结果相对应。
实验一SPSS的方差分析、相关分析与线性回归分析………………………17
1.单因素方差分析的基本操作……………………………………………17
2.单因素方差分析进一步分析的操作……………………………………18
作业一SPSS数据文件的建立和管理、数据的预处理
实验一SPSS数据文件的建立和管理、数据的预处理
【实验目的】
【实验结果与分析】
以上结果是广告形式对销售额的单因素方差的分析结果。可以看到，观测变量销售额的总离差平方和为26169.306；如果仅考虑“广告形式”单个因素的影响，则销售额总变差中，广告形式可解释的变差为5866.083，抽样误差引起的变差为20303.222，它们的方差（平均变差）分别为1955.361和145.023，相除所得的F统计量的观测值为13.483，对应的概率p值近似为0。如果显著性水平α为0.05，由于概率p值小于显著性水平α，则应拒绝零假设，认为不同广告形式对销售产生显著影响，它对销售额的影响效应不全为0。

SPSS分析作业

SPSS分析作业1.研究目的第一步，通过选取A1量表中的引领潮流、追随潮流、中国制造、欧美品牌、保修条款、优惠券、昂贵商品、四处打听、便宜货、羡慕眼光等变量，即消费者的购物频度、多少和购物风格，分析出消费者可以分为几个类别和这些类别的特点，相当于市场营销市场细分的第一步：Segmentation。

好!第二步，选取人口学变量，如年龄、职业、家庭收入、个人可支配收入、文化程度等，来了解各个类别消费者的主要特征，从而通过对消费者个人特征的了解，来判断他们属于那一个类别。

好! 这个判别模型将有利于Targeting.2.模型选取在整个问卷中，没有连续型变量的存在(有两个即消费次数和餐饮次数)。

进行市场细分时，因为我事先不知道消费者可以分为几类，而我依据的变量是分类变量（消费次数、餐饮次数、追随潮流、中国制造、欧美品牌、保修条款、优惠券、昂贵商品、四处打听、便宜货、羡慕眼光），而且是对样本聚类，样本数据也比较大，因此我选取了两步骤聚类（Two-Step Cluster）的方法。

好. 不过注意两步法既可以用于分类也可以用于连续变量!在市场细分的基础上，我将消费者的分类情况作为一个新的变量TSC_7449，因为这个变量是一个三水平的分类变量，所以用了多峰逻辑回归的模型，来看人口学特征对消费者分类情况的预测准确度。

好!3.描述性分析事前，可靠度分析的结果表明，A1量表中，“产地品牌”和“投诉”两个变量会影响分析结果，删除更好，所以，只对剩下的10个变量进行分析。

好, 交待很清楚根据变量的特点，我进行了两种描述性分析：Frequency和Cross Tables。

分析的结果如下：交叉表格可以不要. 用频率分布就可以. 另外最好用一两句话总结每个表格比较好4.输出结果的说明（1）两步骤聚类：Cluster Distribution从表中可以看出，消费者可以分为三类，每一类的人数差别不是很大，但是第一类的人数最多，占到40%。

spss实验一、实验步骤

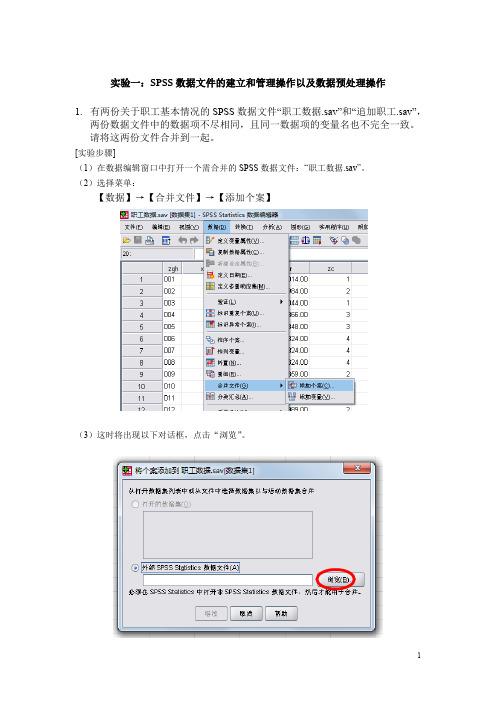
实验一：SPSS数据文件的建立和管理操作以及数据预处理操作1.有两份关于职工基本情况的SPSS数据文件“职工数据.sav”和“追加职工.sav”，两份数据文件中的数据项不尽相同，且同一数据项的变量名也不完全一致。

请将这两份文件合并到一起。

[实验步骤]（1）在数据编辑窗口中打开一个需合并的SPSS数据文件：“职工数据.sav”。

（2）选择菜单：【数据】→【合并文件】→【添加个案】（3）这时将出现以下对话框，点击“浏览”。

（4）打开需进行纵向合并处理的SPSS数据文件“追加职工.sav”。

按“继续”后，显示纵向合并数据文件窗口。

（如下图）（5）对话框右边【新的活动数据集中的变量】框中显示的变量名是两个数据文件中的同名变量，对话框左边【非成对变量】框中显示的变量名是两个文件中的不同名变量。

其中，变量名后面的【*】表示该变量是当前数据编辑窗口中（“职工数据.sav”）的变量，【+】表示该变量是（2）“追加职工.sav”中指定的磁盘文件中的变量。

SPSS默认这些变量的含义不同，且不放入合并后的新文件中。

如果不接受这种默认，可选择其中的两个变量名并按【对】按钮指定配对，表示虽然它们的名称不同但数据含义是相同的，可进入合并后的数据文件中。

本题中，显然职称zc（*）和职称zc1（+）两个变量名需要按【对】按钮指定配对。

方法是：按住“Ctrl键”,同时鼠标点zc（*）和zc1（+），然后按【对】按钮，这时【新的活动数据集中的变量】框中出现“zc&zc1”变量名。

（6）把【非成对变量】框中显示的其他变量名全部标记，按右向箭头。

（7）按【确定】，完成操作。

2.根据“住房状况调查.sav”数据，通过数据排序功能分析本市户口和外地户口家庭的住房面积情况。

（按升序排列）[实验步骤]（1）在数据编辑窗口中打开SPSS数据文件：“住房状况调查.sav”。

（2）选择菜单：【数据】→【排序个案】（3）指定主排序变量“户口状况”到【排序依据】框中，并选择【排序顺序】框中的选项指出该变量按升序还是降序排序。

数据分析spss作业..

数据分析方法及软件应用（作业）题目：4、8、13、16题指导教师：学院：交通运输学院姓名：学号：4、在某化工生产中为了提高收率，选了三种不同浓度，四种不同温度做试验。

在同一浓度与温度组合下各做两次试验，其收率数据如下面计算表所列。

试在α=0.05显著性水平下分析(1)给出SPSS数据集的格式(列举前3个样本即可)；(2)分析浓度对收率有无显著影响；(3)分析浓度、温度以及它们间的交互作用对收率有无显著影响。

解答：（1）分别定义分组变量浓度、温度、收率，在变量视图与数据视图中输入表格数据，具体如下图。

(2)思路：本问是研究一个控制变量即浓度的不同水平是否对观测变量收率产生了显著影响，因而应用单因素方差分析。

假设：浓度对收率无显著影响。

步骤：【分析-比较均值-单因素】，将收率选入到因变量列表中，将浓度选入到因子框中，确定。

输出：變異數分析收率平方和df 平均值平方 F 顯著性群組之間39.083 2 19.542 5.074 .016在群組內80.875 21 3.851總計119.958 23显著性水平α为0.05，由于概率p值小于显著性水平α，则应拒绝原假设，认为浓度对收率有显著影响。

（3）思路：本问首先是研究两个控制变量浓度及温度的不同水平对观测变量收率的独立影响，然后分析两个这控制变量的交互作用能否对收率产生显著影响，因而应该采用多因素方差分析。

假设，H01：浓度对收率无显著影响；H02：温度对收率无显著影响；H03：浓度与温度的交互作用对收率无显著影响。

步骤：【分析-一般线性模型-单变量】，把收率制定到因变量中，把浓度与温度制定到固定因子框中，确定。

输出：主旨間效果檢定因變數: 收率來源第 III 類平方和df 平均值平方 F 顯著性修正的模型70.458a11 6.405 1.553 .230截距2667.042 1 2667.042 646.556 .000浓度39.083 2 19.542 4.737 .030温度13.792 3 4.597 1.114 .382浓度 * 温度17.583 6 2.931 .710 .648錯誤49.500 12 4.125總計2787.000 24校正後總數119.958 23a. R 平方 = .587（調整的 R 平方 = .209）第一列是对观测变量总变差分解的说明；第二列是观测变量变差分解的结果；第三列是自由度；第四列是均方；第五列是Ｆ检验统计量的观测值；第六列是检验统计量的概率ｐ值。

spss练习作业具体步骤

一、调查问卷二、用SPSS Statistics软件进行描述统计分析1、某地区经济增长率的时间序列图形。

解：第一步:数据来源，如图1图 1 某地区经济增长率xls截图图2 Spss软件制作过程截图第二步：将数据输入SPSS软件之中,如图2,制作某地区经济增长率的时间序列图形，如图3.图3某地区1990-2012年经济增长率的时间序列图第三步，从图中可以看出,某地区随时间的变化经济增长率变化趋势较大.2、用SPSS Statistics进行描述统计分析解：第一步，按照题目中的要求，随机选取了148个数据,如图4部分数据：图4 Spss随机数据截图第二步，根据要求，对上月工资进行描述统计分析,主要包括描述数据的集中趋势、离散程度（见表1），绘制直方图（见图5）。

表1 上月工资描述统计表(单位：元）集中趋势离散趋势均值2925 极小值1500中值2900 极大值4800众数2900 全距3300和432900 标准差496.364偏度0。

165 峰度1。

238数据总计148图5 上月工资直方图第三步，分析数据的统计分布状况。

首先，从集中趋势来，上个月平均工资2925元，其中众数和中数也都在2900元，这说明大部分工资水平在2900左右。

其次，从离散趋势来看，最高工资4800元，最低工资1500元，最高工资和最低工资相差3300元，标准差为496。

364，相差较大。

最后，从直方图来看和评述统计表来看，工资在2900元以上的占多数。

可以的该地区整体工资水平大于平均值的占多数，该地区工资水平相对较高。

峰度为1。

238，偏度为0.165符合正态分布。

三、用SPSS Statistics 软件进行参数估计和假设检验及回归分析1、计算总体中上月平均工资95%的置信区间（见表3)。

解：总体中上月平均工资分布未知，但是样本容量大于30,且已知标准误，所以通过SPSS 分析得出总体中上月平均工资95％的置信区间，见表3，假设;H0：总体中上月平均工资95％的不在此在此区间H1：总体中上月平均工资95％的在此区间答，总体中上月平均工资095的置信区间为［2844.37，3005。

spss作业

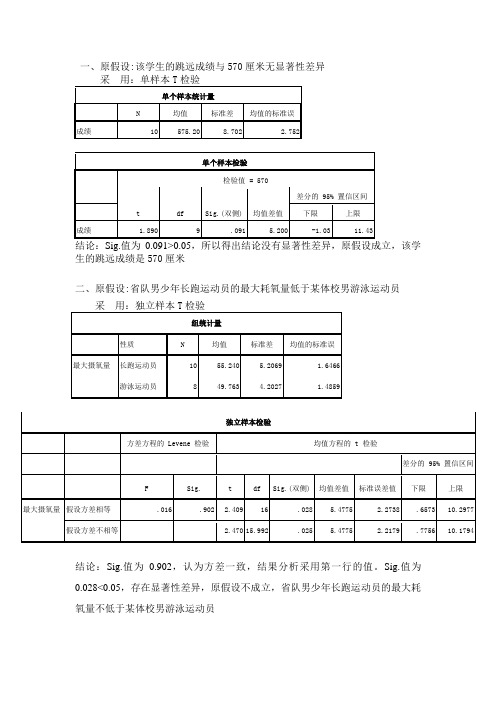
一、原假设:该学生的跳远成绩与570厘米无显著性差异采用：单样本T 检验单个样本统计量N均值标准差均值的标准误成绩10575.208.7022.752单个样本检验检验值 = 570t dfSig.(双侧) 均值差值差分的 95% 置信区间下限上限成绩1.8909.0915.200-1.0311.43结论：Sig.值为0.091>0.05，所以得出结论没有显著性差异，原假设成立，该学生的跳远成绩是570厘米二、原假设:省队男少年长跑运动员的最大耗氧量低于某体校男游泳运动员采用：独立样本T 检验组统计量性质 N 均值标准差均值的标准误最大摄氧量长跑运动员10 55.240 5.2069 1.6466 游泳运动员849.7634.20271.4859结论：Sig.值为0.902，认为方差一致，结果分析采用第一行的值。

Sig.值为0.028<0.05，存在显著性差异，原假设不成立，省队男少年长跑运动员的最大耗氧量不低于某体校男游泳运动员独立样本检验方差方程的 Levene 检验均值方程的 t 检验差分的 95% 置信区间FSig.tdf Sig.(双侧) 均值差值标准误差值下限上限最大摄氧量假设方差相等.016.902 2.409 16.028 5.4775 2.2738 .6573 10.2977 假设方差不相等2.470 15.992.0255.47752.2179.775610.1794三、原假设:两组运动员的血糖含量无显著差异采用：独立样本T检验组统计量性质N 均值标准差均值的标准误血糖量甲组 6 114.367 14.8073 6.0450乙组 6 106.000 17.4056 7.1058独立样本检验方差方程的 Levene 检验均值方程的 t 检验差分的 95% 置信区间F Sig. t df Sig.(双侧) 均值差值标准误差值下限上限血糖量假设方差相等.381 .551 .897 10 .391 8.3667 9.3293 -12.4202 29.1536 假设方差不相等.897 9.750 .391 8.3667 9.3293 -12.4928 29.2262 结论：Sig.值为0.551，认为方差一致，结果分析采用第一行的值。

SPSS操作练习——作业示例 (1)

SPSS操作练习(t检验)要求：1、用SPSS进行统计分析；2、分析说明使用某一统计处理方法的依据；3、将统计结果正确地在论文中进行表达并进行结果分析。

----------------------------------------------------------------------------------1.计算下列两个玉米品种10个果穗长度(cm)的平均值、标准差和变异系数，并解释两个玉米品种的果穗长度有无差异。

【变异系数C·V=（标准偏差SD/平均值MN）×100%】玉米24号：19，21，20，20，18，19，22，21，21，19金皇后玉米：16，21，24，15，26，18，20，19，22，19解：（1）选择分析方法：被比较的玉米24号、金皇后玉米是两个品种的玉米，试验中彼此独立、无配对关系。

先用SPSS对数据是否服从正态分布进行Kolmogorov-Smirnov 检验，得到，玉米24号的p=0.869＞0.05，金皇后玉米的p=0.99＞0.05，说明两个样本均服从正态分布（来自正态总体），因此选择独立样本t检验进行数据分析。

经Levene方差齐性检验，得P=0.028＜0.05，表明方差不齐，因此选择t检验的结果，使用方差不齐时的计算结果。

（2）结果：为比较玉米24号、金皇后两个品种果穗长度的差异，分别随机选定10株进行测定，结果见表1。

表1 玉米24号与金皇后玉米果穗长度的差异性比较(X±SD)品种样品数/株果穗长度/cm 变异系数/% P值(双侧)24号玉米10 20±1.25 6.241.00金皇后玉米10 20±3.40 17.00（3）分析与结论：从表1可以看出，果穗的长度，玉米24号为20±1.25cm，C·V 是6.00%，金皇后为20±3.40cm，C·V为17.00%，虽然两个品种玉米的果穗长度平均值一样，但是，与玉米24号比较，金皇后玉米的标准差、变异系数都较大，表明金皇后玉米果穗长度的变异程度大。

SPSS作业步骤

一、建立变量打开spss→建立variable view窗口→建立变量名。

如在name那一列输入gender；在type选择numeric；label输入性别；点击values出现value labels窗口→在value labels窗口内value 内第一框输入1→第二框输入男→Add，接着重复在第一框输入2→第二框输入女→Add→ok；其它不更改注:如数据小数点后有N位,则在decimals选择N；数值型在type选择numeric，字符型选择string；右对齐左对齐居中在align里设置；missing缺省值二、删数据的方法删女生数据的方法:点击Data→Select Cases→选择性别和if condition is satisfied→点击if→选择性别→点击▶出现gender→= →1(删男生选2)→continue→ok三、输入数据的方法:第一种方法：点击open file打开文件出现open file窗口选择要输入的数据文件→出现text import wizard-step1 of 6窗口→点击下一步→选择fixed widt→下一步→下一步→下一步在data preview选择对应的结尾列点→下一步→点击完成第二种输入数据方法：点击open file打开文件出现open file窗口选择要输入的数据文件→出现text import wizard-step1 of 6窗口→点击下一步(由于有正负号不需选择fixed widt)→下一步→下一步→下一步→下一步→点击完成集中注意、分散注意在label直接修改2.编程语法:点击file→New→syntax→输入（只有一列数据时输入下列语法）data listfile="D:\文本\psych_09\练习二\result1.txt"free (" ")/F_arc1 F_arc2 F_arc3 F_arc4 F_arc5 D_arc1 D_arc2D_arc3 D_arc4 D_arc5.execute.（有两列数据时输入下列语法）data listfile="H:\练习二\教育97.txt"fixedrecords=2/1 alone 1-1 gender 2-2 from 3-3/2 t1 to t40 1-40.Execute.四、合并文件:点击data→merge files→add variables→选择要合并的文件求总平均数:analyze→descriptive statistics→descriptives→年龄▶→options→只选择mean其它不选→continue→ok求女生平均数:先删男生数据(方法同上)，然后同上1.拆分数据:data→select cases→院系→if condition is satisfied→if...→院系▶depar = 1 | depar=3 | depar = 6 | depar= 7 | depar= 10 | depar= 11 | depar= 15→continue求总分:transform→computer variable→第一框输入sum→选择要相加的数据▶+→ok2.反向计分:选择variable view→transform→recode→into different...→选择对应题目▶→在name框内输入新变量名→old and new values→value第一框输入0→value第二框输入2→点击add→重复将2改为0,1改为1→continue→ok五、独立样本T检验：输入数据同练习一；转换数据的行与列data→transpose→选择所有数据▶移到另外一个框→ok；选择var002的全部数据移到var001数据下；在case_lbl中将原来的N个数据改为1，将后来移动的数据改为2；在variable窗口中将name1改为zu，name2改为math，在values 将第一个zu改为1=反馈组2=不反馈组；analyze→compare means→independent...→将math ▶移动到test框内→组▶移动到grouping→点击define→group1输入1 group2输入2→continue→ok报告：本实验为两个水平的独立样本T检验。

SPSS实验上机题

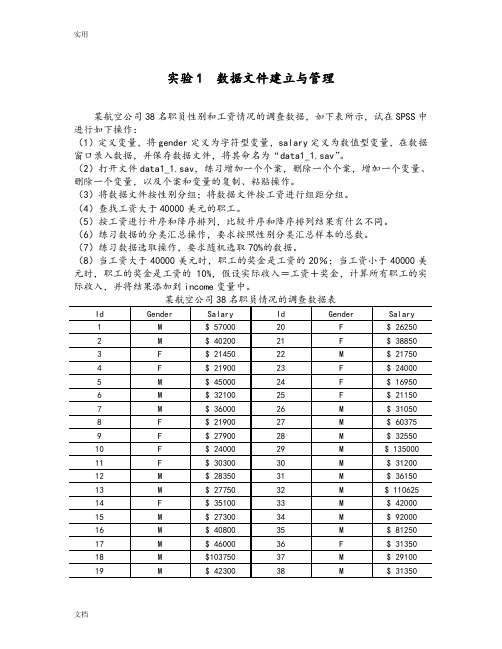
实用实验1 数据文件建立与管理某航空公司38名职员性别和工资情况的调查数据，如下表所示，试在SPSS中进行如下操作：（1）定义变量，将gender定义为字符型变量，salary定义为数值型变量，在数据窗口录入数据，并保存数据文件，将其命名为“data1_1.sav”。

（2）打开文件data1_1.sav，练习增加一个个案，删除一个个案，增加一个变量、删除一个变量，以及个案和变量的复制、粘贴操作。

（3）将数据文件按性别分组；将数据文件按工资进行组距分组。

（4）查找工资大于40000美元的职工。

（5）按工资进行升序和降序排列，比较升序和降序排列结果有什么不同。

（6）练习数据的分类汇总操作，要求按照性别分类汇总样本的总数。

（7）练习数据选取操作，要求随机选取70%的数据。

（8）当工资大于40000美元时，职工的奖金是工资的20％；当工资小于40000美元时，职工的奖金是工资的10%，假设实际收入＝工资＋奖金，计算所有职工的实际收入，并将结果添加到income变量中。

实验2 数据特征的描述统计分析1.下表是一电脑公司某年连续120天的销售量数据(单位：台)。

试对其进行频数分析，计算均值、中位数、众数、四分位数,标准差、最大值、最小值、全距,偏度、峰度系数；画出直方图、茎叶图、箱线图；解释结果并说明其分布特征。

234 159 187 155 158 172 163 183 182 177 156 165 143 198 141 167 203 194 196 225 177 189 203 165 187 160 214 168 188 173 176 178 184 209 175 210161 152 149 211 206 196 196 234 185 189 196 172 150 161 178 168 171 174 160 153 186 190 172 207 228 162 223 170 208 165 197 179 186 175 213 176 153 163 218 180 192 175 197 144 178 191 201 181 166 196 179 171 210 233 174 179 187 173 202 182 154 164 215 233 168 175 198 188 237 194 205 195 174 226 180 172 211 190 200 172 187 189 188 1952.下表是某班同学月生活费资料，试对其进行描述分析，并对结果作出说明。

SPSS实验1-描述分析

SPSS作业1：频数分析（一）大学生消费支出情况调查为研究某高校学生平均每月消费支出情况，现收集到的一些数据，进行描述性分析。

频数分析的基本操作：（1）选择菜单Analyz e－Descriptive Statistics－Frequencies；（2）选择变量“户口”“职业”到Variable框中；（3）单击“Charts”,分别选择Bar Chart、Pie Chart，结果如下：FrequenciesFrequency TableBar ChartPie Chart分析：本次调查的学生人数共120人，其中，城镇人口72人，占总人数的60%。

农村人口48人，占总人数的40%。

城镇户籍的学生明显多于农村户籍的学生，其父母职业大致分为：1国家机关 2企业单位 3个体户 4一般农户 5其他，在这里，职业为企业单位人员，个体户，一般农户的比例不相上下，占了绝大部分。

学生月消费支出金额的分析：基本操作：（1）将消费支出分组：1、500元以下 2、501-1000元 3、1001-1500元 4、1501-2000元 5、2001元以上；（2）选择菜单Analyz e－Descriptive Statistics－Frequencies－变量“xf”－直方图，结果如下：Frequencies分析：从上面表格可以看出，有一半的学生（55.8％）的月消费支出在500-1000元内，有近四分之一（22.5%）的学生月消费支出是在1000-1500元内，其次是消费在500元以下的学生人数占12.5%，消费在1500-2000元的学生人数占5%，最少的是消费在2000元以上的学生人数。

直方图表明学生的月消费支出金额大致呈正态分布，即月消费支出在500-1000元的学生占较大比例，也有少部分消费金额偏低的学生，以及有极少数消费支出较高的学生。

计算基本描述统计量的基本操作：（1）先对数据进行拆分：选择菜单Dat e－Split File－Compare Group—选择变量“性别”－OK；（2）选择菜单Analyz e－Descriptive Statistics－Descriptives—变量“每月消费支出”（3）在Option框中，选择所需计算的基本描述统计量，结果如下：Descriptives分析：男生的平均月消费支出（1084.38元）高于女生（834.82元）。

spss作业,聚类分析

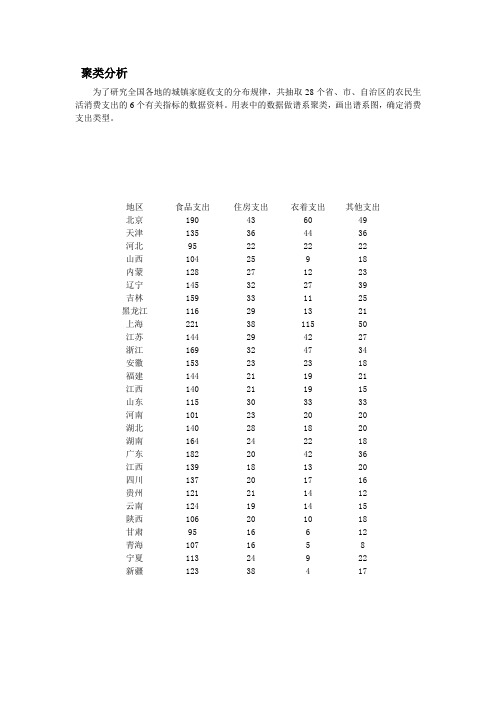
聚类分析为了研究全国各地的城镇家庭收支的分布规律，共抽取28个省、市、自治区的农民生活消费支出的6个有关指标的数据资料。

用表中的数据做谱系聚类，画出谱系图，确定消费支出类型。

地区食品支出住房支出衣着支出其他支出北京190 43 60 49天津135 36 44 36河北95 22 22 22山西104 25 9 18内蒙128 27 12 23辽宁145 32 27 39吉林159 33 11 25黑龙江116 29 13 21上海221 38 115 50江苏144 29 42 27浙江169 32 47 34安徽153 23 23 18福建144 21 19 21江西140 21 19 15山东115 30 33 33河南101 23 20 20湖北140 28 18 20湖南164 24 22 18广东182 20 42 36江西139 18 13 20四川137 20 17 16贵州121 21 14 12云南124 19 14 15陕西106 20 10 18甘肃95 16 6 12青海107 16 5 8宁夏113 24 9 22新疆123 38 4 17【结果与分析】一、欧氏距离平方、组间平均距离连接法Case Processing Summary(a)CasesValid Missing Total N Percent N Percent N Percent28 100.0 0 .0 28 100.0a Average Linkage (Between Groups)上表表示进行聚类分析的有效样品是28个，无缺失值。

Agglomeration ScheduleStageCluster CombinedCoefficientsStage Cluster FirstAppearsNext Stage Cluster 1 Cluster 2 Cluster 1 Cluster 21 14 21 15.000 0 0 62 22 23 22.000 0 0 123 4 24 30.000 0 0 104 3 16 45.000 0 0 155 8 27 51.000 0 0 106 14 20 55.500 1 0 87 13 17 67.000 0 0 88 13 14 82.167 7 6 169 12 18 123.000 0 0 1410 4 8 141.000 3 5 1511 25 26 161.000 0 0 1812 5 22 179.000 0 2 1613 2 10 215.000 0 0 1914 7 12 302.500 0 9 2215 3 4 310.750 4 10 1816 5 13 333.600 12 8 2017 11 19 342.000 0 0 2318 3 25 386.000 15 11 2519 2 6 396.500 13 0 2120 5 28 617.250 16 0 2221 2 15 833.667 19 0 2422 5 7 915.222 20 14 2423 1 11 1021.000 0 17 2624 2 5 1225.875 21 22 2525 2 3 1757.844 24 18 2626 1 2 5112.264 23 25 2727 1 9 18396.630 26 0 0上表表示聚类过程，从中可知，聚类共进行27步；第一步首先合并距离最近的14号和21号样品，形成类G1；因为next stage=6，所以在第6步G1和20号进行复聚类，因此，在Stage Cluster First Appears里列的Cluster 1=1，Cluster 2=0；第二步，合并22号和23号样品，形成类G2；因为next stage=12，所以在第12步，G2和第5号样品进行复聚类，且Cluster 1=0，Cluster 2=2；第一次出现类类的合并在第8步，Cluster 1=7，Cluster 2=6，表示第7步和第6步合并形成的类在第8步合并；其余的类似，不再详细叙述。