运筹学各章的作业题答案
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学(第五版)习题答案

运筹学习题答案第一章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)max 12z x x =+51x +102x £50 1x +2x ³1 2x £4 1x ,2x ³0 (2)min z=1x +1.52x 1x +32x ³3 1x +2x ³2 1x ,2x ³0 (3)max z=21x +22x 1x -2x ³-1 -0.51x +2x £2 1x ,2x ³0 (4)max z=1x +2x 1x -2x ³0 31x -2x £-3 1x ,2x ³0 解:(1)(图略)有唯一可行解,max z=14 (2)(图略)有唯一可行解,min z=9/4 (3)(图略)无界解(4)(图略)无可行解1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)min z=-31x +42x -23x +54x 41x -2x +23x -4x =-2 1x +2x +33x -4x £14 -21x +32x -3x +24x ³2 1x ,2x ,3x ³0,4x 无约束无约束(2)max kk z s p =11nmk ik ik i k z a x ===åå11(1,...,)mikk xi n =-=-=åik x ³0 (i=1(i=1……n; k=1,…,m) (1)解:设z=-z ¢,4x =5x -6x , 5x ,6x ³0 标准型:标准型:Max z ¢=31x -42x +23x -5(5x -6x )+07x +08x -M 9x -M 10x s. t . -41x +2x -23x +5x -6x +10x =2 1x +2x +33x -5x +6x +7x =14 -21x +32x -3x +25x -26x -8x +9x =2 1x ,2x ,3x ,5x ,6x ,7x ,8x ,9x ,10x ³0 初始单纯形表: j c ® 3 -4 2 -5 5 0 0 -M -M i qB C B Xb 1x 2x 3x 5x6x7x 8x9x10x-M 10x 2 -4 1 -2 1 -1 0 0 0 1 2 0 7x14 1 1 3 -1 1 1 0 0 0 14 -M 9x2 -2 [3] -1 2 -2 0 -1 1 0 2/3 -z ¢4M 3-6M 4M-4 2-3M 3M-5 5-3M 0 -M 0 0 (2)解:加入人工变量1x ,2x ,3x ,…n x ,得:,得: Max s=(1/kp )1n i=å1m k =åik a ik x -M 1x -M 2x -…..-M n xs.t. 11mi ik k x x =+=å(i=1,2,3(i=1,2,3……,n) ik x ³0, i x ³0, (i=1,2,3(i=1,2,3……n; k=1,2….,m) M 是任意正整数是任意正整数 初始单纯形表:初始单纯形表: jc-M -M … -M 11k a p 12k a p… 1mk ap (1)n k a p 2n k a p …mnkapi qB C BXb 1x2x … n x11x12x … 1mx … 1n x2n x… nmx -M 1x1 1 0 … 0 1 1 … … 0 0 … 0 -M 2x 1 0 1 … 0 0 … … 0 0 … 0 … … … … … … … … … … … … … … … … -M n x 1 0 0 … 1 0 0 … 0 … 1 1 … 1 -s n M 0 0 … 0 11k a M p +12ka Mp + … 1mk a M p + (1)n k aM p +2n k a M p +…mnk a M p +1.3在下面的线性规划问题中找出满足约束条件的所有基解。
运筹学习题答案(1)

第一章 线性规划及单纯形法(作业)1.4 分别用图解法和单纯型法求解下列线性规划问题,并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解:①图解法:由作图知,目标函数等值线越往右上移动,目标函数越大,故c 点为对应的最优解,最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点,解之得X=(15/4,3/4)T 。
Max z =33/4. ② 单纯形法:将上述问题化成标准形式有: Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为:P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵,构成一个基,对应变量向,x 3,x 4为基变量,令非基变量x 1,x 2为零,找到T 优解,代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题,并指出属哪一类。
(3)Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解:这种情况化为标准形式: Max z '=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z '=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法: Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段,将表中y 1,y 2去掉,目标函数回归到Max z '=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析(作业)2.7给出线性规划问题:Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求:(1)写出其对偶问题;(2)已知原问题最优解为X *=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
运筹学基础及应用课后习题答案(第一二章习题解答)

运筹学基础及应用课后习题答案(第一二章习题解答)第一章:线性规划一、选择题1. 线性规划问题中,目标函数可以是()A. 最大化B. 最小化C. A和B都对D. A和B都不对答案:C解析:线性规划问题中,目标函数可以是最大化也可以是最小化,关键在于问题的实际背景。
2. 在线性规划问题中,约束条件通常表示为()A. 等式B. 不等式C. A和B都对D. A和B都不对答案:C解析:线性规划问题中的约束条件通常包括等式和不等式两种形式。
二、填空题1. 线性规划问题的基本假设是______。
答案:线性性2. 线性规划问题中,若决策变量个数和约束条件个数相等,则该问题称为______。
答案:标准型线性规划问题三、计算题1. 求解以下线性规划问题:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 83x + 4y ≤ 12x, y ≥ 0答案:最优解为 x = 4, y = 2,最大值为 Z = 14。
解析:画出约束条件的图形,找到可行域,再求目标函数的最大值。
具体步骤如下:1) 将约束条件化为等式,画出直线;2) 找到可行域的顶点;3) 将顶点代入目标函数,求解最大值。
第二章:非线性规划一、选择题1. 以下哪个方法适用于求解非线性规划问题()A. 单纯形法B. 拉格朗日乘数法C. 柯西-拉格朗日乘数法D. A和B都对答案:B解析:非线性规划问题通常采用拉格朗日乘数法求解,单纯形法适用于线性规划问题。
2. 非线性规划问题中,以下哪个条件不是K-T条件的必要条件()A. 梯度条件B. 正则性条件C. 互补松弛条件D. 目标函数为凸函数答案:D解析:K-T条件包括梯度条件、正则性条件和互补松弛条件,与目标函数是否为凸函数无关。
二、填空题1. 非线性规划问题中,若目标函数和约束条件都是凸函数,则该问题称为______。
答案:凸非线性规划问题2. 非线性规划问题中,K-T条件是求解______的必要条件。
运筹学1至6章习题参考答案

-0.25
1
1.5
2
C(j)-Z(j)
-1.75
0
0
1.25
0
-12.5
X1
-3
1
0
2
-1
0
2
M
X2
-5
0
1
-0.5
0.5
0
2
4
X5
0
0
0
-1.5
[0.5]
1
0
0
C(j)-Z(j)
0
0
3.5
-0.5
0
-16
X1
-3
1
0
-1
0
2
2
X2
-5
0
1
1
0
-1
2
X4
0
0
0
-3
1
2
0
C(j)-Z(j)
0
0
2
0
1
【解】设xj、yj(j=1,2,…,6)分别为1~6月份的生产量和销售量,则数学模型为
(1)
(2)目标函数不变,前6个约束右端常数800改为1000,第7~11个约束右端常数200改为0,第12个约束“≤200”改为“=-200”。
1.4某投资人现有下列四种投资机会,三年内每年年初都有3万元(不计利息)可供投资:
0
0
0
R. H. S.
Ratio
Basis
C(i)
X1
X2
X3
X4
X5
X6
X4
0
-1
2
3
1
0
0
4
M
X5
0
[4]
《运筹学》(第二版)课后习题参考答案

生产工序
所需时间(小时)
每道工序可用时间(小时)
1
2
3
4
5
成型
3
4
6
2
3
3600
打磨
4
3
5
6
4
3950
上漆
2
3
3
4
3
2800
利润(百元)
2.7
3
4.5
2.5
3
解:设 表示第i种规格的家具的生产量(i=1,2,…,5),则
s.t.
通过LINGO软件计算得: .
11.某厂生产甲、乙、丙三种产品,分别经过A,B,C三种设备加工。已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表2—10所示。
-10/3
-2/3
0
故最优解为 ,又由于 取整数,故四舍五入可得最优解为 , .
(2)产品丙的利润 变化的单纯形法迭代表如下:
10
6
0
0
0
b
6
200/3
0
1
5/6
5/3
-1/6
0
10
100/3
1
0
1/6
-2/3
1/6
0
0
100
0
0
4
-2
0
1
0
0
-20/3
-10/3
-2/3
0
要使原最优计划保持不变,只要 ,即 .故当产品丙每件的利润增加到大于6.67时,才值得安排生产。
答:(1)唯一最优解:只有一个最优点;
(2)多重最优解:无穷多个最优解;
(3)无界解:可行域无界,目标值无限增大;
运筹学第四章习题答案

即:4y1+6y2=﹣8 ① 又由于原问题的最优解X1*>0,X2*<0是松约束,故对偶问题的 约束必为紧约束,即对偶问题的前两个约束必为等式:
y1+y2=﹣2 y1+ky2=﹣2 ∴由①②解得y1*=﹣2 Y*=(﹣2,0)
② ③ y2*=0,即对偶问题的最优解为
将y1*,y2*的值代入③式得k=﹣1
(2)max z=4x1-2x2+3x3-x4
X1+x2+2x3+x4≤7
2x1-x2+2x3-x4=﹣2
s、t
X1-2x2+x4≥﹣3
X1、x3≥0 x2、x4无符号约束
解:其对偶问题为:
Min w=7y1-2y2-3y3
y1+2y2+y3≥4
y1-y2-2y3=﹣2
s、t
2y1+2y2≥3
y1-y2+y3=﹣1
y1≥0 y2无符号约束 y3≤0
4、已知线性规划问题:
Max z=x1+2x2+3x3+4x4
x1+2x2+2x3+3x4≤20
s、t
2x1+x2+3x3+2x4≤20
xj≥0 j=1、2、3、4
其对偶问题最优解为y1=1.2 y2=0.2,由对偶理论直接求出原问题的 最优解。
解:将Y*=(1.2,0.2)代入对偶问题的约束条件:
1、写出下列线性规划问题的对偶问题。
(1)min z=x1+x2+2x3
X1+2x2+3x3≥2
2x1+x2-x3≤4
s.t
3x1+2x2பைடு நூலகம்4x3≤6
运筹学课程作业答案

工厂5
工厂9 工厂6
工厂3
8
线性规划 Linear Programming(LP)
3. 河流污染治理规划问题
曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
工厂2 工厂8
工厂7
工厂1 工厂3
工厂4
工厂5
工厂9
工厂6
今日认识未为晚, 吾辈齐心治环境, 线性规划大有用, 定让江水绿如蓝。 9
10
线性规划 Linear Programming(LP)
背景资料:
表-1 污水排放量
单位:万m3
化工厂1
1.2
化工厂4
2
化工厂7
2
化工厂2
1
化工厂5
1
化工厂8
0.8
化工厂3
3
化工厂6
1
化工厂9
1.5
表-2 流经各化工厂的河流流量
单位:万m3
化工厂1
500
化工厂4 1200 化工厂7 1200
化工厂2
6
第一章作业
3. 河流污染治理规划问题 曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
7
线性规划 Linear Programming(LP)
案 例 河流污染治理规划问题
曾几何时长江水, 哺育华夏代代人, 谁知后代疏珍惜, 清清江水黑如泥。
工厂1
工厂2 工厂8
工厂7
工厂4
5
▪ ▪
对化工厂7应有—— 3 (2-X7)+ 0.8(1.5-X9) / 1200 ≦ 0.2%
13
线性规划 Linear Programming(LP)
▪ 对化工厂4应有——
运筹学课后答案大全
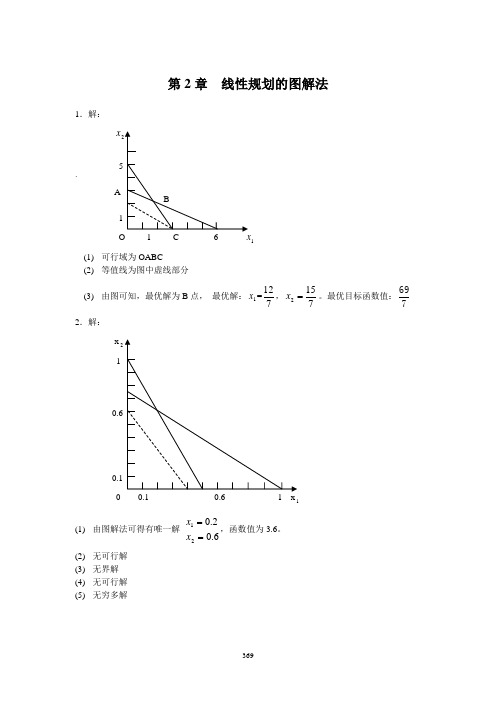
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
运筹学课后习题答案

运筹学课后习题答案第一章线性规划1、由图可得:最优解为2、用图解法求解线性规划:Min z=2x1+x2解:由图可得:最优解x=1.6,y=6.43用图解法求解线性规划:Max z=5x1+6x2解:由图可得:最优解Max z=5x1+6x2, Max z= +4用图解法求解线性规划:Maxz = 2x 1 +x 2 由图可得:最大值==+35121x x x ,所以==2321x xmax Z = 8.6将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’7将线性规划模型化为标准形式Min Z =x1+2x2+3x3解:令Z’ = -z,引进松弛变量x4≥0,引进剩余变量x5≥0,得到一下等价的标准形式。
x2’=-x2 x3=x3’-x3’’Z’ = -min Z = -x1-2x2-3x39用单纯形法求解线性规划问题:Max Z =70x1+120x2解: Max Z =70x1+120x2单纯形表如下Max Z =3908.11.解:(1)引入松弛变量X4,X5,X6,将原问题标准化,得max Z=10X1+6X2+4X3X1+X2+X3+X4=10010 X1+4X2+5X3+X5=6002 X1+2X2+6X3+X6=300X1,X2,X3,X4,X5,X6≥0得到初始单纯形表:(2)其中ρ1 =C1-Z1=10-(0×1+0×10+0×2)=10,同理求得其他根据ρmax =max{10,6,4}=10,对应的X1为换入变量,计算θ得到,θmin =min{100/1,600/10,300/2}=60,X5为换出变量,进行旋转运算。
(3)重复(2)过程得到如下迭代过程ρj≤0,迭代已得到最优解,X*=(100/3,200/3,0,0,0,100)T,Z* =10×100/3+6×200/3+4×0 =2200/3。
运筹学1至6章习题参考答案
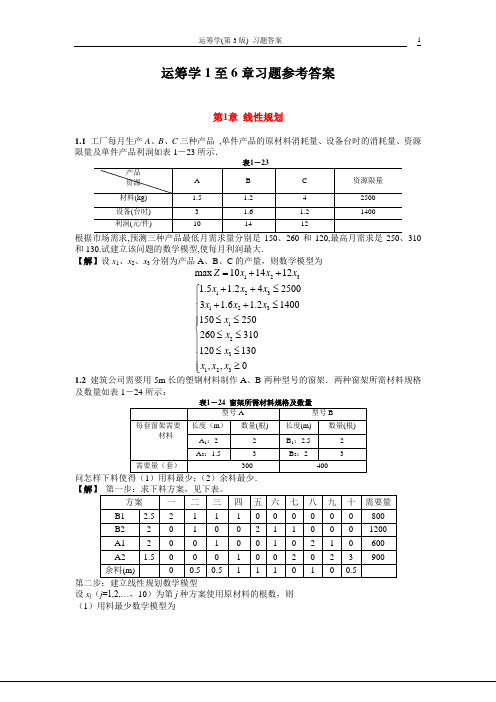
0
2
11/8
0
-3/4
0
9
X4
0
0
0
9/8
1
7/16
-1/4
27/4
6
X1
3
1
0
-1/2
0
1/4
0
3
M
X2
2
0
1
[11/16]
0
-3/32
1/8
1/8
0.181818
C(j)-Z(j)
0
0
0
0
-9/16
-1/4
37/4
X3进基、X2出基,得到另一个基本最优解。
C(j)
3
2
-0.125
6重油
7残油
辛烷值
80
115
105
蒸汽压:公斤/平方厘米
1.0
1.5
0.6
0.05
每天供应数量(桶)
2000
1000
1500
1200
1000
1000
800
问炼油厂每天生产多少桶成品油利润最大,建立数学模型。
解设xij为第i(i=1,2,3,4)种成品油配第j(j=1,2,…,7)种半成品油的数量(桶)。
10
-5
1
0
0
0
* Big M
5
3
1
0
0
0
X1
10
1
3/5
1/5
0
1/5
2
X4
0
0
4
-9
1
1
25
C(j)-Z(j)
0
-11
-1
运筹学课后习题答案

第一章 线性规划及单纯形法1.用X j (j=1.2…5)分别代表5中饲料的采购数,线性规划模型:12345123412341234min 0.20.70.40.30.8.3267000.50.2300.20.8100(1,2,3,4,5,6)0j z x x x x x st x x x x x x x x x x x x x x x x j =+++++++≥+++≥+++≥=≥555 +18 +2 0.5+2 2.解:设123456x x x x x x x 表示在第i 个时期初开始工作的护士人数,z 表示所需的总人数,则123456161223344556min .607060502030(1,2.3.4.5.6)0i z x x x x x x st x x x x x x x x x x x x x i =++++++≥+≥+≥+≥+≥+≥=≥ 3.解:设用i=1,2,3分别表示商品A ,B ,C ,j=1,2,3分别代表前,中,后舱,Xij 表示装于j 舱的i 种商品的数量,Z 表示总运费收入则:111213212223313233111213212223313233112131122232132333112131max 1000()700()600().6001000800105740010575400105715008652000z x x x x x x x x x st x x x x x x x x x x x x x x x x x x x x x =++++++++++≤++≤++≤++≤++≤++≤++≤ 122232132333112131122232132333122232112131132333865300086515008650.158658650.158658650.18650(1,2.3.1,2,3)ij x x x x x x x x x x x x x x x x x x x x x x x x x i j ++≤++≤++≤++++≤++++≤++≥== 5. (1)Z = 4(2)12121212max .6101207051038z x x st x x x x x x =++≤+≥≤≥≤≥ 解:如图:由图可得: **(10,6)16T x Z == ; 即该问题具有唯一最优解*(10,6)Tx =(3)无可行解(4)12121212max 56.22232,0z x x st x x x x x x =+-≥-+≤≥ 如图:由图知,该问题具有无界解。
运筹学清华大学第四版答案

运筹学清华大学第四版答案【篇一:运筹学作业2(清华版第二章部分习题)答案】s=txt>2.1 题(p. 77)写出下列线性规划问题的对偶问题:????(1)?????maxz?2x1?2x2?4x3s.t.x1?3x2?4x3?22x1?x2?3x3?3x1?4x2? 3x3?5x1?0,x2?0,x3无约束;解:根据原—对偶关系表,可得原问题的对偶规划问题为:?maxw?2y1?3y2?5y3?s.t.y1?2y2?y3?2??3y1?y2?4y3?2 ? ?4y1?3y2?3y3?4?y1?0,y2?0,y3?0??mn?minz???cijxij?i?1j?1?n???cijxij?ai,i?1,?,m(2)? j?1?n??cijxij?bj,j?1,?,n?j?1???xij?0,i?1,?,m;j?1,?,n解:根据原—对偶关系表,可得原问题的对偶规划问题为:mn??maxw??aiui??bjvji?1j?1??ui?vj?cij ??i?1,?,m;j?1,?,n???ui无约束,vj无约束2.2判断下列说法是否正确,为什么?(1)如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;答:错。
因为:若线性规划的原问题存在可行解,且其对偶问题有可行解,则原问题和可行问题都将有最优解。
但,现实中肯定有一些问题是无最优解的,故本题说法不对。
maxz?3x1?x2例如原问题s.t.?x1?x2?1?x2?3??x?0,x?02?1有可行解,但其对偶问题minw?y1?3y2s.t.?3?y1?y2?1?y1??y?0,y?02?1无可行解。
(2)如果线性规划的对偶问题无可行解,则原问题也一定无可行解;答:错,如(1)中的例子。
(3)在互为对偶的一对原问题与对偶问题中,不管原问题是求极大或求极小,原问题可行解的目标函数值一定不超过其对偶问题可行解的目标函数值。
答:错。
正确说法是:在互为对偶的一对原问题与对偶问题中,求极大的问题可行解的目标函数值一定不超过求极小的问题可行解的目标函数值。
2-9章运筹学课后题及答案

第二章决策分析2.1 某公司面对五种自然状态、四种行动方案的收益情况如下表:假定不知道各种自然状态出现的概率,分别用以下五种方法选择最优行动方案:1、最大最小准则2、最大最大准则3、等可能性准则4、乐观系数准则(分别取α=0.6、0.7、0.8、0.9)5、后悔值准则解:1、用最大最小准则决策S4为最优方案;2、用最大最大准则决策S2为最优方案;3、用等可能性准则决策S4为最优方案;4、乐观系数准则决策(1) α=0.6,S1为最优方案;(2) α=0.7,S1为最优方案;(3) α=0.8,S1为最优方案;(4) α=0.9,S2为最优方案;可见,随着乐观系数的改变,其决策的最优方案也会随时改变。
5、用后悔值准则决策S4为最优方案。
2.2 在习题1中,若各种自然状态发生的概率分别为P(N1)=0.1、P(N2)=0.3、P(N3)=0.4、P(N4)=0.2、P(N5)=0.1。
请用期望值准则进行决策。
解:期望值准则决策S1为最优方案。
3.3 市场上销售一种打印有生产日期的保鲜鸡蛋,由于确保鸡蛋是新鲜的,所以要比一般鸡蛋贵些。
商场以35元一箱买进,以50元一箱卖出,按规定要求印有日期的鸡蛋在一周内必须售出,若一周内没有售出就按每箱10元处理给指定的奶牛场。
商场与养鸡场的协议是只要商场能售出多少,养鸡场就供应多少,但只有11箱、12箱、15箱、18箱和20箱五种可执行的计划,每周一进货。
1、编制商场保鲜鸡蛋进货问题的收益表。
2、分别用最大最小准则、最大最大准则、等可能性准则、乐观系数准则(α=0.8)和后悔值准则进行决策。
3、根据商场多年销售这种鸡蛋的报表统计,得到平均每周销售完11箱、12箱、15箱、18箱和20箱这种鸡蛋的概率分别为:0.1、0.2、0.3、0.3、0.1。
请用期望值准则进行决策。
1、收益表2、用各准则模型求解(1)最大最小准则得S5为最优方案;(2)最大最大准则得S1为最优方案;(3)等可能性准则得S4为最优方案;(4)乐观系数( =0.8)准则得S1为最优方案;(5)后悔值准则得S3为最优方案。
运筹学知到章节答案智慧树2023年华东交通大学

运筹学知到章节测试答案智慧树2023年最新华东交通大学第一章测试1.用运筹学解决问题时,要对问题进行()。
参考答案:分析和定义2.运筹学是一门()。
参考答案:定量与定性相结合的学科3.规划论内容不包括()。
参考答案:网络分析4.运筹学主要研究对象是各种有组织系统的管理问题及生产经营活动。
()参考答案:对5.研究大量随机现象,从中揭示出事物基本规律的科学方法是指线性规划法。
()参考答案:错6.统筹学是用教学方法研究各种系统最优化问题的学科。
()参考答案:错7.若用图解法求解线性规划问题,则该问题所含决策变量的数目一般为()。
参考答案:二个8.图解法求解极小化线性规划问题,一般目标函数直线放在可行域内,并()移动。
参考答案:沿着梯度反方向移动。
9.在二元线性规划问题中,如果问题有可行解,则一定有最优解。
()参考答案:错10.任何线性规划问题一定有最优解。
()参考答案:错11.下面哪些不是线性规划问题的标准形式所具备的()?参考答案:添加新变量时,可以不考虑变量的正负性12.线性规划标准型中,决策变量()是非负的。
参考答案:一定13.下列哪种解法必须化标准型()?参考答案:单纯形表格法14.线性规划的标准型主要特征为:(1)目标函数为极大化类型;(2)所有的约束条件都是等式;(3)所数学规划有约束方程右端的常数都是非负的;(4)所有决策变量都是非负的。
()参考答案:对15.对于线性规划问题,下列说法正确的是()。
参考答案:说法都正确16.对于任意线性规划问题(含三维以上),它的基可行解和可行域的顶点是一一对应的即基可行解数等于可行域的顶点数。
()参考答案:对17.基可行解的分量都是正的。
()参考答案:错18.如果线性规划问题存在最优解,则最优解一定可以在可行解域的顶点上获得。
()参考答案:对19.可行解是满足约束条件和非负条件的决策变量的一组取值:()参考答案:正确20.用单纯形法求解线性规划时,不论极大化或者是极小化问题,均用最小比值原则确定出基变量:()参考答案:正确21.求极小值,唯一最优解情形,要求所有检验数()时达到最优。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》各章的作业----复习思考题及作业题第一章绪论复习思考题1、从运筹学产生的背景认识本学科研究的内容和意义。
2、了解运筹学的内容和特点,结合自己的理解思考学习的方法和途径。
3、体会运筹学的学习特征和应用领域。
第二章线性规划建模及单纯形法复习思考题1、线性规划问题的一般形式有何特征2、建立一个实际问题的数学模型一般要几步3、两个变量的线性规划问题的图解法的一般步骤是什么4、求解线性规划问题时可能出现几种结果,那种结果反映建模时有错误5、什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。
6、试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。
7、试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。
8、在什么样的情况下采用人工变量法,人工变量法包括哪两种解法9、大M 法中,M 的作用是什么对最小化问题,在目标函数中人工变量的系数取什么最大化问题呢10、什么是单纯形法的两阶段法两阶段法的第一段是为了解决什么问题在怎样的情况下,继续第二阶段作业题:1、把以下线性规划问题化为标准形式:(1)max z=x1-2x2+x3.x1+x2+x3≤122x1+x2-x3≥6-x1+3x2=9x1,x2,x3≥0(2)min z=-2x1-x2+3x3-5x4x1+2x2+4x3-x4≥62x1+3x2-x3+x4=12x1+x3+x4≤4x1,x2,x4≥0(3)max z=x1+3x2+4x3.3x1+2x2≤13x2+3x3≤172x1+x2+x3=13x1,x3≥02、用图解法求解以下线性规划问题(1)max z=x1+3x2.x1+x2≤10-2x1+2x2≤12x1≤7x1,x2≥0(2)min z=x1-3x2.2x1-x2≤4x1+x2≥3x2≤5x1≤4x1,x2≥03、在以下问题中,列出所有的基,指出其中的可行基,基础可行解以及最优解。
max z=2x1+x2-x3.x1+ x2+2x3≤6x1+4x2-x3≤4x1,x2,x3≥04、用单纯形表求解以下线性规划问题(1)max z=x1-2x2+x3.x1+x2+x3≤122x1+x2-x3≤6-x1+3x2≤9x1,x2,x3≥0(2)min z=-2x1-x2+3x3-5x4x1+2x2+4x3-x4≤62x1+3x2-x3+x4≤12x1+x3+x4≤4x1,x2,x3,x4≥05、用大M法和两阶段法求解以下线性规划问题(1)Max z=x1+3x2+4x3.3x1+2x2≤13x2+3x3≤172x1+x2+x3=13x1,x2,x3≥0(2)max z=2x1-x2+x3.x1+x2-2x3≤84x1-x2+x3≤22x1+3x2-x3≥4x1,x2,x3≥06、某饲养场饲养动物,设每头动物每天至少需要700克蛋白质、30克矿物质、100毫克维生素。
现有五种饲料可供选用,各种饲料每公斤营养成分含量及单价如下表所示:7、某工厂生产Ⅰ、Ⅱ、Ⅲ、Ⅳ四种产品,产品Ⅰ需依次经过A、B两种机器加工,产品Ⅱ需依次经过A、C两种机器加工,产品Ⅲ需依次经过B、C两种机器加工,产品Ⅳ需依次经过A、B机器加工。
有关数据如表所示,请为该厂制定一个最优生产计划。
第三章线性规划问题的对偶及灵敏度分析复习思考题1、对偶问题和它的经济意义是什么2、简述对偶单纯形法的计算步骤。
它与单纯形法的异同之处是什么3、什么是资源的影子价格它和相应的市场价格之间有什么区别4、如何根据原问题和对偶问题之间的对应关系,找出两个问题变量之间、解及检验数之间的关系5、利用对偶单纯形法计算时,如何判断原问题有最优解或无可行解6、在线性规划的最优单纯形表中,松弛变量(或剩余变量)0>+k n x ,其经济意义是什么7、在线性规划的最优单纯形表中,松弛变量k n x +的检验数0>+k n σ,其经济意义是什么 8、关于i j j i b c a ,,单个变化对线性规划问题的最优方案及有关因素将会产生什么影响有多少种不同情况如何去处理9、线性规划问题增加一个变量,对它原问题的最优方案及有关因素将会产生什么影响如何去处理10、线性规划问题增加一个约束,对它原问题的最优方案及有关因素将会产生什么影响如何去处理作业题1、写出以下问题的对偶问题(1) min z= 2x 1 +3x 2 +5x 3 +6x 4. x 1 +2x 2 +3x 3 +x 4 ≥2 -2x 1 -x 2 -x 3 +3x 4 ≤-3x 1, x 2, x 3, x 4 ≥0(2) min z= 2x 1 +3x 2 -5x 3 .x 1+x 2-x 3+x 4 ≥52x 1+x 3≤4x 2 +x 3 +x 4 =6x 1≤0, x 2≥0, x 3≥0, x 4无符号限制2、已知如下线性规划问题Max z= 6x 1 -2x 2 +10x 3 . x 2 + 2x 3 ≤5 3x 1 -x 2 + x 3≤10x 1,x 2,x 3≥0其最优单纯形表为(1)写出原始问题的最优解、最优值、最优基 B 及其逆 B -1。
(2)写出原始问题的对偶问题,并从上表中直接求出对偶问题的最优解。
3、用对偶单纯形法求解以下问题(1)min z=4x1+6x2+18x3.x1+3x3≥3x2+2x3≥5x1,x2,x3≥0(2)min z=10x1+6x2.x1+x2≥22x1-x2≥6x1,x2≥04、已知以下线性规划问题max z=2x1+x2-x3.x1+2x2+x3≤8-x1+x2-2x3≤4x1,x2,x3≥0及其最优单纯形表如下:(1) 求使最优基保持不变的c2=1的变化范围。
如果c2从1变成5,最优基是否变化,如果变化,求出新的最优基和最优解。
(2) 对c1=2进行灵敏度分析,求出c1由2变为4时的最优基和最优解。
(3) 对第二个约束中的右端项b2 = 4 进行灵敏度分析,求出b2 从4 变为1 时新的最优基和最优解。
(4) 增加一个新的变量x6,它在目标函数中的系数c6 = 4,在约束条件中的系数向量为a612=⎡⎣⎢⎤⎦⎥,求新的最优基和最优解。
(5) 增加一个新的约束x2+x32,求新的最优基和最优解。
5、某工厂用甲、乙、丙三种原料生产A、B、C、D四种产品,每种产品消耗原料定额以及三种原料的数量如下表所示:(1)求使总利润最大的生产计划和按最优生产计划生产时三种原料的耗用量和剩余量。
(2)求四种产品的利润在什么范围内变化,最优生产计划不会变化。
(3)求三种原料的影子价格。
(4)在最优生产计划下,哪一种原料更为紧缺如果甲原料增加120吨,这时紧缺程度是否有变化第四章运输问题复习思考题1、运输问题的数学模型具有什么特征为什么其约束方程的系数矩阵的秩最多等于+nm-12、用西北角法确定运输问题的初始基本可行解的基本步骤是什么3、最小元素法的基本思想是什么为什么在一般情况下不可能用它直接得到运输问题的最优方案4、试述用闭回路法检验给定的调运方案是否最优的原理,其检验数的经济意义是什么5、用闭回路法检验给定的调运方案时,如何从任意空格出发去寻找一条闭回路这闭回路是否是唯一的6、试述用位势法求检验数的原理、步骤和方法。
7、试给出运输问题的对偶问题(对产销平衡问题)。
8、如何把一个产销不平衡的运输问题(产大于销或销大于产)转化为产销平衡的运输问题。
9、一般线性规划问题应具备什么特征才可以转化为运输问题的数学模型作业题1、求解下列产销平衡的运输问题,下表中列出的为产地到销地之间的运价。
(1)用西北角法、最小元素法求初始基本可行解;(2)由上面所得的初始方案出发,应用表上作业法求最优方案,并比较初始方案2、用表上作业法求下列产销平衡的运输问题的最优解:(表上数字为产地到销地的运价,M 为任意大的正数,表示不可能有运输通道)(1)(2)3、用表上作业法求下列产销不平衡的运输问题的最优解:(表上数字为产地到销地的里程,M 为任意大的正数,表示不可能有运输通道)。
(1)4、某农民承包了5块土地共206亩,打算小麦、玉米和蔬菜三种农作物,各种农作物的计划播种面积(亩)以及每块土地种植各种不同的农作物的亩产数量(公斤)见1200)减去每一个亩产量,得到新的求最小的运输表,再进行计算。
得到求解的结果后,再通过逆运算得到原问题的解。
(想一想为什么)第五章动态规划思考题主要概念及内容:多阶段决策过程;阶段及阶段变量;状态、状态变量及可能的状态集合;决策、决策变量及允许的决策集合;策略、策略集合及最优策略;状态转移方程;K-子过程;阶段指标函数、过程指标函数及最优值函数;边界条件、递推方程及动态规划基本方程;最优性原理;逆序法、顺序法。
复习思考题:1、试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。
2、动态规划的阶段如何划分3、试述用动态规划求解最短路问题的方法和步骤。
4、试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界条件等概念。
5、试述建立动态规划模型的基本方法。
6、试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。
作业题1、用动态规划求解以下网络从A到G的最短路径。
ABBBCCDDDEEF 12312123125216437333254271089711912132、某公司有5台设备,分配给所属A,B,C 三个工厂。
各工厂获得不同的设备台数所能产生效益(万元)的情况如下表。
求最优分配方案,使总效益最大。
3、用动态规划求解以下非线性规划问题: max z = x 1 2 x 2 ·3 x 3 . x 1+3x 2+2x 3 ≤12 x 1 , x 2 , x 3 ≥04、某企业生产某种产品,每月月初按订货单发货,生产的产品随时入库,由于空间的限制,仓库最多能够贮存产品90000件。
在上半年(1至6月)其生产成本(万元/千件)和产品订单的需求数量情况如下表:已知上一年底库存量为40千件,要求6月底库存量仍能够保持40千件。
问:如何安排这6个月的生产量,使既能满足各月的定单需求,同时生产成本最低。
第六章 排队论复习思考题1、排队论主要研究的问题是什么2、试述排队模型的种类及各部分的特征;3、Kendall 符号C B A Z Y X /////中的各字母分别代表什么意义;4、理解平均到达率、平均离去率、平均服务时间和顾客到达间隔时间等概念;5、分别写出泊松分布、负指数分布的密度函数,说明这些分布的主要性质;6、试述队长和排队长;等待时间和逗留时间;忙期和闲期等概念及他们之间的联系与区别。
