二进制、八进制、十进制与十六进制转换计算精华复习过程
2进制、8进制和16进制与10进制的转换过程

2进制、8进制和16进制与10进制的转换过程在数字的世界里,我们经常使用不同的进制来表示数值。
最常用的进制是十进制,但还有其他的进制,如二进制、八进制和十六进制。
这些进制与十进制之间可以进行转换,下面我们来探讨一下这些转换过程。
首先,我们来看一下二进制、八进制和十六进制是如何转换为十进制的。
二进制是基数为2的进制,它只有两个数码:0和1。
例如,二进制数1101转换为十进制数的计算过程如下:1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 13所以,二进制数1101转换为十进制数是13。
八进制是基数为8的进制,它有八个数码:0、1、2、3、4、5、6和7。
例如,八进制数3725转换为十进制数的计算过程如下:3 * 8³ + 7 * 8² + 2 * 8¹ + 5 * 8⁰ = 2021所以,八进制数3725转换为十进制数是2021。
十六进制是基数为16的进制,它有十六个数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E和F。
例如,十六进制数AF12转换为十进制数的计算过程如下:A * 16³ + F * 16² + 1 * 16¹ + 2 * 16⁰ = 419448所以,十六进制数AF12转换为十进制数是419448。
接下来,我们来看一下十进制是如何转换为二进制、八进制和十六进制的。
十进制数转换为二进制数的方法是不断除以2,直到商为0为止。
例如,十进制数13转换为二进制数的计算过程如下:13 / 2 = 6 余 16 / 2 = 3 余 03 / 2 = 1 余 11 /2 = 0 余 1所以,十进制数13转换为二进制数是1101。
十进制数转换为八进制数的方法是不断除以8,直到商为0为止。
例如,十进制数2021转换为八进制数的计算过程如下:2021 / 8 = 252 余 5252 / 8 = 31 余 431 / 8 = 3 余 73 / 8 = 0 余 3所以,十进制数2021转换为八进制数是3725。
c语言各进制转换方法

二进制,八进制,十进制,十六进制之间的转换算法一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
二进制_八进制_十进制_十六进制之间的相互转换

二进制,八进制,十进制,十六进制之间的相互转换和相关概念二进制:计算机只认识0或1,也就是高电平和低电平.所以所有的数据格式最终会转化为2进制形式,计算机硬件才能识别。
二进制逢二进一,八进制逢八进一,十进制逢十进一,十六进制逢十六进一。
下边是各进制之间的转换公式.二进制转十进制0110 0100(2) 换算成十进制第0位0 * 2^0 = 0第1位0 * 2^1 = 0第2位1 * 2^2 = 4第3位0 * 2^3 = 0第4位0 * 2^4 = 0第5位1 * 2^5 = 32第6位1 * 2^6 = 64第7位0 * 2^7 = 0 +---------------------------100二进制转八进制可采用8421法1010011(2)首先每三位分割即: 001,010,011不足三位采用0补位.然后采用8421法: 001=1010=2011=3所以转换成8进制是123二进制转十六进制1101011010100(2)首先每四位分割即: 0001,1010,1101,0100不足四位采用0补位.然后采用8421法: 0001:11010:A1101:D0100:4所以转换成十六进制是1AD4十六进制当数字超过9后将采用A代替10,B代替11,C代替12,D代替13,E代替14,F代替15;下边是十进制的各种转换:十进制转二进制6(10)10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
商余数6/2 3 03/2 1 11/2 0 1最后把余数从下向上排列写出110即是转换后的二进制.十进制转换八进制10进制数转换成八进制数,这是一个连续除8的过程:把要转换的数,除以8,得到商和余数,将商继续除以8,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
120(10)商余数120/8 15 015/8 1 71/8 0 1最后把余数从下向上排列写出170即是转换后的八进制.十进制转换十六进制10进制数转换成十六进制数,这是一个连续除16的过程:把要转换的数,除以16,得到商和余数,将商继续除以16,直到商为0。
(完整版)二进制、八进制、十进制、十六进制之间转换详解

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
计算机进制之间的转换

计算机进制之间的转换进制是计算机中用于表示数值的一组符号系统,包括二进制、八进制、十进制和十六进制等。
在计算机科学中,进制转换是一种常见且重要的操作。
本文将详细介绍计算机进制之间的转换方法。
1. 二进制 (Binary) 转换为十进制 (Decimal):方法1:将二进制数从右往左按位展开,每一位的值与2的幂相乘,然后将得到的结果相加。
例如,二进制数1101转换为十进制,计算过程如下:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=13方法2:使用公式法。
将二进制数从高位到低位按权展开,并将每一位的值乘以相应权重,然后将结果相加。
例如,二进制数1101转换为十进制,计算过程如下:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=132. 十进制 (Decimal) 转换为二进制 (Binary):方法1:使用除二取余法。
将十进制数从右往左不断除以2,直到商为0。
最后,将得到的余数按照从下往上的顺序排列,即为二进制数。
例如,十进制数13转换为二进制,计算过程如下:13÷2=商6、余16÷2=商3、余03÷2=商1、余11÷2=商0、余1将得到的余数按从下往上的顺序排列,即为二进制数1101方法2:使用公式法。
将十进制数转换为相应的二进制幂的和。
例如,十进制数13转换为二进制,计算过程如下:13=(2^3)+(2^2)+(2^0)=11013. 十进制 (Decimal) 转换为八进制 (Octal):方法1:使用除八取余法。
将十进制数从右往左不断除以8,直到商为0。
最后,将得到的余数按从下往上的顺序排列,即为八进制数。
例如,十进制数86转换为八进制,计算过程如下:86÷8=商10、余610÷8=商1、余21÷8=商0、余1将得到的余数按从下往上的顺序排列,即为八进制数126方法2:使用公式法。
将十进制数转换为相应的八进制幂的和。
二进制,八进制,十进制,十六进制之间的转换

二进制,八进制,十进制,十六进
制之间的转换
方法是:小数除以2得到余数,即小数除以2,余数就是砝码上的数,得到的商值继续除以2。
根据这个步骤,它将继续向下操作,直到商360被重新知道为0。
例如:把十进制数 150 转换为二进制数:如下:
•2
二进制转换为十进制的方法是:将二进制数按重量展开,相加得到十进制数。
•3
二进制转换为八进制的方法是:三个二进制数通过重量展开相加得到一个八进制数。
(请注意,3位二进制到八进制的转换是从右向左开始的,不足时加0)。
•4
八进制数转换成二进制数的方法如下:八进制数除以2得到二进制数,每个八进制数由三个二进制数组成。
不足时,在最左边补零。
•5
二进制到十六进制的方法类似于二进制到八进制的方法,八进制是三合一,十六进制是四合一。
(注意,4位二进制到十六进制的转换是从右到左,不足时加0)。
•6
十六进制转换成二进制的方法是:将十六进制数除以2得到二进制数,每个十六进制数为4个二进制数。
油量不足时,在最左边加零。
•7
十进制转八进制或者十六进制
将十进制转换为八进制或十六进制,然后除以8或16,直到商为0。
•8
将八进制或十六进制转换成十进制的方法是:将八进制和十六进制香烟组的二进制数按重量展开相加得到十进制数。
•9
八进制 >十六进制方法:将八进制转换为二进制,然后再将二进制转换为十六进制,小数点位置不变。
•10
十六进制 >八进制
方法:将十六进制转换成二进制,再将二进制转换成八进制,小数点位置不变。
二进制八进制十进制十六进制之间的转换算法

二进制,八进制,十进制,十六进制之间的转换算法一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,()2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
十进制、二进制、八进制、十六进制之间的转换doc

十进制转二进制: 用 2 辗转相除至结果为 1 将余数和最后的 1 从下向上倒序写 就是结果 例如 302 302/2 = 151 余 0 151/2 = 75 余 1 75/2 = 37 余 1 37/2 = 18 余 1 18/2 = 9 余 0 9/2 = 4 余 1 4/2 = 2 余 0 2/2 = 1 余 0 故二进制为 100101110 二进制转十进制 从最后一位开始算,依次列为第 0、1、2...位 第 n 位的数(0 或 1)乘以 2 的 n 次方 得到的结果相加就是答案 例如:01101011.转十进制: 第 0 位:1 乘 2 的 0 次方=1 1 乘 2 的 1 次方=2 0 乘 2 的 2 次方=0 1 乘 2 的 3 次方=8 0 乘 2 的 4 次方=0 1 乘 2 的 5 次方=32 1 乘 2 的 6 次方=64 0 乘 2 的 7 次方=0 然后:1+2+0 +8+0+32+64+0=107.二进制 01101011=十进制 107.二进制转十进制,十进制转二进制的算法 阅读:5915 时间:2008-6-16 6:02:10 整理:华 夏黑盟-----------------------------------------------------------------二进制转十进制,十进制转二进制的算法 十进制转二进制: 用 2 辗转相除至结果为 1 将余数和最后的 1 从下向上倒序写 就是结果 例如 302 302/2 = 151 余 0 151/2 = 75 余 1 75/2 = 37 余 1 37/2 = 18 余 1 18/2 = 9 余 0 9/2 = 4 余 1 4/2 = 2 余 0 2/2 = 1 余 0 故二进制为 100101110 二进制转十进制 从最后一位开始算,依次列为第 0、1、2...位 第 n 位的数(0 或 1)乘以 2 的 n 次方 得到的结果相加就是答案 例如:01101011.转十进制:第 0 位:1 乘 2 的 0 次方=1 1 乘 2 的 1 次方=2 0 乘 2 的 2 次方=0 1 乘 2 的 3 次方=8 0 乘 2 的 4 次方=0 1 乘 2 的 5 次方=32 1 乘 2 的 6 次方=64 0 乘 2 的 7 次方=0 然后:1+2+0 +8+0+32+64+0=107. 二进制 01101011=十进制 107. 一、二进制数转换成十进制数 由二进制数转换成十进制数的基本做法是, 把二进制数首先写成加权 系数展开式, 然后按十进制加法规则求和。
二进制八进制十进制十六进制四种算法之间的互相转换

二进制八进制十进制十六进制四种算法之间的互相转换1.二进制转十进制:二进制数是基于2的数制系统,只包含0和1两个数字。
转换二进制数到十进制数非常简单,只需要将二进制数中的每个数字乘以2的幂次方,然后将结果相加即可。
例如,二进制数"1010"转换为十进制数的计算方法如下:1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=102.八进制转十进制:八进制数是基于8的数制系统,只包含0到7的数字。
转换八进制数到十进制数也非常简单,只需要将八进制数中的每个数字乘以8的幂次方,然后将结果相加即可。
例如,八进制数"753"转换为十进制数的计算方法如下:7*8^2+5*8^1+3*8^0=7*64+5*8+3=448+40+3=4913.十六进制转十进制:十六进制数是基于16的数制系统,包含0到9的数字和A到F的字母。
转换十六进制数到十进制数也非常简单,只需要将每个十六进制数字乘以16的幂次方,然后将结果相加即可。
其中字母A到F分别表示10到15、例如,十六进制数"3AF"转换为十进制数的计算方法如下:3*16^2+10*16^1+15*16^0=3*256+10*16+15=768+160+15=9434.十进制转二进制:十进制数是我们日常生活中最常用的数制系统,包含数字0到9、转换十进制数到二进制数可以使用除2取余法。
具体步骤是:将十进制数除以2,直到商为0,然后将每次的余数倒序排列起来作为二进制数的结果。
例如,将十进制数10转换为二进制数的步骤如下:10/2=5余05/2=2余12/2=1余01/2=0余1倒序排列余数得到二进制数"1010"。
5.十进制转八进制:将十进制数转换为八进制数也可以使用除8取余法。
具体步骤与转换为二进制数相似,只需要将除数改为8即可。
例如,将十进制数25转换为八进制数的步骤如下:25/8=3余13/8=0余3倒序排列余数得到八进制数"31"。
十进制、二进制、八进制、十六进制之间的换算规律

◆十进制转二进制:二进制是计算技术中广泛采用的一种数制。
二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前计算机系统使用的基本上是二进制系统。
用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110◆二进制转十进制从最后一位开始算,依次列为第0、1、2...位第n位的数(0或1)乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.好了,现在对二进制和十进制之间的换算有了初步的了解了吧,下面,我们就进一步深入了解二者之间的其他换算规律:二进制转十进制,十进制转二进制的算法一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
很完整的281016进制转换方法

很完整的2、8、10、16进制转换方法最近在研究C语言,因为要用到各进制间转换,所以收集了一些资料…这是一节“前不着村后不着店”的课。
不同进制之间的转换纯粹是数学上的计算。
不过,你不必担心会有么复杂,无非是乘或除的计算。
生活中其实很多地方的计数方法都多少有点不同进制的影子。
比如我们最常用的10进制,其实起源于人有10个指头。
如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。
至于二进制……没有袜子称为0只袜子,有一只袜子称为1只袜子,但若有两袜子,则我们常说的是:1双袜子。
生活中还有:七进制,比如星期。
十六进制,比如小时或“一打”,六十进制,比如分钟或角度……我们找到问号字符(?)的ASCII值是63,那么我们可以把它转换为八进值:77,然后用‘\77′来表示'?'。
由于是八进制,所以本应写成‘\077′,但因为C,C++规定不允许使用斜杠加10进制数来表示字符,所以这里的0可以不写。
事实上我们很少在实际编程中非要用转义符加八进制数来表示一个字符,所以,6.2.4小节的内容,大家仅仅了解就行。
6.2.5 十六进制数转换成十进制数2进制,用两个阿拉伯数字:0、1;8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;10进制,用十个阿拉伯数字:0到9;16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?用竖式计算:2AF5换算成10进制:第0位: 5 * 16^0 = 5第1位: F * 16^1 = 240第2位: A * 16^2 = 2560第3位: 2 * 16^3 = 8192 +————————————-10997直接计算就是:5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997(别忘了,在上面的计算中,A表示10,而F表示15)现在可以看出,所有进制换算成10进制,关键在于各自的权值不同。
二进制、八进制、十进制与十六进制转换计算精华
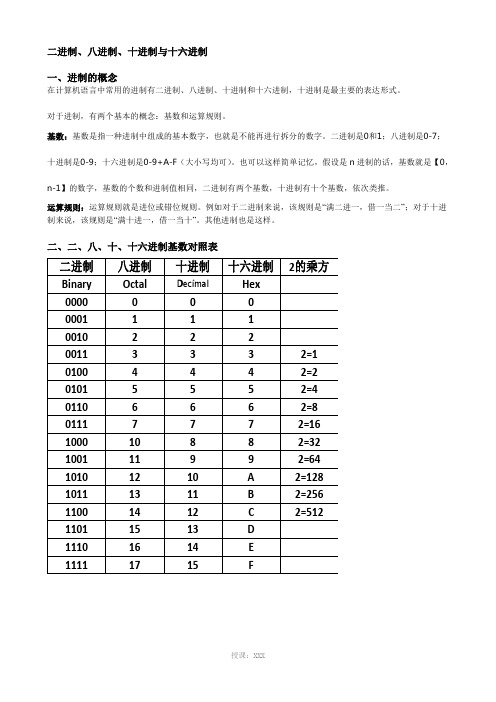
三、二进制转化成其他进制1.二进制(Binary)——>八进制(Octal)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.10101)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2.二进制(Binary)——>十进制(Decimal)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n 位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3.二进制(Binary)——>十六进制(Hex)例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.10101)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
二进制八进制十进制十六进制之间的转换算法

二进制八进制十进制十六进制之间的转换算法二进制、八进制、十进制和十六进制都是常见的数值表示系统。
它们
可以互相转换,以下是在这四个进制之间进行转换的算法:
1.二进制与八进制的转换:
-将二进制数每3位分组(从右往左),不足3位则在左侧补0。
-将每组的二进制数转换为相应的八进制数。
2.二进制与十进制的转换:
-将二进制数每一位乘以2的相应次幂,并将结果相加。
3.二进制与十六进制的转换:
-将二进制数每4位分组(从右往左),不足4位则在左侧补0。
-将每组二进制数转换为相应的十六进制数。
4.八进制与十进制的转换:
-将八进制数每一位乘以8的相应次幂,并将结果相加。
5.八进制与十六进制的转换:
-首先将八进制数转换为二进制数,再将二进制数转换为十六进制数。
6.十进制与十六进制的转换:
-将十进制数每个位上的数字转换为相应的十六进制数。
举例说明:
1.二进制转八进制:
2.二进制转十进制:
-二进制数1101转换为十进制:1*2^3+1*2^2+0*2^1+1*2^0=13
3.二进制转十六进制:
4.八进制转十进制:
-八进制数74转换为十进制:7*8^1+4*8^0=60。
5.八进制转十六进制:
6.十进制转十六进制:
-十进制数255转换为十六进制:255=FF。
以上是二进制、八进制、十进制和十六进制之间的基本转换算法。
根据不同的进制转换需求,我们可以使用这些算法进行相应的转换计算。
(完整版)二进制、八进制、十进制、十六进制之间转换详解.doc

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分① 整数部分方法:除 2 取余法,即每次将整数部分除以 2,余数为该位权上的数,而商继续除以 2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为 0 为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的 168 转换为二进制得出结果将十进制的 168 转换为二进制,(10101000)2分析 : 第一步,将 168 除以 2, 商 84, 余数为 0。
第二步,将商 84 除以 2,商 42 余数为 0。
第三步,将商 42 除以 2,商 21 余数为 0。
第四步,将商 21 除以 2,商 10 余数为 1。
第五步,将商 10 除以 2,商 5 余数为 0。
第六步,将商 5 除以 2,商 2 余数为 1。
第七步,将商 2 除以 2,商 1 余数为 0。
第八步,将商 1 除以 2,商 0 余数为 1。
第九步,读数,因为最后一位是经过多次除以 2 才得到的,因此它是最高位,读数字从最后的余数向前读,即 10101000(2)小数部分方法:乘 2 取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是 0 还是 1,取舍,如果是零,舍掉,如果是 1,向入一位。
换句话说就是 0 舍 1 入。
读数要从前面的整数读到后面的整数,下面举例:例 1:将 0.125 换算为二进制得出结果:将 0.125 换算为二进制( 0.001 )2分析:第一步,将0.125 乘以 2,得 0.25, 则整数部分为0, 小数部分为0.25;第二步 ,将小数部分0.25 乘以 2, 得 0.5, 则整数部分为0, 小数部分为0.5;第三步 ,将小数部分0.5乘以2,得 1.0,则整数部分为1,小数部分为0.0;第四步 , 读数 , 从第一位读起 , 读到最后一位 , 即为 0.001 。
十进制、二进制、八进制、十六进制之间的换算规律资料

◆十进制转二进制:二进制是计算技术中广泛采用的一种数制。
二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前计算机系统使用的基本上是二进制系统。
用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110◆二进制转十进制从最后一位开始算,依次列为第0、1、2...位第n位的数(0或1)乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.好了,现在对二进制和十进制之间的换算有了初步的了解了吧,下面,我们就进一步深入了解二者之间的其他换算规律:二进制转十进制,十进制转二进制的算法一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
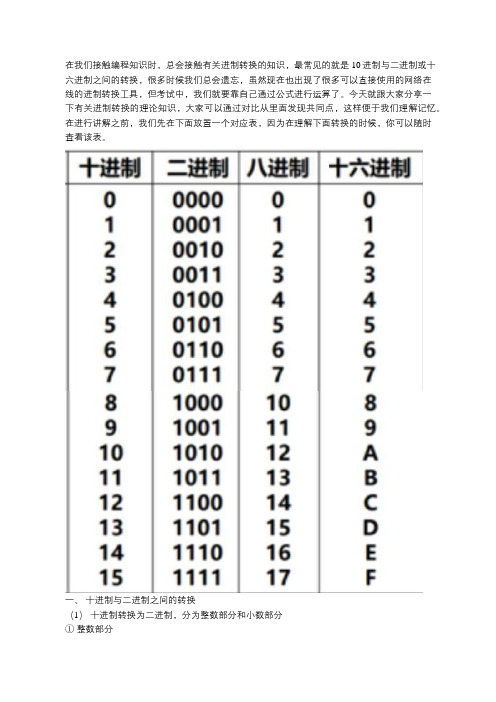
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
很完整的2、8、10、16进制转换方法

很完整的2、8、10、16进制转换方法最近在研究C语言,因为要用到各进制间转换,所以收集了一些资料…这是一节“前不着村后不着店”的课。
不同进制之间的转换纯粹是数学上的计算。
不过,你不必担心会有么复杂,无非是乘或除的计算。
生活中其实很多地方的计数方法都多少有点不同进制的影子。
比如我们最常用的10进制,其实起源于人有10个指头。
如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。
至于二进制……没有袜子称为0只袜子,有一只袜子称为1只袜子,但若有两袜子,则我们常说的是:1双袜子。
生活中还有:七进制,比如星期。
十六进制,比如小时或“一打”,六十进制,比如分钟或角度……我们找到问号字符(?)的ASCII值是63,那么我们可以把它转换为八进值:77,然后用‘\77′来表示’?'。
由于是八进制,所以本应写成‘\077′,但因为C,C++规定不允许使用斜杠加10进制数来表示字符,所以这里的0可以不写。
事实上我们很少在实际编程中非要用转义符加八进制数来表示一个字符,所以,6.2.4小节的内容,大家仅仅了解就行。
6.2.5 十六进制数转换成十进制数2进制,用两个阿拉伯数字:0、1;8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;10进制,用十个阿拉伯数字:0到9;16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?用竖式计算:2AF5换算成10进制:第0位: 5 * 16^0 = 5第1位: F * 16^1 = 240第2位: A * 16^2 = 2560第3位: 2 * 16^3 = 8192 +————————————-10997直接计算就是:5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997(别忘了,在上面的计算中,A表示10,而F表示15)现在可以看出,所有进制换算成10进制,关键在于各自的权值不同。
十进制、二进制、八进制,十六进制之间相互转换方法详解

十进制、二进制、八进制,十六进制之间相互转换方
法详解
1.十进制想要转换为n进制:
整数部分不停地除以n,直到商为0即可,记录下每次的余数,从最后一个余数开始排列即可。
小数部分不停地乘以n,每次乘完后把个位数的数字记录后再变为0,再进行下一次乘法运算,直到小数部分为0即可,记录下每次乘法结束后个位数的数字为多少,从第一个数字开始排列即可。
2.n进制转换为十进制:
n进制上的每一个数字乘以位权再把它们全部加起来。
(如果不懂位权是啥的,请看:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为10^0、10^1、10^2、10^3。
因为:4567=4x10^3+5x10^2+6x10^1+7x10^0),
3.二进制转换为八进制:
从右至左,每3个为一组,不足的补0,通过转换为十进制的方法把它们转换为数字,再依次写下了即可。
4.八进制转换为二进制:
每一个数转化为3位的二进制数即可,不足的补0,再按顺序排列即可。
5.二进制转换为16进制:
从右至左,每4个为一组,不足的补0,通过转换为十进制的
方法把它们转换为数字,需注意的是十六进制中10-15为A-F,再依次写下了即可。
6.十六进制转换为二进制:
每一个数转化为4位的二进制数即可,不足的补0,再按顺序排列即可。
7.八进制转换为十六进制:
先转换为二进制,再转换为十六进制即可。
8。
十六进制转换为八进制:
先转换为二进制,再转换为八进制即可。
二进制八进制十进制十六进制之间的转换算法

二进制,八进制,十进制,十六进制之间的转换算法一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二进制、八进制、十进制与十六进制转换计算精华三、二进制转化成其他进制1.二进制(Binary)——>八进制(Octal)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.10101)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2.二进制(Binary)——>十进制(Decimal)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n 位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3.二进制(Binary)——>十六进制(Hex)例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.10101)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
(10010)2=(22)8=(18) 10=(12)16(0.10101)2=(0.52)8=(0.96875)10=(0.A8)16四、八进制转化成其他进制1.八进制(Octal)——>二进制(Binary)例子1:将八进制数(751)8转换成二进制数。
(751)8=(7 5 1)8=(111 101 001)2=(111101001)2例子2:将八进制数(0.16)8转换成二进制数。
(0.16)8=(0. 1 6)8=(0. 001 110)2=(0.00111)2诀窍:八进制转换成二进制与二进制转换成八进制相反。
2.八进制(Octal)——>十进制(Decimal)例子1:将八进制数(751)8转换成十进制数。
(751)8=(7x8^2+5x8^1+1x8^0)10=(448+40+1)10=(489)10例子2:将八进制数(0.16)8转换成十进制数。
(0.16)8=(0+1x8^-1+6x8^-2)10=(0+0.125+0.09375)10=(0.21875)10诀窍:方法同二进制转换成十进制。
以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0-7)乘以8的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0-7)乘以8的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3.八进制(Octal)——>十六进制(Hex)例子1:将八进制数(751)8转换成十六进制数。
(751)8=(111101001)2=(0001 1110 1001)2=(1 E 9)16=(1E9)16例子2:将八进制数(0.16)8转换成十六进制数。
(0.16)8=(0.00111)2=(0. 0011 1000)2=(0.38)16诀窍:八进制直接转换成十六进制比较费力,因此,最好先将八进制转换成二进制,然后再转换成十六进制。
(751)8=(111101001)2=(489)10=(1E9)16(0.16)8=(0.00111)2=(0.21875)10=(0.38)16五、十进制转化成其他进制1.十进制(Decimal)——>二进制(Binary)例子1:将十进制数(93)10转换成二进制数。
93/2=46 (1)46/2=23 023/2=11 (1)11/2=5 (1)5/2=2 (1)2/2=1 0(93)10=(1011101)2例子2:将十进制数(0.3125)10转换成二进制数。
0.3125x2 = 0 . 6250.625x2 = 1 .250.25x2 = 0 .50.5x2 = 1 .0(0.3125)10=(0.0101)2诀窍:以小数点为界,整数部分除以2,然后取每次得到的商和余数,用商继续和2相除,直到商小于2。
然后把第一次得到的余数作为二进制的个位,第二次得到的余数作为二进制的十位,依次类推,最后一次得到的小于2的商作为二进制的最高位,这样由商+余数组成的数字就是转换后二进制的值(整数部分用除2取余法);小数部分则先乘2,然后获得运算结果的整数部分,将结果中的小数部分再次乘2,直到小数部分为零。
然后把第一次得到的整数部分作为二进制小数的最高位,后续的整数部分依次作为低位,这样由各整数部分组成的数字就是转化后二进制小数的值(小数部分用乘2取整法)。
需要说明的是,有些十进制小数无法准确的用二进制进行表达,所以转换时符合一定的精度即可,这也是为什么计算机的浮点数运算不准确的原因。
2.十进制(Decimal)——>八进制(Octal)例子1:将十进制数(93)10转换成八进制数。
93/8=11 (5)11/8=1 (3)(93)10=(135)8例子2: 将十进制数(0.3125)10转换成八进制数。
0.3125x8 = 2 .50.5x8 = 4 .0(0.3125)10=(0.24)8诀窍:方法同十进制转化成二进制。
以小数点为界,整数部分除以8,然后取每次得到的商和余数,用商继续和8相除,直到商小于8。
然后把第一次得到的余数作为八进制的个位,第二次得到的余数作为八进制的十位,依次类推,最后一次得到的小于8的商作为八进制的最高位,这样由商+余数组成的数字就是转换后八进制的值(整数部分用除8取余法);小数部分则先乘8,然后获得运算结果的整数部分,将结果中的小数部分再次乘8,直到小数部分为零。
然后把第一次得到的整数部分作为八进制小数的最高位,后续的整数部分依次作为低位,这样由各整数部分组成的数字就是转化后八进制小数的值(小数部分用乘8取整法)。
3.十进制(Decimal)——>十六进制(Hex)例子1:将十进制数(93)10转换成十六进制数。
93/16=5……..13(D)(93)10=(5D)16例子2: 将十进制数(0.3125)10转换成十六进制数。
0.3125x16 = 5.0(0.3125)10=(0.5)16诀窍:方法同十进制转化成二进制。
以小数点为界,整数部分除以16,然后取每次得到的商和余数,用商继续和16相除,直到商小于16。
然后把第一次得到的余数作为十六进制的个位,第二次得到的余数作为十六进制的十位,依次类推,最后一次得到的小于16的商作为十六进制的最高位,这样由商+余数组成的数字就是转换后十六进制的值(整数部分用除16取余法);小数部分则先乘16,然后获得运算结果的整数部分,将结果中的小数部分再次乘16,直到小数部分为零。
然后把第一次得到的整数部分作为十六进制小数的最高位,后续的整数部分依次作为低位,这样由各整数部分组成的数字就是转化后十六进制小数的值(小数部分用乘16取整法)。
(93)10=(1011101)2=(135)8=(5D)16(0.3125)10=(0.0101)2=(0.24)8=(0.5)16六、十六进制转换成其他进制1.十六进制(Hex)——>二进制(Binary)例子1:将十六进制数(A7)16转换成二进制数。
(A7)16=(A 7)16=(1010 0111)2=(10100111)2例子2:将十六进制数(0.D4)16转换成二进制数。
(0.D4)16=(0. D 4)16=(0. 1101 0100)2=(0.110101)2诀窍:十六进制转换成二进制与二进制转换成十六进制相反。
2.十六进制(Hex)——>八进制(Octal)例子1:将十六进制数(A7)16转换成八进制数。
(A7)16=(10100111)2=(010 100 111)8=(247)8例子2:将十六进制数(0.D4)16转换成八进制数。
(0.D4)16=(0.110101)2=(0. 110 101)8=(0.65)8诀窍:十六进制直接转换成八进制比较费力,因此,最好先将十六进制转换成二进制,然后再转换成八进制。
3.十六进制(Hex)——>十进制(Decimal)例子1:将十六进制数(A7)16转换成十进制数。
(A7)16=(10x16^1+7x16^0)10=(160+7)10=(167)10例子2:将十六进制数(0.D4)16转换成十进制数。
(0.D4)16=(0+13x16^-1+4x16^-2)10=(0+0.8125+0.015625)10=(0.828125)10诀窍:方法同二进制转换成十进制。
以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0-9,A-F)乘以16的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0-9,A-F)乘以16的-n 次方,然后相加即可得到小数位的十进制数(按权相加法)。
(A7)16=(10100111)2=(247)8=(167)10(0.D4)16=(0.110101)2=(0.65)8=(0.828125)10七、总结1. 其他进制转十进制:将二进制数、八进制数、十六进制数的各位数字分别乘以各自基数的(N-1)次方,其相加之和便是相应的十进制数,这是按权相加法。
2. 十进制转其他进制:整数部分用除基取余法,小数部分用乘基取整法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
3. 二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足。
