基本型曲线测设极坐标计算程序
极坐标法点位测设步骤及原理

极坐标法点位测设步骤及原理1. 极坐标法概述嘿,朋友们,今天咱们聊一聊一个很酷的测量方法——极坐标法。
可能你会问,这和你我有什么关系?哎呀,别小看它!极坐标法可是我们在进行点位测设时的得力助手,像是你口袋里的万能工具,不论干什么都能派上用场。
特别是在一些开阔的地区,极坐标法简直就是如鱼得水,有趣又实用。
1.1 极坐标法的基本原理首先要理清楚这极坐标法的原理,听起来有点难,但其实简单得很。
一句话,极坐标法就像是把地球上的点变成了数值,这样一来,测量就变得更精准了。
有点儿像你在购物时用条形码扫描器,瞬间就可以看到商品的信息。
极坐标法把一个点的位置用一个角度和一个距离来表示,简直就像是在描绘地图上的“宝藏所在地”。
1.2 极坐标法的优势说到这儿,不得不提极坐标法的好处了。
你想啊,当我们在野外测量地形,或者测设建筑位置时,极坐标法能帮助我们快速找到目标,省去很多麻烦。
别以为只是理论上的优势哦,实际操作中,它能让测量变得高效,不像传统方法那样走弯路。
就好比你和朋友们约好在某家新开的餐厅,极坐标法告诉你怎么走能最快到达,而不是让你绕到局。
2. 点位测设的步骤那么,既然原理和优势都了解了,接下来就来说说具体的测设步骤。
说到这儿,大家可得集中精神哦,因为这可是重头戏!2.1 第一步:准备工作首先,我们得进行准备工作。
这就好比出门前你要检查背包,看有没有带水、食物和地图。
极坐标法也一样,首先得确认测量设备是否齐全,比如经纬仪、尺子,最大的敌人就是没准备好,浪费时间就不好玩了。
2.2 第二步:设定基准点接下来,我们要设定一个固定基准点。
可以想象一下,在一片茫茫大海中,找到一个信号岛,才能更好地定位。
这个基准点就是我们这次测量的“信号塔”,从这里出发,一切都变得简单了。
通过测量基准点到目标点的角度和距离,我们就能找到正确的位置。
2.3 第三步:实地测量一切准备就绪之后,就到实地测量的环节了!这时候,大家要把极坐标法的理论应用到实际中。
全站仪极坐标法曲线桥测量计算_pdf

p——内移距(加缓和曲线后,圆曲线在原来两个切点处,沿切线的垂线
方向,向内移动的距离,称为内移距);
E——偏距值(线路中心点与梁工作线交点的间距),在设计图中示出。
预偏心——梁工作线交点与墩中心点间的距离,在墩台定型图中示出。
在第一、三象限,YC′、YC″为正;在第二、四象限 YC′、YC″为负。本桥两条曲
C
B(JD22-1)
E
筑龙网
D
A(JD22-2)
网中 AB 边为设计给定导线边,AD、DC、CE 为三角网基线边。测角采用的是
全圆测回法,基线丈量采用全站仪,经过多次观测及平差,网的精度满足了四等网的
要求。
二、桥墩台线路中心点放样
桥墩台线路中心点即线路中心线与墩台横向轴线的交点。线路中心点位坐标可通
筑龙网
桥台护桩示意图
纵向护桩方向线
α 线路中心线
桥梁工作线
横
台尾
向
胸 墙 线
护 桩 方 向
线
墩的横向十字线为相临两跨梁工作线夹角补角(180°-α)的平分线,其中α
为某墩的梁工作线交角;墩纵向十字线为过墩中心墩横向十字线的垂线。(见下图)
桥墩纵向护桩十字线 工作线交角平分线
8
线在一、三象限,故计算公式与上述相同。
四、曲线墩台细部位置坐标计算
计算原理:(见下图)将先前建立的统一坐标系中的坐标原点移到某墩中心上,
根据纵向轴线相对坐标纵轴的转交及想要计算的点位与墩中心的相对位置关系,计算
WWHZW坐.标Z原点
`
(重庆方向)32#台
第二曲线
筑龙网
第一曲线 0#台(遂宁方向)
二、缓和曲线上墩台线路中心(A)、墩台梁工作线交点(A′)、墩台中心线交
卡西欧FX5800P编程计算器应用及程序

程序示例
U“Z=0 Y≠0”=0
K0+=0 H0=3014.6 ≥=1/74.09 D=2.9 E=2.46 R=1.671
【1】 直线段
实测坐标(m)
圆拱段超欠(m) 直墙超欠(m) 底板超欠(m) 至拱肩高差(m)
111.139 93.763 64.030 94.543 116.748
18°52ˊ49.81" 91°24ˊ13.56" 88°26ˊ53.49" 49°40ˊ03.20" 60°41ˊ09.73"
移 动 值(m)
DV=、0.254 D∧=、0.700 DV=、0.049 DV=、0.140 DV=、0.168
据目录(个数)是利用“ ”,按 FUNCTION->7->2->1->EXE 就可以看到个数了。
在程序中调用统计储存器中的数据时,是利用 List 调用的。具体格式如下: List X[A]+Y[A]i->C
式中 A 是点号,C 是任意储存单元。具体示例详见“程序部分”->“极程序放样” (2)、利用统计计算(SD/REG)
2、以 形式计算。以坐标换算为例:
坐标重合点 A 旧坐标 98042.831->SHIFT->RCL->A 11430.122->SHIFT->RCL->B A+Bi->E 新坐标值均为零,就不必另行输值,新旧坐标方位角差值 69°56"23"->W。 要求计算施工坐标 X=27,Y=29.1 的 B 点的测量坐标。 计算赋值:27->U,29.1->V。U+Vi->F
<=、0.663 =>、0.023 <=、0.218 <=、0.561 =>、0.298
任意点极坐标法测设曲线

任意点极坐标法测设曲线随着测距仪、全站仪的普及应用,任意点击坐标法测设曲线,已在生产者中得到了广泛应用。
用这种方法的优点是:设站灵活,不受地形条件限制,主点和曲线点可同时测设。
但应注意,由于测点彼此独立,应采用一定的方法检核,起点为误差不应大于5cm。
一、任意点极坐标法测设曲线的原理如图1-1所示,M、N为已知的平面控制点,A 、B、C为待定曲线点,设M、N、A、B、C点在相同坐标系下的坐标均已知,则根据坐标反算可得坐标方位角:αM,N、αM,A、αM,B、αM、C。
水平距离D M,A、D M,B、D M,C。
测设时,置镜于M点,后视N点定向,定向后视读数配置为αM,N;旋转仪器当平盘读数为αM,A时,于视线方向上测设D M,A,得A 点;用同样方法可测出B、C等点。
1-1任意点极坐标法测设曲线原理由此可见,任意点极坐标法测设曲线的关键问题是:统一坐标系下控制点、曲线点的坐标计算;测设数据计算。
一、 坐标计算坐标系的建立主要取决于控制点的情况。
如果控制点是为测设曲线而布设的,则坐标系一般采用ZH-xy 坐标系;如果控制点是既有控制点(如初测导线点),则控制点所在的坐标系就是统一坐标系,即既有坐标系统。
1. ZH-xy 测量坐标系下曲线点坐标计算如图1-2所示,以始端缓和曲线ZH 为原点,以ZH 切线为X 轴,且指向交点方向为正向,建立测量中的平面直角坐标系ZH-xy ,则在此坐标系下,ZH-HY 段曲线点的坐标为:错误!未找到引用源。
式1-1错误!未找到引用源。
式中,l A 为A 点到缓和曲线起点的曲线长;l o 为缓和曲线长;R 为圆J α曲线半径;按里程增加方向,当曲线右偏时y A坐标为正,左偏时y A 坐标为负。
HY—YH段曲线点的坐标为:错误!未找到引用源。
式1-2式中错误!未找到引用源。
错误!未找到引用源。
为错误!未找到引用源。
点的里程,错误!未找到引用源。
按里程增加方向,当曲线右偏时,y B坐标为正,左偏时y B坐标为负。
曲线坐标计算程序
I=30/(3.1415926*A*A)*(LF-LT)*(LF+2*LT)
l=L-LF的五次方/(72*A的四次方)*(0.8-LT/LF-LT/LF的平方+LT/LF的3次方+LT/LF的4次方-0.8LT/LF的5次方)
LT=A*A/R-(该曲线起点里程与HY点里程之差) LF=LT+(该曲线起点里程与前视点里程之差)
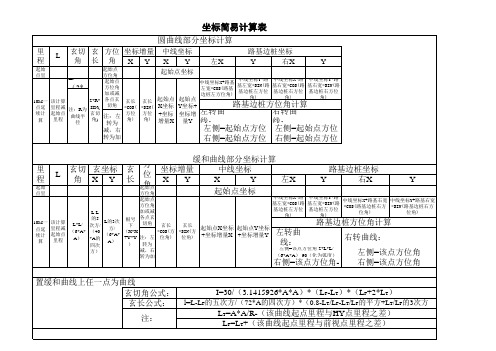
坐标简易计算表
圆曲线部分坐标计算
里程
起始 点里
L 玄切角玄长 方位角
坐标增量 X Y
中线坐标 X Y
左X
路基边桩坐标 Y 右X
Y
起始点 起始点坐标 方位角 起始点 中线坐标X+路基 中线坐标Y+路 中线坐标X+路 中线坐标Y+路 L/(2*R) 方位角 左宽*COS(路基 基左宽*SIN(路 基右宽*COS(路 基右宽*SIN(路 加或减 边桩左方位角) 基边桩左方位 基边桩右方位 基边桩右方位 角) 角) 角) 各点玄 玄长 玄长 起始点 起始点 2*R* 10M一 该计算 点延 里程减 注:R为 SIN( 切角 *COS( *SIN( X坐标 Y坐标+ 续计 起始点 曲线半 玄切 注:左 方位 方位 +坐标 坐标增 角) 角) 里程 角) 增量X 算 量Y 径 转为
Hale Waihona Puke 缓和曲线部分坐标计算 坐标增量 中线坐标 X Y X Y 左X 起始点坐标
路基边桩坐标 Y 右X
Y
路基边桩方位角计算 右转曲线:
右侧=该点方位角-2*L*L/(6*A*A)+90(化为弧度)
右侧=该点方位角+2*L*L/(6*A*A)+90(化为弧度)
置缓和曲线上任一点为曲线起点坐标计算:
简单曲线的极坐标方程课件

(2)过点 A(1,0),倾斜角为34π的直线的直角坐标方程为 y= -(x-1),即 y=1-x,
将 y=ρsin θ,x=ρcos θ 代入上式得 ρsin θ=1-ρcos θ, ∴ρ(cos θ+sin θ)=1 0≤θ<34πρ≥0和74π<θ<2πρ≥0.
直角坐标方程与极坐标方程的互化
(2)将 x=ρcos θ,y=ρsin θ 代入 x2+y2+2ax=0,得 ρ2cos2θ+ρ2sin2 θ+2aρcos θ=0,即 ρ(ρ+2acos θ)=0,又 ρ =0, ∴ρ=-2acos θ, 所以,圆 x2+y2+2ax=0(a≠0)的极坐标方程为 ρ=-2acos θ,圆心为(-a,0),半径为 r=|a|.
极坐标方程涉及的是长度与角度,因此列方程的实质是解直角或斜三角形.
[变式训练] 1.在极坐标系中,求: (1)圆心在极点,半径为2的圆的极坐标方程; (2)圆心为C(2,π),半径为2的圆的极坐标方程.
解析: (1)设所求圆上任意一点 M(ρ,θ), 结合图形(1),得|OM|=2,∴ρ=2,0≤θ<2π.
[规律方法] 化曲线的直角坐标方程 f(x,y)=0 为极坐标方 程 f(ρ,θ)=0,只要将 x=ρcos θ.y=ρsin θ 代入到方程 f(x,y) =0 中即可.化为极坐标方程时,如果不加特殊说明,就认为 ρ≥0.
例如 x2+y2=25 化为极坐标方程时,有 ρ=5 或 ρ=-5 两 种情况,由于 ρ≥0,所以 ρ=5.事实上,这两个方程都是以极点 为圆心,以 5 为半径的圆.
[变式训练] 2.(1)若本例中条件不变,如何求以 A 为端点 且在极轴上方的射线的极坐标方程?
(2)若本例中直线过点 A(1,0)不变,直线的倾斜角变为34π, 如何求直线的极坐标方程?
(完整word版)任务7-3极坐标法测设圆曲线学习指导.

任务7.3 :极坐标法测设圆曲线学习指南一、概述二、任务书极坐标法测设圆曲线工作任务书三、学习内容1.圆曲线逐桩坐标计算在城市道路、高速公路中常设有圆曲线,也就是在两条直线之间加一段圆弧,以便改变方向。
圆曲线线形是由直线→圆曲线→直线组成,分为右偏曲线和左偏曲线(图6-5-1和图6-5-2)。
圆曲线测量就是将线路中线圆曲线段每隔一定的间隔用木桩在地面上表示出来。
1.1 圆曲线要素计算圆曲线的要素包括切线长(T),曲线长(L),外矢距(E0)和切曲差(q)。
(1) 切线长:ZY(或YZ)至JD间的直线长;(2) 曲线长:ZY至YZ间的曲线长;(3) 外矢距:JD沿半径方向至QZ间的直线长;(4) 切曲差:二倍切线长与曲线长之差。
从图6-5-1的几何关系,当圆曲线半径R、转向角α已知时,可得综合要素T、L、E0、q等的计算公式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=-=⋅⋅=⋅=LT q R R E R L R T 22sec 1802tan 0απαα (6-5-1) 上述式中:α----线路转向角,即相邻两直线延长线的夹角; R-----圆曲线半径;1.2 圆曲线主点里程推算(1)圆曲线主点 ZY ——直圆点QZ ——曲中点 YZ ——圆直点 (2)主点里程推算⎪⎩⎪⎨⎧+=+=-=L ZY YZ L ZY QZ T JD 点里程点里程点里程点里程里程点里程2ZY (6-5-2)主点里程检核计算:q T ZY YZ -+=2点里程点里程 (6-5-3)1.3 圆曲线逐桩坐标计算(1). 曲线起点ZY 点线路坐标计算⎩⎨⎧︒++=︒++=)()(切切180sin 180cosZY JD ZYZY JD ZY T Y Y T X X αα (6-5-4) 式中:(JD JD Y X ,)------JD 的线路坐标; (ZY ZY Y X ,)-----ZY 的线路坐标; 切ZY α------ZY 至JD 点的坐标方位角。
简单曲线的极坐标方程(教案)

简单曲线的极坐标方程教案章节:第一章至第五章第一章:引言1.1 极坐标系的介绍极坐标系的定义和基本概念极坐标系与直角坐标系的关系极坐标系的优点和应用领域1.2 极坐标方程的基本形式极坐标方程的定义和表达方式极坐标方程与直角坐标方程的转换方法常见曲线的极坐标方程的例子第二章:圆的极坐标方程2.1 圆的极坐标方程的定义和性质圆的极坐标方程的表达方式圆的半径和角度的关系圆的极坐标方程的图像和特点2.2 圆的极坐标方程的参数方程参数方程的定义和表达方式圆的参数方程与极坐标方程的关系参数方程在圆的极坐标方程中的应用第三章:螺旋线的极坐标方程3.1 螺旋线的极坐标方程的定义和性质螺旋线的极坐标方程的表达方式螺旋线的半径和角度的关系螺旋线的极坐标方程的图像和特点3.2 螺旋线的极坐标方程的参数方程参数方程的定义和表达方式螺旋线的参数方程与极坐标方程的关系参数方程在螺旋线的极坐标方程中的应用第四章:双曲线的极坐标方程4.1 双曲线的极坐标方程的定义和性质双曲线的极坐标方程的表达方式双曲线的半径和角度的关系双曲线的极坐标方程的图像和特点4.2 双曲线的极坐标方程的参数方程参数方程的定义和表达方式双曲线的参数方程与极坐标方程的关系参数方程在双曲线的极坐标方程中的应用第五章:椭圆的极坐标方程5.1 椭圆的极坐标方程的定义和性质椭圆的极坐标方程的表达方式椭圆的半径和角度的关系椭圆的极坐标方程的图像和特点5.2 椭圆的极坐标方程的参数方程参数方程的定义和表达方式椭圆的参数方程与极坐标方程的关系参数方程在椭圆的极坐标方程中的应用第六章:直线的极坐标方程6.1 直线的极坐标方程的定义和性质直线的极坐标方程的表达方式直线的极坐标方程与直角坐标方程的关系直线的极坐标方程的图像和特点6.2 直线的极坐标方程的参数方程参数方程的定义和表达方式直线的参数方程与极坐标方程的关系参数方程在直线的极坐标方程中的应用第七章:抛物线的极坐标方程7.1 抛物线的极坐标方程的定义和性质抛物线的极坐标方程的表达方式抛物线的半径和角度的关系抛物线的极坐标方程的图像和特点7.2 抛物线的极坐标方程的参数方程参数方程的定义和表达方式抛物线的参数方程与极坐标方程的关系参数方程在抛物线的极坐标方程中的应用第八章:渐开线的极坐标方程8.1 渐开线的极坐标方程的定义和性质渐开线的极坐标方程的表达方式渐开线的半径和角度的关系渐开线的极坐标方程的图像和特点8.2 渐开线的极坐标方程的参数方程参数方程的定义和表达方式渐开线的参数方程与极坐标方程的关系参数方程在渐开线的极坐标方程中的应用第九章:双曲线的渐近线的极坐标方程9.1 双曲线的渐近线的极坐标方程的定义和性质双曲线的渐近线的极坐标方程的表达方式双曲线的渐近线的半径和角度的关系双曲线的渐近线的极坐标方程的图像和特点9.2 双曲线的渐近线的极坐标方程的参数方程参数方程的定义和表达方式双曲线的渐近线的参数方程与极坐标方程的关系参数方程在双曲线的渐近线的极坐标方程中的应用第十章:总结与拓展10.1 简单曲线极坐标方程的应用极坐标方程在工程和物理领域的应用极坐标方程在艺术和设计领域的应用极坐标方程在其他领域的应用10.2 极坐标方程的进一步研究复杂曲线的极坐标方程研究极坐标方程与其他数学分支的联系极坐标方程在现代科学技术中的应用重点和难点解析:1. 第一章:引言极坐标系的定义和基本概念:需要重点关注极坐标系与直角坐标系的关系,以及极坐标系的优点和应用领域。
070简单曲线的极坐标系方程(2)

高二数学 序号 高二 年级 班 教师 徐文龙 学生课题 简单曲线的极坐标系方程(2)教学内容:直线的极坐标方程教学目的:了解极坐标方程,会求直线的极坐标方程,会对极坐标方程与直角坐标方程进行互化. 重点难点:直线的极坐标方程的求法与互化。
复习引入1.回顾极坐标和直角坐标的互化公式。
2. 回顾在直角坐标系中的直线方程。
1)直线的一般方程为 2)过点(3,0),且与x 轴垂直的直线方程为 3、回顾求曲线极坐标方程的一般步骤新知教学例1:求过极点,倾斜角为4π的射线的极坐标方程思考:与直角坐标系中直线方程相比较,极坐标系中的直线方程表示起来很不方便,要用两条射线组合而成,原因在哪?应该如何弥补这个不足?(阅读教材P14)例2. 求过点A (a ,0)(a>0)且垂直于极轴的直线l 的极坐标方程.变式:设点P 的极坐标为P (a ,0),直线l 过点P 且与极轴所成的角为α,求直线l 的极坐标方程.课堂练习1. 求直线的极坐标方程:(1)过极点,关于极轴的倾斜角是3π的直线; (2)过点A (2,0)且垂直于极轴的直线;3)过点(2,3π),并且和极轴垂直的直线课堂小结:求直线极坐标方程的一般步骤:1、据题意画出草图;2、设点M (,)ρθ是直线上任意的一点3、连接MO ;4、根据几何条件建立关于,ρθ的方程,并化简5、检验并确定所得方程极为所求课后作业:1、求适合下列条件的直线或圆的极坐标方程:1)过点A (3,6π)且垂直于极轴的直线;(2)垂直于极轴且极点到它的距离是5的直线;(3)过极点,倾斜角是12π的直线2.已知直线的极坐标方程为sin()42πρθ+=,求点A (2,74π)到这条直线的距离.3.把下列直角坐标方程和极坐标方程互化(1)x=4 (2)2x-3y-1=0(3)sin 2ρθ= (4)(2cos 5sin )40ρθθ+-=(5)221x y -=。
简单曲线的极坐标方程 课件

(4)∵ρcos 22θ=1,
∴ρ·1+c2os θ=1,即 ρ+ρcos θ=2.
∴ x2+y2+x=2.化简,得 y2=-4(x-1).
(5)∵ρ2cos 2θ=4,
∴ρ2cos 2θ-ρ2sin 2θ=4,即 x2-y2=4.
(6)∵ρ=2-c1os
, θ
∴2ρ-ρcos θ=1,
∴2 x2+y2-x=1.化简,得 3x2+4y2-2x-1=0.
解析:(1)将 x=ρcos θ,y=ρsin θ 代入 y2=4x, 得(ρsin θ)2=4ρcos θ. 化简,得 ρsin 2θ=4cos θ. (2)将 x=ρcos θ,y=ρsin θ 代入 y2+x2-2x-1=0,得 (ρsin θ)2+(ρcos θ)2-2ρcos θ-1=0. 化简,得 ρ2-2ρcos θ-1=0. (3)∵tan θ=yx,∴tan π3=yx= 3. 化简,得 y= 3x(x≥0).
∴过点 A2,4π且平行于极轴的直线方程为 ρsin θ= 2. (2)如图所示,点 A3,π3,即|OA|=3,∠AOB=π3.由已知 ∠MBx=34π,
∴∠OAB=34π-π3=51π2,∴∠OAM=π-51π2=71π2.
又∵∠OMA=∠MBx-θ=34π-θ,在△MOA 中,根据正
弦定理,得 sin
6.已知曲线C1,C2的极坐标方程分别为ρcos θ=3,ρ=
4cos θ
ρ≥0,0≤θ<,π2 则曲线C1与C2交点的极坐标为
Байду номын сангаас
________.
解析:我们通过联立解方程组ρρc=os4cθo=s 3θ ρ≥0,0≤θ<
π2解得ρθ==2π6 3 , 即两曲线的交点为 2 3,π6.
三、简单曲线的极坐标方程

2=5 3 cos -5 sin 即化为直角坐标为
5 3 2 5 2 x y 5 3 x 5 y 即( x ) ( y ) 25 2 2 5 3 5 所以圆心为( , ), 半径是5 2 2
2 2
练习:
A、双曲线
1、极坐标方程 cos( )所表示的曲线是( D ) 4
B、椭圆
C、抛物线
D、圆
2
2、曲线的极坐标方程=4 sin 表示的圆的 圆心坐标和半径是什么? 圆心坐标是(2,
), 半径是r=2
3、圆=10 cos( )的圆心坐标是( C ) 3 2 D、 (5, ) (5, ) A、 (5,0) B、 C、 (5, ) 3 3 3
5 ( 0) 4
o
M
x
(3)求过极点,倾斜角为 的直线的极坐标方程。 4 5 ( 0) 和 ( 0) M 4 4
﹚
4
o
x
和前面的直角坐标系里直线方程的表示形
式比较起来,极坐标系里的直线表示起来很不
方便,要用两条射线组合而成。原因在哪?
P 点坐标(ρ1cos θ1,ρ1sin θ1), π 当 α≠ 时,直线方程为 y-ρ1sin θ1=tan α(x-ρ1cos θ1) , 2 即 x· tan α-y-ρ1cos θ1·tan α+ρ1sin θ1=0. π 当 α= 时,x=ρ1cos θ1. 2 答
M (,) A
O
C(a,0)
x
曲线的极坐标方程
①曲线C上任一点的坐标(所有坐标中至少有一个)
一 定义:若曲线C上的点与方程f(,)=0有如下关系:
符合方程f(,)=0 ;
导线极坐标法测设曲线方法研究及应用

导线极坐标法测设曲线方法研究及应用摘要:近年来,我国铁路建设事业发展迅速,这对施工测量有了更加严格的要求。
在以往的路线工程测量中我们常用的方法是全站仪极坐标法,本文论述了一种新的施工测量方法—导线极坐标法。
采用导线极坐标法(全站仪配合)设站一次可以进行整条曲线测设,计算简单、测设便捷。
理论和实践都证明导线极坐标法测设公路铁路工程较以往的方法更是灵活、简便、精度高,是一种值得推广应用的新方法。
本文根据全站仪的特点和导线极坐标法放样过程,利用极坐标放样的点位精度估算原理,对影响全站仪配合导线极坐标法放样公路中线精度的因素进行了分析,验证了该方法在施工测量中的优越性。
关键词:导线极坐标法;全站仪;放样;曲线测设Abstract: In recent years,the construction of railways grows in a rapid speed,and this call for more strict demand to the engineering suvey.The total station and the polar coordinate method is the common way in the railway engineering.This article introduces a new way named the traverse polar coordinate method,which is very convienent and not complicated using this method together with the total station.It shows practicely and theorically that it is of great flexibility and convinence,and has compotence for wide use.The design analyze the error that may emerge in the road engineering using this kind of way by analying the charactristics and the processes of setting out,and it indicates that it has a lot of merits.Key words;the polar coordinate way;the total station;lay out;set out the curve0 前言随着科学技术的发展和各种光进测量工具在测量中的应用,工程项目的可靠性、寿命和安全面临着更高的技术要求。
简单曲线的极坐标方程课件

2.求极坐标方程的步骤
剖析求曲线的极坐标方程的步骤与求直角坐标方程的步骤类似,
就是把曲线看作适合某种条件的点的集合或轨迹.将已知条件用曲
线上的点的极坐标ρ,θ的关系式f(ρ,θ)=0表示出来,就得到曲线的极
坐标方程,具体如下:
(1)建立适当的极坐标系,设P(ρ,θ)是曲线上的任意一点.
(2)由曲线上的点所适合的条件,列出曲线上任意一点的极径ρ和
【例3】 将下列曲线的直角坐标方程化为极坐标方程:
(1)射线 y= 3(≤0);
(2)圆x2+y2+2ax=0(a≠0).
= cos,
分析:由公式
化简即可.
= sin
解:(1)将 x=ρcos θ,y=ρsin θ 代入 y= 3,
得ρsin θ= 3cos θ.当 ρ≠0 时,tan θ= 3,
π
4π
∴θ= 或 = .
3
3
∵x≤0,∴ρcos θ≤0,∴θ=
4π
3
.
由于射线过极点,故射线 y= 3(≤0)的极坐标方程为
4π
θ= (≥0).
3
(2)将x=ρcos θ,y=ρsin θ代入x2+y2+2ax=0,得
ρ2cos2θ+ρ2sin2θ+2aρcos θ=0,
即ρ(ρ+2acos θ)=0.
1.直角坐标系与极坐标系的区别
剖析(1)在直角坐标系中,一条曲线如果有方程,那么曲线和它的
方程是一一对应的(解集完全相同且互相可以推导的等价方程,只
看作一个方程).可是在极坐标系中,虽然是一个方程只能与一条曲
线对应,但一条曲线却可以与多个方程对应,所以曲线和它的方程
极坐标法在曲线测设中的应用

要: 传统 的偏 角法曲线测设 , 设站 多、 效率低 , 特别是在 现场条件 复 杂的 山区等地 区测设 曲线 困难 , 多 需
次移动测站 。采 用极 坐标法进行 曲线测设 , 站一次即测 出整条 曲线 , 设 可有效地提 高工作 效率。
Ap l ain o h oa o r iae meh d i h e in a d me s r me to u v s p i to fte p lrc o d n t t o n t e d sg n a u e n fc r e c
卢 西魁 , 张保 东
x 8= X H+尺( Z 1一csp oa )+ , n.
=
式 中: i ——任意放样点 。
a 一
取值 范 围 0 ~30, 根据 直线 Z 。 6。并 J—i 所
在 象 限推算其 最终 值 。
3 测量放样
置镜 于 点 , 视 在 统 一 坐 标 系 中任 意 一 坐 后
随着 国家 经 济 的 发 展 , 交 通 条 件 的要 求 越 来 B, 对 c距 z 点 的距 离 分 别 为 . , B . 。 图 中共 有 3 , s . ,c As s 越 高 , 以高 速公 路 不 断增 加 , 程 不 断 延 长 , 速 个 坐标 系 , 是 始端 缓 和曲线 坐标 系 ( , )2是末 所 里 高 1 ; 公 路事业 飞速 发展 , 高速公 路 建设 过 程 中 , 多地 端缓 和 曲线 坐 标 系 ( , ,; 为 了计 算方 便 选定 在 许 )3是 区障碍物 多 、 形 复杂 , 地 给施 工测 量 带来 了极 大 的 困 的统 一 坐标 系 ( ,,。 l ) 难 。 以往 由于 测 距 工 具 落 后 , 曲线 测 设 一 般 采 用 偏 角法 、 切线 支 距 法 。这 些 测 量 方 法 测 设 一 条 曲线 需 统一 坐标 系原点 ( D) 定应 遵守 以下 原则 : y 选 应使 统一 坐标 系 和始 端 缓 和 曲线 坐 标 系 、 端 末
简单曲线的极坐标方程

7π
或θ= 4 (ρ∈R).
1
1.在极坐标系中,点A(1,π)到直线ρcos θ=2的距离是(
A.1
B.2
C.3
2
3
4
5
)
D.4
解析:点A(1,π)化为直角坐标为(-1,0),直线ρcos θ=2化为直角坐标方程为x=2.
因为点A(-1,0)到直线x=2的距离为3,所以点A(1,π)到直线ρcos θ=2的距离为3.
=1.故ρ
.
2
sin2
即
(3)将x=ρcos θ,y=ρsin θ代入2x2-3y2=4,得2(ρcos θ)2-3(ρsin θ)2=4,
即2ρ2cos2θ-3ρ2sin2θ=4,2ρ2-5ρ2sin2θ=4.
4
故ρ2=
.
2−5sin2
4
5
坐标的互化公式间接求解.
探究一
探究二
探究三
变式训练2
探究四
π
求过点A 2, 4 且平行于极轴的直线l的极坐标方程.
解:如图所示,在直线l上任意取除点A外的一点M(ρ,θ),过点M作极轴的垂线,H为
垂足.
π
π
∵A 2, 4 ,∴|MH|=2sin 4 = 2.
在Rt△OMH中,|MH|=|OM|sin θ,即ρsin θ= 2.
∴动点M的轨迹方程是ρ=4cos θ(ρ≠0).
∵ρ2=4ρcos θ,∴x2+y2=4x,即(x-2)2+y2=4.
故(x-2)2+y2=4(x≠0,且y≠0)为所求的直角坐标方程.
探究一
探究二
探究三
探究四
方法二:设点M的坐标是(ρ,θ)(ρ≠0),N(ρ1,θ1).
全站仪极坐标法曲线桥测量计算_pdf

交点的连线分中点。
3
墩台中心点:自线路中心延墩台横向轴线向曲线外侧偏移 E(偏距)+50cm(预 偏心)的点位。(当设计中无预偏心时墩台中心与墩台梁工作线交点重合,有预偏心 时为不同的两个点位,注意区分。)桥墩中心点为墩的几何中心,桥台中心点为桥台 胸墙 E 值点。
桥台的纵向十字线为胸墙 E 值点和台尾 E 值点连线;桥台横向十字线为过胸墙 E 值点作桥台纵向中心线的垂线(桥台横向十字线即桥台胸墙线)。(见下图)
伐树木等清障工作工作量较大。当地属温带季风气候,施工期间最高气温 45℃,最
底气温 0℃,全年大部分时间雨雾天气较多,空气湿度大,测量时的能见度较差。
该桥设计为单线,平面位置处在两条反向曲线上,两条线间夹一条直线,曲线上
墩台按扇形布置,梁中心线采用平分中矢布置,桥位曲线布置情况如下:
桥位起讫里程:DIK34+240.27~DIK35+277.74,桥梁全长 1037.47 米。 夹直线:在本桥中起止里程 DIK34+444.70~DIK34+804.62,6#墩~17#墩在此直
过公式计算出,需要时利用全站仪极坐标法直接测设即可。
三、桥梁墩台梁工作线交点、墩台中心、墩台中心十字线的定义及放样方法
定义:(前提:此桥桥墩采用扇形布置,桥台采用折线布置。)
梁工作线交点:在单线桥上为相临两孔梁的中心线的交点(即自线路中心延墩台
横向轴线向曲线外侧偏移 E(偏距)的点位);在双线桥上为两线相邻两孔梁中心线
YC″= (R+ p)–(R+E+预偏心)cosαi
式中:β——缓和曲线角(缓和曲线与圆曲线相接处的半径和从圆心作切线垂线的
夹角); li ——计算点至 ZH(或 HZ)的曲线长; R——圆曲线半径;
路线平面曲线定测极坐标原理计算程序

路线平面曲线定测极坐标原理计算程序
戴志国
【期刊名称】《林业勘察设计》
【年(卷),期】1995(000)001
【摘要】文章介绍适用于PC-E500计算器使用的、采用TRUE BASIC语言编制的路线平面线型定测计算程序,论述程序的基本结构、数据输入与结果输出及使用方法,并举例说明源程序的应用。
【总页数】5页(P57-61)
【作者】戴志国
【作者单位】福建省林业勘察设计院
【正文语种】中文
【中图分类】U412.2
【相关文献】
1.平面曲线弧长极坐标公式探讨 [J], 陆小庆;颜超;孔倩
2.任意站极坐标法测设线路平面曲线探讨 [J], 彭仪普
3.浅谈新建铁路线路平面曲线半径的选择 [J], 田要成
4.极坐标原理在定测林区公路平曲线中的应用 [J], 谢再勤;戴志国;林炳淦
5.对公路测设极坐标计算程序的改进与探讨 [J], 苏清松;许合作;刘万宝
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本型曲线测设极坐标计算程序基础理论平面路线的计算和设计是铁路、公路测量工作中的一项重要的内容。
主要包含平面曲线要素和平曲线主点桩号的计算,以及路线中桩逐桩坐标的计算。
随着全站仪、光电测距仪、计算机和Casio可编程系列计算器的广泛应用和飞速发展,测量的方法也随之改进,测量的效率和精度不断提高。
但也存在部分测量基层人员对曲线理论了解不够深入,只会照搬程序和使用程序,如果程序出现问题、需要修改或自己编写时,却不知如何进行。
现在就目前现有的测量理论,将极坐标测设曲线基础由浅入深的介绍给广大测量人员,便于了解和读懂计算程序。
当我们在现场测量时,只需携带编有曲线计算程序的计算器,输入所测点的点号(里程)或与之相关构造物的各点时,即刻得到测点的测量数据。
操作简便灵活、计算快捷、便于掌握。
既减轻了计算工作量,又改善了工作条件,提高了工作效率。
基本型曲线的综合理论目前我国使用的基本型曲线主要分为两种类型:一种是圆曲线;另一种是圆曲线两端加设相等缓和曲线的曲线。
首先介绍圆曲线的综合要素的计算:一、看图学曲线Ⅰ圆曲线的主点和要素的意义:JD……交点,两相邻直线相交的点;ZY……直圆点,按线路前进方向由直线(Ⅰ)进入圆曲线的分界点;QZ……曲中点,圆曲线的中点;ZY……圆直点,按线路前进方向由圆曲线进入直线(Ⅱ)的分界点;T ……切线长,为交点至直圆点或圆直点的长度;L ……曲线长,圆曲线的长度(即ZY至YZ的圆弧长度);E ……外矢距,为交点至曲中点的长度;a……转向角,直线(Ⅰ)与直线(Ⅱ)的夹角,沿线路前进方向,直线(Ⅱ)向左转则为a左,直线(Ⅱ)向右转则为a右;R ……圆曲线的半径。
二、圆曲线要素的计算a、R、交点里程、曲线的转向(左、右)是计算和编程时的必要资料,是已知值。
其它的主要素值一般设计直接提供,也可以通过以下公式计算求得。
圆曲线要素的计算公式:切线长 T=Rtan(a/2)曲线长 L=R aπ/180°外矢距 E=R(sec(a/2)-1)=R(1/cos(a/2)-1)式中计算L时,a以度为单位。
三、圆曲线主点里程的计算主点里程计算是根据计算出的曲线要素,由一已知里程来推算,一般设计直接提供的是交点的里程,我们先依据交点里程计算出直圆点里程,再沿里程增加方向由ZY→QZ→YZ进行推算。
ZY=JD - T;QZ=ZY + L/2;YZ=QZ + L/2圆曲线两端加设相等缓和曲线的计算:一、 看图学曲线上图为右向曲线示意图上图为左向曲线示意图OⅡⅠ圆曲线坐标计算:a y=180(l- l0)/Rπx y=Rsin a yy y=R(1-cos a y)x y y y为测点的曲线坐标,后面需要转换成大地坐标。
有了y y x y的坐标后还要求成ZH点的坐标,公式如下:ZHx = 交点X坐标+T×COS(起始方位角±180度)ZHy = 交点Y坐标+T×SIN(起始方位角±180度)HZx = 交点X坐标+T×COS(起始方位角±转角)HZy = 交点Y坐标+T×SIN(起始方位角±转角)二、缓和曲线的性质1、缓和曲线的作用当车辆以高速由直线进入圆曲线时,就会产生离心力,直接影响车辆的行驶安全和乘客的舒适。
为此需要抵消离心力的影响,考虑直线与圆曲线的连接不能完全消除,就在直线与圆曲线间加入一段曲率半径逐渐变化的过渡曲线,这种曲线称为缓和曲线。
2、缓和曲线的性质缓和曲线是直线逐渐过渡到圆曲线的一种渐变的曲线,是含有辐射螺旋线性质的曲线,它将螺旋线从中截断一部分,与直线连接处的半径为 (无穷大),与圆曲线相接处半径为圆曲线的半径R相等。
由于缓和曲线是一种渐变曲线,如何求得缓和曲线上任意一点的半径、能否找出半径随曲线长度的变化的规律,是深入了解曲线计算的必要条件,也为后一步复曲线计算打下一定的基础。
缓和曲线的曲率半径与缓和曲线计算长度的关系:ρ∝1/ l或ρl=C上式中,C是一个常数,称缓和曲线半径变更率。
按照ρl =C 为必要条件通过求导,导出缓和曲线方程式为:x =l -l 5/40C 2 + l 9/3456C 2 +…… y =l 3/6C - l 7/336 C 3 + l 11/42240C 5 +……式中,x 、y 为缓和曲线上任一点的直角坐标,然而在实际工作中可以根据测设精度的要求,可以将高次项舍去。
当l =l 0,ρ=R 时,可以推出 R l 0=C依据C =R l 0,则缓和曲线方程式变为:x =l -l 5/40R 2 l 02 y =l 3/6 R l 0式中: l-为缓和曲线上任一点P 到ZH (或HZ )的曲线长; l 0-为缓和曲线总长度。
当l =l 0时,则有x =x 0、y =y 0,即为缓圆点(HY )或圆缓点(YH )的 的直角坐标x 0、y 0 。
x 0=l 0-l 0 3/40R 2 y 0=l 02/6 R式中: x 0、y 0为缓圆点(HY )或圆缓点(YH )的直角坐标3、缓和曲线与直线、圆曲线的组合方法缓和曲线的性质是在不改变直线段方向和保持圆曲线半径不变的情况下,插入到直线段和圆曲线之间。
缓和曲线的一半长度处在原圆曲线范围内,另一半处在原直线段范围内,这样就使得圆曲线沿垂直切线方向,向曲线内侧移动了一个距离p (即圆曲线内移量);由此,圆曲线的圆心相应的移动了p ×sec (a/2)的量值,圆心由O ’移至到O ,圆曲线随之也整体向曲线内侧移动。
当然在直线和圆曲线插入缓和曲线之后,使原有的圆曲线长度减少了两个“半条 缓和曲线的长度。
4、缓和曲线常数的计算经过以上的简单介绍,缓和曲线的物理含意和几何关系可以通过缓和曲线常数来表现:β0=180°l 0/2R πδ0=β0/3=180°l 0/6R π m =l 0/2-l 03/240R 2 p =l 0/24R -l 04/2688R 3 x 0=l 0-l 03/40R 2 y 0=l 02/6 R式中β0、δ0、m 、p 、x 0、y 0称为缓和曲线的常数。
ⅠⅡO其中:β0……缓和曲线的切线角,即缓和曲线终点处的切线与直线之间的交角;它也是圆曲线延长ι0/2所对应的圆心角。
δ0……缓和曲线的总偏角,它是缓和曲线起点和缓和曲线终点连线与直线之间的夹角。
m……切垂距,即缓和曲线起点于与圆心O向切线所作垂线垂足的距离。
P ……圆曲线内移量,为垂线长与圆曲线半径R之差。
三、缓和曲线连同圆曲线的要素计算1、曲线综合要素计算在前面我们已经初步了解圆曲线和缓和曲线的性质,以及它们的推论计算公式后,现在只需将它们有机地结合起来,再经过理论推证就得到曲线综合要素计算公式,如下:切线长 T=m +(R + p)tan(a/2)曲线长 L=R aπ/180°+ l0=2 l0 + Rπ(a-2β0) /180°外矢距 E=(R + p)(sec(a/2)-1)=(R + p)(1/cos(a/2)-1) 切曲差 q = 2T-Lι0是计算的必要参数,是设计提供的已知值。
式中,R、a、2、缓和曲线连同圆曲线主点里程的计算主点里程计算是根据计算出的曲线要素,由一已知里程来推算,一般设计直接提供的是交点的里程,我们先依据交点里程计算出直缓点里程,再沿里程增加方向由ZH→HY→QZ→YH→HZ进行推算。
ZH=JD - T;HY=ZH + l0;QZ=HY + L/2;YH=QZ +(L/2-l0);HZ=YH + L基本型曲线极坐标计算基本理论在铁路、公路、市政工程以及其它线路测量中,当采用极坐标法测设线路和与之相关构造物的各点时,通常使用切线支距法先计算测设点的独立坐标;再将独立坐标转换为大地坐标。
为此,我们应建立一个相对应的独立坐标系统。
一、独立坐标系的建立线路计算的独立坐标系统它是以直缓点 (ZH)或直圆点(ZY)为坐标原点,即(X=0,Y=0),以直缓点指向交点的切线为X轴,以垂直切线方向为Y轴;将线路前进方向的X轴的值设定为“+”值,将垂直切线方向指向线路右侧的值设定为“+”值,反之为“-”值。
详见独立坐标系参考图:注:为了清晰的表达x,y值的“+、-”,在编程时设定一个特定的代号表示坐标的“+、-”,通常用“1,-1”来表示曲线的转向,“1”为右向曲线,“-1”为左向曲线;在公式表达时用“±”来表示曲线的转向,“+”表示右向曲线的Y值为正值,“-”表示左向曲线的Y值为负值。
随着目前极坐标在线路测量工作中的广泛应用,切线支距法作为极坐标计算的基础,是我们在理论学习中和编写程序时所必须要掌握的关键部分。
然而,在实际工作中部分基层测量人员只是对第一缓和曲线部分和圆曲线部分的坐标计算公式有所了解,对第二缓和曲线部分坐标计算公式感到困惑,弄不清楚公式中坐标的转换原理。
下面我们将针对第二缓和曲线部分坐标计算进行重点详细的分解。
切线支距法计算坐标公式:1、第一缓和曲线段的坐标计算公式X h1 = l-l 5/ 40R2l02+ l9/3456R4l04y h1 = ±(l3/6Rl0 - l7/336R3l03+ l11/42240R5l05)2、圆曲线段的坐标计算公式a y=180(l- l0)/Rπ+β0x y=Rsin a y + my y=±(R(1-cos a y)+ p)3、第二缓和曲线部分在计算第二缓和曲线的坐标时,首先要弄清楚相对于HZ点建立的坐标系计算出的x’、y’是如何通过坐标转轴公式转换到ZH坐标系的。
a、坐标转换的原理坐标系转换是指两个相对独立,但又具有特定关联的直角坐标系之间的坐标换算的关系。
它含有两层意思,即两个不同的过程,一是两个坐标轴系之间的旋转过程,另一个则是两个轴系之间的移动换位的过程。
首先,我们应先了解和熟悉坐标转换的基本图形。
左侧图形表达的是两个坐标轴系之间的旋转关系,其中X’O Y’坐标系与XOY坐标系之间旋转了a角;右侧图形表达的是两个坐标轴系之间的移动关系,其中X’O’Y’坐标系与XOY坐标系之间是通过距离S和夹角a进行连接的,即X’O’ Y’坐标系中的原点O’的坐标具有双重性,在X’O’ Y’的坐标系中,它的原点坐标为(0,0);在XOY的坐标系中,它的原点坐标为(X0’,Y0’)。
然后我们将旋转和移动结合起来,就构成了坐标系的转换关系。
见左图:b、坐标转轴公式当我们弄清楚坐标系的转换关系之后,再进一步的推论和扩展,将建立在独立坐标系中的点P,通过两个坐标系的几何关系和它们之间的三角函数计算,就不难得出坐标转轴的基础公式。
见右图。
即:X P=X O’ + X P’·Cos a’ + Y P’·Sin a’Y P=Y O’ + (Y P’·Cos a’-X P’·Sin a’)代入公式: X O’= S·Cos aY O’= S·Sin a就可以得出一套完整的坐标转轴公式:X P=S·Cos a + X P’·Cos a’ + Y P’·Sin a’Y P=S·Sin a + (Y P’·Cos a’-X P’·Sin a’)c、第二缓和曲线的坐标计算公式经过上面一系列的推导,下面我们只需将坐标转轴的原理复制到整个曲线中,把以ZH点建立的坐标系当作XOY坐标系;把HZ点建立的坐标系当作X’O’Y’坐标系,就相对容易的得出第二缓和曲线的坐标计算公式了。
