数学竞赛训练题--选择题(每题含详解)

合集下载

小学数学6年级奥数竞赛试题126-149题(含详解)

第126题：有A 、B 、C 、D 四根材料相同的蜡烛，其中A 和B 一样粗，C 和D 一样粗，A 和C 一样长，B 和D 一样长，把四根蜡烛同时点燃，过了6小时，D 首先烧完，此时B 所剩长度是C 的2倍，再过1小时40分钟，C 正好烧完。

请问：A 、B 还可以再燃烧多久？答案： A 还可燃烧575分钟，B 还可燃烧350分钟解析：依题意如图所示，由于C 、D 粗细相同，燃烧时间比为460分钟：360分钟＝23: 18，所以不妨设C 长23米，D 长18米，又当D 燃尽时，C 还剩5米，B 是C 的2倍，长10米，所以B 燃烧了8米，B 与D 的粗度之比为燃烧长度的反比，18:8＝9:4，即B 是D 的49倍，如果把A 、B 换成和C 、D 同样粗细的蜡烛，长度会变为42074923=⨯（米），2814918=⨯（米），又可知1米可燃烧2018360=÷（分钟），所以A 、B 完整燃烧分别为1035分钟和810分钟，当C 正好燃尽时，A 还可燃烧575分钟，B 还可燃烧350分钟。

第127题：将1、2、3、4、5、6分别填在正方体的6个面上，计算具有公共棱的两个面上的数的乘积共有12个，请问：这12个乘积的和最大是多少？答案：147 解析：正方体的每个面都与另4个面有公共棱，只和与它相对的面不相交．我们将题述的12个乘积与1～6这6个数中任取两数相乘得到的1526=C 个乘积相比较即知，缺少的31215=-个乘积恰是正方体3组相对面上的两数之积．全部15个乘积之和是定值，利用乘法对加法的分配律可计算出它为17565)65(4)654(3)6543(2)65432(1=⨯++⨯+++⨯++++⨯+++++⨯．于是为使12个乘积之和最大，需要正方体各对面上两数的乘积相加尽可能小，亦即将1～6分成3对，两两相乘，使乘积之和最小．经计算，这个和最小是28435261=⨯+⨯+⨯，从而所求的最大值是14728175=-．第128题：有一个自然数除以15、17、19所得的商与余数之和都相等，并且商和余数都大于1，那么这个自然数是多少？答案：1082 解析：设除以15时商为a 余b ；除以17时商为c 余d ；除以19时商e 余f 。

【高中数学竞赛专题大全】竞赛专题11 概率(50题竞赛真题强化训练)解析版+原卷版

【高中数学竞赛专题大全】竞赛专题11 概率（50题竞赛真题强化训练）一、填空题1．（2018·安徽·高三竞赛）从1，2，…，10中随机抽取三个各不相同的数字，其样本方差21s ≤的概率=_________. 【答案】115【解析】【详解】123x x x <<的样本方差()3221113i i s x x ==-≤∑，当且仅当1x 、2x 、3x 是连续的正整数.故()231081115P s C ≤==.故答案为1152．（2018·广东·高三竞赛）袋中装有m 个红球和n 个白球，m ＞n≥4.现从中任取两球，若取出的两个球是同色的概率等于取出的两个球是异色的概率，则满足关系40m n +≤的数组（m ，n ）的个数为_______. 【答案】3 【解析】【详解】记“取出两个红球”为事件A ，“取出两个白球”为事件B ，“取出一红一白两个球”为事件C ，则()22m m n C P A C +=，()22n m n C P B C +=，()112m nm nC C P C C +⋅=. 依题意得()()()P A P B P C +=，即2211m n m n C C C C +=.所以()2m n m n +=-，从而m n +为完全平方数.又由4m n >≥及40m n +≤，得940m n ≤+≤. 所以9,3,m n m n +=⎧⎨-=⎩或16,4,m n m n +=⎧⎨-=⎩或25,5,m n m n +=⎧⎨-=⎩或36,6,m n m n +=⎧⎨-=⎩. 解之得（m ，n ）=（6，3）（舍去），或（10，6），或（15，10），或（21，15）. 故符合题意的数组（m ，n ）有3个.故答案为33．（2018·广东·高三竞赛）已知点A （1，1），B （1,02），C （3,02）经过点A 、B 的直线和经过点A 、C 的直线与直线()01y a a =<<所围成的平面区域为G.已知平面矩形区域(){},02,01x y x y <<<<中任意一点进入区域G 的可能性为116，则a=__________. 【答案】12 【解析】【详解】直线AB 方程为21y x =-，直线AC 方程为23y x =-+，直线y a =与它们的交点为D （1,2a a -），E （3,2a a -）.G 的面积等于三角形ADE 的面积()212a -，因此()211416a -=，解之得12a =. 故答案为124．（2019·全国·高三竞赛）已知甲、乙两人进行一种博弈游戏，甲获胜的概率为23，乙获胜的概率为13.若其中一人比另一人多赢两局，则游戏结束那么，需要进行的游戏局数的数学期望为_______. 【答案】185. 【解析】【详解】设所求的数学期望为E ξ.注意到，两局就结束的概率等于22215339⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭.若两局没有结束，则必定恰赢了一局，回到初始状态，此时的数学期望为2E ξ+，从而， ()541822995E E E ξξξ⨯++=⇒=. 故答案为1855．（2019·全国·高三竞赛）两人约定：在某天一同去A 地，早上7点到8点之间在B 地会合，但先到达B 地者最多在原地等待5min 分钟，如果没有见到对方则自己先行.设两人到达B 地的时间是随机的、独立的、等可能的.那么，两人能够在当天一同去A 地的概率是______. 【答案】23144【解析】【详解】设两人到达A 地的时间分别是7点过m 分和7点过n 分（0m ≤、60n ≤）.用数对(),m n 表示两人分别到达A 地的时间.则在直角坐标系中，点(),m n 的存在域是一个边长为60的正方形，其面积为3600.显然，两人能够在当天一同去A 地等价于5m n -≤.此时，相应点的存在域是正方形中位于两直线5m n -=±之间的部分区域（如图），其面积为2360055575-=. 故所求概率为575233600144=. 故答案为231446．（2019·全国·高三竞赛）在面积为1的正方形ABCD 中任取一点P ，则PAB △、PBC 、PCD 、PDA 的面积均大于16的概率是____．【答案】19【解析】【详解】如图，以A 为原点，AB 为x 轴建立直角坐标系.设(),p x y ，01x <<，01y <<. 由题设知x ，y 必满足()()112611261112611126x y x y ⎧>⎪⎪⎪>⎪⎨⎪->⎪⎪⎪->⎩，即12331233x y ⎧<<⎪⎪⎨⎪<<⎪⎩. 因此，满足题设条件的点p 必在直线13x =，23x =和13y =，23y =所围成的正方形区域内.所以所求概率为2211319⎛⎫⎪⎝⎭=. 故答案为197．（2019·全国·高三竞赛）圆周上有10个等分点.则以这10个等分点中的4个点为顶点的凸四边形中，梯形所占的个数比为______. 【答案】27【解析】【详解】任选4点，共有410210C =个凸四边形，其中，梯形的两条平行边既可以从5组平行于直径的5条平行弦中选取，也可以从5组不平行于直的4条平行弦中选取，去除矩形，梯形共有60个.所以，梯形所占的个数比为27. 故答案为278．（2019·全国·高三竞赛）记{}{}1,3,5,7,9,2,4,6,8A B ==．现抛掷硬币从A 、B 中无放回地取出数字组成九位数，规则是：若硬币出现正面时，就从集合A 中取出一个最小的数；若硬币出现反面时，就从集合B 中取出一个最小的数．当一个集合的数字被取完而另一个集合还有数字时，另一集合剩下的数字就按从小到大的顺序添在后面按此规则，取出的数字恰好为123456789的概率为________．【答案】1256【解析】【详解】由规则知，抛掷硬币的正反面序列为：正反正反正反正反．所以，取出的数字恰好为123456789的概率为8112256⎛⎫= ⎪⎝⎭．故答案为12569．（2021·全国·高三竞赛）在1，2，3，…，10这10个正整数中任取4个，记ξ为这四个数中两数相邻的组数，则ξ的数学期望E ξ=__________．【答案】65【解析】【分析】【详解】易知ξ的取值为1,2,3，且：327741013233765C C E C ξ⨯⨯+⨯⨯+⨯==．故答案为：65.10．（2018·全国·高三竞赛）甲、乙、丙、丁各拿一个足球同时进行一次传球，要求每个人可以将球传给另外三人中的任何一人．一次传球后，每个人仍各有一个球的概率为______．【答案】19【解析】【详解】 433139P ⨯== 11．（2018·全国·高三竞赛）袋内有8只白球和2只红球，每次从中随机取出一只球，然后放回1只白球．则第四次恰取完所有红球的概率为______．【答案】0.0434 【解析】【详解】第四次恰取完所有红球的概率为2229182918210.043410101010101010101010⎛⎫⎛⎫⨯⨯+⨯⨯⨯+⨯⨯= ⎪ ⎪⎝⎭⎝⎭．12．（2019·全国·高三竞赛）从{}1,2,,100中任取5个数（可以相同）．则取到合数的个数的数学期望是______．【答案】3710【解析】【详解】{}1,2,,100中合数共有74个，设ξ为取到合数的个数．则()()557426i 05100100iiP C i ξ-⎛⎫⎛⎫==≤≤ ⎪⎪⎝⎭⎝⎭．故ξ服从二项分布．因此，7437510010E ξ=⨯=．故答案为371013．（2018·全国·高三竞赛）甲有一个箱子，里面有红球和白球共4个；乙有一个箱子，里面有2个红球、1个白球、1个黄球.现在，甲从他的箱子中任取2个球，乙从他的箱子中任取1个球，如果取出的3个球颜色全不同，则甲获胜.为了保证甲获胜的概率最大，则甲的箱子中的红球个数为____. 【答案】2 【解析】【详解】设甲的箱子中有()1n n ≥个红球，则白球有4n -个.故甲获胜的概率为()114214414.24n n C C P n n C C -==-422n n +-≤=，即()44n n -≤，当且仅当2n =时，上式等号成立，P 最大.14．（2019·全国·高三竞赛）两人作一种游戏:连续旋转一枚硬币若干次,当正(或反)面向上的次数累计达到5次时游戏结束.游戏结束时,如果正面向上的次数累计达到5次,则A 胜;否则B 胜.那么,旋转不足9次就决出胜负的概率为______.【答案】93128【解析】【详解】考察旋转9次才结束游戏的情形.此时,前8次旋转中正面向上和反面向上各有4次,其概率为488C 352128=,于是,旋转不足9次就结束游戏的概率为35931128128-=. 故答案为9312815．（2019·全国·高三竞赛）设1210,,,a a a 是2000,2001,,2009的一个排列，记数列{}n a 的前n 项和为n S ．则排列1210,,,a a a 满足“()110i S i ≤≤都不是3的倍数”的概率为______.【答案】150【解析】【详解】设2000,2001,,2009的一个排列为一个基本事件M .则基本事件总数为1010N A =.下面计算所求事件M 含的基本事件数．（1）首项不能是3的倍数，除首项以外各项均可是3的倍数，从而，3的倍数有39A 种排法；（2）去掉3的倍数后，考虑模3余2、余1的数的位置（用i a 模3的余数代替i a ）：当11a =时，21a =，32a =，41a =，……此时，含1的项比含2的项多，这与已知矛盾；当12a =时，22a =，31a =，……此时，满足题设要求．综上，模3余2、余l 的数的位置唯一确定，它们的各自排法分别有44A 和33A 种．因此，事件M 含基本事件数为343943m A A A =.故所求概率150m P N ==．故答案为15016．（2019·全国·高三竞赛）一副扑克牌除去大、小王共52张.洗好后，四个人顺次每人抓13张.则两个红A （即红桃A 、方块A ）在同一个人手中的概率为________. 【答案】417【解析】【详解】注意到，牌洗好后每个人的牌就定下来了，即已将52张牌排在了52个位置上. 记四组牌号为：1，5，9，13，⋯，49；2，6，10，14，⋯，50； 3，7，11，15，⋯，51；4，8，12，16，⋯，52．则红桃A 、方块A 在同一组中的排列数为25013504M A A =.从而，所求概率为452!17M P ==. 故答案为41717．（2018·湖北·高三竞赛）一枚骰子连贯投掷四次，从第二次起每次出现的点数都不小于前一次出现的点数的概率为______. 【答案】772【解析】【详解】设1234a a a a 、、、分别是四次投掷骰子得到的点数，那么()1234,,,a a a a 共有46种不同的情况. 如果从第二次起每次出现的点数都不小于前一次出现的点数，则 1234a a a a ≤≤≤.若1234a a a a 、、、的值都相等，则()1234,,,a a a a 有16C 种不同的情况；若1234a a a a 、、、恰好取两个不同的值，则()1234,,,a a a a 有263C 种不同的情况；若1234a a a a 、、、恰好取3个不同的值，则()1234,,,a a a a 有363C 种不同的情况；若1234a a a a 、、、恰好取4个不同的值，则()1234,,,a a a a 有46C 种不同的情况.因此，满足1234a a a a ≤≤≤的情况共有1234666633126C C C C +++=（种）.故所求的概率为41267672=. 18．（2019·上海·高三竞赛）某侦察班有12名战士，其中报务员有3名.现要将这12名战士随机分成3组，分别有3名战士、4名战士、5名战士，那么每一组都有1名报务员的概率是________.【答案】311【解析】【详解】由题意可知，所有的分组方法34129C C N =，满足题意的分组方法23973!C C n =，则满足题意的概率值：2397341293!C C 3C C 11P ==.故答案为：311． 19．（2019·贵州·高三竞赛）已知m ∈{11，13，15，17，19}，n ∈{2000，2001，…，2019}，则mn 的个位数是1的概率为____________ . 【答案】25【解析】【详解】当m =11，n ∈{2000，2001，…，2019}时，mn 的个位数都是1，此时有20种选法；当m =13，n ∈{2000，2004，2008，2012，2016}时，mn 的个位数都是1，此时有5种选法；当m =15时，mn 的个位数不可能为1，此时有0种选法；当m =17，n ∈{2000，2004，2008，2012，2016}时，mn 的个位数都是1，此时有5种选法；当m =19，n ∈{2000，2002，2004，…，2018}时，m 的个位数都是1，此时有10种选法. 综上，所求概率为205051025205++++=⨯.故答案为：25．20．（2021·全国·高三竞赛）有甲乙两个盒子，甲盒中有5个球，乙盒中有6个球（所有球都是一样的）.每次随机选择一个盒子，并从中取出一个球，直到某个盒子中不再有球时结束.则结束时是甲盒中没有球的概率为______. 【答案】319512【解析】【分析】【详解】相当于前十次中至少有五次选择了甲盒的概率，即5101011101051319222512i i p CC ===+=∑.故答案为：319512. 21．（2021·全国·高三竞赛）先后三次掷一颗骰子，则其中某两次的点数和为10的概率为___________．【答案】23108【解析】【分析】【详解】有两次为5的概率为213531166216C C +=，有两次为6和4的概率为211134323306216A C C C +=，所以概率为163023216216108+=. 故答案为：23108. 22．（2018·福建·高三竞赛）从如图所示的，由9个单位小方格组成的，33⨯方格表的16个顶点中任取三个顶点，则这三个点构成直角三角形的概率为______．【答案】514【解析】【详解】先计算矩形的个数，再计算直角三角形的个数．如图所示，根据矩形特点，由这16个点可以构成224436C C ⨯=个不同的矩形．又每个矩形可以分割成4个不同的直角三角形，且不同的矩形，分割所得的直角三角形也不同．因此，可得436144⨯=个直角顶点在矩形顶点的不同的直角三角形．再算直角顶点不在矩形顶点：（1）在12⨯的矩形中，有直角顶点不在矩形顶点，边长分别为()2,2,2的直角三角形两个．而12⨯矩形横向、纵向各有6个，故共有21224⨯=个．（2）在23⨯的矩形中，有直角顶点不在矩形顶点，边长分别为5,5,10的直角三角形4个，边长分别为(2,22,10的直角三角形4个．而23⨯矩形横向、纵向各有两个，故共有()44432+⨯=个．所以，所求的概率31614424322005401414P C ++===⨯． 23．（2018·全国·高三竞赛）从集合{}1,2,,2014中随机地、不放回地取出三个数123a a a 、、，然后再从剩下的2011个数中同样随机地、不放回地取出三个数123b b b 、、.则将123a a a ⨯⨯为长、宽、高的砖能放进以123b b b ⨯⨯为长、宽、高的盒子中的概率为__________．【答案】14【解析】【详解】不妨设123a a a <<，123b b b <<，当且仅当11a b <，22a b <，33a b <时砖可放入盒中. 设126c c c <<<是从{}1,2,,2014中选出的六个数，再从中选出三个，有36C =20种方法.这三个作为123a a a 、、，剩下三个作为123b b b 、、，符合要求的1a 只能为1c . 2a 若为2c ，则3a 可为3c 或4c 或5c ；2a 若为3c ，则3a 可为4c 或5c .故符合要求的取法为5种，概率51204p ==. 24．（2018·全国·高三竞赛）小明、小红分别独立重复投掷均匀的色子，直到第-次出现6点为止．则小明和小红投掷的次数相差不超过1的概率为________．【答案】833【解析】【详解】设小明、小红投掷次数分别为ξη、.则所求为()()()1,11,]i P i P i i P i i ξηξηξη+∞===+==++=+=∑.由独立性,知所求概率为()()()()()()111)i P i P i P i P i P i P i ξηξηξη+∞=⎡⎤==+==++=+=⎣⎦∑=111151515151266666666i i i ii ---+∞=⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⨯⨯⨯+⨯⨯⨯⨯⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦∑=833.25．（2018·全国·高三竞赛）设n 为正整数.从集合{}1,2,,2015中任取一个正整数n 恰为方程236n n n ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦的解的概率为_______（[]x 表示不超过实数x 的最大整数）. 【答案】10072015【解析】【详解】当()6n k k Z +=∈时，6322n k k ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦，66233636n n k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤+=+=+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦.满足题中方程的n 为6，12，…，2010，共335个；当()65n k k Z +=-∈时，653322n k k -⎡⎤⎡⎤==-⎢⎥⎢⎥⎣⎦⎣⎦， 6565221333636n n k k k k k --⎡⎤⎡⎤⎡⎤⎡⎤+=+=-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦. 满足题中方程的n 为1，7，13，…，2011，共336个；当()64n k k Z +=-∈时，643222n k k -⎡⎤⎡⎤==-⎢⎥⎢⎥⎣⎦⎣⎦， 6464221333636n n k k k k k --⎡⎤⎡⎤⎡⎤⎡⎤+=+=-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦. 满足题中方程的n 不存在；当()63n k k Z +=-∈时，633222n k k -⎡⎤⎡⎤==-⎢⎥⎢⎥⎣⎦⎣⎦， 6363211323636n n k k k k k --⎡⎤⎡⎤⎡⎤⎡⎤+=+=-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦. 满足题中方程的n 为3，9，15，…，2013，共336个；当()62n k k Z +=-∈时，623122n k k -⎡⎤⎡⎤==-⎢⎥⎢⎥⎣⎦⎣⎦，6262211323636n n k k k k k --⎡⎤⎡⎤⎡⎤⎡⎤+=+=-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦. 满足题中方程的n 不存在；当()61n k k Z +=-∈时，613122n k k -⎡⎤⎡⎤==-⎢⎥⎢⎥⎣⎦⎣⎦， 6161211323636n n k k k k k --⎡⎤⎡⎤⎡⎤⎡⎤+=+=-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦. 满足题中方程的n 不存在. 因此，从集合{}1,2,,2015中任取一个正整数n 恰为题中方程的解的概率为335336336100720152015++=. 26．（2018·全国·高三竞赛）抛一颗色子三次，所得点数分别为m 、n 、p .则函数322132n y mx x px =--+在[)1,+∞上为增函数的概率为______. 【答案】1124【解析】【详解】注意到，()322132n f x mx x px =--+ 在[)1,+∞上为增函数等价于()220f x mx nx p =-->'在[)1,+∞上恒成立，等价于()10f '>，即2m n p >+.当2m =时，3n p +≤，有3种；当3m =时，5n p +≤，有10种；当4m =时，7n p +≤，有21种；当5m =时，9n p +≤，有30种；当6m =时，11n p +≤，有35种. 故所求概率为331021303511624++++=.27．（2019·全国·高三竞赛）将编号为1，2，…，9的几颗珍珠随机固定在一串项链上，假设每颗珍珠的距离相等，记项链上所有相邻珍珠编号之差的绝对值之和为T 则T 取得最小值的放法的概率为______. 【答案】1315【解析】【详解】由题设，知珍珠的固定方法共有9!47!92=⨯⨯（种）. 在项链所在的圆周上，从1~9有优弧和劣弧两条路径，设12,,,k x x x ⋅⋅⋅是依次排列在这段弧上的珍珠号码.则()()()11211219198k k T x x x x x x x x =-+-+⋅⋅⋅+-≥-+-+⋅⋅⋅+-=，当且仅当1219k x x x <<<⋅⋅⋅<<时，等号成立.因此，T 取得最小值的放法共有0123677772C C C C +++=（种）.故所求概率为62147!315=⨯. 28．（2018·全国·高三竞赛）小张、小李、小华、小明四人玩轮流投掷一枚标准色子的游戏.若有一人投到的数最小，且无人与他并列，则判他获胜；若投出最小数的人多于一个，则将没投出最小数的人先淘汰，再让剩下的人重新做一轮游戏，这样不断地进行下去，直到某个人胜出为止.已知第一个投掷色子的小张投到了数3.则他获胜的概率是______. 【答案】175864【解析】【详解】考虑第一轮次中可能出现的四种情形. （1）小张获胜.这种概率是313168P ⎛⎫== ⎪⎝⎭.（2）小张与另外某一人打成平局.这种概率是213131668C ⎛⎫⨯⨯= ⎪⎝⎭，故形成此情形且小张最终获胜的概率是21118216P =⨯=（注意该游戏永不停止地进行下去的概率是0，下同）.（3）小张与另外某两个人打成平局，这种概率是2231316624C ⎛⎫⨯⨯= ⎪⎝⎭，故形成此情形且小张最终获胜的概率是311124372P =⨯=. （4）所有人均打成平局．这种概率是3116216⎛⎫= ⎪⎝⎭，故形成此情形且小张最终获胜的概率是41112164864P =⨯=. 综上，小张在游戏中获胜的概率为1234111117581672864864P P P P P =+++=+++=. 29．（2018·全国·高三竞赛）从集合{}1,2,,2011⋅⋅⋅中任意选取两个不同的数a 、b ，使得a b n +=（n 为某正整数）的概率为12011．则ab 的最小值为______．【答案】2010．【解析】【详解】记使得a b n +=的方法有k 种．则22011110052011k k C=⇒=．考虑ab 尽量小，且使a b n +=的方法有1005种．取2011n =．则120102************+=+=⋅⋅⋅=+．此时，2011a b +=的选法恰有1005种．于是，ab 的最小值为120102010⨯=．30．（2018·全国·高三竞赛）A B 、两队进行乒乓球团体对抗赛,每队各三名队员,每名队员出场一次. A B 、两队的三名队员分别是1A 、23A A 、,123B B B 、、,且i A 对j B 的胜率为()13ii j i j ≤≤+、.则A 队得分期望的最大可能值是______. 【答案】9160【解析】【详解】设123A A A ，，胜率为123,,,p p p A 则队得分期望为123p p p ++，计算123123123123123123246255336354446435++++++++++++，，，，，，可知,当132132:,:,:A B A B A B 时,期望最大为9160. 31．（2018·全国·高三竞赛）将1~6这16个正整数随机地填入44⨯棋盘的16个格子中（每格填写一数），则使每行、每列填数之和皆为偶数的概率为______．【答案】412145【解析】【详解】首先，将44⨯棋盘染黑白两色，使黑、白两种格子各有8个，且每行（或列）中同色的格子有偶数个．分三种情况讨论：（1）若第一列为两黑两自，则该列有24C 种染法．考虑后三列每行黑格的个数，则有12323223334+⨯⨯+⨯⨯+⨯=种染法．（2）若第一列为四黑，则后三列共有2234321C C +=种染法．（3）若第一列为四白，则后三列共有21种染法．对于以上每种染法，将1~16中的偶数填入黑格中，奇数填入白格中，得到满足条件的填法．故所求概率为()()26342128!4116!2145⨯+⨯⨯=．32．（2019·全国·高三竞赛）某人练习打靶，开始时，他距靶100m ，此时，进行第一次射击.若此次射击不中，则后退50m 进行第二次射击，一直进行下去.每次射击前都后退50m ，直到命中为止，已知他第一次的命中率为14，且命中率与距离的平方成反比.则他能够命中的概率等于_________. 【答案】12 【解析】【详解】记事件“第n 次射击命中”为n A ，其概率为()n P A .则()114P A =. 又第n 次射击时距离靶()()()100501501n n m +-=-，则()()()2122111n P A P A n n ⎛⎫== ⎪+⎝⎭+.于是，前n 次内命中的概率为()()()()121211n n n P P A A A P A P A P A =-⋅⋅⋅⋅⋅⋅=-⋅⋅⋅()21111324211111492233111n n n n n ⎡⎤+⎛⎫⎛⎫=---⋅⋅⋅-=-⋅⋅⋅⋅⋅⋅⋅⋅⋅⎢⎥ ⎪⎪++⎝⎭⎝⎭+⎢⎥⎣⎦()1212121n nn n +=-⋅=++.令n →∞，得1lim 2n n P →∞=. 因此，此人能够命中的概率是12.故答案为1233．（2019·全国·高三竞赛）如图，给定由()12n n +个点组成的正三角形点阵．在其中任意取三个点，以这三点为顶点构成的正三角形的概率为__________．【答案】224n n +-【解析】【详解】设正三角形点阵的凸包为正ABC ∆，边长为1n -.首先，计算正△DEF 的个数，其中，D 、E 、F 为上述正三角形点阵内的点. 如图，将AB 、AC 分别延长到点,B C ''，使得''1BB CC ==.将BB '分成n 等份.对正三角形点阵内任一点X ，过X 作AB 、AC 的平行线与B C ''的交点，并分别记为b c X X 、. 下面分两种情形.1.正△DEF 与正△ABC 的对应边平行，则正△DEF 与边B C ''上有序三点组()b ,,c c E F F 一一对应，有3n+1C 个正三角形.2.正△D E F '''不与正△ABC 对应边平行，作正△D E F '''的外接正△DEF ，使得正△DEF 与正△ABC 的对应边平行，则正△D E F '''与边B’C’上有序四点组()b b ,',',c c E D D F 一一对应，有41n C +个正三角形.综上，共有344n+112n n C C C +++=个正三角形.从而，所求概率为()42321224n n n C C n n ++=+-. 故答案为224n n +-34．（2019·全国·高三竞赛）有7名运动员分别获得某项比赛的一、二、三等奖，已知一等奖的人数不少于1人，二等奖的人数不少于2人，三等奖的人数不少于3人.则恰有2人获一等奖的概率为______. 【答案】613【解析】【详解】按一、二、三等奖的顺序，获奖人数有三种情况：()1,2,4，()1,3,3，()2,2,3.当()1,2,4时，发奖方式有12476465711052C C C ⨯=⨯⨯=（种）；当()1,3,3时，发奖方式有1337636547114032C C C ⨯⨯=⨯⨯=⨯（种）；当()2,2,3时，发奖方式有322742765431210322C C C ⨯⨯⨯=⨯⨯=⨯（种）. 故恰有2人获一等奖的概率为 210621014010513=++.35．（2019·全国·高三竞赛）某校进行投篮比赛，共有64人参加.已知每名参赛者每次投篮的命中率为34.规定：只有连续命中两次才能被录取，一旦录取就停止投篮，否则一直投满4次.设ξ表示录取人数.则E ξ______. 【答案】54 【解析】【详解】每位参赛者被录取的概率为33133113313321644444444434444256p ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故录取人数ξ服从二项分布，即216~64,256B ξ⎛⎫ ⎪⎝⎭.所以，2166454256E ξ=⨯=. 故答案为5436．（2019·全国·高三竞赛）数字钟分别用两个数字显示小时、分、秒（如10:03:18）.在同一天的05:00:00~23:00:00（按小时计算）之间，钟面上的六个数字都不相同的概率是______. 【答案】61540【解析】【详解】为了满足题中的条件，设钟面显示应为()1212121112::6,6,h h m m s s m s h h <<≠. 当16h <，26h <时，1m 和1s 应在小于7中的另外四个数中选择.因而，1m 有四种选择方式，1s 有三种选择方式.由于已选择了四个数字，2m 和2s 就只能从剩余的六个数字中选择，它们分别有六种、五种的选择方式.在05:00:00—23:00:00之间，这种情形共有时间总数是743652520⨯⨯⨯⨯=.当1h 、2h 中只有一个小于6时，类似可求在05:00:00~23:00:00之间，这种情形共有时间总数是854654800⨯⨯⨯⨯=.因此，钟面上的六个数字都不相同的次数是250048007320+=，概率为732061183600540=⨯.37．（2021·浙江金华第一中学高三竞赛）甲，乙两人进行一场七局四胜制的游戏，任何一人累计获胜四局即为胜方，同时游戏结束，另一人为负方．若在每局中，双方各有12的概率获胜，则游戏结束时胜方比负方多获胜的局数的数学期望为______．【答案】3516【解析】【分析】【详解】由题可设游戏结束时胜方比负方多获胜的局数为X ,则X 可能取值为1,2,3,4, 比七局,前六场两人三胜三负,胜方比负方多获胜一场,63615(1)216P X C ⎛⎫=== ⎪⎝⎭;比六局,前五场胜方三胜两负,胜方比负方多获胜两场,63515(2)2216P X C ⎛⎫=== ⎪⎝⎭;比五局,前四场胜方三胜一负,胜方比负方多获胜三场,53411(3)224P X C ⎛⎫=== ⎪⎝⎭,比四局,胜方连胜四局,411(4)228P X ⎛⎫=== ⎪⎝⎭,所以551135()123416164816E X =⨯+⨯+⨯+⨯=. 故答案为：3516. 38．（2019·四川·高三竞赛）设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球(取出某色球的概率均相同)，确定颜色后放回，直到连续两次均取出红色球时为止，记此时取出球的次数为ξ，则ξ的数学期望为_____ . 【答案】12 【解析】【详解】设所求数学期望为E ，第一次取出的球的颜色分别为红、黄、蓝的取法的次数ξ的数学期望为E (a )、E (b )、E (c ).则E (b )=E (c ).因为第一次取出的球的颜色为红、黄、蓝的概率是相同的，所以()2()3E a E b E +=，①先考虑第一次取出的球是红色的，若第二次取出的球是红色的，则操作结束；若不然，第一个为红球，第二个球的颜色为黄或蓝，忽略第一个球，剩下的取球方式可以视为一种新的取法(即第一个球的颜色是黄或蓝)，则12()2(1())33E a E b =⨯++②再考虑第一次取出的球的颜色是黄或蓝，忽略第一个球，剩下的取球方式可以视为一种新的取法，则()1E b E =+③ 由①、②、③，解得E =12. 故答案为：12．39．（2019·广西·高三竞赛）从1，2，…，20中任取3个不同的数，这3个数构成等差数列的概率为____________ . 【答案】338【解析】【详解】设取出的3个不同的数分别为a 、b 、c .不同的取法共有320C 种，若这3个数构成等差数列，则有a +c =2b .故、c 同为奇数或同为偶数，且a 与c 确定后，b 随之而定.从而所求概率为221010320338C C P C +==. 故答案为：338．二、解答题(共0分)40．（2018·黑龙江·高三竞赛）为响应国家“精准扶贫，产业扶贫”的战略，哈市面向全市征如《扶贫政策》义务宣传志愿者，从年龄在[20，45]的500名志愿者中随机抽取100名，其年龄频率分布直方图如图所示.（1）求图中x 的值；（2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动，再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低35岁”的人数为X ，求X 的分布列及数学期望.【答案】（1）0.06x =（2）分布列见解析，期望为1.8 【解析】【详解】（1）根据频率分布直方图可得()0.010.020.040.0751x ++++⨯=，解得0.06x =.（2）.用分层抽样的方法，从100志愿者中选取10名，则其中年龄“低于35岁”的人有6铭，“年龄不低于35岁”的人有4名，故X 的可能取值为0，1，2，3.()343101030C P X C ===，()12643103110C C P X C ===，()2164310122C C P X C ===，()36310136C P X C ===.故X 的分布列为： X 0 1 2 3 P 1303101216所以()13110123 1.8301026E X =⨯+⨯+⨯+⨯=.41．（2018·湖南·高三竞赛）棋盘上标有第0，1，2，⋅⋅⋅，100站，棋子开始时位于第0站，棋手抛掷均匀硬币走跳棋游戏.若掷出正面，棋子向前跳出一站；若掷出反面，棋子向前跳出两站，直到跳到第99站（胜利大本营）或第100站（失败集中营）是，游戏结束.设棋子跳到第n 站的概率为n P . （1）求3P 的值；（2）证明：111()(299)2n n n n P P P P n ++-=--≤≤；（3）求99100P P 、的值.【答案】（1）58（2）111()(2n 99)2n n n n P P P P +--=-≤≤（3）1009911132P ⎛⎫=+ ⎪⎝⎭ 【解析】【详解】（1）棋子跳到第3站有以下三种途径：连续三次掷出正面，其概率在18；第一次掷出反面，第二次掷出正面，其概率为14；第一次掷出正面，第二次掷出反面，其概率为14，因此3P =58.（2）易知棋子先跳到第2n -站，再掷出反面，其概率为212n P -；棋子先跳到第1n -站，再掷出正面，其概率为112n P -，因此有()1212n n n P P P --=+，即()11212n n n n P P P P ----=-+，也即()()1112992n n n n P P P P n +--=-≤≤. （3）由（2）知数列{}()11n n P P n --≥是首项为{}()11n n P P n --≥ 1011122P P -=-=-，公比为12-的等比数列.因此有()()11101122nn n n n P P P P ---⎛⎫-=--= ⎪⎝⎭.由此得到 999899100111211122232P ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 由于若跳到第99站时，自动停止游戏，故有10098991111232P P ⎛⎫==+ ⎪⎝⎭. 42．（2018·全国·高三竞赛）已知数列{}n a 满足10a =，并且对任意的1,11n n n n Z a a a 取或++∈-+的概率均为12．（1）设21n a +的值为随机变量X ，试求X 的概率分布；（2）求X 的绝对值的数学期望E|X|．【答案】（1）见解析；（2）2212n n n nC -．【解析】【详解】（1）设1n n n d a a +=-.则对任意正整数,n n d 取1或-1的概率均为12，且()22211111n nn i i i i i a a a a d ++===+-=∑∑.设21n a k +=.显然，2k n ≤，并设此时122,,,n d d d ⋅⋅⋅中有x 个1,2n-x 个-1.则X-(2n-x)=k. 因此，k=2(x-n)只能取[-2n,2n]之间的偶数值.对于偶数2m(m=0,±1,...,±n)，事件{X=2m}相当于在2n 个数122,,,n d d d ⋅⋅⋅中，有n+m 个取1，n-m 个取-1，因此，X 的概率分布可表示为()()2220,1,,2n mn n C P X m m n +=-==±⋅⋅⋅±（2）对任意1≤i≤n ，易知P(X=-2m)=P(X=2m).从而，()()22121,2,,2n m nn C P X m m n +-===⋅⋅⋅.2222211112?22n m nn n m nn n n m m C E X m mC ++--====∑∑()2222112nn mn mnn n m n m CnC ++-=⎡⎤=+-⎣⎦∑()1212221122nn m n mn nn m nCnC +-+--==-∑ 12122211122n nn m n m n n n m m n C n C +-+--==⎛⎫=- ⎪⎝⎭∑∑ ()212222*********.2222n n n n n n n n nC n C n ---⎡⎤=⨯⨯--=⎢⎥⎣⎦ 43．（2018·全国·高三竞赛）掷骰子（为均匀的正方体，六个面分别标有1、2、3、4、5、6）游戏规则如下：第一次掷9枚骰子，将其中显示为1的骰子拿出放到一边；第二次掷剩下的骰子，再将显示为1的骰子拿出；……，直到未掷出显示为1的骰子或骰子全部拿出，游戏结束.已知恰好掷9次结束游戏的概率为u v uab c d（a、b 、c 、d 为不同的质数，u v N +∈、）.求uv bcd +. 【答案】2012 【解析】【详解】由游戏规则，知若恰好掷9次结束游戏，则前八次中每次恰好有1枚骰子显示为1，第九次无论显示是否为1，游戏均结束，其中，第()1,2,,8k k =⋅⋅⋅次掷10k -枚骰子，恰有1枚显示为1的概率为191010156k k k C ---⨯⨯. 则191891010125566k u k k v u kk k k C ab k c d ----==⨯⨯==∏∏ 363737444040379!5565756632⨯⨯⨯===⨯ 7a ⇒=，5b =，3c =，2d =，37u =，40v =.故37405322012uv bcd +=⨯+=.44．（2018·全国·高三竞赛）从集合{}()1,2,,,2S n n N n +=⋅⋅⋅∈≥的子集中先后取出两个不同的子集P 、Q ，求以下事件发生的概率：（1）PQ ，且Q P ；（2）Card ()()01P Q k k n ⋂=≤≤- 【答案】（1）()1321221n n n n ----；（2）()3221kn n- 【解析】【详解】由集合S 共有2n 个子集，知有序子集对(),P Q 的取法共有()22221n nn A =-种.（1）考虑“P Q ，且Q P ”的对立事件：“P ⊂≠ Q 或Q ⊂≠ P ”.若P ⊂≠ Q ，记Card ()()1Q i i n =≤≤..则Q 有in C 种取法.而P 是Q 的真子集，于是，P 有21i -种取法.从而，满足P ⊂≠ Q 的子集对(),P Q 的取法总数为()121232nn niiiiin n n nn i i i C C C ===-=-=-∑∑∑.由对称性，Q ⊂≠ P 的取法也有32n n -种.因此，P Q ，且Q P 的概率为()()()12323211221221n n nnnnn n----=---. （2）集合{}1,2,,S n =⋅⋅⋅中含有n 的子集的个数为12n -个.于是，事件Card ()()01P Q k k n ⋂=≤≤-等价于在n k -元集合S S '=\()P Q ⋂中先后选取两个子集P '、Q '，使得P Q '⋂'=∅.设Card ()()0P i i k ='≤≤.则P '有ik C 种取法.于是，,s Q C P '⊆'.从而，Q '有2k i -种取法.此时，子集对(),P Q ''共有12k ik C -种选法.故满足P Q '⋂'=∅的子集对(),P Q ''有023kk i i kk i C -==∑（个）.因此，Card ()()01P Q k k n ⋂=≤≤-的概率为()3221kn n-. 45．（2019·全国·高三竞赛）甲乙两人参加竞选，结果是甲得n 票，乙得m 票()n m >. 试求：唱票中甲累计的票数始终超过乙累计的票数的概率. 【答案】n mn m-+ 【解析】【详解】若唱甲当选，则记为1；若唱乙当选，则记为1-. 每一种唱票方式都对应一个由n 个1和m 个1-组成的排列. 用k S 表示谴责k 项的和，在直角坐标系中标出点(),k k S ，并将点(),k k S 与点()11,k k S ++用线段联结()00,1,2,,,0k m n S 其中=⋅⋅⋅+=. 这样，每一种唱票方式都对应一条联结()0,0O 与(),A m n n m +-的折线. 而甲累计的票数始终领先等价于所有的点(),k k S 都在x 轴的上方，即折线与x 轴无交点（我们称为“好折线”，反之为“坏折线”）.显然，联结O 、A 的“自由”（无限定条件）折线有C nm n +条，这是因为在m n +段中选择n 段为上升有C nm n +种方法.对每一条坏折线，有如下两种情形：一是经过点()1,1S -，二是经过点()1,1T . 对于第一种情形，坏折线是由S 到A 的自由折线，从而，这样的折线有1C nn m +-条.对于第二种情形，注意到过()1,1T 的坏折线必与x 轴相交，设其横坐标最小的交点为P . 将此折线位于P 左边的部分作关于x 轴的对称折线，便得到过点()1,1S -的坏折线，于是，坏折线的条数也有1C nn m +-条. 所以，合乎条件的好折线的条数为11111C 2C C C 1C n n n nm n m n m n m n m n m m n -++-+-+-+-⎛⎫-=-=- ⎪⎝⎭.综上所述，所求的概率为()11C C 1C C m mn m n m n nn m n mn m m n mn n n m +-+-++--⎛⎫-⋅== ⎪+⎝⎭. 46．（2019·全国·高三竞赛）如图，正六边形ABCDEF 的中心为O ，对A 、B 、C 、D 、E 、F 、O 这七个点中的任意两点，以其中一点为起点、另一点为终点作向量.任取其中两个向量，以它们的数量积的绝对值作为随机变量ξ.试求ξ的概率分布列及其数学期望E ξ.【答案】见解析【解析】【详解】所作出的向量数为2721C =，则可取221210C =对向量.设所取向量分别为a 、b .由于···cos ,a b a b a b ξ==，因此，可不考虑向量的方向.不妨令所取两向量的夹角均为它们所在直线的夹角（取值范围为[]0,90︒︒），则任意两向量之间的夹角均属于集合{}0,30,60,90︒︒︒︒，每个向量的模值属于集合{}3,2，其中，模为1的个数为1236，模为2的个数为3.若2a b ==，则它们之间的夹角必为60︒，·2a b =，其概率为1321221070⨯⨯=. 若3a b =0︒或60︒.当夹角为0︒时，·3a b =，其概率为1611221070⨯⨯=；当夹角为60︒时，3·2a b =，其概率为1462221035⨯⨯=. 若1a b ==，则它们之间的夹角可能为0︒或60︒.易知其概率分别为。

初中数学竞赛代数专题讲义之代数式求值含例题习题及详解

代数式求值由数与字母经有限次代数运算（加、减、乘、除、乘方、开方）所组成的表达式叫做代数式。

已知一个代数式，把式中的字母用给定数值代替后，运算所得结果叫做在字母取给定数值时代数式的值。

一、专题知识1.基本公式（1）立方和公式：2233()()a b a ab b a b +-+=+（2）立方差公式：2233()()a b a ab b a b-++=-（3）完全立方和：33223()33a b a a b ab b +=+++（4）完全立方差：33223()33a b a a b ab b -=-+-2.基本结论（1）33322()33a b a b a b ab +=+--（2）33322()33a b a b a b ab -=-+-（3）22()()4a b a b ab-=+-二、经典例题例题1已知y z x z x yx y z+++==求代数式y z x +的值。

【解】（1）0x y z ++≠，由等比性质得2()2x y z y zx y z x+++==++；（2）0x y z ++=，则y z x +=-，所以1y zx+=-。

例题2已知234100x y +-=，求代数式y x x y xy y x x 65034203152223--++++的值。

【解】32221532043506x x y xy y x x y++++--322222215205034103410105(3410)(3410)(3410)1010x xy x x y y y x y x x y y x y x y =+-++-++-+=+-++-++-+=例题3实数,,a b c满足条件：231224a b ab -=+=-，求代数式2a b c ++的值。

【解】22222442318224a b a ab b ab c ab ⎧-=⇒-+=⎪⎨+=-⇒+=-⎪⎩两式相加得，()2220a b ++=只有2=0a b +且0c =，所以20a b c ++=。

2020小升初数学专题训练《数学竞赛》(通用含详解)

专题训练《数学竞赛》一、单选题（共7题；共14分）1.“65+26 100－26”，比较大小，在里应填的符号是（）A. ＞B. ＜C. ＝D. －2.“11－6 5”，比较大小，在里应填的符号是（）A. ＞B. ＜C. =D. +3.一列火车长200米，以每分钟1200米的速度经过一座大桥，从车头进到车尾出一共用了2分钟。

求桥的长度是多少米？正确的算式是（）A. 1200×2+200B. 1200×2-200C. （1200+200）×2D. （1200-200）×24.在单摆实验中，如果增加绳长，单位时间内单摆的摆动次数（）A. 减少B. 增加C. 不变5.钟面上是（）时。

A. 6时B. 12时30分C. 12时D. 6时5分6.三个人站成一排照相，有（）种站法．A. 2B. 4C. 67.同学们到动物园去游玩，参观猴山的有28人，参观狮子馆的有32人，两个馆都参观的有18人，去动物园的一共有（）人。

A. 60B. 42C. 50D. 46二、判断题（共7题；共16分）8.25＋25×4＝200。

（）9.小动物们读得正确吗？（1）（）（2）（）10.芳芳中午12点睡觉，闹钟3点准时响起，则时针在这段时间旋转了60°。

（）11.一个盒子里有同样大小的黄球和黑球各4个，只要摸出3个球，就可以保证一定有2个同色的球。

（）12.和一样重。

（）13.从1开始的连续10个奇数中任取6个，一定有两个数的和是20。

（）14.一瓶纯牛奶，亮亮第一次喝了30%，然后在瓶里兑满水，又接着喝去30%．亮亮第一次喝的纯奶多．（）三、填空题（共7题；共8分）15.在横线上填上“＞”、“＜”或“＝”．100cm＋200cm________3m 54÷9×2________24÷8×316.小东买了一个篮球和一个足球，篮球价格是足球的两倍。

高中数学竞赛训练解答题(每题含详解)

高中数学竞赛训练题—解答题1．b a ,是两个不相等的正数，且满足2233b a b a -=-，求所有可能的整数c ,使得ab c 9=.2．已知不等式24131...312111an n n n >++++++++对一切正整数a 均成立，求正整数a 的最大值，并证明你的结论。

3．设{}n a 为14a =的单调递增数列，且满足22111168()2n n n n n n a a a a a a +++++=++，求{n a }的通项公式。

4．（1）设,0,0>>y x 求证：;432yx y x x -≥+ （2）设,0,0,0>>>z y x求证：.2333zxyz xy x z z z y y y x x ++≥+++++5. 设数列 ,1,,12,1,,13,22,31,12,21,11kk k -，问：（1）这个数列第2010项的值是多少；（2）在这个数列中，第2010个值为1的项的序号是多少.6. 设有红、黑、白三种颜色的球各10个。

现将它们全部放入甲、乙两个袋子中，要求每个袋子里三种颜色球都有，且甲乙两个袋子中三种颜色球数之积相等。

问共有多少种放法。

7．已知数列{}n a 满足1a a =（0,1a a ≠≠且），前n 项和为n S ，且(1)1n n aS a a=--，记lg ||n n n b a a =（n *∈N ），当a =时，问是否存在正整数m ，使得对于任意正整数n ，都有m n b b ≥？如果存在，求出m 的值；如果不存在，说明理由．8. 在ABC ∆中，已9,sin cos sin AB AC B A C ==，又ABC ∆的面积等于6.（Ⅰ）求ABC ∆的三边之长；（Ⅱ）设P 是ABC ∆（含边界）内一点，P 到三边AB 、BC 、AB 的距离为1d 、2d 和3d ，求123d d d ++的取值范围.9．在数列{}n a 中，1a ，2a 是给定的非零整数，21n n n a a a ++=-．（1）若152a =，161a =-，求2008a ；（2）证明：从{}n a 中一定可以选取无穷多项组成两个不同的常数数列．10. 已知椭圆)1(1222>=+a y ax ，Rt ABC ∆以A （0，1）为直角顶点，边AB 、BC 与椭圆交于两点B 、C 。

经典--排列组合习题-(含详细答案)

排列组合专项训练1.题1 (方法对比，二星)题面：(1)有5个插班生要分配给3所学校，每校至少分到一个，有多少种不同的分配方法？(2)有5个数学竞赛名额要分配给3所学校，每校至少分到一个名额，有多少种不同的名额分配方法？解析：“名额无差别”——相同元素问题(法1)每所学校各分一个名额后，还有2个名额待分配，可将名额分给2所学校、1所学校，共两类：2133C C +(种)(法2——挡板法)相邻名额间共4个空隙，插入2个挡板，共：246C =(种) 注意：“挡板法”可用于解决待分配的元素无差别，且每个位置至少分配一个元素的问题.(位置有差别，元素无差别)同类题一题面：有10个运动员名额，分给7个班，每班至少一个,有多少种分配方案？答案：69C详解：因为10个名额没有差别，把它们排成一排。

相邻名额之间形成9个空隙。

在9个空档中选6个位置插个隔板，可把名额分成7份，对应地分给7个班级，每一种插板方法对应一种分法共有69C 种分法。

同类题二题面：求方程X+Y+Z=10的正整数解的个数。

答案：36. 详解：将10个球排成一排，球与球之间形成9个空隙，将两个隔板插入这些空隙中（每空至多插一块隔板），规定由隔板分成的左、中、右三部分的球数分别为x 、y 、z 之值, 故解的个数为C 92=36（个）。

2.题2 (插空法，三星)题面：某展室有9个展台，现有3件展品需要展出，要求每件展品独自占用1个展台，并且3件展品所选用的展台既不在两端又不相邻，则不同的展出方法有______种；如果进一步要求3件展品所选用的展台之间间隔不超过两个展位，则不同的展出方法有____种. 答案：60，48同类题一题面：6男4女站成一排，任何2名女生都不相邻有多少种排法？答案：A 66·A 47种.详解：任何2名女生都不相邻，则把女生插空，所以先排男生再让女生插到男生的空中，共有A 66·A 47种不同排法．同类题二题面：有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有( )A ．36种B ．48种C ．72种D ．96种答案：C.详解：恰有两个空座位相邻，相当于两个空位与第三个空位不相邻，先排三个人，然后插空，从而共A 33A 24＝72种排法，故选C.3．题3 (插空法，三星)题面：5个男生到一排12个座位上就座，两个之间至少隔一个空位．1]没有坐人的7个位子先摆好，[2](法1——插空)每个男生占一个位子，插入7个位子所成的8个空当中，有：58A =6720种排法.(法2)[1]5个男生先排好：55A ；[2]每个男生加上相邻的一个座位，共去掉9个位置，当作5个排好的元素，共有6个空，剩下的3个元素往里插空，每个空可以插1个、2个、3个元素，共有：3216662C C C ++种，综上：有55A (3216662C C C ++)=6720种.同类题一题面：文艺团体下基层宣传演出，准备的节目表中原有4个歌舞节目，如果保持这些节目的相对顺序不变，拟再添两个小品节目，则不同的排列方法有多少种？答案：30。

7年级数学培优竞赛试题1-25题(含详解)

七年级第1题：已知0132=+-x x , 则 =++13242x x x 。

答案：0.1第2题：若,,a b c 互异，且x y a b b c c aZ ==---，求x y Z ++的值。

答案：0第3题：a 取什么值时，方程组⎩⎨⎧=+=+3135y x a y x 的解是正数？答案：6.2<a <331第4题：方程 200422=-b a的正整数解有组.答案：2组第5题：用一张长方形的纸，折出一个30°的角，如何折？答案：第6题：（1）若A 和B 都是4次多项式，则A+B 一定是（） A 、8次多项式 B 、4次多项式C 、次数不高于4次的整式D 、次数不低于4次的整式答案: C（2）如果316x +的立方根是4，求24x +的平方根___________。

答案：立方根是4，则这个数是43=64。

3x+16=64，解得x =16。

2x +4=2×16+4=36， 36=±6。

第7题：已知21x x +=，那么 . 答案: 2016解析：x 4+2x 3-x 2-2x +2017= x 4+2x 3+ x 2-2x 2-2x +2017=（x 2+x ）2-2（x 2+x ）+2017=12-2×1+2017=1-2+2017=2016。

第8题：若2a ＋5b ＋4c ＝0，3a ＋b －7c ＝0，则a ＋b －c 的值是___________________答案：2a +5b +4c =0 ① a +b -7c =0 ②将①×3得6a +15b +12c =0 ③将②×2得6a +2b -14c =0 ④由③-④得13b +26c =0 ， b= -2c ⑤将⑤带入① 2a -10c +4c =0 ， 2a =6c ，a =3c ⑥将⑤和⑥带入a +b -c =3c -2c-c =0。

第 9 题：如图所示，四边形ABCD 是矩形，E 、F 分别是AB 、BC 上的点，且AB AE 21=，BC CF 31=，AF 与CE 相交于G ，如果矩形ABCD 的面积为120，那么可知AEG ∆与CGF ∆的面积之和为____________。

五年级上册数学竞赛试题-整除问题进阶人教版(含详解)

第二讲整除问题进阶上次课我们学习了一些比较常用的整除判断方法,如利用末位数字判断、利用数字和判断等．现在我们再来学习一些新的判断方法．一、截断作和【分析】能同时被9和11整除,说明这个六位数能被99整除．想一想,99的整除特性是什么?四位数能同时被9和11整除,这个四位数是多少?【分析】这个九位数是99的倍数,说明两位截断以后,各段之和是99的倍数．这个99的倍数可能是多少呢?已知八位数能被99整除,这个八位数是多少?二、截断作差能被7、11、13整除的数的特征：从个位开始,每三位一截,奇数段之和与偶数段之和的差能被7或11或13整除．123678 已知九位数1234789能被99整除,这个九位数是多少?23六位数2008能同时被9和11整除．这个六位数是多少?【分析】根据能被7整除的数的特征：末三位组成的数与末三位以前的数组成的数之差能被7整除,我们可以由此将问题简化．四位数572能被7整除,那么这个四位数可能是多少?接下来我们处理一些较复杂的问题．【分析】在本题中,255259555999□个个能被13整除．这个数的位数太多,我们可以想办法使它变得简短一些．因为1001是13的倍数,而555555、999999分别是555、999与1001的乘积,说明它们都是13的倍数．那我们是不是可以去掉这个51位数上的一些5和9,并仍然保证它能被13整除?已知多位数2010120103111333个个能被13整除,那么中间方格内的数字是多少?已知51位数255259555999个个能被13整除,中间方格内的数字是多少?阿呆写了一个两位数59,阿瓜写了一个两位数89,他们让小高写一个一位数放在59与89之间拼成一个五位数5989,使得这个五位数能被7整除．请问：小高写的数是多少?用数字6,7,8各两个,要组成能同时被6,7,8整除的六位数．请写出一个满足要求的六位数．【分析】能被6,7,8整除的数有什么特点呢?最难把握的在于这个六位数能被7整除,我们应该怎样安排数字才能使得它的前三位与后三位的差能被7整除呢?题目只要求我们写出一个满足要求的六位数,所以只需要找出一种特殊情况即可．一个五位数,它的末三位为999．如果这个数能被23整除,那么这个五位数最小是多少?【分析】我们没有学过能被23整除的数的特征,而且23也不能拆分成两个特殊数的乘积,因此不可能根据整除特征来考虑．我们尝试从整除的定义来入手,这个五位数能被23整除,就是说它能写成23与另一个数的乘积．接下来,大家想到该怎么办了吗?课堂内外自古成功在尝试枚举法和尝试法在解决数论问题时经常使用．当看到一个问题很难下手时,不妨先从简单情形出发试一试,也许能找出规律和思路．胡适（学者,诗人,1946～1948年任北京大学校长）,在他的作品《尝试集》的序言中写到：“尝试成功自古无,放翁这话未必是．我今为下一转语,自古成功在尝试”．这首诗中第一句为陆游所说,但他所说的尝试只是简单的浅尝辄止,当然不能成功．而最后一句则是胡适对第一句的改编：如果尝试是大胆的,深入的,那么一定能够成功．我们在解决某些数学问题时,需要的正是胡适所说的这种尝试．作业1. 在7315,58674,325702,96723,360360中,7的倍数有哪些?13的倍数有哪些?2. 四位数33能同时被9和11整除,这个四位数是多少?3. 四位数278能被7整除,那么这个四位数是多少?4. 已知多位数201225881258258258□个（2012个258）能同时被7和13整除,方格内的数字是多少?5. 已知多位数2011120113111333个个能被7整除,那么中间方格内的数字是多少?第二讲整除问题进阶例题1. 答案：120087详解：能被9和11整除可以看作是能被99整除,可以两位截断求数段和,那么有208++是99的倍数,只能是99．两个空中先后要填1和7．例题2. 答案：123483789详解：设这个九位数为1234789ab ,两位截断求和1234789160a b ba ++++=+是99的倍数,只能是198．所以a =8,b =3．例题3. 答案：6详解：利用7的整除特性,895930-=能被7整除,只能填6．例题4. 答案：5详解：555555、999999能被13整除,前面依次去掉555555,后面一次去掉999999后仍然是13的倍数．所以只需要满足13|59就可以了．空格中要填5．例题5. 答案：768768详解：形如abcabc 一定能被7整除,可以考虑由两个相同的三位数来组成这个六位数,三位数由6、7、8组成．又可知这个六位数一定能被3整除,所以只要保证后三位能被8整除就可以了．答案不唯一．例题6.答案：20999详解：利用数字谜,从后往前逐位确定．练习1.答案：6237简答：两位截断后的和是99．练习2.答案：12327678简答：两位截断后的和是198．练习3.答案：5712或5782简答：利用7的整除特性,72与5的差是7的倍数,空格中可以填1或8．练习4.答案：0简答：前面依次去掉111111,后面依次去掉333333,最后剩下．它是13的倍数,那么空格中只能填0．作业1.答案：7的倍数有7315,58674,360360；13的倍数有325702,360360 简答：牢记7和13的判断方法．作业2.答案：6336简答：这个四位数是99的倍数,两位截断后求和即可．作业3.答案：2758简答：应用三位截断法,可知能被7整除,框中填5满足条件．76作业4. 答案：9简答：应用三位截断,可知能被7和13整除,即是91的倍数,框中填9满足条件．作业5. 答案：3简答：应用三位截断,可知能被7整除,框中填3满足条件．13 81 81。

2014届八年级全国数学竞赛赛前专项训练_方程(含详解)

初中数学竞赛专项训练（方程）一、选择题：1、方程018)8(2=-++-a x a x 有两个整数根，试求整数a 的值（）A. -8B. 8C. 7D. 9 2、方程1)1(32=-++x x x 的所有整数解的个数是（）A. 2B. 3C. 4D. 53、若0x 是一元二次方程)0(02≠=++a c bx ax 的根，则判别式ac b 42-=∆与平方式20)2(b ax M +=的大小关系是（） A. △＞MB. △=MC. △＜MD. 不能确定4、已知ac b 42-是一元二次方程)0(02≠=++a c bx ax 的一个实数根，则ab 的取值范围为（）A. ab ≥81 B. ab ≤81 C. ab ≥41 D. ab ≤41 5、已知1x 、2x 是方程0)53()2(22=+++--k k x k x 的两个实根，则2221x x +的最大值是（） A. 19B. 18C. 955D. 以上答案都不对6、已知z y x 、、为三个非负实数，且满足132523=-+=++z y x z y x ，　，z y x u 73-+=若，则u 的最大值与最小值之和为（）A. 7762-B. 7764-C. 7768-D. 7774-7、若m 、n 都是正实数，方程022=++n mx x 和方程022=++m nx x 都有实数根，则m+n 的最小值是（） A. 4 B. 6 C. 8 D. 108、气象爱好者孔宗明同学在x （x 为正整数）天中观察到：①有7个是雨天；②有5个下午是晴天；③有6个上午是晴天；④当下午下雨时上午是晴天。

则x 等于（） A. 7 B. 8 C. 9 D. 10 二、填空题1、已知两个方程0022=++=++a bx x b ax x 与有且只有一个公共根，则这两个方程的根应是＿＿＿＿＿＿＿＿＿＿＿＿2、若)(016110161122b a b b a a ≠=++=++，　，则=-baa b ＿＿＿＿＿＿＿3、已知关于x 的方程012)1(2=-+++n x n x 的两根为整数，则整数n 是＿＿＿＿＿4、设1x 、2x 是方程02)1(222=+++-k x k x 的两个实数根，且8)1)(1(21=++x x ，则k 的值是＿＿＿＿＿＿＿＿＿＿5、已知a 、b 是方程042=+-m x x 的两个根，b 、c 是方程0582=+-m x x 的两个根，则m ＝＿＿＿＿＿＿＿＿＿＿6、设1x 、2x 是关于x 的一元二次方程22=++a ax x 的两个实数根，则)2)(2(1221x x x x --的最大值为＿＿＿＿＿＿＿＿＿＿三、解答题1、关于x 的方程01)1(2=+--x k kx 有有理根，求整数k 的值。

小学数学6年级奥数竞赛试题76-100题(含详解)

１＝－ 5
第 87 题：（1）同时含字母 a，b，c，且系数是 1 的 7 次单项式共有_________个；（2）由字母 a，b，c 组成（未必同时含有），且系数是 1 的 7 次单项式共____个。答案：（1） 15 （2）36 解析：（1）方法一：当 a 的次数为 1 时，有 abc 5 , ab 2 c 4 , ab 3 c 3 , ab 4 c 2 , ab 5 c 5 种。当 a 的次数为 2 时，有 a 2 bc 4 , a 2 b 2 c 3 , a 2 b 3c 2 , a 2 b 4 c 4 种。当 a 的次数为 3 时，有 a 3bc 3 , a 3b 2 c 2 , a 3b 3 c 3 种。当 a 的次数为 4 时，有 a 4 bc 2 , a 4 b 2 c 2 种。
2017 a 2 b 2 (a b)(a b) 2017 1 (2017) (1)
当
a b 2017 时 a b 1 a b 2017 时 a b 1
解得 a 1009
b 1008 a 1009 b 1008 a 1009 b =－ 1008 a 1009 b =－ 1008
（2）若折叠后，数 3 表示的点与数－1 表示的点重合，则此时数 5 表示的点与数_____________
表示的点重合；若这样折叠后，数轴上有 A、B 两点也重合，且 A、B 两点之间的距离为 9 （A 在 B 的左侧），则 A 点表示的数为______________，B 点表示的数为_______________．
a 1 2b 则 a 2b 1 。
将 a 2b 1 代入 2a 4b 3 中得 4b 2 4b 3 5 。

2012年浙江省高中数学竞赛试题(含详解答案)

2012 年浙江省高中数学竞赛试题解答
说明：本试卷分为 A 卷和 B 卷： A 卷由本试卷的 2２题组成，即 10 道选择题， 7 道填空题、 3 道解答题和 2 道附加题；B 卷由本试卷的前 20 题组成，即 10 道选择题，7 道填空题和 3 道解答题。
一、选择题（本大题共有 10 小题，每题只有一个正确答案，将正确答案的序号填入题干后的括号里，多选、不选、错选均不得分，每题 5 分，共 50 分） 1 2i 1．已知 i 为虚数单位，则复数（ B ） i2 4 3 4 3 A． i B． i C． i D． i 5 5 5 5
三、解答题（本大题共 3 小题，每小题 17 分，共计 51 分） 18. 已知实数 x1, x2 ,
, x10 满足 xi 1 4, xi 2 6 ，求 x1, x2 ,
i 1 i 1
10
10
, x10 的平均值
x。
18. 解答： 10 所以有
[( xi 1) ( xi 2)] xi 1 xi 2 10 ，……（5）
解答：
1 2i (1 2i )(i 2) i 。正确答案为 B。 i2 (i 2)(i 2)
C ）
2．下列函数中，既是奇函数，又在区间 ( , ) 上单调递增的函数为（ A. y x 2 x B. y x 2sin x C. y x3 x D. y tan x

2011 2011
1 的值为 k 1 lg ai lg ai 1
1 =2011. k 1 lg ai lg ai 1
1 lg a1 lg a2012 2011 1 1 ( ) lg q lg ai 1 k 1 lg ai lg ai 1 k 1 lg ai

7年级数学培优竞赛试题51-75题(含详解)

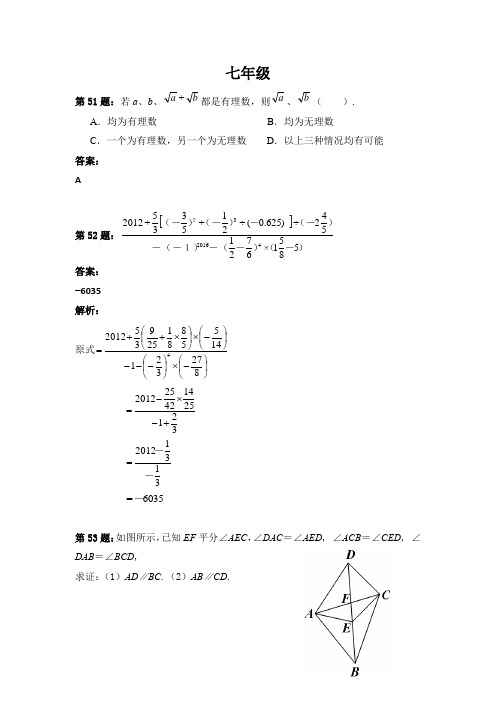
七年级第51题：若a 、b 、ba +都是有理数，则a、b（）.A ．均为有理数B ．均为无理数C ．一个为有理数，另一个为无理数D ．以上三种情况均有可能答案： A第52题：[]）－（）－－（－（－１））（－－）（－）（－２5851×6721542÷)625.0(÷21+5335+2012420163答案： −6035 解析：原式⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛---⎪⎭⎫⎝⎛-⨯⎪⎭⎫ ⎝⎛⨯++=82732114558812593520124321251442252012+-⨯-=31312012=－－6035=－第53题：如图所示，已知EF 平分∠AEC ，∠DAC ＝∠AED , ∠ACB ＝∠CED , ∠DAB ＝∠BCD ,求证：（1）AD ∥BC .（2）AB ∥CD .：证明：（1）∵EF平分∠AEC∴∠AED=∠DEC∵∠AED=∠DEC∠DAC=∠AED∴∠DEC=∠DAC∵∠ACB=∠CED∠DEC=∠DAC∴∠DAC=∠ACB∴AD∥BC（2）∵∠DAB=∠BCD∠DAC=∠ACB∴∠BAC=∠ACD∴AB∥CD第54题：如图所示，在平面直角坐标系中，一颗棋子从点P处开始依次关于点A、B、C做循环对称跳动，即第一次跳到点P关于点A的对称点M处，接着跳到点M关于点B的对称点N处，第三次再跳到点N关于点C的对称点处……如此下去.（1）在图中画出点M、N，并写出M、N的坐标。

（2）求经过第2017次跳动之后，棋子落在的位置与点P的距离。

（1）()0,2-M 、()4,4N（2）经观察可发现跳动为周期数为3的周期，1...67232017=÷所以跳到了M 点，M 点到P 点距离为222222=+第55题：对于给定的正奇数n ，定义f （n ）＝n1++51+31+1计算2017×f （2017）―2[ f （1）+f （3）+……+f （2015）]答案：原式]20151++51+31+1++51+31+1)31+(1+[1×2)20171+...+51+31+(1×2017=）（）＋（－......()201720172015220152017...5201252017320143201720162017+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛-+-=1...1111+++++=1009个11009=第56题：如图所示，△ABC 是周长为20的正三角形，P 是三角形内一点，PD//AB 、PE//BC 、PF//AC ，则PD+PE+PF ＝．答案：320解析：如图延长EP 交AB 与点G ，延长FP 交BC 与点H△GFP 为等边三角形，则FP=GP ，四边形GBDP 为平行四边形，则GP=BD △PDH 为等边三角形，则PD=DH 。

浙江省强基联盟2023-2024学年高一上学期12月综合测试数学试题(含答案)

浙江强基联盟2023学年第一学期高一12月联考数学试题（答案在最后）一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{},a b 的真子集个数为（）A.3B.4C.5D.6【答案】A 【解析】【分析】利用集合元素个数即可求出集合{},a b 共有{}{},,a b ∅三个真子集.【详解】根据题意可知集合{},a b 中有3个元素，所以共有2213-=个，即有{}{},,a b ∅三个真子集.故选：A2.若2:1,320p x x x ∃>-+>，则p 的否定为（）A.21,320x x x ∃>-+≤B.21,320x x x ∃≤-+≤C.21,320x x x ∀≤-+≤D.21,320x x x ∀>-+≤【答案】D 【解析】【分析】根据给定条件，利用存在量词命题的否定求解即可.【详解】命题2:1,320p x x x ∃>-+>是存在量词命题，其否定是全称量词命题，所以命题p 的否定为21,320x x x ∀>-+≤.故选：D .3.若0a >，0b >，则“1a b +≥”是“1≥”的（）A.必要不充分条件 B.充分不必要条件C.充要条件 D.既不充分也不必要条件【答案】A 【解析】【分析】根据充分必要条件的定义判断，注意基本不等式的应用即在0,0a b >>的情况下，判断两个命题11a b +≥⇒和11a b ≥⇒+≥．.【详解】解：取1a =，19b =，满足1a b +≥，但213=<，充分性不满足；反过来，1a b +≥≥成立，故必要性成立.故选：A ．4.若一圆弧长等于其所在圆的内接正三角形的边长，则此圆弧所对的圆心角α的弧度数为（）A.π3B.π2C.D.2【答案】C 【解析】【分析】画图设外接圆半径2r =，利用正三角形性质可得圆弧长l =，再由弧度制定义可得α=【详解】不妨设正ABC 的外接圆半径2r =，圆心为O ，取BC 的中点为D ，连接,AD OC ，易知O 在AD 上，且30OCB ∠= ，AD BC ⊥；如下图所示：在Rt OCD △中，112OD OC ==，所以CD BC ==依题意可知该圆弧长l BC ==所以圆心角2l r α===故选：C5.已知()1,3P 为角α终边上一点，则2sin cos sin 2cos αααα-=+（）A.-7B.1C.2D.3【答案】B【解析】【分析】先根据三角函数的定义求出tan 3α=，再利用齐次化将弦化切进行求解.【详解】()1,3P 为角α终边上一点，故tan 3α=，故2sin cos 2tan 151sin 2cos tan 25αααααα--===++.故选：B6.若m n <，p q <，且()()0p m p n --<，()()0q m q n --<，则（）A.m p n q <<<B.p m q n <<<C.n m p q <<<D.p m n q<<<【答案】C 【解析】【分析】首先根据已知条件判断出p 和m 、n 的关系以及q 和m 、n 的关系，结合p q <即可求解.【详解】因为()()0p m p n --<，所以m 和n 一个大于p ，一个小于p ，因为m n <，所以m p n <<，因为()()0q m q n --<，所以m 和n 一个大于q ，一个小于q ，因为m n <，所以m q n <<，因为p q <，所以m p q n <<<，故选：C.7.已知函数f (x )＝1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y ＝f (1－x )的大致图象是（）A.B.C.D.【答案】D 【解析】【分析】由()f x 得到()1f x -的解析式，根据函数的特殊点和正负判断即可.【详解】因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩，所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩，当x ＝0时，y ＝f (1)＝3，即y ＝f (1－x )的图象过点(0，3)，排除A ；当x ＝－2时，y ＝f (3)＝－1，即y ＝f (1－x )的图象过点(－2，－1)，排除B ；当0x <时，()1311,(1)log 10x f x x ->-=-<，排除C ，故选：D ．8.已知关于x 的一元二次不等式2310mx x -+<的解集为(),a b ，则3aab b+的最小值是（）A.2B. C.3D.【答案】A 【解析】【分析】由一元二次不等式解集可知0,0a b >>,且满足113a b+=，将3aab b +化简变形可得341a ab a b b+=+-，利用基本不等式即可求得当1,12a b ==时3aab b +的最小值是2.【详解】由一元二次不等式2310mx x -+<的解集为(),a b 可得0m >，利用韦达定理可得3010a b mab m ⎧+=>⎪⎪⎨⎪=>⎪⎩，即可得3a b ab +=，且0,0a b >>,113a b +=；所以可得3333141a ab b ab ab a a b a b b b-+=+=-++=+-；易知()11141411521213141334b a b a b a b a a b ⎛⎫⎛⎫++++ ⎪ ⎛+-=+-=-≥+-= ⎝⎪⎝⎭⎝⎭，当且仅当4b aa b=，即1,12a b ==时等号成立；即3aab b+的最小值是2.故选：A二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.已知0a >，0b >，则下列各式正确的是（）A.π3=- B.1=C.m na-=D.121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭【答案】ABD 【解析】【分析】根据指数的运算公式分别判断各选项.【详解】A 选项：由π30->π3=-，A 选项正确；B ()11111123612312600222221a b b a a b a b ⎛⎫⎛⎫-⨯-+⨯ ⎪ --⎝⎭⎝⎭⎡⎤====⎢⎥⎣⎦，B 选项正确；C 选项：m na-=，C 选项错误；D 选项：112121101333333331246663b a b a a b a b b ⎛⎫⎛⎫-------- ⎪ ⎪⎝⎭⎝⎭⎛⎫÷-=-=-=- ⎪⎝⎭，D 选项正确；故选：ABD.10.已知πsin 22α⎛⎫+=⎪⎝⎭，且ππ22α-<<，则()tan πα+的值可能是（）A.B.33-C.33D.【答案】BC 【解析】【分析】由π3sin cos 22αα⎛⎫+==⎪⎝⎭，结合ππ22α-<<分情况讨论即可求解.【详解】由题意得πsin cos 22αα⎛⎫+== ⎪⎝⎭，()tan παtan α+=，因为ππ22α-<<，当π02α-<<时，因为cos 2α=，所以1sin 2α==-，此时sin tan cos 3ααα==-，故B 项正确；当π02α<<时，因为cos 2α=，所以1sin 2α==，此时sin tan cos 3ααα==，故C 项正确.故选：BC.11.已知定义在R 上的偶函数()f x 满足()()20f x f x -+=，则下列命题成立的是（）A.()f x 的图象关于直线1x =对称B.()30f =C.函数()1f x -为偶函数D.函数()1f x +为奇函数【答案】BD 【解析】【分析】由()()20f x f x -+=及奇偶性可得函数的周期性与对称性，进而判断各选项.【详解】因为函数()f x 为偶函数，所以函数()f x 关于y 轴对称，且()()22f x f x -=-，又()()20f x f x -+=，所以()()20f x f x -+=，且()()()()222f x x f x f f x ⎡⎤=-=--+=+⎣⎦-，所以函数()f x 关于点()1,0-中心对称，且周期为4，所以函数()f x 关于()1,0对称，A 选项错误；()()310f f =-=，B 选项正确；()1f x -由()f x 向右平移一个单位得到，则()1f x -关于点()0,0对称，为奇函数，C 选项错误；()1f x +由()f x 向左平移一个单位得到，则()1f x +关于点()0,0对称，为奇函数，D 选项正确；故选：BD.12.函数()ln f x x =，已知实数0m >，0n >，且m n ≠，则下列命题正确的是（）A.若()()f m f n =，则2m n +≥B.若()()f m f n <，则1m n<<C.存在m n >，使得()()22mnf f <D.()()22f m f n m n f ++⎛⎫>⎪⎝⎭恒成立【答案】D 【解析】【分析】根据指数函数与对数函数的单调性可判断B ，C 选项，结合基本不等式可判断A ，D 选项.【详解】由()ln f x x =，可知函数()f x 在()0,∞+上单调递增，若()()f m f n =，则()()f m f n =-，即1ln ln lnm n n=-=，可得1mn =，A 选项：m n +≥m n =时等号成立，又m n ≠，则2m n +>，A 选项错误；B 选项：1mn =，m n ≠，则01m n <<<或01n m <<<，B 选项错误；C 选项：若m n >，则22m n >，则()()22mnf f >恒成立，C 选项错误；D 选项：由ln 22m n m n f ++⎛⎫=⎪⎝⎭，()()ln ln l 2n 2f m f n m n ++==，又2m n+≥，当且仅当m n =时成立，又m n ≠，所以2m n +>ln 2m n +>()()22f m f n m n f ++⎛⎫>⎪⎝⎭，D 选项正确；故选：D.三､填空题：本题共4小题，每小题5分，共20分.（其中第16题第一空2分，第二空3分）13.已知幂函数()()1mf x m x =-的图象过点()2,M a ，则=a __________.【答案】4【解析】【分析】根据幂函数的定义可得2m =，再根据函数图象过点()2,M a ，可得a .【详解】由函数()()1mf x m x =-为幂函数，得10m -=，即2m =，所以()2f x x =，又函数()f x 过点()2,M a ，则()2224a f ===，故答案为：4.14.在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例，其中“弦”指的是直角三角形的斜边.现将两个全等的直角三角形拼接成一个矩形，若其中一个三角形“弦”的长度为4，则该矩形周长的最大值为____________.【答案】【解析】【分析】确定222416a b +==，矩形周长为()2a b +，根据均值不等式计算得到答案.【详解】设直角三角形的两条直角边长分别为a ，b ，则222416a b +==，,0a b >，矩形周长为()2a b +，()()2222222222232a b a b ab a b a b a b +=++≤+++=+=，故a b +≤，当且仅当a b ==时等号成立，故周长的最大值为故答案为：15.已知实数1b a >>，且17log log 4a b b a +=，则ln 4ln b a -=__________.【答案】0【解析】【分析】通过换底公式可得ln ln 17ln ln 4b a a b +=，可得ln 4ln ba =，即可得解.【详解】由17log log 4a b b a +=，换成以e 为底，可得ln ln 17ln ln 4b a a b +=，设ln ln b t a=，则1174t t +=，解得4t =或14t =，又1b a >>，ln ln 0b a >>，则ln 1ln bt a=>，所以4t =，即ln 4ln b a =即ln 4ln 0b a -=，故答案为：0.16.已知函数()221,0lg 1,0x x x f x x x ⎧--≤=⎨->⎩，则函数()f x 的零点为__________；若关于x 的方程()()22130f x mf x m ⎡⎤++-=⎣⎦有5个不同的实数根，则实数m 的取值范围是__________.【答案】①.1x =--和10x =②.52,1,133⎛⎤⎡⎫--⋃ ⎪⎥⎢⎝⎦⎣⎭【解析】【分析】结合分段函数性质令()0f x =即可解得()f x 的两个零点为1x =--和10x =，画出函数图象，利用换元法以及数形结合将方程根的问题转化成关于t 的方程22130t mt m ++-=有两个不相等的实根12,t t 且满足(]12,1t ∈--，21t >-；再由一元二次方程根的分布即可求得实数m 的取值范围.【详解】根据题意可得当0x ≤时，()221f x x x =+-，令()0f x =，解得1x =--或1x =-；当0x >时，()lg 1f x x =-，令()0f x =，解得10x =，所以可得函数()f x 的零点为1x =--和10x =；因此可得()221,0lg 1,0x x x f x x x ⎧+-≤=⎨->⎩，画出函数图象如下图所示：令()f x t =，则方程()()22130f x mf x m ⎡⎤++-=⎣⎦可转化为22130t mt m ++-=；结合图象可知，当(]2,1t ∈--时，函数y t =与函数()f x 有三个交点，当2t =-或1t >-时，函数y t =与函数()f x 有两个交点，当2t <-时，函数y t =与函数()f x 有一个交点；若关于x 的方程()()22130f x mf x m ⎡⎤++-=⎣⎦有5个不同的实数根，则方程22130t mt m ++-=有两个不相等的实根12,t t ，且满足(]122,1,2t t ∈--=-或21t >-；若22t =-可得23250m m +-=，解得11m =，253m =-；经检验当11m =时，方程22130t mt m ++-=即为220t t +-=，解得121,2t t ==-，不合题意；当253m =-时，关于t 的方程可化为232205t t --=，解得1211,23t t ==-，不合题意；所以可知方程22130t mt m ++-=有两个不相等的实根12,t t 需满足(]12,1t ∈--且21t >-；若()12,1t ∈--,故()()()222222Δ4130113022130m m m m m m ⎧=-->⎪⎪--+-<⎨⎪--+->⎪⎩，解得513m -<<-或213m <<，若11t =-，可得2320m m +-=，即31m =-或423m =；检验当31m =-时，关于t 的方程可化为220t t --=，此时121,21t t =-=>-，满足题意；当423m =时，关于t 的方程可化为23210t t +-=，此时1211,13t t =-=>-，满足题意；综上可知，实数m 的取值范围为513m -<≤-或213m ≤<，所以实数m 的取值范围是52,1,133⎛⎤⎡⎫--⋃ ⎪⎥⎢⎝⎦⎣⎭.故答案为：1x =--10x =；52,1,133⎛⎤⎡⎫--⋃ ⎪⎥⎢⎝⎦⎣⎭【点睛】方法点睛：求解方程根的嵌套问题时，经常利用换元法将方程转化，再结合函数图象利用根的分布情况得出参数满足的条件即可求得参数取值范围.四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17.已知集合{}{}28,14A x x B x m x m =≤≤=-≤≤||.（1）若1m =，求A B ⋂；（2）若A B ⊆，求实数m 的取值范围.【答案】（1）{}|24A B x x =≤≤ （2）23m ≤≤【解析】【分析】（1）将1m =代入可得{}|04B x x =≤≤，由交集运算即可求得出结果；（2）根据集合间的包含关系即可求得23m ≤≤.【小问1详解】由1m =可得{}|04B x x =≤≤，由{}28|A x x =≤≤可得{}|24A B x x =≤≤ ；【小问2详解】若A B ⊆可得1248m m -≤⎧⎨≥⎩，解得23m ≤≤，所以实数m 的取值范围是23m ≤≤.18.在平面直角坐标系xOy 中，角α以x 轴的非负半轴为始边，它的终边与单位圆221x y +=交于第二象限内的点(),P m n .（1）若35n =，求tan α及()2sin cos cos 2cos 2πααπαα++⎛⎫++ ⎪⎝⎭的值；（2）若7sin cos 13αα+=，求点P 的坐标.【答案】18.34-；111019.512,1313P ⎛⎫- ⎪⎝⎭【解析】【分析】（1）根据三角函数的定义式，结合同角三角函数关系式及诱导公式化简可得解；（2）根据三角函数定义式列方程，解方程.【小问1详解】由已知角α的终边与单位圆221x y +=交于第二象限内的点(),P m n ，则sin n α=，cos m α=，tan nmα=，221+=m n ，且0m <，由35n =，得45m ==-，则335tan 445n m α===--，再由诱导公式可得()4212sin cos 2sin cos 2tan 11134sin 2cos tan 210cos 2cos 1223παααααπααααα⎛⎫-⨯-+ ⎪++-+-+⎝⎭====-+-+⎛⎫⎛⎫++-⨯-+ ⎪ ⎪⎝⎭⎝⎭【小问2详解】由7sin cos 13αα+=，得713m n +=，0,0m n ，又221+=m n ，则()22249212169m n m n mn mn +=++=+=，解得60169mn =-，所以()22212028921169169n m m n mn -=+-=+=，所以1713n m -=，所以513m =-，1213n =，即512,1313P ⎛⎫-⎪⎝⎭.19.某园林建设公司计划购买一批机器投入施工.据分析，这批机器可获得的利润y （单位：万元）与运转时间x （单位：年）的函数关系式为2144y x x =-+-（13x ≤，且*N x ∈）（1）当这批机器运转第几年时，可获得最大利润？最大利润为多少？（2）当运转多少年时，这批机器的年平均利润最大？【答案】（1）当这批机器运转第7年时，可获得最大利润，最大利润为45（2）当运转2年时，这批机器的年平均利润最大【解析】【分析】（1）根据二次函数性质可得最大利润；（2）根据基本不等式可得年平均利润的最大值.【小问1详解】由()22144745y x x x =-+-=--+，13x ≤，可知当7x =时，y 取最大值为45，即当这批机器运转第7年时，可获得最大利润，最大利润为45；【小问2详解】由已知可得年平均利润2144441414y x x s x x x x x x -+-⎛⎫===--+=-++ ⎪⎝⎭，13x ≤，则4141410s x x ⎛⎫=-++≤-+= ⎪⎝⎭，当且仅当4x x=，即2x =时，等号成立，即当运转2年时，这批机器的年平均利润最大.20.函数()21ax bf x x +=+是定义在()1,1-上的奇函数，且13310f ⎛⎫= ⎪⎝⎭.（1）求()f x 的解析式；（2）利用单调性的定义证明()f x 在()1,1-上为增函数；（3）解不等式()()120f x f x -+<.【答案】（1）()()21,1,1xf x xx +∈-=（2）证明见解析；（3）10,3⎛⎫ ⎪⎝⎭【解析】【分析】（1）利用函数奇偶性定义以及函数值13310f ⎛⎫=⎪⎝⎭可求得1a =，0b =可得解析式；（2）根据单调性定义按照取值、作差、变形定号、下结论等步骤证明即可；（3）利用函数奇偶性和单调性，结合定义域得出不等关系即可解得不等式解集为10,3⎛⎫ ⎪⎝⎭.【小问1详解】对于()1,1x ∀∈-，都有()1,1x -∈-，所以()21ax bf x x-+-=+；又函数()21ax bf x x +=+是定义在()1,1-上的奇函数，所以()()f x f x -=-，即2211ax b ax b x x -++=-++，可得0b =，所以()21axf x x =+；由13310f ⎛⎫= ⎪⎝⎭可得21133331010113af a ⎛⎫=== ⎪⎝⎭⎛⎫+ ⎪⎝⎭，解得1a =；所以()21xf x x =+，因此()f x 的解析式为()()21,1,1xf x xx +∈-=【小问2详解】取()12,1,1x x ∀∈-，且12x x <，则()()()()()()()()()()22122112121212222222121212*********x x x x x x x x x x f x f x x x x x x x +-+---=-==++++++，因为()12,1,1x x ∈-，且12x x <，所以12120,1x x x x -<<，即1210x x ->，可得()()()()121222121011x x x x x x --<++，所以()()120f x f x -<，即()()12f x f x <；所以()f x 在()1,1-上为增函数；【小问3详解】将不等式()()120f x f x -+<转化为()()12f x f x -<-，又()f x 是定义在()1,1-上的奇函数,所以可得()()12f x f x -<-，再根据（2）中的结论可知12111121x xx x -<-⎧⎪-<-<⎨⎪-<<⎩，解得103x <<；即不等式()()120f x f x -+<的解集为10,3⎛⎫ ⎪⎝⎭.21.已知函数()()()22,xf x x a a =--∈R .（1）当1a =时，解关于x 的方程()0f x =；（2）当3x ≥时，恒有()1f x ≥，求实数a 的取值范围；（3）解关于x 的不等式()0f x ≥.【答案】（1）2x =或0x =；（2）(],7-∞；（3）答案见解析；【解析】【分析】（1）将1a =代入即可解出方程()0f x =的根为2x =或0x =；（2）将不等式()1f x ≥恒成立问题转化为[)min12,3,2xa x x ⎛⎫≤-∈+∞ ⎪-⎝⎭，再利用函数单调性即可得7a ≤满足题意；（3）对参数a 的取值进行分类讨论，结合不等式即可求得其解集.【小问1详解】当1a =时，方程()0f x =即为()()()2210xf x x =--=，解得2x =或0x =；【小问2详解】当3x ≥时，不等式()1f x ≥可化为122xa x ≤--，依题意可知，需满足[)min12,3,2xa x x ⎛⎫≤-∈+∞ ⎪-⎝⎭，由于函数2x y =在[)3,+∞上单调递增，函数12y x =--在[)3,+∞上单调递增；所以函数122xy x =--在[)3,+∞上单调递增，因此3min 11227232x a x ⎛⎫≤-=-= ⎪--⎝⎭，即实数a 的取值范围是(],7-∞；【小问3详解】由()0f x ≥可得()()220xx a --≥，①当0a ≤时，可得20x a ->，不等式等价为20x -≥，此时不等式解集为[)2,+∞；②当04a <<时，方程()()220xx a --=有两根，即1222,log x x a ==，且22log a >；此时不等式解集为[)(]22,,log a +∞⋃-∞；③当4a =时，方程()()220xx a --=仅有一根，即2x =，此时不等式解集为R ；④当4a >时，方程()()220xx a --=有两根，即1222,log x x a ==，且22log a <；此时不等式解集为[)(]2log ,,2a +∞⋃-∞；22.设,,a b m ∈R ，若满足22()()a m b m -<-，则称a 比b 更接近m .（1）设比1+更接近0，求x 的取值范围；（2）判断“21x y mx y+-<--”是“x 比y 更接近m ”的什么条件，并说明理由；（3）设0x >且31x x y x +≠=+，试判断x 与y【答案】（1）[)0,1（2）充分不必要条件，理由见解析；（3）y 【解析】【分析】（1）依据定义列出不等式，结合一元二次不等式解法即可求得x 的取值范围；（2）根据已知条件分别判断充分性和必要性是否成立即可得出结论；（3）由0x >且31x x y x +≠=+利用函数单调性，分别对0x <<和x >y x 的大小进行比较，即可得出结论.【小问1详解】根据题意可得())2210-<-，即310x -<；可得()110<，解得01x ≤<；即x 的取值范围为[)0,1；【小问2详解】充分性：显然x y ≠，由21x y m x y +-<--可得()()1x m y m x y-+-<--，①若0x y -<，则()()x m y m y x -+->-，可得0x m ->；又0x y -<可得x y <，所以0y m x m ->->；即可得()()22x m y m -<-，此时可以得出“x 比y 更接近m ”；②若0x y ->，则()()x m y m y x -+-<-，可得0x m -<；又0x y ->可得x y >，所以0x m y m >->-；即可得()()22x m y m -<-，此时可以得出“x 比y 更接近m ”；因此充分性成立必要性：由x 比y 更接近m 可得()()22x m y m -<-，即x m y m -<-，若0,3,1x y m ===，此时2113x y m x y +-=->--，即必要性不成立；所以“21x y mx y+-<--”是“x 比y 更接近m ”的充分不必要条件；【小问3详解】当x >32111x y x x +==+++在)+∞上单调递减，所以31x y x +=<+y <；)13321111x x y x x x -++-===-+++，(()221111y x x x x x ⎡⎤--=---=-++⎢⎥++⎣⎦，由对勾函数性质可知()211y x x =+++在)+∞上单调递增，所以()(2111y x x =++>+++，(()2101y x x x ⎡⎤--=-++<⎢⎥+⎣⎦y x <；同理当0x <<时，由单调性可知31x y x +=>=+y >可知)()211y x x x ⎡⎤=-+++⎢⎥+⎣⎦，又由对勾函数性质可知函数()211y x x =+++在()1上单调递减，在上单调递增；又()(2100,1001⎡⎡⎤-++<-++=⎢⎢+⎣⎦⎣，所以)()2101y x x x ⎡⎤=-+++<⎢⎥+⎣⎦在0x <<时恒成立，即y x <；综上可得满足((22y x <-，即y【点睛】关键点点睛：本题关键在于理解新定义的概念，并结合不等式性质以及函数单调性比较出两绝对值大小，再由定义得出结论.。

【高中数学竞赛专题大全】竞赛专题1 集合(50题竞赛真题强化训练)解析版+原卷版

【高中数学竞赛专题大全】竞赛专题1 集合（50题竞赛真题强化训练）一、单选题1．（2018·天津·高三竞赛）如果集合{}1,2,3,,10A =，{}1,2,3,4B =，C 是A 的子集，且C B ≠∅，则这样的子集C 有（）个.A ．256B ．959C ．960D ．961【答案】C 【解析】【详解】满足C B ⋂=∅的子集C 有62个，所以满足C B ⋂≠∅的子集C 有10622960-=个. 故答案为C2．（2020·浙江温州·高一竞赛）已知集合{}{}2|2,230A x x B x x x =>=--<∣，则A B =( ).A ．{23}xx <<∣ B ．{12}xx -<<∣ C ．{21xx -<<-∣或2}x > D ．{2∣<-xx 或3}x > 【答案】A 【解析】【详解】(,2)(2,)A =-∞-+∞，又223(3)(1)0(1,3)x x x x B --=-+<⇒=-，所以(2,3)A B =. 故选：A.3．（2018·黑龙江·高三竞赛）已知集合(){}2,60A x y x a y =++=，集合()(){},2320B x y a x ay a =-++=.若AB =∅，则a 的值是（）.A ．3或-1B ．0C ．-1D ．0或-1【答案】D 【解析】【详解】A B ⋂=∅，即直线21:60l x a y ++=与()2:2320l a x ay a -++=平行.令()2132a a a ⨯=-，解得0a =或-14．（2019·全国·高三竞赛）已知{}1,2,,216,S A S =⋅⋅⋅⊆.若集合A 中任两个元素的和都不能被6整除，则集合A 中元素的个数最多为（）. A ．36 B ．52 C ．74 D ．90【答案】C 【解析】【详解】记{}()6,0,1,,5k S x S x n k n N k =∈=+∈=⋅⋅⋅，且50k k S S ==⋃.易知()36k card S =.则集合A 中既不能同时有1S 与5S 或2S 与4S 中元素，也不能有6S 中两个元素、3S 中两个元素.要使A 中元素最多，可选1S 与2S 中全部元素，0S 与3S 中各一个元素.故最多共有36361174+++=个元素. 故答案为C5．（2019·吉林·高三竞赛）集合A ={2,0,1,3}，集合B ={x |-x ∈A ,2-x 2∉A }，则集合B 中所有元素的和为 A ．4- B ．5- C ．6- D ．7-【答案】B 【解析】【详解】由题意可得B ={-2，-3}，则集合B 中所有元素的和为-5. 故选：B. 二、填空题6．（2018·四川·高三竞赛）设集合{}1,2,3,4,5,6,7,8I =，若I 的非空子集AB 、满足A B =∅，就称有序集合对(),A B 为I 的“隔离集合对”，则集合I 的“隔离集合对”的个数为______.（用具体数字作答）【答案】6050 【解析】【详解】设A 为I 的()17k k ≤≤元子集，则B 为I 的补集的非空子集.所以，“隔离集合对”的个数为()()()()7778880880808898888888111212122223216050k kk kk k k k CC C C C C C --===-=-=+-+---=-+=∑∑∑. 故答案为6050.7．（2018·湖南·高三竞赛）设集合2{|},{31021|}01A x x x B x m x m =-≤=+≤≤--，若A B B =，则实数m 的取值范围为__________. 【答案】3m ≤ 【解析】【详解】由A B B ⋂=知，B A ⊆，而2{|3100}{|25}A x x x x x =--≤=-≤≤.当B =∅时，121m m +>-，即2m <，此时B A ⊆成立. 当B ≠∅时，121m m +≤-，即2m ≥，由B A ⊆，得21,21 5.m m -≤+⎧⎨-≤⎩ 解得33m -≤≤.又2m ≥，故得23m ≤≤. 综上，有3m ≤. 故答案为3m ≤8．（2021·全国·高三竞赛）已知,a b ∈R ，集合{}2{1,,},,M a b N a ab ==，若N M ⊆，则a b+的值为_________．【答案】1- 【解析】【分析】【详解】依题意，1,0,1,a a b b a ≠≠≠≠．若21a =，则1,{1,1,},{1,}a M b N b =-=-=-，所以,0b b b -==．若2a a =，则0a =或1，矛盾．若2a b =，则{}{}2231,,,,M a a N a a ==，于是31a =或a ，得0a =或±1，舍去．综上所述，1a b +=-．故答案为：1-.9．（2018·山东·高三竞赛）集合A 、B 满足{}1,2,3,,10A B =，A B =∅，若A 中的元素个数不是A 中的元素，B 中的元素个数不是B 中的元素，则满足条件的所有不同的集合A 的个数为______．【答案】186 【解析】【详解】设A 中元素个数为()1,2,,9k k =，则B 中元素个数为10k -，依题意k A ∉，441122m k m ⎛⎫⎛⎫-<<+ ⎪ ⎪⎝⎭⎝⎭．10k B -∉，10k A -∈，此时满足题设要求的A 的个数为1102k C --．其中，当5k =时，不满足题意，故5k ≠．所以A 的个数为018484888882186C C C C C +++-=-=．10．（2018·福建·高三竞赛）将正偶数集合{}2,4,6,从小到大按第n 组有32n -个数进行分组：{}2，{}4,6,8,10，{}12,14,16,18,20,22,24，…，则2018位于第______组．【答案】27 【解析】【详解】设2018在第n 组，由2018为第1009个正偶数，根据题意得()()11132100932n ni i i i -==-<≤-∑∑，即()()223113100922n n n n ----<≤．解得正整数27n =．所以2018位于第27组．11．（2021·全国·高三竞赛）在{1,2,,12}的非空真子集中，满足最大元素与最小元素之和为13的集合个数为___________. 【答案】1364 【解析】【详解】考虑1,12;2,11;3,10;4,9;5,8;6,7这5组数，每一组可作为集合的最大元素和最小元素，故所求集合的个数为()10864221222211364-+++++=，故答案为：136412．（2021·全国·高三竞赛）已知集合{1,2,3,,1995}M =，A 是M 的子集，当x A ∈时，19x A ∉，则集合A 元素个数的最大值为_______．【答案】1895 【解析】【详解】解析：先构造抽屉：{6,114},{7,133},,{105,1995},{1,2,3,4,5,106,107,,1994}．使前100个抽屉中恰均只有2个数，且只有1个数属于A ，可从集合M 中去掉前100个抽屉中的数，剩下199510021795-⨯=个数，作为第101个抽屉．现从第1至100个抽屉中取较大的数，和第101个抽屉中的数，组成集合A ，于是{1,2,3,4,5,106,107,,1995}A =，满足A 包含于M ，且当x A ∈时，19x A ∉．所以card()A 的最大值为199********-=．故答案为：1895.13．（2021·全国·高三竞赛）设111,,,23100X ⎧⎫=⎨⎬⎩⎭，子集G X ⊆之积数定义为G 中所有元素之乘积（空集的积数为零），求X 中所有偶数个元素之子集的积数的总和是_________．【答案】4851200##5124200【解析】【详解】解：设X 中所有偶数个元素之子集的积数的总和是A ，X 中所有奇数个元素之子集的积数之和是B ，则111991*********A B ⎛⎫⎛⎫⎛⎫+=+++-=⎪⎪⎪⎝⎭⎝⎭⎝⎭，11199111123100100A B ⎛⎫⎛⎫⎛⎫-=----=- ⎪⎪⎪⎝⎭⎝⎭⎝⎭．解得4851200A =．故答案为：485120014．（2020·江苏·高三竞赛）设*n N ∈，欧拉函数()n ϕ表示在正整数1，2，3，…，n 中与n 互质的数的个数，例如1，3都与4互质，2，4与4不互质，所以()42ϕ=，则()2020ϕ=__________．【答案】800 【解析】【详解】解析：法一：因为2202025101=⨯⨯，故能被2整除的数有1010个，能被5整除的数有404个，能被101整除的数有20个，既能被2整除又能被5整除的数有202个，既能被2整除又能被101整除的数有10个，既能被5整除又能被101整除的数有4个，既能被2整除又能被5和101整除的数有2个．故与2020不互质的有10104042020210421220++---+=，则()2020800ϕ=．故答案为：800.法二：()()()()2202025101=800ϕϕϕϕ=⨯⨯.故答案为：800.15．（2021·浙江·高二竞赛）给定实数集合A ，B ，定义运算{},,A B x x ab a b a A b B ⊗==++∈∈.设{}0,2,4,,18A =⋅⋅⋅，{}98,99,100B =，则A B ⊗中的所有元素之和为______. 【答案】29970 【解析】【分析】【详解】由(1)(1)1x a b =++-，则可知所有元素之和为(1319)30031029970+++⨯-⨯=.故答案为：29970.16．（2021·全国·高三竞赛）从自然数中删去所有的完全平方数与立方数，剩下的数从小到大排成一个数列{}n a ，则2020a =_________．【答案】2074 【解析】【分析】【详解】注意到23366452025,121728,132197,3729,44096=====，我们考虑1到2025中n a 出现的次数．这里有45个平方数，12个立方数，3个6次方数，所以n a 出现的次数为2025451231971--+=，接下来直至2197前都没有平方数和立方数，所以20202020197120252074a =-+=．17．（2021·全国·高三竞赛）设正整数m 、n ，集合{1,2,,}A n =，{1,2,,}B m =,{(,),}S u v u A v B ⊆∈∈，满足对任意的(,),(,)a b S x y S ∈∈，均有：()()0a x b y --≤，则max ||S =________．【答案】1n m +- 【解析】【分析】【详解】首先对S 中任意两个不同元素(,),(,)a b x y ，必有b a y x -≠-．事实上，若b a y x -=-，则b y ≠（否则a x =，这与(,)(,)a b x y ≠矛盾）．若b y <，则a x <，则()()0a x b y -->，这与题意矛盾，同理，b y >亦与题意矛盾．这样S 中任意元素(,),a b b a -各不相同，而{1,2,,0,1,,1}b a m m n -∈----共1n m +-种情形，则||1S n m ≤+-．再令{(,)S x y y m ==且1x n ≤≤，或x n =且1}y m ≤≤，此时||1S n m =+-．故答案为：1n m +-.18．（2021·全国·高三竞赛）已知A 与B 是集合1,2,3,{},100的两个子集，满足：A 与B 的元素个数相同，且A B 为空集.若当n A ∈时总有22n B +∈，则集合A B 的元素个数最多为_______. 【答案】66 【解析】【分析】【详解】先证||66A B ≤，只须证33A ≤，为此只须证若A 是{}1,2,,49的任一个34元子集，则必存在n A ∈，使得22n A +∈.证明如下：将{}1,2,,49分成如下33个集合：{}{}{}{}1,4,3,8,5,12,,23,48共12个；{}{}{}{}2,6,10,22,14,30,18,38共4个；{}{}{}{}25,27,29,,49共13个；{}{}{}{}26,34,42,46共4个.由于A 是{}1,2,,49的34元子集，从而由抽屉原理可知上述33个集合中至少有一个2元集合中的数均属于A ，即存在n A ∈，使得22n A +∈. 如取{}1,3,5,,23,2,10,14,18,25,27,29,,49,26,34,42,46A =，22{|}B n n A =+∈，则A ､B 满足题设且||66A B =. 故答案为：66.19．（2021·全国·高三竞赛）设集合{1,2,3,,10},{(,,),,S A x y z x y z S ==∈∣，且()}3339x y z ++∣，则A 有_______个元素．【答案】243 【解析】【分析】【详解】将S 中元素按3x 模9余数分类得：123{1,4,7,10},{2,5,8},{3,6,9}S S S ===．对每个(),,x y z A ∈，有,,x y z 分别属于123,,S S S ，或,,x y z 均属于3S ．因此A 中共有()33!4333243⨯⨯⨯+=个元素．故答案为：243.20．（2021·全国·高三竞赛）设S 为集合{}0,1,2,,9的子集，若存在正整数N ，使得对任意整数n N >，总能找到正实数a b 、，满足a b n +=，且a b 、在十进制表示下的所有数字（不包括开头的0）都属于集合S ，则||S 的最小值为___（||S 表示集合S 的元素个数）. 【答案】5 【解析】【分析】【详解】第一步，证明4S ≥，若4S =，则其中两数（可相同）相加共10个值（4个2i x 加上24C 6=个i j x x +），而n 的个位数由这10个值的个位数产生，因此，这10个值的个位数不能重复；在0、1、2、…、9中有五个奇数，五个偶数，若四个元中0或4个奇数，不能加出奇数；若四个元中有1个奇数，只能产生3个奇数；若四个元中有2个奇数，只能产生4个奇数；若四个元中有3个奇数，只能产生3个奇数；因此||4S >.第二步，构造一个五元组满足条件，稍加实验可得下表上表表明，0、1、2、…、9中的每个数字，都可以由{}0,1,2,3,6中的两个相加得到，则对任意正整数n ，从个位数开始依次向高位遍历，将每位数都按表格中表示分解为两个数，赋值给a b 、对应的位置，遍历完毕后自然得到a b 、. 综上min ||5S =. 故答案为：5.21．（2019·江西·高三竞赛）将集合{1，2，……，19}中每两个互异的数作乘积，所有这种乘积的和为_________ . 【答案】16815 【解析】【详解】所求的和为()22221(1219)12192⎡⎤+++-+++⎣⎦1(361002470)2=-16815=.故答案为：16815．22．（2019·河南·高二竞赛）称{1,2,3,4,5,6,7,8,9}的某非空子集为奇子集：如果其中所有数之和为奇数，则奇子集的个数为____________ . 【答案】256 【解析】【详解】全集{1，2，3，…，9}中含有5个奇数、4个偶数.根据奇子集的定义知，奇子集中只能含有1个奇数、3个奇数、5个奇数，而偶数的个数为0、1、2、3、4都有可能. 所以，奇子集共有：()()()101401450144444435454445C C C C C C C C C C C C +++++++++++()()135014555444C C C C C C =+++++()451012256=++⨯=个.故答案为：256．23．（2019·广西·高三竞赛）已知yz ≠0，且集合{2x ，3z ，xy }也可以表示为{y ，2x 2，3xz }，则x =____________.【答案】1 【解析】【详解】易知xyz ≠0，由两集合各元素之积得2366,1x yz x yz x ==. 经验证，x =1符合题意. 故答案为：1．24．（2019·山东·高三竞赛）已知(){}23|log 21,(,](,)A x x x B a b =-=-∞⋃+∞其中a <b ，如果A ∪B =R ，那么a －b 的最小值是_______ . 【答案】1- 【解析】【详解】由已知得[1,0)(2,3]A =-⋃，故b －a ≤1，于是1a b --. 故答案为：1-．25．（2019·重庆·高三竞赛）设A 为三元集合(三个不同实数组成的集合)，集合B ={x +y |x ，y ∈A ，x ≠y }，若{}222log 6,log 10,log 15B =，则集合A =_______ . 【答案】{}221,log 3,log 5 【解析】【详解】设{}222log ,log ,log A a b c =，其中0<a <b <c .则ab =6，ac =10，bc =15. 解得a =2，b =3，c =5，从而{}221,log 3,log 5A =. 故答案为：{}221,log 3,log 5．26．（2018·河北·高二竞赛）已知集合{},,A x xy x y =+，{}0,,B x y =且A=B ，那么20182018x y +=_______.【答案】2 【解析】【详解】由B 中有三个元素知，0x ≠且0y ≠，故A 中0x y +=，即有x y =-，又{}{},,x xy x y =若x x xy y ⎧=⎨=⎩，则11x y =⎧⎨=-⎩.此时{}{}1,1,0,0,1,1A B =-=-. 若x t x xy =⎧⎨=⎩，则00x y =⎧⎨=⎩，或11x y =-⎧⎨=-⎩，或11x y =⎧⎨=⎩，不满足互异性，舍去.故1x =，1y =-，所以201820182x y +=. 27．（2019·全国·高三竞赛）集合{}1,2,,100S =，对于正整数m ，集合S 的任一m 元子集中必有一个数为另外m-1个数乘积的约数.则m 的最小可能值为__________．【答案】26 【解析】【详解】所有不大于100的素数共有25个，记其构成的组合为T=｛2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97｝.注意到，集合T 中每一个元素均不能被T 中其余24个元素之积整除. 故2526m T m >=⇒≥.另一方面，用反证法证明：对于集合S 的任一26元子集，其中必有一个数为另外25个数乘积的约数.为叙述方便，对于素数p 和正整数x ，记()p x α表示x 中缩含p 的幂指数.若存在集合S 的某个26元子集A ，对每个x A ∈，x 均不整除集合A 中其余25个数乘积，则对每个x A ∈，存在x 的素因子p ，使得(){}\p p x A x x z αα∈⎛⎫> ⎪ ⎪⎝⎭∏，称这样的素数p 为x 的特异素因子，这种特异素因子不是唯一的.由于26A =，且所有特异素因子均属于集合S ，而集合S 中只有25个素数，故必有集合A 的两个不同元素x 、y 具有同一个特异素因子p. 由特异性及{}\y A x ∈，知(){}{}\p p p z A x x z y ααα∈⎛⎫>≥ ⎪⎪⎝⎭∏.类似地，(){}()\p p p z A y y z x ααα∈⎛⎫>≥⎪ ⎪⎝⎭∏，矛盾. 综上，m 的最小可能值为26.28．（2018·全国·高三竞赛）若实数集合{}2,3A x y =与{}6,B xy =恰有一个公共元素，则A B 中的所有元素之积为__________．【答案】0 【解析】【详解】将集合A 、B 的唯一公共元素记为a . 若0a ≠，则集合A 、B 的另一个元素均为6xya，矛盾. 进而，A B ⋃中的所有元素之积为0.29．（2021·全国·高三竞赛）已知非空集合{1,2,,2019,2020}X M ⊆=，用()f X 表示集合X中最大数和最小数的和，则所有这样的()f X 的和为_____. 【答案】()2020202121⋅-【解析】【分析】【详解】将M 中的非空子集两两进行配对，对每个非空子集X M ⊆，令{2021}X xx X '=-∈∣，对M 的任意两个子集1X 和2X ，若12X X ≠时，12X X ''≠.则所有非空集合X 可以分成X X '≠和X X '=两类. 当X X '=时，必有()2021f X =，当X X '≠时，必有()()202124042f X f X +'=⨯=.又M 的非空子集共有202021-个，故所有这样的()f X 的和为()2020202121⋅-.故答案为：()2020202121⋅-.30．（2019·浙江·高三竞赛）在复平面上，任取方程10010z -=的三个不同的根为顶点组成三角形，则不同的锐角三角形的数目为____________.【答案】39200 【解析】【详解】易知10010z -=的根在单位圆上，且相邻两根之间弧长相等，都为2100π，即将单位圆均匀分成100段小弧.首先选取任意一点A 为三角形的顶点，共有100种取法.按顺时针方向依次取顶点B 和顶点C ，设AB 弧有x 段小弧，CB 弧有y 段小弧，AC 弧有z 段小弧，则△ABC 为锐角三角形的等价条件为：1001,,49x y z x y z ++=⎧⎨⎩970,,48x y z x y z ++=⎧⇒⎨⎩ ① 计算方程组①的整数解个数，记1{|97,49}P x x y z x =++=，2{|97,49}P y x y z y =++=，3{|97,49}P z x y z z =++=，{(,,)|97,,,0}S x y z x y z x y z =++=，则123123||P P P S P P P ⋂⋂=-⋃⋃2991231C |i j i j P P P P P P <⎛=-++-∑⋂+ ⎝)23|P P ⋂⋂229950C 3C 1176=-=. 由于重复计算3次，所以所求锐角三角形个数为1001176392003⨯=. 故答案为：39200．31．（2019·浙江·高三竞赛）已知集合A ={k +1，k +2，…，k +n }，k 、n 为正整数，若集合A 中所有元素之和为2019，则当n 取最大值时，集合A =________. 【答案】{334，335，336，337，338，339} 【解析】【详解】由已知2136732k n n ++⨯=⨯. 当n =2m 时，得到(221)36733,6,333k m m m n k ++=⨯⇒===；当n =2m +1时，得到(1)(21)36731,3k m m m n +++=⨯⇒==. 所以n 的最大值为6，此时集合{334,335,336,337,338,339}A =. 故答案为：{334,335,336,337,338,339} ．32．（2021·全国·高三竞赛）设集合{1,2,3,4,5,6,7,8,9,10}A =，满足下列性质的集合称为“翔集合”：集合至少含有两个元素，且集合内任意两个元素之差的绝对值大于2.则A 的子集中有___________个“翔集合”. 【答案】49 【解析】【分析】设出集合{1,2,3,,}n 中满足题设性质的子集个数为n a ，写出2340,1a a a ===，在4n >时，要分情况把n a 的递推公式写出来，进而得到10a ，即答案. 【详解】设集合{1,2,3,,}n 中满足题设性质的子集个数为n a ，则2340,1a a a ===.当4n >时，可将满足题设性质的子集分为如下两类：一类是含有n 的子集，去掉n 后剩下小于2n -的单元子集或者是{1,2,3,,3}n -满足题设性质的子集，前者有3n -个，后者有3n a -个；另一类是不含有n 的子集，此时恰好是{1,2,3,,1}n -满足题设性质的子集，有1n a -个.于是，31(3)n n n a n a a --=-++.又2340,1a a a ===，所以56789103,6,11,19,31,49a a a a a a ======.故答案为：49 【点睛】本题的难点是用数列的思想来考虑，设集合{1,2,3,,}n 中满足题设性质的子集个数为n a ，写出n a 的递推公式，再代入求值即可. 三、解答题33．（2021·全国·高三竞赛）已知非空正实数有限集合A ，定义集合{},,,x B x y A C xy x y A y ⎧⎫=∈=∈⎨⎬⎩⎭，证明：2A B C ⋅≤．【答案】证明见解析【解析】【详解】以集合B 作为突破口，取b B ∈，并设有()n b 个数对(),(1,2,,())i i x y i n b =满足：,,ii i ix b x y A y =∈．由条件知,()i i ax ay C a A ∈∈，考虑集合(){}(),,1,2,,()i i X b ax ay a A i n b =∈=⋅⋅⋅，有()()(),(),X b A X b X b b B b b ''=∅∈'≥≠．于是，2||C ≥U ()b BX b ∈=b B∈∑|()|X b ≥||||B A ⋅得证． 34．（2021·浙江·高二竞赛）设数集{}12,,,m P a a a =，它的平均数12mp a a a C m+++=.现将{1,2,,}S n =分成两个非空且不相交子集A ，B ，求A B C C -的最大值，并讨论取到最大值时不同的有序数对(),A B 的数目. 【答案】最大值2n，数目为22n -.【解析】【分析】不妨设A B C C >，记{}12,,,p A a a a =，12p T a a a =+++，可以得到A B C C -=12n T n n p p ⎛⎫+- ⎪-⎝⎭，考虑T 最大的情况是取最大的p 个数，此时可以发现A B C C -的结果正好是与p 无关的定值，从而也就得到了A B C C -的最大值，然后考察p 的可能的值，得到A B C C >时(),A B 的组数，并利用对称性得到A B C C <时(),A B 具有与之相等的组数，从而得到所有可能的(),A B 的组数. 【详解】不妨设A B C C >，记{}12,,,p A a a a =，12p T a a a =+++，所以(1)2A B A Bn n TT C C C C p n p+--=-=-- 11(1)12()2n n n T n T p n p n p n p p ⎛⎫⎛⎫++=+-=- ⎪ ⎪---⎝⎭⎝⎭，又有(21)(1)(2)2p n p T n p n p n -+≤-++-+++=，所以211222A B n n p n nC C n p -++⎛⎫-≤-= ⎪-⎝⎭当且仅当(21)2p n p T -+=时，取到等号，所以A B C C -的最大值2n.此时{1,,}A n p n =-+，由,A B 非空，可知1p =，2，…，1n -，有1n -种情况，利用对称性得到A B C C <时(),A B 具有与之相等的组数，由于A B C C -的最大值2n不可能有A B C C =的情况，所以有序数对(),A B 的数目为22n -. 35．（2020·全国·高三竞赛）设集合{1,2,,19}A =．是否存在集合A 的非空子集12,S S ，满足（1）1212,S S S S A ⋂=∅⋃=；（2）12,S S 都至少有4个元素；（3）1S 的所有元素的和等于2S 的所有元素的乘积？证明你的结论．【答案】证明见解析. 【解析】【分析】不妨设21,2,,,219S x y x y =<<≤，由条件可得2187xy x y ++=，即(21)(21)3751525x y ++==⨯，根据219x y <<≤,,x y N ∈，可得出其一组解，可证明.【详解】解：答案是肯定的．不妨设21,2,,,219S x y x y =<<≤，,x y N ∈ 则1219122x y xy +++----=，所以2187xy x y ++=，故(21)(21)3751525x y ++==⨯，所以7,12x y ==是一组解故取13,4,5,6,7,8,10,11,13,14,15,16,17,18,19S =，21,2,7,12S =，则这样的12,S S 满足条件 36．（2021·全国·高三竞赛）设n 是正整数，我们说集合{1,2,,2}n 的一个排列()122,,,n x x x 具有性质P ，是指在{1,2,,21}n -当中至少有一个i ，使得1i i x x n +-=.求证：对于任何n ，具有性质P 的排列比不具有性质P 的排列的个数多. 【答案】证明见解析【解析】【详解】设A 为不具有性质P 的排列的集合，B 为具有性质P 的排列的集合，显然||||(2)!A B n +=.为了证明||||A B <，只要得到1||(2)!2B n >就够了.设()122,,,n x x x 中，k 与k n +相邻的排列的集合为,1,2,,k A k n =.则22(21)!,2(22)!,1k k j A n A A n k j n =⋅-=⋅-≤<≤，由容斥原理得121||||2(21)!4(22)||!k k kj n n k j nB A A A n nC n =≤<≤≥-=⋅⋅--⋅⋅-∑∑(2)!2(1)(22)!n n n n =--⋅- 2(22)!n n n =⋅⋅-212(22)!2n n n ->⋅⋅- 1(2)!2n = 37．（2021·全国·高三竞赛）平面上有一个(3)n n ≥阶完全图，对其边进行三染色，且每种颜色至少染一条边.现假设在完全图中至多选出k 条边，且把这k 条边的颜色全部变为给定三色中的某种颜色后，此图同时也可以被该种颜色的边连通.若无论初始如何染色，都可以达到目的，求k 的最小值. 【答案】3n ⎡⎤⎢⎥⎣⎦【解析】【详解】先证明：3n k ⎡⎤≥⎢⎥⎣⎦.（这里3n ⎡⎤⎢⎥⎣⎦表示不超过3n 的最大的整数）.假设三种颜色为1、2、3，n 阶完全图的n 个点分成三个点集A ､B ､C ，且||||3n A B ⎡⎤==⎢⎥⎣⎦.做如下染色：集合A 中的点之间连的边染1，集合B 中的点之间连的边染2，集合C 中的点之间连的边染3，集合A 与B 间的点连的边染2，集合B 与C 间的点连的边染3，集合C 与A 间的点连的边染1.从而，若变色后最终得到染1的颜色的边形成的连通图，由于集合B 中的点出发的边均染的是2或3，于是，变色边数不小于||3n B ⎡⎤=⎢⎥⎣⎦.类似地，若变色后最终得到染2或3的颜色的边形成的连通图，则变色边数不小于||A （或C )3n ⎡⎤≥⎢⎥⎣⎦.故3n k ⎡⎤≥⎢⎥⎣⎦.再证明：3n k ⎡⎤≤⎢⎥⎣⎦.对n 用数学归纳法. 当3n =时，结论成立.假设1(4)n n -≥时，结论成立.则n 个点时：（1）若完全图中由某点出发的边有三种不同颜色，由归纳假设，可通过改变其中13n -⎡⎤⎢⎥⎣⎦条边的颜色得到同色连通图.（2）若完全图中由所有点出发的边均最多两种不同颜色，记A 为所有出发的边均染1或2的点组成的集合，记B 为所有出发的边均染2或3的点组成的集合，记C 为所有出发的边均染3或1的点组成的集合. 如果某些点连出的边都染颜色1，则把它归入集合A ；如果某些点连出的边都染颜色2，则把它归入集合B ；如果某些点连出的边都染颜色3，则把它归入集合C .不失一般性，不妨设||||A B C≤≤∣.则||3n A ⎡⎤≤⎢⎥⎣⎦.若B ≠∅，则C ≠∅，集合B 中的点连向集合C 中的点的边均染3.故B C ⋃由颜色3可以连通. 此时，任选集合B 中一点，集合A 中每个点与该点的连线的边颜色均变成3，由||3n A ⎡⎤≤⎢⎥⎣⎦知成立.若B =∅，则A =∅，于是，完全图的边均染的是1或3. 这与条件“每种颜色至少染一条边”不符. 所以由归纳法知原结论成立.38．（2022·全国·高三专题练习）班级里共有()3n n ≥名学生，其中有A ，B ，C ．已知A ，B ，C 中任意两人均为朋友，且三人中每人均与班级里中超过一半的学生为朋友．若对于某三个人，他们当中任意两人均为朋友，则称他们组成一个“朋友圈”．（1）求班级里朋友圈个数的最大值()F n ．（2）求班级里朋友圈个数的最小值()G n ．【答案】（1）()()126n n n --；（2）()4,41,6,,21,2n nn n G n n n =⎧⎪⎪+≥=⎨⎪-⎪⎩为偶数为奇数【解析】【分析】（1）利用组合数可求()F n ；（2）利用容斥原理可求()G n . 【详解】（1）当班级中的任意3人中，任意两个人都是朋友时，班级里朋友圈个数的最大，此时()()()3126n n n n F n C --==.（2）当3n =时，()31G =，当4n =时，A ，B ，C 中的每个人都至少与班级的3个同学是好朋友，故4人彼此是好朋友，故()44G =，当5n ≥时，记a P 为班级中除去,,A B C 且与A 是朋友的同学的集合，b P 为班级中除去,,A B C 且与B 是朋友的同学的集合，Pc 为班级中除去,,A B C 且与C 是朋友的同学的集合，若2(3)n k k =≥，由题设可知，a P 、b P 、Pc 中的元素的个数不小于1k -，余下同学记为：452,,,k Y Y Y ，集合M 中元素的个数记为M ，因为余下人数为23k -，由容斥原理可得23a b c k P P P -≥a b c ab ac bc abc P P P P P P P P P P P P =++---+，所以2333a b a c b c abc k k P P P P P P P P P -≥----+，即ab ac b c abc P P P P P P P P P k ++-≥，故此时()1G n k ≥+，考虑一种特殊情况：{}{}4+2+22,,,,,a k c b k k P Y Y P P Y Y ===，此时朋友圈个数为1111k k -++=+，故()112nG n k =+=+. 若21(2)n k k =+≥，由题设可知，a P 、b P 、Pc 中的元素的个数不小于1k -，余下同学记为：4521,,,k Y Y Y +，集合M 中元素的个数记为M ，因为余下人数为22k -，由容斥原理可得22a b c k P P P -≥a b c ab ac bc abc P P P P P P P P P P P P =++---+，所以2233a b a c b c abc k k P P P P P P P P P -≥----+，即1ab ac b c abc P P P P P P P P P k ++-≥-，故此时()G n k ≥，考虑一种特殊情况：{}{}{}4+2+22+321,,,,,,,,a k b k k c k k P Y Y P Y Y P Y Y +===，此时朋友圈个数为112k k ++-=，故()12n G n k -==. 综上，()4,41,6,,21,2n nn n G n n n =⎧⎪⎪+≥=⎨⎪-⎪⎩为偶数为奇数.39．（2021·浙江·高三竞赛）某班有10名同学计划在暑假举行若干次聚会，要求每名同学至多参加三次聚会，并且任意两名同学至少在一次聚会中相遇.求最大的正整数m ，使得无论如何安排符合上述要求的聚会，都一定存在某次聚会有至少m 名同学参加. 【答案】最大正整数m 是5 【解析】【分析】【详解】解：设有n 次聚会，聚会人数分别为1x ，2x ，…，n x （均为正整数）.我们有： 1210330n x x x +++≤⨯=1210452222n x x x ⎛⎫⎛⎫⎛⎫⎛⎫++⋅⋅⋅+≥= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭记11n S x x =+⋅⋅⋅+，2221n S x x =+⋅⋅⋅+，则2190S S -≥可知214S S ≥，即{}22111max ,,4nn nx x x x x x +⋅⋅⋅+⋅⋅⋅≥≥+⋅⋅⋅+若上式等号成立，则必须14n x x =⋅⋅⋅==，并且1130n S x x =+⋅⋅⋅+=，这样可得7.5n =导致矛盾.所以我们有{}1max ,,5n x x ⋅⋅⋅≥，即一定存在某次聚会有至少5名同学参加，即5m =满足题意.另一方面，我们给出10名同学参加聚会的一种安排方式：共A ，B ，C ，D ，E ，F 六次聚会，每次聚会恰好有5名同学参加，下面的10个三元子集分别表示10名同学各参加哪三次聚会：{}ABC ，{}CDE ，{}AEF ，{}BDF ，{}ABD ，{}ADE ，{}BCE ，{}BEF ，{}CDF ，{}ACF .易知在所有6203⎛⎫= ⎪⎝⎭个三元子集中，互补的两个三元子集在上式中恰好出现一个.这保证了上面的10个三元子集中每两个都相交，即任意两名同学至少在一次聚会中相遇.此外，A ，B ，C ，D ，E ，F 中的每一个在上式的10个三元子集中恰好出现五次，即每次聚会都恰好有5名同学参加，这意味着6m ≥不符合题意. 因此所求的最大正整数m 是5.另一种构造：{}ABC ，{}ABC ，{}BEF ，{}BEF ，{}CDF ，{}CDF ，{}ABD ，{}AEF ，{}ADE ，{}CDE .40．（2021·全国·高三竞赛）设2n ≥为正数，122,,,n A A A 为1,2,{},n 的所有子集的任一个排列．求2111nii ii i A A A A ++=⋅∑的最大值，其中121n A A +=．【答案】()2222n n n -+-【解析】【分析】【详解】先证两个引理．引理1 设122,,,n A A A 是集合1,2,{},n 的所有子集，则存在122,,,n A A A 的一个排列122,,,n B B B ，使得对任意的1,2,,2n i =均满足i B 、1i B +中的一个是另一个的子集，且元素个数差1，其中约定121n B B +=．引理1的证明：对n 用归纳法．当2n =时，集合{1,2}的4个子集排列为∅、{1}、{1,2}、{2}便满足要求．假设当n k =时存在排列122,,,k B B B 满足要求，则当1n k =+时，考虑下面的排列：12211222,,,,{1},{1},,{1},{1}k kk B B B B k B k B k B k -⋅⋅⋅++⋅⋅⋅++，这显然是集合{1,2,,1}k ⋅⋅⋅+的所有子集满足要求的一个排列．引理1证毕．引理2 设A 、B 是任意两个不同的有限集，则2221A B A B A B ⋅≤+-，（1）当A 、B 中一个为另一个的子集，且元素个数差1时等号成立．引理2的证明：设\,\,A B x B A y A B z ===．因为A B ≠，故x 、y 不能同时为0，于是x 、y 中至少有一个大于等于1．（1）22222()()()11x y z z x z y z x y ⇔++≤+++-⇔+≥，（2）显然成立．又当A 、B 中一个为另一个的子集且元素个数差1时，x 、y 中有一个为0，一个为1．（2）中取等号，从而（1）也取等号．引理2证毕．回到原题．由引理2可得()22222211111111122nnnn ii i i i i i i i i AA A A A AB -+++===≤+-=-∑∑∑ ()212211C 222n k n n n n k k n n ---==-=+-∑ ()2222n n n -=+-．又如果将{1,2,,}n ⋅⋅⋅的所有子集按照引理1中的排法便知上式等号成立．故所求的最大值为()2222n n n -+-．41．（2021·全国·高三竞赛）设{}()1,2,3,,2,m M n m n +=⋅∈N 是连续2m n ⋅个正整数组成的集合，求最小的正整数k ，使得M 的任何k 元子集中都存在1m +个数121,,,m a a a +满足1(1,2,,)i i a a i m +=．【答案】21m n n ⋅-+．【解析】【分析】【详解】记{1,2,3,,}A n =，任何一个以i 为首项，2为公比的等比数列与A 的交集设为i A ．一方面，由于M 中2m n n ⋅-个元的子集{}1,2,,2m n n n ++⋅中不存在题设的1m +个数，否则12112mm n a a a n ++≤<<<≤⋅，而1212m m nn a n ⋅+≤≤=，矛盾．故21m k n n ≥⋅-+．另一方面，21m k n n =⋅-+时，题设满足.若非如此，考虑以1212n i i -⎛⎫+≤ ⎪⎝⎭为首项，以2为公比的等比数列．其与M 的交集的元素个数为21i A m ++个．设M 任何k 元子集为T ，则上述等比数列与M 的交集中至少有21i A +个元素不在T 中，而i j ≠时，2121i j A A ++=∅．注意到21112||,i n iA A +-=所以21112|\|||ii n M T A A n +-≥==，可得2m T M n n n ≤⋅=⋅-与21mT k n n ==⋅-+矛盾．综上，所求k 为21m n n ⋅-+．42．（2021·全国·高三竞赛）对两个不全等的矩形A 、B ，称A B >，若A 的长不小于B 的长，且A 的宽也不小于B 的宽.现在若对任意的n 个两两不全等的，长和宽均为不超过2020的正整数的矩形，都必存在其中3个矩形A 、B 、C ，使得A B C >>，求n 的最小值. 【答案】2021 【解析】【分析】【详解】一方面，当2021n =时，若不存在满足要求的3个矩形，我们把所有的矩形如下分类：对一个矩形A ，若在剩下2020个矩形中，存在一个矩形B ，使得A B >，则称A 为“父矩形”，否则称A 为“子矩形”.由抽屉原理，其中必有一类至少含有1011个矩形，设它们的宽为121011x x x ≤≤⋯≤. 但易知所有的“父矩形”之间两两不能比较大小，所有的“子矩形”之间也两两不能比较大小，于是必有121011x x x <<<且相应的它们的长121011y y y >>>，合在一起即121011*********x x x y y y <<<≤<<<，与它们均为不超过2020的正整数矛盾.另一方面，当2020n ≤时，考虑所有长宽满足要求的，周长为4040的矩形，共1010个，及周长为4042的矩形，也共1010个.由于周长相等的两个矩形无法比大小，因此这2020个矩形中不存在满足要求的3个矩形. 综上，n 的最小值为2021.43．（2021·全国·高三竞赛）已知X 是一个有限集.110110,X A A X B B =⋃⋃=⋃⋃是满足如下性质的两个分划：若,110i j A B i j ⋂=∅≤≤≤，则10i j A B ⋃≥.求X 的最小值. 【答案】50 【解析】【分析】【详解】X 的最小值为50.我们先证明||50X ≥. 考虑集合110110,,,,,A A B B 中元素个数最少的集合，不妨设为1A .记1A a =，则1A 至多与110,,B B 中a 个集合相交.不妨设1,1,,i A B i k ⋂≠∅=且1,1,,10i A B i k ⋂=∅=+，其中k a ≤.故110,1,,10i A B i k ⋃≥=+.从而对1i k ∀≥+有11010Bi A a ≥-=-. 由1A 的最小性知1,,k B B 的元素个数均不小于a .从而1101110||k k X B B B B B B +=⋃⋃=++++(10)(10)502(5)(5)k a k a k a ≥⋅+--=+--.（1）若5a ≤，则5k ≤，此时由上式知||50X ≥；（2）若5a >，由1A 是110,,A A 中元素个数最少的集合知||1050X a ≥>.故||50X ≥.另一方面，||X 能取到50，例如，取11221010{1,2,3,4,5},{6,7,8,9,10},,{46,47,48,49,50}A B A B A B ======.显然它们满足条件，这时{}1,2,,50X =⋯.44．（2021·全国·高三竞赛）设集合S 是由平面上任意三点不共线的4039个点构成的集合，且其中2019个点为红色，2020个点为蓝色；在平面上画出一组直线，可以将平面分成若干区域，若一组直线对于点集S 满足下述两个条件，称这是一个“好直线组”：（1）这些直线不经过该点集S 中的任何一个点；（2）每个区域中均不会同时出现两种颜色的点.求k 的最小值，使得对于任意的点集S ，均存在由k 条直线构成的“好直线组”. 【答案】2019. 【解析】【分析】【详解】先证明2019k ≥：在一个圆周上顺次交替标记2019个红点和2019个蓝点，在平面上另外任取一点染为蓝色，这个圆周就被分成了4038段弧，则每一段的两个端点均染了不同的颜色；若要满足题目的要求，则每一段弧均与某条画出的直线相交；因为每条直线和圆周至多有两个交点，所以，至少要有403820192=条直线. 再证明：用2019条直线可以满足要求.对于任意两个同色点AB 、，均可用两条直线将它们与其他的点分离. 作法：在直线AB 的两侧作两条与AB 平行的直线，只要它们足够接近AB ，它们之间的带状区域里就会只有A 和B 这两个染色点. 设P 是所有染色点的凸包，有以下两种情形：（1）假设P 有一个红色顶点，不妨记为A .则可作一条直线，将点A 和所有其他的染色点分离，这样，余下的2018个红点可以组成1009对，每对可以用两条平行直线将它们与所有其他的染色点分离.所以，总共用2019条直线可以达到要求.（2）假设P 的所有顶点均为蓝色.考虑P 上的两个相邻顶点，不妨记为AB 、.则用一条直线就可以将这两个点与所有其他染色点分离.这样，余下的2018个蓝点可以组成1009对，每对可以用两条直线将它们与所有其他染色点分离. 所以，总共也用了2019条直线可以达到要求. 综上：k 的最小值为2019.45．（2021·全国·高三竞赛）设函数:f ++→Z Z 满足对于每个n +∈Z ，均存在一个k +∈Z ，使得2()k f n n k =+，其中，m f 是f 复合m 次．设n k 是满足上述条件的k 中的最小值，证明：数列12,,k k 无界．【答案】证明见解析. 【解析】【分析】【详解】设{}21,(1),(1),S f f =，对于每个正整数n S ∈，存在正整数k ，使得2()kfn n k S =+∈．因此，集合S 是无界的，且函数f 将S 映射到S ．此外，函数f 在集合S 上是单射．事实上，若(1)(1)()i j f f i j =≠，则m f （1）从某个值开始周期性地进行重复．于是，集合S 是有界的，矛盾．定义:g S S →为2()()n kn g n f n n k ==+．首先证明：g 也是单射．假设()()()g a g b a b =<，则22()()a b k ka b a k f a f b b k +===+，于是，>a b k k ．因为函数f 在集合S 上是单射，所以()()2()a b k k a b fa b a k k -==+-．又0a b a k k k <-<，与a k 的最小性矛盾．设T 是集合S 中非形如()()g n n S ∈的元素构成的集合．由于对每个n S ∈，均有()g n n >，则1T ∈．于是，T 是非空集合．对每个t T ∈，记{}2,(),(),t C t g t g t =，且称tC 为从t 开始的“链”．因为g 是单射，所以，不同的链不交．对每个n S T ∈，均有()n g n ='，其中，n n '<，n S '∈．重复上述过程，知存在t T ∈，使得t n C ∈，从而，集合S 是链t C 的并．若(1)n f 是从(1)i nt f =开始的链t C 中的元素，则122t j n n a a =+++，其中，()()()()112221(1)(1)(1)(1)jj i t ta a a n n n n j j f g f ff f f fa a -===+++．故(1)(1)22t n nt tn n n n f f t --=+=+． ① 其次证明：集合T 是无限的．假设集合T 中只有有限个元素则只有有限个链()1212,,,t t t t t C C C t t t <<<．固定N ．若(1)(1)n f n N ≤≤是链t C 中的元素，则由式①知：(1)22nt r n n Nf t t -=+≤+．由于1N +个不同的正整数1，(1),,(1)N f f 均不超过2r N t +，则12r NN t +≤+．当N 足够大时，这是不可能的.因此，集合，T 是无限的．选取任意正整数k ，考虑从集合T 中前1k +个数开始的1k +个链．设t 是这1k +个数中最大的一个．则每个链中均包含一个元素不超过t ，且至少有一个链中不含1,2,,t t t k +++中的任何一个数．于是，在这个链中存在一个元素n ，使得()g n n k ->，即n k k >．。

四年级下册数学试题--第9章《数学广角--鸡兔同笼》单元测评人教版含答案

2020-2021学年人教版四年级下册数学单元测评必刷卷第9章《数学广角—鸡兔同笼》测试时间：90分钟满分：100分+30分题号一二三四五 B 卷总分得分A 卷基础训练（100 分）一、选择题（每题1.5分，共18分）1．（2021·全国四年级单元测试）解放军进行野营拉练。

晴天每天走35km ，雨天每天比晴天少走8km ，一周共走了229km 。

这一周晴天有（）天。

A ．1B ．2C ．5D ．62．（2021·全国四年级单元测试）四年级学生参加“欢度六一”绘画评比，一共选出了52幅优秀作品，贴在6块展板上展出。

每块大展板可以贴10幅作品，每块小展板可以贴6幅作品。

大展板有（）块。

A ．2B ．3C ．4D ．63．（2021·全国四年级培优）王师傅搬40块玻璃，搬一块得4元，如果打碎一块没有搬运费，还要赔6元，最后王师傅拿到了140元，王师傅打碎了（）块。

A ．1B ．2C ．3D ．44．（2021·全国四年级单元测试）某次数学测验共20题，做对一题得5分，做错一题扣1分，不做得0分。

小红得了76分，她做对了几道题呢？（） A ．12B ．14C ．16D ．185．（2021·江苏五年级期中）太和镇某小学植树小分队10人参加植树活动。

男生每人栽了5棵树，女生每人栽了3棵树，一共栽了42棵树。

男生有（）人。

A ．8B ．6C ．46．（2021·全国四年级单元测试）在解决问题“笼子里有若干只鸡和兔。

从上面数，有14个头；从下面数，有44只脚。

鸡、兔各有几只？”时，下面求鸡的只数的算式是（）。

A ．4414()24-⨯÷ B ．()441442(2)-⨯÷- C ．144)4(44⨯-÷ D ．()1444()442⨯-÷- 7．（2021·全国四年级单元测试）42人去划船，一共租了10条船，正好坐满。

【竞赛题】人教版小学五年级下册数学第10讲《比例计算与列表分析》竞赛试题(含详解)

第十讲比例计算与列表分析比例是五年级的重要内容，之前我们已经学习过一些简单的比例问题，如按比例分配、化连比以及比例中的不变量．这一讲中，我们将继续比例的学习．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1．学校组织体检，收费标准如下：老师每人3元，学生每人2元．已知老师和学生的人数比为2:9，共收得体检费3120元．那么老师、学生各有多少人？分析：老师、学生的人数比是多少？所有老师、所有学生支付的体检费之比又是多少？练习1．某高速公路收费站对于过往车辆每辆收费标准是：大客车10元，小客车6元．某日通过该收费站的大客车和小客车数量之比为5∶6，共收取过路费602元．求共有客车多少辆．例题2．徐福记的巧克力糖每6块包成一小袋，水果糖每15块包成一大袋．现有巧克力糖和水果糖各若干袋，而且巧克力糖比水果糖多30袋．如果巧克力糖的总块数与水果糖的总块数之比为7:10，那么它们各有多少块？分析：巧克力糖与水果糖比较，每袋的糖数之比是多少？题中还告诉我们，巧克力糖的总块数与水果糖的总块数之比为7:10，由此能求出两种糖的袋数之比吗？练习2．花店有玫瑰花和康乃馨，一束玫瑰花有9支，一束康乃馨有6支．已知玫瑰花比康乃馨少50束，且玫瑰花与康乃馨的总支数之比为3:7，问：花店共有多少支玫瑰花？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -利用题目中的条件，我们可以将比例进行转化，比如例1中，题目告诉了我们人数比，然后我们要求出钱数之比；例2中，我们要通过块数比求出袋数的比．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3．碧梨超市雇了一些卡车运输苹果、梨和香蕉，这三种水果的重量比是4:2:1．大型卡车专门运输苹果，中型卡车专门运输梨，小型卡车专门运输香蕉．这三种卡车的载重量之比是4:3:2．已知大型卡车比小型卡车多6辆，那么一共雇了多少辆卡车？分析：水果重量、卡车数量和卡车的载重量，这三个量之间有什么关系？练习3．三洋姥姥从超市买来了一些饮料有可乐、雪碧、冰红茶，三种饮料的瓶数比为4:5:9，大洋只喝可乐，二洋只喝雪碧，三洋只喝冰红茶，他们每人每天喝掉饮料的瓶数比是1:2:3，最终大洋比三洋晚10天就把自己的饮料喝完了，那么二洋的雪碧够他喝多少天？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -当题目条件非常多的时候，列出表格来整理题中条件，能够使问题更为清晰明了，容易入手．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题4．某俱乐部男、女会员的人数之比是3:2，分为甲、乙、丙三组．已知甲、乙、丙三组的人数比是10:8:7，甲组中男、女会员的人数之比是3:1，乙组中男、女会员的人数之比是5:3．求丙组中男、女会员人数之比．分析：题中条件较多，不好处理，我们不妨设出其中一个量的“份数”来进行求解．设出哪个量的份数合适，以及设成多少份较好呢？我们所选取的数量最好是能与较多的其他数量关联在一起，同时所设出的份数最好能使得其余数量的份数也“比较整”，这样才最有助于我们的解题．Array练习4．有个工厂有三个分厂，全厂男、女职工人数的比是9:5，三个分厂人数比是8:9:11，第一分厂男、女职工人数比为3:1，第二分厂男、女职工人数比是5:4，第三分厂男职工比女职工多150人．这个厂共有职工多少人？例题5．有三个筐装有苹果和梨，已知苹果和梨的总数之比为4:3，第一个筐中苹果和梨个数比为6:5，第二个筐中苹果和梨个数比为3:5，且第一、第二、第三个筐的水果个数之比为11:16:9，求第三个筐中苹果和梨的个数比．分析：在填份数时，有时会出现除不尽的情况．这时只要适当扩倍就可以解决问题．例题6．某次数学竞赛设一、二、三等奖，已知：①甲、乙两校获一等奖人数比为1:2，且两校获奖总人数之比是5:4；②甲、乙两校获二等奖人数占两校获奖人数总和的14，其中乙校是甲校的3.5倍；③甲校三等奖获奖人数占该校获奖人数的45．请问：乙校获三等奖人数占该校获奖人数的几分之几？分析：本题中除了有比例的条件，还有分数的条件，倍数的条件．这些条件也都可以转化成比例的条件．比例尺地图上的比例尺，表示图上距离比实际距离缩小的程度，因此也叫缩尺．用公式表示为：/ 比例尺图上距离实际距离．比例尺通常有三种表示方法．（1）数字式，用数字的比例式或分数式表示比例尺的大小．例如地图上1厘米代表实地距离500千米，可写成：1:50000000，，或写成：五千万分之一．（2）线段式，在地图上画一条线段，并注明地图上1厘米所代表的实际距离．（3）文字式，在地图上用文字直接写出地图上1厘米代表实地距离多少千米，例如图上1厘米相当于地面距离10千米．三种表示方法可以互换．根据地图上的比例尺，可以量算图上两地之间的实地距离；根据两地的实际距离和比例尺，可计算两地的图上距离；根据两地的图上距离和实际距离，可以计算比例尺．根据地图的用途，所表示地区范围的大小、图幅的大小和表示内容的详略等不同情况，制图选用的比例尺有大有小．地图比例尺中的分子通常为1，分母越大，比例尺就越小．通常比例尺大于二十万分之一的地图称为大比例尺地图；比例尺介于二十万分之一至一百万分之一之间的地图，称为中比例尺地图；比例尺小于一百万分之一的地图，称为小比例尺地图．在同样图幅上，比例尺越大，地图所表示的范围越小，图内表示的内容越详细，精度越高；比例尺越小，地图上所表示的范围越大，反映的内容越简略，精确度越低．1:2000000 1:4000001:100000 1:30000作业1. A 、B 两种商品的价格比是7:3．如果它们的价格分别上涨70元，它们的价格比就变成7:4．B 商品原来的价格是多少？作业2. 某商店有桔子、苹果和梨出售．一斤桔子卖5元，一斤苹果卖4元，一斤梨卖3元，卡莉娅买了10斤水果，其中桔子和苹果的重量之比为5:9，苹果和梨的重量之比为3:2，那么她一共花了多少钱？作业3. 某班同学去野外军训，他们在一起吃午餐，男生每人要吃3个馒头，女生每人要吃2个馒头，已知男生比女生多3人，且男生、女生吃的馒头总数之比为7:4，那么男生和女生各有多少人？作业4. 碧丽小学的五年级有2个班，其中1班的男生和女生的人数比是2:3．全部五年级的学生中，男生和女生的人数比是3:4．又知道1班与2班的人数比是10:11，且1班的男生比2班的女生少10个．那么五年级一共有多少学生？作业5. 有两包糖，每包糖内都装有奶糖、水果糖和巧克力糖．已知：（1）第一包比第二包的奶糖少，且第一包与第二包糖的总数之比是1:2；（2）第一包和第二包中的水果糖总数占全部糖果总数的40%，其中第一包比第二包少；（3）第一包糖中巧克力糖与其它两种糖的总数之比为2:1．那么，第一包与第二包的巧克力糖之比是多少？俗话说，兴趣是最好的老师。

2019-2020年初中数学竞赛初赛试题(一,含详解)

及 x 轴围成的三角形面积为 sk ，则 s1 s2 s3 ... s2006 的值是
。
13．如图，正方形 ABCD和正方形 CGEF的边长分别是 2 和 3，且
点 B、 C、 G 在同一直线上， M 是线段 AE 的中点，连结 MF，则 MF
的长为
。
14．边长为整数的等腰三角形一腰上的中线将其周长分为
心 DEF 的各边与 ABC 的对应边平行，且各对应边的距离都是
1cm,
那么 DEF 的周长是（
）
(A)5cm (B)6cm (C)
( 6 3 )cm (D) ( 3 3 )cm
3．将长为 15cm 的木棒截成长度为整数的三段，使它们构成一个三角形的三边，则不同的截法有 ( ) (A)5 种 (B) 6 种 (C)7 种 (D)8 种
（ 1）随着 m 的变化，该二次函数图象的顶点 P 是否都在某条抛物线上？如果是，请求出该抛物线的表达式；如果不是，请说明理由；
（ 2）如果直线 y x 1 经过二次函数 y x 2 2( m 1 ) x m 1 图象的顶点 P，求
此时 m的值。
全国初中数学竞赛初赛试题（一）参考答案
一、选择题 1．答案 D
4．作抛物线 A 关于 x 轴对称的抛物线 B，再将抛物线 B 向左平移 2 个单位，向上平移 1 个单位，得到的抛物线 C 的函数解析式是 y 2( x 1 ) 2 1，则抛物线 A 所对应的函数表达
式是 ( )
(A) y 2( x 3 )2 2 (B) y 2( x 3) 2 2
(C) y 2( x 1 )2 2 (D) y 2( x 3 )2 2
顶点，棋子停在顶点 D。依这样的规则，在这 10 次移动的过程

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学竞赛训练题—选择题1．当01x <<时，()lg xf x x=，则下列大小关系正确的是（） A ．22()()()f x f x f x << B. 22()()()f x f x f x << C. 22()()()f x f x f x << D. 22()()()f x f x f x <<2．设()f x 在[0,1]上有定义，要使函数()()f x a f x a -++有定义，则a 的取值范围为（）A ．1(,)2-∞-； B. 11[,]22-； C. 1(,)2+∞； D. 11(,][,)22-∞-⋃+∞3．已知P 为三角形ABC 内部任一点（不包括边界），且满足()(2)0PB PA PB PA PC -+-=，则△ABC 一定为 ( )A ．直角三角形；B. 等边三角形；C. 等腰直角三角形；D. 等腰三角形4．已知()()2222212f x x a b x a ab b =++-++-是偶函数，则函数图象与y 轴交点的纵坐标的最大值是（）A B. 2 C. D. 45．已知函数34)(2+-=x x x f ，集合}0)()(|),{(≤+=y f x f y x M ，集合}0)()(|),{(≥-=y f x f y x N ，则在平面直角坐标系内集合M N 所表示的区域的面积是（） A.4π B. 2πC.πD.π26. 函数()f x = ）[]3. 1, . 1, C. 1, D. 1, 22A B ⎡⎤⎡⎡⎢⎥⎣⎣⎣⎦7. 设)(x f 有反函数)(1x f -，将)32(-=x f y 的图象向左平移2个单位，再关于x 轴对称后所得函数的反函数是（） A ．21)(1--=-x fyB ．2)(11x f y --=- C ．2)(11x f y --= D ．21)(1-=-x f y 8.化简三角有理式xx x x xx x x 22662244cos sin 2cos sin cos sin sin cos ++++的值为（）A. 1B. sin cos x x +C. sin cos x xD. 1+sin cos x x9.设a ,b 为两个相互垂直的单位向量。

已知OP =a ，OQ =b ，OR=r a +k b .若△PQR 为等边三角形，则k ，r 的取值为（）A ．k r ==B ．k r ==C ．k r ==D ．k r == 10.设{}n a ，{}n b 分别为等差数列与等比数列，且11444,1a b a b ====，则以下结论正确的是（）A. 22a b >B. 33a b <C. 55a b >D. 66a b >11.若15,(12)x R x +∈+则的二项式展开式中系数最大的项为（） A ．第8项 B. 第9项 C. 第8项和第9项 D. 第11项 12.设()cos5x f x =，12111(log ),(log ),(log )e e a f b f c f e πππ===，则下述关系式正确的是（）。

A ．a b c >> B. b c a >> C. c a b >> D. b a c >> 13．已知－１＜βα+＜3，且２＜βα-＜４，则βα32+的范围是（） A. )217,213(-B. )211,27(-C. )213,27(-D. )213,29(-14．若函数()2log 1a y x ax =-+有最小值，则a 的取值范围是（）．A 01a <<B 02,1a a <<≠C 12a <<D 2a ≥15．已知,1,=>ab b a 则ba b a -+22的最小值是（）．A 22 B2 C 2 D 116．已知cos cos 1x y +=，则sin sin x y -的取值范围是（）．A []11-，B []2-，2C 0⎡⎣D ⎡⎣17．函数()f x 是(0,)+∞上的单调递增函数，当*n N ∈时，*()f n N ∈，且[()]3f f n n =，则(1)f 的值等于（）．A 1 B 2 C 3 D 418.设集合}5,4,3,2,1{},1,0,2{=-=N M ，映射N M f →:使得对任意的M x ∈，都有)()(x xf x f x ++是奇数，则这样的映射f的个数是（）（A ）45 （B ）27 （C ）15 （D ）11 19.设函数xbax x g x x f +==)(,ln )(，它们的图象在x 轴上的公共点处有公切线，则当1>x 时，)(x f 与)(x g 的大小关系是（）（A ）)()(x g x f >（B ）)()(x g x f <（C ）)()(x g x f =（D ）)(x f 与)(x g 的大小不定 20.已知正方体ABCD —A 1B 1C 1D 1，过顶点A 1在空间作直线l ，使直线l 与直线AC 和BC 1所成的角都等于600，这样的直线l 可以作（）（A ）4条（B ）3条（C ）2条（D ）1条21. 从１至169的自然数中任意取出３个数构成以整数为公比的递增等比数列的取法有（） A. 89种 B. 90种 C. 91种 D. 92种22.一个正六面体的各个面和一个正八面体的各个面都是边长为a 的正三角形，这样的两个多面体的内切球的半径之比是一个最简分数nm，那么积n m ⋅等于（）A ．3B ．4C ．6D ．1223.圆周上有10个等分点，则以这10个等分点中的四个点为顶点的凸四边形中，梯形所占的比为（） A ．821 B ．421C ．1126D ．2724．把2008表示成两个整数的平方差形式，则不同的表示方法有（）种．A 4B 6C 8D 1625.12)526(++n 的小数表示中，小数点后至少连续有（）（A ）12+n 个零（B ）22+n 个零（C ）32+n 个零（D ）42+n 个零26.设AB 是椭圆12222=+by a x （0>>b a ）的长轴，若把AB100等分，过每个分点作AB的垂线，交椭圆的上半部分于P 1、P 2、… 、P 99 ，F 1为椭圆的左焦点，则21111P F P F A F +++…B F P F 1991++的值是（）（A ）a 98 （B ）a 99 （C ）a 100 （D ）a 101高中数学竞赛训练题—选择题答案1.解：当01x <<时，()0lg x f x x =<，222()0lg x f x x =<，22()0lg x f x x ⎛⎫=> ⎪⎝⎭。

又因为2222(2)0lg lg 2lg 2lg x x x x x x x x x x---==<。

所以 22()()()f x f x f x <<。

选 C 。

2解：函数()()f x a f x a -++的定义域为 [,1][,1]a a a a +⋂--。

当0a ≥时，应有1a a ≤-，即12a ≤；当0a ≤时，应有1a a -≤+，即12a ≥-。

因此，选 B 。

3解：因为,2PB PA AB PB PA PC CB CA -=+-=+，所以已知条件可改写为()0AB CB CA ⋅+=。

容易得到此三角形为等腰三角形。

因此选 D 。

4解：由已知条件可知，2210a b +-=，函数图象与y 轴交点的纵坐标为222a ab b +-。

令,s cos in b a θθ==，则22222sin cos sin cos2sin 2c s 2o a ab b θθθθθθ+=+=--+≤ 选 A 。

5．C 提示：由已知可得M ={（x ,y )|f (x )+f (y )≤0}={(x ,y )|(x -2)2+(y -2)2≤2},N ={(x ,y )|f (x )-f (y )≥0} ={(x ,y )|(x -y )(x +y -4)≥0}.则22(2)(2)2()(4)0x y M N x y x y ⎧-+-≤=⎨-+-≥⎩ ,作出其交集部分可得如图所示，其面积为圆面积的一半，即为212ππ=，故应选C.6.D .解：()f x 的定义域为34,x ≤≤则031x ≤-≤，令23sin , 02x πθθ-=≤≤，则()f x =sin sin 2sin()3πθθθθ==+=+因5336πππθ≤+≤，则 1sin()1, 12sin()2233ππθθ≤+≤≤+≤ 7. A 解：设)32(-=x f y 上有点),(00y x 左移2 ),2(00y x -关于x 轴对称),2(00y x --取反函数)2,(00--x y ，∴⎩⎨⎧=-=-y x x y 200⇒⎩⎨⎧-=+=xy y x 002代入)32(-=x f y 得)12(+=-y f x ⇒)(121x f y -=+-⇒21)(1--=-x fy ，8.解答为 A 。

22442222sin cos )(sin cos sin cos )2sin cos x x x x x x x x ++-+分母=(4422s i n c o s s i nc o sx x x x =++。

也可以用特殊值法9.解答．C. PQ QR PR ==，12==r=k=。

10.解答：A 。

11444,1a b a b ====设等差数列的公差为d ，等比数列公比为q,由，得223355663,2,0,1,a b a b a b a b =======-=得。

11.解答：D. 11512129322,33r rr r r r r T C T T T T r ++++=≤≤⇒≤≤由，，r=10，第11项最大。

12.解答： D 。

函数()cos5x f x =为偶函数，在（0，2π）上，()cos f x x =为减函数，而121111log log ,log ,log 2log log ee e e e e ππππππ=-=-=， log 2log 105log 554e e e ππππ<<<<，所以b a c >>。

13解：由待定系数法或线性规划可得。

14答案：C ．解：当01a <<时，log a y x =是递减函数，由于21t x ax =-+没有最大值，所以()2log 1a y x ax =-+没有最小值；当1a >时，()2log 1a y x ax =-+有最小值等价于21t x ax =-+有大于0的最小值．这等价于240a ∆=-<，因此12a <<．15答案：A.解：记t b a =-，则0>t ，b a b a -+2222222≥+=+=t t t t ，（当且仅当22t a b ===即时取等号）．故选A ． 16答案：D ．解：设sin sin x y t -=，易得21cos cos sin sin 2t x y x y --=，即()21cos 2t x y -+=．由于()1cos 1x y -≤+≤，所以21112t --≤≤，解得 t ≤≤．17答案：B 解：（用排除法）令1n =，则得[(1)]3f f =．若(1)1f =，则[(1)](1)3f f f ==，与(1)1f =矛盾；若(1)3f =，则[(1)](3)3f f f ==，与“()f x 在(0,)+∞上单调递增”矛盾；若(1)4f =，则[(1)](4)3f f f ==，也与“()f x 在(0,)+∞上单调递增”矛盾．故选B ． 18.A 提示：当2-=x 时，)2(2)()(---=++f x xf x f x 为奇数，则)2(-f 可取1、3、5，有3种取法；当0=x 时，)0()()(f x xf x f x =++为奇数，则)0(f 可取1、3、5，有3种取法；当1=x 时，)1(21)()(f x xf x f x +=++为奇数，则)1(f 可取1、2、3、4、5，有5种取法。