编译原理(龙书)习题(5,6,7,8)章
编译原理课后答案-第二版
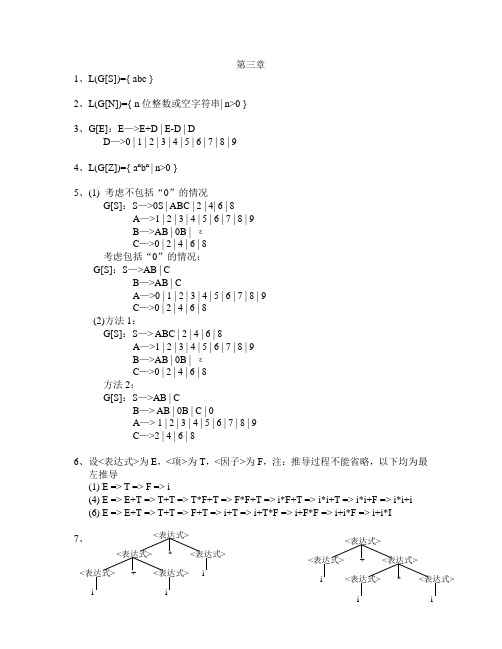
第三章1、L(G[S])={ abc }2、L(G[N])={ n位整数或空字符串| n>0 }3、G[E]:E—>E+D | E-D | DD—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 94、L(G[Z])={ a n b n | n>0 }5、(1) 考虑不包括“0”的情况G[S]:S—>0S | ABC | 2 | 4| 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8考虑包括“0”的情况:G[S]:S—>AB | CB—>AB | CA—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>0 | 2 | 4 | 6 | 8(2)方法1:G[S]:S—> ABC | 2 | 4 | 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8方法2:G[S]:S—>AB | CB—> AB | 0B | C | 0A—> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>2 | 4 | 6 | 86、设<表达式>为E,<项>为T,<因子>为F,注:推导过程不能省略,以下均为最左推导(1) E => T => F => i(4) E => E+T => T+T => T*F+T => F*F+T => i*F+T => i*i+T => i*i+F => i*i+i(6) E => E+T => T+T => F+T => i+T => i+T*F => i+F*F => i+i*F => i+i*I7、<表达式><表达式>*<表达式><表达式>+<表达式>i i i<表达式><表达式>+<表达式>i <表达式>*<表达式>i i8、是有二义性的,因为句子abc 有两棵语法树(或称有两个最左推导或有两个最右推导)最左推导1:S => Ac => abc 最左推导2:S => aB => abc 9、(1)(2) 该文法描述了变量a 和运算符+、*组成的逆波兰表达式10、(1) 该文法描述了各种成对圆括号的语法结构(2) 是有二义性的,因为该文法的句子()()存在两种不同的最左推导: 最左推导1:S => S(S)S => (S)S => ()S => ()S(S)S => ()(S)S => ()()S => ()()最左推导2:S => S(S)S => S(S)S(S)S => (S)S(S)S=> ()S(S)S => ()(S)S => ()()S => ()()11、(1) 因为从文法的开始符E 出发可推导出E+T*F ,推导过程如下:E => E+T =>E+T*F ,所以E+T*F 是句型。
《编译原理》课后习题答案第5章

《编译原理》课后习题答案第5章《编译原理》课后习题答案第5章.pdf《编译原理》课后习题答案第5章.pdf第5章自顶向下语法分析方法第1题对文法G[S] S→a|∧|(T) T→T,S|S(1) 给出(a,(a,a))和(((a,a),∧,(a)),a)的最左推导。
(2) 对文法G,进行改写,然后对每个非终结符写出不带回溯的递归子程序。
(3) 经改写后的文法是否是LL(1)的?给出它的预测分析表。
(4) 给出输入串(a,a)#的分析过程,并说明该串是否为G的句子。
答案:(1) 对(a,(a,a)的最左推导为:S(T) (T,S) (S,S) (a,S) (a,(T)) (a,(T,S)) (a,(S,S)) (a,(a,S)) (a,(a,a))对(((a,a),∧,(a)),a) 的最左推导为:S(T) (T,S) (S,S) ((T),S) ((T,S),S) ((T,S,S),S) ((S,S,S),S) (((T),S,S),S) (((T,S),S,S),S) (((S,S),S,S),S) (((a,S),S,S),S) (((a,a),S,S),S) (((a,a),∧,S),S) (((a,a),∧,(T)),S)(((a,a),∧,(S)),S)《编译原理》课后习题答案第5章.pdf《编译原理》课后习题答案第5章.pdf(((a,a),∧,(a)),S) (((a,a),∧,(a)),a)(2) 改写文法为:0) S→a 1) S→∧ 2) S→( T ) 3) T→S N 4) N→, S N 5) N→ε非终结符FIRST集FOLLOW集S {a,∧,(} {#,,,)} T {a,∧,(} {)} N {,,ε} {)}对左部为N的产生式可知:FIRST (→, S N)={,} FIRST (→ε)={ε} FOLLOW (N)={)}由于SELECT(N →, S N)∩SELECT(N →ε) ={,}∩ { )}= 所以文法是LL(1)的。
编译原理(第2版)课后习题答案详解

第1 章引论第1 题解释下列术语:(1)编译程序(2)源程序(3)目标程序(4)编译程序的前端(5)后端(6)遍答案:(1)编译程序:如果源语言为高级语言,目标语言为某台计算机上的汇编语言或机器语言,则此翻译程序称为编译程序。
(2)源程序:源语言编写的程序称为源程序。
(3)目标程序:目标语言书写的程序称为目标程序。
(4)编译程序的前端:它由这样一些阶段组成:这些阶段的工作主要依赖于源语言而与目标机无关。
通常前端包括词法分析、语法分析、语义分析和中间代码生成这些阶段,某些优化工作也可在前端做,也包括与前端每个阶段相关的出错处理工作和符号表管理等工作。
(5)后端:指那些依赖于目标机而一般不依赖源语言,只与中间代码有关的那些阶段,即目标代码生成,以及相关出错处理和符号表操作。
(6)遍:是对源程序或其等价的中间语言程序从头到尾扫视并完成规定任务的过程。
第2 题一个典型的编译程序通常由哪些部分组成?各部分的主要功能是什么?并画出编译程序的总体结构图。
答案:一个典型的编译程序通常包含8 个组成部分,它们是词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、中间代码优化程序、目标代码生成程序、表格管理程序和错误处理程序。
其各部分的主要功能简述如下。
词法分析程序:输人源程序,拼单词、检查单词和分析单词,输出单词的机内表达形式。
语法分析程序:检查源程序中存在的形式语法错误,输出错误处理信息。
语义分析程序:进行语义检查和分析语义信息,并把分析的结果保存到各类语义信息表中。
中间代码生成程序:按照语义规则,将语法分析程序分析出的语法单位转换成一定形式的中间语言代码,如三元式或四元式。
中间代码优化程序:为了产生高质量的目标代码,对中间代码进行等价变换处理。
目标代码生成程序:将优化后的中间代码程序转换成目标代码程序。
表格管理程序:负责建立、填写和查找等一系列表格工作。
表格的作用是记录源程序的各类信息和编译各阶段的进展情况,编译的每个阶段所需信息多数都从表格中读取,产生的中间结果都记录在相应的表格中。
《编译原理实践及应用》习题的参考答案

附录部分习题参考答案第1章参考答案:1,2,3,4,5,6,7解答:略!第2章参考答案:1,2,3:解答:略!4. 解答:A:① B:③ C:① D:②5. 解答:用E表示<表达式>,T表示<项>,F表示<因子>,上述文法可以写为:E → T | E+TT → F | T*FF → (E) | i最左推导:E=>E+T=>E+T+T=>T+T+T=>F+T+T=>i+T+T=>i+F+T=>i+i+T=>i+i+F=>i+i+iE=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*i 最右推导:E=>E+T=>E+F=>E+i=>E+T+i=>E+F+i=>E+i+i=>T+i+i=>F+i+i=>i+i+iE=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i =>i+i*ii+i+i和i+i*i的语法树如下图所示。
i+i+i、i+i*i的语法树6. 解答:(1) 终结符号为:{or,and,not,(,),true,false}非终结符号为:{bexpr,bterm,bfactor}开始符号为:bexpr(2) 句子not(true or false)的语法树为:7. 解答:(1) 把a n b n c i分成a n b n和c i两部分,分别由两个非终结符号生成,因此,生成此文法的产生式为:S → ABA → aAb|abB → cB|ε(2) 令S为开始符号,产生的w中a的个数恰好比b多一个,令E为一个非终结符号,产生含相同个数的a和b的所有串,则产生式如下:S → aE|Ea|bSS|SbS|SSbE → aEbE|bEaE|ε(3) 设文法开始符号为S,产生的w中满足|a|≤|b|≤2|a|。
编译原理作业题答案编译原理课后题答案

第二章高级语言的语法描述6、令文法G 6为:N →D|ND D → 0|1|2|3|4|5|6|7|8|9(1)G 6 的语言L (G 6)是什么?(2)给出句子01270127、、34和568的最左推导和最右推导。
解答:思路:由N N →→ D|ND 可得出如下推导N =>=>ND ND ND=>=>=>NDD NDD NDD=>…=>=>…=>=>…=>D D n(n >=1=1))可以看出,N 最终可以推导出1个或多个(也可以是无穷)D ,而D D →→ 0|1|2|3|4|5|6|7|8|9可知,每个D 为0~9中的任一个数字,所以,中的任一个数字,所以,N N N 最终推导出的就是由最终推导出的就是由0~9这10个数字组成的字符串。
(1)G 6 的语言L (G 6)是由0~9这10个数字组成的字符串个数字组成的字符串,,或{0{0,,1,1,……,9}+。
(2)(2)句子句子01270127、、34和568的最左推导分别为的最左推导分别为: : N =>=>ND ND ND=>=>=>NDD NDD NDD=>=>=>NDDD NDDD NDDD=>=>=>DDDD DDDD DDDD=>=>=>0DDD 0DDD 0DDD=>=>=>01DD 01DD 01DD=>=>=>012D 012D 012D=>=>=>0127 0127 N =>=>ND ND ND=>=>=>DD DD DD=>=>=>3D 3D 3D=>=>=>34 34N =>=>ND ND ND=>=>=>NDD NDD NDD=>=>=>DDD DDD DDD=>=>=>5DD 5DD 5DD=>=>=>56D 56D 56D=>=>=>568 568 句子01270127、、34和568的最右推导分别为的最右推导分别为: :N =>=>ND ND ND=>=>=>N7N7N7=>=>=>ND7ND7ND7=>=>=>N27N27N27=>=>=>ND27ND27ND27=>=>=>N127N127N127=>=>=>D127D127D127=>=>=>0127 0127 N =>=>ND ND ND=>=>=>N4N4N4=>=>=>D4D4D4=>=>=>34 34N =>=>ND ND ND=>=>=>N8N8N8=>=>=>ND8ND8ND8=>=>=>N68N68N68=>=>=>D68D68D68=>=>=>568 5687、写一个文法,使其语言是奇数集,且每个基数不以0开头。
编译原理 龙书 第二版 第5、6章

2)E->T
E.type=T.type
3)T->num
T.type=integer
4)T->num.num
T.type=float
(2)
产生式
语义规则
1)E->E1+T
If E1.type ==T.type then E.type=E1.type
Else begin
E.type=float
105: goto–
6)按照产生式B->B1 || M B2进行归约
7)按照产生式B->(B1)进行归约
8)按照产生式B->B1 && M B2进行归约
9)各子表达式的truelist和falselist在上图中已标出
3)三元式序列
4)间接三元式序列
答:(1)抽象语法树
(2) 四元式序列
t1=b+c
t2=minus t1
t3=a+t2
op
Arg1
result
0
+
b
c
T1
1
minus
T1
T2
2
+
a
T2
T3
(3)三元式序列
op
Arg1
Arg2
0
+
b
c
1
minus
(0)
2
+
a
(1)
(4)间接三元式序列
10
(0)
E.type=T.type; E.val=T.val
3)T->num
T.type=integer; T.val=num
《编译原理》习题参考答案(六)

《编译原理》习题参考答案(六)第五章5.4 为下列类型写类型表达式:(a) 指向实数的指针数组,数组的下标从1到100。
(b) 两位数组(即数组的数组),他的行下标从1到10,列下标从1到20。
(c) 函数,他的定义域是从整数到整数的指针的函数,它的值域是从一个整数和一个字符组成的纪录。
Solution:(a) array ( 1 . . 100 , pointer ( real ) )(b) array ( 1 . . 10 , array ( 1 . . 20 , type ) )(c) ( integer →pointer(integer) )→record((i : integer) * ( c : char )) 假定作为值域的记录类型的两个域分别叫i和c。
5.6 下列文法定以字面常量表的表。
符号的解释和图5.2文法的那些相同,增加了类型list,它表示类型T的元素表。
→ D ; EP→ D ; D | id : TD→ list of T | char | integerTE→ ( L ) | literal | num | id→ E , L | EL写一个类似5.3节中的翻译方案,以确定表达式( E )和表( L )的类型。
P→ D ; ED→ D ; DD→ id : T { addtype ( id.entry , T.type ) }T→ char { T.type := char }T→ integer { T.type := integer }T→ list of T1 { T.type := list ( T1.type ) }E→ literal { E.type := char }E→ num { E.type := integer }E→ id { E.type := lookup ( id.entry ) }E→ ( L ) { E.type := list ( L.type ) }L→E{L.type:=E.type}L→ E , L1 { L.type := if L1.type = E.type then E.typeelse type_error }5.16 对下面的每对表达式,找出最一般的合一代换:(a) α1 → ( α2 →α1 )(b) array ( β1 ) → ( pointer( β1 ) →β2 )(c) γ1 →γ2(d) δ1 →(δ1 →δ2 )Solution:S(α1) = array ( β1 ) S(α2) = pointer ( β1 ) S(β2) = array ( β1 ) (a)(c):S(γ1) = α1 S(γ2) = α2 → α1 (a)(d):S(α1) = S(α2) = S(δ1) = S(δ2) = α (b)(c):S(γ1) = array ( β1 ) S(γ2) = pointer ( β1 ) → β2 (b)(d): 无 (c)(d):S(γ1) = δ1 S(γ2) = δ1 → δ25.17 仿效例5.5,推到下面map 的多态类型: map: ∀ α . ∀ β . ( ( α → β ) * list ( α ) ) → list ( β ) map 的ML 定义是 fun map ( f , l ) = if null ( l ) then nilelse cons ( f ( hd ( l ) ) , map ( f , tl ( l ) ) );在这个函数体中,内部定义的标识符的类型是: null : ∀α . list (α ) → boolean ; nil : ∀α . list (α ) ;cons : ∀α . ( α * list (α ) ) → list (α ) ;hd:∀α . list (α ) →α;∀α . list (α ) → list (α ) ;tl:Solution:行定型断言代换规则(1) f : α( Exp Id )(2) l : β( Exp Id )(3) map : γ( Exp Id )(4) map ( f , l ) : δγ = ( α * β ) →δ(Exp Funcall)(5) null : list (α0) → boolean ( Exp Id ) 和( Type Fresh )(6) null ( l ) : boolean β = list (α0) (Exp Funcall)(7) nil : list (α1) ( Exp Id ) 和( Type Fresh )(8) l : list (α0) 由(2)可得(9) hd : list (α2) →α2( Exp Id ) 和( Type Fresh )(10) hd ( l ) : α0α2 = α0(Exp Funcall)(11) f ( hd ( l ) ) : α3α = α0→α3( Exp Id )(12) f : α0→α3由(1)可得(13) tl : list (α4)→ list (α4) ( Exp Id ) 和( Type Fresh )(14) tl ( l ) : list (α0) α4 = α0(Exp Funcall)(15) map : ((α0→α3)*list(α0))→δ由(3)可得(16) map ( f , tl ( l ) ) : δ(Exp Funcall)(17) cons : α5 * list(α5) → list(α5) ( Exp Id ) 和( Type Fresh ) (18) cons (…) : list (α3) α5 = α3 , δ=list(α3) (Exp Funcall)(19) if : boolean *α6 * α6→α6( Exp Id ) 和( Type Fresh )(20) if (…) : list (α1) α6 = α1 , α3 = α1(Exp Funcall)(21) match : α7 *α7 →α7( Exp Id ) 和( Type Fresh ) (22) match (…) : list (α1) α7 = list (α1) (Exp Funcall)至此有map : ( (α0→α1)*list(α0) )→list(α1)所以map : ∀α . ∀β . ( ( α→β ) * list ( α ) ) → list ( β )5.18 假定类型名link和cell如5.5节那样定义,下面的表达式中,那些结构等价?那些名字等价?(a) link(b) pointer ( cell )(c) pointer ( link )(d) pointer ( record ( ( info : integer ) * ( next : pointer ( cell ) ) ) ) Solution:(a)、(b)、(d)结构等价,无名字等价。
编译原理5、6、7章解题小结

编译原理5、6、7章解题小结第一篇:编译原理5、6、7章解题小结第5、6、7章小结几种语法分析方法• 自上而下–递归下降分析法–预测(LL(1))分析法• 自下而上–算符优先分析法– LR分析法:LR(0)、SLR(1)、LR(1)、LALR(1)一、自上而下的语法分析方法1.不带回溯确定的自上而下分析法2.对文法的要求:1)文法非左递归2)LL(1)文法i.LL(1)文法的定义:⌝ LL分析表不含多重元素⌝对A∈VT,A->α|β• FIRST(α)⋂ FIRST(β)=φ• α与β至多只有一个为ε• 若β*⇒ε,则FIRST(α)⋂ FOLLOW(A)=φii.LL(1)文法的两个性质⌝ LL(1)文法不含左递归⌝ LL(1)文法无二义i.将方法G改写成LL(1)文法的方法:⌝消去直接左递归⌝提公共左因子3.根据文法规则构造1)递归下降分析程序的方法2)预测分析表的方法EX1:已知文法G:S->aAbDe | dA->BSD | eB->Sac | cD | εD->Se | ε求:1)每个非终结符的FIRST,FOLLOW集2)判定是否为LL(1)文法。
解:FIRST(S)={a,e};FIRST(B)={a,d,c,ε};FIRST(D)={a,d,ε};FIRST(A)={a,d,c,ε,e};FOLLOW(S)={a,e,d,b,#};FOLLOW(B)={a,e};FOLLOW(D)={a,e,b};FOLLOW(A)={b};FIRST()EX2:已知∑={a,b},用高级语言编写一个能够识别集合L={ anbn | n≥0}的程序。
提示:1、求文法G:S->aSb | ε2、判定文法G能用何种方法做。
二、自下而上的语法分析方法(一)、算符优先分析法1.算符优先分析法的定义2.最左素左语3.确定优先关系,构造优先关系表EX3:已知文法G:S->S;D | DD->D(T)| HT->T+S | SH->a |(S)求:1)求优先关系表2)判定是否为OG、OPG文法。
编译原理(龙书)习题(5,6,7,8)章

6.2.1 将算术表达式 a+-(b+c) 翻译成
1)抽象语法树 2)四元式序列 3)三元式序列 4)间接三元式序列
PPT课件整理
15
1)抽象语法树:
PPT课件整理
16
2)四元式序列:
3)三元式序列:
4)间接三元式序列:
PPT课件整理
17
6.4.1 向图6-19的翻译方案中加入对应于下列产生式的规则: 1) EE1*E2 2) EE1(单目加 )
第5章 语法制导的翻译
5.2.3 假设我们有一个产生式 A。BAC,D B,C,D这四个非终 结符号都有两个属性:s是一个综合属性,而i是一个继承属 性。对于下面的每组规则,指出(i)这些规则是否满足S属性 定义的要求。(ii)这些规则是否满足L属性定义的要求。(iii) 是否存在和这些规则一致的求值过程?
1)一个repeat语句,repeat S while B 2)一个for循环语句,for (S1 ; B ; S2) S3
S-->repeat S1 while B
begin=newlabel() S1.next=newlabel() B.true=begin B.false = S.next S.code=label(begin)||
(完整版)编译原理第五章作业参考答案

SELECT(F PF/ )=FIRST(P)={(,a,b,^};
SELECT(F/ *F /)={*}; SELECT(F/ ε )=FOLLOW(F/)={(,a,b,^,+,),#};
SELECT(P (E))={(}
SELECT(P a)={a}
SELECT(P b)={b}
SELECT(P ^)={^} 可见,相同左部产生式的
if(CH== ’ aR’E)AD(CH);// 产生式 S a else if(CH== ’ ^ ’ ) READ(C产H)生;//式 S ^ else if(CH== ’产( ’生)式// S (T) {
READ(CH); P_T(); IF (CH= =’ ) ’TH)EN READ(CH) else ERROR } else ERR; } void P_T()// 非终结符 S 的子程序 { if(IsIn(CH,FIRST_SU)) //FIRST_SU 为 T SU 的右部的 FIRST 集合 { P_S(); P_U(); } } void P_U()// 非终结符 U 的子程序 { if(CH== ’ , ’产生)//式 U , SU
3.已知文法 G[S] :
S MH|a
H LSo| ε K dML|ε
L eHf
M K|bLM 判断 G是否是 LL( 1)文法,如果是,构造 LL( 1)分析表。 解: 首先求各非终结符的 FIRST 集合:
FIRST 集合有:
FIRST(E)=FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^}; FIRST(E / )={+, ε }
FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^}; FIRST(T / )=FIRST(T) ∪ { ε }={(,a,b,^, ε };
编译原理课后习题答案

第一章1.典型的编译程序在逻辑功能上由哪几部分组成?答:编译程序主要由以下几个部分组成:词法分析、语法分析、语义分析、中间代码生成、中间代码优化、目标代码生成、错误处理、表格管理。
2. 实现编译程序的主要方法有哪些?答:主要有:转换法、移植法、自展法、自动生成法。
3. 将用户使用高级语言编写的程序翻译为可直接执行的机器语言程序有哪几种主要的方式?答:编译法、解释法。
4. 编译方式和解释方式的根本区别是什么?答:编译方式:是将源程序经编译得到可执行文件后,就可脱离源程序和编译程序单独执行,所以编译方式的效率高,执行速度快;解释方式:在执行时,必须源程序和解释程序同时参与才能运行,其不产生可执行程序文件,效率低,执行速度慢。
第二章1.乔姆斯基文法体系中将文法分为哪几类?文法的分类同程序设计语言的设计与实现关系如何?答:1)0型文法、1型文法、2型文法、3型文法。
2)2. 写一个文法,使其语言是偶整数的集合,每个偶整数不以0为前导。
答:Z→SME | BS→1|2|3|4|5|6|7|8|9M→ε | D | MDD→0|SB→2|4|6|8E→0|B3. 设文法G为:N→ D|NDD→ 0|1|2|3|4|5|6|7|8|9请给出句子123、301和75431的最右推导和最左推导。
答:N⇒ND⇒N3⇒ND3⇒N23⇒D23⇒123N⇒ND⇒NDD⇒DDD⇒1DD⇒12D⇒123N⇒ND⇒N1⇒ND1⇒N01⇒D01⇒301N⇒ND⇒NDD⇒DDD⇒3DD⇒30D⇒301N⇒ND⇒N1⇒ND1⇒N31⇒ND31⇒N431⇒ND431⇒N5431⇒D5431⇒75431N⇒ND⇒NDD⇒NDDD⇒NDDDD⇒DDDDD⇒7DDDD⇒75DDD⇒754DD⇒7543D⇒75431 4. 证明文法S→iSeS|iS| i是二义性文法。
答:对于句型iiSeS存在两个不同的最左推导:S⇒iSeS⇒iiSesS⇒iS⇒iiSeS所以该文法是二义性文法。
编译原理(第3版)课本习题答案

第二章 高级语言及其语法描述6.(1)L (G 6)={0,1,2,......,9}+(2)最左推导:N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127 N=>ND=>DD=>3D=>34N=>ND=>NDD=>DDD=>5DD=>56D=>568 最右推导:N=>ND =>N7=>ND7=>N27=>ND27=>N127=>D127=>0127 N=>ND=>N4=>D4=>34N=>ND=>N8=>ND8=>N68=>D68=>5687.【答案】G:S →ABC | AC | CA →1|2|3|4|5|6|7|8|9B →BB|0|1|2|3|4|5|6|7|8|9C →1|3|5|7|98.(1)最左推导:E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*iE=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F)=>i*(i+i) 最右推导:E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*iE=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i)=>F*(i+i)=>i*(i+i) (2)9.证明:该文法存在一个句子iiiei 有两棵不同语法分析树,如下所示,因此该文法是二义的。
编译原理课后习题答案

编译原理课后习题答案第三章N=>D=> {0,1,2,3,4,5,6,7,8,9}N=>ND=>NDDL={a |a(0|1|3..|9)n且 n>=1}(0|1|3..|9)n且 n>=1{ab,}a nb n n>=1第6题.(1) <表达式> => <项> => <因子> => i(2) <表达式> => <项> => <因子> => (<表达式>) => (<项>)=> (<因子>)=>(i)(3) <表达式> => <项> => <项>*<因子> => <因子>*<因子> =i*i(4) <表达式> => <表达式> + <项> => <项>+<项> => <项>*<因子>+<项>=> <因子>*<因子>+<项> => <因子>*<因子>+<因子> = i*i+i (5) <表达式> => <表达式>+<项>=><项>+<项> => <因子>+<项>=i+<项> => i+<因子> => i+(<表达式>) => i+(<表达式>+<项>)=> i+(<因子>+<因子>)=> i+(i+i)(6) <表达式> => <表达式>+<项> => <项>+<项> => <因子>+<项> => i+<项> => i+<项>*<因子> => i+<因子>*<因子> = i+i*i第7题第9题语法树ss s* s s+aa a推导: S=>SS*=>SS+S*=>aa+a* 11. 推导:E=>E+T=>E+T*F语法树:E*短语: T*F E+T*F直接短语: T*F句柄: T*F12.短语:直接短语:句柄:13.(1)最左推导:S => ABS => aBS =>aSBBS => aBBS => abBS => abbS => abbAa => abbaa最右推导:S => ABS => ABAa => ABaa => ASBBaa => ASBbaa => ASbbaa => Abbaa => a1b1b2a2a3 (2) 文法:S ABSS Aa S ε A aB b(3) 短语:a1 , b1 , b2, a2 , , bb , aa , abbaa,直接短语: a1 , b1 , b2, a2 , , 句柄:a114 (1)S ABA aAb | εB aBb | ε (2)S 1S0 S AA 0A1 |ε第四章1. 1. 构造下列正规式相应的DFA (1) 1(0|1)*101NFA123114(2) 1(1010*|1(010)*1)*0 NFA(3)NFA(4)NFA2.解:构造DFA 矩阵表示b其中0 表示初态,*表示终态用0,1,2,3,4,5分别代替{X} {Z} {X,Z} {Y} {X,Y} {X,Y,Z}得DFA状态图为:3.解:构造DFA矩阵表示构造DFA的矩阵表示其中表示初态,*表示终态替换后的矩阵4.(1)解构造状态转换矩阵:{2,3} {0,1}{2,3}a={0,3} {2},{3},{0,1}{0,1}a={1,1} {0,1}b={2,2}(2)解:首先把M 的状态分为两组:终态组{0},和非终态组{1,2,3,4,5} 此时G=( {0},{1,2,3,4,5} ) {1,2,3,4,5}a ={1,3,0,5} {1,2,3,4,5}b ={4,3,2,5}由于{4}a ={0} {1,2,3,5}a ={1,3,5}因此应将{1,2,3,4,5}划分为{4},{1,2,3,5} G=({0}{4}{1,2,3,5}) {1,2,3,5}a ={1,3,5} {1,2,3,5}b ={4,3,2}因为{1,5}b ={4} {23}b ={2,3}所以应将{1,2,3,5}划分为{1,5}{2,3} G=({0}{1,5}{2,3}{4}){1,5}a ={1,5} {1,5}b ={4} 所以{1,5} 不用再划分{2,3}a ={1,3} {2,3}b ={3,2}因为 {2}a ={1} {3}a ={3} 所以{2,3}应划分为{2}{3} 所以化简后为G =( {0},{2},{3},{4},{1,5})7.去除多余产生式后,构造NFA 如下确定化,构造DFA 矩阵G={(0,1,3,4,6),(2,5)} {0,1,3,4,6}a={1,3}{0,1,3,4,6}b={2,3,4,5,6}所以将{0,1,3,4,6}划分为 {0,4,6}{1,3} G={(0,4,6),(1,3),(2,5)}{0,4,6}b={3,6,4} 所以划分为{0},{4,6} G={(0),(4,6),(1,3),(2,5)}不能再划分,分别用0,4,1,2代表各状态,构造DFA 状态转换图如下;b8.代入得S = 0(1S|1)| 1(0S|0) = 01(S|ε) | 10(S|ε) = (01|10)(S|ε) = (01|10)S | (01|10)= (01|10)*(01|10)构造NFA由NFA可得正规式为(01|10)*(01|10)=(01|10)+9.状态转换函数不是全函数,增加死状态8,G={(1,2,3,4,5,8),(6,7)}(1,2,3,4,5,8)a=(3,4,8) (3,4)应分出(1,2,3,4,5,8)b=(2,6,7,8)(1,2,3,4,5,8)c=(3,8)(1,2,3,4,5,8)d=(3,8)所以应将(1,2,3,4,5,8)分为(1,2,5,8), (3,4)G={(1,2,5,8),(3,4),(6,7)}(1,2,5,8)a=(3,4,8) 8应分出(1,2,5,8)b=(2,8)(1,2,5,8)c=(8)(1,2,5,8)d=(8)G={(1,2,5),(8),(3,4),(6,7)}(1,2,5)a=(3,4,8) 5应分出G={(1,2), (3,4),5, (6,7) ,(8) }去掉死状态8,最终结果为 (1,2) (3,4) 5,(6,7) 以1,3,5,6代替,最简DFA为b正规式:b*a(da|c)*bb*第五章1.S->a | ^ |( T )T -> T , S | S(a,(a,a))S => ( T ) => ( T , S ) => ( S , S ) => ( a , S) => ( a, ( T )) =>(a , ( T , S ) ) => (a , ( S , S )) => (a , ( a , a ) )S=>(T) => (T,S) => (S,S) => ( ( T ) , S ) => ( ( T , S ) , S ) => ( ( T , S , S ) , S ) => ( ( S , S , S ) , S )=> ( ( ( T ) , S , S ) , S ) => ( ( ( T , S ) , S , S ) , S ) =>( ( ( S , S ) ,S , S ) , S ) => ( ( ( a , S ) , S , S ) , S )=> ( ( ( a , a ) , S , S ) , S ) => ( ( ( a , a ) , ^ , S ) , S ) => ( ( ( a , a ) , ^ , ( T ) ) , S )=> ( ( ( a , a ) , ^ , ( S ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , a )S->a | ^ |( T )T -> T , ST -> S消除直接左递归:S->a | ^ |( T )T -> S T’T’ -> , S T’ | ξSELECT ( S->a) = {a}SELECT ( S->^) = {^}SELECT ( S->( T ) ) = { ( }SELECT ( T -> S T’) = { a , ^ , ( }SELECT ( T’ -> , S T’ ) = { , }SELECT ( T’ ->ξ) = FOLLOW ( T’ ) = FOLLOW ( T ) = { ) } 构造预测分析表分析符号串( a , a )#分析栈剩余输入串所用产生式#S ( a , a) # S -> ( T )# ) T ( ( a , a) # ( 匹配# ) T a , a ) # T -> S T’# ) T’ S a , a ) # S -> a# ) T’ a a , a ) # a 匹配# ) T’,a) # T’ -> , S T’# ) T’ S , , a ) # , 匹配# ) T’ S a ) # S->a# ) T’ a a ) # a匹配# ) T’) # T’ ->ξ# ) ) # )匹配# # 接受2.E->TE’ E’->+E E’->ξ T->FT’ T’->T T’->ξ F->PF’ F’->*F’ F’->ξP->(E) P->a P->b P->∧SELECT(E’->+E)={+}SELECT(E’->ε)=FOLLOW(E’)= {#,)}SELECT(T->FT’)=FIRST(F)= {(,a,b,^}SELECT(T’ —>T)=FIRST(T)= {(,a,b,^)SELECT(T’->ε)=FOLLOW(T’)= {+,#,)}SELECT(F ->P F’)=FIRST(F)= {(,a,b,^}SELECT(F’->*F’)={*}SELECT(F’->ε)=FOLLOW(F’)= {(,a,b,^,+,#,)}3. S->MH S->a H->Lso H->ξ K->dML K->ξ L->eHf M->K M->bLMFIRST ( S ) =FIRST(MH)= FIRST ( M ) ∪ FIRST ( H ) ∪ {ξ} ∪ {a}= {a, d , b , e ,ξ}FIRST( H ) = FIRST ( L ) ∪ {ξ}= { e , ξ}FIRST( K ) = { d , ξ}FIRST( M ) = FIRST ( K ) ∪ { b } = { d , b ,ξ}FOLLOW ( S ) = { # , o }FOLLOW ( H ) = FOLLOW ( S ) ∪ { f } = { f , # , o }FOLLOW ( K ) = FOLLOW ( M ) = { e , # , o }FOLLOW ( L ) ={ FIRST ( S ) –{ξ} } ∪{o} ∪ FOLLOW ( K )∪ { FIRST ( M ) –{ξ} } ∪ FOLLOW ( M )= {a, d , b , e , # , o }FOLLOW ( M ) ={ FIRST ( H ) –{ξ} } ∪ FOLLOW ( S )∪{ FIRST ( L ) –{ξ} } = { e , # , o }SELECT ( S-> M H) = ( FIRST ( M H) –{ξ} ) ∪ FOLLOW ( S )= ( FIRST( M ) ∪ FIRST ( H ) –{ξ} ) ∪ FOLLOW ( S )= { d , b , e , # , o }SELECT ( S-> a ) = { a }SELECT ( H->L S o ) = FIRST(L S o) = { e }SELECT ( H ->ξ ) = FOLLOW ( H ) = { f , # , o }SELECT ( K-> d M L ) = { d }SELECT ( K->ξ ) = FOLLOW ( K ) = { e , # , o }SELECT ( L-> e H f ) = { e }SELECT ( M->K ) = ( FIRST( K ) –{ξ} ) ∪ FOLLOW ( M ) = {d,e , # , o }SELECT ( M -> b L M )= { b }构造LL( 1 ) 分析表4 . 文法含有左公因式,变为S->C $ { b, a }C-> b A { b }C-> a B { a }A -> b A A { b }A-> a A’ { a }A’-> ξ { $ , a, b }A’-> C { a , b }B->a B B { a }B -> b B’ { b }B’->ξ { $ , a , b }B’-> C { a, b }5. <程序> --- S <语句表>――A <语句>――B <无条件语句>――C <条件语句>――D <如果语句>――E<如果子句> --FS->begin A end S->begin A end { begin }A-> B A-> B A’ { a , if }A-> A ; B A’-> ; B A’ { ; }A’->ξ { end }B-> C B-> C { a }B-> D B-> D { if }C-> a C-> a { a }D-> E D-> E D’ { if }D-> E else B D’-> else B { else }D’->ξ {; , end }E-> FC E-> FC { if }F-> if b then F-> if b then { if }非终结符是否为空S-否 A-否A’-是 B-否 C-否 D-否D’-是 E-否 F-否FIRST(S) = { begin }FIRST(A) = FIRST(B) ∪ FIRST(A’) ∪ {ξ} = {a , if , ; , ξ}FIRST(A’) ={ ; , ξ}FIRST(B) = FIRST(C) ∪ FIRST(D) ={ a , if }FIRST(C) = {a}FIRST(D) = FIRST(E)= { if }FIRSR(D’) = {else , ξ}FIRST(E) = FIRST(F) = { if }FIRST(F) = { if }FOLLOW(S) = {# }FOLLOW(A) = {end}FOLLOW(A’) = { end }FOLLOW(B) = {; , end }FOLLOW (C) = {; , end , else }FOLLOW(D) = {; , end }FOLLOW( D’ ) = { ; , end }FOLLOW(E) = { else , ; end }FOLLOW(F) = { a }S A A’ B C D D’ E F if then else begin end a b ;6. 1.(1) S -> A | B(2) A -> aA|a(3)B -> bB |b提取(2),(3)左公因子(1) S -> A | B(2) A -> aA’(3) A’-> A|ξ(4) B -> bB’2.(1) S->AB(2) A->Ba|ξ(3) B->Db|D(4) D-> d|ξ提取(3)左公因子(1) S->AB(2) A->Ba|ξ(3) B->DB’(4) B’->b|ξ(5) D-> d|ξ3.(1) S->aAaB | bAbB(2) A-> S| db(3) B->bB|a4(1)S->i|(E)(2)E->E+S|E-S|S提取(2)左公因子(1)S->i|(E)(2)E->SE’(3)E’->+SE’|-SE’ |ξ5(1)S->SaA | bB(2)A->aB|c(3)B->Bb|d消除(1)(3)直接左递归(1)S->bBS’(2)S’->aAS’|ξ(4) B -> dB’(5)B’->bB’|ξ6.(1) M->MaH | H(2) H->b(M) | (M) |b消除(1)直接左递归,提取(2)左公因子(1)M-> HM’(2)M’-> aHM’ |ξ(3)H->bH’ | ( M )(4)H’->(M) |ξ7. (1)1)A->baB2)A->ξ3)B->Abb4)B->a将1)、2)式代入3)式1)A->baB2)A->ξ3)B->baBbb4)B->bb5)B->a提取3)、4)式左公因子1)A->baB2)A->ξ3)B->bB’4)B’->aBbb | b5)B->a(3)1)S->Aa3)A->SB4)B->ab将3)式代入1)式1)S->SBa2)S->b3)A->SB4)B->ab消除1)式直接左递归1)S->bS’2)S’->BaS’ |ξ3)S->b4)A->SB5)B->ab删除多余产生式4)1)S->bS’2)S’->BaS’ |ξ3)S->b4)B->ab(5)1)S->Ab2)S->Ba3)A->aA4)A->a5)B->a提取3) 4)左公因子1)S->Ab2)S->Ba3)A->aA’4)A’-> A |ξ将3)代入1) 5)代入21)S->aA’b2)S->aa3)A->aA’4)A’-> A |ξ5)B->a提取1) 2)左公因子1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξ5)B->a删除多余产生式5)1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξA A’ S’ S将3)代入4)1)S-> aS’2)S’->A’b | a3)A->aA ’4)A’-> aA’ |ξ将4)代入2)1)S-> aS’2)S’->aA’b3)S’->a4)S’->b5)A->aA ’6)A’-> aA’ |ξ对2)3)提取左公因子1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b5)A->aA ’6)A’-> aA’ |ξ删除多余产生式5)1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b5)A’-> aA’ |ξ第六章1S a | ∧ | ( T )T T , S | S解:(1) 增加辅助产生式S’#S#求 FIRSTVT集FIRSTVT(S’)= {#}FIRSTVT(S)={a ∧ ( }={ a ∧ ( } FIRSTVT (T) ={,} ∪ FIRSTVT( S ) = { , a ∧ ( }求 LASTVT集LASTVT(S’)= { # }LASTVT(S)={ a ∧ )}LASTVT (T) ={ , a ∧ )}(2)算符优先关系表a∧(),# a·>·>·>∧·>·>·> (<·<·<·=·<·)·>·>·>,<·<·<··>·>#<·<·<·=·因为任意两终结符之间至多只有一种优先关系成立,所以是算符优先文法(3)a ∧( ) , #F 1 1 1 1 1 1g 1 1 1 1 1 1f 2 2 1 3 2 1g 2 2 2 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1(4)栈优先关系当前符号剩余输入串移进或规约#<· ( a,a)# 移进#( <· a ,a)# 移进# (a ·> , a)# 规约#(T <· , a)# 移进#(T,<· a )# 移进#(T,a ·> ) # 规约#(T,T ·> ) # 规约#(T =· ) # 移进#(T) ·> #规约#T =·#接受4.扩展后的文法S’#S# S S;G S G G G(T) G H H a H(S)T T+S T S(1)FIRSTVT(S)={;}∪FIRST VT(G) = {; , a , ( }FIRSTVT(G)={ ( }∪FIRSTVT(H) = {a , ( }FIRSTCT(H)={a , ( }FIRSTVT(T) = {+} ∪FIRSTVT(S) = {+ , ; , a , ( }LASTVT(S) = {;} ∪LASTVT(G) = { ; , a , )}LASTVT(G) = { )} ∪ LASTVT(H) = { a , )}LASTVT(H) = {a, )}LASTVT(T) = {+ } ∪LASTVT(S) = {+ , ; , a , ) };()a+#;·><··><··>·> (<·<·=·<·<·)·>·>·>·>·> a·>·>·>·>·> +<·<··><··>#<·<·<·=·因为任意两终结符之间至多只有一种优先关系成立,所以是算符优先文法(2)句型a(T+S);H;(S)的短语有:a(T+S);H;(S) a(T+S);H a(T+S) a T+S (S) H直接短语有: a T+S H (S)句柄: a素短语:a T+S (S)最左素短语:a(3)分析a;(a+a)(4)不能用最右推导推导出上面的两个句子。
编译原理 龙书 第二版 第5、6章

4)L’->BL1’
L1’.m=L’.m*L’.m;L1’.side=L’.side
L1’.inh=L’.inh*L’.side+B*L1’.m
L’.syn=L1’.syn
5)L’->ε
L’.syn=L’.inh
6)B->0
B.val=0
7)B->1
B.val=1
练习5.3.1:下面是涉及运算符+和整数或浮点运算分量的表达式文法。区分浮点数的方法是看它有无小数点。
E-〉E+T|T T-〉num.num|num
1)给出一个SDD来确定每个项T和表达式E的类型
2)扩展(1)中得到的SDD,使得它可以把表达式转换成为后缀表达式。使用一个单目运算符intToFloat把一个整数转换为相等的浮点数
答:
(1)
产生式
语义规则
1)E->E1+T
If E1.type ==T.type then E.type=E1.type
2)四元式序列
3)三元式序列
4)间接三元式序列
答:(1)抽象语法树
(2) 四元式序列
t1=b+c
t2=minus t1
t3=a+t2
op
Arg1
Arg2
result
0
+
b
c
T1
1
minus
T1
T2
2
+
a
T2
T3
(3)三元式序列
op
Arg1
Arg2
0
+
b
c
1
minus
(0)
编译原理龙书第二版课后答案

编译原理龙书第二版课后答案【篇一:编译原理习题答案,1-8 章龙书第二版7.8 章】6 :c 语言函数 f 的定义如下:int f(int x, *py, **ppz){**ppz +=1 ; *py +=2 ;x +=3; return x+*py+**ppz;}变量 a 是一个指向 b 的指针;变量 b 是一个指向 c 的指针,而 c 是一个当前值为 4 的整数变量。
如果我们调用 f(c,b,a), 返回值是什么?答: x 是传值 ,而 b 和 c 是传地址方式;由函数定义可以得到: b=c,a=b, 而**a=**a+1=c+1=5 = c=5; *b=*b+2=c+2=7 =c=7,**a=7;c=c+3=4+3=7所以调用 f(c,b,a) 返回值是 7+7+ 7=21练习7.3.2 :假设我们使用显示表来实现下图中的函数。
请给出对fib0 (1)的第一次调用即将返回时的显示表。
同时指明那时在栈中的各种活动记录中保存的显示表条目答:结果如下第八章练习 8.2.1 :假设所有的变量都存放在内存中,为下面的三地址语句生成代码:5)下面的两个语句序列x=b*cy=a+x答:生成的代码如下练习 8.5.1 :为下面的基本块构造构造dagd=b*ce=a+bb=b*ca=e-d答: dag 如下练习 8.6.1 :为下面的每个 c 语言赋值语句生成三地址代码1)x=a+b*c答:生成的三地址代码如下【篇二:编译原理龙书第二版第4章】.1:考虑上下文无关文法: s-s s +|s s *|a 以及串 aa + a* (1) 给出这个串的一个最左推导 s - s s * - s s + s * - a s + s * - a a + s * - aa+a*(3)给出这个串的一棵语法分析树习题 4.3.1 :下面是一个只包含符号 a 和 b 的正则表达式的文法。
它使用 +替代表示并运算的符号 |,以避免和文法中作为元符号使用的竖线相混淆: rexpr? rexpr + rterm | rterm rterm?rterm rfactor |rfactor rfactor? rfactor * | rprimary rprimary?a | b 1)对这个文法提取公因子2)提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗?3)提取公因子之后,原文法中消除左递归 4) 得到的文法适用于自顶向下的语法分析吗?解1)提取左公因子之后的文法变为rexpr? rexpr + rterm | rterm rterm?rterm rfactor |rfactor rfactor? rfactor * | rprimary rprimary?a | b2)不可以,文法中存在左递归,而自顶向下技术不适合左递归文法3)消除左递归后的文法rexpr - rterm rexpr’rexpr rterm ’-+ rterm rexpr’|? rterm- rfactor rterm’ rterm-rfactor’’ |? rfactor- rprimay rfactor’ rfactor-*rfactor’’ |? rprimary- a| b4)该文法无左递归,适合于自顶向下的语法分析习题 4.4.1 :为下面的每一个文法设计一个预测分析器,并给出预测分析表。
编译原理课后答案第五章代码优化

第五章 代码优化
A= 0 I= 1
B1
B= J+ 1 B′2
L1: C= B+ I
B2
A= C+ A
if I= 100 g2oto L
第五章 代码优化
所以d必有通路到达M中任一结点ni,而M中任一结 点又可以通过n到达d(n→d为回边),从而M中任意两个 结点之间必有一通路,L中任意两个结点之间亦必有一 通路。此外,由M中结点性质可知:d到M中任一结点ni 的通路上所有结点都应属于M,ni到n的通路上所有结 点也都属于M。因此,L中任意两结点间通路上所有结 点都属于L,也即,L是强连通的。
L1: E= B*B
B3
F= F+ 2
E= E+ F
write(E)
if E> 100 g2oto L
halt B4 L2: F= F- B15 goto1 L
图5-1 程序流图
第五章 代码优化
5.4 基本块的DAG如图5-2所示。若: (1) b在该基本块出口处不活跃; (2) b在该基本块出口处活跃; 请分别给出下列代码经过优化之后的代码: (1) a=b+c (2) b=a-d (3) c=b+c (4) d=a-d
if I= 100 g2oto L
F
T
I= I+ 1 B3 goto 1L
L2: write AB4 halt
图5-5 习题5.8的程序流图
第五章 代码优化
(2) 很容易看出,B3→B2是流图中的一条有向边, 并且有B2 DOM B3,故B3→B2为流图中的一条回边。循 环可通过回边求得,即找出由结点B2、结点B3以及有通 路到达B3但不经过B2的所有结点。所以,由回边组成的 B3→B2循环是{ B2,B3}。
《编译原理》第八章习题答案下载

四元式:
100 (+, a, b, t1) 101 (+, c, d, t2) 102 (*, t1, t2, t3) 103 (-, t3, /, t4) 104 (+, a, b, t5) 105 (+, t5, c, t6) 106 (-, t4, t6, t7)
树形:
盛威网()专业的计算机学习网站
如果题目是 S::=L.L | L L::=LB | B B::=0 | 1 则写成: S`::=S {print(S.val);} S::=L1.L2 { S.val:=L1.val+L2.val/2L2.length ;} S::= L { S.val:=L.val; } L::=L1B { L.val:=L1.val*2+B.val; L.length:=L1.length+1; } L::=B { L.val:=B.val; L.length:=1;} B::=0 { B.val:=0; } B::=1 { B.val:=1;}
答案:加入新的开始符号 S`和规则 S`ÆS,得到增广文法。语法制导定义如下:
产生式 S`ÆS SÆL1.L2 SÆL LÆL1B
LÆB
BÆ0 BÆ1
语义规则 print(S.val) S.val:=L1.val+L2.val/2L2.length S.val:=L.val L.val:=L1.val*2+B.val L.length:=L1.length+1 L.val:=B.val L.length:=1 B.val:=0 B.val:=1
end ELSE begin
E.type:=real IF E1.type=integer THEN
编译原理 第二章习题答案

第2章习题解答1.文法G[S]为:S->Ac|aBA->abB->bc写出L(G[S])的全部元素。
[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}==============================================2. 文法G[N]为:N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?[答案]G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D===============================================3.已知文法G[S]:S→dAB A→aA|a B→ε|bB问:相应的正规式是什么?G[S]能否改写成为等价的正规文法?[答案]正规式是daa*b*;相应的正规文法为(由自动机化简来):G[S]:S→dA A→a|aB B→aB|a|b|bC C→bC|b也可为(观察得来):G[S]:S→dA A→a|aA|aB B→bB|ε===================================================================== ==========4.已知文法G[Z]:Z->aZb|ab写出L(G[Z])的全部元素。
[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}===================================================================== =========5.给出语言{a n b n c m|n>=1,m>=0}的上下文无关文法。
最新编译原理(龙书)习题(5,6,7,8)章共39页

谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利最新源自译原理(龙书)习题(5,6,7,8)章
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了求小数部分的值,引入L的综合属性b记录2的 L
的位数次幂值(2 length of L)
S L1.L2 SL L L1 B
LB B0 B1
S.val = L1.val +L2.val / L2.b; S.val = L.val;
L.val = L1.val *2 + B.val; L.b = L1.b*2;
第5章 语法制导的翻译
5.2.3 假设我们有一个产生式 ABCD 。A,B,C,D这
四个非终结符号都有两个属性:s是一个综合属性,而i是
一个继承属性。对于下面的每组规则,指出(i)这些规则是 否满足S属性定义的要求。(ii)这些规则是否满足L属性定 义的要求。(iii)是否存在和这些规则一致的求值过程? 1)A.s = B.i + C.s 不满足S属性定义,满足L属性定义 2)A.s = B.i + C.s 和 D.i = A.i + B.s 不满足S属性定义,满足L属性定义 3)A.s = B.s + D.s 满足S属性定义,满足L属性定义 4)A.s=D.i,B.i=A.s+C.s,C.i=B.s和D.i=B.i+C.i 不满足S属性定义,不满足L属性定义
精品课件
5.2.4 这个文法生成了含“小数点”的二进制: S L.L | L L LB | B B 0 |1
设计一个L属性的SDD来计算S.val,即输入串的十进制 数值。比如,串101.11应该被翻译为十进制数5.635。提 示:使用一个继承属性L.side来指明一个二进制位在小 数点的哪一边。
L.val = B.val; L.b = 2; B.val = 0; B.val = 1;
精品课件
5.3.1 下面是涉及运算符+和整数或浮点运算分量的表达式的 文法。区分浮点数的方法是看它有无小数点。
EET|T T num.num| num
1)给出一个SDD来确定每个项T和表达式E的类型。 2)扩展(1)中得到的SDD,使得它可以把表达式转换成为后缀
D 0 D1 { D .val D1.val ; D .b D1.b 1}
| 1D1 { D .val 1 2 D1.b D1.val ; D .b D1.b 1}
| { D .val 0; D .b 0}
精品课件
第6章 中间代码生成
6.1.1 为下面的表达式构造DAG ((x+y)-((x+y)*(x-y)))+((x+y)*(x-y))
精品课件
6.2.1 将算术表达式 a+-(b+c) 翻译成
1)抽象语法树 2)四元式序列 3)三元式序列 4)间接三元式序列
精品课件
1)抽象语法树:
精品课件
2)四元式序列: 3)三元式序列: 4)间接三元式序列:
精品课件
6.4.1 向图6-19的翻译方案中加入对应于下列产生式的规则: 1) EE1*E2 2) EE1(单目加)
BB10{B.val2B1.va}l | B11{B.val2B1.val1} | 1{B.val1}
改写这个SDT,使得基础文法不再是左递归的,但仍然 可以计算出整个输入串的相同的B.val的值。
精品课件
非终结符D的综合属性b表示二进制数的位数, val表
示:对B应的1十D 进{制B .v数al 的 1数 2值D .b。 消D .除val左} 递归后如下
S1.code||
label(S1.next)|| B.code
精品课件
S-->for ( S1; B; S2 ) S3
S1.next=newlabel() B.true=newlabel() begin=newlabel() B.fale=S.next S2.next =S1.next S3.next=begin S.code=S1.code||label(S1.next )||
B.code||label(begin)|| S2.code|| gen('goto'
S1.next)||
label(B.true)||S3.#39;
6.7.7 使用图6-37中的翻译方案翻译下列表 达式。给出每个子表达式的truelist和 falselist。你可以假设第一条被生成的指 令的地址是100。
精品课件
6.4.2 使用图6-20中的增量式翻译方案重复练习 6.4.1
在增量方式中,gen不仅要构造出一个新的三地址指令,还 要将它添加到至今为止已生成精品的课件指令序列之后。
6.4.3 使用使用图6-22所示的翻译方案来翻译 下列赋值语句:
2) x = a[i][j] + b[i][j]
假设w1为数组a的第一维的宽度,w2为数组b的 第
一维的宽度,整数的宽度为w。
t1 = i * w1;
t2 = j * w;
t3 = t1 + t2;
t4 = a[t3];
精品课件
t6 = j * w; t7 = t5 + t6; t8 = b[t7]; t9 = t4 + t8;
6.6.1 在图6-30的语法制导定义中添加处理下 列控制流构造的规则:
1)一个repeat语句,repeat S while B 2)一个for循环语句,for (S1 ; B ; S2) S3
S-->repeat S1 while B
begin=newlabel() S1.next=newlabel() B.true=begin B.false = S.next S.code=label(begin)||
表达式。使用一个单目运算符intToFloat把一个整数转换 为相等的浮点数。
精品课件
精品课件
(2)设code 为综合属性,代表各非终结符 的代码属性 type为综合属性,代表各非终结符的类型 属性 inttoreal把整型值转换为相等的实型值 vtochar将数值转换为字符串
精品课件
精品课件
精品课件
5.3.3 给出一个SDD对x*(3*x+x*x)这样的表达式 求微分。表达式中涉及运算符+和*,变量x和 常量。假设不进行任何简化,也就是说,比如 3*x将被翻译为3*1+0*x。
exp 为原表达式的字符串,s 为求导后的字 符串。
|| 为串联接符。
精品课件
精品课件
精品课件
5.4.3 下面的SDT计算了一个由0和1组成的串的值。它把输 入的符号串当作按照正二进制数来解释。
