高一数学立体几何测试题
高中数学高一必修2空间立体几何试卷(有详细答案)

高中数学立体几何测试试卷学校:___姓名:___班级:___考号:__一.单选题1.一个圆锥的侧面展开图的圆心角为90°,它的表面积为a,则它的底面积为()A.B.C.D.2.设α为平面,m,n为直线()A.若m,n与α所成角相等,则m∥nB.若m∥α,n∥α,则m∥nC.若m,n与α所成角互余,则m⊥nD.若m∥α,n⊥α,则m⊥n3.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为()A.75°B.60°C.45°D.30°4.设α是空间中的一个平面,l,m,n是三条不同的直线,①若m⊂α,n⊂α,l⊥m,l⊥n,则l⊥α;②若l∥m,m∥n,l⊥α,则n⊥α;③若l∥m,m⊥α,n⊥α,则l∥n;④若m⊂α,n⊥α,l⊥n,则l∥m;则上述命题中正确的是()A.①②B.②③C.②④D.③④5.已知一个铜质的五棱柱的底面积为16cm2,高为4cm,现将它熔化后铸成一个正方体的铜块(不计损耗),那么铸成的铜块的棱长是()A.2cm B.C.4cm D.8cm6、在正方体ABCD-A l B1C1D1中,P是正方体的底面A l B1C1D1(包括边界)内的一动点(不与A1重合),Q是底面ABCD内一动点,线段A1C与线段PQ相交且互相平分,则使得四边形A1QCP面积最大的点P有()A.1个B.2个C.3个D.无数个7.如图所示几个空间图形中,虚线、实线使用不正确的有()A.②③B.①③C.③④D.④二.填空题8、如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是______.9、一个正方体的六个面上分别标有字母A、B、C、D、E、F,如图是此正方体的两种不同放置,则与D面相对的面上的字母是______.10.设α、β为互不重合的平面,m、n为互不重合的直线,下列四个命题中所有正确命题的序号是______.①若m⊥α,n⊂α,则m⊥n;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β.③若m∥α,n∥α,则m∥n.④若α⊥β,α∩β=m,n⊂α,n⊥m,则n⊥β.三.简答题11、在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=,在线段SA上取一点E(不含端点)使EC=AC,截面CDE与SB交于点F.(1)求证:四边形EFCD为直角梯形;(2)设SB的中点为M,当的值是多少时,能使△DMC为直角三角形?请给出证明.12、正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.13、已知三棱椎D-ABC,AB=AC=1,AD=2,∠BAD=∠CAD=∠BAC=90°,点E,F分别是BC,DE的中点,如图所示,(1)求证AF⊥BC(2)求线段AF的长.参考答案一.单选题1.一个圆锥的侧面展开图的圆心角为90°,它的表面积为a,则它的底面积为()A.B.C.D.答案:A解析:解:设圆锥的母线为l,所以圆锥的底面周长为:,底面半径为:=,底面面积为:.圆锥的侧面积为:,所以圆锥的表面积为:+=a,底面面积为:=.故选A.2.设α为平面,m,n为直线()A.若m,n与α所成角相等,则m∥nB.若m∥α,n∥α,则m∥nC.若m,n与α所成角互余,则m⊥nD.若m∥α,n⊥α,则m⊥n答案:D解析:解:对于选项A,若m,n与α所成角相等,m,n也可能相交、平行、异面;故A错误;对于选项B,若m∥α,n∥α,直线m,n也可能平行,也可能相交,还有可能异面;故B 错误;对于选项C,若m,n与α所成角互余,如与α所成角分别为30°和60°,直线m,n所成的角有可能为30°;故C错误;对于选项D,根据线面垂直的性质,容易得到m⊥n;故D正确;故选D.3.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为()A.75°B.60°C.45°D.30°答案:C解析:解析:如图,四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO则AO是AP在底面ABCD上的射影.∴∠PAO即为所求线面角,∵AO=,PA=1,∴cos∠PAO==.∴∠PAO=45°,即所求线面角为45°.故选C.4.设α是空间中的一个平面,l,m,n是三条不同的直线,①若m⊂α,n⊂α,l⊥m,l⊥n,则l⊥α;②若l∥m,m∥n,l⊥α,则n⊥α;③若l∥m,m⊥α,n⊥α,则l∥n;④若m⊂α,n⊥α,l⊥n,则l∥m;则上述命题中正确的是()A.①②B.②③C.②④D.③④答案:B解析:解:①根据线面垂直的判定,当m,n相交时,结论成立,故①不正确;②根据平行线的传递性,可得l∥n,故l⊥α时,一定有n⊥α,故②正确;③由垂直于同一平面的两直线平行得m∥n,再根据平行线的传递性,即可得l∥n,故③正确.④m⊂α,n⊥α,则n⊥m,∵l⊥n,∴可以选用正方体模型,可得l,m平行、相交、异面都有可能,如图所示,故④不正确故正确的命题是②③故选B.5.已知一个铜质的五棱柱的底面积为16cm2,高为4cm,现将它熔化后铸成一个正方体的铜块(不计损耗),那么铸成的铜块的棱长是()A.2cm B.C.4cm D.8cm答案:C解析:解:∵铜质的五棱柱的底面积为16cm2,高为4cm,∴铜质的五棱柱的体积V=16×4=64cm3,设熔化后铸成一个正方体的铜块的棱长为acm,则a3=64解得a=4cm故选C6、在正方体ABCD-A l B1C1D1中,P是正方体的底面A l B1C1D1(包括边界)内的一动点(不与A1重合),Q是底面ABCD内一动点,线段A1C与线段PQ相交且互相平分,则使得四边形A1QCP面积最大的点P有()A.1个B.2个C.3个D.无数个答案:C解:∵线段A1C与线段PQ相交且互相平分,∴四边形A1QCP是平行四边形,因A l C的长为定值,为了使得四边形A1QCP面积最大,只须P到A l C的距离为最大即可,由正方体的特征可知,当点P位于B1、C1、D1时,平行四边形A1QCP面积相等,且最大.则使得四边形A1QCP面积最大的点P有3个.故选C.7.如图所示几个空间图形中,虚线、实线使用不正确的有()A.②③B.①③C.③④D.④答案:D解析:解:根据棱柱的放置和“看见的棱用实线、看不见的棱用虚线”,则①②③正确,④错误,故选D.二.填空题8、如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是______.答案:2解:连接BE,则∵SB⊥底面ABCD,∠SEC=90°,∴BE⊥CE.故问题转化为在梯形ABCD中,点E是线段AD上的动点,求满足BE⊥CE的点E的个数.设AE=x,则DE=3-x,∵AB⊥AD,AB∥CD,AB=1,AD=3,CD=2,∴10=1+x2+4+(3-x)2,∴x2-3x+2=0,∴x=1或2,∴满足BE⊥CE的点E的个数为2,∴满足∠SEC=90°的点E的个数是2.故答案为:2.9、一个正方体的六个面上分别标有字母A、B、C、D、E、F,如图是此正方体的两种不同放置,则与D面相对的面上的字母是______.答案:B解析:解:由此正方体的两种不同放置可知:与C相对的是F,因此D与B相对.故答案为:B.10.设α、β为互不重合的平面,m、n为互不重合的直线,下列四个命题中所有正确命题的序号是______.①若m⊥α,n⊂α,则m⊥n;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β.③若m∥α,n∥α,则m∥n.④若α⊥β,α∩β=m,n⊂α,n⊥m,则n⊥β.答案:①④解析:解:①若m⊥α,n⊂α,利用线面垂直的性质,可得m⊥n,正确;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;两条相交直线才行,不正确.③m∥α,n∥α,则m与n可能平行、相交、异面,不正确.④若α⊥β,α∩β=m,n⊂α,n⊥m,则由面面垂直的性质定理我们易得到n⊥β,正确.故答案为:①④.三.简答题11、在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=,在线段SA上取一点E(不含端点)使EC=AC,截面CDE与SB交于点F.(1)求证:四边形EFCD为直角梯形;(2)设SB的中点为M,当的值是多少时,能使△DMC为直角三角形?请给出证明.答案:解:(1)∵CD∥AB,AB⊂平面SAB,∴CD∥平面SAB面EFCD∩面SAB=EF,∴CD∥EF.∵∠D=90°,∴CD⊥AD,又SD⊥面ABCD,∴SD⊥CD,∴CD⊥平面SAD,∴CD⊥ED又EF<AB<CD,∴EFCD为直角梯形.(2)当=2时,能使DM⊥MC.∵AB=a,∴,∴,∴SD⊥平面ABCD,∴SD⊥BC,∴BC⊥平面SBD.在△SBD中,SD=DB,M为SB中点,∴MD⊥SB.∴MD⊥平面SBC,MC⊂平面SBC,∴MD⊥MC,∴△DMC为直角三角形.12、正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.答案:解:如图所示,正三棱台ABC-A1B1C1中,高OO1=3,底面边长为A1B1=2,AB=4,∴OA=×AB=,O1A1=×A1B1=,∴棱台的侧棱长为AA1==;又OE=×AB=,O1E1=×A1B1=,∴该棱台的斜高为EE1==.13、已知三棱椎D-ABC,AB=AC=1,AD=2,∠BAD=∠CAD=∠BAC=90°,点E,F分别是BC,DE的中点,如图所示,(1)求证AF⊥BC(2)求线段AF的长.答案:解:(1)分别以AB、AC和AD为x、y、z轴,建立空间直角坐标系O-xyz,如图所示:记A(0,0,0),B(1,0,0),C(0,1,0),D(0,0,2),∴E(,,0),F(,,1);∴(,,1),=(-1,1,0),∴•=×(-1)+×1+1×0=0,∴⊥,即AF⊥BC;(2)∵=(,,1),∴||===,即线段AB=.。
高一数学立体几何大题(含答案)

4.in/w).6=4r3.
例 3:如图,PD ⏊ 平面 ABCD,AD ⏊ CD,AB ⎳ CD,PQ ⎳ CD,AD
= CD = DP = 2PQ = 2AB = 2, 点 M 为 BQ 的中点 .
为 的 P Q C -
M-
大小
0 .
Sepm E 却 二
忙=
以 <m (
,
蕊 令 1
二
5 = -
3
※ 琴 㱺 sina.me
㱺 Somc 二 士 心 的 ✗
=r
.
二号 器 Q到 平面 阰 的 距离 为 : d = 2 5
.io
shnoifst.no
,
㱺 VQ-pmc-f-Somc.dk/nEfsio=fs'm0.
PCHEF 进而 1211 平面 ,
在 阳 仲 , PA-E.AE/,PC=0=)PA4AcEpc2=sAc-1A.
所以 又由 题 干 知 : A 4 P B ,
A
C
1
-
平面阳
13
.
13) 易知 SEFG 二 ftp.c , 所以 /7AB=fSopAB-AC.=f-li2nE.iS'm45J-l
1 求二面角 Q - PM - C 的正弦值;
2 若 N 为线段 CQ 上的点,且直线 DN 与平面 PMQ 所成的角为
π 6
,
求线段
QN
的长
.
子 (2) 由 山 知 二面⻆ QPMC 的 大小 为 ,
劝 的平面 PMQ所 成的 ⻆ 为 至
所以 叽 与平面PMC 所 成的 ⻆
2023-2024学年高一下数学《平面向量及立体几何初步》测试卷及答案解析

2023-2024学年高一数学《平面向量及立体几何初步》一.选择题(共12小题)
1.(2022春•鼓楼区校级期中)已知向量,,若∥,则实数m =()
A.1B.﹣1C .D
.﹣
2.(2022春•鼓楼区校级期中)已知向量,是单位向量,若|2﹣|=,
则
与的夹角为()
A .
B .
C .
D .
3.(2022春•鼓楼区校级期中)P是△ABC
所在平面内一点,若,则S△ABP:S
△ABC
=()
A.1:4B.1:3C.2:3D.2:1 4.(2022•福州模拟)已知向量,为单位向量,且⊥,则•(4﹣3)=()A.﹣3B.3C.﹣5D.5 5.(2022春•马尾区校级月考)已知△ABC的内角A,B,C对边分别为a,b,c,若2c sin C =(a+b)(sin B﹣sin A),则当角C取得最大值时,B=()
A .
B .
C .
D .
6.(2022春•福州期中)在四边形ABCD
中,若=,且|﹣|=|
+|,则该四边
形一定是()
A.正方形B.菱形C.矩形D.等腰梯形7.(2022•鼓楼区校级三模)已知AB,CD分别是圆柱上、下底面圆的直径,且AB⊥CD.O1,O分别为上、下底面的圆心,若圆柱的底面圆半径与母线长相等,且三棱锥A﹣BCD的体积为18,则该圆柱的侧面积为()
A.9πB.12πC.16πD.18π8.(2022•福州模拟)在底面半径为1的圆柱OO1中,过旋转轴OO1作圆柱的轴截面ABCD,其中母线AB=2,E是BC的中点,F是AB的中点,则()
A.AE=CF,AC与EF是共面直线
第1页(共25页)。
高一数学(必修二)立体几何初步单元测试卷及答案

高一数学(必修二)立体几何初步单元测试卷及答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图所示,己知正方形O A B C ''''的边长为1,它是水平放置的一个平面图形的直观图,则其原图形的周长为( )A.8B.22C.4D.223+2.下列说法正确的是( ) A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点,则必有无数个公共点D.如果两条直线没有交点,则这两条直线平行3.正方体1111ABCD A B C D -中,P ,Q ,R 分别是AB ,AD ,11B C 的中点,那么正方体中过P ,Q ,R 的截面图形是( ) A.三角形B.四边形C.五边形D.六边形4.某圆柱的高为2,其正视图如图所示,圆柱上下底面圆周及侧面上的点A ,B ,D ,F ,C 在正视图中分别对应点A ,B ,E ,F ,C ,且3AE EF =,2BF BC =,异面直线AB ,CD 所成角的正弦值为45,则该圆柱的外接球的表面积为( )A.20πB.16πC.12πD.10π5.在《九章算术·商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭1111ABCD A B C D -中,1124AB A B ==,四个侧面均为全等的等腰梯形且面积之和为122( ) 282B.283142D.1436.异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线7.如图,在正方体1111ABCD A B C D -中,E ,F 分别是11A D ,11B C 的中点,则与直线CF 互为异面直线的是( )A.1CCB.11B CC.DED.AE8.下列说法中正确的是( ) A.三点确定一个平面 B.四边形一定是平面图形 C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点二、多选题(本题共4小题,每小题5分,共20分。
高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ,
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线,且 a,b 所成角为 40 °,直线 c 与 a,b 均异面,且所成角均为
∵ BD ⊥ AC , MN ∥ BD
∵ PA⊥面 ABCD
θ,若这样的 c 共有四条,则 θ的范围为 (70 °, 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、 已知异面直线 a, b 的公垂线段 AB 的中点为 O,平面 满足 a∥ , b∥ , 且 O , M 、 N 是 a, b 上的任意两点, MN ∩ = P,求证: P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答 案
一、 1- 8 ACDDBDBA
2、已知 m, n 为异面直线, m∥平面 , n∥平面 , ∩ =l ,则 l( ) ( A)与 m, n 都相交 ( B)与 m,n 中至少一条相交 ( C)与 m, n 都不相交 ( D )与 m, n 中一条相交
3、已知 a, b 是两条相交直线, a∥ ,则 b 与 的位置关系是 ( )
A 、 b∥
PAM
∵ AB=2 , BM=1 , CM=1
∴ AM= 5 ,
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1.异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线
高一数学(必修二)立体几何练习题(含答案)
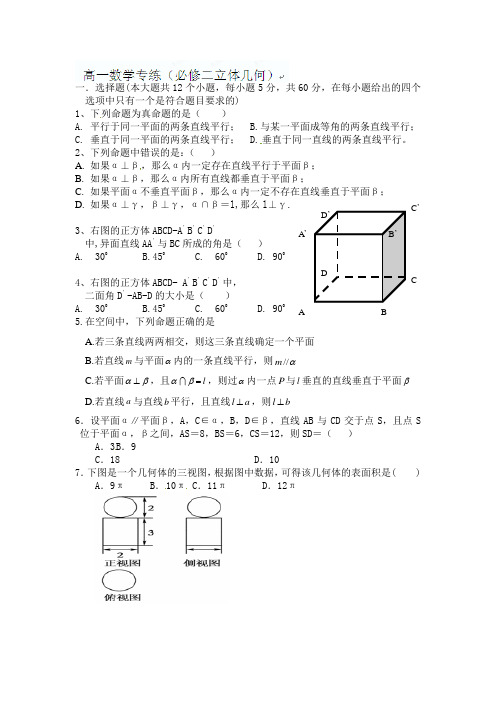
一.选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的) 1、下列命题为真命题的是( )A. 平行于同一平面的两条直线平行;B.与某一平面成等角的两条直线平行;C. 垂直于同一平面的两条直线平行;D.垂直于同一直线的两条直线平行。
2、下列命题中错误的是:( )A. 如果α⊥β,那么α内一定存在直线平行于平面β;B. 如果α⊥β,那么α内所有直线都垂直于平面β;C. 如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;D. 如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是( ) A. 300 B.450 C. 600 D. 900 4、右图的正方体ABCD- A ’B ’C ’D ’中,二面角D ’-AB-D 的大小是( )A. 300B.450C. 600D. 900 5.在空间中,下列命题正确的是A.若三条直线两两相交,则这三条直线确定一个平面B.若直线m 与平面α内的一条直线平行,则α//mC.若平面βα⊥,且l =βα ,则过α内一点P 与l 垂直的直线垂直于平面βD.若直线a 与直线b 平行,且直线a l ⊥,则b l ⊥6.设平面α∥平面β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且点S 位于平面α,β之间,AS =8,BS =6,CS =12,则SD =( )A .3B .9C .18D .10 7.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12πA B DA ’B ’D ’ C C ’ABD CE F8. 正方体的内切球和外接球的半径之比为( )A. 3:1B. 3:2C. 3:3D. 2:39.已知△ABC 是边长为a 2的正三角形,那么它的斜二侧所画直观图A B C 的面积为( )A.32a 2 B.34a 2 C.64a 2 D.6a 210.若正方体的棱长为2,则以该正方体各个面的中心为顶点的多面体的体积为( )A.26B.23C.33D.2311. 在空间四边形ABCD 中,AD=BC=2,E 、F 分别是AB 、CD 的中点,EF=2,求AD 与BC 所成角的大小.( )A. 30B. 45C.60οD. 90 12.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,//EF AB ,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ) A92B 5C 6D 152二、填空题(共4小题,每小题5分,共20分,把答案填在题中的横线上)13. Rt ABC ∆中,3,4,5AB BC AC ===,将三角形绕直角边AB 旋转一周所成的几何体的体积为.14.一个圆台的母线长为5 cm ,两底面面积分别为4πcm 2 和25π cm 2.则圆台的体积 ________. 15. 三棱锥S-ABC 中SA平面ABC ,AB 丄BC,SA= 2,AB =B C=1,则三棱锥S-ABC 的外接球的表面积等于______.16.如图,在直角梯形ABCD 中,,,BC DC AE DC ⊥⊥M 、N 分别是AD 、BE 的中点,将三角形ADE 沿AE 折起。
高一数学立体几何试题答案及解析

高一数学立体几何试题答案及解析1.设三棱柱的体积为,分别是侧棱上的点,且,则四棱锥的体积为()A.B.C.D.【答案】C【解析】假设重合,重合,则【考点】棱柱棱锥的体积2.如图,四棱锥中,,四边形是边长为的正方形,若分别是线段的中点.(1)求证:∥底面;(2)若点为线段的中点,求三角形的面积。
【答案】(1)见解析;(2)【解析】要想证明线面平行,只需证明出该线段与面内的任意一条线段平行即可,在本题中,需要连接辅助线进行解答,在解此问题时主要运用了三角形内中位线平行于底边的性质;首先需要掌握知识,三角形的中位线的长度为底边的一半,先求出所需边的长度,再运用余弦定理,求出角的度数,在运用三角形面积公式即可得到结果。
试题解析:(1)解:连接,由题意知,为中点,为的中位线,平面平面平面(2)连接由(1)知:,同理可得:,,【考点】空间几何的运算3.如图,在四棱台中,底面,四边形为正方形,,,平面.(1)证明:为的中点;(2)求点到平面的距离.【答案】(1)详见解析;(2)【解析】(1)根据线面平行的性质定理,线面平行则,线线平行,所以可证,可证四边形是平行四边形,即证明是中点;(2)根据等体积转化,可证是直角三角形,写出体积公式,求解距离.试题解析:解(1)连接AD1,则D1C1∥DC∥AB,∴A、E、C1、D1四点共面,∵C1E∥平面ADD1A1,则C1E∥AD1,∴AEC1D1为平行四边形,∴AE=D1C1=1,∴E为AB的中点.(6分)(2),∵AD⊥DC,AD⊥DD1,∴AD⊥平面DCC1D1,AD⊥DC1.设点E到平面ADC1的距离为h,则,解得.【考点】1.线面平行的性质定理;2.等体积转化.4.设长方体的长、宽、高分别为2,1, 1,其顶点都在同一个球面上,则该球的体积为_______.【答案】【解析】球直径为长方体的体对角线,故半径为【考点】球内接长方体的性质,球体积的计算5.(本小题12分)如图所示,三棱柱ABC-A1B1C1中,.(1)证明:;(2)若,求三棱柱ABC-A1B1C1的体积.【答案】(1)见解析;(2)3【解析】(1)取AB的中点O,连接OC,OA1,A1B,证得,,则根据线面垂直的判定定理可得,进而得出;(2)先证明,进而证出,再求出,最后利用柱体的体积公式求出体积;试题解析:(1)取AB 的中点O ,连接.因为,所以.由于,故△AA 1B 为等边三角形,所以.因为,所以.又,故.(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形,所以. 又,则,故.因为所以,为三棱柱的高.又△ABC 的面积,故三棱柱的体积.【考点】1.线面垂直的判定定理;2.线线垂直的证明方法;3.柱体的体积公式;6. 如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误的是( ).A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1D .异面直线AD 与CB 1角为60°【答案】D【解析】因为易证∥,由线面平行的判定定理可证得∥面,所以A 选项结论正确; 由正方体可得面,可证得,由为正方体得,因为,所以面,从而可证得.同理可证明,根据线面垂直的判定定理可证得面,所以B ,C 选项结论都正确; 因为∥,所以为异面直线与所成的角,由正方体可得,所以D 选项的内容不正确. 故选D 。
高一立体几何试卷及答案

高一立体几何试卷及答案The document was prepared on January 2, 2021立体几何试题一.选择题每题4分,共40分1.已知AB 0300300150空间,下列命题正确的个数为1有两组对边相等的四边形是平行四边形,2四边相等的四边形是菱形3平行于同一条直线的两条直线平行 ;4有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有A 1个B 2个C 3个D 4个二.填空题每题4分,共16分11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N,设直线AB 与平面α交于点O,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题1510分如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =.求证:四边形1EBFD 是平行四边形1610分如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明:直线PC 与平面ABD 垂直CB1712分如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC1812分如图,长方形的三个面的对角线长分别是a,b,c,求长方体对角线AC'的长C1bC BA答案1三点共线2无数 无数3a 1证明: 1AE C F = 11AB C D =11EAB FC D ∠=∠∴ 11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG 1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++。
高一数学立体几何单元测试及答案

立体几何综合测评(满分:150分时间:120分钟)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.给出下列命题,其中是真命题的为()(1)若两个平面平行,那么其中一个平面内的直线一定平行于另一个平面;(2)若两个平面平行,那么垂直于其中一个平面的直线一定垂直于另一个平面;(3)若两个平面垂直,那么垂直于其中一个平面的直线一定平行于另一个平面;(4)若两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面.A.(1)(2)B.(1)(3)C.(2)(4) D.(3)(4)A[(1)因为两个平面平行,所以两个平面没有公共点,即其中一个平面内的直线与另一个平面也没有公共点,所以(1)正确.(2)因为该直线与其中一个平面垂直,那么该直线必与其中两条相交直线垂直,又两个平面平行,故另一个平面也必定存在两条相交直线与该直线垂直,所以该直线与另一个平面也垂直,故(2)正确.(3)错,反例:该直线可以在另一个平面内.(4)错,反例:其中一个平面内也存在直线与另一个平面平行.综上:(1)(2)为真命题.]2.给出以下四个命题:①不共面的四点中,其中任意三点不共线;②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;③若直线a,b共面,直线a,c共面,则直线b,c共面;④依次首尾相接的四条线段必共面.其中正确命题的个数是()A.0 B.1C.2 D.3B[①假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以①正确;②如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面;③显然不正确;④不正确.因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.]3.在正方体ABCD-A1B1C1D1中,棱所在直线与直线BA1是异面直线的条数为()A.4 B.5C.6 D.7C[如图,在正方体ABCD-A1B1C1D1中,与直线BA1异面的直线有CD,C1D1,C1C,D1D,B1C1,AD,共6条,故选C.]4.设l为直线,α,β是两个不同的平面.下列命题中正确的是()A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥βB[对于A,若l∥α,l∥β,则α和β可能平行也可能相交,故错误;对于B,若l⊥α,l⊥β,则α∥β,故正确;对于C,若l⊥α,l∥β,则α⊥β,故错误;对于D,若α⊥β,l∥α,则l与β的位置关系有三种可能:l⊥β,l∥β,lβ,故错误.故选B.] 5.如图,已知P A⊥矩形ABCD所在的平面,则图中互相垂直的平面有()A.1对B.2对C.3对D.5对D[∵DA⊥AB,DA⊥P A,∴DA⊥平面P AB.同理BC⊥平面P AB,又AB⊥平面P AD,∴DC⊥平面P AD,∴平面P AD⊥平面AC,平面P AB⊥平面AC,平面PBC⊥平面P AB,平面P AB⊥平面P AD,平面PDC⊥平面P AD,共5对.]6.如图,α∩β=l,点A,C∈α,点B∈β,且BA⊥α,BC⊥β,那么直线l与直线AC的关系是()A.异面B.平行C.垂直D.不确定C[∵BA⊥α,α∩β=l,lα,∴BA⊥l.同理BC⊥l.又BA∩BC=B,∴l⊥平面ABC.∵AC平面ABC,∴l⊥AC.]7.下列命题中正确的是()A.将正方形旋转不可能形成圆柱B.以直角梯形的一腰为轴旋转所得的旋转体是圆台C.圆柱、圆锥、圆台的底面都是圆面D.通过圆台侧面上一点,有无数条母线C[将正方形绕其一边所在直线旋转可以形成圆柱,所以A错误;B中必须以垂直于底边的腰为轴旋转才能得到圆台,所以B错误;通过圆台侧面上一点,只有一条母线,所以D错误,故选C.] 8.如图所示的组合体,其构成形式是()A.左边是三棱台,右边是圆柱B.左边是三棱柱,右边是圆柱C.左边是三棱台,右边是长方体D.左边是三棱柱,右边是长方体D[根据三棱柱和长方体的结构特征,可知此组合体左边是三棱柱,右边是长方体.]9.设长方体的长,宽,高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为() A.3πa2B.6πa2C.12πa2D.24πa2B[由题可知,球的直径等于长方体的体对角线的长度,故2R=4a2+a2+a2,解得R=62a,所求球的表面积S=4πR2=6πa2.]10.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为()A.πa2 B.73πa2C.113πa2D.5πa2B[由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.如图,P为三棱柱上底面的中心,O为球心,易知AP=23×32a=33a,OP=12a,所以球的半径R=OA满足R2=⎝⎛⎭⎪⎫33a2+⎝⎛⎭⎪⎫12a2=7 12a 2,故S球=4πR2=73πa2.]11.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为()A.3172B.210C.132D.310C[如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径为R =OA =62+⎝ ⎛⎭⎪⎫522=132.]12.已知l ,m 表示两条不同的直线,α表示平面,则下列说法正确的是( ) A .若l ⊥α,m α,则l ⊥mB .若l ⊥m ,m α,则l ⊥αC .若l ∥m ,m α,则l ∥αD .若l ∥α,m α,则l ∥m A [对于A ,若l ⊥α,m α,则根据直线与平面垂直的性质,知l ⊥m ,故A 正确;对于B ,若l ⊥m ,m α,则l 可能在α内,故B 不正确;对于C ,若l ∥m ,m α,则l ∥α或l α,故C 不正确;对于D ,若l ∥α,m α,则l 与m 可能平行,也可能异面,故D 不正确.故选A.]二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上) 13.已知正六棱柱的侧面积为72 cm 2,高为6 cm ,那么它的体积为__________cm 3. 363 [设正六棱柱的底面边长为x cm ,由题意得6x ·6=72,所以x =2 cm , 于是其体积V =34×22×6×6=36 3 cm 3.]14.圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角的度数为________. 180° [S 底+S 侧=3S 底,2S 底=S 侧,即2πr 2=πrl ,得2r =l . 设侧面展开图的圆心角为θ,则θπl 180°=2πr ,∴θ=180°.]15.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是棱AA 1和AB 上的点,若∠B 1MN 是直角,则∠C1MN等于________.90°[∵B1C1⊥平面A1ABB1,MN平面A1ABB1,∴B1C1⊥MN.又∠B1MN为直角,∴B1M⊥MN.而B1M∩B1C1=B1,∴MN⊥平面MB1C1.又MC1平面MB1C1,∴MN⊥MC1,∴∠C1MN=90°.]16.棱长为1的正四面体内有一点P,由点P向各个面引垂线,垂线段分别为d1,d2,d3,d4,则d 1+d 2+d 3+d 4的值为________.63 [设四面体的高为h ,则h =12-⎝ ⎛⎭⎪⎫23×32×12=63,13Sh =13S (d 1+d 2+d 3+d 4),∴d 1+d 2+d 3+d 4=h =63.]B三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)如图,正方体ABCD -A ′B ′C ′D ′的棱长为a ,连结A ′C ′,A ′D ,A ′B ,BD ,BC ′,C ′D ,得到一个三棱锥.求:(1)三棱锥A ′BC ′D 的表面积与正方体表面积的比值; (2)三棱锥A ′BC ′D 的体积.[解] (1)∵ABCD -A ′B ′C ′D ′是正方体, ∴六个面是互相全等的正方形,∴A ′C ′=A ′B =A ′D =BC ′=BD =C ′D =2a ,∴S 三棱锥=4×34×(2a )2=23a 2,S 正方体=6a 2, ∴S 三棱锥S 正方体=33. (2)显然,三棱锥A ′ABD ,C ′BCD ,D A ′D ′C ′, B A ′B ′C ′是完全一样的, ∴V 三棱锥A ′BC ′D =V 正方体-4V 三棱锥A ′ABD =a 3-4×13×12a 2×a =13a 3.18.(本小题满分12分)如图,在三棱锥A -BCD 中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E ,F (E 与A ,D 不重合)分别在棱AD ,BD上,且EF ⊥AD .求证:(1)EF ∥平面ABC ; (2)AD ⊥AC .[证明] (1)在平面ABD 内,因为AB ⊥AD ,EF ⊥AD , 所以EF ∥AB .又因为EF 平面ABC ,AB 平面ABC , 所以EF ∥平面ABC .(2)因为平面ABD ⊥平面BCD , 平面ABD ∩平面BCD =BD , BC 平面BCD ,BC ⊥BD , 所以BC ⊥平面ABD .因为AD 平面ABD ,所以BC ⊥AD .又AB ⊥AD ,BC ∩AB =B ,AB 平面ABC ,BC 平面ABC , 所以AD ⊥平面ABC . 又因为AC 平面ABC , 所以AD ⊥AC .19.(本小题满分12分)如图,圆锥的轴截面SAB 为等腰直角三角形,Q 为底面圆周上一点.(1)若QB的中点为C,求证:平面SOC⊥平面SBQ;(2)若∠AOQ=120°,QB=3,求圆锥的表面积.[解](1)证明:∵SQ=SB,OQ=OB,C为QB的中点,∴QB⊥SC,QB⊥OC.∵SC∩OC=C,∴QB⊥平面SOC.又∵QB平面SBQ,∴平面SOC⊥平面SBQ.(2)∵∠AOQ=120°,QB=3,∴∠BOQ=60°,即△OBQ为等边三角形,∴OB= 3.∵△SAB为等腰直角三角形,∴SB=6,∴S侧=3·6π=32π,∴S表=S侧+S底=32π+3π=(3+32)π.20.(本小题满分12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:P A∥平面BDE;(2)求证:平面P AC⊥平面BDE;(3)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.[解](1)证明:连结OE,如图所示.∵O,E分别为AC,PC的中点,∴OE∥P A.∵OE平面BDE,P A平面BDE,∴P A∥平面BDE. (2)证明:∵PO⊥平面ABCD,∴PO⊥BD.在正方形ABCD中,BD⊥AC.又∵PO∩AC=O,∴BD⊥平面P AC.又∵BD平面BDE,∴平面P AC⊥平面BDE.(3)取OC 中点F ,连结EF .∵E 为PC 中点,∴EF 为△POC 的中位线,∴EF ∥PO .又∵PO ⊥平面ABCD ,∴EF ⊥平面ABCD ,∴EF ⊥BD .∵OF ⊥BD ,OF ∩EF =F ,∴BD ⊥平面EFO ,∴OE ⊥BD ,∴∠EOF 为二面角E -BD -C 的平面角,∴∠EOF =30°.在Rt △OEF 中,OF =12OC =14AC =24a ,∴EF =OF ·tan 30°=612a ,∴OP =2EF =66a .∴V P ABCD =13×a 2×66a =618a 3.21.(本小题满分12分)如图,三棱锥P -ABC 中,P A ⊥平面ABC ,P A =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥P -ABC 的体积;(2)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PM MC 的值.[解] (1)由题设AB =1,AC =2,∠BAC =60°,可得S △ABC =12·AB ·AC ·sin 60°=32.由P A ⊥平面ABC ,可知P A 是三棱锥P -ABC 的高.又P A =1,所以三棱锥P -ABC 的体积V =13·S △ABC ·P A =36.(2)证明:在平面ABC 内,过点B 作BN ⊥AC ,垂足为N .在平面P AC 内,过点N 作MN ∥P A 交PC 于点M ,连接BM . 由P A ⊥平面ABC 知P A ⊥AC ,所以MN ⊥AC .由于BN ∩MN =N ,故AC ⊥平面MBN .又BM 平面MBN ,所以AC ⊥BM . 在直角△BAN 中,AN =AB ·cos ∠BAC =12,从而NC =AC -AN =32.由MN ∥P A ,得PM MC =AN NC =13.22.(本小题满分12分)如图(1),在Rt △ABC 中,∠C =90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1F ⊥CD ,如图(2).(1) (2)(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ.说明理由.这样的设问该怎么回答?[解](1)证明:∵D,E分别为AC,AB的中点,∴DE∥BC.又∵DE平面A1CB,BC平面A1CB,∴DE∥平面A1CB.(2)证明:由已知得AC⊥BC且DE∥BC,∴DE⊥AC,∴DE⊥A1D,DE⊥CD,A1D∩CD=D,∴DE⊥平面A1DC,而A1F平面A1DC,∴DE⊥A1F.又∵A1F⊥CD,DE∩CD=D,∴A1F⊥平面BCDE,∵BE平面BCDE,∴A1F⊥BE.(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,连接PQ,QE,则PQ∥BC.又∵DE∥BC,∴DE∥PQ,∴平面DEQ即为平面DEP.由(2)知,DE⊥平面A1DC,A1C平面A1DC,∴DE⊥A1C.又∵P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP.又DE∩DP=D,∴A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q(A1B的中点),使得A1C⊥平面DEQ.。
高一数学立体几何试题

高一数学立体几何试题1.设三棱柱的体积为,分别是侧棱上的点,且,则四棱锥的体积为()A.B.C.D.【答案】C【解析】假设重合,重合,则【考点】棱柱棱锥的体积2.一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图如图,则该圆锥的体积为()A.πB.2πC.πD.π【答案】A【解析】由该几何体的三视图得到该圆锥的底面半径是:,高是,所以体积是:.【考点】1.三视图;2.几何体的体积.3.如图所示,正四棱锥中,为底面正方形的中心,侧棱与底面所成的角的正切值为.(1)求侧面与底面所成的二面角的大小;(2)若是的中点,求异面直线与所成角的正切值;(3)问在棱上是否存在一点,使⊥侧面,若存在,试确定点的位置;若不存在,说明理由.【答案】(1)(2)(3)点为的四等分点【解析】(1)取中点,设面,连接则为二面角的平面角,设,则可利用表示出和,从而根据,即可求得,即可求出二面角的大小。
(2)连接为异面直线与所成的角,根据,判断出面,从而可推断,从而可知为直线与所成的角,根据勾股定理求得,从而求出,则即可求得。
(3)延长交于,取中点,连接,先证出平面和平面垂直,再通过已知条件证出平面,取中点,利用,推断出,可知,最后可推断出平面,即为四等分点。
试题解析:(1)取中点,连接,依条件可知,则为所求二面角P-AD-O的平面角.∵面,∴为侧棱与底面所成的角.∴,7(2)连接,∴∠OEA为异面直线PD与AE所成的角.为异面直线与所成的角∵,,∴⊥平面.又平面,∴⊥.(3)延长交于,取中点,连.,∴⊥平面.∴平面⊥平面.又,∴为正三角形..又平面平,∴MG⊥平面PBC.平面取中点,,∴平面.点为的四等分点.【考点】(1)直线与平面垂直的判定(2)二面角的求法4.下列说法不正确的是A.空间中,一组对边平行且相等的四边形是一定是平行四边形;B.同一平面的两条垂线一定共面;C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;D.过一条直线有且只有一个平面与已知平面垂直.【答案】D【解析】A中由平行四边形判定定理可知结论正确;B中两垂线平行,因此确定一个平面;C中由线面垂直的判定定理可知结论正确;D中过一条直线有无数平面与已知平面垂直【考点】线面平行垂直的判定与性质5.已知是直线,是平面,下列命题中:①若垂直于内两条直线,则;②若平行于,则内可有无数条直线与平行;③若m⊥n,n⊥l则m∥l;④若,则;正确的命题个数为()A.1B.2C.3D.4【答案】A【解析】①改为垂直于平面内的两条相交直线;②正确;③改为或相交或异面;④改为或异面.故选A.【考点】线与线,面与面,线与面位置关系6.长方体的表面积是,所有棱长的和是,则对角线的长是()A.B.C.D.【答案】D【解析】设长方体的长、宽、高分别为.则有.则长方体的对角线长为.故D正确.【考点】长方体的表面积,对角线.【思路点晴】本题主要考查的是长方体的表面积,属容易题.应先设出长方体的长、宽、高,表示出长方体的全面积,十二条棱长度之和,然后根据勾股定理可得对角线的长度.7.用到球心距离为2的平面去截球,所得的截面面积为,则球的体积为()A.B.C.D.【答案】B【解析】用到球心距离为2的平面去截球,所得的截面面积为,所以小圆的半径为1,已知球心到该截面的距离为2,所以球的半径为,所以球的体积为:;故选B.【考点】球的体积与表面积8.设是两条不同的直线,是两个不同的平面,下列命题中正确的是A.若,,则B.若,,则C.若,,则D.若,,,则【答案】D【解析】A中,与可垂直、可异面、可平行;B中与可平行、可异面;C中若,仍然满足,故C错误;故D正确.【考点】1.直线与直线的平行与垂直;2.平面与平面平行与垂直的命题判断.9.设是两个不同的平面,是一条直线,以下命题正确的是()A.若,则B.若,则C.若,则D.若,则【答案】C【解析】若,则或∥,故A不正确;若,则或∥,故B不正确;若,则,故C正确;若,则或或∥,故D不正确,所以C为正确答案.【考点】直线与平面的位置关系.10.边长为的正三角形,在斜二测画法下的平面直观图的面积为.【答案】【解析】,所以.【考点】直观图.11.下列说法正确的是()A.底面是正多边形,侧面都是正三角形的棱锥是正棱锥B.各个侧面都是正方形的棱柱一定是正棱柱C.对角面是全等的矩形的直棱柱是长方体D.两底面为相似多边形,且其余各面均为梯形的多面体必为棱台【答案】A【解析】由正棱锥的定义可知A正确;B不正确,例如各个侧面都是正方形的四棱柱的底面一定是菱形,但不一定是正方形,所以此时的四棱柱不一定是正四棱柱;C不正确,对角面是全等的矩形的直棱柱的底面可能是等腰梯形;D不正确,不能保证此多面体的各侧棱交于一点.【考点】几何体的概念问题.12.一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.【答案】A【解析】由已知中的三视图可知该几何体是一个组合体,由一个底面半径为,高为的半圆锥和一个底面边长为的正方形,高为的四棱锥组合而成,分别代入圆锥和棱锥的体积公式,可得这个几何体的体积,故选A.【考点】由三视图求面积、体积.13.(2009•浙江)设α,β是两个不同的平面,l是一条直线,以下命题正确的是()A.若l⊥α,α⊥β,则l⊂βB.若l∥α,α∥β,则l⊂βC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β【答案】C【解析】本题考查的知识点是直线与平面之间的位置关系,逐一分析四个答案中的结论,发现A,B,D中由条件均可能得到l∥β,即A,B,D三个答案均错误,只有C满足平面平行的性质,分析后不难得出答案.解:若l⊥α,α⊥β,则l⊂β或l∥β,故A错误;若l∥α,α∥β,则l⊂β或l∥β,故B错误;若l⊥α,α∥β,由平面平行的性质,我们可得l⊥β,故C正确;若l∥α,α⊥β,则l⊥β或l∥β,故D错误;故选C【考点】空间中直线与平面之间的位置关系.14.(2015秋•鞍山校级期末)正六棱柱ABCDEF﹣A1B1C1D1E1F1的底面边长为,侧棱长为1,则动点从A沿表面移动到点D1时的最短的路程是.【答案】【解析】根据题意,画出图形,结合图形得出从A点沿表面到D1的路程是多少,求出即可.解:将所给的正六棱柱按图1部分展开,则AD′1==,AD1==,∵AD′1<AD1,∴从A点沿正侧面和上底面到D1的路程最短,为.故答案为:.【考点】多面体和旋转体表面上的最短距离问题.15.(2014•埇桥区校级学业考试)已知A(1,0,2),B(1,﹣3,1),点M在z轴上且到A、B两点的距离相等,则M点坐标为()A.(﹣3,0,0) B.(0,﹣3,0)C.(0,0,﹣3) D.(0,0,3)【答案】C【解析】点M(0,0,z),利用A(1,0,2),B(1,﹣3,1),点M到A、B两点的距离相等,建立方程,即可求出M点坐标解:设点M(0,0,z),则∵A(1,0,2),B(1,﹣3,1),点M到A、B两点的距离相等,∴∴z=﹣3∴M点坐标为(0,0,﹣3)故选C.【考点】两点间的距离公式.16.已知向量=(1,2),=(2,3﹣m),且∥,那么实数m的值是()A.﹣1B.1C.4D.7【答案】A【解析】根据向量的平行的条件和向量的坐标运算即可求出.解:向量=(1,2),=(2,3﹣m),且∥,∴1×(3﹣m)=2×2,∴m=﹣1,故选:A.【考点】平面向量共线(平行)的坐标表示.17.如图是一个几何体的三视图(单位:cm).(1)画出这个几何体的直观图(不要求写画法)(2)求这个几何体的表面积及体积.【答案】(1)见解析;(2)表面积;体积3.【解析】(1)由三视图可知该几何体为平放的三棱柱,则可画出其三棱柱;(2)由三视图可知棱柱的两底面为等腰三角形且底边长为2,高为1.一个侧面是长为3宽为2的矩形;另两个侧面都是长为3宽为的矩形,从而可得其表面积和体积.试题解析:(1)由三视图可知该几何体为平放的三棱柱,直观图为:(2)由三视图可知,该棱柱的高,底面等腰的底,的,高为1,.故所求全面积.几何体的体积.【考点】1三视图;2几何体的表面积,体积.18.(2011•南昌三模)如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥底面A1B1C1,主视图是边长为2的正方形,该三棱柱的左视图面积为()A.4B.C.D.【答案】B【解析】由三视图和题意可知三棱柱是正三棱柱,结合正视图,俯视图,不难得到侧视图,然后求出面积.解:由三视图和题意可知三棱柱是正三棱柱,底面边长为2,侧棱长2,结合正视图,俯视图,得到侧视图是矩形,长为2,宽为面积为:故选B.【考点】由三视图求面积、体积.19.(2015秋•沈阳校级月考)如图,四棱锥P﹣ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.求证:(1)PA∥平面EFG;(2)DH⊥平面EFG.【答案】见解析【解析】(1)根据面面平行的性质推出线面平行;(2)由题意可证DH⊥PA,DH⊥AB,可证DH⊥平面PAB,从而证明DH⊥PB,由(1)EF∥AB,EG∥PB,从而证明DH⊥EG,DH⊥EF,即可证明DH⊥平面EFG.证明:(1)∵E、G分别是PC、BC的中点,∴EG是△PBC的中位线,∴EG∥PB,又∵PB⊂平面PAB,EG⊄平面PAB,∴EG∥平面PAB,∵E、F分别是PC、PD的中点,∴EF∥CD,又∵底面ABCD为正方形,∴CD∥AB,∴EF∥AB,又∵AB⊂平面PAB,EF⊄平面PAB,∴EF∥平面PAB,又EF∩EG=E,∴平面EFG∥平面PAB,∵PA⊂平面PAB,∴PA∥平面EFG.(2)∵PD⊥AD,PD=AD,H为的中点,∴DH⊥PA,∵BA⊥平面PDA,DH⊂平面PDA,∴DH⊥AB,∴DH⊥平面PAB,∴DH⊥PB,由(1)EF∥AB,EG∥PB,∴DH⊥EG,DH⊥EF,∴DH⊥平面EFG.【考点】直线与平面垂直的判定;直线与平面平行的判定.20.(2015春•咸宁期末)如图是正方体的平面展开图,则在这个正方体中:①BM与ED平行②CN与BE是异面直线③CN与BM成60°角④DM与BN是异面直线以上四个命题中,正确的命题序号是()A.①②③B.②④C.③④D.②③④【答案】C【解析】根据恢复的正方体可以判断出答案.解:根据展开图,画出立体图形,BM与ED垂直,不平行,CN与BE是平行直线,CN与BM成60°,DM与BN是异面直线,故③④正确.故选:C【考点】空间中直线与直线之间的位置关系.21.(2015秋•河池期末)下列结论判断正确的是()A.任意三点确定一个平面B.任意四点确定一个平面C.三条平行直线最多确定一个平面D.正方体ABCD﹣A1B1C1D1中,AB与CC1异面【答案】D【解析】根据题意,容易得出选项A、B、C错误,画出图形,结合异面直线的定义即可判断D 正确.解:对于A,不在同一直线上的三点确定一个平面,∴命题A错误;对于B,不在同一直线上的四点确定一个平面,∴命题B错误;对于C,三条平行直线可以确定一个或三个平面,∴命题C错误;对于D,如图所示,正方体ABCD﹣A1B1C1D1中,AB与CC1是异面直线,命题D正确.故选:D.【考点】平面的基本性质及推论.22.设点M是等腰直角三角形ABC的斜边BA的中点,P是直线BA上任意一点,PE⊥AC于E,PF⊥BC于F,求证:(1)ME=MF;(2)ME⊥MF.【答案】见解析【解析】(1)以等腰直角三角形的直角顶点C为坐标原点O,以OA为单位长,以直线OA.OB分别为x轴.y轴建立平面直角坐标系,由此能证明ME=MF.(2)分别求出ME2+MF2=,,由此能证明ME⊥MF.证明:(1)如图,以等腰直角三角形的直角顶点C为坐标原点O,以OA为单位长,以直线OA.OB分别为x轴.y轴建立平面直角坐标系,则A(1,0),B(0,1),…(2分)设P(x0,y),则有x+y=1,∵PE⊥OA,PF⊥OB,∴E(x0,0),F(0,y),,,∵,∴ME=MF.…(7分)(2)∵ME2+MF2=()2+++(﹣y)2=,,∴ME2+MF2=EF2,∴ME⊥MF.…(12分)【考点】空间中直线与直线之间的位置关系.23.已知l,m是两条不同的直线,α是一个平面,则下列命题正确的是()A.若l⊥α,m⊂α,则l⊥mB.若l⊥m,m⊂α,则l⊥αC.若l∥α,m⊂α,则l∥mD.若l∥α,m∥α,则l∥m【答案】A【解析】对四个命题分别进行判断,即可得出结论.解:对于A,若l⊥α,m⊂α,则根据直线与平面垂直的性质定理知:l⊥m,故A正确;对于B,若l⊥m,m⊂α,则根据直线与平面垂直的判定定理知:l⊥α不正确,故B不正确;对于C,∵l∥α,m⊂α,∴由直线与平面平行的性质定理知:l与m平行或异面,故C不正确;对于D,若l∥α,m∥α,则l与m平行,异面或相交,故D不正确.故选:A.【考点】平面与平面之间的位置关系;空间中直线与直线之间的位置关系;空间中直线与平面之间的位置关系.24.如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,AA′⊥平面ABCD(1)求证:A′C∥平面BDE;(2)求证:平面A′AC⊥平面BDE.【答案】见解析【解析】(1)首先找到线面平行的充分条件,可以通过中位线找到线线平行,再进一步证明线面平行.(2)要证明平面A′AC⊥平面BDE.可以通过BD⊥平面A'AC来进行转化,进一步找到BD⊥平面A'AC的充分条件,从而得到结果.证明:(1)设BD交AC于M,连结ME.∵ABCD为正方形,所以M为AC中点,又∵E为A'A的中点∴ME为△A'AC的中位线∴ME∥A'C又∵ME⊂平面BDE,A'C⊄平面BDE∴A'C∥平面BDE.(2)∵ABCD为正方形∴BD⊥AC∵A'A⊥平面ABCD∴A'A⊥BD.又AC∩A'A=A AC⊂面A'AC AA'⊂面A'AC∴BD⊥平面A'AC∵BD⊂平面BDE∴平面A'AC⊥平面BDE.【考点】平面与平面垂直的判定;直线与平面平行的判定.25.如图,在正方体中,分别为棱的中点.(Ⅰ)求证:∥平面;(Ⅱ)求异面直线与所成角.【答案】(Ⅰ)详见解析(Ⅱ)【解析】(Ⅰ)证明线面平行可通过证明线线平行或面面平行得以实现,本题证明时利用中点产生的中位线加以证明;(Ⅱ)求异面直线所成角时首先将异面直线平移为相交直线,求其夹角即可,本题中通过平移可知就是异面直线与所成角,通过求解角所在的三角形三边得到角的大小试题解析:(1)连结BD,分别为AD,AB的中点,所以EF∥BD,由所以四边形是平行四边形,所以,平面平面平面(Ⅱ)连接,四边形是平行四边形又∥就是异面直线与所成角在正方体中即异面直线与所成角为【考点】1.线面平行的判定;2.异面直线所成角26.将正方体截取一个四棱锥后得到的几何体如图所示,则有关该几何体的三视图表述正确的是()A.正视图与俯视图形状完全相同B.侧视图与俯视图形状完全相同C.正视图与侧视图形状完全相同D.正视图、侧视图与俯视图形状完全相同【答案】C【解析】根据三视图的特点,画出几何体的三视图,可得答案.解:该几何体的三视图如下所示:主视图:侧视图:俯视图:则正视图与侧视图形状完全相同,故选:C【考点】简单空间图形的三视图.27.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.【答案】(1)见解析;(2)【解析】(1)由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;2)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC⊂平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出;解:(1)∵PA=PD,∴PQ⊥AD,又∵底面ABCD为菱形,∠BAD=60°,∴BQ⊥AD,PQ∩BQ=Q,∴AD⊥平面PQB又AD⊂平面PAD,∴平面PQB⊥平面PAD;(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,∴PQ⊥平面ABCD,BC⊂平面ABCD,∴PQ⊥BC,又BC⊥BQ,QB∩QP=Q,∴BC⊥平面PQB,又PM=3MC,∴V﹣QBM=V M﹣PQB=P【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积.28.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和.过A、B 分别作两平面交线的垂线,垂足为A′、B′,则AB:A′B′=()A.2:1 B.3:1 C.3:2 D.4:3【答案】A【解析】设AB的长度为a用a表示出A'B'的长度,即可得到两线段的比值.解:连接AB'和A'B,设AB=a,可得AB与平面α所成的角为,在Rt△BAB'中有AB'=,同理可得AB与平面β所成的角为,所以,因此在Rt△AA'B'中A'B'=,所以AB:A'B'=,故选A.【考点】平面与平面垂直的性质.29.对于直线m,n和平面α,β,能得出α⊥β的一个条件是()A.m⊥n,m∥α,n∥βB.m⊥n,α∩β=m,n⊂αC.m∥n,n⊥β,m⊂αD.m∥n,m⊥α,n⊥β【答案】C【解析】在A中,α与β相交或相行;在B中,α与β不一定垂直;在C中,由由面面垂直的判定定理得α⊥β;在D中,由面面平行的判定定理得α∥β.解:在A中,m⊥n,m∥α,n∥β,则α与β相交或相行,故A错误;在B中,m⊥n,α∩β=m,n⊂α,则α与β不一定垂直,故B错误;在C中,m∥n,n⊥β,m⊂α,由由面面垂直的判定定理得α⊥β,故C正确;在D中,m∥n,m⊥α,n⊥β,则由面面平行的判定定理得α∥β,故D错误.故选:C.【考点】空间中直线与平面之间的位置关系.30.正方体ABCD﹣A1B1C1D1的棱长为,△AB1D1面积为,三棱锥A﹣A1B1D1的体积为.【答案】,【解析】正方体ABCD﹣A1B1C1D1的棱长为,△AB1D1是边长为=2的等边三角形,由此能求出△AB1D1面积和三棱锥A﹣A1B1D1的体积.解:∵正方体ABCD﹣A1B1C1D1的棱长为,∴△AB1D1是边长为=2的等边三角形,∴△AB1D1面积S==.== =.故答案为:,.【考点】棱柱、棱锥、棱台的体积.31.已知正四面体中,是的中点,则异面直线与所成角的余弦值为()A.B.C.D.【答案】B【解析】如图,取中点,连接,因为是中点,则,或其补角就是异面直线所成的角,设正四面体棱长为1,则,,.故选B.【考点】异面直线所成的角.【名师】求异面直线所成的角的关键是通过平移使其变为相交直线所成角,但平移哪一条直线、平移到什么位置,则依赖于特殊的点的选取,选取特殊点时要尽可能地使它与题设的所有相减条件和解题目标紧密地联系起来.如已知直线上的某一点,特别是线段的中点,几何体的特殊线段.32.对于四面体ABCD,下列命题正确的是________.(写出所有正确命题的编号).①相对棱AB与CD所在的直线是异面直线;②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足重合;④任何三个面的面积之和都大于第四个面的面积;⑤分别作三组相对棱中点的连线,所得的三条线段相交于一点.【答案】①④⑤【解析】本题考查空间几何体的线线关系,以及空间想象能力.如图所示,四面体ABCD中,AB与CD是异面直线,故①正确;当四面体ABCD中,对棱AB与CD不垂直时,由顶点A作四面体的高,其垂足不是△BCD三条高线的交点,故②不正确;若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足不一定重合,故③不正确;如图,过顶点A 作AO ⊥面BCD ,O 为垂足,连结OB 、OC 、OD ,则S △ABC >S △BOC ,S △ACD >S △COD ,S △ABD >S △BOD ,∴S △ABC +S △ACD +S △ABD >S △BOC +S △COD +S △BOD =S △BCD , 故④正确. 如图四面体ABCD 中取AB 、CD 、AD 、BC 的中点分别为E 、F 、M 、N ,连线EF 、MN ,则EF 、MN 分别为▱EMFN 的对角线,∴EF 、MN 相交于点O ,且O 为EF 、MN 的中点,取AC 、BD 的中点分别为R 、H ,则ERFH 为平行四边形,即点O 也是RH 的中点,故⑤正确.33. 一个正三棱柱的三视图如图所示,求这个正三棱柱的体积和表面积。
高一数学立体几何练习题及答案

高一数学立体几何练习题及答案一、选择题1. 下列哪个图形不是立体图形?A. 立方体B. 圆锥C. 圆柱D. 正方形答案:D2. 已知一个立方体的边长为5cm,求它的表面积和体积分别是多少?A. 表面积:150cm²,体积:125cm³B. 表面积:100cm²,体积:125cm³C. 表面积:150cm²,体积:100cm³D. 表面积:100cm²,体积:100cm³答案:A3. 以下哪个选项可以形成一个正方体?A. 六个相等的长方体B. 一个正方形和一个长方体C. 六个相等的正方形D. 一个正方形和一个正方体答案:C4. 以下哪个图形可以形成一个圆柱?A. 一个正方形和一个长方体B. 一个圆和一个长方体C. 一个长方形和一个长方体D. 一个正方形和一个正方体答案:C5. 以下哪个选项可以形成一个圆锥?A. 一个圆和一个长方体B. 一个圆和一个正方体C. 一个正方形和一个长方体D. 一个正方形和一个正方体答案:B二、填空题1. 已知一个正方体的表面积为96cm²,求它的边长是多少?答案:4cm2. 已知一个圆柱的半径为3cm,高为10cm,求它的表面积和体积分别是多少?答案:表面积:198cm²,体积:90π cm³3. 以下哪个选项可以形成一个长方体?A. 六个相等的正方形B. 一个圆和一个长方形C. 六个相等的长方形D. 一个正方形和一个正方体答案:C三、解答题1. 某长方体的长、宽、高分别为3cm、4cm、5cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)表面积 = 2(长×宽 + 长×高 + 宽×高)= 2(3×4 + 3×5 + 4×5)= 2(12 + 15 + 20)= 2(47)= 94cm²(2)体积 = 长×宽×高= 3×4×5= 60cm³2. 某圆锥的半径是5cm,高是12cm,请回答以下问题:(1)它的表面积是多少?(2)它的体积是多少?答案:(1)斜面积= π×半径×斜高= π×5×13≈ 204.2cm²(2)体积= (1/3)π×半径²×高= (1/3)π×5²×12≈ 314.2cm³四、解析题某正方体的表面积是96cm²,它的边长是多少?解答:设正方体的边长为x,由表面积的计算公式可得:表面积 = 6x²96 = 6x²16 = x²x = 4所以,该正方体的边长为4cm。
高中立体几何试题及答案

高中立体几何试题及答案一、选择题(每题3分,共15分)1. 空间中,如果直线a与平面α平行,那么直线a与平面α内的任意直线b的位置关系是:A. 平行B. 异面C. 相交D. 垂直2. 一个正方体的棱长为a,那么它的对角线长度为:A. a√2B. a√3C. 2aD. 3a3. 已知一个圆锥的底面半径为r,高为h,圆锥的体积是:A. πr²hB. 1/3πr²hC. 2πr²hD. 3πr²h4. 一个球的半径为R,那么它的表面积是:A. 4πR²B. 2πR²C. πR²D. R²5. 空间中,如果两个平面α和β相交于直线l,那么直线l与平面α和平面β的位置关系是:A. 平行B. 垂直C. 相交D. 包含二、填空题(每题2分,共10分)6. 空间直角坐标系中,点A(2,3,4)到原点O的距离是________。
7. 一个正四面体的每个顶点都与其它三个顶点相连,那么它的边长与高之比为________。
8. 已知一个长方体的长、宽、高分别为l、w、h,那么它的体积是________。
9. 空间中,如果一个点到平面的距离是d,那么这个点到平面上任意一点的距离的最大值是________。
10. 一个圆柱的底面半径为r,高为h,它的侧面积是________。
三、解答题(共75分)11. (15分)已知空间直角坐标系中,点A(1,2,3),B(4,5,6),点C 在平面ABC内,且AC=BC=2,求点C的坐标。
12. (20分)一个圆锥的底面半径为3,高为4,求圆锥的全面积和表面积。
13. (20分)一个长方体的长、宽、高分别为5、3、2,求其外接球的半径。
14. (20分)已知一个球的表面积为4π,求该球的体积。
答案:一、选择题1. A2. B3. B4. A5. C二、填空题6. √(1²+2²+3²)=√147. √3:18. lwh9. d+R10. 2πrh三、解答题11. 点C的坐标可以通过向量运算求得,设C(x,y,z),则向量AC=向量BC,即(1-x,2-y,3-z)=(x-4,5-y,6-z),解得x=3,y=4,z=5,所以点C的坐标为(3,4,5)。
高中数学立体几何大题练习与答案

一、解答题1.(2023高一下·重庆沙坪坝·百强名校期末)如图,有一个正四棱柱,E 、F 高中数学立体几何大题练习与答案分别为底面棱A D 11,D C 11的中点,=AB 4,=AA 61,点G 在AA 1上,且=AA AG 321.(1)判断直线BG 是否在平面BEF 内?说明理由; (2)求二面角A EF G −−1的余弦值.【答案】(1)直线BG 在平面BEF 内,理由见解析【分析】(1)建立空间直角坐标系,求平面BEF 的法向量,根据法向量与BG 的关系可判断;(2)运用几何法,得到二面角的平面角即可求解.【详解】(1)以D 为坐标原点,DA ,DC ,DD 1分别为x ,y ,z 轴建立空间直角坐标系 则E F B G (2,0,6),(0,2,6),(4,4,0),(4,0,4)所以(2,2,0)EF =−,(2,4,6)BE =−−,(0,4,4)BG =−设平面BEF 的法向量为(,,)n x y z =,则(1,1,1)n ⇒=⎩−−+=⎨⎧−++=x y z x y z 24602200所以其0BG n ⋅=且点B 在平面BEF 内,故直线BG 在平面BEF 内.(2)连接B D 11交EF 于O ,连接BO因为平面EFG 与平面BEF 是同一平面,平面A EF 1与平面B EF 1是同一平面, 则BOB 1为二面角−−B EF B 1的平面角,记为又==B O B D 43111,=BB 61所以==BO所以==θBO B O cos 12.(2023·江苏·百强名校期末)如图,在直三棱柱ABC-A 1B 1C 1中,D ,E 分别为AB ,BC 的中点,点F 在侧棱B 1B 上,且⊥B D A F 11 ,⊥AC A B 1111.求证:(1)直线DE 平面A 1C 1F ;(2)平面B 1DE ⊥平面A 1C 1F. 【答案】(1)详见解析(2)详见解析【详解】试题分析:(1)利用线面平行判定定理证明线面平行,而线线平行的寻找往往结合平面几何的知识,如中位线的性质等;(2)利用面面垂直判定定理证明,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直性质定理与判定定理. 试题解析:证明:(1)在直三棱柱111ABC A B C 中,A C 11,AC 在三角形ABC 中,因为D ,E 分别为AB ,BC 的中点, 所以DE AC ,于是11DE AC ,又因为DE ⊄平面⊂AC F AC ,1111平面AC F 11, 所以直线DE//平面AC F 11.(2)在直三棱柱111ABC A B C 中,面平⊥AA A B C 1111 因为⊂AC 11平面A B C 111,所以⊥AA AC 111,又因为面平面平,⊥⊂⊂⋂=AC A B AA ABB A A B ABB A A B AA A ,,111111*********, 所以⊥AC 11平面ABB A 11.因为⊂B D 1平面ABB A 11,所以⊥AC B D 111.又因为面平面平,⊥⊂⊂⋂=B D A F AC AC F A F AC F AC A F A ,,1111111111111, 所以面平⊥B D AC F 111.因为直线面平⊂B D B DE 11,所以面平B DE 1面平⊥AC F .11 【考点】直线与直线、直线与平面、平面与平面的位置关系【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型:(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直;(4)证明面面垂直,需转化为证明线面垂直,进而转化为证明线线垂直.3.(2023高一下·吉林长春·百强名校期末)在四棱锥−P ABCD 中,底面ABCD 是边长为2的菱形,∠=︒BAD 60,若==PA PD ∠=PAB 10cos .(1)证明:平面⊥PAD 平面ABCD ; (2)求二面角−−B PD A 的正切值.【答案】(1)证明见解析;(2 【分析】(1)取AD 中点O ,连结PO ,BO ,BD ,推导出⊥PO AD ,及⊥PO BO ,从而⊥PO 平面ABCD 由此得到平面⊥PAD 平面ABCD .(2)由面面垂直的性质得到⊥BO 平面ABCD ,作⊥OE PD 于E ,由三垂线定理,得⊥BE PD ,从而∠BEO 就是二面角−−B PD A 的平面角,在POD Rt 中,计算各数据,得到所求角的正切值.【详解】(1)证明:取AD 中点O ,连结PO ,BO ,BD ,在PAD 中,=PA PD=AD 2,则⊥PO AD ,===PO 2.在菱形ABCD 中,∠=︒BAD 60,==AB AD 2,∴===AB AD BD 2,∴⊥BO AD ,且===BO PAB 中,∠=PAB cos ,∴=+−⋅⋅∠=+−=PB PA AB PA AB PAB 2cos 54227222. 在POB 中,+=+==OB PO PB 347222,∴⊥PO BO ,且ADBO O =∴⊥PO 平面ABCD .又⊂PO 平面PAD ∴平面⊥PAD 平面ABCD .(2)由(1)知平面⊥PAD 平面ABCD ,且平面⋂PAD 平面=ABCD AD ,且⊥BO AD , ∴⊥BO 平面ABCD ,作⊥OE PD 于E ,由三垂线定理,得⊥BE PD . ∴∠BEO 就是二面角−−B PD A 的平面角,在POD Rt 中,⊥OE PD ,有⋅=⋅PD OE PO OD =⨯OE 21,∴=OE在BOE Rt 中,∠===OE BEO OBtan∴二面角−−B PD A4.(2023高一下·吉林长春·百强名校期末)如图.已知正三棱柱111ABC A B C 的底面边长=AB 6,D ,E 分别是CC 1,BC 的中点,=AE DE .(1)三棱锥−A ECD 的体积; (2)正三棱柱111ABC A B C 的表面积.【答案】(2)【分析】(1)依题意可得⊥AE BC ,在由正三棱柱的性质得到⊥CC BC 1,利用勾股定理求出线段的长度,最后由A ECD D AEC AECV V SCD ==⋅−−31计算可得;(2)求出上下底面积及侧面积,即可求出棱柱的表面积.【详解】(1)因为E 是BC 的中点,ABC 为等边三角形,所以⊥AE BC , 在正三棱柱111ABC A B C 中⊥CC 1平面ABC ,⊂BC 平面ABC ,所以⊥CC BC 1,又=AB 6,所以=EC 3,AE ===AE DE ,所以==CD所以AECS=⨯⨯=231所以33A ECD D AEC AECV V SCD ==⋅=⨯=−−11.(2)由(1)可知==CC CD 211112ABC A B C S S ==⨯⨯=61ABCS CCC =⋅=⨯⨯=侧366210821,所以棱柱的表面积=⨯=S 25.(2023高一下·四川成都·百强名校期末)如图,在四棱锥−P ABCD 中,⊥PC 底面ABCD ,在直角梯形ABCD 中,⊥AB AD ,BC AD //,==AD AB BC 22,E 是PD 中点.求证:(1)CE //平面PAB ; (2)平面⊥PCD 平面ACE . 【答案】(1)证明见解析 (2)证明见解析【分析】(1)取线段AP 的中点F ,可证得四边形BCEF 为平行四边形,从而得到CE BF //,由线面平行的判定可证得结论;(2)由线面垂直性质和勾股定理可分别证得⊥PC AC ,⊥AC CD ,由线面垂直和面面垂直的判定可证得结论.【详解】(1)取线段AP 的中点F ,连接EF BF ,,,E F 分别为PD AP ,中点,∴EF AD //,=EF AD 21, 又BC AD //,=BC AD 21,∴EF BC //,=EF BC , ∴四边形BCEF 为平行四边形,∴CE BF //,BF ⊂平面PAB ,⊄CE 平面PAB ,∴CE //平面PAB . (2)PC ⊥平面ABCD ,⊂AC 平面ABCD ,∴⊥PC AC ; 设=AD 2,则==AB BC 1,//BC AD ,⊥AB AD ,∴⊥AB BC ,∴=AC ==CD∴+=AC CD AD 222,∴⊥AC CD ;PCCD C =,⊂PC CD ,平面PCD ,∴⊥AC 平面PCD ,AC ⊂平面ACE ,∴平面⊥PCD 平面ACE .6.(2023高一下·安徽六安·百强名校期末)在正三角形ABC 中,E ,F ,P 分别是AB 、AC 、BC 边上的点,满足===AE EB CF FA CP PB :::1:2(如图1).将△AEF 沿EF 折起到的1A EF 位置,使平面⊥A EF 1平面BEF ,连结A B 1,P A 1(如图2).(1)求证:FP //平面A EB 1;(2)求直线A E 1与平面A BP 1所成角的大小. 【答案】(1)证明见解析(2)︒60.【分析】(1)依题意可得FP BA //,即FP BE //,从而得证;(2)法一:设E 到面A BP 1距离为h ,根据=−−V V A BPE E A BP 11,即可求得h 的值,进而求解即可.法二:在图1中过点F 作FD BC //交AB 于点D ,即可得到△ADF 为等边三角形,则⊥FE A E 1,再由面面垂直的性质得到⊥A E 1平面BEP ,设A E 1在平面A BP 1内的射影为A Q 1,且A Q 1交BP 于点Q ,则可得⊥BP 平面A EQ 1,则∠E AQ 1就是A E 1与平面A BP 1所成的角,再由锐角三角函数计算可得.【详解】(1)∵=CP PB CF FA ::,∴FP BA //, ∴FP BE //,∵⊂BE 平面A EB 1,⊄FP 平面A EB 1,∴BP //平面A EB 1; (2)法一:在图1中过点F 作FD BC //交AB 于点D ,因为===AE EB CF FA CP PB :::1:2, 所以==BD AD CF AF ::1:2,即D 、E 为AB 的三等分点,所以E 为AD 的中点,又ABC 为等边三角形,所以△ADF 也为等边三角形, 所以⊥FE AD ,则⊥FE A E 1,又平面⊥A EF 1平面BEF ,平面A EF 1平面=BEF FE ,⊂A E 1平面A EF 1,所以在图2中,⊥A E 1平面BEP ,又⊂BP 平面BEP ,∴⊥A E BP 1,设A E 1在平面A BP 1内的射影为A Q 1,且A Q 1交BP 于点Q , 则可得⊥BP 平面A EQ 1,又⊂AQ 1平面A EQ 1,∴⊥BP AQ 1,则∠E AQ 1就是A E 1与平面A BP 1所成的角,设=AB 3,在△EBP 中,∵==BE BP 2,60=︒∠EBP , ∴△EBP 是等边三角形,∴=BE EP ,又⊥A E 1平面BEP ,∴=A B A P 11,∴Q 为BP 的中点,且=EQ又=A E 11,在1A EQ Rt ,∠==A EEA Q EQtan 11601∠=︒EA Q , 所以直线A E 1与平面A BP 1所成的角为︒60.法二:同法一可得⊥A E 1平面BEP ,设E 到面A BP 1距离为h ,设=AB 3,则==A B A P 11,则=−−V V A BPE E A BP 11,∴△△⋅=⋅S A E S h BPE A BP 331111,∴△△⨯===⋅⨯S h S A E A BP BPE 221221111,设A E 1与面A BP 1所成角为θ,则=θA E h sin 1︒≤≤︒θ090,∴=︒θ60. 所以直线A E 1与平面A BP 1所成的角为︒60.7.(2023高一下·重庆沙坪坝·百强名校期末)如图,四边形ABCD 是圆柱下底面的内接四边形,AC 是圆柱底面的直径,PC 是圆柱的一条母线,=AB AD ,∠=BAD 60,点F 在线段AP 上,=PA PF 4.(1)求证:平面⊥PCD 平面PAD ;(2)若==CP CA 4,求直线AC 与平面FCD 所成角的正弦值. 【答案】(1)证明见解析【分析】(1)先证⊥AD 平面PCD ,再根据面面垂直的判定定理可证平面⊥PCD 平面PAD ;(2)以C 为原点,CA 所在直线为x 轴,过C 且垂直于平面APC 的直线为y 轴,CP 所在直线为z 轴,建立空间直角坐标系,利用线面角的向量公式可求出结果. 【详解】(1)因为PC 是圆柱的一条母线,所以⊥PC 底面ABCD , 又⊂AD 底面ABCD ,所以⊥PC AD , 因为AC 是圆柱底面的直径,所以⊥AD CD , 因为⊂PC CD ,平面PCD ,⋂=PC CD C , 所以⊥AD 平面PCD ,又因为⊂AD 平面PAD ,所以平面⊥PCD 平面PAD .(2)以C 为原点,CA 所在直线为x 轴,过C 且垂直于平面APC 的直线为y 轴,CP 所在直线为z 轴,建立空间直角坐标系, 因为=AB AD ,=AC AC ,∠=∠=ADC ABC 2π, 所以R R t ADC t ABC ≅,又∠=BAD 60,所以π6DAC BAC ==, 因为==CP CA 4,=PA PF 4,所以==CD AC221,=AD所以C (0,0,0),A (4,0,0), D ,F (1,0,3), 所以(4,0,0)AC =−,(1,3,0)CD =,(1,0,3)CF =, 设平面FCD 的一个法向量为(,,)n x y z =,则n CD x y n CF x z ⋅=+=⋅=+=⎩⎪⎨⎪⎧3030,取=−x 3,得y =z 1,则(3,3,1)n =−,设直线AC 与平面FCD 所成角为θ,则sin cos ,||||AC n AC n AC n ⋅=<>=θ==.即直线AC 与平面FCD 所成角的正弦值为13.8.(2023高一下·重庆沙坪坝·百强名校期末)如图,在四棱锥−P ABCD 中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD ,=PD DC ,E 、F 分别是PC 、AD 中点.(1)求证:DE //平面PFB ;(2)求PC 与面PFB 所成角的正弦值.【答案】(1)见解析;(2【分析】(1)取PB 的中点为G ,连接EG FG ,,可证四边形DEGF 为平行四边形,从而可证DE //平面PFB ;(2)利用等积法可求C 到平面PFB 的距离,从而可求PC 与面PFB 所成角的正弦值. 【详解】(1)取PB 的中点为G ,连接EG FG ,, 因为E G ,分别为所在棱的中点,故=EG BC EG BC 2//,1, 而=DF AD 21,=AD BC AD BC //,,故=EG DF EG DF //,, 故四边形DEGF 为平行四边形,所以FG DE //, 而⊂FG 平面PBF ,⊄DE 平面PBF ,故DE //平面PFB .(2)设=DC a ,连接CF ,设C 到平面PBF 的距离为h .因为⊥PD 底面ABCD ,⊂CD 平面ABCD ,故⊥PD CD ,同理⊥⊥PD AD PD BC ,, 而=PD DC,故PC .故=PF a 2,同理=BF a 2. 因为⊥BC CD ,而⋂=PD DC D ,故⊥BC 平面PCD , 而⊂PC 平面PCD ,故⊥BC PC,所以==PB ,故△==S a PFB 2412, 又△=⨯⨯=S a a a FCB2212, 因为=−−V V P FCB C PFB,故⨯⨯=⨯a a h 32311122,故=h ,设PC 与面PFB 所成角为θ,则=θsin9.(2023高一·全国·课后作业)如图,在三棱锥P ABC −中,∠=︒ACB 90,⊥PA 底面ABC(1)证明:平面⊥PBC 平面P AC(2)若==AC BC PA ,M 是PB 中点,求AM 与平面PBC 所成角的正切值 【答案】(1)证明见解析【分析】(1)由∠=︒ACB 90,得到⊥AC CB ,再根据⊥PA 底面ABC ,得到⊥PA CB ,然后利用线面垂直和面面垂直的判定定理证明;(2)作⊥AO PC ,连接OM ,由平面⊥PBC 平面P AC ,得到⊥AO 平面PBC , 则∠AMO 即为AM 与平面PBC 所成的角求解. 【详解】(1)证明:因为∠=︒ACB 90, 所以⊥AC CB ,又⊥PA 底面ABC , 所以⊥PA CB ,又⋂=AC PA A , 所以⊥BC 平面P AC , 因为⊂BC 平面PBC , 所以平面⊥PBC 平面P AC ; (2)如图所示:作⊥AO PC ,连接OM ,因为平面⊥PBC 平面P AC ,平面⋂PBC 平面P AC=PC , 所以⊥AO 平面PBC ,则∠AMO 即为AM 与平面PBC 所成的角,设===AC BC PA t ,则==AB PB ,,所以=AM 2,又=AO 2,所以==OM t 21,所以AM 与平面PBC 所成角的正切值为∠==OMAMO AOtan10.(2023高一下·重庆北碚·百强名校期末)如图,四棱锥S —ABCD 中,底面ABCD 为菱形,602ABC SA SD AB ====,∠,侧面SAB ⊥侧面SBC ,M 为AD 的中点.(1)求证:平面SMC ⊥平面SBC ;(2)若AB 与平面SBC 成30角时,求二面角−−A SC D 的大小, 【答案】(1)证明见解析 (2)︒90【分析】(1)由线面垂直与面面垂直的判定定理求解即可;(2)取BS 的中点N ,连接AN ,由题意可得=BS CS 的中点E ,连接AE DE ,,可证明∠AED 是二面角−=A SC D 的平面角,求出角∠AED 的大小即可求解 【详解】(1)因为=SD SA ,又M 为AD 的中点, 所以⊥SM AD , 又BC AD //, 所以⊥SM BC ,又M 为AD 的中点,底面ABCD 为菱形,∠=︒ABC 60, 所以⊥CM AD AD BC ,//, 所以⊥CM BC ,因为⊥CM BC ,⊥SM BC ,⊥=SM CM M ,⊂SM 平面SCM ,⊂CM 平面SCM ,所以⊥BC 平面SCM ,因为⊂BC 平面SBC , 所以平面⊥SBC 平面SCM ,(2)取BS 的中点N ,连接AN ,又=SA AB , 所以⊥AN BS ,又平面⊥SAB 平面SBC ,平面SAB 平面=SBC SB ,⊂AN 平面SAB ,所以⊥AN 平面SBC ,又AB 与平面SBC 所成的角为︒30, 所以∠=︒ABN 30, 又=⊥AB AN BN 2,,所以===AN BN BS 1,由(1)知⊥BC 平面SCM ,又⊂SC 平面SBC , 所以⊥BC SC ,又==BS BC 2,所以==CS 取CS 的中点E ,连接AE DE ,, 因为===SA AC CD SD , 所以⊥⊥AE CS DE CS ,,所以∠AED 是二面角−=A SC D 的平面角,又====AC CD CE CS 22,1所以==AE 又+=+==AE DE AD 224222, 所以⊥AE DE ,即∠=︒AED 90, 所以二面角−=A SC D 的大小为︒90,11.(2023高一下·重庆北碚·百强名校期末)如图,三棱柱ABC —A B C 111的底面是等腰直角三角形,侧面BB 1C 1C 是矩形,∠=CAB 90,==AB AC AA 1 ,点P 是棱A B 11的中点,且P 在平面ABC 内的射影O 在线段BC 上,=BO BC 41,点M ,N 分别是线段CP ,CA 的中点(1)求证: MN //平面AA B B 11 (2)求二面角−−M AC B 的正切值. 【答案】(1)见解析【分析】(1)连接AP ,则由三角形中位线定理可得MN ∥AP ,然后利用线面平行的判定定理可证得结论,(2)连接OB 1,取CO 的中点E ,连接ME ,过点E 作⊥EF AC 于F ,连接MF ,可证得∠MFE 为 二面角−−M AC B 的平面角,然后计算即可 【详解】(1)证明:连接AP ,因为M ,N 分别是线段CP ,CA 的中点, 所以MN ∥AP ,因为⊄MN 平面AA B B 11,⊂AP 平面AA B B 11, 所以MN ∥平面AA B B 11,(2)解:连接OB 1,取CO 的中点E ,连接ME ,过点E 作⊥EF AC 于F ,连接MF , 因为M ,是线段CP 的中点,所以ME ∥OP ,=ME OP 21,因为⊥OP 平面ABC ,所以⊥ME 平面ABC , 因为⊂AC 平面ABC ,所以⊥ME AC , 因为⋂=ME EF E , 所以⊥AC 平面MEF ,因为⊂MF 平面MEF ,所以⊥AC MF , 所以∠MFE 为 二面角−−M AC B 的平面角, 设===AB AC AA 21,因为∠=CAB 90,所以=BC所以==BO BC 41==CO BC 43,所以==CE CO 21,=︒==EF CE 4sin 453, 在1OBB Rt 中,=+=+=OB OB BB 2241911222, 因为⊥OP 平面ABC ,平面ABC ∥平面A B C 111, 所以⊥OP 平面A B C 111, 因为⊂A B 11平面A B C 111, 所以⊥OP A B 11,所以===OP 2,所以==ME OP 21,在MEF Rt 中,∠===EF MEF ME 43tan 4,所以二面角−−M AC B 的正切值为312.(2023高一下·重庆渝中·百强名校期末)如图;正四棱柱−ABCD A B C D 1111中;=AA AB 21;点P 为DD 1的中点.(1)求证:直线∥BD 1平面PAC ;(2)求直线BC 1与平面APC 所成线面角的正弦值. 【答案】(1)证明见解析(2)15【分析】(1)设AC 和BD 交于点O ,则O 为BD 的中点,连接PO ,可得PO BD //1,可得直线BD //1平面PAC ;(2)设==AA AB 241,利用等体积法可求点D 到平面APC 的距离为d ,进而利用直线BC 1与平面APC 所成线面角与直线AD 1与平面APC 所成线面角相等,可求直线BC 1与平面APC 所成线面角的正弦值.【详解】(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点,连接PO ,P 是DD 1的中点,∴PO BD //1,又PO ⊂平面PAC ,⊂BD 1平面PAC ,∴直线BD //1平面PAC ,(2)设==AA AB 241,则三角形APC为正三角形,===AP AC PC ,APCSAP ==42 设点D 到平面APC 的距离为d ,由等体积法:=−−V V P ADC D APC , 所以1133ADC APCPD Sd S ⋅=⋅,则ADC APC PD S S ===⋅d 233423,由点P 为中点,所以点D ,D 1到平面APC 距离相等,由AD BC //11,所以直线BC1与平面APC 所成线面角与直线AD 1与平面APC 所成线面角相等, 设直线AD1与平面APC 所成线面角为θ,所以==θAD d sin 1∴直线BC 1与平面APC 所成线面角的正弦值为15.13.(2023高一下·重庆沙坪坝·百强名校期末)如图,在直三棱柱111ABC A B C 中,∠=︒BAC 90,===AB AC AA 21,M 为AB 的中点,点G 为△A B C 111的重心.(1)证明:BG 平面ACM 1(2)求三棱锥−G A MC 1的体积. 【答案】(1)证明见解析; (2)32.【分析】(1)先证明平面BGN //平面ACM 1,再由面面平行的性质可得线面平行; (2)利用等体积法求解即可.【详解】(1)连接C G 1并延长交A B 11于点N ,连接BN CM BG ,,,如图,在直三棱柱111ABC A B C 中,点G 为△A B C 111的重心, 所以C N CM //1,又⊄C N 1平面ACM 1,⊂CM 平面ACM 1, 所以C N //1平面ACM 1,因为A N BM A N BM //,=11,所以四边形BMA N 1是平行四边形, 所以BN A M //1,又⊄BN 平面ACM 1,⊂A M 1平面ACM 1, 所以BN //平面ACM 1,又1=BN C N N ,所以平面BGN //平面ACM 1, 又⊂BG 平面BGN ,所以BG 平面ACM 1.(2)由(1)知BG平面ACM 1, 所以==−−−V V V G A MC B A MC A BMC 111, 三棱锥−A BMC 1的高=A A 21,△=⋅=⨯⨯=S BM AC BMC 2212111, 所以△==⋅=⨯⨯=−−V V AA S G A MC A BMC BMC 33321112111. 14.(2023高一下·重庆沙坪坝·百强名校期末)在直三棱柱111ABC A B C 中,=AB 3,=BC 4,=AA 21,︒∠=ABC 90,点D 为AC 的中点.(1)求证:AB 1//平面C BD 1; (2)求三棱锥−B BDC 11的体积. 【答案】(1)证明见详解 (2)2【分析】(1)根据线面平行的判定定理分析证明;(2)根据题意可证⊥AB 平面BCC B 11,再利用转换顶点法求体积. 【详解】(1)连接B C 1交BC 1于点O ,连接DO , 因为BCC B 11为平行四边形,则O 为B C 1的中点, 且点D 为AC 的中点,则AB 1//DO ,又因为⊄AB 1平面C BD 1,⊂DO 平面C BD 1, 所以AB 1//平面C BD 1.(2)因为⊥BB 1平面ABC ,⊂AB 平面ABC ,所以⊥BB AB 1, 又因为⊥AB BC , 且BB BC B =1,⊂BB BC ,1平面BCC B 11,所以⊥AB 平面BCC B 11,且点D 为AC 的中点,故三棱锥−D BB C 11的高为=AB 2213,所以三棱锥−B BDC 11的体积==⨯⨯⨯⨯=−−V V B BDC D BB C 3222421311111.15.(2023·江苏苏州·百强名校期末)如图,在三棱锥P ABC −中,ABC 是边长为等边三角形,且===PA PB PC 6,⊥PD 平面ABC ,垂足为⊥D DE ,平面PAB ,垂足为E ,连接PE 并延长交AB 于点G .(1)求二面角P AB C 的余弦值;(2)在平面PAC 内找一点F ,使得⊥EF 平面PAC ,说明作法及理由,并求四面体PDEF 的体积.【答案】(2)答案见解析,34.【分析】(1)根据条件确定∠PGD 就是二面角PAB C 的平面角,构造三角形求解;(2)根据给定的条件知⊥PB 平面PAC ,过点E 作PB 的平行线与P A 交于F ,则⊥EF 平面P AC ,再求出三棱锥−P EFD 的底面积和高即可.【详解】(1)PA PB PC ==,并且ABC 是等边三角形,∴三棱锥P ABC −是正三棱锥,D 是ABC 的中心,点G 是AB 边的中点;由⊥PD 平面ABC , ⊥DE 平面PAB ,⊂AB 平面PAB ,可知⊥⊥⋂=AB PD AB DE PD DE D ,,,⊂PD 平面PDG ,⊂DE 平面PDG ,所以⊥AB 平面PDG ,进而得⊥⊥AB PG AB DG ,, 所以∠PGD 就是二面角PAB C 的平面角,又ABC 是边长为===PA PB PC 6,+=PA PB AB 222,PAB ∴是等腰直角三角形,同理△△PAC PBC ,都是等腰直角三角形;∴==PG AB 21===GD CG 3311∠==PG PGD GD cos P AB C ;(2),,,PB PC PB PA PA PC P PA ⊥⊥=⊂平面PAC ,⊂PC 平面PAC , ∴⊥PB 平面PAC ,同理⊥PC 平面PAB ,又⊥DE 平面PAB ,∴ED PC //,∴E 与点P ,D ,C 共面,即E 点在线段PG 上,又,2EDGPGC ED PC ∴==31,===PG CG PE PE CD 3,2∠=APG 4π,过E 点在平面P AB 内作PB 的平行线,与P A 交于F ,则⊥EF 平面PAC , PEF 也是等腰直角三角形,==EF2, 又⊥DE 平面P AB ,⊂EF 平面P AB ,∴⊥DE EF ,将PEF 作为底面,则ED 是三棱锥−D PEF 的高,11143323P DEF D PEF PEFV V SDE ∴===⨯⨯⨯⨯=−−222,即四面体PDEF 的体积为34.16.(2023·上海嘉定·百强名校期末)在长方体−ABCD A B C D 1111中,==AD DD 11,=AB E 、F 、G 分别为AB 、BC 、C D 11的中点.(1)求三棱锥−A GEF 的体积;(2)点P 在矩形ABCD 内,若直线D P //1平面EFG ,求线段D P 1长度的最小值.【答案】【分析】(1)等体积由=−−V V A GEF G AEF 可得.(2)先证平面EFG //平面ACD 1,则由直线D P //1平面EFG 可得点P 在直线AC 上,进而可得线段D P 1长度的最小值【详解】(1)依题意有AEFSAE BF =⋅⋅=⋅=22228111,所以三棱锥−A GEF 的体积1133A GEF G AEF AEFV V SDD ==⋅⋅==−−11 (2)如图,连结D A D C AC ,,11,∵E F G ,,分别为AB BC C D ,,11的中点,∴⊄AC EF EF //,平面ACD 1,⊂AC 平面ACD 1, ∴EF //平面ACD ,1∵⊄EG AD EG //,1平面ACD 1,⊂AD 1平面ACD 1,∴EG //平面ACD 1, ∵EFEG E =,∴平面EFG //平面ACD 1,∵D P //1平面EFG ,∴点P 在直线AC 上,在△ACD 1中,AD AC CD ===2,211,1AD CS==21∴当⊥D P AC 1时,线段D P 1的长度最小,最小值为△⨯⨯AC S AD C 22211=21=2. 17.(2023高一下·安徽合肥·百强名校期末)在多面体ABCDE 中,=BC BA ,DE BC //,AE ⊥平面BCDE ,=BC DE 2,F 为AB 的中点.(1)求证:EF //平面ACD ;(2)若==EA EBCD ,求二面角−−B AD E 的平面角正弦值的大小. 【答案】(1)证明见解析【分析】(1)取AC 中点G ,连接DG FG ,,由已知得四边形DEFG 是平行四边形,由此能证明EF //平面ACD .(2)过点B 作BM 垂直DE 的延长线于点M ,过M 作⊥MH AD ,垂足为H ,连接BH ,则∠BHM 是二面角−−B AD E 的平面角,由此即可求出二面角−−B AD E 的正弦值的大小.【详解】(1)证明:取AC 中点G ,连接DG ,FG .因为F 是AB 的中点,所以FG 是ABC 的中位线, 则∥FG BC ,=FG BC 21,所以∥FG DE ,=FG DE , 则四边形DEFG 是平行四边形,所以∥EF DG ,又⊄EF 平面ACD ,⊂DG 平面ACD ,故∥EF 平面ACD . (2)过点B 作BM 垂直DE 的延长线于点M ,因为AE ⊥平面BCDE ,⊂BM 平面ADE ,所以⊥AE BM , 且⊥BM DE ,、DE AE平面ADE ,DEAE E =,则⊥BM 平面ADE ,⊂AD 平面ADE ,⊥BM AD , 过M 作⊥MH AD ,垂足为H ,连接BH ,、⊂BM MH 平面BMH ,BM MH M =,则⊥AD 平面BMH ,所以⊥AD BH ,则∠BHM 是二面角−−B AD E 的平面角.设=DE a ,则==BC AB a 2,在△BEM 中,=EM a2,=BE ,所以=BM .又因为△△∽ADE MDH ,所以=HM ,则∠=BHM 6tan∴∠=BHM 13sin . 18.(2023高一下·浙江绍兴·百强名校期末)如图,四棱锥−P ABCD 中,∠=∠=︒ABC BCD 90,∆PAD 是以AD 为底的等腰直角三角形,===AB BC CD 224,E为BC 中点,且=PE(Ⅰ)求证:平面⊥PAD 平面ABCD ; (Ⅱ)求直线PE 与平面PAB 所成角的正弦值.【答案】(Ⅰ)见解析(Ⅱ【分析】(Ⅰ) 过P 作AD 垂线,垂足为F ,由=+PE PF FE 222得,︒∠=PFE 90.又⊥PF AD ,可得⊥PF 平面ABCD ,即可证明.(Ⅱ)易得E 到平面PAB 距离等于F 到平面PAB 距离.过F 作AB 垂线,垂足为G ,在∆PFG 中,过F 作PG 垂线,垂足为Q ,可证得:⊥FQ 平面PAB .求得:FQ ,从而==θPE FQ sin ,即可求解. 【详解】(Ⅰ) 过P 作AD 垂线,垂足为F ,由=+PE PF FE 222得,︒∠=PFE 90. 又⊥PF AD ,∴⊥PF 平面ABCD , ∴平面⊥PAD 平面ABCD ;(Ⅱ)∵EF AB //,∴E 到平面PAB 距离等于F 到平面PAB 距离. 过F 作AB 垂线,垂足为G ,在∆PFG 中,过F 作PG 垂线,垂足为Q , 可证得:⊥FQ 平面PAB .求得:=FQ ,从而=θPE FQ sin即直线PE 与平面PAB【点睛】本题考查面面垂直的证明,考查线面角的求解、是中档题.19.(2023高一下·湖南长沙·百强名校期末)已知正三棱柱111ABC A B C 中,=AB 2,M是B C 11的中点.(1)求证:AC //1平面A MB 1;(2)点P 是直线AC 1上的一点,当AC 1与平面ABC 所成的角的正切值为2时,求三棱锥−P A MB 1的体积. 【答案】(1)证明见解析【分析】(1)连接AB 1交A B 1于点N ,连接MN ,利用中位线的性质可得出MN AC //1,再利用线面平行的判定定理可证得结论成立;(2)利用线面角的定义可求得CC 1的长,分析可知点P 到平面A MB 1的距离等于点C 1到平面A MB 1的距离,可得出==−−−V V V P A MB C A MB B A C M 11111,结合锥体的体积公式可求得结果. 【详解】(1)证明:连接AB 1交A B 1于点N ,连接MN ,因为四边形AA B B 11为平行四边形,⋂=AB A B N 11,则N 为AB 1的中点, 因为M 为B C 11的中点,则MN AC //1,1AC ⊄平面A MB 1,⊂MN 平面A MB 1,故AC //1平面A MB 1.(2)解:因为⊥CC 1平面ABC ,∴AC 1与平面ABC 所成的角为∠CAC 1, 因为ABC 是边长为2的等边三角形,则=AC 2,1CC ⊥平面ABC ,⊂AC 平面ABC ,∴⊥CC AC 1,则∠==ACCAC CC tan 211, 所以,==CC AC 241,1//AC 平面A MB 1,∈P AC 1,所以,点P 到平面A MB 1的距离等于点C 1到平面A MB 1的距离,因为M 为B C 11的中点,则△△===S S A MC A B C 22211211111则△===⋅=⨯−−−V V V BB S P A MB C A MB B A C M A C M 3341111111111. 20.(2023高一下·湖南长沙·百强名校期末)如图,在棱长为3的正方体ABCD −A'B'C'D'中,M 为AD 的中点.(1)求证:'DB //平面'BMA ;(2)在体对角线'DB 上是否存在动点Q ,使得AQ ⊥平面'BMA ?若存在,求出DQ 的长;若不存在,请说明理由. 【答案】(1)证明见解析 (2)【分析】(1)连接'AB 交'BA 于点E ,连接EM ,证得'EM DB //,结合线面平行的判定定理,即可证得'DB //面'BMA .(2)根据题意,证得BA ⊥'平面'ADB ,得到平面⊥'BMA 平面'ADB ,作⊥'AQ DB ,利用面面垂直的性质,证得⊥AQ 平面'BMA ,再由△△∽'ADB QDA Rt Rt ,即可求得DQ 的长. 【详解】(1)证明:连接'AB ,交'BA 于点E ,连接EM . 因为四边形''ABB A 是正方形,所以E 是'AB 的中点, 又M 是AD 的中点,所以'EM DB //,因为⊂EM 面'BMA ,/⊂'DB 面'BMA ,所以'DB //面'BMA .(2)在对角线'DB 上存在点Q ,且=DQ ⊥AQ 平面'BMA , 证明如下:因为四边形''ABB A 是正方形,所以⊥''AB BA , 因为⊥AD 平面''ABB A ,⊂'BA 面''ABB A ,所以⊥'AD BA , 因为AB AD A =',且⊂'AB AD ,平面'ADB ,所以BA ⊥'平面'ADB ,因为⊂'BA 平面'BMA ,所以平面⊥'BMA 平面'ADB , 作⊥'AQ DB 于Q ,因为'EM DB //,所以⊥AQ EM ,因为⊂AQ 平面'ADB ,平面'ADB 平面='BMA EM ,所以⊥AQ 平面'BMA ,由△△∽'ADB QDA Rt Rt ,可得'==DB DQ AD 2所以当=DQ ⊥AQ 平面'BMA .21.(2023高一下·湖南长沙·百强名校期末)如图,在四棱锥P −中,底面ABCD 为正方形,侧面ADP 是正三角形,侧面ADP ⊥底面ABCD ,M 是DP 的中点.(1)求证:AM ⊥平面CDP ;(2)求直线BP 与底面ABCD 所成角的正弦值. 【答案】(1)证明见解析【分析】(1)先证得⊥AM DP ,由⊥CD AD ,结合面面垂直的性质,证得⊥CD 平面ADP ,进而得到⊥CD AM ,利用线面垂直的判定定理,即可证得⊥AM 平面CDP ; (2)取AD 的中点E ,连BE ,EP ,证得⊥PE 平面ABCD ,得到∠EBP 是所求直线与平面所成角,在直角△BEP 中,即可求解.【详解】(1)证明:因为侧面ADP 为正三角形,且M 为DP 中点,所以⊥AM DP , 又因为底面ABCD 为正方形,所以⊥CD AD .因为平面⊥ADP 平面ABCD 且平面⋂ADP 平面=ABCD AD ,⊂CD 平面ABCD , 所以⊥CD 平面ADP ,又因为⊂AM 平面ADP ,所以⊥CD AM , 因为CDDP D =,且⊂CD DP ,平面CDP ,所以⊥AM 平面CDP .(2)解:取AD 的中点E ,连BE ,EP ,因为△ADP 为正三角形,且E 为AD 中点,所以⊥PE AD ,又因为平面⊥ADP 平面ABCD ,平面⋂ADP 平面=ABCD AD ,且⊂PE 平面PAD , 所以⊥PE 平面ABCD ,所以∠EBP 是所求直线与平面所成角,不妨设=AD a 2,则在等边△ADP 中,可得EP =,在直角ABE 中,==BE ;在直角中,=BP ,故∠==BP EBP EP sin所以直线与底面22.(2023高一下·浙江·百强名校期末)如图,正三棱柱的底面边长为2,高,过的截面与上底面交于PQ ,且点是棱A C 11的中点,点在棱上.(1)试在棱上找一点,使得QD //平面,并加以证明;(2)求四棱锥−C ABQP 的体积. 【答案】(1)点为棱的中点,证明见解析;(2)43.【分析】(1)证法1:取的中点,连接DM ,B M 1,可得A B //11平面ABQP ,再由线面平行的性质可得A B PQ //11,则可得是棱的中点,由三角形中位线定理结合已知可得四边形DMB Q 1是平行四边形,可得QD B M //1,然后由线面平行的判定定理可证得结论;证法2:由已知条件可证得PQ //平面,从而得PDAA 1是平行四边形,PD AA //1,由线面平行的判定可得PD //面,从而得面PDQ //面,再由面面平行的性质可得结论; (2)解法一:连接,四棱锥−C ABQP 可视为三棱锥−C BPQ 和−C ABP 组合而成,然后分别求出两个三棱锥的体积即可;解法二:分别取和的中点,,连接,CM ,连接C N 1交PQ 于点,连接MG ,CG ,可证得平面⊥ABQP 平面CMNC 1,则⊥CG 平面ABQP ,然后结合已知条件求出等腰梯形ABQP 的面积,从而可求得四棱锥的体积【详解】(1)证法1:点为棱的中点,证明如下:取的中点,连接DM ,B M 1.∵AB A B //11,平面ABQP ,⊄A B 11平面ABQP ,∴A B //11平面ABQP ,∵平面,平面ABQP 平面=A B C PQ 111,∴A B PQ //11.又是棱A C 11的中点,∴是棱的中点,∴QB 1∥,=QB BC 211 ∵,分别为棱,的中点,∴DM ∥,=DM BC 21∴QB 1∥DM ,=QB DM 1∴四边形DMB Q 1是平行四边形,∴QD B M //1, ∵⊂B M 1平面,⊄OD 平面,∴QD //平面.证法2:为的中点时,QD //平面.证明如下: ∵AB //平面,平面ABQP ,平面ABQP 平面=A B C PQ 111,∴PQ AB //,⊄PQ 平面,平面,所以PQ //平面,又∵为的中点,为A C 11的中点,∴PDAA 1是平行四边形,∴PD AA //1,又∵⊄PD 平面,⊂AA 1平面,∴PD //面,又∵与PQ 在平面PDQ 内相交,∴面PDQ //面,又∵⊂QD 面PDQ ,∴DQ //平面.(2)解法一:连接,四棱锥−C ABQP 可视为三棱锥−C BPQ 和−C ABP 组合而成,三棱锥−C ABP 可视为,底面积ABCS==22,设=−V V C BAP 1,体积为==V 32111.三棱锥−C BPQ 与−C ABP 等高,体积比为底面积之比,设=−V V C BPQ 2,则△△===V V S S PQ AB BPQ BAP :::1:221,故==V V 241121,因此,=+=−V V V C ABPQ 4312,即为所求. 解法二:分别取和的中点,,连接,CM ,连接C N 1交PQ 于点,连接MG ,CG . ∵和是正三角形,且,分别是和的中点, ∴⊥CM AB ,且CM ∥C N 1,=CM C N 1,则,,,四点共面.∵平面,平面,∴⊥CC AB 1,又平面CMNC 1,⊂CC 1平面CMNC 1,⋂=CM CC C 1,∴平面CMNC 1,∵平面ABQP ,∴平面⊥ABQP 平面CMNC 1.在矩形CMNC 1中,==MN CC 1===CN CM AB 1∴===C G NG CC MN 11,∴∠=∠=︒C GC NGM 451,且==CG 1,∴∠=︒CGM 90,即⊥CG MG .又平面⊥ABQP 平面CMNC 1,平面ABQP 平面=CMNC MG 1,⊂CG 平面CMNC 1,∴⊥CG 平面ABQP .在等腰梯形ABQP 中,==PQ A B 21111,,===BQ AP∴等腰梯形ABQP 的高=h , ∴四棱锥−C ABQP 的体积形梯=⋅=⨯+⨯V CG S CG PQ AB hABQP 332111)(=+=32412113)(.23.(2023高一下·广西玉林·百强名校期末)在如图所示的七面体AA B C D C 1111中,四边形A B C D 1111为边长为2的正方形, ⊥AA 1平面A B C D 1111,∥CC AA 11,且==CC AA 211,,,分别是C C 1,,的中点.(1)求点到平面MNP 的距离;(2)若直线A C 11交PN 于点,直线交平面MNP 于点,证明:,,三点共线.【答案】(1)(2)证明见解析【分析】(1)利用三棱锥体积转换思想,先求三棱锥−C MNP 1的体积,再确定底面积△MNP ,最后得点到平面MNP 的距离即可【详解】(1)解:==⨯⨯⨯⨯=−−V V C MNP M C NP 32611111111记到平面MNP 的距离为d ,在△MNP 中,===MN NP MP △==S MNP 2221,∴△==−S d V MNPC 31MNP 1,(2)证明:∵∥AA CC 11, ∴与确定平面AA C C 11,∵,∈E 平面AA C C 11,且,∈E 平面MNP ,∴平面AAC C11平面=PMN ME ,∵⋂AC 1平面=MPN F ,∴∈F 平面PMN ,∈F 平面AA C C 11, ∴点在直线上,则,,三点共线.24.(2023高一下·福建泉州·百强名校期末)如图所示,在四棱锥中,已知P A ⊥底面ABCD ,且底面ABCD 为梯形,,,====PA AD BC AB 33,点E 在线段PD 上,=PD PE 3.(1)求证:CE //平面P AB ; (2)求证:平面P AC ⊥平面PCD . 【答案】(1)证明见解析 (2)证明见解析【分析】(1)由线面平行的判定定理证明即可; (2)由线面垂直与面面垂直的判定定理证明即可【详解】(1)(1)过E 作EF AD //交P A 于点F ,连接BF , 因为,所以EF BC //.又=PD PE 3,所以=AD EF 3. 又=AD BC 3,所以所以四边形BCEF 为平行四边形, 所以CE BF //,又CE ⊄平面P AB ,BF ⊂平面P AB , 所以CE //平面P AB .。
新人教版高一数学必修2试题立体几何

高一数学(必修2)立体几何试题参考公式一、选择题(本大题共10小题,每小题4分,共40分,将答案直接填在下表中)(1)下列命题为真命题的是()(A)平行于同一平面的两条直线平行(B)垂直于同一平面的两条直线平行(C)与某一平面成等角的两条直线平行(D)垂直于同一直线的两条直线平行(2)若一个角的两边分别和另一个角的两边平行,那么这两个角()(A)相等(B)互补(C)相等或互补(D)无法确定(3)正三棱锥的底面边长为2,侧面均为直角三角形,则此棱锥的体积为()(A(B(C(D(4)已知PD⊥矩形ABCD所在的平面,图中相互垂直的平面有()(A)2对(B)3对(C)4对(D)5对(5)如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是()(A)2(B)12+(C)22+(D)1(C)(1,3,5)(D)(-1,-3,5)二、填空题(本大题共6小题,每小题4分,共24分)(11)底面直径和高都是4cm的圆柱的侧面积为cm2.(12)若两个球的表面积之比是4∶9,则它们的体积之比是.(13)图①中的三视图表示的实物为_____________;PA B CD图②为长方体积木块堆成的几何体的三视图,此几何体共由_______块木块堆成.三、解答题(本大题共4小题,共36分.解答应写出文字说明、演算步骤或推证过程) (17)(本小题满分9分)如图,O 是正方形ABCD 的中心, PO ⊥底面ABCD ,E 是PC 的中点.求证:(Ⅰ)P A ∥平面BDE ;(Ⅱ)平面P AC ⊥平面BDE .(18)(本小题满分9分)已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和. (Ⅰ)求该圆台的母线长; (Ⅱ)求该圆台的体积.高一数学(必修2)训练题参考答案一、选择题二、填空题(11)π16 (12)8∶27 (13)圆锥;4 (14)60° (15)(0,3) (16)8 三、解答题 (17) 证明:(Ⅰ)连结EO ,在△P AC 中,∵O 是AC 的中点,E 是PC ∴OE ∥AP . 又∵OE ⊂平面BDE , P A ⊄平面BDE , ∴P A ∥平面BDE .(Ⅱ)∵PO ⊥底面ABCD ,∴PO ⊥BD .图①正视图 左视图俯视图 正视图 左视图又∵AC ⊥BD ,且AC PO =O , ∴BD ⊥平面P AC . 而BD ⊂平面BDE , ∴平面P AC ⊥平面BDE .(18)解:(Ⅰ)设圆台的母线长为l ,则圆台的上底面面积为224S ππ=⋅=上, 圆台的下底面面积为2636S ππ=⋅=下, 所以圆台的底面面积为40S S S π=+=下上 又圆台的侧面积(26)8S l l ππ=+=侧,于是840l ππ=,即5l =为所求.(Ⅱ)由(Ⅰ)可求得,圆台的高为3h ==.∴ (13V S S h =++圆台下上=(143633ππ+⋅=52π.。
高一数学立体几何综合试题答案及解析

高一数学立体几何综合试题答案及解析1.等腰梯形,上底,腰,下底,以下底所在直线为x轴,则由斜二测画法画出的直观图的面积为_______.【答案】【解析】如上图,,,,因为,所以,所以,在直观图中,【考点】斜二测画法2.在四边形中,∥,,将沿折起,使平面平面,构成三棱锥,则在三棱锥中,下列命题正确的是()A.平面平面B.平面平面C.平面平面D.平面平面【答案】D【解析】∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD.故CD⊥平面ABD,则CD⊥AB,又AD⊥AB,故AB⊥平面ADC,所以平面ABC⊥平面ADC.故选D.【考点】折叠问题,垂直关系。
点评:中档题,对于折叠问题,要特别注意“变”与“不变”的几何元素,及几何元素之间的关系。
3.已知、是不同的平面,、是不同的直线,则下列命题不正确的()A.若∥则B.若∥,则∥C.若∥,,则D.若则∥【答案】B【解析】A项中∥;B项中直线,可能平行可能异面;C项依据线面垂直的判定定理可知成立;D项依据垂直于同一直线的两平面平行可知结论正确【考点】空间线面间平行垂直的判定点评:本题用到了判定定理有:一个平面经过另一平面的一条垂线则两面垂直,两条平行直线中的一条垂直于平面则另一条也垂直于平面,垂直于同一直线的两平面平行4.①分别与两条异面直线都相交的两条直线一定是异面直线;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中为真命题的是()A.①和②B.②和④C.③和④D.②和③【答案】B【解析】解:因为①分别与两条异面直线都相交的两条直线一定是异面直线;可能平行,因此错误。
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;成立③垂直于同一直线的两条直线相互平行;可能相交,错误④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.成立故选B5.如图,正四棱锥中,侧棱与底面所成角的正切值为.(1)求侧面与底面所成二面角的大小;(2)若E是PB中点,求异面直线PD与AE所成角的正切值.【答案】(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,∴∠PAO就是PA与底面ABCD所成的角,∴ tan∠PAO=.设AB=1,则PO=AOtan∠PAO =.设F为AD中点,连FO、PF,易知OF⊥AD,PF⊥AD,所以∠PAO就是侧面PAD与底面ABCD所成二面角的平面角.在Rt中,,∴,即侧面PAD与底面ABCD所成二面角的大小为;(2)连结EO,由于O为BD中点,E为PD中点,所以.∴就是异面直线PD与AE所成的角.在Rt中,.∴.由,可知面.所以,在Rt中,,即异面直线PD与AE所成角的正切值为.【解析】略6.(本小题满分16分)如图,多面体中,两两垂直,平面平面,平面平面,.(1)证明四边形是正方形;(2)判断点是否四点共面,并说明为什么?(3)连结,求证:平面.【答案】证明:(1)…………..2分同理,……..3分则四边形是平行四边形.又四边形是正方形. ……..4分(2) 取中点,连接.在梯形中,且.又且,且.……………………..5分四边形为平行四边形, ……………………..6分. ……………………..7分在梯形中,, ……………………..9分四点共面. …………………….10分(3)同(1)中证明方法知四边形BFGC为平行四边形.且有,从而,. ……………………..12分又故,而,故四边形BFGC为菱形, . ……………………..14分又由知.正方形中,,故.. ……………………..16分【解析】略7.(本小题満分12分)如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.(Ⅰ)证明AD⊥D1F;(Ⅱ)求AE与D1F所成的角;(Ⅲ)证明面AED⊥面A1FD1;【答案】(Ⅰ)∴AD⊥D1F(Ⅱ)∴AE⊥D1FAE与D1F所成的角为900(Ⅲ)由以上可知D1F⊥平面AED∴面AED⊥面A1FD1;【解析】略8.(本小题满分12分)如图,在三棱柱中,面,,,分别为,的中点.(1)求证:∥平面;(2)求证:平面;(3)直线与平面所成的角的正弦值.【答案】(1)证明:连结,与交于点,连结.因为,分别为和的中点,所以∥.又平面,平面,所以∥平面.(2)证明:在直三棱柱中,平面,又平面,所以.因为,为中点,所以.又,所以平面.又平面,所以.因为四边形为正方形,,分别为,的中点,所以△≌△,.所以.所以.又,所以平面.(3)设CE与C1D交于点M,连AM由(2)知点C在面AC1D上的射影为M,故∠CAM为直线AC与面AC1D所成的角,又A1C1//AC所以∠CAM亦为直线A1C1与面AC1D所成的角。
高一数学立体几何综合试题

高一数学立体几何综合试题1.如图是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在的直线是异面直线的有()A.1对B.2对C.3对D.4对【答案】C【解析】如图所示:把展开图再还原成正方体,由经过平面外一点和平面内一点的直线和平面内不进过该点的直线是异面直线可得,AB,CD,EF,GH这四条线段所在直线是异面直线的有:AB和 CD,AB 和 HG,EF 和 HC,共三对,故选 C.【考点】展开图还原几何体,异面直线.2.如图,三棱柱的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。
(I)求证:B1C//平面AC1M;(II)求证:平面AC1M⊥平面AA1B1B.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)由三视图还原为空间几何体的实际形状时,要从三视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体的实际形状时,一般以正视图和俯视图为主,结合侧视图进行综合考虑;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(3)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.试题解析:证明:(I)由三视图可知三棱柱为直三棱柱,底面是等腰直角三角形且,连结A1C,设。
连结MO,由题意可知A1O=CO,A1M=B1M,所以 MO//B1C.又平面;平面,所以平面 6分(II),又为的中点,平面,平面又平面所以平面AC1M⊥平面AA1B1B 12分【考点】(1)直线与平面平行的判定;(2)平面与平面垂直的判定.3.如图所示,直观图四边形是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A.B.C.D.【答案】A【解析】由题可得A¢D¢=A¢B¢=1,B¢C¢=1+,所以原平面图形中AD=1,AB=2,BC=1+,根据梯形的面积计算公式可得【考点】斜二测画法.4.在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形,则实数x的值为()A.-2B.2C.6D.2或6【答案】D【解析】因为在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形.所以可得.有空间两点间的距离公式可得,解得.故选D.【考点】1.空间中的两点的距离公式.2.解二次方程的能力.5.如图,空间四边形的对棱、成的角,且,平行于与的截面分别交、、、于、、、.(1)求证:四边形为平行四边形;(2)在的何处时截面的面积最大?最大面积是多少?【答案】(1)利用线面平行的性质得到线线平行,然后再利用平行四边形的定义即可证明.(2)当E为AB的中点时,截面面积最大,,【解析】(1)平面,平面,平面平面,.同理,,同理,四边形为平行四边形.(2)与成角,或,当E为AB的中点时,截面面积最大,,【考点】本题考查了线面平行的性质及平行四边形的概念、面积点评:证明两直线平行的方法有:①依定义采用反证法;②利用公理4;③线面平行的性质定理;④面面平行的性质定理6.如图:是⊙的直径,垂直于⊙所在的平面,PA="AC," 是圆周上不同于的任意一点,(1) 求证:平面。
高一数学立体几何综合试题答案及解析

高一数学立体几何综合试题答案及解析1.在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形,则实数x的值为()A.-2B.2C.6D.2或6【答案】D【解析】因为在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形.所以可得.有空间两点间的距离公式可得,解得.故选D.【考点】1.空间中的两点的距离公式.2.解二次方程的能力.2.如图:是⊙的直径,垂直于⊙所在的平面,PA="AC," 是圆周上不同于的任意一点,(1) 求证:平面。
(2) 求二面角 P-BC-A 的大小。
【答案】(1)利用线面垂直的性质可得线线垂直,再利用线面垂直的判定定理,可得结论;(2)∠PCA=450【解析】试题分析(1)利用线面垂直的性质可得线线垂直,再利用线面垂直的判定定理,可得结论;(2)利用二面角的求解。
因为因为PA⊥平面ABC,且BC⊂平面ABC,所以PA⊥BC.又△ABC中,AB是圆O的直径,所以BC⊥AC.、又PA∩AC=A,所以BC⊥平面PAC.(2)在第一问的基础上,由于是⊙的直径,垂直于⊙所在的平面,PA="AC," 是圆周上不同于的任意一点,那么可知二面角 P-BC-A 的大小450【考点】空间图形的位置关系点评:本题考查直线与平面垂直的判定定理,平面与平面垂直的判定定理,考查空间图形的位置关系,属于中档题.3.已知正方体中,面中心为.(1)求证:面;(2)求异面直线与所成角.【答案】(1)对于线面平行的证明一般要利用其判定定理来求证。
(2)【解析】(1)证明:连结,设,连结,则四边形为平行四边形,∴又∵,∴面. 6分(2)解:由(1)可知,为异面直线与所成角(或其补角),设正方体的边长2,则在中,,,,∴为直角三角形,∴. 6分【考点】异面直线的角,线面平行点评:解决的关键是熟练的根据几何中的性质定理和判定定理来求解,属于基础题。
4.、经过空间一点作与直线成角的直线共有()条A.0B.1C.2D.无数【答案】D【解析】若点P在直线l上,可以做无数条直线与直线l成角,这些线成一个圆锥形状.若点P不在直线l上,可以过点P作一条直线与l平行,然后以为一个圆锥的高,P为圆锥的顶点,其中母线与轴角,所以能做无数条.5.已知a、b是两条异面直线,c∥a,那么c与b的位置关系()A.一定是异面B.一定是相交C.不可能相交D.不可能平行【答案】D【解析】解:6.已知两直线m、n,两平面α、β,且.下面有四个命题( )(1)若; (2);(3; (4).其中正确命题的个数是A.0B.1C.2D.3【答案】C【解析】,所以,则存在有。
立体几何测试题(共10篇)

立体几何测试题(共10篇)立体几何测试题(一): 立体几何问题立体几何试题已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.1.EF平行于B1D1,B1D1平行于BD,所以EF平行于BD,EFBD四点共面2.F,D,A,C1属于平面A1ACC1,且AC1与PQ不平行,所以AC1与PQ相交A1C交平面DBFE于R点,又因为PQ属于平面DBFE,所以AC1与PQ相交于R 所以R属于PQ,PQR共线立体几何测试题(二): 几个书后练习题立体几何1.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.是否正确2.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.为什么不对谢不对,因为a有可能在经过b的面上,不是平行关系立体几何测试题(三): 一道数学基本的立体几何的题目~在正方形ABCD-A"B"C"D"中,P、Q分别为A"B"、BB"的中点.(1)求直线AP与CQ所成的角的大小(2)求直线AP与BD所成的角的大小我还没学过空间向量,1.取DC中点E,连EC,证明EC平行AP,用余弦定理算2.取AB中点F,连接FB,用余弦定理算【立体几何测试题】立体几何测试题(四): 求大量立体几何难题!立体几何综合试题(自己画图)1、已知正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点.(1)求证:DE‖平面A1B1C1;(2)求二面角A1—DE—B1的大小.2、已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF =BC=2a.(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么证明你的结论3、在底面是直角梯形的四棱锥中,AD‖BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a.(I)求二面角P—CD—A的正切值;(II)求点A到平面PBC的距离.4、在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.5、已知四棱锥P—ABCD,底面ABCD是菱形,平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值6.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P 在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.7、在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明平面;(II)证明平面EFD;(III)求二面角的大小.8、已知在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(I)试确定点F的位置,使得D1E⊥平面AB1F;(II)当D 1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).9、直四棱柱ABCD-A1B1C1D1的底面是梯形,AB‖CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点.点P到直线AD1的距离为⑴求证:AC‖平面BPQ⑵求二面角B-PQ-D的大小10、已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心.(Ⅰ)证明:AF⊥平面FD1B1;(Ⅱ)求异面直线EB与O1F所成角的余弦值;这些题应该还可以!你来试试吧!题不要求多就精就可以了!不懂的或不会做的,我来帮你解答!立体几何测试题(五): 立体几何初步练习题已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱B1C1,C1D1,A1B1,D1A1的中点,求证(1)MN平行于DEF,(2)平面AMN平行于平面CEF(1)连接B1D1因为MN、EF为三角形A1B1D1、B1C1D1的中位线,所以MN平行于EF因为MN不属于面DEF,EF属于面DEF所以MN平行于面DEF(2)这题题目错了吧,应该是DEF吧立体几何测试题(六): 解析几何基础知识练习题靠!一楼的那么多废话那么多选择题:集合,函数(图像),立体几何,圆锥一、数学命题原则 1.普通高等学校招生数学科的考试,按照“考查基础知识的【立体几何测试题】立体几何测试题(七): 高一必修二立体几何习题1-7的题仓库的房顶呈正四棱锥形,量的地面的边长为2.6m,侧棱长2.1m,先要在房顶上铺一层油毡纸,问:需要油毡纸的面积多少运用海伦公式房顶为4个相同的三角形海伦公式a=2.6 b=2.1 c=2.1 p=a+b+c/2=3.4S=根号下p*(p-a)*(p-b)*(p-c)=2.1444S=2.144*4=8.576平方米立体几何测试题(八): 怎么根据题目画数学的立体几何图形搞懂了题目的要求,就照那意思去画,立体几何记住透视很重要.立体几何测试题(九): 求立体几何判断题的解题方法.①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直⑤……等等,诸如此类.见到很多这样的题目,但是却总找不到解题的方法,概念定理也经常记混.本人感激不尽!记一些模型,例如墙角模型什么的这个很重要.遇见不熟悉的题,用书本和笔(手指也可以)比划一下.这种题目主要是找反例!想象力也很重要啦……立体几何测试题(十): 一道高中立体几何的题目.已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,O1是底面A1B1C1D1的中心.E 是CO1上的点,设CE等于X,四棱锥E-ABCD的体积为y,求y关于X的函数关系式..图只有自己画一下了,做EF垂直于平面ABCD 垂足为F易得出CEF相似于O1CC1因为C1O1=根号2 CC1=4 得CO1=3根号2CE/CO1=EF/CC1 得出EF=4X/3根号2Y=底面积*EF/3=4*4X/9根号2Y=8根号2*X/9职高立体几何测试题空间立体几何测试题。
高一立体几何初步测试题及答案

高一立体几何初步测试题及答案1.在空间四点中,无三点共线是四点共面的(充分不必要条件)。
2.若a∥b,b∩c=A,则a,c的位置关系是(相交直线或异面直线)。
3.圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是(等腰直角三角形)。
4.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形,则该几何体的体积为(64)。
5.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是(50π)。
6.已知正方体外接球的体积是π,那么正方体的棱长等于(3)。
7.若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是(若α⊥β,l∈α,n∈β,则l⊥n)。
8.如图,在正方体ABCD-A' B' C' D'中,E,F,G,H分别为AA',AB,BB',B'C'的中点,则异面直线EF与GH所成的角等于(90°)。
9.已知两个平面垂直,其中正确的命题数量是(2)。
10.平面α与平面β平行的条件可以是(直线a//α,a//β)。
三、简答题(本大题共4小题,每小题10分,共40分)1.如何确定一个圆锥的侧面展开图?答:将圆锥展开,使其侧面展开为一段扇形,然后将扇形展开成一个直角三角形,即可得到圆锥的侧面展开图。
2.如何确定一个几何体的三视图?答:俯视图是从正上方看几何体,可以看到几何体的顶面和底面;正视图是从正前方看几何体,可以看到几何体的前面和后面;左视图是从正左方看几何体,可以看到几何体的左面和右面。
通过这三个视图,可以确定一个几何体的形状和尺寸。
3.如何判断两个平面是否平行?答:如果两个平面的法向量平行,则这两个平面平行。
也可以通过判断它们的交线是否平行来确定两个平面是否平行。
4.如何判断两条直线是否相交?答:如果两条直线的方向向量不平行,则它们相交;如果两条直线的方向向量平行但不重合,则它们异面直线;如果两条直线的方向向量重合,则它们可能重合也可能平行。
高一数学立体几何试题答案及解析

高一数学立体几何试题答案及解析1.如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为()A.B.C.D.【答案】A【解析】略2.在正方体ABCD–A1B1C1D1中,已知E是棱C1D1的中点,则异面直线B1D1与CE所成角的余弦值的大小是()A.B.C.D.【答案】D【解析】略3.如图1,正方体中,、是的三等分点,、是的三等分点,、分别是、的中点,则四棱锥的侧视图为()【答案】C【解析】侧视图从左向右投影,对应,对应,对应,对应,因此侧视图为C项【考点】三视图4.已知直线,平面,下列命题正确的是()A.B.C.D.【答案】D【解析】根据两个平面平行的判定定理:一个平面内的两条相交直线和另一个平面平行,则这两个平面平行,符号表示为:;【考点】空间中两个平面平行的判定定理;5.(本小题满分13分)如图,在棱长均为的直三棱柱中,是的中点.(1)求证:平面;(2)求直线与面所成角的正弦值.【答案】(1)见解析;(2).【解析】(1)直三棱柱的侧棱和底面垂直,从而可得到AD⊥BB1,并且AD⊥BC,从而由线面垂直的判定定理可得到AD⊥平面BCC1B1;(2)连接C1D,从而可得到∠AC1D为直线AC1和平面BCC1B1所成角,在Rt△AC1D中,容易求出AD,AC1,从而sin∠AC1D=.试题解析:(1)直三棱柱中,,又,D是BC的中点,,平面;(2)连接,由(1)平面,则即为直线与面所成角,在直角中,,,,.即直线与面所成角的正弦值为.【考点】直线与平面所成的角;直线与平面垂直的判定.6.正方体的表面积为24,则该正方体的内切球的体积为____________.【答案】【解析】正方形边长设为,内切球的直径为2,所以体积为【考点】正方体与球的基本知识7.在正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于()A.30°B.45°C.60°D.90°【答案】B【解析】根据二面角的定义,是所求二面角的平面角,易得:.【考点】二面角8.已知是直线,是平面,下列命题中:①若垂直于内两条直线,则;②若平行于,则内可有无数条直线与平行;③若m⊥n,n⊥l则m∥l;④若,则;正确的命题个数为()A.1B.2C.3D.4【答案】A【解析】①改为垂直于平面内的两条相交直线;②正确;③改为或相交或异面;④改为或异面.故选A.【考点】线与线,面与面,线与面位置关系9.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是________【答案】【解析】直观图中等腰直角三角形斜边长为2,所以两条直角边为,面积为1,因为直观图和平面图面积比为,所以平面图形的面积为【考点】平面直观图10.如图,是一个平面图形的水平放置的斜二测直观图,则这个平面图形的面积等于.【答案】【解析】水平放置的斜二测直观图还原成平面图形如上图,由斜二测画法的定义:平行于轴的线段仍平行于轴,长度不变,平行于轴的线段仍平行于轴,但长度减半,所以,,,所以.【考点】斜二测画法.11.如图,是正方体的棱的中点,给出下列命题①过点有且只有一条直线与直线,都相交;②过点有且只有一条直线与直线,都垂直;③过点有且只有一个平面与直线,都相交;④过点有且只有一个平面与直线,都平行.其中真命题是:A.①②③B.①②④C.①③④D.②③④【答案】B【解析】直线与是两条互相垂直的异面直线,点不在这两异面直线中的任何一条上,如图所示:取的中点,则,且,设与交于,则点共面,直线必与直线相交于某点.所以,过点有且只有一条直线与直线都相交;故①正确;过点有且只有一条直线与直线都垂直,此垂线就是棱,故②正确;过点有无数个平面与直线都相交,故③不正确;过点有且只有一个平面与直线都平行,此平面就是过点与正方体的上下底都平行的平面,故④正确.综上,①②④正确,③不正确,故选B.【考点】1.直线与平面平行的性质;2.平面与平面垂直的性质.【思路点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质,体现了数形结合的数学思想,①需要构造一个过点M且与直线AB、B1C1都相交的平面,就可判断;②利用过空间一点有且只有一条直线与已知平面平行判断;③可举反例,即找到两个或两个以上过点m且与直线AB、B1C1都相交的平面,即可判断.④利用线面平行的性质来判断即可.12.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积________________.【答案】【解析】因为设圆锥的底面半径为,母线为,利用圆锥的底面周长就是圆锥的侧面展开图的弧长,推出底面半径与母线的关系,通过圆锥的表面积求出底面半径,,得,圆锥的高,即圆锥的高为,即圆锥的体积.【考点】锥体的侧面积公式.【思路点睛】设圆锥的底面半径为,母线为,利用圆锥的底面周长就是圆锥的侧面展开图的弧长,推出底面半径与母线的关系,通过圆锥的表面积求出底面半径,求出圆锥的高,然后再根据圆锥的体积公式,即可求出圆锥的体积.13.正六棱柱的底面边长为,侧棱长为1,则动点从沿表面移到点时的最短的路程是.【答案】【解析】如下图所示,作出正六棱柱的展开图,如果动点从经侧面通过移到点时,则路程为;如果动点从经经沿上底面移到点时,根据题目条件,,则路程为;而,所以最短的路程是.【考点】1、棱锥的展开图;2、最值问题.14.若底面为正三角形的几何体的三视图如图所示,则几何体的侧面积为()A.B.C.D.【答案】D【解析】由三视图可知该几何体为底面为正三角形的直三棱柱,底面三角形的高为,棱柱高为4,设底面边长为x,则解得,故几何体的侧面积为故选:D.【考点】三视图,几何体的侧面积15.如下图所示,观察四个几何体,其中判断正确的是()A.①是棱台B.②是圆台C.③不是棱锥D.④是棱柱【答案】D【解析】图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱;很明显③是棱锥,选D.【考点】空间几何体的结构特征.16.在空间直角坐标系中,给定点,若点与点关于平面对称,点与点关于轴对称,则()A.2B.4C.D.【答案】A【解析】由题意知:,,则,故选A.【考点】空间两点间的距离公式.17.某几何体的三视图如图所示(单位:),则该几何体的体积是()A.B.C.D.【答案】C【解析】由三视图可知该几何体的形状是棱长为的正方体上有一个高为的正四棱锥,其体积为.【考点】1、三视图;2、空间几何体的体积.18.(2015秋•大连校级期末)如图,三棱锥P﹣ABC中,平面PAC⊥平面ABC,∠ABC=,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.(1)证明:EF∥BC.(2)证明:AB⊥平面PFE.(3)若四棱锥P﹣DFBC的体积为7,求线段BC的长.【答案】(1)、(2)见解析;(3)BC=3或BC=.【解析】(1)由EF∥面PBC可得出EF∥BC;(2)由PC=PD=CD=4可知△PDC是等边三角形,故PE⊥AC,由平面PAC⊥平面ABC可得PE⊥平面ABC,故PE⊥AB,由EF∥BC,BC⊥AB可得AB⊥EF,从而AB⊥平面PEF;(3)设BC=x,用x表示出四边形DFBC的面积,根据体积列出方程解出x.解:(1)证明:∵EF∥面PBC.EF⊂面ABC,面PBC∩面ABC=BC,∴EF∥BC.(2)∵由CD=DE+EC=4,PD=PC=4,∴△PDC是等边三角形,∴PE⊥AC,又∵平面PAC⊥平面ABC,平面PAC∩面ABC=AC,PE⊂平面PAC,∴PE⊥平面ABC,∵AB⊂平面ABC,∴PE⊥AB,∵∠ABC=,EF∥BC.∴AB⊥EF,又∵PE⊂平面PEF,EF⊂平面PEF,PE∩EF=E,∴AB⊥平面PEF.(3)设BC=x,则AB=,∴=,∵EF∥BC,∴△AFE∽△ABC,∴.∵AD=AE,,∴S=,四边形DFBC由(2)可知PE⊥平面ABC,且PE=,∴V=,解得x=3或者,∴BC=3或BC=.【考点】直线与平面垂直的判定;棱柱、棱锥、棱台的体积.19.(2015秋•鞍山校级期末)如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=.(Ⅰ)求证:AO⊥平面BCD;(Ⅱ)求O点到平面ACD的距离.【答案】(Ⅰ)见解析;(Ⅱ).【解析】(1)连结OC,推导出AO⊥BD,AO⊥OC,由此能证明AO⊥平面BCD.(Ⅱ)设点O到平面ACD的距离为h,由V﹣ACD=V A﹣OCD,能求出点O到平面ACD的距离.O证明:(1)连结OC,∵△ABD为等边三角形,O为BD的中点,∴AO⊥BD.∵△ABD和△CBD为等边三角形,O为BD的中点,,∴.在△AOC中,∵AO2+CO2=AC2,∴∠AOC=90°,即AO⊥OC.∵BD∩OC=0,∴AO⊥平面BCD.解:(Ⅱ)设点O到平面ACD的距离为h.∵V﹣ACD=V A﹣OCD,∴.O在△ACD中,AD=CD=2,.而,,∴.∴点O到平面ACD的距离为.【考点】点、线、面间的距离计算;直线与平面垂直的判定.20.平面截球的球面所得圆的半径为1,球心到平面的距离为,则此球的体积为()A.B.C.D.【答案】B【解析】利用截面圆的性质先求得球的半径长.如图,设截面圆的圆心为,为∴,即球的半径为,∴,故选B.【考点】1、球体的体积;2、球体的性质.【思路点晴】本题考察的是球体的性质,属于中档题目;用平面截球面,得到一个圆,球心到圆心的连线垂直于圆所在的平面,从而得到直角三角形,利用勾股定理即可求出球的半径,再将球的半径代入球的体积公式中,即可求出球的体积.21.某几何体的三视图如图所示,则该几何体的体积为________.【答案】24【解析】由俯视图可以判断该几何体的底面为直角三角形,由正视图和左视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的.在长方体中分析还原,如图(1)所示,故该几何体的直观图如图(2)所示.在图(1)中,,.故几何体的体积为.【考点】1、三视图;2、组合体的体积.【技巧点晴】本题考查的是空间几何体的体积的求法、三视图问题,属于中档题目;要先从三视图的俯视图入手,如果俯视图是圆,几何体为圆锥或三圆柱,如果俯视图是三角形,几何体为三棱柱或三棱锥;根据三视图得出该几何体为三棱柱截去三棱锥后的几何体,用两个体积相减即可.22.如图所示,在四边形ABCD中,AB=AD=CD=1,BD=,BD CD,将四边形ABCD沿对角线BD折成四面体,使平面平面BCD,则下列结论正确的是 .(1);(2);(3)与平面所成的角为;(4)四面体的体积为.【答案】(2)(4)【解析】由BD CD,使平面平面BCD,知平面,所以,又由,得,即,所以平面,即.因此是错误的,是正确的,由上面证明知是与平面所成的角,由知,.故选(2)(4)正确.【考点】命题的真假判断.【名师】折叠问题是考查学生空间想象能力的较好载体.如本题,不仅要求学生象解常规立几综合题一样懂得线线,线面和面面位置关系的判定方法及相互转化,角的作法,还要正确识别出平面图象折叠后的空间图形,更要识得折前折后有关线线、线面位置的变化情况以及有关量(边长与角)的变化情况,否则无法正确解题.这正是折叠问题的价值所在.23.如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=PA,F为PA的中点.(1)求证:PC∥平面BDF.(2)记四棱锥C-PABE的体积为V1,三棱锥P-ACD的体积为V2,求的值.【答案】(1)证明见解析;(2).【解析】(1)要证线面平行,就是要证线线平行,这条平行线就是过的平面与平面的交线,从图中看,设与的交点为,就是要找的平行线,由中位线定理可证得平行;(2)题中四棱锥与三棱锥的体积没有直接的关系,我们可以通过体积公式进行转化,首先,而三棱锥与四棱锥的高相等(同),因此只要求得其底面积之比即可.试题解析:(1)证:连接EF,连接BD交AC与点O,连OF,依题得O为AC中点,又F为PA的中点,所以OF为中位线,所以OF//PC因为所以PC∥平面BDF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修2立体几何测试题
一、选择题(每小题5分)
1、线段AB 在平面α内,则直线AB 与平面α的位置关系是( )
A 、A
B α⊂ B 、AB α⊄
C 、由线段AB 的长短而定
D 、以上都不对
2、下列说法正确的是( )
A 、三点确定一个平面
B 、四边形一定是平面图形
C 、梯形一定是平面图形
D 、平面α和平面β有不同在一条直线上的三个交点 3、垂直于同一条直线的两条直线一定( )
A 、平行
B 、相交
C 、异面
D 、以上都有可能 4、在正方体1111ABCD A B C D -中,下列几种说法正确的是 ( )
A 、11AC AD ⊥
B 、11D
C AB ⊥ C 、1AC 与DC 成45角
D 、11AC 与1B C 成60角 5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是( )
A 、l ∥a
B 、l 与a 异面
C 、l 与a 相交
D 、l 与a 没有公共点 6、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有( )
A 、1
B 、2
C 、3
D 、4 7、在空间四边形ABCD 各边AB BC CD DA 、、、上分别取
E
F
G
H 、、、四点,如果与EF GH 、能相交于点P ,那么( ) A 、点P 必在直线AC 上 B 、点P 必在直线BD 上
C 、点P 必在平面AB
D 内 D 、点P 必在平面ABC 外 8、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有( )
A 、0个
B 、1个
C 、2个
D 、3个 9、一个棱柱是正四棱柱的条件是( )
A 、底面是正方形,有两个侧面是矩形
B 、底面是正方形,有两个侧面垂直于底面
C 、底面是菱形,且有一个顶点处的三条棱两两垂直
D 、底面是正方形,每个侧面都是全等矩形的四棱柱
10、已知二面角AB αβ--的平面角是锐角θ,α内一点C 到β的距离为3,点C 到棱AB
的距离为4,那么tan θ的值等于 ( )
A 、
3
4
B 、
35
C D 二、填空题(每小题5分)
B 1
C 1
A 1D 1
B
A
C
D
11、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体
(填”大于、小于或等于”).
12、正方体1111ABCD A B C D -中,平面11AB D 和平面1BC D 的位置关系为 13、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,则平行四边形ABCD 一定
是 . 14、如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件
_________时,有A 1 B ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
11、 12、 13、 14、
三、解答题(要求写出主要的证明、解答过程)
15、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(10分)
16、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG. 求证:EH ∥BD . (12分) 17、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .(12分)
H G F
E D B A C
S
D C
B A
18、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证:(1)O C 1∥面11AB D ; (2 )1AC ⊥面11AB D . (14分)
一、选择题(每小题5分,共50分)
ACDDD BA B DA
二、填空题(每小题5分)
11、小于 12、平行
13、菱形 14、1111AC B D 对角线与互相垂直
三、解答题(要求写出主要的证明、解答过程)
15、解:设圆台的母线长为l ,则
圆台的上底面面积为224S ππ=⋅=上
圆台的上底面面积为2525S ππ=⋅=下 所以圆台的底面面积为29S S S π=+=下上
又圆台的侧面积(25)7S l l ππ=+=侧 于是725l ππ=
即29
7
l =
为所求. 16、证明:,EH FG EH ⊄面BCD ,FG ⊂面BCD EH ∴面BCD
又EH ⊂面BCD ,面
BCD 面ABD BD =,EH BD ∴
17、证明:
90ACB ∠= BC AC ∴⊥
又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC BC AD ∴⊥ 又,SC AD SC
BC C ⊥=AD ∴⊥面SBC
18、证明:(1)连结11A C ,设11
111AC B D O =
连结1AO
,
1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形
D 1O
D
B A
C 1
B 1
A 1
C
11A C AC ∴且 11A C AC =
又1,O O 分别是11,A C AC 的中点,11
O C AO ∴且11O C AO =
11AOC O ∴是平行四边形
111,C O AO AO ∴⊂面11AB D ,1C O ⊄面11AB D
∴1C O 面11AB D
(2)
1CC ⊥面1111A B C D 11!CC B D ∴⊥
又
1111A C B D ⊥, 1111B D AC C ∴⊥面 1
11AC B D ⊥即 同理可证11A C AB ⊥, 又11
11D B AB B = ∴1A C ⊥面11AB D。
