叠前深度偏移、速度建模、保幅偏移
叠前偏移速度分析方法

叠前偏移速度分析方法叠前偏移是一种常用于地震数据处理中的方法,通过对原始地震数据进行一次波场叠加和反卷积处理,主要用于提高地震剖面分辨率和改善成像质量。
叠前偏移速度是在进行叠前偏移处理时,对地层速度进行精确估计,以便更好地恢复地下结构。
下面将介绍几种常用的叠前偏移速度分析方法。
1.叠前地震偏移速度分析叠前地震偏移速度分析方法的基本原理是拟合地下速度模型,通过将地震数据在多个速度模型上进行偏移处理,分别对比反射事件的位置和形态,找到最佳的速度模型。
这种方法一般采用常规的速度层析技术,将地震道集与速度模型之间进行匹配,通过最小二乘法、全局搜寻等方法调整速度模型的参数,不断优化速度模型,以获得最佳的地下结构成像结果。
2.叠前堆积速度分析叠前堆积速度分析方法是通过将生成的叠前偏移剖面进行叠加,直到消除非叠加区域内的波形差异。
该方法通常用于复杂地质情况下的速度分析,如存在倾斜、断层等情况。
在叠前堆积速度分析过程中,需要进行多次迭代,每次迭代都会生成一个新的叠前偏移剖面,并将其与之前的剖面进行叠加,直到最后产生一个叠加结果,从而获得最佳的速度模型。
3.叠前参数扫描速度分析叠前参数扫描速度分析方法主要用于处理深水区的地震数据,因为深水区的地层速度往往变化较大,且存在不确定性。
该方法通过改变反射面深度等叠前参数,对地震数据进行多次偏移处理,然后对比处理结果,找到最佳的叠前参数。
在叠前参数扫描速度分析过程中,通常采用一维或二维参数空间的策略,通过迭代计算找到最佳的叠前参数。
以上是几种常用的叠前偏移速度分析方法,它们在叠前偏移处理中起到了关键的作用。
这些方法通过采用不同的参数和技术手段,对地震数据进行多次处理和比较,以求得最佳的地下结构成像结果。
在实际应用中,根据地震数据的特点和处理需求,可以选择合适的速度分析方法,以获得高质量的地下成像结果。
叠前深度偏移速度建模保幅偏移
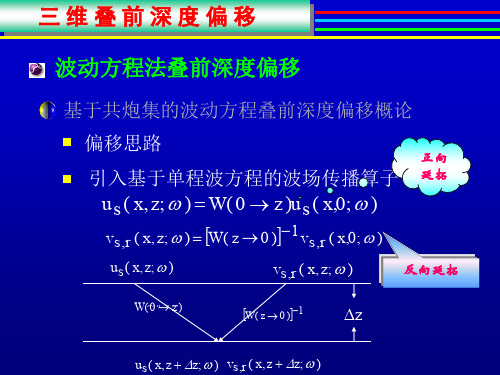
偏移速度建模
模型试算及分析
偏移速度建模
共反射点CRP道集偏移速度建模
CRP道集偏移速度建模是基于叠前深度偏移、 地震层析成像(ST)、和深度聚集分析 (DFA)。在DFA中,若偏移深度和聚焦深 度之间的误差为零,则偏移速度合理;否则, 依据误差修正偏移速度 。
偏移速度建模
共反射点CRP道集偏移速度建模
r
ms ( x, z ) us ( x, z; )vs ( x, z; )
分析:
(2) (3)
可见成像的核心是波场外推算子,目前基于波动方 程的波场延拓算子不外乎:有限差分波场延拓算子 和付立叶波场延拓算子。
三维叠前深度偏移
频率空间域有限差分(FXFD)法叠前深度偏移
基本理论
波动方程保幅偏移
波动方程法三维叠前深度偏移技术在很大程 度上能够实现保幅处理,特别是付立叶有限 差分(FFD)法,综合了付立叶方法与有限 差分法的优点,对陡倾角地层和强横向变速 介质有很好的适应性,是目前精度最高的叠 前深度偏移方法。下面主要在叠前深度偏移 方法的基础上讨论适用于各向异性介质的保 幅偏移,以及基于粘滞声波、弹性波和粘弹 性波动方程的保幅偏移。
2 u 1 2 u 0 (9)
v 2 t 2
2u 2 u 0
v2
(10)
三维叠前深度偏移
s( x, y, z ) s0 ( z ) s( x, y, z ) (11)
u (x, y, z,) u0(x, y, z,) us (x, y, z,) (12)
反演公式如下:
m(x)
1 2
St
H
(x)
L
L
S
叠前深度偏移技术研究及应用

叠前深度偏移技术研究及应用作者:张念崔守凯杨强强来源:《中国化工贸易·下旬刊》2018年第04期摘要:叠前深度偏移技术是复杂地区地震资料成像的关键技术,速度-深度模型精确性及输入道集数据质量影响该技术准确性,通过分析总结做好叠前深度偏移处理工作,对优化叠前深度偏移技术有重要作用。
关键词:地震成像;叠前深度偏移;构造模型;速度模型1 叠前深度偏移技术简介我国油气田勘探开发深入,由寻找简单构造油气藏向寻找复杂断块油气藏、潜山油气藏、隐蔽性油气藏发展,由简单地表勘探向复杂地表勘探转移,勘探开发目标也由简单构造向高陡倾角构造、逆冲构造、盐丘构造、非均质岩性勘探转移。
深度偏移技术成为一种发展趋势,特别在复杂地下地质构造成像方面有不可替代作用。
克希霍夫积分法叠前深度偏移,利用边界积分方法近似求解波动方程实现地震数据成像,地球内部各点声波反射系数由记录在多维曲面的数据加权求和获得,求和曲面形状及求和加权系数用单个散射波传播时的格林函数计算。
克希霍夫积分法叠前深度偏移由两部分组成:一部分是旅行时计算;另一部分是克希霍夫积分。
叠前偏移精度主要取决旅行时的计算精度。
旅行时计算建立在费马原理基础上,即波沿射线传播的旅行时比其他任何路径传播的旅行时小。
叠前深度偏移与时间偏移不同,考虑地震波在地下传播走时和速度界面折射现象。
实际应用须提供反映地下速度变化和速度界面深度模型;处理时,先根据工区先期地质认识和已有地震地质资料,建一个粗略初始模型,再用逐步逼近方法,不断修改模型,直至获得较合理层速度-深度模型。
2 叠前深度偏移技术应用分析以色列Paradigm公司软件产品GeoDepth,用软件中克希霍夫叠前深度偏移对A地区采集的三维资料处理。
主体流程如下:GeoDepth启动与工区建立→数据加载及质量监控→时间构造模型建立→时间速度模型建立→深度速度模型建立→最终叠前深度偏移→成果输出。
A地区地震成像的主要问题:①地表高程变化较大,低速层速度横向不稳定;②地下构造复杂、高陡倾角地层、逆冲断裂带和断层屏蔽区、新老地层交错,速度模型难以建立。
叠前深度偏移处理技术研究

叠前深度偏移处理技术研究作者:熊小娟来源:《中国科技博览》2016年第08期[摘要]叠前深度偏移可以解决复杂构造,陡倾角地层的成像,随着油田勘探开发的不断深入,叠前深度偏移已经越来越多地应用到实际生产中,本文主要介绍了叠前深度偏移的原理,Kirchhoff叠前深度偏移的实现过程及优缺点和实际的应用效果。
[关键词]叠前深度偏移 Kirchhoff、速度模型、陡倾角地层中图分类号:P618.130.8 文献标识码:A 文章编号:1009-914X(2016)08-0105-01引言:叠前深度偏移可以更好的解决复杂构造带地质体成像问题,已成为地球物理界的共识和勘探趋势。
地震偏移成像是一种将地震信息进行重排的反演运算,能使地震波能量归位到真实空间位置,获取地下正确构造图像。
上世纪70 年代初出现了基于几何地震学和绕射理论的射线偏移;同一时期Claerbout等针对标量波动方程提出了有限差分近似解法,实现了地震偏移。
Kirchhoff 积分法是以Hagedoorn“绕射最大凸度曲线”概念为基础建立起来的,表述为沿绕射曲线在地面对所有接收点进行加权积分的过程。
后来Keho等提出了Kirchhoff偏移的算法原型。
一、叠前深度偏移的处理过程(1)叠前深度偏移基本原理Kirchhoff深度偏移算法可应用于大角度倾斜地层和横向速度剧烈变化的情况。
同时还较好地顾及了介质的曲界面、强折射面对地震波射线的折射效应。
它在层状介质模型下的三维深度域偏移计算公式为:式中和为地面上的坐标;为深度;为偏移场在点上的双程旅行时;为轴与连接点和点的直线间的夹角。
上式可以最终归结为根据给定孔径的绕射波空间时距曲线所观测到的地震波场之和。
(2)Kirchhoff叠前深度偏移主要步骤Kirchhoff叠前深度偏移主要包括初始速度模型建立、旅行时计算、Kirchhoff偏移求和、深度速度模型迭代与修正。
①速度模型的建立叠前深度偏移时,首先利用常规处理中获得的叠加速度对目标线进行叠前时间偏移,得到时间偏移的共成像点道集,再对共成像点道集进行反动校,利用反动校后的共成像点道集做速度分析,求得均方根速度。
叠前时间偏移速度分析及速度模型建立技术

【 5 】 符 奇, 张烈辉, 胡书 勇, 等. 底 水油藏
水 平 井 水 平 段 合 理 位 置及 长 度 的 确 定 [ 1 1 . 石 油钻 采工 艺, 2 0 0 9 , 3 1 … 1: 5 1 - 5 5
初期 日产油1 0 . 3 t ,含水率5 4 . 6 %。油藏采 油速 度从 整体 实施 前 0 . 7 8 %达 到最 大 时 2 . 7 6 %,累计 产油 1 2 . 2×1 0 t ,采 出程度
对 常 规速 度 分析 有 以下优 点 。
( 1 )偏移后做速度分析可 以提高道集的信噪比。
( 2 ) 可 以消除绕射波对速度分析的干扰。
( 3 )反 射波 归位 后可 以使速 度 分 析得 到 的 速 度场 位 置 关 系 更正 确 。
2 叠前 时 间偏 移 速度 分析 方 法
学院 学报 , 2 0 0 5 , 2 5 ( 6 ) : 3 1 — 3 4
( 上接6 9 页)( 2) 层 间厚 度 不能 太 厚 ,层 间太 厚 ,速 度 变 化太
在胜 利某地 区做叠前时间偏移 时 ,针对资料的特点 ,采用 两种速度分析方法联合建模 ,偏移结果得到了很大的改善 ( 如 图7 所示 ),首先用D e r e g o ws k i 循环法速度分析得到初始速度模 型 ,在D e r e g o w s k i 循环法速度分析的基础上再利用垂向剩余延迟 分析法对速度进行精细调整得到精确 的速度模型 ,精细速度模 型偏移剖面中断面及断裂系统更加清楚。
对做好 叠前偏 移处理具有 一定 的指 导作用 。
随着对勘探精度 的要求越来越高 ,叠前 时间偏移处理已成 为实现复杂隐蔽构造 精确成像的重要手段。而叠前偏移成像的 质 量又主要依赖于速度分析精度及速度模型 的正确性 ,因此在 叠前时间偏移处理时必须了解叠前时间偏移对速度 的要求 、深 入研 究速度分析及速度模型建立方法和技术 ,为叠前 时间偏移 处理提供准确可靠的速度模型。
Petrel速度建模技术在深度偏移中的应用

钻井完井化 工 设 计 通 讯Drilling CompletionChemical Engineering Design Communications·251·第45卷第8期2019年8月随着油气田勘探开发已经进入到精细挖潜阶段,对于比较复杂的地区,如陡倾角和横向速度变化剧烈地区的地震资料成像问题,采用一般的偏移方法,最终的成像效果无法满足精细构造解释的要求[1]。
目前,叠前深度偏移是改善地震资料质量、提高复杂构造和岩性反射成像精度的最有效的方法。
速度模型的准确与否,在叠前深度偏移过程中起着至关重要的作用,对最终的偏移成像效果有着很大的影响。
特别是当前很多复杂的地区,多数都是地下岩性、构造变化剧烈,如有逆掩断裂、岩浆岩隆起区、盐丘等高陡的地区,需要进行叠前深度偏移处理,以力求更好的成像效果。
但是,这些地区采集的地震资料一般信噪比低,成像效果差,因此建立高精度的速度模型难度也较大。
本论文主要是基于斯伦贝谢公司研发的Petrel 一体化建模软件,以一体化概念引导,把丰富的地质、测井、物探信息融入到深度域速度场建模的过程中,最终创新性地形成了一套比较全面、专业的速度建模流程,为后续的深度偏移奠定了良好的模型基础。
整个的建模过程主要可以分为2个部分:①以地质概念为基础的初始模型;②以地震为基础的速度模型完善[1-2]。
1 构建初始模型为了使速度模型更加可靠、精确,必须减少后期层析反演迭代的次数,确保整个速度模型的准确性。
首先需要建立比较准确的初始速度模型,整个速度模型与地下真实的速度模型差异越小,深度偏移效果就越好。
此次的初始模型的建立,主要是以地质概念为指导,先建立起精细的层位构造解释,同时,结合研究区内分布的多口井数据资料,在地质概念的基础上建立起基本的速度格架。
初始模型的建立包括近地表建模、井控垂向建模、层约束的井速度建模等三个基本内容。
1.1 近地表建模在整个速度建场的过程中,近地表速度模型的好坏对后续的偏移结果影响较大,特别是一些断面、层面、内幕反射。
3---Kirchhoff型保幅叠前深度偏移

能把真振幅偏移的基本思想推广到多波多分量地震资料及各
Gardner, 1998 );另一种是全局方法介绍的是加权真振幅 偏移核的反演( Wu, 1998 )。为了计算合适的保幅叠前深 度偏移的权函数,Philippe等提出了地面道位置的几何研究。 由此把上述两种方法综合成3-D保幅叠前深度偏移方法。在 这种方法中,保幅偏移的权函数包含了振幅补偿和采集观测 系统补偿两大部分。对于采集观测系统补偿应该考虑道密度 和采集效应。把一特定的密度权函数因子直接包含在偏移核 中,这样就考虑了不规则采集的影响,由此能提高最终的保 幅成像结果。
幅反射。如果真振幅偏移的基本思想是通过带权的绕射叠
加偏移来实现,则相应的真振幅偏移被称为是Kirchhoff型 真振幅偏移。
真振幅偏移的基本思想: 真振幅偏移的基本概念和算法由20世纪80年代初期正式 提出。但其基本思想的形成可追溯到 20 世纪 60 年代。最初 Bortfeld的工作只局限在数值试验上。二十世纪80年代初, Bortfeld由产业界转入大学,开始对真振幅的基础进行系统
六、优化偏移孔径
下面给出了一利用一优化成像孔径的Kirchhoff型偏移方法。其算法如下, 首先把自动增益控制应用到各个共炮点道集上,然后用下述方法确定的一
优化孔径逐道偏移炮道集。优化偏移孔径的实现步骤如下:
1)用大于一预定门槛值的振幅拾取反射波至; 2)利用地震道上的局部倾斜叠加对拾取的波至计算入射角 3)从检波点向地下介质发射射线; 4)沿该射线路径寻找镜像反射点;
四、真振幅权函数 真振幅偏移公式与叠前深度偏移公式相似,但真振幅 核项与积分加权项不同。反射点M的成像积分式为:
u ( , t ) u ( M ) 1 d 2K DS ( , M ) | t D ( ; M ) 2 A t
速度模型误差给叠前深度偏移成像带来的假象

1 偏 移方 法 简 介
目前 , 实用 的 波 动 方 程 叠 前 深 度 偏 移 方 法 较 多, 如频 率波 数域 法 m 、 移加 内 差法 …]有 限 相 、
差 分法 ] 分 步 傅 立 叶 法 、 立 叶 有 限法 Ⅲ 、 、 傅
广义 屏法 等 。作 者在 本文 采用 的是 分 步傅 立 叶 方 法 , 由 So a 提 出 , 原理 主要 如下 6: 它 t f 其 1 ]
二 维声波 波动 方程 可表示 为 :
: + ¨ () 1
其 中 U ,,)为 地 震 波 场 ; ( z ( =t ,)为 介 质 速
度 ; 与 :为空 问坐标 ; 为地震 波 的双程 旅行 时 。 t 采用单 程波炮 点或 检波 点外 推方程 :
O z
兰: 一 )u ±(l l 一_ 1
U ,,J = U ( 。甜)+U ( ) ( ) ( 。() c o ,, 1 ,, 5 可通过式 ( ) 4 求取 , U 通过 以下 步骤实 现 :
( 速度模型 a )
,m 0 1 00 0 20 00 30 0 0 4 0 00 50 0 0
对公 式 ( ) 4 中得到 的 G ( 。 o k ,, )作 傅 立 叶反 变换 , 即将 相移后 的波场 变换 到空 间频 率域
6 5
S ,) =S ( )+△ ( : ( 。: . ,) s
() 3
的深 度域层 速度模 型 。由此可 以看出 , 该方 法对 陡 倾地 层 、 断层及 深部 断层 面之 下 的 目标 层 , 能较 都
其中 S ,)为介质慢 度 ; 。 ( : S ( )为背景 慢度 , 只
随深度方 向变化 ; S ,)为慢 度扰 动量 。 A( :
叠前深度偏移、速度建模、保幅偏移

(10)
三维叠前深度偏移
s( x , y , z ) s0 ( z ) s( x , y , z )
u ( x, y, z, ) u0 ( x, y, z, ) us ( x, y, z, )
u 0 ( x, y, z z, ) u ( x, y, z, w)e
iz
FTX T iS ( X T , zi )z u ( X T , zi )
(4.30)
三维叠前深度偏移
还有MRS-ELBF的广义屏算子、ELRF的广义屏算子 及基于Born/Rytov近似的联合广义屏算子。 模型试算
Marmousi模型相屏偏移剖面
三维叠前深度偏移
Marmousi模型ELBF法偏移剖面(dz=2m)
三维叠前深度偏移
叠前深度偏移成像因稳健且效率与精度高,已成为人们关注的重 点和焦点。包括射线法和波动方程法(FXFD,SSF,FFD,GS) 。以 粘滞声波、弹性波波动方程为基础的偏移方法,以及适于各向异 性介质的偏移方法都得到了一定的应用,并取得了较好的效果。
射线法三维叠前深度偏移
Kirchhoff积分法的关键是绕射旅行时的计算
u 1 1 i ( )u z v c
(7)
相关成像条件
1 P ( z m , ) S ( z m , ) ˆ R( z m ) 2 N S ( z m , )
(8)
三维叠前深度偏移
模型试算 下面给出Marmousi模型FXFD的试算结果
Marmousi模型及其FXFD法偏移剖面
2u x
2
2u y
2
2u z
叠前深度偏移技术

叠前深度偏移技术一、技术原理及主要技术内容叠前深度偏移技术已由克希霍夫积分法发展到波动方程法,同时还发展了其它的偏移方法,如:高斯束(Beam)偏移、相移屏偏移技术、转换波叠前深度偏移、各向异性叠前深度偏移等,现把上述各种方法分述如下:(1)克希霍夫积分法叠前深度偏移:该偏移方法一般由两部分组成:一部分是旅行时计算,另外一部分是克希霍夫积分处理。
偏移的精度主要取决于旅行时的精度。
旅行时计算建立在费马原理的基础上,即地下两点间的一切可能路径中实际路径对应于最小旅行时间。
它遵循倒转射线追踪机制,大多数情况下使用对应于体波而不是首波的射线,这样减少了偏移成像的畸变,且输出轨迹是灵活的。
新方法主要改进了原方法中单波至、不保幅的缺点,现在是计算多波至旅行时,并且具有振幅与相位保持特性,最具代表性的方法是由以色列PARADIGM公司发展的共反射角克希霍夫积分法,其原理与方法是:由成像点到地面采用照明式射线追踪;在每个射线均计算旅行时、观测位置、相位旋转因子、慢度;在特定倾角每对射线均是潜在反射;求和某成像点同一层的所有反射形成共反射成像道集;所有到达时的振幅与相位都是保持的。
高斯射线束(Gaussian Beam)偏移方法有别于常规的克希霍夫积分法深度偏移方法,目前只有Chevron公司使用它,它分多组射线束进行研究,采用Gaussian法振幅衰减与相位抛物线近似等。
具体讲它是将震源和接受点波场局部分解成“束”,并利用精确的射线追踪将这些束返回地下。
一个地面位置能发出几个束,不同的束对应不同的初始传播方向,每个束独立于其他束传播,且受单个射线管引导。
射线管可以重叠,所以能量能在成像位置、震源位置及接受点位置间以多个路径传播,因此高斯射线束偏移可处理多路径。
该种方法部分解决了常规克希霍夫积分法精度不高的问题。
(2)波动方程法叠前深度偏移:该种方法研究多波至,易振幅与相位保持,精度高,但费机时,主要方法有有限差分法(FD)与相移校正法(PSPC),它们均基于单程波动方程、平方根算子向下延拓,并使用多个参考速度。
地震勘探中的叠前深度偏移算法

地震勘探中的叠前深度偏移算法地震勘探是一种重要的地球物理探测方法。
通过利用地震波的反射、折射和传播特性,可以了解地下结构和地质情况,为石油、天然气等能源资源的探测和开发提供依据。
在地震勘探中,叠前深度偏移算法是一种重要的数据处理技术,可以提高地震成像质量,提高勘探地震数据的分辨率和准确性。
一、叠前深度偏移算法的基本原理叠前深度偏移算法是一种用于地震数据处理的数学算法,其基本思想是在时间域将地震数据转换为深度域,然后采用折射面模型或者波阵面模型来对地下结构进行成像。
其基本原理可以简单描述如下:1. 叠前深度偏移算法首先对地震数据进行逆时偏移(NMO处理),将时间域的地震数据转换为零偏移距时刻对应的地震数据。
2. 然后,将逆时深度层剖面上的地震数据集合在一起,形成叠前深度域数据。
3. 叠前深度偏移算法的关键是调整不同深度层的地震数据时差,以消除波形的走时差异,实现不同深度维度的波形匹配,进而实现相关波形叠加成像。
4. 此后,根据地震波在不同速度介质中的折射、反射特性,利用Kirchhoff积分公式计算深度域内的各点反射能量,最终形成地下结构的深度成像结果。
二、叠前深度偏移算法的应用叠前深度偏移算法在地震数据处理中广泛应用,可以大大提高地下结构成像质量和解析度。
其应用领域主要包括以下几个方面:1. 沉积物地质研究。
地震勘探可以对深层地质结构进行探测和解析,对于沉积物地质研究具有重要作用。
叠前深度偏移算法可以提高地震数据的分辨率和准确性,更好地揭示岩相、层序等信息。
2. 石油勘探与开发。
地震勘探是石油勘探和开发的核心技术之一,其质量和准确性对于石油勘探和开发的成功具有决定性作用。
叠前深度偏移算法可以提高地震成像质量,更好地勘探目标层位和构造特征。
3. 工程地质勘察。
叠前深度偏移算法可以应用于工程地质勘察中,对于建设工程和地质灾害防治具有重要意义。
其可以准确获取地下结构信息,对于建设工程场地的选址和设计提供重要依据。
地震数据处理第七章:偏移
(1)简单速度+简单构造=叠后时间偏移; (2)复杂速度+简单构造=叠后深度偏移; (3)简单速度+复杂构造=叠前时间偏移; (4)复杂速度+复杂构造=叠前深度偏移;
(5)简单速度=时间偏移 (6)复杂速度=深度偏移;
(7)简单构造=叠后偏移; (8)复杂构造=叠前偏移。
成像中的偏移
偏移孔径
追踪射线的最大出射角
CRP (common reflection point) MVA (Migration Velocity Analysis)
MVA Xsection Window
Interactive Horizon RMO Analysis
View CRP Gathers
叠后偏移:
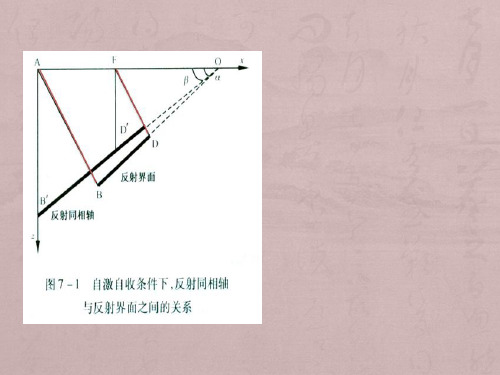
将水平叠加剖面用爆炸反射面概念实现倾斜反射层归位和绕射波收敛 偏移原来及效果见下图
偏移原理图
(1)时间反射层比地质界面长; (2)时间反射层向下倾方向移动; (3)时间反射层倾角小
叠加剖面上的B’D’对应于 BD,且AB=AB’
偏移处理(简称偏移)或偏移成像
是通过数值计算把地面记录延拓为地下波场的 过程,在此过程中,绕射波得到收敛,倾斜界面反 射波得到归位,波场干涉得到分解,波前回转现象 得到消除,界面折射得以校正(深度偏移),从而使 地层构造、断层分布、断点、尖灭点、边缘、异常 体和岩性变化得到清晰成像和准确归位。
简单地下模型
分选叠前数据为共偏移距剖面 使用常用平均法产生初始速度模型 实行共偏移距剖面的叠前偏移 分选偏移道为CRP道集 调整速度使CRP道集上的同相轴变平
速度变异
每个偏移剖面是地 下的冗余成像 无速度变异存在
View Ray Density
Difference Files from MVA Tomography Inversion Small inversion aggressiveness factor
第3章Kirchhoff积分法叠前深度偏移

第三章 Kirchhoff 积分法叠前深度偏移大家知道,叠前偏移的概念早在70年代中期就提出来了,但由于叠前记录的信噪比较低,偏移的初始模型又很难选准,加之当时的计算机无法承受叠前偏移较大的计算量,直到90年代叠前偏移才开始尝试应用于油气勘探地震数据的精细处理中。
常见的叠前深度偏移方法可以分为两类:第一类是基于绕射扫描叠加原理的Kirchhoff 积分法,另一类是基于波动方程的偏移方法(如有限差分偏移方法、Fourier 偏移方法等)。
本章重点讨论Kirchhoff 积分法叠前深度偏移。
Kirchhoff 积分法叠前深度偏移被认为是一种高效实用的叠前深度偏移方法,目前主要完善三维采集和叠前深度偏移软件。
积分法具有高偏移角度、无频散、占用资源少和实现效率高的特点,并且积分法能够适应变化的观测系统和起伏的地表,优化的射线追踪法和改进的有限差分法能够在速度场变化的情况下快速准确地计算绕射波和反射波旅行时,从而使积分法能够适应复杂的构造成像。
地震偏移成像问题,经过最近十多年的研究与发展,已经基本解决了和正在解决三维偏移,叠前深度偏移和多分量地震偏移等诸问题。
但是偏移中有诸多问题尚未解决,例如真振幅偏移问题和各向异性介质中的地震偏移问题。
近年来,解决真振幅偏移问题就是偏移地震数据得到真正的振幅和相位信息,从而为岩性解释服务。
由于积分法具有许多优点,因此研究Kirchhoff 型保幅叠前深度偏移具有很高的理论价值和实用价值。
下面就变速射线追踪法计算走时、有限差分法计算走时以及Kirchhoff 型常规叠前深度偏移和保幅叠前深度偏移做详细讨论和分析。
§3.1 变速射线追踪法计算走时Kirchhoff 积分法叠前深度偏移已在实际生产中应用了多年,并解决了不少复杂构造的成像问题(Zhu & Lines, 1998)。
Kirchhoff 积分法的关键是绕射旅行时的计算,目前常用的计算方法是射线追踪法和有限差分法(Schneider, 1992, 1995)。
叠前深度偏移

7、沿层剩余延迟迭代
东方公司研究院处理中心
叠前时间偏移
8、处理效果 叠前深度偏移
东方公司研究院处理中心
培训内容
叠前深度偏移基本原理 三维各向异性叠前深度偏移流程 二维叠前深度偏移基本流程 几点体会
东方公司研究院处理中心
几点体会与认识
1、GeoDepth软件的速度模型建立以及层速度迭代 优化方法具有行业领先优势; 2、GeoDepth软件产品多、应用模块多、模块中选 件多,需要在今后的项目中逐步消化应用; 3、此次培训收获很多,一是更系统地了解深度偏 移的工作流程与操作,二是掌握了Geodepth的更多 功能,为下一步做好深度偏移、用好深度偏移提供 了保障。
东方公司研究院处理中心
3、建立初始沿层层速度
基本步骤: • 层位网格化,建模 (MAP) • 生成时间域层速度 (CVI) • 沿层抽取沿层层速度并建模 (MAP) 1.编辑层速度平面图并建模 (MAP)很重要
东方公司研究院处理中心
4、更新沿层层速度
初始叠前深度偏移
CRP道集是否拉平
Y
N
计算沿层剩余延迟
理论模型
叠加剖面 时间偏移
叠加剖面 时间偏移
深度偏移
东方公司研究院深处度理偏移中心
各向异性叠前深度偏移工作思路
1
2
工区建立数据加载
道集的加载与检查 速度的加载与检查
初始速度模型的建立
层位模型的建立 创建初始深度域层速度体
4
各向异性深度偏移
井约束求取各向异性参数 各向异性叠前深度偏移
东方公司研究院处理中心
二维叠前深度偏移基本流程
工区建立
1.数据加载
叠前时间偏移与叠前深度偏移1

叠前时间偏移与叠前深度偏移1叠前时间偏移与叠前深度偏移1、叠前偏移从实现方法上可分为叠前时间偏移和叠前深度偏移。
从理论上讲,叠前时间偏移只能解决共反射点叠加的问题,不能解决成像点与地下绕射点位置不重合的问题,因此叠前时间偏移主要应用于地下横向速度变化不太复杂的地区。
当速度存在剧烈的横向变化、速度分界面不是水平层状时,只有叠前深度偏移能够实现共反射点的叠加和绕射点的归位,叠前深度偏移是一种真正的全三维叠前成像技术,但它的成像效果必须依赖于准确的速度-深度模型,而模型的迭代和修改是一个非常复杂和费时的过程,周期长,花费也相当昂贵。
1.1 叠前时间偏移叠前时间偏移是复杂构造成像和速度分析的重要手段,它可以有效地克服常规NMO、DMO和叠后偏移的缺点,实现真正的共反射点叠加。
叠前时间偏移产生的共反射点(CRP)道集,消除了不同倾角和位置的反射带来的影响,不仅可以用来优化速度分析,而且也是进行AVO地震反演的前提。
Kirchhoff叠前时间偏移方法的基础是计算地下散射点的时距曲面。
根据Kirchhoff绕射积分理论,时距曲面上的所有样点相加就得到该绕射点的偏移结果。
具体的实现过程就是沿非零炮检距的绕射曲线旅行时轨迹对振幅求和,速度场决定求和路径的曲率,对每个共炮检距剖面单独成像,然后将所有结果叠加起来形成偏移剖面。
1.2 叠前深度偏移实际上,叠前时间偏移可认为是一种能适应各种倾斜地层的广义NMO叠加,其目的是使各种绕射能量聚焦,而不是把绕射能量归位到其相应的绕射点上去,它基于的速度模型是均匀的,或者仅允许有垂直变化,因此,叠前时间偏移仅能实现真正的共反射点叠加,当地下地层倾角较大,或者上覆地层横向速度变化剧烈,速度分界面不是水平层状的条件下,叠前时间偏移并不能解决成像点与地下绕射点位置不重合的问题。
为了校正这种现象,我们可以在时间剖面的基础上,再做一次校正,使成像点与绕射点位置重合,这就是做叠后深度偏移的目的,但叠后深度偏移有缺点,主要是无法避免NMO校正叠加所产生的畸变,而且在实现过程中缺少模型叠代修正的手段,因此叠后深度偏移一般作为叠前深度偏移流程的一部分,用于深度域模型层位的解释。
叠前深度偏移层析反演速度模型建立及应用

( 1 . R e s e a r c h I n s t i t u t e o f E x p l o r a t i o n a n d D e v e l o p m e n t f o D a q i n g O i ie f l l d C o m p a n y L t d . ,D a q i n g 1 6 3 7 1 2 ,C h i n a ; 2 . N o . 1 O i l P r o d u c t i o n P l a n t f o D a q i n g O i l ie f l d C o m p a n y L t d . ,D a q i n g 1 6 3 0 0 1 ,C h i n a )
( 1 .大庆油 田有限责任公司勘探开发研究院 ,黑龙江 大庆 1 6 3 7 1 2;2 .大庆油 田有限责任公 司第一采油厂 , 黑龙江 大庆 1 6 3 0 0 1)
摘要 :叠前深度偏移技术是 目前解决复杂地质构造精确成 像问题 的重要手段 ,其 成像效果 取决于深度 域速度模 型的准确与否。通常采用 的沿层构造解释速度建模方法 在构造特别 复杂 、层位解 释不合 理时往往得 不到准确 的 速度模型 ,因此研究 了层析反演更新深度域速度模型 的建立方法 。该 方法可利 用偏移成像 数据计算 剩余误差 曲 线和地层倾 角信息 ,迭代更新反射层 的位置和形 态 ,最终获取 准确 的速度模型 。应 用实例表 明 ,层析反演速 度
r e a s o n h o r i z o n i n t e r p r e t a t i o n,t h e r e f o r e t h e mo d e l i n g me t ho d o f r e f r e s h i n g t h e v e l o c i t y i n t h e d e p t h d o ma i n b y t o mo —
叠前深度偏移 (NXPowerLite)

(b)波动方程叠前深度偏移
Kirchhoff积分法叠前深度偏移
一.概述
二.变速射线追踪法计算走时
三.有限差分法计算走时 四.Kirchhoff积分法叠前深度偏移
概
述
Kirchhoff积分法叠前深度偏移具有高偏移角度、
无频散、占用资源少和实现效率高的特点,并且积
分法能够适应变化的观测系统和起伏的地表,优化
t1 min( s0 , s1 )z ( t 32 a ) t 2 min( s0 , s 2 )x
(15) 当(14)式方程的右边根号下出现负值时,我们选取: (16) 当向z方向外推时, z ,当向x方向外推时 l x 。 l
( t 32b ) t 0 min( s0 , s1 )l
特别注意关键参数的试验:反假频距离、反假频频 率和偏移孔径的合理选取
模型试算(叠前深度偏移)
对Marmousi模型数据实现了叠前深度偏移处理。图(a),(b) 分别为使用Kirchhoff积分法和波动方程法偏移的结果。可以看 到,波动方程法对背斜内幕和低速目的层较好的成像。
(a) Kirchhoff叠前深度偏移
(20) 在满足(20)式的条件下,利用方程(19)可实现三维旅行时场的 计算。
模型试算
x/m x/m (z/m)
1000 m/s
(z/m)
1000 m/s
2500 m/s 2500 m/s 图4 层状介质和重叠在其上的震源 位于(40,160)点的等时线图。注意, 上 、 下 层 速 度 分 别 为 1000m/s 和 2500 m/s。 图5 含高速体的均匀介质和重叠在其上 的震源位于(160, 0)点的等时线图。背景 速度为1000m/s,高速体速度为2500m/s
叠前时间偏移与叠前深度偏移讲解

叠前时间偏移与叠前深度偏移摘要:偏移使倾斜反射归位到它们真正的地下界面位置,并使绕射波收敛,即可以提高空间分辨率。
按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。
这里主要讨论叠前偏移。
偏移方法分为时间域和深度域两类,时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的,而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。
这里主要介绍克希霍夫积分法叠前时间偏移、有限差分法叠前时间偏移、Fourier变换法叠前时间偏移三种叠前时间偏移方法。
在叠前深度偏移上面,主要根据其技术的发展历史,现状,及未来趋势进行叙述,并进行了不同偏移技术的成像对比。
关键字:叠前时间偏移叠前深度偏移克希霍夫积分法正文:一、引言偏移使倾斜反射归位到它们真正的地下界面位置,并使绕射波收敛,即可以提高空间分辨率。
按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。
偏移方法分为时间域和深度域两类。
时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的,而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。
从当前技术发展的状况看,目前国内应用的叠前偏移技术基本上可以概括为以下两类。
一种是基于波动方程积分解的克希霍夫积分法叠前偏移。
这种技术,在20世纪90年代以前就在研究,目前,随着多年来持续不断地改进和完善,已经成为一种高效实用的叠前偏移方法,它具有高角度成像、无频散、占用资源少和实现效率高的特点,能适应不均匀的空间采样和起伏地表,比较适合复杂构造的成像。
目前国际上有多种较为成熟的积分法叠前成像软件,是当前实际生产中使用的主要叠前深度偏移方法。
一种是基于波动方程微分解的波动方程叠前偏移。
这种技术目前在国内的应用还处于试验阶段。
叠前时间偏移与叠后时间偏移和叠前深度偏移一样,都是基于三大数学工具,即克希霍夫积分、有限差分和Fourier变换。
二、叠前时间偏移技术叠前时间偏移的可行性分为下面三个方面:①实现这种技术所需的软硬件成本合理。
