Fluent时间步长
Fluent时间步长

用FLUENT计算非稳态问题,是不是在计算时必须保证在每个时间步timestep里都要收敛才行,否则计算结果就不对呢?也就是说,在iteration选项里,max iteration pertime step设为一个值,比如500,就是如果500次迭代后仍未收敛,进入下一步迭代,那对结果会有什么影响。
对于隐式非定常格式,原则上,每个时间步长内必须保证结果收敛。
在fluent 的帮助中就有这样的话:“对于不可压流动,在每个时间步内,不可压解必须迭代直至收敛。
"另外,我们回归到fluent内部计算的本源,它实质就是一种差分算法,通过不断逼近来获得真实解,这样我们就不难理解为什么在每个时间步长内需要收敛了.max iteration pertime step 设定的是最大时间步,在单一步长内,如果结果已经收敛,则会自动跳至下一时间进行计算。
所以其设定要纵观全局。
但对于周期性流动,这种收敛性的要求就相对松动一些.不过你需要多计算几个周期,等计算结果达到对时间的周期状态后,再对结果进行储存。
对于显式非定常格式,在Fluent帮助中这样说:“一定记住,对于显式非定常格式,每一个迭代就是一个时间步。
”如果每个时间步内结果没有得到收敛,则很有可能你所得到的结果是不真实的,但是一个时间步内的不真实性应该不会影响到下一个时间步长内的计算。
因为在每一个时间步开时,fluent 都会进行初始化。
在单个时间步内,它实际是按照稳态进行计算的。
time step size的设定是根据你的计算需要,一般是你的特征长度(比如说管道的长度)除于特征速度(比如平均速度)的值再小一到两个量级即可,如果你的time stip size太大,计算会提示你的,改小即可。
number of time steps是这样设定的:number of time steps X time step size =实际时间积累.比如说,你计算一个射流,你需要计算到1秒时候的情况,那么(number of time steps)=1秒/(time step size).Fluent中非稳态时间步长设置最近所做的非稳态计算,若设置太小,计算时间就太长,设置太大的话就会出现Global Courant Number飙升过大的不能继续进行下去的问题.有网友建议:http://www.efluid。
Fluent时间步长

之阳早格格创做用FLUENT估计非稳态问题,是不是正在估计时必须包管正在每个时间步timestep里皆要支敛才止,可则估计截止便分歧过失呢?也便是道,正在iteration选项里,max iteration pertime step设为一个值,比圆500,便是如果500次迭代后仍已支敛,加进下一步迭代,那对付截止会有什么做用. 对付于隐式非定常要领,准则上,每个时间步少内必须包管截止支敛.正在fluent 的助闲中便有那样的话:“对付于不可压震动,正在每个时间步内,不可压解必须迭代直至支敛.”其余,咱们返回到fluent里里估计的基础,它真量便是一种好分算法,通过不竭迫近去赢得真正在解,那样咱们便不易明白为什么正在每个时间步少内需要支敛了.max iteration pertime step 设定的是最大时间步,正在简单步少内,如果截止已经支敛,则会自动跳至下一时间举止估计.所以其设定要纵瞅齐部.然而对付于周期性震动,那种支敛性的央供便相对付紧动一些.不过您需要多估计几个周期,等估计截止达到对付时间的周期状态后,再对付截止举止储藏. 对付于隐式非定常要领,正在Fluent助闲中那样道:“一定记着,对付于隐式非定常要领,每一个迭代便是一个时间步.”如果每个时间步内截止不得到支敛,则很有大概您所得到的截止是不真正在的,然而是一个时间步内的不真正在性该当不会做用到下一个时间步少内的估计.果为正在每一个时间步启时,fluent 皆市举止初初化.正在单个时间步内,它本量是依照稳态举止估计的.time step size的设定是根据您的估计需要,普遍是您的特性少度(比圆道管讲的少度)除于特性速度(比圆仄衡速度)的值再小一到二个量级即可,如果您的time stip size太大,估计会提示您的,改小即可.number of time steps是那样设定的:number of time steps X time step size=本量时间聚集.比圆道,您估计一个射流,您需要估计到1秒时间的情况,那么(number of time steps)=1秒/(time step size).Fluent中非稳态时间步少树立迩去所搞的非稳态估计,若树立太小,估计时间便太少,树立太大的话便会出现Global Courant Number飙降过大的不克不迭继承举止下去的问题.单元最小少度除于流场仄衡流速,不过那个值大概很小,您不妨以那个值为基准举止安排,一启初不妨与大些,如果不问题,不妨再搁大些,那样不妨支缩估计时间.若按那种要领,估计底下那个例子:2mm,10个网格,流速1m/s.时间步少time steps=0.2/1000=0.0002.然而是尔正在举止估计时,树立为1e-6,皆无法举止下去.所以那种换算要领仍旧只可动做参照.尔当前采与的是自动安排时间步少,暂时瞅去效验还不妨.怎么知讲非稳态估计时间步少是符合的?courant number与支敛 courant number本量上是指时间步少战空间步少的相对付闭系,系统自动减小courant数,那种情况普遍出当前存留尖钝形状的估计域,当局部的流速过大大概者压好过大时堕落,把局部的网格加稀再试一下.正在fluent中,用courant number去安排估计的宁静性与支敛性.普遍去道,随着courant number的从小到大的变更,支敛速度渐渐加快,然而是宁静性渐渐落矮.所以简直的问题,正在估计的历程中,最佳是把courant number从小启初树立,瞅瞅迭代残好的支敛情况,如果支敛速度较缓而且比较宁静的话,不妨适合的减少courant number的大小,根据自己简直的问题,找出一个比较符合的courant number,让支敛速度不妨脚够的快,而且不妨脆持它的宁静性.时间步少与准确性戴自《数值估计与工程仿真》第一期做家gim1 、正在不计模型缺面,而且估计宁静的前提下,数值估计的时间步少的采用存留一个妥当值,过大大概过小皆市做用模拟截止的准确性.2 、简直数值模拟中,最佳能有一定的真验数据大概其余的不妨认为准确的截止动做考证资料,那样才搞妥当的选定时间步少,普及估计的准确性.3 、FLUENT 硬件采与隐式估计,那便需要设定每一次迭代的最大步数(Max Iterations per Time step ) ,如果达到最大步数前估计已经支敛,系统会自动加进下一步迭代.利用那一面不妨采与如下要领决定迭代的时间步少:系统普遍认为每一步的迭代次数应正在10 一20 次之问,设定一个时间步少后如果正在迭代次数内还不支敛便该当减小时间步少,反之则该当减少时间步少.普遍,皆预先给定一个较小的时问步少举止迭代女步,而后逐步调整.天然迭代次数也跟简直问题相闭,还需要估计体味的不竭聚集.tags: fluent,非稳态,时间步少fluent迭代估计中,非定常问题的时间步少怎么样采用隐式时间积分规划:时间步少Δt<ρ(Δx)2 /2Γ;半隐式时间积分规划:时间步少Δt<ρ(Δx)2 /Γ;齐隐式时间积分规划:时间步少不节造.Δx是网格相邻节面的距离,Γ是扩集系数,分歧问题有分歧的物理意思非稳态时间步少与迭代步数的计划正在unsteady的估计供解中,大部分共教该当会对付solver 中树立比较迷惘,正在那里,尔念便尔部分的明白对付其时间步少与迭代步数举止一些分解计划. 1、正在举止unsteady 估计的时间,fluent是从前一个时间算到下一个时间(即time steps),而每个时间步少内的估计便相称于一个准稳态供解,果此需要树立Max Iterations per Time Step;正在那个时间步少内的估计便是一个稳态历程,正在达到iteration次数之前支敛完毕,便跳到下一个time step,可则便将所确定的迭代次数算完正在跳下一个time step. 2、时间步少的树立:(1)特性少度除以特性速度所得的时间小二个量级大概者更小.那是表里值,本量上,如果不是处事站运止的话,耗费的估计时间太少.果此,常常正在fluent中选定那个比率的1/5到1/10,特地是一启初不知讲怎么样设定的时间最佳是挨启adaptive 让它自动定义定义时间步少.然而其中最小的时间尺度,部分认为最小也只可小到那个比率的1/100的那个火仄上.(2)最小网格少度除以流速大概者转动震动速度.那个是包管每一次迭代皆正在一个网格范畴内,不会果跨网格而引导截止缺面,然而本量中估计一段时间后大概加快估计速度,会将时间步少树立较大,末尾为得到最后供解,再将时间步少调小,举止细微的估计.3、时间步少里的迭代步数树立:包管每个时间步少达到支敛,大概者能明隐瞅到主要残好直线趋于火仄.4、时间步数:瞅您需要估计多万古间,自己感触起码需要估计3-5个震动循环周期才大概得到非定常的宁静震动周期状态.。
三十九、Fluent时间步长的估算与库朗数

三十九、Fluent时间步长的估算与库朗数1. 库朗数1.1 概念理解什么是库朗数?库朗数是用来衡量数值计算稳定性的一个物理量,也被称为CFL数、CFL准则在流体力学仿真软件中,都能找到库朗数(Courant number)的解释和定义。
在CFX的帮助文件里给出了一个比较直观的公式来定义一维网格的库朗数(Courant Number):其中,u为流体速度;Δt为时间步长;Δx为网格尺寸;形象点理解,u*Δt表示流体在Δt时间内流动的距离,除以网格尺寸,则表示流体在一个时间步长内流过了多少个网格。
显然一个时间步长内流过的网格越多,计算就越快,但收敛性就会越差。
类似于人赛跑,跑得快固然很快能跑完,但也可能中间摔跟头。
库朗数主要受流速u、时间步长Δt和网格尺寸Δx的影响。
而流速u和网格尺寸Δx主要由实际工况决定,不能人为控制,因此主要由时间步长Δt来控制库朗数。
1.2 取值标准一般来说,考虑收敛性的话,库朗数肯定越低越好,但相应的时间步长也会很小,收敛速度变慢。
一般取值在1~10之间比较合适,当然要根据实际情况,如收敛性比较差,可适当降低这个数值。
收敛性比较好,收敛速度慢,可适当增加库朗数。
Fluent帮助文档认为对于大多数问题,库朗数设置为1能够满足要求。
实际上,Fluent很多案例的库朗数都是50,这主要是选择了隐式算法的原因1.3 库朗数于亚松驰因子亚松驰因子under-relaxation factor单元格内物理量φ取决于旧值φold、变化量△φ和亚松弛因子α。
也就是说亚松弛因子是一个调节物理量变化的系数。
基于压力的耦合算法中库朗数可用亚松驰因子表示出来:2. 库朗数的设置2.1 基于密度求解器Density-based显示格式Explicit Formulation默认是1,对于2维问题可适当增加库朗数,但不要超过2.0。
如果设置没有问题,但是计算发散了,或者残差上升得非常快,就必须降低 Courant number,可能需要降低到0.5,甚至0.1。
FLUENT系列资料:7

多相流算例多相流模拟介绍在自然界和工程问题中会遇到大量的多相流动。
物质一般具有气态、液态和固态三相,但是多相流系统中相的概念具有更为广泛的意义。
在多项流动中,所谓的“相”可以定义为具有相同类别的物质,该类物质在所处的流动中具有特定的惯性响应并与流场相互作用。
多相流动模式根据多相流系统中相的概念,按照下面的原则对多相流分成如下几类:∙气-液或者液-液两相流:o气泡流动:连续流体中的气泡或者液泡。
o液滴流动:连续气体中的离散流体液滴。
o活塞流动: 在连续流体中的大的气泡o分层自由面流动:由明显的分界面隔开的非混合流体流动。
∙气-固两相流:o充满粒子的流动:连续气体流动中有离散的固体粒子。
o气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
∙液-固两相流o泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes数通常小于1。
当Stokes数大于1时,流动成为流化(fluidization)了的液-固流动。
o水力运输: 在连续流体中密布着固体颗粒o沉降运动: 在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
∙三相流(上面各种情况的组合)多相系统的例子各流动模式对应的例子如下:∙气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷∙液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗∙活塞流例子:管道或容器内有大尺度气泡的流动∙分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝∙粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动∙风力输运例子:水泥、谷粒和金属粉末的输运∙流化床例子:流化床反应器,循环流化床∙泥浆流例子:泥浆输运,矿物处理∙水力输运例子:矿物处理,生物医学及物理化学中的流体系统∙沉降例子:矿物处理多相建模方法计算流体力学的进展为深入了解多相流动提供了基础。
fluent稳态收敛曲线

fluent稳态收敛曲线Fluent稳态收敛曲线是一种用于评估数值模拟方法性能的工具。
在流体力学领域,数值模拟方法被广泛应用于解决复杂的流动问题,如湍流、多相流等。
然而,由于数值计算的局限性,我们需要确保所采用的方法能够在一定精度范围内收敛到真实的解。
稳态收敛曲线就是用来评估这种收敛性的。
稳态收敛曲线是通过在不同的时间步长下进行数值模拟,并比较不同时间步长的模拟结果与真实解之间的误差来绘制的。
具体来说,我们首先选择一个初始的时间步长,然后逐渐减小时间步长,直到达到一个足够小的值。
在这个过程中,我们会记录每个时间步长的模拟结果与真实解之间的误差。
最后,我们将这些误差值作为纵坐标,时间步长作为横坐标,绘制出一条曲线,这就是稳态收敛曲线。
稳态收敛曲线具有以下几个特点:1. 收敛性:随着时间步长的减小,模拟结果与真实解之间的误差会逐渐减小。
这意味着数值模拟方法具有一定的收敛性,可以在一定精度范围内逼近真实的解。
2. 稳定性:当时间步长减小到一定程度时,误差值趋于稳定。
这意味着数值模拟方法在这个精度范围内是稳定的,不会因为时间步长的进一步减小而导致误差值的大幅度波动。
3. 最优时间步长:稳态收敛曲线上有一个最优的时间步长,使得模拟结果与真实解之间的误差最小。
这个最优时间步长就是我们应该选择的时间步长,以获得最佳的模拟结果。
4. 过度离散和欠离散:在稳态收敛曲线上,如果误差值在减小到一定程度后开始增大,说明数值模拟方法出现了过度离散现象。
这是因为时间步长过小,导致数值计算的误差过大。
相反,如果误差值在减小到一定程度后不再减小,说明数值模拟方法出现了欠离散现象。
这是因为时间步长过大,导致数值计算无法捕捉到流动过程中的细节。
为了获得准确的稳态收敛曲线,我们需要遵循以下步骤:1. 选择合适的网格和边界条件:网格质量和边界条件的选择对数值模拟结果的准确性至关重要。
我们需要确保网格质量良好,边界条件符合实际流动情况。
FLUENT时间步长的选取对模拟结果的影响

– 将单精度浮点数转换为双精度浮点数来提高数字表示精度
单精度浮点数通常具有十进制中7位精确小数位,双精度浮点数则有约15位精确小数位
– 但使用双精度浮点数的缺点是其占据2倍内存空间,完成计算需要占用更多时间 – 在进行数值积分时,只要条件许可,通常倾向于在积分算法中使用双精度浮点数
2010 Eric
FN1-3
截断误差
截断误差是由不含舍入误差的积分步长产生的
– 截断误差是积分算法的步长在计算机上以无限数值精度执行而引起的误 差 – 每个积分算法都有其自身的截断误差特性
ቤተ መጻሕፍቲ ባይዱ
减小积分步长可将截断误差降低到任意小
– 但减小积分步长会增加仿真执行时间 – 并在解中增加舍入误差
使用高阶积分算法可以减小截断误差
2010 Eric
FN1-5
时间步长的选取对模拟结果的影响
2010 Eric
FN1-1
误差来源的分析
数值模拟可能存在的误差来源于3个方面:
– 模型误差 – 截断误差 – 舍入误差
引起误差的原因
– 引起模型误差的原因主要是,数学模型往往忽略许多次要因素造成的解 与实际真解之间的差值 – 由于事先积分算法的差分方程所得到的总是微分方程精确解的逼近值, 在积分算法的每一步都会在近似解中引入误差,误差的来源有2种:舍入 误差和截断误差
2010 Eric
FN1-2
舍入误差
舍入误差是在计算中用精度有限的有理数逼近精度无限的实数的结果
– 特定计算中,算术运算的数目和类型,以及浮点表示法的精度决定舍入误差的大 小
具体的计算和算术运算序列给定后,唯一能减小舍入误差的方法是增加计算 中数字表示法的精度
fluent能量方程不收敛

fluent能量方程不收敛?
答:Fluent能量方程不收敛的原因可能有以下几点:
1. 网格质量:网格质量是影响Fluent能量方程收敛性的重要因素。
如果网格质量较差,可能导致局部区域的能量方程无法收敛。
优化单元质量,常用方式包括缩小单元尺寸、采用多面体网格等。
2. 湍流模型:Fluent中使用了多种湍流模型,不同的湍流模型对能量方程的收敛性影响不同。
某些湍流模型可能导致能量方程不稳定,难以收敛。
3. 边界条件和初始条件:不合适的边界条件和初始条件可能导致能量方程不收敛。
为了保证能量方程的收敛性,需要合理设置边界条件和初始条件。
4. 物理参数设置:Fluent中涉及到许多物理参数设置,如比热容、密度等。
这些参数的设置会影响能量方程的收敛性。
5. 材料属性和模型设置:材料属性、边界条件等模型设置有问题也可能导致计算不收敛。
例如,某些模型数值稳定性不佳(例如欧拉多相流模型),在模型设置更应该注意。
6. 时间步长:对于瞬态计算,过大的时间步长也会引起计算不收敛。
为了解决Fluent能量方程不收敛的问题,可以尝试以下方法:
1. 检查并优化网格质量,确保网格质量达到要求。
2. 选择合适的湍流模型,确保模型的稳定性和收敛性。
3. 合理设置边界条件和初始条件,确保其与实际情况相符。
4. 调整物理参数设置,确保其在合理范围内。
5. 检查材料属性和模型设置,确保其准确性和合理性。
6. 对于瞬态计算,可以尝试减小时间步长,以提高计算的稳定性和收敛性。
fluent 时间步长 变化 表达式

时间步长是指在数值模拟中,模拟系统在每一次迭代计算中所使用的时间间隔。
在数值模拟中,时间步长的选择对模拟结果的精度和效率具有重要影响。
在本文中,我们将探讨时间步长的变化对数值模拟表达式的影响,并讨论如何根据需要选择适当的时间步长。
1. 时间步长的变化在数值模拟中,通常会通过离散化来将连续的时间变量转化为离散的时间点。
而时间步长就是每个离散时间点之间的间隔。
在一些模拟程序中,时间步长是固定不变的,这种情况下模拟系统在每一步迭代计算中所使用的时间间隔是相同的。
然而,在一些情况下,时间步长需要进行动态调整,以适应模拟系统在不同阶段的变化情况。
时间步长的变化可以通过以下几种方式实现:1)自适应时间步长:根据系统状态的变化动态调整时间步长,以保证模拟结果的精度和计算效率。
2)固定多步长:将整个模拟时间区间分为若干个子区间,在每个子区间内使用不同的时间步长来逼近系统的动态变化。
3)外部控制调整:通过外部控制器的输入来实时调整时间步长,以应对模拟系统外部输入的变化。
2. 时间步长变化对表达式的影响时间步长的变化会对数值模拟表达式的精度和稳定性产生影响。
更小的时间步长能够更准确地刻画系统的动态变化,但也会导致计算量的增加;而较大的时间步长则可能会导致模拟结果的不准确甚至不稳定。
如何选择合适的时间步长是数值模拟中需要解决的重要问题。
1)精度:时间步长越小,数值模拟结果的精度通常会越高。
这是因为较小的时间步长能够更细致地刻画系统在短时间内的变化,从而提高模拟结果的精度。
然而,需要注意的是,过小的时间步长也可能会导致数值模拟结果的误差,因为计算机的精度是有限的。
需要根据具体问题来选择合适的时间步长。
2)稳定性:在一些数值模拟中,系统的稳定性对模拟结果的影响非常重要。
较大的时间步长可能会导致数值模拟系统的不稳定,甚至发散。
需要根据模拟系统的动态特性来选择合适的时间步长,以保证模拟结果的稳定性。
3. 如何选择合适的时间步长根据以上的讨论,我们可以得出一些关于如何选择合适时间步长的建议:1)根据模拟系统的动态特性来选择合适的时间步长。
fluent瞬态求解可变时间步设置
fluent瞬态求解可变时间步设置在fluent计算中,相对于固定的时间步而言,可变时间步(variable time step)的应用更加灵活,若使用得当,可减小计算时长,但不影响求解精度。
以下介绍可变时间步的详细使用方法。
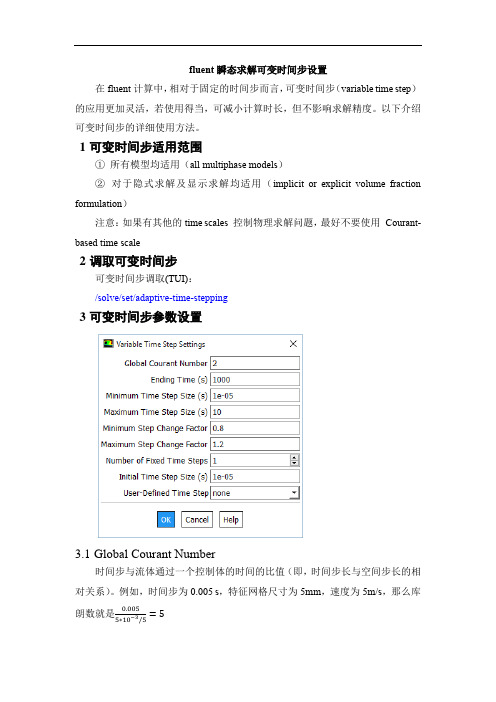
1可变时间步适用范围①所有模型均适用(all multiphase models)②对于隐式求解及显示求解均适用(implicit or explicit volume fraction formulation)注意:如果有其他的time scales 控制物理求解问题,最好不要使用Courant-based time scale2调取可变时间步可变时间步调取(TUI):/solve/set/adaptive-time-stepping3可变时间步参数设置3.1Global Courant Number时间步与流体通过一个控制体的时间的比值(即,时间步长与空间步长的相对关系)。
例如,时间步为0.005 s,特征网格尺寸为5mm,速度为5m/s,那么库=5朗数就是0.0055∗10−3/5控制库朗数的目的是为了在一个时间步内,使流体通过的网格数量不会太多,以此保证迭代效果默认的global Courant number是2推荐的库朗数大小:显式求解explicit volume fraction formulation瞬态求解(transient):2时均求解(time-averaged):可比2稍大,但是不得大于5隐式求解implicit volume fraction formulation瞬态求解(transient):对于一阶时间求解(first order time formulation),推荐库朗数为2,对于二阶时间求解(second order time formulation),推荐库朗数最大为5时均求解(time-averaged):最大为203.2initial time step size在第一个时间步及固定时间步数量(number of fixed time steps)范围内使用,其数值必须介于上图最大和最小时间步范围之内,最好能够使得库朗数接近于1。
fluent特征松弛时间

fluent特征松弛时间摘要:1.Fluent 软件介绍2.特征松弛时间的概念3.特征松弛时间的应用4.特征松弛时间的设置与调整5.总结正文:【1.Fluent 软件介绍】Fluent 是一款广泛应用于流体力学领域的计算流体力学(CFD)软件,可以用于模拟流体流动、传热和化学反应等多种物理现象。
Fluent 提供了丰富的物理模型和数值方法,可以模拟从微观到宏观的各种流体问题,被广泛应用于工程、科学研究和教育等领域。
【2.特征松弛时间的概念】在Fluent 中,特征松弛时间是一个重要的时间步长参数,它控制着流体物理量的更新速度。
特征松弛时间决定了在每个时间步长内,Fluent 软件用于计算流体物理量的时间步长数目。
一般来说,特征松弛时间越小,计算精度越高,但计算时间也会相应增加。
【3.特征松弛时间的应用】特征松弛时间在Fluent 中的应用主要体现在以下几个方面:(1)控制计算精度:通过调整特征松弛时间,可以控制每个时间步长内流体物理量的更新次数,从而影响计算精度。
(2)提高计算效率:在保证计算精度的前提下,可以通过适当增大特征松弛时间,减少每个时间步长的计算次数,提高计算效率。
(3)减小数值扩散:特征松弛时间较小时,数值扩散现象会减轻,从而可以更准确地模拟流体流动。
【4.特征松弛时间的设置与调整】在Fluent 中,特征松弛时间可以通过以下步骤进行设置和调整:(1)打开Fluent 软件,创建或打开一个流体模拟项目。
(2)在主界面的“解决问题”模块中,选择“定义模型”,进入模型定义对话框。
(3)在模型定义对话框中,选择“时间步长控制”,找到“特征松弛时间”参数。
(4)输入合适的特征松弛时间值,并根据实际计算情况进行调整。
(5)点击“关闭”按钮,返回主界面,开始进行流体模拟计算。
【5.总结】Fluent 中的特征松弛时间对于流体模拟计算具有重要意义,可以通过调整特征松弛时间来控制计算精度、计算效率和数值扩散等。
FLUENT控制步长时间courant数的有效的经验

" What is the difference between the time accurate solution of Navier-Stokes equations and the DNS solution? "I'm not sure I understand this question correctly, but as far as I am aware DNS (Direct Numerical Simulation) is defined as a time accurate solution of the Navier-Stokes equations.Perhaps you mean "What is the difference between laminar & turbulent DNS?" ? Believing this to be so from reading the rest of your message I wrote the following:When the DNS is of turbulence rather than a laminar flow the turbulence requires initialization in some way. The same is true of LES (LES is always turbulent, because laminar LES = DNS by definition). I have found little reported work on the proceedures used to accomplish this turbulence initialization.I can only speak for the LES code I use (and the generations of code that preceded it). The turbulence is initialized by setting an initial flow field that has a random fluctation velocity component added to the inital mean velocity.-----------------For example:U_initial_cell =U_initial_mean + (Random_number * U_initial_mean * 0.20)( Random_number has a value in the range -1 to +1 )This function sets the initial cell velocity to that of the initial_mean with a tolerance of 20% (i.e. + or - 20%). So if the U_initial_mean was 1.0 then the initial velocity of the cell could be anywhere between 0.8 and 1.2 depending on the Random_number (an intrinsic computer function).-----------------The value for initial fluctuation (20% etc) is a fairly arbitrary value just required to `kick-start' the turbulence. Once the simulation has been kick-started and run sufficiently long enough for the correct energy cascade to be observed (by monitoring k.e. of the flow) the statistics data from that point onward is o.k to be used for results. This accumulation of statistical data is one of the reasons why LES/DNS turbulent simulations require so much more time to run.Providing the same random_number is used on the same cells during initialization the computations of two DNS cases will be exactly* the same when all other conditions (boundary, geometry, etc) are equivalent.*exactly is defined as Phi(x,t)_simulation_A = Phi(x,t)_simulation_BIf different random_numbers are used then the flow solution would be expected to be slightly numerically different from a previous run, but statistically the same. This would be similar to the case where two experimental turbulent simulations in a wind tunnel do not have exactly* the same flow field, but are expected to be statistically the same and have the same coherent structures in the flow.LES, or turbulent DNS is like journeying along a road. The intial fluctations imposed pre-determine which exact roads you will travel on, and the other boundary conditions determine the general direction in which you will be heading. In industrial problems the concern is with the direction you are heading,N,E,S, or West, and not so much if you are on a particular road at a particular time, e.g. walking by 43 Accacia Road at 5pm.This idea may be seen in the definition of turblence by Hinze (1959) "...so that statistically distinct average values can be discerned." For if Taylor & Von Karman's 1937 definition was taken literally CFD shouldn't exist!The grid size of LES should be small enough. But it is not easy to get the exact size of the smallest cells. Some people use y+, other people use Kolmogorov scales,etc. As you know, the basic assumption is that the flow with SGS is isotropic in the case of using Smagorinsky model.Based on my experience, not only the size of smallest grids but also there are many other facts to be considered in LES. Computational domain size, cell cluster, boundary conditions, wall treatment, etc.So if you want to do LES, some compromise would be necessary. At first, please use reasonable size of computational domain, number of cells and run the problem in your computer. If the result is not accurate enough, then increase the resolution. But even though the resolution is not enough (in the LES viewpoint), you may get satisfactory results.Good luckIdeally, while doing LES you want to have a mesh which resolves all the anisotropic scales leaving only the isotropic scales to be modeled. The modeling of the isotropic scales is similar to the RANS approach. In reality, it is not possible to satisfy all the mesh resolution requiremnts all the time with LES. For the question whether a coarse mesh LES gives a good solution, it depends on the level of accuracy you are lookiing at. This is where your engineering intuition should provide you the answer.。
FLUENT不收敛的解决方法

FLUENT不收敛的解决方法解决FLUENT不收敛的问题是一个复杂的过程,因为它涉及到多个因素的相互影响。
下面是一些解决FLUENT不收敛问题的常用方法:1.初始条件的选择:在开始数值求解之前,需要确定一个合适的初始条件。
初始条件对于解的收敛性至关重要。
初始条件应该尽可能接近真实的解,以便尽快地达到收敛状态。
2.网格的质量:网格的质量对于解的收敛性有重要影响。
不合适的网格质量可能导致剧烈的数值振荡和不收敛。
因此,在进行数值求解之前,要确保网格是充分细化和适当分布的。
3.边界条件的设置:边界条件是数值求解的重要组成部分。
正确选择和设置边界条件可以帮助解决不收敛的问题。
边界条件应该与实际情况相适应,并且在数值上稳定。
4.松弛因子的调整:松弛因子是迭代求解过程中的一个重要参数。
它可以控制数值振荡的幅度和求解的速度。
调整松弛因子可以帮助改善解的收敛性。
通常,可以通过逐步调整松弛因子的值来找到合适的取值。
5.改变求解方法:FLUENT提供了多种求解方法,包括迭代解法、隐式解法等。
在遇到不收敛的情况下,可以尝试改变求解方法。
例如,从显式求解器切换到隐式求解器,或者改变迭代收敛准则等。
6.缩小时间步长:时间步长是时间离散化的重要参数。
当模拟流体现象有快速变化时,时间步长可能需要相应缩小。
缩小时间步长可以提高求解的稳定性和收敛性。
7.考虑物理特性:在建立数学模型和设定边界条件时,要充分考虑物理特性。
不合理的模型和边界条件可能导致不收敛的问题。
合理的物理模型和边界条件可以提高解的收敛性。
8.自适应网格:自适应网格技术可以根据流场的变化情况动态调整网格,从而提高求解的精度和收敛性。
在遇到不收敛的问题时,可以尝试使用自适应网格技术。
9.并行计算:FLUENT支持并行计算,可以利用多个处理器进行求解。
并行计算可以加速求解过程,并有助于解决不收敛的问题。
通过提高计算效率,可以增加求解的稳定性和收敛性。
10.稳定化技术:当遇到不稳定的流场时,可以尝试使用稳定化技术来提高求解的稳定性。
fluent组件参数设定参考

Fluent组件参数设定参考第一部分读入文件1.1 读入文件FLUENT组件读取工况文件(.cas)和网格文件(.msh),并得到一些相关信息,之后运行FL UENT相应的程序,并运行FLUENT读取信息的脚本,点击打开加载网格信息显示在界面中以供用户调试。
1.2 求解器类型二维三维指所导入的模型维数。
单精度与双精度:单精度与双精度指求解器在表示变量的时候采用单精度的float类型或者采用double类型。
在所有的操作系统上都可以进行单精度和双精度计算。
对于大多数情况来说,单精度计算已经足够,但在下面这些情况下需要使用双精度计算:(1)计算域非常狭长(比如细长的管道),用单精度表示节点坐标可能不够精确,这时需要采用双精度求解器。
(2)如果计算域是许多由细长管道连接起来的容器,各个容器内的压强各不相同。
如果某个容器的压强特别高的话,那么在采用同一个参考压强时,用单精度表示其他容器内压强可能产生较大的误差,这时可以考虑使用双精度求解器。
(3)在涉及到两个区域之间存在很大的热交换,或者网格的长细比很大时,用单精度可能无法正确传递边界信息,并导致计算无法收敛,或精度达不到要求,这时也可以考虑采用双精度求解器。
第二部分网格操作2.1 网格刻度网格刻度主要是可以改变原来网格创建的单位,在网格软件中,默认单位一般是毫米,而在FLUENT软件中,默认单位是米,所以需要修改。
在面板上选择网格文件创建的单位,fluent组件将会再fluent里面将默认单位m改为网格文件创建的单位,一般改为mm。
2.2 网格检查网格检查是检查网格的质量信息,要求网格不能有负体积,2.3 网格光顺临近单元体积的快速变化会导致大的截断误差。
截断误差是指控制方程偏导数和离散估计之间的差值。
FLUENT可以改变单元体积或者网格体积梯度来精化网格从而提高网格的光滑性。
拉普拉斯光滑适用于各种类型的网格,当使用拉普拉斯方法时,一个拉普拉斯光滑操作被应用于非结构网格以重新配置节点。
fluent 非定常计算的 自适应时间步控制

fluent 非定常计算的自适应时间步控制fluent 非定常计算的自适应时间步控制一、引言在计算流体力学领域,非定常计算是一项重要的研究内容。
在进行非定常计算时,自适应时间步控制是必不可少的一环。
本文将从何谓非定常计算开始,逐步展开对自适应时间步控制的深入讨论,以帮助读者更好地理解和掌握这一内容。
二、何谓非定常计算在计算流体力学中,非定常计算是指随时间而变化的流场情况。
与定常计算相比,非定常计算需要考虑流场在时间上的演变,因此需要对时间进行离散化处理,计算每个时间步上的流场情况。
非定常计算通常适用于流动速度、压力等随时间变化较大或需要研究流场随时间演变的情况。
三、自适应时间步控制的必要性在进行非定常计算时,选取合适的时间步长对计算结果的精确性和计算效率有着至关重要的影响。
过长的时间步长会导致计算结果的不准确,而过短的时间步长则会增加计算量,降低计算效率。
需要一种能够自适应地根据流场情况调整时间步长的方法,以保证计算结果的准确性和计算效率的平衡。
四、自适应时间步控制的方法和原理1. 时间步长的调整方法在 fluent 软件中,自适应时间步控制通常采用两种方法:局部时间步控制和全局时间步控制。
局部时间步控制是指根据流场的局部情况来调整时间步长,一般适用于流场中存在着不同的时间尺度或流动速度差异较大的情况。
全局时间步控制则是指在整个计算域中使用相同的时间步长,适用于流场情况较为均匀的情况。
2. 时间步长的调整原理时间步长的自适应调整通常基于残差、稳定性和收敛性等指标。
在fluent 中,可以通过设定残差的阈值来判断流场的变化情况,当残差超过设定的阈值时,自适应时间步控制会自动减小时间步长,以保证计算结果的精确性。
另外,流场的稳定性和收敛性也会影响时间步长的调整,通过对流场的数值特征进行评估,可以进一步优化时间步控制的效果。
五、对自适应时间步控制的个人理解自适应时间步控制是非定常计算中的关键技术之一,能够有效地提高计算的精确性和效率。
fluent共轭换热固体时间步长是什么意思

fluent共轭换热固体时间步长是什么意思Fluent共轭换热固体时间步长是什么意思?1. 引言在传热领域,共轭换热问题是一个重要的研究课题。
而在Fluent中,共轭换热固体时间步长是一个关键的参数,对于模拟结果的准确性和收敛性有着重要影响。
本文将深入探讨Fluent共轭换热固体时间步长的具体含义,以及其在实际工程仿真中的作用。
2. Fluent共轭换热固体时间步长的定义在Fluent中,共轭换热固体时间步长是指在求解多物质传热问题时,用于计算固体传热的时间步长参数。
这一参数的设定对于模拟结果的准确性和计算效率有着重要作用。
3. 具体作用和影响3.1 准确性Fluent共轭换热固体时间步长的设定直接影响了固体传热过程的模拟准确性。
时间步长过大会导致模拟结果的精度下降,时间步长过小则会增加计算成本。
合理设定共轭换热固体时间步长对于保证模拟结果的准确性至关重要。
3.2 收敛性另外,共轭换热固体时间步长的设定也对模拟的收敛性有着重要影响。
合理的时间步长能够提高数值模拟的收敛速度,减少计算时间和资源的消耗,从而提高工程仿真的效率和可行性。
4. 个人观点和理解个人认为,在实际工程仿真中,合理的共轭换热固体时间步长设定是保证模拟结果准确性和收敛性的关键之一。
需要根据具体的传热问题和模拟要求,综合考虑时间步长对准确性和计算效率的影响,进行合理的参数设定。
5. 总结本文深入探讨了Fluent共轭换热固体时间步长的具体含义和在实际工程仿真中的作用。
从准确性和收敛性的角度分析了时间步长的影响,并共享了个人观点和理解。
合理设定共轭换热固体时间步长,对于保证传热模拟的准确性和计算效率至关重要。
希望本文对于相关领域的工程师和研究人员有所帮助。
通过以上分析,你对Fluent共轭换热固体时间步长的概念是否已经有了更深入的理解呢?如果还有其他问题需要进一步探讨,欢迎随时与我联系。
在Fluent中,共轭换热固体时间步长是指在多物质传热问题中,用于计算固体传热的时间步长参数。
fluent圆管仿真湍流参数设置

一、概述在工程领域中,流体力学仿真是一项十分重要的工作。
在进行流体力学仿真时,对于湍流参数的设置尤为关键。
本文主要讨论在使用fluent软件进行圆管湍流仿真时,如何设置参数以获得准确可靠的结果。
二、湍流模型的选择1. 简介在进行圆管湍流仿真时,首先需要选择合适的湍流模型。
目前常用的湍流模型包括k-ε模型、k-ω模型、SST湍流模型等。
每种湍流模型都有其适用的范围和局限性。
2. 参数设置在fluent软件中,进行湍流模型选择时需要考虑雷诺数、流场特性等因素。
根据具体情况选择合适的湍流模型,并对相应的参数进行设置。
三、网格划分1. 网格类型在进行圆管湍流仿真时,合适的网格划分也是至关重要的。
常见的网格类型包括结构化网格、非结构化网格等。
2. 网格密度对于圆管湍流仿真,网格的密度对结果的准确性有着直接的影响。
在fluent软件中,可以通过设置不同的网格密度来进行网格划分。
四、边界条件设置1. 入口边界条件对于圆管湍流仿真,入口边界条件的设置对结果有着重要的影响。
在fluent软件中,可以通过设定入口速度、湍流强度等参数来进行设置。
2. 出口边界条件出口边界条件的设置同样十分重要。
在fluent软件中,需要考虑出口压力、流速等参数。
五、求解器设置1. 时间步长在进行湍流仿真时,时间步长的选择对结果的精度有着很大的影响。
需要根据具体情况进行合理的设置。
2. 收敛准则在fluent软件中,收敛准则的设置也是必不可少的。
通过调整收敛准则的值来保证计算结果的准确性。
六、计算结果分析1. 流场分布通过fluent软件进行湍流仿真后,可以获得流场的分布情况。
需要对结果进行仔细的分析和比对。
2. 压降计算在圆管湍流仿真中,压降是一个重要的参数。
需要对压降进行精确的计算和分析。
七、总结圆管湍流仿真是流体力学仿真中的重要内容。
在使用fluent软件进行仿真时,正确的参数设置和合理的操作流程至关重要。
通过本文的讨论,相信读者对圆管湍流仿真的参数设置有了更清晰的认识,能够在实际工程中取得更好的仿真结果。
fluent中time step size

fluent中time step size
在Fluent中,时间步长(time step size)是指在模拟过程中每
次迭代所使用的时间间隔。
它决定了模拟的时间精度和计算效率。
在Fluent中,时间步长可以通过不同的方法进行设置:
1. 自动时间步长(Automatic Time Step):Fluent可以自动根
据模拟中的物理特性和计算条件来确定合适的时间步长。
可以通过在求解设置中将时间步长设置为“自动”来使用这种方法。
2. 手动设置(Manual Setting):用户可以手动设置时间步长,固定在一个特定的值上。
可以通过在求解设置中将时间步长设置为“手动”并指定一个值来使用这种方法。
在选择时间步长时,需要平衡时间精度和计算时间之间的权衡。
如果时间步长设置得太小,模拟将需要更长的计算时间,而如果时间步长设置得太大,可能会导致数值不稳定或模拟结果不准确。
因此,通常需要进行多次模拟试验来确定最佳的时间步长。
fluent 二阶隐式时间格式

fluent 二阶隐式时间格式摘要:一、引言二、二阶隐式时间格式介绍1.概念解析2.应用场景三、fluent 软件中的二阶隐式时间格式实现1.操作方法2.参数设置四、二阶隐式时间格式在fluent 软件中的优势及局限性1.优势2.局限性五、总结正文:一、引言在流体力学领域,数值模拟是一种重要的研究方法。
其中,fluent 软件作为一款功能强大的流体力学模拟软件,被广泛应用于各种工程问题中。
为了提高模拟精度,fluent 软件提供了二阶隐式时间格式,以满足用户在不同场景下的需求。
本文将对fluent 中的二阶隐式时间格式进行详细介绍。
二、二阶隐式时间格式介绍1.概念解析二阶隐式时间格式,是指在时间步进过程中,采用二阶差分方程对物理量进行离散化处理的一种时间格式。
相较于一阶格式,二阶格式具有更高的精度,能够更好地捕捉流场中的细节信息。
2.应用场景二阶隐式时间格式主要应用于以下场景:(1)对流场中变化较为缓慢的物理量进行求解,如压力、速度等;(2)在稳态模拟中,需要更高的精度时;(3)在非稳态模拟中,需要捕捉流场瞬间变化时。
三、fluent 软件中的二阶隐式时间格式实现1.操作方法在fluent 软件中,用户可通过以下步骤实现二阶隐式时间格式的设置:(1)打开fluent 软件,创建或导入模型;(2)在“物理模型”选项卡下,选择“湍流模型”;(3)在“湍流模型”设置中,找到“时间格式”,选择“二阶隐式”;(4)设置其他参数,如湍流参数、边界条件等;(5)进行模拟计算。
2.参数设置在设置二阶隐式时间格式时,用户还需关注以下参数设置:(1)时间步长:根据实际问题需求,选择合适的时间步长;(2)稳态要求:对于稳态模拟,可适当放宽时间步长要求;(3)收敛标准:设置合适的收敛标准,以保证模拟精度和计算效率。
四、二阶隐式时间格式在fluent 软件中的优势及局限性1.优势(1)提高模拟精度:相较于一阶时间格式,二阶隐式时间格式能够提供更准确的数值解;(2)适应多种场景:二阶隐式时间格式在稳态和瞬态模拟中均有较好的表现,能够满足不同用户需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用FLUENT计算非稳态问题,是不是在计算时必须保证在每个时间步timestep里都要收敛才行,否则计算结果就不对呢也就是说,在iteration选项里,max iteration pertime step设为一个值,比如500,就是如果500次迭代后仍未收敛,进入下一步迭代,那对结果会有什么影响。
对于隐式非定常格式,原则上,每个时间步长内必须保证结果收敛。
在fluent 的帮助中就有这样的话:“对于不可压流动,在每个时间步内,不可压解必须迭代直至收敛。
”另外,我们回归到fluent内部计算的本源,它实质就是一种差分算法,通过不断逼近来获得真实解,这样我们就不难理解为什么在每个时间步长内需要收敛了。
max iteration pertime step 设定的是最大时间步,在单一步长内,如果结果已经收敛,则会自动跳至下一时间进行计算。
所以其设定要纵观全局。
但对于周期性流动,这种收敛性的要求就相对松动一些。
不过你需要多计算几个周期,等计算结果达到对时间的周期状态后,再对结果进行储存。
对于显式非定常格式,在Fluent帮助中这样说:“一定记住,对于显式非定常格式,每一个迭代就是一个时间步。
”
如果每个时间步内结果没有得到收敛,则很有可能你所得到的结果是不真实的,但是一个时间步内的不真实性应该不会影响到下一个时间步长内的计算。
因为在每一个时间步开时,fluent 都会进行初始化。
在单个时间步内,它实际是按照稳态进行计算的。
time step size的设定是根据你的计算需要,一般是你的特征长度(比如说管道的长度)除于特征速度(比如平均速度)的值再小一到两个量级即可,如果你的time stip size太大,计算会提示你的,改小即可。
number of time steps是这样设定的:number of time steps X time step size=实际时间积累。
比如说,你计算一个射流,你需要计算到1秒时候的情况,那么(number of time steps)=1秒/(time step size)。
Fluent中非稳态时间步长设置
最近所做的非稳态计算,若设置太小,计算时间就太长,设置太大的话就会出现Global Courant Number飙升过大的不能继续进行下去的问题。
有网友建议:&Id=3782
单元最小长度除于流场平均流速,不过这个值可能很小,你可以以这个值为基准进行调节,一开始可以取大些,如果没有问题,可以再放大些,这样可以缩短计算时间。
若按这种方法,计算下面这个例子:2mm,10个网格,流速1m/s。
时间步长time steps=1000=。
但是我在进行计算时,设置为1e-6,都无法进行下去。
所以这种换算方法还是只能作为参考。
我现在采用的是自动调节时间步长,目前看来效果还可以。
courant number与收敛
courant number实际上是指时间步长和空间步长的相对关系,系统自动减小courant数,这种情况一般出现在存在尖锐外形的计算域,当局部的流速过大或者压差过大时出错,把局部的网格加密再试一下。
在fluent中,用courant number
来调节计算的稳定性与收敛性。
一般来说,随着courant number的从小到大的变化,收敛速度逐渐加快,但是稳定性逐渐降低。
所以具体的问题,在计算的过程中,最好是把courant number从小开始设置,看看迭代残差的收敛情况,如果收敛速度较慢而且比较稳定的话,可以适当的增加courant number的大小,根据自己具体的问题,找出一个比较合适的courant number,让收敛速度能够足够的快,而且能够保持它的稳定性。
时间步长与准确性
摘自《数值计算与工程仿真》第一期作者gim
1 、在不计模型误差,而且计算稳定的前提下,数值计算的时间步长的选取存在一个恰当值,过大或过小都会影响模拟结果的准确性。
2 、具体数值模拟中,最好能有一定的实验数据或其它的可以认为准确的结果作为验证资料,这样才能恰当的选定时间步长,提高计算的准确性。
3 、FLUENT 软件采用隐式计算,这就需要设定每一次迭代的最大步数(Max Iterations per Time step ) ,如果达到最大步数前计算已经收敛,系统会自动进入下一步迭代。
利用这一点可以采取如下方法确定迭代的时间步长:系统一般认为每一步的迭代次数应在10 一20 次之问,设定一个时间步长后如果在迭代次数内还没有收敛就应该减小时间步长,反之则应该增加时间步长。
一般,都事先给定一个较小的时问步长进行迭代儿步,而后逐步调整。
当然迭代次数也跟具体问题相关,还需要计算经验的不断积累。
tags: fluent,非稳态,时间步长
fluent迭代计算中,非定常问题的时间步长如何选取
显式时间积分方案:时间步长Δt<ρ(Δx)2 /2Γ;半隐式时间积分方案:时间步长Δt<ρ(Δx)2 /Γ;全隐式时间积分方案:时间步长没有限制。
Δx是网格相邻节点的距离,Γ是扩散系数,不同问题有不同的物理意义
非稳态时间步长与迭代步数的讨论
在unsteady的计算求解中,大部分同学应该会对solver中设置比较迷惑,在这里,我想就我个人的理解对其时间步长与迭代步数进行一些分析讨论。
1、在进行unsteady 计算的时候,fluent是从前一个时间算到下一个时间(即time steps),而每个时间步长内的计算就相当于一个准稳态求解,因此需要设置Max Iterations per Time Step;在这个时间步长内的计算就是一个稳态过程,在达到iteration次数之前收敛完成,就跳到下一个time step,否则就将所规定的迭代次数算完在跳下一个time step。
2、时间步长的设置:(1)特征长度除以特征速度所得的时间小二个量级或者更小。
这是理论值,实际上,如果不是工作站运行的话,花费的计算时间太长。
因此,通常在fluent 中选定这个比例的1/5到1/10,特别是一开始不知道如何设定的时候最好是打开adaptive 让它自动定义定义时间步长。
但其中最小的时间尺度,个人认为最小也只能小到这个比例的1/100的这个水平上。
(2)最小网格长度除以流速或者旋转流动速度。
这个是保证每一次迭代都在一个网格范围内,不会因跨网格而导致结果误差,但实际中计算一段时间后可能加快计算速度,会将时间步长设置较大,最后为得到最终求解,再将时间步长调小,进行细微的计算。
3、时间步长里的迭代步数设置:保证每个时间步长达到收敛,或者能明显看到主要残差曲线趋于水平。
4、时间步数:看你需要计算多长时间,本人觉得至少需要计算3-5个流动循环周期才可能得到非定常的稳定流动周期状态。
