随机信号分析与处理习题解答罗鹏飞
随机信号分析与处理习题解答罗鹏飞.pdf

P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n
n
∑ 所以 X = Xi 服从参数为 n,p 的二项分布。 i =1
且有 E( Xi ) = 1⋅ P{Xi = 1}+ 0 ⋅ P{Xi = 0} = p ,
E
(
X
2 i
)
= 12
⋅
P{ X i
= 1}+
P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n , 0 < p < 1
求 X 的均值和方差。 解法一:直接按照定义计算
n
n
∑ ∑ E( X ) = mP{X = m} = mCnm pm (1− p)n−m
m=0
m=0
∑n
=m
n!
pm (1− p)n−m
第 1 章 随机变量基础
1.1 设有两个随机变量 X 和 Y,证明
fY|X ( y | x) =
f (x, y) f X (x)
,
f X |Y
(x
|
y)
=
f (x, y) fY (y)
y x+Δx
∫ ∫ f (x, y)dxdy
提示:首先证明 F ( y | x < X ≤ x + Δx) = −∞ x
02
⋅
P{ X i
=
0}
=
p
,
D(Xi )
=
E
(
X
2 i
)
−
E2(Xi)
=
p
−
p2
=
p(1 −
p)
n
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=i i i x X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他0201)](2π[cos 2)()(x x A dx x dF x f 由1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x (2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x x x x F (3)0)]()([)(>--=a a x u x u a xx F (4)0)()()(>---=a a x u axa x u a x x F2解:(1)⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x 当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数; 1)(0≤≤x F 成立;)()(x F x F =+也成立。
《随机信号分析与处理》教学大纲

《随机信号分析与处理》教学⼤纲《随机信号分析与处理》教学⼤纲(执笔⼈:罗鹏飞教授学院:电⼦科学与⼯程学院)课程编号:070504209英⽂名称:Random Signal Analysis and Processing预修课程:概率论与数理统计、信号与系统、数字信号处理学时安排:60学时,其中讲授54学时,实践6学时学分:3⼀、课程概述(⼀)课程性质地位本课程是电⼦⼯程、通信⼯程专业的⼀门学科基础课程。
该课程系统地介绍随机信号的基本概念、随机信号的统计特性分析⽅法以及随机信号通过系统的分析⽅法;介绍信号检测、估计、滤波等信号处理理论的基本原理和信息提取⽅法。
其⽬的是使学⽣通过本课程的学习,掌握随机信号分析与处理的基本概念、基本原理和基本⽅法,培养学⽣运⽤随机信号分析与处理的理论解决⼯程实际问题的能⼒,提⾼综合素质,为后续课程的学习打下必要的理论基础。
本课程是电⼦信息技术核⼼理论基础。
电⼦信息系统中的关键技术是信息获取、信息传输、信息处理,这些技术的理论基础就是随机信号的分析、检测、估计、滤波等理论,这正是本课程的主要内容。
因此,本课程内容是电⼦信息类应⽤型⼈才知识结构中不可或缺的必备知识。
⼆、课程⽬标(⼀)知识与技能通过本课程的学习,掌握随机信号分析与处理基本概念和基本分析⽅法。
内容包括:1.理解和掌握随机过程基本概念和统计描述;2.掌握随机过程通过线性和⾮线性系统分析⽅法3.理解和掌握典型随机过程的特点及分析⽅法;4.掌握参数估计的概念、规则和性能分析⽅法;5.掌握信号检测的概念、规则和性能分析⽅法;6.掌握⾼斯⽩噪声中最佳检测器的结构和性能分析。
通过本课程的学习,要达到的能⼒⽬标是:1.具有正确地理解、阐述、解释⽣活中的随机现象的能⼒,即培养统计思维能⼒;2.运⽤概率、统计的数学⽅法和计算机⽅法分析和处理随机信号的能⼒;3.初步具备雷达、通信、导航等技术领域的信号处理系统的分析、设计、仿真的科学研究能⼒;4.培养⾃主学习能⼒;5.培养技术交流能⼒(包括论⽂写作和⼝头表达);6.培养协作学习的能⼒;(⼆)过程与⽅法依托“理论、实践、第⼆课堂”三个基本教学平台,通过课堂教学、概念测试、课堂研讨、案例研究、作业、实验、课程论⽂、⽹络教学等多种教学形式,采⽤研究型、案例式、互动研讨、基于团队学习、基于MATLAB的教学以及基于多媒体的教学等多种教学⽅法和⼿段,使学⽣加深对随机信号分析与处理的基本概念、基本原理以及应⽤的理解,并使学⽣通过⾃主学习、⼩组作业、案例研究、实验、课题论⽂等主动学习形式,培养⾃学能⼒和协同学习的能⼒,使学⽣不仅获得知识、综合素质得到提⾼。
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x2(2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F (3)0)]()([)(>--=a a x u x u ax x F (4)0)()()(>---=a a x u ax a x u a x x F解:(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数;1)(0≤≤x F 成立; )()(x F x F =+也成立。
随机信号分析罗鹏飞

2 | | 0 R X ( ) lim X e
∴mX =0
2 |0| X
X
X
0 rX ( )d e 0
0
| |
1 1 d e |0
(2)
m X lim R X ( ) lim (1 | |) 0
可算出线性变换矩阵的秩r(L)=3,且 X=[X1,X2, X3]T 的协方差阵为单位矩阵I,易知Y服从三维 正态分布,Y的均值为mY=Lm =O,协方差阵为
LKLT 1 2 1 6 1 3 1 2 1 6 1 3 1 0 2 1 0 0 2 1 0 1 0 2 6 0 0 1 1 0 3 1 6 1 6 2 6 1 6 1 6 2 6 1 3 1 3 1 3
2.4 设随机过程 X (t) = b + Nt,已知 b为常量, N 为正态随机变量,其均值为 m,方差为σ2。 试求随机过程X(t)的一维概率密度及其均值和 方差。 解:∵ N 为正态随机变量,∴X(t)也是正态随 机变量。
2.13 已知随机过程 X (t ) = cosΩt ,其中Ω为均 匀分布于 (ω1,ω2)中的随机变量。试求: (1)均值为mX (t) ; (2)自相关函数 RX (t1, t2) 。 1 解:Ω的概率密度函数为: f () 2 1 (1)均值:mX (t) =E{X(t)} costf ()d 2 1 1 2 sin t |1 cost d 1 (2 1 )t 2 1 sin 2 t sin 1t (2 1 )t
m
m jm m jm a e a e m 0
北邮随机信号分析与处理第2章习题解答_2

不满足严格平稳。
思考:是否满足广义平稳?
3
2.17
随机过程由下述三个样本函数组成,且等概率发生:
X (t, e1 ) 1, X (t, e2 ) sin t, X (t, e3 ) cos t (1)计算均值 mX (t ) 和自相关函数 RX (t1 , t2 );
(2)该过程是否为平稳随机过程? 解: 1 1 1
ftp服务器地址
ftp://10.108.142.57
用户名和密码均为:sjxhfx
包括每次课的课件和部分习题解答
1
2.14
广义平稳随机过程 Y (t ) 的自相关矩阵如下,试确定矩阵中用 表示的元素。 2 1.3 0.4 2 1.2 0.8 RY 0.4 1.2 1.1 0.9 2 解:由自相关函数的性质
2
2.15
根据掷骰子试验,定义随机过程为
K X (t ) cos t ( K 1, 2,3, 4,5,6) 3 (1)求 X (1) 、X (2) 的概率密度; (2) X (t ) 是否为平稳随机过程?
解:
1/ 2, K 1,5 1/ 2, K 2, 4 K X (1) cos 1, K 3 3 1, K 6
E[ A(t1 ) A(t2 )cos t1 cos t2 ] E[ A(t1 ) B(t2 )cos t1 sin t2 ] E[ B(t1 ) A(t2 )sin t1 cos t2 ] E[ B(t1 ) B(t2 )sin t1 sin t2 ] RA (t1, t2 )cos t1 cos t2 RB (t1, t2 )sin t1 sin t2 R( )cos t1 cos t2 R( )sin t1 sin t2 R( )cos(t1 t2 ) R( )cos( )
“随机信号分析与处理”课程军事应用案例式教学实践

2022年6月第24期Jun. 2022No.24教育教学论坛EDUCATION AND TEACHING FORUM“随机信号分析与处理”课程军事应用案例式教学实践田瑞琦,刘晓斌,谢晓霞(国防科技大学 电子科学学院,湖南 长沙 410073)[摘 要] 信号分析与处理技术是电子信息系统中关键技术的理论基石,“随机信号分析与处理”课程是电子信息类本科专业的一门专业必修课程。
在分析国防科技大学“随机信号分析与处理”课程教学现状的基础上,提出军事应用案例式教学改革设想,通过介绍课程相关军事应用案例的收集和制作、课堂施教及教学效果,得出军事应用案例式教学改革能够进一步提高教学效果,促进学员对信号处理基本原理的理解,增强学员动手能力,为学员创新能力和综合素质的提高发挥重要作用。
[关键词] 随机信号;信号分析与处理;军事应用;案例式教学;教学改革[基金项目] 2020年度国防科技大学本科生教改课题“基于导弹试验数据的‘随机信号分析与处理’金课案例库建设”(U2020010)[作者简介] 田瑞琦(1990—),女,湖南常德人,博士,国防科技大学电子科学学院讲师,主要从事信号分析与处理理论及教学研究;刘晓斌(1990—),男,河南郑州人,博士,国防科技大学电子科学学院讲师,主要从事雷达信号处理与目标识别理论及教学研究;谢晓霞(1974—),女,湖南益阳人,硕士,国防科技大学电子科学学院教授,主要从事信号分析与处理理论及教学研究。
[中图分类号] G642.0 [文献标识码] A [文章编号] 1674-9324(2022)24-0140-04 [收稿日期] 2021-06-18引言2017年,习近平总书记向军事科学院、国防大学、国防科技大学授军旗、致训词,出席座谈会并发表重要讲话强调,国防科技大学是高素质新型军事人才培养和国防科技自主创新高地。
要紧跟世界军事科技发展潮流,适应打赢信息化局部战争要求,抓好通用专业人才和联合作战保障人才培养,加强核心关键技术攻关,努力建设世界一流高等教育院校[1]。
(仅供参考)随机信号分析与处理简明教程--第二章习题答案
证明:设τ = t2 − t1
Rz
(τ
)
=
E[z( t1 )z( t 2
)]
≤
E[
z2
(t1)
+ 2
z2
(t2
)]
=
1 2
E[z2
(t1 )
+
z2
(t2
)]
=
1 2
E[z
2
(t1
)]+
1 2
E[z2(t2 Nhomakorabea)]=
1 2
(R
z
(0)
+
R
z
(0))
=
R
z
(0)
(平稳过程)
所以, R z (0)
= σz2
+
可看作一个随机过程 X (t) = Acos(Ωt + Θ) ,其中 A, Ω, Θ 是相互独立的随机变量,且已知
f
A
(a)
=
⎧ ⎪ ⎨
2a A02
,
a ∈ (0, A0 ) ,
fΩ (ω) = ⎪⎨⎧1010 ,
ω
∈ (250,350) ,
fΘ (θ
)
=
⎪⎧ ⎨
1 2π
,
θ ∈ (0, 2π )
⎪⎩0, 其他
第 2 章习题解答
2.1 设有正弦波随机过程 X (t) = V cosωt ,其中 0 ≤ t < ∞ , ω 为常数,V 是均匀分布于 [0,1] 区间的随机变量。
(1)画出该过程两条样本函数;
(2)确定随机变量
X (ti ) 的概率密度,画出 ti
=
0,
π 4ω
信号分析与处理_习题答案.
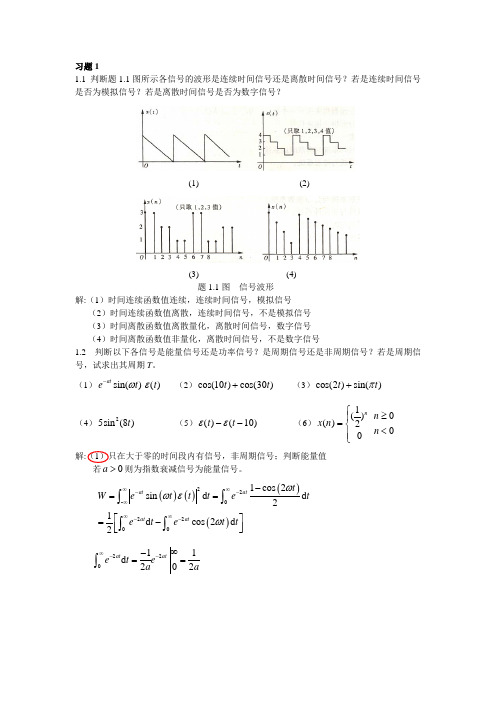
∫ ∫ [ ] T
x(t − t0 )
=
t
−∞ x(τ − t0 )dτ =
t −t0 −∞
x(λ)dλ = y(t − t0 ) ,时不变系统。
因果系统。
(3) y(t) = x 2 (2t)
T ax1 (t ) + bx2 (t ) ≠ aT x1 (t ) + bT x2 (t ) ,非线性系统。
= ay1 (t ) + by2 (t )
,线性系统。
T x (t − t0 )= x(t − t0 − 2) + x(2 − t − t0 ) ≠ y(t − t0 ) ,时变系统。
t 有可能小于 2 − t ,故为非因果系统。
t
∫ (2) y(t) = x(τ )dτ −∞
T ax1 (t ) + bx2 (t )= aT x1 (t ) + bT x2 (t ) ,线性系统。
(2) x(2 − t) ;
dx(t)
(5)
;
dt
(3) x(1 − 2t) ;
t
∫ (6) x(x )dx −∞
x(t)
4
4
4
4
2
2
2
2
-2 o 2
t
-1 o 1 2 3 t
题 1.3 图
o 1 2 3 4 t -1 o 1 2 t
2
t
∫ ξ(ξ)dξ −∞
10
4
-2 o 2 t
8
6
d 2
-2
-4 o 2 4 6 8t
4 2
−2
o 2t
1.4 给定序列
2n + 1 −3 ≤ n ≤ −1
2014年北京邮电大学随机信号分析与处理期末考试试题

北京邮电大学随机信号分析与处理综合练习题一、判断题:1. 设x(t)和Y(t)是相互独立的平稳随机过程,则它们的乘积也是平稳的。
2. X(t)为一个随机过程,对于任意一个固定的时刻t i,X(t i)是一个确定值。
3. 设X和丫是两个随机变量,X和丫不相关且不独立,有D(X Y) D(X) D(Y)。
4. 一般来说,平稳正态随机过程与确定性信号之和仍然为平稳的正态过程。
5. 设X(t)是不含周期分量的零均值平稳随机过程,其自相关函数为R X(),从物理概念上理解,有lim R X ( ) 0。
6. 对于线性系统,假设输入为非平稳随机过程,则不能用频谱法来分析系统输出随机过程的统计特性。
7. 若随机过程X(t)满足;!■:: = i「,HI卅逬与t无关,则X(t)是广义平稳(宽平稳)过程。
8. 随机过程的方差表示消耗在单位电阻上瞬时功率的统计平均值。
9. 广义循环平稳的随机过程本身也是一种广义平稳的随机过程。
10. 高斯白噪声经过匹配滤波器后仍然为高斯白噪声。
•选择填空1 •对于联合平稳随机过程X(t)和Y(t)的互相关函数R XY(),以下关系正确的是(1) 。
(1) A • R XY( ) R XY()B. R XY() -R YX()C. R XY ( ) R YX ( )D. R XY ( ) R XY ()2.随机过程X(t)的自相关函数满足R x(t“t2)m x(tjm x(t2)0,则可以断定X(tJ 和X (t2)之间的关系是(2)。
(2) A.相互独立 B.相关 C.不相关 D.正交3•两个不相关的高斯随机过程 X(t)和丫⑴,均值分别为m x 和m Y ,方差分别为则X(t)和丫(t)的联合概率密度为 (3)。
在0到2之间均匀分布,则X(t)的平均功率谱密度为 (6)。
11(6) A.-[G N ( 0) G N ()]B.—[G N ( 0) G N ()]4 211C.[G N()G N()]D.[G N()G N()]446. 已知 2 10 1,信号m(t) cos 1tcos 2t 的Hilbert 变换为(7).复包络为(8)。
北邮随机信号分析与处理第2章习题解答_1

[ E ( X 2 ) E 2 ( X )] [ E ( XY ) E ( X ) E (Y )] t1 [ E ( XY ) E ( X ) E (Y )] t2 [ E (Y 2 ) E 2 (Y )] t1t2
mY (t ) E[ X (t ) (t )] E[ X (t )] (t ) mX (t ) (t )
协方差函数:
KY (t1 , t2 ) RY (t1, t2 ) mY (t1 )mY (t2 ) E{[( X (t1 ) (t1 )][ X (t2 ) (t2 )]} [mX (t1 ) (t1 )][mX (t2 ) (t2 )] E[ X (t1 ) X (t2 )] E[ X (t1 ) (t2 )] E[ X (t2 ) (t1 )] E[ (t1 ) (t2 )]
2 x1 x1 2 2 2 2 2 2 200 A0 x1 x3 50 A0 x12 x3
7
(0 x1 A0 , 250 x2 350, x1 x3 x1 )
2.5
X 3 的边缘概率分布为
x3
A0
350
250
f X1 X 2 X 3 ( x1 , x2 , x3 )dx2 dx1 2 x1
有
J1
1 a y
2 2
J2
1 a2 y2
于是
1 1 1 fY | A ( y | a ) 2 a 2 y 2 2
( y a)
1 a2 y2
1
a2 y2
9
2.5
由全概率公式
fY ( y ) f A (a ) fY | A ( y | a )dad f A (a) f ( ) fY | A ( y | a )dad
《随机信号分析与处理》教学大纲

《随机信号分析与处理》教学大纲(执笔人:罗鹏飞教授学院:电子科学与工程学院)课程编号:070504209英文名称:Random Signal Analysis and Processing预修课程:概率论与数理统计、信号与系统、数字信号处理学时安排:60学时,其中讲授54学时,实践6学时学分:3一、课程概述(一)课程性质地位本课程是电子工程、通信工程专业的一门学科基础课程。
该课程系统地介绍随机信号的基本概念、随机信号的统计特性分析方法以及随机信号通过系统的分析方法;介绍信号检测、估计、滤波等信号处理理论的基本原理和信息提取方法。
其目的是使学生通过本课程的学习,掌握随机信号分析与处理的基本概念、基本原理和基本方法,培养学生运用随机信号分析与处理的理论解决工程实际问题的能力,提高综合素质,为后续课程的学习打下必要的理论基础。
本课程是电子信息技术核心理论基础。
电子信息系统中的关键技术是信息获取、信息传输、信息处理,这些技术的理论基础就是随机信号的分析、检测、估计、滤波等理论,这正是本课程的主要内容。
因此,本课程内容是电子信息类应用型人才知识结构中不可或缺的必备知识。
二、课程目标(一)知识与技能通过本课程的学习,掌握随机信号分析与处理基本概念和基本分析方法。
内容包括:1.理解和掌握随机过程基本概念和统计描述;2.掌握随机过程通过线性和非线性系统分析方法3.理解和掌握典型随机过程的特点及分析方法;4.掌握参数估计的概念、规则和性能分析方法;5.掌握信号检测的概念、规则和性能分析方法;6.掌握高斯白噪声中最佳检测器的结构和性能分析。
通过本课程的学习,要达到的能力目标是:1.具有正确地理解、阐述、解释生活中的随机现象的能力,即培养统计思维能力;2.运用概率、统计的数学方法和计算机方法分析和处理随机信号的能力;3.初步具备雷达、通信、导航等技术领域的信号处理系统的分析、设计、仿真的科学研究能力;4.培养自主学习能力;5.培养技术交流能力(包括论文写作和口头表达);6.培养协作学习的能力;(二)过程与方法依托“理论、实践、第二课堂”三个基本教学平台,通过课堂教学、概念测试、课堂研讨、案例研究、作业、实验、课程论文、网络教学等多种教学形式,采用研究型、案例式、互动研讨、基于团队学习、基于MATLAB的教学以及基于多媒体的教学等多种教学方法和手段,使学生加深对随机信号分析与处理的基本概念、基本原理以及应用的理解,并使学生通过自主学习、小组作业、案例研究、实验、课题论文等主动学习形式,培养自学能力和协同学习的能力,使学生不仅获得知识、综合素质得到提高。
随机信号分析与处理习题解答_罗鹏飞

P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n
n
∑ 所以 X = Xi 服从参数为 n,p 的二项分布。 i =1
且有 E( Xi ) = 1⋅ P{Xi = 1}+ 0 ⋅ P{Xi = 0} = p ,
E
(
X
2 i
)
= 12
⋅
P{ X i
= 1}+
函数 g(x) 的图像如下
解法一:根据概率分布函数的定义计算。
当 y ≤ 0 时, FY ( y) = P{Y ≤ y} = P{X < x0} + P{X > x1} = P{X < x0}+1− P{X < x1} = F (x0 ) +1− F (x1)
当 y ≤ A 时, FY ( y) = P{Y ≤ y} = P{x0 < X < x1} = FX (x1) − FX (x0 )
所以 Y 的概率分布函数为
FY ( y) = [1− FX (x1) + FX (x0 )]U ( y) + [FX (x1) − FX (x0 )]U ( y − A)
解法二:从概率密度 fY ( y) 入手求概率分布函数 FY ( y) 。 由图可知 g(x) 的取值只可能为 0 或 A,求Y 的概率分布函数,也就是对 g(x) 取 0 或 A
<
X
≤
x2 )
=
P{Y ≤ y, x1 < X ≤ x2} P{x1 < X ≤ x2}
=
y x2 f (x, y)dxdy
−∞ x1
FX (x2 ) − FX (x1 )
随机信号分析与处理答案(罗鹏飞,张文明编著)

H( f )
2 2
f 图 ( 利 用 w 2 f , 得 到
2
4 2si nT)f ( ) H( f ) (注意图中要标出最大值及所对应的频率,且
为正数) 4.
(2)
R(0,1) E[ X (0) X (1)] E[2 cos 2 cos(2 )] 4 E[cos cos ] 1 1 4 [(cos 2 0) (cos 2 ) ] 2 2 2 1 4 2 2
5. P85:2.6 问题还需增加“求均值,自相关函数及验证平稳性”
作业一的参考答案 1. P28:1.10
f XY ( x, y ) fY ( y )
1 0
解:利用 f X /Y ( x / y )
fY ( y )
所以
f XY ( x, y)dx
2ax 2by a 2by dx ab ab
f X /Y ( x / y )
解: (1)
互相关系数 XY
Cov( X , Y ) 2 3 D( X ) D(Y )
CZW Cov(2 X Y , X 2Y )
(2)
E[(2 X Y )( X 2Y )] E (2 X Y ) E ( X 2Y ) 2
(3)
因为 X , Y 为高斯随机变量 所以
解:
因为 A , B 为独立的高斯随机变量 所以
E( AB) E( A) E( B) 0 E[ X ] E( A)cos wt E( B)cos wt 0
随机信号分析与处理答案(罗鹏飞,张文明编著)

作业一的参考答案1. P28:1.10解:利用 /(,)(/)()XY X Y Y f x y f x y f y =10222()(,)Y XY ax by a byf y f x y dx dx a b a b+∞-∞++===++⎰⎰所以 /2()/()2()(/)(2)/()(2)X Y ax by a b ax by f x y a by a b a by +++==+++//1/4(/1/4)(/)12()441224X Y X Y y f x y f x y ax b ax b a b a b ===++==++10(/1/4)(/1/4)48326(2)X Y E X Y xf x y dxax b a b x dx a b a b +∞-∞===++==++⎰⎰(2) 同理利用 /0.50.5(,)(/)()XY Y X x x X f x y f y x f x ===可得到 /134(/)(/1/2)26()Y X a bE Y X yf y x dy a b +∞-∞+====+⎰2. P29:1.15解:由题意可得,1()1,E X = 4()1E X =,1()2D X =,4()2D X =, 1441(,)(,)0Cov X X Cov X X ==。
所以 (1) 均值矩阵'11⎡⎤=⎢⎥⎣⎦m ,协方差矩阵'2002⎡⎤=⎢⎥⎣⎦K Y 的分布为''14(,)(,)TY X X N =m K(2) 1(2)2E X =,23()1E X X +=-,34()1E X X -=-所以 Z 的均值矩阵''211⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦m 1111(2,2)(2)4()428Cov X X D X D X ===⨯=,123123123121312121313(2,)[(2)()](2)()(22)21(10)2[(,)()()(,)()()]22[11(1)010]22Cov X X X E X X X E X E X X E X X X X Cov X X E X E X Cov X X E X E X +=+-+=+-⨯⨯-+=++++=+⨯-++⨯+=同理可得 134341(2,)0(,2)Cov X X X Cov X X X -==-, 23()6D X X +=,23343423(,)(,)2Cov X X X X Cov X X X X +-=-+=,34()2D X X -=所以 协方差矩阵''820262022⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦K , Z 满足的分布为''''(,)Z N m K(3) Z 的特征函数''''1()exp[()]2T T z w j Φ=-m w w K w其中 ''''12328201,262,[ ]1022T w w w ⎡⎤⎡⎤⎢⎥⎢⎥=-==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦m K w3. 随机变量,X Y 具有高斯分布特征,1,2,X Y m m ==,协方差矩阵为44[][]49XXYYXY CC C C C -==-, 其中22,X XY Y C C σσ==,XY C 和YX C 是XY 的两个协方差。
北邮随机信号分析与处理第1章习题解答

记
Y1 Y Y 2 YN
线性变换 Y LX
L 为 N N 矩阵
15
1.12
假定 L 为满秩,得 x L-1y 由多维随机变量的函数的求解表达式
f Y (y ) f X (L-1y ) J f X (L-1y )
1
条件均值为
f XY ( x, y ) 2(ax by) fY | X ( y | x ) (0 x, y 1) f X ( x) 2ax b 将 X 1/ 2 代入,得 a 2by fY | X ( y | x 1/ 2) (0 y 1) ab
E (Y | X 1/ 2)
因此的概率分布函数可写为其中为常数假定随机变量的概率分布函数已知其中为常数假定随机变量的概率分布函数已知设随机变量的联合概率密度为根据条件概率密度可得到条件均值为10已知随机变量由条件均值得到边缘均值为的边缘概率密度为因此11由条件均值得到边缘均值的详细推导过程
ftp服务器地址
ftp://10.108.142.57
n odd
3
1.3 (2/2)
fY ( y )
n
f X ( xn )
dxn dy d (arcsin y n ) d ( arcsin y n ) f X ( arcsin y n ) dy dy n odd
n even
f X (arcsin y n )
n even
f X (arcsin y n )
1 1 y2
f X ( arcsin y n )
(完整版)随机信号处理考题答案

(完整版)随机信号处理考题答案填空:1.假设连续随机变量的概率分布函数为F(x)则F(-∞)=0, F (+∞)=12.随机过程可以看成是样本函数的集合,也可以看成是随机变量的集合3.如果随机过程X(t)满足任意维概率密度不随时间起点的变化而变化,则称X(t)为严平稳随机过程,如果随机过程X(t)满足均值为常数,自相关函数只与时间差相关则称X(t)为广义平稳随机过程4.如果一零均值随机过程的功率谱,在整个频率轴上为一常数,则称该随机过程为白噪声,该过程的任意两个不同时刻的状态是不相关5. 宽带随机过程通过窄带线性系统,其输出近似服从正态分布,窄带正态噪声的包络服从瑞利分布,而相位服从均匀分布6.分析平稳随机信号通过线性系统的两种常用的方法是冲激响应法,频谱法7.若实平稳随机过程相关函数为Rx(τ)=25+4/(1+6τ),则其均值为5或-5,方差为4 7.匹配滤波器是输出信噪比最大作为准则的最佳线性滤波器。
1.广义各态历经过称的信号一定是广义平稳随机信号,反之,广义平稳的随机信号不一定是广义各态历经的随机信号2.具有高斯分布的噪声称为高斯噪声,具有均匀分布的噪声叫均匀噪声,而如果一个随机过程的概率谱密度是常数,则称它为白噪声3.白噪声通过都是带宽的线性系统,输出过程为高斯过程4.平稳高斯过程与确定的信号之和是高斯过程,确定的信号可以认为是该过程的数学期望5.平稳正态随机过程的任意概率密度只由均值和协方差阵确定1.白噪声是指功率谱密度在整个频域内均匀分布的噪声。
3.对于严格平稳的随机过程,它的均值与方差是与时间无关的函数,即自相关函数与时间间隔有关,与时间起点无关。
4.冲激响应满足分析线性输出,其均值为_____________________。
5.偶函数的希尔伯特变换是奇函数。
6.窄带随机过程的互相关函数公式为P138。
1.按照时间和状态是连续还是离散的,随机过程可分为四类,这四类是连续时间随机过程,离散型随机过程、随机序列、离散随机序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
<
X
≤
x2 )
=
P{Y ≤ y, x1 < X ≤ x2} P{x1 < X ≤ x2}
=
y x2 f (x, y)dxdy
−∞ x1
FX (x2 ) − FX (x1 )
上式对 y 求导,得
∫x2 f (x, y)dx
fY|x1< X ≤x2 ( y |
x1
<
X
≤
x2 )
=
x1
FX (x2 ) − FX (x1 )
P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n , 0 < p < 1
求 X 的均值和方差。 解法一:直接按照定义计算
n
n
∑ ∑ E( X ) = mP{X = m} = mCnm pm (1− p)n−m
m=0
m=0
∑n
=m
n!
pm (1− p)n−m
m=1
(m −1)!
∑ = np n−1 (n −1)(n − 2) (n − m) pm (1− p)[(n−1)−m]
m=0
m!
∑ = np n−1 (n −1)(n − 2) [(n −1) − m +1] pm (1− p)[(n−1)−m]
m=0
m!
= np[ p + (1 − p)]n−1 = np
=
lim
Δx→0
fY|x< X ≤x+Δx ( y
|
x
<
X
≤ x + Δx) =
f (x, y) f X (x)
于是有
f X |Y (x | y) =
f (x, y) fY (y)
f (x, y) = f X |Y (x | y) fY ( y) = fY|X ( y | x) f X (x)
1.2 设随机变量 X 服从二项式分布,其概率分布律为
i =1
i =1
1.3 设随机变量 Y 与 X 满足如下函数关系
Y = g( X ) = sin( X + θ)
其中θ是已知常量,求 Y 的概率密度。
解答:显然,若 y > 1,则 fY ( y) = 0 。若 y ≤ 1,这时对于任意的 y ,有无穷多个 x 值与
之对应,即
x2n = arcsin y −θ + 2π n , n = 0, ±1, ±2,… x2n+1 = π − arcsin y −θ + 2π n , n = 0, ±1, ±2,…
故有
P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n
n
∑ 所以 X = Xi 服从参数为 n,p 的二项分布。 i =1
且有 E( Xi ) = 1⋅ P{Xi = 1}+ 0 ⋅ P{Xi = 0} = p ,
E
(
X
2 i
)
= 12
⋅
P{ X i
= 1}+
02
⋅
P{ X i
=
0}
=
p
,
D(Xi )
=
E
(
X
2 i
)
−
E2(Xi)
=
p
−
p2
=
p(1 −
p)
n
∑ 根据 Xi 相互之间的独立性,所以对于服从二项分布的 X = Xi 有 i =1
n
n
E( X ) = E(∑ Xi ) = ∑ E( Xi ) = np
i =1
i =1
n
n
D( X ) = D(∑ Xi ) = ∑ D( Xi ) = np(1− p)
m=0
m!
类似地可得
E( X 2 ) = E[ X ( X −1) + X ] = E[ X ( X −1)] + E( X )
n
∑ =
m( m
−
1)CLeabharlann m npm(1 −
p)n−m
+
np
m=0
= n(n −1) p 2[ p + (1 − p)]n−2 + np
= n(n −1) p 2 + np
所以 X 的方差为
D( X ) = E( X 2 ) − E 2 ( X ) = n(n − 1) p 2 + np − (np)2 = np(1 − p)
解法二:设 X1, X 2 ,…, X n 相互独立,且都服从 (0 −1) 分布,分布规律为 P{Xi = 0} = 1− p , P{Xi = 1} = p , i = 1, 2,…, n ,
,然后对 y 求导得,
FX (x + Δx) − FX (x)
x + Δx
∫ fY|x<X ≤x+Δx ( y | x < X
≤ x + Δx) =
f (x, y)dx
x
≈
FX (x + Δx) − FX (x)
f (x, y)Δx f X (x)Δx
最后求Δx→0 的极限。
∫ ∫ 解答:
F(y
|
x1
m=0 m!(n − m)!
∑ = n m n(n −1)(n − 2) (n − m +1) pm (1− p)n−m
m=0
m!
∑ = n m n(n −1)(n − 2) (n − m +1) pm (1− p)n−m
m=1
m!
∑ = np n (n −1)(n − 2) [n − (m −1)] pm−1(1− p)[(n−1)−(m−1)]
在上式中,假定 x1 = x , x2 = x + Δx ( Δx 无穷小量),则
x + Δx
∫ fY|x<X ≤x+Δx ( y | x < X
≤ x + Δx) =
f (x, y)dx
x
FX (x + Δx) − FX (x)
≈
f (x, y)Δx f X (x)Δx
因此
同理可得
fY|X
(y
|
x)
第 1 章 随机变量基础
1.1 设有两个随机变量 X 和 Y,证明
fY|X ( y | x) =
f (x, y) f X (x)
,
f X |Y
(x
|
y)
=
f (x, y) fY (y)
y x+Δx
∫ ∫ f (x, y)dxdy
提示:首先证明 F ( y | x < X ≤ x + Δx) = −∞ x
n
∑ 则 X = Xi 服从参数为 n,p 的二项分布,即 P{X = m} = Cnm p m (1 − p)n−m 。 i =1 X 的所有可能取值为 0,1, 2,…, n 。由独立性可知,X 以特定的方式取 m(如前 m 个取
1,后 m 个取 0)的概率为 pm (1− p)n−m 。而 X 取 m 的两两互不相容的方式有 Cnm 种可能,
∑ ∑ 注意:根据多项式展开式 (a + b)n
=
n i=0
Cni aibn−i
=
n i=0
n! a bi n−i i!(n − i)!
∑ = n n(n −1)(n − 2) (n − i +1)aibn−i
i=0
i!
所以有
∑n−1 (n −1)(n − 2) [(n −1) − m +1] pm (1− p)[(n−1)−m] = [ p + (1− p)]n−1
