量子力学与统计物理习题解答(理论物理导论)北理工_李卫_修订版
北京理工大学08年研究生入学考试量子力学试题及答案(7)

的零级近似波函数为
(0) N
1 2
(
(0) 1
(0) 2
)
其中
(0) 1
1 exp[ iNx]
L
L
(0) 2
1 exp[ iNx]
L
L
12
五、(20分)设电子处于自旋态
1 ( z
1) ,求 n
n
的
2
可能测量值及相应的概率。
n
(sin
L
L
能量一级修正满足的方程(久期方程)
H11
E
(1) N
H 21
H12 0
H 22
E
(1) N
9
(0) 1
N
1 exp[ iNx]
L
L
(0) 2
N
1 exp[ iNx]
L
L
H11
H12
1 L
1 L
L 2
iNx
e L
cos
0
1
5
i
e E2t0
2
a
1 5
2
[4
2 1
0
2 2
2 (e 1 2
i
(
E2
E1
)t0
e
i
(
E2
E1
)t0
)]dx
2
a
w
1 5
2
[4
2 1
0
2 2
2 (e 1 2
量子力学习题问题详解

量子力学习题问题详解量子力学习题答案1.2 在0k 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解:由德布罗意波粒二象性的关系知:E h =ν;p h /=λ由于所考虑的电子是非相对论的电子(26k e E (3eV)c (0.5110)-μ?),故:2e E P /(2)=μ69h /p h /hc /1.2410/0.7110m 0.71nm--λ====?=?= 1.3氦原子的动能是E=1.5kT ,求T=1K 时,氦原子的德布罗意波长。
解:对于氦原子而言,当K 1=T 时,其能量为J 102.07K 1K J 10381.1232323123---?===kT E 于是有一维谐振子处于22/2()xx Ae αψ-=状态中,其中α为实常数,求:1.归一化系数;2.动能平均值。
(22x e dx /∞-α-∞=α?)解:1.由归一化条件可知:22*2x(x)(x)dx A e dx1A/1∞∞-α-∞-∞ψψ===α=取相因子为零,则归一化系数1/21/4 A/=απ2.2222222222222222222*2x/2x/2222x/2x/222x/22x/22222242x2T(x)T(x)dx A e(P/2)e dx dA e()e dx2dxdA e(xe)dx2dxA{xe(xe)dx}2A x e dx A22∞∞-α-α-∞-∞∞-α-α-∞∞-α-α-∞∞∞-α-α-∞-∞∞-α-∞=-μ=--αμ=--α--αμ=α=μμ=()==2222224x2224x x2222222421()xd(e)21A(){xe e dx}221AA()242∞-α-∞∞∞-α-α-∞-∞α-α=α---μαππααα--μμα若α,则该态为谐振子的基态,T4ω=解法二:对于求力学量在某一体系能量本征态下的平均值问题,用F-H定理是非常方便的。
一维谐振子的哈密顿量为:2222d 1H x2dx2=-+μωμ它的基态能量1E2=ω选择为参量,则:0dE 1d 2=ω;222dH d 2d 2()T d dx 2dx=-=-=μμ dH 20T d= 由F-H 定理知:0dE dH 2100T d d 2===ω 可得:1T 4=ω2.2 由下列定态波函数计算几率流密度: ikr ikr e re r -==1)2( 1)1(21ψψ 从所得结果说明1ψ表示向外传播的球面波,2ψ表示向(即向原点) 传播的球面波。
量子力学课后习题答案

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThcλλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
量子力学填空题答案精选全文完整版

可编辑修改精选全文完整版填空题答案1.量子力学的最早创始人是 普朗克 ,他的主要贡献是于 1900 年提出了 能量量子化 假设,解决了黑体辐射 的问题。
2.按照德布罗意公式λνεh p h ==,,质量为21,μμ的两粒子,若德布罗意波长同为λ,则它们的动量比p 1:p 2= 1:1 ;能量比E 1:E 2=12:μμ;若粒子速度为v=0.9c ,按相对论公式计算,其德布罗意波长'λ=24202//p c c μλ+。
3.用分辨率为1微米的显微镜观察自由电子的德布罗意波长,若电子的能量E=kT 23(k 为玻尔兹曼常数),要能看到它的德布罗意波长,则电子所处的最高温度T max =K h k 221031-≈⎪⎭⎫ ⎝⎛λμ。
4.阱宽为a 的一维无限深势阱,阱宽扩大1倍,粒子质量缩小1倍,则能级间距将扩大(缩小) 缩小1倍;若坐标系原点取在阱中心,而阱宽仍为a ,质量仍为μ,则第n 个能级的能量E n =3,2,12/2222=n a n μπ,相应的波函数=)(x n ψ()a x ax n a n <<=0sin 2πψ和()a x x n≥≤=,00ψ。
5.处于态311ψ的氢原子,在此态中测量能量、角动量的大小,角动量的z 分量的值分别为E=eV eV 51.136.132-=;L= 2;L z = ,轨道磁矩M z =B M 。
6.两个全同粒子组成的体系,单粒子量子态为)(q k ϕ,当它们是玻色子时波函数为),(21q q s ψ=()()()()[]玻色体系1221221121q q q q k k k k ϕϕϕϕ+;为费米子时),(21q q A ψ()()()()]费米体系12212211q q q q k k k k ϕϕϕϕ-7.非简并定态微扰理论中求能量和波函数近似值的公式是E n =()()+-'+'+∑≠020m nn m mn mnnE EH H E ,)(x n ψ = ()()() +-'+∑≠00020m m nnm mnn E EH ψψ,其中微扰矩阵元'mn H =()()⎰'τψψd H n m 00ˆ;而'nn H 表示的物理意义是 在未受微扰体系中,H '的平均值 。
量子力学简答100题及答案

1、简述波函数的统计解释;2、对“轨道”和“电子云”的概念,量子力学的解释是什么?3、力学量Gˆ在自身表象中的矩阵表示有何特点? 4、简述能量的测不准关系;5、电子在位置和自旋z S ˆ表象下,波函数⎪⎪⎭⎫⎝⎛=ψ),,(),,(21z y x z y x ψψ如何归一化?解释各项的几率意义。
6、何为束缚态?7、当体系处于归一化波函数ψ(,) r t 所描述的状态时,简述在ψ(,)r t 状态中测量力学量F 的可能值及其几率的方法。
8、设粒子在位置表象中处于态),(t r ψ,采用Dirac 符号时,若将ψ(,) r t 改写为ψ(,)r t 有何不妥?采用Dirac 符号时,位置表象中的波函数应如何表示? 9、简述定态微扰理论。
10、Stern —Gerlach 实验证实了什么? 11、一个物理体系存在束缚态的条件是什么? 12、两个对易的力学量是否一定同时确定?为什么? 13、测不准关系是否与表象有关?14、在简并定态微扰论中,如 ()H0的某一能级)0(n E ,对应f 个正交归一本征函数i φ(i =1,2,…,f ),为什么一般地i φ不能直接作为()H HH'+=ˆˆˆ0的零级近似波函数? 15、在自旋态χ12()s z 中, S x 和 S y的测不准关系( )( )∆∆S S x y 22•是多少? 16、在定态问题中,不同能量所对应的态的迭加是否为定态Schrodinger 方程的解?同一能量对应的各简并态的迭加是否仍为定态Schrodinger 方程的解?17、两个不对易的算符所表示的力学量是否一定不能同时确定?举例说明。
18说明厄米矩阵的对角元素是实的,关于对角线对称的元素互相共轭。
19何谓选择定则。
20、能否由Schrodinger 方程直接导出自旋?21、叙述量子力学的态迭加原理。
22、厄米算符是如何定义的?23、据[aˆ,+a ˆ]=1,a a Nˆˆˆ+=,n n n N =ˆ,证明:1ˆ-=n n n a 。
量子力学课后习题答案

Wnl (r)dr Rnl2 (r)r 2dr
例如:对于基态 n 1, l 0
W10 (r) R102 (r)r 2
4 a03
r e2 2r / a0
求最可几半径
R e 2 r / a0
10
a03 / 2
dW10 (r) 4 (2r 2 r 2 )e2r / a0
x)
k
2
2
(
x)
0
其解为 2 (x) Asin kx B cos kx
根据波函数的标准条件确定系数A、B,由连续性条件,得
2 (0) 1(0) B 0
2 (a) 3 (a) Asin ka 0
A0
sin ka 0
ka n
(n 1, 2, 3,)
[1 r
eikr
r
(1 r
eikr )
1 r
eikr
r
(1 r
eikr )]er
i1 1 11 1 1
2
[ r
(
r2
ik
) r
r
(
r2
ik
r )]er
k
r2
er
J1与er 同向。 1 表示向外传播的球面波。
习题
(2)
J2
i
2
(
2
* 2
2*
解:U (x)与t 无关,是定态问题
薛定谔方程为
2
2
d2 dx2
(x) U (x) (x)
E (x)
在各区域的具体形式为:
x0
量子力学练习题答案

Wmk =| am (t) |2
∫ ∫ 其中
am
(t)
=
1 i=
t 0
eiωmkτ
H
′
mk
dτ
,
H
′
mk
=
ϕm* Hl ′(t)ϕkdτ ,ωmk = (Em − Ek ) / =
二、 证明题 1. 证明黑体辐射的辐射本领 E(ν ,T ) 与 E(λ,T ) 之间的关系。 证明:黑体的辐射本领是指辐射体单位面积在单位时间辐射出来的、单位 频率间隔内的能量,用 E(ν ,T ) 表示。由于ν = c / λ ,所以黑体的辐射本领也 可以表示成 E(λ,T ) 。由定义得单位面积、单位时间内辐射的能量为
的同时决定,也使得它们的分布同时制约,这种制约就是不确定性原理,
它是任何两个力学量在任何状态下的涨落(用均方差表示)必须满足的相
互制约关系,公式表示为
ΔA⋅ ΔB ≥ 1 ⋅ [lA, Bl] 2
23. 如果算符 Aˆ 的本征值分别为 A1, A2, A3,",在算符 Aˆ 的自身表象中写出
算符 Aˆ 的矩阵形式。
下,所有力学量的概率分布不随时间改变;在一切状态下,守恒量的概率
分布不随时间改变。
25. 在 Sz 表象下,写出算符 Sˆz 及其本征态|↑〉 和|↓〉 的矩阵表达式。
答:在 Sz 表象下,算符 Sˆz 的矩阵表达式为
Sz
=
= ⎛1
2
⎜ ⎝
0
0⎞ − 1⎟⎠
其本征态|↑〉 和|↓〉 的矩阵表达式分别为
v∫ 答: pkdqk = nkh (nk = 1, 2,3,")
其中 (qk , pk ) 代表一对共轭的正则坐标和动量。 7. 利用光波的双缝干涉实验,说明 Born 的概率波解释。 答:Born 认为,微观粒子的运动状态用“波函数”来描述,粒子通过双缝 时,每一个缝都有一个所谓的“波”通过,只不过与经典波的强度对应的, 是粒子在某点附近出现的相对概率。对通过双缝的粒子,其概率“分成” 了两束(波动性),但对某个具体的粒子,它只能通过其中的一个缝(粒子
量子力学练习参考解答

量子力学练习参考解答第一章 波函数与薛定谔方程1.1,1.2,1.3题解答略。
1.4(a )设一维自由粒子的初态为一个Gauss 波包,222412)(1)0,(απαψxx p i e e x -=证明:初始时刻,0=x ,0p p =[]2)(12α=-=∆x x x[]α2)(12=-=∆p p p2 =∆⋅∆p x证:初始时刻012222===-+∞∞-+∞∞-⎰⎰dx exdx x x x απαψ2122222222απαψα===-∞+∞-∞+∞-⎰⎰dx exdx x x x()22122α=-=∆xx x)0,(x ψ的逆变换为⎰+∞∞--=dx ex p ipx/)0,(21)(ψπϕ=⎰+∞∞---dx eeeipx x x p i/2412220)(121απαπ=2220()22214(/)p p eααπ--22202()()p p p eααϕπ--=因此02)(p dp p p p ==⎰+∞∞-ϕ2222222)(0αϕ +==⎰∞+∞-p dp p p p()α22122 =-=∆p p p2 =∆⋅∆p x注:也可由以下式子计算p 和2p :2222(,0)()(,0)(,0)()(,0)dp x ix dx dxd p x x dxdx ψψψψ+∞*-∞+∞*-∞=-=-⎰⎰1.5 设一维自由粒子的初态为)0,(x ψ,证明在足够长时刻后,()[]⎪⎭⎫⎝⎛⋅⎥⎦⎤⎢⎣⎡⋅-=t mx t imx i t m t x ϕπψ2exp 4exp ,2式中()()⎰+∞∞--=dx e x k ikx0,21ψπϕ是)0,(x ψ的Fourier 变换。
提示:利用()x e e x i i δπααπα=-∞→24/lim。
证:依照平面波的时刻转变规律 ()t kx i ikxe e ω-→ , m k E 22==ω,任意时刻的波函数为()()()dk e k t x mtkkx i 2/221, -+∞∞-⎰=ϕπψ()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⋅=⎰∞+∞-22/2ex p 212t mx k m t i k dk etimx ϕπ(1) 那时刻足够长后(所谓∞→t ),上式被积函数中的指数函数具有δ函数的性质,取m t 2 =α , (2)参照此题的解题提示,即得()()⎰+∞∞--⎪⎭⎫ ⎝⎛-⋅≈k d t mx k k e t m et x i timx δϕππψπ4/2221,2⎪⎭⎫⎝⎛=-t mx e e t m t imx i ϕπ2/4/2 (3) 1.6 依照粒子密度散布ρ和粒子流密度散布j的表示式, ()()()t r t r t r ,,,*ψψρ=()()()()()[]t r t r t r t r mi t r j ,,,,2,**ψψψψ∇-∇-=概念粒子的速度散布v()()()()⎥⎦⎤⎢⎣⎡∇-∇-==t r t r t r t r m i j v ,,,,2**ψψψψρ 证明:0=⨯∇v 。
北京理工大学07年研究生入学考试量子力学试题及答案(6)

2 t I
]
8
(3)若系统附加一个能量微扰项 V cos ,求系统第一激 发态能量的一级修正值。 (3)
H cos
( 10) ( )
1 2
e i
E1(1)
1 H11 2
2
cos d 0
0
9
四、(30分) 为泡利算符,试求 (1)在 z 表象中,求 z , x 和 y 的本征态。 (2)在 x 表象中,求 z和 y 的本征态和本征值。 (3)由 z 表象变换到 x 表象的变换矩阵。 (1)在 z 表象中, x 和 y 的矩阵表示 解:
L2 L2 H H 解: (1)转子能量的经典表示: ,对平面转子, z 2I 2I 1 im ˆ2 ( ) m 2 2( ) m 0,1,2, ( ) e Lz 2
m2 2 ˆ 所以 ( ) 也是 H 的属于本征值 E m 的本征函数。 2I
Y00 (3)(已知球谐函数: 1 3 3 , Y10 cos , Y11 sin e i ) 4 8 4 1 i 1 e sin cos 4 4
2 3 i 1 3 2 1 e sin cos Y11 Y10 3 8 3 3 4 3
即得 y 的属于本征值 1的本征态分别为
(2)在 x 表象中,求 z和 y 的本征态和本征值。 利用轮换对称性,在 x表象中, 0 1 1 0 y x 1 0 0 1
y 的本征值和本征态: 1; 2 1
2 2
L z取值可为 ,,0,概率比
值概率
1 1 2 , , 6 6 3
。Lz 0 0
量子力学练习答案

《量子力学》试题(A) 答案及评分标准一、简答题(30分,每小题5分) 1.何谓势垒贯穿?是举例说明。
答:微观粒子在能量E 小于势垒高度时仍能贯穿势垒的现象,称为势垒贯穿。
它是一种量子效应,是微观粒子波粒二象性的体现。
例如金属电子冷发射、α衰变等现象都是由隧道效应产生的,利用微观粒子势垒贯穿效应的特性制造了隧道二极管。
2.波函数()t r ,ψ是应该满足什么样的自然条件?()2,t r ψ的物理含义是什么? 答:波函数是用来描述体系的状态的复函数,除了应满足平方可积的条件之外,它还应该是单值、有限和连续的。
()2,t r ψ表示在t 时刻r 附近τd 体积元中粒子出现的几率密度。
3.分别说明什么样的状态是束缚态、简并态、正宇称态和负宇称态?答:当粒子的坐标趋向无穷远时,波函数趋向零,称之为粒子处于束缚态。
若一个本征值对应一个以上的本征态,则称该本征值是简并的,所对应的本征态即为简并态,本征态的个数就是本征值相应的简并度。
将波函数中的坐标变量改变一个负号,若新波函数与原波函数一样,则称其为正宇称态;将波函数中的坐标变量改变一个负号,若新波函数与原波函数相差一个负号,则称其为负宇称态。
4.物理上可观测量应该对应什么样的算符?为什么?答:物理上可观测量对应线性厄米算符。
线性是状态叠加原理要求的,厄米算符的本征值是实数,可与观测值比较。
5.坐标x 分量算符与动量x 分量算符x pˆ的对易关系是什么?并写出两者满足的测不准关系。
答:对易关系为[] i ˆ,=x px ,测不准关系为2≥∆⋅∆x p x 6.厄米算符F ˆ的本征值nλ与本征矢n 分别具有什么性质? 答:本征值为实数,本征矢为正交、归一和完备的函数系二、证明题:(10分,每小题5分)(1)证明:i z y x =σσσˆˆˆ 证明:由对易关系z x y y x i σσσσσˆ2ˆˆˆˆ=-及反对易关系0ˆˆˆˆ=+x y y x σσσσ ,得z y x i σσσˆˆˆ=上式两边乘z σˆ,得2ˆˆˆˆz z y x i σσσσ= ∵ 1ˆ2=z σ ∴ i z y x =σσσˆˆˆ (2)证明幺正变换不改变矩阵的本征值。
(完整版)量子力学期末考试题及解答

一、 波函数及薛定谔方程1.推导概率(粒子数)守恒的微分表达式;()(),,w r t J r t o t∂+∇•=∂解答:由波函数的概率波解释可知,当(),r t ψ已经归一化时,坐标的取值概率密度为()()()()2,,,,w r t r t r t r t ψψψ*== (1) 将上式的两端分别对时间t 求偏微商,得到()()()()(),,,,,w r t r t r t r t r t t t tψψψψ**∂∂∂=+∂∂∂ (2) 若位势为实数,即()()V r V r *=,则薛定谔方程及其复共轭方程可以分别改写如下形式()()()()2,,,2r t ih ir t V r r t t m h ψψψ∂=∇-∂ (3)()()()()2,,,2r t ih ir t V r r t t m hψψψ***∂=-∇+∂ (4) 将上述两式代入(2)式,得到()()()()()22,,,,,2r t ih r t r t r t r t t mψψψψψ**∂⎡⎤=∇-∇⎣⎦∂ ()()()(),,,,2ihr t r t r t r t mψψψψ**⎡⎤=∇•∇-∇⎣⎦ (5) 若令()()()()(),,,,,2ih J r t r t r t r t r t mψψψψ**⎡⎤=∇-∇⎣⎦ (6) 有()(),,0w r t J r t t∂+∇•=∂ (7) 此即概率(粒子数)守恒的微分表达式。
2.若线性谐振子处于第一激发态()2211exp 2x C x α⎛⎫ψ=- ⎪⎝⎭求其坐标取值概率密度最大的位置,其中实常数0α>。
解答:欲求取值概率必须先将波函数归一化,由波函数的归一化条件可知()()222221exp 1x dx Cx x dx ψα∞∞-∞-∞=-=⎰⎰(1)利用积分公示())2221121!!exp 2n n n n x x dx αα∞++--=⎰ (2) 可以得到归一化常数为C = (3)坐标的取值概率密度为 ()()()322221exp w x x x x ψα==- (4)由坐标概率密度取极值的条件())()3232222exp 0d w x x x x dx αα=--= (5) 知()w x 有五个极值点,它们分别是 10,,x α=±±∞(6)为了确定极大值,需要计算()w x 的二阶导数()()()232222322226222exp d w x x x x x x dx αααα⎤=----⎦)()32244222104exp x x x ααα=-+- (7)于是有()23200x d w x dx ==> 取极小值 (8)()220x d w x dx =±∞= 取极小值 (9)()23120x d w x dx α=±=< 取极大值 (10)最后得到坐标概率密度的最大值为2111w x x ψαα⎛⎫⎛⎫=±==±= ⎪ ⎪⎝⎭⎝⎭(11)3.半壁无限高势垒的位势为()()()()000x v x x a v x a ∞<⎧⎪=≤≤⎨⎪>⎩求粒子能量E 在00E v <<范围内的解。
北京理工大学04年研究生入学考试量子力学试题及答案(3)

1 ˆ ˆ ˆ ˆ ˆ ˆ 1,1 ( L2 L2 L L L L ) 1,1 4
1 1 2 2 ˆ ˆ 1,1 L L 1,1 2 4 4 2
(Lx ) 2 L2 Lx x
2
L 1,1 0
2 2
15
ˆ 1,1 1 1,1 L L 1,1 0 ˆ ˆ Lx 1,1 Lx 2
14
2
ˆ ˆ ˆ ˆ ˆ ˆ ˆ 5.在 Y11 态下,求 (Lx ) 2 的平均值。 L2x ( L2 L2 L L L L )
1 4
ˆ2 1,1 1 1,1 ( L L )( L L ) 1,1 ˆ ˆ ˆ ˆ L 1,1 Lx 4
4.证明 exp( i z ) cos i z
e
i z
sin
参考大连理工2004年题二(3)
(i z ) n (i ) n ( ) ( z ) n n! n! n 0 even odd
n
( ( z ) 2 1 ,所以 n 为偶数时, z ) n 1;n为奇数时, z ) z (
A
2 a
0
3 5 a5 a4 2 a 2 a x ( x a) dx A [ a 2a ] A 1 5 3 4 30 2 2 2
所以
( x)
a
30 x( x a) 5 a
60 a 2 x c1 ( x) 1 ( x) * dx ( x ax) sin dx 6 0 a a 0
a2 1 a2 1 1 2 a2 ( 2 ) 3 2 2 3 2
3
a x 2
1 1 x2 a2 ( 2 ) 3 2
量子力学导论第4章答案参考资料

第四章力学量用算符表达与表象变换1 14.1 )设A 与B 为厄米算符,则—AB BA 和 AB 一 BA 也是厄米算符。
由此证明,任何一个算符2 2i分解为F =F . • iFF 与F_均为厄米算符,且证:i)1AB BA1 -AB BA 为厄米算符。
1 1 1二—B A - A B 二 丄 BA - AB 二丄 AB - BA -2i 2i 2i二1(AB - BA )也为厄米算符。
iii )令 F 二 AB ,则 F 二 AB = B A ;= BA ,由i ) ,ii )得F . = F , F_ = F_,即卩F 和F_皆为厄米算符。
则由(1)式,不难解得F iF4.2)设F (x, p )是x, p 的整函数,证明整函数是指F(X, p)可以展开成F(X,p) = v C mn X m p n 。
m,n =0证: (1)先证 p,x m L -mi x m 4, X, p n]二 ni pn/。
p,xm ] =x m4 lp,x 「p, x m4 xi x m4 x m ^ ip,xk p,x m Q x 2 --2i x m4 x m : b, x 殳2 b,x m ; x 3=-3i x m4 ■ 'p,x m ^x 3 二… =-m -1i 乂心■ b,x m —z x m _ --m -1 i x m4 -i x m J 二 mi x m4同理,F 均可1 ^2i F -F1F =2 F F ,1 11 B A A B BA AB AB BAii)扌 AB 一 BA 且定义F T F「F(1)'p,F:xX, p n .1 - p n二X, p Z- X, p n J Ip=i*p n' + p n~ IX, p】p + X, p n~ 】p2= 2i%n」+ k, p n,】p 2=n卷p n」现在,Ip,F ]= |P, hC mn X”=送C mn b,X m Ip"Q QC mn -mi x mJ p nm,n兰:F 7而-i ——C mn -mi x mJ p n。
《量子力学与统计力学》各章习题

2 《量子力学与统计力学》各章习题习题一1.1、一颗质量为20克的子弹以仰角30º初速率500米/秒从60米的高度处射出。
求在重力作用下该子弹着地前的轨道以及射出50秒后对射出点的位矢、速度、动量、角动量、动能和机械能。
(不考虑空气阻力,重力加速度取10米/秒2,地面为零重力势能面)。
1.2、在极坐标平面中任取两点P 1和P 2,但它们和极点三者不共线。
试分别画出在P 1和P 2处的极坐标单位矢。
1.3、在球坐标系中任取一点P ,试画出P 点的球坐标单位矢。
1.4、对于做斜上抛运动的子弹,以抛出点为坐标系原点建立直角坐标系。
试分别选取两组不同的广义坐标,并用之表示子弹在任一时刻的直角坐标。
1.5、氢原子由一个质子和一个电子组成。
试说明一个孤立氢原子体系是基本形式的Lagrange方程适用的体系。
1.6、证明: Lagrange 方程的基本形式(1.59)式可写为如下的Nielsen 形式:αααQ q T q T =∂∂-∂∂2 ,s ,,2,1 =α 1.7、设一个s 自由度的体系的广义坐标为αq ),,2,1(s =α。
试证明存在一个任意可微函数),,,,(21t q q q F s ,由它与该体系的Lagrange 函数构成的如下函数dtt q q q dF s ),,,,(L L 21 +=' 满足Langrange 方程(1.67)式。
1.8、设一个s 自由度的体系的广义坐标为αq ),,2,1(s =α,满足Langrange 方程(1.67)式的Lagrange 函数为),,,,,,,,(L 2121t q q q q q q s s 。
设存在另一组广义坐标αξ,),,2,1(s =α,且有变换方程),,,,(21t q q s ξξξαα =,s ,,2,1 =α此变换叫做点变换。
证明: 若通过上述点变换将),,,,,,,,(L 2121t q q q q q q s s 变换为),,,,,,,,(L L 2121t s s ξξξξξξ =,则有 s dt d , ,2 ,1 ,0L )L ( ==∂∂-∂∂αξξαα 这就是说,Lagrange 方程的形式与所选用的广义坐标无关。
统计物理习题解答
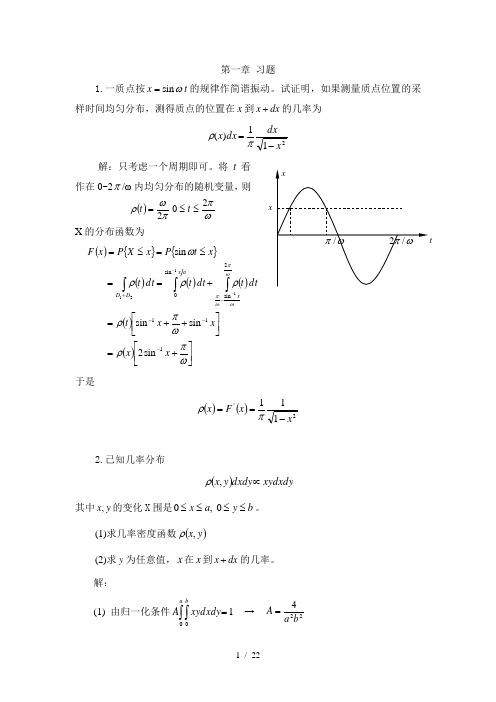
第一章 习题1.一质点按t x sin ω=的规律作简谐振动。
试证明,如果测量质点位置的采样时间均匀分布,测得质点的位置在x 到dx x +的几率为211)(xdxdx x -=πρ解:只考虑一个周期即可。
将t 看作在0~2π/ω内均匀分布的随机变量,则()πωρ2=t ωπ20≤≤t X 的分布函数为(){}{}()()()()()⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡++=+==≤=≤=----+⎰⎰⎰--ωπρωπρρρρωωπωωπx x x x t dtt dt t dt t x t P x X P x F xax D D 1112sin sin 0sin 2 sin sin sin 1121于是()()2'111xx F x -==πρ2.已知几率分布()xydxdy dxdy y x ∝,ρ其中y x ,的变化X 围是b y a x ≤≤≤≤0 ,0。
(1)求几率密度函数()y x ,ρ(2)求y 为任意值,x 在x 到dx x +的几率。
解:(1) 由归一化条件100=⎰⎰a bxydxdy A → 224ba A =t则()⎪⎩⎪⎨⎧≤≤≤≤=其它00,04,22by a x xy b a y x ρ(2) ()()⎰⎰===+∞∞-bX axydy b a x dy y x x 022224,ρρa x ≤≤0 于是()dx a xdx x X 22=ρ3.已知几率分布dx e dx x x )(ααρ-=, +∞<≤x 0其中0>α,x 的变化X 围是0至∞。
试求x 的平均值x ,方均根值2x ,平均平方偏差2)(x x -和相对涨落22)()(x x x -。
解: (1)()()αααααρα101 1100=⎥⎥⎦⎤⎢⎢⎣⎡-∞+-=-=====⎰⎰⎰⎰⎰∞+--+∞-+∞+∞--+∞dt e te tde dt te dx ex dx x X E X tt t tx(2)()220222ααρα===-+∞+∞⎰⎰dx e x dx x x X x则α22=x(3) ()()()()222222112ααα=-=-=-=X E X E X X X D(4) ()()111222==ααX X D4.一光子的能量ε与动量p 有如关系cp =ε,c 为光速。
量子力学课后问题详解

a
a
A2 a 1 [1 cos n (x a)]dx
a 2
d2 dx 2
2
(x)
E
2
(x)
②
Ⅲ: x a
2 2m
d2 dx 2
3
(x)
U
( x)
3
(x)
E
3
(x)
③
由于(1)、(3)方程中,由于U (x) ,要等式成立,必须
1(x) 0 2 (x) 0
即粒子不能运动到势阱以外的地方去。
方程(2)可变为
d
2 2 (x) dx 2
2mE 2
2
(x)
子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短, 因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动 性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才 能显现。
1.3 氦原子的动能是 E 3 kT (k 为玻耳兹曼常数),求 T=1K 时,氦原子的德布罗意波 2
显然,两种情况下的热运动所对应的能量要大于前面的量子化的能量的间隔。
1.5 两个光子在一定条件下可以转化为正负电子对,如果两光子的能量相等,问要实现实
种转化,光子的波长最大是多少?
解 关于两个光子转化为正负电子对的动力学过程,如两个光子以怎样的概率转化为正
负电子对的问题,严格来说,需要用到相对性量子场论的知识去计算,修正当涉及到这个过
(2)
J2
i 2m
(
2
* 2
2*
)
i [1 eikr 2m r
(1 eikr ) 1 eikr
r r
r
r
理论物理导论-李卫1-3章习题解答完整

n 1,2,3,
波函数的两个表达式还可统一为一个表达式
n 1,2,3,
4.带电荷q的一维谐振子在外电场E作用下运动,
U ( x) ( 2 x2 / 2) qEx ,试证明粒子的能量和波函数分别为
1 q 2E 2 En n 2 2 2
(1)归一化因子A; (2)粒子的几率密度; (3)粒子出现在何处的几率最大?
( x 0) ( x 0)
解:(1) ( x) ( x)dx A
2
0
x 2e 2x dx 令
2x ,则
A2
0
A2 2 x 2 e 2 x dx 3 e d 8 0 A2 3 (3) 8 A2 3 2! 8 A2 3 4
n 1,2,3,
证明:势函数与时间无关,是定态问题。 由于是无限深势阱,粒子不可能到达阱外,因此在阱外
( x) 0,
| x | a / 2
| x | a / 2
在阱内,波函数满足定态薛定谔方程
2 ( x) E ( x) 2
上式可变形为 2E ( x) 2 ( x) 0
2 证明:势函数与时间无关,是定态问题。定态薛定谔方程为
2 1 ( x) 2 x 2 qEx ( x) E ( x) 2u 2
n ( x) N n e
1 2 2 x1 2
H n (x1 ),
x1 x
qE
上式可改写为
E , p k
3、用来解释光电效应的爱因斯坦公式为 4、戴微孙-革末 为
E , p k
(理论物理导论)李卫-修订版

理工类可用量子力学与统计物理习题解答 第一章1. 一维运动粒子处于⎩⎨⎧≤>=-)0(0)0()(x x Axe x xλψ的状态,式中>0,求(1)归一化因子A ; (2)粒子的几率密度;(3)粒子出现在何处的几率最大? 解:(1)⎰⎰∞-∞∞-*=0222)()(dx e x A dx x x x λψψ令 x λξ2=,则323232023202224!28)3(88λλλξξλξλA AA d e A dx ex Ax=⨯=Γ==-∞∞-⎰⎰由归一化的定义1)()(=⎰∞∞-*dx x x ψψ得 2/32λ=A(2)粒子的几率密度xe x x x x P λλψψ2234)()()(-*==(3)在极值点,由一阶导数0)(=dxx dP 可得方程0)1(2=--xex x λλ 而方程的根0=x ;∞=x ;λ/1=x 即为极值点。
几率密度在极值点的值0)0(=P ;0)(lim =∞→x P x ;24)/1(-=e P λλ由于P(x)在区间(0,1/)的一阶导数大于零,是升函数;在区间(1/,)的一阶导数小于零,是减函数,故几率密度的最大值为24-e λ,出现在λ/1=x 处。
2. 一维线性谐振子处于状态t i x Aet x ωαψ212122),(--=(1)求归一化因子A ;(2)求谐振子坐标小x 的平均值; (3)求谐振子势能的平均值。
解:(1)⎰⎰∞∞--∞∞-*=dx e A dx x222αψψ⎰∞-=02222dx e A xα⎰∞-=0222ξαξd e Aαπ2A =由归一化的定义1=⎰∞∞-*dx ψψ得 πα=A (2) ⎰⎰∞∞-∞∞--==dx xeA dx x xP x x222)(α因被积函数是奇函数,在对称区间上积分应为0,故 0=x(3)⎰∞∞-=dx x P x U U )()(⎰∞∞--=dx e kx x 22221απα ⎰∞-=0222dx e x k x απα ⎰∞-=222ξξπαξd e k⎥⎦⎤⎢⎣⎡+-=⎰∞-∞-0022221ξξπαξξd e e k⎰∞-=02221ξπαξd e k 2212ππαk=24αk =将2μω=k 、μωα=2代入,可得02141E U ==ω 是总能量的一半,由能量守恒定律U T E +=0可知动能平均值U E U E T ==-=0021和势能平均值相等,也是总能量的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量子力学与统计物理习题解答 第一章1. 一维运动粒子处于⎩⎨⎧≤>=-)0(0)0()(x x Axe x xλψ的状态,式中λ>0,求(1)归一化因子A ; (2)粒子的几率密度;(3)粒子出现在何处的几率最大? 解:(1)⎰⎰∞-∞∞-*=0222)()(dx e x A dx x x x λψψ令 x λξ2=,则323232023202224!28)3(88λλλξξλξλA AA d e A dx ex Ax=⨯=Γ==-∞∞-⎰⎰由归一化的定义1)()(=⎰∞∞-*dx x x ψψ得 2/32λ=A(2)粒子的几率密度xe x x x x P λλψψ2234)()()(-*==(3)在极值点,由一阶导数0)(=dxx dP 可得方程0)1(2=--xex x λλ 而方程的根0=x ;∞=x ;λ/1=x 即为极值点。
几率密度在极值点的值0)0(=P ;0)(lim =∞→x P x ;24)/1(-=e P λλ由于P(x)在区间(0,1/λ)的一阶导数大于零,是升函数;在区间(1/λ,∞)的一阶导数小于零,是减函数,故几率密度的最大值为24-e λ,出现在λ/1=x 处。
2. 一维线性谐振子处于状态t i x Aet x ωαψ212122),(--=(1)求归一化因子A ;(2)求谐振子坐标小x 的平均值;(3)求谐振子势能的平均值。
解:(1)⎰⎰∞∞--∞∞-*=dx e Adx x222αψψ⎰∞-=02222dx e A xα⎰∞-=0222ξαξd e Aαπ2A =由归一化的定义1=⎰∞∞-*dx ψψ得 πα=A (2) ⎰⎰∞∞-∞∞--==dx xe A dx x xP x x222)(α因被积函数是奇函数,在对称区间上积分应为0,故 0=x (3)⎰∞∞-=dx x P x U U )()(⎰∞∞--=dx e kx x 22221απα ⎰∞-=0222dx e x k x απα⎰∞-=222ξξπαξd e k⎥⎦⎤⎢⎣⎡+-=⎰∞-∞-0022221ξξπαξξd e e k⎰∞-=02221ξπαξd e k 2212ππαk=24αk =将2μω=k 、μωα=2代入,可得02141E U ==ω 是总能量的一半,由能量守恒定律U T E +=0可知动能平均值U E U E T ==-=0021和势能平均值相等,也是总能量的一半。
3.设把宽为a 的一维无限深势阱的坐标原点取在势阱中点,有⎩⎨⎧≥∞<=)2/|(|,)2/|(|,0)(a x a x x U试通过具体解定态薛定谔方程,证明势阱中粒子的波函数为2/||,6,4,2,sin 2,5,3,1,cos 2)(a x n x an a n x a n a x n ≤⎪⎪⎩⎪⎪⎨⎧===ππψ粒子的能量为 ,4,3,2,1,22222==n n aE n μπ证明:势函数与时间无关,是定态问题。
由于是无限深势阱,粒子不可能到达阱外,因此在阱外 2/||,0)(a x x ≥=ψ 在阱内,波函数满足定态薛定谔方程2/||)()(22a x x E x ≤=''-ψψμ上式可变形为 0)(2)(2=+''x Ex ψμψ令222 Ek μ=,则方程化为0)()(2=+''x k x ψψ该方程的通解为 kx B kx A x cos sin )(+=ψ 在边界上,波函数应满足连续性条件,即0)(0)(2/2/==+=-=a x a x x x ψψ将通解代入有2cos 2sin 02cos 2sin=+=+-ka B ka A ka B ka A由此可得2cos 02sin==ka B ka AA 和B 不能同时为零,否则解无意义。
0≠A ,则必有,6,4,2,02sin==⇒=n a n k ka n π0≠B ,则必有,5,3,1,02cos ==⇒=n an k ka n π由此可得方程的解为⎪⎩⎪⎨⎧===,6,4,2,sin ,5,3,1,cos )(n x a n A n x a n B x n ππψ 由归一化条件 ⎰∞∞-*=1dx n n ψψ可知12/sin 2/2/222==⎪⎭⎫ ⎝⎛⎰-a A dx x a n A a a π12/cos 2/2/222==⎪⎭⎫ ⎝⎛⎰-a B dx x a n B a a π解得a B A /2== 故在阱内的波函数为⎪⎪⎩⎪⎪⎨⎧===,6,4,2,sin 2,5,3,1,cos 2)(n x an a n x a n a x n ππψ粒子的能量,4,3,2,1,22222222===n n ak E n μπμ波函数的两个表达式还可统一为一个表达式,3,2,1),2(sin 2)(=+=n ax a n a x n πψ书中例题与习题的不同是将坐标原点取在势阱的左边界上,其解为,3,2,1,sin 2)(==n x an a x n πψ 因此只要作坐标平移代换21ax x +=,将坐标原点移到势阱中心,立即可得到习题的结果。
4.带电荷q 的一维谐振子在外电场E 作用下运动,x q x x U E-=)2/()(22μω,试证明粒子的能量和波函数分别为 222221μωωE q n E n -⎪⎭⎫ ⎝⎛+=21121),()(212μωαψαEq x x x H eN x n x n n -==-证明:势函数与时间无关,是定态问题。
定态薛定谔方程为)()(21)(2222x E x x q x x u ψψμωψ=⎪⎭⎫ ⎝⎛-+''-E 上式可改写为)()(2)()2(21)(222242222222x E x q x q x q x x u ψψμωψωμμωμωψ=-+-+''-E E E即)(2)(21)(22222222x q E q x x u ψμωμωμωψ⎪⎪⎭⎫ ⎝⎛+=-+''-E E 作代换21μωEq x x -=,2222μωβE q E E +=,则方程化为标准的一维谐振子方程)(21)(2121212x E x x u ψμωψβ=+''- 其解为 )()(1211212x H eN x n x n n αψα-=能量为ωβ ⎪⎭⎫ ⎝⎛+=21n E n代换回去得能量 2222222212μωωμωβE E q n q E E n -⎪⎭⎫ ⎝⎛+=-=波函数21121),()(212μωαψαEq x x x H eN x n x n n -==-我们看一下谐振子所受的力12222)()(x q x q x dx x dU F μωμωμωμω=-=-==EE 由F =0可知谐振子的平衡点不再是0=x 而是平移到2μωEq x =作代换21μωEq x x -=,无非是将坐标原点移到新的平衡点2μωEq ,移到新的平衡点后,与标准谐振子的力函数表达式完全相同。
5.有一维势垒如下图所示,自由粒子沿x +方向向势垒运动,0U E <<,求粒子的透射系数D 。
提示:写出)(x U 表达式;令E x U =)(,解出积分限b ;利用(2-104)式得D ,并注意简化运算。
解:⎩⎨⎧><≤≤-=ax x a x a x U x U ,0,00),/1()(0E()⎥⎥⎦⎤⎢⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-------------=⎰=⎰=⎰=⎰=2/302/3000000000000003240)(220220])/1([220])([220E U b a U E U U a x aUd x a U E U U a dx x aUE U dxE a x U dxE x U eD e D e D eD e D D b b bbμμμμμ由 b aU U a b U E 000)/1(-=-= 可得000=--b aU E U 故 ()2/3003240E U U a eD D --=μ6.粒子在三维无限深势阱⎩⎨⎧≥≥≥∞<<<=)2/||,2/||,2/|(|,)2/||,2/||,2/|(|,0),,(c z b y a x c z b y a x z y x U中运动,求粒子的波函数和能量。
解:势能不含时间是定态问题。
在阱外,波函数 2/||,2/||,2/||,0),,(c z b y a x z y x ≥≥≥=ψ 在阱内,波函数满足定态薛定谔方程 2/||,2/||,2/||),,(),,(222c z b y a x z y x E z y x ≤≤≤=∇-ψψμ令222Ek μ=,则方程可化为标准形式 0),,(),,(22=+∇z y x k z y x ψψ令 )()()(),,(z Z x Y x X z y x =ψ 代入方程有02222222=+++XYZ k Z dz d XY Y dy d XZ X dx d YZ除以XYZ ,可得01112222222=+++k Z dzd Z Y dy d Y X dx d X 要使上式成立,必然有222222222111z y x k Z dzd Z k Y dy d Y k X dx d X -=-=-=即000222222222=+=+=+Z k Z dzd Y k Y dyd X k X dx d z y x 由波函数的连续性可知在边界上)2/()2/(0)2/()2/(0)2/()2/(==-==-==-c Z c Z b Y b Y a X a X 由方程和边界条件可得⎪⎩⎪⎨⎧='==,6,4,2,sin ,5,3,1,cos )(n x a n A n x a n A x X n ππ⎪⎩⎪⎨⎧='==,6,4,2,sin ,5,3,1,cos )(m x b m B m x b m B y Y m ππ⎪⎩⎪⎨⎧='==,6,4,2,sin ,5,3,1,cos )(l x c l C l x c l C x Z l ππ由归一化条件可得a A A 2='=;bB B 2='=;cC C 2='=⎪⎪⎩⎪⎪⎨⎧=== ,6,4,2,sin 2,5,3,1,cos 2)(n x a n a n x a n a x X n ππ⎪⎪⎩⎪⎪⎨⎧===,6,4,2,sin 2,5,3,1,cos 2)(m x bm b m x b m b y Y m ππ⎪⎪⎩⎪⎪⎨⎧===,6,4,2,sin 2,5,3,1,cos 2)(l x cl c l x c l c x Z l ππ或,3,2,1),2(sin 2)(=+=n a x a n a x X n π,3,2,1),2(sin 2)(=+=m b y b m b y Y m π ,3,2,1),2(sin 2)(=+=l c z c l c z Z l π波函数,2,1;,2,1;,2,1),2(sin )2(sin )2(sin 8),,(===+++=l m n cz c l b y b m a x a n abc z y x nml πππψ 能量 )(2)(22222222222222222cl b m a n k k k k E z y x nml++=++==μπμπμ2、一维谐振子处于基态22122)(x e x απαψ-=,其中μωα=求 ?)()(22=⋅p x ∆∆(要求:按定义计算)⎰⎰∞∞-∞∞--=⋅===22222*2212122ααπαπαπαψψαdx e x dx x x x⎰⎰∞∞--∞∞-===022*dx xe dx x x xαπαψψ222221)(α∆=-=∴x x x ··························3分同理,222)(p p p -=∆ ·························1分 注意到一维情况下,只须考虑x p ,因此dx e x e i dx x i p x x x 22*2222ααπαψψ-∞∞--∞∞-∂∂⋅=∂∂=⎰⎰0)(222=-=⎰∞∞--dx x e i x απαα ···················3分 dx e x ep x x x 2222222222ααπα-∞∞--∂∂-=⎰dx xe dx d e x x ⎰∞∞---⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=22222222αααπαdx e x e e x x x ⎰∞∞----⎥⎥⎦⎤⎢⎢⎣⎡--=2222223222222ααααπα ⎰⎰-∞∞----=dx e x dx e x x 222222523ααπαπα22122222523 ααπαπααππα=⋅-⋅=2)()(222222 α∆∆=-==∴x xx p p p p ·························3分最后得 4221)()(222222=⋅=⋅αα∆∆p x ······················2分第四章1.试证ϕθϕθψ33sin )(),,(i e r f r =为2ˆL 和zL ˆ的共同本征函数,并求出相应的本征值。
