高中数学必修2同步练习第一章1.2.3
2019_2020学年高中数学第一章立体几何初步1.2.3空间中的垂直关系第1课时直线与平面垂直学案新人教B版必修2

第1课时直线与平面垂直1.理解线线垂直、线面垂直的概念.2.掌握直线与平面垂直的判定定理及性质.3.能应用性质定理证明空间位置关系.1.直线与直线的垂直两条直线垂直的定义:如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互相垂直.2.直线与平面垂直(1)直线与平面垂直的定义:如果一条直线和一个平面相交于点O,并且和这个平面内过交点O的任何直线都垂直,则称这条直线和这个平面互相垂直.这条直线叫做平面的垂线,这个平面叫做直线的垂面,交点叫做垂足,垂线上任意一点到垂足间的线段,叫做这个点到这个平面的垂线段,垂线段的长度叫做这个点到平面的距离.(2)直线和平面垂直的判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线就垂直于这个平面. (简而言之:线线垂直,则线面垂直)(3)推论:如果在两条平行直线中,有一条垂直于平面,那么另一条也垂直于这个平面.3.直线与平面垂直的性质(1)由直线和平面垂直的定义知,直线与平面内的所有直线都垂直,除此以外还有性质定理.(2)垂直于同一个平面的两条直线平行.垂直于同一条直线的两个平面平行.1.下列命题正确的是( )A.垂直于同一条直线的两直线平行B.垂直于同一条直线的两直线垂直C.垂直于同一个平面的两直线平行D.垂直于同一条直线的一条直线和平面平行解析:选C.在空间中垂直于同一直线的两条直线,可能平行,可能相交,也可能异面,所以A,B错;垂直于同一直线的直线和平面的位置关系可以是直线在平面内,也可以是直线和平面平行,所以D错;注意分析清楚给定条件下直线和平面可能的位置关系,不要有遗漏.2.在三棱锥ABCD中,AB=AD,CB=CD,求证:AC⊥BD.证明:如图取BD的中点E,连接AE,EC.因为AB=AD,BE=ED,所以AE⊥BD.又因为CB=CD,BE=ED,所以CE⊥BD.又AE∩EC=E,所以BD⊥平面ACE,又AC⊂平面ACE,所以AC⊥BD.3.垂直于同一条直线的两条直线平行吗?解:不一定.平行、相交、异面都有可能.线面垂直的判定如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN ⊥PM,N为垂足.(1)求证:AN⊥平面PBM;(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.【证明】(1)因为AB为⊙O的直径,所以AM⊥BM.又PA⊥平面ABM,所以PA⊥BM.又因为PA∩AM=A,所以BM⊥平面PAM.又AN⊂平面PAM,所以BM⊥AN.又AN⊥PM,且BM∩PM=M,所以AN⊥平面PBM.(2)由第一问知AN⊥平面PBM,PB⊂平面PBM,所以AN⊥PB.又因为AQ⊥PB,AN∩AQ=A,所以PB⊥平面ANQ.又NQ⊂平面ANQ,所以PB⊥NQ.在本例中若条件不变,在四面体PAMB的四个面中共有多少个直角三角形.解:由本例第一问的证明过程知,BM⊥平面PAM,又PM⊂平面PAM,所以BM⊥PM.所以∠PAM=∠PAB=∠AMB=∠BMP=90°.所以四个面都是直角三角形.证明线面垂直的方法(1)线线垂直证明线面垂直①定义法(不常用,但由线面垂直可得出线线垂直);②判定定理法:要着力寻找平面内哪两条相交直线(有时作辅助线);结合平面图形的性质(如勾股定理逆定理、等腰三角形底边中线等)及一条直线与平行线中一条垂直也与另一条垂直等结论来论证线线垂直.(2)平行转化法(利用推论)①a∥b,a⊥α⇒b⊥α;②α∥β,a⊥α⇒a⊥β.如图所示,S为Rt△ABC所在平面外一点,且SA=SB=SC.点D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若直角边BA=BC,求证:BD⊥平面ASC.证明:(1)法一:在等腰三角形SAC中,D为AC的中点,所以SD⊥AC,取AB的中点E,连接DE、SE.则ED∥BC,又AB⊥BC,所以DE⊥AB.又SE⊥AB,SE∩DE=E,所以AB⊥平面SED,所以AB⊥SD,又AB∩AC=A,所以SD⊥平面ABC.法二:因为D为AC中点,△ABC为直角三角形.所以AD=BD,又SA=SB,SD=SD,所以△SAD≌△SBD,所以∠SDB=∠SDA.又SA=SC,所以SD⊥AC,即∠SDA=90°,所以∠SDB=90°,即SD⊥BD,又BD∩AC=D,所以SD⊥平面ABC.(2)因为BA=BC,所以BD⊥AC,又SD⊥平面ABC,所以SD⊥BD,因为SD∩AC=D,所以BD⊥平面ASC.线面垂直的性质的应用如图,已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB于点E,过E作EF⊥SC于点F.(1)求证:AF⊥SC;(2)若平面AEF交SD于点G,求证:AG⊥SD.【证明】(1)因为SA⊥平面AC,BC⊂平面AC,所以SA⊥BC,因为四边形ABCD为矩形,所以AB⊥BC.所以BC⊥平面SAB,所以BC⊥AE.又SB⊥AE,SB∩BC=B,所以AE⊥平面SBC,所以AE⊥SC.又EF⊥SC,AE∩EF=E,所以SC⊥平面AEF.所以AF⊥SC.(2)因为SA⊥平面AC,所以SA⊥DC.又AD⊥DC,AD∩SA=A,所以DC⊥平面SAD.所以DC⊥AG.又由(1)有SC⊥平面AEF,AG⊂面AEF,所以SC ⊥AG ,所以AG ⊥平面SDC ,所以AG ⊥SD .证明线线垂直的常用思路线面垂直――→推出定义线线垂直――→推出判定定理线面垂直――→推出定义线线垂直.如图所示,在正方体ABCD A 1B 1C 1D 1中,M 是AB 上一点,N 是A 1C 的中点,MN ⊥平面A 1DC . 求证:(1)MN ∥AD 1; (2)M 是AB 的中点.证明:(1)因为四边形ADD 1A 1为正方形,所以AD 1⊥A 1D . 又因为CD ⊥平面ADD 1A 1,所以CD ⊥AD 1. 因为A 1D ∩CD =D , 所以AD 1⊥平面A 1DC . 又因为MN ⊥平面A 1DC , 所以MN ∥AD 1.(2)如图,连接ON ,在△A 1DC 中,A 1O =OD ,A 1N =NC . 所以ON ═∥12CD .因为CD ═∥AB , 所以ON ∥AM . 又因为MN ∥OA ,所以四边形AMNO 为平行四边形. 所以ON =AM .因为ON =12CD ,所以AM =12DC =12AB .所以M 是AB 的中点.线面垂直的综合应用如图所示,在直四棱柱ABCD A 1B 1C 1D 1中,已知DC =DD 1=2AD =2AB ,AD ⊥DC ,AB∥DC .(1)求证:D 1C ⊥AC 1;(2)设E 是DC 上一点,试确定E 的位置,使D 1E ∥平面A 1BD ,并说明理由. 【解】 (1)证明:连接C 1D .因为DC =DD 1,所以四边形DCC 1D 1是正方形,所以DC 1⊥D 1C . 因为AD ⊥DC ,AD ⊥DD 1,DC ∩DD 1=D , 所以AD ⊥平面DCC 1D 1,D 1C ⊂平面DCC 1D 1,所以AD ⊥D 1C .又AD ∩DC 1=D ,所以D 1C ⊥平面ADC 1. 又AC 1⊂平面ADC 1,所以D 1C ⊥AC 1.(2)如图,当E 是CD 的中点时满足条件,连接BE 、D 1E ,因为AB ═∥12CD , 所以四边形ABED 为平行四边形. 所以BE ∥AD ∥A 1D 1.所以四边形BED 1A 1为平行四边形, 所以D 1E ∥A 1B .又D 1E ⊄面A 1BD ,A 1B ⊂A 1BD , 所以D 1E ∥平面A 1BD .综上所述,当E 是DC 的中点时,可使D 1E ∥平面A 1BD .线面垂直与平行的相互转化(1)空间中直线与直线垂直、直线与平面垂直、直线与直线平行可以相互转化,每一种垂直与平行的判定都是从某种垂直与平行开始转化为另一种垂直与平行,最终达到目的的.(2)转化关系:线线垂直判定定理定义线面垂直性质判定定理推论线线平行.如图所示,侧棱垂直于底面的三棱柱ABC A 1B 1C 1中,底面ABC 为等腰直角三角形,∠ACB =90°,CE ⊥AB 1,D 为AB 的中点.求证:(1)CD ⊥AA 1; (2)AB 1⊥平面CED .证明:(1)由题意,得AA 1⊥平面ABC ,CD ⊂平面ABC ,所以CD ⊥AA 1.(2)因为D 是AB 的中点,△ABC 为等腰直角三角形,∠ACB =90°,所以CD ⊥AB . 又CD ⊥AA 1,AB ∩A 1A =A ,所以CD ⊥平面A 1B 1BA ,因为AB 1⊂平面A 1B 1BA ,所以CD ⊥AB 1. 又CE ⊥AB 1,CD ∩CE =C , 所以AB 1⊥平面CED .1.直线与直线垂直如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互相垂直.两条直线垂直包括相交垂直和异面垂直. 2.线面垂直、线线垂直的证明方法 (1)线面垂直的证明方法:①定义法;②判定定理法;③判定定理的推论.(2)线线垂直的证明方法:①定义法;②线面垂直的性质. (3)线线垂直与线面垂直可相互转化.1.直线与平面垂直的定义,应注意:①定义中的“任何直线”这一条件,②直线与平面垂直是相交中的特殊情况,③利用定义可得直线和平面垂直则直线与平面内的所有直线垂直.2.直线与平面垂直应注意两点:①定理中的条件,是“平面内的两条相交直线”既不能说是“两条直线”,也不能说“无数条直线”.②应用定理的关键是在平面内,找到两条相交直线与已知直线垂直.3.“垂直于同一条直线的两条直线平行”要求涉及到的三条直线在同一个平面内,否则不正确.这告诉我们平面几何中的一些结论推广到空间时不一定成立,需要多加注意.1.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( )A.平行B.垂直C.相交不垂直D.不确定解析:选B.一条直线垂直于三角形的两条边,那么这条直线必垂直于这个三角形所在的平面,因而必与第三边垂直.2.l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面解析:选B.A答案还有异面或者相交的情况,C、D不一定.3.已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,平行四边形ABCD一定是.解析:因为PA⊥平面ABCD,所以PA⊥BD.又因为PC⊥BD,PA∩PC=P,所以BD⊥平面PAC,所以BD⊥AC,所以平行四边形ABCD一定是菱形.答案:菱形4.点P是等腰三角形ABC所在平面外一点,PA⊥平面ABC,PA=8,在△ABC中,AB=AC=5,BC=6,则点P到BC的距离是.答案:4 5[学生用书P97(单独成册)])[A 基础达标]1.已知直线a⊥平面α,b∥α,则a与b的关系为( )A.a⊥b,且a与b相交B.a⊥b,且a与b不相交D.a与b不一定垂直解析:选C.过b作平面β,β∩α=b′,则b∥b′,因为a⊥平面α,所以a⊥b′,所以a⊥b.2.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( ) A.m⊂α,n⊂α,m∥β,n∥β⇒α∥βB.α∥β,m⊂α,n⊂β⇒m∥nC.m⊥α,m⊥n⇒n∥αD.m∥n,n⊥α⇒m⊥α解析:选D.由直线与平面垂直的判定定理的推论可知D正确.3.E、F分别是正方形ABCD中AB、BC的中点,沿DE、DF及EF把△ADE、△CDF和△BEF 折起,使A、B、C三点重合于一点P,则有( )A.DP⊥平面PEF B.DE⊥平面PEFC.EF⊥平面PEF D.DF⊥平面PEF解析:选A.如图所示,A、B、C三点重合于点P,则PD⊥PE,PD⊥PF,又PE∩PF=P,所以PD⊥平面PEF.4.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是( )A.EF⊥平面αB.EF⊥平面βC.PQ⊥GE解析:选B .因为EG ⊥平面α,PQ ⊂平面α,所以EG ⊥PQ .若EF ⊥平面β,则由PQ ⊂平面β,得EF ⊥PQ .又EG 与EF 为相交直线,所以PQ ⊥平面EFHG ,所以PQ ⊥GH ,故选B .5.在正方体ABCD A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总保持AP ⊥BD 1,则动点P 的轨迹是( )A .线段B 1C B .线段BC 1C .BB 1中点与CC 1中点连成的线段D .BC 中点与B 1C 1中点连成的线段解析:选A .如图,由于BD 1⊥平面AB 1C ,故点P 一定位于B 1C 上.6.如图,▱ADEF 的边AF ⊥平面ABCD ,AF =2,CD =3,则CE =.解析:因为AF ⊥平面ABCD ,AF ∥DE ,所以DE ⊥平面ABCD ,CD ⊂平面ABCD ,所以DE ⊥CD ,因为DE =AF =2,CD =3,所以CE =22+33=13.答案:137.α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线,给出四个论断:①m ∥n ;②α∥β;③m ⊥α;④n ⊥β.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .答案:⎭⎪⎬⎪⎫m ∥n α∥βm ⊥α⇒n ⊥β 8.如图所示,在矩形ABCD 中,AB =1,BC =a (a >0),PA ⊥平面AC ,且PA =1,若BC 边上存在点Q ,使得PQ ⊥QD ,则a 的最小值为 .解析:因为PA ⊥平面ABCD ,所以PA ⊥QD . 若BC 边上存在一点Q ,使得QD ⊥PQ , 则有QD ⊥平面PAQ ,从而QD ⊥AQ .在矩形ABCD 中,当AD =a <2时,直线BC 与以AD 为直径的圆相离,故不存在点Q ,使PQ ⊥DQ .所以当a ≥2时,才存在点Q ,使得PQ ⊥QD .所以a 的最小值为2. 答案:29.如图,在四棱锥P ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AP =AB =2,BC =22,E ,F 分别是AD ,PC 的中点.证明:PC ⊥平面BEF .证明:如图所示,连接PE ,EC , 在Rt △PAE 和Rt △CDE 中,因为PA =AB =CD ,AE =DE ,所以PE =CE ,即△PEC 是等腰三角形. 又因为F 是PC 的中点,所以EF ⊥PC . 又因为BP = AP 2+AB 2=22=BC ,F 是PC 的中点,所以BF ⊥PC .又因为BF ∩EF =F ,所以PC ⊥平面BEF . 10.侧棱垂直于底面的三棱柱ABC A ′B ′C ′满足∠BAC =90°,AB =AC =12AA ′=2,点M ,N 分别为A ′B ,B ′C ′的中点.(1)求证:MN ∥平面A ′ACC ′; (2)求证:A ′N ⊥平面BCN ; (3)求三棱锥C MNB 的体积. 解:(1)证明:如图,连接AB ′,AC ′,因为四边形ABB ′A ′为矩形,M 为A ′B 的中点,所以AB ′与A ′B 交于点M ,且M 为AB ′的中点,又点N 为B ′C ′的中点,所以MN ∥AC ′, 又MN ⊄平面A ′ACC ′,且AC ′⊂平面A ′ACC ′, 所以MN ∥平面A ′ACC ′.(2)证明:因为A ′B ′=A ′C ′=2,点N 为B ′C ′的中点, 所以A ′N ⊥B ′C ′.又BB ′⊥平面A ′B ′C ′,所以A ′N ⊥BB ′, 所以A ′N ⊥平面B ′C ′CB ,所以A ′N ⊥平面BCN . (3)由图可知V C MNB =V M BCN , 因为∠BAC =90°, 所以BC =AB 2+AC 2=22,S △BCN =12×22×4=42.由(2)及∠B ′A ′C ′=90°可得A ′N =2, 因为M 为A ′B 的中点, 所以M 到平面BCN 的距离为22, 所以V C MNB =V M BCN =13×42×22=43.[B 能力提升]11.在正方体ABCD A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( ) A .AC B .BD C .A 1DD .A 1A解析:选B.如图所示,连接AC,BD,因为BD⊥AC,A1C1∥AC,所以BD⊥A1C1,因为BD⊥A1A,A1A∩A1C1=A1,所以BD⊥平面ACC1A1,因为CE⊂平面ACC1A1,所以BD⊥CE.12.如图所示,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的正投影,给出下列结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中,正确结论的序号是.解析:对于①、③,因为PA⊥平面ABC,故PA⊥BC.又BC⊥AC,故BC⊥平面PAC,从而BC⊥AF.故③正确.又AF⊥PC,故AF⊥平面PBC,所以AF⊥PB,故①正确.对于②,由①知AF⊥PB,而AE⊥PB,从而PB⊥平面AEF,故EF⊥PB.故②正确.对于④,AE与平面PBC不垂直,故④不正确.答案:①②③13.如图,四棱锥PABCD中,O是底面正方形ABCD的中心,侧棱PD⊥底面ABCD,PD =DC,E是PC的中点.(1)证明:EO∥平面PAD;(2)证明:DE⊥平面PBC.证明:(1)连接AC,因为点O是底面正方形ABCD的中心,所以点O是AC的中点,又因为E是PC的中点,所以在△PAC中,EO是中位线,所以PA∥EO.因为EO⊄平面PAD,PA⊂平面PAD,所以EO∥平面PAD.(2)因为PD⊥平面ABCD,BC⊂平面ABCD,所以PD⊥BC,因为底面ABCD是正方形,有BC⊥DC,所以BC⊥平面PDC.而DE⊂平面PDC,所以BC⊥DE.因为PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,所以DE⊥PC.又BC,PC⊂平面PBC,且BC∩PC=C,所以DE⊥平面PBC.14.(选做题)如图,A、B、C、D为空间四点,在△ABC中,AC=BC,等边三角形ADB 以AB为轴转动,问是否总有AB⊥CD?证明你的结论.解:当△ADB以AB为轴转动时,总有AB⊥CD.证明如下:①当点D在平面ABC内时,因为AC=BC,AD=BD,所以C、D都在线段AB的垂直平分线上.所以CD⊥AB.②当点D不在平面ABC内时,取AB中点O,连DO,CO.因为AC=BC,AD=BD,所以CO⊥AB,DO⊥AB.又CO∩DO=O,所以AB⊥平面COD.因为CD⊂平面COD,所以AB⊥CD.综上所述,总有AB⊥CD.。
新人教B版高中数学必修二教学课件 第一章 立体几何初步 1.2.3《(第2课时)平面与平面垂直》

∵PA⊥平面ABC,BC⊂平面ABC, ∴PA⊥BC, ∵AD∩PA=A,∴BC⊥平面PAC, 又AC⊂平面PAC,∴BC⊥AC.
[点评]
已知条件是线面垂直和面面垂直,要证明两条直
线垂直,应将两条直线中的一条放入一平面中,使另一条直线 与该平面垂直,即由线面垂直得到线线垂直.在空间图形中, 高一级的垂直关系蕴含着低一级的垂直关系,通过本题可以看 到:面面垂直⇒线面垂直⇒线线垂直.
求证:平面ABC⊥平面SBC.
[ 解析]
解法一:取 BC 的中点 D,连接 AD、SD.
由题意知△ASB 与△ASC 是等边三角 形,则 AB=AC. ∴AD⊥BC,SD⊥BC. 2 令 SA=a,在△SBC 中,SD= 2 a, 2 又∵AD= AC -CD = 2 a,
2 2
∴AD2+SD2=SA2. 即 AD⊥SD.又∵AD⊥BC,∴AD⊥平面 SBC. ∵AD⊂平面 ABC, ∴平面 ABC⊥平面 SBC.
[解析]
∵△ABC为正三角形,D为BC的中点,
∴AD⊥BC. 又∵CC1⊥底面ABC,AD⊂平面ABC, ∴CC1⊥AD. 又BC∩CC1=C, ∴AD⊥平面BCC1B1. 又AD⊂平面AC1D,
∴平面AC1D⊥平面BCC1B1.
三棱锥 S -ABC 中,∠ BSC = 90°,∠ ASB= 60°,∠ ASC =60°,SA=SB=SC.
当 F 为 PC 的中点时,满
足平面 DEF⊥平面 ABCD. 取 AD 的中点 G,PC 的中点 F,连 接 PG、BG、DE、EF、DF,则 PG⊥ AD,而平面 PAD⊥面 ABCD, 所以 PG⊥平面 ABCD.在△PBC 中, EF∥PB; 在菱形 ABCD 中,GB∥DE,而 EF⊂平面 DEF,DE⊂平面 DEF,EF∩DE =E,∴平面 DEF∥平面 PGB.又 PG⊥平面 ABCD,PG⊂平面 PGB, ∴平面 PGB⊥平面 ABCD,∴平面 DEF⊥平面 ABCD.
第一章-1.2.3-充分条件、必要条件高中数学必修第一册人教B版

图1.2.3-3
【解析】如图1.2.3-3(1),闭合开关或者闭合开关都可以使灯泡亮;反之,若要
A.[1, +∞)
)
B.(−∞, 1]
C.[−3, +∞)
D.(−∞, −3]
【解析】¬: − 3 ≤ ≤ 1,¬: ≤ ,∵ ¬是¬的充分不必要条件,
∴ [−3,1] ⫋ (−∞, ],∴ ≥ 1.
例15 在如图1.2.3-3所示的电路图中,“闭合开关”是“灯泡亮”的什么条件?
【解析】∵ −2,2 ⊆ −∞, 2 ,∴ < 2是 < 2的充分条件.
必要条件
(4)“我是中国人”是“我是山东人”的__________.
【解析】∵ {山东人} ⊆ {中国人},∴ “我是中国人”是“我是山东人”的必要条件.
知识点2 充要条件
例2-3 判断下列说法是否正确.若不正确,请说明理由.
.在数轴上表示出 0,3
2
+3
图D 1.2.3-1所示,由题意知 ⇒ , ⇏ ,则
≥ 3,解得
2
围是[3, +∞).
图D 1.2.3-1
和
+3
−∞,
2
,如
≥ 3,即的取值范
4.已知: > 1或 < −3,: > ,且¬是¬的充分不必要条件,则实数的取值范
围为( A
≤ ≤ (答案不唯一)
(2) ⊆ ∩ 的一个充分不必要条件为_________________________.
【解析】 ⊆ ∩ 的一个充分不必要条件可为6 ≤ ≤ 9.
题型3 充要条件的证明
例13 证明: = 是2 + 2 = 2的充要条件.
最新人教版高中数学必修2课时同步测题(全册 共236页 附解析)

最新人教版高中数学必修2课时同步测题(全册共236页附解析)目录1.1 空间几何体的结构1.1.1 棱柱、棱锥、棱台的结构特征1.1.2 圆柱、圆锥、圆台、球、简单组合体的结构特征1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影1.2.2 空间几何体的三视图1.2.3 空间几何体的直观图1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积1.3.2 球的体积和表面积章末复习课第一单元评估验收卷(一)第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 平面第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.2 空间中直线与直线之间的位置关系2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定2.2.3 直线与平面平行的性质2.2.4 平面与平面平行的性质2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定2.3.2 平面与平面垂直的判定2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质章末复习课第二单元评估验收卷(二)第三章直线与方程3.1 直线的倾斜角与斜率3.1.1 倾斜角与斜率3.1.2 两条直线平行与垂直的判定3.2 直线的方程3.2.1 直线的点斜式方程3.2.2 直线的两点式方程第一章空间几何体1.1 空间几何体的结构1.1.1 棱柱、棱锥、棱台的结构特征A级基础巩固一、选择题1.下列几何体中棱柱有()A.5个B.4个C.3个D.2个解析:由棱柱的定义及几何特征,①③为棱柱.答案:D2.对有两个面互相平行,其余各面都是梯形的多面体,以下说法正确的是()A.棱柱B.棱锥C.棱台D.一定不是棱柱、棱锥解析:根据棱柱、棱锥、棱台的特征,一定不是棱柱、棱锥.答案:D3.下列图形经过折叠可以围成一个棱柱的是()解析:A、B、C、中底面多边形的边数与侧面数不相等.答案:D4.由5个面围成的多面体,其中上、下两个面是相似三角形,其余三个面都是梯形,并且这些梯形的腰延长后能相交于一点,则该多面体是()A.三棱柱B.三棱台C.三棱锥D.四棱锥解析:根据棱台的定义可判断知道多面体为三棱台.答案:B5.某同学制作了一个对面图案均相同的正方形礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)()解析:其展开图是沿盒子的棱剪开,无论从哪个棱剪开,剪开的相邻面在展开在图中可以不相邻,但未剪开的相邻面在展开图中一定相邻,又相同的图案是盒子相对的面,展开后绝不能相邻.答案:A二、填空题6.如图所示,正方形ABCD中,E,F分别为CD,BC的中点,沿AE,AF,EF将其折成一个多面体,则此多面体是________.解析:折叠后,各面均为三角形,且点B、C、D重合为一点,因此该多面体为三棱锥(四面体).答案:三棱锥(四面体)7.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为________cm.解析:由题设,该棱柱为五棱柱,共5条侧棱.所以每条侧棱的长为605=12(cm).答案:128.①有两个面互相平行,其余各面都是平行四边形的几何体的侧棱一定不相交于一点,故一定不是棱台;②两个互相平行的面是平行四边形,其余各面是四边形的几何体不一定是棱台;③两个互相平行的面是正方形,其余各面是四边形的几何体一定是棱台.其中正确说法的个数为________.解析:①正确,因为具有这些特征的几何体的侧棱一定不相交于一点,故一定不是棱台;②正确;③不正确,当两个平行的正方形完全相等时,一定不是棱台.答案:29.根据如图所示的几何体的表面展开图,画出立体图形.解:图①是以ABCD为底面,P为顶点的四棱锥.图②是以ABCD和A1B1C1D1为底面的棱柱.其图形如图所示.B级能力提升1.如图所示,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定解析:如图所示,倾斜小角度后,因为平面AA1D1D∥平面BB1C1C,所以有水的部分始终有两个平面平行,而其余各面都易证是平行四边形(水面与两平行平面的交线)因此呈棱柱形状.答案:A2.一个正方体的六个面上分别标有字母A,B,C,D,E,F,下图是此正方体的两种不同放置,则与D面相对的面上的字母是________.解析:由图知,标字母C的平面与标有A、B、D、E的面相邻,则与D面相对的面为E面,或B面,若B面与D面相对,则A面与B面相对,这时图②不可能,故只能与D面相对的面上字母为B.答案:B3.如图所示,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,求沿正方体表面从点A到点M的最短路程.解:若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是13 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是17 cm.故沿正方体表面从点A到点M的最短路程是13 cm.第一章空间几何体1.1 空间几何体的结构1.1.2 圆柱、圆锥、圆台、球、简单组合体的结构特征A级基础巩固一、选择题1.下列几何体中是旋转体的是()①圆柱②六棱锥③正方体④球体⑤四面体A.①和⑤B.①C.③和④D.①和④解析:圆柱、球体是旋转体,其余均为多面体.答案:D2.如图所示的简单组合体的结构特征是()A.由两个四棱锥组合成的B.由一个三棱锥和一个四棱锥组合成的C.由一个四棱锥和一个四棱柱组合成的D.由一个四棱锥和一个四棱台组合成的解析:这个8面体是由两个四棱锥组合而成.答案:A3.下图是由哪个平面图形旋转得到的()解析:图中几何体由圆锥、圆台组合而成,可由A中图形绕图中虚线旋转360°得到.答案:A4.如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面平行于底面,那么截面图形为()解析:截面图形应为图C所示的圆环面.答案:C5.用一张长为8、宽为4的矩形硬纸卷成圆柱的侧面,则相应圆柱的底面半径是()A.2 B.2πC.2π或4πD.π2或π4解析:如图所示,设底面半径为r,若矩形的长8恰好为卷成圆柱底面的周长,则2πr=8,所以r=4π;同理,若矩形的宽4恰好为卷成圆柱的底面周长,则2πr=4,所以r=2π.所以选C.答案:C二、填空题6.等腰三角形绕底边上的高所在的直线旋转180°,所得几何体是________.解析:结合旋转体及圆锥的特征知,所得几何体为圆锥.答案:圆锥7.给出下列说法:①圆柱的母线与它的轴可以不平行;②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线,都可以构成直角三角形;③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是____________(填序号).解析:由旋转体的形成与几何特征可知①③错误,②④正确.答案:②④8.如图是一个几何体的表面展成的平面图形,则这个几何体是__________.答案:圆柱三、解答题9.如图所示的物体是运动器材——空竹,你能描述它的几何特征吗?解:此几何体是由两个大圆柱、两个小圆柱和两个小圆台组合而成的.10.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的半径分别2 cm和5 cm,圆台的母线长是12 cm,求圆锥SO的母线长.解:如图,过圆台的轴作截面,截面为等腰梯形ABCD,由已知可得上底半径O1A=2 cm,下底半径OB=5 cm,且腰长AB=12 cm.设截得此圆台的圆锥的母线长为l,则由△SAO1∽△SBO,可得l-12 l=25,所以l=20 cm.故截得此圆台的圆锥的母线长为20 cm.B级能力提升1.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为()A.一个球体B.一个球体中间挖出一个圆柱C.一个圆柱D.一个球体中间挖去一个长方体解析:外面的圆旋转形成一个球,里面的长方形旋转形成一个圆柱.所有形成的几何为一个球体挖出一个圆柱.答案:B2.一个半径为5 cm的球,被一平面所截,球心到截面圆心的距离为4 cm,则截面圆面积为__________cm2.解析:如图所示,过球心O作轴截面,设截面圆的圆心为O1,其半径为r.由球的性质,OO1⊥CD.在Rt△OO1C中,R=OC=5,OO1=4,则O1C=3,所以截面圆的面积S=π·r2=π·O1C2=9π.答案:9π3.如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?解:把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,即为蚂蚁爬行的最短距离.因为AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π.所以AB′=A′B′2+AA′2=4+(2π)2=21+π2,所以蚂蚁爬行的最短距离为21+π2.第一章空间几何体1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影1.2.2 空间几何体的三视图A级基础巩固一、选择题1.以下关于投影的叙述不正确的是()A.手影就是一种投影B.中心投影的投影线相交于点光源C.斜投影的投影线不平行D.正投影的投影线和投影面垂直解析:平行投影的投影线互相平行,分为正投影和斜投影两种,故C错.2.如图所示,水平放置的圆柱形物体的三视图是()答案:A3.如图,在直角三角形ABC,∠ACB=90°,△ABC绕边AB 所在直线旋转一周形成的几何体的正视图为()解析:由题意,该几何体是两个同底的圆锥组成的简单组合体,且上部分圆锥比底部圆锥高,所以正视图应为选项B.答案:B4.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()A.球B.三棱锥C.正方体D.圆柱解析:球的三视图都是圆;三棱锥的三视图都是全等的三角形;正方体的三视图都是正方形;圆柱的底面放置在水平面上,则其俯视图是圆,正视图是矩形,故几何体不可能是圆柱.5.一个四棱锥S-ABCD,底面是正方形,各侧棱长相等,如图所示,其正视图是一等腰三角形,其腰长与图中等长的线段是()A.AB B.SBC.BC D.SE解析:正视图的投影面应是过点E与底面ABCD垂直的平面,所以侧棱SB在投影面上的投影为线段SE.答案:D二、填空题6.下列几何体各自的三视图中,有且仅有两个视图相同的是________(填序号).①正方体②圆锥③三棱台④正四棱锥解析:在各自的三视图中,①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.所以满足仅有两个视图相同的是②④.答案:②④7.一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为:①长方形;②正方形;③圆.其中满足条件的序号是________.答案:②③8.下图中的三视图表示的几何体是________.解析:根据三视图的生成可知,该几何体为三棱柱.答案:三棱柱三、解答题9.根据三视图(如图所示)想象物体原形,指出其结构特征,并画出物体的实物草图.解:由俯视图知,该几何体的底面是一直角梯形;由正视图知,该几何体是一四棱锥,且有一侧棱与底面垂直.所以该几何体如图所示.10.画出图中3个图形的指定视图.解:如图所示.B级能力提升1.如图所示为一个简单几何体的三视图,则其对应的实物图是()答案:A2.已知正三棱锥V-ABC的正视图、俯视图如图所示,它的侧棱VA=2,底面的边AC=3,则由该三棱锥得到的侧视图的面积为________.解析:正三棱锥V-ABC的侧视图不是一个等腰三角形,而是一个以一条侧棱、该侧棱所对面的斜高和底面正三角形的一条高构成的三角形,如侧视图所示(其中VF是斜高),由所给数据知原几何体的高为3,且CF=3 2.故侧视图的面积为S=12×32×3=334.答案:33 43.如图所示的是某两个几何体的三视图,试判断这两个几何体的形状.解:①由俯视图知该几何体为多面体,结合正视图和侧视图知,几何体应为正六棱锥.②由几何体的三视图知该几何体的底面是圆,相交的一部分是一个与底面同圆心的圆,正视图和侧视图是由两个全等的等腰梯形组成的.故该几何体是两个圆台的组合体.第一章空间几何体1.2 空间几何体的三视图和直观图1.2.3 空间几何体的直观图A级基础巩固一、选择题1.关于斜二测画法所得直观图,以下说法正确的是()A.等腰三角形的直观图仍是等腰三角形B.正方形的直观图为平行四边形C.梯形的直观图不是梯形D.正三角形的直观图一定为等腰三角形解析:由直观图的性质知B正确.答案:B2.利用斜二测画法画边长为3 cm的正方形的直观图,正确的是图中的()解析:正方形的直观图应是平行四边形,且相邻两边的边长之比为2∶1.答案:C3.如图,用斜二测画法画一个水平放置的平面图形为一个正方形,则原来图形的形状是()解析:直观图中正方形的对角线为2,故在平面图形中平行四边形的高为22,只有A项满足条件,故A正确.答案:A4.已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2 cm,另一个圆锥顶点到底面的距离为3 cm,则其直观图中这两个顶点之间的距离为()A.2 cm B.3 cm C.2.5 cm D.5 cm解析:因为这两个顶点连线与圆锥底面垂直,现在距离为5 cm,而在直观图中根据平行于z轴的线段长度不变,仍为5 cm.答案:D5.若一个三角形采用斜二测画法,得到的直观图的面积是原三角形面积的()A.24B.2倍 C.22 D.2倍解析:底不变,只研究高的情况即可,此结论应识记.答案:A二、填空题6.如图所示,△A′B′C′是△ABC的水平放置的直观图,A′B′∥y轴,则△ABC是________三角形.解析:由于A′B′∥y轴,所以在原图中AB∥y轴,故△ABC为直角三角形.答案:直角7.已知△ABC的直观图如图所示,则△ABC的面积为________.解析:△ABC中,∠A=90°,AB=3,AC=6,所以S=12×3×6=9.答案:98.如图所示,水平放置的△ABC的斜二测直观图是图中的△A′B′C′,已知A′C′=6,B′C′=4,则AB边的实际长度是_______.解析:在原图中AC=6,BC=4×2=8,∠AOB=90°,所以AB=62+82=10.答案:10三、解答题9.如图所示,已知水平放置的平面图形的直观图是一等腰直角三角形ABC,且AB=BC=1,试画出它的原图形.解:(1)在如图所示的图形中画相应的x轴、y轴,使∠xOy=90°(O与A′重合);(2)在x轴上取C′,使A′C′=AC,在y轴上取B′,使A′B′=2AB;(3)连接B′C′,则△A′B′C′就是原图形.10.画出底面是正方形、侧棱均相等的四棱锥的直观图(棱锥的高不做具体要求).解:画法:(1)画轴.画Ox轴、Oy轴、Oz轴,∠xOy=45°(135°),∠xOz=90°,如图.(2)画底面.以O为中心在xOy平面内,画出底面正方形的直观图ABCD.(3)画顶点.在Oz轴上截取OP,使OP的长度是四棱锥的高.(4)成图.顺次连接PA、PB、PC、PD,并擦去辅助线,得四棱锥的直观图.B级能力提升1.水平放置的△ABC有一边在水平线上,它的斜二测直观图是正△A′B′C′,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能解析:如下图所示,斜二测直观图还原为平面图形,故△ABC 是钝角三角形.答案:C2.如图,Rt△O′A′B′是一平面图形的直观图,直角边O′B′=1,则这个平面图形的面积是________.解析:因为O′B=1,所以O′A′=2,所以在Rt△OAB中,∠AOB=90°,OB=1,OA=2 2.所以S△AOB=12×1×22= 2.答案:23.如图是一个空间几何体的三视图,试用斜二测画法画出它的直观图.解:根据三视图可以想象出这个几何体是六棱台.(1)画轴.如图①,画x轴、y轴、z轴,使∠xOy=45°,∠xOz =90°.(2)画两底面,由三视图知该几何体为六棱台,用斜二测画法画出底面正六边形ABCDEF,在z轴上截取OO′,使OO′等于三视图中的相应高度,过O′作Ox的平行线O′x′,Oy的平行线O′y′,利用O′x与O′y′画出底面正六边形A′B′C′D′E′F′.(3)成图.连接A′A,B′B,C′C,D′D,E′E,F′F,整理得到三视图表示的几何体的直观图,如图②.第一章空间几何体1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积A级基础巩固一、选择题1.轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( )A .4倍B .3倍 C.2倍D .2倍解析:设轴截面正三角形的边长为2a ,所以S 底=πa 2,S 侧=πa ·2a =2πa 2,因此S 侧=2S 底. 答案:D2.如图所示,ABC A ′B ′C ′是体积为1的棱柱,则四棱锥C -AA ′B ′B 的体积是( )A.13B.12C.23D.34解析:因为V C A ′B ′C ′=13V 柱=13,所以V C AA ′B ′B =1-13=23.答案:C3.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的全面积为( )A .3πB .33πC .6πD .9π解析:由于圆锥的轴截面是等边三角形,所以2r =l , 又S 轴=12×l 2×sin 60°=34l 2=3,所以l =2,r =1.所以S圆锥表=πr2+πrl=π+2π=3π.故选A.答案:A4.(2015·课标全国Ⅰ卷)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依恒内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图所示,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放米约有()A.14斛B.22斛C.36斛D.66斛解析:由l=14×2πr=8得圆锥底面的半径r=16π≈163,所以米堆的体积V=14×13πr2h=14×2569×5=3209(立方尺),所以堆放的米有3209÷1.62≈22(斛).答案:B5.已知正方体的8个顶点中,有4个为侧面是等边三角形的一三棱锥的顶点,则这个三棱锥与正方体的表面积之比为()A.1∶ 2 B.1∶ 3C.2∶ 2 D.3∶ 6解析:棱锥B′ ACD′为适合条件的棱锥,四个面为全等的等边三角形,设正方体的边长为1,则B′C=2,S△B′AC=3 2.三棱锥的表面积S 锥=4×32=23,又正方体的表面积S 正=6. 因此S 锥∶S 正=23∶6=1∶ 3. 答案:B 二、填空题6.若一个圆台的正视图如图所示,则其侧面积为________.解析:由正视图可知,该圆台的上、下底面圆的半径分别为1,2,其高为2,所以其母线长l =⎝ ⎛⎭⎪⎫4-222+22=5, 所以S 侧=π(1+2)×5=35π. 答案:35π7.下图是一个空间几何体的三视图,这个几何体的体积是________.解析:由图可知几何体是一个圆柱内挖去一个圆锥所得的几何体,V =V 圆柱-V 圆锥=π×22×3-13π×22×3=8π.答案:8π8.(2015·福建卷)某几何体的三视图如图所示,则该几何体的表面积等于________.解析:由三视图知,该几何体是直四棱柱,底面是直角梯形,且底面梯形的周长为4+ 2.则S侧=8+22,S底=2×(1+2)2×1=3.故S表=S侧+S底=11+2 2.答案:11+22三、解答题9.已知圆柱的侧面展开图是长、宽分别为2π和4π的矩形,求这个圆柱的体积.解:设圆柱的底面半径为R,高为h,当圆柱的底面周长为2π时,h=4π,由2πR=2π,得R=1,所以V圆柱=πR2h=4π2.当圆柱的底面周长为4π时,h=2π,由2πR=4π,得R=2,所以V圆柱=πR2h=4π·2π=8π2.所以圆柱的体积为4π2或8π2.10.一个正三棱柱的三视图如图所示(单位:cm),求这个正三棱柱的表面积与体积.解:由三视图知直观图如图所示,则高AA′=2 cm,底面高B′D′=23cm ,所以底面边长A ′B ′=23×23=4(cm).一个底面的面积为12×23×4=43(cm 2).所以表面积S =2×43+4×2×3=24+83(cm 2), V =43×2=83(cm 3).所以表面积为(24+83)cm 2,体积为83(cm 3).B 级 能力提升1.某几何体的三视图如图所示,俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )A.203π B.103π C .6πD.163π 解析:该几何体的上方是以2为底面圆的半径,高为2的圆锥的一半,下方是以2为底面圆的半径,高为1的圆柱的一半,其体积为V =π×22×12+12×13π×22×2=2π+43π=103π.答案:B2.(2015·江苏卷)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为__________.解析:底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱的总体积为13π×52×4+π×22×8=196π3.设新的圆锥和圆柱的底面半径为r ,则13π·r 2×4+π·r 2×8=28π3r 2=196π3,解得r =7.答案:73.某几何体的三视图如图所示(单位:cm),求该几何体的体积.解:由三视图知,该几何体是一个四棱柱与一个四棱锥的组合体. V 四棱柱=23=8,V 四棱锥=13×22×2=83.故几何体的体积V =V 四棱柱+V 四棱锥=8+83 =323(cm 3).第一章 空间几何体 1.3 空间几体的表面积与体积 1.3.2 球的体积和表面积A 级 基础巩固一、选择题1.若一个球的体积扩大到原来的27倍,则它的表面积扩大到原来的( )A .3倍B .3 3 倍C .9倍D .9 3 倍解析:由V ′=27 V ,得R ′=3R ,R ′R=3则球的表面积比S ′∶S =⎝ ⎛⎭⎪⎫R ′R 2=9. 答案:C2.把3个半径为R 的铁球熔成一个底面半径为R 的圆柱,则圆柱的高为( )A .RB .2RC .3RD .4R 解析:设圆柱的高为h ,则πR 2h =3×43πR 3,所以h =4R . 答案:D3.如图所示,是某几何体的三视图,则该几何体的体积为( )A .9π+42B .36π+18 C.92π+12 D.92π+18解析:由三视图可知该几何体是一个长方体和球构成的组合体,其体积V=43π⎝⎛⎭⎪⎫323+3×3×2=92π+18.答案:D4.设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为()A.3πa2B.6πa2C.12πa2D.24πa2解析:设该球的半径为R,所以(2R)2=(2a)2+a2+a2=6a2,即4R2=6a2.所以球的表面积为S=4πR2=6πa2.答案:B5.下图是一个几何体的三视图,根据图中数据,可得几何体的表面积是()A.4π+24 B.4π+32C.22πD.12π解析:由三视图可知,该几何体上部分为半径为1的球,下部分为底边长为2,高为3的正四棱柱,几何体的表面积为4π+32.答案:B二、填空题6.将一钢球放入底面半径为3 cm 的圆柱形玻璃容器中,水面升高4 cm ,则钢球的半径是________.解析:圆柱形玻璃容器中水面升高4cm ,则钢球的体积为V =π×32×4=36π,即有43πR 3=36π,所以R =3.答案:3 cm7.两个球的表面积之差为48π,它们的大圆周长之和为12π,则这两个球的半径之差为________.解析:由题意设两球半径分别为R 、r (R >r ),则:⎩⎪⎨⎪⎧4πR 2-4πr 2=48π2πR +2πr =12π即⎩⎪⎨⎪⎧R 2-r 2=12R +r =6.,所以R -r =2. 答案:28.已知某几何体的三视图如图所示,则该几何体的体积为________.解析:由三视图可知几何体为组合体,上方是半径为1的球,下方是长方体,其底面是边长为2的正方形,侧棱长为4,故其体积V =43×π×13+2×2×4=16+4π3. 答案:16+4π3三、解答题9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r =1,l =3,试求该组合体的表面积和体积.解:组合体的表面积S =4πr 2+2πrl =4π×12+2π×1×3=10π. 因为圆柱的体积V 圆柱=πr 2l =π×12×3=3π,又两个半球的体积2V 半球=43πr 3=43π, 因此组合体的体积V =3π+43π=133π. 10.如图,一个圆柱形的玻璃瓶的内半径为3 cm ,瓶里所装的水深为8 cm ,将一个钢球完全浸入水中,瓶中水的高度上升到8.5 cm ,求钢球的半径.解:设球的半径为R ,由题意可得43πR 3=π×32×0.5, 解得:R =1.5 (cm),所以所求球的半径为1.5 cm.B 级 能力提升1.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.8π3B.82π3 C .82π D.32π3解析:截面面积为π,则该小圆的半径为1,设球的半径为R ,则R 2=12+12=2,所以R =2,V =43πR 3=82π3.答案:B2.边长为42的正方形ABCD 的四个顶点在半径为5的球O 的表面上,则四棱锥O -ABCD 的体积是________.解析:因为正方形ABCD 外接圆的半径r =(42)2+(42)22=4.又因为球的半径为5, 所以球心O 到平面ABCD 的距离d =R 2-r 2=3,所以V O ABCD =13×(42)3×3=32. 答案:323.体积相等的正方体、球、等边圆柱(轴截面为正方形的圆柱)的表面积分别是S 1,S 2,S 3,试比较它们的大小.解:设正方体的棱长为a ,球的半径为R ,等边圆柱的底面半径为r ,则S 1=6a 2,S 2=4πR 2,S 3=6πr 2.由题意知,43πR 3=a 3=πr 2·2r , 所以R =334πa ,r =312πa , 所以S 2=4π⎝⎛⎭⎪⎪⎫334πa 2=4π·3916π2a 2=336πa 2, S 3=6π⎝⎛⎭⎪⎪⎫312πa 2=6π·314π2a 2=354πa 2, 所以S 2<S 3.又6a 2>3312πa 2=354πa 2,即S 1>S 3. 所以S 1,S 2,S 3的大小关系是S 2<S 3<S 1.章末复习课[整合·网络构建][警示·易错提醒]1.台体可以看成是由锥体截得的,易忽视截面与底面平行且侧棱(母线)延长后必交于一点.2.空间几何体不同放置时其三视图不一定相同.3.对于简单组合体,若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,易忽视虚线的画法.4.求组合体的表面积时:组合体的衔接部分的面积问题易出错.5.由三视图计算几何体的表面积与体积时,由于几何体的还原不准确及几何体的结构特征认识不准易导致失误.6.易混侧面积与表面积的概念.专题1空间几何体的三视图与直观图三视图是立体几何中的基本内容,能根据三视图识别其所表示的立体模型,并能根据三视图与直观图所提供的数据解决问题.主要考查形式:(1)由三视图中的部分视图确定其他视图;(2)由三视图还原几何体;(3)三视图中的相关量的计算.其中(3)是本章的难点,也是重点之一,解这类题的关键是准确地将三视图中的数据转化为几何体中的数据.[例1](1)若一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为()A.2,23B.22,2C.4,2D.2,4(2)(2016·全国Ⅲ卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36 5 B.54+18 5 C.90 D.81解析:(1)由三视图的画法规则知,正视图与俯视图长度一致,正视图与侧视图高度一致,俯视图与侧视图宽度一致.所以侧视图中2为正三棱柱的高,23为底面等边三角形的高,所以底面等边三角形边长为4.(2)由三视图可知,该几何体的底面是边长为3的正方形,高为6,侧棱长为35,则该几何体的表面积S=2×32+2×3×35+2×3×6=54+18 5.故选B.答案:(1)D(2)B。
人教A版高中数学必修二 1.2.3空间几何体的直观图 同步练习(II)卷(模拟)

人教A版高中数学必修二 1.2.3空间几何体的直观图同步练习(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共9题;共18分)1. (2分) (2018高一上·延边月考) 已知△ABC的平面直观图是边长为的正三角形,那么原△ABC的面积为()A .B .C .D .2. (2分)某工作的三视图如图所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为()(材料利用率=新工件的体积/原工件的体积)A .B .C .D .3. (2分)正方体ABCD-A1B1C1D1的棱线长为1,面对角线B1D1上有两个动点E,F,且,则下列四个结论中①②平面ABCD ③三棱锥A-BEF的体积为定值④异面直线AE,BF所成的角为定值,其中正确的个数是()A . 1B . 2C . 3D . 44. (2分)已知△ABC的平面直观图△A′B′C′是边长为2的正三角形,则△ABC的面积为()A .B .C .D .5. (2分)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A . 1B .C .D . 26. (2分)如图所示的斜二测直观图表示的平面图形是()A . 平行四边形B . 等腰梯形C . 直角梯形D . 长方形7. (2分) (2017高一下·磁县期末) 用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形,其中梯形的上底是下底的,若原平面图形的面积为3 ,则OA的长为()A . 2B .C .D .8. (2分)已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形,则原△ABC 的面积为()A . a2B . a2C . a2D . a29. (2分) (2018高二上·凌源期末) 某几何体的三视图如图所示,则其表面积为()A .B .C .D .二、填空题 (共3题;共3分)10. (1分)用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是________11. (1分)如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△AOB的面积为16,A′B′∥y′轴,过A′作A′C′⊥x′轴,则A′C′=________.12. (1分)如图,△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图,A′B′在x′轴上,B′C′⊥x′轴,且B′C′=3,则△ABC的边AB上的高为________.三、解答题 (共2题;共10分)13. (5分)画棱长为2 cm的正方体的直观图.14. (5分)在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形ABCD并求出其面积.参考答案一、单选题 (共9题;共18分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、二、填空题 (共3题;共3分)10-1、11-1、12-1、三、解答题 (共2题;共10分)13-1、14-1、。
人教b版高中数学必修2同步练习题及答案全册汇编

人B版高中数学必修2同步习题目录第1章1.1.1同步练习第1章1.1.2同步练习第1章1.1.3同步练习第1章1.1.4同步练习第1章1.1.5同步练习第1章1.1.6同步练习第1章1.1.7同步练习第1章1.2.1同步练习第1章1.2.2第一课时同步练习第1章1.2.2第二课时同步练习第1章1.2.3第一课时同步练习第1章1.2.3第二课时同步练习第1章章末综合检测第2章2.1.1同步练习第2章2.1.2同步练习第2章2.2.1同步练习第2章2.2.2第一课时同步练习第2章2.2.2第二课时同步练习第2章2.2.3第一课时同步练习第2章2.2.3第二课时同步练习第2章2.2.4同步练习第2章2.3.1同步练习第2章2.3.2同步练习第2章2.3.3同步练习第2章2.3.4同步练习第2章2.4.1同步练习第2章2.4.2同步练习第2章章末综合检测人教B版必修2同步练习1.关于平面,下列说法正确的是()A.平行四边形是一个平面B.平面是有大小的C.平面是无限延展的D.长方体的一个面是平面答案:C2.如图所示的两个相交平面,其中画法正确的有()A.1个B.2个C.3个D.4个解析:选B.被平面遮住的部分应画虚线,故(1)(4)正确.3.如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上三点,则在正方体盒子中,∠ABC等于()A.45°B.60°C.90°D.120°答案:B4.飞机飞行表演在空中留下漂亮的“彩带”,用数学知识解释为________.答案:点动成线5.一个平面将空间分成________部分;两个平面将空间分成________部分.答案:23或41.下列不属于构成几何体的基本元素的是()A.点B.线段C.曲面D.多边形(不含内部的点)解析:选D.点、线、面是构成几何体的基本元素.2. 如图是一个正方体的展开图,每一个面内都标注了字母,则展开前与B相对的是()A.字母E B.字母CC.字母A D.字母D解析:选B.正方体展开图有很多种,可以通过实物观察,选一个面作为底面,通过空间想象操作完成.不妨选字母D所在的面为底面,可以得到A,F是相对的面,E与D相对;若选F做底面,则仍然得到A,F是相对的面,E与D相对,则与B相对的是字母C.3.如图,下列四个平面图形,每个小四边形皆为正方形,其中可以沿两个正方形的相邻边折叠围成一个立方体的图形是()解析:选C.借助模型进行还原.4.下列命题正确的是()A.直线的平移只能形成平面B.直线绕定直线旋转肯定形成柱面C.直线绕定点旋转可以形成锥面D.曲线的平移一定形成曲面解析:选C.直线的平移,可以形成平面或曲面,命题A不正确;当两直线平行时旋转形成柱面,命题B不正确;曲线平移的方向与曲线本身所在的平面平行时,不能形成曲面,D不正确,只有C正确.故选C.5.下列几何图形中,可能不是平面图形的是()A.梯形B.菱形C.平行四边形D.四边形解析:选D.四边形可能是空间四边形,如将菱形沿一条对角线折叠成4个顶点不共面的四边形.6.下面空间图形的画法中错误的是()解析:选D.被遮住的地方应该画成虚线或不画,故D图错误.7.在以下图形中,正方体ABCD-A1B1C1D1不可以由四边形________(填序号)平移而得到.①ABCD;②A1B1C1D1;③A1B1BA;④A1BCD1.解析:①ABCD,②A1B1C1D1,③A1B1BA,按某一方向平移可以得到正方体ABCD-A1B1C1D1,④A1BCD1平移不能得到正方体ABCD-A1B1C1D1.答案:④8. 把如图的平面沿虚线折叠可以折叠成的几何体是________.解析:图中由六个正方形组成,可以动手折叠试验,得到正方体.答案:正方体9.如右图小明设计了某个产品的包装盒,但是少设计了其中一部分,请你把它补上,使其成为两边均有盖的正方体盒子.你能有________种方法.答案:410. 指出下面几何体的点、线、面.解:顶点A 、B 、C 、D 、M 、N ;棱AB 、BC 、CD 、DA 、MA 、MB 、MC 、MD 、NA 、NB 、NC 、ND ;面MAD 、面MAB 、面MBC 、面MDC 、面NAB 、面NAD 、面NDC 、面NBC .11.搬家公司想把长2.5 m ,宽0.5 m ,高2 m 的长方体家具从正方形窗口穿过,正方形窗口的边长为a ,则a 至少是多少?解:如图,问题实质是求正方形的内接矩形边长为2 m,0.5 m 时正方形的边长a =2+0.52=524≈1.77(m).所以a 至少是1.77 m 时,长方体家具可以通过.12.要将一个正方体模型展开成平面图形,需要剪断多少条棱?你能从中得出什么规律来吗?解:需要剪断7条棱.因为正方体有6个面,12条棱,两个面有一条棱相连,展开后六个面就有5条棱相连,所以剪断7条棱.规律是正方体的平面展开图只能有5条棱相连,但是,有5条棱相连的6个正方形图形不一定是正方体的平面展开图.人教B 版必修2同步练习1.在下列立体图形中,有5个面的是( ) A .四棱锥 B .五棱锥 C .四棱柱 D .五棱柱解析:选A.柱体均有两个底面,锥体只有一个底面.2.如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是( )A .棱柱B .棱台C .棱柱与棱锥组合体D .无法确定 答案:A3.在四棱锥的四个侧面中,直角三角形最多可有( ) A .1个 B .2个 C .3个 D .4个 答案:D4.棱柱的侧面是________形,棱锥的侧面是________形,棱台的侧面是________形. 答案:平行四边 三角 梯5.在正方形ABCD 中,E 、F 分别为BC 、CD 的中点,沿AE 、AF 、EF 将其折成一个多面体,则此多面体是________.答案:三棱锥1.下列命题正确的是( )A .斜棱柱的侧棱有时垂直于底面B .正棱柱的高可以与侧棱不相等C .六个面都是矩形的六面体是长方体D .底面是正多边形的棱柱为正棱柱解析:选C.四个侧面都是矩形的棱柱是直平行六面体.两个底面是矩形的直平行六面体是长方体.故正确答案为C.2.将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体为( )A .棱柱B .棱台C .棱柱与棱锥的组合体D .不能确定 解析:选A.水面始终与固定的一边平行,且满足棱柱的定义.3. 如图所示,正四棱锥S -ABCD 的所有棱长都等于a ,过不相邻的两条棱SA ,SC 作截面SAC ,则截面的面积为( )A.32a 2 B .a 2C.12a 2 D.13a 2 解析:选C.根据正棱锥的性质,底面ABCD 是正方形,∴AC =2a .在等腰三角形SAC中,SA =SC =a ,又AC =2a ,∴∠ASC =90°,即S △SAC =12a 2.故正确答案为C.4.若要使一个多面体是棱台,则应具备的条件是( ) A .两底面是相似多边形 B .侧面是梯形 C .两底面平行D .两底面平行,侧棱延长后交于一点解析:选D.根据棱台的定义可知,棱台必备的两个条件:底面平行,侧棱延长后相交于一点.5.若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( ) A .正三棱锥 B .正四棱锥 C .正五棱锥 D .正六棱锥解析:选D.正三棱锥的底面边长和侧棱相等时叫做正四面体,因此该棱锥可以是正三棱锥,所以不选A ,另外,正四棱锥,正五棱锥也是可能的,故B 、C 也不选,根据正六边形的特点,正六边形的中心到各个顶点的距离相等,在空间中,除中心外,不可能再找到和各顶点的连线都等于底面边长的点,因此该棱锥不可能是正六棱锥.故选D. 6.已知正四棱锥的侧棱长是底面边长的k 倍,则k 的取值范围是( )A .(0,+∞)B .(12,+∞)C .(2,+∞)D .(22,+∞)解析:选D.由正四棱锥的定义知如图,正四棱锥S -ABCD 中,S 在底面ABCD 内的射影O 为正方形的中心,而SA >OA =22AB ,∴SA AB >22,即k >22. 7.长方体表面积为11,十二条棱长度的和为24,则长方体的一条对角线长为________. 解析:设长方体的长、宽、高分别为a 、b 、c ,则4(a +b +c )=24,∴a +b +c =6.又(ab +bc +ac )×2=11.∴长方体的一条对角线长l =a 2+b 2+c 2=(a +b +c )2-2(ab +bc +ac )=62-11=5. 答案:58.在正方体上任意选择4个顶点,它们可能是如下各种几何体(图形)的4个顶点,这些几何体(图形)是________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.解析:本题借助正方体的结构特征解答,4个顶点连成矩形的情形很容易作出;图(1)中四面体A 1D 1B 1A 是③中描述的情形;图(2)中四面体DA 1C 1B 是④中描述的情形;图(3)中四面体A 1D 1B 1D 是⑤中描述的情形.因此正确答案为①③④⑤.答案:①③④⑤9.正四棱台的上、下底面边长分别是5和7,体对角线长为9,则棱台的斜高等于________.解析:如图,四边形BDD 1B 1是等腰梯形,B 1D 1=52,BD =72,BD 1=9,所以OO 1 =BD 21-(BD +B 1D 12)2=3. 又E 1,E 分别为B 1C 1,BC 的中点,所以O 1E 1=52,OE =72.所以在直角梯形OEE 1O 1中,斜高E 1E =OO 21+(OE -O 1E 1)2=10.答案:1010.已知正四棱锥V -ABCD 中,底面面积为16,一条侧棱的长为211,求该棱锥的高.解:取正方形ABCD 的中心O ,连接VO 、AO ,则VO 就是正四棱锥V -ABCD 的高. 因为底面面积为16,所以AO =2 2. 因为一条侧棱长为211, 所以VO =VA 2-AO 2=44-8=6.所以正四棱锥V -ABCD 的高为6.11. 如图所示,长方体ABCD -A 1B 1C 1D 1.(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?(2)用平面BCFE 把这个长方体分成两部分后,各部分形成的几何体还是棱柱吗?如果是,是几棱柱?如果不是,请说明理由.解:(1)是棱柱,并且是四棱柱.因为它可以看成由四边形ADD 1A 1沿AB 方向平移至BCC 1B 1形成的几何体,符合棱柱的定义.(2)截面BCFE 右边的部分是三棱柱BEB 1-CFC 1,其中△BEB 1和△CFC 1是底面.截面BCFE 左边的部分是四棱柱ABEA 1-DCFD 1,其中四边形ABEA 1和四边形DCFD 1是底面.12. 如图所示,正三棱柱ABC -A 1B 1C 1中,AB =3,AA 1=4,M 为AA 1的中点,P 是BC 上一点,且由P 沿棱柱侧面经过棱CC 1到M 的最短路线长为29,设这条最短路线与CC 1的交点为N ,求:(1)该三棱柱的侧面展开图的对角线长; (2)PC 和NC 的长. 解:(1)正三棱柱ABC -A 1B 1C 1的侧面展开图是一个长为9,宽为4的矩形,如图所示,其对角线长为92+42=97.(2)由P 沿棱柱侧面经过棱CC 1到M 的最短路线,即侧面展开图中的线段MP ,设PC 的长为x ,则在Rt △AMP 中,AM =2,MP =29,∴AP 2=PM 2-AM 2=25,即(x +3)2=25, ∴x =2,即PC =2. ∵NC MA =PC P A =25, 又MA =2,∴NC =45,故PC 和NC 的长分别为2,45.人教B 版必修2同步练习1.下列说法正确的是( )A .圆台是直角梯形绕其一边旋转而成的B .圆锥是直角三角形绕其一边旋转而成的C .圆柱不是旋转体D .圆台可以看成是用平行于底面的平面截一个圆锥而得到的解析:选D.A 错误,这里需指明绕直角梯形与底边垂直的一腰旋转.B 错误,圆锥是直角三角形绕一条直角边旋转而成.C 错误,圆柱是旋转体.2.一条直线绕着与它相交但不垂直的直线旋转一周所得的几何图形是( ) A .旋转体 B .两个圆锥 C .圆柱 D .旋转面 答案:D3.一个等腰梯形绕着它的对称轴旋转半周所得的几何体是( ) A .圆柱 B .圆锥 C .圆台 D .以上都不对 答案:C4.一个圆柱的母线长为15 cm ,底面半径为12 cm ,则圆柱的轴截面面积是________.答案:360 cm 25.有下列说法:①球的半径是连接球心和球面上任意一点的线段; ②球的直径是连接球面上两点的线段; ③不过球心的截面截得的圆叫做小圆. 其中正确说法的序号是________.解析:利用球的结构特征判断:①正确;②不正确,因为直径必过球心;③正确. 答案:①③1.正方形ABCD 绕对角线AC 所在直线旋转一周所得组合体的结构特征是( ) A .两个圆台组合成的 B .两个圆锥组合成的C .一个圆锥和一个圆台组合成的D .一个圆柱和一个圆锥组合成的解析:选B.如图△ABO 与△CBO 绕AC 旋转,分别得到一个圆锥.2.边长为5 cm 的正方形EFGH 是圆柱的轴截面,则从E 点沿圆柱的侧面到相对顶点G 的最短距离是( )A .10 cmB .5 2 cmC .5π2+1 cm D.52π2+4 cm解析:选D.圆柱的侧面展开图如图所示,展开后E ′F =12·2π·(52)=52π,∴E ′G = 52+(52π)2=52π2+4(cm).3.若圆柱的轴截面是一个正方形,其面积为4S ,则它的一个底面面积是( ) A .4S B .4πS C .πS D .2πS 解析:选C.由题意知圆柱的母线长为底面圆的直径2R ,则2R ·2R =4S ,得R 2=S .所以底面面积为πR 2=πS .4.用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1∶3,这截面把圆锥母线分为两段的比是( )A .1∶3B .1∶9C .1∶(3-1) D.3∶2解析:选C.由圆锥的截面性质可知,截面仍是圆,设r 1、r 2分别表示截面与底面圆的半径.而l 1与l 2表示母线被截得的线段.则r 1r 2=l 1l 1+l 2=13=13,∴l 1∶l 2=1∶(3-1). 5.设M 、N 是球O 半径OP 上的两点,且NP =MN =OM ,分别过N 、M 、O 作垂直于OP 的平面,截球面得三个圆,则这三个圆的面积之比为( )A .3∶5∶6B .3∶6∶8C .5∶7∶9D .5∶8∶9解析:选D.作出球的轴截面图如图, 设球的半径为3R , 则MM ′=9R 2-R 2=8R ,NN ′=9R 2-4R 2=5R .所截三个圆的面积之比为:π·(5R )2∶π·(8R )2∶π·(3R )2=5∶8∶9.故选D.6.已知一个正方体内接于一个球,过球心作一截面,则截面不可能是( )解析:选D.过球心的任何截面都不可能是圆的内接正方形. 7.一圆锥的轴截面的顶角为120°,母线长为1,过顶点作圆锥的截面中,最大截面的面积为________.解析:当截面顶点为90°时,截面面积最大,为12×1×1=12.答案:128. 如图所示,在透明塑料制成的长方体容器ABCD -A 1B 1C 1D 1中灌进一些水,将固定容器底面的一边BC 置于地面上,再将容器倾斜,随着倾斜程度的不同,以下命题:①水的形状成棱柱形;②水面EFGH 的面积不变;③A 1D 1始终与水面EFGH 平行.其中正确的 序号是________.解析:在倾斜的过程中,因为前后两面平行,侧面(上下、左右)为平行四边形,所以是棱柱.故填①③.答案:①③9.已知一个圆柱的轴截面是一个正方形且其面积是Q ,则此圆的半径为________.解析:设圆柱底面半径为r ,母线为l ,则由题意得⎩⎪⎨⎪⎧2r =l ,2r ·l =Q ,解得r =Q 2.答案:Q210.圆台的两底面面积分别为1,49,平行于底面的截面面积的2倍等于两底面面积之和,求圆台的高被截面分成的两部分的比.解:将圆台还原成圆锥,如图所示.O 2、O 1、O 分别是圆台上底面、截面和下底面的圆心,V 是圆锥的顶点,令VO 2=h, O 2O 1=h 1,O 1O =h 2则⎩⎪⎨⎪⎧h +h 1h=49+121,h +h 1+h 2h =491,所以⎩⎪⎨⎪⎧h 1=4h ,h 2=2h ,即h 1∶h 2=2∶1.11. 如图是一个底面直径为20 cm 的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6 cm ,高为20 cm 的圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降多少?解:因为圆锥形铅锤的体积为13×π×(62)2×20=60π(cm 3).设水面下降的高度为x cm , 则小圆柱的体积为 π(202)2x =100πx (cm 3). 所以有60π=100πx , 解此方程得x =0.6. 故杯里的水下降了0.6 cm.12.用一张4 cm ×8 cm 的矩形硬纸卷成圆柱的侧面,求圆柱轴截面的面积(接头忽略不计).解:分两种情况:(1)以矩形8 cm 的边为母线长,把矩形硬纸卷成圆柱侧面(如图(1))轴截面为矩形A 1ABB 1,根据题意可知底面圆的周长为:2π·OA =4,则OA =2π,于是AB =4π.根据矩形的面积公式得:S 截面=A 1A ·AB =8·4π=32π(cm 2).(2)以矩形4 cm 的边长为母线长,把矩形硬纸卷成圆柱侧面(如图(2)),轴截面为矩形A 1ABB 1,根据题意可知底面圆的周长为:2π·OA =8,则OA =4π,于是AB =8π.根据矩形的面积公式得:S 截面=A 1A ·AB =4·8π=32π(cm 2).综上所述,轴截面的面积为32πcm 2.人教B 版必修2同步练习1.直线的平行投影可能是( ) A .点 B .线段 C .射线 D .曲线 答案:A2.在灯光下,圆形窗框在与窗框平行的墙面上的影子的形状是( ) A .平行四边形 B .椭圆形 C .圆形 D .菱形解析:选C.由点光源的中心投影的性质可知影子应为圆形.3.如图所示的是水平放置的三角形的直观图,D ′是△A ′B ′C ′中B ′C ′边上的一点,且D ′离C ′比D ′离B ′近,又A ′D ′∥y ′轴,那么原△ABC 的AB 、AD 、AC 三条线段中( )A .最长的是AB ,最短的是AC B .最长的是AC ,最短的是AB C .最长的是AB ,最短的是AD D .最长的是AD ,最短的是AC 答案:C4.已知有一个长为5 cm ,宽为4 cm 的矩形,则其斜二测直观图的面积为________. 解析:由于该矩形的面积为S =5×4=20(cm 2). 所以其斜二测直观图的面积为S ′=24S =52(cm 2). 答案:5 2 cm 25.长度相等的两条平行线段的直观图的长度________. 答案:相等1.放晚自习后,小华走路回家,在经过一盏路灯时,他发现自己的身影( ) A .变长 B .变短 C .先变长后变短 D .先变短后变长 答案:D2.下列关于直观图画法的说法中,不正确的是( )A .原图中平行于x 轴的线段,其对应线段仍平行于x ′轴,长度不变B .原图中平行于y 轴的线段,其对应线段仍平行于y ′轴,长度不变C .画与坐标系xOy 对应的坐标系x ′O ′y ′时,∠x ′O ′y ′可以等于135°D .画直观图时,由于选轴不同,所画的直观图可能不同解析:选B.平行于y 轴的线段其长度变为原来的12.3. 如图所示,梯形A ′B ′C ′D ′是平面图形ABCD 的直观图,若A ′D ′∥O ′y ′,A ′B ′∥C ′D ′,A ′B ′=23C ′D ′=2,A ′D ′=1,则四边形ABCD 的面积是( )A .10B .5 2C .5D .10 2解析:选C.还原后的四边形ABCD 为直角梯形,AD 为垂直底边的腰,AD =2,AB =2,CD =3,S 四边形ABCD =5,故正确答案为C.4.如图,在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是BB 1,BC 的中点,则图中阴影部分在平面ADD 1A 1上的射影为( )答案:A5.如果图形所在的平面不平行于投射线,那么下列说法正确的是( ) A .矩形的平行投影一定是矩形 B .梯形的平行投影一定是梯形 C .正方形的平行投影一定是矩形 D .正方形的平行投影一定是菱形解析:选B.因为梯形两底的平行投影仍然平行,故选B.6.如下图所示为一平面图形的直观图,则此平面图形可能是下图中的( )解析:选C.根据斜二测画法的规则:平行于x 轴或在x 轴上的线段的长度在新坐标系中不变,在y 轴上或平行于y 轴的线段的长度在新坐标中变为原来的12,并注意到∠xOy =90°,∠x ′O ′y ′=45°,因此由直观图还原成原图形为选项C.7. 如图所示,已知用斜二测画法画出的△ABC 的直观图△A ′B ′C ′是边长为a 的正三角形,那么原△ABC 的面积为________.解析:过C ′作y ′轴的平行线C ′D ′与x ′轴交于D ′,则C ′D ′=32a sin45°=62a .又∵C ′D ′是原△ABC 的高CD 的直观图, ∴CD =6a .∴S △ABC =12AB ·CD =12a ·6a =62a 2.答案:62a 28.给出下列说法:①正方形的直观图是一个平行四边形,其相邻两边长的比为1∶2,有一内角为45°;②水平放置的正三角形的直观图是一个底边长不变,高为原三角形高的一半的三角形;③不等边三角形水平放置的直观图是不等边三角形;④水平放置的平面图形的直观图是平面图形.写出其中正确说法的序号________.解析:对于①,若以该正方形的一组邻边所在的直线为x 轴、y 轴,则结论正确;但若以该正方形的两条对角线所在的直线为x 轴、y 轴,由于此时该正方形的各边均不在坐标轴上或与坐标轴平行,则其直观图中相邻两边长不一定符合“横不变,纵减半”的规则;对于②,水平放置的正三角形的直观图是一个底边长不变,高比原三角形高的一半还要短的三角形;对于③,只要坐标系选取的恰当,不等边三角形的水平放置的直观图可以是等边三角形.答案:④9. 水平放置的△ABC 的斜二测直观图如图所示,已知A ′C ′=3,B ′C ′=2,则AB 边上的中线的实际长度为________.解析:在直观图中,∠A ′C ′B ′=45°,则在原图形中∠ACB =90°,AC =3,BC =4,则斜边AB =5,故斜边的中线长为52.答案:5210.在有太阳的某时刻,一个大球放在水平地面上,球的影子伸到距离球与地面接触点10 m 处,同一时刻一根长 3 m 的木棒垂直于地面,且影子长1 m ,求此球的半径.解:由题设知BO ′=10,设∠ABO ′=2α(0°<α<45°)(如图),由题意知tan 2α=31=3,即2α=60°,∴α=30°,∴tan α=33. 在Rt △OO ′B 中,tan α=RBO ′,∴R =BO ′·tan α=1033 m.即此球的半径为1033m.11. 如图所示,一建筑物A 高为BC ,眼睛位于点O 处,用一把长为22 cm 的刻度尺EF 在眼前适当地运动,使眼睛刚好看不到建筑物A ,这时量得眼睛和刻度尺的距离MN 为10 cm ,眼睛与建筑物的距离MB 为20 m ,求建筑物A 的高.(假设刻度尺与建筑物平行)解:由题意可知O ,F ,C 三点共线,O ,E ,B 三点共线.因为EF ∥BC ,所以EF BC =OE OB =MNMB.把EF =22 cm ,MN =10 cm ,MB =2000 cm 代入上式,得22BC =102000,解得BC =4400 cm =44 m.即建筑物A 高44 m.12. 某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成60°角,房屋向南的窗户AB 高1.6米,现要在窗子外面的上方安装一个水平遮阳蓬AC ,如图所示,求:(1)当遮阳蓬AC 的宽度在什么范围内时,太阳光线直接射入室内?(2)当遮阳蓬AC 的宽度在什么范围内时,太阳光线不能直接射入室内(精确到0.01米)? 解:(1)在Rt △ABC 中,∠ACB =60°,AB =1.6米, 则AC =AB tan ∠ACB=3AB 3,∴AC =1.63≈0.92(米).当0<AC ≤0.92米时,太阳光可直接射入室内. (2)当AC >0.92米时,太阳光不能直接射入室内.人教B版必修2同步练习1.下列说法中正确的是()A.任何物体的三视图都与物体的摆放位置有关B.任何物体的三视图都与物体的摆放位置无关C.有的物体的三视图与物体的摆放位置无关D.正方体的三视图一定是三个全等的正方形解析:选C.球的三视图与它的摆放位置无关,从任何方向看都是圆.2.如图所示,桌面上放着一个圆锥和一个长方体,其俯视图是()答案:D3.(2011年高考山东卷)下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.其中真命题的个数是()A.3B.2C.1 D.0解析:选A.对于①,可以是放倒的三棱柱;容易判断②③可以.4.一件物体的三视图的排列规则是:俯视图放在主视图的________,长度与主视图一样,左视图放在主视图的______,高度与主视图一样,宽度与俯视图的宽度一样.答案:下面右面5.某个几何体的三视图如图,这个几何体是________.答案:圆锥1. 如图所示的是水平放置的圆柱形物体,其三视图是()解析:选A.此题主要研究从物体到三视图的转化过程,主视图是从正面观察物体的形状;左视图是从左侧面观察物体的形状;俯视图是从上往下观察物体的形状.从正面看是个矩形,从左面看是个圆,从上往下看是一个矩形,对照图中的A,B,C,D,可知A是正确的.2.图中三图顺次为一个建筑物的主视图、左视图、俯视图,则其为________的组合体.()A.圆柱和圆锥B.正方体和圆锥C.正四棱柱和圆锥D.正方形和圆解析:选C.直接画出符合条件的组合体,可以得解.3.如图所示,有且仅有两个视图相同的几何体是()A.(1)(2) B.(1)(3)C.(1)(4) D.(2)(4)解析:选D.在这四个几何体中,图(2)与图(4)均只有主视图和左视图相同.4.如图(1)所示是物体的实物图,在图(2)四个选项中是其俯视图的是()答案:C5.一个几何体由一些小正方体摆成,其主视图与左视图如图所示,其俯视图不可能是()解析:选C.通过分析主视图第一列有两个,而左视图第二列有两个,所以俯视图是选项C时,不符合要求.6. 把10个相同的小正方体按如图所示位置堆放,它的表面有若干个小正方形,如果将图中标了字母A的一个小正方体搬走,这时表面的小正方形个数与搬动前相比()A.不增不减B.减少1个C.减少2个D.减少3个答案:A7.欣赏下列物体的三视图,并写出它们的名称.答案:(1)主视图(2)左视图(3)俯视图(4)主视图(5)左视图(6)俯视图8.下图是某个圆锥的三视图,根据主视图中所标尺寸,则俯视图中圆的面积为________,圆锥母线长为________.解析:由主视图的底边可知俯视图的半径为10,则面积为100π.由主视图知圆锥的高为30,又底面半径为10,则母线长为102+302=1010.答案:100π10109.一个几何体由几个相同的小正方体组合而成,它的主视图、左视图、俯视图如图所示,则这个组合体包含的小正方体的个数是________.解析:由三视图画出几何体如图.观察知,包含小正方体个数为5个.答案:510.如图所示是一些立体图形的视图,但是观察的方向不同,试说明下列各图可能是哪一种立体图形的视图.图(1)可能为球、圆柱,如图(4)所示.图(2)可能为棱锥、圆锥、棱柱,如图(5)所示.图(3)可能为正四棱锥,如图(6)所示.11. 如图是根据某一种型号的滚筒洗衣机抽象出来的几何体,数据如图所示(单位:cm),试画出它的三视图.解:这个几何体是由一个长方体和一个圆柱体构成的.三视图如下图所示.12.如图,BC⊥CD,且CD⊥MN,ABCD绕AD所在直线MN旋转,在旋转前,点A 可以在DM上选定.当点选在射线上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较异同.解:(1)当点A在下图(a)中射线DM的位置时,绕MN旋转一周所得几何体为底面半径为CD的圆柱和圆锥叠加而成,其三视图如下图(a).(2)当点A在下图(b)中射线DM的位置时,即B到MN作垂线的垂足时旋转后的几何体为圆柱,其三视图如下图(b).(3)当点A在下图(c)中所示位置时,其旋转所得几何体为圆柱中挖去同底的圆锥,其三视图如下图(c).(4)当点A位于点D时,如下图(d)中,旋转体为圆柱中挖去同底等高的圆锥,其三视图如下图(d).人教B 版必修2同步练习1.一正四棱锥各棱长均为a ,则其表面积为( ) A.3a 2 B .(1+3)a 2 C .22a 2 D .(1+2)a 2解析:选B.正四棱锥的底面积为S 底=a 2,侧面积为S 侧=4×12×a ×32a =3a 2,故表面积为S 表=S 底+S 侧=(1+3)a 2.2.底面为正方形的直棱柱,它的底面对角线长为2,体对角线长为6,则这个棱柱的侧面积是( )A .2B .4C .6D .8 答案:D3.若球的大圆周长为C ,则这个球的表面积是( ) A.C 24π B.C 22π C.C 2πD .2πC 2 答案:C4.一个圆锥的底面半径为2,高为23,则圆锥的侧面积为________.解析:S 侧=πRl =π×2×22+(23)2=8π. 答案:8π5.已知棱长为1,各面都是正三角形的四面体,则它的表面积是________. 答案: 31.正三棱锥的底面边长为a ,高为66a ,则此棱锥的侧面积等于( ) A.34a 2 B.32a 2 C.334a 2 D.332a 2解析:选A.斜高h ′ =(66a )2+(3a 6)2=12a , 则S 侧=12·3a ·12a =34a 2.2.正六棱柱的高为6,底面边长为4,则它的全面积是( ) A .48(3+3) B .48(3+23) C .24(6+2) D .144解析:选A.S 两底=34×42×6×2=483,S 侧=6×4×6=144.∴S 全=144+483=48(3+3).3.正四棱台两底面边长分别为3 cm 和5 cm ,那么它的中截面面积为( ) A .2 cm 2 B .16 cm 2 C .25 cm 2 D .4 cm 2。
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
高中数学必修2全册教案学案同步练习课堂巩固
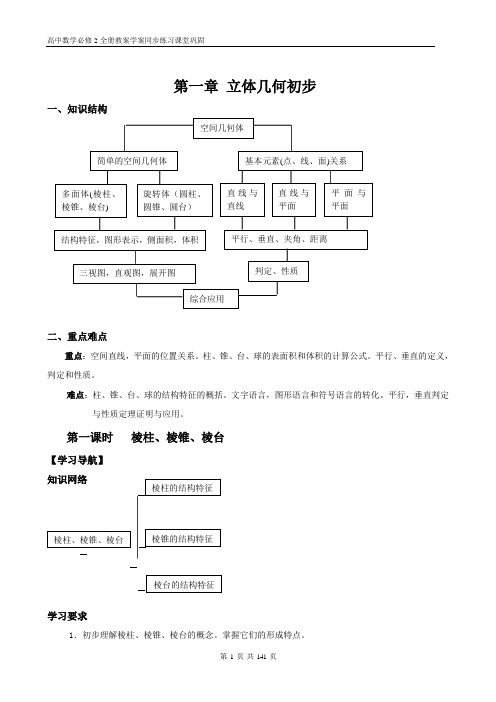
第一章 立体几何初步一、知识结构二、重点难点重点:空间直线,平面的位置关系。
柱、锥、台、球的表面积和体积的计算公式。
平行、垂直的定义,判定和性质。
难点:柱、锥、台、球的结构特征的概括。
文字语言,图形语言和符号语言的转化。
平行,垂直判定与性质定理证明与应用。
第一课时 棱柱、棱锥、棱台【学习导航】知识网络学习要求 1.初步理解棱柱、棱锥、棱台的概念。
掌握它们的形成特点。
2.了解棱柱、棱锥、棱台中一些常用名称的含义。
3.了解棱柱、棱锥、棱台这几种几何体简单作图方法4.了解多面体的概念和分类.【课堂互动】自学评价1.棱柱的定义:表示法:思考:棱柱的特点:.【答】2.棱锥的定义:表示法:思考:棱锥的特点:.【答】3.棱台的定义:表示法:思考:棱台的特点:.【答】4.多面体的定义:5.多面体的分类:⑴棱柱的分类⑵棱锥的分类⑶棱台的分类【精典范例】例1:设有三个命题:甲:有两个面平行,其余各面都是平行四边形所围体一定是棱柱;乙:有一个面是四边形,其余各面都三角形所围成的几何体是棱锥;丙:用一个平行与棱锥底面的平面去截棱锥,得到的几何体叫棱台。
以上各命题中,真命题的个数是(A)A.0 B. 1 C. 2 D. 3例2:画一个四棱柱和一个三棱台。
【解】四棱柱的作法:⑴画上四棱柱的底面----画一个四边形;⑵画侧棱-----从四边形的每一个顶点画平行且相等的线段;⑶画下底面------顺次连结这些线段的另一个端点互助参考7页例1⑷画一个三棱锥,在它的一条侧棱上取一点,从这点开始,顺次在各个侧面画出与底面平行的线段,将多余的线段檫去.互助参考7页例1点评:(1)被遮挡的线要画成虚线(2)画台由锥截得思维点拔:解柱、锥、台概念性问题和画图需要:(2).灵活理解柱、锥、台的特点:例如:棱锥的特点是:⑴两个底面是全等的多边形;⑵多边形的对应边互相平行;⑶棱柱的侧面都是平行四边形。
反过来,若一个几何体,具有上面三条,能构成棱柱吗?或者说,上面三条能作为棱柱的定义吗? 答:不能.点评:就棱柱来验证这三条性质,无一例外,能不能找到反例,是上面三条能作为棱柱的定义的关键。
高中数学必修2第1章-1.3.2球的体积和表面积同步练习题及答案

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】1.3.2球的体积和表面积【课时目标】1.了解球的体积和表面积公式.2.会用球的体积和表面积公式解决实际问题.3.培养学生的空间想象能力和思维能力.1.球的表面积设球的半径为R,则球的表面积S=________,即球的表面积等于它的大圆面积的________倍.2.球的体积设球的半径为R,则球的体积V=________.一、选择题1.一个正方体与一个球表面积相等,那么它们的体积比是()A.6π6B.π2C.2π2D.3ππ2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的() A.2倍B.22倍C.2倍D.32倍3.正方体的内切球和外接球的体积之比为()A.1∶ 3 B.1∶3C.1∶3 3 D.1∶94.若三个球的表面积之比为1∶2∶3,则它们的体积之比为()A.1∶2∶3 B.1∶2∶ 3C.1∶22∶3 3 D.1∶4∶75.长方体的一个顶点上的三条棱长分别为3,4,5,且它的8个顶点都在同一个球面上,则这个球的表面积为()A.25πB.50πC.125πD.以上都不对6.一个圆锥与一个球的体积相等,圆锥的底面半径是球半径的3倍,圆锥的高与球半径之比为()A.4∶9 B.9∶4C.4∶27 D.27∶4二、填空题7.毛泽东在《送瘟神》中写到:“坐地日行八万里”.又知地球的体积大约是火星的8倍,则火星的大圆周长约________万里.8.将一钢球放入底面半径为3 cm的圆柱形玻璃容器中,水面升高4 cm,则钢球的半径是________.9.(1)表面积相等的正方体和球中,体积较大的几何体是________;(2)体积相等的正方体和球中,表面积较小的几何体是________.三、解答题10.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?11.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.能力提升12.已知棱长都相等的正三棱锥内接于一个球,某学生画出了四个过球心的平面截球与三棱锥所得的图形,如图所示,则()A.以上四个图形都是正确的B.只有(2)(4)是正确的C.只有(4)是错误的D.只有(1)(2)是正确的13.有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.1.利用球的半径、球心到截面圆的距离、截面圆的半径可构成直角三角形,进行相关计算.2.解决球与其他几何体的切接问题,通常作截面,将球与几何体的各量体现在平面图形中,再进行相关计算.3.解答组合体问题要注意知识的横向联系,善于把立体几何问题转化为平面几何问题,运用方程思想与函数思想解决,融计算、推理、想象于一体.1.3.2 球的体积和表面积 答案知识梳理1.4πR 2 4 2.43πR 3作业设计1.A [先由面积相等得到棱长a 和半径r 的关系a =6π3r ,再由体积公式求得体积比为6π6.] 2.B [由面积扩大的倍数可知半径扩大为原来的2倍,则体积扩大到原来的22倍.] 3.C [关键要清楚正方体内切球的直径等于棱长a ,外接球的直径等于3a .] 4.C [由表面积之比得到半径之比为r 1∶r 2∶r 3=1∶2∶3,从而得体积之比为V 1∶V 2∶V 3=1∶22∶33.]5.B [外接球的直径2R =长方体的体对角线=a 2+b 2+c 2(a 、b 、c 分别是长、宽、高).]6.A [设球半径为r ,圆锥的高为h ,则13π(3r)2h =43πr 3,可得h ∶r =4∶9.]7.4解析 地球和火星的体积比可知地球半径为火星半径的2倍,日行8万里指地球大圆的周长,即2πR 地球=8,故R 地球=4π(万里),所以火星的半径为2π万里,其大圆的周长为4万里.8.3 cm解析 设球的半径为r ,则36π=43πr 3,可得r =3 cm .9.(1)球 (2)球解析 设正方体的棱长为a ,球的半径为r . (1)当6a 2=4πr 2时,V 球=43πr 3=6πa 3>a 3=V 正方体;(2)当a 3=43πr 3时,S 球=4πr 2=63π6a 2<6a 2=S 正方体.10.解 要使冰淇淋融化后不会溢出杯子,则必须V 圆锥≥V 半球,V 半球=12×43πr 3=12×43π×43,V 圆锥=13Sh =13πr 2h =13π×42×h .依题意:13π×42×h ≥12×43π×43,解得h ≥8.即当圆锥形杯子杯口直径为8 cm ,高大于或等于8 cm 时,冰淇淋融化后不会溢出杯子. 又因为S 圆锥侧=πrl =πr h 2+r 2,当圆锥高取最小值8时,S 圆锥侧最小,所以高为8 cm 时,制造的杯子最省材料.11.解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.根据切线性质知,当球在容器内时,水深为3r ,水面的半径为3r ,则容器内水的体积为V =V 圆锥-V 球=13π·(3r)2·3r -43πr 3=53πr 3,而将球取出后,设容器内水的深度为h ,则水面圆的半径为33h ,从而容器内水的体积是V ′=13π·(33h)2·h =19πh 3,由V =V ′,得h=315r .即容器中水的深度为315r .12.C [正四面体的任何一个面都不能外接于球的大圆(过球心的截面圆).] 13.解 设正方体的棱长为a .如图所示.①正方体的内切球球心是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,所以有2r 1=a ,r 1=a 2,所以S 1=4πr 21=πa 2.②球与正方体的各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,2r 2=2a ,r 2=22a ,所以S 2=4πr 22=2πa 2. ③正方体的各个顶点在球面上,过球心作正方体的对角面得截面,所以有2r 3=3a , r 3=32a ,所以S 3=4πr 23=3πa 2. 综上可得S 1∶S 2∶S 3=1∶2∶3.。
高中数学必修2教学同步讲练第一章《圆柱、圆锥、圆台、球、简单组合体的结构特征》练习题(含答案)

第一章空间几何体1.1 空间几何体的结构1.1.2 圆柱、圆锥、圆台、球、简单组合体的结构特征A级基础巩固一、选择题1.下列几何体中是旋转体的是()①圆柱②六棱锥③正方体④球体⑤四面体A.①和⑤B.①C.③和④D.①和④解析:圆柱、球体是旋转体,其余均为多面体.答案:D2.如图所示的简单组合体的结构特征是()A.由两个四棱锥组合成的B.由一个三棱锥和一个四棱锥组合成的C.由一个四棱锥和一个四棱柱组合成的D.由一个四棱锥和一个四棱台组合成的解析:这个8面体是由两个四棱锥组合而成.答案:A3.下图是由哪个平面图形旋转得到的()解析:图中几何体由圆锥、圆台组合而成,可由A中图形绕图中虚线旋转360°得到.答案:A4.如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面平行于底面,那么截面图形为()解析:截面图形应为图C所示的圆环面.答案:C5.用一张长为8、宽为4的矩形硬纸卷成圆柱的侧面,则相应圆柱的底面半径是()A.2 B.2πC.2π或4πD.π2或π4解析:如图所示,设底面半径为r,若矩形的长8恰好为卷成圆柱底面的周长,则2πr=8,所以r=4;π同理,若矩形的宽4恰好为卷成圆柱的底面周长,则2πr=4,所以r=2.所以选C.π答案:C二、填空题6.等腰三角形绕底边上的高所在的直线旋转180°,所得几何体是________.解析:结合旋转体及圆锥的特征知,所得几何体为圆锥.答案:圆锥7.给出下列说法:①圆柱的母线与它的轴可以不平行;②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线,都可以构成直角三角形;③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是____________(填序号).解析:由旋转体的形成与几何特征可知①③错误,②④正确.答案:②④8.如图是一个几何体的表面展成的平面图形,则这个几何体是__________.答案:圆柱三、解答题9.如图所示的物体是运动器材——空竹,你能描述它的几何特征吗?解:此几何体是由两个大圆柱、两个小圆柱和两个小圆台组合而成的.10.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的半径分别2 cm和5 cm,圆台的母线长是12 cm,求圆锥SO的母线长.解:如图,过圆台的轴作截面,截面为等腰梯形ABCD,由已知可得上底半径O1A=2 cm,下底半径OB=5 cm,且腰长AB=12 cm.设截得此圆台的圆锥的母线长为l,则由△SAO1∽△SBO,可得l -12l =25,所以l =20 cm. 故截得此圆台的圆锥的母线长为20 cm.B 级 能力提升1.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为( )A .一个球体B .一个球体中间挖出一个圆柱C .一个圆柱D .一个球体中间挖去一个长方体解析:外面的圆旋转形成一个球,里面的长方形旋转形成一个圆柱.所有形成的几何为一个球体挖出一个圆柱.答案:B2.一个半径为5 cm 的球,被一平面所截,球心到截面圆心的距离为4 cm ,则截面圆面积为__________cm 2.解析:如图所示,过球心O 作轴截面,设截面圆的圆心为O 1,其半径为r .由球的性质,OO1⊥CD.在Rt△OO1C中,R=OC=5,OO1=4,则O1C=3,所以截面圆的面积S=π·r2=π·O1C2=9π.答案:9π3.如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?解:把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,即为蚂蚁爬行的最短距离.因为AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π.所以AB′=A′B′2+AA′2=4+(2π)2=21+π2,所以蚂蚁爬行的最短距离为21+π2.。
人教a版高中数学选修2-3全册同步练习及单元检测含答案

人教版高中数学选修2~3 全册章节同步检测试题目录第1章《计数原理》同步练习 1.1测试1第1章《计数原理》同步练习 1.1测试2第1章《计数原理》同步练习 1.1测试3第1章《计数原理》同步练习 1.2排列与组合第1章《计数原理》同步练习 1.3二项式定理第1章《计数原理》测试(1)第1章《计数原理》测试(2)第2章同步练习 2.1离散型随机变量及其分布列第2章同步练习 2.2二项分布及其应用第2章测试(1)第2章测试(2)第2章测试(3)第3章练习 3.1回归分析的基本思想及其初步应用第3章练习 3.2独立性检验的基本思想及其初步应用第3章《统计案例》测试(1)第3章《统计案例》测试(2)第3章《统计案例》测试(3)1. 1分类加法计数原理与分步乘法计数原理测试题一、选择题1.一件工作可以用2种方法完成,有3人会用第1种方法完成,另外5人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是( )A.8 B.15 C.16 D.30答案:A2.从甲地去乙地有3班火车,从乙地去丙地有2班轮船,则从甲地去丙地可选择的旅行方式有( )A.5种 B.6种 C.7种 D.8种答案:B3.如图所示为一电路图,从A 到B 共有( )条不同的线路可通电( )A.1 B.2 C.3 D.4答案:D4.由数字0,1,2,3,4可组成无重复数字的两位数的个数是( )A.25 B.20 C.16 D.12答案:C5.李芳有4件不同颜色的衬衣,3件不同花样的裙子,另有两套不同样式的连衣裙.“五一”节需选择一套服装参加歌舞演出,则李芳有( )种不同的选择方式( ) A.24 B.14 C.10 D.9答案:B6.设A ,B 是两个非空集合,定义{}()A B a b a A b B *=∈∈,,|,若{}{}0121234P Q ==,,,,,,,则P *Q 中元素的个数是( )A.4 B.7 C.12 D.16答案:C二、填空题7.商店里有15种上衣,18种裤子,某人要买一件上衣或一条裤子,共有 种不同的选法;要买上衣,裤子各一件,共有 种不同的选法.答案:33,2708.十字路口来往的车辆,如果不允许回头,共有 种行车路线.答案:129.已知{}{}0341278a b ∈∈,,,,,,,则方程22()()25x a y b -+-=表示不同的圆的个数是 .答案:1210.多项式123124534()()()()a a a b b a a b b ++++++··展开后共有 项.答案:1011.如图,从A →C ,有 种不同走法.答案:612.将三封信投入4个邮箱,不同的投法有 种.答案:34三、解答题13.一个口袋内装有5个小球,另一个口袋内装有4个小球,所有这些小球的颜色互不相同.(1)从两个口袋内任取一个小球,有多少种不同的取法?(2)从两个口袋内各取一个小球,有多少种不同的取法?解:(1)549N =+=种;(2)5420N =⨯=种.14.某校学生会由高一年级5人,高二年级6人,高三年级4人组成.(1)选其中1人为学生会主席,有多少种不同的选法?(2)若每年级选1人为校学生会常委,有多少种不同的选法?(3)若要选出不同年级的两人参加市里组织的活动,有多少种不同的选法?解:(1)56415N =++=种;(2)564120N =⨯⨯=种;(3)56644574N =⨯+⨯+⨯=种15.已知集合{}321012()M P a b =---,,,,,,,是平面上的点,a b M ∈,. (1)()P a b ,可表示平面上多少个不同的点?(2)(),可表示多少个坐标轴上的点?P a b解:(1)完成这件事分为两个步骤:a的取法有6种,b的取法也有6种,∴P点个数为N=6×6=36(个);(2)根据分类加法计数原理,分为三类:①x轴上(不含原点)有5个点;②y轴上(不含原点)有5个点;③既在x轴,又在y轴上的点,即原点也适合,∴共有N=5+5+1=11(个).1. 1分类加法计数原理与分步乘法计数原理测试题一、选择题1.从集合{ 0,1,2,3,4,5,6}中任取两个互不相等的数a ,b 组成复数a bi +,其中虚数有( )A .30个B .42个C .36个D .35个答案:C2.把10个苹果分成三堆,要求每堆至少1个,至多5个,则不同的分法共有( )A .4种B .5种C .6种D .7种答案:A3.如图,用4种不同的颜色涂入图中的矩形A ,B ,C ,D 中,要求相邻的矩形涂色不同,则不同的涂法有( )A .72种B .48种C .24种D .12种答案:A4.教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有( )A .10种B .52种 C.25种 D.42种答案:D5.已知集合{}{}023A B x x ab a b A ===∈,,,,,|,则B 的子集的个数是( ) A.4 B.8 C.16 D.15答案:C6.三边长均为正整数,且最大边长为11的三角形的个数为( )A.25 B.26 C.36 D.37答案:C二、填空题7.平面内有7个点,其中有5个点在一条直线上,此外无三点共线,经过这7个点可连成不同直线的条数是 .答案:128.圆周上有2n 个等分点(1n >),以其中三个点为顶点的直角三角形的个数为 .答案:2(1)n n-9.电子计算机的输入纸带每排有8个穿孔位置,每个穿孔位置可穿孔或不穿孔,则每排可产生种不同的信息.答案:25610.椭圆221x ym n+=的焦点在y轴上,且{}{}123451234567m n∈∈,,,,,,,,,,,,则这样的椭圆的个数为.答案:2011.已知集合{}123A,,,且A中至少有一个奇数,则满足条件的集合A分别是.答案:{}{}{}{}{}13122313,,,,,,,12.整数630的正约数(包括1和630)共有个.答案:24三、解答题13.用0,1,2,3,4,5六个数字组成无重复数字的四位数,比3410大的四位数有多少个?解:本题可以从高位到低位进行分类.(1)千位数字比3大.(2)千位数字为3:①百位数字比4大;②百位数字为4:1°十位数字比1大;2°十位数字为1→个位数字比0大.所以比3410大的四位数共有2×5×4×3+4×3+2×3+2=140(个).14.有红、黄、蓝三种颜色旗子各(3)n n>面,任取其中三面,升上旗杆组成纵列信号,可以有多少种不同的信号?若所升旗子中不允许有三面相同颜色的旗子,可以有多少种不同的信号?若所升旗子颜色各不相同,有多少种不同的信号?解:1N=3×3×3=27种;227324N=-=种;33216N=⨯⨯=种.15.某出版社的7名工人中,有3人只会排版,2人只会印刷,还有2人既会排版又会印刷,现从7人中安排2人排版,2人印刷,有几种不同的安排方法.解:首先分类的标准要正确,可以选择“只会排版”、“只会印刷”、“既会排版又会印刷”中的一个作为分类的标准.下面选择“既会排版又会印刷”作为分类的标准,按照被选出的人数,可将问题分为三类:第一类:2人全不被选出,即从只会排版的3人中选2人,有3种选法;只会印刷的2人全被选出,有1种选法,由分步计数原理知共有3×1=3种选法.第二类:2人中被选出一人,有2种选法.若此人去排版,则再从会排版的3人中选1人,有3种选法,只会印刷的2人全被选出,有1种选法,由分步计数原理知共有2×3×1=6种选法;若此人去印刷,则再从会印刷的2人中选1人,有2种选法,从会排版的3人中选2人,有3种选法,由分步计数原理知共有2×3×2=12种选法;再由分类计数原理知共有6+12=18种选法.第三类:2人全被选出,同理共有16种选法.所以共有3+18+16=37种选法.1. 1 分类加法计数原理与分步乘法计数原理综合卷一.选择题:1.一个三层书架,分别放置语文书12本,数学书14本,英语书11本,从中取出一本,则不同的取法共有()(A)37种(B)1848种(C)3种(D)6种2.一个三层书架,分别放置语文书12本,数学书14本,英语书11本,从中取出语文、数学、英语各一本,则不同的取法共有()(A)37种(B)1848种(C)3种(D)6种3.某商业大厦有东南西3个大门,楼内东西两侧各有2个楼梯,从楼外到二楼的不同走法种数是()(A) 5 (B)7 (C)10 (D)124.用1、2、3、4四个数字可以排成不含重复数字的四位数有()(A)265个(B)232个(C)128个(D)24个5.用1、2、3、4四个数字可排成必须含有重复数字的四位数有()(A)265个(B)232个(C)128个(D)24个6.3科老师都布置了作业,在同一时刻4名学生都做作业的可能情况有()(A)43种(B)34种(C)4×3×2种(D)1×2×3种7.把4张同样的参观券分给5个代表,每人最多分一张,参观券全部分完,则不同的分法共有()(A)120种(B)1024种(C)625种(D)5种8.已知集合M={l,-2,3},N={-4,5,6,7},从两个集合中各取一个元素作为点的坐标,则这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数是()(A)18 (B)17 (C)16 (D)109.三边长均为整数,且最大边为11的三角形的个数为()(A)25 (B)36 (C)26 (D)3710.如图,某城市中,M、N两地有整齐的道路网,若规定只能向东或向北两个方向沿途中路线前进,则从M到N 不同的走法共有()(A)25 (B)15 (C)13 (D)10二.填空题:11.某书店有不同年级的语文、数学、英语练习册各10本,买其中一种有种方法;买其中两种有种方法.12.大小不等的两个正方形玩具,分别在各面上标有数字1,2,3,4,5,6,则向上的面标着的两个数字之积不少于20的情形有种.13.从1,2,3,4,7,9中任取不相同的两个数,分别作为对数的底数和真数,可得到个不同的对数值.14.在连结正八边形的三个顶点组成的三角形中,与正八边形有公共边的有个.15.某班宣传小组要出一期向英雄学习的专刊,现有红、黄、白、绿、蓝五种颜色的粉笔供选用,要求在黑板中A、B、C、D每一部分只写一种颜色,如图所示,相邻两块颜色不同,则不同颜色的书写方法共有种.三.解答题:D CB A16.现由某校高一年级四个班学生34人,其中一、二、三、四班分别为7人、8人、9人、10人,他们自愿组成数学课外小组.(1)选其中一人为负责人,有多少种不同的选法?(2)每班选一名组长,有多少种不同的选法?(3)推选二人做中心发言,这二人需来自不同的班级,有多少种不同的选法?17.4名同学分别报名参加足球队,蓝球队、乒乓球队,每人限报其中一个运动队,不同的报名方法有几种?[探究与提高]1.甲、乙两个正整数的最大公约数为60,求甲、乙两数的公约数共有多个?2.从{-3,-2,-1,0,l,2,3}中,任取3个不同的数作为抛物线方程y=ax2+bx+c(a≠0)的系数,如果抛物线过原点,且顶点在第一象限,这样的抛物线共有多少条?3.电视台在“欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的群众来信,甲信箱中有30封,乙信箱中有20封.现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?综合卷1.A 2.B 3.D 4.D 5.B 6.B 7.D 8.B 9.B 10.B11.30;300 12.513.17 14.40 15.1801. 2排列与组合1、 排列综合卷1.90×9l ×92×……×100=( )(A )10100A (B )11100A (C )12100A (D )11101A 2.下列各式中与排列数mn A 相等的是( )(A )!(1)!-+n n m (B )n(n -1)(n -2)……(n -m) (C )11m n nA n m --+ (D )111m n n A A --3.若 n ∈N 且 n<20,则(27-n )(28-n)……(34-n)等于( ) (A )827n A - (B )2734n n A -- (C )734n A - (D )834n A -4.若S=123100123100A A A A ++++,则S 的个位数字是( )(A )0 (B )3 (C )5 (D )85.用1,2,3,4,5这五个数字组成没有重复数字的三位数,其中偶数共有( ) (A )24个 (B )30个 (C )40个 (D )60个6.从0,l ,3,5,7,9中任取两个数做除法,可得到不同的商共有( ) (A )20个 (B )19个 (C )25个 (D )30个7.甲、乙、丙、丁四种不同的种子,在三块不同土地上试种,其中种子甲必须试种,那么不同的试种方法共有( )(A )12种 (B )18种 (C )24种 (D )96种8.某天上午要排语文、数学、体育、计算机四节课,其中体育不排在第一节,那么这天上午课程表的不同排法共有( )(A )6种 (B )9种 (C )18种 (D )24种9.有四位司机、四个售票员组成四个小组,每组有一位司机和一位售票员,则不同的分组方案共有( )(A )88A 种 (B )48A 种 (C )44A ·44A 种 (D )44A 种10.有4位学生和3位老师站在一排拍照,任何两位老师不站在一起的不同排法共有( ) (A )(4!)2种 (B )4!·3!种 (C )34A ·4!种 (D )35A ·4!种11.把5件不同的商品在货架上排成一排,其中a ,b 两种必须排在一起,而c ,d 两种不能排在一起,则不同排法共有( )(A )12种 (B )20种 (C )24种 (D )48种 二.填空题::12.6个人站一排,甲不在排头,共有 种不同排法.13.6个人站一排,甲不在排头,乙不在排尾,共有 种不同排法.14.五男二女排成一排,若男生甲必须排在排头或排尾,二女必须排在一起,不同的排法共有 种.15.将红、黄、蓝、白、黑5种颜色的小球,分别放入红、黄、蓝、白、黑5种颜色的口袋中,但红口袋不能装入红球,则有种不同的放法.16.(1)有5本不同的书,从中选3本送给3名同学,每人各一本,共有种不同的送法;(2)有5种不同的书,要买3本送给3名同学,每人各一本,共有种不同的送法.三、解答题:17.一场晚会有5个唱歌节目和3个舞蹈节目,要求排出一个节目单(1)前4个节目中要有舞蹈,有多少种排法?(2)3个舞蹈节目要排在一起,有多少种排法?(3)3个舞蹈节目彼此要隔开,有多少种排法?18.三个女生和五个男生排成一排.(1)如果女生必须全排在一起,有多少种不同的排法?(2)如果女生必须全分开,有多少种不同的排法?(3)如果两端都不能排女生,有多少种不同的排法?(4)如果两端不能都排女生,有多少种不同的排法?(5)如果三个女生站在前排,五个男生站在后排,有多少种不同的排法?综合卷1.B 2.D 3.D 4.C 5.A 6.B 7.B 8.C 9.D 10.D 11.C12.600 13.504 14.480 15.9616.(1) 60;(2) 12517.(1) 37440;(2) 4320;(3) 1440018.(1) 4320;(2) 14400;(3) 14400;(4) 36000;(5) 7202、组合 综合卷一、选择题:1.下列等式不正确的是( ) (A )!!()!mn n C m n m =- (B )11mm n n m C C n m++=-(C )1111m m n n m C C n +++=+ (D )11m m n n C C ++= 2.下列等式不正确的是( )(A )m n m n n C C -= (B )11m m mm m m C C C -++=(C )123455555552C C C C C ++++= (D )11111m m m m n n n n C C C C --+--=++3.方程2551616x x x CC --=的解共有( ) (A )1个 (B )2个 (C )3个 (D )4个4.若372345n n n C A ---=,则n 的值是( )(A )11 (B )12 (C )13 (D )145.已知7781n n n C C C +-=,那么n 的值是()(A )12 (B )13 (C )14 (D )15 6.从5名男生中挑选3人,4名女生中挑选2人,组成一个小组,不同的挑选方法共有( )(A )3254C C 种(B ) 3254C C 55A 种(C ) 3254A A 种(D ) 3254A A 55A 种7.从4个男生,3个女生中挑选4人参加智力竞赛,要求至少有一个女生参加的选法共有( )(A )12种 (B )34种 (C )35种 (D )340种8.平面上有7个点,除某三点在一直线上外,再无其它三点共线,若过其中两点作一直线,则可作成不同的直线( )(A )18条 (B )19条 (C )20条 (D )21条9.在9件产品中,有一级品4件,二级品3件,三级品2件,现抽取4个检查, 至少有两件一级品的抽法共有( )(A )60种 (B )81种 (C )100种 (D )126种10.某电子元件电路有一个由三节电阻串联组成的回路,共有6个焊点,若其中某一焊点脱落,电路就不通.现今回路不通,焊点脱落情况的可能有( ) (A )5种 (B )6种 (C )63种 (D )64种 二.填空题:11.若11m m n n C xC --=,则x= .12.三名教师教六个班的课,每人教两个班,分配方案共有 种。
最新人教A版高中数学必修二全册同步课时跟踪练习

最新人教A版高中数学必修二全册同步课时跟踪练习棱柱、棱锥、棱台的结构特征圆柱、圆锥、圆台、球及简单组合体的结构特征中心投影与平行投影及空间几何体的三视图空间几何体的直观图柱体、锥体、台体的表面积与体积球的体积和表面积平面空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系平面与平面之间的位置关系直线与平面、平面与平面平行的判定直线与平面、平面与平面平行的性质直线与平面垂直的判定平面与平面垂直的判定直线与平面垂直的性质平面与平面垂直的性质倾斜角与斜率两条直线平行与垂直的判定直线的点斜式方程直线的两点式方程直线的一般式方程两条直线的交点坐标、两点间的距离点到直线的距离、两条平行线间的距离圆的标准方程圆的一般方程直线与圆的位置关系圆与圆的位置关系直线与圆的方程的应用空间直角坐标系棱柱、棱锥、棱台的结构特征一、题组对点训练对点练一棱柱的结构特征1.下面没有体对角线的一种几何体是()A.三棱柱B.四棱柱C.五棱柱D.六棱柱解析:选A三棱柱只有面对角线,没有体对角线.2.关于如图所示的4个几何体,说法正确的是()A.只有②是棱柱B.只有②④是棱柱C.只有①②是棱柱 D.只有①②④是棱柱解析:选D解决这类问题,要紧扣棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行.图①②④满足棱柱的定义,正确;图③不满足侧面都是平行四边形,不正确.3.如图,将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度,则倾斜后水槽中的水形成的几何体的形状是________.解析:由于倾斜角度较小,所以倾斜后水槽中水形成的几何体的形状应为四棱柱.答案:四棱柱对点练二棱锥、棱台的结构特征4.三棱锥的四个面中可以作为底面的有()A.1个B.2个C.3个 D.4个解析:选D三棱锥的每一个面均可作为底面,应选D.5.下面说法中,正确的是()A.上下两个底面平行且是相似四边形的几何体是四棱台B.棱台的所有侧面都是梯形C.棱台的侧棱长必相等D.棱台的上下底面可能不是相似图形解析:选B由棱台的结构特点可知,A、C、D不正确.6.下列四个几何体为棱台的是()解析:选C棱台的底面为多边形,各个侧面为梯形,侧棱延长后又交于一点,只有C 项满足这些要求.对点练三多面体的表面展开图7.下列图形中,不是三棱柱展开图的是()解析:选C本题考查三棱柱展开图的形状.显然C无法将其折成三棱柱,故选C.8.如图所示,不是正四面体(各棱长都相等的三棱锥)的展开图的是()A.①③B.②④C.③④ D.①②解析:选C可选择阴影三角形作为底面进行折叠,发现①②可折成正四面体,③④不论选哪一个三角形作底面折叠都不能折成正四面体.9.如图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D,M,R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是________(把你认为正确命题的序号都填上).解析:将正方体的六个面分别用“前”“后”“左”“右”“上”“下”标记,若记面NPGF为“下”,面PSRN为“后”,则面PQHG,MNFE,EFCB,DEBA分别为“右”“左”“前”“上”.按各面的标记折成正方体,则点D,M,R重合;点G,C重合;点B,H重合;点A,S,Q重合.故②④正确,①③错误.答案:②④二、综合过关训练1.下列图形经过折叠可以围成一个棱柱的是()解析:选D A、B、C中底面边数与侧面个数不一致,故不能围成棱柱.2.以下有三个结论:①有两个面互相平行,其余各面都是四边形的多面体一定是棱柱;②有一个面是多边形,其余各面都是三角形的多面体一定是棱锥;③侧面都是矩形的棱柱是长方体.正确的个数是()A.0 B.1C.2 D.3解析:选A由棱柱、棱锥定义知①②错;侧面都是矩形的棱柱可能是斜棱柱,故③错.3.某同学制作了一个对面图案相同的正方体礼品盒(如图),则这个正方体礼品盒的表面展开图应该为()解析:选A两个☆不能并列相邻,B、D错误;两个※不能并列相邻,C错误,故选A.也可通过实物制作检验来判定.4.下列说法正确的是()A.有2个面平行,其余各面都是梯形的几何体是棱台B.多面体至少有3个面C.各侧面都是正方形的四棱柱一定是正方体D.九棱柱有9条侧棱,9个侧面,侧面为平行四边形解析:选D选项A错误,反例如图1;一个多面体至少有4个面,如三棱锥有4个面,不存在有3个面的多面体,所以选项B错误;选项C错误,反例如图2,上、下底面是全等的菱形,各侧面是全等的正方形,它不是正方体;根据棱柱的定义,知选项D正确.5.若一个棱台共有21条棱,则这个棱台是________棱台.解析:由棱台的概念可知,棱台的上下底面为相似多边形,边数相同;侧面为梯形,侧面个数与底面多边形边数相同,可知该棱台为七棱台.答案:七6.如图所示平面图形沿虚线折起后,(1)为________,(2)为________,(3)为________.解析:结合棱柱、棱锥的概念可知,(1)是四棱柱,(2)是三棱锥,(3)是四棱锥.答案:四棱柱三棱锥四棱锥7.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.解:(1)是上海世博会中国馆,其主体结构是四棱台.(2)是法国卢浮宫,其主体结构是四棱锥.(3)是国家游泳中心“水立方”,其主体结构是四棱柱.(4)是美国五角大楼,其主体结构是五棱柱.8.如图在以O为顶点的三棱锥中,过O的三条棱两两夹角都是30°,在一条棱上取A、B两点,OA=4 cm,OB=3 cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.解:作出三棱锥的侧面展开图,如图A、B两点间最短绳长就是线段AB的长度.在△AOB中,∠AOB=30°×3=90°,OA=4 cm,OB=3 cm,所以AB=OA2+OB2=5 cm.所以此绳在A、B两点间的最短绳长为5 cm.圆柱、圆锥、圆台、球及简单组合体的结构特征一、题组对点训练对点练一旋转体的结构特征1.下列几何体中是旋转体的是()①圆柱;②六棱锥;③正方体;④球体;⑤四面体.A.①和⑤B.①C.③和④ D.①和④解析:选D根据旋转体的概念可知,①和④是旋转体.2.下面几何体的轴截面(过旋转轴的截面)是圆面的是()A.圆柱B.圆锥C.球 D.圆台解析:选C圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形,只有球的轴截面是圆面.3.有下列说法:①球的半径是球面上任意一点与球心的连线;②球的直径是球面上任意两点间的连线;③用一个平面截一个球,得到的是一个圆.其中正确说法的序号是________.解析:利用球的结构特征判断:①正确;②不正确,因为直径必过球心;③不正确,因为得到的是一个圆面.答案:①对点练二简单组合体4.下列几何体是简单组合体的是()解析:选D A选项中的几何体是圆锥,B选项中的几何体是圆柱,C选项中的几何体是球,D选项中的几何体是一个圆台中挖去一个圆锥,是简单组合体.5.以钝角三角形的较小边所在的直线为轴,其他两边旋转一周所得到的几何体是()A.两个圆锥拼接而成的组合体B.一个圆台C.一个圆锥D.一个圆锥挖去一个同底的小圆锥解析:选D如图以AB为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.6.指出如图(1)(2)所示的图形是由哪些简单几何体构成的.解:分割图形,使它的每一部分都是简单几何体.图(1)是由一个三棱柱和一个四棱柱拼接而成的简单组合体.图(2)是由一个圆锥和一个四棱柱拼接而成的简单组合体.对点练三有关几何体的计算7.用长为4,宽为2的矩形作侧面围成一个圆柱,此圆柱轴截面面积为()A.8 B.8π C.4π D.2π解析:选B由题意可知,假设围成的圆柱底面周长为4,高为2,设圆柱底面圆的半径为r,则2πr=4,所以r=2π,所以截面是长为2,宽为4π的矩形,所以截面面积为2×4π=8π.同理,当围成的圆柱底面周长为2,高为4时,截面面积为8π.8.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为________cm.解析:h=20 cos 30°=103(cm).答案:10 3二、综合过关训练1.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为()A.一个球体B.一个球体中间挖出一个圆柱C.一个圆柱D.一个球体中间挖去一个长方体解析:选B圆旋转一周形成球,圆中的矩形旋转一周形成一个圆柱,所以选B.2.下列说法中正确的个数是()①用一个平面去截一个圆锥得到一个圆锥和一个圆台;②圆锥中过轴的截面是一个等腰三角形;③分别以矩形(非正方形)的长和宽所在直线为旋转轴,旋转一周得到的两个几何体是两个不同的圆柱.A.0 B.1 C.2 D.3解析:选C①中,必须用一个平行于底面的平面去截圆锥,才能得到一个圆锥和一个圆台,故①说法错误;显然②③说法正确.故说法正确的有2个.3.若圆柱体被平面截成如图所示的几何体,则它的侧面展开图是()解析:选D结合几何体的实物图,从截面最低点开始高度增加缓慢,然后逐渐变快,最后增加逐渐变慢,不是均衡增加的,所以A、B、C错误.4.两平行平面截半径为5的球,若截面面积分别为9 π和16 π,则这两个平面间的距离是()A.1B.7C.3或4 D.1或7解析:选D如图(1)所示,若两个平行平面在球心同侧,则CD=52-32-52-42=1.如图(2)所示,若两个平行截面在球心两侧,则CD=52-32+52-42=7.5.给出下列说法:①圆柱的底面是圆面;②经过圆柱任意两条母线的截面是一个矩形面;③圆台的任意两条母线的延长线,可能相交,也可能不相交;④夹在圆柱的两个截面间的几何体还是一个旋转体,其中说法正确的是________.解析:①正确,圆柱的底面是圆面;②正确,经过圆柱任意两条母线的截面是一个矩形面;③不正确,圆台的母线延长一定相交于一点;④不正确,夹在圆柱的两个平行于底面的截面间的几何体才是旋转体.答案:①②6.已知圆锥的底面半径为1 cm,高为 2 cm,其内部有一个内接正方体,则这个内接正方体的棱长为________.解析:设正方体的棱长为a,则a2=1-22a1,即a=2 2.答案:22cm7.如图所示,梯形ABCD中,AD∥BC,且AD<BC,当梯形ABCD绕AD所在直线旋转一周时,其他各边旋转围成了一个几何体,试描述该几何体的结构特征.解:如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的简单组合体.8.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.解:圆台的轴截面如图所示,设圆台上、下底面半径分别为x cm,3x cm,延长AA1交OO1的延长线于S,在Rt△SOA中,∠ASO=45°,则∠SAO=45°,所以SO=AO=3x,SO1=A1O1=x,所以OO1=2x.又S轴截面=12(6x+2x)·2x=392,所以x=7.所以圆台的高OO1=14 (cm),母线长l=2OO1=142(cm),两底面半径分别为7 cm,21 cm.中心投影与平行投影及空间几何体的三视图一、题组对点训练对点练一平行投影和中心投影1.直线的平行投影可能是()A.点B.线段C.射线 D.曲线解析:选A直线的平行投影可能是直线也可能是点,故选A.2.下列的四个图形中采用中心投影画法的是()解析:选A根据平行投影和中心投影的画法规则,B、C、D选项中的图形均为平行投影下的图形,而A选项中的图形采用的是中心投影画法.3.如图,E,F分别是正方体ABCD-AB1C1D1的面ADD1A1和面BCC1B1的中心,则四边形BFD1E在该正方体的面上的正投影可能是________(把所有可能图形的序号都填上).解析:图②是在平面DCC1D1或平面ABCD上的正投影;图③是在平面BCC1B1上的正投影.图①④均不符合.答案:②③对点练二简单几何体的三视图4.已知一个几何体的三视图如图所示,则此几何体的组成为()A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱C.上面为圆台,下面为圆柱 D.上面为棱台,下面为圆柱解析:选C结合三视图,易知该几何体上面为圆台,下面为圆柱.5.如图所示的几何体中,正视图与侧视图都是长方形的是________.解析:(2)的侧视图是三角形,(5)的正视图和侧视图都是等腰梯形,其余的都符合条件.答案:(1)(3)(4)6.如图所示的螺栓是由棱柱和圆柱构成的组合体,试画出它的三视图.解:三视图如图所示.对点练三由三视图还原空间几何体7.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为() A.217 B.2 5C.3 D.2解析:选B先画出圆柱的直观图,根据题图的三视图可知点M,N的位置如图①所示.圆柱的侧面展开图及M,N的位置(N为OP的四等分点)如图②所示,连接MN,则图中MN即为M到N的最短路径.∵ON=14×16=4,OM=2,∴MN=OM2+ON2=22+42=2 5.8.如图是一个几何体的三视图,则可以判断此几何体是________.解析:由三视图可知,此几何体为一个正四棱锥.答案:正四棱锥9.如图,图(1)、(2)、(3)是图(4)表示的几何体的三视图,其中图(1)是________,图(2)是________,图(3)是________(写出视图名称).解析:由几何体的位置知,(1)为正视图,(2)为侧视图,(3)为俯视图.答案:正视图侧视图俯视图二、综合过关训练1.下列命题中正确的是()A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的投影可能平行D.一条线段的中点的平行投影仍是这条线段投影的中点解析:选D矩形的平行投影可能是线段,平行四边形或矩形,梯形的平行投影可能是线段或梯形,两条相交直线的投影是两条相交直线或是一条直线.因此A、B、C均错,故D 正确.2.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧视图为()解析:选B依题意,侧视图中棱的方向从左上角到右下角,故选B.3.某个游戏环节,玩家需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为()解析:选A由题意知,图中正方形、圆形、三角形对应某几何体的三视图,结合选项中给出的图形分析可知,A中几何体满足要求.故选A.4.在一个几何体的三视图中,正视图和侧视图是两个完全相同的图形,如图所示,则相应的俯视图可以为()A.①②B.②③C.③④ D.②④解析:选D若俯视图为图①,则该几何体的正视图的上方三角形应该没有高线,故俯视图不可能为图①,排除选项A;若俯视图为图③,则该几何体的侧视图的上方应该没有左边小三角形,故俯视图不可能为图③,排除选项B、C;若俯视图为图②,则该几何体是由上面是正四棱锥,下面是正方体组合而成的简单组合体;若俯视图为图④,则该几何体是由上面是正四棱锥,下面是圆柱组合而成的简单组合体.故选D.5.由小正方体木块搭成的几何体的三视图如图所示,则该几何体由________块小正方体木块搭成.解析:小木块的排列方式如图所示.由图知,几何体由7块小正方体木块搭成.答案:76.若一个正三棱柱(底面为正三角形,侧面为矩形的棱柱)的三视图如图所示,则这个正三棱柱的侧棱长和底面边长分别为________、________.解析:侧视图中尺寸2为正三棱柱的侧棱长,尺寸23为俯视图正三角形的高,所以正三棱柱的底面边长为4.答案:2 47.某组合体的三视图如图所示,试画图说明此组合体的结构特征.解:该三视图表示的几何体是由一个四棱柱和一个四棱台拼接而成的组合体(如图所示).8.如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,求三棱锥P -ABC 的正视图与俯视图的面积的比值的最大值.解:点P 是平面A 1B 1C 1D 1内的一个动点,则三棱锥P -ABC 的正视图始终是一个底为1,高为2的三角形, 其面积S 1=12×1×2=1.当点P 在底面ABCD 内的投影点在△ABC 的内部或边界上时,其俯视图的面积最小, 最小面积S 2=12×1×1=12,所以三棱锥P -ABC 的正视图与俯视图的面积的比值的最大值为S 1S 2=2.空间几何体的直观图一、题组对点训练 对点练一 斜二测画法1.用斜二测画法画水平放置的△ABC 时,若∠A 的两边分别平行于x 轴、y 轴,且∠A =90°,则在直观图中∠A ′=( )A .45°B .135°C .45°或135°D.90°解析:选C 在画直观图时,∠A ′的两边依然分别平行于x ′轴、y ′轴,而∠x ′O ′y ′=45°或135°.2.用斜二测画法画水平放置的平面图形的直观图,对其中的线段说法错误的是( ) A .原来相交的仍相交 B .原来垂直的仍垂直 C .原来平行的仍平行 D .原来共点的仍共点解析:选B 根据斜二测画法,原来垂直的未必垂直. 3.关于斜二测画法所得直观图的说法正确的是( ) A .直角三角形的直观图仍是直角三角形 B .梯形的直观图是平行四边形 C .正方形的直观图是菱形D .平行四边形的直观图仍是平行四边形解析:选D 由斜二测画法规则可知,平行于y 轴的线段长度减半,直角坐标系变成斜坐标系,而平行性没有改变,故只有选项D 正确.4.如图,已知等腰三角形ABC ,则如图所示的四个图中,可能是△ABC 的直观图的是 ( )A.①②B.②③C.②④ D.③④解析:选D原等腰三角形画成直观图后,原来的腰长不相等,③④两图分别是∠x′O′y′成135°和45°的坐标系中的直观图.5.画出水平放置的四边形OBCD(如图所示)的直观图.解:(1)过点C作CE⊥x轴,垂足为E,如图(1)所示,画出对应的x′轴、y′轴,使∠x′O′y′=45°.(2)如图(2)所示,在x′轴上取点B′,E′,使得O′B′=OB,O′E′=OE;在y′轴上取一点D,使得O′D′=12OD;过E′作E′C′∥y′轴,使E′C′=12EC.(3)连接B′C′,C′D′,并擦去x′轴与y′轴及其他一些辅助线,如图(3)所示,四边形O′B′C′D′就是所求的直观图.对点练二由直观图还原平面图形6.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()解析:选A由直观图的画法可知,落在y轴上的对角线的长为22,结合各选项可知选A.7.如图所示,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是()A.AB B.ACC.BC D.AD解析:选B由直观图可知△ABC是以∠B为直角的直角三角形,所以斜边AC最长.8.如图所示,Rt△O′A′B′是一平面图形的直观图,直角边O′B′=1,则这个平面图形的面积是()A.2 2 B.1C. 2D.4 2解析:选C在△AOB中,OB=O′B′=1,OA=2O′A′=22,且∠AOB=90°,S△AOB=12OA·OB=12×1×22= 2.二、综合过关训练1.已知一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,长方体的长、宽、高分别为20 m,5 m,10 m,四棱锥的高为8 m,如果按1∶500的比例画出它的直观图,那么在直观图中,长方体的长、宽、高和棱锥的高应分别为() A.4 cm,1 cm,2 cm,1.6 cmB.4 cm,0.5 cm,2 cm,0.8 cmC.4 cm,0.5 cm,2 cm,1.6 cmD.4 cm,0.5 cm,1 cm,0.8 cm解析:选C直观图中长、宽、高应分别按原尺寸的1500,11 000,1500计算,最后单位转化为cm.2.如图所示的正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,则原图形的周长是()A.6 cm B.8 cmC.(2+32) cm D.(2+23) cm解析:选B直观图中,O′B′=2,原图形中OC=AB=(22)2+12=3,OA=BC =1,∴原图形的周长是2×(3+1)=8.3.如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,A′B′∥y′轴,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为()A.2 2 B. 2C.16 2 D.1解析:选A 因为A ′B ′∥y ′轴,所以在△ABO 中,AB ⊥OB .又△ABO 的面积为16,所以12AB ·OB =16.所以AB =8,所以A ′B ′=4.如图,作A ′C ′⊥O ′B ′于点C ′,所以B ′C ′=A ′C ′,所以A ′C ′的长为4sin 45°=2 2.4.已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2 cm ,另一个圆锥顶点到底面的距离为3 cm ,则其直观图中这两个顶点之间的距离为( )A .2 cmB .3 cmC .2.5 cmD .5 cm解析:选D 圆锥顶点到底面的距离即圆锥的高,故两顶点间距离为2+3=5 cm ,在直观图中与z 轴平行的线段长度不变,仍为5 cm.5.有一个长为5,宽为4 的矩形,则其直观图的面积为________. 解析:由于该矩形的面积为S =5×4=20,所以由公式S ′=24S ,得其直观图的面积为S ′=24S =5 2. 答案:5 26.一个水平放置的平面图形的斜二测直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,则原平面图形的面积为________.解析:过A 作AE ⊥BC ,垂足为E .∵DC ⊥BC 且AD ∥BC ,∴ADCE 是矩形,∴EC =AD =1.由∠ABC =45°,AB =AD =1知BE =22,∴原平面图形是梯形且上、下两底边长分别为1和1+22,高为2, ∴原平面图形的面积为12×⎝⎛⎭⎫1+1+22×2=2+22.答案:2+227.如图,四边形A ′B ′C ′D ′是边长为1的正方形,且它是某个四边形按斜二测画法画出的直观图,请画出该四边形的原图形,并求出原图形的面积.解:画出平面直角坐标系xOy ,使点A 与O 重合, 在x 轴上取点C ,使AC =2, 再在y 轴上取点D ,使AD =2, 取AC 的中点E ,连接DE 并延长至点B , 使DE =EB ,连接DC ,CB ,BA ,则四边形ABCD 为正方形A ′B ′C ′D ′的原图形(也可以过点C 作BC ∥y 轴,且使CB =AD =2,然后连接AB ,DC ),如图所示.易知四边形ABCD 为平行四边形,∵AD =2,AC =2,∴S ▱ABCD =2×2=2 2. 8.如图为一几何体的展开图:沿图中虚线将它们折叠起来,请画出其直观图.解:由题设中所给的展开图可以得出,此几何体是一个四棱锥,其底面是一个边长为2的正方形,垂直于底面的侧棱长为2,其直观图如图所示.柱体、锥体、台体的表面积与体积一、题组对点训练对点练一 柱体、锥体、台体的侧面积与表面积 1.棱长为3的正方体的表面积为( ) A .27 B .64 C .54D.36解析:选C 根据表面积的定义,组成正方体的面共6个,且每个都是边长为3的正方形.从而,其表面积为6×32=54.2.若圆锥的高等于底面直径,则它的底面积与侧面积之比为( ) A .1∶2 B .1∶ 3 C .1∶ 5D.3∶2解析:选C 设圆锥底面半径为r ,则高h =2r ,∴其母线长l =5r .∴S 侧=πrl =5πr 2,S 底=πr 2.则S 底∶S 侧=1∶ 5.3.已知正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4B .16πC .9πD.27π4解析:选A 如图,设球心为O ,半径为r ,则在Rt △AOF 中,(4-r )2+(2)2=r 2,解得r =94,所以该球的表面积为4πr 2=4π×⎝⎛⎭⎫94 2=81π4.4.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D.3解析:选A 设圆台较小底面半径为r ,则另一底面半径为3r .由S =π(r +3r )·3=84π,解得r =7.5.一个高为2的圆柱,底面周长为2π,该圆柱的表面积为________.解析:由底面周长为2π可得底面半径为1.S 底=2πr 2=2π,S 侧=2πr ·h =4π,所以S 表=S底+S 侧=6π. 答案:6π对点练二 柱体、锥体、台体的体积6.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A .2B .4C .6D.8解析:选C 由几何体的三视图可知,该几何体是一个底面为直角梯形,高为2的直四棱柱,直角梯形的两底边长分别为1,2,高为2,∴该几何体的体积为V =12×(2+1)×2×2=6.7.若圆锥的侧面展开图为一个半径为2的半圆,则圆锥的体积是________.解析:易知圆锥的母线长为2,设圆锥的底面半径为r ,则2πr =12×2π×2,∴r =1,则高h =l 2-r 2= 3.∴V 圆锥=13πr 2· h =13π×3=3π3.答案:3π38.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是________.解析:几何体的直观图为正方体去掉以正方体中心为顶点,上底面为底面的四棱锥,其体积为2×2×2-13×1×22=203.答案:203对点练三 求几何体体积的方法9.如图,在正三棱柱ABC -A 1B 1C 1中,AB =4,AA 1=6.若E ,F 分别是棱BB 1,CC 1上的点,则三棱锥A -A 1EF 的体积是________.解析:因为在正三棱柱ABC -A 1B 1C 1中,AA 1∥BB 1,AA 1⊂平面AA 1C 1C ,BB 1⊄平面AA 1C 1C ,所以BB 1∥平面AA 1C 1C ,从而点E 到平面AA 1C 1C 的距离就是点B 到平面AA 1C 1C 的距离,作BH ⊥AC ,垂足为点H ,由于△ABC 是正三角形且边长为4,所以BH =23,从而三棱锥A -A 1EF 的体积VA -A 1EF =VE -A 1AF =13S △A 1AF ·BH =13×12×6×4×23=8 3.答案:8 3 二、综合过关训练1.如图,ABC -A ′B ′C ′是体积为1的棱柱,则四棱锥C -AA ′B ′B 的体积是( )A.13 B.12 C.23D.34解析:选C ∵V C -A ′B ′C ′=13V 棱柱=13,∴V C -AA ′B ′B =1-13=23. 2.已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比值是( )A.1+2π2πB.1+4π4πC.1+2ππD.1+4π2π解析:选A 设圆柱的底面半径为r ,高为h ,。
高中数学 必修二 同步练习 专题1.2.1中心投影与平行投影、空间几何体的三视图(解析版)

一、选择题1.以下关于投影的叙述不正确的是A.手影就是一种投影B.中心投影的投影线相交于点光源C.斜投影的投影线不平行D.正投影的投影线和投影面垂直【答案】C【解析】平行投影的投影线互相平行,分为正投影和斜投影两种,故C错.2.下列哪个实例不是中心投影A.工程图纸B.小孔成像C.相片D.人的视觉【答案】A3.一个几何体的三视图的形状都相同、大小均相等,那么这个几何体不可以是A.球B.三棱锥C.正方体D.圆柱【答案】D【解析】球的三视图均为圆,且大小均相等;对于三棱锥O−ABC,当OA,OB,OC两两垂直且OA=OB=OC 时,其三视图的形状可以都相同,大小均相等;正方体的三视图是三个大小均相等的正方形;圆柱的三视图中必有一个为圆,其他两个为矩形,故一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是圆柱,故选D.4.以下关于几何体的三视图的论述中,正确的是A.球的三视图总是三个全等的圆B.正方体的三视图总是三个全等的正方形C.水平放置的正四面体的三视图都是正三角形D .水平放置的圆台的俯视图是一个圆 【答案】A【解析】球的三视图总是三个全等的圆.5.小周过生日,公司为她预订的生日蛋糕(示意图)如下图所示,则它的正视图应该是【答案】B6.如图,在正方体1111ABCD A B C D -中,P 是线段CD 的中点,则三棱锥11P A B A -的侧视图为A .B .C .D .【答案】D【解析】由直观图可知,三棱锥11P A B A -的侧视图中线段11A B 的投影是线段11C D ,线段1B A 的投影是线段1C D ,是实线;而线段1A P 的投影是线段1D P ,是虚线. 故选D.7.如图是一个几何体的三视图,则此几何体的直观图是A .B .C .D .【答案】D【解析】由已知可得原几何体是一个圆锥和一个圆柱的组合体,上部分是一个圆锥,下部分是一个圆柱,而且圆锥和圆柱的底面积相等,故此几何体的直观图是:.故选D.8.若沿一个正方体三个面的对角线截得的几何体如图所示,则下列说法正确的是A .正视图与侧视图一样B .正视图与俯视图一样C .侧视图与俯视图一样D .正视图、侧视图、俯视图都不一样【答案】C9.如图,在正方体1111ABCD A B C D 中, M N 、分别是1BB 、BC 的中点,则图中阴影部分在平面11ADD A 上的投影为图中的A.B.C.D.【答案】A10.一个几何体的三视图如下图所示,这个几何体可能是一个A.三棱锥B.底面不规则的四棱锥C.三棱柱D.底面为正方形的四棱锥【答案】C【解析】根据三视图可知,该几何体是一个倒放的三棱柱.11.如图是一个几何体的三视图,则该几何体的所有棱中,最大值是A.2B.3C.32D.10【答案】C12.如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h随时间t变化的图象可能是【答案】B【解析】由容器的三视图可知容器是由圆柱和圆台构成.由于水是匀速注入的,故水面的高度随着时间t的变化先是均匀增加,然后逐渐加快,故选B.二、填空题13.夜晚,人在路灯下的影子是________投影,人在月光下的影子是________投影.【答案】中心平行【解析】路灯的光是从一点发出的,故影子是中心投影;而月光可以近似看作平行的,月光下的影子是平行投影.14.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.【答案】①②③⑤15.一物体及其正视图如图:则它的侧视图与俯视图分别是图形中的________.【答案】③②【解析】侧视图是矩形中间有条实线,应选③;俯视图为矩形中间两条实线,且为上下方向,应选②. 16.如图,直三棱柱ABC-A1B1C1的侧棱长为2,底面是边长为2的正三角形,正视图是边长为2的正方形,则其侧视图的面积为________.【答案】2 317.如图,点O为正方体ABCD—A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是(写出所有可能的序号).【答案】①②③【解析】要画出四边形D′OEF在该正方体的各个面上的投影,只需画出四个顶点D′,O,E,F在每个面上的投影,再顺次连接就可得到在该面上的投影.空间四边形D′OEF在正方体的面DCC′D′上的正投影是①;在面BCC′B′上的正投影是②;在面ABCD上的正投影是③.故填①②③.三、解答题18.如图所示的几何体是由一个长方体木块锯成的.(1)判断该几何体是否为棱柱;(2)画出它的三视图.【答案】(1)是棱柱;(2)见解析.【解析】(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.(2)该几何体的三视图如下图:19.用数个小正方体组成一个几何体,使它的正视图和俯视图如图所示,俯视图中小正方形中的字母表示在该位置的小正方体的个数.(1)你能确定哪些字母表示的数?(2)该几何体可能有多少种不同的形状?【答案】见解析.(2)当d,e,f中有一个是2时,有3种不同的形状;当d,e,f中有两个是2时,有3种不同的形状;当d,e,f都是2时,有1种形状. 所以该几何体可能有7种不同的形状.。
金版学案高中数学必修2苏教版1.2.3同步辅导与检测课件.ppt

金品质•高追求 我们让你更放心!
返回
◆数学•必修2•(配苏教版)◆
直线和平面所成的角
平面的一条斜线和它在这个平面内的射影所成的锐角, 叫做这条斜线和这个平面所成的角.包括0°角、直角、锐 角,因此直线和平面所成角的范围是 0,.π2求 斜线与平面所 成的角一般步骤:
①找出斜线在给定平面内的射影;②指出并论证斜线 与平面所成的角;③在含有斜线与平面所成的角的三角形中, 利用平面几何或三角函数知识求出这个角.
金品质•高追求 我们让你更放心!
返回
◆数学•必修2•(配苏教版)◆
5.直线与平面垂直的定义:如果一条直线a与一个平 面a内的____________________,我们就说直线a与平面α互 相垂直.
6.过一点有且只有一条直线与平面垂直,同样, ____________________.
7.从平面外一点引平面的垂线, ____________________,叫做这个点到这个平面的距离.
5.任意一条直线都垂直 6.过一点有且只有一个平面与直线垂直 7.这个点和垂足间的回
◆数学•必修2•(配苏教版)◆
8.直线与平面垂直的判定定理
(1)文字语言:如果一条直线和一个平面内的______, 那么这条直线垂直于这个平面.
(2)符号语言:假设________,________,________, ________,________,那么l⊥α.
(1)文字语言:如果一条直线和一个平面平行,经过这 条直线的平面和这个平面相交,那么这条直线和交线平 行.简称为:“____________________〞.
(2)符号语言:假设______∥________,______, ________,那么l∥m.
高中数学必修2课后习题答案

高中数学必修高中数学必修 2 课后习题答案课后习题答案第一章第一章 空间几何体空间几何体1.1 空间几何体的结构空间几何体的结构练习练习((第 7 页)1.(1)圆锥; (2)长方体; (3)圆柱与圆锥组合而成的组合体; (4)由一个六棱柱挖去一个圆柱体而得到的组合体。
2.(1)五棱柱; (2)圆锥 3.略习题 1.1 A 组1.(1) C; (2)C; (3)D; (4) C 2.(1)不是台体,因为几何体的“侧棱”不相交于一点,不是由平等于“底面”的平面截棱锥得到的。
(2)、(3)也不是台体,因为不是由平行与棱锥和圆锥底面的平面截得的几何体。
3.(1)由圆锥和圆台组合而成的简单组合体;(2)由四棱柱和四棱锥组合而成的简单组合体。
4.两个同心的球面围成的几何体(或在一个球体内部挖去一个同心球得到的简单组合体)。
5.制作过程略。
制作过程说明平面图形可以折叠成立体图形,立体图形可以展开为平面图形。
B 组1.剩下的几何体是棱柱,截去的几何体也是棱柱;它们分别是五棱柱和三棱柱。
2.左侧几何体的主要结构特征:圆柱和棱柱组成的简单组何体;中间几何体的主要结构特征:下部和上部都是一个圆柱截去一个圆柱组成的简单组何体;右侧几何体的主要结构特征:下部是一个圆柱体,上部是一个圆柱截去一个圆柱组成的简单组何体。
1.2 空间几何体的三视图和直观图空间几何体的三视图和直观图练习练习((第 15 页)1.略2.(1)四棱柱(图略);(2)圆锥与半球组成的简单组合体(图略); (3)四棱柱与球组成的简单组合体(图略); (4)两台圆台组合而成的简单组合体(图略)。
3.(1)五棱柱(三视图略);(2)四个圆柱组成的简单组合体(三视图略); 4.三棱柱练习练习((第 19 页)1.略。
2.(1)√ (2)× (3)× (4)√ 3.A 4.略 5.略习题 1.2 A 组1.略 2.(1)三棱柱 (2)圆台 (3)四棱柱 (4)四棱柱与圆柱组合而成的简单组合体 3~5.略B 组1~2.略3.此题答案不唯一,一种答案是由15个小正方体组合而成的简单组合体,如图。
高中数学人教A版必修2第一章1.2.3空间几何体的直观图-斜二侧画法 课件教学课件

(3)已知图形中平行于x轴的线段,在直观图中保持 原长度不变;平行于y轴的线段,长度为原来的一半。
例2.用斜二测画法画长,宽,高分别是4cm,3cm, 2cm的长方体的直观图。
思考:直观图
画法的步骤是 怎样的?
上 分 别 截 取 2 c m 长 的 线 段 A A , B B , C C , D D .
Z
D
C y
A D
BQ C
MO
Nx
AP B
4成 图 .顺 次 连 接 A,B,C,D,并 加 以 整 理
去 掉 辅 助 线 ,将 被 遮 挡 住 的 部 分 改 为 虚 线 ,
就 可 得 到 长 方 体 的 直 观 图 .
1、画轴; 2、画底面; 3、画侧棱;(直棱柱的侧棱和z轴平行,长度保持不变) 4、成图。注意:去掉辅助线,将被遮挡的部分改为虚线.
1 画 轴 . 画 x 轴 , y 轴 , z 轴 , 三 轴 交 于 点 O , 使 x O y = 4 5 ,
x O z 9 0 .
Z
y
O
x
2画 底 面 .以 O为 中 心 ,在 x轴 上 取 线 段 MN,使 MN=4 cm;在
脚踏实地过好每一天,最简单的恰恰是最难的。拿梦想去拼,我怎么能输。只要学不死,就往死里学。我会努力站在万人中央成为别人的光。行为决定性格, 性格决定命运。不曾扬帆,何以至远方。人生充满苦痛,我们有幸来过。如果骄傲没有被现实的大海冷冷拍下,又怎么会明白要多努力才能走到远方。所有的 豪言都收起来,所有的呐喊都咽下去。十年后所有难过都是下酒菜。人生如逆旅,我亦是行人。驾驭命运的舵是奋斗,不抱有一丝幻想,不放弃一点机会,不 停止一日努力。失败时郁郁寡欢,这是懦夫的表现。所有偷过的懒都会变成打脸的巴掌。越努力,越幸运。每一个不起舞的早晨,都是对生命的辜负。死鱼随 波逐流,活鱼逆流而上。墙高万丈,挡的只是不来的人,要来,千军万马也是挡不住的既然选择远方,就注定风雨兼程。漫漫长路,荆棘丛生,待我用双手踏 平。不要忘记最初那颗不倒的心。胸有凌云志,无高不可攀。人的才华就如海绵的水,没有外力的挤压,它是绝对流不出来的。流出来后,海绵才能吸收新的 源泉。感恩生命,感谢她给予我们一个聪明的大脑。思考疑难的问题,生命的意义;赞颂真善美,批判假恶丑。记住精彩的瞬间,激动的时刻,温馨的情景, 甜蜜的镜头。感恩生命赋予我们特有的灵性。善待自己,幸福无比,善待别人,快乐无比,善待生命,健康无比。一切伟大的行动和思想,都有一个微不足道 的开始。在你发怒的时候,要紧闭你的嘴,免得增加你的怒气。获致幸福的不二法门是珍视你所拥有的、遗忘你所没有的。骄傲是胜利下的蛋,孵出来的却是 失败。没有一个朋友比得上健康,没有一个敌人比得上病魔,与其为病痛暗自流泪,不如运动健身为生命添彩。有什么别有病,没什么别没钱,缺什么也别缺 健康,健康不是一切,但是没有健康就没有一切。什么都可以不好,心情不能不好;什么都可以缺乏,自信不能缺乏;什么都可以不要,快乐不能不要;什么 都可以忘掉,健身不能忘掉。选对事业可以成就一生,选对朋友可以智能一生,选对环境可以快乐一生,选对伴侣可以幸福一生,选对生活方式可以健康一生。 含泪播种的人一定能含笑收获一个有信念者所开发出的力量,大于个只有兴趣者。忍耐力较诸脑力,尤胜一筹。影响我们人生的绝不仅仅是环境,其实是心态 在控制个人的行动和思想。同时,心态也决定了一个人的视野、事业和成就,甚至一生。每一发奋努力的背后,必有加倍的赏赐。懒惰像生锈一样,比操劳更 消耗身体。所有的胜利,与征服自己的胜利比起来,都是微不足道。所有的失败,与失去自己的失败比起来,更是微不足道挫折其实就是迈向成功所应缴的学 费。在这个尘世上,虽然有不少寒冷,不少黑暗,但只要人与人之间多些信任,多些关爱,那么,就会增加许多阳光。一个能从别人的观念来看事情,能了解 别人心灵活动的人,永远不必为自己的前途担心。当一个人先从自己的内心开始奋斗,他就是个有价值的人。没有人富有得可以不要别人的帮助,也没有人穷 得不能在某方面给他人帮助。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵,昨天的太阳,晒不干今天的衣裳。今天做别人不 愿做的事,明天就能做别人做不到的事。到了一定年龄,便要学会寡言,每一句话都要有用,有重量。喜怒不形于色,大事淡然,有自己的底线。趁着年轻, 不怕多吃一些苦。这些逆境与磨练,才会让你真正学会谦恭。不然,你那自以为是的聪明和藐视一切的优越感,迟早会毁了你。无论现在的你处于什么状态, 是时候对自己说:不为模糊不清的未来担忧,只为清清楚楚的现在努力。世界上那些最容易的事情中,拖延时间最不费力。崇高的理想就像生长在高山上的鲜 花。如果要搞下它,勤奋才能是攀登的绳索。行动是治愈恐惧的良药,而犹豫、拖延将不断滋养恐惧。海浪的品格,就是无数次被礁石击碎又无数闪地扑向礁 石。人都是矛盾的,渴望被理解,又害怕被看穿。经过大海的一番磨砺,卵石才变得更加美丽光滑。生活可以是甜的,也可以是苦的,但不能是没味的。你可
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.3空间几何体的直观图
一、基础过关
1.下列结论:
①角的水平放置的直观图一定是角;
②相等的角在直观图中仍然相等;
③相等的线段在直观图中仍然相等;
④两条平行线段在直观图中对应的两条线段仍然平行.
其中正确的有() A.①②B.①④C.③④D.①③④
2.在用斜二测画法画水平放置的△ABC时,若∠A的两边分别平行于x轴、y轴,则在直观图中∠A′等于() A.45°B.135°C.90°D.45°或135°
3.下面每个选项的2个边长为1的正△ABC的直观图不是全等三角形的一组是()
4.如图甲所示为一个平面图形的直观图,则此平面图形可能是图乙中的()
5.利用斜二测画法得到:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上结论中,正确的是______________.(填序号)
6.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为____________.
7.如图是一梯形OABC的直观图,其直观图面积为S.求梯形OABC的面积.
8.如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.
二、能力提升
9.如图,正方形O′A′B′C′的边长为1 cm,它是水平放置的一
个平面图形的直观图,则原图的周长是()
A.8 cm B.6 cm
C.2(1+3) cm D.2(1+2) cm
10.如图所示的是水平放置的△ABC在直角坐标系的直观图,其中D′
是A′C′的中点,且∠A′C′B′≠30°,则原图形中与线段BD
的长相等的线段有________条.
11.如图所示,为一个水平放置的正方形ABCO,它在直角坐标系xOy中,点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.
12.如图所示,梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠DAB=30°,AD=3 cm,试画出它的直观图.
三、探究与拓展
13.在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,
如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边
形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出
其面积.
答案
1.B 2.D 3.C 4.C 5.①② 6.2.5
7.解设O′C′=h,则原梯形是一个直角梯形且高为2h.
过C ′作C ′D ′⊥O ′A ′于D ′,
则C ′D ′=
22
h . 由题意知1
2C ′D ′(C ′B ′+O ′A ′)=S .
即2
4
h (C ′B ′+O ′A ′)=S . 又原直角梯形面积为S ′=1
2·2h (C ′B ′+O ′A ′)
=h (C ′B ′+O ′A ′)=4S
2=22S .
所以梯形OABC 的面积为22S .
8.解 (1)作出长方体的直观图ABCD -A 1B 1C 1D 1,如图a 所示;
(2)再以上底面A 1B 1C 1D 1的对角线交点为原点建立x ′,y ′,z ′轴,如图b 所示,在z ′上取点V ′,使得V ′O ′的长度为棱锥的高,连接V ′A 1,V ′B 1,V ′C 1,V ′D 1,得到四棱锥的直观图,如图b ;
(3)擦去辅助线和坐标轴,遮住部分用虚线表示,得到几何体的直观图,如图c.
9.A 10.2 11.
22
12.解 画法:步骤:
(1)如图a 所示,在梯形ABCD 中, 以边AB 所在的直线为x 轴,点A 为原点, 建立平面直角坐标系xOy .如图b 所示,
画出对应的x ′轴,y ′轴,使∠x ′O ′y ′=45°. (2)在图a 中,过D 点作DE ⊥x 轴,垂足为E .在图b 中, 在x ′轴上取A ′B ′=AB =4 cm ,
A ′E ′=AE =3
2
3≈2.598 cm ;
过点E ′作E ′D ′∥y ′轴,使E ′D ′=12ED =12×3
2
=0.75 cm ,再过点D ′作
D′C′∥x′轴,且使D′C′=DC=2 cm.
(3)连接A′D′、B′C′,并擦去x′轴与y′轴及其他一些辅助线,如图c所示,则四
边形A′B′C′D′就是所求作的直观图.
13.解四边形ABCD的真实图形如图所示,
∵A′C′在水平位置,A′B′C′D′为正方形,
∴∠D′A′C′=∠A′C′B′
=45°,
∴在原四边形ABCD中,
DA⊥AC,AC⊥BC,
∵DA=2D′A′=2,
AC=A′C′=2,
∴S四边形ABCD=AC·AD=2 2.。
