(完整版)弹塑性力学习题题库加答案
弹塑性力学部分习题及答案

1 εij = (ui, j +uj,i ) 2
σji, j
(i, j =12,3) ,
E 1 ν = 2(uj,ij +ui, jj ) +1−2νuk,kjδij (1+ν)
5Байду номын сангаас
20112011-2-17
题1-3
E 1 ν (uj,ij +ui,jj ) + σji, j = uk,ki 2 (1+ν) 1−2ν
3
2c
l
y
解: 1、将 Φ 代入
∇ 4Φ =0 满足, 为应力函数。 满足, Φ 为应力函数。
2、求应力(无体力) 求应力(无体力)
20112011-2-17 20
题1-13 3 3F xy q 2 Φ= xy− 2 + y 4c 3 2 c
2
o
x
2c
l
y
2
∂φ 3F xy ∂φ σx = 2 = − 3 +q, σy = 2 =0, ∂y 2c ∂x y2 ∂φ 3F τxy =− = − 1− 2 ∂x∂y 4c c
z l y
F = −ρg bz
x
x
20112011-2-17
8
题1-5 等截面直杆(无体力作用),杆轴 等截面直杆(无体力作用),杆轴 ), 方向为 z 轴,已知直杆的位移解为
u =−kyz v =kxz
w=k ( x, y) ψ
为待定常数, 其中 k 为待定常数,ψ(x‚y)为待定函数, 为待定函数 试写出应力分量的表达式和位移法方程。 试写出应力分量的表达式和位移法方程。
2
工程弹塑性力学题库及答案(修订)

,再求应力偏张量
,
,
,
,
,
。
由此求得:
然后求得:
,
,解出
然后按大小次序排列得到
,
,
1.9 已知应力分量中
,求三个主应力
,以及每个
主应力所对应的方向余弦
。
解:特征方程为
记, , 应满足下列关系
由(a),(b)式,·11得
(a) (b) (c)
, ,由此求得
,代入(c)式,得
解:的定义、物理意义:
;
1) 表征 Sij 的形式;2) 相等,应力莫尔圆相似,Sij 形式相同;3) 由可确定 S1:S2:S3。
1.4设某点应力张量 的分量值已知,求作用在过此点平面
力矢量
,并求该应力矢量的法向分量 。
解:该平面的法线方向的方向余弦为
上的应
而应力矢量的三个分量满足关系
曲线基本上和简单拉伸时的
曲线一样。
7.4 比较两种塑性本构理论的特点: 解:增量理论和全量理论。增量理论将整个加载历史看成是一系列的微小增量加 载过程所组成,研究每个微小增量加载过程中应变增量与应力增量之间的关系, 再沿加载路径依次积分应变增量得最终的应变。全量理论不去考虑应力路径的影 响,直接建立应变全量与应力全量直接的关系。
z
且 利用平衡方程
当
时, 为(e)式。
(3)塑性阶段 平衡方程和几何方程同上。
本构方程 与(2)弹塑性阶段同样步骤:可得
(e) (f) (g)
5.9 如图所示等截面直杆,截面积为 ,且 。在 处作用一个逐渐增加 的力 。该杆材料为理想弹塑性,拉伸和压缩时性能相同。按加载过程分析
结构所处不同状态,并求力 作用截面的位移 与 的关系。 解:基本方程为
弹塑性力学习题及答案

.本教材习题和参考答案及部分习题解答第二章2.1计算:(1)pi iq qj jk δδδδ,(2)pqi ijk jk e e A ,(3)ijp klp ki lj e e B B 。
答案 (1)pi iq qj jkpk δδδδδ=;答案 (2)pqi ijk jk pq qp e e A A A =-;解:(3)()ijp klp ki ljik jl il jk ki lj ii jj ji ij e e B B B B B B B B δδδδ=-=-。
2.2证明:若ijji a a =,则0ijk jk e a =。
(需证明)2.3设a 、b 和c 是三个矢量,试证明:2[,,]⋅⋅⋅⋅⋅⋅=⋅⋅⋅a a a b a cb a b b bc a b c c a c b c c证:因为123111123222123333i i i i i i i i i i i i i ii i i i a a a b a c b a b b b c c a c b c c a a a a b c b b b a b c c c c a b c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, 所以123111123222123333123111123222123333det det()i ii i i i i ii i i i i ii ii i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c a a a a b c b b b a b c c c c a b c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即得 1231112123222123333[,,]i i i i i i i i i i i i i i i i i i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c ⋅⋅⋅⋅⋅⋅=⋅⋅⋅==a a a b a c b a b b b c a b c c a c b c c 。
弹塑性力学部分习题及答案

e kk
2019/8/31
4
题1-3
e kk
ij (1 E )( ij 1 2 e ij) (i,j 1 ,2 ,3 )
j,i j (1 E )( j,i j 1 2 k,jk ij ) (i,j 1 ,2 ,3 )
i1 2ui,j
j
Guj,jiGi,ju j
代入 j,ij F b i0 (i,j 1 ,2 ,3 )
得
G 2 u i G u j,j iF b i0在 V 上
2019/8/31
7
题1-4 等截面柱体在自重作用下,应力解为
x=y=xy=yz=zx=0 , z=gz,试求位移。
,且设 ur 表达式为
ur C1rC r2(18 E 2)2r3
b
ra
x
试由边界条件确定 C1 和 C2 。
y
解: 边界条件为: (r)r=a=0, (r)r=b=0
应力r(平面
应力问题):
r 1E2(ddrururr)
2019/8/31
32
题1-16 由边界条件确定 C1 和 C2 :
v g l x y E
y
l
式中 E、 为弹性模量和泊松系数。
试(1)求应力分量和体积力分量;
hh
(2)确定各边界上的面力。
x
解: 1、求应变
x u x E g l x , y y v E g (l x )
2019/8/31
15
x
x=ax、y=ax、xy= -ax
3、求应变
x=ax、y=a(2x+y-l-h)、 xy= -ax
弹塑性力学习题集_很全有答案_

题 2 —4 图
2—5* 如题 2—5 图,刚架 ABC 在拐角 B 点处受 P 力,已知刚架的 EJ,求 B、C 点的 转角和位移。 (E 为弹性模量、J 为惯性矩) 2—6 悬挂的等直杆在自重 W 的作用下如题 2—6 图所示。材料比重为 γ ,弹性模量为 E,横截面积为 A。试求离固定端 z 处一点 c 的应变 ε z 与杆的总伸长 ∆l 。 2—7* 试按材料力学方法推证各向同性材料三个弹性常数:弹性模量 E、剪切弹性模 量 G、泊松比 v 之间的关系:
1 1 1 , n y = , nz = 的微斜面上的全应力 Pα ,正 2 2 2
试求外法线 n 的方向余弦为: n x = 应力 σ α 和剪应力 τ α 。
2—10 已知物体的应力张量为: 30 − 80 50 σ ij = 0 − 30 MPa 110 (对称)
2—39* 若位移分量 u i 和 u i′ 所对应的应变相同,试说明这两组位移有何差别? 2—40* 试导出平面问题的平面应变状态( ε x = γ zx = γ zy = 0 )的应变分量的不变量及
主应变的表达式。 2—41* 已知如题 2—41 图所示的棱柱形杆在自重作用下的应变分量为: γz νγz εz = , εx =εy = − ; γ xy = γ yz = γ zx = 0; E E 试求位移分量,式中 γ 为杆件单位体积重量,E、ν 为材料的弹性常数。
试确定外法线的三个方向余弦相等时的微斜面上的总应力 Pα ,正应力 σ α 和剪应力 τ α 。 2—11 试求以主应力表示与三个应力主轴成等倾斜面(八面体截面)上的应力分量, 并证明当坐标变换时它们是不变量。 2—12 试写出下列情况的应力边界条件。
题 2—12 图
弹塑性力学试卷及弹性力学教材习题及解答

二、填空题:(每空2分,共8分)1、在表征确定一点应力状态时,只需该点应力状态的-------个独立的应力分量,它们分别是-------。
(参照oxyz直角坐标系)。
2、在弹塑性力学应力理论中,联系应力分量与体力分量间关系的表达式叫---------方程,它的缩写式为-------。
三、选择题(每小题有四个答案,请选择一个正确的结果。
每小题4分,共16分。
)1、试根据由脆性材料制成的封闭圆柱形薄壁容器,受均匀内压作用,当压力过大时,容器出现破裂。
裂纹展布的方向是:_________。
A、沿圆柱纵向(轴向)B、沿圆柱横向(环向)C、与纵向呈45°角D、与纵向呈30°角2、金属薄板受单轴向拉伸,板中有一穿透形小圆孔。
该板危险点的最大拉应力是无孔板最大拉应力__________倍。
A、2B、3C、4D、53、若物体中某一点之位移u、v、w均为零(u、v、w分别为物体内一点,沿x、y、z直角坐标系三轴线方向上的位移分量。
)则在该点处的应变_________。
A、一定不为零B、一定为零C、可能为零D、不能确定4、以下________表示一个二阶张量。
A、B、C、D、四、试根据下标记号法和求和约定展开下列各式:(共8分)1、;(i ,j = 1,2,3 );2、;五、计算题(共计64分。
)1、试说明下列应变状态是否可能存在:;()上式中c为已知常数,且。
2、已知一受力物体中某点的应力状态为:式中a为已知常数,且a>0,试将该应力张量分解为球应力张量与偏应力张量之和。
为平均应力。
并说明这样分解的物理意义。
3、一很长的(沿z轴方向)直角六面体,上表面受均布压q作用,放置在绝对刚性和光滑的基础上,如图所示。
若选取=ay2做应力函数。
试求该物体的应力解、应变解和位移解。
(提示:①基础绝对刚性,则在x=0处,u=0 ;②由于受力和变形的对称性,在y=0处,v=0 。
)题五、3图4、已知一半径为R=50mm,厚度为t=3mm的薄壁圆管,承受轴向拉伸和扭转的联合作用。
(完整版)弹塑性力学习题题库加答案
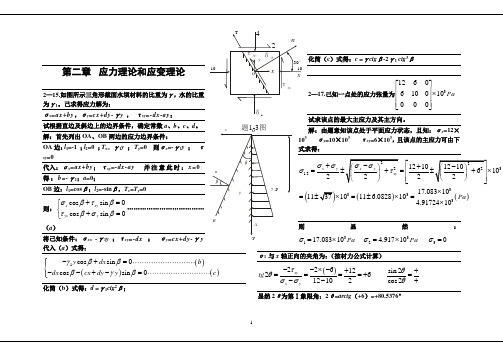
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为:σx =ax+by ,σy =cx+dy-γy , τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件:OA 边:l 1=-1 ;l 2=0 ;T x = γ1y ; T y =0 则σx =-γ1y ; τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0 得:b=-γ1;a =0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0则:cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………(a )将己知条件:σx= -γ1y ;τxy =-dx ; σy =cx+dy-γy 代入(a )式得:()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103 σy =10×103 τxy =6×103,且该点的主应力可由下式求得:(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然:3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为:(按材力公式计算)()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376°题图1-3则:θ=+40.268840°16' 或(-139°44')2—19.己知应力分量为:σx =σy =σz =τxy =0,τzy =a ,τzx =b ,试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
(完整版)弹塑性力学习题题库加答案

第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为:σx =ax+by ,σy =cx+dy-γy , τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件:OA 边:l 1=-1 ;l 2=0 ;T x = γ1y ; T y =0 则σx =-γ1y ; τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0 得:b=-γ1;a =0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0则:cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………(a )将己知条件:σx= -γ1y ;τxy =-dx ; σy =cx+dy-γy 代入(a )式得:()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103 σy =10×103 τxy =6×103,且该点的主应力可由下式求得:(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然:3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为:(按材力公式计算)()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376°题图1-3则:θ=+40.268840°16' 或(-139°44')2—19.己知应力分量为:σx =σy =σz =τxy =0,τzy =a ,τzx =b ,试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
弹塑性力学习题题库加答案(1)

第二章 应力理论和应变理论2—3.试求图示单元体斜截面上的σ30°和τ30°(应力单位为MPa )并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时,其符号及30106.768 6.77()104sin 2cos 2sin 602cos 6022132 3.598 3.60()22x y xy MPa MPa σστατα--=----+=⋅+=⋅-=-⨯-⨯=--代入弹性力学的有关公式得: 己知 σx = -10 σy = -4 τxy = +23030()cos 2sin 2221041041cos 602sin 6073222226.768 6.77()104sin 2cos 2sin 602cos 6022132 3.598 3.60()2x yx yxy x y xy MPa MPa σσσσσατασστατα+-=++---+=++=--⨯+⨯=----+=-⋅+=-⋅+=+⨯=由以上计算知,材力与弹力在计算某一斜截面上的应力时,所使用的公式是不同的,所得结果剪应力的正负值不同,但都反映了同一客观实事。
2—6. 悬挂的等直杆在自重W 作用下(如图所示)。
材料比重为γ弹性模量为 E ,横截面面积为A 。
试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。
解:据题意选点如图所示坐标系xoz ,在距下端(原点)为z 处的c 点取一截面考虑下半段杆的平衡得:题图1-3c 截面的内力:N z =γ·A ·z ; c 截面上的应力:z z N A z z A Aγσγ⋅⋅===⋅; 所以离下端为z 处的任意一点c 的线应变εz 为:zz zEEσγε==;则距下端(原点)为z 的一段杆件在自重作用下,其伸长量为:()22zzzzz z z z y zz l d l d d zd EEEγγγε=⎰⋅∆=⎰⋅=⎰=⎰=;显然该杆件的总的伸长量为(也即下端面的位移):()2222ll A l lW ll d l EEAEAγγ⋅⋅⋅⋅⋅=⎰∆=== ;(W=γAl )2—9.己知物体内一点的应力张量为:σij =50030080030003008003001100-⎡⎤⎢⎥+-⎢⎥⎢⎥--⎣⎦应力单位为kg /cm 2 。
弹塑性力学习题题库加答案(1)

第二章 应力理论和应变理论2—3.试求图示单元体斜截面上的σ30°和τ30°(应力单位为MPa )并说明使用材料力学求斜截面应力为公式应用于弹性力学的应力计算时,其符号及30106.768 6.77()104sin 2cos 2sin 602cos 6022132 3.598 3.60()22x y xy MPa MPa σστατα--=----+=⋅+=⋅-=-⨯-⨯=--代入弹性力学的有关公式得: 己知 σx = -10 σy = -4 τxy = +23030()cos 2sin 2221041041cos 602sin 6073222226.768 6.77()104sin 2cos 2sin 602cos 6022132 3.598 3.60()2x yx yxy x y xy MPa MPa σσσσσατασστατα+-=++---+=++=--⨯+⨯=----+=-⋅+=-⋅+=+⨯=由以上计算知,材力与弹力在计算某一斜截面上的应力时,所使用的公式是不同的,所得结果剪应力的正负值不同,但都反映了同一客观实事。
2—6. 悬挂的等直杆在自重W 作用下(如图所示)。
材料比重为γ弹性模量为 E ,横截面面积为A 。
试求离固定端z 处一点C 的应变εz 与杆的总伸长量Δl 。
解:据题意选点如图所示坐标系xoz ,在距下端(原点)为z 处的c 点取一截面考虑下半段杆的平衡得:题图1-3c 截面的内力:N z =γ·A ·z ; c 截面上的应力:z z N A z z A Aγσγ⋅⋅===⋅; 所以离下端为z 处的任意一点c 的线应变εz 为:zz zEEσγε==;则距下端(原点)为z 的一段杆件在自重作用下,其伸长量为:()22zzzzz z z z y zz l d l d d zd EEEγγγε=⎰⋅∆=⎰⋅=⎰=⎰=;显然该杆件的总的伸长量为(也即下端面的位移):()2222ll A l lW ll d l EEAEAγγ⋅⋅⋅⋅⋅=⎰∆=== ;(W=γAl )2—9.己知物体内一点的应力张量为:σij =50030080030003008003001100-⎡⎤⎢⎥+-⎢⎥⎢⎥--⎣⎦应力单位为kg /cm 2 。
弹塑性力学试题集锦(很全,有答案)

1 / 218弹塑性力学2008级试题一 简述题(60分) 1)弹性与塑性弹性:物体在引起形变的外力被除去以后能恢复原形的这一性质。
塑性:物体在引起形变的外力被除去以后有部分变形不能恢复残留下来的这一性质。
2)应力和应力状态应力:受力物体某一截面上一点处的内力集度。
应力状态:某点处的9个应力分量组成的新的二阶张量∑。
3)球张量和偏量球张量:球形应力张量,即σ=000000m m m σσσ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,其中()13m x y z σσσσ=++ 偏量:偏斜应力张量,即x m xy xz ij yx y m yz zx zy z m S σστττσστττσσ⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦,其中2 / 218()13m x y z σσσσ=++5)转动张量:表示刚体位移部分,即110221102211022u v u w y x z x v u v w ij x y z y w u w v x z y z W ⎡⎤⎛⎫⎛⎫∂∂∂∂--⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎢⎥⎝⎭⎝⎭⎢⎥⎛⎫⎛⎫∂∂∂∂⎢⎥=-- ⎪⎪⎢⎥ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎢⎥⎢⎥⎛⎫⎛⎫∂∂∂∂⎢⎥-- ⎪ ⎪ ⎪⎢⎥∂∂∂∂⎝⎭⎝⎭⎣⎦6)应变张量:表示纯变形部分,即112211221122uu v u w x y x z x v u vv w ij x y yz y w u w v wx z y z zε⎡⎤⎛⎫⎛⎫∂∂∂∂∂++⎢⎥ ⎪ ⎪ ⎪∂∂∂∂∂⎢⎥⎝⎭⎝⎭⎢⎥⎛⎫⎛⎫∂∂∂∂∂⎢⎥=++ ⎪⎪⎢⎥ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭⎢⎥⎢⎥⎛⎫⎛⎫∂∂∂∂∂⎢⎥++ ⎪ ⎪ ⎪⎢⎥∂∂∂∂∂⎝⎭⎝⎭⎣⎦7)应变协调条件:物体变形后必须仍保持其整体性和连续性,因此各应变分量之间,必须要有一定得关3 / 218系,即应变协调条件。
22222y xyx y x x yεγε∂∂∂+=∂∂∂∂。
8)圣维南原理:如作用在弹性体表面上某一不大的局部面积上的力系,为作用在同一局部面积上的另一静力等效力所代替,则荷载的这种重新分布,只造离荷载作用处很近的地方,才使应力的分布发生显著变化,在离荷载较远处只有极小的影响。
弹塑性力学-陈明祥版的-课后习题答案++

◆ 所有与坐标系选取无关的量,统称为物理恒量。
◆ 在一定单位制下,只需指明其大小即足以被说明
的物理量,统称为标量。例如温度、质量、功等。
◆ 在一定单位制下,除指明其大小还应指出其方向
的物理量,称为矢量。例如速度、加速度等。
x j xk
(I-25)
4.张量的分解
张量一般是非对称的。若张量 ai的j 分量满足
aij a ji
(I-27)
则 aij称为对称张量。 如果 的分ai量j 满足
aij a ji
(I-28)
则称为反对称张量。显然反对称张量中标号重复的
分量(也即主对角元素)为零,即 a11 a22 。a33 0
弹塑性力学与材料力学同属固体力学的 分支学科,它们在分析问题解决问题的基本 思路上都是一致的,但在研究问题的基本方 法上各不相同。其基本思路如下:
(1) 受力分析及静力平衡条件 (力的分析)
物体受力作用处于平衡状态,应当满足的条件 是什么?(静力平衡条件)
(2) 变形的几何相容条件 (几何分析)
材料是均匀连续的,在受力变形后仍应是连续 的。固体内既不产生“裂隙”,也不产生“重叠 ”, 此时材料变形应满足的条件是什么?(几何相 容条件)
建立起普 遍适用的理 论与解法。
1、涉及数学理论较复杂,并以其理论与解
法的严密性和普遍适用性为特点;
2、弹塑性的工程解答一般认为是精确的;
3、可对初等力学理论解答的精确度和可靠
进行度量。
四、 弹塑性力学的基本任务
可归纳为以下几点: 1.建立求解固体的应力、应变和位移分布规律的 基本方程和理论; 2.给出初等理论无法求解的问题的理论和方法, 以及对初等理论可靠性与精确度的度量; 3.确定和充分发挥一般工程结构物的承载能力, 提高经济效益; 4.为进一步研究工程结构物的强度、振动、稳定 性、断裂等力学问题,奠定必要的理论基础。
弹塑性力学课后习题答案

(I-4) (I-5)
★ 关于求和标号,即哑标有:
◆ 求和标号可任意变换字母表示。
◆ 求和约定只适用于字母标号,不适用于数字标号。 ◆ 在运算中,括号内的求和标号应在进行其它运算前
优先求和。例:
aii2a121a222a323
(I-12)
(ai) i2(a 1 1a22 a3)3 2 (I-13)
aibjk cijk
(I-21)
◆ 张量乘法不服从交换律,但张量乘法服从分配
律和结合律。例如:
( a i j b i) c j k a i c k j b i c k j; 或 ( a i b k j ) c m a i( b j k c m )
(I-22)
C、张量函数的求导:
◆ 一个张量是坐标函数,则该张量的每个分量都
◆ 绝对标量只需一个量就可确定,而绝对矢量则需
三个分量来确定。
◆ 若我们以r表示维度,以n表示幂次,则关于三维
空间,描述一切物理恒量的分量数目可统一地表 示成:
Mrn (Ⅰ—1)
◆ 现令n为这些物理量的阶次,并统一称这些物
理量为张量。
当n=0时,零阶张量,M=1,标量; 当n=1时,一阶张量,M=3,矢量;
(I-25 )
4.张量的分解
张量一般是非对称的。若张量 aij的分量满足
aij a ji
(I-27)
则 aij 称为对称张量。 如果 的分aij量满足
aij aji
(I-28)
则称为反对称张量。显然反对称张量中标号重复的
分量(也即主对角元素)为零,即 a11a22。a330
第二章 应力理论
七应变莫尔圆41弹性变形与塑性变形的特点塑性力学的附加假设42常用简化力学模型43弹性本构方程弹性应变能函数44屈服函数主应力空间常用屈服条件47塑性本构方程简介静不定问题的解答1静力平衡分析平衡微分方程2几何变形分析几何方程3物理关系分析物理方程表明固体材料产生弹性变形或塑性变形时应力与应变以及应力率与应变率之间关系的物性方程称为本构方程关系
弹塑性力学习题集_很全有答案_
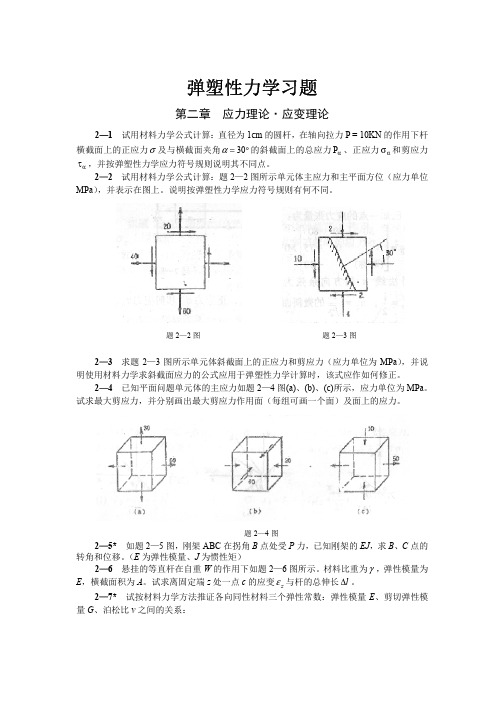
σ y = cx + dy − γy , τ xy = − dx − ay ,其它应力分量为零。试根据
直边及斜边上的边界条件,确定常数 a、b、c、d。 2—16* 已知矩形截面高为 h, 宽为 b 的梁受弯曲时的正 My 12 M 应力 σ z = = y, 试求当非纯弯时横截面上的剪应力公 J bh 3 式。 (利用弹塑性力学平衡微分方程)
题 2—15 图
12 6 0 2—17 已知一点处的应力张量为: σ ij = 6 10 0 MPa ,试求该点的最大主应力及 0 0 0 其主方向。 2—18* 在物体中某一点 σ x = σ y = σ z = τ xy = 0 ,试以 τ yz 和 τ zx 表示主应力。
3—1
为 ε 1 = 1.7 × 10 −4 , ε 2 = 0.4 × 10 −4 。已知ν = 0.3,试求主应变 ε 3 。
3—9 如题 4—9 图示尺寸为 1×1×1cm 的铝方块,无间隙地嵌入——有槽的钢块中。 设钢块不变形,试求:在压力 P = 6KN 的作用下铝块内一点应力状态的三个主应力及主应 变,铝的弹性常数 E=70Gpa,ν = 0.33。 3—10* 直径 D = 40mm 的铝圆柱体, 无间隙地放入厚度为 δ = 2mm 的钢套中, 圆柱受
v = b0 + b1 x + b2 y + b3 z w = c 0 + c1 x + c 2 y + c3 z
式中 a 0 L , a1 L , a 2 L 为常数,试证各点的应变分量为常数。 2—29 设已知下列位移,试求指定点的应变状态。
(1) u = (3x 2 + 20) × 10 −2 , v = (4 yx) × 10 −2 ,在(0,2)点处。 (2) u = (6 x 2 + 15) × 10 −2 , v = (8 zy ) × 10 −2 , w = (3z 2 − 2 xy) × 10 −2 ,在(1,3,4)点处。 2—30 试证在平面问题中下式成立: εx + εy =ε′ x + ε′ y
(完整版)弹塑性力学习题题库加答案.docx
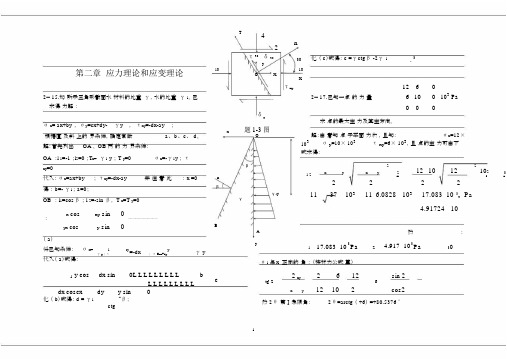
第二章 应力理论和应变理论2— 15.如 所示三角形截面水 材料的比重 γ,水的比重 γ 1。
己求得 力解 :σ x = ax+by , σy =cx+dy- γy , τxy =-dx-ay ;根据直 及斜 上的 界条件,确定常数 a 、b 、c 、 d 。
解:首先列出OA 、 OB 两 的 力 界条件:OA :l 1=-1 ;l 2=0 ;T x= γ1 y ; T y =0σx =-γ1y ; τxy =0代入: σx =ax+by ; τxy =-dx-ay 并 注 意 此 : x =0得 : b=- γ1; a=0;OB : l 1=cos β ; l 2=-sin β, T x =T y =0:x cosxy sin0 yx cosy sin⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( a )将己知条件: σ x=1xy=-dxyγ y-γ y ; τ; σ =cx+dy-代入( a )式得:1 y cos dx sin0L L L L L L L L L bdx coscxdyy sin L L L L L L L L L化 ( b )式得: d = γ12β;ctgT4n2τ 30° δ 30°30°化 ( c )式得: c =γctg β -2γ 13y10x10Ox12 6τxy103 Pa2— 17.己知一点 的 力 量6 10 00 0δ y求 点的最大主 力及其主方向。
x题1-3 图解:由 意知 点 于平面 力状 ,且知:σx =12×O103σ y =10× 103 τ xy =6× 103,且 点的主 力可由下式求得:β212 101221.2xyxy21023n 22xy22610βγ 1y113710311 6.0828 10317.083 10 3 Paγ34.91724 10BA然:y117.083 10 3Pa2 4.917 10 3Pa30σ 1 与 x 正向的 角 : (按材力公式 算)c2 xy2 6 12 sin 2tg 2121026xycos2然 2θ 第Ⅰ象限角: 2θ=arctg ( +6) =+80.5376 °则:θ=+40.2688 B 40° 16'或(-139° 44')2— 19.己知应力分量为:σx=σy=σz=τxy=0,τzy=a,τzx=b,试计算出主应力σ1、σ2、σ3 并求出σ2 的主方向。
弹塑性力学部分习题及答案

解
根据梁的弯曲变形公式,y = Fx/L(L - x),其中y为挠度,F 为力,L为梁的长度。代入题目给定的数据,得y = (frac{300 times (4 - x)}{8})。当x = 2时,y = (frac{300 times (4 - 2)}{8}) = 75mm。
习题三答案及解析
解析
和变形情况。
04
弹塑性力学弹塑性力学的基本假设。
答案
弹塑性力学的基本假设包括连续性假设、均匀性假设、各向同性假设和非线性假设。连 续性假设认为物质是连续的,没有空隙;均匀性假设认为物质的性质在各个位置都是相 同的;各向同性假设认为物质的性质在不同方向上都是相同的;非线性假设认为弹塑性
习题二答案及解析
01 02 03 04
解析
选择题主要考察基本概念的理解,如能量守恒定律、牛顿第二定律等 。
填空题涉及简单的力学计算,如力的合成与分解、牛顿第二定律的应 用等。
计算题要求应用能量守恒定律和牛顿第二定律进行计算,需要掌握基 本的力学原理和公式。
习题三答案及解析
01
答案
02
选择题
03
1. A
2. 解
根据牛顿第二定律,F = ma,其中F为力,m为质量,a 为加速度。代入题目给定的数据,得a = (frac{400}{5}) = 80m/s(}^{2})。再根据运动学公式s = ut + (frac{1}{2})at(}^{2}),得s = 10 × 2 + (frac{1}{2} times 80 times (2)^2) = 108m。
04
计算题要求应用胡克定律和动量守恒定律进行计算,需要掌握基本的 力学原理和公式。
习题二答案及解析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为:σx =ax+by ,σy =cx+dy-γy , τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件:OA 边:l 1=-1 ;l 2=0 ;T x = γ1y ; T y =0 则σx =-γ1y ; τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0 得:b=-γ1;a =0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0则:cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………(a )将己知条件:σx= -γ1y ;τxy =-dx ; σy =cx+dy-γy 代入(a )式得:()()()1cos sin 0cos sin 0y dx b dx cx dy y c γβββγβ-+=⎧⎪⎨--+-=⎪⎩化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103 σy =10×103 τxy =6×103,且该点的主应力可由下式求得:(()()31.233331210102217.0831******* 6.082810 4.9172410x yPa σσσ⎡++⎢=±=⨯⎢⎣⨯=⨯=±⨯=⨯则显然:3312317.08310 4.917100Pa Pa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为:(按材力公式计算)()22612sin 22612102cos 2xyx ytg τθθσσθ--⨯-++====+=--+显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376°题图1-3则:θ=+40.268840°16' 或(-139°44')2—19.己知应力分量为:σx =σy =σz =τxy =0,τzy =a ,τzx =b ,试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
解:由2—11题计算结果知该题的三个主应力分别为:1σ=20σ=;3σ=设σ2与三个坐标轴x 、y 、z 的方向余弦为:l 21、l 22、l 23,于是将方向余弦和σ2值代入下式即可求出σ2的主方向来。
()()()()()()21222232321222232321222322122010203x yx xz xz yx y yz zy zx zy z yx zy l l l l l l l l l l l l l σσττττσσττττσσττ⎧-++==⎪⎪+-+==⎨⎪++-=+=⎪⎩以及:()22221222314l l l ++=由(1)(2)得:l 23=0 由(3)得:2122l a l b =-;2221l b l a=-; 将以上结果代入(4)式分别得:21l ===;22l ===;2122al l b =-22l ∴==同理21l = 于是主应力σ2的一组方向余弦为:(,22b a b+,0);σ3的一组方向余弦为(2±); 2—20.证明下列等式: (1):J 2=I 2+2113I ; (3):()212ii kk ik ik I σσσσ=--; 证明(1):等式的右端为:()()22211223311231133I I σσσσσσσσσ+=-+++++()()22212312233112233112223σσσσσσσσσσσσσσσ=+++++-++ ()()()222123122331122331246666σσσσσσσσσσσσσσσ=+++++-++22212312233126σσσσσσσσσ⎡⎤=++---⎣⎦22222211222233331112226σσσσσσσσσσσσ⎡⎤=-++-++-+⎣⎦()()()222122331216J σσσσσσ⎡⎤=-+-+-=⎣⎦故左端=右端 证明(3):()212ii kk ik ik I σσσσ=-- 右端=()12ii kk ik ik σσσσ- ()()()222222122x y z xy yz zx x y z x y z σσστττσσσσσσ⎡⎤=+++++-++++⎣⎦ ()()2222222221222x y z xy yz zx x y z x y y z z x σσστττσσσσσσσσσ⎡⎤=+++++----++⎣⎦()2222x y y z z x xy yz zx I σσσσσστττ=-++---=2—32:试说明下列应变状态是否可能(式中a 、b 、c 均为常数)(1):()22200000ij c x y cxy cxy cy ε⎡⎤+⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(2): ()()()()222222222210210211022ij axy ax by ax y az by ax by az by ε⎡⎤+⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥++⎢⎥⎣⎦(3): ()22200000ij c x y z cxyz cxyz cy z ε⎡⎤+⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 解(1):由应变张量εij 知:εxz =εyz =εzx =εzy =εz =0 而εx 、εy 、εxy 及εyx 又都是x 、y 坐标的函数,所以这是一个平面应变问题。
将εx 、εy 、εxy 代入二维情况下,应变分量所应满足的变形协调条件知:22222y xyx y x x yεγε∂∂∂+=∂∂∂∂ 也即:2c +0=2c 知满足。
所以说,该应变状态是可能的。
解(2):将己知各应变分量代入空间问题所应满足的变形协调方程得:222222222222222222222y xyx y yzz x zxz xy yz zx x xy yz y zx yz xy zx z y x x yz y y z x z z x x y z x y z y z x y z x z x y z x y εγεεγεεγεγγγεγγεγγγγε⎫∂∂∂+=⎪∂∂∂∂⎪⎪∂∂∂⎪+=∂∂∂∂⎪⎪∂∂∂+=∂∂∂∂⎬∂∂⎛⎫∂∂∂+-= ⎪∂∂∂∂∂∂⎝⎭∂∂∂⎛⎫∂∂+-=⎪∂∂∂∂∂∂⎝⎭∂∂⎛⎫∂∂∂+-= ⎪∂∂∂∂∂∂⎝⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭………………………………(1) 202000002220cz cz cy cy cx +=⎫⎪+≠⎪⎪=⎬⎪=⎪≠⎪⎭不满足,因此该点的应变状态是不可能的。
第三章:弹性变形及其本构方程3-10.直径为D=40mm 的铝圆柱体,紧密地放入厚度为=δ2mm 的钢套中,圆柱受轴向压力P =40KN 。
若铝的弹性常数据E 1=70G a p .V 1=0.35,钢的弹性常数E =210G a p 。
试求筒内的周向应力。
钢钢钢E q q E 10102.02104122=⨯⨯⨯⨯=--ε∵ 钢铝εε= q =2.8MN /m 2钢套 228/2qDMN m t θσ==t qv r 2=σ ; tqr=θσ ; 0=z σ ; 1εσ⋅=E r ;4-14.试证明在弹性范围内剪应力不产生体积应变,并由纯剪状态说明v =0。
证明:在外力作用下,物体将产生变形,也即将产生体积的改变和形状的改变。
前者称为体变,后者称为形变。
并且可将一点的应力张量σij 和应变张量εij 分解为,球应力张量、球应变张量和偏应力张量、偏应变张量。
ij m ij ijijm ij ij s e σσδεεδ=+⎧⎨=+⎩ 而球应变张量只产生体变,偏应变张量只引起形变。
通过推导,我们在小变形的前提下,对于各向同性的线弹体建立了用球应力、球应变分量和偏应力分量,偏应变分量表示的广义胡克定律:()()3122m m e ij ijk k s Ge σε⎧==⎪⎨=⎪⎩ (1) 式中:e 为体积应变 1231x y z e I εεεεεε'=++=++= 由(1)式可知,物体的体积应变是由平均正力σm 确定,由e ij 中的三个正应力之和为令,以及(2)式知,应变偏量只引起形变,而与体变无关。
这说明物体产生体变时,只能是平均正应力σm 作用的结果,而与偏应力张量无关进一步说就是与剪应力无关。
物体的体积变形只能是并且完全是由球应力张量引起的。
由单位体积的应变比能公式:3122o ov od m m ij ij u u u s e σε=+=+;也可说明物体的体变只能是由球应力分量引起的。
当某一单元体处于纯剪切应力状态时:其弹性应变比能为:221102o ov od xy xy v u u u G Eττ+=+=+= 由u o 的正定性知:E >0,1+v >0.得:v >-1。
由于到目前为止还没有v <0的材料,所以,v 必须大于零。
即得:v >0。
3-16.给定单向拉伸曲线如图所示,εs 、E 、E ′均为已知,当知道B 点的应变为ε时,试求该点的塑性应变。
解:由该材料的σ—ε曲线图可知,该种材料为线性强化弹塑性材料。
由于B 点的应变已进入弹塑性阶段,故该点的应变应为:εB =ε=εe +εp 故:εp =ε-εe()()11e e s s E E E EE Eσεεσεεεεεε''=-=-+-=-+-⎡⎤⎡⎤⎣⎦⎣⎦ 111s s s E E E E E E E E E E εεεεεε'''⎛⎫⎛⎫=--+=--- ⎪ ⎪⎝⎭⎝⎭()1s E E εε'⎛⎫=-- ⎪⎝⎭;3-19.已知藻壁圆筒承受拉应力2sz σσ=及扭矩的作用,若使用Mises 条件,试求屈服时扭转应力应为多大?并求出此时塑性应变增量的比值。
解:由于是藻壁圆筒,所可认圆筒上各点的应力状态是均匀分布的。
据题意圆筒内任意一点的应力状态为:(采用柱坐标表示)0θσ=,0r σ=,2sz σσ=;0r θτ=,z θττ=;0zr τ=;于是据miess 屈服条件知,当该藻壁圆筒在轴向拉力(固定不变)ρ及扭矩M (遂渐增大,直到材料产生屈服)的作用下,产生屈服时,有:()()()()122222226s r z z r r z zr θθθθσσσσσσστττ⎡⎤=-+-+-+++⎣⎦11222222266222s s sσσσττ⎡⎤⎡⎤⎛⎫⎛⎫=-++=+⎢⎥⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎦⎣⎦解出τ得:2sστ=;τ就是当圆筒屈服时其横截面上的扭转应力。
