解直角三角形应用中的“双直角三角形”模型
初中几何双直角三角形模型
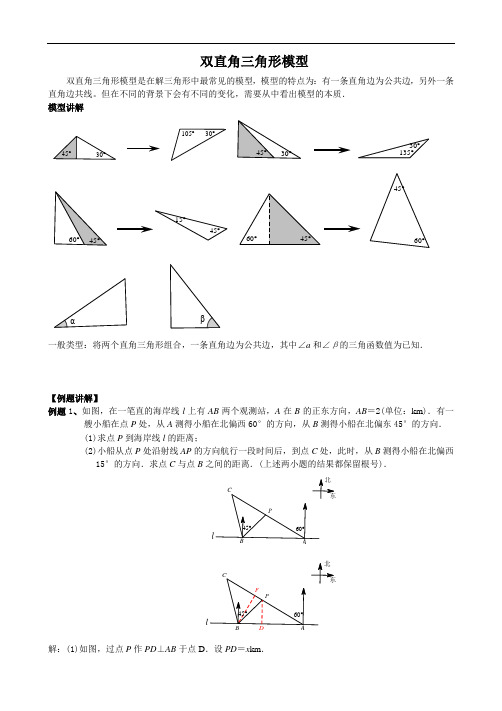
双直角三角形模型双直角三角形模型是在解三角形中最常见的模型,模型的特点为:有一条直角边为公共边,另外一条直角边共线。
但在不同的背景下会有不同的变化,需要从中看出模型的本质.模型讲解105°30°30°135°15°45°60°45°一般类型:将两个直角三角形组合,一条直角边为公共边,其中∠a和∠β的三角函数值为已知.【例题讲解】例题1、如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(1)求点P到海岸线l的距离;(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号).ll解:(1)如图,过点P作PD⊥AB于点D.设PD=x km.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x km.在Rt A△P AD中,∠ADP=90°,∠P AD=90°-60°=30°,∴AD=3PD=3x km.∵BD+AD=AB,∴x+3x=2,x=3-1,∴点P到海岸线l的距离为(3-1)km;(2)如图,过点B作BF⊥AC于点F.在Rt△ABF中,∠AFB=90°,∠BAF=30°,∴BF=12AB=l km.在△ABC中,∠C=180°-∠BAC-∠ABC=45°.在Rt△BCF中,∠BFC=90°,∠C=45°,∴BC=2BF=2km,∴点C与点B之间的距离为2km.例题2、如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.(1)若轮船照此速度与航向航行,何时到达海岸线?(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:2≈1.4,3≈1.7)解:(1)延长AB交海岸线于点D,过点B作BE⊥海岸线于点E,过点A作AF⊥l于F,如图所示.∵∠BEC=∠AFC=90°,∠EBC=60°,∠CAF=30°,∴∠ECB=30°,∠ACF=60°,∴∠BCA=90°,∵BC=12,AB=36×4060=24,∴AB=2BC,∴∠BAC=30°,∠ABC=60°,∵∠ABC=∠BDC+∠BCD=60°,∴∠BDC=∠BCD=30°,∴BD=BC=12,∴时间t=1236=13小时=20分钟,∴轮船照此速度与航向航行,上午11:00到达海岸线.(2)∵BD=BC,BE⊥CD,∴DE=EC,在RT△BEC中,BC=12,∠BCE=30°,∴BE=6,EC=3≈10.2,∴CD=20.4,∵20<20.4<21.5,∴轮船不改变航向,轮船可以停靠在码头.【巩固练习】 1、如图,从热气球C 上测定建筑物A 、B 底部的俯角分别为30°和60°,如果这时气球的高度CD 为150米,且点A 、D 、B 在同一直线上,建筑物A 、B 间的距离为 .2、如图,在高楼前D 点测得楼顶的仰角为30°,向高楼前进60米到C 点,又测得仰角为45°,则该高楼的高度大约为 .(保留整数)3、如图是一山谷的横断面示意图,宽AA ′为15m ,用曲尺(两直尺相交成直角)从山谷两侧测量出OA =1m ,OB =3m ,O ′A ′=0.5m ,O ′B ′=3m (点A ,O ,O ′,A ′在同一条水平线上),则该山谷的深h 为 m .4、如图所示,一条自西向东的观光大道l 上有A 、B 两个景点,A 、B 相距2km ,在A 处测得另一景点C 位于点A 的北偏东60°方向,在B 处测得景点C 位于景点B 的北偏东45°方向,求景点C 到观光大道l 的距离.(结果精确到0.1km )5、如图,在直角坐标系中,直线y =-34x +6与坐标轴分别交于A 、B 两点,AB 中点为点P ,则点P 到直线y =-x 的最短距离PQ 的长度为 .xyQABOP6、如图,在△ABC,AC=3,BC=4,∠ACB=90°,将△ABC绕点C顺时针旋转.(1)当AC平分∠A′CB′时,BD的长为;(2)连接AA′,当△AA′C为等边三角形时,BD的长为.A'B'EAB CD7、如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.(1)若AD=2,求AB;(2)若AB+CD=23+2,求A B.A B CD8、如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度.(结果精确到个位,参考数据:2≈1.41,3≈1.73,6≈2.4)9、2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.飞机上有239名乘客,其中154名是中国同胞,中国政府启动了全面应急和搜救机制,派出多艘中国舰船在相关海域进行搜救.如图,某日在南印度洋海域有两艘自西向东航行的搜救船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两船同时测得在A 的东北方向,B的北偏东15°方向有一疑似物C,求此时疑似物C与搜救船A、B的距离各是多少?(结果保留根号)10、如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A 处测得灯塔P 在船的西北方向.航行40分钟后到达点B 处,这时灯塔P 恰好在船的正北方向.已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?11、学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x °、y °和z °,若满足x 2+y 2=z 2,则称这个三角形为勾股三角形.(1)根据“勾股三角形”的定义,请你直接判断命题:“直角三角形是勾股三角形”是真命题还是假命题?(2)如图,△ABC 内接于⊙0,AB 6AC =13BC =2,⊙O 的直径BE 交AC 于点D , ①求证:△ABC 是勾股三角形;②求DE 的长.CD E O B参考答案1.解:∵∠ECA =30°,∠FCB =60°,又∵CD ⊥AB ,CD ⊥EF ,∴∠ACD =60°,∠BCD =30°,在Rt △ADC 中,tan ∠ACD =ADCD∴4D =tan 60°⋅DC 3×90=3, 在Rt △BCD 中,tan ∠BCD =BDCD, BD =tan 30°⋅DC 390=3∴AB =AD +BD =33=3答:建筑物A 、B 间距离为3米.2.解:设楼高AB 为x .在Rt △ADB 中有:DB =tan30x ︒ =3,在Rt △ACB 中有:BC =tan 45x︒=x . 而CD =BD -BC =31)x =60,解得x =82.3.解:设A 、A ′到谷底的水平距离为AC =m ,A ′C =n ,∴m +n =15,根据题意知,OB ∥CD ∥O ′B ′.∵OA =1,OB =3,0′A ′=0.5,O ′B ′=3.∴h m=OB OA =3,h n =''''O B O A =6, ∴(13+16)h =15,解得h =30(m )4.解:如图,过点C作CD⊥l于点D,设CD=x km,在△ACD中,∵∠ADC=90°,∠CAD=30°,∴AD=3CD=3x km,在△BCD中,∵∠BDC=90°,∠CBD=45°,∴BD=CD=x km,∵AD-BD=AB,∴3x-x=2,∴X=3+1=2.7(k m).答:景点C到观光大道的距离约为2.7km.5.解:可知点P为(4,3),作PH⊥y轴交直线y=-x于点H,则H(4,-4),PH=7,∴最短距离PQ22722xyHPOBAQ6.解:过D作DH⊥BC于H,(1)可知∠BCD=45°,设CH=DH=t,则BH=43t,∴BC=t+43t=4,解得t=127,∴BD=53t=207.(2)可知∠BCD=∠A′CA=60°,设CH=DH=t,则BH3,∴BC=t3=4,解得t=31),∴BD=53×3-1)10310HA'B'EABCD7.解:(1)过D点作DE⊥AB,过点B作BF⊥CD,∵∠A=∠C=45°,∠ADB=∠ABC=105°,∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=360°﹣45°﹣45°﹣105°=165°,∴∠BDF=∠ADC﹣∠ADB=165°﹣105°=60°,△ADE与△BCF为等腰直角三角形,∵AD=2,∴AE=DE22∵∠ABC =105°,∴∠ABD =105°﹣(180°﹣45°﹣60°)=30°, ∴BE =tan30DE︒=233=6,∴AB =2+6; (2)设DE =x ,则AE =x ,BE =tan30x︒=33x =3x ,∴BD =2x , ∵∠BDF =60°,∴∠DBF =30°,∴DF =12BD =x ,∴BF =3x ,∴CF =3x , ∵AB =AE +BE =x +3x ,CD =DF +CF =x +3x ,AB +CD =23+2, ∴AB =3+1AE BCFD8.解:(1)延长BA 交EF 于点G .在Rt △AGE 中,∠E =23°,∴∠GAE =67°,又∵∠BAC =38°,∴∠CAE =180°﹣67°﹣38°=75°. (2)过点A 作AE ⊥CD ,垂足为H .在△ADH 中,∠ADC =60°,AD =8,cos ∠ADC =DHAD, ∴DH =4,sin ∠ADC =AHAD,∴AH =43. 在Rt △ACH 中,∠C =180°﹣75°﹣60°=45°,∴CH =AH =43,AC =46. ∴AB =AC +CD =46+43+4≈20 (米). 答:这棵大树折断前高约20米.9.解:过点B 作BD ⊥AC 于D .由题意可知,∠BAC =45°,∠ABC =90°+15°=105°, ∴∠ACB =180°﹣∠BAC ﹣∠ABC =30°.在Rt △ABD 中,AD =BD =AB •sin ∠BAD =20×22=102 (海里), 在Rt △BCD 中,BC =sin BDBCD∠=10212=202 (海里),DC =tan BDBCD ∠=10233=106 (海里),∴AD +CD =102+106=10(2+6)(海里).答:疑似物C 与搜救船A 的距离是10(2+6)海里,与搜救船B 的距离是20海里.10.解:这艘船能按原方向继续向前航行.理由如下:如图,过点B 作BH ⊥AP 于H ,过点P 作PM ⊥AB ,交AB 延长线于M . 由题意,知AB =24×4060=16(海里),∠BAP =75°﹣45°=30°. ∵PB ∥AC ,∴∠BPH =∠CAP =45°.在Rt △ABH 中,BH =12AB =8,AH =3BH =83. 在Rt △PBH 中,PH =BH =8,∴P A =PH +AH =8+83,∴PM =P A •sin ∠P AM =12P A =4+43>9,∴能按原方向继续向前航行.11.解:(1)∵对于任意的三角形,设其三个角的度数分别为x °、y °和z °,若满足x 2+y 2=z 2,则称这个三角形为勾股三角形,∴无法得到,所有直角三角形是勾股三角形,故是假命题;(2)由题意可得:2221802160x y z xy x y z⎧++=⎪=⎨⎪+=⎩,解得:x +y =102;(3)①证明:过B 作BH ⊥AC 于H ,设AH =x ,Rt △ABH 中,BH 26x -,Rt△CBH中,)2+(1x)2=4,解得:x所以,AH=BH,HC=1,∴∠A=∠ABH=45°,∴tan∠HBC=CHBHHBC=30°,∴∠BCH=60°,∠B=75°,∴452+602=752,∴△ABC是勾股三角形;②连接CE,∵∠A=45°,∴∠BEC=∠BAC=45°,又∵BE是直径,∴∠BCE=90°,∴BC=CE=2,过D作DK⊥AB于K,设KD=h,∵∠EBC=45°,∠ABC=75°,∴∠ABE=30°,∴BK,AK=h,∴hhh∴BD=2KD=2h=BE﹣BD=。
北师大版初中数学9年级下册解直角三角形应用中的“双直角三角形”模型-优课件

.
QC 45°
D
60°
1500米
O
AB
如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m,高度C处
的飞机,测量人员测得正前方A、B两点处的俯角分别为60°和45°,求隧道AB的长
.
QC 45°
D 解:由题意得∠ACO=30°,∠CBO=45°,
60° 1500米
O
AB
在 Rt△COA 中,∵tan30°= OA CO
答:此时轮船所在的 B 处与灯塔 P 的距离是 40 6 海里.
如图,A、B 两地之间有一座山,汽车原来从A地到B 地经过C 地沿折线 A→C→B行驶,现开通隧道后,汽车直接沿直线 AB 行驶. 已知 AC = 10 千米, ∠A = 30°,∠B = 45°. 则隧道开通后,汽车从 A地到B 地比原来少走多少千米?( 结果保留根号)
C
在 Rt△ACD 中,∵∠A= 30°,∴CD = 1 AC=5 千米
2
30°
45°
∴
AD
CD tan 300
5 5 3
3 千米
A
D
B
3
在 Rt△BCD 中,∵∠B= 45°
∴BD = CD = 5,BC=5 2 千米
∴ AC+ BC-AB=10 5 2 (5 3 5)=(5 5 2 5 3 )千米
∴OA=CO×tan30°=1500× 3 =500 3 m, 3
在 Rt△COB 中,OB=OC=1500m,
∴AB=(1500﹣500 3 ) m
答:隧道 AB 的长约为(1500﹣500 3 ) m.
类型二:背靠式
如图,一艘轮船位于灯塔P的北偏东60°方向且与灯塔P的距离为80海里的A处
八年级上册数学专题第7讲 双直角三角形模型
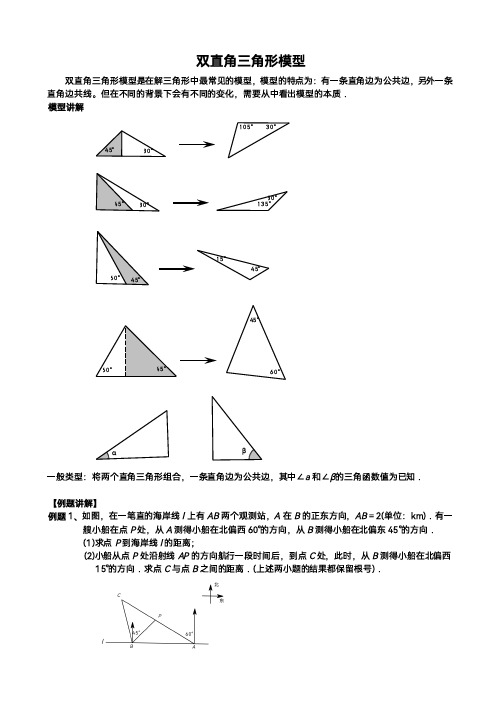
双直角三角形模型双直角三角形模型是在解三角形中最常见的模型,模型的特点为:有一条直角边为公共边,另外一条直角边共线。
但在不同的背景下会有不同的变化,需要从中看出模型的本质.模型讲解105°30°30°45°30°135°30°45°15°45°60°45°60°45°45°60°βα一般类型:将两个直角三角形组合,一条直角边为公共边,其中∠a 和∠β的三角函数值为已知.【例题讲解】例题1、如图,在一笔直的海岸线l 上有AB 两个观测站,A 在B 的正东方向,AB =2(单位:km ).有一艘小船在点P 处,从A 测得小船在北偏西60°的方向,从B 测得小船在北偏东45°的方向.(1)求点P 到海岸线l 的距离;(2)小船从点P 处沿射线AP 的方向航行一段时间后,到点C 处,此时,从B 测得小船在北偏西15°的方向.求点C 与点B 之间的距离.(上述两小题的结果都保留根号).解:(1)如图,过点P作PD⊥AB于点D.设PD=x km.在R t△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x km.在R t A△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,∴AD=3PD=3x km.∵BD+AD=AB,∴x+3x=2,x=3-1,∴点P到海岸线l的距离为(3-1)km;(2)如图,过点B作BF⊥AC于点F.AB=l km.在R t△ABF中,∠AFB=90°,∠BAF=30°,∴BF=12在△ABC中,∠C=180°-∠BAC-∠ABC=45°.在R t△BCF中,∠BFC=90°,∠C=45°,∴BC=2BF=2km,∴点C与点B之间的距离为2km.例题2、如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.(1)若轮船照此速度与航向航行,何时到达海岸线?(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:2≈1.4,3≈1.7)解:(1)延长AB交海岸线于点D,过点B作BE⊥海岸线于点E,过点A作AF⊥l于F,如图所示.∵∠BEC=∠AFC=90°,∠EBC=60°,∠CAF=30°,∴∠ECB=30°,∠ACF=60°,∴∠BCA=90°,∵BC=12,AB=36×40=24,∴AB=2BC,∴∠BAC=30°,∠ABC=60°,60∵∠ABC=∠BDC+∠BCD=60°,∴∠BDC=∠BCD=30°,∴BD=BC=12,∴时间t=1236=13小时=20分钟,∴轮船照此速度与航向航行,上午11:00到达海岸线.(2)∵BD=BC,BE⊥CD,∴DE=EC,在RT△BEC中,BC=12,∠BCE=30°,∴BE=6,EC=63≈10.2,∴CD=20.4,∵20<20.4<21.5,∴轮船不改变航向,轮船可以停靠在码头.【巩固练习】1、如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,建筑物A、B间的距离为.2、如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为.(保留整数)3、如图是一山谷的横断面示意图,宽AA′为15m,用曲尺(两直尺相交成直角)从山谷两侧测量出OA=1m,OB=3m,O′A′=0.5m,O′B′=3m(点A,O,O′,A′在同一条水平线上),则该山谷的深h为m.4、如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l 的距离.(结果精确到0.1km)5、如图,在直角坐标系中,直线y=-34x+6与坐标轴分别交于A、B两点,AB中点为点P,则点P到直线y=-x的最短距离PQ的长度为.6、如图,在△ABC,AC=3,BC=4,∠ACB=90°,将△ABC绕点C顺时针旋转.(1)当AC平分∠A′CB′时,BD的长为;(2)连接AA′,当△AA′C为等边三角形时,BD的长为.A'B'EAB CD7、如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.(1)若AD=2,求AB;(2)若AB+CD=23+2,求A B.A B CD8、如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度.(结果精确到个位,参考数据:2≈1.41,3≈1.73,6≈2.4)9、2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH 370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.飞机上有239名乘客,其中154名是中国同胞,中国政府启动了全面应急和搜救机制,派出多艘中国舰船在相关海域进行搜救.如图,某日在南印度洋海域有两艘自西向东航行的搜救船A 、B ,B 船在A 船的正东方向,且两船保持20海里的距离,某一时刻两船同时测得在A 的东北方向,B 的北偏东15°方向有一疑似物C ,求此时疑似物C 与搜救船A 、B 的距离各是多少?(结果保留根号)10、如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A 处测得灯塔P 在船的西北方向.航行40分钟后到达点B 处,这时灯塔P 恰好在船的正北方向.已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?11、学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x °、y °和z °,若满足x 2+y 2=z 2,则称这个三角形为勾股三角形.(1)根据“勾股三角形”的定义,请你直接判断命题:“直角三角形是勾股三角形”是真命题还是假命题?(2)如图,△ABC 内接于⊙0,AB=6,AC =1+3,BC =2,⊙O 的直径BE 交AC 于点D ,①求证:△ABC 是勾股三角形;②求DE 的长.AC DEOB参考答案1.解:∵∠ECA =30°,∠FCB =60°,又∵CD ⊥AB ,CD ⊥EF ,∴∠ACD =60°,∠BCD =30°,在R t △ADC 中,t a n ∠ACD =A DC D ∴4D =t a n 60° DC =3×90=903,在R t △BCD 中,t a n ∠BCD =B D C D ,BD =t a n 30° DC =33×90=303,∴AB =AD +BD =903+303=1203.答:建筑物A 、B 间距离为1203米.2.解:设楼高AB 为x .在R t △ADB 中有:DB =t a n 30x=3x ,在R t △ACB 中有:BC =t a n 45x =x .而CD =BD -BC =(3-1)x =60,解得x =82.3.解:设A 、A ′到谷底的水平距离为AC =m ,A ′C =n ,∴m +n =15,根据题意知,OB ∥CD ∥O ′B ′.∵OA =1,OB =3,0′A ′=0.5,O ′B ′=3.∴h m =O B O A =3,h n =''''O B O A =6,∴(13+16)h =15,解得h =30(m ).4.解:如图,过点C 作CD ⊥l 于点D ,设CD=x km ,在△ACD 中,∵∠ADC =90°,∠CAD =30°,∴AD =3CD =3x km ,在△BCD 中,∵∠BDC =90°,∠CBD =45°,∴BD =CD =x km ,∵AD -BD =AB ,∴3x -x =2,∴X =3+1=2.7(k m ).答:景点C 到观光大道的距离约为2.7km .5.解:可知点P 为(4,3),作PH ⊥y 轴交直线y=-x 于点H ,则H (4,-4),PH =7,∴最短距离PQ =2P H =72=7226.解:过D 作DH ⊥BC 于H ,(1)可知∠BCD =45°,设CH =DH =t ,则BH =43t ,∴BC =t +43t =4,解得t =127,∴BD =53t =207.(2)可知∠BCD =∠A ′CA =60°,设CH =DH =t ,则BH =3t ,∴BC =t +3t =4,解得t =2(3-1),∴BD =53×2(3-1)=103103 .H A 'B 'E ABC D7.解:(1)过D 点作DE ⊥AB ,过点B 作BF⊥CD ,∵∠A =∠C =45°,∠ADB =∠ABC=105°,∴∠ADC =360°﹣∠A ﹣∠C ﹣∠ABC =360°﹣45°﹣45°﹣105°=165°,∴∠BDF =∠ADC ﹣∠ADB =165°﹣105°=60°,△ADE 与△BCF 为等腰直角三角形,∵AD =2,∴AE =DE =22=2,∵∠ABC =105°,∴∠ABD =105°﹣(180°﹣45°﹣60°)=30°,∴BE =t a n 30D E=233=6,∴AB=2+6;(2)设DE =x ,则AE =x ,BE =t a n 30x=33x =3x ,∴BD =2x ,∵∠BDF =60°,∴∠DBF =30°,∴DF =12BD =x ,∴BF =3x ,∴CF =3x ,∵AB =AE +BE =x +3x ,CD =DF+CF =x +3x ,AB +CD =23+2,∴AB =3+1A E BCFD8.解:(1)延长BA 交EF 于点G .在R t △AGE中,∠E =23°,∴∠GAE =67°,又∵∠BAC =38°,∴∠CAE =180°﹣67°﹣38°=75°.(2)过点A 作AE ⊥CD ,垂足为H .在△ADH中,∠ADC=60°,AD=8,c os∠ADC=D HA D,∴DH=4,sin∠ADC=A HA D,∴AH=43.在R t△ACH中,∠C=180°﹣75°﹣60°=45°,∴CH=AH=43,AC=46.∴AB=AC+CD=46+43+4≈20(米).答:这棵大树折断前高约20米.9.解:过点B作BD⊥AC于D.由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,∴∠ACB=180°﹣∠BAC﹣∠ABC=30°.在R t△ABD中,AD=BD=AB•sin∠BAD=20×22=102(海里),在R t△BCD中,BC=si n B DB C D=10212=202(海里),DC=t a n B DB C D=10233=106(海里),∴AD+CD=102+106=10(2+6)(海里).答:疑似物C与搜救船A的距离是10(2+6)海里,与搜救船B的距离是20海里.10.解:这艘船能按原方向继续向前航行.理由如下:如图,过点B作BH⊥AP于H,过点P作PM⊥AB,交AB延长线于M.由题意,知AB=24×4060=16(海里),∠BAP=75°﹣45°=30°.∵PB∥AC,∴∠BPH=∠CAP=45°.在R t △ABH 中,BH =12AB =8,AH =3BH =83.在R t △PBH 中,PH =BH =8,∴PA =PH +AH =8+83,∴PM=PA •sin ∠PAM =12PA =4+43>9,∴能按原方向继续向前航行.11.解:(1)∵对于任意的三角形,设其三个角的度数分别为x °、y °和z °,若满足x 2+y 2=z 2,则称这个三角形为勾股三角形,∴无法得到,所有直角三角形是勾股三角形,故是假命题;(2)由题意可得:2221802160xy z xy x y z ,解得:x +y =102;(3)①证明:过B 作BH ⊥AC 于H ,设AH=x ,R t △ABH 中,BH =26x ,R t △CBH 中,(26x )2+(1+3﹣x )2=4,解得:x =3,所以,AH =BH =3,HC =1,∴∠A =∠ABH =45°,∴t a n ∠HBC =C HB H =13=33,∴∠HBC =30°,∴∠BCH =60°,∠B =75°,∴452+602=752,∴△ABC 是勾股三角形;②连接CE ,∵∠A =45°,∴∠BEC =∠BAC =45°,又∵BE 是直径,∴∠BCE =90°,∴BC =CE =2,过D 作DK ⊥AB 于K ,设KD =h ,∵∠EBC =45°,∠ABC =75°,∴∠ABE =30°,∴BK =3h ,AK =h ,∴h +3h =6,解得:h =3262 ,∴BD =2KD =2h =32﹣6,∴BE ﹣BD =22﹣(32﹣6)=6﹣2.AC DEHO B K。
【万能解题模型】13 解直角三角形的实际应用中的基本模型(课件)中考数学

解:过点 B 作 BE⊥AD 于点 D,BF⊥CD 于点 F. ∵CD⊥AD, ∴四边形 BEDF 是矩形. ∴FD=BE,FB=DE. 在 Rt△ABE 中,BE∶AE=1∶2.4=5∶12, 设 BE=5x,AE=12x, 根据勾股定理,得 AB=13x, ∴13x=52.
解得 x=4. ∴BE=FD=5x=20,AE=12x=48. ∴DE=FB=AD-AE=72-48=24. ∴在 Rt△CBF 中, CF=FB·tan ∠CBF≈24×43=32. ∴CD=FD+CF=20+32=52. 答:大楼的高度 CD 约为 52 米.
图形演变 2:
3.如图所示,某办公大楼正前方有一根高度是 15 米的旗杆 ED,从办公楼顶 端 A 测得旗杆顶端 E 的俯角α是 45°,旗杆底端 D 到大楼前梯坎底边的距离 DC 是 20 米,梯坎坡长 BC 是 12 米,梯坎坡度 i=1∶ 3,则大楼 AB 的高度约为(精确到 0.1 米,参考数据: 2≈1.41, 3≈1.73, 6≈2.45)( D )
又∵BC=221,即 CD+BD=221, ∴0.85x+0.53x=221, 解得 x≈160. 答:AB 的长约为 160 m.
模型 2 母子型(在三角形外部作高)
模型分析: 通过在三角形外作高,构造出两个直角三角形求解,其中公共边 是解题的关键.
等量关系: 在 Rt△ABC 和 Rt△DBC 中,BC 为公共边,AD+DC=AC. 图形演变 1:
2.如图,A,B 两点被池塘隔开,在 AB 外选一点 C,连接 AC, BC.测得 BC=221 m,∠ACB=45°,∠ABC=58°.根据测得的数据, 求 AB 的长.(结果取整数,参考数据:sin 58°≈0.85,cos 58°≈0.53, tan 58°≈1.60)
发挥典型例题“模型”的解题功能双“直角三角形”在解直角三角形中的应用

发挥典型例题“模型”的解题功能——双“直角三角形”在解直角三角形中的应用例3如图,折叠长方形的一边AD,使点D落在BC的边上的点F处,已知AB=8cm,BC=10cm.求折痕AE的长.分析:这是一道折纸问题,解决这类问题一定要把握折痕是对称轴,深入探究隐含条件,准确找到已知条件,未知条件以及它们之间的关系,构建立方程求解.解:连接AE,A'.'AADE与△AFE重合,.AFE坌ADEB...AF:AD=BC=10.F是通过作辅助线,把四边形分成两个直角三角形,进行求解.但其中一个直角要运用勾股定理的逆定理进行证明,在推理时,应注意将较小的两边的平方和与较大的边的平方相比较.例4如图,在四边形ABCD中,C=90.,AB=13,BC=4,CD=3,AD:12,求四边形ABCD的面积.D分析:连接BD,由勾股DE喜理得茎BABADAc合,边的长运用逆定一c理,~AABD是直角三角F=DE.设EC=,贝4DE=8一.在RtAABF中,AB+B=A..?.BF:,:,:6..'.'C=BC—BF=10—6=4在RtACEF中,FC+CE=EF2,即4+:(8一).解得:3..'.EF=DE=5.在RtAAFE中,AE=AF+EF=10+5.=125.AE=5答:折痕AE的长为5cm.四,运用逆定理求解已知四边形的四边长以及一个直角时,通常形,于是,四边形ABCD的面积不难求出.解:连接BD,在RtACBD中,由勾股定理可得BD=,/B+cD=~/4+3=5.又?.?BD+AD:5+12=169.AB:13=169,.?.BD+AD=AB..'.△ABD是直角三角形...S四边形^BcD=S△^BD+S△i}f_:AD-BD+1-BC.CD:÷×12×5+÷×4×':3624330.=_I×l×)+_××= 发挥典型例题"摸型''-j8Ig禳题功能双"直角三角形''在解直角三角形中的应用◆江苏王锋教材上有这样一道习题:为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为27.,然后他向气球方向前进了50米,此时观测气球,测得仰角为40..若小明的眼睛离地面1.6米,小明如何计算气球的高度?(精确到0.1米)分析:这是一个具有实际情景的数学问题,首先应把它抽象为数学问题,找到其数学A模型.用点c表示气球的位置,为什么胖的人比瘦的人怕热?.$肄潍堡明盈礁酗日D≯l:^栌觏《,点A,B表示小明2次观测气球的位置,点A,曰,D 在同一直线上,CD上AD,CD的长与小明的眼睛离地面的高度的和就是所求的气球的高度.(解答略)课本中有些例题就其使用价值而言,往往不亚于一些重要的定理,法则,可谓璞玉浑金,平面直角坐标系的创始人,着名的法国数学家笛卡儿曾经说过:"我所解决的每一个问题都将成为一个范例,以用于解决其他相关的问题."观察,再现上面习题图形的结构特征,探究,挖掘其中隐含的数学信息可以发现:①2个RtAADC,RtABDC有一个公共的直角边CD:②2个直角边AD,BD存在关系AD—BD=AB.这2个关系式恰是我们将未知量与已知量联系在一起列方程的重要的相等关系. 事实上许多与此相联系解直角三角形的实际应用问题,抓住上述的"双直角三角形"模型所具有的2个特征都可迎刃而解.一,计算遮阳棚的宽度例1在一次课题学习课上,同学们为教室窗户设计一个遮阳棚,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2米,BCD表示直角遮阳棚,已知当地一年中在午时的太阳光与水平线CD的最小夹角Og为18.6.,最大夹角JB为64.5..请你根据以上数据,帮助小明同学计算出遮阳棚中CD的长是多少米?(结果保留两个有效数字)(参考数据:sinl8.6.=0.32,tanl8.6.:0.34,sin64.5.=0.90,tan64.5.:2.1)分析:观察图形,可以发现有2个公共直角边的RtABCD,RtAACD,而且边之间存在AC—BC= AB的关系,若设CD=,借助锐角三角函数在RtABCD,RtAACD中可以表示出AC,BC,通过解方程可以获解.解:设CD为,在RfABCD中,/BDC=Ol=18.6.,皇'..tanZBDC=,}u£,眚...曰c:CD.tanBDC:0.34.数.在R△∞中,ADc卢=64?5~1_._fan/_ADC=,..AC:CD?tan/ADC=2.1.AB=AC—BC..'.2=2.1x一0.34x.故一1.14米.答:CD长约为1.14米.二,轮船是否有触礁危险问题例2如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60.的方向上,继续向东行驶2O分钟后,到达曰处又测得灯塔P在它的北偏东45.方向上,如果海轮不改变方向继续前进有没有触礁的危险?解析:欲判断海轮不改变方向继续前进有无触礁的危险,只要求出点P到线段AB所在直线的距离与6海里比较大小,即可判断有无触礁危险为此过P作PC上AB于C点,构造出"双直角三角形"模型——RlAACP,RtABCP;由题意,得AB=l8X=6,/PAB=90.-60.:30.,/PBC:90.一45.:45.,PCB=90.,所以PC=Bc在RtAPAC,tan30.一=孚=6+P—C?解得Pc:3+3?因为3√3+3>6,所以海轮不改变方向继续前进无触礁危险.三,计算河宽例3如图,小强在江南岸选定建筑物A,并在江北岸的处观察,此时,视线与江岸BE所成的夹角/_ABE=30.,小强沿江岸BE向东走了500m,到C处,再观察A,此时视线AC与江岸所成的夹角/ACE=60..根据小强提供的信息,你能测出河宽吗?若能,写出求解过程(结果可保留根号);若不能,请说明理由.分析:首先我们应在图形中BCDE找到河宽的线段,为此过点A作\\\:AD上船,垂足为D,则线段A口的————蓝色的刀和蓝色的枪(猜4字成语)?.(."Ia)Y尘长度就是河的宽度,容易发现图中的2个"双直角三角形"模型,从而得到下面的解法.在AABC中,BD=30.,LACE=60.,.'.BAC=30O.._.AC=BC=500.在Rt△ACD中,LACD=60.,AD=AC×sin60.=500×=250~/3-m.答:这条河的宽度为250米.四,拯救生命问题某建霎羹援C亲某建筑物废墟下方点处有生命\\: 迹象,已知废墟一侧地面上两探C'测点』4,相距3米,探测线与地面的夹角分别是3O.和6O.(如图),试确定生命所在点C的深度.(结果精确到0.1米.参考数据:1.41,1.73)分析:如图,过点C作cD上B交A曰于D点,则CD的长就是生命所在点c的深度.?.'探测线与地面的夹角为30.或6O.,.'./CAD=30.CBD=60..在RtABDCqb,tan60o_历CD,.?.肋=CD:.在RtAADCt:p,tan30o=CD,.?.=CD=....AB:AD—BD:3.一:3.即∞:半:2.6(米).所以生命所在点c的深度约为2.6米.牛刀小试1.如图,-1~11以每小时30海里的速度向东北方向航行,在A处观测灯塔C在船的北偏东75. 的方向.航行l2分钟后到达B处,这时灯塔C恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域.这艘船可以继续沿东北方向航行Ⅱ马7为什么?(参考数据:一1.4l,一1.73)解析:欲判断船不改变方向继续前进有无触礁的危险,只要求出点C到线段AB所在直线的距离与8海里比较大小,即可判断有无触礁危险.为此过c作CDJ-AB于D点,构造出"双直角三角形"模型——Rt△ACD,RtABCD.解这两个直角三角形方可获解.如图,过点C作CD上直线日于D.设DC=.在Rt△CDB中,'.'CBD:45.,.?.BD=CD=.在Rt△CAD中,...CAD=75.一45.=30...?.AD=—CDtan30:.u_.'AB=3012=6,而AD—BD=AB,.?.AD—BD=6.即√一=6.解得=,/31=3(川——即DC=3(+1)一8.2>8..'.这艘船可以继续沿东北方向航行.2.武当山风景管理区,为提高游客到某点的誊44把倾角由.改为32.,已知原台阶A的长为5米(BC所在的地面为水平面).试求改善后的台阶多占多长一段地面?(精确到0.ol米,sin44.=0.695,cos44.=0.719,tan32.=0.661)弛解析:欲把台阶的倾角由44.改为32.,显然台阶应加长,所占的地面也变长,如图,AD表示加长后的台阶,则BD表示台阶加长后地面上多占的一端,观察图形,显然它具备"双直角三角形"模型的特征.在Rt△ABC中,BC=AB?cos44.=5cos44.一3.597.在RtAACDD=ACta:ta~5.558,njnj..BD=CD—BC=5.558—3.597—1.96.即改善后的台阶多占1.96米长的一段地面.身穿着金色衣服的人(猜4字成语)? .(-y一)Y翊,镪一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:汽车从 A 地到 B 地比原来少走( 5 5 2 5 3 )千米
变式题
C
A
30°
D
45°
B
方法总结 所谓“双直角三角形”是指一条直角边重合,另一条直角边共线的两 个直角三角形. 解决这类问题时,抓住两三角形的公共边,并找到公共边与其它相关
边的关系,直接计算或列方程解决问题.
初中数学知识点精讲课程
优翼 微课
初中数学知识点精讲课程
优翼 微课
初中数学知识点精讲课程
优翼 微课
初中数学知识点精讲课程
如图, A 、 B 两地之 间有 一 座山, 汽车 原 来从 A 地到 B 地经过 C 地沿折线 A→C→B行驶,现开通隧道后,汽车直接沿直线 AB 行驶. 已知 AC = 10 千米, ∠A = 30°,∠B = 45°. 则隧道开通后,汽车从 A地到B 地比原来少走多少千 米?(结果保留根号)
优翼 微课
初中数学知识点精讲课程
解直角三角形应用中的“双直角三角形”模型
所谓“双直角三角形”是指一条直角边重合,另一条直角边共线的两
个直角三角形,
其位置关系有两种:Leabharlann 叠合式背靠式
优翼 微课
初中数学知识点精讲课程
优翼 微课
C
解:作 CD⊥AB,垂足为 D.
A
30°
D
45°
B
1 在 Rt△ACD 中,∵∠A= 30° ,∴CD = AC=5 千米 2 CD 5 ∴ AD 5 3 千米 tan 300 3 3
在 Rt△BCD 中,∵∠B= 45° ∴BD = CD = 5,BC= 5 2 千米 ∴ AC+ BC-AB= 10 5 2 (5 3 5) =( 5 5 2 5 3 )千米
