解析几何第四版习题答案第四章
解析几何第四章习题及解答

第4章 二次曲线和二次曲面习题4.11.在直角坐标系x O y 中,以直线:43120l x y -+=为新坐标系的x '轴,取通过(1,3)A -且垂直于l 的直线为y '轴,写出点的坐标变换公式, 并且求直线1:3250l x y -+=在新坐标系中的方程。
解:直线:43120l x y -+=的方向是(3,4),与它垂直的方向是(4,3)±-,新坐标系的x '轴的坐标向量取为34(,)55,y '轴坐标向量取为43(,)55-,与直线:43120l x y -+=垂直且的直线方程可设为340x y c ++=,由于过点(1,3)A -,得到直线方程是3490x y ++=,两直线的交点(3,0)-是新坐标原点,所以点的坐标变换公式:34355.43055x x y y ⎡⎤-⎢⎥'-⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦直线1:3250l x y -+=在新坐标系中的方程:13443:3(3)2()505555l x y x y ''''---++=,化简有1:18200.l x y ''--=2.作直角坐标变换,已知点(6,5),(1,4)A B --的新坐标分别为(1,3),(0,2)-,求点的坐标变换公式。
解:设同定向的点的坐标变换公式是:cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是:cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1) A B =-变为(1,5)A B ''=-,于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到125s i n ,c o s .1313θθ==于是点的坐标变换公式是:5121313.1251313x x a y y b ⎡⎤-⎢⎥'⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦将点(1,4)B -及它的像点(0,2)代入得到3713,6213a b ⎡⎤⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦所以点的坐标变换公式是: 51237131313.12562131313x x y y ⎡⎤⎡⎤-⎢⎥⎢⎥'⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦设反定向的点的坐标变换公式是:cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是:cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1)A B =-变为(1,5) A B ''=-,于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到s i n 1,c o s 0.θθ=-=于是点的坐标变换公式是:01.10x x a y y b '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'-⎣⎦⎣⎦⎣⎦⎣⎦将点(1,4B -及它的像点(0,2)代入得到3,4a b ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦所以点的坐标变换公式是: 013.104x x y y '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'--⎣⎦⎣⎦⎣⎦⎣⎦3.设新旧坐标系都是右手直角坐标系,点的坐标变换公式为5,3,22(1)(2) 2.3;22x x y x y y x y x y ⎛''=++ '=-+⎧⎨' =-⎩''=-+- ⎝ 其中,(,)x y 与(,)x y ''分别表示同一点的旧坐标与新坐标,求新坐标系的原点的旧坐标,并且求坐标轴旋转的角θ。
解析几何第四版吕林根课后习题答案一至三章

第一章向量与坐标§1.1 向量的概念1.下列情形中的向量终点各构成什么图形?(1)把空间中一切单位向量归结到共同的始点;(2)把平行于某一平面的一切单位向量归结到共同的始点;(3)把平行于某一直线的一切向量归结到共同的始点;(4)把平行于某一直线的一切单位向量归结到共同的始点.[解]:(1)单位球面;(2)单位圆(3)直线;(4)相距为2的两点2. 设点O是正六边形ABCDEF的中心,在向量OA、、OC、、、OF、、BC、CD、、EF和FA中,哪些向量是相等的?[解]:如图1-1,在正六边形ABCDEF中,相等的向量对是:图1-1.DEOFCDOEABOCFAOBEFOA和;和;和;和;和3. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=. 当ABCD是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC, 则在∆BAC中,21AC. KL与AC方向相同;在∆DAC中,21AC. NM与AC方向相同,从而KL=NM且KL与NM方向相同,所以KL=.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对向量中,找出相等的向量和互为相反向量的向量:(1) AB、; (2) AE、; (3) 、;(4) AD、; (5) BE、.[解]:相等的向量对是(2)、(3)和(5);互为反向量的向量对是(1)和(4)。
§1.2 向量的加法1.要使下列各式成立,向量ba,应满足什么条件?(1-=+(2+=+(3-=+(4+=-E(5=[解]:(1),-=+(2),+=+(3≥且,=+ (4),+=-(5),≥-=-§1.3 数量乘向量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从向量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出向量→x ,→y . 解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线向量AL , BM ,可 以构成一个三角形.[证明]: )(21+=)(21BC BA BM +=)(21+=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线向量CN BM AL ,,构成一个三角形。
解析几何第四版吕林根 期末复习 课后习题(重点)详解

第一章 矢量与坐标§1.3 数量乘矢量4、 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.6、 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM ,可 以构成一个三角形.证明: )(21AC AB AL +=)(21+=)(21CB CA CN +=0)(21=+++++=++∴7.、设L 、M 、N 是△ABC 的三边的中点,O 是任意一点,证明 ++=OL +OM +ON .[证明] += MB OM OB += NC ON OC +=)(OM +++++=++∴ =)(CN BM AL ON OM OL ++-++ 由上题结论知:0=++CN BM AL ON OM OL OC OB OA ++=++∴ 从而三中线矢量BM ,,构成一个三角形。
8.、如图1-5,设M 是平行四边形ABCD 的中心,O 是任意一点,证明OA +OB ++OD =4OM .[证明]:因为OM =21(OA +), OM =21(OB +), 所以 2OM =21(OA +OB +OC +) 所以OA +OB ++OD =4OM .10、 用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.图1-5证明 已知梯形ABCD ,两腰中点分别为M 、N ,连接AN 、BN . →→→→→→++=+=DN AD MA AN MA MN ,→→→→→→++=+=CN BC MB BN MB MN ,∴ →→→+=BC AD MN ,即§1.4 矢量的线性关系与矢量的分解3.、设一直线上三点A , B , P 满足AP =λ(λ≠-1),O 是空间任意一点,求证:OP =λλ++1[证明]:如图1-7,因为=-OA ,PB =OB -,所以 -OA =λ (OB -),(1+λ)OP =+λ,从而 OP =λλ++1OB.4.、在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; (2)设AT 是角A 的平分线(它与BC 交于T 点),将分解为21,e e 的线性组合解:(1)()12123131,e e e e -==-=-= , 2111231323131e e e e e BD AB AD +=-+=+=,同理123132e e AE +=(2)因为||||TC =||11e e ,且 BT 与方向相同, 所以 BT ||21e e .由上题结论有AT ||||1||212211e e e e e +||||212112e e e e e e +.5.在四面体OABC 中,设点G 是ABC ∆的重心(三中线之交点),求矢量对于矢量,,,的分解式。
解析几何第四版知识题目解析第四章

第四章 柱面、锥面、旋转曲面与二次曲面§ 4.1柱面1、已知柱面的准线为:⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 且(1)母线平行于x 轴;(2)母线平行于直线c z y x ==,,试求这些柱面的方程。
解:(1)从方程⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 中消去x ,得到:25)2()3()3(222=-+++--z y y z即:0235622=----+z y yz z y 此即为要求的柱面方程。
(2)取准线上一点),,(0000z y x M ,过0M 且平行于直线⎩⎨⎧==cz yx 的直线方程为:⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+=+=z z t y y tx x zz t y y t x x 000000 而0M 在准线上,所以⎩⎨⎧=+--+=-++-+--02225)2()3()1(222t z y x z t y t x 上式中消去t 后得到:02688823222=--+--++z y x xy z y x此即为要求的柱面方程。
2而0M 在准线上,所以:⎩⎨⎧+=-++=-)2(2)2(22t z t x t z y t x消去t ,得到:010*******22=--+++z x xz z y x此即为所求的方程。
3、求过三条平行直线211,11,-=+=--==+==z y x z y x z y x 与的圆柱面方程。
解:过又过准线上一点),,(1111z y x M ,且方向为{}1,1,1的直线方程为: ⎪⎩⎪⎨⎧-=-=-=⇒⎪⎩⎪⎨⎧+=+=+=t z z t y y tx x tz z t y y tx x 111111 将此式代入准线方程,并消去t 得到:013112)(5222=-++---++z y x zx yz xy z y x此即为所求的圆柱面的方程。
解析几何第四版吕林根课后习题答案第四章

第四章 柱面、锥面、旋转曲面与二次曲面§ 4.1柱面1、已知柱面的准线为:⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 且(1)母线平行于x 轴;(2)母线平行于直线c z y x ==,,试求这些柱面的方程。
解:(1)从方程⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 中消去x ,得到:25)2()3()3(222=-+++--z y y z 即:0235622=----+z y yz z y 此即为要求的柱面方程。
(2)取准线上一点),,(0000z y x M ,过0M 且平行于直线⎩⎨⎧==c z yx 的直线方程为:⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+=+=z z t y y tx x zz t y y tx x 000000 而0M 在准线上,所以⎩⎨⎧=+--+=-++-+--02225)2()3()1(222t z y x z t y t x 上式中消去t 后得到:02688823222=--+--++z y x xy z y x 此即为要求的柱面方程。
2、设柱面的准线为⎩⎨⎧=+=z x z y x 222,母线垂直于准线所在的平面,求这柱面的方程。
解:由题意知:母线平行于矢量{}2,0,1- 任取准线上一点),,(0000z y x M ,过0M 的母线方程为:⎪⎩⎪⎨⎧+==-=⇒⎪⎩⎪⎨⎧-==+=t z z yy tx x tz z y y tx x 2200000而0M 在准线上,所以:⎩⎨⎧+=-++=-)2(2)2(22t z t x t z y t x 消去t ,得到:010*******22=--+++z x xz z y x 此即为所求的方程。
3、求过三条平行直线211,11,-=+=--==+==z y x z y x z y x 与的圆柱面方程。
解:过原点且垂直于已知三直线的平面为0=++z y x :它与已知直线的交点为())34,31,31(),1,0,1(,0,0,0--,这三点所定的在平面0=++z y x 上的圆的圆心为)1513,1511,152(0--M ,圆的方程为: ⎪⎩⎪⎨⎧=++=-++++07598)1513()1511()152(222z y x z y x 此即为欲求的圆柱面的准线。
最全 解析几何第四版习题答案第四章(完整版)

第四章 柱面、锥面、旋转曲面与二次曲面§ 4.1柱面1、已知柱面的准线为:⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 且(1)母线平行于x 轴;(2)母线平行于直线c z y x ==,,试求这些柱面的方程。
解:(1)从方程⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 中消去x ,得到:25)2()3()3(222=-+++--z y y z 即:0235622=----+z y yz z y 此即为要求的柱面方程。
(2)取准线上一点),,(0000z y x M ,过0M 且平行于直线⎩⎨⎧==c z yx 的直线方程为:⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+=+=z z t y y tx x zz t y y tx x 000000 而0M 在准线上,所以⎩⎨⎧=+--+=-++-+--02225)2()3()1(222t z y x z t y t x 上式中消去t 后得到:02688823222=--+--++z y x xy z y x此即为要求的柱面方程。
2而0M 在准线上,所以:⎩⎨⎧+=-++=-)2(2)2(22t z t x t z y t x 消去t ,得到:010*******22=--+++z x xz z y x此即为所求的方程。
3、求过三条平行直线211,11,-=+=--==+==z y x z y x z y x 与的圆柱面方程。
解:过又过准线上一点),,(1111z y x M ,且方向为{}1,1,1的直线方程为: ⎪⎩⎪⎨⎧-=-=-=⇒⎪⎩⎪⎨⎧+=+=+=t z z t y y tx x tz z t y y tx x 111111 将此式代入准线方程,并消去t 得到:013112)(5222=-++---++z y x zx yz xy z y x此即为所求的圆柱面的方程。
线性代数与空间解析几何-第四章习题解答

(a − d ) × (b − c ) = a × b − a × c − d × b + d × c = a × b − c × d − a × c + b × d = 0 证:
故a − b与b − c共线。
11
证: AB = {− 1,3,3}
AC = {0,4,2}
AD = {3,1,−4}
i j k n= 1 3 2 = − i + 5 j − 7k 2 −1 −1
(3)
所以 法向量为 { -1,5,-7}
由点法式: -(x-1)+5(y-3)-7(z-2)=0 即 x-5y+7z=0 设平面法向量为 { A, B, C },由点法式平面方程:A(x-2)+B(y-3)=0…………* 因为: 平面平行 Z 轴, 所以:法向量垂直 Z 轴 即
设向量的方向余弦为 cos α . cos β . cos γ。由已知β = α
10 ( 加
A
题
)
1 ∆∆ABC中,D为BC边中点,证明AD = (AB + AC) 。 2
B
D
C
证明:由三角形法则 AD = AB + BD 两式相加得 2 AD = AB + AC , 即 AD =
AD = AC + CD 又 ∵ D为BC中点。 ∴BD = −CD
第四章 空间与向量运算
习题一 1 (1) (2)
AB(1,3,0)
BC (−5,0,0) CA(4,−3,0)
AB = (3 − 2) 2 + (2 + 1) 2 + (1 − 1) 2 = 10
2 A (3,4,0) 在 xoy 面上 B(0,4,3)点在 yoz 面上 C(3,0,0)在 x 轴上 D(0,-1,0)在 y 轴上 3 3u-2v=3(a-b+2c)-2(-3b-c)=3a+3b+8c 4 D C O A B 设四边形 ABCD 中 AC 与 DB 交于 O,由已知 AO=OC,DO=OB 因为 AB=AO+OB=OC+DO=DC,AD=AO+OD=OC+BO=BC 所以 ABCD 为平行四边形。 5
解析几何,吕林根,课后习题解答一到五
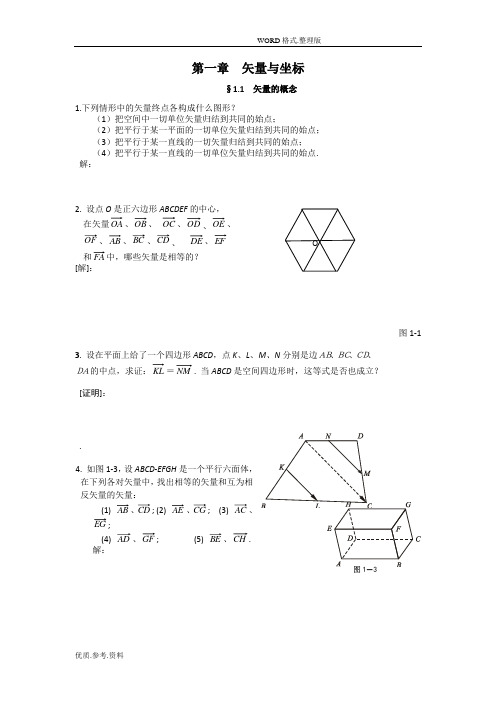
(4) 如 果 a p n,
证明:
b q n,
c r n, 那 么 ,
a,b, c 共 面 .
3. 如果非零矢量 ri (i=1,2,3)满足 r1 r2 r3 , r2 = r3 r1 , r3 = r1 r2 ,那么 r1 , r2 , r3 是彼此 垂直的单位矢量,并且按这次序构成右手系. [证明]:
图 1-11
6 已知△ ABC 的三顶点 A(0, 0,3), B(4, 0, 0), C(0,8, 3)
试
求: (1) △ 三边长 (2) △三内角 (3) 三中线长 (4) 角 A 的角平分线矢量 AD(中点
在 BC 边上),并求 AD 的方向余弦和单位矢量
解:
§1.8 两矢量的失性
1.已知 a 1, b 5, a b 3. 试求: (1) a b (2) (a b) (a b)2 (3) (a 2b) (b 2a)2
10.证明:四面体每一个顶点与对面重心所连的线段共点,且这点到顶点的距离是它到对面 重心距离的三倍. 用四面体的顶点坐标把交点坐标表示出来. [证明] ,
优质.参考.资料
WORD 格式.整理版
, §1.6 矢量在轴上的射影
1.已知矢量 AB 与单位矢量 e 的夹角为150 ,且 AB 10,求射影矢量 e AB 与射影 e AB , 又如果 e e ,求射影矢量 e AB 与射影 e AB .
7.已知 A,B,C 三点坐标如下:
(1)在标架 O;e1,e2 下, A0,1, B2,2,C 2,4. (2)在标架 O;e1,e2 ,e3 下, A0,1,0, B1,0,2,C 2,3,4
判别它们是否共线?若共线,写出 AB 和 AC 的线形关系式.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 柱面、锥面、旋转曲面与二次曲面§ 4.1柱面1、已知柱面的准线为:⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 且(1)母线平行于x 轴;(2)母线平行于直线c z y x ==,,试求这些柱面的方程。
解:(1)从方程⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 中消去x ,得到:25)2()3()3(222=-+++--z y y z 即:0235622=----+z y yz z y 此即为要求的柱面方程。
(2)取准线上一点),,(0000z y x M ,过0M 且平行于直线⎩⎨⎧==c z yx 的直线方程为:⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+=+=z z t y y tx x zz t y y tx x 000000 而0M 在准线上,所以⎩⎨⎧=+--+=-++-+--02225)2()3()1(222t z y x z t y t x 上式中消去t 后得到:02688823222=--+--++z y x xy z y x此即为要求的柱面方程。
2而0M 在准线上,所以:⎩⎨⎧+=-++=-)2(2)2(22t z t x t z y t x 消去t ,得到:010*******22=--+++z x xz z y x此即为所求的方程。
3、求过三条平行直线211,11,-=+=--==+==z y x z y x z y x 与的圆柱面方程。
解:过又过准线上一点),,(1111z y x M ,且方向为{}1,1,1的直线方程为: ⎪⎩⎪⎨⎧-=-=-=⇒⎪⎩⎪⎨⎧+=+=+=t z z t y y tx x tz z t y y tx x 111111 将此式代入准线方程,并消去t 得到:013112)(5222=-++---++z y x zx yz xy z y x此即为所求的圆柱面的方程。
4、已知柱面的准线为{})(),(),()(u z u y u x u =γ,母线的方向平行于矢量{}Z Y X S ,,=,试证明柱面的矢量式参数方程与坐标式参数方程分别为:S v u Y x +=)(与⎪⎩⎪⎨⎧+=+=+=Zv u z z Yv u y y Xv u x x )()()( 式中的v u ,为参数。
证明:对柱面上任一点),,(z y x M ,过M 的母线与准线交于点))(),(),((u z u y u x M ',则,S v M M ='即1、求顶点在原点,准线为01,0122=+-=+-z y z x 的锥面方程。
解:设为锥面上任一点),,(z y x M ,过M 与O 的直线为:zZ y Y x X == 设其与准线交于),,(000Z Y X ,即存在t ,使zt Z yt Y xt X ===000,,,将它们代入准线方程,并消去参数t ,得:0)()(222=-+--y z y z z x即:0222=-+z y x此为所要求的锥面方程。
2、已知锥面的顶点为)2,1,3(--,准线为0,1222=+-=-+z y x z y x ,试求它的方程。
解:设),,(z y x M 为要求的锥面上任一点,它与顶点的连线为:221133++=++=--z Z y Y x X 令它与准线交于),,(000Z Y X ,即存在t ,使⎪⎩⎪⎨⎧++-=++-=-+=t z Z t y Y t x X )2(2)!(1)3(3000 将它们代入准线方程,并消去t 得:044441026753222=+-+-+--+-z y x xz yz xy z y x此为要求的锥面方程。
4、求对锥面上任一点),,(z y x M ,过M 与顶点O 的母线为:zZ y Y x X == 令它与准线的交点为),,(000Z Y X ,即存在t ,使zt Z yt Y xt X ===000,,,将它们代入准线方程,并消去t 得:0=++zx yz xy此即为要求的圆锥面的方程。
5、求顶点为)4,2,1(,轴与平面022=++z y x 垂直,且经过点)1,2,3(的圆锥面的方程。
解:轴线的方程为:142221-=-=-z y x 过点)1,2,3(且垂直于轴的平面为:0)1()2(2)3(2=-+-+-z y x即: 01122=-++z y x 该平面与轴的交点为)937,920,911(,它与)1,2,3(的距离为: 3116)1937()2920()3911(222=-+-+-=d∴要求圆锥面的准线为:的径矢为{}0000,,z y x =γ,试证明锥面的矢量式参数方程与坐标式参数方程分别为:0()(1)v u v γγγ=+-与000()(1)()(1)()(1)x vx u v x y vy u v y z vz u v z=+-⎧⎪=+-⎨⎪=+-⎩式中,v u ,为参数。
证明:对锥面上任一点),,(z y x M ,令OM γ=,它与顶点A 的连线交准线于((),(),())M x u y u z u '=,即OM ()u γ'=。
//AM AM ',且0AM '≠(顶点不在准线上) AM vAM '∴=即00(())v u γγγγ-=- 亦即0()(1)v u v γγγ=+-此为锥面的矢量式参数方程。
若将矢量式参数方程用分量表示,即:000{,,}{(),(),()}(1){,,}x y z v x u y u z u v x y z =+-⎪⎩⎪⎨⎧-+=-+=-+=∴000)1()()1()()1()(zv u vz z y v u vy y x v u vx x 此为锥面的坐标式参数方程,v u ,为参数。
§ 4.3旋转曲面1、求下列旋转曲面的方程:(1);111112x y z -+-==-绕1112x y z -==-旋转 (2);1211x y z -==-绕1112x y z -==-旋转 (3)1133x y z -==-绕z 轴旋转;(4)空间曲线2221z xx y ⎧=⎪⎨+=⎪⎩绕z 轴旋转。
解:(1)设1111(,,)M x y z 是母线111112x y z -+-==-上任一点,过1M 的纬圆为:111222222111()()2()0(1)(1)(1)(2)x x y y z z x y z x y z ---+-=⎧⎨++-=++-⎩因1M 在母线上, 1111211x y z -∴==- (3) 从(1)——(3)消去111,,x y z ,得到:2225523122424242446230x y z xy yz xz x y z ++--+-+-+=此为所求的旋转面的方程。
(3)对母线上任一点1111(,,)M x y z ,过该点的纬圆为:1222222111(1)(2)z z x y z x y z =⎧⎨++=++⎩又1M 在母线上,所以:1111133x y z -==- (3) 从(1)——(3)消去111,,x y z ,得到:2229()10690x y z z +---=此为所求的旋转面方程。
(4)对母线上任一点1111(,,)M x y z ,过1M 的纬圆为:1222222111(1)(2)z z x y z x y z =⎧⎨++=++⎩又1M 在母线上,所以2112211(1)1(2)z x x y ⎧=⎪⎨+=⎪⎩从(1)——(3)消去111,,x y z ,得到:221x y +=211101z z x z ==≤∴≤≤即旋转面的方程为:221x y += (01)z ≤≤2、将直线01xy zβα-==绕z 轴旋转,求这旋转面的方程,并就,αβ可能的值讨论这是什么曲面?解:先求旋转面的方程式:z任取母线上一点1111(,,)M x y z ,过1M 的纬圆为:1222222111(1)(2)z z x y z x y z =⎧⎨++=++⎩又11101x y z βα-== (3) 从(1)——(3)消去111,,x y z ,得到:222220x y z αβ+--=此即为所求旋转面的方程。
当0,0αβ=≠时,旋转面为圆柱面(以z 轴为轴);当0,0αβ≠=时,旋转面为圆锥面(以z 轴为轴,顶点在原点); 当,0αβ≠时,旋转面变为z 轴;当0,0αβ=≠时,旋转面为单叶旋转双曲面。
3、已知曲线Γ的参数方程为(),(),()x x u y y u z z u ===,将曲线Γ绕z 轴旋转,求旋转曲面的参数方程。
解:如图,设((),(),())M x u y u z u 为Γ上任一点,则对经过M 的纬圆上任一点(,,)p x y z ,§4.4椭球面1、做出平面20x -=与椭球面22221494x y z ++=的交线的图形。
解:平面20x -=与椭球面22221494x y z ++=的交线为: 2239442y z x ⎧+=⎪⎨⎪=⎩ ,即 2212734y z ⎧+=⎪⎪⎨⎪ ——椭 图形为y2、设动点与点(1,0,0)的距离等于从这点到平面4x =的距离的一半,试求此动点的轨迹。
解:设动点(,,)M x y z ,要求的轨迹为∑,则条两两相互垂直的射线,分别交曲面123,,p p p ,设112233,,op r op r op r ===,试证:222222123111111r r r a b c++=++ 证明:利用上题结果,有22222221(1,2,3)i i i i i r a b cλμν=++=其中,,i i i λμν是i op 的方向余弦。
若将(1,2,3)i op i =所在的直线看成新的坐标系的三个坐标轴,则123,,λλλ是坐标矢量关于新坐标系的方向余弦,从而2221231λλλ++=,同理,2221231μμμ++=,2221231ννν++= 所以,222222222123123123222222123222111111()()()111r r r a b c a b c λλλμμμννν++=++++++++=++即:222222123111111r r r a b c ++=++ 5、一直线分别交坐标面,,yoz zox xoy 于三点,,A B C ,当直线变动时,直线上的三定点,,A B C 也分别在三个坐标面上变动,另外,直线上有第四点p ,它与三点的距离分别为,,a b c ,当直线按照这样的规定(即保持,,A B C 分别在三坐标面上)变动,试求p 点的轨迹。
解:设112233(0,,),(,0,),(,,0)A y z B x z C x y ,则知:2121331221,x z z yx y z z z z ==--z z21211221(,,0)x z z yC z z z z ∴-- 又设(,,)p x y z ,,,pA a pB b pC c ===222211222222222221211221()()(1)()()(2)()()(3)x y y z z a x x y z z b x z z yx y z c z z z z ⎧⎪+-+-=⎪⎪-++-=⎨⎪⎪-+-+=--⎪⎩又p 在AB 的连线上,111121y y z z x x y z z --∴==--(4) 从(1)——(4)消去1122,,,y z x z ,得到即:22222(1)1a a b cλ-=-2222222a cb c b aλ-=⋅- λ∴=满足要求的平2、给定方程2221(0)x y z A B C A B C λλλ++=>>>--- 试问当λ取异于,,A B C 的各种数值时,它表示怎样的曲面?解:对方程2221(0)x y z A B C A B C λλλ++=>>>--- (*) 1º、当A λ>时,(*)不表示任何实图形; 2º、当A B λ>>时,(*)表示双叶双曲面; 3º、当B C λ>>时,(*)表示单叶双曲面; 4º、当C λ<时,(*)表示椭球面。
