matlab绘制温度场

已知坐标和坐标点温度 3维 matlab

已知坐标和坐标点温度 3维 matlab已知坐标和坐标点温度 3维 matlab1. 背景介绍在数学和计算机科学领域，已知坐标和坐标点温度是一个重要的问题。

在实际应用中，我们经常需要根据已知的坐标和相应的温度信息来进行分析和计算。

而在计算机编程中，特别是在使用Matlab进行数据处理和可视化时，对已知坐标和坐标点温度的处理也经常涉及到。

2. 已知坐标和坐标点温度的基本概念在处理已知坐标和坐标点温度时，首先我们需要了解一些基本的概念。

坐标通常由(x, y, z)三个数值来表示，分别对应空间中的三个方向。

而坐标点的温度则是该点在空间中的温度值。

在3维空间中，已知坐标和坐标点温度可以用矩阵或数组来表示，每一行对应一个坐标点，而温度值则对应该点的温度信息。

3. Matlab中的处理方法在Matlab中，我们可以利用矩阵和数组的运算来处理已知坐标和坐标点温度。

我们可以将已知的坐标点和温度值存储在两个分别对应的矩阵或数组中。

通过Matlab提供的矩阵运算和函数，我们可以进行各种操作，比如计算坐标点之间的距离，查找特定温度范围内的坐标点等。

Matlab还提供了丰富的绘图函数，可以将处理后的坐标点和温度信息直观地展示出来。

4. 深入探讨已知坐标和坐标点温度的应用除了基本的处理方法外，已知坐标和坐标点温度还有许多深层次的应用。

比如在气象学中，我们可以根据已知的气象站坐标和气温信息来绘制气温分布图，以便对气候变化进行分析。

在地理信息系统中，已知坐标和坐标点温度也被广泛应用于地图制作和空间数据分析。

另外，在工程领域中，我们可以利用已知坐标和坐标点温度来进行热传导分析和热能分布计算。

5. 总结和回顾通过对已知坐标和坐标点温度的深入探讨，我们了解了这一问题的基本概念和Matlab中的处理方法。

我们也看到了这一问题在实际应用中的广泛应用，以及与其他领域的密切联系。

在未来的学习和工作中，我们可以进一步深入研究已知坐标和坐标点温度在不同领域的应用，以及利用Matlab中更高级的技术来处理和分析相关数据。

基于DS18B20的温度场可视化测绘系统毕业论文

基于DS18B20的温度场可视化测绘系统专业班级：电气工程与其自动化3班姓名：黄锦指导教师：啸轮机工程学院摘要本文介绍了基于DS18B20和STC89C52RC单片机的多点温度测量的方法和原理，以与利用matlab软件运用插值法对数据进行处理，实现温度的可视化。

首先，利用DSI8B20温度传感器和单片机与其它外围硬件结合在一起，实现温度的测量和显示；然后，通过MATLAB对数据进行处理绘图，模拟温度场的可视。

该设计主要分为以下几个部分：硬件设计、软件设计、系统的调试与实现以与matlab对温度场的模拟测绘。

其中硬件设计主要是由Proteus软件进行电路的设计和仿真，软件设计采用C语言编写实现，绘图通过matlab进行。

采用这种解决方案，实现了基于DS18B20进行的各项软硬件软件的设计，实现了多点温度测量和显示以与温度场的模拟可视化。

关键词：温度测量；温度传感器DS18B20；STC89C52RC单片机；MATLABAbstractThis article describes the multi-point temperature measurement method and principle based on DS18B20 and STC89C52RC，To make the temperature field visual ,interpolation method and matlab software are used for data processing．First,combine DS18B20 and the MCU and other peripheral equiphments to make the measuring temperature is displayed. Then using matlab plot it.The design is mainly divided into the several parts as follows：the hardware design，the software design and the debugging and implementation of the entire system and the matlab plotting．Among the design，the hardware design and circuits drawing by means of Proteus software and the software design is realized by using C language programming,picture drawing by matlab．The DS18B20 based design，debugging and dispose of the all software and hardware items and even the multi-point temperature measuring and displaying have been realized by adopting the solution．Keywords: Temperature Measurement;TemperaturesensorDS18B20; STC89C52RC;MATLAB目录第1章绪论01.1概述01.1.1选题背景与意义01.1.2温度检测技术的研究现状与发展趋势01.2 系统方案论证1第2章硬件基础介绍22.1 DS18B20温度传感器介绍22.1.1 DS18B20温度传感器概述22.1.2 DS18B20接口电路42.1.3 DS18B20工作原理52.1.4 DS18B20工作时序62.2 STC89C52RC单片机简介82.3 LCD1602液晶显示屏简介8第3章硬件电路设计103.1单片机驱动电路设计103.2 温度测量模块电路设计113.3 温度显示模块电路设计 (11)3.4温度报警电路设计123.5系统硬件电路设计123.6小结13第4章软件程序设计13主要讨论温度显示、测量、与报警子程序的设计和调试134.1 DS18B20的测量温度程序设计134.2 LCD1602的显示程序设计164.3 报警控制电路软件设计174.4系统软件程序设计194.5本章小结19第5章利用matlab实现温度场数据可视化205.1可视化的方法205.2 数据的采集和处理205.3 本章小结26结论 (27)参考文献27致 28附录0附录1 测温系统实物图0附录2 本设计测温系统电路图（基于proteus）0附录3 本设计的系统总程序源代码（基于Keil μVison4）1第1章绪论1.1概述本章讨论的主要是本课题的选题背景意义，还有研究现状和发展趋势以与测温系统方案设计。

焊接热过程仿真实验报告

焊接热过程仿真实验一、实验目的1、通过实验加强对瞬时点热源焊接温度场和焊接热循环的概念、影响因素、解析解和数值解的特点等的感性认识。

2、Matlab,Ansys软件的使用。

二、实验内容1、使用Matlab计算绘制瞬时点热源焊接温度分布曲线。

2、使用Aansys软件对瞬时点热源焊接温度场进行仿真计算，观察温度分布云图，绘制指定点的焊接热循环曲线，对瞬时点热源焊接温度场的影响因素进行定量定性的探讨。

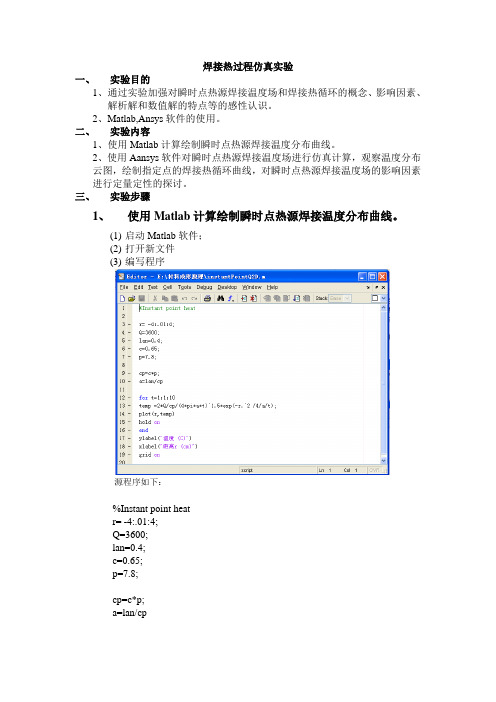
三、实验步骤1、使用Matlab计算绘制瞬时点热源焊接温度分布曲线。

(1)启动Matlab软件；(2)打开新文件(3)编写程序源程序如下：%Instant point heatr= -4:.01:4;Q=3600;lan=0.4;c=0.65;p=7.8;cp=c*p;a=lan/cpfor t=1:1:10temp =2*Q/cp/(4*pi*a*t)^1.5*exp(-r.^2 /4/a/t);plot(r,temp)hold onendylabel('温度(C)')xlabel('距离r (cm)')grid on（4）运行程序（5）记录指定时间的温度，绘制温度分布曲线。

实验结果图如下：2、使用Aansys软件对瞬时点热源焊接温度场进行仿真计算。

ANSYS软件采用有限元方法进行稳态、瞬态热分析，计算各种热载荷引起的温度、热梯度、热流率、热流密度等参数。

这些热载荷包括：对流，辐射，热流率，热流密度（单位面积热流），热生成率（单位体积热流），固定温度的边界条件。

采用ANSYS软件进行热过程分析可以用菜单交互操作和编程两种方式。

由于本次实验仅有两学时，学生又无该软件的使用经验，所以主要以程序调试为主，将重点放在参数影响因素的探讨。

（1）使用文本文件编辑器编写程序（2）以.mac为扩展名存盘（3）运行Ansys软件(4) 设置文件夹到程序所在文件夹（4）运行程序源程序及各步骤所得结果图如下：! 步骤1：项目设置FINISH/CLEAR/FILNAME, Point heating!Give the analysis a title/TITLE,Point Heat! 步骤2：设置单元、材料特性参数/UNITS,SIET,1,SOLID70 !单元类型选择MP,DENS,1,7800 !密度MP,KXX,1,40 !导热系数MP,C,1,650 !比热容!MPTEMP,1,0,227,727,1727,2727!MPDATA,KXX,1,1,83.5,61.5,32.5,42.5,46 !MPDATA,C,1,1,430,540,980,847,400!MPTEMP,1,0,1533,1595,1670!MPDATA,ENTH,1,1,0,7.5E9,9.6E9,1.05E10!步骤3：建模a=0.05 !模型边长an=5 !边长上的单元数b=0.01 !网格密集区边长bn=10 !网格密集区边长上的单元数block,0,b,0,b,0,b !建模block,0,a,0,a,0,avovlap,all/pnum,volu,1!步骤4：网格划分vsel,s,loc,z,0,bvatt,1,,1,0mshkey,1LESIZE,11, , ,bn, , , , ,1 LESIZE,6, , ,bn, , , , ,1LESIZE,7, , ,bn, , , , ,1vmesh,allvsel,invevatt,1,,1,0esize,a/ansmrtsize,6mshape,1,3dmshkey,0vmesh,allvsel,all/VIEW,1,0.5,-1,0.5/TRIAD,OFF !Turn triad symbol off/REPLOT!步骤5：求解/SOLUANTYPE,TRANSIENT,NEWTRNOPT,FULLLUMPM,ONTOFFST,273TUNIF,20 ! 工件初始温度。

MATLAB与VB接口编程实现磨削温度场的仿真

第28卷　第11期2006年11月武　汉　理　工　大　学　学　报JOURNA L OF WUHAN UNIVERSIT Y OF TECHN OLOG Y Vol.28　No.11　Nov.2006MA T LAB 与VB 接口编程实现磨削温度场的仿真汪心立,张建华,任升峰,段彩云,董春杰(山东大学机械工程学院,济南250061)摘　要:　将MA TLAB 的强大数学运算功能和图形绘制功能与VB 在用户界面开发方面的优势结合起来,通过混合编程实现了磨削温度场的仿真研究。

在仿真系统的前端界面输入计算温度场的命令语句或者是直接输入磨削用量后经过调用MA TLAB 软件计算可以得到相应条件下的温度场模型,同时该仿真系统除了应用温度场仿真外还可扩充到其他物理量如磨削力,表面粗糙度等的仿真研究。

关键词:　磨削;　温度场;　MA TLAB ;　VB ;　计算机仿真中图分类号:　TP 391.9文献标志码:　A 文章编号:167124431(2006)1120111203Simulation of G rinding T emperature Field B ased on the Applicationof MAT LAB and VBW A N G Xi n 2li ,ZHA N G Jian 2hua ,R EN S heng 2f eng ,DUA N Cai 2yun ,DON G Chun 2jie(School of Mechanical Engineering ,Shandong University ,Jinan 250061,China )Abstract :　This paper introduced the research of simulation in grinding temperature field based on the hybrid programming between MA TLAB and VB.The simulation integrates their advantages ,which were powerful mathematic calculation capacity and graphic capacity of MA TLAB ,and VB ’s friendly visual interface.When inputting programmed command of temperature pattern or grinding parameters directly ,the temperature distribution could be gained through calculating by MA TLAB ,and be 2sides ,it could also be applied to other physical quantity simulation ,for example grinding force ,surface roughness and so on.K ey w ords :　grinding ;　temperature fields ;　MA TLAB ;　VB ;　computer simulation 收稿日期:2006205220.基金项目:国家自然科学基金(50275087).作者简介:汪心立(19802),男,硕士.E 2mail :wangxinli @在磨削温度场的仿真研究中,应用数学模型和计算机仿真技术能够得出比较准确的温度分布图,可以分析磨削用量对温度场的影响,进而发现磨削温度场的变化规律,通过优化磨削用量,使温度场的温度变化趋向于合理[1],最终能够达到在磨削过程中减少磨削烧伤发生的效果。

24 MATLAB求温度场

理数学模型形式如下 :
椭圆型 PDE
- ·( c u) + ɑu = f
(1)
非线性 PDE
- ·( c ( u) u) + ɑ( u) u = f ( u)
(2)
本征型问题
- ·( c u) + ɑu = ε·d u
(3)
抛物线型 PDE
d ( 9u/ 9t) - ·( c u) + ɑu = f
式 (6) 适用一般非稳态导热的数学模型 ,应用于平壁点热源导热模型的 Parabolic 方程为 : rho ×C × T′- div ( k ×grɑd ( T) ) = Q + h ×( Text - T ) , El2 liptic 方程为 - div ( k ×grɑd ( T) ) = Q + h ×( Text T) ,图 3 为网格精化图 ,图 4 为采用 Elliptic 模型得到的平壁点热源导热温度分布三维图 ,即为稳定时的温度场。采用 Parabolic 模型可以得到动态的温度分布 ,图 5～8 分别为点热源模型在几个不同时刻的温度分布情况 ,其中热源的一边都是绝热。
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
《工业炉》第 27 卷第 3 期 2005 年 5 月
流换热时其温升规律和绝热的温升规律是一致的。
关键词 :温度场 ; PDE 工具箱 ;非稳态导热 ;点热源中图分类号 : T K124 文献标识码 : A
Application of MATLAB in Solving Temperature Field

(完整word版)matlab绘制温度场

通过在室内的某些位置布置适当的节点，采集回来室内的温湿度以及空气质量等实际参数。

首先对室内空间建模，用一个无限细化的三维矩阵来模拟出室内的温度分布情况，针对采集回来的数据，采用插值法和适当次数的拟合函数的拟合，得出三维矩阵的实际值的分布，最后结合matlab软件绘制出计算出的温度场的三维图像。

一．数据的采集与处理因为影响人的舒适感的温度层只是室内的某一高度范围内的温度，而温度传感器虽然是布置在一个平面内，但是采用插值法和拟合函数法是可以大致再现出影响人的舒适感的温度层的温度变化的。

同时，在构建出的三维模型中，用第三维表示传感器层面的温度。

在传感器层面，传感器分布矩阵如下：X=【7.5 36.5 65.5】（模型内单位为cm）Y=【5.5 32.5 59.5】Z=【z1 z2 z3；z4 z5 z6；z7 z8 z9；】（传感器采集到的实时参数）采用meshgrid（xi，yi，zi，…）产生网格矩阵；首先按照人的最小温度分辨值，将室内的分布矩阵按照同样的比例细化，均分，使取值点在坐标一定程度上也是接近于连续变化的，从而才能最大程度上使处理数据得来的分布值按最小分辨值连续变化！根据人体散热量计算公式：C=hc（tb-Ta）其中hc为对流交换系数；结合Gagge教授提出的TSENS热感觉指标可以计算出不同环境下人的对环境温度变化时人体温度感知分辨率，作为插值法的一个参考量，能使绘制出的温度场更加的符合人体的温度变化模式。

例如按照10cm的均差产生网格矩阵（实际上人对温度的分辨率是远远10cm大于这个值的，但是那样产生的网格矩阵也是异常庞大的，例如以0.5cm为例，那么就可以获得116*108=12528个元素，为方便说明现已10cm为例）：[xi yi]=meshgrid(7.5:10:65.5,5.5:10:59.5)xi =7.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.5000yi =5.5000 5.5000 5.5000 5.5000 5.5000 5.500015.5000 15.5000 15.5000 15.5000 15.5000 15.500025.5000 25.5000 25.5000 25.5000 25.5000 25.500035.5000 35.5000 35.5000 35.5000 35.5000 35.500045.5000 45.5000 45.5000 45.5000 45.5000 45.500055.5000 55.5000 55.5000 55.5000 55.5000 55.5000产生网格矩阵之后，就可以在测得的实时数据的基础上，通过相关的温度场的专业的估算函数，以及相关的数值处理函数来估计整个分布面（有最小的分辨率）上的温度了。

(完整word版)西安交通大学——温度场数值模拟(matlab)

温度场模拟matlab代码：clear,clc,clfL1=8;L2=8;N=9;M=9;% 边长为8cm的正方形划分为8*8的格子T0=500;Tw=100; % 初始和稳态温度a=0.05; % 导温系数tmax=600;dt=0.2; % 时间限10min和时间步长0.2sdx=L1/(M-1);dy=L2/(N-1);M1=a*dt/(dx^2);M2=a*dt/(dy^2);T=T0*ones(M,N);T1=T0*ones(M,N);t=0;l=0;k=0;Tc=zeros(1,600);% 中心点温度，每一秒采集一个点for i=1:9for j=1:9if(i==1|i==9|j==1|j==9)T(i,j)=Tw;% 边界点温度为100℃elseT(i,j)=T0;endendendif(2*M1+2*M2<=1) % 判断是否满足稳定性条件while(t<tmax+dt)t=t+dt;k=k+1;for i=2:8for j=2:8T1(i,j)=M1*(T(i-1,j)+T(i+1,j))+M2*(T(i,j-1)+T(i,j+1))+(1-2*M1-2*M2)*T(i,j);endendfor i=2:8for j=2:8T(i,j)=T1(i,j);endendif(k==5)l=l+1;Tc(l)=T(5,5);k=0;endendi=1:9;j=1:9;[x,y]=meshgrid(i); figure(1);subplot(1,2,1);mesh(x,y,T(i,j))% 画出10min 后的温度场 axis tight;xlabel('x','FontSize',14);ylabel('y','FontSize',14);zlabel('T/℃','FontSize',14) title('1min 后二维温度场模拟图','FontSize',18) subplot(1,2,2);[C,H]=contour(x,y,T(i,j)); clabel(C,H);axis square;xlabel('x','FontSize',14);ylabel('y','FontSize',14); title('1min 后模拟等温线图','FontSize',18) figure(2); xx=1:600;plot(xx,Tc,'k-','linewidth',2)xlabel('时间/s','FontSize',14);ylabel('温度/℃','FontSize',14);title('中心点的冷却曲线','FontSize',18)else disp('Error!') % 如果不满足稳定性条件，显示“Error ！” end实验结果：时间/s温度/℃中心点的冷却曲线x1min后二维温度场模拟图T /℃xy1min 后模拟等温线图x5min 后二维温度场模拟图T /℃xy5min 后模拟等温线图x10min后二维温度场模拟图T /℃xy10min 后模拟等温线图x10min 后二维温度场模拟图（不满足稳定性条件）yT /℃21时间/s温度/℃中心点的冷却曲线（不满足稳定性条件）。

某温度控制系统的MATLAB仿真

某温度控制系统的MATLAB仿真1. 简介温度控制是很多工业过程中的一个重要环节，能够保证工业生产过程的稳定性和产品质量。

本文将介绍一个基于MATLAB的温度控制系统的仿真，包括系统的建模和控制算法的实现。

2. 温度控制系统建模温度控制系统一般由一个加热元件和一个温度传感器组成。

加热元件通过对电流或电压的控制来控制温度，温度传感器用于测量当前温度的值。

本文以一个简化的一维加热系统为例进行仿真。

2.1 系统参数设置首先，我们需要设置温度控制系统的一些参数，包括加热元件的功率、温度传感器的灵敏度和环境温度等。

这些参数可以在MATLAB中定义，如下所示：P = 100; % 加热元件功率K = 0.5; % 温度传感器灵敏度T_ambient = 25; % 环境温度2.2 系统动力学建模接下来，我们需要建立温度控制系统的动力学模型。

假设加热元件和温度传感器之间存在一定的传热延迟，我们可以使用一阶惯性模型进行建模。

系统的状态方程可以表示为：T_dot = (P - K * (T - T_ambient)) / C其中，T_dot为温度的变化率，T为温度的值，C为系统的热容量。

根据系统的动力学特性，我们可以选择合适的参数来建立系统模型。

3. 控制算法设计在温度控制系统中，我们需要设计一个控制算法来将温度稳定在设定的目标温度附近。

常用的控制算法包括比例控制、比例积分控制和模糊控制等。

本文选取比例积分控制（PI控制）作为控制算法进行仿真。

3.1 PI控制器设计PI控制器由一个比例项和一个积分项组成，其输出可以表示为：u(t) = K_p * (e(t) + (1 / T_i) * \\int_{0}^{t} e(\\tau) d\\tau)其中，e(t)为温度误差，K_p为比例系数，T_i为积分时间常数。

比例系数和积分时间常数的选择是控制器设计中的关键。

3.2 控制律实现在MATLAB中，我们可以使用控制系统工具箱来实现PI控制器。

基于MATLAB的室温分布监测可视化技术

基于MATLAB的室温分布监测可视化技术摘要：为了使空调的负荷端（恒温恒湿室）温度分布均匀，送风末端设计为全面孔板单向流的送风方式。

通过计算来确定送风量和孔板的规格，并实际测量来获取恒温恒湿室内的温度分布情况，借助MATLAB软件对测取的数据进行二维、三维插值，绘制出温度分布的等高线图、三维图和四维图，最后对温度分布情况进行分析和总结。

关键词：送风末端；温度分布；MATLAB；可视化；三维插值1概述当前空调系统送风末端领域鲜有准确测量温度分布的测试方法，对于温度分布监测的可视化技术更加少见，主要难点集中在温度测取点布置、温度精确测试仪器选取、测量数据的多维度插值和四维可视化的实现。

最难点位于四维可视化技术的实现，目前温度分布主要通过固定点位测温实现，最多能实现平面温度场分布可视化，无法进行空间内温度云图呈现，主要技术难点在于三维插值计算和思维插值计算的融合，以及四维云图的呈现。

若要解决此问题，需要重点对插值算法进行深入研究，并借助MATLAB强大的插值计算模型，求解温度场分布。

恒温恒湿室作为本次实验对象，总面积为25，围护结构采用双面隔热彩钢库板制作，库板厚度为150mm，长宽高尺寸分别为6000mm、3500mm、3080mm。

恒温恒湿室内设有静压室，位于室内最顶部，高度为470mm。

室温20℃时，设计最大冷负荷为12kW，围护结构负荷为3.25kW，温度调节范围-25~55℃。

恒温恒湿室墙壁处挂有冷风机组，主要用于-25℃~10℃的低温需求。

在本文中不作使用，但是其存在会影响恒温恒湿室的温度分布情况。

温度传感器全部采用四线制热电阻，分度号PT100（A），测量精度0.2℃。

在实际测量中，信号传输线的长度普遍在10米以上，线路的阻值对二线制热电阻测温会产生较大的影响，测量误差波动较大。

四线制热电阻不仅可以消除引出线电阻的影响，还可以消除连接导线间接触电阻及其阻值变化的影响，主要用在高精度温度测量方面。

Matlab中的图形绘制技巧

MATLAB中的图形绘制技巧概述：MATLAB是一种用于科学计算和数据可视化的强大工具，它提供了丰富的图形绘制功能，使用户能够清晰地展示和分析数据。

本文将介绍一些MATLAB中的图形绘制技巧，帮助读者更加熟悉和灵活运用这些功能。

一、基本图形绘制1.折线图(Line Plot)：折线图是用于显示随时间、变量或其他条件变化而变化的数据的理想选择。

例如，假设我们想要展示一段时间内气温的变化趋势，可以使用MATLAB中的plot 函数来生成折线图。

通过在X轴上放置时间（日期）或变量，将温度值绘制在Y 轴上，我们可以清晰地看到气温的变化。

2.散点图(Scatter Plot)：散点图用于观察两个连续变量之间的关系。

在MATLAB中，可以使用scatter 函数生成散点图。

例如，我们可以绘制一个散点图来观察身高和体重之间的关系，每个点代表一个人，x轴表示身高，y轴表示体重。

通过观察图形，我们可以直观地看到身高和体重之间是否存在某种关联。

3.柱状图(Bar Plot)：柱状图适用于对各个组或类别之间的数值进行比较。

使用bar函数可以在MATLAB中绘制柱状图。

例如，如果我们想要比较不同地区的人口数量，可以使用柱状图将不同地区的人口数量以柱状图的形式展示出来。

不同地区的柱状图高度不同，可以直观地看到不同地区的人口数量差异。

4.饼图(Pie Chart)：饼图用于表示不同类别之间的比例关系，MATLAB中的pie函数可以用来生成饼图。

例如，我们可以使用饼图展示一份问卷调查中各个选项的比例，饼图的每个扇区表示一个选项，扇区的面积大小代表该选项占总数的比例。

通过观察饼图，我们可以更加直观地了解各个选项之间的比例关系。

二、高级图形绘制技巧1.子图(Subplot)：在MATLAB中，我们可以使用subplot函数创建一个包含多个子图的大图。

通过在subplot函数中指定行数和列数，可以将图形划分为不同的区域，并在每个区域中绘制不同的图形。

热传导方程[整理版]

前言本文只是针对小白而写，可以使新手对热传导理论由很浅到不浅的认识，如想更深学习热传导知识，请转其它文档。

一、概念与常量1、温度场：指某一时刻τ下，物体内各点的温度分布状态。

在直角坐标系中：t=f(x,y,z,τ)；在柱坐标系中：t=f(r,θ,z,τ)；在球坐标系中：t=f(r,θ,∅,τ)。

补充：根据温度场表达式，可分析出导热过程是几维、稳态或非稳态的现象，温度场是几维的、稳态的或非稳态的。

2、等温面与等温线：三维物体内同一时刻所有温度相同的点的集合称为等温面；一个平面与三维物体等温面相交所得的的曲线线条即为平面温度场中的等温线。

3、温度梯度：在具有连续温度场的物体内，过任意一点P温度变化率最大的方向位于等温线的法线方向上。

称过点P的最大温度变化率为温度梯度(temperature gradient)。

用grad t表示。

定义为：grad t=∂t∂nn补充：温度梯度表明了温度在空间上的最大变化率及其方向，是向量，其正向与热流方向恰好相反。

对于连续可导的温度场同样存在连续的温度梯度场。

在直角坐标系中：grad t=∂t∂xi+∂t∂yj+∂t∂zk3、导热系数定义式：λ=q-grad t单位W/(m⋅K)导热系数在数值上等于单位温度降度(即1K/m)下，在垂直于热流密度的单位面积上所传导的热流量。

导热系数是表征物质导热能力强弱的一个物性参数。

补充：由物质的种类、性质、温度、压力、密度以及湿度影响。

二、热量传递的三种基本方式热量传递共有三种基本方式：热传导；热对流；热辐射三、导热微分方程式（统一形式：ρc∂t∂τ=λ∇2t+q）直角坐标系：ρc∂t∂τ=∂∂x(λ∂t∂x)+∂∂y(λ∂t∂y)+∂∂z(λ∂t∂z)+q圆柱坐标系：ρc∂t∂τ=1r∂∂r(λr∂t∂r)+1r2∂∂ϕ(λ∂t∂ϕ)+∂∂z(λ∂t∂z)+q球坐标系：ρc∂t∂τ=1r2∂∂r(λr2∂t∂r)+1r2sinθ∂∂θ(λsinθ∂t∂θ)+1r2sin2θ∂∂ϕ(λ∂t∂ϕ)+ q其中，称α=λρc为热扩散系数，单位m2/s，ρ为物质密度，c为物体比热容，λ为物体导热系数，q为热源的发热率密度，h为物体与外界的对流交换系数。

matlab绘制温度场复习过程

m a t l a b绘制温度场通过在室内的某些位置布置适当的节点，采集回来室内的温湿度以及空气质量等实际参数。

首先对室内空间建模，用一个无限细化的三维矩阵来模拟出室内的温度分布情况，针对采集回来的数据，采用插值法和适当次数的拟合函数的拟合，得出三维矩阵的实际值的分布，最后结合matlab软件绘制出计算出的温度场的三维图像。

一．数据的采集与处理因为影响人的舒适感的温度层只是室内的某一高度范围内的温度，而温度传感器虽然是布置在一个平面内，但是采用插值法和拟合函数法是可以大致再现出影响人的舒适感的温度层的温度变化的。

同时，在构建出的三维模型中，用第三维表示传感器层面的温度。

在传感器层面，传感器分布矩阵如下：X=【7.5 36.5 65.5】（模型内单位为cm）Y=【5.5 32.5 59.5】Z=【z1 z2 z3；z4 z5 z6；z7 z8 z9；】（传感器采集到的实时参数）采用meshgrid（xi，yi，zi，…）产生网格矩阵；首先按照人的最小温度分辨值，将室内的分布矩阵按照同样的比例细化，均分，使取值点在坐标一定程度上也是接近于连续变化的，从而才能最大程度上使处理数据得来的分布值按最小分辨值连续变化！根据人体散热量计算公式：C=hc（tb-Ta）其中hc为对流交换系数；结合Gagge教授提出的TSENS热感觉指标可以计算出不同环境下人的对环境温度变化时人体温度感知分辨率，作为插值法的一个参考量，能使绘制出的温度场更加的符合人体的温度变化模式。

例如按照10cm的均差产生网格矩阵（实际上人对温度的分辨率是远远10cm 大于这个值的，但是那样产生的网格矩阵也是异常庞大的，例如以0.5cm为例，那么就可以获得116*108=12528个元素，为方便说明现已10cm为例）： [xi yi]=meshgrid(7.5:10:65.5,5.5:10:59.5)xi =7.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.5000yi =5.5000 5.5000 5.5000 5.5000 5.5000 5.500015.5000 15.5000 15.5000 15.5000 15.5000 15.500025.5000 25.5000 25.5000 25.5000 25.5000 25.500035.5000 35.5000 35.5000 35.5000 35.5000 35.500045.5000 45.5000 45.5000 45.5000 45.5000 45.500055.5000 55.5000 55.5000 55.5000 55.5000 55.5000产生网格矩阵之后，就可以在测得的实时数据的基础上，通过相关的温度场的专业的估算函数，以及相关的数值处理函数来估计整个分布面（有最小的分辨率）上的温度了。

温度场三维模拟,附matlab程序

and sharing with colleagues.
Other uses, including reproduction and distribution, or selling or licensing copies, or posting to personal, institutional or model
Since the ﬁber length is much larger than the ﬁber cross section, the capability of heat dissipation from the ﬁber end facet is a lot lower than that from the ﬁber side. Therefore the transverse temperature distributions in the DCF at room temperature are gov-
© 2010 Elsevier GmbH. All rights reserved.
1. Introduction
high-power ﬁber lasers are now mature products and have numerous applications in medical, military, industrial processing and modern telecommunication because of some unique advantages including high conversion efﬁciency, excellent beam quality, less thermal effect, small volume and weight, etc. [1–3]. In the continuous-wave (cw) regim, Yb-doped double-clad ﬁber laser (DCFL) with an output power of 1.36 kW has been reported by using large mode area (LMA) ﬁbers [3]. Although the thermal effects can be ignored in low-power ﬁber lasers, the heat dissipation is an important feature and affects laser performance in kilowatt power domain [4,5]. So the thermal effect in high-power ﬁber laser attracted much attention recently [6,7]. However, few investigations focus on the evolution of the temperature and the inﬂuence of the inner-clad shape. In this paper, a theoretical and numerical analysis of 3D temperature ﬁeld is investigated by solving the transient heat conduction equation.

基于MATLAB的焊接温度场数值计算

C W T 中国水运 2019·02 75基于MATLAB 的焊接温度场数值计算DOI 编码：10.13646/ki.42-1395/u.2019.02.027于有生（广东南方职业学院，广东江门 529040）摘　要：本文利用高斯数值积分原理得到厚大焊件点状连续移动热源温度场高斯数值积分表达式，在MATLAB 平台的基础上编写了该温度场的数值计算程序，并通过Q235钢的焊接实例进行数值计算，计算结果说明，利用高斯积分法求解焊接温度场的数值解可以在焊接工程实践中应用。

关键词：焊接温度场；高斯数值积分；MATLAB中图分类号：TG44 文献标识码：A 文章编号：1006—7973（2019）02-0075-021前言焊接温度场特性对提高焊接质量具有重要意义。

焊接温度场的计算属于非线性瞬态热传导问题，焊接过程温度场的急剧变化造成温度分布的不均匀，分析计算比一般的热过程要困难。

焊接温度场研究始于20世纪40年代，近年来随着焊接温度场研究的逐渐深入, 有限元法逐渐应用于焊接温度场的数值模拟过程，研究方向逐渐转向三维焊接模拟，并实现温度、相变及热应力进行多场耦合计算。

但解析法在焊接传热计算中仍然发挥重要的作用。

本文在MATLAB 平台下，通过编程对厚大焊件点状连续移动热源温度场的解析表达式，利用高斯积分法进行数值分析计算。

2点状连续移动热源温度场的高斯积分厚大焊件点状连续移动热源温度场的解析表达式为：式中：；'"t t t −=；C：比热容(J/g ∙°C)；Cρ：容积比热容(J/cm ∙°C)；a：热扩散率(cm 2/s)；v：焊接速度(cm/s)。

式（1）的积分要利用高斯数值积分公式进行变换得到式（2）：式中：p 为高斯积分总步数；n=3——二次三点高斯积分；Δt 为高斯积分步长；t=p*Δt——高斯积分总时间；Ζi 为高斯求积节点；H i 为高斯求积节点处的高斯积分系数。

基于MATLAB的温度检测系统设计

基于MATLAB的温度检测系统设计成人教育学院毕业设计论文2012 年 6 月目录前言 (3)1 系统总体结构 (4)2 系统硬件 (4)2.1 系统的硬件设计 (4)2.2 AT89S52单片机实验开发板 (5)2.2.1 AT89S52单片机介绍 (6)2.2.2 串行接口介绍 (8)2.3 DS18B20传感器简介…………………………………………………………102.3.1 DS18B20内部结构 (10)2.3.2 DS18B20的工作原理 (11)2.3.3 DS18B20的指令系统 (12)2.3.4 DS18B20的通信协议 (13)2.3.5 DS18B20使用中注意事项 (14)2.3.6 DS18B20与单片机的典型接口设计 (15)3 系统的软件设计 (16)3.1下位机程序设计……………………………………………………………163.2 MATLAB程序设计 (17)3.2.1 MATLAB串口通信技术 (18)3.2.2 MATLAB GUI介绍 (20)3.2.3 GUI界面设计 (21)4 系统调试………………………………………………………………………234.1 下位机调试 (23)4.2 串口调试 (23)4.3 系统联调 (24)基于MATLAB的温度检测系统设计前言温度是工业控制中主要的被控参数之一，特别是在冶金、化工、建材、食品、机械、石油等工业中，具有举足重轻的作用。

传统靠人工控制的温度、湿度、液位等信号的测压力控系统，外围电路比较复杂，测量精度较低，分辨率不高，需进行温度校准非线性校准、温度补偿、传感器标定等；且它们的体积较大、使用不够方便，更重要的是参数的设定需要有其它仪表的参与，外界设备多，成本高，因而越来越适应不了社会的要求。

在对多类型、多通道信号同时进行检测和控制中，传统的测控系统能力有限。

如何将计算机与各种设施、设备结合，简化人工操作并实现自动控制，满足社会的需求，成为一个很迫切的问题。

利用matlab求解圆柱内稳定温度分布

数学物理方法论文（圆柱体齐次边界条件以及matlab的可视化）学院: 信息院年级: 2011级班级: 通信一班姓名: ***一、应用背景:现在由于公寓楼采用集体供暖的措施,需要在地下铺设圆柱形长管道,而对于管道的半径选取需要进行一定的计算,才能使得热水在传送过程中不会因温度过低而达不到用户的要求。

对于以上的问题，我们可以简化到应用数学中来解决。

二、简化例题：若一供暖公司采用的运输管道为标准圆柱体，其半径为ρ。

，长为L ，设管入口有均匀分布的强度为q 。

的热流流入，出口有相同的热流流出，管道侧面保持温度为0℃。

求解管道内的稳恒温度。

三、例题解答：解：因为上下底非齐次边界的非齐次项是常数，故可较易化成齐次边界。

这样本征值问题就变成傅里叶级数本征问题，而不是贝塞尔函数本征问题，同时系数的求解也较为简单。

令 z 01kq =νv kq u +=0则v 的定解问题为：⎪⎪⎪⎩⎪⎪⎪⎨⎧=-===∆===z k q v L z z z z 00200,00ρρννν 分离变数得到的本征值问题为：⎪⎩⎪⎨⎧===+==0',0'0"02L z z Z Z Z h Z 解得 ()......2,1,0,==n Ln h n πz Ln A Z n n πcos =，问题在柱内的有限解为：()⎪⎪⎭⎫⎝⎛∞=⋅=∑ρππρνL n n n I z L n A z 00cos ，由初始条件，得z kq IA n z L n L n 00ncos -=∑∞=⋅⎪⎪⎭⎫⎝⎛ππρ将上式右端展为傅里叶余弦级数，则有()dz L zn z k q L n LI n LA ππρcos 2000⋅-=⎰L L z n z n L L z n n L Ln L k I q 02000si n c o s 2-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⋅+=πππππρ()()[]112-2000--⎪⎭⎫ ⎝⎛=nn L L n L k Iq ππρ ()()()⎪⎩⎪⎨⎧+===12,402000220m n L n I n k Lq m n πρπ但不等于，()()()00,2-01000000=-==⎰I kL q zdz k q LI A L ()∑∞=+⋅⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛++=∴0002020012cos 12121242-m z L m L m I m L m I k L q k L q ππρπρπνν+=∴kqu四、以上问题的Matlab 的可视化：建立圆柱体：t=linspace(-pi,pi,200); y=linspace(0,4,200); [T,Y]=meshgrid(t,y); X=sin(T); Z=cos(T); mesh(X,Y,Z); axis equal由于本题中需要四维的数学建模（三维立体图形，再加一维的温度坐标），对于专业知识要求较高，以现有的知识水平还无法对四维进行分析求解，因此采用三维坐标（二维管道的横截面，再加一维的平面温度分布），进行求解。

一维热处理过程matlab仿真

我们以钢、粘土砖、铝合金和钛合金为研究对象（1）相同作用时间，温度随材料厚度的变化图像；（2）铝合金在不同热处理时间时温度随材料厚度的变化图像。考察加热时间100s时，材料距加热表面0.5m内的温度场分布。
Company Logo
材料和热处理参数
方法一）

Company Logo
图像分析
假设存在一种材料A，其导温系数与固态金属铝合金相同，但其熔点1300K以上（即在模拟过程中不会发生液化过程），比较该材料与铝合金加热温度分布曲线。
粘土砖
铝合金（液）
2040
2357
840
1080
1.17
91.9
6.82E-7
3.61E-5

Company Logo
相变过程的模拟方法
方法一：对于铝合金，固态时初始温度293K，最终温度913K；液态时初始温度913K，最终温度1293K。将固态与液态曲线综合。

Company Logo
铝合金不同加热时间图像（方法二）

Company Logo
结论导温系数越高，温度升高越快。
在加热100s时，铝合金热量可传递到距离表面 0.4m处，其余三者热量传递最大距离为0.15m。
铝合金固态传热比液态传热快，在相变点处有明显拐点。由不同加热时间图像可知，温度高时升温速度下降。
Company Logo
方法二存在的问题
对于材料性质的假设可能不够合理猜想：准确的温度分布曲线可能介于方法一所作曲线和方法二所作曲线之间。

wwwthemegallerycomcompanylogo图像方法一wwwthemegallerycomcompanylogo图像分析假设存在一种材料a其导温系数与固态金属铝合金相同但其熔点1300k以上即在模拟过程中不会发生液化过程比较该材料与铝合金加热温度分布曲线

MATLAB 画等温线

测量到不同坐标点的高度值,如何用matlab画三维图附上部分数据：A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077-211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381-225.8973 -33397.5869 5.5587];解：代码在matlab2009a版以上均可运行。

A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077-211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381-225.8973 -33397.5869 5.5587];xData = A(:,1);yData = A(:,2);zData = A(:,3);fitresult = fit( [xData, yData], zData, 'linearinterp');figure( 'Name', '三维图' );plot( fitresult, [xData, yData], zData );xlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -53, 50 );试一试：A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077 -211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381 -225.8973 -33397.5869 5.5587];xData = A(:,1);yData = A(:,2);zData = A(:,3);minx = min(xData);maxx = max(xData);miny = min(yData);maxy = max(yData);tx = linspace(minx,maxx)';ty = linspace(miny,maxy);[XI,YI] = meshgrid(tx,ty);ZI = griddata(xData,yData,zData,XI,YI); mesh(XI,YI,ZI), holdplot3(xData,yData,zData,'o'), hold offxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -53, 50 );.................x=[7392 7392 7392 7392 5608 5608 5608 5608 80 00 5000 6500 6500 6500 6500 6500 6500 6500 6500 6500 6500];y=[476 404 476 404 476 404 476 404 440 440 440 440 500 380 440 440 440 440 440 44 0];z=[17.06 16.93 17.8 17.4 17.17 16.89 17.28 17.26 17.04 16.94 16.92 17.3 17.37 17.17 17.34 17.11 17.22 17.24 17.11 17.2];minx = min(x);maxx = max(x);miny = min(y);maxy = max(y);[X,Y,Z]=griddata(x,y,z,linspace(minx,maxx)',linspace(miny,maxy),'v4') ; %插值figure,surf(X,Y,Z) %三维曲面...%% Initialization.% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: ' fit 1'.ft = 'linearinterp';opts = fitoptions( ft );opts.Weights = zeros(1,0);opts.Normalize = 'on';[fitresult, gof] = fit( [x, y], z, ft, opts );% Plot fit with data.figure( 'Name', 'untitled fit 1' );h = plot( fitresult, [x, y], z );% legend( h, ' fit 1', 'z vs. x, y', 'Location', 'NorthEast' );% Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid on.......................x=[7392 7392 7392 7392 5608 5608 5608 5608 80 00 5000 6500 6500 6500 6500 6500 6500 6500 6500 6500 6500];y=[476 404 476 404 476 404 476 404 440 440440 440 500 380 440 440 440 440 440 44 0];z=[17.06 16.93 17.8 17.4 17.17 16.89 17.28 17.26 17.04 16.94 16.92 17.3 17.37 17.17 17.34 17.11 17.22 17.24 17.11 17.2];% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: ' fit 1'.ft = fittype( 'poly22' );opts = fitoptions( ft );opts.Lower = [-Inf -Inf -Inf -Inf -Inf -Inf];opts.Upper = [Inf Inf Inf Inf Inf Inf];opts.Weights = zeros(1,0);[fitresult, gof] = fit( [x, y], z, ft, opts );fitresult% Plot fit with data.figure( 'Name', 'z' );h = plot( fitresult, [x, y], z );% legend( h, 'z fit 1', 'z vs. x, y', 'Location', 'NorthEast' );% Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -57.5, 42 );.................A=[18467 17001 308 20177 17642 276 26852 16114 225 23785 17643 194 27823 14737 189 18906 16346 173 25981 18051 173 22046 17634 171 23238 6502 169 27696 11621 169 27700 11609 16516607 17365 155 23146 15382 153 14405 18032 152 27232 14482 150 27380 18202 136 26591 13715 126 14074 16516 124 15801 3966 115 21684 13101 114 15255 5110 110 24580 13319 107 23325 16701 105 24065 7353 104 25021 16290 104 15952 18397 103 27346 13331 100 24685 14278 98 17414 15476 97 12778 5799 93 17044 10691 93 17981 18449 93 20983 15862 93 22605 14301 93 5451 2757 92 19041 15769 90 24003 15286 90 7100 2449 89 18413 11721 88 21475 8540 85 19007 11488 84 17008 4775 82 17079 5894 81 13855 3345 79 13920 5354 79 22193 12185 79 16569 6055 78 18993 12371 78 22965 13535 78 15517 17034 77 24631 9422 76 4153 2299 73 11702 4480 71 24153 12450 71 15007 5535 7019569 7348 7015087 3512 6922846 9149 6925461 9834 6816823 4207 6721766 12348 6712625 16259 66];x=A(:,1);y=A(:,2);z=A(:,3);minx = min(x);maxx = max(x);miny = min(y);maxy = max(y);[X,Y,Z]=griddata(x,y,z,linspace(minx,maxx)',linspace(miny,maxy),'v4') ; %插值figure,surf(X,Y,Z) %三维曲面...%% Initialization.% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: 'untitled fit 1'.ft = 'linearinterp';opts = fitoptions( ft );opts.Weights = zeros(1,0);opts.Normalize = 'on';[fitresult, gof] = fit( [x, y], z, ft, opts ); % Plot fit with data.figure( 'Name', ' fit 1' );h = plot( fitresult, [x, y], z );% legend( h, ' fit 1', 'z vs. x, y', 'Location', 'NorthEast' ); % Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid on。