二阶系统的时域性能指标计算
二阶系统的时域分析

n
n
112 2 (阻尼 (阻振 尼荡 振)频 荡率 )频率
n
n
d
d
则 s1 、 2j d 此时
C (s) 1 s (s s )2 2 (s )2 2
d
d
精选课件
14
所 其1中以 cco1(setβ)所 t=12ζ1即以 seβci=1t(neac tr)cotdtc21sodsts ζsei n (iβt nc称c dodo t为 s se阻dtt 尼sc 角io ns d)dts ei n t si ns i dn t( )
2
C n ;C n ;C 1
1 (s s)s 2 (s s)s 3
1 21
1 22
而s1,s2是ζ和ωn的函数,显然c(t)只与ζ ,ωn有关,即ζ ,ωn决
定着c(t)的形式。分别讨论如下:
精选课件
11
① ζ >1时,(过阻尼) s1 ,s2 为一对不等的负实数根。
j
j
s1、s2
0
0
t
9
二阶系统的闭环极点分布
特征根: s1,2 nn 21
j
j
j
n 1 2
n 1 2
n
0
n 12
0
0
n 1 2
n
0 1
1
1 0
j
s1 s2
n
0
1
j
n
0
n
精选课件0
j
0
1 10
2 二阶系统的单位阶跃响应
当r(t) = 1 时 或R(s)=1/s 时, 有:
C (s) (s)R (s)s2 2 n 2s 21 s
第三章 时域分析法
二阶系统的时域分析二阶系统的数学模型

二阶系统的时域分析二阶系统的数学模型二阶系统指的是系统的动态特性可以由一个二阶微分方程描述的系统。
在控制工程中,二阶系统的时域分析主要包括对系统阶跃响应、脉冲响应、频率响应等进行分析。
下面将详细介绍二阶系统的数学模型以及各种时域分析方法。
二阶系统可以由一个二阶微分方程进行描述。
一般而言,二阶系统的数学模型可以写成如下形式:\[a_2\frac{{d^2y(t)}}{{dt^2}} + a_1\frac{{dy(t)}}{{dt}} +a_0y(t) = b_2\frac{{d^2u(t)}}{{dt^2}} + b_1\frac{{du(t)}}{{dt}}+ b_0u(t)\]其中,y(t)为系统的输出,u(t)为系统的输入,a_0、a_1、a_2以及b_0、b_1、b_2分别为系统的系数。
这个方程也可以写成常用的形式:\[\frac{{d^2y(t)}}{{dt^2}} + 2ζω_n\frac{{dy(t)}}{{dt}} +ω_n^2y(t) = K_p\frac{{d^2u(t)}}{{dt^2}} +T_i\frac{{du(t)}}{{dt}} + K_cu(t)\]其中,ζ为阻尼比,ω_n为自然频率,K_p为比例增益,T_i为积分时间常数,K_c为控制器增益。
2.二阶系统的阶跃响应阶跃响应是指系统在接受一个单位阶跃信号作为输入时的响应。
通过对二阶系统的数学模型应用拉普拉斯变换,可以得到系统的传递函数。
对于一个传递函数为G(s)的系统,其阶跃响应可以通过下面的公式得到:\[y(t) = A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))\]其中,A为阶跃响应的幅度,ω_d为阻尼振荡角频率,ϕ为相位角。
3.二阶系统的脉冲响应脉冲响应是指系统在接受一个单位脉冲信号作为输入时的响应。
与阶跃响应类似,通过对二阶系统的数学模型进行拉普拉斯变换,可以得到系统的传递函数。
对于一个传递函数为G(s)的系统,其脉冲响应可以通过下面的公式得到:\[y(t) = \frac{{A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))}}{{\sqrt{1-ζ^2}}}\]其中,A为单位脉冲信号的幅度。
二阶系统的时域分析二阶系统的数学模型

t
n
1
n2 e 1 2
entsinnt
sidnt
dtn101
2
2
e n t
cos d t
h' (t)
1
2n2 edstipnntsindntpd(tn
0 n
01,
1,2e2,nt
si)n
d
t
二阶系统的时域分析
欠阻尼二阶系统阶跃响应的性能指标
2.峰值时间tp tp为输出响应达到第一个峰值所对应的时间所
过阻尼二阶系统调节时间特性
二阶系统的时域分析
临界阻尼二阶系统的暂态响应
当ζ=1时,临界阻尼二阶系统T1=T2,
1 T1
1 T2
n
则临界阻尼二阶系统的单位阶跃响应为
c(s)
s
n2
n 2
1 s
1 s
s
n
n 2
s
1 n
h(t ) 1 (1 nt )ent 过阻尼二阶系统的响应较缓慢,实际应用 的控制系统一般不采用过阻尼系统。
结论
无阻尼系统属于临界稳定系统,不属于稳定 系统
临界阻尼和过阻尼系统虽无超调量,但反应 迟钝
欠阻尼系统虽有超调量,但反应迅速
因此控制系统就是性能指标之间的均衡,一 般设计成欠阻尼系统。
阻尼比一般取0.4~0.8,此时系统反应迅速, 而且超调量也不大
二阶系统的时域分析
阻尼比ζ是二阶系统的一个重要参量,由值ζ的大小 可以间接判断一个二阶系统的暂态品质。在过阻尼 (ζ>1)情况下,暂态特性为单调变化曲线,没有 超调和振荡,但调节时间较长,系统反应迟缓。当 ζ≤0 ,输出量作等幅振荡或发散振荡,系统不能稳 定工作。
不易求出ts,但 可得出ωnts与 ζ的关系曲线
第3讲 二阶系统的时域分析

18
三、典型二阶系统的动态过程分析
(一)衰减振荡瞬态过程 (0 1):欠阻尼
s 1, 2 ζω n jωn 1 ζ
2
ζω n jωd
c (t ) 1 Fra biblioteke ζωn t 1 ζ 2
sin(ωd t β ) ,
t 0
⒈ 上升时间 t r :根据定义,当 t t r时,c(tr ) 1 。
3
s1, 2 n n 1
2
⒊ 当 1 时,特征方程有一对相等的实根,两个极点位于S平 面负实轴上,系统时间响应无振荡,称为临界阻尼系统,系统 的阶跃响应为非振荡过程。 ⒋ 当 1 时,特征方程有一对不等的实根,两个极点位于S 平面负实轴上,系统时间响应无振荡,称为过阻尼系统,系统 的阶跃响应为非振荡过程。 以上 1 属于非振荡情况
于是有:
tr d
ωd ωn 1 ζ 2
n
n
j n 1 2 j d
n
称为阻尼角
j n 1 2
cos
可见,当阻尼比一定时,系统的响应速度与自然频率成正比; 而当阻尼振荡频率一定时,阻尼比越小,上升时间越短。
2 n 1 C ( s) ( s) R( s) 2 2 s 2 n s n s
2 其中, 由特征方程 s 2 2 n s n 0
可求得两个特征根(即闭环极点)
s1, 2 n n 2 1
6
[分析]:
s1, 2 n n 1
s n n 1 2 2 2 2 s s 2 n s n s 2 n s n
控制工程(自动控制)第九次课 二阶系统响应及性能指标

测速反馈控制: 测速反馈控制:
R(s )
E (s )
U (s )
2 ωn s( s + 2ξωn )
C (s )
Kt s
2 ωn 2 2 s 2 + (2ζωn + Ktωn )s + ωn
Φ( s) =
K tωn ζt =ζ + >ζ 2
ω n 不变
结论:测速反馈会降低系统的开环增益, 结论:测速反馈会降低系统的开环增益,从而 加大系统在斜坡输入时的稳态误差, 加大系统在斜坡输入时的稳态误差,但不影 响系统的自然频率,并可增大系统的阻尼比. 响系统的自然频率,并可增大系统的阻尼比.
R (s )
E (s )
2 ωn s( s + 2ξωn )
Td s + 1
U (s )
C (s )
ω (Td s +1) Φ(s) = 2 2 2 s + (2ζωn + Tdωn )s + ωn
2 n
Td ωn ζd =ζ + >ζ 2
ω n 不变
结论:比例 微分控制可以增大系统的阻尼 微分控制可以增大系统的阻尼, 结论:比例-微分控制可以增大系统的阻尼,使 阶跃响应的超调量下降,调节时间缩短, 阶跃响应的超调量下降,调节时间缩短,且 不影响常值稳态误差及系统的自然频率. 不影响常值稳态误差及系统的自然频率.
ess = lim[r (t ) c(t )] =
t →∞
2ζ
ωn
2,临界阻尼情况(ζ =1): ,临界阻尼情况( ):
c(t ) = t 2
ωn
t →∞
+
2e
ωn t
自动控制理论时域分析2--二阶系统

4.调整时间 t s(又称过渡过程时间) :响应曲线达到并 保持与稳态值之差在预定的差值△内(又叫误差带 )所 需要的时间。一般△取±2%或±5%。
二、二阶系统的动态响应性能指标 (1)峰值时间 t P
因为
c (t ) 1 e nt 1
2
sin( d t )
t n p d
dc ( t ) dt
d p
0
ttp
e sin( t ) e cos( t ) 0
t n p n d p
整理得:
tg ( ) dtp
12
p t p 0, ,2 ,3
n
0 Re
s1
s2
0
Re
s2
s1
0
Re
0
Re
s2
(a) 0 1 (b) 1 (c) 1 (d) 0
特征根为:共扼复数 特征根为:
相等实数
不等实数
共扼虚数
1.欠阻尼情况 :
( 0 1 )
2
s n 1 1 , 2 n
s j 1 , 2 n d
c ( t) 1 cos t n
c (t )
( 0)
(t 0)
2
1
0
t
这是一条等幅振荡曲线。
( 0)
c (t )
1
c (t ) r (t )
2
1
1
c (t )
0
t
0
t
( 0 1 )
1
r (t )
3.3二阶系统
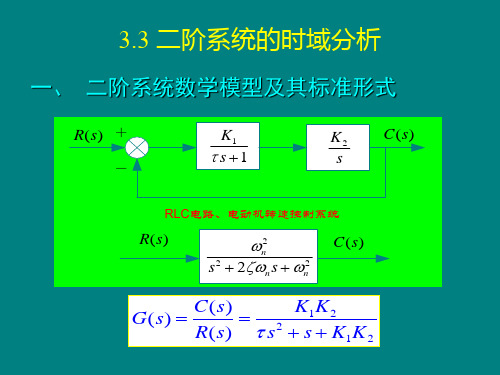
tp d 1 2 n
(6)最大超调量的计算:
p
c(t p ) c() c ( )
n t p
100%
1 2
2
e
e
(cos d t p
sin d t p ) 100%
n t p
(cos
1
sin ) 100%
dc(t ) / dt 0
则
故
n e
nt p
sin(d t p ) d e
tan(d t p )
nt p
cos(d t p ) 0
2
1
tan
到达第一个峰值时应有
d t p 0, , 2 ,3
d t p
s1 , s2 jn 是一对共轭纯虚数根。
三、二阶系统的单位阶跃响应
对于单位阶跃输入
r (t ) 1(t )
1 R( s) s
于是
2 n 1 C ( s) 2 2 s 2n s n s
由拉氏反变换可以得到二阶系统的单位阶跃响应为
c(t ) L1[C ( s)] 下面按阻尼比分别讨论。
欠阻尼系统单位阶跃响应为
c(t ) 1 e nt cos d t
n t e sin d t d
n
1 e nt (cos d t
1
2
sin d t )
(t 0)
或写为
c(t ) 1 e nt 1
2
( 1
解得 t 1/ n 。 整个暂态过程中,临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的 95% 所经历的时 间做为调整时间,则
第三章 控制系统的时域分析—2二阶系统时域分析

2 n
1
s
L1
A0 s
s
A1 s1
s
A2 s2
s2 s1
其 中A0 s C(s) s0 1A1 , A2自 己 求
8
c t
1
A1e s1t
A2e s2t
1
s2
1 s1
s1e s2t s2e s1t
❖单调过程,无超调, 大,内耗大,无法维持能量交换,即
二阶系统的时域响应
快
稳
准
动态性能分析 tr,td,tp,ts,s%
稳定性分析 稳态性能分析
Routh判据
ess
二阶系统的基本性质及结论
2
3-3 二阶系统的时域分析
二阶系统:以二阶微分方程作为运动方程的控制系统。 1 二阶系统的数学模型
一伺服系统,系统框图如下:
R(s) E(s)
K
C(s)
- sTms 1
振荡角频率”
10
(s)
s2
1 2 01s
1
2
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
2
4
6
8 10 12 14 16 18 20
11
❖临界阻尼下单位阶跃响应 1 1
r(t) 1(t) , R(s) 1 s
s1 s2 n
s1 s2
C(s) n2 1 1 n 1
K Tm
n-自然频率(或无阻尼振荡频率)
2
n
1 Tm
1
2 Tm K
-阻尼比(相对阻尼系数)
二阶系统的闭环特征方程为:
s2 2ns n2 0
二阶系统的时域分析.ppt

d ds
[C
(s
)(
s
n
)
2
]s
n
1
2 [C(s) (s n )2 ]sn n
C(t) 1 ent ntent 1 ent (1 nt) (t 0)
j [s]
s1s2
n o
1
C(t) 1
1 是输出响应的单调和振荡过程的分界,通
常称为临界阻尼状态。
o
2020/3/29
3-3二阶系统的时域分析
况,故称为阻尼系数。
2020/3/29
3-3二阶系统的时域分析
10
3.二阶系统的性能指标(1)-上升时间
根据定义,当 t tr时,c(tr ) 1。 令 c(t) 1 et sin (dt+ ) =1
sin
c(t) 1 et sin (dt+ ) , t 0 sin
e t sin (d t+ ) 0 sin
T1 T2
n
T2
1
n
h(t)= 1 -(1临+ω界n阻t)尼0je-ωnt
0<0<ξ<ξ<1 1 S1,2= -ξ ωn ±jj ωn√1-ξξ2 =0
jj 0
0
0
e - h(t)=
ξ=1 0 1
2020/3/2√91-ξ2
-ξωSnt欠1s,2i阻n=(尼ω±d3t-j3+二ωβ阶n)系统的时域分析
为阻尼振荡圆频率。
2020/3/29
3-3二阶系统的时域分析
1 2 是振荡频率。称 d
5
2.二阶系统的单位阶跃响应(4)-过阻尼
极点:s1,2 n n 2 1
阶跃响应:c(t) 1
n
实验二二阶系统时域分析
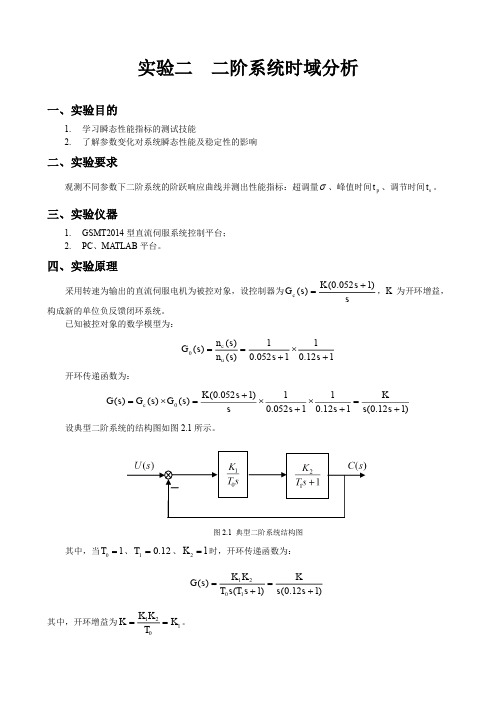
实验二 二阶系统时域分析一、 实验目的1. 学习瞬态性能指标的测试技能2. 了解参数变化对系统瞬态性能及稳定性的影响二、 实验要求观测不同参数下二阶系统的阶跃响应曲线并测出性能指标:超调量σ、峰值时间p t 、调节时间s t 。
三、 实验仪器1. GSMT2014型直流伺服系统控制平台;2. PC 、MA TLAB 平台。
四、 实验原理采用转速为输出的直流伺服电机为被控对象,设控制器为ss K s G c )1052.0()(+=,K 为开环增益,构成新的单位负反馈闭环系统。
已知被控对象的数学模型为:112.011052.01)()()(0+⨯+==s s s n s n s G u c 开环传递函数为:)112.0(112.011052.01)1052.0()()()(0+=+⨯+⨯+=⨯=s s Ks s s s K s G s G s G c 设典型二阶系统的结构图如图2.1所示。
图2.1 典型二阶系统结构图其中,当01T =、12.01=T 、21K =时,开环传递函数为:)112.0()1()(1021+=+=s s Ks T s T K K s G 其中,开环增益为1021K T K K K ==。
闭环传递函数为其中,1T K n =ω 11121T K =ξ (2.1) (1)当10<<ξ,即欠阻尼情况时,二阶系统的阶跃响应为衰减振荡,如图2.2中曲线1所示。
()1)(0)n T d C t t t ξωωθ=-+≥ (2.2)式中 21ξωω-=n d1tgθ-=峰值时间可由式(2.2)对时间求导,并令它为零,得:p d t πω== (2.3)超调量()()()p p C t C t C t σ∞∞-=,求得p eσ= (2.4)调节时间s t ,采用2%允许误差范围时,近似地等于系统时间常数1()n ξω⨯的四倍,即:n s t ξω4=(2.5)(2)当1=ξ,临界阻尼时,系统的阶跃响应为单调的指数曲线,如图2.2中曲线2所示)0()1(1)(≥+-=-t t e t C n t n ωω令输出为98.0可求得s t 。
二阶系统的时域分析二阶系统的数学模型

二阶系统的时域分析二阶系统的数学模型二阶系统是指由两个一阶系统级联或并联组成的动态系统。
它的数学模型可以表示为如下形式:$$s^2Y(s) + 2ξω_nsY(s) + ω_n^2Y(s) = X(s)$$其中,$s$是复频域变量,$Y(s)$和$X(s)$分别是系统的输出和输入拉普拉斯变换形式;$ξ$是阻尼比,$ω_n$是自然频率。
为了进行时域分析,我们需要将模型转换为时域表示。
我们可以通过拉普拉斯逆变换对模型进行求解。
首先,我们可以将拉普拉斯变换模型转换为分母为二次方程的形式:$$s^2 + 2ξω_ns + ω_n^2 = 0$$这是一个特征方程,也称为二阶系统的特征方程。
根据特征方程的解,我们可以获得系统的阻尼比和自然频率。
特别地,当阻尼比$ξ$小于1时,系统被称为欠阻尼;当阻尼比$ξ$等于1时,系统被称为临界阻尼;当阻尼比$ξ$大于1时,系统被称为过阻尼。
根据不同的阻尼比,我们可以对系统的时域响应进行分类:1.欠阻尼情况下,系统的时域响应会产生振荡。
振荡的频率为阻尼比与自然频率的乘积。
2.临界阻尼情况下,系统的时域响应会趋于稳定,但不会产生振荡。
3.过阻尼情况下,系统的时域响应会趋于稳定,没有振荡,并且速度较快。
在实际应用中,我们经常需要对二阶系统的时域响应进行分析和设计。
常见的时域响应指标包括步响应、阶跃响应和频率响应。
这些响应可以通过对特征方程进行求解来获得。
对于步响应,我们可以通过求解特征方程的根来获得系统的过渡时间、最大超调量和静态误差等信息。
通过调整控制器和系统参数,我们可以改变这些指标,以满足系统设计的要求。
对于阶跃响应,我们可以通过求解特征方程的根来获得系统的上升时间、峰值时间和调节时间等信息。
同样,通过调整控制器和系统参数,我们可以改变这些指标,以满足系统设计的要求。
对于频率响应,我们可以通过将特征方程转换为复频域变量来获得系统的频率响应函数。
频率响应函数可以帮助我们分析系统在不同频率下的增益和相位变化。
第三章二阶系统响应与时域性能指标解析

第三章二阶系统响应与时域性能指标解析在控制系统中,二阶系统是指具有二阶传递函数的系统。
二阶系统在工程实践中非常常见,例如机械系统、电子电路系统等。
了解二阶系统的响应和时域性能指标对于设计和分析控制系统非常重要。
二阶系统的传递函数可以表示为$G(s)=\frac{\omega_n^2}{{s^2+2\zeta\omega_ns+\omega_n^2}}$,其中$\omega_n$是系统的自然频率,$\zeta$是系统的阻尼比。
首先我们从系统的阶跃响应来分析二阶系统的时域性能指标。
阶跃响应是系统对阶跃信号输入的响应。
通过对传递函数分母进行因式分解,我们可以将传递函数改写为$G(s)=\frac{\omega_n^2}{(s+s_1)(s+s_2)}$,其中$s_1 = (-\zeta+\sqrt{\zeta^2-1})\omega_n$,$s_2 = (-\zeta-\sqrt{\zeta^2-1})\omega_n$。
1. 峰值超调量(Percent Overshoot):峰值超调量是指系统过渡过程中输出信号的最大超调量与步变幅度之比。
通过阶跃响应曲线可以直观地看出系统的峰值超调量。
2. 调节时间(Settling Time):调节时间是指系统从初始状态到稳定状态所需的时间。
在阶跃响应曲线中,调节时间可以定义为系统的输出信号在峰值超调之后首次进入指定误差范围内所需的时间。
一般来说,稳定误差范围可以选择输出信号与目标信号之差小于目标值的一些百分比,例如5%。
3. 峰值时间(Peak Time):峰值时间是指系统输出信号首次达到峰值超调量的时间。
在阶跃响应曲线中,峰值时间可以直接读取。
4. 上升时间(Rise Time):上升时间是指系统输出信号从初始状态到达峰值的时间。
在阶跃响应曲线中,上升时间可以定义为系统输出信号从0.1倍峰值超调量到0.9倍峰值超调量之间所需的时间。
二阶系统的阶跃响应曲线具有不同的形态,取决于系统的阻尼比$\zeta$。
典型二阶系统的时域响应与性能分析

典型二阶系统的时域响应与性能分析对于一个典型的二阶系统,其数学模型可以表示为以下形式:m*d^2y/dt^2 + c*dy/dt + ky = u(t)其中,m是系统的质量,c是系统的阻尼系数,k是系统的刚度,y(t)是系统的输出,u(t)是系统的输入。
二阶系统的时域响应描述了在给定输入条件下系统的输出变化情况。
常用的描述二阶系统时域性能的指标包括过渡过程、超调量、峰值时间、稳态误差等。
首先是过渡过程。
过渡过程是指系统输出从初始值到达稳定状态所经历的时间。
过渡过程可以通过系统的阻尼比和固有频率来确定。
阻尼比(Damping Ratio)是指系统的阻尼系数与临界阻尼时的阻尼系数之比,表示系统对阻尼变化的敏感程度。
固有频率(Natural Frequency)是指在没有任何阻尼的情况下,系统的振荡频率。
其次是超调量。
超调量是指系统输出达到峰值时的最大偏离幅度与稳态幅值之间的差值。
超调量可以通过系统的阻尼比来衡量,当阻尼比越小时,超调量越大。
峰值时间是指系统输出达到峰值的时间点,通常用稳定时刻的时间点减去起始时间点来衡量。
峰值时间可以通过系统的阻尼比和固有频率来计算,当阻尼比越小时,峰值时间越长。
稳态误差是指系统输出稳定之后与期望输出之间的差值。
稳态误差可以通过系统的阻尼比来衡量,当阻尼比越小时,稳态误差越大。
在实际应用中,我们经常需要对二阶系统的性能进行分析与优化。
一种常见的方法是通过改变系统的阻尼比、固有频率等参数来获得所需的效果。
例如,如果需要减小超调量,可以通过增加阻尼比的方式来实现;如果需要减小过渡时间,可以通过增加固有频率的方式来实现。
此外,对于二阶系统的分析可以采用频域方法,如Bode图和Nyquist图等。
这些图形可以提供系统的频率响应信息,帮助我们更全面地理解和优化系统性能。
总之,典型二阶系统的时域响应与性能分析是控制系统工程中很重要的一部分。
充分理解和分析二阶系统的时域响应特征和性能指标,可以帮助我们更好地设计和控制系统,提高系统的稳定性和性能。
第三章二阶系统响应与时域性能指标

第三章二阶系统响应与时域性能指标第三章介绍了二阶系统的响应和时域性能指标。
二阶系统是指具有两个阶数的系统,常见的二阶系统包括二阶低通滤波器和二阶弹簧质量振动系统等。
了解二阶系统的响应和性能指标对于工程实践和控制系统设计非常重要。
首先,我们先介绍了二阶系统的自由响应和强迫响应。
自由响应是指系统在没有外部输入的情况下的响应,主要由系统的初始条件决定。
强迫响应是指系统在受到外部输入信号刺激后的响应,主要由刺激信号的频率和幅值决定。
在讨论自由响应时,我们介绍了二阶系统的特征方程和特征根。
特征方程是描述系统特征的方程,由系统的传递函数决定。
特征根是特征方程的根,决定了系统的稳定性和响应特性。
特征根可以分为实根和共轭复根两种,分别对应系统的欠阻尼和过阻尼响应。
接着,我们讨论了二阶系统的时域性能指标。
其中包括超调量、峰值时间、调节时间和稳态误差等。
超调量反映了系统响应的振荡程度,峰值时间是达到响应峰值所需要的时间,调节时间是达到稳态的时间。
稳态误差则表征了系统输出与目标值之间的差异。
最后,我们通过实例来说明了如何使用MATLAB来计算和绘制二阶系统的时域性能指标。
MATLAB是一种非常方便的工具,可以极大地简化计算和绘图的过程。
通过使用MATLAB,我们可以更加直观地了解二阶系统的响应特性和时域性能。
总之,了解二阶系统的响应和时域性能指标对于工程实践和控制系统设计非常重要。
通过本章的学习,我们可以更好地理解和分析二阶系统的响应特性,为系统设计和调试提供有力支持。
同时,通过使用MATLAB等工具,我们可以更加方便地进行计算和绘图,提高工作效率和准确性。
自动控制原理--二阶系统的时域响应

y(t ) L-1[Y (s)]
-n
1 - e-nt (cos d t
1 - 2 sin d t )
s2
1-
e - nt (
1- 2
1 - 2 cos d t sin d t )
j jd
0
1-
e - nt 1 - 2 sin(n
1 - 2 t tg-1
1- 2 )
y(t)
单位阶跃响应( 0<<1 )
esst
2
a K
K
0.25
a 0.187
比例微分控制与输出微分反馈的比较
1、增加阻尼的来源不同:两者都增大了系 统阻尼,但来源不同;
2、对于噪声和元件的敏感程度不同; 3、对开环增益和自然振荡角频率的影响不
同; 4、对动态响应的影响不同。
(1)增加阻尼的来源
• 比例微分的阻尼来自误差信号的速度;
1)
阶跃响应:y(t) 1
1
-1t
e T1
1
-1t
e T2
T2 T1 -1
T1 T2 -1
yt
j
1
0
0
t
单位阶跃响应(>1)
无振荡、无超调
2、临界阻尼 =1
j 0
两个相同的负实根
闭环系统的极点为 s1,2 -n
闭环传递函数为
GB
Y (s) R(s)
(s
n2 n )2
阶跃响应: y(t) 1- e-nt (1 nt)
阻尼振荡频率
衰减振荡
d 1- 2n
4、零阻尼 0
阶跃响应y(t)=1-cos nt
n --无阻尼振荡角频率
j 0
一对纯虚根
典型二阶系统的时域响应与性能分析

实验二 典型二阶系统的时域响应与性能分析一、实验目的1、研究二阶系统的特征参量(ζ, ωn )对过渡过程的影响。
2、研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
二、实验设备PC 机一台,TD-ACS 教学实验系统一套。
三、实验原理典型二阶系统开环传递函数为:)1()1()(101101+=+=s T s T K s T s T K s G ;其中,开环放大系数01T K K = 。
系统方块图与模拟电路如图2-1与图2-2所示。
图2-1典型二阶系统方块图图2-2模拟电路图先算出临界阻尼、欠阻尼、过阻尼时电电阻R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性。
设R T K K s T T s T 200,2.0,10110=====,系统闭环传递函数为:2222221)()(n n n s s TK s T s T KK s Ts K s R s C ωζωω++=++=++= 其中,自然振荡频率:RT K n 1010==ω 阻尼比:4102521RTKTn===ωζ 典型二阶系统的瞬态性能指标:超调量:21%ζζπδ--=e峰值时间:21ζωπ-=n p t峰值时间的输出值:211)(ζζπ-=+=e t C p调节时间:1)欠阻尼10<<ζ,⎪⎪⎩⎪⎪⎨⎧=∆=∆≈5324,,t n n s ζωζω2)临界阻尼1=ζ,⎪⎪⎩⎪⎪⎨⎧=∆=∆≈575.4284.5,,t nns ωω3)过阻尼1>ζ,⎩⎨⎧=∆=∆≈532411,p ,p t s ,1p -与2p -为二阶系统两个互异的负实根122,1-±-=-ζωζωnn p ,21p p ->>-,过阻尼系统可由距离虚轴较近的极点1p -的一阶系统来近似表示。
四、实验内容与要求1、实验前预先计算出典型二阶系统性能指标的理论值并填入实验对照表2-1中。
2、按模拟电路图接线,将信号源单元的“ST”端插针与“S”端插针用“短路块”短接,使每个运放单元均设置锁零场效应管,此时运放具有锁零功能。
自动控制原理(3-2)

arccos 1.09(rad )
1 0.7
d n 1 2 3.14(rad / s)
0.65( s ) d
td
n
3.5
0.37( s )
tr
ts
n
4.4
2.15( s ) 0.05
ts
n
2.70( s)
对上式取拉氏反变换,求得单位阶跃响应为:
h(t ) 1 e sin d t cos d t 2 1 1 1 e nt 1 2 cos d t sin d t 1 2
n t
1
1 1 2
e nt sin( d t ) , t 0
式中, arctan( 1 2 ) ,或者
arccos
欠阻尼二阶系统的单位阶跃响应有两部分组成:
稳态分量为1,系统在单位阶跃函数作用下不存在
稳态位臵误差;
瞬态分量为阻尼正弦振荡项,其振荡频率为ωd,
故称为阻尼振荡频率。
t 0
系统的误差为:
e(t ) r (t ) c(t ) 2
n
2
n
1 2 e nt sin 1 2 n t 2arctg 1 2 1
1 2
e t T1 e t T2 h(t ) 1 , t0 T2 T1 1 T1 T2 1
4.无阻尼(ζ=0)二阶系统的单位阶跃响应
h(t ) 1 cos nt , t 0
可见,这是一条平均值为1的正、余弦形式的等幅振 荡,其振荡频率为ωn,故可称为无阻尼振动频率。 实际的控制系统通常都有一定的阻尼比,因此不可能 通过实验方法测得ωn,而只能测得ωd,且小于ωn。
二阶系统频域指标与动态时域指标之间的对应关系

一、概述在控制系统工程中,频域指标和时域指标是评价系统性能的重要标准。
二阶系统是一类简单且常见的动态系统,其频域指标和时域指标之间存在一定的对应关系。
本文将探讨二阶系统频域指标与动态时域指标之间的对应关系,以及在实际工程中的应用。
二、二阶系统概述1. 二阶系统的数学描述二阶系统是指具有两个传递函数零点和两个传递函数极点的动态系统。
其数学模型可以用如下的传递函数形式表示:$$ G(s) = \frac{K}{s^2 + 2ζω_ns + ω_n^2} $$其中,K为系统的增益,ζ为阻尼比,ω_n为自然频率。
2. 二阶系统的特性二阶系统在频域和时域上有着特定的性能指标,包括频域指标如增益裕度、相位裕度、共振峰值等,以及时域指标如上升时间、峰值时间、定时时间等。
三、频域指标与动态时域指标的对应关系1. 增益裕度与峰值时间的关系在频域分析中,增益裕度是指系统在开环增益相对于临界增益时的增益范围。
而峰值时间是指系统的输出响应中出现的最大过渡过程时间。
二者之间存在如下的关系:$$MG = \frac{1}{\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,MG为增益裕度,Tp为峰值时间。
2. 相位裕度与上升时间的关系相位裕度是指系统在开环相位相对于-180°时的相位范围。
上升时间是指系统输出响应从初始稳态值上升到峰值的时间。
二者之间的关系可以表示为:$$PM = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tr = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,PM为相位裕度,Tr为上升时间。
3. 共振峰值与峰值时间的关系共振峰值描述了系统在共振频率处的增益倍数。
而峰值时间则是描述了系统输出响应中的最大过渡过程时间。
二者的关系如下:$$M_p = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中,M_p为共振峰值,Tp为峰值时间。
