不对称短路的分析和计算..
不对称短路故障分析与计算(电力系统课程设计)

不对称短路故障分析
02
不对称短路故障类型
单相接地短路
其中一相电流通过接地电阻,其余两 相保持正常。
两相短路
两相接地短路
两相电流通过接地电阻,另一相保持 正常。
两相之间没有通过任何元件直接短路。
不对称短路故障产生的原因
01
02
03
设备故障
设备老化、绝缘损坏等原 因导致短路。
外部因素
如雷击、鸟类或其他异物 接触线路导致短路。
操作错误
如误操作或维护不当导致 短路。
不对称短路故障的危害
设备损坏
短路可能导致设备过热、烧毁或损坏。
安全隐患
短路可能引发火灾、爆炸等安全事故。
停电
短路可能导致电力系统的局部或全面停电。
经济损失
停电和设备损坏可能导致重大的经济损失。
不对称短路故障计算
03
方法
短路电流的计算
短路电流的计算是电力系统故障分析中的重要步骤,它涉及到电力系统的 运行状态和设备参数。
不对称短路故障分析与 计算(电力系统课程设计)
contents
目录
• 引言 • 不对称短路故障分析 • 不对称短路故障计算方法 • 不对称短路故障的预防与处理 • 电力系统不对称短路故障案例分析 • 结论与展望
引言
01
课程设计的目的和意义
掌握电力系统不对称短路故障的基本原理和计算 方法
培养解决实际问题的能力,提高电力系统安全稳 定运行的水平
故障描述
某高校电力系统在宿舍用电高峰期发生不对称短路故障,导致部 分宿舍楼停电。
故障原因
经调查发现,故障原因为学生私拉乱接电线,导致插座短路。
解决方案
加强学生用电安全教育,规范用电行为;加强宿舍用电管理,定 期检查和维护电路。
不对称短路的分析和计算

不对称短路的分析和计算Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】目录摘要电力系统的安全、稳定、经济运行无疑是历代电力工作者所致力追求的,但是从电力系统建立之初至今电力系统就一直伴随着故障的发生而且电力系统的故障类型多样。
在电力系统运行过程中,时常会发生故障,且大多是短路故障。
短路通常分为三相短路、单相接地短路、两相短路和两相接地短路。
其中三相短路为对称短路,后三者为不对称短路。
电力运行经验指出单相接地短路占大多数,因此分析与计算不对称短路具有非常重要意义。
求解不对称短路,首先应该计算各原件的序参数和画出等值电路。
然后制定各序网络。
根据不同的故障类型,确定出以相分量表示的边界条件,进而列出以序分量表示的边界条件,按边界条件将三个序网联合成复合网,由复合网求出故障处各序电流和电压,进而合成三相电流电压。
关键词: 不对称短路计算、对称分量法、节点导纳矩阵1电力系统短路故障的基本概念短路故障的概述在电力系统运行过程中,时常发生故障,其中大多数是短路故障。
所谓短路:是指电力系统正常运行情况以外的相与相之间或相与地(或中性线)之间的连接。
除中性点外,相与相或相与地之间都是绝缘的。
电力系统短路可分为三相短路,单相接地短路。
两相短路和两相接地短路等。
三相短路的三相回路依旧是对称的,故称为不对称短路。
其他的几种短路的三相回路均不对称,故称为不对称短路。
电力系统运行经念表明,单相短路占大多数,上述短路均是指在同一地点短路,实际上也可能在不同地点同时发生短路,例如两相在不同地点接地短路。
依照短路发生的地点和持续时间不同,它的后果可能使用户的供电情况部分地或全部地发生故障。
当在有由多发电厂组成的电力系统发生端来了时,其后果更为严重,由于短路造成电网电压的大幅度下降,可能导致并行运行的发电机失去同步,或者导致电网枢纽点电压崩溃,所有这些可能引起电力系统瓦解而造成大面积的停电事故,这是最危险的后果。
第八章 三相不对称短路分析

X 2 1.22 X d
无阻尼绕组同步发电机
X 2 1.45 X d
零序电抗:机端零序电压的基频分量与流入定子 的电流零序分量的比值。
" X 0 (0.15 ~ 0.6) X d
第8章 电力系统不对称故障的分析计算
二、异步电动机的各序电抗
异步电机的正序参数常用恒定阻抗表示
等值漏抗:正负零序相同。
励磁电抗:负序励磁电抗与正序相同。
结论:所有静止元件的正负序等值电路及其参 数完全相同。 零序励磁电抗:与变压器的铁芯结构密切相关。
第8章 电力系统不对称故障的分析计算
零序励磁电抗
对于由三个单相变压 器组成的三相变压器 组,每相的零序主磁 通和正序主磁通一样, 都有独立的铁心磁路。 对于三相四柱式变压 器,零序磁通也能在 铁芯形成回路。因此, 零序电抗很大。
(8 12)
式(8-12)表明:在三相参数对称的线性电路中,各序对称分量 相互独立,因此可对正负零序分量分别进行计算。 所谓元件的序阻抗,是指元件三相参数对称时,元件两端某一序 的电压降与通过该元件同一序电流的比值,即:
/I Z1 V a1 a1 /I Z 2 V a2 a2 /I Z 0 V a0 a0
3I0
Xn
3 I0
Xn
XI XII
3Xn
Xm0
第8章 电力系统不对称故障的分析计算
自耦变压器的零序阻抗及其等值电路
(1)中性点直接接地
其参数和等值电路,与外电路的联接,Xm0 ——与 普通变压器相同 中性点的入地电流为:
3( I I ) I n I0 II 0
图7-11
第8章 电力系统不对称故障的分析计算
20不对称短路分析(新)

一、单相短路接地f(1)
以a相为特殊相(a相发生单相接地短路)
1、边界条件: b、c相没有接地,其接地电流
a b
c
Ua
Ub
Uc
Ib 0, Ic 0
Ia Ib Ic
a相短路点的对地电压 Ua 0
f
2、用对称分量表示的边界条件
Ua 0 Ua Ua1 Ua2 Ua0 0
Ia1 Ia2 Ia0 Ia / 3 相当于各序网络相串联
Ua1
n1
jX 2 f2
Ia2 Ua2 n2
jX 0 f0
Ia0
Ua 0
n0
4、短路点各相的电流和电压
Ia 3Ia1 Ib 0 Ic 0 Ua 0 Ub a2Ua1 aUa2 Ua0 Uc aUa1 a2Ua2 Ua0
5.相量图:以 Ia1 为参考相量画电流、电压相量图
Ic 2 Ib1
0
即:Ua1 Ua2 Ua0 0
又 : Ia1 Ia2 Ia0 0
表明:正序网与负序网相并联,零序网络开路,没有 零序电流分量。
3、复合序网 两相短路的复合序网=正序网与负序网络相并联
jX 1
E
Ia1
f1
Ua1
n1
jX 2
Ia 2
f2
Ua 2
n2
由复合序网可求出短路点处的a相的电流和电压的对
Uc2 Ub1
Ua1 Ua 2
Ua
6、结论:
1)短路电流、电压中无零序分量。
2)两相短路电流中的正、负序分量大小相等,方向相反;
两故障相的电流大小相等(幅值=
)3I,a 方向相反。
3)短路点处两故障相的电压大小相等、相位相同,幅值
为非故障相的电压的一半,相位与非故障相电压相反。
第八章电力系统不对称故障的分析

•
U
fc (1)
•
U
fc ( 2 )
•
U
fc ( 0 )
1
•
U
fc
3
同一类型短路故障发生在不同相上时,基准相的序分量 故障边界条件的形式不会改变,于是复合序网的形式不 会改变,计算公式、结论均不会改变,只是表达式中下 脚符号改变而已。
j a2 a X ff (2) a2 1 X ff (0) I&fa(1)
U&fc aU&fa(1) a2U&fa(2) U&fa(0)
j a a2 X ff (2) a 1 X ff (0) I&fa(1)
(四)向量图:
Ifc(2) Ifb(1)
Ifc(1) Ifb(2)
•
I fa(2)
X ff (0)
•
I fa(1)
X ff (2) X ff (0)
•
I fa(2)
X ff (2)
•
I fa(1)
X ff (2) X ff (0)
U&fa(1) U&fa(1) U&fa(1)
j
X X ff (2) ff (0)
•
I fa(1)
X ff (2) X ff (0)
(2)两故障相中的短路电流的绝对值相等,方向相反, 数值上为正序电流的 3 倍;
(3)当在远离发电机的地方发生两相短路时,可通过对序网 进行三相短路计算来近似求两相短路的电流;
(4)两相短路时的正序电流在数值上与在短路点加一个附加阻
抗
Z (2)
构成一个增广正序网而发生三相短路时的电流相等。即
•
•
•
不对称短路的分析和计算

武汉理工大学《电力系统分析》课程设计说明书目录摘要 (3)1 电力系统短路故障的基本概念 (4)1.1短路故障的概述 (4)1.2 三序网络原理 (5)1.2.1 同步发电机的三序电抗 (5)1.2.2 变压器的三序电抗 (5)1.2.3 架空输电线的三序电抗 (6)1.3 标幺制 (6)1.3.1 标幺制概念 (6)1.2.2标幺值的计算 (7)1.4 短路次暂态电流标幺值和短路次暂态电流 (8)2 简单不对称短路的分析与计算 (9)2.1单相(a相)接地短路 (9)2.2 两相(b,c相)短路 (10)2.3两相(b相和c相)短路接地 (12)2.4 正序等效定则 (14)3 不对称短路的计算的实际应用 (14)3.1 设计任务及要求 (14)3.2 等值电路及参数标幺值的计算 (15)3.3 各序网络的化简和计算 (17)3.3.1 正序网络 (17)3.3.2 负序网络 (19)3.3.3 零序网络 (20)3.4 短路点处短路电流、冲击电流的计算 (20)4 实验结果分析 (21)5 心得体会 (22)6 参考文献 (23)2摘要电力系统的安全、稳定、经济运行无疑是历代电力工作者所致力追求的,但是从电力系统建立之初至今电力系统就一直伴随着故障的发生而且电力系统的故障类型多样。
在电力系统运行过程中,时常会发生故障,且大多是短路故障。
短路通常分为三相短路、单相接地短路、两相短路和两相接地短路。
其中三相短路为对称短路,后三者为不对称短路。
电力运行经验指出单相接地短路占大多数,因此分析与计算不对称短路具有非常重要意义。
求解不对称短路,首先应该计算各原件的序参数和画出等值电路。
然后制定各序网络。
根据不同的故障类型,确定出以相分量表示的边界条件,进而列出以序分量表示的边界条件,按边界条件将三个序网联合成复合网,由复合网求出故障处各序电流和电压,进而合成三相电流电压。
关键词: 不对称短路计算、对称分量法、节点导纳矩阵31电力系统短路故障的基本概念1.1短路故障的概述在电力系统运行过程中,时常发生故障,其中大多数是短路故障。
第十章 不对称故障的分析和计算

2
U
a 2
n2
X0∑
图
f0
I a
0
U
a 0
n0 复合序网图
电力系统应用
第十章 不对称故障的分析和计算
短路相短路电流的绝对值为:
3 E I 3 I a 1 X X X 1 2 0
电力系统应用
第十章 不对称故障的分析和计算
X 1∑
f1
X 2∑
f2
E
I a 1
X 0∑
U a 1
n1 f0
I a 2
U a 2
n2
I a 0
图4-41
U a 0
n0
两相短路时的复合序网图
由复合序网可直接解得:
E Ia1 Ia2 j(X1 X2) U jI X U a1 a2 a1 2
j0.0454
f1
l
f 1.1∠0°
(a)
n1 (b)
j0.051
j0.042
j0.0454
f2
j0.042
j0.159
f0
n2 (c) (d)
n0
图4-38 例题4-7附图 (a)原理接线;(b)正序网络;(c)负序网络;(d) 零序网络
LANZHOU RESOURCES&ENVIRONMENT VOC-TECH COLLEGE
U 0 ,LANZHOU I 0 a 0 a 0 RESOURCES&ENVIRONMENT VOC-TECH COLLEGE
电力系统应用
5.3不对称短路时短路点电流和电压的分析及...

第5 章电力系统不对称短路的计算分析5.1 基本认识5.2 元件的序阻抗及系统序网络的拟制及化简5.3 不对称短路时短路点电流和电压的分析及计算前言:1. 不对称短路时短路点的电流和电压出现不对称,短路点电流和电压的计算关键是求出其中一相的各序电流、电压分量。
2. 各序电流、电压分量分量的计算方法:解析法——解方程:上述 5.1 中三序网的基本式+三个补充方程(据不同类短路型的边界条件列出。
——繁,不用有两种复合序网法——将三个序网适当连接———组成复合序网法,求各序电流、电压(该法易记,方便,故广泛用——实际上是由解析法推导出的)3. 何谓“复合序网’——将三个序网适当连接,体现 a 相各序电流、电压关系的网络图。
4. 设对短路点各序网络图以简化到最简单的形式(见下图)——且表达形式有三种正序网E jX1 I a1E jX 1Ia1(n) f ++Ua1X1Ua1__G表达1 表达2 表达3 jX jX2 2I Ia 2a2+(n)f+Ua2Ua 2X2__表达1 表达2 表达3零序网jX jXIIa0a0+(n)f+Ua0Ua 0X_—表达1 表达2 表达3一、复合序网图及相量图(一)单相接地(1)f (如下图所示)a—E+aa 相——故障相,特殊相—E b +bc 相——非故障相—E c +I I b I ca分析:边界条件:I (1)b I (1)cU (1) a 0据对称分量法, 得:I1 1(1) (1) (1) 2 (1) (1) (1)a (I aI a I ) I I I1 3a b c a a23(1)a0——即三序电流相等U (1) (1) (1)a U U Ua1 a2 (1)a0三序电流、电压可用下图5-30 体现,称为复合序网。
E jX1Ia1+Ua1_jX2Ia2+Ua 2jXIa0+Ua 0图5-30 f (1) 复合序网注:(1) 复合序网,体现了三序电流、电压的关系I (1) (1) (1)a I I1 a2a0U (1) (1) (1)a U U1 a2a0(2) 由复合序网, 可直接写出短路点 f (1) 点的各序电流、电压IE(1) (1)aa I I1 ( ) a2j X X X1 2 3(1)a0U (1) (1) (1) (1)a E jI X (U U1 a a1 a2 a01 )(1) (1) U a20 jI a X2 2(1) (1)U a00 jI a X0(3)短路点故障相电流( 31) (1) (1) (1) (1)I a I I I I ——即为正序电流a1 a 2 a0 a1(1)I 的3 倍a1(1) (1) o2. 相量图(设I a I 0 )1 a1注:(1)由相量图可见,短路点:(1) 故障相电压U 0a I (1) 3a I(1)a1非故障相电压(1) (1) 但相位差(1) (1) 0OIb IU b U , 120c c (2)作相量图方法A 先作各相各序分量B 再作各相U、I 相量(二)两相短路( 2)f (如下图所示)b,cbc 相——故障相—E a +a 相——非故障相,特殊相—E +b—E+cI I b I ca分析:边界条件:I (2) a 0I (2)b I ( 2) cU ( 2)b U ( 2)c 0据对称分量法, 得:(2) (2)I a U (无零序网)0, 0 0a0I (2) (2)a I1 a2U (2) ( 2)a U1 a2三序电流、电压可用下图5-31 体现,称为复合序网。
电力系统不对称故障的分析计算

第八章 电力系统不对称故障的分析计算主要内容提示:电力系统中发生的故障分为两类:短路和断路故障。
短路故障包括:单相接地短路、两相短路、三相短路和两相接地短路;断路故障包括:一相断线和两相断线。
除三相短路外,均属于不对称故障,系统中发生不对称故障时,网络中将出现三相不对称的电压和电流,三相电路变成不对称电路。
直接解这种不对称电路相当复杂,这里引用120对称分量法,把不对称的三相电路转换成对称的电路,使解决电力系统中各种不对称故障的计算问题较为方便。
本章主要内容包括:对称分量法,电力系统中主要元件的各序参数及各种不对称故障的分析与计算。
§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量(正序分量、负序分量、零序分量)之和。
设c b a F F F ∙∙∙为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下:()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ∙∙∙∙∙∙∙∙∙∙∙∙++=++=++= 三组序分量如图8-1所示。
正序分量: ()1a F ∙、()1b F ∙、()1c F ∙三相的正序分量大小相等,彼此相位互差120°,与系统正常对称运行方式下的相序相同,达到最大值的顺序a →b →c ,在电机内部产生正转磁场,这就是正序分量。
此正序分量为一平衡的三相系统,因此有:()()()111c b a F F F ∙∙∙++=0。
负序分量:()2a F ∙、()2b F ∙、()2c F ∙三相的负序分量大小相等,彼此相位互差120°,与系图 8-1 三序分量Fc(0) ·零序F b(0) ·F a(0) ·120°120° 120° 正序F b(1)·F a(1)·F c(1) ·ω120°120°120°负序 F a(2)·F c(2)·F b(2)·ω统正常对称运行方式下的相序相反,达到最大值的顺序a →c →b ,在电机内部产生反转磁场,这就是负序分量。
不对称短路的分析和计算

不对称短路的分析和计算不对称短路是指电路中的短路现象不对称地分布在电路中的其中一侧。
简单来说,不对称短路是指电路中其中一侧的短路现象比另一侧更为严重,或者在电路中其中一侧出现了短路而另一侧没有出现短路的情况。
这种情况会导致电压和电流在电路中的分布不平衡,可能会破坏电路元器件,甚至引起火灾事故。
因此,对不对称短路进行分析和计算是非常重要的。
1.电路拓扑分析:首先,对电路的拓扑结构进行研究,分析电路中各个元器件的连接方式和途径,确定电路的供电路径和负载分布,找出可能导致不对称短路的因素。
2.元器件参数分析:对电路中的元器件进行参数分析,包括电阻、电容、电感等参数。
如果在电路中存在不对称短路现象,可能是一些元器件的参数偏离正常范围,导致该侧电流增加,从而引发不对称短路。
3.测试测量:通过使用合适的测试工具和仪器对不对称短路的存在与程度进行测试和测量。
常用的测试仪器包括数字万用表、示波器、短路测试仪等。
通过测试测量可以准确地了解不对称短路的情况,有助于后续的计算和处理。
1.电流计算:根据电路的拓扑结构和元器件参数,计算各个分支电路中的电流大小。
通过电路中的欧姆定律和基尔霍夫定律等电路定律,可以求解各个分支电路的电流。
2.电压计算:根据电路中的电源电压和各个分支电路的电流,计算各个节点处的电压大小。
通过电路中的基尔霍夫定律和电压分压定律等电路定律,可以求解各个节点处的电压。
3.规范检查:对计算得到的电流和电压进行规范检查。
根据电路的设计和规范要求,检查计算结果是否符合规范,包括各个元器件的额定电流、电压、功率等。
4.不对称短路分析:对计算得到的电流和电压进行分析,确定是否存在不对称短路现象。
如果其中一侧的电流明显偏高,而另一侧的电流较小或接近零,可能存在不对称短路。
5.故障诊断:根据不对称短路的分析结果,进行故障诊断,并采取合适的措施进行处理。
可能的处理方法包括更换元器件、调整电路连接方式、增加保护元器件等。
电力系统不对称故障的分析计算

电力系统不对称故障的分析计算6.3 不对称短路时故障处的短路电流和电压字体大小:小中大简单不对称短路包括:利用对称分量法可以求解简单不对称短路,但需要根据不对称短路的边界条件再列出三个方程。
(6-3)➢单相接地短路边界条件:➢两相短路边界条件:复合序网:➢两相接地短路边界条件:复合序网:6.3.1 单相接地短路边界条件:由式6-1直接可以得到(略去了a相的下标a):由式6-2可以得到:所以(略去了a相的下标a):(6-4)将式6-3和式6-4联立求解,则(6-5)根据式6-4可以得到单相接地短路的复合序网。
复合序网—根据边界条件所确定的短路点各序量之间的关系,将各序网络连接起来所形成的网络。
显然,由复合序网也可以直接得到式6-5。
此外:再利用式6-1,可以得到短路点的故障相电流:短路点的非故障相电压:一般X1∑≈X2∑,因此,如果X0∑<X1∑,则单相短路电流大于同一地点的三相短路电流;反之,则单相短路电流小于三相短路电流。
[例6-2] 在图示电力系统中,变压器T2高压侧发生a相接地短路,不计负荷作用,试计算短路瞬间故障点的短路电流。
解:取功率基准值SB=120MVA ,各级电压基准值U B =U av =115、37、10.5kV 。
计算各元件的电抗标幺值,并做出正序、负序和零序等值电路。
X G1=X G2=0.14X L1=105×0.4×120/1152=0.381=X L2 X L0=3×0.381=1.143X T1_1=10.5/100×120/120=0.105=X T1_2=X T1_0 X T2_1=10.5/100×120/60=0.21=X T2_2=X T2_0化简正序、负序和零序等值电路,并做出单相接地短路的复合序网。
X 1∑=X G1+X T1_1+X L1=0.626=X 2∑短路点的故障相电流:短路电流有效值:6.3.2 两相短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:如果,则:短路点的各相对地电压:6.3.3 两相接地短路边界条件:复合序网:由复合序网可以得到:再利用式6-1可以得到短路点的故障相电流:短路点的非故障相电压:6.3.4 正序等效定则及其应用三种不对称短路时,正序电流分别为:单相接地短路两相短路两相接地短路因此,三种不对称短路时,正序电流可以归纳为:正序等效定则—简单不对称短路故障的短路点正序电流分量,与在短路点每一相中加入附加电抗后发生的三相短路时的电流相等。
电力系统不对称故障的分析和计算汇总

( 0)
I fa (1)
( 0) V f j ( X ff (1) X ff ( 2 ) X ff ( 0 ) )
5
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
各序分量确定为:
I
V V V
fa ( 2 )
I
f ( 0)
fa ( 0 )
I
fa (1)
fa(1)
V
jX ff (1) I fa(1) j ( X ff ( 2) X ff ( 0) ) I fa(1)
fa( 2 )
jX ff ( 2) I fa(1) jX ff ( 0) I fa(1)
fa( 0 )
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
各序分量的求解方法:
1. 解方程组
2. 复合序网法
2019/1/2
电力系统分析 第八章 电力系统不对称故障的分析和计算
4
1、解方程组
V X ff (1) I fa(1) V fa(1)
X ff ( 2) I fa( 2) V
X ff ( 0) I fa( 0) V
V
fa (1)
2 2 2
V fc a V fa(1) a V fa( 2) V fa(0)
2
j(a a ) X
2
ff ( 2 )
(a 1) X ff ( 0) I fa(1)
短路电流的计算与影响分析

短路电流的计算与影响分析在电力系统中,短路电流是指由于线路或设备出现故障导致的电流异常增大的现象。
短路电流的计算与影响分析是电力系统运行与规划中关键的一环。
本文将从计算方法和影响分析两个方面来深入探讨短路电流的相关问题。
一、短路电流的计算方法短路电流的计算是建立在电力系统的拓扑结构和电气参数的基础上进行的。
一般来说,短路电流可以分为对称短路电流和不对称短路电流两种情况,下面将介绍它们的计算方法。
1. 对称短路电流的计算对称短路电流是指系统中的三相电流均相等的情况。
在计算对称短路电流时,我们常用的方法是采用对称分解法。
首先,根据系统的拓扑结构和电气参数,我们可以得到系统的节点导纳矩阵Y和节点电压向量U。
然后,通过对称分解法,我们可以将节点导纳矩阵Y分解为正序分量矩阵Y0、负序分量矩阵Y1和零序分量矩阵Y2。
最后,利用节点电压向量U和分解得到的矩阵Y0,我们可以计算得到对称短路电流。
2. 不对称短路电流的计算不对称短路电流是指系统中的三相电流不相等的情况。
在计算不对称短路电流时,我们常用的方法是采用正序不对称分量法。
首先,根据系统的拓扑结构和电气参数,我们可以得到系统的节点导纳矩阵Y和节点电压向量U。
然后,通过正序不对称分量法,我们可以将节点导纳矩阵Y分解为正序分量矩阵Y0、负序分量矩阵Y1和零序分量矩阵Y2。
最后,利用节点电压向量U和分解得到的矩阵Y0、Y1和Y2,我们可以计算得到不对称短路电流。
二、短路电流的影响分析短路电流的异常增大会对电力系统的设备和运行产生一系列的影响,下面将对其进行分析。
1. 设备保护与安全短路电流的计算可以为设备保护提供重要依据。
通过计算得到的短路电流,可以确定合适的保护器件的额定电流和动作时间,从而保护设备免受过载和短路故障的损害。
另外,短路电流的异常增大还可能导致设备的温升过高,进而影响设备的正常运行和寿命。
2. 动态稳定性短路电流的异常增大会对电力系统的动态稳定性产生影响。
电力系统不对称故障的分析-PPT

a1
.
Uc
.
.
aU a1 a 2 U a2
.
U a1
jX 2
. I a1
短路点得电流、电压相量图
Ua
IC
Ia2 Ia1 0
Ub Uc Ua
电压向量图
Ib
电流向量图
三、两相短路接地
Ua Ub Uc
a b c
Ia
Ib
Ic
jX f
➢短路点得边界条件为
U
b U c
Ia 0 j(Ib
.
Ib
.
I a0 a2
.
I a1 a
.
I a2
(a2
X 2 aX 0 X2 X0
)
.
I
a1
.
Ic.Leabharlann I a0.a I a1
a2
.
I a2
(a
X 2
a2 X0
. ) I a1
X2 X0
.
.
.
.
.
U a U a0 U a1 U a2 3U a1 j3
X 2 X 0
.
I a1
X 2 X 0
X 0 X1
E1
1.5
X 0 X1
2
X 0 X1
j
3 2
E1
Uc
j [(a
a2 ) X1
(a 1) X 0 ]
E12 j (2 X1
X0 )
(a
a2) 2
(a 1)
X 0 X1
X 0 X1
E1
1.5
X 0 X1
2 X0 X1
j
3 2
E1
➢非故障相电压得绝对值为
电力系统不对称故障的分析和计算
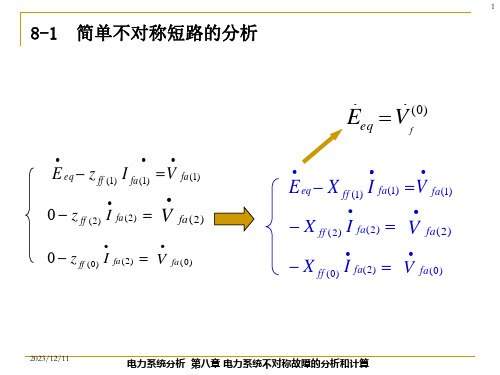
•
•
•
aV fa(1) a2 V fa(2) V fa(0) 0
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
16
化简整理后,得
•
•
•
I fa(1) I fa(2) I fa(0) 0
•
•
•
V fa(1) V fa(2) V fa(0)
2023/12/11
I
fb
2
•
I
•
fa(1) I
•
I fa(2)
fa ( 0)
( 2
X ff (2)
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ) ff (0)
•
I
fc
•
I
•
fa(1) 2 I
•
I fa(2) fa(0)
(
X ff (2)
2
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ff (0) )
9
Vfa(1)
Vfc(2) Vfc(2) Vfc(1)
Vfb(2)
Vfb(1)
V Vfc(0) Vfc Vfa(2) Vfa(0)
fb
Vfb(0)
2023/12/11
电力系统分析 第八章 电力系统不对称故障的分析和计算
10
短路点故障相电流为
• (1) •
•
•
•
•
I f I fa I fa(1) I fa(2) I fa(0) 3 I fa(1)
•
V
fa (1)
电力系统发生简单不对称短路时电流的计算

毕业论文(设计)届电气工程及其自动化专业班级题目电力系统发生简单不对称短路时电流的计算姓名学号指导教师职称内容摘要随着电力事业的快速发展,电力电子新技术得到了广泛应用,出于技术、经济等方面的考虑,500KV及以上的超高压输电线路普遍不换位,再加上大量非线性元件的应用’电力系统的不对称问题日益严重。
因此电力系统不对称故障分析与计算显得尤为重要。
基于对称分量法的基本理论,对称分量法采取的具体方法之一是解析法,即把该网络分解为正、负、零序三个对称序网,这三组对称序分量可分别按对称的三相电路分解。
计算机程序法。
通过计算机形成三个序网的节点导纳矩阵,然后利用高斯消去法通过相应公式对他们进行数据运算,即可求得故障点的等值阻抗。
最后根据故障类型选取相关公式计算故障处个序电流,电压,进而合成三相电流电压。
进行了参数不对称电网故障计算方法的研究。
通过引计算机算法,系统介绍电网参数不对称的计算机算法方法。
根据断相故障和短路故障的特点,通过在故障点引入计算机算法,给出了各种断相故障和短路故障的仿真计算。
此方法以将故障电网分为对称网络不对称网络两部分,在程序法则下建立起不对称电网故障计算统一模型,根据线性电路的基本理论,并借助于相序参数变换技术完成故障计算。
关键词:参数不对称;电网;故障计算AbstractWith the rapid development of power industry ,power electronic technology has been widely used;For technical and economic consideration ,500kV and above transmission lies are generally not transposition ,together with the application of a large number of nonlinear ,the power system the growing problem of asymmetry .therefore ,asymmetric power system fault analysis and calculation is very important .Based on the basic theory of symmetry is one of the specific method to resolve the law ,that to the network is decomposed into positive,negative and zero sequence network of the three symmetric sequence ,these three groups of symmetry by symmetry sequence components,respectively Decomposition of three-phase puterprocedure .Sequence of three computer -based network node admittance matrix,and then use the appropriate formula by Gauss elimination method for data on their operations,one can fault endpoint equivalent impedance.Finally,select the associated fault type fault Department calculated the sequence current voltage,and then synthesis of three-phase voltage and current.Parameters were calculated asymmetry of power failure.By means of a computer algorithm,the system describes a computer algorithm for asymmetric network parameters method.And under short circuit fault in the characteristic of the point of failure through the introduction of computer algorithms,given the various short-circuit fault and the simulation.This method to the fault network is divided into two symmetrical parts of the network and not the network,rules of procedure established under the unified model of asymmetric fault calculation,according to the basic theory of linear circuits,and with the help transform the completion of the order parameter phase fault calculation.Key Words: Parameters of asymmetry,power, fault calculation目录前言电力系统的安全、稳定、经济运行无疑是历代电力工作者所致力追求的,但是从电力系统建立之初至今电力系统就一直伴随着故障的发生而且电力系统的故障类型多样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
武汉理工大学《电力系统分析》课程设计说明书目录摘要 (3)1 电力系统短路故障的基本概念 (4)1.1短路故障的概述 (4)1.2 三序网络原理 (5)1.2.1 同步发电机的三序电抗 (5)1.2.2 变压器的三序电抗 (5)1.2.3 架空输电线的三序电抗 (6)1.3 标幺制 (6)1.3.1 标幺制概念 (6)1.2.2标幺值的计算 (7)1.4 短路次暂态电流标幺值和短路次暂态电流 (8)2 简单不对称短路的分析与计算 (9)2.1单相(a相)接地短路 (9)2.2 两相(b,c相)短路 (10)2.3两相(b相和c相)短路接地 (12)2.4 正序等效定则 (14)3 不对称短路的计算的实际应用 (14)3.1 设计任务及要求 (14)3.2 等值电路及参数标幺值的计算 (15)3.3 各序网络的化简和计算 (17)3.3.1 正序网络 (17)3.3.2 负序网络 (19)3.3.3 零序网络 (20)3.4 短路点处短路电流、冲击电流的计算 (20)4 实验结果分析 (21)5 心得体会 (22)6 参考文献 (23)2摘要电力系统的安全、稳定、经济运行无疑是历代电力工作者所致力追求的,但是从电力系统建立之初至今电力系统就一直伴随着故障的发生而且电力系统的故障类型多样。
在电力系统运行过程中,时常会发生故障,且大多是短路故障。
短路通常分为三相短路、单相接地短路、两相短路和两相接地短路。
其中三相短路为对称短路,后三者为不对称短路。
电力运行经验指出单相接地短路占大多数,因此分析与计算不对称短路具有非常重要意义。
求解不对称短路,首先应该计算各原件的序参数和画出等值电路。
然后制定各序网络。
根据不同的故障类型,确定出以相分量表示的边界条件,进而列出以序分量表示的边界条件,按边界条件将三个序网联合成复合网,由复合网求出故障处各序电流和电压,进而合成三相电流电压。
关键词: 不对称短路计算、对称分量法、节点导纳矩阵31电力系统短路故障的基本概念1.1短路故障的概述在电力系统运行过程中,时常发生故障,其中大多数是短路故障。
所谓短路:是指电力系统正常运行情况以外的相与相之间或相与地(或中性线)之间的连接。
除中性点外,相与相或相与地之间都是绝缘的。
电力系统短路可分为三相短路,单相接地短路。
两相短路和两相接地短路等。
三相短路的三相回路依旧是对称的,故称为不对称短路。
其他的几种短路的三相回路均不对称,故称为不对称短路。
电力系统运行经念表明,单相短路占大多数,上述短路均是指在同一地点短路,实际上也可能在不同地点同时发生短路,例如两相在不同地点接地短路。
依照短路发生的地点和持续时间不同,它的后果可能使用户的供电情况部分地或全部地发生故障。
当在有由多发电厂组成的电力系统发生端来了时,其后果更为严重,由于短路造成电网电压的大幅度下降,可能导致并行运行的发电机失去同步,或者导致电网枢纽点电压崩溃,所有这些可能引起电力系统瓦解而造成大面积的停电事故,这是最危险的后果。
产生短路的原因很多主要有如下几个方面:(1)原件损坏,例如绝缘材料的自然老化,设计,安装及维护不良所带来的设备缺陷发展成短路。
(2)气象条件恶化,例如雷电造成的闪络放电或避雷针动作,架空线路由于大风或导线覆冰引起电杆倒塌等。
(3)违规操作,例如运行人员带负荷拉刀闸。
(4)其他,例如挖沟损伤电缆。
在电力系统和电气设备的设计和运行中,短路计算是解决一系列技术问题所不可缺少的基本计算,比如在选择发电厂和电力系统的主接线时为啦比较不同方案接图,进行电力系统暂态稳定计算,研究短路对用户的影响。
合理配置各种继电保护和自动装置并正确整定其参数都必须进行短路的计算和分析.41.2 三序网络原理对称分量法分析计算不对称故障时,首先要作出电力系统的各序网络,为此要根据电力系统的接线图,中性点接地情况等原始资料,在故障点分别施加各序电势,从故障点开始,逐步查明各序电流流通的情况。
凡是某一序电流能流通的元件,都必须包括在该序网络中,并用相应的序参数和等值电路表示。
三序网络包括正序,负序和零序网络。
正序网络就是通常计算对称短路时所用的等值网络。
除中性点接地阻抗以及空载变压器外,电力系统各元件均应包括在正序网络中,并且用相应的正序参数和等值电路表示。
负序电流能流通的元件和正序电流相同,但所有电源的负序电势为零。
因此,把正序网络中各元件的参数都用负序参数代替,并令电源电势等于零,而在短路点引入代替故障条件的不对称电势电源中的负序分量,便得到负序网络。
1.2.1 同步发电机的三序电抗同步发电机在对称运行时,只有正序电势和正序电流,此时的电机参数,就是正序参数。
当发电机定子通过负序基频电流时,它产生的负序旋转磁场与正序基频电流产生的旋转磁场正好反向,因此,负序旋转磁场同转子之间有两倍同步转速的相对运动。
负序电抗取决于定子负序旋转磁场所遇见的磁阻。
由于转子纵横轴之间不对称,随着序旋转磁场同转子之间的相对位置不同,负序阻抗也就不同。
当发电机定子通过零序基频电流时,由于各相电枢磁势大小相等,相位相同,且在空间上相差120°电角度,它们在气隙中的合成磁势为零,所以,发电机的零序阻抗仅由定子绕组的等值漏磁通决定。
1.2.2 变压器的三序电抗变压器等值电路中的参数不仅同变压器的结构相关,有的参数也同所通过电流的序别有关。
变压器各绕组的电阻,与所通过的电流序别无关。
因此,变压器的正序、负序和零序的等值电阻相等。
5变压器的漏抗,反映了原副方绕组之间磁耦合的紧密程度。
因此,变压器的正序、负序和零序的等值漏抗也相等。
变压器的励磁电抗,取决于主磁通路径的磁导。
变压器通以负序电流时,主磁通的路径与正序完全相同,所以,变压器的正序和负序等值电路完全相同。
关于零序等值电路取决于变压器与外电路的连接情况,如下所述。
(1)当外电路向变压器某侧绕组施加零序电压时,如果能在该绕组产生零序电流,则等值电路中该侧绕组与外电路接通;如不能产生零序电流,则与外电路断开。
因此,只有中性点接地的星形接法才能与外电路接通。
(2)当变压器绕组具有零序电势时,如果它能将零序电势施加到外电路上去并提供零序电流通路,则与外电路连通,不然断开。
也只有中性点接地的星形接法才能与外电路接通。
(3)在三角形接法的绕组中,绕组的零序电势虽然不能作用到外电路去,但能在三绕组中形成零序环流。
因此,在等值电路中该侧绕组断点接零序等值中性点。
1.2.3 架空输电线的三序电抗输电线路的正、负序阻抗及等值电路完全相同,当输电线路通过零序电流时,由于三相零序电流大小相等、相位相同,所以,必须借助大地及架空线来构成零序电流的通路。
1.3标幺制1.3.1 标幺制概念在短路计算中,各电气量如电流.电压.电阻.电抗.功率等数值可以用名值表示,也可以用标幺值表示,为了计算方便,通常在1KV以下的低压系统用有名值,而高压等级中有多个电压等级,存在电抗换算问题,宜采用标幺值。
所谓标幺制,就是把各个物理量均用标幺值来表示的一种相对单位制。
某一物理量的标幺值A的比值,即:A ,等于它的实际值A与所选定的基准值d67dA A A *= 在进行标幺值计算时,首先选定基准值。
基准值原则上可以任意选定,但因物理量之间有内在的必然联系,所以并非所有的基准值都可以任意选取。
在短路计算中经常用到的四个物理量容量S ,电压U ,电流I ,和电抗X 。
通常选定基准容量d S 和基准电压d U则基准电流和基准电抗d X 分别为:d I =2d d d U X S == 为了计算方便,常取基准容量S d =100MV .A ,基准电压用各级线路的平均额定电压,即.d av U U =。
所谓线路平均额定电压,是指线路始端最大额定电压与线路末端最小额定电压的平均值,如表2-1所示。
在产品样本中,电力系统中各电气设备如发电机,变压器,,电抗器等所给出的标幺值,都是以其本身额定值为基准的标幺值或百分值。
由于各电气设备的额定值往往不尽相同,基准值不同的标幺值是不能直接进行运算的,因此,必须把不同基准值的标幺值换算成统一基准值的标幺值。
1.2.2标幺值的计算(1)发电机电抗标幺值:%100G B G NX S X S =⨯8 (2)负载电抗标幺值: 2L L L U X Q S ****= (3) 变压器电抗标幺值:%100K B T NTU S X S =⨯ 22%100BK T NT B S U X U U =⨯⨯(4) 线路电抗标幺值:02BW BS X x L U =1.4 短路次暂态电流标幺值和短路次暂态电流(1)短路次暂态电流标幺值(I *)和短路次暂态电流(K I *):E I Z **=∑)K I I KV **=(2 )短路冲击电流(sh i ):2.55()sh sh K K i K I I KA =≈其各种短路故障点的短路电流为 :()()1n n K a I m I *= ()K K B I I I KA *=⨯()n m ---比例系数,单相接地短路(1)3,m =。
两相短路(2) 1.732,m =两相接地时(1.1)m = 。
9()12101(1)n a U I U Z Z Z Z **=≈=++∑在无限大容量系统中,由于系统母线电压维持不变,所以短路后任何时刻的短路电流周期分量有效值(习惯上用K I 表示)始终不变,所以有 K I I I *∞==(3)短路容量(功率) K S 的计算:(.)BK av K B K SS U I S I MV A Z *=⨯==⨯∑KK K BI S I I **=== 。
2 简单不对称短路的分析与计算2.1单相(a 相)接地短路abc图2-1 单相接地短路单相接地短路时的系统接线图如图2-1所示,故障处的三相的边界条件:0a U •= 0b I •= 0c I •=用对称分量表示为:1200a a a U U U •••++=21200a a a a I aI I •••++=21200a a a aI a I I •••++=即有:10 12013a a a a I I I I ••••=== 根据单相接地短路时的边界条件连接复合网,如图2-2所示。
由复合网图可以写出各序分量:图2-2 单相短路复合网络120120a a a E I I I Z Z Z ••••∑===++∑∑∑111a a U E I Z •••=-∑∑222a a U I Z ••=-∑000a a U I Z ••=-∑于是可以用对称分量法得到短路点的各相电流电压:12013a a a a a I I I I I •••••=++=0b c I I ••==1200a a a a U U U U ••••=++=()()2221201201b a a a a U a U aU U I a a Z a Z •••••⎡⎤=++=-+-⎢⎥∑∑⎣⎦()()221201201c a a a a U aU a U U I a a Z a Z •••••⎡⎤=++=-+-⎢⎥∑∑⎣⎦2.2 两相(b,c 相)短路11a b c图2-3 两相短路两相短路的系统接线如图2-3所示,短路点的边界条件:0a I •= b c I I ••=- 0bc U •= 0b c U U ••== 用对称分量表示为:120a a a I I I•••++=22120120()a a a a a a a I aI I aI a I I ••••••++=-++ 22120120a a a a a a a U aU U aU a U U ••••••++=++于是有:12a a I I ••=- 00a I •= 12a a U U ••=由式可知,故障点不与大地相连,零序电流无通路,因此无零序网络。
