正交试验设计案例
正交试验设计实例

显著性
A
618
B
114
C
234
e
18
S
984
2 309 2 57 2 117 29 8
34.3
**
6.333 ×
13
*
F0.90 (2,2) 9.0 F0.95 (2,2) 19.0 F0.99 (2,2) 99.0
最佳水平组合是A3B2C2 ,考虑B为不显著因素,取经济方案
A3B1C2 。
171
153 T=450
T3
183
144
144
153
T1
41
47
45
48
T2
48
55
57
51 Y = 50
T3
61
48
48
51
R
20
8
12
3
S
618
114
234
18 ST=984
数据分析: 1、直观法:第9方案 y=64 ,最佳方案为:A3B3C2 2、极差法:A>C>B
方差分析计算表
来源 平方和S 自由度f 水平
A温度(℃) B时间 (m) C用碱量(%)
1
80
2
85
3
90
90
5
120
6
150
7
(1)计算数据
1
2
3
4
y
1
1
1
1
1
31
2
1
2
2
2
54
3
1
3
3
3
38
4
2
1
2
3
正交试验设计原理与实例

目录
• 正交试验设计原理 • 正交表及其特性 • 正交试验设计实例 • 正交试验设计在实践中的应用 • 正交试验设计的优缺点 • 正交试验设计的发展趋势与展望
正交试验设计原理
01
定义与特点
定义
正交试验设计是一种通过正交表来安 排多因素多水平的试验,以高效地获 取试验结果的方法。
绿色环保
随着可持续发展理念的深入,正交试验设计将更加注重环 保和资源节约,减少试验过程中的浪费和污染。
定制化服务
针对不同行业和领域的需求,正交试验设计将提供更加定 制化的服务,满足客户特定的试验要求和目标。
展望
拓展应用领域 创新算法研究 强化实际应用 国际化合作与交流
正交试验设计的应用领域将进一步拓展,不仅局限于工程、科 学等领域,还将渗透到医学、经济、管理等领域。
靠性。
试验设计的基本步骤
明确试验目的
确定要解决的问题和目标,明确试验的约束 条件。
确定因素和水平
确定影响试验结果的主要因素及其取值范围或 水平。
选择合适的正交表
根据因素和水平数量,选择合适的正交表进行试 验设计。
制定试验计划
根据正交表,安排具体的试验计划,包括试验条件 、测试指标等。
实施试验
按照试验计划进行试验,并记录每个试验点的结 果。
未来将不断涌现出新的正交试验设计算法,提高试验的准确性 和效率,满足更多复杂试验的需求。
正交试验设计将更加注重与实际问题的结合,通过解决实际问 题来推动其理论和应用的发展。
正交试验设计将加强国际间的合作与交流,促进学术研究的共 同进步和创新。
THANKS.
实例二:农业种植试验
总结词
全面、系统、科学
正交设计应用实例(毕业论文)

2 正交实验设计2.1 正交实验设计概述正交实验设计(Orthogonal experimental design) 11是研究多因素多水平的一种设计方法,它是根据从全面实验中挑选出部分有代表性的点进行实验,正交实验设计又称正交设计或多因素优选设计,是一种合理安排、科学分析各实验因素的一种有效的数理统计方法。
它是在实践经验和理论认识的基础上,借助一种规格化的“正交表”,从众多的实验条件中确定出若干个代表性较强的实验条件,科学地安排实验,然后对实验结果进行综合比较,统计分析,探求各因素水平的最佳组合,从而得到最优或较优实验方案的一种实验设计方法。
正交实验设计的特点是用不太多的实验次数,找出实验因素的最佳水平组合,了解实验因素的重要性程度及交互作用情况,减少实验盲目性,避免资金浪费等。
它能以较少的实验次数找到较好的实验(生产)方案,由正交实验寻找出的优化参数(条件)与全面实验所找出的最优条件有一致的趋势。
正交实验设计具有正交性,使实验具备均衡分散和综合可比性。
此法应用方便,准确性高,在多因素条件下应用有很大的优越性,是一种高效率、快速、经济的实验设计方法。
日本著名的统计学家田口玄一将正交实验选择的水平组合列成表格,称为正交表。
例如作一个三因素三水平的实验,按全面实验要求,须进行33=27种组合的实验,且尚未考虑每一组合的重复数。
若按L9(3)3正交表按排实验,只需作9次,显然大大减少了工作量。
因而正交实验设计在很多领域的研究中已经得到广泛应用。
2.2 正交实验设计基本程序正交设计中常用的术语有:指标、因子和水平。
正交设计把实验设计要考表示第i次实验的指标值;把对实验虑的结果和评价准则称为指标,一般以yi结果和对评价指标可能产生影响且在实验中明确了条件加以对比的因素称为因子,一般以大写字母表示;把每个因子在实验中的具体条件称为因子的水平,简称水平,一般以表示因子的大写字母加上脚标来表示。
对于多因素实验,正交设计是简单常用的一种设计方法,其设计程序12如图4所示。
正交实验法设计测试用例例子

正交实验法设计测试用例例子正交实验法(Orthogonal Experimental Design)是一种设计测试用例的方法,通过合理选择测试用例,可以有效减少测试工作量,提高测试效率。
正交实验法的核心思想是通过一定的设计原则,选择一组具有独立性和均匀性的测试用例,以覆盖系统的各个方面,从而发现系统中的问题。
以下是使用正交实验法设计测试用例的一些例子:1. 网页登录功能测试:通过正交实验法设计测试用例,测试网页登录功能的正确性和稳定性。
测试用例包括用户名和密码长度的不同组合、是否输入正确的用户名和密码、是否支持记住密码等等。
2. 购物车功能测试:通过正交实验法设计测试用例,测试购物车功能的正确性和稳定性。
测试用例包括添加商品到购物车的不同顺序、添加不同数量的商品、删除商品、修改商品数量等等。
3. 文件上传功能测试:通过正交实验法设计测试用例,测试文件上传功能的正确性和稳定性。
测试用例包括上传不同类型的文件、上传不同大小的文件、上传多个文件、上传文件的同时进行其他操作等等。
4. 数据库查询功能测试:通过正交实验法设计测试用例,测试数据库查询功能的正确性和性能。
测试用例包括查询不同条件的数据、查询不同数量的数据、查询数据的同时进行其他操作等等。
5. 网络连接功能测试:通过正交实验法设计测试用例,测试网络连接功能的正确性和稳定性。
测试用例包括连接不同类型的网络、连接不同网络的速度、在连接过程中进行其他操作等等。
6. 手机应用程序测试:通过正交实验法设计测试用例,测试手机应用程序的正确性和稳定性。
测试用例包括不同操作系统的手机、不同型号的手机、在不同网络环境下使用等等。
7. 网络游戏测试:通过正交实验法设计测试用例,测试网络游戏的正确性和稳定性。
测试用例包括不同操作系统的电脑、不同网络环境下使用、同时进行其他操作等等。
8. 电子邮件发送功能测试:通过正交实验法设计测试用例,测试电子邮件发送功能的正确性和稳定性。
正交试验法(含案例)

正交试验设计法一、定义:正交试验设计法就是利用正交表来合理安排多因素试验的一种方法。
二、常用术语1、指标:指标就是试验要考察的效果。
常用X、Y、Z……来表示。
▼定量指标:能够用数量来表示的试验指标,如重量、尺寸、温度。
▼定性指标:不能用数量来表示的试验指标,如颜色、味道、外观。
●定性指标量化:可用打分法、分等法。
2、因素:因素是指对试验指标可能产生影响的原因。
因素是在试验中应当加以考察的重点内容。
一般用大写字母A、B、C……来表示。
3、水平(位级):位级是指因素在试验中所处的状态或条件。
常用阿拉伯数字1、2、3……来表示。
如: A1、A2、A3、B1、B2、B3。
三、正交表 (已设计好的标准化表格,是进行正试验法的基本工具)1、日本型正交表:由日本质量管理专家田口玄一博士创立。
该正交试验设计法,除需试验的因素外,还要研究分析因素与因素之间的交互作用,一起上列,对试验结果的分析用方差分析等方法,过程较复杂。
2、中国型正交表是由以我国张千里教授为首的中国专家所创立。
它不考虑因素之间的交互作用,而将其交互作用融于试验之中,对试验结果的分析采用极差分析法,简单的用“看一看”与“算一算”相结合的分析、简单、易行、同样能得到满意的结论,是一种实用的试验方法,很适合现场应用。
四、正交表的特点:1、均衡分散性:每一列中各种字码出现的次数相同,保证试验条件均衡地分散在配合完全的位级组合之中,因而代表性强,容易出现好条件。
2、整齐可比性:任意两列中全部有序数字对出现次数都是相同的。
保证了在各个位级的效果之中,最大限度地排除了其他因素的干扰,能最有效地进行比较,作出展望。
五、用中国型正交表安排试验的步骤 1、明确试验目的 2、确定考察指标 3、挑因素、选位级,制定因素位级表 ①挑因素的原则: ▼分析影响指标的各种因素,排除: 不可控因素 对指标影响不大的因素 已掌握得好的因素(让其固定在适当位置上) ▼选对指标可能影响大,又无把握的因素。
正交试验设计经典案例

正交试验设计经典案例
一、L9(3^4)正交试验设计
这个实验设计是一个L9(3^4)正交试验设计,用于研究铜锌合金中锌的含量、冶炼时间、冷却速率和成型压力对铜锌合金硬度的影响。
在这个设计中,有四个因素(锌的含量、冶炼时间、冷却速率和成型压力)和三个水平(低、中、高)。
该试验的九个试验条件如下表所示。
2、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计,用于研究发酵生产中,发酵液pH 值、生物量、发酵温度、曲菌培养基和曲菌翻转次数对干酪根的质量影响。
在这个设计中,有五个因素(发酵液pH值、生物量、发酵温度、曲菌培养基和曲菌翻转次数)和四个水平(低、中低、中高、高)。
该试验的十六个试验条件如下表所示。
3、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计,用于研究太阳能集热器的建造,包括集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置对太阳能集热器效率的影响。
在这个设计中,有五个因素(集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置)和四个水平(低、中低、中高、高)。
该试验的十六个试验条件如下表所示。
以上这些都是经典的正交试验设计案例,这些设计都遵循着统计学中的一些原则和方法,有效地结合了多个因素的影响,将因素控制在一定范围内,从而帮助我们更好地理解问题并提出相应的解决方案。
正交表正交试验设计应用案例

正交表正交试验设计应用案例
想象一下,你是个超级大厨,要做一种绝世美味的蛋糕。
这个蛋糕的美味程度可能受到好几个因素的影响呢。
比如说面粉的种类(高筋、低筋、中筋),糖的用量(多、中、少),烤箱的温度(高、中、低),还有烘烤的时间(长、中、短)。
这就像一个谜题,要找到最佳组合才能做出超级好吃的蛋糕。
这时候,正交表正交试验设计就像一个魔法工具闪亮登场啦。
咱们就用这个神奇的工具来安排试验。
比如说,按照正交表的规则,咱们不用把所有可能的组合都试一遍,因为那得试好多好多回,太费时间和材料啦。
咱们根据正交表来做试验。
先做一组是高筋面粉、多糖、高温度烤箱、长时间烘烤的蛋糕。
再做一组低筋面粉、中量糖、中等温度烤箱、中等时间烘烤的蛋糕,就这么按照正交表安排,做了几组不同组合的蛋糕。
然后呢,找一群吃货来试吃这些蛋糕,并且给蛋糕打分,从口感、香气、松软度等方面来评价。
最后通过分析这些数据,就像侦探分析线索一样。
咱们发现哦,原来低筋面粉、少量糖、中等温度烤箱、中等时间烘烤做出来的蛋糕得分最高,是最受欢迎的组合。
你看,通过正交表正交试验设计,咱们大厨就轻松找到了做超级美味蛋糕的最佳配方,既节省了材料和时间,又做出了超棒的蛋糕。
这就是正交表正交试验设计在美食领域的一个超酷应用案例啦。
正交试验设计经典案例

正交试验设计经典案例
一家电子公司想要调查消费者对于他们新研发的智能手表的使用满意度及其对价格的敏感度。
他们采用了L9(3^4)正交试验设计,选择了3个因素进行测试:屏幕大小、电池寿命和价格。
每个因素有3个水平,分别是大、中、小屏幕大小,长、中、短电池寿命以及高、中、低价格。
在9个不同的试验方案中,每个因素的不同水平都得以考虑到,从而提高生产效率和减少测试成本。
通过5星评分,每个试验者对手表的满意度进行评分,1星表示非常不满意,5星表示非常满意。
同时,通过问卷调查的方式确认每个测试样本对于价格的接受程度。
最后,将得到的数据进行分析,得知消费者最钟爱价格中等、电池寿命长、屏幕大小中等的手表,同时也知道消费者对于价格的敏感度相对比较低。
此正交试验设计的成功使用确保了该公司产品采用更高效率且更低成本地生产方式,并为更好地满足目标市场需求提供了重要数据支持。
正交设计举例

正交设计举例正交设计是一种研究多因素多水平的设计方法,它根据正交性从全面试验中挑选出部分有代表性的点进行试验。
这些代表性的点具备了“均匀分散,齐整可比”的特点,是一种高效率、快速、经济的实验设计方法。
以下是正交设计的一个具体例子:假设某建筑材料研究院想要研究如何提高粉煤灰砖的抗折强度。
在这个试验中,有三个因素可能会影响抗折强度,分别是成型用水量、碾压时间和每次碾压的料重。
每个因素都有三个水平,例如成型用水量可以是9%、10%、11%,碾压时间可以是8min、10min、12min,每次碾压的料重可以是330kg、360kg、400kg。
如果进行全面试验,需要进行3^3=27种组合的实验,且尚未考虑每一组合的重复数。
但是,如果采用正交设计,可以选择一个三因素三水平的正交表,例如L9(3^4),只需要进行9次试验。
这9次试验将涵盖所有因素的所有水平,而且每个因素的每个水平都会与其他因素的每个水平组合一次,且仅组合一次。
具体的试验方案可以如下安排:试验1:成型用水量9%、碾压时间8min、每次碾压的料重330kg试验2:成型用水量9%、碾压时间10min、每次碾压的料重360kg试验3:成型用水量9%、碾压时间12min、每次碾压的料重400kg试验4:成型用水量10%、碾压时间8min、每次碾压的料重360kg试验5:成型用水量10%、碾压时间10min、每次碾压的料重400kg试验6:成型用水量10%、碾压时间12min、每次碾压的料重330kg试验7:成型用水量11%、碾压时间8min、每次碾压的料重400kg试验8:成型用水量11%、碾压时间10min、每次碾压的料重330kg试验9:成型用水量11%、碾压时间12min、每次碾压的料重360kg通过这9次试验,可以找出影响抗折强度的最优组合。
这种方法大大减少了试验次数,提高了效率,而且能够得到全面试验的效果。
注塑正交试验(DOE)案例表

4.5 4.4
53 2
4.5
4.2
KJ/m2
73
68
4.3 4.5
3 4.5 4.7
KJ/m2
本方案试验结论 方案测试结果为:4.4 KJ/m2 □建议采用 ■不建议采用 □重新试验 □重新拟定
试验方案号:□ 1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 ■ 8 □ 9 □
shu
试 因素代号
A
4.8
KJ/m2
.
kszl
.
本方案试验结论 方案测试结果为: 4.7 KJ/m2 □建议采用 ■不建议采用 □重新试验 □重新拟定
试验方案号:□ 1 ■ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9 □
shu
因素代号 试
A
B
C
D
E
验 数参
因素名称 位级量值
注射温度 195 (℃)
冷却时间 35 (Min)
4.5 4.4
2
43 4.6 4.5
4.4
KJ/m2
本方案试验结论 方案测试结果为:4.4 KJ/m2 □建议采用 ■不建议采用 □重新试验 □重新拟定
试验方案号:□ 1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 ■ 9 □
shu
因素代号 试
A
B
C
D
E
验 因素名称 注射温度
215
(℃)
B 模温
25
(M i n )
C 注射压力
55
(Mpa)
设定参数 215
25
过
程显示
记 录
Miax
218
27
显示Miin 212
正交设计-案例Z

研究环境因素(温度、湿度、光照时长、温差、光强)对植物生长()的影响1.试验因素及水平本次正交试验考察了温度、湿度、光照时长、温差和光强对新梢长度的影响。
其中,温度、湿度、光照时长三个因素有5水平;温差和光强有3水平。
参考因素、水平如表1所示:2、正交表选择本次试验对5个因素进行了讨论,其中,3个因素选择5水平,2个因素选(56)正交试验表来安排择3水平。
不考虑影响因素之间的交互作用,故选用L25实验。
3、表头设计4、极差分析由极差分析可知:A >B >E >C >D ;较好的因素水平搭配为A 3B 5C 2D 2E 14、 方差分析由上述方差分析表可知,A 因素对试验有着非常显著地影响。
※【部分计算公式如下:】 (1)计算偏差平方和21)(=∑=n K k x n 1P∑==2512k kT x Q∑==a in i A x a Q 12*1P Q SS T T -=P Q SS A A -= PQ SS B B -=P Q SS C C -= P Q SS D D -= PQ SS E E -=PQ SS F F -=)()(E D C B A T SS SS SS SS SS SS SS +-++-=误差 (2)计算自由度 取: α=0.05 df A =df B =df C =n-1=4 df E =df D =n-1=2 df 总=n-1=25-1=24df 误差= df 总-(df A +df B +df C )-(df E +df D )=8 n2= 3*(5-1)+2*(3-1)=16 F A =F(n1,n2)=F(4,16)=3.01 F B =F(n1,n2)=F(4,16)=F C==3.01 F D =F(n1,n2)=F(2,16)=F E =3.63 Fe=(n1,n2)=F(8,16)=2.59 (3)列方差分析表,作F 检验eeA AA n SS n SS F =e eB BB n SS n SS F =。
正交试验设计实例
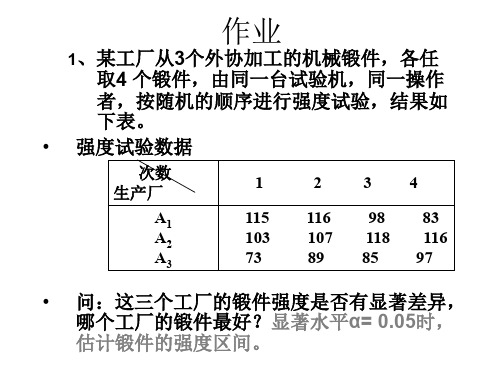
F= 4.923 分 子 分 母 自 由 度 分 别 为 : 2, 9
方差分析表
变异来源
平方和
S
因 子 A( 组 间 ) 误 差 e( 组 内 )
总计
1304 11 9 2 2496
自由度 f 2 9 11
均方 MS 652 132.44
F 4.923
F0.05(2,9)=4.26 F0.1(2,9)=3.01
宜水平组合;3)计算各因素的贡献率。
因素 水平
A温度(℃) B时间 (m) C用碱量(%)
1
80
2
85
3
90
90
5
120
6
150
7
(1)计算数据
1
2
3
4
y
1
1
1
1
1
31
2
1
2
2
2
54
3
1
3
3
3
38
4
2
1
2
3
53
5
2
2
3
1
49
6
2
3
1
2
42
7
3
1
3
2
57
8
3
2
1
3
62
9
3
3
2
1
64
T1
123
141
135
Se ST SA = 2 4 9 6 - 1 3 0 4 = 1 1 9 2 , 组 内 自 由 度 : fe fT fA = 1 1 - 2 = 9 , 组 内 均 方 ( 即 方 差 2 ): MSe Se fe = 1 1 9 2 / 9 = 1 3 2 . 4 4 。
田间正交试验案例

田间正交试验案例
田间正交试验是一种农业试验设计方法,主要用于评估不同因素对作物生长和产量的影响。
以下是一个田间正交试验的案例:
假设我们想要研究三个因素(A、B和C)对某种作物产量的影响。
这三个因素可以是不同的肥料类型、灌溉方式或种植密度。
1. 确定试验目的:评估不同因素对作物产量的影响,并找出最优的组合。
2. 选取因素和水平:选择三个因素A、B和C,并为每个因素设定三个水平(例如,A1、A2、A3;B1、B2、B3;C1、C2、C3)。
3. 制定正交表:根据因素和水平数量,选择合适的正交表。
在本例中,我们可以使用一个3行3列的正交表。
4. 分配试验小区:根据正交表,将每个因素的每个水平分配到一个试验小区中。
例如,第1行第1列的试验小区为A1B1C1,第2行第2列的试验小区为A2B2C2,以此类推。
5. 进行试验:在每个试验小区中种植相同数量的作物,并按照预定的因素和水平进行管理。
6. 收获和测量:在作物成熟后,收获每个小区的作物,并测量其产量。
7. 数据分析和结论:使用统计分析方法(如方差分析)来分析数据,并确定每个因素对产量的影响程度。
通过比较不同组合的产量,可以找出最优的组合。
8. 总结和建议:根据试验结果,总结出各个因素对产量的影响规律,并为农民提供优化种植管理的建议。
需要注意的是,田间正交试验需要合理地安排试验小区的位置和顺序,以确保结果的准确性和可靠性。
同时,试验过程中需要严格遵守随机化和重复原则,以减少误差和偶然因素的影响。
(完整word版)正交试验的方差分析实例1

正交试验设计实例分析正交试验设计是使用正交表来安排多因素、多水平试表验,并采用统计学方法分析实验结果的一种实验设计方法[1]。
对于多因素、多水平的问题,人们一般希望通过若干次的实验找出各因素的主次关系和最优搭配条件,用正交表合理地安排实验,可以省时、省力、省钱,同时又能得到基本满意的实验效果。
因此,这种方法在改进产品质量、优化工艺条件及研发新产品等诸多方面广泛应用。
但是,很多研究人员在使用该方法时,有些细节往往容易被忽视。
作者以姜黄素的提取为例具体阐述这一方法的使用和注意事项。
1.实例:姜黄素是姜黄中的主要活性成分,在优化其提取工艺时,首先应确定正交试验需要考察的因素和水平。
尤本明等[2]考察了三个因素,因素A(作为溶媒的乙醇浓度)、因素 B(溶媒的量)、因素C(渗漉速度),每个因素取三个水平。
试验设计时,一般还应考虑各因素间的交互作用,也就是因素之间的联合作用,这点不可忽视。
根据以往经验可知,本例中因素之间的交互作用可以忽略,故采用 L9(34)正交表来安排试验(见表1)。
该表共有4列,将因素 A 、B 、C 分别安排在正交表的第2、3、4列上,第1列为空白列。
在试验前,各因素及水平在正交表中的位置必须交待清楚,以确定各次试验的条件,避免不必要的错误。
1 正交试验设计与结果2 .直观分析法:表1中的 K1、K2、K3分别表示在各因素各水平下姜黄素提取量的总和,K分别表示在各因素各水平下姜黄素提取量的平均值。
由于有时会遇到各因素水平数不等的情况,因此,一般用提取量的平均值大小来反映同一个因素的各个不同水平对试验结果(提取量)影响的大小,并以此确定该因素应取的最佳水平。
用同一因素各水平下平均提取量的极差R(极差=平均提取量的最大值-平均提取量的最小值)来反映各因素的水平变动对试验结果(提取量)影响的大小。
极差大就表示该因素的水平变动对试验结果的影响大,极差小就表示该因素的水平变动对试验结果的影响小。
正交试验实际应用案例

正交试验实际应用案例正交试验是指在实验设计中通过选择合适的试验方案,使得各个因素之间相互独立,以最小的试验次数获得最多有效信息的一种实验设计方法。
正交试验广泛应用于产品设计、工艺优化、市场调研等领域。
以下是正交试验的几个实际应用案例。
1.产品设计正交试验在产品设计中的应用非常广泛。
例如,在新产品开发过程中,常常需要考虑多个因素的影响,比如材料、结构、工艺等。
通过使用正交试验,可以确定各个因素的最佳取值范围,并找到各个因素的相互作用关系。
这样可以在较少的试验次数内,对多个因素进行优化,提高产品的性能和质量。
2.工艺优化在制造过程中,往往存在多个因素对产品质量的影响。
例如,在其中一种产品的生产过程中,可能有多个因素会影响产品的成品率。
通过使用正交试验,可以确定各个因素对成品率的重要程度,并找出各个因素的最佳取值范围。
这样可以大大提高产品的成品率,并减少废品率和不良品率。
3.市场调研正交试验也可以应用于市场调研领域。
在进行市场调研时,常常需要对多个变量进行分析,并找出影响市场反应的关键因素。
通过使用正交试验,可以确定各个因素的重要性,并进行综合分析,找到影响市场反应的主要因素。
这样可以帮助企业更加准确地了解市场需求,制定更科学的市场策略。
4.药物研发在药物研发过程中,常常需要考虑多个因素对药效的影响。
正交试验可以帮助研发人员确定最佳的药物配方,并找到各个因素对药效的相互作用关系。
这样可以提高药物的疗效,并减少不良反应的发生。
5.网络优化在进行网络优化时,常常需要考虑多个因素对网络性能的影响。
通过使用正交试验,可以确定各个因素的重要程度,并找出最佳的网络配置方案。
这样可以提高网络的传输速度和可靠性,提升用户体验。
综上所述,正交试验在产品设计、工艺优化、市场调研、药物研发和网络优化等领域都有广泛的应用。
通过选择合适的试验方案,正交试验可以帮助研究人员在较少的试验次数内获取更多有效信息,提高工作效率和成果质量。
正交试验设计表案例

退 出
1.3.2.2 代表性
一方面: (1)任一列的各水平都出现,使得部 分试验中包括了所有因素的所有水平; (2)任两列的所有水平组合都出现, 使任意两因素间的试验组合为全面试验。 另一方面:由于正交表的正交性,正交试验的试 验点必然均衡地分布在全面试验点中,具有很强 的代表性。因此,部分试验寻找的最优条件与全 面试验所找的最优条件,应有一致的趋势。
代表正交表;L右下角的数字“8”表示有8行 ,用这张 正交表安排试验包含8个处理(水平组合) ;括号内的底 数“2” 表示因素的水平数,括号内2的指数“7”表示 有7列 ,用这张正交表最多可以安排7个2水平因素。
上一张 下一张 主 页 退 出
表10-2
上一张 下一张 主 页
退 出
常用的正交表已由数学工作者制定出来,供进行 正交设计时选用。2水平正交表除L8(27)外,还有L4(23)、 L16(215) 等 ; 3 水 平 正 交 表 有 L9(34) 、 L27(213)…… 等 (详见附表14及有关参考书)。 1.3.2 正交表的基本性质
在这 9 个水平组合中, A 因素各水平下包括 了 B 、 C 因素的 3个水平,虽然搭配方式不同, 但B、C皆处于同等地位,当比较A因素不同水 平时,B因素不同水平的效应相互抵消,C因素 不同水平的效应也相互抵消。所以A因素3个水 平间具有综合可比性。同样, B 、 C 因素 3个水 平间亦具有综合可比性。
组合)来进行试验。图 10-1 中标有试验号的九
个“ (·)”,就是利用正交表 L9(34) 从 27个试验点
中挑选出来的9个试验点。即:
(1)A1B1C1 (2)A2B1C2 (3)A3B1C3
(4)A1B2C2
(7)A1B3C3
测试用例设计方法正交试验法详解

测试用例设计方法--正交试验法详解正交试验法介绍正交试验法是研究多因素、多水平的一种试验法,它是利用正交表来对试验进行设计,通过少数的试验替代全面试验,根据正交表的正交性从全面试验中挑选适量的、有代表性的点进行试验,这些有代表性的点具备了“均匀分散,整齐可比”的特点。
正交表是一种特制的表格,一般用L n (m k)表示,L 代表是正交表,n 代表试验次数或正交表的行数,k 代表最多可安排影响指标因素的个数或正交表的列数,m 表示每个因素水平数,且有n=k*(m-1)+1。
正交表的特点正交表具有以下两个特点。
正交表必须满足这两个特点,有一条不满足,就不是正交表。
每列中不同数字出现的次数相等。
这一特点表明每个因素的每个水平与其它因素的每个水平参与试验的几率是完全相同的,从而保证了在各个水平中最大限度地排除了其它因素水平的干扰,能有效地比较试验结果并找出最优的试验条件。
在任意2列其横向组成的数字对中,每种数字对出现的次数相等。
这个特点保证了试验点均匀地分散在因素与水平的完全组合之中,因此具有很强的代表性。
使用正交试验法的原因对于单因素或两因素试验,因其因素少,试验的设计、实施与分析都比较简单。
但在实际工作中,常常需要同时考察3个或3个以上的试验因素,若进行全面试验,试验的规模很大,由于时间和成本的限制我们不可能进行全面试验,但是具体挑其中的哪些测试用例进行测试我们心里拿不准,总担心不做不挑选的那些测试用例会遗漏一些严重缺陷。
为了有效的、合理地减少测试的工时与费用,我们利用正交试验法来设计测试用例。
正交试验法就是安排多因素试验、寻求最优水平组合的一种高效率的试验设计方法。
我们用测试实例来进行说明使用正交试验法设计测试用例的好处。
测试需求:某所大学通信系共2个班级,刚考完某一门课程,想通过“性别”、“班级”和“成绩”这三个查询条件对通信系这门课程的成绩分布,男女比例或班级比例进行人员查询: 根据“性别”=“男,女”进行查询 根据“班级”=“1班,2班”查询 根据“成绩”=“及格,不及格”查询按照传统设计——全部测试分析上述测试需求,有3个被测元素,被测元素我们称为因素,每个因素有两个取值,我们称之为水平值,所以全部测试用例个数是2*2*2=8,参见下表序号性别班级成绩1女1班及格2女1班不及格3女2班及格4女2班不及格5男1班及格6男1班不及格7男2班及格8男2班不及格利用正交表设计测试用例,我们得到的测试用例个数是n=3*(2-1)+1=4,对于三因素两水平的刚好有L4(23)的正交表可以套用,于是用正交表试验法得出4个测试用例如下:序号性别班级成绩1女1班及格2女2班不及格3男1班不及格4男2班及格根据实际需要可以在用正交试验法设计用例的基础上补充一些测试用例。
正交实验举例

正交试验设计法正交试验设计法的基本思想正交表正交表试验方案的设计试验数据的直观分析正交试验的方差分析常用正交表1.正交试验设计法的基本思想正交试验设计法,就是使用已经造好了的表格--正交表--来安排试验并进行数据分析的一种方法。
它简单易行,计算表格化,使用者能够迅速掌握。
下边通过一个例子来说明正交试验设计法的基本想法。
[例1]为提高某化工产品的转化率,选择了三个有关因素进行条件试验,反应温度(A),反应时间(B),用碱量(C),并确定了它们的试验范围:A:80-90℃B:90-150分钟C:5-7%试验目的是搞清楚因子A、B、C对转化率有什么影响,哪些是主要的,哪些是次要的,从而确定最适生产条件,即温度、时间及用碱量各为多少才能使转化率高。
试制定试验方案。
这里,对因子A,在试验范围内选了三个水平;因子B和C也都取三个水平:A:Al=80℃,A2=85℃,A3=90℃B:Bl=90分,B2=120分,B3=150分C:Cl=5%,C2=6%,C3=7%当然,在正交试验设计中,因子可以是定量的,也可以是定性的。
而定量因子各水平间的距离可以相等,也可以不相等。
这个三因子三水平的条件试验,通常有两种试验进行方法:(Ⅰ)取三因子所有水平之间的组合,即AlBlC1,A1BlC2,A1B2C1,……,A3B3C3,33=27次试验。
用图表示就是图1 立方体的27个节点。
这种试验法叫做全面试验法。
全面试验对各因子与指标间的关系剖析得比较清楚。
但试验次数太多。
特别是当因子数目多,每个因子的水平数目也多时。
试验量大得惊人。
如选六个因子,每个因子取五个水平时,如欲做全面试验,则需56=15625次试验,这实际上是不可能实现的。
如果应用正交实验法,只做25次试验就行了。
而且在某种意义上讲,这25次试验代表了15625次试验。
图1 全面试验法取点..........(Ⅱ)简单对比法,即变化一个因素而固定其他因素,如首先固定B、C于Bl、Cl,使A变化之:↗A1B1C1 →A2↘A3 (好结果)如得出结果A3最好,则固定A于A3,C还是Cl,使B变化之:↗B1A3C1 →B2 (好结果)↘B3得出结果以B2为最好,则固定B于B2,A于A3,使C变化之:↗C1A3B2→C2 (好结果)↘C3试验结果以C2最好。
含拟水平法正交设计案例

含拟水平法正交设计案例正交设计是一种常用的实验设计方法,可以用于研究多个因素对实验结果的影响。
在正交设计中,因素的水平被组合成一系列实验条件,以寻找最优的组合方案。
下面列举了十个含拟水平法正交设计案例,以展示正交设计的应用范围和实际意义。
1. 药物配方优化:一家制药公司希望优化一种药物的配方,以提高其药效和稳定性。
通过正交设计,可以同时考虑药物中多个成分的不同水平,找到最佳的配方组合。
2. 机械零件设计:一家汽车制造公司需要设计一种新型机械零件,以提高汽车的性能和耐用性。
通过正交设计,可以系统地考虑不同参数(如材料、形状、尺寸等)的影响,找到最佳的设计方案。
3. 农作物种植优化:一个农场主希望优化农作物的种植条件,以提高产量和质量。
通过正交设计,可以考虑不同因素(如土壤水分、施肥量、光照强度等)的影响,找到最佳的种植方案。
4. 食品加工工艺改进:一家食品加工厂希望改进某种食品的加工工艺,以提高产品的口感和营养价值。
通过正交设计,可以考虑不同因素(如温度、时间、pH值等)的影响,找到最佳的加工工艺。
5. 建筑材料性能测试:一家建筑材料公司需要测试新型建筑材料的性能,以评估其适用范围和优势。
通过正交设计,可以考虑不同因素(如材料成分、制备工艺、环境条件等)的影响,找到最佳的测试方案。
6. 环境污染治理:一家环境保护机构希望找到最佳的污染治理方案,以减少环境污染物的排放。
通过正交设计,可以考虑不同因素(如处理方法、处理时间、处理剂量等)的影响,找到最佳的治理方案。
7. 产品包装设计:一家新产品公司需要设计产品的包装,以提高产品的吸引力和市场竞争力。
通过正交设计,可以考虑不同因素(如包装材料、颜色、形状等)的影响,找到最佳的包装设计方案。
8. 市场调研设计:一家市场调研公司需要设计一项调研项目,以了解消费者对某种产品的需求和偏好。
通过正交设计,可以考虑不同因素(如产品价格、品牌知名度、广告宣传等)的影响,找到最佳的调研设计方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四水平L16(45)、 L64(421)、 L256(485) …
五水平L25(56)、 L125(531)、 L625(5156) … 常用非标准表有: (均为等水平表,为缩减标准表试验号间隔而设计,不可考察交互作用) 二水平 L4(23)、 L4(23) 、L4(23) 、L4(23) … 三水平L4(23)、 L4(23)、 L4(23)、 L4(23) … 四水平L4(23)、 L4(23)、 L4(23)、 L4(23) … 五水平L4(23)、 L4(23)、 L4(23)、 L4(23) … 常用混合水平正交表有:(水平不等,一般不可考察交互作用)
因素 水平 1 2 3 TritonX-100(A) 0.8% 1.0% 1.2% DOC浓度(B) 0.2% 0.4% 0.6% 裂解时间(C) 1h 2h 4h
6
三 设计程序
3.1.4选用合适的正交表:所选用的正交表必须包含所有的试验因素和水平,并且试验次数相对较小。
3.1.1.1正交表名称:正交表名称以La(bc) 形式命名 。
1
2
3 4 5 6 7 8 9
A1
A1 A2(1.0%) A2 A2 A3(1.2%) A3 A3
B2(0.4%)
B3(0.6%) B1 B2 B3 B1 B2 B3
C2(2h)
C3(4h) C2 C3 C1 C3 C1 C2
A1B2C2
A1B3C3 A2B1C2 A2B2C3 A2B3C1 A3B1C3 A3B2C1 A3B3C2
L8(4×24)、 L9( 22×32 )、 L12( 3×24 )、 L16( 44×23 )、 L16( 43×26 ) …
8
三 设计程序
3.1.1.2选择正交表
(1)是否考虑交互作用:交互作用为因素间的联合搭配对试验指标的影响。每张标准表都配有一张交 互作用正交表,可考察因素间交互作用的影响。在实际生产活动中,交互作用是普遍存在的现象,但 是如果我们的目的只是为了得到最优化的工艺,而不需要搞清楚因素之间的相互作用的话,交互作用
TritonX-100和去氧胆酸钠,样品总蛋白质含量≤2000ug/ml。这样本试验主要研究TritonX-100和去氧胆 酸钠的作用浓度和裂解时间。即试验因素为TritonX-100浓度、去氧胆酸钠浓度和裂解时间3个因素。 3.1.3因素水平:TritonX-100浓度普遍应用的范围为0.4%~1.2%,根据以往试验和经验我们选择水平为 0.8%、1.0%、1.2%三个水平;同理选定去氧胆酸钠浓度为0.2%、0.4%、0.6%三个水平,裂解时间选 择1h、2h、4h三个水平。 则根据3.1.2和3.1.3我们得到如下因素水平表
9
三 设计程序
3.2设计实例二:研究某病毒在接种某细胞后的最适培养条件 3.2.1试验目的及试验指标:试验目的为确定某病毒的最适培养条件,可以用病毒收获液的抗原含量作 为试验指标。 3.2.2试验因素:影响病毒在细胞上生长的主要因素有接种浓度、培养基种类、培养基pH值、培养时间、 培养温度等,由于培养基是固定因素无水平可选择,我们选定接种浓度、培养基pH值、培养时间、培 养温度4因素进行研究。不同的培养基分为不同的试验批次重复本实验即可。 3.2.3因素水平:根据经验与同类细胞的培养条件,我们可以设定一下本细胞因素水平如下: 接种浓度(M.O.I):0.01,0.1,1.0 培养温度( ℃ ):33,35,37 则根据3.2.2和3.2.3我们得到因素水平表如图
正交试验设计与分析
目录
背景介绍 基本概念 设计程序 结果分析
1 2 3 4
4
项目风险评估
2
一 背景介绍
(3)正交试验表设计 本实验设计包含3因素3水平,使用3水平正交试验表L9(34)确定9次试验。表5为正交试验 表。
表5 正交试验表
试验编号 A A1(0.8%) B B1(0.2%) C C1(1h) D A1B1C1
2.3 试验指标:用来衡量试验效果的特征量,也就是试验结果。 2.4试验因素:对试验指标产生影响的原因都称为试验因素。 2.5 因素水平:试验因素在试验中所处的各种状态或者不同值。
4
三 设计程序
根据试验目的确定试验效 果的评价指标,如纯度、 回收率等
明确试验目的, 选定试验指标
根据知识、以往的试验结 论、经验、对试验指标影 响等选择合适的试验因素
正交设计 因素个数,列数
La(bc)
试验次数,行数 因素水平数
正交表L9(34)
试验号
因
A 1 1 1 2 2 2 3 3 3 B 1 2 3 1 2 3 1 2 3
素
C 1 2 3 2 3 1 3 1 2 D 1 2 3 3 1 2 2 3 1
1 2 3 4 5 6 7 8 9
7
三 设计程序
3.1.1.2正交表分类:正交表可分为标准表和非标准表,也可分为等水平正交表和混合水平正交表。
K1为所有含有相应因素水平1的试验结果之和,K2为所有含有相应因素水平2的试验结果之和,以此类 推。即: A因素 K1=36.5+31.77+38.79+38.02=144.78
K2=31.54+35.02+30.9+35.62=133.08
…… B因素 K1=35.02+32.37+38.79+34.54=140.72 K2=36.2+29.32+35.62+34.02=135.16
列号 试验号
接种浓度 (M.O.I)
培养基种 类
培养时间 ( h)
pH值
1 2 3 4 5 6 7 8
0.01 0.01 0.01 0.01 0.1 0.1 0.1 0.1
33 35 37 35 33 35 37 35
48 72 96 120 72 48 120 96
7.0 7.2 7.4 7.8 7.8 7.4 7.2 7.0
9 10 11 12 13 14 15
1.0 1.0 1.0 1.0 0.01 0.01 0.01
33 35 37 35 33 35 37
96 120 48 72 120 96 72
7.2 7.0 7.8 7.4 7.4 7.8 7.0
16
0.01
35
48
7.2
13
四 结果分析
4.1极差分析法:非常直观、简便的方法,在误差影响不大、精度要求不高的实验中得到广泛的应用。 经过很简单的计算即可得到最优搭配、最优组合、因素主次,能够比较圆满的迅速得到最优工艺。
Hale Waihona Puke 确定需要考察 的因素水平以2~4为宜,如若分 批进行则可“走着瞧”, 于有苗头处加重稀处加密
选取适当的因 素水平
正交表要容得下所有因素 水平,且试验次数最少者 为合适
选用合适正交 表
每一列为一因素,如无交 互作用则不分顺序。如有 交互作用则需单设计表头。
表头设计
将正交表中的数字换做因 素各水平就形成了实验方 案
SST SS因素 SS空列(误差)
15
谢
谢
16
……
…… A因素 k1= K1/4=36.20 k2= K2/4=36.20 …… ……
14
四 结果分析
4.1方差分析法:极差分析法无法估算试验误差,且对于各因素的影响不能给出精确地数量估计。为了 弥补此缺陷我们引入了方差分析法。 方差分析基本思想是将数据的总变异分解成因素引起的变异和误差引起的变异两部分,构造F统计量, 作F检验,即可判断因素作用是否显著。 F检验即方差齐性检验,用于检验两个样本的方差是否相等。
制定方案
5
三 设计程序
3.1 设计实例一:流感病毒裂解正交试验
3.1.1试验目的及试验指标:试验目的为确定流感病毒最适裂解条件。对于裂解效果的影响选择电镜观 察为试验指标。。 3.1.2试验因素:影响裂解条件的因素有裂解剂、裂解剂浓度、裂解时间、裂解温度、样品总蛋白质浓
度等条件,根据以往研究经验及本产品规程规定,我们固定了裂解温度为24~26℃,裂解剂选择
培养温度( ℃ ) 33 35 37 35
培养时间(h) 48 72 96 120
培养液pH值 7.0 7.2 7.4 7.8
这样,我们可以选择标准正交表L16(45)来安排试验。
11
三 设计程序
3.2.5试验方案:将正交表中数字换做试验条件得到试验方案
12
三 设计程序
列号 试验号
接种浓度 (M.O.I) 培养温度 (℃) 培养时间 ( h) pH值
3
二 基本概念
2.1 正交试验:正交试验是利用正交表来安排与分析多因素试验的一种设计 方法。由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行 试验,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水 平组合。 其典型特点是,用部分试验来代替全面试验,通过对部分试验结果的分 析,了解全面试验的情况。 2.2 正交表:学名叫正交阵列(Orthogonal Array),是正交试验设计的 基本工具。它是根据均衡分布思想,运用组合数学理论构造的一种数学表 格。均衡分布思想是正交表的核心。常用的正交表已由数学工作者制作成 标准表格。如:L4(23)、 L8(27) 、 L9(34) 、 L16(45)等
3.2.4 选用合适的正交表:本试验因素水平组合为32 × 42,查询混合水平正交表,并无合适正交表可 用。需要对因素水平进行部分调整。常用的方法有拟水平法、活动水平法、组合因素法、直积法、直 和法等。采用拟水平法虚拟接种浓度1个水平和培养基一个水平后,因素水平变更为:
