激光原理及应用(第2版)(陈家璧)课后答案(全)
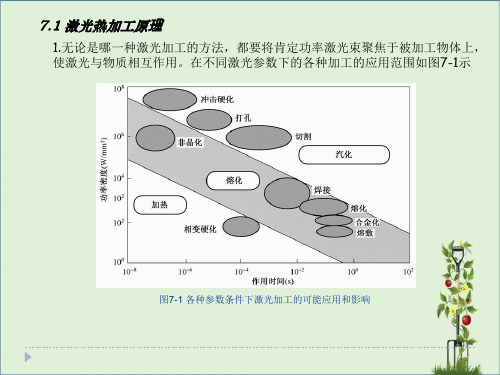
陈家璧版光学信息技术原理及应用习题解答(7-8章)

陈家璧版光学信息技术原理及应用习题解答(7-8章)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第七章 习题解答1. 某种光盘的记录范围为内径80mm,外径180mm 的环形区域,记录轨道的间距为2um.假设各轨道记录位的线密度均相同记录微斑的尺寸为um,试估算其单面记录容量. (注: 内、外径均指直径)解: 记录轨道数为 25000002.0280180=⨯-=N单面记录容量按位计算为 ∑=⨯≈⨯+=Nn n M 110107.10006.0)002.040(2π bits = 17 Gb.按字节数计算的存储容量为 2.1GB.2. 证明布拉格条件式(7-1)等效于(7-17)式中位相失配= 0的情形, 因而(7-18)式描述了体光栅读出不满足布拉格条件时的位相失配。
证明: 将体光栅读出满足布拉格条件时的照明光波长(介质内) 和入射角 (照明光束与峰值条纹面间夹角)分别记为0和θ0, 则根据布拉格条件式(7-1)有: 2sin θ0= 0 其中为峰值条纹面间距.对于任意波长λa (空气中) 和入射角θr (介质内), 由(7-17)式, 位相失配 δ 定义为:24)cos(n K K ar πλθφδ--=其中n 0为介质的平均折射率, K = 2π/Λ为光栅矢量K 的大小,φ为光栅矢量倾斜角,其值为 22πθθφ++=sr ,θr 为再现光束与系统光轴夹角 (参见图7-9).当 δ = 0 时,有2422cos n K K a r s r πλθπθθ=⎪⎭⎫ ⎝⎛-++ 即:Λ=Λ=⎪⎭⎫ ⎝⎛-2422sin 0λππλθθn s rλ为介质中的波长. 由于角度2sr θθ-恰为照明光与峰值条纹面的夹角θ, ∑ ©亦即布拉格条件2Λ sin θ = λ.当读出光偏离布拉格角θo 和布拉格波长λo 的偏移量分别为∆θ和∆λ时,有[]0200200002044sin )sin(cos )cos( 4)()(cos n K n K K K n K K πλπλθθφθθφπλλθθφδ∆--∆--∆-=∆+-∆+-=利用布拉格条件式(7-17), 以及∆θ和∆λ很小时的近似关系 cos ∆θ≈1 和 sin ∆θ≈∆θ, 立即可得:δ =∆θK sin(φ-θ0) - ∆λK 2/4πn 0 即(7-18)式 原题得证。
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l 证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆4.2设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹?答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G 式中12ννν-=∆,复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆ ,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在δντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N 4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
激光原理与应用答案(陈家壁主编)

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
激光原理及应用陈家璧主编习题解答

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kTh 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
激光原理及应用1-6章部分课后答案

激光原理及应用部分课后答案1-4为使He-Ne 激光器的相干长度达到1KM ,它的单色性0λλ∆应是多少?2-2当每个模式内的平均光子数(光子简并数)大于1时,以受激辐射为主。
2-3如果激光器和微波激射器分别在um 10=λm 500n =λ和z 3000MH =ν输出1W 连续功率,问美秒从激光上能级向下能级跃迁的粒子数是多少?2-4当一对激光能级为E2和E1(f1=f2),相应的频率为v (波长为λ),能级上的粒子数密度分别为n2和n1,q 求:(1)当v=3000MHZ ,T=3000K 时,n2/n1=?(2)当λ=1um ,T=3000K 时,n2/n1=?(3)当λ=1um ,n2/n1=0时,温度T=?解:2-5激发态的原子从能级E2跃迁到E1时,释放出λ=5um的光子,求这个两个能级的能量差。
若能级E1和E2上的原子数分别为N1和N2,试计算室温T=300K的N2/N值。
2-7如果工作物质的某一跃迁是波长为100nm的远紫外光,自发辐射跃迁概率1621s10-=A,试问:(1)改跃迁的受激辐射爱因斯坦系数B21是多少?(2)为使受激辐射跃迁概率比自发辐射跃迁概率大三倍,腔内的单色能量密度νρ应为多少?2-9某一物质受光照射,沿物质传播1mm的距离时被吸收了1%,如果该物质的厚度是0.1m,那么入射光中有百分之几能通过该物质?并计算该物质的吸收系数α。
2-10激光在0.2m 长的增益介质中往复运动过程中,其增强了30%。
求该介质的小信号增益系数0G 。
假设激光在往复运动中没有损耗。
3-2CO2激光器的腔长L=100cm,反射镜直径D=1.5cm,两镜的光强反射系数分别为r1=0.985,r2=0.8.求由衍射损耗及输出损耗所分别引起的δ,τ。
3-4,分别按下图中的往返顺序,推导近轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ,并证明这两种情况下的)(D A +21相等。
《激光原理及应用》陈家璧第二版-第七章课件
T0,0,AqS0r
232t
Ø激光功率密度过高,材料在外表汽化,不在深层熔化;激光功率密度过低, 则能量会集中到较大的体积内,使焦点处熔化的深度很小
7.1 激光热加工原理
(4) 激光等离子体屏蔽现象 Ø激光作用于靶外表,引发蒸汽,蒸汽连续吸取激光能量,使温度上升,最终 在靶外表产生高温高密度的等离子体。等离子体快速向外膨胀,在此过程中连 续吸取入射激光,阻挡激光到达靶面,切断了激光与靶的能量耦合。 如图7-2所示,为等离子云变化的过程
Ø简化:假设半无限大〔即物体厚度无限大〕物体外表受到均匀的激光垂直照 射加热,被材料外表吸取的光功率密度不随时间转变,而且光照时间足够长, 以至被吸取的能量、所产生的温度、导热和热辐射之间到达动平衡,此时圆形 激光光斑中心的温度可以由下式确定
T0, AP
r0t
7.1 激光热加工原理
(2) 材料的加热 假设光照时间为有限长(s),考察点离开外表的距离(cm)也不为零,此时圆形激 光光斑中心轴线上考察点的温度为
图7-14离焦量对打孔质量的影响
7.3.1 激光打孔
3. 激光打孔工艺参数的影响 ※ 脉冲激光的重复频率对打孔的影响
用调Q方法取得巨脉冲时,脉冲的平均功率根本不变,脉宽也不变,重复频率越高 ,脉冲的峰值功率越小,单脉冲的能量也越小。这样打出的孔深度要减小。
※ 被加工材料对打孔的影响 材料对激光的吸取率直接影响到打孔的效率。由于不同材料对不同激光波长有不同 的吸取率,必需依据所加工的材料性质选择激光器。
7.3.1 激光打孔
1.激光打孔原理:激光打孔机的根本构造包括激光器、加工头、冷却系统、数控 装置和操作面盘〔图7-13〕。加工头将激光束聚焦在材料上需加工孔的位置,适 中选择各加工参数,激光器发出光脉冲就可以加工出需要的孔。
激光原理与应用课后题答案 陈家壁版

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h qn 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kT n n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kTh e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
《激光原理及应用》陈家璧第二版 - 第七章

图7-15 激光切割头的结构示意图
※ 氧助熔化切割: 金属被激光迅速加热至燃点以上,与氧发生剧烈的氧化反应(即燃 烧),放出大量的热,又加热下一层金属,金属被继续氧化,并借助气体压力将氧 化物从切缝中吹掉。
7.3.2 激光切割
4. 激光切割的工艺参数及其规律 ※ 激光功率: 激光切割时所需功率的大小,是由材料性质和切割机理决定的。 ※ 切割速度: 在一定功率条件下,板厚越大,切割速度越小。切割速度对切口表 面粗糙度也有较大影响。 ※ 气体的压力:在功率和切割材料板厚一定时,有一最佳切割气体流量,这时切 割速度最快。随着激光功率的增加,切割气体的最佳流量是增大的。 ※ 光束在质量、透镜焦距和离焦量:激光器输出光束的模式为基横模时对激光切 割最为有利。光斑大小与聚焦透镜的焦距成正比。短焦距的透镜虽然可以得到较 小光斑,但焦深很小。离焦量对切割速度和切割深度影响较大,切割过程中必须 保持不变,一般离焦量选用负值,即焦点位置置于切割板面下面某一点。 ※ 喷嘴:喷嘴是影响激光切割质量和效率的—个重要部件。激光切割一般采用 同轴(气流与光轴同心)喷嘴,喷嘴出口直径大小应依据板厚加以选择。另外,喷 嘴到工件表面的距离对切割质量也有较大影响,为了保证切割过程稳定,这个距 离必须保持不变。
图7-9 激光熔凝处理后横截面组织示意图
图7-10 T10钢激光熔凝层显微硬度沿淬硬层深度的分布
7.2.3 激光熔覆技术
1.激光熔覆(Laser Cladding)技术亦称激光包覆、激光涂覆、激光熔敷,是一种新 的表面改性技术。它通过在基材表面添加熔覆材料,利用高功率密度的激光束使 之与基材表面一起熔凝的方法,在基材表面形成与其为冶金结合的添料熔覆层, 以改善其表面性能的工艺。 2.激光熔覆技术具有如下优点 3.激光熔覆工艺依据材料的添加方式不同,分为预置涂层法和同步送料法。 4.同步送料法指在激光束照射基材的同时,将待熔覆的材料送入激光熔池,经 熔融、冷凝后形成熔覆层的工艺过程。激光熔覆材料包括金属、陶瓷或者金属 陶瓷,材料的形式可以是粉末、丝材或者板材,工艺过程如图7-11所示。 激光熔覆技术
(完整word版)《激光原理》课后题答案

《激光原理》习题解答第一章习题解答1 为了使氦氖激光器的相干长度达到1KM ,它的单色性0λλ∆应为多少?解答:设相干时间为τ,则相干长度为光速与相干时间的乘积,即c L c ⋅=τ根据相干时间和谱线宽度的关系 cL c ==∆τν1又因为γνλλ∆=∆,0λνc=,nm 8.6320=λ由以上各关系及数据可以得到如下形式: 单色性=ννλλ∆=∆=cL 0λ=101210328.61018.632-⨯=⨯nmnm 解答完毕。
2 如果激光器和微波激射器分别在10μm、500nm 和Z MH 3000=γ输出1瓦连续功率,问每秒钟从激光上能级向下能级跃迁的粒子数是多少。
解答:功率是单位时间内输出的能量,因此,我们设在dt 时间内输出的能量为dE ,则功率=dE/dt激光或微波激射器输出的能量就是电磁波与普朗克常数的乘积,即d νnh E =,其中n 为dt 时间内输出的光子数目,这些光子数就等于腔内处在高能级的激发粒子在dt 时间辐射跃迁到低能级的数目(能级间的频率为ν)。
由以上分析可以得到如下的形式:ννh dth dE n ⨯==功率 每秒钟发射的光子数目为:N=n/dt,带入上式,得到:()()()13410626.61--⨯⋅⨯====s s J h dt n N s J νν功率每秒钟发射的光子数 根据题中给出的数据可知:z H mms c13618111031010103⨯=⨯⨯==--λν z H mms c1591822105.110500103⨯=⨯⨯==--λν z H 63103000⨯=ν把三个数据带入,得到如下结果:19110031.5⨯=N ,182105.2⨯=N ,23310031.5⨯=N3 设一对激光能级为E1和E2(f1=f2),相应的频率为ν(波长为λ),能级上的粒子数密度分别为n2和n1,求(a)当ν=3000兆赫兹,T=300K 的时候,n2/n1=? (b)当λ=1μm ,T=300K 的时候,n2/n1=? (c)当λ=1μm ,n2/n1=0.1时,温度T=?解答:在热平衡下,能级的粒子数按波尔兹曼统计分布,即:TK E E T k h f f n n b b )(ex p ex p 121212--=-=ν (统计权重21f f =) 其中1231038062.1--⨯=JK k b为波尔兹曼常数,T 为热力学温度。
《激光原理及应用》习题参考答案仅供大家学习参考用

《激光原理及应用》习题参考答案思考练习题11•解答:设每秒从上能级跃迁到下能级的粒子数为n 。
单个光子的能量:g = h v = he / Z 连续功率:p 二n ; 则,n = p/ ;a.对发射■ = 0.5000的光:p 1 0.5000 10-6 n — —he 6.63 10 ⑶ 3.0 108-2.514 1018(个)b.对发射、• = 3000 MHz 的光_________ 16.63 10 "4 3000 106= 5.028 1023(个)E 2 a 匹Tn 1hv些=小-1n 1hc 3T6.26 103(K)'■ ln 匹3.解答:(1) 由玻耳兹曼定律可得_E 2 -E 1e '丁 , m/g20且4g 1 =g 2, m • n 2 =10代入上式可得: n 2 :30 (个)(2 )由 (a ), (b ) ,(c)式可得:2.解答:E 2 - E<| = h..(a).(b) (1 )由 ■■■. = c/ ■ .......(a ), (b )式可得:.(c)n 2 /g 2(2) p =108 n 2(E 2 -EJ =5.028 10-(W) 4•解答:(1)由教材(1-43)式可得e kT —1因此:fT ' =2.82kh ,hc同样可求得: 一丄 =4.96九m kT故' m - m = 0.568c8h1 3 A-2000J s/m 3 -3.860 10, J s/m 3 (0.6328 10冷3 5.0 10*8- 6.63 10 ^4= 7.592 10 5•解答:(1)红宝石半径 r = 0.4cm ,长L -8cm ,铬离子浓度匸=2 1018cm‘,发射波长• =0.6943 10 “m ,巨脉冲宽度 -T = 10 ns 则输出最大能量2 ,、he18E - (:r L) 2 1034826.63 1030 108二 0.42 86(J)二 2.304(J)0.6943 10」脉冲的平均功率:P =E /.「23041010"2.304 叫) (2)自发辐射功率 _ hcN 2heP (兀r 2L)Q 自皿z-X663计 3° IO 8 *1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考练习题11.试计算连续功率均为1W 的两光源,分别发射=0.5000m ,=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61c hq n 239342100277.51031063.61h qn 2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g ,求:(1)当原子跃迁时相应频率为=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长=1,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m mkT n nn g e n g )则有:1]3001038.11031063.6exp[2393412kT h e n n (2)K T T e n n kT h 3623834121026.61.0]1011038.11031063.6exp[3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4n n e g n g n kT h 且202110n n 可求出312n (2)功率=W 918810084.51064.131104.(1)普通光源发射=0.6000m 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度为若干?(2)在He —Ne 激光器中若34/100.5m s J ,为0.6328m ,设=1,求q q 激自为若干?答:(1)(2)943436333106.71051063.68)106328.0(88h h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
设红宝石直径0.8cm ,长8cm ,铬离子浓度为2×1018cm -3,巨脉冲宽度为10ns 。
求:(1)输出0.6943m 激光的最大能量和脉冲平均功率;(2)如上能级的寿命=10-2s ,问自发辐射功率为多少瓦?答:(1)最大能量Jch d r h N W 3.2106943.01031063.61010208.0004.0683461822脉冲平均功率=瓦8961030.21010103.2t W (2)瓦自自自145113.2112002021e h N P en dt e n N tA 6.试证单色能量密度公式,用波长来表示应为5811hckT hc e 证明:11811852322kT h kT h e hc c e h c c dVd dw dVd dw 7.试证明,黑体辐射能量密度()为极大值的频率m 由关系112.82m T kh 给出,并求出辐射能量密度为极大值的波长m 与m 的关系。
答:(1)由33811hv kT h c e 可得:))1(113(82323kT hee e c h kT hkT h kT h 令kT h x ,则上式可简化为:xx xee )1(3解上面的方程可得:82.2x 即:1182.282.2kh T kT h m m(2)辐射能量密度为极大值的波长m 与m 的关系仍为mm c 8.由归一化条化证明(1-65a)式中的比例常数1A 证明:2202)2/1()(4)(Af N ,由归一化条件且0是极大的正数可得:1)2/1()(402202d A 1)2/1()(4202202d A 1)41(120222d A 11]'4[4202Aarctg A9.试证明:自发辐射的平均寿命211A ,21A 为自发辐射系数。
证明:自发辐射时在上能级上的粒子数按(1-26)式变化:tA en t n 21202)(=自发辐射的平均寿命可定义为dt t n n 02201式中dt t n 2为t 时刻跃迁的原子已在上能级上停留时间间隔dt 产生的总时间,因此上述广义积分为所有原子在激发态能级停留总时间,再按照激发态能级上原子总数平均,就得到自发辐射的平均寿命。
将(1-26)式代入积分即可得出210121A dt e t A 10.光的多普勒效应中,若光源相对接收器的速度为c ,证明接收器接收到的频率01/1/c c ,在一级近似下为:0(1)c证明:022021220)1()211)(1()1)(1(11c c c c c c c 即证11.静止氖原子的3S 22P 4谱线的中心波长为0.6328m ,设氖原子分别以0.1c ,0.5c 的速度向着接收器运动,问接收到的频率各为多少?答:Hz c c c c 146801.010241.5106328.01039.01.19.01.111同理可求:Hz c 141.010288.4;Hz c 145.010211.8;Hzc 145.010737.212.设氖原子静止时发出0.6328m 红光的中心频率为 4.74×1014Hz ,室温下氖原子的平均速率设为560m/s 。
求此时接收器接收频率与中心频率相差若干?答:Hz c 81460680010848.81074.4108667.1)108667.11()1035601()1(13.(1) 一质地均匀的材料对光的吸收为0.01mm -1、光通过10cm 长的该材料后,出射光强为入射光强的百分之几? (2) —光束通过长度为1m 的均匀激活的工作物质,如果出射光强是入射光强的两倍,试求该物质的增益系数。
答;(1)368.01)0()()0()(10001.0e e I z I e I z I Az (2)11693.02ln 2)0()()0()(m G e I z I e I z I G Gz思考练习题 21.利用下列数据,估算红宝石的光增益系数n 2-n 1=51018cm -3,1/f()=2×1011 s -1,t 自发=211A 310-3s ,λ=0.6943m ,=l.5,g 1=g 2。
答:)(8)(8)(8)()(222133321333212121f A n f h c h c A n G c h B A f h c nB G 11122431871.010215.18)106943.0(1031105)(cm G 2.He-Ne 激光器中,Ne 原子数密度n 0=n 1+n 2=l012cm -3,1/f()=15×109s -1,λ=0.6328m ,t 自发=211A 10-17s ,g 3=3,g 2=5,11,又知E 2、E 1能级数密度之比为4,求此介质的增益系数G 值。
答:11112211211112312210103141081021410n g g n n n n E E cm n n n 比能级数密度之比为和332121333332121888hc A B c h c h B A 192617112212172.0105.118)106328.0(1010314)(8)()(cm f A n f h c nB G 3.(a)要制作一个腔长L =60cm 的对称稳定腔,反射镜的曲率半径取值范围如何?(b)稳定腔的一块反射镜的曲率半径R 1=4L ,求另一面镜的曲率半径取值范围。
答:(a )R R R 21;cm R R L R L 301)1)(1(0(b )L R L R R L R L R L31)1(4301)1)(1(022221或4. 稳定谐振腔的两块反射镜,其曲率半径分别为R 1=40cm ,R 2=100cm ,求腔长L 的取值范围。
答:cmL cm L LL R L R L1401004001)1001)(401(01)1)(1(021或5.试证非均匀增宽型介质中心频率处的小讯号增益系数的表达式(2-28)。
证明:2102100021000210002100)ln2(2)()2ln (2)()()()()(h c B n G f f h c B n G f h c B n G D D D D D D D D 即证。
6.推导均匀增宽型介质,在光强I ,频率为的光波作用下,增益系数的表达式(2-19)。
证明:220022000)2)(1()()(])2()[()()(1)()(s s I I G f f I I G G 而:)()(2)2()(12)()()(2)()()()()(0022000000002100002100G G f f G f f h c B n G f h c B n G 依据上面两式可得:220002)2)(1()()()2()(s I IG G ;即证。
7.设均匀增宽型介质的小讯号增益曲线的宽度为,求证,I =I S 时的稳定工作时讯号增益曲线的线宽为2,并说明其物理意义。
证明:(1)220002220022000)2)(1()()()2()2)(1()()(])2()[()()(1)()(s s s I I G I I G f f I I G G 当1s I I 时,增益系数的最大值为:2)()(000G G ;当增益系数的最大值为增益系数的最大值的一半时,即4)()2(2)()()2()()(1)()(0022000200G G f f G G 时,对应有两个频率为:2)2(2)2(2210201=-=-以及(2)物理意义:当光强s I I 时,介质只在2范围内对光波有增益作用,在此范围外增益可忽略不计,而光波也只在这个线宽范围内对介质有增益饱和作用。
8.研究激光介质增益时,常用到“受激发射截面”()e (cm 2)概念,它与增益系数()G (cm -1)的关系是()()e G n ,n 为反转粒子数密度,试证明:具有上能级寿命为,线型函数为()f 的介质的受激发射截面为222(()8e c f )。
证明:222222333213332121218)()(81)(8)()()(8)()(f c f c f h c h c A n G c h B A f h c nB G e e 9. 饱和光强()s I 是激光介质的一个重要参数。
证明均匀增宽介质在中心频率0处的饱和光强000()()s e hI ,并计算均匀增宽介质染料若丹明6G 在0=0.5950m 处的饱和光强。
(已知=5.5×l 0—9s ,=4.66×1013Hz ,=1.36)答:(1))()(2)()()(2)()()()()(2)(0000000021210e s e s e s hI f f h c c I f h c nB G nG B c I(2) 25322000220020000/10213.34)()(8)()()()(cm W hc hI f c h I e s e e s 10.实验测得He-Ne 激光器以波长=0.6328工作时的小讯号增益系数为G 0=310-4/d(cm -1),d 为腔内毛细管内径(cm)。
