(完整)初二认识概率-知识点,测试题及答案,推荐文档
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、下列试验能够构成事件的是()A.掷一次硬币B.射击一次C.标准大气压下,水烧至100℃D.摸彩票中头奖2、下列说法不正确的是()A.某种彩票中奖的概率是,买1000张该种彩票一定会中奖B.了解一批电视机的使用寿命适合用抽样调查C.若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定 D.在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件3、某学校组织知识竞赛,共设20道题,其中有关中国优秀传统文化试题10道,实践应用题4道,创新能力题6道,小捷从中任选一道试题作答,他选中创新能力试题的概率是()A. B. C. D.4、一个不透明的袋中装有除颜色外均相同的5个红球和n个黄球,从中随机摸出一个,摸到红球的概率是,则n是()A.5B.8C.3D.135、已知:四边形ABCD的对角线AC、BD相交于点O,给出下列4个条件:①AB ∥CD;②OA=OC;③AB=CD;④AD∥BC从中任取两个条件,能推出四边形ABCD 是平行四边形的概率是()A. B. C. D.6、国学经典《声律启蒙》中有这样一段话:“斜对正,假对真,韩卢对苏雁,陆橘对庄椿”,现有四张卡片依次写有一“斜”、“正”、“假”、“真”,四个字(4张卡片除了书写汉字不同外其他完全相同),现从四张卡片中随机抽取两张,则抽到的汉字恰为相反意义的概率是()A. B. C. D.7、在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是()A.随着抛掷次数的增加,正面朝上的频率越来越小B.当抛掷的次数很大时,正面朝上的次数一定占总抛掷次数的C.不同次数的试验,正面朝上的频率可能会不相同D.连续抛掷11次硬币都是正面朝上,第12次抛掷出现正面朝上的概率小于8、在一个不透明的盒子里装有3个红球和2个白球,每个球除颜色外都相同,从中任意摸出3个球.下列事件中,不可能事件是()A.摸出的3个球都是红球B.摸出的3个球都是白球C.摸出的3个球中有2个红球1个白球D.摸出的3个球中有2个白球1个红球9、某商场利用摸奖开展促销活动,中奖率为,则下列说法正确的是()A.若摸奖三次,则至少中奖一次B.若连续摸奖两次,则不会都中奖 C.若只摸奖一次,则也有可能中奖 D.若连续摸奖两次都不中奖,则第三次一定中奖10、在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为,那么口袋中球的总数为()A.12个B.9个C.6个D.3个11、下列说法中正确的是()A.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为B.“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件C.“同位角相等”这一事件是不可能事件D.“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件12、下列说法正确的是()A.一个游戏的中将概率是,则做10次这样的游戏一定会中奖B.一组数据6,8,7,8,8,9,10的众数和中位数都是8C.为了解江苏省中学生的心理健康情况,应该采用普查的方式D.若甲组数据的方差S 2甲=0.1,则乙组数据比甲组数据稳定=0.01,乙组数据方差S 2乙13、某学生书包中有三枝红铅笔,两枝黑铅笔,一支白铅笔,它们的形状、大小一样,从中任意摸出一枝,那么摸到白铅笔的机会是()A. B. C. D.14、下列事件中是必然事件的是()A.打开电视,它正在播广告B.掷两枚质地均匀的骰子,点数之和一定大于6C.某射击运动员射击一次,命中靶心D.早晨的太阳从东方升起15、“抛一枚均匀硬币,落地后正面朝上”这一事件是()A.必然事件B.随机事件C.确定事件D.不可能事件二、填空题(共10题,共计30分)16、在一个不透明的口袋中,有若干个红球和白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率0.75,若白球有3个,则红球有________个.17、如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W,请估计事件W的概率P(W)的值________.18、从点A(-2,3),B(1,-6),C(-2,-4)中任取一个点,在y=- 的图象上的概率是________19、在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:摸球的次数n 100 200 300 500 800 1000 3000摸到白球的次数m 65 124 178 302 481 599 1803摸到白球的频率0.65 0.62 0.593 0.604 0.601 0.599 0.601请估计:当n很大时,摸到白球的频率将会接近________.(精确到0.1)20、某班学生分组做抛掷同一型号的一枚图钉的实验,大量重复实验的结果统计如下表:(顶尖朝上频率精确到 0.001)累计实验次数100 200 300 400 500顶尖朝上次数55 109 161 211 269顶尖朝上频率0.550 0.545 0.536 0.528 0.538根据表格中的信息,估计掷一枚这样的图钉落地后顶尖朝上的概率为________.21、在一个不透明的袋子中装有若干个除颜色外形状大小完全相同的球,如果其中有3个白球,且摸出白球的概率是,那么袋子中共有球________个.22、在中,给出以下4个条件:⑴;⑵;⑶;⑷;从中任取一个条件,可以判定出是直角三角形的概率是________.23、如图,四个完全相同的小球上分别写有:0,,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为________.24、现有6张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使得关于x的一元二次方程x2﹣2x+a﹣2=0有实数根,且关于x的分式方程+2=有解的概率为________.25、在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是________.三、解答题(共6题,共计25分)26、一个不透明的口袋中有三个小球,上面分别标有数字,,,除所标数字不同外,其它完全相同,从中随机摸出一个小球,记下数字后放回并搅匀,再随机摸出一个小球.用画树状图(或列表)的方法,求两次摸出的小球所标数字之和大于的概率.27、从一副扑g牌中任意抽取一张,(1)这张牌是“A”(2)这张牌是“红心的”(3)这张牌是“大王”(4)这张牌是“红色的”估计上述事件发生的可能性的大小,将这些事件的序号按发生的可能性从小到大的顺序排列.28、在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.(1)试求出a的值;(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件).29、有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:(1)可能性最大和最小的事件分别是哪个?(填写序号)(2)将这些事件的序号按发生的可能性从小到大的顺序排列:.30、某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).②若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数.③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).参考答案一、单选题(共15题,共计45分)1、D3、B4、C5、C6、B7、C8、B9、C10、C11、B12、B13、A14、D15、B二、填空题(共10题,共计30分)16、17、19、20、21、22、23、24、25、三、解答题(共6题,共计25分)26、28、29、30、。
八年级数学下册第8章 认识概率测试卷及答案

第八单元认识概率综合测试卷一、选择题(每题3分;共24分)1.“a是实数;I a I≥0”这一事件是( )A.必然事件B.不确定事件C.不可能事件D.随机事件2.在某次国际乒乓球单打比赛中;甲、乙两名中国选手进入最后决赛;那么下列事件为必然事件的是( )A.冠军属于中国选手B.冠军属于外国选手C.冠军属于中国选手甲D.冠军属于中国选手乙3.下列事件是随机事件的是( )A.太阳绕着地球转B.小明骑车经过某个十字路口时遇到红灯C.地球上海洋面积大于陆地面积D.李刚的生日是2月30日4.某商场为促销开展抽奖活动;让顾客转动一次转盘;当转盘停止后;只有指针指向阴影区域时;顾客才能获得奖品;下列有四个大小相同的转盘可供选择;使顾客获得奖品可能性最大的是( )A B C D5.从只装有4个红球的袋中随机摸出一球;若摸到白球的概率是P1;摸到红球的概率是P2;则( )A.P1=1;P2=1 B.P1=0;P2=1C.P1=0;P2=14D.P1=P2=146.如图;一个可以自由转动的转盘被等分成6个扇形区域;并涂上了相应的颜色;转动转盘;转盘停止后;指针指向蓝色区域的概率是( )A.16B.13C.12D.237.投掷一枚普通的正方体骰子;四个同学各自发表了以下见解:①出现“点数为奇数"的概率等于出现“点数为偶数”的概率;②只要连掷6次;一定会“出现1点";③投掷前默念几次“出现6点";投掷结果“出现6点”的可能性就会增大;④连续投掷3次;出现点数之和不可能等于19.其中正确见解的个数是( )A.1个B.2个C.3个D.4个8.甲、乙两位同学在一次实验中统计了某一结果出现的频率;给出的统计图如图所示;则符合这一结果的实验可能是( )A.掷一枚正六面体的骰子;出现5点的概率B.掷一枚硬币;出现正面朝上的概率C.任意写出一个整数;能被2整除的概率D.一个袋子中装着只有颜色不同;其他都相同的两个红球和一个黄球;从中任意取出一个是黄球的概率二、填空题(每空2分;共24分)9.某同学期中考试数学考了100分;则他期末考试数学考100分.(选填“不可能”“可能"或“必然”)10.袋子里有5只红球;3只白球;每只球除颜色以外都相同;从中任意摸出1只球;是红球的可能性选填“大于”“小于”或“等于”)是白球的可能性.11.至少需要调查名同学;才能使“有两个同学的生日在同一天”这个事件为必然事件.12.下列4个事件:①异号两数相加;和为负数;②异号两数相减;差为正数;③异号两数相乘;积为正数;④异号两数相除;商为负数.这4个事件中:必然事件是;不可能事件是;随机事件是.13.如图是一枚图钉被抛起后钉尖触地频率随抛掷次数变化趋势图;则一枚图钉被抛起后钉尖触地的概率估计值是.14.一个圆形转盘的半径为2 cm;现将转盘分成若干个扇形;并分别相间涂上红、黄两种颜色.转盘转动10 000次;指针指向红色部分有2 500次.请问指针指向红色的概率的估计值是;转盘上黄色部分的面积大约是.15.在英语句子“Wish you success”(祝你成功)中任选一个字母;这个字母为“s”的概率是.16.为了帮助残疾人;某地举办“即开型"福利彩票销售活动;规定每10万张为一组;其中有10名一等奖;100名二等奖.1 000名三等奖;5 000名爱心奖;小明买了10张彩票;则他中奖的概率为.17.某射击运动员在相同的条件下的射击成绩记录如下:根据频率的稳定性;估计这名运动员射击一次“射中9环以上”的概率是.三、解答题(共52分)18.(本题6分)一枚普通的正方体骰子;六个面上分别标有1、2、3、4、5、6.在抛掷一枚普通的正方体骰子的过程中;请用语言描述:(1)一个不可能事件;(2).一个必然事件;(3)一个随机事件.19.(本题5分)下面第一排表示十张扑克牌的不同情况;任意摸一张.请你用第二排的语言来描述摸到红色扑克牌的可能性大小;并用线连起来.20.(本题8分)在三个不透明的布袋中分别放人一些除颜色不同外;其他都相同的玻璃球;并搅匀;具体情况如下表:下列事件中;哪些是随机事件?哪些是必然事件?哪些是不可能事件?(1)随机从第一个布袋中摸出一个玻璃球;该球是黄色、绿色或红色的;(2)随机从第二个布袋中摸出两个玻璃球;两个球中至少有一个不是绿色的;(3)随机从第三个布袋中摸出一个玻璃球;该球是红色的;(4)随机从第一个布袋和第二个布袋中各摸出一个玻璃球;两个球的颜色一致.21.(本题8分)下图是甲、乙两个可以自由旋转的转盘;转盘被等分成若干个扇形;并将其涂成红、白两种颜色;转动转盘;分别计算指针指向红色区域的机会;若要使它们的机会相等;则应如何改变涂色方案?22.(本题8分)某公司的一批某品牌衬衣的质量抽检结果如下:(1)求从这批衬衣中任抽1件是次品的概率.(2)如果销售这批衬衣600件;至少要准备多少件正品衬衣供买到次品的顾客退换? 23.(本题9分)下表是光明中学七年级(5)班的40名学生的出生月份的调查记录:(1)请你重新设计一张统计表;使全班同学在每个月出生人数情况一目了然;(2)求出10月份出生的学生的频数和频率;(3)现在是1月份;如果你准备为下个月生日的每一位同学送一份小礼物;那你应该准备多少份礼物?24.(本题8分)小强和小明两个同学设计一种同时抛出两枚1元硬币的游戏;游戏规则如下:如果抛出的硬币落下后朝上的两个面都为1元;则小强得1分;其余情况小明得1分;谁先得到10分谁就赢得比赛。
苏科版八年级下册数学第8章 认识概率含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、一个不透明的盒子里装有2个白球,2个红球,若干个黄球,这些球除了颜色外,没有任何其他区别.若从这个盒子中随机摸出一个是黄球的概率是,则盒子中黄球的个数是()A.2B.4C.6D.82、下列事件发生的概率为0的是()A.掷一枚均匀的硬币两次,至少有一次反面朝上;B.今年冬天如皋会下雪;C.掷两个均匀的骰子,朝上面的点数之和为1;D.一个转盘被分成3个扇形,按红、白、黄排列,转动转盘,指针停在红色区域3、从甲、乙、丙、丁四人中任选1名代表,甲被选中的可能性是()A. B. C. D.14、下列事件为不可能事件的是( ).A.某射击运动员射击一次,命中靶心B.掷一次骰子,向上的一面是5点 C.经过城市中某一有交通信号灯的路口,遇到红灯 D.长为3cm、3cm、7cm的三条线段能围成一个三角形5、抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确是()A.连续抛掷2次必有1次正面朝上B.连续抛掷10次不可能都正面朝上 C.大量反复抛掷每100次出现正面朝上50次 D.通过抛掷硬币确定谁先发球的比赛规则是公平的6、已知:四边形ABCD的对角线AC、BD相交于点O,给出下列4个条件:①AB ∥CD;②OA=OC;③AB=CD;④AD∥BC从中任取两个条件,能推出四边形ABCD 是平行四边形的概率是()A. B. C. D.7、下列说法中错误的是()A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖B.从装有10个红球的袋子中,摸出1个白球是不可能事件C.为了解一批日光灯的使用寿命,可采用抽样调查的方式D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是8、事件①:射击运动员射击一次,命中靶心;事件②:购买一张彩票,没中奖,则( )A.事件①是必然事件,事件②是随机事件B.事件①是随机事件,事件②是必然事件C.事件①和②都是随机事件D.事件①和②都是必然事件9、下列不是必然事件的是()A.角平分线上的点到角两边的距离相等B.三角形内心到三边距离相等 C.三角形任意两边之和大于第三边 D.面积相等的两个三角形全等10、下列说法正确的是()A.对角线相等且互相垂直的四边形是菱形B.对角线相等的四边形是矩形 C.频率就是概率 D.相似三角形对应高的比等于周长的比11、下列命题正确的是()A.概率是1%的事件在一次试验中一定不会发生B.要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定D.随意翻到一本书的某页,页码是奇数是随机事件12、下列事件是随机事件的是()A.没有水分,种子发芽B.小张买了一张彩票中500万大奖C.抛一枚骰子,正面向上的点数是7D.367人中至少有2人的生日相同13、在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是()个.A.12B.24C.36D.4814、下列事件中,不可能事件是( )A.掷一枚六个面分别刻有1~6数码的均匀正方体骰子,向上一面的点数是“5”B.任意选择某个电视频道,正在播放动画片C.肥皂泡会破碎D.在平面内,度量一个三角形的内角度数,其和为360°15、下列说法不正确的是()A.某种彩票中奖的概率是,买1000张该种彩票一定会中奖B.了解一批电视机的使用寿命适合用抽样调查 C.若甲组数据的标准差S甲=0.31,乙组数据的标准差S=0.25,则乙组数据比甲组数据稳定 D.在乙一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件二、填空题(共10题,共计30分)16、如图,△ABC中,D、E、F分别是各边的中点,随机地向△ABC中内掷一粒米,则米粒落到阴影区域内的概率是________.17、抛掷骰子时,若用计算器模拟实验,如果研究恰好出现1的机会,则要在________ 到________ 范围中产生随机数,若产生的随机数是________ ,则代表“出现1”,否则就不是.18、在一个不透明的袋子中,有3个白球和1个红球,它们只有颜色上的区别,从袋子中随机摸出一个球记下颜色放回,再随机地摸出一个球,则两次都摸到白球的概率为________ .19、在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同。
苏科版八年级下册数学第8章 认识概率含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、下列说法正确的是()A.调查湘江河水的水质情况,采用抽样调查的方式B.数据2,0,,1,3的中位数是C.可能性是的事件在一次实验中一定会发生 D.从2000名学生中随机抽取100名学生进行调查,样本容量为2000名学生2、一枚质地均匀的骰子,它的六个面上分别有1到6的点数.下列事件中,是不可能事件的是()A.掷一次这枚骰子,向上一面的点数小于5B.掷一次这枚骰子,向上一面的点数等于5C.掷一次这枚骰子,向上一面的点数等于6D.掷一次这枚骰子,向上一面的点数大于63、下列事件中,必然事件是()A.打开电视,它正在播广告B.掷两枚质地均匀的正方体骰子,点数之和大于6C.早晨的太阳从东方升起D.没有水分,种子发芽4、若在“正三角形、平行四边形、圆、正六边形”这四种图形中随机抽取一种图形,则抽到的图形属于中心对称图形的概率是()A. B. C. D.5、在一个10万人的小镇,随机调查了3000人。
其中450人看某电视台的早间新闻,在该镇随便问一个人,他看该电视台早间新闻的概率大约是()A.0.0045B.0.03C.0.0345D.0.156、下列事件是必然事件的是()A.乘坐公共汽车恰好有空座B.同位角相等C.打开手机就有未接电话D.三角形内角和等于180°7、一名运动员连续射靶10次,其中2次命中10环,2次命中9环,6次命中8环,针对某次射击,下列说法正确的是()A.射中10环的可能性最大B.命中9环的可能性最大C.命中8环的可能性最大D.以上可能性均等8、在一个不透明的袋中装有10个只有颜色不同的球,其中5个红球、3个黄球和2个白球.从袋中任意摸出一个球,是白球的概率为()A. B. C. D.9、同时抛掷两枚硬币,正面都朝上的概率为()A. B. C. D.10、如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则()A. B. C. D.以上都有可能11、一个不透明的信封中装有四张完全相同的卡片上分别画有等腰梯形、矩形、菱形、圆,现从中任取一张,卡片上画的恰好既是中心对称图形又是轴对称图形的概率是( )A. B. C. D.112、如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是()A.1B.C.D.13、“淄博地区明天降水概率是15%”,下列说法中,正确的是().A.淄博地区明天降水的可能性较小B.淄博地区明天将有15%的时间降水 C.淄博地区明天将有15%的地区降水 D.淄博地区明天肯定不降水14、在一个不透明的盒子中,装有2个白球和1个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,要使摸出红球的概率为,应在该盒子中再添加红球()A.2个B.3个C.4个D.5个15、一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球,从中随机摸出一个,摸到黄球的概率是( )A. B. C. D.二、填空题(共10题,共计30分)16、“打开我们七年级下册的数学教科书,正好翻到第60页”,这是________(填“随机”或“必然”)事件.17、有9张卡片,每张卡片上分别写有不同的从1到9中的一个自然数,从中任意抽出一张卡片,则抽到的卡片上的数是2的倍数的概率是________.18、小玲在一次班会中参加知识抢答活动,现有语文题道,数学题道,综合题道,她从中随机抽取道,抽中数学题的概率是________.19、随机掷一枚均匀的骰子,点数是5的概率是________.20、从1,2,3,4中任取3个数,作为一个一元二次方程的系数,则构作的一元二次方程有实根的概率是________。
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是()A.m=3,n=5B.m=n=4C.m+n=4D.m+n=82、在一个不透明的布袋中装有红色.白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到白色球的频率稳定在85%左右,则口袋中红色球可能有().A.34个B.30个C.10个D.6个3、从分别标有数﹣3,﹣2,﹣1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不小于2的概率是()A. B. C. D.4、一个不透明的袋中装有除颜色外均相同的5个红球和n个黄球,从中随机摸出一个,摸到红球的概率是,则n是()A.5B.8C.3D.135、下列说法中正确的是( )A.“打开电视机,正在播放《动物世界》”是必然事件B.某种彩票的中奖率为,说明每买1 000张彩票,一定有一张中奖C.抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为 D.想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查6、天气预报称,明天长沙市全市的降水率为90%,下列理解正确的是()A.明天长沙市全市有90%的地方会下雨B.明天长沙市全市有90%的时间会下雨C.明天长沙市全市下雨的可能性较大D.明天长沙市一定会下雨7、下列判断正确的是( )A.“打开电视机,正在播斯诺g台球赛”是必然事件B.一组数据2,3,4,5,5,6的众数和中位数都是5C.“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就必有1次反面朝上 D.甲组数据的方差S甲2=0.01,则乙组数据比甲组稳定2=0.2,乙组数据的方差S乙8、下面四个实验中,实验结果概率最小的是( )A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率D.有7张卡片,分别标有数字1,2,3,4,6,8,9,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率9、下列说法中不正确的是()A.抛掷一枚质量均匀的硬币,硬币落地时正面朝上是随机事件B.把4个球放入三个抽屉中,其中一个抽屉至少有两个球是必然事件C.为了呈现某个月的气温变化情况,应选择的统计图为扇形统计图D.从一副扑g牌中任意抽取1张,摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小10、下列说法正确的是()A.抛一枚硬币,正面一定朝上B.掷一颗骰子,朝上一面的点数一定不大于6C.为了解一种灯泡的使用寿命,宜采用普查的方法D.“明天的降水概率为80%”,表示明天会有80%的地方下雨11、下列事件是必然事件的是()A.瓶酒会爆B.在一段时间内汽车出现故障C.地球在自转D.下届世界杯在中国举行12、如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是()A. B. C. D.13、如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为()A. B. C. D.14、下列事件发生的概率为0的是()A.随意掷一枚均匀的硬币两次,至少有一次反面朝上B.今年冬天黑龙江会下雪C.随意掷两个均匀的骰子,朝上面的点数之和为1D.一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域15、下列说法正确的是()A.若甲、乙两组数据的平均数相同,S甲2=0.1,S乙2=0.04,则乙组数据较稳定 B.如果明天降水的概率是50%,那么明天有半天都在降雨 C.了解全国中学生的节水意识应选用普查方式 D.早上的太阳从西方升起是必然事件二、填空题(共10题,共计30分)16、一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:实验次数200 300 400 500 600 700 800 1000 摸到红球次数m151 221 289 358 429 497 568 701 摸到红球频率0.75 0.74 0.72 0.72 0.72 0.71 a b (1)表格中a=________ ,b=________;(2)估计从袋子中摸出一个球恰好是红球的概率约为________ ;(精确到0.1)17、从-2,-1,2这三个数中任取两个不同的数作为点的坐标,该点在第四象限的概率是:________ 。
初二认识概率-知识点,测试题及答案

认识概率知识点归纳(1)事件可分为:必然事件、不可能事件(确定事件) 、随机事件(不确定事件) 。
(2)一件事件发生的可能性的大小的数值,叫做这件事件的概率。
概率通常用大写P表示。
(3)O W P (A事件)w 1; P (必然事件)=1; P (不可能事件)=0; 0<P (随机事件 ) <1。
(4)频率与概率的关系。
联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率。
区别:某可能事件发生的概率是一个定值。
而这一事件发生的频率是波动的,当试验次数不大时,事件发生的频率与概率的差异可能很大。
事件发生的频率不能简单地等同于其概率,要通过多次试验,用一事件的频率来估计这一事件发生的概率。
1、确定事件和随机事件。
(1) “必然事件”是指事先可以肯定一定会发生的事件。
(2) “不可能事件”是指事先可以肯定一定不会发生的事件。
( 3) “不确定事件”或“随机事件”是指结果的发生与否具有随机性的事件。
2、可能性的大小(1)很可能发生:如果事件发生的可能性很大,我们也说事件很可能发生.不大可能发生:如果事件发生地可能性很小,我们也说事件不大可能发生。
(2)事件的频数、频率。
设总共做n次重复实验,而事件A发生了m次,则称事件A发生的次数m为频数。
称比值m/n为A发生的频率。
(3)概率:某事件发生的可能性也叫做事件发生的概率。
必然事件发生概率为1,不可能事件发生的概率为0,不确定事件发生的概率在0 到1之间。
一般地,如果一个实验有n 个等可能的结果,而事件A包含其中k个结果,我们定义P (A) =k/n=事件A包含的可能结果数/所有可能结果数。
对概率计算应注意:分清所有基本事件的总和( n)和事件A所包含的基本事件总和( k).3、频率与概率的关系。
(1)事件发生的频率会呈现逐渐稳定的趋势。
(2)频率和概率可以非常接近,单不一定相等(3)如何用频率估计机会的大小。
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、下列事件中,是必然事件的是()A.汽车走过一个红绿灯路口时,前方正好是绿灯B.任意买一张电影票,座位号是3的倍数C.掷一枚质地均匀的硬币,正面向上D.从一个只有白球的盒子里摸出一个球是白球2、下列说法正确的是()A.投掷三枚硬币正好三个都正面朝上是不可能事件B.打开电视正在播新闻联播是随机事件C.随机投掷一枚硬币正面朝上的概率是,是指将一枚硬币随机投掷10次,一定有5次正面朝上D.确定事件的发生概率大于0而小于13、下列说法正确的是()A.367人中至少有2人生日相同B.任意掷一枚均匀的骰子,掷出的点数是偶数的概率是C.天气预报说明天的降水概率为90%,则明天一定会下雨D.某种彩票中奖的概率是1%,则买100张彩票一定有1张中奖4、某电视台每播放18分钟节目便插播2分钟广告,打开电视收看该台恰好遇到广告的概率是().A. B. C. D.5、下列说法中不正确的是()A.抛掷一枚硬币,硬币落地时正面朝上是随机事件B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件C.任意打开七年级下册数学教科书,正好是97页是确定事件D.一个盒子中有白球3个,红球6个,(每个球除了颜色外都相同),如果从中任取一个球,取得红球的可能性大6、在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是()A. B. C. D.7、在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球()A.16个B.20个C.25个D.30个8、一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字是偶数的概率为()A. B. C. D.9、在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是()A.4个B.5个C.不足4个D.6个或6个以上10、下列说法中正确的是()A.同一平面内,过一点有且只有一条直线与已知直线平行B.三张分别画有菱形、等边三角形、圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是 C.一组对边平行,一组对边相等的四边形是平行四边形 D.当时,关于的方程有实数根11、下列说法正确的是()A.扔100次硬币,都是国徽面向上,是不可能事件B.小芳在扔图钉游戏中,扔10次,有6次都是钉尖朝下,所以钉尖朝下的可能性大C.王明同学一直是级部第一名,他能考上重点高中是必然事件D.投掷一枚均匀的骰子,投出的点数是10,是一个确定事件12、如图有三条绳子穿过一木板,两人分别站在木板的左、右两边,各选该边的一条绳子。
初中概率知识要点及习题.docx
概率初步一、有关概念1•必然事件和不可能事件:在一定条件下,有些事件必然会发生,这样的事件称为必然事件.相反地,有些事件必然不会发工,这样的事件称为不可能事件.必然事件与不可能事件统称为确定性事件.2.随机事件:在-定条件下,可能发牛•也可能不发牛的事件,称为随机事件.随机事件属于不确定性事件,即事先无法确定.注意:定义中“在一定条件下”说明当条件改变时,事件发生的可能性也会相应地发生改变。
练习1:下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?说明理由。
(1)篮球运动员在罚球线上投篮一次,未投中;(2)掷一次六面体骰子,向上的-而是6点;(3)度量三角形的内角和,结果是360°;(4)放学回家路上在每一个路口都遇上绿灯;(5)将豆油滴在水中,豆油浮在水面上;(6)今晚打开电视发现在播广告;二、随机事件发生的可能性:一般地,随机事件发牛的可能性是有人小的,不同的随机事件发牛的可能性的大小有可能不同。
验证概念举例:袋了中冇4个彩球和2个白球,这些球的形状、大小、质地完全相同。
在看不到球的条件下,随机地从袋子中摸出一个球。
1•这个球是彩色述是白色?2撲出彩球和摸出白球的可能性一样大吗?怎样來描述一个随机事件的可能性的人小呢?三、概率概率:一般地,对于一个随机事件A,我们把刻画其发生町能性大小的数值,称为随机事件A发生的概率, 记为P (A)o在人量重复试验中,如果事件A发生的频率巴会稳定在某个常数p附近,那么这个常数p就叫做n事件A的概率。
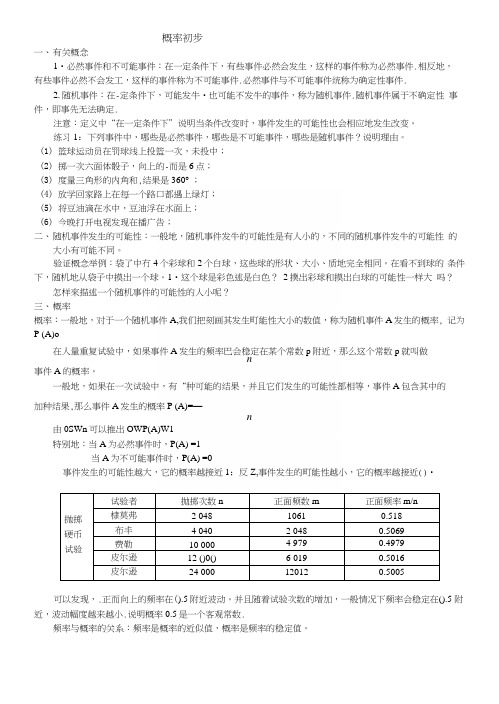
一般地,如果在一次试验中,有“种可能的结果,并且它们发生的可能性都相等,事件A包含其中的加种结果,那么事件A发生的概率P (A)=—n由0SWn可以推出OWP(A)W1特别地:当A为必然事件时,P(A) =1当A为不可能事件时,P(A) =0事件发生的可能性越大,它的概率越接近1;反Z,事件发生的町能性越小,它的概率越接近()•抛掷硬币试验试验者抛掷次数n正面频数m正面频率m/n 棣莫弗 2 04810610.518布丰 4 040 2 0480.5069费勒10 000 4 9790.4979皮尔逊12 ()0() 6 0190.5016皮尔逊24 000120120.5005可以发现,.正而向上的频率在().5附近波动。
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、某同学掷一枚硬币,结果是一连9次都掷出正面朝上,请问他第10次掷出硬币时出现正面朝上的概率为()A.小于B.大于C.D.不能确定2、在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色……如此大量的摸球实验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此实验,他总结出下列结论:①若进行大量的摸球实验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是()A.①②③B.①②C.①③D.②③3、下列说法正确的是( ).A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨B.“抛一枚硬币正面朝上的概率为"表示每抛两次就有一次正面朝上C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖D.“抛一枚均匀的正方体骰子,朝上的点数是2的概率为”表示随着抛掷次数的增加,“抛出朝上的点数是2"这一事件发生的频率稳定在附近4、下列事件中,属于不确定事件的是()A.用长度分别是2 cm, 3 cm, 6 cm的细木条首尾顺次相连可组成一个三角形;B.角平分线上的点到角两边的距离相等;C.如果两个图形关于某条直线对称,则这两个图形一定全等;D.三角形一边上的高线与这条边上的中线互相重合.5、连续四次抛掷一枚硬币都是正面朝上,则“第五次抛掷正面朝上”是()A.必然事件B.不可能事件C.随机事件D.概率为1的事件6、下列说法中,正确的是()A.为检测我市正在销售的酸奶质量,应该采用抽样调查的方式B.两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定C.抛掷一个正方体骰子,点数为奇数的概率是D.“打开电视,正在播放广告”是必然事件7、下列说法中,正确的是()A.不可能事件发生的概率为0B.随机事件发生的概率为C.“明天要降雨的概率为”,表示明天有半天时间都在降雨D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次8、小军旅行箱的密码是一个六位数,但是他忘记了密码的末位数字,则小军能一次打开旅行箱的概率是()A. B. C. D.9、某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是()实验次数100 200 300 500 800 1000 2000频率0.365 0.328 0.330 0.334 0.336 0.332 0.333A.抛一枚硬币,出现正面B.一副去掉大小王的普通扑g牌洗匀后,从中任抽一张牌的花色是红桃C.抛一个质地均匀的正六面体骰子(六个面上分别标有1,2,3,4,5,6),向上的面点数是5D.从一个装有2个白球和1个红球的袋子中任取一球,取到红球10、学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是()A.0.1B.0.15C.0.25D.0.311、下列事件:①掷一次骰子,向上一面的点数是3;②从一个只装有黑色球的袋子摸出一个球,摸到的是白球;③13个人中至少有两个人的生日是在同一个月份;④射击运动员射击一次命中靶心. 其中是必然事件的有()A.1个B.2个C.3个D.4个12、下列说法中,正确的是()A.“明天降雨的概率是80%”表示明天有80%的时间降雨B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖D.在同一年出生的367名学生中,至少有两人的生日是同一天13、不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为()A. B. C. D.14、义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是()A. B. C. D.15、下列事件中必然事件的个数有()①当x时非负实数时,≥0;②打开数学课本时刚好翻到第12页;③13个人中至少有2人的生日是同一个月.A.0个B.1个C.2个D.3个二、填空题(共10题,共计30分)16、现有6张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使得关于x的一元二次方程x2﹣2x+a﹣2=0有实数根,且关于x的分式方程+2=有解的概率为________.17、色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:抽取的体检表数50 100 200 400 500 800 1000 1200 1500 2000 n色盲患者的频数3 7 13 29 37 55 69 85 105 138 m色盲患者的频率0.060 0.070 0.065 0.073 0.074 0.069 0.069 0.071 0.070 0.069 m/n根据表中数据,估计在男性中,男性患色盲的概率为________(结果精确到0.01).18、袋中有4个红球,x个黄球,从中任摸一个恰为黄球的概率为,则x的值为________.19、有一个质地均匀的正方体,六个面上分别标有1~6这六个整数,投掷这个正方体一次,则向上一面的数字是偶数的概率为________.20、一个质地均匀的小正方体,6个面分别标有数字1,1,2,4,5,5,若随机投掷一次小正方体,则朝上一面的数字是5的概率为________.21、任意选择电视的某一频道,正在播放新闻,这个事件是________事件(填“必然”“不可能”或“随机”).22、在一个透明的布袋中,红色、黑色、白色的玻璃球共有80个,它们除颜色外其他完全相同,小李通过多次摸球试验后,发现其中摸到红色球、黑色球的频率分别为15%和45%,则口袋中白色球的数目很可能是________ 个.23、某校体育室里有球类数量如下表,如果随机拿出一个球(每一个球被拿出来的可能性是一样的),那么拿出一个球是足球的可能性是________.球类篮球排球足球数量3 5 424、在2,﹣2,0三个整数中,任取一个,恰好使分式有意义的概率是________.25、若有奖储蓄每1000张奖券中,有一等奖1张,奖金500元,二等奖10张,奖金100元,三等奖50张,奖金20元,纪念奖100张,奖金5元.某人买一张奖券,则他得奖不少于20元的概率为________三、解答题(共6题,共计25分)26、某餐厅新开业,为了吸引顾客,推出“模球有礼”优惠活动,餐厅在一个不透明的纸箱中装入除颜色外完全相同的小球共个,其中红色球个、黄色球个、蓝色球个,剩余为绿色。
完整word版苏科版八年级下册数学第八章 认识概率练习题附解析

……………○),﹣3三个数中,随机抽取两个数相乘,积是正数的概率是(1、从1,…….C.B1D.A.0…………个白球.这些球54个黑球和个红球、2、甲袋装有4个红球和1个黑球,乙袋装有6……除了颜色外没有其他区别,分别搅匀两袋中的球,从袋中分别任意摸出一个球,正确说线线) ( 法是…….从甲袋摸到黑球的概率较大A…….从乙袋摸到黑球的概率较大B……C.从甲、乙两袋摸到黑球的概率相等……D.无法比较从甲、乙两袋摸到黑球的概率○○…3、如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为…………………订订…D..C.A.B……………1关时要将一颗质地均匀的骰子(六个面上分别刻有”规定:在过第n4、一项“过关游戏……2,则算过关;否则不算次,若n次抛掷所出现的点数之和大于n到6的点数)抛掷n○○…过关,则能过第二关的概率是……..DBA..C……………、在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、5装装质地等完全相同.小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机……,如此大量摸球实验后,小新发出其中摸出红球的频率稳定……摸出一球,记下颜色,……若进行大量50%.对此实验,他总结出下列结论:①于20%,摸出黑球的频率稳定于……若从布袋中任意摸出一个球,该球是黑30%;②摸球实验,摸出白球的频率应稳定于……20次摸出的球是红球.其中说法正确的是次,必有球的概率最大;③若再摸球100○②③D.①③.BA.①②③.①②C○………游戏规则如下:是一种竞猜游戏,百宝箱”互动环节,“6、中央电视台幸运52”栏目中的“……个商标牌的背面是一张哭脸,若翻到哭脸,就不能得奖,参与这20个商标中,有5在…。
某观众前两次翻牌均获得若干奖个游戏的观众有三次翻牌机会(翻过的牌不能再翻)……)金,那么他第三次翻牌获奖的概率是(外内1/6 .C.1/4 DBA.1/20 .1/52 …………)7、下列事件是必然事件的是(…….酒瓶会爆炸A…….抛掷一枚硬币,正面朝上B○C.地球在自转○….今天的气温是D100度……………….……………环,针8环,8、一名运动员连续射靶10次,其中2次命中10环,2次命中96次命○)对某次射击,下列说法正确的是(…9A.射中10环的可能性最大B.命中环的可能性最…C.命中8环的可能性最大D.以上可能性均……、如图所示是用相同的正方形砖铺成的地板,一宝物藏在某一块下面,宝物在白色区…域的概率线…………………….A.B.C.D○○………个白球,这些球的形状、大小、质地等完全相同,在看不10、袋子中装有4个黑球和2……)到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是(…A.摸出的三个球中至少有一个球是黑球…….摸出的三个球中至少有一个球是白球B订订.摸出的三个球中至少有两个球是黑球C…….摸出的三个球中至少有两个球是白球D…….个白球,11、口袋中有21个黑球,从中任取一个球,摸到白球的概率为…………大圆的直径把组同心圆分成四等份,假设击中圆面上每、如图所示是一飞镖游戏板,12○. 个点都等可能的,则落在黑色区域的概率○……………………装装……是正方体小木块(质地均匀)的一顶点,将木块随机投掷在水平桌面上,、如图,13A…….A则与桌面接触的概率是…………○○……………的三张扑克、甲、乙两人玩抽扑克牌游戏,游戏规则是:从牌面数字分别为145、6、7…随机抽取一张,放回后,再随机抽取一张,若所抽的两张牌面数字的积为奇数,牌中.……或“公平”(填则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜,这个游戏外内)不公平“”…………(太阳从东边升起)P=_________。
八年级下册数学期末复习第8章《认识概率》知识点归纳与巩固训练(有答案)

八下第8章《认识概率》知识点归纳与巩固训练知识点一:事件的类型1、随机事件:;2、必然事件:;3、不可能事件:;注:必然事件和不可能事件是确定事件。
知识点二:事件可能性的大小1、必然事件的可能性为1(100%),记作P(A)=;2、随机事件的可能性有大有小,在0---1之间,<P(A)<.3、不可能事件的可能性为0,记作P(A)=知识点三:概率与频率1、概率:;表示方法:用A表示一个事件,用P(A)表示事件A发生的概率必然事件记作:P(A)=随机事件记作:<P(A)<.不可能事件记作:P(A)=2、概率与频率的关系:;注:(1)任一随机事件,它发生的概率是由它自身决定的,且是客观存在的,概率是随机事件自身的属性。
它反映这个随机事件发生的可能性大小。
(2)事实上,事件A发生的概率()AP的精确值,即这个常数还是未知的,但是在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值。
(3)在充分多次试验中,一些事件的频率总在一个定值附近摆动,试验次数越多,摆动幅度越小,这个性质称为频率的稳定性。
(4)通过试验用频率估计概率的大小,必须要求试验是在相同条件下进行巩固训练一、选择题1.下列事件中,是必然事件的是()A. 将油滴入水中,油会浮在水面上B. 车辆随机到达一个路口,遇到红灯C. 如果a2=b2,那么a=bD. 掷一枚质地均匀的硬币,一定正面向上2.从概率统计的角度解读下列诗词所描述的事件.其中属于确定事件的是()A. 黄梅时节家家雨,青草池塘处处蛙B. 人间四月芳菲尽,山寺桃花始盛开C. 水面上秤锤浮,直待黄河彻底枯D. 一夜北风紧,开门雪尚飘3.已知抛一枚均匀硬币正面朝上的概率为1,下列说法错误的是()2A. 连续抛一枚均匀硬币2次必有1次正面朝上B. 连续抛一枚均匀硬币10次可能都是正面朝上C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的4.一个不透明的袋子中装有4个红球,2个黄球,这些球除了颜色外都相同,从中随机抽出3个球,下列事件为必然事件的是()A. 至少有1个球是黄球B. 至少有1个球是红球C. 至少有2个球是黄球D. 至少有2个球是红球5.布袋中有大小一样的3个白球和2个黑球,从袋中任意摸出1个球,下列判断正确的是()A. 摸出的球一定是白球B. 摸出的球一定是黑球C. 摸出的球是白球的可能性大D. 摸出的球是黑球的可能性大6.在一个不透明的布袋中,红球、黑球、白球共有若干个,这些球除颜色外其他都相同.小新从布袋中随机摸出一个球,记下颜色后放回布袋中;摇匀后再随机摸出一个球,记下颜色后放回布袋中⋯⋯如此通过大量重复摸球试验后,小新发现其中摸出红球的频率在20%附近摆动,摸出黑球的频率在50%附近摆动.对此试验,他总结出下列结论: ①若进行大量重复摸球试验,则摸出白球的频率在30%附近摆动; ②若从布袋中任意摸出一个球,则该球是黑球的可能性最大; ③若再摸球100次,则必有20次摸出的是红球.其中正确的是()A. ① ② ③B. ① ②C. ① ③D. ② ③7.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是()A. 频率就是概率B. 频率与试验次数无关C. 概率是随机的,与频率无关D. 随着试验次数的增加,频率一般会趋近于概率8.一个不透明的袋子中装有3个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该试验多次,发现摸到白球的频率稳定在0.6,则可判定袋子中黑球的个数为()A. 2B. 3C. 4D. 5二、填空题9.下列事件:①在足球比赛中,弱队战胜强队:②抛掷一枚硬币,落地后正面朝上;③任取两个正整数,其和大于1;④长分别为3、5、9厘米的三条线段能围成一个三角形.其中是确定事件的有________个.10.一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,则n=_____.11.下列事件: ①掷一枚质地均匀的硬币,正面朝上; ②打开电视,正在播放电视剧; ③随意翻开一本有400页的书,正好翻到第200页; ④下雨天,马路潮湿; ⑤你的身高能长到5米; ⑥买大乐透中头奖; ⑦掷一枚质地均匀的正方体骰子,得到的点数小于9.其中不可能事件有;必然事件有;随机事件中,发生可能性最大的是,发生可能性最小的是(填序号).12.某射手在相同条件下进行射击训练,结果如下:该射手击中靶心的概率的估计值是________.(精确到0.01)13.在一个不透明的盒子中装有n个球,它们除了颜色之外其他都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是.14.在一个不透明的盒子里装有黑、白两种颜色的球共40个,这些球除颜色外其余完全相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:摸球的10020030050080010003000次数n摸到白球651241783024815991803的次数m摸到白球0.650.620.5930.6040.6010.5990.601的频率mn(1)请估计:当n很大时,摸到白球的频率将会接近;(精确到0.1)(2)假如你摸一次,则摸到白球的可能性为;(3)估算盒子里黑、白两种颜色球的个数分别为、.三、解答题15.如图,圆盘面被分成8个面积相同的扇形区域,小明转动转盘一次:(1)指针最终所指向的不是奇数就是偶数;(2)指针最终所指向的是奇数;(3)指针最终所指向的是0;(4)指针最终所指向的是8;(5)指针最终所指向的是大于l的数.请指出上面5个事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件,并根据事件发生的可能性的大小按从小到大的顺序排列.16.班里有18个男生,15个女生,从中任意抽取a人打扫卫生.(1)女生被抽到是必然事件,求a的取值范围;(2)女生小丽被抽到是随机事件,求a的取值范围.17.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球试验:每组先将10个与红球大小、形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:(1)表中的a=,b=;(2)请估计:当次数s很大时,摸到白球的频率将会接近(精确到0.1);(3)请推算:摸到红球的概率是(精确到0.1);(4)试估算:这个不透明的口袋中红球的个数.18.有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件: ①指针指向红色; ②指针指向绿色; ③指针指向黄色; ④指针不指向黄色.估计各事件的可能性大小,完成下列问题:(1)可能性最大和最小的事件分别是哪个?(用序号表示)(2)将这些事件的序号按发生的可能性从小到大的顺序排列:.答案和解析1.A解:A.将油滴入水中,油会浮在水面上是必然事件,故A符合题意;B.车辆随机到达一个路口,遇到红灯是随机事件,故B不符合题意;C.如果a2=b2,那么a=b是随机事件,故C不符合题意;D.掷一枚质地均匀的硬币,一定正面向上是随机事件,故D不符合题意.2.C解:A.黄梅时节家家雨,青草池塘处处蛙是随机事件,故A不符合题意;B.人间四月芳菲尽,山寺桃花始盛开是随机事件,故B不符合题意;C.水面上秤锤浮,直待黄河彻底枯是不可能事件,属于确定事件,故C符合题意;D.一夜北风紧,开门雪尚飘是随机事件,故D不符合题意.3.A解:A.连续抛一枚均匀硬币2次,每次正面朝上的概率都是随机的,故本选项错误;B.连续抛一枚均匀硬币10次可能都是正面朝上,故本选项正确;C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次,故本选项正确;D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的,故本选项正确;4.B解:A.至少有1个球是黄球是随机事件,选项不符合题意;B.至少有1个球是红球是必然事件,选项符合题意;C.至少有2个球是黄球是随机事件,选项不符合题意;D.至少有2个球是红球是随机事件,选项不符合题意.5.C解:A∵布袋中有大小一样的3个白球和2个黑球,∴从袋中任意摸出1个球,摸出的球不一定是白球,故此选项错误;B∵布袋中有大小一样的3个白球和2个黑球,∴从袋中任意摸出1个球,摸出的球不一定是黑球,故此选项错误;C.摸出的球是白球的可能性大,故此选项正确;D.摸出的球是黑球的可能性小于是白球的可能性,故此选项6.B解:∵在一个不透明的布袋中,红球、黑球、白球共有若干个,其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,∴①若进行大量摸球实验,摸出白球的频率稳定于:1−20%−50%=30%,故此选项正确;∵摸出黑球的频率稳定于50%,大于其它频率,∴②从布袋中任意摸出一个球,该球是黑球的概率最大,故此选项正确;③若再摸球100次,不一定有20次摸出的是红球,故此选项错误;故正确的有①②.7.D解:随机事件A发生的频率,是指在相同条件下重复n次试验,事件A发生的次数m 与试验总次数n的比值,与试验次数有关,选项B错误;频率不同于概率,频率本身是随机的,在试验前不能确定,无法从根本上来刻画事件发生的可能性的大小,而概率是一个确定的常数,是客观存在的,与试验次数无关,选项A错误,选项C错误;在大量重复试验时,频率会逐步趋于稳定,总在某个常数附近摆动,且摆动幅度很小,这个常数可以作为这个事件发生的概率的估计值.由此可见,随着试验次数的增多,频率会趋近于概率,可以看作是概率的近似值,选项D正确.8.A解:设黑球个数为x,∵重复该试验多次,摸到白球的频率稳=0.6,解得x=2定在0.6,∴估计摸到白球的概率为0.6,∴33+x9.2①,在足球赛中,弱队战胜强队有可能发生,所以是不确定事件;②,抛掷一枚硬币,落地后正面朝上有可能发生,所以是不确定事件;③,由于最小的正整数为1,则任取两个正整数,其和大于1是必然事件,所以是确定事件;④,由于3+5=8<9,不能满足构成三角形的条件,故④是不可能事件,所以属于确定事件,综上所述,确定事件有③和④,共2个.10.13解:摸出12个球可能都是黑球,至少有一个是白球,球的个数大于12,n最小是13.11.⑤;④⑦;①;⑥.解:不可能事件为:⑤;必然事件为:④⑦;随机事件中,发生可能性最大的是①;发生可能性最小的是⑥.12.0.90解:由击中靶心频率都在0.90上下波动,所以该射手击中靶心的概率的估计值是0.90,13.100=0.03,解得n=100.故估计n大约是100.解:由题意可得,3n14.(1)0.6;(2)60%;(3)16,24(1)∵摸到白球的频率为0.6,∴当n很大时,摸到白球的频率将会接近0.6,故答案为0.6;(2)∵摸到白球的频率为0.6,∴假如你摸一次,你摸到白球的概率p(白球)=0.6=60%,故答案为60%;(3)∵白球:40×0.6=24(个),黑球:40−24=16(个),∴盒子里黑、白两种颜色的球各有16个,24个,故答案为16,24.15.解:必然事件有(1);不可能事件有(3);随机事件有(2)(4)(5).可能性由小至大排列为(3)(4)(2)(5)(1).16.解:(1)∵班里有18个男生,15个女生,从中任意抽取a人打扫卫生,女生被抽到是必然事件,又总人数为33人,∴18<a≤33(a为整数).(2)∵班里有18个男生,15个女生,从中任意抽取a人打扫卫生,女生小丽被抽到是随机事件,∴a≥1,∴1≤a<33(a为整数).17.解:(1)123;0.404(2)0.4;(3)0.6.(4)设红球有x个,根据题意得xx+10=0.6,解得x=15.答:这个不透明的口袋中红球大约有15个.解:(1)a=300×0.41=123,b=606÷1500=0.404,故答案为123;0.404;(2)当次数s很大时,摸到白球的频率将会接近0.4,故答案为0.4;(3)摸到红球的概率是1−0.4=0.6,18.解:∵共3红2黄1绿相等的六部分,∴①指针指向红色的概率为36=12;②指针指向绿色的概率为16;③指针指向黄色的概率为26=13;④指针不指向黄色为46=23,(1)可能性最大的是④,最小的是②;(2)②<③<①<④.1、最困难的事就是认识自己。
《概率》知识点总结+典型例题+练习(含答案)

概率考纲要求1.了解随机现象和概率的统计定义,理解必然事件和不可能事件的意义.2.知道概率的性质,理解古典概率模型的含义,掌握求古典概型的方法,并会求古典概型的概率.3.知道互斥事件,会用概率加法公式求互斥事件的概率.4.认识n 次独立重复实验模型,并记住n 次独立重复实验中恰好发生k 次的概率公式,并会简单应用.5.了解随机变量、离散型随机变量及其概率分布;能写出简单的离散型随机变量的概率分布.6.了解二项分布,能写出简单的二项分布. 知识点一:随机事件的概率 1.随机事件的相关概念随机现象:在相同条件下具有多种可能结果,而事先又无法确定会出现哪种结果的现象称为随机现象.随机试验:研究随机现象所进行的观察和试验称为随机试验.随机事件:随机试验的结果称为随机事件,简称事件,常用大写字母A ,B ,C 等来表示. 必然事件:在一定条件下,必然发生的事件称为必然事件,用Ω来表示. 不可能事件:在一定条件下,不可能发生的事件称为不可能事件,用∅来表示. 基本事件:在随机试验中不能再分的最简单的随机事件称为基本事件. 复合事件:可以用基本事件来描述的随机事件称为复合事件. 2.频率与概率频数:设在n 次重复试验中,事件发A 生了m 次(0 ≤m ≤n ),m 称为事件A 的频数. 频率:事件A 的频数在试验的总次数中所占的比例mn,称为事件A 发生的频率. 事件A 发生的概率:当试验次数充分大时,如果事件发A 生的频率mn总稳定在某个常数附近,那么就把这个常数叫做事件A 发生的概率,记作)(A P . 事件A 发生的概率的性质:(1)对于必然事件Ω,()1=P Ω; (2)对于不可能事件∅,0)(=∅P ; (3)0≤P (A )≤1. 知识点2: 古典概型 1. 古典概型:(1)定义:如果一个随机试验的基本事件只有有限个,并且各个基本事件发生的可能性都相等,那么称这个随机试验属于古典概型.特征:试验的所有可能结果的个数是有限的;每个结果出现的机会均等.(2)在古典概型中,若试验共包含有n 个基本事件,并且每一个事件发生的可能性都相同,事件A 包含m 个基本事件,那么事件A 发生的概率()m P A n =2.互斥事件:(1)定义:在随机试验中,不可能同时发生的两个事件称为互斥事件或互不相容事件 (2)和事件:在随机试验中,若事件C 发生意味着事件A 与事件B 中至少有一个发生,则把事件C 称为事件A 与事件B 的和事件,记作C AB =(3)互斥事件的概率加法公式:互斥的事件A 和事件B 中至少有一个发生的概率()()()P A B P A P B =+知识点3:离散型随机变量及其分布 1.随机变量的概念如果随机试验的结果可以用一个变量的取值来表示,这个变量的取值带有随机性,并且取这些值的概率是确定的,那么这个变量叫做随机变量,通常用小写希腊字母ξ、η等表示,或用大写英文字母,,,X Y Z 等表示. 2.离散型随机变量的概念如果随机变量的所有可能取值可以一一列出,则这种随机变量称为离散型随机变量. 3.离散型随机变量的概率分布(1)离散型随机变量的概率分布的定义离散型随机变量ξ的所有可能取值1x ,2x ,3x …,i x …与其对应的概率(x )i i P p ξ==(i =1,2,3,…)所有组成的表叫做随机变量ξ的概率分布(分布列). 离散型随机变量概率分布的性质. ① 0(1,2,3,)i p i =≥;②1231i p p p p +++⋅⋅⋅++⋅⋅⋅=.(2)计算离散型随机变量的概率分布的主要步骤为 ①写出随机变量的所有取值;②计算出各个取值对应的随机事件的概率; ③列出表格.注意验证0(1,2,3,)i p i =≥以及121i p p p ++⋅⋅⋅++⋅⋅⋅=.知识点4:二项分布 1.n 次独立重复实验定义:在相同条件下,重复进行n 次试验,如果每次试验的结果与其他各次试验的结果无关,那么这n 次重复试验叫做n 次独立重复试验. 2.n 次伯努利实验定义:在n 次独立重复试验中,如果每次试验的可能结果只有两个,且它们相互对立,即只考虑两个事件A 和A ,并且在每次试验中事件A 发生的概率都相同,这样的n 次独立重复试验叫做n 次伯努利试验. 3.伯努利公式如果在每次试验中事件A 发生的概率()P A p =,事件A 不发生的概率()1P A p =-,那么在n 次伯努利试验中,事件A 恰好发生k 次的概率为k n k k n n p p k P --=)1(C )((其中0,1,2,,k n =⋅⋅⋅).4.二项分布如果在一次试验中某事件A 发生的概率的p ,随机变量ξ为n 次独立试验中事件发A 生的次数,那么随机变量ξ的概率分布为其中n k p ,,2,1,0,10 =<<我们将这种形式的随机变量ξ的概率分布叫做二项分布.称随机变量ξ服从参数为n 、p 的二项分布,记为(,)B n p ξ.二项分布是以伯努利试验为背景的重要分布. 题型一 基本概念例1 一口袋中有10个小球,其中有8个白球、2个黑球,从中任取3个小球,有以下事件:①3个都是白球. ②至少有一个是黑球. ③3个都是黑球. ④至少有一个白球.其中随机事件是 ;必然事件是 ;不可能事件是 . 分析:本题考察定义的理解及“至少”的含义. 随机事件有①②; 必然事件有④; 不可能事件有③. 解答:①②,④,③ 题型二 古典概型例2 同时抛掷两颗骰子,则所得点数之和为7的概率为 .分析:本题考查古典概型,试验发生包含的事件是抛掷两颗骰子,共有6⨯6=36种结果,满足条件的事件是点数之和为7,可以列举出所有的事件:(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)共有6种结果,根据古典概型概率公式得到61=P . 解答:61. 题型三 互斥事件例3 某地区年降水量在50~100mm 范围内的概率为0.21,在100~150mm 范围内的概率为0.22,则年降水量在50~155mm ,范围内的概率为多少? 分析:应用互斥事件的概率加法公式 解答:0.43题型四 独立重复试验及概率例4 一枚硬币连续抛掷3次,恰好有两次正面向上的概率为( ).A.18B.38C.12 D.23分析:设事件A ={正面向上},则()P A =12,抛掷3次相当于做3次独立重复试验,恰好有两次正面向上的概率为2123113(2)228P C ξ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭. 解答:B .题型五 离散型随机变量的概率分布例5 从含有8个正品、2个次品的产品中,不放回地抽取3次,每次抽取一个,用ξ表示抽到次品的次数,求: (1) ξ的概率分布.(2) 至多有一次抽到次品的概率.解答:(1)随机变量ξ的所有可能取值为0,1,2,且383107(0)15C P C ξ===, 1228310715C C P C ξ=(=1)=, 21283101(2)15C C P C ξ===. 所以ξ的概率分布为(2)至多有一次抽到次品的概率为715+715=1415. 题型六 二项分布例6 在人寿保险中,设一个投保人能活到65岁的概率为0.6,求三个投保人中活到65岁的人数ξ的概率分布.解答:记A ={一个投保人能活到65岁},则A ={一个投保人活不到65岁}.于是()0.6,()10.60.4P A P A ==-=.且随机变量(3,0.6)B ξ.因此0333(0)0.6(10.6)0.064P C =⋅⋅-=, 11233(1)0.6(10.6)0.288P C =⋅⋅-=,22133(2)0.6(10.6)0.432P C =⋅⋅-=,33033(3)0.6(10.6)0.216P C =⋅⋅-=.所以,三个投保人中能活到65岁的人数ξ的概率分布为一、选择题1.在10张奖券中,有1张一等奖,2张二等奖,从中任意抽取1张,则中一等奖的概率为( ). A.310 B.15 C.110 D.132.甲乙两人进行一次射击,甲击中目标的概率为0.7,乙击中的概率为0.2,那么甲乙两人都没击中的概率为( ).A. 0.24 B .0.56 C. 0.06 D. 0.863.某人从一副不含大小王扑克牌中(52张)任意取一张出来,他抽到黑桃或是红桃的概率为( ).A. 0B.152 C. 1352 D. 124.书包里有中文书5本,英文书3本,从中任集抽取2本,则都抽到中文书的概率是( ). A.15 B.25 C.12 D.5145.一个口袋中有5个红球,7个白球,每次取出一个,有放回取三次,观察球的颜色属于( ).A.重复试验B.古典概型C. 3次独立重复试验概率模型D.以上都不是 6.同时抛掷三枚硬币,三枚出现相同一面的概率为( ).A12 B 14 C 16 D 187.某品牌种子的发芽率是0.8,在试验的5粒种子中恰有4粒发芽的概率是( ). A.410.8(10.8)- B.140.8(10.8)-C.41450.8(10.8)C -D.44150.8(10.8)C -8.下列变量中不是随机变量的是( ). A. 射手射击一次的环数 B. 在一个标准大气压下100时会沸腾 C. 城市夏季出现的暴雨次数 D. 某班期末考试数学及格人数9.若从标有3,4,5,6,7的5张卡片中任取3张,取得奇数的个数为ξ,则随机变量ξ的可能取值的个数是( ).A .0 B. 1 C. 2 D .3 10.已知离散型随机变量ξ的概率分布为则n 的值为( ).A .0.31 B. 0.25 C. 0.26 D. 0.2 二、判断题:1. 某人参加射击比赛,一次射击命中的环数为(奇数环)是随机事件( )2. 在重复进行同一试验时,随着试验总次数的增加,事件A 发生的频率一般会越来越接近概率. ( )3. 任一事件A ,其发生的概率为()P A ,则有0≤P (A )≤1 . ( )4. 必然事件的概率为0.( )5. 袋子里有3颗红球6颗白球,从中任取一颗是白球的概率是13.( ) 6. 盒内装有大小相同的3个白球1个黑球,从中摸出2个球,则两个球全是白球的概率是12. ( )7. 同时抛掷3枚硬币,三枚出现相同一面的概率是18. ( )8. 同宿舍8人抓阄决定谁负责周一值日是随机试验.( )9. 运动员进行射击训练,考察一次射击命中的环数,命中2环的概率是110. ()10. 甲、乙两台机床,它们因故障停机的概率分别为0.01和0.02,则这两台机床同时因故障停机的概率为0.03. ( )三、填空题1.在10件产品中有3件次品,若从中任取2件,被抽到的次品数用ξ表示,则2ξ=表示的随机事件为.2.盒中有3个白色的球和5个红色的球,任取出一个球,取出的是红色的概率为.3.10件产品中有2件次品,任取3件,设取出的3件产品中所含正品数为随机变量ξ,则ξ的可能取值为.4.从甲、乙、丙3人中,任选2人参加社会实践,甲被选中的概率为.5.某气象站天气预报的准确率为0.8,一周中播报准确的次数为ξ,则2ξ=的概率为.(用式子表示)四、解答1.口袋里装有3个黑球与2个白球,任取3个球,求取到的白球的个数ξ的概率分布.2.口袋里装有4个黑球与1个白球,每次任取1个球,有放回地取3次,求所取过的3个球中恰有两个黑球的概率.高考链接1.(2014年) 已知离散型随机变量ξ的概率分布为则(1)Pξ==( ).A .0.24 B. 0.28 C.0.48 D.0.522.(2019年) 一口袋里装有4个白球和4个红球现在从中任取3个球,则取到既有白球又有红球的概率 .3.(2018年) 若将一枚硬币抛3次,则至少出现一次正面的概率为 .4.(2016年) 从1,2,3,4,5中任选3个数字组成一个无重复数字的三位数,则这个三位数是偶数的概率为 .5.(2017年) 取一个正方形及其外接圆,在圆内随机取一点,该点取自正方形内的概率为.积石成山1.某单选题要求从A 、B 、C 、D 四个选项中,选择一个正确答案,假设考生不会,随机地选择了一个答案,则他答对此题的概率是().A.1B.12C.13D.142. 某乐队有11名乐师,其中男乐师7人,现该乐队要选出一名指挥,则选出的指挥为女乐师的概率为().A.711B14C.47D.4113. 已知A 、B 是互斥事件,若1()5P A=,1()2P A B+=,则()P B的值是().A .45B.710C.310D.1104. 袋中装有3个黑球和2个白球一次取出两个球,恰好是黑白球各一个的概率().A. 15B.310C.25D.355. 5人站成一排照相,其中甲乙二人相邻的概率为().A. 25B.35C.15D.146. 一个箱子中有6个除了颜色之外完全一样的球,其中2个是红色的,4个是黑色的,那么在里面随机拿出一个是红色的概率是多少?().A. 12B.13C.14D.167. 掷一枚质地均匀且六面上分别有1,2,3,4,5,6点的骰子,则向上一面点数大于4的概率为().A. 12B.13C.23D.148. 抛掷一枚质地均匀的骰子,则向上一面出现偶数点概率是().A.12B.13C.16D.19.把一枚均匀的硬币连抛5次,得到5次国徽向上的概率为().A. 132B.532C.316D.313210.一副扑克牌去掉大小王,任意抽出一张不是黑桃的概率为().A. 14B .13C.12D.34概率答案一、选择题二、判断题三、填空题1.{任抽2件,有2件次品}.2. 58解析:151858CpC==.3. 1,2,3.4. 23解析:枚举法:选派方法有(甲,乙),(甲,丙),(乙,丙)共3种,其中甲被选中有2种,故所求概率为 23P =.5. 22570.8(10.8)C ⨯⨯-解析:设A ={播报一次,准确},则()0.8P A =,所以2257(2)0.8(10.8)P C ξ==⨯⨯-四、解答题1. 分析:任取3球属于古典概型,服从的分布为离散型随机变量的概率分布. 解:随机变量ξ的所有可能取值为0,1,2,则3032351(0)10C C P C ξ===, 2132353(1)5C C P C ξ===, 1232353(2)10C C P C ξ===. 所以概率分布为2. 分析:本题为有放回的抽取,是伯努利试验,服从二项分布. 解:设所取过的3个球中含有黑球的个数为随机变量ξ,则43,5B ξ⎛⎫⎪⎝⎭,于是 21234148(2)55125P C ξ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭ .高考链接1.B2.67解析:古典概率模型,则从中任意取3个球,取到既有白球又有红球的概率为122144443867C C C C C +=.3.78解析:试验发生包含的事件是将一枚硬币抛掷三次,共有328=(种)结果,满足条件的事件的对立事件是三枚硬币都是反面,有1种结果,则至少一次正面向上的概率是17188-=.4.25解析:从1,2,3,4,5这5个数字中任取3个数字组成没有重复的三位数,基本事件总数3560n P ==,这个三位数是偶数包含的基本事件个数122424m C P ==,∴这个三位数是偶数的概率为242605mPn===.5. 2π解析:设正方形的边长为11S=正方形,∴222Sππ⎛=⨯=⎝⎭外接圆∴该点取自正方形内部的概率为122Pππ==.积石成山。
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、下列事件为必然事件的是()A.打开电视机,它正在播广告B.抛掷一枚硬币,一定正面朝上C.投掷一枚普通的正方体骰子,掷得的点数小于7D.某彩票的中奖机会是1%,买1张一定不会中奖2、下列说法正确的是( )A.13名同学中,至少有两人的出生月份相同是必然事件B.“抛一枚硬币正面朝上概率是0.5”表示每抛硬币2次有1次出现正面朝上C.如果一件事发生的机会只有十万分之一,那么它就不可能发生D.从1、2、3、4、5、6中任取一个数是奇数的可能性要大于偶数的可能性3、小明的妈妈让他在无法看到袋子里糖果的情形下从中任抽一颗.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同.如果袋中所有糖果数量统计如图所示,那么小明抽到红色糖果的可能性为()A. B. C. D.4、甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则符合这一结果的实验可能是()A.掷一枚正六面体的骰子,出现5点的概率B.掷一枚硬币,出现正面朝上的概率C.任意写出一个整数,能被2整除的概率D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率5、下列说法正确的是( )A.13名同学中,至少有两人的出生月份相同是必然事件B.“抛一枚硬币正面朝上概率是0.5”表示每抛硬币2次有1次出现正面朝上C.如果一件事发生的机会只有十万分之一,那么它就不可能发生D.从1、2、3、4、5、6中任取一个数是奇数的可能性要大于偶数的可能性6、小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )A. B. C. D.7、口袋中有14个红球和若干个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,记下颜色后放回,多次实验后发现摸到白球的频率稳定在0.3,则白球的个数是( )A.5B.6C.7D.88、必然事件的概率是()A.-1B.0C.0.5D.19、一个布袋中有1个红球,3个黄球,4个蓝球,它们除颜色外完全相同. 从袋中随机取出一个球,取到黄球的概率是()A. B. C. D.10、若从10~99这连续90个正整数中选出一个数,其中每个数被选出的机会相等,则选出的数其十位数字与个位数字的和为9的概率是A. B. C. D.11、书架上有数学书2本,英语书3本,语文书5本,从中任意抽取一本是数学书的概率是()A. B. C. D.12、下列说法正确的是()A.某市“明天降雨的概率是75%”表示明天有75%的时间会降雨B.随机抛掷一枚均匀的硬币,落地后正面一定朝上C.在一次抽奖活动中,“中奖的概率是”表示抽奖l00次就一定会中奖D.在平面内,平行四边形的两条对角线一定相交13、下列事件中,是必然事件的是()A.任意买一张电影票,座位号是2的倍数B.13个人中至少有两个人生肖相同C.车辆随机到达一个路口,遇到红灯D.明天一定会下雨14、一个质地均匀的小正方体的六面上都标有数字,1,2,3,4,5,6。
八年级数学下册第8章《认识概率》精选好题(含答案)

第8章《认识概率》例题精选知识梳理重难点分类解析考点1 确定事件与随机事件【考点解读】事件可以分为不可能事件、必然事件和随机事件,要求学生能够分清事件的类型,为学习概率做好充分的准备,本考点中考命题多以简单选择题的形式出现.例1 (2018·福建)投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )A.两枚骰子向上一面的点数之和大于1B.两枚骰子向上一面的点数之和等于1C.两枚骰子向上一面的点数之和大于12D.两枚骰子向上一面的点数之和等于12分析:本题考查判断随机事件.因为每枚骰子的最小点数是1,所以两枚散子向上一面的点数之和大于1是必然事件,两枚散子向上一面的点数之和等于1是不可能事件;因为每枚骰子的最大点数是6,两枚骰子的点数之和最大是12,所以两枚骰子向上一面的点数之和大于12是不可能事件,两枚骰子向上一面的点数之和等于12是随机事件.答案:D【规律·技法】必然事件是指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.【反馈练习】1.下列诗句所描述的事件中,是不可能事件的是( )A.手可摘星辰B.黄河入海流C.大漠孤烟直D.锄禾日当午点拨:理解不可能事件的概念,并会判断事件的类型.2. (2018·扬州期末)一个不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4 个黑球、2个白球.从袋子中一次摸出3个球,下列事件是不可能事件的是( )A.摸出的是3个白球B.摸出的是3个黑球C.摸出的是2个白球、1个黑球D.摸出的是2个黑球、1个白球点拨:理解不可能事件的概念,并作出正确地判断.考点2 可能性的大小【考点解读】事件发生的可能性大小不一,要求学生能对具体事例进行分析、判断.本考点内容是学习概率的基础,作为了解内容,中考中一般不直接体现.例2 一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是( )A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到白球与摸到红球的可能性相等D.摸到红球比摸到白球的可能性大分析:因为摸到红球是随机事件,故A不符合题意;因为摸到白球是随机事件,故B不符合题意;因为红球比白球多,所以摸到红球比摸到白球的可能性大,故C不符合题意,D符合题意.答案:D【规律·技法】根据事件发生可能性的大小、生活常识,以及随机事件的判断方法,即可解题.【反馈练习】3.如图,有甲、乙、丙3个均匀的转盘(转盘中各个扇形的面积都相等),比较这3个转盘在停止转动后指针停在1号区域的可能性,下列说法正确的是()A.甲转盘最大B.乙转盘最大C.丙转盘最大D.甲、乙、丙转盘一样大点拨:判断转盘中指针停在指定区域可能性大小的基本方法是比较各个指定区域的面积占转盘面积的比值,比值大的可能性就大.4.自由转动如图所示的转盘(被8等分).下列事件中哪些是必然事件?哪些是随机事件?根据你所学的知识,将这些事件的序号按发生的可能性从小到大的顺序排列.(1)转盘停止后指针指向1;(2)转盘停止后指针指向10;(3)转盘停止后指针指向的是偶数;(4)转盘停止后指针指向的不是奇数就是偶数;(5)转盘停止后指针指向的数大于1.点拨:正确辨别事件类型,根据可能性等于所求情况数与总情况数之比分别求出每种情况的可能性,再按发生的可能性从小到大的顺序排列即可.考点3 频率与概率【考点解读】一个事件发生的可能性的大小称为这个事件发生的概率,在多次重复试验中,一个随机事件发生的频率会在某一个常数附近摆动,并趋于稳定,称为频率的稳定性,常把此数作为随机事件发生的概率的估计值.考试要求比较低,多以选择题或填空题的形式出现. 例3 (2018·呼和浩特)某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )A.袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球B.掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数C.先后两次掷一枚质地均匀的硬币,两次都出现反面D.先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9 分析:根据折线统计图易得当实验次数增多时,频率约为0.33,则实验的概率为13.对于选项A,概率为35,不符合;对于选项B,概率为12,不符合;对于选项C,概率为14,不符合; 对于选项D,概率为13,符合.答案:D【规律·技法】根据折线统计图确定实验的概率是解题的关键.【反馈练习】5.关于频率与概率有下列几种说法:①“明天下雨的概率是90%”,表示明天下雨的可能性很大;②“抛一枚硬币正面朝上的概率为12”,表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”,表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为1 2”,表示随着抛掷次数的增力,“抛出正面朝上”这一事件发生的频率稳定在12附近.其中正确的说法有( )A.①④B.②③C.②①D.①③点拨:本题主要考查概率的相关知识,正确理解概率的意义是解题的关键.6.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球试验,他们将30个与红球大小、形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色.再把它放回袋中,多次重复摸球。
苏科版八年级下册数学第8章 认识概率 含答案

苏科版八年级下册数学第8章认识概率含答案一、单选题(共15题,共计45分)1、下列说法中,正确的是()A.在同一年出生的367名学生中,至少有两人的生日是同一天B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖 D.“明天降雨的概率是80%”表示明天有80%的时间降雨2、下列事件为必然事件的是()A.射击一次,中靶B.画一个三角形,其内角和是C.掷一枚质地均匀的硬币,正面朝上D.12人中至少有2人的生日在同一个月3、一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有4个,若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a大约是()A.25B.20C.15D.104、从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为()A.0B.C.D.5、中国抗击疫情最宝贵的经验就是“早发现,早报告,早隔离,早治疗”.在这12个字中“早”字出现的频率是()A. B. C. D.6、在一个不透明的袋子里装有一个黑球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球,两次都摸到黑球的概率是()A. B. C. D.7、在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小敏通过多次实验发现,摸出红球的频率稳定在 0.25 左右,则袋子中红球的个数最有可能是()A.5B.10C.12D.158、以下说法正确的是()A.在同一年出生的400人中至少有两人的生日相同B.一个游戏的中奖率是1%,买100张奖券,一定会中奖C.一副扑g牌中,随意抽取一张是红桃K,这是必然事件D.一个袋中装有3个红球、5个白球,任意摸出一个球是红球的概率是9、下列事件是必然事件的是().A.在足球比赛中,弱队战胜强队B.抛掷1枚硬币,落地时正面朝上 C.任意两个正整数,其和大于1 D.小明在本次数学考试中得150分10、从标有-5a2b , 2a2b2 , ab2 , -5ab的四张同样大小的卡片中,任意抽出两张,“抽出的两张是同类项”这一事件是()A.不可能事件B.不确定事件C.必然事件D.确定事件11、下列事件是随机事件的为()A.度量三角形的内角和,结果是180°B.经过城市中有交通信号灯的路口,遇到红灯C.爸爸的年龄比爷爷大D.通常加热到100℃时,水沸腾12、抛掷一枚均匀的硬币一次,出现正面朝上的概率是()A. B. C. D.113、同时抛掷两枚硬币,正面都朝上的概率为A. B. C. D.14、下列事件中,属于必然事件的是( )A.明年元旦会下雨B.三角形三内角的和为180°C.抛一枚硬币正面向上D.在一个没有红球的盒子里,摸到红球15、一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时是绿灯的概率是()A. B. C. D.二、填空题(共10题,共计30分)16、从,,,,,这个数中任意选一个数作为的值,则使关于的方程的解是负数,且关于的一次函数的图象不经过第一象限的概率为________.17、小强同学从-1,0,1,2,3,4这六个数中任选一个数,满足不等式x+1<2的概率是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
认识概率知识点归纳(1)事件可分为:必然事件、不可能事件(确定事件)、随机事件(不确定事件)。
(2)一件事件发生的可能性的大小的数值,叫做这件事件的概率。
概率通常用大写 P 表示。
(3)0≤P(A 事件)≤1;P(必然事件)=1;P(不可能事件)=0;0<P(随机事件)<1。
(4)频率与概率的关系。
联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率。
区别:某可能事件发生的概率是一个定值。
而这一事件发生的频率是波动的,当试验次数不大时,事件发生的频率与概率的差异可能很大。
事件发生的频率不能简单地等同于其概率,要通过多次试验,用一事件的频率来估计这一事件发生的概率。
1、确定事件和随机事件。
()“必然事件”是指事先可以肯定一定会发生的事件。
()“不可能事件”是指事先可以肯定一定不会发生的事件。
()“不确定事件”或“随机事件”是指结果的发生与否具有随机性的事件。
2、可能性的大小(1)很可能发生:如果事件发生的可能性很大,我们也说事件很可能发生.不大可能发生:如果事件发生地可能性很小,我们也说事件不大可能发生。
(2)事件的频数、频率。
设总共做 n 次重复实验,而事件 A 发生了 m 次,则称事件 A 发生的次数 m 为频数。
称比值 m/n 为A 发生的频率。
(3)概率:某事件发生的可能性也叫做事件发生的概率。
必然事件发生概率为 1,不可能事件发生的概率为 0,不确定事件发生的概率在 0 到1 之间。
一般地,如果一个实验有 n个等可能的结果,而事件 A 包含其中 k 个结果,我们定义 P(A)=k/n=事件 A 包含的可能结果数/所有可能结果数。
对概率计算应注意:分清所有基本事件的总和(n)和事件 A 所包含的基本事件总和(k).3、频率与概率的关系。
(1)事件发生的频率会呈现逐渐稳定的趋势。
(2)频率和概率可以非常接近,单不一定相等(3)如何用频率估计机会的大小。
4、树状图与列表法求解概率测试题一、填空题(共 10 个小题,每题给出四个答案,只有一个是正确的,请将正确答案填在下面的方框内,每题 3 分,共 30 分) 1. 下列成语所描述的事件是必然发生的是 ()A. 水中捞月B. 拔苗助长C. 守株待免D. 瓮中捉鳖2. 一个事件的概率不可能是()13 A.0 B.C.1D.2 23. 小明和三个女生,四个男生玩丢手绢的游戏,小明随意将手绢丢在一名同学后面,那么这名同学不是女生的概率是()3 343A.B. C.D.48 7 7 4. 有六张卡片:上面各写有 1、1、2、3、4、4 六个数,从中任意摸一张,摸到奇数的概率是( ) 1 1 1 2 A.B. C. D.623 3 5. 用 1、2、3 三个数字组成一个三位数,则组成的数是偶数的概率是()1 1A.B.1 1 C.D.34566. 小刚掷一枚硬币,一连 9 次都掷出正面朝上,当他第十次掷硬币时,出现正面朝上的概率是()1 2 A.0B.1C. D.237. 下列说法错误的是()A.彩票的中奖率只有三百八十万分之一,买一张根本不会中奖B.两点确定一条直线C.过一点可画无数条直线D.太阳绕着地球转的概率是 08. 一个袋中有 4 个珠子,其中 2 个红色,2 个蓝色,除颜色外其余特征均相同,若从这个袋中任取 2 个珠子,都是蓝色的概率是( )1111A.B.C.D.23469. (2009,荆门市)从只装有 4 个红球的袋中随机摸出一球,若摸到白球的概率是 p 1,摸到红球的概率是 p 2,则( )A.p 1=1,p 2=1.B.p 1=0,p 2=1.C.p 1=0,p 2= 1 .D.p 1=p 2= 1 4 410. 如图 1 所示是用相同的正方形砖铺成的地板,一宝物藏在某一块下面,宝物在白色区域的概率是()5211A.B.C.D.9 9 6 2二、填空题(共 6 个小题,每题 3 分,共 18 分)11. 任意掷二枚均匀的骰子(六个面分别标有 1 到 6 个点)图 1朝上面的点数之和是数字7 的概率是.12.为了促销,厂家在每一件纯净水中放有两瓶在瓶盖反面写有“再来一瓶”的奖励,每件纯净水24 瓶,小冬任买一瓶,获奖的概率是.13.小明有两件上衣,三条长裤,则他有几种不同的穿法.14.1、3、5、8 路公共汽车都要停靠某个站口(假设这个站只能停靠一辆汽车),小华每天都要在此等候1 路或5 路公共汽车上学(假设当时各路车首先到站的可能性相等),则首先到站的正好是小华要乘坐的公共汽车的概率是.115.从一个不透明的口袋中任意摸出一球是白球的概率为,已知袋中白球有 3 个,6则袋中球的总数是.16.(2009,凉山州,6 分)已知一个口袋中装有7 个只有颜色不同的球,其中3 个白球,4 个黑球.若往口袋中再放入x 个白球和y 个黑球,从口袋中随机取出一个白球的概率是1,4y 与x 之间的函数关系式.三、解答题(17、18 题,每题6 分,其余8 分共52 分)17.小明所在年级共 10 个班,每班 45 名同学,现从每个班中任意抽一名学生,共 10 名学生参加课外活动,问小明被抽到的概率是多少?18.(杭州) 在一张边长为4cm 的正方形纸上做扎针随机试验,纸上有一个半径为1cm 的圆形阴影区域,则针头扎在阴影区域内的概率为多少?19.(2009,江苏,8 分)一家医院某天出生了3 个婴儿,假设生男生女的机会相同,那么这3 个婴儿中,出现1 个男婴、2 个女婴的概率是多少?20.小明与小亮玩摸球游戏,在一个袋子中放有 5 个完全一样的球,分别标有1、2、3、4、5 五个数字,小明从袋中摸出一球,记下号码,然后放回由小亮摸,规定:如果摸到的球号码大于 3 则小明胜,否则小亮胜,你认为这个游戏公平吗?请说明理由-3-2-121. (2009,济南市,8 分)有 3 张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的 k ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b .(注: 本题的第三张背面的-3 应该是 3)(1) 写出 k 为负数的概率; 正面(2) 求一次函数 y = kx + b 的图象经过二、三、四象限的概率.(用树状图或列表法求解)背面22. 一口袋中装有四根长度分别为 1cm ,3cm ,4cm 和 5cm 的细木棒,小明手中有一根长度为 3cm 的细木棒,现随机从袋内取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:(1) 求这三根细木棒能构成三角形的概率;(2) 求这三根细木棒能构成直角三角形的概率; (3) 求这三根细木棒能构成等腰三角形的概率.23.(2009,威海,7 分)除颜色外完全相同的六个小球分别放到两个袋子中,一个袋子中放两个红球和一个白球,另一个袋子中放一个红球和两个白球.随机从两个袋子中分别摸出一个小球,试判断摸出两个异色小球的概率与摸出两个同色小球的概率是否相等,并说明理由.24.附加题(2009,宁德市,10A B C(1)小明的这三件文具中,可以看做是轴对称图形的是(填字母代号);(2)请用这三个图形中的两个拼成一个轴对称图案,在答题卡的指定位置画出草图(只须画出一种);(3)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表计算)答案:一.选择题 1.D 2.D3.C4.B5.A6.C7.A8.D9.B10.A1 1 1二、填空题11. 12. 13.6 14. 15.18 16. y = 3x + 5 根据概率的计算公式表示6 12 2出概率后,再将代数式进行变形写出函数关系式.3 +x 因为取出一个白球的概率P =7 +x +y ∴3 +x=17 +x +y 4∴12 + 4x = 7 +x +y∴y 与x 的函数关系式为:y = 3x + 5三、17.略 18.略19.解:用树状图分析如下:第一个第二个第三个所有结果男(男男男)男女(男男女)男男(男女男)女女(男女女)开始男(女男男)男女(女男女)女男(女女男)女女(女女女)从树状图中可以发现共有8 种等可能的情况,其中出现 1 个男婴、2 个女婴共有3 种3情形,所以出现1 个男婴、2 个女婴的概率为P (1 个男婴,2 个女婴)=.820.略21.解:(1)k 为负数的概率是23(2)画树状图开始第一次-1 -2 3第二次-2 3 -1 3 -2 1第二次第一次-1 -2 3-1 ----- (-1,-2 )(-1,3 )-2 (-2 ,-1)------ (-2 ,3 )3 (3 ,-1)(3 ,-2 )-----共有6 种情况,其中满足一次函数y =kx +b 经过第二、三、四象限,即k < 0,b < 0 的情况有2 种所以一次函数y =kx +b 经过第二、三、四象限的概率为2=1 6 322.解:我们可以先把从四根细木棒中取两根细木棒的所有可能情况列举出来有:(1,3)、(1,4)、(1,5)、(3,4)、(3,5)、(4,5)共有6 种. 然后再配上长度为3cm 的细木棒,(1)根据“两边之和大于第三边”可知能够构成三角形的有:1,3,3;3,4,3;3,5,3;3,4,5 有4 种等可能情形.(2)根据“勾股定理的逆定理”可知能构成直角三角形的有:3,4,5 1 种情形.(3)根据“有两边相等的三角形是等腰三角形” 可知有:1,3,3;3,4,3;3,5,3 3 种情形,所以有:4 2 1(1)P(构成三角形)= =;(2)P(构成直角三角形)= ;(3)P(构成等腰三角6 3 6形)=3 =1 .6 223.解:摸出两个异色小球的概率与摸出两个同色小球的概率不相等.画树状图如下(画出一种情况即可):开始或开始红红白白白红红白白红白白红白白红红白红红白红红白5∴摸出两个异色小球的概率为,94摸出两个同色小球的概率.9即摸出两个异色小球的概率与摸出两个同色小球的概率不相等.24.解:(1)B,C(2)如:等(3)画树状图或列表开始A B CA B C A B C A B C(A,A) (A,B) (A,C) (B,A) (B,B) (B,C) (C,A) (C,B) (C,C)一共有9 种结果,每种结果出现的可能性是相同的.而其中能恰好拼成轴对称图形的结果有五种,分别是(A,A) 、(B,B)、(C,C)、(B,C)、(C,B),所以两件文具可以拼成一个轴对称图5案的概率是9.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
