实验三 用Excel进行方差分析实验报告
实验四用EXCEL实现方差分析

实验四用EXCEL实现方差分析方差分析(Analysis of Variance, ANOVA)是一种用于比较两个或更多个样本均值是否显著不同的统计方法。
它通过比较各样本的方差是否相等来推断样本均值是否有显著差异。
本实验将使用EXCEL软件来实现方差分析。
1.实验目的掌握用EXCEL实现方差分析的方法,能够对不同样本的均值进行比较,并判断是否有显著差异。
2.实验原理方差分析是通过计算组间与组内的均方差(mean square)与自由度(degree of freedom)来推断是否存在差异显著的方法。
在EXCEL中使用方差分析的步骤主要包括数据录入、数据分析工具的使用、方差分析表的解读和结果的判断。
3.实验步骤Step 1: 数据录入首先将要分析的数据录入到EXCEL的工作表中,每组数据占用一列或一行,例如:组1:67,75,62,71,73组2:82,79,85,80,87组3:91,85,89,95,93Step 2: 数据分析工具的使用选择数据分析工具,依次点击"数据"-"数据分析",弹出数据分析对话框,选择"方差分析",点击"确定"。
Step 3: 填写方差分析对话框参数Step 4: 方差分析结果解读与判断EXCEL会生成方差分析表,其中包括组间均方(MSb),组内均方(MSw),总均方(MSt),标准误差(Sb),F值,自由度(df),P值等数据。
根据F值和P值来判断是否有显著差异。
通常,如果P值小于显著性水平(0.05),则拒绝原假设,即表示组间均值有显著差异。
4.实验注意事项(1)确保数据录入准确无误,符合方差分析的前提条件。
(2)需事先安装加载数据分析工具,具体操作方法可参考EXCEL软件帮助手册。
(3)在解读结果时,除了判断P值是否小于显著性水平之外,还要注意观察各组的均值和方差大小关系。
5.结论通过上述步骤,在EXCEL中可以快速实现方差分析,并得到方差分析表。
Excel数据处理之三 方差分析

统计学中的几个基本概念1、同质(homogeneity)与变异(variation)严格地讲,同质是指被研究指标的影响因素完全相同。
但在医学研究中,有些影响因素往往是难以控制的(如遗传、营养等),甚至是未知的。
所以,在统计学中常把同质理解为对研究指标影响较大的、可以控制的主要因素尽可能相同。
例如研究儿童的身高时,要求性别、年龄、民族、地区等影响身高较大的、易控制的因素要相同,而不易控制的遗传、营养等影响因素可以忽略。
同质基础上的个体差异称为变异。
如同性别、同年龄、同民族、同地区的健康儿童的身高、体重不尽相同。
事实上,客观世界充满了变异,生物医学领域更是如此。
哪里有变异,哪里就需要统计学。
若所研究的同质群体中所有个体一模一样,只需观察任一个体即可,无须进行统计研究。
2、总体(population)与样本(sample)任何统计研究都必须首先确定观察单位(observed unit),亦称个体(individual)。
观察单位是统计研究中最基本的单位,可以是一个人、一个家庭、一个地区、一个样品、一个采样点等。
总体是根据研究目的确定的同质观察单位的全体,或者说,是同质的所有观察单位某种观察值(变量值)的集合。
例如欲研究山东省2002年7岁健康男孩的身高,那么,观察对象是山东省2002年的7岁健康男孩,观察单位是每个7岁健康男孩,变量是身高,变量值(观察值)是身高测量值,则山东省2002年全体7岁健康男孩的身高值构成一个总体。
它的同质基础是同地区、同年份、同性别、同为健康儿童。
总体又分为有限总体(finite population)和无限总体(infinite population)。
有限总体是指在某特定的时间与空间范围内,同质研究对象的所有观察单位的某变量值的个数为有限个,如上例;无限总体是抽象的,无时间和空间的限制,观察单位数是无限的,如研究碘盐对缺碘性甲状腺病的防治效果,该总体的同质基础是缺碘性甲状腺病患者,同用碘盐防治;该总体应包括已使用和设想使用碘盐防治的所有缺碘性甲状腺病患者的防治效果,没有时间和空间范围的限制,因而观察单位数无限,该总体为无限总体。
生物统计用Excel和SPSS软件进行方差分析

当处理确定有作用,组间均方是由于误差与不同处理共同导致的结果,各样本来自不同总体,那么组间均方会远远大于组内均方,即
MS组间>> MS组内。
3、因为LSD法实质上是t 检验,故有人指出其最适宜的比较形式是:在进行试验设计时就确定各处理只是固定的两个两个相比,每个
• (二)因素各水平的观测数据的方差均 相等
• (三)观测值是互相独立的
方差分析种类
• 在方差分析中,根据所研究试验因素的 多少,可分为单因素、两因素和多因素 试验资料的方差分析。根据各处理内重 复数是否相等,单因素方差分析又分为 重复数相等和重复数不等两种情况
方差分析的基本步骤
• (一)计算各项平方和与自由度。
多重比较的方法甚多,常用的有最小显著差 数法(LSD法)和最小显著极差法(LSR法)
( 一 ) 最 小 显 著 差 数 法 (LSD 法 , least significant difference) 此法的基本作法是:在F
检验显著的前提下,先计算出显著水平为α的 最小显著差数LSD,然后将任意两个处理平均 数的差数的绝对值 xi. x j. 与其比较。若 xi. x j. > LSDa时则 x i.与x j. 在α水平上差异显著;反之,则 在α水平上差异不显著。
处理平均数在比较中只比较一次。
多重比较的方法甚多,常用的有最小显著差数法(LSD法)和最小显著极差法(LSR法)
常用的LSR法有q-检验法和新复极差法两种。
这些在显著水平α上依秩次距k的不同而采用的不同的检验尺度叫做最小显著极差LSR。
生物统计用Excel和SPSS软件进行方差分析
当处理确定有作用,组间均方是由于误差与不同处理共同导致的结果,各样本来自不同总体,那么组间均方会远远大于组内均方,即
EXCEL中方差分析
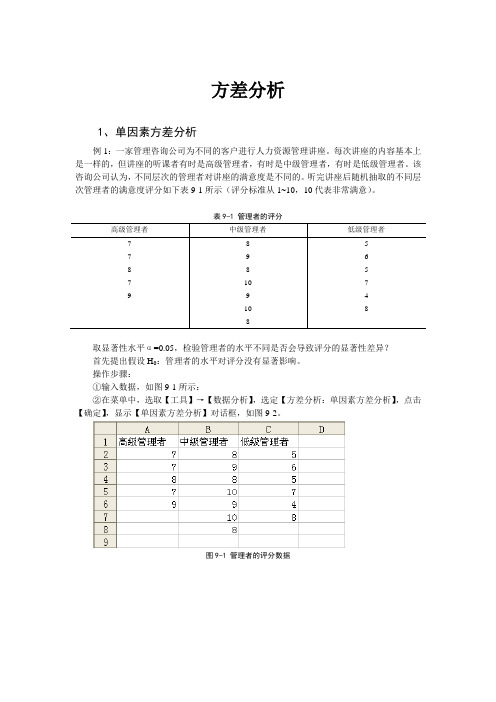
方差分析1、单因素方差分析例1:一家管理咨询公司为不同的客户进行人力资源管理讲座。
每次讲座的内容基本上是一样的,但讲座的听课者有时是高级管理者,有时是中级管理者,有时是低级管理者。
该咨询公司认为,不同层次的管理者对讲座的满意度是不同的。
听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1所示(评分标准从1~10,10代表非常满意)。
表9-1 管理者的评分高级管理者中级管理者低级管理者7 8 57 9 68 8 57 10 79 9 410 88取显著性水平α=0.05,检验管理者的水平不同是否会导致评分的显著性差异?首先提出假设H0:管理者的水平对评分没有显著影响。
操作步骤:①输入数据,如图9-1所示:②在菜单中,选取【工具】→【数据分析】,选定【方差分析:单因素方差分析】,点击【确定】,显示【单因素方差分析】对话框,如图9-2。
图9-1 管理者的评分数据图9-2 单因素方差分析对话框③在“输入区域”框输入数据矩阵(首坐标:尾坐标),可选为“A1:C8”,点选“标志位于第一行”,在“分组方式”框选定“列”,指定显著水平α=0.05,输出选项的输出区域可为工作表的任何位置,本例选择在I4处。
④点击【确定】,则得输出结果,如下图9-3所示。
图9-3 单因素方差分析结果图9-3是一个单因素方差分析结果的报告。
第一个表是有关各样本的一些描述统计量,它可以作为方差分析的参考信息。
第二个表是方差分析结果。
其中SS 表示平方和,df 为自由度,MS 表示均方,F 为检验的统计量,P-value 为用于检验的P 值,F crit 为给定α水平下的临界值。
从方差分析表可以看到,由于68232.375573.11=>=αF F ,所以拒绝原假设,即管理者的水平对评分的影响是显著的。
在进行决策时,可以直接利用方差分析表中的P 值与显著性水平α的值进行比较,若 P <α,则拒绝原假设;若P >α,则不能拒绝原假设。
Excel中的单因素方差分析

Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题,需要应用方差分析。
方差分析是把试验看成一个整体,分解各种变异的原因。
从总的方差中,将可能的变异原因逐个分出,并用误差的方法作为判断其他方差是否显著的标准,如果已知变异原因的方差比误差方差大得多,那么,该方差就不是随机产生的,试验的处理间的差异不会是由于误差原因造成的,这时处理的效应是应该肯定的。
通过学习Excel中方差分析,掌握基本的分析操作,能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法2、例:在五个硼肥试验处理中测得苹果叶内硼含量(ppm),试比较各处理苹果叶内平均含硼量的差异显著性。
3、操作步骤:在Excel统计中,完全随机试验设计的方差分析,只须经过单因素方差分析即可得出结果,具体步骤如下:①打开Excel,向单元格中输入文字与数字,建立表格;②单击“工具”,在出现的对话框中,选择“数据分析”,选取“方差分析: 单因素方差分析”;③单击“确定”,单击“输入区域:”框右边的按钮,用鼠标选中数据,再次单击按钮;其他设置选择a为0.05。
分组方式:行。
点选标志位于第一列④单击“确定”,即可输出单因素方差分析结果。
4、方差分析输出结果: SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.55、多重比较:由方差分析的结果,采用新复极差测验法,再稍加计算比较处理, 即可得出:新复极差测验的LSR值6结论:由方差分析结果F=94.17>F o.o5=Fcrit=2.76,可知5种喷硼处理间差异显著,并可知除E与B二处理间无极显著差异外,其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析,是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题,如各组之间有显著差异,说明这个因素(分类变量)对因变量是有显著影响的,因素的不同水平会影响到因变量的取值。
Excel应用于方差分析的实训教学探究

( S c h o o l o f L i f o S c i e n c e ,Hu n a n U n i v e r s i t y o f A r t s a n d S c i e n c e ,H u n a n C h a n g d e 4 1 5 0 0 0 )
h i g h l i g h t d e t o ma ke he t da t a lo f w f u l l f o r ma t t i n g ,t h e d e c o mp o s i t i o n p r o c e s s mo r e c o n c i s e nd a t he f r e e d o m d e c o mp o s i t i o n a n d F t e s t s t e p l e s s c u b e m r s o me i n t he v a r i nc a e a na l y s i s p r ce o s s o f Ex c e l ,whi c h p ov r i d e d a wi d e a p e r t ur e mo d e t h a t u s i n g Ex c e l e l e c t r o n i c f o m r t o ea r li z e p r a c t i c a l t e a c h i n g f o r n o n - s t a t i s t i c s p r o f e s s i o n a l u n d e r g r a d u a t e s ’p r o b a bi l i t y nd a s t a t i s t i c s c o u r s e .
试验六、 用excel进行方差分析

地区A 方案B B1
A1
354 336
B2
385 392
B3
360 371
A2
342 367
390 377
353 374
A3
330 352
388 380
378 359
数据转换 反正旋转换:
处理 对照
1
2
3
97
95
93
70
91Biblioteka 777868
82
72
75
66
85
64
76
49
78
56
63
55
77
68
71
64
练习:课本122页 例6.14。 127-129页所有的习题 实验报告:P128习题6.9
库”) -------“单因素方差分析”-------点 击确定,根据要求,输入数据,得到结
果。
例:某公司对新销售人员进行不同的销售培训。 为了比较培训课程的有效性,随机选择了三组销 售人员,每组五人,一组接受A课程训练,一组接 受B课程训练,另一组C不接受任何训练。当前两 组的训练课程结束时,收集训练后两个星期内各 组销售人员的销售记录,进行方差分析。
实验六 运用EXCEL进行方差分析 实验目的:熟练掌握运用EXCEl进 行方差分析。 实验材料:计算机,EXCEL软件 实验地点:机房 实验内容:
单向分组资料方差分析
• 此类资料由完全随机试验获得
• 步骤:
•
输入数据-------从菜单中找到“工
具”------- 选择“数据分析”(如没有,
选择“加载宏”,然后选择“分析工具
A课程
2058 2176 3449 2517 944
Excel数据处理之三 方差分析

关于本站 | 版权声明 | 网站地图 | 在线投稿 | 广告合作 | 6SQ工具条
Copyright © 1999-2005 All rights reserved. 贵宾统计
/qtool/stats/1229.html
图 3-7
数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因 素可重复方差分析,出现如图3-8的对话框,对话框的内容基本与双因素无重复
/qtool/stats/1229.html
2011/3/3
w
页码,5/6(W)
方差分析相同,区别在于每一样本的行数选项,在此输入重复试验的次数即 可。
第三节 方差分析
字体大小: 小 中 大
在数据分析工具库中提供了3种
基本类型的方差分析:单因素方差 分析、双因素无重复试验和可重复 试验的方差分析,本节将分别介绍
Custom Tactical Comms Design Your Own SWAT, Military and Covert/Surveillance Comms Systems!
图 3-3 双因素无重复试验方差分析 与单因素方差分析类似,在分析前需将试验数据按一定的格式输入工作表 中,如图3-4所示:
/qtool/stats/1229.html
2011/3/3
w
页码,3/6(W)
图 3-4 数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因 素无重复方差分析,出现如图3-5的对话框,对话框的内容如下: 1. 输入区域:选择数据所在区域,可以包含因素水平标志。 2. 果数据输入时选择了因素水平标志,请选择标志按钮。 3. 显著性水平α:根据实际情况输入,一般选择0.05。 4. 输出选项:按需要选择分析结果存储的位置。
在Excel表中进行多元方差分析

西北农业学报 2006,15(2):174~179A cta A g riculturaeB oreali2occi dentalis S inica在Excel表中进行多元方差分析3胡想顺,刘小凤,赵惠燕,李东鸿,胡祖庆(西北农林科技大学植物保护学院,陕西杨凌 712100)摘 要:应用函数编辑器和简单的复制、粘贴功能即可在Excel表中实现较为复杂的多元方差分析,可用到的命令有求和命令“SUM”,计数器命令“COUN T”,求平均值命令“AV ERA GE”,对应数据相乘的积的求和命令“SUMPRODUCT”,矩阵相乘命令“MMUL T”以及求解矩阵的行列式的值的命令“MDETERM”。
并给出了一个在Excel表中进行双因素不等重复处理的多元方差分析和多重比较的例子。
关键词:Microsoft Excel2000;函数编辑器;多元方差分析;生物统计中图分类号:S11+3 文献标识码:A 文章编号:100421389(2006)022*******Multiple Covariance Analysis in Microsoft Excel2000 HU Xiang2shun,L IU Xiao2feng,ZHAO Hui2yan,L I Dong2hong and HU Zu2qing (College of Plant Protection,Nort hwest A&F University,Yangling Shaanxi 712100,China)Abstract:U sed f unctions editor and simple cop y,stick f unction could do multiple coveriance analysis in Micro soft Excel table.The order include total sum order"SUM",count order"COUN T",mean order"AV ERA GE",and t he order"SUM PRODUC T"t hat about count t he total sum of some data’s p roduct which some group s number corresponding multiply;t he order"MMUL T"t hat used to count p roduct of two mat rixes;t he order"MD ETERM"t hat used to count t he determinant value of one ma2 t rix.An example about two factors multiple covariance analysis and multiple comparisons which have different repetitio n in Micro soft Excel2000had been given.K ey w ords:Micro soft Excel2000;Functions editor;Multiple coveriance analysis;Biostastics 多元方差分析是数理统计的基本方法之一,用于解决2个以上同协方差阵多元(多指标)正态总体均值向量的比较问题[1]。
统计学实验EXCEL实习报告

实验步骤:在Excel中,进行方差分析可以使用公式和函数的方法。
一:单因素方差分析
例:根据学生调查的结果,试用方差分析的方法比较在5%的显著性水平下能否认为学生的学习兴趣对他们的统计成绩有显著影响。
全部选中,再选择插入,插入图表,饼图,得到下图:
实验二描述统计分析过程(用Excel计算描述统计量)
实验目的:用Excel计算描述统计量
实验步骤:Excel中用于描述统计量的方法有两种,函数方法和描述统计工具的方法。
一:用函数计量描述统计量
了解实习生的工资情况,随机抽取了30人。并输入单元格,如图:
实验三用Excel进行参数估计与假设检验
实验目的:用Excel进行参数估计与假设检验
实验步骤:在Excel中,进行参数估计只能使用公式和函数的方法,而假设检验除以上两种方法外,还可以使用假设检验工具。
一.使用Excel进行区间估计
抽查40位顾客的消费额,求在概率90%的保证下,顾客平均消费额的估计区间。
实验一Excel基本操作(用Excel搜集与整理数据)
实验目的:掌握用Excel进行数据的搜集整理与显示
实验步骤:
一:用Excel搜集数据
使用Excel进行抽样,先对各个总体单位进行编号,编号后,可以输入工作表。
例如:有60个总体单位,每个总体单位一个编
选择数据分析选项,打开数据分析对话框,从中选择抽样。如下图。
三:用Excel进行有重复双因素方差分析
与无重复的双因素方差分析不同,有重复双因素方差分析可以分为有交互作用和无交互作用两种情况。
例子:
在Excel表格中输入相应数据,从“数据分析”中选择“方差分析”
Excel在双因素等重复试验方差分析中的应用

Excel在双因素等重复试验方差分析中的应用摘要:本论文旨在说明如何简单地将双因素等重复试验方差分析通过Excel软件来实现,使读者了解如何将数理统计同计算机技术相结合的一种方式。
关键词:方差分析、双因素等重复试验、Excel软件。
引言:方差分析是数理统计中的基本方法之一,是工农业生产和科学研究中分析数据的一种重要方法。
例如在化工生产过程中,众多因素会影响到产品的数量和质量,有些因素影响较大,有些较小,为了保证优质高产,就需要找出对产品数量和质量影响显著的因素,因此,就需要进行试验。
方差分析就是根据试验结果进行分析、推断各相关因素对试验结果的影响是否显著的有效方法,而往往实际需要分析的数据量庞大复杂,人工计算难以适应其速度、精度的要求,就需要引入计算机技术的辅助。
Excel是Microsoft Office家族中的一款应用软件,是一个功能多、技术先进、使用方便的表格式数据综合管理和分析系统,函数库丰富,制图功能较好,可以进行数据处理、统计分析和决策辅助。
将Excel软件应用于方差分析,将使得处理问题的数据规模和复杂性程度极大地提高,精度也更为准确,同时方便省时,结果直观了然。
而双因素等重复试验方差分析在几种简单类型的方差分析中稍微复杂些,计算量更大,更加有必要用Excel来处理。
原理:S E 称为误差平方和,S A 、S B 分别称为因素A 、因素B 的效应平方和,S A ⨯B称为A 、B 交互效应平方和。
S T ,S E ,S A ,S B ,S A ⨯B 的自由度依次为rst ﹣1,rs (t ﹣1),r ﹣1,s ﹣1,(r ﹣1)(s ﹣1)。
记T ...=111rsti j k X===∑∑∑ijk,T ij .=1tk X =∑ijk (i=1,2,…,r ;j=1,2,…,s ),T i ..=11stj k X ==∑∑ijk (i=1,2,…,r ),T .j .=11rti k X ==∑∑ijk (j=1,2,…,s )。
用excel进行方差分析的实验报告

用excel进行方差分析的实验报告实验四:用excel进行方差分析的实验报告实验目的:学会在计算机上利用excel进行单因素方差分析和有交互的双因素分析以及无交互的双因素分析,实验背景:方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
一个复杂的事物,其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显著影响的因素,各因素之间的交互作用,以及显著影响因素的最佳水平等。
方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
对变差的度量,采用离差平方和。
实验内容:实验(1):单因素方差分析条件:单因素方差分析是对成组设计的多个样本均数比较,所以对数据格式有特殊要求,因素的不同水平作为表格的列(或行),在不同水平下的重复次数作为行(或列)。
例1:以下数据来自2009年中国统计年鉴,各地区农村居民家庭平均每人生活消费支出,按不同项目分组的不同地区:其中,1代表生活消费支出合计,2代表食品,3代表衣着,4代表居住, 5代表家庭设施及服务, 6代表交通和通讯, 7代表文教娱乐用品及服务,8代表医疗保健, 9代表其他商品及服务各地区农村居民家庭平均每人生活消费支出 (2009年)单位:元地区项目地区生活消费食品衣着居住家庭设备交通和文教娱乐医疗保健其他品支出合计及服务通讯用品及服务及务地区 1 2 3 4 5 6 7 8北京8897.59 2808.92 654.36 1798.88 528 1132.09 960.41 867.87 14天津4273.15 1848.11 324.63 674.67 187.83 481.27 371.85 299.79 8河北3349.74 1195.65 217.82 796.62 170.4 350.92 263.53 289.27 6山西3304.76 1224.6 283.2 584.07 156.27 324.89 416.94 240.94 7内蒙古3968.42 1578.57 271.88 609.29 148.03 466.34 390.85 416.87 8辽宁4254.03 1563.33 335.93 793.91 185.5 416.41 437.79 409.64 11吉林3902.9 1371.12 286.97 737.07 168.36 355.99 376.76 511.5 9黑龙江4241.27 1331.07 345.69 946.84 161.03 427.35 496.42 434.25 9上海9804.37 3639.14 496.14 2102.96 480.62 1212.38 942.76 738.94 19江苏5804.45 2275.28 306.62 969.76 286.37 691.56 818.45 322.99 13浙江7731.7 2812.39 473.11 1488.95 374.31 968.17 843.34 609.07 16安徽3655.02 1494.19 203.37 813.12 229.66 302.23 312.05 227.1 福建5015.72 2304.14 291.72 821.21 260.68 570.24 421.69 219.02 12江西3532.66 1609.2 162.58 725.11 181.91 295.76 254.77 232.78 7山东4417.18 1618.66 265.59 945.81 273.77 533.55 399.95301.55河南3388.47 1220.36 225.64 875.83 203.81 310.11 234.01 242.87 7湖北3725.24 1668.35 195.45 702.62 229.32 307.22 281.68 236.31 10步骤:(1)、在excel的分析工具库中中选择“方差分析:单因素方差分析”指定相应的数据区域和显著性水平,点击“确定”后输出最终输出结果:表一方差分析:单因素方差分析SUMMARY组观测数求和平均方差列 1 32 129281.5 4040.048 3465440列 2 32 52249.75 1632.805 428309.6列 3 32 7951.16 248.4738 15408.02列 4 32 25251.6 789.1125 162323.1列 5 32 6519.28 203.7275 10263列 6 32 13547.29 423.3528 66285.85列 7 32 11279.63 352.4884 55136列 8 32 9809.81 306.5566 31281.44列 9 32 2716.05 84.87656 1665.067 表一是各组数据的描述统计指标。
实验三 方差分析

一、实验目的
掌握EXCEL提供的函数进行方差分析方法 掌握数据分析工具进行方差分析方法
二、实验内容:
单因素资料方差分析 两因素无重复观察值 两因素有重复观察值 数据转换
三、实验步骤:
利用函数进行——单因素方差分析 利用数据分析工具进行方差分析
1.利用函数进行——单因素方差分析
计算处理项和Ti、总和T和矫正数C DEVSQ(),计算总平方和SST_
DEVSQ = ∑ ( x − x) 2
SUMSQ ()/n-C,计算处理平方和SSt SSe= SST-SSt FINV,得F0.05 SE=(MS/n)^0.5 计算R0.05或R0.01
SUMSQ = ∑ T i
2
2.利用数据分析工具进行方差分析
3.利用函数进行数据转换
反正弦转换
原始数据(以百分数表示) 反正弦值 DEGREES(ASIN(SQRT(P/100))) (SIN(RADIANS(X)))^2*100 工具 百分数 数据分析
单因素方差分析
单因素
输入原始数据 工具 → 数据分析 → 单因素方差分析→确定 → 选中数据 → 确定
双因素无重复观察值
输入原始数据 工具 → 数据分析→ 无重复因素分析→确定 → 选中数据 →确定
双因素有重复观察值
输入原始数据 工具 → 数据分析→ 有重复双因素分析→确定 → 选中数据(带表头) →输入重复次数→确定
excel方差分析

9.3 双因素方差分析
【例 9.3】某农科所试验在水溶液中种植西红柿,采用了三种不同的施肥方式和四种 不同的水温。 三中施肥方式是: 一开始就给以全部可溶性肥料; 每两个月给以 1/2 的溶液; 每月给以 1/4 的溶液。水温分别为: 4℃、 9℃、 16℃、 20℃。试验产量如下表: 施 一次施肥 20 16 9 8 肥 19 15 9 7 方 式 三次施肥 21 14 11 6
本例中,工厂是因素,3 个工厂分别是 3 个水平,混合原料所需的时间是响应变量。 在此假定混合原料所需的时间服从正态分布,并且 3 个工厂混合原料所需时间的方差相 等。符合独立的假定。由于只有一个因素,因此是单因素分析。为检验三家工厂混合一 批原料所需平均时间是否相同,提出假设: 原假设:三个工厂混合原料所需的平均时间相同 备择假设:三个工厂混合原料所需的平均时间不相同 使用 Excel 的“方差分析:单因素方差分析”分析工具进行单因素的方差分析。 操作步骤: 第 1 步:将分析数据输入工作表单元格区域 A1:C6。 第 2 步:单击“工具”菜单,选定“数据分析”命令,出现“数据分析”对话框。 第 3 步:在分析工具列表栏中选择“方差分析:单因素方差分析” (如图 9-1) 。
范霄文:excel 软件与数据分析
程度(响应变量)必须服从正态分布。 2. 因素各水平的观测数据的方差相等。本例意味着上级、同事、下属传播程度的方 差相等。 3. 各观察值是独立的。本例意味着样本各个传播程度的一个观测值与另一个观察值 是独立的。 在实际应用过程中,应用方差分析时应符合以上的假定,至少是近似符合假定条件。
图 9.3-1 数据分析对话框 第 3 步:在对话框中选择“方差分析:无重复双因素分析” ,单击“确定”按钮,出 现“方差分析:无重复双因素分析”对话框。 第 4 步:在“方差分析:无重复双因素分析”对话框中(如图 9.3-2) 。
实验三__方差分析

[实验项目]实验三方差分析[教学时数]2课时。
[实验目的与要求]掌握使用Excel电子表格和统计分析软件进行方差分析的方法。
[实验材料与设备]计算机;有关数据资料。
[实验内容]1、掌握用Excel中的数据分析工具进行方差分析的方法。
2、学习用统计分析软件进行方差分析的方法。
[实验方法]1、用Excel中的数据分析工具进行方差分析的方法。
(1)工具的安装。
(2)工具的使用。
①单因子方差分析。
②两因子无重复资料的方差分析。
③两因子有重复资料的方差分析。
④两因子系统资料的方差分析。
⑤多因子方差分析。
2、用统计分析软件进行方差分析的方法。
(1)单因子方差分析(2)两因子方差分析(3)两因子系统资料的方差分析(4)多因子方差分析[指导与训练方案]1、将本次实验内容整理成实验报告。
2、练习:1、在同样饲养管理条件下,三个品种猪的增重如下表,试对三个品种增重差异是否显著进行检验。
品种增重x ij(kg)A116 12 18 18 13 11 15 10 17 18A210 13 11 9 16 14 8 15 13 8A311 8 13 6 7 15 9 12 10 11 (MS e=8.57,F=6.42)2、用三种酸类处理某牧草种子,观察其对牧草幼苗生长的影响(指标:幼苗干重,单位:mg)。
试验资料如下:处理幼苗干重(mg)对照 4.23 4.38 4.10 3.99 4.25HCl 3.85 3.78 3.91 3.94 3.86丙酸 3.75 3.65 3.82 3.69 3.73丁酸 3.66 3.67 3.62 3.54 3.71(1)进行方差分析(不用LSD法、LSR进行多重比较,F=33.86**)(2)对下列问题通过单一自由度正交比较给以回答:①酸液处理是否能降低牧草幼苗生长?②有机酸的作用是否不同于无机酸?③两种有机酸的作用是否有差异?(F1=86.22**,F2=13.13**,F3=2.26)3、为了比较4种饲料(A)和猪的3个品种(B),从每个品种随机抽取4头猪(共12头)分别喂以4种不同饲料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3种课程训练平均销售记录多重比较表
课程 B课程 A课程 C课程
平均数 x i 2928 2228.8 1951.6
x i 1951 6 . 976.4 277.2
x i 2228.8 699.2
因为MSe 3992323, n 5, 所以标准误 x 为 . s
的提高无显著影响,不 同改革方
q0.01 6.93 5.95 5.41
LSR0.05 1.6996 1.5288 1.4280
LSR0.01 3.0356 2.6063 2.3698
进一步对改革方案各水 平平均经
3.多重比较
品种小麦收获量极显著高于B4品种,但B1、B2和B3品
方案
B2 B3
B1
式为
F值 1.61 20.49**
自由度df 均方MS 4 3.5245 3 44.8818 12 2.1902 19
SS B
1 1 x2j C 3 2 (20 an
2415655 2411208 444
SSAB SSAB SSA SSB 469
因为MSe 3992323, n 5, 所以标准误 x 为 . s
s x MSe / n 3992323 / 5 282.5712 .
q值与LSR值
dfe
12
秩次距 2 3
q0.05 3.08 3.77
q0.01 4.32 5.05
LSR0.05 870.3193 1065.2934
A2
单个观测值试验资料。A因素有5个水平,即a=5
b=5× 4=20个观测值。方差分析如下:
A3
x 3 j
54.32 /(5 4) 214054245 . 2 2 C (32.3 33.2 · 32.82 29.42) 214054245 .
00 21405 .4245 175 .0255
C
1 (125 .8 2 128 .2 2 131 .9 2 134 .6 2 133 .8 2 ) 21405 .4245 4 00 21405 .4245 14.0980
本题A因素有3个水平,即 2 18个观测值。
1.计算各项平方和与自由度 2 C x / abn 65882 /(3 3 2)
SSe SST SSt 73225837300 25317957300 4790788 . .
dfT kn 1 3 5 1 14
dft k 1 3 1 2
dfe dfT dft 14 2 12
2.列出方差分析表,进行F检验
2查临界F值得,F0.05( 4,12 ) 3.26,根据df1 df B 3; 3.49,F0.01(3,12 ) 5.95。
SSe SST SSAB 6014 4695
dfT abn 1 3 3 2 1 17
05 ( 3,12 )
2查临界F值得,F0.05( 4,12 ) 3.26,根据df1 df B 3; 3.49,F0.01(3,12 ) 5.95。
LSR0.01 1220.7076 1426.9846
5.95, p 0.01, F值极显著。说明不同地 块对小麦收获量无显著 获量有极显著影响。
3.多重比较
采用q法,4个品种小麦收获量平均数多重
4个品种小麦收获量平均数多重比较表
品种
B2
B1
B3
B4
平均数 174 172.5 166.1 141.7
2.列出方差分析表,进行F检验 变异来源 A因素 B因素 误差 总变异 平方和SS 14.098 134.6455 26.282 175.0255
多重比较表如下
x i 2228.8
根据df1 df A 4,df2 dfe 12查临界F值得,F0.05( 4,12 ) 3.26, df2 dfe 12查临界F值得,F0.05(3,12 ) 3.49,F0.01(3,12 ) 5.95。
多从结果表明,A、B、C课程训练间平均销售业绩差异均不显著。
两因素试验资料方差分析
小麦产量表.8 2928 1951.6
地块
品种
A1 A2
A3
A4
A5
验资料进行方差分析如下:
合计x j
0442 16812) 84215584.2700 22583 .7300
2
平均x j
B1 32.3 34 34.7 36 35.5 172.5 34.5
B2 33.2 33.6 36.8 34.3 36.1 174 34.8
B3 30.8 34.4 32.3 35.8 32.8 166.1 33.22
合计xi
这是一个两因素交叉分组单个观测值试验资料。A因素有 1.计算各项平方和与自由度 2 矫正数 C x / kn 654.32 /(5 4) 214054245 . 2 2 2 总平方和 SST xij C (32.3 33.2 · 32.82
根据df1 df A 4,df2 dfe 12查临界F值得,F0.05( 4,12 ) 3.26, df2 dfe 12查临界F值得,F0.05(3,12 ) 3.49,F0.01(3,12 ) 5.95。
因为A因素的F值1.61 F0.05( 4,12 ) , p 0.05, F值不显著;B因素
3种课程训练销售记录方差分析表
变异来源 课程间 误差 总变异
平方和SS 2531796 4790788 7322584
自由度df 均方MS 2 1265898 12 399232.3 14
df1 dft 2,df2 dfe 12查临界F值得,F0.05( 2,12) 3.88,因为F F0.05( 2,12) , P 0.05, 表 明3种课程训练间平均销售 业绩差异不显著。
共有ab 3 3 9个水平组合;
1 C (172 .5 2 174 2 166 .12 141 .7 2 ) 21405 .4245 5 700 21405 .4245 134 .6455
SA SSB 175.0255 14.0980 134.6455 26.2820
SS B
1 1 x2j C 5 (172 .5 2 174 2 166 .12 a 21540 .0700 21405 .4245 134 .6455
误差平方和 F值 3.17 总自由度 处理自由度 误差自由度
SSe SST SSA SSB 175.0255 14.0980 1
dfT abn 1 3 3 2 1 17
05 ( 3,12 )
B 4 ,12 ) , p 0.05, F值不显著; 因素的F值20.49 F0.01( 3,12 )
df AB ab 1 3,3 1 8
df A a 1 3 1 2
x i 166.1 7.9**
x i 172.5 1.5
6.4**
变异来源 A因素 B因素 互作(A×B) 误差 总变异
/ a 2.1902/ 5 0.4380
q值与LSR值
查临界F值得,F0.05( 2,9) 4.
FB F0.01( 2,9) , FAB F0.05( 4,9),表
因B因素各水平的重复数为
s x j 146 .5556 /(3 2) 4.942
dfe
9
多重比较结果表明,改 革方 均经济效应差异不显著 。
两因素试验资料方差分析
——有重复两因素方差分析
改革方案效应表
B1
x1 jl
x1 j
x1 j
x2 jl
x2 j
x 2 j
x3 jl
dfT ab 1 5 4 1 19
df A a 1 5 1 4
dfB b 1 4 1 3
为F F0.05( 2,12) , P 0.05, 表
dfe dfT df A dfB 19 4 3 12
资料方差分析表
单因素试验资料方差分析
各组销售人员销售业绩
课程 A课程 B课程 C课程 合计
2058 3339 2228
观测值 xij 2176 3449 2777 3020 2578 1227
2517 2437 2044
944 3067 1681
合计xi 11144 14640 9758 35542
这是一个单因素试验,处理数k=3,重复数n=5。现对此试验资料进行方差分析如下: 1.计算各项平方和与自由度 2 C x / kn 355422 /(3 5) 84215584.2700 矫正数 2 SST xij C (20582 21762 · 20442 16812) 84215584.2700 总平方和 91538168 .0000 84215584 .2700 7322583 .7300 1 1 处理平方和 SS t xi2 C (11144 2 14640 2 9758 2 ) 84215584 .2700 n 5 86747380 .0000 84215584 .2700 2531795 .7300 误差平方和 总自由度 处理自由度 误差自由度
21580 .4500 21405 .4245 175 .0255
9758 ) 84215584 .2700
B因素有4个水平,即b=4,共有a× b=5× 4=20个观测值。方差分析如下:
