c语言用六种方法求定积分
定积分计算方法总结

定积分计算方法总结定积分是微积分中的一种重要概念,用于计算曲线与x轴之间的面积、曲线的弧长、质量、质心等物理量。
本文将总结定积分的计算方法,包括基本定积分的计算、换元积分法、分部积分法等。
一、基本定积分的计算基本定积分是指形如∫f(x)dx的定积分,其中f(x)为已知函数。
基本定积分的计算方法主要包括常数法、分段法和凑微分法。
1. 常数法:当被积函数为常数函数时,可以直接利用积分性质计算。
如∫kdx=kx+C,其中k为常数,C为积分常数。
2. 分段法:当被积函数在不同区间上有不同的表达式时,可以将积分区间划分为不同的子区间,在每个子区间上分别计算积分,然后再求和得到整个区间上的积分值。
3. 凑微分法:当被积函数可以通过凑微分的方式转化为已知函数的微分形式时,可以利用凑微分法进行计算。
凑微分法的关键是找到合适的凑微分项,使得被积函数可以表示为一个函数的微分。
例如,对于∫x^2dx,可以将其转化为∫(x^2+1-1)dx,然后利用积分性质计算。
二、换元积分法换元积分法是一种常用的定积分计算方法,通过引入新的变量进行替换,将原来的积分转化为更容易计算的形式。
换元积分法的关键是选择合适的换元变量和适当的换元公式。
1. 一般换元法:当被积函数中存在形如f(g(x))g'(x)的部分时,可以选择g(x)作为新的变量进行替换。
然后利用链式法则计算新的微分形式,将原来的积分转化为新变量的积分。
2. 三角换元法:当被积函数中存在形如sin(x)或cos(x)等三角函数时,可以选择三角函数的反函数作为新的变量进行替换。
然后利用三角函数的导数和反函数的导数计算新的微分形式,将原来的积分转化为新变量的积分。
三、分部积分法分部积分法是一种常用的定积分计算方法,通过将积分中的乘积拆解为两个函数的乘积,利用分部积分公式进行计算。
分部积分法的关键是选择合适的分部函数和求导函数。
分部积分公式为∫u(x)v'(x)dx=u(x)v(x)-∫v(x)u'(x)dx。
C语言常用算法集合

1.定积分近似计算:/*梯形法*/double integral(double a,double b,long n) { long i;double s,h,x;h=(b-a)/n;s=h*(f(a)+f(b))/2;x=a;for(i=1;i<n;i++){x+=h;s+=h*f(x) ;}return(s);}/*矩形法*/double integral(double a,double b,long n) { long i;double t=0,h,x;h=(b-a)/n;x=a;for(i=0;i<n;i++){t+=h*f(x);x+=h;}return(t);}2. 生成斐波那契数列:/*直接计算*/int fib(int n){ int i,f1=1,f2=1,f;for(i=3;i<=n;i++){f=f1+f2;f1=f2;f2=f;}if(n==1||n==2) return 1;else return f;}/*递归调用*/void fib(int n,int*s){ int f1,f2;if(n==1||n==2) *s=1;else{ fib(n-1,&f1);fib(n-2,&f2);*s=f1+f2;}}3.素数的判断:/*方法一*/for (t=1,i=2;i<n; i++)if(n%i==0) t=0;if(t) printf("%d is prime",n);/*方法二*/for (t=1,i=2;i<n&&t; i++)if(n%i==0) t=0;if(t) printf("%d is prime",n);/*方法三*/for (i=2;i<n; i++)if(n%i==0) break;if(i==n) printf("%d is prime",n); /*方法四*/for(t=1,i=2; i<=(int)sqrt(n); i++)if(n%i==0){t=0;break;}if(t) printf("%d is prime",n);4.反序数:/*求反序数*/long fan(long n){ long k;for(k=0;n>0;n/=10)k=10*k+n%10;return k;}/*求回文数*/int f(long n){ long k,m=n;for(k=0;n>0;n/=10)k=10*k+n%10;if(m==k) return 1;return 0;}/*求整数位数*/int f(long n){ int count;for(count=0;n>0;n/=10)count++;return count;}5.求最大公约数:/*方法一*/int gcd(int x,int y){ int z;z=x<y?x:y;while(!(x%z==0&&y%z==0))/*x%z||y%z*/ z--;return z;}/*方法二*/int gcd(int x,int y){int r;while((r=x%y)!=0){x=y;y=r;}return y;}/*方法三*/int gcd(int a ,int b){ int r ;if((r=a%b)==0)return b;elsereturn gcd(b,r);}6.数组常用算法:查找:/*线性查找*/int find(int num,int x[],int key){ int i,m=-1;for(i=0;i<num;i++)if(x[i]==key){m=i;break;}return m;}/*折半查找*/int find(int x[],int num,int key){ int m=-1,low=0,high=num-1,mid;while(low<=high){mid=(low+high)/2;if(x[mid]==key){m=mid;break;}else if(x[mid]>key) high=mid-1;else low=mid+1;}return m;}/*折半查找(递归)*/int b_search(int x[ ],int low,int high,int key) {int mid;mid=(low+high)/2;if(x[mid]==key) return mid;if(low>=high) return -1;else if(key<x[mid])return b_search(x,low,mid-1,key);elsereturn b_search(x,mid+1,high,key); }/*寻找子串*/int find(char *s1,char *s2){ int i,k=0;while(s1[i]==s2[i]) i++;if(s2[i]==0) return k;s1++;k++;return -1;}分词:/*方法一*/void fen(char s[][10],char str){ int i,j,k;for(i=0,j=0,k=0;str[i]!=0;i++)if(isalpha(a[i]))s[j][k++]=str[i];else {s[j][k]=0;k=0;j++;}}}/*方法二*/#include<stdio.h>#include<string.h>void main(){ int i=0,n=0;char s[80],*p;strcpy(s,"It is a book.");for(p=s;p!='\0';p++)if(*p=='')i=0;elseif(i==0){n++;i=1;}printf("%d\n",n);getch();}排序:/*插入法排序*/void sort(int a[],int n){ int i,j,t;for(i=1;i<n;i++){t=a[i];for(j=i-1;j>=0&&t<a[j];j--)a[j+1]=a[j];a[j]=t;}}/*归并排序*/#define x 10#define y 10void com(int *a,int *b,int *c){ int i,j,k;for(i=0,j=0,k=0;i<=x&&j<=y;){if(a[i]<b[j]){c[k++]=a[i];i++;}else{c[k++]=b[j];j++;}}if(i<x) for(k=k-1;i<x;i++)c[k++]=a[i];if(j<x) for(k=k-1;j<y;j++)c[k++]=a[j]; }/*交换法排序1 冒泡排序*/void sort(int a[],int n){ int i,j,t,flag;for(i=0;i<n-1;i++){flag=1;for(j=0;j<n-1-i;j++)if(a[j]>a[j+1]){t=a[j];a[j]=a[j+1];a[j+1]=t;flag=0;}if(flag) break;}}/*交换法排序2*/void sort(int a[],int n){ int i,j,t;for(i=0;i<n-1;i++)for(j=i+1;j<n;j++)if(a[i]>a[j]){t=a[i];a[i]=a[j];a[j]=t;}}/*选择法排序*/void sort(int a[],int n){ int i,j,point,t;for(i=0;i<n-1;i++){point=i;for(j=i+1;j<n;j++)if(a[point]<a[j]) point=j;if(point!=i){t=a[point];a[point]=a[i];a[i]=t;}}}7.一元非线性方程求根:/*牛顿迭代法求函数跟*/#include <stdio.h>#include <math.h>int main(void){ double x,x1,eps=1e-6,f,f1; /*误差为eps*/x=1.0; /*x=1.0是初值*/do{x1=x;f=6-x1*(5-x1*(4-3*x1)); /*f为f(x)函数*/f1=-5+x1*(8-9*x1); /*f1为f(x)的导函数*/x=x1-f/f1;f=6-x*(5-x*(4-3*x));}while(fabs(f)>=eps &&fabs(x-x1)>=eps);printf("x=%f",x);}/*二分法求函数跟*/#include <stdio.h>#include <math.h>double f(double x){ return 6-x*(5-x*(4-3*x)); /*f(x)函数*/}int main(void){ double a,b,c,x,eps=1e-6;do{scanf("%lf%lf",&a,&b);}while(f(a)*f(b)>0);if(fabs(f(a))<1e-6)x=a;else if (fabs(f(b))<1e-6)x=b;else {c=(b+a)/2;while(fabs(f(c))>eps&&fabs(b-a)>eps){if(f(a)*f(c)<0)b=c;elsea=c;c=(b+a)/2;}x=c;}printf("x=%f",x);}/*弦截法求函数跟*/c=(a*f(b)-b*f(a))/ (f(b)-f(a));while(fabs(f(c))>eps){if(f(a)*f(c)<0)b=c;elsea=c;c=(a*f(b)-b*f(a))/ (f(b)-f(a));}#include <stdio.h>void f();int main(void){ int x, loop=0;do{for(x=1;x<5;x++) {int x=2;printf("%d",x);}printf("%d ",x);f();loop++;}while(loop<1);getch();}void f(){ printf("%d",x++); }8.汉诺塔:#include<stdio.h>void Hanoi(int n, char A, char B, char C){if(n==1)printf("\n move %d from %c to %c",n,A,C);else{Hanoi(n-1,A,C,B);printf("\nmove %d from %c to %c",n,A,C);Hanoi(n-1,B, A, C);}}int main(void){ Hanoi(3,'A','B','C');getch();}9.建立链表:NODE *creat(void) /* void表示无参函数*/{NODE *head=NULL,*p1=NULL,*p2=NULL;long num;unsigned score;int n=0;do{scanf(“%ld%u”,&num,&score);if(num==0) break;n++;p1=(NODE *)malloc(sizeof(NODE));p1->data.num=num,p1->data.score=score;p1->next=NULL;if(n==1)head=p2=p1;else{p2->next=p1;p2=p1;}}while(1);return head;}10.级数的近似计算:#include <stdio.h>#include <math.h>int main(void){ double s=1,a=1,x,eps,f;int n,m;printf("input x and eps:");scanf ("%lf%lf",&x,&eps);for(n=1;fabs(a)>eps; n++){for(f=1,m=1;m<=n;m++)f*=m;a=pow(x,n)/f;s+=a;}printf("%f",s);}。
C语言用六种方法求定积分

C语言用六种方法求定积分C语言中求定积分的方法主要有以下六种:基本公式法、数值积分法、Laplace变换法、微积分概念法、数值积分法和Monte Carlo方法。
下面将详细介绍每种方法的原理和实现。
1.基本公式法:基本公式法是求解定积分的最基本方法,根据不同函数的特点和性质,利用已知的积分公式进行求解。
例如,对于一次函数和常数函数,可以使用基本公式法求解。
2.数值积分法:数值积分法是通过将定积分转化为数值计算问题来求解。
常用的数值积分方法有矩形法、梯形法和辛普森法等。
这些方法基于将求积分区间分割成若干个小区间,然后在每个小区间上近似计算出函数的积分值,再将这些积分值加总得到最终结果。
3. Laplace变换法:Laplace变换法是一种利用Laplace变换求解微分方程的方法,也可以用来求解定积分。
通过将被积函数进行Laplace变换,然后利用Laplace变换公式求解积分,最后再求出反变换得到结果。
4.微积分概念法:微积分概念法是通过将定积分定义为函数曲线下的面积来求解。
具体做法是将被积函数图像与坐标轴围成的面积分为若干个小的矩形、梯形或曲线段以及一个小的区域。
然后根据图形的几何性质进行近似计算,将这些小面积相加得到最终结果。
5.数值积分法:数值积分法也是一种基于数值计算的方法,但与前面提到的数值积分法不同,它通过构造一系列特定形式的插值函数对被积函数进行逼近,然后计算插值函数的积分值来近似求解定积分。
常用的数值积分法有牛顿-科特斯公式和高斯-勒让德公式。
6. Monte Carlo方法:Monte Carlo方法是一种基于统计随机性的数值积分方法,它通过随机抽样来进行数值求解。
具体做法是在被积函数图像下随机抽取一系列点,根据这些随机点的坐标和函数值来估计函数的积分值。
通过对多次随机抽样的结果取平均可以得到定积分的近似值。
以上六种方法都可以用C语言来实现,具体的实现方法可以根据具体问题的特点和要求选择合适的算法和数据结构,然后编写相应的代码实现。
C语言实现定积分求解方法

C语言实现定积分求解方法C语言可以通过数值积分的方法来实现定积分的求解,主要有矩形法、梯形法和辛普森法等几种常见的求解方法。
矩形法是最简单的一种数值积分方法,它将定积分区间等分成若干个小区间,然后在每个小区间上取一个点,将积分区间分成若干个小矩形,对每个小矩形的面积进行求和,即可得到近似的定积分值。
以下是使用矩形法实现定积分求解的C语言代码:```c#include<stdio.h>#include<math.h>double f(double x)//定义需要求解的函数return sqrt(1-x*x);double integrate(double a, double b, int n)//a:积分下限,b:积分上限,n:划分的矩形个数double dx = (b-a)/n; // 求解每个小矩形的宽度double sum = 0.0; // 求和变量int i;for(i=0; i<n; i++)double x = a + i*dx + dx/2; // 计算每个小矩形的横坐标中点sum += f(x)*dx; // 计算每个小矩形的面积并求和}return sum;int maindouble a = 0.0; // 积分下限double b = 1.0; // 积分上限int n = 1000; // 划分的矩形个数double result = integrate(a, b, n); // 求解定积分printf("The definite integral is: %.6f\n", result);return 0;```梯形法是一种比矩形法更精确的数值积分方法,它将积分区间等分成若干个小区间,然后将每个小区间上的函数图像近似为一个梯形,对每个梯形的面积进行求和,即可得到近似的定积分值。
以下是使用梯形法实现定积分求解的C语言代码:```c#include<stdio.h>#include<math.h>double f(double x)//定义需要求解的函数return sqrt(1-x*x);double integrate(double a, double b, int n)//a:积分下限,b:积分上限,n:划分的梯形个数double dx = (b-a)/n; // 求解每个小梯形的底边宽度double sum = 0.0; // 求和变量int i;for(i=0; i<n; i++)double x1 = a + i*dx; // 计算每个小梯形的左边横坐标double x2 = a + (i+1)*dx; // 计算每个小梯形的右边横坐标sum += (f(x1)+f(x2))*dx/2; // 计算每个小梯形的面积并求和}return sum;int maindouble a = 0.0; // 积分下限double b = 1.0; // 积分上限int n = 1000; // 划分的梯形个数double result = integrate(a, b, n); // 求解定积分printf("The definite integral is: %.6f\n", result);return 0;```辛普森法是一种更为精确的数值积分方法,它将积分区间等分成若干个小区间,然后在每个小区间上使用二次多项式来逼近积分函数的曲线,对每个小区间的积分值进行加权求和,即可得到近似的定积分值。
矩形法求函数的定积分

用矩形法求函数的定积分(C 语言实现)
在本程序中,先分别定义了 5 个 C 函数 f1、f2、f3、f4、f5,用来代表 5 个不同的函数。然后 定义了一个求定积分的函数 integral。现在介绍矩形法求函数定积分的数学思想。
设函数 在区间[a,b]上连续,在(a,b)上可导,将[a,b]之间的长度等分成 n 份(n 越大计算越精 确)。于是第 块小矩形的面积为 ,
printf("%lf\n",S[j]); } }
运行结果如图所示:
可以发现,计算值与理论值十分接近,当 N 取的足够大时,可以获得十分精确的值,但是运算 次数也会增加,本函数的时间复杂度为 O(n)。
从指针的用法上来讲,本程序使用了“指向函数的指针”。一个函数的函数名,代表了这个函 数的首地址,在主函数中,5 次调用 integral 函数,实现了对 5 个不同的函数求积分。integral 函 数包含了三个参数,前两个参数表示被积函数的上下限。
sum=sum+d*(*fun)(a+i*d);//定积分近似计算公式 }//fun 是指向函数的指针,该指针所指向的函数带有一个 double 型的形参, //同时,该函数的返回值类型为 double return sum; }
2
C 语言在计算中的应用
void main() {
double S[5]; int j; S[0]=integral(0,1,f1);//fun 指向 f1 S[1]=integral(0,1,f2);//fun 指向 f2 S[2]=integral(0,1,f3);//fun 指向 f3 S[3]=integral(0,1,f4);//fun 指向 f4 S[4]=integral(0,1,f5);//fun 指向 f5 printf("输出各个函数的积分值:\n"); for(j=0;j<5;j++) {
定积分计算方法总结

定积分计算方法总结定积分是微积分中的一个重要概念,用于计算曲线与坐标轴之间的面积、曲线长度、质量、动量等问题。
本文将总结几种常见的定积分计算方法。
1.基本积分法:也称为不定积分法,是定积分的基础。
通过求导的逆过程,可以将一些简单的函数反求积分。
例如,对于常数函数、幂函数、指数函数、三角函数等,都可以直接得到不定积分的表达式。
但对于复杂函数,基本积分法可能不适用。
2. 牛顿-莱布尼茨公式:也称为换元积分法。
该方法通过引入新的变量,将原积分转化为更简单的形式。
常见的换元变量有正弦函数、指数函数、幂函数等。
换元积分法的关键在于选择合适的换元变量,使得被积函数的形式变得更简单。
例如,对于∫sin(2x)dx,可以通过令u=2x进行换元,得到新的积分∫sin(u)du,再求解即可。
3. 分部积分法:也称为乘法积分法,是对乘积形式的积分进行处理的方法。
通过对乘积函数中的一个函数求导,另一个函数积分,可以将原积分转化为更简单的形式。
分部积分法的公式为∫udv=uv-∫vdu,其中u和v是可以求导或积分的函数。
该方法适用于许多复杂函数的积分计算,例如多项式函数与指数函数的积分。
4. 凑微分法:也称为凑常数法,是对积分式进行代换,使得被积函数的微分形式展开后更简单,从而进行积分的方法。
例如,对于∫x/(1+x^2)dx,可以通过令u=1+x^2进行代换,得到新的积分∫(1/u)du,再求解即可。
5. 变限积分法:该方法常用于计算曲线与坐标轴之间的面积。
当被积函数为连续函数时,可以通过使用反函数求解,将定积分转化为一系列不定积分的差值。
例如,对于求解曲线y=f(x)与x轴所围成的面积,可以将其表示为∫[a,b]f(x)dx=[F(x)]a^b,其中F(x)是f(x)的原函数。
通过求F(x)的反函数,可以将定积分简化为计算两个不定积分的差值。
6. 参数方程法:该方法适用于计算平面曲线围成的面积。
当曲线由参数方程给出时,可以通过将x或y表示为参数的函数,进而将面积转化为定积分的形式。
C语言实现定积分求解方法

C语⾔实现定积分求解⽅法求定积分的⽅法有很多种,下⾯是我总结的⼏种⽐较常⽤的⽅法。
#include <stdio.h>#include <stdlib.h>#include <math.h>#include <time.h>#define N 3double fun(double x){double y;y = sqrt(4-(x)*(x));//y = sin(x);return y;}/*随机点法求定积分*/double Darts(int n){double x, y;time_t t;int i = 0;int count = 0;srand((unsigned)time(&t));for (i=0; i<n; i++){x = rand()%100/100.0;y = rand()%100/100.0;if (y <= 1-pow(x,2)){count++;}}return (double)count/(double)n;}/*左矩形法求定积分*/double LeftRect(double down, double up, int n){double h, s;int i;/*计算步长*/h = (up-down)/n;s = fun(down)*h;for (i=1; i<n; i++){s = s + fun(down+i*h)*h;}return s;}/*梯形公式求定积分*/double Trape(double down, double up, int n){double h, s;int i = 0;/*计算步长*/h = (up-down)/n;s = 0.5*(fun(down)+fun(down+h))*h;for (i=1; i<n; i++){s = s + 0.5 * (fun(down+i*h) + fun(down+(i+1)*h))*h;}return s;}/*复合梯形公式*/double T(double x, double y, int z){double h, Tn;int i = 0;h = (y-x)/z;Tn = (fun(x)+fun(y))/2;for (i=0; i<z; i++){Tn = Tn+fun(x+i*h);}Tn = Tn*h;return Tn;}/*⾟普⽣公式求定积分,公式为:S[n]=(4*T[2*n]-T[n])/3,其中T[2n],T[n]为梯形公式计算结果*/ double Simposn(double down, double up, int n){double s;/*⾟普⽣公式*/s = (4*T(down, up, 2*n) - T(down, up, n))/3;return s;}/*⾼斯公式求定积分*/double Gass(double (*func)(double x), double a, double b, int n){int i = 0;//⾼斯点及其求积系数列表float x1[1]={0.0};float A1[1]={2};float x2[2]={-0.5573503,0.5573503};float A2[2]={1,1};float x3[3]={-0.7745967,0.0,0.7745967};float A3[3]={0.555556,0.888889,0.555556};float x4[4]={0.3399810,-0.3399810,0.8611363,-0.8611363};float A4[4]={0.6521452,0.6521452,0.3478548,0.3478548};float x5[5]={0.0,0.5384693,-0.5384693,0.9061799,-0.9061799};float A5[5]={0.5688889,0.4786287,0.4786287,0.2369269,0.2369269};float *p, *t;switch (n){case 1:p = x1;t = A1;break;case 2:p = x2;t = A2;break;case 3:p = x3;t = A3;break;case 4:p = x4;t = A4;break;case 5:p = x5;t = A5;break;default :printf("intput wrong!");}float g = 0;for (i=0; i<n; i++){g += (*func)((b-a)*p[i]/2+(a+b)/2)*t[i];}g *= (b-a)/2;return g;}int main(int argc, char *argv[]){printf("随机点法积分值%f\n", Darts(10000)); double down, up;int n;double sum = 0;printf("积分下限:\n");scanf("%lf", &down);printf("积分上限:\n");scanf("%lf", &up);printf("分隔数⽬:\n");scanf("%d", &n);sum = LeftRect(down, up, n);printf("左矩形法积分值为:%f\n", sum);sum = Trape(down, up, n);printf("梯形公式积分值为:%f\n", sum);sum = Simposn(down, up, n);printf("⾟普⽣公式积分值为:%f\n", sum);sum = Gass(fun, down, up, N);printf("⾼斯公式积分值为:%f\n", sum);return 0;}。
C语言使用矩形法求定积分的通用函数
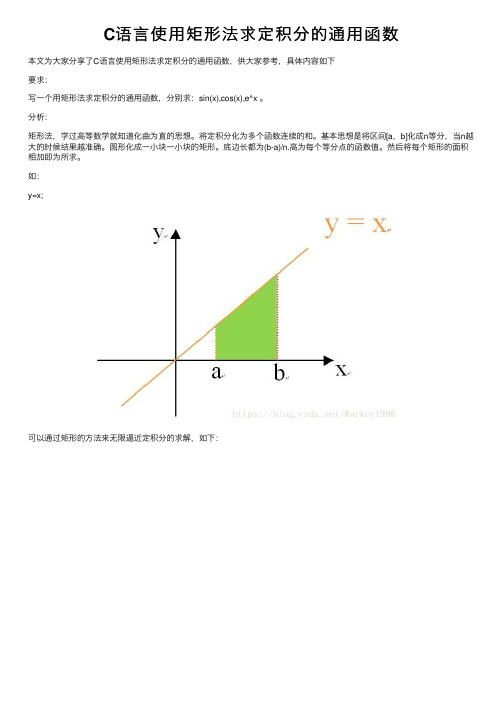
C语⾔使⽤矩形法求定积分的通⽤函数本⽂为⼤家分享了C语⾔使⽤矩形法求定积分的通⽤函数,供⼤家参考,具体内容如下要求:写⼀个⽤矩形法求定积分的通⽤函数,分别求:sin(x),cos(x),e^x 。
分析:矩形法,学过⾼等数学就知道化曲为直的思想。
将定积分化为多个函数连续的和。
基本思想是将区间[a,b]化成n等分,当n越⼤的时候结果越准确。
图形化成⼀⼩块⼀⼩块的矩形。
底边长都为(b-a)/n.⾼为每个等分点的函数值。
然后将每个矩形的⾯积相加即为所求。
如:y=x;可以通过矩形的⽅法来⽆限逼近定积分的求解,如下:因为被分成n等分,就可以认为每⼀等分是⼀个矩形,那么每⼀矩形的⾯积为:每⼀个矩形⾯积为:***Sn=f(x)(b-a)/n 总⾯积为:****S=S1+S2+…+Sn#include <stdio.h>#include <stdlib.h>#include <math.h>//引⼊sin x,cos x,e^x的库//使⽤指向函数的指针变量来复⽤⼀个通⽤函数int main(){int i,j,k,n,m;float res;float (*fun)(float);//定义指向函数的指针变量float integral (float a,float b,float (*fun)(float),int n);//n为将积分区间(b-a)分成n等分,当n的值越⼤的时候结果越精确,数学上的定义是取⽆穷⼤float fsin(float);//sin x函数的声明float fcos(float);//cos x函数的声明float fexp(float);//e^x 函数的声明printf ("请输⼊积分的下限\n");scanf ("%d",&m);printf ("请输⼊积分的上限\n");scanf ("%d",&n);printf("请输⼊你要计算的函数的具体函数\n");printf("1.sin(x) 2.cos(x) 3.e^x\n");scanf ("%d",&i);switch(i){case 1:fun=fsin;//函数地址(⼊⼝)交给指针变量,灵活性强break;case 2:fun=fcos;break;case 3:fun=fexp;}res=(fun)(2.00);//printf("xxxx=%f\n",res);printf ("计算的结果为\n");res=integral(m,n,fun,200000);printf("res=%f",res);return 0;}float fsin(float x){// printf("fsinx=%f\n",x);return sin(x);}float fcos(float x){//printf("fcosx=%f\n",x);return cos(x);}float fexp(float x){//getchar();//printf("fexp=%f\n",x);return exp(x);}float integral(float a,float b,float (*fun)(float),int n){//矩形法计算,定积分转换为连续求和的形式int i=0;float x=a,s=0;float h=(b-a)/n;for (i=1;i<=n;i++){x=x+h;s=s+((*fun)(x)*h);}return s;}结果:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C语言实验报告求定积分班级10信息与计算科学一班姓名戴良伟学号 211.描述问题 利用①左矩形公式,②中矩形公式,③右矩形公式 ,④梯形公式,⑤simpson 公式,⑥Gauss 积分公式求解定积分。
2. 分析问题定积分定积分的定义定积分就是求函数()f x 在区间[],a b 中图线下包围的面积。
即()0,,,y x a x b y f x ====所包围的面积。
这个图形称为曲边梯形,特例是曲边梯形。
如下图:(图1)设一元函数()y f x =,在区间[],a b 内有定义。
将区间[],a b 分成n 个小区间[][][][]00112,,,,,......,i a x x x x x x b 。
设1i i i x x x -∆=-,取区间i x ∆中曲线上任意一点记做()i f ξ,作和式:()1lim n n i f i xi ξ→+∞=⎛⎫∆ ⎪⎝⎭∑ 若记λ为这些小区间中的最长者。
当0λ→时,若此和式的极限存在,则称这个和式是函数()f x 在区间[],a b 上的定积分。
记作:()ba f x dx ⎰ 其中称a 为积分下限,b 为积分上限,()f x 为被积函数,()f x dx 为被积式,∫ 为积分号。
之所以称其为定积分,是因为它积分后得出的值是确定的,是一个数,而不是一个函数。
定积分的几何意义[1]它是介于x 轴、函数f(x)的图形及两条直线x=a ,x=b 之间的各个部分面积的代数和。
在x 轴上方的面积取正号;在x 轴下方的面积取负号。
如图言实现定积分计算的算法利用复合梯形公式实现定积分的计算假设被积函数为()f x ,积分区间为[],a b ,把区间[],a b 等分成n 个小区间,各个区间的长度为h ,即()/h b a n =-,称之为“步长”。
根据定积分的定义及几何意义,定积分就是求函数()f x 在区间[],a b 中图线下包围的面积。
将积分区间n 等分,各子区间的面积近似等于梯形的面积,面积的计算运用梯形公式求解,再累加各区间的面积,所得的和近似等于被积函数的积分值,n 越大,所得结果越精确。
以上就是利用复合梯形公式实现定积分的计算的算法思想。
复合梯形公式:()()()1122n n i i h T f a f x f b -=⎛⎫=++ ⎪⎝⎭∑[2] 具体算法如下:算法一1:输入积分区间的端点值a 和b ;2:输入区间的等分个数n (要求n 尽可能大,以保证程序运行结果有较高的精确度);3:计算步长()/h b a n =-;4:对累加和赋初值()/2a b T f f =-;5:计算累加和()11n i i T f x -==∑6:算出积分值n T T h =⨯;7:输出积分近似值n T ,完毕。
1.2.2利用Smpson 公式实现定积分的计算假设被积函数为()f x ,积分区间为[],a b ,把区间[],a b 等分成n 个小区间,各个区间的长度为h 。
在复合梯形公式的基础上,构造出一种加速计算积分的方法。
作为一种外推算法, 它在不增加计算量的前提下提高了误差的精度。
具体算法如下:算法二1:输入积分上限b 和下限a ;2:输入区间的等分个数n (要求n 尽可能大,以保证程序运行结果有较高的精确度);3:利用辛甫生公式:[][][]()42/3S n T n T n =⨯-[2],实现对定积分的求解(其中[]2T n ,[]T n 均为梯形公式计算所得的结果,由此可见辛甫生公式是以梯形公式为基础的);4:算出积分值S n ;5:输出积分近似值S,完毕。
n利用Guass公式实现定积分计算Guass型求积公式是构造高精度差值积分的最好方法之一。
他是通过让节点和积分系数待定让函数f(x)以此取i=0,1,2....n次多项式使其尽可能多的能够精确成立来求出积分节点和积分系数。
高斯积分的代数精度是2n-1,而且是最高的。
通常运用的是-1---+1的积分节点和积分系数,其他积分域是通过变换x=(b-a)t/2 +(a+b)/2 变换到-1到1之间积分。
算法三1:输入积分上限b和下限a;2:利用Guass公式,求定积分;4:算出积分值Sn5:输出积分近似值S,完毕。
n3.程序的编写程序一(左矩形公式)源程序#include<>#include<>void main(){double f(double x);/*f(x)为函数举例,即被积函数*/int i,n;/*n为区间等分的个数,应尽可能大*/double a,b,h,s;/*a为积分下限,b为积分上限,h为步长*/printf("积分下限 a:\n");scanf("%lf",&a);printf("积分上限 b:\n");scanf("%lf",&b);printf("区间等分个数 n :\n");scanf("%d",&n);h=(b-a)/n; /*步长的计算*/s=f(a)*h;for(i=1;i<n;i++){s=s+f(a+i*h)*h;}printf("函数 f(x) 的积分值为 s=%\n",s);}/*以下为被积函数的定义,即函数举例*/ double f(double x){double y;y=sqrt(4-x*x);return (y);}程序一的编译运行被积函数为f(x)=sqrt4-(x*x)的情况先编译,再运行,屏幕显示及操作如下:输入0+回车输入2+回车输入1000+回车程序二(中矩形公式)源程序#include<>#include<>void main(){double f(double x);/*f(x)为函数举例,即被积函数*/int i,n;/*n为区间等分的个数,应尽可能大*/ double a,b,h,s;/*a为积分下限,b为积分上限,h为步长*/ printf("积分下限 a:\n");scanf("%lf",&a);printf("积分上限 b:\n");scanf("%lf",&b);printf("区间等分个数 n :\n");scanf("%d",&n);h=(b-a)/n; /*步长的计算*/s=*(f(a)+f(a+h))*h;for(i=1;i<n;i++){s=s+*(f(a+i*h)+f(a+(i+1)*h))*h;}printf("函数 f(x) 的积分值为 s=%\n",s); }/*以下为被积函数的定义,即函数举例*/ double f(double x){double y;y=sqrt(4-x*x);return (y);}程序二的编译运行被积函数为f(x)=sqrt4-(x*x)的情况先编译,再运行,屏幕显示及操作如下:输入0+回车输入2+回车输入1000+回车程序三(右矩形公式)源程序#include<>#include<>void main(){double f(double x);/*f(x)为函数举例,即被积函数*/int i,n;/*n为区间等分的个数,应尽可能大*/ double a,b,h,s;/*a为积分下限,b为积分上限,h为步长*/ printf("积分下限 a:\n");scanf("%lf",&a);printf("积分上限 b:\n");scanf("%lf",&b);printf("区间等分个数 n :\n");scanf("%d",&n);h=(b-a)/n; /*步长的计算*/s=f(a+h)*h;for(i=1;i<n-1;i++){s=s+f(a+(i+1*h))*h;}printf("函数 f(x) 的积分值为 s=%\n",s); }/*以下为被积函数的定义,即函数举例*/ double f(double x){double y;y=sqrt(4-x*x);return (y);}程序三的编译运行被积函数为f(x)=sqrt4-(x*x)的情况先编译,再运行,屏幕显示及操作如下:输入0+回车输入2+回车输入1000+回车程序四(梯形公式)源程序#include<>#include<>void main(){double f(double x);/*f(x)为函数举例,即被积函数*/int i,n;/*n为区间等分的个数,应尽可能大*/ double a,b,h,s;/*a为积分下限,b为积分上限,h为步长*/ printf("积分下限 a:\n");scanf("%lf",&a);printf("积分上限 b:\n");scanf("%lf",&b);printf("区间等分个数 n :\n");scanf("%d",&n);h=(b-a)/n; /*步长的计算*/s=*(f(a)+f(a+h))*h;for(i=1;i<n;i++){s=s+*(f(a+i*h)+f(a+(i+1)*h))*h;}printf("函数 f(x) 的积分值为 s=%\n",s); }/*以下为被积函数的定义,即函数举例*/ double f(double x){double y;y=sqrt(4-x*x);return (y);}程序四的编译运行被积函数为f(x)=sqrt4-(x*x)的情况先编译,再运行,屏幕显示及操作如下:输入0+回车输入2+回车输入1000+回车程序五(Simpson公式)源程序#include<>#include<>void main(){double T(double x,double y,int z); double a,b,s;int n;printf("积分下限 a:\n");scanf("%lf",&a);printf("积分上限 b:\n");scanf("%lf",&b);printf("区间等分个数 n :\n");scanf("%d",&n);s=(4*T(a,b,2*n)-T(a,b,n))/3;/*利用辛甫生公式求解定积分*/printf("函数 f(x) 的积分值为 s=%f\n",s);/*以下为复合梯形公式的定义*/double T(double x,double y,int z) {double h,Tn;int i;double f(double t);h=(y-x)/z;Tn=(f(x)+f(y))/2;for(i=1;i<z;i++)Tn=Tn+f(x+i*h);Tn=Tn*h;return (Tn);}/*以下为被积函数的定义,即函数举例*/ double f(double t){double s;s=sqrt(4-t*t);return (s);}程序四的编译运行被积函数为f(x)=sqrt4-(x*x)的情况先编译,再运行,屏幕显示及操作如下:输入0+回车输入2+回车输入1000+回车程序六(Guass公式)源程序#include <>#include <>#define N 3float gass_integral(float (*)(float),float,float,int); void main(){float function_name(float);float a,b;printf("请输入积分上限b\n");scanf("%f",&b);printf("请输入积分下限a\n");scanf("%f",&a);float ans;ans=gass_integral(function_name,a,b,N);printf("ans=%f",ans);}-1---+1 之间float gass_integral(float (*func)(float x), float a,float b ,int n ){左矩形公式误差:%,中矩形公式误差:%,右矩形公式误差:%,梯形公式误差:%,辛普森公式和高斯公式误差几乎等于0,六个程序运行结果对比,在计算相同的函数f(x)=sqrt(4-x*x)的定积分,Simpson公式和Guass公式比矩形和梯形公式更可行,更有效。
