实验六_非线性方程求解
雅各比迭代实验报告(3篇)

第1篇一、实验目的1. 理解雅各比迭代法的原理和应用。
2. 掌握雅各比迭代法的计算步骤和实现方法。
3. 通过实验验证雅各比迭代法在求解线性方程组中的有效性和收敛性。
二、实验原理雅各比迭代法是一种求解线性方程组的迭代方法。
对于形如Ax=b的线性方程组,其中A是n×n的系数矩阵,x是n维未知向量,b是n维常数向量,雅各比迭代法的基本思想是将方程组Ax=b转化为一系列的简单方程进行迭代求解。
设A为对角占优矩阵,则雅各比迭代法的迭代公式为:x_{k+1} = (D - L)^{-1}(b - Ux_k)其中,D是A的对角矩阵,L是A的非对角元素中下三角矩阵,U是A的非对角元素中上三角矩阵。
三、实验内容1. 准备实验环境:安装MATLAB软件,创建实验文件夹。
2. 编写实验程序:(1)定义系数矩阵A和常数向量b。
(2)计算对角矩阵D、下三角矩阵L和上三角矩阵U。
(3)初始化迭代变量x_0。
(4)设置迭代次数N和容许误差ε。
(5)进行雅各比迭代计算,并输出每一步的迭代结果。
(6)判断迭代是否收敛,若收敛则输出最终结果,否则输出未收敛信息。
3. 运行实验程序,观察迭代过程和结果。
四、实验步骤1. 创建实验文件夹,打开MATLAB软件。
2. 编写实验程序,保存为“雅各比迭代法实验.m”。
3. 运行实验程序,观察迭代过程和结果。
4. 分析实验结果,验证雅各比迭代法的有效性和收敛性。
五、实验结果与分析1. 运行实验程序,得到以下迭代过程和结果:迭代次数 | 迭代结果---------|---------1 | x_1 = [0.3333, 0.3333]2 | x_2 = [0.3333, 0.3333]3 | x_3 = [0.3333, 0.3333]...N | x_N = [0.3333, 0.3333]2. 分析实验结果:(1)从实验结果可以看出,雅各比迭代法在求解线性方程组时,经过有限次迭代即可收敛。
2020数学实验任务书
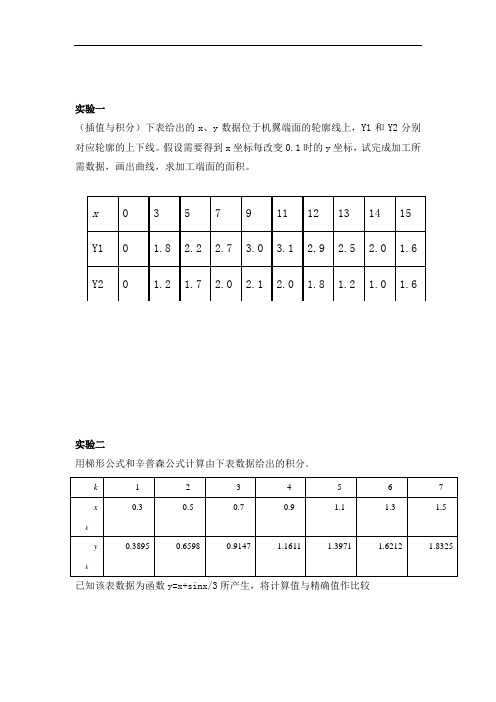
实验一(插值与积分)下表给出的x、y数据位于机翼端面的轮廓线上,Y1和Y2分别对应轮廓的上下线。
假设需要得到x坐标每改变0.1时的y坐标,试完成加工所需数据,画出曲线,求加工端面的面积。
实验二用梯形公式和辛普森公式计算由下表数据给出的积分。
已知该表数据为函数y=x+sinx/3所产生,将计算值与精确值作比较实验三(优化)用matlab 或lingo 求解该问题∑==91i ix Z Min254321≥++++x x x x x 398653≥++++x x x x x29764≥+++x x x x02215≤--x x x076≤-x x058≤-x x02219≤--x x x02213≤--x x x实验四(非线性方程求解)(1)小张夫妇以按揭方式贷款买了一套价值20万的房子,首付了5万元,没有还款1000元,15年还清。
问贷款利率是多少?(2)某人与贷款50万元购房,他咨询了两家银行,第一家银行开出的条件是每月还4500元,15年还清;第二家银行开出的条件是每年还45000元,20年还清。
从利率方面看,那家银行较优惠(简单的假设年利率=月利率*12)?74≤-x x实验五(优化)某厂向用户提供发动机,合同规定,第一,二,三季度分别交货40,60,80台,每季生产费用为分f(x)=ax+bx^2,交货后有剩余,可下季交货,每台每季储存费c元,每季最大生产能力100台,第一季度没有存货,设a=50,b=0.2,c=4,问如何安排生产使总费用最小,并讨论a,b,c的影响,作出合理解释。
实验六(回归分析)矿脉有13个相邻样本点,人为地设定一原点,现测得各样本点对原点的距离x,与该样本点处某种金属含量y的一组数据如下,画出散点图观察二者的关系,试建立合适的回归模型,如二次曲线、双曲线、对数曲线等。
实验五(线性方程组的数值解法和非线性方程求解)

1大学数学实验 实验报告 | 2014/4/5一、 实验目的1、学习用Matlab 软件数值求解线性代数方程组,对迭代法的收敛性和解的稳定性作初步分析;2、通过实例学习用线性代数方程组解决简化问题。
二、 实验内容项目一:种群的繁殖与稳定收获:种群的数量因繁殖而增加,因自然死亡而减少,对于人工饲养的种群(比如家畜)而言,为了保证稳定的收获,各个年龄的种群数量应维持不变。
种群因雌性个体的繁殖而改变,为方便起见以下种群数量均指其中的雌性。
种群年龄记作k=1,2,…,n ,当年年龄k 的种群数量记作x k ,繁殖率记作b k (每个雌性个体1年的繁殖的数量),自然存活率记作s k (s k =1−d k ,d k 为1年的死亡率),收获量记作ℎk ,则来年年龄k 的种群数量x ̌k 应该为x ̌k =∑b k n k=1x k , x ̌k+1=s k x k −ℎk , (k=1,2,…,n -1)。
要求各个年龄的种群数量每年维持不变就是要求使得x ̌k =x k , (k=1,2,…,n -1).(1) 如果b k , s k 已知,给定收获量ℎk ,建立求各个年龄的稳定种群数量x k 的模型(用矩阵、向量表示).(2) 设n =5,b 1=b 2=b 5=0,b 3=5,b 4=3,s 1=s 4=0.4,s 2=s 3=0.6,如要求ℎ1~ℎ5为500,400,200,100,100,求x 1~x 5.(3) 要使ℎ1~ℎ5均为500,如何达到?问题分析:该问题属于简单的种群数量增长模型,在一定的条件(存活率,繁殖率等)下为使各年龄阶段的种群数量保持不变,各个年龄段的种群数量将会满足一定的要求,只要找到种群数量与各个参量之间的关系,建立起种群数量恒定的方程就可以求解出各年龄阶段的种群数量。
模型建立:根据题目中的信息,令x ̌k =x k ,得到方程组如下:{x ̌1=∑b k nk=1x k =x 1x ̌k+1=s k x k −ℎk =x k+1整理得到:{−x 1∑b k nk=1x k =0−x k+1+s k x k =ℎk2 大学数学实验 实验报告 | 2014/4/52写成系数矩阵的形式如下:A =[b 1−1b 2b 3s 1−100s 2−1…b n−1b n0000⋮⋱⋮000000000⋯00−10s n−1−1]令h =[0, ℎ1,ℎ2,ℎ3,…,ℎn−2,ℎn−1]Tx =[x n , x n−1,…,x 1]T则方程组化为矩阵形式:Ax =h ,即为所求模型。
数值分析实验报告——非线性方程求根

数值分析实验报告——非线性方程求根一、实验目的:1.掌握求解非线性方程的常用方法;2.了解非线性方程求根问题的数值解法;3.熟悉使用数值分析软件进行非线性方程求根的实现。
二、实验原理:非线性方程指的是形如f(x)=0的方程,其中f(x)是一个非线性函数。
非线性方程求根的常用方法包括二分法、割线法和牛顿法等。
其中,二分法是通过不断缩小区间范围来逼近方程的解;割线法是通过使用割线来逼近方程的解;牛顿法则是通过使用切线来逼近方程的解。
对于给定的非线性方程,可以根据实际情况选择合适的方法进行求根。
三、实验内容:1.编写求解非线性方程的函数,包括二分法、割线法和牛顿法;2.使用编写的函数求解给定的非线性方程,比较各个方法的收敛速度和精确程度;3.根据实际情况分析和选择合适的方法进行求根。
四、实验步骤:1.针对给定的非线性方程,编写二分法的函数实现:(1)首先确定方程的解存在的区间;(2)根据方程的解存在的区间,使用二分法逐步缩小区间范围;(3)根据设定的精度要求,不断循环迭代,直至满足要求或达到迭代次数限制;2.针对给定的非线性方程,编写割线法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据割线的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;3.针对给定的非线性方程,编写牛顿法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据牛顿法的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;4.根据给定的非线性方程,分别使用二分法、割线法和牛顿法进行求解,并比较各个方法的收敛速度和精确程度;5.分析实际情况,选择合适的方法进行求解。
五、实验结果:4.通过比较,发现割线法和牛顿法的收敛速度较快,精确程度较高,因此选择割线法进行求解。
六、实验总结:通过本次实验,我掌握了求解非线性方程的常用方法,并使用数值分析软件实现了二分法、割线法和牛顿法。
高斯-赛德尔法--数值分析线性方程组的迭代解法

实验六、高斯-塞德尔法
一、实验目的
通过本实验学习线性方程组的迭代解法。掌握高斯-赛德尔迭代法编程。
二、计算公式
}
if(k==T)printf("\nNo");
else
printf("\n",k);
for(i=0;i<M;i++)
printf("x(%d)=%15.7f\n",i+1,x[i]);
}
四、例题
书P189页例6:用高斯-塞德尔迭代解线性方程组:
取 使得
#include<math.h>
#define M 3
#define N 4
main()
{
double a[M][N]={{8,-3,2,20},
{4,11,-1,33},
{6,3,12,36},
};
double x[M]={0,0,0};//初值
double r,t,q,eps=0.0000202;//需要精度
if(j!=i)q=q+a[i][j]*x[j];
x[i]=(a[i][N-1]-q)/a[i][i];
if(fabs(x[i]-t)>r)r=fabs(x[i]-t);
}
if(r<eps)break;
printf("\nk=%d,",k);
for(i=0;i<M;i++)
printf("\nx[%d]=%lf",i,x[i]);
鲍威尔算法实验报告

一、实验目的1. 理解鲍威尔算法的基本原理和步骤。
2. 掌握鲍威尔算法在求解非线性方程组中的应用。
3. 分析鲍威尔算法的收敛速度和精度。
二、实验原理鲍威尔算法是一种迭代算法,用于求解非线性方程组。
该算法的基本思想是利用相邻迭代的残差向量构造一个线性方程组的系数矩阵,进而求出近似解。
具体步骤如下:1. 初始化:选择初始点 \( x_0 \) 和 \( x_1 \),计算初始残差向量\( \mathbf{r}_0 = f(x_0) \) 和 \( \mathbf{r}_1 = f(x_1) \)。
2. 构造系数矩阵:根据残差向量 \( \mathbf{r}_0 \) 和 \( \mathbf{r}_1 \) 构造系数矩阵 \( \mathbf{A} \)。
3. 求解线性方程组:求解线性方程组 \( \mathbf{A} \mathbf{x} =\mathbf{r}_1 \),得到系数 \( \mathbf{x} \)。
4. 更新近似解:根据系数 \( \mathbf{x} \) 更新近似解 \( x_2 = x_1 +\mathbf{x} \)。
5. 检查收敛性:计算新的残差向量 \( \mathbf{r}_2 = f(x_2) \),如果满足收敛条件,则停止迭代;否则,返回步骤2。
三、实验内容1. 选择非线性方程组:设非线性方程组为\[\begin{cases}f_1(x_1, x_2) = x_1^2 + x_2^2 - 1 = 0 \\f_2(x_1, x_2) = x_1^3 - x_2 - 1 = 0\end{cases}\]2. 选择初始点:取 \( x_0 = (0, 0) \) 和 \( x_1 = (1, 1) \)。
3. 运行鲍威尔算法:根据上述步骤,编写程序求解该非线性方程组。
四、实验结果与分析1. 实验结果:经过多次迭代,鲍威尔算法得到近似解为 \( x_1 \approx 0.5285 \),\( x_2 \approx 0.8572 \)。
实验六 用SPSS进行非线性回归分析
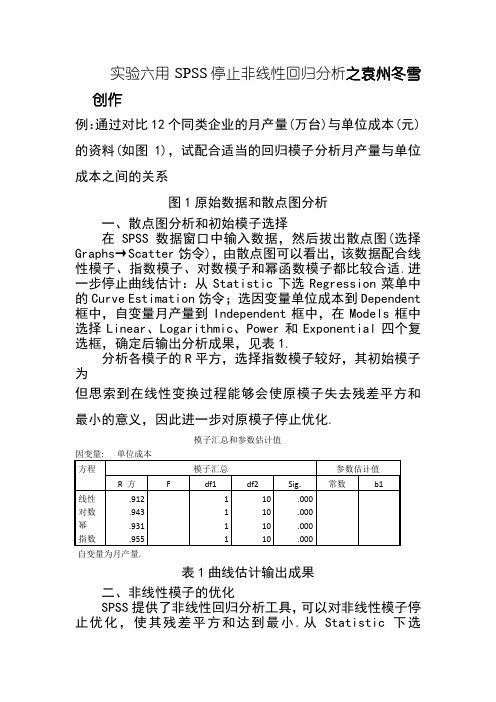
实验六用SPSS停止非线性回归分析之袁州冬雪创作例:通过对比12个同类企业的月产量(万台)与单位成本(元)的资料(如图1),试配合适当的回归模子分析月产量与单位成本之间的关系图1原始数据和散点图分析一、散点图分析和初始模子选择在SPSS数据窗口中输入数据,然后拔出散点图(选择Graphs→Scatter饬令),由散点图可以看出,该数据配合线性模子、指数模子、对数模子和幂函数模子都比较合适.进一步停止曲线估计:从Statistic下选Regression菜单中的Curve Estimation饬令;选因变量单位成本到Dependent 框中,自变量月产量到Independent框中,在Models框中选择Linear、Logarithmic、Power和Exponential四个复选框,确定后输出分析成果,见表1.分析各模子的R平方,选择指数模子较好,其初始模子为但思索到在线性变换过程能够会使原模子失去残差平方和最小的意义,因此进一步对原模子停止优化.表1曲线估计输出成果二、非线性模子的优化SPSS提供了非线性回归分析工具,可以对非线性模子停止优化,使其残差平方和达到最小.从Statistic下选Regression菜单中的Nonlinear饬令;按Paramaters按钮,输入参数A:176.57和B:-.0183;选单位成本到Dependent 框中,在模子表达式框中输入“A*EXP(B*月产量)”,确定.SPSS输出成果见表2.由输出成果可以看出,颠末6次模子迭代过程,残差平方和已有了较大改善,缩小为568.97,误差率小于0.00000001,优化后的模子为:迭代汗青记录b迭代数a残差平方和参数A B5.346E+133.087导数是通过数字计算的.a. 主迭代数在小数左侧显示,次迭代数在小数右侧显示.b. 由于持续残差平方和之间的相对减少量最多为SSCON = 1.000E-008,因此在22 模子评估和10 导数评估之后,系统停止运行.表2非线性回归的输出成果传统手工运算求解,运算量与迭代次数成正比;而使用SPSS求解,只要输入了初始参数值和模子表达式,无论迭代多少次,都可疾速得到最后成果,不但减轻了计算强度,而且提高了数据准确度,相比Excel又有了极大的前进.。
数值分析实验报告总结

一、实验背景数值分析是研究数值计算方法及其理论的学科,是计算机科学、数学、物理学等领域的重要基础。
为了提高自身对数值分析理论和方法的理解,我们进行了数值分析实验,通过实验加深对理论知识的掌握,提高实际操作能力。
二、实验目的1. 理解数值分析的基本理论和方法;2. 掌握数值分析实验的基本步骤和技巧;3. 培养实验设计和数据分析能力;4. 提高编程和计算能力。
三、实验内容本次实验主要分为以下几个部分:1. 线性方程组求解实验:通过高斯消元法、LU分解法等求解线性方程组,并分析算法的稳定性和误差;2. 矩阵特征值问题计算实验:利用幂法、逆幂法等计算矩阵的特征值和特征向量,分析算法的收敛性和精度;3. 非线性方程求根实验:运用二分法、牛顿法、不动点迭代法等求解非线性方程的根,比较不同算法的优缺点;4. 函数插值实验:运用拉格朗日插值、牛顿插值等方法对给定的函数进行插值,分析插值误差;5. 常微分方程初值问题数值解法实验:运用欧拉法、改进的欧拉法、龙格-库塔法等求解常微分方程初值问题,比较不同算法的稳定性和精度。
四、实验过程1. 线性方程组求解实验:首先,编写程序实现高斯消元法、LU分解法等算法;然后,对给定的线性方程组进行求解,记录计算结果;最后,分析算法的稳定性和误差。
2. 矩阵特征值问题计算实验:编写程序实现幂法、逆幂法等算法;然后,对给定的矩阵进行特征值和特征向量的计算,记录计算结果;最后,分析算法的收敛性和精度。
3. 非线性方程求根实验:编写程序实现二分法、牛顿法、不动点迭代法等算法;然后,对给定的非线性方程进行求根,记录计算结果;最后,比较不同算法的优缺点。
4. 函数插值实验:编写程序实现拉格朗日插值、牛顿插值等方法;然后,对给定的函数进行插值,记录计算结果;最后,分析插值误差。
5. 常微分方程初值问题数值解法实验:编写程序实现欧拉法、改进的欧拉法、龙格-库塔法等算法;然后,对给定的常微分方程初值问题进行求解,记录计算结果;最后,比较不同算法的稳定性和精度。
清华大学数学实验报告6

实验六非线性方程求解实验目的1. 掌握用matlab软件求解非线性方程和方程组的基本用法, 并对结果做初步分析.2. 练习用非线性方程和方程组建立实际问题的模型并进行求解.实验内容题目3(1)小张夫妇以按揭方式贷款买了1 套价值20 万元的房子,首付了5 万元,每月还款1000 元,15 年还清。
问贷款利率是多少?(2)某人欲贷款50 万元购房,他咨询了两家银行,第一家银行开出的条件是每月还4500 元,15 年还清;第二家银行开出的条件是每年还450000 元,20 年还清。
从利率方面看,哪家银行较优惠(简单地假设年利率=月利率×12)?建立模型:设房价为b,首付款为b0,银行按照月利率(复利)来计算,月利率为r,月付款(月末支付)为a,共需要支付的月数为n。
根据经济学中资金的时间价值概念,可以得到:房价在n个月之后的实际价值为:b(1+r)n按揭购房期间交的所有款项在第n个月末的实际价值为:b0(1+r)n+a(1+r)n−1+(1+r)n−2+⋯+1=b0(1+r)n+a×(1+r)n−1由于在第n个月末还清了贷款,因此上述两个时间价值相等,则得到下面的关系式,即为解答此问题的方程:b(1+r)n=b0(1+r)n+a×(1+r)n−1即:(b−b0)(1+r)n−a×(1+r)n−1=0(1)代入已知条件:b=200000,b0=50000,a=1000,n=180,利用MATLAB解此非线性方程,经过简单的估测之后,给定初始值为r0=0.001,得到结果为:r=0.0020812,即贷款月利率为0.20812%。
(2)I.第一家银行相应的已知条件为:b=500000,b0=0,a=4500,n=180,利用MATLAB计算,经过简单的估测之后,给定初始值为r0=0.005,得到结果为:r=0.0058508,即这家银行的贷款月利率为0.58508%。
【清华】实验6非线性方程求解

实验六非线性方程求解姓名:李严凯学号:2009011887 班级:化93实验目的1掌握用MATLAB 软件求解非线性方程和方程组的基本用法,并对结果作出初步的分析2 练习用非线性方程组建立实际问题的模型并进行求解实验内容3.问题复述:(1)小张夫妇以按揭方式贷款买了一套价值20万的房子,首付了5万元,每月还款1000元,15年还清。
问贷款利率是多少?(2)某人欲贷款50万元购房,他咨询了两家银行,第一家银行开出的条件是每月还4500元,15年还清;第二家银行开出的条件是每年还45000元,20年还清。
从利率方面看,那家银行较优惠(简单假设年利率=月利率*12)?解答:模型:在实际问题中,购房人在支付首付后,向银行按揭申请贷款,并由银行支付购房人不足以支付的部分房价。
而后购房人将在一定时期内定期定额缴纳月供,直至还清银行的贷款本金及利息。
而银行则每月设定固定的月利率,按照复利的方式计算购房人应需缴纳的房款。
不妨设购房之初,购房人向银行申请了a0的贷款,银行的月利率为x,每月购房人向银行支付的月供为b,则在以后各月(第1、2、3…n个月),购房人所欠银行的贷款为:a1=a0*(1+x)-b;a2=a1*(1+x)-b;a3=a2*(1+x)-b;……an=a(n-1)*(1+x)-b当购房人所欠银行的贷款数an=0时,其贷款还清,还贷过程结束。
到此模型分析完毕,可以进行MATLAB求解。
求解:首先写出函数,表示出第n个月购房人所欠银行贷款:function y = interest( x,n ) %x为月利率n=180; %n为还清贷款的月数a(1)=15*(1+x)-0.1; %第1个月欠款for i=2:na(i)=a(i-1)*(1+x)-0.1; %第n个月欠款endy=a(n);end得到以上表达式后,令其中y=0即可解得月利率x,编程如下:[x,fv,ef,out]=fzero(@interest,0.05)考虑到银行贷款利率的实际情况,初值设为了0.05程序输出结果如下:x = 0.002081163889460fv = -5.287437154777308e-014ef =1out = intervaliterations: 12iterations: 14funcCount: 38algorithm: 'bisection, interpolation'message: 'Zero found in the interval [-0.014, 0.0952548]' 当然,也可以采用fsolve求解,列出:[x,fv,ef,out]=fsolve(@interest,0.05)得到x =0.002081163889460fv =-5.287437154777308e-014ef =1out = iterations: 14funcCount: 30algorithm: 'trust-region dogleg'firstorderopt: 9.769300386433235e-011message: [1x695 char]可以看出,两种解法的结果基本相同,不过fzero的解答时间更快,效果更优。
数学实验-迭代(方程求解)

实验六 迭代(方程求解)一.实验目的:认识迭代数列,考察迭代数列的收敛性.并学会用Mathematica 系统对线性和非线性的方程组进行迭代求解.二.实验环境:计算机,Mathematica 数学软件,Word 文档,课本。
三.实验的基本理论和方法:给定迭代函数f(x)以及一个初值0x 利用1(),0,1,n n x f x n +==⋅⋅⋅迭代得到数列n x ,0,1,n =⋅⋅⋅.如果数列n x 收敛与某个*x ,则有**()x f x =.即*x 是方程()x f x =的解.由此用如下的方法求方程()0g x =的近似解。
将方程()0g x =改写为等价的方程()x f x =,然后选取一初值利用1(),0,1,n n x f x n +==⋅⋅⋅做迭代.迭代数列n x 收敛的极限就是()0g x =的解.线性方程组以及非线性方程组的求解与单变量的方程求解方法类似.实验内容和步骤四.实验内容与结果 1.线性方程组⑴编写给定初值0x 及迭代函数()f x ,迭代n 次产生相应的序列.⑵给函数()(2/)f x x x =+初值为0进行迭代80次所产生的迭代序列并显示. 输入程序:Iterate f_,x0_,n_Integer :Module t ,i,temp x0,AppendTo t,temp ;For i1,in,i ,tempf temp ;AppendTo t,temp;tf x_:x 2x2;Iterate f,1.,80运行结果得:1.,1.5,1.41667,1.41422,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421,1.41421输入程序:NTIterate g_,x0_,n_Integer :Modulei,var x0,t ,h,h x_Dt g x ,x;For i 1,i n,i ,AppendTo t,var ;If h var0,var N var g var h var ,20, Print"Divided by Zero after",i,"'s iterations.";Break ;tg x_:x^32;NTIterate g,1,40运行结果得:1,1.3333333333333333333,1.2638888888888888889,1.2599334934499769665,1.259921050017769774,1.259921049894873165,1.259921049894873165,1.259921049894873165,1.25992104989487316,1.25992104989487316,1.25992104989487316,1.2599210498948732,1.2599210498948732,1.2599210498948732,1.259921049894873,1.259921049894873,1.259921049894873,1.259921049894873,1.25992104989487,1.25992104989487,1.25992104989487,1.2599210498949,1.2599210498949,1.2599210498949,1.259921049895,1.259921049895,1.259921049895,1.259921049895,1.25992104989,1.25992104989,1.25992104989,1.2599210499,1.2599210499,1.2599210499,1.259921050,1.259921050,1.259921050,1.259921050,1.25992105, 1.259921052. 非线性方程组⑴对于给定的矩阵M ,数组f 和初始向量0x ,由迭代1n n x Mx f +=+编写迭代程序,并选择初值分别迭代20和50次所产生的序列. 迭代40次运行结果: 输入程序:LSIterate m_,f_List,f0_List,n_Integer :Modulei,var f0,t Table ,i,n,For i1,in,i,tivar;varm.varf ;t m1,0.4,0.5,1;f1,1;f00,0;LSIterate m,f,f0,40运行结果得:0,0, 1.,1., 2.4,2.5, 4.4,4.7,7.28,7.9,11.44,12.54,17.456,19.26,26.16,28.988,38.7552,43.068,56.9824,63.4456,83.3606,92.9368,121.535,135.617,176.782,197.385,256.736,286.776,372.446,416.144,539.904,603.367,782.251,874.319,1132.98,1266.44,1640.56,1833.93,2375.13,2655.21,3438.22,3843.78,4976.73,5563.88,7203.28,8053.25,10425.6,11655.9,15088.9,16869.7,21837.8,24415.1,31604.9,35335.,45739.9,51138.5,66196.3,74009.4,95801.,107109.,138645.,155010.,200650.,224334.,290385.,324660.,420250.,469854.,608192.,679980.,880185.,984077.,1.27382106,1.42417106, 1.84349106,2.06108106,2.66792106,2.98282106,3.86105106,4.31678106迭代60次运行结果输入程序:LSIterate m_,f_List,f0_List,n_Integer:Modulei,var f0,t Table,i,n,For i1,i n,i,t i var;var m.var f;tm1,0.4,0.5,1;f1,1;f00,0;LSIterate m,f,f0,60运行结果得:1,1.3333333333333333333,1.2638888888888888889,1.2599334934499769665,1.259921050017769774,1.259921049894873165,1.259921049894873165,1.259921049894873165,1.25992104989487316,1.25992104989487316,1.25992104989487316,1.2599210498948732,1.2599210498948732,1.2599210498948732,1.259921049894873,1.259921049894873,1.259921049894873,1.259921049894873,1.25992104989487,1.25992104989487,1.25992104989487,1.2599210498949,1.2599210498949,1.2599210498949,1.259921049895,1.259921049895,1.259921049895,1.259921049895,1.25992104989,1.25992104989,1.25992104989,1.2599210499,1.2599210499,1.2599210499,1.259921050,1.259921050,1.259921050,1.259921050,1.25992105,1.25992105⑵改写矩阵的等价形式,给定数组f 和初始向量0x ,运用迭代格式11()x I D A x D b --=-+编写迭代程序。
哈工大数值分析实验报告

产生逼近解 x*的迭代数列{xk},这就是割线法的思想
.1.
数值分析实验报告
宋俊霖
拟 Newton 法以 X 0 为初始 Nhomakorabea似,利用递推关系
X k 1 X k H k F ( X k ) H k 1 ( F ( X k 1 ) F ( X k )) X k 1 X k H k 1 H k H k , k 0,1,...
其中 r 为要求的方程的根的重数,这就是改进的 Newton 法,当求解已知重数的方程的根 时,在同种条件下其收敛速度要比 Newton 法快的多。 割线法通常预先给出两个猜测初值 x0 , x1 ,然后根据迭代公式
xk 1 xk f ( xk ) ( xk xk 1 ) f ( xk ) f ( xk 1 )
产生近似于方程组 F ( X ) 0 的解 X * 的迭代序列 { X k } , 利用这个递推关系式就是拟 Newton 法, 实际计算时, 只要选择较好的初始近似 X 0 和初始矩阵 H 0 , 一般可得到较好的近似解。
1.2
Python 程序设计
二分法源程序: import math def f(x): return math.sin(x)-0.5*x**2 def binary_method(f, x0, x1, eps, maxi): delta=100 k=0 while delta > eps: x2 = (x1+x0)/2 if f(x0)*f(x2)>0: x0=x2 else : x1=x2 delta=abs(x1-x0) k+=1 print('Root is at: ', x2) print('f(x) at root is: ', f(x2)) x0=1.0 x1=2.0 binary_method(f, x0, x1, 1e-5,100)
实验六-用SPSS进行非线性回归分析

实验六-用SPSS进行非线性回归分析
一、实验目的
通过本次实验,学生应掌握以下内容:
1.掌握非线性回归和SPSS结合的方法
2.掌握非线性回归结果的解读和分析
3.熟悉SPSS软件的使用和应用
二、实验原理与方法
1.非线性回归分析原理
非线性回归分析是一种常见的回归分析方法,其主要目的是找到一个非线性函
数来描述变量之间的关系。
其中,非线性函数的形式可以是指数函数、对数函数、幂函数、多项式函数等等。
在实际应用中,非线性回归分析常用于描述速度、密度、强度、反应等自然界和社会经济现象的关系。
2. SPSS软件的使用
SPSS是目前应用最为广泛的统计学分析软件之一。
通过SPSS可以进行数据的
描述统计、频率分布、方差分析、回归分析、因子分析、判别分析等多种统计分析。
在本次实验中,我们将要使用SPSS软件来进行非线性回归分析,通过SPSS软件,我们可以方便地得出非线性回归方程、残差、R方值等重要数据,并进行数据可视化分析。
三、实验步骤
1. 数据准备
本次实验所使用的数据集为。
《数值分析》_实验

( )
( )
4、另外选取一个近似表达式,尝试拟合效果的比较; 5、* 绘制出曲线拟合图。 三、目的和意义 1、掌握曲线拟合的最小二乘法; 2、最小二乘法亦可用于解超定线代数方程组; 3、探索拟合函数的选择与拟合精度间的关系
第5页
数值分析实验,宋伦继
6
实验四 数值积分与数值微分
一、问题提出 选用复合梯形公式,复合 Simpson 公式,Romberg 算法,计算
x
*
⎡ 0 ⎤ ⎢ −6 ⎥ ⎥ ⎢ ⎢ 20 ⎥ ⎥ ⎢ ⎢ 23 ⎥ ⎢ 9 ⎥ ⎥ ⎢ ⎢− 22⎥ ⎢ − 15 ⎥ ⎥ ⎢ ⎥ ⎢ 45 ⎦ ⎣
=
( 1,
-1,
0,
2,
1,
-1,
0,
2)
T
第7页
数值分析实验,宋伦继
8
3、三对角形线性方程组
⎡ 4 − 1 0 0 0 0 0 0 0 0 ⎤ ⎡ x1 ⎤ ⎡ 7 ⎤ ⎢− 1 4 − 1 0 0 0 0 0 0 0 ⎥ ⎢ x ⎥ ⎢ 5 ⎥ ⎥ ⎢ 2⎥ ⎥ ⎢ ⎢ ⎢ 0 − 1 4 − 1 0 0 0 0 0 0 ⎥ ⎢ x3 ⎥ ⎢ − 13⎥ ⎥⎢ ⎥ ⎥ ⎢ ⎢ ⎢ 0 0 − 1 4 − 1 0 0 0 0 0 ⎥ ⎢ x4 ⎥ ⎢ 2 ⎥ ⎢ 0 0 0 − 1 4 − 1 0 0 0 0 ⎥ ⎢ x5 ⎥ ⎢ 6 ⎥ ⎥⎢ ⎥ = ⎢ ⎥ ⎢ ⎢ 0 0 0 0 − 1 4 − 1 0 0 0 ⎥ ⎢ x6 ⎥ ⎢− 12⎥ ⎢ 0 0 0 0 0 −1 4 −1 0 0 ⎥ ⎢ x ⎥ ⎢ 14 ⎥ ⎥ ⎢ 7⎥ ⎥ ⎢ ⎢ ⎢ 0 0 0 0 0 0 − 1 4 − 1 0 ⎥ ⎢ x8 ⎥ ⎢−4⎥ ⎢ 0 0 0 0 0 0 0 − 1 4 − 1⎥ ⎢ x ⎥ ⎢ 5 ⎥ ⎥ ⎢ 9⎥ ⎥ ⎢ ⎢ ⎥ ⎥⎢ ⎥ ⎢ 0 0 0 0 0 0 0 0 −1 4 ⎦ ⎢ −5⎦ ⎣ ⎣ ⎣ x10 ⎦
求解非线性方程的牛顿迭代法

求解非线性方程的牛顿迭代法作者:李晓辉任伟和程长胜来源:《科技风》2021年第14期摘要:本文主要讲了求解非线性方程的牛顿迭代法。
文章首先引入牛顿迭代法的公式、迭代函数。
紧接着文章又介绍了牛顿迭代法的局部收敛性以及它的收敛速度,并通过数值实验验证了牛顿迭代法求解非线性方程的有效性。
关键词:牛顿迭代法;局部收敛;收敛速度中图分类号:O010224文献标识码:A一、绪论类似于线性方程组Ax=b求解的问题,非线性方程的一般问题可化为f(x)=y,即“对于什么样的x的值,函数f取值为y”,这里可以暂且先把f当成单变量函数,通常把y移项并吸收进f,从而一般形式可记为f(x)=0,因此,一个一般的一元非线性方程的求解问题有如下形式:给定函数f,寻找x(实的或复的),使得f(x)=0。
若存在一点x*满足该性质,称x*是方程f(x)=0的根或函数的零点。
这类问题称为求根问题或求零点问题。
此外,方程的根的情况可分为单根和重根。
一般的非线性方程的重数可以定义如下:若f(x)=(x-x*)m·g(x)且g(x)≠0,其中,m为自然数,称x*为f(x)的m重根,m=1时也称单根。
若区间[a,b]上有方程的一个实根,称该区间为方程的一个有根区间,如果能把方程的有根区间的长度缩短到一定的范围内,那么就求到了一个近似根,通常采用的都是数值求解的办法,因此若假设要求有根区间长度为0(即求到精确解),这些数值求解的办法通常都会产生一个逐渐逼近根的一个无穷序列。
求方程的近似根,一般要考虑如下几个问题:(1)根的存在性问题,即方程有没有实根,有几个根。
(2)有根区间的确定。
本文介绍的算法通常是假设有根的前提下给出求近似根的方法,一般需要以别的辅助工具先确定有根区间。
(3)求出足够近似的根,即在制定精度下缩小有根区间,或通过某些判别条件断定近似根的精度。
二、Newton迭代公式的构造简单迭代是将非线性方程f(x)=0通过代数恒等变形,将原方程化成等价方程x=φ(x),从而形成迭代式xk+1=φ(xk)。
线性方程组的数值解法-安振华-2012011837

实验5:线性方程组的数值解法化学工程系分2 安振华2012011837【实验目的】1、掌握线性方程组的常用数值解法,包括高斯消去法、LU分解法以及校正法。
2、体验数值计算的时间复杂度和计算规模的关系。
3、加深对数值计算误差的理解。
4、学习使用迭代法等算法,求解非线性方程。
5、学习如何使用MATLAB解非线性方程组和方程组。
【实验容】【实验五:习题9】种群的繁殖与稳定收获:种群的数量因繁殖而增加,因自然死亡而减少,对于人工饲养的种群(比如家畜)而言,为了保证稳定的收获,各个年龄的种群数量应保持不变,种群因雌性个体的繁殖而改变,为方便起见以下种群数量均指其中的雌性。
种群年龄记作k=1,2,…,n,当年年龄k的种群数量记作x k,繁殖率记作b k(每个雌性个体在1年繁殖的数量),自然存活率记作s k(s k=1-d k,d k为1年的死亡率),收获量记作h k,则来年年龄k的种群数量k x应为:111,(1,2,,1)n k k k k k k k x b x x s x h k n +===-=⋅⋅⋅-∑要求各个年龄的种群数量每年维持不变就是要使(1,2,,)k k x x k n ==⋅⋅⋅(1) 若b k ,s k 已知,给定收获量h k ,建立求各年龄的稳定种群数量x k 的模型(用矩阵向量表示)(2) 设n=5,b 1=b 2=b 5=0,b 3=5,b 4=3,s 1=s 4=0.4,s 2=s 3=0.6,如果要求h 1~h 5为500,400,200,100,100,求x 1~x 5 (3) 要使h 1~h 5均为500,如何达到? 【分析】为方便起见以下种群数量均指其中的雌性。
我们并且有以下的假设:(1)雌性个体的繁殖率和存活率在特定的时间是不变的。
(2)人工饲养的种群在质量和数量上是不受外界环境和资源的限制的。
(3)模型中不考虑人为的或是自然的灾害所造成的种群数量、繁殖率和存活率的变动。
数值分析实验报告

数值分析实验报告一、实验目的数值分析是一门研究用计算机求解数学问题的数值方法及其理论的学科。
本次实验的目的在于通过实际操作和编程实现,深入理解和掌握数值分析中的常见算法,提高运用数值方法解决实际问题的能力,并对算法的精度、稳定性和效率进行分析和比较。
二、实验环境本次实验使用的编程语言为 Python,使用的开发工具为 PyCharm。
实验所依赖的主要库包括 NumPy、Matplotlib 等。
三、实验内容(一)函数逼近与插值1、拉格朗日插值法通过给定的离散数据点,构建拉格朗日插值多项式,对未知点进行函数值的估计。
2、牛顿插值法与拉格朗日插值法类似,但采用了不同的形式和计算方式。
(二)数值积分1、梯形公式将积分区间划分为若干个梯形,通过计算梯形面积之和来近似积分值。
2、辛普森公式基于抛物线拟合的方法,提高积分近似的精度。
(三)线性方程组求解1、高斯消元法通过逐行消元将线性方程组化为上三角形式,然后回代求解。
2、 LU 分解法将系数矩阵分解为下三角矩阵 L 和上三角矩阵 U,然后通过两次前代和回代求解。
(四)非线性方程求解1、二分法通过不断将区间一分为二,逐步缩小根所在的区间,直到满足精度要求。
2、牛顿迭代法利用函数的切线来逼近根,通过迭代逐步收敛到根的近似值。
四、实验步骤(一)函数逼近与插值1、拉格朗日插值法定义计算拉格朗日基函数的函数。
根据给定的数据点和待求点,计算插值多项式的值。
输出插值结果,并与真实值进行比较。
2、牛顿插值法计算差商表。
构建牛顿插值多项式。
进行插值计算和结果分析。
(二)数值积分1、梯形公式定义积分区间和被积函数。
按照梯形公式计算积分近似值。
分析误差。
2、辛普森公式同样定义积分区间和被积函数。
运用辛普森公式计算积分近似值。
比较与梯形公式的精度差异。
(三)线性方程组求解1、高斯消元法输入系数矩阵和右端项向量。
进行消元操作。
回代求解方程。
输出解向量。
2、 LU 分解法对系数矩阵进行 LU 分解。
《数值分析》课程实验报告范文

《数值分析》课程实验报告范文《数值分析》课程实验报告姓名:学号:学院:机电学院日期:2022年某月某日目录实验一函数插值方法1实验二函数逼近与曲线拟合5实验三数值积分与数值微分7实验四线方程组的直接解法9实验五解线性方程组的迭代法15实验六非线性方程求根19实验七矩阵特征值问题计算21实验八常微分方程初值问题数值解法24实验一函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。
试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。
实验二函数逼近与曲线拟合一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量与时间t的拟合曲线。
t(分)051015202530354045505501.272.162.863.443.874.154.374.51 4.584.024.64二、要求1、用最小二乘法进行曲线拟合;2、近似解析表达式为;3、打印出拟合函数,并打印出与的误差,;4、另外选取一个近似表达式,尝试拟合效果的比较;5、某绘制出曲线拟合图。
三、目的和意义1、掌握曲线拟合的最小二乘法;2、最小二乘法亦可用于解超定线代数方程组;3、探索拟合函数的选择与拟合精度间的关系四、实验步骤:第一步先写出线性最小二乘法的M文件functionc=lpoly(某,y,m)n=length(某);b=zero(1:m+1);f=zero(n,m+1); fork=1:m+1f(:,k)=某.^(k-1);enda=f'某f;b=f'某y';c=a\b;c=flipud(c);第二步在命令窗口输入:>>lpoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到:an=-0.00240.20370.2305即所求的拟合曲线为y=-0.0024某2+0.2037某+0.2305在编辑窗口输入如下命令:>>某=[0,5,10,15,20,25,30,35,40,45,50,55];>>y=-0.0024某某.^2+0.2037某某+0.2305;>>plot(某,y)命令执行得到如下图五、实验结论分析复杂实验数据时,常采用分段曲线拟合方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
i 1
4
i
1, xi 0
均相共沸混合物应该满足稳定条件,即共沸混合物的每个组分在气体状态下和在液 体状态下具有相同的化学势能。在压强 P 不大的情况下,这个条件可以表示为:
P iP i , i 1, 2,3, 4
Pi 是组分 i 的饱和气相压强,与温度 T 有关,可以根据如下表达式确定:
x2 = 1.4044 out2 = iterations: 6 初值取 1.2 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),1.2) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),1.2) 得到如下结果 x1 = 1.4044 out1 = iterations: 6 x2 = 1.4044 out2 = iterations: 4 初值取 1.5 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),1.5) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),1.5) 得到如下结果 x1 = 1.4044 out1 = iterations: 5 x2 = 1.4044 out2 = iterations: 3 查 workspace 得到精确结果
10
,取不同
的初值计算,输出初值、根的近似值和迭代次数,分析不同根的收敛域;自己构造 某个迭代公式用迭代法求解,并自己编写牛顿法的程序进行求解和比较。 编写程序确定根的大致位置 x=-1.5:0.01:1.5; y=sin(x)-x.^2/2; z=0*x; plot(x,y,'b',x,z,'k') 画出 sin x x 2 在区间 -1.5,1.5 上的图像
迭代次数 1 2 3 4 5 6 7 8 9 10 11 12 普通迭代法(迭代次数 12) 1.2972825327 1.3876798689 1.4023415974 1.4041688094 1.4043857914 1.4044114001 1.4044144203 1.4044147765 1.4044148185 1.4044148234 1.4044148240 1.4044148241 牛顿法(迭代次数 6) 1.7428163969 1.4640982835 1.4070280250 1.4044202764 1.4044148241 1.4044148241
ln Pi ai bi , i 1, 2,3, 4 T ci
其中 ai , bi , ci 为常数。 i 是组分 i 的液相活度系数,可以根据如下表达式确定:
xq j ji ln i 1 ln x j qij 4 j 1 j 1 x q k jk k 1
得到如下结果 x1 = 0 out1 = iterations: 0 x2 = 0 out2 = iterations: 0 初值取 0.3 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),0.3) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),0.3) 得到如下结果 x1 = -2.4455e-029 out1 = iterations: 7 x2 = -9.6022e-012 out2 = iterations: 4 初值取 0.6 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),0.6) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),0.6) 得到如下结果 x1 = -1.0173e-026 out1 = iterations: 8 x2 = -2.4368e-010 out2 = iterations: 6 初值取 0.9 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),0.9) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),0.9) 得到如下结果 x1 = 1.4044 out1 = iterations: 7
实验六 非线性方程求解
材料系 材 93 2009011976 邓陟
一.
实验目的
1. 用 MATLAB 软件掌握求解非线性方程的迭代法和牛顿法,并对结果作初步分析。 2. 通过实例练习用非线性方程求解的实际问题。
二.
实验内容
2
1. 分别用 fzero 和 fsolve 程序求方程 sin x x 2 0 的所有根,准确到 10
k
0 1 2 3
xk a 5
x1
0 0
x2
0.7803 0.5858
x3
0 0.4142
x4
0.2197 0
T
76.9613 71.9657
3. 用迭代公式 xk 1 axk exp bxk 计算序列 xk ,分析其收敛性,其中 a 分别取 5, 11,15; b (>0)任意,初值 x0 1 。观察是否有混沌现象出现,并找出前几个分叉 点,观察分叉点的极限趋势是否符合 Feigenbaum 常数揭示的规律。 编写 M 文件 iter.m function x=iter(a,b) x0=1; x(1)=x0; for i=2:50 x(i)=a*x(i-1)*exp(-b*x(i-1)); end x=x'; 令 b 1 ,分别计算 a 5,11,15 时的 xk 编写程序 x1=iter(5,1); x2=iter(11,1); x3=iter(15,1); 不同 a 的计算结果如下
4 4
1 ai ln P 0, i 1, 2,3, 4
由于只有当组分 i 参与到该共沸混合物中时才需要满足上式,所以将上式进一步写 成
b xq 4 4 j ji xi i ln x j qij 4 T ci j 1 j 1 x q k jk k 1
命令 初值 0 0.3 0.6 0.9 1.2 1.5 fzero 根的近似值 0 0 0 1.4044148241 1.4044148241 1.4044148241 迭代次数 0 7 8 7 6 5 fsolve 根的近似值 0 0 -0.0000000002 1.4044148244 1.4044148241 1.4044148249 迭代次数 0 4 6 6 4 3
2
由图像可知 sin x x 2 0 有两个根,一个在 x 0 附近,另一个在 x 1.5 附近。
2
取不同初值 0,0.1,,
1.4,1.5 用 fzero 和 fsolve 求解 sin x x 2 2 0 的所有根
初值取 0 编写程序 [x1,fv1,ef1,out1]=fzero(inline('sin(x)-x^2/2'),0) [x2,fv2,ef2,out2]=fsolve(inline('sin(x)-x^2/2'),0)
从上表可以看出,对于方程求根,fzero 命令求出的解的稳定性要好于 fsolve 命令。 构造迭代公式 x
2sin x 用迭代法求解
编写程序 x(1)=1;b=1;k=1; while or(k==1,abs(b)>1e-10*abs(x(k))) x(k+1)=sqrt(2*sin(x(k))); b=x(k+1)-x(k); k=k+1; end n=k-1 得到如下结果 n= 12 用牛顿法求解 编写程序 x(1)=1;b=1;k=1; while or(k==1,abs(b)>1e-10*abs(x(k))) x(k+1)=x(k)-(sin(x(k))-(x(k)^2)/2)/(cos(x(k))-x(k)); b=x(k+1)-x(k); k=k+1; end n=k-1 得到如下结果 n= 6 两种方法所求结果如下
在压强 p 760 mmHg 下,为了形成均相共沸混合物,温度和组分分别是多少?请 尽量找出所有可能的解。 共沸混合物,是指由两种或两种以上物质组成的液体混合物,当在某种压力下被蒸 馏或局部汽化时,在气体状态下和液体状态下保持相同的组分。 该混合物由 4 个组分组成,组分 i 所占的比例为 xi i 1, 2,3, 4 ,则
4 4
, i 1, 2,3, 4
其中 qij 表示组分 i 与组分 j 的交互作用参数, qij 构成交互作用矩阵 Q 。 对 P iP i 两边取对数,并带入 P i ,i
xq bi ln x j qij 4 j ji T ci j 1 j 1 x q k jk k 1
a4 19.293;
b4 4117.07;
c1 239.73,
c2 219.16,
c3 252.64,
c4 227.44;
1.0 0.192 2.169 1.611 0.316 1.0 0.477 0.524 Q 0.377 0.360 1.0 0.296 0.524 0.282 2.065 1.0
从以上结果可知,牛顿法的收敛速度要快于根据方程直接构造迭代式的迭代法。 2. 给定 4 种物质对应的参数 ai , bi , ci 和交互作用矩阵 Q 如下:
a1 18.607,
b1 2643.31,
