静电场与恒定电流场
实验八用恒定电流场模拟静电场

实验八用恒定电流场模拟静电场
一、实验目的
本实验的目的是利用恒定电流场模拟静电场,由而探究静电场特性及其影响力。
二、实验原理
本实验利用恒定电流场模拟静电场,即在已确定的空间上设置恒定电流场,模拟静电场的形成。
静电场实际上是由固定电荷内部产生的静态电场,由外部静电力引起,其方向垂直于电荷分布。
随着距离的增加,静电场在空间上的强度会逐渐减弱,最终在某个距离外消失。
三、实验准备
本实验准备的主要设备包括:示波器、恒定电流源、特技电极、石英板以及相关仪器仪表等。
四、实验过程
(1)设定实验条件:首先在示波器上设置参数,以满足实验要求;接着将恒定电流源的输出电压调节至一定值,同时将接地端与石英板的一面相连,将恒定电流源的输出端与石英板的另一面相连,这样设定可使得石英板上形成恒定电流场;最后,将特技电极放置于石英板的表面,以检测石英板上的电势变化。
(2)采集数据:示波器将侦测到的电势变化投入图形拟合程序,根据线性规律拟合出基本分布储存,计算出所需数据,从而确定恒定电流场半径和静电场实验强度。
五、实验总结
本实验利用恒定电流场模拟静电场,主要依靠示波器侦测出电势变化,然后根据线性规律将电势变化拟合出其基本构型,从而计算出所需数据。
本实验给予了对静电场的大致把握,观察到静电场的传播特性,有助于对静电场未来的深入研究。
静电场与恒定电流场的转化与统一

一
注意 到
× ), ×H) + V ・ 1 H :=( : ( D)
( .)(. +/(×)7 : (z 秀j , , )v) c
我们 务必 记 得 , 于两 种 场 的 媒 质 环 境 相 异 。 由 式( ) 5 中不 能 同时 出现 和 P 这 里进 一步 分 两种 情 ,
出 : 于工 程实 际 由于 (/ 《 l因 而 对 vc) ,
r lt n hp i e txb o sa al be yu i gt e E n ti lt i .te s t lcr e d a d c n tn u rn ed eai s i t e to k v i l .B s i s n r ai t h t i ee t c f l n o s t r t l o n h a n h e e vy ac i i a c e f i
V ×H =J
J = E
(
(
×
・
z ,+ =
,
D )= p+(/ J vc) J
l
( 6 )
1 两种 场 的转 化 和 统 一
已经提 及 , 电场 与恒 定 电流 场是 目前 电磁学 静 中独立 的两 大 部 分 。而 且 所 处 的 媒 质 环 境 互 不 交 叉 。这里 , 我们 把两 者用 Mawe 方程 联 系起 来 , x l l 有
表 1给 出了他们 之 间的 比较 。
文 中涉 及 的 主 题 是 静 电 场 和 恒 定 电流 场 。众 所周 知 , Frdy和 Maw l为 杰 出代表 的学者 首 以 aaa xe l
次把 电和磁 联 系 起 来 , 构 成 著 名 的 Maw l 方 程 并 xe l
高中物理 第二章静电场和恒定电流电场

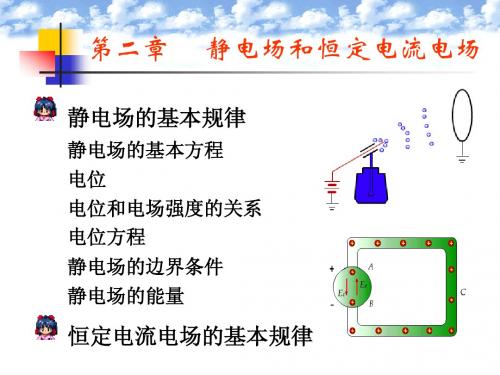
第二章 静电场和恒定电流电场§2.1 静电场的基本方程1 静电场的定义:场的源-电荷,相对于观察者(坐标系)静止。
2 静电场的基本方程:0=∂∂t,因此有 ⎪⎪⎩⎪⎪⎨⎧=⋅∇==⋅∇==⨯∇=⨯∇000B HB D E D E H μρε 可以发现电场量(ε,,D E )与磁场量(μ,,B H)无耦合,故可以单独研究静电场和静磁场。
于是静电场的基本方程是⎪⎩⎪⎨⎧=⋅∇==⨯∇ρεD ED E3 静电场的物理特性;1)场源:电荷,散度源,旋度为零,是保守场,可以定义势能。
2)电力线:非环,始于正电荷或带正电荷的导体或无穷远,终于负电荷或带负电荷的导体或无穷远。
3)与磁场关系:无关。
§2.2 电位1 为什么需要电位:1)电位作辅助量,简化求解过程,矢量变标量。
2)静电场电位有物理意义:电位是单位正电荷的势能。
3)电位比电场易测量。
2 电位定义:前提是旋度为零。
任何标量梯度的旋度恒等于零:0=∇⨯∇ϕ (梯度的物理解释:最陡)因此只要让ϕ-∇=E静电场的旋度方程自然满足。
3 电位的物理意义:任意一点A 的电位等于把单位正电荷从该点移到电位参考点P (零电位点)电场力所做的功,也就是外力克服电场力把单位正电荷从电位参考点(零电位点)移到该点所做的功。
数值上也就是单位正电荷所具有的势能。
⎰⎰⎰⎰⎰⎰=-==⋅∇=⋅∇-=⋅→⋅=⋅=PAA PA PA P A PAP AP AAP d l d l d l d E l d E q l d F W ϕϕϕϕϕϕ上式结果与A 点到P 点的具体路径无关,这是因为⎰=⋅=+=-AMPNAANPAMP ANP AMP l d E W W W W 0AMNP所以 A N P A M P W W =因此我们才可以说(在静电场条件下)电位是单位正电荷的势能。
势能本身就意味着它只与状态有关,与过程无关。
4 电位参考点的选择:1)电荷在有限区域,无穷远点为参考点。
静电场与恒定电流电场

电 场 力
同性相斥
异性相吸
离 散 电 荷 系 的 电 场
假设静电场是由置于不同位置的一组 N个离散点电荷 q1 、 ˆ R 2 的线性函数 q2 、 qN 所产生,由于电场强度是 Rq 、 (满足迭加原理),某一点的总场 E 为所有各电荷产生 的场的矢量和。
1 E r 40
检查是否可以利用对称性简化计算 代入积分公式,求出待求场点的电场
例 题
dE
dq ldl dE 1 ldl ˆ R 40 R 2 z R
dE
R
R
dl ad
cos
R a2 z2 az ld 1 3 40 2 2 2 a z
P r 0e r E r
非均匀
各向同性:极化强度的某一坐标分量仅决定于相应的电 场强度的坐标分量;否则,称为各向异性介质
静电场为保守场或无旋场 静电场的环路积分为零(环路定理)
E dl 0
C
E 0
静电场与电位有如下关系
E
等 位 面
E
电力线与等位面垂直 电力线与等位线的疏密相同 沿电力线方向电位降低
解 题 策 略
离散电荷分布:
1 r 40
i 1
N
0 8.85 1012 F/m
CGS制:高斯制。
长度:厘米,cm; 质量:克,g; 时间:秒,s。
ke 1
迭 加 原 理
如果真空中存在多个点电荷,那么作用于每一个点电荷 上的静电力等于其它点电荷单独存在时作用于该点电荷 上的静电力的矢量和。
F3
ˆ R 31
F31
q1q 3 ˆ q 2q 3 ˆ 1 R F3 F31 F32 R 31 32 2 2 40 R32 R31
对恒定电流场模拟静电场的等势线实验讨论

对恒定电流场模拟静电场的等势线实验讨论
恒定电流场模拟静电场的等势线实验是一种常用的物理实验,它可以用来研究静电场的等势线分布。
实验中,首先要准备一个恒定电流源,然后将它连接到一个电阻网络中,电阻网络中的电阻可以调节,以模拟不同的静电场等势线分布。
实验中,首先要测量电阻网络中的电阻,然后将恒定电流源连接到电阻网络中,并调节电阻,使电流在电阻网络中均匀分布。
接着,可以使用一个示波器来测量电阻网络中的电压,从而得到电压的分布情况,从而得到静电场的等势线分布。
实验结果可以用来检验电动势定律,即电动势的变化等于电势差乘以电路中的电阻。
此外,实验结果还可以用来研究电荷的分布情况,以及电荷的分布对静电场的影响。
总之,恒定电流场模拟静电场的等势线实验是一种有效的物理实验,它可以用来研究静电场的等势线分布,以及电荷的分布情况,从而检验电动势定律,并研究电荷的分布对静电场的影响。
用恒定电流场模拟静电场 (1)

用恒定电流场模拟静电场实验设计思想及背景场强和电势是描述静电场的两个基本物理量,其空间分布常用电场线及等势面来描述。
一般不规则带电体的场强、电势数学表达式复杂,因此常采用实验方法来研究。
但如果用静电仪表来测量静电场,因测量仪器的介入会改变原静电场的分布,所以采用模拟法,即用稳恒电流场模拟静电场的分布。
实验目的1.了解用模拟法测绘静电场的原理; 2.加深对电场强度和电势概念的理解。
实验原理 一.模拟依据以长直同轴圆柱面间的电场分布为例 1.静电场图1(a)为一均匀带电的长直同轴圆柱面。
a 是半径为0r 的长直圆柱导体(中心电极),b 是内半径为0R 的同轴长直导体圆筒(同轴外电极)。
设电极a ,b 各带等量异号电荷,两电极之间将产生静电场,两极的电势分别为0a U U =和0b U =(接地)。
由于对称性,在垂直于轴线的任一个截面S内,有均匀分布的辐射状电场线,见图1(b)。
由电磁学理论,均匀带电的长直同轴导体柱面之间的电场强度rk r E 1π2==ελ (1) 式中,λ为导体上电荷的线密度;ε为均匀电介质的介电常数(亦称为电容率);r 为两导体间任一点到轴线的距离,ελπ2/=k 。
由电势差定义,两电极间任意—点与外电极之间的电势差r R dr r Edr U U R rR rb 0ln π2π20ελελ===-⎰⎰ 因为0b U =,所以到轴线距离为r 的一点的电势为 rRU 0ln π2ελ=(2) 由上式r 相同处电势相等,因此均匀带电长直同轴圆柱面电场中等势面为一系列同轴圆柱面。
2.恒定电流场(模拟场)一根长直同轴圆柱面横断面的二维结构如图2所示。
选模拟电极a 为中心电极,b 为同轴外电极,将其置于导电微晶或导电溶液中。
在a ,b 电极之间加上稳恒电压0U (中心电极a 接正,外电极b 接负),导电介质中就建立起恒定的电流场。
由于电极是对称的,电极间导电介质是均匀的,所以将有恒定电流均匀地沿径向从中心电极流向外电极。
静电场与恒定电流场

球体 均匀带 球面 电的: 点电荷
无限大
平板
平面
例1-6 均匀带电球面 求半径为R, 均匀地带有总电量q (设q>0)的球面的静电场分布 分析空间中任一点的电场
看作同心球面上一点 带电球面切洋葱 例1-3
空间任一点和电场都垂直球面且 同一球面上每点电场强度相同 2 e E ds Eds E ds E 4 r
r
dE
Q
P
E
Q
dE
dq e 2 r 4 0 r
E Ex Ey Ez
dE dEx dE y dEz
Ex dE x E y dE y Ez dE z
Q
dV
ds
dl
体分布,体电荷密度
电磁学
电荷的相互作用
数学准备 常用坐标系下的线、面和体积分 矢量运算 简单的矢量分析 引言 电磁现象的普遍性 人类对电磁现象认识的悠久历史
物质与运动,物理永恒主题下的重要组成部分
系统的学习: 电磁学
电动力学
量子电动力学
……
0.1 电荷 电荷是物质的基本属性 两种电荷:正电荷和负电荷 电性力:同号相斥、异号相吸 电荷量:物体带电的多少
EP 2E cos
EP 4 0 r l 4
2
P r
l/2
2 l r2 4
ql
-q
l
q
r l
EP ql 4 0 r
3
电偶极矩
p ql
p EP 3 4 0 r
例1-2 P15 真空中一均匀带电直线,电荷线密度为 。线外有一点 P ,离开直线的垂直距离为 a ,P 点和直线两端连线的夹角分别为 1 和 2 。求 P 点 的场强。 dq dx 取一段电荷微元dq dE 2 4 0 r 4 0 r 2
用恒定电流场模拟静电场实验报告

用恒定电流场模拟静电场实验报告示例文章篇一:《用恒定电流场模拟静电场实验报告》嘿,亲爱的小伙伴们!今天我要给你们讲讲我做的那个超级有趣的用恒定电流场模拟静电场的实验!实验前,老师就跟我们说这个实验可神奇啦,能让我们看到平时看不到的电场“模样”。
我心里那个好奇呀,就像有只小猫在挠痒痒,迫不及待地想开始。
我们先准备了一堆东西,什么导电纸、电极、电源、电压表等等。
看着这些家伙什儿,我心里直犯嘀咕:“它们真能帮我们模拟出静电场?”实验开始啦!我和小组的小伙伴们眼睛都瞪得大大的。
我们把导电纸铺平,就像给小电场准备了一张舒适的大床。
然后把电极小心翼翼地放上去,那模样,简直比照顾小宝宝还小心。
我看着小伙伴操作,着急地说:“轻点儿,轻点儿,别把电极弄歪啦!”小伙伴白了我一眼:“知道啦,你别在旁边瞎嚷嚷!”电源接通的那一刻,我感觉自己的心都跟着“砰砰”跳起来。
电压表的指针开始摆动,就像一个小精灵在跳舞。
我们赶紧记录下数据,那认真劲儿,仿佛我们是大科学家在做超级重要的研究。
测量的时候可费劲啦!一会儿这个数据不太对,一会儿那个位置又偏了。
我忍不住抱怨:“哎呀,这也太难搞了吧!”另一个小伙伴鼓励我说:“别灰心,咱们再仔细点儿!”经过好一番折腾,数据终于收集得差不多了。
我们看着那些密密麻麻的数字,脑袋都有点大了。
“这可怎么分析呀?”我愁眉苦脸地说。
不过,办法总比困难多!我们一起讨论,一起计算,慢慢地好像摸到了一些门道。
就好像在黑暗中走了好久,终于看到了一丝亮光。
你说这静电场看不见摸不着的,我们居然能用恒定电流场来模拟它,这难道不神奇吗?这就好比我们看不到风,但能通过飘动的树叶感受到风的存在一样。
最后得出的结论就是,通过这个实验,我们成功地用恒定电流场模拟出了静电场,让那些原本抽象的东西变得具体起来。
这让我深深感受到,科学的世界真是充满了奇妙和惊喜,只要我们敢于探索,就能发现更多的奥秘!怎么样,小伙伴们,你们是不是也觉得这个实验很有趣呢?示例文章篇二:《用恒定电流场模拟静电场实验报告》嘿!同学们,今天我要跟你们分享一个超级有趣的实验——用恒定电流场模拟静电场!在开始之前,我满怀着好奇和期待,心里一直在想:这到底能不能成功呢?老师把我们分成了几个小组,我和我的小伙伴们都摩拳擦掌,准备大干一场。
用恒定电流场模拟静电场

用恒定电流场模拟静电场静电场是由电荷散布决定的。
带电导体在空间形成的静电场,对部份比较简单的情形,可通过理论计算取得其电场散布。
但对大多数情形都无法取得其数学表达式,也就不能求解出其电场散布。
因此,为了解这些情形下的电场散布,通常借助实验的方式来测定出其电场散布。
由于直接测量静电场是很困难的,因此实验中采纳间接的模拟法来进行测量,用恒定电流场来模拟静电场,即通过测绘恒定电流场的散布来刻画对应的静电场。
一、教学目的1.学习用模拟法刻画和研究静电场的散布。
2.测绘同轴柱形电极和平行板电极间的电场散布。
二、教学要求1.本实验三小时完成。
2.了解模拟法应用的条件,加深对电场强度,电势概念的明白得。
3.把握水槽式静电场模拟仪的利用方式。
4.正确测绘出两种电极状况下的电场散布图并学会用单对数坐标纸作图。
5.对测量结果进行评判,写出合格的实验报告。
三、教学重点和难点1.模拟法应用的条件和特点。
2.刻画电场散布图及用单对数坐标纸作图。
四、讲解内容1.提问:本实验对静电场的测绘采纳的是什么方式?什么缘故要用此方式?回答:采纳的是模拟法测绘静电场。
因为直接测量静电场的散布,需用探针对空间各点逐点进行测量。
当把探针放入静电场后,由于静电感应,探针上会产生感应电荷,而形成一个新电场与原电场迭加,从而引发原电场的畸变。
显然直接测量不可行,因此采纳模拟法来进行测绘。
2.提问:模拟法分为哪两种模拟,其应用的条件是什么?本实验采纳的是哪一种模拟?回答:模拟法分为物理模拟和数学模拟。
物理模拟的应用条件为物理相似和几何相似,即模型和原型都遵从一样的物理规律;模型的几何尺寸与原型的几何尺寸成比例的放大或缩小。
数学模拟应用的条件为模型与原型在物理实质上能够完全不同,但它们都遵从相同的数学规律,即知足相似的数学方程。
用恒定电流场模拟静电场采纳的是数学模拟。
3.提问:用恒定电流场模拟静电场的理论依据是什么?回答:其理论依据是恒定电流场与静电场知足相同形式的数学方程(极间电势及电场公式对照)。
1-2 电场 电场强度

解
E dE
由对称性有 E E i x
q ( ) 2π R
q R
y dq dl r
o
x
P
dE
x
1 dl er 2 4π 0 r
z
1 – 2 电场 电场强度
第一章静电场 恒定电流场
q R
y dq dl r
o
q ( ) 2π R
1 dl er z 2 4π 0 r d l x E dEx dE cos 2 l l 4 π 0 r r 2π R qx xdl 2 2 32 3 0 4π 0 (x R ) 4π 0r dE
o
2 R 2
x
Q Q
r r
q0
E
E
q0
E
Q
E
Q
r 0 E ?
1 – 2 电场 电场强度
四 电场强度的叠加原理 点电荷 qi 对 q0 的作用力
第一章静电场 恒定电流场
q1
Fi
由力的叠加原理得 q0 所受合力 F Fi i Fi F q 故 0 处总电场强度 E q0 i q0
1 – 2 电场 电场强度
一 静电场
第一章静电场 恒定电流场
实验证实了两静止电荷间存在相互作用的静电力,
但其相互作用是怎样实现的?
电 场 电荷
电荷
场是一种特殊形态的物质
场 实物
物 质
1 – 2 电场 电场强度
二 电场强度于该点处的单位试验电荷 (试验电荷为点电 所受的力,其方向为正电荷受力 荷、且足够小,故对 方向. 原电场几乎无影响)
电荷体密度
静电场和稳恒电流场的异同

静电场和稳恒电流场的异同
静电场与稳恒电流场是两种完全不同的电场。
静电场主要是指电荷在不动或静止状态下所产生的电场,而稳恒电流场则主要是指电流在稳定状态下所产生的电场。
两者的本质差异在于电荷的移动情况。
静电场中电荷不动,电场只由电荷所引起,故其场线密集,以直线为主,场强较大,且不能传递信息和能量。
而稳恒电流场中电流稳定地流动,基本上呈匀速直线流动形态,故其场线则是环路状,场强较小,且能传递信息和能量。
此外,两者的应用领域也不同。
静电场主要应用于电荷分布的研究及电场作用下的物理现象,如静电感应、静电力、高压电场等。
而稳恒电流场则主要应用于电路中电阻的热效应、磁场感应、电磁铁等方面。
总之,静电场和稳恒电流场都是电场的表现形式,但在电荷状态及应用领域等方面存在着较大的差异。
大学电磁场与电磁波第三章3.4恒定电流场与静电场的比拟

图3.4.5深埋球形接地器
解法一 直接用电流场的计算方法I→J= NhomakorabeaI
4πr 2
→
E
=
J
γ
=
I
4πγr 2
R = 1 4πγa
∫ → U =
∞ a
I
4πγr 2
dr
=
I
4πγa
解法二 静电比拟法
C =ε Gγ
C = 4πεa, G = 4πγa , R = 1 4πγa
接地电阻越大越好吗?
2.直立管形接地器
即
G C
=
σ ε
静电系统的部分电容可与多导体电极系统的部分电导相互比拟。(自学)
例2 求同轴电缆的绝缘电阻。设内外的半径分别为R1、R2,长度为 l,中间媒质的
电导率为σ,介电常数为ε 。
解法一 直接用电流场的计算方法
设
I→J = I →E= J = I
2πρl
σ 2πρlσ
图3.4.3 同轴电缆横截面
解: 考虑地面的影响,可用镜像法。
图3.4.6 直立管形接地器
由静电比拟法
C
=
4πεl
ln 4l
,
d
则 C=ε, Gσ
G
=
4πσl
ln 4l
(2l
>>
d)
d
实际电导 G′ = I 2 = 1 G, 即 R = 1 ln 4l
U2
2πσl d
3.非深埋的球形接地器
解:考虑地面的影响,可用镜像法处理。
图3.4.7 非深埋的球形接地器
1)直接用电流场计算
设 I→ J
→
E=J
γ
→ U = ∫ E ⋅ dl
静电场恒定电流场

02
静电除尘器的工作原理是:在高压电场中,气体分子被电离 成正离子和电子,电子在向集尘极移动的过程中与粉尘颗粒 碰撞并使其带电,然后在电场力的作用下向集尘极移动并被 吸附。通过定期清理集尘极,可以去除收集到的粉尘颗粒。
03
静电除尘器的优点包括高效除尘、低能耗、稳定可靠等。 然而,其缺点包括设备庞大、维护成本高、需要高压电源 等。
探索静电场与恒定电流场在生物医学工程中的应 用,如电疗、电刺激等。
环境监测与治理
利用静电场与恒定电流场的特性,开发环境监测 和治理的新技术和方法。
感谢观看
THANKS
恒定电流场中,电流 密度矢量与电场强度 矢量垂直。
恒定电流场的形成
恒定电流场的形成需要电源、导 线和负载等组成部分,其中电源 提供电能,导线传输电流,负载
消耗电能。
恒定电流场的形成需要满足一定 的条件,如电源的稳定输出、导 线的恒定阻抗、负载的恒定阻抗
等。
恒定电流场的形成过程中,电荷 在电场力的作用下移动形成电流, 而电流的ห้องสมุดไป่ตู้动又会产生新的电场。
运用数学工具,建立更精确的数学模型,以描述静电场与恒定电流场的分布、变化和相互 作用。
探索非线性效应
研究静电场与恒定电流场中的非线性效应,如混沌、分形等复杂现象,以揭示其内在的动 态特性。
静电场与恒定电流场的实验研究
实验验证理论模型
通过实验手段验证理论模型的正确性和有效性,为理论提供实证 支持。
发展高精度测量技术
等领域。
了解静电场与恒定电流场的相 互作用有助于更好地理解和应 用电磁波的传播和电磁场的性
质。
04
静电场与恒定电流场的实际 应用
静电除尘器
01
第2章静电场和恒定电流电场
ϕ = C E1t = E2t Et = 0 ρs ⇒ ⇔ ∂ϕ D n − D2n = 1 Dn = ρs ε ∂n = −ρs 0
E = −∇ϕ, ∇⋅ D = ρ Q v v v ∇⋅ (ϕD) = ϕ∇⋅ D +∇ϕ ⋅ D v v v v v v ∴E ⋅ D = −∇ϕ ⋅ D = −∇⋅ (ϕD) +ϕ∇⋅ D = −∇⋅ (ϕD) + ρϕ v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫∫ ∇⋅ (ϕD)dv 2 2 v v v 高斯定理) Q∫∫∫ ∇⋅ (ϕD)dv = ∫∫ ϕD⋅ dS (高斯定理) v v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫ ϕD⋅ dS 2 2 1 v v 1 Q ∫∫ ϕD⋅ dS 通常 = 0 ∴W = ∫∫∫ ρϕdv (2) 2 2
−ρ 0 ≤ x ≤ d 2 , ∇ ϕ1 = 2 ε d ∇2ϕ = 0, ≤ x≤d 2 2 ϕ 因为ϕ1 , 2与坐标y,z 无
+
x
d
−
2
ρ
2
O
关,电位方程可简化为: 电位方程可简化为:
d ϕ1 −ρ ∇ ϕ1 = = , 2 dx ε
2 2
d ϕ2 ∇ ϕ2 = = 0, 2 dx
v v 1 W = ∫∫∫ E ⋅ Ddv (1) 六 静电场的能量 v v 2
例1 平行板电容器极板平面的尺寸远大于它们之间的距 离d,两极板间加恒定电压 U 0 ,极板间的介电常数为ε, 其中一半空间有体电荷均匀分布, 其中一半空间有体电荷均匀分布,体电荷密度为 ρ ,分 界面与极板平行。试求极板间的电位分布。 界面与极板平行。试求极板间的电位分布。 解
当分界面为导体与电介质的交界 面时,由于导体的特殊性质, 面时,由于导体的特殊性质,在导体和介质的分解面上 的边界条件有其特点。导体在静电场中有以下性质: 的边界条件有其特点。导体在静电场中有以下性质: 1)导体内部不带电,电荷只分布在导体表面上; 导体内部不带电,电荷只分布在导体表面上; 导体内部电场为零; 2)导体内部电场为零; 3)导体表面电场方向为法线方向,导体是个等势体, 导体表面电场方向为法线方向,导体是个等势体, 表面是等势面。 表面是等势面。 导体和电介质分界面上的边界条件为: 导体和电介质分界面上的边界条件为:
实验八 用恒定电流场模拟静电场

实验八用稳恒电流场模拟测绘静电场静电场的分布由空间的电荷分布决定。
已知空间的电荷分布以及电介质和边界条件来求解静电场的分布,绝大多数情况下无法求出解析解,因此,要用数值或实验的方法来测量静电场的分布。
直接测量静电场的分布通常比较困难,因为将电表等仪器放入待测场中会使待测场发生变化。
此外,除了静电式仪器之外的大多数仪器也不能用于静电场的直接测量,因为在静电场中无电流流过,这些仪器是不起作用的。
因此,在这个实验中用恒定电流场来模拟静电场。
具体做法是根据测量结果来描绘出与静电场对应的恒定电流场电势分布,从而确定静电场的电势分布。
模拟法的本质是用一种易于实现、便于测量的物理过程来模拟不易实现、不便测量的过程,只要这两种过程有一一对应的物理量,并且这些物理量在两个过程中满足数学形式基本相同的方程和边界条件。
[实验目的]1. 学会用模拟法测量和研究静电场;2. 加深对电场强度和电势等概念的理解。
[实验原理]根据电磁学理论,导电介质中恒定电流产生的场的基本方程和边界条件,和静电场中无电荷空间的对应方程和边界条件有相似的形式,如下表所示:由上表可见,两个场之间的物理量存在一一对应关系。
两个场的电势都是方程的解,静电场中导体的表面为等势面,而电流场中电极上各点的电势相等,所以两个场用电势来表示时的边界条件相同,所以两个场的解相等。
因此,可以用恒定电流场来模拟静电场,即用恒定电流场的电势分布来模拟静电场的电势分布。
如图8-1是一圆柱形同轴电缆,内圆筒半径1r ,外圆筒半径2r ,所带电量电荷线密度为λ±。
根据高斯定理,圆柱形同轴电缆电场的电位移矢量:rD π2λ=电场强度为:2πE rλε=式中,r 为场中任一点到轴的垂直距离。
两极之间的电位差为:212121d ln 2π2πr r rU U r r r λλεε-==⎰设 =2U 0V 211ln 2πr U r λε= (8-1)任一半径r 处的电位为:22d ln 2π2πr rr U r rλλεε==⎰(8-2) 把(8-1)式代入(8-2)式消去λ,得: r rr r U U 2121ln ln =(8-3) 现在要设计一稳恒电流场来模拟同轴电缆的圆柱形电场,使它们具有电位分布相同的数学形式,其要求为 (1)设计的电极与圆柱形带电导体相似,尺寸与实际场有一定比例,保证边界条件相同。
用恒定电流模拟静电场实验报告思考题

用恒定电流模拟静电场实验报告思考题静电场是由电荷分布决定的。
给定区域内的电荷分布和介质分布及边界条件,可根据麦克斯韦议程组和边界条件来求得电场分布。
但大多数情况下求出解析解,因此,要靠数字解法求出或实验方法测出电场分布。
【实验目的】1.学会用模拟法描绘和研究静电场的分布状况。
2.掌握了解模拟法应用的条件和方法。
3.加深对电场强度及电势等基本概念的理解。
【实验仪器】导电液体式电场描绘仪,同轴电极,平行板电极,白纸(自备)【实验原理】直接测量静电场是很困难的,因为仪表(或其探测头)放入静电场中会使被测电场发生一定变化。
如果用静电式仪表测量,由于场中无电流流过,不起作用。
因此,在实验中采用恒定电流场来模拟静电场。
即通过测绘点定电流场的分布来测绘对应的静电场分布。
模拟法的要求是:仿造一个场(称为模拟场),使它的分布和静电场的分布完全一样,当用探针去探测曲势分布时,不会使电场分布发生畸变,这样就可以间接测出静电场。
1用模拟法测量静电场的方法之一是用电流场代替静电场。
由电磁学理论可知电解质(或水液)中稳恒电流的电流场与电介质(或真空)中的静电场具有相似性。
在电流场的无源区域中,电流密度矢量和静电场中的电场强度矢量所遵从的物理规律具有相同的数学形式,所以这两种场具有相似性。
在相似的场源分布和相似的边界条件下,它们的解的表达式具有相同的数学模型。
如果把连接电源的两个电极放在不良导体如稀薄溶液(或水液)中,在溶液中将产生电流场。
电流场中有许多电位彼此相等的点,测出这些电位相等的点,描绘成面就是等位面。
这些面也是静电场中的等位面。
通常电场分布是在三维空间中,但在水液中进行模拟实验时,测出的电场是在一个水平面内的分布。
这样等位面就变成了等位线,根据电力线与等位线正交的关系,即可画出电力线。
这些电力线上每一点切线方向就是该点电场强度的方向。
这就可以用等位线和电力线形象地表示静电场的分布了。
检测电流中各等位点时,不影响电流线的分布,测量支路不能从电流场中取出电流,因此,必须使用高内阻电压就能消除这种影响。
静电场和恒定电流常用公式

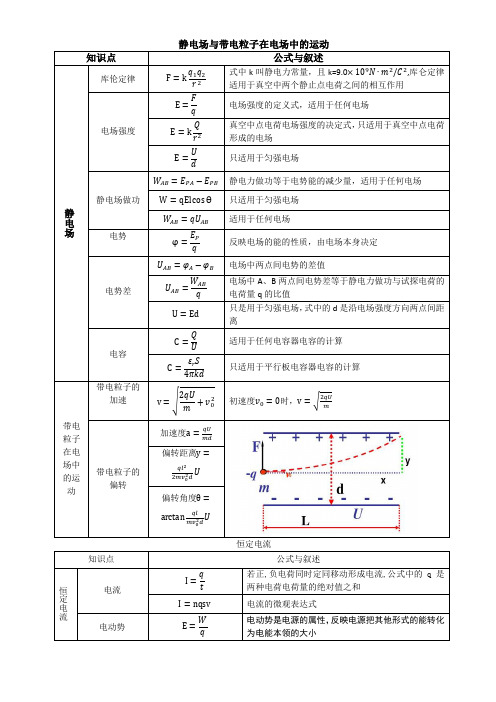
静电场和恒定电流常用公式电场元电荷e=1.6×10-19C(k=9.0×109Nm 2/C 2) 库仑定律:电场强度:(定义式)点电荷的电场强度:电场力:F=qE注:以上公式中各物理量均以绝对值代入计算。
电势: (ε为电势能)(公式中各物理量均以正、负值代入计算)电势差:(公式中各物理量均以正、负值代入计算)电场力做的功:qEd qU W ==电容:(定义式)决定式:平行板电容器两极板间的电场强度为(由E=U/d,C=Q/U 和得出):带点粒子在电场中的运动①粒子穿越电场的加速度:mdqU m qE m F ===a ②粒子穿越电场的运动时间:0L t v = ③粒子离开电场的侧移距离:202202222121mdv qUL mv qEL at y === ④粒子离开电场时的偏角θ:200y tan mdv qUL v v ==θ 恒定电流电流强度:neSv R U t Q I ===电阻:Sl I U R ρ==(ρ为导体的电阻率,单位Ω•m )(1)串联电路 221r Q Q k F =q F E =2r Q k E =q εϕ=q W U AB B A AB =-=ϕϕU Q C =S kQ E επ4=kd S C πε4=①各处的电流强度相等:I 1=I 2=…… =I n ②分压原理:n n 2211R U R U R U =⋯⋯== ③电路的总电阻:R=R 1+R 2+……+R n ④电路总电压:U=U 1+U 2+……+U n(2)并联电路①各支路电压相等:U=U 1=U 2=……=U n ②分流原理:I 1R 1=I 2R 2=……=I n R n ③电路的总电阻:n211111R R R R +⋯⋯++= ④电路中的总电流:I=I 1+I 2+……+I n 焦耳定律 t R U Rt I Pt Q W 22==== R U UI R I P P 22热==== 无论串联电路还是并联电路,电路的总功率等于各用电器功率之和,即: n P P PP +⋯⋯++=21总 闭合电路欧姆定律(1)路端电压与外电阻R 的关系:Rr E r R ER IR U +=+==1(外电路为纯电阻电路) (2)路端电压与电流的关系:U=E -Ir (普适式)电源的总功率(电源消耗的功率)P 总=IE电源的输出功率(外电路消耗的功率)P 输=IU电源内部损耗的功率:P 损=I 2r由能量守恒有:IE=IU +I 2r外电路为纯电阻电路时:()()r R r R E r R R E R I IU P 422222+-=+===输 由上式可以看出,当外电阻等于电源内部电阻(R=r )时,电源输出功率最大,其最大输出功率为r42max E P =出电源的效率:电源的输出功率与电源功率之比,即%100%100%100⨯=⨯=⨯=EU IE IU P P 出η 对纯电阻电路,电源的效率为()%10011%100r %100r 22⨯+=⨯+=⨯+=RR R R I R I η 由上式看出:外电阻越大,电源的效率越高。
静电场与恒定电流公式
带电粒子的偏转
加速度
偏转距离
偏转角度
恒定电流
知识点
公式与叙述
恒定电流
电流
若正,负电荷同时定同移动形成电流,公式中的q是两种电荷电荷量的绝对值之和
电流的微观表达式
电动势
电动势是电源的属性,反映电源把其他形式的能转化为电能本领的大小
电动势等干内外电路电势降落之和
欧姆定律
部分电路欧姆定律,只适川于金属导体和解质溶液
并联电路中通过各电阻的电流跟它的阻值成反比
多用电表
原理
满偏电流
半偏电流
电阻的决定式,电阻的大小面导体的材料、横截面积和长度共同决定
闭合电路能量转化关系
电路闭合后,非静电力所做的功等于内外电路中电能转化为其他形式的能的总和
电源的最大输出功率
当外电路的电阻等于电源的内阻时,电源的输出功率最大
电源的效率
输出功率和电源总功率的比值
电路的基本关系
串联电路
电流关系:
串联电路各处的电流相等
电压关系
申联电路两端的总电压等于各部分电路电压之和
电阻关系
串联电路的总电阻等于各部分电路电阻之和
串联电路分压:
串联电路中各电压两端电压跟它的阻值或正比
并联电路
电流关系
并联电路的总电流等于各支路电流之和
电压关系
井联电路的总电压与各支路电压相等
电阻关系
并联电路总电阻的倒数等于各支路电阻的倒数之和
并联电路分流
闭合电路欧姆定律,只适用于外电路为纯电的情况
电功
适用于任何电路
只适用于纯电阻电路
焦耳定律
对于非纯电阻电路W>Q;对于纯电阻电路,W=Q
用恒定电流场模拟静电场

y 2
z 2
在相同的边界条件下,这两个方程的特解相同,即这两种场的电势分布相似。实验中只 要两种场的带电体的形状和大小,相对位置以及边界条件一样,就可以用电流场来研究和测 绘静电场的分布。
下面以同轴圆柱形电极的静电场和相应的模拟场——稳恒电流场来讨论这种等效性。
图 1 同轴圆柱电极(a)及其静电场分布图(b)
2、 同轴圆柱电极模拟场等势线电压分布表
等势线测量点 r1 (cm) r2 (cm) r3 (cm) r4 (cm) 平均值 r (cm)
理论值 r 理(cm)
U1 (7.0V)
1.43
1.30
1.25
1.21
1.37
1.34
U2 (5.0V)
1.90
1.90
1.78
1.85
1.91
1.88
U3 (3.0V)
实验中把连接电源的两个电极放在不良导体如稀薄溶液(或水)中,在溶液中将产生电
流场。电流场中有许多电势彼此相等的点,测出这些电势相等的点,描绘成面就是等势面。
这些面也是静电场中的等势面。通常电场分布是在三维空间中,但在水中进行模拟实验时,
测出的电场是在一个水平面内的分布。这样等势面就变成了等势线,根据电场线与等势线正
述困难,本实验采用数学模拟法,仿造一个与待测静电场分布完全一样的电流场(称为模拟
场),使它的分布和静电场的分布完全一样,当用探针去探测模拟场时,它不受干扰,因此可
以间接测出被模拟的静电场。
一般情况下,要进行数学模拟,模拟者和被模拟者在数学形式上要有相同的方程,在相
同的初始条件和边界条件下,方程的特解相同,这样才可以进行模拟。由电磁学理论可知,
4、 将电表转换开关拨向“探测”,让探针接触中心电极,调节电压至 10V(细调)。若 中心电极的电压显示为 0V,则改变电源电压输出极性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S侧
S侧
S侧
SE dS 2rhE
qi h
i
E 2 0 r
同例1-2
例1-9 计算无限大均匀带电平面
的场强分布(电荷密度为)
面对称性 E垂直于平面
E
E
例1-4的结论
E S
dS
2底
侧
侧 0 底 2ES
SE dS 2ES
qi S
i
E 2 0
2ES S 0
同例1-4
例1-10 计算两无限大均匀带异号电荷平面的场
d e
E
dS
EdS
q
4 0 R 2
dS
e
S
q
4 0 R 2
dS
q
4 0 R 2
dS q
S
0
E
dS
+
2. 点电荷在任意形状的高斯面内
一定可以重新做一个球面让
电荷在圆心所有电场线通过
e
E dS
S
E dS
q
S'
0
S
S’
++
3. 点电荷在闭合曲面以外
做两个同心球面
e
E dS 0
强分布。
1-9 结论 EA EB 20
平面之间:
+
-
EA
E内 EA EB 0
平面之外:
EB
A
B
E外 EA EB 0
1.4 电势及其梯度 静电场的功能关系
1.4.1 静电场的保守性
保守性
做工与路径无关
1、点电荷的电场
b
E
q
40r 2
q
r dr
将一检验电荷沿任意路径L 从a点到b点,电场力的功
i 1
Ei
in i 1
qi
4 0
ri
2
eri
电荷连续分布带电体场强
dE
dq
4 0r 2
er
E dE
Q
dq
4 0r 2 er
qi
ri
Q r P
dE
E Ex Ey Ez
Q
dV
dE dEx dEy dEz
Ex dEx Ey dEy Ez dEz
ds
dl
体分布,体电荷密度 面分布,面电荷密度 线分布,线电荷密度
dq dv dq ds
dq dl
例题 1-1 P12 电偶极子轴线的中垂线上静电场 r >> l
电偶极子:一对等值异号的点电
荷构成的电荷系。
q
E E 40 r 2 l 2 4
EP 2E cos
E+
EP
P
cos
l/2 r2 l2
4
EP
4 0
ql r2 l2
32
4
E-
r
-q l q
对于 a >> L 离导线很远的地方
Ex 0
E
Ey
a
2 cos
L 4a(a2
L2
/
4)1/ 2
点电荷
L 4 a 2
q
4 a 2
例1-3 电荷 q 均匀地分布在一半径为 R 的圆环上。 计算在圆环的轴线上任一给定点 P 的场强。
取圆环上一段电荷微元dq
r
R
x
P
x
dE//
dq
dq
0.3 物质的电结构 原子物理
0.2 电荷的相互作用
静止电 荷q0
电场
静止电 荷q
磁 场
电场力 两个电荷之间的相互作用 电场 传递电场力的矢量场
非超距作用
第1章 静电场 恒定电流场
静止电 荷q0
静止电 荷q
静电场
电场
导体中 的运动 电荷q
恒定电流场
对称性分析
1.2 电场和电场强度
1.2.1电场的描述
更一般的情况
de
E
dS
E
cosdS
e
E dS
S
E cos dS
S
如果是闭合曲面
e
E dS
S
E cosdS
S
规定面积元方向从闭 合面内指向面外
电力线穿入 电力线穿出
E
ds
0
E ds > 0
n
dS
E
(9c) E
S
dS
dS
1.3.2 高斯定理的表述与证明
库伦定律
静止电荷
电场
qi
E ds i
S
0
是高斯面上各点的场强,由闭合面内、外电荷 E 的分布决定,是全部电荷共同产生的的合场强
E dS
S
只取决于闭合面内的电量
电场的基本规律,有源场
1.3.3 高斯定理求静电场分布
E ds
i
qi
S
0
求解
E
利用对称性, 将E作为标量 提出积分式!
电荷的对称分布
k 9 109 N m2 / C 2
F
1
4
q1q2 r2
0
1
4k
8.851012
(
N 1m 2 C 2
)
静电力常量
真空介电常数(真空电容率)
矢量形式
F
1
4 0
q1q2 r2
er
电场强度分布
E
1
4 0
q r2
er
er
从场源电荷q指 向场点
球对称 正电荷受力方向
点电荷系场强
E
E
f
q
in i 1
fi
in
fi
q
i1 q
in
Ei i 1
1.2.2 库伦定律与静电场的计算
库伦定律
F
在真空中,两个静止点电荷之间的
相互作用力大小,与它们的电量的乘 积成正比,与它们之间距离的平方成
r
q2
反比;作用力的方向沿着它们的联线,
同号电荷相斥,异号电荷相吸。
q1
F
k
q1q2 r2
利用上一题结论,取一个
dr
同心圆环为电荷微元dq
r
dE
R
xP
dE
4 0
xdq x2 r2
3/2
dq 2 rdr
x 2 rdr
dE 4 0
x2 r2 3 2
R
E dE
0
x 2 rdr 40 x2 r 2 3 2
x
2 0
1
(x2
R2 )1
2
E
2 0
1
(x2
r a
q0
dl
E
dA q0E dl
q0E cos dl
A
L q0 E dl
L
q0q
40r 2
dr
q0q
40r 2
dr
q0q
4 0
1 ra
1 rb
2、任意带电体系的电场
将带电体系分割为许多点电 荷元,根据电场的叠加性
E Ei
i
电场力做功为:
A q0
E dl
L
q0
+++++++++ --------------
+ +
–
几种电荷的 E 线分布的实验现象:
单个点电极
正负点电极
单个带电板
正负带电板
电场通量 通过某一曲面电场线数的代数和
n E
S
S
S
n
S
S
E
E N S
e N ES
S Sen
表征电场线穿过面的方向
e ES ES cos E S
r >> l
EP
ql
4 0 r 3
电偶极矩
p ql
EP
p
4 0 r 3
例1-2 P15 真空中一均匀带电直线,电荷线密度为
。线外有一点 P ,离开直线的垂直距离为 a ,P
点和直线两端连线的夹角分别为 1 和 2 。求 P 点
的场强。
取一段电荷微元dq
dE
dq
40r 2
dx 40r 2
pE
1.3 高斯定理 1.3.1 电场线与电通量
电场线
用一簇假象空间曲线形象描述场强 分布通常把这些曲线称为电场线
电场线对电场的 描述
E
电场方向:电场线上每一 点的切线方向
电场大小:在电场中任一 点,取一垂直于该点场强 方向的面积元,通过的电 场线数目为该点场强的量 值
电场线的特点
始于正电荷终于负电荷 电场线永不闭合 电场线永不相交
电场的对称分布
常见的电荷分布的对称性
球对称
柱对称
面对称
球体 均匀带 球面 电的: 点电荷
柱体 无限长 柱面
带电线
平板 无限大
平面
例1-6 均匀带电球面 求半径为R, 均匀地带有总电量q (设q>0)的球面的静电场分布
分析空间中任一点的电场
看作同心球面上一点
带电球面切洋葱 例1-3
空间任一点和电场都垂直球面且 同一球面上每点电场强度相同
Q++
场源电荷 检验电荷 场点
场力 电场强度
E
f
q0
q0 P
f
(q0静止)
注意 点电荷(尺寸小) q0足够小,对待测电场影响小
静电场
静止的场源电荷产生的电场
电场是位置函数,是矢量场
E
Er
Ex
y
z
单位
