运筹学实验报告二

合集下载

运筹学实验报告2讲解

实验报告《运筹学》2015～2016学年第一学期实验目的：加强学生分析问题的能力，锻炼数学建模的能力。

掌握WinQSB/Matlab 软件中线性规划、灵敏度问题的求解和分析。

用 WORD 书写实验报告：包括详细规划模型、试验步骤和结果分析。

实验内容：题1：某厂的一个车间有1B ，2B 两个工段可以生产123,,A A A 三种产品，各工段开工一天生产三种产品的数量和成本，以及合同对三种产品的每周最低需求量由表1给出。

问每周各工段对该生产任务应开工几天，可使生产合同的要求得到满足，并使成本最低。

建立模型。

表1生产定额(吨/天)工段B生产合同每周最低需求量（吨）ib iA 产品1A 2A 3A 1B 2B 11311310002000599成本（元/天）建立模型：WinQSB录入模型界面：运行结果界面：结果分析：决策变量：X1，X2最优解：X1=3，X2=2；目标系数：C1=1000，C2=2000；最优值：7000；其中X1贡献3000，X2贡献4000；检验数，或称缩减成本：0，0。

即当非基变量增加一个单位时，目标值的变动量。

目标系数的允许减量和允许增量；目标系数在此范围变量时，最优基不变。

约束条件约束条件：C1，C2，C3左端：5，11，9右端：5，9，9松弛变量或剩余变量：该端等于约束左端与约束优端之差；为0表示资源达到限制值。

题2：明兴公司面临一个是外包协作还是自行生产的问题。

该公司生产甲、乙、丙三种产品，这三种产品都要经过铸造、机加工和装配三个车间。

甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。

有关情况见表2；公司中可利用的总工时为：铸造8000小时，机加工12000小时和装配10000小时。

建立模型：解；假设公司选择甲产品自产X1件，外包协作X2件，乙产品自产X3件，外包协作X4件，丙产品生产X5件，则有；maxZ=15X1+13X2+10X3+9X4+7X5s.t. 5X1+10X3+7X5<=80006X1+6X2+4X3+4X4+8X5<=12000 3X1+3X2+2X3+2X4+2X5<=10000 X1-5>=0WinQSB录入模型界面：运行结果界面：结果分析：(1)X*=(1600,0,0,600,0), Z*=29400元，即：公司为了获得最大利润29400元，甲、乙、丙三种产品各生产1600件、600件、0件。

运筹学实验报告

运筹学实验报告运筹学实验报告一、实验目的：本实验旨在了解运筹学的基本概念和方法，并通过实践，掌握运筹学在实际问题中的应用。

二、实验过程：1.确定运筹学的应用领域：本次实验选择了物流配送问题作为运筹学的应用领域。

2.收集数据：我们选择了一个小型企业的物流配送数据进行分析，并将数据录入到计算机中。

3.建立模型：根据所收集的数据，我们建立了一个代表物流配送问题的数学模型。

4.运用运筹学方法进行求解：我们运用了线性规划的方法对物流配送问题进行求解，并得到了最优解。

5.分析结果：通过分析最优解，我们得出了一些有关物流配送问题的结论，并提出了一些优化建议。

三、实验结果：通过运用运筹学方法对物流配送问题进行求解，我们得到了一个最优解，即使得物流成本最低的配送方案。

将最优解与原始的配送方案进行对比，我们发现最优解的物流成本降低了20%，节省了货物运输的时间，减少了仓储成本。

四、实验结论：通过本次实验，我们了解了运筹学的基本概念和方法，并成功应用运筹学方法解决了物流配送问题。

通过分析最优解，我们发现采用最优解可以降低物流成本，提高配送效率。

因此，我们得出结论：运筹学在物流配送问题中的应用具有重要意义，可以帮助企业降低成本、提高效率。

五、实验心得：通过本次实验，我对运筹学有了更深入的了解。

通过实践应用运筹学方法，我明白了运筹学的实用性和价值。

在以后的工作中，我会更加注重运筹学方法的应用，以解决实际问题，提高工作效率。

本次实验不仅增强了我的动手实践能力，也培养了我分析和解决问题的能力。

我将继续学习和探索运筹学的知识，为将来的工作打下坚实的基础。

运筹学实验报告

实验二案例4.3 便民超市的网点布设一、背景资料介绍便民超市的网点布设：南平市规划在其远郊建一卫星城镇，下设20个街区，如图所示。

各街区居民数预期为1、4、9、13、17、20各12000人；2、3、5、8、11、14、19各14000人；6、7、10、12、15、16、18各15000人。

便民超市准备在上述街区进行布点。

根据方便就近的原则，在某一街区设点，该点将服务于该街区及相邻街区。

例如在编号为3的街区设一超市点，它服务的街区为1、2、3、4、6。

由于受到经费限制，便民超市将在上述20个街区内先设两个点。

请提供你的建议：在哪两个街区设点，使其服务范围的居民人数为最多。

二、数学模型的建立1、根据图示及材料可以总结出以下表格：2、设街区编号为Xi,在第i个街区设点能服务到的人数为a i令Xi=1时，表示在第i街区设点；Xi=0时，表示在第i街区不设点{10,2..m ax )20,193,2,1(01201201或目标函数：个街区不设点，在第个街区设点，在第==⎩⎨⎧=⋯⋯==∑∑==i i i i i i i i x x a t s x aZ i i i x三、数据输入方法1、打开运筹学软件，点击整数规划，选择纯整数规划，单击菜单中的“新建”2、在变量个数中输入：20，在约束条件中输入：21，选择Max ，然后单击确定3、在目标函数中变量X1，X2，……X19，X20所对应的系数分别填入：4、共设21个约束条件(j=21)，前20个约束条件是为了保证Xi=0或1，第21个约束条件是为了保证从20个街区中选2个。

（1）在约束条件j （j=1、2、3…18、19、20）中：除了变量Xi （当i=j 时）的系数填“1”，其余变量的系数都填“0”，符号都选择“≤”，b 的值都为“1”；（2）在约束条件j （j=21）中：所有变量Xi 的系数都填“1”，符号选择“=”，b 的值为“2”四、数据输出解读1、所有数据输入完后，单击“解决”按钮，得到如下“提示信息”对话框2、单击“确定”后，得到“结果输出”表格3、结果表明：当便民超市在街区6和14设点时，其服务范围内的居民人数为最多；此时，预期最多服务人数为208000人。

运筹学实验报告

运筹学实验报告学院：安全与环境工程姓名：***学号： **********专业：物流工程班级：物流1302班实验时间： 5月8日、 5月9日5月13日、5月14日5月20日、5月21日湖南工学院安全与环境工程学院2015年5月实验一线性规划一、实验目的1、理解线性规划的概念。

2、对于一个问题，能够建立基本的线性规划模型。

3、会运用Excel解决线性规划电子表格模型。

二、实验内容线性规划的一大应用适用于联邦航空公司的工作人员排程，为每年节省开支超过600万美元。

联邦航空公司正准备增加其中心机场的往来航班，因此需要雇佣更多的客户服务代理商，但是不知道到底要雇用多少数量的代理商。

管理层意识到在向公司的客户提供令人满意的服务水平的同时必须进行成本控制，因此，必须寻找成本与收益之间合意的平衡。

于是，要求管理团队研究如何规划人员才能以最小的成本提供令人满意的服务。

分析研究新的航班时间表，以确定一天之中不同时段为实现客户满意水平必须工作的代理商数目。

在表1.2的最后一栏显示了这些数目，其中第一列给出对应的时段。

表中的其它数据反映了公司与客户服务代理商协会所定协议上的一项规定，这一规定要求每一代理商工作8小时为一班，各班的时间安排如下：轮班1：6:00AM～2:00PM轮班2：8:00AM～4:00PM轮班3：中午～8:00PM轮班4：4:00PM～午夜轮班5：10:00PM～6:00AM表中打勾的部分表示这段时间是有相应轮班的。

因为轮班之间的重要程度有差异，所以协议中工资也因轮班所处的时间而不同。

每一轮班对代理商的补偿（包括收益）如最低行所示。

问题就是，在最低行数据的基础上，确定将多少代理商分派到一天之中的各个轮班中去，以使得人员费用最小，同时，必须保证最后一栏中所要求的服务水平的实现。

表1.1 联邦航空公司人员排程问题的数据轮班的时段时段 1 2 3 4 5 最少需要代理商的数量6:00AM～8:00AM √ 488:00AM～10:00AM √√ 7910:00AM～中午√√ 65中午～2:00PM √√√ 872:00PM～4:00PM √√ 644:00PM～6:00PM √√ 736:00PM～8:00PM √√ 828:00PM～10:00PM √ 4310:00PM～午夜√√ 52午夜～6:00AM √ 15每个代理商的每日成本 170 160 175 180 195三、实验步骤（1）明确实验目的：科学规划人员以最小的成本提供令人满意的服务。

运筹学实践教学报告范文(3篇)

第1篇一、引言运筹学作为一门应用数学分支，广泛应用于经济管理、工程技术、军事决策等领域。

本报告旨在通过运筹学实践教学，验证理论知识在实际问题中的应用效果，提高学生的实践能力和创新能力。

以下是对本次实践教学的总结和反思。

二、实践教学内容1. 线性规划问题本次实践教学选择了线性规划问题作为研究对象。

通过建立线性规划模型，我们尝试解决生产计划、资源分配等实际问题。

- 案例一：生产计划问题某公司生产A、B两种产品，每单位A产品需消耗2小时机器时间和3小时人工时间，每单位B产品需消耗1小时机器时间和2小时人工时间。

公司每天可利用机器时间为8小时，人工时间为10小时。

假设A、B产品的利润分别为50元和30元，请问如何安排生产计划以获得最大利润？- 建模：设A产品生产量为x，B产品生产量为y，目标函数为最大化利润Z = 50x + 30y，约束条件为：\[\begin{cases}2x + y \leq 8 \\3x + 2y \leq 10 \\x, y \geq 0\end{cases}\]- 求解：利用单纯形法求解该线性规划问题，得到最优解为x = 3，y = 2，最大利润为240元。

- 案例二：资源分配问题某项目需要分配三种资源：人力、物力和财力。

人力为50人，物力为100台设备，财力为500万元。

根据项目需求，每种资源的需求量如下：- 人力：研发阶段需20人，生产阶段需30人；- 物力：研发阶段需30台设备，生产阶段需50台设备；- 财力：研发阶段需100万元，生产阶段需200万元。

请问如何合理分配资源以满足项目需求？- 建模：设人力分配量为x，物力分配量为y，财力分配量为z，目标函数为最大化总效用U = x + y + z，约束条件为：\[\begin{cases}x \leq 20 \\y \leq 30 \\z \leq 100 \\x + y + z \leq 500\end{cases}\]- 求解：利用线性规划软件求解该问题，得到最优解为x = 20，y = 30，z = 100，总效用为150。

运筹学第二次实验报告

实验课程名称运筹学实验项目名称熟悉LINDO软件Repart功能及其他功能年级 09级专业信息与计算科学学生姓名曾权学号 0907010215理学院实验时间：2011 年10 月12 日学生实验室守则一、按教学安排准时到实验室上实验课，不得迟到、早退和旷课。

二、进入实验室必须遵守实验室的各项规章制度，保持室内安静、整洁，不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物，不准做与实验内容无关的事，非实验用品一律不准带进实验室。

三、实验前必须做好预习（或按要求写好预习报告），未做预习者不准参加实验。

四、实验必须服从教师的安排和指导，认真按规程操作，未经教师允许不得擅自动用仪器设备，特别是与本实验无关的仪器设备和设施，如擅自动用或违反操作规程造成损坏，应按规定赔偿，严重者给予纪律处分。

五、实验中要节约水、电、气及其它消耗材料。

六、细心观察、如实记录实验现象和结果，不得抄袭或随意更改原始记录和数据，不得擅离操作岗位和干扰他人实验。

七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验，应特别注意规范操作，注意防护；若发生意外，要保持冷静，并及时向指导教师和管理人员报告，不得自行处理。

仪器设备发生故障和损坏，应立即停止实验，并主动向指导教师报告，不得自行拆卸查看和拼装。

八、实验完毕，应清理好实验仪器设备并放回原位，清扫好实验现场，经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。

九、无故不参加实验者，应写出检查，提出申请并缴纳相应的实验费及材料消耗费，经批准后，方可补做。

十、自选实验，应事先预约，拟订出实验方案，经实验室主任同意后，在指导教师或实验技术人员的指导下进行。

十一、实验室内一切物品未经允许严禁带出室外，确需带出，必须经过批准并办理手续。

学生所在学院：理学院专业：信息与计算科学班级：信计091姓名曾权学号 0907010215 实验组实验时间2011/10/12 指导教师杨光惠成绩实验项目名称熟悉LINDO软件的Repart功能及其它功能实验目的及要求：熟悉LINDO软件的Repart功能及其它功能如：Tableau（给出标准型的单纯形法）Formulation（给出整数后的模型）Picture实验（或算法）原理：LINDO软件的Tableau（给出标准型的单纯形法）Formulation（给出整数后的模型）Picture功能实验硬件及软件平台：windows操作系统、LINDO平台、计算机实验步骤：1、打开计算机并运行LINDO软件2、输入模型并检查错误3、调试程序并得出最后结果4、问题反馈实验内容（包括实验具体内容、算法分析、源代码等等）：输入的模型，及相关操作结果：实验结果与讨论：1、结果出来的图看不懂2、对picture的功能掌握不够指导教师意见：签名：年月日。

大学生运筹学实训报告范文

一、引言运筹学是一门应用数学的分支，它运用数学模型、统计方法和计算机技术等工具，对复杂系统进行优化和决策。

为了更好地理解和掌握运筹学的理论和方法，提高实际操作能力，我们开展了大学生运筹学实训。

以下是本次实训的报告。

二、实训目的1. 理解运筹学的基本概念、原理和方法；2. 学会运用运筹学解决实际问题；3. 提高团队协作和沟通能力；4. 培养独立思考和创新能力。

三、实训内容1. 线性规划（1）实训目的：通过线性规划实训，掌握线性规划问题的建模、求解和结果分析。

（2）实训内容：以生产问题为例，建立线性规划模型，运用单纯形法求解最优解。

2. 整数规划（1）实训目的：通过整数规划实训，掌握整数规划问题的建模、求解和结果分析。

（2）实训内容：以背包问题为例，建立整数规划模型，运用分支定界法求解最优解。

3. 非线性规划（1）实训目的：通过非线性规划实训，掌握非线性规划问题的建模、求解和结果分析。

（2）实训内容：以旅行商问题为例，建立非线性规划模型，运用序列二次规划法求解最优解。

4. 网络流（1）实训目的：通过网络流实训，掌握网络流问题的建模、求解和结果分析。

（2）实训内容：以运输问题为例，建立网络流模型，运用最大流最小割定理求解最优解。

5. 概率论与数理统计（1）实训目的：通过概率论与数理统计实训，掌握概率论与数理统计的基本概念、原理和方法。

（2）实训内容：以排队论为例，建立概率模型，运用排队论公式求解系统性能指标。

四、实训过程1. 组建团队，明确分工；2. 针对每个实训内容，查阅相关资料，了解理论背景；3. 根据实际问题，建立数学模型；4. 选择合适的算法，进行编程实现；5. 对结果进行分析，总结经验教训。

五、实训成果1. 理解了运筹学的基本概念、原理和方法；2. 掌握了线性规划、整数规划、非线性规划、网络流和概率论与数理统计等运筹学工具；3. 提高了团队协作和沟通能力；4. 培养了独立思考和创新能力。

六、实训心得1. 运筹学是一门实用性很强的学科，它可以帮助我们解决实际问题，提高工作效率；2. 在实训过程中，我们要注重理论联系实际，将所学知识应用于实际问题的解决；3. 团队协作和沟通能力在实训过程中至关重要，要学会与团队成员共同进步；4. 实训过程中，我们要敢于尝试，勇于创新，不断提高自己的实践能力。

运筹学实验报告

运筹学实验报告运筹学实验报告2实验内容：线性规划问题的建模和求解。

“炼油厂生产计划安排”，“长征医院的护士值班计划”两题目任选其一，每个小组最多3名同学，共同完成实验报告。

一、问题提出长征医院是长宁市的一所区级医院,该院每天各时间区段内需求的值班护士数如表1所示.该医院护士上班分五个班次,每班8h,具体上班时间为第一班2:00~10:00,第二班6:00~14:00,第三班10:00~18:00,第四班14:00~22:00,第五班18:00~2:00（次日）.每名护士每周上5个班,并被安排在不同日子,有一名总护士长负责护士的值班安排计划.值班方案要做到在人员或经济上比较节省,又做到尽可能合情合理.下面是一些正在考虑中的值班方案:方案1 每名护士连续上班5天,休息2天,并从上班第一天起按从上第一班到第五班顺序安排.例如第一名护士从周一开始上班,则她于周一上第一班,周二上第二班,……,周五上第五班；另一名护士若从周三起上班,则她于周三上第一班,周四上第二班,……,周日上第五班,等等.方案2 考虑到按上述方案中每名护士在周末（周六、周日）两天内休息安排不均匀.于是规定每名护士在周六、周日两天内安排一天、且只安排一天休息,再在周一至周五期间安排4个班,同样上班的五天内分别顺序安排5个不同班次.在对第1、2方案建立线性规划模型并求解后,发现方案2虽然在安排周末休息上比较合理,但所需值班人数要比第1方案有较多增加,经济上不太合算,于是又提出了第3方案.方案3 在方案2基础上,动员一部分护士放弃周末休息,即每周在周一至周五间由总护士长给安排三天值班,加周六周日共上五个班,同样五个班分别安排不同班次.作为奖励,规定放弃周末休息的护士,其工资和奖金总额比其他护士增加a%.根据上述,帮助长征医院的总护士长分析研究:(x)对方案1、2建立使值班护士人数为最少的线性规划模型并求解；(b)对方案3,同样建立使值班护士人数为最少的线性规划模型并求解,然后回答a的值为多大时,第3方案较第2方案更经济；二、问题简述从该医院各时间段护士值班表可看出：五个时间段所需护士人数分别为18,20,19,17,12。

运筹学实验心得(精选5篇)

运筹学实验心得(精选5篇)运筹学实验心得篇1实验心得：1.背景与目标：运筹学是一门决策支持学科，它使用数学模型和算法来解决实际生活中的优化问题。

本实验的目标是通过学习运筹学的基本理论和方法，提高自己在实际问题中的决策能力和解决问题的能力。

2.实验内容：本实验包括了几个重要的运筹学主题，包括线性规划、整数规划、非线性规划和动态规划等。

我们首先学习了这些基本概念和算法，然后通过具体案例进行了实践操作，并运用所学知识对实际生活中的一些问题进行了分析和解决。

3.实验结果与收获：通过实验，我们成功地运用运筹学方法解决了一些实际问题。

例如，我们使用线性规划算法解决了货物配送问题，并使用整数规划算法解决了人员调度问题。

同时，我们也收获了一些理论知识和实践经验。

我们学会了如何使用数学模型和算法来解决实际问题，并提高了自己的决策能力和解决问题的能力。

4.反思与建议：在实验过程中，我们遇到了一些困难和挑战。

例如，有时候我们无法理解复杂的数学模型和算法，或者无法找到合适的实际问题来验证我们的知识。

因此，我们建议在学习运筹学时，应该注重基本概念和算法的学习，并积极寻找合适的实际问题来巩固和应用所学知识。

总的来说，这次实验让我们更加深入地了解了运筹学的魅力和价值，也让我们更加坚定了自己的学习方向和目标。

运筹学实验心得篇2当然，我可以帮助您撰写一篇运筹学实验的心得体会。

以下是一个可能的示例：---标题：运筹学实验：理论到实践的桥梁摘要：这篇*分享了一次运筹学实验的经历，描述了实验中的问题、解决方法以及所学到的经验教训。

关键词：运筹学，实验，问题解决，学习经验---运筹学是我在大学期间最喜爱的科目之一。

它提供了一种实用且富有挑战性的方法来理解和解决现实世界中的优化问题。

然而，真正将理论与实际联系起来的，是我的第一次运筹学实验。

实验开始时，我被一大堆复杂的数学模型和计算机程序搞得眼花缭乱。

理论知识和抽象的模型使我有些晕头转向，但我还是勇敢地面对了挑战。

运筹学实验总结

运筹学实验总结引言：运筹学是一门综合了数学、经济学和工程学等多学科知识的学科，它通过建立数学模型和运用各种优化方法，帮助我们在现实问题中寻找最优解决方案。

在这学期的运筹学课程中，我们进行了一系列实验。

这些实验不仅加深了对运筹学理论的理解，还提供了一种应用运筹学方法解决问题的实践平台。

在本文中，我将总结我参与的运筹学实验，并分享我的体会和收获。

实验一：线性规划问题求解在这个实验中，我们学习了线性规划的基本概念和求解方法。

我选择了一个典型的生产调度问题作为实验题目。

通过建立数学模型，并运用线性规划软件，我成功地解决了这个问题。

通过这个实验，我深刻理解了线性规划问题的本质，以及如何利用线性规划方法找到最优解。

实验二：整数规划问题求解整数规划是线性规划的扩展，它在决策问题中更加实用。

在这个实验中，我选择了货物配送路线问题作为研究对象。

通过构建整数规划模型，并运用求解软件，我得到了最佳的货物配送方案。

这个实验不仅对我的数学建模能力提出了要求，还培养了我的实际问题解决能力。

实验三：动态规划动态规划是一种重要的优化方法，它广泛应用于最优化问题的求解。

在这个实验中，我们学习了动态规划的基本原理和设计思想。

我选择了旅行商问题作为研究对象，通过建立递推关系和寻找最优子结构，我成功地解决了该问题。

这个实验让我意识到了动态规划方法的强大威力，同时也对我的算法设计能力提出了更高的要求。

实验四：模拟退火算法模拟退火算法是一种全局搜索优化算法，具有很强的应用能力。

在这个实验中，我选择了旅行商问题作为研究对象，通过模拟退火算法的迭代和优化，我得到了一个较好的解。

通过这个实验，我掌握了模拟退火算法的基本原理和实现过程，也了解到了算法的优越性。

实验五：遗传算法遗传算法是一种模拟自然选择和遗传机制的优化算法。

在这个实验中，我选择了装箱问题作为研究对象。

通过运用遗传算法的交叉、变异和适应度选择，我得到了一个较好的装箱方案。

这个实验不仅对我的算法设计能力提出了更高的要求，还让我意识到了遗传算法的创新性和解决复杂问题的能力。

运筹学实验报告2

运筹学实验报告2《运筹学》课程实验第 2 次实验报告实验内容及基本要求:实验项目名称:运输问题实验实验类型: 验证每组人数: 1实验内容及要求:内容:运输问题建模与求解要求:能够写出求解模型、运用软件进行求解并对求解结果进行分析实验考核办法:实验结束要求写出实验报告，并于实验结束一周内(5月29日)上交。

实验结果:(附后)内容主要包括以下3点:1. 问题分析与建立模型，阐明建立模型的过程(一定要给出模型)。

2. 实验步骤，包含使用什么软件以及详细的实验过程。

3. 实验结果及其分析。

成绩评定:该生对待本次实验的态度 ?认真 ?良好 ?一般 ?比较差。

本次实验的过程情况 ?很好 ?较好 ?一般 ?比较差对实验结果的分析 ?很好 ?良好 ?一般 ?比较差文档书写符合规范程度 ?很好 ?良好 ?一般 ?比较差综合意见: 成绩指导教师签名刘长贤日期 2012.5.31实验背景:某农民承包了五块土地工206亩，打算种小麦、玉米和蔬菜三种农作物。

各种农作物的计划播种面积(亩)以及每块土地各种不同农作物的亩产量(公斤)如表1所示。

问如何安排种植计划，可使总产量最高,表1 每块土地种植不同农作物的亩产数量土地块别计划1 2 34 5 播种作物种类面积小麦 500 600650 1050 80086850 800 700 900 95070 玉米1000 950 850550 70050 蔬菜44 32 46 36 48土地亩数一(问题分析与建立模型 1.问题分析:总产量为目标函数maxZ;计划播种面积和土地亩数是约束条件;每块土地种植的不同农作物的亩产数量是决策变量2数学模型:目标函数1112131415MaxZ,500x，600x，650x，1050x，800x，2122232425 850x，800x，700x，900x，950x，1000x31，950x32，850x33，550x34，700x35约束条件x，x，x，x，x,861112131415x，x，x，x，x,702122232425x，x，x，x，x,503132333435x，x，x,36112131x，x，x,48122232x，x，x,44132333x，x，x,32142434 x，x，x,46152535xi,j,0,i,1,2,3,4,5;j,1,2,3二(实验步骤1.根据数学模型和题目要求，使用Excel软件建立如下表格2.单元格名称指定:选中要指定名称的单元格，点击“插入-名称-定义/指定”，则可对上图中的“亩产数量(=Sheet1!$C$3:$G$5)，种植量(=Sheet1!$C$8:$G$10)，实际面积(=Sheet1!$H$8:$H$10)，计划面积(=Sheet1!$J$8:$J$10)，实际亩数(=Sheet1!$C$11:$G$11)，土地亩数(=Sheet1!$C$13:$G$13)，总产量(=Sheet1!$L$12)”进行名称的指定3.单元格赋值:(1)利用“求和”函数对“实际面积”和“实际亩数”相应的单元格进行赋值，例如H8=SUM(小麦)，C11=SUM(土地1)(2)利用“SUMPRODUCT”函数对“总产量”对应的单元格L12进行赋值，由于之前指定了单元格名称，故总产量=SUMPRODUCT(亩产数量,种植量) (3)由于当前各决策变量的值为0，故相应的实际面积，实际亩数，总产量为0 4.单击“工具”>“加载宏”>“规划求解”设置相关参数，如下图目标单元格为总产量可变单元格为每块土地种植的不同农作物对应的单元格约束条件为实际面积=计划面积;实际亩数=计划亩数5.设置完目标单元格、可变单元格和约束条件后，点击“选项”，选定“采用线性模型”和“假定非负”，点击“确定”进行规划求解，结果如下图三(实验结果及分析由上图可知:应这样安排种植计划能使总产量最大1.在土地1上种植34亩玉米和2亩蔬菜2.在土地2上种植48亩蔬菜3.在土地3上种植44亩小麦4.在土地4上种植32亩小麦5.在土地5上种植10亩小麦和36亩玉米。

运筹学实验报告2

实验报告《运筹学》2015～2016学年第一学期学院（部）管理学院指导教师阎瑞霞班级代号 1511131姓名/学号周云佳2同组人无提交时间成绩评定实验目的：加强学生分析问题的能力，锻炼数学建模的能力。

掌握WinQSB/Matlab 软件中线性规划、灵敏度问题的求解和分析。

用 WORD 书写实验报告：包括详细规划模型、试验步骤和结果分析。

问每周各工段对该生产任务应开工几天，可使生产合同的要求得到满足，并使成本最低。

建立模型。

即当非基变量增加一个单位时，目标值的变动量。

目标系数的允许减量和允许增量；目标系数在此范围变量时，最优基不变。

约束条件约束条件：C1，C2，C3左端：5，11，9右端：5，9，9松弛变量或剩余变量：该端等于约束左端与约束优端之差；为0表示资源达到限制值。

题2：明兴公司面临一个是外包协作还是自行生产的问题。

该公司生产甲、乙、丙三种产品，这三种产品都要经过铸造、机加工和装配三个车间。

甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。

有关情况见表2；公司中可利用的总工时为：铸造8000小时，机加工12000小时和装配10000小时。

建立模型：解；假设公司选择甲产品自产X1件，外包协作X2件，乙产品自产X3件，外包协作X4件，丙产品生产X5件，则有；maxZ=15X1+13X2+10X3+9X4+7X5. 5X1+10X3+7X5<=80006X1+6X2+4X3+4X4+8X5<=120003X1+3X2+2X3+2X4+2X5<=10000X1-5>=0WinQSB录入模型界面：运行结果界面：结果分析：(1)X*=(1600,0,0,600,0), Z*=29400元，即：公司为了获得最大利润29400元，甲、乙、丙三种产品各生产1600件、600件、0件。

运筹学(二)实验报告

《运筹学（二）》实验报告2011～2012学年第二学期学院（部）：姓名/学号：实验目的：加强学生分析问题的能力，锻炼数学建模的能力。

利用所学知识，设计动态规划和决策树算法，并完成程序设计。

实验内容：题1（动态规划）：（投资问题）现有资金5百万元，可对3个项目进行投资。

假设2#项目的投资不得超过3百万元，1#和3#项目的投资均不得超过4百万元，3#项目至少要投资1百万元。

投资5年后每个项目预计可获得的收益由表1给出。

问如何投资可获得最大的收益。

表1实验过程参考答案：建立模型：MATLAB程序代码：题2：在某单人理发店顾客到达为普阿松流，平均到达间隔为20分钟，理发时间服从负指数分布，平均时间为15分钟。

求（1）顾客来理发不必等待的概率；（2）理发店内顾客平均数；（3）顾客在理发馆内平均逗留时间；（4）若顾客在店内平均逗留时间超过1.25小时，则店主将考虑增加设备及理发员，问平均到达率提高多少时店主才做这样考虑呢？MATLAB程序代码：function[PO,Ls,Lp,Ws,Wq]=model6lenda=input('请输入到达速率:');mhu=input('请输入服务速率:');rho=lenda/mhu;PO=1-rho;Ls=lenda/(mhu-lenda);Lq=Ls-rho;Ws=1/(mhu-lenda);Wq=Ws-1/mhu;POLsLqWsWq结果分析：>> model6请输入到达速率:1/20请输入服务速率:1/15PO =0.2500Ls =3.0000Lq =2.2500Ws =60.0000Wq =45.0000ans =0.25001．PO=0.252.Ls=33.Ws=604.lenda=4/75(人/分钟)5.题3：某企业为了扩大某产品的生产，拟建设新厂。

据市场预测，产品销路好的概率为0.7，销路差的概率为0.3。

有三种方案可供企业选择：方案一、新建大厂，需投资300万元。

运筹学实验报告

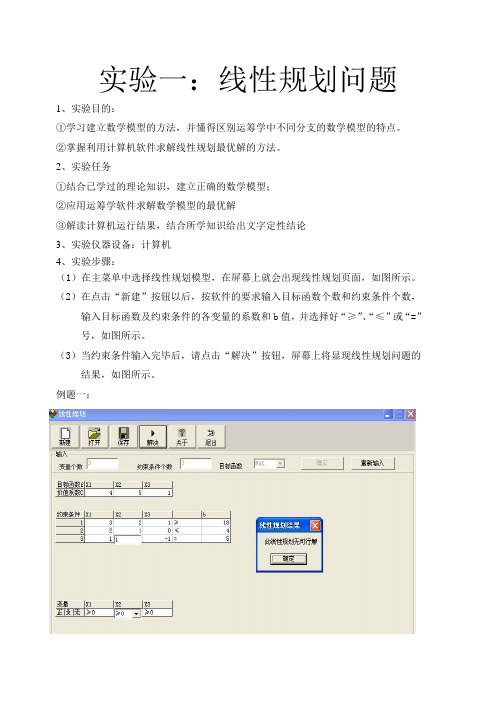
实验一：线性规划问题1、实验目的：①学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。

②掌握利用计算机软件求解线性规划最优解的方法。

2、实验任务①结合已学过的理论知识，建立正确的数学模型；②应用运筹学软件求解数学模型的最优解③解读计算机运行结果，结合所学知识给出文字定性结论3、实验仪器设备：计算机4、实验步骤：（1）在主菜单中选择线性规划模型，在屏幕上就会出现线性规划页面，如图所示。

（2）在点击“新建”按钮以后，按软件的要求输入目标函数个数和约束条件个数，输入目标函数及约束条件的各变量的系数和b值，并选择好“≥”、“≤”或“=”号，如图所示。

（3）当约束条件输入完毕后，请点击“解决”按钮，屏幕上将显现线性规划问题的结果，如图所示。

例题一：例题二：例题三：例题四：例题五5、试验体会或心得运筹学是一门实用的学科，学习运筹学，结合生活实际运用运筹学，我们可以将资源最大化利用。

学习理论的目的就是为了解决实际问题。

线性规划的理论对我们的实际生活指导意义很大。

当我们遇到一个问题，需要认真考察该问题。

如果它适合线性规划的条件，那么我们就利用线性规划的理论解决该问题。

线性规划指的是在资源有限的条件下，为达到预期目标最优，而寻找资源消耗最少的方案。

其数学模型有目标函数和约束条件组成。

一个问题要满足一下条件时才能归结为线性规划的模型：⑴要求解的问题的目标能用效益指标度量大小，并能用线性函数描述目标的要求；⑵为达到这个目标存在很多种方案；⑶要到达的目标是在一定约束条件下实现的，这些条件可以用线性等式或者不等式描述。

所以，通过这次实验，不仅对运筹学的有关知识有了进一步的掌握，同时对在自己的计算机操作水准也有了很大的提高。

这次实验让我懂得了运筹学在电脑的应用，让我对运输与数学相结合的应用理解更深了。

实验二：整数规划与运输问题1、实验目的：①学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。

运筹学实验报告2

运筹学实验报告2交通与汽车工程学院课程名称: 运筹学(汽车) 课程代码: 7100570 学院(直属系): 交通与汽车工程学院年级/专业/班: 2009级物流管理3班学生姓名: 学号: 实验总成绩: 任课教师: 黎青松开课学院: 交通与汽车工程学院实验中心名称: 物流管理实验室第 2 组西华大学实验报告西华大学实验报告开课学院及实验室:交通与汽车学院计算机中心实验时间: 年月日学生姓名学号实验成绩课程名称运筹学(汽车学院) 课程代码 8245050 实验项目名称炼油厂计划、菜篮子工程项目代码指导教师黎青松项目学分实验课考勤 10% 实验工作表现 20% 实验报告 70% 1、实验目的1.1训练建模能力1.2.应用EXCEL建模及求解的方法应用;1.3通过实验进一步掌握运筹学有关方法原理、求解过程，提高学生分析问题和解决问题能力。

2、实验设备、仪器及材料计算机、Excel3、实验内容3.1炼油厂产计划安排问题例一炼油厂的生产计划某炼油厂的工艺流程图如图 1-1所示。

炼油厂输入两种原油(原油 1和原油2)。

原油先进入蒸馏装置，每桶原油经蒸馏后的产品及份额见表1-1，其中轻、中、重石脑油的辛烷值分别为90、80和70。

1西华大学实验报告石脑油部分直接用于发动机油混合，部分输入重整装置，得辛烷值为115的重整汽油。

1桶轻、中、重石脑油经重整后得到的重整汽油分别为0.6、0.52、0.45桶。

蒸馏得到的轻油和重油，一部分直接用于煤油和燃料油的混合，一部分经裂解装置得到裂解汽油和裂解油。

裂解汽油的辛烷值为105。

1桶轻油经裂解后得0.68桶裂解油和0.28桶裂桶汽油;1桶重油裂解后得0.75桶裂解油和0.2桶裂解汽油。

其中裂解汽油用于发动机油混合，裂解油用于煤油和燃料油的混合。

渣油可直接用于煤油和燃料油的混合，或用于生产润滑油。

1桶渣油经处理后可得0.5桶润滑油。

混合成的高档发动机油的辛烷值应不低于 94，普通的发动机油辛烷值不低于84。

运筹学实验报告2

国际商学院实验报告
专业班级：专业信管姓名：_ ___学号：___成绩：________
课程名称：运筹学
指导师：
实验项目：用EXCEL软件求解线性规划模型-大M法法
实验日期：
本课程共____次实验
本次实验为第_2__次
实验目的：
1．熟悉大M算法。
2．熟练使用EXCEL软件之规划求解功能求解非典则式线性规划模型。
2.10
最优化结果：
X*=（1.67，1.67，0，0）T Z*=13.33
灵敏度分析：
（1）价格灵敏度分析：由于C变化只影响检验数。因此，当σj=(cj+△C j)-CBB-1pj≤0时，最优解保持不变。
-2≤△C1≤+∞, -0.615≤△C2≤10, -∞≤△C3≤0.444,-∞≤△C3≤3.333
2.11
此问题无可行解。
实验内容：
求解下列线性规划模型：
P25例2.9；P26例2.10；P27例2.11
实验结果（实验体会）：
2.9
最优化结果：
X*=（0，2，2）T Z*=10
灵敏度分析：
（1）价格灵敏度分析：由于C变化只影响检验数。因此，当σj=(cj+△C j)-CBB-1pj≤0时，最优解保持不变。
-1≤△C1≤+∞,-1≤△C2≤+∞,-1≤△C3≤+∞,
（3）影子价格分析：影子价格（阴影价格）是模型中某个约束条件的右端项增加（或减少）一个单位而导致的目标值的增量（或减量），它是最优单纯形表中松弛变量检验数的相反数。它的大小反映了资源在系统内的稀缺程度。影子价格越高，这种资源越稀缺，而影子价格为0的约束资源为赋余资源。影子价格也是一种机会成本，对资源的购买决策具有重要的参考价值。当资源的实际价格低于影子价格时，可以适当购进该种资源以增加收益；当资源的实际价格高于影子价格时，可以适当售出该种资源。本例中3种资源的影子价格依次为0，3，-1。

运筹学实验报告 2

运筹学实验报告学院：专业班级：姓名：学号：实验一线性规划一、实验目的学习WinQSB软件的基本操作，利用Linear Programming功能求解线性规划问题。

掌握线性规划的基本理论与求解方法，重点在于单纯形法的应用以及灵敏度分析方法。

二、实验内容安装WinQSB软件，了解WinQSB软件在Windows环境下的文件管理操作，熟悉软件界面内容，掌握操作命令。

利用Linear Programming功能建立线性模型，输入模型，求解模型，并对求解结果进行简单分析。

三、实验步骤1．将WinQSB文件复制到本地硬盘；在WinQSB文件夹中双击setup.exe。

2．指定安装WinQSB软件的目标目录（默认为C:\ WinQSB）。

3．安装过程需要输入用户名和单位名称（任意输入），安装完毕之后，WinQSB菜单自动生成在系统程序中。

4．熟悉WinQSB软件子菜单内容及其功能，掌握操作命令。

5．求解下面线性规划问题：某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。

已知产品的规格要求，产品单价，每天能供应的原材料数量及原材料单价分别见下表1和2。

该厂应如何安排生产，使利润收入为最大？表1产品名称规格要求单价（元/kg）A 原材料C不少于50%原材料P不超过25%50B 原材料C不少于25%原材料P 不超过50%35D 不限25表2原材料名称每天最多供应量（kg）单价（元/kg）C P H 10010060652535列出该线性规划问题的模型如下：以A C 表示产品A 中C 的成分，A P 表示产品A 中P 的成分，依次类推。

则约束条件为：A C +BC +D C ≤100 A P +B P +D P ≤100 A H +B H +D H ≤60在约束条件中共有9个变量，为计算和叙述方便，分别用x 1,…,x 9表示。

令x 1=A c , x 2=A p , x 3=A H , x 4=B C , x 5=B P , x 6=B H , x 7=D C , x 8=D P , x 9=D H . 则：启动程序开始→程序→WinQSB →Linear and Integer Programming ，点击菜单栏File 中的New Problem 项，建立新问题。

实验二运筹学

实验二线性规划模型的对偶问题及灵敏度分析一、实验目的：进一步掌握线性规划模型的基本原理，理解线性规划的对偶问题，掌握R软件在线性规划问题灵敏度分析中的运用。

二、实验内容：（1）教材P127 习题1。

利用线性规划的最终单纯形表，对目标函数系数和约束方程的常数项进行灵敏度分析，并在R软件中验证你的计算结果；（2）教材P131 习题11。

写出该问题的对偶问题，并用R 软件求解原问题和对偶问题。

指出二者最优解与对偶价格之间的联系。

（3）建立教材P130 习题7的数学模型并用R软件分析。

三、实验要求：（1）利用线性规划基本原理对所求解问题建立数学模型；（2）熟练写出线性规划问题的对偶问题；（3）给出R软件中的输入并求解；（4）对目标函数系数及约束方程的常数项进行灵敏度分析四、实验报告要求：实验过程描述（包括变量定义、分析过程、分析结果及其解释、实验过程遇到的问题及体会）。

（1）maxz=20X1+8X2+6X38X1+3X2+2X3<=2502X1+X2<=504X1+3X3<=150X 1,X2,X3>=0> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$sens.coef.from;x$sens.coef.to[1] -1e+30 6e+00 3e+00[1] 2.4e+01 1.0e+30 1.0e+30C1范围是（-∞，24），C2范围是（6，+∞），C3范围是（3，+∞）> library(lpSolve)> obj<-c(20,8,6)> mat<-matrix(c(8,3,2,2,1,0,4,0,3),nrow=3,byrow=T) > dir<-c("<=","<=","<=")> rhs<-c(250,50,150)> x<-lp("max",obj,mat,dir,rhs,compute.sens=1)> x$status;x$solution;x$objval[1] 0[1] 0 50 50[1] 700> x$duals;x$duals.from;x$duals.to[1] 0 8 2 -4 0 0[1] -1.000000e+30 7.105427e-15 -2.842171e-14 0.000000e +00 -1.000000e+30 -1.000000e+30[1] 1.0e+30 5.0e+01 1.5e+02 2.5e+01 1.0e+30 1.0e+30b1,b2,b3的对偶价格分别为0、8、2；b1范围为(250，∞)，b2范围为(0, 50)，b3范围为(0, 150)。

运筹学实验报告二

运筹学实验报告2讲解

运筹学实验报告

运筹学实验报告

运筹学实验报告

运筹学实践教学报告范文(3篇)

运筹学第二次实验报告

大学生运筹学实训报告范文

运筹学实验报告

运筹学实验心得(精选5篇)

运筹学实验总结

运筹学实验报告2

运筹学实验报告2

运筹学(二)实 验 报 告

运筹学实验报告

运筹学实验报告2

运筹学实验报告2

运筹学实验报告 2

实验二运筹学

运筹学(二)实验报告