ansys确定边坡安全系数

运用 ANSYS 模拟边坡开挖并计算安全系数

程实践有一定的参考意义。
１）以有限元数值迭代不收敛作为边坡失稳的标志；２）以特征应变从坡脚到坡顶贯通作为边坡失稳的标志Ｊ。本次分析设定计算模型最终计算数值迭代不收敛为边坡失稳依据。
ＡＮＳＹＳ中能用于岩土材料的只有Ｄ．Ｐ模型，Ｄ — Ｐ模型是理想
但是无法计算出安全系数。在现今的工程中，有限元极限随着我国经济建设的飞速发展，能源消耗严重与道路交通运性广，它既适用于工业设计，且适应性广，对输能力不足是当前社会主义建设面临的两大难题，其中，水电站分析法运用的越来越广泛，
运用ＡＮＳＹＳ模拟边坡开挖并计算安全系数
贾正
摘
涂兴怀
６１００３９）
（西华大学能源与环境学院，四川成都
要：利用ＡＮＳＹＳ有限元强度折减法，对某边坡开挖施工进行了模拟分析，通过计算两种开挖坡率、三种不同工况下对应的边
的原则吸收社会资金完成。
分析评价，进行了危险性分区，并对建设规划提出了要求，为城市
３）中危险区（较安全区）：主要分布在长寿沟一金陵河段滑坡用地选择和项目选址提供了依据。４）鉴于北坡地质灾害以浅层前后缘和金陵河一南坡村段古老滑坡中部平台，人员建筑密集但滑塌和崩塌为主，故应改变北坡地质灾害的整体防治思路，应将
ＮＳＹＳ有限元强度折减法。的就是稳定性与安全性，因为一旦边坡失稳就会产生严重后果，本次分析采用Ａ

ANSYS课程作业-边坡稳定性分析

边坡稳定性分析、问题描述边坡围岩分别选择3种材料，用强度折减法判断稳定性及安全系数。

、建模三、材料参数单元类型：PLANE82受力状态：平面应变Plain strain四、载荷1. 位移条件两侧边约束X方向位移，底边约束X、Y方向位移。

2. 受力条件重力10g/cm21NODESU五、结果分析1•收敛结果ANSYSR15XJJUN 28 Z01513:03:04丄塔丄』；；冷：忖:£ K :伴随强度折减系数的增加，边坡的塑性应变增大，塑性区也随之扩大，当塑性区发展成一个贯通区域，边坡就不稳定，此时求解也不收敛。

与此同时，边坡水平位移也变大。

因此, 主要通过观察后处理中边坡变形图、应力图、塑形区来判断稳定性与否。

2. F=1.0结果分析F=1.0时边坡变形图311^1KY5-€W —.0S3TMMH-.C5S*44 -.SLSil■“”戸呂0^36C"? ,0315^3 .eCSTgflAN SYSR15.0JUK 冲12：aa：Z4F=1.0时边坡X方向位移云图F=1.0时边坡X方向应力云图AN SYSR15.0JOE品p冨耶43 12：DO15Q T.[?SE-LEPFLE J JV悵V⑹MtSME --34&E-34M 强“阴.1&91-0< .2A0K-Q4 .HCS«-CI3»K-«& . ll&E-CH . I^lE-04 . E ECB-O^ . J：4fiE-CHF=1.0时边坡塑性变形云图此时边坡坡趾处有微小塑性应变，塑性区范围较小。

-.aiaifii-.osasi«r'.aitSi4fl ： ' _fi9-s27H -■frilJ*1! rd 如 9"卍财 Ml4片轴*ll«at边坡水平方向最大位移为116.21mm 。

3. F=1.2结果分析F=1.2时边坡变形图SOUL SDUJT IQN STEP*：SnE 7IlKt-： us ixmi MT5-C聊-ai«i.J1ZT 才9 WisHlMinF=1.2时边坡X 方向应力云图F=1.2时边坡塑性变形云图边坡塑性区进一步扩大，在边坡右侧边界出现塑性区。

用ANSYS分析边坡稳定性

用ANSYS分析边坡稳定性提纲：第一章：绪论1.1 研究背景及意义1.2 国内外研究现状及进展1.3 研究内容和目的1.4 论文结构安排第二章：边坡稳定性分析方法及原理2.1 边坡稳定性分析方法概述2.2 常用边坡稳定分析软件简介2.3 复杂地形边坡分析方法2.4 常用岩土参数测定方法第三章：基岩边坡稳定性分析3.1 基岩边坡的稳定性分析3.2 基岩边坡的模型建立3.3 基岩边坡的计算第四章：典型边坡案例分析4.1 案例选取理由及数据来源4.2 案例基本情况介绍4.3 数值计算结果分析4.4 结果分析和比较第五章：结论与展望5.1 研究结论5.2 研究不足和未来研究方向5.3 工程实践中的应用5.4 论文总结与展望以上是一篇用ANSYS分析边坡稳定性的论文提纲，涵盖了绪论、边坡稳定性分析方法及原理、基岩边坡稳定性分析、典型边坡案例分析和结论与展望五个章节。

其中，绪论阐述了研究的背景、意义以及研究目的和内容，为后续的分析工作打下基础。

在边坡稳定性分析方法及原理章节中，详细介绍常用的边坡稳定分析方法和软件，以及复杂地形边坡分析方法和岩土参数测定方法。

第三章以基岩边坡为例，介绍了基岩边坡的稳定性分析及其模型建立和计算。

第四章选取典型边坡案例进行分析，对比结果，进一步验证本文方法的可行性。

最后，结论与展望章节总结了本文研究的结论和展望未来的研究方向，为工程实践提供参考。

第一章：绪论1.1 研究背景及意义在建设工程和地质灾害监测过程中，边坡是一种常见的岩土工程地质体。

针对边坡的稳定性分析，可以提前发现潜在的危险，掌握岩土地质构造，确定合适的工程措施和预防措施，有效保障人民生命和财产的安全，减少工程投入，推进工程建设。

因此，研究边坡的稳定性，对岩土工程领域的实践具有十分重要的实际意义。

1.2 国内外研究现状及进展近年来，岩土工程领域的研究在发展，已经出现了多种边坡稳定性分析方法。

数据智能算法在数据分析和识别矿井边坡稳定性方面得到了广泛应用，例如神经网络，支持向量机，粒子群优化算法。

基于ANSYS有限元软件的边坡稳定性分析

基于ANSYS有限元软件的边坡稳定性分析摘要：随着计算力学、计算数学、工程管理学与计算机科学的快速发展，数值模拟的技术随之变得越来越成熟。

本文使用ANSYS有限元软件来模拟边坡，运用强度折减法，分析凝聚力和内摩擦角对边坡安全系数的影响，获得相应的位移云图。

把安全系数作为判断边坡稳定性的一个重要的指标，从而及时地发现和避免可能发生的滑坡、崩塌等自然灾害，尽可能地降低人民生命和财产的损失。

关键词：边坡；稳定性；有限元软件；数值模拟；强度折减法引言边坡是指地壳表面具有侧向临空面的地质体，由坡面、坡顶与其下方一定深度的岩土体构成。

边坡存在于大量的工程中，包括但不限于铁路、公路和水利工程等。

近年来，滑坡，泥石流，山体崩塌等灾害时有发生，严重危害了人民的生命及财产安全，给人们的生活造成了重大的威胁，边坡稳定成为社会各界广泛关注的一个问题。

不仅如此，边坡是否稳定会严重影响工程的施工安全、运营安全和建设成本，因此，边坡的稳定性有分析研究的充分必要。

运用数值模拟的方法研究边坡稳定性最早使用的就是有限元法，也是现在最常用的数值模拟方法。

有限元法充分考虑了介质的变形特征，能够正确地反应边坡的受力状态。

既能考虑到边坡沿软弱结构面破坏，还能分析边坡的整体稳定破坏。

1ANSYS有限元软件简介FEA(Finite Element Analysis)是一种高效的，常用的计算方法，它是将连续的对象离散化成若干个有限大小的单元体的集合，从而求解连续体的力学问题。

ANSYS有限元软件包含多中有限元分析类型，从简单的线性静态分析到复杂的非线性动态分析都能够进行计算求解。

2参数选取及计算模型建立2.1 选取背景参数本次数值模拟以国内某矿边坡为对象，采用有限元软件ANSYS分析该边坡结构在不同力学参数条件下的应力应变情况，并判断其稳定性。

边坡的材料属性如表1所示。

2.2 建立计算模型对于边坡这种纵向比较长的实体，计算模型可简化成平面应变问题，即认为边坡所受的外力不随Z轴变化，其在外力作用下所发生的位移和应变都只在自身平面内。

ansys边坡开挖案例

基于ANSYS 的边坡开挖模拟摘要:基于ANSYS 软件对边坡的开挖进行了模拟分析,并对该过程中涉及到的生死单元、有限元强度折减法做了介绍,提出了用生死单元在建模过程中的优点,最后以工程算例做计算分析,计算了开挖边坡的稳定系数。

关键词:ANSYS 边坡开挖,生死单元,强度折减边坡的开挖在一些边坡工程中是经常会遇到的,边坡开挖是一个卸荷的过程,在卸荷前后边坡的稳定性状况直接关系着工程的施工安全、施工进度和经费预算等,因此有必要对边坡的稳定性进行定性定量的综合分析。

边坡开挖前后的应力场和位移场的变化规律是边坡稳定性评价的基础,准确评价和预测边坡的稳定状况和发展趋势将为边坡的处理措施提供可靠的依据。

随着计算机模拟数值计算技术的发展,可采用ANSYS 有限元软件对边坡开挖进行验算。

1ANSYS 中的生死单元在边坡工程的开挖过程是一个动态的连续施工过程,而不是一次成型的,而且工程上关心的是施工过程中以及施工结束时土工结构物的应力应变分布。

充分应用生死单元的优点能收到事半功倍的效果。

单元生死是指在有限元分析过程中,在力学模型中加入或删除材料,模型中的相应单元就会“虚化”或“激活”。

应用单元虚化和激活的优点是:1) 观察每一个荷载步结束后的求解结果并进行对比分析,因而能够模拟整个开挖过程的力学状况的变化。

2) 只需要建立一次模型,通过虚化单元来模拟进程,而其他方法需要建立多个模型进行过程分析。

2边坡稳定性有限元分析的强度折减法将强度折减法应用于边坡稳定性分析中,折减土体强度,代入有限元程序进行计算,直至计算不收敛,此时的折减系数即为安全系数。

在考虑屈服准则时,一般采用Drucker2Prager 屈服准则,它既考虑了中间主应力σ 2 对屈服强度的影响,又考虑了静水压力对屈服强度的影响,对土体材料有较好的适用性,已广泛应用于土体分析。

Drucker2Prager 屈服准则表达式如下:F = 3βσm + [{ S } T [ M ]{ S } ]1/ 2 - σy = 0 。

用ANSYS分析边坡稳定性

用ANSYS分析边坡稳定性高恭星【摘要】传统方法分析边坡稳定性时,需要假设滑动面的形状；而用ANSYS分析边坡的稳定性时,不需做任何假设,就能得到安全系数,还能直观地得出边坡破坏的类型和形状.用ANSYS分析边坡的稳定性时一般采用强度折减法,ANSYS中常用准则为DP准则,如果要采用其他近似的修正准则则需进行转化.该文在c和φ取不同值时,用ANSYS (DP3)与用瑞典条分法和Janbu法分别计算得出不同的边坡稳定性安全系数,分析c、φ值对边坡稳定性的影响.【期刊名称】《重庆建筑》【年(卷),期】2012(011)009【总页数】4页(P80-83)【关键词】边坡稳定性;有限元折减法;ANSYS;屈服准则【作者】高恭星【作者单位】重庆大学土木工程学院,重庆400030【正文语种】中文【中图分类】TU4310 引言边坡的稳定性可以用安全系数K来表示。

K>1,边坡稳定；K=1，为临界状态；K<1，边坡失稳。

目前，在工程中计算边坡的稳定性的方法主要是建立在极限平衡理论的基础上如Janbu法、瑞典条分法、Bishop法等。

在计算安全系数时需要假设滑动面的形状。

而用有限元法分析，考虑材料的属性，应力应变的关系，满足力的平衡，不用做任何假设，计算完成后不仅能得到比较准确的安全系数，而且还能得到破坏时的滑移面，塑性应变区域、应力场、位移场等结果。

用有限元法分析边坡，可以考虑复杂土层介质，边坡内部的介质的应力应变，分析各种形状的边坡。

在得出安全系数的同时还可以清楚认识边坡滑移的类型，这对边坡加固工程具有指导性作用。

用有限元分析边坡的稳定性一般采用强度折减法。

本文基于强度折减法理论，运用ANSYS分析边坡的稳定性。

1 有限元强度折减法的原理有限元强度折减法的原理就是将岩土体的抗剪强度指标减小为c/K，tamφ/K，把经计算出的c'和φ'代替原来的c和φ，重新代入有限元中进行计算，反复迭代。

运用 ANSYS 模拟边坡开挖并计算安全系数

运用 ANSYS 模拟边坡开挖并计算安全系数贾正;涂兴怀【摘要】This paper made simulation analysis on a side slope excavation construction using ANSYS finite element strength reduction method, through the calculation on two excavation slope rate, the corresponding side slope safety factor under three different construction conditions, made comprehensive analysis on side slope safety and stability under various construction conditions, obtained some valuable conclusions.%利用ANSYS有限元强度折减法，对某边坡开挖施工进行了模拟分析，通过计算两种开挖坡率、三种不同工况下对应的边坡安全系数，综合分析了各种工况下边坡的稳定性与安全性，得出了一些有应用价值的结论。

【期刊名称】《山西建筑》【年(卷),期】2014(000)028【总页数】3页(P56-57,58)【关键词】ANSYS软件;边坡开挖;支护;安全系数【作者】贾正;涂兴怀【作者单位】西华大学能源与环境学院，四川成都 610039;西华大学能源与环境学院，四川成都 610039【正文语种】中文【中图分类】TU413.62随着我国经济建设的飞速发展，能源消耗严重与道路交通运输能力不足是当前社会主义建设面临的两大难题，其中，水电站开发和高速公路的修建是这两大难题中的重要组成部分。

在这两大建设工程领域都会遇到大量的边坡工程，而边坡工程最重要的就是稳定性与安全性，因为一旦边坡失稳就会产生严重后果，给工程带来巨大损失，由此可见对边坡的稳定性与安全性进行综合分析是多么重要。

用ANSYS和FLAC3D软件求解边坡稳定安全系数的比较分析_陈飞

以有限元静力平衡计算不收敛作为边坡整体失稳的标志 ,文
献[14 ]认为塑性区从坡脚到坡顶贯通并不一定意味着破坏 ,
塑性区贯通是破坏的必要条件 ,但不是充分条件 ,还要看是
否产生很大的且无限发展的塑性变形和位移。综合以上观
点并结合 FLAC3D 程序特点 ,采用静力平衡计算是否收敛作
为边坡是否失稳的评判依据 ,并结合边坡剪应变增量是否贯
边坡稳定分析理论具有十分丰富的内容。而基于强度折减的有限元稳定分析方法是目前应用及研究较多的一种分析方法。边坡稳定性分析有限元分析一般采用强度折减法来求得边坡的安全系数。多年来 ,许多学者致力于这方面的研究 , Ugai[7] 、Matsui[8] 、Griffiths[9] 、宋二祥[10] 、张鲁渝[11] 、赵尚毅[12～14 ] 、郑颖人[12～14 ] 、栾茂田[15 ] 等学者在有限元强度折减法应用方面做了大量的工作。
第 8 卷第 1 期 2010年2月
水利与建筑工程学报
Journal of Water Resources and Architectural Engineering
Vol. 8 No. 1 Feb . , 2 0 1 0
用 ANSYS 和 FLAC3D 软件求解边坡稳定安全系数的比较分析
陈飞 , 杨诗义 , 王家成 , 别小平
图 5 程序界面图
图 6 未达到移动时的位移云图
图 7 塑性区贯通时的位移云图如图 6 所示 ,折减系数为 1. 348 ,算法收敛 ,塑性区没有贯通。当折减系数为 1. 349 时 ,算法收敛 ,土坡产生较大位移 , 同时塑性区贯通坡脚至坡顶. 可判断此折减系数下 ,边坡稳定性急剧下降 ,产生滑动。根据边坡失稳破坏判据确定土坡稳定系数 Fs 为 1. 349 。图 7 可以看出塑性区的分布情况 ,这有助于了解边坡整

ANSYS有限元技术在边坡稳定性分析中的应用

1975年 , 英国科学家 Z ienkiew icz等首次在土工弹塑性有限元数值分析中提出抗剪强度折减系数概念 , 由此所确定的强度储备安全系数与 B ishop 在极限平衡法中的稳定安全系数在概念上是一致的 ( 栾茂田等, 2003)。有限元强度折减法原理是将材料的强度参数 c、 tan 值同时除以一个折减系数 F, 这时就会得到一个新的强度参数 c,' , ' 然后再用这个强度参数进行试算 , 继续调整系数 F, 反复计算 , 直到所研究对象达到临界破坏 , 这个时候的系数 F 就是该研究对象的安全系数。计算方程为 c = ' c /F , 土体的内聚力, 为岩土体的内摩擦角。 = ' arctan ( tan /F ); c 为岩
L i Jie Ouyang Zuxi L i Yujiang Zhou H ao W ei Xueyong
( Institute o f Crusta l Dyna m ics, CEA, Be ijing 100085)
B ased on the com parison o f characters betw een the li m it equilib riu m m e th od and the fin ite el em ent m ethod in slope stability ana ly sis , th e paper introduces the basic princip le o f strength reduc t io n fin ite elem ent m ethod , and then expla in s its applica tio n and advantage in the slo pe stab ility analysis w ith an exam ple.

基于ANSYS的有限元强度折减法确定边坡安全系数

基于 ANSYS的有限元强度折减法确定边坡安全系数摘要：本文基于ANSYS，采用D-P外角点外接圆屈服准则对国内某矿区边坡进行稳定性计算分析，通过不断对边坡强度参数黏聚力和内摩擦角进行折减，直到软件计算不收敛为止，其折减的倍数即为边坡稳定安全系数。

计算结果显示，利用ANSYS自带D-P本构模型计算得到的边坡安全系数远大于极限平衡法计算得到的边坡安全系数。

最后应用不同屈服准则安全系数的转换关系得到该边坡平面应变下与M-C匹配的D-P准则的安全系数，并与极限平衡法结果对比，吻合较好。

据此得出结论：在估算边坡安全系数方面，采用有限元强度折减法是一种值得信赖的方法，但计算中采用理想弹塑性材料模型时，屈服准则的选择会对边坡安全系数的计算产生较大影响。

关键词：有限元；强度折减；屈服准则；边坡稳定；安全系数1 引言目前，边坡稳定性分析发方法较多，主要有定性分析法（图解法、类比法）、定量分析法（极限平衡法、数值分析法）、非确定分析法（模糊分析评判法、可靠性分析法）。

而对于边坡安全系数，许多学者大多用定量分析法[1-2]。

传统的极限平衡法首先要确定一个潜在的滑动面，基于一系列简化假定后，由力系平衡或能量守恒求得滑动面的安全系数，用它作为评价边坡安全性的指标。

这些方法有瑞典条分法、简化毕肖普法、简布法、不平衡系数传递法等。

这些方法的基本出发点是一样的，即刚塑性假定，不同之处在于对条间力所作的假定不同。

由于这些假定的物理意义不一样，因此它们所能满足的平衡条件也不相同，计算步骤有繁有简，为了检验所列的各方法和其他边坡稳定性分析方法的精确性，许多学者在过去几十年里从不同角度做了大量研究并进行了系统总结[3-7]。

传统的极限平衡法由于没有考虑土体内部应力与应变的关系，故无法模拟分析土体发生变形甚至破坏的过程。

随着计算机技术的发展，数值计算方法在边坡稳定分析中得到了广泛的应用。

其最大的优点是求解安全系数时，不需要假定滑移面的形状和位置，也无需进行条分，可以分析任何形状的几何体，不但能进行线性分析还可进行非线性分析。

基于ANSYS验证某基坑工程施工坡道及周边岩土的稳定性

基于ANSYS验证某基坑工程施工坡道及周边岩土的稳定性作者：宋加兴张伟孟宪伟刘毅来源：《科技资讯》2024年第06期作者简介：宋加兴（1993—），男，本科，工程师，研究方向为土木工程。

张伟（1974—），男，本科，工程师，研究方向为土木工程。

孟宪伟（1980—），男，本科，高级工程师，研究方向为土地管理。

摘要：施工坡道是施工单位为保证基坑工程顺利实施采取的施工措施，一般根据以往工程经验设置，施工期间坡道及周边支护未施工部位的土体是否稳定，并不在设计考虑范围内，依据工程经验设置的施工坡道有时并不能满足规范要求，但却能够满足施工期间使用要求。

基于某建筑基坑实例尝试采用ANSYS有限元软件对施工单位根据经验设置的施工坡道进行分析验证，希望能够为施工坡道的设置提供一种理论支持。

关键词：基坑工程施工坡道边坡稳定性强度折减法中图分类号：TU43建筑基坑在施工时为了便于土方作业往往需要设置施工坡道，无法按照设计要求做到整体分层开挖。

坡道按留置位置可以分为边侧留置和中部留置两种情形。

对于宽度较小的基坑，由于坡道两侧均靠近支护结构，故无须考虑坡道横向稳定问题，仅仅按照规范要求沿纵向留置好坡度即可。

但对于面积较大的深基坑，施工坡道往往会留置在基坑中部或边侧，特别是坡道设置在基坑边侧时，坡道土体范围内支护结构尚未施工，依靠预留坡道的土体是否能够满足边坡稳定及坡道施工荷载要求，目前主要由现场技术人员通过经验判断，无法从计算上给出准确结论。

此外，有时施工坡道设置并不能满足规范要求，但直至项目完工依然保持平稳运行，这需要一线技术人员对其进行总结分析。

笔者查阅大量资料未发现对施工坡道进行稳定分析的相关案例及文献资料。

由于施工坡道属于三维边坡稳定问题，通过查阅文献发现在某些大型水利工程中有使用ANSYS有限元软件进行三维稳定分析的相关实践案例，且与二维分析相比，三维边坡稳定分析得到的结果更加符合工程实际[1]，笔者尝试将该方法应用于建筑基坑施工坡道及周边土体的稳定性，同时为施工单位的工程经验提供计算依据。

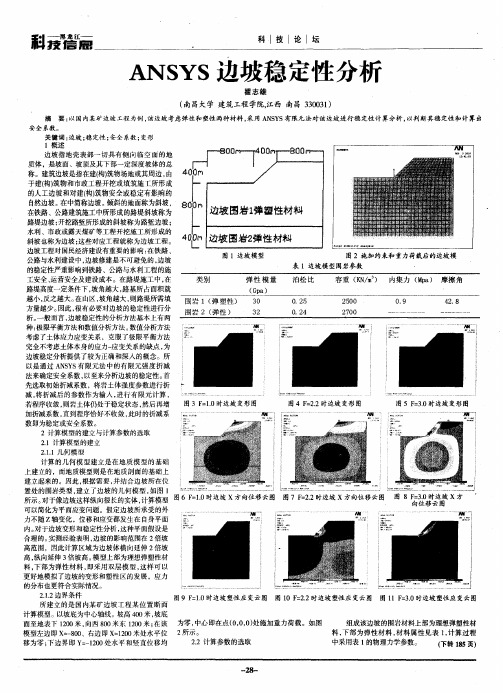
ANSYS边坡稳定性分析

一
２ — ８
科ｌ１｝教文化
笔者在２０年申请内蒙古自治区教育科学０９规划课题《信息技术与中小学学科教学整合的研究》的子课题，课题名称为｛ｏｌ在高中历史教Ｍｏｅｄ学中的应用》作为课题负责人，，克服了重重困难，最终使得课题顺利开展。因为是在内蒙，整体信息技术水平相对落后，要进行信息技术与课程整合的难度较大。首先是思想上难以更新观念，所在地鄂尔多斯，经济较为发达，硬件设备也较为先进，但是在人们的思想观念里，信息技术就是简单的为课堂教学的辅助工具，尤其是最开始在找参与课题的老师时，多次碰壁，有经验的老师不愿参与或者不想冒险，免以影响班级成绩，在笔者向学科教师演示了Ｍｏｈｏｄ的丰富功能后，最终找到的一位是很有冒险精神并敢于创新的年轻的历史老师，实验才得以开始。由此可见，信息技术与课程整合的最大阻力并不全是来自外部，而是有可能来自学科教师本身。众所周知，信息技术教师在中小学工作比较繁琐，在课题批下几个月后课题研究都没有什么
２１．．２边界条件
田
图９ＦＩ＝．０时边坡塑性应变云图图１＝．０Ｆ２２时边坡塑性应变云图图ｌＦ３ｌ＝．０时边坡塑性应变云图
所建立的是国内某矿边坡工程某位置断面计算模型。以坡底为中心轴线。坡商４０米，０坡底中心即在点（，，）Ｏ００处施加重力荷载。如图组成该边坡的围岩材料上部为理想弹塑性材面至地表下１０米，２０向西８０东１００米２０米；在该为零，料，下部为弹性材料，材料属性见表１计算过程，模型左边即ｘ一０：８０、右边即Ｘ１０处水平位２所示。＝２０米２．２计算参数的选取中采用表１的物理力学参数。（下转１５页）８移为零；边界即Ｙ：１０水平和竖直位移均下一２０处

某边坡基于ANSYS的稳定性分析

某边坡基于ANSYS的稳定性分析摘要：目前许多边坡受人类工程活动或者自然灾害的强烈扰动，造成许多了许多的灾难，例如滑坡、崩塌、泥石流等众多边坡问题屡见不鲜，严重损害了人类的经济以及威胁着人类的生命安全。

针对以上问题本文采用一个实际的案例，来分析该边坡的稳定性问题。

主要内容是：利用ANSYS有限元强度折减法来分析和判定某边坡的稳定性，根据ANSYS软件求得的塑性应变云图和位移图，来判定边坡发生失稳时的折减系数，从最后的计算结果不收敛求得边坡的安全系数。

关键词：ANSYS；边坡稳定性；强度折减法；屈服准则；安全性系数0引言近年来，许多边坡灾害事故频发，威胁着人类的生命安全和财产安全。

因此对边坡的稳定性进行分析是非常重要的。

本文研究内容是结合某工程实例，依据有限元强度折减法，用内摩擦角和粘聚力分别除以折减系数得到折减后的参数，运用ANSYS软件进行边坡数值模拟来分析和评价该边坡的稳定性。

1 有限元强度折减法1.1有限元强度折减法当边坡的土体满足莫尔-库伦剪切破坏准则时，可采用强度折减法。

具体的计算步骤是：①选取合适的折减系数。

②用土体的粘聚力和摩擦角除以折减系数。

③把折减后参数代入ANSYS数值模型中进行运算[1]。

如果在ANSYS软件计算时计算恰好不收敛，此时把折减系数定义为安全系数。

本文采用的强度折减法计算公式如下：，（1）式中：为折减系数；和分别为折减前后的粘聚力；和折减前后的内摩擦角。

1.2 屈服准则选取1.2.1 D-P屈服准则Drucker-Prager（D-P屈服准则）的屈服面在主应力空间中是一圆锥面，相较于六棱锥面来说，更利于数值计算，因此，大多数数值分析中使用D-P准则[2]。

由于不同的屈服准则所对应的的安全性系数不同，在实际应用时发现用ANSYS软件进行数值模拟时，DP3误差仅在1％左右，因此本文采用DP3。

1.2.2 参数换算换算与M-C屈服准则相匹配的D-P[3]屈服准则，设粘聚力和摩擦角为岩土实际的材料参数，令，。

不同边坡软件计算边坡安全系数的比较

不同边坡软件计算边坡安全系数的比较李守华【摘要】基于有限元强度折减理论和极限平衡理论,分别采用3种边坡分析软件ANSYS、FLAC和SLIDE对一土质边坡进行稳定性分析.结果表明,ANSYS所得安全系数误差较大,而FLAC和SLIDE结果相对一致,在工程计算中具有一定的实用性和可靠性.【期刊名称】《甘肃科技》【年(卷),期】2012(028)019【总页数】2页(P136-137)【关键词】边坡分析软件;有限元强度折减法;极限平衡法;安全系数【作者】李守华【作者单位】西北民族大学土木工程学院,甘肃兰州730030【正文语种】中文【中图分类】TU413边坡工程对国民经济建设有着重要的影响。

边坡的稳定性将严重影响到铁路、公路与水利工程的施工安全、运营安全及建设成本。

近年来，随着计算机技术的进一步发展，数值分析方法倍受关注，同传统的边坡分析方法相比，数值分析不仅能解决传统分析方法所能解决的问题，而且能更好地描述土体的应力应变和土与结构的相互关系。

其在边坡工程领域中作用是不可或缺的。

同时，数值分析可将研究成果及时地应用于工程实际，对工程决策具有重要的参考价值。

限于篇幅，本文仅介绍目前常用的边坡数值分析软件:ANSYS、FLAC及SLIDE，并利用典型算例比较了这些软件计算的安全系数。

1.1 边坡稳定分析软件简介ANSYS软件［1，2］是由世界上最大的有限元分析软件公司之一的美国ANSYS 开发，融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。

对于土木工程而言，可以进行结构的静力分析、非线性分析、动力学分析、热分析及流体力学分析等。

对于边坡稳定分析ANSYS软件较常采用的是有限元强度折减法。

对于边坡稳定分析可以采用点安全系数等值线法和有限元强度折减法。

本文计算实例采用的是有限元强度折减法。

土体弹塑性模型采用Druker－Prager准则(简称D－P准则)。

DP准则在主应力空间的屈服面为光滑圆锥面，在π平面上的图形为圆形，表述极其简单且数值计算效率很高。

基于ANSYS的强度折减法求解边坡安全系数

基于ANSYS的强度折减法求解边坡安全系数摘要：介绍了一种基于有限元的强度折减法的边坡稳定性分析方法,讨论了该方法的基本原理、安全系数的物理意义、屈服准则和流动法则的选用及边坡破坏的判据等。

算例通过不断减小边坡强度参数黏聚力和内摩擦角,得到新的一组黏聚力和内摩擦角,再输入软件计算至不收敛,此时的折减系数就是边坡的安全系数。

计算结果显示,用ANSYS计算边坡的安全系数有一定的实用性和可靠性。

关键词：强度折减；边坡稳定；ANSYS中图分类号：O 319.56 文献标志码：A 文章编号：1674-0696（2011）基金项目：重庆市科学基金重点资助项目(035679)；2022年高等学校博士学科点专项科研资助项目(20020183061)0 引言当前,研究边坡稳定性的传统方法主要有:瑞典条分法,简化的毕肖普法等。

这些方法主要是建立在极限平衡理论基础上的,在进行稳定性分析时没有考虑土体内部的应力应变关系,无法分析边坡破坏的发生和发展过程,在求安全系数时通常需要假定滑裂面形状为折线、圆弧、对数螺旋线等。

而有限单元法不但满足力的平衡条件,而且考虑了材料的应力应变关系。

求解安全系数时,不需要假定滑移面的形状和位置,也无需进行条分,这使得计算结果更加合理精确。

有限元法较传统的方法有如下优点:①能够对具有复杂地貌、地质的边坡进行计算;②考虑了土体的非线性弹塑性本构关系,以及变形对应力的影响;③能够模拟土坡的失稳过程及其滑移面形状。

滑移面大致在水平位移突变的地方及塑性变形发展严重的部位，成条带状；性变形发展严重的部位,呈条带状;④能够模拟土体与支护的共同作用。

1.强度折减法在 ANSYS 中的实现有限元法全面满足边坡静力许可、应变相容和应力、应变之间的本构关系，使得有限元分析边坡稳定成为近年来的发展趋势，因为有限元法不仅仅能计算出土体的内应力场分布，还可以了解边坡逐步破坏机理，跟踪边坡内塑性区的发展情况。

1.1 边坡失稳的判别依据边坡滑动面塑性区贯通是边坡发生破坏的必要条件，但不是充分条件，采用塑性区贯通来判别趋于保守。

基于ANSYS中PDS模块边坡可靠性分析

基于ANSYS中PDS模块边坡可靠性分析李原;武清玺【摘要】基于ANSYS中PDS模块,在强度折减法确定边坡工程的安全稳定系数后,使用可靠性理论中的蒙特卡洛法,结合有限元软件进行概率设计.通过一个典型的边坡工程实例,在输入多个边坡材料的随机参数情况下,求得边坡最大沉降量以及目标控制值下边坡的失效概率.分析结果形象合理,较传统边坡稳定分析方法更加客观有效.【期刊名称】《低温建筑技术》【年(卷),期】2015(037)002【总页数】3页(P105-107)【关键词】边坡工程;ANSYS中PDS模块;强度折减法;蒙特卡洛法【作者】李原;武清玺【作者单位】河海大学力学与材料学院,南京210098;河海大学力学与材料学院,南京210098【正文语种】中文【中图分类】TU753.7在边坡稳定性数值分析法中，基于有限元的强度折减法作为一种确定性方法，因其简便有效而被广泛地应用。

然而由于没有考虑实际情况和材料参数的不确定性，使计算结果和实际情况相差较大。

将可靠性理论中的蒙特卡洛法和有限元技术结合起来，考虑强度折减，把输入的边坡材料参数作为具有一定统计特征的随机变量，使用有限元软件进行分析，可以较准确的反应边坡实际情况[1]。

在此方法下进行可靠性分析，有助于通过控制最大沉降量的失效概率来保证边坡稳定性，本文使用大型有限元软件ANSYS中的PDS模块可以很好地解决此类问题。

建立在强度折减有限元分析基础上的边坡稳定性分析的基本原理就是将关于边坡稳定的两个参数内聚力c和摩擦角φ同时除以一个折减系数F，得到新的内聚力c′和摩擦角φ′，即:将折减后的参数输入并使用有限元软件分析计算。

开始时F取小一些，保证近乎于一个弹性问题，若程序收敛则说明边坡稳定。

然后慢慢增加F直至某一值使得程序恰好不收敛，此时的折减系数即为边坡的稳定安全系数，即边坡达到到极限状态[2]。

本文计算采用理想弹塑性模型，在大型有限元分析软件ANSYS中采用D-P准则，这是Drucker和Prager于1952年在Mises准则的基础上进行修正，消除了M-C屈服面的棱线，考虑平均静水压力对屈服的影响，其屈服函数为：I1=σ1+σ2+σ3式中，I1与J2为应力张量的第一不变量和应力偏张量的第二不变量；α与k为材料常数，通过与M-C屈服模型的比较可确定其值。