信号与系统第7章
信号与系统课后习题与解答第七章

15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5-1(a)所示。
)()2(n x 序列的图形如图5-1(b)所示。
)()3(n x 序列的图形如图5-1(c)所示。
)()4(n x 序列的图形如图5-1(d)所示。
)()5(n x 序列的图形如图5-1(e)所示。
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5-2(b)所示。
x()2(n 序列的图形如图5-2(c)所示。
x))3(n(x 序列的图形如图5-2(d)所示。
)4(n())5(n 序列的图形如图5-2(e)所示。
x()x 序列的图形如图5-2(f)所示。
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-3(a)所示。
)()2(n x 序列的图形如图5-3(b)所示。
)()3(n x 序列的图形如图5-3(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的,如果是周期性的,试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数,所以)(n x 是周期性的,且周期为14。
信号与系统第七章 系统函数

=
K
N1N 2 " N m e j(ψ1+ψ2 +"ψm ) M1 M2 " Mn ej(θ1+θ2 +"θn )
H (jω)
=
K
N1N2 " Nm M1M2 "Mn
ϕ (ω) = (ψ1 +ψ2 + "ψm ) − (θ1 +θ 2 + "θ n )
当ω 沿虚轴移动时,各复数因子(矢量)的模和辐角都
①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时,响应均趋于0。 ②H(z)在单位圆上的一阶极点所对应的响应函数为稳 态响应。
③H(z)在单位圆上的高阶极点或单位圆外的极点,其 所对应的响应序列都是递增的。即当k→∞时,响应 均趋于∞。
第 19 页
三、由系统函数零、极点分布 决定频响特性
v1(t ) −
R
+
C v2(t )
−
写出网络转移函数表达式
H (s)
=
V2 (s) V1 (s )
=
1 RC
⎜⎛ ⋅⎜ ⎜⎜⎝
s
1 +1
RC
⎟⎞ ⎟ ⎟⎟⎠
=
1 RC
1 M1 ejθ1
= V2 ejϕ (ω) V1
M1
θ1
−1 RC
jω
O
σ
第 28 页
频响特性
jω
M1
V2 1 V1 1
2 θ1
−1 RC
O
σ
O1 RC
( ) H
jω
=
1 RC
1 M1 e jθ1
= V2 ejϕ (ω) V1
信号与系统课件第七章离散时间系统

两序列的样值 ======= 新序列
2)相乘:z(n) x(n) y(n)
逐项对应相加
两序列的样值 ======= 新序列
3)延时:z(n) x(n m)
逐项对应相乘
原序列 ============ 新序列
2016/1/21 信号与系统 11
逐项依次左移或右移m位
离散信号的运算
4)反褶:z(n) x(n)
1 n 0 u ( n) 0 n 0
n=0,其 值=1
u (n i )
n
1 n i u (n i ) 0 n i
n
3 2 1 0
1
i
u ( n) ( n k ) k 0 (n) u (n) u (n 1)
序列:信号的时间函数只在某些离散瞬时nT 有定义值,即x(nT )
其中T为均匀的离散时刻之间隔隔; nT 称函数的宗量, n 0, 1, 2,
样值:离散信号处理的非实时性 x(n)表示序列
其中n表示各函数值在序列中出现的序号
某序列n的函值x(n)=== 在第n个样值的“样值”
2016/1/21 信号与系统 9
2016/1/21 信号与系统 30
五、离散、时间系统的数学模型联系
离散、连续模型之间联系 差分方程与 微分方程:
对连续y(t ), 若在t nT 各点取样值y(nT ), 且T 足够小
y(nT ) n 1 T dy(t ) y 则 dt T
2016/1/21
x ( n)
6
3
3 2 1 0 1 2 3 4 5 6
n
x(2n)
6 4 2
陈后金《信号与系统》(第2版)章节题库(连续时间信号与系统的复频域分析)

(5)
由微分性质
得:
。
(6)
(7) (8)
12.已知 F(s)和收敛域,求 f(t)。
17 / 76
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1) 由于 <-3,f(t)是反因果信号,所以 (2) 由于 <-1,f(t)是反因果信号,所以 (3)
(1)f(-t)u(-t)↔F(-s);(2)f(t)u(-t)↔—F(s);
(3)f(-t)u(t)↔F(-s)。
证明:用定义式来证明
,则
(1)
令-t=λ,则
(2)
(3)
7.已知
求下列信号的拉氏变换:
(1)
解:从收敛域知 f(t)是因果信号,利用拉氏变换的性质求解。
(1) (2)
(3)
12 / 76
的单边拉普拉斯
2.因果信号 f(t)的拉普拉斯变换为 度为________。
【答案】2
2 / 76
则 f(t)在 t=0 的冲激强
圣才电子书
【解析】用长除法得
十万种考研考证电子书、题库视频学习平台
则
由于 F(s)含常数项 2,其逆变换正好对应 F(t),故 f(t)在 t=0 的冲激强度为 2。
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)
8.已知 f(t)的波形如图 7-3 所示,求下列信号的拉氏变换。
解:(1)
图 7-3
(2) (3) (4) (5) (6)
9.用拉氏变换性质求以下各题(f(t)是因果信号)。
13 / 76
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1) (2) (3) (4)
信号与系统奥本海姆课件第7章

如果采样时,不满足采样定理的要求,就一定
会在 xp (t)的频谱周期延拓时出现频谱混(Aliasing)
的现象。 此时,即使通过理想内插也得不到原信号。但
是无论怎样,恢复所得的信号 xr (t)与原信号 x(t)在
采样点上将具有相同的值。
xr (nT ) x(nT )
24
7.3 The Effect of Under-Sampling :Aliasing (混叠)
t
2T T 0 T 2T
11
在频域由于 p(t) P( j) 2 ( 2 k)
T n
T
所以
X p(
j)
1
2
X(
j) P( j)
1
2
X ( j) 2
T
( ks )
k
1 T
k
X
(
j(
ks ))
s
2
T
(Sampling Frequency)
可见,在时域对连续时间信号进行冲激串采
xr t xt cos0t
28
Chapter 7
Sampling
a s 60
29
Chapter 7
b
0
s
3
s
30
xr t xt cos0t
H j
Sampling
s
s
0
0
0 s
s
2
2
Figure (b)
30
Chapter 7
c
0
2s
3
s
3 2
0
xr t coss 0 t x t
X r ( j) X ( j)
t F
信号与系统第七、八章课后习题

N k
当
2
2.线性时不变离散时间系统 ①线性 线性=叠加性+均匀性(齐次性)
c1 x1 (n) c2 x2 (n)
系统
c1 y1 (n) c2 y2 (n)
②时不变
x(n N )
系统
y (n N )
x ( n)
1 E
y ( n)
y ( n)
a
ay(n)
单位延时
1 T D z ( )
已知激励初始状态y(-1)=0,y(-2)=1/2, fk=2ku(k),求系统 的零输入响应,零状态响应和全响应. 解: (1) 零输入响应 根据定义,零输入响应满足方程:
yx (k ) 3 yx (k 1) 2 yx (k 2) 0
其初始状态
1 yx (1) y (1) 0, yx 2 y 2 2
x(n)(n n0 ) x(n0 )(n n0 )
n
x(n)(n) x(0) (n) x(0)
n
n
x(n)(n n ) x(n ) (n n ) x(n )
0 0 n 0 0
x ( n)
k k 零状态响应
2 1 k k k (1) (2) (2) , k 0 3 3
离散时间系统的单位样值响应
(n)
零状态系统
h( n)
单位样值响应h(n)是系统在零状态时,由单位样值信 号作用之下产生的响应。因此,它是一个零状态响应。
同样,单位样值信号δ(n)仅在n=0时刻等于1,其它时 刻δ(n)=0,因此系统在n>0时的响应是零输入响应。
奥本海姆《信号与系统》(第2版)知识点归纳考研复习(下册)

第7章采样第8章通信系统第9章拉普拉斯变换第10章Z变换第11章线性反馈系统第7章采样7.2连续时间信号x(t)从一个截止频率为的理想低通滤波器的输出得到,如果对x(t)完成冲激串采样,那么下列采样周期中的哪一些可能保证x(t)在利用一个合适的低通滤波器后能从它的样本中得到恢复?7.3在采样定理中,采样频率必须要超过的那个频率称为奈奎斯特率。
试确定下列各信号的奈奎斯特率:7.4设x(t)是一个奈奎斯特率为ω0的信号,试确定下列各信号的奈奎斯特率:7.5设x(t)是一个奈奎斯特率为ω0的信号,同时设其中。
7.6在如图7-1所示系统中,有两个时间函数x1(t)和x2(t)相乘,其乘积W (t)由一冲激串采样,x1(t)带限于ω17.7信号x(t)用采样周期T经过一个零阶保持的处理产生一个信号x0(t),设x1(t)是在x(t)的样本上经过一阶保持处理的结果,即7.8有一实值且为奇函数的周期信号x(t),它的傅里叶级数表示为7.9考虑信号x(t)为7.10判断下面每一种说法是否正确。
7.11设是一连续时间信号,它的傅里叶变换具有如下特点:7.12有一离散时间信号其傅里叶变换具有如下性质:7.13参照如图7-7所示的滤波方法,假定所用的采样周期为T,输入xc(t)为带限,而有7.14假定在上题中有重做习题7.13。
7.15对进行脉冲串采样,得到若7.16关于及其傅里叶变换7.17考虑理想离散时间带阻滤波器,其单位脉冲响应为频率响应在条件下为7.18假设截止频率为π/2的一个理想离散时间低通滤波器的单位脉冲响应是用于内插的,以得到一个2倍的增采样序列,求对应于这个增采样单位脉冲响应的频率响应。
7.19考虑如图7-11所示的系统,输入为x[n],输出为y[n]。
零值插入系统在每一序列x[n]值之间插入两个零值点,抽取系统定义为其中W[n]是抽取系统的输入序列。
若输入x[n]为试确定下列ω1值时的输出y[n]:7.20有两个离散时间系统S1和S2用于实现一个截止频率为π/4的理想低通滤波器。
信号与系统(奥本海默第二版)第7章

(a) 脉冲抽样
First-order fold interpolation
|t | 1 sin(T / 2) h1 (t ) 1 , | t | T H1 ( j ) T T /2
2
x1 (t ) x p (t ) * h1 (t )
h1 (t ) * x(nT ) (t nT )
n
x(t ) (t nT )
x2(kT) x2(kT)
n
x(nT ) (t nT )
7.1.1 Impulse-train sampling
p(t)
N
x p (t )
(t nT)
In frequency domain
Band limited interpolation
cT sin(ct) 内插 h(t) ct 函数
xr (t ) x p (t ) * h(t ),
[ x(nT) (t nT)] * h(t)
n
n
[x(nT) (t nT)ቤተ መጻሕፍቲ ባይዱ* h(t)]
x0 (t ) h0 (t ) * x p (t )
n
x(nT)h (t nT)
0
Examples for the applications of zero-order fold interpolation (c )图(a)的1/4间隔抽样, (b)零级保持-重建 零级保持-重建
1 X d (e ) X c ( j ( / T 2k )) T k
1 2k X p ( j ) X ( ) T k T
《信号与系统》奥本海姆第七章

采样频率: 1 f s 2 f M 或 s 2M T
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
信号重建:
x(t)
连续信号
∞
xp(t)
FT
x1 (t ) X1 ( j) 0,| | 1 ;
FT
x2 (t ) X 2 ( j) 0,| | 2 ;
[1 2 ]
计算 x(t ) x1 (t ) x2 (t ) 的采样频率.
20
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
1 1 n 0时, X p j X j , 包 T 含原信号的全部信息, 幅度差T倍。
Xp( j)
A/ T
2
X p j 以s为周期的连续谱 , 有 新的频率成分 ,即 X j 的周期 性延拓。
s
0
s
A
X ( j)
s s M
M M
离散信号与系统的主要优点:
(1) 信号稳定性好 (2) 信号可靠性高 (3) 信号处理简便 (4) 系统灵活性强
4
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
7.0 引言
采样定理是从连续信号到离散信号的桥梁, 也是对信号进行数字处理的第一个环节。
fs (t )
f (t )
A/ D
量化编码
f (n)
数字 滤波器
g(n)
信号与系统第7章(陈后金)3

一、系统函数
2. H(z)与h[k]的关系
[k]
h[k] yzs [k] = [k]*h[k] h[k ]
Z { yzs [k ]} Z {h[k ]} H ( z) Z {h[k ]} Z { [k ]} 1
H ( z ) Z {h[k ]}
h[k ] Z [H ( z)]
H(z)
2.5 1.25 z 1 0.5 z 2 H ( z) 1 0.25 z 2
二、系统函数的零极点分布
系统函数可以表达为零极点增益形式,即
( z r1 )( z r2 )( z rm ) N ( z) H ( z) K D( z ) ( z z1 )( z z2 )( z zn )
-
-
-
W(z)
an-1 an
z域框图
二、离散系统的模拟框图
2. 级联型结构
将系统函数的N(z) 和D(z)分解为一阶或二阶实系
数因子形式,将它们组成一阶和二阶子系统,即
H(z) = H1(z) H2(z) ….. Hn(z)
画出每个子系统直接型模拟流图,然后将各 子系统级联。
X(z)
H1(z)
H2(z)
D(z)=0的根是H(z)的极点,在z平面用表示。 N(z)=0的根是H(z)的零点,在z平面用 表示。 例如
(2) 1 Im (z) j 0. 5j (3) 0. 5 0 0. 5j j Re (z) 0. 5 1
H (z)
z3(z 1 j)(z 1 j)
(z 0.5)(z 1)2(z 0.5 j0.5)(z 0.5 j0.5)
w[k ] a j w[k j ] x[k ]
信号与系统分析——宗伟 7

4.离散时间与离散频率的傅里叶变换(DFS) 离散时间与离散频率的傅里叶变换(DFS)
离散周期时间信号 x ( k ) 的傅里叶变换 X ( n ) 也是离 散周期, 与 构成一对傅里叶变换对, 散周期, x ( k ) X ( n )构成一对傅里叶变换对,又称 为离散傅里叶级数. 为离散傅里叶级数. 傅里叶级数对为
D F T [ x1 ( k )] = X 1 ( n ), D F T [ x 2 ( k )] = X 2 ( n ),
则
D F T [ x1 ( k ) ⊗ x 2 ( k )] = X 1 ( n ) X 2 ( n )
证明: 证明
D F T [ x1 ( k ) ⊗ x 2 ( k )] = D F T [ ∑ x1 ( i ) x 2 (( k − i )) N G N ( i )]
N
)k
的离散傅里叶变换
W 40 W 40 W 40 x (0) 1 1 1 1 0 0 W 41 W 42 W 43 x (1) 1 − j − 1 j 1 − 2 j = = 2 4 6 W 4 W 4 W 4 x (2) 1 − 1 1 − 1 0 0 3 6 9 x (3) 1 j − 1 − j − 1 2 j W4 W4 W4
频域:周期 连续 频域 周期,连续 周期
综合以上三对傅里叶变换的规律可以得出: 综合以上三对傅里叶变换的规律可以得出 一个域中的连续性对应于另一个域中的非周期 性;一个域中的周期性对应于另一个域中的离散 一个域中的周期性对应于另一个域中的离散 性. 除了以上三种变换外,还有第四种变换存在,时 除了以上三种变换外,还有第四种变换存在, 域中周期离散函数对应于频域中离散周期函数, 域中周期离散函数对应于频域中离散周期函数, 即时域频域之间的傅里叶变换规律4: 即时域频域之间的傅里叶变换规律4: 时域:离散, 时域:离散,周期 DFS 频域:周期, 频域:周期,离散
信号与系统课后习题答案第7章

143
第7章 离散信号与系统的Z域分析 144
第7章 离散信号与系统的Z域分析
题图 7.7
145
第7章 离散信号与系统的Z域分析 146
第7章 离散信号与系统的Z域分析
题解图 7.31
147
第7章 离散信号与系统的Z域分析
(2) 由H(z)写出系统传输算子: 对应算子方程和差分方程为
148
7.25 已知一阶、二阶因果离散系统的系统函数分别如下, 求离散系统的差分方程。
111
第7章 离散信号与系统的Z域分析 112
第7章 离散信号与系统的Z域分析 113
第7章 离散信号与系统的Z域分析 114
第7章 离散信号与系统的Z域分析
7.26 已知离散系统如题图7.5所示。 (1) 画出系统的信号流图; (2) 用梅森公式求系统函数H(z); (3) 写出系统的差分方程。
① 或者
② 容易验证式①、②表示同一序列。
57
第7章 离散信号与系统的Z域分析 58
第7章 离散信号与系统的Z域分析 59
第7章 离散信号与系统的Z域分析 60
第7章 离散信号与系统的Z域分析 61
第7章 离散信号与系统的Z域分析
也可以将Yzs(z)表示为
再取Z逆变换,得 ②
自然,式①、②为同一序列。
44
第7章 离散信号与系统的Z域分析 45
第7章 离散信号与系统的Z域分析 46
第7章 离散信号与系统的Z域分析
7.10 已知因果序列f(k)满足的方程如下,求f(k)。
47
第7章 离散信号与系统的Z域分析 48
第7章 离散信号与系统的Z域分析
(2) 已知K域方程为
49
信号与系统课后答案郑君里第7章

信号与系统课后答案:郑君里第7章简介本文是《信号与系统》课程的第7章课后答案,该章节由著名作者郑君里所撰写。
本章主要介绍了信号与系统的离散傅里叶变换(DFT)和离散时间傅里叶变换(DTFT)。
信号处理是一门研究如何用数学方法描述和处理各种信号的科学。
信号是信息的载体,而系统是对信号进行处理的载体。
离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一,它们具有广泛的应用。
理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。
第7章课后题答案第1题根据定义,离散傅里叶变换(DFT)的计算公式如下:$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中,N表示信号的长度,N(N)表示输入信号的离散采样值,N(N)表示变换结果中的频谱系数。
根据公式,我们可以计算出给定信号的DFT变换。
第2题离散傅里叶变换的逆变换公式如下:$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。
第3题离散时间傅里叶变换(DTFT)的计算公式如下:$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示,它不仅适用于周期信号,也适用于非周期信号。
第4题DTFT的逆变换公式如下:$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。
第5题离散时间傅里叶变换的频谱无法在计算机中实现,因为DTFT变换结果是连续的函数。
《信号与系统》第二版第七章:离散信号、离散系统

第七章:离散信号、离散系统
第七章:离散信号、离散系统
§7.1 基本概念(《信号与系统》第二版(郑君里)7.1,7.2,7.3,7.5)
离散时间信号——序列:
9 定义:自变量(宗量)为离散点的信号(函数),记为 f (n), n ∈ Z 。
f
(i)
⎧⎪(离散)
⎨ ⎪⎩
信号或采样或采后信号(取值无限精确)
图 7-5
2
《信号与系统》
9 求和:
第七章:离散信号、离散系统
9 相乘: 9 分支:
图 7-6 图 7-7
图 7-8 9 一步延迟(一步右移)算子: z−1
图 7-9
z−1x (n) = x (n −1)
图 7-10
3
(7-9)
《信号与系统》
第七章:离散信号、离散系统
z−mx(n) = x(n − m)
pN
(n)
=
⎧⎪1 , ⎨⎪⎩0 ,
n n
≤ >
N N
(7-2) (7-3)
图 7-4
pN (n) = u (n + N ) − u ⎡⎣n − ( N +1)⎤⎦
9 正弦序列:
x(n)
=
sin
nω0
=
sin
nT
2π T0
9 复指数序列:
( ) ( ) x n = e jnω0 = x n ejarg⎡⎣x(n)⎤⎦
h(n) = h(n)u(n)
因果信号:
f (n) = f (n)u(n)
BIBO 稳定:
5
(7-16) (7-17) (7-18) (7-19)
(7-20) (7-21)
信号与系统第七章(3)信号流图

7.3 信号流图
本节主要内容:
一、信号流图 1、信号流图的术语 2、信号流图的基本性质 3、信号流图化简的基本规则 二、梅森公式
本节重点、难点
重点:
一、信号流图 二、梅森公式
难点: 梅森公式的应用
§.3 信号流图
一、信号流图的概念
如图 (a)的框图,
它表征了输入 F () F(s) 与输出Y (的) 关系,
由方程211sususcsi????322sususcsi????433sususcsi????212sisirsu????323sisirsu????34srisu??可画出信号流图scscscscscscrrrrru1u2u3u4i1i2i3scscscscscscrrrrru1u2u3u4i1i2i322求转移电压比14susush??32314651scrscrscrscrsusush??????????33求输入阻抗11sisuszin??先求1111susisusisyin????scu1scscscscscrrrrru2u3u4i1i2i31i1scu1scscscscrrrru2u3u4i1i2i31i132211651341scrscrscrscrscrscsusisyin??????????????34165123211scrscrscscrscrscrsisuszin??????????????本节小结一掌握信号流图的基本概念性质和系统的信号流图表示方法
x2
(2)当结点有多个输入时,该结点将所有输
入支路的信号相加,并将和信号传输给所有与该结
点相连的输出支路。
x4 ax1 bx2 cx3
x5 dx4 dax1 bx2 cx3 x6 ex4 eax1 bx2 cx3
信号与系统教案第7章2

cn1
1 an1
an an1
an2 an3
cn3
1
an1
an an1
an4 an5
…
第4行由2,3行同样方法得到。一直排到第n+1行。
罗斯准则指出:若第一列元素具有相同的符号,则 A(s)=0所有的根均在左半开平面。若第一列元素出现符 号改变,则符号改变的总次数就是右半平面根的个数。
第7-17页
解:设加法器的输出信号X(s)
∑ X(s) G(s)
F(s)
Y(s)
X(s)=KY(s)= G(s)X(s)=K G(s)Y(s)+ G(s)F(s)
H(s)=Y(s)/F(s)=G(s)/[1-KG(s)]=1/(s2+3s+2-k)
H(s)的极点为
p1,2
3 2
3 2 2 k 2
第7-9页
■
信号与系统
7.2 系统的稳定性
7.2 系统的稳定性
一、因果系统
因果系统是指,系统的零状态响应yf(.)不会出现 于f(.)之前的系统。
连续因果系统的充分必要条件是:冲激响应 h(t)=0,t<0 或者,系统函数H(s)的收敛域为:Re[s]>σ0
离散因果系统的充分必要条件是:单位响应 h(k)=0, k<0 或者,系统函数H(z)的收敛域为:|z|>ρ0
凡极点位于左半开平面,零点位于右半开平面, 并且所有零点与极点对于虚轴为一一镜像对称的系统 函数即为全通函数。
第7-8页
■
信号与系统
7.1 系统函数与系统特性
(2)最小相移函数
右半开平面没有零点的系统函数称为最小相移函数。 解释见p336 2、离散因果系统
信号与系统教案(吴大正)第7章

l
2s + 4 H 例: ( s ) = 3 s + 3s 2 + 5s + 3
用级联型, 用级联型,并联型实现
1 .级联型实现 级联型实现
2( s + 2 ) H( s ) = ( s + 1 )( s 2 + 2 s + 3 )
2 (s+2) . 2 = ( s + 1 ) ( s + 2s + 3 )
连续因果系统稳定性判断准则 ——罗斯-霍尔维兹准则 罗斯罗斯
对因果系统,只要判断 的极点, 对因果系统,只要判断H(s)的极点,即A(s)=0的根 的极点 的根 称为系统特征根)是否都在左半平面上, (称为系统特征根)是否都在左半平面上,即可判定系统 是否稳定,不必知道极点的确切值. 是否稳定,不必知道极点的确切值. 所有的根均在左半平面的多项式称为霍尔维兹多项式. 所有的根均在左半平面的多项式称为霍尔维兹多项式. 1,必要条件—简单方法 必要条件— 一实系数多项式A(s)=a =0的所有根位于左半开 一实系数多项式A(s)=ansn+…+a0=0的所有根位于左半开 平面的必要条件是: 平面的必要条件是:
c n 1 = 1 a n 1 an a n 1 an 2 an 3
cn 3 = 1 an an 4 an 5
…
a n 1 a n 1
行由2, 行同样方法得到 一直排到第n+1行. 行同样方法得到. 第4行由 ,3行同样方法得到.一直排到第 行由 行 罗斯准则指出:若第一列元素大于零,则A(s)=0所有的 罗斯准则指出:若第一列元素大于零, A(s)=0所有的 根均在左半开平面.若第一列元素出现符号改变, 根均在左半开平面.若第一列元素出现符号改变,则符 号改变的总次数就是右半平面根的个数. 号改变的总次数就是右半平面根的个数.
信号与系统王明泉第七章习题解答
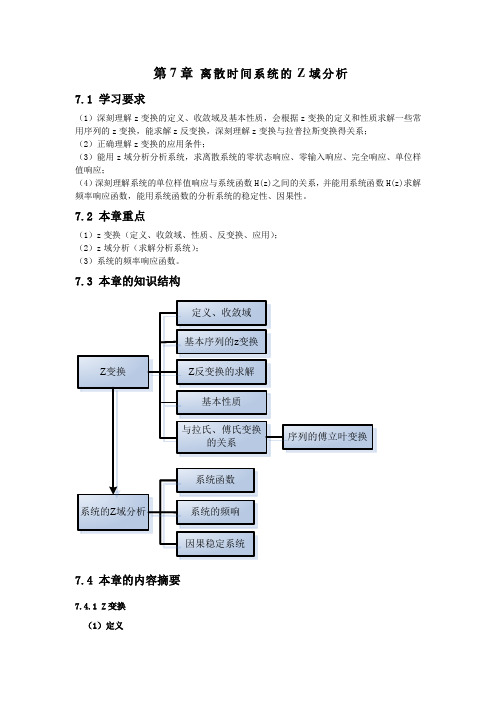
第7章离散时间系统的Z域分析7.1 学习要求(1)深刻理解z变换的定义、收敛域及基本性质,会根据z变换的定义和性质求解一些常用序列的z变换,能求解z反变换,深刻理解z变换与拉普拉斯变换得关系;(2)正确理解z变换的应用条件;(3)能用z域分析分析系统,求离散系统的零状态响应、零输入响应、完全响应、单位样值响应;(4)深刻理解系统的单位样值响应与系统函数H(z)之间的关系,并能用系统函数H(z)求解频率响应函数,能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点(1)z变换(定义、收敛域、性质、反变换、应用);(2)z域分析(求解分析系统);(3)系统的频率响应函数。
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换(1)定义∑∞-∞=-=n nzn x z X )()( 表示为:)()]([z X n x Z =。
(2)收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 (1)当0,021>>n n 时,n 始终为正,收敛条件为0>z ; (2)当0,021<<n n 时,n 始终为负,收敛条件为∞<z ;(3)当0,021><n n 时,n 既取正值,又取负值,收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ (1)当01>n 时,n 始终为正,由阿贝尔定理可知,其收敛域为1x R z >,1x R 为最小收敛半径;(2)当01<n 时,)(z X 分解为两项级数的和,第一项为有限长序列,其收敛域为∞<z ;第二项为z 的负幂次级数,由阿贝尔定理可知,其收敛域为1x R z >;取其交集得到该右边序列的收敛域为∞<<z R x 1。
3.左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他(1)当02<n ,n 始终为负,收敛域为2x R z <,2x R 为最大收敛半径; (2)当02>n ,)(z X 可分解为两项级数的和,第一项为z 的正幂次级数,根据阿贝尔定理,其收敛域为2x R z <,2x R 为最大收敛半径;第二项为有限长序列,其收敛域为0>z ;取其交集,该左边序列的收敛域为20x R z <<。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.1 用样本表示连续时间信号: 采样定理
(Theorem of Sampling) 一. 采样: Sampling
在某些离散的时间点上提取连续时间信号值的 过程称为采样。
是否任何信号都可以由它的离散时间样本来表 示?
对一维连续时间信号采样的例子:
6
在没有任何条件限制的情况下,从连续时间信 号采样所得到的样本序列不能唯一地代表原来的 连续时间信号。
T
T
t
ω
26
一阶保持内插的结果(采样间隔为T/4)
27
一阶保持内插的结果(采样间隔为T/4)
28
7.3 欠采样的效果—频谱混叠
The Effect of Undersampling : Aliasing
一. 欠采样与频谱混叠: 如果采样时,不满足采样定理的要求,就一定会
在 x(t) 的频谱周期延拓时,出现频谱混叠的现象。
1. x(t) 必须是带限的,最高频率分量为ωM 。
2. 采样间隔(周期)不能是任意的,必须保证采样
频率 ωs > 2ωM 。其中 ωs =2π /T 为采样频率。
在满足上述要求时,可以通过理想低通滤波器 从 X p ( jω) 中不失真地分离出X ( jω)。
12
Xp( jω)
1
TT
ω
−ωs −ωM 0 ωMωcωs
为周期进行延拓。
10
∑ X
p(
jω )
=
1 T
∞ k =−∞
X
(
j(ω
−
kωs
))
ωs
=
2π
T
11
要想使采样后的信号样本能完全代表原来的信 号,就意味着要能够从 X p ( jω) 中不失真地分离 出 X ( jω) 。这就要求 X p ( jω) 在周期性延拓时不能 发生频谱的混叠。为此必须要求:
0
x (0 ) x(T )
x(2T )
0T t
∞
p(t) = ∑ δ (t − nT )
−2T −T
x0 (t)
0 T 2T
n=−∞
15
x(t) ⊗xp(t)
1 h0 (t)
t
∞
0T
p(t) = ∑ δ (t − nT )
n=−∞
x0 (t)
δ (t)
−⊕ ∫
延时T
零阶保持系统
h0 (t)
h0 (t)
xd (n) = xc (nT )
∑ 在频域:
X
p(
jω)
=
1 T
∞ k =−∞
Xc[
j(ω
−
kωs )],
ωs
=
2π
T
36
以Ω表示离散时间的频率变量,ω表示连续时间
的频率变量
xd (n) = xc (nT )
∑ X d (e jΩ ) =
+∞ n=−∞
xc
(nT
)e
−
jΩn
∑ xp (t) = xc (t) ⋅ p(t) =
一. 理想内插:
若 h(t) 为理想低通的单位冲激响应,则
∞
x(t) = xp (t) ∗ h(t) = ∑ x(nT )δ (t − nT ) ∗ h(t)
∞
n=−∞
= ∑ x(nT )h(t − nT )
n = −∞
20
表明:理想内插以理想低通滤波器的单位冲激 响应作为内插函数。
h(t) = Tωc Sinc(ωc t) = Tωc Sin ωct = T ⋅ Sinωct
此时,即使通过理想内插也得不到原信号。但是 无论怎样,恢复所得的信号 xr (t)与原信号 x(t) 在采 样点上将具有相同的值。
xr (nT ) = x(nT )
29
例: x(t) = cosω0t
x(t)的频谱 X ( jω)
当 ω0 <ωs <2ω0 时,
产生频谱混叠。
恢复的信号为
xr (t) = cos(ω s −ω0 )t
∞
∑
δ
(ω
−
2π
k)
T n=−∞
T
所以
X p ( jω ) =
1
2π
X ( jω) ∗ P( jω )
∑ =
1
2π
X ( jω) ∗ 2π
T
∞
δ (ω − kωs )
k =−∞
∑ =
1 T
∞ k =−∞
X
(
j(ω
−
kωs ))
ωs
=
2π
T
可见,在时域对连续时间信号进行理想采样,
就相当于在频域将连续时间信号的频谱以 ωs
X ( jω)
π
π
ω
−ω0 0 ω0
πT πT
X p ( jω ) πT
πT
−ω s
ωs
ω
−−ωω0s + ω00 ωs −ωω0 0
πT πT
T Xr ( jω) π T
πT
−ω s
ωs
ω
−ω0 0
−ωs + ω0
ωs ω−0ω0
30
显然当 t = nT 时有
xr (nT) = cos(ω s −ω0)nT
第7章 采 样
本章主要内容
1.如何用连续时间信号的离散时间样本来表示 连续时间信号——采样定理。
2.如何从采样所得到的样本重建连续时间信号。 3.欠采样导致的后果——频谱混叠。 4.连续时间信号的离散时间处理。 5.离散时间信号的采样、抽取及内插。
1
7.0 引言:( Introduction )
在日常生活中,常可以看到用离散时间信号表 示连续时间信号的例子。如传真的照片、电视屏幕 的画面、电影胶片等等,这些都表明连续时间信号 与离散时间信号之间存在着密切的联系。在一定条 件下,可以用离散时间信号代替连续时间信号而并 不丢失原来信号所包含的信息。
Nyquist (奈奎斯特) 采样定理:
对带限于最高频率ωM 的连续时间信号x(t) ,
如果以 ωs > 2ωM 的频率进行理想采样,则 x(t) 可
以唯一的由其样本 x(nT ) 来确定。
2ωM 一般称为奈奎斯特率。
13
• 滤波器应具有T 倍的通带增益,
以补偿采样时频谱幅度的减小。 • 低通滤波器的截止频率必须满足:
ωM < ωc < (ωs − ωM )
14
四. 零阶保持采样: x0 (t)
信号的样本经零阶保持后, 得到一个阶梯形信号。
零阶保持采样相当于理想采样后,再级联一个零阶保持系统。
零阶
x(t )
保持系统
t
x(t) ⊗ xp(t)
1 h0 (t)
t
x0 (t)
x p (t)
x(−2T ) x(−T )
1 Xp( jω)
T
−ωM 0 ω M
ωs
ω
X d (e jΩ )
1 T
−ωMT 0 ωMT
+∞ n = −∞
xc
(nT
)δ
(t
−
nT)
∑ X p ( jω) =
+∞ n=−∞
xc
(nT
)e−
jωnT
X p ( jω ) = X d (e jωT )
∑ X d
(e
jΩ
)
=
X
p
(
j
Ω )
T
=
1 T
∞ k =−∞
Xc[
j
1 T
(Ω
−
2π
k )]
39
−ωs
− 2π
X c ( jω)
1
ω
−ωM 0 ω M
jω )
=
2 Sin(ωT ω
/
2)
−
e
jωT 2
所以
H r ( jω )
=
H ( jω ) 2 Sin ωT
2
jωT
⋅e 2
ω
17
以 H ( jω) 表示理想低通滤波器的特性,则:
H 0 ( jω )
T
2π
Tω
0
H ( jω)
T
ω
−π 0 π
T
T
若
ωc
=
1 2
ω
s
=
π
T
则
H r ( jω ) =
= cosωsnT ⋅ cosω0nT + sinωsnT ⋅sinω0nT
= cosω0nT = x(nT )
ωs = 2π / T
如果 x(t) = cos(ω0t +ϕ) ,则在上述情况下:
{ } Xr( jω) =π δ[ω−(ωs −ω0)]⋅e−jϕ +δ[ω+(ωs −ω0)]⋅ejϕ
2
例1.一幅新闻照片
3
局部放大后的图片
4
研究连续时间信号与离散时间信号之间的关系 主要包括: 1. 在什么条件下,一个连续时间信号可以用它的 离散时间样本来代替而不致丢失原有的信息。 2. 如何从连续时间信号的离散时间样本不失真地 恢复成原来的连续时间信号。 3. 如何对一个连续时间信号进行离散时间处理。 4. 对离散时间信号如何进行采样、抽取及内插。
x(nT ) = cosϕ cosω0nT
这和对 x1(t) = cosϕ cosω0t 采样的结果一样。
从用样本代替信号的角度出发,出现欠采样的
情况是工程应用中不希望的。
32
二. 欠采样在工程实际中的举例:
1. 车轮倒转现象
1
2
3
ωs = 4ω0
