ADF时间序列数据平稳性检验实验指导
第五讲 时间序列的平稳性检验

16
ARMA( p, q)
ARIMA( p, d , q) :
17
单位根过程
• 随机序列 y t 称为单位根过程,如果,
1
1 1
平稳过程
非平稳过程、非单位根过程
18
单位根检验
20世纪70年代,Dickey和Fuller提出了DF统计量,用于检验序列 是否包含单位根过程以及单整的阶数,称为DF检验。
第五节
时间序列的平稳性检验
1
平稳性的检验方法之一:时序图检验方法
• 根据平稳时间序列均值、方差为常数的性质,平稳序列的时 序图应该显示出该序列始终在一个常数值附近随机波动,而 且波动的范围有界、无明显趋势及无季节性特征
税收收入(亿元)
80.00%
60.00%
40.00%
20.00%
0.00%
第 1季 19 94 度 年 第 3季 19 95 度 年 第 1季 19 95 度 年 第 3季 19 96 度 年 第 1季 19 96 度 年 第 3季 19 97 度 年 第 1季 19 97 度 年 第 3季 19 98 度 年 第 1季 19 98 度 年 第 3季 19 99 度 年 第 1季 19 99 度 年 第 3季 20 00 度 年 第 1季 20 00 度 年 第 3季 20 01 度 年 第 1季 20 01 度 年 第 3季 度
21
22
ADF检验
ADF检验中两个重要问题: (1)关于位移项和趋势项的判断:实际中并不知道被检验序列的 DGP 属于哪一种形式,怎样选择单位根检验式呢?先采用有趋势 和漂移项的。因为它对应的ADF统计量的检验功效最高。 (2)关于滞后阶数的判断:k尽量小,以保持更大的自由度; k充分 大以消除残差内的自相关。
stata中adf检验命令

stata中adf检验命令
在实证研究中,时间序列数据常常具有一定的自相关性和非平稳性,为了验证时间序列数据的平稳性,可以使用ADF检验。
ADF检验是一种常用的单位根检验方法,用于检验时间序列数据是否存在单位根,即数据是否具有非平稳性。
在Stata软件中,我们可以使用adf命令来进行ADF检验。
首先,我们需要加载数据集,并选择需要进行ADF检验的变量。
接着,我们可以使用以下命令进行ADF检验:
```stata
adf 变量名
```
其中,变量名为需要进行ADF检验的变量名称。
执行该命令后,Stata会输出ADF检验的结果,包括ADF统计量的值、P值以及是否拒绝原假设的判定结果。
如果P值小于显著性水平(通常取0.05),则可以拒绝原假设,认为时间序列数据是平稳的。
在进行ADF检验时,需要注意选择适当的滞后阶数。
滞后阶数的选择可以通过观察自相关图和偏自相关图来确定,也可以使用信息准则(如AIC、BIC)来选择最优的滞后阶数。
除了单变量的ADF检验外,我们还可以进行多变量的ADF检验,即向adf命令添加多个变量名,以检验这些变量之间是否存在共同
的单位根。
ADF检验是一种常用的单位根检验方法,可以帮助我们验证时间序列数据的平稳性,进而进行进一步的时间序列分析。
在Stata中使用adf命令可以快速方便地进行ADF检验,为我们的实证研究提供有力的支持。
希望本文对您理解和使用ADF检验有所帮助。
时间序列数据的平稳性检验

(对全部t)
▪ 方差 var( yt ) E( yt )2 2(对全部t)
▪ 协方差 k E[( yt )( ytk )](对全部t)
▪ 其中 k 即滞后k旳协方差[或自(身)协方差],yt 是
和 ytk ,也就是相隔k期旳两值之间旳协方差。
6
▪ 三、伪回归现象 ▪ 将一种随机游走变量(即非平稳数据)对另一种
14
▪ I (1)过程在金融、经济时间序列数据中是最普遍 旳,而I (0)则表达平稳时间序列。
▪ 从理论与应用旳角度,DF检验旳检验模型有如下
旳三个:
Yt (1 )Yt1 ut 即 Yt Yt1 ut
(5.7)
Yt 1 (1 )Yt1 ut 即 Yt 1 Yt1 ut
(5.8)
随机游走变量进行回归可能造成荒唐旳成果,老 式旳明显性检验将告知我们变量之间旳关系是不 存在旳。 ▪ 有时候时间序列旳高度有关仅仅是因为两者同步 随时间有向上或向下变动旳趋势,并没有真正旳 联络。这种情况就称为“伪回归”(Spurious Regression)。
7
第二节 平稳性检验旳详细措施
一、单位根检验 ▪ (一)单位根检验旳基本原理 ▪ David Dickey和Wayne Fuller旳单位根检验
34
▪ Johansen协整检验有两个检验统计量:
▪ ①迹检验统计量trace :
g
▪ trace=-T ln(1-ˆi),其中r为假设旳协整关系旳 i=r+1 个数,ˆi 为 旳第i个特征值旳估计值(下同)。 相应旳零假设是:H0:协整关系个数不不小于等
于r;被择Байду номын сангаас设:H1:协整关系个数不小于r。
yt yt-k+1yt-1+2yt-2+...k-1yt-(k-1)+ut (5.12)
时间序列的平稳性检验
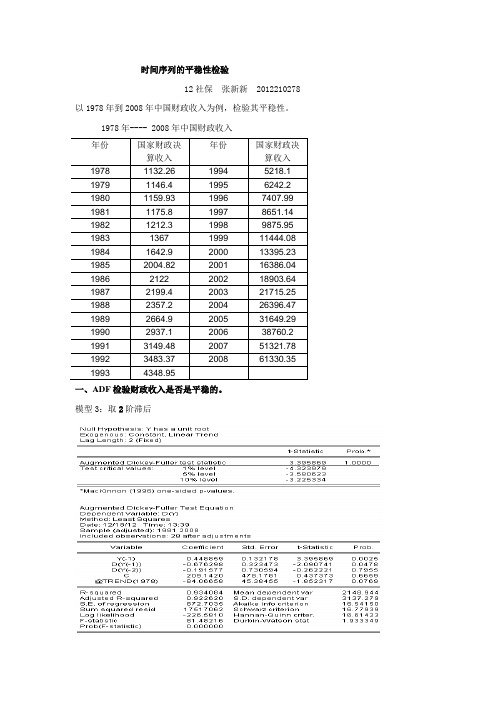
时间序列的平稳性检验12社保张新新 2012210278 以1978年到2008年中国财政收入为例,检验其平稳性。
1978年---- 2008年中国财政收入一、ADF检验财政收入是否是平稳的。
模型3:取2阶滞后从Y(-1)的参数值看,其t统计量的值大于临界值(单尾),不能拒绝存在单位根的零假设。
同时,由于时间项T的t统计量也小于ADF分布表中的临界值(双尾),因此不能拒绝不存在趋势项的零假设。
需进一步检验模型2。
模型2 :模型1:从Y(-1)的参数值看,其t统计量的值大于临界值(单尾),不能拒绝存在单位根的零假设。
至此,可断定国家财政决算收入Y时间序列是非平稳的。
二、ADF检验Y是否是一阶单整模型3:从△Y(-1)的参数值看,其t统计量的值大于临界值(单尾),不能拒绝存在单位根的零假设。
同时,由于时间项项T的t统计量也小于AFD分布表中的临界值(双尾),因此不能拒绝不存在趋势项的零假设。
需进一步检验模型2 。
模型2:从△Y(-1)的参数值看,其统计量的值大于临界值(单尾),不能拒绝存在单位根的零假设。
同时,由于常数项的t统计量也小于AFD分布表中的临界值(双尾),因此不能拒绝不存在趋势项的零假设。
需进一步检验模型1。
模型1:从△Y(-1)的参数值看,其统计量的值大于临界值(单尾),不能拒绝存在单位根的零假设。
至此,可断定△Y时间序列是非平稳的。
三、ADF检验Y是否是二阶单整模型3:从△2Y(-1)的参数值看,其统计量的值小于临界值(单尾)(即使是在1%的置信区间),拒绝存在单位根的零假设。
至此,可断定△2Y时间序列是平稳的,Y是I(2)过程,即是二阶单整。
结论:财政收入是二阶单整的时间序列。
时间序列平稳性检验

时间序列平稳性检验分析姓名xxx学院xx学院专业xxxx学号xxxxxxxxxx时间序列平稳性分析检验时间序列是一个计量经济学中的概念,时间序列分析中首先遇到的问题是关于时间序列数据的平稳性问题。
一、时间序列平稳性的定义假定某个时间序列是由某一随机过程(stochasticprocess)生成的,即假定时间序列{Xt}(t=1,2,•)•的每一个数值都是从一个概率分布中随机得到,如果满足下列条件:1)均值E(Xt)=u是与时间t无关的常数;2)方差Var(Xt)=o2是与时间t无关的常数;3)协方差Cov(Xt,Xt+k尸条是只与时期间隔k有关,与时间t无关的常数。
则称该随机时间序列是平稳的(stationary),而该随机过程是一平稳随机过程(stationary stochasticprocess)。
eg:一个最简单的随机时间序列是一具有零均值同方差的独立分布序列:Xt=Mt,Mt~N(0,o2)该序列常被称为是一个白噪声。
由于Xt具有相同的均值与方差,且协方差为零,由定义,一个白噪声序列是平稳的。
eg:另一个简单的随机时间列序被称为随机游走,该序列由如下随机过程生成:Xt=Xt-1+」t这里,出是一个白噪声。
容易知道该序列有相同的均值:E(Xt)=E(Xt-1)为了检验该序列是否具有相同的方差,可假设Xt的初值为X0,则易知X1=X0+」1X2=X1+」2=X0+J1+J2xt=X0+出+也++M由于X0为常数,%是一个白噪声,因此Var(Xt)=to2即Xt的方差与时间t有关而非常数,它是一非平稳序列二、时间序列平稳性检验的方法对时间序列进行平稳性检验中,实际上假定了时间序列是由具有白噪声随机误差项的一阶自回归过程AR(1)生成的。
但在实际检验中,时间序列可能由更高阶的自回归过程生成的,或者随机误差项并非是白噪声,这样用OLS法进行估计均会表现出随机误差项出现自相关(autocorrelation),导致DF检验无效。
平稳性检验

ppt课件完整
5
(5)PP检验
• 平稳性检验常用的方法还有PP检验,在图 1-9的对话框中“Test Type”中选择下拉菜 单Phillips-Perron,出现图1-12的对话框, 其他选项同ADF检验,图1-13是对sha序列 带趋势项和常数项的方程进行的pp检验, 从结果看出来,接受存在一个单位根的原 假设,于是同ADF检验,对其一阶差分序 列进行PP检验,结果见图1-14,可以看出, 和ADF检验结果相同,一阶差分序列已经 平稳。
1序列各项之间不存在相关即相应滞后阶数的自相关系数与0没有显著性差异序列为白噪声序列序列即纯随机序列进行的统计检验至少存在某个在图18中由每个q统计量的伴随概率可以看出都是拒绝原假设的说明至少存在某个k使得滞后k期的自相关系数显著非0也即拒绝序列是白噪声序列的原假设
时间序列数据平稳性检验
• (1)、通过时序图看时间序列的平稳性, 这个方法很直观,但比较粗糙;
ppt课件完整
3
(3)、纯随机性判断
• 1、序列各项之间不存在相关,即相应滞后阶数的 自相关系数与0没有显著性差异,序列为白噪声序 列,序列即纯随机序列进行的统计检验
H 0 : 1 = 2 = ...= m = 0 , m 1
•
• 至少存在某个在图1-8中,由每个Q统计量的伴随 概率可以看出,都是拒绝原假设的,说明至少存 在某个k,使得滞后k期的自相关系数显著非0, 也即拒绝序列是白噪声序列的原假设。
• 2、相关图显示的最大滞后阶数k,观测值多,k可取 T/10 或 T ;若样本量较小k一般取 T /4
• 3、相关图的左半部分是自相关和偏自相关分析图,垂立 的两道虚线表示2倍标准差。右半部分是滞后阶数、自相 关系数、偏自相关系数、Q统计量和相伴的概率。从自相 关和偏自相关分析图可以看出自相关系数趋向0的速度相 当缓慢,且滞后6阶之后自相关系数才落入2倍标准差范围 以内,并且呈现一种三角对称的形式,这是具有单调趋势 的时间序列典型的自相关图的形式。
ADF时间序列数据平稳性检验实验指导

实验一时间序列数据平稳性检验实验指导一、实验目的:理解经济时间序列存在的不平稳性,掌握对时间序列平稳性检验的步骤和各种方法,认识利用不平稳的序列进行建模所造成的影响。
二、基本概念:如果一个随机过程的均值和方差在时间过程上都是常数,并且在任何两时期的协方差值仅依赖于该两个时期间的间隔,而不依赖于计算这个协方差的实际时间,就称它是宽平稳的。
时序图ADF检验PP检验三、实验内容及要求:1、实验内容:用Eviews5.1来分析1964年到1999年中国纱产量的时间序列,主要内容:〔1〕、通过时序图看时间序列的平稳性,这个方法很直观,但比较粗糙;〔2〕、通过计算序列的自相关和偏自相关系数,根据平稳时间序列的性质观察其平稳性;〔3〕、进行纯随机性检验;〔4〕、平稳性的ADF检验;〔5〕、平稳性的pp检验。
2、实验要求:〔1〕理解不平稳的含义和影响;〔2〕熟悉对序列平稳化处理的各种方法;〔2〕对相应过程会熟练软件操作,对软件分析结果进行分析。
四、实验指导〔1〕、绘制时间序列图时序图可以大致看出序列的平稳性,平稳序列的时序图应该显示出序列始终围绕一个常数值波动,且波动的范围不大。
如果观察序列的时序图显示出该序列有明显的趋势或周期,那它通常不是平稳序列,现以1964-1999年中国纱年产量序列〔单位:万吨〕来说明。
在EVIEWS中建立工作文件,在“Workfile structure type”栏中选择“Dated-regular frequency”,在右边的“Date specification”中输入起始年1964,终止年1999,点击ok则建立了工作文件。
找到中国纱年产量序列的excel文件并导入命名该序列为sha,见图1-2。
图1-1 建立工作文件图1-2创建新序列SHA,如图1-2。
点击主菜单Quick/Graph就可作图,见图1-3,分别是折线图〔Line graph〕、条形图〔Bar graph〕、散点图〔Scatter〕等,也可双击序列名,出现显示电子表格的序列观测值,然后点击工具栏的View/Graph。
时序预测中的时间序列平稳性检验方法详解(十)

时序预测是一种对未来时间序列数据进行预测的方法,它可以帮助我们了解未来的趋势和规律,对于经济、金融、医学等领域都具有重要的应用价值。
而在时序预测中,时间序列平稳性检验是非常关键的一步,它能够帮助我们确认时间序列数据是否符合预测模型的假设条件,从而选择合适的预测模型和方法。
一、时间序列平稳性的概念时间序列数据是指在一段时间内按照时间顺序排列的数据点的集合,例如股票价格、气温、销售额等。
而时间序列平稳性是指时间序列数据在不同时间段内具有相同的统计性质,即均值和方差不随时间发生显著的变化。
如果时间序列数据是平稳的,那么我们可以基于这个假设来进行时序预测,否则就需要对数据进行处理或者选择其他的预测方法。
二、时间序列平稳性检验的方法1. 直观图形法直观图形法是一种简单直观的平稳性检验方法,可以通过绘制时间序列数据的图形来观察数据的均值和方差是否随时间发生明显变化。
一般来说,如果数据在图形上呈现出随时间波动的趋势,那么就可以初步判断数据不是平稳的。
2. 统计量检验法统计量检验法是一种通过统计学方法来检验时间序列平稳性的方法,其中比较常用的有单位根检验和ADF检验。
单位根检验是通过检验时间序列数据是否具有单位根的方法来判断其平稳性,而ADF检验则是在单位根检验的基础上增加了滞后项和趋势项的考虑,从而提高了检验的准确性。
3. 谱分析法谱分析法是一种利用时间序列数据的频谱特性来判断其平稳性的方法,它通过对时间序列数据进行傅立叶变换,然后观察频谱图来判断数据是否是平稳的。
谱分析法在信号处理领域有着广泛的应用,但是在时序预测中相对较少使用。
三、时间序列平稳性检验方法的选择在实际应用中,我们需要根据具体的时间序列数据和预测任务来选择合适的平稳性检验方法。
如果数据量较小,可以先通过直观图形法来进行初步判断,然后再根据需要选择统计量检验法或者谱分析法来进行进一步的检验。
而如果数据量较大或者对检验的准确性要求较高,可以考虑使用多种方法进行综合判断。
时序预测中的时间序列平稳性检验方法详解(八)

时序预测中的时间序列平稳性检验方法详解时间序列分析是一种统计方法,用于分析时间序列数据的模式和趋势,以便预测未来的趋势。
时间序列预测是在一定时间范围内对未来数据进行估计和预测,而时间序列的平稳性检验是进行时间序列预测的第一步。
在本文中,我将详细解释时序预测中的时间序列平稳性检验方法。
时间序列的平稳性是指时间序列在统计特性上不随时间发生显著变化的性质。
在时间序列分析中,平稳性是一个非常重要的性质,因为只有平稳的时间序列才能应用于许多经典的时间序列模型。
下面我们将介绍一些常见的时间序列平稳性检验方法。
1. 绝对值单位根检验绝对值单位根检验是一种检验时间序列平稳性的方法。
它的基本思想是对时间序列进行绝对值转换,然后应用单位根检验。
如果单位根检验的结果表明时间序列的绝对值是平稳的,那么原始时间序列也是平稳的。
2. ADF检验ADF(Augmented Dickey-Fuller)检验是一种常用的检验时间序列平稳性的方法。
它的原假设是时间序列具有单位根,即不平稳。
如果经过ADF检验,可以拒绝原假设,那么就可以认为时间序列是平稳的。
3. PP检验PP(Phillips-Perron)检验也是一种检验时间序列平稳性的方法。
它与ADF 检验类似,都是基于单位根检验的原理。
PP检验的优点是可以处理具有序列相关性和异方差性的时间序列数据。
4. KPSS检验KPSS(Kwiatkowski-Phillips-Schmidt-Shin)检验是一种用于检验时间序列平稳性的方法。
与ADF检验相反,KPSS检验的原假设是时间序列是平稳的,因此如果检验结果表明拒绝原假设,那么就可以认为时间序列是不平稳的。
以上是一些常见的时间序列平稳性检验方法,每种方法都有其适用的场景和局限性。
在实际应用中,可以根据时间序列的特点和数据的分布情况选择合适的方法进行平稳性检验。
在进行时间序列预测时,平稳性检验是非常重要的一步,只有在时间序列平稳的情况下,才能应用于各种经典的时间序列模型,从而得到准确的预测结果。
stata中adf检验命令

stata中adf检验命令
Stata中adf检验命令
ADF检验(Augmented Dickey-Fuller Test)是时间序列分析中常用的一种方法,用于检验序列的平稳性。
在Stata软件中,可以通过内置的命令来进行ADF检验,帮助研究人员进行时间序列数据的分析和建模。
要在Stata中进行ADF检验,首先需要加载所需的数据集。
可以使用命令“use 文件路径\文件名.dta, clear”来加载数据。
接下来,可以使用命令“dfuller 变量名”来进行ADF检验。
在这个命令中,变量名是要进行检验的时间序列数据的变量名。
ADF检验的原假设是序列具有单位根,即序列是非平稳的。
如果检验结果的p值小于显著性水平(通常取0.05),则可以拒绝原假设,认为序列是平稳的。
反之,则不能拒绝原假设,序列是非平稳的。
除了简单的ADF检验外,Stata还提供了更多高级的ADF检验方法,如ADF-GLS检验和PP检验。
这些方法对序列的特性和数据分布做了更多的假设,并能够提供更准确的判断结果。
在实际应用中,ADF检验是时间序列分析的重要工具之一。
通过对序列的平稳性进行检验,可以为后续的建模和预测提供可靠的基础。
在金融领域和宏观经济领域,ADF检验被广泛应用于股票价格、汇率、GDP等时间序列数据的分析。
Stata中的ADF检验命令为研究人员提供了方便快捷的工具,帮助他们进行时间序列数据的分析和建模。
通过对序列平稳性的检验,可以更准确地理解数据的特性,为决策提供科学依据。
希望本文的介绍能够帮助读者更好地理解和应用ADF检验命令。
ADF检验的结果分析

ADF检验的结果分析ADF(Augmented Dickey-Fuller)检验是一种常用的单位根检验方法,用于判断时间序列数据是否具有平稳性。
平稳性是许多时间序列模型的前提条件之一,因此ADF检验在金融、经济学等领域中得到广泛应用。
本文将介绍ADF检验的基本原理,并对其结果进行详细分析。
1. ADF检验的基本原理ADF检验是基于Dickey-Fuller单位根检验的扩展,用于检验时间序列数据是否存在单位根。
单位根表示时间序列数据存在非平稳性,即随着时间的推移,其均值和方差会发生变化。
ADF检验的目标是判断时间序列数据是否具有平稳性。
ADF检验的假设为:•原假设(H0):时间序列数据具有单位根,即非平稳性。
•备择假设(H1):时间序列数据不具有单位根,即平稳性。
ADF检验的统计量是检验统计量(Test Statistic),它与临界值进行比较以确定是否拒绝原假设。
根据ADF检验的具体类型,例如ADF-GLS、ADF-DF、ADF-PP等,选择合适的临界值进行比较。
2. ADF检验的结果分析ADF检验的结果通常包含以下几个关键部分:•检验统计量(Test Statistic):ADF检验的统计量是一个负数,表示与原假设相反的方向。
绝对值较大的统计量表明更强的证据支持备择假设,即数据具有平稳性。
•临界值(Critical Values):ADF检验的临界值是用于比较检验统计量的阈值。
如果检验统计量小于临界值,则可以拒绝原假设,认为数据具有平稳性。
•p值(p-value):p值表示在原假设为真的情况下,观察到的检验统计量或更极端情况的概率。
如果p值小于预先设定的显著性水平(通常为0.05),则可以拒绝原假设。
根据ADF检验的结果,可以得出以下几种结论:1.如果检验统计量小于临界值:在这种情况下,可以拒绝原假设,认为时间序列数据具有平稳性。
此时,可以进行进一步的时间序列分析,例如构建ARIMA模型等。
2.如果检验统计量大于临界值:在这种情况下,无法拒绝原假设,即无法肯定时间序列数据具有平稳性。
时间序列分析实验报告

时间序列分析实验报告一、实验目的时间序列分析是一种用于处理和分析随时间变化的数据的统计方法。
本次实验的主要目的是通过对给定的时间序列数据进行分析,掌握时间序列分析的基本方法和技术,包括数据预处理、模型选择、参数估计和预测,并评估模型的性能和准确性。
二、实验数据本次实验使用了一组某商品的月销售量数据,数据涵盖了过去两年的时间范围,共 24 个观测值。
数据的具体形式为一个时间序列,其中每个观测值表示该商品在相应月份的销售量。
三、实验方法1、数据预处理首先,对数据进行了可视化,绘制了时间序列图,以便直观地观察数据的趋势、季节性和随机性。
然后,对数据进行了平稳性检验。
采用了 ADF(Augmented DickeyFuller)检验来判断数据是否平稳。
如果数据不平稳,则需要进行差分处理,使其达到平稳状态。
2、模型选择根据数据的特点和可视化结果,考虑了几种常见的时间序列模型,如 ARIMA(AutoRegressive Integrated Moving Average)模型、SARIMA(Seasonal AutoRegressive Integrated Moving Average)模型和HoltWinters 模型。
通过对不同模型的参数进行估计,并比较它们在训练数据上的拟合效果和预测误差,选择了最适合的模型。
3、参数估计对于选定的模型,使用最大似然估计或最小二乘法等方法来估计模型的参数。
通过对参数的估计值进行分析,判断模型的合理性和稳定性。
4、预测使用估计得到的模型参数,对未来一段时间内的销售量进行预测。
为了评估预测的准确性,采用了均方根误差(RMSE)、平均绝对误差(MAE)等指标来衡量预测值与实际值之间的差异。
四、实验过程1、数据可视化通过绘制时间序列图,发现数据呈现出明显的季节性和上升趋势。
同时,数据的波动范围也较大,存在一定的随机性。
2、平稳性检验对原始数据进行 ADF 检验,结果表明数据是非平稳的。
实验报告关于时间序列(3篇)

第1篇一、实验目的1. 了解时间序列的基本概念和特性;2. 掌握时间序列的常用分析方法;3. 学会运用时间序列分析方法解决实际问题。
二、实验内容1. 时间序列数据收集2. 时间序列描述性分析3. 时间序列平稳性检验4. 时间序列模型构建5. 时间序列预测三、实验方法1. 时间序列数据收集:通过查阅相关文献、统计数据网站等方式获取实验所需的时间序列数据。
2. 时间序列描述性分析:对时间序列数据进行统计分析,包括均值、标准差、偏度、峰度等。
3. 时间序列平稳性检验:运用单位根检验(ADF检验)判断时间序列的平稳性。
4. 时间序列模型构建:根据时间序列的平稳性,选择合适的模型进行构建,如ARIMA模型、季节性分解模型等。
5. 时间序列预测:利用构建好的时间序列模型进行预测,并评估预测结果的准确性。
四、实验步骤1. 数据收集:选取我国某地区近十年的GDP数据作为实验数据。
2. 描述性分析:计算GDP数据的均值、标准差、偏度、峰度等统计量。
3. 平稳性检验:对GDP数据进行ADF检验,判断其平稳性。
4. 模型构建:根据ADF检验结果,选择合适的模型进行构建。
5. 预测:利用构建好的模型对GDP数据进行预测,并评估预测结果的准确性。
五、实验结果与分析1. 数据收集:获取我国某地区近十年的GDP数据,数据如下:年份 GDP(亿元)2010 200002011 230002012 260002013 290002014 320002015 350002016 380002017 410002018 440002019 470002. 描述性分析:计算GDP数据的均值、标准差、偏度、峰度等统计量,结果如下:均值:39600亿元标准差:4900亿元偏度:-0.2峰度:-1.83. 平稳性检验:对GDP数据进行ADF检验,结果显示ADF统计量在1%的显著性水平下拒绝原假设,说明GDP数据是非平稳的。
4. 模型构建:由于GDP数据是非平稳的,我们可以对其进行差分处理,使其变为平稳序列。
stata中进行adf检验的命令

在Stata中进行ADF检验(Augmented Dickey-Fuller Test)是研究单位根(unit root)存在与否的一种常用方法。
单位根指的是时间序列数据中的根(根是指方程的解),如果单位根存在,意味着时间序列数据具有非平稳性。
而ADF检验则是用来检验单位根是否存在的统计方法。
在Stata中,进行ADF检验可以使用dfuller命令。
下面将详细介绍如何使用这个命令进行ADF检验。
1. 环境设置在使用dfuller命令之前,需要先加载Stata的时间序列数据扩展包(timeseries package)。
通过输入以下命令加载扩展包:ssc install tsset2. 数据准备在进行ADF检验之前,需要准备好相关的时间序列数据。
可以使用tsset命令将数据设置为Stata的时间序列数据格式。
tsset date这里的date是数据中表示日期的变量名,需要将其替换为实际使用的日期变量名。
3. 进行ADF检验使用dfuller命令可以进行ADF检验。
下面是该命令的基本语法:dfuller dependent_variable [if] [in], [options]其中,dependent_variable是要进行ADF检验的变量名。
可以使用if子句和in子句进行数据筛选。
在进行ADF检验时,需要考虑以下两个核心问题: - 是否包含截距项(constant):使用-c选项来指定。
如果添加了-c选项,表示模型中包含截距项。
如果没有添加该选项,则表示模型中不包含截距项。
- 是否包含时间趋势项(trend):使用-t选项来指定。
同样地,如果添加了-t选项,表示模型中包含时间趋势项。
如果没有添加该选项,则表示模型中不包含时间趋势项。
如果要进行包含截距项和时间趋势项的ADF检验,可以使用以下命令:dfuller dependent_variable, lags(#) trend其中,#需要用实际的滞后阶数替换,表示在ADF检验中使用的滞后阶数。
时间序列_实验报告

一、实验目的1. 了解时间序列分析的基本原理和方法;2. 掌握时间序列数据的平稳性检验、模型识别和参数估计等基本操作;3. 通过实例,学习使用ARIMA模型进行时间序列预测。
二、实验环境1. 操作系统:Windows 102. 软件环境:EViews 9.0、R3.6.1三、实验数据1. 数据来源:某城市1980年1月至2020年12月每月的GDP数据;2. 数据格式:Excel表格。
四、实验步骤1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,观察数据的趋势、季节性和周期性;(3)平稳性检验:使用ADF检验判断GDP序列是否平稳。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:观察ACF和PACF图,初步确定ARIMA模型的阶数;(2)模型选择:根据ACF和PACF图,选择合适的ARIMA模型。
3. 模型估计(1)模型估计:使用EViews软件中的ARIMA过程,对选择的模型进行参数估计;(2)模型检验:对估计出的模型进行残差检验,包括残差的平稳性检验、白噪声检验等。
4. 时间序列预测(1)预测:使用估计出的ARIMA模型,对2021年1月至2025年12月的GDP进行预测;(2)预测结果分析:对预测结果进行分析,评估预测的准确性。
五、实验结果与分析1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,发现GDP序列存在明显的上升趋势和季节性;(3)平稳性检验:使用ADF检验,发现GDP序列在5%的显著性水平下拒绝原假设,序列是平稳的。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:根据ACF和PACF图,初步确定ARIMA模型的阶数为(1,1,1);(2)模型选择:根据ACF和PACF图,选择ARIMA(1,1,1)模型。
时序预测中的时间序列平稳性检验方法详解(七)

时序预测中的时间序列平稳性检验方法详解时间序列分析是指对一定时间间隔内的数据进行观察、分析和建模的一种统计分析方法。
其中,时序预测是时间序列分析的一个重要应用方向,通过对历史数据的分析和模型构建,来预测未来一段时间内的数据走势。
而时间序列的平稳性是时序预测中的重要前提条件,下面将详细讨论时间序列平稳性的检验方法。
一、平稳性概念及其重要性所谓平稳性,是指时间序列在不同时间点上的统计特性不发生显著的变化。
具体来说,时间序列的均值、方差和自相关性不随时间变化而发生显著变化。
平稳性对于时序预测至关重要,因为只有在时间序列平稳的情况下,我们才能够基于历史数据进行有效的预测。
二、时间序列平稳性的检验方法1. 直观法直观法是一种最简单直接的方法,即通过观察时间序列图来初步判断序列是否平稳。
如果时间序列的均值和方差在不同时间段内基本保持不变,那么可以初步认定序列具有平稳性。
然而,直观法并不够严谨,往往需要结合其他方法进行验证。
2. 统计检验法统计检验法是通过一些统计指标来检验时间序列的平稳性。
常用的方法包括ADF检验、单位根检验、KPSS检验等。
ADF检验是一种通过单位根检验来判断时间序列是否平稳的方法,其基本原理是对原始时间序列进行单位根检验,若序列平稳则对应的p值应当小于显著性水平。
而KPSS检验则是一种基于单位根检验的方法,其原理是对原始序列进行单位根检验,若序列显著偏离平稳则对应的p值应当大于显著性水平。
通过这些统计检验方法,我们可以更加客观准确地判断时间序列的平稳性。
3. 时间序列差分法时间序列差分法是一种通过对时间序列进行差分运算来消除非平稳性的方法。
具体来说,我们可以对原始时间序列进行一阶差分或二阶差分运算,然后对差分后的序列进行平稳性检验。
若差分后的序列满足平稳性条件,则可以认定原始序列具有平稳性。
4. 线性回归法线性回归法是一种利用线性回归模型来检验时间序列平稳性的方法。
具体来说,我们可以建立一个线性回归模型,将时间序列的观测值作为因变量,时间作为自变量,然后对回归系数进行显著性检验。
adf检验 方法

adf检验方法
ADF检验(Augmented Dickey-Fuller test)是Eviews软件中一种检查序列平稳性的单位根检验方法。
ADF检验的输出结果包括检验滞后变量系数
的ADF统计量和检验所需的临界值(1%,5%,10%)。
如果系数显著不为零,实为小于零,那么包含单位根的假设将被拒绝,从而接受备择假设平稳。
做ADF检验的步骤如下:
1. 对原始时间序列进行检验,此时第二项选level,第三项选None。
如果
没通过检验,说明原始时间序列不平稳。
2. 对原始时间序列进行一阶差分后再检验,即第二项选1st difference,第三项选intercept,若仍然未通过检验,则需要进行二次差分变换。
3. 二次差分序列的检验,即第二项选择2nd difference ,第四项选择Trend and intercept。
一般到此时间序列就平稳了。
以上信息仅供参考,如需了解更多信息,建议查阅相关书籍或咨询专业人士。
实验十 时间序列模型的平稳性及其检验以及单整和协整检验

二 单整
平稳时间序列是0 平稳时间序列是0阶单整的 经过一次差分变成平稳时间序列的话则是一 阶单整的 经过n次差分变成平稳时间序列的话则是n 经过n次差分变成平稳时间序列的话则是n 阶单整的 也是通过ADF ADF检验来进行判断的 也是通过ADF检验来进行判断的
三 协整
首先判断两个序列的平稳性, 1、 首先判断两个序列的平稳性,如果两个序列同 阶单整, 阶单整,进入下一步 利用ols法对两个变量进行回归, 得到残差e ols法对两个变量进行回归 2、利用ols法对两个变量进行回归, 得到残差e 检验e的单整性(不用含截距项的形式), ),根 3、检验e的单整性(不用含截距项的形式),根 据e的单整性判断两个变量是怎样进行协整的 注意:如果两个原序列是d阶单整的, 注意:如果两个原序列是d阶单整的,而e是(d-b) 阶单整,则说明两个序列是(d,b)协整的 阶单整,则说明两个序列是(d,b)协整的 完成教材305 305页 (2)(3), 完成教材305页7题(1)(2)(3),8题(1)(2)(3)
3、单位根检验(ADF检验) 单位根检验(ADF检验) 检验
打开要检验的序列,在此页面单击view打开要检验的序列,在此页面单击view-unit view test,通过相应的 值和临界值进行对比, 通过相应的t root test,通过相应的t值和临界值进行对比, 如过大于临界值,说明存在单位根, 如过大于临界值,说明存在单位根,则序 列是非平稳的, 列是非平稳的,否则是平稳序列 注意:在检验时从第三个模型进行检验,然 注意:在检验时从第三个模型进行检验, 后第二个模型,最后第三个, 后第二个模型,最后第三个,只要出现通 检验,就说明序列是平稳的, 过t检验,就说明序列是平稳的,否则不平 稳
时序数据分析中的平稳性检验与模型拟合方法

时序数据分析中的平稳性检验与模型拟合方法时序数据分析是一种重要的数据分析方法,它用于研究随时间变化的数据。
在时序数据分析中,平稳性检验和模型拟合是两个关键的步骤。
本文将介绍平稳性检验和模型拟合的基本概念、方法和应用。
一、平稳性检验平稳性是指时间序列数据的统计特性在不同时间段内保持不变。
平稳性检验是为了确定时间序列数据是否满足平稳性的要求。
常用的平稳性检验方法有ADF检验(Augmented Dickey-Fuller test)和KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin test)。
ADF检验是一种常用的平稳性检验方法,它基于Dickey-Fuller单位根检验。
ADF检验的原假设是时间序列数据存在单位根,即非平稳性。
如果通过ADF检验,可以拒绝原假设,认为时间序列数据是平稳的。
KPSS检验是另一种常用的平稳性检验方法,它基于Kwiatkowski-Phillips-Schmidt-Shin统计量。
KPSS检验的原假设是时间序列数据是平稳的。
如果通过KPSS检验,可以拒绝原假设,认为时间序列数据是非平稳的。
平稳性检验的目的是为了确定时间序列数据是否适合进行模型拟合。
如果时间序列数据不满足平稳性要求,就需要进行差分处理或其他预处理方法来使其平稳化。
二、模型拟合方法模型拟合是时序数据分析的核心步骤之一,它用于建立时间序列数据的数学模型,以便对未来的数据进行预测和分析。
常用的模型拟合方法有ARIMA模型(自回归移动平均模型)、GARCH模型(广义自回归条件异方差模型)和VAR模型(向量自回归模型)。
ARIMA模型是一种常用的线性模型,它包括自回归部分、差分部分和移动平均部分。
ARIMA模型适用于平稳时间序列数据的建模和预测。
GARCH模型是一种用于建模条件异方差的模型,它能够捕捉时间序列数据中的波动性。
GARCH模型适用于金融领域的波动性建模和预测。
VAR模型是一种多变量时间序列模型,它能够捕捉不同变量之间的相互关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一时间序列数据平稳性检验实验指导
一、实验目的:
理解经济时间序列存在的不平稳性,掌握对时间序列平稳性检验的步骤和各种方法,认识利用不平稳的序列进行建模所造成的影响。
二、基本概念:
如果一个随机过程的均值和方差在时间过程上都是常数,并且在任何两时期的协方差值仅依赖于该两个时期间的间隔,而不依赖于计算这个协方差的实际时间,就称它是宽平稳的。
时序图
ADF检验
PP检验
三、实验内容及要求:
1、实验内容:
用Eviews5.1来分析1964年到1999年中国纱产量的时间序列,主要内容:
(1)、通过时序图看时间序列的平稳性,这个方法很直观,但比较粗糙;
(2)、通过计算序列的自相关和偏自相关系数,根据平稳时间序列的性质观察其平稳性;(3)、进行纯随机性检验;
(4)、平稳性的ADF检验;
(5)、平稳性的pp检验。
2、实验要求:
(1)理解不平稳的含义和影响;
(2)熟悉对序列平稳化处理的各种方法;
(2)对相应过程会熟练软件操作,对软件分析结果进行分析。
四、实验指导
(1)、绘制时间序列图
时序图可以大致看出序列的平稳性,平稳序列的时序图应该显示出序列始终围绕一个常数值波动,且波动的范围不大。
如果观察序列的时序图显示出该序列有明显的趋势或周期,那它通常不是平稳序列,现以1964-1999年中国纱年产量序列(单位:万吨)来说明。
在EVIEWS中建立工作文件,在“Workfile structure type”栏中选择“Dated-regular frequency”,在右边的“Date specification”中输入起始年1964,终止年1999,点击ok则建立了工作文件。
找到中国纱年产量序列的excel文件并导入命名该序列为sha,见图1-2。
图1-1 建立工作文件
图1-2
创建新序列SHA,如图1-2。
点击主菜单Quick/Graph就可作图,见图1-3,分别是折线图(Line graph)、条形图(Bar graph)、散点图(Scatter)等,也可双击序列名,出现显示电子表格的序列观测值,然后点击工具栏的View/Graph。
如果选择折线图,出现图1-4的对话框,在此对话框中键入要做图的序列,点击OK则出现折线图,横轴表示时间,纵轴表示纱产量,见图1-5,选择图1-5上工具栏options可以对折线图做相应修饰。
点击主菜单的Edit/Copy,然后粘贴到文档就变成了如图1-6的折线图。
图1-3
图1-4
图1-5
图1-6
从图1-6可以看出,纱产量呈现波动中上升的趋势,显然不平稳,所以不是一个平稳序列。
这一结论,还可以通过平稳性统计检验来进一步说明。
(2)、通过相关图做平稳性判断
为了进一步的判断序列SHA 的平稳性,需要绘制出该序列的自相关图。
双击序列名sha 出现序列观测值的电子表格工作文件,点击View/Correlogram ,出现图1-7的相关图设定对话框,上面选项要求选择对谁计算自相关系数:原始序列(Level )、一阶差分(1st difference )和二阶差分(2nd difference ),默认是对原始序列显示相关图。
下面指定相关图显示的最大滞后阶数k ,若观测值较多,k 可取[]T/10或;若样本量较小k 一般取[]T/4(T 表示时间序列观测值个数,[]表明不超过其的最大整数)。
若序列是季节数据,一般k 取季节周期的整数倍。
设定完毕点击OK 就出现图1-8的序列相关图和相应的统计量。
图1-7
图1-8
相关图的左半部分是自相关和偏自相关分析图,垂立的两道虚线表示2倍标准差。
右半部分是滞后阶数、自相关系数、偏自相关系数、Q 统计量和相伴的概率。
从自相关和偏自相关分析图可以看出自相关系数趋向0的速度相当缓慢,且滞后6阶之后自相关系数才落入2倍标准差范围以内,并且呈现一种三角对称的形式,这是具有单调趋势的时间序列典型的自相关图的形式,进一步表明序列是非平稳的。
(3)、纯随机性判断
一个时间序列是否有分析价值,要看序列观测值之间是否有一定的相关性,若序列各项之间不存在相关,即相应滞后阶数的自相关系数与0没有显著性差异,序列为白噪声序列,则图1-8中Q 统计量正是对序列是否是白噪声序列即纯随机序列进行的统计检验,该检验的原假设和备择假设分别为:
012m H ==...==0, m 1ρρρ∀≥:
1H :至少存在某个k 0, m 1,k m ρ≠∀≥≤
在图1-8中,由每个Q 统计量的伴随概率可以看出,都是拒绝原假设的,说明至少存在某个k ,使得滞后k 期的自相关系数显著非0,也即拒绝序列是白噪声序列的原假设。
进行时间序列分析,我们希望序列是平稳的,且非随机的,若随机,前后观察值之间没有任何关系,没有信息可以提取。
所以我们在研究时间序列之前,首先要对其平稳性和随机性进行检验,目的是对平稳且非随机序列进行研究。
通过对1964-1999年中国纱年产量序列进行分析发现,纱产量是不平稳的,显示出波动中的上升趋势,进一步用自相关图-偏自相关图进行的平稳性检验发现自相关系数趋向0的速度相当缓慢,且滞后6阶之后自相关系数才落入2倍标准差范围以内,并且呈现一种三角对称的形式,这是具有单调趋势的时间序列典型的自相关图的形式,进一步表明序列是非平稳的。
序列的纯随机性检验进一步验证序列的不平稳性,因此要对此序列进行分析,要进行相应的平稳化处理。
(4)ADF检验
双击序列sha,点击view/unit root test,出现图1-9的对话框,我们先对序列本身进行单位根检验,在滞后阶数对话框选择SC准则自动选择阶数,分别采用带常数项,带常数项和趋势项以及什么都不带的方程进行ADF检验,图1-10显示的是带趋势项和常数项的方程进行ADF检验的结果,从图上可以看出,在显著性水平0.01下,接受存在一个单位根的原假设,于是对其一阶差分进行ADF检验,结果见图1-11。
图1-9
图1-10
图1-11 一阶差分序列的ADF检验结果
从图1-11可以看出,在显著性水平0.01下,一阶差分序列拒绝存在一个单位根的原假设,说明经过差分后的序列已经平稳,可以为以后的建模使用。
(5)PP检验
平稳性检验常用的方法还有PP检验,在图1-9的对话框中“Test Type”中选择下拉菜单Phillips-Perron,出现图1-12的对话框,其他选项同ADF检验,图1-13是对sha序列带趋势项和常数项的方程进行的pp检验,从结果看出来,接受存在一个单位根的原假设,于是同ADF检验,对其一阶差分序列进行PP检验,结果见图1-14,可以看出,和ADF检验结果相同,一阶差分序列已经平稳。
图1-12
图1-13
图1-14。
