中考数学填空题压轴题(含答案)
中考数学压轴题精选5(含答案)

一.选择题(共1小题)1.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为()A.(1345,0)B.(1345.5,)C.(1345,)D.(1345.5,0)二.填空题(共1小题)2.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E 是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F 处,连接AF,则线段AF的长取最小值时,BF的长为.三.解答题(共10小题)3.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是,位置关系是;(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.4.如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.(1)求抛物线L的解析式;(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC 内(包括△OBC的边界),求h的取值范围;(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.5.在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE=∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;(2)通过观察、测量、猜想:=,并结合图②证明你的猜想;(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求的值.(用含α的式子表示)6.如图,直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为﹣1和﹣4,且抛物线过原点.(1)求抛物线的解析式;(2)在坐标轴上是否存在点C,使△ABC为等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;(3)若点P是线段AB上不与A,B重合的动点,过点P作PE∥OA,与抛物线=3S 第三象限的部分交于一点E,过点E作EG⊥x轴于点G,交AB于点F,若S△BGF,求的值.△EFP7.如图1(注:与图2完全相同),二次函数y=x2+bx+c的图象与x轴交于A (3,0),B(﹣1,0)两点,与y轴交于点C.(1)求该二次函数的解析式;(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC 边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).8.如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=,BC=.(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.9.如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.10.如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.11.将△ABC绕点B逆时针旋转α(0°<α<180°)得到△DBE,直线DE与直线AC相交于点F,连接BF.(1)如图1,若α=60°,DF=2AF,请直接写等于;(2)若DF=mAF,(m>0,且m≠1)①如图2,求;(用含α,m的式子表示)②如图3,依题意补全图形,请直接写出等于.(用含α,m的式子表示)12.已知:△ABC,△DEF都是等边三角形,M是BC与EF的中点,连接AD,BE.(1)如图1,当EF与BC在同一条直线上时,直接写出AD与BE的数量关系和位置关系;(2)△ABC固定不动,将图1中的△DEF绕点M顺时针旋转α(0°≤α≤90°)角,如图2,判断(1)中的结论是否仍然成立,若成立,请加以证明;若不成立,说明理由;(3)△ABC固定不动,将图1中的△DEF绕点M旋转α(0°≤α≤90°)角,作DH⊥BC于点H.设BH=x,线段AB,BE,ED,DA所围成的图形面积为S.当AB=6,DE=2时,求S关于x的函数关系式,并写出相应的x的取值范围.一.选择题(共1小题)1.B;二.填空题(共1小题)2.;三.解答题(共10小题)3.AG=EG;AG⊥EG;4.;5.;6.;7.;8.;9.﹣m+4;﹣m2﹣m+4;10.;11.1;sin;12.;。
中考数学 专题17 四川中考填空题压轴专题(解析版)

专题17 四川中考填空题压轴专题【典例1】(2019•眉山)如图,反比例函数y =kx (x >0)的图象经过矩形OABC 对角线的交点M ,分别交AB ,BC 于点D 、E .若四边形ODBE 的面积为12,则k 的值为 4 .【点拨】本题可从反比例函数图象上的点E 、M 、D 入手,分别找出△OCE 、△OAD 、▱OABC 的面积与|k |的关系,列出等式求出k 值.【解答】解:由题意得:E 、M 、D 位于反比例函数图象上,则S △OCE =12|k |,S △OAD =12|k |, 过点M 作MG ⊥y 轴于点G ,作MN ⊥x 轴于点N ,则S ▱ONMG =|k |, 又∵M 为矩形ABCO 对角线的交点,则S 矩形ABCO =4S ▱ONMG =4|k |, 由于函数图象在第一象限, ∴k >0,则k2+k 2+12=4k ,∴k =4.【点睛】本题考查了反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k |.本知识点是中考的重要考点,同学们应高度关注.【典例2】(2019•凉山州)如图,正方形ABCD 中,AB =12,AE =14AB ,点P 在BC 上运动(不与B 、C 重合),过点P 作PQ ⊥EP ,交CD 于点Q ,则CQ 的最大值为 4 .【点拨】先证明△BPE ∽△CQP ,得到与CQ 有关的比例式,设CQ =y ,BP =x ,则CP =12﹣x ,代入解析式,得到y 与x 的二次函数式,根据二次函数的性质可求最值. 【解答】解:∵∠BEP +∠BPE =90°,∠QPC +∠BPE =90°, ∴∠BEP =∠CPQ . 又∠B =∠C =90°, ∴△BPE ∽△CQP . ∴BE PC=BP CQ.设CQ =y ,BP =x ,则CP =12﹣x . ∴912−x=xy ,化简得y =−19(x 2﹣12x ),整理得y =−19(x ﹣6)2+4, 所以当x =6时,y 有最大值为4. 故答案为4.【点睛】本题主要考查了正方形的性质、相似三角形的判定和性质,以及二次函数最值问题,几何最值用二次函数最值求解考查了树形结合思想.【典例3】(2019•自贡)如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos (α+β)=√217.【点拨】给图中相关点标上字母,连接DE ,利用等腰三角形的性质及三角形内角和定理可得出∠α=30°,同理,可得出:∠CDE =∠CED =30°=∠α,由∠AEC =60°结合∠AED =∠AEC +∠CED 可得出∠AED =90°,设等边三角形的边长为a ,则AE =2a ,DE =√3a ,利用勾股定理可得出AD 的长,再结合余弦的定义即可求出cos (α+β)的值.【解答】解:给图中相关点标上字母,连接DE ,如图所示. 在△ABC 中,∠ABC =120°,BA =BC , ∴∠α=30°.同理,可得出:∠CDE =∠CED =30°=∠α. 又∵∠AEC =60°,∴∠AED =∠AEC +∠CED =90°.设等边三角形的边长为a ,则AE =2a ,DE =2×sin60°•a =√3a , ∴AD =√AE 2+DE 2=√7a , ∴cos (α+β)=DE AD =√217. 故答案为:√217.【点睛】本题考查了解直角三角形、等边三角形的性质以及规律型:图形的变化类,构造出含一个锐角等于∠α+∠β的直角三角形是解题的关键.【典例4】(2019•雅安)已知函数y ={−x 2+2x(x >0)−x(x ≤0)的图象如图所示,若直线y =x +m 与该图象恰有三个不同的交点,则m 的取值范围为 0<m <14 .【点拨】直线与y =﹣x 有一个交点,与y =﹣x 2+2x 有两个交点,则有m >0,x +m =﹣x 2+2x 时,△=1﹣4m >0,即可求解.【解答】解:直线y =x +m 与该图象恰有三个不同的交点, 则直线与y =﹣x 有一个交点, ∴m >0,∵与y=﹣x2+2x有两个交点,∴x+m=﹣x2+2x,△=1﹣4m>0,∴m<1 4,∴0<m<1 4;故答案为0<m<1 4.【点睛】本题考查二次函数与一次函数的图象及性质;能够根据条件,数形结合的进行分析,可以确定m的范围.【典例5】(2019•广元)如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是﹣6<M<6.【点拨】将(﹣1,0)与(0,2)代入y=ax2+bx+c,可知b=a+2,利用对称轴可知:a>﹣2,从而可知M的取值范围.【解答】解:将(﹣1,0)与(0,2)代入y=ax2+bx+c,∴0=a﹣b+c,2=c,∴b=a+2,∵−b2a>0,a<0,∴b>0,∴a>﹣2,∴﹣2<a<0,∴M=4a+2(a+2)+2 =6a+6=6(a+1)∴﹣6<M<6,故答案为:﹣6<M<6;【点睛】本题考查二次函数,解题的关键是熟练运用二次函数的图象与性质,本题属于中等题型.【典例6】(2019•巴中)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC=24+16√3.【点拨】将△BPC绕点B逆时针旋转60°后得△AP'B,根据旋转的性质可得∠PBP′=∠CAB=60°,BP=BP′,可得△BPP′为等边三角形,可得BP′=BP=8=PP',由勾股定理的逆定理可得,△APP′是直角三角形,由三角形的面积公式可求解.【解答】解:如图,将△BPC绕点B逆时针旋转60°后得△AP'B,连接PP′,根据旋转的性质可知,旋转角∠PBP′=∠CAB=60°,BP=BP′,∴△BPP′为等边三角形,∴BP′=BP=8=PP';由旋转的性质可知,AP′=PC=10,在△BPP′中,PP′=8,AP=6,由勾股定理的逆定理得,△APP′是直角三角形,∴S△ABP+S△BPC=S四边形AP'BP=S△BP'B+S△AP'P=√34BP2+12×PP'×AP=24+16√3故答案为:24+16√3【点评】本题考查了旋转的性质,等边三角形的性质,勾股定理,作辅助线构造出等边三角形和直角三角形是解题的关键,也是本题的难点.【典例7】(2019•内江)如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为2π3+√3.【点拨】连接OE ,作OF ⊥DE ,先求出∠COE =2∠D =60°、OF =12OD =1,DF =OD cos ∠ODF =√3,DE =2DF =2√3,再根据阴影部分面积是扇形与三角形的面积和求解可得. 【解答】解:如图,连接OE ,作OF ⊥DE 于点F ,∵四边形ABCD 是平行四边形,且∠A =150°, ∴∠D =30°,则∠COE =2∠D =60°, ∵CD =4, ∴CO =DO =2,∴OF =12OD =1,DF =OD cos ∠ODF =2×√32=√3, ∴DE =2DF =2√3, ∴图中阴影部分的面积为60⋅π⋅22360+12×2√3×1=2π3+√3, 故答案为:2π3+√3.【点睛】本题考查的是扇形面积计算、平行四边形的性质,掌握扇形面积公式:S =nπr 2360是解题的关键.【典例8】(2019•泸州)如图,在等腰Rt △ABC 中,∠C =90°,AC =15,点E 在边CB 上,CE =2EB ,点D 在边AB 上,CD ⊥AE ,垂足为F ,则AD 的长为 9√2 .【点拨】过D 作DH ⊥AC 于H ,根据等腰三角形的性质得到AC =BC =15,∠CAD =45°,求得AH =DH ,得到CH =15﹣DH ,根据相似三角形的性质即可得到结论.【解答】解:过D 作DH ⊥AC 于H , ∵在等腰Rt △ABC 中,∠C =90°,AC =15, ∴AC =BC =15, ∴∠CAD =45°, ∴AH =DH , ∴CH =15﹣DH , ∵CF ⊥AE ,∴∠DHA =∠DF A =90°, ∴∠HAF =∠HDF , ∴△ACE ∽△DHC , ∴DH AC=CH CE,∵CE =2EB , ∴CE =10, ∴DH 15=15−DH 10,∴DH =9, ∴AD =9√2, 故答案为:9√2.【点睛】本题考查了相似三角形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.【典例9】(2019•乐山)如图1,在四边形ABCD 中,AD ∥BC ,∠B =30°,直线l ⊥AB .当直线l 沿射线BC 方向,从点B 开始向右平移时,直线l 与四边形ABCD 的边分别相交于点E 、F .设直线l 向右平移的距离为x ,线段EF 的长为y ,且y 与x 的函数关系如图2所示,则四边形ABCD 的周长是 .【点拨】根据题意和函数图象中的数据,可以得到AB、BC、AD的长,再根据平行线的性质和图形中的数据可以得到CD的长,从而可以求得四边形ABCD的周长.【解答】解:∵∠B=30°,直线l⊥AB,∴BE=2EF,由图可得,AB=4cos30°=4×√32=2√3,BC=5,AD=7﹣4=3,由图象可得,AN=5﹣4=1,ND=CM=7﹣5=2,DM=2,∵∠B=30°,EF⊥AB,∴∠M=60°,又∵DM=MC=2,∴△DMC是等边三角形,∴DC=DM=2,∴四边形ABCD的周长是:AB+BC+AD+CD=2√3+5+3+2=10+2√3,故答案为:10+2√3.【点睛】本题考查动点问题的函数图象,解答本题的关键是明确题意,利用数形结合的思想解答.【典例10】(2019•攀枝花)正方形A1B1C1A2,A2B2C2A3,A3B3C3A4,…按如图所示的方式放置,点A1,A2,A3,…和点B1,B2,B3,…分别在直线y=kx+b(k>0)和x轴上.已知点A1(0,1),点B1(1,0),则C5的坐标是(47,16),.【点拨】由题意可知A1纵坐标为1,A2的纵坐标为2,A3的纵坐标为4,A4的纵坐标为8,…,即可得到C1,C2,C3,C4,C5的纵坐标,根据图象得出C1(2,1),C2(5,2),C3(11,4),即可得到C1,C2,C3,C4,C5…在一条直线上,直线的解析式为y=13x+13,把C5的纵坐标代入即可求得横坐标.【解答】解:由题意可知A1纵坐标为1,A2的纵坐标为2,A3的纵坐标为4,A4的纵坐标为8,…,∵A1和C1,A2和C2,A3和C3,A4和C4的纵坐标相同,∴C1,C2,C3,C4,C5的纵坐标分别为1,2,4,8,16,…∴根据图象得出C1(2,1),C2(5,2),C3(11,4),∴直线C1C2的解析式为y=13x+13,∵A5的纵坐标为16,∴C5的纵坐标为16,把y=16代入y=13x+13,解得x=47,∴C5的坐标是(47,16),故答案为(47,16).【点睛】此题考查了待定系数法求一次函数的解析式、等腰直角三角形和正方形的性质.此题难度适中,属于规律型题目,注意掌握数形结合思想的应用.【典例11】(2019•广安)如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3,并使∠A2OA3=60°,再以OA3为直角边作Rt △OA3A4,并使∠A3OA4=60°…按此规律进行下去,则点A2019的坐标为(﹣22017,22017√3).【点拨】通过解直角三角形,依次求A1,A2,A3,A4,…各点的坐标,再从其中找出规律,便可得结论.【解答】解:由题意得,A1的坐标为(1,0),A2的坐标为(1,√3),A3的坐标为(﹣2,2√3),A4的坐标为(﹣8,0),A5的坐标为(﹣8,﹣8√3),A6的坐标为(16,﹣16√3),A7的坐标为(64,0),…由上可知,A点的方位是每6个循环,与第一点方位相同的点在x正半轴上,其横坐标为2n﹣1,其纵坐标为0,与第二点方位相同的点在第一象限内,其横坐标为2n﹣2,纵坐标为2n﹣2√3,与第三点方位相同的点在第二象限内,其横坐标为﹣2n﹣2,纵坐标为2n﹣2√3,与第四点方位相同的点在x负半轴上,其横坐标为﹣2n﹣1,纵坐标为0,与第五点方位相同的点在第三象限内,其横坐标为﹣2n﹣2,纵坐标为﹣2n﹣2√3,与第六点方位相同的点在第四象限内,其横坐标为2n﹣2,纵坐标为﹣2n﹣2√3,∵2019÷6=336…3,∴点A2019的方位与点A3的方位相同,在第二象限内,其横坐标为﹣2n﹣2=﹣22017,纵坐标为22017√3,故答案为:(﹣22017,22017√3).【点睛】本题主点的坐标的规律题,主要考查了解直角三角形的知识,关键是求出前面7个点的坐标,找出其存在的规律.【典例12】(2019•南充)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,AB =24,BC =5.给出下列结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;②△OAB 的面积最大值为144;③当OD 最大时,点D 的坐标为(25√2626,125√2626).其中正确的结论是 ②③ .(填写序号)【点拨】①由条件可知AB =24,则AB 的中点E 的运动轨迹是圆弧,最后根据弧长公式即可计算出点E 所经过的路径长;②当△OAB 的面积最大时,因为AB =24,所以△OAB 为等腰直角三角形,即OA =OB ,可求出最大面积为144;③当O 、E 、D 三点共线时,OD 最大,过点D 作DF ⊥y 轴于点F ,可求出OD =25,证明△DF A ∽△AOB 和△DFO ∽△BOA ,可求出DF 长,则D 点坐标可求出. 【解答】解:∵点E 为AB 的中点,AB =24, ∴OE =12AB =12,∴AB 的中点E 的运动轨迹是以点O 为圆心,12为半径的一段圆弧, ∵∠AOB =90°, ∴点E 经过的路径长为90×12×π180=6π,故①错误;当△OAB 的面积最大时,因为AB =24,所以△OAB 为等腰直角三角形,即OA =OB , ∵E 为AB 的中点,∴OE ⊥AB ,OE =12AB =12,∴S △AOB =12×24×12=144,故②正确;如图,当O 、E 、D 三点共线时,OD 最大,过点D 作DF ⊥y 轴于点F ,∵AD =BC =5,AE =12AB =12, ∴DE =√AD 2+AE 2=√52+122=13, ∴OD =DE +OE =13+12=25, 设DF =x ,∴OF =√OD 2−DF 2=√252−x 2, ∵四边形ABCD 是矩形, ∴∠DAB =90°, ∴∠DF A =∠AOB , ∴∠DAF =∠ABO , ∴△DF A ∽△AOB ∴DF OA =DA AB ,∴x OA=524,∴OA =24x5, ∵E 为AB 的中点,∠AOB =90°, ∴AE =OE , ∴∠AOE =∠OAE , ∴△DFO ∽△BOA , ∴OD AB =OF OA,∴2524=√252−x 224x 5,解得x =25√2626,x =−25√2626舍去,∴OF=125√26 26,∴D(25√2626,125√2626).故③正确.故答案为:②③.【点睛】本题考查四边形综合题、直角形的性质、矩形的性质、相似三角形的判定和性质等知识.解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.【典例13】(2019•绵阳)如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2√2.将△BDE绕点B逆时针方向旋转后得△BD′E′,当点E′恰好落在线段AD′上时,则CE′=√2+√6.【点拨】如图,连接CE′,根据等腰三角形的性质得到AB=BC=2√2,BD=BE=2,根据性质的性质得到D′B=BE′=BD=2,∠D′BE′=90′,∠D′BD=∠ABE′,由全等三角形的性质得到∠D′=∠CE′B=45°,过B作BH⊥CE′于H,解直角三角形即可得到结论.【解答】解:如图,连接CE′,∵△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2√2,∴AB=BC=2√2,BD=BE=2,∵将△BDE绕点B逆时针方向旋转后得△BD′E′,∴D′B=BE′=BD=2,∠D′BE′=90°,∠D′BD=∠ABE′,∴∠ABD′=∠CBE′,∴△ABD′≌△CBE′(SAS),∴∠D′=∠CE′B=45°,过B作BH⊥CE′于H,在Rt△BHE′中,BH=E′H=√22BE′=√2,在Rt△BCH中,CH=√BC2−BH2=√6,∴CE′=√2+√6,故答案为:√2+√6.【点睛】本题考查了旋转的性质,全等三角形的判定和性质,等腰直角三角形的性质,解直角三角形,正确的作出辅助线是解题的关键.【典例14】(2019•宜宾)如图,△ABC 和△CDE 都是等边三角形,且点A 、C 、E 在同一直线上,AD 与BE 、BC 分别交于点F 、M ,BE 与CD 交于点N .下列结论正确的是 ①③④ (写出所有正确结论的序号).①AM =BN ;②△ABF ≌△DNF ;③∠FMC +∠FNC =180°;④1MN=1AC+1CE【点拨】①根据等边三角形性质得出AC =BC ,CE =CD ,∠ACB =∠ECD =60°,求出∠BCE =∠ACD ,根据SAS 推出两三角形全等即可;②根据∠ABC =60°=∠BCD ,求出AB ∥CD ,可推出△ABF ∽△DNF ,找不出全等的条件; ③根据角的关系可以求得∠AFB =60°,可求得MFN =120°,根据∠BCD =60°可解题; ④根据CM =CN ,∠MCN =60°,可求得∠CNM =60°,可判定MN ∥AE ,可求得MN AC=DN CD=CD−CN CD,可解题.【解答】证明:①∵△ABC 和△CDE 都是等边三角形, ∴AC =BC ,CE =CD ,∠ACB =∠ECD =60°, ∴∠ACB +∠ACE =∠ECD +∠ACE , 即∠BCE =∠ACD , 在△BCE 和△ACD 中, {BC =AC∠BCE =∠ACD CE =CD,∴△BCE ≌△ACD (SAS ),∴AD =BE ,∠ADC =∠BEC ,∠CAD =∠CBE , 在△DMC 和△ENC 中, {∠MDC =∠NEC DC =BC ∠MCD =∠NCE =60°, ∴△DMC ≌△ENC (ASA ), ∴DM =EN ,CM =CN ,∴AD ﹣DM =BE ﹣EN ,即AM =BN ; ②∵∠ABC =60°=∠BCD , ∴AB ∥CD , ∴∠BAF =∠CDF , ∵∠AFB =∠DFN ,∴△ABF ∽△DNF ,找不出全等的条件;③∵∠AFB +∠ABF +∠BAF =180°,∠FBC =∠CAF , ∴∠AFB +∠ABC +∠BAC =180°, ∴∠AFB =60°, ∴∠MFN =120°, ∵∠MCN =60°, ∴∠FMC +∠FNC =180°; ④∵CM =CN ,∠MCN =60°, ∴△MCN 是等边三角形, ∴∠MNC =60°, ∵∠DCE =60°, ∴MN ∥AE , ∴MN AC=DN CD=CD−CN CD,∵CD =CE ,MN =CN , ∴MN AC =CE−MN CE ,∴MNAC=1−MNCE ,两边同时除MN 得1AC=1MN−1CE,∴1MN=1AC+1CE.故答案为①③④【点睛】本题考查了全等三角形的判定,考查了全等三角形的对应边、对应角相等的性质,考查了平行线的运用,考查了正三角形的判定,本题属于中档题.【典例15】(2019•资阳)如图,在△ABC 中,已知AC =3,BC =4,点D 为边AB 的中点,连结CD ,过点A 作AE ⊥CD 于点E ,将△ACE 沿直线AC 翻折到△ACE ′的位置.若CE ′∥AB ,则CE ′=95.【点拨】如图,作CH ⊥AB 于H .首先证明∠ACB =90°,解直角三角形求出AH ,再证明CE ′=AH 即可.【解答】解:如图,作CH ⊥AB 于H .由翻折可知:∠AE ′C =∠AEC =90°,∠ACE =∠ACE ′, ∵CE ′∥AB , ∴∠ACE ′=∠CAD , ∴∠ACD =∠CAD , ∴DC =DA , ∵AD =DB , ∴DC =DA =DB , ∴∠ACB =90°, ∴AB =√AC 2+BC 2=5, ∵12•AB •CH =12•AC •BC ,∴CH =125,∴AH =√AC 2−CH 2=95, ∵CE ′∥AB ,∴∠E ′CH +∠AHC =180°, ∵∠AHC =90°, ∴∠E ′CH =90°, ∴四边形AHCE ′是矩形, ∴CE ′=AH =95, 故答案为95.【点睛】本题考查翻折变换,平行线的性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.【典例16】(2019•达州)如图,抛物线y =﹣x 2+2x +m +1(m 为常数)交y 轴于点A ,与x 轴的一个交点在2和3之间,顶点为B .①抛物线y =﹣x 2+2x +m +1与直线y =m +2有且只有一个交点;②若点M (﹣2,y 1)、点N (12,y 2)、点P (2,y 3)在该函数图象上,则y 1<y 2<y 3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y =﹣(x +1)2+m ; ④点A 关于直线x =1的对称点为C ,点D 、E 分别在x 轴和y 轴上,当m =1时,四边形BCDE 周长的最小值为√34+√2.其中正确判断的序号是 ①③④ .【点拨】①把y =m +2代入y =﹣x 2+2x +m +1中,判断所得一元二次方程的根的情况便可得判断正确; ②根据二次函数的性质进行判断;③根据平移的公式求出平移后的解析式便可;④因BC 边一定,只要其他三边和最小便可,作点B 关于y 轴的对称点B ′,作C 点关于x 轴的对称点C′,连接B′C′,与x轴、y轴分别交于D、E点,求出B′C′便是其他三边和的最小值.【解答】解:①把y=m+2代入y=﹣x2+2x+m+1中,得x2﹣2x+1=0,∵△=4﹣4=0,∴此方程两个相等的实数根,则抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点,故此小题结论正确;②∵抛物线的对称轴为x=1,∴点P(2,y3)关于x=1的对称点为P′(0,y3),∵a=﹣1<0,∴当x<1时,y随x增大而增大,又∵﹣2<0<12,点M(﹣2,y1)、点N(12,y2)、点P′(0,y3)在该函数图象上,∴y2>y3>y1,故此小题结论错误;③将该抛物线向左平移2个单位,再向下平移2个单位,抛物线的解析式为:y=﹣(x+2)2+2(x+2)x+m+1﹣2,即y=﹣(x+1)2+m,故此小题结论正确;④当m=1时,抛物线的解析式为:y=﹣x2+2x+2,∴A(0,2),C(2,2),B(1,3),作点B关于y轴的对称点B′(﹣1,3),作C点关于x轴的对称点C′(2,﹣2),连接B′C′,与x轴、y轴分别交于D、E点,如图,则BE+ED+CD+BC=B′E+ED+C′D+BC=B′C′+BC,根据两点之间线段最短,知B′C′最短,而BC的长度一定,∴此时,四边形BCDE周长=B′C′+BC最小,为:√B′M2+C′M2+√BM2+CM2=√32+52+√12+12=√34+√2,故此小题结论正确;故答案为:①③④.【点睛】本题考查二次函数的应用、二次函数的图象与性质、二次函数与坐标轴的交点、求线段和的最小值等知识,解题的关键是灵活运用所学知识解决问题,属于中考填空题中的压轴题.【典例17】(2019•遂宁)如图,在平面直角坐标系中,矩形OABC的顶点O落在坐标原点,点A、点C分别位于x轴,y轴的正半轴,G为线段OA上一点,将△OCG沿CG翻折,O点恰好落在对角线AC上的点P处,反比例函数y=12x经过点B.二次函数y=ax2+bx+c(a≠0)的图象经过C(0,3)、G、A三点,则该二次函数的解析式为y=12x2−114x+3.(填一般式)【点拨】点C (0,3),反比例函数y =12x 经过点B ,则点B (4,3),由勾股定理得:(4﹣x )2=4+x 2,故点G (32,0),将点C 、G 、A 坐标代入二次函数表达式,即可求解.【解答】解:点C (0,3),反比例函数y =12x经过点B ,则点B (4,3), 则OC =3,OA =4, ∴AC =5,设OG =PG =x ,则GA =4﹣x ,P A =AC ﹣CP =AC ﹣OC =5﹣3=2, 由勾股定理得:(4﹣x )2=4+x 2, 解得:x =32,故点G (32,0),将点C 、G 、A 坐标代入二次函数表达式得:{c =394a +32b +c =014a +4b +c =0,解得:{ a =12b =−114c =3,故答案为:y =12x 2−114x +3.【点睛】本题考查的是二次函数综合运用,涉及到矩形基本性质、反比例函数基本性质与应用,其中用勾股定理求OG 的长度,是本题解题的关键.【典例18】(2018•凉山州)△AOC 在平面直角坐标系中的位置如图所示,OA =4,将△AOC 绕O 点,逆时针旋转90°得到△A 1OC 1,A 1C 1,交y 轴于B (0,2),若△C 1OB ∽△C 1A 1O ,则点C 1的坐标 (43,83) .【点拨】如图作C 1H ⊥x 轴于H .由△C 1OB ∽△C 1A 1O ,推出OC 1A 1C 1=OB OA 1=12,由tan ∠C 1A 1H =OBOA 1=C 1K A 1H =12,设C 1H =m ,则A 1H =2m ,OH =2m ﹣4,构建方程即可解决问题; 【解答】解:如图作C 1H ⊥x 轴于H .∵△C 1OB ∽△C 1A 1O , ∴OC 1A 1C 1=OB OA 1=12,∵tan ∠C 1A 1H =OBOA 1=C 1HA 1H =12,设C 1H =m ,则A 1H =2m ,OH =2m ﹣4,∴A 1C 1=√5m ,OC 1=√m 2+(2m −4)2, ∴√5m =2√m 2+(2m −4)2, 解得m =83或85(舍弃),∴C 1(43,83).(本题也可以证明tan ∠OC 1H =OH HC 1=12,S 设C 1(m ,2m ),根据A 1H =4m ,构建方程)【点睛】本题考查相似三角形的性质、坐标与图形的旋转等知识,解题的关键是学会利用参数构建方程解决问题,属于中考填空题中的压轴题.【精练1】(2019秋•河东区期末)如图,在反比例函数y =−6x (x <0)的图象上任取一点P ,过P 点分别作x 轴,y 轴的垂线,垂足分别为M ,N ,那么四边形PMON 的面积为 .【点拨】设出点P 的坐标,四边形PMON 的面积等于点P 的横纵坐标的积的绝对值,把相关数值代入即可.【解答】解:设点P 的坐标为(x ,y ),∵点P 的反比例函数解析式上, ∴xy =﹣6,易得四边形PMON 为矩形, ∴四边形PMON 的面积为|xy |=6, 故答案为6.【点睛】考查反比例函数的比例系数的意义;用到的知识点为:在反比例函数图象上的点的横纵坐标的积等于反比例函数的比例系数.注意面积应为正值.【精练2】(2016秋•江阴市校级月考)如图,正方形ABCD 的边长为1cm ,M 、N 分别是BC 、CD 上两个动点,且始终保持AM ⊥MN ,则△ADN 的最小面积为 .【点拨】设BM =xcm ,则MC =(1﹣x )cm ,当AM ⊥MN 时,利用互余关系可证△ABM ∽△MCN ,利用相似比求CN ,根据三角形的面积公式表示出△ADN 的面积,用二次函数的性质求面积的最小值. 【解答】解:设BM =xcm ,则MC =(1﹣x )cm , ∵∠AMN =90°,∴∠AMB +∠NMC =90°,∠NMC +∠MNC =90°, ∴∠AMB =∠MNC , 又∵∠B =∠C , ∴△ABM ∽△MCN ,则AB MC=BM CN,即11−x=x CN,解得:CN =x(1−x)1=x (1﹣x ), ∴S △ADN =S 正方形ABCD =12×1×[1﹣x (1﹣x )]=12x 2−12x +12, ∵12<0,∴当x =12cm 时,S △ADN 最小,最小值是4×12×12−(−12)24×12=38(cm 2).故答案是:38cm 2.【点睛】本题考查了二次函数的性质的运用.关键是根据已知条件判断相似三角形,利用相似比求函数关系式.【精练3】(2019秋•香坊区期末)等边△ABC 中,点P 是BC 所在直线上一点,且PC :BC =1:4,则tan ∠APB 的值是 .【点拨】过A 作AD ⊥BC 于D ,设等边△ABC 的边长为4a ,则DC =2a ,AD =2√3a ,PC =a ,分类讨论:当P 在BC 的延长线上时,DP =DC +CP =2a +a =3a ;当P 点在线段BC 上,即在P ′的位置,则DP ′=DC ﹣CP ′=a ,然后分别利用正切的定义求解即可. 【解答】解:如图,过A 作AD ⊥BC 于D ,设等边△ABC 的边长为4a ,则DC =2a ,AD =2√3a ,PC =a , 当P 在BC 的延长线上时,DP =DC +CP =2a +a =3a , 在Rt △ADP 中,tan ∠APD =AD DP =2√3a 3a =2√33; 当P 点在线段BC 上,即在P ′的位置,则DP ′=DC ﹣CP ′=a , 在Rt △ADP ′中,tan ∠AP ′D =AD DP′=2√3aa =2√3.故答案为2√3或2√33.【点睛】本题考查了解直角三角形:利用三角函数和勾股定理求三角形中未知的边或角的过程叫解直角三角形.也考查了分类讨论思想的运用.【精练4】(2019秋•长清区期中)如图,在△ABC 中,∠BAC =90°,AB =AC =√2,点D 、E 分别在BC 、AC 上(点D 不与点B 、C 重合),且∠ADE =45°,若△ADE 是等腰三角形,则CE = .【点拨】可得∠B =∠C =45°,可证得△DCE ∽△ABD ,由于D 与B 、C 不重合,显然∠ADE =∠AED=45°不符合题意,即AD≠AE,所以此题分两种情况讨论:①AD=DE,此时(2)的相似三角形全等,由此可求得CD、BD的长,进而可得CE、AE的值.【解答】解:∵点D不能与B点重合,∴AD=AE不能成立,(或:∵∠ADE=45°,若AD=AE,则∠AED=ADE=45°,从而∠DAE=90°,即B与D重合,这与已知条件矛盾).①当AE、DE为腰,即AE=DE时(如图1),∠EAD=∠EDA=45°,此时,AD平分∠BAC,∴D为BC边的中点(“三线合一”性质),且E也为AC边的中点,∴CE=AE=√2 2;②当AD、DE为腰,即AD=DE时(如图2),∵∠BAC=90°,AB=AC=2,∴∠B=∠C=45°.∵∠ADE=45°,∴∠B=∠C=∠ADE.∵∠ADB=∠C+∠DAC,∠DEC=∠ADE+∠DAC,∴∠ADB=∠DEC.∵∠ADC +∠B +∠BAD =180,∠DEC +∠C +∠CDE =180°, ∴∠ADC +∠B +∠BAD =∠DEC +∠C +∠CDE , ∴∠EDC =∠BAD , ∴△ABD ∽△DCE 此时AD 与DE 为对应边,∴△ABD ≌△DCE ,DC =AB =√2, CE =BD =BC ﹣CD =2−√2. 因此CE 的长为2−√2或√22. 故答案为:2−√2或√22. 【点睛】本题考查了相似三角形的判定与性质,等腰三角形的判定,解答时证明三角形相似是关键. 【精练5】(2019秋•江岸区校级月考)我们把函数y ={x 2−2x −3(x ≥0)x 2+2x −3(x ≤0)的图象记为C ,若直线y =x +b与图象C 有且只有三个公共点,则b 的取值是 .【点拨】画出分段函数的图象,结合图象找到直线与该图象有三个交点的两端情况:直线经过点(0,﹣3)时;直线y =x +b 与y =x 2+2x ﹣3(x ≤0)部分只有一个交点时. 【解答】解:根据函数解析式分别画出函数图象,如图所示: 当直线经过点(0,﹣3)时,此时函数与直线y =x +b 恰有三个交点, ∴b =﹣3,当直线y =x +b 与y =x 2+2x ﹣3(x ≤0)部分只有一个交点时, ∴x 2+2x ﹣3=x +b , ∴b =−134; ∴b =﹣3或b =−134时两图象有三个交点; 故答案为−134或﹣3.【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.【精练6】(2018秋•越秀区期末)抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④6a﹣2b+c<0;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2,其中正确的判断是(填写所有正确判断的序号)【点拨】根据抛物线的开口方向,对称轴,抛物线与x轴的交点情况,二次函数图象上点的坐标特征判断即可.【解答】解:∵抛物线对称轴x=﹣1,经过(1,0),∴−b2a=−1,a+b+c=0,∴b=2a,c=﹣3a,∵抛物线开口向上,∴a>0,∴b>0,c<0,∴abc<0,故①错误;∵抛物线与x轴有两个交点,∴b2﹣4ac>0,故②正确;∵抛物线与x轴交于(﹣3,0),∴9a﹣3b+c=0,故③正确;∵9a﹣3b+c=0,b=2a,c=﹣3a,∴6a﹣2b+c=6a﹣4a﹣3a=﹣a<0,故④正确;∵抛物线对称轴x=﹣1,∴x=﹣0.5与x=﹣1.5的函数值相等,∵﹣1.5>﹣2,∴则y1<y2;故⑤错误;故答案为:②③④.【点睛】本题考查二次函数与系数的关系,二次函数图象上的点的特征,解题的关键是灵活运用所学知识解决问题,灵活运用数形结合思想.【精练7】(2019春•东海县期中)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°,得到线段AQ,连接BQ,若P A=3,PB=4,PC=5,则四边形APBQ的面积为【点拨】连结PQ,如图,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=AQ=3,∠P AQ=60°,则可判断△APQ为等边三角形,所以PQ=AP=3,接着证明△APC≌△ABQ得到PC=QB=5,然后利用勾股定理的逆定理证明△PBQ为直角三角形,再根据三角形面积公式,利用S=S△BPQ+S△APQ进行计算.四边形APBQ【解答】解:连结PQ,如图,∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∵线段AP绕点A顺时针旋转60°得到线段AQ,∴AP=AQ=3,∠P AQ=60°,∴△APQ为等边三角形,∴PQ=AP=3,∵∠CAP+∠BAP=60°,∠BAP+∠BAQ=60°,∴∠CAP=∠BAQ,且AC=AB,AP=AQ∴△APC≌△ABQ(SAS),∴PC=QB=5,在△BPQ中,∵PB2=42=16,PQ2=32=9,BQ2=52=25,∴PB2+PQ2=BQ2,∴△PBQ为直角三角形,∠BPQ=90°,∴S四边形APBQ=S△BPQ+S△APQ=12BP×PQ+√34×PQ2=6+9√34故答案为:6+9√3 4【点睛】本题考查了旋转的性质,全等三角形的性质,勾股定理以及逆定理,证明△APQ为等边三角形是本题的关键.【精练8】(2019•吉林)如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的▱ODCE的顶点C在AB̂上.若OD=8,OE=6,则阴影部分图形的面积是(结果保留π).【点拨】连接OC,根据同样只统计得到▱ODCE是矩形,由矩形的性质得到∠ODC=90°.根据勾股定理得到OC=10,根据扇形的面积公式和矩形的面积公式即可得到结论.【解答】解:连接OC,∵∠AOB=90°,四边形ODCE是平行四边形,∴▱ODCE是矩形,∴∠ODC=90°.∵OD=8,OE=6,∴OC=10,∴阴影部分图形的面积=90⋅π×102360−8×6=25π﹣48.故答案为:25π﹣48.【点睛】本题考查了扇形的面积的计算,矩形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.【精练9】(2019•虞城县一模)如图1,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s.设P、Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系如图2所示(其中曲线OM为抛物线的一部分,其余各部分均为线段)当点P在ED上运动时,连接QD,若QD平分∠PQC,则t的值为.【点拨】根据题意和函数图象可以得到BE和BC的长,然后根据当t=5时,y=10可以得到AB的长,然后根据QD平分∠PQC,可得DG=DC,进而可以求得相应的t的值.【解答】解:由题意可得,BE =5,BC =12, ∵当t =5时,S =10, ∴10=5×AB2,得AB =4, 作EH ⊥BC 于点H ,作EF ∥PQ ,P 1Q 2∥EF ,作DG ⊥P 1Q 2于点G , 则EH =AB =4,BE =BF =5, ∵∠EHB =90°, ∴BH =√52−42=3, ∴HF =2,∴EF =√42+22=2√5, ∴P 1Q 2=2√5,设当点P 运动到P 1时,Q 2D 平分∠P 1Q 2C ,则DG =DC =4,P 1D =17﹣AE ﹣EP 1=12﹣3﹣(t ﹣5)=14﹣t , ∴(14−t)×42=2√5×42,解得,t =14﹣2√5, 故答案为:14﹣2√5.【点睛】本题考查动点问题的函数图象,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.【精练10】(2018秋•市中区期末)将正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2按如图所示方式放置,点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y =x +1和x 轴上,则点B 2019的横坐标是 .【点拨】根据直线y=x+1可求与x轴、y轴的交点坐标,得出第一个正方形的边长,得出点B1的横坐标,根据第二个正方形与第一个正方形的关系,可求出第二个正方形的边长,进而确定B2的横坐标,依此类推,可得出B2019的横坐标.【解答】解:当x=0时,y=x+1=1,∴A(0,1),当y=0时,x=﹣1,∴直线与x轴的交点(﹣1,0)∴B1(1,1),易得△A1B1A2、△A2B2A3、△A3B3A4、△A4B4A5……均是等腰直角三角形,可得:每一个正方形的边长都是它前一个正方形边长的2倍,因此:B2的横坐标为1+1×2=1+2=20+21=3=22﹣1,B3的横坐标为1+1×2+2×2=1+2+4=20+21+22=7=23﹣1,B4的横坐标为24﹣1,B5的横坐标为25﹣1,……B2019的横坐标为22019﹣1,故答案为:22019﹣1.【点睛】此题主要考查了一次函数图形上的点与坐标特征,规律型问题常用的方法是,分别求出前几个数据,然后依据变化规律,得出一般的结论.本题就是先求出B1的横坐标为21﹣1,B2的横坐标为22﹣1,B3的横坐标为23﹣1,B4的横坐标为24﹣1,……进而得到B n的横坐标为2n﹣1.【精练11】(2019•鄂尔多斯模拟)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),根据这个规律探索可得,第56个点的坐标为.【点拨】根据题意和图象中的点的坐标,可以发现这些点的变化规律,从而可以求得第56个点的坐标.【解答】解:由题意可得,横坐标是1的点有1个,横坐标是2的点有2个,横坐标是3的点有3个,…,∵56=(1+2+3+…+10)+1,∴第56个点的坐标为(11,10),故答案为:(11,10)【点睛】本题考查规律性:点的坐标,解答本题的关键是明确题意,发现题目中点的变化规律,求出相应的点的坐标.【精练12】(2019春•徐州期中)如图,在矩形ABCD中,AB=2cm,BC=3cm,现有一根长为2cm的棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P 在运动过程中所经过的路径长度为cm.【点拨】根据题意可以判断出点P的运动轨迹是4段弧长和2段线段的长度.【解答】解:连接BP,如图所示:∵P是EF的中点,∴BP=12EF=12×2=1,如图所示,点P的运动轨迹是4段弧长+2段线段的长度,即4×90π×1180+2×1=2π+2.故答案为:2π+2.【点睛】本题考查了轨迹、矩形的性质、直角三角形斜边上的中线等于斜边的一半的性质以及弧长的计算.判断出点的P运动的轨迹是解题的关键.【精练13】(2018秋•雨花区校级期末)如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=12S△ABC;③EF=BD;④∠BFE=∠CDF;⑤△DEF是等腰直角三角形,当∠EDF在△ABC内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有个.。
填空压轴题(几何篇)-2023年中考数学压轴题专项训练(学生版)
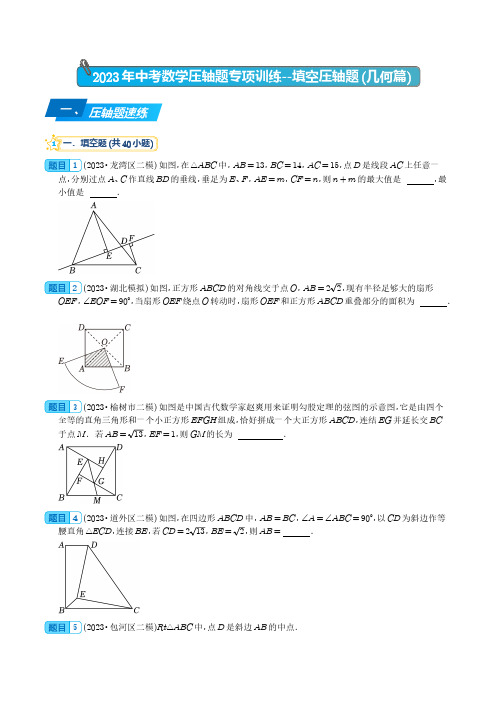
2023年中考数学压轴题专项训练--填空压轴题(几何篇)一、压轴题速练1一.填空题(共40小题)1(2023•龙湾区二模)如图,在△ABC中,AB=13,BC=14,AC=15,点D是线段AC上任意一点,分别过点A、C作直线BD的垂线,垂足为E、F,AE=m,CF=n,则n+m的最大值是,最小值是.2(2023•湖北模拟)如图,正方形ABCD的对角线交于点O,AB=22,现有半径足够大的扇形OEF,∠EOF=90°,当扇形OEF绕点O转动时,扇形OEF和正方形ABCD重叠部分的面积为.3(2023•榆树市二模)如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD,连结EG并延长交BC于点M.若AB=13,EF=1,则GM的长为.4(2023•道外区二模)如图,在四边形ABCD中,AB=BC,∠A=∠ABC=90°,以CD为斜边作等腰直角△ECD,连接BE,若CD=213,BE=2,则AB=.5(2023•包河区二模)Rt△ABC中,点D是斜边AB的中点.(1)如图1,若DE ⊥BC 与E ,DF ⊥AC 于F ,DE =3,DF =4,则AB =;(2)如图2,若点P 是CD 的中点,且CP =52,则PA 2+PB 2=.6(2023•庐江县三模)如图,四边形ABCD 中,AB =AC =AD ,点M 、N 分别是BC 、CD 的中点,连接MN ,若∠DAM =105°,∠BAN =75°,若AM AN=3+12,则∠ANM =°.7(2023•中山市二模)如图,△ABC 与△BDE 均为等腰直角三角形,点A ,B ,E 在同一直线上,BD ⊥AE ,垂足为点B ,点C 在BD 上,AB =4,BE =10.将△ABC 沿BE 方向平移,当这两个三角形重叠部分的面积等于△ABC 面积的一半时,△ABC 平移的距离为.8(2023•新都区模拟)青朱出入图,是魏晋时期数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂.开方除之,即弦也.”,若图中DF =1,CF =2,则AE 的长为.9(2023•黄埔区一模)△ABC为等腰直角三角形,AB=AC=6,∠BAC=90°,动点D在边BC上运动.以A为直角顶点,在AD右侧作等腰直角三角形△ADE(如图).M为DE中点,N为BC三等分点,CN=13BC,连接MN,则线段MN的最小值为.10(2023•雁塔区校级模拟)如图,菱形ABCD的边长为5,将一个直角的顶点放置在菱形的中心O 处,此时直角的两边分别交边AD,CD于点E,F,当OE⊥AD时,OE的长为2,则EF的长是.11(2023•奉贤区二模)如果四边形有一组邻边相等,且一条对角线平分这组邻边的夹角,我们把这样的四边形称为“准菱形”.有一个四边形是“准菱形”,它相等的邻边长为2,这两条边的夹角是90°,那么这个“准菱形”的另外一组邻边的中点间的距离是 2 .12(2023•吕梁一模)如图,在正方形ABCD中,点P在对角线BD上,点E,F分别在边AB和BC 上,且∠EPF=45°,若CF=2DP=4,AE=12,则AB的长度为.13(2023•蚌埠二模)如图,点E为正方形ABCD的边CD上一点,以点A为圆心,AE长为半径画弧EF,交边BC于点F,已知正方形边长为1.(1)若∠DAE=15°,则DE的长为;(2)△AEF的面积为S的最大值是.14(2023•兰考县一模)如图,方形ABCD中,AB=8,点P为射线BC上任意一点(与点B、C不重合),连接AP,在AP的右侧作正方形APGH,连接AG,交射线CD于E,当ED长为2时,点BP的长为.15(2023•本溪一模)由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C,D都在格点上,∠A=60°,则cos∠CDB的值为.16(2023•沂南县校级一模)如图,矩形ABCD中,AC、BD相交于点O,过点B作BF⊥AC交CD 于点F,交AC与点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN、EM,则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是.17(2023•琼海一模)如图,菱形ABCD,AE⊥BC,点E为垂足,点F为AE的中点,连接BF并延长交AD于点G,连接CG,CE=2,CG=211,则DG=,AG=,AF=.18(2023•镇江一模)如图,在矩形ABCD中,AB=6,BC=8,△BEF的顶点E在对角线AC上运动,且∠BFE=90°,∠EBF=∠BAC,连接AF,则AF的最小值为.19(2023•泉州模拟)如图,在菱形ABCD 中,∠A =60°,点E 在边AD 上,以BE 为边在菱形ABCD 的内部作等边三角形BEF ,若∠DEF =α,∠EBD =β,则α与β之间的数量关系可用等式表示为.20(2023•市南区一模)如图,正方形ABCD 中,E 、F 分别为BC 、CD 边上的点,∠EAF =45°,则下列结论中正确的有.(填序号)①BE +DF =EF ;②tan ∠AMD =CD DF; ③BM 2+DN 2=MN 2;④若EF =1.5,S △AEF =3,则.S 正方形ABCD =4.21(2023•大连一模)学习菱形时,我们从它的边、角和对角线等方面进行研究,可以发现并证明:菱形的每一条对角线平分一组对角.小明参考平行四边形、矩形判定方法的研究过程,得出下面的猜想:①一条对角线平分一组对角的四边形是菱形;②每一条对角线平分一组对角的四边形是菱形;③一条对角线平分一组对角的平行四边形是菱形.其中正确的是(填序号,填写一个即可).22(2023•石景山区一模)如图,在菱形ABCD 中,点E ,F 分别在BC ,AD 上,BE =DF .只需添加一个条件即可证明四边形AECF 是矩形,这个条件可以是(写出一个即可).23(2023•河东区一模)已知,如图,已知菱形ABCD 的边长为6,∠ABC =60°,点E ,F 分别在AB ,CB 的延长线上,且BE =BF =13AB ,G 是DF 的中点,连接GE ,则GE 的长是.24(2023•合肥模拟)如图,点P在正方形ABCD内,∠BPC=135°,连接PA、PB、PC、PD.(1)若PA=AB,则∠CPD=;(2)若PB=2,PC=3,则PD的长为.25(2023•鄞州区一模)如图,Rt△ABC中,∠C=90°,AC=BC=8,作正方形CDEF,其中顶点E 在边AB上.(1)若正方形CDEF的边长为26,则线段AE的长是;(2)若点D到AB的距离是2,则正方形CDEF的边长是.26(2023•郓城县校级模拟)如图,在平行四边形ABCD中,对角线AC、BD交于点O.点M是BC 边的中点,连接AM、OM,作CF∥AM.已知OC平分∠BCF,OB平分∠AOM,若BD=32,则sin∠BAM的值为.27(2023•三原县二模)如图,点M是▱ABCD内一点,连接MA,MB,MC,MD,过点A作AP∥BM,过点D作DP∥CM,AP与DP交于点P,若四边形AMDP的面积为6,则▱ABCD的面积为.28(2023•和平区二模)如图,已知正方形ABCD的边长为4,点E为边BC上一点,BE=3,在AE的右侧,以AE为边作正方形AEFG,H为BG的中点,则AH的长等于.29(2023•鼓楼区校级模拟)如图,在矩形ABCD中,AD=3,AB=4,B是边AB上一点,△BCE与△FCE关于直线CE对称,连接BF并延长交AD于点G,过点F作FH⊥AD,垂足为点H,设BE=a,若点H为AG的中点,则BE的长为.30(2023•呼和浩特一模)如图在菱形ABCD中,O为对角线AC与BD的交点,点P为边AB上的任一点(不与A、B重合),过点P分别作PM⊥AC,PN⊥BD,M、N为垂足,则可以判断四边形MPNO 的形状为.若菱形的边长为a,∠ADC=120°,则MN的最小值为.(用含a的式子表示)31(2023•洛阳一模)在扇形OAB中,∠AOB=60°,点C是半径OA上一点,且OC=6,将线段OC 沿OB方向平移,当平移距离是6时,点C的对应点C'恰好落在弧AB上,则图中阴影部分的面积为.32(2023•临渭区二模)如图,正六边形纸片ABCDEF的边长为6cm,从这个正六边形纸片上剪出一个扇形(图中阴影部分),则这个扇形的面积为cm2.(结果保留π)33(2023•桂林二模)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,半径为1的⊙O在Rt△ABC内移动,当⊙O与∠A的两边都相切时,圆心O到点B的距离为2 .34(2023•万州区模拟)如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,以点B为圆心,AB为半径作圆弧交CB的延长线于点D,以点A为圆心,AC为半径作圆弧交AD于点E.则图中阴影部分的面积为.35(2023•九龙坡区校级模拟)如图,AC、AD是⊙O中关于直径AB对称的两条弦,以弦AC、AD 为折线将弧AC、弧AD折叠后过圆心O,若⊙O的半径r=4,则圆中阴影部分的面积为.36(2023•烟台一模)如图,GC,GB是⊙O的切线,AB是⊙O的直径,延长GC,与BA的延长线交于点E,过点C作弦CD∥AB,连接DO并延长与圆交于点F,连接CF,若AE=2,CE=4,则CD的长度为.37(2023•历下区二模)如图,已知扇形AOB的半径OA=2,∠AOB=120°将扇形AOB绕点A顺时针旋转30°得到扇形AO′B′,则图中阴影部分的面积是.38(2023•邓州市一模)如图,在扇形AOB中,∠AOB=60°,OA=3,半径OC平分AB,点D为半径OA中点,点E为半径OC上一动点,当AE+DE取得最小值时,由AC,AE,CE围成的阴影部分的面积为.39(2023•龙口市二模)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB 为直径的圆经过点C,D,则cos∠ADC的值为.40(2023•渝中区校级二模)如图,扇形纸片AOB的半径为2,沿AB折叠扇形纸片,点O恰好落在AB上的点C处,图中阴影部分的面积为.。
(完整版)九年级数学选择、填空压轴题训练(含答案),推荐文档

九年级数学综合训练一、选择题(本大题共9 小题,共27.0 分)1.如图,在平面直角坐标系中2 条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x 轴于点A,交y 轴于点B,直线l2交x 轴于点D,过点B 作x 轴的平行线交l2于点C,点A、E 关于y 轴对称,抛物线y=ax2+bx+c 过E、B、C 三点,下列判断中:①a-b+c=0;②2a+b+c=5;③抛物线关于直线x=1 对称;④抛物线过点(b,c);⑤S 四边形ABCD=5,其中正确的个数有()A. 5B. 4C. 3D. 22.如图,10 个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如,表示a1=a2+a3,则a1的最小值为()A.32B.36C.38D.403.如图,直线y= ��x -6 分别交x 轴,y 轴于A,B,M 是反比例函数y=�(x>0)的图象上位于直线上方的一点,MC∥x 轴交AB 于C,MD⊥MC 交AB 于D,AC•BD=43,则k 的值为()A. ‒ 3B. ‒ 4C. ‒ 5D. ‒ 64.在平面直角坐标系xOy 中,将一块含有45°角的直角三角板如图放置,直角顶点C 的坐标为(1,0),顶点A 的坐标为(0,2),顶点B 恰好落在第一象限的双曲线上,现将直角三角板沿x 轴正方向平移,当顶点A 恰好落在该双曲线上时停止运动,则此时点C 的对应点C′的坐标为()(3,0) (2,0) (5,0) (3,0)A. 2B.C. 2D.5.如图,在矩形ABCD 中,AB<BC,E 为CD 边的中点,将△ADE 绕点E 顺时针旋转180°,点D 的对应点为C,点A 的对应点为F,过点E 作ME⊥AF 交BC 于点M,连接AM、BD 交于点N,现有下列结论:35 ①AM =AD +MC ;②AM =DE +BM ;③DE 2=AD •CM ;④点 N 为△ABM 的外心. 其中正确的个数为()A. 1 个B. 2 个C. 3 个D. 4 个6. 规定:如果关于 x 的一元二次方程 ax 2+bx +c =0(a ≠0)有两个实数根,且其中一个根是另一个根的 2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程 x 2+2x -8=0 是倍根方程;②若关于 x 的方程 x 2+ax +2=0 是倍根方程,则 a =±3;③若关于 x 的方程 ax 2-6ax +c =0(a ≠0)是倍根方程,则抛物线 y =ax 2-6ax +c 与 x 轴的公共点的坐标是 (2,0)和(4,0); 4 ④若点(m ,n )在反比例函数 y =x 的图象上,则关于 x 的方程 mx 2+5x +n =0 是倍根方程. 上述结论中正确的有( )A. ①②B. ③④C. ②③D. ②④7. 如图,六边形 ABCDEF 的内角都相等,∠DAB =60°,AB =DE ,则下列结论成立的个数是() ①AB ∥DE ;②EF ∥AD ∥BC ;③AF =CD ;④四边形 ACDF 是平行四边形;⑤六边形 ABCDEF 既是中心对称图形,又是轴对称图形.A. 2B. 3C. 4D. 58. 如图,在 Rt △ABC 中,∠C =90°,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )A. 4B. 5C. 6D. 79. 如图,矩形 ABCD 中,AE ⊥BD 于点 E ,CF 平分∠BCD ,交 EA 的延长线于点 F ,且 BC =4,CD =2,给出下列结论:①∠BAE =∠CAD ;4②∠DBC =30°;③AE =5 5;④AF =2 ,其中正确结论的个数有( )A. 1 个B. 2 个C. 3 个D. 4 个二、填空题(本大题共 10 小题,共 30.0 分)10.如图,在Rt△ABC 中,∠BAC=30°,以直角边AB 为直径作半圆交AC 于点D,以AD 为边作等边△ADE,延长ED 交BC 于点F,BC=2 3,则图中阴影部分的面积为.(结果不取近似值)11.如图,在6×6 的网格内填入1 至6 的数字后,使每行、每列、每个小粗线宫中的数字不重复,则a×c=.12.如图,正方形ABCD 中,BE=EF=FC,CG=2GD,BG 分别交AE,AF 于M,N.下列结论:4 �M 3 1①AF⊥BG;②BN=3NF;③M G=8;④S 四边形CGNF=2S 四边形ANGD.其中正确的结论的序号是.13.已知:如图,在△AOB 中,∠AOB=90°,AO=3cm,BO=4cm.将△AOB 绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB 的交点D 恰好为AB 的中点,则线段B1D= cm.14.如图,边长为4 的正六边形ABCDEF 的中心与坐标原点O 重合,AF∥x 轴,将正六边形ABCDEF 绕原点O 顺时针旋转n 次,每次旋转60°.当n=2017 时,顶点A 的坐标为.15.如图,在Rt△ABC 中,BC=2,∠BAC=30°,斜边AB 的两个端点分别在相互垂直的射线OM、ON 上滑动,下列结论:①若C、O 两点关于AB 对称,则OA=2 3;②C、O 两点距离的最大值为4;③若AB 平分CO,则AB⊥CO;�④斜边AB 的中点D 运动路径的长为2;其中正确的是(把你认为正确结论的序号都填上).16.如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N(3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB=30°,要使PM+PN 最小,则点P 的坐标为.17.在一条笔直的公路上有A、B、C 三地,C 地位于A、B 两地之间,甲车从A地沿这条公路匀速驶向C 地,乙车从B 地沿这条公路匀速驶向A 地,在甲车出发至甲车到达C 地的过程中,甲、乙两车各自与C 地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h 时,两车相遇;②乙车出发1.5h 时,两车相距170km;③乙车出5发27h 时,两车相遇;④甲车到达C 地时,两车相距40km.其中正确的是(填写所有正确结论的序号).�18.如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=x(x>0)的图象经过A,B 两点.若点A 的坐标为(n,1),则k 的值为.19.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A 旋转180°得到点P1,点P1绕点B 旋转180°得到点P2,点P2绕点C 旋转180°得到点P3,点P3绕点A 旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为.答案和解析1.【答案】C【解析】解:∵直线l1:y=-3x+3 交x 轴于点A,交y 轴于点B,∴A(1,0),B(0,3),∵点A、E 关于y 轴对称,∴E(-1,0).∵直线l2:y=-3x+9 交x 轴于点D,过点B 作x 轴的平行线交l2 于点C,∴D(3,0),C 点纵坐标与B 点纵坐标相同都是3,把y=3 代入y=-3x+9,得3=-3x+9,解得x=2,∴C(2,3).∵抛物线y=ax2+bx+c 过E、B、C 三点,∴,解得,∴y=-x2+2x+3.①∵抛物线y=ax2+bx+c 过E(-1,0),∴a-b+c=0,故①正确;②∵a=-1,b=2,c=3,∴2a+b+c=-2+2+3=3≠5,故②错误;③∵抛物线过B(0,3),C(2,3)两点,∴对称轴是直线x=1,∴抛物线关于直线x=1 对称,故③正确;④∵b=2,c=3,抛物线过C(2,3)点,∴抛物线过点(b,c),故④正确;⑤∵直线l1∥l2,即AB∥CD,又BC∥AD,∴四边形ABCD 是平行四边形,∴S 四边形ABCD=BC•OB=2×3=6≠5,故⑤错误.综上可知,正确的结论有3个.故选:C.根据直线l1的解析式求出A(1,0),B(0,3),根据关于y 轴对称的两点坐标特征求出E(- 1,0).根据平行于x 轴的直线上任意两点纵坐标相同得出C 点纵坐标与B 点纵坐标相同都是3,再根据二次函数图象上点的坐标特征求出C(2,3).利用待定系数法求出抛物线的解析式为y=-x2+2x+3,进而判断各选项即可.本题考查了抛物线与x 轴的交点,一次函数、二次函数图象上点的坐标特征,关于y 轴对称的两点坐标特征,平行于x 轴的直线上任意两点坐标特征,待定系数法求抛物线的解析式,平行四边形的判定及面积公式,综合性较强,求出抛物线的解析式是解题的关键.2.【答案】D【解析】解:∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3(a8+a9)+a10,∴要使a1 取得最小值,则a8+a9 应尽可能的小,取a8=2、a9=4,∵a5=a8+a9=6,则a7、a10 中不能有6,若a7=8、a10=10,则a4=10=a10,不符合题意,舍去;若a7=10、a10=8,则a4=12、a6=4+8=12,不符合题意,舍去;若a7=10、a10=12,则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40,符合题意;综上,a1的最小值为40,故选:D.由a1=a7+3(a8+a9)+a10 知要使a1 取得最小值,则a8+a9 应尽可能的小,取a8=2、a9=4,根据a5=a8+a9=6,则a7、a10 中不能有6,据此对于a7、a8,分别取8、10、12 检验可得,从而得出答案.本题主要考查数字的变化类,根据题目要求得出a1取得最小值的切入点是解题的关键.3.【答案】A【解析】解:过点D 作DE⊥y 轴于点E,过点C 作CF⊥x 轴于点F,令x=0 代入y= x-6,∴y=-6,∴B(0,-6),∴OB=6,令y=0 代入y= x-6,∴x=2 ,∴(2 ,0),∴OA=2 ,∴勾股定理可知:AB=4 ,∴sin∠OAB= = ,cos∠OAB= =设M(x,y),∴CF=-y,ED=x,∴sin∠OAB= ,∴AC=- y,∵cos∠OAB=cos∠EDB= ,∴BD=2x,∵AC•BD=4,∴- y×2x=4 ,∴xy=-3,∵M 在反比例函数的图象上,∴k=xy=-3,故选(A)过点D 作DE⊥y 轴于点E,过点C 作CF⊥x 轴于点F,然后求出OA 与OB 的长度,即可求出∠OAB 的正弦值与余弦值,再设M(x,y),从而可表示出BD 与AC 的长度,根据AC•BD=4列出即可求出k 的值.本题考查反比例函数与一次函数的综合问题,解题的关键是根据∠OAB 的锐角三角函数值求出BD、AC,本题属于中等题型.4.【答案】C【解析】解:过点B 作BD⊥x 轴于点D,∵∠ACO+∠BCD=90°,∠OAC+∠ACO=90°,∴∠OAC=∠BCD,在△ACO 与△BCD 中,∴△ACO➴△BCD(AAS)∴OC=BD,OA=CD,∵A(0,2),C(1,0)∴OD=3,BD=1,∴B(3,1),∴设反比例函数的解析式为y= ,将B(3,1)代入y= ,∴k=3,∴y= ,∴把y=2 代入y= ,∴x= ,当顶点A 恰好落在该双曲线上时,此时点A 移动了个单位长度,∴C 也移动了个单位长度,此时点C 的对应点C′的坐标为(,0)故选:C.过点B 作BD⊥x 轴于点D,易证△ACO➴△BCD(AAS),从而可求出B 的坐标,进而可求出反比例函数的解析式,根据解析式与 A 的坐标即可得知平移的单位长度,从而求出 C 的对应点.本题考查反比例函数的综合问题,涉及全等三角形的性质与判定,反比例函数的解析式,平移的性质等知识,综合程度较高,属于中等题型.5.【答案】B【解析】解:∵E 为CD 边的中点,∴DE=CE,又∵∠D=∠ECF=90°,∠AED=∠FEC,∴△ADE➴△FCE,∴AD=CF,AE=FE,又∵ME⊥AF,∴ME 垂直平分AF,∴AM=MF=MC+CF,∴AM=MC+AD,故①正确;如图,延长CB 至G,使得∠BAG=∠DAE,由AM=MF,AD∥BF,可得∠DAE=∠F=∠EAM,可设∠BAG=∠DAE=∠EAM=α,∠BAM=β,则∠AED=∠EAB=∠GAM=α+β,由∠BAG=∠DAE,∠ABG=∠ADE=90°,可得△ABG∽△ADE,∴∠G=∠AED=α+β,∴∠G=∠GAM,∴AM=GM=BG+BM,由△ABG∽△ADE,可得= ,而AB<BC=AD,∴BG<DE,∴BG+BM<DE+BM,即AM<DE+BM,∴AM=DE+BM 不成立,故②错误;∵ME⊥FF,EC⊥MF,∴EC2=CM×CF,又∵EC=DE,AD=CF,∴DE2=AD•CM,故③正确;∵∠ABM=90°,∴AM 是△ABM 的❧➓圆的直径,∵BM<AD,∴当BM∥AD 时,= <1,∴N 不是AM 的中点,∴点N 不是△ABM 的❧心,故④错误.综上所述,正确的结论有2 个,故选:B.根据全等三角形的性质以及线段垂直平分线的性质,即可得出AM=MC+AD;根据△ABG∽△ ADE,且AB<BC,即可得出BG<DE,再根据AM=GM=BG+BM,即可得出AM=DE+BM 不成立;根据ME⊥FF,EC⊥MF,运用射影定理即可得出EC2=CM×CF,据此可得DE2=AD•CM 成立;根据N 不是AM 的中点,可得点N 不是△ABM 的❧心.本题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,矩形的性质以及旋转的性质的综合应用,解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导,解题时注意:三角形❧➓圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的❧心,故❧心到三角形三个顶点的距离相等.6.【答案】C【解析】解:①由x2-2x-8=0,得(x-4)(x+2)=0,解得x1=4,x2=-2,∵x1≠2x2,或x2≠2x1,1 1 ∴方程 x 2-2x-8=0 不是倍根方程. 故①错误;②关于 x 的方程 x 2+ax+2=0 是倍根方程,∴设 x 2=2x 1,∴x 1•x 2=2x 2=2,∴x 1=±1,当 x 1=1 时 ,x 2=2,当 x 1=-1 时 ,x 2=-2,∴x 1+x 2=-a=±3,∴a=±3,故②正确;③关于 x 的方程 ax 2-6ax+c=0(a≠0)是倍根方程,∴x 2=2x 1,∵抛物线 y=ax 2-6ax+c 的对称轴是直线 x=3,∴抛物线 y=ax 2-6ax+c 与 x 轴的交点的坐标是(2,0)和(4,0),故③正确;④∵点(m ,n )在反比例函数 y= 的图象上,∴mn=4,解 mx 2+5x+n=0 得 x 1=- ,x 2=- ,∴x 2=4x 1,∴关于 x 的方程 mx 2+5x+n=0 不是倍根方程;故选:C .①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;②设 x 2=2x 1,得到 x 1•x 2=2x 2=2,得到当 x 1=1 时,x 2=2,当 x 1=-1 时,x 2=-2,于是得到结论;③根据“倍根方程”的定义即可得到结论;④若点(m,n)在反比例函数y= 的图象上,得到mn=4,然后解方程mx2+5x+n=0 即可得到正确的结论;本题考查了反比例函数图象上点的坐标特征,根与系数的关系,正确的理解倍根方程的定义是解题的关键.7.【答案】D【解析】解:∵六边形ABCDEF 的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,∴AD∥EF∥CB,故②正确,∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA 是等腰梯形,∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,连➓CF 与AD 交于点O,连➓DF、AC、AE、DB、BE.∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC 是平行四边形,故④正确,同法可证四边形AEDB 是平行四边形,∴AD 与CF,AD 与BE 互相平分,∴OF=OC,OE=OB,OA=OD,∴六边形ABCDEF 既是中心对称图形,故⑤正确,故选D.根据六边形ABCDEF 的内角都相等,∠DAB=60°,平行线的判定,平行四边形的判定,中心对称图形的定义一一判断即可.本题考查平行四边形的判定和性质、平行线的判定和性质、轴对称图形、中心对称图形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.【答案】D【解析】解:如图:故选:D.①以B 为圆心,BC 长为半径画弧,交AB 于点D,△BCD 就是等腰三角形;②以A 为圆心,AC 长为半径画弧,交AB 于点E,△ACE 就是等腰三角形;③以C 为圆心,BC 长为半径画弧,交AC 于点F,△BCF 就是等腰三角形;④以C 为圆心,BC 长为半径画弧,交AB 于点K,△BCK 就是等腰三角形;⑤作AB 的垂直平分线交AC 于G,则△AGB 是等腰三角形;➅作BC 的垂直平分线交AB 于I,则△BCI 和△ACI 是等腰三角形.本题考查了等腰三角形的判定的应用,主要考查学生的理解能力和动手操作能力.9.【答案】C【解析】解:在矩形ABCD 中,∵∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠ADE+∠DAE=∠DAE+∠BAE=90°,∴∠BAE=∠ADB,∵∠CAD=∠ADB,∴∠BAE=∠CAD,故①正确;∵BC=4,CD=2,∴tan∠DBC= = ,∴∠DBC≠30°,故②错误;∵BD= =2 ,∵AB=CD=2,AD=BC=4,∵△ABE∽△DBA,∴,即,∴AE= ;故③正确;∵CF 平分∠BCD,∴∠BCF=45°,∴∠ACF=45°-∠ACB,∵AD∥BC,∴∠DAC=∠BAE=∠ACB,∴∠EAC=90°-2∠ACB,∴∠EAC=2∠ACF,∵∠EAC=∠ACF+∠F,∴∠ACF=∠F,∴AF=AC,∵AC=BD=2 ,∴AF=2 ,故④正确;故选C.根据余角的性质得到∠BAE=∠ADB,等量代换得到∠BAE=∠CAD,故①正确;根据三角函数的定义得到tan∠DBC= = ,于是得到∠DBC≠30°,故②错误;由勾股定理得到BD==2 ,根据相似三角形的性质得到AE= ;故③正确;根据角平分线的定义得到∠BCF=45°,求得∠ACF=45°-∠ACB,推出∠EAC=2∠ACF,根据❧角的性质得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根据等腰三角形的判定得到AF=AC,于是得到AF=2 ,故④正确.本题考查了矩形的性质,相似三角形的判定和性质,三角形的❧角的性质,角平分线的定义,熟练掌握相似三角形的判定和性质是解题的关键.10.【答案】3【解析】3 3-2π解:如图所示:设半圆的圆心为O,连➓DO,过D 作DG⊥AB 于点G,过D 作DN⊥CB 于点N,∵在Rt△ABC 中,∠BAC=30°,∴∠ACB=60°,∠ABC=90°,∵以AD 为边作等边△ADE,∴∠EAD=60°,∴∠EAB=60°+30°=90°,可得:AE∥BC,则△ADE∽△CDF,∴△CDF 是等边三角形,∵在Rt△ABC 中,∠BAC=30°,BC=2 ,∴AC=4 ,AB=6,∠DOG=60°,则AO=BO=3,故DG=DO•sin60°=,则AD=3 ,DC=AC-AD= ,故DN=DC•sin60°=×= ,则S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF= ×2 ×6- ×3×- - × ×=3 - π.故答案为:3 - π.根据题意结合等边三角形的性质分别得出AB,AC,AD,DC 的长,进而利用S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF 求出答案.此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识,正确分割图形是解题关键.11.【答案】2【解析】解:对各个小宫格编号如下:先看己:已经有了数字3、5、6,缺少1、2、4;观察发现:4 不能在第四列,2 不能在第五列,而2 不能在第六列;所以2 只能在第六行第四列,即a=2;则b 和c 有一个是1,有一个是4,不确定,如下:观察上图发现:第四列已经有数字2、3、4、6,缺少1 和5,由于5 不能在第二行,所以5 在第四行,那么1 在第二行;如下:再看乙部分:已经有了数字1、2、3,缺少数字4、5、6,观察上图发现:5 不能在第六列,所以5在第五列的第一行;4 和6 在第六列的第一行和第二行,不确定,分两种情况:①当4 在第一行时,6 在第二行;那么第二行第二列就是4,如下:再看甲部分:已经有了数字1、3、4、5,缺少数字2、6,观察上图发现:2 不能在第三列,所以2 在第二列,则6 在第三列的第一行,如下:观察上图可知:第三列少1 和4,4 不能在第三行,所以4 在第五行,则1 在第三行,如下:观察上图可知:第五行缺少1 和2,1 不能在第1 列,所以1 在第五列,则2 在第一列,即c=1,所以b=4,如下:观察上图可知:第六列缺少1 和2,1 不能在第三行,则在第四行,所以2 在第三行,如下:再看戊部分:已经有了数字2、3、4、5,缺少数字1、6,观察上图发现:1 不能在第一列,所以1 在第二列,则6 在第一列,如下:观察上图可知:第一列缺少3 和4,4 不能在第三行,所以4 在第四行,则3 在第三行,如下:观察上图可知:第二列缺少5 和6,5 不能在第四行,所以5 在第三行,则6 在第四行,如下:观察上图可知:第三行第五列少6,第四行第五列少3,如下:所以,a=2,c=1,ac=2;②当6 在第一行,4 在第二行时,那么第二行第二列就是6,如下:再看甲部分:已经有了数字1、3、5、6,缺少数字2、4,观察上图发现:2 不能在第三列,所以2 在第2 列,4 在第三列,如下:观察上图可知:第三列缺少数字1 和6,6 不能在第五行,所以6 在第三行,则1 在第五行,所以c=4,b=1,如下:观察上图可知:第五列缺少数字3 和6,6 不能在第三行,所以6 在第四行,则3 在第三行,如下:观察上图可知:第六列缺少数字1 和2,2 不能在第四行,所以2 在第三行,则1 在第四行,如下:观察上图可知:第三行缺少数字1 和5,1 和5 都不能在第一列,所以此种情况不成立;综上所述:a=2,c=1,a×c=2;故答案为:2.粗线把这个数独分成了6 块,为了便于解答,对各部分进行编号:甲、乙、丙、丁、戊、己,先从各部分中数字最多的己出发,找出其各个小方格里面的数,再根据每行、每列、每小宫格都不出现重复的数字进行推算.本题是六阶数独,比较复杂,关键是找出突破口,先推算出一个区域或者一行、一列,再逐步的进行推算.12.【答案】①③【解析】解:①∵四边形ABCD 为正方形,∴AB=BC=CD,∵BE=EF=FC,CG=2GD,∴BF=CG,∵在△ABF 和△BCG 中,,∴△ABF➴△BCG,∴∠BAF=∠CBG,∵∠BAF+∠BFA=90°,∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;②∵在△BNF 和△BCG 中,,∴△BNF∽△BCG,∴ = = ,∴BN= NF;②错误;③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,AF= = ,∵S△ABF= AF•BN=AB•BF,∴BN= ,NF= BN= ,∴AN=AF-NF= ,∵E 是BF 中点,∴EH 是△BFN 的中位线,∴EH= ,NH= ,BN∥EH,∴AH= , = ,解得:MN= ,∴BM=BN-MN= ,MG=BG-BM= ,∴ = ;③正确;④连➓AG,FG,根据③中结论,则NG=BG-BN= ,∵S 四边形CGNF=S△CFG+S△GNF= CG•CF+NF•NG=1+= ,S 四边形ANGD=S△ANG+S△ADG= AN•GN+AD•DG= + = ,∴S 四边形CGNF≠S 四边形ANGD,④错误;故答案为①③.①易证△ABF➴△BCG,即可解题;②易证△BNF∽△BCG,即可求得的值,即可解题;③作EH⊥AF,令AB=3,即可求得MN,BM 的值,即可解题;④连➓AG,FG,根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD,即可解题.本题考查了全等三角形的判定和性质,考查了相似三角形的判定和对应边成比例的性质,本题中令AB=3 求得AN,BN,NG,NF 的值是解题的关键.13.【答案】1.5【解析】解:∵在△AOB 中,∠AOB=90°,AO=3cm,BO=4cm,∴AB= =5cm,∵点D 为AB 的中点,∴OD= AB=2.5cm.∵将△AOB 绕顶点O,按顺时针方向旋转到△A1OB1 处,∴OB1=OB=4cm,∴B1D=OB1-OD=1.5cm.故答案为1.5.先在直角△AOB 中利用勾股定理求出AB= =5cm,再利用直角三角形斜边上的中线等于斜边的一半得出OD= AB=2.5cm.然后根据旋转的性质得到OB1=OB=4cm,那么B1D=OB1-OD=1.5cm.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理.14.【答案】(2,2 3)【解析】解:2017×60°÷360°=336…1,即与正六边形ABCDEF 绕原点O 顺时针旋转1 次时点A 的坐标是一样的.当点A 按顺时针旋转60°时,与原F 点重合.连➓OF,过点F 作FH⊥x 轴,垂足为H;由已知EF=4,∠FOE=60°(正六边形的性质),∴△OEF 是等边三角形,∴OF=EF=4,∴F(2,2 ),即旋转2017 后点A 的坐标是(2,2 ),故答案是:(2,2 ).将正六边形ABCDEF 绕原点O 顺时针旋转2017 次时,点A 所在的位置就是原F 点所在的位置.此题主要考查了正六边形的性质,坐标与图形的性质-旋转.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.15.【答案】①②③【解析】解:在Rt△ABC 中,∵BC=2,∠BAC=30°,∴AB=4,AC= =2 ,①若C、O 两点关于AB 对称,如图1,∴AB 是OC 的垂直平分线,则OA=AC=2 ;所以①正确;②如图1,取AB 的中点为E,连➓OE、CE,∵∠AOB=∠ACB=90°,∴OE=CE= AB=2,当OC 经过点E 时,OC 最大,则C、O 两点距离的最大值为4;所以②正确;③如图2,同理取AB 的中点E,则OE=CE,∵AB 平分CO,∴OF=CF,∴AB⊥OC,所以③正确;④如图3,斜边AB 的中点D 运动路径是:以O 为圆心,以2 为半径的圆周的,则:=π.所以④不正确;综上所述,本题正确的有:①②③;故答案为:①②③.①先根据直角三角形30°的性质和勾股定理分别求AC 和AB,由对称的性质可知:AB 是OC 的垂直平分线,所以OA=AC;②当OC 经过AB 的中点E 时,OC 最大,则C、O 两点距离的最大值为4;③如图2,根据等腰三角形三线合一可知:AB⊥OC;④如图3,半径为2,圆心角为90°,根据弧长公式进行计算即可.本题是三角形的综合题,考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式,熟练掌握直角三角形斜边中线等于斜边一半是本题的关键,难度适中.3 316.【答案】(2, 2 )【解析】解:作N 关于OA 的对称点N′,连➓N′M 交OA 于P,则此时,PM+PN 最小,∵OA 垂直平分NN′,∴ON=ON′,∠N′ON=2∠AON=60°,∴△NON′是等边三角形,∵点M 是ON 的中点,∴N′M⊥ON,∵点N(3,0),∴ON=3,∵点M 是ON 的中点,∴OM=1.5,∴PM= ,∴P(,).故答案为:(,).作N 关于OA 的对称点N′,连➓N′M 交OA 于P,则此时,PM+PN 最小,由作图得到ON=ON′,∠N′ON=2∠AON=60°,求得△NON′是等边三角形,根据等边三角形的性质得到N′M⊥ON,解直角三角形即可得到结论.本题考查了轴对称-最短路线问题,等边三角形的判定和性质,解直角三角形,关键是确定P 的位置.17.【答案】②③④【解析】解:①观察函数图象可知,当t=2 时,两函数图象相交,∵C 地位于A、B 两地之间,∴交点代表了两车离C 地的距离相等,并不是两车相遇,结论①错误;②甲车的速度为240÷4=60(km/h),乙车的速度为200÷(3.5-1)=80(km/h),∵(240+200-60-170)÷(60+80)=1.5(h),∴乙车出发1.5h 时,两车相距170km,结论②正确;③∵(240+200-60)÷(60+80)=2 (h),∴乙车出发2 h 时,两车相遇,结论③正确;④∵80×(4-3.5)=40(km),∴甲车到达C 地时,两车相距40km,结论④正确.综上所述,正确的结论有:②③④.故答案为:②③④.①观察函数图象可知,当t=2 时,两函数图象相交,结合交点代表的意义,即可得出结论①错误;②根据速度=路程÷时间分别求出甲、乙两车的速度,再根据时间=路程÷速度和可求出乙车出发1.5h 时,两车相距170km,结论②正确;③根据时间=路程÷速度和可求出乙车出发2 h 时,两车相遇,结论③正确;④结合函数图象可知当甲到C 地时,乙车离开C 地0.5 小时,根据路程=速度×时间,即可得出结论④正确.综上即可得出结论.本题考查了一次函数的应用,根据函数图象逐一分析四条结论的正误是解题的关键.18.【答案】【解析】5 ‒ 1 2解:作AE⊥x 轴于E,BF⊥x 轴于F,过B 点作BC⊥y 轴于C,交AE 于G,如图所示:则AG⊥BC,∵∠OAB=90°,∴∠OAE+∠BAG=90°,∵∠OAE+∠AOE=90°,∴∠AOE=∠GAB ,在△AOE 和△BAG 中,,∴△AOE ➴△BAG (AAS ),∴OE=AG ,AE=BG ,∵点 A (n ,1),∴AG=OE=n ,BG=AE=1,∴B (n+1,1-n ),∴k=n×1=(n+1)(1-n ),整理得:n 2+n-1=0,解得:n= ∴n=,(负值舍去), ∴k=故答案为: ;.作 AE ⊥x 轴于 E ,BF ⊥x 轴于 F ,过 B 点作 BC ⊥y 轴于 C ,交 AE 于 G ,则 AG ⊥BC ,先求得△ AOE ➴△BAG ,得出 AG=OE=n ,BG=AE=1,从而求得 B (n+1,1-n ),根据 k=n×1=(n+1)(1-n )得出方程,解方程即可.本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识;熟练掌握反比例函数图象上点的坐标特征,证明三角形全等是解决问题的关键.19.【答案】(-2,0)【解析】解:如图所示,P 1(-2,0),P 2(2,-4),P 3(0,4),P 4(-2,-2),P 5(2,-2),P 6(0,2),发现 6 次一个循环,∵2017÷6=336…1,∴点 P 2017 的坐标与 P 1 的坐标相同,即 P 2017(-2,0),故答案为(-2,0).画出P1~P6,寻找规律后即可解决问题.本题考查坐标与图形的性质、点的坐标等知识,解题的关键是循环探究问题的方法,属于中考常考题型.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
填空压轴题(函数篇)-2023年中考数学压轴题专项训练(解析版)

填空压轴题(函数篇)1.压轴题速练1一.填空题(共40小题)1(2023•上虞区模拟)已知点A 在反比例函数y =12x(x >0)的图象上,点B 在x 轴正半轴上,若△OAB 为等腰直角三角形,则AB 的长为23或26 .【答案】23或26.【分析】因为等腰三角形的腰不确定,所以分三种情况分别计算即可.【详解】解:当AO =AB 时,此时∠OAB =90°;∵A 在函数y =12x(x >0)上,∴S △OAB =12,∴12×OA ×AB =12,即12AB 2=12,∴AB =24=26;当AB =BO 时,此时∠ABO =90°;∵A 在函数y =12x (x >0)上,∴S △AOB =122=6,∴12×OB ×AB =6,即12AB 2=6,∴AB =23,当OA =OB 时,A 点落在y 轴上,故不合题意,综上所述,AB 的长为23或26.故答案为:23或26.2(2023•姑苏区校级一模)在平面直角坐标系xOy 中,对于点P (a ,b ),若点P '的坐标为ka +b ,a +b k(其中k 为常数且k ≠0),则称点P '为点P 的“k -关联点”.已知点A 在函数y =3x (x >0)的图象上运动,且A 是点B 的“3-关联点”,若C (-1,0),则BC 的最小值为 3105 .【答案】3105.【分析】由A 是点B 的“3-关联点”,可设点B 坐标,表示出点A 坐标,由点A 在函数y =3x(x >0)的图象上,就得到点B 在一个一次函数的图象上,可求出这条直线与坐标轴的交点M 、N ,过C 作这条直线的垂线,这点到垂足之间的线段CB ,此时CB 最小,由题中的数据,可以证明出△MON ∽△MBC ,进而得出MNMC =ONBC,进而求出BC .【详解】解:过点B 作QB ⊥MN ,垂足为B ,设B (x ,y ),∵A 是点B 的“3-关联点”,∴A 3x +y ,x +y3 ,∵点A 在函数y =3x (x >0)的图象上,∴(3x +y )x +y3=3,即:3x +y =3或2x +y =-3(舍去x <0,y <0),∴y =-3x +3,∴点B 在直线y =-3x +3上,直线y =-3x +3与x 轴、y 轴相交于点M 、N ,则M (1,0)、N (0,3),∴MN =12+32=10,MC =MO +OC =1+1=2,当CB ⊥MN 时,线段BC 最短,∵∠CBM =∠NOM =90°,∠CMB =∠NMO ,∴△MON ∽△MBC ,∴MN MC =ON BC ,即102=3BC,解得:BC =3105,故答案为:3105.3(2023•海门市一模)如图,在平面直角坐标系xOy 中,已知点A (m ,n ),B (m +4,n -2)是函数y =kx(k >0,x >0)图象上的两点,过点B 作x 轴的垂线与射线OA 交于点C .若BC =8,则k 的值为6.【答案】6.【分析】作AD ⊥x 轴于点D ,设直线CB 与x 轴交于点E ,根据AD ∥CE ,得AD CE =ODOE,所以n =32m ,即可得到点A m ,32m ,B m +4,32m -2 ,代入y =kx (k >0,x >0)即可求出答案.【详解】解:如图,作AD ⊥x 轴于点D ,设直线CB 与x 轴交于点E ,∵点A (m ,n ),B (m +4,n -2),BC =8,∴点D (m ,0),E (m +4,0),CE =n +6,∵AD ∥CE ,∴AD CE =ODOE ,∴n n +6=m m +4,∴n =32m ,∴点A m ,32m ,B m +4,32m -2 ,∵点A ,B 是函数y =kx(k >0,x >0)图象上的两点,∴k =m ⋅32m =(m +4)•32m -2 ,解得m =2,∴k =m ⋅32m =6,故答案为:6.【点睛】此题考查了反比例函数图象上点的坐标特征,平行线分线段成比例定理,关键是根据AD ∥CE ,得AD CE =OD OE,求出n =32m .4(2023•建昌县一模)如图,在平面直角坐标系中,点A ,B 在反比例函数y =kx(k ≠0,x >0)的图象上,点C 在y 轴上,AB =AC ,AC ∥x 轴,BD ⊥AC 于点D ,若点A 的横坐标为5,BD =3CD ,则k 值为 154 .【答案】154.【分析】延长BD 交x 轴于点E ,过点B 作BG ⊥y 轴于点G ,过点A 作AF ⊥x 轴于点F ,设B (m ,n ),可得BD =3m ,AD =5-m ,根据勾股定理求出m =1,进一步得出AF =n -3,再根据n =5(n -3)求出n =154即可得出结论.【详解】解:延长BD 交x 轴于点E ,过点B 作BG ⊥y 轴于点G ,过点A 作AF ⊥x 轴于点F ,则四边形BGCD ,COED ,ADEF 均为矩形,∴BG =CD ,AF =DE ,CD =OE ,设B (m ,n ),则有BG =CD =OE =m ,BE =n ,∵AC =AB =5,∴AD =AC -CD =5-m ,∵BD =3CD =3m ,∴AF =DE =n -3m ,在Rt △ABD 中,BD 2+AD 2=AB 2,∴(3m )2+(5-m )2=52,解得m 1=1,m 2=0(不符合题意,舍去),∴DE =n -3,AF =n -3,∴B (1,n ),A (5,n -3),∵点A ,B 在反比例函数y =kx(k ≠0,k >0)的图象上,∴n =5(n -3),解得n =154,∴k =1×154=154.故答案为:154.【点睛】本题主要考查了反比例函数图象上点的坐标特征,矩形的判定与性质以及勾股定理等知识,熟练掌握反比例函数图象上点的坐标一定满足该函数解析式是解答本题的关键.5(2023•碑林区校级模拟)如图,等腰直角△ABC的顶点A 坐标为(-3,0),直角顶点B 坐标为(0,1),反比例函数y =kx(x <0)的图象经过点C ,则k =-4.【答案】-4.【分析】先利用等角的余角相等证明∠CBD =∠BAO ,则可根据“AAS ”判断△AOB ≌△BDA ,所以OB =CD =1,OA =BD =3,则OD =OC +CD =4,从而得到点C 的坐标,代入y =kx(x <0)即可求得k 的值.【详解】解:作CD ⊥y 轴于D ,∵A (3,0),B (0,1),∴OA =3,OB =1,∵∠ABC =90°,∴∠ABO +∠CBD =90°,∵∠ABO +∠BAO =90°,∴∠CBD =∠BAO ,在△AOB 和△BDC 中,∠CBD =∠BAO ∠AOB =∠BDC =90°AB =BC ,∴△AOB ≌△BDA (AAS ),∴OB =CD =1,OA =BD =3,∴点C 的坐标(-1,4),∵反比例函数y =kx(x <0)的图象经过点C ,∴k =-1×4=-4.故答案为:-4.6(2023•宁波模拟)如图,在平面直角坐标系xOy 中,△OAB 为等腰直角三角形,且∠A =90°,点B 的坐标为(4,0).反比例函数y =kx(k ≠0)的图象交AB 于点C ,交OA 于点D .若C 为AB 的中点,则OD OA=32 .【答案】32.【分析】由等腰直角三角形的性质得到A (2,2),直线OA 为y =x ,进一步求得点C (3,1),利用待定系数法求得反比例函数的解析式,与直线OA 的解析式联立,解方程组求得点D 的坐标,从而求得ODOA=32.【详解】解:∵点B 的坐标为(4,0),∴OB =4,∵△OAB 为等腰直角三角形,且∠A =90°,∴A (2,2),∴直线OA 为y =x ,∵C 为AB 的中点,∴C (3,1),∵反比例函数y =kx(k ≠0)的图象交AB 于点C ,交OA 于点D ,∴k =3×1=3,∴反比例函数为y =3x,由y =3x y =x,解得x =3y =3 或x =-3y =-3 ,∴D (3,3),∴OD OA=32.故答案为:32.7(2023•龙港市二模)如图,Rt △ABO 放置在平面直角坐标系中,∠ABO =Rt ∠,A 的坐标为(-4,0).将△ABO 绕点O 顺时针旋转得到△A ′B ′O ,使点B 落在边A ′O 的中点.若反比例函数y =kx(x >0)的图象经过点B ',则k 的值为 3 .【答案】3.【分析】连接BB′,交y轴于D,由题意可知OB=12OA,得出∠A′OB′=∠AOB=60°,证得△BOB′是等边三角形,然后证得BB′垂直于y轴,BD=B′D,从而求得BD=B′D=1,OD=3,得到B′(1,3),代入y=k x(x>0)即可求得k的值.【详解】解:连接BB′,交y轴于D,由题意可知OB=12OA,∴∠OAB=30°,∴∠A′OB′=∠AOB=60°,∵BO=B′O,∴△BOB′是等边三角形,∵∠BOD=90°-60°=30°,∴OD平分∠BOB′,∴BB′垂直于y轴,BD=B′D,∴BB′∥x轴,∵A的坐标为(-4,0),∴OA=4,∴OB=2,∴等边△BOB′的边长为2,∴BD=B′D=1,OD=3,∴B′(1,3),∵反比例函数y=k x(x>0)的图象经过点B',∴k=1×3=3,故答案为:3.8(2023•温州二模)如图,点A在x轴上,以OA为边作矩形OABC,反比例函数y=kx(k>0,x>0)的图象经过AB的中点E,交边BC于点D,连结OE.若OE=OC,CD=2,则k的值为 1633 .【答案】1633.【分析】设OC =AB =m ,则AE =12OE =12m ,利用勾股定理求得OA =32m ,即可得到D (2,m ),E 32m ,12m,由k =xy 得到k =2m =32m •12m ,解得m =833,即可求得k =2m =1633.【详解】解:设OC =AB =m ,∵点E 是AB 的中点,∴AE =12AB∵OE =OC ,CD =2,∴AE =12OE =12m ,∴OA =OE 2-12OE 2=32OE =32m ,∴D (2,m ),E 32m ,12m ,∵反比例函数y =kx (k >0,x >0)的图象经过点D 、E ,∴k =2m =32m •12m ,解得m 1=833,m 2=0(舍去),∴k =2m =1633,故答案为:1633.9(2023•石家庄二模)已知A ,B ,C 三点的坐标如图所示.(1)若反比例函数y =kx的图象过点A ,B ,C 中的两点,则不在反比例函数图象上的是点C ;(2)当反比例函数的图象与线段AC (含端点)有且只有一个y =kx公共点时,k 的取值范围是3≤k <4或k =12424 .【答案】(1)C ;(2)3≤k <4或k =12124.【分析】(1)根据反比例函数系数k =xy 判断即可;(2)求得直线AC 的解析式,与反比例函数解析式联立,整理得3x 2-11x +2k =0,当Δ=0时,反比例函数的图象与直线AC 有且只有一个公共点,求得此时k 的值,根据k =4时,反比例函数经过A 、B 两点,k =3时,反比例函数经过C 点,根据图象即可得出3≤k <4时,反比例函数y =kx的图象与线段AC (含端点)有且只有一个公共点,从而得出3≤k <4或k =12124.【详解】解:(1)由坐标系可知,A (1,4),B (2,2),C (3,1),∵1×4=2×2≠3×1,∴反比例函数y =kx的图象过点A 、B ,点C 不在反比例函数图象上,故答案为:C ;(2)设直线AC 为y =kx +b ,代入A 、C 的坐标得k +b =43k +b =1 ,解得k =-32b =112,∴直线AC 为y =-32x +112,令k x =-32x +112,整理得3x 2-11x +2k =0,当反比例函数的图象与直线AC 有且只有一个公共点时,Δ=0,∴(-11)2-4×3×2k =0,解得k =12124,由(1)可知k =4时,反比例函数图象过A (1,4),B (2,2)两点,k =3时,反比例函数图象过C 点,∴3≤k <4时,反比例函数y =kx 的图象与线段AC (含端点)有且只有一个公共点,综上,当反比例函数y =kx的图象与线段AC (含端点)有且只有一个公共点时,k 的取值范围是3≤k<4或k =12124.故答案为:3≤k <4或k =12124.10(2023•郫都区二模)定义:若一个函数图象上存在横纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点(-1,-1)是函数y =2x +1的图象的“等值点”.若函数y =x 2-2(x ≥m )的图象记为W 1,将其沿直线x =m 翻折后的图象记为W 2.当W 1、W 2两部分组成的图象上恰有2个“等值点”时,m 的取值范围为m <-98或-1<m <2.【答案】m <-98或-1<m <2.【分析】先求出函数y =x 2-2的图象上有两个“等值点”(-1,-1)或(2,2),再利用翻折的性质分类讨论即可.【详解】解:令x =x 2-2,解得:x 1=-1,x2=2,∴函数y =x 2-2的图象上有两个“等值点”(-1,-1)或(2,2),①当m <-1时,W 1,W 2两部分组成的图象上必有2个“等值点”(-1,-1)或(2,2),W 1:y =x 2-2(x ≥m ),W 2:y =(x -2m )2-2(x <m ),令x =(x -2m )2-2,整理得:x2-(4m+1)x+4m2-2=0,∵W2的图象上不存在“等值点”,∴Δ<0,∴(4m+1)2-4(4m2-2)<0,∴m<-98,②当m=-1时,有3个“等值点”(-2,-2)、(-1,-1)、(2,2),③当-1<m<2时,W1,W2两部分组成的图象上恰有2个“等值点”,④当m=2时,W1,W2两部分组成的图象上恰有1个“等值点”(2,2),⑤当m>2时,W1,W2两部分组成的图象上没有“等值点”,综上所述,当W1,W2两部分组成的图象上恰有2个“等值点”时,m<-98或-1<m<2.故答案为:m<-98或-1<m<2.11(2023•双阳区一模)如图,抛物线y=-0.25x2+4与y轴交于点A,过AO的中点作BC∥x轴,交抛物线y=x2于B、C两点(点B在C的左边),连接BO、CO,若将△BOC向上平移使得B、C两点恰好落在抛物线y=-0.25x2+4上,则点O平移后的坐标为(0,1.5).【答案】(0,1.5).【分析】先求得A的坐标,进而根据题意得到B、C两点的纵坐标为2,把y=2代入y=x2得x=±2,即可求得B(-2,2),进一步求得x=-2时,函数y=-0.25x2+4的值,即可求得平移的距离,得到点O平移后的坐标.【详解】解:∵抛物线y=-0.25x2+4与y轴交于点A,∴A(0,4),∴OA=4,∵过AO的中点作BC∥x轴,交抛物线y=x2于B、C两点(点B在C的左边),∴B、C两点的纵坐标为2,把y=2代入y=x2得x=±2,∴B(-2,2),把x=-2代入y=-0.25x2+4得y=-0.5+4=3.5,∴此时点B的坐标为(-2,3.5),∴平移的距离为3.5-2=1.5,∴点O平移后的坐标为(0,1.5),故答案为:(0,1.5).12(2023•衡水二模)如图,点A a,-3 a(a<0)是反比例函数y=k x图象上的一点,点M(m,0),将点A绕点M顺时针旋转90°得到点B,连接AM,BM.(1)k的值为-3;(2)当a=-3,m=0时,点B的坐标为(1,3);(3)若a=-1,无论m取何值时,点B始终在某个函数图象上,这个函数图象所对应的表达式.【答案】(1)-3;(2)(1,3);(3)点B始终在函数y=x-2的图象上.【分析】(1)把A的坐标代入反比例函数反比例函数y=kx即可求得;(2)作AC⊥x轴于C,BD⊥x轴于D,根据旋转的性质得出△BDM≌△MCA,从而得出AC=MD,CM=BD,即可得出点B的坐标;(3)由(2)可知AC=MD,CM=BD,根据题意得出B(3+m,m+1),从而得出点B始终在函数y= x-2的图象上.【详解】解:(1)∵点A a,-3 a(a<0)是反比例函数y=k x图象上的一点,∴k=a•-3a=-3.故答案为:-3;(2)作AC⊥x轴于C,BD⊥x轴于D,∵∠AMB=90°,∴∠AMC+∠BMD=90°,∵∠AMC+∠MAC=90°,∴∠BMD=∠MAC,∵∠BDM=∠MCA=90°,BM=AM,∴△BDM≌△MCA(AAS),∴AC=MD,CM=BD,∵a=-3,m=0,∴A(-3,1),M(0,0),∴AC=1,MC=3,∴MD=1,BD=3,∴B(1,3);故答案为:(1,3);(3)若a=-1,则A(-1,3),由(2)可知AC=MD,CM=BD,∵M(m,0),∴B(3+m,m+1),∴点B始终在函数y=x-2的图象上.13(2023•市中区二模)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)⋯根据这个规律,第2023个点的坐标(45,2).【答案】(45,2).【分析】观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,横坐标是奇数时,最后以横坐标为该数,纵坐标以0结束;据此求解即可.【详解】解:观察图形可知,到每一个横坐标结束,经过整数点的个数等于最后横坐标的平方,∴横坐标以n结束的有n2个点,∵452=2025,∴第2025个点的坐标是(45,0),∴2023个点的纵坐标往上数2个单位为2,∴2023个点的坐标是(45,2);故答案为:(45,2).【点睛】本题考查了点坐标规律探究,观察出点的个数与横坐标存在平方关系是解题的关键.14(2023•沈阳二模)某商厦将进货单价为70元的某种商品,按销售单价100元出售时,每天能卖出20个,通过市场调查发现,这种商品的销售单价每降价1元,日销量就增加1个,为了获取最大利润,该种商品的销售单价应降5元.【答案】5.【分析】设降价x元时,则日销售可以获得利润为W,由销售问题的数量关系表示出W与x之间的关系,根据关系式的性质就可以求出结论.【详解】解:设该种商品的销售单价应降价x元时,日销售可以获得利润为W元,由题意,得W=(100-70-x)(20+x)=-x2+10x+600=-(x-5)2+625,∵a=-1<0,∴当x=5时,W=625.最大故答案为:5.【点睛】本题考查了销售问题的数量关系的运用,利润=(售价-进价)×销量的运用,二次函数的顶点式的运用,解答时求出二次函数的解析式是解题的关键15(2023•贵港二模)如图,抛物线y1截得坐标轴上的线段长AB=OD=6,D为y1的顶点,抛物线y2由y 1平移得到,y2截得x轴上的线段长BC=9.若过原点的直线被抛物线y1,y2所截得的线段长相等,则这条直线的解析式为y =x .【答案】y =x .【分析】根据已知条件,待定系数求得抛物线y 1,y 2的解析式,设过原点的直线解析式为y =kx ,过原点的直线被抛物线y 1,y 2所截得的线段长相等,即可求解.【详解】解:∵抛物线y 1截得坐标轴上的线段长AB =OD =6,D 为y 1的顶点,∴A (-3,0),B (3,0),D (0,6),设y 1的解析式为y =ax 2+6,代入(3,0),得9a +6=0,解得:a =-23,∴y 1的解析式为y 1=-23x 2+6,∵抛物线y 2由y 1平移得到,y 2截得x 轴上的线段长BC =9,∴C (12,0),则y 2的解析式为y =-23(x -3)(x -12),即y 2=-23x 2+10x -24,设过原点的直线解析式为y =kx ,与y 1,y 2分别交于点F ,G ,H ,K ,如图所示,联立y =kx y 1=-23x 2+6,即-23x 2-kx +6=0,∴x 1+x 2=-3k2,x 1•x 2=-9,∴F 、G 两点横坐标之差为|x 1-x 2|=(x 1+x 2)2-4x 1⋅x 2=94k 2+36,联立y =kx y 2=-23x 2+10x -24,即-23x 2+(10-k )x -24=0,∴x 1+x 2=-3k -302,x 1⋅x 2=36,∴H 、K 两点横坐标之差为|x 1-x 2|=(x 1+x 2)2-4x 1⋅x 2=-3k -302 2-144,∵FG =HK ,∴94k 2+36=-3k -3022-144,解得k =1,故直线解析式为y =x .故答案为:y =x .16(2023•江都区一模)如图,在平面直角坐标系中,点A ,B 坐标分别为(3,4),(-1,1),点C 在线段AB 上,且AC BC=13,则点C 的坐标为 2,134 .【答案】2,134.【分析】分别过点A ,B ,C 作x 轴的垂线垂足分别为E ,D ,F ,过点B 作BG ⊥AE 于点G ,交CF 于点H ,则CF ∥AE ,BH ⊥CF ,BD =HF =EG ,设点C 的坐标为(m ,n ),则CF =n ,OF =m ,可得CH=n -1,BH =m +1,根据△BHC ∽△BGA ,可得m +14=n -13=34,即可求解.【详解】解:如图,分别过点A ,B ,C 作x 轴的垂线垂足分别为E ,D ,F ,过点B 作BG ⊥AE 于点G ,交CF 于点H ,则CF ∥AE ,BH ⊥CF ,BD =HF =EG ,∵点A ,B 坐标分别为(3,4),(-1,1),∴BD =HF =EG =1,AE =4,BG =4,∴AG =3,设点C 的坐标为(m ,n ),则CF =n ,OF =m ,∴CH =n -1,BH =m +1,∵AC BC=13,∴BC AB=34,∵CF ∥AE ,∴△BHC ∽△BGA ,∴BH BG =CH AG =BC AB ,∴m +14=n -13=34,解得:m =2,n =134,∴点C 的坐标为2,134 .故答案为:2,134 .17(2023•龙华区二模)如图,在平面直角坐标系中,OA =3,将OA 沿y 轴向上平移3个单位至CB ,连接AB ,若反比例函数y =kx(x >0)的图象恰好过点A 与BC 的中点D ,则k =25 .【答案】25.【分析】设A (m ,n ),则由题意B (m ,n +3),进而求得D m 2,n +62,根据反比例函数系数k =xy ,得到k =mn =m 2•n +62,解得n =2,利用勾股定理求得m 的值,得到A (5,2),代入解析式即可求得k 的值.【详解】解:设A (m ,n ),则B (m ,n +3),∵点D 是BC 的中点,C (0,3),∴D m 2,n +62,∵反比例函数y =kx (x >0)的图象恰好过点A 与BC 的中点D ,∴k =mn =m 2•n +62,解得n =2,∴A (m ,2),∵OA =3,∴m 2+22=32,∴m =5(负数舍去),∴A (5,2),∴k =5×2=25,故答案为:25.18(2023•乐至县模拟)如图,在平面直角坐标系中,点A 、A 1、A 2、A 3⋯A n 在x 轴上,B 1、B 2、B 3⋯B n 在直线y =-33x +33上,若A (1,0),且△A 1B 1O 、△A 2B 2A 1⋯△A n B n A n -1都是等边三角形,则点B n 的横坐标为1-3×2n -2(n 为正整数).【答案】1-3×2n -2(n 为正整数).【分析】过点B n 作B n ∁n ⊥x 轴于点∁n ,利用一次函数图象上点的坐标特征,可得出该直线与y 轴的交点,解直角三角形,可得出∠OAB 1=30°,利用等边三角形的性质及三角形的外角性质,可得出OA 1的长度,结合B 1C 1=32OA 1可得出B 1C 1的长,同理,可求出B n ∁n =3•2n -2(n ≥2,且n 为整数),再结合一次函数图象上点的坐标特征,即可求出点B n 的横坐标.【详解】解:过点B n 作B n ∁n ⊥x 轴于点∁n ,如图所示.∵直线的解析式为y =-33x +33,∴该直线与y 轴交于点0,33,∴tan ∠OAB 1=331=33,∴∠OAB 1=30°.∵△A 1B 1O 是等边三角形,∴∠A 1OB 1=60°,∴∠AB 1O =30°=∠OAB 1,∴OA 1=OB 1=OA =1,∴B 1C 1=32OA 1=32;同理:A 1A 2=AA 1=2,A 2A 3=AA 2=4,A 3A 4=AA 3=8,⋯,∴A n -1A n =AA n -1=2n -1(n ≥2,且n 为整数),∴B n ∁n =32A n -1A n =3•2n -2(n ≥2,且n 为整数),∴点B n 的纵坐标为3•2n -2(n 为正整数).当y =3•2n -2时,3•2n -2=-33x +33,解得:x =1-3×2n -2,∴点B n 的横坐标为1-3×2n -2(n 为正整数).故答案为:1-3×2n -2(n 为正整数).19(2023•玄武区一模)已知函数y =2x 2-(m +2)x +m (m 为常数),当-2≤x ≤2时,y 的最小值记为a .a 的值随m 的值变化而变化,当m =2时,a 取得最大值.【答案】2.【分析】分类讨论抛物线对称轴的位置确定出m 的范围即可.【详解】解:由二次函数y =2x 2-(m +2)x +m (m 为常数),得到对称轴为直线x =m +24,抛物线开口向上,当m +24≥2,即m ≥6时,由题意得:当x =2时,a =8-2m -4+m =4-m ,a 随m 增大而减小,a 的最大值为-2;当-2<m +24<2,-10<m <6时,由题意得:当x =m +24时,a =2×m +24 2-(m +2)•m +24 +m =-18(m -2)2+32,则m =2时,a 取得最大值32;当m +24≤-2,即m ≤-10时,由题意得:当x =-2时,a =8+2m +4+m =3m +12,a 随m 增大而增大,a 的最大值为-18;综上,当m =2时,a 取得最大值.故答案为:2.20(2023•萧山区一模)已知点P (x 1,y 1)Q (x 2,y 2)在反比例函数y =6x图象上.(1)若x 1x 2=2,则y 1y 2= 12 .(2)若x 1=x 2+2,y 1=3y 2,则当自变量x >x 1+x 2时,函数y 的取值范围是y <-32 .【答案】(1)12;(2)y <-32.【分析】(1)把P 、Q 代入解析式得到y 1=6x 1,y 2=6x 2,进一步得到y 1y 2=6x 16x 2=x 2x 1=12;(2)由x 1=x 2+2,y 1=3y 2得到x 1=-1,x 2=-3,即可得到x 1+x 2=-4,求得x =-4时的函数值,然后根据反比例函数的性质即可得到函数y 的取值范围.【详解】解:(1)∵点P (x 1,y 1)Q (x 2,y 2)在反比例函数y =6x图象上,∴y 1=6x 1,y 2=6x 2,∵x 1x 2=2,∴y 1y 2=6x 16x 2=x 2x 1=12,故答案为:12;(2)∵点P (x 1,y 1)Q (x 2,y 2)在反比例函数y =6x图象上,∴y 1=6x 1,y 2=6x 2,∵y 1=3y 2,∴6x 1=3×6x 2,∴x 2=3x 1,∵x 1=x 2+2,∴x 1=3x 1+2,∴x 1=-1,x 2=-3,∴x 1+x 2=-4,当x =-4时,y =6-4=-32,∵反比例函数y =6x中k >0,∴x <0时,y 随x 的增大而减小,∴当自变量x >x 1+x 2时,函数y 的取值范围是y <-32,故答案为:y <-32.21(2023•灞桥区校级模拟)如图,点A ,B 分别在y 轴正半轴、x 轴正半轴上,以AB 为边构造正方形ABCD,点C,D恰好都落在反比例函数y=k x(k≠0)的图象上,点E在BC延长线上,CE=BC,EF⊥BE,交x轴于点F,边EF交反比例函数y=k x(k≠0)的图象于点P,记△BEF的面积为S,若S=k2+12,则k的值为8.【答案】8.【分析】作DM⊥y轴于M,CN⊥x轴于N.设OA=b,OB=a.首先利用全等三角形的性质求出D、C两点坐标,再证明a=b,再构建方程求出k的值.【详解】解:如图作DM⊥y轴于M,CN⊥x轴于N.设OA=b,OB=a.∵四边形ABCD是正方形,∴∠DAB=90°,AD=AB,∴∠DAM+∠BAO=90°,∵∠BAO+∠ABO=90°,∴∠DAM=∠ABO,∵∠AOB=∠DAM=90°,∴△AOB≌△BNC(AAS),同理△BNC≌△DMA,∴DM=OA=BN=b,AM=OB=CN=a,∴D(b,a+b),C(a+b,a),∵点C,D恰好都落在反比例函数y=k x(k≠0)的图象上,∴b(a+b)=a(a+b),∵a+b≠0,∴a=b,∴OA=OB,∴∠ABO=45°,∠EBF=45°,∵BE⊥EF,∴△BEF是等腰直角三角形,∵BC=EC,∴可得E(3a,2a),F(5a,0),∴12×4a×2a=k2+12,∴4a2=k2+12,∵D(a,2a),∴2a2=k,∴2k=k2+12,∴k =8.故答案为:8.【点睛】本题考查反比例函数图象的点的特征,正方形的性质、全等三角形的判定和性质,解题的关键是学会利用参数解决问题,属于中考选择题中的压轴题.22(2023•东莞市校级一模)如图,在平面直角坐标系中,点A 在y 轴上,点B 在x 轴上.以AB 为边长作正方形ABCD ,S 正方形ABCD =50,点C 在反比例函数y =k /x (k ≠0,x >0)的图象上,将正方形沿x 轴的负半轴方向平移6个单位长度后,点D 刚好落在该函数图象上,则k 的值是8.【答案】8.【分析】作DF ⊥y 轴于点F ,CE ⊥x 轴于点E ,通过证得△OAB ≌△EBC ≌△FDA 可得出BE =OA =DF ,CE =OB =AF ,设OA =a ,OB =b ,即可得出C (a +b ,b ),D (a ,a +b ),进而把点C 和平移后的D 点坐标代入反比例函数的解析式求出k 的值即可.【详解】解:作DF ⊥y 轴于点F ,CE ⊥x 轴于点E ,正方形ABCD 中,AB =BC ,∠ABC =90°,∴∠ABO +∠CBE =90°,Rt △ABO 中,∠BAO +∠ABO =90°,∴∠CBE =∠BAO ,在△OAB 与△EBC 中,∠CBE =∠BAO ∠BEC =∠AOB =90°BC =AB ,∴△OAB ≌△EBC (AAS ),∴BE =OA ,CE =OB ,同理△OAB ≌△FDA ,∴DF =OA ,AF =OB ,设OA =a ,OB =b ,则C (a +b ,b ),D (a ,a +b ),∵点C 在反比例函数y =k /x (k ≠0,x >0)的图象上,将正方形沿x 轴的负半轴方向平移6个单位长度后,点D 刚好落在该函数图象上,∴k =b (a +b )=(a -6)•(a +b ),∴a -6=b ,∵S 正方形ABCD =50,∴AB 2=50,∵OA 2+OB 2=AB 2,∴a 2+b 2=50,即a 2+(a -6)2=50,解得a =7(负数舍去),∴b =a -6=1,∴k =b (a +b )=8.故答案为:8.23(2023•长春一模)如图,正方形ABCD 、CEFG 的顶点D 、F 都在抛物线y =-12x 2上,点B 、C 、E 均在y 轴上.若点O 是BC 边的中点,则正方形CEFG 的边长为1+2 .【答案】1+2.【分析】设OB =OC =12BC =a ,且a >0,即可得D (-2a ,-a ),根据D (-2a ,-a )在抛物线y =-12x 2上,可得a =12,设正方形CEFG 的边长为b ,且b >0,同理可得F b ,-12-b ,代入y =-12x 2中,问题得解.【详解】解:∵点O 是BC 边的中点,∴设OB =OC =12BC =a ,且a >0,在正方形ABCD 中,DC =BC =2a ,DC ⊥BC ,∴D (-2a ,-a ),∵D (-2a ,-a )在抛物线y =-12x 2上,∴-a =-12(-2a )2,解得:a =12,设正方形CEFG 的边长为b ,且b >0,∴CE =EF =b ,∴OE =OC +CE =12+b ,∴结合正方形的性质,可知F b ,-12-b ,∵F b ,-12-b 在抛物线y =-12x 2上,∴-12-b =-12b 2,解得:b =1+2(负值舍去),故答案为:1+2.24(2023•成都模拟)如图,在△AOB 中,AO =AB ,射线AB 分别交y 轴于点D ,交双曲线y =kx(k >0,x >0)于点B ,C ,连接OB ,OC ,当OB 平分∠DOC 时,AO 与AC 满足AO AC=23,若△OBD 的面积为4,则k = 407 .【答案】407.【分析】通过证得△AOD ∽△ACO ,得到AD AB=23,即可求得△AOB 的面积为12,进一步求得△BOC 的面积为6,根据S △BOC =S 梯形BMNC 得出k 的值即可.【详解】解:作BM ⊥x 轴于M ,CN ⊥x 轴于N ,∵AO =AB ,∴∠AOB =∠ABO ,∴∠AOD +∠BOD =∠OCB +∠BOC ,∵∠BOD =∠BOC ,∴∠AOD =∠ACO ,∵∠OAD =∠CAO ,∴△AOD ∽△ACO ,∴AD OA =AO AC=23,∴AD AB=23,∵△OBD 的面积为4,∴△AOB 的面积为12,∵AO AC=23,∴AB AC=23,∴△BOC 的面积为6,∴COD 的面积为10,∴x B x C =410=25,∴设B 2x ,k 2x ,则C 5x ,k5x,∵S △BOC =S △BOM +S 梯形BMNC -S △CON ,S △BOM =S △CON =12|k |,∴S △BOC =S 梯形BMNC =12k 2x +k5x⋅(5x -2x )=6,解得k =407,故答案为:407.25(2023•北仑区二模)如图,将矩形OABC 的顶点O 与原点重合,边AO 、CO 分别与x 、y 轴重合.将矩形沿DE 折叠,使得点O 落在边AB 上的点F 处,反比例函数y =kx(k >0)上恰好经过E 、F 两点,若B 点的坐标为(2,1),则k 的值为10-221 .【答案】10-221.【分析】连结OF ,过E 作EH ⊥OA 于H ,由B 点坐标为(2,1),即可得出E 点的坐标为(k ,1),F 点的坐标为2,k 2 ,证得△EHD ∽△OAF ,得到EH OA =HD AF,求得HD =k4,进而求得OD =HD +OH =k 4+k =5k 4,AD =2-5k 4,由折叠可得DF =OD =5k 4,利用勾股定理得到关于k 的方程,解方程即可求得k 的值.【详解】解:连结OF ,过E 作EH ⊥OA 于H .∵B 点坐标为(2,1),∴E 点的纵坐标为1,F 点的横坐标为2,∵反比例函数y =kx(k >0)上恰好经过E 、F 两点,∴E 点的坐标为(k ,1),F 点的坐标为2,k2,∵∠EDH +∠AOF =∠EDH +∠HED =90°,∴∠AOF =∠HED ,又∠EHD =∠OAF =90°,∴△EHD ∽△OAF ,∴EH OA =HD AF,即12=HD k 2,∴HD =k4,∴OD =HD +OH =k 4+k =5k 4,AD =2-5k4,由折叠可得DF =OD =5k4,在Rt △DAF 中,由勾股定理可得2-5k 4 2+k 2 2=5k 44,解得k 1=10-221,k 2=10+221(舍).∴k 的值为10-221.故答案为:10-221.26(2023•合肥二模)已知函数y =x 2+mx (m 为常数)的图形经过点(-5,5).(1)m =4.(2)当-5≤x ≤n 时,y 的最大值与最小值之和为2,则n 的值n =-3或n =10-2 .【答案】(1)4;(2)n =-3或n =10-2.【分析】(1)把已知坐标代入解析式计算即可.(2)根据抛物线额性质,分类计算.【详解】解:(1)∵函数y=x2+mx(m为常数)的图形经过点(-5,5),∴5=(-5)2-5m,解得m=4,故答案为:4;(2)由(1)得m=4,∴函数的解析式为y=x2+4x,∴y=x2+4x=(x+2)2-4,故抛物线的对称轴为直线x=-2,二次函数的最小值为-4,∵(-5,5)的对称点为(1,5),当-5≤x≤n时,y的最大值与最小值之和为2,当-5≤n<-2时,最大值为5,x=n时,取得最小值,且为y=n2+4n,根据题意,得n2+4n+5=2,解得n=-3,n=-1(舍去),故n=-3;当-2≤n≤1时,最大值为5,x=-2时,取得最小值,且为-4,根据题意,得5-4=1,不符合题意;当n>1时,x=-2时,取得最小值,且为-4,x=n时,取得最大值,且为y=n2+4n,根据题意,得n2+4n-4=2,解得n=10-2,n=-10-2(舍去),故n=10-2;故答案为n=-3或n=10-2.27(2023•仓山区校级模拟)下表记录了二次函数y=ax2+bx+2(a≠0)中两个变量x与y的6组对应值,x⋯-5x1x21x33⋯y⋯m020n m⋯其中-5<x1<x2<1<x3<3.根据表中信息,当-52<x<0时,直线y=k与该二次函数图象有两个公共点,则k的取值范围为2<k<83 .【答案】2<k<8 3.【分析】由抛物线经过(-5,m),(3,m)可得抛物线对称轴,从而可得a与b的关系,再将(1,0)代入解析式可得二次函数解析式,将二次函数解析式化为顶点式求解.【详解】解:∵抛物线经过(-5,m),(3,m),∴抛物线对称轴为直线x=-b2a=-1,∴b=2a,y=ax2+2ax+2,将(1,0)代入y=ax2+2ax+2得0=a+2a+2,解得a=-2 3,∴y =-23x 2-43x +2=-23(x +1)2+83,∴x =-1时,y =83为函数最大值,将x =-52代入y =-23x 2-43x +2得y =76,将x =0代入代入y =-23x 2-43x +2得y =2,∴2<k <83满足题意.故答案为:2<k <83.28(2023•西安二模)如图,在平面直角坐标系中,直线y =-x +1与x 轴,y 轴分别交于点A ,B ,与反比例函数y =kx(k <0)的图象在第二象限交于点C ,若AB =BC ,则k 的值为-2.【答案】-2.【分析】过点C 作CH ⊥x 轴于点H .求出点C 的坐标,可得结论.【详解】解:过点C 作CH ⊥x 轴于点H .∵直线y =-x +1与x 轴,y 轴分别交于点A ,B ,∴A (1,0),B (0,1),∴OA =OB =1,∵OB ∥CH ,∴△AOB ∽△AHC ,∴OA AH =AB AC ,∴AO OH =AB CB=1,∴OA =OH =1,∴CH =2OB =2,∴C (-1,2),∵点C 在y =kx的图象上,∴k =-2,故答案为:-2.29(2023•龙泉驿区模拟)在某函数的给定自变量取值范围内,该函数的最大值与最小值的差叫做该函数在此范围内的界值.当t ≤x ≤t +1时,一次函数y =kx +1(k >0)的界值大于3,则k 的取值范围是k >3;当t ≤x ≤t +2时,二次函数y =x 2+2tx -3的界值为2,则t =-1+22或-22 .【答案】k >3;-1+22或-22.【分析】y =kx +1:根据k >0时,y 随x 的增大而增大,根据最大值-最小值>3列不等式可解答;y=x2+2tx-3:先求得二次函数的对称轴,得到函数的增减性,分情况讨论,根据二次函数y=x2 +2tx-3的界值为2列方程可解答.【详解】解:当t≤x≤t+1时,一次函数y=kx+1(k>0)的界值大于3,∴y最大值-y最小值>3,∵k>0,y随x的增大而增大,∴x=t时,y最小值=tk+1,x=t+1时,y最大值=k(t+1)+1,∴k(t+1)+1-(tk+1)>3,∴k>3;y=x2+2tx-3=(x+t)2-3-t2,当x=-t时,y最小值=-3-t2,当x=t时,y=3t2-3,当x=t+2时,y=3t2+8t+1,①当-t≤t≤t+2时,t≥0,此时,当x=t时,y取最小值,当x=a+2时,y取最大值,∴y最大值=3t2+8t+1,y最小值=3t2-3,∴3t2+8t+1-(3t2-3)=2,解得t=-14(舍去);②当t≤-t≤t+2时,-1≤t≤0,当-12≤t≤0时,y最大值=3t2+8t+1,y最小值=-3-t2,∴3t2+8t+1-(-t2-3)=2,解得t=-1+22或t=-1-22(舍);当-1≤t≤-12时,y最大值=3t2-3,y最小值=-3-t2,3t2-3-(-t2-3)=2,解得t=-22或t=22(舍);③当t≤t+2≤-t时,t≤-1,y最小值=3t2+8t+1,y最大值=3t2-3,∴3t2-3-(3t2+8t+1)=2,解得t=-34(舍去);综上所述,t的值为-1+22或-22.故答案为:k>3;-1+22或-22.30(2023•姑苏区一模)如图①,四边形ABCD中,AB∥DC,AB>AD.动点P,Q均以1cm/s的速度同时从点A出发,其中点P沿折线AD-DC-CB运动到点B停止,点Q沿AB运动到点B停止,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数图象如图②所示,则AB=15cm.【答案】15.【分析】结合图象可知当t =13时,点P 到达点D ,此时y =90,AQ =13cm ,从而可求出此时△APQ 的高DE =12cm ,当t =18时,点P 到达点C ,点Q 已经停止,此时y =90,AQ =AB .由AB ∥DC ,可知此时△APQ 的高也为12cm ,再根据三角形的面积公式即可求出AB 的长.【详解】解:过点D 作DE ⊥AB 于E ,如图所示:当t =13时,P 到达D 点,即AD =AQ =13cm ,此时y =78,∴12AQ •DE =12×13•DE =78,∴DE =12,当t =18时,点P 到达点C ,此时点Q 已停止运动,此时y =90cm 2,AQ =AB ,∵AB ∥DC ,∴此时△APQ 的高也为12cm ,∴S △APQ =12AB •DE =12AB ×12=90,∴AB =15(cm ),故答案为:15.【点睛】本题考查动点问题的函数图象,平行线间的距离,三角形的面积公式等知识.利用数形结合的思想是解题关键.31(2023•宁波模拟)如图,点B 是反比例函数y =8x(x >0)图象上一点,过点B 分别向坐标轴作垂线,垂足为A ,C .反比例函数y =kx(x >0)的图象经过OB 的中点M ,与AB ,BC 分别相交于点D ,E .连接DE 并延长交x 轴于点F ,点G 与点O 关于点C 对称,连接BF ,BG .则k =2;△BDF 的面积=3.【答案】2,3.【分析】连接OD ,表示出点M 的坐标,即可求得k 的值,根据△BDF 的面积=△OBD 的面积=S △BOA -S △OAD ,即可求得.【详解】解:连接OD ,设点B (m ,n ),则点M 12m ,12n,∵点B 是反比例函数y =8x(x >0)图象上一点,∴mn =8,∵反比例函数y =kx(x >0)的图象经过OB 的中点M ,∴k =12m ⋅12n =14mn =14×8=2,∴△BDF 的面积=△OBD 的面积=S △BOA -S △OAD =12×8-12×2=3.故答案为:2,3.32(2023•青羊区模拟)如图,在平面直角坐标系中,一次函数y =3x 与反比例函数y =kx(k ≠0)的图象交于A ,B 两点,C 是反比例函数位于第一象限内的图象上的一点,作射线CA 交y 轴于点D ,连接BC ,BD ,若CD BC=45,△BCD 的面积为30,则k =6.【答案】6.【分析】作CF ⊥y 于点I ,BF ⊥x ,交CI 的延长线于点F ,作AE ⊥CF 于点E ,设BC 交y 轴于点M ,设A (m ,3m ),则B (-m ,-3m ),k =3m 2,设点C 的横坐标为a ,则C a ,3m 2a,可证明tan ∠CAE =tan ∠CBF =a 3m ,则∠CAE =∠CBF ,即可推导出∠CDM =∠CMD ,则CD =CM ,所以CI CF =CMBC=CD BC=45,则CI =4FI ,所以a =4m ,C 4m ,3m 4 ,由CI MI =tan ∠CMD =tan ∠CBF =43,得DI=MI =3m ,则DM =6m ,于是得12×6m ×m +12×6m ×4m =30,则m 2=2,所以k =3m 2=6.【详解】解:作CF ⊥y 于点I ,BF ⊥x ,交CI 的延长线于点F ,作AE ⊥CF 于点E ,设BC 交y 轴于点M ,∵直线y =3x 经过原点,且与双曲线y =kx交于A ,B 两点,∴点A 与点B 关于原点对称,设A (m ,3m ),则B (-m ,-3m ),k =3m 2,设点C 的横坐标为a ,则C a ,3m 2a ,F -m ,3m 2a,∵tan ∠CAE =CE AE =a -m 3m -3m 2a =a 3m ,tan ∠CBF =CF BF =a +m 3m 2a+3m=a3m ,∴tan ∠CAE =tan ∠CBF ,∴∠CAE =∠CBF ,∵AE ∥BF ∥DM ,∠CAE =∠CDM ,∠CBF =∠CMD ,∴∠CDM =∠CMD ,∴CD =CM ,∵CI CF =CM BC =CD BC=45,∴CI =4FI ,∴a =4m ,∴C 4m ,3m4 ,∵CI MI=tan ∠CMD =tan ∠CBF =a 3m =4m 3m =43,∴DI =MI =34CI =34×4m =3m ,∴DM =DI +MI =6m ,∵12DM •FI +12DM •CI =S △BCD =30,∴12×6m ×m +12×6m ×4m =30,∴m 2=2,∴k =3m 2=3×2=6,故答案为:6.33(2023•锦江区模拟)已知关于x 的多项式ax 2+bx +c (a ≠0),二次项系数、一次项系数和常数项分别a ,b ,c ,且满足a 2+2ac +c 2<b 2.若当x =t +2和x =-t +2(t 为任意实数)时ax 2+bx +c 的值相同;当x =-2时,ax 2+bx +c 的值为2,则二次项系数a 的取值范围是 215<x <27 .【答案】215<a <27.【分析】先根据二次函数的对称性可得其对称轴是:-b 2a =t +2-t +22=2,得b 与a 的关系:b =-4a ,将(-2,2)代入y =ax 2+bx +c 中可得:c =2-12a ,代入a 2+2ac +c 2<b 2中可解答.【详解】解:∵当x =t +2和x =-t +2(t 为任意实数)时ax 2+bx +c 的值相同,∴-b 2a =t +2-t +22=2,∴b =-4a ,∵当x =-2时,ax 2+bx +c 的值为2,∴函数y =ax 2+bx +c 经过点(-2,2),∴4a -2b +c =2,∴4a +8a +c =2,∴c =2-12a ,∵a 2+2ac +c 2<b 2,∴(a +c )2<b 2,∴(a +c )2-b 2<0,∴(a +c +b )(a +c -b )<0,∵b =-4a ,c =2-12a ,∴(a +2-12a -4a )(a +2-12a +4a )<0,∴(2-15a )(2-7a )<0,∴215<a <27.故答案为:215<a <27.34(2023•江北区一模)如图,菱形ABCO 的顶点A 与对角线交点D 都在反比例函数y =kx(k >0)的图象上,对角线AC 交y 轴于点E ,CE =2DE ,且△ADB 的面积为15,则k =8;延长BA 交x 轴于点F ,则点F 的坐标为 607,0 .【答案】8,607,0.【分析】通过构造延长线得到直角三角形EOM ,再用射影定理求出ED 、DA 、DO 之间的数量关系,在通过△ODA 面积为15求出ED 、DA 、DO 实际长度,再通过求D 点到y 轴的距离求出D 点坐标,也解出k ,进而得出B 点坐标.再过点A 作AH ⊥ND 于H ,然后通过相似求出A 点坐标,进而得出AB 直线解析式,最后得出F 点坐标.【详解】解:延长DA 交x 轴于点M ,设DE =a ,则CE =2a ,CD =AD =3a ,∵ED =a ,∴AM =a ,∴Rt △MOE 中,OD ⊥EM ,OD 2=ED ⋅DM ,∴OD =2a ,∵S △AOD =12OD ⋅DA =15,∴2a ⋅3a 2=15,∴a =5过D 作DN ⊥y 轴,则tan ∠DOE =12,即ON =2DN ,∵OD =25,∴D (2,4),即k =8.∵D (2,4),∴B (4,8),过点A 作AH ⊥ND 于H ,∵∠OND =∠H =90°,∠EDN +∠NDO =90°,∠NDO +∠HDA =90°,∴∠NDO =∠HDA ,∴△DHA ∽△OND ,∵DA =35,∴DH =6,AH =3,。
2023北京中考数学专题突破——填空压轴题(学生版)

2023北京中考数学专题突破——填空压轴题1.张老师准备为书法兴趣小组的同学购买上课的用具,在文具商店看到商店有A、B两种组合和C、D、E、F商品及它们的售价,组合及单件商品质量一样.若该小组共有12人,其中,笔和本每人各需要一份,砚台2人一方即可,墨汁n瓶(n≥3).张老师共带了200元钱,请给出一个满足条件的购买方案(购买数量写前面商品代码写后面即可,例如:2A+3B+……);n最多买瓶.商品价格组合A(1支笔+1个本+1方砚台+1瓶墨汁)25元组合B(1支笔+1个本+1瓶墨汁)18元C:1支笔5元D:1个本4元E:一方砚台10元F:一瓶墨汁12元2.某跨学科综合实践小组准备购买一些盒子存放实验材料.现有A,B,C三种型号的盒子,盒子容量和单价如表所示:盒子型号A B C盒子容量/升234盒子单价/元569其中A型号盒子做促销活动:购买三个及三个以上可一次性返现金4元,现有28升材料需要存放且每个盒子要装满材料.(1)若购买A,B,C三种型号的盒子的个数分别为2,3,4,则购买费用为元;(2)若一次性购买所需盒子且使购买费用不超过58元,则购买A,B,C三种型号的盒子的个数分别为.(写出一种即可)3.某快递员负责为A,B,C,D,E五个小区取送快递,每送一个快递收益1元,每取一个快递收益2元,某天5个小区需要取送快递数量如表小区需送快递数量需取快递数量A156B105C85D47E134(1)如果快递员一个上午最多前往3个小区,且要求他最少送快递30件,最少取快递15件,写出一种满足条件的方案(写出小区编号);(2)在(1)的条件下,如果快递员想要在上午达到最大收益,写出他的最优方案(写出小区编号).4.某快递公司的快递件分为甲类件和乙类件,快递员送甲类件每件收入1元,送乙类件每件收入2元.累计工作1小时,只送甲类件,最多可送30件,只送乙类件,最多可送10件;累计工作2小时,只送甲类件,最多可送55件,只送乙类件,最多可送20件;…,经整理形成统计表如表:12345678累计工作时长最多件数(时)种类(件)甲类件305580100115125135145乙类件1020304050607080(1)如果快递员一天工作8小时,且只送某一类件,那么他一天的最大收入为元;(2)如果快递员一天累计送x小时甲类件,y小时乙类件,且x+y=8,x,y均为正整数,那么他一天的最大收入为元.5.甲、乙两人分别在A,B两条生产线上加工零件,在A生产线,甲、乙均是每天最少可以加工2个A零件.当连续生产时,甲第一天能加工10个A零件,每连续加工一天,加工的零件数比前一天少2个;乙第一天能加工8个A零件,每连续加工一天,加工的零件数比前一天少1个.在B生产线,甲每天加工7个B零件,乙每天加工8个B零件.在同一天内,甲和乙不能在同一条生产线上工作,且在一条生产线连续工作不少于3天时可改变生产线,改变生产线后加工时间重新计算.根据题意,得:(1)甲在A生产线连续工作3天最多能加工A零件个;(2)若一个A零件、一个B零件组成一套产品,则14天最多能加工套产品.6.某甜品店会员购买本店甜品可享受八折优惠.“五一”期间该店又推出购物满200元减20元的“满减”活动.说明:①“满减”是指购买的甜品标价总额达到或超过200元时减20元.“满减”活动只享受一次;②会员可按先享“满减”优惠再享八折优惠的方式付款,也可按先享八折优惠再享“满减”优惠的方式付款.小红是该店会员.若购买标价总额为220元的甜品,则最少需支付元;若购买标价总额为x元的甜品,按先享八折优惠再享“满减”优惠的方式付款最划算,则x的取值范围是.7.某跨学科综合实践小组准备购买一些盒子存放实验材料.现有A,B,C三种型号的盒子,盒子容量和单价如表所示:盒子型号A B C盒子容量/升234盒子单价/元569其中A型号盒子做促销活动:购买三个及三个以上可一次性返现金4元,现有28升材料需要存放且每个盒子要装满材料.(1)若购买A,B,C三种型号的盒子的个数分别为2,4,3,则购买费用为元;(2)若一次性购买所需盒子且使购买费用不超过58元,则购买A,B,C三种型号的盒子的个数分别为.(写出一种即可)8.如图,在8个格子中依次放着分别写有字母a~h的小球.甲、乙两人轮流从中取走小球,规则如下:①每人首次取球时,只能取走2个或3个球;后续每次可取走1个,2个或3个球;②取走2个或3个球时,必须从相邻的格子中取走;③最后一个将球取完的人获胜.(1)若甲首次取走写有b,c,d的3个球,接着乙首次也取走3个球,则(填“甲”或“乙”)一定获胜;(2)若甲首次取走写有a,b的2个球,乙想要一定获胜,则乙首次取球的方案是.9.为了鼓励本次模拟练习取得进步的同学,某班决定给该部分同学发放奖品,学习用品商店为了提高营业额,将商品打包促销(每个大礼包限购1个),老师发现了编号分别为A,B,C,D,E,F的六个大礼包中均含有老师需要的一、二、三等奖的奖品,每个大礼包中的各类奖品数量如下:大礼包编号一等奖(个)二等奖(个)三等奖(个)总奖品数(个)A15410B2338C3148D42511E5139F34512该班需要的总的奖品个数不超过41个,且一等奖的个数不少于8个,不超过14个,二等奖的个数不少于7个,不超过13个,且三等奖的个数最多,请同学们帮助老师写出满足条件的购买方案.(写出要购买的大礼包编号)10.现在有三个仓库A1、A2、A3,分别存有7吨、12吨、11吨某原材料;要将这种原材料运往三个加工厂B1、B2、B3,每个加工厂都需要10吨原材料.从每个仓库运送1吨材料到每个加工厂的成本如表所示(单位:元/吨):B1B2B3 A1(7t)126A2(12t)042A3(11t)315现在要让每个仓库清仓、每个加工厂都得到足够的材料,(1)如果从A3运10吨到B1、运1吨到B2,从A1运7吨到B2,那么从A2需要运吨到B2;(2)考虑各种方案,运费最低为元.11.某公园划船项目收费标准如下:船型两人船(限乘两人)四人船(限乘四人)六人船(限乘六人)八人船(限乘八人)每船租金(元/小时)90100130150某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为元.12.盲盒为消费市场注入了活力,既能够营造消费者购物过程中的趣味体验,也为商家实现销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个,搭配为A,B,C三种盲盒各一个,其中A盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音箱;B 盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音箱的数量之比为3:2;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱.经核算,A盒的成本为145元,B盒的成本为245元(每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和),则C盒的成本为元.13.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某校初三(5)班举办了“古诗词”大赛,现有小恩、小王、小奕三位同学进入了最后冠军的角逐,决赛共分为六轮,规定:每轮分别决出第一、二、三名(没有并列),对应名次的得分分别为a,b,c(a>b>c且a,b,c均为正整数)分,选手最后得分为各轮得分之和,得分最高者为冠军.下表是三位选手在每轮比赛中的部分得分情况,小恩同学第三轮的得分为.第一轮第二轮第三轮第四轮第五轮第六轮总分小恩a a27小王a b c11小奕c b10 14.以下是小亮的妈妈做晚饭的食材准备及加工时间列表,有一个炒菜锅,一个电饭煲,一个煲汤锅,两个燃气灶可用,做好这顿晚餐一般情况下至少需要分钟.准备时间(分钟)加工时间(分钟)用时种类米饭330炒菜156炒菜258汤5615.高速公路某收费站出城方向有编号为A,B,C,D,E的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:收费出口编号A,B B,C C,D D,E E,A260330300360240通过小客车数量(辆)在A,B,C,D,E五个收费出口中,每20分钟通过小客车数量最多的一个收费出口的编号是.16.某生产线在同一时间只能生产一笔订单,即在完成一笔订单后才能开始生产下一笔订单中的产品.一笔订单的“相对等待时间”定义为该笔订单的等待时间与生产线完成该订单所需时间之比.例如,该生产线完成第一笔订单用时5小时,之后完成第二笔订单用时2小时,则第一笔订单的“相对等待时间”为0,第二笔订单的“相对等待时间”为,现有甲、乙、丙三笔订单,管理员估测这三笔汀单的生产时间(单位:小时)依次为a,b,c,其中a>b>c,则使三笔订单“相对等待时间”之和最小的生产顺序是.17.某生产基地有五台机器设备,现有五项工作待完成,每台机器完成每项工作获得的效益值如下表所示.若每台机器只完成一项工作,则完成五项工作的效益值总和的最大值为.工作一二三四五效益机器甲1517141715乙2223212020丙913141210丁7911911戊1315141511 18.某学习兴趣小组由学生和教师组成,人员构成同时满足以下三个条件:(ⅰ)男学生人数多于女学生人数;(ⅱ)女学生人数多于教师人数;(ⅲ)教师人数的两倍多于男学生人数,①若教师人数为4,则女学生人数的最大值为;②该小组人数的最小值为.19.某陶艺工坊有A和B两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.大中小尺寸数量(个)款式A81525B01020烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.某批次需要生产10个大尺寸陶艺品,50个中尺寸陶艺品,76个小尺寸陶艺品.(1)烧制这批陶艺品,A款电热窑至少使用次;(2)若A款电热窑每次烧制成本为55元,B款电热窑每次烧制成本为25元,则烧制这批陶艺品成本最低为元.20.某单位有10000名职工,想通过验血的方式筛查出某种病毒的携带者.如果对每个人的血样逐一化验,需要化验10000次.统计专家提出了一种化验方法:随机地按5人一组分组,然后将各组5个人的血样混合再化验.如果混合血样呈阴性,说明这5个人全部阴性;如果混合血样呈阳性,说明其中至少有一个人呈阳性,就需要对这组的每个人再分别化验一次.假设携带该病毒的人数占0.05%.回答下列问题:(1)按照这种化验方法是否能减少化验次数(填“是”或“否”);(2)按照这种化验方法至多需要次化验,就能筛查出这10000名职工中该种病毒的携带者.21.为美化广场环境要建花坛,一个花坛由四季海棠、三色堇、蔷薇三种花卉组成,这三种花卉的盆数同时满足以下三个条件:a.三色堇的盆数多于四季海棠的盆数;b.四季海棠的盆数多于蔷薇的盆数;c.蔷薇盆数的2倍多于三色堇的盆数.①若蔷薇的盆数为4,则四季海棠盆数的最大值为;②一个花坛花盆数量的最小值为.22.某咖啡店提供三种咖啡,其对应两种容量的价格如下表所示:咖啡品种中杯(300ml)大杯(450ml)A30元/杯45元/杯B34元/杯55元/杯C45元/杯65元/杯咖啡店开展回馈活动,凡自备容器购买咖啡者,每种中杯咖啡价格可减免2元、大杯咖啡价格可减免5元.请根据上述信息,回答下列问题:(1)店长收到顾客反映,有的咖啡品种在自备容器后,同种大杯咖啡的每毫升价格还是比中杯的贵,请问是表中的品种(填“A”,“B”或“C”);(2)若要让所有咖啡品种在自备容器后,同种大杯咖啡的每毫升价格都比中杯的便宜,则应将大杯咖啡的价格至少减免元(减免的钱数为整数).23.我校学生会正在策划一次儿童福利院的慰问活动.为了筹集到600元活动资金,学生会计划定制一批穿校服的毛绒小熊和带有校徽图案的钥匙扣,表格中有这两种商品的进价和售价.另外,若将一个小熊和一个钥匙扣组成一份套装出售,则将售价打九折.为了更好的制定进货方案,学生会利用抽样调查的方式统计了校内学生对商品购买意向的百分比情况(见表格),若按照这个百分比情况定制商品,至少定制小熊个和钥匙扣个,才能筹集到600元资金(即获得600元利润).小熊钥匙扣套装进价13316售价16418购买意向40%30%25%24.某超市对某品牌袋装茶叶搞促销活动,商家将该品牌袋装茶叶按以下五种类型出售:A 类只有一袋茶叶,B类有二袋茶叶,C类有三袋茶叶,D类有五袋茶叶,E类有七袋茶叶,价格如表:种类A B C D E 单价(元/类)2036426590小云准备在该超市购买6袋上述品牌的茶叶,则购买茶叶的总费用最低为元.25.某公司生产一种营养品,每日购进所需食材500千克,制成A,B两种包装的营养品,并恰好全部用完.信息如表:规格每包食材含量每包售价A包装1千克45元B包装0.25千克12元已知生产的营养品当日全部售出.若A包装的数量不少于B包装的数量,则A为包时,每日所获总售价最大,最大总售价为元.26.小宜跟几位同学在某快餐厅吃饭,如下为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.A套餐:一份盖饭加一杯饮料B套餐:一份盖饭加一份凉拌菜C套餐:一份盖饭加一杯饮料与一份凉拌菜(1)他们点了份A套餐(用含x或y的代数式表示);(2)若x=6,且A、B、C套餐均至少点了1份,则最多有种点餐方案.27.小周自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为40元/盒、55元/盒、60元/盒、70元/盒.为增加销量,小周对这四种水果进行促销:一次购买水果的总价达到80元,顾客就少付x元.每笔订单顾客网上支付成功后,小周会得到支付款的80%.(1)当x=6时,顾客一次购买草莓和西瓜各1盒,需要支付元;(2)在促销活动中,为保证小周每笔订单得到的金额均不低于促销前总价的七折,则x 的最大值为.28.为了加强学生的交通意识,保证学生的交通安全,某附中和交警大队联合举行了“交通志愿者”活动,选派部分同学和家长志愿者到学校东门和南门的若干个交通路口协助警察维持交通秩序,若每个路口安排4人,那么每个路口安排完后还剩下18人,若每个路口安排6人,那么每个路口安排完后还剩下人数不足4人,若每个路口安排7人,只有最后一个路口不足7人,则这个中学一共选派的同学和家长志愿者的总人数为.29.某快餐店的价目表如下:菜品价格汉堡(个)21元薯条(份)9元汽水(杯)12元1个汉堡+1份薯条(A套餐)28元1个汉堡+1杯汽水(B套餐)30元1个汉堡+1份薯条+1杯汽水(C套餐)38元小明和同学们一共需要10个汉堡,5份薯条,6杯汽水,那么最低需要元.30.某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:车型大巴车(最多可坐55人)中巴车(最多可坐39人)小巴车(最多可坐26人)每车租金(元∕天)900800550则租车一天的最低费用为元.第11页(共11页)。
中考数学成都中考二诊数学专题汇编B卷:填空题(含答案)压轴题

一.填空题(共60小题)1.如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP 交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=.2.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为.3.如图,在Rt△ABC中,∠C=90°,BC=2,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为.4.如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D,若BC=6,sin∠BAC=,则AC=,CD=.5.如图,在Rt△ABC中,∠ACB=90°,AB=,D是CB延长线上一点,以BD为边向上作等边三角形EBD,连接AD,若AD=11,且∠ABE=2∠ADE,则tan∠ADE的值为.6.如图,点A是反比例函数y=(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan ∠OAB=.点C是反比例函数y=(x>0)图象上一动点,连接AC,OC,若△AOC的面积为,则点C的坐标为.7.如图,在等腰Rt△ABC中,AC=BC=6,∠EDF的顶点D是AB的中点,且∠EDF=45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH 沿DH折叠,点G落在点M处,连接AM,若=,则AH的长为.8.如图,直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为.9.如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=(k>0)的图象经过点A、B,则k=.10.如图,四边形ABCD内接于⊙O,对角线AC、BD交于点P,且AB=AD,若AC=7,AB=3,则BC•CD=.11.如图,将反比例函数y=(k>0)的图象向左平移2个单位长度后记为图象c,c与y轴相交于点A,点P为x轴上一点,点A关于点P的对称点B在图象c上,以线段AB为边作等边△ABC,顶点C恰好在反比例函数y=﹣(x>0)的图象上,则k=.12.如图,点O是矩形ABCD的对角线的交点,AB=15,BC=8,直线EF经过点O,分别与边CD,AB相交于点E,F(其中0<DE<).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是,此时折痕EF的长为.13.如图,直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,C是AB的中点,点D在直线y=﹣2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是.14.如图1,点A在第一象限,AB⊥x轴于B点连接OA,将Rt△AOB折叠,使A′点落在x轴上,折痕交AB边于D点,交斜边OA于E点.(1)若A点的坐标为(4,3),当EA′∥AB时点A′的坐标是.(2)若A′与原点O重合,OA=4,双曲线y=(x>0)的图象恰好经过D,E两点(如图2),则k =.15.如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=24cm,点P为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长为;现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当α从0°到90°的变化过程中,点Q移动的路径长为.(结果保留根号)16.为了庆祝“六一儿童节”,育才初一年级同学在班会课进行了趣味活动,小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=4cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为.17.如图,在Rt△ABC中,∠ACB=90°,D为AB边上一点,且点D到BC的距离等于点D到AC的距离.将△ABC绕点D旋转得到△A′B′C′,连接BB′,CC′.若=,则的值为.18.已知直线y=kx+2与y轴交于点A,与双曲线y=相交于B,C两点,若AB=3AC,则k的值为.19.如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为.20.如图,点O为坐标原点,▱ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=(x>0)的图象经过点C且S△BEF=,则k的值为.21.如果点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点.已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF的费马点,则PD+PE+PF=.22.一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是.现将三角板DEF 绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为.(结果保留根号)23.如图所示,在△ABC中,∠B=90°,BA=BC=2,以B为圆心作圆B与AC相切,点P是圆B上任一动点,连接P A、PC,则P A+PC的最小值为.24.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y=9x﹣1的图象上,则点P的坐标为.25.如图,在△ABC中,D,E分别是△ABC两边的中点,如果(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称为△ABC的中内弧,例如,图中是△ABC其中的某一条中内弧.若在平面直角坐标系中,已知点F(0,4),O(0,0),H(4,0),在△FOH中,M,N分别是FO,FH 的中点,△FOH的中内弧所在圆的圆心P的纵坐标m的取值范围是.26.已知,△ABC和△ADE均为等腰三角形,AB=AC=5,AD=AE=2,且∠BAC=∠DAE=120°,把△ADE绕点A在平面内自由旋转.如图,连接BD,CD,CE,点M,P,N分别为DE,DC,BC的中点,连接MP,PN,MN,则△PMN的面积最大值为.27.△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN②③△PMN为等边三角形④若BN=CP,则∠ACB=75°.则正确结论是.28.如图,点A、B在x轴的上方,∠AOB=90°,OA、OB分别与函数y=、y=﹣的图象交于A、B 两点,以OA、OB为邻边作矩形AOBC.当点C在y轴上时,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则=.29.已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:①2a+b<0;②﹣1≤a≤﹣;③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.其中结论正确的序号是.30.如图,在△ABC中,已知AB=AC=6,BC=8,P是BC边上的一动点(P不与点B、C重合),∠B=∠APE,边PE与AC交于点D,当△APD为等腰三角形时,则PB的长为.31.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在边BC上,且BM=b,连AM、MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF.给出以下四个结论:①∠MAD=∠AND;②CP=b﹣;③△ABM≌△NGF;④A、M、P、D 四点共圆,其中正确的结论是(填序号).32.如图,反比例函数y=(x>0)经过A、B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD、AB,已知AC=1,BE=1,S矩形BEOD=4,则点D到AB的最短距离为.33.如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是.34.在直角坐标系中,我们将圆心坐标和半径均为整数的圆称为“整圆”.如图所示,直线l:y=kx+4与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是个.35.如图,四边形ABCD内接于以AC为直径的⊙O,AD=,CD=2,BC=BA,AC与BD相交于点F,将△ABF沿AB翻折,得到△ABG,连接CG交AB于E,则BE长为.36.如图,在△AOC中,∠OAC=90°,AO=AC,OC=2,将△AOC放置于平面直角坐标系中,点O与坐标原点重合,斜边OC在x轴上.反比例函数y=(x>0)的图象经过点A.将△AOC沿x轴向右平移2个单位长度,记平移后三角形的边与反比例函数图象的交点为A1,A2.重复平移操作,依次记交点为A3,A4,A5,A6…分别过点A,A1,A2,A3,A4,A5…作x轴的垂线,垂足依次记为P,P1,P2,P3,P4,P5…若四边形APP1A1的面积记为S1,四边形A2P2P3A3的面积记为S2…,则S n=.(用含n 的代数式表示,n为正整数)37.如图,在矩形ABCD中,AB=9,AD=6,点O为对角线AC的中点,点E在DC的延长线上且CE=1.5,连接OE,过点O作OF⊥OE交CB延长线于点F,连接FE并延长交AC的延长线于点G,则=.38.如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD 上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=的解析式为.39.如图,曲线l是由函数y=在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4,4),B(2,2)的直线与曲线l相交于点M、N,则△OMN的面积为.40.已知一个矩形纸片ABCD,AB=12,BC=6,点E在BC边上,将△CDE沿DE折叠,点C落在C'处;DC',EC'分别交AB于F,G,若GE=GF,则sin∠CDE的值为.41.如图,在△ABC中,已知AB=AC=4,BC=6,P是BC边上的一动点(P不与点B、C重合),连接AP,∠B=∠APE,边PE与AC交于点D,当△APD为等腰三角形时,则PB之长为.42.如图,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q 从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示,给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=24cm2;③当14<t<22时,y=100﹣6t;④在运动过程中,使得△ABP是等腰三角形的P点一共3个;⑤当△BPQ与△BEA相似时,t=14.5,其中正确结论的序号是.43.如图,在矩形ABCD中,AB=2,BC=2,将矩形ABCD绕点C顺时针旋转,得到矩形A1B1CD1,点E是A1B1的中点,过B作BF⊥B1C于点F,连接DE,DF,则线段DE长度的最大值是,线段DF长度的最小值是.44.如图,已知直线AB交x轴于点A,分别与函数y=(x>0,a>0)和y=(x>0,b>a>0)的图象相交于点B,C,过点B作BD∥x轴交函数y=的图象于点D,过点C作CE∥x轴交函数y=的图象于点E,连接AD,BE,若=,S△ABD=2,则S△BCE=.45.如图,在矩形ABCD中,AB=3,AD=4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,连接PD,PG,则PD+PG的最小值为.46.如图,一次函数y=kx+4的图象与反比例函数y=(x>0,m>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,点E为线段AB的中点,点P(2,0)是x轴上一点,连接EP.若△COD的面积是△AOB的面积的倍,且AB=2PE,则m的值为.47.如图,在等腰直角三角形ABC中,∠ACB=90°,在△ABC内一点P,已知∠1=∠2=∠3,将△BCP 以直线PC为对称轴翻折,使点B与点D重合,PD与AB交于点E,连接AD,将△APD的面积记为S1,将△BPE的面积记为S2,则的值为.48.已知一次函数y=﹣x+m的图象与反比例函数y=的图象交于A、B两(点A在点B的左侧),点P 为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为.49.如图,△ABC,△EFG分别是边长为2和1的等边三角形,D是边BC,EF的中点,直线AG,FC相交于点M,当△EFG绕点D旋转一周时,点M经过的路径长为.50.如图,过原点的直线与反比例函数y=(x>0)、反比例函数y=(x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y=(x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为.51.如图,二次函数Y=﹣x2﹣x+2象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是.52.如果m,n是两个不相等的实数,且满足m2﹣m=3,n2﹣n=3,那么代数式n3+4m+2019=.53.已知:如图,△ABC中,∠A=45°,AB=6,AC=,点D、E、F分别是三边AB、BC、CA上的点,则△DEF周长的最小值是.54.若关于x的不等式组无解,且关于y的分式方程有正整数解,则满足条件的整数a的值为.55.如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM=.56.如图,反比例函数y=图象与直线y=﹣x交于A,B两点,将双曲线右半支沿射线AB方向平移与左半支交于C,D.点A到达A′点,A′B=BO,CE=6,则k=.57.如图,在平面直角坐标系中,矩形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,AC长为,若将边AC平移至A'C'处,此时A'坐标为(﹣4,2),分别连接A'B,C'O,反比例函数y=的图象与四边形A'BOC'对角线A'O交于D点,连接BD.则当BD取得最小值时,k的值是.58.如图,在Rt△ABC中,∠C=90°,AC=4,cos A=,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为.59.如图所示,直线y=x分别与双曲线y=(k1>0,x>0),双曲线y=(k2>0,x>0)交于点A、点B,且OA=2AB,将直线向上平移2个单位长度后,与双曲线y=交于点C,若S△ABC=1,则k1k2的值为.60.已知如图,正方形ABCD的边长为4,取AB边上的中点E,连接CE,过点B作BF⊥CE于点F,连接DF.过点A作AH⊥DF于点H,交CE于点M,交BC于点N,则MN=.参考答案一.填空题(共60小题)1.;2.2;3.3或;4.3;;5.;6.(4,)或(1,10);7.或或3;8.﹣;9.﹣1;10.40;11.2;12.;;13.3;14.(,0);;15.24(﹣1)cm;4cm;16.2﹣;17.;18.1或﹣;19.7+;20.12;21.+1;22.(12﹣12)cm;(12﹣18)cm;23.;24.(3,3);25.m≤1或m≥2;26.;27.①②③④;28.4;29.②③;30.2或;31.①②③④;32.2;33.;34.6;35.;36.;37.;38.y=;39.8;40.;41.2或;42.①②⑤;43.2+;﹣;44.;45.3﹣2;46.m=2或6;47.;48.4或﹣4;49.π;50.4﹣4;51.8;52.2026;53.;54.﹣8、0、4;55.或;56.﹣;57.﹣;58.1或3;59.9;60.1;。
中考数学选择填空压轴题专题(含答案)

专题01代数式的求值问题例1.观察下列等式:1=2=3=4=5=6=64,…,根据这个规律,则1)+2\S\UP6(2)+2\S\UP6(3)+2\S\UP6(4)+…+2\S\UP6(2017的末位数字是()A.0 B.2 C.4 D.6同类题型1.1计算:1=2=3=4=5=31,…归纳各计算结果中的个位数字规律,猜测2016的个位数字是()A.1 B.3 C.7 D.5同类题型1.2观察下列算式1=2=3=4=5=6=7=2187…根据上述算式中的规律,你认为2018的末位数字是()A.3 B.9 C.7 D.1例2.下列定义一种关于n的运算:①当n是奇数时,结果为3n+5②n为偶数时结果是n2\S\UP6(k)(其中k是使n2\S\UP6(k)是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是()A.1 B.2 C.7 D.8同类题型2.1定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为n2\S\UP6(k) (其中k是使n2\S\UP6(k)为奇数的正整数),并且运算重复进行.例如,取n=26,那么当n=26时,第2016次“F运算”的结果是________.同类题型2.2对于任意正整数n,定义"n!!"如下:当n是偶数时,n!!=n﹒(n-2)﹒(n-4)…6﹒4﹒2,当n是奇数时,n!!=n﹒(n-2)﹒(n-4)…5﹒3﹒1,且有n!=n﹒(n-1)﹒(n-2)…3﹒2﹒1则有四个命题:①(2015!!)﹒(2016!!)=2016!②2016!!=2018③2015!!的个位数是5④2014!!的个位数是0其中正确的命题有()A.1个B.2个C.3个D.4个例3.一列数123满足条件:1=12n=1n-1且n为整数),则2017等于()A.-1 B.12C.1 D.2同类题型 3.1一列数123满足条件:1=12n=1n-1且n为整数),则1)+a\S\DO(2)+a\S\DO(3)+…+a\S\DO(2017=________.同类题型3.2 1、2、3、20是20个由1,0,-1组成的数,且满足下列两个等式:①1)+x\S\DO(2)+x\S\DO(3)+…+x\S\DO(20=4,②(\l(x\S\DO(1)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(2)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(3)-1))\S\UP6(2)+…+\b\bc\((\l(x\S\DO(20)-1))\S\UP6(2=32,则这列数中1的个数为()A.8 B.10 C.12 D.14例4.设△ABC的面积为1.如图1,分别将AC,BC边2等分1),E\S\DO(1是其分点,连接1)BD\S\DO(1交于点1得到四边形1)F\S\DO(1)E\S\DO(1其面积1=13.如图2,分别将AC,BC边3等分1),D\S\DO(2),E\S\DO(1),E\S\DO(2是其分点,连接2)BD\S\DO(2交于点2得到四边形2)F\S\DO(2)E\S\DO(2其面积2=16如图3,分别将AC,BC边4等分1),D\S\DO(2),D\S\DO(3),E\S\DO(1),E\S\DO(2),E\S\DO(3是其分点,连接3)BD\S\DO(3交于点3得到四边形3)F\S\DO(3)E\S\DO(3其面积3=110…按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形n)F\S\DO(n)E\S\DO(n其面积n =________.同类题型4.1庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=112)3)n.4.2图图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作1于点1再过点1作1)C\S\DO(2于点2又过点2作2)C\S\DO(3于点3如此无限继续下去,则可将利△ABC分割成1、1)C\S\DO(2、1)C\S\DO(2)C\S\DO(3、2)C\S\DO(3)C\S\DO(4、…、n-2)C\S\DO(n-1)C\S\DO(n、….假设AC=2,这些三角形的面积和可以得到一个等式是________________________________.同类题型4.2 如图,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,如此操作下去,则第n个小三角形的面积为________.例5.如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的()A.aa+b B.ba+b C.ha+b D.ha+h例5图 5.1图同类题型5.1如图,一个啤酒瓶的高度为30cm,瓶中装有高度12cm的水,将瓶盖盖好后倒置,这时瓶中水面高度20cm,则瓶中水的体积和瓶子的容积之比为________.(瓶底的厚度不计)同类题型5.2一艘轮船往返甲、乙两港之间,第一次往返航行时,水流速度为a千米/时,第二次往返航行时,正遇上发大水,水流速度为b千米/时(b>a),已知该船在两次航行中的静水速度相同,则该船这两次往返航行所用时间的关系是()A.第一次往返航行用的时间少B.第二次往返航行用的时间少C.两种情况所用时间相等D.以上均有可能例6.若1x=3,求2)x\S\UP6(4)+x\S\UP6(2)+1的值是()A.18 B.110 C.12 D.14同类题型6.1 已知a,b,c满足|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2=2+2ac,则a-b+c的值为()A.2 B.4 C.6 D.8同类题型6.2已知a,b,c满足ab-ca+c5,则a+c2a+b的值为()A.12 B.34 C.1 D.2参考答案例1.观察下列等式:1=2=3=4=5=6=64,…,根据这个规律,则1)+2\S\UP6(2)+2\S\UP6(3)+2\S\UP6(4)+…+2\S\UP6(2017的末位数字是()A.0 B.2 C.4 D.6解:∵1=2=3=4=5=6=64,…,∴2017÷4=504…1,∵(2+4+8+6)×504的末尾数字是0,∴1)+2\S\UP6(2)+2\S\UP6(3)+2\S\UP6(4)+…+2\S\UP6(2017的末位数字是2,选B.同类题型1.1计算:1=2=3=4=5=31,…归纳各计算结果中的个位数字规律,猜测2016的个位数字是()A.1 B.3 C.7 D.5解:∵1=2=3=4=15,5=6=7=8=255…∴由此可以猜测个位数字以4为周期按照1,3,7,5的顺序进行循环,知道2016除以4为504,而第4个数字为5,所以可以猜测2016的个位数字是5.选D.同类题型1.2观察下列算式1=2=3=4=5=6=7=2187…根据上述算式中的规律,你认为2018的末位数字是()A.3 B.9 C.7 D.1解:以3为底的幂的末位数字是3,9,7,1依次循环的,2018÷4=504…2,所以2018的个位数字是9,选B.例2.下列定义一种关于n的运算:①当n是奇数时,结果为3n+5②n为偶数时结果是n2\S\UP6(k)(其中k是使n2\S\UP6(k)是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是()A.1 B.2 C.7 D.8解:第一次:3×449+5=1352,第二次:1352k根据题意k=3时结果为169;第三次:3×169+5=512,第四次:因为512是2的9次方,所以k=9,计算结果是1;第五次:1×3+5=8;第六次:8k因为8是2的3次方,所以k=3,计算结果是1,此后计算结果8和1循环.因为449是奇数,所以第449次运算结果是8.选D.同类题型2.1定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为n2\S\UP6(k) (其中k是使n2\S\UP6(k)为奇数的正整数),并且运算重复进行.例如,取n=26,那么当n=26时,第2016次“F运算”的结果是________.解:根据题意,得当n=26时,第1次的计算结果是262=13,第2次的计算结果是13×3+5=44,第3次的计算结果是442\S\UP6(2)=11,第4次的计算结果是11×3+5=38,第5次的计算结果是382=19,第6次的计算结果是19×3+5=62,第7次的计算结果是622=31,第8次的计算结果是31×3+5=98,第9次的计算结果是982=49,第10次的计算结果是49×3+5=152,第11次的计算结果是1522\S\UP6(3)=19,以下每6次运算一循环,∵(2016-4)÷6=335…2,∴第2016次“F运算”的结果与第6次的计算结果相同,为62,故答案为:62.同类题型2.2对于任意正整数n,定义"n!!"如下:当n是偶数时,n!!=n﹒(n-2)﹒(n-4)…6﹒4﹒2,当n是奇数时,n!!=n﹒(n-2)﹒(n-4)…5﹒3﹒1,且有n!=n﹒(n-1)﹒(n-2)…3﹒2﹒1则有四个命题:①(2015!!)﹒(2016!!)=2016!②2016!!=2018③2015!!的个位数是5④2014!!的个位数是0其中正确的命题有()A.1个B.2个C.3个D.4个解:根据题意,依次分析四个命题可得:对于①,(2015!!)﹒(2016!!)=(2﹒4﹒6﹒8…2008﹒2010﹒2012﹒2014﹒2016)﹒(1﹒3﹒5﹒7…2009﹒2011﹒2013﹒2015)=1﹒2﹒3﹒4﹒5…﹒2012﹒2013﹒2014﹒2015﹒2016=2016!,故①正确;对于②,2016!!=2﹒4﹒6﹒8﹒10…2008﹒2010﹒2012﹒2014﹒2016=1008)(1﹒2﹒3﹒4…1008=1008故②正确;对于③,2015!=2015×2011×2009×…×3×1,其个位数字与1×3×5×7×9的个位数字相同,故其个位数字为5,故正确;对于④,2014!!=2﹒4﹒6﹒8…2008﹒2010﹒2012﹒2014,其中含有10,故个位数字为0,故正确;选D.例3.一列数123满足条件:1=12n=1n-1且n为整数),则2017等于()A.-1 B.12C.1 D.2解:∵1=12n=1n-1∴2=11-a\S\DO(1)=112=2,3=11-a\S\DO(2)=11-2=-1,4=11-a\S\DO(3)=11-(-1)=12…∴这列数每3个数为一循环周期,∵2017÷3=672…1,∴2017=1=12选B.同类题型 3.1一列数123满足条件:1=12n=1n-1且n为整数),则1)+a\S\DO(2)+a\S\DO(3)+…+a\S\DO(2017=________.解:∵1=12n=1n-1∴2=11-a\S\DO(1)=112=2,3=11-a\S\DO(2)=11-2=-1,4=11-a\S\DO(3)=11-(-1)=12…∴这列数每3个数为一循环周期,∵2017÷3=672…1,∴2017=1=12又∵1)+a\S\DO(2)+a\S\DO(3=12=32∴1)+a\S\DO(2)+a\S\DO(3)+…+a\S\DO(2017=312=12.答案为12.同类题型3.2 1、2、3、20是20个由1,0,-1组成的数,且满足下列两个等式:①1)+x\S\DO(2)+x\S\DO(3)+…+x\S\DO(20=4,②(\l(x\S\DO(1)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(2)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(3)-1))\S\UP6(2)+…+\b\bc\((\l(x\S\DO(20)-1))\S\UP6(2=32,则这列数中1的个数为()A.8 B.10 C.12 D.14解:∵1、2、3、20是20个由1,0,-1组成的数,且满足下列两个等式:①1)+x\S\DO(2)+x\S\DO(3)+…+x\S\DO(20=4,②(\l(x\S\DO(1)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(2)-1))\S\UP6(2)+\b\bc\((\l(x\S\DO(3)-1))\S\UP6(2)+…+\b\bc\((\l(x\S\DO(20)-1))\S\UP6(2=32,∴-1的个数有8个,则1的个数有12个.故选C.例4.设△ABC的面积为1.如图1,分别将AC,BC边2等分1),E\S\DO(1是其分点,连接1)BD\S\DO(1交于点1得到四边形1)F\S\DO(1)E\S\DO(1其面积1=13.如图2,分别将AC,BC边3等分1),D\S\DO(2),E\S\DO(1),E\S\DO(2是其分点,连接2)BD\S\DO(2交于点2得到四边形2)F\S\DO(2)E\S\DO(2其面积2=16如图3,分别将AC,BC边4等分1),D\S\DO(2),D\S\DO(3),E\S\DO(1),E\S\DO(2),E\S\DO(3是其分点,连接3)BD\S\DO(3交于点3得到四边形3)F\S\DO(3)E\S\DO(3其面积3=110…按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形n)F\S\DO(n)E\S\DO(n其面积n =________.解:如图所示,连接12)E\S\DO(23∵图1中1),E\S\DO(1是△ABC两边的中点,∴1)∥ABD\S\DO(1)E\S\DO(1=12∴1)E\S\DO(1且1)E\S\DO(1)BF\S\DO(1)=1)E\S\DO(1)AB=12∴△CD1E1=14)S\S\DO(△ABC=14∵1是BC的中点,∴△BD1E1=△CD1E1=14∴△D1E1F1=13)S\S\DO(△BD1E1=114=112∴1=△CD1E1)+S\S\DO(△D1E1F1=1112=13同理可得:图2中2=△CD2E2)+S\S\DO(△D2E2F2=1118=16图3中3=△CD3E3)+S\S\DO(△D3E3F3=1380=110以此类推,将AC,BC边(n+1)等分,得到四边形n)E\S\DO(n)F\S\DO(n其面积n=1n+1)\S\UP6(2)n+1)\S\UP6(2)1+n+1=2n+1)(n+2答案为2(n+1)(n+2).同类题型4.1庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=112)3)n.图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作1于点1再过点1作1)C\S\DO(2于点2又过点2作2)C\S\DO(3于点3如此无限继续下去,则可将利△ABC分割成1、1)C\S\DO(2、1)C\S\DO(2)C\S\DO(3、2)C\S\DO(3)C\S\DO(4、…、n-2)C\S\DO(n-1)C\S\DO(n、….假设AC=2,这些三角形的面积和可以得到一个等式是________.解:如图2,∵AC=2,∠B=1∴1中1=30°,且BC=3∴1=12=1=3)AC\S\DO(1=3∴△ACC1=12)﹒AC\S\DO(1)﹒CC\S\DO(1=13=32∵1)C\S\DO(2∴1)C\S\DO(2=1=30°,∴2=12)CC\S\DO(1=321=3)CC\S\DO(2=32∴△CC)\S\DO(1)C\S\DO(2=12)﹒CC\S\DO(2)﹒C\S\DO(1)C\S\DO(2=1\R(332=334同理可得,△C)\S\DO(1)C\S\DO(2)C\S\DO(3=3(\l(\F(32△C)\S\DO(2)C\S\DO(3)C\S\DO(4=3(\l(\F(33…∴△C)\S\DO(n-2)C\S\DO(n-1)C\S\DO(n=3(\l(\F(3n-1又∵△ABC=12=13=3∴3=3\R(33\R(3(\l(\F(323(\l(\F(333(\l(\F(3n-1∴3=3\l(1+\F(3(\l(\F(323n-1n)+….答案为3=3\l(1+\F(3(\l(\F(323n-1n)+….同类题型4.2 如图,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,如此操作下去,则第n个小三角形的面积为________.解:记原来三角形的面积为s,第一个小三角形的面积为1第二个小三角形的面积为2∵1=14=122=114=143=16∴n=12\S\UP6(2n)=12n)2=12n-1答案为12\S\UP6(2n-1).例5.如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的()A.aa+b B.ba+b C.ha+b D.ha+h解:设规则瓶体部分的底面积为S平方厘米.倒立放置时,空余部分的体积为bS立方厘米,正立放置时,有墨水部分的体积是aS立方厘米,因此墨水的体积约占玻璃瓶容积的asas+bs=aa+b.选A.同类题型5.1如图,一个啤酒瓶的高度为30cm,瓶中装有高度12cm的水,将瓶盖盖好后倒置,这时瓶中水面高度20cm,则瓶中水的体积和瓶子的容积之比为________.(瓶底的厚度不计)解:设瓶的底面积为2,则左图V水=12S cm3,右图V空=10S cm3,∵V瓶=V水+V空=22S cm3,∴V水:V瓶=6:11.故答案为611.同类题型5.2一艘轮船往返甲、乙两港之间,第一次往返航行时,水流速度为a千米/时,第二次往返航行时,正遇上发大水,水流速度为b千米/时(b>a),已知该船在两次航行中的静水速度相同,则该船这两次往返航行所用时间的关系是()A.第一次往返航行用的时间少B.第二次往返航行用的时间少C.两种情况所用时间相等D.以上均有可能解:设两次航行的路程都为S,静水速度设为v,第一次所用时间为:SS2vS2)-a\S\UP6(2第二次所用时间为:SS2vS2)-b\S\UP6(2∵b>a,∴2)>a\S\UP6(2,∴2)-b\S\UP6(2)<v\S\UP6(2)-a\S\UP6(2∴2vS2)-b\S\UP6(2)2)-a\S\UP6(2∴第一次的时间要短些.选A.例6.若1x=3,求2)x\S\UP6(4)+x\S\UP6(2)+1的值是()A.18 B.110 C.12 D.14解:∵1x=3,∴1x))\S\UP6(2=9,即1x\S\UP6(2)=9-2=7,∴4)+x\S\UP6(22))=x\S\UP6(22=7+1=8,∴24)+x\S\UP6(2)+18.选A.同类题型6.1 已知a,b,c满足|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2=2+2ac,则a-b+c的值为()A.2 B.4 C.6 D.8解:∵已知a,b,c满足|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2=2+2ac,∴|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2-2ac=2,…①且(a-3)b\S\UP6(2)必有意义,又∵2≥0,∴a-3≥0①当a-3>0时,|2a-4|>2,有|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2-2ac>2,则这与①式相矛盾,即a-3>0不成立;②当a-3=0时,a=3,则|2a-4|+|b+2|(a-3)b\S\UP6(2))+a\S\UP6(2)+c\S\UP6(2-2ac=2+|b+2|2=2,|b+2|2=0,又∵|b+2|≥0,2≥0,∴必有b+2=0,c-3=0即:b=-2,c=3∴a-b+c=3-(-2)+3=8选D.同类题型6.2已知a,b,c满足ab-ca+c5,则a+c2a+b的值为()A.12 B.34 C.1 D.2解:设ab-ca+c5=k,则a=2k①,b-c=3k②,a+c=5k③.①+②+③得:2a+b=10k.∴a+c5k12.选A.专题02方程、不等式中的含参问题例1.已知三个非负实数a,b,c满足:3a+2b+c=5和2a+b-3c=1,若m=3a+b-7c,则m的最小值为__________.同类题型1.1 已知x+2y-3z=0,2x+3y+5z=0,则x+y+zx-y+z=________.同类题型1.2 方程组4x+3m=28x-3y=m)的解x,y满足x>y,则m的取值范围是()A.910 B.109 C.1910 D.1019例2.关于x的方程2+mx-9=0和2)-3x+m\S\UP6(2+6m=0有公共根,则m的值为________.同类题型2.1 已知a是一元二次方程2-2018x+1=0的一个根,则代数式2018a\S\UP6(2)+1的值是___.同类题型2.2 已知关于x的方程2)-1)x\S\UP6(2+(2k-1)x+1=0有两个不相等的实数根,那么实数k的取值范围为_____________.同类题型2.3 已知α、β是方程2-2x-4=0的两个实数根,则3+8β+6的值为()A.-1B.2C.22D.30例3.已知方程11a的两根分别为a,1a,则方程11a-1的根是()A.a,1a-1 B.1a-1,a-1C.1a,a-1D.a,aa-1同类题型3.1 若关于x的方程2x-bx-1=3的解是非负数,则b的取值范围是________.同类题型3.2 观察分析下列方程:①2x=3;②6x=5;③12x=7.请利用它们所蕴含的规律,求关于x的方程2)+nx-4=2n+5(n为正整数)的根,你的答案是_________________.同类题型3.3 已知关于x的方程2a+13a x-1)(x+2只有整数解,则整数a的值为_____________.例4.[x]表示不超过x的最大整数.如,[π]=3,[2]=2,[-2.1]=-3.则下列结论:①[-x]=-[x];②若[x]=n,则x的取值范围是n≤x<n+1;③当-1<x<1时,[1+x]+[1-x]的值为1或2;④x=-2.75是方程4x-2[x]+5=0的唯一一个解.其中正确的结论有_________(写出所有正确结论的序号).同类题型4.1 设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,(x)表示最接近x的整数(x ≠n+0.5,n为整数).例如[3.4]=3,{3.4}=4,(3.4)=3.则不等式8≤2x+[x]+3{x}+4(x)≤14的解为()A.0.5≤x≤2 B.0.5<x<1.5或1.5<x<2C.0.5<x<1.5D.1.5<x<2同类题型4.2规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是___________.(写出所有正确说法的序号)①当x=1.7时,[x]+(x)+[x)=6;②当x=-2.1时,[x]+(x)+[x)=-7;③方程4[x]+3(x)+[x)=11的解为1<x<1.5;④当-1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.同类题型4.3 如果关于x的不等式(a+b)x+2a-b>0的解集是52,那么关于x的不等式(b-a)x+a +2b≤0的解集是____________.同类题型4.4 若关于x的不等式组\F(x+4x2x-a<0解集为x<2,则a的取值范围是___________.同类题型4.5 按如图的程序计算,若开始输入的值x为正数,最后输出的结果为656,则满足条件的x的不同值最多有___________.参考答案例1.已知三个非负实数a,b,c满足:3a+2b+c=5和2a+b-3c=1,若m=3a+b-7c,则m的最小值为__________.解:由题意可得3a+2b+c=52a+b-3c=1m=3a+b-7c,解得7﹒(m+2)3-3,11﹒(m+2)3,m+23,由于a,b,c是三个非负实数,∴a≥0,b≥0,c≥0,∴157.所以m_(最小值)=57.故本题答案为:-57.同类题型1.1 已知x+2y-3z=0,2x+3y+5z=0,则x+y+zx-y+z=________.解:由题意得:x+2y-3z=0①2x+3y+5z=0②),①×2-②得y=11z,代入①得x=-19z,原式x+y+z-19z+11z+z729.同类题型1.2 方程组4x+3m=28x-3y=m)的解x,y满足x>y,则m的取值范围是()A.910 B.109 C.1910 D.1019解:4x+3m=2①8x-3y=m②)由①得2-3m4,代入②得,2-3m4-3y=m,4-7m3.∵x>y,即2-3m4-7m3,解得1019.选D.例2.关于x的方程2+mx-9=0和2)-3x+m\S\UP6(2+6m=0有公共根,则m的值为________.解:设这个公共根为α.则方程2+mx-9=0的两根为α、-m-α;方程2)-3x+m\S\UP6(2+6m=0的两根为α、3-α,由根与系数的关系有:α(-m-α)=-9,2+6m,整理得,2+mα=9①,2)-3α+m\S\UP6(2+6m=0②,②-①得,2+6m-3α-mα=-9,即2-α(m+3)=0,(m+3)(m+3-α)=0,所以m+3=0或m+3-α=0,解得m=-3或α=m+3,把α=m+3代入①得,2+m(m+3)=9,2)+6m+9+m\S\UP6(2+3m=9,m(2m+9)=0,所以m=0或2m+9=0,解得m=0或m=-4.5,综上所述,m的值为-3,0,-4.5.同类题型2.1 已知a是一元二次方程2-2018x+1=0的一个根,则代数式2018a\S\UP6(2)+1的值是___.解:由题意,把根a代入2-2018x+1=0,可得:2-2018a+1=0,∴2-2017a-a+1=0,2+1=2018a;∴2-2017a=a-1,∴20182)+11a-122018a a-1=2018-1,=2017.同类题型2.2 已知关于x的方程2)-1)x\S\UP6(2+(2k-1)x+1=0有两个不相等的实数根,那么实数k的取值范围为_____________.解:由题意知,k≠±1,2)-4(k\S\UP6(2-1)=5-4k>0∴54且k≠±1.同类题型2.3 已知α、β是方程2-2x-4=0的两个实数根,则3+8β+6的值为()A.-1 B.2 C.22 D.30解:∵α、β是方程2-2x-4=0的两个实数根,∴α+β=2,2-2α-4=0,∴2=2α+4∴3)+8β+6=α﹒α\S\UP6(2+8β+6=α﹒(2α+4)+8β+62+4α+8β+6=2(2α+4)+4α+8β+6=8α+8β+14=8(α+β)+14=30,故选D.例3.已知方程11a的两根分别为a,1a,则方程11a-1的根是()A.a,1a-1 B.1a-1,a-1 C.1a,a-1 D.a,aa-1解:方程11a-1可以写成11a-1的形式,∵方程11a的两根分别为a,1a,∴方程11a-1的两根的关系式为x-1=a-1,1a-1,即方程的根为x=a或aa-1,∴方程11a-1的根是a,aa-1.选D.同类题型3.1 若关于x的方程2x-bx-1=3的解是非负数,则b的取值范围是________.解:去分母得,2x-b=3x-3∴x=3-b∵x≥0∴3-b≥0解得,b≤3又∵x-1≠0∴x≠1即3-b≠1,b≠2则b的取值范围是b≤3且b≠2.同类题型3.2 观察分析下列方程:①2x=3;②6x=5;③12x=7.请利用它们所蕴含的规律,求关于x的方程2)+nx-4=2n+5(n为正整数)的根,你的答案是_________________.解:1×2x=3,解得:x=2或x=1;2×3x=5,解得:x=2或x=3;3×4x=7,解得:x=3或x=4,得到规律mnx=m+n的解为:x=m或x=n,所求方程整理得:n(n+1)x-4=2n+1,根据规律得:x-4=n或x-4=n+1,解得:x=n+4或x=n+5.同类题型3.3 已知关于x的方程2a+13a x-1)(x+2只有整数解,则整数a的值为_____________.解:方程两边同乘以(x-1)(x+2),得:2(x+2)-(a+1)(x-1)=3a,解得:2a-531-a,∵方程只有整数解,∴1-a=3或1或-3或-1,当1-a=3,即a=-2时,x=-2-1=-3,检验,将x=-3代入(x-1)(x+2)=4≠0,故x=-3是原分式方程的解;当1-a=1,即a=0时,x=-2-3=-5,检验,将x=-5代入(x-1)(x+2)=18≠0,故x=-7是原分式方程的解;当1-a=-3,即a=4时,x=-2+1=-1,检验,将x=-1代入(x-1)(x+2)=-2≠0,故x=-1是原分式方程的解;当1-a=-1,即a=2时,x=1,检验,将x=1代入(x-1)(x+2)=0,故x=1不是原分式方程的解;∴整数a的值为:-2,0或4.例4.[x]表示不超过x的最大整数.如,[π]=3,[2]=2,[-2.1]=-3.则下列结论:①[-x]=-[x];②若[x]=n,则x的取值范围是n≤x<n+1;③当-1<x<1时,[1+x]+[1-x]的值为1或2;④x=-2.75是方程4x-2[x]+5=0的唯一一个解.其中正确的结论有_________(写出所有正确结论的序号).解:①当x=-3.5时,[-3.5]=-4,-[x]=-3,不相等,故原来的说法错误;②若[x]=n,则x的取值范围是n≤x<n+1是正确的;③当-1<x<0时,[1+x]+[1-x]=0+1=1;当x=0时,[1+x]+[1-x]=1+1=2;当0<x<1时,[1+x]+[1-x]=1+0=1;故当-1<x<1时,[1+x]+[1-x]的值为1或2是正确的;④x-[x]的范围为0~1,4x-2[x]+5=0,-5≤2x<-7,即-2.5≤x<-3.5,x=-2.75或x=-3.25都是方程4x-2[x]+5=0,故原来的说法错误.故答案为:②③.同类题型4.1 设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,(x)表示最接近x的整数(x ≠n+0.5,n为整数).例如[3.4]=3,{3.4}=4,(3.4)=3.则不等式8≤2x+[x]+3{x}+4(x)≤14的解为()A.0.5≤x≤2 B.0.5<x<1.5或1.5<x<2C.0.5<x<1.5 D.1.5<x<2解:根据题意得:x>0,若x≥2,则2x≥4,[x]≥2,3{x}≥6,4(x)≥8,不等式不成立.故只需分析0<x<2时的情形即可,①0<x≤0.5时,不等式可化为:8≤2x+0+3+0≤14,解得:2.5≤x≤5.5,不符合不等式;②当0.5<x≤1时,不等式可化为:8≤2x+0+3+4≤14,解得:0.5≤x≤3,因此0.5<x≤1,符合不等式;③当1<x<1.5时,不等式可化为:8≤2x+1+6+4≤14,解得:-1.5≤x≤1.5,因此1<x<1.5,符合不等式;④当1.5<x<2时,不等式可化为:8≤2x+1+6+8≤14,解得:-3.5≤x≤-0.5,不符合不等式.故原不等式的解集为:0.5<x<1.5.故选C.同类题型4.2规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是___________.(写出所有正确说法的序号)①当x=1.7时,[x]+(x)+[x)=6;②当x=-2.1时,[x]+(x)+[x)=-7;③方程4[x]+3(x)+[x)=11的解为1<x<1.5;④当-1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.解:①当x=1.7时,[x]+(x)+[x)=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;②当x=-2.1时,[x]+(x)+[x)=[-2.1]+(-2.1)+[-2.1)=(-3)+(-2)+(-2)=-7,故②正确;③4[x]+3(x)+[x)=11,7[x]+3+[x)=11,7[x]+[x)=8,1<x<1.5,故③正确;④∵-1<x<1时,∴当-1<x<-0.5时,y=[x]+(x)+x=-1+0+x=x-1,当-0.5<x<0时,y=[x]+(x)+x=-1+0+x=x-1,当x=0时,y=[x]+(x)+x=0+0+0=0,当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,∵y=4x,则x-1=4x时,得13;x+1=4x时,得13;当x=0时,y=4x=0,∴当-1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,故答案为:②③.同类题型4.3 如果关于x的不等式(a+b)x+2a-b>0的解集是52,那么关于x的不等式(b-a)x+a +2b≤0的解集是____________.解:∵关于x的不等式(a+b)x+2a-b>0的解集是52,∴b-2aa+b,∴b-2a52,且a+b<0,即b=-3a,a+b<0,∴a-3a<0,即a>0,∴b-a=-4a<0,∴关于x的不等式(b-a)x+a+2b≤0的解集是-a-2bb-a,∵-a-2b-a+6a54,∴关于x的不等式(b-a)x+a+2b≤0的解集是54.同类题型4.4 若关于x的不等式组\F(x+4x2x-a<0解集为x<2,则a的取值范围是___________.解:由x+4x2+1,得2x+8>3x+6,解得x<2,由x-a<0,得x<a,又因关于x的不等式组\F(x+4x2x-a<0解集为x<2,所以a≥2.同类题型4.5 按如图的程序计算,若开始输入的值x为正数,最后输出的结果为656,则满足条件的x的不同值最多有___________.解:∵最后输出的数为656,∴5x+1=656,得:x=131>0,∴5x+1=131,得:x=26>0,∴5x+1=26,得:x=5>0,∴5x+1=5,得:x=0.8>0;∴5x+1=0.8,得:x=-0.04<0,不符合题意,故x的值可取131,26,5,0.8共4个.专题03函数的几何综合问题例1.如图,在平面直角坐标系中,直线l:3\R(33与x轴交于点1,以1为边长作等边三角形1)OB\S\DO(1,过点1作1)B\S\DO(2平行于x轴,交直线l于点2,以1)B\S\DO(2为边长作等边三角形2)A\S\DO(1)B\S\DO(2,过点2作2)B\S\DO(3平行于x轴,交直线l于点3,以2)B\S\DO(3为边长作等边三角形3)A\S\DO(2)B\S\DO(3,…,则点2017的横坐标是____________.同类题型1.1 如图,直线l:y=x+1交y轴于点1,在x轴正方向上取点1,使1)=OA\S\DO(1;过点1作2)B\S\DO(1⊥x轴,交l于点2,在x轴正方向上取点2,使1)B\S\DO(2)=B\S\DO(1)A\S\DO(2;过点2作3)B\S\DO(2⊥x轴,交l于点3,在x轴正方向上取点3,使2)B\S\DO(3)=B\S\DO(2)A\S\DO(3;…记1)B\S\DO(1面积为1,1)A\S\DO(2)B\S\DO(2面积为2,2)A\S\DO(3)B\S\DO(3面积为3,…则2017等于()A.4030 B.4031 C.4032 D.4033同类题型1.2 如图,已知直线l:33x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点1;过点1作y轴的垂线交直线l于点1,过点1作直线l的垂线交y轴于点2;…;按此作法继续下去,则点4的坐标为()A.(0,128)B.(0,256)C.(0,512)D.(0,1024)同类题型1.3 如图,在平面直角坐标系中,直线l:33x+1交x轴于点B,交y轴于点A,过点A作1⊥AB 交x轴于点1,过点1作1)A\S\DO(1⊥x轴交直线l于点2…依次作下去,则点n的横坐标为____________.例2.高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离1、2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有_________(把所有正确结论的序号都填在横线上).同类题型2.1 甲、乙两辆汽车沿同一路线从A地前往B地,甲车以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为1小时;③两车在途中第二次相遇时t的值为5.25;④当t=3时,两车相距40千米,其中不正确的个数为()A.0个B.1个C.2个D.3个同类题型2.2 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟74h到达B地;(4)乙车行驶94小时或194小时,两车恰好相距50km.正确的个数是()A.1B.2C.3D.4同类题型2.3 甲、乙两人从科技馆出发,沿相同的路线分别以不同的速度匀速跑向极地馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极地馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.则下列四种说法:①甲的速度为1.5米/秒;②a=750;③乙在途中等候甲100秒;④乙出发后第一次与甲相遇时乙跑了375米.其中正确的个数是()A.1个B.2个C.3个D.4个例3.如图,已知动点P在函数12x(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E,F,则AF﹒BE的值为()A.4B.2C.1D.12同类题型3.1 如图,在反比例函数32x的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数kx的图象上运动,若tan∠CAB=2,则k的值为()A.-3B.-6C.-9D.-12同类题型3.2 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在第一象限,点C在线段AB上,点D在AB的右侧,△OAB和△BCD都是等腰直角三角形,∠OAB=∠BCD=90°,若函数6x(x>0)的图象经过点D,则△OAB与△BCD的面积之差为()A.12 B.6 C.3 D.2同类题型3.3 如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数1x和9x在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交1x的图象于点C,连结A C.若△ABC是等腰三角形,则k的值是___________.例4.如图,一次函数y=x+b的图象与反比例函数kx的图象交于点A(3,6)与点B,且与y轴交于点C,若点P是反比例函数kx图象上的一个动点,作直线AP与x轴、y轴分别交于点M、N,连结BN、CM.若△ACM)=S\S\DO(△ABN,则APAN的值为__________.同类题型4.1 当12≤x≤2时,函数y=-2x+b的图象上至少有一点在函数1x的图象下方,则b的取值范围为()A.2 B.92 C.b<3D.92同类题型4.2 方程2+3x-1=0的根可视为函数y=x+3的图象与函数1x的图象交点的横坐标,那么用此方法可推断出方程2+2x-1=0的实数根0所在的范围是()A.0<0 B.0<1 C.0<2 D.0<3例5.在平面直角坐标系xOy中,抛物线2)+2mx-m\S\UP6(2-m+1交y轴于点为A,顶点为D,对称轴与x轴交于点H.当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,则m=__________.同类题型5.1 已知抛物线14)x\S\UP6(2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为3,3),P是抛物线14)x\S\UP6(2+1上一个动点,则△PMF周长的最小值是()A.3 B.4 C.5 D.6同类题型5.2 抛物线2+bx+3(a≠0)经过点A(-1,0),32,0),且与y轴相交于点C.设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.同类题型5.3小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为__________cm.参考答案例1.如图,在平面直角坐标系中,直线l:3\R(33与x轴交于点1,以1为边长作等边三角形1)OB\S\DO(1,过点1作1)B\S\DO(2平行于x轴,交直线l于点2,以1)B\S\DO(2为边长作等边三角形2)A\S\DO(1)B\S\DO(2,过点2作2)B\S\DO(3平行于x轴,交直线l于点3,以2)B\S\DO(3为边长作等边三角形3)A\S\DO(2)B\S\DO(3,…,则点2017的横坐标是____________.解:由直线l:3\R(33与x轴交于点1,可得1(1,0),D(0,33),∴1=1,1D=30°,如图所示,过1作1)A⊥OB\S\DO(1于A,则112,即1的横坐标为12\S\UP6(12,由题可得1)B\S\DO(2)B\S\DO(1)=∠OB\S\DO(1D=30°,2)A\S\DO(1)B\S\DO(1)=∠A\S\DO(1)B\S\DO(1O =60°,∴1)B\S\DO(1)B\S\DO(2=90°,∴1)B\S\DO(2)=2A\S\DO(1)B\S\DO(1=2,过2作2)B⊥A\S\DO(1)B\S\DO(2于B,则12)A\S\DO(1)B\S\DO(2=1,即2的横坐标为132\S\UP6(22,过3作3)C⊥A\S\DO(2)B\S\DO(3于C,同理可得,2)B\S\DO(3)=2A\S\DO(2)B\S\DO(2=4,12)A\S\DO(2)B\S\DO(3=2,即3的横坐标为172\S\UP6(32,同理可得,4的横坐标为1152\S\UP6(42,由此可得,n的横坐标为n)-12,∴点2017的横坐标是2017)-12.同类题型1.1 如图,直线l:y=x+1交y轴于点1,在x轴正方向上取点1,使1)=OA\S\DO(1;过点1作2)B\S\DO(1⊥x轴,交l于点2,在x轴正方向上取点2,使1)B\S\DO(2)=B\S\DO(1)A\S\DO(2;过点2作3)B\S\DO(2⊥x轴,交l于点3,在x轴正方向上取点3,使2)B\S\DO(3)=B\S\DO(2)A\S\DO(3;…记1)B\S\DO(1面积为1,1)A\S\DO(2)B\S\DO(2面积为2,2)A\S\DO(3)B\S\DO(3面积为3,…则2017等于()A.4030 B.4031 C.4032 D.4033解:∵1)=OA\S\DO(1;过点1作2)B\S\DO(1⊥x轴,1)B\S\DO(2)=B\S\DO(1)A\S\DO(2);A\S\DO(3)B\S\DO(2⊥x轴,2)B\S\DO(3)=B\S\DO(2)A\S\DO(3;…∴1)B\S\DO(1,1)A\S\DO(2)B\S\DO(2,2)A\S\DO(3)B\S\DO(3是等腰直角三角形,∵y=x+1交y轴于点1,∴1(0,1),∴1(1,0),∴1)=OA\S\DO(1=1,∴112,同理112,112;…∴12)×2\S\UP6(2n-2)=2\S\UP6(2n-3,∴2017)=2\S\UP6(2×2017-3)=2\S\UP6(4031,选B.同类题型1.2 如图,已知直线l:33x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点1;过点1作y轴的垂线交直线l于点1,过点1作直线l的垂线交y轴于点2;…;按此作法继续下去,则点4的坐标为()A.(0,128)B.(0,256)C.(0,512)D.(0,1024)解:∵直线l的解析式为33x,∴l与x轴的夹角为30°,∵AB∥x轴,∴∠ABO=30°,∵OA=1,∴OB=2,∴3,∵1B⊥l,∴1=60°,∴1O=4,∴1(0,4),同理可得2(0,16),…∴4纵坐标为4=256,∴4(0,256).选B.同类题型1.3 如图,在平面直角坐标系中,直线l:33x+1交x轴于点B,交y轴于点A,过点A作1⊥AB 交x轴于点1,过点1作1)A\S\DO(1⊥x轴交直线l于点2…依次作下去,则点n的横坐标为____________.解:由直线l:33x+1交x轴于点B,交y轴于点A,可得A(0,1),3,0),∴33,即∠ABO=30°,∴BA=2AO=2,又∵1⊥AB交x轴于点1,AO=1,∴23,∴1中,43;由题可得83,∴23,∴1)B\S\DO(2中,163;由题可得329,∴33,∴2)B\S\DO(3中,643,…以此类推,\F(4n3,又∵3,∴\F(4n3,∴点n的横坐标为4n3.例2.高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离1、2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的坐标为(7,180),其中正确的有_________(把所有正确结论的序号都填在横线上).解:①450+240=690(千米).故A、C之间的路程为690千米是正确的;②450÷5-240÷4=90-60=30(千米/小时).故乙车比甲车每小时快30千米是正确的;③690÷(450÷5+240÷4)=690÷(90+60)=690÷150=4.6(小时).故4.6小时两车相遇,原来的说法是错误的;④(450-240)÷(450÷5-240÷4)=210÷(90-60)=210÷30=7(小时),450÷5×7-450=630-450=180(千米).故点E的坐标为(7,180)是正确的,故其中正确的有①②④.同类题型2.1 甲、乙两辆汽车沿同一路线从A地前往B地,甲车以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为1小时;③两车在途中第二次相遇时t的值为5.25;④当t=3时,两车相距40千米,其中不正确的个数为()A.0个B.1个C.2个D.3个解:①由函数图象,得a=120÷3=40故①正确,②由题意,得5.5-3-120÷(40×2),=2.5-1.5,=1.∴甲车维修的时间为1小时;故②正确,③如图:∵甲车维修的时间是1小时,∴B(4,120).∵乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.∴E(5,240).∴乙行驶的速度为:240÷3=80,∴乙返回的时间为:240÷80=3,∴F(8,0).设BC的解析式为1)=k\S\DO(1)t+b\S\DO(1,EF的解析式为2)=k\S\DO(2)t+b\S\DO(2,由图象,得120=4k\S\DO(1)+b\S\DO(1)240=5.5k\S\DO(1)+b\S\DO(,)),240=5k\S\DO(2)+b\S\DO(2)0=8k\S\DO(2)+b\S\DO(2))解得k\S\DO(1)=80b\S\DO(1)=-200),k\S\DO(2)=-80b\S\DO(2)=640),∴1=80t-200,2=-80t+640,当1)=y\S\DO(2时,80t-200=-80t+640,t=5.25.∴两车在途中第二次相遇时t的值为5.25小时,故弄③正确,④当t=3时,甲车行的路程为:120km,乙车行的路程为:80×(3-2)=80km,∴两车相距的路程为:120-80=40千米,故④正确,选A.同类题型2.2 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟74h到达B地;(4)乙车行驶94小时或194小时,两车恰好相距50km.。
2022年中考数学复习之挑战压轴题(填空题):图像的平移、折叠、旋转(含答案)

2022年中考数学复习之挑战压轴题(填空题):图像的平移、折叠、旋转一.填空题(共10小题)1.(2021秋•鼓楼区校级期末)如图,在△ABC中,AB=AC,BC=6,tan∠ACB=2,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,CD,则CD长的最小值为.2.(2021秋•历城区期末)如图,在矩形ABCD中,AB=3,AD=9,点E,F分别在边AD,BC上,且AE=2,沿直线EF翻折,点A的对应点A′恰好落在对角线AC上,点B的对应点为B′,分别在线段EF,A′B′上取点M,N,沿直线MN二次翻折,使点F与点E重合,则线段MN的长为.3.(2021•綦江区校级三模)如图,在矩形ABCD中,E为AB边上的一点,将△ADE沿DE 翻折,得到△DEF,且F在BC边上,G为AD边上的一点,过点G作AD的垂线交DF 于点H,连接AH交DE于点P,连接AF,若AB=7,BF=3,HA平分∠GHF,则AG 的长度为.4.(2021•马鞍山模拟)如图,将边长为4的正方形ABCD纸片沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q连接PQ,则△GPQ的周长最小值是.5.(2020•海安市模拟)如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.6.(2021春•东阳市期末)在综合实践课上,小明把边长为2cm的正方形纸片沿着对角线AC剪开,如图1所示.然后固定纸片△ABC,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′B,D′C,在平移过程中:(1)四边形A′BCD′的形状始终是;(2)A′B+D′B的最小值为.7.(2021•路北区一模)如图,边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止.第一次滚动时正方形旋转了°,点A在滚动过程中到出发点的最大距离是.8.(2021•河北区模拟)如图,四边形ABCD是边长为2的正方形,E是BC边的中点,F 是直线DE上的动点.连接CF,将线段CF逆时针旋转90°得到CG,连接EG,则EG 的最小值是.9.在正方形ABCD中,点P是对角线AC上一点,连接DP,将DP绕点D逆时针旋转90°后得到线段DE,连接PE,点C关于直线PE的对称点是C′,连接C′E、C′P、C′A.若四边形AC′ED是平行四边形,PC=2,则平行四边形AC′ED的面积是.10.(2020•衢州二模)如图,在矩形ABCD中,AD=8,AB=6,点E是CD的中点,过点E作EF∥BC,交对角线BD于点F.将△DEF绕点D逆时针方向旋转得到△DE1F1,连接CE1,BF1,设旋转角度为α(0°<α<180°),则=;连接CF1,当△DF1B 为直角三角形时,CF1=.2022年中考数学复习之挑战压轴题(填空题):图像的平移、折叠、旋转(10题)参考答案与试题解析一.填空题(共10小题)1.(2021秋•鼓楼区校级期末)如图,在△ABC中,AB=AC,BC=6,tan∠ACB=2,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,CD,则CD长的最小值为.【考点】轴对称﹣最短路线问题;旋转的性质;解直角三角形;等腰三角形的性质.【专题】图形的相似;推理能力.【分析】以BC为边构建出和△BPD相似的三角形,通过将CD边转化为其他边来求值.【解答】解:如图所示,以BC为底边向上作三等腰△BQC,连接BP.由题意可得△BQC和△BPQ均为顶角为120°的等腰三角形,可得,∠QBC=∠PBD=30°,∴∠QBC﹣∠QBD=∠PBD﹣∠QBD,∴∠PBQ=∠DBC,∴△PBQ∽△DBC,∴,∴当PQ⊥AC时,有PQ最小,即此时CD最小,如图所示,设OP′⊥AC,延长AQ与BC交K,此时QP'为QP的最小值,可得AK⊥BC,∵△BQC中,∠BQC=120°,BC=6,∴BK=3,∠QBK=30°,∴QK==,∵tan∠ACB==,KC=3,∴AK==,∴AQ=AK﹣QK=,AC==,∵∠AP'Q=∠AKC=90°,∠QAP'=∠CAK,∴△AQP'∽△ACK,∴,∴,∴QP'=,∴CD==.【点评】本题考查的是瓜豆原理的知识点,重难点在于构造相似三角形的手拉手模型,属于难题.2.(2021秋•历城区期末)如图,在矩形ABCD中,AB=3,AD=9,点E,F分别在边AD,BC上,且AE=2,沿直线EF翻折,点A的对应点A′恰好落在对角线AC上,点B的对应点为B′,分别在线段EF,A′B′上取点M,N,沿直线MN二次翻折,使点F与点E重合,则线段MN的长为.【考点】翻折变换(折叠问题);相似三角形的判定与性质;矩形的性质.【专题】几何综合题;压轴题;推理能力.【分析】如图,过点F作FT⊥AD于T,则四边形ABFT是矩形,连接FN,EN,设AC 交EF于J.证明△FTE∽△ADC,求出ET=1,EF=,设A′N=x,根据NF=NE,可得12+(3﹣x)2=22+x2,解方程求出x,可得结论.【解答】解:如图,过点F作FT⊥AD于T,则四边形ABFT是矩形,连接FN,EN,设AC交EF于J.∵四边形ABFT是矩形,∴AB=FT=3,BF=AT,∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=9,∠B=∠D=90°∴AC===3,∵∠TFE+∠AEJ=90°,∠DAC+∠AEJ=90°,∴∠TFE=∠DAC,∵∠FTE=∠D=90°,∴△FTE∽△ADC,∴==,∴==,∴TE=1,EF=,∴BF=AT=AE﹣ET=2﹣1=1,设A′N=x,∵NM垂直平分线段EF,∴NF=NE,∴12+(3﹣x)2=22+x2,∴x=1,∴FN===,∴MN===,故答案为:.【点评】本题属于几何综合题,考查矩形的性质,翻折变换,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数构建方程解决问题,属于中考填空题中的压轴题.3.(2021•綦江区校级三模)如图,在矩形ABCD中,E为AB边上的一点,将△ADE沿DE 翻折,得到△DEF,且F在BC边上,G为AD边上的一点,过点G作AD的垂线交DF 于点H,连接AH交DE于点P,连接AF,若AB=7,BF=3,HA平分∠GHF,则AG 的长度为7.【考点】翻折变换(折叠问题);相似三角形的判定与性质;角平分线的性质;矩形的性质.【专题】推理填空题;矩形菱形正方形;推理能力.【分析】过点A作AN⊥DF于点N,延长AB,DF交于点M,设AE=x,AD=y,由翻折可知:EF=AE=x,DF=AD=BC=y,则BE=AB﹣AE=7﹣x,CF=BC﹣BF=y﹣3,在Rt△BEF和Rt△DFC中,根据勾股定理得x=,y=,证明△BFM∽△ADM,可得BM=,证明△EFM∽△ANM,可得AN=7,然后根据角平分线的性质可以解决问题.【解答】解:如图,过点A作AN⊥DF于点N,延长AB,DF交于点M,设AE=x,AD=y,由翻折可知:EF=AE=x,DF=AD=BC=y,则BE=AB﹣AE=7﹣x,CF=BC﹣BF=y﹣3,在Rt△BEF和Rt△DFC中,根据勾股定理,得:BE2+BF2=EF2,DC2+CF2=DF2,∴(7﹣x)2+32=x2,72+(y﹣3)2=y2,解得x=,y=,∴EF=,AD=,∴BE=7﹣x=,CF=y﹣3=,∵BF∥AD,∴△BFM∽△ADM,∴=,∴=,∴BM=,∴EM=BM+BE=+=,∴AM=AB+BM=7+=,由翻折可知:∠EFD=∠EAD=90°,∵AN⊥DF,∴∠EFM=∠ANM=90°,∴EF∥AN,∴△EFM∽△ANM,∴=,∴=,∴AN=7,∵HA平分∠GHF,AN⊥DF,HG⊥AD,∴AG=AN=7.故答案为:7.【点评】本题考查了矩形的相关证明与计算,相似三角形的判定与性质,熟练掌握矩形的性质与相似三角形的性质与判定是解题的关键.4.(2021•马鞍山模拟)如图,将边长为4的正方形ABCD纸片沿EF折叠,点C落在AB 边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q连接PQ,则△GPQ的周长最小值是2+2.【考点】翻折变换(折叠问题);正方形的性质;轴对称﹣最短路线问题.【专题】平移、旋转与对称.【分析】如图,取CD的中点N,连接PN,PB,BN.首先证明PQ=PN,PB=PG,推出PQ+PG=PN+PB≥BN,求出BN即可解决问题.【解答】解:如图,取CD的中点N,连接PN,PB,BN.由翻折的性质以及对称性可知;PQ=PN,PG=PC,HG=CD=4,∵QH=QG,∴QG=2,在Rt△BCN中,BN==2,∵∠CBG=90°,PC=PG,∴PB=PG=PC,∴PQ+PG=PN+PB≥BN=2,∴PQ+PG的最小值为2,∴△GPQ的周长的最小值为2+2,故答案为2+2.【点评】本题考查翻折变换,正方形的性质,直角三角形斜边中线的性质,勾股定理等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考填空题中的压轴题.5.(2020•海安市模拟)如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.【考点】翻折变换(折叠问题);三角形的面积;矩形的性质.【专题】推理填空题;平移、旋转与对称;几何直观;运算能力;推理能力.【分析】根据矩形ABCD中,AB=3,BC=4,可得AC=5,由AE=可得点F是边BC上的任意位置时,点C始终在AC的下方,设点G到AC的距离为h,要使四边形AGCD 的面积的最小,即h最小.所以点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD 的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.根据锐角三角函数先求得h 的值,再分别求得三角形ACD和三角形ACG的面积即可得结论.【解答】解:如图,在矩形ABCD中,AB=3,BC=4,∠B=∠D=90°,连接AC,∴AC=5,∵AB=3,AE=,∴点F是边BC上的任意位置时,点G始终在AC的下方,设点G到AC的距离为h,S四边形AGCD=S△ACD+S△ACG=3×4+×5h,=6+h.要使四边形AGCD的面积最小,即h最小.∵点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.在Rt△ABC中,sin∠BAC==,在Rt△AEH中,AE=,sin∠BAC==,解得EH=AE=,EG=BE=AB﹣AE=3﹣,∴h=EH﹣EG=﹣(3﹣)=﹣3.∴S四边形AGCD=6+×(﹣3)=﹣=.故答案为:.【点评】本题考查了翻折变换,解决本题的关键是确定满足条件的点G的位置,运用相似、锐角三角函数等知识解决问题.6.(2021春•东阳市期末)在综合实践课上,小明把边长为2cm的正方形纸片沿着对角线AC剪开,如图1所示.然后固定纸片△ABC,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′B,D′C,在平移过程中:(1)四边形A′BCD′的形状始终是平行四边形;(2)A′B+D′B的最小值为2.【考点】作图﹣平移变换;正方形的性质;轴对称﹣最短路线问题.【专题】作图题;推理能力.【分析】(1)利用平移的性质证明即可.(2)如图2中,作直线DD′,作点C关于直线DD′的对称点C″,连接D′C″,BC″,过点B作BH⊥CC″于H.求出BC″,证明A′B+BD′=BD′+CD′=BD′+D′C″≥BC″,可得结论.【解答】解:(1)如图2中,∵A′D′=BC,A′D′∥BC,∴四边形A′BCD′是平行四边形,故答案为:平行四边形.(2)如图2中,作直线DD′,作点C关于直线DD′的对称点C″,连接D′C″,BC″,过点B作BH⊥CC″于H.∵四边形ABCD是正方形,∴AB=BC=2,∠ABC=90°,∴AC=AB=2,∵BJ⊥AC,∴AJ=JC,∴BJ=AC=,∵∠BJC=∠JCH=∠H=90°,∴四边形BHCJ是矩形,∵BJ=CJ,∴四边形BHCJ是正方形,∴BH=CH=,在Rt△BHC″中,BH=,HC″=3,∴BC″===2,∵四边形A′BCD′是平行四边形,∴A′B=CD′,∴A′B+BD′=BD′+CD′=BD′+D′C″≥BC″,∴A′B+BD′≥2,∴A′B+D′B的最小值为2,故答案为:2【点评】本题考查作图﹣平移变换,轴对称最短问题,勾股定理等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.7.(2021•路北区一模)如图,边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止.第一次滚动时正方形旋转了150°,点A在滚动过程中到出发点的最大距离是+.【考点】旋转的性质;正多边形和圆;轨迹.【专题】平移、旋转与对称;解直角三角形及其应用.【分析】如图,点A的运动轨迹是图中红线.延长AE交红线于H,线段AH的长,即为点A在滚动过程中到出发点的最大距离.【解答】解:第一次滚动正方形旋转了240°﹣90°=150°.如图,点A的运动轨迹是图中红线.延长AE交红线于H,线段AH的长,即为点A在滚动过程中到出发点的最大距离.易知EH=EA2==,在△AEF中,∵AF=EF=1,∠AFE=120°,∴AE=,∴AH=AE+EH=+.∴点A在滚动过程中到出发点的最大距离为+.故答案为:150,+【点评】本题考查旋转变换,正方形的性质,正六边形的性质,解直角三角形等知识,解题的关键是理解题意,学会正确寻找点A的运动轨迹,属于中考填空题中的压轴题.8.(2021•河北区模拟)如图,四边形ABCD是边长为2的正方形,E是BC边的中点,F 是直线DE上的动点.连接CF,将线段CF逆时针旋转90°得到CG,连接EG,则EG的最小值是.【考点】旋转的性质;正方形的性质.【专题】矩形菱形正方形.【分析】如图,作直线BG.由△CBG≌△CDF,推出∠CBG=∠CDF,因为∠CDF是定值,推出点G在直线BG上运动,且tan∠CBG=tan∠CDF==,根据垂线段最短可知,当EG⊥BG时,EG的长最短.【解答】解:如图,作直线BG.∵四边形ABCD是正方形,∴CB=CD,∠BCD=90°,∵∠FCG=∠DCB=90°,∴∠BCG=∠DCF,∵CG=CF,∴△CBG≌△CDF,∴∠CBG=∠CDF,∵∠CDF是定值,∴点G在直线BG上运动,且tan∠CBG=tan∠CDF==,根据垂线段最短可知,当EG⊥BG时,EG的长最短,此时tan∠EBG==,设EG=m,则BG=2m,在Rt△BEG中,∵BE2=BG2+EG2,∴1=m2+4m2,∴m=(负根已经舍弃),∴EG的最小值为,故答案为.【点评】本题考查旋转变换、正方形的性质、全等三角形的判定和性质、垂线段最短、解直角三角形等知识,解题的关键是准确寻找全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考填空题中的压轴题.9.在正方形ABCD中,点P是对角线AC上一点,连接DP,将DP绕点D逆时针旋转90°后得到线段DE,连接PE,点C关于直线PE的对称点是C′,连接C′E、C′P、C′A.若四边形AC′ED是平行四边形,PC=2,则平行四边形AC′ED的面积是2+4.【考点】旋转的性质;平行四边形的性质;正方形的性质;轴对称的性质.【专题】矩形菱形正方形.【分析】如图,连接DC′,作PH⊥CD于H,设CD交EC′于K.只要证明△ADC′≌△CDP,△DKC′,△PCH是等腰直角三角形即可解决问题;【解答】解:如图,连接DC′,作PH⊥CD于H,设CD交EC′于K.∵四边形ABCD是正方形,∴AD=CD,∵四边形ADEC′是平行四边形,∴DE=AC′=DP,∠DAC′=∠DEK,∵AD⊥CD,AD∥EC′,∴CD⊥EC′,∵∠PDE=90°,∴∠PDC+∠CDE=90°,∠CDE+∠DEK=90°,∴∠CDP=∠DAC′,∴△ADC′≌△CDP,∴DC′=PC=2,∠ADC′=∠DCP=45°,∵∠ADC=∠PHC=90°,∴∠KDC′=45°,∴△DKC′,△PCH是等腰直角三角形,∴DK=KC′=CH=PH=,∴C′K=PH,CK′∥PH,∴四边形PHKC′是平行四边形,∵∠PHK=90°,∴四边形PHKC′是矩形,∴PH=PC′=PC=2,∴AD=CD=2+2,∴四边形AC′ED的面积=(2+2)=2+4.故答案为2+4.【点评】本题考查旋转变换、正方形的性质、平行四边形的性质、等腰直角三角形的判定和性质、全等三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.10.(2020•衢州二模)如图,在矩形ABCD中,AD=8,AB=6,点E是CD的中点,过点E作EF∥BC,交对角线BD于点F.将△DEF绕点D逆时针方向旋转得到△DE1F1,连接CE1,BF1,设旋转角度为α(0°<α<180°),则=;连接CF1,当△DF1B 为直角三角形时,CF1=或.【考点】旋转的性质;勾股定理;矩形的性质.【专题】平移、旋转与对称;图形的相似;解直角三角形及其应用;运算能力;推理能力.【分析】由△BDF1∽△CDE1可得=;分为∠BDF1=90°,∠DF1B=90°两种情形,分别解斜△CDF1即可得.【解答】解:如图1,∵△DEF绕点D逆时针方向旋转得到△DE1F1,∴∠EDF=∠E1DF1,∴∠EDF﹣∠EDF1=∠E1DF1﹣∠EDF1,∴∠F1DB=∠E1DC,∵==,==,∴=,∴△BDF1∽△CDE1,∴===,故答案是;如图2,当∠BDF1=90°时,在△CDF1中,CD=6,DF1=5,∠CDF1=90°﹣∠BDC,作F1G⊥CD于G,在Rt△AGF1中,DF1=5,∠AF1G=∠BDC,∴F1G=DF1•cos∠AF1G=5•cos∠BDC=5•=5×=3,DG=5•sin∠BDC=4,∴CG=CD﹣DG=2,∴CF==,如图3,当∠DF1B=90°时(图中F1′),∵,∴∠DCF1′=∠DBF1′=30°,作F1′H⊥CD于H,∴设F1′H=a,则CH=a,∴DH=6﹣,在Rt△DHF1′中,由勾股定理得,(6﹣)2+a2=52,∴,(舍去),\∴CF1′=2a=3﹣4,故答案是或3﹣4.【点评】本题以旋转为背景,考查了三角形相似和解直角三角形,解决问题的关键是正确分类和数量熟练掌握基本图形.考点卡片1.三角形的面积(1)三角形的面积等于底边长与高线乘积的一半,即S△=×底×高.(2)三角形的中线将三角形分成面积相等的两部分.2.角平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.注意:①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直角平分线的性质语言:如图,∵C在∠AOB的平分线上,CD⊥OA,CE⊥OB∴CD=CE3.等腰三角形的性质(1)等腰三角形的概念有两条边相等的三角形叫做等腰三角形.(2)等腰三角形的性质①等腰三角形的两腰相等②等腰三角形的两个底角相等.【简称:等边对等角】③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】(3)在①等腰;②底边上的高;③底边上的中线;④顶角平分线.以上四个元素中,从中任意取出两个元素当成条件,就可以得到另外两个元素为结论.4.勾股定理(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.(2)勾股定理应用的前提条件是在直角三角形中.(3)勾股定理公式a2+b2=c2的变形有:a=,b=及c=.(4)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.5.平行四边形的性质(1)平行四边形的概念:有两组对边分别平行的四边形叫做平行四边形.(2)平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.(3)平行线间的距离处处相等.(4)平行四边形的面积:①平行四边形的面积等于它的底和这个底上的高的积.②同底(等底)同高(等高)的平行四边形面积相等.6.矩形的性质(1)矩形的定义:有一个角是直角的平行四边形是矩形.(2)矩形的性质①平行四边形的性质矩形都具有;②角:矩形的四个角都是直角;③边:邻边垂直;④对角线:矩形的对角线相等;⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.(3)由矩形的性质,可以得到直角三角形的一个重要性质,直角三角形斜边上的中线等于斜边的一半.7.正方形的性质(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.(2)正方形的性质①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形、平行四边形、矩形、菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.8.正多边形和圆(1)正多边形与圆的关系把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.(2)正多边形的有关概念①中心:正多边形的外接圆的圆心叫做正多边形的中心.②正多边形的半径:外接圆的半径叫做正多边形的半径.③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.9.轨迹10.轴对称的性质(1)如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.由轴对称的性质得到一下结论:①如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称;②如果两个图形成轴对称,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.11.轴对称-最短路线问题1、最短路线问题在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L 的交点就是所要找的点.2、凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.12.翻折变换(折叠问题)1、翻折变换(折叠问题)实质上就是轴对称变换.2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数.13.作图-平移变换(1)确定平移后图形的基本要素有两个:平移方向、平移距离.(2)作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.14.旋转的性质(1)旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.(2)旋转三要素:①旋转中心;②旋转方向;③旋转角度.注意:三要素中只要任意改变一个,图形就会不一样.15.相似三角形的判定与性质(1)相似三角形相似多边形的特殊情形,它沿袭相似多边形的定义,从对应边的比相等和对应角相等两方面下定义;反过来,两个三角形相似也有对应角相等,对应边的比相等.(2)三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.16.解直角三角形(1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.(2)解直角三角形要用到的关系①锐角、直角之间的关系:∠A+∠B=90°;②三边之间的关系:a2+b2=c2;③边角之间的关系:sin A==,cos A==,tan A==.(a,b,c分别是∠A、∠B、∠C的对边)。
中考数学填空题压轴答案详细
中考填空压轴题1.如 ,在矩形 片 ABCD 中, AB = 3,BC = 5,点 E 、F 分 在 段 AB 、BC 上,将 △ BEF 沿 EF 折叠,点 B 落在 B ′ .如 1,当 B ′在 AD 上 , B ′在 AD 上可移 的最大距离_________;如 2,当 B ′在矩形 ABCD 内部 , AB ′的最小 ______________.AB ′ D AB ′DEFEFACFBBFF CFB FFCF图 1图 22.如 , 器上一根弦固定在 器面板上 A 、 B 两点,支撑点 C 是凑近点 B 的黄金切割 点,若 AB =80cm , AC = ______________cm .( 果保存根号)3.已知抛物 y = ax 2- 2ax -1+a ( a >0)与直 x = 2,x = 3, y =1, y = 2 成的正方形有公共点, a 的取 范 是 ___________________.4.如 , 7 根 柱形木棒的横截面 的半径均 _______________.1, 捆扎7 根木棒一周的 子 度yAAA859x4A A AD14OA 3 2 x27ABCAAA 1075.如 ,已知 A 1(1,0),A 2(1,- 1),A 3(- 1,- 1),A 4(- 1,1),A 5(2,1), ⋯, 点 A 2010 的坐 是 __________________.6.在 Rt △ ABC 中, ∠ C = 90°, AC = 3, BC = 4.若以 C 点 心, r 半径所作的 与斜 AB 只有一个公共点, r 的取 范 是 _________________.7.已知 ⊙ A 和⊙ B 订交, ⊙ A 的半径 5, AB = 8,那么 ⊙B 的半径 r 的取 范 是_________________.8.已知抛物 12- 4x -1,抛物 F 2112F :y = x与 F 对于点( 1,0)中心 称, 在F 和 F成的封 形上,平行于y 的 段 度的最大 _____________.9.如 ,四 形 ABCD 中, AB =4, BC = 7,CD = 2,AD = x , x 的取 范 是().10.已知正数 a 、 b 、 c 足 a 2+ c 2= 16, b 2+ c 2= 25, k = a 2+b 2 的取 范 是 _________________.AADBCBDC11.如 ,在 △ABC 中, AB =AC , D 在 AB 上, BD =AB , ∠A 的取 范 是 _________________.12.函数 y = 2x 2+ 4| x| -1 的最小 是 ____________.13.已知抛物 y = ax 2 +2ax +4( 0< a <3), A ( x 1, y 1),B ( x 2,y 2)是抛物 上两点,若 x 1< x 2,且 x 1+x 2=1-a , y 1 __________ y 2(填 “>”、 “< ”或“= ”)14.如 , △ ABC 中, ∠A 的均分 交 BC 于 D ,若 AB = 6, AC = 4, ∠ A =60°, AD 的___________.15.如 , Rt △ABC 中, ∠ C =90°, AC =6,BC =8,点 D 在 AB 上, DE ⊥AC 交 AC 于 E , DF ⊥ AB 交 BC 于 F , AD =x ,四 形 CEDF 的面 y , y 对于 x 的函数分析式__________________________,自 量 x 的取 范 是 _____________________.yBA DFDBPkHKGy =Ax1y =CAOCxBED F CxEk1k16.两个反比率函数 y = x 和 y = x 在第一象限内的 象如 所示,点 P 在 y = x 的 象上,11PC ⊥ x 于点 C ,交 y = x 的 象于点 A ,PD ⊥y 于点 D ,交 y = x的 象于点 B ,当点 Pk在 y = x 的 象上运 ,以下 : ① △ ODB 与△ OCA 的面 相等; ② 四 形 PAOB 的面 不会 生 化; ③ PA 与 PB 始 相等; ④ 当点 A 是 PC 的中点 ,点 B 必定是 PD 的中点.此中必定正确的选项是 _________________.(把你 正确 的序号都填上,少填 或 填不 分).17.如 , △ ABC 中, BC = 8,高 AD = 6,矩形 EFGH 的一 EF 在 BC 上,其他两个 点 G 、 H 分 在 AC 、 AB 上, 矩形 EFGH 的面 最大 ___________.18.已知二次函数 y =a(a + 1)x 2- (2a + 1)x +1,当 a 挨次取 1,2,⋯,2010 ,函数的像在 x 上所截得的 段 A 11 22 ,⋯,A 2010 2010的 度之和 _____________. B ,AB B19.如 是一个矩形桌子,一小球从 P 撞 到 Q ,反射到 R ,又从 R 反射到 S ,从 S 反射 回原 P ,入射角与反射角相等 (比如 ∠PQA = ∠RQB 等),已知 AB = 8,BC =15,DP = 3.小球所走的路径的 _____________.ADCRBAFDQEGGSBCFCBD PAE1120.如,在平行四形ABCD中,点 E、F 分在 AB、AD 上,且 AE=3AB,AF=4AD,AGEF交角 AC 于 G,AC= _____________.21.已知 m,n 是对于 x 的方程 x2-2ax+a+ 6=0 的两根, (m-1)2+ (n- 1)2的最小_____________.22.如,四形ABCD和 BEFG均正方形,AG: DF: CE= _____________.23.如,在△ ABC中,∠ABC= 60°,点 P 是△ ABC内的一点,且∠APB=∠BPC=∠CPA,且 PA=8,PC= 6, PB=________.ACD ADD1D3O 2DP AB C B C1234BC C C C24.如, AB、 CD 是⊙O 的两条弦,∠AOB与∠ C互,∠COD与∠A 相等,∠ AOB 的度数是 ________.25.如,一个半径2的一个半径 2 的的心,中暗影部分的面_____________.26.如,在 Rt△ ABC中,∠ACB= 90°,∠ B=30°,AC= 2.作△ ABC的高 CD,作△ CDB 的高 DC11 1 1,作△ DC B 的高 C D ,⋯⋯,这样下去,获得的全部暗影三角形的面之和__________.27.已知抛物y= x 2- (2m+ 4)x+ m 2-10 与 x 交于 A、 B 两点, C 是抛物点,若△ABC直角三角形, m= __________.28.已知抛物 y=x 2-(2m+ 4)x+m 2- 10 与 x 交于 A、B 两点, C 是抛物点,若△ ABC等三角形,抛物的分析式 ___________________________.429.已知抛物 y=ax 2+( 3+ 3a)x+4 与 x 交于 A、 B 两点,与 y 交于点 C.若△ ABC直角三角形, a=__________.30.如,在直角三角形 ABC 中,∠ A=90°,点 D 在斜 BC上,点E、 F 分在直角 AB、 AC 上,且 BD= 5,CD=9,四形 AEDF是正方形,暗影部分的面 __________.31.小同学想用“描点法”画二次函数 y= ax2+ bx+c( a≠0)的象,取自量 x 的 5 个,分算出的 y ,以下表:AFEB D Cx⋯-2-1012⋯y⋯112-125⋯因为马虎,小算了此中的一个y ,你指出个算的y 所的 x= __________.32.等三角形ABC 的 6,将其搁置在如所示的平面直角坐系中,此中BC在 x 轴上, BC边上的高 OA 在 y 轴上。
2020中考数学专题突破训练_填空压轴题_含解析_-1

2020中考数学专题突破训练:填空压轴题(含解析)1.如图,矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30°,将△ABE沿BE翻折,得到△A′BE,连接CA′并延长,与AD相交于点F,则DF的长为.解:如图作A′H⊥BC于H.∵∠ABC=90°,∠ABE=∠EBA′=30°,∴∠A′BH=30°,∴A′H=BA′=1,BH=A′H=,∴CH=3﹣.∵△CDF∽△A′HC,∴ =,∴ =,∴DF=6﹣2.故答案为:6﹣2.2.数学课上,老师提出如下问题:△ABC是⊙O的内接三角形,OD⊥BC于点D.请借助直尺,画出△ABC中∠BAC的平分线.晓龙同学的画图步骤如下:(1)延长OD交»BC于点M;(2)连接AM交BC于点N.所以线段AN为所求△ABC中∠BAC的平分线.请回答:晓龙同学画图的依据是.【答案】垂径定理,等弧所对的圆周角相等.3.如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣x+4上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,依据图形所反映的规律,S2018=.【分析】分别过点P1.P2.P3作x轴的垂线段,先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高,继而求得三角形的面积,得出面积的规律即可得出答案.【解答】解:如图,分别过点P1.P2.P3作x轴的垂线段,垂足分别为点C.D.E,∵P1(3,3),且△P1OA1是等腰直角三角形,∴OC=CA1=P1C=3,设A1D=a,则P2D=a,∴OD=6+a,∴点P2坐标为(6+a,a),将点P 2坐标代入y=﹣x+4,得:﹣(6+a )+4=a ,解得:a=,∴A 1A 2=2a=3,P 2D=,同理求得P 3E=、A 2A 3=,∵S 1=×6×3=9.S 2=×3×=、S 3=××=、……∴S 2018=,故答案为:.4.阅读下面材料:小亮的作法如下:C老师说:“小亮的作法正确”请回答:小亮的作图依据是_________________________________________________.【答案】两点确定一条直线;同圆或等圆中半径相等;5.如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A 逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为BC=DC+EC ;探索:如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;应用:如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.【分析】(1)证明△BAD≌△CAE,根据全等三角形的性质解答;(2)连接CE,根据全等三角形的性质得到BD=CE,∠ACE=∠B,得到∠DCE=90°,根据勾股定理计算即可;(3)作AE⊥AD,使AE=AD,连接CE,DE,证明△BAD≌△CAE,得到BD=CE=9,根据勾股定理计算即可.【解答】解:(1)BC=DC+EC,理由如下:∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE,∴BD=CE,∴BC=BD+CD=EC+CD,故答案为:BC=DC+EC;(2)BD2+CD2=2AD2,理由如下:连接CE,由(1)得,△BAD≌△CAE,∴BD=CE,∠ACE=∠B,∴∠DCE=90°,∴CE2+CD2=ED2,在Rt△ADE中,AD2+AE2=ED2,又AD=AE,∴BD2+CD2=2AD2;(3)作AE⊥AD,使AE=AD,连接CE,DE,∵∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAD′,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE=9,∵∠ADC=45°,∠EDA=45°,∴∠EDC=90°,∴DE==6,∵∠DAE=90°,∴AD=AE=DE=6.6.如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是【分析】由图形可知,第n行最后一个数为=,据此可得答案.【解答】解:由图形可知,第n行最后一个数为=,∴第8行最后一个数为==6,则第9行从左至右第5个数是=,故答案是 7.已知:在四边形ABCD 中,∠ABC =∠ADC =90º,M 、N 分别是CD 和BC 上的点.求作:点M 、N ,使△AMN 的周长最小.作法:如图,(1)延长AD ,在AD 的延长线上截取DA ´=DA ;(2)延长AB ,在AB 的延长线上截取B A″=BA ;(3)连接A′A″,分别交CD 、BC 于点M 、N .则点M 、N 即为所求作的点.请回答:这种作法的依据是_____________.【答案】①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的 连线段被对称轴垂直平分)②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);③两点之间线段最短.8.如图,∠MON=30°,点B 1在边OM 上,且OB 1=2,过点B 1作B 1A 1⊥OM 交ON 于点A 1,以A 1B 1为边在A 1B 1右侧作等边三角形A 1B 1C 1;过点C 1作OM 的垂线分别交OM 、ON 于点B 2.A 2,以A 2B 2ABC D A ''A 'N M DC BA为边在A2B2的右侧作等边三角形A2B2C2;过点C2作OM的垂线分别交OM、ON于点B3.A3,以A3B3为边在A3B3的右侧作等边三角形A3B3C3,…;按此规律进行下去,则△A n B n+1C n的面积为()2n﹣2×.(用含正整数n的代数式表示)【解答】解:由题意△A1A2C1是等边三角形,边长为,△A2A3C2是等边三角形,边长为×,△A3A4C3是等边三角形,边长为××=()2×,△A4A5C4是等边三角形,边长为×××=()3×,…,△A n B n+1C n的边长为()n﹣1×,∴△A n B n+1C n的面积为×[()n﹣1×]2=()2n﹣2×.9.如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为23 °.解∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠DBC=46°,由翻折不变性可知,∠DBE=∠EBC=∠DBC=23°,故答案为23.10. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy 中,矩形ABCD 的边AB 在x 轴上,,,边AD 长为5. 现固定边AB ,“推”矩形使点D 落在y 轴的正半轴上(落点记为),相应地,点C 的对应点的坐标为 .【答案】(7,4)11.如图,正方形AOBO 2的顶点A 的坐标为A (0,2),O 1为正方形AOBO 2的中心;以正方形AOBO 2的对角线AB 为边,在AB 的右侧作正方形ABO 3A 1,O 2为正方形ABO 3A 1的中心;再以正方形ABO 3A 1的对角线A 1B 为边,在A 1B 的右侧作正方形A 1BB 1O 4,O 3为正方形A 1BB 1O 4的中心;再以正方形A 1BB 1O 4的对角线A 1B 1为边在A 1B 1的右侧作正方形A 1B 1O 5A 2,O 4为正方形A 1B 1O 5A 2的中心:…;按照此规律继续下去,则点O 2018的坐标为 (21010﹣2,21009) .【分析】由题意Q 1(1,1),O 2(2,2),O 3(,4,2),O 4(,6,4),O 5(10,4),O 6(14,8)…观察可知,下标为偶数的点的纵坐标为2,下标为偶数的点在直线y=x+1上,点O 2018的纵坐标为21009,可得21009=x+1,同侧x=21010﹣2,可得点O 2018的坐标为(21010﹣2,21009).【解答】解:由题意Q 1(1,1),O 2(2,2),O 3(,4,2),O 4(,6,4),O 5(10,4),O 6(14,8)…观察可知,下标为偶数的点的纵坐标为2,(3,0)A -(4,0)B D 'C'下标为偶数的点在直线y=x+1上,∵点O 2018的纵坐标为21009, ∴21009=x+1,∴x=21010﹣2,∴点O 2018的坐标为(21010﹣2,21009). 故答案为(21010﹣2,21009). 12.在平面直角坐标系xOy 中,点(2,)A m -绕坐标原点O 顺时针旋转90︒后,恰好落在右图中阴影区域(包括边界)内,则m 的取值范围是 .【答案】532m ≤≤ 13.为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是 1024 .【解答】解:∵将这些金蛋按1﹣2018的顺序进行标号,第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,∴剩余的数字都是偶数,是2的倍数,;∵他将剩下的金蛋在原来的位置上又按1﹣1009编了号,又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋,∴剩余的数字为4的倍数,以此类推:2018→1009→504→252→126→63→31→15→7→3→1共经历10次重新编号,故最后剩余的数字为:210=1024.故答案为:1024.14.下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.请回答:在上面的作图过程中,①ABC △是直角三角形的依据是 ;②ABC △是等腰三角形的依据是 .【答案】①直径所对的圆周角为直角OQB②线段垂直平分线上的点与这条线段两个端点的距离相等15.按一定顺序排列的一列数叫做数列,如数列:,,,,…,则这个数列前2018个数的和为_____.【答案】【解析】【分析】根据数列得出第n个数为,据此可得前2018个数的和为,再用裂项求和计算可得.【详解】由数列知第n个数为,则前2018个数的和为===1﹣=,故答案为:.16.下面是“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:如图,(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;请回答:该尺规作图的依据是.【答案】与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;三角形的高的定义.17.下面是按一定规律排列的代数式:a2,3a4,5a6,7a8,…则第8个代数式是15a16.【分析】直接利用已知单项式的次数与系数特点得出答案.【解答】解:∵a2,3a4,5a6,7a8,…∴单项式的次数是连续的偶数,系数是连续的奇数,∴第8个代数式是:(2×8﹣1)a2×8=15a16.故答案为:15a16.。
中考数学几何选择填空压轴题四边形难题(含答案))

1、 《求长度》 (答案)1、(容易)如图1的矩形ABCD 中,有一点E 在AD 上,今以BE 为折线将A 点往右折,如图2所示,再作过A 点且与CD 垂直的直线,交CD 于F 点,如图3所示,若AB= 36,BC=13,∠BEA=60°,则图3中AF 的长度为 4【解】作AH ⊥BC 于H2、(难)如图,矩形ABCD 与菱形EFGH 的对角线均交于点O ,且EG ∥BC ,将矩形折叠,使点C 与点O 重合,折痕MN 恰好过点G 若AB=6,EF=2,∠H=120°,则DN 的长为36-【解】长EG 交DC 于P 点,连接GC 、FH ;如图所示: 则CP=DP=21CD=26,△GCP 为直角三角形,∵四边形EFGH 是菱形,∠EHG=120°,∴GH=EF=2,∠OHG=60°,EG ⊥FH ,∴OG=GH•sin60°=2×23=3,由折叠的性质得:CG=OG=3,OM=CM ,∠MOG=∠MCG ,∴PG==26,∵OG ∥CM ,∴∠MOG+∠OMC=180°,∴∠MCG+∠OMC=180°,∴OM ∥CG ,∴四边形OGCM 为平行四边形,∵OM=CM ,∴四边形OGCM 为菱形,∴CM=OG=3,根据题意得:PG 是梯形MCDN 的中位线,∴DN+CM=2PG=6,∴DN=36-3、(中等)如图,△ABC 的周长为19,点D ,E 在边BC 上,∠ABC 的平分线垂直于AE ,垂足为N ,∠ACB 的平分线垂直于AD ,垂足为M ,若BC=7,则MN 的长度为25【解】△BNA ≅△BNE∴BA=BE ,∴△BAE 是等腰三角形,同理△CAD 是等腰三角形,∴点N 是AE 中点,点M 是AD 中点(三线合一),∴MN 是△ADE 的中位线, ∵BE+CD=AB+AC=19-BC=19-7=12,∴DE=BE+CD-BC=5,∴MN=21DE=25.4、(难度)如图,在菱形ABCD 中,∠ABC=120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B 、D 重合),折痕为EF ,若DG=2,BG=6,则BE 的长为______2.8【解】作EH ⊥BD ,设BE=x在Rt △EHG 中,EG 2=EH 2+GH 2,即(8-x )2=(23x )2+(6-21x )2,解得,x =2.8,即BE=2.8, 故答案为:2.85、如图,▱ABCD 中,AB=7,BC=3,连接AC ,分别以点A 和点C 为圆心,大于21AC 的长为半径作弧, 两弧相交于点M ,N ,作直线MN ,交CD 于点E ,连接AE ,则△AED 的周长是_____ 10.6、(容易)如图,ABCD 的对角线相交于点O ,且AD CD ,过点O 作OM AC ,交AD 于点M .如果CDM 的周长为8,那么ABCD 的周长是_ 16【解】∵四边形ABCD 是平行四边形,∴OA=OC ,∵OM ⊥AC ,∴AM=CM ,∵△CDM 的周长为8, ∴CM+DM+CD=AM+DM+CD=AD+CD=8,∴平行四边形ABCD 的周长是:2×8=16.7、(中等)如图,正方形ABCD 的边长为12,点E 在边AB 上,BE=8,过点E 作EF ∥BC ,分别交BD 、CD 于G 、F 两点.若点P 、Q 分别为DG 、CE 的中点,则PQ 的长为_____ 1328、(难度)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,AB=OB ,点E 、点F 分别是OA 、OD 的中点,连接EF ,∠CEF=45°,EM ⊥BC 于点M ,EM 交BD 于点N ,FN=,则线段BC 的长为_____249、(难度)如图,平行四边形ABCD 中,AM ⊥BC 于M ,AN ⊥CD 于N ,已知AB =10,BM =6,MC =3,则MN 的长为___________5734【方法】将目标量置入直角三角形中10、(容易)如上图,在矩形ABCD 中,AB =6,BC =8,点E 是BC 中点,点F 是边CD 上的任意一点,当△AEF 的周长最小时,则DF 的长为 4【解】以CD 为对称轴作对称变换11、如图,在矩形ABCD 中,E 是BC 边上的点,连接AE 、DE ,将△DEC 沿线段DE 翻折,点C 恰好落在线段AE 上的点F 处.若AB =6,BE : EC =4 : 1,则线段DE 的长为 ____102_______.【方法】AD = AE=10;勾股定理12、如图,矩形ABCD 中,AB =8,BC =4.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则AE 的长是 [5【解】连接EF 交AC 于O ,∵四边形EGFH 是菱形,∴EF ⊥AC ,OE =OF , ∵四边形ABCD 是矩形,∴∠B =∠D =90°,AB ∥CD ,∴∠ACD =∠CAB , 在△CFO 与△AOE 中,,∴△CFO ≌△AOE ,∴AO =CO ,A BDCM NAE BDC F∵AC ==4,∴AO =21AC =2,∵∠CAB =∠CAB ,∠AOE =∠B =90°,∴△AOE ∽△ABC ,∴,∴,∴AE =5.13、(难度)如图,矩形ABCD 中,AB =2,AD =2.点E 是BC 边上的一个动点,连接AE ,过点D 作DF ⊥AE 于点F .当△CDF 是等腰三角形时,BE 的长为 1、2、22-【解】①CF =CD 时,过点C 作CM ⊥DF ,垂足为点M ,则CM ∥AE ,DM =MF ,延长CM 交AD 于点G ,∴AG =GD =1,∴CE =1, ∵CG ∥AE ,AD ∥BC ,∴四边形AGCE 是平行四边形,∴CE =AG =1,∴BE =1 ∴当BE =1时,△CDF 是等腰三角形;②DF =DC 时,则DC =DF =2,∵DF ⊥AE ,AD =2,∴∠DAE =45°,则BE =2, ∴当BE =2时,△CDF 是等腰三角形;③FD =FC 时,则点F 在CD 的垂直平分线上,故F 为AE 中点. ∵AB =2,BE =x ,∴AE =,AF =,∵△ADF ∽△EAB ,∴=,,x 2﹣4x +2=0,解得:x =2±2,∴当BE =22-时,△CDF 是等腰三角形.综上,当BE =1、2、22-时,△CDF 是等腰三角形.14、如图,边长为1的菱形ABCD 中,∠DAB=60度.连接对角线AC ,以AC 为边作第二个菱形ACC 1D 1,使∠D 1AC=60°;连接AC 1,再以AC 1为边作第三个菱形AC 1C 2D 2,使∠D 2AC 1=60°;…,按此规律所作的第n 个菱形的边长为 1)3(-n .解:连接DB ,∵四边形ABCD 是菱形,∴AD=AB .AC ⊥DB , ∵∠DAB=60°,∴△ADB 是等边三角形,∴DB=AD=1,∴BM=21, ∴AM==23,∴AC=3,同理AC 1=3AC=(3)2,AC 2=3AC 1=33=(3)3, 按此规律所作的第n 个菱形的边长为1)3(-n15、如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ,设正方形的中心为O ,连接AO ,如果AB=4,AO=26,那么AC 的长等于 16 .【解】如图,过O 点作OG 垂直AC ,G 点是垂足.∵∠BAC=∠BOC=90°,∴ABCO 四点共圆,∴∠OAG=∠OBC=45° ∴△AGO 是等腰直角三角形,∴2AG 2=2GO 2=AO 2=2)26(=72, ∴OG=AG=6,∵∠BAH=∠OGH=90°,∠AHB=∠OHG ,∴△ABH ∽△GOH ,∴AB/OG=AH/(AG ﹣AH ),∵AB=4,OG=AG=6,∴AH=2.4 在直角△OHC 中,∵HG=AG ﹣AH=6﹣2.4=3.6,OG 又是斜边HC 上的高, ∴OG 2=HG×GC ,而OG=6,GH=3.6,∴GC=10.∴AC=AG+GC=6+10=16. 故AC 边的长是16.16、如图,在梯形ABCD 中,AD ∥BC ,∠B=90°,AD=2,BC=5,E 为DC 中点,tanC=34.则AE 的长度为265【解】过点E 作BC 的垂线交BC 于点F ,交AD 的延长线于点M , 在梯形ABCD 中,AD ∥BC ,E 是DC 的中点,∴∠M=∠MFC ,DE=CE ;在△MDE 和△FCE 中,∠M=∠MFC ,∠DEM=∠CEF ,DE=CE ;∴△MDE ≌△FCE ,∴EF=ME ,DM=CF . ∵AD=2,BC=5,∴DM=CF=23, 在Rt △FCE 中,tanC=CFEF =34,∴EF=ME=2,在Rt △AME 中,AE=265)232(222=++ 17、如图,平行四边形ABCD 中,AE 平分∠BAD 交BC 边于E ,EF ⊥AE 交CD 边于F ,延长BA 到点G ,使AG = CF ,连接GF .若BC = 7,DF = 3,tan ∠AEB =3 ,则GF 的长为 23【解】连接AC ,羊场AE 与DC 延长线交于一点H18、(容易)如图,梯形ABCD 中,AD ∥BC ,AB = 3,BC=4,连结BD ,∠BAD 的平分线交BD 于 点E ,且AE ∥CD ,则AD 的长为1DG ABCDEMABC DEF【解】构造平行四边形。
中考数学压轴题含答案

中考数学压轴题含答案一、选择题1、下列图形中,既是轴对称图形,又是中心对称图形的是()A.菱形B.平行四边形C.矩形(答案:C)2、如果一个三角形的三条边的平方相等,那么这个三角形一定是()A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形(答案:A)3、下列说法正确的是()A.所有的质数都是奇数B.所有的偶数都是合数C.一个数的因数一定比它的倍数小D.自然数一定是正数(答案:A)二、填空题1、若a-b=2,a+b=7,则a²-b²=(答案:14)2、我们学过的数有整数和分数,整数的运算律在分数运算中(答案:同样适用)。
3、一个长方形的周长是20cm,长和宽的比是3:2,则长方形的面积是(答案:60平方厘米)。
三、解答题1、一个圆柱体底面半径为r,高为h,它的体积是多少?(答案:πr²h)2、有一块三角形的土地,底边长为120米,高为90米,这块土地的面积是多少?(答案:5400平方米)3、对于一个给定的整数n,如果它是3的倍数,那么我们就称它为“三的倍数”,否则我们就称它为“非三的倍数”。
现在有一个整数n,它是“三的倍数”,我们可以得出哪些结论?(答案:n+1、n+2、n+3、...、2n都是“三的倍数”,因为它们都可以被3整除。
)中考数学压轴题100题及答案在中考数学考试中,压轴题往往是最具挑战性和最能检验考生数学能力的题目。
为了帮助同学们更好地理解和掌握中考数学的压轴题,本文将分享100道经典的中考数学压轴题及其答案。
一、选择题1、在一个等边三角形中,边长为6,下列哪个选项的面积最接近这个等边三角形的面积?A. 20B. 25C. 30D. 35答案:B解析:等边三角形的面积可以通过计算得出,边长为6的等边三角形的面积为:436293约为28.2,因此选项B最接近。
2、如果一个多边形的内角和是外角和的2倍,那么这个多边形的边数是多少?A. 4B. 6C. 8D. 10答案:C解析:根据多边形的内角和公式和外角和为360度,可列出方程求解。
2024年中考数学复习几何专项练习:动点运动路径之瓜豆原理(含答案解析)

2024年中考数学复习几何专项练习:动点运动路径之瓜豆原理(含答案解析)一、填空题1.如图,等边三角形ABC 中,AB =4,高线AHD 是线段AH 上一动点,以BD 为边向下作等边三角形BDE ,当点D 从点A 运动到点H 的过程中,点E 所经过的路径为线段CM ,则线段CM 的长为,当点D 运动到点H ,此时线段BE 的长为.【答案】2【分析】由“SAS ”可得△ABD ≌△CBE ,推出AD =EC ,可得结论,再由勾股定理求解2,BH =当,D H 重合时,2,BE BH ==从而可得答案.【详解】解:如图,连接EC .∵△ABC ,△BDE 都是等边三角形,∴BA =BC ,BD =BE ,∠ABC =∠DBE =60°,∴∠ABD =∠CBE ,在△ABD 和△CBE 中,BA BC ABD CBE BD BE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△CBE (SAS ),∴AD =EC ,∵点D 从点A 运动到点H ,∴点E的运动路径的长为CM AH ==,当,D H 重合,而BDE △(即BHE )为等边三角形,,BE BH \=4,,AB AH AH BC ==^Q2,BH ==2,BE ∴=故答案为:.【点睛】本题考查等边三角形的性质,全等三角形的判定和性质,动点的轨迹等知识,解题的关键是正确寻找全等三角形解决问题.2.如图,正方形ABCD 的边长为4,E 为BC 上一点,且1BE =,F 为AB 边上的一个动点,连接EF ,以EF 为边向右侧作等边EFG∆,连接CG ,则CG 的最小值为.【答案】52【分析】由题意分析可知,点F 为主动点,G 为从动点,所以以点E 为旋转中心构造全等关系,得到点G 的运动轨迹,之后通过垂线段最短构造直角三角形获得CG 最小值.【详解】由题意可知,点F 是主动点,点G 是从动点,点F 在线段上运动,点G 也一定在直线轨迹上运动将EFB ∆绕点E 旋转60︒,使EF 与EG 重合,得到EFB EHG ∆≅∆,从而可知EBH ∆为等边三角形,点G 在垂直于HE 的直线HN 上,作CM HN ⊥,则CM 即为CG 的最小值,作EP CM ⊥,可知四边形HEPM 为矩形,则1351222CM MP CP HE EC =+=+=+=.故答案为52.【点睛】本题考查了线段极值问题,分清主动点和从动点,通过旋转构造全等,从而判断出点G 的运动轨迹,是本题的关键.3.如图,等边ABC 中,8AB =,O 是BC 上一点,且14BO BC =,点M 为AB 边上一动点,连接OM ,将线段OM 绕点O 按逆时针方向旋转60︒至ON ,连接BN CN 、,则BCN △周长的最小值为.【答案】8+8【分析】过点N 作ND BC ⊥于点D ,过点O 作OH BM ⊥于点H ,则90OHM ODN ∠=∠=︒,证明HOM DNO ≌,可得DN OH =,从而得到点N 的运动轨迹是直线,且该直线与直线BC 平行,在BC 的左侧,与BCC 关于该直线的对称点E ,连接BE 交该直线于N ,即当点B ,N ,E 三点共线时,BCN △的周长最小,连接CE 交该直线于G ,则22CE CG DN ===CE BC ⊥,求出BE ,即可求解.【详解】解:如图,过点N 作ND BC ⊥于点D ,过点O 作OH BM ⊥于点H ,则90OHM ODN ∠=∠=︒,∵ABC 为等边三角形,∴60ABC ∠=︒,8BC AB ==,∴120BMO BOM ∠+∠=︒,根据题意得:60MON ∠=︒,OM ON =,∴120NOD BOM ∠+∠=︒,∴NOD BMO ∠=∠,∴HOM DNO ≌,∴DN OH =,∵14BO BC =,∴2BO =,∵60ABC ∠=︒,∴30BOH ∠=︒,∴112BH OB ==,∴DN OH ==∴点N 的运动轨迹是直线,且该直线与直线BC 平行,在BC 的左侧,与BC作点C 关于该直线的对称点E ,连接BE 交该直线于N ,即当点B ,N ,E 三点共线时,BCN △的周长最小,连接CE 交该直线于G ,则22CE CG DN ===,CE BC ⊥,∴BE =∴△ACN 的周长的最小值为8+故答案为:8+.【点睛】本题考查旋转变换,全等三角形的判定和性质,轴对称,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.4.如图,正方形ABCD 的边长为P 是CD 边上的一动点,连接AP ,将AP 绕点A 顺时针方旋转60︒后得到AQ ,连接CQ ,则点P 在整个运动过程中,线段CQ 所扫过的图形面积为.【答案】3-【分析】根据题意画出点P 在CD 上移动的过程,线段CQ 所扫过的面积就是COQ 的面积,根据正方形的性质,等边三角形的性质以及全等三角形的判定和性质,得出线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- ,再根据等边三角形,等腰直角三角形面积的计算方法进行计算即可.【详解】解:如图,当点P 在点D 时,相应的点Q 落在点O ,当点P 移动到点C 时,相应的点Q 在点Q ,CQ 扫过的面积就是COQ 的面积,由题意可知,AOD △、ACQ 都是等边三角形,AO DO AD ∴===AQ CQ AC ====,四边形ABCD 是正方形,AOD △是等边三角形,906030ODC ∴∠=︒-︒=︒,45ACD ∠=︒,OD CD = ,18030752DOC DCO ︒-︒∴∠=∠==︒,754530ACO ∴∠=︒-︒=︒,45607530QCO QCD DCO ∠=∠-∠=︒+︒-︒=︒,ACO QCO ∴∠=∠,AC QC = ,CO CO =,AOC ∴ ≌()SAS QOC ,AO QO ∴=,604515CQO CAO ∠=∠=︒-︒=︒,()3601801530290AOQ ∴∠=︒-︒-︒-︒⨯=︒,即AOQ △是等腰直角三角形,∴线段CQ 所扫过的图形面积()12ACQ AOQ S S S =- 111222⎛=⨯⨯⨯ ⎝3=,故答案为:3.【点睛】本题考查正方形、等边三角形,等腰直角三角形以及全等三角形的判定和性质,掌握正方形、等边三角形,等腰直角三角形以及全等三角形的判定和性质是正确解答的前提.5.如图,点D 是等边ABC 边AB 上的一动点(不与端点重合),点D 绕点C 引顺时针方向旋转60 得点E ,所得的CDE 边DE 与BC 交于点F ,则CF DE的最小值为.【分析】由旋转的性质得CDE 为等边三角形,由CEF CAD ∽△△得到CF CE CD AC =,即CF CD DE AC =,从而得到当CD 最小时,比值最小,再由“垂线段最短”得到当CD AB ⊥时,CD 值最小,作出对应图形,利用“ACD 是含30︒角的直角三角形”求出CD AC,从而得解.【详解】解:由旋转的性质得:CD CE =,60DCE ∠=︒,CDE ∴ 为等边三角形,DE CD CE ∴==,60A DEC ∠=∠=︒60ACD DCB ∠+∠=︒60DCB ECF ∠+∠=︒ACD ECF∴∠=∠∵60A DEC ∠=∠= ,ACD ECF∠=∠CEF CAD∴ ∽CF CE CD AC ∴=,即CF CD DE AC=AC 为定值,∴当CD 最小时,比值最小.根据“垂线段最短”可知:当CD AB ⊥时,CD 值最小,过点C 作CD AB ⊥于D ,并补全图形如下:ABC 是等边三角形,CD AB ⊥,60ACB ∠=︒∴1302ACD ACB ∠=∠=︒设AC 2a =,则12AD AC a ==∴CD ==,∴此时CF CD DE AC ==即CF DE 的最小值为2.故答案为:2.【点睛】此题考查图形的旋转变化与性质,等边三角形的判定和性质,相似三角形的判定与性质,含30︒角的直角三角形的性质,垂线段最短,理解“垂线段最短”和利用相似三角形的性质将CF DE转化为CD AC 是解题的关键.6.如图,在ACB △中,60ACB ∠=︒,75BAC ∠=︒,12AC =,点D 是边BC 上的一动点,连接AD ,将线段AD 绕点A 按逆时针方向旋转75︒得到线段AE ,连接CE ,则线段CE 长度的最小值是.【答案】/-【分析】过点A 作AF BC ⊥于点F ,在AB 上取点N ,使12AN AC ==,连接DN ,过点N 作点NM BD ⊥于点M ,证明()SAS NAD DAE ≌,求出CE DN =,得出当DN 最小时,CE 最小,根据垂线段最短,得出当点D 与点M 重合时,DN 最小,则CE 最小,求出最小结果即可.【详解】解:过点A 作AF BC ⊥于点F ,在AB 上取点N ,使12AN AC ==,连接DN ,过点N 作点NM BD ⊥于点M ,如图所示:根据旋转可知,AD AE =,75DAE ∠=︒,∵75BAC DAE ==︒∠∠,∴BAC DAC DAE DAC ∠-∠=∠-∠,即NAD CAE =∠∠,∵AN AC =,AD AE =,∴()SAS NAD CAE ≌,∴CE DN =,∴当DN 最小时,CE 最小,∵垂线段最短,∴当点D 与点M 重合时,DN 最小,则CE 最小,∵90AFC ∠=︒,60BCA ∠=︒,∴906030CAF ∠=︒-︒=︒,∴162CF AC ==,∴AF ==,∵45BAF BAC CAF =-=︒∠∠∠,90AFB ∠=︒,∴904545B ∠=︒-︒=︒,∴B BAF ∠=∠,∴BF AF ==∴AB ==∴12BN AB AN =-=-,∵90BMN ∠=︒,45B ∠=︒,∴904545BNM =︒-︒=︒∠,∴B BNM =∠∠,∴BM NM =,∵222BN NM BM =+,∴()22212NM =-,解得:NM =-,∴CE 的最小值为-.故答案为:【点睛】本题主要考查了全等三角形的判定和性质,勾股定理,等腰三角形的判断和性质,直角三角形的性质,垂线段最短,解题的关键是作出辅助线,构造全等三角形,证明CE DN =.7.如图,点A 的坐标为3⎫⎪⎪⎝⎭,点B 是x 轴正半轴上的一点,将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC .若点C 的坐标为(,4)k ,则k 的值为.【分析】连接BC ,过A 点作AF x ⊥轴于F ,C 作CD x ⊥轴于点D ,CE AF ⊥于点E ,则四边形DCEF 是矩形,根据将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ,可得ABC 是等边三角形,AB AC BC ==,由点A 的坐标为,(,4)C k ,有AC ==,而BD ==FB ==OF BF BD OD k ++==,可得k =,解方程可得答案.【详解】解:连接BC ,过A 点作AF x ⊥轴于F ,C 作CD x ⊥轴于点D ,CE AF ⊥于点E ,则四边形DCEF 是矩形,如图:∵将线段AB 绕点A 按逆时针方向旋转60︒得到线段AC ,∴AB AC =,60BAC ∠=︒,∴ABC 是等边三角形,∴AB AC BC ==,∵点A 的坐标为,(,4)C k ,,∴3CE k FD =-=,4CD =,3AF =,∴1AE EF AF CD AF =-=-=,∴AC BC AB ====,在Rt BCD 中,BD =,在Rt AFB 中,FB =∵OF BF BD OD k ++==,∴3k =,设k x =x =,化简变形得:42346490x x -=-,解得21x =-(舍去)或2493x =,∴3x =或3x =-(不符合题意,舍去),∴k ,∴k =,.【点睛】本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含k 的代数式表示相关线段的长度.8.如图,在边长为6的等边ABC 中,直线AD BC ⊥,E 是AD 上的一个动点连接EC ,将线段EC 绕点C 逆时针方向旋转60︒得到FC ,连接DF ,则点E 运动过程中,DF 的最小值是.【答案】32【分析】取线段AC 的中点G ,连接EG ,根据等边三角形的性质可得出CD CG =以及FCD ECG Ð=Ð,由旋转的性质可得出EC FC =,由此即可利用全等三角形的判定定理SAS 证出FCD ≌ECG ,进而即可得出DF GE =,再根据点G 为AC 的中点,即可得出EG 的最小值,此题得解.【详解】解:取线段AC 的中点G ,连接EG ,如图所示.ABC 为等边三角形,6AC BC ==,且AD 为ABC 的对称轴,132CD CG AB ∴===,60ACD ∠=︒,60ECF =︒∠ ,FCD ECG \Ð=Ð.FCD ∴ ≌()ECG SAS ,DF GE ∴=.当EG BC ∥时,EG 最小,点G 为AC 的中点,∴此时1133222EG DF CD ===⨯=.故答案为:32.【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出DF GE =.9.如图,在ABC ∆中,90ACB ︒∠=,点D 在BC 边上,5BC =,2CD =,点E 是边AC 所在直线上的一动点,连接DE ,将DE 绕点D 顺时针方向旋转60︒得到DF ,连接BF ,则BF 的最小值为.【答案】72【分析】当E 与点C 重合时,点F 与等边三角形CDG 的点G 重合,当点F 开始运动时,△ECD ≌△FGD ,故点F 在线段GF 上运动,根据垂线段最短原理,当BF ⊥GF 时,BF 有最小值,根据直角三角形的性质计算即可.【详解】当E与点C重合时,点F与等边三角形CDG的点G重合,∵DE绕点D顺时针方向旋转60 得到DF,∴△DEF是等边三角形,∴∠GDC=∠FDE=60°,ED=FD,∴∠GDC-∠GDE=∠FDE-∠GDE,∴∠EDC=∠FDG,∵△DEF是等边三角形,∴CD=GD,∴△ECD≌△FGD,∴EC=GF,∠ECD=∠FGD=90°,∴点F在线段GF上运动,根据垂线段最短原理,当BF⊥GF时,BF有最小值,如图,当旋转到BF∥DG 时,BF⊥GF,垂足为F,过点D作DH⊥BF,垂足为H,∵∠FGD=90°,∴四边形FGDH是矩形,∴∠GDH=90°,GD=FH=2,∵∠GDC=60°,∴∠BDH=30°,∵BD=BC-CD=5-2=3,∴BH=1232 BD=,∴BF=FH+BH=2+32=72,故答案为:7 2.【点睛】本题考查了等边三角形的判定和性质,矩形的判定和性质,垂线段最短,直角三角形的性质,熟练掌握等边三角形的判定,灵活运用直角的判定和直角三角形的性质是解题的关键.10.如图,正方形ABCD的边长为4,E为BC上一点,且1BE=,F为AB边上的一个动点,连接EF,将EF 烧点E顺时什旋转60°得到EG,连接CG,则CG的最小值为.【答案】5 2【分析】由题意分析可知,点F为主动点,G为从动点,所以以点E为旋转中心构造全等关系,得到点G 的运动轨迹,之后通过垂线段最短构造直角三角形获得CG最小值.【详解】解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动,将△EFB绕点E旋转60°,使EF与EG重合,得到△EBH为等边三角形,△EBF≌△EHG,∴∠EHG=∠ABC=90°,HE=BE=1,∠BEH=60°,∴点G在垂直于HE的直线HN上.作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,∴∠CEP=180°-60°-90°=30°,∴CP=12CE=12×(4-1)=32,则CM=MP+CP=35122 HE PC+=+=,即CG的最小值为5 2.故答案为5 2.【点睛】本题考查了旋转的性质,线段最值问题,全等三角形的性质,正方形的性质,矩形的判定与性质,含30°角的直角三角形的性质,以及垂线段最短等知识,分清主动点和从动点,通过旋转构造全等,从而判断出点G的运动轨迹,是本题的关键,之后运用垂线段最短,构造图形计算,是极值问题中比较典型的类型.11.如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值【答案】.【分析】由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD ,由垂线段最短得到当CD ⊥AB 时,△BDE 的周长最小,于是得到结论.【详解】∵将△ACD 绕点C 逆时针方向旋转60°得到△BCE ,∴∠DCE=60°,DC=EC ,∴△CDE 是等边三角形,由旋转的性质得,BE=AD ,∴C △DBE =BE+DB+DE=AB+DE=4+DE ,∵△CDE 是等边三角形,∴DE=CD ,∴C △DBE =CD+4,由垂线段最短可知,当CD ⊥AB 时,△BDE 的周长最小,此时,∴△BDE 的最小周长,故答案为.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,三角形周长的计算,熟练掌握旋转的性质是解题的关键.12.如图,在ABC 中,8AC BC ==,60BCA ∠= ,直线AD BC ⊥,E 是AD 上的一个动点,连接EC ,将线段EC 绕点C 按逆时针方向旋转60 得到FC ,连接DF ,则点E 运动过程中,DF 的最小值是.【答案】2【分析】根据题意取线段AC 的中点G ,连接EG ,根据等边三角形的性质以及角的计算即可得出CD=CG 以及∠FCD=∠ECG ,由旋转的性质可得出EC=FC ,由此即可利用全等三角形的判定定理SAS 证出△FCD ≌△ECG ,进而即可得出DF=GE ,再根据点G 为AC 的中点,即可得出EG 的最小值.【详解】取线段AC 的中点G ,连接EG,如图所示.8AC BC == ,60BCA ∠= ,ABC ∴为等边三角形,且AD 为ABC 的对称轴,142CD CG AB ∴===,60ACD ∠= ,60ECF ∠= ,FCD ECG ∴∠=∠.在FCD 和ECG 中,FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩,FCD ∴ ≌()ECG SAS ,DF GE ∴=.当//EG BC 时,EG 最小,点G 为AC 的中点,∴此时11224EG DF CD BC ====.故答案为2.【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出.DF GE =本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边是关键.13.如图,等边△AOB 的边长为4,点P 从点O 出发,沿OA 以每秒1个单位的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间是t 秒.将线段BP 的中点绕点P 按顺时针方向旋转60°得点C ,点C 随点P 的运动而运动,连接CP 、CA .在点P 从O 向A 运动的过程中,当△PCA 为直角三角形时t 的值为.【答案】2或83【详解】如图(1)过点P 作PD ⊥OB 于点D ,过C 作CE ⊥OA 于E ,∴∠PDO=∠PEC=90°,∵∠O=60°,∴∠OPD=30°,∴OD=12t ,∴BD=4-12t ,,∵线段BP 的中点绕点P 按顺时针方向旋转60°得点C ,∴∠BPC=60°,BP=2PC ,∵∠OPD=30°,∴∠BPD+∠CPE=90°,∴∠DBP=∠CPE ,∴△PCE ∽△BPD ,∴CE PE PC PD BD PB==,11242PE t ==-,∴,PE=2-14t ,OE=2+34t ,如图(2)当∠PCA=90度时,作CF ⊥PA ,∴△PCF ∽△ACF ,∴△PCF ∽△ACF ,∴PF CF CF AF =,∴CF 2=PF•AF ,∵PF=2-14t ,AF=4-OF=2-34t ,,)2=(2-14t )(=2-34t ),∴t=2,这时P 是OA 的中点;如图(3)当∠CAP=90°时,此时OA=OE ,∴2+34t=4,∴t=83,故答案为2或83.【点睛】本题考查了相似三角形的判定与性质,勾股定理的运用,等边三角形的性质,直角三角形的性质,旋转的性质等,正确地添加辅助线,求出OE 的长是解题的关键.二、解答题14.在平面直角坐标系中,A (a ,0)、B (b ,0),且a ,b 满足26930a a b -+++=,C 、D 两点分别是y 轴正半轴、x 轴负半轴上的两个动点;(1)如图1,若C (0,4),求△ABC 的面积;(2)如图1,若C (0,4),BC =5,BD=AE ,且∠CBA=∠CDE ,求D 点的坐标;(3)如图2,若∠CBA =60°,以CD 为边,在CD 的右侧作等边△CDE ,连接OE ,当OE 最短时,求A ,E 两点之间的距离.【答案】(1)△ABC 的面积为12;(2)D 点的坐标为(-2,0);(3)A ,E 两点之间的距离为32【分析】(1)利用完全平方式和绝对值的性质求出a ,b ,然后确定A 、B 两点坐标,从而利用三角形面积公式求解即可;(2)根据题意判断出CBD DAE △≌△,从而得到CB AD =,然后利用勾股定理求出CB ,及可求出结论;(3)首先根据“双等边”模型推出DCB ECA ≌,得到120DBC EAC ∠=∠=︒,进一步推出AE BC ∥,从而确定随着D 点的运动,点E 在过点A 且平行于BC 的直线PQ 上运动,再根据点到直线的最短距离为垂线段的长度,确定OE 最短时,各点的位置关系,最后根据含30°角的直角三角形的性质求解即可.【详解】解:(1)∵26930a a b -+++=,∴()2330a b -++=,由非负性可知,3030a b -=⎧⎨+=⎩,解得:33a b =⎧⎨=-⎩,∴()3,0A ,()3,0B -,()336AB =--=,∵()0,4C ,∴4OC =,∴11641222ABC S AB OC ==⨯⨯= ;(2)由(1)知()3,0A ,()3,0B -,∴OA OB =,∵OC AB ⊥,∴90AOC BOC ∠=∠=︒,在AOC 和BOC 中,OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴()AOC BOC SAS △≌△,∴CBO CAO ∠=∠,∵CDA CDE ADE BCD CBA ∠=∠+∠=∠+∠,CBA CDE ∠=∠,∴ADE BCD ∠=∠,在BCD △和ADE V 中,BCD ADE CBD DAE BD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BCD ADE AAS ≌,∴CB AD =,∵()3,0B -,()0,4C ,∴3OB =,4OC =,∴5BC ==,∴5AD BC ==,∵()3,0A ,∴()2,0D -;(3)由(2)可知CB =CA ,∵∠CBA =60°,∴△ABC 为等边三角形,∠BCA =60°,∠DBC =120°,∵△CDE 为等边三角形,∴CD =CE ,∠DCE =60°,∵∠DCE =∠DCB +∠BCE ,∠BCA =∠BCE +∠ECA ,∴∠DCB =∠ECA ,在△DCB 和△ECA 中,CD CE DCB ECA CB CA =⎧⎪∠=∠⎨⎪=⎩∴()DCB ECA SAS ≌,∴120DBC EAC ∠=∠=︒,∵12060180EAC ACB ∠+∠=︒+︒=︒,∴AE BC ∥,即:随着D 点的运动,点E 在过点A 且平行于BC 的直线PQ 上运动,∵要使得OE 最短,∴如图所示,当OE ⊥PQ 时,满足OE 最短,此时∠OEA =90°,∵120DBC EAC ∠=∠=︒,60CAB ∠=︒,∴60OAE EAC CAB ∠=∠-∠=︒,30AOE ∠=︒,∵()3,0A ,∴3OA =,∴1322AE OA ==,∴当OE 最短时,A ,E 两点之间的距离为32.【点睛】本题考查坐标与图形,全等三角形的判定与性质,等腰三角形和等边三角形的判定与性质等,理解平面直角坐标系中点坐标的特征,掌握等腰或等边三角形的性质,熟练使用全等三角形的判定与性质是解题关键.15.在▱ABCD中,∠ABC=60°,AB=4,BC=6.点E'在BC边上且BE'=4,将B E'绕点B逆时针旋转a°得到BE(0°<a<180°).(1)如图1,当∠EBA=90°时,求S△BCE;(2)如图2,在旋转过程中,连接CE,取CE中点F,作射线BF交直线AD于点G.①求线段BF的取值范围;②当∠EBF=120°时,求证:BC﹣DG=2BF;(3)如图3.当∠EBA=90°时,点S为线段BE上一动点,过点E作EM⊥射线AS于点M,N为AM中点,直接写出BN的最大值与最小值.=6;【答案】(1)S△BCE(2)①1<BF<5;②证明见解答;(3)BNBN的最大值为【分析】(1)如图1,过点E 作EF ⊥BC 交CB 的延长线于点F ,根据题意求得∠EBF =180°-∠EBA -∠ABC =180°-90°-60°=30°,再根据特殊直角三角形的性质进而求得BC 上的高EF =2,代入面积公式算出结果;(2)①如图,在线段FG 上截取FK =BF ,连接EK 、CK ,可证得四边形BCKE 是平行四边形,得出:BE =CK =BE '=4,BC =6,再运用三角形三边关系即可求得答案;②可证△EKB ≌△BGA (AAS ),得出BK =AG ,由AG =AD -DG ,即可推出结论;(3)连接AE ,取AE 的中点P ,PA 的中点Q ,连接BP 、NP 、NQ 、BQ ,可证△ABE 是等腰直角三角形,得出:AE AB P 是AE 的中点,可得:BP ⊥AE ,且BP =AP =EP ,利用勾股定理得BQ,当B 、Q 、N 三点共线时,BN 的最小值=BQ -NQ,当点S 与点E 重合时,EM =0,PN =0,此时,BN 的最大值=BP 【详解】(1)解:如图1,过点E 作EH ⊥BC 交CB 的延长线于点H ,∴∠EHC =90°,∵∠ABC =60°,∠EBA =90°,∴∠EBH =180°-∠EBA -∠ABC =180°-90°-60°=30°,∵点E '在BC 边上且BE '=4,将B E '绕点B 逆时针旋转α°得到BE ,∴BE =B E '=4,∴EH =12BE =12×4=2,又∵BC =6,∴S △BCE =12BC •EH =12×6×2=6;(2)解:①如图,在线段FG 上截取FK =BF ,连接EK 、CK ,∵EF=FC,BF=FK,∴四边形BCKE是平行四边形,∴BE=CK=BE'=4,BC=6,在△BCK中,BC-CK<BK<BC+CK,∴6-4<BK<6+4,即2<2BF<10,∴1<BF<5;②证明:∵四边形ABCD是平行四边形,且∠ABC=60°,AB=4,∴∠A=180°-∠ABC=180°-60°=120°,AD∥BC,AD=BC,BE=AB,∵∠EBF=120°,即∠EBK=120°,∴∠EBK=∠A,∵EK∥BC,∴EK∥AD,∴∠EKB=∠BGA,在△EKB和△BGA中,EKB BGAEBK ABE AB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EKB≌△BGA(AAS),∴BK=AG,由①知:BK=2BF,又∵AG=AD-DG,∴2BF =BC -DG ;(3)解:连接AE ,取AE 的中点P ,PA 的中点Q ,连接BP 、NP 、NQ 、BQ ,∵∠ABE =90°,AB =BE =4,∴△ABE 是等腰直角三角形,∴AE ,∵点P 是AE 的中点,∴BP ⊥AE ,且BP =AP =EP ,∵N 是AM 的中点,P 是AE 的中点,∴PN 是△AEM 的中位线,∴PN ∥EM ,∴∠ANP =∠AME =90°,∵点Q 是AP 的中点,∴QN =PQ =12AP在Rt △BPQ 中,BQ =当B 、Q 、N 三点共线时,BN 的最小值=BQ -NQ 当点S 与点E 重合时,EM =0,PN =0,此时,BN 的最大值=BP 【点睛】本题是几何变换综合题,主要考查了旋转的性质,平行四边形的性质,等腰直角三角形的性质,全等三角形的判定与性质,三角形中位线定理及勾股定理等知识,解题的关键是灵活运用所学知识解决问题.16.如图,线段AB =10cm ,C 是线段AB 上的一个动点(不与A 、B 重合),在AB 上方分别以AC 、BC 为边作正△ACD 和正△BCE ,连接AE ,交CD 于M ,连接BD ,交CE 于N ,AE 、BD 交于H ,连接CH .(1)求sin ∠AHC ;(2)连接DE ,设AD =x ,DE =y ,求y 与x 之间的函数关系式;(3)把正△BCE 绕C 顺时针旋转一个小于60°的角,在旋转过程中H 到△DCE 的三个顶点距离和最小,即HC +HD +HE 的值最小,HC +HD +HE 的值总等于线段BD 的长.若AC =,旋转过程中某一时刻2AH =3DH ,此刻△ADH 内有一点P ,求PA +PD +PH 的最小值.【答案】(1)2;(2)y0<x <10);【分析】(1)过点C 作CT ⊥AE 于点T ,CR ⊥BD 于点R ,先证△ACE ≌△DCB 得∠CAM =∠HDM ,由直角三角函数可得sin sin =CT CA CAM CD HDM CR ∠=∠= ,从而得CH 平分∠AHB ,进而求得∠AHC =∠BHC =60°即可求解;(2)如图2中,如图,过点D 作DP ⊥CE 于点P ,先由三角函数求得CP =12CD =12x ,DP =2x ,又由AB =10cm ,得CE =CB =(10﹣x )cm ,进而得PE =|10﹣x ﹣12x |=|10﹣32x |,最后由勾股定理即可求得y 与x 之间的函数关系式;(3)如图3中,以AD 为边向外作等边△ADW ,连接WH ,由题意WH 是PA +PD +PH .过点D 作DS ⊥AH 于H ,过点W 作WG ⊥AD 于点G ,过点H 作HK ⊥AD 于K ,过点W 作WQ ⊥HK 于点Q .假设AH =3k ,DH =2k ,由勾股定理得AH =6,DH =4,DSHKDKWQ =KGGW =KWHQWH 的长即PA +PD +PH 的最小值.【详解】(1)解:过点C 作CT ⊥AE 于点T ,CR ⊥BD 于点R.∵△ADC ,△ECB 都是等边三角形,∴CA =CD ,CE =CB ,∠ACD =∠ECB =60°,∴∠ACE =∠DCB ,在△ACE 和△DCB 中,CA CD ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△DCB (SAS ),∴∠CAM =∠HDM ,∵CT ⊥AE ,CR ⊥BD ,∴sin sin =CT CA CAM CD HDM CR ∠=∠= ,∴CH 平分∠AHB ,∵∠AMC =∠DMH ,∴∠AHM =∠ACM =60°,∴∠AHC =∠BHC =60°,∴sin ∠AHC =2;(2)解:如图2中,如图,过点D 作DP ⊥CE 于点P .∵AC =CD =x (cm ),∠DCE =60°,∴CP =12CD =12x ,DP ,∵AB =10cm ,∴BC =AB ﹣AC =(10﹣x )cm ,∴CE =CB =(10﹣x )cm ,∴PE =|10﹣x ﹣12x |=|10﹣32x |,∴y =DE (0<x <10);(3)解:如图3中,以AD 为边向外作等边△ADW ,连接WH ,由题意WH 是PA +PD +PH .过点D 作DS ⊥AH 于H ,过点W 作WG ⊥AD 于点G ,过点H 作HK ⊥AD 于K ,过点W 作WQ ⊥HK 于点Q .∵2AH =3DH ,∴可以假设AH =3k ,DH =2k ,∵∠DHS =60°,DS ⊥AH ,∴SH =12DH =k ,DS ,AM =2k ,∵AD 2=AS 2+DS 2,∴()2=(2k )2+)2,∴k =2(负根已经舍弃),∴AH =6,DH =4,DS∵12•AH •DS =12•AD •HK ,∴HK =7,DK 7,∵AG =DG WQKG 是矩形,∴WQ =KG GW =KW∴HQ =KH +KQ =7,∴WH =∴PA +PD +PH 的最小值为【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,解直角三角形等知识,添加常用辅助线,构造直角三角形解决问题是解本题的关键.17.在学习了图形的旋转知识后,某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究.(1)问题梳理,问题呈现:如图1,点D 在等边ABC 的边BC 上,过点C 画AB 的平行线l ,在l 上取CE BD =,连接AE ,则在图1中会产生一对旋转图形.请结合问题中的条件,证明:ABD ACE ≌△△;(2)初步尝试:如图2,在ABC 中,AB AC =,点D 在BC 边上,且BD DC <,将ABD △沿某条直线翻折,使得AB 与AC 重合,点D 与BC 边上点F 重合,再将ACF △沿AC 所在直线翻折,得到ACE △,则在图2中会产生一对旋转图形.若30BAC ∠=︒,6AD =,连接DE ,求ADE V 的面积;(3)深入探究:如图3,在ABC 中,60ACB ∠=︒,75BAC ∠=︒,6AC =,点D 是边BC 上的任意一点,连接AD ,将线段AD 绕点A 按逆时针方向旋转75°,得到线段AE ,连接CE ,求线段CE 长度的最小值.【答案】(1)见解析;(2)9;(3)【分析】(1)根据△ABC 是等边三角形,可得AB =AC ,∠BAC =∠B =60°,进而利用SAS 可证明△ABD ≌△ACE .(2)如图2,过点E 作EH ⊥AD 于H ,由翻折可得△ACE ≌△ABD ≌△ACF ,可得AE =AD =6,EH =3,再运用S △ADE =12×AD ×EH ,即可求得答案.(3)如图3中,在AB 上截取AN =AC ,连接DN ,作NH ⊥BC 于H ,作AM ⊥BC 于M .利用SAS 证明△EAC ≌△DAN ,推出当DN 的值最小时,EC 的值最小,求出HN 的值即可解决问题.【详解】(1)如图1,∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠B =60°,∵CE ∥AB ,∴∠ACE =∠BAC =60°,∴∠B =∠ACE ,在△ABD 和△ACE 中,AB AC B ACE BD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS );(2)如图2,过点E 作EH ⊥AD 于H,∵由翻折可得:△ACF ≌△ABD ,△ACE ≌△ACF ,∴△ACE ≌△ABD ≌△ACF ,∴AE =AD =6,∠CAE =∠BAD ,∴∠DAE =∠BAC =30°,∵EH ⊥AD ,∴EH =12AE =3,∴S △ADE =12×AD ×EH =12×6×3=9;(3)如图3中,在AB 上截取AN =AC ,连接DN ,作NH ⊥BC 于H ,作AM ⊥BC 于M.∵∠CAB =∠DAE ,∴∠EAC =∠DAN ,∵AE =AD ,AC =AN ,∴△EAC ≌△DAN (SAS ),∴CE =DN ,∴当DN 的值最小时,EC 的值最小,在Rt △ACM 中,∵∠ACM =60°,AC =6,∴30CAM ∠=︒,∴132CM AC ==,∴AM∵∠MAB =∠BAC −∠CAM =75°−30°=45°,∴AMB 为等腰直角三角形,∴AB=,∴NB =AB −AN =−6,在Rt △NHB 中,∵∠B =45°,∴NBH △为等腰直角三角形,∴NH根据垂线段最短可知,当点D 与H 重合时,DN 的值最小,∴CE 的最小值为.【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.18.(一)发现探究在△ABC中AB=AC,点P在平面内,连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度,得到线段AQ,连接BQ;【发现】如图1如果点P是BC边上任意一点,则线段BQ和线段PC的数量关系是;【探究】如图2,如果点P为平面内任意一点.前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.请仅以图2所示的位置关系加以证明(或说明);(二)拓展应用【应用】如图3,在△DEF中,DE=6,∠EDF=60°,∠DEF=90°,P是线段EF上的任意一点连接DP,将线段DP绕点D顺时针方向旋转60°,得到线段DQ,连接EQ请求出线段EQ长度的最小值.【答案】【发现】BQ=PC;【探究】BQ=PC仍然成立,证明见解析;【应用】线段EQ长度的最小值为3.【分析】[发现]先判断出∠BAQ=∠CAP,进而用SAS判断出△BAQ≌△CAP,即可得出结论;[探究]结论BQ=PC仍然成立,理由同【发现】的方法;[应用]在DF上取一点H,使DH=DE,连接PH,过点H作HM⊥EF于M,构造出△DEQ≌△DHP,得出EQ=HP,当HP⊥EF(点P和点M重合)时,EQ最小,求HM即可.【详解】[发现]由旋转知,AQ=AP,∵∠PAQ=∠BAC,∴∠PAQ﹣∠BAP=∠BAC﹣∠BAP,∴∠BAQ=∠CAP,∵AB=AC,∴△BAQ≌△CAP(SAS),∴BQ=CP,故答案为:BQ=PC;【探究】结论:BQ=PC仍然成立,理由:由旋转知,AQ=AP,∵∠PAQ=∠BAC,∴∠PAQ﹣∠BAP=∠BAC﹣∠BAP,∴∠BAQ=∠CAP,∵AB=AC,∴△BAQ≌△CAP(SAS),∴BQ=CP,【应用】如图3,在DF上取一点H,使DH=DE,连接PH,过点H作HM⊥EF于M,由旋转知,DQ=DP,∠PDQ=60°,∵∠EDF=60°,∴∠PDQ=∠EDF,∴∠EDQ=∠HDP,∴△DEQ≌△DHP(SAS),∴EQ=HP,求EQ最小,就是求HP最小,当HP⊥EF(点P和点M重合)时,HP最小,最小值为HM,∵∠EDF=60°,∠DEF=90°,∴∠F=30°,∵DE=6,∴DF=2DE=12,∵DH=DE=6,∴FH=6,∵∠F=30°,∴HM=3.线段EQ长度的最小值为3..【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,含30°角的直角三角形的性质,恰当的作辅助线,把所求线段转化为与动点P有关的线段,根据垂线段最短确定线段位置是解本题的关键.。
压轴题28填空压轴题(函数篇)-2023年中考数学压轴题专项训练(全国通用)(原卷版)

2023年中考数学压轴题专项训练压轴题28填空压轴题(函数篇)一.填空题(共40小题)1.(2023•上虞区模拟)已知点A在反比例函数y=12x(x>0)的图象上,点B在x轴正半轴上,若△OAB为等腰直角三角形,则AB的长为.2.(2023•姑苏区校级一模)在平面直角坐标系xOy中,对于点P(a,b),若点P'的坐标为(ka+b,a+b k)(其中k为常数且k≠0),则称点P'为点P的“k—关联点”.已知点A在函数y=3x(x>0)的图象上运动,且A是点B的“3—关联点”,若C(﹣1,0),则BC的最小值为.3.(2023•海门市一模)如图,在平面直角坐标系xOy中,已知点A(m,n),B(m+4,n﹣2)是函数y=kx(k>0,x>0)图象上的两点,过点B作x轴的垂线与射线OA交于点C.若BC=8,则k的值为.4.(2023•建昌县一模)如图,在平面直角坐标系中,点A,B在反比例函数y=kx(k≠0,x>0)的图象上,点C在y轴上,AB=AC,AC∥x轴,BD⊥AC于点D,若点A的横坐标为5,BD=3CD,则k值为.5.(2023•碑林区校级模拟)如图,等腰直角△ABC的顶点A坐标为(﹣3,0),直角顶点B坐标为(0,1),反比例函数y=kx(x<0)的图象经过点C,则k=.6.(2023•宁波模拟)如图,在平面直角坐标系xOy中,△OAB为等腰直角三角形,且∠A=90°,点B的坐标为(4,0).反比例函数y=kx(k≠0)的图象交AB于点C,交OA于点D.若C为AB的中点,则ODOA=.7.(2023•龙港市二模)如图,Rt△ABO放置在平面直角坐标系中,∠ABO=Rt∠,A的坐标为(﹣4,0).将△ABO绕点O顺时针旋转得到△A′B′O,使点B落在边A′O的中点.若反比例函数y=kx(x>0)的图象经过点B',则k的值为.8.(2023•温州二模)如图,点A在x轴上,以OA为边作矩形OABC,反比例函数y=kx(k>0,x>0)的图象经过AB的中点E,交边BC于点D,连结OE.若OE=OC,CD=2,则k的值为.9.(2023•石家庄二模)已知A,B,C三点的坐标如图所示.(1)若反比例函数y=kx的图象过点A,B,C中的两点,则不在反比例函数图象上的是点;(2)当反比例函数的图象与线段AC(含端点)有且只有一个y=kx公共点时,k的取值范围是.10.(2023•郫都区二模)定义:若一个函数图象上存在横纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点(﹣1,﹣1)是函数y=2x+1的图象的“等值点”.若函数y=x2﹣2(x≥m)的图象记为W1,将其沿直线x=m翻折后的图象记为W2.当W1、W2两部分组成的图象上恰有2个“等值点”时,m的取值范围为.11.(2023•双阳区一模)如图,抛物线y=﹣0.25x2+4与y轴交于点A,过AO的中点作BC∥x轴,交抛物线y=x2于B、C两点(点B在C的左边),连接BO、CO,若将△BOC向上平移使得B、C两点恰好落在抛物线y=﹣0.25x2+4上,则点O平移后的坐标为.12.(2023•衡水二模)如图,点A(a,−3a)(a<0)是反比例函数y=k x图象上的一点,点M(m,0),将点A绕点M顺时针旋转90°得到点B,连接AM,BM.(1)k的值为;(2)当a=﹣3,m=0时,点B的坐标为;(3)若a=﹣1,无论m取何值时,点B始终在某个函数图象上,这个函数图象所对应的表达式.13.(2023•市中区二模)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2023个点的坐标.14.(2023•沈阳二模)某商厦将进货单价为70元的某种商品,按销售单价100元出售时,每天能卖出20个,通过市场调查发现,这种商品的销售单价每降价1元,日销量就增加1个,为了获取最大利润,该种商品的销售单价应降 元.15.(2023•贵港二模)如图,抛物线y 1截得坐标轴上的线段长AB =OD =6,D 为y 1的顶点,抛物线y 2由y 1平移得到,y 2截得x 轴上的线段长BC =9.若过原点的直线被抛物线y 1,y 2所截得的线段长相等,则这条直线的解析式为 .16.(2023•江都区一模)如图,在平面直角坐标系中,点A ,B 坐标分别为(3,4),(﹣1,1),点C 在线段AB 上,且AC BC=13,则点C 的坐标为 .17.(2023•龙华区二模)如图,在平面直角坐标系中,OA =3,将OA 沿y 轴向上平移3个单位至CB ,连接AB ,若反比例函数y =kx (x >0)的图象恰好过点A 与BC 的中点D ,则k = .18.(2023•乐至县模拟)如图,在平面直角坐标系中,点A 、A 1、A 2、A 3…A n 在x 轴上,B 1、B 2、B 3…B n在直线y =−√33x +√33上,若A (1,0),且△A 1B 1O 、△A 2B 2A 1…△A n B n A n ﹣1都是等边三角形,则点B n的横坐标为 .19.(2023•玄武区一模)已知函数y =2x 2﹣(m +2)x +m (m 为常数),当﹣2≤x ≤2时,y 的最小值记为a .a 的值随m 的值变化而变化,当m = 时,a 取得最大值.20.(2023•萧山区一模)已知点P (x 1,y 1)Q (x 2,y 2)在反比例函数y =6x图象上. (1)若x 1x 2=2,则y 1y 2= .(2)若x 1=x 2+2,y 1=3y 2,则当自变量x >x 1+x 2时,函数y 的取值范围是 . 21.(2023•灞桥区校级模拟)如图,点A ,B 分别在y 轴正半轴、x 轴正半轴上,以AB 为边构造正方形ABCD ,点C ,D 恰好都落在反比例函数y =k x(k ≠0)的图象上,点E 在BC 延长线上,CE =BC ,EF ⊥BE ,交x 轴于点F ,边EF 交反比例函数y =kx(k ≠0)的图象于点P ,记△BEF 的面积为S ,若S =k2+12,则k 的值为 .22.(2023•东莞市校级一模)如图,在平面直角坐标系中,点A 在y 轴上,点B 在x 轴上.以AB 为边长作正方形ABCD ,S 正方形ABCD =50,点C 在反比例函数y =k /x (k ≠0,x >0)的图象上,将正方形沿x 轴的负半轴方向平移6个单位长度后,点D 刚好落在该函数图象上,则k 的值是 .23.(2023•长春一模)如图,正方形ABCD 、CEFG 的顶点D 、F 都在抛物线y =−12x 2上,点B 、C 、E 均在y 轴上.若点O 是BC 边的中点,则正方形CEFG 的边长为 .24.(2023•成都模拟)如图,在△AOB 中,AO =AB ,射线AB 分别交y 轴于点D ,交双曲线y =kx (k >0,x >0)于点B ,C ,连接OB ,OC ,当OB 平分∠DOC 时,AO 与AC 满足AO AC=23,若△OBD 的面积为4,则k= .25.(2023•北仑区二模)如图,将矩形OABC 的顶点O 与原点重合,边AO 、CO 分别与x 、y 轴重合.将矩形沿DE 折叠,使得点O 落在边AB 上的点F 处,反比例函数y =kx (k >0)上恰好经过E 、F 两点,若B 点的坐标为(2,1),则k 的值为 .26.(2023•合肥二模)已知函数y =x 2+mx (m 为常数)的图形经过点(﹣5,5). (1)m = .(2)当﹣5≤x ≤n 时,y 的最大值与最小值之和为2,则n 的值 .27.(2023•仓山区校级模拟)下表记录了二次函数y =ax 2+bx +2(a ≠0)中两个变量x 与y 的6组对应值,x … ﹣5 x 1 x 2 1 x 3 3 … y…m2nm…其中﹣5<x 1<x 2<1<x 3<3.根据表中信息,当−52<x <0时,直线y =k 与该二次函数图象有两个公共点,则k 的取值范围为 .28.(2023•西安二模)如图,在平面直角坐标系中,直线y =﹣x +1与x 轴,y 轴分别交于点A ,B ,与反比例函数y =kx (k <0)的图象在第二象限交于点C ,若AB =BC ,则k 的值为 .29.(2023•龙泉驿区模拟)在某函数的给定自变量取值范围内,该函数的最大值与最小值的差叫做该函数在此范围内的界值.当t ≤x ≤t +1时,一次函数y =kx +1(k >0)的界值大于3,则k 的取值范围是 ;当t ≤x ≤t +2时,二次函数y =x 2+2tx ﹣3的界值为2,则t = .30.(2023•姑苏区一模)如图①,四边形ABCD 中,AB ∥DC ,AB >AD .动点P ,Q 均以1cm /s 的速度同时从点A 出发,其中点P 沿折线AD ﹣DC ﹣CB 运动到点B 停止,点Q 沿AB 运动到点B 停止,设运动时间为t (s ),△APQ 的面积为y (cm 2),则y 与t 的函数图象如图②所示,则AB = cm .31.(2023•宁波模拟)如图,点B 是反比例函数y =8x(x >0)图象上一点,过点B 分别向坐标轴作垂线,垂足为A ,C .反比例函数y =kx (x >0)的图象经过OB 的中点M ,与AB ,BC 分别相交于点D ,E .连接DE 并延长交x 轴于点F ,点G 与点O 关于点C 对称,连接BF ,BG .则k = ;△BDF 的面积= .32.(2023•青羊区模拟)如图,在平面直角坐标系中,一次函数y =3x 与反比例函数y =kx (k ≠0)的图象交于A ,B 两点,C 是反比例函数位于第一象限内的图象上的一点,作射线CA 交y 轴于点D ,连接BC ,BD ,若CD BC=45,△BCD 的面积为30,则k = .33.(2023•锦江区模拟)已知关于x的多项式ax2+bx+c(a≠0),二次项系数、一次项系数和常数项分别a,b,c,且满足a2+2ac+c2<b2.若当x=t+2和x=﹣t+2(t为任意实数)时ax2+bx+c的值相同;当x=﹣2时,ax2+bx+c的值为2,则二次项系数a的取值范围是.34.(2023•江北区一模)如图,菱形ABCO的顶点A与对角线交点D都在反比例函数y=kx(k>0)的图象上,对角线AC交y轴于点E,CE=2DE,且△ADB的面积为15,则k=;延长BA交x轴于点F,则点F的坐标为.35.(2023•吴兴区一模)如图1,点A是反比例函数y=kx(k>0)的图象上一点,连接OA,过点A作AA1∥y轴交y=1x(x>0)的图象于点A1,连接OA1并延长交y=k x(k>0)的图象于点B,过点B作BB1∥y轴交y=kx(k>0)的图象于点B1,已知点A的横坐标为1,S△AOA1=2S△BA1B1,连接OB1,小明通过对△AOA1和△BOB1的面积与k的关系展开探究,发现k的值为;如图2,延长OB1交y=kx(k>0)的图象于点C,过点C作CC1∥y轴交y=kx(k>0)的图象于点C1,依此进行下去.记S△BA1B1=S1,S△CB1C1=S2,…则S2023=.36.(2023•徐汇区二模)如图,抛物线C1:y=x2+2x−3与抛物线C2:y=ax2+bx+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A、B(点B在点A右侧),与y轴的交点分别为C、D.如果BD=CD,那么抛物线C2的表达式是.37.(2023•蜀山区校级模拟)距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h (米)与物体运动的时间t(秒)之间满足函数关系h=﹣5t2+mt+n,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差).(1)m=,n=;(2)当2≤t≤3时,w的取值范围是.38.(2023•南充模拟)如图,平移抛物线y=ax2+bx+c,使顶点在线段AB上运动,与x轴交于C,D两点.若A(﹣2,﹣3),B(4,﹣3),四边形ABDC的面积为15,则a=.39.(2023•通州区一模)某学校带领150名学生到农场参加植树劳动,学校同时租用A,B,C三种型号客车去农场,其中A,B,C三种型号客车载客量分别为40人、30人、10人,租金分别为700元、500元、200元.为了节省资金,学校要求每辆车必须满载,并将学生一次性送到农场植树,请你写出一种满足要求的租车方案,满足要求的几种租车方案中,最低租车费用是元.40.(2023•武侯区模拟)某投球发射装置斜向上发射进行投球实验,球离地面的高度h(米)与球运行时间t(秒)之间满足函数关系式h=﹣5t2+mt+n,该装置的发射点离地面10米,球筐中心点离地面35米.如图,若某次投球正好中心入筐,球到达球筐中心点所需时间为5秒,那么这次投球过程中球离地面的高度h(米)与球运行时间t(秒)之间满足的函数关系式为(不要求写自变量的取值范围);我们把球在每2秒内运行的最高点离地面的高度与最低点离地面的高度的差称为“投射矩”,常用字母“L”表示.那么在这次投球过程中,球入筐前L的取值范围是.。
2024北京中考数学二轮复习 专题一 选择、填空压轴题 (含答案)

2024北京中考数学二轮复习专题一选择、填空压轴题类型一分析统计图(表)1.根据国家统计局2019—2023年中国普通本专科、中等职业教育及普通高中招生人数的相关数据,绘制统计图如下:2019—2023年普遍本专科、中等职业教育及普遍高中招生人数第1题图下面有四个推断:①2019—2023年,普通本专科招生人数逐年增多;②2023年普通高中招生人数比2019年增加约4%;③2019—2023年,中等职业教育招生人数逐年减少;④2019年普通高中招生人数约是中等职业教育招生人数的1.4倍.所有合理推断的序号是()A.①④ B.②③ C.①②④D.①②③④2.为了解某校学生每周课外阅读时间的情况,随机抽取该校a 名学生进行调查,获得的数据整理后绘制成统计表如下:每周课外阅读时间x (小时)0≤x <22≤x <44≤x <66≤x <8x ≥8合计频数817b 15a 频率0.080.17c 0.151表中4≤x <6组的频数b 满足25≤b ≤35.下面有四个推断:①表中a的值为100;②表中c的值可以为0.31;③这a名学生每周课外阅读时间的中位数一定不在6~8之间;④这a名学生每周课外阅读时间的平均数不会超过6.所有合理推断的序号是()A.①②B.③④C.①②③D.②③④3.密云水库是首都北京重要水源地,水源地生态保护对保障首都水源安全及北京市生态和城市可持续发展具有不可替代的作用.以下是1986—2023年密云水库水体面积和年降水量变化图.1986—2023年密云水库水体面积和年降水量变化图第3题图(以上数据来源于《全国生态气象公报(2023年)》,部分年份缺数据)对于现有数据有以下结论:①2004年的密云水库水体面积最小,仅约为20km2;②2015—2023年,密云水库的水体面积呈持续增加趋势.表明水资源储备增多;③在1986—2023年中,2023年的密云水库水体面积最大,约为170km2;④在1986—2023年中,密云水库年降水量最大的年份,水体面积也最大.其中结论正确的是()A.②③B.②④C.①②③D.③④4.某公司计划招募一批技术人员,他们对25名面试合格人员又进行了理论知识和实践操作测试,其中25名入围者的面试成绩排名,理论知识成绩排名与实践操作成绩的排名情况如图所示第4题图下面有3个推断:①甲的理论知识成绩排名比面试成绩排名靠前;②甲的实践操作成绩排名与理论知识成绩排名相同;③乙的理论知识成绩排名比甲的理论知识成绩排名靠前.其中合理的是()A.①B.①②C.①③D.①②③5.多年来,北京市以强有力的措施和力度治理大气污染,空气质量持续改善,主要污染物的年平均浓度值全面下降.下图是1998年至2019年二氧化硫(SO2)和二氧化氮(NO2)的年平均浓度值变化趋势图.第5题图下列说法错误的是()A.1998年至2019年,SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数B.1998年至2019年,SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数C.1998年至2019年,SO2的年平均浓度值的方差小于NO2的年平均浓度值的方差D.1998年至2019年,SO2的年平均浓度值比NO2的年平均浓度值下降得更快6.“实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标.某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为A,B两组,从A,B组各抽取10位客户的电动汽车的实际平均续航里程数据整理成图.其中“⊙”表示A组的客户,“*”表示B组的客户.第6题图下列推断不正确的是()A.A组客户的电动汽车的“实际平均续航里程”的最大值低于B组B.A组客户的电动汽车的“实际平均续航里程”的方差低于B组C.A组客户的电动汽车的“实际平均续航里程”的平均值低于B组D.这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组7.某种预防病虫害的农药即将于三月15日之前喷洒,需要连续三天完成,又知当最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度时药物效果最佳,为此农广站工作人员查看了三月1—15日的天气预报,请你结合气温图给出一条合理建议,药剂喷洒可以安排在________日开始进行.1—15日天气情况第7题图类型二分析与判断函数图象1.如图,一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同.用t 表示小球滚动的时间,v 表示小球的速度.下列图象中,能表示小球在斜坡上时v 与t 的函数关系的图象大致是()第1题图2.某农科所响应“乡村振兴”号召,为某村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗先在农科所的温室中生长,平均高度长到大约20cm 时,移至该村的大棚内继续生长.研究表明,60天内,这种瓜苗的平均高度y (cm)与生长时间x (天)的函数关系的图象如图所示.当这种瓜苗长到大约80cm 时,开始开花结果,此时瓜苗在该村大棚内生长的天数是()第2题图A.10天B.18天C.33天D.48天3.有一圆形苗圃如图①所示,中间有两条交叉过道AB ,CD ,它们为苗圃⊙O 的直径,且AB ⊥C D.入口K位于AD ︵中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为t ,与入口K 的距离为S ,表示S 与t 的函数关系的图象大致如图②所示,则该园丁行进的路线可能是()第3题图A.A →O →DB.C →A →O →BC.D →O →CD.O →D →B →C4.(2023通州区一模)为满足人民对美好生活的向往,造福子孙后代,环保部门要求相关企业加强污水治理能力,污水排放未达标的企业要限期整改.甲、乙两个企业的污水排放量W 与时间t 的关系如图所示,我们用W t表示t时刻某企业的污水排放量,用-Wt1-Wt2t1-t2的大小评价在t1至t2这段时间内某企业污水治理能力的强弱.已知甲、乙两企业在整改期间排放的污水排放量与时间的关系如下图所示.第4题图给出下列四个结论:①在t1≤t≤t2这段时间内,甲企业的污水治理能力比乙企业强;②在t1时刻,乙企业的污水排放量高;③在t3时刻,甲、乙两企业的污水排放量都已达标;④在0≤t≤t1,t1≤t≤t2,t2≤t≤t3这三段时间中,甲企业在t2≤t≤t3的污水治理能力最强.其中所有正确结论的序号是()A.①②③B.①③④C.②④D.①③5.(2023房山区一模)在平面直角坐标系xOy中,若函数图象上任意两点P(x1,y1),Q(x2,y2)均满足(x1-x2)(y1-y2)>0.下列四个函数图象中,所有正确的函数图象的序号是()第5题图A.①②B.③④C.①③D.②④类型三代数类问题1.(2023西城区期末)现有函数y +4(x <a ),2-2x (x ≥a ),如果对于任意的实数n ,都存在实数m ,使得当x =m 时,y =n ,那么实数a 的取值范围是()A.-5≤a ≤4 B.-1≤a ≤4 C.-4≤a ≤1D.-4≤a ≤52.在平面直角坐标系xOy 中,对于自变量为x 的函数y 1和y 2,若当-1≤x ≤1时,都满足|y 1-y 2|≤1成立,则称函数y 1和y 2互为“关联的”.下列函数中,不与y =x 2互为“关联的”函数是()A.y =x 2-1B.y =2x 2C.y =(x -1)2D.y =-x 2+13.(2023人大附中模拟)在数轴上有三个互不重合的点A ,B ,C ,它们代表的实数分别为a ,b ,c ,下列结论中:①若abc >0,则A ,B ,C 三点中,至少有一个点在原点右侧;②若a +b +c =0,则A ,B ,C 三点中,至少有一个点在原点右侧;③若a +c =2b ,则点B 为线段AC 的中点;④O 为坐标原点且A ,B ,C 均不与O 重合,若OB -OC =AB -AC ,则bc >0.所有正确结论的序号是()A.①② B.③④ C.①②③D.①②③④4.(2023西城区二模)从1,2,3,4,5中选择四个数字组成四位数abcd ,其中a ,b ,c ,d 分别代表千位、百位、十位、个位数字.若要求这个四位数同时满足以下条件:①abcd 是偶数;②a >b >c ;③a +c =b +d ,请写出一个符合要求的数________.5.(2023燕山区期末)在实数范围内定义一种运算“*”,其运算法则为a *b =a 2-a b.根据这个法则,下列结论中错误的是________.(把所有错误结论的序号都填在横线上)①2*3=2-6;②若a +b =0,则a *b =b *a ;③(x +2)*(x +1)=0是一元二次方程;④方程(x +2)*1=3的根是x 1=-3-52,x 2=-3+52.6.(2023丰台区一模)京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系xOy 中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G .点A ,B ,C ,D 分别是图形G 与坐标轴的交点,已知点D 的坐标为(0,-3),AB 为半圆的直径,且AB =4,半圆圆心M 的坐标为(1,0).关于图形G 给出下列四个结论,其中正确的是________(填序号).①图形G 关于直线x =1对称;②线段CD 的长为3+3;③图形G 围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点);④当-4≤a ≤2时,直线y =a 与图形G 有两个公共点.第6题图7.(2023石景山区二模)在平面直角坐标系xOy 中,A (0,1),B (1,1),有以下4种说法:①一次函数y =x 的图象与线段AB 无公共点;②当b <0时,一次函数y =x +b 的图象与线段AB 无公共点;③当k >1时,反比例函数y =k x的图象与线段AB 无公共点;④当b >1时,二次函数y =x 2-bx +1的图象与线段AB 无公共点.上述说法中正确的是________.8.(2023一七一中学模拟)小聪用描点法画出了函数y =x (x ≥0)的图象F ,如图所示.结合旋转的知识,他尝试着将图象F 绕原点逆时针旋转90°得到图象F 1,再将图象F 1绕原点逆时针旋转90°得到图象F 2,如此继续下去,得到图象F n .在尝试的过程中,他发现点P (4,2)在图象________上(写出一个正确的即可);若点P (a ,b )在图象F 2021上,则a =________(用含b 的代数式表示).第8题图9.如图,A (0,1),B (1,5),曲线BC 是双曲线y =k x(k ≠0)的一部分,曲线AB 与BC 组成图形G ,由点C 开始不断重复图形G 形成一线“波浪线”,若点P (2023,m ),Q (x ,n )在该“波浪线”上,则m 的值为________.n 的最大值为________.第9题图类型四几何类问题1.(2023海淀区一模)如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR 边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是()第1题图A.AB和CDB.AB和EFC.CD和GHD.EF和GH2.程老师制作了如图①所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动.图②是操作学具时,所对应某个位置的图形的示意图.第2题图有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ;②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ;③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ;④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ.其中所有正确结论的序号是()A.②③B.③④C.②③④D.①②③④3.(2021东城区二模)数学课上,李老师提出如下问题:已知:如图,AB是⊙O的直径,射线AC交⊙O于C.求作:弧BC的中点D.同学们分享了如下四种方案:第3题图①如图①,连接BC,作BC的垂直平分线,交⊙O于点D;②如图②,过点O作AC的平行线,交⊙O于点D;③如图③,作∠BAC的平分线,交⊙O于点D;④如图④,在射线AC上截取AE,使AE=AB,连接BE,交⊙O于点D.上述四种方案中,正确的方案的序号是________.4.(20231大兴区一模)如图,在▱ABCD中,AD>AB,E,F分别为边AD,BC上的点(E,F 不与端点重合).对于任意▱ABCD,下面四个结论中:①存在无数个四边形ABFE,使得四边形ABFE是平行四边形;②至少存在一个四边形ABFE,使得四边形ABFE是菱形;③至少存在一个四边形ABFE,使得四边形ABFE是矩形;④存在无数个四边形ABFE,使得四边形ABFE的面积是▱ABCD面积的一半.所有正确结论的序号是________.第4题图5.(2021西城区期末)如图,在平面直角坐标系xOy中,P(4,3),⊙O经过点P.点A,点B 在y轴上,PA=PB,延长PA,PB分别交⊙O于点C,点D,设直线CD与x轴正方向所夹的锐角为α.(1)⊙O的半径为________;(2)tanα=________第5题图参考答案类型一分析统计图(表)1.C【解析】由题图知2019—2023年,普通本专科招生人数逐年增多,故①正确;2023年普通高中招生人数比2019年增加约876-839×100%≈4%,故②正确;从2019—2018839年,中等职业教育招生人数逐年减少,从2019—2023年,中等职业教育招生人数在增加,故③错误;2019年普通高中招生人数约是中等职业教育招生人数的839÷600≈1.4倍,故④正确.2.A【解析】①8÷0.08=100,故表中a的值为100,是合理推断;②25÷100=0.25,35÷100=0.35,1-0.08-0.17-0.35-0.15=0.25,1-0.08-0.17-0.25-0.15=0.35,故表中c的值为0.25≤c≤0.35,表中c的值可以为0.31,是合理推断;③∵表中4≤x<6组的频数b满足25≤b≤35,∴8+17+25=50,8+17+35=60,∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.3.A【解析】由题图知①2004年的水体面积超过60km2,不符合题意;②2015—2023年,密云水库的水体面积呈持续增加趋势,表明水资源储备增多,符合题意;③在1986—2023年中,2023年的密云水库水体面积最大,约为170km2,符合题意;④水体面积最大的年份是2023年,但年降水量不是最大,不符合题意.4.D【解析】由题图知,甲的面试成绩排名为11,理论知识成绩排名为8,实践操作成绩排名为8;乙的面试成绩排名为7,实践操作成绩排名为15,理论知识成绩排名为5,故①②③都合理,故选D.5.C【解析】由题图可得,A.2000年至2019年,SO2的年平均浓度值都在NO2的年平均浓度值以下,由此可得SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数,此选项正确,不合题意;B.2000年至2019年,SO2的年平均浓度值都在NO2的年平均浓度值以下,由此可得SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数,此选项正确,不合题意;C.根据图中两折线中点的离散程度可得SO2的年平均浓度值的方差大于NO2的年平均浓度值的方差,此选项错误,符合题意;D.1998年至2019年,根据图中两折线的起止点可得SO2的年平均浓度值比NO2的年平均浓度值下降得更快,此选项正确,不合题意.6.C 【解析】由图象可得,A 组客户的电动汽车的“实际平均续航里程”的最大值在350左右,B 组客户的电动汽车的“实际平均续航里程”的最大值在450左右,故A 选项不符合题意;A 组客户的电动汽车的“实际平均续航里程”的数据波动比B 组客户的电动汽车的“实际平均续航里程”的数据波动小,即A 组客户的电动汽车的“实际平均续航里程”的方差比B 组客户的电动汽车的“实际平均续航里程”的方差小,故B 选项不符合题意;A 组客户的电动汽车的“实际平均续航里程”的平均值不一定低于B 组,故C 选项符合题意;这20位客户的电动汽车的“实际平均续航里程”按从大到小排序,第10位,第11位均在B 组,故D 选项不符合题意.7.3或12(任写一个即可)【解析】由题图可知,3日、4日、5日最低温度分别是1摄氏度、2摄氏度、0摄氏度,且昼夜温差分别是8-1=7摄氏度,4-2=2摄氏度,9-0=9摄氏度,最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度,可以药剂喷洒,12日、13日、14日最低温度分别是6摄氏度、7摄氏度、8摄氏度,且昼夜温差分别是12-6=6摄氏度,16-7=9摄氏度,14-8=6摄氏度,最低温度不低于0摄氏度,且昼夜温差不大于10摄氏度,可以药剂喷洒.类型二分析与判断函数图象1.D 【解析】∵一个小球由静止开始沿一个斜坡滚下,其速度每秒增加的值相同,∴v t为定值,∴v 与t 是正比例函数的关系.∴选项D 符合题意.2.B 【解析】当15<x ≤60时,设y =kx +b (k ≠0),k +b =20,k +b =170,=103,=-30,∴y =103x -30.当y =80时,103x -30=80,解得x =33,33-15=18(天),∴开始开花结果,此时瓜苗在该村大棚内生长的天数是18天.3.B 【解析】若按A →O →D 路线,图象应呈现对称性,故A 错误;若按C →A →O →B ,则从C →A 距离逐渐减少,A →O →B 距离先减少,再增大,符合题图中函数图象的大致走势,故B 正确;C 、D 中,起始点处S 值小于终点处S 值,由题图可知在起点和终点时,S 值最大且相等,故C 、D 错误.4.D 【解析】①在t 1≤t ≤t 2这段时间内,甲企业的图象比乙企业的图象倾斜角度大,故①正确;②在t 1时刻,甲企业的污水排放量高,故②错误;③在t 3时刻,甲、乙两企业的污水排放量在达标量以下,故③正确;④在0≤t ≤t 1,t 1≤t ≤t 2,t 2≤t ≤t 3这三段时间中,甲企业在t 1≤t ≤t 2的图象倾斜角度最大,即治理污水能力最强,故④错误.5.D 【解析】由题意中(x 1-x 2)(y 1-y 2)>0可知,x 1-x 2>0,y 1-y 2>0或x 1-x 2<0,y 1-y 2<0,即当x 1>x 2时,y 1>y 2或当x 1<x 2时,y 1<y 2.故函数中y 随着x 的增大而增大,故②④正确.类型三代数类问题1.A 【解析】如解图,由图象可知,当-5≤a ≤4时,对于任意的实数n ,都存在实数m ,使得当x =m 时,函数y =n .第1题解图2.C 【解析】A .∵|y 1-y 2|=|x 2-(x 2-1)|=1≤1,故A 选项与y =x 2互为“关联的”函数;B .∵|y 1-y 2|=|x 2-2x 2|=x 2,又∵-1≤x ≤1,∴x 2≤1,故B 选项与y =x 2互为“关联的”函数;C .∵|y 1-y 2|=|x 2-(x -1)2|=|2x -1|,又∵-1≤x ≤1,∴|2x -1|≤3,故C 选项不与y =x 2互为“关联的”函数;D .∵|y 1-y 2|=|x 2-(-x 2+1)|=|2x 2-1|,又∵-1≤x ≤1,∴|2x 2-1|≤1,故D 选项与y =x 2互为“关联的”函数.3.D 【解析】若全在原点的左侧,则a <0,b <0,c <0,与abc >0矛盾,∴三点中至少有一个在原点的右侧,故①正确;若全在原点的左侧,则a <0,b <0,c <0,∴a +b +c <0.又∵a ,b ,c 不全为0,与a +b +c =0矛盾,∴至少有一个点在原点右侧,故②正确;∵a +c =2b ,∴b =a +c 2,∴B 为AC 的中点,故③正确;由绝对值的意义:OB =|b |,OC =|c |,AB =|b -a |,AC =|c -a |,|b |-|c |=|b -a |-|c -a |,∴A 在最左或最右时,上面等式的右边=b -c 或c -b ,∴|b |-|c |=b -c ,∴b >0,c >0,∴bc >0,|b |-|c |=c -b ,∴b <0,c <0,∴bc >0,故④正确.4.4312(答案不唯一)【解析】∵abcd 是偶数,∴d =2或4.∵a >b >c ,a +c =b +d ,∴a =4,b =3,c =1,d =2,或a =5,b =4,c =1,d =2,或a =5,b =3,c =2,d =4,或a =5,b =2,c =1,d =4,∴abcd =4312或5412或5324或5214.5.③④【解析】根据题中的定义得:2*3=(2)2-2×3=2-6,①正确,不符合题意;若a +b =0,则有a =-b ,a *b =a 2-ab =b 2+b 2=2b 2,b *a =b 2-ab =b 2+b 2=2b 2,即a *b =b *a ,②正确,不符合题意;已知等式变形得:(x +2)2-(x +2)(x +1)=0,即x 2+4x +4-x 2-3x -2=0,合并得:x +2=0,是一元一次方程,③错误,符合题意;④方程变形得:(x +2)2-(x +2)=3,整理得:x 2+4x +4-x -2-3=0,即x 2+3x -1=0,∵a =1,b =3,c =-1,∴x =-b ±b 2-4ac 2a =-3±132,解得x 1=-3+132,x 2=-3-132,④错误,符合题意.6.①②【解析】由半圆M 可知A (-1,0),B (3,0),M (1,0),且点A ,B 在抛物线上,∴图形G 关于直线x =1对称,故①正确;如解图,连接CM ,第6题解图在Rt △MOC 中,∵OM =1,CM =2,∴OC =22-12= 3.又∵D (0,-3),∴OD =3,∴CD =OC +OD =3+3,故②正确;根据题图得,图形G 围成区域内(不含边界)恰有13个整点(即横、纵坐标均为整数的点),故③错误;由题意得A (-1,0),B (3,0),当a =-4时,直线y =-4与图形G 有一个公共点,当a =2时,直线y =2与图形G 有一个公共点,故④错误.综上所述,正确的有①②.7.②③【解析】一次函数y =x 图象经过点B (1,1),即一次函数y =x 的图象与线段AB 有公共点,故①错误;一次函数y =x 图象刚好经过点B (1,1),向下平移直线y =x ,此时b <0,直线y =x +b 与线段AB 无公共点,故②正确;反比例函数y =1x的图象刚好经过点B (1,1),当k >1时,反比例函数y =k x的图象沿着y =x 向远离原点的方向平移,与线段AB 无公共点,故③正确;二次函数y =x 2-bx +1的图象一定经过A (0,1),即二次函数的图象与线段AB 有公共点,故④错误.8.F 4,-b 【解析】根据旋转的规律得,F 1的解析式为y =x 2,其图象位于第二象限;F 2的解析式为y =--x ,其图象位于第三象限;F 3的解析式为y =-x 2,其图象位于第四象限;F 4的解析式为y =x ,其图象位于第一象限;…则2021÷4=505……1,即F 2021的图象位于第二象限,该图象的函数解析式是y =x 2.∵P (4,2)位于第一象限,∴点P 所在的图象是F 4.∵点P (a ,b )在图象F 2021上,∴b =a 2,∴a =-b .9.1,5【解析】∵B (1,5)在y =k x 的图象上,∴k =1×5=5.当x =5时,y =55=1.∴C (5,1).又∵2023÷5=404,∴m =1.∵Q (x ,n )在该“波浪线”上,∴n 的最大值是5.类型四几何类问题1.D 【解析】如解图,连接OQ ,则∠POQ =45°,sin 45°=cos 45°=22,当点M 在AB 和CD 上时,α<45°,则sin α<cos α,当点M 在EF 和GH 上时,α>45°,sin α>cos α.第1题解图2.C 【解析】①当∠PAQ =30°,PQ =6时,以P 为圆心,6为半径画弧,与射线AM 有两个交点,则△PAQ 的形状不能唯一确定,故①错误;②当∠PAQ =30°,PQ =9时,以P 为圆心,9为半径画弧,与射线AM 有两个交点,但左边位置的Q 不符合题意,∴Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故②正确;③当∠PAQ =90°,PQ =10时,以P 为圆心,10为半径画弧,与射线AM 有两个交点,但此时两个三角形全等,Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故③正确;④当∠PAQ =150°,PQ =12时,以P 为圆心,12为半径画弧,与射线AM 有两个交点,左边的Q 不符合题意,∴Q 点位置唯一确定,则可得到形状唯一确定的△PAQ ,故④正确,故选C .3.①②③④【解析】①如题图①,由作图可知,BC 的垂直平分线经过圆心O ,∵OD⊥BC ,∴点D 是BC ︵的中点;②如解图①,连接BC ,∵AB 是⊙O 的直径,∴∠ACB =90°.∵OD ∥AC ,∴OD ⊥BC ,∴点D 是BC ︵的中点;③如题图③,∵∠BAD =∠CAD ,∴点D 是BC ︵的中点;④如解图②,连接AD ,∵AB 是⊙O 的直径,∴∠ADB =90°.∵AE =AB ,∴∠BAD =∠CAD ,∴点D 是BC ︵的中点.图①图②第3题解图4.①②④【解析】只要满足AB ∥EF ,则四边形ABFE 是平行四边形,这样的EF 有无数条,故①正确;∵AD >AB ,∴在AD 上截取AE =AB ,再满足AB ∥EF ,就能使得四边形ABFE 是菱形,故②正确;∵∠B 不是直角,∴矩形ABFE 不存在,故③错误;只要当EF 经过▱ABCD 对角线交点时,四边形ABFE 的面积是▱ABCD 面积的一半,这样的EF 有无数条,故④正确.5.(1)5;(2)43【解析】(1)如解图,连接OP ,∵P (4,3),∴OP =32+42=5;(2)如解图,设CD 交x 轴于点J ,过点P 作PT ⊥AB 交⊙O 于点T ,交AB 于点E ,连接CT ,DT ,OT ,∵P (4,3),∴PE =4,OE =3.在Rt △OPE 中,tan ∠POE =PE OE =43,∵OE ⊥PT ,OP =OT ,∴∠POE =∠TOE ,∴∠PDT =12∠POT =∠POE ,∵PA =PB ,PE ⊥AB ,∴∠APT =∠DPT ,∴TC ︵=DT ︵,∴∠TDC =∠TCD ,∵PT ∥x 轴,∴∠CJO =∠CKP ,∵∠CKP =∠TCK+∠CTK ,∠CTP =∠CDP ,∠PDT =∠TDC +∠CDP ,∴∠TDP =∠CJO ,∴∠CJO =∠POE ,∴tan α=tan ∠CJO =tan ∠POE =43.第5题解图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据考试大纲,填空压轴题仍将以探究规律类型题为主要考察方向。
题型一:数字规律【例1】一组按一定规律排列的式子:-,,-,,…,(0a ≠),则第n 个式子是 (n为正整数).【答案】【例2】按一定规律排列的一列数依次为:,916,79,54,31 ……,按此规律排列下去,这列数中的第5个数是 ,第n 个数是 .【答案】1125,122+n n【例3】一组按规律排列的整数5,7,11,19,…,第6个整数为____ _,根据上述规律,第n 个整数为____ (n 为正整数).【答案】67;32+n (n 为正整数)【例4】将除去零以外的自然数按以下规律排列,根据第一列的奇数行的数的规律,写出第一列第9行的数为 ,再结合第一行的偶数列的数的规律,判断2011所在的位置是第 行第 列.【答案】81;第45行第15列2a 52a 83a 114a 31(1)n na n --例题精讲填空题压轴题【例5】某些植物发芽有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为a )第n 年 1 2 3 4 5 … 老芽率 a a 2a 3a 5a … 新芽率 0 a a 2a 3a … 总芽率a2 a3a5a8a…照这样下去,第8年老芽数与总芽数的比值为 .【解析】由规律可以看出,从第3年开始,老芽率、新芽率,总芽率都分别是前两年之和,因此,第8年的老芽为21,总芽为34,因此答案为2134. 【解析】2134题型二:多边形上存在的点数【例6】如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .【解析】此类型题首先要找到边数的特点,然后找每条边上点的数目,第n 个图形是2n +边形,而且每个边上有n 个点。
【答案】(2)n n +或22n n +或2(1)1n +-【例7】用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n 个“口”字需用棋子___________【答案】4n【例8】用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第10个图案需要 个“O”.① ② ③ ④ 【答案】181第2个“口”第1个“口” 第3个“口”第n 个“口”………………第1个图形第2个图形第3个图形第4个图形题型三:藏头露尾型【例9】如下图是一组有规律的图案,第1个 图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n 是正整数)个图案中由 个基础图形组成.【解析】此类问题重点要找到“头是谁”“尾是谁”,①13+;②132+⨯;③133+⨯,……第n 个31n + 【答案】31n +【例10】搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②,图③的方式串起来搭建,则串7顶这样的帐篷需要 根钢管.图1 图2 图3【答案】83.题型四:成倍数变化型【例11】如图,ABC ∆中,90ACB ∠=︒,1AC BC ==,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与ABC ∆的BC 边重叠为止,此时这个三角形的斜边长为_____.【解析】注意每一次变化所变化的倍数 【答案】81;11(2)2n n - 【例12】如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,......依次作下去,图中所作的第三个四边形的周长为________; 所作的第n 个四边形的周长为_________________.【答案】2,24()2n【例13】如图,在ABC ∆中,A α∠=,ABC ∠的平分线与ACD ∠的平分线交于点1A ,得1A ∠,则1______A ∠=.1A BC ∠的平分线与1ACD ∠的平分线交于点2A ,得2A ∠,……,2009A BC ∠的平分线与2009A CD ∠的平分线交于点2010A ,得2010A ∠,则2010A ∠= .【答案】2α,20102α(1)(2)(3)……A 2A 1DC A【例14】如图,小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形1111A B C D ,正方形1111A B C D 的面积为 ; 再把正方形1111A B C D 的各边延长一倍得到正方形2222A B C D , 如此进行下去,正方形n n n n D C B A 的面积为 . (用含有n 的式子表示,n 为正整数)【答案】5,n5【例15】把一个正三角形分成四个全等的三角形,第一次挖去中间的一个小三角形,对剩下的三个小正三角形再重复以上做法……一直到第n 次挖去后剩下的三角形有 个.第一次 第二次 第三次 第四次【答案】3n题型五:相似与探究规律【例16】已知ABC AB AC m ∆==中,,72ABC ∠=︒,1BB 平分ABC ∠交AC 于1B ,过1B 作12B B //BC交AB 于2B ,作23B B 平分21AB B ∠,交AC 于3B ,过3B 作34//B B BC ,交AB 于4B ……依次进行下去,则910B B 线段的长度用含有m 的代数式可以表示为 .【答案】m 6215⎪⎪⎭⎫⎝⎛-【例17】如图,矩形纸片ABCD 中,6,10AB BC ==.第一次将纸片折叠,使点B 与点D 重合,折痕与BD交于点1O ;设1O D 的中点为1D ,第二次将纸片折叠使 点B 与点1D 重合,折痕与BD 交于点2O ;设21O D 的中点 为2D ,第三次将纸片折叠使点B 与点2D 重合,折痕与BD 交于点3O ,… .按上述方法折叠,第n 次折叠后的折痕与BD 交于点n O ,则1BO = ,n BO = .第一次折叠 第二次折叠 第三次折叠【答案】2;12332n n -- B AD C 1O 1O 2O 1D 1D 2D 1O 2O 3O B AD C B ADCBA DC【例18】如图,直线x y 33=,点1A 坐标为(1,0),过点1A 作x 轴的垂线交直线于点1B ,以原点O 为圆心,1OB 长为半径画弧交x 轴于点2A ;再过点2A 作x 轴的垂线 交直线于点2B ,以原点O 为圆心,2OB 长为半径画弧交x 轴于 点3A ,…,按此做法进行下去,点4A 的坐标为( , ); 点n A ( , ).【答案】(938,0)(1)332(-n ,0) 【例19】如图,以等腰三角形AOB 的斜边为直角边向外作第2个等腰直角三角形1ABA ,再以等腰直角三角形1ABA 的斜边为直角边向外作第3个等腰直角三角形11A BB ,……,如此作下去,若1OA OB ==,则第n 个等腰直角三角形的面积n S = ________(n 为正整数).【解析】由题干可知:123124 (222)S S S ===,,可知22n n S -=【答案】22n -【例20】如图,n +1个边长为2的等边三角形有一条边在同一直线上,设211B D C ∆的面积为1S ,322B D C ∆的面积为2S ,…,1n n n B D C +∆的面积为n S ,则2S = ;n S =____ (用含n 的式子表示).【答案】233,31nn + 【例21】如图,P 为ABC ∆的边BC 上的任意一点,设BC a =,当1B 、1C 分别为AB 、AC 的中点时,1112B C a =,当2B 、2C 分别为1BB 、1CC 的中点时,2234B C a =,当3B 、3C 分别为2BB 、2CC 的中点时,3378B C a =,当4B 、4C 分别为3BB 、3CC 的中点时,441516B C a =当5B 、5C 分别为4BB 、4CC 的中点时,55_____B C =当n B 、n C 分别为1n BB -、1n CC -的中点时,则n n B C = ;设ABC ∆中BC 边上的高为h ,则n n PB C ∆的面积为______(用含a 、h 的式子表示).【答案】a 3231,a n n 212-, ah n n 12212+-D 4D 3D 2D 1C 5C 4C 3C 2C 1B 5B 4B 3B 2B 1A……B 2B 1A 1BOAC 3B 3B 2C 2C 1B 1CBA【例22】如图,在梯形ABCD 中,AB CD ∥,AB a =,CD b =,E 为边AD 上的任意一点,EF AB ∥,且EF 交BC 于点F .若E 为边AD 上的中点,则______EF =(用含有a ,b 的式子表示);若E 为边AD 上距点A 最近的n 等分点(2n ≥,且n 为整数),则______EF =(用含有n ,a ,b 的式子表示).【答案】2a b +;(1)b n an+-【例23】已知在ABC ∆中,BC a =.如图1,点1B 、1C 分别是AB 、AC 的中点,则线段11B C 的长是_______; 如图2,点1B 、2B ,1C 、2C 分别是AB 、AC 的三等分点,则线段1122B C B C +的值是__________;如图3, 点12......、、、n B B B ,12......、、、n C C C 分别是AB 、AC 的(1)n +等分点,则线段1122n n B C B C B C ++⋅⋅⋅+的值是 ______.【答案】1,2a a ,12na 【例24】已知:如图,在Rt ABC ∆中,点1D 是斜边AB 的中点,过点1D 作11D E AC ⊥于点1E ,连接1BE 交1CD 于点2D ;过点2D 作22D E AC ⊥于点2E ,连接2BE ,交1CD 于点3D ;过点3D 作33D E AC ⊥于点3E ,如此继续,可以依次得到点4D 、5D 、…n D , 分别记11BD E ∆、22BD E ∆、33BD E ∆、…n n BD E ∆的面积 为1S 、2S 、3S …n S .设ABC ∆的面积是1,则1______S =, ______n S =(用含n 的代数式表示).【答案】14,21(1)n +题型六:折叠与探究规律【例25】如图,将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN .设2AB =,当12CE CD =时,则________AMBN=. 若1CE CD n =(n 为整数),则_______AM BN=.(用含n 的式子表示) 【答案】15;1)1(22+-n n【例26】如图,正方形ABCD ,E 为AB 上的动点,(E 不与A 、B 重合)连接DE ,作DE 的中垂线,交图3图2图12n-1B 2C 2A BCB 1C 1C 1B 1CBA FE D CBANMFEDCBAB321AD 于点F .⑴若E 为AB 中点,则______DFAE= ⑵若E 为AB 的n 等分点(靠近点A ),则________DFAE= 【答案】251,42n n+题型七:其他类型【例27】图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+3中线段AB 的长为 .图1 图2 图31+【例28】如图,1P 是一块半径为1的半圆形纸板,在1P 的左下端剪去一个半径为12的半圆后得到图形2P ,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形34,,,,n P P P ,记纸板n P 的面积为n S ,试计算求出=-23S S ;并猜想得到1n n S S --=()2n ≥【答案】1)41(2,32---n ππ【例29】如图,图①是一块边长为1,周长记为1P 的正三角形纸板,沿图①的底边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第)3(≥n n 块纸板的周长为n P ,则=-34P P ;1--n n P P = .P 3P 2P 1【答案】81,121-⎪⎭⎫⎝⎛n【例30】已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).当8n =时,共向外作出了 个小等边三角形;当n k =时,共向外作出了 个小等边三角形,这些小等边三角形的面积和是 (用含k 的式子表示).【答案】18; 【例31】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(10),,点D 的坐标为(02),.延长CB 交x 轴于点1A ,作正方形111A B C C ;延长11C B 交x 轴于点2A ,作正方形2221A B C C …按这样 的规律进行下去,第3个正方形的面积为________;第n 个正方形的面积为___________(用含n 的代数式表示).【答案】4235)(,22235-⎪⎭⎫ ⎝⎛n【例32】如图所示,111()P x y ,、222()P x y ,,……()n n n P x y ,在函数4y x=(0x >)的图象上,11OP A ∆,212P A A ∆,323P A A ∆…1n n n P A A -∆都是等腰三角形,斜边1OA 、12A A …1n n A A -,都在x 轴上, 则1_____y =,12______n y y y ++⋅⋅⋅+=【答案】2 , 2n【例33】如图所示,直线1+=x y 与y 轴交于点1A ,以1OA 为边作正方形111OA B C ,然后延长11C B 与直线1+=x y 交于点2A ,得到第一个梯形112AOC A ;再以12C A 为边作正方形1222C A B C ,同样延长22C B 与直线1+=x y 交于点3A 得到第二个梯形2123A C C A ;,再以23C A 为边作正方形2333C A B C ,延长33C B ,得到第三个梯形;……则第2个梯形2123A C C A 的面积是 ;第n (n 是正整数)个梯形的面积是 (用含n 的式子表示).3(-2)k 23(2)k s k-n =3n =5……n =4① ② ③ ④C 2B 2A 2C 1B 1A 1DC B AO yx【答案】6;2n 2223-⨯或1n 423-⨯【例34】在平面直角坐标系中,我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点 正方形,如图,菱形ABCD 的四个顶点坐标分别是(80)-,,(04),,(80),,(04)-,,则菱形ABCD 能覆盖的单位格点正方形的个数是_______个;若菱形n n n n A B C D 的四个顶点坐标分别为(20)-,n , (0),n ,(20),n ,(0)-,n (n 为正整数), 则菱形n n n n A B C D 能覆盖的单位格点正方形的 个数为_________(用含有n 的式子表示).【答案】单位格点个数为48,单位格点个数为n n 442-【例35】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形1111A B C D 、2222A B C D 、3333A B C D 每个正方形四条边上的整点的个数.按此规律推算出正方形10101010A B C D 四条边上的整点共有 个.【答案】80【例36】对于每个正整数n ,抛物线2211(1)(1)n n n n n y x x +++=-+与x 轴交于n A ,n B 两点,若n n A B 表示这两点间的距离,则n n A B = (用含n 的代数式表示);112220112011A B A B A B +++的值为 .【答案】()20122011,11+n nyxOD 1D 2D 3C 1C 2C 3B 1B 2B 3A 3A 2A 1123-1-2-3-3-2-1321-8-448ODC BAyx。
