北京市西城区2014 — 2015学年度第一学期期末试卷高一数学基础薄弱校(试题)
20142015西城高三第一学期期末数学(理)试题及答案

北京市西城区2014—2015学年度第一学期期末试卷高三数学(理科)2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1{}A -=,2{|2}B x x x =-<,则集合A B =I ( ) (A ){1,0,1}-(B ){1,0}-(C ){0,1}(D ){1,1}-3.在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若A 为锐角,2a b =,sin B =,则( ) (A )3A π= (B )6A π=(C)sin 3A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为((A )4 (B )5 (C )6 (D )72.设命题p :∀平面向量a 和b ,||||||-<+a b a b ,则p ⌝为( ) (A )∀平面向量a 和b ,||||||-+≥a b a b (B )∃平面向量a 和b ,||||||-<+a b a b (C )∃平面向量a 和b ,||||||->+a b a b (D )∃平面向量a 和b ,||||||-+≥a b a b5.设函数()3cos f x x b x =+,x ∈R ,则“0b =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域,点(,)B a b 为坐标平面xOy 内一点,若对于区域D 内的任一点(,)A x y ,都有1OA OB ⋅u u u r u u u r≤成立,则a b +的最大值等于( )(A )2 (B )1 (C )0 (D )36.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) (A(B )最长棱的棱长为3(C )侧面四个三角形中有且仅有一个是正三角形 (D )侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( )(A )(4,8) (B )(4,)+? (C )(0,4) (D )(8,)+?侧(左)视图正(主)视图俯视图第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i12iz -=+,则||z = _____.10.设12,F F 为双曲线C :2221(0)16x y a a -=>的左、右焦点,点P 为双曲线C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为____.11.在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么x y z ++=______.12.如图,在ABC ∆中,以BC 为直径的半圆分别交AB ,AC 于点E ,F , 且2AC AE =,那么AFAB=____;A ∠= _____.13.现要给4个唱歌节目和2个小品节目排列演出顺序,要求2个小品节目 之间恰好有3个唱歌节目,那么演出顺序的排列种数是______.(用数字作答)14.设P ,Q 为一个正方体表面上的两点,已知此正方体绕着直线PQ 旋转θ(02θπ<<)角后能与自身重合,那么符合条件的直线PQ 有_____条.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.16.(本小题满分13分)现有两种投资方案,一年后投资盈亏的情况如下: (1)投资股市:(2)购买基金:(Ⅰ)当4p =时,求q 的值; (Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于45,求p 的取值范围; (Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知12p =,16q =,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.17.(本小题满分14分)如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面ABCD ,90BAD ∠=o ,BC AD //,且122A A AB AD BC ==== ,点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)证明:1A F ∥平面1B CE ;(Ⅱ)若E 是棱AB 的中点,求二面角1A EC D --的余弦值; (Ⅲ)求三棱锥11B A EF -的体积的最大值.18.(本小题满分13分)已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ,且在点P 处的切线相同. (Ⅰ)若点P 的坐标为1(,1)e-,求,a b 的值; (Ⅱ)已知a b =,求切点P 的坐标.19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,求证:12||||S PM S PN =.B CDA B 1C 1E FA 1 D 120.(本小题满分13分)设函数()(9)f x x x =-,对于任意给定的m 位自然数0121m m n a a a a -=L (其中1a 是个位数字,2a 是十位数字,L ),定义变换A :012()()()()m A n f a f a f a =+++L . 并规定(0)0A =.记10()n A n =,21()n A n =,L , 1()k k n A n -=,L .(Ⅰ)若02015n =,求2015n ;(Ⅱ)当3m ≥时,证明:对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<; (Ⅲ)如果*010(,3)m n m m <∈≥N ,写出m n 的所有可能取值.(只需写出结论)北京市西城区2014 — 2015学年度第一学期期末高三数学(理科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.D 3.A 4.C 5.C 6.D 7.B 8.A 二、填空题:本大题共6小题,每小题5分,共30分.9.1 10.221416x y -=11.17412.12 π313.96 14.13 注:第10,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +, ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意,得πππ2π2π2262x k k -++≤≤, 解得4π2π4π4π+33k x k -≤≤,所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . (9)分(Ⅱ)解:如图过点B 作线段BC 垂直于x由题意,得33π4TAC ==,2=BC ,所以2tan 3πBC BAO AC ∠==. ………… 13分16.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立,所以p +13+q =1. ……………… 2分又因为14p =, 所以q =512. ……………… 3分 (Ⅱ)解:记事件A 为 “甲投资股市且盈利”,事件B 为“乙购买基金且盈利”,事件C 为“一年后甲、乙两人中至少有一人投资获利”, ……………… 4分则C AB AB AB =U U ,且A ,B 独立. 由上表可知, 1()2P A =,()P B p =. 所以()()()()P C P AB P AB P AB =++ ……………… 5分 111(1)222p p p =?+?? 1122p =+. ……………… 6分因为114()225P C p =+>,所以35p >. ……………… 7分又因为113p q ++=,0q ≥, 所以23p ≤.所以3253p ≤<. (8)分(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X 为丙投资股票的获利金额(单位:万元),所以随机变量X 的分布列为:X 4 02- P12 1838…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资,且记Y 为丙购买基金的获利金额(单位:万元),所以随机变量Y 的分布列为:Y2 01-P121316…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.…… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D .又因为平面ABCD I 平面1A ECF EC =,平面1111A B C D I 平面11A ECF A F =, 所以1A F ∥EC . …………………2分 又因为1A F ⊄平面1B CE ,EC ⊂平面1B CE ,所以1A F ∥平面1B CE . …………………4分B CA 1 D 1DA B 1 C 1 E F x yzM(Ⅱ)解:因为1AA ⊥底面ABCD ,90BAD ∠=o ,所以1AA ,AB ,AD 两两垂直,以A 为原点,以AB ,AD ,1AA 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系. …………………5分则1(0,0,2)A ,(1,0,0)E ,(2,1,0)C , 所以 1(1,0,2)A E =-u u u r ,1(2,1,2)AC =-u u u r . 设平面1A ECF 的法向量为(,,),m x y z =u r由10A E m ⋅=u u u r u r ,10AC m ⋅=u u u r u r , 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-u r. …………………7分又因为平面DEC 的法向量为(0,0,1)n =r, (8)分所以1cos ,3||||m n m n m n ⋅<>==⋅u r ru r r ur r , 由图可知,二面角1A EC D --的平面角为锐角,所以二面角1A EC D --的余弦值为13. …………………10分(Ⅲ)解:过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A B C D ,FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时,FM 取到最大值2(此时点E 与点B 重合), 所以当F 与点1D 重合时,三棱锥11B A EF -的体积的最大值为43. (14)分18.(本小题满分13分) (Ⅰ)解:由题意,得21()1e e ea bf =-=-, …………………1分且()2f x ax b '=-,1()g x x'=, …………………3分由已知,得11()()e ef g ''=,即2e eab -=, 解得22e a =,3e b =. …………………5分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………6分 由②,得 1(21)a s s =-,其中12s ≠,代入①,得 1ln 21s s s -=-. (*) (7)分因为 10(21)a s s =>-,且0s >,所以 12s >. …………………8分 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. (9)分令()0F x '= ,解得1x =或14x =(舍). …………………10分 当x 变化时,()F x '与()F x 的变化情况如下表所示,()F x '+ 0 -()F x↗↘…………………12分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞U 时()0F x <.因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,23b =,222c a b =-=, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为||21||42FA AP m ==-, 所以 8m =. ………………5分 (Ⅱ)解:若直线l 的斜率不存在, 则有 21S S =,||||PM PN =,符合题意. …………6分若直线l 的斜率存在,则设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N . 由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分)8)(8()8)(2()8)(2(211221----+--=x x x x k x x k)8)(8(32)(102212121--++-=x x kx x k x kx0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k ,所以 MPF NPF ∠=∠. ……………… 12分因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠, 21||||sin 2S PF PN NPF =⋅⋅∠, ……………… 13分所以12||||S PM S PN =. ……………… 14分20.(本小题满分13分)(Ⅰ)解:114082042n =+++=,2201434n =+=,3182038n =+=,418826n =+=,5141832n =+=,6181432n =+=,……所以 201532n =. (3)分(Ⅱ)证明:因为函数2981()(9)()24f x x x x =-=--+,所以对于非负整数x ,知()(9)20f x x x =-≤.(当4x =或5时,取到最大值)… 4分 因为 12()()()()m A n f a f a f a =+++L ,所以 ()20A n m ≤. ……………… 6分令 1()1020m g m m -=-,则31(3)102030g -=-⨯>.当3m ≥时,11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->, 所以 (1)g()0g m m +->,函数()g m ,(m ∈N ,且3m ≥)单调递增. 故 g()g(3)0m >≥,即11020()m m A n ->≥.所以当3m ≥时,对于任意的m 位自然数n 均有1()10m A n -<. …………………9分(Ⅲ)答:m n 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38. (14)分。
北京市西城区2014 — 2015学年高三(文)第一学期期末试卷

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(文科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1,2{}A -=,2{|}B x x x =>,则集合A B = ( ) (A ){1,0,1}-(B ){1,2}-(C ){0,1,2}(D ){1,1,2}-【答案】B 【解析】“0x ∀>”的否定为“0x ∃>”,“2log 2x x >”的否定为“2log 2x x ≤” 所以,p ⌝为:2log 0,2x x x ∃>≤ 故答案为:B 【考点】全称量词与存在性量词 【难度】 13.在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若A 为锐角,2a b =,sin B =,则( )【答案】B 【解析】{}01B x x x =<>或,所以{}1,2A B =-故答案为:B 【考点】 集合的运算 【难度】 12.设命题p :2log 0,2x x x ∀>>,则p ⌝为( ) (A )2log 0,2x x x ∀>< (B )2log 0,2x x x ∃>≤ (C )2log 0,2x x x ∃>< (D )2log 0,2x x x ∃>≥(A )3A π= (B )6A π=(C)sin 3A =(D )2sin 3A =【答案】A 【解析】由正弦定理得sin sin a b A B =,所以sin 2sin A aB b==,所以sin A =。
因为ABC ∆为锐角三角形,所以3A π=故答案为:A【考点】 正弦定理 【难度】 14.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )7【答案】C【解析】3x =时,328y ==,833<; 4x =时,4216y ==,1643<; 5x =时,5232y ==,3253<;6x =时,6264y ==,6463>,输出6x =。
北京市西城区2014-2015学年度高三第一学期期末试数学理-含答案
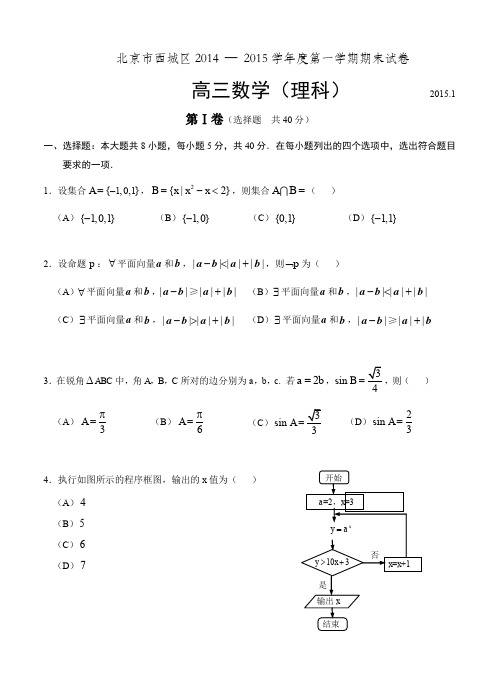
北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(理科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1{}A -=,2{|2}B x x x =-<,则集合A B =( )(A ){1,0,1}-(B ){1,0}-(C ){0,1}(D ){1,1}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin B =,则( ) (A )3A π= (B )6A π=(C)sin A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )72.设命题p :∀平面向量a 和b ,||||||-<+a b a b ,则p ⌝为( )(A )∀平面向量a 和b ,||||||-+≥a b a b (B )∃平面向量a 和b ,||||||-<+a b a b (C )∃平面向量a 和b ,||||||->+a b a b (D )∃平面向量a 和b ,||||||-+≥a b a b5.设函数()3cos f x x b x =+,x ∈R ,则“0b =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域,点(,)B a b 为坐标平面xOy 内一点,若对于区域D内的任一点(,)A x y ,都有1OA OB ⋅≤成立,则a b +的最大值等于( ) (A )2 (B )1 (C )0(D )36.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) (A(B )最长棱的棱长为3(C )侧面四个三角形中有且仅有一个是正三角形 (D )侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( )(A )(4,8) (B )(4,)+? (C )(0,4)(D )(8,)+?侧(左)视图正(主)视图俯视图第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i12iz -=+,则||z = _____.10.设12,F F 为双曲线C :2221(0)16x y a a -=>的左、右焦点,点P 为双曲线C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为____.11.在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么x y z ++=______.12. 如图,在ABC ∆中,以BC 为直径的半圆分别交AB ,AC 于点E ,F ,且2AC AE =,那么AFAB=____;A ∠= _____.13.现要给4个唱歌节目和2个小品节目排列演出顺序,要求2个小品节目之间恰好有3个唱歌节目,那么演出顺序的排列种数是______. (用数字作答)14. 设P ,Q 为一个正方体表面上的两点,已知此正方体绕着直线PQ 旋转()角后能与自身重合,那么符合条件的直线PQ 有_____条.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.16.(本小题满分13分)现有两种投资方案,一年后投资盈亏的情况如下: (1)投资股市:(2)购买基金:(Ⅰ)当4p =时,求q 的值; (Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于45,求p 的取值范围; (Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知12p =,16q =,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面A B CD ,90BAD ∠=,BC AD //,且122A A AB AD BC ==== ,点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)证明:1A F ∥平面1B CE ;(Ⅱ)若E 是棱AB 的中点,求二面角1A EC D --的余弦值; (Ⅲ)求三棱锥11B A EF -的体积的最大值.18.(本小题满分13分)已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ,且在点P 处的切线相同.(Ⅰ)若点P 的坐标为1(,1)e-,求,a b 的值; (Ⅱ)已知a b =,求切点P 的坐标.19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,求证:12||||S PM S PN =.B CDA B 1C 1E FA 1 D 1设函数()(9)f x x x =-,对于任意给定的m 位自然数0121m m n a a a a -=(其中1a 是个位数字,2a 是十位数字,),定义变换A :012()()()()m A n f a f a f a =+++. 并规定(0)0A =.记10()n A n =,21()n A n =,, 1()k k n A n -=,.(Ⅰ)若02015n =,求2015n ;(Ⅱ)当3m ≥时,证明:对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<; (Ⅲ)如果*010(,3)m n m m <∈≥N ,写出m n 的所有可能取值.(只需写出结论)北京市西城区2014 — 2015学年度第一学期期末高三数学(理科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.D 3.A 4.C 5.C 6.D 7.B 8.A 二、填空题:本大题共6小题,每小题5分,共30分.9.1 10.221416x y -=11.17412.12 π313.9614.13注:第10,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +, ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意,得πππ2π2π2262x k k -++≤≤, 解得4π2π4π4π+33k x k -≤≤,所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . ……………… 9分(Ⅱ)解:如图过点B 作线段BC 垂直于x由题意,得33π4TAC ==,2=BC , 所以2tan 3πBC BAO AC ∠==.16.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立, 所以p +13+q =1. ……………… 2分 又因为14p =, 所以q =512. ……………… 3分 (Ⅱ)解:记事件A 为 “甲投资股市且盈利”,事件B 为“乙购买基金且盈利”,事件C 为“一年后甲、乙两人中至少有一人投资获利”, ……………… 4分则C AB AB AB =U U ,且A ,B 独立. 由上表可知, 1()2P A =,()P B p =.所以()()()()P C P AB P AB P AB =++ ……………… 5分 111(1)222p p p =?+?? 1122p =+. ……………… 6分因为114()225P C p =+>,所以35p >. ……………… 7分 又因为113p q ++=,0q ≥,所以23p ≤.所以3253p ≤<. ……………… 8分(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X 为丙投资股票的获利金额(单位:万元),所以随机变量X 的分布列为:…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资,且记Y 为丙购买基金的获利金额(单位:万元),所以随机变量Y 的分布列为:…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.……… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D .又因为平面ABCD 平面1A ECF EC =,平面1111A B C D 平面11A ECF A F =,所以1A F ∥EC . …………………2分 又因为1A F ⊄平面1B CE ,EC ⊂平面1B CE ,所以1A F ∥平面1B CE . …………………4分 (Ⅱ)解:因为1AA ⊥底面ABCD ,90BAD ∠=,所以1AA ,AB ,AD 两两垂直,以A 为原点,以AB ,AD ,1AA 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系. …………………5分则1(0,0,2)A ,(1,0,0)E ,(2,1,0)C , 所以 1(1,0,2)A E =-,1(2,1,2)AC =-. 设平面1A ECF 的法向量为(,,),m x y z = 由10A E m ⋅=,10AC m ⋅=, 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-. …………………7分 又因为平面DEC 的法向量为(0,0,1)n =, …………………8分所以1cos ,3||||m n m n m n ⋅<>==⋅,由图可知,二面角1A EC D --的平面角为锐角,所以二面角1A EC D --的余弦值为13. …………………10分(Ⅲ)解:过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A B C D ,FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时,FM 取到最大值2(此时点E 与点B 重合), 所以当F 与点1D 重合时,三棱锥11B A EF -的体积的最大值为43. ………………14分18.(本小题满分13分) (Ⅰ)解:由题意,得21()1e e ea bf =-=-, …………………1分 且()2f x ax b '=-,1()g x x'=, …………………3分 由已知,得11()()e ef g ''=,即2e eab -=, 解得22e a =,3e b =. …………………5分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………6分 由②,得 1(21)a s s =-,其中12s ≠,代入①,得 1ln 21s s s -=-. (*) …………………7分因为 10(21)a s s =>-,且0s >,所以 12s >. …………………8分 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………9分 令()0F x '= ,解得1x =或14x =(舍). …………………10分当x 变化时,()F x '与()F x 的变化情况如下表所示,…………………12分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞时()0F x <.因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,b =2c =, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为||21||42FA AP m ==-, 所以 8m =. ………………5分(Ⅱ)解:若直线l 的斜率不存在, 则有 21S S =,||||PM PN =,符合题意. …………6分若直线l 的斜率存在,则设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N . 由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分 )8)(8()8)(2()8)(2(211221----+--=x x x x k x x k)8)(8(32)(102212121--++-=x x kx x k x kx0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k ,所以 MPF NPF ∠=∠. ……………… 12分 因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠, 21||||sin 2S PF PN NPF =⋅⋅∠, ……………… 13分 所以12||||S PM S PN =. ……………… 14分20.(本小题满分13分)(Ⅰ)解:114082042n =+++=,2201434n =+=,3182038n =+=,418826n =+=,5141832n =+=,6181432n =+=,……所以 201532n =. ……………… 3分(Ⅱ)证明:因为函数2981()(9)()24f x x x x =-=--+,所以对于非负整数x ,知()(9)20f x x x =-≤.(当4x =或5时,取到最大值)… 4分 因为 12()()()()m A n f a f a f a =+++,所以 ()20A n m ≤. ……………… 6分 令 1()1020m g m m -=-,则31(3)102030g -=-⨯>.当3m ≥时,11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->, 所以 (1)g()0g m m +->,函数()g m ,(m ∈N ,且3m ≥)单调递增. 故 g()g(3)0m >≥,即11020()m m A n ->≥.所以当3m ≥时,对于任意的m 位自然数n 均有1()10m A n -<. …………………9分 (Ⅲ)答:m n 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38.…………………14分。
北京市西城区-第一学期期末考试高三数学理及答案
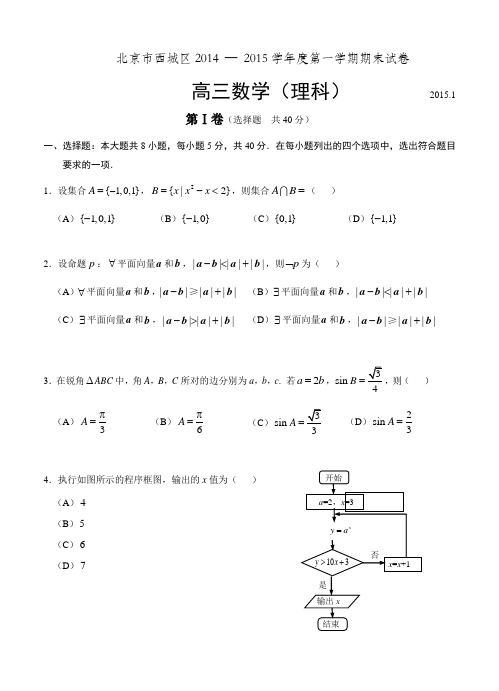
北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(理科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1{}A -=,2{|2}B x x x =-<,则集合A B =( )(A ){1,0,1}-(B ){1,0}-(C ){0,1}(D ){1,1}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin B =,则( ) (A )3A π= (B )6A π=(C)sin 3A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )72.设命题p :∀平面向量a 和b ,||||||-<+a b a b ,则p ⌝为( )(A )∀平面向量a 和b ,||||||-+≥a b a b (B )∃平面向量a 和b ,||||||-<+a b a b (C )∃平面向量a 和b ,||||||->+a b a b (D )∃平面向量a 和b ,||||||-+≥a b a b5.设函数()3cos f x x b x =+,x ∈R ,则“0b =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域,点(,)B a b 为坐标平面xOy 内一点,若对于区域D内的任一点(,)A x y ,都有1OA OB ⋅≤成立,则a b +的最大值等于( ) (A )2 (B )1 (C )0(D )36.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) (A(B )最长棱的棱长为3(C )侧面四个三角形中有且仅有一个是正三角形 (D )侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP ,则实数m 的取值范围是( )(A )(4,8) (B )(4,) (C )(0,4)(D )(8,)侧(左)视图正(主)视图俯视图第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i12iz -=+,则||z = _____.10.设12,F F 为双曲线C :2221(0)16x y a a -=>的左、右焦点,点P 为双曲线C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为____.11.在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么x y z ++=______.12. 如图,在ABC ∆中,以BC 为直径的半圆分别交AB ,AC 于点E ,F ,且2AC AE =,那么AFAB=____;A ∠= _____.13.现要给4个唱歌节目和2个小品节目排列演出顺序,要求2个小品节目之间恰好有3个唱歌节目,那么演出顺序的排列种数是______. (用数字作答)14. 设P ,Q 为一个正方体表面上的两点,已知此正方体绕着直线PQ 旋转()角后能与自身重合,那么符合条件的直线PQ 有_____条.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)2 x3ya321258zE FCB A已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.16.(本小题满分13分)现有两种投资方案,一年后投资盈亏的情况如下: (1)投资股市:(2)购买基金:(Ⅰ)当4p时,求q 的值; (Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于45,求p 的取值范围; (Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知12p,16q ,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面ABCD ,90BAD ∠=,BC AD //,且122A A AB AD BC ==== ,点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)证明:1A F ∥平面1B CE ;(Ⅱ)若E 是棱AB 的中点,求二面角1A EC D --的余弦值; (Ⅲ)求三棱锥11B A EF -的体积的最大值.18.(本小题满分13分)已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ,且在点P 处的切线相同.(Ⅰ)若点P 的坐标为1(,1)e-,求,a b 的值; (Ⅱ)已知a b =,求切点P 的坐标.19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,求证:12||||S PM S PN =.B CDA B 1C 1E FA 1 D 1设函数()(9)f x x x =-,对于任意给定的m 位自然数0121m m n a a a a -=(其中1a 是个位数字,2a 是十位数字,),定义变换A :012()()()()m A n f a f a f a =+++. 并规定(0)0A =.记10()n A n =,21()n A n =,, 1()k k n A n -=,.(Ⅰ)若02015n =,求2015n ;(Ⅱ)当3m ≥时,证明:对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<; (Ⅲ)如果*010(,3)m n m m <∈≥N ,写出m n 的所有可能取值.(只需写出结论)北京市西城区2014 — 2015学年度第一学期期末高三数学(理科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.D 3.A 4.C 5.C 6.D 7.B 8.A 二、填空题:本大题共6小题,每小题5分,共30分.9.1 10.221416x y -=11.17412.12 π313.9614.13注:第10,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +, ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意,得πππ2π2π2262x k k -++≤≤, 解得4π2π4π4π+33k x k -≤≤,所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . ……………… 9分(Ⅱ)解:如图过点B 作线段BC 垂直于x由题意,得33π4TAC ==,2=BC , 所以2tan 3πBC BAO AC ∠==.16.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立, 所以p +13+q =1. ……………… 2分 又因为14p, 所以q =512. ……………… 3分 (Ⅱ)解:记事件A 为 “甲投资股市且盈利”,事件B 为“乙购买基金且盈利”,事件C 为“一年后甲、乙两人中至少有一人投资获利”, ……………… 4分则CAB AB AB ,且A ,B 独立.由上表可知, 1()2P A ,()P B p .所以()()()()P C P AB P AB P AB ……………… 5分111(1)222p pp1122p . ……………… 6分 因为114()225P C p , 所以35p. ……………… 7分 又因为113p q ,0q ≥,所以23p ≤.所以3253p ≤. ……………… 8分(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X 为丙投资股票的获利金额(单位:万元),所以随机变量X 的分布列为:…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资,且记Y 为丙购买基金的获利金额(单位:万元),所以随机变量Y 的分布列为:…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.……… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D .又因为平面ABCD 平面1A ECF EC =,平面1111A B C D 平面11A ECF A F =,所以1A F ∥EC . …………………2分 又因为1A F ⊄平面1B CE ,EC ⊂平面1B CE ,所以1A F ∥平面1B CE . …………………4分 (Ⅱ)解:因为1AA ⊥底面ABCD ,90BAD ∠=,所以1AA ,AB ,AD 两两垂直,以A 为原点,以AB ,AD ,1AA 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系. …………………5分则1(0,0,2)A ,(1,0,0)E ,(2,1,0)C , 所以 1(1,0,2)A E =-,1(2,1,2)AC =-. 设平面1A ECF 的法向量为(,,),m x y z = 由10A E m ⋅=,10AC m ⋅=, 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-. …………………7分 又因为平面DEC 的法向量为(0,0,1)n =, …………………8分所以1cos ,3||||m n m n m n ⋅<>==⋅,由图可知,二面角1A EC D --的平面角为锐角,所以二面角1A EC D --的余弦值为13. …………………10分(Ⅲ)解:过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A B C D ,FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时,FM 取到最大值2(此时点E 与点B 重合), 所以当F 与点1D 重合时,三棱锥11B A EF -的体积的最大值为43. ………………14分18.(本小题满分13分) (Ⅰ)解:由题意,得21()1e e ea bf =-=-, …………………1分 且()2f x ax b '=-,1()g x x'=, …………………3分 由已知,得11()()e ef g ''=,即2e eab -=, 解得22e a =,3e b =. …………………5分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………6分 由②,得 1(21)a s s =-,其中12s ≠,代入①,得 1ln 21s s s -=-. (*) …………………7分因为 10(21)a s s =>-,且0s >, 所以 12s >. …………………8分 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………9分 令()0F x '= ,解得1x =或14x =(舍). …………………10分 当x 变化时,()F x '与()F x 的变化情况如下表所示,…………………12分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞时()0F x <. 因此,当且仅当1x =时()0F x =.所以方程(*)有且仅有一解1s =.于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………13分19.(本小题满分14分) (Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,b =2c =, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为 ||21||42FA AP m ==-, 所以 8m =. ………………5分(Ⅱ)解:若直线l 的斜率不存在, 则有 21S S =,||||PM PN =,符合题意. …………6分若直线l 的斜率存在,则设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分 因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分 )8)(8()8)(2()8)(2(211221----+--=x x x x k x x k )8)(8(32)(102212121--++-=x x k x x k x kx 0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k , 所以 MPF NPF ∠=∠. ……………… 12分 因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠, 21||||sin 2S PF PN NPF =⋅⋅∠, ……………… 13分 所以12||||S PM S PN =. ……………… 14分20.(本小题满分13分)(Ⅰ)解:114082042n =+++=,2201434n =+=,3182038n =+=,418826n =+=,5141832n =+=,6181432n =+=,……所以 201532n =. ……………… 3分(Ⅱ)证明:因为函数2981()(9)()24f x x x x =-=--+,所以对于非负整数x ,知()(9)20f x x x =-≤.(当4x =或5时,取到最大值)… 4分 因为 12()()()()m A n f a f a f a =+++,所以 ()20A n m ≤. ……………… 6分 令 1()1020m g m m -=-,则31(3)102030g -=-⨯>.当3m ≥时,11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->, 所以 (1)g()0g m m +->,函数()g m ,(m ∈N ,且3m ≥)单调递增.故 g()g(3)0m >≥,即11020()m m A n ->≥.所以当3m ≥时,对于任意的m 位自然数n 均有1()10m A n -<. …………………9分 (Ⅲ)答:m n 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38.…………………14分。
【数学】北京市西城区(普通校)2014-2015学年高一上学期期末考试

北京市西城区2014 — 2015学年度第一学期期末试卷高一数学试卷满分:150分 考试时间:120分钟 A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)22.已知向量(2,8)=a ,(4,2)=-b .若2=-c a b ,则向量=c ( ) (A )(0,18)(B )(8,14)(C )(12,12)(D )(4,20)-3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )35(B )45-(C )34(D )34-4.在△ABC 中,D 是BC 的中点,则AD =( )(A )1()2AB AC + (B )1()2AB AC - (C )1()2AB BC +(D )1()2AB BC -5.函数2(sin cos )y x x =-的最小正周期为( ) (A )2π(B )3π2(C )π(D )π26.如果函数cos()y x =+ϕ的一个零点是3π,那么ϕ可以是( ) (A )6π (B )6π-(C )3π(D )3π-7.如图,在矩形ABCD 中,2AB =,BC =, E 是CD 的中点,那么AE DC ⋅=( )(A )4(B )2(C (D )18.当[0,π]x ∈时,函数()cos f x x x =的值域是( )(A )[2,1]-(B )[1,2]-(C )[1,1]-(D )[-9.为得到函数πcos()6y x =+的图象,只需将函数sin y x =的图象( ) (A )向左平移π3个单位 (B )向右平移π3个单位(C )向左平移2π3个单位 (D )向右平移2π3个单位10.已知a ,b 为单位向量,且m ⋅=a b ,则||t +a b ()t ∈R 的最小值为( )(A (B )1(C )||m(D二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11.若向量(1,2)=a 与向量(,1)=-λb 共线,则实数=λ_____. 12.已知α是第二象限的角,且5sin 13α=,则cos =α_____. 13.若(,)22ππ∈-θ,且tan 1>θ,则θ的取值范围是_____. 14.已知向量(1,3)=a ,(2,1)=-b ,(1,1)=c .若(,)=∈R c a +b λμλμ,则=λμ_____. 15.函数2()sin sin cos f x x x x =+⋅的最大值是_____. 16.关于函数()sin(2)()6f x x x π=-∈R ,给出下列三个结论:① 对于任意的x ∈R ,都有2()cos(2)3f x x π=-; ② 对于任意的x ∈R ,都有()()22f x f x ππ+=-;③ 对于任意的x ∈R ,都有()()33f x f x ππ-=+.其中,全部正确结论的序号是_____.三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知tan 2=-α,其中(,)2π∈πα. (Ⅰ)求πtan()4-α的值; (Ⅱ)求sin 2α的值. 18.(本小题满分14分)已知向量(cos ,sin )=ααa,1(2=-b ,其中α是锐角. (Ⅰ)当30︒=α时,求||+a b ; (Ⅱ)证明:向量+a b 与-a b 垂直; (Ⅲ)若向量a 与b 夹角为60︒,求角α. 19.(本小题满分10分)已知函数()sin cos f x a x b x =+,其中a ∈Z ,b ∈Z .设集合{|()0}A x f x ==,{|(())0}B x f f x ==,且A B =.(Ⅰ)证明:0b =; (Ⅱ)求a 的最大值.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分. 把答案填在题中横线上. 1.已知集合{,}A a b =,则满足{,,}AB a b c =的不同集合B 的个数是_____.2.若幂函数y x =α的图象过点(4,2),则=α_____.3.函数2lg ,0,()4,0,x x f x x x >⎧=⎨-<⎩的零点是_____.4.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若()(2)f m f >,则实数m 的取值范围是_____.5.已知函数()f x 的定义域为D .若对于任意的1x D ∈,存在唯一的2x D ∈,使得M =成立,则称函数()f x 在D 上的几何平均数为M .已知函数()31([0,1])g x x x =+∈,则()g x 在区间[0,1]上的几何平均数为_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值. 7.(本小题满分10分)已知函数()23x x f x a b =⋅+⋅,其中,a b 为常数. (Ⅰ)若0ab >,判断()f x 的单调性,并加以证明; (Ⅱ)若0ab <,解不等式:(1)()f x f x +>. 8.(本小题满分10分)定义在R 上的函数()f x 同时满足下列两个条件: ① 对任意x ∈R ,有(2)()2f x f x +≥+;② 对任意x ∈R ,有(3)()3f x f x +≤+.设()()g x f x x =-.(Ⅰ)证明:(3)()(2)g x g x g x +≤≤+; (Ⅱ)若(4)5f =,求(2014)f 的值.北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1.D ;2.B ;3.B ;4.A ;5.C ;6.A ;7.B ;8.A ;9.C ; 10.D. 二、填空题:本大题共6小题,每小题4分,共24分.11.12-; 12.1213-; 13. (,)42ππ; 14.32;15.12+; 16. ① ② ③. 注:16题,少解不给分.三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 tan 2=-α,所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 3=. 【 6分】(Ⅱ)解:由π(,π)2∈α,tan 2α=-, 得sin α=, 【 8分】cos α=. 【10分】 所以 4sin 22sin cos 5==-ααα. 【12分】 18.(本小题满分14分) (Ⅰ)解:当30︒=α时,1)2=a , 【 1分】所以+a b =, 【 2分】所以||+=a b = 【 4分】(Ⅱ)证明:由向量(cos sin )αα=,a,1(,22=-b ,得 1(cos ,sin 22+=-+ααa b ,1(cos ,sin 22-=+-ααa b , 由 π(0,)2∈α,得向量+a b ,-a b 均为非零向量. 【 5分】因为 222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b , 【 7分】所以向量+a b 与-a b 垂直. 【 8分】 (Ⅲ)解:因为||||1==a b ,且向量a 与b 夹角为60︒,所以 1||||cos 602︒⋅=⋅=a b a b . 【10分】所以 11cos 22-=αα, 即 π1sin()62-=α. 【12分】 因为 π02<<α, 所以 πππ663-<-<α, 【13分】 所以 ππ66-=α, 即3π=α. 【14分】 19.(本小题满分10分) (Ⅰ)证明:显然集合A ≠∅.设 0x A ∈,则0()0f x =. 【 1分】 因为 A B =,所以 0x B ∈, 即 0(())0f f x =,所以 (0)0f =, 【 3分】 所以 0b =. 【 4分】 (Ⅱ)解:由(Ⅰ)得()sin f x a x =,a ∈Z .① 当0a =时,显然满足A B =. 【 5分】 ② 当0a ≠时,此时{|sin 0}A x a x ==;{|sin(sin )0}B x a a x ==, 即{|sin ,}B x a x k k ==π∈Z . 【 6分】 因为 A B =,所以对于任意x ∈R ,必有sin a x k ≠π (k ∈Z ,且0)k ≠成立. 【 7分】 所以对于任意x ∈R ,sin k x a π≠,所以 1k aπ>, 【 8分】 即 ||||a k <⋅π,其中k ∈Z ,且0k ≠.所以 ||a <π, 【 9分】 所以整数a 的最大值是3. 【10分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1. 4;2.12; 3. 2-,1; 4. (2,2)-; 5. 2. 注:3题,少解得2分,有错解不给分. 二、解答题:本大题共3小题,共30分. 6.(本小题满分10分)(Ⅰ)解法一:因为2()(2)()(2)2f x x x a x a x a =-+=+--, 所以,()f x 的图象的对称轴方程为22ax -=. 【 2分】 由212a-=,得0a =. 【 4分】 解法二:因为函数()f x 的图象关于直线1x =对称,所以必有(0)(2)f f =成立, 【 2分】 所以 20a -=, 得0a =. 【 4分】 (Ⅱ)解:函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤,即 2a ≥时, 因为()f x 在区间(0,1)上单调递增,所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】 ② 当2012a-<<,即 02a <<时,因为()f x 在区间2(0,)2a -上单调递减,在区间2(,1)2a-上单调递增, 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥,即 0a ≤时, 因为()f x 在区间(0,1)上单调递减,所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】 7.(本小题满分10分)(Ⅰ)解:当0,0a b >>时,()f x 在R 上是增函数;当0,0a b <<时,()f x 在R 上是减函数; 【 1分】 证明如下:当0,0a b >>时,任取12,x x ∈R ,且12x x <,则210x x x ∆=->, 则 212121()()(22)(33)x x x x y f x f x a b ∆=-=-+-.因为 122122,0(22)0x x x x a a <>⇒->;又122133,0(33)0x x x xb b <>⇒->, 所以 21()()0y f x f x ∆=->,所以,当0,0a b >>时,()f x 在R 上是增函数.当0,0a b <<时,同理可得,()f x 在R 上是减函数. 【 5分】 (Ⅱ)解:由(1)()2230x xf x f x a b +-=⋅+⋅>,得 32()2xb a >-. (*) 【 6分】① 当0,0a b <>时,(*)式化为3()22xa b->, 解得32log ()2ax b>-.【 8分】 ② 当0,0a b ><时,(*)式化为3()22xa b-<, 解得32log ()2ax b<-.【10分】 8.(本小题满分10分)(Ⅰ)证明:因为()()g x f x x =-,所以(2)(2)2g x f x x +=+--,(3)(3)3g x f x x +=+--.由条件①,②可得(2)(2)2()22()()g x f x x f x x f x x g x +=+--≥+--=-=;③ 【 2分】 (3)(3)3()33()()g x f x x f x x f x x g x +=+--≤+--=-=. ④ 【 4分】 所以(3)()(2)g x g x g x +≤≤+. (Ⅱ)解:由③得 (2)()g x g x +≥,所以(6)(4)(2)()g x g x g x g x +≥+≥+≥. 【 6分】由④得 (3)()g x g x +≤,所以(6)(3)()g x g x g x +≤+≤. 【 7分】 所以必有(6)()g x g x +=,即()g x 是以6为周期的周期函数. 【 8分】 所以(2014)(33564)(4)(4)41g g g f =⨯+==-=. 【 9分】 所以(2014)(2014)20142015f g =+=. 【10分】。
北京市西城区2013-2014学年高一数学上学期期末考试试题(基础薄弱校试题)北师大版

市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分:150分 考试时间:120分钟 A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知[0,2)∈πα,且角α与角π6-终边相同,则=α( ) (A )11π6(B )7π6 (C )5π6(D )π62.若sin 0<α,且cos 0>α,则角α是( ) (A )第一象限的角 (B )第二象限的角 (C )第三象限的角(D )第四象限的角3.已知向量1(1,0)=e ,2(0,1)=e ,那么向量122+e e 的坐标是( ) (A )(1,2)-(B )(1,2)-(C )(1,2)--(D )(1,2)4.若角α的终边经过点(1,2)P -,则tan =α( )(A (B )(C )2- (D )12-5.已知正方形ABCD 的边长为1,则AB AC ⋅=( )(A (B )1(C(D )26.在平面直角坐标系xOy 中,函数sin y x =的图象( ) (A )关于x 轴对称 (B )关于y 轴对称 (C )关于原点对称(D )关于点(,0)2π对称7.在△ABC 中,D 是BC 的中点,则向量AD =( )(A )1122AB AC + (B )AB AC + (C )1122AB AC -(D )AB AC -8.已知函数1()sin cos 22f x x x =+,则()12f π=( )(A )2 (B (C )1(D9.设a ,b 是两个非零向量,且+=-a b a b ,则a 与b 夹角的大小为( ) (A )120︒(B )90︒(C )60︒(D )30︒10.已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增,则正数ω的最大值是( ) (A )32(B )43(C )34 (D )23二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11.sin()3π-=______. 12. 若1cos 2=-α,且(0,)∈πα,则α=______. 13.已知向量(1,3)=a ,(2,)k =-b .若向量a 与b 共线,则实数k =_____. 14.若tan 2=α,且32π∈(π,)α,则sin()2π+=α______. 15. 定义在R 上的函数()f x 满足:对任意的x ∈R ,都有(2)()f x f x +=.若(1)2f -=,则(3)f =_____.16. 已知向量(cos ,sin )αα=a ,(cos ,sin )ββ=b .若π,3〈〉=a b ,则cos()-=αβ_____.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)已知3tan 4=-α. (Ⅰ)求πtan()4-α的值; (Ⅱ)求2sin 3cos 3sin 2cos --αααα的值.18.(本小题满分12分)已知函数2()(sin 2cos 2)1f x x x =++. (Ⅰ)求()f x 的最小正周期; (Ⅱ)若[,]124x ππ∈,求()f x 的最大值与最小值.19.(本小题满分12分)如图,正六边形ABCDEF 的边长为1,O 为其中心,,M N 分别是,BC DE 上的动点,且BM DN =.(Ⅰ)若,M N 分别是,BC DE 的中点,求OM ON ⋅的值; (Ⅱ)求OM ON ⋅的取值X 围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>,{|02}B x x =<≤,那么A B =_____.2. 已知2log 3a =,3log 2b =,21log 3c =.将,,a b c 按从小到大排列为_____. 3. 函数()121()2xf x x =-的零点个数为_____.4.若函数2()2f x x x =-在区间(,)a +∞上是增函数,则a 的取值X 围是_____.5. 给定数集A .若对于任意,a b A ∈,有a b A +∈,且a b A -∈,则称集合A 为闭集合.给出如下三个结论:① 集合{4,2,0,2,4}A =--为闭集合; ② 集合{|2,}A n n k k ==∈Z 为闭集合; ③ 若集合12,A A 为闭集合,则12A A 为闭集合.其中,全部正确结论的序号是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知函数21()x f x x-=.(Ⅰ)证明:()f x 是奇函数;(Ⅱ)用函数单调性的定义证明:()f x 在(0,)+∞上为增函数.7.(本小题满分10分)已知函数()log (2)1a f x x =+-,其中1a >.(Ⅰ)若()f x 在[0,1]上的最大值与最小值互为相反数,求a 的值; (Ⅱ)若()f x 的图象不经过第二象限,求a 的取值X 围. 8.(本小题满分10分)已知函数()|2|f x x x =-. (Ⅰ)解不等式()3f x <;(Ⅱ)设0a >,求()f x 在区间[0,]a 上的最大值.市西城区2013 — 2014学年度第一学期期末试卷高一数学参考答案及评分标准 2014.1 A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1. A ;2. D ;3. D ;4. C ;5. B ;6. C ;7.A ;8. A ;9. B ; 10. C. 二、填空题:本大题共6小题,每小题4分,共24分.11. 12.32π; 13.6-;14. 15.2; 16.12. 三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 3tan 4=-α, 所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 7=-. 【 6分】(Ⅱ)解:因为3tan 4=-α, 所以2sin 3cos 2tan 33sin 2cos 3tan 2--=--αααααα 【 9分】 1817=. 【12分】18.(本小题满分12分)(Ⅰ)解:2()(sin 2cos 2)1f x x x =++22sin 22sin 2cos 2cos 21x x x x =+⋅++【 2分】sin 42x =+.【 4分】 因为 242T ππ==, 所以()f x 的最小正周期是2π. 【 6分】 (Ⅱ)解:由(Ⅰ)得,()sin 42f x x =+.因为124x ππ≤≤, 所以 43x π≤≤π, 【 8分】所以 0sin 41x ≤≤,所以 2sin 423x ≤+≤. 【10分】 所以,当8x π=时,()f x 取得最大值3;当4x π=时,()f x 取得最小值2.【12分】19.(本小题满分12分)(Ⅰ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,且,M N 分别是,BC DE 的中点,所以 32OM ON ==,120MON ︒∠=, 【 2分】 所以 3cos1208OM ON OM ON ︒⋅==-. 【 4分】 (Ⅱ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,BM DN =,所以 △DON ≌△BOM . 【 6分】 所以 OM ON =,且DON BOM ∠=∠,即 OM ON =,且120MON ︒∠=. 【 8分】所以 21cos1202OM ON OM ON ON ︒⋅==-. 【10分】当点N 重合于点D 或E 时,ON 取得最大值1,OM ON ⋅取得最小值12-;【11分】当点N 是DE 的中点时,ON取得最小值2,OM ON ⋅取得最大值38-.【12分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1.{|01}x x <<;2.c b a <<;3.1;4.[1,)+∞;5.②. 二、解答题:本大题共3小题,共30分.6.(本小题满分10分)(Ⅰ)证明:由已知,函数()f x 的定义域为{0}D x x =∈≠R . 【 1分】设x D ∈,则x D -∈,22()11()()x x f x f x x x----==-=--. 【 3分】所以函数()f x 为奇函数. 【 4分】 (Ⅱ)证明:设12,x x 是(0,)+∞上的两个任意实数,且12x x <,则210x x x ∆=->.2221212111()()x x y f x f x x x --∆=-=-【 6分】 22122121121212(1)(1)()(1)x x x x x x x x x x x x ----+==. 【 8分】 因为 120x x <<, 所以 120x x >,210x x ->,1210x x +>,所以 0y ∆>, 【 9分】 所以 ()f x 在(0,)+∞上是增函数. 【10分】7.(本小题满分10分)(Ⅰ)解:函数()log (2)1a f x x =+-的定义域是(2,)-+∞.【 1分】因为 1a >,所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】 所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-;最小值是(0)log 21a f =-. 【 4分】依题意,得 log 31(log 21)a a -=--, 【 5分】 解得a =【 6分】(Ⅱ)解:由(Ⅰ)知,()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中,令0x =,得(0)log 21a f =-, 所以,()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】 依题意,得(0)log 210a f =-≤, 【 9分】 解得 2a ≥. 【10分】8.(本小题满分10分)(Ⅰ)解:原不等式可化为22230x x x ≥⎧⎨--<⎩,, (1) 或22230.x x x <⎧⎨-+>⎩,(2) 【 1分】解不等式组(1),得 23x ≤<;解不等式组(2),得2x <. 【 3分】 所以原不等式的解集为{|3}x x <.【 4分】(Ⅱ)解:222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩【 5分】① 当01a <<时,()f x 是[0,]a 上的增函数,此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】 ② 当12a ≤≤时,()f x 在[0,1]上是增函数,在[1,]a 上是减函数,此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③当2a >时,令()(1)(2)10f a f a a -=-->,解得1a >.所以,当21a <≤+此时()(1)f a f ≤,()f x 在[0,]a 上的最大值是(1)1f =;当1a >+()(1)f a f >,()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】 记()f x 在区间[0,]a 上的最大值为()g a ,所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤⎨⎪->⎪⎩【10分】。
2014-2015年北京市西城区高一上学期期末数学试卷与答案Word版

2014-2015学年北京市西城区高一(上)期末数学试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(4分)已知α∈(0,2π),且sinα<0,cosα>0,则角α的取值范围是()A.B.C.D.2.(4分)已知向量=(2,8),=(﹣4,2).若=2﹣,则向量=()A.(0,18)B.(8,14)C.(12,12)D.(﹣4,20)3.(4分)已知角α的终边经过点P(3,﹣4),那么sinα=()A.B.C.D.4.(4分)在△ABC中,D是BC的中点,则=()A.B.C.D.5.(4分)函数y=(sinx﹣cosx)2的最小正周期为()A.2πB. C.πD.6.(4分)如果函数y=cos(x+φ)的一个零点是,那么φ可以是()A.B.C.D.7.(4分)如图,在矩形ABCD中,AB=2,,E是CD的中点,那么=()A.4 B.2 C.D.18.(4分)当x∈[0,π]时,函数f(x)=cosx﹣sinx的值域是()A.[﹣2,1]B.[﹣1,2]C.[﹣1,1]D.9.(4分)为得到函数的图象,只需将函数y=sinx的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位10.(4分)已知,为单位向量,且•=m,则|+t|(t∈R)的最小值为()A.B.1 C.|m| D.二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上. 11.(4分)若向量=(1,2)与向量=(λ,﹣1)共线,则实数λ=.12.(4分)设α是第二象限角,sinα=,则cosα=.13.(4分)若,且tanθ>1,则θ的取值范围是.14.(4分)已知向量=(1,3),=(2,﹣1),=(1,1).若=λ+μ(λ,μ∈R),则=.15.(4分)函数f(x)=sin2x+sinx•cosx的最大值是.16.(4分)关于函数f(x)=sin (2x﹣)(x∈R),给出下列三个结论:①对于任意的x∈R,都有f(x)=cos (2x﹣);②对于任意的x∈in R,都有f(x+)=f(x﹣);③对于任意的x∈R,都有f(﹣x)=f(+x).其中,全部正确结论的序号是.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知tanα=﹣2,其中.(Ⅰ)求的值;(Ⅱ)求sin2α的值.18.(14分)已知向量=(cosα,sinα),=(﹣,),其中α是锐角.(Ⅰ)当α=30°时,求|+|;(Ⅱ)证明:向量+与﹣垂直;(Ⅲ)若向量与夹角为60°,求角α.19.(10分)已知函数f(x)=asinx+bcosx,其中a∈Z,b∈Z.设集合A={x|f(x)=0},B={x|f(f(x))=0},且A=B.(Ⅰ)证明:b=0;(Ⅱ)求a的最大值.一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 20.(4分)已知集合A={a,b},则满足A∪B={a,b,c}的不同集合B的个数是.21.(4分)已知幂函数f(x)=xα的图象过点(4,2),则α=.22.(4分)函数f(x)=的零点是.23.(4分)设f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数.若f(m)>f(2),则实数m的取值范围是.24.(4分)已知函数f(x)的定义域为D.若对于任意的x1∈D,存在唯一的x2∈D,使得=M成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤.25.(10分)已知函数f(x)=(x﹣2)(x+a),其中a∈R.(Ⅰ)若f(x)的图象关于直线x=1对称,求a的值;(Ⅱ)求f(x)在区间[0,1]上的最小值.26.(10分)已知函数f(x)=a•2x+b•3x,其中a,b为常数.(Ⅰ)若ab>0,判断f(x)的单调性,并加以证明;(Ⅱ)若ab<0,解不等式:f(x+1)>f(x).27.(10分)定义在R上的函数f(x)同时满足下列两个条件:①对任意x∈R,有f(x+2)≥f(x)+2;②对任意x∈R,有f(x+3)≤f(x)+3.设g(x)=f(x)﹣x.(Ⅰ)证明:g(x+3)≤g(x)≤g(x+2);(Ⅱ)若f(4)=5,求f(2014)的值.2014-2015学年北京市西城区高一(上)期末数学试卷参考答案与试题解析一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(4分)已知α∈(0,2π),且sinα<0,cosα>0,则角α的取值范围是()A.B.C.D.【解答】解:由sinα<0,cosα>0,可得α为第四象限的角,又α∈(0,2π),∴α∈.故选:D.2.(4分)已知向量=(2,8),=(﹣4,2).若=2﹣,则向量=()A.(0,18)B.(8,14)C.(12,12)D.(﹣4,20)【解答】解:向量=(2,8),=(﹣4,2),若=2﹣,则=(4,16)﹣(﹣4,2)=(8,14).故选:B.3.(4分)已知角α的终边经过点P(3,﹣4),那么sinα=()A.B.C.D.【解答】解:由于角α的终边经过点P(3,﹣4),∴x=3,y=﹣4,r=|OP|=5,∴sinα==﹣,故选:B.4.(4分)在△ABC中,D是BC的中点,则=()A.B.C.D.【解答】解:∵D是BC的中点,∴=,故选:A.5.(4分)函数y=(sinx﹣cosx)2的最小正周期为()A.2πB. C.πD.【解答】解:化简可得y=(sinx﹣cosx)2=1﹣sin2x,∴由周期公式可得T==π,故选:C.6.(4分)如果函数y=cos(x+φ)的一个零点是,那么φ可以是()A.B.C.D.【解答】解:若y=cos(x+φ)的一个零点是,则cos(+φ)=0,即+φ=kπ+,k∈Z即φ=kπ+,当k=0时,φ=,故选:A.7.(4分)如图,在矩形ABCD中,AB=2,,E是CD的中点,那么=()A.4 B.2 C.D.1【解答】解:=(+)•=+=+=0+==2.故选:B.8.(4分)当x∈[0,π]时,函数f(x)=cosx﹣sinx的值域是()A.[﹣2,1]B.[﹣1,2]C.[﹣1,1]D.【解答】解:∵f(x)=cosx﹣sinx=2cos(x+),∴当x∈[0,π]时,x+∈[,],∴由余弦函数的图象和性质可知:2cos(x+)∈[﹣2,1].故选:A.9.(4分)为得到函数的图象,只需将函数y=sinx的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【解答】解:y=sinx=cos(x﹣),,故只需将函数y=sinx的图象向左平移个长度单位.故选:C.10.(4分)已知,为单位向量,且•=m,则|+t|(t∈R)的最小值为()A.B.1 C.|m| D.【解答】解:,为单位向量,且•=m,则|+t|2=+t2+2t=1+t2+2tm=(t+m)2+1﹣m2,当t=﹣m时,|+t|2取得最小值1﹣m2,则|+t|(t∈R)的最小值为.故选:D.二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.11.(4分)若向量=(1,2)与向量=(λ,﹣1)共线,则实数λ=.【解答】解:∵∴﹣1=2λ∴故答案为:.12.(4分)设α是第二象限角,sinα=,则cosα=﹣.【解答】解:∵sinα=,α是第二象限角,∴cosα=﹣=﹣=﹣.故答案为:﹣.13.(4分)若,且tanθ>1,则θ的取值范围是(,).【解答】解:若,且tanθ>1,则θ∈(,),故答案为:(,).14.(4分)已知向量=(1,3),=(2,﹣1),=(1,1).若=λ+μ(λ,μ∈R),则=.【解答】解:∵向量=(1,3),=(2,﹣1),=(1,1).=λ+μ(λ,μ∈R),∴,解得,∴=.故答案为:.15.(4分)函数f(x)=sin2x+sinx•cosx的最大值是.【解答】解:化简可得f(x)=sin2x+sinx•cosx=+sin2x=sin(2x﹣)+,∴当sin(2x﹣)=1时函数取最大故答案为:16.(4分)关于函数f(x)=sin (2x﹣)(x∈R),给出下列三个结论:①对于任意的x∈R,都有f(x)=cos (2x﹣);②对于任意的x∈in R,都有f(x+)=f(x﹣);③对于任意的x∈R,都有f(﹣x)=f(+x).其中,全部正确结论的序号是①②③..【解答】解:①f(x)=cos[﹣(2x﹣)]=cos(﹣2x)=cos(2x﹣),故①正确,②f(x+)=sin[2(x+)﹣)]=﹣sin(2x﹣)],f(x﹣)=sin[2(x ﹣)﹣)]=﹣sin(2x﹣),则f(x+)=f(x﹣)故②正确③f()=sin(2×﹣)=sin=1为最大值,故x=是函数的对称轴,故③正确,故答案为:①②③.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知tanα=﹣2,其中.(Ⅰ)求的值;(Ⅱ)求sin2α的值.【解答】解:(Ⅰ)∵tanα=﹣2,∴tan(α﹣)===3;(Ⅱ)∵α∈(,π),tanα=﹣2,∴cosα=﹣=﹣,sinα==,则sin2α=2sinαcosα=﹣.18.(14分)已知向量=(cosα,sinα),=(﹣,),其中α是锐角.(Ⅰ)当α=30°时,求|+|;(Ⅱ)证明:向量+与﹣垂直;(Ⅲ)若向量与夹角为60°,求角α.【解答】(Ⅰ)解:当α=30°时,=(,),所以,+=(,),所以,|+|==.(Ⅱ)证明:由向量=(cosα,sinα),=(﹣,),得+=(cosα﹣,sinα+),﹣=(cosα+,sinα﹣),由,得向量+,﹣均为非零向量.因为(+)•(﹣)=﹣=(cos2α+sin2α)﹣(+)=0,所以向量+与向量﹣垂直.(Ⅲ)解:因为||=||=1,且向量与夹角为60°,所以=||•||•cos60°=,所以,即.因为,所以,所以,即.19.(10分)已知函数f(x)=asinx+bcosx,其中a∈Z,b∈Z.设集合A={x|f(x)=0},B={x|f(f(x))=0},且A=B.(Ⅰ)证明:b=0;(Ⅱ)求a的最大值.【解答】(Ⅰ)证明:显然集合A≠∅.设x0∈A,则f(x0)=0.(1分)因为A=B,所以x0∈B,即f(f(x0))=0,所以f(0)=0,(3分)所以b=0.(4分)(Ⅱ)解:由(Ⅰ)得f(x)=asinx,a∈Z.①当a=0时,显然满足A=B.(5分)②当a≠0时,此时A={x|asinx=0};B={x|asin(asinx)=0},即B={x|asinx=kπ,k∈Z}.(6分)因为A=B,所以对于任意x∈A,必有asinx≠kπ(k∈Z,且k≠0)成立.(7分)所以对于任意x∈A,,所以,(8分)即|a|<|k|•π,其中k∈Z,且k≠0.所以|a|<π,(9分)所以整数a的最大值是3.(10分)一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 20.(4分)已知集合A={a,b},则满足A∪B={a,b,c}的不同集合B的个数是4.【解答】解:因为集合A={a,b},满足A∪B={a,b,c},所以B={c}、{a,c}、{b,c}、{a,b,c}共4个,故答案为:4.21.(4分)已知幂函数f(x)=xα的图象过点(4,2),则α=.【解答】解:∵4α=2,解得,故答案为:22.(4分)函数f(x)=的零点是﹣2或1.【解答】解:∵函数f(x)=∴或解得:x=1,或x=﹣2故答案:﹣2,1;23.(4分)设f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数.若f(m)>f(2),则实数m的取值范围是(﹣2,2).【解答】解:∵f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数,∴不等式f(m)>f(2),等价为f(|m|)>f(2),即|m|<2,解得﹣2<m<2,故答案为:(﹣2,2);24.(4分)已知函数f(x)的定义域为D.若对于任意的x1∈D,存在唯一的x2∈D,使得=M成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为2.【解答】解:根据已知中关于函数g(x)在D上的几何平均数为C的定义,结合g(x)=3x+1在区间[0,1]单调递增则x1=0时,存在唯一的x2=1与之对应C==2,故答案为:2.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤.25.(10分)已知函数f(x)=(x﹣2)(x+a),其中a∈R.(Ⅰ)若f(x)的图象关于直线x=1对称,求a的值;(Ⅱ)求f(x)在区间[0,1]上的最小值.【解答】(Ⅰ)解法一:因为f(x)=(x﹣2)(x+a)=x2+(a﹣2)x﹣2a,所以,f(x)的图象的对称轴方程为.由,得a=0.解法二:因为函数f(x)的图象关于直线x=1对称,所以必有f(0)=f(2)成立,所以﹣2a=0,得a=0.(Ⅱ)解:函数f(x)的图象的对称轴方程为.①当,即a≥2时,因为f(x)在区间(0,1)上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=﹣2a.②当,即0<a<2时,因为f(x)在区间上单调递减,在区间上单调递增,所以f(x)在区间[0,1]上的最小值为.③当,即a≤0时,因为f(x)在区间(0,1)上单调递减,所以f(x)在区间[0,1]上的最小值为f(1)=﹣(1+a).26.(10分)已知函数f(x)=a•2x+b•3x,其中a,b为常数.(Ⅰ)若ab>0,判断f(x)的单调性,并加以证明;(Ⅱ)若ab<0,解不等式:f(x+1)>f(x).【解答】(Ⅰ)解:当a>0,b>0时,f(x)在R上是增函数;当a<0,b<0时,f(x)在R上是减函数.证明如下:当a>0,b>0时,任取x1,x2∈R,且x1<x2,则△x=x2﹣x1>0,则.因为;又,所以△y=f(x2)﹣f(x1)>0,所以,当a>0,b>0时,f(x)在R上是增函数.当a<0,b<0时,同理可得,f(x)在R上是减函数.(Ⅱ)解:由f(x+1)﹣f(x)=a•2x+2b•3x>0,得.(*)①当a<0,b>0时,(*)式化为,解得.②当a>0,b<0时,(*)式化为,解得.27.(10分)定义在R上的函数f(x)同时满足下列两个条件:①对任意x∈R,有f(x+2)≥f(x)+2;②对任意x∈R,有f(x+3)≤f(x)+3.设g(x)=f(x)﹣x.(Ⅰ)证明:g(x+3)≤g(x)≤g(x+2);(Ⅱ)若f(4)=5,求f(2014)的值.【解答】(本小题满分10分)(Ⅰ)证明:因为g(x)=f(x)﹣x,所以g(x+2)=f(x+2)﹣x﹣2,g(x+3)=f(x+3)﹣x﹣3.由条件①,②可得g(x+2)=f(x+2)﹣x﹣2≥f(x)+2﹣x﹣2=f(x)﹣x=g(x);【(2分)】③g(x+3)=f(x+3)﹣x﹣3≤f(x)+3﹣x﹣3=f(x)﹣x=g(x).④【(4分)】所以g (x +3)≤g (x )≤g (x +2). (Ⅱ)解:由③得 g (x +2)≥g (x ),所以g (x +6)≥g (x +4)≥g (x +2)≥g (x ).【(6分)】 由④得 g (x +3)≤g (x ),所以g (x +6)≤g (x +3)≤g (x ).【(7分)】 所以必有g (x +6)=g (x ),即g (x )是以6为周期的周期函数.【(8分)】所以g (2014)=g (335×6+4)=g (4)=f (4)﹣4=1.【(9分)】赠送—高中数学知识点【1.3.1】单调性与最大(小)值 (1)函数的单调性 ①定义及判定方法函数的 性 质定义图象判定方法函数的单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< .x .2.时,都有f(x ...1.)<f(x .....2.).,那么就说f(x)在这个区间上是增函..数..x 1x 2y=f(X)xy f(x )1f(x )2o(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图 象上升为增) (4)利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< .x .2.时,都有f(x ...1.)>f(x .....2.).,那么就说f(x)在这个区间上是减函数.... y=f(X)yx ox x 2f(x )f(x )211(1)利用定义 (2)利用已知函数的单调性(3)利用函数图象(在某个区间图 象下降为减)(4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为yxo增,()u g x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数,分别在[,0)a -、]a 上为减函数.(3)最大(小)值定义①一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M ≤;(2)存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法函数的 性 质定义图象 判定方法 函数的奇偶性如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...-.f(x ...).,那么函数f(x)叫做奇函数....(1)利用定义(要先判断定义域是否关于原点对称) (2)利用图象(图象关于原点对称) 如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...f(x)....,那么函数f(x)叫做偶函数....(1)利用定义(要先判断定义域是否关于原点对称) (2)利用图象(图象关于y 轴对称)②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y轴两侧相对称的区间增减性相同,偶函数在y轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.所以f(2014)=g(2014)+2014=2015.【(10分)】。
2015西城文科数学-期末

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(文科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.设集合1,0,1,2{}A -=,2{|}B x x x =>,则集合A B =( )(A ){1,0,1}-(B ){1,2}-(C ){0,1,2}(D ){1,1,2}-3.在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若A 为锐角,2a b =,3sin 4B =,则( ) (A )3A π= (B )6A π=(C )3sin 3A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )75.设函数()y f x =的定义域为R ,则“(0)0f =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件(B )必要而不充分条件2.设命题p :2log 0,2xx x ∀>>,则p ⌝为( ) (A )2log 0,2xx x ∀>< (B )2log 0,2xx x ∃>≤ (C )2log 0,2xx x ∃><(D )2log 0,2xx x ∃>≥a =2,x =3开始 x y a =x =x +1103y x >+ 输出x 结束否是(C )充分必要条件 (D )既不充分也不必要条件6. 某天,甲要去银行办理储蓄业务,已知银行的营业时间为9:00至17:00,设甲在当天13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是( ) (A )13 (B )34 (C )58 (D )458. 如图,在空间四边形ABCD 中,两条对角线,AC BD 互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边,,,AB BC CD DA 分别相交于点,,,E F G H ,记四边形EFGH 的面积为y ,设BEx AB=,则( ) (A )函数()y f x =的值域为(0,4] (B )函数()y f x =的最大值为8(C )函数()y f x =在2(0,)3上单调递减(D )函数()y f x =满足()(1)f x f x =-第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数i1iz =+,则||z =______.10.设平面向量,a b 满足||3=a ,||2=b ,3⋅=-a b ,那么,a b 的夹角θ=____.7. 设抛物线2:4W y x =的焦点为F ,过F 的直线与W 相交于A ,B 两点,记点F 到直线l :1x =-的距离为d ,则有( )(A )2||d AB ≥ (B )2||d AB = (C )2||d AB ≤(D )2||d AB <A BE CD GH F侧(左)视图正(主)视图 22 11111.一个四棱锥的三视图如图所示,那么这个四棱锥最长棱的棱长为_____.12.设12,F F 为双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,且直线2y x =为双曲线C 的一条渐近线,点P 为C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为_____.13. 某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元. 为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有_______种不同的购买奖品方案.14. 设函数3||, 1,()log , 1.x a x f x x x -⎧=⎨>⎩≤(1)如果(1)3f =,那么实数a =___;(2)如果函数()2y f x =-有且仅有两个零点,那么实数a 的取值范围是___.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2π()12sin ()4f x x =--,x ∈R . (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)判断函数()f x 在区间ππ[,]66-上是否为增函数?并说明理由.16.(本小题满分13分)已知数列{}n a 满足25a =,且其前n 项和2n S pn n =-. (Ⅰ)求p 的值和数列{}n a 的通项公式;(Ⅱ)设数列{}n b 为等比数列,公比为p ,且其前n 项和n T 满足55T S <,求1b 的取值范围. 17.(本小题满分14分)如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面ABCD ,90BAD ∠=,BC AD //,且122A A AD BC ===,1AB =. 点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)求证:1A F ∥平面1B CE ;(Ⅱ)求证: AC ⊥平面11CDD C ;(Ⅲ)写出三棱锥11B A EF -体积的取值范围. (结论不要求证明)18.(本小题满分13分)最近,张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案,且一年后投资盈亏的情况如下:(1) 投资股市:投资结果 获利不赔不赚亏损概 率12 18 38(2) 购买基金:投资结果 获利不赔不赚亏损概 率p13q(Ⅰ)当12p =时,求q 的值; (Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p 的取值范围;(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率. 19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,若122S S =,求直线l 的方程.20.(本小题满分13分)对于函数(),()f x g x ,如果它们的图象有公共点P ,且在点P 处的切线相同,则称函数()f x 和()g x 在点P 处相切,称点P 为这两个函数的切点.设函数2()(0)f x ax bx a =-≠,()ln g x x =.B CA 1 D 1DA B 1C 1E F(Ⅰ)当1a =-,0b =时, 判断函数()f x 和()g x 是否相切?并说明理由; (Ⅱ)已知a b =,0a >,且函数()f x 和()g x 相切,求切点P 的坐标;(Ⅲ)设0a >,点P 的坐标为1(,1)e-,问是否存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切?若点P 的坐标为2(e ,2)呢?(结论不要求证明)北京市西城区2014 — 2015学年度第一学期期末高三数学(文科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.B 3.A 4.C 5.B 6.D 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分. 9.22 10.2π311. 22 12.221416x y -=513.9 14.2-或4 (1,3]- 注:第12,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为2π()12sin ()4f x x =--πcos 2()4x =- ……………… 3分sin 2x =, ……………… 5分所以函数()f x 的最小正周期2ππ2T ==.……………… 7分 (Ⅱ)解:结论:函数()f x 在区间ππ[,]66-上是增函数. ……………… 9分理由如下:由ππ2π22π22k x k -+≤≤,解得ππππ44k x k -+≤≤,所以函数()f x 的单调递增区间为ππ[π,π]44k k -+,()k ∈Z .……………… 12分 当0=k 时,知)(x f 在区间ππ[,]44-上单调递增, 所以函数()f x 在区间ππ[,]66-上是增函数. ……………… 13分16.(本小题满分13分)(Ⅰ)解:由题意,得11S p =-,242S p =-,因为 25a =,212S a a =+, 所以 24215S p p =-=-+,解得 2p =. ……………… 3分所以 22n S n n =-.当2n ≥时,由1n n n a S S -=-, ……………… 5分 得 22(2)[2(1)(1)]43n a n n n n n =-----=-. ……………… 7分 验证知1n =时,1a 符合上式,所以43n a n =-,*n ∈N . ……………… 8分(Ⅱ)解:由(Ⅰ),得11(12)(21)12n n n b T b -==--. ……………… 10分 因为 55T S <,所以 521(21)255b -<⨯-,解得 14531b <. ……………… 12分 又因为10b ≠,所以1b 的取值范围是45(,0)(0,)31-∞. ……………… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,A 1 D 1B 1C 1F所以平面ABCD ∥平面1111A B C D . 又因为平面ABCD 平面1A ECF EC =,平面1111A B C D 平面11A ECF A F =,所以 1A F ∥CE . …………………3分 又 1A F ⊄平面1B CE ,CE ⊂平面1B CE ,所以 1A F ∥平面1B CE . …………………6分 (Ⅱ)证明:在四边形ABCD 中,因为 90BAD ∠=,BC AD //,且BC AD 2=,2AD =,1AB =, 所以 222112AC =+=,222112CD =+=. 所以 222AC CD AD +=,所以 90ACD ∠=,即AC CD ⊥. …………………7分 因为 1A A ⊥平面ABCD AC ⊂,平面ABCD , 所以 1A A AC ⊥.因为在四棱柱1111D C B A ABCD -中,11//A A C C ,所以 1C C AC ⊥. …………………9分 又因为 1,CD C C ⊂平面11CDD C ,1CDC C C =,所以 AC ⊥平面11CDD C . …………………11分(Ⅲ)解:三棱锥11B A EF -的体积的取值范围是12[,]33. …………………14分18.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种 且三种投资结果相互独立,所以 p +13+q =1. ……………… 2分又因为 12p =, 所以 q =61. ……………… 3分(Ⅱ)解:由“购买基金”亏损的概率比“投资股市”亏损的概率小,得 38q <, ……………… 4分 因为 p +13+q =1,所以 2338q p =-<,解得 724p >. ……………… 7分 又因为 113p q ++=,0q ≥, 所以 23p ≤. 所以72243p ≤<. ……………… 8分 (Ⅲ)解:记事件A 为 “一年后张师傅和李师傅两人中至少有一人获利”, ………… 9分用a ,b ,c 分别表示一年后张师傅购买基金“获利”、“不赔不赚”、“亏损”,用x ,y ,z 分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”,则一年后张师傅和李师傅购买基金,所有可能的投资结果有339⨯=种, 它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)b y ,(,)b z ,(,)c x ,(,)c y ,(,)c z , ……………10分所以事件A 的结果有5种,它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)c x . …………… 11分 因此这一年后张师傅和李师傅两人中至少有一人获利的概率5()9P A =. …………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,23b =,222c a b =-=, ………………2分则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为 ||21||42FA AP m ==-,所以 8m =. ………………5分 (Ⅱ)解:若直线l 的斜率不存在,则有 21S S =,不合题意. ………………6分若直线l 的斜率存在,设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分 因为PMF ∆和PNF ∆的面积分别为111||||2S PF y =⋅,221||||2S PF y =⋅,所以2||||212121=-==y yy y S S . ……………… 9分 即 212y y -=.所以 221y y y -=+,2212221)(22y y y y y +-=-=, ……………… 11分则 22121)]2()2([2)2()2(-+--=-⋅-x k x k x k x k , 即 2212121)4(24)(2-+-=++-x x x x x x ,即 2222222)43416(2434162344816-+-=++⋅-+-k k k k k k , 解得 25±=k . ……………… 13分所以直线l 的方程为 )2(25-=x y 或 )2(25--=x y . ……………… 14分20.(本小题满分13分)(Ⅰ)解:结论:当1a =-,0b =时,函数()f x 和()g x 不相切. …………………1分 理由如下:由条件知2()f x x =-, 由()ln g x x =,得0x >,又因为 ()2f x x '=-,1()g x x'=, …………………2分 所以当0x >时,()20f x x '=-<,1()0g x x '=>,所以对于任意的0x >,()()f x g x ''≠.当1a =-,0b =时,函数()f x 和()g x 不相切. …………………3分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………4分由②,得 1(21)a s s =-,代入①,得 1ln 21s s s -=-. (*) …………………5分因为 10(21)a s s =>-,且0s >, 所以 12s >. 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………6分 令()0F x '= ,解得1x =或14x =(舍). …………………7分当x 变化时,()F x '与()F x 的变化情况如下表所示,x1(,1)21 (1,)+∞()F x ' +0 -()F x↗↘…………………8分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞时()0F x <. 因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………9分 (Ⅲ)解:当点P 的坐标为1(,1)e-时,存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切; …………………11分当点P 的坐标为2(e ,2)时,不存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切. …………………13分。
北京市西城区2014-2015学年高一上学期期末考试数学试题 Word版含答案

北京市西城区2014 — 2015学年度第一学期期末试卷高一数学 2015.1试卷满分:150分 考试时间:120分钟A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)22.已知向量(2,8)=a ,(4,2)=-b .若2=-c a b ,则向量=c ( ) (A )(0,18)(B )(12,12)(C )(8,14)(D )(4,20)-3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )35(B )34(C )34-(D )45-4.已知函数sin y x =和cos y x =在区间M 上都是增函数,那么区间M 可以是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)25.在△ABC 中,D 是BC 的中点,则AB AC +=( ) (A )2AD(B )2DA(C )2BD(D )2DB6.下列函数中,偶函数是( ) (A )()sin()f x x =π+ (B )()tan()f x x =π- (C )()sin()2f x x π=+ (D )()cos()2f x x π=-7.为得到函数πcos()6y x =+的图象,只需将函数cos y x =的图象( ) (A )向左平移π3个单位 (B )向右平移π3个单位(C )向左平移π6个单位 (D )向右平移π6个单位8.如图,在矩形ABCD 中,2AB =,BC =, E 是CD 的中点,那么AE DC ⋅=( )(A )4(B )2(C (D )19.函数2sin y x =的最小正周期为( ) (A )2π(B )π(C )π2(D )π410.已知向量(1,sin )θ=a ,(cos θ=b ,其中R θ∈,则||-a b 的最大值是( ) (A )4(B )3(C )2(D )1二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11.若(0,)∈πα,且α与角53π-终边相同,则=α_____. 12.若向量(1,2)=a 与向量(,1)=-λb 共线,则实数=λ_____. 13.已知α是第二象限的角,且5sin 13α=,则cos =α_____. 14. 已知向量(1,3)=a ,(2,1)=-b ,(1,1)=c .若(,)=∈R c a +b λμλμ,则=λμ_____. 15.函数2()(sin cos )f x x x =+的最大值是_____.16.关于函数()sin(2)()6f x x x π=-∈R ,给出下列三个结论:① 函数()f x 的图象与2()cos(2)3g x x π=-的图象重合; ② 函数()f x 的图象关于点(,0)12π对称; ③ 函数()f x 的图象关于直线3x π=对称.其中,全部正确结论的序号是_____.三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知tan 2=-α,且(,)2π∈πα. (Ⅰ)求πtan()4-α的值; (Ⅱ)求sin 2α的值.18.(本小题满分12分)已知向量(cos ,sin )=ααa ,1(2=-b ,其中α是锐角. (Ⅰ)证明:向量+a b 与-a b 垂直; (Ⅱ)当|2||2|+=-a b a b 时,求角α.19.(本小题满分12分)已知函数()sin 21f x x x =+. (Ⅰ)求()f x 的单调递减区间;(Ⅱ)若对于任意ππ[,]42x ∈,都有()2f x m -<成立,求实数m 的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分. 把答案填在题中横线上. 1.函数1lg y x=的定义域是_____. 2.若幂函数y x =α的图象过点(4,2),则=α_____. 3.662log 2log 9+=_____. 4.函数21,0,()4,0,x x f x x x ->⎧=⎨-<⎩的零点是_____.5.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若(21)()f m f m ->,则实数m 的取值范围是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知全集U =R ,集合{|(2)0}P x x x =-≥,{|26}M x a x a =<<+. (Ⅰ)求集合U P ð;(Ⅱ)若U P M ⊆ð,求实数a 的取值范围.7.(本小题满分10分)已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值.8.(本小题满分10分)已知函数()23x x f x a b =⋅+⋅,其中,a b 为常数. (Ⅰ)若0ab >,判断()f x 的单调性,并加以证明; (Ⅱ)若0ab <,解不等式:(1)()f x f x +>.北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1.D ;2.C ;3.D ;4. D ;5. A ;6. C ;7. C ;8.B ;9. B ; 10.B . 二、填空题:本大题共6小题,每小题4分,共24分.11.3π; 12. 12-; 13. 1213-; 14.32; 15. 2; 16. ① ② ③.注:16题,少解不给分.三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 tan 2=-α,所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 3=. 【 6分】(Ⅱ)解:由π(,π)2∈α,tan 2α=-, 得sin α=, 【 8分】cos α=. 【10分】 所以 4sin 22sin cos 5==-ααα. 【12分】18.(本小题满分12分)(Ⅰ)证明:由向量(cos sin )αα=,a,1(22=-b , 得1(cos ,sin )22+=-+ααa b ,1(cos ,sin )22-=+-ααa b , 【 1分】 由π(0,)2∈α,得向量+a b ,-a b 均为非零向量. 【 2分】因为222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b , 【 5分】 所以向量+a b 与-a b 垂直. 【 6分】 (Ⅱ)解:将|2||2|+=-a b a b 两边平方,化简得223(||||)80-+⋅=a b a b . 【 8分】 由||||1==a b , 得 0⋅=a b , 【 9分】所以 1cos 022αα-+=,所以 tan =α. 【11分】 注意到 π(0,)2∈α, 所以 π6α=. 【12分】19.(本小题满分12分)(Ⅰ)解:()sin 21f x x x =+π12sin(2)3x =+-. 【 2分】因为函数sin y x =的单调递减区间为π3π[2π,2π]()22k k k ++∈Z . 由 ππ3π2π22π232k x k +≤-≤+()k ∈Z , 【 4分】 得 5π11πππ1212k x k +≤≤+()k ∈Z . 所以()f x 的单调递减区间为5π11π[π,π]1212k k ++()k ∈Z . 【 6分】 (Ⅱ)解: 因为 ππ[,]42x ∈, 所以 ππ2π2633x -≤≤,由(Ⅰ)得 π212sin(2)33x +-≤≤,所以 ()f x 的值域是[23],. 【 8分】 ()2()2()2f x m f x m f x -<⇔-<<+,ππ[,]42x ∈. 【10分】所以 max ()2m f x >-,且 min ()2m f x <+,所以 14m <<, 即m 的取值范围是(1,4). 【12分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1. {|01x x ∈<<R ,或1}x >;2. 12; 3. 2; 4. 2-,1; 5. 1(,1)3.注:4题,少解得2分,有错解不给分. 二、解答题:本大题共3小题,共30分. 6.(本小题满分10分)(Ⅰ)解:因为全集U =R ,集合{|(2)0}P x x x =-≥,所以 {|(2)0}U P x x x =-<ð, 【 2分】 即集合{|02}U P x x =<<ð. 【 4分】 (Ⅱ)解:因为 U P M ⊆ð,所以 0,262,a a ≤⎧⎨+≥⎩ 【 6分】解得 0,2.a a ≤⎧⎨≥-⎩ 【 8分】所以 [2,0]a ∈-. 【10分】 注:第(Ⅱ)小问没有等号扣1分. 7.(本小题满分10分)(Ⅰ)解法一:因为2()(2)()(2)2f x x x a x a x a =-+=+--, 所以,()f x 的图象的对称轴方程为22ax -=. 【 2分】 由212a-=,得0a =. 【 4分】 解法二:因为函数()f x 的图象关于直线1x =对称,所以必有(0)(2)f f =成立, 【 2分】 所以 20a -=, 得0a =. 【 4分】 (Ⅱ)解:函数()f x 的图象的对称轴方程为22ax -=.① 当202a-≤,即 2a ≥时, 因为()f x 在区间(0,1)上单调递增,所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<,即 02a <<时, 因为()f x 在区间2(0,)2a -上单调递减,在区间2(,1)2a-上单调递增, 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥,即 0a ≤时, 因为()f x 在区间(0,1)上单调递减,所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】 8.(本小题满分10分)(Ⅰ)解:当0,0a b >>时,()f x 在R 上是增函数;当0,0a b <<时,()f x 在R 上是减函数; 【 1分】证明如下:当0,0a b >>时,任取12,x x ∈R ,且12x x <,则210x x x ∆=->, 则212121()()(22)(33)x x x xy f x f x a b ∆=-=-+-.因为 122122,0(22)0xxxxa a <>⇒->;又122133,0(33)0xxxxb b <>⇒->, 所以 21()()0y f x f x ∆=->,所以,当0,0a b >>时,()f x 在R 上是增函数.当0,0a b <<时,同理可得,()f x 在R 上是减函数. 【 5分】 (Ⅱ)解:由(1)()2230xxf x f x a b +-=⋅+⋅>,得 32()2xb a >-. (*) 【 6分】 ① 当0,0a b <>时,(*)式化为3()22xa b->,解得32log ()2ax b>-. 【 8分】 ② 当0,0a b ><时,(*)式化为3()22xab-<, 解得32log ()2ax b<-. 【10分】。
北京市西城区2015届高三上学期期末考试数学(文)试题(有答案)AqUwMq

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(文科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1,2{}A -=,2{|}B x x x =>,则集合A B =I ( ) (A ){1,0,1}-(B ){1,2}-(C ){0,1,2}(D ){1,1,2}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,3sin B =,则( ) (A )3A π= (B )6A π=(C )3sin A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )75.设函数()y f x =的定义域为R ,则“(0)0f =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件6. 某天,甲要去银行办理储蓄业务,已知银行的营业时间为9:00至17:00,设甲在当天2.设命题p :2log 0,2xx x ∀>>,则p ⌝为( ) (A )2log 0,2xx x ∀>< (B )2log 0,2xx x ∃>≤ (C )2log 0,2xx x ∃><(D )2log 0,2xx x ∃>≥a =2,x =3开始 x y a =x =x +1103y x >+ 输出x结束否是13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是( ) (A )13 (B )34 (C )58 (D )458. 如图,在空间四边形ABCD 中,两条对角线,AC BD 互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边,,,AB BC CD DA 分别相交于点,,,E F G H ,记四边形EFGH 的面积为y ,设BEx AB=,则( ) (A )函数()y f x =的值域为(0,4] (B )函数()y f x =的最大值为8(C )函数()y f x =在2(0,)3上单调递减(D )函数()y f x =满足()(1)f x f x =-第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数i1iz =+,则||z =______.10.设平面向量,a b 满足||3=a ,||2=b ,3⋅=-a b ,那么,a b的夹角θ=____.11.一个四棱锥的三视图如图所示,那么这个四棱锥最长棱的棱7. 设抛物线2:4W y x =的焦点为F ,过F 的直线与W 相交于A ,B 两点,记点F 到直线l :1x =-的距离为d ,则有( )(A )2||d AB ≥ (B )2||d AB = (C )2||d AB ≤(D )2||d AB <A BE CD GH F侧(左)视图正(主)视图俯视图 22111 11长为_____.12.设12,F F 为双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,且直线2y x =为双曲线C 的一条渐近线,点P 为C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为_____.13. 某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元. 为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有_______种不同的购买奖品方案.14. 设函数3||, 1,()log , 1.x a x f x x x -⎧=⎨>⎩≤(1)如果(1)3f =,那么实数a =___;(2)如果函数()2y f x =-有且仅有两个零点,那么实数a 的取值范围是___.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2π()12sin ()4f x x =--,x ∈R . (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)判断函数()f x 在区间ππ[,]66-上是否为增函数?并说明理由.16.(本小题满分13分)已知数列{}n a 满足25a =,且其前n 项和2n S pn n =-. (Ⅰ)求p 的值和数列{}n a 的通项公式;(Ⅱ)设数列{}n b 为等比数列,公比为p ,且其前n 项和n T 满足55T S <,求1b 的取值范围.17.(本小题满分14分)如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面ABCD ,90BAD ∠=o,BC AD //,且122A A AD BC ===,B CA 1 D 1 DA B 1C 1E F1AB =. 点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)求证:1A F ∥平面1B CE ; (Ⅱ)求证: AC ⊥平面11CDD C ;(Ⅲ)写出三棱锥11B A EF -体积的取值范围. (结论不要求证明)18.(本小题满分13分)最近,张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案,且一年后投资盈亏的情况如下:(1) 投资股市:投资结果 获利不赔不赚亏损概 率121838(2) 购买基金:投资结果 获利不赔不赚亏损概 率p13q(Ⅰ)当2p =时,求q 的值; (Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p 的取值范围;(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率. 19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,若122S S =,求直线l 的方程.20.(本小题满分13分)对于函数(),()f x g x ,如果它们的图象有公共点P ,且在点P 处的切线相同,则称函数()f x 和()g x 在点P 处相切,称点P 为这两个函数的切点. 设函数2()(0)f x ax bx a =-≠,()ln g x x =.(Ⅰ)当1a =-,0b =时, 判断函数()f x 和()g x 是否相切?并说明理由;(Ⅱ)已知a b =,0a >,且函数()f x 和()g x 相切,求切点P 的坐标;(Ⅲ)设0a >,点P 的坐标为1(,1)e-,问是否存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切?若点P 的坐标为2(e ,2)呢?(结论不要求证明)北京市西城区2014 — 2015学年度第一学期期末高三数学(文科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.B 3.A 4.C 5.B 6.D 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分. 9.22 10.2π311. 22 12.221416x y -=513.9 14.2-或4 (1,3]- 注:第12,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为2π()12sin ()4f x x =--πcos 2()4x =- ……………… 3分sin 2x =, ……………… 5分所以函数()f x 的最小正周期2ππ2T ==.……………… 7分(Ⅱ)解:结论:函数()f x 在区间ππ[,]66-上是增函数. ……………… 9分 理由如下:由ππ2π22π22k x k -+≤≤,解得ππππ44k x k -+≤≤,所以函数()f x 的单调递增区间为ππ[π,π]44k k -+,()k ∈Z .……………… 12分当0=k 时,知)(x f 在区间ππ[,]44-上单调递增, 所以函数()f x 在区间ππ[,]66-上是增函数. ……………… 13分16.(本小题满分13分)(Ⅰ)解:由题意,得11S p =-,242S p =-,因为 25a =,212S a a =+, 所以 24215S p p =-=-+,解得 2p =. ……………… 3分所以 22n S n n =-.当2n ≥时,由1n n n a S S -=-, ……………… 5分得 22(2)[2(1)(1)]43n a n n n n n =-----=-. ……………… 7分 验证知1n =时,1a 符合上式,所以43n a n =-,*n ∈N . ……………… 8分(Ⅱ)解:由(Ⅰ),得11(12)(21)12n n n b T b -==--. ……………… 10分 因为 55T S <, 所以 521(21)255b -<⨯-,解得 14531b <. ……………… 12分 又因为10b ≠,所以1b 的取值范围是45(,0)(0,)31-∞U . ……………… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D . 又因为平面ABCD I 平面1A ECF EC =, 平面1111A B C D I 平面11A ECF A F =,所以1A F∥CE.…………………3分又 1A F ⊄平面1B CE ,CE ⊂平面1B CE ,所以 1A F ∥平面1B CE . …………………6分 (Ⅱ)证明:在四边形ABCD 中,因为 90BAD ∠=o ,BC AD //,且BC AD 2=,2AD =,1AB =, 所以 222112AC =+=,222112CD =+=. 所以 222AC CD AD +=,B CA 1 D 1 DAB 1C 1EF所以 90ACD ∠=o ,即AC CD ⊥. …………………7分 因为 1A A ⊥平面ABCD AC ⊂,平面ABCD , 所以 1A A AC ⊥.因为在四棱柱1111D C B A ABCD -中,11//A A C C ,所以 1C C AC ⊥. …………………9分 又因为 1,CD C C ⊂平面11CDD C ,1CD C C C =I ,所以 AC ⊥平面11CDD C . …………………11分(Ⅲ)解:三棱锥11B A EF -的体积的取值范围是12[,]33. …………………14分18.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种 且三种投资结果相互独立,所以 p +13+q =1. ……………… 2分又因为 12p =, 所以 q =61. ……………… 3分(Ⅱ)解:由“购买基金”亏损的概率比“投资股市”亏损的概率小, 得 38q <, ……………… 4分 因为 p +13+q =1,所以 2338q p =-<,解得 724p >. ……………… 7分 又因为 113p q ++=,0q ≥, 所以 23p ≤. 所以72243p ≤<. ……………… 8分 (Ⅲ)解:记事件A 为 “一年后张师傅和李师傅两人中至少有一人获利”, ………… 9分用a ,b ,c 分别表示一年后张师傅购买基金“获利”、“不赔不赚”、“亏损”,用x ,y ,z 分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”,则一年后张师傅和李师傅购买基金,所有可能的投资结果有339⨯=种, 它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)b y ,(,)b z ,(,)c x ,(,)c y ,(,)c z , ……………10分所以事件A 的结果有5种,它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)c x .…………… 11分 因此这一年后张师傅和李师傅两人中至少有一人获利的概率5()9P A =. …………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,23b =,222c a b =-=, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为||21||42FA AP m ==-, 所以 8m =. ………………5分 (Ⅱ)解:若直线l 的斜率不存在,则有 21S S =,不合题意. ………………6分若直线l 的斜率存在,设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分 因为PMF ∆和PNF ∆的面积分别为111||||2S PF y =⋅,221||||2S PF y =⋅, 所以2||||212121=-==y yy y S S . ……………… 9分 即 212y y -=.所以 221y y y -=+,2212221)(22y y y y y +-=-=, ……………… 11分则 22121)]2()2([2)2()2(-+--=-⋅-x k x k x k x k , 即 2212121)4(24)(2-+-=++-x x x x x x ,即 2222222)43416(2434162344816-+-=++⋅-+-k k k k k k , 解得 25±=k . ……………… 13分 所以直线l 的方程为 )2(25-=x y 或 )2(25--=x y . ……………… 14分20.(本小题满分13分)(Ⅰ)解:结论:当1a =-,0b =时,函数()f x 和()g x 不相切. …………………1分 理由如下:由条件知2()f x x =-, 由()ln g x x =,得0x >,又因为 ()2f x x '=-,1()g x x'=, …………………2分所以当0x >时,()20f x x '=-<,1()0g x x '=>,所以对于任意的0x >,()()f x g x ''≠.当1a =-,0b =时,函数()f x 和()g x 不相切. …………………3分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………4分 由②,得 1(21)a s s =-,代入①,得 1ln 21s s s -=-. (*) …………………5分 因为 10(21)a s s =>-,且0s >,所以 12s >. 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………6分 令()0F x '= ,解得1x =或14x =(舍). …………………7分 当x 变化时,()F x '与()F x 的变化情况如下表所示,x1(,1)21 (1,)+∞()F x '+0 -()F x↗↘…………………8分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞U 时()0F x <. 因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………9分 (Ⅲ)解:当点P 的坐标为1(,1)e-时,存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切; …………………11分 当点P 的坐标为2(e ,2)时,不存在符合条件的函数()f x 和()g x ,使得它们在点P 处相 切. …………………13分。
北京市西城区2013-2014学年高一上学期期末考试数学试题(基础薄弱校试题)Word版含答案

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分:150分 考试时间:120分钟A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知[0,2)∈πα,且角α与角π6-终边相同,则=α( ) (A )11π6(B )7π6 (C )5π6(D )π62.若sin 0<α,且cos 0>α,则角α是( ) (A )第一象限的角 (B )第二象限的角 (C )第三象限的角(D )第四象限的角3.已知向量1(1,0)=e ,2(0,1)=e ,那么向量122+e e 的坐标是( ) (A )(1,2)-(B )(1,2)-(C )(1,2)--(D )(1,2)4.若角α的终边经过点(1,2)P -,则tan =α( )(A )5(B )5-(C )2- (D )12-5.已知正方形ABCD 的边长为1,则AB AC ⋅=( )(A )2(B )1(C (D )26.在平面直角坐标系xOy 中,函数sin y x =的图象( ) (A )关于x 轴对称 (B )关于y 轴对称 (C )关于原点对称(D )关于点(,0)2π对称7.在△ABC 中,D 是BC 的中点,则向量AD =( )(A )1122AB AC + (B )AB AC + (C )1122AB AC -(D )AB AC -8.已知函数1()cos 2f x x x =+,则()12f π=( )(A (B (C )1(D 9.设a ,b 是两个非零向量,且+=-a b a b ,则a 与b 夹角的大小为( ) (A )120︒(B )90︒(C )60︒(D )30︒10.已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增,则正数ω的最大值是( ) (A )32(B )43(C )34 (D )23二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11. sin()3π-=______. 12. 若1cos 2=-α,且(0,)∈πα,则α=______. 13. 已知向量(1,3)=a ,(2,)k =-b .若向量a 与b 共线,则实数k =_____. 14. 若tan 2=α,且32π∈(π,)α,则sin()2π+=α______. 15. 定义在R 上的函数()f x 满足:对任意的x ∈R ,都有(2)()f x f x +=.若(1)2f -=,则(3)f =_____.16. 已知向量(cos ,sin )αα=a ,(cos ,sin )ββ=b .若π,3〈〉=a b ,则c o s ()-=αβ_____.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)已知3tan 4=-α. (Ⅰ)求πtan()4-α的值; (Ⅱ)求2sin 3cos 3sin 2cos --αααα的值.18.(本小题满分12分)已知函数2()(sin 2cos2)1f x x x =++. (Ⅰ)求()f x 的最小正周期; (Ⅱ)若[,]124x ππ∈,求()f x 的最大值与最小值.19.(本小题满分12分)如图,正六边形ABCDEF 的边长为1,O 为其中心,,M N 分别是,BC DE 上的动点,且BM DN =.(Ⅰ)若,M N 分别是,BC DE 的中点,求OM ON ⋅的值; (Ⅱ)求OM ON ⋅的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>,{|02}B x x =<≤,那么A B =_____.2. 已知2log 3a =,3log 2b =,21log 3c =.将,,a b c 按从小到大排列为_____. 3. 函数()121()2xf x x =-的零点个数为_____.4. 若函数2()2f x x x =-在区间(,)a +∞上是增函数,则a 的取值范围是_____.5. 给定数集A .若对于任意,a b A ∈,有a b A +∈,且a b A -∈,则称集合A 为闭集合.给出如下三个结论:① 集合{4,2,0,2,4}A =--为闭集合; ② 集合{|2,}A n n k k ==∈Z 为闭集合; ③ 若集合12,A A 为闭集合,则12A A 为闭集合.其中,全部正确结论的序号是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知函数21()x f x x-=.(Ⅰ)证明:()f x 是奇函数;(Ⅱ)用函数单调性的定义证明:()f x 在(0,)+∞上为增函数.7.(本小题满分10分)已知函数()log (2)1a f x x =+-,其中1a >.(Ⅰ)若()f x 在[0,1]上的最大值与最小值互为相反数,求a 的值; (Ⅱ)若()f x 的图象不经过第二象限,求a 的取值范围.8.(本小题满分10分)已知函数()|2|f x x x =-. (Ⅰ)解不等式()3f x <;(Ⅱ)设0a >,求()f x 在区间[0,]a 上的最大值.北京市西城区2013 — 2014学年度第一学期期末试卷高一数学参考答案及评分标准 2014.1A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1. A ;2. D ;3. D ;4. C ;5. B ;6. C ;7.A ;8. A ;9. B ; 10. C . 二、填空题:本大题共6小题,每小题4分,共24分.11.2-; 12. 32π; 13.6-;14.5-; 15.2; 16. 12.三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 3tan 4=-α, 所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】7=-. 【 6分】(Ⅱ)解:因为3tan 4=-α, 所以2sin 3cos 2tan 33sin 2cos 3tan 2--=--αααααα 【 9分】1817=. 【12分】18.(本小题满分12分)(Ⅰ)解:2()(sin 2cos2)1f x x x =++22sin 22sin 2cos 2cos 21x x x x =+⋅++ 【 2分】 sin 42x =+. 【 4分】因为 242T ππ==, 所以()f x 的最小正周期是2π. 【 6分】 (Ⅱ)解:由(Ⅰ)得,()sin 42f x x =+.因为124x ππ≤≤, 所以 43x π≤≤π, 【 8分】所以 0sin 41x ≤≤,所以 2sin 423x ≤+≤. 【10分】 所以,当8x π=时,()f x 取得最大值3;当4x π=时,()f x 取得最小值2.【12分】19.(本小题满分12分)(Ⅰ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,且,M N 分别是,BC DE 的中点,所以 32OM ON ==,120MON ︒∠=, 【 2分】 所以 3cos1208OM ON OM ON ︒⋅==-. 【 4分】 (Ⅱ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,BM DN =,所以 △DON ≌△BOM . 【 6分】 所以 OM ON =,且DON BOM ∠=∠,即 OM ON =,且120MON ︒∠=. 【 8分】所以 21cos1202OM ON OM ON ON ︒⋅==-. 【10分】 当点N 重合于点D 或E 时,ON 取得最大值1,OM ON ⋅取得最小值12-;【11分】当点N 是DE 的中点时,ON 取得最小值2,OM ON ⋅取得最大值38-.【12分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1.{|01}x x <<;2.c b a <<;3. 1;4. [1,)+∞;5.②. 二、解答题:本大题共3小题,共30分.6.(本小题满分10分)(Ⅰ)证明:由已知,函数()f x 的定义域为{0}D x x =∈≠R . 【 1分】设x D ∈,则x D -∈,22()11()()x x f x f x x x----==-=--. 【 3分】所以函数()f x 为奇函数. 【 4分】 (Ⅱ)证明:设12,x x 是(0,)+∞上的两个任意实数,且12x x <,则210x x x ∆=->.2221212111()()x x y f x f x x x --∆=-=-【 6分】 22122121121212(1)(1)()(1)x x x x x x x x x x x x ----+==. 【 8分】 因为 120x x <<, 所以 120x x >,210x x ->,1210x x +>,所以 0y ∆>, 【 9分】 所以 ()f x 在(0,)+∞上是增函数. 【10分】7.(本小题满分10分)(Ⅰ)解:函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >,所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】 所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-;最小值是(0)log 21a f =-.【 4分】 依题意,得 log 31(log 21)a a -=--, 【 5分】 解得a =【 6分】(Ⅱ)解:由(Ⅰ)知,()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中,令0x =,得(0)log 21a f =-, 所以,()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】 依题意,得(0)log 210a f =-≤, 【 9分】 解得 2a ≥. 【10分】8.(本小题满分10分) (Ⅰ)解:原不等式可化为22230x x x ≥⎧⎨--<⎩,,(1) 或22230.x x x <⎧⎨-+>⎩,(2) 【 1分】解不等式组(1),得 23x ≤<;解不等式组(2),得2x <. 【 3分】 所以原不等式的解集为{|3}x x <. 【 4分】(Ⅱ)解:222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时,()f x 是[0,]a 上的增函数,此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】② 当12a ≤≤时,()f x 在[0,1]上是增函数,在[1,]a 上是减函数,此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时,令()(1)(2)10f a f a a -=-->,解得1a > 所以,当21a <≤此时()(1)f a f ≤,()f x 在[0,]a 上的最大值是(1)1f =;当1a >此时()(1)f a f >,()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】记()f x 在区间[0,]a 上的最大值为()g a ,所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤+⎨⎪->+⎪⎩ 【10分】高考资源网版权所有!投稿可联系QQ :1084591801。
北京市西城区高三数学上学期期末考试试题 文

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(文科)第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1,2{}A -=,2{|}B x x x =>,则集合A B =I ( ) (A ){1,0,1}-(B ){1,2}-(C ){0,1,2}(D ){1,1,2}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin B =,则( ) (A )3A π=(B )6A π=(C)sin 3A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )75.设函数()y f x =的定义域为R ,则“(0)0f =”是“函数()f x 为奇函数”的( )2.设命题p :2log 0,2xx x ∀>>,则p ⌝为( ) (A )2log 0,2xx x ∀>< (B )2log 0,2xx x ∃>≤ (C )2log 0,2xx x ∃><(D )2log 0,2xx x ∃>≥(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件6. 某天,甲要去银行办理储蓄业务,已知银行的营业时间为9:00至17:00,设甲在当天 13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是( )(A )13 (B )34 (C )58 (D )458. 如图,在空间四边形ABCD 中,两条对角线,AC BD 互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边,,,AB BC CD DA 分别相交于点,,,E F G H ,记四边形EFGH 的面积为y ,设BEx AB=,则( ) (A )函数()y f x =的值域为(0,4] (B )函数()y f x =的最大值为8(C )函数()y f x =在2(0,)3上单调递减(D )函数()y f x =满足()(1)f x f x =-第Ⅱ卷(非选择题 共110分)7. 设抛物线2:4W y x =的焦点为F ,过F 的直线与W 相交于A ,B 两点,记点F 到直线l :1x =-的距离为d ,则有( ) (A )2||d AB ≥ (B )2||d AB = (C )2||d AB ≤ (D )2||d AB <A BE CD GH F二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数i1iz =+,则||z =______.10.设平面向量,a b 满足||3=a ,||2=b ,3⋅=-a b ,那么,a b 的夹角θ=____.11.一个四棱锥的三视图如图所示,那么这个四棱锥最长棱的棱长为_____.12.设12,F F 为双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,且直线2y x =为双曲线C的一条渐近线,点P 为C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为_____.13. 某小学教师准备购买一些签字笔和铅笔盒作为奖品,已知签字笔每支5元,铅笔盒每个6元,花费总额不能超过50元. 为了便于学生选择,购买签字笔和铅笔盒的个数均不能少于3个,那么该教师有_______种不同的购买奖品方案.14. 设函数3||, 1,()log , 1.x a x f x x x -⎧=⎨>⎩≤(1)如果(1)3f =,那么实数a =___;(2)如果函数()2y f x =-有且仅有两个零点,那么实数a 的取值范围是___.侧(左)视图正(主)视图俯视图三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2π()12sin ()4f x x =--,x ∈R . (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)判断函数()f x 在区间ππ[,]66-上是否为增函数?并说明理由.16.(本小题满分13分)已知数列{}n a 满足25a =,且其前n 项和2n S pn n =-. (Ⅰ)求p 的值和数列{}n a 的通项公式;(Ⅱ)设数列{}n b 为等比数列,公比为p ,且其前n 项和n T 满足55T S <,求1b 的取值范围.17.(本小题满分14分)如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面ABCD ,90BAD ∠=o ,BC AD //,且122A A AD BC ===,1AB =. 点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)求证:1A F ∥平面1B CE ;(Ⅱ)求证: AC ⊥平面11CDD C ;(Ⅲ)写出三棱锥11B A EF -体积的取值范围. (结论不要求证明)18.(本小题满分13分)最近,张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案,且一年后投资盈亏的情况如下:(1) 投资股市:B CA 1 D 1DA B 1C 1E F(2) 购买基金:(Ⅰ)当2p =时,求q 的值; (Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p 的取值范围; (Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率. 19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,若122S S =,求直线l 的方程.20.(本小题满分13分)对于函数(),()f x g x ,如果它们的图象有公共点P ,且在点P 处的切线相同,则称函数()f x 和()g x 在点P 处相切,称点P 为这两个函数的切点. 设函数2()(0)f x ax bx a =-≠,()ln g x x =.(Ⅰ)当1a =-,0b =时, 判断函数()f x 和()g x 是否相切?并说明理由; (Ⅱ)已知a b =,0a >,且函数()f x 和()g x 相切,求切点P 的坐标;(Ⅲ)设0a >,点P 的坐标为1(,1)e-,问是否存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切?若点P 的坐标为2(e ,2)呢?(结论不要求证明)北京市西城区2014 — 2015学年度第一学期期末高三数学(文科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.B 3.A 4.C 5.B 6.D 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分.9.2 10.2π311. .221416x y -=13.9 14.2-或4 (1,3]- 注:第12,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为2π()12sin ()4f x x =--πcos 2()4x =- ……………… 3分sin 2x =, ……………… 5分所以函数()f x 的最小正周期2ππ2T ==.……………… 7分 (Ⅱ)解:结论:函数()f x 在区间ππ[,]66-上是增函数. ……………… 9分理由如下:由ππ2π22π22k x k -+≤≤, 解得ππππ44k x k -+≤≤,所以函数()f x 的单调递增区间为ππ[π,π]44k k -+,()k ∈Z .……………… 12分 当0=k 时,知)(x f 在区间ππ[,]44-上单调递增, 所以函数()f x 在区间ππ[,]66-上是增函数. ……………… 13分16.(本小题满分13分)(Ⅰ)解:由题意,得11S p =-,242S p =-,因为 25a =,212S a a =+, 所以 24215S p p =-=-+,解得 2p =. ……………… 3分所以 22n S n n =-.当2n ≥时,由1n n n a S S -=-, ……………… 5分 得 22(2)[2(1)(1)]43n a n n n n n =-----=-. ……………… 7分 验证知1n =时,1a 符合上式,所以43n a n =-,*n ∈N . ……………… 8分(Ⅱ)解:由(Ⅰ),得11(12)(21)12n n n b T b -==--. ……………… 10分 因为 55T S <,所以 521(21)255b -<⨯-,解得 14531b <. ……………… 12分 又因为10b ≠,所以1b 的取值范围是45(,0)(0,)31-∞U . ……………… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D . 又因为平面ABCD I 平面1A ECF EC =, 平面1111A B C D I 平面11A ECF A F =,所以 1A F ∥CE . …………………3分B CA 1 D 1DA B 1C 1E F又 1A F ⊄平面1B CE ,CE ⊂平面1B CE ,所以 1A F ∥平面1B CE . …………………6分 (Ⅱ)证明:在四边形ABCD 中,因为 90BAD ∠=o ,BC AD //,且BC AD 2=,2AD =,1AB =, 所以 222112AC =+=,222112CD =+=. 所以 222AC CD AD +=,所以 90ACD ∠=o ,即AC CD ⊥. …………………7分 因为 1A A ⊥平面ABCD AC ⊂,平面ABCD , 所以 1A A AC ⊥.因为在四棱柱1111D C B A ABCD -中,11//A A C C ,所以 1C C AC ⊥. …………………9分 又因为 1,CD C C ⊂平面11CDD C ,1CD C C C =I ,所以 AC ⊥平面11CDD C . …………………11分(Ⅲ)解:三棱锥11B A EF -的体积的取值范围是12[,]33. …………………14分18.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种 且三种投资结果相互独立,所以 p +13+q =1. ……………… 2分又因为 12p =, 所以 q =61. ……………… 3分 (Ⅱ)解:由“购买基金”亏损的概率比“投资股市”亏损的概率小, 得 38q <, ……………… 4分 因为 p +13+q =1,所以 2338q p =-<,解得 724p >. ……………… 7分 又因为 113p q ++=,0q ≥, 所以 23p ≤. 所以72243p ≤<. ……………… 8分 (Ⅲ)解:记事件A 为 “一年后张师傅和李师傅两人中至少有一人获利”, ………… 9分用a ,b ,c 分别表示一年后张师傅购买基金“获利”、“不赔不赚”、“亏损”,用x ,y ,z 分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”,则一年后张师傅和李师傅购买基金,所有可能的投资结果有339⨯=种, 它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)b y ,(,)b z ,(,)c x ,(,)c y ,(,)c z , ……………10分所以事件A 的结果有5种,它们是:(,)a x ,(,)a y ,(,)a z ,(,)b x ,(,)c x .…………… 11分 因此这一年后张师傅和李师傅两人中至少有一人获利的概率5()9P A =. …………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,b =2c =, ………………2分则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为 ||21||42FA AP m ==-,所以 8m =. ………………5分 (Ⅱ)解:若直线l 的斜率不存在,则有 21S S =,不合题意. ………………6分若直线l 的斜率存在,设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分因为PMF ∆和PNF ∆的面积分别为111||||2S PF y =⋅,221||||2S PF y =⋅,所以2||||212121=-==y yy y S S . ……………… 9分 即 212y y -=.所以 221y y y -=+,2212221)(22y y y y y +-=-=, ………………11分 则 22121)]2()2([2)2()2(-+--=-⋅-x k x k x k x k , 即 2212121)4(24)(2-+-=++-x x x x x x ,即 2222222)43416(2434162344816-+-=++⋅-+-k k k k k k , 解得 25±=k . ……………… 13分所以直线l 的方程为 )2(25-=x y 或 )2(25--=x y . ……………… 14分20.(本小题满分13分)(Ⅰ)解:结论:当1a =-,0b =时,函数()f x 和()g x 不相切. …………………1分 理由如下:由条件知2()f x x =-, 由()ln g x x =,得0x >,又因为 ()2f x x '=-,1()g x x'=, …………………2分 所以当0x >时,()20f x x '=-<,1()0g x x '=>,所以对于任意的0x >,()()f x g x ''≠.当1a =-,0b =时,函数()f x 和()g x 不相切. …………………3分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >, 由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………4分- 11 - 由②,得 1(21)a s s =-, 代入①,得 1ln 21s s s -=-. (*) …………………5分 因为 10(21)a s s =>-,且0s >, 所以 12s >. 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………6分 令()0F x '= ,解得1x =或14x =(舍). …………………7分 当x 变化时,()F x '与()F x 的变化情况如下表所示,…………………8分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞U 时()0F x <.因此,当且仅当1x =时()0F x =.所以方程(*)有且仅有一解1s =.于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………9分 (Ⅲ)解:当点P 的坐标为1(,1)e -时,存在符合条件的函数()f x 和()g x ,使得它们在点P 处相切; …………………11分 当点P 的坐标为2(e ,2)时,不存在符合条件的函数()f x 和()g x ,使得它们在点P 处相 切. …………………13分。
北京市西城区2014-2015学年度第一学期期末试卷

北京市西城区2014-2015学年度第一学期期末试卷高三语文2015.1本试卷共10页,150分。
考试时长150分钟。
考生务必将答案写在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、本大题共7小题,共22分。
阅读下面的文字,完成1-4题。
大家都知道,韩愈因反佛被皇帝贬谪,在半道上写下了“云横秦岭家何在,□□□□□□□”这样杰出的诗句。
应该说,捍.卫儒家“道统”的甲(热情/激情),使韩愈在这方面的论述带有明显的臆断式排他倾.(qīng)向。
例如他对佛教传入前后的漫长历史的总体判断,以及他误以为佛教是在炫耀信奉者的长寿,或追求一种惩.(chěng)罚性的灵验等等,都是义.气用事的草率之言。
他不明白,他所排列的从尧到孟子的所谓“道统”是一种理论假设,而一个泱泱..大国的广大民众却需要有自己的宗教信仰,这种宗教信仰在实际展开时,往往伴有特殊的非理性仪式。
儒家学者再高明,也不应该以自己的思维逻辑.来框范天下。
尤其是对于他们很少有发言权的关于生命的终极意义和彼岸世界等课题,乙(更/但)不应该阻止别人去思考。
其实更多文人没有韩愈这么极端。
正因为如此,我们看到,三种完全不同的审美境界出现在中华文化之中。
一种..是逍遥自由,直觉天籁;一...是温柔敦厚,载.(zài)道言志;一种种.是拈.(niān)花一笑,妙悟真如。
中国文化人最丙(熟习/熟悉)的是第一种,但如果从更高的精神层面和审美等级上来看,真正不可缺少的是后面两种。
1.文中加点字的注音和字形都不正确....的一项是(2分)A.倾.(qīng)向捍.卫B.惩.(chěng)罚义.气用事C.载.(zài)道言志泱泱..大国D.拈.(niān)花一笑逻辑.2.在文中方格处填入下列语句,恰当的一项是(2分)A.雨打芭蕉叶带愁B.影入平羌江水流C.遥望洞庭山水翠D.雪拥蓝关马不前3.在文中甲乙丙处依次填入词语,恰当的一项是(2分)A.热情更熟习B.激情更熟悉C.热情但熟悉D.激情但熟习4.对末段文字中三个“一种”依次指代的对象,理解正确的一项是(2分)A.儒家道家佛家B.儒家佛家道家C.道家佛家儒家D.佛家道家儒家5.下列句子中加点的成语,使用不正确...的一项是(3分)---WORD格式--可编辑--A.自两只大熊猫入驻多伦多动物园以来,每天入园的游客可谓摩肩接踵....,这样大增的人气令园方非常满意。
北京市西城区2014-2015学年度高三第一学期期末试理科数学(含答案)
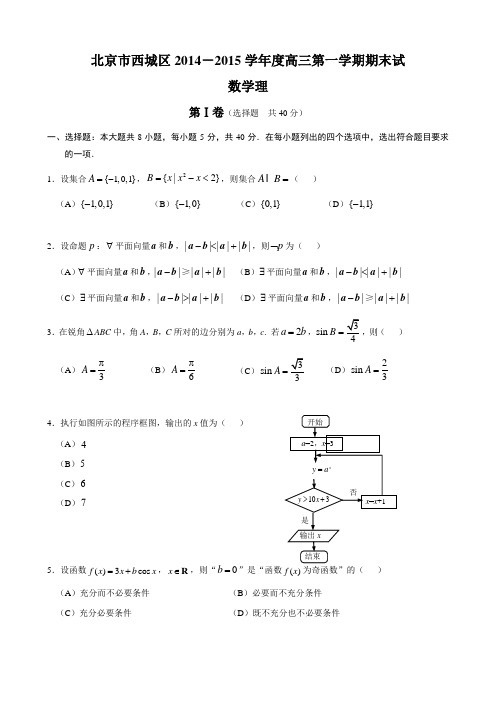
北京市西城区2014-2015学年度高三第一学期期末试数学理第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1{}A -=,2{|2}B x x x =-<,则集合A B =( )(A ){1,0,1}-(B ){1,0}-(C ){0,1}(D ){1,1}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin 4B =,则( ) (A )3A π= (B )6A π=(C)sin A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )75.设函数()3cos f x x b x =+,x ∈R ,则“0b =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件2.设命题p :∀平面向量a 和b ,||||||-<+a b a b ,则p ⌝为( )(A )∀平面向量a 和b ,||||||-+≥a b a b (B )∃平面向量a 和b ,||||||-<+a b a b (C )∃平面向量a 和b ,||||||->+a b a b(D )∃平面向量a 和b ,||||||-+≥a b a b8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域,点(,)B a b 为坐标平面x O 内一点,若对于区域D 内的任一点(,)A x y ,都有1OA OB ⋅≤成立,则a b +的最大值等于( ) (A )2 (B )1 (C )0(D )3第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i12iz -=+,则||z = _____.10.设12,F F 为双曲线C :2221(0)16x y a a -=>的左、右焦点,点P 为双曲线C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为____.6.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) (A(B )最长棱的棱长为3(C )侧面四个三角形中有且仅有一个是正三角形 (D )侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( )(A )(4,8) (B )(4,)+ (C )(0,4)(D )(8,)+侧(左)视图正(主)视图俯视图11.在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么x y z ++=______.12. 如图,在ABC ∆中,以BC 为直径的半圆分别交AB ,AC 于点E ,F ,且2AC AE =,那么AFAB=____;A ∠= _____. 13.现要给4个唱歌节目和2个小品节目排列演出顺序,要求2个小品节目之间恰好有3个唱歌节目,那么演出顺序的排列种数是______. (用数字作答)14. 设P ,Q 为一个正方体表面上的两点,已知此正方体绕着直线PQ 旋转()角后能与自身重合,那么符合条件的直线PQ 有_____条.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.16.(本小题满分13分)现有两种投资方案,一年后投资盈亏的情况如下: (1)投资股市:(2)购买基金:(Ⅰ)当4p =时,求q 的值; (Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于45,求p 的取值范围; (Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知12p =,16q =,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.17.(本小题满分14分)如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面A B C D ,90BAD ∠=,BC AD //,且122A A AB AD BC ==== ,点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)证明:1A F ∥平面1BCE ; (Ⅱ)若E 是棱AB 的中点,求二面角1A EC D --的余弦值; (Ⅲ)求三棱锥11B A EF -的体积的最大值.18.(本小题满分13分)已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ,且在点P 处的切线相同.(Ⅰ)若点P 的坐标为1(,1)e-,求,a b 的值; (Ⅱ)已知a b =,求切点P 的坐标.19.(本小题满分14分)B CDA B 1C 1E FA 1 D 1已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)Pm m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,求证:12||||S PM S PN =.20.(本小题满分13分)设函数()(9)f x x x =-,对于任意给定的m 位自然数0121m m n a a a a -=(其中1a 是个位数字,2a 是十位数字,),定义变换A :012()()()()m A n f a f a f a =+++. 并规定(0)0A =.记10()n A n =,21()n A n =,, 1()k k n A n -=,.(Ⅰ)若02015n =,求2015n ;(Ⅱ)当3m ≥时,证明:对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<; (Ⅲ)如果*010(,3)m n m m <∈≥N ,写出m n 的所有可能取值.(只需写出结论)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.D 3.A 4.C 5.C 6.D 7.B 8.A 二、填空题:本大题共6小题,每小题5分,共30分.9.1 10.221416x y -=11.17412.12 π313.9614.13注:第10,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +, ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意,得πππ2π2π2262x k k -++≤≤, 解得4π2π4π4π+33k x k -≤≤, 所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . ……………… 9分(Ⅱ)解:如图过点B 作线段BC 垂直于x由题意,得33π4TAC ==,2=BC ,所以2tan 3πBC BAO AC ∠==.16.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立, 所以p +13+q =1. ……………… 2分 又因为14p =, 所以q =512. ……………… 3分 (Ⅱ)解:记事件A 为 “甲投资股市且盈利”,事件B 为“乙购买基金且盈利”,事 件C 为“一年后甲、乙两人中至少有一人投资获利”, ……………… 4分则C AB AB AB =U U ,且A ,B 独立.由上表可知, 1()2P A =,()P B p =. 所以()()()()P C P AB P AB P AB =++ ……………… 5分 111(1)222p p p =?+? 1122p =+. ……………… 6分因为114()225P C p =+>,所以35p >. ……………… 7分 又因为113p q ++=,0q ≥,所以23p ≤.所以3253p ≤<. ……………… 8分(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X 为丙投资股票的获利金额(单位:万元),所以随机变量X 的分布列为:…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资,且记Y 为丙购买基金的获利金额(单位:万元),所以随机变量Y 的分布列为:…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.……… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D .又因为平面ABCD 平面1A ECF EC =,平面1111A BC D 平面11A ECF A F =,所以1A F ∥EC . …………………2分 又因为1A F ⊄平面1BCE ,EC ⊂平面1BCE , 所以1A F ∥平面1BCE . …………………4分 (Ⅱ)解:因为1AA ⊥底面ABCD ,90BAD ∠=,所以1AA ,AB ,AD 两两垂直,以A 为原点,以AB ,AD ,1AA 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系. …………………5分则1(0,0,2)A ,(1,0,0)E ,(2,1,0)C ,所以 1(1,0,2)A E =-,1(2,1,2)AC =-. 设平面1A ECF 的法向量为(,,),m x y z = 由10AE m ⋅=,10AC m ⋅=, 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-. …………………7分 又因为平面DEC 的法向量为(0,0,1)n =, …………………8分 所以1cos ,3||||m n m n m n ⋅<>==⋅,由图可知,二面角1A EC D --的平面角为锐角,所以二面角1A EC D --的余弦值为13. …………………10分(Ⅲ)解:过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A BCD ,FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时,FM 取到最大值2(此时点E 与点B 重合), 所以当F 与点1D 重合时,三棱锥11B A EF -的体积的最大值为43. ………………14分18.(本小题满分13分) (Ⅰ)解:由题意,得21()1e e ea bf =-=-, …………………1分 且()2f x ax b '=-,1()g x x'=, …………………3分 由已知,得11()()e ef g ''=,即2e eab -=, 解得22e a =,3e b =. …………………5分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………6分 由②,得 1(21)a s s =-,其中12s ≠,代入①,得 1ln 21s s s -=-. (*) …………………7分因为 10(21)a s s =>-,且0s >, 所以 12s >. …………………8分设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞,则 2(41)(1)()(21)x x F x x x ---'=-. …………………9分 令()0F x '= ,解得1x =或14x =(舍). …………………10分当x 变化时,()F x '与()F x 的变化情况如下表所示,…………………12分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞时()0F x <.因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,b =2c =, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为||21||42FA AP m ==-, 所以 8m =. ………………5分 (Ⅱ)解:若直线l 的斜率不存在, 则有 21S S =,||||PM PN =,符合题意. …………6分若直线l 的斜率存在,则设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N . 由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分 因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分 )8)(8()8)(2()8)(2(211221----+--=x x x x k x x k)8)(8(32)(102212121--++-=x x kx x k x kx0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k ,所以 MPF NPF ∠=∠. ……………… 12分因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠, 21||||sin 2S PF PN NPF =⋅⋅∠, ……………… 13分 所以12||||S PM S PN =. ……………… 14分20.(本小题满分13分)(Ⅰ)解:114082042n =+++=,2201434n =+=,3182038n =+=,418826n =+=,5141832n =+=,6181432n =+=,……所以 201532n =. ……………… 3分(Ⅱ)证明:因为函数2981()(9)()24f x x x x =-=--+,所以对于非负整数x ,知()(9)20f x x x =-≤.(当4x =或5时,取到最大值)… 4分 因为 12()()()()m A n f a f a f a =+++,所以 ()20A n m ≤. ……………… 6分 令 1()1020m g m m -=-,则31(3)102030g -=-⨯>.当3m ≥时,11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->, 所以 (1)g()0g m m +->,函数()g m ,(m ∈N ,且3m ≥)单调递增.故 g()g(3)0m >≥,即11020()m m A n ->≥.所以当3m ≥时,对于任意的m 位自然数n 均有1()10m A n -<. …………………9分 (Ⅲ)答:m n 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38.…………………14分。
北京市西城区高一数学上学期期末考试试题(基础薄弱校试题)北师大版

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学2014.1试卷满分:150分 考试时间:120分钟 A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知[0,2)∈πα,且角α与角π6-终边相同,则=α( ) (A )11π6(B )7π6 (C )5π6(D )π62.若sin 0<α,且cos 0>α,则角α是( ) (A )第一象限的角 (B )第二象限的角 (C )第三象限的角(D )第四象限的角3.已知向量1(1,0)=e ,2(0,1)=e ,那么向量122+e e 的坐标是( ) (A )(1,2)-(B )(1,2)-(C )(1,2)--(D )(1,2)4.若角α的终边经过点(1,2)P -,则tan =α( )(A )5(B )5-(C )2- (D )12-5.已知正方形ABCD 的边长为1,则AB AC ⋅=( )(A )2(B )1(C (D )26.在平面直角坐标系xOy 中,函数sin y x =的图象( ) (A )关于x 轴对称 (B )关于y 轴对称 (C )关于原点对称(D )关于点(,0)2π对称7.在△ABC 中,D 是BC 的中点,则向量AD =( )(A )1122AB AC + (B )AB AC + (C )1122AB AC -(D )AB AC -8.已知函数1()cos 2f x x x =+,则()12f π=( )(A (B (C )1(D 9.设a ,b 是两个非零向量,且+=-a b a b ,则a 与b 夹角的大小为( ) (A )120︒(B )90︒(C )60︒(D )30︒10.已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增,则正数ω的最大值是( ) (A )32(B )43(C )34 (D )23二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11. sin()3π-=______. 12. 若1cos 2=-α,且(0,)∈πα,则α=______. 13. 已知向量(1,3)=a ,(2,)k =-b .若向量a 与b 共线,则实数k =_____. 14. 若tan 2=α,且32π∈(π,)α,则sin()2π+=α______. 15. 定义在R 上的函数()f x 满足:对任意的x ∈R ,都有(2)()f x f x +=.若(1)2f -=,则(3)f =_____.16. 已知向量(cos ,sin )αα=a ,(cos ,sin )ββ=b .若π,3〈〉=a b ,则c o s ()-=αβ_____.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)已知3tan 4=-α. (Ⅰ)求πtan()4-α的值; (Ⅱ)求2sin 3cos 3sin 2cos --αααα的值.18.(本小题满分12分)已知函数2()(sin 2cos2)1f x x x =++. (Ⅰ)求()f x 的最小正周期; (Ⅱ)若[,]124x ππ∈,求()f x 的最大值与最小值.19.(本小题满分12分)如图,正六边形ABCDEF 的边长为1,O 为其中心,,M N 分别是,BC DE 上的动点,且BM DN =.(Ⅰ)若,M N 分别是,BC DE 的中点,求OM ON ⋅的值; (Ⅱ)求OM ON ⋅的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>,{|02}B x x =<≤,那么A B =_____.2. 已知2log 3a =,3log 2b =,21log 3c =.将,,a b c 按从小到大排列为_____. 3. 函数()121()2xf x x =-的零点个数为_____.4. 若函数2()2f x x x =-在区间(,)a +∞上是增函数,则a 的取值范围是_____.5. 给定数集A .若对于任意,a b A ∈,有a b A +∈,且a b A -∈,则称集合A 为闭集合.给出如下三个结论:① 集合{4,2,0,2,4}A =--为闭集合; ② 集合{|2,}A n n k k ==∈Z 为闭集合; ③ 若集合12,A A 为闭集合,则12A A 为闭集合.其中,全部正确结论的序号是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知函数21()x f x x-=.(Ⅰ)证明:()f x 是奇函数;(Ⅱ)用函数单调性的定义证明:()f x 在(0,)+∞上为增函数.7.(本小题满分10分)已知函数()log (2)1a f x x =+-,其中1a >.(Ⅰ)若()f x 在[0,1]上的最大值与最小值互为相反数,求a 的值; (Ⅱ)若()f x 的图象不经过第二象限,求a 的取值范围. 8.(本小题满分10分)已知函数()|2|f x x x =-. (Ⅰ)解不等式()3f x <;(Ⅱ)设0a ,求()f x 在区间[0,]a 上的最大值.北京市西城区2013 — 2014学年度第一学期期末试卷高一数学参考答案及评分标准 2014.1 A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1. A ;2. D ;3. D ;4. C ;5. B ;6. C ;7.A ;8. A ;9. B ; 10. C. 二、填空题:本大题共6小题,每小题4分,共24分.11.2-; 12. 32π; 13.6-;14. 15.2; 16. 12.三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 3tan 4=-α, 所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 7=-. 【 6分】(Ⅱ)解:因为3tan 4=-α, 所以2sin 3cos 2tan 33sin 2cos 3tan 2--=--αααααα 【 9分】1817=. 【12分】18.(本小题满分12分)(Ⅰ)解:2()(sin 2cos2)1f x x x =++22sin 22sin 2cos 2cos 21x x x x =+⋅++ 【 2分】 sin 42x =+. 【 4分】因为 242T ππ==, 所以()f x 的最小正周期是2π. 【 6分】 (Ⅱ)解:由(Ⅰ)得,()sin 42f x x =+. 因为124x ππ≤≤,所以43x π≤≤π, 【 8分】 所以 0sin 41x ≤≤,所以 2sin 423x ≤+≤. 【10分】 所以,当8x π=时,()f x 取得最大值3;当4x π=时,()f x 取得最小值2.【12分】19.(本小题满分12分)(Ⅰ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,且,M N 分别是,BC DE 的中点,所以 32OM ON ==,120MON ︒∠=, 【 2分】 所以 3cos1208OM ON OM ON ︒⋅==-. 【 4分】 (Ⅱ)解:因为ABCDEF 是边长为1的正六边形,O 为其中心,BM DN =,所以 △DON ≌△BOM . 【 6分】 所以 OM ON =,且DON BOM ∠=∠,即 OM ON =,且120MON ︒∠=. 【 8分】所以 21cos1202OM ON OM ON ON ︒⋅==-. 【10分】当点N 重合于点D 或E 时,ON 取得最大值1,OM ON ⋅取得最小值12-;【11分】当点N 是DE 的中点时,ON 取得最小值2,OM ON ⋅取得最大值38-.【12分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1.{|01}x x <<;2.c b a <<;3. 1;4. [1,)+∞;5.②. 二、解答题:本大题共3小题,共30分.6.(本小题满分10分)(Ⅰ)证明:由已知,函数()f x 的定义域为{0}D x x =∈≠R . 【 1分】设x D ∈,则x D -∈,22()11()()x x f x f x x x----==-=--. 【 3分】所以函数()f x 为奇函数. 【 4分】 (Ⅱ)证明:设12,x x 是(0,)+∞上的两个任意实数,且12x x <,则210x x x ∆=->.2221212111()()x x y f x f x x x --∆=-=-【 6分】 22122121121212(1)(1)()(1)x x x x x x x x x x x x ----+==. 【 8分】 因为 120x x <<, 所以 120x x >,210x x ->,1210x x +>,所以 0y ∆>, 【 9分】 所以 ()f x 在(0,)+∞上是增函数. 【10分】7.(本小题满分10分)(Ⅰ)解:函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >,所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】 所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-;最小值是(0)log 21a f =-. 【 4分】依题意,得 log 31(log 21)a a -=--, 【 5分】 解得a =【 6分】(Ⅱ)解:由(Ⅰ)知,()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中,令0x =,得(0)log 21a f =-, 所以,()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】 依题意,得(0)log 210a f =-≤, 【 9分】 解得 2a ≥. 【10分】8.(本小题满分10分)(Ⅰ)解:原不等式可化为22230x x x ≥⎧⎨--<⎩,, (1) 或22230.x x x <⎧⎨-+>⎩,(2) 【 1分】解不等式组(1),得 23x ≤<;解不等式组(2),得2x <. 【 3分】 所以原不等式的解集为{|3}x x <. 【 4分】(Ⅱ)解:222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩【 5分】① 当01a <<时,()f x 是[0,]a 上的增函数,此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】② 当12a ≤≤时,()f x 在[0,1]上是增函数,在[1,]a 上是减函数,此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时,令()(1)(2)10f a f a a -=-->,解得1a >. 所以,当21a <≤此时()(1)f a f ≤,()f x 在[0,]a 上的最大值是(1)1f =;当1a >()(1)f a f >,()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】 记()f x 在区间[0,]a 上的最大值为()g a ,所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤+⎨⎪->+⎪⎩ 【10分】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2014 — 2015学年度第一学期期末试卷
高一数学 2015.1
试卷满分:150分 考试时间:120分钟
A 卷 [必修 模块4] 本卷满分:100分
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有
一项是符合要求的.
1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2
(B )π(,π)2
(C )3π(π,
)2
(D )3π
(
,2π)2
2.已知向量(2,8)=a ,(4,2)=-b .若2=-c a b ,则向量=c ( ) (A )(0,18)
(B )(12,12)
(C )(8,14)
(D )(4,20)-
3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )
35
(B )
34
(C )34
-
(D )45
-
4.已知函数sin y x =和cos y x =在区间M 上都是增函数,那么区间M 可以是( ) (A )π(0,)2
(B )π(,π)2
(C )3π(π,
)2
(D )3π
(
,2π)2
5.在△ABC 中,D 是BC 的中点,则AB AC +=( ) (A )2AD
(B )2DA
(C )2BD
(D )2DB
6.下列函数中,偶函数是( ) (A )()sin()f x x =π+ (B )()tan()f x x =π- (C )()sin()2f x x π
=+ (D )()cos(
)2
f x x π
=-
7.为得到函数π
cos()6
y x =+
的图象,只需将函数cos y x =的图象( ) (A )向左平移π3个单位 (B )向右平移π
3个单位
(C )向左平移π6个单位 (D )向右平移π
6
个单位
8.如图,在矩形ABCD 中,2AB =,BC , E 是CD 的中点,那么AE DC ⋅=( )
(A )4
(B )2
(C (D )1
9.函数2
sin y x =的最小正周期为( ) (A )2π
(B )π
(C )
π
2
(D )
π4
10.已知向量(1,sin )θ=a ,(cos θ=b ,其中R θ∈,则||-a b 的最大值是( ) (A )4
(B )3
(C )2
(D )1
二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11.若(0,)∈πα,且α与角53
π
-
终边相同,则=α_____. 12.若向量(1,2)=a 与向量(,1)=-λb 共线,则实数=λ_____. 13.已知α是第二象限的角,且5
sin 13
α=
,则cos =α_____. 14. 已知向量(1,3)=a ,(2,1)=-b ,(1,1)=c .若(,)=∈R c a +b λμλμ,则
=λ
μ
_____. 15.函数2
()(sin cos )f x x x =+的最大值是_____.
16.关于函数()sin(2)()6
f x x x π=-∈R ,给出下列三个结论:
① 函数()f x 的图象与2()cos(2)3
g x x π
=-的图象重合; ② 函数()f x 的图象关于点(
,0)12
π
对称; ③ 函数()f x 的图象关于直线3
x π
=对称.
其中,全部正确结论的序号是_____.
三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)
已知tan 2=-α,且(,)2
π
∈πα. (Ⅰ)求π
tan()4
-
α的值; (Ⅱ)求sin 2α的值.
18.(本小题满分12分)
已知向量(cos ,sin )=ααa ,1(2=-b ,其中α是锐角. (Ⅰ)证明:向量+a b 与-a b 垂直; (Ⅱ)当|2||2|+=-a b a b 时,求角α.
19.(本小题满分12分)
已知函数()sin 21f x x x =+. (Ⅰ)求()f x 的单调递减区间;
(Ⅱ)若对于任意ππ[,]42
x ∈,都有()2f x m -<成立,求实数m 的取值范围.
B 卷 [学期综合] 本卷满分:50分
一、填空题:本大题共5小题,每小题4分,共20分. 把答案填在题中横线上. 1.函数1
lg y x
=
的定义域是_____. 2.若幂函数y x =α的图象过点(4,2),则=α_____. 3.662log 2log 9+=_____. 4.函数2
1,
0,
()4,0,
x x f x x x ->⎧=⎨
-<⎩的零点是_____.
5.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若(21)()f m f m ->,则实数m 的取值范围是_____.
二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)
已知全集U =R ,集合{|(2)0}P x x x =-≥,{|26}M x a x a =<<+. (Ⅰ)求集合U P ð;
(Ⅱ)若U P M ⊆ð,求实数a 的取值范围.
7.(本小题满分10分)
已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值.
8.(本小题满分10分)
已知函数()23x x f x a b =⋅+⋅,其中,a b 为常数. (Ⅰ)若0ab >,判断()f x 的单调性,并加以证明; (Ⅱ)若0ab <,解不等式:(1)()f x f x +>.。
