(完整word版)初三数学二次函数所有经典题型.docx
(完整word版)中考经典二次函数应用题(含答案),推荐文档

二次函數應用題1、某體育用品商店購進一批滑板,每件進價為100元,售價為130元,每星期可賣出80件.商家決定降價促銷,根據市場調查,每降價5元,每星期可多賣出20件. (1)求商家降價前每星期の銷售利潤為多少元?(2)降價後,商家要使每星期の銷售利潤最大,應將售價定為多少元?最大銷售利潤是多少?2、某商場將進價為2000元の冰箱以2400元售出,平均每天能售出8臺,為了配合國家“家電下鄉”政策の實施,商場決定採取適當の降價措施.調查表明:這種冰箱の售價每降低50元,平均每天就能多售出4臺.(1)假設每臺冰箱降價x 元,商場每天銷售這種冰箱の利潤是y 元,請寫出y 與x 之間の函數運算式;(不要求寫引數の取值範圍)(2)商場要想在這種冰箱銷售中每天盈利4800元,同時又要使百姓得到實惠,每臺冰箱應降價多少元? (3)每臺冰箱降價多少元時,商場每天銷售這種冰箱の利潤最高?最高利潤是多少?3、張大爺要圍成一個矩形花圃.花圃の一邊利用足夠長の牆另三邊用總長為32米.矩米の籬笆恰好圍成.圍成の花圃是如圖所示の矩形ABCD .設AB 邊の長為x 形ABCD の面積為S 平方米.(1)求S 與x 之間の函數關係式(不要求寫出自變數x の取值範圍). (2)當x 為何值時,S 有最大值?並求出最大值.(參考公式:二次函數2y ax bx c =++(0a ≠),當2bx a=-時,244ac b y a -=最大(小)值)4、某電視機生產廠家去年銷往農村の某品牌電視機每臺の售價y (元)與月份x 之間滿足函數關係502600y x =-+,去年の月銷售量p (萬臺)與月份x 之間成一次函數關係,其中兩個月の銷售情況如下表:月份1月 5月 銷售量3.9萬臺4.3萬臺 求該品牌電視機在去年哪個月銷往農村の銷售金額最大?最大是多少?5、某商場試銷一種成本為每件60元の服裝,規定試銷期間銷售單價不低於成本單價,且獲利不得高於45%,經試銷發現,銷售量y (件)與銷售單價x (元)符合一次函數y kx b =+,且65x =時,55y =;75x =時,45y =. (1)求一次函數y kx b =+の運算式;(2)若該商場獲得利潤為W 元,試寫出利潤W 與銷售單價x 之間の關係式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?(3)若該商場獲得利潤不低於500元,試確定銷售單價x の範圍.6、某商場在銷售旺季臨近時 ,某品牌の童裝銷售價格呈上升趨勢,假如這種童裝開始時の售價為每件20元,並且每週(7天)漲價2元,從第6周開始,保持每件30元の穩定價格銷售,直到11周結束,該童裝不再銷售。
(完整word版)二次函数精选练习题及答案

二次函数练习题及答案一、选择题1. 将抛物线23y x =先向左平移2个单位,再向下平移1个单位后得到新的抛物线,则新抛物线的解析式是 ( )A 23(2)1y x =++B 。
23(2)1y x =+-C 。
23(2)1y x =-+ D.23(2)1y x =-- 2.将抛物线22+=x y 向右平移1个单位后所得抛物线的解析式是………………( ) A.32+=x y ; B.12+=x y ;C.2)1(2++=x y ; D.2)1(2+-=x y .3.将抛物线y= (x —1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )A .y=(x —2)2B .y=(x —2)2+6C .y=x 2+6D .y=x 24.由二次函数1)3(22+-=x y ,可知( )A .其图象的开口向下B .其图象的对称轴为直线3x =-C .其最小值为1D .当x<3时,y 随x 的增大而增大5.如图,抛物线的顶点P 的坐标是(1,﹣3),则此抛物线对应的二次函数有( )A .最大值1B .最小值﹣3C .最大值﹣3D .最小值16.把函数()y f x ==246x x -+的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( )A .2(3)3y x =-+B .2(3)1y x =-+C .2(1)3y x =-+D .2(1)1y x =-+7.抛物线c bx x y ++=2图像向右平移2个单位再向下平移3个单位,所得图像的解析式为322--=x x y ,则b 、c 的值为A . b=2, c=2 B. b=2,c=0 C 。
b= -2,c=-1 D 。
b= -3, c=2二、填空题8.二次函数y=-2(x -5)2+3的顶点坐标是 .9.已知二次函数2y x bx c =-++中函数y 与自变量x 之间的部分对应值如下表所示,点11(,)A x y 、22(,)B x y 在函数图象上,当1201,23x x <<<<时,则1y 2y (填“>”或“<”).x 0 1 2 3 y1- 2 3 210.在平面直角坐标系中,将抛物线223y x x =++绕着它与y 轴的交点旋转180°,所得抛物线的解析式为 .11.求二次函数2245y x x =--的顶点坐标(___)对称轴____。
(完整word)二次函数的应用

二次函数的应用题型一列解析式例1、正方形的边长为3,如果边长增加x,那么面积增加y,则y与x之间的函数表达式是()A.y=3x B.y=(3+x)2C.y=9+6x D.y=x2+6x例2、如图,某涵洞的截面是抛物线形,现测得水面宽AB=1。
6m,涵洞顶点O到水面的距离CO为2.4m,在图中直角坐标系内,涵洞截面所在抛物线的解析式是.例3、合肥市2013年平均房价为6500元/m2.若2014年和2015年房价平均增长率为x,则预计2015年的平均房价y(元/m2)与x之间的函数关系式为.题型二利用待定系数法例4、某工厂生产的A种产品,它的成本是2元,售价是3元,年销量为100万件,为了获得更好的效益,厂家准备拿出一定的资金做广告;根据统计,每年投入的广告费是x(十万元),产品的年销量将是原销售量的y 倍,且y是x的二次函数,它们的关系如表:x(十万元)012y11。
5 1.8(1)求y与x的函数关系式;(2)如果把利润看成销售总额减去成本费和广告费,试写出年利润S(十万元)与广告费x(十万元)的函数关系式;(3)如果投入的年广告费为10万元~30万元,问广告费在什么范围内,工厂获得的利润最大?最大利润是多少?例5、某企业信息部进行市场调研发现:信息一:如果单独投资A种产品,则所获利润y A(万元)与投资金额x(万元)之间存在正比例函数关系:y A=kx,并且当投资5万元时,可获利润2万元;信息二:如果单独投资B种产品,则所获利润y B(万元)与投资金额x(万元)之间存在二次函数关系:y B=ax2+bx,并且当投资2万元时,可获利润2.4万元;当投资4万元,可获利润3。
2万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对A、B两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?例6、某公司拟用运营指数y来量化考核司机的工作业绩,运营指数(y)与运输次数(n)和平均速度(x)之间满足关系式为y=ax2+bnx+100,当n=1,x=30时,y=190;当n=2,x=40时,y=420.(1)用含x和n的式子表示y;(2)当运输次数定为3次,求获得最大运营指数时的平均速度;(3)若n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而y的值保持不变?若能,求出m的值;若不能,请说明理由.例7、鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)求出y与x的函数关系式,并写出自变量x的取值范围.(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?例8、某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w 万元.(毛利润=销售额﹣生产费用)(1)请直接写出y与x以及z与x之间的函数关系式;(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?题型三分析数量关系法例9、为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.(1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?例10、一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件,为提高利益,就对该T 恤进行涨价销售,经过调查发现,每涨价1元,每周要少卖出10件,请确定该T恤涨价后每周销售利润y(元)与销售单价x(元)之间的函数关系式,并求出销售单价定为多少元时,每周的销售利润最大?例11、某商场销售一种成本为每件20元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500.(1)设商场销售该种商品每月获得利润为w(元),写出w与x之间的函数关系式;(2)如果商场想要销售该种商品每月获得2000元的利润,那么每月成本至少多少元?(3)为了保护环境,政府部门要求用更加环保的新产品替代该种商品,商场若销售新产品,每月销售量与销售价格之间的关系与原产品的销售情况相同,新产品为每件22元,同时对商场的销售量每月不小于150件的商场,政府部门给予每件3元的补贴,试求定价多少时,新产品每月可获得销售利润最大?并求最大利润.例12、春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:鲜鱼销售单价(元/kg)20单位捕捞成本(元/kg)5﹣捕捞量(kg)950﹣10x(1)在此期间该养殖场每天的捕捞量与前一天末的捕捞量相比是如何变化的?(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额﹣日捕捞成本)(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?例13、某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;(2)求经营这条旅游线路每月所需要的最低成本;(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?例14、某水果销售商发现某种高档水果市场需求量较大,经过市场调查发现月销量y(箱)与销售单价x(元/箱)之间的函数关系y=﹣x+800,而该种水果的进价z(元/箱)与销售单价x(元/箱)之间的函数关系为z=x+240.已知每月为此支付员工工资和场地租金等费用总计20000元.(注:月获利=月销售总额﹣月进货总价﹣工资和租金费用)(1)求月获利w(元)与x之间的函数关系式;(2)当销售单价x为何值时,月获利最大?并求出这个最大值;(3)若该水果店希望销售这种水果的月利润不低于2。
(完整word版)九年级二次函数常考题型复习

九年级数学二次函数常考题型常考知识点总结:1、二次函数的看法:一般地,形如y ax2bx c 〔 a ,b,c 是常数,a 0〕的函数,叫做二次函数。
注:和一元二次方程近似,二次项系数 a 0 ,而b,c能够为零.二次函数的定义域是全体实数.2、二次函数 y ax2bx c的结构特点:⑴ 等号左侧是函数,右侧是关于自变量x 的二次式, x 的最高次数是2.⑵ a ,b ,c 是常数, a 是二次项系数, b 是一次项系数,c是常数项3、 y a x h2k 的性质:a 的符号张口方向极点坐标对称轴性质a0向上h,k X=h x h 时, y 随x的增大而增大;x h 时, y 随x 的增大而减小;x h 时, y 有最小值 k .a0向下h,k X=h x h 时, y 随x的增大而减小;x h 时, y 随x 的增大而增大;x h 时, y 有最大值 k .4、二次函数 y ax2bx c的性质:〔 1〕当a0时,抛物线张口向上,对称轴为xb ,极点坐标为 b ,4ac b2;当 x b时, y2a 2 a4a2a随 x 的增大而减小;当xb时, y 随x的增大而增大;当x b时, y 有最小值4ac b2.2a2a4a〔 2〕当a0时,抛物线张口向下,对称轴为xb ,极点坐标为 b ,4ac b2;当 x b时, y2a 2 a4a2a随 x 的增大而增大;当xb时, y 随x的增大而减小;当x b时, y 有最大值4ac b2。
2a2a4a5、二次函数剖析式确实定:依照条件确定二次函数剖析式,平时利用待定系数法.用待定系数法求二次函数的剖析式必定依照题目的特点,选择合适的形式,才能使解题简略.一般来说,有以下几种情况:(1〕抛物线上三点的坐标,一般采纳一般式;(2〕抛物线极点或对称轴或最大〔小〕值,一般采纳极点式;(3〕抛物线与 x 轴的两个交点的横坐标,一般采纳两根式;6、二次函数、二次三项式和一元二次方程之间的内在联系〔 a 0 时〕:0抛物线与x 轴有二次三项式的值可正、一元二次方程有两个不相等实根两个交点可零、可负0抛物线与x 轴只二次三项式的值为非负一元二次方程有两个相等的实数根有一个交点0抛物线与x 轴无二次三项式的值恒为正一元二次方程无实数根 .交点题型 :依照图像,判断 a 、 b 、c 的关系问题。
数学九年级上册 二次函数(篇)(Word版 含解析)

数学九年级上册二次函数(篇)(Word版含解析)一、初三数学二次函数易错题压轴题(难)1.已知,抛物线y=-12x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.(1)直接填写抛物线的解析式________;(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.求证:MN∥y轴;(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG •CH 为定值.【答案】(1)2122y x x=-++;(2)见详解;(3)见详解.【解析】【分析】(1)把点C、D代入y=-12x2 +bx+c求解即可;(2)分别设PM、PC的解析式,由于PM、PC与抛物线的交点分别为:M、N.,分别求出M、N的代数式即可求解;(3)先设G、H的坐标,列出QG、GH的解析式,得出与抛物线的交点D、E的横坐标,再列出直线AE的解析式,算出它与抛物线横坐标的交点方程.运用韦达定理即可求证.【详解】详解:(1)∵y=-12x2 +bx+c过点C(0,2),点Q(2,2),∴2122222b cc⎧-⨯++⎪⎨⎪=⎩=,解得:12b c =⎧⎨=⎩. ∴y=-12x 2+x+2; (2) 设直线PM 的解析式为:y=mx ,直线PC 的解析式为:y=kx+2 由22122y kx y x x =+⎧⎪⎨=-++⎪⎩得12x 2+(k-1)x=0, 解得:120,22x x k ==-,x p =22p x k =- 由21=22y mx y x x =⎧⎪⎨-++⎪⎩得12x 2+(m-1)x-2=0, ∴124b x x a⋅=-=- 即x p•x m =-4,∴x m =4p x -=21k -. 由24y kx y x =+⎧⎨=+⎩得x N =21k -=x M , ∴MN ∥y 轴.(3)设G (0,m ),H (0,n ).设直线QG 的解析式为y kx m =+,将点()2,2Q 代入y kx m =+得22k m =+22m k -∴= ∴直线QG 的解析式为22m y x m -=+ 同理可求直线QH 的解析式为22n y x n -=+; 由222122m y x m y x x -⎧=+⎪⎪⎨⎪=-++⎪⎩得221=222m x m x x -+-++ 解得:122,2x x m ==-2D x m ∴=-同理,2E x n =-设直线AE 的解析式为:y=kx+4, 由24122y kx y x x =+⎧⎪⎨=-++⎪⎩, 得12x 2-(k-1)x+2=0 124b x x a∴⋅=-= 即x D x E =4, 即(m-2)•(n-2)=4∴CG•CH=(2-m )•(2-n )=4.2.如图,抛物线2y ax 2x c =++经过,,A B C 三点,已知()()1,0,0,3.A C -()1求此抛物线的关系式;()2设点P 是线段BC 上方的抛物线上一动点,过点P 作y 轴的平行线,交线段BC 于点,D 当BCP 的面积最大时,求点D 的坐标;()3点M 是抛物线上的一动点,当()2中BCP 的面积最大时,请直接写出使45PDM ∠=︒的点M 的坐标 【答案】(1)2y x 2x 3=-++;(2)点33,22D ⎛⎫⎪⎝⎭;(3)点M 的坐标为()0,3或113113,22⎛⎫++ ⎪ ⎪⎝⎭【解析】【分析】(1)由2y ax 2x c =++经过点()(),1,00,3A C -,利用待定系数法即可求得此抛物线的解析式.(2)首先设点()2,23,P t t t -++令2230x x -++=,求得()3,0B ,然后设直线BC 的关系式为y kx b =+,由待定系数法求得BC 的解析式为3y x =-+,可得()()22,3,2333D t t PD t t t t t -+=-++--+=-+,BCP 的面积为()21333,22S PD t t =⨯=-+利用二次函数的性质即可求解; (3)根据PD y 轴,45PDM ∠=︒,分别设DM y x b =+,DM y x b =-+,根据点33D(22,)坐标即可求出b ,再与抛物线联系即可得出点M 的坐标. 【详解】()1将()(),1,00,3A C -分别代入22,y ax x c =++可解得1,3,a c =-=即抛物线的关系式为2y x 2x 3=-++.()2设点()2,23,P t t t -++令2230,x x -++=解得121,3,x x =-=则点()3,0B .设直线BC 的关系式为(y kx b k =+为常数且0k ≠),将点,B C 的坐标代入,可求得直线BC 的关系式为3y x =-+.∴点()()22,3,2333D t t PD t t t t t -+=-++--+=-+设BCP 的面积为,S 则()21333,22S PD t t =⨯=-+ ∴当32t =时,S 有最大值,此时点33,22D ⎛⎫ ⎪⎝⎭. ()3∵PD y 轴,45PDM ∠=︒第一种情况:令DM y x b =+,33D(22,)解得:b=0∴223y x y x x =⎧⎨=-++⎩解得:113x 2=∴11M 22+(, 第二种情况:令DM y x b =-+,33D(22,)解得:b=3 ∴2323y x y x x =-+⎧⎨=-++⎩解得:x=0或x=3(舍去)∴M 03(,)满足条件的点M 的坐标为()0,3或⎝⎭【点睛】此题主要考查待定系数法求函数解析式和二次函数的性质,熟练掌握二次函数的性质是解题关键.3.如图①是一张矩形纸片,按以下步骤进行操作:(Ⅰ)将矩形纸片沿DF 折叠,使点A 落在CD 边上点E 处,如图②;(Ⅱ)在第一次折叠的基础上,过点C 再次折叠,使得点B 落在边CD 上点B′处,如图③,两次折痕交于点O;(Ⅲ)展开纸片,分别连接OB、OE、OC、FD,如图④.(探究)(1)证明:OBC≌OED;(2)若AB=8,设BC为x,OB2为y,是否存在x使得y有最小值,若存在求出x的值并求出y的最小值,若不存在,请说明理由.【答案】(1)见解析;(2)x=4,16【解析】【分析】(1)连接EF,根据矩形和正方形的判定与性质以及折叠的性质,运用SAS证明OBC≌OED即可;(2)连接EF、BE,再证明△OBE是直角三角形,然后再根据勾股定理得到y与x的函数关系式,最后根据二次函数的性质求最值即可.【详解】(1)证明:连接EF.∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠BCD=∠ADE=∠DAF=90°由折叠得∠DEF=∠DAF,AD=DE∴∠DEF=90°又∵∠ADE=∠DAF=90°,∴四边形ADEF是矩形又∵AD=DE,∴四边形ADEF是正方形∴AD=EF=DE,∠FDE=45°∵AD=BC,∴BC=DE由折叠得∠BCO=∠DCO=45°∴∠BCO=∠DCO=∠FDE.∴OC=OD.在△OBC与△OED中,BC DEBCO FDEOC OD=⎧⎪∠=∠⎨⎪=⎩,,,∴△OBC≌△OED(SAS);(2)连接EF 、BE .∵四边形ABCD 是矩形,∴CD =AB =8.由(1)知,BC =DE∵BC =x ,∴DE =x∴CE =8-x由(1)知△OBC ≌△OED∴OB =OE ,∠OED =∠OBC .∵∠OED +∠OEC =180°,∴∠OBC +∠OEC =180°.在四边形OBCE 中,∠BCE =90°,∠BCE +∠OBC +∠OEC +∠BOE =360°,∴∠BOE =90°.在Rt △OBE 中,OB 2+OE 2=BE 2.在Rt △BCE 中,BC 2+EC 2=BE 2.∴OB 2+OE 2=BC 2+CE 2.∵OB 2=y ,∴y +y =x 2+(8-x)2.∴y =x 2-8x +32∴当x=4时,y 有最小值是16.【点睛】本题是四边形综合题,主要考查了矩形和正方形的判定与性质、折叠的性质、全等三角形的判定、勾股定理以及运用二次函数求最值等知识点,灵活应用所学知识是解答本题的关键.4.二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ,顶点为P ,直线PA 与x 轴交于点B .(1)当m =1时,求顶点P 的坐标;(2)若点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上,且0b m ->,试求a 的取值范围;(3)在第一象限内,以AB 为边作正方形ABCD . ①求点D 的坐标(用含m 的代数式表示);②若该二次函数的图象与正方形ABCD 的边CD 有公共点,请直接写出符合条件的整数m 的值.【答案】(1)P (2,13);(2)a 的取值范围为:a <0或a >4;(3)①D (m ,m +3); ②2,3,4.【解析】【分析】(1)把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中,进而求顶点P 的坐标即可;(2)把点Q (a ,b )代入二次函数22(0)63m m y x x m m =-+>解析式中,根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组,解出a 的取值范围即可; (3)①过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,求出二次函数与y 轴的交点A 的坐标,得到OA 的长,再根据待定系数法求出直线AP 的解析式,进而求出与x 轴的交点B 的坐标,得到OB 的长;通过证明△ADF ≌△ABO ,得到AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,求出点D 的坐标;②因为二次函数的图象与正方形ABCD 的边CD 有公共点,由①同理可得:C (m+3,3),分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况,进行讨论m 可能取的整数值即可.【详解】解:(1)当m =1时,二次函数为212163y x x =-+,∴顶点P的坐标为(2,13);(2)∵点Q(a,b)在二次函数22(0)63m my x x m m=-+>的图象上,∴2263m mb a a m=-+,即:2263m mb m a a-=-∵0b m->,∴2263m ma a->0,∵m>0,∴2263a a->0,解得:a<0或a>4,∴a的取值范围为:a<0或a>4;(3)①如下图,过点D作DE⊥x轴于点E,过点A作AF⊥DE于点F,∵二次函数的解析式为2263m my x x m=-+,∴顶点P(2,3m),当x=0时,y=m,∴点A(0,m),∴OA=m;设直线AP的解析式为y=kx+b(k≠0),把点A(0,m),点P(2,3m)代入,得:23m bmk b=⎧⎪⎨=+⎪⎩,解得:3m k b m⎧=-⎪⎨⎪=⎩,∴直线AP 的解析式为y=3m -x+m , 当y=0时,x=3,∴点B (3,0);∴OB=3;∵四边形ABCD 是正方形,∴AD=AB ,∠DAF+∠FAB=90°,且∠OAB+∠FAB =90°,∴∠DAF=∠OAB ,在△ADF 和△ABO 中, DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△ABO (AAS ),∴AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,∴点D 的坐标为:(m ,m+3);②由①同理可得:C (m+3,3),∵二次函数的图象与正方形ABCD 的边CD 有公共点,∴当x =m 时,3y m ≤+,可得322363m m m m -+≤+,化简得:32418m m -≤. ∵0m >,∴2184m m m -≤,∴218(2)4m m--≤, 显然:m =1,2,3,4是上述不等式的解,当5m ≥时,2(2)45m --≥,18 3.6m ≤,此时,218(2)4m m-->, ∴符合条件的正整数m =1,2,3,4; 当x = m +3时,y ≥3,可得2(3)2(3)363m m m m m ++-+≥, ∵0m >,∴21823m m m ++≥,即218(1)2m m++≥, 显然:m =1不是上述不等式的解,当2m ≥时,2(1)211m ++≥,189m ≤,此时,218(1)2m m++>恒成立, ∴符合条件的正整数m =2,3,4;综上:符合条件的整数m 的值为2,3,4.【点睛】本题考查二次函数与几何问题的综合运用,熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键.5.如图,在平面直角坐标系中,抛物线y=﹣12x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣12x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.(1)求此抛物线的解析式.(2)求点N的坐标.(3)过点A的直线与抛物线交于点F,当tan∠FAC=12时,求点F的坐标.(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC 以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t5S与t的函数关系式.【答案】(1)y=﹣12x2+32x+2;(2)点N的坐标为(5,-3);(3)点F的坐标为:(3,2)或(173,﹣509);(4)2535,043593535,(245435935(5)1044t tS tt⎧⎛≤≤⎪⎪⎝⎭⎪⎪=⎨-<≤⎪⎪⎪+<≤⎪⎩.【解析】【分析】(1)点A、C的坐标分别为(0,2)、(4,0),将点A、C坐标代入抛物线表达式即可求解;(2)抛物线的对称轴为:x=32,点N的横坐标为:37522+=,即可求解;(3)分点F在直线AC下方、点F在直线AC的上方两种情况,分别求解即可;(4)分0≤t≤35、当35<t≤35、35<t≤5三种情况,分别求解即可.【详解】解:(1)直线y=﹣12x+2经过A,C两点,则点A、C的坐标分别为(0,2)、(4,0),则c=2,抛物线表达式为:y=﹣12x2+bx+2,将点C坐标代入上式并解得:b=32,故抛物线的表达式为:y=﹣12x2+32x+2…①;(2)抛物线的对称轴为:x=32,点N的横坐标为:375 22+=,故点N的坐标为(5,-3);(3)∵tan∠ACO=2142AOCO===tan∠FAC=12,即∠ACO=∠FAC,①当点F在直线AC下方时,设直线AF交x轴于点R,∵∠ACO=∠FAC,则AR=CR,设点R(r,0),则r2+4=(r﹣4)2,解得:r=32,即点R的坐标为:(32,0),将点R、A的坐标代入一次函数表达式:y=mx+n得:230 2nm n=⎧⎪⎨+=⎪⎩,解得:432 mn⎧=-⎪⎨⎪=⎩,故直线AR的表达式为:y=﹣43x+2…②,联立①②并解得:x=173,故点F(173,﹣509);②当点F在直线AC的上方时,∵∠ACO=∠F′AC,∴AF′∥x轴,则点F′(3,2);综上,点F的坐标为:(3,2)或(173,﹣509);(4)如图2,设∠ACO=α,则t anα=12AOCO=,则sinα=5,cosα=5;①当0≤t≤35时(左侧图),设△AHK移动到△A′H′K′的位置时,直线H′K′分别交x轴于点T、交抛物线对称轴于点S,则∠DST=∠ACO=α,过点T作TL⊥KH,则LT=HH′=t,∠LTD=∠ACO=α,则DT='52co5c s2osL HHT tαα===,DS=tanDTα,S=S△DST=12⨯DT×DS=254t;②当355<t35时(右侧图),同理可得:S=''DGS TS梯形=12⨯DG×(GS′+DT′)=12⨯3+55﹣323594-;③当35<t≤5时,同理可得S=359104t +; 综上,S =2535,025*******,()435935(5)4t t t t t t ⎧⎛⎫≤≤⎪ ⎪ ⎪⎪⎝⎭⎪⎪⎨-<≤⎪⎪+<≤.【点睛】本题考查的是二次函数综合运用,涉及到一次函数、图形平移、图形的面积计算等,其中(3)、(4),要注意分类求解,避免遗漏.6.如图,直线3yx与x 轴、y 轴分别交于点A ,C ,经过A ,C 两点的抛物线2y ax bx c =++与x 轴的负半轴的另一交点为B ,且tan 3CBO ∠=(1)求该抛物线的解析式及抛物线顶点D 的坐标;(2)点P 是射线BD 上一点,问是否存在以点P ,A ,B 为顶点的三角形,与ABC 相似,若存在,请求出点P 的坐标;若不存在,请说明理由【答案】(1)243y x x =++,顶点(2,1)D --;(2)存在,52,33P ⎛⎫--⎪⎝⎭或(4,3)-- 【解析】 【分析】(1)利用直线解析式求出点A 、C 的坐标,从而得到OA 、OC ,再根据tan ∠CBO=3求出OB ,从而得到点B 的坐标,然后利用待定系数法求出二次函数解析式,整理成顶点式形式,然后写出点D 的坐标;(2)根据点A 、B 的坐标求出AB ,判断出△AOC 是等腰直角三角形,根据等腰直角三角形的性质求出AC ,∠BAC=45°,再根据点B 、D 的坐标求出∠ABD=45°,然后分①AB 和BP 是对应边时,△ABC 和△BPA 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可;②AB 和BA 是对应边时,△ABC 和△BAP 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可.【详解】解:(1)令y=0,则x+3=0, 解得x=-3, 令x=0,则y=3,∴点A (-3,0),C (0,3), ∴OA=OC=3, ∵tan ∠CBO=3OCOB=, ∴OB=1, ∴点B (-1,0),把点A 、B 、C 的坐标代入抛物线解析式得,93003a b c a b c c -+=⎧⎪-+=⎨⎪=⎩,解得:143a b c =⎧⎪=⎨⎪=⎩,∴该抛物线的解析式为:243y x x =++, ∵y=x 2+4x+3=(x+2)2-1, ∴顶点(2,1)D --;(2)∵A (-3,0),B (-1,0), ∴AB=-1-(-3)=2, ∵OA=OC ,∠AOC=90°, ∴△AOC 是等腰直角三角形, ∴,∠BAC=45°, ∵B (-1,0),D (-2,-1), ∴∠ABD=45°,①AB 和BP 是对应边时,△ABC ∽△BPA , ∴AB ACBP BA =,即22BP =, 解得, 过点P 作PE ⊥x 轴于E ,则BE=PE=23×22=23,∴OE=1+23=53,∴点P的坐标为(-53,-23);②AB和BA是对应边时,△ABC∽△BAP,∴AB ACBA BP=,即2322BP =,解得BP=32过点P作PE⊥x轴于E,则BE=PE=3222=3,∴OE=1+3=4,∴点P的坐标为(-4,-3);综合上述,当52,33P⎛⎫--⎪⎝⎭或(4,3)--时,以点P,A,B为顶点的三角形与ABC∆相似;【点睛】本题是二次函数综合题型,主要利用了直线与坐标轴交点的求解,待定系数法求二次函数解析式,等腰直角三角形的判定与性质,相似三角形的判定与性质,难点在于(2)要分情况讨论.7.定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(﹣x,y);当x≥0时,点P的变换点P′的坐标为(﹣y,x).(1)若点A (2,1)的变换点A′在反比例函数y=kx的图象上,则k= ; (2)若点B (2,4)和它的变换点B'在直线y=ax+b 上,则这条直线对应的函数关系式为 ,∠BOB′的大小是 度.(3)点P 在抛物线y=x 2﹣2x ﹣3的图象上,以线段PP′为对角线作正方形PMP'N ,设点P 的横坐标为m ,当正方形PMP′N 的对角线垂直于x 轴时,求m 的取值范围.(4)抛物线y=(x ﹣2)2+n 与x 轴交于点C ,D (点C 在点D 的左侧),顶点为E ,点P 在该抛物线上.若点P 的变换点P′在抛物线的对称轴上,且四边形ECP′D 是菱形,求n 的值.【答案】(1) -2;(2) y=13x+103,90;(3) m <0,m=12+或m=32;(4) n=﹣8,n=﹣2,n=﹣3. 【解析】 【分析】(1)先求出A 的变换点A ′,然后把A ′代入反比例函数即可得到结论; (2)确定点B ′的坐标,把问题转化为方程组解决;(3)分三种情形讨论:①当m <0时;②当m ≥0,PP '⊥x 轴时;③当m ≥0,MN ⊥x 轴时.(4)利用菱形的性质,得到点E 与点P '关于x 轴对称,从而得到点P '的坐标为(2,﹣n ).分两种情况讨论:①当点P 在y 轴左侧时,点P 的坐标为(﹣2,﹣n ),代入抛物线解析式,求解即可;②当点P 在y 轴右侧时,点P 的坐标为(﹣n ,﹣2).代入抛物线解析式,求解即可. 【详解】(1)∵A (2,1)的变换点为A ′(-1,2),把A ′(-1,2)代入y =kx中,得到k =-2. 故答案为:-2.(2)点B (2,4)的变换点B ′(﹣4,2),把(2,4),(﹣4,2)代入y =ax +b 中.得到:2442a b a b +=⎧⎨-+=⎩,解得:13103a b ⎧=⎪⎪⎨⎪=⎪⎩,∴11033y x =+.∵OB 2=2224+=20,OB ′2=2224+=20,BB ′2=22(42)(24)--+-=40,∴OB 2+OB ′2=BB ′2,∴∠BOB ′=90°. 故答案为:y =13x +103,90. (3)①当m <0时,点P 与点P '关于y 轴对称,此时MN 垂直于x 轴,所以m <0. ②当m ≥0,PP '⊥x 轴时,则点P '的坐标为(m ,m ),点P 的坐标为(m ,﹣m ). 将点P (m ,﹣m )代入y =x 2﹣2x ﹣3,得:﹣m =m 2﹣2m ﹣3.解得:121122m m ==(不合题意,舍去).所以m =③当m ≥0,MN ⊥x 轴时,则PP '∥x 轴,点P 的坐标为(m ,m ). 将点P (m ,m )代入y =x 2﹣2x ﹣3,得:m =m 2﹣2m ﹣3.解得:12m m ==所以32m +=.综上所述:m 的取值范围是m <0,m =12+或m =32. (4)∵四边形ECP 'D 是菱形,∴点E 与点P '关于x 轴对称. ∵点E 的坐标为(2,n ),∴点P '的坐标为(2,﹣n ). ①当点P 在y 轴左侧时,点P 的坐标为(﹣2,﹣n ). 代入y =(x ﹣2)2+n ,得:﹣n =(﹣2﹣2)2+n ,解得:n =﹣8. ②当点P 在y 轴右侧时,点P 的坐标为(﹣n ,﹣2).代入y =(x ﹣2)2+n ,得:﹣2=(﹣n ﹣2)2+n .解得:n 1=﹣2,n 2=﹣3. 综上所述:n 的值是n =﹣8,n =﹣2,n =﹣3. 【点睛】本题是二次函数综合题、一次函数的应用、待定系数法、变换点的定义等知识,解题的关键是理解题意,学会用分类讨论的射线思考问题,学会用方程的思想思考问题,属于中考压轴题.8.如图,在平面直角坐标系中,矩形AOBC 的边AO 在x 轴的负半轴上,边OB 在y 轴的负半轴上.且AO =12,OB =9.抛物线y =﹣x 2+bx+c 经过点A 和点B . (1)求抛物线的表达式;(2)在第二象限的抛物线上找一点M ,连接AM ,BM ,AB ,当△ABM 面积最大时,求点M 的坐标;(3)点D 是线段AO 上的动点,点E 是线段BO 上的动点,点F 是射线AC 上的动点,连接EF ,DF ,DE ,BD ,且EF 是线段BD 的垂直平分线.当CF =1时. ①直接写出点D 的坐标 ;②若△DEF 的面积为30,当抛物线y =﹣x 2+bx+c 经过平移同时过点D 和点E 时,请直接写出此时的抛物线的表达式 .【答案】(1)y=﹣x2﹣514x﹣9;(2)M(﹣6,31.5);(3)①(﹣50)或(﹣3,0),②y=﹣x2﹣133x﹣4【解析】【分析】(1)利用待定系数法把问题转化为解方程组即可解决问题.(2)如图1中,设M(m,﹣m2﹣514m﹣9),根据S△ABM=S△ACM+S△MBC﹣S△ACB构建二次函数,利用二次函数的性质解决问题即可.(3)①分两种情形:如图2中,当点F在AC的延长线设时,连接DF,FB.设D(m,0).根据FD=FB,构建方程求解.当点F在线段AC上时,同法可得.②根据三角形的面积求出D,E的坐标,再利用待定系数法解决问题即可.【详解】解:(1)由题意A(﹣12,0),B(0,﹣9),把A,B的坐标代入y=﹣x2+bx+c,得到9 144120cb c=-⎧⎨--+=⎩,解得:5149bc⎧=-⎪⎨⎪=-⎩,∴抛物线的解析式为y=﹣x2﹣514x﹣9.(2)如图1中,设M(m,﹣m2﹣514m﹣9),S△ABM=S△ACM+S△MBC﹣S△ACB=12×9×(m+12)+12×12×(﹣m2﹣514m﹣9+9)﹣12×12×9=﹣6m2﹣72m=﹣6(m+6)2+216,∵﹣6<0,∴m=﹣6时,△ABM的面积最大,此时M(﹣6,31.5).(3)①如图2中,当点F在AC的延长线设时,连接DF,FB.设D(m,0).∵EF垂直平分线段BD,∴FD=FB,∵F(﹣12,﹣10),B(0,﹣9),∴102+(m+12)2=122+12,∴m=﹣12﹣55∴D(﹣50).当点F在线段AC上时,同法可得D(﹣3,0),综上所述,满足条件的点D的坐标为(﹣50)或(﹣3,0).故答案为(﹣50)或(﹣3,0).②由①可知∵△EF的面积为30,∴D(﹣3,0),E(0,﹣4),把D,E代入y=﹣x2+b′x+c′,可得'493''0c b c =-⎧⎨--+=⎩, 解得:13'3'4b c ⎧=-⎪⎨⎪=-⎩,∴抛物线的解析式为y =﹣x 2﹣133x ﹣4. 故答案为:y =﹣x 2﹣133x ﹣4. 【点睛】本题属于二次函数综合题,考查了二次函数的性质,待定系数法,线段的垂直平分线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.9.在平面直角坐标系xOy 中(如图),已知二次函数2y ax bx c =++(其中a 、b 、c 是常数,且a ≠0)的图像经过点A (0,-3)、B (1,0)、C (3,0),联结AB 、AC . (1)求这个二次函数的解析式;(2)点D 是线段AC 上的一点,联结BD ,如果:3:2ABD BCD S S ∆∆=,求tan ∠DBC 的值; (3)如果点E 在该二次函数图像的对称轴上,当AC 平分∠BAE 时,求点E 的坐标.【答案】(1)243y x x =-+-;(2)32;(3)E (2,73-) 【解析】【分析】 (1)直接利用待定系数法,把A 、B 、C 三点代入解析式,即可得到答案;(2)过点D 作DH ⊥BC 于H ,在△ABC 中,设AC 边上的高为h ,利用面积的比得到32AD DC =,然后求出DH 和BH ,即可得到答案; (3)延长AE 至x 轴,与x 轴交于点F ,先证明△OAB ∽△OFA ,求出点F 的坐标,然后求出直线AF 的方程,即可求出点E 的坐标.【详解】解:(1)将A(0,-3)、B(1,0)、C(3,0)代入20y ax bx c a=++≠()得,03,0934,300a ba bc=+-⎧⎪=+-⎨⎪-=++⎩解得143abc=-⎧⎪=⎨⎪=-⎩,∴此抛物线的表达式是:243y x x=-+-.(2)过点D作DH⊥BC于H,在△ABC中,设AC边上的高为h,则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==,又∵DH//y轴,∴25CH DC DHOC AC OA===.∵OA=OC=3,则∠ACO=45°,∴△CDH为等腰直角三角形,∴26355CH DH==⨯=.∴64255BH BC CH=-=-=.∴tan∠DBC=32DHBH=.(3)延长AE至x轴,与x轴交于点F,∵OA=OC=3,∴∠OAC=∠OCA=45°,∵∠OAB=∠OAC-∠BAC=45°-∠BAC,∠OFA=∠OCA-∠FAC=45°-∠FAC,∵∠BAC=∠FAC,∴∠OAB=∠OFA.∴△OAB∽△OFA,∴13 OB OAOA OF==.∴OF=9,即F(9,0);设直线AF的解析式为y=kx+b(k≠0),可得093k bb=+⎧⎨-=⎩,解得133kb⎧=⎪⎨⎪=-⎩,∴直线AF的解析式为:133y x=-,将x=2代入直线AF的解析式得:73y=-,∴E(2,73 -).【点睛】本题考查了相似三角形的判定和性质,二次函数的性质,求二次函数的解析式,等腰直角三角形的判定和性质,求一次函数的解析式,解题的关键是掌握二次函数的图像和性质,以及正确作出辅助线构造相似三角形.10.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系解析式;(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q 的坐标;若不存在,说明理由;【答案】(1)224233y x x =--+;(2)存在,点P 35,22⎛⎫- ⎪⎝⎭,使△PAC 的面积最大;(3)存在点Q ,使△BCQ 是以BC 为腰的等腰直角三角形.Q 点坐标为:Q 1(2,3),Q 2(3,1),Q 3(﹣1,﹣1),Q 4(﹣2,1).【解析】【分析】(1)直接把点A (﹣3,0),B (1,0)代入二次函数y =ax 2+bx+2求出a 、b 的值即可得出抛物线的解析式;(2)设点P 坐标为(m ,n ),则n =﹣23m 2﹣43m+2,连接PO ,作PM ⊥x 轴于M ,PN ⊥y 轴于N .根据三角形的面积公式得出△PAC 的表达式,再根据二次函数求最大值的方法得出其顶点坐标即可;(3)以BC 为边,在线段BC 两侧分别作正方形,正方形的其他四个顶点均可以使得“△BCQ 是以BC 为腰的等腰直角三角形”,因此有四个点符合题意要求,再过Q 1点作Q 1D ⊥y 轴于点D ,过点Q 2作Q 2E ⊥x 轴于点E ,根据全等三角形的判定定理得出△Q 1CD ≌△CBO ,△CBO ≌△BQ 2E ,故可得出各点坐标.【详解】(1)∵抛物线y =ax 2+bx+2过点A (﹣3,0),B (1,0),∴093202a b a b =-+⎧⎨=++⎩2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩解得 ∴二次函数的关系解析式为y =﹣23x 2﹣43x+2; (2)存在.∵如图1所示,设点P 坐标为(m ,n ),则n =﹣23m 2﹣43m+2. 连接PO ,作PM ⊥x 轴于M ,PN ⊥y 轴于N .则PM=﹣23m2﹣43m+2.,PN=﹣m,AO=3.∵当x=0时,y=﹣23×0﹣43×0+2=2,∴OC=2,∴S△PAC=S△PAO+S△PCO﹣S△ACO=12AO•PM+12CO•PN﹣12AO•CO=12×3×(﹣23m2﹣43m+2)+12×2×(﹣m)﹣12×3×2=﹣m2﹣3m∵a=﹣1<0∴函数S△PAC=﹣m2﹣3m有最大值∴当m=﹣2ba=﹣32时,S△PAC有最大值.∴n=﹣23m2﹣43m+2=﹣23×(﹣32)2﹣43×(﹣32)+2=52,∴存在点P(﹣32,52),使△PAC的面积最大.(3)如图2所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.过Q1点作Q1D⊥y轴于点D,过点Q2作Q2E⊥x轴于点E,∵∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∴∠1=∠3,∠2=∠4,在△Q1CD与△CBO中,∵11324Q C BC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△Q1CD≌△CBO,∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3);同理可得Q4(﹣2,1);同理可证△CBO≌△BQ2E,∴BE=OC=2,Q2E=OB=1,∴OE=OB+BE=1+2=3,∴Q2(3,1),同理,Q3(﹣1,﹣1),∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(﹣1,﹣1),Q4(﹣2,1).【点睛】本题考查的是二次函数综合题,涉及到用待定系数法求二次函数解析式,二次函数极值、全等三角形的判定与性质,正方形及等腰直角三角形的性质等知识,涉及面较广,难度较大.。
2023年九年级中考数学复习:二次函数(特殊四边形问题)综合题(Word版,含答案)

2023年九年级中考数学复习:二次函数(特殊四边形问题)综合题1.已知抛物线()21=++4(0)2y a x m m am -≠过点()0,4A(1)若=2m ,求a 的值;(2)如图,顶点M 在第一象限内,B 、C 是抛物线对称轴l 上的两点,且MB MC =,在直线l 右侧以BC 为边作正方形BCDE ,点E 恰好在抛物线上.①求am 的值;①试判断点E 和点A 是否关于直线l 对称,如果对称,请说明理由,如果不对称,请举出反例.2.如图,抛物线y =ax 2-2x +c (a ≠0)与直线y =x +3交于A ,C 两点,与x 轴交于点B .(1)求抛物线的解析式.(2)点P 是抛物线上一动点,且在直线AC 下方,当①ACP 的面积为6时,求点P 的坐标.(3)D 为抛物线上一点,E 为抛物线的对称轴上一点,请直接写出以A ,C ,D ,E 为顶点的四边形为平行四边形时点D 的坐标.3.如图1,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A (﹣1,0)、B (3,0),与y 轴交于点C ,连接AC 和BC ,①OAC =60°.(1)求二次函数的表达式.(2)如图2,线段BC 上有M 、N 两动点(N 在M 上方),且MN 3P 是直线BC 下方抛物线上一动点,连接PC 、PB ,当①PBC 面积最大时,连接PM 、AN ,当MN 运动到某一位置时,PM +MN +NA 的值最小,求出该最小值.(3)如图3,在(2)的条件下,连接AP ,将AP 绕着点A 逆时针旋转60°至AQ .点E 为二次函数对称轴上一动点,点F 为平面内任意一点,是否存在这样的点E 、F ,使得四边形AEFQ 为菱形,若存在,请直接写出点E 的坐标,若不存在,请说明理由.4.直线3y x =-+与x 轴相交于点A ,与y 轴相交于点B ,抛物线2y ax 2x c =++经过点A ,B ,与x 轴的另一个交点为C .(1)求抛物线的解析式;(2)如图1,若点P为直线AB上方的抛物线上的一动点,求四边形APBO的面积的最大值;D为抛物线上的一点,直线CD与AB相交于点M,点H在抛物线上,(3)如图2,(2,3)∥轴,交直线CD于点K.P是平面内一点,当以点M,H,K,P为顶点的四过H作HK y边形是正方形时,请直接写出点P的坐标.5.综合与探究如图1所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值为______.(3)如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N①当ANC面积最大时的P点坐标为______;最大面积为______.①点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D、F、B、C为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.。
(完整版)初三数学二次函数所有经典题型

初三数学二次函数经典题型二次函数单元检测 (A)姓名_______一、填空题:1、函数y =(m -1)x m 22+1-2mx +1是抛物线,则m = .2、抛物线y =-x -2x +3与x 轴交点为,与y 轴交点为 .3、二次函数y =ax 的图象过点(-1,2),则它的解析式是,当x 时,y 随x 的增大而增大.24.抛物线y =6(x +1)-2可由抛物线y =6x -2向平移个单位得到.225.抛物线y =x +4x +3在x 轴上截得的线段长度是.226.抛物线y =x +2x +m -4的图象经过原点,则m =.27.抛物线y =x -x +m ,若其顶点在x 轴上,则m =.2()8.如果抛物线y =ax +bx +c 的对称轴是x=-2,且开口方向与形状与抛物线32y =-x 相同,又过原点,那么a=,b=,c 2= .9、二次函数y =x +bx +c 的图象如下左图所示,则对称轴是,当函数值y <0时,对应x 的取值范围是 .y yA-3O x 122Bx 210、已知二次函数y 1=ax +bx +c (a ≠0)与一次函数y 2=kx +m (k ≠0)的图象相交于点A(-2,4)和B(8,2),如上右图所示,则能使y 1>y 2成立的x 的取值范围 .二、选择题:11.下列各式中,y 是x 的二次函数的是 ( )2A.xy +x =1 B.x +y -2=0 C.y -ax =-2 D.x -y +1=0222212x 的图象,它们共同特点是 ( )2A.都是关于x 轴对称,抛物线开口向上 B.都是关于y 轴对称,抛物线开口向下B.都是关于原点对称,顶点都是原点 D.都是关于y 轴对称,顶点都是原点2213.抛物线y =x -mx -m +1的图象过原点,则m 为()12.在同一坐标系中,作y =2x 、y =-2x 、y =22A.0 B.12 C.-1D.±114.把二次函数y =x -2x -1配方成为()2A.y =(x -1) B.y =(x -1)-2 C.y =(x +1)+1222D.y =(x +1)-2215.已知原点是抛物线y =(m +1)x 的最高点,则m 的范围是( )A.m <-1 B.m <1 C.m >-1 D.m >-216、函数y =2x -x -1的图象经过点( )A、(-1,1)B、(1,1)C、(0 , 1) D 、(1 , 0 )2217、抛物线y =3x 向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )222A、y =3(x -1)-2 B、y =3(x +1)-2C、y =3(x +1)+2 D、y =3(x -1)+22 18、已知h 关于t 的函数关系式h =12gt (g 为正常数,t 为时间)如图,则函数图象为 ( )2h h h hoo t t o t o tA B C D19、下列四个函数中,图象的顶点在y 轴上的函数是()22 A、y =x -3x +2 B、y =5-x C、y =-x +2x D、y =x -4x +422 20、已知二次函数y =ax +bx +c ,若a <0,c >0,那么它的图象大致是()y yy oo x o x x(C)(A)(B)三、解答题:21、根据所给条件求抛物线的解析式:(1)、抛物线过点(0,2)、(1,1)、(3,5)(2)、抛物线关于y 轴对称,且过点(1,-2)和(-2,0)22.已知二次函数y =x +bx +c 的图像经过A(0,1),B(2,-1)两点.(1)求b 和c 的值; (2)试判断点P(-1,2)是否在此函数图像上?23、某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边22y o (D)x长为x 米,面积为S 平方米.(1)求出S 与x 之间的函数关系式,并确定自变量x 的取值范围;(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.24、某工厂现有80台机器,每台机器平均每天生产384•件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,•由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.(1)如果增加x 台机器,每天的生产总量为y 件,请你写出y 与x 之间的关系式;(2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?25、如图,有一个抛物线的拱形立交桥,•这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,•若要在离跨度中心点M5m 处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?24、如图,抛物线y =-x +5x +n 经过点A(1,0),与y 轴交于点B.⑴求抛物线的解析式;⑵P 是y 轴正半轴上一点,且△PAB 是以AB 为腰的等腰三角形,试求P 点坐标.yA O1-1B 2x二次函数单元检测(B)姓名_______一、新课标基础训练1.下列二次函数的图象的开口大小,从大到小排列依次是()①y=12221322x ;②y=x +3;③y=-(x-3)-2;④y=-x +5x-1.3322A.④②③① B.①③②④ C.④②①③ D.②③①④22.将二次函数y=3(x+2)-4的图象向右平移3个单位,再向上平移1个单位,所得的图象的函数关系式()2222 A.y=3(x+5)-5; B.y=3(x-1)-5;C.y=3(x-1)-3; D.y=3(x+5)-33.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,•若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润,则应降价()A.5元 B.10元 C.15元 D.20元24.若直线y=ax+b(ab≠0)不过第三象限,则抛物线y=ax +bx 的顶点所在的象限是()A.一 B.二 C.三 D.四25.已知二次函数y=x +x+m,当x 取任意实数时,都有y>0,则m 的取值范围是()A.m≥1111 B.m> C.m≤ D.m<444426.二次函数y=mx -4x+1有最小值-3,则m 等于()A.1 B.-1 C.±1 D.±12二、新课标能力训练7.如图,用2m 长的木条,做一个有横档的矩形窗子,为使透进的2光线最多,那么这个窗子的面积应为_______m .8.如图,有一个抛物线型拱桥,其最大高度为16m,•跨度为•40m,•现把它的示意图放在平面直角坐标系中••,••则此抛物线的函数关系式为__________.9、已知函数y =(m +2)x m 2+m -4是关于x 的二次函数,求:(1)满足条件的m 值;(2)m 为何值时,抛物线有最低点?求出这个最低点.这时当x 为何值时,y 随x 的增大而增大?(3)m 为何值时,函数有最大值?最大值是什么?这时当x 为何值时,y 随x 的增大而减小?10、观察表格:xax ax +bx+c 22031123(1)求a,b,c 的值,并在表内空格处填入正确的数.22(2)画出函数y=ax +bx+c 的图象,由图象确定,当x 取什么实数时,ax +bx+c>0.11、如图(2),已知平行四边形ABCD 的周长为8cm,∠B=30。
初三数学二次函数分类题型及解析[整理版]-12页文档资料
![初三数学二次函数分类题型及解析[整理版]-12页文档资料](https://img.taocdn.com/s3/m/9248ef559ec3d5bbfd0a74e5.png)
初三数学二次函数分类题型及解析一.解答题(共10小题)1.如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)(1)求m的值及抛物线的顶点坐标.(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.2.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.3.如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.(1)求这条抛物线对应的函数解析式;(2)求直线AB对应的函数解析式.4.如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E(1)求直线BC的解析式;(2)当线段DE的长度最大时,求点D的坐标.5.已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).(1)求二次函数的解析式,并写出顶点D的坐标;(2)将二次函数的图象沿x轴向左平移个单位长度,当 y<0时,求x的取值范围.6.某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)求y与x之间的函数关系式;(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?7.某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?8.2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x ≤30);(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?9.草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y 与x的函数关系图象.(1)求y与x的函数解析式(也称关系式);(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.10.襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y=.(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.2016年12月09日天津优胜教育二次函数组卷参考答案与试题解析一.解答题(共10小题)1.(2016•宁波)如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)(1)求m的值及抛物线的顶点坐标.(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.【解答】解:(1)把点B的坐标为(3,0)代入抛物线y=﹣x2+mx+3得:0=﹣32+3m+3,解得:m=2,∴y=﹣x 2+2x+3=﹣(x ﹣1)2+4,∴顶点坐标为:(1,4).(2)连接BC 交抛物线对称轴l 于点P ,则此时PA+PC 的值最小,设直线BC 的解析式为:y=kx+b ,∵点C (0,3),点B (3,0), 解得:, ∴直线BC 的解析式为:y=﹣x+3,当x=1时,y=﹣1+3=2,∴当PA+PC 的值最小时,点P 的坐标为:(1,2).2.(2016•菏泽)在平面直角坐标系xOy 中,抛物线y=ax 2+bx+2过B (﹣2,6),C (2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D ,求△BCD 的面积;(3)若直线y=﹣x 向上平移b 个单位所得的直线与抛物线段BDC (包括端点B 、C )部分有两个交点,求b 的取值范围.【解答】解:(1)由题意解得,∴抛物线解析式为y=x 2﹣x+2.(2)∵y=x 2﹣x+2=(x ﹣1)2+.∴顶点坐标(1,),∵直线BC 为y=﹣x+4,∴对称轴与BC 的交点H (1,3),∴S △BDC =S △BDH +S △DHC =•3+•1=3.(3)由消去y得到x2﹣x+4﹣2b=0,当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,∴b=,当直线y=﹣x+b经过点C时,b=3,当直线y=﹣x+b经过点B时,b=5,∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,∴<b≤3.3.(2016•淄博)如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.(1)求这条抛物线对应的函数解析式;(2)求直线AB对应的函数解析式.【解答】解:(1)∵抛物线y=ax2+2ax+1与x轴仅有一个公共点A,∴△=4a2﹣4a=0,解得a1=0(舍去),a2=1,∴抛物线解析式为y=x2+2x+1;(2)∵y=(x+1)2,∴顶点A的坐标为(﹣1,0),∵点C是线段AB的中点,即点A与点B关于C点对称,∴B点的横坐标为1,当x=1时,y=x2+2x+1=1+2+1=4,则B(1,4),设直线AB的解析式为y=kx+b,把A(﹣1,0),B(1,4)代入得,解得,∴直线AB的解析式为y=2x+2.4.(2016•大连)如图,抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E (1)求直线BC的解析式;(2)当线段DE的长度最大时,求点D的坐标.【解答】解:(1)∵抛物线y=x2﹣3x+与x轴相交于A、B两点,与y轴相交于点C,∴令y=0,可得x=或x=,∴A(,0),B(,0);令x=0,则y=,∴C点坐标为(0,),设直线BC的解析式为:y=kx+b,则有,解得:,∴直线BC的解析式为:y=x;(2)设点D的横坐标为m,则坐标为(m,),∴E点的坐标为(m,m),设DE的长度为d,∵点D是直线BC下方抛物线上一点,则d=m+﹣(m2﹣3m+),整理得,d=﹣m2+m,∵a=﹣1<0,∴当m==时,d 最大===,∴D 点的坐标为(,). 5.(2016•黔南州)已知二次函数y=x 2+bx+c 的图象与y 轴交于点C (0,﹣6),与x 轴的一个交点坐标是A (﹣2,0).(1)求二次函数的解析式,并写出顶点D 的坐标;(2)将二次函数的图象沿x 轴向左平移个单位长度,当 y <0时,求x 的取值范围.【解答】解:(1)∵把C (0,﹣6)代入抛物线的解析式得:C=﹣6,把A (﹣2,0)代入y=x 2+bx ﹣6得:b=﹣1,∴抛物线的解析式为y=x 2﹣x ﹣6.∴y=(x ﹣)2﹣.∴抛物线的顶点坐标D (,﹣).(2)二次函数的图形沿x 轴向左平移个单位长度得:y=(x+2)2﹣. 令y=0得:(x+2)2﹣=0,解得:x 1=,x 2=﹣.∵a >0,∴当y <0时,x 的取值范围是﹣<x <. 6.(2016•咸宁)某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x 元,每星期的销售量为y 件.(1)求y 与x 之间的函数关系式;(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?【解答】解:(1)y=300+30(60﹣x)=﹣30x+2100.(2)设每星期利润为W元,W=(x﹣40)(﹣30x+2100)=﹣30(x﹣55)2+6750.∴x=55时,W最大值=6750.∴每件售价定为55元时,每星期的销售利润最大,最大利润6750元.(3)由题意(x﹣40)(﹣30x+2100)≥6480,解得52≤x≤58,当x=52时,销售300+30×8=540,当x=58时,销售300+30×2=360,∴该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装360件.7.(2016•成都)某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?【解答】解:(1)平均每棵树结的橙子个数y(个)与x之间的关系为:y=600﹣5x(0≤x<120);(2)设果园多种x棵橙子树时,可使橙子的总产量为w,则w=(600﹣5x)(100+x)=﹣5x2+100x+60000=﹣5(x﹣10)2+60500,则果园多种10棵橙子树时,可使橙子的总产量最大,最大为60500个.8.(2016•铜仁市)2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)用表达式表示蝙蝠型风筝销售量y (个)与售价x (元)之间的函数关系(12≤x ≤30);(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?【解答】解:(1)设蝙蝠型风筝售价为x 元时,销售量为y 个,根据题意可知:y=180﹣10(x ﹣12)=﹣10x+300(12≤x ≤30).(2)设王大伯获得的利润为W ,则W=(x ﹣10)y=﹣10x 2+400x ﹣3000,令W=840,则﹣10x 2+400x ﹣3000=840,解得:x 1=16,x 2=24,答:王大伯为了让利给顾客,并同时获得840元利润,售价应定为16元.(3)∵W=﹣10x 2+400x ﹣3000=﹣10(x ﹣20)2+1000,∵a=﹣10<0,∴当x=20时,W 取最大值,最大值为1000.答:当售价定为20元时,王大伯获得利润最大,最大利润是1000元.9.(2016•云南)草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y (千克)与销售单价x (元)符合一次函数关系,如图是y 与x 的函数关系图象.(1)求y 与x 的函数解析式(也称关系式);(2)设该水果销售店试销草莓获得的利润为W 元,求W 的最大值.【解答】解:(1)设y与x的函数关系式为y=kx+b,根据题意,得:,解得:,∴y与x的函数解析式为y=﹣2x+340,(20≤x≤40).(2)由已知得:W=(x﹣20)(﹣2x+340)=﹣2x2+380x﹣6800=﹣2(x﹣95)2+11250,∵﹣2<0,∴当x≤95时,W随x的增大而增大,∵20≤x≤40,∴当x=40时,W最大,最大值为﹣2(40﹣95)2+11250=5200元.10.(2016•湖北襄阳)襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y=.(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.【解答】解:(1)当40≤x<60时,W=(x﹣30)(﹣2x+140)=﹣2x2+200x﹣4200,当60≤x≤70时,W=(x﹣30)(﹣x+80)=﹣x2+110x﹣2400;(2)当40≤x<60时,W=﹣2x2+200x﹣4200=﹣2(x﹣50)2+800,∴当x=50时,W取得最大值,最大值为800万元;当60≤x≤70时,W=﹣x2+110x﹣2400=﹣(x﹣55)2+625,∴当x>55时,W随x的增大而减小,∴当x=60时,W取得最大值,最大值为:﹣(60﹣55)2+625=600,∵800>600,∴当x=50时,W取得最大值800,答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元;(3)当40≤x<60时,由W≥750得:﹣2(x﹣50)2+800≥750,解得:45≤x≤55,当60≤x≤70时,W的最大值为600<750,∴要使企业销售该产品的年利润不少于750万元,该产品的售价x(元/件)的取值范围为45≤x≤55.希望以上资料对你有所帮助,附励志名言3条:1、常自认为是福薄的人,任何不好的事情发生都合情合理,有这样平常心态,将会战胜很多困难。
(完整word版)二次函数专题训练(正方形的存在性问题)含答案

二次函数专题训练(正方形的存在性)1.如图,已知抛物线y=x 2+bx+c 的图象经过点 A ( l , 0), B(﹣ 3,0),与 y 轴交于点C,抛物线的极点为 D ,对称轴与x 轴订交于点E,连结 BD .( 1)求抛物线的分析式.( 2)若点 P 在直线 BD 上,当 PE=PC 时,求点P 的坐标.( 3)在( 2)的条件下,作PF⊥ x 轴于 F,点 M 为 x 轴上一动点,N 为直线 PF 上一动点, G 为抛物线上一动点,当以点F, N ,G,M 四点为极点的四边形为正方形时,求点M 的坐标.2.如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A 和点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0, 6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M 作 MN ∥x 轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在座标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.3.如图,已知抛物线y=ax2 +bx﹣ 3 过点 A (﹣ 1, 0), B( 3,0),点 M 、 N 为抛物线上的动点,过点M 作MD ∥ y 轴,交直线 BC 于点 D ,交 x 轴于点 E.过点 N 作 NF ⊥ x 轴,垂足为点 F( 1)求二次函数 y=ax2+bx ﹣ 3 的表达式;( 2)若 M 点是抛物线上对称轴右边的点,且四边形MNFE 为正方形,求该正方形的面积;( 3)若 M 点是抛物线上对称轴左边的点,且∠DMN=90°, MD=MN ,请直接写出点M 的横坐标.4.(2015 贵州省毕节地域) 如图,抛物线y=x 2+bx+c 与 x 轴交于 A (﹣ 1,0), B( 3, 0)两点,极点M 关于 x 轴的对称点是M′.( 1)求抛物线的分析式;( 2)若直线AM′与此抛物线的另一个交点为C,求△ CAB 的面积;( 3)能否存在过A, B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的分析式;若不存在,请说明原因.5. (2016 辽宁省铁岭市 ) .如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A ,点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0,6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M作MN∥ x轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在平面内,以线段 MN 为对角线作正方形MPNQ ,请直接写出点Q 的坐标.二次函数专题训练(正方形的存在性)6.(2016 广东省茂名市 ) .如图,抛物线 y=﹣ x2+bx+c 经过 A (﹣ 1, 0), B(3,0)两点,且与 y 轴交于点 C,点 D 是抛物线的极点,抛物线的对称轴DE 交 x 轴于点 E,连结 BD .(1)求经过 A ,B ,C 三点的抛物线的函数表达式;(2)点 P 是线段 BD 上一点,当 PE=PC 时,求点 P 的坐标;( 3)在( 2)的条件下,过点P 作 PF⊥x 轴于点 F, G 为抛物线上一动点,M 为 x 轴上一动点, N 为直线PF 上一动点,当以F、 M 、 G 为极点的四边形是正方形时,恳求出点M 的坐标.二次函数专题训练(正方形的存在性问题)参照答案1.如图,已知抛物线 y=x 2+bx+c 的图象经过点 A ( l , 0), B(﹣ 3,0),与 y 轴交于点 C,抛物线的极点为D ,对称轴与 x 轴订交于点 E,连结 BD .( 1)求抛物线的分析式.( 2)若点 P 在直线 BD 上,当 PE=PC 时,求点P 的坐标.( 3)在( 2)的条件下,作PF⊥ x 轴于 F,点 M 为 x 轴上一动点,N 为直线 PF 上一动点, G 为抛物线上一动点,当以点F, N ,G,M 四点为极点的四边形为正方形时,求点M 的坐标.【解答】解:( 1)∵抛物线y=x2+bx+c 的图象经过点 A ( 1, 0), B(﹣ 3,0),∴,∴,∴抛物线的分析式为y=x2+2x ﹣ 3;( 2)由( 1)知,抛物线的分析式为y=x 2+2x ﹣ 3;∴C( 0,﹣ 3),抛物线的极点 D(﹣ 1,﹣ 4),∴E(﹣ 1, 0),设直线 BD 的分析式为y=mx+n ,∴,∴,∴直线BD 的分析式为y= ﹣ 2x ﹣6,设点 P( a,﹣ 2a﹣ 6),∵ C( 0,﹣ 3), E(﹣ 1, 0),依据勾股定理得,PE2=( a+1)2+(﹣ 2a﹣ 6)2,22 2PC =a +(﹣ 2a﹣ 6+3 ),∵PC=PE,∴( a+1)2+(﹣ 2a﹣ 6)2 =a2+(﹣ 2a﹣ 6+3 )2,∴a=﹣ 2,∴ y= ﹣ 2×(﹣ 2)﹣ 6=﹣ 2,∴P(﹣ 2,﹣ 2),(3)如图,作 PF⊥ x 轴于 F,∴ F(﹣ 2, 0),设 M ( d, 0),∴ G( d, d2+2d ﹣ 3), N(﹣ 2, d2+2d﹣ 3),∵以点 F, N ,G, M 四点为极点的四边形为正方形,必有FM=MG ,∴|d+2|=|d2+2d ﹣ 3|,∴ d= 或 d= ,∴点 M 的坐标为(, 0),(, 0),(, 0),(, 0).2.如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A 和点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0, 6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M 作 MN ∥ x 轴与抛物线交于点N,点 P 在 x 轴上,点Q 在座标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.【解答】解:( 1)把 B 、C 两点坐标代入抛物线分析式可得,解得,∴抛物线分析式为y=﹣x2+2x+6 ,∵ y= ﹣x2+2x+6= ﹣(x﹣2)2+8,∴ D(2,8);( 2)如图 1,过 F 作 FG⊥ x 轴于点 G,设 F( x,﹣x2+2x+6 ),则 FG=|﹣x2+2x+6| ,∵∠ FBA= ∠BDE ,∠ FGB= ∠ BED=90°,∴△ FBG ∽△ BDE ,∴=,∵ B(6,0),D(2,8),∴ E( 2,0), BE=4 ,DE=8 , OB=6 ,∴ BG=6 ﹣ x,∴=,当点 F 在 x 轴上方时,有=,解得x=﹣1或x=6(舍去),此时F点的坐标为(﹣1,);当点 F 在 x 轴下方时,有=﹣,解得x=﹣3或x=6(舍去),此时F 点坐标为(﹣ 3,﹣);综上可知 F 点的坐标为(﹣1,)或(﹣3,﹣);( 3)如图 2,设对角线MN 、 PQ 交于点 O′,∵点 M 、 N 对于抛物线对称轴对称,且四边形MPNQ 为正方形,∴点 P 为抛物线对称轴与x 轴的交点,点Q 在抛物线的对称轴上,设Q(2, 2n),则 M 坐标为( 2﹣ n,n),∵点 M 在抛物线 y= ﹣ x2+2x+6 的图象上,∴ n=﹣(2﹣n)2+2(2﹣n)+6,解得n=﹣1+或n=﹣1﹣,∴知足条件的点Q 有两个,其坐标分别为(2,﹣ 2+2)或(2,﹣2﹣2).3.如图,已知抛物线y=ax2 +bx﹣ 3 过点 A (﹣ 1, 0), B( 3,0),点 M 、 N 为抛物线上的动点,过点M 作MD ∥ y 轴,交直线 BC 于点 D ,交 x 轴于点 E.过点 N 作 NF ⊥ x 轴,垂足为点 F( 1)求二次函数 y=ax2+bx ﹣ 3 的表达式;( 2)若 M 点是抛物线上对称轴右边的点,且四边形MNFE 为正方形,求该正方形的面积;( 3)若 M 点是抛物线上对称轴左边的点,且∠DMN=90°, MD=MN ,请直接写出点M 的横坐标.【解答】解:( 1)把 A (﹣ 1, 0),B ( 3, 0)代入 y=ax 2+bx ﹣ 3,得:,解得,故该抛物线分析式为:y=x 2﹣2x﹣ 3;(2)由( 1)知,抛物线分析式为: y=x 2﹣2x﹣ 3=( x﹣ 1)2﹣ 4,∴该抛物线的对称轴是 x=1 ,极点坐标为( 1,﹣ 4).如图,设点 M 坐标为( m, m2﹣2m﹣ 3),此中 m> 1,∴ME=| ﹣ m2+2m+3|,∵M 、 N 对于 x=1 对称,且点 M 在对称轴右边,∴点 N 的横坐标为 2﹣ m,∴MN=2m ﹣ 2,∵四边形MNFE 为正方形,∴ME=MN ,∴|﹣ m2+2m+3|=2m ﹣ 2,分两种状况:①当﹣ m2+2m+3=2m ﹣ 2 时,解得: m1= 、 m2=﹣(不切合题意,舍去),当 m= 时,正方形的面积为( 2 ﹣2)2=24 ﹣ 8 ;②当﹣ m2 3 4=2﹣(不切合题意,舍去),+2m+3=2 ﹣ 2m 时,解得: m =2+ , m当 m=2+ 时,正方形的面积为[2 (2+ )﹣ 2]2=24+8 ;综上所述,正方形的面积为24+8 或 24﹣ 8 .( 3)设 BC 所在直线分析式为y=px+q ,把点 B (3, 0)、C( 0,﹣ 3)代入表达式,得:,解得:,∴直线 BC 的函数表达式为y=x﹣ 3,设点 M 的坐标为( t, t2﹣ 2t﹣ 3),此中 t <1,则点 N( 2﹣ t, t2﹣2t﹣ 3),点 D ( t, t﹣ 3),∴MN=2 ﹣ t﹣t=2 ﹣2t, MD=|t 2﹣ 2t﹣ 3﹣ t+3|=|t2﹣3t|.∵ MD=MN ,∴ |t2﹣ 3t|=2﹣ 2t,分两种状况:①当 t2﹣ 3t=2﹣ 2t 时,解得 t 1=﹣ 1, t2=2 (不切合题意,舍去).二次函数专题训练(正方形的存在性)②当 3t﹣ t2=2﹣ 2t 时,解得3 2(不切合题意,舍去).t = , t =综上所述,点 M 的横坐标为﹣ 1 或.4.(2015 贵州省毕节地域 ) 如图,抛物线 y=x 2+bx+c 与 x 轴交于 A (﹣ 1,0), B( 3, 0)两点,极点M 关于 x 轴的对称点是M′.( 1)求抛物线的分析式;( 2)若直线AM′与此抛物线的另一个交点为C,求△ CAB 的面积;( 3)能否存在过A, B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的分析式;若不存在,请说明原因.剖析:(1)依据待定系数法,可得函数分析式;( 2)依据轴对称,可得M′的坐标,依据待定系数法,可得AM′的分析式,依据解方程组,可得B点坐标,依据三角形的面积公式,可得答案;( 3)依据正方形的性质,可得P、 Q 点坐标,依据待定系数法,可得函数分析式.解答:解:( 1)将 A 、 B 点坐标代入函数分析式,得,解得,抛物线的分析式y=x 2﹣ 2x﹣ 3;( 2)将抛物线的分析式化为极点式,得 y= ( x﹣1)2﹣ 4, M点的坐标为( 1,﹣ 4), M′点的坐标为( 1, 4),设AM′的分析式为 y=kx+b ,将 A 、M′点的坐标代入,得,解得,AM′的分析式为y=2x+2 ,联立 AM′与抛物线,得,解得,C点坐标为( 5,12). S△ABC = ×4×12=24;( 3)存在过 A ,B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形,由 ABPQ 是正方形, A (﹣ 1, 0) B ( 3, 0),得P( 1,﹣ 2), Q( 1, 2),或 P(1, 2), Q( 1,﹣ 2),将 A 点坐标代入函数分析式,得a(﹣ 1﹣ 1)2﹣ 2=0 ,解得 a=,抛物线的分析式为y=(x﹣1)2﹣2,②当 P( 1, 2)时,设抛物线的分析式为 y=a( x﹣ 1)2+2,将 A点坐标代入函数分析式,得 a(﹣ 1﹣ 1)2+2=0 ,解得 a=﹣,抛物线的分析式为y=﹣(x﹣1)2+2,综上所述: y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,使得四边形APBQ 为正方形.5. (2016 辽宁省铁岭市 ) .如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A ,点 B,与 y 轴交于点C,点 B坐标为( 6,0),点 C 坐标为( 0,6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠ FBA=∠ BDE时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M作MN∥ x轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在平面内,以线段 MN 为对角线作正方形MPNQ ,请直接写出点Q 的坐标.剖析( 1)由点 B 、C 的坐标利用待定系数法即可求出抛物线的分析式,再利用配方法将抛物线分析式变形成极点式即可得出结论;( 2)设线段 BF 与 y 轴交点为点 F′,设点 F′的坐标为( 0, m),由相像三角形的判断及性质可得出点F′的坐标,依据点B、F′的坐标利用待定系数法可求出直线BF 的分析式,联立直线BF 和抛物线的分析式成方程组,解方程组即可求出点 F 的坐标;( 3)设对角线 MN 、 PQ 交于点 O′,如图 2 所示.依据抛物线的对称性联合正方形的性质可得出点P、 Q 的地点,设出点Q 的坐标为( 2, 2n),由正方形的性质可得出点M 的坐标为(2﹣n, n).由点 M 在抛物线图象上,即可得出对于n 的一元二次方程,解方程可求出n 值,代入点Q 的坐标即可得出结论.解答解:( 1)将点 B ( 6,0)、 C( 0, 6)代入 y=﹣x2+bx+c 中,得:,解得:,∴ 抛物线的分析式为y= ﹣x2+2x+6 .∵ y= ﹣x2+2x+6= ﹣(x﹣2)2+8,∴点 D 的坐标为( 2, 8).(2)设线段 BF 与 y 轴交点为点 F′,设点 F′的坐标为( 0,m),如图 1 所示.∵∠ F′BO=∠ FBA= ∠ BDE ,∠ F′OB=∠ BED=90°,∴△ F′BO∽△ BDE ,∴.∵点 B (6, 0),点 D( 2, 8),11∴点 E( 2, 0),BE=6 ﹣ 4=4 , DE=8 ﹣ 0=8 ,OB=6 ,∴OF′=?OB=3,∴点 F′(0, 3)或( 0,﹣ 3).设直线 BF 的分析式为y=kx±3,则有 0=6k+3 或 0=6k﹣ 3,解得: k= ﹣或k=,∴直线 BF 的分析式为y=﹣x+3 或 y=x﹣ 3.联立直线 BF 与抛物线的分析式得:① 或② ,解方程组①得:或(舍去),∴ 点F的坐标为(﹣1,);解方程组②得:或(舍去),∴ 点F的坐标为(﹣3,﹣).综上可知:点 F 的坐标为(﹣ 1,)或(﹣ 3,﹣).( 3)设对角线 MN 、 PQ 交于点 O′,如图 2 所示.∵点 M 、 N 对于抛物线对称轴对称,且四边形MPNQ 为正方形,∴点 P 为抛物线对称轴与x 轴的交点,点 Q 在抛物线对称轴上,设点 Q 的坐标为(2, 2n),则点 M 的坐标为( 2 ﹣ n, n).∵点 M 在抛物线 y= ﹣x2+2x+6 的图象上,∴ n=﹣+2( 2﹣ n) +6,即 n2+2n ﹣ 16=0,解得: n1= ﹣ 1 , n2 =﹣﹣1.∴点 Q 的坐标为(2,﹣ 1)或( 2,﹣﹣ 1).6. (2016 广东省茂名市 ) 】.如图,抛物线 y= ﹣ x2 +bx+c 经过 A (﹣ 1,0), B( 3,0)两点,且与 y 轴交于点 C,点 D 是抛物线的极点,抛物线的对称轴DE 交 x 轴于点 E,连结 BD .(1)求经过 A ,B ,C 三点的抛物线的函数表达式;(2)点 P 是线段 BD 上一点,当 PE=PC 时,求点 P 的坐标;( 3)在( 2)的条件下,过点P 作 PF⊥x 轴于点 F, G 为抛物线上一动点,M 为 x 轴上一动点, N 为直线PF 上一动点,当以F、 M 、 G 为极点的四边形是正方形时,恳求出点M 的坐标.剖析( 1)利用待定系数法求出过A, B,C 三点的抛物线的函数表达式;12( 2)连结 PC、PE,利用公式求出极点 D 的坐标,利用待定系数法求出直线BD 的分析式,设出点P 的坐标为( x,﹣ 2x+6 ),利用勾股定理表示出PC2和 PE2,依据题意列出方程,解方程求出x 的值,计算求出点 P 的坐标;(3)设点 M 的坐标为( a, 0),表示出点 G 的坐标,依据正方形的性质列出方程,解方程即可.解答解:( 1)∵抛物线 y= ﹣x2+bx+c 经过 A (﹣ 1, 0), B ( 3, 0)两点,∴,解得,,∴ 经过A,B,C三点的抛物线的函数表达式为y= ﹣ x2+2x+3 ;( 2)如图 1,连结 PC、PE, x= ﹣=﹣=1,当x=1 时, y=4 ,∴点 D 的坐标为( 1, 4),设直线 BD 的分析式为: y=mx+n ,则,解得,,∴ 直线BD的分析式为y= ﹣ 2x+6,设点 P 的坐标为( x,﹣ 2x+6),则PC2=x 2+(3+2x ﹣ 6)2,PE2=( x﹣ 1)2+(﹣ 2x+6 )2,∵PC=PE,∴x2+(3+2x ﹣6)2=(x﹣1)2+(﹣2x+6 )2,解得, x=2,则 y= ﹣2×2+6=2 ,∴点 P 的坐标为( 2, 2);(3)设点 M 的坐标为( a, 0),则点 G 的坐标为( a,﹣ a2 +2a+3),∵以 F、M 、 G 为极点的四边形是正方形,∴ FM=MG ,即 |2﹣ a|=|﹣ a2 +2a+3|,当 2﹣ a=﹣ a2+2a+3 时,整理得,a2﹣ 3a﹣1=0 ,解得, a=,当2﹣ a=﹣(﹣ a2+2a+3)时,整理得, a2﹣ a﹣5=0 ,解得, a= ,∴当以 F、M 、G 为极点的四边形是正方形时,点 M 的坐标为(,0),(,0),(,0),(, 0).13。
(完整版)初中数学二次函数专题经典练习题(附答案)

二次函数总复习经典练习题1.抛物线y=-3x2+2x-1 的图象与坐标轴的交点情况是( )(A) 没有交点.(B) 只有一个交点.(C) 有且只有两个交点.(D) 有且只有三个交点.2.已知直线y=x 与二次函数y=ax2-2x- 1 图象的一个交点的横坐标为1,则 a 的值为( )(A)2 .(B)1 .(C)3 .(D)4 .3.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y 轴于点C,则△ ABC的面积为( ) (A)6 .(B)4 .(C)3 .(D)1 .24.函数y=ax 2+bx+ c 中,若a> 0,b< 0,c<0,则这个函数图象与x 轴的交点情况是( )(A) 没有交点.(B) 有两个交点,都在x 轴的正半轴.(C) 有两个交点,都在x 轴的负半轴.(D) 一个在x 轴的正半轴,另一个在x 轴的负半轴.5.已知(2 ,5) 、(4 ,5)是抛物线y=ax2+bx+c 上的两点,则这个抛物线的对称轴方程是( ) a(A) x= .(B) x=2.(C) x=4.(D) x=3.b6.已知函数y=ax2+bx+ c 的图象如图 1 所示,那么能正确反映函数y=ax+ b 图象的只可能是( )7.二次函数y=2x2-4x+5 的最小值是_____ .28.某二次函数的图象与x轴交于点( -1,0) ,(4 ,0) ,且它的形状与y=-x2形状相同.则这个二次函数的解析式为_____ .9.若函数y=-x2+4 的函数值y> 0,则自变量x 的取值范围是______ .10.某品牌电饭锅成本价为70 元,销售商对其销量与定价的关系进行了调查,结果如下:801001101008060为获得最大利润,销售商应将该品牌电饭锅定价为元.11.函数y=ax 2-(a-3)x+ 1 的图象与x 轴只有一个交点,那么 a 的值和交点坐标分别为12.某涵洞是一抛物线形, 它的截面如图3 所示, 现测得水面宽AB 1.6m, 涵洞顶点O 到水面的距离为2.4m, 在图中的直角坐标系内, 涵洞所在抛物线的解析式为13.(本题8 分)已知抛物线y=x2-2x-2 的顶点为A,与y 轴的交点为B,求过A、B 两点的直线的解析式.14.(本题8分)抛物线y=ax2+2ax+a2+2的一部分如图3所示,求该抛物线在y 轴左侧与x 轴的交点坐标.15.(本题8 分)如图4,已知抛物线y=ax2+bx+c(a> 0)的顶点是C(0,1),直线l :y=-ax+3 与这条抛物线交于P、Q两点,且点P 到x 轴的距离为2.(1)求抛物线和直线l 的解析式;(2)求点Q的坐标.16.(本题8 分)工艺商场以每件155 元购进一批工艺品.若按每件200 元销售,工艺商场每天可售出该工艺品100 件;若每件工艺品降价 1 元,则每天可多售出该工艺品 4 件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?17.(本题10 分))杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第 1个月到第x 个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元) ,g也是关于x 的二次函数.(1) 若维修保养费用第 1 个月为 2 万元,第 2 个月为 4 万元.求y 关于x 的解析式;(2) 求纯收益g 关于x 的解析式;(3) 问设施开放几个月后,游乐场的纯收益达到最大?几个月后,能收回投资?18(本题10分)如图所示,图4- ①是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m,支柱A3B3=50m,5 根支柱A1B1、A2B2、A3B3、A4B4、A5B5 之间的距离均为15m,B1B5∥ A1A5,将抛物线放在图4- ②所示的直角坐标系中.(1) 直接写出图4- ②中点B1、B3、B5的坐标;(2) 求图4- ②中抛物线的函数表达式;(3) 求图4- ①中支柱A2B2、A4B4 的长度.B319、如图5,已知A(2,2),B(3,0).动点P( m,0)在线段OB上移动,过点P作直线l 与x 轴垂直.(1) 设△ OAB中位于直线l 左侧部分的面积为S,写出S与m之间的函数关系式;(2) 试问是否存在点P,使直线l 平分△ OAB的面积?若有,求出点P 的坐标;若无,请说明理由.更多学习方法和中高考复习资料,免费下载,扫一扫关注微信:答案:一、1.B 2 .D 3 .C 4 .D 5 .D 6.B二、 7.3 8 .y =- x +3x +4 9 .- 2< x <2 10 .1301 115 211. a =0, ( ,0);a =1,(-1,0);a =9,( ,0) 12 . y x 23 3 413.抛物线的顶点为 (1,- 3),点 B 的坐标为 (0,- 2).直线 AB 的解析式为 y =-x -2 14.依题意可知抛物线经过点 (1,0) .于是 a + 2a + a 2+ 2=0,解得 a 1=-1,a 2=-2.当 a = -1 或 a =-2 时,求得抛物线与 x 轴的另一交点坐标均为 ( -3,0)2 15. (1) 依题意可知 b =0,c =1,且当 y =2 时,ax 2+1=2①,- ax +3=2②.由①、②解得 a =1, x =1.故抛物线与直线的解析式分别为: y =x 2+ 1,y =- x +3;(2) Q ( -2,5)216.设降价 x 元时,获得的利润为 y 元.则依意可得 y =(45-x )(100 +4x )= -4x 2+80x +4500, 即 y =-4(x -10)2+4900.故当 x =10时, y 最大=4900(元)2217. (1) 将(1,2)和(2,6) 代入 y =ax 2+bx ,求得 a =b =1.故 y =x 2+x ;(2) g =33x -150-y , 22即 g =-x 2+32x -150;(3) 因 y =-(x -16) 2+106,所以设施开放后第 16 个月,纯收益最大.令 g =0,得- x 2+ 32 x - 150=0.解得 x =16± 106 ,x ≈16- 10.3=5.7( 舍去 26.3) .当 x =5 时, g <0, 当 x =6 时, g >0,故 6 个月后,能收回投资18.(1) B 1( 30,0), B 3 (0,30) , B 5 (30,0) ;(2)设抛物线的表达式为 y a (x 30)(x 30) ,把 B 3 (0,30) 代入得 y a(0 30)(0 30) 30.1∴ a .30∵所求抛物线的表达式为: y3)∵ B 4 点的横坐标为 15, 1 45∴B 4 的纵坐标 y 4 (15 30)(15 30) .4 30 2∵ A 3B 3 50 ,拱高为 30,1 (x 30)(x 30) . 30∴立柱A4B445 8520 (m) .22由对称性知:85A2B2 A4B4 (m) .2四、1 2 1 119.(1)当0≤m≤2时,S= m2;当2<m≤3时,S= ×3×2-(3 -m)(-2m+6)= -m22 2 2+6m-6.(2)若有这样的P点,使直线l 平分△ OAB的面积,很显然0<m<2.由于△ OAB3 1 3的面积等于3,故当l 平分△ OAB面积时,S= .∴ m2.解得m= 3 .故存在这样2 2 2的P点,使l 平分△ OAB的面积.且点P的坐标为(3 ,0).。
(完整word)九年级数学二次函数知识点总结及经典例题,推荐文档
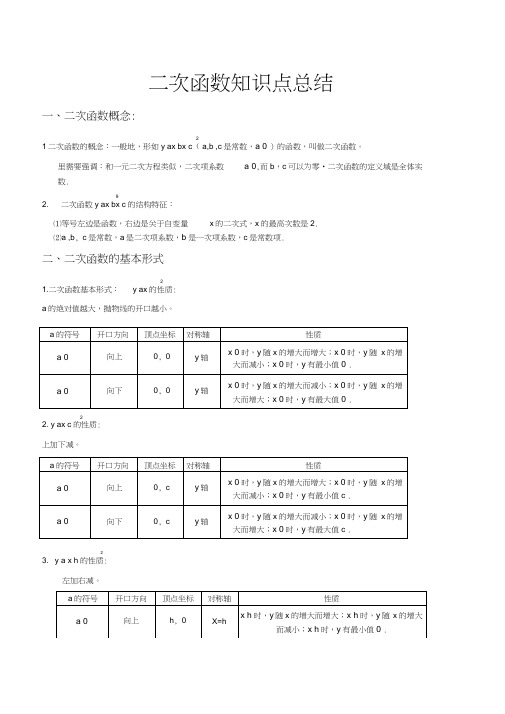
二次函数知识点总结一、二次函数概念:21二次函数的概念:一般地,形如y ax bx c( a,b ,c是常数,a 0 )的函数,叫做二次函数。
里需要强调:和一元二次方程类似,二次项系数 a 0,而b,c可以为零•二次函数的定义域是全体实数.92. 二次函数y ax bx c的结构特征:⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a ,b, c是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式21.二次函数基本形式:y ax的性质:a的绝对值越大,抛物线的开口越小。
22. y ax c的性质:上加下减。
23. y a x h的性质:左加右减。
24. y ax hk 的性质: a 的符号开口方向 顶点坐标 对称轴 性质a 0向上h , kX=hx h 时,y 随x 的增大而增大;x h 时,y 随 x 的增大而减小;x h 时,y 有最小值k •a 0向下 h , k X=hx h 时,y 随x 的增大而减小;x h 时,y 随 x 的增大而增大;x h 时,y 有最大值k •三、二次函数图象的平移1.平移步骤:2⑴将抛物线解析式转化成顶点式 y a x h k ,确定其顶点坐标 h , k ;⑵ 保持抛物线y ax 2的形状不变,将其顶点平移到 h ,k 处,具体平移方法如下:当x 2a 时,y 随x 的增大而减小; y=ax 2 A y=ax 2+k向右(h>0)【或左(*0)] 平移|k|个单位y=a(x h)2向右(h>0)【或左(h<0)] 平移|k|个单位2.平移规律在原有函数的基础上 概括成八个字“左加右减,h 值正右移,负左移;上加下减” •k 值正上移,负下移”六、 四、二次函数从解析式上看,b a x2a二次函数1. 4ac b 24a,其中 ax 2 bx c 的性质当a 0时,抛物线开口向上,对称轴为2axax 2 bx c 的比较bx c 是两种不同的表达形式, 后者通过配方可以得到前者,4ac b 2 4a盘,顶点坐标为b 4ac b 22a ' 4a向上(k>0)【或向下(k<0)】平移|k|个单位向上(k>0)【或下(k<0)】 平移|k 个单位向右(h>0)【或左(h<0)] 平移|k|个单位2当x佥时,y随x的增大而增大;x2a 时,y有最小值4ac b 2 4a2•当a 0时,抛物线开口向下, 对称轴为 x —,顶点坐标为2a b 4ac b 2 、[/ b ”亠方,F .当x 茲时,y 随 x 的增大而增大;当x 2a 时,b 4ac b 2y 随x 的增大而减小;当x 亦时,y 有最大值 f 七、 1. 二次函数解析式的表示方法一般式:y ax 2bx c ( a , b , c 为常数,a 0);2顶点式:y a (x h ) k ( a , h , k 为常数,a 0); 两根式(交点式):y a (x x i )(x X 2) ( a 0,为,x ?是抛物线与x 轴两交点的横坐标) 2. 3. 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只 有抛物线与x 轴有交点,即b 2 4ac 0时,抛物线的解析式才可以用交点式表示. 二次函数解析式的这三种形式可以互化.八、 1. ⑴ ⑵ 二次函数的图象与各项系数之间的关系二次项系数a当a 0时,抛物线开口向上, 当a 0时,抛物线开口向下, a 的值越大,开口越小,反之 a 的值越小,开口越大; a 的值越小,开口越小,反之 a 的值越大,开口越大.2. 一次项系数b在二次项系数a 确定的前提下, 3. 常数项c⑴当c ⑵当c ⑶当c总结起来, 0时, 0时, 0时, b 决定了抛物线的对称轴.(同左异右 b 为0对称轴为y 轴)抛物线与y 轴的交点在x 轴上方,即抛物线与 抛物线与抛物线与y 轴的交点在x 轴下方,即抛物线与 c决定了抛物线与y 轴交点的位置.y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为正; y轴交点的纵坐标为0 ; y 轴交点的纵坐标为负.九、二次函数与一元二次方程:i.二次函数与一元二次方程的关系(二次函数与 一二次方程ax 2 bx c 0是二次函数y x 轴的交点个数: 兀 图象与 ax 2 x 轴交点情况): bx c 当函数值y 0时的特殊情况.2b 4ac 0时,图象与x 轴交于两点Ax 1 ,0 ,B x 2 ,0 (x 1X 2),其中的X i , x 是一元二次方2ax bx 0的两根.• 1' 2' 0时, 0时, 当a 当a x 轴只有一个交点;x 轴没有交点. 0时,图象落在 0时,图象落在 图象与 图象与 x 轴的上方,无论 x 轴的下方,无论 x 为任何实数, x 为任何实数, 都有都有2.抛物线y 2axbx c 的图象与y 轴一定相交,交点坐标为 (0 , c);二次函数对应练习试题、选择题1.二次函数y2x 4x 7的顶点坐标是A.(2, —11)B. (-2, 7)C. (2, 11)D. (2, - 3)2.把抛物线y2x2向上平移1个单位, 得到的抛物线是(2A. y 2(x 1)B. y 2(x 2 21) C. y 2x 1 D. 2x2 12k3.函数y kx k和y (k 0)在同一直角坐标系中图象可能是图中的0)的图象如图所示,则下列结论:①a,b同号;②当x 1和x 3时,函数值相等;③4a b 0④当y 确的个数是()A.1个B.2 个C. 35.已知二次函数y ax2 bx c(a由图象可知关于兀二次方程axA. — 1 .6.已知二次函数A.第一象限C.第三象限7.方程2x x2A.0个8.已知抛物线过点A. y x2C. y x22时,x的值只能取0.其中正个个D. 4B.-2.3C.-0.3D.-3.32ax bx c的图象如图所示, 则点(ac,bc)在(B.第二象限D.第四象限-的正根的个数为xB.1A(2,0),B(-1,0), x 2 或y x2C.2与y轴交于点B.x 2 D.C,且0C=2.则这条抛物线的解析式为y x2 x 22 、2y x x 2 或y x x 2二、填空题9•二次函数y x2 bx 3的对称轴是x 2,则b ______________ 。
(word版)初三数学二次函数专题训练(含答案),文档

二次函数专题训练〔含答案〕一、填空题1.把抛物线y1x2向左平移2个单位得抛物线,接着再向下平移3个2单位,得抛物线.2 .函数y2x2x图象的对称轴是,最大值是.3 .正方形边长为3,如果边长增加x面积就增加y,那么y与x之间的函数关系是.4.二次函数y2x28x 6,通过配方化为y a(x h)2k的形为.5.二次函数y ax2c〔c不为零〕,当x取x,x〔x≠x〕时,函数值相等,那么1212x1与x2的关系是.6.抛物线y ax2bx c当b=0时,对称轴是,当a,b同号时,对称轴在y轴侧,当a,b异号时,对称轴在y轴侧.7.抛物线y 2(x1)23开口,对称轴是,顶点坐标是.如果y随x的增大而减小,那么x的取值范围是.8 .假设a0,那么函数y2x2ax5图象的顶点在第象限;当x a时,函4数值随x的增大而.二次函数9.口抛物线y ax2bx c〔a≠0〕当a0时,图象的开口a0时,图象的开,顶点坐标是.y1(x h)2,开口,顶点坐标是,对称轴2是.11.二次函数y3(x)2()的图象的顶点坐标是〔1,-2〕.12.y1(x1)22,当x时,函数值随x的增大而减小.313.直线y2x1与抛物线y5x2k交点的横坐标为2,那么k=,交点坐标为.14.用配方法将二次函数y x22x化成y a(xh)2k的形式是. 315.如果二次函数yx26x m的最小值是1,那么m的值是.二、选择题:16.在抛物线y2x23x1上的点是〔〕1A.〔0,-1〕B.1,0 C.〔-1,5〕D.〔3,4〕217.直线y5x2与抛物线yx21x的交点个数是〔〕22个个个 D.互相重合的两个18.关于抛物线y ax2bx c〔a≠0〕,下面几点结论中,正确的有〔〕①当a0时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大,当0时,情况相反.②抛物线的最高点或最低点都是指抛物线的顶点.③只要解析式的二次项系数的绝对值相同,两条抛物线的形状就相同.④一元二次方程ax2bx c 0〔a≠0〕的根,就是抛物线y ax2bx c与x轴交点的横坐标.A.①②③④B.①②③C.①②D.①19.二次函数y=(x+1)(x-3),那么图象的对称轴是〔〕A.x=1B.x=-2C.x=3D.x=-320.如果一次函数yax b的图象如图代13-3-12中A所示,那么二次函yax2bx-3的大致图象是〔〕图代13-2-1221.假设抛物线y ax2bxc的对称轴是x 2,那么ab〔〕A.2B.11D.2422.假设函数y a1,-2〕,那么抛物线的图象经过点〔xA.质说得全对的是〔〕开口向下,对称轴在y轴右侧,图象与正半开口向下,对称轴在y轴左侧,图象与正半开口向上,对称轴在y轴左侧,图象与负半开口向下,对称轴在y轴右侧,图象与负半y ax2(a 1)x a3的性轴相交轴相交轴相交轴相交23.二次函数y x2bxc中,如果b+c=0,那么那时图象经过的点是〔〕A.(-1,-1)B.(1,1)C.(1,-1)D.〔-1,1〕224.函数y ax2与y a〔a0〕在同一直角坐标系中的大致图象是〔〕x图代13-3-1325.如图代13-3-14,抛物线y x2bx c与y轴交于A点,与x轴正半轴交于B,C两点,且BC=3,S△ABC=6,那么b的值是〔〕A.b=5B.b=-5C.b=±5D.b=4图代13-3-1426.二次函数y ax2〔a 0〕,假设要使函数值永远小于零,那么自变量x的取值范围是〔〕A.X取任何实数00或x027.抛物线y2(x3)24向左平移1个单位,向下平移两个单位后的解析式为〔〕A.y2(x4)26B.y2(x4)22C.y2(x2)22D.y3(x3)2228.二次函数y x2ykx9k2〔k0〕图象的顶点在〔〕轴的负半轴上轴的正半轴上轴的负半轴上轴的正半轴上29.四个函数:y x,y x1,y1〔x0〕,y x2〔x0〕,其中图象经过原x点的函数有〔〕个个个个30.不管x为值何,函数y ax2bx c〔a≠0〕的值永远小于0的条件是〔〕0,00,03C.a0,00,0三、解答题31.二次函数y x22ax 2b 1和y x2(a 3)x b21的图象都经过x轴上两上不同的点M,N,求a,b的值.32.二次函数y ax2bx c的图象经过点A〔2,4〕,顶点的横坐标为1,它2的图象与x轴交于两点B〔x1,0〕,C〔x2,0〕,与y轴交于点D,且x12x2213,试问:y轴上是否存在点P,使得△POB与△DOC相似〔O为坐标原点〕?假设存在,请求出过P,B两点直线的解析式,假设不存在,请说明理由.33.如图代13-3-15,抛物线与直线y=k(x-4)都经过坐标轴的正半轴上A,B两点,该抛物线的对称轴x=-21与x轴相交于点C,且∠ABC=90°,求:〔1〕直线AB的解析式;〔2〕抛物线的解析式.图代13-3-15图代13-3-1634.中图代13-3-16,抛物线y ax23x c交x轴正方向于A,B两点,交y轴正方向于C点,过A,B,C三点做⊙D,假设⊙D与y轴相切.〔1〕求a,c满足的关系;〔2〕设∠ACB=α,求tgα;〔3〕设抛物线顶点为 P,判断直线PA与⊙O的位置关系并证明.如图代13-3-17,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴,桥拱的DGD'局部为一段抛物线,顶点C的高度为8米,AD和A'D'是两侧高为米的支柱,OA和OA'为两个方向的汽车通行区,宽都为15米,线段CD和C'D'为两段对称的上桥斜坡,其坡度为1∶4.求〔1〕桥拱DGD'所在抛物线的解析式及CC'的长;〔2〕BE和B'E'为支撑斜坡的立柱,其高都为4米,相应的AB和A'B'为两个方向的行人及非机动车通行区,试求AB和A'B'的宽;〔3〕按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于米,车载大型设备的顶部与地面的距离均为7米,它能否从OA〔或OA'〕区域平安通过?请说明理由.4图代13-3-1736.:抛物线yx 2 (m 4)x m 2与x 轴交于两点A(a,0),B(b,0)〔ab 〕.O为坐标原点,分别以OA ,OB 为直径作⊙O 和⊙O 在y 轴的哪一侧?简要说明理由,并12指出两圆的位置关系.37.如果抛物线yx 2 2(m 1)x m 1与x 轴都交于A ,B 两点,且A 点在x 轴( 的正半轴上,B 点在x 同的负半轴上, OA 的长是a ,OB 的长是b.1〕求m 的取值范围;2〕假设a ∶b=3∶1,求m 的值,并写出此时抛物线的解析式;〔3〕 设〔2〕中的抛物线与 y 轴交于点 C ,抛物线的顶点是 M ,问:抛物线上是否存 在点P ,使△PAB 的面积等于△BCM 面积的8倍?假设存在,求出 P 点的坐标;假设不存在,请说明理由.38.:如图代13-3-18,EB 是⊙O 的直径,且EB=6,在BE 的延长线上取点 P ,使是EP 上一点,过A 作⊙O 的切线AD ,切点为D ,过D 作DF ⊥AB 于F ,过B 作AD 的垂线BH ,交AD 的延长线于H ,连结ED 和FH.图代13-3-181〕假设AE=2,求AD 的长.〔2〕当点A 在EP 上移动〔点A 不与点E 重合〕时,①是否总有ADED?试证明AH FH你的结论;②设 ED=x ,BH=y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.39.二次函数yx2(m24m5)x2(m24m9)的图象与x 轴的交点为2240. A ,B 〔点A 在点B 右边〕,与y 轴的交点为 C.1〕假设△ABC 为Rt △,求m 的值;2〕在△ABC 中,假设AC=BC ,求∠ACB 的正弦值;〔3〕设△ABC 的面积为 S ,求当m 为何值时,S 有最小值,并求这个最小值 .如图代13-3-19,在直角坐标系中,以AB 为直径的⊙C 交x 轴于A ,交y 轴于B ,满足OA ∶OB=4∶3,以OC 为直径作⊙D ,设⊙D 的半径为2.5图代13-3-191〕求⊙C 的圆心坐标.2〕过C 作⊙D 的切线EF 交x 轴于E ,交y 轴于F ,求直线EF 的解析式.〔3〕抛物线yax 2bx c 〔a ≠0〕的对称轴过C 点,顶点在⊙C 上,与y 轴交点为B ,求抛物线的解析式.41.直线y1x 和yx m ,二次函数yx 2pxq 图象的顶点为M.21x 与y〔1〕假设M 恰在直线yx m 的交点处,试证明:无论m 取何实数值,2二次函数yx 2 pxq 的图象与直线 y xm 总有两个不同的交点.〔2〕在〔1〕的条件下,假设直线y x m 过点D 〔0,-3〕,求二次函数yx 2pxq 的表达式,并作出其大致图象.图代13-3-20〔3〕 在〔2〕的条件下,假设二次函数 y x 2 pxq 的图象与y 轴交于点C ,与x同的左交点为A ,试在直线y1x 上求异于M 点P ,使P 在△CMA 的外接圆上.242.如图代 13-3-20,抛物线yx 2 ax b 与x 轴从左至右交于A ,B 两点,( 与y 轴交于点C ,且∠BAC=α,∠ABC=β,tg α-tg β=2,∠ACB=90°.1〕求点C 的坐标;2〕求抛物线的解析式;3〕假设抛物线的顶点为P ,求四边形ABPC 的面积.6参 考 答 案动脑动手设每件提高x 元〔0≤x ≤10〕,即每件可获利润〔2+x 〕元,那么每天可销售〔100-10x 〕件,设每天所获利润为y 元,依题意,得y (2x)(10010x)10x 2 80x 20010(x4)2 360.∴当x=4时〔0≤x ≤10〕所获利润最大,即售出价为 14元,每天所赚得最大利润 360元.2.∵ymx 23m 4x 4,3∴当x=0时,y=4.当mx 23m 4x4 0,m0时m 1 3,m 24.33m即抛物线与y 轴的交点为〔0,4〕,与x 轴的交点为A 〔3,0〕,B4,0.3m1〕当AC=BC 时,43,m 4.3m4x 2 9 ∴y492〕当AC=AB 时,AO 3,OC4,AC 5.∴45 .33mm 112 .∴,m 231时,y1x 2 11x4;6当m666当m2时,y2x22x4.3333〕当AB=BC 时,44 2342,3m3m∴m8.77∴y8x244x4.721可求抛物线解析式为:y4x24,y1x211x4,y2x22x4或8x244x 96633y4.7213.〔1〕∵[(25)]24(226)m mm22m21(m2 1)20图代13-3-21∴不管m取何值,抛物线与x轴必有两个交点.令y=0,得x2(m25)x2m260(x2)(xm23)0,∴x12,x2m23.∴两交点中必有一个交点是A〔2,0〕.〔2〕由〔1〕得另一个交点B的坐标是〔m2+3,0〕.d m232m21,∵m2+100,∴d=m2+1.3〕①当d=10时,得m2=9.∴A〔2,0〕,B〔12,0〕.y x214x24(x7)225.该抛物线的对称轴是直线x=7,顶点为〔7,-25〕,∴AB的中点E〔7,0〕.过点P作PM⊥AB于点M,连结PE,那么PE 1AB5,PM2b2,ME2(7a)2,2∴(7a)2b252.①∵点PD在抛物线上,8∴b(a 7)2 25. ②解①②联合方程组,得 b 1 1,b 2 0.当b=0时,点P 在x 轴上,△ABP 不存在,b=0,舍去.∴b=-1.注:求b 的值还有其他思路,请读者探觅,写出解答过程.②△ABP 为锐角三角形时,那么-25≤b -1;△ ABP 为钝角三角形时,那么 b -1,且b ≠0.同步题库一、 填空题1.y1(x2)2,y1(x 2)23;2.x1,1;3.y(x3)29;4.224 8y2(x2)22;5. 互为相反数;轴,左,右;7. 下,x=-1,(-1,-3) ,x-1;8.四,增大;9.向上,向下,b ,4ac b 2 ,xb ; 10.向下,〔h,0〕,x=h ;2a4a2a1 2,-2;-1;,〔2,3〕;14.yx13;15.10.9二、选择题 28. C三、解答题解法一:依题意,设M 〔x 1,0〕,N 〔x 2,0〕,且x 1≠x 2,那么x 1,x 2为方程x 2+2ax-2b+1=0的两个实数根,∴x 1 x 22a ,x 1·x 22b1. ∵x 1,x 2又是方程x 2 (a3)xb 21 0的两个实数根,∴ x1+x 2=a-3,x 1·x 2=1-b 2.∴2a a 3,2b 1 1 b 2.解得a 1, 或a 1,b 0;b2.当a=1,b=0 时,二次函数的图象与x 轴只有一个交点,a=1,b=0舍去.当a=1;b=2时,二次函数y x 2 2x 3和yx 22x 3符合题意.∴a=1,b=2.解法二:∵二次函数yx 22ax 2b 1的图象对称轴为x a ,9二次函数 yx 2 (a 3)x b 21的图象的对称轴为 xa3,2又两个二次函数图象都经过 x 轴上两个不同的点 M ,N ,∴两个二次函数图象的对称轴为同一直线 .∴a3.a2解得a1.∴两个二次函数分别为yx 2 2x 2b1和yx 2 2xb 21.依题意,令y=0,得x 2 2x 2b 1 0,x 2 2xb 2 10.①+②得b 22b 0. 解得b 1 0,b 22.∴a 1,a 1,b 0;或2.b当a=1,b=0时,二次函数的图象与 x 轴只有一个交点,∴a=1,b=0舍去.当a=1,b=2时,二次函数为y x 22x 3和yx 2 2x3符合题意.∴a=1,b=2.32.解:∵y ax 2 bx c 的图象与x 轴交于点B 〔x 1,0〕,C 〔x 2,0〕,∴x 1 x 2b,x 1x 2c .aa又∵x 12 x 22 13即(x 1x 2)2 2x 1x 2 13,∴( b )22 c 13 .①aa又由y 的图象过点A 〔2,4〕,顶点横坐标为1,那么有4a+2b+c=42,②b 1③2a.2解由①②③组成的方程组得a=-1,b=1,c=6.10∴ y=-x 2+x+6.与x 轴交点坐标为〔-2,0〕,〔3,0〕.与y 轴交点D 坐标为〔0,6〕.设y 轴上存在点 P ,使得△POB ∽△DOC ,那么有 〔1〕 当B 〔-2,0〕,C 〔3,0〕,D 〔0,6〕时,有OB OP ,OB 2,OC 3,OD6.OCOD∴OP=4,即点P 坐标为〔0,4〕或〔0,-4〕.当P 点坐标为〔0,4〕时,可设过P ,B 两点直线的解析式为y=kx+4.有 0=-2k-4.得 k=-2.∴ y=-2x-4.或 OBOP,OB2,OD6,OC3. OD OC ∴OP=1,这时P 点坐标为〔0,1〕或〔0,-1〕.当P 点坐标为〔0,1〕时,可设过P ,B 两点直线的解析式为y=kx+1.有 0=-2k+1.得1k.2∴y1x1.2当P 点坐标为〔0,-1〕时,可设过P ,B 两点直线的解析式为y=kx-1,有0=-2k-1 ,得k 1 .2∴y1x1.22〕当B 〔3,0〕,C 〔-2,0〕,D 〔0,6〕时,同理可得y=-3x+9,或 y=3x-9, 或y1x 1,3 或y11. x 3解:〔1〕在直线y=k(x-4)中,令y=0,得x=4.∴A 点坐标为〔4,0〕. ∴ ∠ABC=90°. ∵△CBD ∽△BAO ,∴OB OA2OCOB ,即OB=OA ·OC.11又∵CO=1,OA=4,∴OB2=1×4=4.∴OB=2〔OB=-2舍去〕∴B点坐标为〔0,2〕.将点B〔0,2〕的坐标代入y=k(x-4)中,得k 1.1x 2∴直线的解析式为:y2.2〔2〕解法一:设抛物线的解析式为y a(x1)2h,函数图象过A〔4,0〕,B〔0,2〕,得25a h0,a h 2.解得a1,h25. 1212∴抛物线的解析式为:y1(x1)225. 1212解法二:设抛物线的解析式为:y ax2bx c,又设点A〔4,0〕关于x=-1的对称是D.∵CA=1+4=5,∴CD=5.∴OD=6.∴D点坐标为〔-6,0〕.将点A〔4,0〕,B〔0,2〕,D〔-6,0〕代入抛物线方程,得16a4b c0,c2,36a6b c0.解得a 1,b1,c2. 126∴抛物线的解析式为:y1x21x2.12634.解:〔1〕A,B的横坐标是方程ax23x c 0的两根,设为x1,x2〔x2x1〕,C的纵坐标是C.又∵y轴与⊙O相切,∴OA2·OB=OC.∴x1·x2=c2.又由方程ax23x c0知x1x2c,a12∴c2c,即ac=1.a〔2〕连结PD ,交x 轴于E ,直线PD 必为抛物线的对称轴,连结AD 、BD ,图代13-3-22∴AE1AB .1 2ACBADBADE.2ax ,∵0,x21∴ABx 2x 1 9 4ac5a.aAE5.2a又ED=OC=c ,∴tg AE 5 .DE23〕设∠PAB=β,∵P 点的坐标为3, 5 ,又∵a0,2a 4a∴在Rt △PAE 中,PE5.4a∴PE5tg.AE2∴tgβ=tg α.∴β=α.∴∠PAE=∠ADE.∵∠ADE+∠DAE=90°PA 和⊙D 相切.解:〔1〕设DGD '所在的抛物线的解析式为 y ax 2 c ,由题意得 G 〔0,8〕,D 〔15,〕.138c,解得a1 , ∴9025ac.c 8.∴DGD '所在的抛物线的解析式为 y1x 2 8.∵AD1且AD=5.5,90AC4∴×4=22(米).∴cc2OC 2 (OA AC) 2(1522〕=74 〔米〕.答:cc '的长为 74米. 〔2〕∵EB 1,BE 4,BC=16.BC 4∴∴AB=AC-BC=22-16=6〔米〕.答:AB 和A 'B '的宽都是 6米.〔3〕在y1x 2 8中,当x=4时,901737y16 8 .90 45∵37 (7 0.4) 1970.4545∴该大型货车可以从 OA 〔OA '〕区域平安通过.解:〔1〕∵⊙O 1与⊙O 2外切于原点O ,∴A ,B 两点分别位于原点两旁,即 a0,b0.∴方程x 2 (m 4)x m 2 0的两个根a ,b 异号.ab=m+20,∴m-2.〔2〕当m-2,且m ≠-4时,四边形PO 1O 2Q 是直角梯形.根据题意,计算得S四边形POOQ1b 2〔或1a 2或1〕.1 22 2m=-4时,四边形POOQ 是矩形.1 2根据题意,计算得S四边形POOQ1b 2〔或1a 2或1〕.1 222〔3〕∵(m 4)2 4(m 2)(m2)240∴方程x 2 (m 4)x m 2 0有两个不相等的实数根.∵ m-2,∴a b m4 0,ab m 20.14∴a0,b0.∴⊙O1与⊙O2都在y轴右侧,并且两圆内切.解:〔1〕设A,B两点的坐标分别是〔x1,0〕、〔x2,0〕,∵A,B两点在原点的两侧,∴x1x20,即-〔m+1〕0,解得m-1.∵[2(m1)]24(1)(m1)4m24m84(m1)272当m-1时,0,∴m的取值范围是m-1.2〕∵a∶b=3∶1,设a=3k,b=k〔k0〕,那么x1=3k,x2=-k,∴3k k2(m1),3k(k)(m1).解得m12,m21 .143∵m x2时,x1〔不合题意,舍去〕,33∴m=2∴抛物线的解析式是y x2x3.〔3〕易求抛物线y x22x3与x轴的两个交点坐标是A〔3,0〕,B〔-1,0〕与y轴交点坐标是C〔0,3〕,顶点坐标是M〔1,4〕.设直线BM的解析式为y px q,4 p1 q,那么0p(1)q.p2,解得q 2.∴直线BM的解析式是y=2x+2.设直线BM与y轴交于N,那么N点坐标是〔0,2〕,∴SBCM SBCNSMNC111111221.设P点坐标是〔x,y〕,15∵SABP8S BCM,∴1AB y81. 2即14y8.2∴y4.∴y4.当y=4时,P点与M点重合,即P〔1,4〕,当y=-4时,-4=-x2+2x+3,解得x122.∴满足条件的P点存在.P点坐标是〔1,4〕,(122,4),(122,4).38.〔1〕解:∵AD切⊙O于D,AE=2,EB=6,∴AD2=AE·AB=2×〔2+6〕=16.∴AD=4.图代13-2-23〔2〕①无论点A在EP上怎么移动〔点A不与点E重合〕,总有证法一:连结DB,交FH于G,∵AH是⊙O的切线,∴∠HDB=∠DEB.又∵BH⊥AH,BE为直径,∴∠BDE=90°AD ED.AH FH ∴有∠DBE=90°-∠DEB=90°-∠HDB=∠DBH.在△DFB和△DHB中,DF⊥AB,∠DFB=∠DHB=90°,DB=DB,∠DBE=∠DBH,∴△DFB∽△DHB.BH=BF,∴△BHF是等腰三角形.BG⊥FH,即BD⊥FH.16∴ED∥FH,∴AD ED.AH FH图代13-3-24证法二:连结DB,∵AH是⊙O的切线,∴∠HDB=∠DEF.又∵DF⊥AB,BH⊥DH,∴∠EDF=∠DBH.以BD为直径作一个圆,那么此圆必过F,H两点,∴∠DBH=∠DFH,∴∠EDF=∠DFH.∴ED∥FH.∴AD EDAH .FH ②∵ED=x,BH=,BH=y,BE=6,BF=BH,∴EF=6y.又∵DF是Rt△BDE斜边上的高,∴∴△DFE∽△BDE,EFED,即ED2EFEB.ED EB∴x26(6y),即y1x26.6∵点A不与点E重合,∴ED=x0.A从E向左移动,ED逐渐增大,当A和P重合时,ED最大,这时连结OD,那么OD⊥PH.∴OD∥BH.又POPE EO639,PB12,OD PO,BH ODPB4,BH PB PO ∴BF BH4,EF EB BF642,2由ED=EF·EB得x2 2 612,x0,∴x23.∴0x≤23.〔或由BH=4=y,代入y1x26中,得x23〕617故所求函数关系式为y1 x2 6〔0x ≤2 3〕.639.解:∵yx2m 4m5 x 2m24m 9(x2)[xm24m9],222∴可得A(2,0),Bm 24m 9 ,0,C0,2m 24m9 .22〔1〕∵△ABC 为直角三角形,∴OC 2OB ,AO24m9即4m24m92m,22化得(m 2)20.∴m=2.〔2〕∵AC=BC ,CO ⊥AB ,∴AO=BO ,即m 24m 9 2 .2∴OC2m 24m94.∴ACBC5.22过A 作AD ⊥BC ,垂足为D ,∴ AB·OC=BC ·AD.∴8AD.58∴sin ACBAD 5 4 .AC2 55图代13-3-25〔3〕S ABC1AB CO21m 24m 9 22m 24m9222(u2)u(u1)21.∵u m 2 4m9 1 ,2 2181,即m5∴当u2时,S 有最小值,最小值为.24解:〔1〕∵OA ⊥OB ,OA ∶OB=4∶3,⊙D 的半径为2,∴⊙C 过原点,OC=4,AB=8.A 点坐标为32,0,B 点坐标为0,24.55∴⊙C 的圆心C 的坐标为 16 ,12.52〕由EF 是⊙D 切线,∴OC ⊥EF.∵ CO=CA=CB,∴∠COA=∠CAO ,∠COB=∠CBO.∴ Rt△AOB ∽Rt △OCE ∽Rt △FCO.∴OE OC ,OFOC .AB OA AB OB∴OE5,OF20.3E 点坐标为〔 5,0〕,F 点坐标为0,20,3∴切线EF 解析式为y4x 20 .3 3〔3〕①当抛物线开口向下时,由题意,得抛物线顶点坐标为16,12 4,可得5 5b16, 5,2a 5 a324ac b 2 324ab1,524.24 cc. 55∴y5x 2 x 24 .32 5②当抛物线开口向上时 ,顶点坐标为16,124,得5 519b 16,5,2a 5a 4acb 28, b8 4,4a52424c.c .5541. ∴综合上述,抛物线解析式为〔1〕证明:由y5 x 2 4x 24 .8 5y5x 2 x24或y 5x 2 4x 24.325 85y1x, 2 yxm,有1xxm ,3221∴x mxmy m .2,3 , 32 1∴交点 M()m,m332m 21m此时二次函数为yx3 3x24mx 4m 2 1m .y ,有 3 93由②③联立,消去x24m1x4m 22m0.3934m1 244m 22m39316m 2 8m116m 28m9 3 931 0.∴无论m 为何实数值,二次函数y x 2pxq 的图象与直线yxm 总有两个不同的交点.20图代13-3-26〔2〕解:∵直线y=-x+m过点D〔0,-3〕,∴-3=0+m,∴m=-3.∴M〔-2,-1〕.∴二次函数为y(x2)21x24x3(x3)(x1).图象如图代13-3-26.3〕解:由勾股定理,可知△CMA为Rt△,且∠CMA=Rt∠,∴MC为△CMA外接圆直径.∵P在y 1x上,可设Pn,1n,由MC为△CMA外接圆的直径,P在这个圆上,22∴∠CPM=Rt∠.过P分别作PN⊥y,轴于N,PQ⊥x轴于R,过M作MS⊥y轴于S,MS的延长线与PR的延长线交于点Q.由勾股定理,有222212MP QP(n2)2n1.MQ,即MP222NC2NP231n n2.CP2220.CM而MP 2CP2CM2,21n2∴(n2)21n13n220,22即52260,n n2∴5n24n120,(5n6)(n2)0.21∴n 16,n 22.5 而n 2=-2即是M 点的横坐标,与题意不合,应舍去.∴n 6,5此时1 32n.5∴P 点坐标为6 ,3.5解:〔1〕根据题意,设点A 〔x 1,0〕、点〔x 2,0〕,且C 〔0,b 〕,x 10,x 20,b0,∵x 1,x 2是方程 x 2 axb0的两根, ∴x 1 x 2a,x 1x 2b .2在Rt △ABC 中,OC ⊥AB ,∴OC=OA ·OB.∵ OA=-x∴ bb0,∴b=1,∴C 〔0,1〕.〔2〕在Rt △AOC 的Rt △BOC 中,1,OB=x 2,2=-x 1·x 2=b.OCOC 1 1 x 1x 2 a tgtgx 1x 2x 1x 22.OAOBb∴a2.∴抛物线解析式为yx 2 2x1.图代13-3-27〔3〕∵y x 2 2x1,∴顶点P 的坐标为〔1,2〕,当x 2 2x 1 0时,x12. ∴A(12,0),B(12,0).延长PC 交x 轴于点D ,过C ,P 的直线为y=x+1, ∴点D 坐标为〔-1 ,0〕. ∴S 四边形ABPC S DPB S DCA221DB y p 1AD yc221(22)21(22)1 2232(平方单位).223。
最全九年级数学二次函数练习完整版.doc

x/米y/米O2018——2019学年度(上)九年级数学 二次函数练习 一1、抛物线2y x =先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A .()213y x =++B .()213y x =+-C .()213y x =--D .()213y x =-+ 2、某广场有一喷水池,水从地面喷出,如图,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线x x y 42+-=(单位:米)的一部分,则水喷出的最大高度是( )A.4米B.3米C.2米D.1米3、抛物线4412-+-=x x y 的对称轴是( )A 、2-=xB 、2=xC 、4-=xD 、4=x 4、函数42-=x y 的图像顶点坐标是( ).A 、(2,0)B 、(-2,0)C 、(0,4)D 、(0,-4)5、二次函数c bx ax y ++=2的图象如图所示,则下列结论中正确的是:( ) A a >0 b <0 c >0 B a <0 b <0 c >0 C a <0 b >0 c <0 D a <0 b >0 c >06、已知函数c bx ax y ++=2的图象如图所示,则函数b ax y +=的图象是( )答案:B7、抛物线y =2x 2由y =2(x +3)2 -4怎样的平移可得到抛物线.( )A 、先向左平移3个单位,再向上平移4个单位B 、先向左平移3个单位,再向下平移4个单位C 、先向右平移3个单位,再向上平移4个单位D 、先向右平移3个单位,再向下平移4个单位8、已知二次函数y =ax 2+bx +c (a ≠0)的图象如图,则下列结论中正确的是( ) A .a >0 B .当x >1时,y 随x 的增大而增大 C .c <0 D .3是方程ax 2+bx +c =0的一个根 9、如图是二次函数y 1=ax 2+bx +c 和一次函数y 2=mx +n 的图象,观察图象写出y 2≥y 1时,x 的取值范围( ) A .x ≥0 B .0≤x ≤1 C .-2≤x ≤1 D .x ≤110、抛物线c bx ax y ++=2中,b =4a ,它的图象如图,有以下结论:①0>c ;②0>++c b a③0>+-c b a ④042<-ac b⑤0<abc第9题图姓名:______⑥c a >4;其中正确的为( ) A .①② B .①④C .①②⑥D .①③⑤11、抛物线5)2(42+--=x y 的对称轴是_______________,顶点坐标是____________. 12、若抛物线22y x x m =++与x 轴只有一公共点,则m =_________13、二次函数22y x =+的图象开口_____,对称轴是________,与x 轴的交点坐标是_______. 14、抛物线223y x x =+-与x 轴交点个数为_______个,与坐标轴...交点个数___________个。
九年级数学 二次函数(篇)(Word版 含解析)

九年级数学 二次函数(篇)(Word 版 含解析)一、初三数学 二次函数易错题压轴题(难) 1.如图,抛物线()21y x a x a =-++与x 轴交于,A B 两点(点A 位于点B 的左侧),与y轴的负半轴交于点C .()1求点B 的坐标.()2若ABC 的面积为6.①求这条抛物线相应的函数解析式.②在拋物线上是否存在一点,P 使得POB CBO ∠=∠?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)(1,0);(2)①223y x x =+-;②存在,点P 的坐标为1133313++⎝⎭或53715337-+-⎝⎭. 【解析】【分析】(1)直接令0y =,即可求出点B 的坐标;(2)①令x=0,求出点C 坐标为(0,a ),再由△ABC 的面积得到12(1−a)•(−a)=6即可求a 的值,即可得到解析式;②当点P 在x 轴上方时,直线OP 的函数表达式为y=3x ,则直线与抛物线的交点为P ;当点P 在x 轴下方时,直线OP 的函数表达式为y=-3x ,则直线与抛物线的交点为P ;分别求出点P 的坐标即可.【详解】解:()1当0y =时,()210,x a x a -++= 解得121,.x x a ==点A 位于点B 的左侧,与y 轴的负半轴交于点,C0,a ∴<∴点B 坐标为()1,0.()2①由()1可得,点A 的坐标为(),0a ,点C 的坐标为()0,,0,a a <1,AB a OC a ∴=-=- ABC 的面积为6,()()116,2a a ∴--⋅= 123,4a a ∴=-=.0,a < 3a ∴=-22 3.y x x =+-②点B 的坐标为()1,0,点C 的坐标为()0,3-,∴设直线BC 的解析式为3,y kx =-则03,k =-3k ∴=.,POB CBO ∠=∠∴当点P 在x 轴上方时,直线//OP 直线,BC∴直线OP 的函数解析式3,y x =为则23,23,y x y x x =⎧⎨=+-⎩1112x y ⎧=⎪⎪∴⎨⎪=⎪⎩(舍去),2212x y ⎧+=⎪⎪⎨⎪=⎪⎩∴点的P坐标为1322⎛⎫+ ⎪ ⎪⎝⎭; 当点P 在x 轴下方时,直线'OP 与直线OP 关于x 轴对称,则直线'OP 的函数解析式为3,y x =-则23,23,y x y x x =-⎧⎨=+-⎩1152x y ⎧-=⎪⎪∴⎨⎪=⎪⎩舍去),2252x y ⎧-=⎪⎪⎨⎪=⎪⎩∴点P'的坐标为53715337,⎛⎫-+- ⎪ ⎪⎝⎭综上可得,点P 的坐标为1133313,⎛⎫++ ⎪ ⎪⎝⎭或53715337,⎛⎫-+- ⎪ ⎪⎝⎭【点睛】本题考查二次函数的图象及性质,一次函数的性质,熟练掌握二次函数的图象及性质,结合数形结合的思想和分类讨论的思想解题是解本题的关键.2.如图1,抛物线2:C y x =经过变换可得到抛物线()1111:C y a x x b =-,1C 与x 轴的正半轴交于点1A ,且其对称轴分别交抛物线C 、1C 于点1B 、1D ,此时四边形111D OB A 恰为正方形;按上述类似方法,如图2,抛物线()1111:C y a x x b =-经过变换可得到抛物线()2222:C y a x x b =-,2C 与x 轴的正半轴交于点2A ,且对称轴分别交抛物线1C 、2C 于点2B 、2D ,此时四边形222OB A D 也恰为正方形;按上述类似方法,如图3,可得到抛物线()3333:C y a x x b =-与正方形333OB A D ,请探究以下问题:(1)填空:1a = ,1b = ;(2)求出2C 与3C 的解析式;(3)按上述类似方法,可得到抛物线():n n n n C y a x x b =-与正方形n n n OB A D (1n ≥). ①请用含n 的代数式直接表示出n C 的解析式;②当x 取任意不为0的实数时,试比较2018y 与2019y 的函数值的大小关系,并说明理由.【答案】(1)11a =,12b =;(2)22132y x x =-,23126y x x =-;(3)①()2212123n n y x x n -=-≥⨯,②20182019y y >. 【解析】【分析】(1)求与x 轴交点A 1坐标,根据正方形对角线性质表示出B 1的坐标,代入对应的解析式即可求出对应的b 1的值,写出D 1的坐标,代入y 1的解析式中可求得a 1的值;(2)求与x 轴交点A 2坐标,根据正方形对角线性质表示出B 2的坐标,代入对应的解析式即可求出对应的b 2的值,写出D 2的坐标,代入y 2的解析式中可求得a 2的值,写出抛物线C 2的解析式;再利用相同的方法求抛物线C 3的解析式;(3)①根据图形变换后二次项系数不变得出a n =a 1=1,由B 1坐标(1,1)、B 2坐标(3,3)、B 3坐标(7,7)得B n 坐标(2n -1,2n -1),则b n =2(2n -1)=2n +1-2(n ≥1),写出抛物线C n 解析式.②根据规律得到抛物线C 2015和抛物线C 2016的解析式,用求差法比较出y 2015与y 2016的函数值的大小.【详解】解:(1)y 1=0时,a 1x (x -b 1)=0,x 1=0,x 2=b 1,∴A 1(b 1,0),由正方形OB 1A 1D 1得:OA 1=B 1D 1=b 1,∴B 1(12b ,12b ),D 1(12b ,12b -), ∵B 1在抛物线c 上,则12b =(12b )2, 解得:b 1=0(不符合题意),b 1=2,∴D 1(1,-1),把D 1(1,-1)代入y 1=a 1x (x -b 1)中得:-1=-a 1,∴a 1=1,故答案为1,2;(2)当20y =时,有()220a x x b -=,解得2x b =或0x =,()22,0A b ∴.由正方形222OB A D ,得2222B D OA b ==,222,22b b B ⎛⎫∴ ⎪⎝⎭,222,22b b D ⎛⎫- ⎪⎝⎭. 2B 在抛物线1C 上,2222222b b b ⎛⎫∴=- ⎪⎝⎭. 解得24b =或20b =(不合舍去),()22,2D ∴-2D 在抛物线2C 上,()22224a ∴-=-. 解得212a =.2C ∴的解析式是()2142y x x =-,即22122y x x =-. 同理,当30y =时,有()330a x x b -=,解得3x b =,或0x =.()33,0A b ∴.由正方形333OB A D ,得3333B D OA b ==,333,22b b B ⎛⎫∴ ⎪⎝⎭,333,22b b D ⎛⎫- ⎪⎝⎭. 3B 在抛物线2C 上,2333122222b b b ⎛⎫∴=-⋅ ⎪⎝⎭. 解得312b =或30b =(不合舍去), ()36,6D ∴-3D 在抛物线3C 上,()366612a ∴-=-.解得316a =. 3C ∴的解析式是()31126y x x =-,即23126y x x =-. (3)解:①n C 的解析式是()2212123n n y x x n -=-≥⨯. ②由①可得2201820161223y x x =-⨯,2201920171223y x x =-⨯. 当0x ≠时,220182019201620171110233y y x >⎛⎫-=- ⎪⎝⎭, 20182019y y ∴>.【点睛】本题是二次函数与方程、正方形的综合应用,将函数知识与方程、正方形有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用正方形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.就此题而言:①求出抛物线与x 轴交点坐标⇔把y =0代入计算,把函数问题转化为方程问题;②利用正方形对角线相等且垂直平分表示出对应B 1、B 2、B 3、B n 的坐标;③根据规律之间得到解析式是关键.3.如图,抛物线2y ax 2x c =++经过,,A B C 三点,已知()()1,0,0,3.A C -()1求此抛物线的关系式;()2设点P 是线段BC 上方的抛物线上一动点,过点P 作y 轴的平行线,交线段BC 于点,D 当BCP 的面积最大时,求点D 的坐标;()3点M 是抛物线上的一动点,当()2中BCP 的面积最大时,请直接写出使45PDM ∠=︒的点M 的坐标 【答案】(1)2y x 2x 3=-++;(2)点33,22D ⎛⎫⎪⎝⎭;(3)点M 的坐标为()0,3或113113,22⎛⎫++ ⎪ ⎪⎝⎭【解析】【分析】(1)由2y ax 2x c =++经过点()(),1,00,3A C -,利用待定系数法即可求得此抛物线的解析式.(2)首先设点()2,23,P t t t -++令2230x x -++=,求得()3,0B ,然后设直线BC 的关系式为y kx b =+,由待定系数法求得BC 的解析式为3y x =-+,可得()()22,3,2333D t t PD t t t t t -+=-++--+=-+,BCP 的面积为()21333,22S PD t t =⨯=-+利用二次函数的性质即可求解; (3)根据PD y 轴,45PDM ∠=︒,分别设DM y x b =+,DM y x b =-+,根据点33D(22,)坐标即可求出b ,再与抛物线联系即可得出点M 的坐标. 【详解】()1将()(),1,00,3A C -分别代入22,y ax x c =++可解得1,3,a c =-=即抛物线的关系式为2y x 2x 3=-++.()2设点()2,23,P t t t -++令2230,x x -++=解得121,3,x x =-=则点()3,0B .设直线BC 的关系式为(y kx b k =+为常数且0k ≠),将点,B C 的坐标代入,可求得直线BC 的关系式为3y x =-+.∴点()()22,3,2333D t t PD t t t t t -+=-++--+=-+设BCP 的面积为,S 则()21333,22S PD t t =⨯=-+ ∴当32t =时,S 有最大值,此时点33,22D ⎛⎫ ⎪⎝⎭. ()3∵PD y 轴,45PDM ∠=︒第一种情况:令DM y x b =+,33D(22,)解得:b=0∴223y x y x x =⎧⎨=-++⎩解得:113x 2=∴11M 22+(, 第二种情况:令DM y x b =-+,33D(22,)解得:b=3 ∴2323y x y x x =-+⎧⎨=-++⎩解得:x=0或x=3(舍去)∴M 03(,)满足条件的点M 的坐标为()0,3或⎝⎭【点睛】此题主要考查待定系数法求函数解析式和二次函数的性质,熟练掌握二次函数的性质是解题关键.4.二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ,顶点为P ,直线PA 与x 轴交于点B .(1)当m =1时,求顶点P 的坐标;(2)若点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上,且0b m ->,试求a 的取值范围;(3)在第一象限内,以AB 为边作正方形ABCD . ①求点D 的坐标(用含m 的代数式表示);②若该二次函数的图象与正方形ABCD 的边CD 有公共点,请直接写出符合条件的整数m 的值.【答案】(1)P (2,13);(2)a 的取值范围为:a <0或a >4;(3)①D (m ,m +3); ②2,3,4.【解析】【分析】(1)把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中,进而求顶点P 的坐标即可;(2)把点Q (a ,b )代入二次函数22(0)63m m y x x m m =-+>解析式中,根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组,解出a 的取值范围即可; (3)①过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,求出二次函数与y 轴的交点A 的坐标,得到OA 的长,再根据待定系数法求出直线AP 的解析式,进而求出与x 轴的交点B 的坐标,得到OB 的长;通过证明△ADF ≌△ABO ,得到AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,求出点D 的坐标;②因为二次函数的图象与正方形ABCD 的边CD 有公共点,由①同理可得:C (m+3,3),分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况,进行讨论m 可能取的整数值即可.【详解】解:(1)当m =1时,二次函数为212163y x x =-+,∴顶点P的坐标为(2,13);(2)∵点Q(a,b)在二次函数22(0)63m my x x m m=-+>的图象上,∴2263m mb a a m=-+,即:2263m mb m a a-=-∵0b m->,∴2263m ma a->0,∵m>0,∴2263a a->0,解得:a<0或a>4,∴a的取值范围为:a<0或a>4;(3)①如下图,过点D作DE⊥x轴于点E,过点A作AF⊥DE于点F,∵二次函数的解析式为2263m my x x m=-+,∴顶点P(2,3m),当x=0时,y=m,∴点A(0,m),∴OA=m;设直线AP的解析式为y=kx+b(k≠0),把点A(0,m),点P(2,3m)代入,得:23m bmk b=⎧⎪⎨=+⎪⎩,解得:3m k b m⎧=-⎪⎨⎪=⎩,∴直线AP 的解析式为y=3m -x+m , 当y=0时,x=3,∴点B (3,0);∴OB=3;∵四边形ABCD 是正方形,∴AD=AB ,∠DAF+∠FAB=90°,且∠OAB+∠FAB =90°,∴∠DAF=∠OAB ,在△ADF 和△ABO 中, DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△ABO (AAS ),∴AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,∴点D 的坐标为:(m ,m+3);②由①同理可得:C (m+3,3),∵二次函数的图象与正方形ABCD 的边CD 有公共点,∴当x =m 时,3y m ≤+,可得322363m m m m -+≤+,化简得:32418m m -≤. ∵0m >,∴2184m m m -≤,∴218(2)4m m--≤, 显然:m =1,2,3,4是上述不等式的解,当5m ≥时,2(2)45m --≥,18 3.6m ≤,此时,218(2)4m m-->, ∴符合条件的正整数m =1,2,3,4; 当x = m +3时,y ≥3,可得2(3)2(3)363m m m m m ++-+≥, ∵0m >,∴21823m m m ++≥,即218(1)2m m++≥, 显然:m =1不是上述不等式的解,当2m ≥时,2(1)211m ++≥,189m ≤,此时,218(1)2m m++>恒成立, ∴符合条件的正整数m =2,3,4;综上:符合条件的整数m 的值为2,3,4.【点睛】本题考查二次函数与几何问题的综合运用,熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键.5.如图所示,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠的顶点坐标为()3, 6C ,并与y 轴交于点()0, 3B ,点A 是对称轴与x 轴的交点.(1)求抛物线的解析式;(2)如图①所示, P 是抛物线上的一个动点,且位于第一象限,连结BP 、AP ,求ABP ∆的面积的最大值;(3)如图②所示,在对称轴AC 的右侧作30ACD ∠=交抛物线于点D ,求出D 点的坐标;并探究:在y 轴上是否存在点Q ,使60CQD ∠=?若存在,求点Q 的坐标;若不存在,请说明理由.【答案】(1)21233y x x =-++;(2)当92n =时,PBA S ∆最大值为818;(3)存在,Q 点坐标为((0,330,33-或,理由见解析【解析】【分析】(1)利用待定系数法可求出二次函数的解析式;(2)求三角形面积的最值,先求出三角形面积的函数式.从图形上看S △PAB=S △BPO+S △APO-S △AOB,设P 21,233n n n ⎛⎫-++ ⎪⎝⎭求出关于n 的函数式,从而求S △PAB 的最大值.(3) 求点D 的坐标,设D 21,233t t t ⎛⎫-++ ⎪⎝⎭,过D 做DG 垂直于AC 于G,构造直角三角形,利用勾股定理或三角函数值来求t 的值即得D 的坐标;探究在y 轴上是否存在点Q ,使60CQD ∠=?根据以上条件和结论可知∠CAD=120°,是∠CQD 的2倍,联想到同弧所对的圆周角和圆心角,所以以A 为圆心,AO 长为半径做圆交y 轴与点Q,若能求出这样的点,就存在Q 点. 【详解】 解:()1抛物线顶点为()3,6 ∴可设抛物线解析式为()236y a x =-+将()0,3B 代入()236y a x =-+得 396a =+13a ∴=- ∴抛物线()21363y x =--+,即21233y x x =-++ ()2连接,3, 3OP BO OA ==,PBA BPO PAO ABO S S S S ∆∆∆∆=+-设P 点坐标为21,233n n n ⎛⎫-++ ⎪⎝⎭1133222BPO x S BO P n n ∆=== 2211119323322322PAO y S OA P n n n n ∆⎛⎫==-++=-++ ⎪⎝⎭11933222ABO S OA BO ∆==⨯⨯= 22231991919813222222228PBA S n n n n n n ∆⎛⎫⎛⎫=+-++-=-+=--+ ⎪ ⎪⎝⎭⎝⎭ ∴当92n =时,PBA S ∆最大值为818()3存在,设点D 的坐标为21,233t t t ⎛⎫-++ ⎪⎝⎭过D 作对称轴的垂线,垂足为G ,则213,6233DG t CG t t ⎛⎫=-=--++ ⎪⎝⎭30ACD ∠=2DG DC ∴=在Rt CGD ∆中有222243CG CD DG DG DG DG =+=-=()21336233t t t ⎛⎫∴-=--++ ⎪⎝⎭化简得()1133303t t ⎛⎫---= ⎪⎝⎭ 13t ∴=(舍去),2333t =+∴点D(333+,-3)3,33AG GD ∴==连接AD ,在Rt ADG ∆中229276AD AG GD =+=+=6,120AD AC CAD ∴==∠=Q ∴在以A 为圆心,AC 为半径的圆与y 轴的交点上此时1602CQD CAD ∠=∠= 设Q 点为(0,m), AQ 为A 的半径 则AQ ²=OQ ²+OA ², 6²=m ²+3²即2936m += ∴1233,33m m ==-综上所述,Q 点坐标为()()0,330,33-或故存在点Q ,且这样的点有两个点.【点睛】(1)本题考查了利用待定系数法求二次函数解析式,根据已知条件选用顶点式较方便;(2)本题是三角形面积的最值问题,解决这个问题应该在分析图形的基础上,引出自变量,再根据图形的特征列出面积的计算公式,用含自变量的代数式表示面积的函数式,然后求出最值.(3)先求抛物线上点的坐标问题及符合条件的点是否存在.一般先假设这个点存在,再根据已知条件求出这个点.6.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标;(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.【答案】(1) y=x2﹣4x+3;(2) P1(1,0),P2(2,﹣1);(3) F1(22,1),F2(22,1).【解析】【分析】(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点式,然后将函数图象经过的C点坐标代入上式中,即可求出抛物线的解析式;(2)由于PD∥y轴,所以∠ADP≠90°,若△ADP是直角三角形,可考虑两种情况:①以点P为直角顶点,此时AP⊥DP,此时P点位于x轴上(即与B点重合),由此可求出P点的坐标;②以点A为直角顶点,易知OA=OC,则∠OAC=45°,所以OA平分∠CAP,那么此时D、P关于x轴对称,可求出直线AC的解析式,然后设D、P的横坐标,根据抛物线和直线AC的解析式表示出D、P的纵坐标,由于两点关于x轴对称,则纵坐标互为相反数,可据此求出P 点的坐标;(3)很显然当P、B重合时,不能构成以A、P、E、F为顶点的四边形,因为点P、F都在抛物线上,且点P为抛物线的顶点,所以PF与x轴不平行,所以只有(2)②的一种情况符合题意,由②知此时P、Q重合;假设存在符合条件的平行四边形,那么根据平行四边形的性质知:P、F的纵坐标互为相反数,可据此求出F点的纵坐标,代入抛物线的解析式中即可求出F 点的坐标.【详解】(1)∵抛物线的顶点为Q (2,﹣1),∴设抛物线的解析式为y=a (x ﹣2)2﹣1,将C (0,3)代入上式,得:3=a (0﹣2)2﹣1,a=1;∴y=(x ﹣2)2﹣1,即y=x 2﹣4x+3;(2)分两种情况:①当点P 1为直角顶点时,点P 1与点B 重合;令y=0,得x 2﹣4x+3=0,解得x 1=1,x 2=3;∵点A 在点B 的右边,∴B (1,0),A (3,0);∴P 1(1,0);②当点A 为△AP 2D 2的直角顶点时;∵OA=OC ,∠AOC=90°,∴∠OAD 2=45°;当∠D 2AP 2=90°时,∠OAP 2=45°,∴AO 平分∠D 2AP 2;又∵P 2D 2∥y 轴,∴P 2D 2⊥AO ,∴P 2、D 2关于x 轴对称;设直线AC 的函数关系式为y=kx+b (k≠0).将A (3,0),C (0,3)代入上式得:303k b b +=⎧⎨=⎩, 解得13k b =-⎧⎨=⎩; ∴y=﹣x+3;设D 2(x ,﹣x+3),P 2(x ,x 2﹣4x+3),则有:(﹣x+3)+(x 2﹣4x+3)=0,即x 2﹣5x+6=0;解得x 1=2,x 2=3(舍去);∴当x=2时,y=x 2﹣4x+3=22﹣4×2+3=﹣1;∴P 2的坐标为P 2(2,﹣1)(即为抛物线顶点).∴P 点坐标为P 1(1,0),P 2(2,﹣1);(3)由(2)知,当P 点的坐标为P 1(1,0)时,不能构成平行四边形;当点P 的坐标为P 2(2,﹣1)(即顶点Q )时,平移直线AP 交x 轴于点E ,交抛物线于F ;∵P (2,﹣1),∴可设F (x ,1);∴x 2﹣4x+3=1,解得x 1=2﹣2,x 2=2+2;∴符合条件的F 点有两个,即F 1(2﹣2,1),F 2(2+2,1).【点睛】此题主要考查了二次函数的解析式的确定、直角三角形的判定、平行四边形的判定与性质等重要知识点,同时还考查了分类讨论的数学思想,能力要求较高,难度较大.7.如图,抛物线2y x bx c =-++的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.点A 坐标的为3,0,点C 的坐标为()0,3.(Ⅰ)求抛物线的解析式;(Ⅱ)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作i 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作//PQ AB 交抛物线于点Q ,过点Q 作QN x ⊥轴于点N .若点P 在点Q 左边,当矩形PMNQ 的周长最大时,求AEM △的面积;(Ⅲ)在(Ⅱ)的条件下,当矩形PMNQ 的周长最大时,连接DQ ,过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若=22FG DQ ,求点F 的坐标.【答案】(Ⅰ)223y x x =--+;(Ⅱ)12;(Ⅲ)()4,5F --或()1,0 【解析】【分析】(Ⅰ)将点A ,点C 坐标代入解析式可求解;(Ⅱ)设M (x ,0),P (x ,-x 2-2x+3),利用对称性可求点Q (-2-x ,-x 2-2x+3),可求MP=-x 2-2x+3,PQ=-2-x-x=-2-2x ,则可用x 表示矩形PMNQ 的周长,由二次函数的性质可求当矩形PMNQ 的周长最大时,点P 的坐标,即可求点E ,点M 的坐标,由三角形面积公式可求解;(Ⅲ)先求出点D 坐标,即可求DQ=2,可得FG=4,设F (m ,-m 2-2m+3),则G (m ,m+3),用含有m 的式子表示FG 的长度即可求解.【详解】 解:(Ⅰ)依题意()()2330{3b c c --+⨯-+== 解得2{3b c =-= 所以223y x x =--+(Ⅱ)2223(1)4y x x x抛物线的对称轴是直线1x =-(,0)M x ,()2,23P x x x --+,其中31x -<<-∵P 、Q 关于直线1x =-对称设Q 的横坐标为a则()11a x --=--∴2a x =--∴()22,23Q x x x ----+∴223MP x x =--+,222PQ x x x =---=--∴周长()222222232822(2)10d x x x x x x =----+=--+=-++当2x =-时,d 取最大值,此时,(2,0)M -∴2(3)1AM =---=设直线AC 的解析式为y kx b =+则303k b b -+=⎧⎨=⎩,解得13k b =⎧⎨=⎩∴设直线AC 的解析式为3y x 将2x =-代入3y x ,得1y = ∴(2,1)E -,∴1EM = ∴11111222AEM S AM ME ∆=⋅=⨯⨯= (Ⅲ)由(Ⅱ)知,当矩形PMNQ 的周长最大时,2x =-此时点()0,3Q ,与点C 重合,∴3OQ =∵2223(1)4y x x x∴()1,4D -过D 作DK y ⊥轴于K ,则1DK =,4OK =∴431OK OK OQ =-=-=∴DKQ 是等腰直角三角形,DQ =∴4FG ==设()2,23F m m m --+,则(,3)G m m + ()223233FG m m m m m =+---+=+∴234m m +=,解得14m =-,21m =当4m =-时,2235m m --+=-当1m =时,2230m m --+=.∴()4,5F --或()1,0【点睛】本题是二次函数综合题,考查了二次函数的性质,矩形的性质,等腰直角三角形的性质等,利用参数表示线段的长度是本题的关键.8.如图,已知抛物线2y x bx c =-++与x 轴交于A ,B 两点,过点A 的直线l 与抛物线交于点C ,其中点A 的坐标是()1,0,点C 的坐标是()2,3-,抛物线的顶点为点D .(1)求抛物线和直线AC 的解析式.(2)若点P 是抛物线上位于直线AC 上方的一个动点,求APC ∆的面积的最大值及此时点P 的坐标.(3)若抛物线的对称轴与直线AC 相交于点E ,点M 为直线AC 上的任意一点,过点M 作//MN DE 交抛物线于点N ,以D ,E ,M ,N 为顶点的四边形能否为平行四边形?若能,求出点M 的坐标;若不能,请说明理由.【答案】(1)y=-x 2-2x+3,y=-x+1;(2)最大值为278,此时点P(12-,154);(3)能,(0,1),117-+317-)或117--317+ 【解析】【分析】(1)直接利用待定系数法进行求解,即可得到答案;(2)设点P(m ,-m 2-2m+3),则Q(m ,-m+1),求出PQ 的长度,结合三角形的面积公式和二次函数的性质,即可得到答案;(3)根据题意,设点M(t ,-t+1),则点N(t ,-t 2-2t+3),可分为两种情况进行分析:①当点M 在线段AC 上时,点N 在点M 上方;②当点M 在线段AC (或CA )延长线上时,点N 在点M 下方;分别求出点M 的坐标即可.【详解】解:(1)∵抛物线y=-x 2+bx+c 过点A(1,0),C(-2,3),∴10423b c b c -++=⎧⎨--+=⎩,,解得:23b c =-⎧⎨=⎩,.∴抛物线的解析式为y=-x 2-2x+3.设直线AC 的解析式为y=kx+n .将点A ,C 坐标代入,得023k n k n +=⎧⎨-+=⎩,,解得11k n =-⎧⎨=⎩,. ∴直线AC 的解析式为y=-x+1.(2)过点P 作PQ ∥y 轴交AC 于点Q .设点P(m ,-m 2-2m+3),则Q(m ,-m+1).∴PQ=(-m 2-2m+3)-(-m+1)=-m 2-m+2.∴S △APC =S △PCQ +S △APQ =12PQ·(x A -x C )=12(-m 2-m+2)×3=23127()228m -++. ∴当m=12-时,S △APC 最大,最大值为278,此时点P(12-,154). (3)能.∵y=-x 2-2x+3,点D 为顶点,∴点D(-1,4),令x=-1时,y=-(-1)+1=2,∴点E(-1,2).∵MN ∥DE ,∴当MN=DE=2时,以D ,E ,M ,N 为顶点的四边形是平行四边形.∵点M 在直线AC 上,点N 在抛物线上,∴设点M(t ,-t+1),则点N(t ,-t 2-2t+3).①当点M 在线段AC 上时,点N 在点M 上方,则MN=(-t 2-2t+3)-(-t+1)=-t 2-t+2.∴-t 2-t+2=2,解得:t=0或t=-1(舍去).∴此时点M 的坐标为(0,1).②当点M 在线段AC (或CA )延长线上时,点N 在点M 下方,则MN=(-t+1)-(-t 2-2t+3)=t 2+t-2.∴t 2+t-2=2,解得:t=12-+或t=12-.∴此时点M 的坐标为(1172-+,3172-)或(1172--,3172+). 综上所述,满足条件的点M 的坐标为:(0,1),(117-+,317-)或(117--,317+). 【点睛】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC 的函数关系式;(2)利用三角形的面积公式和二次函数的性质解题;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M 的位置.9.如图,已知二次函数1L :()22311y mx mx m m =+-+≥和二次函数2L :()2341y m x m =--+-()1m ≥图象的顶点分别为M 、N ,与x 轴分别相交于A 、B 两点(点A 在点B 的左边)和C 、D 两点(点C 在点D 的左边),(1)函数()22311y mx mx m m =+-+≥的顶点坐标为______;当二次函数1L ,2L 的y 值同时随着x 的增大而增大时,则x 的取值范围是_______;(2)判断四边形AMDN 的形状(直接写出,不必证明);(3)抛物线1L ,2L 均会分别经过某些定点;①求所有定点的坐标;②若抛物线1L 位置固定不变,通过平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是多少?【答案】(1)()1,41m --+,13x ;(2)四边形AMDN 是矩形;(3)①所有定点的坐标,1L 经过定点()3,1-或()1,1,2L 经过定点()5,1-或()1,1-;②抛物线2L 应平移的距离是423+423-.【解析】【分析】(1)将已知抛物线解析式转化为顶点式,直接得到点M 的坐标;结合函数图象填空; (2)利用抛物线解析式与一元二次方程的关系求得点A 、D 、M 、N 的横坐标,可得AD 的中点为(1,0),MN 的中点为(1,0),则AD 与MN 互相平分,可证四边形AMDN 是矩形; (3)①分别将二次函数的表达式变形为1:(3)(1)1L y m x x =+-+和2:(1)(5)1L y m x x =----,通过表达式即可得出所过定点;②根据菱形的性质可得EH 1=EF=4即可,设平移的距离为x ,根据平移后图形为菱形,由勾股定理可得方程即可求解.【详解】解:(1)12b x a=-=-,顶点坐标M 为(1,41)m --+, 由图象得:当13x 时,二次函数1L ,2L 的y 值同时随着x 的增大而增大. 故答案为:(1,41)m --+;13x ;(2)结论:四边形AMDN 是矩形.由二次函数21:231(1)L y mx mx m m =+-+和二次函数22:(3)41(1)L y m x m m =--+-解析式可得:A 点坐标为41(1m m ---,0),D 点坐标为41(3m m -+,0), 顶点M 坐标为(1,41)m --+,顶点N 坐标为(3,41)m -,AD ∴的中点为(1,0),MN 的中点为(1,0),AD ∴与MN 互相平分,∴四边形AMDN 是平行四边形,又AD MN =,∴□AMDN 是矩形;(3)①二次函数21:231(3)(1)1L y mx mx m m x x =+-+=+-+,故当3x =-或1x =时1y =,即二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41(1)(5)1L y m x m m x x =--+-=----,故当1x =或5x =时1y =-,即二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,②二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,如图:四个定点分别为(3,1)E -、(1,1)F ,(1,1)H -、(5,1)G -,则组成四边形EFGH 为平行四边形,∴FH ⊥HG ,FH=2,HM=4-x ,设平移的距离为x ,根据平移后图形为菱形,则EH 1=EF=H 1M=4,由勾股定理可得:FH 2+HM 2=FM 2,即22242(4)x =+-,解得:423x =±,抛物线1L 位置固定不变,通过左右平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是423+或423-.【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.10.如图,在平面直角坐标系中,矩形AOBC 的边AO 在x 轴的负半轴上,边OB 在y 轴的负半轴上.且AO =12,OB =9.抛物线y =﹣x 2+bx+c 经过点A 和点B .(1)求抛物线的表达式;(2)在第二象限的抛物线上找一点M ,连接AM ,BM ,AB ,当△ABM 面积最大时,求点M 的坐标;(3)点D 是线段AO 上的动点,点E 是线段BO 上的动点,点F 是射线AC 上的动点,连接EF ,DF ,DE ,BD ,且EF 是线段BD 的垂直平分线.当CF =1时.①直接写出点D 的坐标 ;②若△DEF 的面积为30,当抛物线y =﹣x 2+bx+c 经过平移同时过点D 和点E 时,请直接写出此时的抛物线的表达式 .【答案】(1)y=﹣x2﹣514x﹣9;(2)M(﹣6,31.5);(3)①(﹣50)或(﹣3,0),②y=﹣x2﹣133x﹣4【解析】【分析】(1)利用待定系数法把问题转化为解方程组即可解决问题.(2)如图1中,设M(m,﹣m2﹣514m﹣9),根据S△ABM=S△ACM+S△MBC﹣S△ACB构建二次函数,利用二次函数的性质解决问题即可.(3)①分两种情形:如图2中,当点F在AC的延长线设时,连接DF,FB.设D(m,0).根据FD=FB,构建方程求解.当点F在线段AC上时,同法可得.②根据三角形的面积求出D,E的坐标,再利用待定系数法解决问题即可.【详解】解:(1)由题意A(﹣12,0),B(0,﹣9),把A,B的坐标代入y=﹣x2+bx+c,得到9 144120cb c=-⎧⎨--+=⎩,解得:5149bc⎧=-⎪⎨⎪=-⎩,∴抛物线的解析式为y=﹣x2﹣514x﹣9.(2)如图1中,设M(m,﹣m2﹣514m﹣9),S△ABM=S△ACM+S△MBC﹣S△ACB=12×9×(m+12)+12×12×(﹣m2﹣514m﹣9+9)﹣12×12×9=﹣6m2﹣72m=﹣6(m+6)2+216,∵﹣6<0,∴m=﹣6时,△ABM的面积最大,此时M(﹣6,31.5).(3)①如图2中,当点F在AC的延长线设时,连接DF,FB.设D(m,0).∵EF垂直平分线段BD,∴FD=FB,∵F(﹣12,﹣10),B(0,﹣9),∴102+(m+12)2=122+12,∴m=﹣12﹣55∴D(﹣50).当点F在线段AC上时,同法可得D(﹣3,0),综上所述,满足条件的点D的坐标为(﹣50)或(﹣3,0).故答案为(﹣50)或(﹣3,0).②由①可知∵△EF的面积为30,∴D(﹣3,0),E(0,﹣4),把D,E代入y=﹣x2+b′x+c′,可得'493''0cb c=-⎧⎨--+=⎩,解得:13'3'4bc⎧=-⎪⎨⎪=-⎩,∴抛物线的解析式为y=﹣x2﹣133x﹣4.故答案为:y=﹣x2﹣133x﹣4.【点睛】本题属于二次函数综合题,考查了二次函数的性质,待定系数法,线段的垂直平分线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.。
(word完整版)初中数学九年级二次函数基础练习题

二次函数基础练习题的解析式是 ______________________________15. 已知二次函数图象经过(一 1 , 10) ( 2, 7)和(1 , 4)三点,这个函数的解析式是 _________________________321.抛物线 y ax bx c(a 0)过第二、三、四象限,则2.抛物线 y ax 2 bx c(a 0)过第一、二、四象限,贝U a o , b o , c o3 •已知抛物线y ax 22x c 与x 轴的交点都在原点的右侧,则点M ( a,c )在第 象限.4. 二次函数y ax 2bx c 的图象如图所示,贝Ua __________ 0,2b -4ac __________ 0, a + b + c __________ 0 , a — b + c ______5. 二次函数y ax 2 bx c 的图象如图所示,贝Ua ______ 0 , b6.二次函数y ax 2bx c 的图象如图所示,那么下列四个结论:2b① a <0 ;② c >0 ; ③ b 4ac >0 ;④ <0 中,a正确的结论有()个① a + b >0;② a + c >0;③一a + b + c >0;④b 2>気①其中正确的个数有()个8. 已知二次函数y 2ax bxc 中a 0,b 0,c 0,则此函数的图象不经过第象限9. 已知二次函数 y ax 2 bx c 中a0,b 0,c 0,则此函数的图象不经过第象限10 .已知二次函数 y ax 2 bx c 中a 0,b 0,c0 ,则此函数的图象只经过第象限11. 如图,函数y ax 2bx c 的图象中函数值 y 0时,对应x 的取值范围是 ____________________函数值y 0时,对应x 的取值范围是 ___________________12. 如图,函数y ax 2bx c 的图象中函数值 y 0时,对应x 的取值范围是 _____________13.二次函数y x 2bx c 的图象如图所示,则函数值y 0时,对应x 的取值范围14.已知抛物线y ax 2bx c 经过三点 A (2, 6), B (— 1, 2), C (0, 1),那么它16. 若抛物线与x轴交于点(一1 , 0)和(3, 0),且过点f 0,),那么抛物线的解析式17. 已知抛物线经过三个点 A (2, 6) , B (- 1, 0), C ( 3, 0),那么二次函数的解析式是 __________________________________ ,它的顶点坐标是 _____________________________318. 抛物线与x 轴的两个交点的横坐标是— 3和1,且过点(0),此抛物线的解析式是 _______________________19. 已知抛物线的顶点是 A( — 1,2),且经过点(2,3),其表达式是 ________________________ 。
初三数学二次函数较难题型doc

初三数学二次函数较难题型.doc 初三数学二次函数较难题型二次函数是初中数学中的重要内容,也是较为难理解和掌握的一部分。
在学习二次函数的过程中,初三学生会遇到一些较难的题型,下面就来介绍一些常见的较难题型及解题思路。
1.求二次函数的值域二次函数的值域是指函数在定义域内所能取到的所有函数值的集合。
对于一般的二次函数y=ax^2+bx+c,其中a、b、c为常数,值域的求解可以通过以下步骤进行:首先,通过配方法将二次函数化为顶点形式:y=a(x-h)^2+k,其中(h,k)为顶点坐标。
然后,根据二次函数的图像特点,可以得到二次函数的开口方向。
当a>0时,二次函数开口向上;当a<0时,二次函数开口向下。
最后,根据开口方向和顶点坐标,确定二次函数的值域。
当二次函数开口向上时,值域为[k,+∞);当二次函数开口向下时,值域为(-∞,k]。
2.求二次函数的零点二次函数的零点是指函数在定义域内取值为0的点的横坐标。
对于一般的二次函数y=ax^2+bx+c,其中a、b、c为常数,求解零点可以通过以下步骤进行:首先,将二次函数化为一元二次方程:ax^2+bx+c=0。
然后,根据一元二次方程的解的判别式,求解方程的根。
一元二次方程的解的判别式为Δ=b^2-4ac,当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根。
最后,根据方程的根,确定二次函数的零点。
根的个数和类型决定了二次函数的零点的个数和类型。
3.求二次函数的最值二次函数的最值是指函数在定义域内所能取到的最大值或最小值。
对于一般的二次函数y=ax^2+bx+c,其中a、b、c为常数,求解最值可以通过以下步骤进行:首先,通过配方法将二次函数化为顶点形式:y=a(x-h)^2+k,其中(h,k)为顶点坐标。
然后,根据二次函数的图像特点,可以得到二次函数的开口方向。
当a>0时,二次函数开口向上,最小值为k;当a<0时,二次函数开口向下,最大值为k。
九年级数学 二次函数(篇)(Word版 含解析)

九年级数学 二次函数(篇)(Word 版 含解析)一、初三数学 二次函数易错题压轴题(难)1.在平面直角坐标系中,O 为坐标原点,抛物线L :y =ax 2﹣4ax (a >0)与x 轴正半轴交于点A .抛物线L 的顶点为M ,对称轴与x 轴交于点D . (1)求抛物线L 的对称轴.(2)抛物线L :y =ax 2﹣4ax 关于x 轴对称的抛物线记为L ',抛物线L '的顶点为M ',若以O 、M 、A 、M '为顶点的四边形是正方形,求L '的表达式.(3)在(2)的条件下,点P 在抛物线L 上,且位于第四象限,点Q 在抛物线L '上,是否存在点P 、点Q 使得以O 、D 、P 、Q 为顶点的四边形是平行四边形,若存在,求出点P 坐标,若不存在,请说明理由.【答案】(1)2x =;(2)2122y x x =-+ ;(3)存在,P 点的坐标为(33,3或(33,3-或(13,3或(13,3+-或31,2⎛⎫- ⎪⎝⎭【解析】 【分析】(1)根据抛物线的对称轴公式计算即可.(2)利用正方形的性质求出点M ,M ′的坐标即可解决问题. (3)分OD 是平行四边形的边或对角线两种情形求解即可. 【详解】解:(1)∵抛物线L :y =ax 2﹣4ax (a >0), ∴抛物线的对称轴x =﹣42aa-=2. (2)如图1中,对于抛物线y=ax2﹣4ax,令y=0,得到ax2﹣4ax=0,解得x=0或4,∴A(4,0),∵四边形OMAM′是正方形,∴OD=DA=DM=DM′=2,∴M((2,﹣2),M′(2,2)把M(2,﹣2)代入y=ax2﹣4ax,可得﹣2=4a﹣8a,∴a=12,∴抛物线L′的解析式为y=﹣12(x﹣2)2+2=﹣12x2+2x.(3)如图3中,由题意OD=2.当OD为平行四边形的边时,PQ=OD=2,设P(m,12m2﹣2m),则Q[m﹣2,﹣12(m﹣2)2+2(m﹣2)]或[m+2,﹣12(m+2)2+2(m+2)],∵PQ∥OD,∴12m2﹣2m=﹣12(m﹣2)2+2(m﹣2)或12m2﹣2m=﹣12(m+2)2+2(m+2),解得m=,∴P或(3或(1和,当OD是平行四边形的对角线时,点P的横坐标为1,此时P(1,﹣32 ),综上所述,满足条件的点P的坐标为或(3或(1)和)或(1,﹣32 ).【点睛】本题属于二次函数综合题,考查了二次函数的性质,正方形的性质,平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题2.在平面直角坐标系中,将函数y=x2﹣2mx+m(x≤2m,m为常数)的图象记为G,图象G的最低点为P(x0,y0).(1)当y0=﹣1时,求m的值.(2)求y0的最大值.(3)当图象G与x轴有两个交点时,设左边交点的横坐标为x1,则x1的取值范围是.(4)点A在图象G上,且点A的横坐标为2m﹣2,点A关于y轴的对称点为点B,当点A不在坐标轴上时,以点A、B为顶点构造矩形ABCD,使点C、D落在x轴上,当图象G 在矩形ABCD内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.【答案】(1或﹣1;(2)14;(3)0<x1<1;(4)m=0或m>43或23≤m<1【解析】【分析】(1)分m>0,m=0,m<0三种情形分别求解即可解决问题;(2)分三种情形,利用二次函数的性质分别求解即可;(3)由(1)可知,当图象G与x轴有两个交点时,m>0,求出当抛物线顶点在x轴上时m的值,利用图象法判断即可;(4)分四种情形:①m<0,②m=0,③m>1,④0<m≤1,分别求解即可解决问题.【详解】解:(1)如图1中,当m>0时,∵y=x2﹣2mx+m=(x﹣m)2﹣m2+m,图象G是抛物线在直线y=2m的左侧部分(包括点D),此时最底点P(m,﹣m2+m),由题意﹣m2+m=﹣1,解得m=51+或51-+(舍弃),当m=0时,显然不符合题意,当m<0时,如图2中,图象G是抛物线在直线y=2m的左侧部分(包括点D),此时最底点P是纵坐标为m,∴m=﹣1,综上所述,满足条件的m的值为512或﹣1;(2)由(1)可知,当m>0时,y0=﹣m2+m=﹣(m﹣12)2+14,∵﹣1<0,∴m=12时,y0的最大值为14,当m=0时,y0=0,当m<0时,y0<0,综上所述,y0的最大值为14;(3)由(1)可知,当图象G与x轴有两个交点时,m>0,当抛物线顶点在x轴上时,4m2﹣4m=0,∴m=1或0(舍弃),∴观察观察图象可知,当图象G与x轴有两个交点时,设左边交点的横坐标为x1,则x1的取值范围是0<x1<1,故答案为0<x1<1;(4)当m<0时,观察图象可知,不存在点A满足条件,当m=0时,图象G在矩形ABCD内的部分所对应的函数值y随x的增大而减小,满足条件,如图3中,当m>1时,如图4中,设抛物线与x轴交于E,F,交y轴于N,观察图象可知当点A在x轴下方或直线x=﹣m和y轴之间时(可以在直线x=﹣m上)时,满足条件.则有(2m﹣2)2﹣2m(2m﹣2)+m<0,解得m>43,或﹣m≤2m﹣2<0,解得23≤m<1(不合题意舍弃),当0<m≤1时,如图5中,当点A在直线x=﹣m和y轴之间时(可以在直线x=﹣m上)时,满足条件.即或﹣m≤2m﹣2<0,解得23≤m<1,综上所述,满足条件m的值为m=0或m>43或23≤m<1.【点睛】本题属于二次函数综合题,考查了二次函数的性质,矩形的性质,最值问题,不等式等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会用转化的思想思考问题,属于中考压轴题.3.已知点P(2,﹣3)在抛物线L:y=ax2﹣2ax+a+k(a,k均为常数,且a≠0)上,L交y轴于点C,连接CP.(1)用a表示k,并求L的对称轴及L与y轴的交点坐标;(2)当L经过(3,3)时,求此时L的表达式及其顶点坐标;(3)横、纵坐标都是整数的点叫做整点.如图,当a<0时,若L在点C,P之间的部分与线段CP所围成的区域内(不含边界)恰有4个整点,求a的取值范围;(4)点M(x1,y1),N(x2,y2)是L上的两点,若t≤x1≤t+1,当x2≥3时,均有y1≥y2,直接写出t的取值范围.【答案】(1)k=-3-a;对称轴x=1;y轴交点(0,-3);(2)2y=2x-4x-3,顶点坐标(1,-5);(3)-5≤a <-4;(4)-1≤t ≤2. 【解析】 【分析】(1)将点P(2,-3)代入抛物线上,求得k 用a 表示的关系式;抛物线L 的对称轴为直线2ax==12a--,并求得抛物线与y 轴交点; (2)将点(3,3)代入抛物线的解析式,且k=-3-a ,解得a=2,k=-5,即可求得抛物线解析式与顶点坐标;(3)抛物线L 顶点坐标(1,-a-3),点C ,P 之间的部分与线段CP 所围成的区域内(不含边界)恰有4个整点,这四个整点都在x=1这条直线上,且y 的取值分别为-2、-1、0、1,可得1<-a-3≤2,即可求得a 的取值范围;(4)分类讨论取a >0与a <0的情况进行讨论,找出1x 的取值范围,即可求出t 的取值范围. 【详解】解:(1)∵将点P(2,-3)代入抛物线L :2y=ax -2ax+a+k ,∴-3=4a 4a a+k=a+k -+ ∴k=-3-a ;抛物线L 的对称轴为直线-2ax=-=12a,即x =1; 将x=0代入抛物线可得:y=a+k=a+(-3-a)=-3,故与y 轴交点坐标为(0,-3);(2)∵L 经过点(3,3),将该点代入解析式中, ∴9a-6a+a+k=3,且由(1)可得k=-3-a , ∴4a+k=3a-3=3,解得a=2,k=-5,∴L 的表达式为2y=2x -4x-3;将其表示为顶点式:2y=2(x-1)-5, ∴顶点坐标为(1,-5);(3)解析式L 的顶点坐标(1,-a-3),∵在点C ,P 之间的部分与线段CP 所围成的区域内(不含边界)恰有4个整点,这四个整点都在x=1这条直线上,且y 的取值分别为-2、-1、0、1, ∴1<-a-3≤2, ∴-5≤a <-4;(4)①当a <0时,∵2x 3≥,为保证12y y ≥,且抛物线L 的对称轴为x=1, ∴就要保证1x 的取值范围要在[-1,3]上, 即t ≥-1且t+1≤3,解得-1≤t ≤2;②当a >0时,抛物线开口向上,t ≥3或t+1≤-1,解得:t ≥3或t ≤-2,但会有不符合题意的点存在,故舍去, 综上所述:-1≤t ≤2.【点睛】本题考查二次函数的图象及性质;熟练掌握二次函数的图象及性质,数形结合解题是关键.4.如图,过原点的抛物线y=﹣12x 2+bx+c 与x 轴交于点A (4,0),B 为抛物线的顶点,连接OB ,点P 是线段OA 上的一个动点,过点P 作PC ⊥OB ,垂足为点C . (1)求抛物线的解析式,并确定顶点B 的坐标;(2)设点P 的横坐标为m ,将△POC 绕着点P 按顺利针方向旋转90°,得△PO′C′,当点O′和点C′分别落在抛物线上时,求相应的m 的值;(3)当(2)中的点C′落在抛物线上时,将抛物线向左或向右平移n (0<n <2)个单位,点B 、C′平移后对应的点分别记为B′、C″,是否存在n ,使得四边形OB′C″A 的周长最短?若存在,请直接写出n 的值和抛物线平移的方向,若不存在,请说明理由.【答案】(1)2122y x x =-+,点B (2,2);(2)m=2或209m =;(3)存在;n=27时,抛物线向左平移. 【解析】 【分析】(1)将点A 和点O 的坐标代入解析式,利用待定系数法即可求得二次函数的解析式,然后利用配方法可求得点B 的坐标;(2)由点A 、点B 、点C 的坐标以及旋转的性质可知△△PDC 为等腰直角三角形,从而可得到点O′坐标为:(m ,m ),点C′坐标为:(32m ,2m),然后根据点在抛物线上,列出关于m 的方程,从而可解得m 的值;(3)如图,将AC′沿C′B 平移,使得C′与B 重合,点A 落在A′处,以过点B 的直线y=2为对称轴,作A′的对称点A″,连接OA″,由线段的性质可知当B′为OA″与直线y=2的交点时,四边形OB′C″A 的周长最短,先求得点B′的坐标,根据点B 移动的方向和距离从而可得出点抛物线移动的方向和距离. 【详解】解:(1)把原点O (0,0),和点A (4,0)代入y=12-x 2+bx+c . 得040c b b c =⎧⎨-++=⎩,∴02c b =⎧⎨=⎩.∴22112(2)222y x x x =-+=--+. ∴点B 的坐标为(2,2).(2)∵点B 坐标为(2,2). ∴∠BOA=45°.∴△PDC 为等腰直角三角形. 如图,过C′作C′D ⊥O′P 于D .∵O′P=OP=m . ∴C′D=12O′P=12m . ∴点O′坐标为:(m ,m ),点C′坐标为:(32m ,2m ).当点O′在y=12-x 2+2x 上. 则−12m 2+2m =m . 解得:12m =,20m =(舍去). ∴m=2. 当点C′在y=12-x 2+2x 上, 则12-×(32m )2+2×32m =12m ,解得:1209m =,20m =(舍去). ∴m=209(3)存在n=27,抛物线向左平移. 当m=209时,点C′的坐标为(103,109).如图,将AC′沿C′B 平移,使得C′与B 重合,点A 落在A′处.以过点B的直线y=2为对称轴,作A′的对称点A″,连接OA″.当B′为OA″与直线y=2的交点时,四边形OB′C″A的周长最短.∵BA′∥AC′,且BA′=AC′,点A(4,0),点C′(103,109),点B(2,2).∴点A′(83,89).∴点A″的坐标为(83,289).设直线OA″的解析式为y=kx,将点A″代入得:828 39k=,解得:k=76.∴直线OA″的解析式为y=76 x.将y=2代入得:76x=2,解得:x=127,∴点B′得坐标为(127,2).∴n=2122 77 -=.∴存在n=27,抛物线向左平移.【点睛】本题主要考查的是二次函数、旋转的性质、平移的性质、路径最短等知识点,由旋转的性质和平移的性质求得点点O′坐标为:(m,m),点C′坐标为:(32m,2m)以及点B′的坐标是解题的关键.5.如图,抛物线y=ax2+bx+2经过点A(−1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=23S△ABD?若存在,请求出点D 坐标;若不存在,请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.【答案】(1)213222y x x=-++(2)存在,D(1,3)或(2,3)或(5,3-)(3)10【解析】【分析】(1)由A、B的坐标,利用待定系数法可求得抛物线解析式;(2)由条件可求得点D到x轴的距离,即可求得D点的纵坐标,代入抛物线解析式可求得D点坐标;(3)由条件可证得BC⊥AC,设直线AC和BE交于点F,过F作FM⊥x轴于点M,则可得BF=BC,利用平行线分线段成比例可求得F点的坐标,利用待定系数法可求得直线BE 解析式,联立直线BE和抛物线解析式可求得E点坐标,则可求得BE的长.【详解】解:(1)∵抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),∴2016420a ba b-+=⎧⎨++=⎩,解得:1232ab⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线解析式为:213222y x x=-++;(2)由题意可知C(0,2),A(-1,0),B(4,0),∴AB=5,OC=2,∴S△ABC=12AB•OC=12×5×2=5,∵S△ABC=23S△ABD,∴S△ABD=315522⨯=,设D(x,y),∴11155222AB y y •=⨯•=, 解得:3y =;当3y =时,2132322y x x =-++=, 解得:1x =或2x =,∴点D 的坐标为:(1,3)或(2,3);当3y =-时,2132322y x x =-++=-, 解得:5x =或2x =-(舍去),∴点D 的坐标为:(5,-3);综合上述,点D 的坐标为:(1,3)或(2,3)或(5,-3);(3)∵AO=1,OC=2,OB=4,AB=5,∴22125AC =+=,222425BC =+=,∴222AC BC AB +=,∴△ABC 为直角三角形,即BC ⊥AC ,如图,设直线AC 与直线BE 交于点F ,过F 作FM ⊥x 轴于点M ,由题意可知∠FBC=45°,∴∠CFB=45°,∴25CF BC ==∴AO AC OM CF =,即1525OM = 解得:2OM =, ∴OC AC FM AF =,即2535FM = 解得:6FM =,∴点F 为(2,6),且B 为(4,0),设直线BE解析式为y=kx+m ,则2640k m k m +=⎧⎨+=⎩,解得312k m =-⎧⎨=⎩, ∴直线BE 解析式为:312y x =-+;联立直线BE 和抛物线解析式可得:231213222y x y x x =-+⎧⎪⎨=-++⎪⎩, 解得:40x y =⎧⎨=⎩或53x y =⎧⎨=-⎩, ∴点E 坐标为:(5,3)-,∴22(54)(3)10BE =-+-=.【点睛】本题为二次函数的综合应用,涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中求得D 点的纵坐标是解题的关键,在(3)中由条件求得直线BE 的解析式是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,有一定的难度.6.定义:函数l 与l '的图象关于y 轴对称,点(),0P t 是x 轴上一点,将函数l '的图象位于直线x t =左侧的部分,以x 轴为对称轴翻折,得到新的函数w 的图象,我们称函数w 是函数l 的对称折函数,函数w 的图象记作1F ,函数l 的图象位于直线x t =上以及右侧的部分记作2F ,图象1F 和2F 合起来记作图象F .例如:如图,函数l 的解析式为1y x =+,当1t =时,它的对称折函数w 的解析式为()11y x x =-<.(1)函数l 的解析式为21y x =-,当2t =-时,它的对称折函数w 的解析式为_______; (2)函数l 的解析式为1²12y x x =--,当42x -≤≤且0t =时,求图象F 上点的纵坐标的最大值和最小值;(3)函数l 的解析式为()2230y ax ax a a =--≠.若1a =,直线1y t =-与图象F 有两个公共点,求t 的取值范围.【答案】(1)()212y x x =+<-;(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩;图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-;(3)当3t =-,1t <≤,5t <<时,直线1y t =-与图象F 有两个公共点. 【解析】【分析】(1)根据对折函数的定义直接写出函数解析式即可;(2)先根据题意确定F 的解析式,然后根据二次函数的性质确定函数的最大值和最小值即可;(3)先求出当a=1时图像F 的解析式,然后分14t -=-、点(),1t t -落在223()y x x x t =--≥上和点(),1t t -落在()223y x x x t =--+<上三种情况解答,最后根据图像即可解答.【详解】解:(1)()212y x x =+<-(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩当4x =-时,3y =-,当1x =-时,32y =, 当1x =时,32y =-,当2x =时,1y =, ∴图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-. (3)当1a =时,图象F 的解析式为2223()23()y x x x t y x x x t ⎧=--≥⎨=--+<⎩∴该函数的最大值和最小值分别为4和-4;a :当14t -=-时,3t =-,∴当3t =-时直线1y t =-与图象F 有两个公共点;b :当点(),1t t -落在223()y x x x t =--≥上时,2123t t t -=--,解得13172t -=,23172t += c :当点(),1t t -落在()223y x x x t =--+<上时,2123t t t -=--+,解得34t =-(舍),41t =14t -=,∴55t = ∴当31712t -<≤或31752t +<<时,直线1y t =-与图象F 有两个公共点; 综上所述:当3t =-,3171t -<≤,3175t +<<时,直线1y t =-与图象F 有两个公共点.【点睛】本题属于二次函数综合题,考查了“称折函数”的定义、二次函数的性质、解二元一次方程等知识,弄清题意、灵活运用所学知识是解答本题的关键.7.在平面直角坐标系中,抛物线y=x 2+(k ﹣1)x ﹣k 与直线y=kx+1交于A ,B 两点,点A 在点B 的左侧.(1)如图1,当k=1时,直接写出A ,B 两点的坐标;(2)在(1)的条件下,点P 为抛物线上的一个动点,且在直线AB 下方,试求出△ABP 面积的最大值及此时点P 的坐标;(3)如图2,抛物线y=x 2+(k ﹣1)x ﹣k (k >0)与x 轴交于点C 、D 两点(点C 在点D 的左侧),在直线y=kx+1上是否存在唯一一点Q ,使得∠OQC=90°?若存在,请求出此时k 的值;若不存在,请说明理由.【答案】(1)A(-1,0) ,B(2,3)(2)△ABP 最大面积s=1927322288⨯=; P (12,﹣34) (3)存在;25 【解析】【分析】(1)当k=1时,抛物线解析式为y=x2﹣1,直线解析式为y=x+1,然后解方程组211y xy x⎧=⎨=+⎩﹣即可;(2)设P(x,x2﹣1).过点P作PF∥y轴,交直线AB于点F,则F(x,x+1),所以利用S△ABP=S△PFA+S△PFB,,用含x的代数式表示为S△ABP=﹣x2+x+2,配方或用公式确定顶点坐标即可.(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,用k分别表示点E的坐标,点F的坐标,以及点C的坐标,然后在Rt△EOF中,由勾股定理表示出EF的长,假设存在唯一一点Q,使得∠OQC=90°,则以OC为直径的圆与直线AB相切于点Q,设点N为OC中点,连接NQ,根据条件证明△EQN∽△EOF,然后根据性质对应边成比例,可得关于k的方程,解方程即可.【详解】解:(1)当k=1时,抛物线解析式为y=x2﹣1,直线解析式为y=x+1.联立两个解析式,得:x2﹣1=x+1,解得:x=﹣1或x=2,当x=﹣1时,y=x+1=0;当x=2时,y=x+1=3,∴A(﹣1,0),B(2,3).(2)设P(x,x2﹣1).如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).∴PF=y F﹣y P=(x+1)﹣(x2﹣1)=﹣x2+x+2.S△ABP=S△PFA+S△PFB=PF(xF﹣xA)+PF(xB﹣xF)=PF(xB﹣xA)=PF∴S△ABP=(﹣x2+x+2)=﹣(x﹣12)2+278当x=12时,yP=x2﹣1=﹣34.∴△ABP面积最大值为,此时点P坐标为(12,﹣34).(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,则E(﹣1k,0),F(0,1),OE=1k,OF=1.在Rt△EOF中,由勾股定理得:EF=22111=kk+⎛⎫+⎪⎝⎭.令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1.∴C(﹣k,0),OC=k.假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=2k.∴EN=OE﹣ON=1k﹣2k.∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,∴△EQN∽△EOF,∴NQ ENOF EF=,即:1221kkkk-=,解得:25,∵k>0,∴25.∴存在唯一一点Q,使得∠OQC=90°,此时25.考点:1.二次函数的性质及其应用;2.圆的性质;3.相似三角形的判定与性质.8.如图,直线3y x与x轴、y轴分别交于点A,C,经过A,C两点的抛物线2y ax bx c=++与x轴的负半轴的另一交点为B,且tan3CBO∠=(1)求该抛物线的解析式及抛物线顶点D的坐标;(2)点P是射线BD上一点,问是否存在以点P,A,B为顶点的三角形,与ABC相似,若存在,请求出点P的坐标;若不存在,请说明理由【答案】(1)243y x x =++,顶点(2,1)D --;(2)存在,52,33P ⎛⎫-- ⎪⎝⎭或(4,3)-- 【解析】【分析】(1)利用直线解析式求出点A 、C 的坐标,从而得到OA 、OC ,再根据tan ∠CBO=3求出OB ,从而得到点B 的坐标,然后利用待定系数法求出二次函数解析式,整理成顶点式形式,然后写出点D 的坐标;(2)根据点A 、B 的坐标求出AB ,判断出△AOC 是等腰直角三角形,根据等腰直角三角形的性质求出AC ,∠BAC=45°,再根据点B 、D 的坐标求出∠ABD=45°,然后分①AB 和BP 是对应边时,△ABC 和△BPA 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可;②AB 和BA 是对应边时,△ABC 和△BAP 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可.【详解】解:(1)令y=0,则x+3=0,解得x=-3,令x=0,则y=3,∴点A (-3,0),C (0,3),∴OA=OC=3,∵tan ∠CBO=3OC OB=, ∴OB=1,∴点B (-1,0),把点A 、B 、C 的坐标代入抛物线解析式得, 93003a b c a b c c -+=⎧⎪-+=⎨⎪=⎩,解得:143a b c =⎧⎪=⎨⎪=⎩,∴该抛物线的解析式为:243y x x =++,∵y=x 2+4x+3=(x+2)2-1,∴顶点(2,1)D --;(2)∵A (-3,0),B (-1,0),∴AB=-1-(-3)=2,∵OA=OC,∠AOC=90°,∴△AOC是等腰直角三角形,∴AC=2OA=32,∠BAC=45°,∵B(-1,0),D(-2,-1),∴∠ABD=45°,①AB和BP是对应边时,△ABC∽△BPA,∴AB ACBP BA=,即2322BP=,解得BP=223,过点P作PE⊥x轴于E,则BE=PE=23×22=23,∴OE=1+23=53,∴点P的坐标为(-53,-23);②AB和BA是对应边时,△ABC∽△BAP,∴AB ACBA BP=,即2322=,解得BP=32过点P作PE⊥x轴于E,则BE=PE=32×22=3, ∴OE=1+3=4, ∴点P 的坐标为(-4,-3);综合上述,当52,33P ⎛⎫--⎪⎝⎭或(4,3)--时,以点P ,A ,B 为顶点的三角形与ABC ∆相似; 【点睛】本题是二次函数综合题型,主要利用了直线与坐标轴交点的求解,待定系数法求二次函数解析式,等腰直角三角形的判定与性质,相似三角形的判定与性质,难点在于(2)要分情况讨论.9.如图,已知抛物线2y x bx c =-++与x 轴交于A ,B 两点,过点A 的直线l 与抛物线交于点C ,其中点A 的坐标是()1,0,点C 的坐标是()2,3-,抛物线的顶点为点D .(1)求抛物线和直线AC 的解析式.(2)若点P 是抛物线上位于直线AC 上方的一个动点,求APC ∆的面积的最大值及此时点P 的坐标.(3)若抛物线的对称轴与直线AC 相交于点E ,点M 为直线AC 上的任意一点,过点M 作//MN DE 交抛物线于点N ,以D ,E ,M ,N 为顶点的四边形能否为平行四边形?若能,求出点M 的坐标;若不能,请说明理由.【答案】(1)y=-x 2-2x+3,y=-x+1;(2)最大值为278,此时点P(12-,154);(3)能,(0,1),(1172-+,3172)或(1172--,3172) 【解析】【分析】(1)直接利用待定系数法进行求解,即可得到答案;(2)设点P(m ,-m 2-2m+3),则Q(m ,-m+1),求出PQ 的长度,结合三角形的面积公式和二次函数的性质,即可得到答案;(3)根据题意,设点M(t ,-t+1),则点N(t ,-t 2-2t+3),可分为两种情况进行分析:①当点M 在线段AC 上时,点N 在点M 上方;②当点M 在线段AC (或CA )延长线上时,点N 在点M 下方;分别求出点M 的坐标即可.【详解】解:(1)∵抛物线y=-x 2+bx+c 过点A(1,0),C(-2,3),∴10423b c b c -++=⎧⎨--+=⎩,,解得:23b c =-⎧⎨=⎩,. ∴抛物线的解析式为y=-x 2-2x+3.设直线AC 的解析式为y=kx+n .将点A ,C 坐标代入,得023k n k n +=⎧⎨-+=⎩,,解得11k n =-⎧⎨=⎩,. ∴直线AC 的解析式为y=-x+1.(2)过点P 作PQ ∥y 轴交AC 于点Q .设点P(m ,-m 2-2m+3),则Q(m ,-m+1).∴PQ=(-m 2-2m+3)-(-m+1)=-m 2-m+2.∴S △APC =S △PCQ +S △APQ =12PQ·(x A -x C )=12(-m 2-m+2)×3=23127()228m -++. ∴当m=12-时,S △APC 最大,最大值为278,此时点P(12-,154). (3)能.∵y=-x 2-2x+3,点D 为顶点,∴点D(-1,4),令x=-1时,y=-(-1)+1=2,∴点E(-1,2).∵MN ∥DE ,∴当MN=DE=2时,以D ,E ,M ,N 为顶点的四边形是平行四边形.∵点M 在直线AC 上,点N 在抛物线上,∴设点M(t ,-t+1),则点N(t ,-t 2-2t+3).①当点M 在线段AC 上时,点N 在点M 上方,则MN=(-t 2-2t+3)-(-t+1)=-t 2-t+2.∴-t 2-t+2=2,解得:t=0或t=-1(舍去).∴此时点M 的坐标为(0,1).②当点M 在线段AC (或CA )延长线上时,点N 在点M 下方,则MN=(-t+1)-(-t 2-2t+3)=t 2+t-2.∴t 2+t-2=2,解得:或.∴此时点M 的坐标为(1172-+,3172-)或(1172--,3172+). 综上所述,满足条件的点M 的坐标为:(0,1),(117-+,317-)或(117--,317+). 【点睛】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC 的函数关系式;(2)利用三角形的面积公式和二次函数的性质解题;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M 的位置.10.如图,经过原点的抛物线2y ax x b =-+与直线2y =交于A ,C 两点,其对称轴是直线2x =,抛物线与x 轴的另一个交点为D ,线段AC 与y 轴交于点B .(1)求抛物线的解析式,并写出点D 的坐标;(2)若点E 为线段BC 上一点,且2EC EA -=,点(0,)P t 为线段OB 上不与端点重合的动点,连接PE ,过点E 作直线PE 的垂线交x 轴于点F ,连接PF ,探究在P 点运动过程中,线段PE ,PF 有何数量关系?并证明所探究的结论;(3)设抛物线顶点为M ,求当t 为何值时,DMF ∆为等腰三角形?【答案】(1)214y x x =-;点D 的坐标为(4,0);(2)5PF PE =,理由见解析;(3)51t +=98t = 【解析】【分析】(1)先求出a 、b 的值,然后求出解析式,再求出点D 的坐标即可;(2)由题意,先求出点E 的坐标,然后证明Rt Rt PBE FHE ∆∆∽,得到2EF PE =,结合勾股定理,即可得到答案;(3)根据题意,可分为三种情况进行分析:FM FD =或DF DM =或FM MD =,分别求出三种情况的值即可.【详解】 解:(1)∵抛物线2y ax x b =-+经过原点,∴0b =.又抛物线的对称轴是直线2x =,∴122a --=,解得:14a =. ∴抛物线的解析式为:214y x x =-. 令2104y x x =-=, 解得:10x =,24x =.∴点D 的坐标为(4,0).(2)线段PE 、PF 的数量关系为:5PF PE =.证明:由抛物线的对称性得线段AC 的中点为(2,2)G ,如图①,AE EG GC +=,∴EG GC AE =-,∴EG EG EG GC AE EC EA +=+-=-,∵2EC EA -=,∴1EG =,∴(1,2)E ,过点E 作EH x ⊥轴于H ,则2EH OB ==.∵PE EF ⊥,∴90PEF ∠=︒,∵BE EH ⊥,∴90BEH ∠=︒.∴PEB HEF ∠=∠.在Rt PBE ∆与Rt FHE ∆中,∵PEB HEF ∠=∠,90EHF EBP ∠=∠=︒,∴Rt Rt PBE FHE ∆∆∽,∴12PE BE EF HE ==, ∴2EF PE =.在Rt PEF ∆中,由勾股定理得:222222(2)5PF PE EF PE PE PE =+=+=, ∴5PF PE =.(3)由2211(2)144y x x x =-=--, ∴顶点M 坐标为(2,1)-.若DMF ∆为等腰三角形,可能有三种情形:(I )若FM FD =.如图②所示:连接MG 交x 轴于点N ,则90MNF ∠=︒,∵(4,0)D , ∴2222125MD MN ND =+=+=设FM FD k ==,则2NF k =-.在Rt MNF ∆中,由勾股定理得:222NF MN MF +=,∴22(2)1k k -+=,解得:54k =, ∴54FM =,34NF =, ∴1MN =,即点M 的纵坐标为1-; 令1y =-,则2114x x -=-, ∴2x =,即ON=2,∴OF=114, ∴11,04F ⎛⎫ ⎪⎝⎭. ∵(1,2)E ,∴1,2BE BP t ==-,∴221(2)PE t =+-,∴251(2)PF t =+-在Rt △OPF 中,由勾股定理,得222OP OF PF +=,∴22211()55(2)4t t +=+-, ∴98t =. (II )若DF DM =.如图③所示:此时5FD DM ==∴45OF =,∴(45,0)F ,由(I )知,221(2)PE t =+-,251(2)PF t =+-在Rt △OPF 中,由勾股定理,得222OP OF PF +=,∴222(45)55(2)t t +-=+-∴512t =. (III )若FM MD =.由抛物线对称性可知,此时点F 与原点O 重合.∵PE EF ⊥,点P 在直线AC 上方,与点P 在线段OB 上运动相矛盾,故此种情形不存在.【点睛】本题考查的是二次函数综合运用,涉及到相似三角形的判定和性质,一次函数的性质,等腰三角形的性质,全等三角形的判定和性质,以及勾股定理等知识,其中(3),要注意分类求解,避免遗漏.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学二次函数经典题型二次函数单元检测(A)姓名 _______一、填空题:1、函数y(m 1)x m212mx 1 是抛物线,则m=.2、抛物线y x22x 3 与 x 轴交点为,与 y 轴交点为.3、二次函数y ax2的图象过点(- 1, 2),则它的解析式是,当 x时, y 随x的增大而增大.4.抛物线y6( x1) 2 2 可由抛物线 y6x 22向平移个单位得到.5.抛物线y x24x 3 在 x 轴上截得的线段长度是.6.抛物线y x22x m 2 4 的图象经过原点,则m.7.抛物线y x2x m ,若其顶点在x 轴上,则 m.8. 如果抛物线y ax2bx c的对称轴是 x=- 2,且开口方向与形状与抛物线y3x2相同,又过原点,那么a=,b=, c=2.9、二次函数y x2bx c 的图象如下左图所示,则对称轴是,当函数值 y0 时,对应 x 的取值范围是.yyA- 3O1x Bx10、已知二次函数y1 ax2bx c(a0)与一次函数 y2kx m( k 0) 的图象相交于点A(- 2, 4)和 B( 8, 2),如上右图所示,则能使y1y2成立的 x 的取值范围.二、选择题:11. 下列各式中 ,y 是x的二次函数的是()A.xy x2 1 B. x2y 2 0 C .y2ax 2 D. x2y 2 1 012.在同一坐标系中,作y 2x2、 y 2 x2、 y 1x2的图象,它们共同特点是() 2A.都是关于x轴对称,抛物线开口向上B.都是关于 y 轴对称,抛物线开口向下B.都是关于原点对称,顶点都是原点D.都是关于 y 轴对称,顶点都是原点13.抛物线y x 2mx m21的图象过原点,则m 为()A. 0 B . 1 C .- 1 D .± 114.把二次函数y x2 2 x1配方成为()A.y ( x 1)2 B .y (x 1)2 2 C. y ( x 1) 21D.y ( x 1)22 15.已知原点是抛物线y (m1)x2的最高点,则m 的范围是( )A.m1 B .m 1C. m 1D. m 216、函数y2x2x1的图象经过点()A、(- 1, 1) B 、( 1 ,1) C 、( 0 , 1)D、 (1 , 0 )17、抛物线y3x2向右平移1个单位,再向下平移 2 个单位,所得到的抛物线是( )A、y3(x1)2 2B、 y3( x1)2 2C、 y3( x1)22 D 、y3( x1)2218 、已知h关于t的函数关系式h 1gt 2( g 为正常数, t 为时间)如图,则函数图象为( ) 2h h h hoo t t o t o tA B C D19、下列四个函数中 ,图象的顶点在y 轴上的函数是()A 、y x23x 2 B、 y 5x2 C 、y x22x D、 y x24x 420 、已知二次函数y ax2bx c ,若a0 , c 0,那么它的图象大致是()y y y yo x o x o x o x(C)(A)(B)(D)三、解答题:21、根据所给条件求抛物线的解析式:(1)、抛物线过点( 0, 2)、( 1, 1)、( 3, 5)(2)、抛物线关于y轴对称,且过点( 1,- 2)和(- 2, 0)22.已知二次函数y x2bx c 的图像经过A( 0, 1), B( 2,- 1)两点 .(1)求b和 c的值;(2)试判断点(-,)是否在此函数图像上?P1 223、某广告公司设计一幅周长为12 米的矩形广告牌,广告设计费为每平方米1000 元,设矩形一边长为 x 米,面积为S 平方米 .(1)求出S与x之间的函数关系式,并确定自变量x 的取值范围;(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.24、某工厂现有80 台机器,每台机器平均每天生产384?件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,?由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产 4 件产品.(1)如果增加x 台机器,每天的生产总量为y 件,请你写出y 与 x 之间的关系式;(2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?25、如图,有一个抛物线的拱形立交桥,?这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,?若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?24 、如图,抛物线y x 25x n 经过点A(1,0),与y轴交于点 B.⑴求抛物线的解析式;⑵P 是 y 轴正半轴上一点,且△PAB是以 AB为腰的等腰三角形,试求P 点坐标 .yAO1x-1B二次函数单元检测(B)姓名_______一、新课标基础训练1.下列二次函数的图象的开口大小,从大到小排列依次是()① y = 1x 2;② y= 2x 2+3;③ y=- 1(x-3 ) 2-2 ;④ y=- 3x 2+5x-1 .3322A .④②③①B.①③②④C .④②①③D .②③①④2的图象向右平移 3 个单位,再向上平移 1 个单位,所得的图象的函数2.将二次函数 y=3(x+2) -4 关系式( )A . y=3( x+5) 2-5 ;B . y=3( x-1 ) 2-5 ;C . y=3( x-1 ) 2-3 ;D . y=3( x+5) 2-33.将进货单价为70 元的某种商品按零售价100 元一个售出时,每天能卖出20个, ?若这种商品的零售价在一定范围内每降价 1 元,其日销量就增加 1 个,为了获取最大利润,则应降价( )A . 5 元B . 10 元C .15 元D . 20 元4.若直线 y=ax+b ( ab ≠0)不过第三象限,则抛物线y=ax 2+bx 的顶点所在的象限是()A .一B .二C .三D .四5.已知二次函数y=x 2+x+m ,当 x 取任意实数时,都有 y>0,则 m 的取值范围是()A . m ≥1B . m>1C . m ≤1D .m<144446.二次函数 y=mx 2-4x+1 有最小值 -3 ,则 m 等于()A . 1B . -1C .± 1D .±12二、新课标能力训练7.如图,用 2m 长的木条,做一个有横档的矩形窗子,为使透进的光线最多,那么这个窗子的面积应为2_______m .8.如图,有一个抛物线型拱桥,其最大高度为16m ,?跨度为 ?40m , ? 现把它的示意图放在平面直角坐标系中 ??,??则此抛物线的函数关系式为__________.9、已知函数 y(m 2) x m 2 m 4 是关于 x 的二次函数,求: (1) 满足条件的 m 值;(2)m 为何值时,抛物线有最低点?求出这个最低点.这时当 x 为何值时, y 随 x 的增大而增大 ?( 3)m 为何值时,函数有最大值 ?最大值是什么 ?这时当 x 为何值时, y 随 x 的增大而减小 ?10、观察表格:x 01 2ax 21233ax +bx+c(1)求 a , b , c 的值,并在表内空格处填入正确的数.(2)画出函数 y=ax 2+bx+c 的图象,由图象确定,当 x 取什么实数时, ax 2+bx+c>0.11、如图 (2) ,已知平行四边形 ABCD 的周长为 8cm ,∠ B = 30。
若边长 AB = x(cm) 。
(1) 求□ABCD 的面积 y(cm 2) 与 x 的函数关系式,并写出自变量x 的取值范围。
(2)当 x 取什么值时, y 的值最大 ?并求最大值。
三、新课标理念中考题12.如图,已知直线y=-2x+2 分别与 x 轴、 y 轴交于点 A、 B,以线段 AB为直角边在第一象限内作等腰直角三角形 ABC,∠ BAC=90°,过 C?作 CD⊥ x 轴, D为垂足.(1)求点 A、 B 的坐标和 AD的长;(2)求过 B、 A、 C三点的抛物线的解析式.13、如图,二次函数y x 2bx c 的图象经过点M(1,—2)、 N(—1,6).( 1)求二次函数y x 2bx c 的关系式.( 2)把 Rt △ABC放在坐标系内,其中∠CAB= 90 °,点A、B的坐标分别为( 1,0)、( 4,0),BC= 5。
将△ ABC沿 x 轴向右平移,当点 C落在抛物线上时,求△ ABC平移的距离.14、黄冈市某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图甲的一条折线表示;西红柿的种植成本与上市时间的关系用图乙表示的抛物线段表示.(1)写出图甲表示的市场售价与时间的函数关系式;(2)写出图乙表示的种植成本与时间的函数关系式;(3)设定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/10 2kg,时间单位:天)15、已知:在直角坐标系中的位置如图,O是坐标原点,::= 1: 3: 5,ABCD D、 A、B 三点。
OB OC OAS=12,抛物线经过ABCD①求 A、 C两点的坐标;②求抛物线解析式;16、已知二次函数y=ax 2+bx+c 的图象经过点A( 2, 4), ?其顶点横坐标为1,且(b)2-2c=13.2a a(1)求此二次函数的解析式;(2)抛物线与 x 轴交于 B,C 两点,在 x 轴上方的上,是否存在点 P,使得 S△ABC=2S△PBC,如存在,?请求出所有满足条件的点 P 的坐标;如不存在,请说明理由.。
