数学建模线性规划上机题汇编

合集下载

大学生数学建模练习题

大学生数学建模练习题一、线性规划问题假设你是一家制造公司的经理，公司生产两种产品A和B。

生产一个产品A需要3小时的机器时间和2小时的人工时间，产品B需要2小时的机器时间和4小时的人工时间。

公司每天有24小时的机器时间和40小时的人工时间可用。

如果产品A的销售价格是50元，产品B是80元，如何安排生产计划以最大化利润？二、排队论问题一家银行有3个服务窗口，平均每天接待200名顾客。

每名顾客的平均服务时间是5分钟。

假设顾客到达银行是随机的，服从泊松分布，服务时间服从指数分布。

请计算银行的平均排队长度和顾客的平均等待时间。

三、库存管理问题一家零售商销售一种季节性产品，该产品的需求量在一年中波动很大。

产品的成本是每个20元，存储成本是每个每年2元，缺货成本是每个10元。

如果零售商希望在一年内保持至少95%的服务水平，应该如何确定最优的订货量和订货频率？四、网络流问题在一个供水系统中，有四个水库和五个城市。

水库1和2可以向城市A 供水，水库2和3可以向城市B供水，水库3和4可以向城市C和D供水。

每个水库的供水能力不同，每个城市的需求也不同。

如果需要确保所有城市的需求都得到满足，如何确定最优的供水方案？五、预测问题给定一个公司过去5年的季度销售额数据，使用时间序列分析方法预测下个季度的销售额。

请考虑季节性因素和趋势，并给出预测的置信区间。

六、优化问题一个农场主有一块矩形土地，打算围成一个矩形的牧场。

如果围栏的总长度是固定的，比如400米，如何确定牧场的长和宽，使得牧场的面积最大？七、多目标决策问题一家公司需要在多个项目中做出选择，每个项目都有不同的预期收益、风险和实施时间。

如果公司需要在风险和收益之间做出权衡，并且希望项目尽快完成，如何使用多目标决策方法来选择最合适的项目组合？通过解决这些练习题，大学生可以加深对数学建模的理解，提高分析和解决实际问题的能力。

希望这些练习题能够帮助学生在数学建模的道路上更进一步。

线性规划题及答案

线性规划题及答案一、问题描述某公司生产两种产品A和B，每一个产品的生产需要消耗不同的资源，并且每一个产品的销售利润也不同。

公司希翼通过线性规划来确定生产计划，以最大化利润。

已知产品A每一个单位的生产需要消耗2个资源1和3个资源2，每一个单位的销售利润为10元；产品B每一个单位的生产需要消耗4个资源1和1个资源2，每一个单位的销售利润为15元。

公司目前有10个资源1和12个资源2可供使用。

二、数学建模1. 假设生产产品A的数量为x，生产产品B的数量为y。

2. 根据资源的消耗情况，可以得到以下约束条件：2x + 4y ≤ 10 （资源1的消耗）3x + y ≤ 12 （资源2的消耗）x ≥ 0, y ≥ 0 （生产数量为非负数）3. 目标是最大化利润，即最大化销售收入减去生产成本：最大化 Z = 10x + 15y三、线性规划求解1. 将目标函数和约束条件转化为标准形式：目标函数：最大化 Z = 10x + 15y约束条件：2x + 4y ≤ 103x + y ≤ 12x ≥ 0, y ≥ 02. 通过图形法求解线性规划问题：a. 绘制约束条件的图形：画出2x + 4y = 10和3x + y = 12的直线，并标出可行域。

b. 确定可行域内的顶点：可行域的顶点为(0, 0)，(0, 2.5)，(4, 0)，(2, 3)。

c. 计算目标函数在每一个顶点处的值：分别计算Z = 10x + 15y在(0, 0)，(0, 2.5)，(4, 0)，(2, 3)四个顶点处的值。

Z(0, 0) = 0Z(0, 2.5) = 37.5Z(4, 0) = 40Z(2, 3) = 80d. 比较所有顶点处的目标函数值，确定最优解：最优解为Z = 80，即在生产2个单位的产品A和3个单位的产品B时，可以获得最大利润80元。

四、结论根据线性规划的结果，公司在资源充足的情况下，应该生产2个单位的产品A和3个单位的产品B，以最大化利润。

建模补充-线性规划练习题(带答案)

线性规划建模习题2.某医院昼夜24小时各时间段内需要的护士数量如下：2:00～6:00 10人；6:00～10:00 15人；10:00～14:00 25人；14:00～18:00 20人；18:00～22:00 18人；22:00～2:00 12人。

护士分别于2:00、6:00、10:00、14:00、18:00、22:00分六批上班，并连续工作8小时。

试确定：(a)该医院至少应设多少名护士，才能满足值班需要；(b)若医院可聘用合同工护士，上班时间同正式工护士。

若正式工护士报酬为10元/小时，合同工护士为15元/小时，问医院聘用正式工和合同工护士各多少人成本最低？3.某人有一笔30万元的资金，在今后三年内有以下投资项目：(1)三年内的每年年初均可投资，每年获利为投资额的20%，其本利可一起用于下一年投资；(2)只允许第一年年初投入，第二年年末可收回，本利合计为投资额的150%，但此类投资限额不超过15万元；(3)于三年内第二年初允许投资，可于第三年末收回，本利合计为投资额的160%，这类投资限额20万元；(4)于三年内的第三年初允许投资，一年收回，可获利40%，投资限额为10万元。

试为该人确定一个使第三年末本利和为最大的投资计划。

8.市场对I、II两种产品的需求量为：产品I在1～4月每月需10000件，5 ～9月每月30000件，10 ～12月每月需100000件；产品II在3 ～9月每月15000件，其他月每月50000件。

某厂生产这两种产品成本为：产品I在1 ～5月内生产每件5元，6 ～12月内生产每件4.5元；产品II 在1 ～5月内生产每件8元，6 ～12月内生产每件7元。

该厂每月生产两种产品能力总和不超过120000件。

产品I容积每件0.2立方米，产品II每件0.4立方米，而该厂仓库容积为15000立方米。

要求：(1)若占用本厂每月每立方米库容需1元，该厂应如何安排生产计划，才能在满足市场需求的前提下，确保生产加库存费用最低？(2)上述问题是否有可行解？(3)若该厂仓库不足时，可从外厂租借，租用外厂仓库时上述费用增加为1.5元，试问在满足市场需求情况下，该厂应如何安排生产，使总的生产加库存费用为最少？15.一个大的造纸公司下设10个造纸厂，供应1000个用户。

数学线性规划试题答案及解析

数学线性规划试题答案及解析1.在平面直角坐标系中，为不等式组所表示的区域上一动点，则直线斜率的最小值为 .【答案】【解析】不等式组表示的区域如图，当取得点时，直线斜率取得最小，最小值为．故选C．2.若实数满足其中，若使得取得最小值的解有无穷多个，则等于．【答案】2．【解析】表达式可看成是定点与动点连线斜率（点在所给不等式组表示的平面区域内），如图，动直线过定点，为使满足题意的点有无穷多个，此时直线应过，从而【考点】本题考查含参数的二元一次不等式组表示平面区域等知识，意在考查画图、用图及计算能力.3.设实数满足条件，则的最大值是（）A．B．C．D．【答案】A【解析】画出可行域，如图所示，目标函数变形为，直线经过可行域，尽可能地向下平移经过点时取到最大值，即的最大值为.【考点】本题考查线性规划等基础知识，意在考查学生数形结合思想的运用能力和基本运算能力．4.已知实数满足：，则的最小值为 .【答案】【解析】画出可行域及直线..，如图所示.平移直线，当经过点时，直线的纵截距最大，所以，．【考点】本题考查简单线性规划的应用等知识，意在考查作图、识图、用图的能力及数形结合思想．5.某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车．某天需送往A地至少72吨的货物，派用的每辆车需满载且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人，运送一次可得利润350元．该公司合理计划当天派用两类卡车的车辆数，可得最大利润z＝ () A．4 650元B．4 700元C．4 900元D．5 000元【答案】C【解析】设派用甲型卡车x辆，乙型卡车y辆，则，目标函数z＝450x＋350y，画出可行域如图，当目标函数经过A(7,5)时，利润z最大，为4 900元6.若x，y满足约束条件则z＝3x－y的最小值为________．【答案】－1【解析】本小题主要考查线性规划最优解的应用，解题的突破口是正确作出可行域和平移目标函数曲线．利用不等式组，作出可行域，则目标函数直线过(0,1)时，z取最小值－1.7.已知变量满足约束条件，若的最大值为，则实数 .【答案】或（对1个得3分，对2个得5分）【解析】利用线性规划的知识画出不等式组表示的可行域如下图所示:其中点,根据线性规划的知识可得目标函数的最优解在只能是,当目标函数在点A处取得最优解时,有符合题意,当目标函数在点B处取得最优解时, 符合题意,当目标函数在C点取得最优解时, 无解,所以或,故填或.8.已知点满足约束条件，为坐标原点，则的最大值为．【答案】5【解析】作出可行域，得到当位于时，最大，其值为5.9.浙江理）设，其中实数满足，若的最大值为12，则实数________。

线性规划题及答案

线性规划题及答案线性规划是一种优化问题的数学建模方法，通过线性函数的约束条件来求解目标函数的最大或最小值。

在实际问题中，线性规划经常被用来解决资源分配、生产计划、运输问题等。

下面我将为您提供一道线性规划题及其答案，以帮助您更好地理解线性规划的应用。

题目：某公司生产两种产品A和B，每个单位的产品A需要2个单位的原材料X和1个单位的原材料Y，每个单位的产品B需要1个单位的原材料X和3个单位的原材料Y。

公司每天可用的原材料X和Y分别为10个单位和15个单位。

产品A的售价为100元/单位，产品B的售价为150元/单位。

假设公司希望最大化每天的总收入，请问应该生产多少单位的产品A和产品B？解答：首先，我们需要定义决策变量。

设产品A的产量为x个单位，产品B的产量为y个单位。

然后，我们需要建立目标函数和约束条件。

目标函数：总收入 = 100x + 150y约束条件：1. 原材料X的使用量：2x + y ≤ 102. 原材料Y的使用量：x + 3y ≤ 153. 产量非负：x ≥ 0, y ≥ 0接下来，我们可以使用线性规划的方法来求解最优解。

首先，将目标函数和约束条件转化为标准的线性规划形式：目标函数：Maximize 100x + 150y约束条件：2x + y ≤ 10x + 3y ≤ 15x ≥ 0, y ≥ 0然后，我们可以使用单纯形法或其他线性规划求解方法来求解最优解。

在这里，为了简化计算，我们使用图形法来求解。

首先，将约束条件转化为直线的形式：2x + y = 10x + 3y = 15然后，我们可以画出约束条件所对应的直线。

在坐标系中，标出两个直线的交点，即可确定可行域。

接下来，我们需要计算目标函数在可行域内的各个顶点的值，并比较得出最优解。

通过计算，我们得到以下结果：顶点A(0, 5)：总收入 = 100 * 0 + 150 * 5 = 750顶点B(5, 0)：总收入 = 100 * 5 + 150 * 0 = 500顶点C(3, 2)：总收入 = 100 * 3 + 150 * 2 = 750因此，最优解为在顶点A和顶点C处取得，即生产5个单位的产品A和2个单位的产品B，总收入为750元。

线性规划题及答案

线性规划题及答案一、问题描述假设某公司生产两种产品：产品A和产品B。

每天生产的产品A需要花费3小时的人工时间和2小时的机器时间，每天生产的产品B需要花费2小时的人工时间和4小时的机器时间。

公司每天有8小时的人工时间和10小时的机器时间可供使用。

产品A的利润为200元/件，产品B的利润为300元/件。

公司希望通过合理安排生产计划，使得每天的总利润最大化。

二、数学建模1. 定义变量：设产品A的生产量为x，产品B的生产量为y。

2. 建立目标函数：总利润最大化，即Maximize Z = 200x + 300y。

3. 建立约束条件：3x + 2y ≤ 8（人工时间约束）2x + 4y ≤ 10（机器时间约束）x ≥ 0，y ≥ 0（非负约束）三、线性规划模型Maximize Z = 200x + 300ysubject to3x + 2y ≤ 82x + 4y ≤ 10x ≥ 0, y ≥ 0四、求解线性规划问题通过线性规划求解器进行计算，得到最优解。

1. 求解目标函数最大值：Z = 200x + 300y最大值为Z = 200 * 2 + 300 * 1 = 700。

2. 求解最优生产量：当x = 2，y = 1时，总利润最大，即每天生产2件产品A和1件产品B，总利润为700元。

五、结论根据线性规划模型的计算结果，为了使得公司每天的总利润最大化，应该安排每天生产2件产品A和1件产品B。

这样可以获得每天700元的总利润。

六、灵敏度分析在线性规划问题中，灵敏度分析可以帮助我们了解模型的稳定性和可行性。

下面对人工时间和机器时间的变化进行灵敏度分析。

1. 人工时间的变化：当每天的人工时间增加1小时，即约束条件变为3x + 2y ≤ 9时，重新求解线性规划问题。

结果显示，最大总利润仍然为700元，最优生产量为每天生产2件产品A和1件产品B。

2. 机器时间的变化：当每天的机器时间增加1小时，即约束条件变为2x + 4y ≤ 11时，重新求解线性规划问题。

数学建模习题——线性规划

某银行经理计划用一笔资金进行有价证券的投资，可供购进的证券以及其信用等级、到期年限、收益如下表所示．按照规定，市政证券的收益可以免税，其他证券的收益需按50%的税率纳税．此外还有表四问：（1）若该经理有1000万元资金，应如何投资？（2）如果能够以2.75%的利率借到不超过100万元资金，该经理应如何操作？（3）在1000万元资金情况下，若证券A 的税前收益增加为4.5%，投资应否改变？若证券C 的税前收益减少为4.8%，投资应否改变？解：设利润函数为M(x),投资A 、B 、C 、D 、E 五种类型的证券资金分别为12345,,,,x x x x x 万元，则由题设条件可知12345123452341234512345123451234512345()0.0430.0270.0250.0220.0451000400225 1.4()9154325(),,,,0M x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++≤++≥++++≤++++++++≤++++≥利用MATLAB 求解最优解，代码如下： c=[-0.043 -0.027 -0.025 -0.022 -0.045];A=[1 1 1 1 1;0 -1 -1 -1 0;0.6 0.6 -0.4 -0.4 3.6;4 10 -1 -2 -3];b=[1000;-400;0;0]; Aeq=[]; beq=[];vlb=[0;0;0;0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub) 运行结果如下：即12345218.1818,0,736.3636,0,45.4545x x x x x =====因此，应投资A 证券218.1818万元，B 证券0万元，C 证券736.3636万元，D 证券45.4545万元，最大利润为29.8364万元。

数学建模测试题-线性规划部分

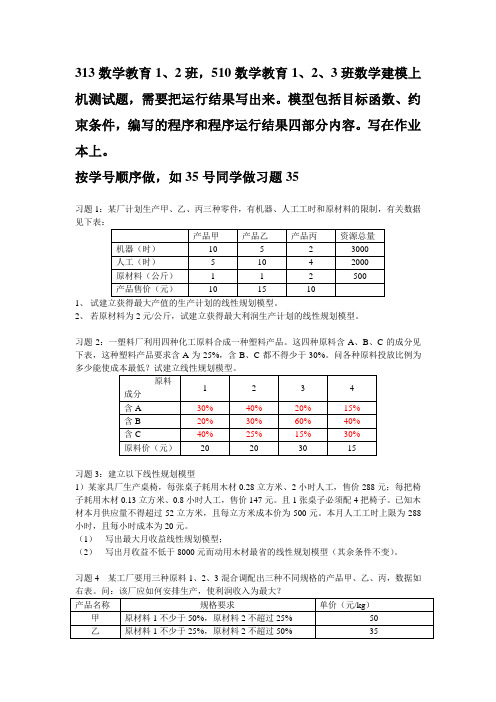
313数学教育1、2班，510数学教育1、2、3班数学建模上机测试题，需要把运行结果写出来。

模型包括目标函数、约束条件，编写的程序和程序运行结果四部分内容。

写在作业本上。

按学号顺序做，如35号同学做习题35习题1：某厂计划生产甲、乙、丙三种零件，有机器、人工工时和原材料的限制，有关数据1、2、若原材料为2元/公斤，试建立获得最大利润生产计划的线性规划模型。

习题2：一塑料厂利用四种化工原料合成一种塑料产品。

这四种原料含A、B、C的成分见下表，这种塑料产品要求含A为25%，含B、C都不得少于30%。

问各种原料投放比例为习题3：建立以下线性规划模型1）某家具厂生产桌椅，每张桌子耗用木材0.28立方米、2小时人工，售价288元；每把椅子耗用木材0.13立方米、0.8小时人工，售价147元。

且1张桌子必须配4把椅子。

已知木材本月供应量不得超过52立方米，且每立方米成本价为500元。

本月人工工时上限为288小时，且每小时成本为20元。

（1）写出最大月收益线性规划模型；（2）写出月收益不低于8000元而动用木材最省的线性规划模型（其余条件不变）。

习题4 某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙，数据如右表。

问：该厂应如何安排生产，使利润收入为最大？习题5、某部门现有资金200万元，今后五年内考虑给以下的项目投资。

已知：项目A ：从第一年到第五年每年年初都可投资，当年末能收回本利110%；项目B ：从第一年到第四年每年年初都可投资，次年末能收回本利125%，但规定每年最大投资额不超过30万元；项目C ：需在第三年年初投资，第五年末能收回本利140%，但规定最大投资额不能超过80万元；项目D ：需在第二年年初投资，第五年末能收回本利155%，但规定最大投资额不能超过100万元；问：a.应如何确定这些项目的每年投资额，使得第五年年末拥有资金的本利金额为最大？ b.应如何确定这些项目的每年投资额，使得第五年年末拥有资金的本利在330万元的基础上使得其投资总的风险系数为最小？习题6 某公司计划在三年的计划期内，有四个建设项目可以投资：项目Ⅰ从第一年到第三年年初都可以投资。

线性规划题及答案

线性规划题及答案引言概述：线性规划是运筹学中的一种数学方法，用于寻觅最优解决方案。

在实际生活和工作中，线性规划问题时常浮现，通过对问题进行建模和求解，可以得到最优的决策方案。

本文将介绍一些常见的线性规划题目，并给出详细的答案解析。

一、生产规划问题1.1 生产规划问题描述：某工厂生产两种产品A和B，产品A每单位利润为100元，产品B每单位利润为150元。

每天工厂有8小时的生产时间，产品A每单位需要2小时，产品B每单位需要3小时。

问工厂每天应该生产多少单位的产品A 和产品B，才干使利润最大化？1.2 生产规划问题答案：设产品A的生产单位为x，产品B的生产单位为y，则目标函数为Max Z=100x+150y，约束条件为2x+3y≤8，x≥0，y≥0。

通过线性规划方法求解，得出最优解为x=2，y=2，最大利润为400元。

二、资源分配问题2.1 资源分配问题描述：某公司有两个项目需要投资，项目A每万元投资可获得利润2万元，项目B每万元投资可获得利润3万元。

公司总共有100万元的投资额度，问如何分配投资额度才干使利润最大化？2.2 资源分配问题答案：设投资项目A的金额为x万元，投资项目B的金额为y万元，则目标函数为Max Z=2x+3y，约束条件为x+y≤100，x≥0，y≥0。

通过线性规划方法求解，得出最优解为x=40，y=60，最大利润为240万元。

三、运输问题3.1 运输问题描述：某公司有两个仓库和三个销售点，每一个销售点的需求量分别为100、150、200，每一个仓库的库存量分别为80、120。

仓库到销售点的运输成本如下表所示，问如何安排运输方案使得总成本最小？3.2 运输问题答案：设从仓库i到销售点j的运输量为xij，则目标函数为Min Z=∑(i,j) cij*xij，约束条件为每一个销售点的需求量得到满足，每一个仓库的库存量不超出。

通过线性规划方法求解，得出最优的运输方案，使得总成本最小。

四、投资组合问题4.1 投资组合问题描述：某投资者有三种投资标的可选择，预期收益率和风险如下表所示。

1、线性规划(数学建模)

⎧2 x1 + x2 ≤ 10 ⎪x + x ≤ 8 ⎪ 1 2 s.t.（约束条件） ⎨ ⎪ x2 ≤ 7 ⎪ ⎩ x1 , x2 ≥ 0
（2）
（1）式被称为问题的目标函数，（2）中的几个不等式这里变量 x1 , x 2 称之为决策变量，是问题的约束条件，记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性函数，故被称为线性规划问题。总之，线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选适当的决策变量，是我们建立有效模型的关键之一。 1.2 线性规划的 Matlab 标准形式线性规划的目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便，Matlab 中规定线性规划的标准形式为
max z = 2 x1 + 3x2 − 5 x3 s.t. x1 + x2 + x3 = 7 2 x1 − 5 x2 + x3 ≥ 10 x1 + 3 x2 + x3 ≤ 12 x1 , x2 , x3 ≥ 0
-3-
解（i）编写 M 文件 c=[2;3;-5]; a=[-2,5,-1;1,3,1]; b=[-10;12]; aeq=[1,1,1]; beq=7; x=linprog(-c,a,b,aeq,beq,zeros(3,1)) value=c'*x （ii）将M文件存盘，并命名为example1.m。（iii）在Matlab指令窗运行example1即可得所求结果。例3 求解线性规划问题

数学建模线性规划问题超全共54页文档

数学建模线性规划问题超全
11、获得的成功越大，就越令人高兴。野心是使人勤奋的原因，节制使人枯萎。 12、不问收获，只问耕耘。如同种树，先有根茎，再有枝叶，尔后花实，好好劳动，不要想太多，那样只会使人胆孝懒惰，因为不实践，甚至不接触社会，难道你是野人。(名言网) 13、不怕，不悔(虽然只有四个字，但常看常新。 14、我在心里默默地为每一个人祝福。我爱自己，我用清洁与节制来珍惜我的身体，我用智慧和知识充实我的头脑。 15、这世上的一切都借希望而完成。农夫不会播下一粒玉米，如果他不曾希望它长成种籽；单身汉不会娶妻，如果他不曾希望有小孩；商人或手艺人不会工作，如果他不曾希望因此而有收益。-- 马钉路德。
谢谢！
51、天下之事常成于困约，而败于奢靡。—陆游 52、生命不等于是呼吸，生命是活动。——卢梭
53、伟大的事业，需要决心，能力，组织和责任感。 ——易卜生 54、唯书籍不朽。——乔特
55、为中华之崛起而读书。 ——周恩来

线性规划经典例题

线性规划经典例题一、问题描述某工厂生产两种产品A和B，每单位产品A需要2个工时和3个材料单位，每单位产品B需要3个工时和2个材料单位。

已知该工厂每天有40个工时和50个材料单位可用。

产品A的利润为每单位100元，产品B的利润为每单位80元。

问该工厂应该生产多少单位的产品A和产品B才能使利润最大化？二、数学建模1. 假设生产产品A的单位数量为x，生产产品B的单位数量为y。

2. 根据题目要求，可以得到以下约束条件：- 工时约束：2x + 3y ≤ 40- 材料约束：3x + 2y ≤ 50- 非负约束：x ≥ 0，y ≥ 03. 目标函数：利润最大化，即最大化目标函数 Z = 100x + 80y。

三、标准格式的线性规划模型最大化目标函数：Z = 100x + 80y约束条件：2x + 3y ≤ 403x + 2y ≤ 50x ≥ 0，y ≥ 0四、求解方法可以使用线性规划的求解方法，如单纯形法或者求解器进行求解。

以下是使用求解器求解的步骤：1. 打开线性规划求解器，输入目标函数和约束条件。

2. 设置目标为最大化。

3. 添加约束条件：2x + 3y ≤ 40，3x + 2y ≤ 50，x ≥ 0，y ≥ 0。

4. 点击求解按钮，得到最优解及最优值。

5. 解释结果并作出决策。

五、求解结果与决策分析经过求解器计算，得到最优解为x = 10，y = 10，最优值为Z = 1800。

根据最优解，该工厂应该生产10个单位的产品A和10个单位的产品B，才能使利润最大化，最大利润为1800元。

六、敏感性分析对于该线性规划问题，我们可以进行敏感性分析来了解目标函数系数的变化对最优解的影响。

1. 目标函数系数变化：- 如果产品A的利润系数从100变为110，产品B的利润系数从80变为90，重新求解得到新的最优解为x = 10，y = 10，最优值为Z = 2000。

可以看出，利润系数的变化对最优解有一定的影响，但最优解仍然是生产10个单位的产品A和10个单位的产品B。

线性规划模型例题——数学模型

Reduced Cost 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.350000 0.3500000 0.3500000 Dual Price 1.000000 1.300000 0.8000000 1.300000 -1.000000 0.000000
3
22
+0.4 x +0.5 x
3
23
<=0 <=0
-0.5 x -0.5 x
3
31
3
32
3
33
（1）、在 LINGO 软件中输入如下程序：
model: max=0.9*x11+1.4*x12+1.9*x13+0.45*x21+0.95*x22+1.45*x23-0.05*x31+0.45* x32+0.95*x33; x11+x21+x31<2000; x12+x22+x32<2500; x13+x23+x33<1200; 0.4*x11-0.6*x12-0.6*x13>0; -0.2*x11-0.2*x12+0.8*x13<0; 0.85*x21-0.15*x22-0.15*x23>0; -0.6*x21-0.6*x22+0.4*x23<0; -0.5*x31-0.5*x32+0.5*x33<0; end
线性规划例题线性规划模型高中数学线性规划非线性规划模型数学建模非线性规划数学线性规划数学建模线性规划线性规划数学题一元线性回归例题线性代数例题
规划模型
模型假设：

线性规划经典例题

线性规划经典例题一、问题描述某公司生产两种产品A和B，每个产品的生产需要消耗不同的资源。

现在公司希望通过线性规划来确定每种产品的生产数量，以最大化利润。

已知产品A每个单位的利润为10元，产品B每个单位的利润为15元。

同时，产品A每个单位需要消耗2个资源X和3个资源Y，产品B每个单位需要消耗4个资源X和1个资源Y。

公司总共有40个资源X和30个资源Y可供使用。

二、数学建模1. 假设产品A的生产数量为x，产品B的生产数量为y。

2. 目标函数：最大化利润。

利润可以表示为10x + 15y。

3. 约束条件：a) 资源X的约束条件：2x + 4y ≤ 40b) 资源Y的约束条件：3x + y ≤ 30c) 非负约束条件：x ≥ 0，y ≥ 0三、求解过程1. 根据数学建模中的目标函数和约束条件，可以得到如下线性规划模型：最大化：10x + 15y约束条件：2x + 4y ≤ 403x + y ≤ 30x ≥ 0，y ≥ 02. 使用线性规划求解方法，可以得到最优解。

通过计算，得到最优解为x = 6，y = 6，利润最大化为180元。

四、结果分析根据最优解，可以得知最大利润为180元，其中产品A的生产数量为6个，产品B的生产数量为6个。

同时，资源X还剩余28个，资源Y还剩余24个。

五、灵敏度分析对于线性规划问题，灵敏度分析可以帮助我们了解目标函数系数和约束条件右端项的变化对最优解的影响。

1. 目标函数系数的变化：a) 如果产品A的利润提高到12元，产品B的利润保持不变，重新求解线性规划模型可以得到新的最优解。

新的最优解为x = 8，y = 4，利润最大化为168元。

b) 如果产品A的利润保持不变，产品B的利润提高到20元，重新求解线性规划模型可以得到新的最优解。

新的最优解为x = 4，y = 7，利润最大化为190元。

2. 约束条件右端项的变化：a) 如果资源X的数量增加到50个，资源Y的数量保持不变，重新求解线性规划模型可以得到新的最优解。

线性规划题及答案

线性规划题及答案线性规划是一种优化问题的数学建模方法，它在各个领域中都有广泛的应用。

本文将为您提供一道线性规划题目及其详细的解答过程。

题目描述：某公司生产两种产品A和B，产品A每单位利润为300元，产品B每单位利润为500元。

生产一个单位产品A需要消耗2个单位的原料X和3个单位的原料Y；生产一个单位产品B需要消耗1个单位的原料X和4个单位的原料Y。

公司每天有100个单位的原料X和150个单位的原料Y可供使用。

公司希望在满足原料供应的情况下，最大化每天的利润。

解答过程：1. 定义变量：设产品A的产量为x，产品B的产量为y。

2. 建立目标函数：目标函数即每天的利润，由题目可知，每单位产品A的利润为300元，每单位产品B的利润为500元。

因此，目标函数为：最大化 Z = 300x + 500y3. 建立约束条件：a) 原料X的供应限制：每单位产品A需要消耗2个单位的原料X，每单位产品B需要消耗1个单位的原料X。

因此，原料X的供应限制可以表示为：2x + y ≤ 100b) 原料Y的供应限制：每单位产品A需要消耗3个单位的原料Y，每单位产品B需要消耗4个单位的原料Y。

因此，原料Y的供应限制可以表示为：3x + 4y ≤ 150c) 产量非负限制：产品的产量必须为非负数，即：x ≥ 0y ≥ 04. 求解线性规划问题：将目标函数和约束条件进行整理，得到线性规划模型为：最大化 Z = 300x + 500y约束条件：2x + y ≤ 1003x + 4y ≤ 150x ≥ 0y ≥ 0使用线性规划求解器或图形法等方法，可以得到最优解。

5. 最优解及结论：经过计算，得到最优解为：x = 25，y = 25此时，最大利润为：Z = 300 * 25 + 500 * 25 = 20000元因此，当公司每天生产25个单位的产品A和25个单位的产品B时，可以实现每天最大利润为20000元。

总结：本文提供了一道线性规划题目及详细的解答过程。

第一篇线性规划建模习题答案

第一章习题1•设用原料A生产甲、乙、丙的数量分别为x11,x12,x i3，用原料B生产甲、乙、丙的数量分别为X21,X22,X23，原料C生产甲、乙、丙的数量分别为X31,X32,X33，则可以建立线性规划问题的数学模型：max S =3.6x11 1.8x12—0.2x13 5.6x21 3.8x22 1.8x23 7.6x31 5.8x32 3.8x33X" +x12+x13兰2000X21 + X22 + X23 兰2500X31 +X32 +X33 <200 —0.6x21—0.6x31 30st.«—0.2x21 +0.8x31 W00.85x12—0.15x22 - 0.15x32±0—0.6x12—0.6x22 +0.4x32 W0—0.5x13—0.5x23 +0.5X33兰0X j -0,(i, j =1,2,3)LINGO求解程序见程序max=3.6*x11+5.6*x21+7.6*x31+1.8*x12+3.8*x22+5.8*x32-0.2*x13+1.8*x23+ 3.8*x33;-0.4*x11+0.6*x21+0.6*x31<0;0.2*x11+0.2*x21-0.8*x31>0; -0.85*x12+0.15*x22+0.15*x32<0;0.6*x12+0.6*x22-0.4*x32>0;0.5*x13+0.5*x23-0.5*x33>0;x11+x12+x13<=2000;x21+x22+x23<=2500;x31+x32+x33<=1200;求解结果：X11 = 1526.66, X21 = 1017.78, X31 = 0, X12 = 473.33, X22 = 1482.22, X32 = 1200X13 = 0, X23 = 0,X33 = 0 ，max S = 24640 (兀)。

数学建模线性规划matlib

姓名：黄威学号：11L1002104题目：某厂生产甲乙两种口味的饮料,每百箱甲饮料需用原料6千克,工人10名,可获利10万元;每百箱乙饮料需用原料5千克,工人20名,可获利9万元.今工厂共有原料60千克,工人150名,又由于其他条件所限甲饮料产量不超过8百箱.问如何安排生产计划,即两种饮料各生产多少使获利最大.进一步讨论:1)若投资0.8万元可增加原料1千克,问应否作这项投资.2)若每百箱甲饮料获利可增加1万元,问应否改变生产计划.⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤++=0,815020106056910max 21121212121x x x x x x x x x Z x x 则由题意可知：百箱。

百箱，已生产设甲生产>> c=[-10;-9];A=[6 5;10 20];b=[60;150];Aeq=[];beq=[];>> lb=[0;0]lb =>> ub=[8;inf]ub =8Inf>> x=linprog(c,A,b,Aeq,beq,lb,ub)Optimization terminated.x =6.42864.2857>> [x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)Optimization terminated.x =6.42864.2857fval =-102.85718571.1022857.4,4286.621===Z Z x x 取得最大值，即时函数因此当（一）>> c=[-10;-9];A=[6 5;10 20];b=[61;150];Aeq=[];beq=[];>> lb=[0;0]lb =>> ub=[8;inf]ub =8Inf>> x=linprog(c,A,b,Aeq,beq,lb,ub) Optimization terminated.x =6.71434.1429>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub) Optimization terminated.x =6.71434.1429fval =-104.4286万元；净利润为万元；万元获取利润为也就相当于投资；）相比之前增加了（万元；时，所获得总利润为当原料增加7715 .05715.18.05715.18571.102-4286.1044286.104kg1（二）>> c=[-11;-9];A=[6 5;10 20];b=[60;150];Aeq=[];beq=[];lb=[0;0]lb =>> ub=[8;inf]ub =8Inf>> x = linprog(c,A,b,Aeq,beq,lb,ub) Optimization terminated.x =8.00002.4000>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub) Optimization terminated.x =8.00002.4000fval =-109.6000因此需要改变方案。

数学建模线性规划上机题汇编

大学生数学建模练习题

线性规划题及答案

建模补充-线性规划练习题(带答案)

数学线性规划试题答案及解析

线性规划题及答案

线性规划题及答案

数学建模习题——线性规划

数学建模测试题-线性规划部分

线性规划题及答案

1、线性规划(数学建模)

数学建模线性规划问题超全共54页文档

线性规划经典例题

线性规划模型例题——数学模型

线性规划经典例题

线性规划题及答案

最新数学建模线性规划上机题

第一篇线性规划建模习题答案

数学建模线性规划matlib