系统辨识实验1·哈工大
(哈工大)系统辨识与自适应控制——第一讲..

第一讲 系统辨识的基本概念
一、什么是系统辨识?
1. 机理分析建模方法 (白箱法)
图1 单级倒立摆实验装置 2010-02-20 控制理论与制导技术研究中心 第2 页
Harbin Institute of Technology– HIT
m
u
M
F
r
O
图2 单级倒立摆示意图 2010-02-20 控制理论与制导技术研究中心 第3 页
Harbin Institute of Technology– HIT
图中所示变量名的物理含义如表1所示。
2010-02-20
控制理论与制导技术研究中心
第4 页
Harbin Institute of Technology– HIT
步骤一:对小车进行受力分析,小车的受力分析如图3所 P 示。
u M
N
F
r
图3 小车受力分析图
图中,P表示摆杆对小车水平方向上的作用力,单位N; N 表示摆杆对小车垂直方向上的作用力,单位(N)。 根据牛顿定律,小车水平方向上的力平衡方程为:
2010-02-20 控制理论与制导技术研究中心 第5 页
Harbin Institute of Technology– HIT
步骤四:化成状态空间描述。
1 x 2 x 2 m 2 l 2 x2 cos x1 sin x1 m lucos x1 x 4 m l cos x1 ( M m)m glsin x1 ( M m) fx2 x 2 ( M m)(J m l2 ) m 2 l 2 cos2 x1 3 x4 x 2 m lfx2 cos x1 m 2 l 2 g sin x1 cos x1 ( J m l2 ) x 4 ( J m l2 )m lx2 sin x1 ( J m l2 )u 4 x ( M m)(J m l2 ) m 2 l 2 cos2 x1
系统辨识及自适应控制实验..

Harbin Institute of Technology系统辨识与自适应控制实验报告题目:渐消记忆最小二乘法、MIT方案与卫星振动抑制仿真实验专业:控制科学与工程姓名:学号: 15S******指导老师:日期: 2015.12.06哈尔滨工业大学2015年11月本实验第一部分是辨识部分,仿真了渐消记忆递推最小二乘辨识法,研究了这种方法对减缓数据饱和作用现象的作用;第二部分是自适应控制部分,对MIT 方案模型参考自适应系统作出了仿真,分别探究了改变系统增益、自适应参数的输出,并研究了输入信号对该系统稳定性的影响;第三部分探究自适应控制的实际应用情况,来自我本科毕设的课题,我从自适应控制角度重新考虑了这一问题并相应节选了一段实验。
针对挠性卫星姿态变化前后导致参数改变的特点,探究了用模糊自适应理论中的模糊PID 法对这种变参数系统挠性振动抑制效果,并与传统PID 法比较仿真。
一、系统辨识1. 最小二乘法的引出在系统辨识中用得最广泛的估计方法是最小二乘法(LS)。
设单输入-单输出线性定长系统的差分方程为:()()()()()101123n n x k a x k a k n b u k b u x k n k +-+⋯+-=+⋯+-=,,,, (1.1) 错误!未找到引用源。
式中:()u k 错误!未找到引用源。
为控制量;错误!未找到引用源。
为理论上的输出值。
错误!未找到引用源。
只有通过观测才能得到,在观测过程中往往附加有随机干扰。
错误!未找到引用源。
的观测值错误!未找到引用源。
可表示为: 错误!未找到引用源。
(1.2)式中:()n k 为随机干扰。
由式(1.2)得错误!未找到引用源。
()()()x k y k n k =- (1.3)将式(1.3)带入式(1.1)得()()()()()()()101111()nn n i i y k a y k a y k n b u k b u k b u k n n k a k i n =+-+⋯+-=+-+⋯+-++-∑ (1.4)我们可能不知道()n k 错误!未找到引用源。
系统辨识实验报告30288
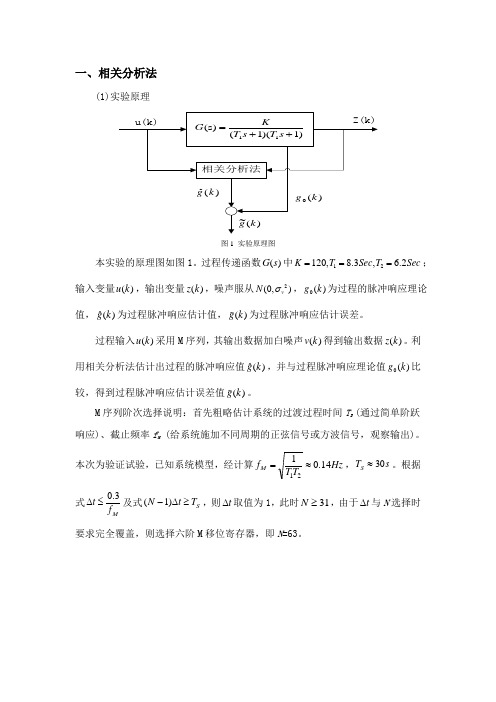
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
数学模型-哈尔滨工业大学

系统建模的抽象过程
(可观测) 输入变量 (可观测) 输出变量
真实系统
观测屏障
抽象
真实系统
ω(t) ρ(t)
黑箱 灰箱 白箱
数学描述 ω(t)、ρ(t)---输入输出变量对
17
数学建模信息源
数据
2.先验知识
3.试验数据
先验 知识
建模
模型应用
目的 达到否?
目标
1.目标和目的
18
图2.1 数学建模的信息源
在定义一个系统时,首先要确定系统的边界。尽管世界上的事物是 相互联系的,但当我们研究某一对象时,总是要将该对象与其环境区别开 来。边界确定了系统的范围,边界以外对系统的作用称为系统的输入,系 统对边界以外的环境的作用称为系统的输出。
边界 输出
环境
输入
系统
8
研究上述系统时,可分为三类问题: (1)系统的分析问题 (2)系统的控制问题 (3)系统的辨识问题
K 0 s W0 ( s ) e (Ts 1) n
15
1.1.3 数学模型
本质上讲,系统数学模型是从系统概念出发的关 于现实世界的一小部分或几个方面的抽象的“映像”。
系统数学模型的建立需要建立如下抽象:输入、 输出、状态变量及其间的函数关系。这种抽象过程称 为模型构造。
系统数学建模就是将真实系统抽象成相应的数学 表达式(一些规则、指令的集合)。
2
主要内容安排
第一章 绪论 第二章 系统辨识常用输入信号 第三章 系统数学描述及经典辨识法 第四章 最小二乘法辨识
第五章 极大似然法辨识
第六章 系统结构辨识
3
实验1 白噪声和M序列的产生 实验2 相关分析法辨识脉冲响应
系统辨识实验报告

自动化09-3 宋佳瑛09051304系统辨识实验报告实验一:系统辨识的经典方法实验目的:掌握系统的数学模型与系统的输入,输出信号之间的关系,掌握经典辨识的实验测试方法和数据处理方法。
熟悉matlab/Simulink 环境。
实验内容:1.用系统阶跃响应法测试给定系统的数学模型。
在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或二阶加纯滞后模型,对模型进行验证。
2.在被辨识的系统加入噪声干扰,重复上述1的实验过程。
1.没有噪声搭建对象测试对象流程图实验结果为:2、加入噪声干扰搭建对象实验结果:加入噪声干扰之后水箱输出不平稳,有波动。
实验二:相关分析法搭建对象:处理程序:for i=1:15m(i,:)=UY(32-i:46-i,1); endy=UY(31:45,2);gg=ones(15)+eye(15);g=1/(25*16*2)*gg*m*y; plot(g);hold on;stem(g);实验结果:相关分析法最小二乘法建模:二、三次实验本次实验要完成的内容:1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS);2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说明;实验内容结果与程序代码:以下给出RLS中的参数估计过程曲线和误差曲线程序清单:LS(二阶):M=UY(:,1);z=UY(:,2);H=zeros(199,5);for i=1:199H(i,1)=-z(i+1);H(i,2)=-z(i);H(i,3)=M(i+2);H(i,4)=M(i+1);H(i,5)=M(i);endEstimate=inv(H'*H)*H'*(z(3:201))RLS(二阶):clcM=UY(:,1);z=UY(:,2);P=100*eye(5); %估计方差Pstore=zeros(5,200);Pstore(:,1)=[P(1,1),P(2,2),P(3,3),P(4,4),P(5,5)]';Theta=zeros(5,200); %参数的估计值,存放中间过程估值Theta(:,1)=[0;0;0;0;0];K=[10;10;10;10;10;10;10];for i=3:201h=[-z(i-1);-z(i-2);M(i);M(i-1);M(i-2)];K=P*h*inv(h'*P*h+1);Theta(:,i-1)=Theta(:,i-2)+K*(z(i)-h'*Theta(:,i-2));P=(eye(5)-K*h')*P;Pstore(:,i-1)=[P(1,1),P(2,2),P(3,3),P(4,4),P(5,5)]';endi=1:200;figure(1)plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:)) title('待估参数过渡过程')figure(2)plot(i,Pstore(1,:),i,Pstore(2,:),i,Pstore(3,:),i,Pstore(4,:),i,Pstore(5,:)) title('估计方差变化过程')同理可以写出三阶的LS以及RLS算法,此处略去。
哈工大智能控制神经网络第十一课神经网络系统辨识

m
n
y(k) biu(k d i) ai y(k i)
i0
i 1
或
y(k) qd B(q1) u(k) B(q1) u(k d)
A(q1 )
A(q1 )
第一式为 ARMA 模型:
右边第 2 项为输出 y(k)的过去值组合称自回归部分; 第 1 项为输入 u(k)的过去值组合称滑动平均部分。
定义:
P(z)
Y (z) U (z)
Zy(k) Z u (k )
用迟后移位定理求 Z 变换,经整理得 Z 传递函数:
P( z)
b0 + b1z 1 + b2 z 2 + + bm z m 1 + a1z 1 + a2 z 2 + + an z n
z d
m
b0 (1 pi z 1)
i1
n
z d P0 (z)z d
确定性系统NN辨识——改进算法
引入加权因子,此时
h [ c 1 y (k 1 ), y c 2 (k 2 ), , c ny (k n );
c n + 1 u (k d ),c n + 2 u (k d 1 ), c n + m + 1 u (k d m )]T
可取 ci i,01
则参数估计更新:w ( k + 1 ) w ( k ) + R ( k ) e ( k ) h ( k )
系统辨识理论基础
定义:在输入/输出数据基础上,从一组给 定模型类中确定一个所测系统等价的模型。 辨识三要素: 输入/输出数据 模型类(系统结构) 等价准则 e.g. J e
符号
P: 待辨识系统; Pˆ 辨识系统模型
哈尔滨工业大学(威海)操作系统实验报告及答案

哈尔滨工业大学(威海)操作系统实验报告说明:本实验报告实验答案,是本人在上实验时的测试数据,由于操作系统实验中后面实验与当时所做实验的计算机的配置有关,因此本实验报的数据仅供参考。
实验1进程的描述与控制Windows 2000编程(实验估计时间:100分钟)1.1 背景知识Windows 2000 可以识别的应用程序包括控制台应用程序、GUI应用程序和服务应用程序。
控制台应用程序可以创建GUI,GUI应用程序可以作为服务来运行,服务也可以向标准的输出流写入数据。
不同类型应用程序间的惟一重要区别是其启动方法。
Windows 2000是以NT技术构建的,它提供了创建控制台应用程序的能力,使用户可以利用标准的C++工具,如iostream库中的cout和cin对象,来创建小型应用程序。
当系统运行时,Windows 2000的服务通常要向系统用户提供所需功能。
服务应用程序类型需要ServiceMail()函数,由服务控制管理器(SCM)加以调用。
SCM是操作系统的集成部分,负责响应系统启动以开始服务、指导用户控制或从另一个服务中来的请求。
其本身负责使应用程序的行为像一个服务,通常,服务登录到特殊的LocalSystem账号下,此账号具有与开发人员创建的服务不同的权限。
当C++编译器创建可执行程序时,编译器将源代码编译成OBJ文件,然后将其与标准库相链接。
产生的EXE文件是装载器指令、机器指令和应用程序的数据的集合。
装载器指令告诉系统从哪里装载机器代码。
另一个装载器指令告诉系统从哪里开始执行进程的主线程。
在进行某些设置后,进入开发者提供的main()、Servicemain()或WinMain()函数的低级入口点。
机器代码中包括控制逻辑,它所做的事包括跳转到Windows API函数,进行计算或向磁盘写入数据等。
Windows允许开发人员将大型应用程序分为较小的、互相有关系的服务模块,即动态链接库(DLL)代码块,在其中包含应用程序所使用的机器代码和应用程序的数据。
哈工大模式识别实验报告
模式识别实验报告本次报告选做第一个实验,实验报告如下:1 实验要求构造1个三层神经网络,输出节点数1个,即多输入单输出型结构,训练它用来将表中的第一类样本和第二类样本分开。
采用逐个样本修正的BP算法,设隐层节点数为4,学习效率η=0.1,惯性系数α=0.0;训练控制总的迭代次数N=100000;训练控制误差:e=0.3。
在采用0~1内均匀分布随机数初始化所有权值。
对1)分析学习效率η,惯性系数α;总的迭代次数N;训练控制误差e、初始化权值以及隐层节点数对网络性能的影响。
要求绘出学习曲线----训练误差与迭代次数的关系曲线。
并将得到的网络对训练样本分类,给出错误率。
采用批处理BP算法重复1)。
比较两者结果。
表1 神经网络用于模式识别数据(X1、X2、X3是样本的特征)2 BP 网络的构建三层前馈神经网络示意图,见图1.图1三层前馈神经网络①网络初始化,用一组随机数对网络赋初始权值,设置学习步长η、允许误差ε、网络结构(即网络层数L 和每层节点数n l );②为网络提供一组学习样本; ③对每个学习样本p 循环a .逐层正向计算网络各节点的输入和输出;b .计算第p 个样本的输出的误差Ep 和网络的总误差E ;c .当E 小于允许误差ε或者达到指定的迭代次数时,学习过程结束,否则,进行误差反向传播。
d .反向逐层计算网络各节点误差)(l jp δ如果l f 取为S 型函数,即xl e x f -+=11)(,则 对于输出层))(1()()()()(l jp jdp l jp l jp l jp O y O O --=δ 对于隐含层∑+-=)1()()()()()1(l kj l jp l jp l jp l jp w O O δδe .修正网络连接权值)1()()()1(-+=+l ip l jp ij ij O k W k W ηδ式中,k 为学习次数,η为学习因子。
η取值越大,每次权值的改变越剧烈,可能导致学习过程振荡,因此,为了使学习因子的取值足够大,又不至产生振荡,通常在权值修正公式中加入一个附加动量法。
哈工大《操作系统》实验1

(5)重新编写一个setup.s,然后将其中的显示的信息改为:“Now we are in SETUP”。
再次编译,重新用make命令生成BootImage,结合提示信息和makefile文修改build.c,具体将setup.s改动如下:mov cx,#27mov bx,#0x0007 ! page 0, attribute 7 (normal)mov bp,#msg1mov ax,#0x1301 ! write string, move cursorint 0x10dieLoop:j dieLoopmsg1:.byte 13,10,13,10.ascii "Now we are in SETUP".byte 13,10,13,10将build.c改动如下:if(strcmp("none",argv[3]) == 0)//添加判断return 0;if ((id=open(argv[3],O_RDONLY,0))<0)die("Unable to open 'system'");// if (read(id,buf,GCC_HEADER) != GCC_HEADER)// die("Unable to read header of 'system'");// if (((long *) buf)[5] != 0)// die("Non-GCC header of 'system'");for (i=0 ; (c=read(id,buf,sizeof buf))>0 ; i+=c )if (write(1,buf,c)!=c)die("Write call failed");close(id);fprintf(stderr,"System is %d bytes.\n",i);if (i > SYS_SIZE*16)die("System is too big");return(0);(6)验证:用make是否能成功生成BootImage,运行run命令验证运行结果。
(哈工大)系统辨识与自适应控制——第一讲

2010-02-20
第5页
Harbin Institute of Technology– HIT
uFPM d2r d t2
F d r
dt
步骤二:对摆杆进行受力分析,摆杆的受力如图4所示。
θ
N
mg
P
图4 摆杆受力分析图
摆杆水平方向上的力平衡方程如下,
2010-02-20
第6页
Harbin Institute of Technology– HIT
x1 x2
x2
(Mm)mgl1x(Mm)fx2 mlx4
(Mm)(J ml2) m2l2
mlu
x3 x4
x4
m2l2gx1
mlfx2 (J ml2)x4 (J
(Mm)(J ml2) m2l2
ml2)u
(12)
2010-02-20
第10页
Harbin Institute of Technology– HIT
问题:
(1). 效率低:随着系统复杂程度的增加,建模过程愈加复 杂; (2). 不方便“计算机〞在线决策。
2010-02-20
第11页
Harbin Institute of Technology– HIT
2. 系统辨识法(黑箱法)
能否根据“输入、输出数据〞获取“对象〞的数学模型 呢?
例:原被控对象的差分形式为:
x2
m2l2x22c
ox1ss
ixn1mlcuox1sx4mclox1s(Mm)m
(Mm)(Jm2)lm2l2c o2xs1
g s ilxn1(Mm)fx2
x3x4
x4
m
l2fcxox1sm2l2gs
ixn1c ox1s(Jm2)lx4(Jm2)lm22lsxixn1(Jm2)lu
哈工大《操作系统》实验1

(5)重新编写一个setup.s,然后将其中的显示的信息改为:“Now we are in SETUP”。
再次编译,重新用make命令生成BootImage,结合提示信息和makefile文修改build.c,具体将setup.s改动如下:mov cx,#27mov bx,#0x0007 ! page 0, attribute 7 (normal)mov bp,#msg1mov ax,#0x1301 ! write string, move cursorint 0x10dieLoop:j dieLoopmsg1:.byte 13,10,13,10.ascii "Now we are in SETUP".byte 13,10,13,10将build.c改动如下:if(strcmp("none",argv[3]) == 0)//添加判断return 0;if ((id=open(argv[3],O_RDONLY,0))<0)die("Unable to open 'system'");// if (read(id,buf,GCC_HEADER) != GCC_HEADER)// die("Unable to read header of 'system'");// if (((long *) buf)[5] != 0)// die("Non-GCC header of 'system'");for (i=0 ; (c=read(id,buf,sizeof buf))>0 ; i+=c )if (write(1,buf,c)!=c)die("Write call failed");close(id);fprintf(stderr,"System is %d bytes.\n",i);if (i > SYS_SIZE*16)die("System is too big");return(0);(6)验证:用make是否能成功生成BootImage,运行run命令验证运行结果。
系统辩识实验报告

一、实验目的1. 理解系统辨识的基本概念和原理。
2. 掌握递推最小二乘算法在系统辨识中的应用。
3. 通过实验,验证算法的有效性,并分析参数估计误差。
二、实验原理系统辨识是利用系统输入输出数据,对系统模型进行估计和识别的过程。
在本实验中,我们采用递推最小二乘算法对系统进行辨识。
递推最小二乘算法是一种参数估计方法,其基本思想是利用当前观测值对系统参数进行修正,使参数估计值与实际值之间的误差最小。
递推最小二乘算法具有计算简单、收敛速度快等优点。
三、实验设备1. 电脑一台,装有MATLAB软件。
2. 系统辨识实验模块。
四、实验步骤1. 打开MATLAB软件,运行系统辨识实验模块。
2. 在模块中输入已知的系数a1、a2、b1、b2。
3. 生成输入序列u(t)和噪声序列v(t)。
4. 将输入序列u(t)和噪声序列v(t)加入系统,产生输出序列y(t)。
5. 利用递推最小二乘算法对系统参数进行辨识。
6. 将得到的参数估计值代入公式计算参数估计误差。
7. 仿真出参数估计误差随时间的变化曲线。
五、实验结果与分析1. 实验结果根据实验步骤,我们得到了参数估计值和参数估计误差随时间的变化曲线。
2. 结果分析(1)参数估计值:通过递推最小二乘算法,我们得到了系统参数的估计值。
这些估计值与实际参数存在一定的误差,这是由于噪声和系统模型的不确定性所导致的。
(2)参数估计误差:从参数估计误差随时间的变化曲线可以看出,递推最小二乘算法在短时间内就能使参数估计误差达到较低水平。
这说明递推最小二乘算法具有较好的收敛性能。
(3)参数估计误差曲线:在实验过程中,我们发现参数估计误差曲线在初期变化较快,随后逐渐趋于平稳。
这表明系统辨识过程在初期具有较高的灵敏度,但随着时间的推移,参数估计误差逐渐减小,系统辨识过程逐渐稳定。
六、实验结论1. 递推最小二乘算法在系统辨识中具有较好的收敛性能,能够快速、准确地估计系统参数。
2. 实验结果表明,递推最小二乘算法能够有效减小参数估计误差,提高系统辨识精度。
【VIP专享】模糊系统辨识

Harbin Institute of Technology–HIT模糊系统辨识(基于模糊关系)基于模糊关系班晓军banxiaojun@哈尔滨工业大学2014-12-27控制理论与制导技术研究中心第1页Harbin Institute of Technology–HIT一、模糊关系模型2014-12-27控制理论与制导技术研究中心第2页Harbin Institute of Technology–HIT2014-12-27控制理论与制导技术研究中心第3页图1. 模糊模型参考学习控制系统结构图Harbin Institute of Technology–HIT2014-12-27控制理论与制导技术研究中心第4页Harbin Institute of Technology–HIT二、指标2014-12-27控制理论与制导技术研究中心第5页Harbin Institute of Technology–HIT三、建模方法32014-12-27控制理论与制导技术研究中心第6页图3. 货船自动驾驶仪系统Harbin Institute of Technology–HIT第二步:对输入输出数据进行模糊化="12[()]max{[()][()][()]}i mA A A A u k u k u k u k µµµµ,,,u A ()()iu k k →:()()jy k y k C → :[(1)(1)][(2)(2)][()()]u y u y u L y L ↓",,,,,,1122[][][]i j i j iL jL A C A C A C ↓↓",,,,,,2014-12-27控制理论与制导技术研究中心第7页Harbin Institute of Technology–HIT第三步:确定“规则的结构”(),(1),,();(1),(2),,()()u t u t u t k y t y t y t l y t ⎡−−−−−⎤⎣⎦""↓()()⎡⎤ ();u t k y t l y t −−⎣⎦2014-12-27控制理论与制导技术研究中心第8页Harbin Institute of Technology–HIT2014-12-27控制理论与制导技术研究中心第9页Harbin Institute of Technology–HIT2014-12-27控制理论与制导技术研究中心第10页Harbin Institute of Technology–HIT第五步:对以上规则的化简1. 去掉重复的规则;2. 处理相互矛盾的规则;相矛盾的规则2014-12-27控制理论与制导技术研究中心第11页Harbin Institute of Technology–HIT四、举例(煤气炉数据)参见P115 -P116;五、自适应模糊预测模型五自适应模糊预测模型2014-12-27控制理论与制导技术研究中心第12页Harbin Institute of Technology–HIT基于T-S模糊模型的辨识、T S模糊系统(静态)一、T-S2014-12-27控制理论与制导技术研究中心第13页Harbin Institute of Technology–HIT二、辨识1. 前提“结构”辨识(前件“结构”辨识)前提结构辨前件结构辨“前件变量的个数”“每个前件变量对应的语言值的个数”“语言值对应的隶属函数的类型”2. 前提(前件)参数辨识3. 结论“结构”辨识(后件“结构”辨识)例如,“n”的确定4. 结论“参数”辨识(后件“参数”辨识)2014-12-27控制理论与制导技术研究中心第14页Harbin Institute of Technology–HIT三、“前件”“后件”分开辨识的方法“前件”部分:模糊聚类方法(Fuzzy clustering: Fuzzy C-Means Algorithm)“前件”部分辨识完成后,对应的问题可转化为“线性模型辨识”——最小二乘类辨识方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
end M(6) = M(5); M(5) = M(4); M(4) = M(3); M(3) = M(2); M(2) = M(1); M(1) = temp; end
stairs(M_XuLie); ylim([-1.5 1.5]);
7.实验结果及分析 1、生成均匀分布随机序列
run = run + 1; if(M_XuLie_Ext(n) ~= M_XuLie_Ext(n + 1))
if(M_XuLie_Ext(n) == a) test_number_a(run) = test_number_a(run) + 1;
else test_number_a_c(run) = test_number_a_c(run) +
G(SEQ_LENGTH) = 0;
for n = 1 : SEQ_LENGTH for t = 1 : N G(n) = G(n) + R(N * (n - 1) + t); end
end G = G - 6;
figure(3); plot(G); figure(4); hist(G);
实验 3 Num3
E( X k ) , D( X k ) 2 0, (k 1, 2,...)
n
Xk
则随机变量之和 i1 的标准化变量:
n
n
n
Xk E( Xk ) Xk n
Y i1
i 1
i1
n
D( Xk ) i 1
n
近似服从 N (0,1) 分布。
如果
Xn
服从[0,
1]均匀分布,则上式中
0.5 ,
R(Xulie_Length) = 0; X(1) = 20140104; R(1) = X(1) / M; for n = 1 : (Xulie_Length - 1) X(n + 1) = mod((A * X(n) + b), M);
R(n + 1) = X(n + 1) / M; end
N = 12; SEQ_LENGTH = 100;
A = 65539; M = 2147483647; b = 0;
R(Xulie_Length) = 0; X(1) = 20140104; R(1) = X(1) / M; for n = 1 : (Xulie_Length - 1) X(n + 1) = mod((A * X(n) + b), M);
结果: M_result =
1 结论:从测试结果看性质成立
25 20 15
10 5
0 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
结论:从结果图知,生成的白噪声基本服从 N(0,1)分布。
3、生成 M 序列 生成的 M 序列如下(n = 63):
1.5
1
0.5
0
-0.5
-1
-1.5 0
10
20
30
40
50
60
70
验证 M 序列性质: 均衡特性:m 序列每一周期中 1 的个数比 0 的个数多 1 个 (-a 和 a 的个数差 1) 测试程序: number_a = sum(M_XuLie == a); number_a_c = sum(M_XuLie == -a); number_a
测试程序: M_XuLie = M_XuLie'; M_XuLie = -0.5 * (M_XuLie - 1); M_result = 1; % 验证成功则为 1 for n = 1 : (length(M_XuLie) - 1)
M_XuLie_Shift = circshift(M_XuLie, n); M_XuLie_Add = mod((M_XuLie + M_XuLie_Shift), 2); is_shift_found = 0; % false for k = 0 : (length(M_XuLie) - 1)
1; end run = 0;
end end display(test_number_a); display(test_number_a_c); 结果: test_number_a =
842110 test_number_a_c =
10 3 2 1 0 1 结论:从测试结果看性质成立 移位相加特性:m 序列和它的位移序列模二相加后所得序列 仍是该 m 序列的某个位移序列。
(1)生成的 0-1 均布随机序列如下所示:
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 0
200
400
600
均值和方差的实际值:
num1
800
1000
1200
mean_R =
0.4799
var_R = 0.0834
均值和方差理论值: mean_R =0.5
var_R =1/12( = 0.083333) 结论:实际值与理论值已经相当接近。 (2)该随机序列落在 10 个子区间的频率曲线图如下:
number = 2^6 - 1; a = 1; %手动初始化 M M(1)=1; M(2)=0; M(3)=0; M(4)=1; M(5)=1; M(6)=0; M_XuLie(number) = 0;
for n = 1 : number temp = xor(M(6), M(5));
if(temp == 0) M_XuLie(n) = a;
3.实验主要原理
1、混合同余法
混合同余法是加同余法和乘同余法的混合形式,其迭代式如下:
xn1 Rn1
(a xn
*
1
xn /M
b)
mod
M
式中 a 为乘子, x0 为种子,b 为常数,M 为模。混合同余法是一
种递归算法,即先提供一个种子 x0 ,逐次递归即得到一个不超过模
M 的整数数列。
2、正态分布随机数产生方法 由独立同分布中心极限定理有:设随机变量 X1, X 2,...., X n ,... 相互 独立,服从同一分布,且具有数学期望和方差:
2
1 12
。即
n
X k 0.5n
Y i1 n
12 近似服从 N (0,1) 分布。
3、M 序列生成原理 用移位寄存器产生 M 序列的简化框图如下图所示。该图表示 一个由 4 个双稳态触发器顺序连接而成的 4 级移位寄存器,它带有 一个反馈通道。当移位脉冲来到时,每级触发器的状态移到下一级 触发器中,而反馈通道按模 2 加法规则反馈到第一级的输入端。
实验 1 白噪声和 M 序列的产生 实验报告
专业:
哈尔滨工业大学 航天学院控制科学与工程系 自动化
班级: 1004105
姓名:
学号: 11004005**
日期: 2013 年 9 月 24 日
1.实验题目: 白噪声和 M 序列的产生
2.实验目的 1、熟悉并掌握产生均匀分布随机序列方法以及进而产生高斯 白噪声方法 2、熟悉并掌握 M 序列生成原理及仿真生成方法
number_a_c 结果: number_a =
31 number_a_c =
32 结论:从测试结果看性质成立 游程特性:m 序列的一个周期(p=2n-1)中,游程总数为 2n-1。其 中长度为 k 的游程个数占游程总数的 1/2k=2-k,而且,在长度为 k 游程中,连 1 游程与连 0 游程各占一半,其中 1≤k≤(n-2)。长为 (n-1)的游程是连 0 游程, 长为 n 的游程是连 1 游程。 测试程序: M_XuLie_Ext = [M_XuLie, -M_XuLie(end)]; run = int8(0); test_number_a(6) = int8(0); test_number_a_c(6) = int8(0); for n = 1 : length(M_XuLie)
150
100
50
0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
结论:由图像可知,均匀性良好。 2、生成高斯白噪-0.5
-1 -1.5
-2 -2.5
-3 0
10 20
30 40
50 60 70
80 90 100
生成的白噪声的频率统计图如下:
4.实验对象或参数
1、生成均匀分布随机序列 (1)利用混合同余法生成[0, 1]区间上符合均匀分布的随机序列, 并计算该序列的均值和方差,与理论值进行对比分析。要求序列长 度为 1200,推荐参数为 a=65539,M=2147483647,0<x0<M。 (2)将[0, 1]区间分为不重叠的等长的 10 个子区间,绘制该随机 序列落在每个子区间的频率曲线图,辅助验证该序列的均匀性。 (3)对上述随机序列进行独立性检验。(该部分为选作内容)
%if(isequal(circshift(M_XuLie, k), M_XuLie_Add)) if(circshift(M_XuLie, k) == M_XuLie_Add)
is_shift_found = 1; end end if(is_shift_found == 0) M_result = 0; end end display(M_result);
2、生成高斯白噪声 利用上一步产生的均匀分布随机序列,令 n=12,生成服从 N(0,1) 的白噪声,序列长度为 100,并绘制曲线。
3、生成 M 序列 M 序列的循环周期取为 N P 26 1 63,时钟节拍 t 1Sec ,幅度 a 1,逻辑“0”为 a,逻辑“1”为-a,特征多项式 F (s) s6 s5 。 生成 M 序列的结构图如下所示。
+
C
