c++课程设计二叉树

合集下载

数据结构c语言课设-二叉树排序

题目:二叉排序树的实现1 内容和要求1）编程实现二叉排序树，包括生成、插入，删除；2）对二叉排序树进展先根、中根、和后根非递归遍历；3）每次对树的修改操作和遍历操作的显示结果都需要在屏幕上用树的形状表示出来。

4）分别用二叉排序树和数组去存储一个班(50 人以上)的成员信息(至少包括学号、姓名、成绩3 项),比照查找效率，并说明在什么情况下二叉排序树效率高,为什么?2 解决方案和关键代码2.1 解决方案：先实现二叉排序树的生成、插入、删除，编写DisplayBST函数把遍历结果用树的形状表示出来。

前中后根遍历需要用到栈的数据构造，分模块编写栈与遍历代码。

要求比照二叉排序树和数组的查找效率，首先建立一个数组存储一个班的成员信息，分别用二叉树和数组查找，利用clock〔〕函数记录查找时间来比照查找效率。

2.2关键代码树的根本构造定义及根本函数typedef struct{KeyType key;} ElemType;typedef struct BiTNode//定义链表{ElemType data;struct BiTNode *lchild, *rchild;}BiTNode, *BiTree, *SElemType;//销毁树int DestroyBiTree(BiTree &T){if (T != NULL)free(T);return 0;}//清空树int ClearBiTree(BiTree &T){if (T != NULL){T->lchild = NULL;T->rchild = NULL;T = NULL;}return 0;}//查找关键字,指针p返回int SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p) {if (!T){p = f;return FALSE;}else if EQ(key, T->data.key){p = T;return TRUE;}else if LT(key, T->data.key)return SearchBST(T->lchild, key, T, p);elsereturn SearchBST(T->rchild, key, T, p);}二叉树的生成、插入，删除生成void CreateBST(BiTree &BT, BiTree p){int i;ElemType k;printf("请输入元素值以创立排序二叉树:\n");scanf_s("%d", &k.key);for (i = 0; k.key != NULL; i++){//判断是否重复if (!SearchBST(BT, k.key, NULL, p)){InsertBST(BT, k);scanf_s("%d", &k.key);}else{printf("输入数据重复！\n");return;}}}插入int InsertBST(BiTree &T, ElemType e){BiTree s, p;if (!SearchBST(T, e.key, NULL, p)){s = (BiTree)malloc(sizeof(BiTNode));s->data = e;s->lchild = s->rchild = NULL;if (!p)T = s;else if LT(e.key, p->data.key)p->lchild = s;elsep->rchild = s;return TRUE;}else return FALSE;}删除//某个节点元素的删除int DeleteEle(BiTree &p){BiTree q, s;if (!p->rchild) //右子树为空{q = p;p = p->lchild;free(q);}else if (!p->lchild) //左子树为空{q = p;p = p->rchild;free(q);}else{q = p;s = p->lchild;while (s->rchild){q = s;s = s->rchild;}p->data = s->data;if (q != p)q->rchild = s->lchild;elseq->lchild = s->lchild;delete s;}return TRUE;}//整棵树的删除int DeleteBST(BiTree &T, KeyType key) //实现二叉排序树的删除操作{if (!T){return FALSE;}else{if (EQ(key, T->data.key)) //是否相等return DeleteEle(T);else if (LT(key, T->data.key)) //是否小于return DeleteBST(T->lchild, key);elsereturn DeleteBST(T->rchild, key);}return 0;}二叉树的前中后根遍历栈的定义typedef struct{SElemType *base;SElemType *top;int stacksize;}SqStack;int InitStack(SqStack &S) //构造空栈{S.base = (SElemType*)malloc(STACK_INIT_SIZE *sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base;S.stacksize = STACK_INIT_SIZE;return OK;}//InitStackint Push(SqStack &S, SElemType e) //插入元素e为新栈顶{if (S.top - S.base >= S.stacksize){S.base = (SElemType*)realloc(S.base, (S.stacksize + STACKINCREMENT)*sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;return OK;}//Pushint Pop(SqStack &S, SElemType &e) //删除栈顶,应用e返回其值{if (S.top == S.base) return ERROR;e = *--S.top;return OK;}//Popint StackEmpty(SqStack S) //判断是否为空栈{if (S.base == S.top) return TRUE;return FALSE;}先根遍历int PreOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);if (!Visit(p->data)) return ERROR;p = p->lchild;}else{Pop(S, p);p = p->rchild;}}return OK;}中根遍历int InOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);p = p->lchild;}else{Pop(S, p);if (!Visit(p->data)) return ERROR;p = p->rchild;}}return OK;}后根遍历int PostOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S, SS;BiTree p;InitStack(S);InitStack(SS);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);Push(SS, p);p = p->rchild;}else{if (!StackEmpty(S)){Pop(S, p);p = p->lchild;}}}while (!StackEmpty(SS)){Pop(SS, p);if (!Visit(p->data)) return ERROR;}return OK;}利用数组存储一个班学生信息ElemType a[] = { 51, "陈继真", 88,82, "黄景元", 89,53, "贾成", 88,44, "呼颜", 90,25, "鲁修德", 88,56, "须成", 88,47, "孙祥", 87, 38, "柏有患", 89, 9, " 革高", 89, 10, "考鬲", 87, 31, "李燧", 86, 12, "夏祥", 89, 53, "余惠", 84, 4, "鲁芝", 90, 75, "黄丙庆", 88, 16, "李应", 89, 87, "杨志", 86, 18, "李逵", 89, 9, "阮小五", 85, 20, "史进", 88, 21, "秦明", 88, 82, "杨雄", 89, 23, "刘唐", 85, 64, "武松", 88, 25, "李俊", 88, 86, "卢俊义", 88, 27, "华荣", 87, 28, "杨胜", 88, 29, "林冲", 89, 70, "李跃", 85, 31, "蓝虎", 90, 32, "宋禄", 84, 73, "鲁智深", 89, 34, "关斌", 90, 55, "龚成", 87, 36, "黄乌", 87, 57, "孔道灵", 87, 38, "张焕", 84, 59, "李信", 88, 30, "徐山", 83, 41, "秦祥", 85, 42, "葛公", 85, 23, "武衍公", 87, 94, "范斌", 83, 45, "黄乌", 60, 67, "叶景昌", 99, 7, "焦龙", 89, 78, "星姚烨", 85, 49, "孙吉", 90, 60, "陈梦庚", 95,};数组查询函数void ArraySearch(ElemType a[], int key, int length){int i;for (i = 0; i <= length; i++){if (key == a[i].key){cout << "学号：" << a[i].key << " 姓名：" << a[i].name << " 成绩：" << a[i].grade << endl;break;}}}二叉树查询函数上文二叉树根本函数中的SearchBST()即为二叉树查询函数。

c++课程设计报告(二叉树运算)

课程设计报告设计题目：二叉树解决四则运算问题院系:自动化院班级：XXX学号：XXX姓名：XX指导老师：XX时间：XX一．程序功能简介利用二叉树的结构解决带括号的四则运算的问题。

程序利用二叉树的堆栈将二叉树的结点变成结点中的数据时运算符，左右子树是标准结点形式，或是另外的标准二叉树形式，通过后序遍历，经标准结点中的表达式求出。

二．课程设计要求(1)读懂程序，将程序的运算步骤完整的描述出来。

(2)四则运算的表达式可以接受空格输入(3)依照运算顺序依次输出四则运算每一步的算式及及结果，最后输出最终计算结果三．课程设计思想这个课题设计要求最关键的就是读懂程序，用类实现四则运算其实不是很难，只是利用二叉树实现带括号的四则运算有些难度。

初读源程序觉得摸不到头脑，几遍下来还是能够理解的。

在程序中先计算的式子放在栈顶，首先赋值右子树，再赋值左子树，保证优先级。

如图：二叉树类栈运算符栈）—* （+输入“+”，“（”，“*”三个运算符没有优先级冲突，按顺序压栈，然后输入“—”，优先级低于“*”，binary_tree temp_tree; //生成二叉树string thisstring="";thisstring = thisstring + OpStack.top();OpStack.pop() //将栈顶优先级高的运算符移除（即这边的乘号）etree.root = build_node(thisstring);//将优先级高的运算符作为二叉树的根结点copy(temp_tree.root,NodeStack.top().root);//将二叉树堆栈栈顶的二叉树复制到新生成的二叉树中（即把1复制到新的二叉树中）NodeStack.pop();//移除二叉树栈栈顶etree.root->right_child = temp_tree.root;//将二叉树作为新二叉树的右分支temp_tree.root = NULL;copy(temp_tree.root,NodeStack.top().root); //继续将下一个栈顶二叉树复制（即把5复制）etree.root->left_child = temp_tree.root;//成为新二叉树的左分支NodeStack.pop();//移除temp_tree.root = NULL;copy(temp_tree.root, etree.root);NodeStack.push(temp_tree);//新二叉树进栈etree.root = NULL;OpStack.push(c);//优先级低的运算符压栈过程如图：栈顶二叉树temp_tree二叉树Etree二叉树将temp_tree作为etree的右结点新的二叉树类栈最后进行一个遍历，判断运算符栈是否处理完，算出最后结果。

二叉树课程设计报告

一、设计目标二叉树是形象地说既树中每个节点最多只有两个分支，它是一中重要的数据类型。

可以运用于建立家谱，公司所有的员工的职位图，以及各种事物的分类和各种机构的职位图表。

二叉树是通过建立一个链式存储结构，达到能够实现前序遍历，中序遍历，后序遍历。

以及能够从输入的数据中得知二叉树的叶子结点的个数，二叉树的深度。

在此，二叉树的每一个结点中必须包括：值域，左指针域，右指针域。

二、总体设计1．对程序中定义的核心数据结构及对其说明：typedef struct BiTNode{//创建二叉树char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;在开头定义了二叉树的链式存储结构，此处采用了每个结点中设置三个域，即值域，左指针域和右指针域。

2.模块的划分及其功能：本程序分为：7大模块。

二叉树的建立链式存储结构、前序遍历、求叶子结点的个数计算、中序遍历、后序遍历、深度、主函数。

1、二叉树的建立链式存储结构；首先typedef struct BiTNode：定义二叉树的链式存储结构，此处采用了每个结点中设置三个域，即值域，*lchild：左指针域和rchild：右指针域。

2、二叉树的前序遍历；利用二叉链表作为存储结构的前序遍历：先访问根结点，再依次访问左右子树。

3、二叉树的求叶子结点的个数计算；先分别求得左右子树中各叶子结点的个数，再计算出两者之和即为二叉树的叶子结点数。

4、二叉树的中序遍历；利用二叉链表作为存储结构的中序遍历：先访问左子数，再访问根结点，最后访问右子树。

5、二叉树的后序遍历；利用二叉链表作为存储结构的前序遍历：先访问左右子树，再访问根结点。

6、求二叉树的深度：首先判断二叉树是否为空，若为空则此二叉树的深度为0。

否则，就先别求出左右子树的深度并进行比较，取较大的+1就为二叉树的深度。

7、主函数。

核心算法的设计：二叉树是n个节点的有穷个集合，它或者是空集（n=0），或者同时满足以下两个条件：（1）：有且仅有一个称为根的节点；（2）：其余节点分为两个互不相交的集合T1，T2，并且T1，T2都是二叉树，分别称为根的左子树和右子树。

二叉树课程设计

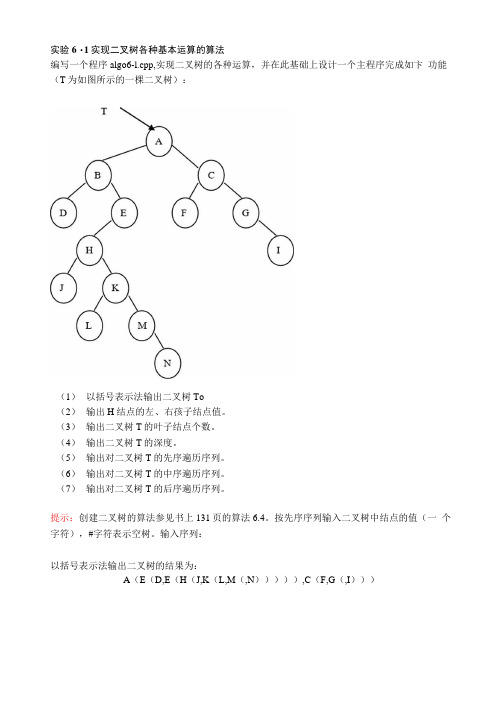
实验6・1实现二叉树各种基本运算的算法编写一个程序algo6-l.cpp,实现二叉树的各种运算，并在此基础上设计一个主程序完成如卞功能（T为如图所示的一棵二叉树）：（1）以括号表示法输出二叉树To（2）输出H结点的左、右孩子结点值。

（3）输出二叉树T的叶子结点个数。

（4）输出二叉树T的深度。

（5）输出对二叉树T的先序遍历序列。

（6）输出对二叉树T的中序遍历序列。

（7）输出对二叉树T的后序遍历序列。

提示：创建二叉树的算法参见书上131页的算法6.4。

按先序序列输入二叉树中结点的值（一个字符），#字符表示空树。

输入序列：以括号表示法输出二叉树的结果为：A（E（D,E（H（J,K（L,M（,N）））））,C（F,G（,I）））程序段#iiiclude<stdio.h>#mclude<stdlib.h>#mclude<sy&/tmieb.h>//#defiiie MAX 50^define OK 1tvpedef stmct btnode{chai Data;//VSapaEv%YAUEYstnict btiiode *Lliiik;//x 6 x OE^O ,Oe stnict btiiode *Rliiik;Z OO xOE^O ,Oe } btnode. *btreetype;//n di6d^p2jeE-mt IiiitBiTiee(btreetype &T){T=NULL;return OK;}〃％・・A绷咗茁void CreatBiTree(btieetype &T) {char ch;scanf(”％c”,&ch);if(ch— ?T=NULL;else{T=(btreetype)malloc(sizeof(btnode));if(!T)exit(-l);T->Data=ch;CreatBiTree(T->Llu±);CreatBiTiee(T->Rlu±);}}//Ea3d56apanAx6o0xOvoid LeftCluld(btreetype &M,chai e) btreetvpe p;p=M;if(p!=NULL){if(p->Data==e){printf(n%c|iAx6o0x6E(^%c\n,\e,p->Llink->Data);} LeftCliild(p->Lliiik.e);LeftCluld(p->Rliiik.e);}}//Ea3dVSapapAOd o0x6void RightCluld(btieetvpe &Machar 亡)btreetvpe p;p=M;if(p!=NULL){if(p->Data==e){prmtf(n%cpA6d o0x6E(^%c\ii,\e,p->Rluik->Data);} RightChild(p->Llink,e);RightChild(p->Rluik,e);}}//P%^6<jx6!4apa,dEymt LeafPoint(btreetype t) return 0;elseif(! t->Lluik&&! t->Rliiik)return 1;elsereturn (LeafPoint(t->Lliiik) + LeafPoint(t->Rlink));}mt Depth(btieetype T)int ij; if(!T)iettun 0; if(T->Llink) i=Depth(T->Llink);else i=0;if<T->Rluik)j=Depth(T->Rliiik);elsej=O;return i>j?i+l:j+l;//A，，o A±iE^- •宅护6他逸応一void DispBiTiee(btreetype T){ if(T!=NULL){pnntfC%c”T>Data);if (T>Llmk!=NULL||T丄・Rhnk!=NULL) {pnntfCC);DispBiTree(T->Llink);if (T->Rlink!=NULL)pniitf(T);DispBiTree(T->Rluik);}}}//IEDdieAu^^E-void PreOider(btieetype T){】f(T){ pnntfC%c”T>Data); PreOrder(T->Llink); PreOrder(T->Rlink);}}//ODDd±eAu>2KE-void InOrder(btreetype T){】f(T){IiiOider(T->LlH±); pnntfC%c”T>Data);IiiOider(T->Rlnik);}}//°6Dd±eAu>z ieE-void PostOrder(btreetype T){】f(T){PostOrder(T->LlHik); PostOider(T->Rliiik); pnntfC%c”T>Data);void main(){timeb tl,t2;ftune(&tl);long m.n;卩门11耳2合6龙1^4£05\2它6口日企即(人6車卩461&良・・・£一注・・・6方6左1)2応±6注&存伙0・丫4£7 亘AiT6ldi(E\jr)；btreetype T;InitBiTree(T);CieatBiTiee(T);pnntf(M A，，o A±iE%--Ea3d>2zeE-:\ii M);DispBiTree(T);prmtf(n\n H);LeftChild(I；H);RightCluld(T：H,);m=LeafPoint(T);pimtf(n6D%d,d6|x6!6apa\ir\m);n=Depth(T);printf(,,^2a5E-^-|LiAEi1]EE(7%d\n l,,n);prmtf(H iEDd=eAu<jl)2ieE-:H);PreOrder(T);pimtf(n\n H);pimtf(n ODDd±eAu>2JEE-:M);InOrder(T);pimtf(,,o6Dd^eAu>2«E-:n);PostOrder(T);prmtf(n\n H);ftime(&t2);t=(t2.time-tl .time)* 10004-(t2.nullitm-tl .nullitm); pnntf(,,d，DD±%3iDd126AE±%ld o AAe\ir\t);}。

c语言编写求二叉树t中叶子结点所在的最小层次与最大层次的函数

c语言编写求二叉树t中叶子结点所在的最小层次与最大层次的函数二叉树是一种常见的数据结构，广泛应用于计算机科学中。

在二叉树中，叶子节点是没有子节点的节点。

找出二叉树中的叶子节点所在的最小层次和最大层次是一个重要的问题，因为它可以帮助我们了解二叉树的结构，以及如何有效地遍历和操作它。

一、二叉树的基本概念在二叉树中，每个节点最多有两个子节点，通常被称为左子节点和右子节点。

树的深度是指从根节点到最远叶子节点的最长路径上的节点数。

叶子节点是没有子节点的节点。

二、编写求最小层次和最大层次的函数1. 函数设计为了找出二叉树中叶子节点所在的最小层次和最大层次，我们可以使用递归的方法。

对于每个节点，我们可以递归地向上遍历，直到到达根节点。

在遍历过程中，我们可以记录下当前层次和叶子节点的层次，从而找出最小层次和最大层次。

下面是一个示例的C语言代码实现：2. 函数实现函数原型：int get_leaf_levels(struct TreeNode* t, int& min_level, int& max_level)函数功能：返回二叉树t中叶子节点的最小层次和最大层次，并更新全局变量min_level和max_level。

函数参数：* t：指向二叉树根节点的指针* min_level：叶子节点的最小层次* max_level：叶子节点的最大层次函数实现：* 首先，初始化全局变量min_level和max_level为INT_MAX。

* 然后，使用递归的方式遍历二叉树t。

对于每个节点，如果它是一个叶子节点，那么更新min_level和max_level为当前层次（当前节点到根节点的层次减一）的最小值和最大值。

如果它不是叶子节点，那么递归地向上遍历，直到到达根节点。

* 最后，返回min_level和max_level的值。

示例代码：struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;};int get_leaf_levels(struct TreeNode* t, int& min_level, int& max_level) {if (t == NULL) { // 空节点没有层次，返回-1return -1;} else if (t->left == NULL && t->right == NULL) { // 叶子节点，更新最小层次和最大层次min_level = max(min_level, t->val); // 更新min_level为当前值与min_level的较大值max_level = min(max_level, t->val); // 更新max_level为当前值与max_level的最小值} else { // 非叶子节点向上遍历，直到根节点int left = get_leaf_levels(t->left, min_level, max_level); // 递归左子树int right = get_leaf_levels(t->right, min_level, max_level); // 递归右子树if (left != -1 || right != -1) { // 如果至少有一个子节点是叶子节点，更新min_level和max_levelmin_level = min(min_level, left); // 更新min_level为当前值的最小值（可能来自左子树）max_level = max(max_level, right); // 更新max_level为当前值的最大值（可能来自右子树）} else { // 如果左右子树都没有叶子节点，那么当前节点就是最小层次的终点（根节点）min_level = t->val; // min_level设置为当前值（根节点的值）}}return min_level; // 返回最小层次的值（可能是根节点的值）}三、总结与展望通过使用C语言编写求二叉树T中叶子结点所在的最小层次与最大层次的函数，我们可以有效地找出二叉树中叶子节点的层次，从而帮助我们了解二叉树的结构和高效地遍历和操作它。

C 二叉树结构的建立与基本操作课案

C++二叉树结构的建立与基本操作二叉树是数据结构中的树的一种特殊情况，有关二叉树的相关概念，这里不再赘述，如果不了解二叉树相关概念，建议先学习数据结构中的二叉树的知识点准备数据定义二叉树结构操作中需要用到的变量及数据等。

复制代码代码如下:#define MAXLEN 20 //最大长度typedef char DATA; //定义元素类型struct CBTType //定义二叉树结点类型{DATA data; //元素数据CBTType * left; //左子树结点指针CBTType * right; //右子树结点指针};定义二叉树结构数据元素的类型DATA以及二叉树结构的数据结构CBTType。

结点的具体数据保存在一个姐都DATA中，而指针left用来指向左子树结点，指针right用来指向右子树结点初始化二叉树初始化二叉树，将一个结点设置为二叉树的根结点。

复制代码代码如下:CBTType * InitTree(){CBTType * node;if(node = new CBTType) //申请内存{cout<<"请先输入一个根节点数据："<<endl;cin>>node->data;node->left=NULL;node->right=NULL;if(node!=NULL) //如果二叉树结点不为空{return node;} else{return NULL;}}return NULL;}首先申请一个结点，然后用户输入根结点的数据，并将左子树和右子树的指针置为空，即可完成二叉树的初始化工作。

查找结点查找结点就是遍历二叉树中的每一个节点，逐个比较数据，当找到目标数据时将返回该数据所在结点的指针。

复制代码代码如下:CBTType *TreeFindNode(CBTType *treeNode,DATA data){CBTType *ptr;if(treeNode==NULL){return NULL;}else{if(treeNode->data==data){return treeNode;}else //分别向左右子树查找{if(ptr=TreeFindNode(treeNode->left,data)) //左子树递归查找{return ptr;}else if(ptr=TreeFindNode(treeNode->right,data)) //右子树递归查找{return ptr;}else{return NULL;}}}}输入参数treeNode为待查找的二叉树的根结点，输入参数data为待查找的结点数据。

c语言数据结构二叉树的基本操作 -回复

c语言数据结构二叉树的基本操作-回复C语言数据结构：二叉树的基本操作概述：二叉树是一种常用的数据结构，在计算机科学中广泛应用于各种算法和问题的解决方案中。

它的特点是每个节点至多有两个子节点，即左子节点和右子节点，且子节点的顺序不能颠倒。

本文将介绍常见的二叉树基本操作，包括创建二叉树、插入节点、删除节点、查找节点、遍历等。

1. 创建二叉树：创建一个二叉树的方法是从根节点开始，逐个插入子节点。

首先定义一个二叉树的结构体，包含一个值和指向左右子节点的指针。

然后使用malloc 函数分配内存空间，并将值赋给根节点的指针。

接着创建左子节点和右子节点，将子节点的指针分别赋给根节点的左右指针。

这样就完成了一个简单的二叉树的创建。

2. 插入节点：插入节点是在现有的二叉树上新增一个节点。

首先找到插入节点的位置，可以从根节点开始逐级比较。

如果插入节点的值小于当前节点，则向左子树查找，否则向右子树查找，直到找到合适的位置。

然后创建一个新节点，并将新节点的指针赋给找到位置的节点的左或右指针。

3. 删除节点：删除节点是将现有的二叉树中的一个节点删除。

首先找到要删除的节点位置，可以通过比较节点的值进行查找，直到找到要删除的节点。

然后根据删除节点的情况分三种情况考虑：若删除节点为叶子节点，直接删除即可；若删除节点只有一个子节点，将子节点的指针赋给删除节点的父节点，然后删除删除节点；若删除节点有两个子节点，需要找到删除节点的左子树中的最大节点或右子树中的最小节点，将其值赋给删除节点，然后删除此最大或最小节点。

4. 查找节点：查找节点是在现有的二叉树中寻找一个特定的节点。

与插入和删除类似，从根节点开始比较节点的值，若要查找的节点值小于当前节点，则继续向左子树查找，否则向右子树查找，直到找到要查找的节点。

若找到了节点，返回此节点的指针；若未找到，返回空指针。

5. 遍历：遍历二叉树是按照一定的顺序访问树中的所有节点。

常见的遍历方式有三种：前序遍历、中序遍历和后序遍历。

二叉树的遍历课程设计(C++)含源代码

《数据结构》课程设计报告设计题目：二叉树的遍历*名：**学号： *********专业：计算机科学与技术院系：计算机科学与技术班级： 1002指导教师：***2012年 3 月1日摘要：本文主要说明如何实现二叉树的遍历。

此次二叉树的遍历基于二叉树的二叉链表存储结构。

遍历方式包括：前序遍历，中序遍历，后续遍历，层序遍历。

其中前序遍历和后续遍历采用非递归算法实现。

编程环境为VC++，除了遍历操作外，还增加了求二叉树的深度，总结点数，每层结点数，以及最近共同祖先（LCA）问题的算法。

关键字：二叉树遍历非递归C++ LCAAbstract: This paper mainly describes how to implement binary tree traversal. The binary tree traversal is based on binary tree binary storage structure. Traversal method includes: preorder traversal,inorder traversal, postorder traversal, levelorder traversal. The former preorder traversal and postorder use of non - recursive algorithm. Programming environment is VC + +, in addition to traversal operation, also increased for solving the binary tree depth 、summary points and each layer of nodes, as well as the most recent common ancestor ( LCA ) algorithm.Keywords: binary tree traversal non-recursive C++ LCA目录一、问题描述 (4)问题描述：创建二叉树并遍历 (4)基本要求： (4)二、需求分析 (4)三、概要设计 (4)1．创建二叉树 (4)2．二叉树的非递归前序遍历示意图 (4)3．二叉树的后序非递归遍历示意图 (5)四、数据结构设计 (5)1．二叉树结点数据类型定义为： (5)2．二叉树数据类型定义为： (5)五、算法设计 (6)1、创建二叉树 (6)2、非递归前序遍历 (7)3、非递归后序遍历 (7)4、求二叉树的高度 (8)5、求二叉树每一层的结点数 (9)6、求两节点最近共同祖先 (9)6、算法流程图 (10)六、程序测试与实现 (11)1、函数之间的调用关系 (11)2、主程序 (11)3、测试数据 (13)4、测试结果 (13)七、调试分析 (14)八、遇到的问题及解决办法 (15)九、心得体会 (15)十、参考文献 (15)一、问题描述问题描述：创建二叉树并遍历基本要求：1、分别运用非递归的方式完成对二叉树的先序和后序遍历2、输出二叉树的高度3、输出每一层的结点数4、查找结点P 和结点Q的最近共同祖先二、需求分析1．本程序的功能包括二叉树的建立，二叉树的递归遍历，二叉树的非递归遍历，查询二叉树的深度，查询每层的结点数，查找两个结点的最近共同祖先，二叉树的打印。

数据结构(C语言版)树、二叉树详细举例介绍

四. 中序遍历算法的非递归描述
BiTNode *GoFarLeft(BiTree T, Stack &S) { if (!T ) return NULL; while (T->lchild ) { // 直到最左端 Push(S, T); T = T->lchild; } return T; }
一.二叉树的顺序存储表示
A B D C E F
A
B
C
D
E
F
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14…
2
5
1
14
37例如:来自二叉链表0520+21+ +2k-1 = 2k-1
性质 3 ：对任何一棵二叉树，若它含有n0 个叶子结点、n2 个度为 2 的结点，则必存在关系式：n0 = n2+1
证明：
设二叉树上结点总数 n = n0 + n1 + n2 又二叉树上分支总数 b = n1+2n2 而 b = n-1 = n0 + n1 + n2 - 1 由此， n0 = n2 + 1
若D为空集，则称为空树；否则: (1) 在D中存在唯一的称为根的数据元素root, (2) 当n>1时，其余结点可分为m (m>0)个互不相交的有限集T1, T2, …, Tm, 其中每一个子集本身又是一棵符合本定义的树，称为根root的子树。
数据关系 R：
因为 k 只能是整数，因此， k =log2n + 1
证明：
则根据第二条性质得 2k-1≤ n < 2k
性质 5 ：
若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点： (1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 i/2 的结点为其双亲结点; (2) 若 2i>n，则该结点无左孩子，否则，编号为 2i 的结点为其左孩子结点； (3) 若 2i+1>n，则该结点无右孩子结点，否则，编号为2i+1 的结点为其右孩子结点。

二叉树程序设计_C语言(打印)

T->lchild=Create(T->lchild); T->rchild=Create(T->rchild); } return T; }
2.先序、中序、后序遍历二叉的函数
void xianxu(BiTree T) {
if(T) {
printf("%c",T->data); xianxu(T->lchild); xianxu(T->rchild); } }
3.求二叉树的叶子结点数和深度的函数
int Sumleaf(BiTree T) {
int sum=0,m,n; if(T){ if((!T->lchild)&&(!T->rchild)) sum++;
m=Sumleaf(T->lchild); sum+=m; n=Sumleaf(T->rchild); sum+=n; } return sum; }
我喜欢实验，因为实验让我更加理解课本上的知识，学会应用所学的知识。而且，实验让我更加喜欢数据结构和 C 语言，更加喜欢代码，更加喜欢编程。
六、小组成员
组长：张毅
成员：楚阿慧郑龙珍
printf(" 1.JianLi 2.DaYin 3.X Xu 4.Z Xu 5.H Xu 6.S Du 7.YZ Shu 8.Menu 9.X Hui 0.Quit\n");
printf("**************************************MENU****************** ********************\n"); }
if(x>g) zuo=(x-g)/2+g; if(x<g) zuo=(x-g)/2+x; line(x-1,y,zuo,y+40); } if(T->rchild!=NULL) { you=2*x-zuo; line(x-1,y,you,y+40); } Paint(T->lchild,zuo,y+40,x);

二叉树课程设计c语言

二叉树是计算机科学中常用的一种数据结构，可以用于表示各种类型的数据。

以下是一个简单的二叉树课程设计，使用C语言实现。

```c#include <stdio.h>#include <stdlib.h>// 定义二叉树节点结构体typedef struct Node {int data;struct Node *left;struct Node *right;} Node;// 创建新节点Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node));if (!newNode) {printf("内存分配失败\n");return NULL;}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}// 插入节点Node* insertNode(Node* root, int data) {if (root == NULL) {return createNode(data);}if (data <= root->data) {root->left = insertNode(root->left, data); } else {root->right = insertNode(root->right, data); }return root;}// 中序遍历二叉树void inorderTraversal(Node* root) {if (root == NULL) {return;}inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);}int main() {Node* root = NULL; // 初始时，根节点为空int arr[] = {8, 3, 10, 1, 6, 14, 4, 7, 13}; // 要插入的节点数据数组int n = sizeof(arr) / sizeof(arr[0]); // 数组元素个数for (int i = 0; i < n; i++) { // 插入节点到二叉树中 root = insertNode(root, arr[i]);}printf("中序遍历二叉树的结果为："); // 中序遍历二叉树，输出结果为升序排列的节点数据数组inorderTraversal(root);printf("\n");return 0;}```。

C语言综合实验设计报告---数据结构：二叉树的遍历

C语言综合实验设计报告题目：数据结构：二叉树的遍历学院:化学工程学院专业:班级:一选题背景数据结构是由若干特性相同的数据元素构成的集合，且在集合上存在一种或多种关系。

由关系不同可将数据结构分为四类：线性结构、树形结构、图状结构和集合结构。

数据的存储结构是数据逻辑结构在计算机中的映象，由关系的两种映象方法可得到两类存储结构：一类是顺序存储结构，它以数据元素相对的存储位置表示关系，则存储结构中只包含数据元素本身的信息；另一类是链式存储结构，它以附加的指针信息（后继元素的存储地址）表示关系。

数据结构课程是离散数学的后续课程，并是操作系统、编译原理、数据库系统、计算机算法设计与分析、计算机网络、软件工程、人工智能等的基础课程，是将来进行大型程序设计的一个训练过程。

二设计思想通过调用函数的方法进行二叉树的遍历，定义坐标固定结点的位置。

自动建立树和手动建立树的标志,选择：2手动,1自动。

文本模式下创建树的过程，如果选择1自动，电脑自动建立树，如果选择2手动，，需要人工手动建立。

手动提示输入结点，创建好树。

再用图形显示创建好的树，进行先序，中序，后序遍历。

遍历时显示每个结点的过程。

最后关闭图形。

三主要问题的解决方法及技术关键存在的主要问题是在手动创建树时怎样输入结点，当选择“人工手动建立”时，在提示后依次输入26个字符或数字，每行一个。

此时树就能建立，然后用图形显示出来。

本程序的技术关键是建立二叉树和图形显示遍历的过程，分别用到Tree *CreatTree(),Void DrawTree(Tree *t)等函数。

遍历结束后，图形关闭。

四流程图五程序清单/********tree2.c二叉树演示********/#include <graphics.h>#include <stdio.h>#include <stdlib.h>#include <dos.h>#include <time.h>typedef struct TREE{char data;/*树的结点数据*/struct TREE *lchild;struct TREE *rchild;int x;/*树的x坐标*/int y;/*树的y坐标*/}Tree;struct OUTPUT{int x;/*三种遍历的x坐标*/int y;/*三种遍历的y坐标*/int num;}s;int nodeNUM=0;/*统计当前的结点数字,最多26个*/char way;/*自动建立树和手动建立树的标志,2手动,1自动*/ char str[3];/*显示结点数据的字符串*/void Init();/*图形初始化*/void Close();/*图形关闭*/Tree *CreatTree();/*文本模式下创建树的过程*/Tree *InitTree(int h,int t,int w);/*创建树,h层次,t横坐标,w 树之间的宽度,n树的建立方式*/void DrawTree(Tree *t);/*用图形显示创建好的树*/void Preorder(Tree *t);/*前序遍历*/void Midorder(Tree *t);/*中序遍历*/void Posorder(Tree *t);/*后序遍历*/void DrawNode(Tree *t,int color);/*遍历时显示每个结点的过程*/ void ClrScr();/*清空树的区域*/void main(){Tree *root;randomize();root=CreatTree();/*创建树*/Init();DrawTree(root);/*每次遍历前显示白色的树*/sleep(1);s.x=100;s.y=300;s.num=1;/*每次遍历前设置显示遍历顺序显示的x,y坐标*/Preorder(root);/*前序遍历*/getch();ClrScr();DrawTree(root);sleep(1);s.x=100;s.y=350;s.num=1;Midorder(root);/*中序遍历*/ getch();ClrScr();DrawTree(root);sleep(1);s.x=100;s.y=400;s.num=1;Posorder(root);/*后序遍历*/ Close();}/*清空树的区域*/void ClrScr(){setcolor(BLACK);setfillstyle(SOLID_FILL,BLACK);bar(0,20,640,280);}/*文本模式下创建树的过程*/Tree *CreatTree(){Tree *root;clrscr();printf("please input n\n");printf("puter creat\n");printf("2.people creat\n");way=getch();/*输入创建树的方法,1电脑自动建立,2人工手动建立*/if(way!='2')way='1';/*其他数字默认自动建立*/if(way=='2')/*手动建立提示输入结点*/printf("Please creat the tree\n");root=InitTree(1,320,150);system("pause");return root;}/*生成二叉树，h表示层次，t表示横坐标，w表示结点左右子树的宽度，随机数n确定结点是空或非空，如n为0，则为空*，但要限定确保结点数不少于三个*/Tree *InitTree(int h,int t,int w){char ch;int n;/*自动建立时随机赋值判断是否是NULL的标志*/Tree *node;if(way=='2')/*手动建立需要自己输入*/scanf("%c",&ch);else/*自动建立的赋值*/{n=random(5);if(n==0&&nodeNUM>=3)/*随机赋值时候确保自动建立的二叉树有三个结点*/ch='.';elsech=65+random(25);}if(ch=='.')/*输入空格代表NULL*/return NULL;else{if(h==6||nodeNUM==26)/*如果树的层次已经到5或者结点树到达26个就自动返回NULL*/return NULL;node=(Tree*)malloc(sizeof(Tree));node->data=ch;node->x=t;/*树的x坐标是传递过来的横坐标*/node->y=h*50;/*树的y坐标与层次大小有关*/nodeNUM++;node->lchild=InitTree(h+1,t-w,w/2);node->rchild=InitTree(h+1,t+w,w/2);}return node;}/*用图形显示创建好的树*/void DrawTree(Tree *t){if(t!=NULL){setcolor(BLACK);setfillstyle(SOLID_FILL,BLACK);fillellipse(t->x,t->y,9,9);setcolor(WHITE);circle(t->x,t->y,10); /*画圆*/sprintf(str,"%c",t->data);/*将内容转换成字符串输出*/ outtextxy(t->x-3,t->y-2,str);if(t->lchild!=NULL)/*左子树*/{line(t->x-5,t->y+12,t->lchild->x+5,t->lchild->y-12);DrawTree(t->lchild);}if(t->rchild!=NULL)/*右子树*/{line(t->x+5,t->y+12,t->rchild->x-5,t->rchild->y-12);DrawTree(t->rchild);}}}/*遍历时显示每个结点的过程*/void DrawNode(Tree *t,int color){setcolor(YELLOW);setfillstyle(SOLID_FILL,YELLOW);fillellipse(t->x,t->y,10,10);setcolor(RED);sprintf(str,"%c",t->data);/*将内容转换成字符串输出*/outtextxy(t->x-3,t->y-2,str);setcolor(color);outtextxy(s.x,s.y,str);setcolor(RED);sprintf(str,"%d",s.num);/*将遍历次序用数字显示在树的结点上*/outtextxy(t->x-3,t->y-20,str);s.num++;sleep(1);}/*前序遍历*/void Preorder(Tree *t){if(t!=NULL){s.x+=15;DrawNode(t,GREEN);Preorder(t->lchild);Preorder(t->rchild);}}/*中序遍历*/void Midorder(Tree *t) {if(t!=NULL){Midorder(t->lchild); s.x+=15;DrawNode(t,YELLOW); Midorder(t->rchild); }}/*后序遍历*/void Posorder(Tree *t) {if(t!=NULL){Posorder(t->lchild); Posorder(t->rchild); s.x+=15;DrawNode(t,BLUE);}}/*图形初始化*/void Init(){int gd=DETECT,gm;initgraph(&gd,&gm,"c:\\tc");cleardevice();setcolor(YELLOW);outtextxy(250,10,"anykey to continue");setcolor(RED);outtextxy(20,300,"preorder");outtextxy(20,350,"midorder");outtextxy(20,400,"posorder");getch();}/*图形关闭*/void Close(){getch();closegraph();}六设计结果说明本程序主函数简洁易懂，用了坐标设定树结点的位置，使运算方便。

二叉搜索树课程设计

二叉搜索树课程设计一、课程目标知识目标：1. 学生能理解二叉搜索树的定义、性质和基本操作。

2. 学生能掌握二叉搜索树的插入、删除和查找算法。

3. 学生能了解二叉搜索树的中序遍历、前序遍历和后序遍历算法。

技能目标：1. 学生能运用所学知识，实现二叉搜索树的构建和操作。

2. 学生能通过编程实践，解决与二叉搜索树相关的问题。

3. 学生能分析二叉搜索树在实际应用中的优缺点，并进行优化。

情感态度价值观目标：1. 学生培养对数据结构和算法的兴趣，增强计算机科学素养。

2. 学生培养团队协作意识，学会与他人共同解决问题。

3. 学生通过学习二叉搜索树，认识到数据结构在实际应用中的重要性，激发学习动力。

课程性质：本课程为计算机科学领域的数据结构与算法课程，以二叉搜索树为研究对象，结合编程实践，提高学生的数据分析和问题解决能力。

学生特点：学生已具备基本的编程能力，对数据结构有一定了解，但可能对二叉搜索树的具体应用和实现细节掌握不足。

教学要求：注重理论与实践相结合，通过讲解、示例、编程实践等环节，使学生掌握二叉搜索树的相关知识，提高编程能力。

同时，关注学生的情感态度价值观培养，激发学习兴趣。

在教学过程中，将课程目标分解为具体的学习成果，便于教学设计和评估。

二、教学内容1. 二叉搜索树的定义及性质- 理解二叉搜索树的定义- 掌握二叉搜索树的性质：左子树所有节点小于根节点，右子树所有节点大于根节点2. 二叉搜索树的插入、删除和查找操作- 学习插入算法，包括递归和非递归实现- 学习删除算法，包括三种情况的处理：删除叶子节点、删除只有一个子节点的节点、删除有两个子节点的节点- 学习查找算法，掌握如何在二叉搜索树中查找特定值3. 二叉搜索树的遍历算法- 学习中序遍历、前序遍历和后序遍历的原理及实现- 分析遍历算法在实际应用中的用途4. 二叉搜索树的应用及优化- 探讨二叉搜索树在实际编程中的应用场景- 分析二叉搜索树的性能，了解平衡二叉搜索树的概念及优势5. 编程实践- 结合教材，完成二叉搜索树的构建、插入、删除、查找等操作的编程实践- 实现二叉搜索树的中序、前序、后序遍历算法- 分析编程实践中遇到的问题，进行优化和改进教学内容安排和进度：第一课时：二叉搜索树的定义及性质，插入算法第二课时：删除算法，查找算法第三课时：遍历算法，应用及优化第四课时：编程实践与讨论教材章节关联：《数据结构与算法分析》第四章：二叉树《算法导论》第三章：二叉树和红黑树三、教学方法1. 讲授法：- 采用引导式讲授，通过问题驱动的形式，激发学生对二叉搜索树知识的探究欲望。

c语言二叉树实例

c语言二叉树实例C语言二叉树实例一、引言二叉树是一种常见的数据结构，在计算机科学中有着广泛的应用。

而C语言作为一种常用的编程语言，也提供了丰富的数据结构和算法支持，使得实现二叉树成为一项相对简单的任务。

本文将以C语言为基础，介绍如何实现一个二叉树，并通过一个实例来演示其使用方法。

二、二叉树的定义二叉树是一种特殊的树形结构，其中每个节点最多有两个子节点。

每个节点包含一个数据元素和指向其左右子节点的指针。

二叉树的特点是具有递归的结构，即每个子树也是二叉树。

三、二叉树的实现在C语言中，可以通过定义一个结构体来表示二叉树的节点。

结构体中包含一个数据元素和两个指针，分别指向左右子节点。

下面是一个简单的二叉树节点的定义：```ctypedef struct TreeNode {int data;struct TreeNode* left;struct TreeNode* right;} TreeNode;```四、二叉树的操作1. 创建节点可以通过动态分配内存的方式创建一个二叉树节点，然后为节点的数据元素赋值，并将左右子节点指针初始化为NULL。

2. 插入节点插入节点是二叉树的一个重要操作，可以根据节点的值来确定其插入位置。

如果插入的值小于当前节点的值，则将其插入到左子树中；如果插入的值大于当前节点的值，则将其插入到右子树中。

插入操作可以通过递归或循环实现。

3. 删除节点删除节点是另一个常用的操作，可以根据节点的值来确定删除的位置。

删除节点时需要考虑三种情况：节点没有子节点、节点只有一个子节点、节点有两个子节点。

删除操作同样可以通过递归或循环实现。

4. 查找节点查找节点可以根据节点的值来确定其位置。

可以通过递归或循环的方式进行查找，当找到对应的节点时，可以返回该节点的指针。

5. 遍历二叉树常见的二叉树遍历方式有三种：前序遍历、中序遍历和后序遍历。

前序遍历是先访问根节点，然后递归遍历左子树和右子树；中序遍历是先递归遍历左子树，然后访问根节点，再递归遍历右子树；后序遍历是先递归遍历左子树和右子树，然后访问根节点。

数据结构课程设计-二叉树的基本操作

二叉树的基本操作摘要：本次课程设计通过对二叉树的一系列操作主要练习了二叉树的建立、四种遍历方式：先序遍历、中序遍历、后序遍历和层序遍历以及节点数和深度的统计等算法。

增加了对二叉树这一数据结构的理解，掌握了使用c语言对二叉树进行一些基本的操作。

关键字：递归、二叉树、层序遍历、子树交换一、程序简介本程序名为“二叉树基本操作的实现”，其主要为练习二叉树的基本操作而开发，其中包含了建立、遍历、统计叶子结点和深度等一系列操作。

其中定义二叉链表来表示二叉树，用一个字符类型的数据来表示每一个节点中存储的数据。

由于没有进行图形界面的设计，用户可以通过程序中的遍历二叉树一功能来查看操作的二叉树。

二、功能模块2.1功能模块图2.2功能模块详解2.2.1建立二叉树输入要建立的二叉树的扩展二叉树的先序遍历序列，来建立二叉树，建立成功会给出提示。

2.2.2遍历二叉树执行操作之后会有四个选项可供选择：先序遍历、中序遍历、后序遍历、层序遍历。

输入对应的序号即可调动相关函数输出相应的遍历序列。

2.2.3统计叶子节点树执行之后输出叶子结点的个数。

2.2.4求二叉树深度执行之后输出二叉树的深度。

2.2.5子树交换交换成功则会给出提示，用户可通过遍历二叉树来观察子树交换之后的二叉树。

三、数据结构和算法设计3.1二叉链表的设计1.typedef struct BiNode {2.char data;3.struct BiNode* lchild; //左孩子4.struct BiNode* rchild; //右孩子5.}BiTree;用一个字符型保存节点数据，分别定义两个struct BiNode类型的指针来指向左孩子和右孩子。

在BiTree.h中实现相关的功能。

3.2队列的实现1.typedef struct {2. ElemType* data;3.int head;//队头指针4.int tail;//队尾指针5.} SqQueue;队列主要用于二叉树遍历过程中的层序遍历，从根节点开始分别将左右孩子放入队列，然后从对头开始输出。

c语言二叉树实验报告

C语言二叉树实验报告摘要本实验报告旨在详细介绍C语言中二叉树的实现方法，并深入探讨二叉树在计算机科学中的应用。

报告内容包括二叉树的定义、创建与遍历方法、二叉树的特性、二叉树的应用领域等方面的内容。

通过对二叉树的学习和实践，我们可以加深对数据结构的理解和应用能力。

1. 引言在计算机科学中，二叉树是一种重要的数据结构，被广泛应用于各种算法和实际问题的解决。

二叉树由节点组成，每个节点最多有两个子节点，分别为左子节点和右子节点。

本实验旨在通过使用C语言来实现二叉树，加深对二叉树的理解和运用能力。

2. 二叉树的定义与创建2.1 二叉树的定义二叉树是一种树形数据结构，在计算机科学中具有广泛的应用。

二叉树由节点组成，每个节点最多有两个子节点，分别为左子节点和右子节点。

根节点是二叉树的起点，也是唯一没有父节点的节点。

2.2 创建二叉树可以通过以下步骤创建一个二叉树：1.定义二叉树的节点结构，包括数据域和左右子节点指针域。

2.使用动态内存分配函数malloc为根节点分配内存空间。

3.输入根节点的值，并将左右子节点指针指向NULL。

4.递归地创建左子树和右子树。

3. 二叉树的遍历方法二叉树的遍历是指以某种顺序访问二叉树中的节点，可以分为前序遍历、中序遍历和后序遍历三种方式。

3.1 前序遍历前序遍历是指先访问根节点，然后递归地遍历左子树和右子树。

在前序遍历中，根节点总是最先被访问。

算法的伪代码如下所示：preorderTraversal(node) {if (node is not NULL) {print node.valuepreorderTraversal(node.left)preorderTraversal(node.right)}}3.2 中序遍历中序遍历是指先递归地遍历左子树，然后访问根节点，最后再递归地遍历右子树。

在中序遍历中，根节点总是被访问在中间位置。

算法的伪代码如下所示：inorderTraversal(node) {if (node is not NULL) {inorderTraversal(node.left)print node.valueinorderTraversal(node.right)}}3.3 后序遍历后序遍历是指先递归地遍历左子树和右子树，最后访问根节点。

C语言二叉树

递归实现
先递归遍历左子树，然后访问根节点，最后递归遍历右子树
非递归实现
利用栈来辅助遍历，先将根节点入栈，然后循环执行出栈、访问、将右子节点入栈的操作，同时在访问节点前，需将其左子树中的所有节点依次入栈
后序遍历
遍历顺序
左子树 -> 右子树 -> 根节点
递归实现
先递归遍历左子树，然后递归遍历右子树，最后访问根节点
if (root == NULL) return;
遍历算法实现
01
postOrder(root->left); // 递归遍历左子树
02
postOrder(root->right); // 递归遍历右子树
03
printf("%d ", root->data); // 访问根节点
遍历算法实现
}
```
XX
PART 03
二叉树遍历方法
REPORTING
前序遍历
遍历顺序
根节点 -> 左子树 -> 右子树
递归实现
先访问根节点，然后递归Байду номын сангаас历左子树，最后递归遍历右子树
非递归实现
利用栈来辅助遍历，先将根节点入栈，然后循环执行出栈、访问、将右子节点和左子节点依次入栈的操作
中序遍历
遍历顺序
左子树 -> 根节点 -> 右子树
结构体定义与初始化
```
初始化：在创建二叉树之前，需要对节点进行初始化，分配内存空间并设置初始值。
结构体定义与初始化
01
```c
02
TreeNode* createNode(int data) {

c语言实现二叉树各种基本运算的算法

c语言实现二叉树各种基本运算的算法二叉树是一种常见的数据结构，可以应用于许多算法和问题中。

在C语言中，我们可以使用指针和结构体来实现二叉树的各种基本运算。

本文将详细介绍二叉树的创建、插入、删除、查找以及遍历等基本操作的算法。

1.创建二叉树创建二叉树可以通过递归的方式来实现。

首先定义一个表示二叉树节点的结构体，包含一个值和左右子节点指针。

然后，通过递归地创建左右子树来构建整个二叉树。

```ctypedef struct TreeNode {int data;struct TreeNode* left;struct TreeNode* right;} TreeNode;//创建二叉树TreeNode* createBinaryTree() {int data;scanf("%d", &data);if (data == -1) { // -1表示空节点return NULL;}TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode)); node->data = data;node->left = createBinaryTree();node->right = createBinaryTree();return node;}```2.插入节点在二叉树中插入节点可以按照二叉搜索树的性质进行。

如果要插入的值小于当前节点的值，则将其插入到左子树中，否则插入到右子树中。

如果子树为空，则直接创建一个新节点作为子树。

```c//插入节点TreeNode* insertNode(TreeNode* root, int data) {if (root == NULL) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}if (data < root->data) {root->left = insertNode(root->left, data);} else {root->right = insertNode(root->right, data);}return root;}```3.删除节点删除二叉树中的节点可以分为三种情况：删除叶子节点、删除只有一个子节点的节点、删除有两个子节点的节点。