等效抗弯刚度计算表
强度和刚度的计算公式

强度和刚度的计算公式强度和刚度是材料力学性能的两个重要指标,用于评估材料在受力作用下的变形和破坏性能。
强度指的是材料抵抗外力作用下发生破坏时所能承受的最大应力,常用于衡量材料的抗拉强度、抗压强度、抗弯强度等。
刚度指的是在给定应力下材料的变形程度,常用于表征材料的刚性和变形能力。
本文将介绍强度和刚度的计算公式和相关知识。
不同材料和应力状态下的强度计算公式有所不同,下面将分别介绍常见的三种情况。
1.抗拉强度(拉伸强度)抗拉强度是材料在受拉力作用下发生破坏时所能承受的最大应力。
计算公式为:σt=F/A其中,σt表示抗拉强度(拉伸强度),F表示施加在材料上的拉力,A表示材料的横截面积。
2.抗压强度抗压强度是材料在受压力作用下发生破坏时所能承受的最大应力。
计算公式为:σc=F/A其中,σc表示抗压强度,F表示施加在材料上的压力,A表示材料的横截面积。
3.抗弯强度抗弯强度是材料在受弯矩作用下发生破坏时所能承受的最大应力。
计算公式为:σb=M/S其中,σb表示抗弯强度,M表示施加在材料上的弯矩,S表示材料的截面模数。
刚度可以通过材料的弹性模量和几何参数来计算,下面介绍两个刚度的计算公式。
1.弯曲刚度弯曲刚度是指在给定弯矩作用下,材料发生弯曲时所产生的刚度。
计算公式为:EI=M/δ其中,EI表示弯曲刚度,M表示施加在材料上的弯矩,δ表示材料的弯曲变形。
2.剪切刚度剪切刚度是指在给定剪切力作用下,材料发生剪切变形时所产生的刚度。
计算公式为:G=τ/γ其中,G表示剪切刚度,τ表示施加在材料上的剪切力,γ表示材料的剪切应变。
以上是强度和刚度的计算公式的介绍,不同材料和材料状态下的计算公式可能略有差异。
同时,需要注意的是,材料的强度和刚度还受到其他因素的影响,例如温度、湿度、应力速率等。
因此,在实际计算中要综合考虑这些因素,以准确评估材料的强度和刚度。
砌体墙刚度计算

一、抗娱布at 1. 结构宿置仃〉底层混凝七抗責墙和檢支柱及承巫砌体境的布遂,児国1291・:松艾墙梁和混駐 土梁的布腎也反映IT 该图上°不考虑承亟创体墙承把底层水半地丧作用'(2>二泾砌体杭震堆和构造拄的布盘见图12-9-2 .各抗窝署上均布起齧梁;三层以上 抗孫墙、构造柱和圈梁布置基本同二戌°<3)二层楼面采用现浇混凝土楼盖•板厚120mg 托梁和一般梁布胃更映圧图12-9-1 k 0 二层以上楼面和屋面均釆用现浇混凝土楼盖和屋盖■板片80nw 股梁布晋基本同二层。
2. 构件和材料(0构件尺寸同第十二联第九卩计算实例.⑵ 材料獺度等级同第|二敢第九节计篦实例“ 二.御務刚度笑算 【・無移刚度计算公式(I)框架柱办一购造柱参与抗靈墙工作系数,对于騎柱和角柱,当凡//叭亠0.5肘,取0.3;当 H, /心VO.5拄: 相架:(2)馄凝卜•抗蕊堆_ ______ 3H 祀 + «r/嗅人和3EJ W(13-M)(13-2-2)(13 2-3)12H.2/.・■ ■时,取0.26:对于培中柱乘以增大系数1.2,对于墙边註乘以增人系数1.5;H: --- i层层高;抗赛墙的长度;巩——洞口宽度之和;心 --- 弯曲变形影响系数.当时,取几=1;血——洞口影响系数」J按表13M 采用乙2.横向刚度验算(1)底层側移刚度讨算0)混炭土抗養墙侧移刚度计算按公式(13-2-3 )或fl 3-2-4)计算底层横向混凝上抗農墙蝕移刚度见表13-2-20 ②混疑土框支柱侧移刚度计算ii I-2.窗泡岛小千“气H.B4•沖«ThtX 10%:3・涧口心心伐備肉斥I中心浅人十旳・业应*«少10 ^・EJ 7.1.2-2单氏框条的柔度和刚皮⑷柔度:(6)刚度12E C-S/C 框架的侧移刚度(图7.1.2-2/;)为一]2E/h 一根柱子的侧移刚度为忑-皆式中瓦——混擬土的弾性摸虽:;Z c—柱的截面惯性矩;h—柱的计算髙度。
混凝土梁受弯刚度原理

混凝土梁受弯刚度原理一、概述混凝土梁是建筑结构中常用的结构元件,其主要承受的是弯曲力。
因此,混凝土梁的抗弯刚度是评估其承载能力的重要指标。
本文将从混凝土梁受弯刚度的原理出发,分析其主要影响因素并探讨其计算方法。
二、混凝土梁受弯刚度的原理混凝土梁受弯刚度的本质是指梁在受到弯曲力矩作用时所表现出的抵抗弯曲变形的能力。
这种能力主要来自混凝土梁的几何形状和材料性质两个方面。
1. 几何形状梁的几何形状是影响其受弯刚度的重要因素。
梁的受弯刚度与梁截面的形状和大小有关。
通常情况下,梁的截面越大,其受弯刚度越大。
此外,梁截面形状也会影响其受弯刚度。
常见的梁截面形状有矩形、圆形、T形和L形等。
这些形状的梁在受到相同载荷时抵抗弯曲变形的能力是不同的。
2. 材料性质混凝土梁的材料性质也是影响其受弯刚度的重要因素。
混凝土的弹性模量和抗拉强度都是影响梁受弯刚度的重要参数。
通常情况下,弹性模量越大,抗拉强度越高的混凝土梁其受弯刚度也越大。
三、影响混凝土梁受弯刚度的因素1. 梁截面形状梁截面形状是影响混凝土梁受弯刚度的主要因素之一。
常见的梁截面形状有矩形、圆形、T形和L形等。
不同形状的梁在承受相同载荷时,其受弯刚度是不同的。
一般情况下,矩形截面的梁受弯刚度最大,其次是T形截面和L形截面的梁,圆形截面的梁受弯刚度最小。
2. 梁截面尺寸梁截面尺寸也是影响混凝土梁受弯刚度的重要因素。
在一定范围内,梁截面尺寸越大,其受弯刚度也越大。
因此,在设计混凝土梁时,应尽量选择尺寸较大的梁截面。
3. 混凝土强度混凝土的强度是影响混凝土梁受弯刚度的另一个关键因素。
混凝土的强度主要包括抗压强度和抗拉强度。
一般情况下,抗压强度越大的混凝土梁其受弯刚度也越大。
此外,抗拉强度也是影响混凝土梁受弯刚度的重要参数。
抗拉强度低的混凝土梁在受到弯曲力矩作用时容易发生开裂,从而导致其受弯刚度降低。
4. 钢筋配筋率混凝土梁中的钢筋起到增强混凝土抗拉强度的作用。
因此,钢筋配筋率也是影响混凝土梁受弯刚度的重要因素之一。
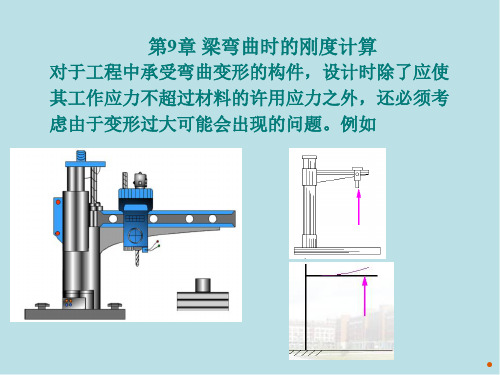
工程力学第9章 梁弯曲时的刚度计算
w
x
qx
F
x
9.1 挠曲线近似微分方程
9.1.2 挠度和转角的关系
◆挠曲线方程 : w f x
w
挠曲线
w
x
qx
F
x
tan dw
dx
dw
dx
9.1.3 挠曲线近似微分方程
一、挠曲线的曲率公式
1M EI
1
x
M x
EI
d2w
1
x
6EI 2l
l 2
2l 2
l 2
2
11Fl3 96EI
未知约束力单独作用引起的B处挠度
wB FB
FB 2l 3
48EI
FBl 3 6EI
将上述结果代入式(b),得到补充方程
11Fl3 FBl3 0 96EI 6EI
w Mex x2 l2 6EIl
(c)
Me 3x2 l2 6EIl
(d)
(4)计算最大挠度与截面的转角
作出梁的弯矩图如下图所示,全梁弯矩为正。其最大 挠度处的转角为零。故由式(c)有
dw Me 3x2 l2 0 dx 6EIl
从而得最大挠度所在截面的坐标为
2
在集中力 F 单独作用下,大梁跨度中点C的挠度由教材表
7–1第5栏中查出为
wC
F
Fl 3 48EI
将以上结果叠加,即得在均布载荷 和q 集中力 的F 共同作用
下,大梁跨度中点C的挠度
复合材料层合管等效抗弯刚度的试验分析

复合材料层合管等效抗弯刚度的试验分析【摘要】本文通过试验分析复合材料层合管的等效抗弯刚度,着重探讨了其定义与公式推导、试验方法与步骤、试验结果分析、参数优化与讨论以及模拟分析。
研究发现,复合材料层合管的等效抗弯刚度受多种因素影响,包括材料组成、层数、厚度等。
通过试验和模拟分析,可以优化管材设计和制备工艺,提高其抗弯性能。
本文还对未来研究方向进行展望,如进一步探究复合材料层合管的其他力学性能及其在工程中的应用前景。
综合以上内容,本研究有助于深入了解复合材料层合管的力学特性,为相关领域的进一步研究和实践提供参考。
【关键词】复合材料、层合管、抗弯刚度、试验分析、参数优化、模拟分析、影响因素、结论、展望1. 引言1.1 研究目的本文旨在通过试验分析,研究复合材料层合管的等效抗弯刚度特性。
具体而言,研究目的包括:1. 探究复合材料层合管在弯曲加载下的变形和破坏行为,以深入理解其力学性能;2. 对比不同材料组合、层厚比和层序排布等因素对抗弯刚度的影响,为优化复合材料层合管设计提供依据;3. 基于实验结果,探讨复合材料层合管等效抗弯刚度的计算方法及其在工程应用中的可靠性。
通过本研究,可为复合材料层合管结构设计和工程应用提供具体数据支持,推动复合材料在航空航天、汽车制造等领域的应用和发展。
1.2 研究意义在工程实践中,复合材料层合管的抗弯刚度是评估其结构性能的重要指标之一。
通过研究复合材料层合管的等效抗弯刚度,可以为工程设计提供对应的理论基础,从而优化结构设计,提高结构的承载能力和安全性。
对于复合材料层合管的抗弯性能进行试验分析,还可以为相关领域的研究和开发工作提供参考和指导。
研究复合材料层合管等效抗弯刚度的意义重大,对于推动复合材料技术的发展具有重要的实际意义。
1.3 研究内容本研究的主要内容是通过试验分析复合材料层合管的等效抗弯刚度,通过实验数据和数学模型的结合,探究复合材料层合管在抗弯性能方面的表现。
具体包括对复合材料层合管等效抗弯刚度的定义与公式推导,试验方法与步骤的设计与实施,试验结果的分析和数据处理,参数的优化与讨论,以及通过模拟分析来进一步验证实验结果。
梁的弯曲-变形刚度计算

一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
1'
y
C'
1
在小变形下: 即:
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al , AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0
砌体墙刚度计算

无洞、小洞混凝土墙考虑剪切、弯曲变形(3);无洞、小洞砖墙仅考虑剪切变形。
上部砖墙考虑的考虑弯曲(12)、剪切底框结构是我国现阶段经济条件下特有的一种结构,从抗震上讲它是一种不合理的结构形式,但限于我国当今的经济发展水平,目前还无法取消,因此在我国内地及广大中西部地区临街建筑中仍普遍采用。
其具有“头重脚轻”、上刚下柔、的特点,为保证实现“小震不坏,中震可修,大震用不倒”的抗震原则,《建筑设计抗震规范》(GB50011-2001)对底框结构底部框架层与上层刚度比做出了明确规定,其中底层框架,第二层与底层侧向刚度比,6、7度时不应大于2.5,8度不应大于1.5,且均不应小于1.要做到这一点,必须在底部框架中布置一定数量的的抗震墙。
结构设计中抗震墙如何设置,有时需要反复计算,多次与建筑专业协调。
作者在总结多年底框架结构工程设计的基础上,对剪力墙布置中的若干问题提出以下解决办法。
1 剪力墙布置原则底框架结构中的剪力墙既是承担竖向荷载的主要构件,更是承担水平力的主要构件,在地震中起第一道防线作用,因此在设计时要考虑底部剪力墙承担100%的水平地震作用,而框架只承担小部分的地震力作为安全储备。
震害观测表明,底框砖房在地震时底层将发生变形集中,会出现过大的侧移而严重破坏甚至倒塌。
有鉴于此,新规范在近十几年各地试验研究的基础上,对底框架结构剪力墙的布置做出了更科学的调整。
首先抗震墙间距要满足最大横墙间距限制,6、7、8度设防区最大横墙间距分别为21m、18m、和1 5m。
其次,剪力墙应沿2个主轴方向都有布置,使之形成直角以更好地发挥抗震作用。
另外要克服矫枉过正的偏见,有些设计人员认为既然底框结构底层薄弱就多布置一点剪力墙越强越好,实际上是走向另一个极端。
剪力墙的设置应与上部砌体结构相协调,抗震设计的原则是沿楼层间侧移刚度应均匀变化,而不允许各层间发生突变。
2 剪力墙使用材料规范中规定6、7度且总层数不超过5层的底框房屋,应允许采用嵌砌于框架之间的砌体抗震墙砌体抗震墙适用于总层数少、柱距较小、平面规整的建筑,它造价低,施工方便。
1剪力墙惯性矩,等效抗弯刚度计算

12.8 17.0 20.4 25.5
1.589 1.48 1.418 1.37
B 2.40E+00 1.80E+00 1.50E+00 1.20E+00 抗弯刚度 3.14E+08 2.30E+08 1.92E+08 1.57E+08 1.47E+08
h
B/t
1.4
6.00E+00
1.4
6.00E+00
加权平均 值
加权平均 值
应力不均匀系数
12
1.264 1.432 1.614 1.800 1.988 2.178
15
1.245 1.374 1.519 1.669 1.820 1.973
20
1.228 1.317 1.422 1.534 1.648 1.763
30
1.214 1.264 1.328 1.399 1.473 1.549
形心位置 0.826 0.853 0.849 0.906 0.948
楼层高度 6.55 4.2 4.2 3 3
35.95
8.662
3.75E+00 3.75E+00 3.75E+00 3.75E+00
0.4 0.3 0.25 0.2
9.4 12.5 15.0 18.8
1.746 1.605 1.519 1.445
楼层高度 6.55 4.2 4.2 3 3
层号
1 2 3 4 7
层号
1 2 3 4 7
1
2
2.19E+08 89942525 1.61E+08 66177557 1.35E+08 55428091 99820926 40927997 93298203 38227394
抗弯刚度概念及其计算方法范文

抗弯刚度概念是指物体抵抗其弯曲变形的能力。
早期用于纺织。
抗弯刚度大的织物,悬垂性较差;纱支粗,重量大的织物,悬垂性亦较差,影响因素很多,有纤维的弯曲性能、纱线的结构、还有织物的组织特性及后整理等。
抗弯刚度现多用于材料力学和混凝土理论中,其英文名称为:bending rigidity。
以材料的弹性模量与被弯构件横截面绕其中性轴的惯性矩的乘积来表示材料抵抗弯曲变形的能力。
编辑本段抗弯刚度计算公式EI中EI的取值E是弹性模量,即产生单位应变时所需的应力,不同材料弹性模量不同,可以从材料手册上查得I是材料横截面对弯曲中性轴的惯性矩,各常规型钢惯性矩也可以从材料手册上查得,<石油化工设备设计便查手册>中也可查到。
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
抗弯强度计算公式

工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型基本参数:长L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*1.2+40*1.4=104 KN工字钢抗弯强度计算方法二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性:Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3 G= 80.1kg/m翼缘厚度tf= 16.5mm 腹板厚度tw= 14.5mm工字钢抗弯强度计算方法三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制〔v〕:L/250工字钢抗弯强度计算方法四、内力计算结果1、支座反力RA = RB =52 KN2、支座反力RB = Pd / 2 =52 KN3、最大弯矩Mmax = Pd * L / 4 =156 KN.M工字钢抗弯强度计算方法五、强度及刚度验算结果1、弯曲正应力σmax = Mmax/ (γx * Wx)=124.85 N/mm22、A处剪应力τA = RA * Sx / (Ix * tw)=10.69 N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)=10.69 N/mm24、最大挠度fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=7.33 mm5、相对挠度v = fmax / L =1/ 818.8弯曲正应力σmax= 124.85 N/mm2 < 抗弯设计值f : 205 N/mm2 ok!支座最大剪应力τmax= 10.69 N/mm2 < 抗剪设计值fv : 125 N/mm2 ok!跨中挠度相对值v=L/ 818.8 < 挠度控制值〔v〕:L/ 250 ok! 验算通过!钢板抗弯强度计算公式钢板强度校核公式是:σmax= Mmax / Wz ≤ [σ]4x壁厚x(边长-壁厚)x7.85其中,边长和壁厚都以毫米为单位,直接把数值代入上述公式,得出即为每米方管的重量,以克为单位。
SMW工法桩设计计算表格
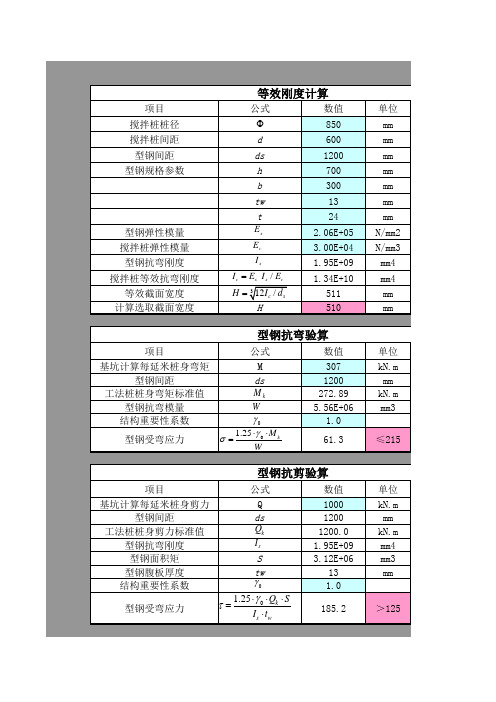
计算依据 型钢水泥土搅拌墙技术规程JGJ/T 199 - 2010
钢材抗弯强度设计 值
备注 标准值
计算依据 型钢水泥土搅拌墙技术规程JGJ/T 199 - 2010
Q235钢fv取值: 壁厚t≤16,125; 钢材抗剪强度设计 壁厚t16~40,120; 值 壁厚t40~60,115
三轴水泥土搅拌桩常采用20%的水泥掺量,被搅动土体 的质量按1800kN/m3取,单位立方米水泥用量为360kg,渗透 性系数应小于1×10-7cm/s,28天无侧限抗压强度需≥ 1.2MPa。
等效刚度计算
项目 搅拌桩桩径 搅拌桩间距 型钢间距 型钢规格参数 公式
数值 850 600 1200 700 300 13 24 2.06E+05 3.00E+04 1.95E+09 1.34E+10 511 510
单位 mm mm mm mm mm mm mm N/mm2 N/mm3 mm4 mm4 mm mm
1
公式
qk L1 Q1 qk L1 / 2
数值 0.2 900 90 1.0 748 0.4 0.250 0.150
单位 N/mm2 mm N/mm mm N/mm2 N/mm2 满足要求
0
d e1 ck
1.25 0 Q1 d e1
型钢与水泥土之间的错动受剪承载力
项目 计算截面处侧压力标准值 型钢翼缘之间的净距 单位深度错动剪力标准值 结构重要性系数 型钢翼缘处墙体有效厚度 水泥土抗剪强度标准值 水泥土抗剪强度设计值 错动剪应力设计值 公式
公式 M
ds
Mk
W
0 1.2.89 5.56E+06 1.0 61.3
第四章 结构刚度计算
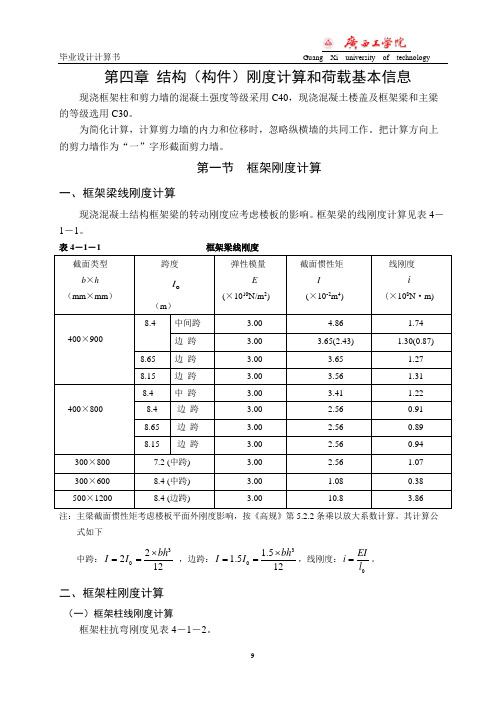
毕业设计计算书Guang Xi university of technology 第四章结构(构件)刚度计算和荷载基本信息现浇框架柱和剪力墙的混凝土强度等级采用C40,现浇混凝土楼盖及框架梁和主梁的等级选用C30。
为简化计算,计算剪力墙的内力和位移时,忽略纵横墙的共同工作。
把计算方向上的剪力墙作为“一”字形截面剪力墙。
第一节框架刚度计算一、框架梁线刚度计算现浇混凝土结构框架梁的转动刚度应考虑楼板的影响。
框架梁的线刚度计算见表4-1-1。
表4-1-1框架梁线刚度注:主梁截面惯性矩考虑楼板平面外刚度影响,按《高规》第5.2.2条乘以放大系数计算。
其计算公式如下中跨:32212bhI I⨯==,边跨:31.51.512bhI I⨯==,线刚度:EIil=。
二、框架柱刚度计算(一)框架柱线刚度计算框架柱抗弯刚度见表4-1-2。
毕业设计计算书Guang Xi university of technology表4-1-2 框架柱线刚度(二)框架柱抗侧刚度和抗推刚度计算对于高宽比小于50m,且高宽比小于4的建筑物,仅考虑梁柱弯曲变形引起的柱侧移刚度,忽略柱的轴向变形。
框架柱的抗侧刚度应考虑与其相连的框架梁的影响,以梁、柱线刚度的比值K和抗侧刚度修正系数α来衡量。
柱的抗侧刚度和抗推刚度计算见表4-1-3。
表4-1-3 框架柱抗侧刚度(D值)注:1.系数K 为梁柱线刚度比,其值为2b c i K i ∑=(一般层),bci K i ∑=(底层)。
b i 为计算平面内与柱子两端刚接的梁的线刚度。
2.修正系数α的值计算如下:2K K α=+(一般层),0.5K Kα+=(底层)。
3.H 为层高。
三、框-剪抗侧力模型中框架刚度框剪结构协同工作中框架抗推刚度可取各层延高度的加权平均值,即NHhCC iFi F 9910563.3104.415.3175.345.3385.34.3645.34.374.322.4478.32.449.35.4446.4⨯=⨯⨯+⨯⨯+⨯+⨯+⨯⨯+⨯+⨯==∑第二节 剪力墙刚度计算剪力墙的等效抗侧刚度计算采用连梁连续化的假定,即假定:1)连梁是延整片墙高度连续均匀分布的,且忽略连梁的轴向变形;2)剪力墙的截面几何特征和材料性能延高度无变化;3)结构各层层高均匀相等。
框架-剪力墙结构近似计算方法

各剪力墙、框架和连梁的内力计算
剪力墙内力
一般取楼板标高处的M、V作为设计内力
求出各楼板标高(第j层)处的总弯矩Mwj、剪力Vwj后,按各片墙的等效刚度进行分配,第j层第i片墙的内力为
02
框-剪结构在水平力作用下的变形曲线呈反S形的弯剪型位移曲线
04
框-剪结构协同工作原力特点:
在下部楼层,剪力墙拉住框架按弯曲型变形,使剪力墙承担了大部分剪力
在上部楼层,框架除承受水平力作用下的那部分剪力外,还要负担拉回剪力墙变形的附加剪力
在上部楼层即使水平力产生的楼层剪力很小,而框架中仍有相当数值的剪力
梁刚域长度:lb1=a1 - hb/4; lb2=a2 - hb/4。 柱刚域长度:lc1=c1 – hc/4; lc2=c2 – hc/4。
图 8-7 连梁刚域长度
约束弯矩系数 刚结连梁两端都产生单位转角时梁端所需施加的力矩,称为梁端约束弯矩系数,以m表示。 两端带刚域:
框架和剪力墙相互间 在顶部有集中力作用。
各层刚度变化不大(用沿高度加权平均的方法,按平均刚度计算)。
01
剪力墙的hw/H≤1/4,连梁的hb/lb≤1/4(剪切变形的影响不大)。
02
框架的H/B<4(柱子轴向变形的影响不大)
03
二、本章计算方法的应用条件
高层建筑结构设计
湖北工业大学土木工程与建筑学院
②水平荷载分配
(a)p图; (b) pw图; (c) pF图
框架承受的荷载(即 框架给剪力墙的弹性 反力)在上部为正, 在下部出现负值。这 是因为框架和剪力墙 单独承受荷载时,其 变形曲线不同
基于等效截面惯性矩的钢筋混凝土梁抗弯刚度计算方法

基于等效截面惯性矩的钢筋混凝土梁抗弯刚度计算方法李长永;康星星;钱晓军;潘丽云【摘要】In view of simplifying the calculation of flexural stiffness of reinforced concrete beam, based on the concept of the equivalent cross-sectional inertia moment and the characteristics of loading vs deflection curves of reinforced concrete beams changing as three sta-ges, a formulas of flexural stiffness related to the loading moment of reinforced concrete beam in the former two stages, namely, before the cracking of normal-cross sectional concrete and before the yield of longitudinal rebar, is established. Taking the ratio of longitudinal tensile rebar and the strength grade of concrete as the variable parameters, the flexural behaviors of 12 reinforced concrete beams were studied in test, and the results show that the measured and calculated values are consistent. Therefore, the proposed calculation method is scientific and practical.%基于等效截面惯性矩概念,结合钢筋混凝土梁荷载-挠度曲线呈3阶段变化的特征,建立了钢筋混凝土梁在正截面开裂前和开裂后至纵向受拉钢筋屈服前的2阶段与作用弯矩相关的抗弯刚度计算公式.以纵向受拉钢筋配筋率和混凝土强度等级为变化参数,对12根钢筋混凝土梁进行受弯性能荷载试验.通过对比分析试验梁抗弯刚度的实测值与计算值,验证了所提计算方法的科学性和实用性.【期刊名称】《华北水利水电学院学报》【年(卷),期】2015(036)006【总页数】4页(P36-39)【关键词】钢筋混凝土梁;抗弯刚度;等效截面惯性矩;配筋率;混凝土强度【作者】李长永;康星星;钱晓军;潘丽云【作者单位】华北水利水电大学土木与交通学院,河南郑州450045;华北水利水电大学土木与交通学院,河南郑州450045;华北水利水电大学土木与交通学院,河南郑州450045;华北水利水电大学土木与交通学院,河南郑州450045【正文语种】中文【中图分类】TU528;TV332钢筋混凝土梁在适筋破坏试验加载过程中,其正截面抗弯刚度经历了从截面弹性至混凝土开裂,再到纵向受拉钢筋屈服,最后至受压区混凝土压碎3个特征阶段[1].结构设计计算时,钢筋混凝土梁的正常使用极限状态挠度验算,对应于从混凝土开裂至纵向受拉钢筋屈服的某个区间,规范GB 50010—2010基于钢筋混凝土梁挠度计算的正截面抗弯“最小刚度原则”,根据正截面弯矩与曲率平均值的相互关系,考虑裂缝截面钢筋和混凝土应变的不均匀性、受压区混凝土的弹塑性变形和应变不均匀性等,建立了钢筋混凝土梁带裂缝工作时的正截面抗弯刚度计算公式[2].对于钢筋混凝土梁自受力至混凝土开裂阶段的抗弯刚度,可依据规范DL 5057—1996的有关规定,采用换算截面刚度的85%作为等效截面刚度进行计算[3].然而,从钢筋混凝土梁受弯挠度全过程非线性分析的需要出发,这些规定均未考虑其受荷大小对正截面抗弯刚度的影响,即在自受载至混凝土开裂的过程中未考虑混凝土内部损伤的累积发展历程,在混凝土开裂至纵向受拉钢筋屈服的某个区间验算正常使用性能时未考虑梁上裂缝发展对截面刚度降低的影响.为此,笔者所在团队曾在研究正常使用荷载作用下(对应于第2阶段的某一区间)钢筋钢纤维轻骨料混凝土叠浇梁的抗弯刚度计算方法时,考虑了荷载作用弯矩对刚度的影响,提出了相应的计算方法[4].本文结合钢筋混凝土梁的正截面受力性能试验研究成果,对其在前2个阶段的抗弯刚度进行了分析,提出了可用于挠度全过程分析的抗弯刚度计算方法.试验设计制作了12根钢筋混凝土梁,截面尺寸(b×h)为150 mm×300 mm,长度为3.0 m,跨度为2.7 m.纵向受力钢筋均配置2根带肋钢筋,纵向受力钢筋的混凝土保护层厚度均为25 mm.架立筋为2φ10 mm,剪跨段的箍筋为φ8@100 mm,纯弯段不配置箍筋.试验设计考虑混凝土强度等级和纵向受拉钢筋配筋率变化.试验梁成型48 h后,拆模并洒水养护7 d,然后置于室内环境下自然养护.在浇筑梁的同时,浇筑边长为150 mm的立方体试块和150 mm×150 mm×300 mm的棱柱体试件,以测定混凝土的实际强度.试验梁采用反力架及液压千斤顶加力装置,两端简支、跨中三分点对称集中加载,由荷载传感器控制荷载值,各级荷载作用下的跨中挠度由布置在跨中截面和支座处的位移计测试,采用英国Solatron高精度全自动数据采集系统进行数据采集[5].主要测试成果见表1.其中梁的编号为:C混凝土强度等级-0-钢筋直径-0a/b.a/b表示每组有2根梁.试验梁的跨中挠度-弯矩关系曲线如图1所示.由图1可知,随着荷载的增大,挠度经历了因截面开裂而明显增大、随裂缝开展与条数增多而逐渐增大以及随纵向受拉钢筋屈服或受压区混凝土压碎而突然增大3个阶段.将图1纵坐标改为各级荷载作用下跨中截面弯矩M与极限承载弯矩Mu的比值M/Mu,重新绘制曲线如图2所示.由图2可以更加清晰地看出,随着弯矩的增加,混凝土的内部损伤逐渐累积,导致混凝土开裂(曲线出现第1个拐点);比值M/Mu随着梁的纵向受拉钢筋配筋率的增大而减小,随着混凝土强度的提高而增大;在混凝土开裂后,随着梁纯弯段裂缝条数的增加、裂缝宽度的增大和延伸高度的发展,挠度逐渐增大.从便于工程设计应用的角度,将混凝土开裂前和正常使用状态(一般M/Mu<0.70)2个阶段分别简化为直线是基本合理的[1-3].根据钢筋混凝土受弯构件挠度计算的最小刚度原则[1-3],按材料力学的简支梁挠度计算公式,可以换算得到梁的抗弯刚度Bs:式中:M为梁的跨中弯矩;l为梁的跨度;s为与荷载形式、支撑条件有关的系数,本试验条件下s=23/216.取每组2根试验梁抗弯刚度的平均值,绘制试验梁在纵向受拉钢筋屈服前荷载作用下的抗弯刚度-弯矩关系曲线,如图3所示.由图3可知,钢筋混凝土梁的抗弯刚度随荷载的变化规律与其挠度变化规律相一致;随着配筋率的增加,梁在混凝土开裂后的抗弯刚度增大;随着混凝土强度的提高,梁的抗弯刚度有所增大.基于材料力学的计算原理,将纵向配筋截面面积折算为等效混凝土截面面积,得到换算截面,然后以换算截面计算其惯性矩I0和抵抗矩W0,从而得到换算截面的抗弯刚度EcI0,乘以折减系数β后即为钢筋混凝土梁的正截面抗弯刚度Bs:式中:Bs为钢筋混凝土梁的正截面抗弯刚度;β为正截面抗弯刚度折减系数,当M=Mcr时,β取式(3)和(4)计算结果的平均值;Ec为混凝土的弹性模量;I0为换算截面的惯性矩.混凝土开裂前的抗弯刚度折减系数与钢筋混凝土梁受拉区混凝土的内部损伤累积有关.可采用弯矩M与开裂弯矩Mcr的比值M/Mcr表征.即:混凝土开裂后的抗弯刚度折减系数与钢筋混凝土梁受压区混凝土的弹塑性变形、受拉区混凝土裂缝的开展与延伸及数量增多、开裂截面受拉钢筋应力及裂缝间钢筋应变的均匀性等有关.参考预应力混凝土梁和钢纤维全轻混凝土叠浇梁在正常使用阶段时的截面抗弯刚度计算模式[4,6],采用M/Mcr和等效配筋率αEρ表征为:式中:W0为换算截面对受拉边缘的弹性抵抗矩;h为梁的截面高度;γ为截面抵抗矩塑性系数;ft为混凝土的抗拉强度;αE为钢筋与混凝土的弹性模量比;ρ为截面配筋率[7-8].试验梁正截面抗裂弯矩实测值Mcr0与式(5)计算值Mcr的比值Mcr0/Mcr的统计结果为:平均值0.962,离散系数0.098.两者符合良好.试验梁抗弯刚度折减系数按式(3)和(4)的计算结果如图4所示.由图4可见,折减系数随着M/Mu的增大而持续减小,科学合理地反映了钢筋混凝土梁从开始受荷至纵向受拉钢筋屈服阶段的正截面抗弯刚度渐变过程.为比较试验梁抗弯刚度的实测值Bs0与计算值Bs的符合程度,将Bs0/Bs随跨中弯矩变化的情况示于图5.Bs0/Bs的统计结果为:平均值0.914,离散系数0.091.实测值与计算值符合良好.试验研究了钢筋混凝土梁的抗弯刚度,分析了纵向受拉钢筋配筋率和混凝土强度对抗弯刚度的影响规律.依据材料力学原理和等效截面惯性矩的概念,建立了钢筋混凝土梁抗弯刚度计算模型,提出了考虑从受荷至纵向受拉钢筋屈服阶段的混凝土和钢筋变形影响的抗弯刚度折减系数的计算公式.试验结果与计算结果对比表明,采用等效截面惯性矩计算钢筋混凝土梁的抗弯刚度是可行的.【相关文献】[1]赵顺波.混凝土结构设计原理[M].2版.上海:同济大学出版社,2013:207-210.[2]中国建筑科学研究院.混凝土结构设计规范:GB 50010—2010[S].北京:中国建筑工业出版社,2011:97-100.[3]西北水电勘测设计研究院.水工混凝土结构设计规范:DL 5057—1996[S].北京:中国电力出版社,1996:78.[4]潘丽云,尚亚琼,康星星,等.钢筋钢纤维全轻混凝土叠浇梁的抗弯刚度[J].华北水利水电大学学报(自然科学版),2015,36(1):43-46.[5]李长永.钢纤维轻骨料混凝土性能与叠浇梁受弯性能研究[D].郑州:郑州大学,2014:21-32.[6]张利梅,赵顺波,黄承逵.高性能预应力混凝土梁挠度试验与计算方法[J].大连理工大学学报,2005,45(1):96-101.[7]赵顺波,管俊风,程晓天,等.钢筋混凝土梁正截面抗裂的相似性试验研究[J].长江科学院院报,2007,24(4):64-66.[8]赵顺波,邵文静,李长永.机制砂再生粗骨料混凝土配筋梁正截面抗裂试验研究[J].华北水利水电学院学报,2013,34(4):46-49.。
第九章弯曲变形和刚度计算

3. 转角θ:横截面绕中性轴转过的角度,即 y 轴与挠曲线法线 的夹角,或 x 轴与挠曲线切线的夹角。逆时针方 d 向为正。 tan dx d f x 小变形: tan dx 即:截面转角近似等于挠曲线在该截面处的斜率。
M 纯弯曲时曲率与弯矩的关系式为: EI
不可能
A B
不可能
问题讨论:
y
A B
问题的边界条件、连续条件 ?
q c x
O A
边界条件
分几段? 连续条件
A处: wA=0 B处: wB=0
A处: wA=0, A =0 分OA一段。
AB、BC两段
B处: w1=w2 1 = 2
11
例:图示一抗弯刚度为 EI的悬臂梁, 在自由端受一集 中力 F作用。试求梁的挠度方程和转角方程 , 并确定 其最大挠度wmax和最大转角max 。
(a x l )
17
(2)建立挠曲线近似微分方程并积分来自梁段I ( 0 x a)
挠曲线近似 微分方程
b EIw1 M 1 F x l
梁段II ( a x l)
EIw2 M 2 F b x F ( x a) l
2 积分一次 b x 转角方程 EIw1 F l 2 C1
P x1 a 2 C1 2 P EI1 x1 a 3 6 C1 x1 a D1 EI1
EIw M ( x) Fl Fx
Fx 2 EIw Flx C1 (a) 2 2 Flx Fx3 EIw C1 x C2 (b) 2 6
(3) 由边界条件确定积分常数 在x=0处: w=0 θ= 0 y
A
输电导线弯曲刚度计算方法研究

输电导线弯曲刚度计算方法研究摘要:导线的弯曲刚度是影响导线力学性能的重要的参数。
通过对导线弯曲刚度进行实测与分析,提出导线抗弯刚度计算方法,为导线微风振动动力响应计算打下了基础。
关键词:导线;弯曲刚度;计算方法;动力响应1引言针对目前绝大多数线路设计中把导线作为柔性线来研究的现状,文献[1,2]在对导线弯曲刚度研究的基础上,分析了考虑弯曲刚度的导线在应力、弧垂方面所存在的差异,通过计算得出,当考虑弯曲刚度时导线应力值大于不考虑弯曲刚度时的应力值,而实际的弧垂值小于设计的弧垂值。
此外,在计算架空线线夹出口处的应力时,不考虑弯曲刚度的影响,也无法得到正确的结果。
本文以理论模型为依据,设计制作了一种新型架空线弯曲刚度测量装置,对典型架空导线LGJ-400/35的静态弯曲刚度进行初步的试验研究。
国外对于考虑弯曲刚度的架空线的研究最早可追溯到二十世纪三十年代。
Varney[3]研究结果表明绞制导线的弯曲刚度值EI是一个变化的量,同时他还指出导线弯曲刚度的取值必定是一个介于最大值EImax 与最小值EImin间的量。
2架空线抗弯刚度计算当自阻尼导线张力为零(T=0)时,导线截面的惯性矩就是各根铝线和钢丝的惯性矩的代数和;弯曲刚度的分股计算法如果假设导线股与股之间不存在摩擦,各股都是单独弯曲的,分股计算法可求得导线弯曲刚度的下限值(1)其中Ei 是第i股的弹性模量;di是第i股的直径;q是总的股数;分股计算法的缺点在于没有考虑架空线内部结构,尤其是每层各股间的绞合摩擦。
架空线受力很大是(T=∞)时,弯曲刚度的整体计算法如果假设架空线每层各股间相互“焊接”,而使同一层导线形成一个实体结构,这种整体假设计算法求得的弯曲刚度值为实际导线弯曲刚度值的上限。
(2)式中Ei 是第i股的弹性模量;di是第i股的直径;q是总的股数;ai为中性轴到第i股的横截面中心的垂直距离。
根据文献[4~5]结论可知,对于架空线弯曲刚度EI存在一个范围而不是一个定值。
梁的强度和刚度计算

梁的强度和刚度计算1.梁的强度计算梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力,设计时要求在荷载设计值作用下,均不超过《规范》规定的相应的强度设计值。
(1)梁的抗弯强度作用在梁上的荷载不断增加时正应力的发展过程可分为三个阶段,以双轴对称工字形截面为例说明如下:梁的抗弯强度按下列公式计算:单向弯曲时(5-3)f W M nx x x ≤=γσ双向弯曲时(5-4)f W M W M ny y y nx x x ≤+=γγσ式中:M x 、M y ——绕x 轴和y 轴的弯矩(对工字形和H 形截面,x 轴为强轴,y 轴为弱轴);W nx 、W ny ——梁对x 轴和y 轴的净截面模量;——截面塑性发展系数,对工字形截面,;对y x γγ,20.1,05.1==y x γγ箱形截面,;对其他截面,可查表得到;05.1==y x γγf ——钢材的抗弯强度设计值。
为避免梁失去强度之前受压翼缘局部失稳,当梁受压翼缘的外伸宽度b 与其厚度t 之比大于 ,但不超过时,应取。
y f /23513y f /235150.1=x γ需要计算疲劳的梁,按弹性工作阶段进行计算,宜取。
0.1==y x γγ(2)梁的抗剪强度一般情况下,梁同时承受弯矩和剪力的共同作用。
工字形和槽形截面梁腹板上的剪应力分布如图5-3所示。
截面上的最大剪应力发生在腹板中和轴处。
在主平面受弯的实腹式梁,以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。
因此,设计的抗剪强度应按下式计算(5-5)v w f It ≤=τ式中:V ——计算截面沿腹板平面作用的剪力设计值;S ——中和轴以上毛截面对中和轴的面积矩;I ——毛截面惯性矩;t w ——腹板厚度;f v ——钢材的抗剪强度设计值。
图5-3 腹板剪应力当梁的抗剪强度不满足设计要求时,最常采用加大腹板厚度的办法来增大梁的抗剪强度。
型钢由于腹板较厚,一般均能满足上式要求,因此只在剪力最大截面处有较大削弱时,才需进行剪应力的计算。
高层建筑结构思考题

《高层建筑结构》课程思考题1.高层建筑结构体系主要有哪些?试述各体系的组成、主要优缺点、基本受力变形特点及适用范围。
答:主要结构体系有框架结构体系,剪力墙结构体系,框架-剪力墙结构体系,筒体结构体系。
①框架结构体系:结构全部由梁柱组成。
优点:建筑平面布置灵活,可以做成大空间,使用灵活,延性好,自重轻,节省材料。
缺点:框架结构的侧向刚度小,侧向变形大,框架结构使用高度有所限制。
框架结构在水平作用下的侧移由两部分组成:第一部分侧移由梁柱的弯矩变形产生,柱和梁都有反弯点,形成侧向变形。
框架下部的梁柱内力大,层间变形大,往上部去变形愈来愈小。
第二部分是由柱的轴向变形产生,柱的拉伸和压缩使结构出现侧移。
这些变形在柱的上部比较大,下部比较小,使结构呈现弯曲型变形。
框架结构体系适用于非抗震地区和层数较少的建筑,建筑高度不要太高,一般15-20层以下为宜。
②剪力墙结构体系:建筑物墙体作为沉重竖向荷载和水平荷载的结构,称为剪力墙结构体系。
优点:整体性好,刚度大,侧向变形较小,抗震效果好。
缺点:剪力墙的间距不能太大,平面布置不灵活,结构自重较大。
剪力墙是一个受弯矩为主的悬臂墙,侧向变形是弯曲型。
剪力墙结构体系在非地震区和地震区的高层建筑中都得到广泛使用,10-30层的住宅及旅馆也可以使用剪力墙结构体系。
③框架-剪力墙结构体系:把框架和剪力墙两种结构共同组合在一起形成的结构体系。
优点:兼有框架和剪力墙的优点,比框架结构的水平承载力和侧向刚度都有很大提高,比剪力墙结构布置灵活,提供较大的空间,有较大的刚度和较强的抗震能力。
缺点:由于剪力墙的存在,一定程度上限制了建筑平面布置的灵活性。
框架剪力墙中的剪力墙是抗侧力的主体,框架则是承受竖向荷载的主体。
框架本身在水平荷载下呈剪切型变形,剪力墙呈弯曲型变形。
两者通过楼板协同工作,共同抵抗水平荷载。
主要适用于25层以下的房屋,最高不宜超过30层;地震区的五层以上的工业厂房;这种体系用于旅馆、公寓、住宅等建筑最为适宜。
