2020年重庆中考数学复习含根号3的几何题专题训练(Word修改版)

合集下载

2020年中考数学精选考点试卷实数(含二次根式)(附标准答案)

2020年中考数学精选考点试卷实数（含二次根式）考试范围：实数（含二次根式)；考试时间：90分钟；总分：120分一、单选题（每小题3分，共30分)1．（2019·重庆初二期末）4的算术平方根是（） A ．-2B ．2C ．±2D ．√22．（2019·湖北初一期末）计算36的结果为（） A ．6B ．－6C ．18D ．－183．（2019·河南初二期中）16的平方根是（） A ．±2B ．2C ．±4D ．44．（2018·湖南中考真题）下列各式中正确的是( ) A ．93=± B ．()233-=-C ．393=D ．1233-=5．（2015·甘肃中考真题）64的立方根是（） A ．4B ．±4C ．8D ．±86．（2013·广西中考真题）在下列实数中，无理数是 A ．0 B ．14C ．5D ．6 7．（2012·天津中考真题）估计6+1的值在（） A ．2到3之间 B ．3到4之间C ．4到5之间D ．5到6之间8．（2016·甘肃中考真题）下列根式中是最简二次根式的是( ) A ．23B ．3C ．9D ．129．（2016·广西中考真题）下列计算正确的是( ) A ．532-=B ．3523615⨯=C ．2(22)16= D ．13= 10．（2018·四川中考真题）二次根式2+4x 中的x 的取值范围是（） A ．x ＜﹣2B ．x≤﹣2C ．x ＞﹣2D ．x≥﹣2二、填空题（每小题4分，共28分)11．（2011·江苏中考真题）计算：82-=_______________． 12．（2013·吉林中考真题）计算：26⨯=___． 13．（2015·四川中考真题）若332y x x =-+-+，则y x = ．14．（2018·吉林中考真题）比较大小：10_____3．（填“＞”、“=”或“＜”） 15．（2013·福建中考真题）计算：√273= ． 16．（2012·辽宁中考真题）3-的绝对值是．17．（2018·山东中考真题）观察下列各式：221111++=1+1212⨯， 221111++=1+2323⨯， 221111++=1+3434⨯， ……请利用你所发现的规律，计算22111++12+22111++23+22111++34+…+22111++910，其结果为_______．三、解答题一（每小题6分，共30分)18．（2019·湖北华中师大一附中美联实验学校初二期末）计算：2118(21)2⨯+- 19．（2019·吉林初三期中）计算：()21543422sin 602⎛⎫----+︒ ⎪⎝⎭20．（2019·上海市长宁中学初一月考）计算：20190-2311(2019)-23π-+-++（）（）21．（2019·广西中考真题）计算：()()201901 3.14162sin30π-+--+．22．（2019·江苏中考真题）计算：012sin 364tan 452⎛⎫-+︒--+︒ ⎪⎝⎭．四、解答题二（每小题8分，共32分))23．（2018·四川中考真题）计算：200121(12)(1)sin 45()22----++24．（2018·贵州中考真题）计算：()220181132tan 60 3.142π-⎛⎫-+-+︒--+ ⎪⎝⎭.25．（2019·山东中考模拟）计算：212cos 3024(12)243︒--⨯+--⨯26．（2019·贵州中考真题）计算：()()12019201929cos 60201920188(0.125)--+-⨯-︒-++.解析1．B【解析】试题分析：因22=4，根据算术平方根的定义即可得4的算术平方根是2．故答案选B ．考点：算术平方根的定义． 2．A【解析】根据算术平方根的定义计算即可求解．【详解】∵62=36，6．故选：A．【点睛】考查了算术平方根，关键是熟练掌握算术平方根的计算法则．3．A【解析】先求出16的算术平方根为4，再根据平方根的定义求出4的平方根即可．【详解】解：=4，4的平方根为±2，的平方根为±2．故选A【点睛】此题考查了平方根，以及算术平方根，熟练掌握平方根的定义是解本题的关键．4．D【解析】原式利用平方根、立方根定义计算即可求出值．【详解】A.原式=3，不符合题意；B.原式=|-3|=3，不符合题意；C.原式不能化简，不符合题意；D.原式故选D．【点睛】本题考查了立方根，以及算术平方根，熟练掌握各自的性质是解题的关键．5．A【解析】试题分析：∵43=64，∵64的立方根是4，故选A考点：立方根．6．C【解析】试题分析：有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数。

重庆中考复习重庆中考几何题分类汇编含答案

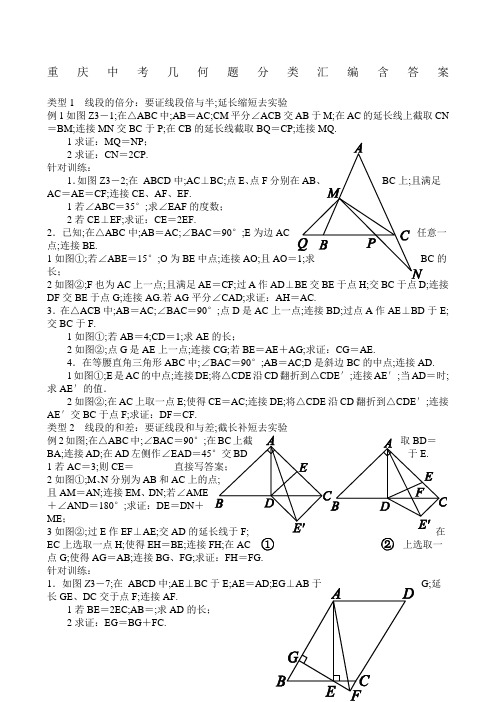
重庆中考几何题分类汇编含答案类型1线段的倍分：要证线段倍与半;延长缩短去实验例1如图Z3－1;在△ABC中;AB＝AC;CM平分∠ACB交AB于M;在AC的延长线上截取CN ＝BM;连接MN交BC于P;在CB的延长线截取BQ＝CP;连接MQ.1求证：MQ＝NP；2求证：CN＝2CP.针对训练：1．如图Z3－2;在ABCD中;AC⊥BC;点E、点FAC＝AE＝CF;连接CE、AF、EF.1若∠ABC＝35°;求∠EAF的度数；2若CE⊥EF;求证：CE＝2EF.2．已知;在△ABC中;AB＝AC;∠BAC＝90°;E为边AC点;连接BE.1如图①;若∠ABE＝15°;O为BE中点;连接AO;且AO的长；2如图②;F也为AC上一点;且满足AE＝CF;过A作AD⊥连接DF交BE于点G;连接AG.若AG平分∠CAD;求证：AH＝AC.3．在△ACB中;AB＝AC;∠BAC＝90°;点D是AC上一点;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点G是AE上一点;连接CG;若BE＝AE＋AG;求证：CG＝AE.4．在等腰直角三角形ABC中;∠BAC＝90°;AB＝AC;D是斜边BC的中点;连接AD.1如图①;E是AC的中点;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′;当AD＝时;求AE′的值．2如图②;在AC上取一点E;使得CE＝AC;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′交BC于点F;求证：DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2如图;在△ABC中;∠BAC＝90°;BA;连接AD;在AD左侧作∠EAD＝451若AC＝3;则CE＝________2如图①;M、N分别为AB和AC且AM＝AN;连接EM、DN;若∠AME＋∠AND＝180°;求证：DE＝DN＋ME；3如图②;过E作EF⊥AE;交ADEC上选取一点H;使得EH＝BE;连接FH;在AC上选取一点G;使得AG＝AB;连接BG、FG;求证：FH＝FG.针对训练：1．如图Z3－7;在ABCD中;AE⊥BC于E;AE＝G;延长GE、DC交于点F;连接AF.1若BE＝2EC;AB＝;求AD的长；2求证：EG＝BG＋FC.2．如图;在正方形ABCD中;点P为AD延长线上一点;连接AC、CP;过点C作CF⊥CP 于点C;交AB于点F;过点B作BM⊥CF于点N;交AC于点M.1若AP＝AC;BC＝4;求S△ACP；2若CP－BM＝2FN;求证：BC＝MC.3．如图;在△ABC中;AB＝BC;以AB为一边向形ABDE;连接DC;EB并延长EB交AC于F;且AE 于G.1若∠EBG＝20°;求∠AFE；2试问线段AE;AF;CF之间的数量关系并证明．类型3倍长中线：三角形中有中线;延长中线等中线例3如图Z3－10①;在Rt△ABC中;∠ABC＝90°;D为斜边AC上两点;且AD＝AB;CE＝CB;连接BD、1求∠EBD的度数；2如图Z3－10②;过点D作FD⊥BD于点D;交BEF;在AB上选取一点H;使得BH＝BC;连接CH;在一点G;使得GD＝CD;连接FH、FG;求证：FH＝FG.针对训练：1．如图;已知在ABCD中;G为BC的中点;点E在AD边上;且∠1＝∠2.1求证：E是AD中点；2若F为CD延长线上一点;连接BF;且满足∠3＝∠2;求证：CD＝BF＋DF.2．如图Z3－12;在菱形ABCD中;点E、F分别是BC、CD上的点;连接AE;AF;DE、EF;∠DAE＝∠BAF.1求证：CE＝CF；2若∠ABC＝120°;点G是线段AF的中点;连接DG;EG.求证：DG⊥GE.3．在Rt△ABC中;∠ACB＝90°;点D与点B在;∠ADC＞∠BAC;且DA＝DC;过点B作BE∥DA交于点E;M为AB的中点;连接MD;ME.1如图①;当∠ADC＝90°时;线段MD与ME________；2如图②;当∠ADC＝60°时;试探究线段MD数量关系;并证明你的结论；3如图③;当∠ADC＝α时;求的值．4．如图①;等边三角形ABC中;CE平分∠ACB;D为BC边上一点;且DE＝CD;连接BE.1若CE＝4;BC＝6;求线段BE的长；2如图②;取BE中点P;连接AP;PD;AD;求证：AP⊥PD且AP＝PD；3如图③;把图Z3－14②中的△CDE绕点C顺时针旋转任意角度;然后连接BE;点P为BE中点;连接AP;PD;AD;问第2问中的结论还成立吗若成立;请证明；若不成立;请说明理由．5．在△ABC中;以AB为斜边;作直角三角形ABD;使点D落在△ABC内;∠ADB＝90°.1如图①;若AB＝AC;∠BAD＝30°;AD＝6;点P、M分别为BC、AB边的中点;连接PM;求线段PM的长；2如图②;若AB＝AC;把△ABD绕点A逆时针旋转一定角度;得到△ACE;连接ED并延长交BC于点P;求证：BP＝CP；3如图③;若AD＝BD;过点D的直线交AC于点E;交BC于点F;EF⊥AC;且AE＝EC;请直接写出线段BF、FC、AD之间的关系不需要证明．类型4中位线：三角形中两中点;连接则成中位线例42017·河南如图①;在Rt△ABC中;∠A＝90°;AB＝AC;点D;E分别在边AB;AC上;AD＝AE;连接DC;点M;P;N分别为DE;DC;BC的中点．1观察猜想：图①中;线段PM与PN的数量关系是__________;位置关系是__________；2探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置;连接MN;BD;CE;判断△PMN 的形状;并说明理由；3拓展延伸：把△ADE绕点A＝10;请直接写出△PMN面积的最大值．针对训练：1．如图①;在任意的三角形ABC以AB和AC为一边作等腰三角形ABE和等腰三角形ACD;AB＝AE;AC＝AD;且∠BAE＋∠CAD＝180°;连接DE;延长CA交DE于F.1求证：∠CAB＝∠AED＋∠ADE；2若∠ACB＝∠BAE＝∠CAD＝90°;如图②;求证：BC＝2AF；3若在△ABC中;如图③所示;作等腰三角形ABE和等腰三角形ACD;AB与DE交于点F;F为DE的中点;请问2中的结论还成立吗若成立;请给出证明;若不成立;请说明理由．2．如图;在△ABC和△ADE中;AB＝AC;AD＝AE;∠BAC＋∠EAD＝180°;△ABC不动;△ADE绕点A旋转;连接BE、CD;F为BE的中点;连接AF.1如图①;当∠BAE＝90°时;求证：CD＝2AF；2当∠BAE≠90°时;1的结论是否成立请结合图②说明理由．3．如图①;在等腰三角形ABC中;AB＝AC;在底边BC上取一点D;在边AC上取一点E;使AE＝AD;连接DE;在∠ABD的内部作∠ABF＝2∠EDC;交AD于点F.1求证：△ABF是等腰三角形；2如图②;BF的延长交AC于点G.若∠DAC＝∠CBG;延长AC至点M;使GM＝AB;连接BM;点N是BG的中点;连接AN;试判断线段AN、BM之间的数量关系;并证明你的结论．类型5角的和差倍分图中有角平分线;关系现．角平分线平行线;;三线合一试试看．例5．如图;把△EFP放置在菱形ABCD中;顶点E;F;P分别在线段AB;AD;AC上;EP＝FP＝6;EF＝6;∠BAD＝60°;且＞6.1求∠EPF的大小；2若AP＝10;求AE＋AF的值．针对训练：1．已知：如图①;AD平分∠BAC;∠B＋∠C＝180°°;易知：DB＝DC.探究：如图②;AD平分∠BAC;∠ABD＋∠ACD;∠ABD＜90°;求证：DB＝DC.2．在△ACB中;AB＝AC;∠BAC＝90°;点D;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点P是AC上一点;连接FP;若AP＝CD;求证：∠ADB＝∠CPF.3．已知;在ABCD中;∠BAD＝45°;AB＝BD;E为BC上一点;连接AE交BD于F;过点D 作DG⊥AE于G;延长DG交BC于H.1如图①;若点E与点C重合;且AF＝;求AD的长；2如图②;连接FH;求证：∠AFB＝∠HFB.4．如图;将正方形纸片ABCD沿EF折叠点E、F分别在边AB、CD上;使点B落在AD边上的点M处;点C落在点N处;MN与CD交于点P;连接EP.当点M在边AD上移动时;连接BM、BP.1求证：BM是∠AMP的平分线；2△PDM的周长是否发生变化证明你的结论．类型6旋转型全等问题：图中若有边相等;可用旋转做例6．△ABC中;∠BAC＝90°;AB＝AC;点D为直线点点D不与B;C重合;以AD为边在AD右侧作正方形ADEF;连接CF.1观察猜想：如图①;当点D在线段BC上时;①BC与CF关系为：________．②BC;CD;CF之间的数量关系为：___________；将结写在横线上2数学思考：如图Z3－25②;当点D在线段CB的延长线上时;结论①;②是否仍然成立若成立;请给予证明；若不成立;请你写出正确结论再给予证明．3拓展延伸：如图Z3－25③;当点D在线段BC的延长线上时;延长BA交CF于点G;连接GE.若已知AB＝2;CD＝BC;请求出GE的长．针对训练：1．在四边形ABCD中;∠B＋∠180°;对角线AC平分∠BAD.1如图①;若∠DAB＝120°;且∠B＝90°;试探究边AD、AB与对角线AC2如图②;若将1中的条件“∠B＝去掉;1中的结论是否成立请说明理由．3如图③;若∠DAB＝90°;探究边AD、AB与对角线AC的数量关系并说明理由．2．如图①;在正方形ABCD中;点E为边BC上一点;将△ABE沿AE翻折得△AHE;延长EH交边CD于F;连接AF.1求证：∠EAF＝45°；2延长AB;AD;如图②;射线AE、AF分别交正方形两个外角的平分线于M、N;连接MN;若以BM、DN、MN为三边围成三角形;试猜想三角形的形状;并证明你的结论．3．如图①;在正方形ABCD内有一点P;PA＝;PB＝;PC＝1;求∠BPC的度数．分析问题根据已知条件比较分散的特点;我们可以通过旋转变换将分散的已知条件集中在一起;于是将△BPC绕点B逆时针旋转90°;得到了△BP′A如图Z3－28②;然后连接PP′.1请你通过计算求出图Z3－28②中∠BPC的度数；2如图③;若在正六边形ABCDEF内有一点P;且PA＝2;PB＝4;PC＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1.证明：1∵AB＝AC;∴∠ABC＝∠ACB.∵∠MBQ＋∠ABC＝180°;∠ACB＋∠PCN＝180°;∴∠MBQ＝∠PCN.在△QBM和△PCN中;∴△QBM≌△PCNSAS．∴MQ＝NP.2过M作MG∥AC交BC于G;∵MG∥AC;∴∠MGB＝∠ACB;∠MGC＝∠PCN;∵由1知;∠ABC＝∠ACB;∴∠ABC＝∠MGB;∴MB＝MG;∵MB＝CN;∴MG＝CN.在△MGP和△NCP中;∴△MGP≌△NCPAAS．∴PG＝CP;∴CG＝CP＋PG;即CG＝2CP.∵CM平分∠ACB;∴∠BCM＝∠MCA;∵MG∥AC;∴∠MCA＝∠GMC;∴∠BCM＝∠GMC;∴MG＝CG;∵MG＝CN;∴CN＝CG;∴CN＝2CP.针对训练1.解：1∵AC⊥BC;∴∠ACB＝90°;又∵AC＝CF;∴∠45°;∵∠ABC＝35°;∴∠EAF＝10°；2证明：方法1：取CF的中点M;连接EM、AM;∵CE⊥EF;∴EM＝CM＝FM＝CF;又∵AC＝AE;∴AM为EC的中垂线;∴∠CAM＋°; 又∵∠ECF＋∠ACE＝90°;∴∠CAM＝∠FCE;又∵∠CEF＝∠ACM＝90°;∴△ACM∽△CEF;∴＝;又∵CF＝AC＝2CM;∴＝＝;即CE＝2EF；方法2：延长FE至M;使EF＝EM;连接CM;∵CE⊥EF;∴△CMF为等腰三角形;又∵AC＝AE＝CF;且∠ACE＝∠CFE易证;∴△CMF≌△CEA;∴FM＝CE＝2EF.2.解：1如图①;在AB上取一点M;使得BM＝ME;连在Rt△ABE中;∵OB＝OE;∴BE＝2OA＝2;∵MB＝ME;∴∠MBE＝∠MEB＝15°;∴∠AME＝∠MBE＋∠MEB＝30°;设AE＝x;则ME＝BM＝2x;AM＝x;∵AB2＋AE2＝BE2;∴2x＋x2＋x2＝22;∴x＝负根舍弃;∴AB＝AC＝2＋·;∴BC＝AB＝＋1.2证明：如图②;作CP⊥AC;交AD的延长线于P;GM⊥AC 于M.∵BE⊥AP;∴∠AHB＝90°;∴∠ABH＋∠BAH＝90°;∵∠BAH＋∠PAC＝90°;∴∠ABE＝∠PAC;又∵AB＝AC;∠BAE＝∠ACP＝90°;∴△ABE≌△CAP;∴AE＝CP＝CF;∠AEB＝∠P;在△DCF和△DCP中;∴△DCF≌△DCP;∴∠DFC＝∠P;∴∠GFE＝∠GEF;∴GE＝GF;∵GM⊥EF;∴FM＝ME;∵AE＝CF;∴AF＝CE;∴AM＝CM;在△GAH和△GAM中;∴△AGH≌△AGM;∴AH＝AM＝CM＝AC.3.解：1∵AB＝4;∴AC＝AB＝4.∵CD＝1;∴AD＝AC－CD＝3.∵在Rt△ABD中;∠BAC＝90°;∴BD＝＝5;∵S＝AB·AD＝AE·BD;∴AE＝2.4.△ABD2证明：如图;在线段EB上截取EH＝AE;并连接∵AE⊥BD;EH＝AE;∴AH＝AE.∵BE＝AE＋AG;∴BH＝BE－HE＝AG.∵∠BAD＝∠BEA＝90°;∴∠ABE＋∠BAE＝∠CAG＋∠BAE＝90°;∴∠ABE＝∠CAG.∵BA＝AC;∴△ABH≌△CAG;∴CG＝AH＝AE.4.解：1∵∠BAC＝90°;AB＝AC;D是斜边BC的中点;∴∠ADC＝90°;∠ACD＝45°.在Rt△ADC中;AC＝AD÷sin45°＝2.∵E是AC的中点;∴CE＝AC＝.∵将△CDE沿CD翻折到△CDE′;∴CE′＝CE＝;∠ACE由勾股定理;得AE′＝＝.2证明：如图;过B作AE′的垂线交AD于点G;交AC于点∵∠ABH＋∠BAF＝90°;∠CAF＋∠BAF＝90°;∴∠ABH＝∠CAF.又∵AB＝AC;∠BAH＝∠ACE′＝90°;∴△ABH≌△CAE′.∴AH＝CE′＝CE;∵CE＝AC;∴AH＝HE＝CE.∵D是BC中点;∴DE∥BH;∴G是AD中点．在△ABG和△CAF中：AB＝AC;∠BAD＝∠ACD＝45°;∠ABH＝∠CAF; ∴△ABG≌△CAF.∴AG＝CF.∵AG＝AD;∴CF＝AD＝CD.∴DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2：解：132证明：延长DN到K;使得NK＝ME;连接AK;如图①;因为∠1＋∠3＝180°;∠1＋∠2＝180°;∴∠2＝∠3.在△AME和△ANK中;∴△AME≌△ANK SAS．∴AE＝AK;∠4＝∠5;∴∠4＋∠EAC＝90°;∴∠5＋∠EAC＝90°;即∠EAK＝∵∠EAD＝45°;∴∠KAD＝∠EAK－∠EAD＝90°－45∴∠EAD＝∠KAD.在△EAD和△KAD中;∴△EAD≌△KAD SAS;∴ED＝KD.∵DK＝DN＋KN;∴ED＝DN＋KN;又NK＝ME;∴ED＝DN＋ME.3证明：延长AE到J;使得EJ＝AE;连接JH;JF.如图②;在△ABE和△JHE中;∴△ABE≌△JHESAS;∴JH＝AB;∠1＝∠2;∵AB＝AG;∴JH＝AG;∵AE＝EJ;EF⊥AJ;∴AF＝JF;∴∠JAF＝∠AJF＝45°;即∠2＋∠3＝45°;∵∠BAC＝90°;∴∠1＋∠EAD＋∠4＝90°;∴∠1＋∠4＝90°－∠EAD;＝90°－45°＝45°;∵∠1＝∠2;∴∠3＝∠4;在△JHF和△AGF中;∴△JHF≌△AGFSAS;∴FH＝FG.针对训练：1.解：1∵四边形ABCD是平行四边形;∴AD＝BC.∵BE＝2EC;设CE＝x;BE＝2x;∴BC＝AD＝AE＝3x.又∵EG⊥AB;∴∠AEB＝90°;∴AB2＝AE2＋BE2;即13＝9x2＋4x2;∴x＝1;∴AD＝3x＝3.2证明：如图;过C作CH⊥AB于H;则四边形CHGF为矩形．∴CF＝HG;∠CHB＝90°;GF＝CH.∵AE⊥BC;EG⊥AB;∴∠AEB＝∠CHB＝90°;∠BCH＋∠B＝90°;∠BAE＋∠B＝90°;∴∠BCH＝∠BAE.又∵AE＝BC;∴△AGE≌△CHB;∴GE＝BH;AG＝GF;∴GE＝BH＝BG＋GH＝BG＋CF.2.解：1∵四边形ABCD是正方形;BC＝4;∴AB＝AD＝CD＝BC＝4;∠ADC＝∠ABC＝90°.∵在Rt△ABC中;AC＝＝4;∴AP＝AC＝;∴S＝AP·CD＝7.△ACP2证明：方法一：如图①;在NC上截取NK＝NF;连接BK.∵四边形ABCD是正方形;∴AB＝BC＝DC;∠ABC＝∠BCD＝∠ADC＝90°.∵∠BCD＝90°;CF⊥CP;∴∠1＋∠DCF＝∠2＋∠DCF＝90°;∴∠1＝∠2;∵在△FBC和△PDC中;∴△FBC≌△PDCASA;∴CF＝CP;∵CP－2FN＝BM;∴CF－FK＝BM;即CK＝BM;∵∠FBC＝90°;BM⊥CF;∴∠1＋∠NBC＝∠4＋∠NBC; ∴∠1＝∠4;∵在△ABM和△BCK中;∴△ABM≌△BCKSAS;∴∠7＝∠6.∵BM⊥CF;NK＝NF;∴BF＝BK;∵BF＝BK;BM⊥CF;∴∠4＝∠∴∠4＋∠7＝∠5＋∠6;∵∠8＝∠4＋∠7;∴∠8＝∠MBC;∴BC＝MC.解：方法二：如图②;延长BM交AD于点G;过A作AE⊥BGE先证△AEB≌△BNCAAS;∴AE＝BN;又证△AEG≌△BNFAAS;∴EG＝NF;再证四边形BCPG为平行四边形;∴BG＝CP;∵CP－BM＝2FN;∴BG－BM＝2EG;∴MG＝2EG;∴点E为MG中点;∵AE⊥MG;EM＝EG;∴AM＝AG;∴∠3＝∠4;∵∠2＝∠3;∠1＝∠4;∴∠1＝∠2;∴BC＝MC.3.解：1∵∠EBG＝20°;CB⊥AE;∴∠BEG＝70o;∠CBF＝∠EBG＝20°;∵四边形ABDE是菱形;∴∠ABE＝∠BEG＝70°;∴∠ABG＝50°;∵AB＝BC;∴∠FCB＝25°;∴∠AFE＝∠CBF＋∠FCB＝45°；2AE;AF;CF之间的数量关系是AF2＋CF2＝2AE2;证明如下：连接DF;∵四边形ABDE是菱形;∴AB＝DB;∠DBE＝∠ABE;∴∠DBF＝∠ABF;∵BF＝BF;∴△DBF≌△ABFSAS;∴DF＝AF;∠BDF＝∠BAF;∵∠BCF＝∠BAF;∴∠BCF＝∠BDF; ∵CB⊥AE;AE∥DB;∴DB⊥CB;∵CB＝AB＝BD;∴△DBC是等腰直角三角形;∴DC＝BD＝AE;∵∠DPB＝∠CPF;∴∠CFP＝∠DBP＝90°;∴DF2＋CF2＝DC2; 即有：AF2＋CF2＝2AE2.类型3倍长中线：三角形中有中线;延长中线等中线例3解：1设∠BEC＝α;∠BDA＝β;则∠C＝180°－2α;∠A＝180°－2β.∵在Rt△ABC中;∠ABC＝90°;∴∠A＋∠C＝90°;即180°－2α＋180°－2β＝90°;∴α＋β＝135°;∴∠EBD＝45°.2证明：法一：如图①;延长BD至点B′;使得DB′＝在△GDB′和△CDB中;∴△GDB′≌△CDB.∴GB′＝BC＝BH;∠GB′D∵FD⊥BD;BD＝DB′;∴FB＝FB′.∵∠FB′G＝45°－∠GB′D;∠HBF＝90°－45°－∠CBD＝45°－∠CBD;∴∠FB′G＝∠HBF.在△FHB和△FGB′中;∴△FHB≌△FGB′;∴HF＝GF.法二：如图②;延长FD至点F′;使得DF′＝DF;先证△DGF≌△DCF′;再证△BHF≌△BCF′;∴HF＝GF.针对训练1.证明：1∵四边形ABCD是平行四边形;∴AB＝CD;AD＝BC;∠A＝∠C.又∵∠1＝∠2;∴△ABE≌△CDG ASA;∴AE＝CG.∵G为BC中点;∴CG＝BC;∴AE＝CG＝BC＝AD;∴E是AD中点．2如图;延长BE;CD交于点H.∵四边形ABCD是平行四边形;∴AB綊CD;∴∠A＝∠ADH;∠1＝∠4;又∵∠1＝∠2;∠3＝∠2;∴∠1＝∠2＝∠3＝∠4;∴FH＝FB.由1;E是AD中点;∴AE＝DE;∴△ABE≌△DHEAAS;∴AB＝DH;∴CD＝AB＝DH＝DF＋FH＝DF＋BF;即CD＝BF＋DF.2.证明：1在菱形ABCD中;AB＝BC＝CD＝AD;∠ADF＝∠ABE; ∵∠DAE＝∠BAF;∴∠DAE－∠EAF＝∠BAF－∠EAF;即∠DAF＝∠BAE.∴△DAF≌△BAE;∴BE＝DF.又∵BC＝CD;∴CE＝CF2如图;延长DG交AB于H;连接EH;∵在菱形ABCD中;AB∥CD;∴∠DFA＝∠GAH.∵G为AF中点;∴AG＝GF.又∵∠DGF＝∠AGH;∴△DGF≌△HGA.∴DG＝又∵AB＝CD;∴BH＝CF.又∵AB∥CD;∠ABC＝120°;∴∠C＝60°.又∵CE＝CF;∴△CEF为等边三角形;∴CF＝EF;∠CFE＝60°;∴EF＝BH;∠DFE＝∠ABC＝120°.又∵BE＝DF;∴△EFD≌△HBE;∴HE＝ED;又∵HG＝DG;∴DG⊥GE.3.解：1MD=ME2MD＝ME.理由如下：如图①;延长EM交DA于点F.∵BE∥DA;∴∠FAM＝∠EBM.又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.∵DA＝DC;∠ADC＝60°;∴∠BED＝∠ADC＝60°;∠ACD＝60°.∵∠ACB＝90°;∴∠ECB＝30°;∴∠EBC＝30°;∴CE＝BE;∴AF＝EC;∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∴∠MDE＝30°.在Rt△MDE中;tan∠MDE＝＝.∴MD＝ME.3如图②;延长EM交DA于点F;∵BE∥DA;∴∠FAM＝∠EBM;又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.延长BE交AC于点N;∴∠BNC＝∠DAC.∵DA＝DC;∴∠DCA＝∠DAC;∴∠BNC＝∠DCA;∵∠ACB＝90°;∴∠ECB＝∠EBC;∴CE＝BE;∴AF＝CE.∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∵∠ADC＝α;∴∠MDE＝.∴在Rt△MDE中;＝tan∠MDE＝tan.4.解：1如图①;作EH⊥BC于点H.∵△ABC是等边三角形;∴∠ACB＝60°.∵CE平分∠ACB;∴∠ECH＝∠ACB＝30°;∵EC＝4;∠ECH＝30°;∴EH＝2;HC＝2.∵BC＝6;∴BH＝6－2＝4.在Rt△BHE中;BE2＝42＋22＝52;∴BE＝2.2如图②;延长DP至M;使DP＝PM;连接BM、AM.在△PDE和△PMB中;∴△PDE≌△PMB SAS．∴BM＝DE;∠1＝∠2.∴BM∥DE.∴∠MBD＋∠BDE＝180°.∵CE平分∠ACB;DE＝CD;∴∠BDE＝30°＋30°＝60∴∠MBD＝120°.∵△ABC是等边三角形;∴∠ABC＝60°;∴∠3＝60°.∵BM＝DE;DE＝CD;∴BM＝CD.在△ABM和△ACD中;∴△ABM≌△ACD SAS．∴AD＝AM;∠4＝∠5.∵PD＝PM;∴AP⊥PD.∵∠4＝∠5;∠BAD＋∠5＝60°;∴∠4＋∠BAD＝60°;即∠MAD＝60°.∴∠PAD＝∠MAD＝30°.∵在Rt△APD中;tan30°＝;∴AP＝PD.3第2问中的结论成立;理由如下：如图③;延长DP至使DP＝PN;连接BN、AN;取BE、AC交于点O.在△PDE∴△PDE≌△PNBSAS．∴BN＝DE;∠1＝∠2.∵DE＝CD;∴BN＝CD.∵∠AOB＝∠EOC;∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO＝60°;∠DEC＝∠DCE＝30°;∴∠1＋∠3∴∠3＝∠4.在△ABN和△ACD中;∴△ABN≌△ACDSAS．∴∠5＝∠6;AN＝AD.∵PD＝PN;∴AP⊥PD.∵∠NAC＋∠5＝60°;∴∠NAC＋∠6＝60°;即∠NAD＝60°.∴∠PAD＝∠NAD＝30°; ∵在Rt△APD中;tan∠PAD＝;∴AP＝PD.5.解：1∵∠ADB＝90°;∠BAD＝30°;AD＝6;∴cos∠BAD＝;∴＝;∴AB＝12.又∵AB＝AC;∴AC＝12;∴PM为△ABC的中位线;∴PM＝AC＝6.2证明：方法一：如图①;在截取ED上截取EQ＝PD;∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4.在△BDP和△CEQ中;PD＝QE;∠1＝∠4;BD＝CE;∴△BDP≌△CEQ.∴BP＝CQ;∠DBP＝∠QCE;又∵∠5＝∠1＋∠DBP;∠6＝∠4＋∠QCE;∴∠5＝∠6;∴PC＝CQ;∴BP＝CP.方法二：如图②;过点B作EP的垂线交EP的延长线于点M;过C EP的垂线交EP于点N.∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4;在△BMD和△CNE中;∠1＝∠4;∠BMD＝∠CNE＝90°;BD＝CE;∴△BMD≌△CNE.∴BM＝CN.在△BMP和△CNP中;∠5＝∠6;∠BMP＝∠CNP;BM＝CN;∴△BMP≌△CNP;∴BP＝CP.方法三：如图③;过点B作BM∥CE交EP略证△BMP≌△CEP;∴BP＝CP.3BF2＋FC2＝2AD2.类型4中位线：三角形中两中点;连接则成中位线例4:解：1PM=PN;PM⊥PN2△PMN为等腰直角三角形;理由如下：由题意知△ABC和△ADE均为等腰直角三角形;∴AB＝AC;AD＝AE;∠BAC＝∠DAE＝90°;∴∠BAD＋∠DAC＝∠CAE＋∠DAC;∴∠BAD＝∠CAE;∴△BAD≌△CAE;∴∠ABD＝∠ACE;BD＝CE.又∵M、P、N分别是DE、CD、BC的中点;∴PM是△CDE的中位线;∴PM∥CE且PM＝CE;∠MPD＝∠ECD＝∠ACD＋∠ACE.同理;PN∥BD且PN＝BD;∠DBC＝∠PNC;又∵BD＝CE;∠ABD＝∠ACE;∴PM＝PN;∴∠MPN＝∠MPD＋∠DPN＝∠ECD＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°;∴PM⊥PN;∴△PMN为等腰直角三角形；3△PMN面积的最大值为.提示：在旋转的过程中;由2中的结论知△PMN为等腰直角三角形;S＝PN2＝BD2;当S△PMN有最大值时;则BD的值最大;由三角形三边关系可推断出当B、A、D三△PMN点共线时;BD的值最大;其最大值为14;此时S△PMN＝PN2＝BD2＝×14×14＝.针对训练：1.解：1证明：延长DA交BE于G点．∵∠BAE＋∠CAD＝180°;即∠EAG＋∠GAB＋∠CAD＝180°;∵∠GAB＋∠BAC＋∠CAD＝180°;∴∠EAG＝∠CAB.∵∠EAG＝∠AED＋∠ADE;∴∠CAB＝∠AED＋∠ADE.2证明：如图①;过E点作DA延长线的垂线;垂足为H.∴∠AHE＝∠ACB＝90°;由1可知;∠EAH＝∠BAC;又∵AE＝AB;∴△AHE≌△ACB;∴EH＝BC;AH＝AC.∵AC＝AD;∴AH＝AD.∵∠EHA＝∠FAD＝90°;∴AF∥EH.∵A为DH中点;∴AF为△DHE中位线;∴EH＝2AF;∴BC＝2AF.3成立．证明如下：如图②;延长DA至M点;使AM＝DA;连接EM;∵∠BAE＋∠CAD＝180°;∠CAD＋∠CAM＝180°;∴∠BAE＝∠CAM;∴∠BAE＋∠CAC＝∠CAM＋∠EAC;即∠BAC＝∠CAM.∵AM＝AD;AD＝AC;∴AM＝AC.又∵AB＝AE;∠BAC＝∠EAM;∴△BAC≌△EAM;∴BC＝EM.∵F、A分别为DE、DM中点;∴AF为△DEM中位线;∴EM＝2AF;∴BC＝2AF.2.解：1证明：∵∠BAC＋∠EAD＝180°;∠BAE＝90°;∴∠DAC＝90°;在△ABE与△ACD中;AE＝AD;∠BAE＝∠CAD＝90°;AB＝AC;∴△ABE≌△ACDSAS;∴CD＝BE;∵在Rt△ABE中;F为BE的中点;∴BE＝2AF;∴CD＝2AF.2成立;证明：如图;延长EA交BC于G;在AG上截取AH＝∵∠BAC＋∠EAD＝180°;∴∠EAB＋∠DAC＝180°;∵∠EAB＋∠BAH＝180°;∴∠DAC＝∠BAH;在△ABH与△ACD中;AH＝AD;∠BAH＝∠CAD;AB＝AC;∴△ABH≌△ACDSAS;∴BH＝DC;∵AD＝AE;AH＝AD;∴AE＝AH;∵EF＝FB;∴BH＝2AF;∴CD＝2AF.3.解：1证明：∵AB＝AC;∴∠ABD＝∠ACD;∵AE＝AD;∴∠ADE＝∠AED;∵∠BAD＋∠ABD＝∠ADE＋∠EDC;∠EDC＋∠ACD∴∠BAD＝2∠EDC;∵∠ABF＝2∠EDC;∴∠BAD＝∠ABF;∴△ABF是等腰三角形；2方法一：如图①;延长CA至点H;使AG＝AH;连接BH;∵点N是BG的中点;∴AN＝BH;∵∠BAD＝∠ABF;∠DAC＝∠CBG;∴∠CAB＝∠CBA;∴△ABC是等边三角形．∴AB＝BC＝AC;∠BAC＝∠BCA＝∵GM＝AB;AB＝AC;∴CM＝AG;∴AH＝CM;在△BAH和△BCM中;∴△BAH≌△BCMSAS;∴BH＝BM;∴AN＝BM;方法二：如图②;延长AN至K;使NK＝AN;连接KB;同方法一;先证△ABC是等边三角形;再证△ANG≌△KNB SAS;所以BK＝AG＝CM;然后可以证得∠ABK＝∠BCN＝120°;最后证△ABK≌△BCN SAS;所以BM＝AK＝2AN.类型5角的和差倍分例5：解：1如图;过点P作PG⊥EF于G.∵PE＝PF＝6;EF＝6;∴FG＝EG＝3;∠FPG＝∠EPG＝∠EPF.在Rt△FPG中;sin∠FPG＝＝＝.∴∠FPG＝60°;∴∠EPF＝2∠FPG＝120°.2如图;作PM⊥AB于M;PN⊥AD于N.∵AC为菱形ABCD的对角线;∴∠DAC＝∠BAC;AM＝AN;PM＝PN.在Rt△PME和Rt△PNF中;PM＝PN;PE＝∴Rt△PME≌Rt△PNF;∴NF＝ME.又∵AP＝10;∠PAM＝∠DAB＝30°;∴AM＝AN＝AP cos30°＝10×＝5.∴AE＋AF＝AM＋ME＋AN－NF＝AM＋AN针对训练：1.证明：如图;过D作DE⊥AB于E;过D作DF⊥AC于F;∵DA平分∠BAC;DE⊥AB;DF⊥AC;∴DE＝DF;∵∠B＋∠ACD＝180°;∠ACD＋∠FCD＝180°∴∠B＝∠FCD;在△DFC和△DEB中;∴△DFC≌△DEB;∴DC＝DB.2.解：1∵AC＝AB＝4;且CD＝1;∴AD＝AC－CD＝3.在Rt△ABD中;∠BAD＝90°;∴BD＝＝5;＝AB·AD＝AE·BD;∵S△ABD∴AE＝2.4.2证明：如图;取BC的中点M;连接AM交BD于点N.∵∠BAC＝90°;AB＝AC;点M为BC的中点;∴AM＝BM＝CM;AM⊥BC;∠NAD＝∠FCP＝45°;∴∠AMF＝∠BMN＝90°.∵AE⊥BD;∴∠MAF＋∠ANE＝∠MBN＋∠BNM＝90°;又∠ANE＝∠BNM;∴∠MAF＝∠MBN;∴△AMF≌△BMN;∴MF＝MN;∴AM－MN＝CM－MF;即AN＝CF.∵AP＝CD;∴AC－CD＝AC－AP;即AD＝CP.∴△ADN≌△CPF;∴∠ADB＝∠CPF.3.解：1∵AB＝BD;∠BAD＝45°;∴∠BDA＝45°;即∠ABD＝90°.∵四边形ABCD是平行四边形;∴当E、C重合时;BF＝BD＝AB.∵在Rt△ABF中;AB2＋BF2＝AF2;∴2BF2＋BF2＝2;∴BF＝1;AB＝2.在Rt△ABD中;AD＝＝＝2.2证明：如图;在AF上截取AK＝HD;连接BK.∵∠AFD＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°; ∴∠2＝∠3.在△ABK与△DBH中;∴△ABK≌△DBH;∴BK＝BH;∠6＝∠5.∵四边形ABCD是平行四边形;∴AD∥BC;∴∠5＝∠4＝45°;∴∠6＝∠5＝45°;∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK与△BFH中;∴△BFK≌△BFH.∴∠BFK＝∠BFH;即∠AFB＝∠HFB.4.解：1证明：由折叠知∠EMN＝∠ABC＝90°∴∠EMB＝∠EBM;∴∠EMN－∠EMB＝∠ABC－∠EBM;即∠BMP＝∠MBC.∵在正方形ABCD中;AD∥BC;∴∠AMB＝∠MBC;∴∠AMB＝∠BMP;∴BM是∠AMP的平分线．2△PDM的周长没有发生变化．证明如下：如图;过B作BQ∵∠A＝90°;且由1知BM是∠AMP的平分线;∴BA＝BQ;∵∠A＝∠MQB＝90°;∠AMB＝∠BMP;MB＝MB;∴△AMB≌△QMB AAS．∴MA＝MQ.∵BA＝BC;∴BQ＝BC;又∵∠BQP＝90°＝∠C;BP＝BP;∴Rt△BPC≌Rt△BPQ HL．∴PC＝PQ;∴△PDM的周长＝MD＋MP＋DP＝MD＋MQ＋QP＋PD＝MD＋MA＋PC＋PD＝AD＋DC＝2AD.∴△PDM的周长没有发生变化．类型6旋转型全等问题：图中若有边相等;可用旋转做实验例6：解：1①∵四边形ADEF是正方形;∴AD＝AF;AB＝AC;∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠B＝∠ACF;∴∠ACB＋∠ACF＝90°;即CF⊥BC；②∵△DAB≌△FAC;∴CF＝BD;∵BC＝BD＋CD;∴BC＝CF＋CD.2结论①成立;结论②不成立．∵四边形ADEF是正方形;∴AD＝AF;AB＝AC.∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠ABD＝∠ACF;CF＝BD;∴∠BCF＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°;即CF⊥BC；∵BC＝CD－BD;∴BC＝CD－CF.3如图;过A作AH⊥BC于H;过E作EM⊥BD于M;EN∵∠BAC＝90°;AB＝AC;∴BC＝AB＝4;AH＝CH＝BC∴CD＝BC＝1;∴DH＝3;同2证得△BAD≌△CAF;∴∠ABD＝∠ACF＝45°;∴∠BCF＝∠ACB＋∠ACF＝∴BC⊥CF;CF＝BD＝5.∵四边形ADEF是正方形;∴AD＝DE;∠ADE＝90°;∵BC⊥CF;EM⊥BD;EN⊥CF;∴四边形CMEN是矩形;∴NE＝CM;EM＝CN;∵∠AHD＝∠ADE＝∠EMD＝90°;∴∠ADH＋∠EDM＝∠EDM＋∠DEM＝90°;∴∠ADH＝∠DEM;∴△ADH≌△DEM;∴EM＝DH＝3;DM＝AH＝2;∴CN＝EM＝3;EN＝CM＝3;∵∠ABC＝45°;∴∠BGC＝45°;∴△BCG是等腰直角三角形;∴CG＝BC＝4;∴GN＝1;∴EG＝＝.针对训练：1.解：1AC＝AD＋AB.证明如下：∵∠B＋∠D＝180°;∠B＝90°;∴∠D＝90°.∵∠DAB＝120°;AC平分∠DAB;∴∠DAC＝∠BAC＝60°;∵∠B＝90°;∴AB＝AC;同理AD＝AC.∴AC＝AD＋AB.21中的结论成立;理由如下：如图①;以C为顶点;AC为一边作∠ACE＝60°;∠ACE的另一边交AB的延长线于点E;∵∠BAC＝60°;∴△AEC为等边三角形;∴AC＝AE＝CE;∠E＝60°;∵∠ABC＋∠D＝180°;∠DAB＝120°;∴∠DCB＝60°;∴∠DCA＝∠ECB.在△DAC和△BEC中;∴△DAC≌△BEC;∴AD＝BE;∴AC＝AE＝AD＋AB.3AD＋AB＝AC.理由如下：如图②;过点C作CE⊥AC交AB的延长于点E;∵∠ABC＋∠D＝180°;∠DAB＝90°;∴∠DCB＝90°;∵∠ACE＝90°;∴∠DCA＝∠BCE;又∵AC平分∠DAB;∴∠CAB＝45°;∴∠E＝45°;∴AC＝CE.∴△CDA≌△CBE;∴AD＝BE;∴AD＋AB＝AE.∵在Rt△ACE中;∠CAB＝45°;∴AE＝＝AC;∴AD＋AB＝AC.2.解：1证明：∵四边形ABCD是正方形;∴∠B＝∠D＝∠BAD＝90°;AB＝AD;∵△ABE沿AE翻折得到△AHE;∴△ABE≌△AHE;∴AH＝AB＝AD;BE＝EH;∠AHE＝∠AHF＝∠B＝∠D＝90°.在Rt△AHF和Rt△ADF中;∴Rt△AHF≌Rt△ADFHL;∴∠HAF＝∠DAF;∴∠EAF＝∠EAH＋∠FAH＝∠BAH＋∠HAD＝∠BAD＝45°;2以BM;DN;MN为三边围成的三角形为直角三角形．证明如下：如图;过点A作AH⊥AN并截取AH＝AN;连接BH、HM;∵∠1＋∠BAN＝90°;∠3＋∠BAN＝90°;∴∠1＝∠3;在△ABH和△ADN中;∴△ABH≌△ADN SAS;∴BH＝DN;∠HBA＝∠NDA＝135°;∵∠HAN＝90°;∠MAN＝45°;∴∠1＋∠2＝∠HAM＝∠MAN＝45°;在△AHM和△ANM中;∴△AHM≌△ANM SAS;∴HM＝NM;∴∠HBP＝180°－∠HBA＝180°－135°＝45°;∴∠HBP＋∠PBM＝45°＋45°＝90°;∴△HBM是直角三角形;∵HB＝DN;HM＝MN;∴以BM;DN;MN为三边围成的三角形为直角三角形．3.解：1如图①;将△PBC绕点B逆时针旋转90°得△P△AP′B≌△CPB;∴P′B＝PB＝;P′A＝PC＝1;∠1＝∠2;∠AP′B＝∠BPC.∵四边形ABCD是正方形;∴AB＝BC;∠ABC＝90°;∴∠2＋∠3＝90°;∴∠1＋∠3＝90°;即∠P′BP＝90°;∴∠BP′P＝45°.在Rt△P′BP中;由勾股定理;得PP′2＝ 4. ∵P′A＝1;AP＝∴P′A2＝1;AP2＝5;∴P′A2＋PP′2＝AP2;∴△P′AP是直角三角形;∴∠AP′P＝90°;∴∠AP′B＝45°＋90°＝135°;∴∠BPC＝135°.2仿照分析中的思路;将△BPC绕点B逆时针旋转120°;得到了△BP′A;连接PP′;如图②.则△PBC≌△P′BA;∴P′B＝PB＝4;P′A＝PC＝2;∠BPC＝∠BP′A;∴△BPP′为等腰三角形;∵∠ABC＝120°;∴∠PBP′＝120°;∴∠BP′P＝30°;过点B作BG⊥PP′于G;则∠P′GB＝90°;∴PP′＝2P′G.∵P′B＝PB＝4;∠BP′P＝30°;∴BG＝2;∴P′G＝2.∴PP′＝4;在△APP′中;∵PA＝2;P′A＝2;PP′＝4;∴P′A2＋P′P2＝PA2;∴△PP′A是直角三角形;∴∠AP′P＝90°;∴∠BPC＝∠BP′A＝∠PP′B＋∠AP′P＝30°＋90°＝120°.。

2020年中考数学三轮限时训练实数与二次根式(含答案) (1)

2020中考数学三轮限时训练实数与二次根式（含答案）1.－16的相反数是()A. 16 B. －6 C. 6D．－162.－6的绝对值是()A. －6B. 6C. 16 D. －163.四个数－3，0，1，2，其中负数是()A. －3B. 0C. 1D. 24.下列实数中的无理数是()A. 0.7B. 12 C. π D. －85.4的平方根是()A. ±2B. －2C. 2D. ±1 26.冰箱冷藏室的温度零上5 ℃，记作＋5 ℃，保鲜室的温度零下7 ℃，记作()A. 7 ℃B. －7 ℃C. 2 ℃D. －12 ℃7.大家翘首以盼的长株潭城际铁路将于2019年年底通车，通车后，从长沙到株洲只需24分钟，从长沙到湘潭只需25分钟，这条铁路线全长95500米，则数据95500用科学记数法表示为()A. 0.955×105B. 9.55×105C. 9.55×104D. 9.5×1048.成都地铁自开通以来，发展速度不断加快，现已成为成都市民主要出行方式之一．今年4月29日成都地铁安全运输乘客约181万乘次，又一次刷新客流记录，这也是今年以来第四次客流记录的刷新，用科学记数法表示181万为()A. 18.1×105B. 1.81×106C. 1.81×107D. 181×1049.宁波栎社国际机场三期扩建工程建设总投资84.5亿元，其中84.5亿元用科学记数法表示为()A. 0.845×1010元B. 84.5×108元C. 8.45×109元D. 8.45×1010元10.人体中红细胞的直径约为0.0000077 m，将数0.0000077用科学记数法表示为()A. 77×10－5B. 0.77×10－7C. 7.7×10－6D. 7.7×10－7第17题图11.2019年7月，第四十五届“世界超级计算机500强排行榜”榜单发布，我国国防科技大学研制的“天河二号”以每秒3386×1013次的浮点运算速度第五次蝉联冠军，若将3386×1013用科学记数法表示成a×10n的形式，则n的值是________．12.9的算术平方根是__________．13.38＝________．14.|－0.3|的相反数等于________．15.计算：|38－4|－(12)－2＝________．16.计算：(－1)2020－(2－3)0＋25.17.计算：55－(2－5)0＋(12)－2.18.计算：(－1)3＋|－12|－(－32)0×(－23)．19. 计算： 27－(－1)2020－3tan60°＋(－2016)0.20. 计算：|－3|－(2020＋sin30°)0－(－12)－1.21. 计算：(12)－1＋(sin60°－1)0－2cos30°＋|3－1|.22. 计算：2－2－2cos60°＋|－12|＋(π－3.14)0.答案1.A 2.B 3.A 4.C 5.A 6.C 7.B 8.C 9.B 10.C 11.3 12.3 13.2 14.-0.3 15. -2 16. 解：原式＝1－1＋5(4分)＝5.(6分)17. 解：原式＝5－1＋4(2分)＝5＋3.(4分)18. 解：原式＝－1＋12－1×(－23)(4分) ＝－12＋23(6分) ＝16.(8分) 19. 解：原式＝33－1－3×3＋1 (4分) ＝0.(6分)20. 解：原式＝3－1＋2(3分)＝2＋2＝4.(6分)21. 解：原式＝2＋1－2×32＋3－1(4分) ＝2＋1－3＋3－1(6分)＝2.(8分)22. 解：原式＝14－2×12＋23＋1(2分) ＝14－1＋23＋1(4分) ＝14＋2 3.(6分)。

2024年重庆市中考数学压轴题

2024年重庆市中考数学压轴题一、在直角三角形ABC中，角C为直角，AC等于3，BC等于4，以点C为圆心，半径为2的圆与AB边的位置关系是？A. 相离B. 相切C. 相交D. 无法确定（答案）B。

解析：首先利用勾股定理计算出斜边AB的长度，AB等于根号下（AC平方加BC 平方）等于5。

接着计算点C到AB边的距离，即直角三角形ABC的面积除以AB边的一半，面积等于二分之一乘以AC乘以BC等于6，所以点C到AB边的距离为6除以5等于1.2，小于圆的半径2，但圆的半径又小于AB边的一半（5除以2等于2.5），因此圆与AB边相切。

二、已知二次函数y等于ax平方加bx加c的图像经过点（1，0），（2，0），（0，2），则a的值为？A. 1B. -1C. 2D. -2（答案）B。

解析：将三个点的坐标代入二次函数，可以得到三个方程：a加b加c等于0，4a加2b加c等于0，c等于2。

解这个方程组，可以得到a等于-1，b等于1，c等于2。

三、一个正方体的内切球半径为2，则这个正方体的体积为？A. 8B. 32C. 64D. 128（答案）C。

解析：正方体的内切球半径等于正方体边长的一半，所以正方体的边长为4，体积为边长的三次方，即4的三次方等于64。

四、在平行四边形ABCD中，E为AD的中点，F为BC上的一点，且BF等于四分之一BC，连接EF，与对角线AC相交于点G，则AG与GC的比值为？A. 1:2B. 1:3C. 2:3D. 3:4（答案）C。

解析：过E做BC的平行线，交AC于H，则EH等于四分之一BC，且EH平行于FC，所以三角形EHG与三角形CFG相似，且相似比为1:3，所以AG与GC的比值为2:3。

五、已知等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为？A. 9B. 12C. 15D. 18（答案）C。

解析：等腰三角形的两边长相等，且大于第三边，所以腰长为6，底边长为3，周长为6加6加3等于15。

2020年中考数学人教版专题复习：平方根、立方根

2020年中考数学人教版专题复习：平方根、立方根一、学习目标：1. 了解一个数的平方根和算术平方根的意义，理解和掌握平方根的性质；2. 会求一个非负数的平方根、算术平方根；3. 掌握立方根的意义，会求一个数的立方根；4. 理解开立方与立方的关系。

二、重点、难点：重点：算术平方根、平方根以及立方根的概念和性质。

难点：算术平方根与平方根的区别与联系。

三、考点分析：中考命题以考查对平方根、算术平方根、立方根的概念的理解程度和估算为主，多以选择题和填空题的形式出现，试题的难度不大，只要对平方根、算术平方根、立方根的有关概念和性质熟练掌握，就能解决中考试题，比较容易得分。

知识梳理一. 平方根：1. 算术平方根的概念及表示方法如果一个正数x的平方等于a，即2x a=，那么这个正数x叫做a的算术平方根。

当0a≥时，a a”，a叫做被开方数。

2. 平方根的概念及其性质（1）平方根的定义如果一个数的平方等于a，即2x a=，那么这个数叫做a的平方根或二次方根。

即如果2=，那么x叫做a的平方根。

x a（2）一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根。

当a≥时，a的平方根表示为。

（3）求一个数a的平方根的运算，叫做开平方，其中a叫做被开方数。

3. 用计算器求一个正数的算术平方根用计算器可以求出任何一个正数的算术平方根（或其近似值）。

二. 立方根：1. 立方根的概念及表示方法如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根。

即如果3x a=，那么x叫做a的立方根，记作0的立方根是0。

2. 开立方的概念求一个数的立方根的运算，叫做开立方。

正如开平方与平方互为逆运算一样，开立方与立方也互为逆运算。

3. 用计算器求立方根很多有理数的立方根是无限不循环小数，我们可用计算器求出它们的近似值。

典例精析知识点一：算术平方根例1. 下列各数有算术平方根吗？如果有，求出它的算术平方根；如果没有，请说明理由。

2020年九年级数学中考几何图形综合题专题训练(含答案)

2020年九年级数学中考几何图形综合题专题训练1、如图，在▱ABCD 中，点E 在边BC 上，点F 在边AD 的延长线上，且DF=BE ，BE 与CD 交于点G（1）求证：BD ∥EF ；（2）若=，BE=4，求EC 的长．2、如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，∠BAC ＝60°，AD 平分∠BAC 交BC 于点D ，过点D 作DE ∥AC 交AB 于点E .点M 是线段AD 上的动点，连接BM 并延长分别交DE ，AC 于点F ，G .(1)求CD 的长；(2)若点M 是线段AD 的中点，求EF DF的值；(3)请问当DM 的长满足什么条件时，在线段DE 上恰好只有一点P ，使得∠CPG ＝60°？3、如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．（1）求证：△AC D∽△BFD；（2）当tan∠ABD=1，AC=3时，求BF的长．4、如图，▱ABCD的对角线AC、BD交于点O，EF过点O且与BC、AD分别交于点E、F．试猜想线段AE、CF的关系，并说明理由．5、如图，平行四边形ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF（1）根据题意，补全原形；（2）求证：BE=DF．6、如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G.(1)猜想并证明线段FG与CG的数量关系；(2)若将图①中的正方形改成矩形，其他条件不变，如图②，那么线段FG与CG之间的数量关系是否改变？请证明你的结论；(3)若将图①中的正方形改成平行四边形，其他条件不变，如图③，那么线段FG与CG 之间的数量关系是否会改变？请证明你的结论．7、如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．8、如图，□A BCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。

2020年重庆中考复习数学最值专题训练(含答案)

2020重庆中考复习最值问题专题训练类型一、利用将军饮马求最值1、如图，正方形ABCD的边长为3，E在BC上，且BE＝2，P在BD上，则PE+PC的最小值为（）A．B．C．D．2、如图，在菱形ABCD中，AB＝6，点E在BC上，BE＝3，∠BAD＝120°，P点在BD上，则PE+PC的最小值为．类型二、利用垂线段最短求最值1、如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P是AB上的任意一点，作PD⊥AC于点D，PE⊥CB于点E，连接DE，则DE的最小值为_________2、在边长为2菱形ABCD中，∠ABC=60°，M、N分别为线段BC和BD上两个动点，则MN+CN的最小值是。

类型三、利用平行线间的距离求最值1.如图，菱形ABCD的边长为5，面积为20，P为CD边上一动点（异于C、D），点M、N分别在BD、BC上运动，则PM+MN的最小值为2.如上左图，菱形ABCD中，AB＝4，∠A＝120°，点M、N、P分别为线段AB、AD、BD上的任意一点，则PM＋PN的最小值为________类型四、利用三角形三边关系、三点共线求最值1、如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB＝2，BC＝1，运动过程中，点D到点O的最大距离为（）A、2+1 B、5C、1455D、522、如图，在矩形纸片ABCD中，AB＝2，AD＝3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是（）A．﹣1 B．C．D．2﹣13、如图，在平行四边形ABCD中，AB＝6，AD＝2，∠A＝45°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．4、如图，在矩形ABCD中，已知AB＝2，BC＝4，点O、P分别是边AB、AD的中点，点H是边CD上的一个动点，连接OH，将四边形OBCH沿OH折叠，得到四边形OFEH，连接PE，则PE长度的最小值是．5、如图，矩形ABCD中，AB＝6，BC＝8，P是边CD上一点，Q是以AD为直径的半圆上一点，则BP+PQ的最小值为（）A．10 B．2+4 C．+1 D．6﹣46、（2019•怀柔区一模）如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C顺时针旋转得到△A'B'C，D是A'B'的中点，连接BD，若BC＝2，∠ABC＝60°，则线段BD的最大值为．类型五、利用中位线+三点共线求最值如图，已知△ABC中，∠ACB＝90°，BC＝6，AC＝12，点D在AC上，且AD＝8，将线段AD绕点A旋转至AD′，F为BD′的中点，线段CF的最大值为类型六、利用胡不归问题求最值1、（2019•南通）如图，▱ABCD中，∠DAB＝60°，AB＝6，BC＝2，P为边CD上的一动点，则PB+PD 的最小值等于．2、（2019•长沙）如图，△ABC中，AB＝AC＝10，tan A＝2，BE⊥AC于点E，D是线段BE上的一个动点，则CD+BD的最小值是（）A．2B．4C．5D．10类型六、利用旋转+三点共线求最值1、如图，P A＝，PB＝3，以AB为一边作正方形ABCD，使P、D两点落在直线AB的两侧，当P与D的距离最大时，正方形ABCD的面积为．''，M是AC的中点，2、如图，在Rt ABCACB∆中，90∆绕顶点C顺时针旋转得到△A B C∠=︒，将ABC∠=︒，则线段MN的最小值为．ABCAC=，30N是A B''的中点，连接MN，若4作业练习1、如图，矩形ABCD中，AB＝6，BC＝8，P是边AD上一动点，将△ABP沿BP折叠后得△BPM，当线段DM的长最短时，AP＝．2、如图，∠MON＝90°，正方形ABCD的顶点A、B分别在OM、ON上运动，当正方形边长为2时，OD 的最大值为．3、如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB＝8，BC＝3，运动过程中，点D到点O的最大距离为．4、（2017秋•梁子湖区期中）如图，在△ABC中，∠ACB＝90°，BC＝2，AC＝6，D为AC上一点，AD＝4，将AD绕点A旋转至AD′，连接BD′，F为BD′的中点，则CF的最大值为．5、如图，菱形ABCD中，∠A＝60°，AB＝6，⊙A、⊙B的半径分别为4和2，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最大值是（）A．6+12 B．6+16 C．18 D．66、如图，P A＝2，PB＝4，将线段P A绕P点旋转一周，以AB为边作正方形ABCD，则PD的最大值为．7、已知：AD＝2，BD＝4，以AB为一边作等边三角形ABC．使C、D两点落在直线AB的两侧．（1）如图，当∠ADB＝60°时，求AB及CD的长；（2）当∠ADB变化，且其它条件不变时，求CD的最大值，及相应∠ADB的大小．2020重庆中考复习最值问题专题训练类型一、将军饮马1、如图，正方形ABCD的边长为3，E在BC上，且BE＝2，P在BD上，则PE+PC的最小值为（）A．B．C．D．解：如图，连接AE，因为点C关于BD的对称点为点A，所以PE+PC＝PE+AP，根据两点之间线段最短可得AE就是AP+PE的最小值，∵正方形ABCD的边长为3，BE＝2，∴AE＝＝，∴PE+PC的最小值是．故选：B．2、如图，在菱形ABCD中，AB＝6，点E在BC上，BE＝3，∠BAD＝120°，P点在BD上，则PE+PC的最小值为3．解：如图，在菱形ABCD中，点A、C关于BD对称，连接AE，与BD的交点即为所求作的点P，∵∠BAD＝120°，∴∠ABC＝180°﹣120°＝60°，∴△ABC是等边三角形，∵AB＝6，BE＝3，∴点E是BC的中点，∴AE⊥BC，∴AE＝＝＝3，即PE+PC的最小值为3．类型二、点到直线距离垂线段最短2、如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P是AB上的任意一点，作PD⊥AC于点D，PE⊥CB于点E，连接DE，则DE的最小值为_________解：∵Rt△ABC中，∠C＝90°，AC＝8，BC＝6，∴AB＝10，连接CP，∵PD⊥AC于点D，PE⊥CB于点E，∴四边形DPEC是矩形，∴DE＝CP，当DE最小时，则CP最小，根据垂线段最短可知当CP⊥AB时，则CP最小，∴DE＝CP＝＝4.82、在边长为2菱形ABCD中，∠ABC=60°，M、N分别为线段BC和BD上两个动点，则MN+CN的最小值是。

中考数学专题特训第六讲：二次根式(含详细参考答案)

中考数学专题复习第六讲：二次根式【基础知识回顾】一、二次根式式子a （）叫做二次根式【赵老师提醒：①次根式a 必须注意a___o 这一条件，其结果也是一个非数即：a ___o②二次根式a （a ≥o ）中，a 可以表示数，也可以是一切符合条件的代数式】二、二次根式的性质：①（a ）2= （a ≥0）= （a ≥0 ,b ≥0）(a ≥0, b ≥0)【赵老师提醒：二次根式的性质注意其逆用：如比较23和的大小，可逆用（a ）2=a(a ≥0)将根号外的整数移到根号内再比较被开方数的大小】三、最简二次根式：最简二次根式必须同时满足条件：1、被开方数的因数是，因式是整式2、被开方数不含的因数或因式四、二次根式的运算：1、二次根式的加减：先将二次根式化简，再将的二次根式进行合并，合并的方法同合并同类项法则相同2、二次根式的乘除：= （a ≥0 ,b ≥0）（a ≥0，b ＞0） 3、二次根式的混合运算顺序：先算再算最后算【赵老师提醒：1、二次根式除法运算过程一般情况下是用将分母中的根号化= = 2、二次根式混合运算过程要特别注意两个乘法公式的运用 3、二次根式运算的结果一定要化成】【重点考点例析】考点一：二次根式有意义的条件（a ≥o ）（a ＜o ）例1 （2012•潍坊）如果代数式43x -有意义，则x 的取值范围是（） A ．x ≠3 B ．x ＜3 C ．x ＞3 D ．x ≥3思路分析：根据二次根式的意义得出x-3≥0，根据分式得出x-3≠0，即可得出x-3＞0，求出即可．解：要使代数式43x -有意义，必须x-3＞0，解得：x ＞3．故选C ．点评：本题考查了二次根式有意义的条件，分式有意义的条件的应用，注意：分式B A中A ≠0，二次根式a 中a ≥0．对应训练1．（2012•德阳）使代数式21xx -有意义的x 的取值范围是（） A ．x≥0 B ．x≠12 C ．x≥0且x≠12D ．一切实数 1．C1．解：由题意得：2x-1≠0，x≥0，解得：x≥0，且x≠12，故选：C ．考点二：二次根式的性质例2 （2012•张家界）实数a 、b 在轴上的位置如图所示，且|a|＞|b|，则化简2||a a b -+的结果为（）A ．2a+bB ．-2a+bC ．bD ．2a-b思路分析：现根据数轴可知a ＜0，b ＞0，而|a|＞|b|，那么可知a+b ＜0，再结合二次根式的性质、绝对值的计算进行化简计算即可．解：根据数轴可知，a ＜0，b ＞0，原式=-a-[-（a+b ）]=-a+a+b=b ．故选C ．点评：本题考查了二次根式的化简和性质、实数与数轴，解题的关键是注意开方结果是非负数、以及绝对值结果的非负性．对应训练为． 1．-b2．解：∵由数轴可知：b ＜0＜a ，|b|＞|a|，=|a+b|+a =-a-b+a =-b ，故答案为：-b ．考点三：二次根式的混合运算思路分析：利用二次根式的分母有理化以及分数指数幂的性质和负整数指数幂的性质，分别化简，进而利用有理数的混合运算法则计算即可．=3．点评：此题主要考查了二次根式的混合运算以及负整数指数幂的性质，熟练利用这些性质将各式进行化简是解题关键．对应训练4=+考点四：与二次根式有关的求值问题222)(1)(x x x ++-思路分析：先根据分式混合运算的法则把原式进行化简，再把x 的值代入进行计算即可．2(1)1)4x x x+0，(1)1)4x x x +=本题考查的是二次根式及分式的化简求值，解答此题的关键是当1，此题难度不大．对应训练A ．0B ．25C ．50D ．804．D分析：根据平方差公式求出1142-642=（114+64）×（114-64）=178×50，再提出50得出50×（178-50）=50×128，分解后开出即可．=80，故选D ．点评：本题考查了平方差公式，因式分解，二次根式的运算等知识点的应用，解此题的关键是能选择适当的方法进行计算，本题主要考查学生的思维能力和应变能力，题目比较好，是一道具有代表性的题目．【聚焦山东中考】1．（2012•泰安）下列运算正确的是（）A 5=-B ．21()164--=C ．x 6÷x 3=x 2 D ．（x 3）2=x 5 1．B ．2.（2012•临沂）计算：= ． 2．03．7【备考真题过关】一、选择题A ．x ＞0B ．x≥-2C ．x≥2D ．x≤2 1．DA B ．5 C ．2 D ．22．AA ．3BC ．D ．3．C ．A ．5＜m ＜6B ．4＜m ＜5C ．-5＜m ＜-4D ．-6＜m ＜-5 4．A即5＜m ＜6，故选A ．5．（2012•南充）下列计算正确的是（）A ．x 3+x 3=x 6B ．m 2•m 3=m 6C ．3=D = 5．D6．（2012•黔东南州）下列等式一定成立的是（）A ．945-=B ．5315⨯=C ．93=±D ．2(9)9--=6．B7．（2012•广西）使式子有意义的x 的取值范围是（）A ． x ≥﹣1B ． ﹣1≤x ≤2C ． x ≤2D ．﹣1＜x ＜2 考点：二次根式有意义的条件。

重庆市中考数学一轮复习第一章数与式第4节数的开方与二次根式配套巩固训练题级答案85.doc

学校班级姓名【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】第4节数的开方与二次根式(建议答题时间：20分钟)命题点一二次根式的概念及性质1. (2017贵港)下列二次根式中，最简二次根式是( )A. － 2B. 12C. 15D. a22. (2016巴中)下列二次根式中，与3是同类二次根式的是( )A. 18B. 13C. 24D. 0.33. (2017益阳)下列各式化简后的结果为32的是( )A. 6B. 12C. 18D. 36命题点二二次根式有意义的条件4. (2017广安) 要使二次根式2x－4在实数范围内有意义，则x的取值范围是( )A. x＞2B. x≥2C. x＜2D. x＝25. 式子a＋1a－2有意义，则实数a的取值范围是______________.6. 使代数式1x＋3＋4－3x有意义的整数x有________个．命题点三平方根、算术平方根、立方根7. (2017甘肃)4的平方根是( )A. 16B. 2C. ±2D. ± 28. (2017武汉)计算36的结果为( )A. 6B. －6C. 18D. －18命题点四二次根式的估值9. (2017天津)估计38的值在( )A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间10. (2017重庆八中一模)下列实数，介于5和6之间的是( )A. 21B. 35C. 42D. 36411. 已知M＝2×8＋5，则M的取值范围是( )A. 8＜M＜9B. 7＜M＜8C. 6＜M＜7D. 5＜M＜612. (2017重庆一中二模)估计7＋3的值在哪两个连续整数之间( )A. 3和4B. 4和5C. 5和6D. 6和713. (2017南京)若3＜a＜10，则下列结论中正确的是( )A. 1＜a＜3B. 1＜a＜4C. 2＜a＜3D. 2＜a＜414. (2017重庆九龙坡区模拟)在数轴上标注了四段范围，如图，则表示8的点落在( )第14题图A. 段①B. 段②C. 段③D. 段④15. (2017连云港)关于8的叙述正确的是( )A. 在数轴上不存在表示8的点B. 8＝2＋ 6C. 8＝±2 2D. 与8最接近的整数是3命题点五二次根式的运算16. (2017十堰)下列运算正确的是( )A. 2＋3＝ 5B. 22×32＝6 2C. 8÷2＝2D. 32－2＝317. (2017 枣庄 )实数a，b在数轴上对应点的位置如图所示，化简|a|＋（a－b）2的结果是( )A. －2a＋bB. 2a－bC. －bD. b第17题图18. (2017黄冈)计算27－613的结果是________．19. (2017山西) 计算：418－92＝________.20. (2017 南京 )计算12＋8×6的结果是________．21. (2017青岛) 计算：(24＋16)×6＝________.22. (2017呼和浩特)计算：|2－5|－2(18－102)＋32.答案1. A2. B3. C4. B5. a ≥－1，且a ≠26. 47. C8. A9. C 10. B11. C 【解析】∵M ＝16＋5＝4＋5，∵4＜5＜9，∴2＜5＜3，∴6＜M ＜7.12. B 【解析】∵ 6.25＜7＜9，∴2.5＜7＜3，∵ 2.25＜3＜4，∴1.5＜3＜2，∴4＜7＋3＜5，∴7＋3的值在4和5之间．13. B14. C 【解析】∵32＝9，2.92＝8.41，2.82＝7.84，∴7.84＜8＜8.41，∴8应介于 2.8与2.9之间．15. D 【解析】选项逐项分析正误 A任何实数在数轴上都有唯一的对应点 × B2＋6＝2(1＋3)≠8 × C8＝22≠±2 2 × D因为8＝22≈2.828，所以与8最接近的整数是3 √16. C17. A 【解析】由题图可知：a ＜0，a －b ＜0，则|a |＋（a －b ）2＝－a －(a －b )＝－2a ＋b .18. 3 19. 3 2 20. 6 3 21. 1322. 解：原式＝5－2－12＋5＋32＝25－1.。

2020年重庆市中考数学试卷word 版(含答案)

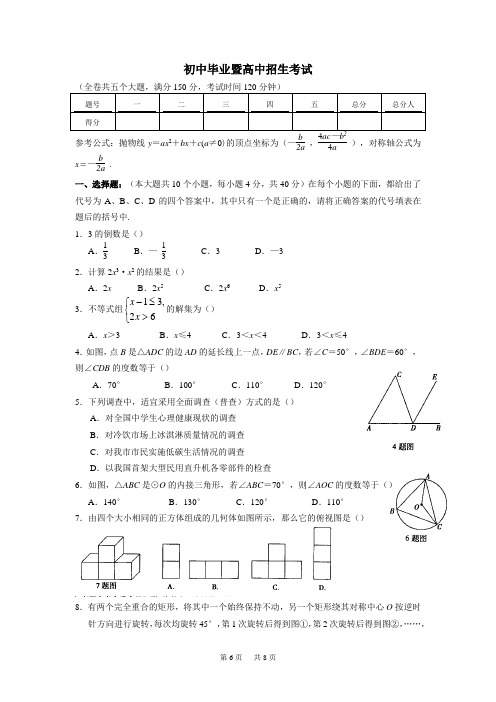
初中毕业暨高中招生考试题号一二三四五总分总分人得分参考公式：抛物线y ＝ax 2＋bx ＋c (a ≠0)的顶点坐标为（—b 2a ，4ac b 4a），对称轴公式为x ＝—b 2a.一、选择题：（本大题共10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案中，其中只有一个是正确的，请将正确答案的代号填表在题后的括号中.1．3的倒数是（）A ．13B ．— 13 C ．3 D ．—32．计算2x 3·x 2的结果是（）A ．2xB ．2x 5C ．2x 6D ．x 5 3．不等式组⎩⎨⎧>≤-62,31x x 的解集为（）A ．x ＞3B ．x ≤4C ．3＜x ＜4D ．3＜x ≤44．如图，点B 是△ADC 的边AD 的延长线上一点，DE ∥BC ，若∠C ＝50°，∠BDE ＝60°，则∠CDB 的度数等于（）A ．70°B ．100°C ．110°D ．120° 5．下列调查中，适宜采用全面调查（普查）方式的是（）A ．对全国中学生心理健康现状的调查B ．对冷饮市场上冰淇淋质量情况的调查C ．对我市市民实施低碳生活情况的调查D ．以我国首架大型民用直升机各零部件的检查6．如图，△ABC 是⊙O 的内接三角形，若∠ABC ＝70°，则∠AOC 的度数等于（） A ．140° B ．130° C ．120° D ．110° 7．由四个大小相同的正方体组成的几何体如图所示，那么它的俯视图是（）8．有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O 按逆时针方向进行旋转，每次均旋转45°，第1次旋转后得到图①，第2次旋转后得到图②，……，则第10次旋转后得到的图形与图①～④中相同的是（）A．图①B．图②C．图③D．图④9．小华的爷爷每天坚持体育锻炼，某天他慢步到离家较远的绿岛公园，打了一会儿太极拳后跑步回家。

2020年重庆市第一一〇中学校初九年级下学期中考实数复习测试卷(解析版)

D. ( 3)2
2. 在272，3.33，2，−2 12，0，0.454455444555…，− 0.9，127，3 217中，无理数的个数有( )
A. 2 个
B. 3 个
3. 下列说法正确的是( )
C. 4 个
D. 5 个
16. 若单项式−5 4 2 + 与 2017 − 2是同类项，则 − 7 的算术平方根是______ ． 17. 定义新运算“☆”： ☆ = + 1，则 2☆(3☆5) =______．
8.【答案】A
【解析】【分析】
本题主要考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0 的平方根是 0；负数没有平方根．根据正数的平方根有两个列方程求解即可．
【解答】解：∵ ( ± 2)2 = 4， ∴ 4 的平方根是±2， ∵ − 3 是 4 的平方根， ∴ − 3 = 2 或 − 3 =− 2，解得 = 5 或 = 1．故选 C．
24. 已知 a、b 满足 + 1 + | − 3 − 1| = 0，求 2 − 4 的立方根．
25. 在平面直角坐标系中， ( , )， (2,2)，且| − + 8| + 3 + 2 − 6 = 0．
(1)求点 A 的坐标； (2)过点 A 作 ⊥ 轴于点 C，连接 BC，AB，求三角形 ABC 的面积； (3)在(2)的条件下，延长 AB 交 x 轴于点 D，AB 交 y 轴于点 E，那么 OD 与 OE 是否相等，请说明理由．
D. + > 0
D. 3 个 D. ± 3
A. 2a
B. 2b
C. 2 − 2
D. 2 + 2
9. 下列说法：

2020年重庆中考数学复习几何最值专题复习八(含答案解析)

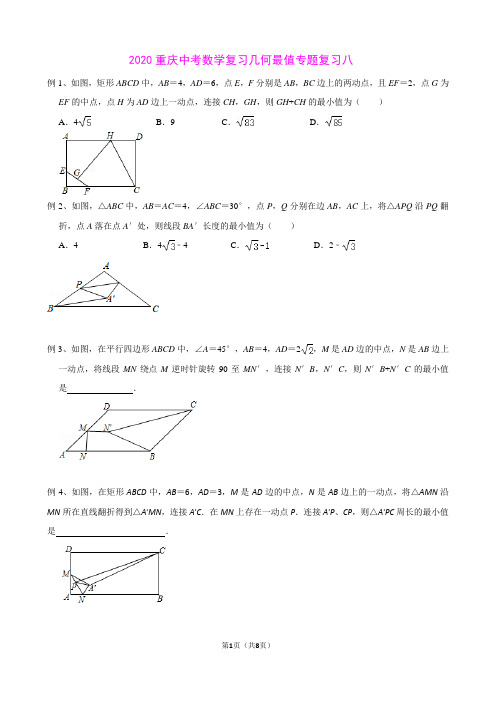
2020重庆中考数学复习几何最值专题复习八例1、如图，矩形ABCD中，AB＝4，AD＝6，点E，F分别是AB，BC边上的两动点，且EF＝2，点G为EF的中点，点H为AD边上一动点，连接CH，GH，则GH+CH的最小值为（）A．4B．9C．D．例2、如图，△ABC中，AB＝AC＝4，∠ABC＝30°，点P，Q分别在边AB，AC上，将△APQ沿PQ翻折，点A落在点A′处，则线段BA′长度的最小值为（）A．4B．4﹣4C．D．2﹣例3、如图，在平行四边形ABCD中，∠A＝45°，AB＝4，AD＝2，M是AD边的中点，N是AB边上一动点，将线段MN绕点M逆时针旋转90至MN′，连接N′B，N′C，则N′B+N′C的最小值是．例4、如图，在矩形ABCD中，AB＝6，AD＝3，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A'MN，连接A'C．在MN上存在一动点P．连接A'P、CP，则△A'PC周长的最小值是．例5、（2018•无锡）如图，矩形ABCD中，AB＝4，AD＝2，E为边AD上一个动点，连结BE，取BE的中点G，点G绕点E逆时针旋转90°得到点F，连结CF，则△CEF面积的最小值是（）A．4B．C．3D．练习：1、（2019秋•罗湖区期末）如图，矩形ABCD中，AB＝20，AD＝30，点E，F分别是AB，BC边上的两个动点，且EF＝10，点G为EF的中点，点H为AD边上一动点，连接CH、GH，则GH+CH的最小值为45．2、如图，在△ABC，AB＝AC＝2，△ABC＝30°，点P、Q分别在边AB、AC上，将△APQ沿PQ翻折，点A落到点A′处，则线段BA′长度的最小值是．3、如图，在△ABC中，∠BAC＝120°，AB＝AC＝4，点M，N分别在边AB，AC上，将△AMN沿MN 翻折，点A的对应点为A′，连接BA′，则BA′长度的最小值为．4如图，点E为正方形ABCD中AD边上的动点，AB＝2，以BE为边画正方形BEFG，连结CF和CE，则△CEF面积的最小值为．2020重庆中考数学复习几何最值专题复习八参考答案例1、如图，矩形ABCD中，AB＝4，AD＝6，点E，F分别是AB，BC边上的两动点，且EF＝2，点G为EF的中点，点H为AD边上一动点，连接CH，GH，则GH+CH的最小值为（）A．4B．9C．D．解：由已知，点G在以B圆心，1为半径的圆在与长方形重合的弧上运动．作C关于AD的对称点C′，连接C′B，交AD于H，交以D为圆心，以1为半径的圆于G由两点之间线段最短，此时C′B的值最小为，则GH+CH的最小值C′G＝10﹣1＝9，故选：B．例2、（2018春•碑林区校级期末）如图，△ABC中，AB＝AC＝4，∠ABC＝30°，点P，Q分别在边AB，AC上，将△APQ沿PQ翻折，点A落在点A′处，则线段BA′长度的最小值为（）A．4B．4﹣4C．D．2﹣解：如图，当点Q与点C重合，A′点落在BC上时，BA′的长度最小．（圆外一点到圆上的点的最短的线段就是BA′，QA最长时，BA′最短），∵AB＝AC＝4，∠ABC＝30°，∴∠B＝∠ACB＝30°，∠BAC＝180°﹣∠A﹣∠ACB＝120°，∵△PCA′是由△PCA翻折得到，∴∠BAC＝∠PA′C＝120°，∴∠PA′B＝180°﹣∠PA′C＝60°，∴∠BPA′＝90°，过A作AD⊥BC于D，则BD＝CD，∵AB＝4，∠B＝30°，∴AD＝AB＝2，BD＝＝2，∴BC＝2AD＝4，AC＝A′C＝4，∴BA′＝4﹣4，∴BA′的最小值为4﹣4，故选：B．例3、（2018春•金牛区期末）如图，在平行四边形ABCD中，∠A＝45°，AB＝4，AD＝2，M是AD 边的中点，N是AB边上一动点，将线段MN绕点M逆时针旋转90至MN′，连接N′B，N′C，则N′B+N′C的最小值是2．解：如图，作ME⊥AD交AB于E，连接EN′、AC、作CF⊥AB于F．∵∠MAE＝45°，∴△MAE是等腰直角三角形，∴MA＝ME，∵∠AME＝∠NMN′＝90°，∴∠AMN＝∠EMN′，∵MN＝MN′，∴△AMN≌△EMN′，∴∠MAN＝∠MEN′＝45°，∴∠AEN′＝90°，∴EN′⊥AB，∵AM＝DM＝，AB＝4，∴AE＝2，EB＝2，∴AE＝EB，∴N′B＝N′A，∴N′B+N′C＝N′A+N′C，∴当A、N′、C共线时，N′B+N′C的值最小，最小值＝AC，在Rt△BCF中，∵BC＝AD＝2，∠CBF＝∠DAB＝45°，∴CF＝BF＝2，在Rt△ACF中，AC＝＝2例4、（2018秋•成都期末）如图，在矩形ABCD中，AB＝6，AD＝3，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A'MN，连接A'C．在MN上存在一动点P．连接A'P、CP，则△A'PC周长的最小值是﹣+3．解：分两步：①连接AP，则AP＝AP′，∴△A'PC周长＝A′P+PC+A′C＝AP+PC+A′C，∵A′P+PC≥AC，当A、P、C三点共线时，A′P+PC有最小值，是AC的长，∴AC与MN的交点就是点P，由勾股定理得：AC＝＝3，②连接CM，∵A′C≥CM﹣A′M，∴当M、A′、C三点共线时，A′C有最小值，此时，∵M是AD的中点，∴AM＝DM＝1.5，∴MC＝＝，由折叠得：AM＝A′M＝1.5，∴A′C＝MC﹣A′M＝﹣1.5，∴△A'PC周长的最小值是：﹣+3，例5、（2018•无锡）如图，矩形ABCD中，AB＝4，AD＝2，E为边AD上一个动点，连结BE，取BE的中点G，点G绕点E逆时针旋转90°得到点F，连结CF，则△CEF面积的最小值是（）A．4B．C．3D．解：过点F作AD的垂线交AD的延长线于点H，∵∠A＝∠H＝90°，∠FEB＝90°，∴∠FEH＝90°﹣∠BEA＝∠EBA，∴△FEH∽△EBA，∴，设AE＝x，∵AB＝4，AD＝2，∴HF＝x，EH＝2，DH＝x，∴△CEF面积＝＝，∴当x＝1时，△CEF面积的最小值是．故选：B．练习：1、（2019秋•罗湖区期末）如图，矩形ABCD中，AB＝20，AD＝30，点E，F分别是AB，BC边上的两个动点，且EF＝10，点G为EF的中点，点H为AD边上一动点，连接CH、GH，则GH+CH的最小值为45．解：由已知，点G在以B圆心，5为半径的圆在与长方形重合的弧上运动．作C关于AD的对称点C′，连接C′B，交AD于H，交以D为圆心，以5为半径的圆于G由两点之间线段最短，此时C′B的值最小值为＝＝50，则GH+CH的最小值＝50﹣5＝45，2、（2018•瑶海区二模）如图，矩形ABCD中，AB＝2，AD＝3，点E、F分别为AD、DC边上的点，且EF＝2，点G为EF的中点，点P为BC上一动点，则P A+PG的最小值为（）A．3B．4C．2D．5解：∵EF＝2，点G为EF的中点，∴DG＝1，∴G是以D为圆心，以1为半径的圆弧上的点，作A关于BC的对称点A′，连接A′D，交BC于P，交以D为圆心，以1为半径的圆于G，此时PA+PG的值最小，最小值为A′G的长；∵AB＝2，AD＝3，∴AA′＝4，∴A′D＝5，∴A′G＝A′D﹣DG＝5﹣1＝4，∴PA+PG的最小值为4，故选：B．3、（2018•射阳县二模）如图，在矩形ABCD中，AB＝3，AD＝4，现有长为3的小木棒EF紧贴AD、DC边滑动（即EF的两个端点始终落在AD、DC边上），G为EF的中点，P为BC边上一动点，则P A+PG 的最小值为2﹣．解：∵EF＝3，点G为EF的中点，∴DG＝，∴G是以D为圆心，以为半径的圆弧上的点，作A关于BC的对称点A′，连接A′D，交BC于P，交以D为圆心，以为半径的圆于G，此时PA+PG的值最小，最小值为A′G的长；∵AB＝3，AD＝4，∴AA′＝6，∴A′D＝2，∴A′G＝A′D﹣DG＝2﹣，∴PA+PG的最小值为2﹣.4、如图，在△ABC，AB＝AC＝2，△ABC＝30°，点P、Q分别在边AB、AC上，将△APQ沿PQ翻折，点A落到点A′处，则线段BA′长度的最小值是2﹣2．解：如图所示过点A作AD⊥BC于点D．∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD＝×120°＝60°，BD＝DC．∴sin∠BAD＝，即＝．∴BD＝．∴BC＝2．由翻折的性质可知：A′Q＝AQ∵AQ+NQ＝AC＝2，∴A′Q+QC＝2．要求BA′的最小值，只需BA′+A′Q+QC有最小值，由两点之间线段最短可知：当点B、Q、C、A′在同一条直线上时，BA′的长度最小．如图所示由翻折的性质可知：A′C＝AC．∴BA′＝BC﹣A′C＝2﹣2．5、如图，在△ABC中，∠BAC＝120°，AB＝AC＝4，点M，N分别在边AB，AC上，将△AMN沿MN 翻折，点A的对应点为A′，连接BA′，则BA′长度的最小值为4．解：如图所示过点A作AD⊥BC于点D．∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD＝×120°＝60°，BD＝DC．∴sin∠BAD＝，即．∴BD＝2．∴BC＝4．由翻折的性质可知：A′N＝AN，∵AN+NC＝AC＝4，∴A′N+NC＝4．要求BA′的最小值，只需BA′+A′N+NC有最小值，由两点之间线段最短可知：当点B、N、C、A′在同一条直线上时，BA′的长度最小．如图所示：由翻折的性质可知：A′C＝AC．∴BA′＝BC﹣A′C＝4﹣4．6、（2016•江东区一模）如图，点E为正方形ABCD中AD边上的动点，AB＝2，以BE为边画正方形BEFG，连结CF和CE，则△CEF面积的最小值为．解：（方法一）过点F作FM⊥AD延长线于点M，令EF与CD的交点为N点，如图所示．则S△CEF＝CN•ME．∵四边形ABCD为正方形，四边形BEFG为正方形，∴∠A＝90°，∠BEF＝90°，BE＝EF，∴∠AEB+∠ABE＝90°，∠MEF+∠MFE＝90°，∠AEB+∠BEF+∠MEF＝180°，∴∠AEB＝∠MFE，∠ABE＝∠MEF．在△ABE和△MEF中，，∴△ABE≌△MEF（ASA）．∴MF＝AE，ME＝AB．∵CD⊥AD，FM⊥AD，∴ND∥FM，∴△EDN∽△EMF，∴．设AE＝x，则ED＝AD﹣AE＝2﹣x，EM＝AB＝2，MF＝AE＝x，∴DN＝＝﹣x2+x＝﹣（x﹣1）2+≤．∴CN＝CD﹣DN≥2﹣≥．∴△CEF面积的最小值为CN•ME＝××2＝．（方法二）连接CG，如图所示．在△ABE和△CBG中，，∴△ABE≌△CBG（SAS）．设AE＝x，则BE2＝AB2+AE2＝4+x2，∴S正方形BEFG＝BE2＝4+x2．∴S△CEF+S BCG＝S正方形BEFG＝2+x2，∴S△CEF＝S正方形BEFG﹣S BCG＝2+x2﹣S△ABE＝2+x2﹣x＝（x﹣1）2+，当x＝1时，△CEF面积最小，最小值为．。

2020重庆中考复习数学几何最值专题训练24(含答案解析)

2020重庆中考复习数学几何最值专题训练二十四例1、（2020•北碚区自主招生）如图，在平行四边形ABCD中，AB＝2，∠ABC＝45°，点E为射线AD 上一动点，连接BE，将BE绕点B逆时针旋转60°得到BF，连接AF，则AF的最小值是．解：如图，以AB为边向下作等边△ABK，连接EK，在EK上取一点T，使得AT＝TK．∵BE＝BF，BK＝BA，∠EBF＝∠ABK＝60°，∴∠ABF＝∠KBE，∴△ABF≌△KBE（SAS），∴AF＝EK，根据垂线段最短可知，当KE⊥AD时，KE的值最小，∵四边形ABCD是平行四边形，∴AD∥BC，∵∠ABC＝45°，∴∠BAD＝180°﹣∠ABC＝135°，∵∠BAK＝60°，∴∠EAK＝75°，∵∠AEK＝90°，∴∠AKE＝15°，∵TA＝TK，∴∠TAK＝∠AKT＝15°，∴∠ATE＝∠TAK+∠AKT＝30°，设AE＝a，则AT＝TK＝2a，ET＝a，在Rt△AEK中，∵AK2＝AE2+EK2，∴a2+（2a+a）2＝4，∴a＝，∴EK＝2a+a＝，∴AF的最小值为．例2、（2020•沙坪坝区自主招生）如图，Rt△ABC中，∠ACB＝90°，AB＝2AC，BC＝3，点E是AB上的一动点，将△ACE沿CE翻折，得到△A'CE，过点B作BF∥AC交∠BAC的平分线于点F，连接A′F，则A′F长度的最小值为3．解：如图，过点A作AH∥BC交FB的延长线于H，连接AA'，过点C作CP⊥AF于P，∵∠ACB＝90°，AB＝2AC，∴cos∠CAB＝，∴∠CAB＝60°，∴tan∠CAB＝＝，∴AC＝，∵BF∥AC，AH∥BC，∴四边形ACBH是平行四边形，又∵∠ACB＝90°，∴四边形ACBH是矩形，∴∠H＝90°，AH＝BC＝3，∵AF平分∠BAC，∴∠BAF＝∠CAF＝30°，∵BF∥AC，∴∠BFA＝∠FAC＝30°，∴AF ＝2AH ＝6，∵CP ⊥AF ，∠CAF ＝30°，∴CP ＝AC ＝，AP ＝CP ＝，在△AA 'F 中，A 'F ≥AF ﹣AA '，∴当点A '在线段AF 上时，A 'F 有最小值，∵将△ACE 沿CE 翻折，得到△A 'CE ，∴AC ＝A 'C ，又∵CP ⊥AF ，∴AA '＝2AP ＝3， ∴A 'F 的最小值＝6﹣3＝3，例3、已知矩形ABCD 中，P 为CD 上边一点, 8AB =，23AD =,∠PAB=60°,M 为△PAB 内一个动点,则3BM 的最小值为 413DMCMGDCMGP例4、如图,在R △ABC 中，0604B=AB ∠=，，D 为线段AB 上一个动点，以CD 为斜边在CD 的左侧作一个等腰Rt CDE,在点D移动的过程中AE的最小值是322A BCED A BCFGMED A BCFGE例5、（2020•蜀山区校级模拟）如图，等边△ABC的边长为4，点D是边AC上的一动点，连接BD，以BD为斜边向上作等腰Rt△BDE，连接AE，则AE的最小值为（）A．1B．C．2D．2解：如图，过点B作BH⊥AC于H点，作射线HE，∵△ABC是等边三角形，BH⊥AC，∴AH＝2＝CH，∵∠BED＝∠BHD＝90°，∴点B，点D，点H，点E四点共圆，∴∠BHE＝∠BDE＝45°，∴点E在∠AHB的角平分线上运动，∴当AE⊥EH时，AE的长度有最小值，∵∠AHE＝45°，∴AH＝AE＝2，∴AE的最小值为，故选：B．例6、（2019•宝应县一模）如图，点D是等边△ABC的边BC上的一个动点，连结AD，将射线DA绕点D顺时针旋转60°交AC于点E，若AB＝4，则AE的最小值是3．解：∵△ABC为等边三角形，∴∠B＝∠C＝60°，AB＝BC＝AC＝4，∵∠B+∠BAD＝∠ADC＝∠ADE+∠EDC，∠ADE＝60°，∴∠BAD＝∠EDC，∴△ABD∽△DCE，∴＝，设BD＝x，则CD＝4﹣x，∴＝，∴CE＝﹣x2+x，∴AE＝AC﹣CE＝4﹣（﹣x2+x）＝x2﹣x+4＝（x﹣2）2+3，∵＞0，由二次函数的性质可知，当x的值为2时，AE有最小值，最小值为3，例7、（2020春•锡山区期中）如图，在△ABC中，∠BAC＝90°，AB＝AC＝3，D为BC边上一点，且BD：DC＝1：2，以D为一个顶点作正方形DEFG，且DE＝BC，连接AE，将正方形DEFG绕点D 旋转一周，在整个旋转过程中，当AE取得最大值时AG的长为．解：当点A、D、E在同一条直线上时，AE取得最大值．过点A作AM⊥BC于点M，∵∠BAC＝90°，AB＝AC＝3，∴BC＝AB＝3，∴BM＝CM＝，∵BD：DC＝1：2，DE＝BC，∴BD＝，DE＝EF＝DG＝FG＝3，∴DM＝﹣＝，在Rt△ADM中，AD＝＝，在Rt△ADG中，AG＝＝．例8、（2020•萧山区一模）如图，已知△ABC中，∠BAC＝120°，AB＝AC＝2．D为BC边一点，且BD：DC＝1：2．以D为一个点作等边△DEF，且DE＝DC连接AE，将等边△DEF绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AF的长为2．解：如图，点E，F在以D为圆心，DC为半径的圆上，当A，D，E在同一直线上时AE取最大值，过点A作AH⊥BC交BC于H，∴∠BAC＝120°，AB＝AC＝2，∴∠B＝∠ACB＝30°，BH＝CH，∴在Rt△ABH中，AH＝AB＝，BH＝AH＝3，∴BC＝2BH＝6，∵BD：DC＝1：2，∴BD＝2，CD＝4，∴DH＝BH﹣BD＝1，在Rt△ADH中，AH＝，DH＝1，∴tan∠DAH＝＝，∴∠DAH＝30°，∠ADH＝60°，∵△DEF是等边三角形，∴∠E＝60°，DE＝EF＝DC，∵∠ADC＝∠E＝60°，∴DC∥EF，∵DC＝EF，∴四边形DEFC为平行四边形，又∵DE＝DC，∴平行四边形DEFC为菱形，∴FC＝DC＝4，∠DCF＝∠E＝60°，∴∠ACF＝∠ACB+∠DCF＝90°，在Rt△ACF中，AF＝＝＝2，例9、（2019秋•温州期中）如图，AB是半圆O的直径，弦AC＝4，∠CAB＝60°，点D是弧BC上的一个动点，作CG⊥AD，连结BG，在点D移动的过程中，BG的最小值是2﹣2．解：如图，以AC为直径作圆O′，连接BO′、BC，O'G，∵CG⊥AD，∴∠AGC＝90°，∴在点D移动的过程中，点G在以AC为直径的圆上运动，∵AB是直径，∴∠ACB＝90°，在Rt△ABC中，∵AC＝4，∠CAB＝60°，∴AO'＝CO'＝2，AB＝AC÷cos60°＝8，BC＝AB•sin60°＝4，∴BO'＝＝＝2，∵O′G+BG≥O′B，∴当O′、G、B共线时，BG的值最小，最小值为O′B﹣O′G＝2﹣2．例10、如图，AB是半⊙O的直径，点C在半⊙O上，AB＝5cm，AC＝4cm．D是上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE．在点D移动的过程中，BE的最小值为（）A．1B．﹣2C．2﹣1D．3解：如图，连接BO′、BC．∵CE⊥AD，∴∠AEC＝90°，∴在点D移动的过程中，点E在以AC为直径的圆上运动，∵AB是直径，∴∠ACB＝90°，在Rt△ABC中，∵AC＝4，AB＝5，∴BC＝＝＝3，O′E＝2，在Rt△BCO′中，BO′＝＝＝，∵O′E+BE≥O′B，∴当O′、E、B共线时，BE的值最小，最小值为O′B﹣O′E＝﹣2，故选：B．例11、（2016•姜堰区三模）如图，AB是半圆O的直径，点C在半圆O上，AB＝5cm，AC＝4cm．D是弧BC上的一个动点（含端点B，不含端点C），连接AD，过点C作CE⊥AD于E，连接BE，在点D 移动的过程中，BE的取值范围是﹣2≤BE＜3．解：如图，由题意知，∠AEC＝90°，∴E在以AC为直径的⊙M的上（不含点C、可含点N），∴BE最短时，即为连接BM与⊙M的交点（图中点E′点），∵AB＝5，AC＝4，∴BC＝3，CM＝2，则BM＝＝＝，∴BE长度的最小值BE′＝BM﹣ME′＝﹣2，BE最长时，即E与C重合，∵BC＝3，且点E与点C不重合，∴BE＜3，综上，﹣2≤BE＜3，例12、（2020•铁西区二模）如图，△ABC中，AB＝AC，∠ABC＝α，tanα＝，AD⊥BC于点D，点E 是线段AD上的一个动点，连接EB，将线段EB绕点E逆时针旋转2α后得到线段EF，连接AF，若BC＝24，则线段AF的最小值为2．解：如图，作BT∥AD，在BT上取一点使得AT＝BT，连接AT，TE，过点E作EH⊥BF于H．∵BE＝EF，∠BEF＝2α，∴∠EBF＝∠EFB，∴∠EBF+α＝90°，∵AB＝AC，AD⊥BD，∴∠BAD+∠ABD＝90°，即∠BAD+α＝90°，∵AD∥BT，∴∠ABT＝∠BAD，∴∠ABT+α＝90°，∴∠ABT＝∠EBF，∵TA＝TB，∴∠ABT＝∠TAB＝∠EBF＝∠EFB，∵EH⊥BF，∴BH＝FH，∵tan∠BEH＝＝，设BH＝5k，则EH＝6k，BE＝k，∴＝＝，同理可证＝，∴＝，∵∠TBE＝∠ABF，∴△TBE∽△ABF，∴＝＝，∴AF＝TE，∵CD＝DB＝12，tan∠ABC＝＝，∴AD＝10，AB＝＝＝2，∴BT＝AT＝，∵ET最小时，AF的值最小，观察图象可知当E与A重合时，ET的值最小，最小值为，∴AF的最小值＝×＝2．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

含3的几何题专题训练
1、如图，在菱形ABCD中，AC，BD相交于点O，BC＝2OC，E为BC边上一点.
（1）若CE＝6，∠ACE＝15°，求BC的长；
（2）若F为BO上一点，且BF＝EF，G为CE中点，连接FG，AG，求证：AG=3FG．
G F O
D
C
E
O D
A
B
E
2、如图1,在ABCD中,BD为对角线,且AB⊥BD,AB=BD.将BD绕点B顺时针旋转0
60得到BE,连接AE 与∠ABD的角平分线交于点F,连接DF.
（1）若AF=2,求CD的长度
（2）如图2,以AD为边在ABCD外作△DAG,且∠DGA=60°,连接GF.求证3GF
D
F
E
D
F
E
G
图1 图2
3、已知ABCD 中,点P 为AD 上一点,连CP ，交对角线BD 于点E ，使∠EPD=∠EDP ，过点E 作EH ⊥BC 于点H ，点F 为EH 上一点，连接DF 、CF ，且DFC ∆是等边三角形.
（1）
若13,5,BD DC FH EH ====求DP 的长度；（2）
求证：
+.3
DE EF BC =
A
4、如图,已知ABCD 中,E 为AD 上一点，连接BE ，CE ，BF 平分EBC ∠交CD 于F.且FH 为EC 的直平分线, 060CBE ∠=
.
（1）若BF=12,FC=8，求AD 的长度；（2）求证：.BC BE +=
A
5、在菱形ABCD 中,∠ABC=60°,BD 为菱形的一条对角线.
(1)如图1,过A 作AE ⊥BC 于点E,交BD 于点F,若EF=2,求菱形ABCD 的面积；
(2)如图2,M 为菱形ABCD 外一点,过A 作AN ⊥BM 交BM 的延长线于点M,连接AM ，DM ，AG ⊥DM 于点G,且∠AMN=∠AMD,求证:3.DM BM AM =+
6、如图,平行四边形ABCD 中,DB=DC, 0
120BDC ∠=,点M 是底边上一动点,连接DM,以线段DM 为边向线段DM 的右侧作等边△DME,连接BE,点F 是线段BE 中点,连接DF 。

(1)如图1，当点E 恰好落在边CD 上，若BC=8,求线段BE 的长； (2)如图2，连接MF,求证: 33.BC MF DF =+
7、如图,在正方形ABCD 中,对角线AC,BD 相较于点O ，,以AD 为边向外作等边△ADE,连接CE,交BD 于F
（1）如图1,若6AE =
，求DF 的长；
（2）如图2,点M 为AB 的延长线上一点,连接CM,连接FM 且FM 平分∠AMC 求证: 3.CM FM AM =-
F
O
D
A
C B E
F
O
D
A
C
B
E
M
图1 图2
8、如图，已知等腰Rt △ABC ，∠ACB ＝90°，CA ＝CB ，以BC 为边向外作等边△CBD ，连接AD ，过点C 作∠ACB 的角平分线与AD 交于点E ，连接BE ．（1）若AE ＝2，求CE 的长度；
（2）以AB 为边向下作△AFB ，∠AFB ＝60°，连接FE ，求证：F A +FB ＝
FE ．
9、在菱形ABCD 中，0
60,DAB ∠=对角线AC BC 、相交于点,O ，点E 在线段BD 上，连接,CE CD 延长线上一点F ，且,DF DE =连接,.DE AD
（1）如图1
，若
6,OE AB OC ==求线段BE 的长；（2）如图2，若G 是线段CE 的中点，连接,BG FG ,若0
60FBG ∠=
时，求证：.EG =
A
A
图1 图2
10、如图,在平行四边形ABCD 中,030D ∠=，AC=AD,AF ⊥CD ，CM ⊥AN ，点E 在AM 上，且∠CEM=0
30 (1)若
AF=3,求AB 的长；(2)
求证：.BN AE +
=
D
11、已知等边△ABC 和底角是30°的等腰△DFB 且BF=DF,按如图1所示的位置摆放点F 在线
段BC 上连接AD,点E 是AD 中点,连接EF.
(1)如图1,已知EF=3
2,求线段FC 的长;(2)将图1中的△DFB 绕着点B 顺时针旋转任意角度至
如图2的位置时,连接CE 求证:CE⊥EF
且.CE =
B
B
图1 图2
12、如图，等边ABC ∆的边AC 上一点D ，作ACB ∠的平分线CF ，连接DF ，使得CF=DF ，连接BD ，点E 为BD 的中点，连接AE 、EF 。

（1）015DBC ∠=，2AD =,求
AC 的长；（2）求证：.AE =
B
C
13、在等边△ABC 中,AD ⊥BC 于点D 点F 为AD 上任一点,连接BF,点G 为BF 的中点,点E 为AB 上一点,且AE=EF 连接EG 、GC 、CE.
(1)若AF=6,10 3.AB =求FB 的长:(2)求证: 3.CG EG =
14、如图1,在矩形ABCD 中,AC 为对角线,延长CD 至点E 使CE=CA,连接AE.F 为AB 上一点,且BF=DE.连接FC
(1)若DE=1,2 2.CF =求CD 的长；
(2)如图2,点G 为线段AE 的中点,连接BG 交AC 于H 若∠BHC+∠ABG=60°,求证:3.AF CE AC +=
15、已知△ABC 中,AB=AC,∠BAC=120°,点D 是底边上一动点,连接AD,以线段AD 为边向线段AD 的右侧作等边△ADE,连接BE,点F 是线段BE 中点,连接AF.
(1)如图1,当点E 恰好落在边AC 上时,若BC=8,求线段BE 的长; (2)如图2,求证:33.BC DF AF =
+
16、在菱形ABCD 中，∠B=60º，E 是边CD 上一点，以CE 为边作等边∆CEF. （1）如图1，当CE ⊥AD ，CF=23ABCD 的面积；
（2）如图2，过点E 作∠CEF 的平分线交CF 于H ，连接DH ，并延长DH 与AC 的延长交于点P ，若∠ECD=1523.CF CP =
17、如图，在平行四边形ABCD 中, AB AC ⊥,过D 作DE⊥AD 交直线AC 于点E,点O 是对角线
AC 的中点且点F 是线段AD 上一点,连FO 开延长交BC 于点G 。

(1)如图1，若4
=45
AC CAD ∠，cos =,求∆ADE 的面积；
(2)如图2，点H 为DC 延长线上一点,连HF,若∠H=030,DE=BG,求证:
.DH CE FH =+
18、如图，□ABCD 中，∠BAC ＝90°，AB ＝AC ，点E 是边AD 上一点，且BE ＝BC ，BE 交AC 于点F ，过点C 作BE 的垂线，垂足为点O ，与AD 交于点G ．
（1）若AB ＝ 2 ，求AE 的长；（2）求证：BF ＝CO ＋3EO ．
O G F E
D
C
B A。