(完整版)解一元一次方程习题精选附答案
解一元一次方程专项练习60题+解析答案

解一元一次方程-红老师一.解答题(共60小题)1.解方程:.2.解方程:.3.解方程:.4.解方程:.5.解方程:.6.解方程:(1)2﹣=x﹣;(2).7.解方程:.8.解方程:﹣1=.9.解方程:.10.解方程:.11.解方程:.12.解方程.13.解方程:.14.解方程:.15.解方程:.16.解方程:﹣=1.17.解方程:=1.18.解方程:=1﹣.19.解方程:﹣2=.20.解方程:.21.解方程:.22.解关于x的一元一次方程.23.解方程:.24.解方程:.25.解方程:.26.解方程:y﹣=2﹣27.解方程:.28.解方程:.29.解方程:3x+.30.解方程:.31.解方程:.32.解方程:.33.解方程:.34.解方程:.35.解方程:.36.解方程:.37.解方程:﹣=1.38.解方程:.39.解方程:.40.解方程:.41.解方程:.42.解方程:﹣1=.43.解方程:=1﹣.44.解方程:.45.解方程:.46.解方程.47.解方程:(1)3(5﹣x)=18+2x;(2);(3).48.解方程:(1);(2).49.解方程:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x);(2);(3).50.解下列方程(1)(2)51.解方程(1)x=﹣1;(2)﹣=1.52.解方程:(1)3x﹣7(x﹣1)=3﹣2(x+3);(2);(3).53.解方程:(1)3x+=3﹣;(2)+2=.54.解方程(1)4x+3(x﹣20)=8x﹣7(20﹣x)(2)﹣=1.55.解方程:﹣=.56.若3x+1的值比的值少1,求x的值.57.k取何值时,代数式值比的值小1.58.当x为何值时,代数式的值与的值的和等于3?59.已知代数式与代数式.(1)当x为何值时,两个代数式的值相等?(2)当x为何值时,代数式的值比代数式的值大2?60.我们规定一种运算:=ad﹣bc,例如=3×6﹣4×5=﹣2,=4x+6,按照这种运算规定,当x等于多少时,=0.解一元一次方程-红老师参考答案与试题解析一.解答题(共60小题)1.解方程:.【解答】解:去分母得:6﹣2(3﹣5x)=3(3x+1),去括号得:6﹣6+10x=9x+3,移项合并得:x=3.2.解方程:.【解答】解:去分母得:5(3x+1)=2(4x+2),去括号得:15x+5=8x+4,移项得:15x﹣8x=4﹣5,合并同类项得:7x=﹣1,解得:x=﹣.3.解方程:.【解答】解:,去分母,3(2x﹣1)=60﹣5(x﹣5),去括号,6x﹣3=60﹣5x+25,移项,6x+5x=60+3+25,合并同类项,11x=88,化系数为1,x=8.4.解方程:.【解答】解:去分母,得3(x﹣2)=12﹣4x,去括号,得3x﹣6=12﹣4x,移项、合并同类项,得7x=18,系数化为1,得.5.解方程:.【解答】解:去分母得:10x﹣5(x﹣1)=20﹣2(x+18),去括号得:10x﹣5x+5=20﹣2x﹣36,移项合并得:7x=﹣21,解得:x=﹣3.6.解方程:(1)2﹣=x﹣;(2).【解答】解:(1)去分母得:12﹣(x+5)=6x﹣2(x﹣1),去括号得:12﹣x﹣5=6x﹣2x+2,移项得:﹣x﹣6x+2x=2﹣12+5,合并得:﹣5x=﹣5,系数化为1得:x=1;(2)方程整理得:﹣2=,即2x﹣2=5x ﹣2,移项得:2x﹣5x=﹣2+2,合并得:﹣3x=0,系数化为1得:x=0.7.解方程:.【解答】解:去分母,得2(3x﹣2)﹣6=5﹣4x,去括号,得6x﹣4﹣6=5﹣4x,移项,合并同类项,得10x=15,系数化为1,得x=1.5.8.解方程:﹣1=.【解答】解:﹣1=3(x+1)﹣6=2(x﹣2)3x+3﹣6=2x﹣43x﹣2x=﹣1x=﹣1.9.解方程:.【解答】解:去分母得:6x﹣3=12﹣4x﹣8,移项合并得:10x=7,解得:x=0.7.10.解方程:.【解答】解:去分母得:4x﹣10=5﹣2x,移项得:4x+2x=5+10,合并同类项得:6x=15,系数化为1得:x=.11.解方程:.【解答】解:,去分母,得3(x﹣1)+12=4(2x+1),去括号,得3x﹣3+12=8x+4,移项,得3x﹣8x=4+3﹣12,合并同类项,得﹣5x=﹣5,系数化成1,得x=1.12.解方程.【解答】解:去分母得:3(3y﹣1)﹣12=2(5y﹣7),去括号得:9y﹣3﹣12=10y﹣14,移项得:9y﹣10y=﹣14+3+12,合并得:﹣y=1,解得:y=﹣1.13.解方程:.【解答】解:去分母,得3(4x﹣3)﹣15=5(2x﹣2),去括号,得12x﹣9﹣15=10x﹣10,移项,得12x﹣10x=﹣10+9+15,合并同类项,得2x=14,系数化为1,得x=7.14.解方程:.【解答】解:原方程去分母,得:2(3x+2)﹣4=2x ﹣1,去括号,得:6x+4﹣4=2x﹣1,移项,合并同类项,得:4x=﹣1,系数化为1,得:.15.解方程:.【解答】解:4﹣(3x﹣1)=2(3+x),去分母,得4﹣3x+1=6+2x,移项,得﹣3x﹣2x=6﹣4﹣1,合并同类项,得﹣5x=1,系数化1,得x=﹣.16.解方程:﹣=1.【解答】解:方程两边同乘以12得:12×﹣12×=12,则3(x+2)﹣2(2x﹣3)=12,故3x+6﹣4x+6=12,移项合并同类项得:﹣x=0,解得:x=0.17.解方程:=1.【解答】解:,去分母,得4x﹣1=6﹣2(3x﹣1),去括号,得4x﹣1=6﹣6x+2,移项,得4x+6x=6+2+1,合并,得10x=9,系数化为1,得.18.解方程:=1﹣.【解答】解:去分母得:3(x﹣1)=6﹣2(x﹣3),去括号得:3x﹣3=6﹣2x+6,移项得:3x+2x=6+6+3,合并同类项得:5x=15,系数化1得:x=3.19.解方程:﹣2=.【解答】解:去分母:2(x+1)﹣8=x,去括号:2x+2﹣8=x,移项:2x﹣x=8﹣2,合并同类项:x=6.20.解方程:.【解答】解:方程两边同乘以12得:12×﹣12×=12,则3(x+2)﹣2(2x﹣5)=12,故3x+6﹣4x+10=12,移项合并同类项得:﹣x=﹣4,解得:x=4.21.解方程:.【解答】解:,去分母,得2x﹣1﹣6=3(2x+3),去括号,得2x﹣1﹣6=6x+9,移项,得2x﹣6x=9+1+6,合并同类项,得﹣4x=16,系数化为1,得x=﹣4.22.解关于x的一元一次方程.【解答】解:去分母得:3(4x﹣3)﹣15=5(2x﹣2),去括号得:12x﹣9﹣15=10x﹣10,移项得:12x﹣10x=24﹣10,合并同类项得:2x=14,解得:x=7.23.解方程:.【解答】解:,去分母,得2(2x﹣1)+3(x+1)=4,去括号,得4x﹣2+3x+3=4,移项、合并同类项,得7x=3,系数化为1,得.24.解方程:.【解答】解:,去分母得,3(x+2)﹣(4x+3)=6,去括号得,3x+6﹣4x﹣3=6,移项得,3x﹣4x=6﹣6+3,合并同类项得,﹣x=3,系数化为1得,x=﹣3.25.解方程:.【解答】解:去分母得:6x﹣(3x﹣3)=2x+4+6,去括号得:6x﹣3x+3=2x+4+6,移项合并得:x=7.26.解方程:y﹣=2﹣【解答】解:10y﹣5(y﹣1)=20﹣2(y+3),10y﹣5y+5=20﹣2y﹣6,10y﹣5y+2y=20﹣6﹣5,7y=9,y=.27.解方程:.【解答】解:×6﹣×6=2×6,3(x﹣1)﹣2(2﹣x)=12,3x﹣3﹣4+2x=12,5x=19,∴x=.28.解方程:.【解答】解:去分母,得5(1﹣2x)=3(3x+4)﹣15,去括号,得5﹣10x=9x+12﹣15,移项,得﹣10x﹣9x=12﹣15﹣5,合并同类项,得﹣19x=﹣8,系数化为1,得.29.解方程:3x+.【解答】解:去分母得,18x+3(x﹣1)=18﹣2(2x ﹣1),去括号得,18x+3x﹣3=18﹣4x+2,移项得,18x+3x+4x=18+2+3,合并同类项得,25x=23,系数化为1得,x=.30.解方程:.【解答】解:去分母得:3(2x+1)﹣(4x﹣1)=6,去括号得:6x+3﹣4x+1=6,移项得:6x﹣4x=6﹣3﹣1,合并得:2x=2,系数化为1得:x=1.31.解方程:.【解答】解:去分母,可得:3(x﹣3)﹣2(4x+1)=6,去括号,可得:3x﹣9﹣8x﹣2=6,移项,可得:3x﹣8x=6+9+2,合并同类项,可得:﹣5x=17,系数化为1,可得:x=﹣3.4.32.解方程:.【解答】解:去分母,方程两边同时乘以6,得:3(x+2)=12﹣2(x﹣2).去括号,得:3x+6=12﹣2x+4.移项、合并同类项,得:5x=10.未知数的系数化为1,得:x=2.33.解方程:.【解答】解:去分母,可得:3(2x﹣3)﹣12=4(x ﹣4),去括号,可得:6x﹣9﹣12=4x﹣16,移项,可得:6x﹣4x=﹣16+9+12,合并同类项,可得:2x=5,系数化为1,可得:x=2.5.34.解方程:.【解答】解:,去分母,得2(x+1)﹣3(x﹣3)=6,去括号,得2x+2﹣3x+9=6,移项,得2x﹣3x=6﹣9﹣2,合并同类项,得﹣x=﹣5,系数化为1,得x=5.35.解方程:.【解答】解:,去分母,得3(x+1)﹣6=2(3x﹣2),去括号,得3x+3﹣6=6x﹣4,移项,得3x﹣6x=﹣4﹣3+6,合并同类项,﹣3x=﹣1,系数化为1,得.36.解方程:.【解答】解:,3(3y﹣1)﹣12=4(2y+7),9y﹣3﹣12=8y+28,9y﹣8y=28+3+12y=43.37.解方程:﹣=1.【解答】解:2(x﹣3)﹣3(4x+1)=6,2x﹣6﹣12x﹣3=6,2x﹣12x=6+6+3,﹣10x=15,x=﹣.38.解方程:.【解答】解:,去分母,得4(2x+1)﹣(x﹣3)=12,去括号,得8x+4﹣x+3=12,移项,得8x﹣x=12﹣4﹣3,合并同类项,得7x=5,系数化成1,得x=.39.解方程:.【解答】解:去分母得:2x=12+3(2x﹣1),去括号得:2x=12+6x﹣3,移项得:2x﹣6x=12﹣3,合并同类项得:﹣4x=9,系数化为1得:x=﹣.40.解方程:.【解答】解:,去分母,得3(3y+2)﹣12=2(2y﹣1),去括号,得9y+6﹣12=4y﹣2,合并同类项,得9y﹣6=4y﹣2,移项,得9y﹣4y=﹣2+6,合并同类项,得5y=4,系数化为1,得.41.解方程:.【解答】解:去分母得,4(x﹣2)=12﹣3(3x﹣2),去括号得,4x﹣8=12﹣9x+6,移项得,4x+9x=12+6+8,合并同类项得,13x=26,系数化1得,x=2.42.解方程:﹣1=.【解答】解:﹣1=,5x﹣3﹣6=3x,5x﹣3x=3+6,2x=9,x=.43.解方程:=1﹣.【解答】解:方程=1﹣,去分母得:5(2x﹣1)=10﹣2(x﹣3),去括号得:10x﹣5=10﹣2x+6,移项合并得:12x=21,解得:x=.44.解方程:.【解答】解:,两边同时乘以6得:2(2x+1)﹣12=﹣x,整理得:4x﹣10=﹣x,解得x=2,45.解方程:.【解答】解:∵,∴+=3,去分母,可得:2(10x﹣20)+5(10x﹣10)=30,去括号,可得:20x﹣40+50x﹣50=30,移项,可得:20x+50x=30+40+50,合并同类项,可得:70x=120,系数化为1,可得:x=.46.解方程.【解答】解:方程整理得:﹣=1,即﹣2x+1=1,去分母得:2x﹣4﹣6x+3=3,移项得:2x﹣6x=3+4﹣3,合并同类项得:﹣4x=4,解得:x=﹣1.47.解方程:(1)3(5﹣x)=18+2x;(2);(3).【解答】解:(1)去括号得:15﹣3x=18+2x,移项得:﹣3x﹣2x=18﹣15,合并同类项得:﹣5x=3,解得:x=﹣;(2)去括号得:﹣=(x﹣4),去分母得:2﹣(2x﹣5)=x﹣4,去括号得:2﹣2x+5=x﹣4,移项得:﹣2x﹣x=﹣4﹣2﹣5,合并同类项得:﹣3x=﹣11,解得:x=;(3)方程整理得:﹣(2x+4)=1.2,去分母得:10x﹣10﹣3(2x+4)=3.6,去括号得:10x﹣10﹣6x﹣12=3.6,移项得:10x﹣6x=3.6+10+12,合并同类项得:4x=25.6,解得:x=6.4.48.解方程:(1);(2).【解答】解:(1)去分母得:3(3x﹣1)﹣12=2(5x﹣7),去括号得:9x﹣3﹣12=10x﹣14,移项得:9x﹣10x=﹣14+3+12,合并同类项得:﹣x=1,系数化为1得:x=﹣1.(2)化整得:,去分母得:3(3x﹣1)﹣2(2x+9)=﹣36,去括号得:9x﹣3﹣4x﹣18=﹣36,移项得:9x﹣4x=﹣36+3+18,合并同类项得:5x=﹣15,系数化为1得:x=﹣3.49.解方程:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x);(2);(3).【解答】解:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x),2x﹣8﹣12x+3=5﹣5x,2x﹣12x+5x=5+8﹣3,﹣5x=10,x=﹣2;(2),2(2x+1)﹣6=6x﹣(10x+1),4x+2﹣6=6x﹣10x﹣1,4x﹣6x+10x=﹣1﹣2+6,8x=3,x=;(3),﹣1=,15x﹣6=2(17﹣20x),15x﹣6=34﹣40x,15x+40x=34+6,55x=40,x=.50.解下列方程(1)(2)【解答】解:(1)去分母得:15x﹣10=8x+4﹣10,移项合并得:7x=4,解得:x=;(2)方程整理得:=1+,去分母得:1﹣20x=3+20x,移项合并得:40x=﹣2,解得:x=﹣.51.解方程(1)x=﹣1;(2)﹣=1.【解答】解:(1)去分母,可得:6x+2(1﹣x)=x+2﹣6,去括号,可得:6x+2﹣2x=x+2﹣6,移项,可得:6x﹣2x﹣x=2﹣6﹣2,合并同类项,可得:3x=﹣6,系数化为1,可得:x=﹣2.(2)∵﹣=1,∴﹣=1,去分母,可得:30x﹣7(17﹣20x)=21,去括号,可得:30x﹣119+140x=21,移项,可得:30x+140x=21+119,合并同类项,可得:170x=140,系数化为1,可得:x=.52.解方程:(1)3x﹣7(x﹣1)=3﹣2(x+3);(2);(3).【解答】解:(1)3x﹣7(x﹣1)=3﹣2(x+3),去括号得:3x﹣7x+7=3﹣2x﹣6,移项得:3x﹣7x+2x=3﹣6﹣7,合并同类项得:﹣2x=﹣10,系数化为1得:x=5;(2),去分母得:2(1﹣2x)﹣18x=3(x﹣1)﹣18,去括号得:2﹣4x﹣18x=3x﹣3﹣18,移项得:2+3+18=3x+4x+18x,合并同类项得:25x=23,系数化为1得:x=;(3)﹣=x,分母化为整数得:﹣=x,去分母得:3(3x﹣5)﹣2(12﹣5x)=6x,去括号得:9x﹣15﹣24+10x=6x,移项得:9x+10x﹣6x=15+24,合并同类项得:13x=39,系数化为1得:x=3.53.解方程:(1)3x+=3﹣;(2)+2=.【解答】解:(1)3x+=3﹣,去分母得:18x+3(x﹣1)=18﹣2(2x﹣1),去括号得:18x+3x﹣3=18﹣4x+2,移项得:18x+3x+4x=18+3+2,合并同类项得:25x=23,系数化为1得:x=;(2)+2=化简得,去分母得:3(3x﹣4)+12=2(5x﹣2),去括号得:9x﹣12+12=10x﹣4,移项得:9x﹣10x=﹣4,合并同类项得:﹣x=﹣4,系数化为1得:x=4.54.解方程(1)4x+3(x﹣20)=8x﹣7(20﹣x)(2)﹣=1.【解答】解:(1)去括号得:4x+3x﹣60=8x﹣140+7x,移项合并得:8x=80,解得:x=10;(2)方程整理得:﹣=1,去分母得:30y﹣119+140y=21,解得:y=.55.解方程:﹣=.【解答】解:化简得:﹣=,去分母得:9(30x﹣15)﹣2(20x﹣10)=18(4﹣8x),去括号得:270x﹣135﹣40x+20=72﹣144x,移项合并同类项得:374x=187,系数化为1得:x=0.5.56.若3x+1的值比的值少1,求x的值.【解答】解:由题意,得,去分母,得6x+2=5x+1﹣2,移项合并,得x=﹣3.57.k取何值时,代数式值比的值小1.【解答】解:由题意得:﹣=﹣1,去分母得2(k+1)﹣3(3k+1)=﹣6,去括号得2k+2﹣9k﹣3=﹣6,移项、合并同类项得:﹣7k=﹣5,系数化1得:.58.当x为何值时,代数式的值与的值的和等于3?【解答】解:根据题意得:+=3,去分母得:6﹣3x+2x+2=18,移项合并得:﹣x=10,解得:x=﹣10.59.已知代数式与代数式.(1)当x为何值时,两个代数式的值相等?(2)当x为何值时,代数式的值比代数式的值大2?【解答】解:(1)根据题意列式为:,去分母得:3x=4(2﹣x),去括号得:3x=8﹣4x,移项、合并同类项,得:7x=8,系数化为1得:.(2)根据题意列式为:,去分母得:3x﹣4(2﹣x)=24,去括号得:3x﹣8+4x=24,移项、合并同类项得:7x=32,系数化为1得:.60.我们规定一种运算:=ad﹣bc,例如=3×6﹣4×5=﹣2,=4x+6,按照这种运算规定,当x等于多少时,=0.【解答】解:∵=ad﹣bc,∴(+1)×(﹣1)=(﹣2)x,解得:x=,故当x=时,=0.。
解一元一次方程习题精选含答案解析
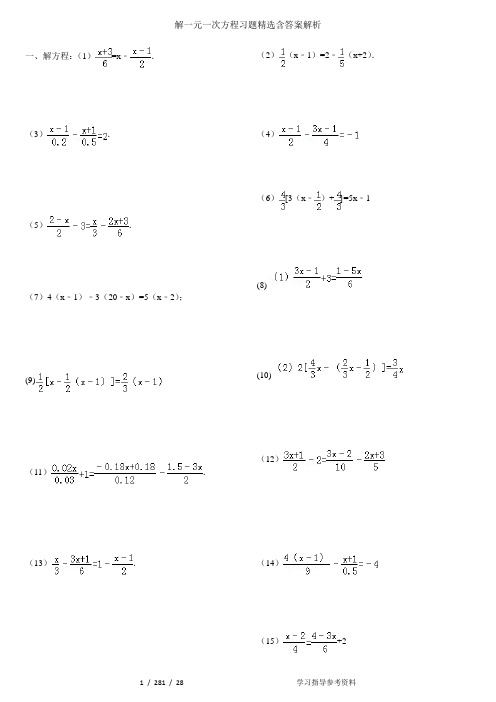
一、解方程:(1)=x ﹣.(3).(5).(7)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(9)(11).(13).(2)(x﹣1)=2﹣(x+2).(4)(6)[3(x ﹣)+]=5x﹣1 (8)(10)(12)(14)(17)(19)x ﹣﹣3(21).(23).20.解方程(1).(2).(I8)12y﹣2.5y=7.5y+5(20).(22).二、计算:(1)(2)÷(4)﹣42×+|﹣2|3×(﹣)3(5)当k 为什么数时,式子比的值少3.6.2.4解一元一次方程(三)参考答案与试题解析一.解答题(共30小题)1.(2005•宁德)解方程:2x+1=7考点:解一元一次方程.专题:计算题;压轴题.分析:此题直接通过移项,合并同类项,系数化为1可求解.解答:解:原方程可化为:2x=7﹣1 合并得:2x=6系数化为1得:x=3点评:解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.2.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),化简可得:3x+3=8x﹣8,移项可得:5x=11,解可得x=.故原方程的解为x=.点评:若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;移项得:﹣x+3x=6﹣4,合并得:2x=2,系数化为1得:x=1.(2)去分母得:5(x﹣1)﹣2(x+1)=2,去括号得:5x﹣5﹣2x﹣2=2,移项得:5x﹣2x=2+5+2,合并得:3x=9,系数化1得:x=3.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.4.解方程:.考点:解一元一次方程.专题:计算题.分析:此题两边都含有分数,分母不相同,如果直接通分,有一定的难度,但将方程左右同时乘以公分母6,难度就会降低.解答:解:去分母得:3(2﹣x)﹣18=2x﹣(2x+3),去括号得:6﹣3x﹣18=﹣3,移项合并得:﹣3x=9,∴x=﹣3.点评:本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x﹣=2﹣.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项、合并同类项、化系数为1,从而得到方程的解;(2)先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣4﹣60+3x=5x﹣10(2分)移项得:4x+3x﹣5x=4+60﹣10(3分)合并得:2x=54(5分)系数化为1得:x=27;(6分)(2)去分母得:6x﹣3(x﹣1)=12﹣2(x+2)(2分)去括号得:6x﹣3x+3=12﹣2x﹣4(3分)移项得:6x﹣3x+2x=12﹣4﹣3(4分)合并得:5x=5(5分)多项式)作为一个整体加上括号.去括号时要注意符号的变化.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x﹣.考点:解一元一次方程.专题:计算题.分析:(1)是简单的一元一次方程,通过移项,系数化为1即可得到;(2)是较为复杂的去分母,本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)3x﹣3=2x+33x﹣2x=3+3x=6;(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0.点评:本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.7.﹣(1﹣2x)=(3x+1)考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:﹣7(1﹣2x)=3×2(3x+1)﹣7+14x=18x+6﹣4x=13x=﹣.点评:解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1.此题去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.8.解方程:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1;(2).点:专题:计算题.分析:(1)可采用去括号,移项,合并同类项,系数化1的方式进行;(2)本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+13x﹣7=4x﹣2∴x=﹣5;(2)原方程可化为:去分母得:40x+60=5(18﹣18x)﹣3(15﹣30x),去括号得:40x+60=90﹣90x﹣45+90x,移项、合并得:40x=﹣15,系数化为1得:x=.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果;(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.9.解方程:.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:,去分母得:2x﹣(3x+1)=6﹣3(x﹣1),去括号得:2x﹣3x﹣1=6﹣3x+3,移项、合并同点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,合并同类项,系数化1,即可求出方程的解;(2)先去分母,再去括号,移项,合并同类项,系数化1可求出方程的解.解答:解:(1)4x﹣3(4﹣x)=2去括号,得4x﹣12+3x=2移项,合并同类项7x=14系数化1,得x=2.(2)(x﹣1)=2﹣(x+2)去分母,得5﹣4移项、合并同类项,得7x=21系数化1,得x=3.点评:(1)此题主要是去括号,移项,合并同类项,系数化1.(2)方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.11.计算:(1)计算:(2)解方程:考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)根据有理数的混合运算法则计减;(2)两边同时乘以最简公分母4,即可去掉分母.解答:解:(1)原式=,=,=.(2)去分母得:2(x﹣1)﹣(3x﹣1)=﹣4,解得:x=3.点评:解答此题要注意:(1)去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数;(2)去分母就是方程两边同时乘以分母的最简公分母.12.解方程:考点:解一元一次方程.专题:计算题.分析:(1)这是一个带分母的方程,所以要为1,从而得到方程的解.(2)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.解答:解:(1)去分母得:3(3x﹣1)+18=1﹣5x,去括号得:9x﹣3+18=1﹣5x,移项、合并得:14x=﹣14,系数化为1得:x=﹣1;(2)去括号得:x﹣x+1=x,移项、合并同类项得:x=﹣1,系数化为1得:x=﹣.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.13.解方程:(2)考点:解一元一次方程.专题:计算题.分析:(1)去分母、去括号、移项、合并同类项、化系数为1.(2)去分母、去括号、移项、合并同类项、化系数为1.解答:(1)解:去分母得:5(3x+1)﹣2×10=3x﹣2﹣2(2x+3),去括号得:15x+5﹣20=3x﹣2﹣4x﹣6,移项得:15x+x=﹣8+15,合并得:16x=7,解得:;(2)解:,4(x﹣1)﹣18(x+1)=﹣36,4x﹣4﹣18x﹣18=﹣36,﹣14x=﹣14,x=1.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+2(3)[3(x﹣)+]=5x﹣1考点:解一元一次方程.专题:计算题.分析:(2)通过去括号、移项、合并同类项、系数化为1,解得x的值;(3)乘最小公倍数去分母即可;(4)主要是去括号,也可以把分数转化成整数进行计算.解答:解:(1)去括号得:10x+5﹣4x+6=6移项、合并得:6x=﹣5,方程两边都除以6,得x=﹣;(2)去分母得:3(x﹣2)=2(4﹣3x)+24,去括号得:3x﹣6=8﹣6x+24,移项、合并得:9x=38,方程两边都除以9,得x=;(3)整理得:[3(x﹣)+]=5x﹣1,4x﹣2+1=5x﹣1,移项、合并得:x=0.点评:一元一次方程的解法:一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.解题时,要灵活运用这些步骤.15.(A类)解方程:5x﹣2=7x+8;(B类)解方程:(x﹣1)﹣(x+5)=﹣;(C类)解方程:.考点:解一元一次方程.专题:计算题.分析:通过去分母、去括号、移项、系数化为1等方法,求得各方程的解.解答:解:A类:5x﹣2=7x+8移项:5x﹣7x=8+2化简:﹣2x=10即:x=﹣5;B类:(x﹣1)﹣(x+5)=﹣去括号:x﹣﹣x﹣5=﹣化简:x=5即:x=﹣;C类:﹣=1去分母:3(4﹣x)﹣2(2x+1)=6去括号:12﹣3x﹣4x﹣2=6化简:﹣7x=﹣4即:x=.点评:本题主要考查一元一次方程的解法,比较简单,但要细心运算.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)考点:解一元一次方程.专题:计算题.分析:(1)去括号以后,移项,合并同类项,系数化为1即可求解;(2)(3)首先去掉分母,再去括号以后,移项,合并同类项,系数化为1以后即可求解;(4)首先根据分数的基本性质,把第一项分母中的0.3化为整数,再去分母,求解.解答:解:(1)去括号得:3x+18=9﹣5+10x 移项得:3x﹣10x=9﹣5﹣18合并同类项得:﹣7x=﹣14则x=2;(2)去分母得:2x+1=x+3﹣5移项,合并同类项得:x=﹣3;(3)去分母得:10y+2(y+2)=20﹣5(y﹣1)去括号得:10y+2y+4=20﹣5y+5移项,合并同类项得:17y=21系数化为1得:;(4)原方程可以变形为:﹣5x=﹣1去分母得:17+20x﹣15x=﹣3移项,合并同类项得:5x=﹣20系数化为1得:x=﹣4.解方程的过程中要注意每步的依据,这几个题目都是基础的题目,需要熟练掌握.点评:17.解方程:(1)解方程:4x﹣3(5﹣x)=13(2)解方程:x﹣﹣3考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,化系数为1,从而得到方程的解.(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣15+3x=13,移项合并得:7x=28,系数化为1得:得x=4;(2)原式变形为x+3=,去分母得:5(2x﹣5)+3(x﹣2)=15(x+3),去括号得10x﹣25+3x﹣6=15x+45,移项合并得﹣2x=76,系数化为1得:x=﹣38.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.18.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2](3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.考点:解一元一次方程;有理数的混合运算.分析:(1)利用平方和立方的定义进行计算.(2)按四则混合运算的顺序进行计算.(3)主要是去括号,移项合并.乘最小公倍数去分母,再求值.解答:解:(1)﹣42×+|﹣2|3×(﹣)3==﹣1﹣1=﹣2.(2)﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2]====.(3)解方程:4x﹣3(5﹣x)=2去括号,得4x﹣15+3x)=2移项,得4x+3x=2+15合并同类项,得7x=17系数化为1,得.(4)解方程:去分母,得15x﹣3(x﹣﹣3×15去括号,得15x﹣3x+6=10x﹣25﹣45移项,得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项,得2x=﹣76系数化为1,得x=﹣38.点评:前两道题考查了学生有理数的混合运算,后两道考查了学生解一元一次方程的能力.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:.考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)和(2)要熟练掌握有理数的混合运算;(3)和(4)首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1.解答:解:(1)(1﹣2﹣4)×=﹣=﹣13;(2)原式=﹣1×(﹣4﹣2)×(﹣)=6×(﹣)=﹣9;(3)解方程:3x+3=2x+7移项,得3x﹣2x=7﹣3合并同类项,得x=4;(4)解方程:去分母,得6(x+15)=15﹣10(x﹣7)去括号,得6x+90=15﹣10x+70移项,得6x+10x=15+70﹣90合并同类项,得16x=﹣5系数化为1,得x=.点评:(1)和(2)要注意符号的处理;(4)要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括号法则以及合并同类项法则.20.解方程(1)﹣0.2(x﹣5)=1;(2).考点:解一元一次方程.分析:(1)通过去括号、移项、系数化为1等过程,求得x的值;(2)通过去分母以及去括号、移项、系数化为1等过程,求得x的值.解答:解:(1)﹣0.2(x﹣5)=1;去括号得:﹣0.2x+1=1,∴﹣0.2x=0,∴x=0;(2).去分母得:2(x﹣2)+6x=9(3x+5)﹣(1﹣2x),∴﹣21x=48,∴x=﹣.点评:此题主要考查了一元一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.考点:解一元一次方程.专题:计算题.分析:先去括号得x+3﹣2x+2=9﹣3x,然后移项、合并同类得到2x=4,然后把x的系数化为1即可.解答:解:去括号得x+3﹣2x+2=9﹣3x,移项得x﹣2x+3x=9﹣3﹣2,合并得2x=4,系数化为1得x=2.点评:本题考查了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知数的项移到方程右边,然后合并同类项,最后把未知数的系数化为1得到原方程的解.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x)...考点:解一元一次方程.专题:方程思想.分析:本题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化1求解.第二个先去括号再通过移项、合并同类项及系数化1求解.第三个先去分母再同第二个.第四个先分子分母乘以10,再同第三个求解.解答:8x﹣3=9+5x,解:8x﹣5x=9+3,3x=12,∴x=4.∴x=4是原方程的解;5x+2(3x﹣7)=9﹣4(2+x),解:5x+6x﹣14=9﹣8﹣4x,5x+6x+4x=9﹣8+14,15x=15,∴x=1.∴x=1是原方程的解..解:3(x﹣1)﹣2(2x+1)=12,3x﹣3﹣4x﹣2=12,3x﹣4x=12+3+2,﹣x=17,∴x=﹣17.∴x=﹣17是原方程的解.,解:,5(10x﹣3)=4(10x+1)+40,50x﹣15=40x+4+40,50x﹣40x=4+40+15,10x=59,∴x=.∴x=是原方程的解.点评:此题考查的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号.23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.考点:解一元一次方程.分析:(1)首先去括号,然后移项、合并同类项,系数化成1,即可求解;(2)首先去分母,然后去括号,移项、合并同类项,系数化成1,即可求解解答:解:(1)去括号,得:0.5x﹣0.7=5.2﹣1.3x+1.3移项,得:0.5x+1.3x=5.2+1.3+0.7合并同类项,得:1.8x=7.2,则x=4;(2)去分母得:7(1﹣2x)=3(3x+1)﹣42,去括号,得:7﹣14x=9x+3﹣42,移项,得:﹣14x﹣9x=3﹣42﹣7,合并同类项,得:﹣23x=﹣46,则x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).考点:解一元一次方程.分析:(1)移项,合并同类项,然后系数化成1即可求解;(2)移项,合并同类项,然后系数化成1即可求解;(3)去括号、移项,合并同类项,然后系数化成1即可求解;(4)首先去分母,然后去括号、移项,合并同类项,然后系数化成1即可求解.解答:解:(1)3x=10.5,x=3.5;(2)3x﹣2x=6﹣8,x=﹣2;(3)2x+3x+3=5﹣4x+4,2x+3x+4x=5+4﹣3,9x=6,x=;(4)2(x+1)+6=3(3x﹣2),2x+2+6=9x﹣6,2x﹣9x=﹣6﹣2﹣6,﹣7x=﹣14,x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.解方程:.考点:解一元一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,移项合并,将x系数化为1,即可求出解.解答:解:去分母得:5(3x﹣1)﹣2(5x﹣6)=2,去括号得:15x﹣5﹣10x+12=2,移项合并得:5x=﹣5,解得:x=﹣1.点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.26.解方程:(1)10x﹣12=5x+15;(2)考点:解一元一次方程.专题:计算题.分析:(1)先移项,再合并同类项,最后化系数为1,从而得到方程的解;(2)先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解答:解:(1)移项,得10x﹣5x=12+15,合并同类项,得5x=27,方程的两边同时除以5,得x=;(2)去括号,得=,方程的两边同时乘以6,得x+1=4x﹣2,移项、合并同类项,得3x=3,方程的两边同时除以3,得x=1.点评:本题考查解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.27.解方程:(1)8y﹣3(3y+2)=7(2).考点:解一元一次方程.专题:计算题.分析:(1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(1)去括号得,8y﹣9y﹣6=7,移项、合并得,﹣y=13,系数化为1得,y=﹣13;(2)去分母得,3(3x﹣1)﹣12=2(5x﹣7),去括号得,9x﹣3﹣12=10x﹣14,移项得,9x﹣10x=﹣14+3+12,合并同类项得,﹣x=1,系数化为1得,x=﹣1.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.28.当k 为什么数时,式子比的值少3.考点:解一元一次方程.专题:计算题.分析:先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解答:解:依题意,得=+3,去分母得,5(2k+1)=3(17﹣k)+45,去括号得,10k+5=51﹣3k+45,移项得,10k+3k=51+45﹣5,合并同类项得,13k=91,系数化为1得,k=7,∴当k=7时,式子比的值少3.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.29.解下列方程:(I)12y﹣2.5y=7.5y+5(II ).考点:解一元一次方程.专题:计算题.分析:(Ⅰ)根据一元一次方程的解法,移项,合并同类项,系数化为1即可得解;(Ⅱ)是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(Ⅰ)移项得,12y﹣2.5y﹣7.5y=5,合并同类项得,2y=5,系数化为1得,y=2.5;(Ⅱ)去分母得,5(x+1)﹣10=(3x﹣2)﹣2(2x+3),去括号得,5x+5﹣10=3x﹣2﹣4x﹣6,移项得,5x﹣3x+4x=﹣2﹣6﹣5+10,合并同类项得,6x=﹣3,系数化为1得,x=﹣.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.30.解方程:.考点:解一元一次方程.专题:计算题.分析:由于方程的分子、分母均有小数,利用分数的基本性质,分子、分母同时扩大相同的倍数,可将小数化成整数.解答:解:原方程变形为,(3分)去分母,得3×(30x﹣11)﹣4×(40x﹣2)=2×(16﹣70x),(4分)去括号,得90x﹣33﹣160x+8=32﹣140x,(5分)移项,得90x﹣160x+140x=32+33﹣8,(6分)合并同类项,得70x=57,(7分)系数化为1,得.(8分)点评:本题考查一元一次方程的解法.解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.本题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.。
解一元一次方程习题及答案

3.2解一元一次方程(1)一、单选题1.方程的解是().A.B.C.D.2.下列方程变形正确的是()A.由得B.由得C.由得D.由得3.已知关于x的方程2x+a=1-x与方程2x-3=1的解相同,则a的值为()A.2B.-2C.5D.-5 4.解方程5x-3=2x+2,移项正确的是()A.5x-2x=3+2B.5x+2x=3+2C.5x-2x=2-3D.5x+2x=2-3 5.下列解方程的过程中,移项错误的是()A.方程变形为B.方程变形为C.方程变形为D.方程变形为6.在解方程x﹣2=4x+5时,下列移项正确的是()A.x+4x=5﹣2B.x+4x=2+5C.x﹣4x=5+2D.x﹣4x=﹣2﹣57.下列式子的变形中,正确的是()A.由6+x=10得x=10+6B.由3x+5=4x得3x-4x=-5C.由8x=4-3x得8x-3x=4D.由2(x-1)=3得2x-1=38.如果x=1是关于x的方程-x+a=3x-2的解,则a的值为()A.1B.-1C.2D.-2 9.将方程移项,可以得到()A.B.C.D.10.下列方程移项、系数化为1正确的是()A.由3+x=5,得x=5+3B.由2x+3=x+7,得2x+x=7+3C.由7x=﹣4,得x=﹣D.由y=2,得y=4二、填空题11.方程的解是.12.如图是正方体的展开图,相对两个面上的数互为倒数,则x=,y=.13.若方程2x+a=1与方程3x﹣1=2x+2的解相同,则a的值为.14.若3x m+5y3与x2y n的差仍为单项式,则m+n=.15.若2a+3与3互为相反数,则a=.三、计算题16.解下列方程:.17.解方程:.18.解方程:.四、解答题19.已知关于x的一元一次方程ax-2=7与方程2x-1=5的解互为相反数,求a的值.20.若整式的值比整式的值大1,求x的值.21.现规定一种新运算,规则如下:※,已知3※,求x的值.22.若方程与关于的方程有相同的解,求的值.23.小莹在解关于的方程时,误将看作,得方程的解为,求原方程的解为多少?24.(1)解方程:(2)先化简,再求值:,其中,答案解析部分1.【答案】A【解析】【解答】解:,移项得,,合并同类项得,,故答案为:A.【分析】根据解一元一次方程的解题步骤“移项、合并同类项”求出方程的解,即可得出答案. 2.【答案】C【解析】【解答】解:A.由得,不符合题意;B.由得,不符合题意;C.由得,符合题意;D.由得,不符合题意.故答案为:C.【分析】利用等式的性质逐项判断即可。
完整版)解一元一次方程习题精选附答案

完整版)解一元一次方程习题精选附答案6.2.4 解一元一次方程一、解答题(共30小题)1.解方程:2x+1=7.2.删除此题。
3.(1)解方程:4-x=3(2-x);2)解方程:删除此题。
4.解方程:删除此题。
5.解方程:1)4(x-1)-3(20-x)=5(x-2);2)x-1=2(x+1)。
6.(1)解方程:3(x-1)=2x+3;2)解方程:x-1=3(x-2)。
7.-1+2x=3x+1.8.解方程:1)5(x-1)-2(x+1)=3(x-1)+x+1;2)删除此题。
9.解方程:删除此题。
10.解方程:1)4x-3(4-x)=2;2)(x-1)+2=2-(x+2)。
11.(1)计算:删除此题。
2)解方程:删除此题。
12.解方程:删除此题。
13.解方程:1)删除此题。
2)删除此题。
14.解方程:1)5(2x+1)-2(2x-3)=6;2)x+2;3)3(x-1)+2=5x-1.15.(A类)解方程:5x-2=7x+8;B类)解方程:(x-1)-(x+5)=-2;C类)解方程:删除此题。
16.解方程:1)3(x+6)=9-5(1-2x);2)删除此题;3)删除此题;4)删除此题。
17.解方程:1)4x-3(5-x)=13;2)x+3.18.(1)计算:-42x+|-2|3x(-1);2)计算:-12-|0.5-2|÷2×[-2-(-3)2];3)4x-3(5-x)=2;4)(x+1)+2=4(x-1)。
19.(1)计算:-1-2-4×(-2);2)计算:-6÷2;3)3x+3=2x+7;4)2x-3=5x+1.20.解方程:1)-0.2(x-5)=1;2)删除此题。
21.解方程:(x+3)-2(x-1)=9-3x。
22.8x-3=9+5x;5x+2(3x-7)=9-4(2+x)。
23.解下列方程:1)0.5x-0.7=5.2-1.3(x-1);2)x+3=-2.24.解方程:1)-0.5+3x=10;2)x= -1;3)5x+3=1;4)删除此题。
七年级解一元一次方程经典50道练习题(带答案)-精选

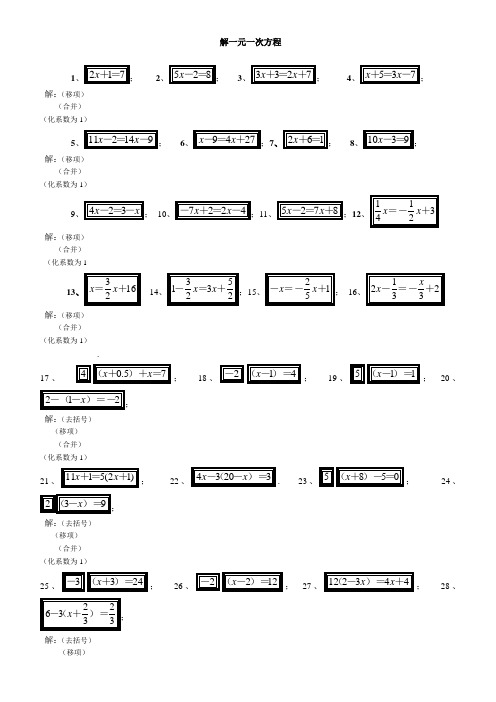
自我测试 60 分钟看看准确率 牛刀小试 相信自己一定行1、2x +1=7;2、5x -2=8;3、3x +3=2x +7;4、x +5=3x -7 ;解:(移项)(合并) (化系数为 1)5、11x -2=14x -9;6、x -9=4x +27 ;7、 2x +6=1;8、10 x -3=9;解:(移项)(合并) (化系数为 1)1 1 9、4x -2=3-x ; 10、-7x +2=2x -4 ;11、5x -2=7x +8 ;12、 x =- x 3 42+解:(移项)(合并) (化系数为 1313、 x = x 1614、+ 23 5 21 x1- x =3x + ;15、1-xx + ; 16、 x2=-2 - =- +2253 3解:(移项)(合并)(化系数为 1).17、4(x +0 .5)+x =7 ; 18、-2(x -1)=4;19、5(x -1)=1; 20、 2-(1-x )=- 2 ;解:(去括号) (移项) (合并) (化系数为 1)21、11x +1=5(2x +1) ;22、4x -(3 2 0-x )=3.23、5(x +8)-5=0;24、2(3-x )=9 ;解:(去括号) (移项) (合并) (化系数为 1)25、-3(x +3)=24 ; 26、-2(x -2)=12 ; 27、1(2 2-3x )=4x +4 ; 28、2 26-(3 x + )= ;3 3解:(去括号)(移项) (合并) (化系数为 1)29、(2 200-15x )=70+25x ;30、(3 2x +1)=12 .31、解:(去分母)x +2x = 5 4; 32、3-xx +4 = 2 3;(去括号) (移项) (合并) (化系数为 1)1 1 1 1 2x-1 x 2+33、(x+1)=(2x-3);34、(x+1)=(x-1);35、 1=-;3 74 3 3 4解:(去分母)(去括号)(移项)(合并)(化系数为 11 1 1 1 1 1 136、(x-1)=2-(x+2). 37、(x+14)=(x+20);38、(x+15)=-(x-7).2 5 7 4 5 2 3解:(去分母)(去括号)(移项)(合并)(化系数为 139、1413x;40、-=247 x5-4=38;41、2x-1 5x+1=68;42、19x-2x-;7=26解:(去分母)(去括号)(移项)(合并)(化系数为 11 1 2x+1 5x 1-43、x- 3 2x 1;44、 1(-)=-=5 2 3 6解:(去分母)1;45、2x14 4 2x(+)=-;7(去括号)(移项)(合并)(化系数为 146、3 29(200 x 300 x 300 .47、(8 3x-1)-(9 5x-11)-(2 2x-7)=30;+)-(-)=10 1025解:(去分母)(去括号)(移项)(合并)(化系数为 148、121 1 1 0.5 x-1 0 .1x 2+x+x ;49、 1=--=-;50、3 4 5 0.2 0.3x 1-0.3-x+20.5=12 .解:(化整)(去分母)(去括号)(移项)(合并)(化系数为1【参考答案】 1、【答案】(1)x =3 ;(2)x =2; (3)x =4 ;(4)x =6;(5)7x ; (6) x =-12 ; (7) x =4 ; (8) x =- 32. = 31.1、【答案】 (9) 5 x ; (10) =- 2 6 x = ; (11) x =- 5; (12) 51x ;=- 3( 13) x =1; ( 14) 2 x ; ( 15) = 3 5x ; (16) x =1.=- 32、【答案】(17) x =1;(18) x =-1;(19)6x ; ( 20) x =-3 ; ( 21) x =4 ; (22) x =9.= 52.1、【答案】 (23) x =- 7 ;(24)3x =- ; (25) x =-11; (26) x =- 4 ; (27)2 1 x = ; (28) 2 10 x = ;9(29) x =6;(30)3x = .23、【答案】(31) x =8 ;(32)1x = ;(33) x =-16 ;(34) x =7 ;(35)52 x =- ;5(36) x =3 ; ( 37) x =- 28 ;(38)5x =-.163.1、【答案】 (39) x =5;(40)13x = ;(41) x =- 1;(42)1420 x ; (43) =- 325 x = ; 12(44) x =- 3;(45)7x = ; (46) x =216 .84、【答案】(47) x =3 ; (48)32x =- ; (49) 15 64 x = ; (50) 13 29x = .2。
解一元一次方程习题精选附答案

考点:
解一元一次方程.
专题:
计算题.
分析:
这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.
解答:
解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),
化简可得:3x+3=8x﹣8,
移项可得:5x=11,
解可得x= .
故原方程的解为x= .
点评:
若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.
解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1
3x﹣7=4x﹣2
∴x=﹣5;
(2)原方程可化为:
去括号得:6﹣3x﹣18=﹣3,
移项合并得:﹣3x=9,
∴x=﹣3.
点评:
本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.
5.解方程
(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);
(2)x﹣ =2﹣ .
考点:
解答:
解:(1)3x﹣3=2x+3
3x﹣2x=3+3
x=6;
(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)
x+3=6x﹣3x+3
x﹣6x+3x=3﹣3
﹣2x=0
∴x=0.
点评:
本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.
专题 解一元一方程计算题(50题)(解析版)

七年级上册数学《第三章一元一次方程》专题训练解一元一次方程计算题(50题)步骤依据具体做法注意事项等式的性质2方程两边同时乘各分母的最小公倍数.(1)不要漏乘不含分母的项.(2)当分子是多项式时,去分母后应将分子作为一个整体加上括号.乘法分配律、去括号法则先去小括号,再去中括号,最后去大括号(也可以先去大括号,再去中括号,最后去小括号).(1)不要漏乘括号里的任何一项.(2)不要弄错符号.等式的性质1把含未知数的项移到方程的一边,常数项移到方程的另一边.(1)移项一定要变号.(2)不移的项不要变号.合并同类项法则系数相加,字母及字母的指数不变,把方程化成ax =b (a ≠0)的形式.未知数的系数不要弄错.等式的性质2在方程ax =b (a ≠0)的两边同除以a (或乘),得到方程的解为x=.不要将分子、分母的位置颠倒.1.(2022秋•宁津县校级期中)解下列方程:(1)﹣3x+3=1﹣x﹣4x;(2)﹣4x+6=5x﹣3;【分析】(1)根据解一元一次方程——移项合并同类项进行计算即可;(2)根据解一元一次方程——移项合并同类项进行计算即可.【解答】解:(1)移项得﹣3x+x+4x=1﹣3,合并得2x=﹣2,系数化为1得x=﹣1;(2)移项得﹣4x﹣5x=﹣3﹣6,合并得﹣9x=﹣9,系数化为1得x=1.【点评】本题考查解一元一次方程——移项合并同类项,掌握一元一次方程的解法是解决此题的关键.2.(2023秋•洛阳期中)解下列方程:(1)−3=12+1;(2)9+3x=4x+3.【分析】(1)先去分母,然后移项,合并同类项即可;(2)通过移项,合并同类项,系数化为1解方程即可.【解答】解:(1)原方程去分母得:2x﹣6=x+2,移项得:2x﹣x=2+6,合并同类项得:x=8;(2)原方程移项得:3x﹣4x=3﹣9,合并同类项得:﹣x=﹣6,系数化为1得:x=6.【点评】本题考查解一元一次方程,熟练掌握解方程的方法是解题的关键.3.(2023秋•西丰县期中)解方程:(1)3x﹣2=4+2x;(2)6x﹣7=9x+8.【分析】(1)根据等式的性质,移项、合并同类项即可;(2)根据等式的性质,移项、合并同类项系数化为1即可.【解答】解:(1)移项,得3x﹣2x=4+2,合并同类项,得x=6.(2)移项,得6x﹣9x=7+8,合并同类项,得﹣3x=15,系数化1,得x=﹣5.【点评】本题考查的是解一元一次方程,熟知解一元一次方程的基本步骤是解题的关键.4.(2023秋•郧阳区期中)解方程:(1)2x﹣x+3=1.5﹣2x;(2)7x+2=5x+8.【分析】利用解一元一次方程的步骤:移项,合并同类项,系数化为1解各方程即可.【解答】解:(1)原方程移项得:2x﹣x+2x=1.5﹣3,合并同类项得:3x=﹣1.5,系数化为1得:x=﹣0.5;(2)原方程移项得:7x﹣5x=8﹣2,合并同类项得:2x=6,系数化为1得:x=3.【点评】本题考查解一元一次方程,熟练掌握解方程的方法是解题的关键.5.(2022秋•莲湖区校级月考)解方程:(1)3x﹣2=5x﹣4;(2)2x+3(x﹣1)=2(x+3).【分析】(1)根据解一元一次方程的步骤,移项,合并同类项,最后将x的系数化为1即可求解.(2)根据解一元一次方程的步骤,先去括号,然后移项,合并同类项,最后将x的系数化为1即可求解.【解答】解:(1)3x﹣2=5x﹣4移项得,3x﹣5x=2﹣4,合并同类项得,﹣2x=﹣2,将x的系数化为1得,x=1.(2)2x+3(x﹣1)=2(x+3)去括号得,2x+3x﹣3=2x+6,移项得,2x+3x﹣2x=6+3,合并同类项得,3x=9,将x的系数化为1得,x=3.【点评】本题主要考查一元一次方程的解法,掌握解方程的基本步骤是解题的关键.6.(2023秋•青秀区校级期中)解下列方程:(1)3x+6=31﹣2x;(2)1−8(14+0.5p=3(1−2p.【分析】根据一元一次方程的解法,经历去括号、移项、合并同类项以及系数化为1进行计算即可.【解答】解:(1)移项得,3x+2x=31﹣6,合并同类项得,5x=25,两边都除以5得,x=5;(2)去括号得,1﹣2﹣4x=3﹣6x,移项得,﹣4x+6x=3+2﹣1,合并同类项得,2x=4,两边都除以2得,x=2.【点评】本题考查解一元一次方程,掌握一元一次方程的解法,理解去括号、移项、合并同类项以及系数化为1的依据是正确解答的前提.7.(2023秋•西城区校级期中)解下列方程:(1)3x﹣4=2x+8;(2)5﹣2x=3(x﹣2).【分析】(1)移项,合并同类项即可;(2)去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)3x﹣4=2x+8,移项,得3x﹣2x=8+4,合并同类项,得x=12;(2)5﹣2x=3(x﹣2),去括号,得5﹣2x=3x﹣6,移项,得﹣2x﹣3x=﹣6﹣5,合并同类项,得﹣5x=﹣11,系数化成1,得x=115.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.8.(2023秋•海珠区校级期中)解方程:(1)x+5=8;(2)3x+4=5﹣2x;(3)8(2x﹣1)﹣(x﹣1)=﹣2(2x﹣1).【分析】根据一元一次方程的解法,经历去括号、移项、合并同类项以及系数化为1等过程,进而求出未知数x的值即可.【解答】解:(1)移项得,x=8﹣5,合并同类项得,x=3;(2)移项得,3x+2x=5﹣4,合并同类项得,5x=1,两边都除以5得,x=15;(3)去括号得,16x﹣8﹣x+1=﹣4x+2,移项得,16x﹣x+4x=2﹣1+8,合并同类项得,19x=9,两边都除以19得,x=919.【点评】本题考查解一元一次方程,掌握一元一次方程的解法和步骤是正确解答的前提,理解去括号、移项、合并同类项以及系数化为1的做法的依据是正确解答的关键.9.(2023秋•重庆期中)解方程:(1)2x﹣6=﹣3x+9;(2)−32−1=−+1.【分析】根据一元一次方程的解法,依次进行移项、合并同类项以及系数化为1进行计算即可.【解答】解:(1)移项得,2x+3x=9+6,合并同类项得,5x=15,两边都除以5得,x=3;(2)移项得,32x﹣x=﹣1﹣1,合并同类项得,12x=﹣2,两边都乘以2得,x=﹣4.【点评】本题考查解一元一次方程,掌握一元一次方程的解法步骤是正确解答的前提.10.(2023秋•新吴区校级期中)解下列方程:(1)3(2x﹣1)=5﹣2(x+2);(2)2(x﹣2)﹣3(4x﹣1)=5(1﹣x).【分析】根据解一元一次方程的步骤解答即可.【解答】解:(1)6x﹣3=5﹣2x﹣4,6x+2x=5﹣4+3,8x=4,x=12;(2)2x﹣4﹣12x+3=5﹣5x,2x﹣12x+5x=5+4﹣3,﹣5x=6,x=−65.【点评】本题考查解一元一次方程,理解并熟练掌握解一元一次方程的步骤是解题的关键.11.(2022秋•陵城区期末)解方程(1)18(x﹣1)﹣2x=﹣2(2x﹣1);(2)3K110−1=5K74.【分析】(1)先去括号,再移项、合并同类项、系数化为1即可;(2)先去分母,再去括号、移项、合并同类项、系数化为1即可.【解答】解:(1)去括号得,18x﹣18﹣2x=﹣4x+2,移项得,18x﹣2x+4x=2+18,合并同类项得,20x=20,x的系数化为1得,x=1;(2)去分母得,2(3y﹣1)﹣20=5(5y﹣7)去括号得,6y﹣2﹣20=25y﹣35,移项得,6y﹣25y=﹣35+20+2,合并同类项得,﹣19y=﹣13,x的系数化为1得,y=1319.【点评】本题考查的是解一元一次方程,熟知去分母、去括号、移项、合并同类项、系数化为1是解一元一次方程的一般步骤是解题的关键.12.(2023秋•九龙坡区校级期中)解下列一元一次方程:(1)3x+4=2﹣x;(2)1−r12=1−25.【分析】根据一元一次方程的解法,经过去分母、去括号、移项、合并同类项以及系数化为1进行解答即可.【解答】解:(1)移项得,3x+x=2﹣4,合并同类项得,4x=﹣2,两边都除以4得,x=−12;(2)两边都乘以10得,10﹣5(x+1)=2(1﹣2x),去括号得,10﹣5x﹣5=2﹣4x,移项得,5x﹣4x=10﹣5﹣2,合并同类项得,x=3.【点评】本题考查解一元一次方程,掌握一元一次方程的解法是正确解答的前提.13.(2022秋•青川县期末)解下列方程:(1)2x﹣(x+10)=3x+2(x+1);(2)K12−2K13=+1.【分析】(1)根据去括号、移项、合并同类项、系数化为1,解一元一次方程的一般步骤解出方程;(2)根据去分母、去括号、移项、合并同类项、系数化为1,解一元一次方程的一般步骤解出方程.【解答】解:(1)2x﹣(x+10)=3x+2(x+1),去括号,得2x﹣x﹣10=3x+2x+2,移项,得2x﹣x﹣3x﹣2x=2+10,合并同类项,得﹣4x=12,系数化为1,得x=﹣3;(2)K12−2K13=+1,去分母,得3(x﹣1)﹣2(2x﹣1)=6x+6,去括号,得3x﹣3﹣4x+2=6x+6,移项,得3x﹣4x﹣6x=6+3﹣2,合并同类项,得﹣7x=7,系数化为1,得x=﹣1.【点评】本题考查解一元一次方程的解法,掌握解一元一次方程的步骤,使方程逐渐向x=a形式转化是解题关键.14.(2022秋•安次区校级月考)解方程:(1)3x﹣4(x+1)=6﹣2(2x﹣5);(2)0.3K0.10.2−2r93=−8.【分析】(1)按照去括号,移项,合并同类项,系数化为1的步骤解方程即可;(2)按照去分母,去括号,移项,合并同类项,系数化为1的步骤解方程即可.【解答】解:(1)3x﹣4(x+1)=6﹣2(2x﹣5)去括号得:3x﹣4x﹣4=6﹣4x+10,移项得:3x﹣4x+4x=6+10+4,合并同类项得:3x=20,系数化为1得;=203;(2)0.3K0.10.2−2r93=−8整理得:3K12−2r93=−8,去分母得:3(3x﹣1)﹣2(2x+9)=﹣48,去括号得:9x﹣3﹣4x﹣18=﹣48,移项得:9x﹣4x=﹣48+18+3,合并同类项得:5x=﹣27,系数化为1得;=−275.【点评】本题主要考查了解一元一次方程,熟知解一元一次方程的步骤是解题的关键.15.(2022秋•工业园区校级月考)解方程:(1)5(x﹣1)=8x﹣2(x+1);(2)3K14−1=5K76.【分析】(1)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.【解答】解:(1)5(x﹣1)=8x﹣2(x+1)去括号得:5x﹣5=8x﹣2x﹣2,移项得:5x﹣8x+2x=﹣2+5,合并得:﹣x=3,解得:x=﹣3;(2)3K14−1=5K76去分母得:3(3x﹣1)﹣12=2(5x﹣7),去括号得:9x﹣3﹣12=10x﹣14,移项得:9x﹣10x=3+12﹣14,合并得:﹣x=1,解得:x=﹣1【点评】此题考查了解一元一次方程,熟练掌握一元一次方程的解法是解本题的关键.16.(2022秋•青川县期末)解下列方程:(1)2x﹣(x+10)=3x+2(x+1);(2)K12−2K13=+1.【分析】(1)根据去括号、移项、合并同类项、系数化为1,解一元一次方程的一般步骤解出方程;(2)根据去分母、去括号、移项、合并同类项、系数化为1,解一元一次方程的一般步骤解出方程.【解答】解:(1)2x﹣(x+10)=3x+2(x+1),去括号,得2x﹣x﹣10=3x+2x+2,移项,得2x﹣x﹣3x﹣2x=2+10,合并同类项,得﹣4x=12,系数化为1,得x=﹣3;(2)K12−2K13=+1,去分母,得3(x﹣1)﹣2(2x﹣1)=6x+6,去括号,得3x﹣3﹣4x+2=6x+6,移项,得3x﹣4x﹣6x=6+3﹣2,合并同类项,得﹣7x=7,系数化为1,得x=﹣1.【点评】本题考查解一元一次方程的解法,掌握解一元一次方程的步骤,使方程逐渐向x=a形式转化是解题关键.17.(2022秋•平桥区校级月考)解方程:(1)8y﹣3(3y+2)=6;(2)r12−1=2+2−4.【分析】(1)依次去括号,移项,合并同类项,系数化为1,即可得到答案,(2)依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案.【解答】解:(1)去括号得:8y﹣9y﹣6=6,移项得:8y﹣9y=6+6,合并同类项得:﹣y=12,系数化为1得:y=﹣12;(2)方程两边同时乘4得:2(x+1)﹣4=8+(2﹣x),去括号得:2x+2﹣4=8+2﹣x,移项得:2x+x=8+2﹣2+4,合并同类项得:3x=12,系数化为1得:x=4.【点评】本题考查了解一元一次方程,正确掌握解一元一次方程的方法和步骤是解题的关键.18.(2022秋•汉阳区期末)解方程:(1)4x+3(2x﹣3)=12﹣(x+4);(2)3r22−1=2K14−2r15.【分析】(1)去括号、移项、合并同类项、系数化为1,依此即可求解;(2)去分母、去括号、移项、合并同类项、系数化为1,依此即可求解.【解答】解:(1)4x+3(2x﹣3)=12﹣(x+4),去括号得:4x+6x﹣9=12﹣x﹣4,10x﹣9=8﹣x,移项得:10x+x=9+8,合并同类项得:11x=17,系数化1得:x=1711;(2))3r22−1=2K14−2r15,去分母得:10(3x+2)﹣20=5(2x﹣1)﹣4(2x+1),去括号得:30x+20﹣20=10x﹣5﹣8x﹣4,移项得:30x﹣10x+8x=﹣5﹣4﹣20+20,合并得:28x=﹣9,化系数为1得:x=−928.【点评】本题考查一元一次方程的解法,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.19.(2023秋•蜀山区校级期中)解方程.(1)3(x﹣7)+5(x﹣4)=15;(2)5r16=9r18−1−3.【分析】(1)根据去括号、移项、合并同类项、系数化1计算即可.(2)根据去分母、去括号、移项、合并同类项、系数化1计算即可.【解答】解:(1)去括号得:3x﹣21+5x﹣20=15,移项、合并同类项得:8x=56,系数化1得:x=7.(2)去分母得:4(5y+1)=3(9y+1)﹣8(1﹣y),去括号得:20y+4=27y+3﹣8+8y,移项、合并同类项得:﹣15y=﹣9,系数化1得:=35.【点评】本题考查解一元一次方程,熟练掌握一元一次方程的解法是解答本题的关键.20.(2023秋•裕安区校级期中)解方程:(1)2(x﹣1)=2﹣5(x+2);(2)5r12−6r24=1.【分析】(1)方程去括号,移项,合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项,合并,把x系数化为1,即可求出解.【解答】解:(1)去括号得:2x﹣2=2﹣5x﹣10,移项得:2x+5x=2﹣10+2,合并得:7x=﹣6,解得:x=−67;(2)去分母得:2(5x+1)﹣(6x+2)=4,去括号得:10x+2﹣6x﹣2=4,移项得:10x﹣6x=4﹣2+2,合并得:4x=4,解得:x=1.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项,合并,把未知数系数化为1,求出解.20.(2023秋•越秀区校级期中)解方程:(1)3x+20=4x﹣25;(2)2K13=1−2K16.【分析】根据解一元一次方程的步骤,依次经过去分母,去括号、移项、合并同类项、系数化为1求出未知数x的值即可.【解答】解:(1)移项得,4x﹣3x=20+25,合并同类项得,x=45;(2)两边都乘以6得,2(2x﹣1)=6﹣(2x﹣1),去括号得,4x﹣2=6﹣2x+1,移项得,4x+2x=6+1+2,合并同类项得,6x=9,两边都除以6得,x=32.【点评】本题考查解一元一次方程,掌握一元一次方程的解法是正确解答的关键.21.(2023秋•工业园区校级期中)解方程:(1)3=1+2(4﹣x);(2)1−K56=r12.【分析】(1)去括号、移项、合并同类项、系数化为1,据此求出方程的解即可;(2)去分母、去括号、移项、合并同类项、系数化为1,据此求出方程的解即可.【解答】解:(1)去括号,可得:3=1+8﹣2x,移项,可得:2x=1+8﹣3,合并同类项,可得:2x=6,系数化为1,可得:x=3.(2)去分母,可得:6﹣(x﹣5)=3(x+1),去括号,可得:6﹣x+5=3x+3,移项,可得:﹣x﹣3x=3﹣6﹣5,合并同类项,可得:﹣4x=﹣8,系数化为1,可得:x=2.【点评】此题主要考查了解一元一次方程的方法,解答此题的关键是要明确解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.22.(2023秋•富川县期中)解方程:(1)3(x﹣1)﹣4=2(1﹣3x);(2)K74−5r82=1.【分析】(1)先去括号,再移项,合并同类项,把x的系数化为1即可;(2)先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.【解答】解:(1)3(x﹣1)﹣4=2(1﹣3x),3x﹣3﹣4=2﹣6x,3x+6x=2+3+4,9x=9,x=1;(2)K74−5r82=1,x﹣7﹣2(5x+8)=4,x﹣7﹣10x﹣16=4,x﹣10x=4+16+7,﹣9x=27,x=﹣3.【点评】本题考查的是解一元一次方程,熟知解一元一次方程的一般步骤是解题的关键.23.(2022秋•丰都县期末)解下列方程:(1)2(x+3)=3(x﹣3);(2)K40.2−2.5=K30.05.【分析】(1)按解一元一次方程的步骤求解即可;(2)利用分数的基本性质先去分母,再按解一元一次方程的步骤求解即可.【解答】解:(1)去括号,得2x+6=3x﹣9,移项,得2x﹣3x=﹣6﹣9,合并同类项,得﹣x=﹣15,系数化为1,得x=15.(2)K40.2−2.5=K30.05,5(K4)5×0.2−2.5=20(K3)0.05×20,5(x﹣4)﹣2.5=20x﹣60,5x﹣20﹣2.5=20x﹣60,﹣15x=﹣37.5,x=2.5.【点评】本题考查了解一元一次方程,掌握解一元一次方程的一般步骤是解决本题的关键.24.(2023秋•天河区校级期中)解方程:(1)4x=3x+7;(2)r12−2K13=1.【分析】(1)方程移项,合并同类项,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.【解答】解:(1)移项得:4x﹣3x=7,合并同类项得:x=7;(2)去分母得:3(x+1)﹣2(2x﹣1)=6,去括号得:3x+3﹣4x+2=6,移项得:3x﹣4x=6﹣3﹣2,合并同类项得:﹣x=1,解得:x=﹣1.【点评】此题考查了解一元一次方程,熟练掌握一元一次方程的解法是解本题的关键.25.(2023秋•南岗区校级期中)解方程:(1)2(x+6)=3(x﹣1);(2)K72−1+3=1.【分析】(1)去括号、移项、合并同类项、系数化为1,据此求出方程的解即可;(2)去分母、去括号、移项、合并同类项,据此求出方程的解即可.【解答】解:(1)去括号,可得:2x+12=3x﹣3,移项,可得:2x﹣3x=﹣3﹣12,合并同类项,可得:﹣x=﹣15,系数化为1,可得:x=15.(2)去分母,可得:3(x﹣7)﹣2(1+x)=6,去括号,可得:3x﹣21﹣2﹣2x=6,移项,可得:3x﹣2x=6+21+2,合并同类项,可得:x=29.【点评】此题主要考查了解一元一次方程的方法,解答此题的关键是要明确解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.26.(2023秋•武昌区期中)解方程:(1)2x+10=2(2x﹣1);(2)K35−r42=−2.【分析】(1)去括号、移项、合并同类项、系数化为1,解出x的值即可;(2)去分母、去括号、移项、合并同类项、系数化为1,解出x的值即可.【解答】解:(1)2x+10=2(2x﹣1),去括号得:2x+10=4x﹣2,移项得:2x﹣4x=﹣2﹣10,合并同类项得:﹣2x=﹣12,系数化为1得:x=6;(2)K35−r42=−2.去括号得:2(x﹣3)﹣5(x+4)=﹣20,去括号得:2x﹣6﹣5x﹣20=﹣20,移项得:2x﹣5x=﹣20+20+6,合并同类项得:﹣3x=6,系数化为1得:x=﹣2.【点评】本题考查了解一元一次方程,解一元一次方程时先观察方程的形式和特点,若有分母一般先去分母;若既有分母又有括号,且括号外的项在乘括号内各项后能消去分母,就先去括号.27.(2023秋•金安区校级期中)解下列方程:(1)3x+5=5x﹣7;(2)3K23=r26−1.【分析】(1)方程移项合并,将x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,将x系数化为1,即可求出解.【解答】解:(1)移项合并得:2x=12,解得:x=6;(2)去分母得:6x﹣4=x+2﹣6,移项合并得:5x=0,解得:x=0.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.28.(2023秋•西城区校级期中)解方程:(1)3x﹣4=2x+5;(2)K34−2r12=1.【分析】(1)移项,合并同类项即可;(2)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)3x﹣4=2x+5,移项,得3x﹣2x=5+4,合并同类项,得x=9;(2)K34−2r12=1,去分母,得x﹣3﹣2(2x+1)=4,去括号,得x﹣3﹣4x﹣2=4,移项,得x﹣4x=4+3+2,合并同类项,得﹣3x=9,系数化成1,得x=﹣3.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.29.(2022秋•枣阳市期末)解方程:(1)2K13−10r16=2r14−1;(2)0.7−0.17−0.20.03=2.【分析】(1)按解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,求解即可;(2)先利用分数的基本性质,把分子、分母化为整数,再按解一元一次方程的一般步骤求解即可.【解答】解:去分母,得4(2x﹣1)﹣2(10x+1)=3(2x+1)﹣12,去括号,得8x﹣4﹣20x﹣2=6x+3﹣12,移项,得8x﹣20x﹣6x=3﹣12+4+2,合并,得﹣18x=﹣3,系数化为1,得x=16.(2)原方程可变形为:107−17−203=2,去分母,得30x﹣7(17﹣20x)=42,去括号,得30x﹣119+140x=42,移项,得30x+140x=119+42,合并,得170x=161,系数化为1,得x=161170.【点评】本题考查了解一元一次方程,掌握解一元一次方程的一般步骤是解决本题的关键.30.(2022秋•虎丘区校级月考)解方程:(1)2K13=2r16−2;(2)2K50.6−3r10.2=10.【分析】(1)去分母,去括号,移项,合并同类项可得结果;(2)去分母,去括号,移项,合并同类项可得结果.【解答】解:(1)2K13=2r16−2,去分母得,2(2x﹣1)=2x+1﹣2×6,去括号得,4x﹣2=2x+1﹣12,移项得,4x﹣2x=1﹣12+2,合并同类项得,2x=﹣9,系数化为1得,=−92;(2)2K50.6−3r10.2=10,去分母得,2x﹣5﹣3(3x+1)=6,去括号得,2x﹣5﹣9x﹣3=6,移项得,2x﹣9x=6+5+3,合并同类项得,﹣7x=14,系数化为1得,x=﹣2.【点评】本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.31.(2023秋•鼓楼区期中)解方程:(1)2x﹣2(3x+1)=6;(2)r12−1=2−33.【分析】(1)去括号,移项,合并同类项,系数化成1即可;(2)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)2x﹣2(3x+1)=6,去括号,得2x﹣6x﹣2=6,移项,得2x﹣6x=6+2,合并同类项,得﹣4x=8,系数化成1,得x=﹣2;(2)r12−1=2−33,去分母,得3(x+1)﹣6=2(2﹣3x),去括号,得3x+3﹣6=4﹣6x,移项,得3x+6x=4﹣3+6,合并同类项,得9x=7,系数化成1,得x=79.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.32.(2022秋•连云港期末)解下列方程:(1)3(x+2)=5x;(2)r12−2=K34.【分析】(1)先去括号移项,然后合并后把x的系数化为1即可;(2)先去分母,再去括号,然后移项、合并后把x的系数化为1即可.【解答】解:(1)3(x+2)=5x,3x+6=5x,3x﹣5x=﹣6,﹣2x=﹣6,x=3;(2)r12−2=K34,2x+2﹣8=x﹣3,2x﹣x=﹣3﹣2+8,x=3.【点评】本题考查了解一元一次方程,掌握解一元一次方程的步骤是关键.33.(2022秋•射阳县校级期末)解方程:(1)2(x﹣2)=3x﹣7;(2)K12−2r36=1.【分析】(1)按照去括号、移项、合并同类项、系数化为1的步骤解一元一次方程;(2)按照去分母、去括号、移项、合并同类项、系数化为1的步骤解一元一次方程即可求解.【解答】解:(1)2(x﹣2)=3x﹣7,去括号,得:2x﹣4=3x﹣7,移项,得:2x﹣3x=﹣7+4,合并同类项,得:﹣x=﹣3,系数化为1:x=3;(2)K12−2r36=1,去分母,得:3(x﹣1)﹣(2x+3)=6,去括号,得:3x﹣3﹣2x﹣3=6,移项,得:3x﹣2x=6+3+3,合并同类项,得:x=12.【点评】本题考查了解一元一次方程,掌握解一元一次方程的步骤是解题的关键.34.(2022秋•硚口区期中)解方程:(1)2﹣3(x+1)=1﹣2(1+0.5x);(2)3+K12=3−2K13.【分析】(1)根据去括号、移项、合并同类项、化系数为1的步骤解一元一次方程即可;(2)根据去分母、去括号、移项、合并同类项、化系数为1的步骤解一元一次方程即可.【解答】解:(1)去括号,得2﹣3x﹣3=1﹣2﹣x,移项、合并同类项,得﹣2x=0,化系数为1,得x=0,∴原方程的解为x=0;(2)去分母,得18x+3(x﹣1)=18﹣2(2x﹣1),去括号,得18x+3x﹣3=18﹣4x+2,移项、合并同类项,得25x=23,化系数为1,得=2325,∴原方程的解为=2325.【点评】本题考查解一元一次方程,熟练掌握一元一次方程的解法步骤并正确求解是解答的关键.35.(2022秋•湖北期末)解方程:(1)2﹣(4﹣x)=6x﹣2(x+1);(2)r32−1=2−5−4.【分析】(1)通过去括号、移项、合并同类项、系数化成1,几个步骤进行解答;(2)通过去分母、去括号、移项、合并同类项、系数化成1,几个步骤进行解答.【解答】(1)解:去括号,得,2﹣4+x=6x﹣2x﹣2,移项,得,x﹣6x+2x=﹣2﹣2+4,合并同类项,得,﹣3x=0,系数化为1,得,x=0;(2)去分母得:2(x+3)﹣4=8x﹣(5﹣x),去括号得:2x+6﹣4=8x﹣5+x,移项得:2x﹣8x﹣x=﹣5﹣6+4,合并得:﹣7x=﹣7,解得:x=1.【点评】本题考查了解一元一次方程,解题关键是熟记解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化成1.36.(2023春•太康县期中)解方程:(1)3x﹣5=2x+3;(2)1−K32=2+3+2.【分析】(1)移项,合并同类项即可;(2)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)3x﹣5=2x+3,移项得:3x﹣2x=3+5,合并同类项得:x=8;(2)1−K32=2+3+2,去分母得:6﹣3(x﹣3)=2(2+x)+12,去括号得:6﹣3x+9=4+2x+12,移项得:﹣3x﹣2x=4+12﹣6﹣9,合并同类项得:﹣5x=1,系数化成1得:x=−15.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.37.(2022秋•万源市校级期末)解方程(1)4﹣3(2﹣x)=5x(2)K22−1=r13−r86.【分析】(1)方程去括号,移项合并,将x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,将x系数化为1,即可求出解.【解答】解:(1)方程去括号得:4﹣6+3x=5x,移项合并得:2x=﹣2,解得:x=﹣1;(2)去分母得:3(x﹣2)﹣6=2(x+1)﹣(x+8),去括号得:3x﹣6﹣6=2x+2﹣x﹣8,移项合并得:2x=6,解得:x=3.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.38.(2023秋•五华区校级期中)解方程:(1)7x+2(3x﹣3)=20;(2)2K13=3r52−1.【分析】(1)先去括号,再移项,合并同类项,把x的系数化为1即可;(2)先去分母,再去括号,移项,合并同类项,把x的系数化为1即可.【解答】解:(1)去括号得,7x+6x﹣6=20,移项得,7x+6x=20+6,合并同类项得,13x=26,x的系数化为1得,x=2;(2)去分母得,2(2x﹣1)=3(3x+5)﹣6,去括号得,4x﹣2=9x+15﹣6,移项得,4x﹣9x=15﹣6+2,合并同类项得,﹣5x=11,x的系数化为1得,x=−115.【点评】本题考查的是解一元一次方程,熟知解一元一次方程的一般步骤是解题的关键.39.(2023•开州区校级开学)解方程:(1)5x+34=2x+534;(2)K20.2=r10.5.【分析】(1)按照解一元一次方程的步骤:移项,合并同类项,系数化为1,进行计算即可解答;(2)先把分母的系数化为整数,然后再按照解一元一次方程的步骤进行计算,即可解答.【解答】解:(1)5x+34=2x+534,5x﹣2x=534−34,3x=5,x=53;(2)K20.2=r10.5,5x﹣10=2x+2,5x﹣2x=2+10,3x=12,x=4.【点评】本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.40.(2023秋•镇海区校级期中)解方程:(1)3(20﹣y)=6y﹣4(y﹣11);(2)0.4r30.2−2=0.45−0.3.【分析】(1)方程去括号,移项合并,把y系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去括号得:60﹣3y=6y﹣4y+44,移项合并得:5y=16,解得:y=3.2;(2)去分母得:1.2x+9﹣1.2=0.9﹣2x,移项合并得:3.2x=﹣6.9,解得:x=−6932.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.41.(2022秋•张店区期末)解方程:(1)3(y﹣7)﹣5(4﹣y)=15;(2)r20.4−2K10.2=−0.5.【分析】(1)去括号,移项合并同类项,系数化为1即可得到答案;(2)去分母,去括号,移项合并同类项,系数化为1即可得到答案.【解答】解:(1)去括号得,3y﹣21﹣20+5y=15,移项得,3y+5y=15+21+20,合并同类项可得,8y=56系数化为1得,y=7;(2)去分母可得,10(x+2)﹣20(2x﹣1)=﹣2,去括号得,10x+20﹣40x+20=﹣2,移项得,10x﹣40x=﹣2﹣20﹣20,合并同类项得,﹣30x=﹣42,系数化为1得,=75.【点评】本题考查了解一元一次方程,掌握解一元一次方程的步骤是关键.42.(2022秋•莲湖区校级月考)解方程:(1)K32−2r13=1.(2)r12−3K14=1.【分析】(1)去分母、去括号、移项、合并同类项、系数化为1即可求解;(2)去分母、去括号、移项、合并同类项、系数化为1即可求解.【解答】解:(1)K32−2r13=1,3(x﹣3)﹣2(2x+1)=6,3x﹣9﹣4x﹣2=6,3x﹣4x=6+9+2,﹣x=17,x=﹣17;(2)r12−3K14=1,2(x+1)﹣(3x﹣1)=4,2x+2﹣3x+1=4,﹣x=4﹣2﹣1,x=﹣1.【点评】本题考查了解一元一次方程,解答本题的关键是掌握解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a的形式转化.43.解下列方程:(1)2r13−10r16=1;(2)4K1.50.5−5K0.80.2=1.2−0.1.【分析】(1)利用等式的性质先去分母,再求解一元一次方程;(2)利用分数的基本性质去分母后,再解一元一次方程.【解答】解:(1)2r13−10r16=1,去分母,得2(2x+1)﹣(10x+1)=6,去括号,得4x+2﹣10x﹣1=6,移项,得4x﹣10x=6﹣2+1,合并同类项,得﹣6x=5,系数化为1,得x=−56;(2)4K1.50.5−5K0.80.2=1.2−0.1.去分母,得2(4x﹣1.5)﹣5(5x﹣0.8)=10(1.2﹣x),去括号,得8x﹣3﹣25x+4=12﹣10x,移项,得8x﹣25x+10x=12+3﹣4,合并同类项,得﹣7x=11,系数化为1,得x=−117.【点评】本题考查了解一元一次方程,掌握解一元一次方程的一般步骤,灵活运用等式的性质和分数的性质去分母是解决本题的关键.44.解方程;(1)2K366−33−23=−1﹣x;(2)K10.2−r10.05=3.【分析】(1)利用等式的性质去分母后,求解一元一次方程;(2)利用分数的性质去分母后,求解一元一次方程.【解答】解:(1)2K366−33−23=−1﹣x,去分母,得2x﹣36﹣2(33﹣2x)=6(﹣1﹣x),去括号,得2x﹣36﹣66+4x=﹣6﹣6x,移项,得2x+4x+6x=﹣6+36+66,合并同类项,得12x=96,系数化为1,得x=8;(2)K10.2−r10.05=3.去分母,得5(x﹣1)﹣20(x+1)=3,去括号,得5x﹣5﹣20x﹣20=3,移项,得5x﹣20x=3+5+20,合并同类项,得﹣15x=28系数化为1,得x=−2815.【点评】本题考查了解一元一次方程,掌握解一元一次方程的一般步骤,灵活运用等式的性质和分数的性质去分母是解决本题的关键.45.(2023春•周口月考)解方程:(1)34[2(+1)+13p=3;(2)3−2K83=−r54.【分析】(1)按照解一元一次方程的步骤,进行计算即可解答;(2)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1,进行计算即可解答.【解答】解:(1)34[2(+1)+13p=3,32(x+1)+14x=3x,6(x+1)+x=12x,6x+6+x=12x,6x+x﹣12x=﹣6,﹣5x=﹣6,x=1.2;(2)3−2K83=−r54,36﹣4(2x﹣8)=﹣3(x+5),36﹣8x+32=﹣3x﹣15,﹣8x+3x=﹣15﹣36﹣32,﹣5x=﹣83,x=835.【点评】本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.46.(2022秋•文登区期末)解方程:(1)4﹣2(x+4)=2(x﹣1);(2)13(+7)=25−12(−5);(3)0.3K0.40.2+2=0.5K0.20.3.【分析】(1)去括号,移项,合并同类项,系数化为1,求解即可;(2)去分母,去括号,移项,合并同类项,系数化为1,求解即可;(3)分母化为整数,去分母,去括号,移项,合并同类项,系数化为1,求解即可.【解答】解:(1)4﹣2(x+4)=2(x﹣1),去括号得:4﹣2x﹣8=2x﹣2,移项得:2x+2x=4﹣8+2,合并同类项得:4x=﹣2,系数化为1得:x=−12;(2)13(+7)=25−12(−5),去分母得:10(x+7)=12﹣15(x﹣5),去括号得:10x+70=12﹣15x+75,移项得:10x+15x=12+75﹣70,合并同类项得:25x=17,系数化为1得:x=1725;(3)0.3K0.40.2+2=0.5K0.20.3,分母化为整数得:3K42+2=5K23,去分母得:3(3x﹣4)+12=2(5x﹣2),去括号得:9x﹣12+12=10x﹣4,合并同类项得:9x=10x﹣4,移项、合并同类项得:x=4.【点评】本题考查了解一元一次方程,解题的关键是熟练掌握一元一次方程的解题步骤.47.解下列方程:(1)(5x﹣2)×30%=(7x+8)×20%;(2)34[43(14−1)+8]=73+23;(3)4K1.50.5−5K0.80.2=1.2−0.1.【分析】(1)方程去括号,移项,合并同类项,即可求出解;(2)方程去括号,去分母,移项,合并同类项,把x系数化为1,即可求出解;(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)(5x﹣2)×30%=(7x+8)×20%,去括号得:15x﹣6=14x+16,移项得:15x﹣14x=16+6,合并同类项得:x=22;(2)34[43(14−1)+8]=73+23;去括号得:14x﹣1+6=73+23,去分母得:3x+60=28+8x,移项得:3x﹣8x=28﹣60,合并同类项得:﹣5x=﹣32,解得:x=325;(3)4K1.50.5−5K0.80.2=1.2−0.1.去分母得:2(4x﹣1.5)﹣5(5x﹣0.8)=10(1.2﹣x),去括号得:8x﹣3﹣25x+4=12﹣10x,移项得:8x﹣25x+10x=12﹣4+3,合并同类项得:﹣7x=11,解得:x=−117.【点评】此题考查了解一元一次方程,解决本题的关键是掌握解一元一次方程的步骤,为:去分母,去括号,移项合并,把未知数系数化为1,求出解.48.(2023春•朝阳区校级月考)解下列方程:(1)2x﹣19=7x+6;(2)4(x﹣2)﹣1=3(x﹣1);(3)K12=23+1;(4)2K13−10r112=2r14−1.【分析】(1)方程移项,合并同类项,把x系数化为1,即可求出解;(2)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;(3)方程去分母,去括号,移项,合并同类项,把m系数化为1,即可求出解;(4)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.【解答】解:(1)移项得:2x﹣7x=6+19,合并同类项得:﹣5x=25,解得:x=﹣5;(2)去括号得:4x﹣8﹣1=3x﹣3,移项得:4x﹣3x=﹣3+8+1,合并同类项得:x=6;(3)去分母得:3(m﹣1)=4m+6,去括号得:3m﹣3=4m+6,移项得:3m﹣4m=6+3,合并同类项得:﹣m=9,解得:m=﹣9;(4)去分母得:4(2x﹣1)﹣(10x+1)=3(2x+1)﹣12,去括号得:8x﹣4﹣10x﹣1=6x+3﹣12,移项得:8x﹣10x﹣6x=3﹣12+4+1,合并同类项得:﹣8x=﹣4,解得:x=0.5.【点评】此题考查了解一元一次方程,熟练掌握方程的解法是解本题的关键.49.(2023秋•香坊区校级月考)解方程:(1)3x﹣8=x+4;(2)1﹣3(x+1)=2(1﹣0.5x);(3)16(3−6)=25x﹣3;(4)3K14−1=5K76.【分析】(1)按照解一元一次方程的步骤:移项,合并同类项,系数化为1,进行计算即可解答;(2)按照解一元一次方程的步骤:去括号,移项,合并同类项,系数化为1,进行计算即可解答;(3)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1,进行计算即可解答;(4)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1,进行计算即可解答.【解答】解:(1)3x﹣8=x+4,3x﹣x=4+8,2x=12,x=6;(2)1﹣3(x+1)=2(1﹣0.5x),1﹣3x﹣3=2﹣x,﹣3x+x=2+3﹣1,﹣2x=4,x=﹣2;。
初中数学解一元一次方程经典练习题(含答案)

初中数学解一元一次方程经典练习题(含答案)解下列一元一次方程:1、3x+7 =2x+14;2、59 x + 2.5 = 23 x + 2.4;3、6(x+1)+7(x+2)= 8(x+3);4、x=2−x 3 + 2+x 4 ;5、2x +3(21+x )=6x +5(9+x );6、5−x 3 + 6-x = 1−x 2 + 20+x 4 ;7、23 [ x - 15( x +1)]= 14(x+14);8、4+3x−10.7 =2- 2x−30.5 ;9、5(x-2)+6x= 0.8(x+4)-3;10、3x+4(x+1)+5(x+2)=50;11、 13 - 15(16 x -1;12、1= x + x 2 + x 4 + x 6 + x12 ;参考答案1、3x+7=2x+14;解:3x+7=2x+143x-2x=14-7x=7故原方程的解是:x=72、59 x + 2.5 = 23 x + 2.4; 解:59 x + 2.5 = 23 x + 2.4 59 x - 23 x =2.4-2.5 5−2×39 x= -0.1 −19x= -0.1x= -0.9故原方程的解是:x= -0.93、6(x+1)+7(x+2)= 8(x+3);解:6(x+1)+7(x+2)= 8(x+3)6x+6+7x+14 =8x+2413x+20 =8x+2413x-8x=24-205x= 4x= 45故原方程的解是:x= 454、x= 2−x3 + 2+x4;解:x= 2−x3 + 2+x412x =4(2-x)+3(2+x)12x=8-4x+6+3x12x=14-x12x+x =1413x=14x= 1413故原方程的解是:x= 14135、2x +3(21+x)=6x +5(9+x);解:2x +3(21+x)=6x +5(9+x)2x+63+3x =6x+45+5x5x+63 =11x+455x-11x=45-63-6x= -18x=3故原方程的解是:x=36、5−x3 + 6-x = 1−x2+ 20+x4;解:5−x3 + 6-x = 1−x2+ 20+x4等式两边同时乘以124(5-x)+12(6-x)=6(1-x)+3(20+x)20-4x+72-12x =6-6x+60+3x-16x+92 =-3x+66-16x+3x =-92+66-13x= -26x=2故原方程的解是:x=27、23[ x - 15( x +1)]=14(x+14);解:23[ x - 15( x +1)]=14(x+14)等式两边同时乘以128 [ x - 15( x +1)]=3(x+14)8x- 85( x +1)=3x+42- 85( x +1)= 3x-8x+42- 85( x +1)= -5x+42等式两边同时乘以5-8(x+1)=5(-5x+42)-8x-8 =-25x+21025x-8x=210+817x=218x= 21817故原方程的解是:x=218178、4+ 3x−10.7 =2- 2x−30.5 ;解:4+ 3x−10.7 =2- 2x−30.5等式两边同时乘以0.7×0.54×0.7×0.5 +0.5(3x-1)=2×0.7×0.5 -0.7(2x-3)1.4+1.5x-0.5= 0.7-1.4x+2.10.9+1.5x= -1.4x+2.81.5x+1.4x=2.8-0.92.9x= 1.9x= 1929 故原方程的解是:x= 19299、5(x -2)+6x= 0.8(x+4)-3;解:5(x -2)+6x= 0.8(x+4)-35x-10+6x =0.8x+3.2-35x+6x-0.8x =3.2-3+10(5+6-0.8)x=10.210.2x=10.2x=1故原方程的解是:x=110、3x+4(x+1)+5(x+2)=50; 解:3x+4(x+1)+5(x+2)=503x+4x+4+5x+10=503x+4x+5x= 50-4-10(3+4+5)x= 3612x= 36x= 3故原方程的解是:x=311、 13 - 15(16 x -1;解: 13 - 15(16 x -1等号两边同时乘以15 - 15(16 x -1)] = x 等号左边去中括号(16 x -1)=x 等号左边去小括号- 16 x +1=x等号两边同时乘以2430x-4x+24=24x26x+24=24x2x= -24x= -12故原方程的解是:x= -1212、1= x + x2 + x4+ x6+ x12;解:1= x + x2 + x4+ x6+ x12等式两边同时乘以12 12=12x+6x+3x+2x+x12=24xx= 12故原方程的解是:x= 12。
解一元一次方程50道练习题(带答案)

解一元一次方程50道练习题(带答案)解一元一次方程50道练习题(带答案)
1. 问题:解方程2x + 5 = 9
解答:将已知方程写成标准形式,得到2x = 9 - 5 = 4
将方程两边同时除以2,得到x = 2
答案:x = 2
2. 问题:解方程3(x - 4) = 5
解答:将已知方程通过分配律展开,得到3x - 12 = 5
将方程两边同时加上12,得到3x = 17
将方程两边同时除以3,得到x = 17/3
答案:x = 17/3
3. 问题:解方程4 - 2x = 6x - 8
解答:将已知方程进行整理,得到-2x - 6x = -8 - 4
将方程进行合并,得到-8x = -12
将方程两边同时除以-8,注意要将负号带到分子,得到x = -12/-8
答案:x = 3/2
4. 问题:解方程6(x + 3) = 4(x - 2)
解答:将已知方程展开,得到6x + 18 = 4x - 8
将方程两边同时减去4x,得到2x + 18 = -8
将方程两边同时减去18,得到2x = -8 - 18
将方程两边同时除以2,得到x = -26/2
答案:x = -13
5. 问题:解方程2(x + 1) - 3(x - 2) = 4 - 2x
解答:将已知方程进行整理,得到2x + 2 - 3x + 6 = 4 - 2x 将方程两边同时减去2x,得到-2x + 8 = 4 - 2x
将方程两边同时加上2x,得到8 = 4
答案:此方程无解
......依次类推,解答剩下的题目。
一元一次方程习题精选附答案

一元一次方程习题精选附答案6.2.4 解一元一次方程(三)一、解答题(共30小题)1.解方程:2x+1=72.删除此题3.1)解方程:4-x=3(2-x);2)解方程:删除此题4.解方程:删除此题5.解方程1)4(x-1)-3(20-x)=5(x-2);2)x-1=2(x-3)。
6.1)解方程:3(x-1)=2x+3;2)解方程:x-1=1/x。
7.-1+2x=3x+18.解方程:5(x-1)-2(x+1)=3(x-1)+x+1;9.解方程:删除此题10.1)4x-3(4-x)=2;2)(x-1)+2=2-(x+2)。
11.1)计算:删除此题2)解方程:删除此题12.解方程:删除此题13.1)删除此题2)删除此题14.1)5(2x+1)-2(2x-3)=6;2)删除此题3)3(x-1)+|x-2|=5x-1.15.A类)解方程:5x-2=7x+8;B类)解方程:(x-1)-(x+5)=-2;C类)解方程:删除此题16.1)3(x+6)=9-5(1-2x);2)删除此题17.1)4x-3(5-x)=13;2)x+3=2x-3.18.1)计算:-42×|-2|÷(3-|3|);2)计算:-12-|0.5-|-2-(-3)|÷2;3)解方程:4x-3(5-x)=2;4)解方程:删除此题19.1)计算:-7×(-1/3)÷(4/5);2)删除此题3)解方程:3x+3=2x+7;4)解方程:6x-2=4x+10.20.1)-0.2(x-5)=1;2)删除此题21.解方程:4x+5=9.22.3x=-12.23.1)0.5x-0.7=5.2-1.3(x-1);2)5x+2(3x-7)=9-4(2+x);3)2x+3(x+1)=5-4(x-1);4)删除此题24.解方程:x=21/6.25.解方程:-2x+5=3x+4.26.1)5x=27;2)删除此题27.解方程:x^2+3x-4=0.28.当k=3时,式子比值少3.29.I)7.5y=14;II)删除此题。
一元一次方程计算练习300道(含答案)

一元一次方程计算300道(含答案)一.解答题(共50小题)1.解下列方程:(1)2+x=﹣5(x﹣1);(2)﹣=x2.解方程:(1)4x﹣3(20﹣x)+4=0(2)=13.解下列方程:(1)2x﹣(x+10)=5x+2(x﹣1);(2)3x+;(3);(4).4.解方程:(1)x﹣1=2(x+1);(2)=﹣15.解方程:(标明解题步骤)(1)﹣=﹣1 (2)﹣=x﹣6.解下列方程:(1)2(10﹣0.5y)=﹣(1.5y+2 (2)(x﹣5)=3﹣(x﹣5)(3)﹣1=(4)x﹣(x﹣9)=[x+(x﹣9)](5)﹣=0.5x+27.解方程(1)﹣2x﹣9=8x+1 (2)﹣=18.解下列方程:(1)3x+1=x﹣7(2)﹣=9.解方程:x﹣=﹣110.按要求完成下列各小题(1)计算:(﹣2)4÷(﹣2)2+5×(﹣)﹣0.25;(2)解方程:﹣1=11.解方程.(1)=1﹣(2)[(x﹣2)﹣6]=112.解方程:(1)5x+1=2x﹣8(2)3(x﹣2)﹣5(3x+2)=2x+6(3)﹣=113.解方程:(1)4x﹣3=2(x﹣1)(2)﹣=1(1)2(3x+4)﹣5(x+1)=3 (2)﹣=1﹣15.解方程:(1)3﹣4x=2x﹣21 (2)﹣1=16.解方程(1)3x﹣2=4+5x (2)17.解方程(1)2(x﹣2)﹣8(x﹣1)=3(1﹣x)(2)18.解方程(1)5(y+8)﹣5=6(2y﹣7)(2)=219.解下列方程:(1)5x=8+2(x﹣1)(2)3x﹣(1)2x﹣(x﹣3)=2(2)21.解方程(1)60﹣20(x+1)=30(x﹣2)(2)22.解方程(1)6x+7=4x﹣5(2)=123.解方程(1)6(2x﹣5)+20=4(1﹣2x)(2)﹣=124.解下列方程:(1)5x=3(x﹣4)(2)1﹣25.解方程:(1)x﹣2(3x﹣1)=6x(2)(x﹣3)﹣2=(2x+3)(1)x﹣﹣2=0(2)﹣1=﹣27.解方程:(1)2(x﹣1)﹣5(2x﹣3)=0(2)﹣1=28.解方程:(1)2x+3=12﹣3(x﹣3)(2)29.解方程:(1)3x+2x=5(2)+=130.解方程:(1)2(2x﹣3)﹣3x=3﹣3(x﹣1)(2)31.解方程:(1)5x﹣2=7x+8(2)x﹣(1﹣)=.(1)3x+3=x+7;(2)5(x﹣5)﹣2(x+1)=3;(3)﹣1.33.解方程(1)4x+3=2x+7(2)﹣2(x﹣1)=4(3)(4)34.解方程与计算.(1)2(x+3)=﹣3(x﹣1)+2(2)﹣x=3﹣(3)(﹣2)4+(﹣4)×()2﹣(﹣1)3(4)(﹣﹣)÷(﹣)35.解下列方程:(1)4x+3=12﹣(x﹣6);(2)=2﹣.(1)a﹣6=a+1(2)3x+=3﹣.37.解方程:(1)5x+6=3x+2(2).38.解下列方程:(1)4x+7=12x﹣5;(2)4y﹣3(5﹣y)=6;(3)﹣=1;(4)﹣=1.39.解方程:(1)﹣=1(2)﹣=0.5 40.解方程:﹣=0.5(1)3x﹣7(x﹣1)=3﹣2(x+3);(2)﹣1=42.解方程:(1)5(x﹣2)﹣2=2(2+x)+x(2)43.解下列方程:(1)x﹣6=x;(2)=1﹣44.解一元一次方程:(1)3(2x﹣1)=4x+3;(2)﹣=145.解方程:(1)﹣x﹣2=2x+1;(2)(x﹣1)﹣x=﹣0.5(x﹣1).46.解方程:(1)4x=1+3x(2)﹣=1(1)4x+5=﹣3x+12;(2).48.解下列方程:(1)3(x﹣2)=x﹣(7﹣8x);(2)=2﹣49.解下列方程:(1)5x﹣3=3x﹣9 (2)=1﹣50.解方程:(1)3x+7=2x﹣5 (2)2(x﹣1)﹣3(2+x)=5;(3)(4)[(﹣)]=x+1二.解答题(共50小题)1.解下列方程:(1)0.5x﹣0.7=6.5﹣1.3x (2)(1﹣2x)=(3x+1)2.解下列方程:(1)6x﹣7=4x﹣5 (2)3.解方程(1)12(2﹣3x)=4+4x (2)﹣=4.解方程:(1)2(3﹣x)=﹣4(x+5)(2)5.解下列方程:(1)8x=﹣2(x+4)(2)6.解方程(1)3x﹣7(x﹣1)=3﹣2(x+3)(2)﹣=17.解下列方程:(1)8x﹣7=2x+11 (2)﹣1=.8.解方程:(1)4x=﹣0.5x﹣9 (2)9.解方程:(1)x﹣(3x﹣2)=2(5﹣x)(2)x+=3+10.解方程:(Ⅰ)3(x﹣1)=2x+3 (Ⅱ)=111.解方程:(1)10x﹣3=7x+3 (2)(1)2(x﹣3)=5x (2)13.解下列方程(1)4﹣x=3(2﹣x);(2)﹣1.14.解方程:(1)5(x+8)﹣5=6(2x﹣7)(2)﹣x=3﹣15.解方程:(1)6x﹣7=4(x﹣1)﹣5(2)﹣1=+216.解方程(1)2x﹣6=2(3x﹣5)(2)(1)﹣2=.(2)=﹣.18.解方程:(1)2(x+1)=﹣2 (2)x﹣﹣119.解方程(1)3﹣(1+2x)=5x (2)=1﹣20.解下列方程:(1)2(x+3)=5x (2)21.解方程:(1)8﹣x=3x+2 (2)(1)4﹣x=3(2﹣x)(2)23.解方程:(1)3x+4﹣5(x+1)=﹣1;(2)﹣=1.24.解方程(1)4x﹣5=3x+2 (2)=﹣1(3)2x﹣3(6﹣x)=3x﹣4(5﹣x)(4)﹣=1.225.解方程(1)﹣5x+1=(2)(x+2)=(x+3)26.解方程:(1)4x﹣2=3﹣x (2)27.解方程:(1)5x﹣2=﹣3(x﹣2)(2)28.解方程:(1)3(x+4)=5﹣2(x﹣1);(2)=1﹣29.解方程(1)2(t﹣3)﹣(4t﹣1)=2﹣4t (2)30.解方程:(1)5x﹣2=2x+1;(2)﹣=1.31.解下列方程:(1)2(x+3)=5(x﹣3)(2)=﹣x(1)3(x﹣4)﹣2(3x+4)=﹣15 (2)33.解方程:(1)3(x﹣1)+2(x+1)=﹣6 (2)=1+34.解方程:(1)3(x﹣3)﹣2(5x﹣7)=6(1﹣x);(2)﹣=1﹣.35.解下列方程:(1)+1=(2)﹣=1.636.解方程:(1)5x=3x﹣12 (2)=1﹣37.解方程:(1)2x﹣3=﹣5(x﹣2)(2)﹣1=(1)4x+3(2x﹣3)=12﹣(x﹣1)(2)y﹣=2﹣39.解方程:(1)3x+7=﹣2x﹣3 (2).40.解方程:(1)4x﹣3(5﹣x)=6 (2)﹣=1.41.解方程:(1)2(10﹣0.5y)=﹣(3y+4);(2)42.解方程:(1)4x﹣6=2(3x﹣1)(2)=1.43.解方程:(1)﹣3(x+1)=9;(2).44.解方程:(1)x﹣(2)45.解方程:(1)2(x+2)=1﹣(x+3)(2)﹣=﹣146.解方程;(1)3(x﹣4)+1=x﹣5 (2)1+=47.解方程:(1)2(x+3)=5x;(2)2﹣.48.解方程:(1)2(y+2)﹣3(4y﹣1)=9(1﹣y);(2)x﹣.49.解下列方程:(1)3x+4=x;(2)50.解方程:(1)2(x﹣2)+2=x+1 (2).一元一次方程计算300道参考答案与试题解析一.解答题(共50小题)1.【解答】解:(1)2+x=﹣5x+5,x+5x=5﹣2,6x=3,x=;(2)2x﹣5(3﹣2x)=10x,2x﹣15+10x=10x,2x+10x﹣10x=15,2x=15,x=.2.【解答】解:(1)4x﹣60+3x+4=0,4x+3x=60﹣4,7x=56,x=8;(2)2(2x+1)﹣(5x﹣1)=6,4x+2﹣5x+1=6,4x﹣5x=6﹣2﹣1,﹣x=3,x=﹣3.3.【解答】解:(1)2x﹣(x+10)=5x+2(x﹣1),去括号得2x﹣x﹣10=5x+2x﹣2,移项得2x﹣x﹣5x﹣2x=10﹣2合并同类项得﹣6x=8,系数化为1,得x=﹣;(2)3x+,18x+3(x﹣1)=18﹣2(2x﹣1),18x+3x﹣3=18﹣4x+2,18x+3x+4x=18+2+3,25x=23,x=;(3),4x+5(x﹣1)=15(x﹣1)﹣16x,4x+5x﹣5=15x﹣15﹣16x,4x+5x﹣15x+16x=﹣15+5,10x=﹣10,x=﹣1;(4),原方程可化为﹣x=﹣1,3(x﹣4)﹣12x=2(10﹣x)﹣12,3x﹣12﹣12x=20﹣2x﹣12,3x﹣12x+2x=20﹣12+12,﹣7x=20,x=﹣.4.【解答】解:(1)去分母得:x﹣2=4x+4,移项合并得:3x=﹣6,解得:x=﹣2;(2)去分母得:15x+5﹣8x+4=﹣10,移项合并得:7x=﹣19,解得:x=﹣.5.【解答】解:(1)去分母得:4(2x﹣1)﹣3(x+2)=﹣12,去括号得:8x﹣4﹣3x﹣6=﹣12,移项合并得:5x=﹣2,解得:x=﹣;(2)方程整理得:﹣=x﹣,去分母得:3x﹣(x﹣1)=6x﹣2,去括号得:3x ﹣x+1=6x﹣2,移项合并得:﹣4x=﹣3,解得:x=.6.【解答】解:(1)去括号得:20﹣y=﹣1.5y﹣2,移项合并得:0.5y=﹣22,解得:y=﹣44;(2)去分母得:x﹣5=9﹣2x+10,移项合并得:3x=24,解得:x=8;(3)去分母得:3x+6﹣12=6﹣4x,移项合并得:7x=12,解得:x=;(4)去括号得:x﹣x+1=x+x ﹣1,去分母得:9x﹣x+9=3x+x﹣9,移项合并得:4x=﹣18,解得:x=﹣;(5)方程整理得:4x﹣2﹣=0.5x+2,去分母得:12x﹣6﹣5x﹣15=1.5x+6,移项合并得:5.5x=27,解得:x=.7.【解答】解:(1)﹣2x﹣9=8x+1,﹣2x﹣8x=1+9,﹣10x=10,x=﹣1;(2)﹣=1,2(2x+1)﹣(5x﹣1)=6,4x+2﹣5x+1=6,4x﹣5x=6﹣2﹣1,﹣x=3,x=﹣3.8.【解答】解:(1)3x+1=x﹣7,移项,合并得2x=﹣8,两边同除以2得x=﹣4;(2)﹣=,去分母,得2(7x﹣1)﹣2(4x+1)=3x+2,去括号,得14x﹣2﹣8x﹣2=3x+2,移项,合并得3x=6,两边同除以3得x=2.9.【解答】解:去分母,得:6x﹣3(x﹣1)=2x+3﹣6,去括号,得:6x﹣3x+3=2x+3﹣6,移项,得:6x﹣3x﹣2x=3﹣6﹣3,合并同类项,得:x=﹣6.10.【解答】解:(1)原式=16÷()﹣33﹣0.25=﹣31;(2)去分母得:3(3x﹣1)﹣12=2(5x﹣7)去括号得:9x﹣10x=15﹣14,解得:x=﹣1.11.【解答】解:(1)=1﹣2(x+3)=12﹣3(3﹣2x),则2x+6=12﹣9+6x,故﹣4x=﹣3解得:x=;(2)[(x﹣2)﹣6]=1x ﹣2﹣8=1,则x=11,解得:x=55.12.【解答】解:(1)5x+1=2x﹣83x=﹣8﹣1,解得:x=﹣3;(2)3(x﹣2)﹣5(3x+2)=2x+63x﹣6﹣15x﹣10=2x+6,移项得:3x﹣15x﹣2x=6+6+10,解得:x=﹣;(3)﹣=12(5x﹣1)﹣3(3+x)=6,则10x﹣2﹣9﹣3x=6,解得:x=.13.【解答】解:(1)4x﹣3=2(x﹣1)4x﹣3=2x﹣2,则2x=1,解得:x=;(2)﹣=12(x﹣3)﹣(x﹣4)=10,则2x﹣6﹣x+4=10,解得:x=12.14.【解答】解:(1)6x+8﹣5x ﹣5=36x﹣5x=3+5﹣8x=0;(2)2x﹣3x﹣1=6﹣3x+32x﹣3x+3x=6+3+12x=10x=5 15.【解答】解:(1)3﹣4x=2x﹣21,﹣4x﹣2x=﹣21﹣3,﹣6x=﹣24,x=4;(2)﹣1=,4(2x﹣1)﹣12=3(3+x),8x﹣4﹣12=9+3x,8x﹣3x=9+4+12,5x=25,x=5.16.【解答】解:(1)3x﹣2=4+5x,3x﹣5x=4+2,﹣2x=6,x=﹣3;(2),3(x﹣2)=6﹣2(2x﹣1),3x﹣6=6﹣4x+2,3x+4x=6+2+6,7x=14,x=2.17.【解答】解:(1)2x﹣4﹣8x+8=3﹣3x2x﹣8x+3x=3+4﹣8﹣3x=﹣1x=;(2)2(5x+1)﹣6=2x﹣110x+2﹣6=2x﹣110x﹣2x=﹣1+6﹣28x=3x= 18.【解答】解:(1)5y+40﹣5=12y﹣4212y﹣5y=42+40﹣57y=77y=11(2)4(7x﹣1)﹣6(5x+1)=24﹣3(3x+2)28x﹣4﹣30x﹣6=24﹣9x﹣628x﹣30x+9x=24﹣6+4+67x=28x=419.【解答】解:(1)5x=8+2x﹣2,5x﹣2x=6,3x=6 x=2,解:(2)36x﹣3(3x﹣1)=2x,36x﹣9x+3=2x 36x﹣9x﹣2x=﹣3,25x=﹣3x=﹣20.【解答】解:(1)2x﹣(x﹣3)=2,2x﹣x+3=2,2x﹣x=2﹣3,x=﹣1;(2),4(2x﹣1)=12﹣3(x﹣2),8x﹣4=12﹣3x+6,8x+3x=12+6+4,11x=22,x=2.21.【解答】解:(1)60﹣20(x+1)=30(x﹣2)60﹣20x﹣20=30x﹣60,﹣20x﹣30x=﹣60﹣60+20,﹣50x=﹣100,x=2;(2),2(x+2)=6﹣3(x﹣1),2x+4=6﹣3x+3,2x+3x=6+3﹣4,5x=5,x=1.22.【解答】解:(1)6x+7=4x﹣5,6x﹣4x=﹣5﹣7,2x=﹣12,x=﹣6;(2)=1,3(x+1)﹣(2﹣3x)=6,3x+3﹣2+3x=6,6x=5,x=.23.【解答】解:(1)6(2x﹣5)+20=4(1﹣2x),12x﹣30+20=4﹣8x,12x+8x=4+30﹣20,20x=14,x=;(2)﹣=1,3(x﹣1)﹣2(2x﹣3)=6,3x﹣3﹣4x+6=6,﹣x=3,x=﹣3.24.【解答】解:(1)5x=3(x﹣4),5x=3x﹣12,5x﹣3x=﹣12,2x=﹣12,x=﹣6;(2)1﹣,6﹣2(x﹣1)=6x﹣(x+6),6﹣2x+2=6x﹣x﹣6,﹣2x﹣6x+x=﹣6﹣6﹣2,﹣7x=﹣14,x=2.25.【解答】解:(1)x﹣2(3x﹣1)=6x,x﹣6x+2=6x,x﹣6x﹣6x=﹣2,﹣11x=﹣2,x=;(2)(x﹣3)﹣2=(2x+3),3(x﹣3)﹣24=2(2x+3),3x﹣9﹣24=4x+6,3x﹣4x=6+9+24,﹣x=39,x=﹣39.26.【解答】解:(1)x﹣﹣2=0,去分母,得3x﹣(9x﹣2)﹣12=0,去括号,得3x﹣9x+2﹣12=0,移项,得3x﹣9x=﹣2+12,合并同类项,得﹣6x=10,系数化为1,得x=﹣;(2)﹣1=﹣,去分母,得3(x﹣2)﹣6=2(x+1)﹣(x+8),去括号,得3x﹣6﹣6=2x+2﹣x﹣8,移项,得3x﹣2x+x=2﹣8+6+6,合并同类项,得2x=6,系数化为1,得x=3.27.【解答】解:(1)去括号得:2x﹣2﹣10x+15=0,移项合并得:﹣8x=﹣13,解得:x=;(2)去分母得:6x+3﹣6=2x﹣2,移项合并得:4x=1,解得:x=.28.【解答】解:(1)去括号得:2x+3=12﹣3x+9,移项合并得:5x=18,解得:x=3.6;(2)去分母得:9x﹣6=24﹣8x+4,移项合并得:17x=34,解得:x=2.29.【解答】解:(1)合并同类项,得:5x=5,系数化为1,得:x=1;(2)去分母,得:3(x+1)+2(x﹣2)=6,去括号,得:3x+3+2x﹣4=6,移项,得:3x+2x=6﹣3+4,合并同类项,得:5x=7,系数化为1,得:x=.30.【解答】解:(1)2(2x﹣3)﹣3x=3﹣3(x﹣1),4x﹣6﹣3x=3﹣3x+3,4x﹣3x+3x=3+3+6,4x=12,x=3;(2),3(x﹣3)﹣6=2(2x+1),3x﹣9﹣6=4x+2,3x﹣4x=2+9+6,﹣x=17,x=﹣17.31.【解答】解:(1)5x﹣7x=8+2﹣2x=10x=﹣5(2)6x﹣9﹣3(3﹣x)=26x﹣9﹣9+3x=26x+3x=2+9+99x=20x=32.【解答】解:(1)3x﹣x=7﹣3,2x=4,x=2;(2)5x﹣25﹣2x﹣2=3,5x﹣2x=3+25+2,3x=30,x=10;(3)4(2y﹣1)=3(y+2)﹣12,8y﹣4=3y+6﹣12,8y﹣3y=6﹣12+4,5y=﹣2,y=﹣.33.【解答】解:(1)4x﹣2x=7﹣3,2x=4,x=2;(2)﹣2x+2=4,﹣2x=4﹣2,﹣2x=2,x=﹣1;(3)3(3﹣x)=2(x+4),9﹣3x=2x+8,﹣3x﹣2x=8﹣9,﹣5x=﹣1,x=;(4)2(7x﹣1)﹣3(5x+1)=12,14x﹣2﹣15x﹣3=12,14x﹣15x=12+2+3,﹣x=17,x=﹣17.34.【解答】解:(1)2(x+3)=﹣3(x﹣1)+2,去括号得:2x+6=﹣3x+3+2,移项合并得:5x=﹣1,解得:x=﹣;(2)去分母得:4﹣4x﹣12=36﹣3x﹣6,移项合并得:﹣x=38,解得:x=﹣38;(3)原式=16﹣1+1=16;(4)原式=(﹣﹣)×(﹣60)=﹣12+30+25=43.35.【解答】解:(1)去括号得:4x+3=12﹣x+6,移项合并得:5x=15,解得:x=3;(2)去分母得:9y+3=24﹣8y+4,移项合并得:17y=25,解得:y=.36.【解答】解:(1)去分母得:2a﹣24=3a+4,移项合并得:﹣a=28,解得:a=﹣28;(2)去分母得:18x+3x﹣3=18﹣4x﹣2,移项合并得:25x=19,解得:x=.37.【解答】解:(1)移项,得:5x﹣3x=2﹣6,合并同类项,得:2x=﹣4,系数化为1,得:x=﹣2;(2)去分母得:2x+4=20﹣5x+5,移项,得:2x+5x=20+5﹣4,合并同类项,得:7x=21,系数化为1,得:x=3.38.【解答】解:(1)移项,得:4x﹣12x=﹣5﹣7,合并同类项,得:﹣8x=﹣12,系数化为1,得:x=;(2)去括号,得:4y﹣15+3y=6,移项,得:4y+3y=6+15,合并同类项,得:7y=21,系数化为1,得:y=3;(3)去分母,得:3(3x﹣1)﹣2(5x﹣7)=12,去括号,得:9x﹣3﹣10x+14=12,移项,得:9x﹣10x=12+3﹣14,合并同类项,得:﹣x=1,系数化为1,得:x=﹣1;(4)整理,得:﹣=1,去分母,得:3(20a﹣3)﹣5(10a+4)=15,去括号,得:60a﹣9﹣50a﹣20=15,移项,得:60a﹣50a=15+9+20,合并同类项,得:10a=44,系数化为1,得:a=4.4.39.【解答】解:(1)去分母得:10+4x﹣30+9x=6,移项合并得:13x=26,解得:x=2;(2)方程整理得:﹣=0.5,去分母得:5x﹣1.5+x=1,移项合并得:6x=2.5,解得:x=.40.【解答】解:10x﹣(3﹣2x)=210x﹣3+2x=210x+2x=2+312x=5x=.41.【解答】解:(1)去括号,得3x﹣7x+7=3﹣2x﹣6,移项,得3x﹣7x+2x=3﹣6﹣7,合并同类项,得﹣2x=﹣10,系数化为1,得x=5;(2)去分母,得9y﹣3﹣12=10y﹣14,移项合并得:y=﹣1.42.【解答】解:(1)去括号得:5x﹣10﹣2=4+2x+x,移项合并得:2x=16,解得:x=8;(2)方程整理得:x﹣2﹣5=﹣1,去分母得:3x﹣21=7﹣4x﹣3,移项合并得:7x=25,解得:x=.43.【解答】解:(1)去分母得:2x﹣24=3x,解得:x=﹣24;(2)去分母得:3x﹣3=6﹣4x﹣2,移项合并得:7x=7,解得:x=1.44.【解答】解:(1)6x﹣3=4x+36x﹣4x=3+32x=6x=3;(2)3(3x﹣1)﹣2(5x﹣7)=129x﹣3﹣10x+14=129x﹣10x=12+3﹣14﹣x=1x=﹣1.45.【解答】解:(1)移项,得:﹣x﹣2x=1+2,合并同类项,得:﹣3x=3,系数化为1,得:x=﹣1;(2)去分母,得:15(x﹣1)﹣16x=﹣5(x﹣1),去括号,得:15x﹣15﹣16x=﹣5x+5,移项,得:15x﹣16x+5x=5+15,合并同类项,得:4x=20,系数化为1,得:x=5.46.【解答】解:(1)4x=1+3x4x ﹣3x=1x=1;(2)﹣=15(x﹣1)﹣2x=105x﹣5﹣2x=105x﹣2x=10+53x=15x=5.47.【解答】解:(1)移项,得:4x+3x=12﹣5,合并同类项,得:7x=7,系数化为1,得:x=1;(2)去分母,得:3(y+2)﹣2(2y﹣1)=12,去括号,得:3y+6﹣4y+2=12,移项,得:3y﹣4y=12﹣6﹣2,合并同类项,得:﹣y=4,系数化为1,得:y=﹣4.48.【解答】解:(1)去括号得:3x﹣6=x﹣7+8x,移项合并得:6x=1,解得:x=;(2)去分母得:3(3y﹣2)=24﹣4(5y﹣7),去括号得:9y﹣6=24﹣20y+28,移项合并得:29y=58,解得:y=2.49.【解答】解:(1)2x=﹣6,x=﹣3;(2)4(x+1)=12﹣3(2x+1)4x+4=12﹣6x﹣34x+6x=12﹣3﹣410x=5x=0.550.【解答】解:(1)3x﹣2x=﹣5﹣7,x=﹣12;(2)2x﹣2﹣6﹣3x=5,2x﹣3x=5+2+6,﹣x=13,x=﹣13;(3)4(2x﹣1)=24+3(3x﹣1),8x﹣4=24+9x﹣3,8x﹣9x=24﹣3+4,﹣x=25,x=﹣25;(4)﹣=x+1,x﹣x=1+,﹣x=,x=﹣.二.解答题1.【解答】解:(1)0.5x﹣0.7=6.5﹣1.3x0.5x+1.3x=6.5+0.7,1.8x=7.2,x=4;(2)(1﹣2x)=(3x+1),7(1﹣2x)=6(3x+1),7﹣14x=18x+6,﹣14x ﹣18x=6﹣7,﹣32x=﹣1,x=.2.【解答】解:(1)6x﹣4x=﹣5+7,2x=2,x=1;(2)4(5y+4)+3(y﹣1)=24﹣(5y﹣5),20y+16+3y﹣3=24﹣5y+5,20y+3y+5y=24+5﹣16+3,28y=16,.3.【解答】解:(1)24﹣36x=4+4x,﹣36x﹣4x=4﹣24,﹣40x=﹣20,x=0.5;(2)3(x﹣3)﹣2(x+1)=1,3x﹣9﹣2x﹣2=1,3x﹣2x=1+9+2,x=12.4.【解答】解:(1)去括号得:6﹣2x=﹣4x ﹣20,移项合并得:2x=﹣26,解得:x=﹣13;(2)去分母得:9+3x﹣6=2x+4,移项合并得:x=1.5.【解答】解:(1)去括号得:8x=﹣2x﹣8,移项合并得:10x=﹣8,解得:x=﹣0.8;(2)去分母得:7﹣14x=9x+3﹣42,移项合并得:﹣23x=﹣46,解得:x=2.6.【解答】解:(1)去括号得:3x﹣7x+7=3﹣2x﹣6,移项合并得:﹣2x=﹣10,解得:x=5;(2)方程整理得:﹣=1,去分母得:35x+35﹣4x+20=14,移项合并得:31x=﹣41,解得:x=﹣.7.【解答】解:(1)8x﹣2x=11+7,6x=18,x=3;(2)3(3y﹣1)﹣12=2(5y﹣7),9y﹣3﹣12=10y ﹣14,9y﹣10y=﹣14+3+12,﹣y=1,y=﹣1.8.【解答】解:(1)4x+0.5x=﹣9,4.5x=﹣9,x=﹣2;(2)6﹣3(x﹣1)=12﹣2(x+2),6﹣3x+3=12﹣2x﹣4,﹣3x+2x=12﹣4﹣6﹣3,﹣x=﹣1,x=1.9.【解答】解:(1)2x﹣(3x﹣2)=4(5﹣x),2x﹣3x+2=20﹣4x,2x﹣3x+4x=20﹣2,3x=18,x=6;(2)6x+3(x﹣3)=18+2(2x ﹣1),6x+3x﹣9=18+4x﹣2,6x+3x﹣4x=18﹣2+9,5x=25,x=5.10.【解答】解:(Ⅰ)去括号得:3x﹣3=2x+3,移项合并得:x=6;(Ⅱ)去分母得:3x+3+6﹣4x=6,移项合并得:﹣x=﹣3,解得:x=3.11.【解答】解:(1)10x﹣3=7x+310x﹣7x=3+33x=6x=2;(2)10(3x+2)﹣20=5(2x﹣1)﹣4(2x+1)30x+20﹣20=10x﹣5﹣8x﹣430x﹣10x+8x=﹣5﹣428x=﹣9x=﹣.12.【解答】解:(1)2(x﹣3)=5x2x﹣6=5x2x﹣5x=6﹣3x=6x=﹣2;(2)2(3x+1)﹣(x﹣3)=306x+2﹣x+3=305x=25x=5.13.【解答】解:(1)去括号得:4﹣x=6﹣3x,移项合并得:2x=2,解得:x=1;(2)去分母得:20﹣5x=3x﹣9﹣15,移项合并得:﹣2x=﹣11,解得:x=5.5.14.【解答】解:(1)5x+40﹣5=12x﹣42,则5x﹣12x=﹣35﹣42,故﹣7x=﹣77,解得:x=11;(2)去分母得:4(1﹣x)﹣12x=36﹣3(x+2),则4﹣4x﹣12x=36﹣3x﹣6,则﹣13x=26,解得:x=﹣2.15.【解答】解:(1)6x﹣7=4x﹣4﹣5,则6x﹣4x=7﹣4﹣5合并同类项得:2x=﹣2,解得:x=﹣1;(2)3(3y﹣1)﹣12=2(5y﹣7)+24,9y﹣3﹣12=10y ﹣14+24,9y﹣10y=15+10,解得:y=﹣25.16.【解答】解:(1)2x﹣6=2(3x ﹣5),2x﹣6=6x﹣10,2x﹣6x=6﹣10,﹣4x=﹣4,解得:x=1;(2)去分母得:3(x+1)﹣6=2(2﹣x),则3x+3﹣6=4﹣2x,则3x+2x=4+3,解得:x=.17.【解答】解:(1)去分母得:3x﹣3﹣24=4x﹣6,移项合并得:x=﹣21;(2)原方程可化为:=﹣,去分母,得3(3x+5)=﹣2(2x﹣1),去括号,得:9x+15=﹣4x+2,移项,得:9x+4x=﹣15+2,合并同类项,得:13x=﹣13,系数化为1,得:x=﹣1.18.【解答】解:(1)去括号得:2x+2=﹣2,移项合并得:2x=﹣4,解得:x=﹣2;(2)去分母得:6x﹣2+2x=x+2﹣6,移项合并得:7x=﹣2,解得:x=﹣.19.【解答】解:(1)去括号得:3﹣1﹣2x=5x,移项合并得:7x=2,解得:x=;(2)去分母得:4x﹣2=6﹣2x﹣1,移项合并得:6x=7,解得:x=.20.【解答】解:(1)去括号得:2x+6=5x,移项合并得:﹣3x=﹣6,解得:x=2;(2)去分母得:2y+2﹣4=8+2﹣y,移项合并得:3y=12,解得:y=4.21.【解答】解:(1)移项合并得:﹣4x=﹣6,解得:x=1.5;(2)去分母得:12﹣12+9x=10x+6﹣12x,移项合并得:11x=6,解得:x=.22.【解答】解:(1)4﹣x=6﹣3x ﹣x+3x=6﹣4 2x=2 x=1 (2)3(x+1)﹣2(2﹣3x)=63x+3﹣4+6x=69x=7 x=23.【解答】解:(1)3x+4﹣5(x+1)=﹣1;3x+4﹣5x﹣5=﹣13x﹣5x=﹣1+5﹣4﹣2x=0x=0;(2)﹣=1.2(2x+1)﹣(5x﹣1)=64x+2﹣5x+1=64x﹣5x=6﹣1﹣2﹣x=3x=﹣3.24.【解答】解:(1)移项,得:4x﹣3x=2+5,合并同类项,得:x=7;(2)去分母,得:3(x+2)=2(2x+3)﹣12,去括号,得:3x+6=4x+6﹣12,移项,得:3x﹣4x=6﹣12﹣6,合并同类项,得:﹣x=﹣12,系数化为1,得:x=12;(3)去括号,得:2x﹣18+3x=3x ﹣20+4x,移项,得:2x+3x﹣3x﹣4x=﹣20+18,合并同类项,得:﹣2x=﹣2,系数化为1,得:x=1;(4)去分母,得:5(x﹣1)﹣3(x+2)=1.8,去括号,得:5x﹣5﹣3x﹣6=1.8,移项,得:5x﹣3x=1.8+5+6,合并同类项,得:2x=12.8,系数化为1,得:x=6.425.【解答】解:(1)去分母得:﹣10x+2=﹣9x+8,移项合并得:﹣x=6,解得:x=﹣6;(2)去分母得:2x+4=3x+9,解得:x=﹣5.26.【解答】解:(1)4x﹣2=3﹣x 移项得:4x+x=3+2,合并同类项得:5x=5,系数化为1得:x=1;(2)去分母得:2(x﹣1)﹣(x+2)=6,去括号得:2x﹣2﹣x﹣2=6,移项得:2x﹣x=6+2+2,合并同类项得:x=10.27.【解答】解:(1)5x﹣2=﹣3(x﹣2)去括号得:5x﹣2=3x﹣6,移项得:5x﹣3x=﹣6+2,合并同类项得:2x=﹣4,系数化为1得:x=﹣2;(2)1﹣=去分母得:6﹣(2x﹣1)=2(2x+1),去括号得:6﹣2x+1=4x+2,移项得:﹣2x﹣4x=2﹣6﹣1,合并同类项得:﹣2x=﹣5,系数化为1得:x=2.5.28.【解答】解:(1)去括号,得:3x+12=5﹣2x+2,移项,得:3x+2x=5+2﹣12,合并同类项,得:5x=﹣5,系数化为1,得:x=﹣1;(2)去分母,得:2(y+3)=12﹣3(3﹣2y),去括号,得:2y+6=12﹣9+6y,移项,得:2y﹣6y=12﹣9﹣6,合并同类项,得:﹣4y=﹣3,系数化为1,得:y=.29.【解答】解:(1)2(t﹣3)﹣(4t ﹣1)=2﹣4t去括号,得2t﹣6﹣4t+1=2﹣4t移项及合并同类项,得2t=7系数化为1,得t=3.5;(2)去分母,得2(2x+1)﹣(10x+1)=6去括号,得4x+2﹣10x﹣1=6移项及合并同类项,得﹣6x=5系数化为1,得x=﹣.30.【解答】解:(1)5x﹣2=2x+1移项及合并同类项,得3x=3系数化为1,得x=1;(2)﹣=1去分母,得4(2x+1)﹣2(5x﹣1)=12去括号,得8x+4﹣10x+2=12移项及合并同类项,得﹣2x=6系数化为1,得x=﹣3.31.【解答】解:(1)2x+6=5x﹣15﹣3x=﹣21x=7(2)10x﹣5=12﹣9x﹣15x34x=17x= 32.【解答】解:(1)3(x﹣4)﹣2(3x+4)=﹣153x﹣12﹣6x﹣8=﹣15﹣3x=5x=;(2)3(x﹣7)=12+4(5x+8)3x﹣21=12+20x+32﹣17x=65x=.33.【解答】(每小题(4分),本题共8分)解:(1)3x﹣3+2x+2=﹣65x﹣1=﹣65x=﹣5x=﹣1(2)3(x﹣1)=12+4(x+1)3x﹣3=12+4x+43x﹣3=16+4x3x ﹣4x=19x=﹣1934.【解答】解:(1)3x﹣9﹣10x+14=6﹣6x﹣7x+5=6﹣6x﹣7x+6x=6﹣5﹣x=1x=﹣1(2)3(2x﹣3)﹣(x﹣5)=6﹣2(7﹣3x)6x﹣9﹣x+5=6﹣14+6x5x ﹣4=6x﹣75x﹣6x=4﹣7﹣x=﹣3x=335.【解答】解:(1)去分母,得:2(2x+1)+6=3(x+2),去括号,得:4x+2+6=3x+6,移项,得:4x﹣3x=6﹣2﹣6,合并同类项,得:x=﹣2;(2)去分母,得:5(x﹣4)﹣2(x﹣3)=1.6,去括号,得:5x﹣20﹣2x+6=1.6,移项,得:5x﹣2x=1.6+20﹣6,合并同类项,得:3x=15.6,系数化为1,得:x=5.2.36.【解答】解:(1)移项合并得:2x=﹣12,系数化为1,得:x=﹣6;(2)去分母得:2(x+3)=12﹣3(3﹣2x),去括号得:2x+6=12﹣9+6x,移项合并得:﹣4x=﹣3,解得:x=.37.【解答】解:(1)去括号得:2x﹣3=﹣5x+10,移项合并得:7x=13,解得:x=;(2)去分母得:3x+3﹣6=4+6x,移项合并得:3x=﹣7,解得:x=﹣.38.【解答】解:(1)去括号得:4x+6x﹣9=12﹣x+1,移项,得:4x+6x+x=12+1+9,合并同类项,得:11x=2,系数化为1,得:x=2;(2)去分母,得:10y﹣2(y+2)=10﹣5(y﹣3),去括号,得:10y﹣2y﹣4=20﹣5y+15,移项,得:10y﹣2y+5y=20+15+4,合并同类项,得:13y=39,系数化为1,得:y=3.39.【解答】解:(1)移项,得3x+2x=﹣3﹣7,合并同类项,得5x=﹣10,系数化为1,得x=﹣2;(2)方程两边同乘6,得2(x﹣4)=﹣3(x+2),去括号,得2x﹣8=﹣3x﹣6,移项,得2x+3x=﹣6+8,合并同类项,得5x=2,系数化为1,得x=0.4.40.【解答】解:(1)去括号得,4x﹣15+3x=6移项、合并同类项得,7x=21系数化为1得,x=3;(2)去分母得,2(5x+1)﹣(2x﹣1)=6去括号得,10x+2﹣2x+1=6移项得,10x﹣2x=6﹣2﹣1合并同类项得,8x=3系数化为1得,.41.【解答】解:(1)去括号得:20﹣y=﹣3y﹣4,移项合并得:2y=﹣24,解得:y=﹣12;(2)去分母得:5x﹣15﹣12x﹣3=15,移项合并得:﹣7x=33,解得:x=﹣.42.【解答】解:(1)去括号得:4x﹣6=6x﹣2,移项合并得:﹣2x=4,解得:x=﹣2;(2)去分母得:10+4x﹣30+9x=6,移项合并得:13x=26,解得:x=2.43.【解答】解:(1)两边除以﹣3得:x+1=﹣3,解得:x=﹣4;(2)去分母得:5(x﹣2)﹣2(x+1)=3,去括号得:5x﹣10﹣2x﹣2=3,移项合并得:3x=15,解得:x=5.44.【解答】解:(1)去分母得:6x﹣9+6x=6﹣x﹣2,移项合并得:13x=13,解得:x=1;(2)去分母得:2﹣4x+4x+4=12﹣6x﹣3,移项合并得:6x=3,解得:x=0.5.45.【解答】解:(1)去括号得:2x+4=1﹣x﹣3,移项合并得:3x=﹣6,解得:x=﹣2;(2)去分母得:8y﹣4﹣3y﹣6=﹣12,移项合并得:5y=﹣2,解得:x=﹣0.4.46.【解答】解:(1)3(x﹣4)+1=x﹣53x﹣12+1=x﹣53x﹣x=﹣5+12﹣12x=6x=3;(2)1+=12+2(x﹣2)=3(3x+7)12+2x﹣4=9x+212x﹣9x=21﹣12+4﹣7x=13x=﹣.47.【解答】解:(1)2(x+3)=5x;2x+6=5x2x﹣5x=﹣6﹣3x=﹣6x=2;(2)2﹣.12﹣2(2x+1)=3(1+x)12﹣4x﹣2=3+3x﹣4x﹣3x=3﹣12+2﹣7x=﹣7x=1.48.【解答】解:(1)去括号得2y+4﹣12y+3=9﹣9y,移项,得2y﹣12y+9y=9﹣4﹣3合并同类项,得﹣y=2,系数化为1,得y=﹣2;(2)去分母,得6x﹣2(3x+2)=6﹣3(x﹣2)去括号,得6x﹣6x﹣4=6﹣3x+6,移项,得6x ﹣6x+3x=6+6+4合并同类项,得3x=16,系数化为1,得x=.49.【解答】解:(1)移项,得3x﹣x=﹣4,合并同类项,得2x=﹣4,系数化为1,得x=﹣2;(2)去分母,得2(2x﹣1)﹣(x+3)=4,去括号,得4x﹣2﹣x﹣3=4移项,得4x﹣x=4+2+3合并同类项,得3x=9,系数化为1,得x=3.50.【解答】解:(1)去括号,得2x﹣4+2=x+1,移项,得2x﹣x=1﹣2+4合并同类项,得x=3;(2)去分母,得3(3x﹣2)=2(x+4)﹣6去括号,得9x﹣6=2x+8﹣6移项,得9x﹣2x=8﹣6+6合并同类项,得7x=8系数化为1,得x=.。
解一元一次方程50道练习题(经典、强化、带答案)
解一元一次方程1234解:(移项)(合并)(化系数为1)5678解:(移项)(合并)(化系数为1)9101112解:(移项)(合并)(化系数为113141516解:(移项)(合并)(化系数为1).17、;18、;19、;20、解:(去括号)(移项)(合并)(化系数为1)21222324、解:(去括号)(移项)(合并)(化系数为1)25;26、;27;28、解:(去括号)(移项)(合并)(化系数为1)293032解:(去分母)(去括号)(移项)(合并)(化系数为1)333435解:(去分母)(去括号)(移项)(合并)(化系数为1363738解:(去分母)(去括号)(移项)(合并)(化系数为139404142解:(去分母)(去括号)(移项)(合并)(化系数为1434445解:(去分母)(去括号)(移项)(合并)(化系数为14647解:(去分母)(去括号)(移项)(合并)(化系数为1484950解:(化整)(去分母)(去括号)(移项)(合并)(化系数为1【参考答案】1、【答案】(1(2(3(4(5(6(7(81.1、【答案】(9(10(11(12(13(14(15(162、【答案】(17(18(19(20(21(22)2.1、【答案】(23(24(25(26(27(28)(29(303、【答案】(31(32(33(34(35(36(37(383.1、【答案】(39(40(41(42(43(44(45(464、【答案】(47(48(49(50。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.2.4解一元一次方程一.解答题(共30小题)1.(2005•宁德)解方程:2x+1=72.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.4.解方程:.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x ﹣=2﹣.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x ﹣.7.﹣(1﹣2x)=(3x+1)8.解方程:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1;(2).9.解方程:.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).11.计算:(1)计算:(2)解方程:12.解方程:13.解方程:(1)(2)14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+2(3)[3(x﹣)+]=5x﹣115.(A 类)解方程:5x﹣2=7x+8;(B类)解方程:(x﹣1)﹣(x+5)=﹣;(C类)解方程:.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)17.解方程:(1)解方程:4x﹣3(5﹣x)=13 (2)解方程:x﹣﹣3 18.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2](3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:.20.解方程(1)﹣0.2(x﹣5)=1;(2).21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x)...23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).25.解方程:.26.解方程:(1)10x﹣12=5x+15;(2)27.解方程:(1)8y﹣3(3y+2)=7 (2).28.当k 为什么数时,式子比的值少3.29.解下列方程:(I)12y﹣2.5y=7.5y+5(II).30.解方程:.6.2.4解一元一次方程(三)参考答案与试题解析一.解答题(共30小题)1.(2005•宁德)解方程:2x+1=7考点:解一元一次方程.专题:计算题;压轴题.分析:此题直接通过移项,合并同类项,系数化为1可求解.解答:解:原方程可化为:2x=7﹣1 合并得:2x=6系数化为1得:x=3点评:解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.2.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),化简可得:3x+3=8x﹣8,移项可得:5x=11,解可得x=.故原方程的解为x=.点评:若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;(2)题的方程中含有分数系数,应先对各式进行化简、整理,然后再按(1)的步骤求解.解答:解:(1)去括号得:4﹣x=6﹣3x,移项得:﹣x+3x=6﹣4,合并得:2x=2,系数化为1得:x=1.(2)去分母得:5(x﹣1)﹣2(x+1)=2,去括号得:5x﹣5﹣2x﹣2=2,移项得:5x﹣2x=2+5+2,合并得:3x=9,系数化1得:x=3.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.4.解方程:.考点:解一元一次方程.专题:计算题.分析:此题两边都含有分数,分母不相同,如果直接通分,有一定的难度,但将方程左右同时乘以公分母6,难度就会降低.解答:解:去分母得:3(2﹣x)﹣18=2x﹣(2x+3),去括号得:6﹣3x﹣18=﹣3,移项合并得:﹣3x=9,∴x=﹣3.点评:本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x﹣=2﹣.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项、合并同类项、化系数为1,从而得到方程的解;(2)先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣4﹣60+3x=5x﹣10(2分)移项得:4x+3x﹣5x=4+60﹣10(3分)合并得:2x=54(5分)系数化为1得:x=27;(6分)(2)去分母得:6x﹣3(x﹣1)=12﹣2(x+2)(2分)去括号得:6x﹣3x+3=12﹣2x﹣4(3分)移项得:6x﹣3x+2x=12﹣4﹣3(4分)合并得:5x=5(5分)系数化为1得:x=1.(6分)点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.去括号时要注意符号的变化.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x﹣.考点:解一元一次方程.专题:计算题.分析:(1)是简单的一元一次方程,通过移项,系数化为1即可得到;(2)是较为复杂的去分母,本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)3x﹣3=2x+33x﹣2x=3+3x=6;(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0.点评:本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.7.﹣(1﹣2x)=(3x+1)考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:﹣7(1﹣2x)=3×2(3x+1)﹣7+14x=18x+6﹣4x=13x=﹣.点评:解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1.此题去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.8.解方程:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1;(2).考解一元一次方程.点:专题:计算题.分析:(1)可采用去括号,移项,合并同类项,系数化1的方式进行;(2)本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+13x﹣7=4x﹣2∴x=﹣5;(2)原方程可化为:去分母得:40x+60=5(18﹣18x)﹣3(15﹣30x),去括号得:40x+60=90﹣90x﹣45+90x,移项、合并得:40x=﹣15,系数化为1得:x=.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果;(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.9.解方程:.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:,去分母得:2x﹣(3x+1)=6﹣3(x﹣1),去括号得:2x﹣3x﹣1=6﹣3x+3,移项、合并同类项得:2x=10,系数化为1得:x=5.点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,合并同类项,系数化1,即可求出方程的解;(2)先去分母,再去括号,移项,合并同类项,系数化1可求出方程的解.解答:解:(1)4x﹣3(4﹣x)=2去括号,得4x﹣12+3x=2移项,合并同类项7x=14系数化1,得x=2.(2)(x﹣1)=2﹣(x+2)去分母,得5(x﹣1)=20﹣2(x+2)去括号,得5x﹣5=20﹣2x﹣4移项、合并同类项,得7x=21系数化1,得x=3.点评:(1)此题主要是去括号,移项,合并同类项,系数化1.(2)方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.11.计算:(1)计算:(2)解方程:考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)根据有理数的混合运算法则计减;(2)两边同时乘以最简公分母4,即可去掉分母.解答:解:(1)原式=,=,=.(2)去分母得:2(x﹣1)﹣(3x﹣1)=﹣4,解得:x=3.点评:解答此题要注意:(1)去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数;(2)去分母就是方程两边同时乘以分母的最简公分母.12.解方程:考点:解一元一次方程.专题:计算题.分析:(1)这是一个带分母的方程,所以要为1,从而得到方程的解.(2)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.解答:解:(1)去分母得:3(3x﹣1)+18=1﹣5x,去括号得:9x﹣3+18=1﹣5x,移项、合并得:14x=﹣14,系数化为1得:x=﹣1;(2)去括号得:x﹣x+1=x,移项、合并同类项得:x=﹣1,系数化为1得:x=﹣.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.13.解方程:(2)考点:解一元一次方程.专题:计算题.分析:(1)去分母、去括号、移项、合并同类项、化系数为1.(2)去分母、去括号、移项、合并同类项、化系数为1.解答:(1)解:去分母得:5(3x+1)﹣2×10=3x﹣2﹣2(2x+3),去括号得:15x+5﹣20=3x﹣2﹣4x﹣6,移项得:15x+x=﹣8+15,合并得:16x=7,解得:;(2)解:,4(x﹣1)﹣18(x+1)=﹣36,4x﹣4﹣18x﹣18=﹣36,﹣14x=﹣14,x=1.点评:本题考查解一元一次方程,正确掌握解一元一次项要变号、去分母时“1”也要乘以最小公倍数.14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+2(3)[3(x﹣)+]=5x﹣1考点:解一元一次方程.专题:计算题.分析:(2)通过去括号、移项、合并同类项、系数化为1,解得x的值;(3)乘最小公倍数去分母即可;(4)主要是去括号,也可以把分数转化成整数进行计算.解答:解:(1)去括号得:10x+5﹣4x+6=6移项、合并得:6x=﹣5,方程两边都除以6,得x=﹣;(2)去分母得:3(x﹣2)=2(4﹣3x)+24,去括号得:3x﹣6=8﹣6x+24,移项、合并得:9x=38,方程两边都除以9,得(3)整理得:[3(x﹣)+]=5x﹣1,4x﹣2+1=5x﹣1,移项、合并得:x=0.点评:一元一次方程的解法:一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.解题时,要灵活运用这些步骤.15.(A类)解方程:5x﹣2=7x+8;(B类)解方程:(x﹣1)﹣(x+5)=﹣;(C类)解方程:.考点:解一元一次方程.专题:计算题.分析:通过去分母、去括号、移项、系数化为1等方法,求得各方程的解.解答:解:A类:5x﹣2=7x+8移项:5x﹣7x=8+2化简:﹣2x=10即:x=﹣5;=﹣去括号:x﹣﹣x﹣5=﹣化简:x=5即:x=﹣;C类:﹣=1去分母:3(4﹣x)﹣2(2x+1)=6去括号:12﹣3x﹣4x﹣2=6化简:﹣7x=﹣4即:x=.点评:本题主要考查一元一次方程的解法,比较简单,但要细心运算.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)考点:解一元一次方程.专题:计算题.分析:(1)去括号以后,移项,合并同类项,系数化为1即可求解;(2)(3)首先去掉分母,再去括号以后,移项,合并同类项,系数化为1以后即可求解;(4)首先根据分数的基本性质,把第一项分母中的0.3化为整数,再去分母,求解.合并同类项得:﹣7x=﹣14则x=2;(2)去分母得:2x+1=x+3﹣5移项,合并同类项得:x=﹣3;(3)去分母得:10y+2(y+2)=20﹣5(y﹣1)去括号得:10y+2y+4=20﹣5y+5移项,合并同类项得:17y=21系数化为1得:;(4)原方程可以变形为:﹣5x=﹣1去分母得:17+20x﹣15x=﹣3移项,合并同类项得:5x=﹣20系数化为1得:x=﹣4.解方程的过程中要注意每步的依据,这几个题目都是基础的题目,需要熟练掌握.点评:17.解方程:(1)解方程:4x﹣3(5﹣x)=13(2)解方程:x﹣﹣3考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,化系数为1,从而得到方程的解.(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣15+3x=13,移项合并得:7x=28,系数化为1得:得x=4;(2)原式变形为,去分母得:5(2x﹣5)+3(x﹣2)=15(x+3),去括号得10x﹣25+3x﹣6=15x+45,移项合并得﹣2x=76,系数化为1得:x=﹣38.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.18.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2](3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.考点:解一元一次方程;有理数的混合运算.分析:(1)利用平方和立方的定义进行计算.(2)按四则混合运算的顺序进行计算.(3)主要是(4)两边同乘最小公倍数去分母,再求值.解答:解:(1)﹣42×+|﹣2|3×(﹣)3==﹣1﹣1=﹣2.(2)﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2]====.(3)解方程:4x﹣3(5﹣x)=2去括号,得4x﹣15+3x)=2移项,得4x+3x=2+15合并同类项,得7x=17系数化为1,得.(4)解方程:2)=5(2x﹣5)﹣3×15去括号,得15x﹣3x+6=10x﹣25﹣45移项,得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项,得2x=﹣76系数化为1,得x=﹣38.点评:前两道题考查了学生有理数的混合运算,后两道考查了学生解一元一次方程的能力.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:.考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)和(2)要熟练掌握有理数的混合运算;(3)和(4)首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1.解答:解:(1)(1﹣2﹣4)×=﹣=﹣13;(2)原式=﹣1×(﹣4﹣2)×(﹣)=6×(﹣)=﹣9;(3)解方程:3x+3=2x+7移项,得3x﹣2x=7﹣3合并同类项,得x=4;(4)解方程:去分母,得6(x+15)=15﹣10(x﹣7)去括号,得6x+90=15﹣10x+70移项,得6x+10x=15+70﹣90合并同类项,得16x=﹣5系数化为1,得x=.点评:(1)和(2)要注意符号的处理;(4)要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括号法则以及合并同类项法则.20.解方程(1)﹣0.2(x﹣5)=1;(2).考点:解一元一次方程.分析:(1)通过去括号、移项、系数化为1等过程,求得x的值;(2)通过去分母以及去括号、移项、系数化为1等过程,求得x的值.解答:解:(1)﹣0.2(x﹣5)=1;去括号得:﹣0.2x+1=1,∴﹣0.2x=0,∴x=0;(2).去分母得:2(x﹣2)+6x=9(3x+5)﹣(1﹣2x),∴﹣21x=48,∴x=﹣.点评:此题主要考查了一元一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.考点:解一元一次方程.专题:计算题.分析:先去括号得x+3﹣2x+2=9﹣3x,然后移项、合并同类得到2x=4,然后把x的系数化为1即可.解答:解:去括号得x+3﹣2x+2=9﹣3x,移项得x﹣2x+3x=9﹣3﹣2,合并得2x=4,系数化为1得x=2.点评:本题考查了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知数的项移到方程右边,然后合并同类项,最后把未知数的系数化为1得到原方程的解.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x)...考点:解一元一次方程.专题:方程思想.分析:本题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化1求解.第二个先去括号再通过移项、合并同类项及系数化1求解.第三个先去分母再同第二个.第四个先分子分母乘以10,再同第三个求解.解答:8x﹣3=9+5x,解:8x﹣5x=9+3,3x=12,∴x=4.∴x=4是原方程的解;5x+2(3x﹣7)=9﹣4(2+x),解:5x+6x﹣14=9﹣8﹣4x,5x+6x+4x=9﹣8+14,15x=15,∴x=1.∴x=1是原方程的解..解:3(x﹣1)﹣2(2x+1)=12,3x﹣3﹣4x﹣2=12,3x﹣4x=12+3+2,﹣x=17,∴x=﹣17.∴x=﹣17是原方程的解.,解:,5(10x﹣3)=4(10x+1)+40,50x﹣15=40x+4+40,50x﹣40x=4+40+15,10x=59,∴x=.∴x=是原方程的解.点评:此题考查的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号.23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.考点:解一元一次方程.分析:(1)首先去括号,然后移项、合并同类项,系数化成1,即可求解;(2)首先去分母,然后去括号,移项、合并同类项,系数化成1,即可求解解答:解:(1)去括号,得:0.5x﹣0.7=5.2﹣1.3x+1.3移项,得:0.5x+1.3x=5.2+1.3+0.7合并同类项,得:1.8x=7.2,则x=4;(2)去分母得:7(1﹣2x)=3(3x+1)﹣42,去括号,得:7﹣14x=9x+3﹣42,移项,得:﹣14x﹣9x=3﹣42﹣7,合并同类项,得:﹣23x=﹣46,则x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).考点:解一元一次方程.分析:(1)移项,合并同类项,然后系数化成1即可求解;(2)移项,合并同类项,然后系数化成1即可求解;(3)去括号、移项,合并同类项,然后系数化成1即可求解;(4)首先去分母,然后去括号、移项,合并同类项,然后系数化成1即可求解.解答:解:(1)3x=10.5,x=3.5;(2)3x﹣2x=6﹣8,x=﹣2;(3)2x+3x+3=5﹣4x+4,2x+3x+4x=5+4﹣3,9x=6,x=;(4)2(x+1)+6=3(3x﹣2),2x+2+6=9x﹣6,2x﹣9x=﹣6﹣2﹣6,﹣7x=﹣14,x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.解方程:.考点:解一元一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,移项合并,将x系数化为1,即可求出解.解答:解:去分母得:5(3x﹣1)﹣2(5x﹣6)=2,去括号得:15x﹣5﹣10x+12=2,移项合并得:5x=﹣5,解得:x=﹣1.点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.26.解方程:(1)10x﹣12=5x+15;(2)考点:解一元一次方程.专题:计算题.分析:(1)先移项,再合并同类项,最后化系数为1,从而得到方程的解;(2)先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解答:解:(1)移项,得10x﹣5x=12+15,合并同类项,得5x=27,方程的两边同时除以5,得x=;(2)去括号,得=,方程的两边同时乘以6,得x+1=4x﹣2,移项、合并同类项,得3x=3,方程的两边同时除以3,得x=1.点评:本题考查解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.27.解方程:(1)8y﹣3(3y+2)=7(2).考点:解一元一次方程.专题:计算题.分析:(1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(1)去括号得,8y ﹣9y﹣6=7,移项、合并得,﹣y=13,系数化为1得,y=﹣13;(2)去分母得,3(3x﹣1)﹣12=2(5x﹣7),去括号得,9x﹣3﹣12=10x﹣14,移项得,9x﹣10x=﹣14+3+12,合并同类项得,﹣x=1,系数化为1得,x=﹣1.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.28.当k为什么数时,式子比的值少3.考点:解一元一次方程.专题:计算题.分析:先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解答:解:依题意,得=+3,去分母得,5(2k+1)=3(17﹣k)+45,去括号得,10k+5=51﹣3k+45,移项得,10k+3k=51+45﹣5,合并同类项得,13k=91,系数化为1得,k=7,∴当k=7时,式子比的值少3.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.29.解下列方程:(I)12y﹣2.5y=7.5y+5(II).考点:解一元一次方程.专题:计算题.分析:(Ⅰ)根据一元一次方程的解法,移项,合并同类项,系数化为1即可得解;(Ⅱ)是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(Ⅰ)移项得,12y﹣2.5y﹣7.5y=5,合并同类项得,2y=5,系数化为1得,y=2.5;(Ⅱ)去分母得,5(x+1)﹣10=(3x﹣2)﹣2(2x+3),去括号得,5x+5﹣10=3x﹣2﹣4x﹣6,移项得,5x﹣3x+4x=﹣2﹣6﹣5+10,合并同类项得,6x=﹣3,系数化为1得,x=﹣.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.30.解方程:.考点:解一元一次方程.专题:计算题.分析:由于方程的分子、分母均有小数,利用分数的基本性质,分子、分母同时扩大相同的倍数,可将小数化成整数.解答:解:原方程变形为,(3分)去分母,得3×(30x﹣11)﹣4×(40x﹣2)=2×(16﹣70x),(4分)去括号,得90x﹣33﹣160x+8=32﹣140x,(5分)移项,得90x﹣160x+140x=32+33﹣8,(6分)合并同类项,得70x=57,(7分)系数化为1,得.(8分)点评:本题考查一元一次方程的解法.解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.本题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.31。
